Free Printable algebra Worksheets for 11th Grade
Algebra-focused math worksheets for Grade 11 students, created to help educators discover new ways to teach and reinforce essential concepts. Download and print these free resources from Quizizz.


Recommended Topics for you
- conic sections
- complex numbers
- radical equations and functions
- dependent variables
- graphing parabolas
- two variable inequalities
- binomial theorem
- absolute value equations functions and inequalities
- rational expressions equations and functions
- sigma notation
- algebraic modeling
- permutations

11th - 12th
10th - 11th

Explore algebra Worksheets by Grades
- kindergarten
Explore algebra Worksheets for grade 11 by Topic
Explore other subject worksheets for grade 11.
- social studies
Explore printable algebra worksheets for 11th Grade
Algebra worksheets for Grade 11 are essential tools for teachers looking to engage their students in the world of mathematics. These worksheets provide a comprehensive and structured approach to learning algebra, ensuring that students have a solid foundation in this critical subject area. Teachers can utilize these worksheets to create lesson plans, homework assignments, and in-class activities that cater to the diverse learning needs of their Grade 11 students. By incorporating a variety of algebraic concepts, such as linear equations, quadratic functions, and exponential growth, these worksheets help students develop their problem-solving skills and mathematical reasoning abilities. With a wide range of algebra worksheets for Grade 11 available, teachers can easily find the perfect resources to support their students' learning and growth in math.
Quizizz is an excellent platform for teachers to access a vast collection of algebra worksheets for Grade 11, as well as other math-related resources. This interactive platform allows teachers to create engaging quizzes and games that can be used in the classroom or assigned as homework. In addition to algebra worksheets, Quizizz offers a plethora of other math resources, including geometry, trigonometry, and calculus materials, ensuring that teachers have everything they need to support their Grade 11 students' mathematical development. The platform also provides valuable analytics and insights, allowing teachers to track their students' progress and identify areas where additional support may be needed. By incorporating Quizizz into their lesson plans, teachers can create a dynamic and interactive learning environment that fosters a deep understanding of algebra and other math concepts for their Grade 11 students.

- State Test Prep Blended program
- State Test Prep Online Program
- Summer Learning
- Writing Program
- Oral Reading Fluency Program
- Reading Skills Improvement Program
- After School Program
- High School Program
- Professional Development Platform
- Teacher PD Online Course
- Smart Communication Platform
- State Assessment Prep
- Classroom Tools
- State Test Teacher PD Course
- State Test Prep Blended Program
- Oral Reading Fluency Online Program
- Oral Reading Fluency Workbooks
- College Readiness – SAT/ACT
- High School Math & ELA
- Curious Reader Series
- For Libraries
- High School Math, Reading and Writing
- Online Professional Certification Exams
- Job Interview Practice Tool
- HR Software
- Online Pre-employment Assessment Platform
- Online Employee Training & Development Platform
- Enterprise Video Library
- Association Software
- Association Learning Management System
- Online Course Platform
- After-event Success Platform
- Self-service FAQ and Help Center
- Free Resources
- Success Stories
- Program Evaluation Reports
Grade 11 Math Questions and Solutions
The Smarter Balanced Assessment Consortium (SBAC) is a standardized test that includes various new technology-enhanced questions.
Some of them are Multiple choice-single correct responses, Multiple choice-multiple correct responses, Matching Tables, Drag and Drop, Hot text, Table Fill in, Graphing, Equation/numeric, Extended constructed response, Short answer, and many more.
This page contains several sample questions and practice test links for Grade 11 Math that give you an idea of questions that your students are likely to see on the test. After each sample question, an answer explanation follows. The explanation includes essential aspects of the task that you may need to consider for the skills, processes, and information your students need to know.
Domain: Grade 11 >> Number and quantity – The Real Number System
Sample Question: Multiply 36/49 and 21/63. What type of number is the result
- The numbers cannot be multiplied
- 57/112,rational
- 12/49,rational
- 12/49,irrational
Answer Explanation: Recall that a rational number is any number that can be expressed as a ratio or quotient of two integers (fractions). Irrational numbers are numbers that cannot be expressed as a fraction. Both numbers are fractions. Therefore, they are both rational numbers. Multiply them together and simplify the answer: 36/49.21/63=(4/7.9/7).3/9.7/7=12/49. The answer is a fraction. Thus, it is a rational number.
Standards: HSN.RN.B.3
Click here to practice: Number and quantity – The Real Number System Questions on Grade 11 Math
Domain: Grade 11 >> Number and Quantity – Quantities
Sample Question: The graph below shows the vibrations one of the strings on a violin when it is being played. What is true about the scale of the y-axis of the graph?

- Each mark on the y-axis could probably be one foot.
- Each mark on the y-axis could probably be one centimeter.
- Each mark on the y-axis could probably be one millimeter.
- Each mark on the y-axis could probably be one inch.
Answer Explanation: The graph represents the amplitude of the vibrating violin string. When the violin string follows this graph, the string is stretched in one direction and then in the other direction. Each time the string crosses the x-axis, it is in its original position. This motion is so small it is almost not seen by the human eye. Therefore the unit has to be very small. The smallest choice is millimeter.
Standards: HSN.RN.A.1
Click here to practice: Grade 11 Number and Quantity – Quantities Questions
Domain: Grade 11 >> Number and Quantity – The Complex Number System
Sample Question: What is the conjugate of the complex number 7+3i ?

Click here to practice: Grade 11 Math Number and Quantity – The Complex Number System Questions
Domain: Grade 11 >> Number and Quantity – Vector & Matrix Quantities
Sample Question: Subtract these two vectors ⟨−12,−23⟩−⟨−8,−14⟩.
Answer Explanation: The question asks us to subtract these two vectors ⟨−12,−23⟩−⟨−8,−14⟩ . If we have two vectors, v→=(x 1 ,y 1 )and w→=(x 2 ,y 2 ), then the difference of the two vectors is v→−w→=⟨x 1 −x 2 ,y 1 −y 2 ⟩ . In this question, we are subtracting ⟨−12,−23⟩−⟨−8,−14⟩ . The difference is ⟨−12−(−8),−23−(−14)⟩=⟨−4,−9⟩
Standards: HSN.VM.B.4
Click here to practice: Number and Quantity – Vector & Matrix Quantities Questions for Grade 11 Math
Domain: Grade 11 >> Algebra – Arithmetic with Polynomials & Rational Expressions
Sample Question: Subtract (x 3 +2x 2 -x+7) from (4x 3 +6x 2 +2x-7)
- -3x 3 +4x 2 +3x-14
- -3x 3 -4x 2 -3x+14
- 3x 3 +4x 2 +3x
- 3x 3 +4x 2 +3x-14
Answer Explanation: When combining polynomials, combine like terms by combining the coefficients. Subtract (x 3 +2x 2 -x+7) from (4x 3 +6x 2 +2x-7) (4x 3 }+6x 2 +2x-7) – (x 3 +2x 2 -x+7) (4x 3 -x 3 ) +(6x 2 -2x 2 ) +(2x-(-x)) +(-7-7) 3x 3 +4x 2 +3x-14
Standards: HSA.APR.A.1
Click here to practice: Algebra – Arithmetic with Polynomials & Rational Expressions Questions for Grade 11 Math
Domain: Grade 11 >> Algebra – Seeing Structure in Expressions
Sample Question: What is the coefficient of the third term the expression 5x 3 y 4 +7x 2 y 3 −6xy 2 −8xy?
Answer Explanation: The expression 5x 3 y 4 +7x 2 y 3 −6xy 2 −8xy is a polynomial expression with four terms. The coefficient of a term is the number in the front of the term. If the term begins with a negative, then the coefficient is a negative number, whether or not the term has variables. The third term is −6xy 2 and the number in the front of the term is -6.
Standards: HSA.SSE.A.1
Click here to practice: Algebra – Seeing Structure in Expressions Questions for Grade 11 Math
Domain: Grade 11 >> Algebra – Creating Equations
Sample Question: Madison is a sales associate for a transportation options dealer. Each month she sells two cars for every 10 bicycles and four motorcycles for every car. If she makes 40 sales per month, and the variable x represents the number of cars she sells, which equation could you use to find how many cars she sells?
- 2x+10x+8x=40
- 2x+10x+8x=20
Answer Explanation: If we use the variable x for the number of cars Madison sells, and she sells two cars for every 10 bicycles, then she sells five times as many bicycles as cars. Thus she sells 5x bicycles. Then, if she sells four motorcycles for every car, the number of motorcycles she sells is 4x. The problem states that she makes 40 sales per month, so add the cars, bicycles, and motorcycles up and make that sum equal to 40. The equation is x+5x+4x=40.
Standards: HSA.CED.A.1
Click here to practice: Algebra – Creating Equations Questions for Grade 11 Math
Domain: Grade 11 >> Algebra – Reasoning with Equations & Inequalities
Sample Question: What is the solution to 6x+5=101?
Answer Explanation: The question asks you to find the solution to 6x+5=101. Begin by subtracting 5 from both sides of the equation. This gives you 6x=96. Next, divide both sides by 6 and x=16.
Standards: HSA.CED.A.4
Click here to practice: Algebra – Reasoning with Equations & Inequalities Questions for Grade 11 Math
Domain: Grade 11 >> Functions – Interpreting Functions
Sample Question: The function f(x)=−1/8(x−7/2)2+3/2 is the path of a football at a practice game. Its graph is shown below. What portion of the domain of this function actually models this situation?

Answer Explanation: The function is a polynomial function. The domain of all polynomial functions, in a mathematical context, is (−∞,∞). However, in a real world context, the domain must allow the function to obey the rules of the real world. The ball is hit at time equals 0 seconds, and the ball lands, according to the graph, at time equals 7 seconds. Therefore, the domain is [0,7].
Standards: HSF.IF.B.5
Click here to practice: Functions – Interpreting Functions Questions for Grade 11 Math
Domain: Grade 11 >> Functions – Building Functions
Sample Question: How is the graph of f(x) = x + 7 different from g(x) = x + 12?
- When f(x) is shifted up 5 units, g(x) will be obtained
- g(x) is obtained by shifting f(x) down 5 units
- When g(x) is shifted up 5 units, f(x) will be obtained
- f(x) is obtained by shifting g(x) up 5 units
Answer Explanation: The value added to the function causes a vertical shift in the graph. Since 12 is 5 units larger than 7, the graph of g(x) is obtained by shifting f(x) 5 units up.
Standards: HSF.BF.B.3
Click here to practice: Functions – Building Functions Questions for Grade 11 Math
Domain: Grade 11 >> Functions – Linear, Quadratic, & Exponential Models
Sample Question: Which function is graphed below?

- f(x)=5(0.5) x
- f(x)=5(0.4) x
- f(x)=4(0.5) x
- f(x)=5(1.5) x
Answer Explanation: The graph shows that the function is an exponential growth function. The formula for an exponential function is f(x)=ab x , where a is the y-intercept and b is the growth factor. If the exponential function is a growth function, then b>1. If the exponential function is a decay function, then 0 x .
Standards: HSF.LE.A.2
Click here to practice: Functions – Linear, Quadratic, & Exponential Models Questions for Grade 11 Math
Domain: Grade 11 >> Functions – Trigonometric Functions
Sample Question: If cosσ=−1, what is the value of sinσ ?
Answer Explanation: Rule :
.PNG)
Standards: HSF.TF.C.8
Click here to practice: Functions – Trigonometric Functions Questions for Grade 11 Math
Domain: Grade 11 >> Geometry – Congruence
Sample Question: Suppose PQRS is translated as shown in the figure below. How is the parallelogram translated?

Answer Explanation: The figure shows that the translation is to the right and downward. Based on the figure, the distance the parallelogram is translated toward the right is the same as the length of side PQ. Additionally, based on the figure, the distance the parallelogram is translated downward appears to be approximately one-half of the length of side QR.
Standards: HSG.CO.A.4
Click here to practice: Geometry – Congruence Questions for Grade 11 Math
Domain: Grade 11 >> Geometry – Similarity, Right Triangles, & Trigonometry
Sample Question: Perform a dilation on point C centered at the origin with scale factor equal to 1/2. What is the coordinate of the resulting image point C’?

Answer Explanation: When dilation is performed about the origin, the coordinates of the image point are the product of the scale factor and the coordinates of the original point. ½*4 = 2. ½* -3 = -3/2.
Standards: HSG.SRT.A.1
Click here to practice: Geometry – Similarity, Right Triangles, & Trigonometry Questions for Grade 11 Math
Domain: Grade 11 >> Geometry – Circles
Sample Question: A tangent line is drawn to a circle from a point outside a circle. A radius is drawn from the center of the circle to the point of tangency of the line. What angle does the radius make with the tangent line?
Answer Explanation: A radius of a circle drawn to the point of tangency of a tangent line is perpendicular to the tangent line.
Standards: HSG.C.A.2
Click here to practice: Geometry – Circles Questions for Grade 11 Math
Domain: Grade 11 >> Geometry – Expressing Geometric Properties with Equations
Sample Question: When writing the equation y=x 2 +6x+7, Angelica used the following steps. If she made any mistakes, explain them and write the correct equation. y=x 2 +6x+7 y−7=x 2 +6x y−7−9=x 2 +6x+9 y−16=(x+3) 2 y=(x+3) 2 +16
Answer Explanation: To put the equation in standard form, we have to complete the square to get the squared binomial that is necessary for standard form. To complete the square, we take half of the coefficient of the linear term which will be 3, then square it and add it to both sides. Then factor the perfect square trinomial to get the squared binomial. Then solve for y.
Standards: HSG.GPE.A.2
Click here to practice: Geometry – Expressing Geometric Properties with Equations Questions for Grade 11 Math
Domain: Grade 11 >> Geometry – Modeling with Geometry
Sample Question: What is the density of a brick that occupies 310cm 3 with a mass of 853 g?
Answer Explanation: V = Bh = lwh Volume of a Rectangular Prism
The formula for density is d = m/V. The volume is given to be 310cm 3 and the mass is 853 g. Plug those values into the formula to find density.
Standards: HSG.MG.A.2
Click here to practice: Geometry – Modeling with Geometry Questions for Grade 11 Math
Domain: Grade 11 >> Geometry – Geometric Measurement & Dimension
Sample Question: A hemisphere with radius 3 cm sits atop a cone of equal diameter and height of 10 cm, as shown in the diagram below. Find the combined volume of the composite object.
.PNG)
Answer Explanation: The total volume of the object is the sum of the volumes of the hemisphere and the cone. V = ½ (4/3) πr 3 +(1/3)πr 2 h V = ½ (4/3) π(3m) 3 +(1/3)π(3m) 2 (10cm)V=48πcm 3
Standards: HSG.GMD.A.3
Click here to practice: Geometry – Geometric Measurement & Dimension Questions for Grade 11 Math
Domain: Grade 11 >> Statistics & Probability – Interpreting Categorical & Quantitative Data
Sample Question: What effect does a group of very large values have on the mean and median of a data set?
- The mean and the median are both increased
- The mean is not changed, but the median is increased
- The mean and median are not changed
- The mean is increased, but the median is decreased
Answer Explanation: The figure below shows the effect on the mean and median as a result of adding some very large elements to a data set. Since the new elements are very large, they have a significant effect on the mean because their very large values are averaged with the other values in the set. The median is also affected, and moves in the same direction as the mean moves.

Standards: HSS.ID.A.3
Click here to practice: Statistics & Probability – Interpreting Categorical & Quantitative Data Questions for Grade 11 Math
Domain: Grade 11 >> Statistics & Probability – Making Inferences & Justifying Conclusions
Sample Question: There are ten playing cards, four of them are red and six of them are black. Julian picks a card at random. What is the probability that he picks a red card?
Answer Explanation: Probability is calculated using the ratio of the number of successes divided by the number of possible choices.
The question asks for the probability of selecting a red card. There are four red cards out of a total of ten cards.
Thus, the probability of selecting a red card is four out of ten, which reduces to two out of five. That ratio is 2/5
Standards: HSS.IC.A.1
Click here to practice: Statistics & Probability – Making Inferences & Justifying Conclusions Questions for Grade 11 Math
Domain: Grade 11 >> Statistics and Probability – Conditional Probability & the Rules of Probability
Sample Question: The Venn diagram below shows the results of a survey on which sport people like to watch on television. Survey participants could choose one sport, two sports or all three sports. Which region(s) contains(s) responses in which a survey participant indicated that he/she like to watch only one sport?

Answer Explanation: Each circle contains the responses that like that specific color. Therefore, Regions A, B, C, E contain the responses that like to watch Baseball. Regions D, A, D, G contain the responses that like to watch Basketball. Regions A, B, D, F contain the responses that like to watch Football. If a letter is in two circles, the region contains responses that liked to watch the sports represented by both circles. If the region is in all three circles, that region contains the responses that like to watch all three sports. If the region is in only one circle, that region contains responses that stated that they only like to watch the sport represented by that circle. The regions that are in only one circle are E, F, G.
Standards: HSS.CP.A.1
Click here to practice: Statistics and Probability – Conditional Probability & the Rules of Probability Questions for Grade 11 Math
Domain: Grade 11 >> Statistics and Probability – Using Probability to Make Decisions
Sample Question: The Census Bureau provided a report that stated that the median income level of Floridians is 47,463. Based on this information, if you took a survey of 100 random workers in Florida, what is the probability the respondents’ income is greater than 47,463?
Answer Explanation: Median is the middle number when all numbers in the set are arranged from the least value to the greatest value. The question states that the median income level in Florida is 47,463, so one-half of the workers in Florida make less than 47,463 and one-half of the workers in Florida make more than 47,463. This means that, based on the Census Bureau’s report, the probability that a randomly selected person’s income is greater than 47,463 is 50% .
Standards: HSS.MD.A.4
Click here to practice: Statistics and Probability – Using Probability to Make Decisions Questions for Grade 11 Math
Looking for online practice tests? Here is the link to practice more of SBAC Grade 11 Math questions.
Related Links
Back-to-school Worksheets
Related posts:
No related posts.

Jenny Watson
One thought on “ grade 11 math questions and solutions ”.
Pingback: Summer is Here! Keep Your Child’s Literacy Skills Sharp with Online Games | Lumos Learning
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Notify me of follow-up comments by email.
Notify me of new posts by email.
Grade 11 math
IXL offers hundreds of grade 11 math skills to explore and learn! Not sure where to start? Go to your personalized Recommendations wall to find a skill that looks interesting, or select a skill plan that aligns to your textbook, provincial curriculum, or standardized test.
A. Measurement
- 1 Unit rates
- 2 Scale drawings: word problems
B. Equations
- 1 Solve linear equations
- 2 Solve linear equations: word problems
- 3 Absolute value and opposites
- 4 Solve absolute value equations
- 5 Graph solutions to absolute value equations
C. Inequalities
- 1 Graph a linear inequality in one variable
- 2 Graph a linear inequality in the coordinate plane
- 3 Write inequalities from graphs
- 4 Write a linear inequality: word problems
- 5 Solve linear inequalities
- 6 Graph solutions to linear inequalities
- 7 Solve absolute value inequalities
- 8 Graph solutions to absolute value inequalities
- 9 Graph solutions to quadratic inequalities
- 10 Solve quadratic inequalities
D. Functions
- 1 Domain and range
- 2 Identify functions
- 3 Evaluate functions
- 4 Find values using function graphs
- 5 Complete a table for a function graph
- 6 Find the slope of a linear function
- 7 Graph a linear function
- 8 Write the equation of a linear function
- 9 Linear functions over unit intervals
- 10 Complete a function table: absolute value functions
- 11 Graph an absolute value function
E. Systems of equations
- 1 Is (x, y) a solution to the system of equations?
- 2 Solve a system of equations by graphing
- 3 Solve a system of equations by graphing: word problems
- 4 Find the number of solutions to a system of equations
- 5 Classify a system of equations
- 6 Solve a system of equations using substitution
- 7 Solve a system of equations using substitution: word problems
- 8 Solve a system of equations using elimination
- 9 Solve a system of equations using elimination: word problems
- 10 Solve a system of equations using any method
- 11 Solve a system of equations using any method: word problems
- 12 Solve a nonlinear system of equations
F. Systems of inequalities
- 1 Is (x, y) a solution to the system of inequalities?
- 2 Solve systems of inequalities by graphing
- 3 Find the vertices of a solution set
- 4 Linear programming
G. Factoring
- 1 Factor monomials
- 2 Factor quadratics
- 3 Factor quadratics using algebra tiles
- 4 Factor using a quadratic pattern
- 5 Factor by grouping
- 6 Factor sums and differences of cubes
- 7 Factor polynomials
H. Quadratic relations
- 1 Characteristics of quadratic functions
- 2 Complete a function table: quadratic functions
- 3 Find a quadratic function
- 4 Graph quadratic functions in vertex form
- 5 Match quadratic functions and graphs
- 6 Solve a quadratic equation using square roots
- 7 Solve a quadratic equation using the zero product property
- 8 Solve a quadratic equation by factoring
- 9 Complete the square
- 10 Graph quadratic functions in standard form
- 11 Solve a quadratic equation using the quadratic formula
- 12 Using the discriminant
I. Parabolas
- 1 Identify the direction a parabola opens
- 2 Find the vertex of a parabola
- 3 Find the axis of symmetry of a parabola
- 4 Write equations of parabolas in vertex form from graphs
- 5 Write equations of parabolas in vertex form using properties
- 6 Graph parabolas
J. Polynomials
- 1 Polynomial vocabulary
- 2 Add and subtract polynomials
- 3 Multiply a polynomial by a monomial
- 4 Multiply two binomials
- 5 Multiply two binomials: special cases
- 6 Multiply polynomials
- 7 Divide polynomials using long division
K. Radical functions and expressions
- 1 Roots of integers
- 2 Roots of rational numbers
- 3 Find roots using a calculator
- 4 Nth roots
- 5 Simplify radical expressions with variables I
- 6 Simplify radical expressions with variables II
- 7 Multiply radical expressions
- 8 Divide radical expressions
- 9 Add and subtract radical expressions
- 10 Simplify radical expressions using the distributive property
- 11 Simplify radical expressions using conjugates
- 12 Domain and range of radical functions
- 13 Solve radical equations
L. Rational exponents
- 1 Evaluate rational exponents
- 2 Multiplication with rational exponents
- 3 Division with rational exponents
- 4 Power rule
- 5 Simplify expressions involving rational exponents I
- 6 Simplify expressions involving rational exponents II
- • New! Solve equations with rational exponents
M. Rational functions and expressions
- 1 Rational functions: asymptotes and excluded values
- 2 Evaluate rational expressions I
- 3 Evaluate rational expressions II
- 4 Simplify rational expressions
- 5 Multiply and divide rational expressions
- 6 Add and subtract rational expressions
- 7 Solve rational equations
N. Exponential functions
- 1 Evaluate exponential functions
- 2 Match exponential functions and graphs I
- 3 Match exponential functions and graphs II
- 4 Solve exponential equations by rewriting the base
- 5 Identify linear and exponential functions
- 6 Exponential functions over unit intervals
- 7 Describe linear and exponential growth and decay
- 8 Exponential growth and decay: word problems
- 9 Compound interest: word problems
- 10 Continuously compounded interest: word problems
O. Angle measures
- 1 Quadrants
- 2 Graphs of angles I
- 3 Graphs of angles II
- 4 Coterminal angles
- 5 Reference angles
P. Right triangles
- 1 Pythagorean Theorem
- 2 Converse of the Pythagorean theorem
- 3 Pythagorean Inequality Theorems
- 4 Special right triangles
Q. Trigonometry
- 1 Trigonometric ratios: sin, cos and tan
- 2 Trigonometric ratios: csc, sec and cot
- 3 Trigonometric ratios in similar right triangles
- 4 Find trigonometric ratios using the unit circle
- 5 Sin, cos and tan of special angles
- 6 Csc, sec and cot of special angles
- 7 Find trigonometric functions using a calculator
- 8 Inverses of sin, cos and tan
- 9 Inverses of csc, sec and cot
- 10 Solve trigonometric equations I
- 11 Solve trigonometric equations II
- 12 Trigonometric ratios: find a side length
- 13 Trigonometric ratios: find an angle measure
- 14 Solve a right triangle
- 15 Law of Sines
- 16 Law of Cosines
- 17 Solve a triangle
- 18 Area of a triangle: sine formula
- 19 Area of a triangle: Law of Sines
R. Two-dimensional figures
- 1 Polygon vocabulary
- 2 Interior angles of polygons
- 3 Perimeter
- 4 Area of triangles and quadrilaterals
- 5 Area and perimeter in the coordinate plane I
- 6 Area and perimeter in the coordinate plane II
- 7 Area and circumference of circles
- 8 Area of compound figures
- 9 Area between two shapes
- 10 Area and perimeter of similar figures
- 11 Classify quadrilaterals
- 12 Properties of parallelograms
S. Three-dimensional figures
- 1 Three-dimensional figure vocabulary
- 2 Parts of three-dimensional figures
- 3 Nets and drawings of three-dimensional figures
- 4 Introduction to surface area and volume
- 5 Surface area of prisms and cylinders
- 6 Surface area of pyramids and cones
- 7 Volume of prisms and cylinders
- 8 Volume of pyramids and cones
- 9 Surface area and volume of spheres
- 10 Introduction to similar solids
- 11 Surface area and volume of similar solids
- 12 Surface area and volume review
- 13 Cross-sections of three-dimensional figures
- 14 Solids of revolution
T. Congruent figures
- 1 Congruence statements and corresponding parts
- 2 Solve problems involving corresponding parts
- 3 Identify congruent figures
- 4 Proofs involving angles
- 5 Proofs involving parallel lines I
- 6 Proofs involving parallel lines II
- 7 SSS and SAS Theorems
- 8 ASA and AAS Theorems
- 9 SSS, SAS, ASA and AAS Theorems
- 10 SSS Theorem in the coordinate plane
- 11 Congruency in isosceles and equilateral triangles
- 12 Hypotenuse-Leg Theorem
- 13 Proofs involving triangles I
- 14 Proofs involving triangles II
U. Triangles
- 1 Classify triangles
- 2 Triangle Angle-Sum Theorem
- 3 Midsegments of triangles
- 4 Triangles and bisectors
- 5 Identify medians, altitudes, angle bisectors and perpendicular bisectors
- 6 Angle-side relationships in triangles
- 7 Triangle Inequality Theorem
V. Similarity
- 1 Identify similar figures
- 2 Ratios in similar figures
- 3 Similarity statements
- 4 Side lengths and angle measures in similar figures
- 5 Similar triangles and indirect measurement
- 6 Perimeters of similar figures
- 7 Similarity rules for triangles
- 8 Similar triangles and similarity transformations
- 9 Similarity of circles
- 10 Triangle Proportionality Theorem
- 11 Areas of similar figures
- 1 Identify hypotheses and conclusions
- 2 Counterexamples
- 3 Truth tables
- 4 Truth values
- 5 Conditionals
- 6 Negations
- 7 Converses, inverses and contrapositives
- 8 Biconditionals
X. Sequences and series
- 1 Classify formulas and sequences
- 2 Find terms of an arithmetic sequence
- 3 Find terms of a geometric sequence
- 4 Find terms of a recursive sequence
- 5 Evaluate formulas for sequences
- 6 Write a formula for an arithmetic sequence
- 7 Write a formula for a geometric sequence
- 8 Write a formula for a recursive sequence
- 9 Sequences: mixed review
- 10 Introduction to sigma notation
- 11 Identify arithmetic and geometric series
- 12 Find the sum of a finite arithmetic or geometric series
- 13 Introduction to partial sums
- 14 Partial sums of arithmetic series
- 15 Partial sums of geometric series
- 16 Partial sums: mixed review
- 17 Convergent and divergent geometric series
- 18 Find the value of an infinite geometric series
- 19 Write a repeating decimal as a fraction
Y. Probability
- 1 Introduction to probability
- 2 Calculate probabilities of events
- 3 Permutations
- 4 Counting principle
- 5 Permutation and combination notation
- 6 Find probabilities using permutations and combinations
- 7 Find probabilities using two-way frequency tables
- 8 Identify independent events
- 9 Probability of independent and dependent events
- 10 Find conditional probabilities
- 11 Independence and conditional probability
- 12 Find conditional probabilities using two-way frequency tables
- 13 Find probabilities using the addition rule
- 14 Find probabilities using the normal distribution
Would you like to explore a topic?
- LEARNING OUTSIDE OF SCHOOL
Or read some of our popular articles?
Free downloadable english gcse past papers with mark scheme.
- 19 May 2022
The Best Free Homeschooling Resources UK Parents Need to Start Using Today
- Joseph McCrossan
- 18 February 2022
How Will GCSE Grade Boundaries Affect My Child’s Results?
- Akshat Biyani
- 13 December 2021
11+ Maths Topics (With Free 11+ Maths worksheet PDF)
- July 12, 2022

What topics do you need to know for the 11+?
What maths is in the 11+, are the 11+ maths topics hard.
- How much should I prepare for 11+
If you have your heart set on your kid attending an independent or grammar school , they will need to do well in the entrance exam . Knowing how to prepare for each subject is the most important step you can take.
We’re going to share what the 11+ maths topics are and how you can help your child nail the 11 plus maths section of the exam . Giving your kid plenty of time to study all of the 11 plus maths topics is key, so let’s get started.
Different secondary schools set their own admission criteria but most will require your kid to ace an 11+ exam on the following: Maths, English and often Verbal Reasoning and/or Non-Verbal Reasoning. These exams will be more challenging than your kid is used to at school and a little bit of planning and studying will go a long way. 📆
You just need to know what to study for in advance. That’s the tricky part but we’re here to help. Let’s focus on the 11+ maths topics today, which many kids find the most challenging aspect. Our guide to the 11 plus maths topics includes those 11 plus tricky maths questions which can catch students out.
While different regions and schools have different maths exams to sit, there are some common 11+ maths topics your kid should expect to see on the paper. If you know which school/s you’re going to apply for, get in touch with us and one of our tutors can help your kid study the right topics the right way, covering all 11 plus topics. At GoStudent we know how to integrate 11 plus problem solving for year 6 pupils into their prep for the 11+.
Here are the 11+ maths topics that appear on different papers across the country.
Venn diagrams
11 plus Venn diagrams are composed of a set of information (numbers and elements), usually with circles or ovals around them. Your kid will need to work out how many x represent x (e.g. how many students like maths and English?).
Many kids enjoy practising questions around 11 plus Venn diagrams. Once they get the hang of it, there is usually no stopping them with this topic.
Time and distance
The 11 plus time and distance questions are about working out how long x will last or at what time it will finish and distance covered or how many kilometres an hour x is. This is often one of the more challenging 11+ maths topics to study for. That’s because there are many variables and different ways the questions can be presented (e.g. a timetable). ⌚
Ratio proportion and scale
The 11 plus ratio questions, proportion questions and scale questions will require your kid to determine the ratio (x:x) from given information. Once your kid learns some simple tricks for working the ratio questions 11+ out, they should feel very confident answering ratio 11+ questions.
Probability
11 plus probability questions can appear in a number of formats. There are often questions about rolling dice and the probability of an outcome or to do with playing cards and questions about the suits, colours and/or numbers.
Profit and loss
11 plus profit and loss questions rely heavily on your kid using division, multiplication, addition, and subtraction. Some of the problems may require your kid to work backwards e.g. if Ann sells a chair for £78 and loses 10 percent what was the cost price of the chair?
Ordering numbers
When it comes to problems around 11 plus ordering numbers your kid will need to arrange a set of given numbers in ascending or descending order. While this sounds fairly straightforward, the questions usually involve decimals or negative numbers to make it more challenging.
Percentages
As the name suggests, 11 plus percentages as a topic is purely about percentages. Some questions can be relatively simple but others will ask your kid to solve multiple percentages in just one problem e.g. what is 5 percent of 15 percent of 40 percent of 200? As long as your kid practises these a lot, they should feel comfortable and have no issue with this topic.
11 plus pie chart questions can include a pie chart that comes with a key to read, percentages on the pie chart or numbers to mark up a section of the pie. Your kid will need to interpret what the data says and answer related questions.
2d and 3d shapes
11 plus maths 2d and 3d shapes are often considered some of the most complex topics. 11 plus shape questions asked are often around volume, for example, and include shapes such as cubes, cylinders and pyramids. A straight-up maths topic they will need to learn but once they understand it they will know exactly how to answer these questions.
11 plus matrices is a topic that has to be practised repeatedly. It involves identifying missing parts to complete a pattern. As this doesn’t rely on a mathematical formula, doing as many sample exercises as possible is the only way to ensure speed and fluency in this area.
Negative numbers
11 plus negative numbers refer to numbers that are less than zero. Example types of questions that your kid may get include adding or subtracting multiple negative and positive numbers. There are some clear rules your child should learn relating to this topic that never deviate so once your kid has mastered them they will be fine.
Number sequences
11 plus number sequences are lists of numbers that are connected but your kid will need to work out how by following the pattern. The pattern will always follow a rule e.g. x2 to reach the next number (= 2, 4, 8, x) or +3 (= 3, 6, 9, x) to work out the missing number.
Units of measurement
11 plus units of measurement are related to area (e.g. square metre), length (e.g. centimetre), volume (e.g litre), and time (e.g. hour). Questions can take a number of forms such as converting measurements from one unit to another (e.g. centimetres into metres).
11 plus symmetry can test your kid’s understanding about line (or reflection) and rotational symmetry. Line symmetry is when half of a shape is the same as the other half and rotational symmetry is when a shape looks the same after being rotated around a point.
11 plus angles focus on the angle sizes of a triangle or where two lines meet. For example, questions can ask to judge which angles appear bigger or work out clock face angles (big hand and little hand). This is a challenging topic and one that requires adequate knowledge and studying beforehand in order to finish the questions in time and correctly.
Short maths
11 plus short maths relates to those questions where an algorithm can be used to work out the answer (e.g. 12.3-2.6=x). Your child should be able to do all of these types of questions or at least know what they need to do because they would have been taught these over and over in primary school. These questions are straightforward, however, the numbers used in the questions are usually more advanced. ➕
Problem solving
11 plus problem solving questions (or long maths) on the other hand will require more time to work through and the maths problem won’t be initially clear. Problem-solving questions can be very challenging, even for kids who are mathematically oriented. Your kid should practise many of these by writing down the problem that is being asked of them and figuring it out.
11 plus algebra
11 plus algebra questions expect your kid to know basic algebraic equations. Your kid will have started some of the algebra 11 plus topic already by filling in missing numbers from an equation at school and should have started learning simple formulae in Year 6. You should give them extra practice in the form of dedicated puzzles and number problems to help with this topic in their maths 11+.
Free maths 11+ practice paper (Free download PDF)
So your child can get in enough practice ahead of time, you can download your very own GoStudent 11+ maths practice paper and answer booklet right here:

As you can see, the possible 11+ maths topics your kid will be presented with on their exam are wide-reaching. This means they need to feel comfortable with all of them because all of the 11plus maths topics have scope to be tricky. This will also help them in secondary school maths and not just on this one exam.
Parents often ask us “are the 11+ maths topics hard?”. We can only give this answer: yes and no. Since the 11+ maths topics are so varied your kid will inevitably find some easy and others more difficult. It will also depend on what they have been focusing on more at school. More importantly, your kid needs to have a good grasp of what is on the eleven + maths exam by being familiar with each topic, though some topics will be the subject of hard 11 plus maths questions while other topics will be presented with easier questions.
The good news is that the exam is designed to be challenging but with good grades still attainable. Most kids that do really well in this exam put in a lot of preparation, so let’s look at how you can support your child.
How much should my child prepare for 11+?
You should encourage your child to prepare as much as they can (within reason) for each of the 11+ maths topics to improve their maths skills . They are still young and not used to studying long hours so practice should take place steadily and regularly but they still need their fun time and to do homework for their regular schoolwork. ⚽
We recommend creating a 11 plus diy learning plan with them that allows for plenty of free time, extra-curricular activities, and also study time. There are many ways to make learning the 11+ maths topics fun. Getting a dedicated tutor will help save time and make practising engaging and rewarding. That’s because an 11+ tutor knows exactly what to focus on and already has the material prepared with a good understanding of the type of 11 plus maths questions that crop up year on year.
At GoStudent , our tutors create a tailored learning plan for each of their students and your kid will receive one too. This includes 11 plus maths papers. That takes some of the pressure off you and your child instantly. Plus, we love to make classes fun and your kid will find the lessons interesting and learn more as a result. If you would like to try a class, the first session is free so you can see for yourself just how much your child benefits.

Popular posts

- By Guy Doza

- By Joseph McCrossan
- In LEARNING TRENDS

- By Akshat Biyani

4 Surprising Disadvantages of Homeschooling
- By Andrea Butler

What are the Hardest GCSEs? Should You Avoid or Embrace Them?
- By Clarissa Joshua
1:1 tutoring to unlock the full potential of your child
More great reads:.

Advice From a Teacher: How Can I Help My Child If They Fail Their Mock Exams?
- By Natalie Lever
- January 9, 2024
- 11 min read


What Are Mock Exams and Why Are They Important?
- January 8, 2024

SQA Results Day 2023: Important Information About How to Get Scottish Exam Results
- By Sharlene Matharu
- August 3, 2023
Book a free trial session
Sign up for your free tutoring lesson..
- Grade 5 Lessons and Practice
- Grade 6 Lessons and Practice
- Grade 7 Lessons and Practice
- Grade 8 Lessons and Practice
- Grade 9 Lessons and Practice
- Grade 10 Lessons and Practice
- Grade 11 Lessons and Practice
- Grade 12 Lessons and Practice
- Financial Literacy
- Whiteboard Templates
- Grade 5 Math Quizzes
- Grade 6 Math Quizzes
- Grade 7 Math Quizzes
- Grade 8 Math Quizzes
- Grade 9 Math Quizzes
- Grade 10 Math Quizzes
Grade 11 Math Quizzes
- Grade 12 Math Quizzes
Check Out Grade 11 Lessons
Introduction to Functions
Basic functions and their characteristics
Domain and range of a function
Transformations of functions
Quadratics and Rational Expressions
Standard, vertex and factored forms of parabola
Factoring quadratics
Completing the square
Simplifying rational expressions
Restrictions in rational expressions
Multiplying and dividing rational expressions
Adding and subtracting rational expressions
Operating radicals
Exponential Functions
Rational exponents
Solving exponential equations
Exponential function and its graph
Exponential growth and decay
Doubling period and half-life problems
Trigonometry
Right triangle trigonometry
Sine Law and Cosine Law
2D and 3D Trig word problems
Trigonometric identities
Unit Circle and special angles ( degrees )
Graphing periodic functions
Solving trigonometric equations
Word problems modeling periodic functions
Sequences/Series and Finance
Arithmetic and geometric sequences
Arithmetic and geometric series
Compound interest
Future Value of Annuities
Also check out IntoMath Financial Literacy section
- Class 11 Maths
- Chapter 3: Trigonometric Functions

Important Questions For Class 11 Maths Chapter 3 - Trigonometric Functions
Important Questions For Class 11 Maths Chapter 3 Trigonometric Functions are provided at BYJU’S to help the students with their examination preparation for the board exams of 2022-2023. Students can go through with these important questions of Trigonometric Functions which are given based on the new pattern prescribed by CBSE .
In Class 11 Trigonometric Functions is the easiest one among all other chapters. Though there are a number of formulas, students can easily score the marks for this chapter. The chapter contains more weightage. Students can refer to the detailed explanations of all the important questions of this chapter here, along with the practice questions. Also, get important questions for Class 11 Maths for all the chapters at BYJU’S.
- Trigonometric Functions Class 11
- Trigonometric Functions Domain Range
- Inverse Trigonometric Functions
Important Questions & Answers For Class 11 Maths Chapter 3 Trigonometric Functions
Q. No.1: In any triangle ABC, prove that a sin (B – C) + b sin (C – A) + c sin (A – B) = 0.
In any triangle ABC,
a/sin A = b/sin B = c/sin C = k
a = k sin A, b = k sin B, c = k sin C
= a sin (B – C) + b sin (C – A) + c sin (A – B)
= k sin A sin B cos C – k sin A cos B sin C + k sin B sin C cos A – k sin B cos C sin A + k sin C sin A cos B – k sin C cos A sin B
Hence proved that a sin (B – C) + b sin (C – A) + c sin (A – B) = 0.
Q.No.2: Find the radius of the circle in which a central angle of 60° intercepts an arc of length 37.4 cm (use π = 22/7).
Length of the arc = l = 37.4 cm
Central angle = θ = 60° = 60π/180 radian = π/3 radians
We know that,
= (37.4) * (π / 3)
Hence, the radius of the circle is 35.7 cm.
Q. No.3: A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?
Number of revolutions made by the wheel in 1 minute = 360
1 minute = 60 seconds
Number of revolutions in 1 second = 360/60 = 6
Angle made in 1 revolution = 360°
Angles made in 6 revolutions = 6 × 360°
Radian measure of the angle in 6 revolutions = 6 × 360 × π/180
= 6 × 2 × π
Hence, the wheel turns 12π radians in one second.
Q. No. 4: Find the value of √3 cosec 20° – sec 20°.
√3 cosec 20° – sec 20°

Q. No. 5: Show that tan 3x tan 2x tan x = tan 3x – tan 2x – tan x.
Let 3x = 2x + x
Taking “tan” on both sides,
tan 3x = tan (2x + x)
tan 3x = (tan 2x + tan x)/ (1- tan 2x tan x)
tan 3x(1 – tan 2x tan x) = tan 2x + tan x
tan 3x – tan 3x tan 2x tan x = tan 2x + tan x
tan 3x – (tan 2x + tan x) = tan 3x tan 2x tan x
Therefore, tan 3x – tan 2x – tan x = tan 3x tan 2x tan x.
Q. No. 6: Prove that:

Hence proved.
Q. No. 7: Find the value of cos 570° sin 510° + sin (-330°) cos (-390°).
LHS =cos (570)sin (510) + sin (- 330)cos (- 390)
= cos (570)sin(510) – sin (330)
= cos (90 * 6 + 30) sin (90 * 5 + 60) – sin (90 * 3 + 60) cos (90 * 4 + 30)
= – cos (30) cos (60) – [ – cos (60) ] cos (30)
= – cos (30) cos (60) + cos (30) sin (60)
Q. No. 8: Find the general solution of the following equation.

cos 2 θ + 3 sin θ + 3 sin 2 θ = 0
1 – sin 2 θ + 3 sin θ + 3 sin 2 θ = 0
2 sin 2 θ + 3 sin θ + 1 = 0
2sin 2 θ + 2 sin θ + sin θ + 1 = 0
2 sin θ (sin θ +1 ) + 1 (sin θ + 1) = 0
(2 sin θ + 1) (sin θ + 1) = 0
2 sin θ + 1 = 0, sin θ + 1 = 0
sin θ = -½, sin θ = -1
θ = nπ – (-1) n π/6, θ = nπ – (-1) n π/2; n ∈ Z
Q. No. 9: Show that 2 sin 2 β + 4 cos (α + β) sin α sin β + cos 2 (α + β) = cos 2α.
LHS = 2 sin 2 β + 4 cos (α + β) sin α sin β + cos 2(α + β)
= 2 sin 2 β + 4 (cos α cos β – sin α sin β) sin α sin β + (cos 2α cos 2β – sin 2α sin 2β)
= 2 sin 2 β + 4 sin α cos α sin β cos β – 4 sin 2 α sin 2 β + cos 2α cos 2β – sin 2α sin 2β
= 2 sin 2 β + sin 2α sin 2β – 4 sin 2 α sin 2 β + cos 2α cos 2β – sin 2α sin 2β
= (1 – cos 2β) – (2 sin 2 α) (2 sin 2 β) + cos 2α cos 2β
= (1 – cos 2β) – (1 – cos 2α) (1 – cos 2β) + cos 2α cos 2β
Therefore, 2 sin 2 β + 4 cos (α + β) sin α sin β + cos 2 (α + β) = cos 2α
Q. No. 10: Prove that:
LHS=(sec 8θ -1 )/ (sec4θ -1)
=(1/(cos8θ) -1 )/ (1/(cos4θ) -1)
=((1-cos8θ)cos4θ )/ ((1-cos4θ) cos8θ)
=(2sin 2 4θcos4θ )/ ((2sin 2 2θ) cos8θ)
=(2sin4θcos4θsin4θ )/ ((2sin 2 2θ) cos8θ)
=(sin8θ * 2sin2θcos2θ )/ ((2sin 2 2θ) cos8θ)
=(tan8θ * cos2θ )/ (sin2θ)
= (tan8θ) /(tan 2θ)
Video Lesson on Trigonometry

Practice Questions For Class 11 Maths Chapter 3 Trigonometric Functions
- Find the general solution of the equation 5cos 2 θ + 7sin 2 θ – 6 = 0.
- If θ lies in the first quadrant and cos θ = 8/17, then find the value of cos (30° + θ) + cos (45° – θ) + cos (120° – θ).
- Prove that cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x).

- Find the general solution of the following equation: tan 2 θ +(1 – √3) tan θ – √3 = 0
- Find the value of tan 225° cot 405° + tan 765° cot 675°.
- If a cos 2θ + b sin 2θ = c has α and β as its roots, then prove that tan α + tan β = 2b/(a + c).
- If cos + cos = 0 = sin + sin β, then prove that cos 2 + cos 2β = -2 cos (α + ).
- Find the most general value of θ satisfying the equation tan θ = -1 and cos θ = 1/√2 .
- The value of cos 1 0 cos 2 0 cos 3 0 …………cos 179 0 is (a) 1/√2 (b) 0 (c) 1 (d) -1
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Please send all important questions from all lesson
Please visit: https://byjus.com/maths/important-questions-class-11-maths/
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
- Skip to main content
- Skip to primary sidebar
- Skip to footer
Additional menu
Khan Academy Blog
Free Math Worksheets — Over 100k free practice problems on Khan Academy
Looking for free math worksheets.
You’ve found something even better!
That’s because Khan Academy has over 100,000 free practice questions. And they’re even better than traditional math worksheets – more instantaneous, more interactive, and more fun!
Just choose your grade level or topic to get access to 100% free practice questions:
Kindergarten, basic geometry, pre-algebra, algebra basics, high school geometry.
- Trigonometry
Statistics and probability
High school statistics, ap®︎/college statistics, precalculus, differential calculus, integral calculus, ap®︎/college calculus ab, ap®︎/college calculus bc, multivariable calculus, differential equations, linear algebra.
- Addition and subtraction
- Place value (tens and hundreds)
- Addition and subtraction within 20
- Addition and subtraction within 100
- Addition and subtraction within 1000
- Measurement and data
- Counting and place value
- Measurement and geometry
- Place value
- Measurement, data, and geometry
- Add and subtract within 20
- Add and subtract within 100
- Add and subtract within 1,000
- Money and time
- Measurement
- Intro to multiplication
- 1-digit multiplication
- Addition, subtraction, and estimation
- Intro to division
- Understand fractions
- Equivalent fractions and comparing fractions
- More with multiplication and division
- Arithmetic patterns and problem solving
- Quadrilaterals
- Represent and interpret data
- Multiply by 1-digit numbers
- Multiply by 2-digit numbers
- Factors, multiples and patterns
- Add and subtract fractions
- Multiply fractions
- Understand decimals
- Plane figures
- Measuring angles
- Area and perimeter
- Units of measurement
- Decimal place value
- Add decimals
- Subtract decimals
- Multi-digit multiplication and division
- Divide fractions
- Multiply decimals
- Divide decimals
- Powers of ten
- Coordinate plane
- Algebraic thinking
- Converting units of measure
- Properties of shapes
- Ratios, rates, & percentages
- Arithmetic operations
- Negative numbers
- Properties of numbers
- Variables & expressions
- Equations & inequalities introduction
- Data and statistics
- Negative numbers: addition and subtraction
- Negative numbers: multiplication and division
- Fractions, decimals, & percentages
- Rates & proportional relationships
- Expressions, equations, & inequalities
- Numbers and operations
- Solving equations with one unknown
- Linear equations and functions
- Systems of equations
- Geometric transformations
- Data and modeling
- Volume and surface area
- Pythagorean theorem
- Transformations, congruence, and similarity
- Arithmetic properties
- Factors and multiples
- Reading and interpreting data
- Negative numbers and coordinate plane
- Ratios, rates, proportions
- Equations, expressions, and inequalities
- Exponents, radicals, and scientific notation
- Foundations
- Algebraic expressions
- Linear equations and inequalities
- Graphing lines and slope
- Expressions with exponents
- Quadratics and polynomials
- Equations and geometry
- Algebra foundations
- Solving equations & inequalities
- Working with units
- Linear equations & graphs
- Forms of linear equations
- Inequalities (systems & graphs)
- Absolute value & piecewise functions
- Exponents & radicals
- Exponential growth & decay
- Quadratics: Multiplying & factoring
- Quadratic functions & equations
- Irrational numbers
- Performing transformations
- Transformation properties and proofs
- Right triangles & trigonometry
- Non-right triangles & trigonometry (Advanced)
- Analytic geometry
- Conic sections
- Solid geometry
- Polynomial arithmetic
- Complex numbers
- Polynomial factorization
- Polynomial division
- Polynomial graphs
- Rational exponents and radicals
- Exponential models
- Transformations of functions
- Rational functions
- Trigonometric functions
- Non-right triangles & trigonometry
- Trigonometric equations and identities
- Analyzing categorical data
- Displaying and comparing quantitative data
- Summarizing quantitative data
- Modeling data distributions
- Exploring bivariate numerical data
- Study design
- Probability
- Counting, permutations, and combinations
- Random variables
- Sampling distributions
- Confidence intervals
- Significance tests (hypothesis testing)
- Two-sample inference for the difference between groups
- Inference for categorical data (chi-square tests)
- Advanced regression (inference and transforming)
- Analysis of variance (ANOVA)
- Scatterplots
- Data distributions
- Two-way tables
- Binomial probability
- Normal distributions
- Displaying and describing quantitative data
- Inference comparing two groups or populations
- Chi-square tests for categorical data
- More on regression
- Prepare for the 2020 AP®︎ Statistics Exam
- AP®︎ Statistics Standards mappings
- Polynomials
- Composite functions
- Probability and combinatorics
- Limits and continuity
- Derivatives: definition and basic rules
- Derivatives: chain rule and other advanced topics
- Applications of derivatives
- Analyzing functions
- Parametric equations, polar coordinates, and vector-valued functions
- Applications of integrals
- Differentiation: definition and basic derivative rules
- Differentiation: composite, implicit, and inverse functions
- Contextual applications of differentiation
- Applying derivatives to analyze functions
- Integration and accumulation of change
- Applications of integration
- AP Calculus AB solved free response questions from past exams
- AP®︎ Calculus AB Standards mappings
- Infinite sequences and series
- AP Calculus BC solved exams
- AP®︎ Calculus BC Standards mappings
- Integrals review
- Integration techniques
- Thinking about multivariable functions
- Derivatives of multivariable functions
- Applications of multivariable derivatives
- Integrating multivariable functions
- Green’s, Stokes’, and the divergence theorems
- First order differential equations
- Second order linear equations
- Laplace transform
- Vectors and spaces
- Matrix transformations
- Alternate coordinate systems (bases)
Frequently Asked Questions about Khan Academy and Math Worksheets
Why is khan academy even better than traditional math worksheets.
Khan Academy’s 100,000+ free practice questions give instant feedback, don’t need to be graded, and don’t require a printer.
| Math Worksheets | Khan Academy |
|---|---|
| Math worksheets take forever to hunt down across the internet | Khan Academy is your one-stop-shop for practice from arithmetic to calculus |
| Math worksheets can vary in quality from site to site | Every Khan Academy question was written by a math expert with a strong education background |
| Math worksheets can have ads or cost money | Khan Academy is a nonprofit whose resources are always free to teachers and learners – no ads, no subscriptions |
| Printing math worksheets use up a significant amount of paper and are hard to distribute during virtual learning | Khan Academy practice requires no paper and can be distributed whether your students are in-person or online |
| Math worksheets can lead to cheating or a lack of differentiation since every student works on the same questions | Khan Academy has a full question bank to draw from, ensuring that each student works on different questions – and at their perfect skill level |
| Math worksheets can slow down student learning since they need to wait for feedback | Khan Academy gives instant feedback after every answer – including hints and video support if students are stuck |
| Math worksheets take up time to collect and take up valuable planning time to grade | Khan Academy questions are graded instantly and automatically for you |
What do Khan Academy’s interactive math worksheets look like?
Here’s an example:
What are teachers saying about Khan Academy’s interactive math worksheets?
“My students love Khan Academy because they can immediately learn from their mistakes, unlike traditional worksheets.”
Is Khan Academy free?
Khan Academy’s practice questions are 100% free—with no ads or subscriptions.
What do Khan Academy’s interactive math worksheets cover?
Our 100,000+ practice questions cover every math topic from arithmetic to calculus, as well as ELA, Science, Social Studies, and more.
Is Khan Academy a company?
Khan Academy is a nonprofit with a mission to provide a free, world-class education to anyone, anywhere.
Want to get even more out of Khan Academy?
Then be sure to check out our teacher tools . They’ll help you assign the perfect practice for each student from our full math curriculum and track your students’ progress across the year. Plus, they’re also 100% free — with no subscriptions and no ads.
Get Khanmigo
The best way to learn and teach with AI is here. Ace the school year with our AI-powered guide, Khanmigo.
For learners For teachers For parents
PRACTICE QUESTIONS ON MATRICES WORKSHEET FOR GRADE 11
(1) Construct an m × n matrix A = [a ij ], where a ij is given by
(i) a ij = (i - 2j) 2 /2 with m = 2 and n = 3 Solution
(ii) a ij = |3i - 4j|/4 with m = 3 and n = 4 Solution
(2) Find the values of p, q, r, and s if
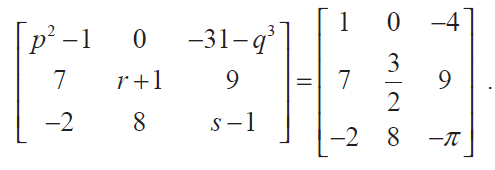
(3) Determine the value of x + y if
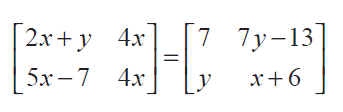
(4) Determine the matrices A and B if they satisfy
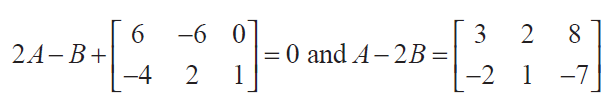
(5) If A =
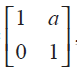
then compute A 4 Solution
(6) Consider the matrix
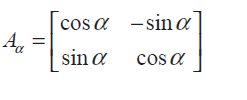
(i) Show that A α A β = A (α+β)
(ii) Find all possible real values of α satisfying the condition A α + A α T = I Solution
(7) If A =
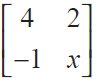
and such that (A− 2I)(A− 3I) = O, find the value of x.
(8) If A =
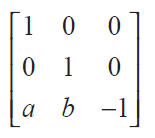
(9) If A =
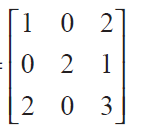
and A 3 - 6A 2 + 7A + KI = 0, then find the value of k.
(10) Give your own examples of matrices satisfying the following conditions in each case:
(i) A and B such that AB ≠ BA .
(ii) A and B such that AB = O = BA, A ≠ O and B ≠ O.
(iii) A and B such that AB = O and BA ≠ O.
(11) Show that f (x) f ( y) = f (x + y), where f(x) =
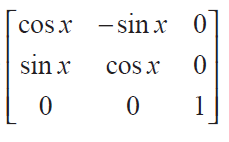
(12) If A is a square matrix such that A 2 = A, find the value of 7A - (I + A) 3 . Solution
(13) Verify the property A(B + C) = AB + AC, when the matrices A, B, and C are given by
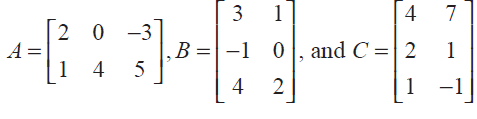
(14) Find the matrix A which satisfies the matrix relation
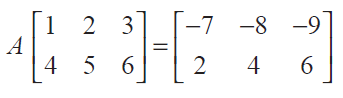
(15)
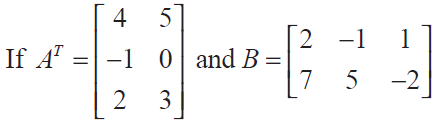
verify the following (i) (A+ B) T = A T + B T = B T + A T
(ii) (A− B) T = A T − B T
(iii) (B T ) T = B .
(16) If A is a 3 × 4 matrix and B is a matrix such that both A T B and BA T are defined, what is the order of the matrix B? Solution
(17) Express the following matrices as the sum of a symmetric matrix and a skew-symmetric matrix:
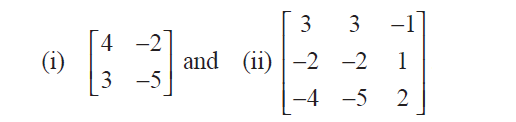
Solution
(18) Find the matrix A such that
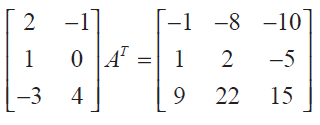
(19) If A
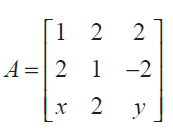
is a matrix such that AA T = 9I , find the values of x and y. Solution
(20) (i) For what value of x, the matrix
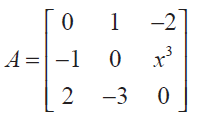
is skew-symmetric Solution
(ii) If A =
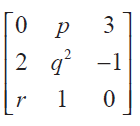
is skew-symmetric, find the values of p, q, and r.
(21) Construct the matrix A = [a ij ] 3x3 , where a ij = i - j. State whether A is symmetric or skew-symmetric
(22) Let A and B be two symmetric matrices. Prove that AB = BA if and only if AB is a symmetric matrix.
(23) If A and B are symmetric matrices of same order, prove that
(i) AB + BA is a symmetric matrix.
(ii) AB - BA is a skew-symmetric matrix Solution
(24) A shopkeeper in a Nuts and Spices shop makes gift packs of cashew nuts, raisins and almonds.
Pack I contains 100 gm of cashew nuts, 100 gm of raisins and 50 gm of almonds.
Pack-II contains 200 gm of cashew nuts, 100 gm of raisins and 100 gm of almonds.
Pack-III contains 250 gm of cashew nuts, 250 gm of raisins and 150 gm of almonds.
The cost of 50 gm of cashew nuts is $50, 50 gm of raisins is $10, and 50 gm of almonds is $60. What is the cost of each gift pack? Solution

Apart from the stuff given above, i f you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to [email protected]
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
- Sat Math Practice
- SAT Math Worksheets
- PEMDAS Rule
- BODMAS rule
- GEMDAS Order of Operations
- Math Calculators
- Transformations of Functions
- Order of rotational symmetry
- Lines of symmetry
- Compound Angles
- Quantitative Aptitude Tricks
- Trigonometric ratio table
- Word Problems
- Times Table Shortcuts
- 10th CBSE solution
- PSAT Math Preparation
- Privacy Policy
- Laws of Exponents
Recent Articles
Best way to learn mathematics.
Jun 25, 24 07:32 PM
Problems on Solving Logarithmic Equations
Jun 24, 24 05:48 PM
SAT Math Preparation Videos (Part - 2)
Jun 24, 24 01:38 AM

Every Question Helps You Learn
Well done, you scored out of 10. Your Streak will increase and as a reward for completing the quiz, meet “Butch” one of our favourite pets!
Bad Luck, you only scored out of 10. Your Streak will not increase but as a reward for completing the quiz, meet “Butch” one of our favourite pets!
Play more quizzes to see other favorite pooches

Back to Maths
Solving Problems (Difficult)

When you answer 8 or more questions correctly your red streak will increase in length. The green streak shows the best player so far today. See our Hall of Fame for previous daily winners.
.jpg)
You should have learnt a few methods for solving real life problems from the previous three groups of 11-plus Maths quizzes: see how well you can apply your skills to these problems.
This is a difficult group of quizzes compared to the previous ones, so remember to read the questions carefully. Look at the four options before choosing your answer.
You may find it helpful to have pencil & paper by your side so you can jot any notes down. Take your time and if you get any wrong, read the helpful comment that appears after you've answered the question - this should help when playing the quiz again.
If you haven't already, it would be a good idea to do the previous quizzes BEFORE doing this one.

Contact Details
Education quizzes, customer service, here to help, our social circles.
© Copyright 2016-2024 - Education Quizzes Work Innovate Ltd - Design | Development | Marketing
We use cookies to enhance your experience on our website.
To comply with the e-Privacy directive, we need your consent - I agree - No thanks - Learn more

Free Mathematics Tutorials
Parabola questions and problems with detailed solutions.
Parabola problems with answers and detailed solutions , in the bottom of the page, are presented.
Questions and Problems
- Find the x and y intercepts, the vertex and the axis of symmetry of the parabola with equation \( y = - x^2 + 2 x + 3 \)?
- What are the points of intersection of the line with equation \( 2x + 3y = 7 \) and the parabola with equation \( y = - 2 x^2 + 2 x + 5\)?
- Find the points of intersection of the two parabolas with equation \( y = -(x - 3)^2 + 2\) and \( y = x^2 - 4x + 1\).
- Find the equation of the parabola \( y = 2 x^2 + b x + c\) that passes through the points \( (-1,-5)\) and \( (2,10)\).
- What is the equation of the parabola with x intercepts at \( x = 2\) and \( x = -3\), and a y - intercept at \( y = 5\)?
- Find the equation of the parabola \( y = a x^2 + b x + c \) that passes through the points \( (0,3) \) , \( (1,-4)\) and \( (-1 , 4)\).
- Find the equation of the parabola, with vertical axis of symmetry, which is tangent to the line \( y = 3 \) at \( x = -2 \) and its graph passes through the point \((0,5) \ ).
- For what value of the slope m is the line, of equation \( y = m x - 3 \), tangent to the parabola of equation \( y = 3 x^2 - x \)?
- For what values of parameter b does the line of equation \( y = 2 x + b \) intersect the parabola of equation \( y = - x^2 - 2 x + 1\) in two points?
- Find the equation \( y = a x^2 + x\) of the tangent parabola to the line of equation \( y = 3 x + 1\).
- Shift the graph of the parabola \( y = x^2 \) to the left 3 units, then reflect the resulting graph in the x-axis, and then shift it up 4 units. What is the equation of the new parabola after these transformations?
- What transformations are needed to transform the graph of the parabola \( y = x^2 \) into the graph of the parabola \( y = - x^2 + 4 x + 6 \)?
Solutions to previous questions and problems
- The points \((-1,-5)\) and \((2,10) \) are on the graph of the parabola \( y = 2 x^2 + b x + c\), therefore. \( -5 = 2 (-1)^2 + b (-1) + c\) \( 10 = 2 (2)^2 + b (2) + c\) Rewrite the above system in b and c in standard form. \( - b + c = - 7\) \( 2b + c = 2\) Solve the above system of equations to obtain: \( c = - 4 \) and \( b = 3\) Equation of the parabola that passes through the points \( (-1,-5)\) and \( (2,10)\) is: \( y = 2 x^2 + b x + c = 2 x^2 + 3 x - 4\) Use a graph plotter to check your answer by graphing \( y = 2 x^2 + 3 x - 4 \) and Check that the graph passes through the points \( (-1,-5) \) and \((2,10)\).
- The equation of a parabola with x-intercepts at \( x = 2 \) and \( x = -3 \) can be written as the product of two factors whose zeros are the x-intercepts as follows: \( y = a(x - 2)(x + 3) \) We now use the y-intercept at (0, 5), which is a point through which the parabola passes, to write: \( 5 = a(0 - 2)(0 + 3) \) Solve for \(a\) \( a = - 5 / 6 \) Equation: \( y = (-5/6)(x - 2)(x + 3)\) Graph \( y = (-5/6)(x - 2)(x + 3)\) and verify that the graph has an x-intercept at \( x = 2 , x = -3 \) and an x-intercept at y in \( y = 5\).
- The points \( (0,3), (1,-4) \) and \( (-1,4) \) lie on the graph of the parabola \( y = a x^2 + b x + c \) and are therefore solutions to the equation of the parabola. Therefore, we write the system of 3 equations as follows: The point \( (0,3) \) gives the equation: \( 3 = a (0)^2 + b (0) + c \quad (I) \) The point \( (1,-4) \) gives the equation: \( - 4 = a (1)^2 + b (1) + c \quad (II) \) The point \( (-1,4) \) gives the equation: \( 4 = a (-1)^2 + b (-1) + c \quad (III) \) Equation (I) gives: \( c = 3 \) Substitute 3 for c in equations (II) and (III) \( a + b = -7 \) \( a - b = 1 \) Solve the system in a and b \( a = - 3 \) and \( b = - 4 \) Equation: \( y = a x^2 + b x + c = -3 x^2 - 4x + 3 \) Graph the graphs of \( y = -3 x^2 - 4x + 3 \) and verify that the graph passes through the points \( (0,3), (1,-4) \) and \( (-1 ,4) \).
- The equation of the parabola, with vertical axis of symmetry, has the form \( y = a x^2 + b x + c \) or in vertex form \( y = a(x - h)^2 + k \) where the vertex is at the point \( (h , k)\) . In this case it is tangent to a horizontal line \( y = 3 \) at \( x = -2 \) which means that its vertex is at the point \( (h , k) = (-2 , 3) \ ). Therefore, the equation of this parabola can be written as: \( y = a(x - h)^2 + k = a(x - (-2))^2 + 3 = a(x + 2)^2 + 3 \) Its graph passes through the point \( (0 , 5) \). That's why \( 5 = a(0 + 2)^2 + 3 = 4 a+ 3 \) Solve the above for \( a \) \( a = 1 / 2 \) Equation: \( y = (1/2)(x + 2)^2 + 3 \) Sketch the graphs of \( y = (1/2)(x + 2)^2 + 3 \) and verify that the graph is tangent to the horizontal line \( y = 3 \) at \( x = -2 \ ) and also the graph passes through the point \( (0 , 5) \).
- A line and a parabola are tangent if they have only one point of intersection, which is the point where they touch. The points of intersection are found by solving the system \( y = m x - 3 \) y \( y = 3 x^2 - x \) \( mx - 3 = 3 x^2 - x \) Write as a standard quadratic equation: \( 3 x^2 - x(1 + m) + 3 = 0 \) The discriminant of the above quadratic equation is given by: \( \Delta = (1 + m)^2 - 4(3)(3) \) The line is tangent to the parabola of the graphs of the two curves have a point of intersection if: \( \Delta = 0 \) (case of a solution of a quadratic equation) Hence the equation: \( (1 + m)^2 - 4(3)(3) = 0 \) solve for me \( (1 + m)^2 = 36 \) Solutions: \( m = 5 \) and \( m = -7 \) Use a graph plotter to check your answer by plotting the graphs of the lines: \( y = 5 x - 3 \) (m = 5 solution ), \( y = -7 x - 3 \) (m = 7 solution) and the parabola \( y = 3 x^2 - x\) and check that the two lines are tangent to the graph of the parabola \( y = 3 x^2 - x\).
- The points of intersection are found by solving the system \( y = 2 x + b \) and \( y = - x^2 - 2x + 1 \) \( 2x + b = - x^2 - 2x + 1 \) Write as a standard quadratic equation: \( - x^2 - 4x + 1 - b = 0 \) The discriminant of the above equation is given by: \( \Delta = (-4)^2 - 4(-1)(1 - b) = 20 - 4b \) The graphs of \( y = 2 x + b \) and \( y = - x^2 - 2 x + 1 \) have two points of intersection if \( \Delta \gt 0 \) (case of two real solutions of a quadratic equation) \( 20 - 4 b \gt 0 \) Solve for b \( b \lt 5 \) Use a graph plotter to check your answer by plotting graphs of \( y = - x^2 - 2 x + 1 \) and lines through equations \( y = 2 x + b \) for values of \( b \gt 5 \) , \( b \lt 5 \) and \( b = 5 \) to see how many points of intersection of the parabola and the line there are for each of these values of \( b \).
- The points of intersection are found by solving the system \( y = a x^2 + x \) y \( y = 3 x + 1 \) \( 3 x + 1 = a x^2 + x \) Write as a standard quadratic equation: \( a x^2 - 2 x - 1 = 0 \) Discriminant: \( \Delta = (-2)^2 - 4(a)(-1) = 4 + 4 a \) The graphs are tangent if they have a point of intersection (case for a solution of a quadratic equation) if \( \Delta = 0 \). That's why \( 4 + 4 a = 0 \) Solve for \(a\) \( a = -1 \) Parabola equation: \( y = -x^2 + x \) Graph \( y = - x^2 + x \) and \( y = 3 x + 1 \) to verify the answer above.
- Beginning: \( y = x^2 \) Shift 3 units to the left: \( y = (x + 3)^2 \) Reflect about the x-axis: \( y = -(x + 3)^2 \) Shift up 4 units: \( y = -(x + 3)^2 + 4 \)
- Given: \( y = - x^2 + 4 x + 6 \) Rewrite in vertex form by completing the square: \( y = - x^2 + 4 x + 6 = - (x - 2)^2 + 10\) Beginning: \( y = x^2\) Shift 2 units to the right: \( y = (x - 2)^2\) Reflect about the x-axis: \( y = -(x - 2)^2 \) Shift up 10 units: \( y = -(x - 2)^2 + 10\)
- Any point identified on the given graph can be used to find the equation of the parabola. However, using the x and y intercepts and the vertex are better ways to find the equation of the parabola whose graph is shown below. Two methods are presented to solve the problem: method 1: The graph has two x-intercepts: (-5, 0) and (-1, 0) Use the two x-intercepts at (-5, 0) and (-1, 0) to write the equation of the parabola as follows: \( y = a(x + 1)(x + 5)\) Use the y-intercept at (0, -5) to write \( - 5 = a(0 + 1)(0 + 5) = 5 a\) Solve for \(a \) \(a = -1\) Write the equation of the parabola: \( y = -(x + 1)(x + 5) = - x^2 -6 x - 5\) method 2: Use the vertex at \( ( h , k) = (-3 , 4) \) to write the equation of the parabola in vertex form as follows: \( y = a(x - h)^2 + k = a(x + 3)^2 + 4 \) Use the y-intercept (0, -5) to find \(a\). \( - 5 = a(0 + 3)^2 + 4 \) Solve the above for \(a\): \( a = -1 \) The equation of the parabola is given by \(y = -(x + 3)^2 + 4 = - x^2 -6 x - 5 \)
More references and links on parables
Popular pages, stay in touch.
- Privacy Policy

- Master weak areas with 10,000+ Questions & Answers
- Best for 11+ Grammar & Independent School Exams
- Improve Speed, Accuracy & Time Management
- Includes 180, Maths Solved Past Papers
Word Problems Questions and Answers

These detailed answers are visible only for premium members
Please register to unlock over one hundred and sixty 11+ Exam Papers. 10,000+ Questions with Answers

Interpreting Word Problems for 11 Plus Exams
1.what are word problems.
Word problems are mathematical problems that are presented in the form of a real-life situation or scenario. They often require students to use their critical thinking skills to analyze and interpret the information given in the problem and apply their mathematical knowledge to find a solution. Word problems can involve a range of mathematical concepts such as addition, subtraction, multiplication, division, fractions, percentages, ratios, and more. They are commonly used in math textbooks, tests, and exams to test students' understanding of mathematical concepts and their ability to apply them in real-life situations.
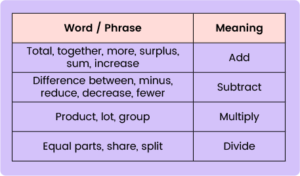
1.1 Vocabulary used in Word Problems
Children must be aware about the vocabulary associated while solving word problems: Look at the table below to understand the logic of how to analyse a word problem:
1.2 What sort of Word Problems may you encounter in your 11 plus exam?
You may encounter Word Problems from the following nine strands in your 11 plus exams:
- Number and Place Value
- Calculations
- Fractions, Decimals & Percentages
- Ratio and Proportion
- Measurement
- Geometry: Properties of Shapes
- Geometry: Position & Direction
1.3 Solved Examples
Example 1: Jessica has 5 cards with the digits 9, 5, 7, 1 and 8 written on them.
| 9 | 5 | 7 | 1 | 8 |
Write down the smallest number Jessica can make using all of these cards:
Solution: The cards given are: 9, 5, 7, 1, 8 Arranging the cards in ascending order: 1, 5, 7, 8, 9 Smallest five digit number formed is: 15789
Example 2: Six friends shared the cost of a tennis court (priced at 3 million pounds) equally. How much did each of them pay?
3 million pounds = £3,000,000
£3,000,000 ÷ 6 = £500,000
Each of the friends have to pay £500000.
Sam spends 1/3 of his money. He then spends 1/3 of what he has left. What fraction of his money did he spend altogether?
First time, Sam spends = 1/3 of his money
Remaining money = 1 - 1/3 = 2/3 of his money
Second time, Sam spends = 1/3 of his remaining money
= 1/3 × 2/3 of his money
= 2/9 of his money
Total spending = 1/3 of his money + 2/9 of his money
= 1/3 + 2/9
= 3/9 + 2/9
Sam spends 5/9 of his money altogether.
Example 4: A drink is made by mixing fruit juice with water. 39 ml of fruit juice is needed to make 600 ml of the drink. How much water is needed to make 800 ml of the drink?
39 ml of fruit juice is required to make 600 ml of the drink.
(600 - 39) = 561 ml of water required to make 600 ml of drink
Required water to make 200 ml of the drink = 561 ÷ 3 = 187 ml
Required water to make 800 ml of the drink = 187 x 4 = 748 ml
Example 5: Miley and Seema are collecting money for charity. Miley collects £10 more than Seema. Altogether they collect £240. How much did Seema collect?
Let Seema collect = £x
Then, Miley collected = £(x + 10)
Total money = £240
x + x + 10 = 240
2x + 10 = 240
2x = 240 - 10
x = 230 ÷ 2
x = £115
Seema collected £115.
Add together 5 metres, 5 centimetres and 5 millimetres. Give your answer in millimetres.
5 m = 5000 mm & 5 cm = 50 mm
5 m+ 5 cm + 5 mm
= 5000 mm + 50 mm + 5 mm
Saif puts five dots on a piece of paper in such a way that no three dots are in a straight line. He joins every dot to every other dot with a straight line. How many lines does he draw?
Saif draws 5 dots such that no three dots are in a straight line. The dots represent the vertices of a pentagon Thus, the number of lines can be found using,
Thus, 10 lines can be drawn.
Give the size of the obtuse angle between the compass directions NE and S.
The angle between Northeast to East = 45°
The angle between East to South = 90°
The obtuse angle between NE and S = 45° + 90° = 135°
Example 9: The bar graph below shows the number of pet sets in each house in a street.
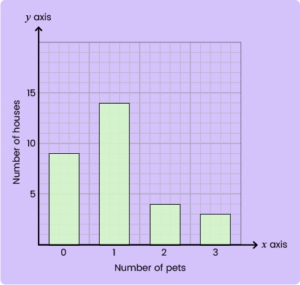
(a) How many houses have 1 pet?
(b) How many houses are there in the street?
(c) How many pets are there in the street?
(a) 14 houses have 1 pet.
(b) 9 + 14 + 4 + 3 = 30
There are 30 houses in the street.
(c) (9 x 0) + (14 x 1) + (2 x 4) + (3 x 3)
= 0 + 14 + 8 + 9
There are 31 pets in the street.

Quiz Summary
0 of 5 Questions completed
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You must first complete the following:
0 of 5 Questions answered correctly
Time has elapsed
You have reached 0 of 0 point(s), ( 0 )
Earned Point(s): 0 of 0 , ( 0 ) 0 Essay(s) Pending (Possible Point(s): 0 )
- Not categorized 0%
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
1 . Question
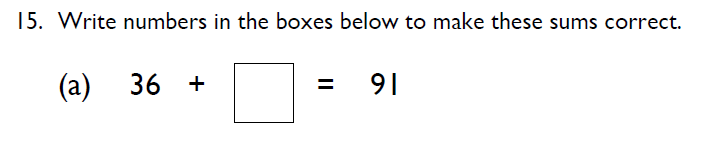
2 . Question

3 . Question

4 . Question
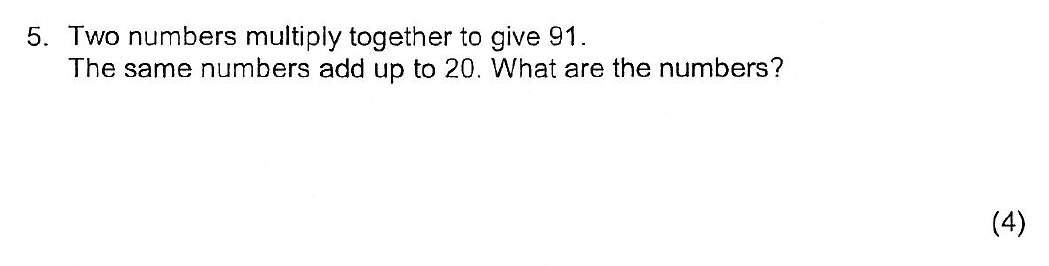
5 . Question
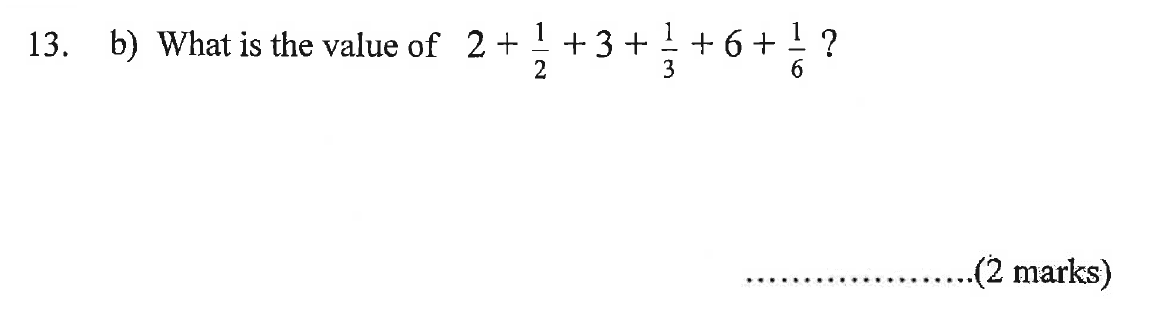
11+ Maths Topics
- Average (2)
- Line symmetry (89)
- Symmetry (28)
- Cubes and Cuboids (111)
- Compound Shapes (102)
- Reflection (70)
- Nets of Solids (51)
- Squares (149)
- Bearings (2)
- Rotational Symmetry (14)
- Translations (19)
- Area and Perimeter (451)
- Parallelogram (15)
- Shapes (37)
- 3D Shapes (45)
- Trapezium (9)
- Triangle (228)
- 2D Shapes (87)
- Slicing (13)
- Rotations (25)
- Angles (199)
- Volume (70)
- Identification of Shapes (20)
- Directions (22)
- Rhombus (4)
- Rectangle (233)
- Polygons (61)
- Reflections (9)
- Coordinates (153)
- Magic square (27)
- Scale Drawings (37)
- Logical Word Problems (8)
- Composite Shapes (1)
- Unit Conversions (262)
- Capacity (7)
- Sorting Tree (3)
- Number Patterns and Sequences (346)
- Temperature (60)
- Data Collection and Presentation (19)
- Networks (12)
- Shortest time (1)
- Factors (153)
- square numbers (112)
- Sequence and Series (6)
- Place Value (57)
- Word Problems (613)
- Ratio & Proportion Medium (3)
- Fractions (789)
- Multiples (141)
- Decimals (412)
- Cube Numbers (24)
- Order and Compare Numbers (205)
- Prime Factorization (12)
- Palindromes (7)
- Unitary Methods (21)
- Read and Write Numbers (15)
- Number Line (27)
- Indices (12)
- Fraction Decimal Percentage Conversion (1)
- Even Numbers (41)
- Percentages (329)
- Equivalent Fraction (1)
- Odd Numbers (27)
- Counting (47)
- Reading and Writing Numbers (103)
- Roman Numbers (4)
- Operations with fractions (2)
- Addition (580)
- Rounding (93)
- Subtraction (529)
- Word Problems (98)
- Word Problems (67)
- Multi Level Word Problems (156)
- Prime Numbers (113)
- decimal manipulation (66)
- Recipes and Proportions (23)
- Speed Distance Time (112)
- Profit and loss (5)
- Alphabet codes (10)
- Money (418)
- Logical Problems (744)
- Time table (14)
- Age Problems (44)
- Seating Arrangement (20)
- Probability (109)
- Patterns and Sequences (123)
- Scale reading (42)
- Train Timetables (33)
- BIDMAS (184)
- Algebraic Equations (109)
- Linear Equations (295)
- Function Machines (79)
- Quadratic Equations (4)
- Simultaneous Equations (86)
- Simplifying expressions (40)
- Substitution (84)
- Algebra Inverse Problems (10)
- Algebra Dependent Problems (204)
- Time and Distance Tables (25)
- Time graph (22)
- Tables (85)
- Venn Diagram (38)
- Pictograms (20)
- Pie Chart (67)
- Bar Chart (103)
- Line Graph (59)
- Mean Median Mode Range (156)
- Tally Marks (6)
- Recipe Problems (18)
- Currency Conversions (75)

What counts as a "good" score will vary depending on the school you want to attend. The standardized 11 Plus test score average across the country is roughly 100. The highest average in some areas is 111. The lowest scores would often fall between 60 and 70, while the highest scores would normally fall between 130 and 140. To achieve excellent marks on 11+ Maths Exams, practice 11+ Maths topic-wise questions .
The best way to prepare for the 11+ Maths Exam is by practicing 11+ Maths topic-wise questions regularly.
Maths online subscriptions are “ Non-Refundable “. No refunds can be issued for any reason. This is because of the nature of digital products.
You should, therefore, make sure that the Maths online subscriptions fulfil your needs before you subscribe.
As these are digital products, we advise parents to go through our Free Past Papers provided on our website and once decided they can buy subscriptions.
Maths: 11+ Sample Paper with answers - 1
11+ Sample Paper with answers - 2
The majority of the 11 Plus Maths questions are mathematical problem-solving, where pupils need to understand and apply mathematical concepts. With regular practice of 11+ Maths Topic-wise questions , you will pass the 11-plus Maths Exam with a high score.
The children must master the following topics for the 11 plus exams
- Number and place value.
- Addition, subtraction, multiplication, and division.
- Fractions, percentages, decimals.
- Ratio and proportion.
- Measurement.
- Geometry (properties and position of shapes, coordinates)
- Statistics.
Get 10,000+ Topic-wise questions by subscribing to our 11+ Maths Topic-wise questions . These questions are collected from 180+ Maths past papers.
11 Plus Maths Past Papers Subscription
Any PiAcademy Memberships are for 1 year (366 days), We give Instant unlock to all exam Resources So that you can plan your 11+ Preparation according to your convenience and as per our Planner Spreadsheets.

Hurry! 11+ Exams are approaching in 6 months. High competition. Most parents fail to do structured planning for the 11+ Exam preparation.
Get a plan and strategy from 11+ Expert Tutors. Avoid the common mistakes that other parents make.
Subscribe to Newsletter
** Get 10% off coupon code on your first order, valid sitewide.
PiAcademy Partners

Follow us on
More than 20,000 registered members!
Exam papers.
© 2014 - 2024 PiAcademy Limited, All Rights Reserved
11plus Problem Solving sample papers
Solve this Question
A quote says “A comedy is a tragedy that happens to others” and a kid tries to read all the letters one-by-one in the quote and it took 1 second to pass onto next letter. Find out the total time taken by the kid to complete the quote?
| 2. 36 seconds |
| 3. 35 seconds |
| 4. 37 seconds |
Click here to see the answer
Answer and Explanation
Answer: 36 seconds
Explanation:
| 2. X |
| 3. Z |
| 4. W |
A B (C D) E (F G) H (I J) K (L M) N (O P) Q (R S) T (U V) W (X Y) Z.
| 2. 121 |
| 3. 134 |
| 4. 123 |
Answer: 123
A farmer measures his field with his bare foot and estimated the length to be 25 feet and the width to be 19 feet. Help the farmer to convert the length and width into meters. (1 meter = 3.28 feet)
| 2. 7.62 m, 5.79 m |
| 3. 5.66 m, 7.33 m |
| 4. 5.5 m, 7.5 m |
Answer: 7.62 m, 5.79 m
Length of the field 25 feet = 25 x 1/3.28 = 7.62 m
Width of the field = 19 feet = 19 x 1/3.28 = 5.79 m
| 2. 6 |
| 3. 1 |
| 4. 2 |
Sum of numbers in each row or column is equal to 14.
Let required number be ‘a’
4 + 9 + a = 14
Free Register
Please register to access free tests, questions, videos, flashcards, vocabulary, mocks and resources:.
- Comprehension
- Spell Check
- Jumbled Words
- Misspelt Words
- Figures Of Speech
- Silent Letters
- Phrasal Verbs
- Model Grammar
- Abbreviations
- Mixed Grammar
- Prepositions
- Active Passive
- Short Maths
- Probability
- Area And Perimeter
- Independent Schools Papers
- Place Value And Rounding
- Writing Numbers
- Addition Subtraction Multiplication Division
- Function Machines
- Hcf And Lcf
- Number Sequences
- Money And Cost
- Percentages
- Ratio Proportion And Scale
- Problem Solving
- 2d And 3d Shapes
- Nets Of 3d Shapes
- Measurement
- Time And Distance
- Inverse Operations
- Times Tables
- Pie Charts And Bar Charts
- Data Tables
- Ordering Numbers
- Negative Numbers
- Gl Assessment
- Coordinates
- Number Equations
- Unit Conversion
- Unit Formula
- Profit And Loss
- Venn Diagrams
- Temperature Calculation
- Powers And Roots
- Relationship
- Odd One Out
- Complete Pattern
- Mirror Image
- Folding Paper
- Placing Dots
- Embedded Figure
- Combining Pieces
- 3letter Missing Word
- Hidden Word
- Insert A Letter
- Shuffled Sentences
- Letter Sequences
- Compound Words
- Similar Meaning
- Letters For Numbers
- Related Numbers
- Misplaced Words
- Move A Letter
- Make A Word
- Vocabulary - Words
Unlimited access to all 11 Plus Grammar & Independent School Tests and Resources for 1 year
Unlimited access to 11 Plus Practice Tests and Resources for 1 month

Let Us Start Preparation with 11PluseHelp – Join Us Today!
Quick links, our services.
- 11Plus-MockExams.co.uk
- MyFlashCards.co.uk
- GCSEMaths4fun.co.uk
- 11PlusIndependent.co.uk
- 11Plus4Fun.co.uk
- GCSEPapers.co.uk
© 2020 11PluseHelp.co.uk , All text and information on the 11PluseHelp.co.uk is copyright and may not be copied or used by individuals or websites without written permission from the Administrator. Any infringement of copyright will be vigorously defended by legal action.
Full-Length SAT Suite Practice Tests
Find full-length practice tests on Bluebook™ as well as downloadable paper (nonadaptive) practice tests to help you prepare for the SAT, PSAT/NMSQT, PSAT 10, and PSAT 8/9.
Paris 2024 Summer Olympics 12 Math Word Problems (Printable + Digital)

Also included in

Description
This NO PREP printable or digital math activity is an easy way to help your students celebrate the 2024 Paris Olympics in the summer! There are 12 total questions, all designed for middle school aged students. This could also be used for lower performing high school students or upper elementary students, although scaffolding may be required.
Math Skills Covered:
- Total (Sums)
- Cost in Euros
- Average Speed
- Mean (Average)
- Distance over Time
- Difference (subtracting)
- Quotient (division)
- Product (multiplication)
- Volume of Rectangular Prism
- Percentage of Whole Number
- Elapsed Time
Looking for more Paris 2024 Olympics Resources? Try these!
Olympics Growing Bundle - includes below resources
Paris 2024 Summer Olympics Friendship Bracelet Craft- FREEBIE
Paris Summer Olympics 2024 Crossword Puzzle Printable - FREEBIE
Paris Summer Olympics 2024 Coloring Pages and Mazes - FREEBIE
Paris 2024 History Reading + Writing Task
Paris 2024 Summer Olympics 10 Math Word Problems
Paris Summer Olympics 2024 11 Math Word Problems
Paris 2024 Summer Olympics 12 Math Word Problems
Paris 2024 Summer Olympics Math Data Analysis Task
Paris 2024 Summer Olympics: Katie Ledecky Reading + Writing Task
Paris 2024 Summer Olympics: Simone Biles Reading + Writing Task
Paris 2024 Olympics: Sha'Carri Richardson Reading + Writing Task
Paris 2024 Olympics: Scottie Scheffler Reading + Writing Task
Olympics Integers Color by Number Math Task - FREEBIE
Olympics Event Matching Trivia - FREEBIE
Questions & Answers
In our middle school era.
- We're hiring
- Help & FAQ
- Privacy policy
- Student privacy
- Terms of service
- Tell us what you think

COMMENTS
Grade 11 Math Problems with Solutions. Questions and problems for grade 11 math including detailed solutions and answers are presented. These problems are designed to gain deep understanding of math concepts and computational procedures and better prepare for math tests and grade 12 Math. Grade 11 Math. Grade 11 Math Practice Test
Grade 11 math practice test questions are presented along with their solutions on videos. Find x . a) 2x x −1 − 1 x +2 − 6 2x2 + 2x − 4 2 x x − 1 − 1 x + 2 − 6 2 x 2 + 2 x − 4 . b) 2x2 + 2x − 4 x2 +8x + 15 ÷ 2x2 +6x + 4 x2 + 10x + 21 2 x 2 + 2 x − 4 x 2 + 8 x + 15 ÷ 2 x 2 + 6 x + 4 x 2 + 10 x + 21 . Simplify the expression ...
Maths Problems with Solutions. Grade 11 maths problems with answers and solutions are presented. Problems. An airplane flies against the wind from A to B in 8 hours. The same airplane returns from B to A, in the same direction as the wind, in 7 hours. Find the ratio of the speed of the airplane (in still air) to the speed of the wind.
Welcome to a collection of 25 challenging math problems designed specifically for 11th graders. These problems will push the boundaries of your mathematical knowledge and problem-solving skills. Each question is tailored to suit the 11th-grade level, covering topics such as algebra, trigonometry, calculus, statistics, and more.
Explore printable Math worksheets for 11th Grade. Math worksheets for Grade 11 are essential tools for teachers to help their students develop a strong foundation in various mathematical concepts. These worksheets cover a wide range of topics, including algebra, geometry, trigonometry, and calculus, which are crucial for students at this level.
Explore printable algebra worksheets for 11th Grade. Algebra worksheets for Grade 11 are essential tools for teachers looking to engage their students in the world of mathematics. These worksheets provide a comprehensive and structured approach to learning algebra, ensuring that students have a solid foundation in this critical subject area.
Grade 11 Math Questions and Solutions. The Smarter Balanced Assessment Consortium (SBAC) is a standardized test that includes various new technology-enhanced questions. Some of them are Multiple choice-single correct responses, Multiple choice-multiple correct responses, Matching Tables, Drag and Drop, Hot text, Table Fill in, Graphing ...
Grade 11 math. 240 skills 179 videos. IXL offers hundreds of grade 11 math skills to explore and learn! Not sure where to start? Go to your personalized Recommendations wall to find a skill that looks interesting, or select a skill plan that aligns to your textbook, provincial curriculum, or standardized test. Solve quadratic inequalities.
2d and 3d shapes. 11 plus maths 2d and 3d shapes are often considered some of the most complex topics. 11 plus shape questions asked are often around volume, for example, and include shapes such as cubes, cylinders and pyramids. A straight-up maths topic they will need to learn but once they understand it they will know exactly how to answer ...
Trigonometry. Right triangle trigonometry. Sine Law and Cosine Law. 2D and 3D Trig word problems. Trigonometric identities. Unit Circle and special angles ( degrees) Graphing periodic functions. Solving trigonometric equations. Word problems modeling periodic functions.
tability-Mathematics (NeSA-M).Each question will ask you to select. an answer from among four choices.For all questions: Read each question ca. efully and choose the best answer. You may use s. ratch paper to solve the problems.The Mathematics Reference Sheet is provid. d in the back of the test booklet. You may refer to.
ALL OF GRADE 11 MATH IN 1 HOUR! (exam review part 3) | jensenmath.ca. Review all of the units of the grade 11 MCR3U math course with practice questions and the 'grade 11 math in 1 hour' review video series. The topics reviewed include: quadratic functions, radicals, simplifying rational expressions, transformations, exact values of trig ratios ...
Free lessons, worksheets, and video tutorials for students and teachers. Topics in this unit include: what is a function, domain and range, vertical line test, quadratics, max and min of quadratics, solving quadratic equations, simplifying radicals. This follows chapter 1 of the grade 11 Functions McGraw Hill textbook and chapter 1 of the grade ...
High school math for grades 10, 11, and 12 math questions and problems to test deep understanding of math concepts and computational procedures are presented. Detailed solutions and answers to the questions are provided. Grade 12 Math . Use Sinusoidal Functions to Solve Applications Problems with Solutions; Grade 12 Math Practice Test
Practice Questions For Class 11 Maths Chapter 3 Trigonometric Functions. Find the value of the below expression. Hint: Simplify the expression to. Find the general solution of the equation 5cos 2 θ + 7sin 2 θ - 6 = 0. If θ lies in the first quadrant and cos θ = 8/17, then find the value of cos (30° + θ) + cos (45° - θ) + cos (120 ...
Khan Academy's 100,000+ free practice questions give instant feedback, don't need to be graded, and don't require a printer. Math Worksheets. Khan Academy. Math worksheets take forever to hunt down across the internet. Khan Academy is your one-stop-shop for practice from arithmetic to calculus. Math worksheets can vary in quality from ...
Free lessons, worksheets, and video tutorials for students and teachers. Topics in this unit include: periodic functions, graphs of sine and cosine, transformations of trig functions, and applications of trig functions. This follows chapter 5 of the grade 11 Functions McGraw Hill textbook and chapter 6 of the grade 11 Functions Nelson textbook.
Math 11 Ch 9: Linear and Quadratic Inequalities : Assignments • 9.1 Graphing Linear Inequalities with Two Variables • 9.2 Solving Quadratic Inequalities with One Variable • 9.3 Graphing Quadratic Inequalities with Two Variables • Ch 9 Review • Final Exam Review. SOL 9.1 9.2 9.3 9R. Practice Test and Quiz • Quiz 9.1 to 9.2 • Quiz 9 ...
Solution. (21) Construct the matrix A = [aij]3x3, where aij = i - j. State whether A is symmetric or skew-symmetric. Solution. (22) Let A and B be two symmetric matrices. Prove that AB = BA if and only if AB is a symmetric matrix. Solution. (23) If A and B are symmetric matrices of same order, prove that. (i) AB + BA is a symmetric matrix.
You should have learnt a few methods for solving real life problems from the previous three groups of 11-plus Maths quizzes: see how well you can apply your skills to these problems. This is a difficult group of quizzes compared to the previous ones, so remember to read the questions carefully. Look at the four options before choosing your answer.
Questions and Problems. Find the x and y intercepts, the vertex and the axis of symmetry of the parabola with equation \( y = - x^2 + 2 x + 3 \)? ... The points of intersection are found by solving the system \( y = 2 x + b \) and \( y = - x^2 ... High School Math (Grades 10, 11, 12): Free Questions and Problems with Answers ...
The standardized 11 Plus test score average across the country is roughly 100. The highest average in some areas is 111. The lowest scores would often fall between 60 and 70, while the highest scores would normally fall between 130 and 140. To achieve excellent marks on 11+ Maths Exams, practice 11+ Maths topic-wise questions.
11 Plus Problem-Solving questions test the analytical, problem solving and logical ability of the children. At the end of 11 plus maths question paper in 11 Plus Entrance Exam, most of the questions are on problem-solving only. Questions on this topic are framed in such a way that children need to identify the logic behind it. You can practice 11+ Maths Papers any times at 11PluseHelp.co.uk ...
Find full-length practice tests on Bluebook™ as well as downloadable paper (nonadaptive) practice tests to help you prepare for the SAT, PSAT/NMSQT, PSAT 10, and PSAT 8/9.
1st grade math. 2nd grade math. 3rd grade math. 4th grade math. 5th grade math. 6th grade math. 7th grade math. ... There are 12 total questions, all designed for middle school aged students. ... Paris Summer Olympics 2024 11 Math Word Problems. Paris 2024 Summer Olympics Math Data Analysis Task. Total Pages. 2 pages. Answer Key.