2 3 formulas and problem solving answer key

Get step-by-step solutions to your math problems

Try Math Solver

Get step-by-step explanations

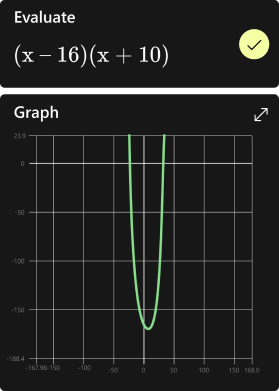
Graph your math problems

Practice, practice, practice

Get math help in your language

Intermediate Algebra (6th Edition)

By martin-gay, elayn, chapter 2 - section 2.3 - formulas and problem solving - exercise set - page 76: 79, work step by step, update this answer.

You can help us out by revising, improving and updating this answer.

After you claim an answer you’ll have 24 hours to send in a draft. An editor will review the submission and either publish your submission or provide feedback.

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

What can QuickMath do?

QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.

• The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
• The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
• The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
• The calculus section will carry out differentiation as well as definite and indefinite integration.
• The matrices section contains commands for the arithmetic manipulation of matrices.
• The graphs section contains commands for plotting equations and inequalities.
• The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.

Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

3.1 Functions and Function Notation

• ⓑ yes (Note: If two players had been tied for, say, 4th place, then the name would not have been a function of rank.)

w = f ( d ) w = f ( d )

g ( 5 ) = 1 g ( 5 ) = 1

m = 8 m = 8

y = f ( x ) = x 3 2 y = f ( x ) = x 3 2

g ( 1 ) = 8 g ( 1 ) = 8

x = 0 x = 0 or x = 2 x = 2

• ⓐ yes, because each bank account has a single balance at any given time;
• ⓑ no, because several bank account numbers may have the same balance;
• ⓒ no, because the same output may correspond to more than one input.
• ⓐ Yes, letter grade is a function of percent grade;
• ⓑ No, it is not one-to-one. There are 100 different percent numbers we could get but only about five possible letter grades, so there cannot be only one percent number that corresponds to each letter grade.

No, because it does not pass the horizontal line test.

3.2 Domain and Range

{ − 5 , 0 , 5 , 10 , 15 } { − 5 , 0 , 5 , 10 , 15 }

( − ∞ , ∞ ) ( − ∞ , ∞ )

( − ∞ , 1 2 ) ∪ ( 1 2 , ∞ ) ( − ∞ , 1 2 ) ∪ ( 1 2 , ∞ )

[ − 5 2 , ∞ ) [ − 5 2 , ∞ )

• ⓐ values that are less than or equal to –2, or values that are greater than or equal to –1 and less than 3
• ⓑ { x | x ≤ − 2 or − 1 ≤ x < 3 } { x | x ≤ − 2 or − 1 ≤ x < 3 }
• ⓒ ( − ∞ , − 2 ] ∪ [ − 1 , 3 ) ( − ∞ , − 2 ] ∪ [ − 1 , 3 )

domain =[1950,2002] range = [47,000,000,89,000,000]

domain: ( − ∞ , 2 ] ; ( − ∞ , 2 ] ; range: ( − ∞ , 0 ] ( − ∞ , 0 ]

3.3 Rates of Change and Behavior of Graphs

$ 2.84 − $ 2.31 5 years = $ 0.53 5 years = $ 0.106 $ 2.84 − $ 2.31 5 years = $ 0.53 5 years = $ 0.106 per year.

a + 7 a + 7

The local maximum appears to occur at ( − 1 , 28 ) , ( − 1 , 28 ) , and the local minimum occurs at ( 5 , − 80 ) . ( 5 , − 80 ) . The function is increasing on ( − ∞ , − 1 ) ∪ ( 5 , ∞ ) ( − ∞ , − 1 ) ∪ ( 5 , ∞ ) and decreasing on ( − 1 , 5 ) . ( − 1 , 5 ) .

3.4 Composition of Functions

( f g ) ( x ) = f ( x ) g ( x ) = ( x − 1 ) ( x 2 − 1 ) = x 3 − x 2 − x + 1 ( f − g ) ( x ) = f ( x ) − g ( x ) = ( x − 1 ) − ( x 2 − 1 ) = x − x 2 ( f g ) ( x ) = f ( x ) g ( x ) = ( x − 1 ) ( x 2 − 1 ) = x 3 − x 2 − x + 1 ( f − g ) ( x ) = f ( x ) − g ( x ) = ( x − 1 ) − ( x 2 − 1 ) = x − x 2

No, the functions are not the same.

A gravitational force is still a force, so a ( G ( r ) ) a ( G ( r ) ) makes sense as the acceleration of a planet at a distance r from the Sun (due to gravity), but G ( a ( F ) ) G ( a ( F ) ) does not make sense.

f ( g ( 1 ) ) = f ( 3 ) = 3 f ( g ( 1 ) ) = f ( 3 ) = 3 and g ( f ( 4 ) ) = g ( 1 ) = 3 g ( f ( 4 ) ) = g ( 1 ) = 3

g ( f ( 2 ) ) = g ( 5 ) = 3 g ( f ( 2 ) ) = g ( 5 ) = 3

[ − 4 , 0 ) ∪ ( 0 , ∞ ) [ − 4 , 0 ) ∪ ( 0 , ∞ )

Possible answer:

g ( x ) = 4 + x 2 h ( x ) = 4 3 − x f = h ∘ g g ( x ) = 4 + x 2 h ( x ) = 4 3 − x f = h ∘ g

3.5 Transformation of Functions

The graphs of f ( x ) f ( x ) and g ( x ) g ( x ) are shown below. The transformation is a horizontal shift. The function is shifted to the left by 2 units.

g ( x ) = 1 x - 1 + 1 g ( x ) = 1 x - 1 + 1

g ( x ) = − f ( x ) g ( x ) = − f ( x )

h ( x ) = f ( − x ) h ( x ) = f ( − x )

Notice: g ( x ) = f ( − x ) g ( x ) = f ( − x ) looks the same as f ( x ) f ( x ) .

g ( x ) = 3 x - 2 g ( x ) = 3 x - 2

g ( x ) = f ( 1 3 x ) g ( x ) = f ( 1 3 x ) so using the square root function we get g ( x ) = 1 3 x g ( x ) = 1 3 x

3.6 Absolute Value Functions

using the variable p p for passing, | p − 80 | ≤ 20 | p − 80 | ≤ 20

f ( x ) = − | x + 2 | + 3 f ( x ) = − | x + 2 | + 3

x = − 1 x = − 1 or x = 2 x = 2

3.7 Inverse Functions

h ( 2 ) = 6 h ( 2 ) = 6

The domain of function f − 1 f − 1 is ( − ∞ , − 2 ) ( − ∞ , − 2 ) and the range of function f − 1 f − 1 is ( 1 , ∞ ) . ( 1 , ∞ ) .

• ⓐ f ( 60 ) = 50. f ( 60 ) = 50. In 60 minutes, 50 miles are traveled.
• ⓑ f − 1 ( 60 ) = 70. f − 1 ( 60 ) = 70. To travel 60 miles, it will take 70 minutes.

x = 3 y + 5 x = 3 y + 5

f − 1 ( x ) = ( 2 − x ) 2 ; domain of f : [ 0 , ∞ ) ; domain of f − 1 : ( − ∞ , 2 ] f − 1 ( x ) = ( 2 − x ) 2 ; domain of f : [ 0 , ∞ ) ; domain of f − 1 : ( − ∞ , 2 ]

3.1 Section Exercises

A relation is a set of ordered pairs. A function is a special kind of relation in which no two ordered pairs have the same first coordinate.

When a vertical line intersects the graph of a relation more than once, that indicates that for that input there is more than one output. At any particular input value, there can be only one output if the relation is to be a function.

When a horizontal line intersects the graph of a function more than once, that indicates that for that output there is more than one input. A function is one-to-one if each output corresponds to only one input.

not a function

f ( − 3 ) = − 11 ; f ( − 3 ) = − 11 ; f ( 2 ) = − 1 ; f ( 2 ) = − 1 ; f ( − a ) = − 2 a − 5 ; f ( − a ) = − 2 a − 5 ; − f ( a ) = − 2 a + 5 ; − f ( a ) = − 2 a + 5 ; f ( a + h ) = 2 a + 2 h − 5 f ( a + h ) = 2 a + 2 h − 5

f ( − 3 ) = 5 + 5 ; f ( − 3 ) = 5 + 5 ; f ( 2 ) = 5 ; f ( 2 ) = 5 ; f ( − a ) = 2 + a + 5 ; f ( − a ) = 2 + a + 5 ; − f ( a ) = − 2 − a − 5 ; − f ( a ) = − 2 − a − 5 ; f ( a + h ) = 2 − a − h + 5 f ( a + h ) = 2 − a − h + 5

f ( − 3 ) = 2 ; f ( − 3 ) = 2 ; f ( 2 ) = 1 − 3 = − 2 ; f ( 2 ) = 1 − 3 = − 2 ; f ( − a ) = | − a − 1 | − | − a + 1 | ; f ( − a ) = | − a − 1 | − | − a + 1 | ; − f ( a ) = − | a − 1 | + | a + 1 | ; − f ( a ) = − | a − 1 | + | a + 1 | ; f ( a + h ) = | a + h − 1 | − | a + h + 1 | f ( a + h ) = | a + h − 1 | − | a + h + 1 |

g ( x ) − g ( a ) x − a = x + a + 2 , x ≠ a g ( x ) − g ( a ) x − a = x + a + 2 , x ≠ a

a. f ( − 2 ) = 14 ; f ( − 2 ) = 14 ; b. x = 3 x = 3

a. f ( 5 ) = 10 ; f ( 5 ) = 10 ; b. x = − 1 x = − 1 or x = 4 x = 4

• ⓐ f ( t ) = 6 − 2 3 t ; f ( t ) = 6 − 2 3 t ;
• ⓑ f ( − 3 ) = 8 ; f ( − 3 ) = 8 ;
• ⓒ t = 6 t = 6
• ⓐ f ( 0 ) = 1 ; f ( 0 ) = 1 ;
• ⓑ f ( x ) = − 3 , x = − 2 f ( x ) = − 3 , x = − 2 or x = 2 x = 2

not a function so it is also not a one-to-one function

one-to- one function

function, but not one-to-one

f ( x ) = 1 , x = 2 f ( x ) = 1 , x = 2

f ( − 2 ) = 14 ; f ( − 1 ) = 11 ; f ( 0 ) = 8 ; f ( 1 ) = 5 ; f ( 2 ) = 2 f ( − 2 ) = 14 ; f ( − 1 ) = 11 ; f ( 0 ) = 8 ; f ( 1 ) = 5 ; f ( 2 ) = 2

f ( − 2 ) = 4 ;    f ( − 1 ) = 4.414 ; f ( 0 ) = 4.732 ; f ( 1 ) = 5 ; f ( 2 ) = 5.236 f ( − 2 ) = 4 ;    f ( − 1 ) = 4.414 ; f ( 0 ) = 4.732 ; f ( 1 ) = 5 ; f ( 2 ) = 5.236

f ( − 2 ) = 1 9 ; f ( − 1 ) = 1 3 ; f ( 0 ) = 1 ; f ( 1 ) = 3 ; f ( 2 ) = 9 f ( − 2 ) = 1 9 ; f ( − 1 ) = 1 3 ; f ( 0 ) = 1 ; f ( 1 ) = 3 ; f ( 2 ) = 9

[ 0 , 100 ] [ 0 , 100 ]

[ − 0.001 , 0 .001 ] [ − 0.001 , 0 .001 ]

[ − 1 , 000 , 000 , 1,000,000 ] [ − 1 , 000 , 000 , 1,000,000 ]

[ 0 , 10 ] [ 0 , 10 ]

[ −0.1 , 0.1 ] [ −0.1 , 0.1 ]

[ − 100 , 100 ] [ − 100 , 100 ]

• ⓐ g ( 5000 ) = 50 ; g ( 5000 ) = 50 ;
• ⓑ The number of cubic yards of dirt required for a garden of 100 square feet is 1.
• ⓐ The height of a rocket above ground after 1 second is 200 ft.
• ⓑ The height of a rocket above ground after 2 seconds is 350 ft.

3.2 Section Exercises

The domain of a function depends upon what values of the independent variable make the function undefined or imaginary.

There is no restriction on x x for f ( x ) = x 3 f ( x ) = x 3 because you can take the cube root of any real number. So the domain is all real numbers, ( − ∞ , ∞ ) . ( − ∞ , ∞ ) . When dealing with the set of real numbers, you cannot take the square root of negative numbers. So x x -values are restricted for f ( x ) = x f ( x ) = x to nonnegative numbers and the domain is [ 0 , ∞ ) . [ 0 , ∞ ) .

Graph each formula of the piecewise function over its corresponding domain. Use the same scale for the x x -axis and y y -axis for each graph. Indicate inclusive endpoints with a solid circle and exclusive endpoints with an open circle. Use an arrow to indicate − ∞ − ∞ or ∞ . ∞ . Combine the graphs to find the graph of the piecewise function.

( − ∞ , 3 ] ( − ∞ , 3 ]

( − ∞ , − 1 2 ) ∪ ( − 1 2 , ∞ ) ( − ∞ , − 1 2 ) ∪ ( − 1 2 , ∞ )

( − ∞ , − 11 ) ∪ ( − 11 , 2 ) ∪ ( 2 , ∞ ) ( − ∞ , − 11 ) ∪ ( − 11 , 2 ) ∪ ( 2 , ∞ )

( − ∞ , − 3 ) ∪ ( − 3 , 5 ) ∪ ( 5 , ∞ ) ( − ∞ , − 3 ) ∪ ( − 3 , 5 ) ∪ ( 5 , ∞ )

( − ∞ , 5 ) ( − ∞ , 5 )

[ 6 , ∞ ) [ 6 , ∞ )

( − ∞ , − 9 ) ∪ ( − 9 , 9 ) ∪ ( 9 , ∞ ) ( − ∞ , − 9 ) ∪ ( − 9 , 9 ) ∪ ( 9 , ∞ )

domain: ( 2 , 8 ] , ( 2 , 8 ] , range [ 6 , 8 ) [ 6 , 8 )

domain: [ − 4 , 4], [ − 4 , 4], range: [ 0 , 2] [ 0 , 2]

domain: [ − 5 , 3 ) , [ − 5 , 3 ) , range: [ 0 , 2 ] [ 0 , 2 ]

domain: ( − ∞ , 1 ] , ( − ∞ , 1 ] , range: [ 0 , ∞ ) [ 0 , ∞ )

domain: [ − 6 , − 1 6 ] ∪ [ 1 6 , 6 ] ; [ − 6 , − 1 6 ] ∪ [ 1 6 , 6 ] ; range: [ − 6 , − 1 6 ] ∪ [ 1 6 , 6 ] [ − 6 , − 1 6 ] ∪ [ 1 6 , 6 ]

domain: [ − 3 , ∞ ) ; [ − 3 , ∞ ) ; range: [ 0 , ∞ ) [ 0 , ∞ )

domain: ( − ∞ , ∞ ) ( − ∞ , ∞ )

f ( − 3 ) = 1 ; f ( − 2 ) = 0 ; f ( − 1 ) = 0 ; f ( 0 ) = 0 f ( − 3 ) = 1 ; f ( − 2 ) = 0 ; f ( − 1 ) = 0 ; f ( 0 ) = 0

f ( − 1 ) = − 4 ; f ( 0 ) = 6 ; f ( 2 ) = 20 ; f ( 4 ) = 34 f ( − 1 ) = − 4 ; f ( 0 ) = 6 ; f ( 2 ) = 20 ; f ( 4 ) = 34

f ( − 1 ) = − 5 ; f ( 0 ) = 3 ; f ( 2 ) = 3 ; f ( 4 ) = 16 f ( − 1 ) = − 5 ; f ( 0 ) = 3 ; f ( 2 ) = 3 ; f ( 4 ) = 16

domain: ( − ∞ , 1 ) ∪ ( 1 , ∞ ) ( − ∞ , 1 ) ∪ ( 1 , ∞ )

window: [ − 0.5 , − 0.1 ] ; [ − 0.5 , − 0.1 ] ; range: [ 4 , 100 ] [ 4 , 100 ]

window: [ 0.1 , 0.5 ] ; [ 0.1 , 0.5 ] ; range: [ 4 , 100 ] [ 4 , 100 ]

[ 0 , 8 ] [ 0 , 8 ]

Many answers. One function is f ( x ) = 1 x − 2 . f ( x ) = 1 x − 2 .

• ⓐ The fixed cost is $500.
• ⓑ The cost of making 25 items is $750.
• ⓒ The domain is [0, 100] and the range is [500, 1500].

3.3 Section Exercises

Yes, the average rate of change of all linear functions is constant.

The absolute maximum and minimum relate to the entire graph, whereas the local extrema relate only to a specific region around an open interval.

4 ( b + 1 ) 4 ( b + 1 )

4 x + 2 h 4 x + 2 h

− 1 13 ( 13 + h ) − 1 13 ( 13 + h )

3 h 2 + 9 h + 9 3 h 2 + 9 h + 9

4 x + 2 h − 3 4 x + 2 h − 3

increasing on ( − ∞ , − 2.5 ) ∪ ( 1 , ∞ ) , ( − ∞ , − 2.5 ) ∪ ( 1 , ∞ ) , decreasing on ( − 2.5 , 1 ) ( − 2.5 , 1 )

increasing on ( − ∞ , 1 ) ∪ ( 3 , 4 ) , ( − ∞ , 1 ) ∪ ( 3 , 4 ) , decreasing on ( 1 , 3 ) ∪ ( 4 , ∞ ) ( 1 , 3 ) ∪ ( 4 , ∞ )

local maximum: ( − 3 , 60 ) , ( − 3 , 60 ) , local minimum: ( 3 , − 60 ) ( 3 , − 60 )

absolute maximum at approximately ( 7 , 150 ) , ( 7 , 150 ) , absolute minimum at approximately ( −7.5 , −220 ) ( −7.5 , −220 )

Local minimum at ( 3 , − 22 ) , ( 3 , − 22 ) , decreasing on ( − ∞ , 3 ) , ( − ∞ , 3 ) , increasing on ( 3 , ∞ ) ( 3 , ∞ )

Local minimum at ( − 2 , − 2 ) , ( − 2 , − 2 ) , decreasing on ( − 3 , − 2 ) , ( − 3 , − 2 ) , increasing on ( − 2 , ∞ ) ( − 2 , ∞ )

Local maximum at ( − 0.5 , 6 ) , ( − 0.5 , 6 ) , local minima at ( − 3.25 , − 47 ) ( − 3.25 , − 47 ) and ( 2.1 , − 32 ) , ( 2.1 , − 32 ) , decreasing on ( − ∞ , − 3.25 ) ( − ∞ , − 3.25 ) and ( − 0.5 , 2.1 ) , ( − 0.5 , 2.1 ) , increasing on ( − 3.25 , − 0.5 ) ( − 3.25 , − 0.5 ) and ( 2.1 , ∞ ) ( 2.1 , ∞ )

b = 5 b = 5

2.7 gallons per minute

approximately –0.6 milligrams per day

3.4 Section Exercises

Find the numbers that make the function in the denominator g g equal to zero, and check for any other domain restrictions on f f and g , g , such as an even-indexed root or zeros in the denominator.

Yes. Sample answer: Let f ( x ) = x + 1 and  g ( x ) = x − 1. f ( x ) = x + 1 and  g ( x ) = x − 1. Then f ( g ( x ) ) = f ( x − 1 ) = ( x − 1 ) + 1 = x f ( g ( x ) ) = f ( x − 1 ) = ( x − 1 ) + 1 = x and g ( f ( x ) ) = g ( x + 1 ) = ( x + 1 ) − 1 = x . g ( f ( x ) ) = g ( x + 1 ) = ( x + 1 ) − 1 = x . So f ∘ g = g ∘ f . f ∘ g = g ∘ f .

( f + g ) ( x ) = 2 x + 6 , ( f + g ) ( x ) = 2 x + 6 , domain: ( − ∞ , ∞ ) ( − ∞ , ∞ )

( f − g ) ( x ) = 2 x 2 + 2 x − 6 , ( f − g ) ( x ) = 2 x 2 + 2 x − 6 , domain: ( − ∞ , ∞ ) ( − ∞ , ∞ )

( f g ) ( x ) = − x 4 − 2 x 3 + 6 x 2 + 12 x , ( f g ) ( x ) = − x 4 − 2 x 3 + 6 x 2 + 12 x , domain: ( − ∞ , ∞ ) ( − ∞ , ∞ )

( f g ) ( x ) = x 2 + 2 x 6 − x 2 , ( f g ) ( x ) = x 2 + 2 x 6 − x 2 , domain: ( − ∞ , − 6 ) ∪ ( − 6 , 6 ) ∪ ( 6 , ∞ ) ( − ∞ , − 6 ) ∪ ( − 6 , 6 ) ∪ ( 6 , ∞ )

( f + g ) ( x ) = 4 x 3 + 8 x 2 + 1 2 x , ( f + g ) ( x ) = 4 x 3 + 8 x 2 + 1 2 x , domain: ( − ∞ , 0 ) ∪ ( 0 , ∞ ) ( − ∞ , 0 ) ∪ ( 0 , ∞ )

( f − g ) ( x ) = 4 x 3 + 8 x 2 − 1 2 x , ( f − g ) ( x ) = 4 x 3 + 8 x 2 − 1 2 x , domain: ( − ∞ , 0 ) ∪ ( 0 , ∞ ) ( − ∞ , 0 ) ∪ ( 0 , ∞ )

( f g ) ( x ) = x + 2 , ( f g ) ( x ) = x + 2 , domain: ( − ∞ , 0 ) ∪ ( 0 , ∞ ) ( − ∞ , 0 ) ∪ ( 0 , ∞ )

( f g ) ( x ) = 4 x 3 + 8 x 2 , ( f g ) ( x ) = 4 x 3 + 8 x 2 , domain: ( − ∞ , 0 ) ∪ ( 0 , ∞ ) ( − ∞ , 0 ) ∪ ( 0 , ∞ )

( f + g ) ( x ) = 3 x 2 + x − 5 , ( f + g ) ( x ) = 3 x 2 + x − 5 , domain: [ 5 , ∞ ) [ 5 , ∞ )

( f − g ) ( x ) = 3 x 2 − x − 5 , ( f − g ) ( x ) = 3 x 2 − x − 5 , domain: [ 5 , ∞ ) [ 5 , ∞ )

( f g ) ( x ) = 3 x 2 x − 5 , ( f g ) ( x ) = 3 x 2 x − 5 , domain: [ 5 , ∞ ) [ 5 , ∞ )

( f g ) ( x ) = 3 x 2 x − 5 , ( f g ) ( x ) = 3 x 2 x − 5 , domain: ( 5 , ∞ ) ( 5 , ∞ )

• ⓑ f ( g ( x ) ) = 2 ( 3 x − 5 ) 2 + 1 f ( g ( x ) ) = 2 ( 3 x − 5 ) 2 + 1
• ⓒ f ( g ( x ) ) = 6 x 2 − 2 f ( g ( x ) ) = 6 x 2 − 2
• ⓓ ( g ∘ g ) ( x ) = 3 ( 3 x − 5 ) − 5 = 9 x − 20 ( g ∘ g ) ( x ) = 3 ( 3 x − 5 ) − 5 = 9 x − 20
• ⓔ ( f ∘ f ) ( − 2 ) = 163 ( f ∘ f ) ( − 2 ) = 163

f ( g ( x ) ) = x 2 + 3 + 2 , g ( f ( x ) ) = x + 4 x + 7 f ( g ( x ) ) = x 2 + 3 + 2 , g ( f ( x ) ) = x + 4 x + 7

f ( g ( x ) ) = x + 1 x 3 3 = x + 1 3 x , g ( f ( x ) ) = x 3 + 1 x f ( g ( x ) ) = x + 1 x 3 3 = x + 1 3 x , g ( f ( x ) ) = x 3 + 1 x

( f ∘ g ) ( x ) = 1 2 x + 4 − 4 = x 2 , ( g ∘ f ) ( x ) = 2 x − 4 ( f ∘ g ) ( x ) = 1 2 x + 4 − 4 = x 2 , ( g ∘ f ) ( x ) = 2 x − 4

f ( g ( h ( x ) ) ) = ( 1 x + 3 ) 2 + 1 f ( g ( h ( x ) ) ) = ( 1 x + 3 ) 2 + 1

• ⓐ ( g ∘ f ) ( x ) = − 3 2 − 4 x ( g ∘ f ) ( x ) = − 3 2 − 4 x
• ⓑ ( − ∞ , 1 2 ) ( − ∞ , 1 2 )
• ⓐ ( 0 , 2 ) ∪ ( 2 , ∞ ) ; ( 0 , 2 ) ∪ ( 2 , ∞ ) ;
• ⓑ ( − ∞ , − 2 ) ∪ ( 2 , ∞ ) ; ( − ∞ , − 2 ) ∪ ( 2 , ∞ ) ;
• ⓒ ( 0 , ∞ ) ( 0 , ∞ )

( 1 , ∞ ) ( 1 , ∞ )

sample: f ( x ) = x 3 g ( x ) = x − 5 f ( x ) = x 3 g ( x ) = x − 5

sample: f ( x ) = 4 x g ( x ) = ( x + 2 ) 2 f ( x ) = 4 x g ( x ) = ( x + 2 ) 2

sample: f ( x ) = x 3 g ( x ) = 1 2 x − 3 f ( x ) = x 3 g ( x ) = 1 2 x − 3

sample: f ( x ) = x 4 g ( x ) = 3 x − 2 x + 5 f ( x ) = x 4 g ( x ) = 3 x − 2 x + 5

sample: f ( x ) = x g ( x ) = 2 x + 6 f ( x ) = x g ( x ) = 2 x + 6

sample: f ( x ) = x 3 g ( x ) = ( x − 1 ) f ( x ) = x 3 g ( x ) = ( x − 1 )

sample: f ( x ) = x 3 g ( x ) = 1 x − 2 f ( x ) = x 3 g ( x ) = 1 x − 2

sample: f ( x ) = x g ( x ) = 2 x − 1 3 x + 4 f ( x ) = x g ( x ) = 2 x − 1 3 x + 4

f ( g ( 0 ) ) = 27 , g ( f ( 0 ) ) = − 94 f ( g ( 0 ) ) = 27 , g ( f ( 0 ) ) = − 94

f ( g ( 0 ) ) = 1 5 , g ( f ( 0 ) ) = 5 f ( g ( 0 ) ) = 1 5 , g ( f ( 0 ) ) = 5

18 x 2 + 60 x + 51 18 x 2 + 60 x + 51

g ∘ g ( x ) = 9 x + 20 g ∘ g ( x ) = 9 x + 20

( f ∘ g ) ( 6 ) = 6 ( f ∘ g ) ( 6 ) = 6 ; ( g ∘ f ) ( 6 ) = 6 ( g ∘ f ) ( 6 ) = 6

( f ∘ g ) ( 11 ) = 11 , ( g ∘ f ) ( 11 ) = 11 ( f ∘ g ) ( 11 ) = 11 , ( g ∘ f ) ( 11 ) = 11

A ( t ) = π ( 25 t + 2 ) 2 A ( t ) = π ( 25 t + 2 ) 2 and A ( 2 ) = π ( 25 4 ) 2 = 2500 π A ( 2 ) = π ( 25 4 ) 2 = 2500 π square inches

A ( 5 ) = π ( 2 ( 5 ) + 1 ) 2 = 121 π A ( 5 ) = π ( 2 ( 5 ) + 1 ) 2 = 121 π square units

• ⓐ N ( T ( t ) ) = 23 ( 5 t + 1.5 ) 2 − 56 ( 5 t + 1.5 ) + 1 N ( T ( t ) ) = 23 ( 5 t + 1.5 ) 2 − 56 ( 5 t + 1.5 ) + 1
• ⓑ 3.38 hours

3.5 Section Exercises

A horizontal shift results when a constant is added to or subtracted from the input. A vertical shifts results when a constant is added to or subtracted from the output.

A horizontal compression results when a constant greater than 1 is multiplied by the input. A vertical compression results when a constant between 0 and 1 is multiplied by the output.

For a function f , f , substitute ( − x ) ( − x ) for ( x ) ( x ) in f ( x ) . f ( x ) . Simplify. If the resulting function is the same as the original function, f ( − x ) = f ( x ) , f ( − x ) = f ( x ) , then the function is even. If the resulting function is the opposite of the original function, f ( − x ) = − f ( x ) , f ( − x ) = − f ( x ) , then the original function is odd. If the function is not the same or the opposite, then the function is neither odd nor even.

g ( x ) = | x - 1 | − 3 g ( x ) = | x - 1 | − 3

g ( x ) = 1 ( x + 4 ) 2 + 2 g ( x ) = 1 ( x + 4 ) 2 + 2

The graph of f ( x + 43 ) f ( x + 43 ) is a horizontal shift to the left 43 units of the graph of f . f .

The graph of f ( x - 4 ) f ( x - 4 ) is a horizontal shift to the right 4 units of the graph of f . f .

The graph of f ( x ) + 8 f ( x ) + 8 is a vertical shift up 8 units of the graph of f . f .

The graph of f ( x ) − 7 f ( x ) − 7 is a vertical shift down 7 units of the graph of f . f .

The graph of f ( x + 4 ) − 1 f ( x + 4 ) − 1 is a horizontal shift to the left 4 units and a vertical shift down 1 unit of the graph of f . f .

decreasing on ( − ∞ , − 3 ) ( − ∞ , − 3 ) and increasing on ( − 3 , ∞ ) ( − 3 , ∞ )

decreasing on ( 0 , ∞ ) ( 0 , ∞ )

g ( x ) = f ( x - 1 ) , h ( x ) = f ( x ) + 1 g ( x ) = f ( x - 1 ) , h ( x ) = f ( x ) + 1

f ( x ) = | x - 3 | − 2 f ( x ) = | x - 3 | − 2

f ( x ) = x + 3 − 1 f ( x ) = x + 3 − 1

f ( x ) = ( x - 2 ) 2 f ( x ) = ( x - 2 ) 2

f ( x ) = | x + 3 | − 2 f ( x ) = | x + 3 | − 2

f ( x ) = − x f ( x ) = − x

f ( x ) = − ( x + 1 ) 2 + 2 f ( x ) = − ( x + 1 ) 2 + 2

f ( x ) = − x + 1 f ( x ) = − x + 1

The graph of g g is a vertical reflection (across the x x -axis) of the graph of f . f .

The graph of g g is a vertical stretch by a factor of 4 of the graph of f . f .

The graph of g g is a horizontal compression by a factor of 1 5 1 5 of the graph of f . f .

The graph of g g is a horizontal stretch by a factor of 3 of the graph of f . f .

The graph of g g is a horizontal reflection across the y y -axis and a vertical stretch by a factor of 3 of the graph of f . f .

g ( x ) = | − 4 x | g ( x ) = | − 4 x |

g ( x ) = 1 3 ( x + 2 ) 2 − 3 g ( x ) = 1 3 ( x + 2 ) 2 − 3

g ( x ) = 1 2 ( x - 5 ) 2 + 1 g ( x ) = 1 2 ( x - 5 ) 2 + 1

The graph of the function f ( x ) = x 2 f ( x ) = x 2 is shifted to the left 1 unit, stretched vertically by a factor of 4, and shifted down 5 units.

The graph of f ( x ) = | x | f ( x ) = | x | is stretched vertically by a factor of 2, shifted horizontally 4 units to the right, reflected across the horizontal axis, and then shifted vertically 3 units up.

The graph of the function f ( x ) = x 3 f ( x ) = x 3 is compressed vertically by a factor of 1 2 . 1 2 .

The graph of the function is stretched horizontally by a factor of 3 and then shifted vertically downward by 3 units.

The graph of f ( x ) = x f ( x ) = x is shifted right 4 units and then reflected across the vertical line x = 4. x = 4.

3.6 Section Exercises

Isolate the absolute value term so that the equation is of the form | A | = B . | A | = B . Form one equation by setting the expression inside the absolute value symbol, A , A , equal to the expression on the other side of the equation, B . B . Form a second equation by setting A A equal to the opposite of the expression on the other side of the equation, − B . − B . Solve each equation for the variable.

The graph of the absolute value function does not cross the x x -axis, so the graph is either completely above or completely below the x x -axis.

The distance from x to 8 can be represented using the absolute value statement: ∣ x − 8 ∣ = 4.

∣ x − 10 ∣ ≥ 15

There are no x-intercepts.

(−4, 0) and (2, 0)

( 0 , − 4 ) , ( 4 , 0 ) , ( − 2 , 0 ) ( 0 , − 4 ) , ( 4 , 0 ) , ( − 2 , 0 )

( 0 , 7 ) , ( 25 , 0 ) , ( − 7 , 0 ) ( 0 , 7 ) , ( 25 , 0 ) , ( − 7 , 0 )

range: [ – 400 , 100 ] [ – 400 , 100 ]

There is no solution for a a that will keep the function from having a y y -intercept. The absolute value function always crosses the y y -intercept when x = 0. x = 0.

| p − 0.08 | ≤ 0.015 | p − 0.08 | ≤ 0.015

| x − 5.0 | ≤ 0.01 | x − 5.0 | ≤ 0.01

3.7 Section Exercises

Each output of a function must have exactly one output for the function to be one-to-one. If any horizontal line crosses the graph of a function more than once, that means that y y -values repeat and the function is not one-to-one. If no horizontal line crosses the graph of the function more than once, then no y y -values repeat and the function is one-to-one.

Yes. For example, f ( x ) = 1 x f ( x ) = 1 x is its own inverse.

Given a function y = f ( x ) , y = f ( x ) , solve for x x in terms of y . y . Interchange the x x and y . y . Solve the new equation for y . y . The expression for y y is the inverse, y = f − 1 ( x ) . y = f − 1 ( x ) .

f − 1 ( x ) = x − 3 f − 1 ( x ) = x − 3

f − 1 ( x ) = 2 − x f − 1 ( x ) = 2 − x

f − 1 ( x ) = − 2 x x − 1 f − 1 ( x ) = − 2 x x − 1

domain of f ( x ) : [ − 7 , ∞ ) ; f − 1 ( x ) = x − 7 f ( x ) : [ − 7 , ∞ ) ; f − 1 ( x ) = x − 7

domain of f ( x ) : [ 0 , ∞ ) ; f − 1 ( x ) = x + 5 f ( x ) : [ 0 , ∞ ) ; f − 1 ( x ) = x + 5

a. f ( g ( x ) ) = x f ( g ( x ) ) = x and g ( f ( x ) ) = x . g ( f ( x ) ) = x . b. This tells us that f f and g g are inverse functions

  f ( g ( x ) ) = x , g ( f ( x ) ) = x   f ( g ( x ) ) = x , g ( f ( x ) ) = x

not one-to-one

[ 2 , 10 ] [ 2 , 10 ]

f − 1 ( x ) = ( 1 + x ) 1 / 3 f − 1 ( x ) = ( 1 + x ) 1 / 3

f − 1 ( x ) = 5 9 ( x − 32 ) . f − 1 ( x ) = 5 9 ( x − 32 ) . Given the Fahrenheit temperature, x , x , this formula allows you to calculate the Celsius temperature.

t ( d ) = d 50 , t ( d ) = d 50 , t ( 180 ) = 180 50 . t ( 180 ) = 180 50 . The time for the car to travel 180 miles is 3.6 hours.

Review Exercises

f ( − 3 ) = − 27 ; f ( − 3 ) = − 27 ; f ( 2 ) = − 2 ; f ( 2 ) = − 2 ; f ( − a ) = − 2 a 2 − 3 a ; f ( − a ) = − 2 a 2 − 3 a ; − f ( a ) = 2 a 2 − 3 a ; − f ( a ) = 2 a 2 − 3 a ; f ( a + h ) = − 2 a 2 + 3 a − 4 a h + 3 h − 2 h 2 f ( a + h ) = − 2 a 2 + 3 a − 4 a h + 3 h − 2 h 2

x = − 1.8 x = − 1.8 or or  x = 1.8 or  x = 1.8

− 64 + 80 a − 16 a 2 − 1 + a = − 16 a + 64 − 64 + 80 a − 16 a 2 − 1 + a = − 16 a + 64

( − ∞ , − 2 ) ∪ ( − 2 , 6 ) ∪ ( 6 , ∞ ) ( − ∞ , − 2 ) ∪ ( − 2 , 6 ) ∪ ( 6 , ∞ )

increasing ( 2 , ∞ ) ; ( 2 , ∞ ) ; decreasing ( − ∞ , 2 ) ( − ∞ , 2 )

increasing ( − 3 , 1 ) ; ( − 3 , 1 ) ; constant ( − ∞ , − 3 ) ∪ ( 1 , ∞ ) ( − ∞ , − 3 ) ∪ ( 1 , ∞ )

local minimum ( − 2 , − 3 ) ; ( − 2 , − 3 ) ; local maximum ( 1 , 3 ) ( 1 , 3 )

( − 1.8 , 10 ) ( − 1.8 , 10 )

( f ∘ g ) ( x ) = 17 − 18 x ; ( g ∘ f ) ( x ) = − 7 − 18 x ( f ∘ g ) ( x ) = 17 − 18 x ; ( g ∘ f ) ( x ) = − 7 − 18 x

( f ∘ g ) ( x ) = 1 x + 2 ; ( g ∘ f ) ( x ) = 1 x + 2 ( f ∘ g ) ( x ) = 1 x + 2 ; ( g ∘ f ) ( x ) = 1 x + 2

( f ∘ g ) ( x ) = 1 + x 1 + 4 x ,   x ≠ 0 ,   x ≠ − 1 4 ( f ∘ g ) ( x ) = 1 + x 1 + 4 x ,   x ≠ 0 ,   x ≠ − 1 4

( f ∘ g ) ( x ) = 1 x , x > 0 ( f ∘ g ) ( x ) = 1 x , x > 0

sample: g ( x ) = 2 x − 1 3 x + 4 ; f ( x ) = x g ( x ) = 2 x − 1 3 x + 4 ; f ( x ) = x

f ( x ) = | x − 3 | f ( x ) = | x − 3 |

f ( x ) = 1 2 | x + 2 | + 1 f ( x ) = 1 2 | x + 2 | + 1

f ( x ) = − 3 | x − 3 | + 3 f ( x ) = − 3 | x − 3 | + 3

f − 1 ( x ) = x - 9 10 f − 1 ( x ) = x - 9 10

f − 1 ( x ) = x - 1 f − 1 ( x ) = x - 1

The function is one-to-one.

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^{2}-x-6=0
• -x+3\gt 2x+1
• line\:(1,\:2),\:(3,\:1)
• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• \frac{d}{dx}(\frac{3x+9}{2-x})
• (\sin^2(\theta))'
• \lim _{x\to 0}(x\ln (x))
• \int e^x\cos (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \sum_{n=0}^{\infty}\frac{3}{2^n}
• Is there a step by step calculator for math?
• Symbolab is the best step by step calculator for a wide range of math problems, from basic arithmetic to advanced calculus and linear algebra. It shows you the solution, graph, detailed steps and explanations for each problem.
• Is there a step by step calculator for physics?
• Symbolab is the best step by step calculator for a wide range of physics problems, including mechanics, electricity and magnetism, and thermodynamics. It shows you the steps and explanations for each problem, so you can learn as you go.
• How to solve math problems step-by-step?
• To solve math problems step-by-step start by reading the problem carefully and understand what you are being asked to find. Next, identify the relevant information, define the variables, and plan a strategy for solving the problem.
• Practice Makes Perfect Learning math takes practice, lots of practice. Just like running, it takes practice and dedication. If you want...

Please add a message.

Message received. Thanks for the feedback.

Algebra 2 Worksheets with answer keys

Enjoy these free printable math worksheets . Each one has model problems worked out step by step, practice problems, as well as challenge questions at the sheets end. Plus each one comes with an answer key.

• Absolute Value Equations
• Simplify Imaginary Numbers
• Adding and Subtracting Complex Numbers
• Multiplying Complex Numbers
• Dividing Complex Numbers
• Dividing Complex Number (advanced)
• End of Unit, Review Sheet
• Exponential Growth (no answer key on this one, sorry)
• Compound Interest Worksheet #1 (no logs)
• Compound Interest Worksheet (logarithms required)
• Simplify Rational Exponents
• Solve Equations with Rational Exponents
• Solve Equations with variables in Exponents
• Factor by Grouping
• 1 to 1 functions
• Evaluating Functions
• Composition of Functions
• Inverse Functions
• Operations with Functions
• Functions Review Worksheet
• Product Rule of Logarithms
• Power Rule of Logarithms
• Quotient Rule of Logarithms
• Logarithmic Equations Worksheet
• Dividing Polynomials Worksheet
• Solve Quadratic Equations by Factoring
• Solve Quadratic Equations by Completing the Square
• Quadratic formula Worksheet (real solutions)
• Quadratic Formula Worksheet (complex solutions)
• Quadratic Formula Worksheet (both real and complex solutions)
• Discriminant Worksheet
• Sum and Product of Roots
• Radical Equations
• Rationalizing the Denominator
• Simplify Rational Expressions Worksheet
• Dividing Rational Expressions
• Multiplying Rational Expressions
• Adding and Subtracting Rational Expressions (with like denominators)
• Adding and Subtracting Ratioal Expressions with Unlike Denominators
• Mixed Review on Rational Expressions

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.3: Separable Equations

• Last updated
• Save as PDF
• Page ID 153922

• Gilbert Strang & Edwin “Jed” Herman

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Use separation of variables to solve a differential equation.
• Solve applications using separation of variables.

We now examine a solution technique for finding exact solutions to a class of differential equations known as separable differential equations. These equations are common in a wide variety of disciplines, including physics, chemistry, and engineering. We illustrate a few applications at the end of the section.

Separation of Variables

We start with a definition and some examples.

Definition: Separable Differential Equations

A separable differential equation is any equation that can be written in the form

\[y'=f(x)g(y). \label{sep} \]

The term ‘separable’ refers to the fact that the right-hand side of Equation \ref{sep} can be separated into a function of \(x\) times a function of \(y\). Examples of separable differential equations include

\[ \begin{align} y' &=(x^2−4)(3y+2) \label{eq1} \\[4pt] y' &=6x^2+4x \label{eq2}\\[4pt] y' &=\sec y+\tan y \label{eq3} \\[4pt] y' &=xy+3x−2y−6. \label{eq4} \end{align} \]

Equation \ref{eq2} is separable with \(f(x)=6x^2+4x\) and \(g(y)=1\), Equation \ref{eq3} is separable with \(f(x)=1\) and \(g(y)=\sec y+\tan y,\) and the right-hand side of Equation \ref{eq4} can be factored as \((x+3)(y−2)\), so it is separable as well. Equation \ref{eq3} is also called an autonomous differential equation because the right-hand side of the equation is a function of \(y\) alone. If a differential equation is separable, then it is possible to solve the equation using the method of separation of variables.

Problem-Solving Strategy: Separation of Variables

• Check for any values of \(y\) that make \(g(y)=0.\) These correspond to constant solutions.
• Rewrite the differential equation in the form \[ \dfrac{dy}{g(y)}=f(x)dx. \nonumber \]
• Integrate both sides of the equation.
• Solve the resulting equation for \(y\) if possible.
• If an initial condition exists, substitute the appropriate values for \(x\) and \(y\) into the equation and solve for the constant.

Note that Step 4 states “Solve the resulting equation for \(y\) if possible.” It is not always possible to obtain \(y\) as an explicit function of \(x\). Quite often we have to be satisfied with finding y as an implicit function of \(x\).

Example \(\PageIndex{1}\): Using Separation of Variables

Find a general solution to the differential equation \(y'=(x^2−4)(3y+2)\) using the method of separation of variables.

Follow the five-step method of separation of variables.

1. In this example, \(f(x)=x^2−4\) and \(g(y)=3y+2\). Setting \(g(y)=0\) gives \(y=−\dfrac{2}{3}\) as a constant solution.

2. Rewrite the differential equation in the form

\[ \dfrac{dy}{3y+2}=(x^2−4)\,dx.\nonumber \]

3. Integrate both sides of the equation:

\[ ∫\dfrac{dy}{3y+2}=∫(x^2−4)\,dx.\nonumber \]

Let \(u=3y+2\). Then \(du=3\dfrac{dy}{dx}\,dx\), so the equation becomes

\[ \dfrac{1}{3}∫\dfrac{1}{u}\,du=\dfrac{1}{3}x^3−4x+C\nonumber \]

\[ \dfrac{1}{3}\ln|u|=\dfrac{1}{3}x^3−4x+C\nonumber \]

\[ \dfrac{1}{3}\ln|3y+2|=\dfrac{1}{3}x^3−4x+C.\nonumber \]

4. To solve this equation for \(y\), first multiply both sides of the equation by \(3\).

\[ \ln|3y+2|=x^3−12x+3C\nonumber \]

Now we use some logic in dealing with the constant \(C\). Since \(C\) represents an arbitrary constant, \(3C\) also represents an arbitrary constant. If we call the second arbitrary constant \(C_1,\) where \(C_1 = 3C,\) the equation becomes

\[ \ln|3y+2|=x^3−12x+C_1.\nonumber \]

Now exponentiate both sides of the equation (i.e., make each side of the equation the exponent for the base \(e\)).

\[ \begin{align*} e^{\ln|3y+2|} &=e^{x^3−12x+C_1} \\ |3y+2| &=e^{C_1}e^{x^3−12x} \end{align*}\]

Again define a new constant \(C_2= e^{C_1}\) (note that \(C_2 > 0\)):

\[ |3y+2|=C_2e^{x^3−12x}.\nonumber \]

Because of the absolute value on the left side of the equation, this corresponds to two separate equations:

\[3y+2=C_2e^{x^3−12x}\nonumber \]

\[3y+2=−C_2e^{x^3−12x}.\nonumber \]

The solution to either equation can be written in the form

\[y=\dfrac{−2±C_2e^{x^3−12x}}{3}.\nonumber \]

Since \(C_2>0\), it does not matter whether we use plus or minus, so the constant can actually have either sign. Furthermore, the subscript on the constant \(C\) is entirely arbitrary, and can be dropped. Therefore the solution can be written as

\[ y=\dfrac{−2+Ce^{x^3−12x}}{3}, \text{ where }C = \pm C_2\text{ or } C = 0.\nonumber \]

Note that in writing a single general solution in this way, we are also allowing \(C\) to equal \(0\). This gives us the singular solution, \(y = -\dfrac{2}{3}\), for the given differential equation. Check that this is indeed a solution of this differential equation!

5. No initial condition is imposed, so we are finished.

Exercise \(\PageIndex{1}\)

Use the method of separation of variables to find a general solution to the differential equation

\[ y'=2xy+3y−4x−6. \nonumber \]

First factor the right-hand side of the equation by grouping, then use the five-step strategy of separation of variables.

\[ y=2+Ce^{x^2+3x} \nonumber \]

Example \(\PageIndex{2}\): Solving an Initial-Value Problem

Using the method of separation of variables, solve the initial-value problem

\[ y'=(2x+3)(y^2−4),\quad y(0)=−1.\nonumber \]

1. In this example, \(f(x)=2x+3\) and \(g(y)=y^2−4\). Setting \(g(y)=0\) gives \(y=±2\) as constant solutions.

2. Divide both sides of the equation by \(y^2−4\) and multiply by \(dx\). This gives the equation

\[\dfrac{dy}{y^2−4}=(2x+3)\,dx.\nonumber \]

3. Next integrate both sides:

\[∫\dfrac{1}{y^2−4}dy=∫(2x+3)\,dx. \label{Ex2.2} \]

To evaluate the left-hand side, use the method of partial fraction decomposition. This leads to the identity

\[\dfrac{1}{y^2−4}=\dfrac{1}{4}\left(\dfrac{1}{y−2}−\dfrac{1}{y+2}\right).\nonumber \]

Then Equation \ref{Ex2.2} becomes

\[\dfrac{1}{4}∫\left(\dfrac{1}{y−2}−\dfrac{1}{y+2}\right)dy=∫(2x+3)\,dx\nonumber \]

\[\dfrac{1}{4}\left (\ln|y−2|−\ln|y+2| \right)=x^2+3x+C.\nonumber \]

Multiplying both sides of this equation by \(4\) and replacing \(4C\) with \(C_1\) gives

\[\ln|y−2|−\ln|y+2|=4x^2+12x+C_1\nonumber \]

\[\ln \left|\dfrac{y−2}{y+2}\right|=4x^2+12x+C_1.\nonumber \]

4. It is possible to solve this equation for \(y.\) First exponentiate both sides of the equation and define \(C_2=e^{C_1}\):

\[\left|\dfrac{y−2}{y+2}\right|=C_2e^{4x^2+12x}.\nonumber \]

Next we can remove the absolute value and let a new constant \(C_3\) be positive, negative, or zero, i.e., \(C_3 =\pm C_2\) or \(C_3 = 0.\)

Then multiply both sides by \(y+2\).

\[y−2=C_3(y+2)e^{4x^2+12x}\nonumber \]

\[y−2=C_3ye^{4x^2+12x}+2C_3e^{4x^2+12x}.\nonumber \]

Now collect all terms involving \(y\) on one side of the equation, and solve for \(y\):

\[y−C_3ye^{4x^2+12x}=2+2C_3e^{4x^2+12x}\nonumber \]

\[y\big(1−C_3e^{4x^2+12x}\big)=2+2C_3e^{4x^2+12x}\nonumber \]

\[y=\dfrac{2+2C_3e^{4x^2+12x}}{1−C_3e^{4x^2+12x}}.\nonumber \]

5. To determine the value of \(C_3\), substitute \(x=0\) and \(y=−1\) into the general solution. Alternatively, we can put the same values into an earlier equation, namely the equation \(\dfrac{y−2}{y+2}=C_3e^{4x^2+12}\). This is much easier to solve for \(C_3\):

\[\dfrac{y−2}{y+2}=C_3e^{4x^2+12x}\nonumber \]

\[\dfrac{−1−2}{−1+2}=C_3e^{4(0)^2+12(0)}\nonumber \]

\[C_3=−3.\nonumber \]

Therefore the solution to the initial-value problem is

\[y=\dfrac{2−6e^{4x^2+12x}}{1+3e^{4x^2+12x}}.\nonumber \]

A graph of this solution appears in Figure \(\PageIndex{1}\).

Exercise \(\PageIndex{2}\)

Find the solution to the initial-value problem

\[ 6y'=(2x+1)(y^2−2y−8) \nonumber \]

with \(y(0)=−3\) using the method of separation of variables.

Follow the steps for separation of variables to solve the initial-value problem.

\[ y=\dfrac{4+14e^{x^2+x}}{1−7e^{x^2+x}} \nonumber \]

Applications of Separation of Variables

Many interesting problems can be described by separable equations. We illustrate two types of problems: solution concentrations and Newton’s law of cooling.

Solution concentrations

Consider a tank being filled with a salt solution. We would like to determine the amount of salt present in the tank as a function of time. We can apply the process of separation of variables to solve this problem and similar problems involving solution concentrations .

Example \(\PageIndex{3}\): Determining Salt Concentration over Time

A tank containing \(100\) L of a brine solution initially has \(4\) kg of salt dissolved in the solution. At time \(t=0\), another brine solution flows into the tank at a rate of \(2\) L/min. This brine solution contains a concentration of \(0.5\) kg/L of salt. At the same time, a stopcock is opened at the bottom of the tank, allowing the combined solution to flow out at a rate of \(2\) L/min, so that the level of liquid in the tank remains constant (Figure \(\PageIndex{2}\)). Find the amount of salt in the tank as a function of time (measured in minutes), and find the limiting amount of salt in the tank, assuming that the solution in the tank is well mixed at all times.

First we define a function \(u(t)\) that represents the amount of salt in kilograms in the tank as a function of time. Then \(\dfrac{du}{dt}\) represents the rate at which the amount of salt in the tank changes as a function of time. Also, \(u(0)\) represents the amount of salt in the tank at time \(t=0\), which is \(4\) kilograms.

The general setup for the differential equation we will solve is of the form

\[\dfrac{du}{dt}=\text{INFLOW RATE − OUTFLOW RATE.} \nonumber \]

INFLOW RATE represents the rate at which salt enters the tank, and OUTFLOW RATE represents the rate at which salt leaves the tank. Because solution enters the tank at a rate of \(2\) L/min, and each liter of solution contains \(0.5\) kilogram of salt, every minute \(2(0.5)=1\) kilogram of salt enters the tank. Therefore INFLOW RATE = \(1\).

To calculate the rate at which salt leaves the tank, we need the concentration of salt in the tank at any point in time. Since the actual amount of salt varies over time, so does the concentration of salt. However, the volume of the solution remains fixed at 100 liters. The number of kilograms of salt in the tank at time \(t\) is equal to \(u(t)\). Thus, the concentration of salt is \(\dfrac{u(t)}{100}\) kg/L, and the solution leaves the tank at a rate of \(2\) L/min. Therefore salt leaves the tank at a rate of \(\dfrac{u(t)}{100}⋅2=\dfrac{u(t)}{50}\) kg/min, and OUTFLOW RATE is equal to \(\dfrac{u(t)}{50}\). Therefore the differential equation becomes \(\dfrac{du}{dt}=1−\dfrac{u}{50}\), and the initial condition is \(u(0)=4.\) The initial-value problem to be solved is

\[\dfrac{du}{dt}=1−\dfrac{u}{50},u(0)=4.\nonumber \]

The differential equation is a separable equation, so we can apply the five-step strategy for solution.

Step 1. Setting \(1−\dfrac{u}{50}=0\) gives \(u=50\) as a constant solution. Since the initial amount of salt in the tank is \(4\) kilograms, this solution does not apply.

Step 2. Rewrite the equation as

\[\dfrac{du}{dt}=\dfrac{50−u}{50}.\nonumber \]

Then multiply both sides by \(dt\) and divide both sides by \(50−u:\)

\[\dfrac{du}{50−u}=\dfrac{dt}{50}.\nonumber \]

Step 3. Integrate both sides:

\[\begin{align*} ∫\dfrac{du}{50−u} &=∫\dfrac{dt}{50} \\ −\ln|50−u| &=\dfrac{t}{50}+C. \end{align*}\]

Step 4. Solve for \(u(t)\):

\[\ln|50−u|=−\dfrac{t}{50}−C\nonumber \]

\[e^{\ln|50−u|}=e^{−(t/50)−C}\nonumber \]

\[|50−u|=C_1e^{−t/50}, \text{ where } C_1 = e^{-C}.\nonumber \]

Eliminate the absolute value by allowing the constant to be positive, negative, or zero, i.e., \(C_1 = \pm e^{-C}\) or \(C_1 = 0\):

\[50−u=C_1e^{−t/50}.\nonumber \]

Finally, solve for \(u(t)\):

\[u(t)=50−C_1e^{−t/50}.\nonumber \]

Step 5. Solve for \(C_1\):

\[\begin{align*} u(0) &=50−C_1e^{−0/50} \\ 4 &=50−C_1 \\ C_1 &=46. \end{align*}\]

The solution to the initial value problem is \(u(t)=50−46e^{−t/50}.\) To find the limiting amount of salt in the tank, take the limit as \(t\) approaches infinity:

\[\begin{align*} \lim_{t→∞}u(t) &=50−46e^{−t/50} \\ &=50−46(0)=50. \end{align*}\]

Note that this was the constant solution to the differential equation. If the initial amount of salt in the tank is \(50\) kilograms, then it remains constant. If it starts at less than \(50\) kilograms, then it approaches \(50\) kilograms over time.

Exercise \(\PageIndex{3}\)

A tank contains \(3\) kilograms of salt dissolved in \(75\) liters of water. A salt solution of \(0.4\) kg salt/L is pumped into the tank at a rate of \(6\) L/min and is drained at the same rate. Solve for the salt concentration at time \(t\). Assume the tank is well mixed at all times.

Follow the steps in Example \(\PageIndex{3}\) and determine an expression for INFLOW and OUTFLOW. Formulate an initial-value problem, and then solve it.

Initial value problem:

\[ \dfrac{du}{dt}=2.4−\dfrac{2u}{25},\, u(0)=3 \nonumber \]

\[u(t)=30−27e^{−t/50} \nonumber \]

Newton’s Law of Cooling

Newton’s law of cooling states that the rate of change of an object’s temperature is proportional to the difference between its own temperature and the ambient temperature (i.e., the temperature of its surroundings). If we let \(T(t)\) represent the temperature of an object as a function of time, then \(\dfrac{dT}{dt}\) represents the rate at which that temperature changes. The temperature of the object’s surroundings can be represented by \(T_s\). Then Newton’s law of cooling can be written in the form

\[ \dfrac{dT}{dt}=k(T(t)−T_s) \nonumber \]

\[ \dfrac{dT}{dt}=k(T−T_s). \nonumber \]

The temperature of the object at the beginning of any experiment is the initial value for the initial-value problem. We call this temperature \(T_0\). Therefore the initial-value problem that needs to be solved takes the form

\[ \dfrac{dT}{dt}=k(T−T_s) \label{newton} \]

with \(T(0)=T_0\), where \(k\) is a constant that needs to be either given or determined in the context of the problem. We use these equations in Example \(\PageIndex{4}\).

Example \(\PageIndex{4}\): Waiting for a Pizza to Cool

A pizza is removed from the oven after baking thoroughly, and the temperature of the oven is \(350°F.\) The temperature of the kitchen is \(75°F\), and after \(5\) minutes the temperature of the pizza is \(340°F\). We would like to wait until the temperature of the pizza reaches \(300°F\) before cutting and serving it (Figure \(\PageIndex{3}\)). How much longer will we have to wait?

The ambient temperature (surrounding temperature) is \(75°F\), so \(T_s=75\). The temperature of the pizza when it comes out of the oven is \(350°F\), which is the initial temperature (i.e., initial value), so \(T_0=350\). Therefore Equation \ref{newton} becomes

\[\dfrac{dT}{dt}=k(T−75) \nonumber \]

with \(T(0)=350.\)

To solve the differential equation, we use the five-step technique for solving separable equations.

1. Setting the right-hand side equal to zero gives \(T=75\) as a constant solution. Since the pizza starts at \(350°F,\) this is not the solution we are seeking.

2. Rewrite the differential equation by multiplying both sides by \(dt\) and dividing both sides by \(T−75\):

\[\dfrac{dT}{T−75}=k\,dt. \nonumber \]

3. Integrate both sides:

\[\begin{align*} ∫\dfrac{dT}{T−75} &=∫k\,dt \\ \ln|T−75| &=kt+C.\end{align*} \nonumber \]

4. Solve for \(T\) by first exponentiating both sides:

\[\begin{align*}e^{\ln|T−75|} &=e^{kt+C} \\ |T−75| &=C_1e^{kt}, & & \text{where } C_1 = e^C. \\ T−75 &=\pm C_1e^{kt} \\ T−75 &=Ce^{kt}, & & \text{where } C = \pm C_1\text{ or } C = 0.\\ T(t) &=75+Ce^{kt}. \end{align*} \nonumber \]

5. Solve for \(C\) by using the initial condition \(T(0)=350:\)

\[\begin{align*}T(t) &=75+Ce^{kt}\\ T(0) &=75+Ce^{k(0)} \\ 350 &=75+C \\ C &=275.\end{align*} \nonumber \]

\[T(t)=75+275e^{kt}.\nonumber \]

To determine the value of \(k\), we need to use the fact that after \(5\) minutes the temperature of the pizza is \(340°F\). Therefore \(T(5)=340.\) Substituting this information into the solution to the initial-value problem, we have

\[T(t)=75+275e^{kt}\nonumber \]

\[T(5)=340=75+275e^{5k}\nonumber \]

\[265=275e^{5k}\nonumber \]

\[e^{5k}=\dfrac{53}{55}\nonumber \]

\[\ln e^{5k}=\ln(\dfrac{53}{55})\nonumber \]

\[5k=\ln(\dfrac{53}{55})\nonumber \]

\[k=\dfrac{1}{5}\ln(\dfrac{53}{55})≈−0.007408.\nonumber \]

So now we have \(T(t)=75+275e^{−0.007048t}.\) When is the temperature \(300°F\)? Solving for \(t,\) we find

\[T(t)=75+275e^{−0.007048t}\nonumber \]

\[300=75+275e^{−0.007048t}\nonumber \]

\[225=275e^{−0.007048t}\nonumber \]

\[e^{−0.007048t}=\dfrac{9}{11}\nonumber \]

\[\ln e^{−0.007048t}=\ln\dfrac{9}{11}\nonumber \]

\[−0.007048t=\ln\dfrac{9}{11}\nonumber \]

\[t=−\dfrac{1}{0.007048}\ln\dfrac{9}{11}≈28.5.\nonumber \]

Therefore we need to wait an additional \(23.5\) minutes (after the temperature of the pizza reached \(340°F\)). That should be just enough time to finish this calculation.

Exercise \(\PageIndex{4}\)

A cake is removed from the oven after baking thoroughly, and the temperature of the oven is \(450°F\). The temperature of the kitchen is \(70°F\), and after \(10\) minutes the temperature of the cake is \(430°F\).

• Write the appropriate initial-value problem to describe this situation.
• Solve the initial-value problem for \(T(t)\).
• How long will it take until the temperature of the cake is within \(5°F\) of room temperature?

Determine the values of \(T_s\) and \(T_0\) then use Equation \ref{newton}.

Initial-value problem \[\dfrac{dT}{dt}=k(T−70),\quad T(0)=450\nonumber \]

\[T(t)=70+380e^{kt}\nonumber \]

Approximately \(114\) minutes.

Key Concepts

• A separable differential equation is any equation that can be written in the form \(y'=f(x)g(y).\)
• The method of separation of variables is used to find the general solution to a separable differential equation.

Key Equations

• Separable differential equation

\(y′=f(x)g(y)\)

• Solution concentration

\(\dfrac{du}{dt}=\text{INFLOW RATE − OUTFLOW RATE}\)

• Newton’s law of cooling

\(\dfrac{dT}{dt}=k(T−T_s)\)

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&