case study questions based on surface area and volume

Class 9 Maths Case Study Questions of Chapter 13 Surface Areas and Volumes

• Post author: studyrate
• Post published:
• Post category: class 9th
• Post comments: 0 Comments

Case study Questions in Class 9 Mathematics Chapter 13  are very important to solve for your exam. Class 9 Maths Chapter 13 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving case study-based questions for Class 9 Maths Case Study Questions  Chapter 13 Surface Areas and Volumes

Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.

These case study questions challenge students to apply their knowledge of quadrilaterals in practical scenarios, enhancing their problem-solving abilities. This article provides the Class 9 Maths Case Study Questions of Chapter 13 Surface Areas and Volumes, enabling students to practice and excel in their examinations.

Surface Areas and Volumes Case Study Questions With Answers

Here, we have provided case-based/passage-based questions for Class 9 Maths Chapter 13 Surface Areas and Volumes

Case Study/Passage-Based Questions

Case Study 1: A class teacher brings some clay in the classroom to teach the topic of mensuration. First she forms a cylinder of radius 6 cm and height 8 cm and then she molds that cylinder into sphere.

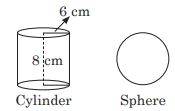
Find the volume of the cylindrical shape. (a) 288 π cm 3 (b) 244 π cm 3 (c) 240 π cm 3 (d) 216 π cm 3

Answer: (a) 288 π cm3

When clay changes into one shape to other, which of the following remains same? (a) Area (b) C.S.A (c) Radius (d) Volume

Answer: (d) Volume

The radius of the sphere is (a) 2 cm (b) 4 cm (c) 5 cm (d) 6 cm

Answer: (d) 6 cm

Find the volume of sphere, the teacher made. (a) 288 π cm 3 (b) 184 π cm 3 (c) 240 π cm 3 (d) 216 π cm 3

Case Study 2: Ankita realised the need of food for birds on her terrace and decided to make a bird feeder. She got a flexible plastic rectangular sheet of size 44 cm × 15 cm. She rolled it along its length and joined the two opposite ends using a tape for circular base of cylinder. She found a square sheet of size 15 cm × 15 cm by cutting it into required circular shape she prepared the bird feeder as shown in figure.

The curved surface area of the cylinder formed is (a) 550 cm 2 (b) 660 cm 2 (c) 430 cm 2 (d) 840 cm 2

Answer: (b) 660 cm2

The radius of the base of the cylinder is (a) 5 cm (b) 6 cm (c) 7 cm (d) 8 cm

Answer: (c) 7 cm

The area of the circular base required for the cylinder is (a) 154 cm 2 (b) 164 cm 2 (c) 240 cm 2 (d) 184 cm 2

Answer: (a) 154 cm2

How much will be the area of square sheet left unused after removing the circular base of the cylinder from it? (a) 78 cm 2 (b) 62 cm 2 (c) 75 cm 2 (d) 71 cm 2

Answer: (d) 71 cm2

Topics Covered in the Case Studies of Chapter 13: Surface Areas and Volumes

The case studies in the Class 9 Maths Case Study Questions of Chapter 13: Surface Areas and Volumes cover the following topics:

• Surface Areas of Solids (Cuboid, Cylinder, Cone, and Sphere)
• Volumes of Solids (Cuboid, Cylinder, Cone, and Sphere)
• Conversion of Units
• Application of Surface Areas and Volumes in Real-Life Scenarios

Hope the information shed above regarding Case Study and Passage Based Questions for Class 9 Mathematics Chapter 13 Surface Areas and Volumes with Answers Pdf free download has been useful to an extent. If you have any other queries about CBSE Class 9 Maths Surface Areas and Volumes Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible By Team Study Rate

You Might Also Like

Mcq questions of class 9 maths chapter 7 triangles with answers, class 9 geography case study questions of chapter 3 drainage, class 9 mcq questions for chapter 8 motion with answers, leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.

• Bihar Board

MBOSE 10th Result 2024

Cfa institute, srm university.

• MBOSE Result 2024
• TBSE Result 2024
• Maharashtra SSC Result
• Odisha Board Result
• RBSE 10th Result 2024
• CBSE Board Result 2024
• Shiv Khera Special
• Education News
• Web Stories
• Current Affairs
• नए भारत का नया उत्तर प्रदेश
• School & Boards
• College Admission
• Govt Jobs Alert & Prep
• GK & Aptitude
• CBSE Class 10 Study Material

CBSE Class 10 Maths Case Study Questions for Chapter 13 - Surface Areas and Volumes (Published By CBSE)

Check case study questions for cbse class 10 maths chapter 13 - surface areas and volumes. this question bank based on case study has been published by the board for class 10 mathematics..

Case study questions for CBSE Class 10 Maths Chapter 13 - Surface Areas and Volumes are published by the CBSE board. Students can solve these questions to acquaint themselves with the new type of questions. Answers to all the questions have been provided with them. These case study questions are quite helpful to prepare for the CBSE Class 10 Maths Exam 2021-2022.

Case Study Questions for Class 10 Maths Chapter 10 - Surface Areas and Volumes

CASE STUDY 1:

Adventure camps are the perfect place for the children to practice decision making for themselves without parents and teachers guiding their every move. Some students of a school reached for adventure at Sakleshpur. At the camp, the waiters served some students with a welcome drink in a cylindrical glass and some students in a hemispherical cup whose dimensions are shown below. After that they went for a jungle trek. The jungle trek was enjoyable but tiring. As dusk fell, it was time to take shelter. Each group of four students was given a canvas of area 551m2 . Each group had to make a conical tent to accommodate all the four students. Assuming that all the stitching and wasting incurred while cutting, would amount to 1m2 , the students put the tents. The radius of the tent is 7m.

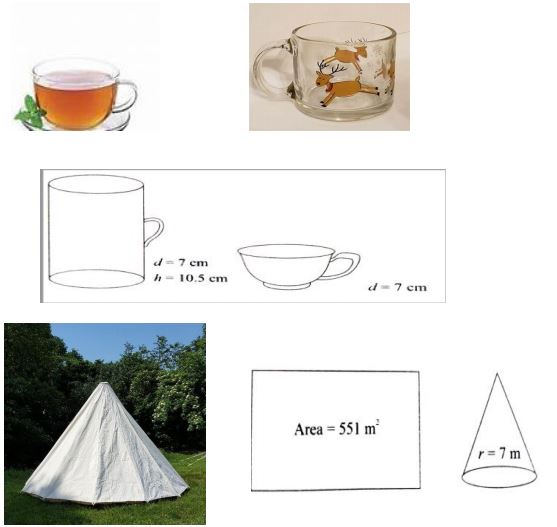
1. The volume of cylindrical cup is

a) 295.75 cm 3

b) 7415.5 cm 3

c) 384.88 cm 3

d) 404.25 cm 3

Answer: d) 404.25 cm 3

2. The volume of hemispherical cup is

a) 179.67 cm 3

b) 89.83 cm 3

c) 172.25 cm 3

d) 210.60 cm 3

Answer: b) 89.83 cm 3

3. Which container had more juice and by how much?

a) Hemispherical cup, 195 cm 3

b) Cylindrical glass, 207 cm 3

c) Hemispherical cup, 280.85 cm 3

d) Cylindrical glass, 314.42 cm 3

Answer: d) Cylindrical glass, 314.42 cm 3

4. The height of the conical tent prepared to accommodate four students is

Answer: c) 24m

5. How much space on the ground is occupied by each student in the conical tent

b) 38.5 m 2

Answer: b) 38.5 m 2

CASE STUDY 2:

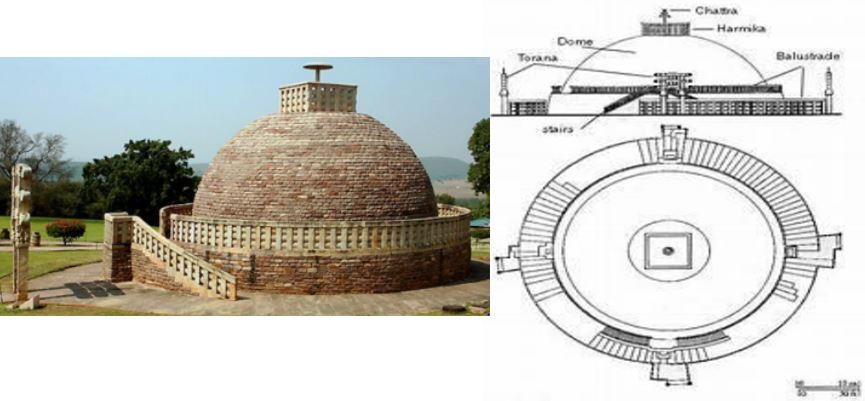
The Great Stupa at Sanchi is one of the oldest stone structures in India, and an important monument of Indian Architecture. It was originally commissioned by the emperor Ashoka in the 3rd century BCE. Its nucleus was a simple hemispherical brick structure built over the relics of the Buddha. .It is a perfect example of combination of solid figures. A big hemispherical dome with a cuboidal structure mounted on it. (Take π = 22/7)

1. Calculate the volume of the hemispherical dome if the height of the dome is 21 m –

a) 19404 cu. m

b) 2000 cu .m

c) 15000 cu. m

d) 19000 cu. m

Answer: a) 19404 cu. m

2. The formula to find the Volume of Sphere is -

a) 2/3 πr 3

b) 4/3 πr 3

c) 4 πr 2

d) 2 πr 2

Answer: b) 4/3 πr 3

3. The cloth require to cover the hemispherical dome if the radius of its base is 14m is

a) 1222 sq.m

b) 1232 sq.m

c) 1200 sq.m

d) 1400 sq.m

Answer: b) 1232 sq.m

4. The total surface area of the combined figure i.e. hemispherical dome with radius 14m and cuboidal shaped top with dimensions 8m 6m 4m is

a)1200 sq. m

b) 1232 sq. m

c) 1392 sq.m

d) 1932 sq. m

Answer: c) 1392 sq.m

5. The volume of the cuboidal shaped top is with dimensions mentioned in question 4

a) 182.45 m 3

b) 282.45 m 3

Answer: d) 192 m 3

CASE STUDY 3:

On a Sunday, your Parents took you to a fair. You could see lot of toys displayed, and you wanted them to buy a RUBIK’s cube and strawberry ice-cream for you. Observe the figures and answer the questions:-

1. The length of the diagonal if each edge measures 6cm is

a) 3√3

b) 3√6

c) √12

d) 6√3

Answers: d) 6√3

2. Volume of the solid figure if the length of the edge is 7cm is

b) 196 cm 3

c) 343 cm 3

d) 434 cm 3

Answers: c) 343 cm 3

3. What is the curved surface area of hemisphere (ice cream) if the base radius is 7cm?

a) 309 cm 2

b) 308 cm 2

c) 803 cm 2

d) 903 cm 2

Answers: b) 308 cm 2

4. Slant height of a cone if the radius is 7cm and the height is 24 cm___

Answers: b) 25 cm

5. The total surface area of cone with hemispherical ice cream is

a) 858 cm 2

b) 885 cm 2

c) 588 cm 2

d) 855 cm 2

Answers: a) 858 cm 2

Also Check:

CBSE Class 10 Maths Case Study Questions - All Chapters

Tips to Solve Case Study Based Questions Accurately

Get here latest School , CBSE and Govt Jobs notification in English and Hindi for Sarkari Naukari and Sarkari Result . Download the Jagran Josh Sarkari Naukri App . Check  Board Result 2024  for Class 10 and Class 12 like  CBSE Board Result ,  UP Board Result ,  Bihar Board Result ,  MP Board Result ,  Rajasthan Board Result  and Other States Boards.

• OAVS Admit Card 2024
• MPPSC VAS Interview Call Letter 2024
• Bihar DElEd Answer Key 2024
• BPSC BHO Recruitment 2024
• 12th Result 2024 Maharashtra Board
• Maharashtra Board 12th Result 2024 Roll Number
• hscresult.mkcl.org Result 2024
• MBSE Result 2024 Class 12
• Mizoram HSSLC Toppers List 2024
• Bihar Deled Answer Key 2024
• CBSE Study Material
• CBSE Class 10

Latest Education News

Brother’s Day 2024: List Of Famous Brothers In The World Who Changed The History Forever

How Fast You Can Find All The 10 Animals Hidden In This Optical Illusion? Timer Is On!

TBSE Result 2024 LIVE: Tripura Board 10th, 12th Results at tbse.tripura.gov.in by Roll No, Registration Number

[Official] Meghalaya Board 10th Result 2024 Releasing Tomorrow, Check Latest News and Updates Here

MBOSE HSSLC Arts Result 2024 LIVE: Check Meghalaya Board Class 12 Arts Stream Results Online at Jagran Josh and megresults.nic.in by Roll Number

JKSSB Answer Key 2024 OUT at jkssb.nic.in: Check Download Link

MGSU Result 2024 OUT at mgsubikaner.ac.in, Direct Link to Download UG and PG Marksheet

HNGU Result 2024 OUT at ngu.ac.in, Direct Link to Download UG and PG Marksheet

School Holiday List in India for 2024-25: Check Summer Vacation Dates and Upcoming Holidays

Brain Teaser: Only the Sharpest Minds Will Find the Hidden Letter 'C' in 17 Seconds

IPL 2024 Qualifier 2: हैदराबाद के सामने रॉयल चैलेंज, कब, कहां और कैसे देखें क्वालीफायर 2, Tickets और Live Streaming डिटेल्स भी देखें

TBSE 12th Arts Result 2024 : Tripura Board Class 12th Arts Result Date And Time at tbse.tripura.gov.in

TBSE 12th Commerce Result 2024 : Tripura Board Class 12th Commerce Result Date And Time at tbse.tripura.gov.in

TBSE 12th Science Result 2024 : Tripura Board Class 12th Science Result Date And Time at tbse.tripura.gov.in

CBSE Class 12 Syllabus 2024-25 PDF (All Subjects)

Today’s School Assembly Headlines (24 May):  Accordion, Virat Kohli, Buddha Purnima, Adani group, RCB v RR, Pune Porsche crash and Other News in English

PSEB Class 11 Environment Education Syllabus 2024-2025: Download in PDF

TBSE Result 2024: Tripura Board Result at Jagran Josh, tbse.tripura.gov.in

TBSE 10th Result 2024: Tripura Madhyamik Result at Jagran Josh, tbse.tripura.gov.in

TBSE 12th Result 2024: Tripura HS Madhyamik Result at Jagran Josh, tbse.tripura.gov.in

CBSE Case Study Questions for Class 9 Maths Surface Areas and Volumes Free PDF

Mere Bacchon, you must practice the CBSE Case Study Questions Class 9 Maths Surface Areas and Volumes  in order to fully complete your preparation . They are very very important from exam point of view. These tricky Case Study Based Questions can act as a villain in your heroic exams!

I have made sure the questions (along with the solutions) prepare you fully for the upcoming exams. To download the latest CBSE Case Study Questions , just click ‘ Download PDF ’.

CBSE Case Study Questions for Class 9 Maths Surface Areas and Volumes PDF

Checkout our case study questions for other chapters.

• Chapter 11 Constructions Case Study Questions
• Chapter 12 Heron’s Formula Case Study Questions
• Chapter 14 Statistics Case Study Questions
• Chapter 15 Probability Case Study Questions

How should I study for my upcoming exams?

First, learn to sit for at least 2 hours at a stretch

Solve every question of NCERT by hand, without looking at the solution.

Solve NCERT Exemplar (if available)

Sit through chapter wise FULLY INVIGILATED TESTS

Practice MCQ Questions (Very Important)

Practice Assertion Reason & Case Study Based Questions

Sit through FULLY INVIGILATED TESTS involving MCQs. Assertion reason & Case Study Based Questions

After Completing everything mentioned above, Sit for atleast 6 full syllabus TESTS.

Comments are closed.

Contact Form

Privacy Policy

• Book Solutions
• State Boards

Case Study Questions Class 10 Maths Surface Areas And Volumes

Case study questions class 10 maths chapter 13 surface areas and volumes.

CBSE Class 10 Case Study Questions Maths Surface Areas And Volumes. Term 2 Important Case Study Questions for Class 10 Board Exam Students. Here we have arranged some Important Case Base Questions for students who are searching for Paragraph Based Questions Surface Areas And Volumes.

At Case Study Questions there will given a Paragraph. In where some Important Questions will made on that respective Case Based Study. There will various types of marks will given 1 marks, 2 marks, 3 marks, 4 marks.

CBSE Case Study Questions Class 10 Maths Surface Areas And Volumes

CASE STUDY 1:

Adventure camps are the perfect place for the children to practice decision making for themselves without parents and teachers guiding their every move. Some students of a school reached for adventure at Sakleshpur. At the camp, the waiters served some students with a welcome drink in a cylindrical glass and some students in a hemispherical cup whose dimensions are shown below. After that they went for a jungle trek. The jungle trek was enjoyable but tiring. As dusk fell, it was time to take shelter. Each group of four students was given a canvas of area 551m 2 . Each group had to make a conical tent to accommodate all the four students. Assuming that all the stitching and wasting incurred while cutting, would amount to 1m 2 , the students put the tents. The radius of the tent is 7m.

[ CBSE Academic Question Paper ]

1.) How much space on the ground is occupied by each student in the conical tent

Answer- b) 38.5 m 2

2.) Which container had more juice and by how much?

• a) Hemispherical cup, 195 cm 3
• b) Cylindrical glass, 207 cm 3
• c) Hemispherical cup, 280.85 cm 3
• d) Cylindrical glass, 314.42 cm 3

Answer- d) Cylindrical glass, 314.42 cm 3

3.) The volume of cylindrical cup is

• a) 295.75 cm 3
• b) 7415.5 cm 3
• c) 384.88 cm 3
• d) 404.25 cm 3

Answer- d) 404.25 cm 3

4.) The volume of hemispherical cup is

• a) 179.67 cm 3
• b) 89.83 cm 3
• c) 172.25 cm 3
• d) 210.60 cm 3

Answer- b) 89.83 cm 3

5.) The height of the conical tent prepared to accommodate four students is

CASE STUDY 2:

On a Sunday, your Parents took you to a fair. You could see lot of toys displayed, and you wanted them to buy a RUBIK’s cube and strawberry ice-cream for you. Observe the figures and answer the questions-:

[ KVS Raipur 2021 – 22 ]

1.) The total surface area of cone with hemispherical ice cream is

Answer- a) 858 cm2 

2.) What is the curved surface area of hemisphere (ice cream) if the base radius is 7cm?

Answer- b) 308 cm2 

3.) The length of the diagonal if each edge measures 6cm is

Answer- d) 6√ 3

4.) Slant height of a cone if the radius is 7cm and the height is 24 cm__

Answer- b) 25 cm

5.) Volume of the solid figure if the length of the edge is 7cm is

Answer- c) 343 cm3 

We hope that above case study questions will help you for your upcoming exams. To see more click below – 

• CBSE Class 10 Maths (standard)
• CBSE Class 10 Maths (Basic)

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

We have a strong team of experienced Teachers who are here to solve all your exam preparation doubts

Sikkim scert class 4 evs chapter 2 games we play solution, sikkim scert class 4 evs chapter 1 changing families solution, assam scert class 8 geography and economics chapter 1 solutions, tripura board class 6 bengali solutions chapter 2 তালগাছ.

Sign in to your account

Username or Email Address

Remember Me

• Andhra Pradesh
• Chhattisgarh
• West Bengal
• Madhya Pradesh
• Maharashtra
• Jammu & Kashmir
• NCERT Books 2022-23
• NCERT Solutions
• NCERT Notes
• NCERT Exemplar Books
• NCERT Exemplar Solution
• States UT Book
• School Kits & Lab Manual
• NCERT Books 2021-22
• NCERT Books 2020-21
• NCERT Book 2019-2020
• NCERT Book 2015-2016
• RD Sharma Solution
• TS Grewal Solution
• TR Jain Solution
• Selina Solution
• Frank Solution
• ML Aggarwal Solution
• Lakhmir Singh and Manjit Kaur Solution
• I.E.Irodov solutions
• ICSE - Goyal Brothers Park
• ICSE - Dorothy M. Noronhe
• Sandeep Garg Textbook Solution
• Micheal Vaz Solution
• S.S. Krotov Solution
• Evergreen Science
• KC Sinha Solution
• ICSE - ISC Jayanti Sengupta, Oxford
• ICSE Focus on History
• ICSE GeoGraphy Voyage
• ICSE Hindi Solution
• ICSE Treasure Trove Solution
• Thomas & Finney Solution
• SL Loney Solution
• SB Mathur Solution
• P Bahadur Solution
• Narendra Awasthi Solution
• MS Chauhan Solution
• LA Sena Solution
• Integral Calculus Amit Agarwal Solution
• IA Maron Solution
• Hall & Knight Solution
• Errorless Solution
• Pradeep's KL Gogia Solution
• OP Tandon Solutions
• Sample Papers
• Previous Year Question Paper
• Value Based Questions
• CBSE Syllabus
• CBSE MCQs PDF
• Assertion & Reason
• New Revision Notes
• Revision Notes
• HOTS Question
• Marks Wise Question
• Toppers Answer Sheets
• Exam Paper Aalysis
• Concept Map
• CBSE Text Book
• Additional Practice Questions
• Vocational Book
• CBSE - Concept
• KVS NCERT CBSE Worksheets
• Formula Class Wise
• Formula Chapter Wise
• JEE Crash Course
• JEE Previous Year Paper
• Important Info
• JEE Mock Test
• JEE Sample Papers
• SRM-JEEE Mock Test
• VITEEE Mock Test
• BITSAT Mock Test
• Manipal Engineering Mock Test
• AP EAMCET Previous Year Paper
• COMEDK Previous Year Paper
• GUJCET Previous Year Paper
• KCET Previous Year Paper
• KEAM Previous Year Paper
• Manipal Previous Year Paper
• MHT CET Previous Year Paper
• WBJEE Previous Year Paper
• AMU Previous Year Paper
• TS EAMCET Previous Year Paper
• SRM-JEEE Previous Year Paper
• VITEEE Previous Year Paper
• BITSAT Previous Year Paper
• UPSEE Previous Year Paper
• CGPET Previous Year Paper
• CUSAT Previous Year Paper
• AEEE Previous Year Paper
• Crash Course
• Previous Year Paper
• NCERT Based Short Notes
• NCERT Based Tests
• NEET Sample Paper
• Previous Year Papers
• Quantitative Aptitude
• Numerical Aptitude Data Interpretation
• General Knowledge
• Mathematics
• Agriculture
• Accountancy
• Business Studies
• Political science
• Enviromental Studies
• Mass Media Communication
• Teaching Aptitude
• NAVODAYA VIDYALAYA
• SAINIK SCHOOL (AISSEE)
• Mechanical Engineering
• Electrical Engineering
• Electronics & Communication Engineering
• Civil Engineering
• Computer Science Engineering
• CBSE Board News
• Scholarship Olympiad
• School Admissions
• Entrance Exams
• All Board Updates
• Miscellaneous
• State Wise Books
• Engineering Exam

Case Study on Surface Areas & Volumes Class 10 Maths PDF

The passage-based questions are commonly known as case study questions. Students looking for Case Study on Surface Areas & Volumes Class 10 Maths can use this page to download the PDF file. 

The case study questions on Surface Areas & Volumes are based on the CBSE Class 10 Maths Syllabus, and therefore, referring to the Surface Areas & Volumes case study questions enable students to gain the appropriate knowledge and prepare better for the Class 10 Maths board examination. Continue reading to know how should students answer it and why it is essential to solve it, etc.

Case Study on Surface Areas & Volumes Class 10 Maths with Solutions in PDF

Our experts have also kept in mind the challenges students may face while solving the case study on Surface Areas & Volumes, therefore, they prepared a set of solutions along with the case study questions on Surface Areas & Volumes.

The case study on Surface Areas & Volumes Class 10 Maths with solutions in PDF helps students tackle questions that appear confusing or difficult to answer. The answers to the Surface Areas & Volumes case study questions are very easy to grasp from the PDF - download links are given on this page.

Why Solve Surface Areas & Volumes Case Study Questions on Class 10 Maths?

There are three major reasons why one should solve Surface Areas & Volumes case study questions on Class 10 Maths - all those major reasons are discussed below:

• To Prepare for the Board Examination: For many years CBSE board is asking case-based questions to the Class 10 Maths students, therefore, it is important to solve Surface Areas & Volumes Case study questions as it will help better prepare for the Class 10 board exam preparation.
• Develop Problem-Solving Skills: Class 10 Maths Surface Areas & Volumes case study questions require students to analyze a given situation, identify the key issues, and apply relevant concepts to find out a solution. This can help CBSE Class 10 students develop their problem-solving skills, which are essential for success in any profession rather than Class 10 board exam preparation.
• Understand Real-Life Applications: Several Surface Areas & Volumes Class 10 Maths Case Study questions are linked with real-life applications, therefore, solving them enables students to gain the theoretical knowledge of Surface Areas & Volumes as well as real-life implications of those learnings too.

How to Answer Case Study Questions on Surface Areas & Volumes?

Students can choose their own way to answer Case Study on Surface Areas & Volumes Class 10 Maths, however, we believe following these three steps would help a lot in answering Class 10 Maths Surface Areas & Volumes Case Study questions.

• Read Question Properly: Many make mistakes in the first step which is not reading the questions properly, therefore, it is important to read the question properly and answer questions accordingly.
• Highlight Important Points Discussed in the Clause: While reading the paragraph, highlight the important points discussed as it will help you save your time and answer Surface Areas & Volumes questions quickly.
• Go Through Each Question One-By-One: Ideally, going through each question gradually is advised so, that a sync between each question and the answer can be maintained. When you are solving Surface Areas & Volumes Class 10 Maths case study questions make sure you are approaching each question in a step-wise manner.

What to Know to Solve Case Study Questions on Class 10 Surface Areas & Volumes?

 A few essential things to know to solve Case Study Questions on Class 10 Surface Areas & Volumes are -

• Basic Formulas of Surface Areas & Volumes: One of the most important things to know to solve Case Study Questions on Class 10 Surface Areas & Volumes is to learn about the basic formulas or revise them before solving the case-based questions on Surface Areas & Volumes.
• To Think Analytically: Analytical thinkers have the ability to detect patterns and that is why it is an essential skill to learn to solve the CBSE Class 10 Maths Surface Areas & Volumes case study questions.
• Strong Command of Calculations: Another important thing to do is to build a strong command of calculations especially, mental Maths calculations.

Where to Find Case Study on Surface Areas & Volumes Class 10 Maths?

Use Selfstudys.com to find Case Study on Surface Areas & Volumes Class 10 Maths. For ease, here is a step-wise procedure to download the Surface Areas & Volumes Case Study for Class 10 Maths in PDF for free of cost.

Since you are already on this page, you can scroll to the top section of this page to get access to the Case Study on Surface Areas & Volumes. To help others reach this page let them know these steps:

• Open Selfstudys.com on your computer/laptop or Smartphone 
• Once the website gets loaded, click on the navigation button

• Find CBSE from the given menu

• Click on Case Study

• Choose Class 10 
• Search Maths and then navigate to the Surface Areas & Volumes Class 10 Maths Case Study

• NCERT Solutions for Class 12 Maths
• NCERT Solutions for Class 10 Maths
• CBSE Syllabus 2023-24
• Social Media Channels
• Login Customize Your Notification Preferences

One Last Step...

• Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.

Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.

Provide prime users with access to exclusive PDF study materials that are not available to regular users.

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Join our Telegram Channel for Free PDF Download

Case Study Questions for Class 9 Maths Chapter 13 Surface Area and Volume

• Last modified on: 2 years ago
• Reading Time: 3 Minutes

Case Study Questions

Question 1:

Nakul was doing an experiment to find the radius r of a ball. For this he took a cylindrical container with radius R = 7 cm and height 10 cm. He filled the container almost half by water as shown in the figure-1. Now he dropped the ball into the container as in figure-2. He observed that in figure-2, the water level in the container raised from P to Q i.e, to 3.4 cm.

(i) What is the approximate radius of the ball? (a) 3 cm (b) 5 cm (c) 7 cm (d) 9 cm

(ii) What is the volume of the cylinder? (a) 1260 cm 2 (b) 540 cm 3 (c) 1620 cm 3 (d) 1540 cm 3

(iii) What is the volume of the spherical ball? (a) 620 cm 3 (b) 824.26 cm 3 (c) 523.81 cm 3 (d) 430.1 cm 3

(iv) How many litres of water can be filled in the full container ? (a) 1.54 litres (b) 2 litres (c) 5 litres (d) 7.5 litres

(v) What is the total surface area of the spherical ball? (a) 441.34 cm 2 (b) 314.29 cm 2 (c) 620 cm 2 (d) 816 cm 2

Download CBSE Books

Exam Special Series:

• Sample Question Paper for CBSE Class 10 Science (for 2024)
• Sample Question Paper for CBSE Class 10 Maths (for 2024)
• CBSE Most Repeated Questions for Class 10 Science Board Exams
• CBSE Important Diagram Based Questions Class 10 Physics Board Exams
• CBSE Important Numericals Class 10 Physics Board Exams
• CBSE Practical Based Questions for Class 10 Science Board Exams
• CBSE Important “Differentiate Between” Based Questions Class 10 Social Science
• Sample Question Papers for CBSE Class 12 Physics (for 2024)
• Sample Question Papers for CBSE Class 12 Chemistry (for 2024)
• Sample Question Papers for CBSE Class 12 Maths (for 2024)
• Sample Question Papers for CBSE Class 12 Biology (for 2024)
• CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
• Master Organic Conversions CBSE Class 12 Chemistry Board Exams
• CBSE Important Numericals Class 12 Physics Board Exams
• CBSE Important Definitions Class 12 Physics Board Exams
• CBSE Important Laws & Principles Class 12 Physics Board Exams
• 10 Years CBSE Class 12 Chemistry Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Physics Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Maths Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Biology Previous Year-Wise Solved Papers (2023-2024)
• ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
• ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
• ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
• ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
• ICSE Important Functions and Locations Based Questions Class 10 Biology
• ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)

✨ Join our Online JEE Test Series for 499/- Only (Web + App) for 1 Year

✨ Join our Online NEET Test Series for 499/- Only for 1 Year

Leave a Reply Cancel reply

Join our Online Test Series for CBSE, ICSE, JEE, NEET and Other Exams

Editable Study Materials for Your Institute - CBSE, ICSE, State Boards (Maharashtra & Karnataka), JEE, NEET, FOUNDATION, OLYMPIADS, PPTs

Discover more from Gurukul of Excellence

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading

CBSE Expert

CBSE Case Study Questions Class 9 Maths Chapter 13 Surface Areas and Volumes PDF Download

Case Study Questions Class 9 Maths Chapter 13  are very important to solve for your exam. Class 9 Maths Chapter 13 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving case study-based questions for Class 9 Maths Chapter 13 Surface Areas and Volumes

Case Study Questions Class 9 Maths Chapter 13

Case Study/Passage-Based Questions

Case Study 1: A class teacher brings some clay into the classroom to teach the topic of mensuration. First, she forms a cylinder of radius 6 cm and height 8 cm and then she molds that cylinder into a sphere.

Find the volume of the cylindrical shape. (a) 288 π cm 3 (b) 244 π cm 3 (c) 240 π cm 3 (d) 216 π cm 3

Answer: (a) 288 π cm3

When clay changes into one shape to other, which of the following remains same? (a) Area (b) C.S.A (c) Radius (d) Volume

Answer: (d) Volume

The radius of the sphere is (a) 2 cm (b) 4 cm (c) 5 cm (d) 6 cm

Answer: (d) 6 cm

Find the volume of sphere, the teacher made. (a) 288 π cm 3 (b) 184 π cm 3 (c) 240 π cm 3 (d) 216 π cm 3

Case Study 2: Ankita realized the need for food for birds on her terrace and decided to make a bird feeder. She got a flexible plastic rectangular sheet of size 44 cm × 15 cm. She rolled it along its length and joined the two opposite ends using a tape for the circular base of the cylinder. She found a square sheet of size 15 cm × 15 cm by cutting it into the required circular shape she prepared the bird feeder as shown in the figure.

The curved surface area of the cylinder formed is (a) 550 cm 2 (b) 660 cm 2 (c) 430 cm 2 (d) 840 cm 2

Answer: (b) 660 cm2

The radius of the base of the cylinder is (a) 5 cm (b) 6 cm (c) 7 cm (d) 8 cm

Answer: (c) 7 cm

The area of the circular base required for the cylinder is (a) 154 cm 2 (b) 164 cm 2 (c) 240 cm 2 (d) 184 cm 2

Answer: (a) 154 cm2

How much will be the area of square sheet left unused after removing the circular base of the cylinder from it? (a) 78 cm 2 (b) 62 cm 2 (c) 75 cm 2 (d) 71 cm 2

Answer: (d) 71 cm2

Hope the information shed above regarding Case Study and Passage Based Questions for Case Study Questions Class 9 Maths Chapter 13 Surface Areas and Volumes with Answers Pdf free download has been useful to an extent. If you have any other queries about Case Study Questions Class 9 Maths Chapter 13 Surface Areas and Volumes and Passage-Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible.

Leave a Comment Cancel reply

Save my name, email, and website in this browser for the next time I comment.

Download India's best Exam Preparation App Now.

Key Features

• Revision Notes
• Important Questions
• Previous Years Questions
• Case-Based Questions
• Assertion and Reason Questions

No thanks, I’m not interested!

Join NOW to get access to exclusive study material for best results

• Case Study Questions
• Surface Areas and Volumes

Please Login or Sign up to continue!

Surface Areas and Volumes Case Study Questions (CSQ’s)

Select the number of questions for the test:

Instructions

• Keep paper and pencil ready but keep your books away.
• Click the "Begin Test" button to start the test.
• You can move between questions and answer them in any order you like.
• Click on "End Test" when you are done.
• These tests are unlimited in nature…take as many as you like.
• You will be able to view the solutions only after you end the test.

All the best – Happy Studying!

Kindly subscribe to continue

Get in Touch

Call / Whats App

• - Class 11 Science
• - Class 11 Commerce
• - Class 12 Science
• - Class 12 Commerce

Case Based Questions Test: Surface Area & Volumes - Class 10 MCQ

10 questions mcq test - case based questions test: surface area & volumes, read the following text and answer the following questions on the basis of the same: mathematics teacher of a school took her 10th standard students to show red fort. it was a part of their educational trip. the teacher had interest in history as well. she narrated the facts of red fort to students. then the teacher said in this monument one can find combination of solid figures. there are 2 pillars which are cylindrical in shape. also 2 domes at the corners which are hemispherical. 7 smaller domes at the centre. flag hoisting ceremony on independence day takes place near these domes. q. write the formula to find the volume of a cylindrical pillar..

• C. πr(l + r)

Read the following text and answer the following questions on the basis of the same: Mathematics teacher of a school took her 10th standard students to show Red fort. It was a part of their Educational trip. The teacher had interest in history as well. She narrated the facts of Red fort to students. Then the teacher said in this monument one can find combination of solid figures. There are 2 pillars which are cylindrical in shape. Also 2 domes at the corners which are hemispherical. 7 smaller domes at the centre. Flag hoisting ceremony on Independence Day takes place near these domes. Q. How much is the volume of a hemisphere if the radius of the base is 3.5 m?

• A. 85.9 m 3
• D. 89.83 m 3

= 89.83 m 3

Read the following text and answer the following questions on the basis of the same: Mathematics teacher of a school took her 10th standard students to show Red fort. It was a part of their Educational trip. The teacher had interest in history as well. She narrated the facts of Red fort to students. Then the teacher said in this monument one can find combination of solid figures. There are 2 pillars which are cylindrical in shape. Also 2 domes at the corners which are hemispherical. 7 smaller domes at the centre. Flag hoisting ceremony on Independence Day takes place near these domes. Q. How much cloth material will be required to cover 2 big domes each of radius 2.5 metres?

• B. 78.57 m 2
• C. 87.47 m 2
• D. 25.8 m 2

= 2 × S.A.of hemispherical dome

= 2 × 2πr 2

= 78.57 m 2

Read the following text and answer the following questions on the basis of the same:

Mathematics teacher of a school took her 10th standard students to show Red fort. It was a part of their Educational trip. The teacher had interest in history as well. She narrated the facts of Red fort to students. Then the teacher said in this monument one can find combination of solid figures. There are 2 pillars which are cylindrical in shape. Also 2 domes at the corners which are hemispherical. 7 smaller domes at the centre. Flag hoisting ceremony on Independence Day takes place near these domes.

• A. 112.3 cm 2
• B. 123.2 m 2
• D. 345.2 cm 2

= 123.2 m 2

Volume of sphere of radius 2 cm

Read the following text and answer the following questions on the basis of same.

A pen stand made of wood is in the shape of a cuboid with 4 conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm.

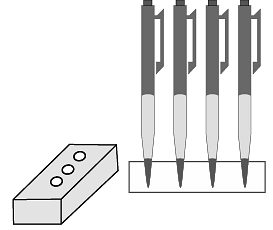
Q. Find the volume of the cuboid?

• A. 520 cm 3
• B. 550 cm 3
• C. 525 cm 3
• D. 528 cm 3

Q. Find the volume of wood taken out to make four cavities.

• A. 30.5 cm 3
• B. 3.02 cm 3
• C. 32.5 cm 3
• D. 1.47 cm 3

Q. Find the diameter of each conical depression.

Q. Write the formula to find out volume of conical depression

myCBSEguide

• Mathematics
• CBSE Class 9 Mathematics...

CBSE Class 9 Mathematics Case Study Questions

Table of Contents

myCBSEguide App

Download the app to get CBSE Sample Papers 2023-24, NCERT Solutions (Revised), Most Important Questions, Previous Year Question Bank, Mock Tests, and Detailed Notes.

If you’re looking for a comprehensive and reliable study resource and case study questions for class 9 CBSE, myCBSEguide is the perfect door to enter. With over 10,000 study notes, solved sample papers and practice questions, it’s got everything you need to ace your exams. Plus, it’s updated regularly to keep you aligned with the latest CBSE syllabus . So why wait? Start your journey to success with myCBSEguide today!

Significance of Mathematics in Class 9

Mathematics is an important subject for students of all ages. It helps students to develop problem-solving and critical-thinking skills, and to think logically and creatively. In addition, mathematics is essential for understanding and using many other subjects, such as science, engineering, and finance.

CBSE Class 9 is an important year for students, as it is the foundation year for the Class 10 board exams. In Class 9, students learn many important concepts in mathematics that will help them to succeed in their board exams and in their future studies. Therefore, it is essential for students to understand and master the concepts taught in Class 9 Mathematics .

Case studies in Class 9 Mathematics

A case study in mathematics is a detailed analysis of a particular mathematical problem or situation. Case studies are often used to examine the relationship between theory and practice, and to explore the connections between different areas of mathematics. Often, a case study will focus on a single problem or situation and will use a variety of methods to examine it. These methods may include algebraic, geometric, and/or statistical analysis.

Example of Case study questions in Class 9 Mathematics

The Central Board of Secondary Education (CBSE) has included case study questions in the Class 9 Mathematics paper. This means that Class 9 Mathematics students will have to solve questions based on real-life scenarios. This is a departure from the usual theoretical questions that are asked in Class 9 Mathematics exams.

The following are some examples of case study questions from Class 9 Mathematics:

Class 9 Mathematics Case study question 1

There is a square park ABCD in the middle of Saket colony in Delhi. Four children Deepak, Ashok, Arjun and Deepa went to play with their balls. The colour of the ball of Ashok, Deepak,  Arjun and Deepa are red, blue, yellow and green respectively. All four children roll their ball from centre point O in the direction of   XOY, X’OY, X’OY’ and XOY’ . Their balls stopped as shown in the above image.

Answer the following questions:

Answer Key:

Class 9 Mathematics Case study question 2

• Now he told Raju to draw another line CD as in the figure
• The teacher told Ajay to mark  ∠ AOD  as 2z
• Suraj was told to mark  ∠ AOC as 4y
• Clive Made and angle  ∠ COE = 60°
• Peter marked  ∠ BOE and  ∠ BOD as y and x respectively

Now answer the following questions:

• 2y + z = 90°
• 2y + z = 180°
• 4y + 2z = 120°
• (a) 2y + z = 90°

Class 9 Mathematics Case study question 3

• (a) 31.6 m²
• (c) 513.3 m³
• (b) 422.4 m²

Class 9 Mathematics Case study question 4

How to Answer Class 9 Mathematics Case study questions

To crack case study questions, Class 9 Mathematics students need to apply their mathematical knowledge to real-life situations. They should first read the question carefully and identify the key information. They should then identify the relevant mathematical concepts that can be applied to solve the question. Once they have done this, they can start solving the Class 9 Mathematics case study question.

Students need to be careful while solving the Class 9 Mathematics case study questions. They should not make any assumptions and should always check their answers. If they are stuck on a question, they should take a break and come back to it later. With some practice, the Class 9 Mathematics students will be able to crack case study questions with ease.

Class 9 Mathematics Curriculum at Glance

At the secondary level, the curriculum focuses on improving students’ ability to use Mathematics to solve real-world problems and to study the subject as a separate discipline. Students are expected to learn how to solve issues using algebraic approaches and how to apply their understanding of simple trigonometry to height and distance problems. Experimenting with numbers and geometric forms, making hypotheses, and validating them with more observations are all part of Math learning at this level.

The suggested curriculum covers number systems, algebra, geometry, trigonometry, mensuration, statistics, graphing, and coordinate geometry, among other topics. Math should be taught through activities that include the use of concrete materials, models, patterns, charts, photographs, posters, and other visual aids.

CBSE Class 9 Mathematics (Code No. 041)

Class 9 Mathematics question paper design

The CBSE Class 9 mathematics question paper design is intended to measure students’ grasp of the subject’s fundamental ideas. The paper will put their problem-solving and analytical skills to the test. Class 9 mathematics students are advised to go through the question paper pattern thoroughly before they start preparing for their examinations. This will help them understand the paper better and enable them to score maximum marks. Refer to the given Class 9 Mathematics question paper design.

QUESTION PAPER DESIGN (CLASS 9 MATHEMATICS)

Mycbseguide: blessing in disguise.

Class 9 is an important milestone in a student’s life. It is the last year of high school and the last chance to score well in the CBSE board exams. myCBSEguide is the perfect platform for students to get started on their preparations for Class 9 Mathematics. myCBSEguide provides comprehensive study material for all subjects, including practice questions, sample papers, case study questions and mock tests. It also offers tips and tricks on how to score well in exams. myCBSEguide is the perfect door to enter for class 9 CBSE preparations.

Test Generator

Create question paper PDF and online tests with your own name & logo in minutes.

Question Bank, Mock Tests, Exam Papers, NCERT Solutions, Sample Papers, Notes

Related Posts

• Competency Based Learning in CBSE Schools
• Class 11 Physical Education Case Study Questions
• Class 11 Sociology Case Study Questions
• Class 12 Applied Mathematics Case Study Questions
• Class 11 Applied Mathematics Case Study Questions
• Class 11 Mathematics Case Study Questions
• Class 11 Biology Case Study Questions
• Class 12 Physical Education Case Study Questions

14 thoughts on “CBSE Class 9 Mathematics Case Study Questions”

This method is not easy for me

aarti and rashika are two classmates. due to exams approaching in some days both decided to study together. during revision hour both find difficulties and they solved each other’s problems. aarti explains simplification of 2+ ?2 by rationalising the denominator and rashika explains 4+ ?2 simplification of (v10-?5)(v10+ ?5) by using the identity (a – b)(a+b). based on above information, answer the following questions: 1) what is the rationalising factor of the denominator of 2+ ?2 a) 2-?2 b) 2?2 c) 2+ ?2 by rationalising the denominator of aarti got the answer d) a) 4+3?2 b) 3+?2 c) 3-?2 4+ ?2 2+ ?2 d) 2-?3 the identity applied to solve (?10-?5) (v10+ ?5) is a) (a+b)(a – b) = (a – b)² c) (a – b)(a+b) = a² – b² d) (a-b)(a+b)=2(a² + b²) ii) b) (a+b)(a – b) = (a + b

MATHS PAAGAL HAI

All questions was easy but search ? hard questions. These questions was not comparable with cbse. It was totally wastage of time.

Where is search ? bar

maths is love

Can I have more questions without downloading the app.

I love math

Hello l am Devanshu chahal and l am an entorpinior. I am started my card bord business and remanded all the existing things this all possible by math now my business is 120 crore and my business profit is 25 crore in a month. l find the worker team because my business is going well Thanks

Leave a Comment

Save my name, email, and website in this browser for the next time I comment.

• Neet Online Test Pack

12th Standard stateboard question papers & Study material

தமிழ் subjects.

கணினி பயன்பாடுகள்

கணினி அறிவியல்

வணிகக் கணிதம் மற்றும் புள்ளியியல்.

கணினி தொழில்நுட்பம்

கணக்குப்பதிவியல்

English Subjects

Computer Science

Business Maths and Statistics

Accountancy

Computer Applications

Computer Technology

11th Standard stateboard question papers & Study material

9th Standard stateboard question papers & Study material

Social Science

சமூக அறிவியல்

6th standard stateboard question papers & study material.

10th Standard stateboard question papers & Study material

7th Standard stateboard question papers & Study material

8th Standard stateboard question papers & Study material

கணிதம் - old

12th Standard CBSE Subject Question Paper & Study Material

Introductory Micro and Macroeconomics

Business Studies

Indian Society

Physical Education

Bio Technology

Engineering Graphics

Entrepreneurship

Hindi Elective

Home Science

Legal Studies

Political Science

11th Standard CBSE Subject Question Paper & Study Material

Mathematics

Enterprenership

Applied Mathematics

10th standard cbse subject question paper & study material.

9th Standard CBSE Subject Question Paper & Study Material

8th Standard CBSE Subject Question Paper & Study Material

7th Standard CBSE Subject Question Paper & Study Material

6th Standard CBSE Subject Question Paper & Study Material

School Exams

Tamil Nadu State Board Exams

Scholarship Exams

Study Materials , News and Scholarships

Stateboard Tamil Nadu

Free Online Tests

Educational News

Scholarships

Entrance Exams India

Video Materials

9th Standard CBSE

Class 9th Maths - Surface Case Study Questions and Answers 2022 - 2023

Class 9th Maths - Surface Case Study Questions and Answers 2022 - 2023 Study Materials Sep-08 , 2022

QB365 provides a detailed and simple solution for every Possible Case Study Questions in Class 9th Maths Subject - Surface, CBSE. It will help Students to get more practice questions, Students can Practice these question papers in addition to score best marks.

A PHP Error was encountered

Severity: Warning

Message: in_array() expects parameter 2 to be array, null given

Filename: material/details.php

Line Number: 1436

Message: Use of undefined constant EXAM - assumed 'EXAM' (this will throw an Error in a future version of PHP)

Line Number: 1438

QB365 - Question Bank Software

Surface areas and volumes case study questions with answer key.

Final Semester - June 2015

(b) What is the curved surface area of hemispherical dome ?

(c) What is the height of the cubodial part ?

d) What is the circumference of the base of the dome ?

(v) The total surface area of a hemispherical dome having radius 7 cm is:

(ii) Write the formula to find the volume of one pillar (including hemispherical dome) :

(iii) The volume of the hemispherical dome at the centre if base radius is 7 m is :

(iv) What is the lateral surface area of all 4 pillars if height of the each pillar is 14 m and base radius is 1.4 m (without dome)?

(v) The cost of polishing all the four pillars if the cost of 1 m 2 is Rs. 270, will be :

Mathematics teacher of a school took his 10th standard students to show Taj Mahal. It was a part of their Educational trip. The teacher had interest in history as well. He narrated the facts of Taj Mahal to the students. Then the teacher said in this monument one can find combination of solid figures. There are 4 pillars which are cylindrical in shape. Also, 2 domes at the back side which are hemispherical. 1 big domes at the centre. It is the finest example of the symmetry. (Use π = 22/7) (i)How much cloth material will be required to cover 2 small domes each of radius  4.2 metres?

(ii) Write the formula to find the volume of a cylindrical pillar:

(iii) Find the lateral surface area of two pillars if height of the pillar is 7 m and radius of the base is 1.4 m.

(iv) How much is the volume of a hemisphere if the radius of the base is 3.5 m?

(v) What is the ratio of sum of volumes of two hemispheres of radius 1 cm each to the volume of a sphere of radius 2 cm?

(ii) If the area of windows and doors is 22 sq m.  The area of the walls to be painted

(iii) What is the area of the tiles to be used for flooring?

(iv) The total area of the room is (including windows and doors):

(v) What is the volume of the air in the room?

(b) The radius of the base of the cylinder is

(c) The area of the circular base required for the cylinder is

(d) How much will be the area of square sheet left unused after removing the circular base of the cylinder from it?

(e) Find the volume of water that can be filled in the cylinder.

(ii) What is the volume of cylindrical shape?

(iii) What is the formula of volume of sphere?

(iv) When clay changes into on shape to other which of the following remains same. 

(v) The radius of the sphere formed is :

(ii) What is formula for calculating the lateral surface area of the cylinder?

(iii) What is the volume of two cylinders?

(iv) If the cuboid needs to be painted red, how much area need to be painted?

(v)  If a cloth is needed to cover the cylindrical part, how much cloth is needed?

(ii) What is the formula for calculating the total surface area of the cylindrical container i.e., milk container?

(iii) If the cube shown in the picture is of dimension 6 cm each. Find the capacity of this cubic container.

(iv) Find the ratio between the volume and C.S.A. of the cylindrical container.

(v)  What is the formula for calculating the total surface area of the hemisphere?

*****************************************

• Previous Class 9th Maths - Probability Case Study Questions and Answers 2022 - 2023
• Next Class 9th Maths - Statistics Case Study Questions and Answers 2022 - 2023

Reviews & Comments about Class 9th Maths - Surface Case Study Questions and Answers 2022 - 2023

Write your Comment

9th Standard CBSE Mathematics Usefull Links

• 10th Standard

Other 9th Standard CBSE Subjects

Other 9th Standard CBSE Mathematics Study material

Class 9th maths - probability case study questions and answers 2022 - 2023 click to view, class 9th maths - statistics case study questions and answers 2022 - 2023 click to view, class 9th maths - surface case study questions and answers 2022 - 2023 click to view, class 9th maths - linear equations in ... click to view, class 9th maths - coordinate geometry case ... click to view, 9th standard cbse mathematics annual exam model question 2020 click to view, 9th standard cbse mathematics public exam sample question 2020 click to view, 9th standard cbse mathematics public exam important question 2019-2020 click to view, 9th standard mathematics board exam sample question 2020 click to view, 9th standard mathematics board exam model question 2019-2020 click to view, cbse 9th mathematics - probability model question paper click to view, cbse 9th mathematics - statistics model question paper click to view, cbse 9th mathematics - surface areas and volumes model question paper click to view, cbse 9th mathematics - heron's formula model question paper click to view, cbse 9th mathematics - constructions model question paper click to view, register & get the solution for class 9th maths - surface case study questions and answers 2022 - 2023.

• School Solutions
• Star Program
• NCERT Solutions Class 12 Maths
• NCERT Solutions Class 12 Physics
• NCERT Solutions Class 12 Chemistry
• NCERT Solutions Class 12 Biology
• NCERT Solutions Class 12 Commerce
• NCERT Solutions Class 12 Economics
• NCERT Solutions Class 12 Accountancy
• NCERT Solutions Class 12 English
• NCERT Solutions Class 12 Hindi
• NCERT Solutions Class 11 Maths
• NCERT Solutions Class 11 Physics
• NCERT Solutions Class 11 Chemistry
• NCERT Solutions Class 11 Biology
• NCERT Solutions Class 11 Commerce
• NCERT Solutions Class 11 Accountancy
• NCERT Solutions Class 11 English
• NCERT Solutions Class 11 Hindi
• NCERT Solutions Class 11 Statistics
• NCERT Solutions Class 10 Maths
• NCERT Solutions Class 10 Science
• NCERT Solutions Class 10 English
• NCERT Solutions Class 10 Hindi
• NCERT Solutions Class 10 Social Science
• NCERT Solutions Class 9 Maths
• NCERT Solutions Class 9 Science
• NCERT Solutions Class 9 English
• NCERT Solutions Class 9 Hindi
• NCERT Solutions Class 9 Social Science
• NCERT Solutions Class 8 Maths
• NCERT Solutions Class 8 Science
• NCERT Solutions Class 8 English
• NCERT Solutions Class 8 Hindi
• NCERT Solutions Class 8 Social Science
• NCERT Solutions Class 7 Maths
• NCERT Solutions Class 7 Science
• NCERT Solutions Class 7 English
• NCERT Solutions Class 7 Hindi
• NCERT Solutions Class 7 Social Science
• NCERT Solutions Class 6 Maths
• NCERT Solutions Class 6 Science
• NCERT Solutions Class 6 English
• NCERT Solutions Class 6 Hindi
• NCERT Solutions Class 6 Social Science
• NCERT Solutions Class 5 Maths
• NCERT Solutions Class 5 English
• NCERT Solutions Class 5 EVS
• NCERT Solutions Class 4 Maths
• NCERT Solutions Class 4 English
• NCERT Solutions Class 4 EVS
• NCERT Solutions Class 4 Hindi
• NCERT Solutions Class 3 Maths
• NCERT Solutions Class 3 English
• NCERT Solutions Class 3 EVS
• NCERT Solutions Class 3 Hindi
• NCERT Solutions Class 2 Maths
• NCERT Solutions Class 2 English
• NCERT Solutions Class 2 Hindi
• NCERT Solutions Class 1 Maths
• NCERT Solutions Class 1 English
• NCERT Solutions Class 1 Hindi
• NCERT Books Class 12
• NCERT Books Class 11
• NCERT Books Class 10
• NCERT Books Class 9
• NCERT Books Class 8
• NCERT Books Class 7
• NCERT Books Class 6
• NCERT Books Class 5
• NCERT Books Class 4
• NCERT Books Class 3
• NCERT Books Class 2
• NCERT Books Class 1
• Important Questions Class 12
• Important Questions Class 11
• Important Questions Class 10
• Important Questions Class 9
• Important Questions Class 8
• Important Questions Class 7
• important questions class 6
• CBSE Class 12 Revision Notes
• CBSE Class 11 Revision Notes
• CBSE Class 10 Revision Notes
• CBSE Class 9 Revision Notes
• CBSE Class 8 Revision Notes
• CBSE Class 7 Revision Notes
• CBSE Class 6 Revision Notes
• CBSE Class 12 Syllabus
• CBSE Class 11 Syllabus
• CBSE Class 10 Syllabus
• CBSE Class 9 Syllabus
• CBSE Class 8 Syllabus
• CBSE Class 7 Syllabus
• CBSE Class 6 Syllabus
• CBSE Class 5 Syllabus
• CBSE Class 4 Syllabus
• CBSE Class 3 Syllabus
• CBSE Class 2 Syllabus
• CBSE Class 1 Syllabus
• CBSE Sample Question Papers For Class 12
• CBSE Sample Question Papers For Class 11
• CBSE Sample Question Papers For Class 10
• CBSE Sample Question Papers For Class 9
• CBSE Sample Question Papers For Class 8
• CBSE Sample Question Papers For Class 7
• CBSE Sample Question Papers For Class 6
• CBSE Sample Question Papers For Class 5
• CBSE Sample Question Papers For Class 4
• CBSE Sample Question Papers For Class 3
• CBSE Sample Question Papers For Class 2
• CBSE Sample Question Papers For Class 1
• CBSE Previous Year Question Papers Class 12
• CBSE Previous Year Question Papers Class 10
• Extra Questions For Class 8 Maths
• Extra Questions For Class 8 Science
• Extra Questions For Class 9 Maths
• Extra Questions For Class 9 Science
• Extra Questions For Class 10 Maths
• Extra Questions For Class 10 Science
• NEET 2021 Question Paper
• NEET 2020 Question Paper
• NEET 2019 Question Paper
• NEET 2018 Question Paper
• NEET 2017 Question Paper
• NEET 2016 Question Paper
• NEET 2015 Question Paper
• NEET Physics Questions
• NEET Chemistry Questions
• NEET Biology Questions
• NEET Sample Papers
• NEET Physics Syllabus
• NEET Chemistry Syllabus
• NEET Biology Syllabus
• NEET Mock Test
• NEET Eligibility Criteria
• JEE Main 2021 Question Paper
• JEE Main 2020 Question Paper
• JEE Main 2019 Question Paper
• JEE Main 2018 Question Paper
• JEE Main 2017 Question Paper
• JEE Main 2016 Question Paper
• JEE Main 2015 Question Paper
• JEE Main Sample Papers
• JEE Main Physics Syllabus
• JEE Main Chemistry Syllabus
• JEE Main Maths Syllabus
• JEE Main Physics Questions
• JEE Main Chemistry Questions
• JEE Main Maths Questions
• JEE main revision notes
• JEE Main Mock Test
• JEE Advanced Physics Questions
• JEE Advanced Chemistry Questions
• JEE Advanced Maths Questions
• JEE Advanced 2021 Question Paper
• JEE Advanced 2020 Question Paper
• JEE Advanced 2019 Question Paper
• JEE Advanced 2018 Question Paper
• JEE Advanced 2017 Question Paper
• JEE Advanced 2016 Question Paper
• JEE Advanced 2015 Question Paper
• JEE Advanced Physics Syllabus
• JEE Advanced Chemistry Syllabus
• JEE Advanced Maths Syllabus
• JEE Advanced Mock Test
• ISC Class 12 Syllabus
• ISC Class 11 Syllabus
• ICSE Class 10 Syllabus
• ICSE Class 9 Syllabus
• ICSE Class 8 Syllabus
• ICSE Class 7 Syllabus
• ICSE Class 6 Syllabus
• ISC Sample Question Papers for Class 12
• ISC Sample Question Papers for Class 11
• ICSE Sample Question Papers for Class 10
• ICSE Sample Question Papers for Class 9
• ICSE Sample Question Papers for Class 8
• ICSE Sample Question Papers for Class 7
• ICSE Sample Question Papers for Class 6
• ICSE Class 10 Revision Notes
• ICSE Class 9 Revision Notes
• ISC Important Questions for Class 12
• ISC Important Questions for Class 11
• ICSE Important Questions for Class 10
• ICSE Important Questions for Class 9
• ICSE Important Questions for Class 8
• ICSE Important Questions for Class 7
• ICSE Important Questions for Class 6
• ISC Class 12 Question Paper
• ICSE Class 10 Question Paper
• Maharashtra Board Syllabus
• Maharashtra Board Sample Question Paper
• Maharashtra Board Previous Year Question Paper
• AP Board Syllabus
• AP Board Sample Question Paper
• AP Board Previous Year Question Paper
• Tamilnadu Board Syllabus
• Tamilnadu Board Sample Question Paper
• Tamilnadu Board Previous Year Question Paper
• Telangana Board Syllabus
• Telangana Board Sample Question Paper
• Telangana Board Previous Year Question Paper
• Karnataka Board Syllabus
• Karnataka Board Sample Question Paper
• Karnataka Board Previous Year Question Paper
• Examination Full Forms
• Physics Full Forms
• Chemistry Full Forms
• Biology Full Forms
• Educational Full Form
• CUET Eligibility Criteria
• CUET Exam Pattern
• CUET Cutoff
• CUET Syllabus
• CUET Admit Card
• CUET Counselling
• CUET Previous Year Question Papers
• CUET Application Form
• CUET Sample Papers
• CUET Exam Centers
• CUET Exam Dates
• CUET Results
• Physics Formulas
• Chemistry Formulas
• Math Formulas
• Algebra Formulas
• Geometry Formulas
• Trigonometry Formulas
• Subscription

Important Questions Class 9 Maths Chapter 13

Home » CBSE » Important Questions Class 9 Maths Chapter 13

• CBSE Important Questions
• Important Questions Class 6
• CBSE Previous Year Question Papers
• CBSE Revision Notes
• CBSE Syllabus
• CBSE Extra Questions
• CBSE Sample Papers
• ISC & ICSE Syllabus
• ICSE Syllabus Class 9
• ICSE Syllabus Class 8
• ICSE Syllabus Class 7
• ICSE Syllabus Class 6
• ICSE Syllabus Class 10
• ICSE Question Paper
• ICSE Sample Question Papers
• ISC Sample Question Papers For Class 12
• ISC Sample Question Papers For Class 11
• ICSE Sample Question Papers For Class 10
• ICSE Sample Question Papers For Class 9
• ICSE Sample Question Papers For Class 8
• ICSE Sample Question Papers For Class 7
• ICSE Sample Question Papers For Class 6
• ICSE Revision Notes
• ICSE Important Questions
• ISC Important Questions For Class 12
• ISC Important Questions For Class 11
• ICSE Important Questions For Class 10
• ICSE Important Questions For Class 9
• ICSE Important Questions For Class 8
• ICSE Important Questions For Class 7
• ICSE Important Questions For Class 6
• Maharashtra board
• Rajasthan-Board
• Andhrapradesh Board
• AP Board syllabus
• Telangana Board
• Tamilnadu Board
• Tamilnadu Sample Question Paper
• Tamilnadu Syllabus
• Tamilnadu Previous Year Question Paper
• NCERT Solutions Class 12
• NCERT Solutions Class 10
• NCERT Solutions Class 11
• NCERT Solutions Class 9
• NCERT Solutions Class 8
• NCERT Solutions Class 7
• NCERT Solutions Class 6
• NCERT Solutions Class 5
• NCERT Solutions Class 4
• NCERT Solutions Class 3
• NCERT Solutions Class 2
• NCERT Solutions Class 1
• JEE Main Question Papers
• JEE Main Syllabus
• JEE Main Questions
• JEE Main Revision Notes
• JEE Advanced Question Papers
• JEE Advanced Syllabus
• JEE Advanced Questions
• JEE Advanced Sample Papers
• NEET Question Papers
• Neet 2021 Question Paper
• Neet 2020 Question Paper
• Neet 2019 Question Paper
• Neet 2018 Question Paper
• Neet 2017 Question Paper
• Neet 2016 Question Paper
• Neet 2015 Question Paper
• NEET Syllabus

Important Questions Class 9  Mathematics Chapter 13 – Surface Areas and Volumes

 Mathematics syllabus Chapter 13 of CBSE Class 9 is about ‘Surface Areas and Volumes’.The surface area and volume are computed for any three-dimensional geometrical shape. The surface area of any type of given object is the area or region occupied by the surface of the object. At the same time, the volume is the total amount of space accessible in any object. In geometry, there are numerous shapes and sizes, like spheres, cubes, cuboids, cones, cylinders, etc. Every shape has its surface area as well as volume. But in the case of two-dimensional figures like squares, circles, rectangles, triangles, etc., we can calculate only the area covered by these figures, and there is no volume involved. 

Quick Links

Extramarks is one of the leading online educational platforms whose credibility lies in providing the best study materials for all classes from 1 through 12.  Teachers and students across the country have unshakable faith and trust in Extramarks. Students may register on the Extramarks website to access our comprehensive suite of study materials, including NCERT solutions, CBSE sample papers, revision notes, etc. Our experienced mathematics faculty experts have made these study notes by referring to the NCERT books which adhere to the CBSE syllabus.

To maximise your potential during exam preparations, students can always register on  Extramarks website and get complete access to Important Questions Class 9 Mathematics Chapter 13 and other study materials, including NCERT solutions, CBSE revision notes, etc. In case you just want to clarify your doubts, you may attend live sessions by experts on any of the topics to ace the exam. 

Important Questions Class 9 Mathematics Chapter 13 – With Solutions

Our in-house Mathematics faculty experts have compiled a set of  Important Questions for  Class 9 Mathematics Chapter 13  by referring to various sources. For every question, the entire team has prepared a step-by-step explanation that will help students understand the concepts used in each question. Also, the questions are chosen in a way that would cover full chapter topics. So by practising from our question bank of Important Questions Class 9 Mathematics Chapter 13, students will be able to revise their chapters and grasp their strong and weak points. And upgrade their preparation by strengthening weak areas and aiming for a  100% score during the exams.  .

Given below are a few of the questions and answers from our question bank of Important Questions Class 9 Mathematics Chapter 13:

 Question 1: Hameed had built a cubical water tank along with a lid for his house, with every outer edge 1.5 m long. He buys the tank’s outer surface, not including the base, covered with square tiles of each side 25 cm (observe the figure given below). Find how much he would have to spend on the tiles if the cost of the tiles is Rs.360 per dozen.                                                  

Image Source: NCERT Textbook

Answer 1: Given,

The edge of the given cubical tank (a) = 1.5 m = 150 cm 

Thus, the surface area of the given tank = 5 × 150 × 150 cm²

The measure of each side of a square tile = 25 cm

Area of every square tile = side × side = 25 × 25 cm²

The required number of tiles in the cubical water tank= (Surface area of the tank)/(Area of each and every tile)

= (5 × 150 × 150)/(25 × 25)

Also, the cost of the tiles per dozen is Rs. 360.

Hence, the cost of each tile = Rs. 360/12 = Rs. 30

Therefore, the total cost of all the 180 tiles = 180 × Rs. 30

                                                              = Rs. 5400

Question 2: A particular plastic box 1.5 m long, 1.25 m wide and 65 cm deep are to be made. It is opened at the top. Ignoring the estimated thickness of the plastic sheet, determine the:

(i)The area of the sheet needed for making the box.

(ii)The cost of the separate sheet for it, if a sheet measuring 1m² cost Rs. 20.

Answer 2: Given: The length (l) of the given box = 1.5m

The breadth (b) of the given box = 1.25 m

The depth (h) of the given box = 0.65m

(i) Box is to be open at the top

The area of the sheet needed.

= 2 x length x height + 2 x breadth x height + 2 x length x breadth.

= [ 2 × 1.5 × 0.65 + 2 × 1.25 × 0.65 + 1.5 × 1.25 ]m²

= (1.95 + 1.625 + 1.875) m²

(ii) The cost of a sheet per m² Area = Rs.20.

The cost of a sheet of 5.45 m² area = Rs (5.45×20)

Question 3: Find out 

(i) the curved surface area of a closed given cylindrical petrol storage tank that is 4.2 m in

diameter and 4.5m high.

(ii) How a small amount of steel actually used if 1/12 of the steel actually used was wasted in making the tank? (Assume π = 22/7)

Answer 3:  The height of the given cylindrical tank, h = 4.5m

The radius of the given circular end, r = (4.2/2)m = 2.1m

(i) The curved surface area of the cylindrical tank is 2πrh

= 2×(22/7)×2.1×4.5 m²

= (44×0.3×4.5) m²

Thus, the Curved Surface Area of the tank is 59.4 m².

(ii) The total surface area of given tank = 2πradius (radius + height)

= 2 × (22/7) × 2.1 × ( 2.1 + 4.5 )

= 44 × 0.3 × 6.6

Now, Let S m² steel sheet be actually used in making the tank.

S(1 -1/12) = 87.12 m²

This implies that S = 95.04 m²

Thus, 95.04 m² steel was used in actuality while making such a tank.

Question 4: The total surface area of a certain cube is 96 cm². The volume of the cube is:

(A) 8 cm³ (B) 512 cm³(C) 64 cm³ (D) 27 cm³

Answer 4: (C) 64 cm³

Explanation:

The surface area of the given cube is 96 cm²

Let the length of the given cube is l cm.

According to the given formula

Thus the length of the given cube is 4 cm.

The volume of a cube = l³

Thus the volume is 64 cm³ which is option c.

Hence, option C is the correct answer.

Question 5:A particular right circular cylinder encloses a sphere of radius r (see fig. 13.22). Find out

(i) surface area of the given sphere,

(ii) curved surface area of the given cylinder,

(iii) ratio of the given areas obtained in (i) and (ii).

(i) The surface area of the given sphere = 4πr², where r is the radius of the given sphere

(ii) The height of the given cylinder, h = r+r =2r

The radius of the given cylinder = r

Curved Surface Area of cylinder formula = 2πrh = 2πr(2r) (using value of h)

(iii) Ratio between areas = (Surface area of the sphere)/(CSA of Cylinder)

= 4πr²/4πr²= 1/1

The ratio of the given areas obtained in (i) and (ii) is 1:1.

Question 6: A particular lead pencil consists of a wooden cylinder with a solid cylinder of graphite filled in the interior. The diameter of the particular pencil is 7 mm, and the diameter of the graphite is 1 mm. If the pencil length is 14 cm, find out the volume of the wood and that of the graphite. (Assume π = 22/7)

The radius of the given pencil, r1 = 7/2 mm = 0.7/2 cm = 0.35 cm

The radius of the given graphite, r2 = 1/2 mm = 0.1/2 cm = 0.05 cm

The height of the given pencil, h = 14 cm

The volume of wood in pencil = (r1²-r2²)h cubic units

Substitute the values we have

= [(22/7)×(0.35²-0.05²)×14]

This implies the volume of wood in pencil = 5.28 cm³

The volume of graphite = r2²h cubic units

Substituting the values we obtained

= (22/7)×0.052×14

= 44×0.0025

Thus, the volume of graphite is 0.11 cm³.

Question 7: In a cylinder, the radius is doubled, and the height is halved; the curved surface area 

(A) is halved (B)is doubled (C) is the same (D) is four times

Answer 7: (C) same

Let the radius of the given cylinder = r unit

Let the height of the given cylinder = h unit.

As per the question,

Radius is doubled = 2r

Height is halved = h/2

The required curved surface area of the given cylinder = 2 × π × r × h

And as per the above condition,

The curved surface area = 2 × π × 2 × r × h/2

= 2 × π × r × h

This is the same as the curved surface area of the cylinder with radius r and height h.

Question 8: A patient in a certain hospital is given soup daily in a cylindrical bowl of diameter 7cm. If the cylindrical bowl is served with soup up to a height of 4cm, how much soup ought to call the hospital to prepare daily to serve 250 patients? (Assume π = 22/7)

The diameter of the given cylindrical bowl = 7 cm

The given radius of the cylindrical bowl, r = 7/2 cm = 3.5 cm

The bowl is served with soup up to a height of 4cm, so h = 4 cm

The volume of soup in one bowl= πr²h

(22/7)×3.5²×4 = 154

The volume of soup in one bowl is 154 cm³

The volume of soup served to 250 patients = (250×154) cm³= 38500 cm³

= 38.5litres.

Question 9: The paint present in a particular container is sufficient to paint the required area of 9.375 sq.m. How many bricks of dimensions 22.5 cm × 10 cm × 7.5 cm can be painted out of this container?

The dimensions of the given brick = 22.5 cm × 10 cm × 7.5 cm

Now, l = 22.5 cm, b = 10 cm, h = 7.5 cm

Surface area of each brick = 2(length x breadth + breadth x height  + height  x length) 

= 2 ( 22.5 × 10 + 10 × 7.5 + 7.5 × 22.5 ) cm²

= 2 ( 225 + 75 + 168.75 ) cm² 

= 2 x 468.75 cm² 

= 937.5 cm² 

The Area that can be painted by the container = 9.375 m² (given)

= 9.375 × 10000 cm²

= 93750 cm²

Hence, the required number of bricks = (Area that the container can paint)/(Surface area of 1 brick)

= 93750/937.5

= 937500/9375

Question 10: In a certain right circular cone, height, radius and slant height are not always sides of a right triangle.

Answer 10: In the required right circular cone, height, radius and slant height are not always sides of a right triangle.

Consider a given right circular cone with height h, slant height l and radius r.

In a required right-angled triangle, one angle = 90°

Evaluating triangle AOB,

By utilising the Pythagorean theorem

AB² = OA² + OB²

l² = h² + r²

This indicates that the cone’s height, radius and slant height can consistently be the sides of a right triangle.

Hence, the provided statement is true.

Question 11:A room’s given length, breadth, and height are 5 m, 4 m and 3 m, respectively. Find out the cost of whitewashing the walls of the room and ceiling at the given rate of Rs 7.50 per m

Answer 11: The length (l) of the given room = 5m

The breadth (b) of the given room = 4m

The height (h) of the given room = 3m

It can be seen that the four walls and the room’s ceiling are to be whitewashed.

The total area required to be whitewashed = Area of the given walls + Area of the ceiling of the given room

= 2 x length x height + 2 x breadth x height +length x breadth

= [ 2 × 5 × 3 + 2 × 4 × 3 + 5 × 4 ]

= ( 30 + 24 + 20 )

The area is 74 m²

Cost of whitewash per m² Area = Rs.7.50 (Given)

Cost of whitewashing 74 m² areas = Rs. (74×7.50)

Question 12: In the figure, you can observe the frame of a lampshade. It is to be covered with a certain decorative cloth.

The required frame has a base diameter of 20 cm and a height of 30 cm. A margin of 2.5 cm is given for folding it over the top and bottom of the frame. Find out how much cloth is needed to cover the lampshade. (Assume π = 22/7)

Answer 12: Say h = height of the frame of the lampshade, looks similar to a cylindrical shape

where, r = radius

The total height is h = (2.5+30+2.5) cm = 35cm and

r = (20/2) cm = 10cm

Use the curved surface area formula to find the cloth required for covering the lampshade, which is 2πrh

= (2×(22/7)×10×35) cm²

Hence, 2200 cm² cloth is required to cover the lampshade .

Question 13: If the radius of a certain cylinder is doubled and its curved surface area is not changed, the height is to be halved.

Answer 13: True

Justification:

Let the radius of the cylinder = r

Height of the cylinder = h

Then, the curved surface area of the cylinder, CSA = 2πrh

According to the question,

The radius is doubled, and the curved surface area is not changed.

The new radius of the cylinder, R = 2r

The new curved surface area of the cylinder, CSA’ = 2πrh …(i)

Alternate case:

When R = 2r and CSA’ = 2πrh

The curved surface area of the required cylinder, in this case, Curved Surface Area’= 2πRh = 2π(2r)h = 4πrh …(ii)

Comparing the given equations (i) and (ii),

But, 2πrh ≠ 4πrh

equation (i) ≠ equation (ii)

Hence, if h = h/2 (height is halved)

Curved Surface Area’ = 2π(2r)(h/2) = 2πrh

Thus, the given statement, “If the radius of a given cylinder is doubled and its curved surface area is not modified, the height must be halved”, is true.

Question 14: The diameter of the base of a given cone is 10.5 cm, and its required slant height is 10 cm. Find out its curved surface area (Assume π=22/7)

Answer 14: The radius of the given base of cone = diameter/ 2 = (10.5/2)cm = 5.25cm

The slant height of the given cone, say l = 10 cm

Curved Surface Area of cone = πrl

= (22/7)×5.25×10 = 165 cm²

Thus, the curved surface area of the required cone is 165cm².

Question 15: A matchbox measures 4 cm×2.5cm×1.5cm. What will be the required volume of a packet containing 12 such boxes?

Answer 15: The dimensions of a given matchbox (a cuboid) are l×b×h = 4 cm×2.5 cm×1.5 cm, respectively

The volume of the given matchbox = l×b×h = (4×2.5×1.5) = 15

Volume of matchbox = 15 cm³

The volume of 12 such matchboxes = (15×12) cm³ = 180 cm³

Therefore, the volume of 12 matchboxes is 180 cm³.

Question 16: Find out the volume of the given right circular cone with

(i) the radius is 6cm, height is 7 cm (ii) the radius is 3.5 cm, height is 12 cm (Assume π = 22/7)

Answer 16: The volume of cone = (1/3) πr²h cube units

 let r be the required radius and h be the height of the cone

(i) The radius of the radius cone, r = 6 cm

The height of the given cone, h = 7cm

Say V be the volume of the given cone; we obtain

V = (1/3)×(22/7)×36×7

The volume of the given cone is 264 cm³.

(ii) The radius of the given cone, r = 3.5cm

The height of the given cone, h = 12cm

The volume of the given cone = (1/3)×(22/7)×3.5²×7 = 154

The volume of the given cone is 154 cm³.

Question 17: The volume of the largest given right circular cone that can be accommodated in a cube whose edge is 2r is the same as the volume of the required hemisphere of radius r.

Answer 17: According to the question,

Edge of the cube, l = 2r

Then, the diameter of the given cone = 2r

The radius of the given cone = 2r/2

The height of the given cone, h = height of the cube

The volume of the cone is given by,

The volume of cone = 1/3 πr²h

= 1/3 πr²(2r)

= Volume of the given hemisphere of radius r

Thus, the required statement “the volume of the given largest right circular cone that can be accommodated in a cube whose edge is 2r equals the volume of the required hemisphere of radius r” is true.

Question 18:The height of a given cone is 15cm. If its volume is 1570cm ³ , find out the diameter of its base. (Use π = 3.14)

Answer 18: Height of the cone, h = 15 cm

The volume of the cone =1570 cm³

Let r be the needed radius of the given cone.

The volume of the cone, V = (1/3) πr²h

So, (1/3) πr²h = 1570

(1/3)×3.14×r² ×15 = 1570

The radius of the base of the required cone is 10 cm.

Question 19: A room’s length, breadth and height are 5 m, 4 m and 3 m, respectively. Find the cost of whitewashing the room’s walls and the ceiling at Rs.7.50 per sq.m.

Answer 19:  Given,

The length of the given room (l) = 5 m

The breadth of the given room (b) = 4 m

The height of the room (h) = 3 m

Area of walls of the given room = Lateral surface area of a cuboid

= 2h(l + b)

= 2 × 3(5 + 4)

Area of the given ceiling = Area of base of the cuboid

Area required to be whitewashed = (54 + 20) sq.m = 74 sq.m

 The cost of whitewashing per sq.m = Rs. 7.50

Hence, the total amount of whitewashing the walls and ceiling of the room = 74 × Rs. 7.50 = Rs. 555

Question 20: The floor of a particular rectangular hall has a given perimeter of 250 m. If the cost of painting the four given walls is Rs.10 per m² is Rs.15000, find out the height of the particular hall.

Answer 20: Let the length, breadth, and height of the given rectangular hall be l, b, and h, respectively.

The Area of four walls = 2lh+2bh

The perimeter of the given floor of the hall = 2(l+b)

The area of four walls = 2(l+b) h = 250h m2

The cost of painting per square metre  area = Rs.10

The cost of painting 250h square meter area = Rs (250h×10) = Rs.2500h

Although, it is given that the cost of painting the walls is Rs. 15000.

15000 = 2500h

Thus, the height of the given hall is 6 m.

Question 21: Metal spheres, separately of radius 2 cm, are loaded into a rectangular box of the required internal dimensions 16 cm × 8 cm × 8 cm. When 16 spheres are compacted, the box is loaded with preservative liquid. Find the volume of this liquid. Give your answer to the nearest integer. [Use π =3.14]

Answer 21: According to the question,

Radius of each sphere, r = 2 cm

The volume of a given sphere 

Volume of 1 sphere = 4/3 πr³

Hence, there are 16 spheres in our question,

Volume of 16 spheres = 16 × 4/3 πr³

= 16 × 4/3 × 3.14 × 2³

= 535.89 cm³

The dimensions of the given rectangular box = 16 cm × 8 cm × 8 cm

The volume of the given rectangular box = 16 × 8 × 8 = 1024 cm³

In order to find the volume of the liquid that is filled in a rectangular box,

We need to find the space left in the given rectangular box after the space occupied by the spheres.

The volume of the given liquid = (Volume of the given rectangular box) – (Volume of the given 16 spheres)

⇒ Volume of the given liquid = 1024 – 535.89

= 488.11 cm³

Thus, the volume of this liquid is 488.11 cm³.

Question 22: The students of a particular Vidyalaya were asked to partake in a competition for creating and embellishing penholders in the form of a cylinder with a base utilising cardboard. Per penholder was to be of radius 3 cm and height 10.5 cm. The Vidyalaya was to provide the competitors with cardboard. If there were around 35 competitors, how much cardboard was needed to be bought for the competition? (Assume π =22/7)

Answer 22: The radius of the circular end of the given cylindrical penholder, r = 3cm

The height of the given penholder, h = 10.5cm

The surface area of a given pen holder = Curved Surface Area of pen holder + Area of base of the given penholder

= 2πrh+πr² 

= 2 × (22/7) × 3 × 10.5 + (22/7) × 3² = 1584/7

Thus, the Area of cardboard sheet used by one competitor is 1584/7 cm²

So, the Area of cardboard sheets used by 35 competitors = 35×1584/7 = 7920 cm²

Therefore, a 7920 cm² cardboard sheet will be needed for the competition.

Question 23: Find out the total surface area of a cone if its slant height is 21 m and the diameter of the required base is 24 m. (Assume π = 22/7)

Answer 23: The radius of the given cone, r = 24/2 m = 12m

The slant height of the given cone, l = 21 m

The total surface area of the given cone = πradius (length+radius)

The total Surface area of the required cone = (22/7)×12×(21+12) m²

= 1244.57m²

Question 24: A particular cuboidal water tank is around 6m long, 5m wide and 4.5m deep. How many litres of water can the water tank hold? (1 m³= 1000 l)

Answer 24: Dimensions of a cuboidal water tank are: l = 6 m and b = 5 m and h = 4.5 m

Formula to find the volume of the tank, V = l×b×h

Put the values, we get

V = (6×5×4.5) = 135

The volume of the water tank is 135 m³

The amount of water that 1 m³ volume can hold = 1000 l

The required amount of water, 135 m³ volume hold = (135×1000) litres = 135000 litres

Thus, given cuboidal water tank can hold up to135000 litres of water.

Question 25: A particular storage tank is in the form of a cube. When it is filled with water, the volume of water is 15.625 m³. If the current depth of water is 1.3 m, find out the volume of water already used from the tank.

Answer 25: When the cubical tank is full:

The volume of water = Volume of cube = 15.625 m³

So, we know that

The volume of cube = (length of the edge of cube)³

⇒ (length of the edge of cube)³ = 15.625

⇒ The required length of the edge of the given cube = ∛15.625

The length of the edge of the given cube = 2.5 m.

When the current depth of the water is 1.3 m:

The length of the given tank = 2.5 m

The breadth of the given tank = 2.5 m

So, the volume of water up to 1.3 m depth = length × breadth × depth

= 2.5 × 2.5 × 1.3

The volume of water already utilised from the tank = (Volume of the tank when it was full of water) –

(Volume of water when its depth is 1.3 m)

= 15.625 – 8.125

Thus, the volume of water already used from the tank is 7.5 m³.

Question 26: If the volume of a right circular cone of height 9cm is 48πcm³, find the diameter of its base.

Answer 26: Height of cone, h = 9cm

The volume of the cone =48π cm³

Let r be the necessary radius of the given cone.

 The volume of the required cone, V = (1/3) ²

So, 1/3 π r²(9) = 48 π

The radius of the given cone is 4 cm.

So, diameter = 2 × Radius = 8

Thus, the diameter of the base is 8 cm.

Question 27: The curved surface area of the given right circular cylinder of height 14 cm is 88 sq. cm. Find out the diameter of the base of the cylinder.

Answer 27: Let d be the diameter and r be the radius of a right circular cylinder.

Height of cylinder (h) = 14 cm 

The curved surface area of the given right circular cylinder = 88 cm2

⇒ 2πrh = 88 cm²

⇒ πdh = 88 cm² (d = 2r) 

⇒ 22/7 x d x 14 cm = 88 cm²

⇒ d = 2 cm 

Accordingly, the diameter of the required base of the cylinder is 2 cm.

Question 28: A certain storage tank is in the form of a cube. When it is filled with water, the volume of water is 15.625 m³. If the present water depth is 1.3 m, find the volume of water already used from the tank.

Answer 28:   When the given cubical tank is full:

The required volume of water = The required volume of cube = 15.625 m³

So, we know that,

⇒ length of the edge of cube = ∛15.625

We know that,

The length of the edge of the cube = 2.5 m.

When the present depth of the given water is 1.3 m:

The required volume of water already utilised from the tank = (Volume of the tank when it was filled with water) –

(Volume of water if the depth is 1.3 m)

Question 29: The paint in a particular container is sufficient to paint an area equal to 9.375 m2. How many bricks of dimensions are required, 22.5 cm×10 cm×7.5 cm and can be painted out of this particular container?

Answer 29: The total surface area of one particular brick = 2 (length x breadth + breadth x height + length x breadth)

= [2 ( 22.5 × 10 + 10 × 7.5 + 22.5 × 7.5 )] cm²

= 2(225+75+168.75) cm²

= (2×468.75) cm²

= 937.5 cm²

Let n be the required number of bricks that can be painted out by the paint of the certain container.

The area of n bricks = (n×937.5) cm²= 937.5n cm²

As per the given data, the Area that can be painted by the paint of the container = 9.375 m² = 93750 cm²

So, we have 93750 = 937.5n

Hence, 100 bricks can be painted out by the paint of the container.

Question 30: The curved surface area of a particular cone is 308 cm2, and its required slant height is 14 cm. Find out

(i) the required radius of the base and (ii) the total surface area of the cone.

(Assume π = 22/7)

Answer 30: The slant height of the given cone, l = 14 cm

Let the required radius of the cone be r.

(i) We know the Curved Surface Area of the cone = πrl

The required Curved surface area of a cone is 308 cm²

(308 ) = (22/7)×r×14

r = 308/44 = 7 cm

The required radius of a cone base is 7 cm.

(ii) Total surface area of cone = Curved Surface Area of cone + Area of base (πr2)

The total surface area of the cone = 308+(22/7)×72 = 308+154 = 462 cm².

Therefore, the required total surface area of the cone is 462 cm².

Question 31: Find out the amount of water displaced by a solid spherical ball of diameter 4.2 cm when completely immersed in water.

Answer 31: Water displaced when a solid spherical ball is immersed completely in water equals its volume.

The diameter of the given spherical ball = 4.2 cm

The radius of the given spherical ball = 4.2/2 = 2.1 cm

So, the volume of a sphere = 4/3 πr³

(4/3) (22/7)(2.1)³ = 38.81

Thus, the volume of water displaced is 38.81 cm³.

Question 32: A particular cuboidal vessel is 10m long and 8m wide. How high must the vessel be made to hold 380 cubic metres of liquid?

Answer 32: The length of the given cuboidal vessel, l = 10 m

The width of the given cuboidal vessel, b = 8m

The volume of the given cuboidal vessel, V = 380 m³

Let the height of the required vessel be h.

 The volume of the given cuboid, V = l×b×h

Using the formula, we have

l×b×h = 380

10×8×h= 380

Or h = 4.75

Thus, the height of the vessels is 4.75 m.

Question 33: A conical pit with a top diameter of 3.5m is 12m deep. What is its capacity in kiloliters?

Answer 33: The diameter of the given conical pit = 3.5 m

The radius of the given conical pit, r = diameter/ 2 = (3.5/2)m = 1.75m

The height of the given pit, h = Depth of pit = 12m

Volume of cone, V = (1/3) πr²h

V = (1/3)×(22/7) ×(1.75)²×12 = 38.5

The volume of a cone is 38.5 m³

Thus,the capacity of the given pit = (38.5×1) kiloliters = 38.5 kiloliters.

Question 34: How many square metres of the canvas are required for a conical tent whose height is to be 3.5 m, and the radius of the base is 12 m?

Answer 34: According to the question,

Dimensions of the conical tent are:

Height = 3.5 m

Radius = 12 m

The required curved surface area of the given cone = πr√(r² + h²)

= 22/7 × 12 √(122 + 3.52)

= 22/7 × 12 × √156.25

= 22/7 × 12 × 12.5

= 471.43 m²

Since the Area of canvas = curved surface area of conical tent

Therefore, the Area of canvas required is 471.43 m².

Question 35: A particular right triangle ABC with sides 5cm, 12cm and 13cm is revolved about the side 12 cm. Find out the volume of the required solid so obtained.

Height (h)= 12 cm

Radius (r) = 5 cm, and

Slant height (l) = 13 cm

V = (1/3)×π×5²×12

The volume of the given cone  formed is 100π cm³.

Question 36: If the triangle ABC revolves around the side 5cm, find out the volume of the given solids so obtained. Find out also the ratio of the volumes of the two solids obtained.

In a right-angled ΔABC is revolved about its side 5cm; a cone will be formed with a radius of 12 cm, a height of 5 cm, and a slant height of 13 cm.

The volume of the cone = (1/3) πr²h; where r is the radius and h is the height of the cone

= (1/3)×π×12×12×5

The volume of the cones formed is 240π cm³.

Hence, required ratio = (result of question 35) / (result of question 36) = (100π)/(240π) = 5/12 = 5:12.

 Question 37: The curved surface area of the given right circular cylinder is 4.4 sq.m. If the required radius of the base of the cylinder is 0.7 m, find its height.

Answer 37: Let h be the height of the given cylinder.

The necessary radius of the base of the given cylinder (r) = 0.7 m 

The required curved surface area of the given cylinder = 4.4 m².

2πrh = 4.4  

2 × 3.14 × 0.7 × h = 4.4

4.4 × h = 4.4 

h = 4.4/4.4

Thus, the required height of the cylinder is 1 m.

Question 38: A certain cubical box has an edge of 10 cm, and the other cuboidal box is 12.5cm long, 10 cm wide, and 8 cm high.

(i) Which box has the greater lateral surface area, and by how much?

(ii) Which box has the smaller total surface area, and by how much?

Answer 38: As per the given question, we have

The edge of a particular cube = 10cm

The length of a particular cube, l = 12.5 cm

The breadth of a particular cube, b = 10cm

The height of a particular cube, h = 8 cm

(i) Find out the lateral surface area for both the given figures

The lateral surface area of the given cubical box = 4 (edge)²

= 400 cm² …(1)

The lateral surface area of cuboidal box = 2[lh+bh]

= [2(12.5×8+10×8)]

= (2×180) = 360

Therefore, the Lateral surface area of the cuboidal box is 360 cm². …(2)

From (1) and (2), the lateral surface area of the cubical box is more than the lateral surface area of the cuboidal box. The difference between both lateral surfaces is 40 cm².

(Lateral surface area of the given cubical box – Lateral surface area of the given cuboidal box =400 cm²–360cm² = 40 cm²)

(ii) Find out the total surface area for both the figures

The total surface area of the given cubical box = 6(edge)²

 = 6(10 cm)²

2 = 600 cm²…(3)

The total surface area of a given cuboidal box

= 2[ length x height + breadth x height + length x breadth]

= [ 2 ( 12.5 × 8 + 10 × 8+ 12.5 × 100 )]

The total surface area of the given cuboidal box is 610 cm²..(4)

From (3) and (4), we can see that the total surface area of the given cubical box is smaller than that of the given cuboidal box. And their difference is 10 cm².

Accordingly, the required total surface area of the given cubical box is smaller than that of the given cuboidal box by 10. As per the given question, we have

Question 39: A particular cylindrical tube open at both ends is made of an iron sheet, which is 2 cm thick. If the required outer diameter is 16 cm and its length is 100 cm, find out how many cubic centimetres of iron have been used in making the tube.

Answer 39: According to the question,

Outer diameter d = 16cm

Outer radius r – 16/2 = 8cm

Height = length = 100cm

The thickness of the iron sheet = 2cm

Volume of cylinder = πr²h, where r= outer radius and π = 3.14

Thus, Volume of cylinder = πr²h

= 3.14 × (8)²× 100

= 20,096 cm³

Here, inner diameter = outer diameter – 2× thickness of the iron sheet

Inner diameter = 16-(2× 2) = 12cm

Inner radius R = 12/2 = 6cm

Thus, Volume of hollow space = πR² h, where R= inner radius and π = 3.14

= 3.14 × (6)²× 100

= 11,304 cm³

The volume of iron used = Volume of the cylinder – Volume of hollow space

= (20,096 – 11,304 ) cm³

Question 40: Find out the cost required for digging a cuboidal pit which is around 8m in length, 6m in breadth and 3m in depth at the rate of Rs 30 per m³.

Answer 40 : The pit has its given length(l) as 8m, breadth (b)as 6m and depth (h)as 3 m.

The volume of the given cuboidal pit = l×b×h = (8×6×3) = 144 (using formula)

The required Volume is 144 m³

Cost of digging per m³ volume = Rs 30

Cost of digging 144 m³ volume = Rs (144×30) = Rs 4320

Question 41:Find out the volume of a sphere whose radius is

(i) 7 cm (ii) 0.63 m

(Assume π =22/7)

Answer 41: (i) Radius of sphere, r = 7 cm

Using, Volume of sphere = (4/3) πr³

= (4/3)×(22/7)×7³

Hence, the volume of the sphere is 1437.33 cm³

(ii) The radius of the given sphere, r = 0.63 m

Using the volume of sphere = (4/3) πr³

= (4/3)×(22/7)×0.63³

= 1.0478 m³

Thus, the volume of the sphere is 1.05 m³ (approx).

Question 42: Find out the amount of water displaced by a solid spherical ball of diameter

(i) 28 cm (ii) 0.21 m

Answer 42: (i) Diameter = 28 cm

Radius, r = 28/2 cm = 14cm

The volume of the solid spherical ball = (4/3) πr³

The required volume of the ball = (4/3)×(22/7)×14³ = 34496/3

Hence, the volume of the ball is 34496/3 cm³

(ii) Diameter = 0.21 m

The required radius of the ball =0.21/2 m= 0.105 m

The volume of the ball = (4/3 )πr³

The required volume of the ball = (4/3)× (22/7)×0.105³ m³

Hence, the volume of the ball = 0.004851 m³

Question 43: In a given hot water heating system, there is a certain cylindrical pipe of length 28 m and diameter 5 cm. Find out the required total radiating surface in the given system.

Answer 43: Given,

The length of the given cylindrical pipe = h = 28 m

The diameter of the given pipe = 5 cm

 The radius of the given piper (r) = 5/ 2 cm = 2.5 cm = 0.025 m

The total radiating surface in the system = Total surface area of the cylinder  

= 2πr(h + r)  

= 2 × (22/7) × 0.025 (28 + 0.025) m²  

= (44 x 0.025 x 28.025)/7 m²

= 4.4 m² (approx)

Question 44:A little indoor greenhouse (herbarium) is constructed entirely of glass panes (including base) carried together with tape. It is around 30cm long, 25 cm wide, and 25 cm high.

(i)What is the required Area of the glass?

(ii)How much tape is required for all 12 edges?

Length of the greenhouse, say l = 30cm

The breadth of the greenhouse, say b = 25 cm

Height of greenhouse, say h = 25 cm

(i) Total surface area of given greenhouse = Area of the glass = 2[lb+lh+bh]

= [2(30×25+30×25+25×25)]

= [2(750+750+625)]

= (2×2125) = 4250

The required total surface area of the glass is 4250 cm²

From the figure, the length of the tape  needed for all the 12 edges  AB, BC, CD, DA, EF, FG, GH, HE AH, BE, DG, and CF.

Full length of tape = 4(l+b+h)

= [4 ( 30 + 25 + 25 )] (after replacing the values)

Thus, 320 cm tape is required for all 12 edges.

From the figure, the length of the tape needed for all the 12 edges AB, BC, CD, DA, EF, FG, GH, HE AH, BE, DG, and CF.

Total length of tape = 4 ( length + breadth + height)

= [ 4 ( 30 + 25 + 25 )] (after replacing the values)

Hence, 320 cm tape is required for all 12 edges.

Question 45: A particular conical tent is 10 m high, and the radius of its base is 24 m. Find out

(i) the slant height of the particular tent.

(ii) cost of the canvas needed to make the tent if the cost of 1 m2 canvas is Rs 70.

(Assume π=22/7)

Image Source: Internet

Let ABC be a conical tent

Height of conical tent, h = 10 m

The radius of the given conical tent, r = 24m

Let the slant height of the given tent be l.

(i) In the right triangle ABO, we have

AB² = AO²+BO²(using Pythagoras theorem)

= (10)²+(24)²

Accordingly, the required slant height of the tent is 26 m.

(ii) Curved Surface Area of tent = πrl

= (22/7)×24×26 m2

Cost of 1 m² canvas = Rs 70

The cost of (13728/7)m² canvas is equal to Rs (13728/7)×70 = Rs 137280

Hence, the cost of the canvas needed to make such a tent is Rs 137280.

Question 46:The diameter of a particular metallic ball is 4.2cm. What is the required mass of the ball if the density of the given metal is 8.9 g per cm3? (Assume π=22/7)

Answer 46: 

The diameter of a given metallic ball = 4.2 cm

The radius(r) of the metallic ball, r = 4.2/2 cm = 2.1 cm

Volume formula = 4/3 πr³

The volume of the metallic ball = (4/3)×(22/7)×2.1 cm³

The volume of the metallic ball = 38.808 cm³

Now, using the relationship between density, mass and volume,

Density = Mass/Volume

Mass = Density × volume

= (8.9×38.808) g

= 345.3912 g

The required mass of the ball is 345.39 g (approx).

Question 47: The height of a particular cone is 16 cm, and its base radius is 12 cm. Find out the curved surface area and the total surface area of the cone. (Take π = 3.14)

Answer 47: i) Height of a cone (h) = 16 cm

Radius of the base (r) = 12 cm

Slant height of cone (l) = √(r2 + h2)

= √(256 + 144)

• ii) The curved surface area of the cone = πrl

= 3.14 × 12 × 20 cm²

= 753.6 cm²

Total surface area = πrl + πr²

= (753.6 + 3.14 × 12 × 12) cm²

= (753.6 + 452.16) cm²

= 1205.76 cm²

Question 48: Shanti Sweets Stall placed an order for preparing cardboard boxes for packing their sweets. Two sizes of boxes were required. The bigger dimensions are 25 cm×20cm×5cm, and the smaller dimension is 15cm×12cm×5cm. 5% of the total surface area is needed extra for all the required overlaps. If the cardboard cost is Rs. 4 for 1000 cm², find out the cost of cardboard needed for supplying 250 boxes of each kind.

Answer 48: Let l, b and h be the box’s length, breadth and height.

Bigger Box:

length = 25cm

breadth = 20 cm

height = 5 cm

Total surface area of the given bigger box = 2(lb+lh+bh)

= [2(25×20+25×5+20×5)]

= [2(500+125+100)]

Extra Area needed for overlapping 1450×5/100 cm2

While considering all overlaps, the total surface area of the bigger box

= (1450+72.5) cm2 = 1522.5 cm²

Area of cardboard sheet needed for 250 such bigger boxes

= (1522.5×250) cm2 = 380625 cm²

Smaller Box:

Similarly, the total surface area of smaller box = [2(15×12+15×5+12×5)] cm²

= [2(180+75+60)] cm²

= (2×315) cm²

Therefore, the extra Area required for overlapping 630×5/100 cm² = 31.5 cm²

The total surface area of 1 smaller box while considering all overlaps

= (630+31.5) cm² = 661.5 cm²

Area of cardboard sheet needed for 250 smaller boxes = (250×661.5) cm² = 165375 cm²

Now, Total cardboard sheet required = (380625+165375) cm²

= 546000 cm²

Given: Cost of 1000 cm² cardboard sheet = Rs. 4

Therefore, the Cost of 546000 cm² cardboard sheet =Rs. (546000×4)/1000 = Rs. 2184

Hence, the cost of cardboard required for supplying 250 boxes of each kind will be Rs. 2184.

Question 49: How many litres of milk can a separate hemispherical bowl of diameter 10.5cm hold? (Assume π = 22/7)

Answer 49: Diameter of hemispherical bowl = 10.5 cm

The radius of the given hemispherical bowl, r = 10.5/2 cm = 5.25 cm

The formula for the volume of the hemispherical bowl = (2/3) πr³

The volume of the given hemispherical bowl = (2/3)×(22/7)×5.25³ = 303.1875

The volume of the given hemispherical bowl is 303.1875 cm³

The capacity of the bowl = (303.1875)/1000 L = 0.303 litres(approx.)

Therefore, the hemispherical bowl can hold 0.303 litres of milk.

Question 50: Find out the total surface area of a cone if its given slant height is 21 m and the given diameter of its required base is 24 m.

Answer 50: Given,

The diameter of the given cone = 24 m 

The radius of the given cone (r) = 24/2 = 12 m 

The slant height of the given cone (l) = 21 m 

The required total surface area of a given cone = πr(l + r) 

= (22/7) × 12 × (21 + 12) 

= (22/7) × 12 × 33 

= 1244.57 m²

Question 51: Praveen needed to make a temporary shelter for her car by making a box-like structure with a tarpaulin that covers all four sides and the canopy of the car (with the front face as a flap which can be rolled up). Presuming that the stitching margins are very small and therefore negligible, how many tarpaulins would be needed to construct the shelter of height 2.5m, with base dimensions 4m×3m?

Answer 51: Let l, b and h be the length, breadth and height of the temporary shelter.

Tarpaulins will be required for the top and four wall sides of the shelter.

Using the given formula, 

Area of required tarpaulin = 2(lh+bh)+lb

On substituting the values of l, b and h, we obtain

= [2(4×2.5+3×2.5)+4×3] m²

= [2(10+7.5)+12]m²

Hence, 47 m² tarpaulins will be required.

Question 52: What is the length of tarpaulin 3 m wide needed to make a conical tent of the given height 8 m and base radius 6m? Presume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm. [Use π=3.14]

Answer 52: Height of conical tent, h = 8m

The required radius of the base of the given tent, r = 6m

Slant height of tent, l2 = (r2+h2)

l2 = (62+82) = (36+64) = (100)

or l = 10 m

Again, CSA of conical tent = πrl

= (3.14×6×10) m2

Let the length of the tarpaulin sheet needed by L

As 20 cm will be wasted, therefore,

The effective length will be (L-0.2m).

Breadth of tarpaulin = 3m (given)

The required area of sheet = The required curved Surface Area of the tent

[(L–0.2)×3] = 188.4

L-0.2 = 62.8

Thus, the length of the required tarpaulin sheet will be 63 m.

Question 53:A particular village, having a population of 4000, needs 150 litres of water per head per day. It has a tank which measures 20 m×15 m×6 m. For how long will the water of this tank last?

Answer 53: The length of the given tank = l = 20 m

The breadth of the given tank = b = 15 m

The height of the given tank = h = 6 m

The total population of a particular village = 4000

The consumption of water per head per day = 150 litres

Water consumed by the individuals in 1 day = (4000×150) litres = 600000 litres …(1)

 the capacity of the given tank, C = l×b×h

Using the given data, we have

C = (20×15×6) m³= 1800 m³

Or C = 1800000 litres

Let the required water in this tank last for d number of days.

The water consumed by all people in d days = Capacity of the tank (using equation (1))

600000 d =1800000

Hence, the water in this tank will last for 3 days.

Question 54: A particular hemispherical tank is made up of an iron sheet 1cm thick. If the essential inner radius is 1 m, then find out the volume of the iron used to make the tank. (Assume π = 22/7)

Answer 54: The inner Radius of the given tank, (r ) = 1m

The outer Radius of the given (R ) = 1.01m

The required volume of the given iron used in the given tank = (2/3) π(R³– r³)

Putting values,

The required volume of the given iron used in the given hemispherical tank = (2/3)×(22/7)×(1.01³– 1³) = 0.06348

So, the volume of the iron used in the hemispherical tank is 0.06348 m³.

Question 55: A particular dome of a building is in the shape of a hemisphere. From inside, it was white-washed at the price of Rs. 4989.60. If the cost of white-washing is Rs 20 per square metre, find the

(i) The required inside surface area of the dome (ii) The volume of the air inside the dome

Answer 55: (i) The cost of white-washing the dome from inside = Rs 4989.60

Cost of white-washing 1m² area = Rs 20

The curved surface area of the inner side of the dome = 498.96/2 m² = 249.48 m²

(ii) Let the required inner radius of the hemispherical dome be r.

Curved Surface Area of the inner side of dome = 249.48 m² (from (i))

Formula to find CSA of a hemisphere = 2πr²

2πr = 249.48

2×(22/7)×r² = 249.48

r² = (249.48×7)/(2×22)

So, the radius is 6.3 m

The volume of air inside the given dome = Volume of hemispherical dome

Using the formula, the volume of the hemisphere = 2/3 πr³

= (2/3)×(22/7)×6.3×6.3×6.3

= 523.9(approx.)

 The required volume of air inside the dome is 523.9 m³.

Question 56: Twenty-seven solid iron spheres, each of radius r and surface area S, are melted to assemble a sphere with surface area S’. Find the

(i) the radius r’ of the new sphere,

(ii) the ratio of Sand S’.

Answer 56: The volume of the solid sphere = (4/3)πr³

The required volume of the given twenty-seven solid sphere = 27×(4/3)πr³ = 36 π r³

(i) New solid iron sphere radius = r’

The required volume of this new sphere = (4/3)π(r’)³

(4/3)π(r’)³ = 36 π r³

(r’)³ = 27r³

The required radius of the new given sphere will be 3r (thrice the radius of the original sphere)

(ii) Surface area of an iron sphere of radius r, S =4πr²

The surface area of a given iron sphere of radius r’= 4π (r’)²

S/S’ = (4πr²)/( 4π (r’)²)

S/S’ = r²/(3r’)² = 1/9

The required ratio of S and S’ is 1: 9.

Question 57: A particular capsule of medicine is in the shape of a sphere of diameter 3.5mm. How much medicine (in mm³) is required to fill this capsule? (Assume π = 22/7)

Answer 57: The diameter of the given capsule = 3.5 mm

The radius of the given capsule, say r = diameter/ 2 = (3.5/2) mm = 1.75mm

The volume of the given spherical capsule = 4/3 πr³

The volume of the given spherical capsule = (4/3)×(22/7)×(1.75)³ = 22.458

 The required volume of the spherical capsule is 22.46 mm³.

Question 58: The required slant height and base diameter of a given conical tomb are 25 m and 14 m, respectively. Find out the cost of white-washing its curved surface at the rate of Rs.210 per 100 sq.m.

Answer 58: Given,

The slant height of a given cone (l) = 25 m  

The diameter of the given base of cone = 2r = 14 m  

∴ Radius = r = 7 m  

Curved Surface Area = πrl 

= (22/7) x 7 x 25 

= 22 × 25  

= 550 sq.m  

Also, given that the cost of white-washing 100 sq.m = Rs. 210 

Thus, the required total cost of white-washing for 550 sq.m = (Rs. 210 × 550)/100 = Rs. 1155

Question 59: The required curved surface area of a given right circular cylinder of height 14 cm is 88 cm2. Find out the diameter of the base of the cylinder. (Assume π =22/7 )

Answer 59: The height of the given cylinder, h = 14cm

Let the diameter of the given cylinder be d

The curved surface area of the cylinder = 88 cm²

We know that the formula to find the Curved surface area of a cylinder is 2πrh.

So 2πrh =88 cm² (r is the radius of the base of the cylinder)

2×(22/7)×r×14 = 88 cm²

Thus, the required diameter of the base of the given cylinder is 2 cm.

Question 60: A godown measures 40 m×25m×15 m. Find out the maximum number of wooden crates, each measuring 1.5m×1.25 m×0.5 m, that can be stored in the godown.

Answer 60: From the statement, we have

The length of the given godown = 40 m

The breadth of the given godown = 25 m

The height of the given godown = 15 m

The length of the wooden crate = 1.5 m

Breadth = 1.25 m

Height = 0.5 m

Since the godown and wooden crate are in cuboidal shape, find the volume of each using the formula V = length x breadth x height.

Volume of a godown = (40×25×15) m³= 15000 m³

The volume of a wooden crate = (1.5×1.25×0.5) m³ = 0.9375 m³

Let us say that n wooden crates can be stored in the godown, then

The volume of n wooden crates = Volume of godown

0.9375×n =15000

Or n= 15000/0.9375 = 16000

Hence, the required number of wooden crates that can be stored in the godown is 16,000.

Question 61: The respective capacity of a cuboidal tank is 50000 litres of water. Find out the breadth of the tank if its length and depth are respectively 2.5 m and 10 m.

Answer 61: The tank’s length (l) and depth (h) is 2.5 m and 10 m, respectively.

 The value of breadth, says b.

 The volume of a given tank = l×b×h = (2.5× b×10) m³= 25b m³

The capacity of the tank= 25b m³, which is equal to 25000b litres

Also, the capacity of a given cuboidal tank is 50000 litres of water (Given)

Therefore, 25000 b = 50000

This implies that b = 2

Thus, the required breadth of the tank is 2 m.

Question 62: A particular wooden bookshelf has external dimensions as follows: Height = 110cm, Depth = 25cm,

Breadth = 85cm . The required thickness of the plank is 5cm everywhere. The required external faces are to be polished, and the required inner faces are to be painted. If the required rate of polishing is 20 paise per cm²6 and the rate of painting is 10 paise per cm², find the total expenses required for polishing and painting the surface of the bookshelf.

Answer 62: External dimensions of book self,

The length, l = 85cm

The breadth, b = 25 cm

The height, h = 110 cm

The external surface area of the shelf while leaving out the front face of the shelf

= length x height + 2 ( length x breadth + breadth x height)

= [85 × 110 + 2 ( 85 × 25 + 25 × 110 )] = ( 9350 + 9750 ) = 19100

The external surface area of the shelf is 19100 cm²

The area of the given front face = [85×110-75×100+2(75×5)] = 1850+750

So, the Area is 2600 cm²

Area to be polished = (19100+2600) cm² = 21700 cm².

Cost of polishing 1 cm² area = Rs 0.20

Cost of polishing 21700 cm² area Rs. (21700×0.20) = Rs 4340

Dimensions of a row of the bookshelf

The length(l) = 75 cm

The breadth (b) = 20 cm and

The height(h) = 30 cm

The area to be painted in one row= 2(l+h)b+lh = [2(75+30)× 20+75×30] = (4200+2250) = 6450

 The Area is 6450 cm².

The area to be painted in 3 rows = (3×6450)cm² = 19350 cm².

The cost of painting 1 cm² area = Rs. 0.10

The cost of painting 19350 cm² area = Rs (19350 x 0.1) = Rs 1935

The total expense needed for polishing and painting the given book shelf= Rs. (4340+1935) = Rs. 6275

 The cost for polishing and painting the book shelf’s surface is Rs. 6275.

Question 63: The pillars of a certain temple are cylindrically shaped. Every pillar has a circular base of a radius of 20cm and a height of 10m. How much would concrete mixture be required to build 14 such pillars?

Answer 63:   It is given that

Radius of the pillar = 20cm = 0.2m

Height of pillar = 10m

We know that

The volume of one pillar = πr²h

By substituting the values

Volume of one pillar = (22/7) × (0.2)² × 10

The volume of one pillar = 1.2571 m³

So the volume of concrete mixture in 14 pillars = 14 × 1.2571 = 17.6m³

Therefore, the volume of concrete mixture required in 14 pillars is 17.6m³.

Question 64: The hollow sphere in which the particular circus motorcyclist carries out his stunts has a diameter of 7 m. Find out the Area available to the motorcyclist for riding.

Answer 64: 

The diameter of the given sphere = 7 m

The radius (r) of the sphere = 7/2 = 3.5 m 

Here, the riding space available for the motorcyclist = Surface area of the sphere

= 4 × (22/7) × 3.5 × 3.5

Question 65: It is essential to make a closed cylindrical tank of height 1m and base diameter 140cm from a given metal sheet. How many square metres of the sheet is required for the same? Assume π = 22/7

Answer 65 : Let h be the height and r be the radius of a cylindrical tank.

Height of the given cylindrical tank, h = 1m

Radius = half of diameter = (140/2) cm = 70cm = 0.7m

The area of sheet needed = Total surface area of the given tank = 2πr(r+h) m²

= [2×(22/7)×0.7(0.7+1)]

Hence, 7.48 square metres  of the sheet are required.

Question 66: A required joker’s cap is in the form of a particular right circular cone of the required base radius of 7 cm and height of 24cm. Find out the Area of the sheet required to make 10 such caps. (Assume π =22/7)

Answer 66: The radius of the given conical cap, r = 7 cm

The height of the given conical cap, h = 24cm

The slant height, l² = (r²+h²)

Or l = 25 cm

The curved surface area of 1 conical cap = πrl

= (22/7)×7×25

Curved Surface Area of 10 caps = (10×550) cm² = 5500 cm²

Hence, the Area of the sheet required to make 10 such caps is 5500 cm².

Question 67: A particular solid cube of side 12 cm is cut into eight cubes of equal volume. What will be the side of the newly formed cube? Also, find out the ratio between their surface areas.

Answer 67: Side of a cube = 12cm (Given)

Find the volume of the cube:

The volume of cube = (Side)³ = (12)³= 1728cm³

The surface area of a given cube with a side 12 cm = 6a² = 6(12) ² cm² …(1)

The required cube is cut into eight small cubes of equal volume; say the side of each cube is p.

The volume of a given small cube = p³

The surface area = 6p² …(2)

The volume of each small cube = (1728/8) cm³ = 216 cm³

Or (p)³ = 216 cm³

Or p = 6 cm

Now, The surface areas of the cubes ratios = (Surface area of the bigger cube)/(Surface area of smaller cubes)

From equations (1) and (2), we get

The surface areas of the cubes ratios = (6a²)/(6p²) = a²/p²= 122/62 = 4

Therefore, the required ratio is 4: 1.

Question 68: The radius of a particular spherical balloon increases from 7 cm to 14 cm as air is pumped into it. Find out the ratio of surface areas of the balloon in the two cases.

Answer 68: 

The radius of the given balloon = r = 7 cm

The radius of the given pumped balloon = R = 14 cm

The ratio of the given surface area = (TSA of the balloon with r = 7 cm)/(TSA of the balloon with R = 14 cm)

= (4πr²)/(4πR²)

= (7)²/(14)²

Thus, the ratio of surface areas of the balloon in the two given cases is 1: 4.

Question 69: A metal pipe is 77 cm long. The inner diameter of a given cross-section is 4 cm, the outer diameter being 4.4cm. 

(i) inner curved surface area,

(ii) outer curved surface area

(iii) total surface area

Answer 69: Let r1 and r2 Inner and outer radii of a cylindrical pipe

r1 = 4/2 cm = 2 cm

r2 = 4.4/2 cm = 2.2 cm

The height of cylindrical pipe, h = length of cylindrical pipe = 77 cm

(i) curved surface area of the outer surface of pipe = 2πr1h

= 2×(22/7)×2×77 cm²

(ii) curved surface area of the outer surface of pipe = 2πr2h

= 2×(22/7)×2.2×77 cm²

= (22×22×2.2) cm²

= 1064.8 cm²

(iii) Total surface area of the given pipe = inner curved surface area + outer curved surface area + Area of both circular ends of the pipe.

= 2r1h+2r2h+2π(r1²-r2²)

= 9668+1064.8+2×(22/7)×(2.2²-2²)

= 2031.8+5.28

= 2038.08 cm²

Accordingly, the required total surface area of the given cylindrical pipe is 2038.08 cm².

Question 70: A particular cloth having an area of 165 m² is shaped into the form of a conical tent of radius 5m.

How many students can sit in the tent if a student, on average, occupies 5/7 m2 on the ground?

Answer 70: A cone is a solid three-dimensional geometric object with a circular base and a pointed apex at the top. A cone consists of one face and one vertex. For a cone, there are no edges.

The required area of the floor of the given tent = πr²

The required area of the floor of the given tent = (22/7) × 5² = 550/7 m²

We know that the required Area required by one student is 5/7 m²

So the required number of students = (550/7)/ (5/7) = 110

Question 71: A bus stop is barricaded from the remaining part of the road using 50 hollow cones made of recycled cardboard. Every cone has a base diameter of 40 cm and a height of 1 m. If the outer side of each cone is to be painted and the cost of painting is Rs. 12 per m², what will be the required cost of painting all these cones? (Using π = 3.14 and take √(1.04) =1.02)

Answer 71: The radius of the required cone, r = diameter/2 = 40/2 cm = 20cm = 0.2 m

The height of the required cone, h = 1m

The slant height of the required cone is l, and l2 = (r2+h2)

Using given values, l2 = (0.22+12)

Or l = 1.02 m

The slant height of the required cone is 1.02 m

Curved Surface Area of each cone = πrl

= (3.14×0.2×1.02)

= 0.64056 m

The curved Surface Area of 50 such cones = (50×0.64056) = 32.028

The curved Surface Area of 50 such cones = 32.028 m2

The cost of painting 1 m² area = Rs 12 (given)

The cost of painting is 32.028 m² Area = Rs (32.028×12)

= Rs.384.336

= Rs.384.34 (approximately)

Hence, the cost of painting all these cones is Rs. 384.34.

Question 72:The circumference of the base of the cylindrical vessel is 132cm, and its height is 25cm. How many litres of water does the cylindrical vessel hold? (1000 cm³= 1L) (Assume π = 22/7)

Answer 72: The circumference of the base of the given cylindrical vessel = 132 cm

The height of the given vessel, h = 25 cm

 r be the radius of the given cylindrical vessel.

Step 1: Find out the radius of the vessel

circumference of base = 2πr, so

2πr = 132 (given)

r = (132/(2 π))

r = 66×7/22 = 21

The radius is 21 cm

Step 2: Find the volume of the vessel

Formula: Volume of cylindrical vessel = πr²h

= (22/7)×21²×25

Therefore, the volume is 34650 cm³

Since, 1000 cm³ = 1L

So, Volume = 34650/1000 L= 34.65L

Hence, the vessel can hold 34.65 litres of water.

Question 73: How many spheres 12cm in diameter can be made from a metallic cylinder of diameter 8cm and a height of 90cm?

Answer 73: It is given that

Diameter of the sphere = 12cm

Radius of the sphere = 12/2 = 6cm

The volume of the sphere = 4/3 πr³

The volume of the sphere = 4/3 × (22/7) × 6³

The volume of the sphere = 905.142 cm³

It is given that

Diameter of the cylinder = 8cm

Radius of the cylinder = 8/2 = 4cm

Height of the cylinder = 90cm

The volume of the cylinder = πr²h

The volume of the cylinder = (22/7) × 4² × 90

Volume of the cylinder = 4525.714 cm³

The required number of spheres = The required volume of cylinder/ Volume of a sphere

Number of spheres = 4525.714/ 905.142 = 5

Thus, 5 spheres can be made from a metallic cylinder.

Question 74:A river 3 m deep and 40 m wide flows at a rate of 2 km per hour. How much water will be needed to fall into the sea in a minute?

Answer 74: Given,

The depth of the given river (h) = 3 m

The width of the given river (w) = 40 m

The flow rate of water = 2 km/hr

i.e. Flow of water in an hour = 2 km = 2000 m

Flow of water in a minute = 2000/60 = 100/3 m

Hence, length (l) = 100/3 m

The required volume of water falling into the sea in 1 minute = Volume of a given cuboid with dimensions l, w, h

= l × w × h

= (100/3) × 40 × 3

= 4000 x 1000 L 

= 4000000 L 

Question 75: The diameter of a given roller is 84 cm, and its length is 120 cm. It takes around 500 complete revolutions to move once over to level a playground. Find out the Area of the playground in m². (Assume π = 22/7)

Answer 75: A roller is in the shape of a cylinder.

Let h be the height of the given roller and r be the given radius.

h = Length of the given roller = 120 cm

The radius of the given circular end of roller = r = (84/2) cm = 42 cm

Now, the Curved Surface Area of the roller = 2πrh

= 2×(22/7)×42×120

= 31680 cm²

Area of field = 500×CSA of roller

= (500×31680) cm²

= 15840000 cm²

Therefore, the  area of the playground is 1584 m²

Question 76: A sphere of diameter 15.6cm is melted and cast into a right circular cone of height 31.2cm. Find out the diameter of the base of the cone.

Answer 76: It the question it is given:

The diameter of sphere = 15.6 cm

The radius of  sphere = 15.6/2 = 7.8 cm

The height of  cone = 31.2 cm

It is known that

4/3 πR3 = 1/3 πr2h

So we would get, 

4/3 × (22/7) × 7.83 = 1/3 × (22/7) × r2 × 31.2

Furthermore

r2 = (4/3 × (22/7) × 7.83)/ (1/3 × (22/7) × 31.2)

Therefore we get

r2 = (4 × 474.552)/ 31.2 = 60.84

Now by taking square root on the RHS

Diameter = 2 (7.8) = 15.6cm

Thus, the required diameter of the base of the given cone is 15.6cm.

Question 77: Find out the surface area of a given sphere of radius:

(i) 10.5cm (ii) 5.6cm (iii) 14cm

Answer 77: Formula: Surface area of a sphere (SA) = 4πr²

(i) The radius of the given sphere, r = 10.5 cm

SA = 4×(22/7)×10.5² = 1386

The surface area of a given sphere is 1386 cm²

(ii) The radius of the given sphere, r = 5.6cm

Using formula, Surface area = 4×(22/ 7)×5.62 = 394.24

The surface area of a sphere is 394.24 cm²

(iii) Radius of sphere, r = 14cm

= 4×(22/7)×(14)²

The surface area of a sphere is 2464 cm²

Question 78: The inner diameter of a certain cylindrical wooden pipe is 24cm, and its outer diameter is 28 cm. The length of the pipe is 35cm. Find the mass of the pipe if 1cm³ of wood has a mass of 0.6g. (Assume π = 22/7)

Answer 78: The inner radius of the given cylindrical pipe, say r1 = diameter 1/ 2 = 24/2 cm = 12cm

The outer radius of the given cylindrical pipe, say r2 = diameter2/ 2 = 28/2 cm = 14 cm

The height of pipe, h = Length of pipe = 35cm

Now, the Volume of pipe = π(r2²-r1²)h cm³

Substitute the values.

Volume of pipe = 110×52 cm³ = 5720 cm³

Since, Mass of 1 cm³ wood = 0.6 g

Mass of 5720 cm³ wood = (5720×0.6) g = 3432 g or 3.432 kg.

Question 79: A particular lead pencil consists of a wooden cylinder with a solid cylinder of graphite filled in the interior. The diameter of the particular pencil is 7 mm, and the diameter of the graphite is 1 mm. If the length of the particular pencil is 14 cm, find out the volume of the wood and that of the graphite.

Answer 79: Given,

Diameter of the pencil = 7 mm

The radius of the given pencil (R) = 7/2 mm

The diameter of the given graphite cylinder = 1 mm

The radius of the given graphite (r) = 1/2 mm

The height of the given graphite (h) = 14 cm = 140 mm (since 1 cm = 10 mm)

The volume of a cylinder = πr²h

Volume of graphite cylinder = πr2h 

= (22/7) × (1/2) × (1/2) × 140

The volume of pencil = πR²h

= (22/7) × (7/2) × (7/2) × 140

= 490 × 11 

The volume of wood = Volume of a penciler – Volume of the given graphite

= 5390- 110 = 5280 mm³

= 5280/1000 (since 1 mm³ = 1/1000 cm³)

Question 80: The radii of two spheres are in the ratio 1:2. Find the ratio of their surface 

Answer 80: Consider x and 2x as the radius of two spheres and S1 and S2 as the surface areas.

It can be written as

S1/ S2 = 4πx²/ 4π (2x)²

On further calculation

S1/ S2 = x²/ 4x²

S1/ S2 = 1/4

Hence, the ratio of their given surface areas is 1:4.

Question 81: Find out the surface area of a sphere of diameter:

(i) 14cm (ii) 21cm (iii) 3.5cm

Answer 81: (i) Radius of sphere, r = diameter/2 = 14/2 cm = 7 cm

The required Surface area of the sphere = 4πr²

= 4×(22/7)×72 = 616

The surface area of a given sphere is 616 cm²

(ii) Radius (r) of the given sphere = 21/2 = 10.5 cm

The surface area of the sphere = 4πr²

= 4×(22/7)×10.5² = 1386

The surface area of a particular sphere is 1386 cm²

Hence, the surface area of a sphere having a diameter of 21cm is 1386 cm²

(iii) The radius(r) of sphere = 3.5/2 = 1.75 cm

= 4×(22/7)×1.75² = 38.5

The surface area of a sphere is 38.5 cm²

Question 82: Find out the total surface area of a hemisphere of radius 10 cm. [Use π=3.14]

Answer 82: The radius of the hemisphere, r = 10cm

 The required total surface area of the hemisphere = 3πr²

= 3×3.14×10² = 942

The required total surface area of the given hemisphere is 942 cm².

Question 83:A particular soft drink is obtainable in two packs – (i) a tin can with a rectangular base of the given length of 5cm and the given width of 4cm, having the required height of 15 cm and (ii) the required plastic cylinder with a given circular base of diameter 7cm and height 10cm. Which container has greater capacity, and by how much? (Assume π=22/7)

Answer 83: (i) tin can will be cuboidal in shape

Dimensions of the tin can are

The length of the given tin, l = 5 cm

The breadth of the given tin, b = 4 cm

The height of the given tin, h = 15 cm

The capacity of the given tin can = l×b×h= (5×4×15) cm³ = 300 cm³

(ii) Plastic cylinder will be cylindrical

Dimensions of the plastic can are:

The radius of the circular end of a given plastic cylinder, r = 3.5cm

Height of the circular end of a given plastic cylinder, H = 10 cm

The capacity of the given plastic cylinder = πr²H

The capacity of the given plastic cylinder = (22/7)×(3.5)²×10 = 385

The capacity of a plastic cylinder is 385 cm³

The plastic cylinder has more capacity from the results of (i) and (ii).

Difference in capacity = (385-300) cm³ = 85cm³

Question 84: The volume and surface area of a certain solid hemisphere are numerically equal. What is the diameter of the hemisphere?

Answer 84: We know that

The volume of a solid hemisphere = Surface area of a solid hemisphere

2/3 πr³ = 3 πr²

r3/ r2 = (3 × π × 3)/ (2 × π)

r = 9/2 units

So the given diameter = 2 (9/2) = 9 units

Accordingly, the required diameter of the hemisphere is 9 units .

Question 85: Meera owns a piece of canvas whose Area is 551 m². She uses it to prepare a conical tent with a base radius of 7 m. Presuming that all the stitching margins and the wastage incurred while cutting amount to approximately 1 m2, find out the volume of the tent that can be made with it.

The Area of the particular canvas = 551 m²

The Area of the canvas lost in wastage = 1 m²

Hence, the area of canvas available for making the tent = (551 – 1) m² = 550 m²

Let l be the slant height

 h be the vertical height,

 then slant height (l)=Areaπr=550×7/22×7=25 m.

∴ The Vertical height (h)=√l ² −r ²

                                           =√25 ² −7 ² m

                                          =√625−49

                                          =√576m

                                          =24 m

Now the volume of the tent=13πr ² h=13×22/7×7×7×24 m ³

                                                               = 1232 m³

Question 86: The diameter of a sphere is 6cm. It is melted and drawn into an individual wire of diameter 2mm. Find the length of the wire .

Answer 86: In the question, below details are given

The diameter of  sphere = 6cm

So the radius of sphere = 6/2 = 3cm

The  diameter of wire = 2mm = 0.2 cm

So the radius of  wire = 2/2 = 1mm = 0.1 cm

Now let us consider h cm as the required length

πr2h = 4/3 πR³

By substituting the values we get

(22/7) × 0.12 × h = 4/3 × (22/7) × 3³

On further simplification we get

h = (4/3 × (22/7) × 27)/ ((22/7) × 0.12)

Therefore by solving we get

h = 36/0.01 = 3600cm = 36m

Hence, the length of the wire is 36m.

Question 87: A particular cylindrical pillar is 50 cm in diameter and 3.5 m in height. Find out the cost of painting the given curved surface of the pillar at the rate of Rs. 12.50 per m².

Answer 87: Let h be the height of a cylindrical pillar and r be the radius.

Height cylindrical pillar = h = 3.5 m

Radius of the circular end of given pillar = r = diameter/2 = 50/2 = 25cm = 0.25m

Curved Surface Area of pillar = 2πrh

= 2×(22/7)×0.25×3.5

The cost of painting 1 m² area = Rs. 12.50

The cost of painting 5.5 m² Area = Rs (5.5×12.50)

Hence, the cost of painting the curved pillar’s curved surface at Rs. 12.50 per m² is Rs 68.75.

Question 88:The required radius of a spherical balloon increases from 7cm to 14cm as air is pumped into it. Find out the ratio of the given surface areas of the balloon in the two cases.

Answer 88: Let r1 and r2 be the given radii of the spherical balloon and spherical balloon when air is pumped into it, respectively. 

Now, the Required ratio = (initial surface area)/(Surface area after pumping air into the balloon)

= 4πr1²/4πr2²

= (7/14)² = (1/2)² = 1/4

Hence, the ratio between the surface areas is 1:4.

Question 89: If the lateral surface of a particular cylinder is 94.2cm² and its height is 5cm, then find out 

(i)the required radius of its base, (ii) its volume.[Use π= 3.14]

Answer 89: CSA of cylinder = 94.2 cm²

Height of cylinder, h = 5cm

(i) Let the radius of the given cylinder be r.

Using the CSA of the cylinder, we get

2πrh = 94.2

2×3.14×r×5 = 94.2

radius is 3 cm

(ii) Volume of cylinder

The formula for the volume of the cylinder = πr²h

Now, πr2h = (3.14×(3)²×5) (using value of r from (i))

Volume is 141.3 cm³

Question 90: A particular capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm³) is needed to fill this capsule?

Answer 90: 

The diameter of the given capsule = 3.5 mm

The radius of the given capsule = (r) = 3.5/2 = 1.75 mm

The volume of the spherical capsule = (4/3)πr³

= (4/3) × (22/7) × 1.75 × 1.75 × 1.75

= 22.458 mm³

Hence, the volume of the capsule is 22.46 mm³

Question 91: The curved surface area of a given right circular cylinder is 4.4 m². If the radius of the base of the given cylinder is 0.7 m, find its height. (Assume π = 22/7)

Answer 91: Let h be the height of the circular cylinder and r be the radius.

The required radius of the base of the given cylinder, r = 0.7m

CSA of cylinder = 2πrh

CSA of cylinder = 4.4m²

By equating both equations, we obtain

2×(22/7)×0.7×h = 4.4

Hence, the height of the cylinder is 1 m.

Question 92: A separate hemispherical bowl made of brass has an inner diameter of 10.5cm. Find out the cost of tin-plating, which is Rs 16 per 100 cm ² . (Assume π = 22/7)

Answer 92: Inner radius of hemispherical bowl, say r = diameter/2 = (10.5)/2 cm = 5.25 cm

The given formula for the Surface area of a hemispherical bowl = 2πr²

= 2×(22/7)×(5.25)² = 173.25

The surface area of the hemispherical bowl is 173.25 cm²

The required cost of tin-plating 100 cm² area = Rs 16

The required cost of tin-plating 1 cm² area = Rs 16 /100

The required cost of tin-plating 173.25 cm² area = Rs. (16×173.25)/100 = Rs 27.72

Hence, the cost of tin-plating the inner side of the hemispherical bowl at the rate of Rs 16 per 100 cm² is Rs 27.72.

Question 93: Calculate the amount of ice cream that can be put into a cone with a base radius of 3.5 cm and height of 12 cm.

Answer 93: Given,

Base radius = r = 3.5 cm

Height = h = 12 cm

The amount of ice cream that can be put into a cone = Volume of a given cone

= (1/3) πr²h

= (1/3) × (22/7) × 3.5 × 3.5 × 12

Question 94:The inner diameter of a certain circular well is 3.5m. It is 10m deep. Find out 

(i) its required inner curved surface area,

(ii) the cost required of plastering this curved surface at Rs. 40 per m ² .

Answer 94: Inner radius of circular well, r = 3.5/2m = 1.75m

Depth of circular well, say h = 10m

(i) Inner curved surface area = 2πrh

= (2×(22/7 )×1.75×10)

Hence, the inner curved surface area of the circular well is 110 m².

(ii)The cost of plastering 1 m² area = Rs.40

The cost of plastering 110 m² area = Rs (110×40)

Thus, the cost of plastering the curved surface of the well is Rs. 4400.

Question 95: Find out the radius of a sphere whose surface area is 154 cm². (Assume π = 22/7)

Answer 95: Let the radius of the sphere be r.

Surface area of sphere = 154 (given)

r2 = (154×7)/(4×22) = (49/4)

r = (7/2) = 3.5

Hence, The radius of the given sphere is 3.5 cm.

Question 96: The capacity of a certain closed cylindrical vessel of height 1m is15.4 litres. How many square metres of the given metal sheet would be required to make it? (Assume π = 22/7)

Answer 96: The height of the given cylindrical vessel, h = 1 m

The capacity of the given cylindrical vessel = 15.4 litres = 0.0154 m³

 r be the radius of the given circular end.

Capacity of cylindrical vessel = (22/7)×r²×1 = 0.0154

After simplifying, we obtain r = 0.07 m

The total surface area of the given vessel = 2πr(r+h)

= 2×22/7×0.07(0.07+1)

= 0.44×1.07

The total surface area of the given vessel is 0.4708 m²

Therefore, 0.4708 m² of the metal sheet would be required to make the cylindrical vessel.

Question 97: A particular spherical ball is broken up into two equal halves. The curved surface area of each and every half is 56.57 cm. What will be the given volume of the spherical ball?

Answer 97: Given,

The curved surface area of half of the spherical ball = 56.57 cm²

(1/2) 4πr² = 56.57

2 × 3.14 × r² = 56.57

r² = 56.57/6.28

r² = 9 (approx)

The volume of spherical ball = (4/3)πr³

= (4/3) × 3.14 × 3 × 3 × 3

= 113.04 cm³

Question 98: A hot water heating system has a cylindrical pipe of length 28 m and a diameter of 5 cm. Find out the whole radiating surface in the system. (Assume π = 22/7)

Answer 98: The height of cylindrical pipe = Length of cylindrical pipe = 28m

The radius of circular end of pipe = diameter/ 2 = 5/2 cm = 2.5cm = 0.025m

Now, the Curved Surface Area of cylindrical pipe = 2πrh, where the r = radius and h = height of the cylinder

= 2×(22/7)×0.025×28 m²

Hence, The Area of the radiating surface of the system is 4.4m².

Question 99: The required diameter of the moon is approximately one-fourth of the diameter of the earth.

Find out the ratio of their surface areas.

Answer 99: If the diameter of the earth is said d, then the diameter of the moon will be d/4 (as per the given statement)

The radius of earth = d/2

The radius of moon = ½×d/4 = d/8

The surface area of the moon = 4π(d/8)²

The surface area of earth = 4π(d/2)²

The ratio of their surface areas = 4π(d/8)²/ 4π(d/2)² = 4/ 64= 1/16

The ratio between their given surface areas is 1:16.

Question 100: A separate hemispherical bowl is made up of steel 0.25 cm thick. The required inner radius of the bowl is 5 cm. Find out the outer curved surface of the bowl. (Assume π =22/7)

Answer 100: The inner radius of the hemispherical bowl = 5 cm

The thickness of the given bowl = 0.25 cm

The outer radius of the given hemispherical bowl = (5+0.25) cm = 5.25 cm

The formula for the outer Curved Surface Area of a hemispherical bowl = 2πr², where r is the radius of the hemisphere

= 2×(22/7)×(5.25)² = 173.25 cm².

Accordingly, the outer curved surface area of the bowl is 173.25 cm².

Question 101: It costs Rs 2200 to paint the curved inner surface of a cylindrical vessel 10m deep. If the cost of painting is Rs 20 per m², find out. 

(i) The required inner curved surface area of the given vessel

(ii) The radius of the base

(iii) The capacity of the vessel

Answer 101: (i)The cost of painting a 1 m² area =Rs 20.

Rs 1 is the cost to paint a 1/20 m² area.

Here, Rs 2200 is the cost of painting = (1/20×2200) m² 

= 110 m² area

The inner surface area of the given vessel is 110m².

(ii) The radius of the base of the vessel, let us say r.

The height (h) = 10 m and

Surface area formula = 2πrh

Using the result of (i)

2πrh = 110 m² 

2×22/7×r×10 = 110

The radius is 1.75 m.

(iii) The volume of vessel formula = πr² h

Here r = 1.75 and h = 10

The volume = (22/7)×(1.75)² ×10 = 96.25

The volume of the vessel is 96.25 m³

Hence, the capacity of the vessel is 96.25 m³ or 96250 litres.

Question 102: The required slant height and base diameter of a particular conical tomb are 25m and 14 m, respectively. Find out the cost of white-washing its curved surface at the rate of Rs. 210 per 100 m2. (Assume π = 22/7)

Answer 102: The slant height of the given conical tomb, l = 25m

The base radius, r = diameter/2 = 14/2 m = 7m

CSA of conical tomb = πrl

= (22/7)×7×25 = 550

CSA of conical tomb= 550m²

Cost of white-washing 550 m² area, which is Rs (210×550)/100

Therefore, the cost will be Rs. 1155 while white-washing the tomb.

Question 103: The volume and surface area of a certain solid hemisphere are numerically equal. What is the diameter of the hemisphere?

Answer 103: We know that

So the given diameter = 2 (9/2) = 9 units,

Therefore, the required diameter of the hemisphere is 9 units .

Benefits Of Solving Important Questions Class 9 Mathematics Chapter 13

Consistently solving questions is pivotal to mastering the concepts and getting good marks in Mathematics. By solving Mathematics Class 9 Chapter 13 Important Questions, students can attain lucidity in the basics of the chapter Surface Areas and Volumes. You can effortlessly find the Important Questions Class 9 Mathematics Chapter 13 on the Extramarks website by registering on our website.

Some other benefits of solving Important Questions Class 9 Mathematics Chapter 13 are: 

• Class 9 Mathematics Chapter 13 Important Questions provide  information about the types of questions that can be expected  in the  examination, which also helps in minimising stress and examination anxiety. 
• Studying something just once may help you grasp the concepts, but going through it over and over again will help you remember it well.. Your chances of scoring better marks in an exam increase as you keep solving more important questions Class 9 Mathematics Chapter 13. It enhances your speed and accuracy.
• The questions and solutions provided are entirely based on the latest CBSE syllabus and as per CBSE guidelines. Hence, The students can completely bank  on it.
• By solving our Chapter 9 Class 13 Mathematics Important Questions, students will get an idea about  the question paper pattern.. Practising these questions similar to the exam questions would help the students gain  confidence, perform much better in their examinations, and eventually top them.

Extramarks provides comprehensive learning solutions for students from Class 1 to Class 12. Our website has abundant resources, along with important questions and solutions. Students can click on the given links to access some of these resources:

• Click to share on Facebook (Opens in new window)
• Click to share on Twitter (Opens in new window)
• Click to share on LinkedIn (Opens in new window)
• Click to share on WhatsApp (Opens in new window)

Q.1 The internal measurements of a cuboidal room are 10 m × 4 m × 6 m. Find the cost of white washing of the walls at the rate of 5 per square metre.

Marks: 3 Ans

Area of four walls of room = 2(l + b)h = 2—(10 + 4)—6 = 168 m 2 Rate of white washing = 5 per m 2 So, the total cost of white washing = 5—168 = 840

Q.2 How many bricks will be required for a wall 8 m long, 6 m high and 22.5 cm thick if each brick measures 25 cm x 11.25 cm x 6 cm

Lengthofthewall= 8—100 =800cm Breadthofthewall =22.5cm Heightofthewall = 6—100 = 600cm. Volumeofthewall = 800—22.5—600 cm 3 Numberofbricksrequired = Volumeofwall Volumeofbrick = 800—22.5—600 25—11.25—6 So,thenumberofbricksrequired=6400.

Q.3 Three equal cubes are placed adjacently in a row. Find the ratio of total surface area of the new cuboid to that of sum of the surface areas of the three cubes.

three equal cubes are placed in row. Let the side of each cubeislunit. Total lenght of thecuboidformed=3lunit Width=lunit,Height=lunit Totalsurfaceareaofcuboid=2 3l 2 +l 2 +3l 2 =14l 2 Totalsurfaceareaofthreecubes=3—6l 2 =18l 2 Therequiredratio= 14l 2 18l 2 =7:9

Q.4 The radius and slant height of a cone are in the ratio 4:7. If its curved surface area is 792 sq cm, find its radius.

let radius of cone = r and slant height = lcm. Therefore, r l = 4 7 curved surface area of cone = rl r 2 l r =792 on multiply and divide by rinLHS r 2 =792— 4 7 r 2 = 792—4—7 22—7 =144 r=12cm.

Q.5 The diameter of a sphere is decreased by 50%. By what percent will its curved surface area decrease

Letthediameterofthesphere=D radius r = D 2 Curvedsurfaceareaofthesphere, =4r 2 =4 D 2 4 So,thecurvedsurfaceareaofthesphere, =D 2 . .. 1 Now,diameterdecreasesby50%. Curvedsurfaceareaofthenewsphere = D 2 2 = D 2 4 . .. 2 Decreaseincurvedsurfaceareaofsphere =D 2 – D 2 4 = 3D 2 4 Therefore,requireddecreasepercent= 3D 2 4 D 2 —100% =75%

Please register to view this section

Faqs (frequently asked questions), 1. what can i get from the extramarks website.

Extramarks is one of the best educational platforms as it has its own archive of educational resources, which assists students in acing their exams. You can get all the NCERT-related material like NCERT solutions, solved exemplar solutions, NCERT-based mock tests, CBSE revision notes, and Important Questions Class 9 Mathematics Chapter 13 on the Extramarks website. Apart from this, you can get comprehensive guidance from our subject experts and take doubt-clearing sessions once you sign up on our official website for all the study resources.      

2. How many total chapters will students study in Class 9 Mathematics?

  There are 15 chapters in Class 9 Mathematics. The list is given below:

• Chapter 1- Number System
• Chapter 2 –Polynomials
• Chapter 3 – Coordinate Geometry
• Chapter 4 –Linear Equations In Two Variables
• Chapter 5 – Introduction To Euclid’s Geometry
• Chapter 6 – Lines And Angles
• Chapter 7 –Triangles
• Chapter 8 – Quadrilaterals
• Chapter 9 –Areas Of Parallelograms And Triangles
• Chapter 10 – Circles
• Chapter 11- Constructions
• Chapter 12- Heron’s Formula
• Chapter 13-Surface Area And Volumes
• Chapter 14- Statistics
• Chapter 15- Probability

CBSE Related Links

Fill this form to view question paper

Otp verification.

• CBSE Maths Important Questions
• Class 9 Maths
• Chapter 13: Surface Areas Volumes

Important Questions CBSE Class 9 Maths Chapter 13 Surface Areas Volumes

Important questions for CBSE Class 9 Maths Chapter 13 Surface Areas and Volumes are given here for students who are preparing for their final exams. All these questions are prepared by our subject experts based on the CBSE syllabus (2022-2023) and are relevant to the NCERT book. The important questions are formulated as per the latest exam pattern.  Practising these questions will help students to score well in their exams. Students can revise by accessing the Class-wise important questions for CBSE Class 9 Maths  at BYJU’S.

Chapter 13 of Class 9 maths deals with various solid shapes such as cubes, cuboids, cones, cylinders and spheres. In this chapter, students will learn how to find the surface area and volumes of all these solids and how we can apply these formulas in word problems based on real-world scenarios.

Also Check:

• Important 2 Marks Questions for CBSE 9th Maths
• Important 3 Marks Questions for CBSE 9th Maths
• Important 4 Marks Questions for CBSE 9th Maths

Important Questions For CBSE Class 9 Surface Areas and Volumes  (Chapter 13)

Q.1: Hameed has built a cubical water tank with a lid for his house, with each outer edge 1.5 m long. He gets the outer surface of the tank excluding the base, covered with square tiles of side 25 cm (see in the figure below). Find how much he would spend on the tiles if the cost of the tiles is Rs.360 per dozen.

Edge of the cubical tank (a) = 1.5 m = 150 cm 

So, surface area of the tank = 5 × 150 × 150 cm 2

The measure of side of a square tile = 25 cm

Area of each square tile = side × side = 25 × 25 cm 2

Required number of tiles = (Surface area of the tank)/(area of each tile)

= (5 × 150 × 150)/(25 × 25)

Also, given that the cost of the tiles is Rs. 360 per dozen.

Thus, the cost of each tile = Rs. 360/12 = Rs. 30

Hence, the total cost of 180 tiles = 180 × Rs. 30 = Rs. 5400

Q.2: The paint in a certain container is sufficient to paint an area equal to 9.375 sq.m. How many bricks of dimensions 22.5 cm × 10 cm × 7.5 cm can be painted out of this container?

Dimensions of the brick = 22.5 cm × 10 cm × 7.5 cm

Here, l = 22.5 cm, b = 10 cm, h = 7.5 cm

Surface area of 1 brick  = 2(lb + bh + hl) 

= 2(22.5 × 10 + 10 × 7.5 + 7.5 × 22.5) cm 2

= 2(225 + 75 + 168.75) cm 2  

= 2 x 468.75 cm 2  

= 937.5 cm 2  

Area that can be painted by the container = 9.375 m 2  (given)

= 9.375 × 10000 cm 2

= 93750 cm 2

Thus, the required number of bricks = (Area that can be painted by the container)/(Surface area of 1 brick)

= 93750/937.5

= 937500/9375

Q.3:   The length, breadth and height of a room are 5 m, 4 m and 3 m respectively. Find the cost of whitewashing the walls of the room and the ceiling at the rate of  Rs.7.50 per sq.m.

Length of the room (l) = 5 m

Breadth of the room (b) = 4 m

Height of the room (h) = 3 m

Area of walls of the room = Lateral surface area of cuboid

= 2h(l + b)

= 2 × 3(5 + 4)

Area of ceiling = Area of base of the cuboid

Area to be white washed = (54 + 20) sq.m = 74 sq.m

Given that, the cost of white washing 1 sq.m = Rs. 7.50

Therefore, the total cost of white washing the walls and ceiling of the room = 74 × Rs. 7.50 = Rs. 555

Q.4:   The curved surface area of a right circular cylinder of height 14 cm is 88 sq.cm. Find the diameter of the base of the cylinder.

Let d be the diameter and r be the radius of a right circular cylinder.

Height of cylinder (h) = 14 cm 

Curved surface area of right circular cylinder = 88 cm 2

⇒ 2πrh = 88 cm 2

⇒ πdh = 88 cm 2 (since d = 2r) 

⇒ 22/7 x d x 14 cm = 88 cm 2

⇒ d = 2 cm 

Hence, the diameter of the base of the cylinder is 2 cm.

Q.5:   Curved surface area of a right circular cylinder is 4.4 sq.m. If the radius of the base of the cylinder is 0.7 m, find its height.

Let h be the height of the cylinder.

Radius of the base of the cylinder (r) = 0.7 m 

Curved surface area of cylinder = 4.4 m 2

2πrh = 4.4  

2 × 3.14 × 0.7 × h = 4.4

4.4 × h = 4.4 

h = 4.4/4.4

Therefore, the height of the cylinder is 1 m.

Q.6:   In a hot water heating system, there is a cylindrical pipe of length 28 m and diameter 5 cm. Find the total radiating surface in the system.

Length of the cylindrical pipe = h = 28 m

Diameter of the pipe = 5 cm

Now, the radius of piper (r) = 5/ 2 cm = 2.5 cm = 0.025 m

Total radiating surface in the system = Total surface area of the cylinder  

= 2πr(h + r)  

= 2 × (22/7) × 0.025 (28 + 0.025) m 2  

= (44 x 0.025 x 28.025)/7 m 2

= 4.4 m 2 (approx)

Q.7:   The height of a cone is 16 cm and its base radius is 12 cm. Find the curved surface area and the total surface area of the cone. (Take π = 3.14)

Height of a cone (h) = 16 cm

Radius of the base (r) = 12 cm

Slant height of cone (l) = √(r 2  + h 2 )

= √(256 + 144)

Curved surface area of cone = πrl

= 3.14 × 12 × 20 cm 2

= 753.6 cm 2

Total surface area = πrl + πr 2

= (753.6 + 3.14 × 12 × 12) cm 2

= (753.6 + 452.16) cm 2

= 1205.76 cm 2

Q.8: Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.

Diameter of the cone = 24 m 

Radius of the cone (r) = 24/2 = 12 m 

Slant height of the cone (l) = 21 m 

Total surface area of a cone = πr(l + r) 

= (22/7) × 12 × (21 + 12) 

= (22/7) × 12 × 33 

= 1244.57 m 2

Q.9: The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of Rs.210 per 100 sq.m.

Slant height of a cone (l) = 25 m  

Diameter of the base of cone = 2r = 14 m  

∴ Radius = r = 7 m  

Curved Surface Area = πrl 

= (22/7) x 7 x 25 

= 22 × 25  

= 550 sq.m  

Also, given that the cost of white-washing 100 sq.m = Rs. 210 

Hence, the total cost of white-washing for 550 sq.m = (Rs. 210 × 550)/100 = Rs. 1155

Q.10: The hollow sphere, in which the circus motorcyclist performs his stunts, has a diameter of 7 m. Find the area available to the motorcyclist for riding.

Diameter of the sphere = 7 m

Radius (r) = 7/2 = 3.5 m 

Now, the riding space available for the motorcyclist = Surface area of the sphere

= 4 × (22/7) × 3.5 × 3.5

Q.11:   The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.

Radius of balloon = r =  7 cm

Radius of pumped balloon = R = 14 cm

Ratio of surface area = (TSA of balloon with r = 7 cm)/(TSA of balloon with R = 14 cm)

= (4πr 2 )/(4πR 2 )

= (7) 2 /(14) 2

Hence, the ratio of surface areas of the balloon in the two cases is 1 : 4.

Q.12: A river 3 m deep and 40 m wide is flowing at the rate of 2 km per hour. How much water will fall into the sea in a minute?

Depth of the river (h) = 3 m

Width of the river (w) = 40 m

Flow rate of water = 2 km/hr

i.e. Flow of water in 1 hour = 2 km = 2000 m

Flow of water in 1 minute = 2000/60 = 100/3 m

Thus, length (l) = 100/3 m

Volume of water falling into the sea in 1 minute = Volume of cuboid with dimension l, w, h

= l × w × h

= (100/3) × 40 × 3

= 4000 x 1000 L 

= 4000000 L

Q.13:   A lead pencil consists of a cylinder of wood with a solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of the pencil is 14 cm, find the volume of the wood and that of the graphite.

Diameter of the pencil = 7  mm

Radius of the pencil (R) = 7/2 mm

Diameter of the graphite cylinder = 1 mm

Radius of the graphite (r) = 1/2 mm

Height (h) = 14 cm = 140 mm (since 1 cm = 10 mm)

Volume of a cylinder = πr²h

Volume of graphite cylinder = πr2h 

= (22/7) × (1/2) × (1/2) × 140

Volume of pencil = πR²h

= (22/7) × (7/2) × (7/2) × 140

= 490 × 11 

Volume of wood = Volume of pencil – Volume of graphite

= 5390- 110 = 5280 mm³

= 5280/1000 (since 1 mm³ = 1/1000 cm³)

Q.14:   Meera has a piece of canvas whose area is 551 m 2 . She uses it to have a conical tent made, with a base radius of 7 m. Assuming that all the stitching margins and the wastage incurred while cutting, amounts to approximately 1 m 2 , find the volume of the tent that can be made with it.

Area of the canvas = 551 m 2

Area of the canvas lost in wastage = 1 m 2

Thus, the area of canvas available for making the tent = (551 – 1) m 2 = 550 m 2

Now, the surface area of the tent = 550 m 2

The required base radius of the conical tent = 7 m

Curved surface area of tent = 550 m 2

That means,

(22/7) × 7 × l = 550

Now, l 2 = h 2 + r 2

h 2 = l 2 – r 2 = (25) 2 – (7) 2 = 625 – 49 = 576

So, the volume of the conical tent = (1/3)πr 2 h

= (1/3) × (22/7) × 7 × 7 × 24

Q.15:   A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm 3 ) is needed to fill this capsule?

Diameter of capsule = 3.5 mm

Radius of capsule = (r) = 3.5/2 = 1.75 mm

Volume of spherical capsule = (4/3)πr 3

= (4/3) × (22/7) × 1.75 × 1.75 × 1.75

= 22.458 mm 3

Therefore, the volume of the capsule is 22.46 mm 3  approx.

Q.16:   Calculate the amount of ice-cream that can be put into a cone with base radius 3.5 cm and height 12 cm.

Base radius = r = 3.5 cm

Height = h = 12 cm

The amount of ice-cream that can be put into a cone = Volume of cone

= (1/3)πr 2 h

= (1/3) × (22/7) × 3.5 × 3.5 × 12

Q.17:   A spherical ball is divided into two equal halves. Given that the curved surface area of each half is 56.57 cm, what will be the volume of the spherical ball?

Curved surface area of of half of the spherical ball = 56.57 cm 2

(1/2) 4πr 2 = 56.57

2 × 3.14 × r 2 = 56.57

r 2 = 56.57/6.28

r 2 = 9 (approx)

Volume of spherical ball = (4/3)πr 3

= (4/3) × 3.14 × 3 × 3 × 3

= 113.04 cm 3

Articles for Class 9

• Algebraic Identities For Class 9
• Areas Of Parallelograms And Triangles Class 9 Notes
• Circles Class 9
• Class 9 Maths MCQs
• Congruence of Triangles Class 9
• Constructions Class 9
• Coordinate Geometry Class 9 Notes
• Heron’s Formula Class 9 Notes
• Linear Equations in Two Variables Class 9 Notes
• Lines and Angles Class 9
• Maths Formulas for Class 9
• Number System for Class 9
• Polynomial Class 9 Notes
• Probability Class 9 Notes
• Quadrilaterals Class 9 Notes
• Surface Area and Volume Class 9

Practice Problems for Surface Areas and Volumes Class 9 Maths

• How many shots, each having a diameter 3 cm, can be made from a cuboidal lead solid of dimensions 9cm × 11cm × 12cm?
• Two identical cubes, each of volume 64 cm 3 are joined together end to end. What is the surface area of the resulting cuboid?
• The barrel of a fountain pen, cylindrical in shape, is 7 cm long and 5 mm in diameter. A full barrel of ink in pen is used up on writing 3300 words on an average. How many words can be written in a bottle of ink containing one-fifth of a litre?
• Water is flowing at the rate of 15 km/h through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide. In what time will the level of water in the pond rise by 21 cm?
• 500 persons are taking a dip into a cuboidal pond which is 80 m long and 50 m broad. What is the rise of water level in the pond, if the average displacement of the water by a person is 0.04 m 3 ?
• Find the curved surface area of a right circular cone whose slant height is 10 cm and base radius is 7 cm. 
• A joker’s cap is in the form of a right circular cone with a base radius of 7 cm and a height of 24 cm. Find the area of the sheet required to make 10 such caps. 
• A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl. 

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.