m8 unit 1 real number system homework page 19

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.1: Real Numbers - Algebra Essentials

• Last updated
• Save as PDF
• Page ID 106313

The following text includes many examples. At the end of the text are supplemental help videos, then the homework exercises.

Learning Objectives

• Classify a real number as a natural, whole, integer, rational, or irrational number.
• Perform calculations using order of operations.
• Use the following properties of real numbers: commutative, associative, distributive, inverse, and identity.
• Evaluate algebraic expressions.
• Simplify algebraic expressions.

It is often said that mathematics is the language of science. If this is true, then the language of mathematics is numbers. The earliest use of numbers occurred \(100\) centuries ago in the Middle East to count, or enumerate items. Farmers, cattlemen, and tradesmen used tokens, stones, or markers to signify a single quantity—a sheaf of grain, a head of livestock, or a fixed length of cloth, for example. Doing so made commerce possible, leading to improved communications and the spread of civilization.

Three to four thousand years ago, Egyptians introduced fractions. They first used them to show reciprocals. Later, they used them to represent the amount when a quantity was divided into equal parts.

But what if there were no cattle to trade or an entire crop of grain was lost in a flood? How could someone indicate the existence of nothing? From earliest times, people had thought of a “base state” while counting and used various symbols to represent this null condition. However, it was not until about the fifth century A.D. in India that zero was added to the number system and used as a numeral in calculations.

Clearly, there was also a need for numbers to represent loss or debt. In India, in the seventh century A.D., negative numbers were used as solutions to mathematical equations and commercial debts. The opposites of the counting numbers expanded the number system even further.

Because of the evolution of the number system, we can now perform complex calculations using these and other categories of real numbers. In this section, we will explore sets of numbers, calculations with different kinds of numbers, and the use of numbers in expressions.

Classifying a Real Number

The numbers we use for counting, or enumerating items, are the natural numbers: \(1, 2, 3, 4, 5\) and so on. We describe them in set notation as \(\{1,2,3,...\}\) where the ellipsis \((\cdots)\) indicates that the numbers continue to infinity. The natural numbers are, of course, also called the counting numbers. Any time we enumerate the members of a team, count the coins in a collection, or tally the trees in a grove, we are using the set of natural numbers. The set of whole numbers is the set of natural numbers plus zero: \(\{0,1,2,3,...\}\).

The set of integers adds the opposites of the natural numbers to the set of whole numbers: \(\{\cdots,-3,-2,-1,0,1,2,3,\cdots\}\). It is useful to note that the set of integers is made up of three distinct subsets: negative integers, zero, and positive integers. In this sense, the positive integers are just the natural numbers. Another way to think about it is that the natural numbers are a subset of the integers.

\[ \overbrace{\cdots, -3,-2,-1}^{\text{negative integers}}, \underbrace{0}_{\text{zero}}, \overbrace{1,\, 2,\,3,\, \cdots}^{\text{positive integers}} \nonumber\]

The set of rational numbers is written as \(\{\frac{m}{n}| \text{m and n are integers and } n \neq 0\}\).Notice from the definition that rational numbers are fractions (or quotients) containing integers in both the numerator and the denominator, and the denominator is never \(0\). We can also see that every natural number, whole number, and integer is a rational number with a denominator of \(1\).

Because they are fractions, any rational number can also be expressed in decimal form. Any rational number can be represented as either:

• a terminating decimal: \(\frac{15}{8} =1.875\), or
• a repeating decimal: \(\frac{4}{11} =0.36363636\cdots = 0.\bar{36}\)

We use a line drawn over the repeating block of numbers instead of writing the group multiple times.

Example \(\PageIndex{1}\): Writing Integers as Rational Numbers

Write each of the following as a rational number. Write a fraction with the integer in the numerator and \(1\) in the denominator.

a. \(7= \frac{7}{1}\)

b. \(0= \frac{0}{1}\)

c. \(-8= \frac{-8}{1}\)

Exercise \(\PageIndex{1}\)

Write each of the following as a rational number.

• \(\frac{11}{1}\)
• \(\frac{3}{1}\)
• \(-\frac{4}{1}\)

Example \(\PageIndex{2}\): Identifying Rational Numbers

Write each of the following rational numbers as either a terminating or repeating decimal.

• \(-\frac{5}{7}\)
• \(\frac{15}{5}\)
• \(\frac{13}{25}\)

a. a repeating decimal

b. \(\frac{15}{5} = 3\)(or \(3.0\)), a terminating decimal

c. \(\frac{13}{25} =0.52\), a terminating decimal

Exercise \(\PageIndex{2}\)

• \(\frac{68}{17}\)
• \(\frac{8}{13}\)
• \(-\frac{13}{25}\)
• \(4\) (or \(4.0\)), terminating
• \(0.\overline{615384}\), repeating
• \(-0.85\), terminating

Irrational Numbers

At some point in the ancient past, someone discovered that not all numbers are rational numbers. A builder, for instance, may have found that the diagonal of a square with unit sides was not \(2\) or even \(32\), but was something else. Or a garment maker might have observed that the ratio of the circumference to the diameter of a roll of cloth was a little bit more than \(3\), but still not a rational number. Such numbers are said to be irrational because they cannot be written as fractions. These numbers make up the set of irrational numbers. Irrational numbers cannot be expressed as a fraction of two integers. It is impossible to describe this set of numbers by a single rule except to say that a number is irrational if it is not rational. So we write this as shown.

\[\{h\mid h \text { is not a rational number}\}\]

Example \(\PageIndex{3}\): Differentiating Rational and Irrational Numbers

Determine whether each of the following numbers is rational or irrational. If it is rational, determine whether it is a terminating or repeating decimal.

• \(\sqrt{25}\)
• \(\frac{33}{9}\)
• \(\sqrt{11}\)
• \(\frac{17}{34}\)
• \(0.3033033303333…\)
• \(\sqrt{25}\): This can be simplified as \(\sqrt{25} = 5\). Therefore,\(\sqrt{25}\)is rational.
• \(\frac{33}{9}\): Because it is a fraction,\(\frac{33}{9}\) is a rational number. Next, simplify and divide. \[\frac{33}{9}=\cancel{\frac{33}{9}} \nonumber\] So, \(\frac{33}{9}\) is rational and a repeating decimal.
• \(\sqrt{11}\): This cannot be simplified any further. Therefore, \(\sqrt{11}\) is an irrational number.
• \(\frac{17}{34}\): Because it is a fraction, \(\frac{17}{34}\) is a rational number. Simplify and divide. \[\frac{17}{34} = 0.5 \nonumber\] So, \(\frac{17}{34}\) is rational and a terminating decimal.
• \(0.3033033303333…\) is not a terminating decimal. Also note that there is no repeating pattern because the group of \(3s\) increases each time. Therefore it is neither a terminating nor a repeating decimal and, hence, not a rational number. It is an irrational number.

Exercise \(\PageIndex{3}\)

• \(\frac{7}{77}\)
• \(\sqrt{81}\)
• \(4.27027002700027…\)
• \(\frac{91}{13}\)
• \(\sqrt{39}\)
• rational and repeating;
• rational and terminating;
• irrational;

Real Numbers

Given any number \(n\), we know that \(n\) is either rational or irrational. It cannot be both. The sets of rational and irrational numbers together make up the set of real numbers. As we saw with integers, the real numbers can be divided into three subsets: negative real numbers, zero, and positive real numbers. Each subset includes fractions, decimals, and irrational numbers according to their algebraic sign (+ or –). Zero is considered neither positive nor negative.

The real numbers can be visualized on a horizontal number line with an arbitrary point chosen as \(0\), with negative numbers to the left of \(0\) and positive numbers to the right of \(0\). A fixed unit distance is then used to mark off each integer (or other basic value) on either side of \(0\). Any real number corresponds to a unique position on the number line.The converse is also true: Each location on the number line corresponds to exactly one real number. This is known as a one-to-one correspondence. We refer to this as the real number line as shown in Figure (\(\PageIndex{1}\).

Example \(\PageIndex{4}\): Classifying Real Numbers

Classify each number as either positive or negative and as either rational or irrational. Does the number lie to the left or the right of \(0\) on the number line?

• \(-\frac{10}{3}\)
• \(\sqrt{5}\)
• \(-\sqrt{289}\)
• \(0.615384615384…\)
• \(-\frac{10}{3}\) is negative and rational. It lies to the left of \(0\) on the number line.
• \(\sqrt{5}\) is positive and irrational. It lies to the right of \(0\).
• \(-\sqrt{289} = -\sqrt{17^2} = -17\) is negative and rational. It lies to the left of \(0\).
• \(-6π\) is negative and irrational. It lies to the left of \(0\).
• \(0.615384615384…\) is a repeating decimal so it is rational and positive. It lies to the right of \(0\).

Exercise \(\PageIndex{4}\)

• \(\sqrt{73}\)
• \(-11.411411411…\)
• \(\frac{47}{19}\)
• \(-\frac{\sqrt{5}}{2}\)
• \(6.210735\)
• positive, irrational; right
• negative, rational; left
• positive, rational; right
• negative, irrational; left
• positive, rational; right

Sets of Numbers as Subsets

Beginning with the natural numbers, we have expanded each set to form a larger set, meaning that there is a subset relationship between the sets of numbers we have encountered so far. These relationships become more obvious when seen as a diagram, such as Figure(\(\PageIndex{2}\)).

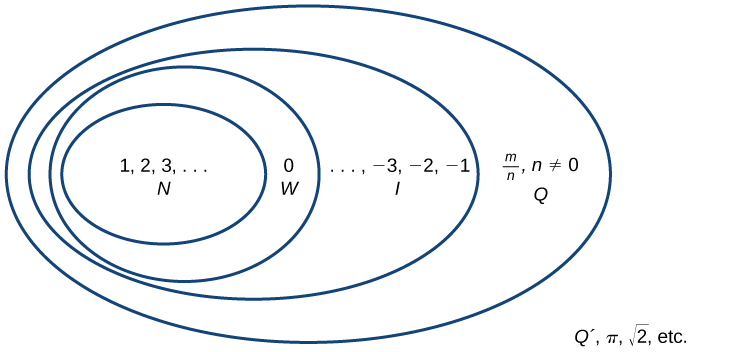
SETS OF NUMBERS

The set of natural numbers includes the numbers used for counting: \(\{1,2,3,...\}\).

The set of whole numbers is the set of natural numbers plus zero: \(\{0,1,2,3,...\}\).

The set of integers adds the negative natural numbers to the set of whole numbers: \(\{...,-3,-2,-1,0,1,2,3,...\}\).

The set of rational numbers includes fractions written as \(\{\frac{m}{n} | \text{m and n are integers and } n \neq 0\}\).

The set of irrational numbers is the set of numbers that are not rational, are nonrepeating, and are nonterminating: \(\{h\parallel \text{h is not a rational number}\}\).

Example \(\PageIndex{5}\): Differentiating the Sets of Numbers

Classify each number as being a natural number (N), whole number (W), integer (I), rational number (Q), and/or irrational number (Q′).

• \(\sqrt{36}\)
• \(\frac{8}{3}\)
• \(3.2121121112…\)

Exercise \(\PageIndex{5}\)

• \(-\frac{35}{7}\)
• \(\sqrt{169}\)
• \(\sqrt{24}\)
• \(4.763763763...\)

Performing Calculations Using the Order of Operations

When we multiply a number by itself, we square it or raise it to a power of \(2\). For example, \(4^2 =4\times4=16\). We can raise any number to any power. In general, the exponential notation an means that the number or variable \(a\) is used as a factor \(n\) times.

\[a^n=a\cdot a\cdot a\cdots a \qquad \text{ n factors} \nonumber \]

In this notation, \(a^n\) is read as the \(n^{th}\) power of \(a\), where \(a\) is called the base and \(n\) is called the exponent. A term in exponential notation may be part of a mathematical expression, which is a combination of numbers and operations. For example, \(24+6 \times \dfrac{2}{3} − 4^2\) is a mathematical expression.

To evaluate a mathematical expression, we perform the various operations. However, we do not perform them in any random order. We use the order of operations. This is a sequence of rules for evaluating such expressions.

Recall that in mathematics we use parentheses ( ), brackets [ ], and braces { } to group numbers and expressions so that anything appearing within the symbols is treated as a unit. Additionally, fraction bars, radicals, and absolute value bars are treated as grouping symbols. When evaluating a mathematical expression, begin by simplifying expressions within grouping symbols.

The next step is to address any exponents or radicals. Afterward, perform multiplication and division from left to right and finally addition and subtraction from left to right.

Let’s take a look at the expression provided.

\[24+6 \times \dfrac{2}{3} − 4^2 \nonumber\]

There are no grouping symbols, so we move on to exponents or radicals. The number \(4\) is raised to a power of \(2\), so simplify \(4^2\) as \(16\).

\[24+6 \times \dfrac{2}{3} − 4^2 \nonumber \]

\[24+6 \times \dfrac{2}{3} − 16 \nonumber\]

Next, perform multiplication or division, left to right.

\[24+4-16 \nonumber\]

Lastly, perform addition or subtraction, left to right.

\[24+4−16 \nonumber\]

\[28−16 \nonumber\]

\[12 \nonumber\]

\[24+6 \times \dfrac{2}{3} − 4^2 =12 \nonumber\]

For some complicated expressions, several passes through the order of operations will be needed. For instance, there may be a radical expression inside parentheses that must be simplified before the parentheses are evaluated. Following the order of operations ensures that anyone simplifying the same mathematical expression will get the same result.

ORDER OF OPERATIONS

Operations in mathematical expressions must be evaluated in a systematic order, which can be simplified using the acronym PEMDAS :

• P (arentheses)
• E (xponents)
• M( ultiplication) and D (ivision)
• A (ddition) and S (ubtraction)

HOW TO: Given a mathematical expression, simplify it using the order of operations.

• Simplify any expressions within grouping symbols.
• Simplify any expressions containing exponents or radicals.
• Perform any multiplication and division in order, from left to right.
• Perform any addition and subtraction in order, from left to right.

Example \(\PageIndex{6}\): Using the Order of Operations

Use the order of operations to evaluate each of the following expressions.

• \((3\times2)^2-4\times(6+2)\)
• \(\dfrac{5^2-4}{7}- \sqrt{11-2}\)
• \(6-\mid 5-8\mid +3\times(4-1)\)
• \(\dfrac{14-3 \times2}{2 \times5-3^2}\)
• \(7\times(5\times3)−2\times[(6−3)−4^2]+1\)
• \(\begin{align*} (3\times2)^2-4\times(6+2)&=(6)^2-4\times(8) && \qquad \text{Simplify parentheses}\\ &=36-4\times8 && \qquad \text{Simplify exponent}\\ &=36-32 && \qquad \text{Simplify multiplication}\\ &=4 && \qquad \text{Simplify subtraction}\\ \end{align*}\)
• \(\begin{align*} \dfrac{5^2-4}{7}- \sqrt{11-2}&= \dfrac{5^2-4}{7}-\sqrt{9} && \qquad \text{Simplify grouping symbols (radical)}\\ &=\dfrac{5^2-4}{7}-3 && \qquad \text{Simplify radical}\\ &=\dfrac{25-4}{7}-3 && \qquad \text{Simplify exponent}\\ &=\dfrac{21}{7}-3 && \qquad \text{Simplify subtraction in numerator}\\ &=3-3 && \qquad \text{Simplify division}\\ &=0 && \qquad \text{Simplify subtraction} \end{align*}\)

Note that in the first step, the radical is treated as a grouping symbol, like parentheses. Also, in the third step, the fraction bar is considered a grouping symbol so the numerator is considered to be grouped.

• \(\begin{align*} 6-\mid 5-8\mid +3\times(4-1)&=6-|-3|+3\times3 && \qquad \text{Simplify inside grouping symbols}\\ &=6-3+3\times3 && \qquad \text{Simplify absolute value}\\ &=6-3+9 && \qquad \text{Simplify multiplication}\\ &=3+9 && \qquad \text{Simplify subtraction}\\ &=12 && \qquad \text{Simplify addition}\\ \end{align*}\)
• \(\begin{align*} \dfrac{14-3 \times2}{2 \times5-3^2}&=\dfrac{14-3 \times2}{2 \times5-9} && \qquad \text{Simplify exponent}\\ &=\dfrac{14-6}{10-9} && \qquad \text{Simplify products}\\ &=\dfrac{8}{1} && \qquad \text{Simplify differences}\\ &=8 && \qquad \text{Simplify quotient}\\ \end{align*}\)

In this example, the fraction bar separates the numerator and denominator, which we simplify separately until the last step.

• \(\begin{align*} 7\times(5\times3)-2\times[(6-3)-4^2]+1&=7\times(15)-2\times[(3)-4^2]+1 && \qquad \text{Simplify inside parentheses}\\ &=7\times(15)-2\times(3-16)+1 && \qquad \text{Simplify exponent}\\ &=7\times(15)-2\times(-13)+1 && \qquad \text{Subtract}\\ &=105+26+1 && \qquad \text{Multiply}\\ &=132 && \qquad \text{Add} \end{align*}\)

Exercise \(\PageIndex{6}\)

• \(\sqrt{5^2-4^2}+7\times(5-4)^2\)
• \(1+\dfrac{7\times5-8\times4}{9-6}\)
• \(|1.8-4.3|+0.4\times\sqrt{15+10}\)
• \(\dfrac{1}{2}\times[5\times3^2-7^2]+\dfrac{1}{3}\times9^2\)
• \([(3-8^2)-4]-(3-8)\)

Using Properties of Real Numbers

For some activities we perform, the order of certain operations does not matter, but the order of other operations does. For example, it does not make a difference if we put on the right shoe before the left or vice-versa. However, it does matter whether we put on shoes or socks first. The same thing is true for operations in mathematics.

Commutative Properties

The commutative property of addition states that numbers may be added in any order without affecting the sum.

\[a+b=b+a\]

We can better see this relationship when using real numbers.

\((−2)+7 = 5 \text{ and } 7+(−2)=5\)

Similarly, the commutative property of multiplication states that numbers may be multiplied in any order without affecting the product.

\[a\times b=b\times a\]

Again, consider an example with real numbers.

It is important to note that neither subtraction nor division is commutative. For example, \(17−5\) is not the same as \(5−17\). Similarly, \(20÷5≠5÷20\).

Associative Properties

The associative property of multiplication tells us that it does not matter how we group numbers when multiplying. We can move the grouping symbols to make the calculation easier, and the product remains the same.

\[a(bc)=(ab)c\]

Consider this example.

\((3\times4)\times5=60 \text{ and } 3\times(4\times5)=60\)

The associative property of addition tells us that numbers may be grouped differently without affecting the sum.

\[a+(b+c)=(a+b)+c\]

This property can be especially helpful when dealing with negative integers. Consider this example.

\([15+(−9)]+23=29 \text{ and } 15+[(−9)+23]=29\)

Are subtraction and division associative? Review these examples.

\[\begin{align*} 8-(3-15)\overset{?}{=}&(8-3)-15\\ 8-(-12)\overset{?}{=}&5-15\\ 20 \neq &10\\ 64\div (8\div 4)\overset{?}{=}&(64\div 8)\div 4\\ 64\div 2\overset{?}{=}&8\div 4\\ 32 \neq & 2 \end{align*}\]

As we can see, neither subtraction nor division is associative.

Distributive Property

The distributive property states that the product of a factor times a sum is the sum of the factor times each term in the sum.

\[a\times(b+c)=a\times b+a\times c\]

This property combines both addition and multiplication (and is the only property to do so). Let us consider an example.

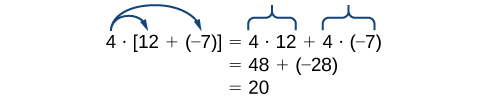
Note that \(4\) is outside the grouping symbols, so we distribute the \(4\) by multiplying it by \(12\), multiplying it by \(–7\), and adding the products.

Example \(\PageIndex{7}\)

To be more precise when describing this property, we say that multiplication distributes over addition. The reverse is not true, as we can see in this example.

\[\begin{align*} 6+(3\times5)\overset{?}{=}&(6+3)\times(6\times5)\\ 6+(15)\overset{?}{=}&(9)\times(11)\\ 21 \neq &99 \end{align*}\]

Multiplication does not distribute over subtraction, and division distributes over neither addition nor subtraction.

A special case of the distributive property occurs when a sum of terms is subtracted.

\[a−b=a+(−b)\]

For example, consider the difference \(12−(5+3)\). We can rewrite the difference of the two terms \(12\) and \((5+3)\) by turning the subtraction expression into addition of the opposite. So instead of subtracting \( (5+3)\), we add the opposite.

Now, distribute \(-1\) and simplify the result.

\[\begin{align*} 12-(5+3)&=12+(-1)\times(5+3)\\ &=12+[(-1)\times5+(-1)\times3]\\ &=12+(-8)\\ &=4 \end{align*}\]

This seems like a lot of trouble for a simple sum, but it illustrates a powerful result that will be useful once we introduce algebraic terms. To subtract a sum of terms, change the sign of each term and add the results. With this in mind, we can rewrite the last example.

\[\begin{align*} 12-(5+3)&=12+(-5-3)\\ &=12-8\\ &=4 \end{align*}\]

Identity Properties

The identity property of addition states that there is a unique number, called the additive identity \((0)\) that, when added to a number, results in the original number.

The identity property of multiplication states that there is a unique number, called the multiplicative identity \((1)\) that, when multiplied by a number, results in the original number.

\[a\times 1=a\]

For example, we have \( (−6)+0=−6\) and \( 23\times1=23\). There are no exceptions for these properties; they work for every real number, including \(0\) and \(1\).

Inverse Properties

The inverse property of addition states that, for every real number a, there is a unique number, called the additive inverse (or opposite), denoted \(−a\), that, when added to the original number, results in the additive identity, \(0\).

\[a+(−a)=0\]

For example, if \(a =−8\), the additive inverse is \(8\), since \((−8)+8=0\).

The inverse property of multiplication holds for all real numbers except \(0\) because the reciprocal of \(0\) is not defined. The property states that, for every real number \(a\), there is a unique number, called the multiplicative inverse (or reciprocal), denoted \(1a\), that, when multiplied by the original number, results in the multiplicative identity, \(1\).

\[a\times \dfrac{1}{a}=1\]

For example, if \(a =−\dfrac{2}{3}\), the reciprocal, denoted \(\dfrac{1}{a}\), is \(-\dfrac{3}{2}\) because

\[a⋅\dfrac{1}{a}=\left(−\dfrac{2}{3}\right)\times\left(−\dfrac{3}{2}\right)=1 \nonumber\]

PROPERTIES OF REAL NUMBERS

The following properties hold for real numbers \(a\), \(b\), and \(c\).

Example \(\PageIndex{8}\): Using Properties of Real Numbers

Use the properties of real numbers to rewrite and simplify each expression. State which properties apply.

• \(3\times 6+3\times 4\)
• \((5+8)+(−8)\)
• \(6−(15+9)\)
• \(\dfrac{4}{7}\times\left(\dfrac{2}{3}\times \dfrac{7}{4}\right)\)
• \(100\times[0.75+(−2.38)]\)
• \(\begin{align*} 3\times6+3\times4&=3\times(6+4) & & \text{Distributive property}\\ &=3\times10 & & \text{Simplify}\\ &=30 & & \text{Simplify}\\ \end{align*}\)
• \(\begin{align*} (5+8)+(-8)&=5+[8+(-8)] & &  \text{Associative property of addition}\\ &=5+0 & &  \text{Inverse property of addition}\\ &=5 & &  \text{Identity property of addition}\\ \end{align*}\)
• \(\begin{align*} 6-(15+9)&=6+[(-15)+(-9)] & &  \text{Distributive property}\\ &=6+(-24) & &  \text{Simplify}\\ &=-18 & &  \text{Simplify}\\ \end{align*}\)
• \(\begin{align*} \dfrac{4}{7}\times\left(\dfrac{2}{3}\times\dfrac{7}{4}\right)&=\dfrac{4}{7}\times\left(\dfrac{7}{4}\times\dfrac{2}{3}\right) & &  \text{Commutative property of multiplication}\\ &=\left(\dfrac{4}{7}\times\dfrac{7}{4}\right)\times\dfrac{2}{3} & &  \text{Associative property of multiplication}\\ &=1\times\dfrac{2}{3} & &  \text{Inverse property of multiplication}\\ &=\dfrac{2}{3} & &  \text{Identity property of multiplication}\\ \end{align*}\)
• \(\begin{align*} 100\times[0.75+(-2.38)]&=100\times0.75+100\times(-2.38) & &  \text{Distributive property}\\ &=75+(-238) & &  \text{Simplify}\\ &=-163 & &  \text{Simplify} \end{align*}\)

Exercise \(\PageIndex{7}\)

• \(\left(-\dfrac{23}{5}\right)\times\left[11\times\left(-\dfrac{5}{23}\right)\right]\)
• \(5\times(6.2+0.4)\)
• \(18-(7-15)\)
• \(\dfrac{17}{18}+\left[\dfrac{4}{9}+\left(-\dfrac{17}{18}\right)\right]\)
• \(6\times(-3)+6\times3\)
• \(11\), commutative property of multiplication
• \(33\), distributive property
• \(26\), distributive property
• \(\dfrac{4}{9}\) ,  commutative property of addition, associative property of addition, inverse property of addition, identity property of addition
• \(0\),  distributive property, inverse property of addition, identity property of addition

Evaluating Algebraic Expressions

So far, the mathematical expressions we have seen have involved real numbers only. In mathematics, we may see expressions such as \(x +5\), \(\dfrac{4}{3}\pi r^3\), or \(\sqrt{2m^3 n^2}\). In the expression \(x +5\), \(5\) is called a constant because it does not vary and \(x\) is called a variable because it does. (In naming the variable, ignore any exponents or radicals containing the variable.) An algebraic expression is a collection of constants and variables joined together by the algebraic operations of addition, subtraction, multiplication, and division.

We have already seen some real number examples of exponential notation, a shorthand method of writing products of the same factor. When variables are used, the constants and variables are treated the same way.

\[\begin{align*} (-3)^5 &=(-3)\times(-3)\times(-3)\times(-3)\times(-3)\Rightarrow x^5=x\times x\times x\times x\times x\\ (2\times7)^3&=(2\times7)\times(2\times7)\times(2\times7)\qquad \; \; \Rightarrow (yz)^3=(yz)\times(yz)\times(yz) \end{align*}\]

In each case, the exponent tells us how many factors of the base to use, whether the base consists of constants or variables.

Any variable in an algebraic expression may take on or be assigned different values. When that happens, the value of the algebraic expression changes. To evaluate an algebraic expression means to determine the value of the expression for a given value of each variable in the expression. Replace each variable in the expression with the given value, then simplify the resulting expression using the order of operations. If the algebraic expression contains more than one variable, replace each variable with its assigned value and simplify the expression as before.

Example \(\PageIndex{9}\): Describing Algebraic Expressions

List the constants and variables for each algebraic expression.

• \(\dfrac{4}{3}\pi r^3\)
• \(\sqrt{2m^3 n^2}\)

Exercise \(\PageIndex{8}\)

• \(2(L + W)\)

Example \(\PageIndex{10}\): Evaluating an Algebraic Expression at Different Values

Evaluate the expression \(2x−7\) for each value for \(x\).

• \(x=−4\)
• Substitute \(0\) for \(x\). \[\begin{align*} 2x-7 &= 2(0)-7 \\ &= 0-7\\ &= -7\\ \end{align*}\]
• Substitute \(1\) for \(x\). \[\begin{align*} 2x-7 &= 2(1)-7 \\ &= 2-7\\ &= -5\\ \end{align*}\]
• Substitute \(\dfrac{1}{2}\) for \(x\). \[\begin{align*} 2x-7 &= 2\left (\dfrac{1}{2} \right )-7 \\ &= 1-7\\ &= -6\\ \end{align*}\]
• Substitute \(-4\) for \(x\). \[\begin{align*} 2x-7 &= 2(-4)-7 \\ &= -8-7\\ &= -15\\ \end{align*}\]

Exercise \(\PageIndex{9}\)

Evaluate the expression \(11−3y\) for each value for \(y\).

• \(y=\dfrac{2}{3}\)
• \(y=−5\)

Example \(\PageIndex{11}\): Evaluating Algebraic Expressions

Evaluate each expression for the given values.

• ​\(x+5\) for \(x=-5\)
• \(\dfrac{t}{2t-1}\) for \(t=10\)
• \(\dfrac{4}{3}\pi r^3\) for \(r=5\)
• \(a+ab+b\) for \(a=11\), \(b=-8\)
• \(\sqrt{2m^3 n^2}\) for \(m=2\), \(n=3\)
• Substitute \(-5\) for \(x\). \[\begin{align*} x+5 &= (-5)+5 \\ &= 0\\ \end{align*}\]
• Substitute \(10\) for \(t\). \[\begin{align*} \dfrac{t}{2t-1} &= \dfrac{(10)}{2(10)-1} \\ &= \dfrac{10}{20-1}\\ &= \dfrac{10}{19}\\ \end{align*}\]
• Substitute \(5\) for \(r\) . \[\begin{align*} \dfrac{4}{3} \pi r^3 &= \dfrac{4}{3}\pi (5)^3 \\ &= \dfrac{4}{3}\pi (125)\\ &= \dfrac{500}{3}\pi\\ \end{align*}\]
• Substitute \(11\) for \(a\) and \(-8\) for \(b\) . \[\begin{align*} a+ab+b &= (11)+(11)(-8)+(-8) \\ &= 11-88-8 \\ &= -85\\ \end{align*}\]
• Substitute \(2\) for \(m\) and \(3\) for \(n\). \[\begin{align*} \sqrt{2m^3 n^2} &= \sqrt{2(2)^3 (3)^2} \\ &= \sqrt{2(8)(9)} \\ &= \sqrt{144} \\ &= 12 \end{align*}\]

Exercise \(\PageIndex{10}\)

• \(\dfrac{y+3}{y-3}\) for \(y=5\)
• \(7-2t\) for \(t=-2\)
• \(\dfrac{1}{3}\pi r^2\) for \(r=11\)
• \((p^2 q)^3\) for \(p=-2\), \(q=3\)
• \(4(m-n)-5(n-m)\) for \(m=\dfrac{2}{3}\) \(n=\dfrac{1}{3}\)
• \(\dfrac{121}{3}\pi\)

An equation is a mathematical statement indicating that two expressions are equal. The expressions can be numerical or algebraic. The equation is not inherently true or false, but only a proposition. The values that make the equation true, the solutions, are found using the properties of real numbers and other results. For example, the equation \(2x +1= 7\) has the unique solution of \(3\) because when we substitute \(3\) for \(x\) in the equation, we obtain the true statement \(2(3)+1=7\).

A formula is an equation expressing a relationship between constant and variable quantities. Very often, the equation is a means of finding the value of one quantity (often a single variable) in terms of another or other quantities. One of the most common examples is the formula for finding the area \(A\) of a circle in terms of the radius \(r\) of the circle: \( A= \pi r^2\). For any value of \(r\), the area \(A\) can be found by evaluating the expression \(\pi r^2\).

Example \(\PageIndex{12}\): Using a Formula

A right circular cylinder with radius \(r\) and height \(h\) has the surface area \(S\) (in square units) given by the formula \(S=2\pi r(r+h)\). See Figure \(\PageIndex{3}\). Find the surface area of a cylinder with radius \(6\) in. and height \(9\) in. Leave the answer in terms of \(\pi\).

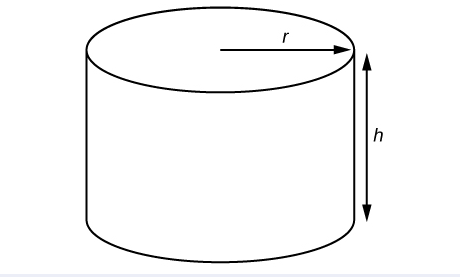
Evaluate the expression \(2\pi r(r+h)\) for \(r=6\) and \(h=9\).

\[\begin{align*} S &= 2\pi r(r+h) \\ &= 2\pi (6)[(6)+(9)] \\ &= 2\pi(6)(15) \\ &= 180\pi \end{align*}\]

The surface area is \(180\pi\) square inches.

Exercise \(\PageIndex{11}\)

A photograph with length \(L\) and width \(W\) is placed in a matte of width \(8\) centimeters (cm). The area of the matte (in square centimeters, or \(cm^2\) is found to be \(A=(L+16)(W+16) - L\)⋅W .See Figure \(\PageIndex{4}\). Find the area of a matte for a photograph with length \(32\)cm and width \(24\)cm.

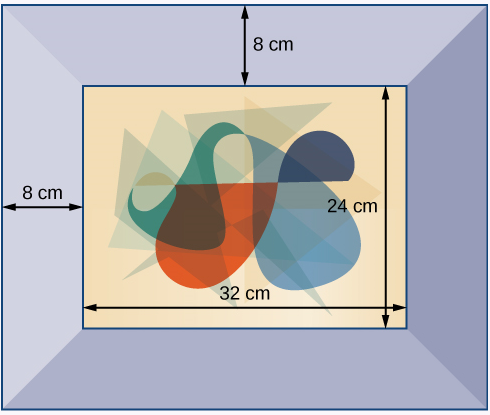
\(1152cm^2\)

Simplifying Algebraic Expressions

Sometimes we can simplify an algebraic expression to make it easier to evaluate or to use in some other way. To do so, we use the properties of real numbers. We can use the same properties in formulas because they contain algebraic expressions.

Example \(\PageIndex{13}\): Simplifying Algebraic Expressions

Simplify each algebraic expression.

• \(3x-2y+x-3y-7\)
• \(2r-5(3-r)+4\)
• \(\left(4t-\dfrac{5}{4}s\right)-\left(\dfrac{2}{3}t+2s\right)\)
• \(2mn-5m+3mn+n\)
• \[\begin{align*} 3x-2y+x-3y-7&=3x+x-2y-3y-7 && \qquad \text{Commutative property of addition}\\ &=4x-5y-7 && \qquad \text{Simplify}\\ \end{align*}\]
• \[\begin{align*} 2r-5(3-r)+4&=2r-15+5r+4 && \qquad \qquad \qquad \text {Distributive property}\\ &=2r+5y-15+4 && \qquad \qquad \qquad \text{Commutative property of addition}\\ &=7r-11 && \qquad \qquad \qquad \text{Simplify}\\ \end{align*}\]
• \[\begin{align*} \left(4t-\dfrac{5}{4}s\right)-\left(\dfrac{2}{3}t+2s\right)&=4t-\dfrac{5}{4}s-\dfrac{2}{3}t-2s && \qquad \text{Distributive property}\\ &=4t-\dfrac{2}{3}t-\dfrac{5}{4}s-2s && \qquad \text{Commutative property of addition}\\ &=\dfrac{10}{3}t-\dfrac{13}{4}s && \qquad \text{Simplify}\\ \end{align*}\]
• \[\begin{align*} 2mn-5m+3mn+n&=2mn+3mn-5m+n && \qquad \text{Commutative property of addition}\\ &=5mn-5m+n && \qquad \text{Simplify}\\ \end{align*}\]

Exercise \(\PageIndex{12}\)

• \(\dfrac{2}{3}y−2\left(\dfrac{4}{3}y+z\right)\)
• \(\dfrac{5}{t}−2−\dfrac{3}{t}+1\)
• \(4p(q−1)+q(1−p)\)
• \(9r−(s+2r)+(6−s)\)
• \(−2y−2z\) or \(−2(y+z)\)
• \(\dfrac{2}{t}−1\)
• \(3pq−4p+q\)
• \(7r−2s+6\)

Example \(\PageIndex{14}\): Simplifying a Formula

A rectangle with length \(L\) and width \(W\) has a perimeter \(P\) given by \(P =L+W+L+W\). Simplify this expression.

\[\begin{align*} P &=L+W+L+W\\ P &=L+L+W+W && \qquad \text{Commutative property of addition}\\ P &=2L+2W && \qquad \text{Simplify}\\ P &=2(L+W) && \qquad \text{Distributive property} \end{align*}\]

Exercise \(\PageIndex{13}\)

If the amount \(P\) is deposited into an account paying simple interest \(r\) for time \(t\), the total value of the deposit \(A\) is given by \(A =P+Prt\). Simplify the expression. (This formula will be explored in more detail later in the course.)

\(A=P(1+rt)\)

Access these online resources for additional instruction and practice with real numbers.

• Simplify an Expression
• Evaluate an Expression1
• Evaluate an Expression2

Key Concepts

• Rational numbers may be written as fractions or terminating or repeating decimals. See Example and Example .
• Determine whether a number is rational or irrational by writing it as a decimal. See Example .
• The rational numbers and irrational numbers make up the set of real numbers. See Example . A number can be classified as natural, whole, integer, rational, or irrational. See Example .
• The order of operations is used to evaluate expressions. See Example .
• The real numbers under the operations of addition and multiplication obey basic rules, known as the properties of real numbers. These are the commutative properties, the associative properties, the distributive property, the identity properties, and the inverse properties. See Example .
• Algebraic expressions are composed of constants and variables that are combined using addition, subtraction, multiplication, and division. See Example . They take on a numerical value when evaluated by replacing variables with constants. See Example , Example , and Example
• Formulas are equations in which one quantity is represented in terms of other quantities. They may be simplified or evaluated as any mathematical expression. See Example and Example .

Supplemental Help videos

Introduction to order of operations:

Homework Exercises 1.1

The following WeBWorK problems will be auto-graded. After submitting them, complete the problems that follow on paper to submit in class. Make sure to write down essential information from the problems and all of your work including short explanations. Leave space on your paper for instructor feedback.

ADAPT \(\PageIndex{1}\)

ADAPT \(\PageIndex{2}\)

ADAPT \(\PageIndex{3}\)

 Written Homework

1.   What do the Associative Properties allow us to do when following the order of operations? Explain your answer with examples.

2.   Simplify \(-2\times{[16\div{(8-4)^2}]^2}\)

3.   Simplify \(4^2-25\times{\frac{1}{5}}\)

4.   Simplify \(9-18\div{3^2}\)

5 .  Solve \(4z-2z(1+4)-36\) for \(z=5\)

6.   Simplify \(8b-4b(3)+1\)

7.   Simplify \(18y-2(1+7y)\)

8.   Simplify \(9x+4x(2+5)-4(2x+3x)\)

9.   Simplify \(\frac{a}{2^3}(64)-12a\div{6}\)

10.  Jessica and her roommate, Adriana, have decided to share a change jar for joint expenses. Jessica put her loose change in the jar first, and then Adriana put her change in the jar. We know that it does not matter in which order the change was added to the jar. What property of addition describes this fact?

11.  If a whole number is not a natural number, what must the number be?

12. Simplify the expression and state whether the number is real or not real. If it is real, state whether the number is rational or irrational: \(\sqrt{-18-4(5)(-1)}\).

13.   What property of real numbers would simplify the following expression: \(4+7(x-1)\)?

The Real Numbers (Pre-Algebra Curriculum - Unit 1) | All Things Algebra®

• Google Apps™

What educators are saying

Also included in.

Description

This Real Numbers Unit Bundle includes guided notes, homework assignments, three quizzes, a study guide, and a unit test that cover the following topics:

• Integers and Integer Operations

• Absolute Value

• Simplifying Fractions

• Converting Fractions, Decimals, and Percents

• Adding and Subtracting Fractions

• Multiplying and Dividing Fractions

• Exponents

• Zero Exponent and Negative Exponents

• Perfect Squares and Perfect Cubes

• Square Roots and Cube Roots

• Scientific Notation

• Comparing & Ordering Number Forms

• Order of Operations

• Evaluating Expressions

• The Real Number System

• Properties

ADDITIONAL COMPONENTS INCLUDED:

(1) Links to Instructional Videos: Links to videos of each lesson in the unit are included. Videos were created by fellow teachers for their students using the guided notes and shared in March 2020 when schools closed with no notice.  Please watch through first before sharing with your students. Many teachers still use these in emergency substitute situations. (2) Editable Assessments: Editable versions of each quiz and the unit test are included. PowerPoint is required to edit these files. Individual problems can be changed to create multiple versions of the assessment. The layout of the assessment itself is not editable. If your Equation Editor is incompatible with mine (I use MathType), simply delete my equation and insert your own.

(3) Google Slides Version of the PDF: The second page of the Video links document contains a link to a Google Slides version of the PDF. Each page is set to the background in Google Slides. There are no text boxes;  this is the PDF in Google Slides.  I am unable to do text boxes at this time but hope this saves you a step if you wish to use it in Slides instead! 

This resource is included in the following bundle(s):

Pre-Algebra Curriculum

More Pre-Algebra Units:

Unit 2 – Algebraic Expressions

Unit 3 – Equations and Inequalities

Unit 4 – Ratios, Proportions, and Percents

Unit 5 – Functions and Linear Representations

Unit 6 – Systems of Equations

Unit 7 – Geometry

Unit 8 – Measurement: Area and Volume

Unit 9 – Probability and Statistics

LICENSING TERMS: This purchase includes a license for one teacher only for personal use in their classroom. Licenses are non-transferable , meaning they can not be passed from one teacher to another. No part of this resource is to be shared with colleagues or used by an entire grade level, school, or district without purchasing the proper number of licenses. If you are a coach, principal, or district interested in transferable licenses to accommodate yearly staff changes, please contact me for a quote at [email protected].

COPYRIGHT TERMS: This resource may not be uploaded to the internet in any form, including classroom/personal websites or network drives, unless the site is password protected and can only be accessed by students.

© All Things Algebra (Gina Wilson), 2012-present

Questions & Answers

All things algebra.

• We're hiring
• Help & FAQ
• Privacy policy
• Student privacy
• Terms of service
• Tell us what you think

• Abby Reinke Elementary School
• Alamos Elementary School
• Bella Vista Middle School
• Chaparral High School
• Crowne Hill Elementary School
• Erle Stanley Gardner Middle School
• French Valley Elementary School
• Great Oak High School
• Helen Hunt Jackson Elementary School
• Home INstead Innovation Academy
• James L. Day Middle School
• Margarita Middle School
• Nicolas Valley Elementary School
• Paloma Elementary School
• Pauba Valley Elementary School
• Rancho Elementary School
• Rancho Vista High School
• Red Hawk Elementary School
• Susan H. Nelson School
• Susan LaVorgna Elementary School
• Temecula Elementary School
• Temecula Luiseño Elementary School
• Temecula Middle School
• Temecula Valley High School
• Tony Tobin Elementary School
• Vail Elementary School
• Vail Ranch Middle School
• Vintage Hills Elementary School
• Ysabel Barnett Elementary School
• Summit Academy
• Temecula Valley Adult School

One Heart One Mind

• M8 Unit 1 - Real Number System

Triggs, Michelle

Page navigation.

• After-School Help Schedule, Expectations & Policies, and Supplies List
• Grades & Grading Policies
• The Parent Zone
• Questions or Feedback? |
• Web Community Manager Privacy Policy (Updated) |

• Kindergarten
• Greater Than Less Than
• Measurement
• Multiplication
• Place Value
• Subtraction
• Punctuation
• 1st Grade Reading
• 2nd Grade Reading
• 3rd Grade Reading
• Cursive Writing

Unit 1 Algebra Basics Homework 1 The Real Numbers

Unit 1 Algebra Basics Homework 1 The Real Numbers - Displaying top 8 worksheets found for this concept.

Some of the worksheets for this concept are Unit 1 real number system homework, Lesson 1 classification and real numbers, Just the maths, Order of operations, Unit 1 the real number system, Prentice hall mathematics courses 1 3, Two step equations date period, Coordinate geometry mathematics 1.

Found worksheet you are looking for? To download/print, click on pop-out icon or print icon to worksheet to print or download. Worksheet will open in a new window. You can & download or print using the browser document reader options.

1. Unit 1 Real Number System Homework

2. lesson 1 (classification and real numbers), 3. ''just the maths'', 4. order of operations -, 5. unit 1: the real number system, 6. prentice hall mathematics courses 1-3, 7. two-step equations date period, 8. coordinate geometry mathematics 1 -.