problem solving for research

Problem Solving

• Reference work entry
• pp 2680–2683
• Cite this reference work entry

• David H. Jonassen 2 &
• Woei Hung 3  

1876 Accesses

12 Citations

Cognition ; Problem typology ; Problem-based learning ; Problems ; Reasoning

Problem solving is the process of constructing and applying mental representations of problems to finding solutions to those problems that are encountered in nearly every context.

Theoretical Background

Problem solving is the process of articulating solutions to problems. Problems have two critical attributes. First, a problem is an unknown in some context. That is, there is a situation in which there is something that is unknown (the difference between a goal state and a current state). Those situations vary from algorithmic math problems to vexing and complex social problems, such as violence in society (see Problem Typology ). Second, finding or solving for the unknown must have some social, cultural, or intellectual value. That is, someone believes that it is worth finding the unknown. If no one perceives an unknown or a need to determine an unknown, there is no perceived problem. Finding...

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Durable hardcover edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Bransford, J., & Stein, B. S. (1984). The IDEAL problem solver: A guide for improving thinking, learning, and creativity . New York: WH Freeman.

Google Scholar  

Frensch, P. A., & Funke, J. (Eds.). (1995). Complex problem solving: The European perspective . Hillsdale: Erlbaum.

Gick, M. L., & Holyoak, K. J. (1983). Schema induction and analogical transfer. Cognitive Psychology, 15 , 1–38.

Article   Google Scholar  

Jonassen, D. H. (2010). Learning to solve problems: A handbook . New York: Routledge.

Jonassen, D. H., & Hung, W. (2008). All problems are not equal: Implications for PBL. Interdisciplinary Journal of Problem-Based Learning, 2 (2), 6–28.

Jonassen, D. H. (2000). Toward a design theory of problem solving. Educational Technology: Research & Development, 48 (4), 63–85.

Jonassen, D. H. (2011). Learning to solve problems: A handbook for designing problem-solving learning environments . New York: Routledge.

Klein, G. A. (1998). Sources of power: How people make decisions . Cambridge, MA: MIT Press.

Lehman, D., Lempert, R., & Nisbett, R. E. (1988). The effects of graduate training on reasoning: Formal discipline and thinking about everyday-life events. Educational Psychologist, 43 , 431–442.

Newell, A., & Simon, H. (1972). Human problem solving . Englewood Cliffs: Prentice Hall.

Rumelhart, D. E., & Norman, D. A. (1988). Representation in memory. In R. C. Atkinson, R. J. Herrnstein, G. Lindzey, & R. D. Luce (Eds.), Steven’s handbook of experimental psychology (Learning and cognition 2nd ed., Vol. 2, pp. 511–587). New York: Wiley.

Sinnott, J. D. (1989). Everyday problem solving: Theory and applications (pp. 72–99). New York: Praeger.

Wood, P. K. (1983). Inquiring systems and problem structures: Implications for cognitive development. Human Development, 26 , 249–265.

Download references

Author information

Authors and affiliations.

School of Information Science and Learning Technologies, University of Missouri, 221C Townsend Hall, 65211, Columbia, MO, USA

Dr. David H. Jonassen

College of Education and Human Development, University of North Dakota, 231 Centennial Drive, Stop 7189, 58202, Grand Forks, ND, USA

Dr. Woei Hung

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to David H. Jonassen .

Editor information

Editors and affiliations.

Faculty of Economics and Behavioral Sciences, Department of Education, University of Freiburg, 79085, Freiburg, Germany

Norbert M. Seel

Rights and permissions

Reprints and permissions

Copyright information

© 2012 Springer Science+Business Media, LLC

About this entry

Cite this entry.

Jonassen, D.H., Hung, W. (2012). Problem Solving. In: Seel, N.M. (eds) Encyclopedia of the Sciences of Learning. Springer, Boston, MA. https://doi.org/10.1007/978-1-4419-1428-6_208

Download citation

DOI : https://doi.org/10.1007/978-1-4419-1428-6_208

Publisher Name : Springer, Boston, MA

Print ISBN : 978-1-4419-1427-9

Online ISBN : 978-1-4419-1428-6

eBook Packages : Humanities, Social Sciences and Law

Share this entry

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

• SUGGESTED TOPICS
• The Magazine
• Newsletters
• Managing Yourself
• Managing Teams
• Work-life Balance
• The Big Idea
• Data & Visuals
• Reading Lists
• Case Selections
• HBR Learning
• Topic Feeds
• Account Settings
• Email Preferences

How to Solve Problems

• Laura Amico

To bring the best ideas forward, teams must build psychological safety.

Teams today aren’t just asked to execute tasks: They’re called upon to solve problems. You’d think that many brains working together would mean better solutions, but the reality is that too often problem-solving teams fall victim to inefficiency, conflict, and cautious conclusions. The two charts below will help your team think about how to collaborate better and come up with the best solutions for the thorniest challenges.

• Laura Amico is a former senior editor at Harvard Business Review.

Partner Center

• Search Menu
• Sign in through your institution
• Browse content in Arts and Humanities
• Browse content in Archaeology
• Anglo-Saxon and Medieval Archaeology
• Archaeological Methodology and Techniques
• Archaeology by Region
• Archaeology of Religion
• Archaeology of Trade and Exchange
• Biblical Archaeology
• Contemporary and Public Archaeology
• Environmental Archaeology
• Historical Archaeology
• History and Theory of Archaeology
• Industrial Archaeology
• Landscape Archaeology
• Mortuary Archaeology
• Prehistoric Archaeology
• Underwater Archaeology
• Urban Archaeology
• Zooarchaeology
• Browse content in Architecture
• Architectural Structure and Design
• History of Architecture
• Residential and Domestic Buildings
• Theory of Architecture
• Browse content in Art
• Art Subjects and Themes
• History of Art
• Industrial and Commercial Art
• Theory of Art
• Biographical Studies
• Byzantine Studies
• Browse content in Classical Studies
• Classical History
• Classical Philosophy
• Classical Mythology
• Classical Literature
• Classical Reception
• Classical Art and Architecture
• Classical Oratory and Rhetoric
• Greek and Roman Epigraphy
• Greek and Roman Law
• Greek and Roman Archaeology
• Greek and Roman Papyrology
• Late Antiquity
• Religion in the Ancient World
• Digital Humanities
• Browse content in History
• Colonialism and Imperialism
• Diplomatic History
• Environmental History
• Genealogy, Heraldry, Names, and Honours
• Genocide and Ethnic Cleansing
• Historical Geography
• History by Period
• History of Agriculture
• History of Education
• History of Emotions
• History of Gender and Sexuality
• Industrial History
• Intellectual History
• International History
• Labour History
• Legal and Constitutional History
• Local and Family History
• Maritime History
• Military History
• National Liberation and Post-Colonialism
• Oral History
• Political History
• Public History
• Regional and National History
• Revolutions and Rebellions
• Slavery and Abolition of Slavery
• Social and Cultural History
• Theory, Methods, and Historiography
• Urban History
• World History
• Browse content in Language Teaching and Learning
• Language Learning (Specific Skills)
• Language Teaching Theory and Methods
• Browse content in Linguistics
• Applied Linguistics
• Cognitive Linguistics
• Computational Linguistics
• Forensic Linguistics
• Grammar, Syntax and Morphology
• Historical and Diachronic Linguistics
• History of English
• Language Acquisition
• Language Variation
• Language Families
• Language Evolution
• Language Reference
• Lexicography
• Linguistic Theories
• Linguistic Typology
• Linguistic Anthropology
• Phonetics and Phonology
• Psycholinguistics
• Sociolinguistics
• Translation and Interpretation
• Writing Systems
• Browse content in Literature
• Bibliography
• Children's Literature Studies
• Literary Studies (Asian)
• Literary Studies (European)
• Literary Studies (Eco-criticism)
• Literary Studies (Modernism)
• Literary Studies (Romanticism)
• Literary Studies (American)
• Literary Studies - World
• Literary Studies (1500 to 1800)
• Literary Studies (19th Century)
• Literary Studies (20th Century onwards)
• Literary Studies (African American Literature)
• Literary Studies (British and Irish)
• Literary Studies (Early and Medieval)
• Literary Studies (Fiction, Novelists, and Prose Writers)
• Literary Studies (Gender Studies)
• Literary Studies (Graphic Novels)
• Literary Studies (History of the Book)
• Literary Studies (Plays and Playwrights)
• Literary Studies (Poetry and Poets)
• Literary Studies (Postcolonial Literature)
• Literary Studies (Queer Studies)
• Literary Studies (Science Fiction)
• Literary Studies (Travel Literature)
• Literary Studies (War Literature)
• Literary Studies (Women's Writing)
• Literary Theory and Cultural Studies
• Mythology and Folklore
• Shakespeare Studies and Criticism
• Browse content in Media Studies
• Browse content in Music
• Applied Music
• Dance and Music
• Ethics in Music
• Ethnomusicology
• Gender and Sexuality in Music
• Medicine and Music
• Music Cultures
• Music and Religion
• Music and Culture
• Music and Media
• Music Education and Pedagogy
• Music Theory and Analysis
• Musical Scores, Lyrics, and Libretti
• Musical Structures, Styles, and Techniques
• Musicology and Music History
• Performance Practice and Studies
• Race and Ethnicity in Music
• Sound Studies
• Browse content in Performing Arts
• Browse content in Philosophy
• Aesthetics and Philosophy of Art
• Epistemology
• Feminist Philosophy
• History of Western Philosophy
• Metaphysics
• Moral Philosophy
• Non-Western Philosophy
• Philosophy of Science
• Philosophy of Action
• Philosophy of Law
• Philosophy of Religion
• Philosophy of Language
• Philosophy of Mind
• Philosophy of Perception
• Philosophy of Mathematics and Logic
• Practical Ethics
• Social and Political Philosophy
• Browse content in Religion
• Biblical Studies
• Christianity
• East Asian Religions
• History of Religion
• Judaism and Jewish Studies
• Qumran Studies
• Religion and Education
• Religion and Health
• Religion and Politics
• Religion and Science
• Religion and Law
• Religion and Art, Literature, and Music
• Religious Studies
• Browse content in Society and Culture
• Cookery, Food, and Drink
• Cultural Studies
• Customs and Traditions
• Ethical Issues and Debates
• Hobbies, Games, Arts and Crafts
• Lifestyle, Home, and Garden
• Natural world, Country Life, and Pets
• Popular Beliefs and Controversial Knowledge
• Sports and Outdoor Recreation
• Technology and Society
• Travel and Holiday
• Visual Culture
• Browse content in Law
• Arbitration
• Browse content in Company and Commercial Law
• Commercial Law
• Company Law
• Browse content in Comparative Law
• Systems of Law
• Competition Law
• Browse content in Constitutional and Administrative Law
• Government Powers
• Judicial Review
• Local Government Law
• Military and Defence Law
• Parliamentary and Legislative Practice
• Construction Law
• Contract Law
• Browse content in Criminal Law
• Criminal Procedure
• Criminal Evidence Law
• Sentencing and Punishment
• Employment and Labour Law
• Environment and Energy Law
• Browse content in Financial Law
• Banking Law
• Insolvency Law
• History of Law
• Human Rights and Immigration
• Intellectual Property Law
• Browse content in International Law
• Private International Law and Conflict of Laws
• Public International Law
• IT and Communications Law
• Jurisprudence and Philosophy of Law
• Law and Politics
• Law and Society
• Browse content in Legal System and Practice
• Courts and Procedure
• Legal Skills and Practice
• Primary Sources of Law
• Regulation of Legal Profession
• Medical and Healthcare Law
• Browse content in Policing
• Criminal Investigation and Detection
• Police and Security Services
• Police Procedure and Law
• Police Regional Planning
• Browse content in Property Law
• Personal Property Law
• Study and Revision
• Terrorism and National Security Law
• Browse content in Trusts Law
• Wills and Probate or Succession
• Browse content in Medicine and Health
• Browse content in Allied Health Professions
• Arts Therapies
• Clinical Science
• Dietetics and Nutrition
• Occupational Therapy
• Operating Department Practice
• Physiotherapy
• Radiography
• Speech and Language Therapy
• Browse content in Anaesthetics
• General Anaesthesia
• Neuroanaesthesia
• Browse content in Clinical Medicine
• Acute Medicine
• Cardiovascular Medicine
• Clinical Genetics
• Clinical Pharmacology and Therapeutics
• Dermatology
• Endocrinology and Diabetes
• Gastroenterology
• Genito-urinary Medicine
• Geriatric Medicine
• Infectious Diseases
• Medical Oncology
• Medical Toxicology
• Pain Medicine
• Palliative Medicine
• Rehabilitation Medicine
• Respiratory Medicine and Pulmonology
• Rheumatology
• Sleep Medicine
• Sports and Exercise Medicine
• Clinical Neuroscience
• Community Medical Services
• Critical Care
• Emergency Medicine
• Forensic Medicine
• Haematology
• History of Medicine
• Browse content in Medical Dentistry
• Oral and Maxillofacial Surgery
• Paediatric Dentistry
• Restorative Dentistry and Orthodontics
• Surgical Dentistry
• Medical Ethics
• Browse content in Medical Skills
• Clinical Skills
• Communication Skills
• Nursing Skills
• Surgical Skills
• Medical Statistics and Methodology
• Browse content in Neurology
• Clinical Neurophysiology
• Neuropathology
• Nursing Studies
• Browse content in Obstetrics and Gynaecology
• Gynaecology
• Occupational Medicine
• Ophthalmology
• Otolaryngology (ENT)
• Browse content in Paediatrics
• Neonatology
• Browse content in Pathology
• Chemical Pathology
• Clinical Cytogenetics and Molecular Genetics
• Histopathology
• Medical Microbiology and Virology
• Patient Education and Information
• Browse content in Pharmacology
• Psychopharmacology
• Browse content in Popular Health
• Caring for Others
• Complementary and Alternative Medicine
• Self-help and Personal Development
• Browse content in Preclinical Medicine
• Cell Biology
• Molecular Biology and Genetics
• Reproduction, Growth and Development
• Primary Care
• Professional Development in Medicine
• Browse content in Psychiatry
• Addiction Medicine
• Child and Adolescent Psychiatry
• Forensic Psychiatry
• Learning Disabilities
• Old Age Psychiatry
• Psychotherapy
• Browse content in Public Health and Epidemiology
• Epidemiology
• Public Health
• Browse content in Radiology
• Clinical Radiology
• Interventional Radiology
• Nuclear Medicine
• Radiation Oncology
• Reproductive Medicine
• Browse content in Surgery
• Cardiothoracic Surgery
• Gastro-intestinal and Colorectal Surgery
• General Surgery
• Neurosurgery
• Paediatric Surgery
• Peri-operative Care
• Plastic and Reconstructive Surgery
• Surgical Oncology
• Transplant Surgery
• Trauma and Orthopaedic Surgery
• Vascular Surgery
• Browse content in Science and Mathematics
• Browse content in Biological Sciences
• Aquatic Biology
• Biochemistry
• Bioinformatics and Computational Biology
• Developmental Biology
• Ecology and Conservation
• Evolutionary Biology
• Genetics and Genomics
• Microbiology
• Molecular and Cell Biology
• Natural History
• Plant Sciences and Forestry
• Research Methods in Life Sciences
• Structural Biology
• Systems Biology
• Zoology and Animal Sciences
• Browse content in Chemistry
• Analytical Chemistry
• Computational Chemistry
• Crystallography
• Environmental Chemistry
• Industrial Chemistry
• Inorganic Chemistry
• Materials Chemistry
• Medicinal Chemistry
• Mineralogy and Gems
• Organic Chemistry
• Physical Chemistry
• Polymer Chemistry
• Study and Communication Skills in Chemistry
• Theoretical Chemistry
• Browse content in Computer Science
• Artificial Intelligence
• Computer Architecture and Logic Design
• Game Studies
• Human-Computer Interaction
• Mathematical Theory of Computation
• Programming Languages
• Software Engineering
• Systems Analysis and Design
• Virtual Reality
• Browse content in Computing
• Business Applications
• Computer Security
• Computer Games
• Computer Networking and Communications
• Digital Lifestyle
• Graphical and Digital Media Applications
• Operating Systems
• Browse content in Earth Sciences and Geography
• Atmospheric Sciences
• Environmental Geography
• Geology and the Lithosphere
• Maps and Map-making
• Meteorology and Climatology
• Oceanography and Hydrology
• Palaeontology
• Physical Geography and Topography
• Regional Geography
• Soil Science
• Urban Geography
• Browse content in Engineering and Technology
• Agriculture and Farming
• Biological Engineering
• Civil Engineering, Surveying, and Building
• Electronics and Communications Engineering
• Energy Technology
• Engineering (General)
• Environmental Science, Engineering, and Technology
• History of Engineering and Technology
• Mechanical Engineering and Materials
• Technology of Industrial Chemistry
• Transport Technology and Trades
• Browse content in Environmental Science
• Applied Ecology (Environmental Science)
• Conservation of the Environment (Environmental Science)
• Environmental Sustainability
• Environmentalist Thought and Ideology (Environmental Science)
• Management of Land and Natural Resources (Environmental Science)
• Natural Disasters (Environmental Science)
• Nuclear Issues (Environmental Science)
• Pollution and Threats to the Environment (Environmental Science)
• Social Impact of Environmental Issues (Environmental Science)
• History of Science and Technology
• Browse content in Materials Science
• Ceramics and Glasses
• Composite Materials
• Metals, Alloying, and Corrosion
• Nanotechnology
• Browse content in Mathematics
• Applied Mathematics
• Biomathematics and Statistics
• History of Mathematics
• Mathematical Education
• Mathematical Finance
• Mathematical Analysis
• Numerical and Computational Mathematics
• Probability and Statistics
• Pure Mathematics
• Browse content in Neuroscience
• Cognition and Behavioural Neuroscience
• Development of the Nervous System
• Disorders of the Nervous System
• History of Neuroscience
• Invertebrate Neurobiology
• Molecular and Cellular Systems
• Neuroendocrinology and Autonomic Nervous System
• Neuroscientific Techniques
• Sensory and Motor Systems
• Browse content in Physics
• Astronomy and Astrophysics
• Atomic, Molecular, and Optical Physics
• Biological and Medical Physics
• Classical Mechanics
• Computational Physics
• Condensed Matter Physics
• Electromagnetism, Optics, and Acoustics
• History of Physics
• Mathematical and Statistical Physics
• Measurement Science
• Nuclear Physics
• Particles and Fields
• Plasma Physics
• Quantum Physics
• Relativity and Gravitation
• Semiconductor and Mesoscopic Physics
• Browse content in Psychology
• Affective Sciences
• Clinical Psychology
• Cognitive Neuroscience
• Cognitive Psychology
• Criminal and Forensic Psychology
• Developmental Psychology
• Educational Psychology
• Evolutionary Psychology
• Health Psychology
• History and Systems in Psychology
• Music Psychology
• Neuropsychology
• Organizational Psychology
• Psychological Assessment and Testing
• Psychology of Human-Technology Interaction
• Psychology Professional Development and Training
• Research Methods in Psychology
• Social Psychology
• Browse content in Social Sciences
• Browse content in Anthropology
• Anthropology of Religion
• Human Evolution
• Medical Anthropology
• Physical Anthropology
• Regional Anthropology
• Social and Cultural Anthropology
• Theory and Practice of Anthropology
• Browse content in Business and Management
• Business Strategy
• Business History
• Business Ethics
• Business and Government
• Business and Technology
• Business and the Environment
• Comparative Management
• Corporate Governance
• Corporate Social Responsibility
• Entrepreneurship
• Health Management
• Human Resource Management
• Industrial and Employment Relations
• Industry Studies
• Information and Communication Technologies
• International Business
• Knowledge Management
• Management and Management Techniques
• Operations Management
• Organizational Theory and Behaviour
• Pensions and Pension Management
• Public and Nonprofit Management
• Strategic Management
• Supply Chain Management
• Browse content in Criminology and Criminal Justice
• Criminal Justice
• Criminology
• Forms of Crime
• International and Comparative Criminology
• Youth Violence and Juvenile Justice
• Development Studies
• Browse content in Economics
• Agricultural, Environmental, and Natural Resource Economics
• Asian Economics
• Behavioural Finance
• Behavioural Economics and Neuroeconomics
• Econometrics and Mathematical Economics
• Economic Systems
• Economic Methodology
• Economic History
• Economic Development and Growth
• Financial Markets
• Financial Institutions and Services
• General Economics and Teaching
• Health, Education, and Welfare
• History of Economic Thought
• International Economics
• Labour and Demographic Economics
• Law and Economics
• Macroeconomics and Monetary Economics
• Microeconomics
• Public Economics
• Urban, Rural, and Regional Economics
• Welfare Economics
• Browse content in Education
• Adult Education and Continuous Learning
• Care and Counselling of Students
• Early Childhood and Elementary Education
• Educational Equipment and Technology
• Educational Strategies and Policy
• Higher and Further Education
• Organization and Management of Education
• Philosophy and Theory of Education
• Schools Studies
• Secondary Education
• Teaching of a Specific Subject
• Teaching of Specific Groups and Special Educational Needs
• Teaching Skills and Techniques
• Browse content in Environment
• Applied Ecology (Social Science)
• Climate Change
• Conservation of the Environment (Social Science)
• Environmentalist Thought and Ideology (Social Science)
• Natural Disasters (Environment)
• Social Impact of Environmental Issues (Social Science)
• Browse content in Human Geography
• Cultural Geography
• Economic Geography
• Political Geography
• Browse content in Interdisciplinary Studies
• Communication Studies
• Museums, Libraries, and Information Sciences
• Browse content in Politics
• African Politics
• Asian Politics
• Chinese Politics
• Comparative Politics
• Conflict Politics
• Elections and Electoral Studies
• Environmental Politics
• European Union
• Foreign Policy
• Gender and Politics
• Human Rights and Politics
• Indian Politics
• International Relations
• International Organization (Politics)
• International Political Economy
• Irish Politics
• Latin American Politics
• Middle Eastern Politics
• Political Methodology
• Political Communication
• Political Philosophy
• Political Sociology
• Political Theory
• Political Behaviour
• Political Economy
• Political Institutions
• Politics and Law
• Politics of Development
• Public Administration
• Public Policy
• Quantitative Political Methodology
• Regional Political Studies
• Russian Politics
• Security Studies
• State and Local Government
• UK Politics
• US Politics
• Browse content in Regional and Area Studies
• African Studies
• Asian Studies
• East Asian Studies
• Japanese Studies
• Latin American Studies
• Middle Eastern Studies
• Native American Studies
• Scottish Studies
• Browse content in Research and Information
• Research Methods
• Browse content in Social Work
• Addictions and Substance Misuse
• Adoption and Fostering
• Care of the Elderly
• Child and Adolescent Social Work
• Couple and Family Social Work
• Developmental and Physical Disabilities Social Work
• Direct Practice and Clinical Social Work
• Emergency Services
• Human Behaviour and the Social Environment
• International and Global Issues in Social Work
• Mental and Behavioural Health
• Social Justice and Human Rights
• Social Policy and Advocacy
• Social Work and Crime and Justice
• Social Work Macro Practice
• Social Work Practice Settings
• Social Work Research and Evidence-based Practice
• Welfare and Benefit Systems
• Browse content in Sociology
• Childhood Studies
• Community Development
• Comparative and Historical Sociology
• Economic Sociology
• Gender and Sexuality
• Gerontology and Ageing
• Health, Illness, and Medicine
• Marriage and the Family
• Migration Studies
• Occupations, Professions, and Work
• Organizations
• Population and Demography
• Race and Ethnicity
• Social Theory
• Social Movements and Social Change
• Social Research and Statistics
• Social Stratification, Inequality, and Mobility
• Sociology of Religion
• Sociology of Education
• Sport and Leisure
• Urban and Rural Studies
• Browse content in Warfare and Defence
• Defence Strategy, Planning, and Research
• Land Forces and Warfare
• Military Administration
• Military Life and Institutions
• Naval Forces and Warfare
• Other Warfare and Defence Issues
• Peace Studies and Conflict Resolution
• Weapons and Equipment

• < Previous chapter
• Next chapter >

21 Problem Solving

Miriam Bassok, Department of Psychology, University of Washington, Seattle, WA

Laura R. Novick, Department of Psychology and Human Development, Vanderbilt University, Nashville, TN

• Published: 21 November 2012
• Cite Icon Cite
• Permissions Icon Permissions

This chapter follows the historical development of research on problem solving. It begins with a description of two research traditions that addressed different aspects of the problem-solving process: ( 1 ) research on problem representation (the Gestalt legacy) that examined how people understand the problem at hand, and ( 2 ) research on search in a problem space (the legacy of Newell and Simon) that examined how people generate the problem's solution. It then describes some developments in the field that fueled the integration of these two lines of research: work on problem isomorphs, on expertise in specific knowledge domains (e.g., chess, mathematics), and on insight solutions. Next, it presents examples of recent work on problem solving in science and mathematics that highlight the impact of visual perception and background knowledge on how people represent problems and search for problem solutions. The final section considers possible directions for future research.

People are confronted with problems on a daily basis, be it trying to extract a broken light bulb from a socket, finding a detour when the regular route is blocked, fixing dinner for unexpected guests, dealing with a medical emergency, or deciding what house to buy. Obviously, the problems people encounter differ in many ways, and their solutions require different types of knowledge and skills. Yet we have a sense that all the situations we classify as problems share a common core. Karl Duncker defined this core as follows: “A problem arises when a living creature has a goal but does not know how this goal is to be reached. Whenever one cannot go from the given situation to the desired situation simply by action [i.e., by the performance of obvious operations], then there has to be recourse to thinking” (Duncker, 1945 , p. 1). Consider the broken light bulb. The obvious operation—holding the glass part of the bulb with one's fingers while unscrewing the base from the socket—is prevented by the fact that the glass is broken. Thus, there must be “recourse to thinking” about possible ways to solve the problem. For example, one might try mounting half a potato on the broken bulb (we do not know the source of this creative solution, which is described on many “how to” Web sites).

The above definition and examples make it clear that what constitutes a problem for one person may not be a problem for another person, or for that same person at another point in time. For example, the second time one has to remove a broken light bulb from a socket, the solution likely can be retrieved from memory; there is no problem. Similarly, tying shoes may be considered a problem for 5-year-olds but not for readers of this chapter. And, of course, people may change their goal and either no longer have a problem (e.g., take the guests to a restaurant instead of fixing dinner) or attempt to solve a different problem (e.g., decide what restaurant to go to). Given the highly subjective nature of what constitutes a problem, researchers who study problem solving have often presented people with novel problems that they should be capable of solving and attempted to find regularities in the resulting problem-solving behavior. Despite the variety of possible problem situations, researchers have identified important regularities in the thinking processes by which people (a) represent , or understand, problem situations and (b) search for possible ways to get to their goal.

A problem representation is a model constructed by the solver that summarizes his or her understanding of the problem components—the initial state (e.g., a broken light bulb in a socket), the goal state (the light bulb extracted), and the set of possible operators one may apply to get from the initial state to the goal state (e.g., use pliers). According to Reitman ( 1965 ), problem components differ in the extent to which they are well defined . Some components leave little room for interpretation (e.g., the initial state in the broken light bulb example is relatively well defined), whereas other components may be ill defined and have to be defined by the solver (e.g., the possible actions one may take to extract the broken bulb). The solver's representation of the problem guides the search for a possible solution (e.g., possible attempts at extracting the light bulb). This search may, in turn, change the representation of the problem (e.g., finding that the goal cannot be achieved using pliers) and lead to a new search. Such a recursive process of representation and search continues until the problem is solved or until the solver decides to abort the goal.

Duncker ( 1945 , pp. 28–37) documented the interplay between representation and search based on his careful analysis of one person's solution to the “Radiation Problem” (later to be used extensively in research analogy, see Holyoak, Chapter 13 ). This problem requires using some rays to destroy a patient's stomach tumor without harming the patient. At sufficiently high intensity, the rays will destroy the tumor. However, at that intensity, they will also destroy the healthy tissue surrounding the tumor. At lower intensity, the rays will not harm the healthy tissue, but they also will not destroy the tumor. Duncker's analysis revealed that the solver's solution attempts were guided by three distinct problem representations. He depicted these solution attempts as an inverted search tree in which the three main branches correspond to the three general problem representations (Duncker, 1945 , p. 32). We reproduce this diagram in Figure 21.1 . The desired solution appears on the rightmost branch of the tree, within the general problem representation in which the solver aims to “lower the intensity of the rays on their way through healthy tissue.” The actual solution is to project multiple low-intensity rays at the tumor from several points around the patient “by use of lens.” The low-intensity rays will converge on the tumor, where their individual intensities will sum to a level sufficient to destroy the tumor.

A search-tree representation of one subject's solution to the radiation problem, reproduced from Duncker ( 1945 , p. 32).

Although there are inherent interactions between representation and search, some researchers focus their efforts on understanding the factors that affect how solvers represent problems, whereas others look for regularities in how they search for a solution within a particular representation. Based on their main focus of interest, researchers devise or select problems with solutions that mainly require either constructing a particular representation or finding the appropriate sequence of steps leading from the initial state to the goal state. In most cases, researchers who are interested in problem representation select problems in which one or more of the components are ill defined, whereas those who are interested in search select problems in which the components are well defined. The following examples illustrate, respectively, these two problem types.

The Bird-and-Trains problem (Posner, 1973 , pp. 150–151) is a mathematical word problem that tends to elicit two distinct problem representations (see Fig. 21.2a and b ):

Two train stations are 50 miles apart. At 2 p.m. one Saturday afternoon two trains start toward each other, one from each station. Just as the trains pull out of the stations, a bird springs into the air in front of the first train and flies ahead to the front of the second train. When the bird reaches the second train, it turns back and flies toward the first train. The bird continues to do this until the trains meet. If both trains travel at the rate of 25 miles per hour and the bird flies at 100 miles per hour, how many miles will the bird have flown before the trains meet? Fig. 21.2 Open in new tab Download slide Alternative representations of Posner's ( 1973 ) trains-and-bird problem. Adapted from Novick and Hmelo ( 1994 ).

Some solvers focus on the back-and-forth path of the bird (Fig. 21.2a ). This representation yields a problem that would be difficult for most people to solve (e.g., a series of differential equations). Other solvers focus on the paths of the trains (Fig. 21.2b ), a representation that yields a relatively easy distance-rate-time problem.

The Tower of Hanoi problem falls on the other end of the representation-search continuum. It leaves little room for differences in problem representations, and the primary work is to discover a solution path (or the best solution path) from the initial state to the goal state .

There are three pegs mounted on a base. On the leftmost peg, there are three disks of differing sizes. The disks are arranged in order of size with the largest disk on the bottom and the smallest disk on the top. The disks may be moved one at a time, but only the top disk on a peg may be moved, and at no time may a larger disk be placed on a smaller disk. The goal is to move the three-disk tower from the leftmost peg to the rightmost peg.

Figure 21.3 shows all the possible legal arrangements of disks on pegs. The arrows indicate transitions between states that result from moving a single disk, with the thicker gray arrows indicating the shortest path that connects the initial state to the goal state.

The division of labor between research on representation versus search has distinct historical antecedents and research traditions. In the next two sections, we review the main findings from these two historical traditions. Then, we describe some developments in the field that fueled the integration of these lines of research—work on problem isomorphs, on expertise in specific knowledge domains (e.g., chess, mathematics), and on insight solutions. In the fifth section, we present some examples of recent work on problem solving in science and mathematics. This work highlights the role of visual perception and background knowledge in the way people represent problems and search for problem solutions. In the final section, we consider possible directions for future research.

Our review is by no means an exhaustive one. It follows the historical development of the field and highlights findings that pertain to a wide variety of problems. Research pertaining to specific types of problems (e.g., medical problems), specific processes that are involved in problem solving (e.g., analogical inferences), and developmental changes in problem solving due to learning and maturation may be found elsewhere in this volume (e.g., Holyoak, Chapter 13 ; Smith & Ward, Chapter 23 ; van Steenburgh et al., Chapter 24 ; Simonton, Chapter 25 ; Opfer & Siegler, Chapter 30 ; Hegarty & Stull, Chapter 31 ; Dunbar & Klahr, Chapter 35 ; Patel et al., Chapter 37 ; Lowenstein, Chapter 38 ; Koedinger & Roll, Chapter 40 ).

All possible problem states for the three-disk Tower of Hanoi problem. The thicker gray arrows show the optimum solution path connecting the initial state (State #1) to the goal state (State #27).

Problem Representation: The Gestalt Legacy

Research on problem representation has its origins in Gestalt psychology, an influential approach in European psychology during the first half of the 20th century. (Behaviorism was the dominant perspective in American psychology at this time.) Karl Duncker published a book on the topic in his native German in 1935, which was translated into English and published 10 years later as the monograph On Problem-Solving (Duncker, 1945 ). Max Wertheimer also published a book on the topic in 1945, titled Productive Thinking . An enlarged edition published posthumously includes previously unpublished material (Wertheimer, 1959 ). Interestingly, 1945 seems to have been a watershed year for problem solving, as mathematician George Polya's book, How to Solve It , also appeared then (a second edition was published 12 years later; Polya, 1957 ).

The Gestalt psychologists extended the organizational principles of visual perception to the domain of problem solving. They showed that various visual aspects of the problem, as well the solver's prior knowledge, affect how people understand problems and, therefore, generate problem solutions. The principles of visual perception (e.g., proximity, closure, grouping, good continuation) are directly relevant to problem solving when the physical layout of the problem, or a diagram that accompanies the problem description, elicits inferences that solvers include in their problem representations. Such effects are nicely illustrated by Maier's ( 1930 ) nine-dot problem: Nine dots are arrayed in a 3x3 grid, and the task is to connect all the dots by drawing four straight lines without lifting one's pencil from the paper. People have difficulty solving this problem because their initial representations generally include a constraint, inferred from the configuration of the dots, that the lines should not go outside the boundary of the imaginary square formed by the outer dots. With this constraint, the problem cannot be solved (but see Adams, 1979 ). Without this constraint, the problem may be solved as shown in Figure 21.4 (though the problem is still difficult for many people; see Weisberg & Alba, 1981 ).

The nine-dot problem is a classic insight problem (see van Steenburgh et al., Chapter 24 ). According to the Gestalt view (e.g., Duncker, 1945 ; Kohler, 1925 ; Maier, 1931 ; see Ohlsson, 1984 , for a review), the solution to an insight problem appears suddenly, accompanied by an “aha!” sensation, immediately following the sudden “restructuring” of one's understanding of the problem (i.e., a change in the problem representation): “The decisive points in thought-processes, the moments of sudden comprehension, of the ‘Aha!,’ of the new, are always at the same time moments in which such a sudden restructuring of the thought-material takes place” (Duncker, 1945 , p. 29). For the nine-dot problem, one view of the required restructuring is that the solver relaxes the constraint implied by the perceptual form of the problem and realizes that the lines may, in fact, extend past the boundary of the imaginary square. Later in the chapter, we present more recent accounts of insight.

The entities that appear in a problem also tend to evoke various inferences that people incorporate into their problem representations. A classic demonstration of this is the phenomenon of functional fixedness , introduced by Duncker ( 1945 ): If an object is habitually used for a certain purpose (e.g., a box serves as a container), it is difficult to see

A solution to the nine-dot problem.

that object as having properties that would enable it to be used for a dissimilar purpose. Duncker's basic experimental paradigm involved two conditions that varied in terms of whether the object that was crucial for solution was initially used for a function other than that required for solution.

Consider the candles problem—the best known of the five “practical problems” Duncker ( 1945 ) investigated. Three candles are to be mounted at eye height on a door. On the table, for use in completing this task, are some tacks and three boxes. The solution is to tack the three boxes to the door to serve as platforms for the candles. In the control condition, the three boxes were presented to subjects empty. In the functional-fixedness condition, they were filled with candles, tacks, and matches. Thus, in the latter condition, the boxes initially served the function of container, whereas the solution requires that they serve the function of platform. The results showed that 100% of the subjects who received empty boxes solved the candles problem, compared with only 43% of subjects who received filled boxes. Every one of the five problems in this study showed a difference favoring the control condition over the functional-fixedness condition, with average solution rates across the five problems of 97% and 58%, respectively.

The function of the objects in a problem can be also “fixed” by their most recent use. For example, Birch and Rabinowitz ( 1951 ) had subjects perform two consecutive tasks. In the first task, people had to use either a switch or a relay to form an electric circuit. After completing this task, both groups of subjects were asked to solve Maier's ( 1931 ) two-ropes problem. The solution to this problem requires tying an object to one of the ropes and making the rope swing as a pendulum. Subjects could create the pendulum using either the object from the electric-circuit task or the other object. Birch and Rabinowitz found that subjects avoided using the same object for two unrelated functions. That is, those who used the switch in the first task made the pendulum using the relay, and vice versa. The explanations subjects subsequently gave for their object choices revealed that they were unaware of the functional-fixedness constraint they imposed on themselves.

In addition to investigating people's solutions to such practical problems as irradiating a tumor, mounting candles on the wall, or tying ropes, the Gestalt psychologists examined how people understand and solve mathematical problems that require domain-specific knowledge. For example, Wertheimer ( 1959 ) observed individual differences in students' learning and subsequent application of the formula for finding the area of a parallelogram (see Fig. 21.5a ). Some students understood the logic underlying the learned formula (i.e., the fact that a parallelogram can be transformed into a rectangle by cutting off a triangle from one side and pasting it onto the other side) and exhibited “productive thinking”—using the same logic to find the area of the quadrilateral in Figure 21.5b and the irregularly shaped geometric figure in Figure 21.5c . Other students memorized the formula and exhibited “reproductive thinking”—reproducing the learned solution only to novel parallelograms that were highly similar to the original one.

The psychological study of human problem solving faded into the background after the demise of the Gestalt tradition (during World War II), and problem solving was investigated only sporadically until Allen Newell and Herbert Simon's ( 1972 ) landmark book Human Problem Solving sparked a flurry of research on this topic. Newell and Simon adopted and refined Duncker's ( 1945 ) methodology of collecting and analyzing the think-aloud protocols that accompany problem solutions and extended Duncker's conceptualization of a problem solution as a search tree. However, their initial work did not aim to extend the Gestalt findings

Finding the area of ( a ) a parallelogram, ( b ) a quadrilateral, and ( c ) an irregularly shaped geometric figure. The solid lines indicate the geometric figures whose areas are desired. The dashed lines show how to convert the given figures into rectangles (i.e., they show solutions with understanding).

pertaining to problem representation. Instead, as we explain in the next section, their objective was to identify the general-purpose strategies people use in searching for a problem solution.

Search in a Problem Space: The Legacy of Newell and Simon

Newell and Simon ( 1972 ) wrote a magnum opus detailing their theory of problem solving and the supporting research they conducted with various collaborators. This theory was grounded in the information-processing approach to cognitive psychology and guided by an analogy between human and artificial intelligence (i.e., both people and computers being “Physical Symbol Systems,” Newell & Simon, 1976 ; see Doumas & Hummel, Chapter 5 ). They conceptualized problem solving as a process of search through a problem space for a path that connects the initial state to the goal state—a metaphor that alludes to the visual or spatial nature of problem solving (Simon, 1990 ). The term problem space refers to the solver's representation of the task as presented (Simon, 1978 ). It consists of ( 1 ) a set of knowledge states (the initial state, the goal state, and all possible intermediate states), ( 2 ) a set of operators that allow movement from one knowledge state to another, ( 3 ) a set of constraints, and ( 4 ) local information about the path one is taking through the space (e.g., the current knowledge state and how one got there).

We illustrate the components of a problem space for the three-disk Tower of Hanoi problem, as depicted in Figure 21.3 . The initial state appears at the top (State #1) and the goal state at the bottom right (State #27). The remaining knowledge states in the figure are possible intermediate states. The current knowledge state is the one at which the solver is located at any given point in the solution process. For example, the current state for a solver who has made three moves along the optimum solution path would be State #9. The solver presumably would know that he or she arrived at this state from State #5. This knowledge allows the solver to recognize a move that involves backtracking. The three operators in this problem are moving each of the three disks from one peg to another. These operators are subject to the constraint that a larger disk may not be placed on a smaller disk.

Newell and Simon ( 1972 ), as well as other contemporaneous researchers (e.g., Atwood & Polson, 1976 ; Greeno, 1974 ; Thomas, 1974 ), examined how people traverse the spaces of various well-defined problems (e.g., the Tower of Hanoi, Hobbits and Orcs). They discovered that solvers' search is guided by a number of shortcut strategies, or heuristics , which are likely to get the solver to the goal state without an extensive amount of search. Heuristics are often contrasted with algorithms —methods that are guaranteed to yield the correct solution. For example, one could try every possible move in the three-disk Tower of Hanoi problem and, eventually, find the correct solution. Although such an exhaustive search is a valid algorithm for this problem, for many problems its application is very time consuming and impractical (e.g., consider the game of chess).

In their attempts to identify people's search heuristics, Newell and Simon ( 1972 ) relied on two primary methodologies: think-aloud protocols and computer simulations. Their use of think-aloud protocols brought a high degree of scientific rigor to the methodology used by Duncker ( 1945 ; see Ericsson & Simon, 1980 ). Solvers were required to say out loud everything they were thinking as they solved the problem, that is, everything that went through their verbal working memory. Subjects' verbalizations—their think-aloud protocols—were tape-recorded and then transcribed verbatim for analysis. This method is extremely time consuming (e.g., a transcript of one person's solution to the cryptarithmetic problem DONALD + GERALD = ROBERT, with D = 5, generated a 17-page transcript), but it provides a detailed record of the solver's ongoing solution process.

An important caveat to keep in mind while interpreting a subject's verbalizations is that “a protocol is relatively reliable only for what it positively contains, but not for that which it omits” (Duncker, 1945 , p. 11). Ericsson and Simon ( 1980 ) provided an in-depth discussion of the conditions under which this method is valid (but see Russo, Johnson, & Stephens, 1989 , for an alternative perspective). To test their interpretation of a subject's problem solution, inferred from the subject's verbal protocol, Newell and Simon ( 1972 ) created a computer simulation program and examined whether it solved the problem the same way the subject did. To the extent that the computer simulation provided a close approximation of the solver's step-by-step solution process, it lent credence to the researcher's interpretation of the verbal protocol.

Newell and Simon's ( 1972 ) most famous simulation was the General Problem Solver or GPS (Ernst & Newell, 1969 ). GPS successfully modeled human solutions to problems as different as the Tower of Hanoi and the construction of logic proofs using a single general-purpose heuristic: means-ends analysis . This heuristic captures people's tendency to devise a solution plan by setting subgoals that could help them achieve their final goal. It consists of the following steps: ( 1 ) Identify a difference between the current state and the goal (or subgoal ) state; ( 2 ) Find an operator that will remove (or reduce) the difference; (3a) If the operator can be directly applied, do so, or (3b) If the operator cannot be directly applied, set a subgoal to remove the obstacle that is preventing execution of the desired operator; ( 4 ) Repeat steps 1–3 until the problem is solved. Next, we illustrate the implementation of this heuristic for the Tower of Hanoi problem, using the problem space in Figure 21.3 .

As can be seen in Figure 21.3 , a key difference between the initial state and the goal state is that the large disk is on the wrong peg (step 1). To remove this difference (step 2), one needs to apply the operator “move-large-disk.” However, this operator cannot be applied because of the presence of the medium and small disks on top of the large disk. Therefore, the solver may set a subgoal to move that two-disk tower to the middle peg (step 3b), leaving the rightmost peg free for the large disk. A key difference between the initial state and this new subgoal state is that the medium disk is on the wrong peg. Because application of the move-medium-disk operator is blocked, the solver sets another subgoal to move the small disk to the right peg. This subgoal can be satisfied immediately by applying the move-small-disk operator (step 3a), generating State #3. The solver then returns to the previous subgoal—moving the tower consisting of the small and medium disks to the middle peg. The differences between the current state (#3) and the subgoal state (#9) can be removed by first applying the move-medium-disk operator (yielding State #5) and then the move-small-disk operator (yielding State #9). Finally, the move-large-disk operator is no longer blocked. Hence, the solver moves the large disk to the right peg, yielding State #11.

Notice that the subgoals are stacked up in the order in which they are generated, so that they pop up in the order of last in first out. Given the first subgoal in our example, repeated application of the means-ends analysis heuristic will yield the shortest-path solution, indicated by the large gray arrows. In general, subgoals provide direction to the search and allow solvers to plan several moves ahead. By assessing progress toward a required subgoal rather than the final goal, solvers may be able to make moves that otherwise seem unwise. To take a concrete example, consider the transition from State #1 to State #3 in Figure 21.3 . Comparing the initial state to the goal state, this move seems unwise because it places the small disk on the bottom of the right peg, whereas it ultimately needs to be at the top of the tower on that peg. But comparing the initial state to the solver-generated subgoal state of having the medium disk on the middle peg, this is exactly where the small disk needs to go.

Means-ends analysis and various other heuristics (e.g., the hill-climbing heuristic that exploits the similarity, or distance, between the state generated by the next operator and the goal state; working backward from the goal state to the initial state) are flexible strategies that people often use to successfully solve a large variety of problems. However, the generality of these heuristics comes at a cost: They are relatively weak and fallible (e.g., in the means-ends solution to the problem of fixing a hole in a bucket, “Dear Liza” leads “Dear Henry” in a loop that ends back at the initial state; the lyrics of this famous song can be readily found on the Web). Hence, although people use general-purpose heuristics when they encounter novel problems, they replace them as soon as they acquire experience with and sufficient knowledge about the particular problem space (e.g., Anzai & Simon, 1979 ).

Despite the fruitfulness of this research agenda, it soon became evident that a fundamental weakness was that it minimized the importance of people's background knowledge. Of course, Newell and Simon ( 1972 ) were aware that problem solutions require relevant knowledge (e.g., the rules of logical proofs, or rules for stacking disks). Hence, in programming GPS, they supplemented every problem they modeled with the necessary background knowledge. This practice highlighted the generality and flexibility of means-ends analysis but failed to capture how people's background knowledge affects their solutions. As we discussed in the previous section, domain knowledge is likely to affect how people represent problems and, therefore, how they generate problem solutions. Moreover, as people gain experience solving problems in a particular knowledge domain (e.g., math, physics), they change their representations of these problems (e.g., Chi, Feltovich, & Glaser, 1981 ; Haverty, Koedinger, Klahr, & Alibali, 2000 ; Schoenfeld & Herrmann, 1982 ) and learn domain-specific heuristics (e.g., Polya, 1957 ; Schoenfeld, 1979 ) that trump the general-purpose strategies.

It is perhaps inevitable that the two traditions in problem-solving research—one emphasizing representation and the other emphasizing search strategies—would eventually come together. In the next section we review developments that led to this integration.

The Two Legacies Converge

Because Newell and Simon ( 1972 ) aimed to discover the strategies people use in searching for a solution, they investigated problems that minimized the impact of factors that tend to evoke differences in problem representations, of the sort documented by the Gestalt psychologists. In subsequent work, however, Simon and his collaborators showed that such factors are highly relevant to people's solutions of well-defined problems, and Simon ( 1986 ) incorporated these findings into the theoretical framework that views problem solving as search in a problem space.

In this section, we first describe illustrative examples of this work. We then describe research on insight solutions that incorporates ideas from the two legacies described in the previous sections.

Relevance of the Gestalt Ideas to the Solution of Search Problems

In this subsection we describe two lines of research by Simon and his colleagues, and by other researchers, that document the importance of perception and of background knowledge to the way people search for a problem solution. The first line of research used variants of relatively well-defined riddle problems that had the same structure (i.e., “problem isomorphs”) and, therefore, supposedly the same problem space. It documented that people's search depended on various perceptual and conceptual inferences they tended to draw from a specific instantiation of the problem's structure. The second line of research documented that people's search strategies crucially depend on their domain knowledge and on their prior experience with related problems.

Problem Isomorphs

Hayes and Simon ( 1977 ) used two variants of the Tower of Hanoi problem that, instead of disks and pegs, involved monsters and globes that differed in size (small, medium, and large). In both variants, the initial state had the small monster holding the large globe, the medium-sized monster holding the small globe, and the large monster holding the medium-sized globe. Moreover, in both variants the goal was for each monster to hold a globe proportionate to its own size. The only difference between the problems concerned the description of the operators. In one variant (“transfer”), subjects were told that the monsters could transfer the globes from one to another as long as they followed a set of rules, adapted from the rules in the original Tower of Hanoi problem (e.g., only one globe may be transferred at a time). In the other variant (“change”), subjects were told that the monsters could shrink and expand themselves according to a set of rules, which corresponded to the rules in the transfer version of the problem (e.g., only one monster may change its size at a time). Despite the isomorphism of the two variants, subjects conducted their search in two qualitatively different problem spaces, which led to solution times for the change variant being almost twice as long as those for the transfer variant. This difference arose because subjects could more readily envision and track an object that was changing its location with every move than one that was changing its size.

Recent work by Patsenko and Altmann ( 2010 ) found that, even in the standard Tower of Hanoi problem, people's solutions involve object-bound routines that depend on perception and selective attention. The subjects in their study solved various Tower of Hanoi problems on a computer. During the solution of a particular “critical” problem, the computer screen changed at various points without subjects' awareness (e.g., a disk was added, such that a subject who started with a five-disc tower ended with a six-disc tower). Patsenko and Altmann found that subjects' moves were guided by the configurations of the objects on the screen rather than by solution plans they had stored in memory (e.g., the next subgoal).

The Gestalt psychologists highlighted the role of perceptual factors in the formation of problem representations (e.g., Maier's, 1930 , nine-dot problem) but were generally silent about the corresponding implications for how the problem was solved (although they did note effects on solution accuracy). An important contribution of the work on people's solutions of the Tower of Hanoi problem and its variants was to show the relevance of perceptual factors to the application of various operators during search for a problem solution—that is, to the how of problem solving. In the next section, we describe recent work that documents the involvement of perceptual factors in how people understand and use equations and diagrams in the context of solving math and science problems.

Kotovsky, Hayes, and Simon ( 1985 ) further investigated factors that affect people's representation and search in isomorphs of the Tower of Hanoi problem. In one of their isomorphs, three disks were stacked on top of each other to form an inverted pyramid, with the smallest disc on the bottom and the largest on top. Subjects' solutions of the inverted pyramid version were similar to their solutions of the standard version that has the largest disc on the bottom and the smallest on top. However, the two versions were solved very differently when subjects were told that the discs represent acrobats. Subjects readily solved the version in which they had to place a small acrobat on the shoulders of a large one, but they refrained from letting a large acrobat stand on the shoulders of a small one. In other words, object-based inferences that draw on people's semantic knowledge affected the solution of search problems, much as they affect the solution of the ill-defined problems investigated by the Gestalt psychologists (e.g., Duncker's, 1945 , candles problem). In the next section, we describe more recent work that shows similar effects in people's solutions to mathematical word problems.

The work on differences in the representation and solution of problem isomorphs is highly relevant to research on analogical problem solving (or analogical transfer), which examines when and how people realize that two problems that differ in their cover stories have a similar structure (or a similar problem space) and, therefore, can be solved in a similar way. This research shows that minor differences between example problems, such as the use of X-rays versus ultrasound waves to fuse a broken filament of a light bulb, can elicit different problem representations that significantly affect the likelihood of subsequent transfer to novel problem analogs (Holyoak & Koh, 1987 ). Analogical transfer has played a central role in research on human problem solving, in part because it can shed light on people's understanding of a given problem and its solution and in part because it is believed to provide a window onto understanding and investigating creativity (see Smith & Ward, Chapter 23 ). We briefly mention some findings from the analogy literature in the next subsection on expertise, but we do not discuss analogical transfer in detail because this topic is covered elsewhere in this volume (Holyoak, Chapter 13 ).

Expertise and Its Development

In another line of research, Simon and his colleagues examined how people solve ecologically valid problems from various rule-governed and knowledge-rich domains. They found that people's level of expertise in such domains, be it in chess (Chase & Simon, 1973 ; Gobet & Simon, 1996 ), mathematics (Hinsley, Hayes, & Simon, 1977 ; Paige & Simon, 1966 ), or physics (Larkin, McDermott, Simon, & Simon, 1980 ; Simon & Simon, 1978 ), plays a crucial role in how they represent problems and search for solutions. This work, and the work of numerous other researchers, led to the discovery (and rediscovery, see Duncker, 1945 ) of important differences between experts and novices, and between “good” and “poor” students.

One difference between experts and novices pertains to pattern recognition. Experts' attention is quickly captured by familiar configurations within a problem situation (e.g., a familiar configuration of pieces in a chess game). In contrast, novices' attention is focused on isolated components of the problem (e.g., individual chess pieces). This difference, which has been found in numerous domains, indicates that experts have stored in memory many meaningful groups (chunks) of information: for example, chess (Chase & Simon, 1973 ), circuit diagrams (Egan & Schwartz, 1979 ), computer programs (McKeithen, Reitman, Rueter, & Hirtle, 1981 ), medicine (Coughlin & Patel, 1987 ; Myles-Worsley, Johnston, & Simons, 1988 ), basketball and field hockey (Allard & Starkes, 1991 ), and figure skating (Deakin & Allard, 1991 ).

The perceptual configurations that domain experts readily recognize are associated with stored solution plans and/or compiled procedures (Anderson, 1982 ). As a result, experts' solutions are much faster than, and often qualitatively different from, the piecemeal solutions that novice solvers tend to construct (e.g., Larkin et al., 1980 ). In effect, experts often see the solutions that novices have yet to compute (e.g., Chase & Simon, 1973 ; Novick & Sherman, 2003 , 2008 ). These findings have led to the design of various successful instructional interventions (e.g., Catrambone, 1998 ; Kellman et al., 2008 ). For example, Catrambone ( 1998 ) perceptually isolated the subgoals of a statistics problem. This perceptual chunking of meaningful components of the problem prompted novice students to self-explain the meaning of the chunks, leading to a conceptual understanding of the learned solution. In the next section, we describe some recent work that shows the beneficial effects of perceptual pattern recognition on the solution of familiar mathematics problems, as well as the potentially detrimental effects of familiar perceptual chunks to understanding and reasoning with diagrams depicting evolutionary relationships among taxa.

Another difference between experts and novices pertains to their understanding of the solution-relevant problem structure. Experts' knowledge is highly organized around domain principles, and their problem representations tend to reflect this principled understanding. In particular, they can extract the solution-relevant structure of the problems they encounter (e.g., meaningful causal relations among the objects in the problem; see Cheng & Buehner, Chapter 12 ). In contrast, novices' representations tend to be bound to surface features of the problems that may be irrelevant to solution (e.g., the particular objects in a problem). For example, Chi, Feltovich, and Glaser ( 1981 ) examined how students with different levels of physics expertise group mechanics word problems. They found that advanced graduate students grouped the problems based on the physics principles relevant to the problems' solutions (e.g., conservation of energy, Newton's second law). In contrast, undergraduates who had successfully completed an introductory course in mechanics grouped the problems based on the specific objects involved (e.g., pulley problems, inclined plane problems). Other researchers have found similar results in the domains of biology, chemistry, computer programming, and math (Adelson, 1981 ; Kindfield, 1993 / 1994 ; Kozma & Russell, 1997 ; McKeithen et al., 1981 ; Silver, 1979 , 1981 ; Weiser & Shertz, 1983 ).

The level of domain expertise and the corresponding representational differences are, of course, a matter of degree. With increasing expertise, there is a gradual change in people's focus of attention from aspects that are not relevant to solution to those that are (e.g., Deakin & Allard, 1991 ; Hardiman, Dufresne, & Mestre, 1989 ; McKeithen et al., 1981 ; Myles-Worsley et al., 1988 ; Schoenfeld & Herrmann, 1982 ; Silver, 1981 ). Interestingly, Chi, Bassok, Lewis, Reimann, and Glaser ( 1989 ) found similar differences in focus on structural versus surface features among a group of novices who studied worked-out examples of mechanics problems. These differences, which echo Wertheimer's ( 1959 ) observations of individual differences in students' learning about the area of parallelograms, suggest that individual differences in people's interests and natural abilities may affect whether, or how quickly, they acquire domain expertise.

An important benefit of experts' ability to focus their attention on solution-relevant aspects of problems is that they are more likely than novices to recognize analogous problems that involve different objects and cover stories (e.g., Chi et al., 1989 ; Novick, 1988 ; Novick & Holyoak, 1991 ; Wertheimer, 1959 ) or that come from other knowledge domains (e.g., Bassok & Holyoak, 1989 ; Dunbar, 2001 ; Goldstone & Sakamoto, 2003 ). For example, Bassok and Holyoak ( 1989 ) found that, after learning to solve arithmetic-progression problems in algebra, subjects spontaneously applied these algebraic solutions to analogous physics problems that dealt with constantly accelerated motion. Note, however, that experts and good students do not simply ignore the surface features of problems. Rather, as was the case in the problem isomorphs we described earlier (Kotovsky et al., 1985 ), they tend to use such features to infer what the problem's structure could be (e.g., Alibali, Bassok, Solomon, Syc, & Goldin-Meadow, 1999 ; Blessing & Ross, 1996 ). For example, Hinsley et al. ( 1977 ) found that, after reading no more than the first few words of an algebra word problem, expert solvers classified the problem into a likely problem category (e.g., a work problem, a distance problem) and could predict what questions they might be asked and the equations they likely would need to use.

Surface-based problem categorization has a heuristic value (Medin & Ross, 1989 ): It does not ensure a correct categorization (Blessing & Ross, 1996 ), but it does allow solvers to retrieve potentially appropriate solutions from memory and to use them, possibly with some adaptation, to solve a variety of novel problems. Indeed, although experts exploit surface-structure correlations to save cognitive effort, they have the capability to realize that a particular surface cue is misleading (Hegarty, Mayer, & Green, 1992 ; Lewis & Mayer, 1987 ; Martin & Bassok, 2005 ; Novick 1988 , 1995 ; Novick & Holyoak, 1991 ). It is not surprising, therefore, that experts may revert to novice-like heuristic methods when solving problems under pressure (e.g., Beilock, 2008 ) or in subdomains in which they have general but not specific expertise (e.g., Patel, Groen, & Arocha, 1990 ).

Relevance of Search to Insight Solutions

We introduced the notion of insight in our discussion of the nine-dot problem in the section on the Gestalt tradition. The Gestalt view (e.g., Duncker, 1945 ; Maier, 1931 ; see Ohlsson, 1984 , for a review) was that insight problem solving is characterized by an initial work period during which no progress toward solution is made (i.e., an impasse), a sudden restructuring of one's problem representation to a more suitable form, followed immediately by the sudden appearance of the solution. Thus, solving problems by insight was believed to be all about representation, with essentially no role for a step-by-step solution process (i.e., search). Subsequent and contemporary researchers have generally concurred with the Gestalt view that getting the right representation is crucial. However, research has shown that insight solutions do not necessarily arise suddenly or full blown after restructuring (e.g., Weisberg & Alba, 1981 ); and even when they do, the underlying solution process (in this case outside of awareness) may reflect incremental progress toward the goal (Bowden & Jung-Beeman, 2003 ; Durso, Rea, & Dayton, 1994 ; Novick & Sherman, 2003 ).

“Demystifying insight,” to borrow a phrase from Bowden, Jung-Beeman, Fleck, and Kounios ( 2005 ), requires explaining ( 1 ) why solvers initially reach an impasse in solving a problem for which they have the necessary knowledge to generate the solution, ( 2 ) how the restructuring occurred, and ( 3 ) how it led to the solution. A detailed discussion of these topics appears elsewhere in this volume (van Steenburgh et al., Chapter 24 ). Here, we describe briefly three recent theories that have attempted to account for various aspects of these phenomena: Knoblich, Ohlsson, Haider, and Rhenius's ( 1999 ) representational change theory, MacGregor, Ormerod, and Chronicle's ( 2001 ) progress monitoring theory, and Bowden et al.'s ( 2005 ) neurological model. We then propose the need for an integrated approach to demystifying insight that considers both representation and search.

According to Knoblich et al.'s ( 1999 ) representational change theory, problems that are solved with insight are highly likely to evoke initial representations in which solvers place inappropriate constraints on their solution attempts, leading to an impasse. An impasse can be resolved by revising one's representation of the problem. Knoblich and his colleagues tested this theory using Roman numeral matchstick arithmetic problems in which solvers must move one stick to a new location to change a false numerical statement (e.g., I = II + II ) into a statement that is true. According to representational change theory, re-representation may occur through either constraint relaxation or chunk decomposition. (The solution to the example problem is to change II + to III – , which requires both methods of re-representation, yielding I = III – II ). Good support for this theory has been found based on measures of solution rate, solution time, and eye fixation (Knoblich et al., 1999 ; Knoblich, Ohlsson, & Raney, 2001 ; Öllinger, Jones, & Knoblich, 2008 ).

Progress monitoring theory (MacGregor et al., 2001 ) was proposed to account for subjects' difficulty in solving the nine-dot problem, which has traditionally been classified as an insight problem. According to this theory, solvers use the hill-climbing search heuristic to solve this problem, just as they do for traditional search problems (e.g., Hobbits and Orcs). In particular, solvers are hypothesized to monitor their progress toward solution using a criterion generated from the problem's current state. If solvers reach criterion failure, they seek alternative solutions by trying to relax one or more problem constraints. MacGregor et al. found support for this theory using several variants of the nine-dot problem (also see Ormerod, MacGregor, & Chronicle, 2002 ). Jones ( 2003 ) suggested that progress monitoring theory provides an account of the solution process up to the point an impasse is reached and representational change is sought, at which point representational change theory picks up and explains how insight may be achieved. Hence, it appears that a complete account of insight may require an integration of concepts from the Gestalt (representation) and Newell and Simon's (search) legacies.

Bowden et al.'s ( 2005 ) neurological model emphasizes the overlap between problem solving and language comprehension, and it hinges on differential processing in the right and left hemispheres. They proposed that an impasse is reached because initial processing of the problem produces strong activation of information irrelevant to solution in the left hemisphere. At the same time, weak semantic activation of alternative semantic interpretations, critical for solution, occurs in the right hemisphere. Insight arises when the weakly activated concepts reinforce each other, eventually rising above the threshold required for conscious awareness. Several studies of problem solving using compound remote associates problems, involving both behavioral and neuroimaging data, have found support for this model (Bowden & Jung-Beeman, 1998 , 2003 ; Jung-Beeman & Bowden, 2000 ; Jung-Beeman et al., 2004 ; also see Moss, Kotovsky, & Cagan, 2011 ).

Note that these three views of insight have received support using three quite distinct types of problems (Roman numeral matchstick arithmetic problems, the nine-dot problem, and compound remote associates problems, respectively). It remains to be established, therefore, whether these accounts can be generalized across problems. Kershaw and Ohlsson ( 2004 ) argued that insight problems are difficult because the key behavior required for solution may be hindered by perceptual factors (the Gestalt view), background knowledge (so expertise may be important; e.g., see Novick & Sherman, 2003 , 2008 ), and/or process factors (e.g., those affecting search). From this perspective, solving visual problems (e.g., the nine-dot problem) with insight may call upon more general visual processes, whereas solving verbal problems (e.g., anagrams, compound remote associates) with insight may call upon general verbal/semantic processes.

The work we reviewed in this section shows the relevance of problem representation (the Gestalt legacy) to the way people search the problem space (the legacy of Newell and Simon), and the relevance of search to the solution of insight problems that require a representational change. In addition to this inevitable integration of the two legacies, the work we described here underscores the fact that problem solving crucially depends on perceptual factors and on the solvers' background knowledge. In the next section, we describe some recent work that shows the involvement of these factors in the solution of problems in math and science.

Effects of Perception and Knowledge in Problem Solving in Academic Disciplines

Although the use of puzzle problems continues in research on problem solving, especially in investigations of insight, many contemporary researchers tackle problem solving in knowledge-rich domains, often in academic disciplines (e.g., mathematics, biology, physics, chemistry, meteorology). In this section, we provide a sampling of this research that highlights the importance of visual perception and background knowledge for successful problem solving.

The Role of Visual Perception

We stated at the outset that a problem representation (e.g., the problem space) is a model of the problem constructed by solvers to summarize their understanding of the problem's essential nature. This informal definition refers to the internal representations people construct and hold in working memory. Of course, people may also construct various external representations (Markman, 1999 ) and even manipulate those representations to aid in solution (see Hegarty & Stull, Chapter 31 ). For example, solvers often use paper and pencil to write notes or draw diagrams, especially when solving problems from formal domains (e.g., Cox, 1999 ; Kindfield, 1993 / 1994 ; S. Schwartz, 1971 ). In problems that provide solvers with external representation, such as the Tower of Hanoi problem, people's planning and memory of the current state is guided by the actual configurations of disks on pegs (Garber & Goldin-Meadow, 2002 ) or by the displays they see on a computer screen (Chen & Holyoak, 2010 ; Patsenko & Altmann, 2010 ).

In STEM (science, technology, engineering, and mathematics) disciplines, it is common for problems to be accompanied by diagrams or other external representations (e.g., equations) to be used in determining the solution. Larkin and Simon ( 1987 ) examined whether isomorphic sentential and diagrammatic representations are interchangeable in terms of facilitating solution. They argued that although the two formats may be equivalent in the sense that all of the information in each format can be inferred from the other format (informational equivalence), the ease or speed of making inferences from the two formats might differ (lack of computational equivalence). Based on their analysis of several problems in physics and math, Larkin and Simon further argued for the general superiority of diagrammatic representations (but see Mayer & Gallini, 1990 , for constraints on this general conclusion).

Novick and Hurley ( 2001 , p. 221) succinctly summarized the reasons for the general superiority of diagrams (especially abstract or schematic diagrams) over verbal representations: They “(a) simplify complex situations by discarding unnecessary details (e.g., Lynch, 1990 ; Winn, 1989 ), (b) make abstract concepts more concrete by mapping them onto spatial layouts with familiar interpretational conventions (e.g., Winn, 1989 ), and (c) substitute easier perceptual inferences for more computationally intensive search processes and sentential deductive inferences (Barwise & Etchemendy, 1991 ; Larkin & Simon, 1987 ).” Despite these benefits of diagrammatic representations, there is an important caveat, noted by Larkin and Simon ( 1987 , p. 99) at the very end of their paper: “Although every diagram supports some easy perceptual inferences, nothing ensures that these inferences must be useful in the problem-solving process.” We will see evidence of this in several of the studies reviewed in this section.

Next we describe recent work on perceptual factors that are involved in people's use of two types of external representations that are provided as part of the problem in two STEM disciplines: equations in algebra and diagrams in evolutionary biology. Although we focus here on effects of perceptual factors per se, it is important to note that such factors only influence performance when subjects have background knowledge that supports differential interpretation of the alternative diagrammatic depictions presented (Hegarty, Canham, & Fabricant, 2010 ).

In the previous section, we described the work of Patsenko and Altmann ( 2010 ) that shows direct involvement of visual attention and perception in the sequential application of move operators during the solution of the Tower of Hanoi problem. A related body of work documents similar effects in tasks that require the interpretation and use of mathematical equations (Goldstone, Landy, & Son, 2010 ; Landy & Goldstone, 2007a , b). For example, Landy and Goldstone ( 2007b ) varied the spatial proximity of arguments to the addition (+) and multiplication (*) operators in algebraic equations, such that the spatial layout of the equation was either consistent or inconsistent with the order-of-operations rule that multiplication precedes addition. In consistent equations , the space was narrower around multiplication than around addition (e.g., g*m + r*w = m*g + w*r ), whereas in inconsistent equations this relative spacing was reversed (e.g., s * n+e * c = n * s+c * e ). Subjects' judgments of the validity of such equations (i.e., whether the expressions on the two sides of the equal sign are equivalent) were significantly faster and more accurate for consistent than inconsistent equations.

In discussing these findings and related work with other external representations, Goldstone et al. ( 2010 ) proposed that experience with solving domain-specific problems leads people to “rig up” their perceptual system such that it allows them to look at the problem in a way that is consistent with the correct rules. Similar logic guides the Perceptual Learning Modules developed by Kellman and his collaborators to help students interpret and use algebraic equations and graphs (Kellman et al., 2008 ; Kellman, Massey, & Son, 2009 ). These authors argued and showed that, consistent with the previously reviewed work on expertise, perceptual training with particular external representations supports the development of perceptual fluency. This fluency, in turn, supports students' subsequent use of these external representations for problem solving.

This research suggests that extensive experience with particular equations or graphs may lead to perceptual fluency that could replace the more mindful application of domain-specific rules. Fisher, Borchert, and Bassok ( 2011 ) reported results from algebraic-modeling tasks that are consistent with this hypothesis. For example, college students were asked to represent verbal statements with algebraic equations, a task that typically elicits systematic errors (e.g., Clement, Lochhead, & Monk, 1981 ). Fisher et al. found that such errors were very common when subjects were asked to construct “standard form” equations ( y = ax ), which support fluent left-to-right translation of words to equations, but were relatively rare when subjects were asked to construct nonstandard division-format equations (x = y/a) that do not afford such translation fluency.

In part because of the left-to-right order in which people process equations, which mirrors the linear order in which they process text, equations have traditionally been viewed as sentential representations. However, Landy and Goldstone ( 2007a ) have proposed that equations also share some properties with diagrammatic displays and that, in fact, in some ways they are processed like diagrams. That is, spatial information is used to represent and to support inferences about syntactic structure. This hypothesis received support from Landy and Goldstone's ( 2007b ) results, described earlier, in which subjects' judgments of the validity of equations were affected by the Gestalt principle of grouping: Subjects did better when the grouping was consistent rather than inconsistent with the underlying structure of the problem (order of operations). Moreover, Landy and Goldstone ( 2007a ) found that when subjects wrote their own equations they grouped numbers and operators (+, *, =) in a way that reflected the hierarchical structure imposed by the order-of-operations rule.

In a recent line of research, Novick and Catley ( 2007 ; Novick, Catley, & Funk, 2010 ; Novick, Shade, & Catley, 2011 ) have examined effects of the spatial layout of diagrams depicting the evolutionary history of a set of taxa on people's ability to reason about patterns of relationship among those taxa. We consider here their work that investigates the role of another Gestalt perceptual principle—good continuation—in guiding students' reasoning. According to this principle, a continuous line is perceived as a single entity (Kellman, 2000 ). Consider the diagrams shown in Figure 21.6 . Each is a cladogram, a diagram that depicts nested sets of taxa that are related in terms of levels of most recent common ancestry. For example, chimpanzees and starfish are more closely related to each other than either is to spiders. The supporting evidence for their close relationship is their most recent common ancestor, which evolved the novel character of having radial cleavage. Spiders do not share this ancestor and thus do not have this character.

Cladograms are typically drawn in two isomorphic formats, which Novick and Catley ( 2007 ) referred to as trees and ladders. Although these formats are informationally equivalent (Larkin & Simon, 1987 ), Novick and Catley's ( 2007 ) research shows that they are not computationally equivalent (Larkin & Simon, 1987 ). Imagine that you are given evolutionary relationships in the ladder format, such as in Figure 21.6a (but without the four characters—hydrostatic skeleton, bilateral symmetry, radial cleavage, and trocophore larvae—and associated short lines indicating their locations on the cladogram), and your task is to translate that diagram to the tree format. A correct translation is shown in Figure 21.6b . Novick and Catley ( 2007 ) found that college students were much more likely to get such problems correct when the presented cladogram was in the nested circles (e.g., Figure 21.6d ) rather than the ladder format. Because the Gestalt principle of good continuation makes the long slanted line at the base of the ladder appear to represent a single hierarchical level, a common translation error for the ladder to tree problems was to draw a diagram such as that shown in Figure 21.6c .

The difficulty that good continuation presents for interpreting relationships depicted in the ladder format extends to answering reasoning questions as well. Novick and Catley (unpublished data) asked comparable questions about relationships depicted in the ladder and tree formats. For example, using the cladograms depicted in Figures 21.6a and 21.6b , consider the following questions: (a) Which taxon—jellyfish or earthworm—is the closest evolutionary relation to starfish, and what evidence supports your answer? (b) Do the bracketed taxa comprise a clade (a set of taxa consisting of the most recent common ancestor and all of its descendants), and what evidence supports your answer? For both such questions, students had higher accuracy and evidence quality composite scores when the relationships were depicted in the tree than the ladder format.

Four cladograms depicting evolutionary relationships among six animal taxa. Cladogram ( a ) is in the ladder format, cladograms ( b ) and ( c ) are in the tree format, and cladogram ( d ) is in the nested circles format. Cladograms ( a ), ( b ), and ( d ) are isomorphic.

If the difficulty in extracting the hierarchical structure of the ladder format is due to good continuation (which leads problem solvers to interpret continuous lines that depict multiple hierarchical levels as depicting only a single level), then a manipulation that breaks good continuation at the points where a new hierarchical level occurs should improve understanding. Novick et al. ( 2010 ) tested this hypothesis using a translation task by manipulating whether characters that are the markers for the most recent common ancestor of each nested set of taxa were included on the ladders. Figure 21.6a shows a ladder with such characters. As predicted, translation accuracy increased dramatically simply by adding these characters to the ladders, despite the additional information subjects had to account for in their translations.

The Role of Background Knowledge

As we mentioned earlier, the specific entities in the problems people encounter evoke inferences that affect how people represent these problems (e.g., the candle problem; Duncker, 1945 ) and how they apply the operators in searching for the solution (e.g., the disks vs. acrobats versions of the Tower of Hanoi problem; Kotovsky et al., 1985 ). Such object-based inferences draw on people's knowledge about the properties of the objects (e.g., a box is a container, an acrobat is a person who can be hurt). Here, we describe the work of Bassok and her colleagues, who found that similar inferences affect how people select mathematical procedures to solve problems in various formal domains. This work shows that the objects in the texts of mathematical word problems affect how people represent the problem situation (i.e., the situation model they construct; Kintsch & Greeno, 1985 ) and, in turn, lead them to select mathematical models that have a corresponding structure. To illustrate, a word problem that describes constant change in the rate at which ice is melting off a glacier evokes a model of continuous change, whereas a word problem that describes constant change in the rate at which ice is delivered to a restaurant evokes a model of discrete change. These distinct situation models lead subjects to select corresponding visual representations (e.g., Bassok & Olseth, 1995 ) and solutions methods, such as calculating the average change over time versus adding the consecutive changes (e.g., Alibali et al., 1999 ).

In a similar manner, people draw on their general knowledge to infer how the objects in a given problem are related to each other and construct mathematical solutions that correspond to these inferred object relations. For example, a word problem that involves doctors from two hospitals elicits a situation model in which the two sets of doctors play symmetric roles (e.g., work with each other), whereas a mathematically isomorphic problem that involves mechanics and cars elicits a situation model in which the sets play asymmetric roles (e.g., mechanics fix cars). The mathematical solutions people construct to such problems reflect this difference in symmetry (Bassok, Wu, & Olseth, 1995 ). In general, people tend to add objects that belong to the same taxonomic category (e.g., doctors + doctors) but divide functionally related objects (e.g., cars ÷ mechanics). People establish this correspondence by a process of analogical alignment between semantic and arithmetic relations, which Bassok and her colleagues refer to as “semantic alignment” (Bassok, Chase, & Martin, 1998 ; Doumas, Bassok, Guthormsen, & Hummel, 2006 ; Fisher, Bassok, & Osterhout, 2010 ).

Semantic alignment occurs very early in the solution process and can prime arithmetic facts that are potentially relevant to the problem solution (Bassok, Pedigo, & Oskarsson, 2008 ). Although such alignments can lead to erroneous solutions, they have a high heuristic value because, in most textbook problems, object relations indeed correspond to analogous mathematical relations (Bassok et al., 1998 ). Interestingly, unlike in the case of reliance on specific surface-structure correlations (e.g., the keyword “more” typically appears in word problems that require addition; Lewis & Mayer, 1987 ), people are more likely to exploit semantic alignment when they have more, rather than less modeling experience. For example, Martin and Bassok ( 2005 ) found very strong semantic-alignment effects when subjects solved simple division word problems, but not when they constructed algebraic equations to represent the relational statements that appeared in the problems. Of course, these subjects had significantly more experience with solving numerical word problems than with constructing algebraic models of relational statements. In a subsequent study, Fisher and Bassok ( 2009 ) found semantic-alignment effects for subjects who constructed correct algebraic models, but not for those who committed modeling errors.

Conclusions and Future Directions

In this chapter, we examined two broad components of the problem-solving process: representation (the Gestalt legacy) and search (the legacy of Newell and Simon). Although many researchers choose to focus their investigation on one or the other of these components, both Duncker ( 1945 ) and Simon ( 1986 ) underscored the necessity to investigate their interaction, as the representation one constructs for a problem determines (or at least constrains) how one goes about trying to generate a solution, and searching the problem space may lead to a change in problem representation. Indeed, Duncker's ( 1945 ) initial account of one subject's solution to the radiation problem was followed up by extensive and experimentally sophisticated work by Simon and his colleagues and by other researchers, documenting the involvement of visual perception and background knowledge in how people represent problems and search for problem solutions.

The relevance of perception and background knowledge to problem solving illustrates the fact that, when people attempt to find or devise ways to reach their goals, they draw on a variety of cognitive resources and engage in a host of cognitive activities. According to Duncker ( 1945 ), such goal-directed activities may include (a) placing objects into categories and making inferences based on category membership, (b) making inductive inferences from multiple instances, (c) reasoning by analogy, (d) identifying the causes of events, (e) deducing logical implications of given information, (f) making legal judgments, and (g) diagnosing medical conditions from historical and laboratory data. As this list suggests, many of the chapters in the present volume describe research that is highly relevant to the understanding of problem-solving behavior. We believe that important advancements in problem-solving research would emerge by integrating it with research in other areas of thinking and reasoning, and that research in these other areas could be similarly advanced by incorporating the insights gained from research on what has more traditionally been identified as problem solving.

As we have described in this chapter, many of the important findings in the field have been established by a careful investigation of various riddle problems. Although there are good methodological reasons for using such problems, many researchers choose to investigate problem solving using ecologically valid educational materials. This choice, which is increasingly common in contemporary research, provides researchers with the opportunity to apply their basic understanding of problem solving to benefit the design of instruction and, at the same time, allows them to gain a better understanding of the processes by which domain knowledge and educational conventions affect the solution process. We believe that the trend of conducting educationally relevant research is likely to continue, and we expect a significant expansion of research on people's understanding and use of dynamic and technologically rich external representations (e.g., Kellman et al., 2008 ; Mayer, Griffith, Jurkowitz, & Rothman, 2008 ; Richland & McDonough, 2010 ; Son & Goldstone, 2009 ). Such investigations are likely to yield both practical and theoretical payoffs.

Adams, J. L. ( 1979 ). Conceptual blockbusting: A guide to better ideas (2nd ed.). New York: Norton.

Google Scholar

Google Preview

Adelson, B. ( 1981 ). Problem solving and the development of abstract categories in programming languages.   Memory and Cognition , 9 , 422–433.

Alibali, M. W., Bassok, M., Solomon, K. O., Syc, S. E., & Goldin-Meadow, S. ( 1999 ). Illuminating mental representations through speech and gesture.   Psychological Science , 10 , 327–333.

Allard, F., & Starkes, J. L. ( 1991 ). Motor-skill experts in sports, dance, and other domains. In K. A. Ericsson & J. Smith (Eds.), Toward a general theory of expertise: Prospects and limits (pp. 126–152). New York: Cambridge University Press.

Anderson, J. R. ( 1982 ). Acquisition of cognitive skill.   Psychological Review , 89 , 369–406.

Anzai, Y., & Simon, H. A. ( 1979 ). The theory of learning by doing.   Psychological Review , 86 , 124–140.

Atwood, M. E, & Polson, P.G. ( 1976 ). A process model for water jug problems.   Cognitive Psychology , 8 , 191–216.

Barwise, J., & Etchemendy, J. ( 1991 ). Visual information and valid reasoning. In W. Zimmermann & S. Cunningham (Eds.), Visualization in teaching and learning mathematics (pp. 9–24). Washington, DC: Mathematical Association of America.

Bassok, M., Chase, V. M., & Martin, S. A. ( 1998 ). Adding apples and oranges: Alignment of semantic and formal knowledge.   Cognitive Psychology , 35 , 99–134.

Bassok, M., & Holyoak, K. J. ( 1989 ). Interdomain transfer between isomorphic topics in algebra and physics.   Journal of Experimental Psychology: Learning, Memory, and Cognition , 15 , 153–166.

Bassok, M., & Olseth, K. L. ( 1995 ). Object-based representations: Transfer between cases of continuous and discrete models of change.   Journal of Experimental Psychology: Learning, Memory, and Cognition , 21 , 1522–1538.

Bassok, M., Pedigo, S. F., & Oskarsson, A. T. ( 2008 ). Priming addition facts with semantic relations.   Journal of Experimental Psychology: Learning, Memory, and Cognition , 34 , 343–352.

Bassok, M., Wu, L., & Olseth, L. K. ( 1995 ). Judging a book by its cover: Interpretative effects of content on problem solving transfer.   Memory and Cognition , 23 , 354–367.

Beilock, S. L. ( 2008 ). Math performance in stressful situations.   Current Directions in Psychological Science , 17 , 339–343.

Birch, H. G. & Rabinowitz, H. S. ( 1951 ). The negative effect of previous experience on productive thinking.   Journal of Experimental Psychology , 41 , 122–126.

Blessing, S. B., & Ross, B. H. ( 1996 ). Content effects in problem categorization and problem solving.   Journal of Experimental Psychology: Learning, Memory, and Cognition , 22 , 792–810.

Bowden, E. M., & Jung-Beeman, M. ( 1998 ). Getting the right idea: Semantic activation in the right hemisphere may help solve insight problems.   Psychological Science , 6 , 435–440.

Bowden, E. M., & Jung-Beeman, M. ( 2003 ). Aha! Insight experience correlates with solution activation in the right hemisphere.   Psychonomic Bulletin and Review , 10 , 730–737.

Bowden, E. M., Jung-Beeman, M., Fleck, J., & Kounios, J. ( 2005 ). New approaches to demystifying insight.   Trends in Cognitive Sciences , 9 , 322–328.

Catrambone, R. ( 1998 ). The subgoal-learning model: Creating better examples so that students can solve novel problems.   Journal of Experimental Psychology: General , 127 , 355–376.

Chase, W. G., & Simon, H. A. ( 1973 ). Perception in chess.   Cognitive Psychology , 4 , 55–81.

Chen, D., & Holyoak, K. J. ( 2010 ). Enhancing acquisition of intuition versus planning in problem solving. In S. Ohlsson & R. Catrambone (Eds.), Proceedings of the 32nd Annual Conference of the Cognitive Science Society (pp. 1875–1880). Austin, TX: Cognitive Science Society.

Chi, M. T. H., Bassok, M., Lewis, M. W., Reimann, P., & Glaser, R. ( 1989 ). Self-explanations: How students study and use examples in learning to solve problems.   Cognitive Science , 13 , 145–182.

Chi, M. T. H., Feltovich, P. J., & Glaser, R. ( 1981 ). Categorization and representation of physics problems by experts and novices.   Cognitive Science , 5 , 121–152.

Clement, J., Lochhead, J., & Monk, G. S. ( 1981 ). Translation difficulties in learning mathematics.   The American Mathematical Monthly , 88 , 286–290.

Coughlin, L. D., & Patel, V. L. ( 1987 ). Processing of critical information by physicians and medical students.   Journal of Medical Education , 62 , 818–828.

Cox, R. ( 1999 ). Representation construction, externalised cognition and individual differences.   Learning and Instruction , 9 , 343–363.

Deakin, J. M., & Allard, F. ( 1991 ). Skilled memory in expert figure skaters.   Memory and Cognition , 19 , 79–86.

Doumas, L. A. A., Bassok, M., Guthormsen, A., & Hummel, J. E. ( 2006 ). Theory of reflexive relational generalization. In R. Sun & N. Miyake (Eds.), Proceedings of the 28th Annual Conference of the Cognitive Science Society (pp. 1246–1250). Mahwah, NJ: Erlbaum.

Dunbar, K. ( 2001 ). The analogical paradox: Why analogy is so easy in naturalistic settings, yet so difficult in the psychological laboratory. In D. Gentner, K. J. Holyoak, & B. Kokinov (Eds.), Analogy: Perspectives from cognitive science (pp. 313–362). Cambridge, MA: MIT Press.

Duncker, K. ( 1945 ). On problem-solving (L. S. Lees, Trans.). Psychological Monographs , 58 (Whole No. 270). (Original work published 1935).

Durso, F. T., Rea, C. B., & Dayton, T. ( 1994 ). Graph-theoretic confirmation of restructuring during insight.   Psychological Science , 5 , 94–98.

Egan, D. E., & Schwartz, B. J. ( 1979 ). Chunking in the recall of symbolic drawings.   Memory and Cognition , 7 , 149–158.

Ericsson, K. A., & Simon, H. A. ( 1980 ). Verbal reports as data.   Psychological Review , 87 , 215–251.

Ernst, G. W., & Newell, A. ( 1969 ). GPS: A case study in generality and problem solving . New York: Academic Press.

Fisher, K. J., & Bassok, M. ( 2009 ). Analogical alignments in algebraic modeling. In B. Kokinov, D. Gentner, & K. J. Holyoak (Eds.), Proceedings of the 2nd International Analogy Conference (pp. 137–144). Sofia, Bulgaria: New Bulgarian University Press.

Fisher, K. J., Bassok, M., & Osterhout, L. ( 2010 ). When two plus two does not equal four: Event-related potential responses to semantically incongruous arithmetic word problems. In S. Ohlsson & R. Catrambone (Eds.), Proceedings of the 32nd Annual Conference of the Cognitive Science Society (pp. 1571–1576). Austin, TX: Cognitive Science Society.

Fisher, K. J., Borchert, K., & Bassok, M. ( 2011 ). Following the standard form: Effects of equation format on algebraic modeling.   Memory and Cognition , 39 , 502–515.

Garber, P., & Goldin-Meadow, S. ( 2002 ). Gesture offers insight into problem solving in adults and children.   Cognitive Science , 26 , 817–831.

Gobet, F., & Simon, H. ( 1996 ). Recall of rapidly presented random chess positions is a function of skill.   Psychonomic Bulletin and Review , 3 , 159–163.

Goldstone, R. L., Landy, D. H., & Son, J. Y. ( 2010 ). The education of perception.   Topics in Cognitive Science , 2 , 265–284.

Goldstone, R. L., & Sakamoto, J. Y. ( 2003 ). The transfer of abstract principles governing complex adaptive systems.   Cognitive Psychology , 46 , 414–466.

Greeno, J. G. ( 1974 ). Hobbits and orcs: Acquisition of a sequential concept.   Cognitive Psychology , 6 , 270–292.

Hardiman, P. T., Dufresne, R., & Mestre, J. P. ( 1989 ). The relation between problem categorization and problem solving among experts and novices.   Memory and Cognition , 17 , 627–638.

Haverty, L. A., Koedinger, K. R., Klahr, D., & Alibali, M. W. ( 2000 ). Solving induction problems in mathematics: Not-so-trivial Pursuit.   Cognitive Science , 24 , 249–298.

Hayes, J. R., & Simon, H. A. ( 1977 ). Psychological differences among problem isomorphs. In N. J. Castellan, D. B. Pisoni, & G. R. Potts (Eds.), Cognitive theory (Vol. 2, pp. 21–44). Hillsdale, NJ: Erlbaum.

Hegarty, M., Canham, M. S., & Fabricant, S. I. ( 2010 ). Thinking about the weather: How display salience and knowledge affect performance in a graphic inference task.   Journal of Experimental Psychology: Learning, Memory, and Cognition , 36 , 37–53.

Hegarty, M., Mayer, R. E., & Green, C. E. ( 1992 ). Comprehension of arithmetic word problems: Evidence from students' eye fixations.   Journal of Educational Psychology , 84 , 76–84.

Hinsley, D. A., Hayes, J. R., & Simon, H. A. ( 1977 ). From words to equations: Meaning and representation in algebra word problems. In D. Hinsley, M. Just., & P. Carpenter (Eds.), Cognitive processes in comprehension (pp. 89–106). Hillsdale, NJ: Erlbaum.

Holyoak, K. J., & Koh, K. ( 1987 ). Surface and structural similarity in analogical transfer.   Memory and Cognition , 15 , 332–340.

Jones, G. ( 2003 ). Testing two cognitive theories of insight.   Journal of Experimental Psychology: Learning, Memory, and Cognition , 29 , 1017–1027.

Jung-Beeman, M., & Bowden, E. M. ( 2000 ). The right hemisphere maintains solution-related activation for yet-to-be solved insight problems.   Memory and Cognition , 28 , 1231–1241.

Jung-Beeman, M., Bowden, E. M., Haberman, J., Frymiare, J. L., Arambel-Liu, S., Greenblatt, R., … Kounios, J. ( 2004 ). Neural activity when people solve verbal problems with insight.   PLOS Biology , 2 , 500–510.

Kellman, P. J. ( 2000 ). An update on Gestalt psychology. In B. Landau, J. Sabini, J. Jonides, & E. Newport (Eds.), Perception, cognition, and language: Essays in honor of Henry and Lila Gleitman (pp. 157–190). Cambridge, MA: MIT Press.

Kellman, P. J., Massey, C. M., & Son, J. Y ( 2009 ). Perceptual learning modules in mathematics: Enhancing students' pattern recognition, structure extraction, and fluency.   Topics in Cognitive Science , 1 , 1–21.

Kellman, P. J., Massey, C., Roth, Z., Burke, T., Zucker, J., Saw, A., … Wise, J. A. ( 2008 ). Perceptual learning and the technology of expertise.   Pragmatics and Cognition , 16 , 356–405.

Kershaw, T. C., & Ohlsson, S. ( 2004 ). Multiple causes of difficulty in insight: The case of the nine-dot problem.   Journal of Experimental Psychology: Learning, Memory, and Cognition , 30 , 3–13.

Kindfield, A. C. H. ( 1993 /1994). Biology diagrams: Tools to think with.   Journal of the Learning Sciences , 3 , 1–36.

Kintsch, W., & Greeno, J. G. ( 1985 ). Understanding and solving word arithmetic problems.   Psychological Review , 92 , 109–129.

Knoblich, G., Ohlsson, S., Haider, H., & Rhenius, D. ( 1999 ). Constraint relaxation and chunk decomposition in insight problem solving.   Journal of Experimental Psychology: Learning, Memory, and Cognition , 25 , 1534–1555.

Knoblich, G., Ohlsson, S., & Raney, G. E. ( 2001 ). An eye movement study of insight problem solving.   Memory and Cognition , 29 , 1000–1009.

Kohler, W. ( 1925 ). The mentality of apes . New York: Harcourt Brace.

Kotovsky, K., Hayes, J. R., & Simon, H. A. ( 1985 ). Why are some problems hard? Evidence from Tower of Hanoi.   Cognitive Psychology , 17 , 248–294.

Kozma, R. B., & Russell, J. ( 1997 ). Multimedia and understanding: Expert and novice responses to different representations of chemical phenomena.   Journal of Research in Science Teaching , 34 , 949–968.

Landy, D., & Goldstone, R. L. ( 2007 a). Formal notations are diagrams: Evidence from a production task.   Memory and Cognition , 35, 2033–2040.

Landy, D., & Goldstone, R. L. ( 2007 b). How abstract is symbolic thought?   Journal of Experimental Psychology: Learning, Memory, and Cognition , 33, 720–733.

Larkin, J. H., McDermott, J., Simon, D. P., & Simon, H. A. ( 1980 ). Models of competence in solving physics problems.   Cognitive Science , 4 , 317–345.

Larkin, J. H., & Simon, H. A. ( 1987 ). Why a diagram is (sometimes) worth ten thousand words.   Cognitive Science , 11 , 65–99.

Lewis, A. B., & Mayer, R. E. ( 1987 ). students' miscomprehension of relational statements in arithmetic word problems.   Journal of Educational Psychology , 79 , 363–371.

Lynch, M. ( 1990 ). The externalized retina: Selection and mathematization in the visual documentation of objects in the life sciences. In M. Lynch & S. Woolgar (Eds.), Representation in scientific practice (pp. 153–186). Cambridge, MA: MIT Press.

MacGregor, J. N., Ormerod, T. C., & Chronicle, E. P. ( 2001 ). Information processing and insight: A process model of performance on the nine-dot and related problems.   Journal of Experimental Psychology: Learning, Memory, and Cognition , 27 , 176–201.

Maier, N. ( 1930 ). Reasoning in humans. I. On direction.   Journal of Comparative Psychology , 10 , 15–43.

Maier, N. ( 1931 ). Reasoning in humans. II. The solution of a problem and its appearance in consciousness.   Journal of Comparative Psychology , 12 , 181–194.

Markman, A. B. ( 1999 ). Knowledge representation . Mahwah, NJ: Erlbaum.

Martin, S. A., & Bassok, M. ( 2005 ). Effects of semantic cues on mathematical modeling: Evidence from word-problem solving and equation construction tasks.   Memory and Cognition , 33 , 471–478.

Mayer, R. E., & Gallini, J. K. ( 1990 ). When is an illustration worth ten thousand words?   Journal of Educational Psychology , 82 , 715–726.

Mayer, R. E., Griffith, E., Jurkowitz, I. T. N., & Rothman, D. ( 2008 ). Increased interestingness of extraneous details in a multimedia science presentation leads to decreased learning.   Journal of Experimental Psychology: Applied , 14 , 329–339.

McKeithen, K. B., Reitman, J. S., Rueter, H. H., & Hirtle, S. C. ( 1981 ). Knowledge organization and skill differences in computer programmers.   Cognitive Psychology , 13 , 307–325.

Medin, D. L., & Ross, B. H. ( 1989 ). The specific character of abstract thought: Categorization, problem solving, and induction. In R. J. Sternberg (Ed.), Advances in the psychology of human intelligence (Vol. 5, pp. 189–223). Hillsdale, NJ: Erlbaum.

Moss, J., Kotovsky, K., & Cagan, J. ( 2011 ). The effect of incidental hints when problems are suspended before, during, and after an impasse.   Journal of Experimental Psychology: Learning, Memory, and Cognition , 37 , 140–148.

Myles-Worsley, M., Johnston, W. A., & Simons, M. A ( 1988 ). The influence of expertise on X-ray image processing.   Journal of Experimental Psychology: Learning, Memory, and Cognition , 14 , 553–557.

Newell, A., & Simon, H. A. ( 1972 ). Human problem solving . Englewood Cliffs, NJ: Prentice-Hall.

Newell, A., & Simon, H. A. ( 1976 ). Computer science as empirical enquiry: Symbols and search.   Communications of the ACM , 19 , 113–126.

Novick, L. R. ( 1988 ). Analogical transfer, problem similarity, and expertise.   Journal of Experimental Psychology: Learning, Memory, and Cognition , 14 , 510–520.

Novick, L. R. ( 1995 ). Some determinants of successful analogical transfer in the solution of algebra word problems.   Thinking and Reasoning , 1 , 5–30.

Novick, L. R., & Catley, K. M. ( 2007 ). Understanding phylogenies in biology: The influence of a Gestalt perceptual principle.   Journal of Experimental Psychology: Applied , 13 , 197–223.

Novick, L. R., Catley, K. M., & Funk, D. J. ( 2010 ). Characters are key: The effect of synapomorphies on cladogram comprehension.   Evolution: Education and Outreach , 3 , 539–547.

Novick, L. R., & Hmelo, C. E. ( 1994 ). Transferring symbolic representations across non-isomorphic problems.   Journal of Experimental Psychology: Learning, Memory, and Cognition , 20 , 1296–1321.

Novick, L. R., & Holyoak, K. J. ( 1991 ). Mathematical problem solving by analogy.   Journal of Experimental Psychology: Learning, Memory, and Cognition , 17 , 398–415.

Novick, L. R., & Hurley, S. M. ( 2001 ). To matrix, network, or hierarchy: That is the question.   Cognitive Psychology , 42 , 158–216.

Novick, L. R., Shade, C. K., & Catley, K. M. ( 2011 ). Linear versus branching depictions of evolutionary history: Implications for diagram design.   Topics in Cognitive Science , 3 (3), 536–559.

Novick, L. R., & Sherman, S. J. ( 2003 ). On the nature of insight solutions: Evidence from skill differences in anagram solution.   The Quarterly Journal of Experimental Psychology , 56A , 351–382.

Novick, L. R., & Sherman, S. J. ( 2008 ). The effects of superficial and structural information on on-line problem solving for good versus poor anagram solvers.   The Quarterly Journal of Experimental Psychology , 61 , 1098–1120.

Ohlsson, S. ( 1984 ). Restructuring revisited I. Summary and critique of the Gestalt theory of problem solving.   Scandinavian Journal of Psychology , 25 , 65–78.

Öllinger, M., Jones, G., & Knoblich, G. ( 2008 ). Investigating the effect of mental set on insight problem solving.   Experimental Psychology , 55 , 269–282.

Ormerod, T. C., MacGregor, J. N., & Chronicle, E. P. ( 2002 ). Dynamics and constraints in insight problem solving.   Journal of Experimental Psychology: Learning, Memory, and Cognition , 28 , 791–799.

Paige, J. M., & Simon, H. A. ( 1966 ). Cognitive processes in solving algebra word problems. In B. Kleinmuntz (Ed.), Problem solving: Research, method, and theory (pp. 51–119). New York: Wiley

Patel, V. L., Groen, G. J., & Arocha, J. F. ( 1990 ). Medical expertise as a function of task difficulty.   Memory and Cognition , 18 , 394–406.

Patsenko, E. G., & Altmann, E. M. ( 2010 ). How planful is routine behavior? A selective attention model of performance in the Tower of Hanoi.   Journal of Experimental Psychology: General , 139 , 95–116.

Polya, G. ( 1957 ). How to solve it (2nd ed.). Princeton, NJ: Princeton University Press.

Posner, M. I. ( 1973 ). Cognition: An introduction . Glenview, IL: Scott, Foresman and Company.

Reitman, W. R. ( 1965 ). Cognition and thought . New York: Wiley.

Richland, L. E., & McDonough, I. M. ( 2010 ), Learning by analogy: Discriminating between potential analogs.   Contemporary Educational Psychology , 35 , 28–43.

Russo, J. E., Johnson, E. J., & Stephens, D. L. ( 1989 ). The validity of verbal protocols.   Memory and Cognition , 17 , 759–769.

Schoenfeld, A. H. ( 1979 ). Explicit heuristic training as a variable in problem-solving performance.   Journal for Research in Mathematics Education , 10 , 173–187.

Schoenfeld, A. H., & Herrmann, D. J. ( 1982 ). Problem perception and knowledge structure in expert and novice mathematical problem solvers.   Journal of Experimental Psychology: Learning, Memory, and Cognition , 8 , 484–494.

Schwartz, S. H. ( 1971 ). Modes of representation and problem solving: Well evolved is half solved.   Journal of Experimental Psychology , 91 , 347–350.

Silver, E. A. ( 1979 ). Student perceptions of relatedness among mathematical verbal problems.   Journal for Research in Mathematics Education , 10 , 195–210.

Silver, E. A. ( 1981 ). Recall of mathematical problem information: Solving related problems.   Journal for Research in Mathematics Education , 12 , 54–64.

Simon, D. P., & Simon, H. A. ( 1978 ). Individual differences in solving physics problems. In R. Siegler (Ed.), Children's thinking: What develops? (pp. 325–348). Hillsdale, NJ: Erlbaum.

Simon, H. A. ( 1978 ). Information-processing theory of human problem solving. In W. K. Estes (Ed.), Handbook of learning and cognitive processes (Vol. 5, pp. 271–295). Hillsdale, NJ: Erlbaum.

Simon, H. A. ( 1986 ). The information processing explanation of Gestalt Phenomena.   Computers in Human Behavior , 2 , 241–255.

Simon, H. A. ( 1990 ). Invariants of human behavior.   Annual Review of Psychology , 41 , 1–19.

Son, J. Y., & Goldstone, R. L. ( 2009 ). Fostering general transfer with specific simulations.   Pragmatics and Cognition , 17 , 1–42.

Thomas, J. C., Jr., ( 1974 ). An analysis of behavior in the hobbits-orcs problem.   Cognitive Psychology , 6 , 257–269.

Weisberg, R. W., & Alba, J. W. ( 1981 ). An examination of the alleged role of “fixation” in the solution of several “insight” problems.   Journal of Experimental Psychology: General , 110 , 169–192.

Weiser, M., & Shertz, J. ( 1983 ). Programming problem representation in novice and expert programmers.   International Journal of Man-Machine Studies , 19 , 391–398.

Wertheimer, M. ( 1959 ). Productive thinking (Rev. ed.). Chicago, IL: University of Chicago Press.

Winn, W. ( 1989 ). The design and use of instructional graphics. In H. Mandl & J. R. Levin (Eds.), Knowledge acquisition from text and pictures (pp. 125–144). Amsterdam, Netherlands: Elsevier

• About Oxford Academic
• Publish journals with us
• University press partners
• What we publish
• New features  
• Open access
• Institutional account management
• Rights and permissions
• Get help with access
• Accessibility
• Advertising
• Media enquiries
• Oxford University Press
• Oxford Languages
• University of Oxford

Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide

• Copyright © 2024 Oxford University Press
• Cookie settings
• Cookie policy
• Privacy policy
• Legal notice

This Feature Is Available To Subscribers Only

Sign In or Create an Account

This PDF is available to Subscribers Only

For full access to this pdf, sign in to an existing account, or purchase an annual subscription.

• Utility Menu

Google Fonts

Creativity & problem-solving.

The Laboratory for Innovation Science at Harvard (LISH) is conducting research and creating evidence-based approaches to problem-solving. Researchers at LISH are identifying the best way to approach a problem, starting with problem formulation, and experimenting with solvers on the best way to find solutions.

Key Questions

How does the nature of the problem to be solved impact the most optimal problem-solving approaches to be used?

How can problems be best formulated so that outsiders can help solve them, how does diversity in knowledge and skills impact problem-solving, can creativity be enhanced through teams and/or exposure to peers, these four research questions frame projects in this track, pushing the boundaries of medical imaging and computational biology through artificial intelligence and algorithm development, extensive crowdsourcing work with nasa and other federal agencies, and using data science to help create a history of the partition of british india. see below for more information on each of the individual projects in this research track., nasa tournament lab.

The NASA Tournament Lab was originally established in 2010 as a joint initiative between NASA’s Center of Excellence for Collaborative Innovation (CoECI), Harvard Business School, and the Institute for Quantitative Social Science, to design and field challenges and contests... Read more about NASA Tournament Lab

Computational Biology Algorithms

Drivers of medical imaging diagnoses, integrating crowds into academic labs, advanced analytics challenges.

With the digital transformation in business and academia, the demand for advanced data analytics is increasing. LISH partners with foundations, government agencies, and research labs to access data analytics solutions through the crowd.... Read more about Advanced Analytics Challenges

Crowdsourcing for Social Good

Crowdsourcing memories from the 1947 partition of british india.

Working with the Lakshmi Mittal and Family South Asia Institute at Harvard University, this project aims to collect and analyze oral histories and memories of the 1947 Partition of British India with a focus on minority voices. Aspects of this project include gathering discrete historical data such as locations and descriptions of refugee camps; mapping geographical locations... Read more about Crowdsourcing Memories from the 1947 Partition of British India

Developing a Process to Foster Co-creation by Patients and Caretakers and our Research Communities

A joint project with Harvard Catalyst — Reactor , this initiative aims to pair patient- and caregiver-derived solutions with research labs at Boston-area medical schools to develop innovative tools to benefit the patients, their disease communities, and others with similar needs.... Read more about Developing a Process to Foster Co-creation by Patients and Caretakers and our Research Communities

City Challenges

LISH researchers are designing experiments wrapped around NYU GovLab’s City Challenges. The City Challenges program aims to use competitions and coaching to solve urban problems. See here for information on a prior challenge.

Related Publications

Free and Open Source Software (FOSS) has become a critical part of the modern economy. There are tens of millions of FOSS projects, many of which are built into software and products we use every day. However, it is difficult to fully understand the health, economic value, and security of FOSS because it is produced in a decentralized and distributed manner. This distributed development approach makes it unclear how much FOSS, and precisely what FOSS projects, are most widely used. This lack of understanding is a critical problem faced by those who want to help enhance the security of FOSS (e.g., companies, governments, individuals), yet do not know what projects to start with. This problem has garnered widespread attention with the Heartbleed and log4shell vulnerabilities that resulted in the susceptibility of hundreds of millions of devices to exploitation.

This report, Census II, is the second investigation into the widespread use of FOSS and aggregates data from over half a million observations of FOSS libraries used in production applications at thousands of companies, which aims to shed light on the most commonly used FOSS packages at the application library level. This effort builds on the Census I report that focused on the lower level critical operating system libraries and utilities, improving our understanding of the FOSS packages that software applications rely on. Such insights will help to identify critical FOSS packages to allow for resource prioritization to address security issues in this widely used software.

The Census II effort utilizes data from partner Software Composition Analysis (SCA) companies including Snyk, the Synopsys Cybersecurity Research Center (CyRC), and FOSSA, which partnered with Harvard to advance the state of open source research. Our goal is to not only identify the most widely used FOSS, but to also provide an example of how the distributed nature of FOSS requires a multi-party effort to fully understand the value and security of the FOSS ecosystem. Only through data-sharing, coordination, and investment will the value of this critical component of the digital economy be preserved for generations to come.

In addition to the detailed results on FOSS usage provided in the report, we identified five high-level findings: 1) the need for a standardized naming schema for software components, 2) the complexities associated with package versions, 3) much of the most widely used FOSS is developed by only a handful of contributors, 4) the increasing importance of individual developer account security, and 5) the persistence of legacy software in the open source space.

Karim R. Lakhani, Anne-Laure Fayard, Manos Gkeredakis, and Jin Hyun Paik . 10/5/2020. “ OpenIDEO (B) ”. Publisher's Version Abstract In the midst of 2020, as the coronavirus pandemic was unfolding, OpenIDEO - an online open innovation platform focused on design-driven solutions to social issues - rapidly launched a new challenge to improve access to health information, empower communities to stay safe during the COVID-19 crisis, and inspire global leaders to communicate effectively. OpenIDEO was particularly suited to challenges which required cross-system or sector-wide collaboration due to its focus on social impact and ecosystem design, but its leadership pondered how they could continue to improve virtual collaboration and to share their insights from nearly a decade of running online challenges. Conceived as an exercise of disruptive digital innovation, OpenIDEO successfully created a strong open innovation community, but how could they sustain - or even improve - their support to community members and increase the social impact of their online challenges in the coming years?

This paper presents NASA’s experience using a Center of Excellence (CoE) to scale and sustain an open innovation program as an effective problem-solving tool and includes strategic management recommendations for other organizations based on lessons learned.

This paper defines four phases of implementing an open innovation program: Learn, Pilot, Scale and Sustain. It provides guidance on the time required for each phase and recommendations for how to utilize a CoE to succeed. Recommendations are based upon the experience of NASA’s Human Health and Performance Directorate, and experience at the Laboratory for Innovation Science at Harvard running hundreds of challenges with research and development organizations.

Lessons learned include the importance of grounding innovation initiatives in the business strategy, assessing the portfolio of work to select problems most amenable to solving via crowdsourcing methodology, framing problems that external parties can solve, thinking strategically about early wins, selecting the right platforms, developing criteria for evaluation, and advancing a culture of innovation. Establishing a CoE provides an effective infrastructure to address both technical and cultural issues.

The NASA experience spanned more than seven years from initial learnings about open innovation concepts to the successful scaling and sustaining of an open innovation program; this paper provides recommendations on how to decrease this timeline to three years.

Tomohiro Ishibashi (Bashi), chief executive officer for B to S, and Julia Foote LeStage, chief innovation officer of Weathernews Inc., were addressing a panel at the HBS Digital Summit on creative uses of big data. They told the summit attendees about how the Sakura (cherry blossoms) Project, where the company asked users in Japan to report about how cherry blossoms were blooming near them day by day, had opened up opportunities for the company's consumer business in Japan. The project ultimately garnered positive publicity and became a foothold to building the company's crowdsourcing weather-forecasting service in Japan. It changed the face of weather forecasting in Japan. Bashi and LeStage wondered whether the experience could be applied to the U.S. market.

BACKGROUND: The association of differing genotypes with disease-related phenotypic traits offers great potential to both help identify new therapeutic targets and support stratification of patients who would gain the greatest benefit from specific drug classes. Development of low-cost genotyping and sequencing has made collecting large-scale genotyping data routine in population and therapeutic intervention studies. In addition, a range of new technologies is being used to capture numerous new and complex phenotypic descriptors. As a result, genotype and phenotype datasets have grown exponentially. Genome-wide association studies associate genotypes and phenotypes using methods such as logistic regression. As existing tools for association analysis limit the efficiency by which value can be extracted from increasing volumes of data, there is a pressing need for new software tools that can accelerate association analyses on large genotype-phenotype datasets.

RESULTS: Using open innovation (OI) and contest-based crowdsourcing, the logistic regression analysis in a leading, community-standard genetics software package (PLINK 1.07) was substantially accelerated. OI allowed us to do this in <6 months by providing rapid access to highly skilled programmers with specialized, difficult-to-find skill sets. Through a crowd-based contest a combination of computational, numeric, and algorithmic approaches was identified that accelerated the logistic regression in PLINK 1.07 by 18- to 45-fold. Combining contest-derived logistic regression code with coarse-grained parallelization, multithreading, and associated changes to data initialization code further developed through distributed innovation, we achieved an end-to-end speedup of 591-fold for a data set size of 6678 subjects by 645 863 variants, compared to PLINK 1.07's logistic regression. This represents a reduction in run time from 4.8 hours to 29 seconds. Accelerated logistic regression code developed in this project has been incorporated into the PLINK2 project.

CONCLUSIONS: Using iterative competition-based OI, we have developed a new, faster implementation of logistic regression for genome-wide association studies analysis. We present lessons learned and recommendations on running a successful OI process for bioinformatics.

Most United States Patent and Trademark Office (USPTO) patent documents contain drawing pages which describe inventions graphically. By convention and by rule, these drawings contain figures and parts that are annotated with numbered labels but not with text. As a result, readers must scan the document to find the description of a given part label. To make progress toward automatic creation of ‘tool-tips’ and hyperlinks from part labels to their associated descriptions, the USPTO hosted a monthlong online competition in which participants developed algorithms to detect figures and diagram part labels. The challenge drew 232 teams of two, of which 70 teams (30 %) submitted solutions. An unusual feature was that each patent was represented by a 300-dpi page scan along with an HTML file containing patent text, allowing integration of text processing and graphics recognition in participant algorithms. The design and performance of the top-5 systems are presented along with a system developed after the competition, illustrating that the winning teams produced near state-of-the-art results under strict time and computation constraints. The first place system used the provided HTML text, obtaining a harmonic mean of recall and precision (F-measure) of 88.57 % for figure region detection, 78.81 % for figure regions with correctly recognized figure titles, and 70.98 % for part label detection and recognition. Data and source code for the top-5 systems are available through the online UCI Machine Learning Repository to support follow-on work by others in the document recognition community.

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Review Article
• Open access
• Published: 11 January 2023

The effectiveness of collaborative problem solving in promoting students’ critical thinking: A meta-analysis based on empirical literature

• Enwei Xu   ORCID: orcid.org/0000-0001-6424-8169 1 ,
• Wei Wang 1 &
• Qingxia Wang 1  

Humanities and Social Sciences Communications volume  10 , Article number:  16 ( 2023 ) Cite this article

15k Accesses

15 Citations

3 Altmetric

Metrics details

• Science, technology and society

Collaborative problem-solving has been widely embraced in the classroom instruction of critical thinking, which is regarded as the core of curriculum reform based on key competencies in the field of education as well as a key competence for learners in the 21st century. However, the effectiveness of collaborative problem-solving in promoting students’ critical thinking remains uncertain. This current research presents the major findings of a meta-analysis of 36 pieces of the literature revealed in worldwide educational periodicals during the 21st century to identify the effectiveness of collaborative problem-solving in promoting students’ critical thinking and to determine, based on evidence, whether and to what extent collaborative problem solving can result in a rise or decrease in critical thinking. The findings show that (1) collaborative problem solving is an effective teaching approach to foster students’ critical thinking, with a significant overall effect size (ES = 0.82, z  = 12.78, P  < 0.01, 95% CI [0.69, 0.95]); (2) in respect to the dimensions of critical thinking, collaborative problem solving can significantly and successfully enhance students’ attitudinal tendencies (ES = 1.17, z  = 7.62, P  < 0.01, 95% CI[0.87, 1.47]); nevertheless, it falls short in terms of improving students’ cognitive skills, having only an upper-middle impact (ES = 0.70, z  = 11.55, P  < 0.01, 95% CI[0.58, 0.82]); and (3) the teaching type (chi 2  = 7.20, P  < 0.05), intervention duration (chi 2  = 12.18, P  < 0.01), subject area (chi 2  = 13.36, P  < 0.05), group size (chi 2  = 8.77, P  < 0.05), and learning scaffold (chi 2  = 9.03, P  < 0.01) all have an impact on critical thinking, and they can be viewed as important moderating factors that affect how critical thinking develops. On the basis of these results, recommendations are made for further study and instruction to better support students’ critical thinking in the context of collaborative problem-solving.

Similar content being viewed by others

Impact of artificial intelligence on human loss in decision making, laziness and safety in education

Testing theory of mind in large language models and humans

Interviews in the social sciences

Introduction.

Although critical thinking has a long history in research, the concept of critical thinking, which is regarded as an essential competence for learners in the 21st century, has recently attracted more attention from researchers and teaching practitioners (National Research Council, 2012 ). Critical thinking should be the core of curriculum reform based on key competencies in the field of education (Peng and Deng, 2017 ) because students with critical thinking can not only understand the meaning of knowledge but also effectively solve practical problems in real life even after knowledge is forgotten (Kek and Huijser, 2011 ). The definition of critical thinking is not universal (Ennis, 1989 ; Castle, 2009 ; Niu et al., 2013 ). In general, the definition of critical thinking is a self-aware and self-regulated thought process (Facione, 1990 ; Niu et al., 2013 ). It refers to the cognitive skills needed to interpret, analyze, synthesize, reason, and evaluate information as well as the attitudinal tendency to apply these abilities (Halpern, 2001 ). The view that critical thinking can be taught and learned through curriculum teaching has been widely supported by many researchers (e.g., Kuncel, 2011 ; Leng and Lu, 2020 ), leading to educators’ efforts to foster it among students. In the field of teaching practice, there are three types of courses for teaching critical thinking (Ennis, 1989 ). The first is an independent curriculum in which critical thinking is taught and cultivated without involving the knowledge of specific disciplines; the second is an integrated curriculum in which critical thinking is integrated into the teaching of other disciplines as a clear teaching goal; and the third is a mixed curriculum in which critical thinking is taught in parallel to the teaching of other disciplines for mixed teaching training. Furthermore, numerous measuring tools have been developed by researchers and educators to measure critical thinking in the context of teaching practice. These include standardized measurement tools, such as WGCTA, CCTST, CCTT, and CCTDI, which have been verified by repeated experiments and are considered effective and reliable by international scholars (Facione and Facione, 1992 ). In short, descriptions of critical thinking, including its two dimensions of attitudinal tendency and cognitive skills, different types of teaching courses, and standardized measurement tools provide a complex normative framework for understanding, teaching, and evaluating critical thinking.

Cultivating critical thinking in curriculum teaching can start with a problem, and one of the most popular critical thinking instructional approaches is problem-based learning (Liu et al., 2020 ). Duch et al. ( 2001 ) noted that problem-based learning in group collaboration is progressive active learning, which can improve students’ critical thinking and problem-solving skills. Collaborative problem-solving is the organic integration of collaborative learning and problem-based learning, which takes learners as the center of the learning process and uses problems with poor structure in real-world situations as the starting point for the learning process (Liang et al., 2017 ). Students learn the knowledge needed to solve problems in a collaborative group, reach a consensus on problems in the field, and form solutions through social cooperation methods, such as dialogue, interpretation, questioning, debate, negotiation, and reflection, thus promoting the development of learners’ domain knowledge and critical thinking (Cindy, 2004 ; Liang et al., 2017 ).

Collaborative problem-solving has been widely used in the teaching practice of critical thinking, and several studies have attempted to conduct a systematic review and meta-analysis of the empirical literature on critical thinking from various perspectives. However, little attention has been paid to the impact of collaborative problem-solving on critical thinking. Therefore, the best approach for developing and enhancing critical thinking throughout collaborative problem-solving is to examine how to implement critical thinking instruction; however, this issue is still unexplored, which means that many teachers are incapable of better instructing critical thinking (Leng and Lu, 2020 ; Niu et al., 2013 ). For example, Huber ( 2016 ) provided the meta-analysis findings of 71 publications on gaining critical thinking over various time frames in college with the aim of determining whether critical thinking was truly teachable. These authors found that learners significantly improve their critical thinking while in college and that critical thinking differs with factors such as teaching strategies, intervention duration, subject area, and teaching type. The usefulness of collaborative problem-solving in fostering students’ critical thinking, however, was not determined by this study, nor did it reveal whether there existed significant variations among the different elements. A meta-analysis of 31 pieces of educational literature was conducted by Liu et al. ( 2020 ) to assess the impact of problem-solving on college students’ critical thinking. These authors found that problem-solving could promote the development of critical thinking among college students and proposed establishing a reasonable group structure for problem-solving in a follow-up study to improve students’ critical thinking. Additionally, previous empirical studies have reached inconclusive and even contradictory conclusions about whether and to what extent collaborative problem-solving increases or decreases critical thinking levels. As an illustration, Yang et al. ( 2008 ) carried out an experiment on the integrated curriculum teaching of college students based on a web bulletin board with the goal of fostering participants’ critical thinking in the context of collaborative problem-solving. These authors’ research revealed that through sharing, debating, examining, and reflecting on various experiences and ideas, collaborative problem-solving can considerably enhance students’ critical thinking in real-life problem situations. In contrast, collaborative problem-solving had a positive impact on learners’ interaction and could improve learning interest and motivation but could not significantly improve students’ critical thinking when compared to traditional classroom teaching, according to research by Naber and Wyatt ( 2014 ) and Sendag and Odabasi ( 2009 ) on undergraduate and high school students, respectively.

The above studies show that there is inconsistency regarding the effectiveness of collaborative problem-solving in promoting students’ critical thinking. Therefore, it is essential to conduct a thorough and trustworthy review to detect and decide whether and to what degree collaborative problem-solving can result in a rise or decrease in critical thinking. Meta-analysis is a quantitative analysis approach that is utilized to examine quantitative data from various separate studies that are all focused on the same research topic. This approach characterizes the effectiveness of its impact by averaging the effect sizes of numerous qualitative studies in an effort to reduce the uncertainty brought on by independent research and produce more conclusive findings (Lipsey and Wilson, 2001 ).

This paper used a meta-analytic approach and carried out a meta-analysis to examine the effectiveness of collaborative problem-solving in promoting students’ critical thinking in order to make a contribution to both research and practice. The following research questions were addressed by this meta-analysis:

What is the overall effect size of collaborative problem-solving in promoting students’ critical thinking and its impact on the two dimensions of critical thinking (i.e., attitudinal tendency and cognitive skills)?

How are the disparities between the study conclusions impacted by various moderating variables if the impacts of various experimental designs in the included studies are heterogeneous?

This research followed the strict procedures (e.g., database searching, identification, screening, eligibility, merging, duplicate removal, and analysis of included studies) of Cooper’s ( 2010 ) proposed meta-analysis approach for examining quantitative data from various separate studies that are all focused on the same research topic. The relevant empirical research that appeared in worldwide educational periodicals within the 21st century was subjected to this meta-analysis using Rev-Man 5.4. The consistency of the data extracted separately by two researchers was tested using Cohen’s kappa coefficient, and a publication bias test and a heterogeneity test were run on the sample data to ascertain the quality of this meta-analysis.

Data sources and search strategies

There were three stages to the data collection process for this meta-analysis, as shown in Fig. 1 , which shows the number of articles included and eliminated during the selection process based on the statement and study eligibility criteria.

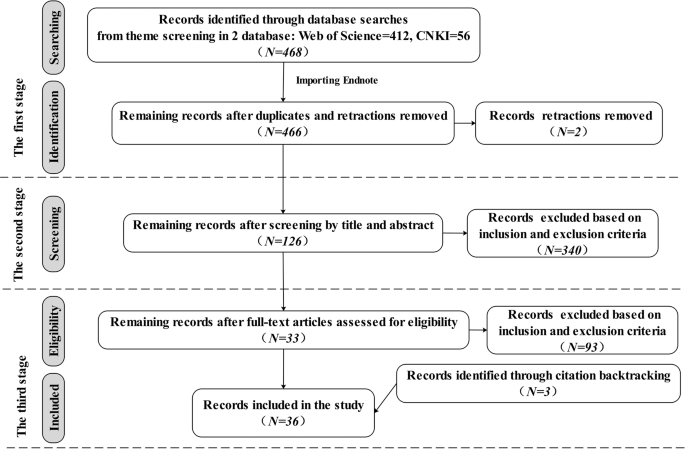
This flowchart shows the number of records identified, included and excluded in the article.

First, the databases used to systematically search for relevant articles were the journal papers of the Web of Science Core Collection and the Chinese Core source journal, as well as the Chinese Social Science Citation Index (CSSCI) source journal papers included in CNKI. These databases were selected because they are credible platforms that are sources of scholarly and peer-reviewed information with advanced search tools and contain literature relevant to the subject of our topic from reliable researchers and experts. The search string with the Boolean operator used in the Web of Science was “TS = (((“critical thinking” or “ct” and “pretest” or “posttest”) or (“critical thinking” or “ct” and “control group” or “quasi experiment” or “experiment”)) and (“collaboration” or “collaborative learning” or “CSCL”) and (“problem solving” or “problem-based learning” or “PBL”))”. The research area was “Education Educational Research”, and the search period was “January 1, 2000, to December 30, 2021”. A total of 412 papers were obtained. The search string with the Boolean operator used in the CNKI was “SU = (‘critical thinking’*‘collaboration’ + ‘critical thinking’*‘collaborative learning’ + ‘critical thinking’*‘CSCL’ + ‘critical thinking’*‘problem solving’ + ‘critical thinking’*‘problem-based learning’ + ‘critical thinking’*‘PBL’ + ‘critical thinking’*‘problem oriented’) AND FT = (‘experiment’ + ‘quasi experiment’ + ‘pretest’ + ‘posttest’ + ‘empirical study’)” (translated into Chinese when searching). A total of 56 studies were found throughout the search period of “January 2000 to December 2021”. From the databases, all duplicates and retractions were eliminated before exporting the references into Endnote, a program for managing bibliographic references. In all, 466 studies were found.

Second, the studies that matched the inclusion and exclusion criteria for the meta-analysis were chosen by two researchers after they had reviewed the abstracts and titles of the gathered articles, yielding a total of 126 studies.

Third, two researchers thoroughly reviewed each included article’s whole text in accordance with the inclusion and exclusion criteria. Meanwhile, a snowball search was performed using the references and citations of the included articles to ensure complete coverage of the articles. Ultimately, 36 articles were kept.

Two researchers worked together to carry out this entire process, and a consensus rate of almost 94.7% was reached after discussion and negotiation to clarify any emerging differences.

Eligibility criteria

Since not all the retrieved studies matched the criteria for this meta-analysis, eligibility criteria for both inclusion and exclusion were developed as follows:

The publication language of the included studies was limited to English and Chinese, and the full text could be obtained. Articles that did not meet the publication language and articles not published between 2000 and 2021 were excluded.

The research design of the included studies must be empirical and quantitative studies that can assess the effect of collaborative problem-solving on the development of critical thinking. Articles that could not identify the causal mechanisms by which collaborative problem-solving affects critical thinking, such as review articles and theoretical articles, were excluded.

The research method of the included studies must feature a randomized control experiment or a quasi-experiment, or a natural experiment, which have a higher degree of internal validity with strong experimental designs and can all plausibly provide evidence that critical thinking and collaborative problem-solving are causally related. Articles with non-experimental research methods, such as purely correlational or observational studies, were excluded.

The participants of the included studies were only students in school, including K-12 students and college students. Articles in which the participants were non-school students, such as social workers or adult learners, were excluded.

The research results of the included studies must mention definite signs that may be utilized to gauge critical thinking’s impact (e.g., sample size, mean value, or standard deviation). Articles that lacked specific measurement indicators for critical thinking and could not calculate the effect size were excluded.

Data coding design

In order to perform a meta-analysis, it is necessary to collect the most important information from the articles, codify that information’s properties, and convert descriptive data into quantitative data. Therefore, this study designed a data coding template (see Table 1 ). Ultimately, 16 coding fields were retained.

The designed data-coding template consisted of three pieces of information. Basic information about the papers was included in the descriptive information: the publishing year, author, serial number, and title of the paper.

The variable information for the experimental design had three variables: the independent variable (instruction method), the dependent variable (critical thinking), and the moderating variable (learning stage, teaching type, intervention duration, learning scaffold, group size, measuring tool, and subject area). Depending on the topic of this study, the intervention strategy, as the independent variable, was coded into collaborative and non-collaborative problem-solving. The dependent variable, critical thinking, was coded as a cognitive skill and an attitudinal tendency. And seven moderating variables were created by grouping and combining the experimental design variables discovered within the 36 studies (see Table 1 ), where learning stages were encoded as higher education, high school, middle school, and primary school or lower; teaching types were encoded as mixed courses, integrated courses, and independent courses; intervention durations were encoded as 0–1 weeks, 1–4 weeks, 4–12 weeks, and more than 12 weeks; group sizes were encoded as 2–3 persons, 4–6 persons, 7–10 persons, and more than 10 persons; learning scaffolds were encoded as teacher-supported learning scaffold, technique-supported learning scaffold, and resource-supported learning scaffold; measuring tools were encoded as standardized measurement tools (e.g., WGCTA, CCTT, CCTST, and CCTDI) and self-adapting measurement tools (e.g., modified or made by researchers); and subject areas were encoded according to the specific subjects used in the 36 included studies.

The data information contained three metrics for measuring critical thinking: sample size, average value, and standard deviation. It is vital to remember that studies with various experimental designs frequently adopt various formulas to determine the effect size. And this paper used Morris’ proposed standardized mean difference (SMD) calculation formula ( 2008 , p. 369; see Supplementary Table S3 ).

Procedure for extracting and coding data

According to the data coding template (see Table 1 ), the 36 papers’ information was retrieved by two researchers, who then entered them into Excel (see Supplementary Table S1 ). The results of each study were extracted separately in the data extraction procedure if an article contained numerous studies on critical thinking, or if a study assessed different critical thinking dimensions. For instance, Tiwari et al. ( 2010 ) used four time points, which were viewed as numerous different studies, to examine the outcomes of critical thinking, and Chen ( 2013 ) included the two outcome variables of attitudinal tendency and cognitive skills, which were regarded as two studies. After discussion and negotiation during data extraction, the two researchers’ consistency test coefficients were roughly 93.27%. Supplementary Table S2 details the key characteristics of the 36 included articles with 79 effect quantities, including descriptive information (e.g., the publishing year, author, serial number, and title of the paper), variable information (e.g., independent variables, dependent variables, and moderating variables), and data information (e.g., mean values, standard deviations, and sample size). Following that, testing for publication bias and heterogeneity was done on the sample data using the Rev-Man 5.4 software, and then the test results were used to conduct a meta-analysis.

Publication bias test

When the sample of studies included in a meta-analysis does not accurately reflect the general status of research on the relevant subject, publication bias is said to be exhibited in this research. The reliability and accuracy of the meta-analysis may be impacted by publication bias. Due to this, the meta-analysis needs to check the sample data for publication bias (Stewart et al., 2006 ). A popular method to check for publication bias is the funnel plot; and it is unlikely that there will be publishing bias when the data are equally dispersed on either side of the average effect size and targeted within the higher region. The data are equally dispersed within the higher portion of the efficient zone, consistent with the funnel plot connected with this analysis (see Fig. 2 ), indicating that publication bias is unlikely in this situation.

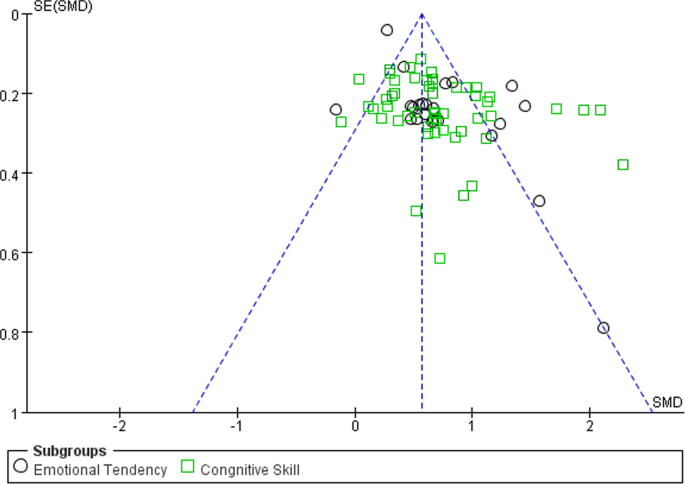
This funnel plot shows the result of publication bias of 79 effect quantities across 36 studies.

Heterogeneity test

To select the appropriate effect models for the meta-analysis, one might use the results of a heterogeneity test on the data effect sizes. In a meta-analysis, it is common practice to gauge the degree of data heterogeneity using the I 2 value, and I 2  ≥ 50% is typically understood to denote medium-high heterogeneity, which calls for the adoption of a random effect model; if not, a fixed effect model ought to be applied (Lipsey and Wilson, 2001 ). The findings of the heterogeneity test in this paper (see Table 2 ) revealed that I 2 was 86% and displayed significant heterogeneity ( P  < 0.01). To ensure accuracy and reliability, the overall effect size ought to be calculated utilizing the random effect model.

The analysis of the overall effect size

This meta-analysis utilized a random effect model to examine 79 effect quantities from 36 studies after eliminating heterogeneity. In accordance with Cohen’s criterion (Cohen, 1992 ), it is abundantly clear from the analysis results, which are shown in the forest plot of the overall effect (see Fig. 3 ), that the cumulative impact size of cooperative problem-solving is 0.82, which is statistically significant ( z  = 12.78, P  < 0.01, 95% CI [0.69, 0.95]), and can encourage learners to practice critical thinking.

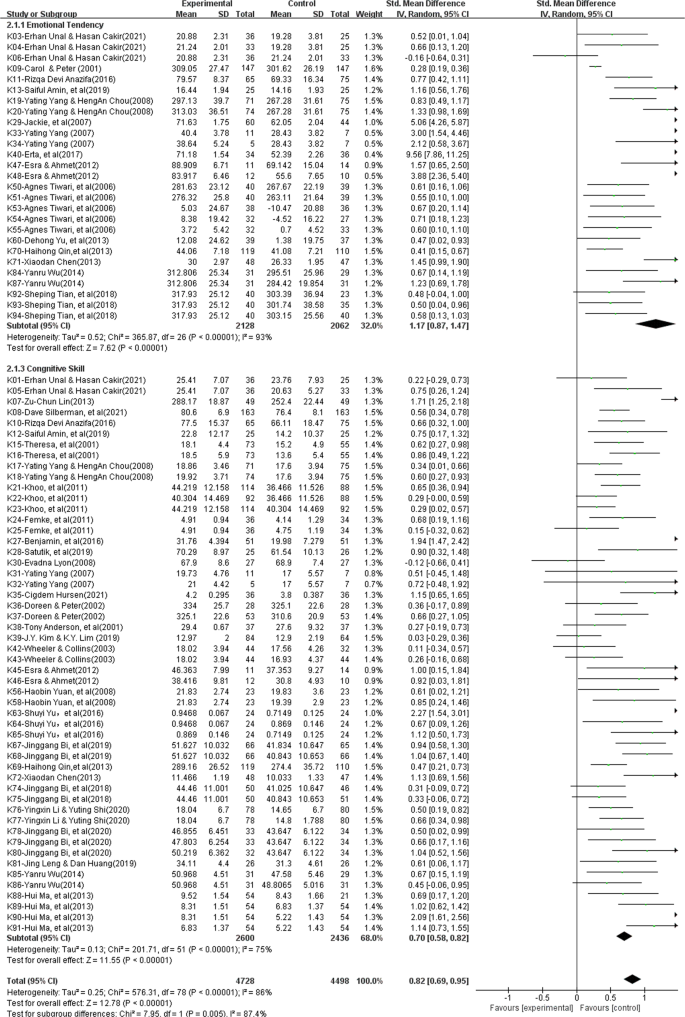
This forest plot shows the analysis result of the overall effect size across 36 studies.

In addition, this study examined two distinct dimensions of critical thinking to better understand the precise contributions that collaborative problem-solving makes to the growth of critical thinking. The findings (see Table 3 ) indicate that collaborative problem-solving improves cognitive skills (ES = 0.70) and attitudinal tendency (ES = 1.17), with significant intergroup differences (chi 2  = 7.95, P  < 0.01). Although collaborative problem-solving improves both dimensions of critical thinking, it is essential to point out that the improvements in students’ attitudinal tendency are much more pronounced and have a significant comprehensive effect (ES = 1.17, z  = 7.62, P  < 0.01, 95% CI [0.87, 1.47]), whereas gains in learners’ cognitive skill are slightly improved and are just above average. (ES = 0.70, z  = 11.55, P  < 0.01, 95% CI [0.58, 0.82]).

The analysis of moderator effect size

The whole forest plot’s 79 effect quantities underwent a two-tailed test, which revealed significant heterogeneity ( I 2  = 86%, z  = 12.78, P  < 0.01), indicating differences between various effect sizes that may have been influenced by moderating factors other than sampling error. Therefore, exploring possible moderating factors that might produce considerable heterogeneity was done using subgroup analysis, such as the learning stage, learning scaffold, teaching type, group size, duration of the intervention, measuring tool, and the subject area included in the 36 experimental designs, in order to further explore the key factors that influence critical thinking. The findings (see Table 4 ) indicate that various moderating factors have advantageous effects on critical thinking. In this situation, the subject area (chi 2  = 13.36, P  < 0.05), group size (chi 2  = 8.77, P  < 0.05), intervention duration (chi 2  = 12.18, P  < 0.01), learning scaffold (chi 2  = 9.03, P  < 0.01), and teaching type (chi 2  = 7.20, P  < 0.05) are all significant moderators that can be applied to support the cultivation of critical thinking. However, since the learning stage and the measuring tools did not significantly differ among intergroup (chi 2  = 3.15, P  = 0.21 > 0.05, and chi 2  = 0.08, P  = 0.78 > 0.05), we are unable to explain why these two factors are crucial in supporting the cultivation of critical thinking in the context of collaborative problem-solving. These are the precise outcomes, as follows:

Various learning stages influenced critical thinking positively, without significant intergroup differences (chi 2  = 3.15, P  = 0.21 > 0.05). High school was first on the list of effect sizes (ES = 1.36, P  < 0.01), then higher education (ES = 0.78, P  < 0.01), and middle school (ES = 0.73, P  < 0.01). These results show that, despite the learning stage’s beneficial influence on cultivating learners’ critical thinking, we are unable to explain why it is essential for cultivating critical thinking in the context of collaborative problem-solving.

Different teaching types had varying degrees of positive impact on critical thinking, with significant intergroup differences (chi 2  = 7.20, P  < 0.05). The effect size was ranked as follows: mixed courses (ES = 1.34, P  < 0.01), integrated courses (ES = 0.81, P  < 0.01), and independent courses (ES = 0.27, P  < 0.01). These results indicate that the most effective approach to cultivate critical thinking utilizing collaborative problem solving is through the teaching type of mixed courses.

Various intervention durations significantly improved critical thinking, and there were significant intergroup differences (chi 2  = 12.18, P  < 0.01). The effect sizes related to this variable showed a tendency to increase with longer intervention durations. The improvement in critical thinking reached a significant level (ES = 0.85, P  < 0.01) after more than 12 weeks of training. These findings indicate that the intervention duration and critical thinking’s impact are positively correlated, with a longer intervention duration having a greater effect.

Different learning scaffolds influenced critical thinking positively, with significant intergroup differences (chi 2  = 9.03, P  < 0.01). The resource-supported learning scaffold (ES = 0.69, P  < 0.01) acquired a medium-to-higher level of impact, the technique-supported learning scaffold (ES = 0.63, P  < 0.01) also attained a medium-to-higher level of impact, and the teacher-supported learning scaffold (ES = 0.92, P  < 0.01) displayed a high level of significant impact. These results show that the learning scaffold with teacher support has the greatest impact on cultivating critical thinking.

Various group sizes influenced critical thinking positively, and the intergroup differences were statistically significant (chi 2  = 8.77, P  < 0.05). Critical thinking showed a general declining trend with increasing group size. The overall effect size of 2–3 people in this situation was the biggest (ES = 0.99, P  < 0.01), and when the group size was greater than 7 people, the improvement in critical thinking was at the lower-middle level (ES < 0.5, P  < 0.01). These results show that the impact on critical thinking is positively connected with group size, and as group size grows, so does the overall impact.

Various measuring tools influenced critical thinking positively, with significant intergroup differences (chi 2  = 0.08, P  = 0.78 > 0.05). In this situation, the self-adapting measurement tools obtained an upper-medium level of effect (ES = 0.78), whereas the complete effect size of the standardized measurement tools was the largest, achieving a significant level of effect (ES = 0.84, P  < 0.01). These results show that, despite the beneficial influence of the measuring tool on cultivating critical thinking, we are unable to explain why it is crucial in fostering the growth of critical thinking by utilizing the approach of collaborative problem-solving.

Different subject areas had a greater impact on critical thinking, and the intergroup differences were statistically significant (chi 2  = 13.36, P  < 0.05). Mathematics had the greatest overall impact, achieving a significant level of effect (ES = 1.68, P  < 0.01), followed by science (ES = 1.25, P  < 0.01) and medical science (ES = 0.87, P  < 0.01), both of which also achieved a significant level of effect. Programming technology was the least effective (ES = 0.39, P  < 0.01), only having a medium-low degree of effect compared to education (ES = 0.72, P  < 0.01) and other fields (such as language, art, and social sciences) (ES = 0.58, P  < 0.01). These results suggest that scientific fields (e.g., mathematics, science) may be the most effective subject areas for cultivating critical thinking utilizing the approach of collaborative problem-solving.

The effectiveness of collaborative problem solving with regard to teaching critical thinking

According to this meta-analysis, using collaborative problem-solving as an intervention strategy in critical thinking teaching has a considerable amount of impact on cultivating learners’ critical thinking as a whole and has a favorable promotional effect on the two dimensions of critical thinking. According to certain studies, collaborative problem solving, the most frequently used critical thinking teaching strategy in curriculum instruction can considerably enhance students’ critical thinking (e.g., Liang et al., 2017 ; Liu et al., 2020 ; Cindy, 2004 ). This meta-analysis provides convergent data support for the above research views. Thus, the findings of this meta-analysis not only effectively address the first research query regarding the overall effect of cultivating critical thinking and its impact on the two dimensions of critical thinking (i.e., attitudinal tendency and cognitive skills) utilizing the approach of collaborative problem-solving, but also enhance our confidence in cultivating critical thinking by using collaborative problem-solving intervention approach in the context of classroom teaching.

Furthermore, the associated improvements in attitudinal tendency are much stronger, but the corresponding improvements in cognitive skill are only marginally better. According to certain studies, cognitive skill differs from the attitudinal tendency in classroom instruction; the cultivation and development of the former as a key ability is a process of gradual accumulation, while the latter as an attitude is affected by the context of the teaching situation (e.g., a novel and exciting teaching approach, challenging and rewarding tasks) (Halpern, 2001 ; Wei and Hong, 2022 ). Collaborative problem-solving as a teaching approach is exciting and interesting, as well as rewarding and challenging; because it takes the learners as the focus and examines problems with poor structure in real situations, and it can inspire students to fully realize their potential for problem-solving, which will significantly improve their attitudinal tendency toward solving problems (Liu et al., 2020 ). Similar to how collaborative problem-solving influences attitudinal tendency, attitudinal tendency impacts cognitive skill when attempting to solve a problem (Liu et al., 2020 ; Zhang et al., 2022 ), and stronger attitudinal tendencies are associated with improved learning achievement and cognitive ability in students (Sison, 2008 ; Zhang et al., 2022 ). It can be seen that the two specific dimensions of critical thinking as well as critical thinking as a whole are affected by collaborative problem-solving, and this study illuminates the nuanced links between cognitive skills and attitudinal tendencies with regard to these two dimensions of critical thinking. To fully develop students’ capacity for critical thinking, future empirical research should pay closer attention to cognitive skills.

The moderating effects of collaborative problem solving with regard to teaching critical thinking

In order to further explore the key factors that influence critical thinking, exploring possible moderating effects that might produce considerable heterogeneity was done using subgroup analysis. The findings show that the moderating factors, such as the teaching type, learning stage, group size, learning scaffold, duration of the intervention, measuring tool, and the subject area included in the 36 experimental designs, could all support the cultivation of collaborative problem-solving in critical thinking. Among them, the effect size differences between the learning stage and measuring tool are not significant, which does not explain why these two factors are crucial in supporting the cultivation of critical thinking utilizing the approach of collaborative problem-solving.

In terms of the learning stage, various learning stages influenced critical thinking positively without significant intergroup differences, indicating that we are unable to explain why it is crucial in fostering the growth of critical thinking.

Although high education accounts for 70.89% of all empirical studies performed by researchers, high school may be the appropriate learning stage to foster students’ critical thinking by utilizing the approach of collaborative problem-solving since it has the largest overall effect size. This phenomenon may be related to student’s cognitive development, which needs to be further studied in follow-up research.

With regard to teaching type, mixed course teaching may be the best teaching method to cultivate students’ critical thinking. Relevant studies have shown that in the actual teaching process if students are trained in thinking methods alone, the methods they learn are isolated and divorced from subject knowledge, which is not conducive to their transfer of thinking methods; therefore, if students’ thinking is trained only in subject teaching without systematic method training, it is challenging to apply to real-world circumstances (Ruggiero, 2012 ; Hu and Liu, 2015 ). Teaching critical thinking as mixed course teaching in parallel to other subject teachings can achieve the best effect on learners’ critical thinking, and explicit critical thinking instruction is more effective than less explicit critical thinking instruction (Bensley and Spero, 2014 ).

In terms of the intervention duration, with longer intervention times, the overall effect size shows an upward tendency. Thus, the intervention duration and critical thinking’s impact are positively correlated. Critical thinking, as a key competency for students in the 21st century, is difficult to get a meaningful improvement in a brief intervention duration. Instead, it could be developed over a lengthy period of time through consistent teaching and the progressive accumulation of knowledge (Halpern, 2001 ; Hu and Liu, 2015 ). Therefore, future empirical studies ought to take these restrictions into account throughout a longer period of critical thinking instruction.

With regard to group size, a group size of 2–3 persons has the highest effect size, and the comprehensive effect size decreases with increasing group size in general. This outcome is in line with some research findings; as an example, a group composed of two to four members is most appropriate for collaborative learning (Schellens and Valcke, 2006 ). However, the meta-analysis results also indicate that once the group size exceeds 7 people, small groups cannot produce better interaction and performance than large groups. This may be because the learning scaffolds of technique support, resource support, and teacher support improve the frequency and effectiveness of interaction among group members, and a collaborative group with more members may increase the diversity of views, which is helpful to cultivate critical thinking utilizing the approach of collaborative problem-solving.

With regard to the learning scaffold, the three different kinds of learning scaffolds can all enhance critical thinking. Among them, the teacher-supported learning scaffold has the largest overall effect size, demonstrating the interdependence of effective learning scaffolds and collaborative problem-solving. This outcome is in line with some research findings; as an example, a successful strategy is to encourage learners to collaborate, come up with solutions, and develop critical thinking skills by using learning scaffolds (Reiser, 2004 ; Xu et al., 2022 ); learning scaffolds can lower task complexity and unpleasant feelings while also enticing students to engage in learning activities (Wood et al., 2006 ); learning scaffolds are designed to assist students in using learning approaches more successfully to adapt the collaborative problem-solving process, and the teacher-supported learning scaffolds have the greatest influence on critical thinking in this process because they are more targeted, informative, and timely (Xu et al., 2022 ).

With respect to the measuring tool, despite the fact that standardized measurement tools (such as the WGCTA, CCTT, and CCTST) have been acknowledged as trustworthy and effective by worldwide experts, only 54.43% of the research included in this meta-analysis adopted them for assessment, and the results indicated no intergroup differences. These results suggest that not all teaching circumstances are appropriate for measuring critical thinking using standardized measurement tools. “The measuring tools for measuring thinking ability have limits in assessing learners in educational situations and should be adapted appropriately to accurately assess the changes in learners’ critical thinking.”, according to Simpson and Courtney ( 2002 , p. 91). As a result, in order to more fully and precisely gauge how learners’ critical thinking has evolved, we must properly modify standardized measuring tools based on collaborative problem-solving learning contexts.

With regard to the subject area, the comprehensive effect size of science departments (e.g., mathematics, science, medical science) is larger than that of language arts and social sciences. Some recent international education reforms have noted that critical thinking is a basic part of scientific literacy. Students with scientific literacy can prove the rationality of their judgment according to accurate evidence and reasonable standards when they face challenges or poorly structured problems (Kyndt et al., 2013 ), which makes critical thinking crucial for developing scientific understanding and applying this understanding to practical problem solving for problems related to science, technology, and society (Yore et al., 2007 ).

Suggestions for critical thinking teaching

Other than those stated in the discussion above, the following suggestions are offered for critical thinking instruction utilizing the approach of collaborative problem-solving.

First, teachers should put a special emphasis on the two core elements, which are collaboration and problem-solving, to design real problems based on collaborative situations. This meta-analysis provides evidence to support the view that collaborative problem-solving has a strong synergistic effect on promoting students’ critical thinking. Asking questions about real situations and allowing learners to take part in critical discussions on real problems during class instruction are key ways to teach critical thinking rather than simply reading speculative articles without practice (Mulnix, 2012 ). Furthermore, the improvement of students’ critical thinking is realized through cognitive conflict with other learners in the problem situation (Yang et al., 2008 ). Consequently, it is essential for teachers to put a special emphasis on the two core elements, which are collaboration and problem-solving, and design real problems and encourage students to discuss, negotiate, and argue based on collaborative problem-solving situations.

Second, teachers should design and implement mixed courses to cultivate learners’ critical thinking, utilizing the approach of collaborative problem-solving. Critical thinking can be taught through curriculum instruction (Kuncel, 2011 ; Leng and Lu, 2020 ), with the goal of cultivating learners’ critical thinking for flexible transfer and application in real problem-solving situations. This meta-analysis shows that mixed course teaching has a highly substantial impact on the cultivation and promotion of learners’ critical thinking. Therefore, teachers should design and implement mixed course teaching with real collaborative problem-solving situations in combination with the knowledge content of specific disciplines in conventional teaching, teach methods and strategies of critical thinking based on poorly structured problems to help students master critical thinking, and provide practical activities in which students can interact with each other to develop knowledge construction and critical thinking utilizing the approach of collaborative problem-solving.

Third, teachers should be more trained in critical thinking, particularly preservice teachers, and they also should be conscious of the ways in which teachers’ support for learning scaffolds can promote critical thinking. The learning scaffold supported by teachers had the greatest impact on learners’ critical thinking, in addition to being more directive, targeted, and timely (Wood et al., 2006 ). Critical thinking can only be effectively taught when teachers recognize the significance of critical thinking for students’ growth and use the proper approaches while designing instructional activities (Forawi, 2016 ). Therefore, with the intention of enabling teachers to create learning scaffolds to cultivate learners’ critical thinking utilizing the approach of collaborative problem solving, it is essential to concentrate on the teacher-supported learning scaffolds and enhance the instruction for teaching critical thinking to teachers, especially preservice teachers.

Implications and limitations

There are certain limitations in this meta-analysis, but future research can correct them. First, the search languages were restricted to English and Chinese, so it is possible that pertinent studies that were written in other languages were overlooked, resulting in an inadequate number of articles for review. Second, these data provided by the included studies are partially missing, such as whether teachers were trained in the theory and practice of critical thinking, the average age and gender of learners, and the differences in critical thinking among learners of various ages and genders. Third, as is typical for review articles, more studies were released while this meta-analysis was being done; therefore, it had a time limit. With the development of relevant research, future studies focusing on these issues are highly relevant and needed.

Conclusions

The subject of the magnitude of collaborative problem-solving’s impact on fostering students’ critical thinking, which received scant attention from other studies, was successfully addressed by this study. The question of the effectiveness of collaborative problem-solving in promoting students’ critical thinking was addressed in this study, which addressed a topic that had gotten little attention in earlier research. The following conclusions can be made:

Regarding the results obtained, collaborative problem solving is an effective teaching approach to foster learners’ critical thinking, with a significant overall effect size (ES = 0.82, z  = 12.78, P  < 0.01, 95% CI [0.69, 0.95]). With respect to the dimensions of critical thinking, collaborative problem-solving can significantly and effectively improve students’ attitudinal tendency, and the comprehensive effect is significant (ES = 1.17, z  = 7.62, P  < 0.01, 95% CI [0.87, 1.47]); nevertheless, it falls short in terms of improving students’ cognitive skills, having only an upper-middle impact (ES = 0.70, z  = 11.55, P  < 0.01, 95% CI [0.58, 0.82]).

As demonstrated by both the results and the discussion, there are varying degrees of beneficial effects on students’ critical thinking from all seven moderating factors, which were found across 36 studies. In this context, the teaching type (chi 2  = 7.20, P  < 0.05), intervention duration (chi 2  = 12.18, P  < 0.01), subject area (chi 2  = 13.36, P  < 0.05), group size (chi 2  = 8.77, P  < 0.05), and learning scaffold (chi 2  = 9.03, P  < 0.01) all have a positive impact on critical thinking, and they can be viewed as important moderating factors that affect how critical thinking develops. Since the learning stage (chi 2  = 3.15, P  = 0.21 > 0.05) and measuring tools (chi 2  = 0.08, P  = 0.78 > 0.05) did not demonstrate any significant intergroup differences, we are unable to explain why these two factors are crucial in supporting the cultivation of critical thinking in the context of collaborative problem-solving.

Data availability

All data generated or analyzed during this study are included within the article and its supplementary information files, and the supplementary information files are available in the Dataverse repository: https://doi.org/10.7910/DVN/IPFJO6 .

Bensley DA, Spero RA (2014) Improving critical thinking skills and meta-cognitive monitoring through direct infusion. Think Skills Creat 12:55–68. https://doi.org/10.1016/j.tsc.2014.02.001

Article   Google Scholar  

Castle A (2009) Defining and assessing critical thinking skills for student radiographers. Radiography 15(1):70–76. https://doi.org/10.1016/j.radi.2007.10.007

Chen XD (2013) An empirical study on the influence of PBL teaching model on critical thinking ability of non-English majors. J PLA Foreign Lang College 36 (04):68–72

Google Scholar  

Cohen A (1992) Antecedents of organizational commitment across occupational groups: a meta-analysis. J Organ Behav. https://doi.org/10.1002/job.4030130602

Cooper H (2010) Research synthesis and meta-analysis: a step-by-step approach, 4th edn. Sage, London, England

Cindy HS (2004) Problem-based learning: what and how do students learn? Educ Psychol Rev 51(1):31–39

Duch BJ, Gron SD, Allen DE (2001) The power of problem-based learning: a practical “how to” for teaching undergraduate courses in any discipline. Stylus Educ Sci 2:190–198

Ennis RH (1989) Critical thinking and subject specificity: clarification and needed research. Educ Res 18(3):4–10. https://doi.org/10.3102/0013189x018003004

Facione PA (1990) Critical thinking: a statement of expert consensus for purposes of educational assessment and instruction. Research findings and recommendations. Eric document reproduction service. https://eric.ed.gov/?id=ed315423

Facione PA, Facione NC (1992) The California Critical Thinking Dispositions Inventory (CCTDI) and the CCTDI test manual. California Academic Press, Millbrae, CA

Forawi SA (2016) Standard-based science education and critical thinking. Think Skills Creat 20:52–62. https://doi.org/10.1016/j.tsc.2016.02.005

Halpern DF (2001) Assessing the effectiveness of critical thinking instruction. J Gen Educ 50(4):270–286. https://doi.org/10.2307/27797889

Hu WP, Liu J (2015) Cultivation of pupils’ thinking ability: a five-year follow-up study. Psychol Behav Res 13(05):648–654. https://doi.org/10.3969/j.issn.1672-0628.2015.05.010

Huber K (2016) Does college teach critical thinking? A meta-analysis. Rev Educ Res 86(2):431–468. https://doi.org/10.3102/0034654315605917

Kek MYCA, Huijser H (2011) The power of problem-based learning in developing critical thinking skills: preparing students for tomorrow’s digital futures in today’s classrooms. High Educ Res Dev 30(3):329–341. https://doi.org/10.1080/07294360.2010.501074

Kuncel NR (2011) Measurement and meaning of critical thinking (Research report for the NRC 21st Century Skills Workshop). National Research Council, Washington, DC

Kyndt E, Raes E, Lismont B, Timmers F, Cascallar E, Dochy F (2013) A meta-analysis of the effects of face-to-face cooperative learning. Do recent studies falsify or verify earlier findings? Educ Res Rev 10(2):133–149. https://doi.org/10.1016/j.edurev.2013.02.002

Leng J, Lu XX (2020) Is critical thinking really teachable?—A meta-analysis based on 79 experimental or quasi experimental studies. Open Educ Res 26(06):110–118. https://doi.org/10.13966/j.cnki.kfjyyj.2020.06.011

Liang YZ, Zhu K, Zhao CL (2017) An empirical study on the depth of interaction promoted by collaborative problem solving learning activities. J E-educ Res 38(10):87–92. https://doi.org/10.13811/j.cnki.eer.2017.10.014

Lipsey M, Wilson D (2001) Practical meta-analysis. International Educational and Professional, London, pp. 92–160

Liu Z, Wu W, Jiang Q (2020) A study on the influence of problem based learning on college students’ critical thinking-based on a meta-analysis of 31 studies. Explor High Educ 03:43–49

Morris SB (2008) Estimating effect sizes from pretest-posttest-control group designs. Organ Res Methods 11(2):364–386. https://doi.org/10.1177/1094428106291059

Article   ADS   Google Scholar  

Mulnix JW (2012) Thinking critically about critical thinking. Educ Philos Theory 44(5):464–479. https://doi.org/10.1111/j.1469-5812.2010.00673.x

Naber J, Wyatt TH (2014) The effect of reflective writing interventions on the critical thinking skills and dispositions of baccalaureate nursing students. Nurse Educ Today 34(1):67–72. https://doi.org/10.1016/j.nedt.2013.04.002

National Research Council (2012) Education for life and work: developing transferable knowledge and skills in the 21st century. The National Academies Press, Washington, DC

Niu L, Behar HLS, Garvan CW (2013) Do instructional interventions influence college students’ critical thinking skills? A meta-analysis. Educ Res Rev 9(12):114–128. https://doi.org/10.1016/j.edurev.2012.12.002

Peng ZM, Deng L (2017) Towards the core of education reform: cultivating critical thinking skills as the core of skills in the 21st century. Res Educ Dev 24:57–63. https://doi.org/10.14121/j.cnki.1008-3855.2017.24.011

Reiser BJ (2004) Scaffolding complex learning: the mechanisms of structuring and problematizing student work. J Learn Sci 13(3):273–304. https://doi.org/10.1207/s15327809jls1303_2

Ruggiero VR (2012) The art of thinking: a guide to critical and creative thought, 4th edn. Harper Collins College Publishers, New York

Schellens T, Valcke M (2006) Fostering knowledge construction in university students through asynchronous discussion groups. Comput Educ 46(4):349–370. https://doi.org/10.1016/j.compedu.2004.07.010

Sendag S, Odabasi HF (2009) Effects of an online problem based learning course on content knowledge acquisition and critical thinking skills. Comput Educ 53(1):132–141. https://doi.org/10.1016/j.compedu.2009.01.008

Sison R (2008) Investigating Pair Programming in a Software Engineering Course in an Asian Setting. 2008 15th Asia-Pacific Software Engineering Conference, pp. 325–331. https://doi.org/10.1109/APSEC.2008.61

Simpson E, Courtney M (2002) Critical thinking in nursing education: literature review. Mary Courtney 8(2):89–98

Stewart L, Tierney J, Burdett S (2006) Do systematic reviews based on individual patient data offer a means of circumventing biases associated with trial publications? Publication bias in meta-analysis. John Wiley and Sons Inc, New York, pp. 261–286

Tiwari A, Lai P, So M, Yuen K (2010) A comparison of the effects of problem-based learning and lecturing on the development of students’ critical thinking. Med Educ 40(6):547–554. https://doi.org/10.1111/j.1365-2929.2006.02481.x

Wood D, Bruner JS, Ross G (2006) The role of tutoring in problem solving. J Child Psychol Psychiatry 17(2):89–100. https://doi.org/10.1111/j.1469-7610.1976.tb00381.x

Wei T, Hong S (2022) The meaning and realization of teachable critical thinking. Educ Theory Practice 10:51–57

Xu EW, Wang W, Wang QX (2022) A meta-analysis of the effectiveness of programming teaching in promoting K-12 students’ computational thinking. Educ Inf Technol. https://doi.org/10.1007/s10639-022-11445-2

Yang YC, Newby T, Bill R (2008) Facilitating interactions through structured web-based bulletin boards: a quasi-experimental study on promoting learners’ critical thinking skills. Comput Educ 50(4):1572–1585. https://doi.org/10.1016/j.compedu.2007.04.006

Yore LD, Pimm D, Tuan HL (2007) The literacy component of mathematical and scientific literacy. Int J Sci Math Educ 5(4):559–589. https://doi.org/10.1007/s10763-007-9089-4

Zhang T, Zhang S, Gao QQ, Wang JH (2022) Research on the development of learners’ critical thinking in online peer review. Audio Visual Educ Res 6:53–60. https://doi.org/10.13811/j.cnki.eer.2022.06.08

Download references

Acknowledgements

This research was supported by the graduate scientific research and innovation project of Xinjiang Uygur Autonomous Region named “Research on in-depth learning of high school information technology courses for the cultivation of computing thinking” (No. XJ2022G190) and the independent innovation fund project for doctoral students of the College of Educational Science of Xinjiang Normal University named “Research on project-based teaching of high school information technology courses from the perspective of discipline core literacy” (No. XJNUJKYA2003).

Author information

Authors and affiliations.

College of Educational Science, Xinjiang Normal University, 830017, Urumqi, Xinjiang, China

Enwei Xu, Wei Wang & Qingxia Wang

You can also search for this author in PubMed   Google Scholar

Corresponding authors

Correspondence to Enwei Xu or Wei Wang .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Ethical approval

This article does not contain any studies with human participants performed by any of the authors.

Informed consent

Additional information.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary tables, rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Xu, E., Wang, W. & Wang, Q. The effectiveness of collaborative problem solving in promoting students’ critical thinking: A meta-analysis based on empirical literature. Humanit Soc Sci Commun 10 , 16 (2023). https://doi.org/10.1057/s41599-023-01508-1

Download citation

Received : 07 August 2022

Accepted : 04 January 2023

Published : 11 January 2023

DOI : https://doi.org/10.1057/s41599-023-01508-1

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Impacts of online collaborative learning on students’ intercultural communication apprehension and intercultural communicative competence.

• Hoa Thi Hoang Chau
• Hung Phu Bui
• Quynh Thi Huong Dinh

Education and Information Technologies (2024)

Exploring the effects of digital technology on deep learning: a meta-analysis

Sustainable electricity generation and farm-grid utilization from photovoltaic aquaculture: a bibliometric analysis.

• A. A. Amusa
• M. Alhassan

International Journal of Environmental Science and Technology (2024)

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

• Reference Manager
• Simple TEXT file

People also looked at

Original research article, creative problem solving as overcoming a misunderstanding.

• Department of Psychology, University of Milano-Bicocca, Milan, Italy

Solving or attempting to solve problems is the typical and, hence, general function of thought. A theory of problem solving must first explain how the problem is constituted, and then how the solution happens, but also how it happens that it is not solved; it must explain the correct answer and with the same means the failure. The identification of the way in which the problem is formatted should help to understand how the solution of the problems happens, but even before that, the source of the difficulty. Sometimes the difficulty lies in the calculation, the number of operations to be performed, and the quantity of data to be processed and remembered. There are, however, other problems – the insight problems – in which the difficulty does not lie so much in the complexity of the calculations, but in one or more critical points that are susceptible to misinterpretation , incompatible with the solution. In our view, the way of thinking involved in insight problem solving is very close to the process involved in the understanding of an utterance, when a misunderstanding occurs. In this case, a more appropriate meaning has to be selected to resolve the misunderstanding (the “impasse”), the default interpretation (the “fixation”) has to be dropped in order to “restructure.” to grasp another meaning which appears more relevant to the context and the speaker’s intention (the “aim of the task”). In this article we support our view with experimental evidence, focusing on how a misunderstanding is formed. We have studied a paradigmatic insight problem, an apparent trivial arithmetical task, the Ties problem. We also reviewed other classical insight problems, reconsidering in particular one of the most intriguing one, which at first sight appears impossible to solve, the Study Window problem. By identifying the problem knots that alter the aim of the task, the reformulation technique has made it possible to eliminate misunderstanding, without changing the mathematical nature of the problem. With the experimental versions of the problems exposed we have obtained a significant increase in correct answers. Studying how an insight problem is formed, and not just how it is solved, may well become an important topic in education. We focus on undergraduate students’ strategies and their errors while solving problems, and the specific cognitive processes involved in misunderstanding, which are crucial to better exploit what could be beneficial to reach the solution and to teach how to improve the ability to solve problems.

Introduction

“A problem arises when a living creature has a goal but does not know how this goal is to be reached. Whenever one cannot go from the given situation to the desired situation simply by action, then there has to be recourse to thinking. (…) Such thinking has the task of devising some action which may mediate between the existing and the desired situations.” ( Duncker, 1945 , p. 1). We agree with Duncker’s general description of every situation we call a problem: the problem solving activity takes a central role in the general function of thought, if not even identifies with it.

So far, psychologists have been mainly interested in the solution and the solvers. But the formation of the problem remained in the shadows.

Let’s consider for example the two fundamental theoretical approaches to the study of problem solving. “What questions should a theory of problem solving answer? First, it should predict the performance of a problem solver handling specified tasks. It should explain how human problem solving takes place: what processes are used, and what mechanisms perform these processes.” ( Newell et al., 1958 , p. 151). In turn, authors of different orientations indicate as central in their research “How does the solution arise from the problem situation? In what ways is the solution of a problem attained?” ( Duncker, 1945 , p. 1) or that of what happens when you solve a problem, when you suddenly see the point ( Wertheimer, 1959 ). It is obvious, and it was inevitable, that the formation of the problem would remain in the shadows.

A theory of problem solving must first explain how the problem is constituted, and then how the solution happens, but also how it happens that it is not solved; it must explain the correct answer and with the same means the failure. The identification of the way in which the problem is constituted – the formation of the problem – and the awareness that this moment is decisive for everything that follows imply that failures are considered in a new way, the study of which should help to understand how the solution of the problems happens, but even before that, the source of the difficulty.

Sometimes the difficulty lies in the calculation, the number of operations to be performed, and the quantity of data to be processed and remembered. Take the well-known problems studied by Simon, Crypto-arithmetic task, for example, or the Cannibals and Missionaries problem ( Simon, 1979 ). The difficulty in these problems lies in the complexity of the calculation which characterizes them. But, the text and the request of the problem is univocally understood by the experimenter and by the participant in both the explicit ( said )and implicit ( implied ) parts. 1 As Simon says, “Subjects do not initially choose deliberately among problem representations, but almost always adopt the representation suggested by the verbal problem statement” ( Kaplan and Simon, 1990 , p. 376). The verbal problem statement determines a problem representation, implicit presuppositions of which are shared by both.

There are, however, other problems where the usual (generalized) interpretation of the text of the problem (and/or the associated figure) prevents and does not allow a solution to be found, so that we are soon faced with an impasse. We’ll call this kind of problems insight problems . “In these cases, where the complexity of the calculations does not play a relevant part in the difficulty of the problem, a misunderstanding would appear to be a more appropriate abstract model than the labyrinth” ( Mosconi, 2016 , p. 356). Insight problems do not arise from a fortuitous misunderstanding, but from a deliberate violation of Gricean conversational rules, since the implicit layer of the discourse (the implied ) is not shared both by experimenter and participant. Take for example the problem of how to remove a one-hundred dollar bill without causing a pyramid balanced atop the bill to topple: “A giant inverted steel pyramid is perfectly balanced on its point. Any movement of the pyramid will cause it to topple over. Underneath the pyramid is a $100 bill. How would you remove the bill without disturbing the pyramid?” ( Schooler et al., 1993 , p. 183). The solution is burn or tear the dollar bill but people assume that the 100 dollar bill must not be damaged, but contrary to his assumption, this is in fact the solution. Obviously this is not a trivial error of understanding between the two parties, but rather a misunderstanding due to social conventions, and dictated by conversational rules. It is the essential condition for the forming of the problem and the experimenter has played on the very fact that the condition was not explicitly stated (see also Bulbrook, 1932 ).

When insight problems are used in research, it could be said that the researcher sets a trap, more or less intentionally, inducing an interpretation that appears to be pertinent to the data and to the text; this interpretation is adopted more or less automatically because it has been validated by use but the default interpretation does not support understanding, and misunderstanding is inevitable; as a result, sooner or later we come up against an impasse. The theory of misunderstanding is supported by experimental evidence obtained by Mosconi in his research on insight problem solving ( Mosconi, 1990 ), and by Bagassi and Macchi on problem solving, decision making and probabilistic reasoning ( Bagassi and Macchi, 2006 , 2016 ; Macchi and Bagassi, 2012 , 2014 , 2015 , 2020 ; Macchi, 1995 , 2000 ; Mosconi and Macchi, 2001 ; Politzer and Macchi, 2000 ).

The implication of the focus on problem forming for education is remarkable: everything we say generates a communicative and therefore interpretative context, which is given by cultural and social assumptions, default interpretations, and attribution of intention to the speaker. Since the text of the problem is expressed in natural language, it is affected, it shares the characteristics of the language itself. Natural language is ambiguous in itself, differently from specialized languages (i.e., logical and statistical ones), which presuppose a univocal, unambiguous interpretation. The understanding of what a speaker means requires a disambiguation process centered on the intention attribution.

Restructuring as Reinterpreting

Traditionally, according to the Gestaltists, finding the solution to an insight problem is an example of “productive thought.” In addition to the reproductive activities of thought, there are processes which create, “produce” that which does not yet exist. It is characterized by a switch in direction which occurs together with the transformation of the problem or a change in our understanding of an essential relationship. The famous “aha!” experience of genuine insight accompanies this change in representation, or restructuring. As Wertheimer says: “… Solution becomes possible only when the central features of the problem are clearly recognized, and paths to a possible approach emerge. Irrelevant features must be stripped away, core features must become salient, and some representation must be developed that accurately reflects how various parts of the problem fit together; relevant relations among parts, and between parts and whole, must be understood, must make sense” ( Wertheimer, 1985 , p. 23).

The restructuring process circumscribed by the Gestaltists to the representation of the perceptual stimulus is actually a general feature of every human cognitive activity and, in particular, of communicative interaction, which allows the understanding, the attribution of meaning, thus extending to the solution of verbal insight problems. In this sense, restructuring becomes a process of reinterpretation.

We are able to get out of the impasse by neglecting the default interpretation and looking for another one that is more pertinent to the situation and which helps us grasp the meaning that matches both the context and the speaker’s intention; this requires continuous adjustments until all makes sense.

In our perspective, this interpretative function is a characteristic inherent to all reasoning processes and is an adaptive characteristic of the human cognitive system in general ( Levinson, 1995 , 2013 ; Macchi and Bagassi, 2019 ; Mercier and Sperber, 2011 ; Sperber and Wilson, 1986/1995 ; Tomasello, 2009 ). It guarantees cognitive economy when meanings and relations are familiar, permitting recognition in a “blink of an eye.” This same process becomes much more arduous when meanings and relations are unfamiliar, obliging us to face the novel. When this happens, we have to come to terms with the fact that the usual, default interpretation will not work, and this is a necessary condition for exploring other ways of interpreting the situation. A restless, conscious and unconscious search for other possible relations between the parts and the whole ensues until everything falls into place and nothing is left unexplained, with an interpretative heuristic-type process. Indeed, the solution restructuring – is a re -interpretation of the relationship between the data and the aim of the task, a search for the appropriate meaning carried out at a deeper level, not by automaticity. If this is true, then a disambiguant reformulation of the problem that eliminates the trap into which the subject has fallen, should produce restructuring and the way to the solution.

Insight Problem Solving as the Overcoming of a Misunderstanding: The Effect of Reformulation

In this article we support our view with experimental evidence, focusing on how a misunderstanding is formed, and how a pragmatic reformulation of the problem, more relevant to the aim of the task, allows the text of the problem to be interpreted in accordance with the solution.

We consider two paradigmatic insight problems, the intriguing Study Window problem, which at first sight appears impossible to solve, and an apparent trivial arithmetical task, the Ties problem ( Mosconi and D’Urso, 1974 ).

The Study Window problem

The study window measures 1 m in height and 1 m wide. The owner decides to enlarge it and calls in a workman. He instructs the man to double the area of the window without changing its shape and so that it still measures 1 m by 1 m. The workman carried out the commission. How did he do it?

This problem was investigated in a previous study ( Macchi and Bagassi, 2015 ). For all the participants the problem appeared impossible to solve, and nobody actually solved it. The explanation we gave for the difficulty was the following: “The information provided regarding the dimensions brings a square form to mind. The problem solver interprets the window to be a square 1 m high by 1 m wide, resting on one side. Furthermore, the problem states “without changing its shape,” intending geometric shape of the two windows (square, independently of the orientation of the window), while the problem solver interprets this as meaning the phenomenic shape of the two windows (two squares with the same orthogonal orientation)” ( Macchi and Bagassi, 2015 , p. 156). And this is where the difficulty of the problem lies, in the mental representation of the window and the concurrent interpretation of the text of the problem. Actually, spatial orientation is a decisive factor in the perception of forms. “Two identical shapes seen from different orientations take on a different phenomenic identity” ( Mach, 1914 ).

The solution is to be found in a square (geometric form) that “rests” on one of its angles, thus becoming a rhombus (phenomenic form). Now the dimensions given are those of the two diagonals of the represented rhombus (ABCD).

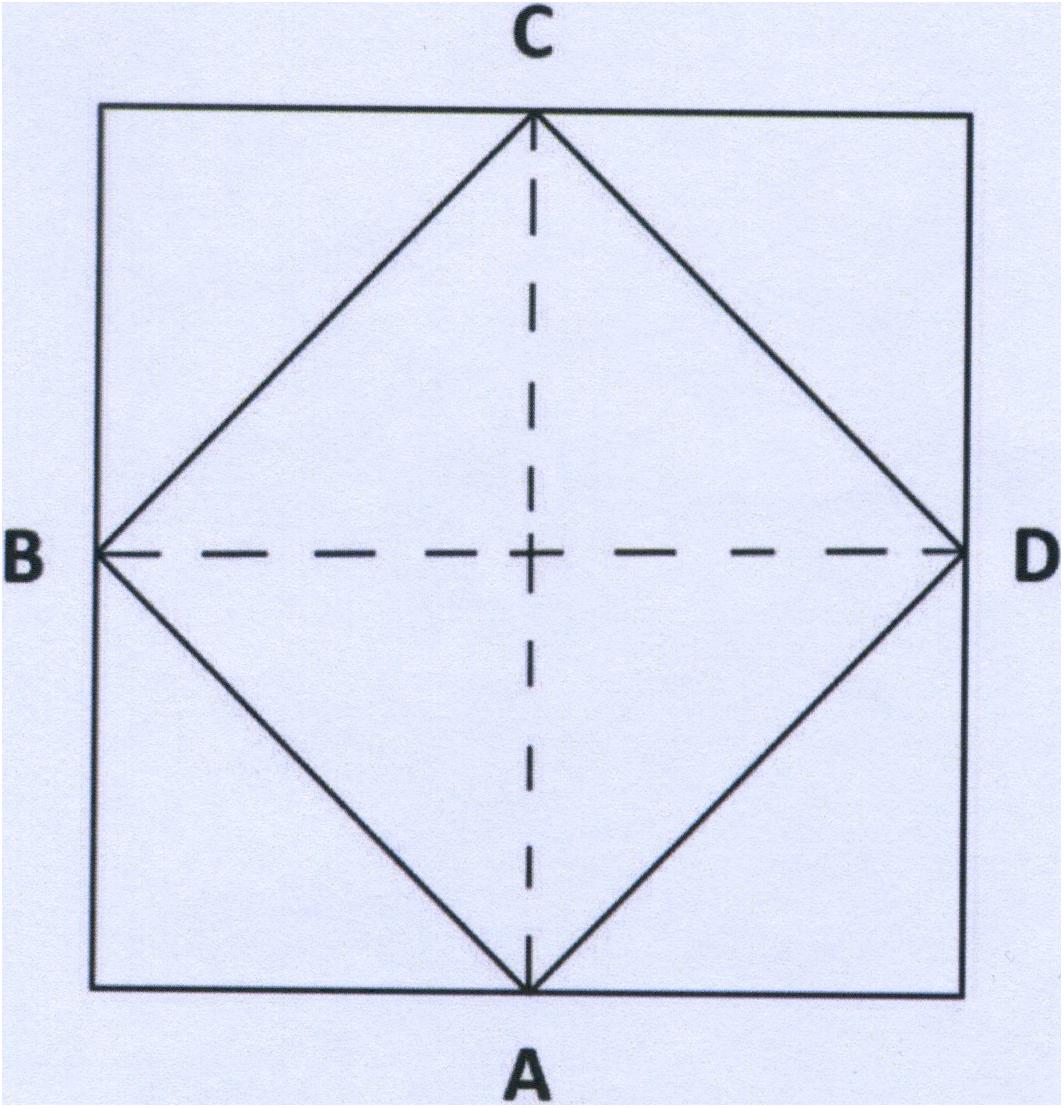
Figure 1. The study window problem solution.

The “inverted” version of the problem gave less trouble:

[…] The owner decides to make it smaller and calls in a workman. He instructs the man to halve the area of the window […].

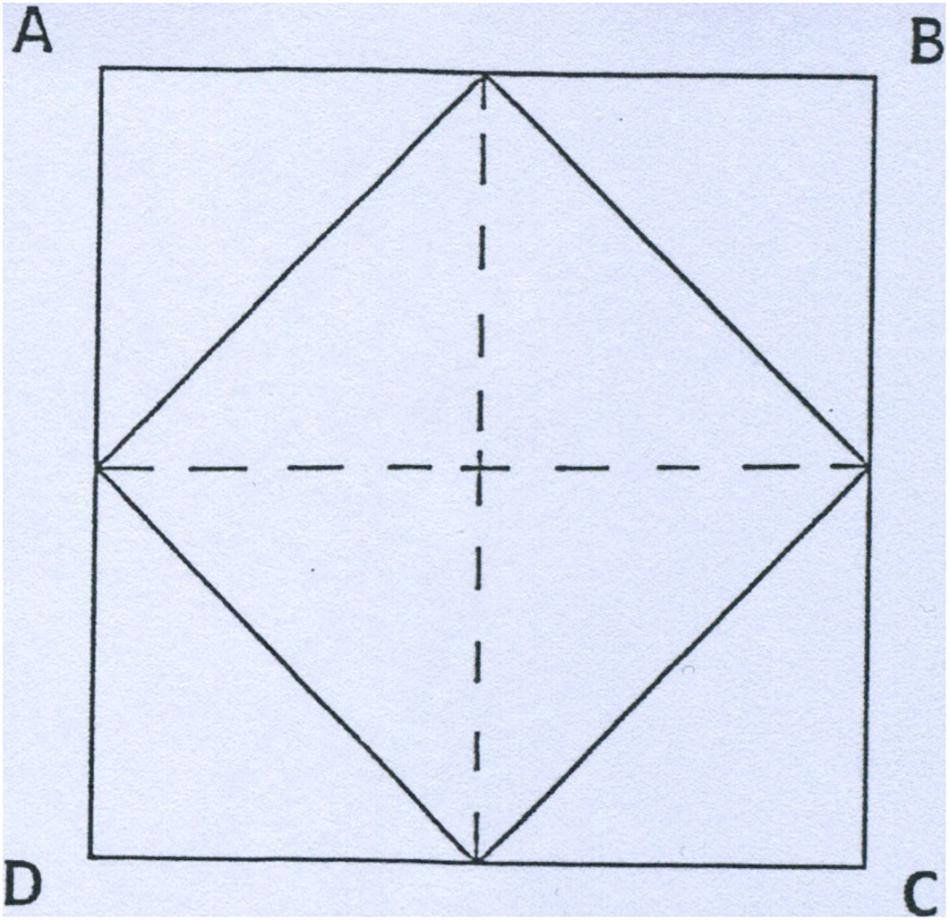
Figure 2. The inverted version.

With this version, 30% of the participants solved the problem ( n = 30). They started from the representation of the orthogonal square (ABCD) and looked for the solution within the square, trying to respect the required height and width of the window, and inevitably changing the orientation of the internal square. This time the height and width are the diagonals, rather than the side (base and height) of the square.

Eventually, in another version (the “orientation” version) it was explicit that orientation was not a mandatory attribute of the shape, and this time 66% of the participants found the solution immediately ( n = 30). This confirms the hypothesis that an inappropriate representation of the relation between the orthogonal orientation of the square and its geometric shape is the origin of the misunderstanding .

The “orientation” version:

A study window measures 1 m in height and 1 m wide. The owner decides to make it smaller and calls in a workman. He instructs the man to halve the area of the window: the workman can change the orientation of the window, but not its shape and in such a way that it still measures one meter by one meter. The workman carries out the commission. How did he do it?

While with the Study window problem the subjects who do not arrive at the solution, and who are the totality, know they are wrong, with the problem we are now going to examine, the Ties problem, those who are wrong do not realize it at all and the solution they propose is experienced as the correct solution.

The Ties Problem ( Mosconi and D’Urso, 1974 )

Peter and John have the same number of ties.

Peter gives John five of his ties.

How many ties does John have now more than Peter?

We believe that the seemingly trivial problem is actually the result of the simultaneous activation and mutual interference of complex cognitive processes that prevent its solution.

The problem has been submitted to 50 undergraduate students of the Humanities Faculty of the University of Milano-Bicocca. The participants were tested individually and were randomly assigned to three groups: control version ( n = 50), experimental version 2 ( n = 20), and experimental version 3 ( n = 23). All groups were tested in Italian. Each participant was randomly assigned to one of the conditions and received a form containing only one version of the two assigned problems. There was no time limit. They were invited to think aloud and their spontaneous justifications were recorded and then transcribed.

The correct answer is obviously “ten,” but it must not be so obvious if it is given by only one third of the subjects (32%), while the remaining two thirds give the wrong answer “five,” which is so dominant.

If we consider the text of the problem from the point of view of the information explicitly transmitted ( said ), we have that it only theoretically provides the necessary information to reach the solution and precisely that: (a) the number of ties initially owned by P. and J. is equal, (b) P. gives J. five of his ties. However, the subjects are wrong. What emerges, however, from the spontaneous justifications given by the subjects who give the wrong answer is that they see only the increase of J. and not the consequent loss of P. by five ties. We report two typical justifications: “P. gives five of his to J., J. has five more ties than P., the five P. gave him” and also “They started from the same number of ties, so if P. gives J. five ties, J. should have five more than P.”

Slightly different from the previous ones is the following recurrent answer, in which the participants also consider the decrease of P. as well as the increase of J.: “I see five ties at stake, which are the ones that move,” or also “There are these five ties that go from one to the other, so one has five ties less and the other has five more,” reaching however the conclusion similar to the previous one that “J. has five ties more, because the other gave them to him.” 2

Almost always the participants who answer “five” use a numerical example to justify the answer given or to find a solution to the problem, after some unsuccessful attempts. It is paradoxical how many of these participants accept that the problem has two solutions, one “five ties” obtained by reasoning without considering a concrete number of initial ties, owned by P. and J., the other “ten ties” obtained by using a numerical example. So, for example, we read in the protocol of a participant who, after having answered “five more ties,” using a numerical example, finds “ten” of difference between the ties of P. and those of J.: “Well! I think the “five” is still more and more exact; for me this one has five more, period and that’s it.” “Making the concrete example: “ten” – he chases another subject on an abstract level. I would be more inclined to another formula, to five.”

About half of the subjects who give the answer “five,” in fact, at first refuse to answer because “we don’t know the initial number and therefore we can’t know how many ties J. has more than P.,” or at the most they answer: “J. has five ties more, P. five less, more we can’t know, because a data is missing.”

Even before this difficulty, so to speak, operational, the text of the problem is difficult because in it the quantity relative to the decrease of P. remains implicit (−5). The resulting misunderstanding is that if the quantity transferred is five ties, the resulting difference is only five ties: if the ties that P. gives to J. are five, how can J. have 10 ties more than P.?

So the difficulty of the problem lies in the discrepancy between the quantity transferred and the bidirectional effect that this quantity determines with its displacement. Resolving implies a restructuring of the sentence: “Peter gives John five of his ties (and therefore he loses five).” And this is precisely the reasoning carried out by those subjects who give the right answer “ten.”

We have therefore formulated a new version in which a pair of verbs should make explicit the loss of P.:

Peter loses five of his ties and John takes them.

However, the results obtained with this version, submitted to 20 other subjects, substantially confirm the results obtained with the original version: the correct answers are 17% (3/20) and the wrong ones 75% (15/20). From a Chi-square test (χ 2 = 2,088 p = 0.148) it results no significant difference between the two versions.

If we go to read the spontaneous justifications, we find that the subjects who give the answer “five” motivate it in a similar way to the subjects of the original version. So, for example: “P. loses five, J. gets them, so J. has five ties more than P.”

The decrease of P. is still not perceived, and the discrepancy between the lost amount of ties and the double effect that this quantity determines with its displacement persists.

Therefore, a new version has been realized in which the amount of ties lost by P. has nothing to do with J’s acquisition of five ties, the two amounts of ties are different and then they are perceived as decoupled, so as to neutralize the perceptual-conceptual factor underlying it.

Peter loses five of his ties and John buys five new ones.

It was submitted to 23 participants. Of them, 17 (74%) gave the answer “ten” and only 3 (13%) the answer “five.” There was a significant difference (χ 2 = 16,104 p = 0.000) between the results obtained using the present experimental version and the results from the control version. The participants who give the correct solution “ten” mostly motivate their answer as follows: “P. loses five and therefore J. has also those five that P. lost; he buys another five, there are ten,” declaring that he “added to the five that P. had lost the five that J. had bought.” The effectiveness of the experimental manipulation adopted is confirmed. 3

The satisfactory results obtained with this version cannot be attributed to the use of two different verbs, which proved to be ineffective (see version 2), but to the splitting, and consequent differentiation (J. has in addition five new ties), of the two quantities.

This time, the increase of J. and the decrease of P. are grasped as simultaneous and distinct and their combined effect is not identified with one or the other, but is equal to the sum of +5 and −5 in absolute terms.

The hypothesis regarding the effect of reformulation has also been confirmed in classical insight problems such as the Square and the Parallelogram ( Wertheimer, 1925 ), the Pigs in a Pen ( Schooler et al., 1993 ), the Bat & Ball ( Frederick, 2005 ) in recent studies ( Macchi and Bagassi, 2012 , 2015 ) which showed a dramatic increase in the number of solutions.

In their original version these problems are true brain teasers, and the majority of participants in these studies needed them to be reformulated in order to reach the solution. In Appendix B we present in detail the results obtained (see Table 1 ). Below we report, for each problem, the text of the original version in comparison with the reformulated experimental version.

Table 1. Percentages of correct solutions with reformulated experimental versions.

Square and Parallelogram Problem ( Wertheimer, 1925 )

Given that AB = a and AG = b, find the sum of the areas of square ABCD and parallelogram EBGD ( Figures 3 , 4 ).

Figure 3. The square and parallelogram problem.

Figure 4. Solution.

Experimental Version

Given that AB = a and AG = b , find the sum of the areas of the two partially overlapping figures .

Pigs in a Pen Problem ( Schooler et al., 1993 )

Nine pigs are kept in a square pen . Build two more square enclosures that would put each pig in a pen by itself ( Figures 5 , 6 ).

Figure 5. The pigs in a pen problem.

Figure 6. Solution.

Nine pigs are kept in a square pen. Build two more squares that would put each pig in a by itself .

Bat and Ball Problem ( Frederick, 2005 )

A bat and a ball cost $1.10 in total. The bat costs $ 1.00 more than the ball. How much does the ball cost? ___cents.

A bat and a ball cost $1.10 in total. The bat costs $ 1.00 more than the ball. Find the cost of the bat and of the ball .

Once the problem knots that alter the aim of the task have been identified, the reformulation technique can be a valid didactic tool, as it allows to reveal the misunderstanding and to eliminate it without changing the mathematical nature of the problem. The training to creativity would consist in this sense in training to have interpretative keys different from the usual, when the difficulty cannot be addressed through computational techniques.

Closing Thoughts

By identifying the misunderstanding in problem solving, the reformulation technique has made it possible to eliminate the problem knots, without changing the mathematical nature of the problem. With the experimental reformulated versions of paradigmatic problems, both apparent trivial tasks or brain teasers have obtained a significant increase in correct answers.

Studying how an insight problem is formed, and not just how it is solved, may well become an important topic in education. We focus on undergraduate students’ strategies and their errors while solving problems, and the specific cognitive processes involved in misunderstanding, which are crucial to better exploit what could be beneficial to reach the solution and to teach how to improve the ability to solve problems.

Without violating the need for the necessary rigor of a demonstration, for example, it is possible to organize the problem-demonstration discourse according to a different criterion, precisely by favoring the psychological needs of the subject to whom the explanation discourse is addressed, taking care to organize the explanation with regard to the way his mind works, to what can favor its comprehension and facilitate its memory.

On the other hand, one of the criteria traditionally followed by mathematicians in constructing, for example, demonstrations, or at least in explaining them, is to never make any statement that is not supported by the elements provided above. In essence, in the course of the demonstration nothing is anticipated, and indeed it happens frequently that the propositions directly relevant and relevant to the development of the reasoning (for example, the steps of a geometric demonstration) are preceded by digressions intended to introduce and deal with the elements that legitimize them. As a consequence of such an expositive formalism, the recipient of the speech (the student) often finds himself in the situation of being led to the final conclusion a bit like a blind man who, even though he knows the goal, does not see the way, but can only control step by step the road he is walking along and with difficulty becomes aware of the itinerary.

The text of every problem, if formulated in natural language, has a psychorhetoric dimension, in the sense that in every speech, that is in the production and reception of every speech, there are aspects related to the way the mind works – and therefore psychological and rhetorical – that are decisive for comprehensibility, expressive adequacy and communicative effectiveness. It is precisely to these aspects that we refer to when we talk about the psychorhetoric dimension. Rhetoric, from the point of view of the broadcaster, has studied discourse in relation to the recipient, and therefore to its acceptability, comprehensibility and effectiveness, so that we can say that rhetoric has studied discourse “psychologically.”

Adopting this perspective, the commonplace that the rhetorical dimension only concerns the common discourse, i.e., the discourse that concerns debatable issues, and not the scientific discourse (logical-mathematical-demonstrative), which would be exempt from it, is falling away. The matter dealt with, the truth of what is actually said, is not sufficient to guarantee comprehension.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Ethics Statement

Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent for participation was not required for this study in accordance with the national legislation and the institutional requirements.

Author Contributions

LM and MB devised the project, developed the theory, carried out the experiment and wrote the manuscript. Both authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

• ^ The theoretical framework assumed here is Paul Grice’s theory of communication (1975) based on the existence in communication of the explicit layer ( said ) and of the implicit ( implied ), so that the recognition of the communicative intention of the speaker by the interlocutor is crucial for comprehension.
• ^ A participant who after having given the solution “five” corrects himself in “ten” explains the first answer as follows: “it is more immediate, in my opinion, to see the real five ties that are moved, because they are five things that are moved; then as a more immediate answer is ‘five,’ because it is something more real, less mathematical.”
• ^ The factor indicated is certainly the main responsible for the answer “five,” but not the only one (see the Appendix for a pragmatic analysis of the text).
• ^ Versions and results of the problems exposed are already published in Macchi e Bagassi 2012, 2014, 2015.

Bagassi, M., and Macchi, L. (2006). Pragmatic approach to decision making under uncertainty: the case of the disjunction effect. Think. Reason. 12, 329–350. doi: 10.1080/13546780500375663

CrossRef Full Text | Google Scholar

Bagassi, M., and Macchi, L. (2016). “The interpretative function and the emergence of unconscious analytic thought,” in Cognitive Unconscious and Human Rationality , eds L. Macchi, M. Bagassi, and R. Viale (Cambridge, MA: MIT Press), 43–76.

Google Scholar

Bulbrook, M. E. (1932). An experimental inquiry into the existence and nature of “insight”. Am. J. Psycho. 44, 409–453. doi: 10.2307/1415348

Duncker, K. (1945). “On problem solving,” in Psychological Monographs , Vol. 58, (Berlin: Springer), I–IX;1–113. Original in German, Psychologie des produktiven Denkens. doi: 10.1037/h0093599

Frederick, S. (2005). Cognitive reflection and decision making. J. Econ. Perspect. 19, 25–42. doi: 10.1257/089533005775196732

Kahneman, D. (2003). A perspective on judgment and choice: mapping bounded rationality. Am. Psychol. 58, 697–720. doi: 10.1037/0003-066x.58.9.697

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaplan, C. A., and Simon, H. A. (1990). In search of insight. Cogn. Psychol. 22, 374–419. doi: 10.1016/0010-0285(90)90008-R

Levinson, S. C. (1995). “Interactional biases in human thinking,” in Social Intelligence and Interaction , ed. E. N. Goody (Cambridge: Cambridge University Press), 221–261. doi: 10.1017/cbo9780511621710.014

Levinson, S. C. (2013). “Cross-cultural universals and communication structures,” in Language, Music, and the Brain: A Mysterious Relationship , ed. M. A. Arbib (Cambridge, MA: MIT Press), 67–80. doi: 10.7551/mitpress/9780262018104.003.0003

Macchi, L. (1995). Pragmatic aspects of the base-rate fallacy. Q. J. Exp. Psychol. 4, 188–207. doi: 10.1080/14640749508401384

Macchi, L. (2000). Partitive formulation of information in probabilistic reasoning: beyond heuristics and frequency format explanations. Organ. Behav. Hum. 82, 217–236. doi: 10.1006/obhd.2000.2895

Macchi, L., and Bagassi, M. (2012). Intuitive and analytical processes in insight problem solving: a psycho-rhetorical approach to the study of reasoning. Mind Soc. 11, 53–67. doi: 10.1007/s11299-012-0103-3

Macchi, L., and Bagassi, M. (2014). The interpretative heuristic in insight problem solving. Mind Soc. 13, 97–108. doi: 10.1007/s11299-014-0139-7

Macchi, L., and Bagassi, M. (2015). When analytic thought is challenged by a misunderstanding. Think. Reas. 21, 147–164. doi: 10.4324/9781315144061-9

Macchi, L., and Bagassi, M. (2019). The argumentative and the interpretative functions of thought: two adaptive characteristics of the human cognitive system. Teorema 38, 87–96.

Macchi, L., and Bagassi, M. (2020). “Bounded rationality and problem solving: the interpretative function of thought,” in Handbook of Bounded Rationality , ed. Riccardo Viale (London: Routledge).

Mach, E. (1914). The Analysis of Sensations. Chicago IL: Open Court.

Mercier, H., and Sperber, D. (2011). Why do human reason? Arguments for an argumentative theory. Behav. Brain Sci. 34, 57–74. doi: 10.1017/s0140525x10000968

Mosconi, G. (1990). Discorso e Pensiero. Bologna: Il Mulino.

Mosconi, G. (2016). “Closing thoughts,” in Cognive Unconscious and Human rationality , eds L. Macchi, M. Bagassi, and R. Viale (Cambridge, MA: MIT Press), 355–363. Original in Italian Discorso e pensiero.

Mosconi, G., and D’Urso, V. (1974). Il Farsi e il Disfarsi del Problema. Firenze: Giunti-Barbera.

Mosconi, G., and Macchi, L. (2001). The role of pragmatic rules in the conjunction fallacy. Mind Soc. 3, 31–57. doi: 10.1007/bf02512074

Newell, A., Shaw, J. C., and Simon, H. A. (1958). Elements of a theory of human problem solving. Psychol. Rev. 65, 151–166. doi: 10.1037/h0048495

Politzer, G., and Macchi, L. (2000). Reasoning and pragmatics. Mind Soc. 1, 73–93. doi: 10.1007/BF02512230

Schooler, J. W., Ohlsson, S., and Brooks, K. (1993). Thoughts beyond words: when language overshadows insight. J. Exp. Psychol. 122, 166–183. doi: 10.1037/0096-3445.122.2.166

Simon, H. A. (1979). Information processing models of cognition. Annu. Rev. Psychol. 30, 363–396. doi: 10.1146/annurev.ps.30.020179.002051

Sperber, D., and Wilson, D. (1986/1995). Relevance: Communication and cognition. Oxford: Blackwell.

Tomasello, M. (2009). Why We Cooperate. Cambridge, Mass: MIT Press. doi: 10.7551/mitpress/8470.001.0001

Wertheimer, M. (1925). Drei Abhandlungen zur Gestalttheorie. Erlangen: Verlag der Philosophischen Akademie.

Wertheimer, M. (1959). Productive Thinking. New York, NY: Harper & Row.

Wertheimer, M. (1985). A gestalt perspective on computer simulations of cognitive processes. Comput. Hum. Behav. 1, 19–33. doi: 10.1016/0747-5632(85)90004-4

Pragmatic analysis of the problematic loci of the Ties problem, which emerged from the spontaneous verbalizations of the participants:

- “the same number of ties”

This expression is understood as a neutral information, a kind of base or sliding plane on which the transfer of the five ties takes place and, in fact, these subjects motivate their answer “five” with: “there is this transfer of five ties from P. to J. ….”

- “5 more, 5 less”

We frequently resort to similar expressions in situations where, if I have five units more than another, the other has five less than me and the difference between us is five.

Consider, for example, the case of the years: say that J. is five years older than P. means to say that P. is five years younger than J. and that the difference in years between the two is five, not ten.

In comparisons, we evaluate the difference with something used as a term of reference, for example the age of P., which serves as a basis, the benchmark, precisely.

- “he gives”

The verb “to give” conveys the concept of the growth of the recipient, not the decrease of the giver, therefore, contributes to the crystallization of the “same number,” preventing to grasp the decrease of P.

Appendix B 4

Given that AB = a and AG = b, find the sum of the areas of square ABCD and parallelogram EBGD .

Typically, problem solvers find the problem difficult and fail to see that a is also the altitude of parallelogram EBGD. They tend to calculate its area with onerous and futile methods, while the solution can be reached with a smart method, consisting of restructuring the entire given shape into two partially overlapping triangles ABG and ECD. The sum of their areas is 2 x a b /2 = a b . Moreover, by shifting one of the triangles so that DE coincides with GB, the answer is “ a b ,” which is the area of the resultant rectangle. Referring to a square and a parallelogram fixes a favored interpretation of the perceptive stimuli, according to those principles of perceptive organization thoroughly studied by the Gestalt Theory. It firmly sets the calculation of the area on the sum of the two specific shapes dealt with in the text, while, the problem actually requires calculation of the area of the shape, however organized, as the sum of two triangles rectangles, or the area of only one rectangle, as well as the sum of square and parallelogram. Hence, the process of restructuring is quite difficult.

To test our hypotheses we formulated an experimental version:

In this formulation of the problem, the text does not impose constraints on the interpretation/organization of the figure, and the spontaneous, default interpretation is no longer fixed. Instead of asking for “the areas of square and parallelogram,” the problem asks for the areas of “the two partially overlapping figures.” We predicted that the experimental version would allow the subjects to see and consider the two triangles also.

Actually, we found that 80% of the participants (28 out of 35) gave a correct answer, and most of them (21 out of 28) gave the smart “two triangles” solution. In the control version, on the other hand, only 19% (9 out of 47) gave the correct response, and of these only two gave the “two triangles” solution.

The findings were replicated in the “Pigs in a pen” problem:

Nine pigs are kept in a square pen . Build two more square enclosures that would put each pig in a pen by itself.

The difficulty of this problem lies in the interpretation of the request, nine pigs each individually enclosed in a square pen, having only two more square enclosures. This interpretation is supported by the favored, orthogonal reference scheme, with which we represent the square. This privileged organization, according to our hypothesis, is fixed by the text which transmits the implicature that the pens in which the piglets are individually isolated must be square in shape too. The function of enclosure wrongfully implies the concept of a square. The task, on the contrary, only requires to pen each pig.

Once again, we created an experimental version by reformulating the problem, eliminating the word “enclosure” and the phrase “in a pen.” The implicit inference that the pen is necessarily square is not drawn.

The experimental version yielded 87% correct answers (20 out of 23), while the control version yielded only 38% correct answers (8 out of 25).

The formulation of the experimental versions was more relevant to the aim of the task, and allowed the perceptual stimuli to be interpreted in accordance with the solution.

The relevance of text and the re-interpretation of perceptual stimuli, goal oriented to the aim of the task, were worked out in unison in an interrelated interpretative “game.”

We further investigated the interpretative activity of thinking, by studying the “Bat and ball” problem, which is part of the CRT. Correct performance is usually considered to be evidence of reflective cognitive ability (correlated with high IQ scores), versus intuitive, erroneous answers to the problem ( Frederick, 2005 ).

Bat and Ball problem

A bat and a ball cost $1.10 in total. The bat costs $ 1.00 more than the ball. How much does the ball cost?___cents

Of course the answer which immediately comes to mind is 10 cents, which is incorrect as, in this case, the difference between $ 1.00 and 10 cents is only 90 cents, not $1.00 as the problem stipulates. The correct response is 5 cents.

Number physiognomics and the plausibility of the cost are traditionally considered responsible for this kind of error ( Frederick, 2005 ; Kahneman, 2003 ).

These factors aside, we argue that if the rhetoric structure of the text is analyzed, the question as formulated concerns only the ball, implying that the cost of the bat is already known. The question gives the key to the interpretation of what has been said in each problem and, generally speaking, in every discourse. Given data, therefore, is interpreted in the light of the question. Hence, “The bat costs $ 1.00 more than” becomes “The bat costs $ 1.00,” by leaving out “more than.”

According to our hypothesis, independently of the different cognitive styles, erroneous responses could be the effect of the rhetorical structure of the text, where the question is not adequate to the aim of the task. Consequently, we predicted that if the question were to be reformulated to become more relevant, the subjects would find it easier to grasp the correct response. In the light of our perspective, the cognitive abilities involved in the correct response were also reinterpreted. Consequently, we reformulated the text as follows in order to eliminate this misleading inference:

This time we predicted an increase in the number of correct answers. The difference in the percentages of correct solutions was significant: in the experimental version 90% of the participants gave a correct answer (28 out of 31), and only 10% (2 out of 20) answered correctly in the control condition.

The simple reformulation of the question, which expresses the real aim of the task (to find the cost of both items), does not favor the “short circuit” of considering the cost of the bat as already known (“$1,” by leaving out part of the phrase “more than”).

It still remains to be verified if those subjects who gave the correct response in the control version have a higher level of cognitive reflexive ability compared to the “intuitive” respondents. This has been the general interpretation given in the literature to the difference in performance.

We think it is a matter of a particular kind of reflexive ability, due to which the task is interpreted in the light of the context and not abstracting from it. The difficulty which the problem implicates does not so much involve a high level of abstract reasoning ability as high levels of pragmatic competence, which disambiguates the text. So much so that, intervening only on the pragmatic level, keeping numbers physiognomics and maintaining the plausible costs identical, the problem becomes a trivial arithmetical task.

Keywords : creative problem solving, insight, misunderstanding, pragmatics, language and thought

Citation: Bagassi M and Macchi L (2020) Creative Problem Solving as Overcoming a Misunderstanding. Front. Educ. 5:538202. doi: 10.3389/feduc.2020.538202

Received: 26 February 2020; Accepted: 29 October 2020; Published: 03 December 2020.

Reviewed by:

Copyright © 2020 Bagassi and Macchi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY) . The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Laura Macchi, [email protected]

This article is part of the Research Topic

Psychology and Mathematics Education

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Front Hum Neurosci

Real World Problem-Solving

Real world problem-solving (RWPS) is what we do every day. It requires flexibility, resilience, resourcefulness, and a certain degree of creativity. A crucial feature of RWPS is that it involves continuous interaction with the environment during the problem-solving process. In this process, the environment can be seen as not only a source of inspiration for new ideas but also as a tool to facilitate creative thinking. The cognitive neuroscience literature in creativity and problem-solving is extensive, but it has largely focused on neural networks that are active when subjects are not focused on the outside world, i.e., not using their environment. In this paper, I attempt to combine the relevant literature on creativity and problem-solving with the scattered and nascent work in perceptually-driven learning from the environment. I present my synthesis as a potential new theory for real world problem-solving and map out its hypothesized neural basis. I outline some testable predictions made by the model and provide some considerations and ideas for experimental paradigms that could be used to evaluate the model more thoroughly.

1. Introduction

In the Apollo 13 space mission, astronauts together with ground control had to overcome several challenges to bring the team safely back to Earth (Lovell and Kluger, 2006 ). One of these challenges was controlling carbon dioxide levels onboard the space craft: “For 2 days straight [they] had worked on how to jury-rig the Odysseys canisters to the Aquarius's life support system. Now, using materials known to be available onboard the spacecraft—a sock, a plastic bag, the cover of a flight manual, lots of duct tape, and so on—the crew assembled a strange contraption and taped it into place. Carbon dioxide levels immediately began to fall into the safe range” (Team, 1970 ; Cass, 2005 ).

The success of Apollo 13's recovery from failure is often cited as a glowing example of human resourcefulness and inventiveness alongside more well-known inventions and innovations over the course of human history. However, this sort of inventive capability is not restricted to a few creative geniuses, but an ability present in all of us, and exemplified in the following mundane example. Consider a situation when your only suit is covered in lint and you do not own a lint remover. You see a roll of duct tape, and being resourceful you reason that it might be a good substitute. You then solve the problem of lint removal by peeling a full turn's worth of tape and re-attaching it backwards onto the roll to expose the sticky side all around the roll. By rolling it over your suit, you can now pick up all the lint.

In both these examples (historic as well as everyday), we see evidence for our innate ability to problem-solve in the real world. Solving real world problems in real time given constraints posed by one's environment are crucial for survival. At the core of this skill is our mental capability to get out of “sticky situations” or impasses, i.e., difficulties that appear unexpectedly as impassable roadblocks to solving the problem at hand. But, what are the cognitive processes that enable a problem solver to overcome such impasses and arrive at a solution, or at least a set of promising next steps?

A central aspect of this type of real world problem solving, is the role played by the solver's surrounding environment during the problem-solving process. Is it possible that interaction with one's environment can facilitate creative thinking? The answer to this question seems somewhat obvious when one considers the most famous anecdotal account of creative problem solving, namely that of Archimedes of Syracuse. During a bath, he found a novel way to check if the King's crown contained non-gold impurities. The story has traditionally been associated with the so-called “Eureka moment,” the sudden affective experience when a solution to a particularly thorny problem emerges. In this paper, I want to temporarily turn our attention away from the specific “aha!” experience itself and take particular note that Archimedes made this discovery, not with his eyes closed at a desk, but in a real-world context of a bath 1 . The bath was not only a passive, relaxing environment for Archimedes, but also a specific source of inspiration. Indeed it was his noticing the displacement of water that gave him a specific methodology for measuring the purity of the crown; by comparing how much water a solid gold bar of the same weight would displace as compared with the crown. This sort of continuous environmental interaction was present when the Apollo 13 engineers discovered their life-saving solution, and when you solved the suit-lint-removal problem with duct tape.

The neural mechanisms underlying problem-solving have been extensively studied in the literature, and there is general agreement about the key functional networks and nodes involved in various stages of problem-solving. In addition, there has been a great deal of work in studying the neural basis for creativity and insight problem solving, which is associated with the sudden emergence of solutions. However, in the context of problem-solving, creativity, and insight have been researched as largely an internal process without much interaction with and influence from the external environment (Wegbreit et al., 2012 ; Abraham, 2013 ; Kounios and Beeman, 2014 ) 2 . Thus, there are open questions of what role the environment plays during real world problem-solving (RWPS) and how the brain enables the assimilation of novel items during these external interactions.

In this paper, I synthesize the literature on problem-solving, creativity and insight, and particularly focus on how the environment can inform RWPS. I explore three environmentally-informed mechanisms that could play a critical role: (1) partial-cue driven context-shifting, (2) heuristic prototyping and learning novel associations, and (3) learning novel physical inferences. I begin first with some intuitions about real world problem solving, that might help ground this discussion and providing some key distinctions from more traditional problem solving research. Then, I turn to a review of the relevant literature on problem-solving, creativity, and insight first, before discussing the three above-mentioned environmentally-driven mechanisms. I conclude with a potential new model and map out its hypothesized neural basis.

2. Problem solving, creativity, and insight

2.1. what is real world problem-solving.

Archimedes was embodied in the real world when he found his solution. In fact, the real world helped him solve the problem. Whether or not these sorts of historic accounts of creative inspiration are accurate 3 , they do correlate with some of our own key intuitions about how problem solving occurs “in the wild.” Real world problem solving (RWPS) is different from those that occur in a classroom or in a laboratory during an experiment. They are often dynamic and discontinuous, accompanied by many starts and stops. Solvers are never working on just one problem. Instead, they are simultaneously juggling several problems of varying difficulties and alternating their attention between them. Real world problems are typically ill-defined, and even when they are well-defined, often have open-ended solutions. Coupled with that is the added aspect of uncertainty associated with the solver's problem solving strategies. As introduced earlier, an important dimension of RWPS is the continuous interaction between the solver and their environment. During these interactions, the solver might be inspired or arrive at an “aha!” moment. However, more often than not, the solver experiences dozens of minor discovery events— “hmmm, interesting…” or “wait, what?…” moments. Like discovery events, there's typically never one singular impasse or distraction event. The solver must iterate through the problem solving process experiencing and managing these sorts of intervening events (including impasses and discoveries). In summary, RWPS is quite messy and involves a tight interplay between problem solving, creativity, and insight. Next, I explore each of these processes in more detail and explicate a possible role of memory, attention, conflict management and perception.

2.2. Analytical problem-solving

In psychology and neuroscience, problem-solving broadly refers to the inferential steps taken by an agent 4 that leads from a given state of affairs to a desired goal state (Barbey and Barsalou, 2009 ). The agent does not immediately know how this goal can be reached and must perform some mental operations (i.e., thinking) to determine a solution (Duncker, 1945 ).

The problem solving literature divides problems based on clarity (well-defined vs. ill-defined) or on the underlying cognitive processes (analytical, memory retrieval, and insight) (Sprugnoli et al., 2017 ). While memory retrieval is an important process, I consider it as a sub-process to problem solving more generally. I first focus on analytical problem-solving process, which typically involves problem-representation and encoding, and the process of forming and executing a solution plan (Robertson, 2016 ).

2.2.1. Problem definition and representation

An important initial phase of problem-solving involves defining the problem and forming a representation in the working memory. During this phase, components of the prefrontal cortex (PFC), default mode network (DMN), and the dorsal anterior cingulate cortex (dACC) have been found to be activated. If the problem is familiar and well-structured, top-down executive control mechanisms are engaged and the left prefrontal cortex including the frontopolar, dorso-lateral (dlPFC), and ventro-lateral (vlPFC) are activated (Barbey and Barsalou, 2009 ). The DMN along with the various structures in the medial temporal lobe (MTL) including the hippocampus (HF), parahippocampal cortex, perirhinal and entorhinal cortices are also believed to have limited involvement, especially in episodic memory retrieval activities during this phase (Beaty et al., 2016 ). The problem representation requires encoding problem information for which certain visual and parietal areas are also involved, although the extent of their involvement is less clear (Anderson and Fincham, 2014 ; Anderson et al., 2014 ).

2.2.1.1. Working memory

An important aspect of problem representation is the engagement and use of working memory (WM). The WM allows for the maintenance of relevant problem information and description in the mind (Gazzaley and Nobre, 2012 ). Research has shown that WM tasks consistently recruit the dlPFC and left inferior frontal cortex (IC) for encoding an manipulating information; dACC for error detection and performance adjustment; and vlPFC and the anterior insula (AI) for retrieving, selecting information and inhibitory control (Chung and Weyandt, 2014 ; Fang et al., 2016 ).

2.2.1.2. Representation

While we generally have a sense for the brain regions that are functionally influential in problem definition, less is known about how exactly events are represented within these regions. One theory for how events are represented in the PFC is the structured event complex theory (SEC), in which components of the event knowledge are represented by increasingly higher-order convergence zones localized within the PFC, akin to the convergence zones (from posterior to anterior) that integrate sensory information in the brain (Barbey et al., 2009 ). Under this theory, different zones in the PFC (left vs. right, anterior vs. posterior, lateral vs. medial, and dorsal vs. ventral) represent different aspects of the information contained in the events (e.g., number of events to be integrated together, the complexity of the event, whether planning, and action is needed). Other studies have also suggested the CEN's role in tasks requiring cognitive flexibility, and functions to switch thinking modes, levels of abstraction of thought and consider multiple concepts simultaneously (Miyake et al., 2000 ).

Thus, when the problem is well-structured, problem representation is largely an executive control activity coordinated by the PFC in which problem information from memory populates WM in a potentially structured representation. Once the problem is defined and encoded, planning and execution of a solution can begin.

2.2.2. Planning

The central executive network (CEN), particularly the PFC, is largely involved in plan formation and in plan execution. Planning is the process of generating a strategy to advance from the current state to a goal state. This in turn involves retrieving a suitable solution strategy from memory and then coordinating its execution.

2.2.2.1. Plan formation

The dlPFC supports sequential planning and plan formation, which includes the generation of hypothesis and construction of plan steps (Barbey and Barsalou, 2009 ). Interestingly, the vlPFC and the angular gyrus (AG), implicated in a variety of functions including memory retrieval, are also involved in plan formation (Anderson et al., 2014 ). Indeed, the AG together with the regions in the MTL (including the HF) and several other regions form a what is known as the “core” network. The core network is believed to be activated when recalling past experiences, imagining fictitious, and future events and navigating large-scale spaces (Summerfield et al., 2010 ), all key functions for generating plan hypotheses. A recent study suggests that the AG is critical to both episodic simulation, representation, and episodic memory (Thakral et al., 2017 ). One possibility for how plans are formulated could involve a dynamic process of retrieving an optimal strategy from memory. Research has shown significant interaction between striatal and frontal regions (Scimeca and Badre, 2012 ; Horner et al., 2015 ). The striatum is believed to play a key role in declarative memory retrieval, and specifically helping retrieve optimal (or previously rewarded) memories (Scimeca and Badre, 2012 ). Relevant to planning and plan formation, Scimeca & Badre have suggested that the striatum plays two important roles: (1) in mapping acquired value/utility to action selection, and thereby helping plan formation, and (2) modulation and re-encoding of actions and other plan parameters. Different types of problems require different sets of specialized knowledge. For example, the knowledge needed to solve mathematical problems might be quite different (albeit overlapping) from the knowledge needed to select appropriate tools in the environment.

Thus far, I have discussed planning and problem representation as being domain-independent, which has allowed me to outline key areas of the PFC, MTL, and other regions relevant to all problem-solving. However, some types of problems require domain-specific knowledge for which other regions might need to be recruited. For example, when planning for tool-use, the superior parietal lobe (SPL), supramarginal gyrus (SMG), anterior inferior parietal lobe (AIPL), and certain portions of the temporal and occipital lobe involved in visual and spatial integration have been found to be recruited (Brandi et al., 2014 ). It is believed that domain-specific information stored in these regions is recovered and used for planning.

2.2.2.2. Plan execution

Once a solution plan has been recruited from memory and suitably tuned for the problem on hand, the left-rostral PFC, caudate nucleus (CN), and bilateral posterior parietal cortices (PPC) are responsible for translating the plan into executable form (Stocco et al., 2012 ). The PPC stores and maintains “mental template” of the executable form. Hemispherical division of labor is particularly relevant in planning where it was shown that when planning to solve a Tower of Hanoi (block moving) problem, the right PFC is involved in plan construction whereas the left PFC is involved in controlling processes necessary to supervise the execution of the plan (Newman and Green, 2015 ). On a separate note and not the focus of this paper, plan execution and problem-solving can require the recruitment of affective and motivational processing in order to supply the agent with the resolve to solve problems, and the vmPFC has been found to be involved in coordinating this process (Barbey and Barsalou, 2009 ).

2.3. Creativity

During the gestalt movement in the 1930s, Maier noted that “most instances of “real” problem solving involves creative thinking” (Maier, 1930 ). Maier performed several experiments to study mental fixation and insight problem solving. This close tie between insight and creativity continues to be a recurring theme, one that will be central to the current discussion. If creativity and insight are linked to RWPS as noted by Maier, then it is reasonable to turn to the creativity and insight literature for understanding the role played by the environment. A large portion of the creativity literature has focused on viewing creativity as an internal process, one in which the solvers attention is directed inwards, and toward internal stimuli, to facilitate the generation of novel ideas and associations in memory (Beaty et al., 2016 ). Focusing on imagination, a number of researchers have looked at blinking, eye fixation, closing eyes, and looking nowhere behavior and suggested that there is a shift of attention from external to internal stimuli during creative problem solving (Salvi and Bowden, 2016 ). The idea is that shutting down external stimuli reduces cognitive load and focuses attention internally. Other experiments studying sleep behavior have also noted the beneficial role of internal stimuli in problem solving. The notion of ideas popping into ones consciousness, suddenly, during a shower is highly intuitive for many and researchers have attempted to study this phenomena through the lens of incubation, and unconscious thought that is internally-driven. There have been several theories and counter-theories proposed to account specifically for the cognitive processes underlying incubation (Ritter and Dijksterhuis, 2014 ; Gilhooly, 2016 ), but none of these theories specifically address the role of the external environment.

The neuroscience of creativity has also been extensively studied and I do not focus on an exhaustive literature review in this paper (a nice review can be found in Sawyer, 2011 ). From a problem-solving perspective, it has been found that unlike well-structured problems, ill-structured problems activate the right dlPFC. Most of the past work on creativity and creative problem-solving has focused on exploring memory structures and performing internally-directed searches. Creative idea generation has primarily been viewed as internally directed attention (Jauk et al., 2012 ; Benedek et al., 2016 ) and a primary mechanism involved is divergent thinking , which is the ability to produce a variety of responses in a given situation (Guilford, 1962 ). Divergent thinking is generally thought to involve interactions between the DMN, CEN, and the salience network (Yoruk and Runco, 2014 ; Heinonen et al., 2016 ). One psychological model of creative cognition is the Geneplore model that considers two major phases of generation (memory retrieval and mental synthesis) and exploration (conceptual interpretation and functional inference) (Finke et al., 1992 ; Boccia et al., 2015 ). It has been suggested that the associative mode of processing to generate new creative association is supported by the DMN, which includes the medial PFC, posterior cingulate cortex (PCC), tempororparietal juntion (TPJ), MTL, and IPC (Beaty et al., 2014 , 2016 ).

That said, the creativity literature is not completely devoid of acknowledging the role of the environment. In fact, it is quite the opposite. Researchers have looked closely at the role played by externally provided hints from the time of the early gestalt psychologists and through to present day studies (Öllinger et al., 2017 ). In addition to studying how hints can help problem solving, researchers have also looked at how directed action can influence subsequent problem solving—e.g., swinging arms prior to solving the two-string puzzle, which requires swinging the string (Thomas and Lleras, 2009 ). There have also been numerous studies looking at how certain external perceptual cues are correlated with creativity measures. Vohs et al. suggested that untidiness in the environment and the increased number of potential distractions helps with creativity (Vohs et al., 2013 ). Certain colors such as blue have been shown to help with creativity and attention to detail (Mehta and Zhu, 2009 ). Even environmental illumination, or lack thereof, have been shown to promote creativity (Steidle and Werth, 2013 ). However, it is important to note that while these and the substantial body of similar literature show the relationship of the environment to creative problem solving, they do not specifically account for the cognitive processes underlying the RWPS when external stimuli are received.

2.4. Insight problem solving

Analytical problem solving is believed to involve deliberate and conscious processing that advances step by step, allowing solvers to be able to explain exactly how they solved it. Inability to solve these problems is often associated with lack of required prior knowledge, which if provided, immediately makes the solution tractable. Insight, on the other hand, is believed to involve a sudden and unexpected emergence of an obvious solution or strategy sometimes accompanied by an affective aha! experience. Solvers find it difficult to consciously explain how they generated a solution in a sequential manner. That said, research has shown that having an aha! moment is neither necessary nor sufficient to insight and vice versa (Danek et al., 2016 ). Generally, it is believed that insight solvers acquire a full and deep understanding of the problem when they have solved it (Chu and Macgregor, 2011 ). There has been an active debate in the problem solving community about whether insight is something special. Some have argued that it is not, and that there are no special or spontaneous processes, but simply a good old-fashioned search of a large problem space (Kaplan and Simon, 1990 ; MacGregor et al., 2001 ; Ash and Wiley, 2006 ; Fleck, 2008 ). Others have argued that insight is special and suggested that it is likely a different process (Duncker, 1945 ; Metcalfe, 1986 ; Kounios and Beeman, 2014 ). This debate lead to two theories for insight problem solving. MacGregor et al. proposed the Criterion for Satisfactory Progress Theory (CSPT), which is based on Newell and Simons original notion of problem solving as being a heuristic search through the problem space (MacGregor et al., 2001 ). The key aspect of CSPT is that the solver is continually monitoring their progress with some set of criteria. Impasses arise when there is a criterion failure, at which point the solver tries non-maximal but promising states. The representational change theory (RCT) proposed by Ohlsson et al., on the other hand, suggests that impasses occur when the goal state is not reachable from an initial problem representation (which may have been generated through unconscious spreading activation) (Ohlsson, 1992 ). In order to overcome an impasse, the solver needs to restructure the problem representation, which they can do by (1) elaboration (noticing new features of a problem), (2) re-encoding fixing mistaken or incomplete representations of the problem, and by (3) changing constraints. Changing constraints is believed to involve two sub-processes of constraint relaxation and chunk-decomposition.

The current position is that these two theories do not compete with each other, but instead complement each other by addressing different stages of problem solving: pre- and post-impasse. Along these lines, Ollinger et al. proposed an extended RCT (eRCT) in which revising the search space and using heuristics was suggested as being a dynamic and iterative and recursive process that involves repeated instances of search, impasse and representational change (Öllinger et al., 2014 , 2017 ). Under this theory, a solver first forms a problem representation and begins searching for solutions, presumably using analytical problem solving processes as described earlier. When a solution cannot be found, the solver encounters an impasse, at which point the solver must restructure or change the problem representation and once again search for a solution. The model combines both analytical problem solving (through heuristic searches, hill climbing and progress monitoring), and creative mechanisms of constraint relaxation and chunk decomposition to enable restructuring.

Ollingers model appears to comprehensively account for both analytical and insight problem solving and, therefore, could be a strong candidate to model RWPS. However, while compelling, it is nevertheless an insufficient model of RWPS for many reasons, of which two are particularly significant for the current paper. First, the model does explicitly address mechanisms by which external stimuli might be assimilated. Second, the model is not sufficiently flexible to account for other events (beyond impasse) occurring during problem solving, such as distraction, mind-wandering and the like.

So, where does this leave us? I have shown the interplay between problem solving, creativity and insight. In particular, using Ollinger's proposal, I have suggested (maybe not quite explicitly up until now) that RWPS involves some degree of analytical problem solving as well as the post-impasse more creative modes of problem restructuring. I have also suggested that this model might need to be extended for RWPS along two dimensions. First, events such as impasses might just be an instance of a larger class of events that intervene during problem solving. Thus, there needs to be an accounting of the cognitive mechanisms that are potentially influenced by impasses and these other intervening events. It is possible that these sorts of events are crucial and trigger a switch in attentional focus, which in turn facilitates switching between different problem solving modes. Second, we need to consider when and how externally-triggered stimuli from the solver's environment can influence the problem solving process. I detail three different mechanisms by which external knowledge might influence problem solving. I address each of these ideas in more detail in the next two sections.

3. Event-triggered mode switching during problem-solving

3.1. impasse.

When solving certain types of problems, the agent might encounter an impasse, i.e., some block in its ability to solve the problem (Sprugnoli et al., 2017 ). The impasse may arise because the problem may have been ill-defined to begin with causing incomplete and unduly constrained representations to have been formed. Alternatively, impasses can occur when suitable solution strategies cannot be retrieved from memory or fail on execution. In certain instances, the solution strategies may not exist and may need to be generated from scratch. Regardless of the reason, an impasse is an interruption in the problem solving process; one that was running conflict-free up until the point when a seemingly unresolvable issue or an error in the predicted solution path was encountered. Seen as a conflict encountered in the problem-solving process it activates the anterior cingulate cortex (ACC). It is believed that the ACC not only helps detect the conflict, but also switch modes from one of “exploitation” (planning) to “exploration” (search) (Quilodran et al., 2008 ; Tang et al., 2012 ), and monitors progress during resolution (Chu and Macgregor, 2011 ). Some mode switching duties are also found to be shared with the AI (the ACC's partner in the salience network), however, it is unclear exactly the extent of this function-sharing.

Even though it is debatable if impasses are a necessary component of insight, they are still important as they provide a starting point for the creativity (Sprugnoli et al., 2017 ). Indeed, it is possible that around the moment of impasse, the AI and ACC together, as part of the salience network play a crucial role in switching thought modes from analytical planning mode to creative search and discovery mode. In the latter mode, various creative mechanisms might be activated allowing for a solution plan to emerge. Sowden et al. and many others have suggested that the salience network is potentially a candidate neurobiological mechanism for shifting between thinking processes, more generally (Sowden et al., 2015 ). When discussing various dual-process models as they relate to creative cognition, Sowden et al. have even noted that the ACC activation could be useful marker to identify shifting as participants work creative problems.

3.2. Defocused attention

As noted earlier, in the presence of an impasse there is a shift from an exploitative (analytical) thinking mode to an exploratory (creative) thinking mode. This shift impacts several networks including, for example, the attention network. It is believed attention can switch between a focused mode and a defocused mode. Focused attention facilitates analytic thought by constraining activation such that items are considered in a compact form that is amenable to complex mental operations. In the defocused mode, agents expand their attention allowing new associations to be considered. Sowden et al. ( 2015 ) note that the mechanism responsible for adjustments in cognitive control may be linked to the mechanisms responsible for attentional focus. The generally agreed position is that during generative thinking, unconscious cognitive processes activated through defocused attention are more prevalent, whereas during exploratory thinking, controlled cognition activated by focused attention becomes more prevalent (Kaufman, 2011 ; Sowden et al., 2015 ).

Defocused attention allows agents to not only process different aspects of a situation, but to also activate additional neural structures in long term memory and find new associations (Mendelsohn, 1976 ; Yoruk and Runco, 2014 ). It is believed that cognitive material attended to and cued by positive affective state results in defocused attention, allowing for more complex cognitive contexts and therefore a greater range of interpretation and integration of information (Isen et al., 1987 ). High attentional levels are commonly considered a typical feature of highly creative subjects (Sprugnoli et al., 2017 ).

4. Role of the environment

In much of the past work the focus has been on treating creativity as largely an internal process engaging the DMN to assist in making novel connections in memory. The suggestion has been that “individual needs to suppress external stimuli and concentrate on the inner creative process during idea generation” (Heinonen et al., 2016 ). These ideas can then function as seeds for testing and problem-solving. While true of many creative acts, this characterization does not capture how creative ideas arise in many real-world creative problems. In these types of problems, the agent is functioning and interacting with its environment before, during and after problem-solving. It is natural then to expect that stimuli from the environment might play a role in problem-solving. More specifically, it can be expected that through passive and active involvement with the environment, the agent is (1) able to trigger an unrelated, but potentially useful memory relevant for problem-solving, (2) make novel connections between two events in memory with the environmental cue serving as the missing link, and (3) incorporate a completely novel information from events occuring in the environment directly into the problem-solving process. I explore potential neural mechanisms for these three types of environmentally informed creative cognition, which I hypothesize are enabled by defocused attention.

4.1. Partial cues trigger relevant memories through context-shifting

I have previously discussed the interaction between the MTL and PFC in helping select task-relevant and critical memories for problem-solving. It is well-known that pattern completion is an important function of the MTL and one that enables memory retrieval. Complementary Learning Theory (CLS) and its recently updated version suggest that the MTL and related structures support initial storage as well as retrieval of item and context-specific information (Kumaran et al., 2016 ). According to CLS theory, the dentate gyrus (DG) and the CA3 regions of the HF are critical to selecting neural activity patterns that correspond to particular experiences (Kumaran et al., 2016 ). These patterns might be distinct even if experiences are similar and are stabilized through increases in connection strengths between the DG and CA3. Crucially, because of the connection strengths, reactivation of part of the pattern can activate the rest of it (i.e., pattern completion). Kumaran et al. have further noted that if consistent with existing knowledge, these new experiences can be quickly replayed and interleaved into structured representations that form part of the semantic memory.

Cues in the environment provided by these experiences hold partial information about past stimuli or events and this partial information converges in the MTL. CLS accounts for how these cues might serve to reactivate partial patterns, thereby triggering pattern completion. When attention is defocused I hypothesize that (1) previously unnoticed partial cues are considered, and (2) previously noticed partial cues are decomposed to produce previously unnoticed sub-cues, which in turn are considered. Zabelina et al. ( 2016 ) have shown that real-world creativity and creative achievement is associated with “leaky attention,” i.e., attention that allows for irrelevant information to be noticed. In two experiments they systematically explored the relationship between two notions of creativity— divergent thinking and real-world creative achievement—and the use of attention. They found that attentional use is associated in different ways for each of the two notions of creativity. While divergent thinking was associated with flexible attention, it does not appear to be leaky. Instead, selective focus and inhibition components of attention were likely facilitating successful performance on divergent thinking tasks. On the other hand, real-world creative achievement was linked to leaky attention. RWPS involves elements of both divergent thinking and of real-world creative achievement, thus I would expect some amount of attentional leaks to be part of the problem solving process.

Thus, it might be the case that a new set of cues or sub-cues “leak” in and activate memories that may not have been previously considered. These cues serve to reactivate a diverse set of patterns that then enable accessing a wide range of memories. Some of these memories are extra-contextual, in that they consider the newly noticed cues in several contexts. For example, when unable to find a screwdriver, we might consider using a coin. It is possible that defocused attention allows us to consider the coin's edge as being a potentially relevant cue that triggers uses for the thin edge outside of its current context in a coin. The new cues (or contexts) may allow new associations to emerge with cues stored in memory, which can occur during incubation. Objects and contexts are integrated into memory automatically into a blended representation and changing contexts disrupts this recognition (Hayes et al., 2007 ; Gabora, 2016 ). Cue-triggered context shifting allows an agent to break-apart a memory representation, which can then facilitate problem-solving in new ways.

4.2. Heuristic prototyping facilitates novel associations

It has long been the case that many scientific innovations have been inspired by events in nature and the surrounding environment. As noted earlier, Archimedes realized the relationship between the volume of an irregularly shaped object and the volume of water it displaced. This is an example of heuristic prototyping where the problem-solver notices an event in the environment, which then triggers the automatic activation of a heuristic prototype and the formation of novel associations (between the function of the prototype and the problem) which they can then use to solve the problem (Luo et al., 2013 ). Although still in its relative infancy, there has been some recent research into the neural basis for heuristic prototyping. Heuristic prototype has generally been defined as an enlightening prototype event with a similar element to the current problem and is often composed of a feature and a function (Hao et al., 2013 ). For example, in designing a faster and more efficient submarine hull, a heuristic prototype might be a shark's skin, while an unrelated prototype might be a fisheye camera (Dandan et al., 2013 ).

Research has shown that activating the feature function of the right heuristic prototype and linking it by way of semantic similarity to the required function of the problem was the key mechanism people used to solve several scienitific insight problems (Yang et al., 2016 ). A key region activated during heuristic prototyping is the dlPFC and it is believed to be generally responsible for encoding the events into memory and may play an important role in selecting and retrieving the matched unsolved technical problem from memory (Dandan et al., 2013 ). It is also believed that the precuneus plays a role in automatic retrieval of heuristic information allowing the heuristic prototype and the problem to combine (Luo et al., 2013 ). In addition to semantic processing, certain aspects of visual imagery have also been implicated in heuristic prototyping leading to the suggestion of the involvement of Broadman's area BA 19 in the occipital cortex.

There is some degree of overlap between the notions of heuristic prototyping and analogical transfer (the mapping of relations from one domain to another). Analogical transfer is believed to activate regions in the left medial fronto-parietal system (dlPFC and the PPC) (Barbey and Barsalou, 2009 ). I suggest here that analogical reasoning is largely an internally-guided process that is aided by heuristic prototyping which is an externally-guided process. One possible way this could work is if heuristic prototyping mechanisms help locate the relevant memory with which to then subsequently analogize.

4.3. Making physical inferences to acquire novel information

The agent might also be able to learn novel facts about their environment through passive observation as well as active experimentation. There has been some research into the neural basis for causal reasoning (Barbey and Barsalou, 2009 ; Operskalski and Barbey, 2016 ), but beyond its generally distributed nature, we do not know too much more. Beyond abstract causal reasoning, some studies looked into the cortical regions that are activated when people watch and predict physical events unfolding in real-time and in the real-world (Fischer et al., 2016 ). It was found that certain regions were associated with representing types of physical concepts, with the left intraparietal sulcus (IPS) and left middle frontal gyrus (MFG) shown to play a role in attributing causality when viewing colliding objects (Mason and Just, 2013 ). The parahippocampus (PHC) was associated with linking causal theory to observed data and the TPJ was involved in visualizing movement of objects and actions in space (Mason and Just, 2013 ).

5. Proposed theory

I noted earlier that Ollinger's model for insight problem solving, while serving as a good candidate for RWPS, requires extension. In this section, I propose a candidate model that includes some necessary extensions to Ollinger's framework. I begin by laying out some preliminary notions that underlie the proposed model.

5.1. Dual attentional modes

I propose that the attention-switching mechanism described earlier is at the heart of RWPS and enables two modes of operation: focused and defocused mode. In the focused mode, the problem representation is more or less fixed, and problem solving proceeds in a focused and goal directed manner through search, planning, and execution mechanisms. In the defocused mode, problem solving is not necessarily goal directed, but attempts to generate ideas, driven by both internal and external items.

At first glance, these modes might seem similar to convergent and divergent thinking modes postulated by numerous others to account for creative problem solving. Divergent thinking allows for the generation of new ideas and convergent thinking allows for verification and selection of generated ideas. So, it might seem that focused mode and convergent thinking are similar and likewise divergent and defocused mode. They are, however, quite different. The modes relate less to idea generation and verification, and more to the specific mechanisms that are operating with regard to a particular problem at a particular moment in time. Convergent and divergent processes may be occurring during both defocused and focused modes. Some degree of divergent processes may be used to search and identify specific solution strategies in focused mode. Also, there might be some degree of convergent idea verification occuring in defocused mode as candidate items are evaluated for their fit with the problem and goal. Thus, convergent and divergent thinking are one amongst many mechanisms that are utilized in focused and defocused mode. Each of these two modes has to do with degree of attention placed on a particular problem.

There have been numerous dual-process and dual-systems models of cognition proposed over the years. To address criticisms raised against these models and to unify some of the terminology, Evans & Stanovich proposed a dual-process model comprising Type 1 and Type 2 thought (Evans and Stanovich, 2013 ; Sowden et al., 2015 ). Type 1 processes are those that are believed to be autonomous and do not require working memory. Type 2 processes, on the other hand, are believed to require working memory and are cognitively decoupled to prevent real-world representations from becoming confused with mental simulations (Sowden et al., 2015 ). While acknowledging various other attributes that are often used to describe dual process models (e.g., fast/slow, associative/rule-based, automatic/controlled), Evans & Stanovich note that these attributes are merely frequent correlates and not defining characteristics of Type 1 or Type 2 processes. The proposed dual attentional modes share some similarities with the Evans & Stanovich Type 1 and 2 models. Specifically, Type 2 processes might occur in focused attentional mode in the proposed model as they typically involve the working memory and certain amount of analytical thought and planning. Similarly, Type 1 processes are likely engaged in defocused attentional mode as there are notions of associative and generative thinking that might be facilitated when attention has been defocused. The crucial difference between the proposed model and other dual-process models is that the dividing line between focused and defocused attentional modes is the degree of openness to internal and external stimuli (by various networks and functional units in the brain) when problem solving. Many dual process models were designed to classify the “type” of thinking process or a form of cognitive processing. In some sense, the “processes” in dual process theories are characterized by the type of mechanism of operation or the type of output they produced. Here, I instead characterize and differentiate the modes of thinking by the receptivity of different functional units in the brain to input during problem solving.

This, however, raises a different question of the relationship between these attentional modes and conscious vs. unconscious thinking. It is clear that both the conscious and unconscious are involved in problem solving, as well as in RWPS. Here, I claim that a problem being handled is, at any given point in time, in either a focused mode or in a defocused mode. When in the focused mode, problem solving primarily proceeds in a manner that is available for conscious deliberation. More specifically, problem space elements and representations are tightly managed and plans and strategies are available in the working memory and consciously accessible. There are, however, secondary unconscious operations in the focused modes that includes targeted memory retrieval and heuristic-based searches. In the defocused mode, the problem is primarily managed in an unconscious way. The problem space elements are broken apart and loosely managed by various mechanisms that do not allow for conscious deliberation. That said, it is possible that some problem parameters remain accessible. For example, it is possible that certain goal information is still maintained consciously. It is also possible that indexes to all the problems being considered by the solver are maintained and available to conscious awareness.

5.2. RWPS model

Returning to Ollinger's model for insight problem solving, it now becomes readily apparent how this model can be modified to incorporate environmental effects as well as generalizing the notion of intervening events beyond that of impasses. I propose a theory for RWPS that begins with standard analytical problem-solving process (See Figures ​ Figures1, 1 , ​ ,2 2 ).

Summary of neural activations during focused problem-solving (Left) and defocused problem-solving (Right) . During defocused problem-solving, the salience network (insula and ACC) coordinates the switching of several networks into a defocused attention mode that permits the reception of a more varied set of stimuli and interpretations via both the internally-guided networks (default mode network DMN) and externally guided networks (Attention). PFC, prefrontal cortex; ACC, anterior cingulate cortex; PCC, posterior cingulate cortex; IPC, inferior parietal cortex; PPC, posterior parietal cortex; IPS, intra-parietal sulcus; TPJ, temporoparietal junction; MTL, medial temporal lobe; FEF, frontal eye field.

Proposed Model for Real World Problem Solving (RWPS). The corresponding neural correlates are shown in italics. During problem-solving, an initial problem representation is formed based on prior knowledge and available perceptual information. The problem-solving then proceeds in a focused, goal-directed mode until the goal is achieved or a defocusing event (e.g., impasse or distraction) occurs. During focused mode operation, the solver interacts with the environment in directed manner, executing focused plans, and allowing for predicted items to be activated by the environment. When a defocusing event occurs, the problem-solving then switches into a defocused mode until a focusing event (e.g., discovery) occurs. In defocused mode, the solver performs actions unrelated to the problem (or is inactive) and is receptive to a set of environmental triggers that activate novel aspects using the three mechanisms discussed in this paper. When a focusing event occurs, the diffused problem elements cohere into a restructured representation and problem-solving returns into a focused mode.

5.2.1. Focused problem solving mode

Initially, both prior knowledge and perceptual entities help guide the creation of problem representations in working memory. Prior optimal or rewarding solution strategies are obtained from LTM and encoded in the working memory as well. This process is largely analytical and the solver interacts with their environment through focused plan or idea execution, targeted observation of prescribed entities, and estimating prediction error of these known entities. More specifically, when a problem is presented, the problem representations are activated and populated into working memory in the PFC, possibly in structured representations along convergence zones. The PFC along with the Striatum and the MTL together attempt at retrieving an optimal or previously rewarded solution strategy from long term memory. If successfully retrieved, the solution strategy is encoded into the PPC as a mental template, which then guides relevant motor control regions to execute the plan.

5.2.2. Defocusing event-triggered mode switching

The search and solve strategy then proceeds analytically until a “defocusing event” is encountered. The salience network (AI and ACC) monitor for conflicts and attempt to detect any such events in the problem-solving process. As long as no conflicts are detected, the salience network focuses on recruiting networks to achieve goals and suppresses the DMN (Beaty et al., 2016 ). If the plan execution or retrieval of the solution strategy fails, then a defocusing event is detected and the salience network performs mode switching. The salience network dynamically switches from the focused problem-solving mode to a defocused problem-solving mode (Menon, 2015 ). Ollinger's current model does not account for other defocusing events beyond an impasse, but it is not inconceivable that there could be other such events triggered by external stimuli (e.g., distraction or an affective event) or by internal stimuli (e.g., mind wandering).

5.2.3. Defocused problem solving mode

In defocused mode, the problem is operated on by mechanisms that allow for the generation and testing of novel ideas. Several large-scale brain networks are recruited to explore and generate new ideas. The search for novel ideas is facilitated by generally defocused attention, which in turn allows for creative idea generation from both internal as well as external sources. The salience network switches operations from defocused event detection to focused event or discovery detection, whereby for example, environmental events or ideas that are deemed interesting can be detected. During this idea exploration phase, internally, the DMN is no longer suppressed and attempts to generate new ideas for problem-solving. It is known that the IPC is involved in the generation of new ideas (Benedek et al., 2014 ) and together with the PPC in coupling different information together (Simone Sandkühler, 2008 ; Stocco et al., 2012 ). Beaty et al. ( 2016 ) have proposed that even this internal idea-generation process can be goal directed, thereby allowing for a closer working relationship between the CEN and the DMN. They point to neuroimaging evidence that support the possibility that the executive control network (comprising the lateral prefrontal and inferior parietal regions) can constrain and direct the DMN in its process of generating ideas to meet task-specific goals via top down monitoring and executive control (Beaty et al., 2016 ). The control network is believed to maintain an “internal train of thought” by keeping the task goal activated, thereby allowing for strategic and goal-congruent searches for ideas. Moreover, they suggest that the extent of CEN involvement in the DMN idea-generation may depend on the extent to which the creative task is constrained. In the RWPS setting, I would suspect that the internal search for creative solutions is not entirely unconstrained, even in the defocused mode. Instead, the solver is working on a specified problem and thus, must maintain the problem-thread while searching for solutions. Moreover, self-generated ideas must be evaluated against the problem parameters and thereby might need some top-down processing. This would suggest that in such circumstances, we would expect to see an increased involvement of the CEN in constraining the DMN.

On the external front, several mechanisms are operating in this defocused mode. Of particular note are the dorsal attention network, composed of the visual cortex (V), IPS and the frontal eye field (FEF) along with the precuneus and the caudate nucleus allow for partial cues to be considered. The MTL receives synthesized cue and contextual information and populates the WM in the PFC with a potentially expanded set of information that might be relevant for problem-solving. The precuneus, dlPFC and PPC together trigger the activation and use of a heuristic prototype based on an event in the environment. The caudate nucleus facilitates information routing between the PFC and PPC and is involved in learning and skill acquisition.

5.2.4. Focusing event-triggered mode switching

The problem's life in this defocused mode continues until a focusing event occurs, which could be triggered by either external (e.g., notification of impending deadline, discovery of a novel property in the environment) or internal items (e.g., goal completion, discovery of novel association or updated relevancy of a previously irrelevant item). As noted earlier, an internal train of thought may be maintained that facilitates top-down evaluation of ideas and tracking of these triggers (Beaty et al., 2016 ). The salience network switches various networks back to the focused problem-solving mode, but not without the potential for problem restructuring. As noted earlier, problem space elements are maintained somewhat loosely in the defocused mode. Thus, upon a focusing event, a set or subset of these elements cohere into a tight (restructured) representation suitable for focused mode problem solving. The process then repeats itself until the goal has been achieved.

5.3. Model predictions

5.3.1. single-mode operation.

The proposed RWPS model provides several interesting hypotheses, which I discuss next. First, the model assumes that any given problem being worked on is in one mode or another, but not both. Thus, the model predicts that there cannot be focused plan execution on a problem that is in defocused mode. The corollary prediction is that novel perceptual cues (as those discussed in section 4) cannot help the solver when in focused mode. The corollary prediction, presumably has some support from the inattentional blindness literature. Inattentional blindness is when perceptual cues are not noticed during a task (e.g., counting the number of basketball passes between several people, but not noticing a gorilla in the scene) (Simons and Chabris, 1999 ). It is possible that during focused problem solving, that external and internally generated novel ideas are simply not considered for problem solving. I am not claiming that these perceptual cues are always ignored, but that they are not considered within the problem. Sometimes external cues (like distracting occurrences) can serve as defocusing events, but the model predicts that the actual content of these cues are not themselves useful for solving the specific problem at hand.

When comparing dual-process models Sowden et al. ( 2015 ) discuss shifting from one type of thinking to another and explore how this shift relates to creativity. In this regard, they weigh the pros and cons of serial vs. parallel shifts. In dual-process models that suggest serial shifts, it is necessary to disengage one type of thought prior to engaging the other or to shift along a continuum. Whereas, in models that suggest parallel shifts, each of the thinking types can operate in parallel. Per this construction, the proposed RWPS model is serial, however, not quite in the same sense. As noted earlier, the RWPS model is not a dual-process model in the same sense as other dual process model. Instead, here, the thrust is on when the brain is receptive or not receptive to certain kinds of internal and external stimuli that can influence problem solving. Thus, while the modes may be serial with respect to a certain problem, it does not preclude the possibility of serial and parallel thinking processes that might be involved within these modes.

5.3.2. Event-driven transitions

The model requires an event (defocusing or focusing) to transition from one mode to another. After all why else would a problem that is successfully being resolved in the focused mode (toward completion) need to necessarily be transferred to defocused mode? These events are interpreted as conflicts in the brain and therefore the mode-switching is enabled by the saliency network and the ACC. Thus, the model predicts that there can be no transition from one mode to another without an event. This is a bit circular, as an event is really what triggers the transition in the first place. But, here I am suggesting that an external or internal cue triggered event is what drives the transition, and that transitions cannot happen organically without such an event. In some sense, the argument is that the transition is discontinuous, rather than a smooth one. Mind-wandering is good example of when we might drift into defocused mode, which I suggest is an example of an internally driven event caused by an alternative thought that takes attention away from the problem.

A model assumption underlying RWPS is that events such as impasses have a similar effect to other events such as distraction or mind wandering. Thus, it is crucial to be able to establish that there exists of class of such events and they have a shared effect on RWPS, which is to switch attentional modes.

5.3.3. Focused mode completion

The model also predicts that problems cannot be solved (i.e., completed) within the defocused mode. A problem can be considered solved when a goal is reached. However, if a goal is reached and a problem is completed in the defocused mode, then there must have not been any converging event or coherence of problem elements. While it is possible that the solver arbitrarily arrived at the goal in a diffused problem space and without conscious awareness of completing the task or even any converging event or problem recompiling, it appears somewhat unlikely. It is true that there are many tasks that we complete without actively thinking about it. We do not think about what foot to place in front of another while walking, but this is not an instance of problem solving. Instead, this is an instance of unconscious task completion.

5.3.4. Restructuring required

The model predicts that a problem cannot return to a focused mode without some amount of restructuring. That is, once defocused, the problem is essentially never the same again. The problem elements begin interacting with other internally and externally-generated items, which in turn become absorbed into the problem representation. This prediction can potentially be tested by establishing some preliminary knowledge, and then showing one group of subjects the same knowledge as before, while showing the another group of subjects different stimuli. If the model's predictions hold, the problem representation will be restructured in some way for both groups.

There are numerous other such predictions, which are beyond the scope of this paper. One of the biggest challenges then becomes evaluating the model to set up suitable experiments aimed at testing the predictions and falsifying the theory, which I address next.

6. Experimental challenges and paradigms

One of challenges in evaluating the RWPS is that real world factors cannot realistically be accounted for and sufficiently controlled within a laboratory environment. So, how can one controllably test the various predictions and model assumptions of “real world” problem solving, especially given that by definition RWPS involves the external environment and unconscious processing? At the expense of ecological validity, much of insight problem solving research has employed an experimental paradigm that involves providing participants single instances of suitably difficult problems as stimuli and observing various physiological, neurological and behavioral measures. In addition, through verbal protocols, experimenters have been able to capture subjective accounts and problem solving processes that are available to the participants' conscious. These experiments have been made more sophisticated through the use of timed-hints and/or distractions. One challenge with this paradigm has been the selection of a suitable set of appropriately difficult problems. The classic insight problems (e.g., Nine-dot, eight-coin) can be quite difficult, requiring complicated problem solving processes, and also might not generalize to other problems or real world problems. Some in the insight research community have moved in the direction of verbal tasks (e.g., riddles, anagrams, matchstick rebus, remote associates tasks, and compound remote associates tasks). Unfortunately, these puzzles, while providing a great degree of controllability and repeatability, are even less realistic. These problems are not entirely congruent with the kinds of problems that humans are solving every day.

The other challenge with insight experiments is the selection of appropriate performance and process tracking measures. Most commonly, insight researchers use measures such as time to solution, probability of finding solution, and the like for performance measures. For process tracking, verbal protocols, coded solution attempts, and eye tracking are increasingly common. In neuroscientific studies of insight various neurological measures using functional magnetic resonance imaging (fMRI), electroencephalography (EEGs), transcranial direct current stimulation (tDCS), and transcranial magnetic stimulation (tMS) are popular and allow for spatially and temporally localizing an insight event.

Thus, the challenge for RWPS is two-fold: (1) selection of stimuli (real world problems) that are generalizable, and (2) selection of measures (or a set of measures) that can capture key aspects of the problem solving process. Unfortunately, these two challenges are somewhat at odds with each other. While fMRI and various neuroscientific measures can capture the problem solving process in real time, it is practically difficult to provide participants a realistic scenario while they are laying flat on their back in an fMRI machine and allowed to move nothing more than a finger. To begin addressing this conundrum, I suggest returning to object manipulation problems (not all that different from those originally introduced by Maier and Duncker nearly a century ago), but using modern computing and user-interface technologies.

One pseudo-realistic approach is to generate challenging object manipulation problems in Virtual Reality (VR). VR has been used to describe 3-D environment displays that allows participants to interact with artificially projected, but experientially realistic scenarios. It has been suggested that virtual environments (VE) invoke the same cognitive modules as real equivalent environmental experience (Foreman, 2010 ). Crucially, since VE's can be scaled and designed as desired, they provide a unique opportunity to study pseudo-RWPS. However, a VR-based research approach has its limitations, one of which is that it is nearly impossible to track participant progress through a virtual problem using popular neuroscientific measures such as fMRI because of the limited mobility of connected participants.

Most of the studies cited in this paper utilized an fMRI-based approach in conjunction with a verbal or visual task involving problem-solving or creative thinking. Very few, if any, studies involved the use physical manipulation, and those physical manipulations were restricted to limited finger movements. Thus, another pseudo-realistic approach is allowing subjects to teleoperate robotic arms and legs from inside the fMRI machine. This paradigm has seen limited usage in psychology and robotics, in studies focused on Human-Robot interaction (Loth et al., 2015 ). It could be an invaluable tool in studying real-time dynamic problem-solving through the control of a robotic arm. In this paradigm a problem solving task involving physical manipulation is presented to the subject via the cameras of a robot. The subject (in an fMRI) can push buttons to operate the robot and interact with its environment. While the subjects are not themselves moving, they can still manipulate objects in the real world. What makes this paradigm all the more interesting is that the subject's manipulation-capabilities can be systematically controlled. Thus, for a particular problem, different robotic perceptual and manipulation capabilities can be exposed, allowing researchers to study solver-problem dynamics in a new way. For example, even simple manipulation problems (e.g., re-arranging and stacking blocks on a table) can be turned into challenging problems when the robotic movements are restricted. Here, the problem space restrictions are imposed not necessarily on the underlying problem, but on the solver's own capabilities. Problems of this nature, given their simple structure, may enable studying everyday practical creativity without the burden of devising complex creative puzzles. Crucial to note, both these pseudo-realistic paradigms proposed demonstrate a tight interplay between the solver's own capabilities and their environment.

7. Conclusion

While the neural basis for problem-solving, creativity and insight have been studied extensively in the past, there is still a lack of understanding of the role of the environment in informing the problem-solving process. Current research has primarily focused on internally-guided mental processes for idea generation and evaluation. However, the type of real world problem-solving (RWPS) that is often considered a hallmark of human intelligence has involved both a dynamic interaction with the environment and the ability to handle intervening and interrupting events. In this paper, I have attempted to synthesize the literature into a unified theory of RWPS, with a specific focus on ways in which the environment can help problem-solve and the key neural networks involved in processing and utilizing relevant and useful environmental information. Understanding the neural basis for RWPS will allow us to be better situated to solve difficult problems. Moreover, for researchers in computer science and artificial intelligence, clues into the neural underpinnings of the computations taking place during creative RWPS, can inform the design the next generation of helper and exploration robots which need these capabilities in order to be resourceful and resilient in the open-world.

Author contributions

The author confirms being the sole contributor of this work and approved it for publication.

Conflict of interest statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I am indebted to Professor Matthias Scheutz, Professor Elizabeth Race, Professor Ayanna Thomas, and Professor. Shaun Patel for providing guidance with the research and the manuscript. I am also grateful for the facilities provided by Tufts University, Medford, MA, USA.

1 My intention is not to ignore the benefits of a concentrated internal thought process which likely occurred as well, but merely to acknowledge the possibility that the environment might have also helped.

2 The research in insight does extensively use “hints” which are, arguably, a form of external influence. But these hints are highly targeted and might not be available in this explicit form when solving problems in the real world.

3 The accuracy of these accounts has been placed in doubt. They often are recounted years later, with inaccuracies, and embellished for dramatic effect.

4 I use the term “agent” to refer to the problem-solver. The term agent is more general than “creature” or “person” or “you" and is intentionally selected to broadly reference humans, animals as well as artificial agents. I also selectively use the term “solver.”

Funding. The research for this Hypothesis/Theory Article was funded by the authors private means. Publication costs will be covered by my institution: Tufts University, Medford, MA, USA.

• Abraham A. (2013). The promises and perils of the neuroscience of creativity . Front. Hum. Neurosci. 7 :246. 10.3389/fnhum.2013.00246 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Anderson J. R., Fincham J. M. (2014). Discovering the sequential structure of thought . Cogn. Sci. 38 , 322–352. 10.1111/cogs.12068 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Anderson J. R., Seung H., Fincham J. M. (2014). Neuroimage discovering the structure of mathematical problem solving . Neuroimage 97 , 163–177. 10.1016/j.neuroimage.2014.04.031 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Ash I. K., Wiley J. (2006). The nature of restructuring in insight: an individual-differences approach . Psychon. Bull. Rev. 13 , 66–73. 10.3758/BF03193814 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Barbey A. K., Barsalou L. W. (2009). Reasoning and problem solving : models , in Encyclopedia of Neuroscience , ed Squire L. (Oxford: Academic Press; ), 35–43. [ Google Scholar ]
• Barbey A. K., Krueger F., Grafman J. (2009). Structured event complexes in the medial prefrontal cortex support counterfactual representations for future planning . Philos. Trans. R. Soc. Lond. B Biol. Sci. 364 , 1291–1300. 10.1098/rstb.2008.0315 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Beaty R. E., Benedek M., Silvia P. J., Schacter D. L. (2016). Creative cognition and brain network dynamics . Trends Cogn. Sci. 20 , 87–95. 10.1016/j.tics.2015.10.004 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Beaty R. E., Benedek M., Wilkins R. W., Jauk E., Fink A., Silvia P. J., et al.. (2014). Creativity and the default network: a functional connectivity analysis of the creative brain at rest . Neuropsychologia 64 , 92–98. 10.1016/j.neuropsychologia.2014.09.019 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Benedek M., Jauk E., Beaty R. E., Fink A., Koschutnig K., Neubauer A. C. (2016). Brain mechanisms associated with internally directed attention and self-generated thought . Sci. Rep. 6 :22959. 10.1038/srep22959 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Benedek M., Jauk E., Fink A., Koschutnig K., Reishofer G., Ebner F., et al.. (2014). To create or to recall? Neural mechanisms underlying the generation of creative new ideas . Neuroimage 88 , 125–133. 10.1016/j.neuroimage.2013.11.021 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Boccia M., Piccardi L., Palermo L., Nori R., Palmiero M. (2015). Where do bright ideas occur in ourbrain? Meta-analytic evidence from neuroimaging studies of domain-specific creativity . Front. Psychol. 6 :1195. 10.3389/fpsyg.2015.01195 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Brandi M. l., Wohlschläger A., Sorg C., Hermsdörfer J. (2014). The neural correlates of planning and executing actual tool use . J. Neurosci. 34 , 13183–13194. 10.1523/JNEUROSCI.0597-14.2014 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Cass S. (2005). Apollo 13, we have a solution , in IEEE Spectrum On-line, 04 , 1. Available online at: https://spectrum.ieee.org/tech-history/space-age/apollo-13-we-have-a-solution
• Chu Y., Macgregor J. N. (2011). Human performance on insight problem solving : a review J. Probl. Solv. 3 , 119–150. 10.7771/1932-6246.1094 [ CrossRef ] [ Google Scholar ]
• Chung H. J., Weyandt L. L. (2014). The physiology of executive functioning , Handbook of Executive Functioning (Springer; ), 13–28. [ Google Scholar ]
• Dandan T., Haixue Z., Wenfu L., Wenjing Y., Jiang Q., Qinglin Z. (2013). Brain activity in using heuristic prototype to solve insightful problems . Behav. Brain Res. 253 , 139–144. 10.1016/j.bbr.2013.07.017 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Danek A. H., Wiley J., Öllinger M. (2016). Solving classical insight problems without aha! experience: 9 dot, 8 coin, and matchstick arithmetic problems . J. Probl. Solv. 9 :4 10.7771/1932-6246.1183 [ CrossRef ] [ Google Scholar ]
• Duncker K. (1945). On problem-solving . Psychol. Monogr. 58 , i–113. [ Google Scholar ]
• Evans J. S., Stanovich K. E. (2013). Dual-process theories of higher cognition: advancing the debate . Perspect. Psychol. Sci. 8 , 223–241. 10.1177/1745691612460685 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Fang X., Zhang Y., Zhou Y., Cheng L., Li J., Wang Y., et al.. (2016). Resting-state coupling between core regions within the central-executive and salience networks contributes to working memory performance . Front. Behav. Neurosci. 10 :27. 10.3389/fnbeh.2016.00027 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Finke R. A., Ward T. B., Smith S. M. (1992). Creative Cognition: Theory, Research, and Applications . Cambridge, MA: MIT press. [ Google Scholar ]
• Fischer J., Mikhael J. G., Tenenbaum J. B., Kanwisher N. (2016). Functional neuroanatomy of intuitive physical inference . Proc. Natl. Acad. Sci. U.S.A. 113 , E5072–E5081. 10.1073/pnas.1610344113 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Fleck J. I. (2008). Working memory demands in insight versus analytic problem solving . Eur. J. Cogn. Psychol. 20 , 139–176. 10.1080/09541440601016954 [ CrossRef ] [ Google Scholar ]
• Foreman N. (2010). Virtual reality in psychology . Themes Sci. Technol. Educ. 2 , 225–252. Available online at: http://earthlab.uoi.gr/theste/index.php/theste/article/view/33 [ Google Scholar ]
• Gabora L. (2016). The neural basis and evolution of divergent and convergent thought . arXiv preprint arXiv:1611.03609 . [ Google Scholar ]
• Gazzaley A., Nobre A. C. (2012). Top-down modulation: bridging selective attention and working memory . Trends Cogn. Sci. 60 , 830–846. 10.1016/j.tics.2011.11.014 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Gilhooly K. J. (2016). Incubation and intuition in creative problem solving . Front. Psychol. 7 :1076. 10.3389/fpsyg.2016.01076 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Guilford J. P. (1962). Creativity: its measurement and development , in A Source Book for Creative Thinking (New York, NY: Charles Scribner's Sons; ), 151–167. [ Google Scholar ]
• Hao X., Cui S., Li W., Yang W., Qiu J., Zhang Q. (2013). Enhancing insight in scientific problem solving by highlighting the functional features of prototypes: an fMRI study . Brain Res. 1534 , 46–54. 10.1016/j.brainres.2013.08.041 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Hayes S. M., Nadel L., Ryan L. (2007). The effect of scene context on episodic object recognition: parahippocampal cortex mediates memory encoding and retrieval success . Hippocampus 9 , 19–22. 10.1002/hipo.20319 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Heinonen J., Numminen J., Hlushchuk Y., Antell H., Taatila V., Suomala J. (2016). Default mode and executive networks areas: association with the serial order in divergent thinking . PLoS ONE 11 :e0162234. 10.1371/journal.pone.0162234 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Horner A. J., Bisby J. A., Bush D., Lin W.-J., Burgess N. (2015). Evidence for holistic episodic recollection via hippocampal pattern completion . Nat. Commun. 6 :7462. 10.1038/ncomms8462 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Isen A. M., Daubman K. A., Nowicki G. P. (1987). Positive affect facilitates creative problem solving . J. Pers. Soc. Psychol. 52 , 1122–1131. 10.1037/0022-3514.52.6.1122 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Jauk E., Benedek M., Neubauer A. C. (2012). Tackling creativity at its roots: evidence for different patterns of EEG alpha activity related to convergent and divergent modes of task processing . Int. J. Psychophysiol. 84 , 219–225. 10.1016/j.ijpsycho.2012.02.012 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Kaplan C. A., Simon H. A. (1990). In search of insight . Cogn. Psychol. 22 , 374–419. [ Google Scholar ]
• Kaufman S. B. (2011). Intelligence and the cognitive unconscious , in The Cambridge Handbook of Intelligence (New York, NY: Cambridge University Press; ), 442–467. [ Google Scholar ]
• Kounios J., Beeman M. (2014). The cognitive neuroscience of insight . Annu. Rev. Psychol. 65 , 71–93. 10.1146/annurev-psych-010213-115154 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Kumaran D., Hassabis D., McClelland J. L. (2016). What learning systems do intelligent agents need? complementary learning systems theory updated . Trends Cogn. Sci. 20 , 512–534. 10.1016/j.tics.2016.05.004 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Loth S., Jettka K., Giuliani M., De Ruiter J. P. (2015). Ghost-in-the-machine reveals human social signals for human–robot interaction . Front. Psychol. 6 :1641. 10.3389/fpsyg.2015.01641 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lovell J., Kluger J. (2006). Apollo 13 . New York, NY: Houghton Mifflin Harcourt. [ Google Scholar ]
• Luo J., Li W., Qiu J., Wei D., Liu Y., Zhang Q. (2013). Neural basis of scientific innovation induced by heuristic prototype . PLoS ONE 8 :e49231. 10.1371/journal.pone.0049231 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• MacGregor J. N., Ormerod T. C., Chronicle E. P. (2001). Information processing and insight: a process model of performance on the nine-dot and related problems . J. Exp. Psychol. Learn. Mem. Cogn. 27 :176. 10.1037/0278-7393.27.1.176 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Maier N. R. (1930). Reasoning in humans. i. on direction . J. Comp. Psychol. 10 :115. [ Google Scholar ]
• Mason R. A., Just M. A. (2013). Neural representations of physics concepts . Psychol. Sci. 27 , 904–913. 10.1177/0956797616641941 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Mehta R., Zhu R. J. (2009). Blue or red? exploring the effect of color on cognitive task performances . Science 323 , 1226–1229. 10.1126/science.1169144 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Mendelsohn G. (1976). Associative and attentional processes in creative performance . J. Pers. 44 , 341–369. [ Google Scholar ]
• Menon V. (2015). Salience network , in Brain Mapping: An Encyclopedic Reference, Vol. 2 , ed Toga A. W. (London: Academic Press; Elsevier; ), 597–611. [ Google Scholar ]
• Metcalfe J. (1986). Premonitions of insight predict impending error . J. Exp. Psychol. Learn. Mem. Cogn. 12 , 623. [ Google Scholar ]
• Miyake A., Friedman N. P., Emerson M. J., Witzki A. H., Howerter A., Wager T. D. (2000). The unity and diversity of executive functions and their contributions to complex “Frontal Lobe” tasks: a latent variable analysis . Cogn. Psychol. 41 , 49–100. 10.1006/cogp.1999.0734 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Newman S. D., Green S. R. (2015). Complex problem solving . Brain Mapp. 3 , 543–549. 10.1016/B978-0-12-397025-1.00282-7 [ CrossRef ] [ Google Scholar ]
• Ohlsson S. (1992). Information-processing explanations of insight and related phenomena . Adv. Psychol. Think. 1 , 1–44. [ Google Scholar ]
• Öllinger M., Fedor A., Brodt S., Szathmáry E. (2017). Insight into the ten-penny problem: guiding search by constraints and maximization . Psychol. Res. 81 , 925–938. 10.1007/s00426-016-0800-3 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Öllinger M., Jones G., Knoblich G. (2014). The dynamics of search, impasse, and representational change provide a coherent explanation of difficulty in the nine-dot problem . Psychol. Res. 78 , 266–275. 10.1007/s00426-013-0494-8 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Operskalski J. T., Barbey A. K. (2016). Cognitive neuroscience of causal reasoning , in Oxford Handbook of Causal Reasoning , ed Waldmann M. R. (New York, NY: Oxford University Press; ), 217–242. [ Google Scholar ]
• Quilodran R., Rothé M., Procyk E. (2008). Behavioral shifts and action valuation in the anterior cingulate cortex . Neuron 57 , 314–325. 10.1016/j.neuron.2007.11.031 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Ritter S. M., Dijksterhuis A. (2014). Creativity the unconscious foundations of the incubation period . Front. Hum. Neurosci. 8 :215. 10.3389/fnhum.2014.00215 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Robertson S. (2016). Problem Solving: Perspectives from Cognition and Neuroscience . New York, NY: Psychology Press. [ Google Scholar ]
• Salvi C., Bowden E. M. (2016). Looking for creativity: where do we look when we look for new ideas? Front. Psychol. 7 :161. 10.3389/fpsyg.2016.00161 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Sawyer K. (2011). The cognitive neuroscience of creativity: a critical review . Creat. Res. J. 23 , 137–154. 10.1080/10400419.2011.571191 [ CrossRef ] [ Google Scholar ]
• Scimeca J. M., Badre D. (2012). Striatal contributions to declarative memory retrieval Jason . Neuron 75 , 380–392. 10.1016/j.neuron.2012.07.014 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Simone Sandkühler J. B. (2008). Deconstructing insight: EEG correlates of insightful problem solving . PLoS ONE 3 :e1459. 10.1371/journal.pone.0001459 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Simons D. J., Chabris C. F. (1999). Gorillas in our midst: sustained inattentional blindness for dynamic events . Perception 28 , 1059–1074. [ PubMed ] [ Google Scholar ]
• Sowden P. T., Pringle A., Gabora L. (2015). The shifting sands of creative thinking: connections to dual-process theory . Think. Reason. 21 , 40–60. 10.1080/13546783.2014.885464 [ CrossRef ] [ Google Scholar ]
• Sprugnoli G., Rossi S., Emmendorfer A., Rossi A., Liew S.-L., Tatti E., et al. (2017). Neural correlates of Eureka moment . Intelligence 62 , 99–118. 10.1016/j.intell.2017.03.004 [ CrossRef ] [ Google Scholar ]
• Steidle A., Werth L. (2013). Freedom from constraints: darkness and dim illumination promote creativity . J. Environ. Psychol. 35 , 67–80. 10.1016/j.jenvp.2013.05.003 [ CrossRef ] [ Google Scholar ]
• Stocco A., Lebiere C., O'Reilly R. C., Anderson J. R. (2012). Distinct contributions of the caudate nucleus, rostral prefrontal cortex, and parietal cortex to the execution of instructed tasks . Cogn. Affect. Behav. Neurosci. 12 , 611–628. 10.3758/s13415-012-0117-7 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Summerfield J. J., Hassabis D., Maguire E. A. (2010). Differential engagement of brain regions within a corenetwork during scene construction . Neuropsychologia 48 , 1501–1509. 10.1016/j.neuropsychologia.2010.01.022 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Tang Y.-Y., Rothbart M. K., Posner M. I. (2012). Neural Correlates of stablishing, maintaining and switching brain states . Trends Cogn. Sci. 16 , 330–337. 10.1016/j.tics.2012.05.001 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Team M. E. (1970). Mission Operations Report apollo 13 . [ Google Scholar ]
• Thakral P. P., Madore K. P., Schacter D. L. (2017). A role for the left angular gyrus in episodic simulation and memory . J. Neurosci. 37 , 8142–8149. 10.1523/JNEUROSCI.1319-17.2017 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Thomas L. E., Lleras A. (2009). Swinging into thought: directed movement guides insight in problem solving . Psychon. Bull. Rev. 16 , 719–723. 10.3758/PBR.16.4.719 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Vohs K. D., Redden J. P., Rahinel R. (2013). Physical order produces healthy choices, generosity, and conventionality, whereas disorder produces creativity . Psychol. Sci. 24 , 1860–1867. 10.1177/0956797613480186 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Wegbreit E., Suzuki S., Grabowecky M., Kounios J., Beeman M. (2012). Visual attention modulates insight versus analytic solving of verbal problems . J. Probl. Solv. 144 , 724–732. 10.7771/1932-6246.1127 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Yang W., Dietrich A., Liu P., Ming D., Jin Y., Nusbaum H. C., et al. (2016). Prototypes are key heuristic information in insight problem solving . Creat. Res. J. 28 , 67–77. 10.1080/10400419.2016.1125274 [ CrossRef ] [ Google Scholar ]
• Yoruk S., Runco M. A. (2014). Neuroscience of divergent thinking . Activ. Nervosa Superior 56 , 1–16. 10.1007/BF03379602 [ CrossRef ] [ Google Scholar ]
• Zabelina D., Saporta A., Beeman M. (2016). Flexible or leaky attention in creative people? Distinct patterns of attention for different types of creative thinking . Mem Cognit . 44 , 488–498. 10.3758/s13421-015-0569-4 [ PubMed ] [ CrossRef ] [ Google Scholar ]

• Bipolar Disorder
• Therapy Center
• When To See a Therapist
• Types of Therapy
• Best Online Therapy
• Best Couples Therapy
• Best Family Therapy
• Managing Stress
• Sleep and Dreaming
• Understanding Emotions
• Self-Improvement
• Healthy Relationships
• Student Resources
• Personality Types
• Guided Meditations
• Verywell Mind Insights
• 2024 Verywell Mind 25
• Mental Health in the Classroom
• Editorial Process
• Meet Our Review Board
• Crisis Support

Problem-Solving Strategies and Obstacles

Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Sean is a fact-checker and researcher with experience in sociology, field research, and data analytics.

JGI / Jamie Grill / Getty Images

• Application
• Improvement

From deciding what to eat for dinner to considering whether it's the right time to buy a house, problem-solving is a large part of our daily lives. Learn some of the problem-solving strategies that exist and how to use them in real life, along with ways to overcome obstacles that are making it harder to resolve the issues you face.

What Is Problem-Solving?

In cognitive psychology , the term 'problem-solving' refers to the mental process that people go through to discover, analyze, and solve problems.

A problem exists when there is a goal that we want to achieve but the process by which we will achieve it is not obvious to us. Put another way, there is something that we want to occur in our life, yet we are not immediately certain how to make it happen.

Maybe you want a better relationship with your spouse or another family member but you're not sure how to improve it. Or you want to start a business but are unsure what steps to take. Problem-solving helps you figure out how to achieve these desires.

The problem-solving process involves:

• Discovery of the problem
• Deciding to tackle the issue
• Seeking to understand the problem more fully
• Researching available options or solutions
• Taking action to resolve the issue

Before problem-solving can occur, it is important to first understand the exact nature of the problem itself. If your understanding of the issue is faulty, your attempts to resolve it will also be incorrect or flawed.

Problem-Solving Mental Processes

Several mental processes are at work during problem-solving. Among them are:

• Perceptually recognizing the problem
• Representing the problem in memory
• Considering relevant information that applies to the problem
• Identifying different aspects of the problem
• Labeling and describing the problem

Problem-Solving Strategies

There are many ways to go about solving a problem. Some of these strategies might be used on their own, or you may decide to employ multiple approaches when working to figure out and fix a problem.

An algorithm is a step-by-step procedure that, by following certain "rules" produces a solution. Algorithms are commonly used in mathematics to solve division or multiplication problems. But they can be used in other fields as well.

In psychology, algorithms can be used to help identify individuals with a greater risk of mental health issues. For instance, research suggests that certain algorithms might help us recognize children with an elevated risk of suicide or self-harm.

One benefit of algorithms is that they guarantee an accurate answer. However, they aren't always the best approach to problem-solving, in part because detecting patterns can be incredibly time-consuming.

There are also concerns when machine learning is involved—also known as artificial intelligence (AI)—such as whether they can accurately predict human behaviors.

Heuristics are shortcut strategies that people can use to solve a problem at hand. These "rule of thumb" approaches allow you to simplify complex problems, reducing the total number of possible solutions to a more manageable set.

If you find yourself sitting in a traffic jam, for example, you may quickly consider other routes, taking one to get moving once again. When shopping for a new car, you might think back to a prior experience when negotiating got you a lower price, then employ the same tactics.

While heuristics may be helpful when facing smaller issues, major decisions shouldn't necessarily be made using a shortcut approach. Heuristics also don't guarantee an effective solution, such as when trying to drive around a traffic jam only to find yourself on an equally crowded route.

Trial and Error

A trial-and-error approach to problem-solving involves trying a number of potential solutions to a particular issue, then ruling out those that do not work. If you're not sure whether to buy a shirt in blue or green, for instance, you may try on each before deciding which one to purchase.

This can be a good strategy to use if you have a limited number of solutions available. But if there are many different choices available, narrowing down the possible options using another problem-solving technique can be helpful before attempting trial and error.

In some cases, the solution to a problem can appear as a sudden insight. You are facing an issue in a relationship or your career when, out of nowhere, the solution appears in your mind and you know exactly what to do.

Insight can occur when the problem in front of you is similar to an issue that you've dealt with in the past. Although, you may not recognize what is occurring since the underlying mental processes that lead to insight often happen outside of conscious awareness .

Research indicates that insight is most likely to occur during times when you are alone—such as when going on a walk by yourself, when you're in the shower, or when lying in bed after waking up.

How to Apply Problem-Solving Strategies in Real Life

If you're facing a problem, you can implement one or more of these strategies to find a potential solution. Here's how to use them in real life:

• Create a flow chart . If you have time, you can take advantage of the algorithm approach to problem-solving by sitting down and making a flow chart of each potential solution, its consequences, and what happens next.
• Recall your past experiences . When a problem needs to be solved fairly quickly, heuristics may be a better approach. Think back to when you faced a similar issue, then use your knowledge and experience to choose the best option possible.
• Start trying potential solutions . If your options are limited, start trying them one by one to see which solution is best for achieving your desired goal. If a particular solution doesn't work, move on to the next.
• Take some time alone . Since insight is often achieved when you're alone, carve out time to be by yourself for a while. The answer to your problem may come to you, seemingly out of the blue, if you spend some time away from others.

Obstacles to Problem-Solving

Problem-solving is not a flawless process as there are a number of obstacles that can interfere with our ability to solve a problem quickly and efficiently. These obstacles include:

• Assumptions: When dealing with a problem, people can make assumptions about the constraints and obstacles that prevent certain solutions. Thus, they may not even try some potential options.
• Functional fixedness : This term refers to the tendency to view problems only in their customary manner. Functional fixedness prevents people from fully seeing all of the different options that might be available to find a solution.
• Irrelevant or misleading information: When trying to solve a problem, it's important to distinguish between information that is relevant to the issue and irrelevant data that can lead to faulty solutions. The more complex the problem, the easier it is to focus on misleading or irrelevant information.
• Mental set: A mental set is a tendency to only use solutions that have worked in the past rather than looking for alternative ideas. A mental set can work as a heuristic, making it a useful problem-solving tool. However, mental sets can also lead to inflexibility, making it more difficult to find effective solutions.

How to Improve Your Problem-Solving Skills

In the end, if your goal is to become a better problem-solver, it's helpful to remember that this is a process. Thus, if you want to improve your problem-solving skills, following these steps can help lead you to your solution:

• Recognize that a problem exists . If you are facing a problem, there are generally signs. For instance, if you have a mental illness , you may experience excessive fear or sadness, mood changes, and changes in sleeping or eating habits. Recognizing these signs can help you realize that an issue exists.
• Decide to solve the problem . Make a conscious decision to solve the issue at hand. Commit to yourself that you will go through the steps necessary to find a solution.
• Seek to fully understand the issue . Analyze the problem you face, looking at it from all sides. If your problem is relationship-related, for instance, ask yourself how the other person may be interpreting the issue. You might also consider how your actions might be contributing to the situation.
• Research potential options . Using the problem-solving strategies mentioned, research potential solutions. Make a list of options, then consider each one individually. What are some pros and cons of taking the available routes? What would you need to do to make them happen?
• Take action . Select the best solution possible and take action. Action is one of the steps required for change . So, go through the motions needed to resolve the issue.
• Try another option, if needed . If the solution you chose didn't work, don't give up. Either go through the problem-solving process again or simply try another option.

You can find a way to solve your problems as long as you keep working toward this goal—even if the best solution is simply to let go because no other good solution exists.

Sarathy V. Real world problem-solving .  Front Hum Neurosci . 2018;12:261. doi:10.3389/fnhum.2018.00261

Dunbar K. Problem solving . A Companion to Cognitive Science . 2017. doi:10.1002/9781405164535.ch20

Stewart SL, Celebre A, Hirdes JP, Poss JW. Risk of suicide and self-harm in kids: The development of an algorithm to identify high-risk individuals within the children's mental health system . Child Psychiat Human Develop . 2020;51:913-924. doi:10.1007/s10578-020-00968-9

Rosenbusch H, Soldner F, Evans AM, Zeelenberg M. Supervised machine learning methods in psychology: A practical introduction with annotated R code . Soc Personal Psychol Compass . 2021;15(2):e12579. doi:10.1111/spc3.12579

Mishra S. Decision-making under risk: Integrating perspectives from biology, economics, and psychology . Personal Soc Psychol Rev . 2014;18(3):280-307. doi:10.1177/1088868314530517

Csikszentmihalyi M, Sawyer K. Creative insight: The social dimension of a solitary moment . In: The Systems Model of Creativity . 2015:73-98. doi:10.1007/978-94-017-9085-7_7

Chrysikou EG, Motyka K, Nigro C, Yang SI, Thompson-Schill SL. Functional fixedness in creative thinking tasks depends on stimulus modality .  Psychol Aesthet Creat Arts . 2016;10(4):425‐435. doi:10.1037/aca0000050

Huang F, Tang S, Hu Z. Unconditional perseveration of the short-term mental set in chunk decomposition .  Front Psychol . 2018;9:2568. doi:10.3389/fpsyg.2018.02568

National Alliance on Mental Illness. Warning signs and symptoms .

Mayer RE. Thinking, problem solving, cognition, 2nd ed .

Schooler JW, Ohlsson S, Brooks K. Thoughts beyond words: When language overshadows insight. J Experiment Psychol: General . 1993;122:166-183. doi:10.1037/0096-3445.2.166

By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

35 problem-solving techniques and methods for solving complex problems

Design your next session with SessionLab

Join the 150,000+ facilitators 
using SessionLab.

Recommended Articles

A step-by-step guide to planning a workshop, how to create an unforgettable training session in 8 simple steps, 47 useful online tools for workshop planning and meeting facilitation.

All teams and organizations encounter challenges as they grow. There are problems that might occur for teams when it comes to miscommunication or resolving business-critical issues . You may face challenges around growth , design , user engagement, and even team culture and happiness. In short, problem-solving techniques should be part of every team’s skillset.

Problem-solving methods are primarily designed to help a group or team through a process of first identifying problems and challenges , ideating possible solutions , and then evaluating the most suitable .

Finding effective solutions to complex problems isn’t easy, but by using the right process and techniques, you can help your team be more efficient in the process.

So how do you develop strategies that are engaging, and empower your team to solve problems effectively?

In this blog post, we share a series of problem-solving tools you can use in your next workshop or team meeting. You’ll also find some tips for facilitating the process and how to enable others to solve complex problems.

Let’s get started! 

How do you identify problems?

How do you identify the right solution.

• Tips for more effective problem-solving

Complete problem-solving methods

• Problem-solving techniques to identify and analyze problems
• Problem-solving techniques for developing solutions

Problem-solving warm-up activities

Closing activities for a problem-solving process.

Before you can move towards finding the right solution for a given problem, you first need to identify and define the problem you wish to solve. 

Here, you want to clearly articulate what the problem is and allow your group to do the same. Remember that everyone in a group is likely to have differing perspectives and alignment is necessary in order to help the group move forward. 

Identifying a problem accurately also requires that all members of a group are able to contribute their views in an open and safe manner. It can be scary for people to stand up and contribute, especially if the problems or challenges are emotive or personal in nature. Be sure to try and create a psychologically safe space for these kinds of discussions.

Remember that problem analysis and further discussion are also important. Not taking the time to fully analyze and discuss a challenge can result in the development of solutions that are not fit for purpose or do not address the underlying issue.

Successfully identifying and then analyzing a problem means facilitating a group through activities designed to help them clearly and honestly articulate their thoughts and produce usable insight.

With this data, you might then produce a problem statement that clearly describes the problem you wish to be addressed and also state the goal of any process you undertake to tackle this issue.  

Finding solutions is the end goal of any process. Complex organizational challenges can only be solved with an appropriate solution but discovering them requires using the right problem-solving tool.

After you’ve explored a problem and discussed ideas, you need to help a team discuss and choose the right solution. Consensus tools and methods such as those below help a group explore possible solutions before then voting for the best. They’re a great way to tap into the collective intelligence of the group for great results!

Remember that the process is often iterative. Great problem solvers often roadtest a viable solution in a measured way to see what works too. While you might not get the right solution on your first try, the methods below help teams land on the most likely to succeed solution while also holding space for improvement.

Every effective problem solving process begins with an agenda . A well-structured workshop is one of the best methods for successfully guiding a group from exploring a problem to implementing a solution.

In SessionLab, it’s easy to go from an idea to a complete agenda . Start by dragging and dropping your core problem solving activities into place . Add timings, breaks and necessary materials before sharing your agenda with your colleagues.

The resulting agenda will be your guide to an effective and productive problem solving session that will also help you stay organized on the day!

Tips for more effective problem solving

Problem-solving activities are only one part of the puzzle. While a great method can help unlock your team’s ability to solve problems, without a thoughtful approach and strong facilitation the solutions may not be fit for purpose.

Let’s take a look at some problem-solving tips you can apply to any process to help it be a success!

Clearly define the problem

Jumping straight to solutions can be tempting, though without first clearly articulating a problem, the solution might not be the right one. Many of the problem-solving activities below include sections where the problem is explored and clearly defined before moving on.

This is a vital part of the problem-solving process and taking the time to fully define an issue can save time and effort later. A clear definition helps identify irrelevant information and it also ensures that your team sets off on the right track.

Don’t jump to conclusions

It’s easy for groups to exhibit cognitive bias or have preconceived ideas about both problems and potential solutions. Be sure to back up any problem statements or potential solutions with facts, research, and adequate forethought.

The best techniques ask participants to be methodical and challenge preconceived notions. Make sure you give the group enough time and space to collect relevant information and consider the problem in a new way. By approaching the process with a clear, rational mindset, you’ll often find that better solutions are more forthcoming.  

Try different approaches  

Problems come in all shapes and sizes and so too should the methods you use to solve them. If you find that one approach isn’t yielding results and your team isn’t finding different solutions, try mixing it up. You’ll be surprised at how using a new creative activity can unblock your team and generate great solutions.

Don’t take it personally 

Depending on the nature of your team or organizational problems, it’s easy for conversations to get heated. While it’s good for participants to be engaged in the discussions, ensure that emotions don’t run too high and that blame isn’t thrown around while finding solutions.

You’re all in it together, and even if your team or area is seeing problems, that isn’t necessarily a disparagement of you personally. Using facilitation skills to manage group dynamics is one effective method of helping conversations be more constructive.

Get the right people in the room

Your problem-solving method is often only as effective as the group using it. Getting the right people on the job and managing the number of people present is important too!

If the group is too small, you may not get enough different perspectives to effectively solve a problem. If the group is too large, you can go round and round during the ideation stages.

Creating the right group makeup is also important in ensuring you have the necessary expertise and skillset to both identify and follow up on potential solutions. Carefully consider who to include at each stage to help ensure your problem-solving method is followed and positioned for success.

Document everything

The best solutions can take refinement, iteration, and reflection to come out. Get into a habit of documenting your process in order to keep all the learnings from the session and to allow ideas to mature and develop. Many of the methods below involve the creation of documents or shared resources. Be sure to keep and share these so everyone can benefit from the work done!

Bring a facilitator 

Facilitation is all about making group processes easier. With a subject as potentially emotive and important as problem-solving, having an impartial third party in the form of a facilitator can make all the difference in finding great solutions and keeping the process moving. Consider bringing a facilitator to your problem-solving session to get better results and generate meaningful solutions!

Develop your problem-solving skills

It takes time and practice to be an effective problem solver. While some roles or participants might more naturally gravitate towards problem-solving, it can take development and planning to help everyone create better solutions.

You might develop a training program, run a problem-solving workshop or simply ask your team to practice using the techniques below. Check out our post on problem-solving skills to see how you and your group can develop the right mental process and be more resilient to issues too!

Design a great agenda

Workshops are a great format for solving problems. With the right approach, you can focus a group and help them find the solutions to their own problems. But designing a process can be time-consuming and finding the right activities can be difficult.

Check out our workshop planning guide to level-up your agenda design and start running more effective workshops. Need inspiration? Check out templates designed by expert facilitators to help you kickstart your process!

In this section, we’ll look at in-depth problem-solving methods that provide a complete end-to-end process for developing effective solutions. These will help guide your team from the discovery and definition of a problem through to delivering the right solution.

If you’re looking for an all-encompassing method or problem-solving model, these processes are a great place to start. They’ll ask your team to challenge preconceived ideas and adopt a mindset for solving problems more effectively.

• Six Thinking Hats
• Lightning Decision Jam
• Problem Definition Process
• Discovery & Action Dialogue

Design Sprint 2.0

• Open Space Technology

1. Six Thinking Hats

Individual approaches to solving a problem can be very different based on what team or role an individual holds. It can be easy for existing biases or perspectives to find their way into the mix, or for internal politics to direct a conversation.

Six Thinking Hats is a classic method for identifying the problems that need to be solved and enables your team to consider them from different angles, whether that is by focusing on facts and data, creative solutions, or by considering why a particular solution might not work.

Like all problem-solving frameworks, Six Thinking Hats is effective at helping teams remove roadblocks from a conversation or discussion and come to terms with all the aspects necessary to solve complex problems.

2. Lightning Decision Jam

Featured courtesy of Jonathan Courtney of AJ&Smart Berlin, Lightning Decision Jam is one of those strategies that should be in every facilitation toolbox. Exploring problems and finding solutions is often creative in nature, though as with any creative process, there is the potential to lose focus and get lost.

Unstructured discussions might get you there in the end, but it’s much more effective to use a method that creates a clear process and team focus.

In Lightning Decision Jam, participants are invited to begin by writing challenges, concerns, or mistakes on post-its without discussing them before then being invited by the moderator to present them to the group.

From there, the team vote on which problems to solve and are guided through steps that will allow them to reframe those problems, create solutions and then decide what to execute on. 

By deciding the problems that need to be solved as a team before moving on, this group process is great for ensuring the whole team is aligned and can take ownership over the next stages. 

Lightning Decision Jam (LDJ)   #action   #decision making   #problem solving   #issue analysis   #innovation   #design   #remote-friendly   The problem with anything that requires creative thinking is that it’s easy to get lost—lose focus and fall into the trap of having useless, open-ended, unstructured discussions. Here’s the most effective solution I’ve found: Replace all open, unstructured discussion with a clear process. What to use this exercise for: Anything which requires a group of people to make decisions, solve problems or discuss challenges. It’s always good to frame an LDJ session with a broad topic, here are some examples: The conversion flow of our checkout Our internal design process How we organise events Keeping up with our competition Improving sales flow

3. Problem Definition Process

While problems can be complex, the problem-solving methods you use to identify and solve those problems can often be simple in design. 

By taking the time to truly identify and define a problem before asking the group to reframe the challenge as an opportunity, this method is a great way to enable change.

Begin by identifying a focus question and exploring the ways in which it manifests before splitting into five teams who will each consider the problem using a different method: escape, reversal, exaggeration, distortion or wishful. Teams develop a problem objective and create ideas in line with their method before then feeding them back to the group.

This method is great for enabling in-depth discussions while also creating space for finding creative solutions too!

Problem Definition   #problem solving   #idea generation   #creativity   #online   #remote-friendly   A problem solving technique to define a problem, challenge or opportunity and to generate ideas.

4. The 5 Whys 

Sometimes, a group needs to go further with their strategies and analyze the root cause at the heart of organizational issues. An RCA or root cause analysis is the process of identifying what is at the heart of business problems or recurring challenges. 

The 5 Whys is a simple and effective method of helping a group go find the root cause of any problem or challenge and conduct analysis that will deliver results. 

By beginning with the creation of a problem statement and going through five stages to refine it, The 5 Whys provides everything you need to truly discover the cause of an issue.

The 5 Whys   #hyperisland   #innovation   This simple and powerful method is useful for getting to the core of a problem or challenge. As the title suggests, the group defines a problems, then asks the question “why” five times, often using the resulting explanation as a starting point for creative problem solving.

5. World Cafe

World Cafe is a simple but powerful facilitation technique to help bigger groups to focus their energy and attention on solving complex problems.

World Cafe enables this approach by creating a relaxed atmosphere where participants are able to self-organize and explore topics relevant and important to them which are themed around a central problem-solving purpose. Create the right atmosphere by modeling your space after a cafe and after guiding the group through the method, let them take the lead!

Making problem-solving a part of your organization’s culture in the long term can be a difficult undertaking. More approachable formats like World Cafe can be especially effective in bringing people unfamiliar with workshops into the fold. 

World Cafe   #hyperisland   #innovation   #issue analysis   World Café is a simple yet powerful method, originated by Juanita Brown, for enabling meaningful conversations driven completely by participants and the topics that are relevant and important to them. Facilitators create a cafe-style space and provide simple guidelines. Participants then self-organize and explore a set of relevant topics or questions for conversation.

6. Discovery & Action Dialogue (DAD)

One of the best approaches is to create a safe space for a group to share and discover practices and behaviors that can help them find their own solutions.

With DAD, you can help a group choose which problems they wish to solve and which approaches they will take to do so. It’s great at helping remove resistance to change and can help get buy-in at every level too!

This process of enabling frontline ownership is great in ensuring follow-through and is one of the methods you will want in your toolbox as a facilitator.

Discovery & Action Dialogue (DAD)   #idea generation   #liberating structures   #action   #issue analysis   #remote-friendly   DADs make it easy for a group or community to discover practices and behaviors that enable some individuals (without access to special resources and facing the same constraints) to find better solutions than their peers to common problems. These are called positive deviant (PD) behaviors and practices. DADs make it possible for people in the group, unit, or community to discover by themselves these PD practices. DADs also create favorable conditions for stimulating participants’ creativity in spaces where they can feel safe to invent new and more effective practices. Resistance to change evaporates as participants are unleashed to choose freely which practices they will adopt or try and which problems they will tackle. DADs make it possible to achieve frontline ownership of solutions.

7. Design Sprint 2.0

Want to see how a team can solve big problems and move forward with prototyping and testing solutions in a few days? The Design Sprint 2.0 template from Jake Knapp, author of Sprint, is a complete agenda for a with proven results.

Developing the right agenda can involve difficult but necessary planning. Ensuring all the correct steps are followed can also be stressful or time-consuming depending on your level of experience.

Use this complete 4-day workshop template if you are finding there is no obvious solution to your challenge and want to focus your team around a specific problem that might require a shortcut to launching a minimum viable product or waiting for the organization-wide implementation of a solution.

8. Open space technology

Open space technology- developed by Harrison Owen – creates a space where large groups are invited to take ownership of their problem solving and lead individual sessions. Open space technology is a great format when you have a great deal of expertise and insight in the room and want to allow for different takes and approaches on a particular theme or problem you need to be solved.

Start by bringing your participants together to align around a central theme and focus their efforts. Explain the ground rules to help guide the problem-solving process and then invite members to identify any issue connecting to the central theme that they are interested in and are prepared to take responsibility for.

Once participants have decided on their approach to the core theme, they write their issue on a piece of paper, announce it to the group, pick a session time and place, and post the paper on the wall. As the wall fills up with sessions, the group is then invited to join the sessions that interest them the most and which they can contribute to, then you’re ready to begin!

Everyone joins the problem-solving group they’ve signed up to, record the discussion and if appropriate, findings can then be shared with the rest of the group afterward.

Open Space Technology   #action plan   #idea generation   #problem solving   #issue analysis   #large group   #online   #remote-friendly   Open Space is a methodology for large groups to create their agenda discerning important topics for discussion, suitable for conferences, community gatherings and whole system facilitation

Techniques to identify and analyze problems

Using a problem-solving method to help a team identify and analyze a problem can be a quick and effective addition to any workshop or meeting.

While further actions are always necessary, you can generate momentum and alignment easily, and these activities are a great place to get started.

We’ve put together this list of techniques to help you and your team with problem identification, analysis, and discussion that sets the foundation for developing effective solutions.

Let’s take a look!

• The Creativity Dice
• Fishbone Analysis
• Problem Tree
• SWOT Analysis
• Agreement-Certainty Matrix
• The Journalistic Six
• LEGO Challenge
• What, So What, Now What?
• Journalists

Individual and group perspectives are incredibly important, but what happens if people are set in their minds and need a change of perspective in order to approach a problem more effectively?

Flip It is a method we love because it is both simple to understand and run, and allows groups to understand how their perspectives and biases are formed. 

Participants in Flip It are first invited to consider concerns, issues, or problems from a perspective of fear and write them on a flip chart. Then, the group is asked to consider those same issues from a perspective of hope and flip their understanding.  

No problem and solution is free from existing bias and by changing perspectives with Flip It, you can then develop a problem solving model quickly and effectively.

Flip It!   #gamestorming   #problem solving   #action   Often, a change in a problem or situation comes simply from a change in our perspectives. Flip It! is a quick game designed to show players that perspectives are made, not born.

10. The Creativity Dice

One of the most useful problem solving skills you can teach your team is of approaching challenges with creativity, flexibility, and openness. Games like The Creativity Dice allow teams to overcome the potential hurdle of too much linear thinking and approach the process with a sense of fun and speed. 

In The Creativity Dice, participants are organized around a topic and roll a dice to determine what they will work on for a period of 3 minutes at a time. They might roll a 3 and work on investigating factual information on the chosen topic. They might roll a 1 and work on identifying the specific goals, standards, or criteria for the session.

Encouraging rapid work and iteration while asking participants to be flexible are great skills to cultivate. Having a stage for idea incubation in this game is also important. Moments of pause can help ensure the ideas that are put forward are the most suitable. 

The Creativity Dice   #creativity   #problem solving   #thiagi   #issue analysis   Too much linear thinking is hazardous to creative problem solving. To be creative, you should approach the problem (or the opportunity) from different points of view. You should leave a thought hanging in mid-air and move to another. This skipping around prevents premature closure and lets your brain incubate one line of thought while you consciously pursue another.

11. Fishbone Analysis

Organizational or team challenges are rarely simple, and it’s important to remember that one problem can be an indication of something that goes deeper and may require further consideration to be solved.

Fishbone Analysis helps groups to dig deeper and understand the origins of a problem. It’s a great example of a root cause analysis method that is simple for everyone on a team to get their head around. 

Participants in this activity are asked to annotate a diagram of a fish, first adding the problem or issue to be worked on at the head of a fish before then brainstorming the root causes of the problem and adding them as bones on the fish. 

Using abstractions such as a diagram of a fish can really help a team break out of their regular thinking and develop a creative approach.

Fishbone Analysis   #problem solving   ##root cause analysis   #decision making   #online facilitation   A process to help identify and understand the origins of problems, issues or observations.

12. Problem Tree 

Encouraging visual thinking can be an essential part of many strategies. By simply reframing and clarifying problems, a group can move towards developing a problem solving model that works for them. 

In Problem Tree, groups are asked to first brainstorm a list of problems – these can be design problems, team problems or larger business problems – and then organize them into a hierarchy. The hierarchy could be from most important to least important or abstract to practical, though the key thing with problem solving games that involve this aspect is that your group has some way of managing and sorting all the issues that are raised.

Once you have a list of problems that need to be solved and have organized them accordingly, you’re then well-positioned for the next problem solving steps.

Problem tree   #define intentions   #create   #design   #issue analysis   A problem tree is a tool to clarify the hierarchy of problems addressed by the team within a design project; it represents high level problems or related sublevel problems.

13. SWOT Analysis

Chances are you’ve heard of the SWOT Analysis before. This problem-solving method focuses on identifying strengths, weaknesses, opportunities, and threats is a tried and tested method for both individuals and teams.

Start by creating a desired end state or outcome and bare this in mind – any process solving model is made more effective by knowing what you are moving towards. Create a quadrant made up of the four categories of a SWOT analysis and ask participants to generate ideas based on each of those quadrants.

Once you have those ideas assembled in their quadrants, cluster them together based on their affinity with other ideas. These clusters are then used to facilitate group conversations and move things forward. 

SWOT analysis   #gamestorming   #problem solving   #action   #meeting facilitation   The SWOT Analysis is a long-standing technique of looking at what we have, with respect to the desired end state, as well as what we could improve on. It gives us an opportunity to gauge approaching opportunities and dangers, and assess the seriousness of the conditions that affect our future. When we understand those conditions, we can influence what comes next.

14. Agreement-Certainty Matrix

Not every problem-solving approach is right for every challenge, and deciding on the right method for the challenge at hand is a key part of being an effective team.

The Agreement Certainty matrix helps teams align on the nature of the challenges facing them. By sorting problems from simple to chaotic, your team can understand what methods are suitable for each problem and what they can do to ensure effective results. 

If you are already using Liberating Structures techniques as part of your problem-solving strategy, the Agreement-Certainty Matrix can be an invaluable addition to your process. We’ve found it particularly if you are having issues with recurring problems in your organization and want to go deeper in understanding the root cause. 

Agreement-Certainty Matrix   #issue analysis   #liberating structures   #problem solving   You can help individuals or groups avoid the frequent mistake of trying to solve a problem with methods that are not adapted to the nature of their challenge. The combination of two questions makes it possible to easily sort challenges into four categories: simple, complicated, complex , and chaotic .  A problem is simple when it can be solved reliably with practices that are easy to duplicate.  It is complicated when experts are required to devise a sophisticated solution that will yield the desired results predictably.  A problem is complex when there are several valid ways to proceed but outcomes are not predictable in detail.  Chaotic is when the context is too turbulent to identify a path forward.  A loose analogy may be used to describe these differences: simple is like following a recipe, complicated like sending a rocket to the moon, complex like raising a child, and chaotic is like the game “Pin the Tail on the Donkey.”  The Liberating Structures Matching Matrix in Chapter 5 can be used as the first step to clarify the nature of a challenge and avoid the mismatches between problems and solutions that are frequently at the root of chronic, recurring problems.

Organizing and charting a team’s progress can be important in ensuring its success. SQUID (Sequential Question and Insight Diagram) is a great model that allows a team to effectively switch between giving questions and answers and develop the skills they need to stay on track throughout the process. 

Begin with two different colored sticky notes – one for questions and one for answers – and with your central topic (the head of the squid) on the board. Ask the group to first come up with a series of questions connected to their best guess of how to approach the topic. Ask the group to come up with answers to those questions, fix them to the board and connect them with a line. After some discussion, go back to question mode by responding to the generated answers or other points on the board.

It’s rewarding to see a diagram grow throughout the exercise, and a completed SQUID can provide a visual resource for future effort and as an example for other teams.

SQUID   #gamestorming   #project planning   #issue analysis   #problem solving   When exploring an information space, it’s important for a group to know where they are at any given time. By using SQUID, a group charts out the territory as they go and can navigate accordingly. SQUID stands for Sequential Question and Insight Diagram.

16. Speed Boat

To continue with our nautical theme, Speed Boat is a short and sweet activity that can help a team quickly identify what employees, clients or service users might have a problem with and analyze what might be standing in the way of achieving a solution.

Methods that allow for a group to make observations, have insights and obtain those eureka moments quickly are invaluable when trying to solve complex problems.

In Speed Boat, the approach is to first consider what anchors and challenges might be holding an organization (or boat) back. Bonus points if you are able to identify any sharks in the water and develop ideas that can also deal with competitors!   

Speed Boat   #gamestorming   #problem solving   #action   Speedboat is a short and sweet way to identify what your employees or clients don’t like about your product/service or what’s standing in the way of a desired goal.

17. The Journalistic Six

Some of the most effective ways of solving problems is by encouraging teams to be more inclusive and diverse in their thinking.

Based on the six key questions journalism students are taught to answer in articles and news stories, The Journalistic Six helps create teams to see the whole picture. By using who, what, when, where, why, and how to facilitate the conversation and encourage creative thinking, your team can make sure that the problem identification and problem analysis stages of the are covered exhaustively and thoughtfully. Reporter’s notebook and dictaphone optional.

The Journalistic Six – Who What When Where Why How   #idea generation   #issue analysis   #problem solving   #online   #creative thinking   #remote-friendly   A questioning method for generating, explaining, investigating ideas.

18. LEGO Challenge

Now for an activity that is a little out of the (toy) box. LEGO Serious Play is a facilitation methodology that can be used to improve creative thinking and problem-solving skills. 

The LEGO Challenge includes giving each member of the team an assignment that is hidden from the rest of the group while they create a structure without speaking.

What the LEGO challenge brings to the table is a fun working example of working with stakeholders who might not be on the same page to solve problems. Also, it’s LEGO! Who doesn’t love LEGO! 

LEGO Challenge   #hyperisland   #team   A team-building activity in which groups must work together to build a structure out of LEGO, but each individual has a secret “assignment” which makes the collaborative process more challenging. It emphasizes group communication, leadership dynamics, conflict, cooperation, patience and problem solving strategy.

19. What, So What, Now What?

If not carefully managed, the problem identification and problem analysis stages of the problem-solving process can actually create more problems and misunderstandings.

The What, So What, Now What? problem-solving activity is designed to help collect insights and move forward while also eliminating the possibility of disagreement when it comes to identifying, clarifying, and analyzing organizational or work problems. 

Facilitation is all about bringing groups together so that might work on a shared goal and the best problem-solving strategies ensure that teams are aligned in purpose, if not initially in opinion or insight.

Throughout the three steps of this game, you give everyone on a team to reflect on a problem by asking what happened, why it is important, and what actions should then be taken. 

This can be a great activity for bringing our individual perceptions about a problem or challenge and contextualizing it in a larger group setting. This is one of the most important problem-solving skills you can bring to your organization.

W³ – What, So What, Now What?   #issue analysis   #innovation   #liberating structures   You can help groups reflect on a shared experience in a way that builds understanding and spurs coordinated action while avoiding unproductive conflict. It is possible for every voice to be heard while simultaneously sifting for insights and shaping new direction. Progressing in stages makes this practical—from collecting facts about What Happened to making sense of these facts with So What and finally to what actions logically follow with Now What . The shared progression eliminates most of the misunderstandings that otherwise fuel disagreements about what to do. Voila!

20. Journalists  

Problem analysis can be one of the most important and decisive stages of all problem-solving tools. Sometimes, a team can become bogged down in the details and are unable to move forward.

Journalists is an activity that can avoid a group from getting stuck in the problem identification or problem analysis stages of the process.

In Journalists, the group is invited to draft the front page of a fictional newspaper and figure out what stories deserve to be on the cover and what headlines those stories will have. By reframing how your problems and challenges are approached, you can help a team move productively through the process and be better prepared for the steps to follow.

Journalists   #vision   #big picture   #issue analysis   #remote-friendly   This is an exercise to use when the group gets stuck in details and struggles to see the big picture. Also good for defining a vision.

Problem-solving techniques for developing solutions 

The success of any problem-solving process can be measured by the solutions it produces. After you’ve defined the issue, explored existing ideas, and ideated, it’s time to narrow down to the correct solution.

Use these problem-solving techniques when you want to help your team find consensus, compare possible solutions, and move towards taking action on a particular problem.

• Improved Solutions
• Four-Step Sketch
• 15% Solutions
• How-Now-Wow matrix
• Impact Effort Matrix

21. Mindspin  

Brainstorming is part of the bread and butter of the problem-solving process and all problem-solving strategies benefit from getting ideas out and challenging a team to generate solutions quickly. 

With Mindspin, participants are encouraged not only to generate ideas but to do so under time constraints and by slamming down cards and passing them on. By doing multiple rounds, your team can begin with a free generation of possible solutions before moving on to developing those solutions and encouraging further ideation. 

This is one of our favorite problem-solving activities and can be great for keeping the energy up throughout the workshop. Remember the importance of helping people become engaged in the process – energizing problem-solving techniques like Mindspin can help ensure your team stays engaged and happy, even when the problems they’re coming together to solve are complex. 

MindSpin   #teampedia   #idea generation   #problem solving   #action   A fast and loud method to enhance brainstorming within a team. Since this activity has more than round ideas that are repetitive can be ruled out leaving more creative and innovative answers to the challenge.

22. Improved Solutions

After a team has successfully identified a problem and come up with a few solutions, it can be tempting to call the work of the problem-solving process complete. That said, the first solution is not necessarily the best, and by including a further review and reflection activity into your problem-solving model, you can ensure your group reaches the best possible result. 

One of a number of problem-solving games from Thiagi Group, Improved Solutions helps you go the extra mile and develop suggested solutions with close consideration and peer review. By supporting the discussion of several problems at once and by shifting team roles throughout, this problem-solving technique is a dynamic way of finding the best solution. 

Improved Solutions   #creativity   #thiagi   #problem solving   #action   #team   You can improve any solution by objectively reviewing its strengths and weaknesses and making suitable adjustments. In this creativity framegame, you improve the solutions to several problems. To maintain objective detachment, you deal with a different problem during each of six rounds and assume different roles (problem owner, consultant, basher, booster, enhancer, and evaluator) during each round. At the conclusion of the activity, each player ends up with two solutions to her problem.

23. Four Step Sketch

Creative thinking and visual ideation does not need to be confined to the opening stages of your problem-solving strategies. Exercises that include sketching and prototyping on paper can be effective at the solution finding and development stage of the process, and can be great for keeping a team engaged. 

By going from simple notes to a crazy 8s round that involves rapidly sketching 8 variations on their ideas before then producing a final solution sketch, the group is able to iterate quickly and visually. Problem-solving techniques like Four-Step Sketch are great if you have a group of different thinkers and want to change things up from a more textual or discussion-based approach.

Four-Step Sketch   #design sprint   #innovation   #idea generation   #remote-friendly   The four-step sketch is an exercise that helps people to create well-formed concepts through a structured process that includes: Review key information Start design work on paper,  Consider multiple variations , Create a detailed solution . This exercise is preceded by a set of other activities allowing the group to clarify the challenge they want to solve. See how the Four Step Sketch exercise fits into a Design Sprint

24. 15% Solutions

Some problems are simpler than others and with the right problem-solving activities, you can empower people to take immediate actions that can help create organizational change. 

Part of the liberating structures toolkit, 15% solutions is a problem-solving technique that focuses on finding and implementing solutions quickly. A process of iterating and making small changes quickly can help generate momentum and an appetite for solving complex problems.

Problem-solving strategies can live and die on whether people are onboard. Getting some quick wins is a great way of getting people behind the process.   

It can be extremely empowering for a team to realize that problem-solving techniques can be deployed quickly and easily and delineate between things they can positively impact and those things they cannot change. 

15% Solutions   #action   #liberating structures   #remote-friendly   You can reveal the actions, however small, that everyone can do immediately. At a minimum, these will create momentum, and that may make a BIG difference.  15% Solutions show that there is no reason to wait around, feel powerless, or fearful. They help people pick it up a level. They get individuals and the group to focus on what is within their discretion instead of what they cannot change.  With a very simple question, you can flip the conversation to what can be done and find solutions to big problems that are often distributed widely in places not known in advance. Shifting a few grains of sand may trigger a landslide and change the whole landscape.

25. How-Now-Wow Matrix

The problem-solving process is often creative, as complex problems usually require a change of thinking and creative response in order to find the best solutions. While it’s common for the first stages to encourage creative thinking, groups can often gravitate to familiar solutions when it comes to the end of the process. 

When selecting solutions, you don’t want to lose your creative energy! The How-Now-Wow Matrix from Gamestorming is a great problem-solving activity that enables a group to stay creative and think out of the box when it comes to selecting the right solution for a given problem.

Problem-solving techniques that encourage creative thinking and the ideation and selection of new solutions can be the most effective in organisational change. Give the How-Now-Wow Matrix a go, and not just for how pleasant it is to say out loud. 

How-Now-Wow Matrix   #gamestorming   #idea generation   #remote-friendly   When people want to develop new ideas, they most often think out of the box in the brainstorming or divergent phase. However, when it comes to convergence, people often end up picking ideas that are most familiar to them. This is called a ‘creative paradox’ or a ‘creadox’. The How-Now-Wow matrix is an idea selection tool that breaks the creadox by forcing people to weigh each idea on 2 parameters.

26. Impact and Effort Matrix

All problem-solving techniques hope to not only find solutions to a given problem or challenge but to find the best solution. When it comes to finding a solution, groups are invited to put on their decision-making hats and really think about how a proposed idea would work in practice. 

The Impact and Effort Matrix is one of the problem-solving techniques that fall into this camp, empowering participants to first generate ideas and then categorize them into a 2×2 matrix based on impact and effort.

Activities that invite critical thinking while remaining simple are invaluable. Use the Impact and Effort Matrix to move from ideation and towards evaluating potential solutions before then committing to them. 

Impact and Effort Matrix   #gamestorming   #decision making   #action   #remote-friendly   In this decision-making exercise, possible actions are mapped based on two factors: effort required to implement and potential impact. Categorizing ideas along these lines is a useful technique in decision making, as it obliges contributors to balance and evaluate suggested actions before committing to them.

27. Dotmocracy

If you’ve followed each of the problem-solving steps with your group successfully, you should move towards the end of your process with heaps of possible solutions developed with a specific problem in mind. But how do you help a group go from ideation to putting a solution into action? 

Dotmocracy – or Dot Voting -is a tried and tested method of helping a team in the problem-solving process make decisions and put actions in place with a degree of oversight and consensus. 

One of the problem-solving techniques that should be in every facilitator’s toolbox, Dot Voting is fast and effective and can help identify the most popular and best solutions and help bring a group to a decision effectively. 

Dotmocracy   #action   #decision making   #group prioritization   #hyperisland   #remote-friendly   Dotmocracy is a simple method for group prioritization or decision-making. It is not an activity on its own, but a method to use in processes where prioritization or decision-making is the aim. The method supports a group to quickly see which options are most popular or relevant. The options or ideas are written on post-its and stuck up on a wall for the whole group to see. Each person votes for the options they think are the strongest, and that information is used to inform a decision.

All facilitators know that warm-ups and icebreakers are useful for any workshop or group process. Problem-solving workshops are no different.

Use these problem-solving techniques to warm up a group and prepare them for the rest of the process. Activating your group by tapping into some of the top problem-solving skills can be one of the best ways to see great outcomes from your session.

• Check-in/Check-out
• Doodling Together
• Show and Tell
• Constellations
• Draw a Tree

28. Check-in / Check-out

Solid processes are planned from beginning to end, and the best facilitators know that setting the tone and establishing a safe, open environment can be integral to a successful problem-solving process.

Check-in / Check-out is a great way to begin and/or bookend a problem-solving workshop. Checking in to a session emphasizes that everyone will be seen, heard, and expected to contribute. 

If you are running a series of meetings, setting a consistent pattern of checking in and checking out can really help your team get into a groove. We recommend this opening-closing activity for small to medium-sized groups though it can work with large groups if they’re disciplined!

Check-in / Check-out   #team   #opening   #closing   #hyperisland   #remote-friendly   Either checking-in or checking-out is a simple way for a team to open or close a process, symbolically and in a collaborative way. Checking-in/out invites each member in a group to be present, seen and heard, and to express a reflection or a feeling. Checking-in emphasizes presence, focus and group commitment; checking-out emphasizes reflection and symbolic closure.

29. Doodling Together  

Thinking creatively and not being afraid to make suggestions are important problem-solving skills for any group or team, and warming up by encouraging these behaviors is a great way to start. 

Doodling Together is one of our favorite creative ice breaker games – it’s quick, effective, and fun and can make all following problem-solving steps easier by encouraging a group to collaborate visually. By passing cards and adding additional items as they go, the workshop group gets into a groove of co-creation and idea development that is crucial to finding solutions to problems. 

Doodling Together   #collaboration   #creativity   #teamwork   #fun   #team   #visual methods   #energiser   #icebreaker   #remote-friendly   Create wild, weird and often funny postcards together & establish a group’s creative confidence.

30. Show and Tell

You might remember some version of Show and Tell from being a kid in school and it’s a great problem-solving activity to kick off a session.

Asking participants to prepare a little something before a workshop by bringing an object for show and tell can help them warm up before the session has even begun! Games that include a physical object can also help encourage early engagement before moving onto more big-picture thinking.

By asking your participants to tell stories about why they chose to bring a particular item to the group, you can help teams see things from new perspectives and see both differences and similarities in the way they approach a topic. Great groundwork for approaching a problem-solving process as a team! 

Show and Tell   #gamestorming   #action   #opening   #meeting facilitation   Show and Tell taps into the power of metaphors to reveal players’ underlying assumptions and associations around a topic The aim of the game is to get a deeper understanding of stakeholders’ perspectives on anything—a new project, an organizational restructuring, a shift in the company’s vision or team dynamic.

31. Constellations

Who doesn’t love stars? Constellations is a great warm-up activity for any workshop as it gets people up off their feet, energized, and ready to engage in new ways with established topics. It’s also great for showing existing beliefs, biases, and patterns that can come into play as part of your session.

Using warm-up games that help build trust and connection while also allowing for non-verbal responses can be great for easing people into the problem-solving process and encouraging engagement from everyone in the group. Constellations is great in large spaces that allow for movement and is definitely a practical exercise to allow the group to see patterns that are otherwise invisible. 

Constellations   #trust   #connection   #opening   #coaching   #patterns   #system   Individuals express their response to a statement or idea by standing closer or further from a central object. Used with teams to reveal system, hidden patterns, perspectives.

32. Draw a Tree

Problem-solving games that help raise group awareness through a central, unifying metaphor can be effective ways to warm-up a group in any problem-solving model.

Draw a Tree is a simple warm-up activity you can use in any group and which can provide a quick jolt of energy. Start by asking your participants to draw a tree in just 45 seconds – they can choose whether it will be abstract or realistic. 

Once the timer is up, ask the group how many people included the roots of the tree and use this as a means to discuss how we can ignore important parts of any system simply because they are not visible.

All problem-solving strategies are made more effective by thinking of problems critically and by exposing things that may not normally come to light. Warm-up games like Draw a Tree are great in that they quickly demonstrate some key problem-solving skills in an accessible and effective way.

Draw a Tree   #thiagi   #opening   #perspectives   #remote-friendly   With this game you can raise awarness about being more mindful, and aware of the environment we live in.

Each step of the problem-solving workshop benefits from an intelligent deployment of activities, games, and techniques. Bringing your session to an effective close helps ensure that solutions are followed through on and that you also celebrate what has been achieved.

Here are some problem-solving activities you can use to effectively close a workshop or meeting and ensure the great work you’ve done can continue afterward.

• One Breath Feedback
• Who What When Matrix
• Response Cards

How do I conclude a problem-solving process?

All good things must come to an end. With the bulk of the work done, it can be tempting to conclude your workshop swiftly and without a moment to debrief and align. This can be problematic in that it doesn’t allow your team to fully process the results or reflect on the process.

At the end of an effective session, your team will have gone through a process that, while productive, can be exhausting. It’s important to give your group a moment to take a breath, ensure that they are clear on future actions, and provide short feedback before leaving the space. 

The primary purpose of any problem-solving method is to generate solutions and then implement them. Be sure to take the opportunity to ensure everyone is aligned and ready to effectively implement the solutions you produced in the workshop.

Remember that every process can be improved and by giving a short moment to collect feedback in the session, you can further refine your problem-solving methods and see further success in the future too.

33. One Breath Feedback

Maintaining attention and focus during the closing stages of a problem-solving workshop can be tricky and so being concise when giving feedback can be important. It’s easy to incur “death by feedback” should some team members go on for too long sharing their perspectives in a quick feedback round. 

One Breath Feedback is a great closing activity for workshops. You give everyone an opportunity to provide feedback on what they’ve done but only in the space of a single breath. This keeps feedback short and to the point and means that everyone is encouraged to provide the most important piece of feedback to them. 

One breath feedback   #closing   #feedback   #action   This is a feedback round in just one breath that excels in maintaining attention: each participants is able to speak during just one breath … for most people that’s around 20 to 25 seconds … unless of course you’ve been a deep sea diver in which case you’ll be able to do it for longer.

34. Who What When Matrix 

Matrices feature as part of many effective problem-solving strategies and with good reason. They are easily recognizable, simple to use, and generate results.

The Who What When Matrix is a great tool to use when closing your problem-solving session by attributing a who, what and when to the actions and solutions you have decided upon. The resulting matrix is a simple, easy-to-follow way of ensuring your team can move forward. 

Great solutions can’t be enacted without action and ownership. Your problem-solving process should include a stage for allocating tasks to individuals or teams and creating a realistic timeframe for those solutions to be implemented or checked out. Use this method to keep the solution implementation process clear and simple for all involved. 

Who/What/When Matrix   #gamestorming   #action   #project planning   With Who/What/When matrix, you can connect people with clear actions they have defined and have committed to.

35. Response cards

Group discussion can comprise the bulk of most problem-solving activities and by the end of the process, you might find that your team is talked out! 

Providing a means for your team to give feedback with short written notes can ensure everyone is head and can contribute without the need to stand up and talk. Depending on the needs of the group, giving an alternative can help ensure everyone can contribute to your problem-solving model in the way that makes the most sense for them.

Response Cards is a great way to close a workshop if you are looking for a gentle warm-down and want to get some swift discussion around some of the feedback that is raised. 

Response Cards   #debriefing   #closing   #structured sharing   #questions and answers   #thiagi   #action   It can be hard to involve everyone during a closing of a session. Some might stay in the background or get unheard because of louder participants. However, with the use of Response Cards, everyone will be involved in providing feedback or clarify questions at the end of a session.

Save time and effort discovering the right solutions

A structured problem solving process is a surefire way of solving tough problems, discovering creative solutions and driving organizational change. But how can you design for successful outcomes?

With SessionLab, it’s easy to design engaging workshops that deliver results. Drag, drop and reorder blocks  to build your agenda. When you make changes or update your agenda, your session  timing   adjusts automatically , saving you time on manual adjustments.

Collaborating with stakeholders or clients? Share your agenda with a single click and collaborate in real-time. No more sending documents back and forth over email.

Explore  how to use SessionLab  to design effective problem solving workshops or  watch this five minute video  to see the planner in action!

Over to you

The problem-solving process can often be as complicated and multifaceted as the problems they are set-up to solve. With the right problem-solving techniques and a mix of creative exercises designed to guide discussion and generate purposeful ideas, we hope we’ve given you the tools to find the best solutions as simply and easily as possible.

Is there a problem-solving technique that you are missing here? Do you have a favorite activity or method you use when facilitating? Let us know in the comments below, we’d love to hear from you! 

thank you very much for these excellent techniques

Certainly wonderful article, very detailed. Shared!

Your list of techniques for problem solving can be helpfully extended by adding TRIZ to the list of techniques. TRIZ has 40 problem solving techniques derived from methods inventros and patent holders used to get new patents. About 10-12 are general approaches. many organization sponsor classes in TRIZ that are used to solve business problems or general organiztational problems. You can take a look at TRIZ and dwonload a free internet booklet to see if you feel it shound be included per your selection process.

Leave a Comment Cancel reply

Your email address will not be published. Required fields are marked *

Going from a mere idea to a workshop that delivers results for your clients can feel like a daunting task. In this piece, we will shine a light on all the work behind the scenes and help you learn how to plan a workshop from start to finish. On a good day, facilitation can feel like effortless magic, but that is mostly the result of backstage work, foresight, and a lot of careful planning. Read on to learn a step-by-step approach to breaking the process of planning a workshop into small, manageable chunks.  The flow starts with the first meeting with a client to define the purposes of a workshop.…

How does learning work? A clever 9-year-old once told me: “I know I am learning something new when I am surprised.” The science of adult learning tells us that, in order to learn new skills (which, unsurprisingly, is harder for adults to do than kids) grown-ups need to first get into a specific headspace.  In a business, this approach is often employed in a training session where employees learn new skills or work on professional development. But how do you ensure your training is effective? In this guide, we'll explore how to create an effective training session plan and run engaging training sessions. As team leader, project manager, or consultant,…

Effective online tools are a necessity for smooth and engaging virtual workshops and meetings. But how do you choose the right ones? Do you sometimes feel that the good old pen and paper or MS Office toolkit and email leaves you struggling to stay on top of managing and delivering your workshop? Fortunately, there are plenty of online tools to make your life easier when you need to facilitate a meeting and lead workshops. In this post, we’ll share our favorite online tools you can use to make your job as a facilitator easier. In fact, there are plenty of free online workshop tools and meeting facilitation software you can…

Design your next workshop with SessionLab

Join the 150,000 facilitators using SessionLab

Sign up for free

Suggested Searches

• Climate Change
• Expedition 64
• Mars perseverance
• SpaceX Crew-2
• International Space Station
• View All Topics A-Z
• Humans in Space

Earth & Climate

The solar system, the universe, aeronautics, learning resources, news & events.

Welcome Back to Planet Earth, Expedition 70 Crew! 

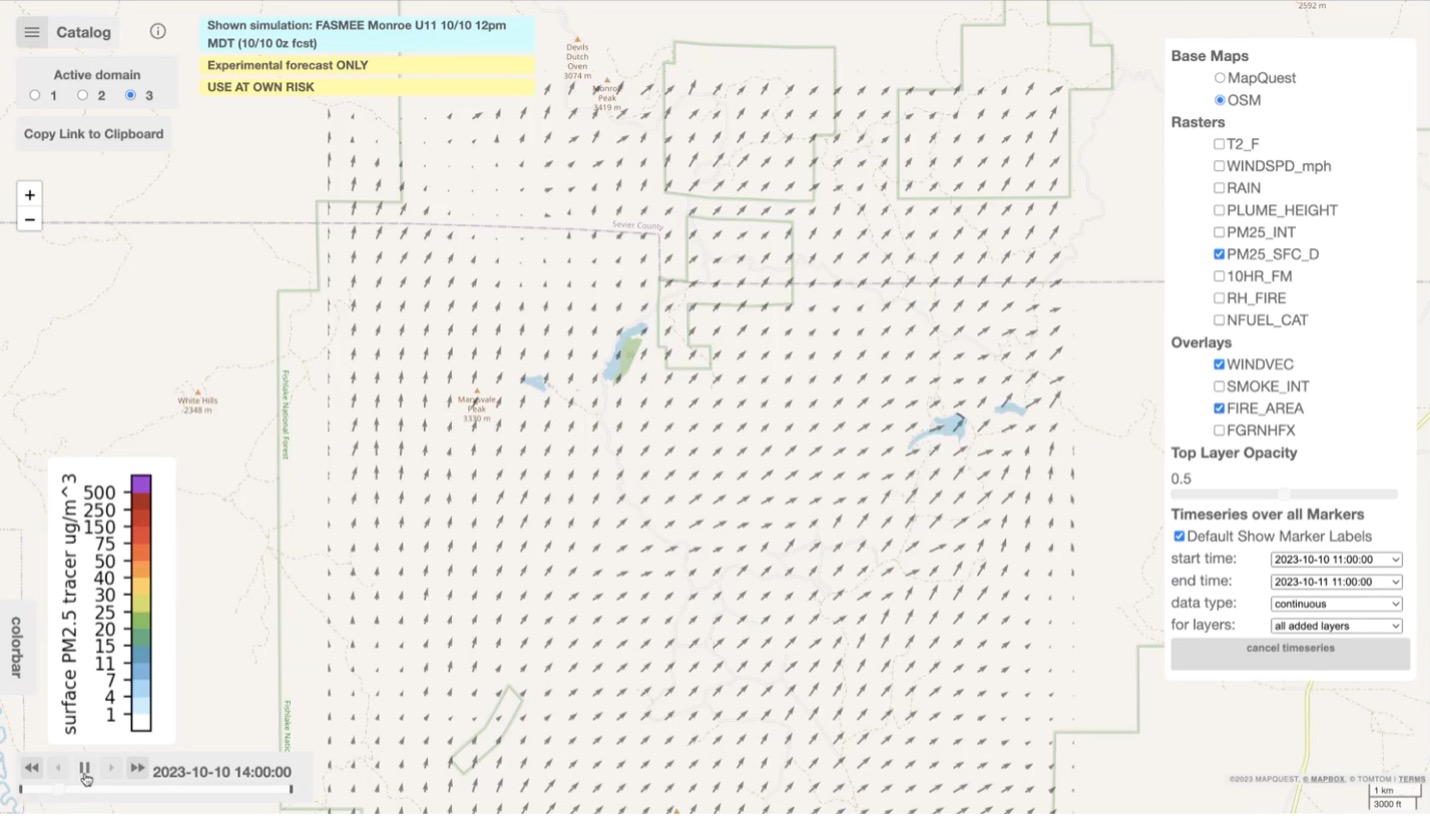
NASA “Wildfire Digital Twin” Pioneers New AI Models and Streaming Data Techniques for Forecasting Fire and Smoke

NASA Study Provides New Look at Orbital Debris, Potential Solutions 

• Search All NASA Missions
• A to Z List of Missions
• Upcoming Launches and Landings
• Spaceships and Rockets
• Communicating with Missions
• James Webb Space Telescope
• Hubble Space Telescope
• Why Go to Space
• Astronauts Home
• Commercial Space
• Destinations
• Living in Space
• Explore Earth Science
• Earth, Our Planet
• Earth Science in Action
• Earth Multimedia
• Earth Science Researchers
• Pluto & Dwarf Planets
• Asteroids, Comets & Meteors
• The Kuiper Belt
• The Oort Cloud
• Skywatching
• The Search for Life in the Universe
• Black Holes
• The Big Bang
• Dark Energy & Dark Matter
• Earth Science
• Planetary Science
• Astrophysics & Space Science
• The Sun & Heliophysics
• Biological & Physical Sciences
• Lunar Science
• Citizen Science
• Astromaterials
• Aeronautics Research
• Human Space Travel Research
• Science in the Air
• NASA Aircraft
• Flight Innovation
• Supersonic Flight
• Air Traffic Solutions
• Green Aviation Tech
• Drones & You
• Technology Transfer & Spinoffs
• Space Travel Technology
• Technology Living in Space
• Manufacturing and Materials
• Science Instruments
• For Kids and Students
• For Educators
• For Colleges and Universities
• For Professionals
• Science for Everyone
• Requests for Exhibits, Artifacts, or Speakers
• STEM Engagement at NASA
• NASA's Impacts
• Centers and Facilities
• Directorates
• Organizations
• People of NASA
• Internships
• Our History
• Doing Business with NASA
• Get Involved
• Aeronáutica
• Ciencias Terrestres
• Sistema Solar
• All NASA News
• Video Series on NASA+
• Newsletters
• Social Media
• Media Resources
• Upcoming Launches & Landings
• Virtual Events
• Sounds and Ringtones
• Interactives
• STEM Multimedia

Discovery Alert: Mini-Neptune in Double Star System is a Planetary Puzzle

NASA Tool Gets Ready to Image Faraway Planets

Astronaut Exercise

Eleasa Kim: Pioneering CLDP Payload Operations and Cultural Integration

5 Things to Know About NASA’s Tiny Twin Polar Satellites

How ‘Glowing’ Plants Could Help Scientists Predict Flash Drought

NASA’s Juno Provides High-Definition Views of Europa’s Icy Shell

The Next Full Moon is the Flower, Corn, or Corn Planting Moon

Binoculars: A Great First Telescope

Webb Cracks Case of Inflated Exoplanet

NASA, Industry to Start Designing More Sustainable Jet Engine Core

Aviary: A New NASA Software Platform for Aircraft Modelling

NASA’s X-59 Passes Milestone Toward Safe First Flight 

Tech Today: From Spacesuits to Racing Suits

Tech Today: A NASA-Inspired Bike Helmet with Aerodynamics of a Jet  

NASA Challenge Gives Artemis Generation Coders a Chance to Shine

Kan Yang: Translating Science Ideas into Engineering Concepts

Aurorasaurus Roars During Historic Solar Storm

Johnson Celebrates AA and NHPI Heritage Month: Anima Patil-Sabale

Diez maneras en que los estudiantes pueden prepararse para ser astronautas

Astronauta de la NASA Marcos Berríos

Resultados científicos revolucionarios en la estación espacial de 2023

Station science 101 | research in microgravity: higher, faster, longer.

Melissa L. Gaskill

Microgravity, a unique orbit, crewed laboratory, twenty years and counting, adding subjects adds time.

The International Space Station provides unique features that enable innovative research, including microgravity, exposure to space, a unique orbit, and hands-on operation by crew members.

The space station provides consistent, long-term access to microgravity. Eliminating the effects of Earth’s gravity on experiments is a game-changer across many disciplines, including research on living things and physical and chemical processes. For example, without gravity hot air does not rise, so flames become spherical and behave differently. Removing the forces of surface tension and capillary movement allows scientists to examine fluid behavior more closely.

The speed, pattern, and altitude of the space station’s orbit provide unique advantages. Traveling at 17,500 miles per hour, it circles the planet every 90 minutes, passing over a majority of Earth’s landmass and population centers in daylight and darkness. Its 250-mile-high altitude is low enough for detailed observation of features, atmospheric phenomena, and natural disasters from different angles and with varying lighting conditions. At the same time, the station is high enough to study how space radiation affects material durability and how organisms adapt and examine phenomena such as neutron stars and blackholes. The spacecraft also places observing instruments outside Earth’s atmosphere and magnetic field, which can interfere with observations from the ground.

Other satellites in orbit contain scientific experiments and conduct Earth observations, but the space station also has crew members aboard to manage and maintain scientific activities. Human operators can respond to and assess events in real time, swap out experiment samples, troubleshoot, and observe results first-hand. Crew members also pack experiment samples and send them back to the ground for detailed analysis.

Thanks to the space station’s longevity, experiments can continue for months or even years. Scientists can design follow-up studies based on previous results, and every expedition offers the chance to expand the number of subjects for human research.

One area of long-term human research is on changes in vision, first observed when astronauts began spending months at a time in space. Scientists wondered whether fluids shifting from the lower to the upper body in microgravity caused increased pressure inside the head that changed eye shape. The Fluid Shifts investigation began in 2015 and continued to measure the extent of fluid shifts in multiple astronauts through 2020. 1

Whether the original study is long or short, it can take years for research to go from the lab into practical applications. Many steps are involved, some of them lengthy. First, researchers must come up with a question and a possible answer, or hypothesis. For example, Fluid Shifts questioned what was causing vision changes and a possible answer was increased fluid pressure in the head. Scientists must then design an experiment to test the hypothesis, determining what data to collect and how to do so.

Getting research onto the space station in the first place takes time, too. NASA reviews proposals for scientific merit and relevance to the agency’s goals. Selected investigations are assigned to a mission, typically months in the future. NASA works with investigators to meet their science requirements, obtain approvals, schedule crew training, develop flight procedures, launch hardware and supplies, and collect any preflight data needed. Once the study launches, in-flight data collection begins. When scientists complete their data collection, they need time to analyze the data and determine what it means. This may take a year or more.

Scientists then write a paper about the results – which can take many months – and submit it to a scientific journal. Journals send the paper to other experts in the same field, a process known as peer review. According to one analysis, this review takes an average of 100 days. 2 The editors may request additional analysis and revisions based on this review before publishing.

Aspects of research on the space station can add more time to the process. Generally, the more test subjects, the better – from 100 to 1,000 subjects for statistically significant results for clinical research. But the space station typically only houses about six people at a time.

Lighting Effects shows how the need for more subjects adds time to a study. This investigation examined whether adjusting the intensity and color of lighting inside the station could help improve crew circadian rhythms, sleep, and cognitive performance. To collect data from enough crew members, the study ran from 2016 until 2020.

Other lengthy studies about how humans adapt to life in space include research on loss of heart muscle and a suite of long-term studies on nutrition, including producing fresh food in space.

For physical science studies, investigators can send batches of samples to the space station and collect data more quickly, but results can create a need for additional research. Burning and Suppression of Solids ( BASS ) examined the characteristics of a wide variety of fuel samples from 2011 to 2013, and BASS-II continued that work through 2017. The Saffire series of fire safety demonstrations began in 2016 and wrapped up in 2024. Researchers have answered many burning (pun intended) questions, but still have much to learn about preventing, detecting, and extinguishing fires in space.

The timeline for scientific results can run long, especially in microgravity. But those results can be well worth the wait.

Melissa Gaskill International Space Station Research Communications Team Johnson Space Center

Search this database of scientific experiments to learn more about those mentioned above.

1 Macias BR, Liu JHK, Grande-Gutierrez N, Hargens AR. Intraocular and intracranial pressures during head-down tilt with lower body negative pressure. Aerosp Med Hum Perform. 2015; 86(1):3–7.  https://www.ingentaconnect.com/content/asma/amhp/2015/00000086/00000001/art00004;jsessionid=31bonpcj2e8tj.x-ic-live-01

2 Powell K. Does it take too long to publish research? Nature 530, pages148–151 (2016). https://www.nature.com/articles/530148a

Discover More Topics

Station Science 101

Latest News from Space Station Research

Space Station Research and Technology Resources

Station Benefits for Humanity

Related Terms

• ISS Research
• International Space Station (ISS)
• Johnson Space Center

Envisioning Proteins: John Jumper, BS’07, uses AI to work on the “protein folding problem”

Media inquiries.

• 615-322-6397 Email

Latest Stories

• Vanderbilt Poll: Majority of Tennessee voters now pro-choice, gender gap developing on key issues
• How patent law can protect public health
• Driving Tennessee Innovation: Insights from Competitiveness Conversations Across America

Share this Story

May 17, 2024, 5:00 PM

It’s one thing to know what a protein looks like on paper—it’s another to know how it looks in real life.

The “protein folding problem” has been one of the most vexing in biology. Even if a scientist knows the DNA sequence for a protein, it’s virtually impossible to predict how the long chains of amino acids will interact and fold in upon themselves to create a three-dimensional model.

“The genome gives us the wrong view of proteins—it gives us a linear view,” John Jumper, BS’07, said at the Apex Lecture, a series sponsored by the Vanderbilt School of Medicine Basic Sciences this past August. You might see several mutations associated with cancer spread out along the chain “and then you look at the structure, and they are all right next to each other,” he said. Such particularities are essential in understanding how a protein functions and how it might be targeted. “It gives us a great tool for making hypotheses about how the cell works that we can ultimately test.”

Jumper is a senior staff research scientist for DeepMind, a London-based company that made a huge leap forward in solving the protein folding problem using artificial intelligence. It first released its prediction software, AlphaFold, in 2018, following it up with the even more accurate AlphaFold 2 in late 2020. The method has produced extremely accurate 3D models of all 200 million or so proteins known to science—all freely available on the cloud. In a competition, it outperformed all other methods of protein structure prediction, including those that are much more labor intensive and time-consuming. The work is so significant that Jumper was awarded the 2023 Albert Lasker Award for Basic Medical Research, which is often considered a precursor prize to the Nobel.

The implications of AlphaFold’s work are vast, allowing for quick, cost-effective predictions that let scientists custom-design drugs to target certain proteins involved in disease, design synthetic enzymes for chemical reactions, speed production of new vaccines and even personalize medical treatments. “AlphaFold represents a revolutionary advance in structural biology, one that has brought the holy grail of predictive protein folding into the toolkit of biochemistry and molecular biology,” said John Kuriyan, dean of the School of Medicine Basic Sciences, in announcing Jumper’s selection for the Apex Lecture, which focuses on breakthroughs in biomedical science. “The impact of these advances on drug discovery and, ultimately, on human health will be enormous.”

At the lecture, Jumper took a deep dive into how he and his fellow scientists trained a neural network on the Protein Database (PDB) to create the model that became AlphaFold. There was no magic bullet, he said. Rather, researchers painstakingly trained the model on pairs and sequences of amino acids using various techniques, knocked out particular genes to observe effects, and even asked the model to critique itself on the road to ever more accurate predictions. “We had many small effects that we were able to put together and many, many ways in which we got a little bit better,” Jumper said. “We found that everything mattered a bit, and nothing mattered a lot.”

— MICHAEL BLANDING

Keep Reading

Combining unique methods, kuriyan lab discovers new protein functions; explores physical space of proteins.

Vanderbilt chemist Ben Brown awarded $2.375M to develop nonaddictive painkillers with AI

Daring to Grow: The stories that shaped Vanderbilt in 2023

Explore story topics.

• Cover Feature
• Featured VMAG
• Features - VMAGAZINE
• publications
• Vanderbilt Magazine
• Winter/Spring 2024
• Apex Lecture Series
• artificial intelligence
• John Jumper
• protein folding problem
• Vanderbilt Magazine – Featured
• Vanderbilt School of Medicine Basic Sciences

Northeastern researcher creates AI tools that help gig workers solve problems

• Search Search

Northeastern professor Saiph Savage works with gig workers to create AI-enhanced collective bargaining tools to change the power dynamic on the gig labor market.

• Copy Link Link Copied!

Researchers at Northeastern University have created artificial intelligence tools to help gig workers organize, collect their own job-related data, analyze their work problems and come up with a strategy to implement solutions.

“Building solid AI-enhanced solutions to enable gig workers’ collective action will pave the way for a fair and ethical gig economy — one with fair wages, humane working conditions and increased job security,” says Saiph Savage , assistant professor and director of the Civic A.I. Lab at Northeastern’s Khoury College of Computer Sciences.

Gig work is typically performed by a freelancer or independent contractor. It is used by rideshare apps such as Uber and Lyft, grocery-delivery services like Instacart, and Upwork, a marketplace that connects companies with temporary on-demand workers.

Gig work provides flexibility to workers and employers, Savage says, and offers economic opportunities to disadvantaged groups. But it also presents challenges for some gig workers such as irregular schedules and unsteady income, lack of job security, isolation and surveillance associated with online work.

The Massachusetts attorney general recently took Uber and Lyft to court over the employment status of its gig workers. The rideshare apps have threatened to leave markets if its drivers are converted from independent contractors to employees.

For Savage, it’s all about giving gig workers the tools — in this case AI tools — to make the most-informed decisions with the greatest amount of data.

“At Northeastern, we have been developing a lot of AI tools that can support gig workers in their collective action to fight for better opportunities,” Savage says.

Featured Stories

Is gig work compatible with employment status? Study finds reclassification benefits both workers and platforms

Do you know where your burger comes from? Memorial Day cookout attendees unaware, food safety expert says

Fascism of the past still casts a shadow on Italy’s politics and anti-immigration rhetoric, Northeastern researcher says

Can airplane turbulence really kill you? Aircraft propulsion expert weighs in on Singapore Airlines death

Tools recently released by the Civic A.I. Lab include GigSousveillance, GigSense and GigAction.

The tools use large language models and social theories to create “intelligent assistants” that help gig workers understand their collective problems, propose solutions and take collective action. The tools strengthen gig workers’ collective opinion and negotiation power, Savage says.

GigSousveillance allows workers to collect their own job-related data and use that data to measure how big a workplace problem has become.

GigSense equips workers with an online AI assistant that helps make sense of their workplace problems and strategically come up with solutions.

GigAction is an AI assistant that guides workers to implement the solutions.

The AI tools help reinforce gig workers’ collective identity, potentially inspiring them to undertake actions that benefit them as a whole, Savage says.

As part of her research, Savage conducted interviews and collaborative design sessions with gig workers from Upwork, Amazon Mechanical Turk, an Amazon platform that allows businesses to connect with a global workforce, and Toloka, a crowdsourcing platform. Later, she analyzed their answers about using the new AI tools. 

“We focus a lot on helping them to identify what are the key points that they should be aiming to negotiate,” Savage says. “What are the main problems that they should be aiming to address collectively, as well as what things should they aim to bargain for with the companies.”

Savage sees potential in attracting more gig workers through social media groups. 

“From there, we move them into our platforms,” she says.

Science & Technology

Recent Stories

Numbers, Facts and Trends Shaping Your World

Read our research on:

Full Topic List

Regions & Countries

• Publications
• Our Methods
• Short Reads
• Tools & Resources

Read Our Research On:

Teens and Video Games Today

85% of u.s. teens say they play video games, and about four-in-ten do so daily. teens see both positive and negative sides of video games – from problem-solving and making friends to harassment and sleep loss, table of contents.

• Who plays video games?
• How often do teens play video games?
• What devices do teens play video games on?
• Social media use among gamers
• Teen views on how much they play video games and efforts to cut back
• Are teens social with others through video games?
• Do teens think video games positively or negatively impact their lives?
• Why do teens play video games?
• Bullying and violence in video games
• Appendix A: Detailed charts
• Acknowledgments
• Methodology

Pew Research Center conducted this analysis to better understand teens’ use of and experiences with video games.

The Center conducted an online survey of 1,453 U.S. teens from Sept. 26 to Oct. 23, 2023, through Ipsos. Ipsos recruited the teens via their parents, who were part of its KnowledgePanel . The KnowledgePanel is a probability-based web panel recruited primarily through national, random sampling of residential addresses. The survey was weighted to be representative of U.S. teens ages 13 to 17 who live with their parents by age, gender, race and ethnicity, household income, and other categories.

This research was reviewed and approved by an external institutional review board (IRB), Advarra, an independent committee of experts specializing in helping to protect the rights of research participants.

Here are the questions used for this analysis , along with responses, and  its methodology .

There are long-standing debates about the impact of video games on youth. Some credit them for helping young people form friendships and teaching them about teamwork and problem-solving . Others say video games expose teenagers to violent content, negatively impact their sleep and can even lead to addiction.

With this in mind, Pew Research Center surveyed 1,423 U.S. teens ages 13 to 17 about their own video game habits – from how often they play to the friends they’ve made and whether it gets in the way of them doing well in school or getting a good night’s sleep. 1

Key findings from the survey

• Video games as a part of daily teen life: 85% of U.S. teens report playing video games, and 41% say they play them at least once a day. Four-in-ten identify as a gamer.
• Gaming as a social experience: 72% of teens who play video games say that a reason why they play them is to spend time with others. And some have even made a friend online from playing them – 47% of teen video game players say they’ve done this.
• Helpful with problem-solving, less so for sleep: Over half of teens who play video games say it has helped their problem-solving skills, but 41% also say it has hurt their sleep.
• Bullying is a problem: 80% of all teens think harassment over video games is a problem for people their age. And 41% of those who play them say they’ve been called an offensive name when playing.
• Boys’ and girls’ experiences differ: Most teen boys and girls play video games, but larger shares of boys identify as gamers (62% vs. 17%) and play every day (61% vs. 22%). Boys who play them are also more likely to experience positive things from it, like making friends, and more troubling things like harassment.

Jump to read about: Who plays video games | Socializing over video games | Views about video games’ impact | Harassment and violence in video games      

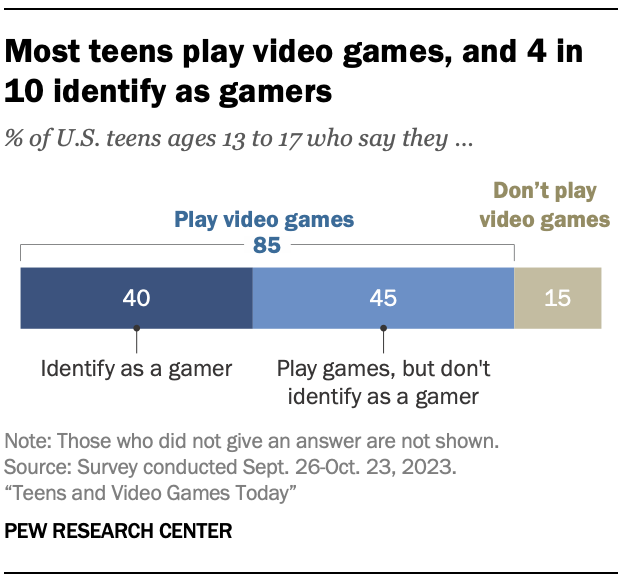
Playing video games is widespread among teens. The vast majority of U.S. teens (85%) say they play them. Just 15% say they never do, according to the survey conducted Sept. 26-Oct. 23, 2023.

In addition to asking whether teens play video games, we also wanted to learn whether they consider themselves gamers. Overall, four-in-ten U.S. teens think of themselves as gamers. Just under half of teens (45%) play video games but do not think of themselves as gamers.

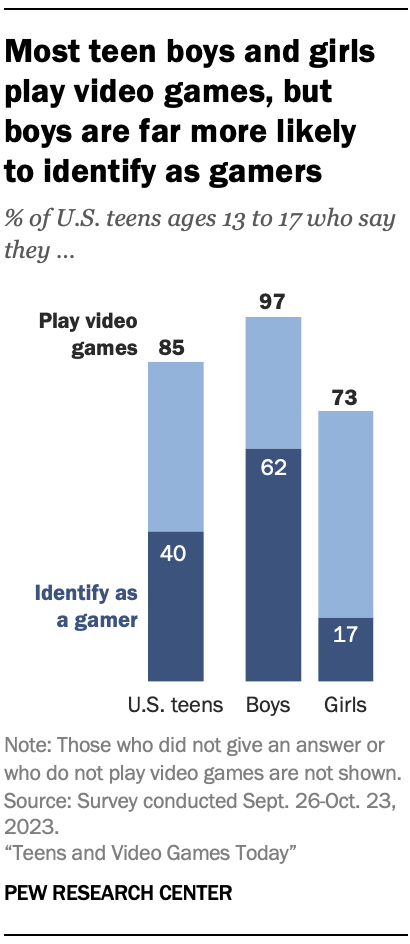
Nearly all boys (97%) say they play video games, compared with about three-quarters of teen girls. There is a substantial gap by gender in whether teens identify as gamers: 62% of teen boys do, compared with 17% of girls. 2

By gender and age

Younger teen girls are more likely than older girls to say they play video games: 81% of girls ages 13 to 14 compared with 67% of those ages 15 to 17. But among boys, nearly all play video games regardless of age. 

Similar shares of teens play video games across different racial and ethnic groups and among those who live in households with different annual incomes. Go to Appendix A for more detail on which teens play video games and which teens identify as gamers.

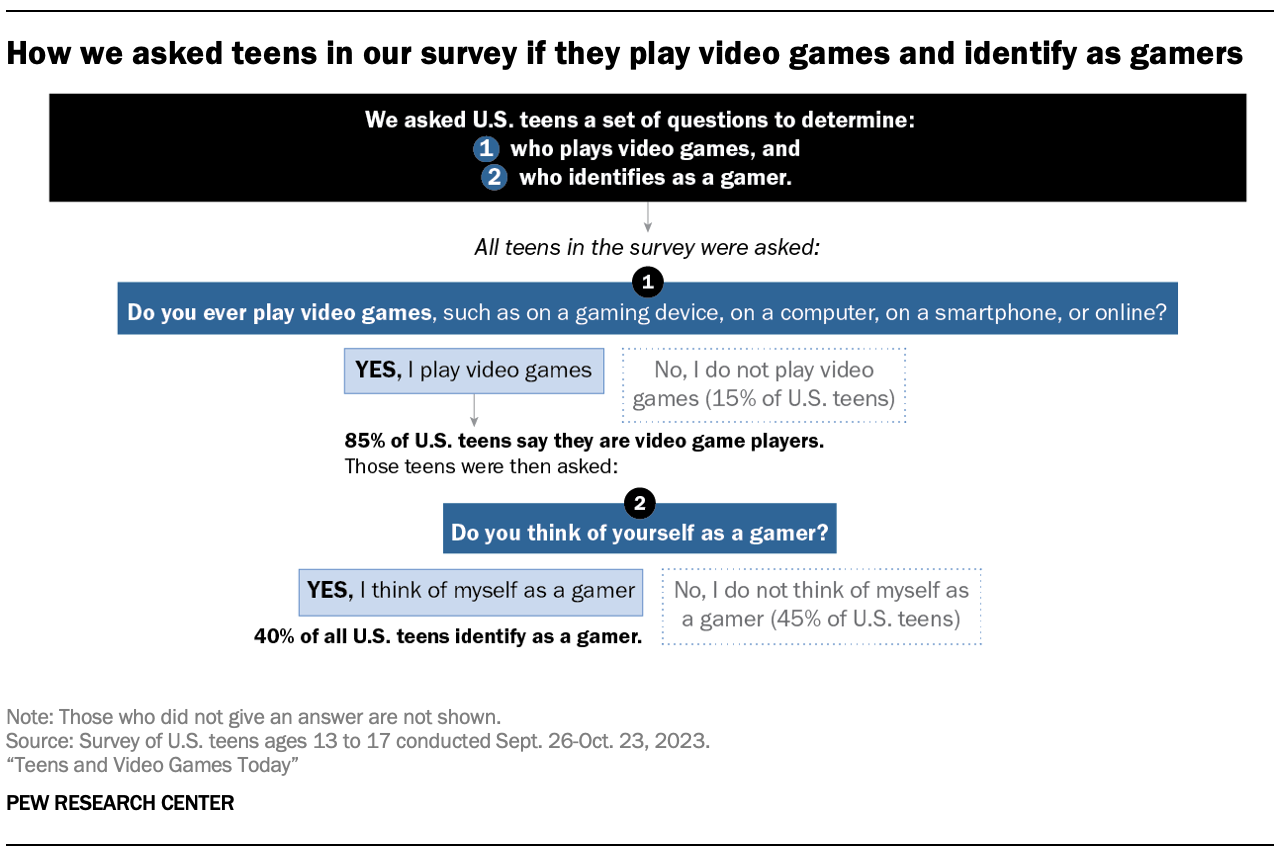
We also asked teens how often they play video games. About four-in-ten U.S. teens say they play video games daily, including 23% who do so several times a day.

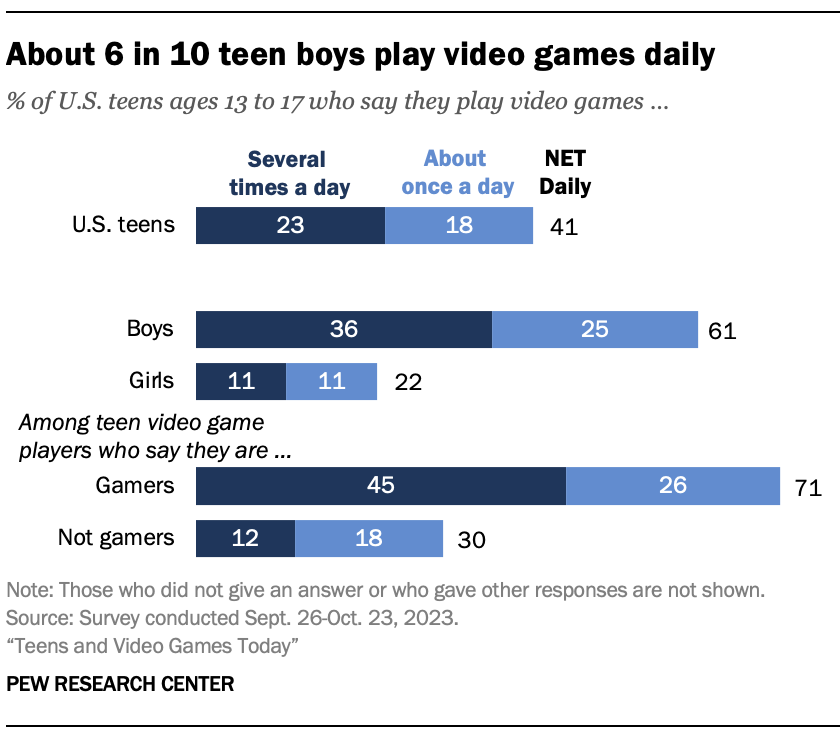
Another 22% say they play several times a week, while 21% play them about once a week or less.

Teen boys are far more likely than girls to say they play video games daily (61% vs. 22%). They are also much more likely to say they play them several times a day (36% vs. 11%).

By whether someone identifies as a gamer

About seven-in-ten teens who identify as gamers (71%) say they play video games daily. This drops to 30% among those who play them but aren’t gamers.

By household income

Roughly half of teens living in households with an annual income of less than $30,000 (53%) say they play video games at least daily. This is higher than those in households with an annual income of $30,000 to $74,999 (42%) and $75,000 or more (39%).

Go to Appendix A to see more details about who plays video games and identifies as a gamer by gender, age, race and ethnicity, and household income.

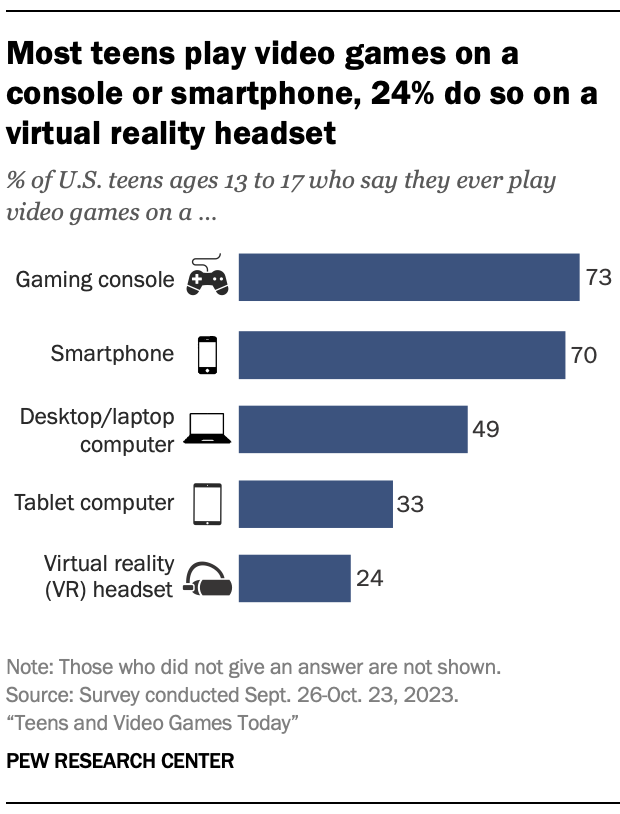
Most teens play video games on a gaming console or a smartphone. When asked about five devices, most teens report playing video games on a gaming console (73%), such as PlayStation, Switch or Xbox. And 70% do so on a smartphone. Fewer – though still sizable shares – play them on each of the following:

• 49% say they play them on a desktop or laptop computer
• 33% do so on a tablet  
• 24% play them on a virtual reality (VR) headset such as Oculus, Meta Quest or PlayStation VR

Many teens play video games on multiple devices. About a quarter of teens (27%) do so on at least four of the five devices asked about, and about half (49%) play on two or three of them. Just 8% play video games on one device.

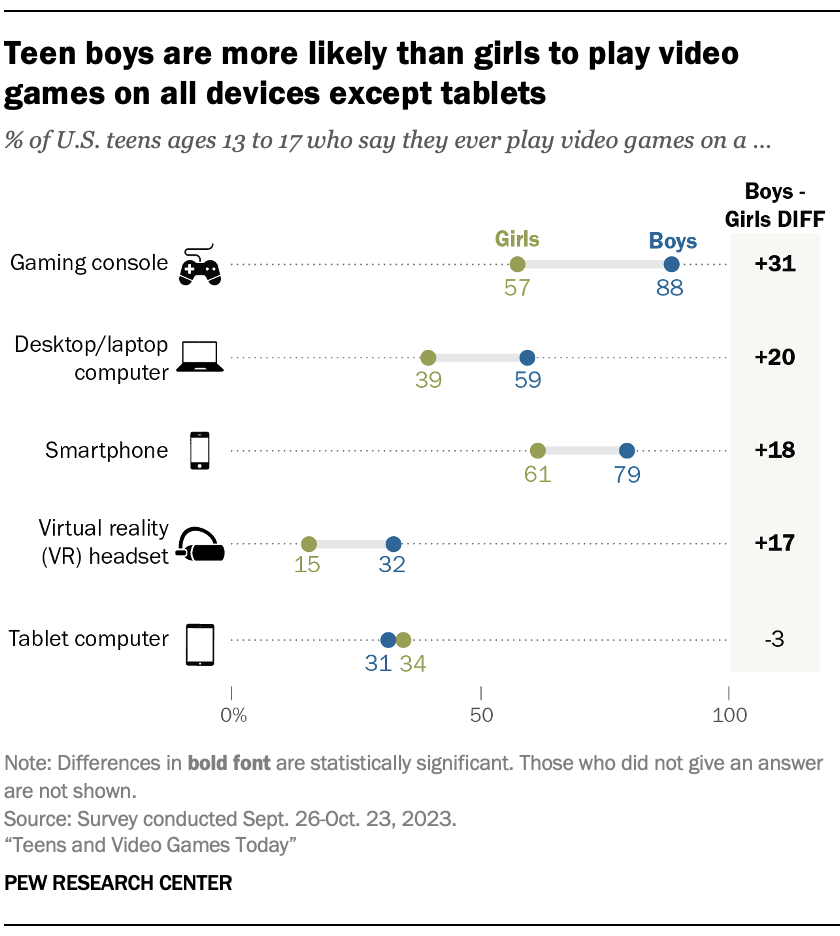
Teen boys are more likely than girls to play video games on four of the five devices asked about – all expect tablets. For instance, roughly nine-in-ten teen boys say they ever play video games on a gaming console, compared with 57% of girls. Equal shares of teen boys and girls play them on tablets.  

Teens who consider themselves gamers are more likely than those who play video games but aren’t gamers to play on a gaming console (95% vs. 78%), desktop or laptop computer (72% vs. 45%) or a virtual reality (VR) headset (39% vs. 19%). Similar shares of both groups play them on smartphones and tablets.

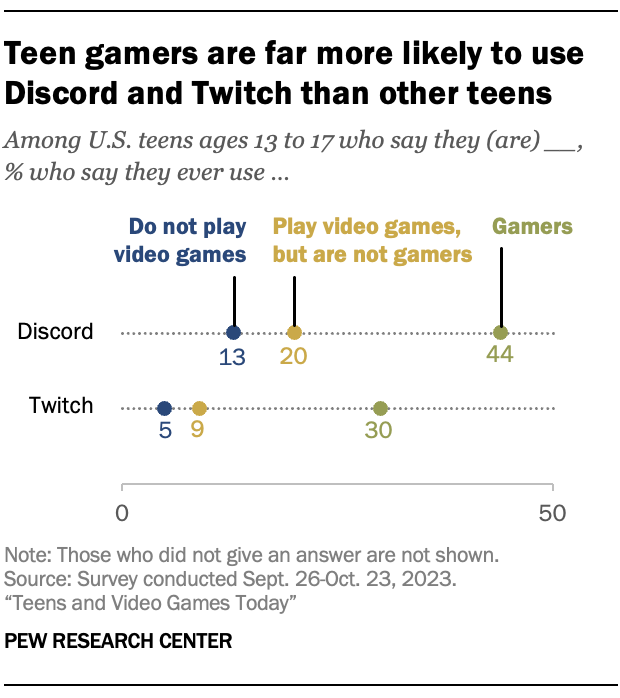
One way that teens engage with others about video games is through online platforms. And our survey findings show that teen gamers stand out for their use of two online platforms that are known for their gaming communities – Discord and Twitch :

• 44% of teen gamers say they use Discord, far higher than video game players who don’t identify as gamers or those who use the platform but do not play video games at all. About three-in-ten teens overall (28%) use Discord.
• 30% of teens gamers say they use Twitch. About one-in-ten other teens or fewer say the same; 17% of teens overall use the platform.

Previous Center research shows that U.S. teens use online platforms at high rates .

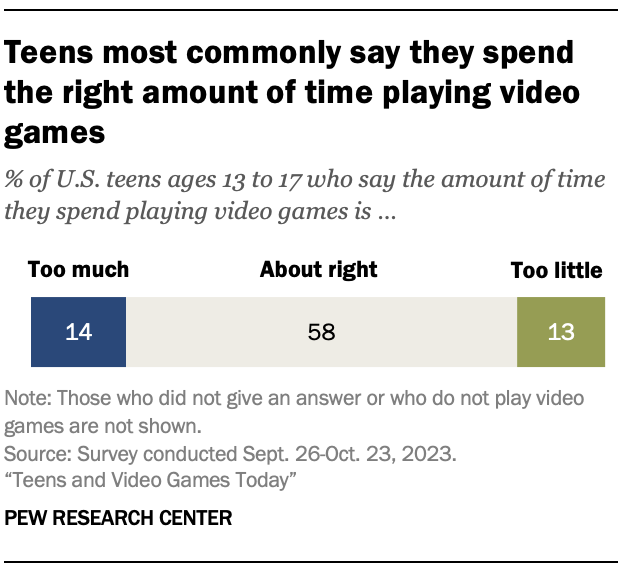
Teens largely say they spend the right amount of time playing video games. When asked about how much time they spend playing them, the largest share of teens (58%) say they spend the right amount of time. Far fewer feel they spend too much (14%) or too little (13%) time playing them.

Teen boys are more likely than girls to say they spend too much time playing video games (22% vs. 6%).

By race and ethnicity

Black (17%) and Hispanic (18%) teens are about twice as likely than White teens (8%) to say they spend too little time playing video games. 3

A quarter of teens who consider themselves gamers say they spend too much time playing video games, compared with 9% of those who play video games but don’t identify as gamers. Teen gamers are also less likely to think they spend too little time playing them (19% vs. 10%).

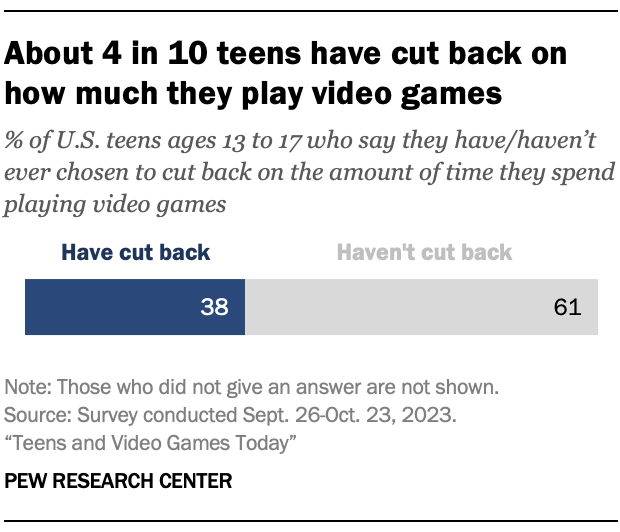
Fewer than half of teens have reduced how much they play video games. About four-in-ten (38%) say they have ever chosen to cut back on the amount of time they spend playing them. A majority (61%) report that they have not cut back at all.

This share is on par with findings about whether teenagers have cut back with their screen time – on social media or their smartphone.

Although boys are more likely to say they play video games too much, boys and girls are on par for whether they have ever cut back. About four-in-ten teen boys (39%) and girls (38%) say that they have ever cut back.

And gamers are as likely to say they have cut back as those who play video games but don’t identify as gamers (39% and 41%).

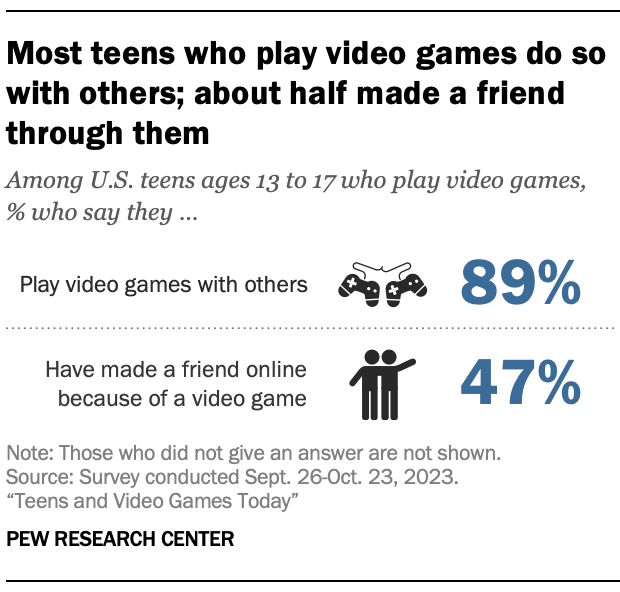
A main goal of our survey was to ask teens about their own experiences playing video games. For this section of the report, we focus on teens who say they play video games.

Socializing with others is a key part of the video game experience. Most teens who play video games do so with others, and some have developed friendships through them.

About nine-in-ten teen video game players (89%) say they play them with other people, in person or online. Far fewer (11%) play them only on their own.

Additionally, about half (47%) report that they have ever made a friend online because of a video game they both play. This equals 40% of all U.S. teens who have made a friend online because of a video game.

These experiences vary by:  

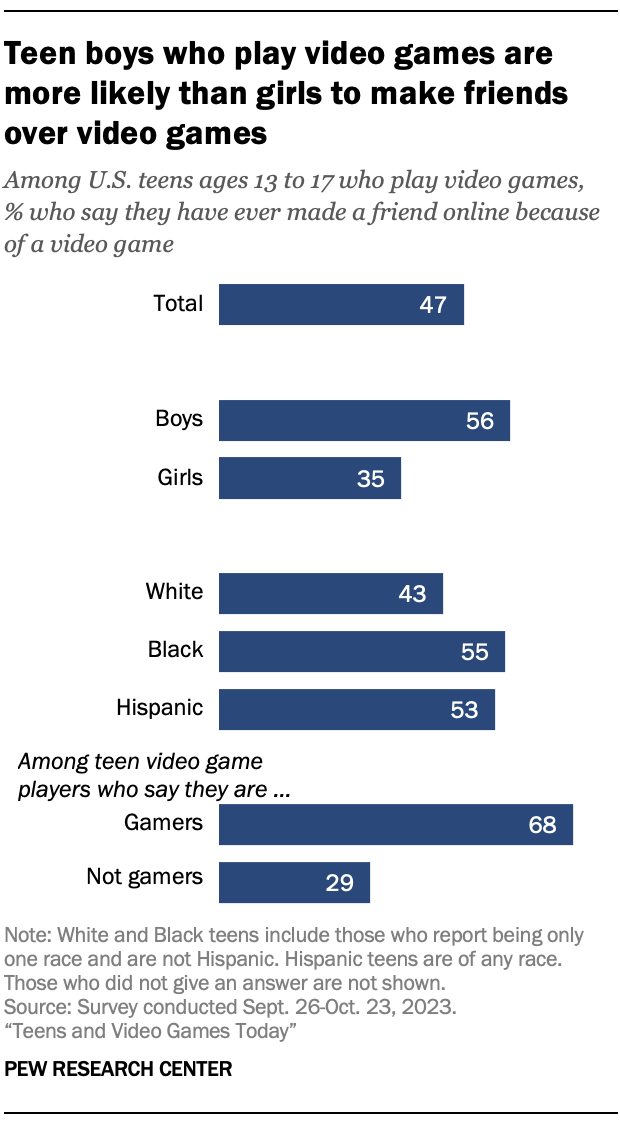
• Gender: Most teen boy and girl video game players play them with others, though it’s more common among boys (94% vs. 82%). Boys who play video games are much more likely to say they have made a friend online because of a video game (56% vs. 35%).
• Race and ethnicity: Black (55%) and Hispanic (53%) teen video game players are more likely than White teen video game players (43%) to say they have made a friend online because of them.
• Whether someone identifies as a gamer: Nearly all teen gamers report playing video games with others (98%). Fewer – though still most – of those who play video games but aren’t gamers (81%) also play them with others. And about seven-in-ten (68%) say they have made a friend online because of a video game, compared with 29% of those who play them but don’t identify as gamers.

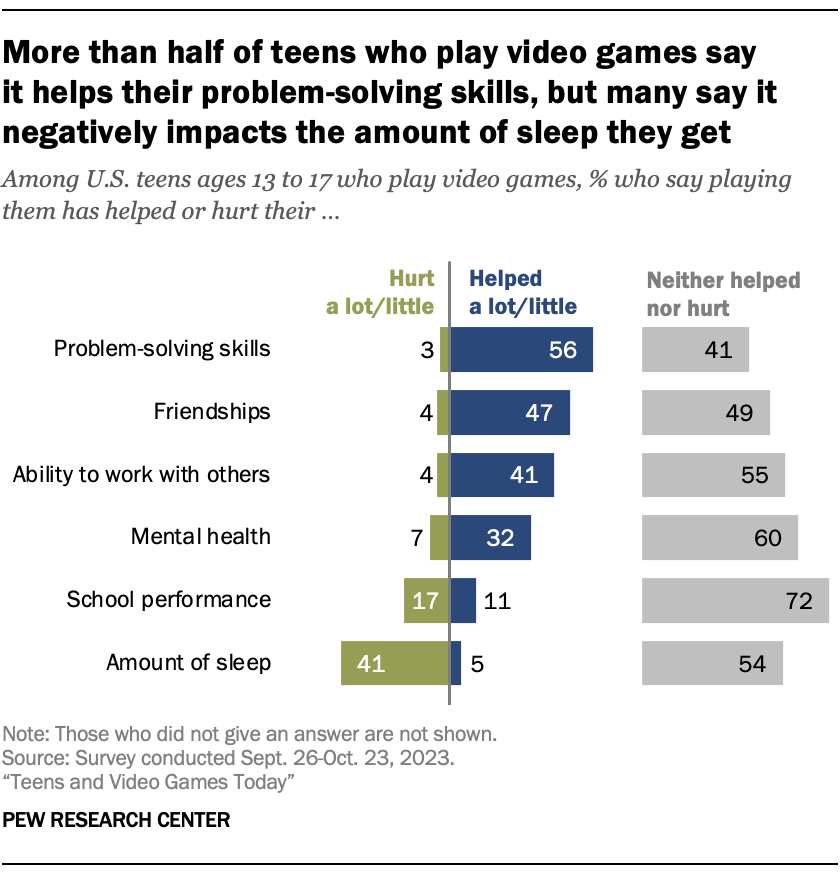
Teens who play video games are particularly likely to say video games help their problem-solving skills. More than half of teens who play video games (56%) say this.

Additionally, more think that video games help, rather than hurt, three other parts of their lives that the survey asked about. Among teens who play video games:

• Roughly half (47%) say it has helped their friendships
• 41% say it has helped how they work with others
• 32% say it has helped their mental health

No more than 7% say playing video games has hurt any of these.

More teens who play video games say it hurts, rather than helps, their sleep. Among these teens, 41% say it has hurt how much sleep they get, while just 5% say it helps. And small shares say playing video games has impacted how well they do in school in either a positive or a negative way.

Still, many teens who play video games think playing them doesn’t have much an impact in any of these areas. For instance, at least six-in-ten teens who play video games say it has neither a positive nor a negative impact on their mental health (60%) or their school performance (72%). Fewer (41%) say this of their problem-solving skills.

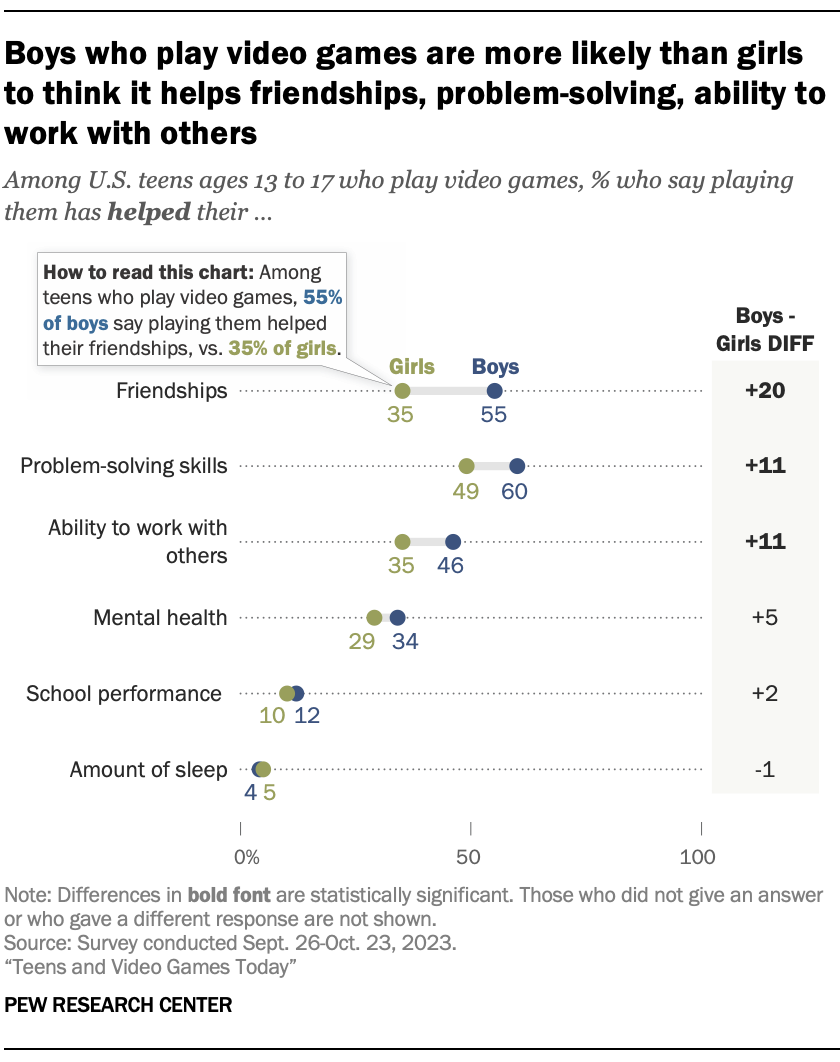
Teen boys who play video games are more likely than girls to think playing them has helped their problem-solving skills, friendships and ability to work with others. For instance, 55% of teen boys who play video games say this has helped their friendships, compared with 35% of teen girls.

As for ways that it may hurt their lives, boys who play them are more likely than girls to say that it has hurt the amount of sleep they get (45% vs. 37%) and how well they do in school (21% vs. 11%). 

Teens who consider themselves gamers are more likely than those who aren’t gamers but play video games to say video games have helped their friendships (60% vs. 35%), ability to work with others (52% vs. 32%), problem-solving skills (66% vs. 47%) and mental health (41% vs. 24%).

Gamers, though, are somewhat more likely to say playing them hurt their sleep (48% vs. 36%) and how well they do in school (20% vs. 14%).

By whether teens play too much, too little or the right amount

Teens who report playing video games too much stand out for thinking video games have hurt their sleep and school performance. Two-thirds of these teens say it has hurt the amount of sleep they get, and 39% say it hurt their schoolwork. Far fewer of those who say they play the right amount (38%) or too little (32%) say it has hurt their sleep, or say it hurt their schoolwork (12% and 16%).

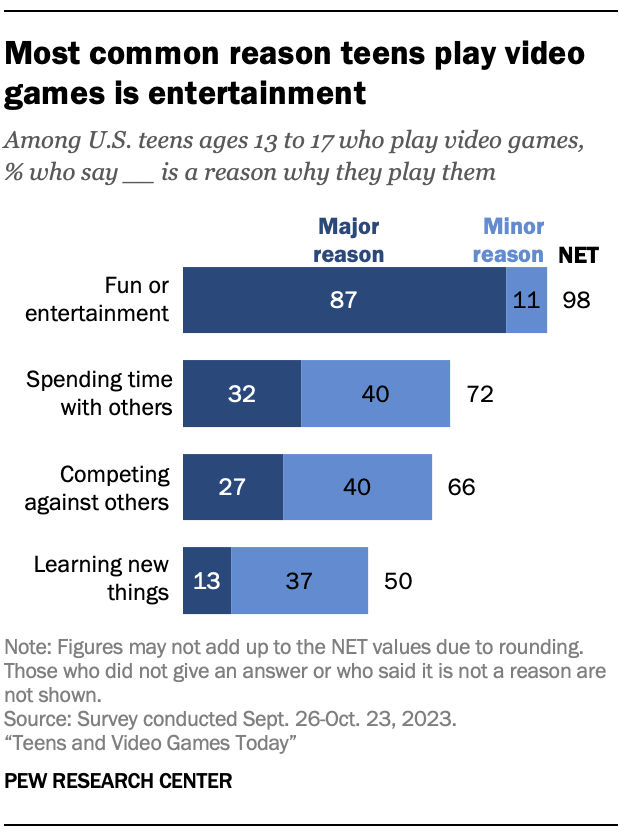
Teens who play video games say they largely do so to be entertained. And many also play them to be social with and interact with others. Teens who play video games were asked about four reasons why they play video games. Among those who play video games:

• Nearly all say fun or entertainment is a major or minor reason why they play video games – with a large majority (87%) saying it’s a major reason.
• Roughly three-quarters say spending time with others is a reason, and two-thirds say this of competing with others. Roughly three-in-ten say each is a major reason.
• Fewer – 50% – see learning something as a reason, with just 13% saying it’s a major reason.

While entertainment is by far the most common reason given by teens who play video games, differences emerge across groups in why they play video games.

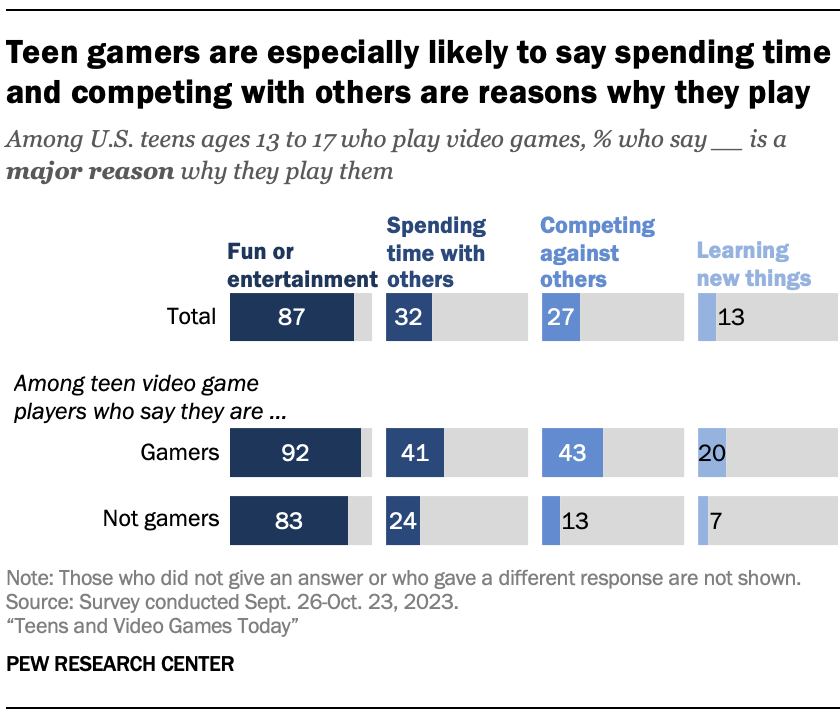
Teens who identify as gamers are particularly likely to say each is major reason, especially when it comes to competing against others. About four-in-ten gamers (43%) say this is a major reason, compared with 13% of those who play video games but aren’t gamers.

Teen boys who play video games are more likely than girls to say competing (36% vs. 15%), spending time with others (36% vs. 27%) and entertainment (90% vs. 83%) are major reasons they play video games.

Black and Hispanic teens who play video games are more likely than White teens to say that learning new things and competing against others are major reasons they play them. For instance, 29% of Black teen video game players say learning something new is a major reason, higher than 17% of Hispanic teen video game players. Both are higher than the 7% of White teen video game players who say the same.

Teens who play video games and live in lower-income households are especially likely to say competing against others and learning new things are major reasons. For instance, four-in-ten teen video game players who live in households with an annual income of less than $30,000 say competing against others is a major reason they play. This is higher than among those in households with annual incomes of $30,000 to $74,999 (29%) and $75,000 or more (23%).

Cyberbullying can happen in many online environments, but many teens encounter this in the video game world.

Our survey finds that name-calling is a relatively common feature of video game life – especially for boys. Roughly four-in-ten teen video game players (43%) say they have been harassed or bullied while playing a video game in one of three ways: 

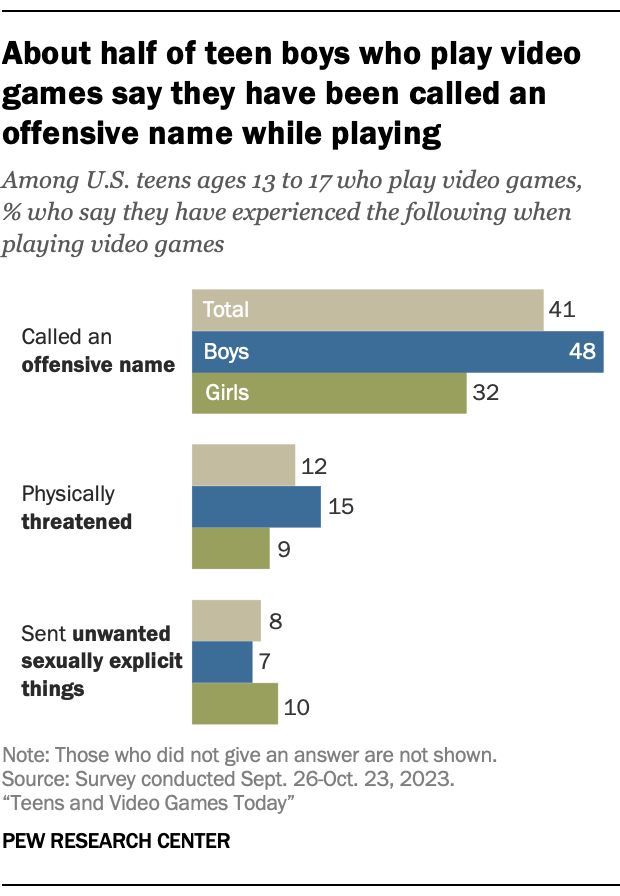
• 41% have been called an offensive name
• 12% have been physically threatened
• 8% have been sent unwanted sexually explicit things

Teen boys are particularly likely to say they have been called an offensive name. About half of teen boys who play video games (48%) say this has happened while playing them, compared with about a third of girls (32%). And they are somewhat more likely than girls to have been physically threatened (15% vs. 9%).

Teen gamers are more likely than those who play video games but aren’t gamers to say they been called and offensive name (53% vs. 30%), been physically threatened (17% vs. 8%) and sent unwanted sexually explicit things (10% vs. 6%).

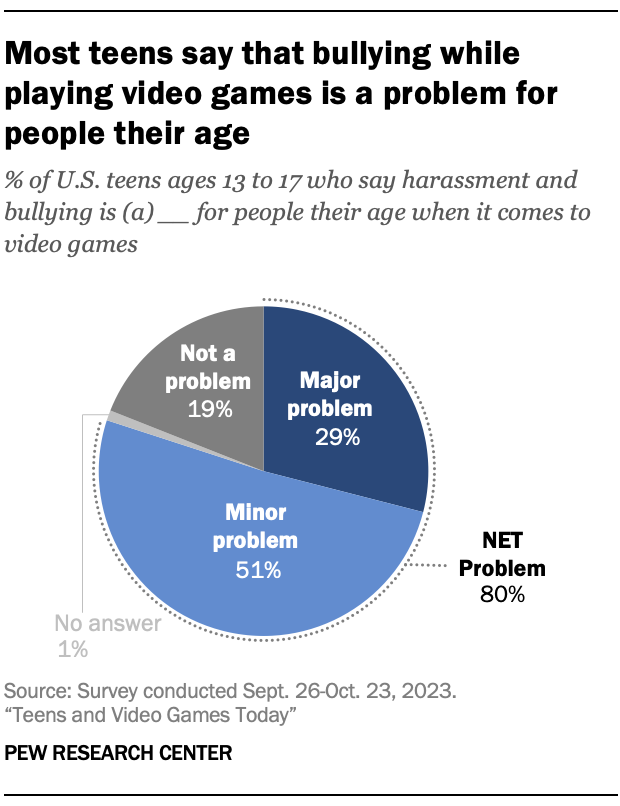
Teens – regardless of whether they’ve had these experiences – think bullying is a problem in gaming. Eight-in-ten U.S. teens say that when it comes to video games, harassment and bullying is a problem for people their age. This includes 29% who say it is a major problem.

It’s common for teens to think harassment while playing video games is a problem, but girls are somewhat more likely than boys to say it’s a major problem (33% vs. 25%).

There have also been decades-long debates about how violent video games can influence youth behavior , if at all – such as by encouraging or desensitizing them to violence. We wanted to get a sense of how commonly violence shows up in the video games teens are playing.

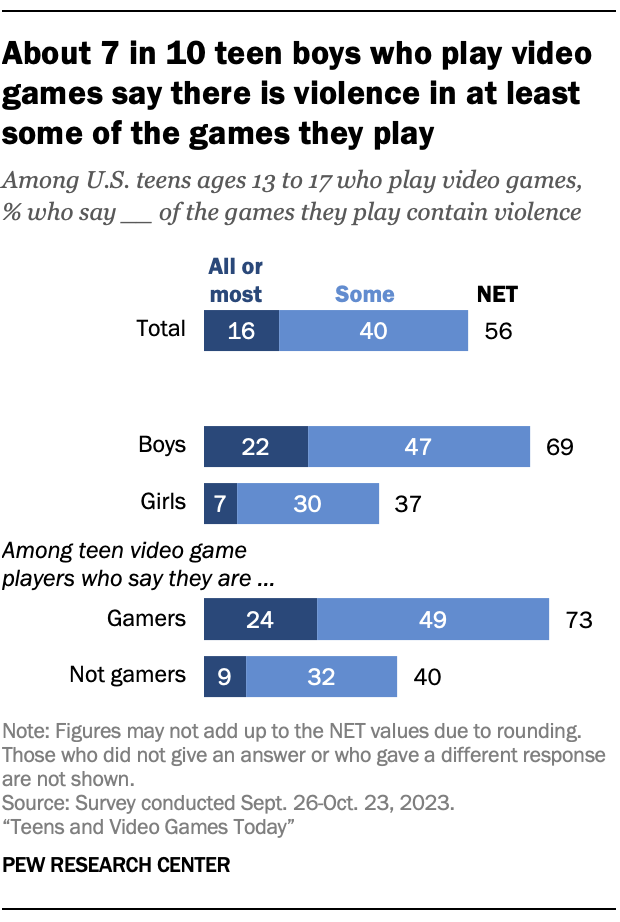
Just over half of teens who play video games (56%) say at least some of the games they play contain violence. This includes 16% who say it’s in all or most of the games they play.

Teen boys who play video games are far more likely than girls to say that at least some of the games they play contain violence (69% vs. 37%).

About three-quarters of teen gamers (73%) say that at least some of the games they play contain violence, compared with 40% among video game players who aren’t gamers.   

• Throughout this report, “teens” refers to those ages 13 to 17. ↩
• Previous Center research of U.S. adults shows that men are more likely than women to identify as gamers – especially the youngest adults. ↩
• There were not enough Asian American respondents in the sample to be broken out into a separate analysis. As always, their responses are incorporated into the general population figures throughout the report. ↩

Sign up for our weekly newsletter

Fresh data delivery Saturday mornings

Sign up for The Briefing

Weekly updates on the world of news & information

• Friendships
• Online Harassment & Bullying
• Teens & Tech
• Teens & Youth

How Teens and Parents Approach Screen Time

Teens and internet, device access fact sheet, teens and social media fact sheet, teens, social media and technology 2023, what the data says about americans’ views of artificial intelligence, most popular, report materials.

1615 L St. NW, Suite 800 Washington, DC 20036 USA (+1) 202-419-4300 | Main (+1) 202-857-8562 | Fax (+1) 202-419-4372 |  Media Inquiries

Research Topics

• Email Newsletters

ABOUT PEW RESEARCH CENTER  Pew Research Center is a nonpartisan fact tank that informs the public about the issues, attitudes and trends shaping the world. It conducts public opinion polling, demographic research, media content analysis and other empirical social science research. Pew Research Center does not take policy positions. It is a subsidiary of  The Pew Charitable Trusts .

Copyright 2024 Pew Research Center

Facility for Rare Isotope Beams

At michigan state university, international research team uses wavefunction matching to solve quantum many-body problems, new approach makes calculations with realistic interactions possible.

FRIB researchers are part of an international research team solving challenging computational problems in quantum physics using a new method called wavefunction matching. The new approach has applications to fields such as nuclear physics, where it is enabling theoretical calculations of atomic nuclei that were previously not possible. The details are published in Nature (“Wavefunction matching for solving quantum many-body problems”) .

Ab initio methods and their computational challenges

An ab initio method describes a complex system by starting from a description of its elementary components and their interactions. For the case of nuclear physics, the elementary components are protons and neutrons. Some key questions that ab initio calculations can help address are the binding energies and properties of atomic nuclei not yet observed and linking nuclear structure to the underlying interactions among protons and neutrons.

Yet, some ab initio methods struggle to produce reliable calculations for systems with complex interactions. One such method is quantum Monte Carlo simulations. In quantum Monte Carlo simulations, quantities are computed using random or stochastic processes. While quantum Monte Carlo simulations can be efficient and powerful, they have a significant weakness: the sign problem. The sign problem develops when positive and negative weight contributions cancel each other out. This cancellation results in inaccurate final predictions. It is often the case that quantum Monte Carlo simulations can be performed for an approximate or simplified interaction, but the corresponding simulations for realistic interactions produce severe sign problems and are therefore not possible.

Using ‘plastic surgery’ to make calculations possible

The new wavefunction-matching approach is designed to solve such computational problems. The research team—from Gaziantep Islam Science and Technology University in Turkey; University of Bonn, Ruhr University Bochum, and Forschungszentrum Jülich in Germany; Institute for Basic Science in South Korea; South China Normal University, Sun Yat-Sen University, and Graduate School of China Academy of Engineering Physics in China; Tbilisi State University in Georgia; CEA Paris-Saclay and Université Paris-Saclay in France; and Mississippi State University and the Facility for Rare Isotope Beams (FRIB) at Michigan State University (MSU)—includes  Dean Lee , professor of physics at FRIB and in MSU’s Department of Physics and Astronomy and head of the Theoretical Nuclear Science department at FRIB, and  Yuan-Zhuo Ma , postdoctoral research associate at FRIB.

“We are often faced with the situation that we can perform calculations using a simple approximate interaction, but realistic high-fidelity interactions cause severe computational problems,” said Lee. “Wavefunction matching solves this problem by doing plastic surgery. It removes the short-distance part of the high-fidelity interaction, and replaces it with the short-distance part of an easily computable interaction.”

This transformation is done in a way that preserves all of the important properties of the original realistic interaction. Since the new wavefunctions look similar to that of the easily computable interaction, researchers can now perform calculations using the easily computable interaction and apply a standard procedure for handling small corrections called perturbation theory.  A team effort

The research team applied this new method to lattice quantum Monte Carlo simulations for light nuclei, medium-mass nuclei, neutron matter, and nuclear matter. Using precise ab initio calculations, the results closely matched real-world data on nuclear properties such as size, structure, and binding energies. Calculations that were once impossible due to the sign problem can now be performed using wavefunction matching.

“It is a fantastic project and an excellent opportunity to work with the brightest nuclear scientist s in FRIB and around the globe,” said Ma. “As a theorist , I'm also very excited about programming and conducting research on the world's most powerful exascale supercomputers, such as Frontier , which allows us to implement wavefunction matching to explore the mysteries of nuclear physics.”

While the research team focused solely on quantum Monte Carlo simulations, wavefunction matching should be useful for many different ab initio approaches, including both classical and  quantum computing calculations. The researchers at FRIB worked with collaborators at institutions in China, France, Germany, South Korea, Turkey, and United States.

“The work is the culmination of effort over many years to handle the computational problems associated with realistic high-fidelity nuclear interactions,” said Lee. “It is very satisfying to see that the computational problems are cleanly resolved with this new approach. We are grateful to all of the collaboration members who contributed to this project, in particular, the lead author, Serdar Elhatisari.”

This material is based upon work supported by the U.S. Department of Energy, the U.S. National Science Foundation, the German Research Foundation, the National Natural Science Foundation of China, the Chinese Academy of Sciences President’s International Fellowship Initiative, Volkswagen Stiftung, the European Research Council, the Scientific and Technological Research Council of Turkey, the National Natural Science Foundation of China, the National Security Academic Fund, the Rare Isotope Science Project of the Institute for Basic Science, the National Research Foundation of Korea, the Institute for Basic Science, and the Espace de Structure et de réactions Nucléaires Théorique.

Michigan State University operates the Facility for Rare Isotope Beams (FRIB) as a user facility for the U.S. Department of Energy Office of Science (DOE-SC), supporting the mission of the DOE-SC Office of Nuclear Physics. Hosting what is designed to be the most powerful heavy-ion accelerator, FRIB enables scientists to make discoveries about the properties of rare isotopes in order to better understand the physics of nuclei, nuclear astrophysics, fundamental interactions, and applications for society, including in medicine, homeland security, and industry.

The U.S. Department of Energy Office of Science is the single largest supporter of basic research in the physical sciences in the United States and is working to address some of today’s most pressing challenges. For more information, visit energy.gov/science.