solve the following assignment problem machine

Procedure, Example Solved Problem | Operations Research - Solution of assignment problems (Hungarian Method) | 12th Business Maths and Statistics : Chapter 10 : Operations Research

Chapter: 12th business maths and statistics : chapter 10 : operations research.

Solution of assignment problems (Hungarian Method)

First check whether the number of rows is equal to the numbers of columns, if it is so, the assignment problem is said to be balanced.

Step :1 Choose the least element in each row and subtract it from all the elements of that row.

Step :2 Choose the least element in each column and subtract it from all the elements of that column. Step 2 has to be performed from the table obtained in step 1.

Step:3 Check whether there is atleast one zero in each row and each column and make an assignment as follows.

Step :4 If each row and each column contains exactly one assignment, then the solution is optimal.

Example 10.7

Solve the following assignment problem. Cell values represent cost of assigning job A, B, C and D to the machines I, II, III and IV.

Here the number of rows and columns are equal.

∴ The given assignment problem is balanced. Now let us find the solution.

Step 1: Select a smallest element in each row and subtract this from all the elements in its row.

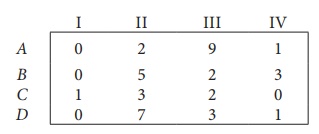
Look for atleast one zero in each row and each column.Otherwise go to step 2.

Step 2: Select the smallest element in each column and subtract this from all the elements in its column.

Since each row and column contains atleast one zero, assignments can be made.

Step 3 (Assignment):

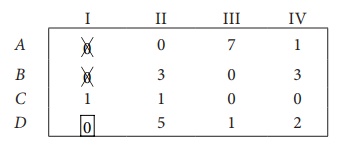
Thus all the four assignments have been made. The optimal assignment schedule and total cost is

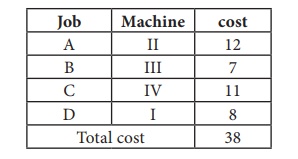
The optimal assignment (minimum) cost

Example 10.8

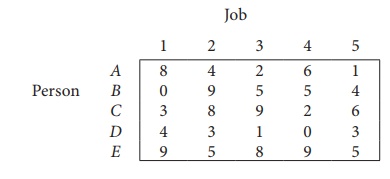
Consider the problem of assigning five jobs to five persons. The assignment costs are given as follows. Determine the optimum assignment schedule.

∴ The given assignment problem is balanced.

Now let us find the solution.

The cost matrix of the given assignment problem is

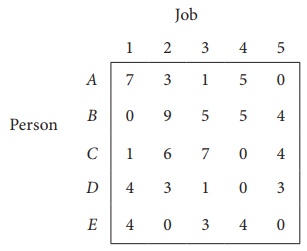
Column 3 contains no zero. Go to Step 2.

Thus all the five assignments have been made. The Optimal assignment schedule and total cost is

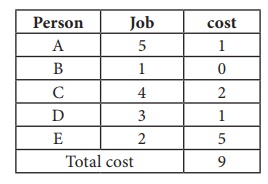
The optimal assignment (minimum) cost = ` 9

Example 10.9

Solve the following assignment problem.

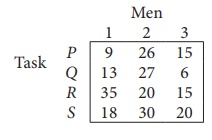
Since the number of columns is less than the number of rows, given assignment problem is unbalanced one. To balance it , introduce a dummy column with all the entries zero. The revised assignment problem is

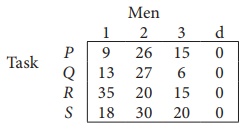
Here only 3 tasks can be assigned to 3 men.

Step 1: is not necessary, since each row contains zero entry. Go to Step 2.

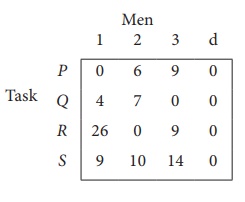
Step 3 (Assignment) :

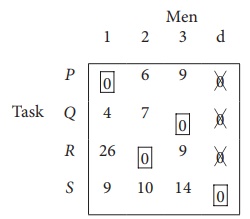
Since each row and each columncontains exactly one assignment,all the three men have been assigned a task. But task S is not assigned to any Man. The optimal assignment schedule and total cost is

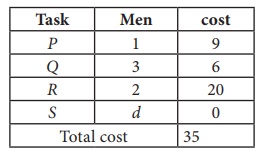
The optimal assignment (minimum) cost = ₹ 35

Related Topics

Privacy Policy , Terms and Conditions , DMCA Policy and Compliant

Copyright © 2018-2024 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.

• Google OR-Tools
• Español – América Latina
• Português – Brasil
• Tiếng Việt

One of the most well-known combinatorial optimization problems is the assignment problem . Here's an example: suppose a group of workers needs to perform a set of tasks, and for each worker and task, there is a cost for assigning the worker to the task. The problem is to assign each worker to at most one task, with no two workers performing the same task, while minimizing the total cost.

You can visualize this problem by the graph below, in which there are four workers and four tasks. The edges represent all possible ways to assign workers to tasks. The labels on the edges are the costs of assigning workers to tasks.

An assignment corresponds to a subset of the edges, in which each worker has at most one edge leading out, and no two workers have edges leading to the same task. One possible assignment is shown below.

The total cost of the assignment is 70 + 55 + 95 + 45 = 265 .

The next section shows how solve an assignment problem, using both the MIP solver and the CP-SAT solver.

Other tools for solving assignment problems

OR-Tools also provides a couple of other tools for solving assignment problems, which can be faster than the MIP or CP solvers:

• Linear sum assignment solver
• Minimum cost flow solver

However, these tools can only solve simple types of assignment problems. So for general solvers that can handle a wide variety of problems (and are fast enough for most applications), we recommend the MIP and CP-SAT solvers.

Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.

Last updated 2023-01-02 UTC.

• MapReduce Algorithm
• Linear Programming using Pyomo
• Networking and Professional Development for Machine Learning Careers in the USA
• Predicting Employee Churn in Python
• Airflow Operators

Solving Assignment Problem using Linear Programming in Python

Learn how to use Python PuLP to solve Assignment problems using Linear Programming.

In earlier articles, we have seen various applications of Linear programming such as transportation, transshipment problem, Cargo Loading problem, and shift-scheduling problem. Now In this tutorial, we will focus on another model that comes under the class of linear programming model known as the Assignment problem. Its objective function is similar to transportation problems. Here we minimize the objective function time or cost of manufacturing the products by allocating one job to one machine.

If we want to solve the maximization problem assignment problem then we subtract all the elements of the matrix from the highest element in the matrix or multiply the entire matrix by –1 and continue with the procedure. For solving the assignment problem, we use the Assignment technique or Hungarian method, or Flood’s technique.

The transportation problem is a special case of the linear programming model and the assignment problem is a special case of transportation problem, therefore it is also a special case of the linear programming problem.

In this tutorial, we are going to cover the following topics:

Assignment Problem

A problem that requires pairing two sets of items given a set of paired costs or profit in such a way that the total cost of the pairings is minimized or maximized. The assignment problem is a special case of linear programming.

For example, an operation manager needs to assign four jobs to four machines. The project manager needs to assign four projects to four staff members. Similarly, the marketing manager needs to assign the 4 salespersons to 4 territories. The manager’s goal is to minimize the total time or cost.

Problem Formulation

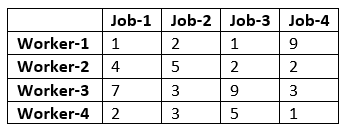
A manager has prepared a table that shows the cost of performing each of four jobs by each of four employees. The manager has stated his goal is to develop a set of job assignments that will minimize the total cost of getting all 4 jobs.  

Initialize LP Model

In this step, we will import all the classes and functions of pulp module and create a Minimization LP problem using LpProblem class.

Define Decision Variable

In this step, we will define the decision variables. In our problem, we have two variable lists: workers and jobs. Let’s create them using  LpVariable.dicts()  class.  LpVariable.dicts()  used with Python’s list comprehension.  LpVariable.dicts()  will take the following four values:

• First, prefix name of what this variable represents.
• Second is the list of all the variables.
• Third is the lower bound on this variable.
• Fourth variable is the upper bound.
• Fourth is essentially the type of data (discrete or continuous). The options for the fourth parameter are  LpContinuous  or  LpInteger .

Let’s first create a list route for the route between warehouse and project site and create the decision variables using LpVariable.dicts() the method.

Define Objective Function

In this step, we will define the minimum objective function by adding it to the LpProblem  object. lpSum(vector)is used here to define multiple linear expressions. It also used list comprehension to add multiple variables.

Define the Constraints

Here, we are adding two types of constraints: Each job can be assigned to only one employee constraint and Each employee can be assigned to only one job. We have added the 2 constraints defined in the problem by adding them to the LpProblem  object.

Solve Model

In this step, we will solve the LP problem by calling solve() method. We can print the final value by using the following for loop.

From the above results, we can infer that Worker-1 will be assigned to Job-1, Worker-2 will be assigned to job-3, Worker-3 will be assigned to Job-2, and Worker-4 will assign with job-4.

In this article, we have learned about Assignment problems, Problem Formulation, and implementation using the python PuLp library. We have solved the Assignment problem using a Linear programming problem in Python. Of course, this is just a simple case study, we can add more constraints to it and make it more complicated. You can also run other case studies on Cargo Loading problems , Staff scheduling problems . In upcoming articles, we will write more on different optimization problems such as transshipment problem, balanced diet problem. You can revise the basics of mathematical concepts in  this article  and learn about Linear Programming  in this article .

• Solving Blending Problem in Python using Gurobi
• Transshipment Problem in Python Using PuLP

You May Also Like

Agglomerative Clustering

K-Means Clustering

KNN Classification using Scikit-learn

Assignment Problem: Meaning, Methods and Variations | Operations Research

After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:

An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.

The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.

Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.

Definition of Assignment Problem:

ADVERTISEMENTS:

Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.

The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:

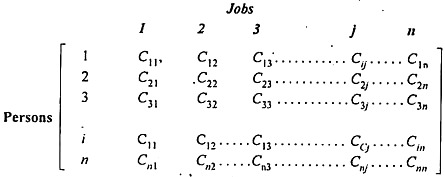
How to Solve the Assignment Problem: A Complete Guide

Table of Contents

Assignment problem is a special type of linear programming problem that deals with assigning a number of resources to an equal number of tasks in the most efficient way. The goal is to minimize the total cost of assignments while ensuring that each task is assigned to only one resource and each resource is assigned to only one task. In this blog, we will discuss the solution of the assignment problem using the Hungarian method, which is a popular algorithm for solving the problem.

Understanding the Assignment Problem

Before we dive into the solution, it is important to understand the problem itself. In the assignment problem, we have a matrix of costs, where each row represents a resource and each column represents a task. The objective is to assign each resource to a task in such a way that the total cost of assignments is minimized. However, there are certain constraints that need to be satisfied – each resource can be assigned to only one task and each task can be assigned to only one resource.

Solving the Assignment Problem

There are various methods for solving the assignment problem, including the Hungarian method, the brute force method, and the auction algorithm. Here, we will focus on the steps involved in solving the assignment problem using the Hungarian method, which is the most commonly used and efficient method.

Step 1: Set up the cost matrix

The first step in solving the assignment problem is to set up the cost matrix, which represents the cost of assigning a task to an agent. The matrix should be square and have the same number of rows and columns as the number of tasks and agents, respectively.

Step 2: Subtract the smallest element from each row and column

To simplify the calculations, we need to reduce the size of the cost matrix by subtracting the smallest element from each row and column. This step is called matrix reduction.

Step 3: Cover all zeros with the minimum number of lines

The next step is to cover all zeros in the matrix with the minimum number of horizontal and vertical lines. This step is called matrix covering.

Step 4: Test for optimality and adjust the matrix

To test for optimality, we need to calculate the minimum number of lines required to cover all zeros in the matrix. If the number of lines equals the number of rows or columns, the solution is optimal. If not, we need to adjust the matrix and repeat steps 3 and 4 until we get an optimal solution.

Step 5: Assign the tasks to the agents

The final step is to assign the tasks to the agents based on the optimal solution obtained in step 4. This will give us the most cost-effective or profit-maximizing assignment.

Solution of the Assignment Problem using the Hungarian Method

The Hungarian method is an algorithm that uses a step-by-step approach to find the optimal assignment. The algorithm consists of the following steps:

• Subtract the smallest entry in each row from all the entries of the row.
• Subtract the smallest entry in each column from all the entries of the column.
• Draw the minimum number of lines to cover all zeros in the matrix. If the number of lines drawn is equal to the number of rows, we have an optimal solution. If not, go to step 4.
• Determine the smallest entry not covered by any line. Subtract it from all uncovered entries and add it to all entries covered by two lines. Go to step 3.

The above steps are repeated until an optimal solution is obtained. The optimal solution will have all zeros covered by the minimum number of lines. The assignments can be made by selecting the rows and columns with a single zero in the final matrix.

Applications of the Assignment Problem

The assignment problem has various applications in different fields, including computer science, economics, logistics, and management. In this section, we will provide some examples of how the assignment problem is used in real-life situations.

Applications in Computer Science

The assignment problem can be used in computer science to allocate resources to different tasks, such as allocating memory to processes or assigning threads to processors.

Applications in Economics

The assignment problem can be used in economics to allocate resources to different agents, such as allocating workers to jobs or assigning projects to contractors.

Applications in Logistics

The assignment problem can be used in logistics to allocate resources to different activities, such as allocating vehicles to routes or assigning warehouses to customers.

Applications in Management

The assignment problem can be used in management to allocate resources to different projects, such as allocating employees to tasks or assigning budgets to departments.

Let’s consider the following scenario: a manager needs to assign three employees to three different tasks. Each employee has different skills, and each task requires specific skills. The manager wants to minimize the total time it takes to complete all the tasks. The skills and the time required for each task are given in the table below:

The assignment problem is to determine which employee should be assigned to which task to minimize the total time required. To solve this problem, we can use the Hungarian method, which we discussed in the previous blog.

Using the Hungarian method, we first subtract the smallest entry in each row from all the entries of the row:

Next, we subtract the smallest entry in each column from all the entries of the column:

We draw the minimum number of lines to cover all the zeros in the matrix, which in this case is three:

Since the number of lines is equal to the number of rows, we have an optimal solution. The assignments can be made by selecting the rows and columns with a single zero in the final matrix. In this case, the optimal assignments are:

• Emp 1 to Task 3
• Emp 2 to Task 2
• Emp 3 to Task 1

This assignment results in a total time of 9 units.

I hope this example helps you better understand the assignment problem and how to solve it using the Hungarian method.

Solving the assignment problem may seem daunting, but with the right approach, it can be a straightforward process. By following the steps outlined in this guide, you can confidently tackle any assignment problem that comes your way.

How useful was this post?

Click on a star to rate it!

Average rating 0 / 5. Vote count: 0

No votes so far! Be the first to rate this post.

We are sorry that this post was not useful for you! 😔

Let us improve this post!

Tell us how we can improve this post?

Operations Research

1 Operations Research-An Overview

• History of O.R.
• Approach, Techniques and Tools
• Phases and Processes of O.R. Study
• Typical Applications of O.R
• Limitations of Operations Research
• Models in Operations Research
• O.R. in real world

2 Linear Programming: Formulation and Graphical Method

• General formulation of Linear Programming Problem
• Optimisation Models
• Basics of Graphic Method
• Important steps to draw graph
• Multiple, Unbounded Solution and Infeasible Problems
• Solving Linear Programming Graphically Using Computer
• Application of Linear Programming in Business and Industry

3 Linear Programming-Simplex Method

• Principle of Simplex Method
• Computational aspect of Simplex Method
• Simplex Method with several Decision Variables
• Two Phase and M-method
• Multiple Solution, Unbounded Solution and Infeasible Problem
• Sensitivity Analysis
• Dual Linear Programming Problem

4 Transportation Problem

• Basic Feasible Solution of a Transportation Problem
• Modified Distribution Method
• Stepping Stone Method
• Unbalanced Transportation Problem
• Degenerate Transportation Problem
• Transhipment Problem
• Maximisation in a Transportation Problem

5 Assignment Problem

• Solution of the Assignment Problem
• Unbalanced Assignment Problem
• Problem with some Infeasible Assignments
• Maximisation in an Assignment Problem
• Crew Assignment Problem

6 Application of Excel Solver to Solve LPP

• Building Excel model for solving LP: An Illustrative Example

7 Goal Programming

• Concepts of goal programming
• Goal programming model formulation
• Graphical method of goal programming
• The simplex method of goal programming
• Using Excel Solver to Solve Goal Programming Models
• Application areas of goal programming

8 Integer Programming

• Some Integer Programming Formulation Techniques
• Binary Representation of General Integer Variables
• Unimodularity
• Cutting Plane Method
• Branch and Bound Method
• Solver Solution

9 Dynamic Programming

• Dynamic Programming Methodology: An Example
• Definitions and Notations
• Dynamic Programming Applications

10 Non-Linear Programming

• Solution of a Non-linear Programming Problem
• Convex and Concave Functions
• Kuhn-Tucker Conditions for Constrained Optimisation
• Quadratic Programming
• Separable Programming
• NLP Models with Solver

11 Introduction to game theory and its Applications

• Important terms in Game Theory
• Saddle points
• Mixed strategies: Games without saddle points
• 2 x n games
• Exploiting an opponent’s mistakes

12 Monte Carlo Simulation

• Reasons for using simulation
• Monte Carlo simulation
• Limitations of simulation
• Steps in the simulation process
• Some practical applications of simulation
• Two typical examples of hand-computed simulation
• Computer simulation

13 Queueing Models

• Characteristics of a queueing model
• Notations and Symbols
• Statistical methods in queueing
• The M/M/I System
• The M/M/C System
• The M/Ek/I System
• Decision problems in queueing

• Branch and Bound Tutorial
• Backtracking Vs Branch-N-Bound
• 0/1 Knapsack
• 8 Puzzle Problem
• Job Assignment Problem
• N-Queen Problem
• Travelling Salesman Problem
• Branch and Bound Algorithm
• Introduction to Branch and Bound - Data Structures and Algorithms Tutorial
• 0/1 Knapsack using Branch and Bound
• Implementation of 0/1 Knapsack using Branch and Bound
• 8 puzzle Problem using Branch And Bound

Job Assignment Problem using Branch And Bound

• N Queen Problem using Branch And Bound
• Traveling Salesman Problem using Branch And Bound

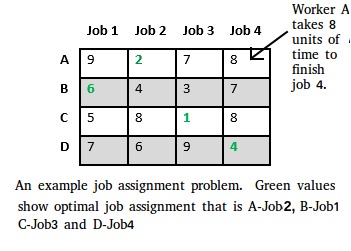
Let there be N workers and N jobs. Any worker can be assigned to perform any job, incurring some cost that may vary depending on the work-job assignment. It is required to perform all jobs by assigning exactly one worker to each job and exactly one job to each agent in such a way that the total cost of the assignment is minimized.

Let us explore all approaches for this problem.

Solution 1: Brute Force  

We generate n! possible job assignments and for each such assignment, we compute its total cost and return the less expensive assignment. Since the solution is a permutation of the n jobs, its complexity is O(n!).

Solution 2: Hungarian Algorithm  

The optimal assignment can be found using the Hungarian algorithm. The Hungarian algorithm has worst case run-time complexity of O(n^3).

Solution 3: DFS/BFS on state space tree  

A state space tree is a N-ary tree with property that any path from root to leaf node holds one of many solutions to given problem. We can perform depth-first search on state space tree and but successive moves can take us away from the goal rather than bringing closer. The search of state space tree follows leftmost path from the root regardless of initial state. An answer node may never be found in this approach. We can also perform a Breadth-first search on state space tree. But no matter what the initial state is, the algorithm attempts the same sequence of moves like DFS.

Solution 4: Finding Optimal Solution using Branch and Bound  

The selection rule for the next node in BFS and DFS is “blind”. i.e. the selection rule does not give any preference to a node that has a very good chance of getting the search to an answer node quickly. The search for an optimal solution can often be speeded by using an “intelligent” ranking function, also called an approximate cost function to avoid searching in sub-trees that do not contain an optimal solution. It is similar to BFS-like search but with one major optimization. Instead of following FIFO order, we choose a live node with least cost. We may not get optimal solution by following node with least promising cost, but it will provide very good chance of getting the search to an answer node quickly.

There are two approaches to calculate the cost function:  

• For each worker, we choose job with minimum cost from list of unassigned jobs (take minimum entry from each row).
• For each job, we choose a worker with lowest cost for that job from list of unassigned workers (take minimum entry from each column).

In this article, the first approach is followed.

Let’s take below example and try to calculate promising cost when Job 2 is assigned to worker A. 

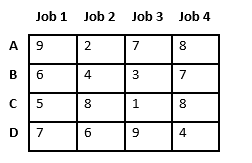
Since Job 2 is assigned to worker A (marked in green), cost becomes 2 and Job 2 and worker A becomes unavailable (marked in red). 

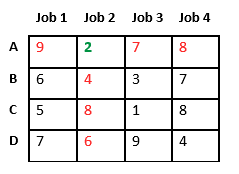
Now we assign job 3 to worker B as it has minimum cost from list of unassigned jobs. Cost becomes 2 + 3 = 5 and Job 3 and worker B also becomes unavailable. 

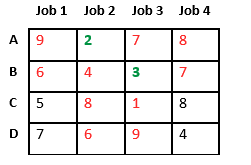
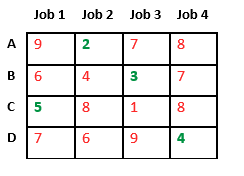
Finally, job 1 gets assigned to worker C as it has minimum cost among unassigned jobs and job 4 gets assigned to worker D as it is only Job left. Total cost becomes 2 + 3 + 5 + 4 = 14. 

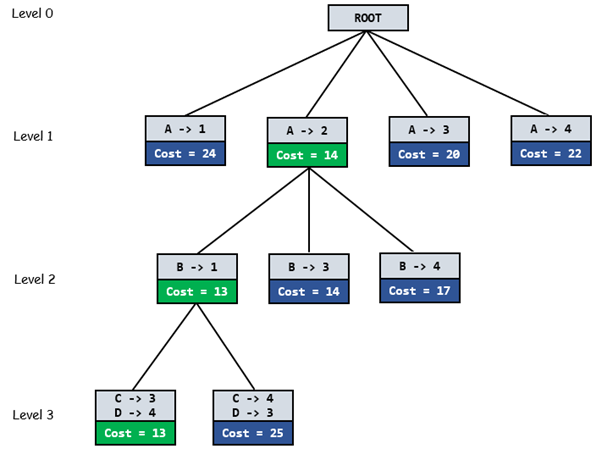
Below diagram shows complete search space diagram showing optimal solution path in green. 

Complete Algorithm:  

Below is the implementation of the above approach:

Time Complexity: O(M*N). This is because the algorithm uses a double for loop to iterate through the M x N matrix.  Auxiliary Space: O(M+N). This is because it uses two arrays of size M and N to track the applicants and jobs.

Please Login to comment...

Similar reads.

• Branch and Bound

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

Solving the Generalized Machine Assignment Problem in Group Technology

• Theoretical Paper
• Published: 01 June 1996
• Volume 47 , pages 794–802, ( 1996 )

Cite this article

• Chun Hung Cheng 1 ,
• Chon-Huat Goh 2 &
• Anita Lee 2  

24 Accesses

22 Citations

Explore all metrics

Many existing solution methodologies for machine assignment problems in group technology do not consider factors such as part demand, operation sequence and cost of intercellular moves. We formulate a 0-1 quadratic programming model that takes into account these factors in machine assignment. Two approaches are proposed to solve this problem. The first is an A*-based approach that generates optimal solutions. The second is a heuristic approach developed to solve problems with large number of machines and/or parts. The heuristic approach is shown to be efficient in producing good solutions in a computational study.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

On optimal due date assignment without restriction and resource allocation in group technology scheduling

Group Scheduling and Due Date Assignment Without Restriction on a Single Machine

Optimal Due Date Assignment Without Restriction and Convex Resource Allocation in Group Technology Scheduling

Author information, authors and affiliations.

The Chinese University of Hong Kong,

Chun Hung Cheng

University of Kentucky, Lexington, USA

Chon-Huat Goh & Anita Lee

You can also search for this author in PubMed   Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cheng, C., Goh, CH. & Lee, A. Solving the Generalized Machine Assignment Problem in Group Technology. J Oper Res Soc 47 , 794–802 (1996). https://doi.org/10.1057/jors.1996.99

Download citation

Received : 01 May 1994

Accepted : 01 November 1995

Published : 01 June 1996

Issue Date : 01 June 1996

DOI : https://doi.org/10.1057/jors.1996.99

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Group Technology
• Quadratic Programming
• Find a journal
• Publish with us
• Track your research