case study questions on current electricity class 12

CBSE Expert

Class 12 Physics Chapter 3 Case Study Question Current Electricity PDF Download

In Class 12 Boards there will be Case studies and Passage Based Questions will be asked, So practice these types of questions. Study Rate is always there to help you. Free PDF Download of CBSE Class 12 Physics Chapter 3 Current Electricity Case Study and Passage Based Questions with Answers were Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 12 Physics Current Electricity  to know their preparation level.

In CBSE Class 12 Physics Paper, Students will have to answer some questions based on  Assertion and Reason . There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.

Current Electricity Case Study Questions With answers

Here, we have provided case-based/passage-based questions for Class 12 Physics  Chapter 3 Current Electricity

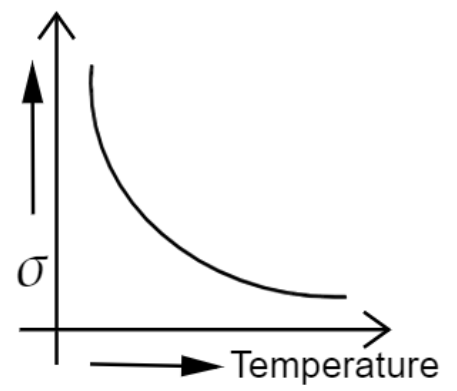
Case Study/Passage-Based Questions

Question 1:

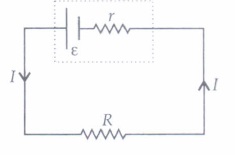
(i) The terminal potential difference of two electrodes of a cell is equal to emf of the cell when

(a) I≠0

(b) I=0

(c) both (a) and (b)

(d) neither (a)nor (b)

Answer: (b) I=0

(ii) A cell of emf E and internal resistance r gives a current of 0.5 A with an external resistance of 12Ω and a current of 0.25 A with an external resistance of 25Ω . What is the value of the internal resistance of the cell?

(a) 5Ω

(b) 1Ω

(c) 7Ω

(d) 3Ω

Answer:  (b) 1Ω 

(iii) Choose the wrong statement.

(a) Potential difference across the terminals of a cell in a closed circuit is always less than its emf.

(b) Internal resistance of a cell decrease with the decrease in temperature of the electrolyte.

(c) Potential difference versus current graph for a cell is a straight line with a -ve slope

(d) Terminal potential difference of the cell when it is being charged is given as V = E + Ir.

Answer: (b) Internal resistance of a cell decrease with the decrease in temperature of the electrolyte.

(iv) An external resistance R is connected to a cell of internal resistance r, the maximum current flows in the external resistance, when

(a) R = r

(b) R < r

(c) R> r

(d) R=l/r

Answer: (a) R = r

(v) IF external resistance connected to a cell has been increased to 5 times, the potential difference across the terminals of the cell increases from 10 V to 30 V. Then, the emf of the cell is

(a) 30 V

(b) 60V

(c) 50 V

(d) 40 V

Answer: (b) 60V

Question 2:

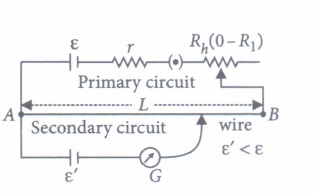
(a) Its sensitivity is low

(b) It measures the emf of a cell very accurately

(c) It is based on the deflection method

(d) None of the above

Answer: (b) It measures the emf of a cell very accurately

(iii) Sensitivity of a potentiometer can be increased by

(a) decreasing potential gradient along the wire	(b) increasing potential gradient along the wire
(c) decreasing current through the wire	(d) increasing current through the wire

Answer: (a) decreasing potential gradient along the wire.

(iv) A potentiometer is an accurate and versatile device to make electrical measurements of EMF because the method involves

(a) potential gradients

(b) a condition of no current flow through the galvanometer

(c) a combination of cells, galvanometer and resistances

(d) cells

Answer: (b) a condition of no current flow through the galvanometer

(v) In a potentiometer experiment, the balancing length is 8 m, when the two cells E l  and E 2  are joined in series. When the two cells are connected in opposition the balancing length is 4 m. The ratio of the e. m. f. of two cells (E l /E 2 ) is

(a) 1: 2

(b) 2: 1

(c) 1: 3

(d) 3: 1

Answer: (d) 3: 1

Hope the information shed above regarding Case Study and Passage Based Questions for Class 12 Physics Chapter 3 Current Electricity with Answers Pdf free download has been useful to an extent. If you have any other queries about CBSE Class 12 Physics Current Electricity Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible.

Leave a Comment Cancel reply

Save my name, email, and website in this browser for the next time I comment.

Download India's best Exam Preparation App Now.

Key Features

• Revision Notes
• Important Questions
• Previous Years Questions
• Case-Based Questions
• Assertion and Reason Questions

No thanks, I’m not interested!

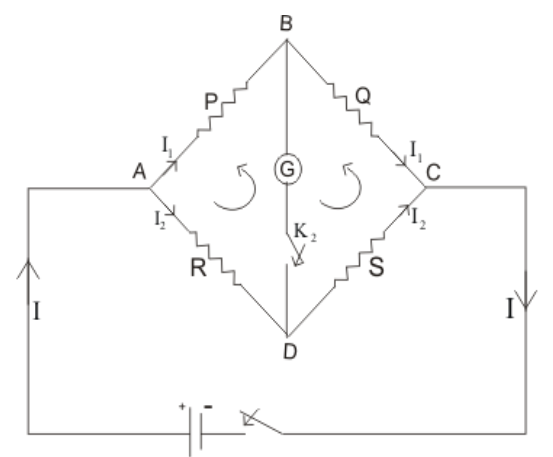
Current Electricity | Case Study-01

(relation between v, e and r of a cell).

Relation Between V, E and r of a Cell-

Emf of a cell is the maximum potential difference between two electrodes of the cell when no current is drawn from the cell. Internal resistance is the resistance offered by the electrolyte of a cell when the electric current flows through it. The internal resistance of a cell depends upon the following factors-

• distance between the electrodes
• nature and temperature of the electrolyte
• nature of electrodes
• area of electrodes

For a freshly prepared cell, the value of internal resistance is generally low and goes on increasing as the cell is put to more and more use. The potential difference between the two electrodes of a cell in a closed circuit is called terminal potential difference and its value is always less than the emf of a cell in a closed circuit. It can be written as V = E – Ir.

All the best!

Time's up

Follow us on Facebook

Current Electricity Quizzes

Topic based quizzes.

• Basics of Electric Current
• Current Density
• Drift Velocity & Relaxation Time
• Relation Between Electric Current & Drift Velocity
• Mobility of Charge Carriers
• Resistance & Conductance
• Temperature Dependence of Resistance
• Resistivity & Conductivity
• Temperature Dependence of Resistivity
• Kirchoff’s Laws
• Combination of Resistors
• Wheatstone Bridge
• EMF & Terminal Voltage of Electric Cell
• Series Combination of Cells
• Parallel Combination of Cells
• Joule’s Law of Heating
• Rating of an Appliance

Chapter Based Quizzes

• Practice Quiz-01
• Practice Quiz-02

Current Electricity Case Studies

• Case Study-01

Class-12 Physics Quizzes

1. Electric Charges & Fields

2. Electrostatic Potential & Capacitance

3. Current Electricity

4. Moving Charges & Magnetism

5. Magnetism & Matter

6. Electromagnetic Induction

7. Alternating Current

8. Electromagnetic Waves

9. Ray Optics

10. Wave Optics

11. Dual Nature of Radiation & Matter

14. Semiconductors

Class-12 Physics Notes

• Physics Important Questions
• Class 12 Physics
• Chapter 3: Current Electricity

Important Questions For Class 12 - Physics - Chapter 3 - Current Electricity

When an electric field is present, an electric charge is subject to a force, which causes it to move if it is free to do so. This movement of charge is known as a current. There are some instances in nature where free-charged particles can be found, such as in the ionosphere. However, in most matters, such as atoms and molecules, the negatively charged electrons and positively charged nuclei are bound together and unable to move freely. A large amount of matter, such as a gram of water, is made up of numerous molecules that are so densely packed that the electrons are no longer connected to specific nuclei. Some materials, like insulators, have electrons that are bound and will not accelerate when an electric field is applied, but other materials, like conductors, have electrons that are largely free to move within the bulk material. As a result, when an electric field is applied, these materials develop electric currents.

When there is no electric field present, the electrons will still be in motion due to random collisions with fixed ions caused by thermal energy. These collisions do not affect the speed of the electrons, but they can change the direction of their movement. As there is no preference for the direction of the velocities of electrons at a particular time, the number of electrons moving in any given direction will be equal to the number moving in the opposite direction. As a result, on average, there is no net movement of charge, and no electric current will be observed.

In metallic conductors, the charges that are able to move and contribute to electrical current are the electrons. These electrons come from the outermost (valence) shells of atoms in the metal and are able to move freely within the metal but are not able to leave it. They move randomly, colliding with each other and with the metal ions, and in the presence of an external electric field, they will drift in the opposite direction of the field. The positive charges in metal are made up of the nuclei of atoms, which remain in fixed positions, and the negatively charged electrons in the inner shells of atoms, which also remain fixed. In electrolytic conductors, the charge carriers are positive and negative ions, and their movement is influenced not only by an external electric field but also by chemical forces within the material.

Important Questions for Class 12 Physics Chapter 3 – Current Electricity are provided here. Students must go through these questions and solve them to prepare for their Physics papers. They can also refer to these questions for quick revision. These questions are more likely to be asked in the exam; hence, students must practise them thoroughly.

Very Short Answer Type Questions

1. Which of the options given is non-ohmic resistance?

(a) Copper wire

(b) Lamp filament

(d) Carbon resistor.

Answer: (C) Diode has non-ohmic resistance in nature.

Explanation: A diode delivers a constant voltage drop even if there is a change in the current, so it does not follow Ohm’s law.

2. What is the unit of conductance?

Answer: (a) Siemen

Explanation: The unit used to measure conductance is called siemen.

3. Current density is a __________.

(a) vector quantity

(b) dimensionless quantity

(c) scalar quantity

(e) None of the choices is suitable

Answer : (a) vector quantity

Explanation : Current density is a vector that describes the flow of electric current per unit area. It is a product of charge density and velocity. Here charge density is a scalar quantity, and velocity is a vector quantity, which makes current density a vector quantity.

4. _________ is the phenomenon in which the resistance of certain materials drops to zero when cooled below a specific temperature.

(a) Conductivity

(b) Superconductivity

(c) Partial conductivity

(d) Insulation

Answer: (b) Superconductivity

Explanation: Superconductivity is the phenomenon in which the resistance of certain materials drops to zero when cooled below a specific temperature.

5. Is the following statement true or false: The overall resistance in a series circuit is higher than the greatest resistance present in the circuit?

(a) True (b) False

Answer: (a) True

Explanation : In a series circuit, the overall resistance is greater than the highest individual resistance present in the circuit.

6. What is the resistance that the electrolyte in a cell provides to the flow of current through it is referred to as?

(a) Internal resistance

(b) Non-resistance

(c) External resistance

(d) None of the choices is suitable

Answer: (a) Internal resistance

Explanation: The internal resistance of a cell refers to the resistance provided by the electrolyte to the flow of current through it.

Short Answer Type Questions

1. Is the motion of a charge across junction momentum conserving? Why or why not?

If the motion of a charge is occurring across a junction, the momentum of the charge is not at all conserved. This is because when the charge (electron) approaches the junction, apart from the uniform electric field that it typically encounters (which maintains the drift velocity fixed), there will be an accumulation of charges on the wires’ at the junction. This also generates an electric field, enabling the change in the direction of the charge’s momentum.

2. The relaxation time ‘t’ is nearly independent of the applied E field, whereas it changes significantly with temperature T. First fact is (in part) responsible for Ohm’s law, whereas the second fact leads to the variation of p (rho) with temperature. Elaborate why?

When the drift velocity rises, the relaxation time ‘t’ (the average time between consecutive collisions) falls, which increases‘p (rho)’ by the relation given below:

\(\begin{array}{l}\rho = \frac{ m }{ n e^2 \tau }\end{array} \)

The drift velocity v d varies in the range of one mm on the rising electric field. On the other hand, the drift velocity rises of the order 10 2 ms -1 when the count of free electrons rises with increasing temperature.

Therefore, due to the rise in v d the relation time considerably decreases in conductors.

3. What are the advantages of the null-point method in a Wheatstone bridge? What additional measurements would be required to calculate R unknown by any other method?

In the case of a Wheatstone bridge, the technique of null point uses balanced Wheatstone bridges, in which the galvanometer’s resistance does not influence the balance point. There is no requirement to find the currents in the galvanometer and resistances. The unbalanced Wheatstone bridge can also be utilised to determine the unknown resistance. However, in this technique, we need the additional accurate measurement of every current in the galvanometer and resistors as well as the galvanometer’s internal resistance.

4. What is the advantage of using thick metallic strips to join wires in a potentiometer?

Resistance is given by the relation

\(\begin{array}{l}R = \frac{ \rho l }{ A }\end{array} \)

So, as the cross-sectional area of the wire increases, the resistance of the wire reduces. Therefore, the metal strips possess very low resistance and can be easily neglected while determining the wire’s length used to find the null point.

5. For wiring in the home, one uses Cu wires or Al wires. What considerations are involved in this?

In the case of electrical wiring in houses, two factors are involved while choosing the wiring materials, the cost of the conducting material (in most cases metal) and the conductivity of the wire. Silver has the greatest conductivity, but it is generally ignored due to its high cost. Just after silver, aluminium and copper are the next ideal conductors. Their production cost is also lower than silver. Thus, aluminium and copper are used for electrical wiring in houses.

6. Why are alloys used for making standard resistance coils?

Alloys are employed for constructing conventional resistance coils as they possess high resistivity and a small resistivity temperature coefficient.

7. Power P is to be delivered to a device via transmission cables having resistance R c . If V is the voltage across R and I is the current through it; find the power wasted and how it can be reduced.

Power Delivered (P) = Current × Voltage = VI

\(\begin{array}{l}\Rightarrow I = P/V \end{array} \)

If R c is taken as the resistance of the electrical transmission line, then the power wasted is

\(\begin{array}{l}P_c = l^2 R_c \end{array} \)

\(\begin{array}{l}= \frac{P^2}{v^2} R_c\end{array} \)

In order to decrease P C , V must be large. Thus, the power must be transmitted at a large voltage.

8. AB is a potentiometer wire (Fig 3.4). If the value of R is increased, in which direction will the balance point J shift?

When R is increased, the electric current in the main circuit will reduce (by V = IR) as the potential is constant. In turn, the potential difference along AB will decrease. Since the R of AB is constant, the potential gradient K = V/AB will decline. In order to balance potential along AB equivalent to the secondary circuit’s potential, the length AJ’ should be bigger than the earlier AJ. Thus, point J changes towards B.

9. While doing an experiment with the potentiometer (Fig 3.5), it was found that the deflection was one-sided, and (i) the deflection decreased while moving from one end A of the wire to the end B: (ii) the deflection increased while the jockey was moved towards end B.

• (a) Which terminal of + or -ve of the cell E 1 , is connected at X in case (i) and how is E 1 related to E?
• (a) Which terminal of cell E 1 is connected at X in case (ii)?

(a) If the electric current in the auxiliary circuit (lower circuit having primary cell) reduces and the potential difference along jockey and A increases. Then deflection in the galvanometer will be one-sided, and the deflection will decrease while displacing from one end A of the wire to the end S. This is only possible when the positive end of the cell E 1 is attached to X and E 1 > E.

(b) If the electric current in the auxiliary circuit rises, the potential difference between jockey and A rises. Then deflection in the galvanometer is one-sided.

10. A cell of emf E and internal resistance r is connected across an external resistance R. Plot a graph showing the variation of P.D. across R versus R.

It is known that

\(\begin{array}{l}I = \frac{ E }{ R + r }\end{array} \)

\(\begin{array}{l}V = IR\end{array} \)

\(\begin{array}{l}\therefore V = \frac{ ER }{ R + r } \,\, ….. \textup{(i)}\end{array} \)

\(\begin{array}{l}V = \frac{ E }{ 1 + \frac{ r }{ R } }\end{array} \)

In this case, r, E are constants.

\(\begin{array}{l}\textup{So, }V \propto \frac{ 1 }{ 1 + \frac{ r }{ R } }\end{array} \)

\(\begin{array}{l}V \propto R\end{array} \)

With the rise in R, the potential difference across R is risen up to the maximum value of E.

11 First, a set of n equal resistors of R each is connected in series to a battery of emf E and internal resistance R. A current I is observed to flow. Then the n resistors are connected in parallel to the same battery. It is observed that the current is increased ten times. What is ‘n’?

If n resistance of R O are linked in parallel and series, then

\(\begin{array}{l}R_s = R + R + R \,\, ….. \textup{n times} \end{array} \)

\(\begin{array}{l}\Rightarrow R_p = nR \end{array} \)

\(\begin{array}{l}\frac{1}{R_p} = \frac{1}{R} + \frac{1}{R} + \frac{1}{R} \,\, ….. \textup{ n times} \end{array} \)

\(\begin{array}{l}\Rightarrow \frac{1}{R_p} = \frac{n}{R} \end{array} \)

\(\begin{array}{l}\Rightarrow R_p = \frac{R}{n} \end{array} \)

When n resistors are linked in series and attached to a battery (with emf E), then electric current flows. Therefore,

\(\begin{array}{l}\frac{ E }{ R + nR } = I\end{array} \)

When n resistances are linked in parallel combination, then the electric current in the circuit increases to ten times of I.

\(\begin{array}{l}\therefore \frac{ E }{ R + \frac{ R }{ n } } = 10 I \end{array} \)

\(\begin{array}{l}\frac{ E }{ R + \frac{ R }{ n } } = \frac{ 10 E }{ R + nR }\end{array} \)

\(\begin{array}{l}\frac{ 1 }{ R \left ( 1 + \frac{1}{n} \right ) } = \frac{ 10 }{ R(1 + n) }\end{array} \)

\(\begin{array}{l}10 \left ( 1 + \frac{1}{n} \right ) = 1 + n\end{array} \)

\(\begin{array}{l}10 + \frac{10}{n} – 1 – n = 0\end{array} \)

\(\begin{array}{l}-n + \frac{10}{n} + 9 = 0 ( \textup{multiply both sides by -n} )\end{array} \)

\(\begin{array}{l}n^2 – 10 – 9n = 0 \end{array} \)

\(\begin{array}{l}n^2 – 9n – 10 = 0\end{array} \)

\(\begin{array}{l}n^2 – 10n + 1n – 10 = 0\end{array} \)

\(\begin{array}{l}n(n – 10) + 1(n-10) = 0\end{array} \)

\(\begin{array}{l}\textup{Therefore, }(n+1)(n-10) = 0\end{array} \)

\(\begin{array}{l}n = -1 \textup{ is not possible or } n = 10\end{array} \)

Therefore, there are ten transistors in combination.

12. Let there be n resistors R 1 ………. R n with R max = max (R 1 …….. R n ) and R min = min {R 1 ….. R n }. Show that when they are connected in parallel, the resultant resistance R p < R min and when they are connected in series, the resultant resistance R s > R max . Interpret the result physically.

Take R max and R min are maximum and minimum resistances among all resistance R 1 R 2 ….. R 1 . When resistors are linked in parallel, then the equivalent resistance R p is \(\begin{array}{l}\frac{ 1 }{ R_v } = \frac{ 1 }{ R_1 } + \frac{ 1 }{ R_2 } + \, …… + \frac{ 1 }{ R }\end{array} \)

Multiplying the two sides by R min ,

\(\begin{array}{l}\frac{ R_{min} }{ R_p } = \frac{ R_{min} }{ R_1} + \frac{ R_{min} }{ R_2 } + \, …..\, \frac{ R_{min} }{ R_n } \,\,\,\,\, (\textup{among }R_1, R_2, ….., R_n).\end{array} \)

\(\begin{array}{l}\textup{ In this case, in RHS, there exists one term } \frac{ R_{min} }{R_{min} } = 1 \textup{ and the rest of the terms are positive, so we have }\end{array} \)

\(\begin{array}{l}\frac{R_{min}}{R_P} = \frac{R_{min}}{R_1} + \frac{R_{min}}{R_2} + ….. + \frac{R_{min}}{R_{n}} > 1\end{array} \)

This represents the resultant resistance R p < R min . Therefore, in parallel combination, the resistors’ equivalent resistance R p is less than any smallest resistance in connection.

If the ‘n’ number of resistance is linked in series, then net resistance is

\(\begin{array}{l}R_s = R_1 + R_2 + R_3 + …… + R_n \,\,\,\,\,\, (b)\end{array} \)

In this case, there is one term possessing resistance R max Thus, in RHS, there should be a term R max which possesses maximum value among R 1 , R 2 , …….. R n .

Since every term of equation (b) are positive, \(\begin{array}{l}R_s = R_1 + R_2 + R_3^+ …….. R_{max} + …… + R_m > R_{max}\end{array} \)

\(\begin{array}{l}R_s > R_{max}\end{array} \)

Thus, in equivalent resistance of the series combination is always more than the maximum resistance (R max ) among R 1 , R 2 , ………. R n .

13. The circuit in the figure shows two cells connected in opposition to each other. Cell E 1 is of emf 6V and internal resistance 2O; cell E 2 is of emf 4V and internal resistance 8O. Find the potential difference between points A and B.

The current direction in the circuit will be exactly as represented in the diagram. Therefore, point B has a greater potential than A (V B > V A ).

\(\begin{array}{l}\textup{Current in the circuit, } I = \frac{ E_1 + E_2 }{r_1 + r_2}\end{array} \)

\(\begin{array}{l}= \frac{ (6 – 4) }V { (2 + 8)\Omega } = 0.2 \textup{amp}\end{array} \)

The potential across E 1 and E 2 are \(\begin{array}{l}E_1 = V – Ir_1 = 6 – 0.2 \times 2 = 6 – 0.4 = 5.6 V\end{array} \)

\(\begin{array}{l}E_2 = V + Ir_2 = 4 + 0.2 \times 8 = 4 + 1.6 = 5.6V\end{array} \)

Therefore, the potential between B and A is \(\begin{array}{l}E_2 = 5.6 Volt\end{array} \)

Since the current is flowing from B to A, the potential at point B is greater than A.

14. Two cells of the same emf E but internal resistance r 1 and r 2 are connected in series to an external resistor R. What should be the value of R so that the potential difference across the terminals of the first cell becomes zero?

The current flowing through the circuit is

\(\begin{array}{l}I = \frac{ E_{eq} }{ R + r_1 + r_2} \, …………… (i) \, (\textup{ In series, } E + E = 2E)\end{array} \)

Then, the potential drop along the first cell is \(\begin{array}{l}V_1 = E – Ir_1\end{array} \)

As per the given scenario

\(\begin{array}{l}V_1 = 0\end{array} \)

\(\begin{array}{l}E – Ir_1 = 0\end{array} \)

\(\begin{array}{l}E- \left ( \frac{ 2E }{ r_1 + r_2 + R } \right )r_1 = 0 \, ……. \textup{from } (i)\end{array} \)

\(\begin{array}{l}\frac{ 2r_1E }{ r_1 + r_2 + R } = E\end{array} \)

\(\begin{array}{l}\Rightarrow r_1 + r_2 + R = 2r_1 \end{array} \)

\(\begin{array}{l}R = r_1 – r_2\end{array} \)

15. Two conductors are made of the same material and have the same length. Conductor A is a solid wire of diameter 1mm. Conductor B is a hollow tube with an outer diameter of 2mm and an inner diameter of 1mm. Find the ratio of resistance R A to R B .

We know that

\(\begin{array}{l}R = \frac{ \rho l }{A}\end{array} \)

Let us assume that the conductor is made up of a substance of resistivity ‘p (rho)’ and the conductor’s length be ‘I’. The diameter of the wire A, d = 1mm

\(\begin{array}{l}\textup{Radius of the wire, } r = \frac{d}{2} = 0.5 \times 10^{-3}m\end{array} \)

\(\begin{array}{l}\textup{ Resistance of the Wire A, } R_A = \frac{ \rho l }{ \pi (0.5 \times 10^{-3})^2 }\end{array} \)

Now let’s find the resistance of wire B.

Let us assume that the conductor is composed of a substance of resistivity ‘p (rho)’ and the conductor’s length be ‘I’. The diameter of the wire B, d 1 = 1mm

The inner radius of the wire is

\(\begin{array}{l}r_1 = \frac{ d_1 }{ 2} = 0.5 \times 10^{-3}\end{array} \)

The outer diameter of the wire B, d 2 = 2mm

\(\begin{array}{l}\textup{ Outer radius of the wire, } r_2 = \frac{ d_2 }{ 2 } = 1 \times 10^{-3}m\end{array} \)

The resistance of the wire B,

\(\begin{array}{l}R_B = \frac{ \rho l }{ \pi ( (r_2)^2 – (r_1)^2 ) }\end{array} \)

\(\begin{array}{l}= \frac{ \rho 1 }{ \pi ( ( 1 \times 10^{-3} )^2 – (0.5 \times 10^{-3})^2 ) }\end{array} \)

The ration of R A and R B is

\(\begin{array}{l}\frac{ R_A }{ R_B } = \frac{ (1 \times 10^{-3} )^2 – (0.5 \times 10^{-3})^2 }{ (0.5 \times 10^{-3})^2 }\end{array} \)

\(\begin{array}{l}\frac{ R_A }{ R_B } = \frac{ 3 }{ 1 }\end{array} \)

The ratio of resistance R A to R B is 3:1.

16. Suppose there is a circuit consisting of only resistances and batteries. Suppose one is to double (or increase it to n-times) all voltages and all resistances. Show that currents are unaltered. Do this for the circuit shown here.

Scenario A: Let us assume a circuit composed of external resistance R 1 , R 2 ………, linked with some batteries E 1 , E 2 , E 3 ……. possessing their internal resistances r 1 , r 2 , r 3 ………..

Take the emf, internal resistance, and equivalent resistance of the given combination as R eq , E eq , and r eq, respectively. Therefore, the current passing in the circuit is

\(\begin{array}{l}I_1 = \frac{ nE_{eq}}{ R_{eq} + r_{eq} }\end{array} \)

Then the cells and resistance are again linked in a way that their resultant resistance, emf, and internal resistance are nR eq , nE eq , and nr eq and respectively. Therefore, again electric current in the new circuit is \(\begin{array}{l}I_2 = \frac{ nE_{eq} }{ nR_{eq} + nr_{eq} }\end{array} \)

\(\begin{array}{l}I_2 = \frac{ nE_{eq} }{ n[ R_{eq} + r_{eq} ] }\end{array} \)

\(\begin{array}{l}= \frac{ E_{\theta q} }{ R_{ \theta q} + r_{eq} } = I_1\end{array} \)

Thus, the electric current stays the same if the R, E, and r of a circuit are raised by n times, i.e. nR, nE, nr.

Long Answer Type Questions

1. Two cells of voltage 10V and 2V and internal resistances 10O and 5O, respectively, are connected in parallel with the positive end of the 10V battery connected to the negative pole of the 2V battery (Fig 3.8). Find the effective voltage and effective resistance of the combination.

According to the junction rule, at A \(\begin{array}{l}I_1 = I + I_2\end{array} \)

When Kirchhoffs rule on loop ADEF and loop BCEF

\(\begin{array}{l}10 = IR + 10I_1\end{array} \)

\(\begin{array}{l}2 = 5I_2 – IR\end{array} \)

\(\begin{array}{l}\therefore 2 = 5(I_1 – I ) – IR \end{array} \)

\(\begin{array}{l}\textup{ From the above equations, we get } 4 = 10 I_{1} – 10I – 2IR\end{array} \)

Subtract the above equation from the first equation,

\(\begin{array}{l}6 = 3 I R + 10 I\end{array} \)

\(\begin{array}{l}3 IR + 10I = 6\end{array} \)

\(\begin{array}{l}I(3R + 10) = 2 \times 3\end{array} \)

\(\begin{array}{l}\frac{ I (3R +10) }{ 3 } = 2\end{array} \)

\(\begin{array}{l}2 = I \left ( R + \frac{10}{3} \right )\end{array} \)

The resultant potential difference due to the two batteries is V eq . It is will be along resistance R.

\(\begin{array}{l}\therefore V_{eq} = I (R + R_{eq}) \end{array} \)

R eq is the circuit’s resistance except for R.

\(\begin{array}{l}V_{eq} = 2 \textup{ Volts and } R_{eq} = \frac{10}{3} \Omega \end{array} \)

2. A room has AC run for 5 hours a day at a voltage of 220V. The wiring of the room consists of Cu of 1 mm radius and a length of 10m, and power consumption per day is ten commercial units. What fraction of it goes in the joule heating in wires? What would happen if the wiring is made of the same dimensions?

\(\begin{array}{l}[ \rho _{cu} = 1.7 \times 10^{-8} \Omega m, \,\, \rho _{Al} = 2.7 \times 10^{-8} \Omega m] \end{array} \)

The entire energy used in five hours a day by AC and wiring is 10kWh

Therefore, the energy used in one hour by AC and wiring is 2kWh.

The total power of the AC and wire is 2000W.

\(\begin{array}{l}P = VI\end{array} \)

\(\begin{array}{l}I = \frac{P}{V} \end{array} \)

\(\begin{array}{l}= \frac{2000}{220} \cong 9.0A\end{array} \)

Take P 0 as the power of wiring then,

\(\begin{array}{l}P_{0} = I^2 R_{W} \, [R_W = \textup{resistance of wiring}]\end{array} \)

\(\begin{array}{l}= 9 \times 9\cdot \frac{P!}{A}\end{array} \)

\(\begin{array}{l}= \frac{ 9 \times 9 \times 1.7 \times 10^{-8} \times 10 }{ 3.14 \times 1 \times 10^{-3} \times 1 \times 10^{-3} }\end{array} \)

\(\begin{array}{l}= \frac{ 81 \times 17 \times 10^{-8 + 6} }{ 3.14 }\end{array} \)

\(\begin{array}{l}= \frac{ 1377 }{ 3.14 } \times 10^{-2}\end{array} \)

\(\begin{array}{l}= 4.38 = 4.4 Watt\end{array} \)

Thus, the energy loss in the wiring

\(\begin{array}{l}\cong 4.4 J/sec \end{array} \)

The fractional loss due to wire heating

\(\begin{array}{l}= \frac{ 4.4 }{ 2000 } \times 100 \% \end{array} \)

\(\begin{array}{l}= 0.22 \% \end{array} \)

\(\begin{array}{l}\frac{ P_A \,(wiring) }{ P_{Cu} \, (wiring) } = \frac{ I^2R_A }{I^2R_{Cu}}\end{array} \)

\(\begin{array}{l}= \frac{ \rho Ai \frac{I_A}{A_{Ai}} }{ \rho Cu \frac{I_{Cu}}{ A_{Cu} }} \textup{ as } 1_{AI} = L_{Cu} \textup{ and } A_{AI} = A_{Cu} \end{array} \)

\(\begin{array}{l}\frac{ P_{A} }{ P_{Cu}} = \frac{ \rho _{A} }{ \rho _{Cu} }\end{array} \)

\(\begin{array}{l}P_{A} = \frac{ 2.7 \times 10^{-8} }{ 1.7 \times 10^{-8} } \times 4.4 Watt\end{array} \)

Therefore, the loss of power in Al wiring is 7 Watts.

3. In an experiment with a potentiometer, VB = 10V. R is adjusted to be 50O (Fig. 3.9). A student wanting to measure voltage E 1 of a battery (approx 8V) finds no null point possible. He then diminishes R to 10O and is able to locate the null point on the last (4th) segment of the potentiometer. Find the resistance of the potentiometer wire and potential drop per unit length across the wire in the second case.

Consider R as the potentiometer wire’s resistance.

\(\begin{array}{l}\textup{Variable resistance, R} = 50\Omega \end{array} \)

I is the electrical current in the primary, which is located at E B = 10V.

\(\begin{array}{l}I \frac{ V_B }{ R + R’ } \Rightarrow \frac{10}{ 50 + R } = I ( \textup{ in primary circuit})\end{array} \)

Potential difference along the potentiometer wire is

\(\begin{array}{l}V’ = IR'\end{array} \)

\(\begin{array}{l}\textup{ From } I \, V’ = \frac{10R’}{50 + R}\end{array} \)

Since R = 50O, the null point cannot be acquired by 8 Volt. Therefore, V < 8 Volt.

\(\begin{array}{l}\frac{ 10 R’ }{ 50 + R’}\,\, (\textup{no balance point})\end{array} \)

As 50 + R’ is positive, therefore, we can multiply the above relation by a positive number, and we get 10R’ < 400 + 8R’

2R’ < 400 R’ < 200

The null point acquired by R = 10O.

V’ > 8 at balance point. Thus, it is possible when

\(\begin{array}{l}\frac{ 10R’ }{ 10 + R } > 8 \, ( \textup{as from I, R = 10})\end{array} \)

Multiply the above equation by the positive value 10 + R’ to both sides

10R’ > 80 + 8R 2R’ > 80 R’ > 40

Since the null point is acquired on the fourth segment or at 3\4 of the total length. Thus, at (3\4)R’ (no balance point) \(\begin{array}{l}\textup{Or } \frac{ 10 \times \frac{3}{4}R’ }{ 10 + R } < 8 \end{array} \)

\(\begin{array}{l}\therefore 7.5R’ < 80 + 8R \end{array} \)

\(\begin{array}{l}-0.5R’ < 80\end{array} \)

\(\begin{array}{l}- R’ < 160 \end{array} \)

\(\begin{array}{l}R’ > -160\end{array} \)

R’ can never be a negative value. Therefore -160O is considered as 160O

\(\begin{array}{l}\textup{So, }[160 < R’ < 200] …. V\end{array} \)

Any of the R’s between 200O and 160O will attaina null point. As the null point is on the last fourth segment of the potentiometer wire, the potential drop along 400cm wire > 7 Volt.

Therefore, K(400cm) > 8V (at balance point)

\(\begin{array}{l}K > \frac{8}{400}Volt/cm \end{array} \)

\(\begin{array}{l}K > \frac{8}{4}Volt/,\end{array} \)

\(\begin{array}{l}K > 2Volt/m\end{array} \)

Since the balance point is at the fourth wire, therefore no balance point at 3m.

\(\begin{array}{l}K (3) < 8 (\textup{no balance point})\end{array} \)

\(\begin{array}{l}K < \frac{ 8 }{ 3 } Volt/m\end{array} \)

\(\begin{array}{l}K < 2 \frac{2}{3}Volt/m\end{array} \)

\(\begin{array}{l}\therefore \left [ 2 \frac{2}{3}V/m \right > K > 2Volt/m ] \end{array} \)

\(\begin{array}{l}\therefore \left [ 2 \frac{2}{3} V/m > K > 2Volt/m \right ] \end{array} \)

4. (a) Consider the circuit in the Figure. How much energy is absorbed by electrons from the initial state of no current (ignore thermal motion) to the state of drift velocity?

(b) Electrons give up energy at the rate of RI 2 per second to the internal energy. What time scale would one associate with energy in problem (a)? N = no of electrons/volume = 10 29 /m 3 , length of circuit = 10cm, cross-section = A = (1mm) 2 .

(a) By using ohm’s law, current I is represented by

\(\begin{array}{l}I = \frac{6V}{6\Omega } = 1A\end{array} \)

\(\begin{array}{l}i = neAv_d\end{array} \)

\(\begin{array}{l}v_d = \frac{i}{neA}\end{array} \)

On substituting the quantities,

\(\begin{array}{l}n \textup{ = the number of electrons/volume } = 10^{29}/m^3\end{array} \)

Circuit length = 10cm

Cross section area A = 1(mm) 2

\(\begin{array}{l}v_d = \frac{ 1 }{ 10^{29} \times 1.6 \times 10^{-19} \times 10^{-6} }\end{array} \)

\(\begin{array}{l}= \frac{1}{1.6} \times 10^{-4} m/s\end{array} \)

Thus, the energy absorbed in the form of kinetic energy is represented by

\(\begin{array}{l}KE = \frac{1}{2} m_ev^2_d \times nAI\end{array} \)

\(\begin{array}{l}= \frac{1}{2} \times 9.1 \times 10^{31} \times \frac{1}{2.56} \times 10^{20} \times 10^{8} \times 10^6 \times 10^1\end{array} \)

\(\begin{array}{l}= 2 \times 10^{-17} J\end{array} \)

(b) Loss of power is represented by

\(\begin{array}{l}P = I^2R = 6 \times 1^2 = 6W = 6J/s\end{array} \)

\(\begin{array}{l}P = \frac{E}{t}\end{array} \)

\(\begin{array}{l}\therefore E = P \times t \end{array} \)

\(\begin{array}{l}\textup{or } t = \frac{E}{P}\end{array} \)

\(\begin{array}{l}= \frac{2 \times 10^{-17} }{ 6 } = 10^{-17}s\end{array} \)

Current Electricity Class 12 Physics One Shot & Mind Maps (Chapter 3)

Current Electricity Class 12 Physics One Shot (Full Chapter Revision)

Current Electricity Class 12 Physics One Shot

Current Electricity Class 12 Physics Crash Course

PHYSICS Related Links

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Talk to our experts

1800-120-456-456

Important Questions for CBSE Class 12 Physics Chapter 3 - Current Electricity 2024-25

• Class 12 Important Question

CBSE Class 12 Physics Chapter-3 Important Questions - Free PDF Download

In terms of physics, chapter 3 on current electricity is both crucial and fascinating. As a result, it is crucial for the pupils to have current electricity class 12 vital questions prepared. This will enable students to fully comprehend the chapter with clarity and precision.

These important questions can be downloaded from Vedantu where expert teachers curate the entire content by verifying it with the guidelines and patterns followed by the CBSE board . Students can excel in this chapter and score better marks by following the study materials containing the physics chapter 3 class 12 important questions . It will also help the students to create notes from the chapter based on the relevant questions. 

Download CBSE Class 12 Physics Important Questions 2024-25 PDF

Also, check CBSE Class 12 Physics Important Questions for other chapters:

CBSE Class 12 Physics Important Questions
Sl.No	Chapter No	Chapter Name
1	Chapter 1
2	Chapter 2
3	Chapter 3	Current Electricity
4	Chapter 4
5	Chapter 5
6	Chapter 6
7	Chapter 7
8	Chapter 8
9	Chapter 9
10	Chapter 10
11	Chapter 11
12	Chapter 12
13	Chapter 13
14	Chapter 14
15	Chapter 15

Related Chapters

Study Important Questions for Class 12 Physics Chapter 3 - Current Electricity

Very Short Answer Questions: (1 Marks)

1. If the temperature of a good conductor decreases, how does the relaxation time of electrons in the conductor change? 

Ans: It is known that,  

$\rho =\frac{m}{n{{e}^{2}}\tau }$ 

Therefore, if the temperature of a good conductor decreases, collision decreases and thus the relaxation time of electrons increases which in turn decreases the resistivity. 

2. If potential difference $V$ applied across a conductor is increased to $2V$, how will the drift velocity of the electron change?

Ans: It is known that,

${{V}_{d}}=\frac{eE\tau }{m}=\frac{eV\tau }{lm}$

When the potential difference across a conductor is doubled, the drift velocity of the electron gets doubled.

3. What is the value of current $I$ at $O$ in the adjoining circuit?

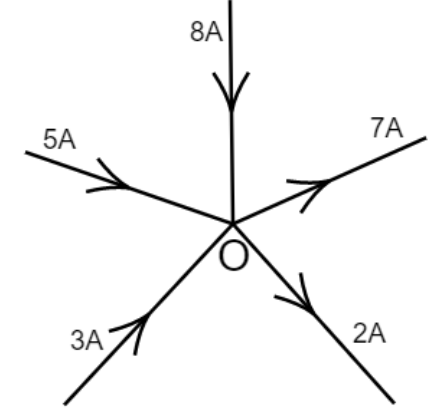
Ans: Total current at O is given by,

$i=5+3-2-7+8$ 

$\Rightarrow i=16-9$

$\Rightarrow i=7A$

Therefore, the current $I$ at $O$is $i=7A$.

4. State one condition for maximum current to be drawn from the cell?

$I=\frac{E}{R+r}$

To find maximum current, internal resistance must be zero.

5. Resistivities of copper, silver and manganin are $1.7\times {{10}^{-8}}m$ , $1.0\times {{10}^{-8}}m$ and $44\times {{10}^{-8}}m$ respectively which of these is the best conductor?

Ans: The resistance is directly proportional to specific resistance (resistivity), when length and area of cross-section is made constant.$R=\frac{\rho l}{A}$

Hence, silver is the best conductor as its specific resistance is less.

6. Draw the graph showing the variation of conductivity with temperature for a metallic conductor? 

Ans: The conductivity for a metallic conductor decreases with the increase in temperature.   

7. If a wire is stretched to double its length, what will be its new resistivity? 

Ans: There will be no change in resistivity because resistivity depends only on the nature of the material. 

8. Name any one material having a small value of temperature coefficient of resistance. Write one use of this material?

Ans: Material having a small value of temperature coefficient of resistance is Nichrome. It is an alloy used for making standard resistance coil. 

9. Two wires $A$ and $B$ are of the same metal and of same length have their areas of cross section in the ratio $2:1$ if the same potential difference is applied across each wire in turn, what will be the ratio of current flowing in $A$ & $B$ ?

$I=\frac{V}{R}$ and $R<\frac{1}{A}$

When area of cross section is $2:1$ then the ratio of current flowing in $A$ & $B$ will be $1:2$.

Very Short Answer Questions: (2 Marks)

1. Two electric bulbs A and B are marked \[\mathbf{220V}\],$40W$ and $220V$$60W$ respectively. Which one has a higher resistance?

$R=\frac{{{V}^{2}}}{p}$ 

For Bulb $A$, ${{R}_{1}}=\frac{{{(220)}^{2}}}{40}=1210\Omega $ 

For Bulb $B$, ${{R}_{2}}=\frac{{{(220)}^{2}}}{60}=806.67\Omega $ 

Therefore, bulb $A$ has higher resistance.

2. A Carbon resistor has three strips of red colour and a gold strip. What is the value of the resistor? What is its tolerance? 

Ans: It is given that,

\[R\text{ }R\text{ }R\text{ }Gold=(22\times {{10}^{2}})\pm 5%\]

Therefore, value of the resistor$=2200\Omega $ and tolerance$=\pm 5%$

3. Determine the voltage drop across the resistor ${{R}_{1}}$ in the circuit given below with \[\mathbf{E}=\text{ }\mathbf{60V}\], ${{R}_{1}}=18\Omega $, ${{R}_{2}}=10\Omega $, ${{R}_{3}}=5\Omega $ and ${{R}_{4}}=10\Omega $.

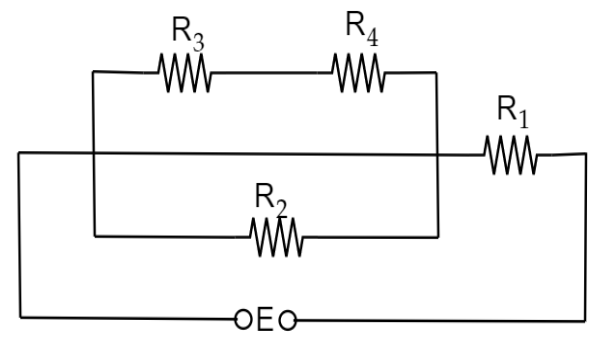
Ans: In the given circuit,

${{R}_{3}}\And {{R}_{4}}$ are in series

$R'={{R}_{3}}+{{R}_{4}}$

\[\Rightarrow R'=5+10=15\Omega \]

Then, $R'\And {{R}_{2}}$ are in parallel

$\frac{1}{R''}=\frac{1}{{{R}^{1}}}+\frac{1}{{{R}_{2}}}$ 

$\Rightarrow \frac{1}{R''}=\frac{1}{15}+\frac{1}{10}$

$\Rightarrow \frac{1}{R''}=\frac{4+6}{60}=\frac{10}{60}$

$\Rightarrow R''=\frac{60}{10}=6\Omega $

Then ${{R}_{1}},R''$ are series

${{R}_{net}}=R''+{{R}_{1}}$ 

$\Rightarrow {{R}_{net}}=6+18=24\Omega $ 

Current: $I=\frac{V}{R}=\frac{60}{24}\text{ampere}$ 

Voltage drop across ${{R}_{1}}=I{{R}_{1}}=\frac{60}{24}\times 18$ 

$\Rightarrow {{V}_{1}}=45v\text{olts}$

Therefore, voltage drop across the resistor ${{R}_{1}}$ is $45volts$.

4. Two heated wires of the same dimensions are first connected in series and then it’s parallel to a source of supply. What will be the ratio of heat produced in the two cases? 

$\text{ }H={{I}^{2}}\operatorname{R}t$    $\left( I=\frac{V}{R} \right)$

$\Rightarrow H=\frac{{{V}^{2}}}{{{R}^{2}}}\times R\times t$ 

$\Rightarrow H=\frac{{{V}^{2}}}{R}t$

$\Rightarrow H\propto \frac{1}{R}$

\[\frac{\text{ }{{\text{H}}_{\text{series}}}\text{ }}{\text{ }{{\text{H}}_{\text{parallel}}}\text{ }}=\frac{\text{ }{{\text{R}}_{\text{parallel}}}\text{ }}{\text{ }{{\text{R}}_{\text{series}}}\text{ }}\]

\[\Rightarrow \frac{\frac{1}{\left( \frac{1}{R}+\frac{1}{R} \right)}}{R+R}=\frac{R/2}{2R}=\frac{R}{2R\times 2}=\frac{1}{4}\]

Therefore, the ratio of heat produced is$1:4$.

5. V.i graph for a metallic wire at two different temperatures is shown in the figure. Which of these two temperatures is higher and why? 

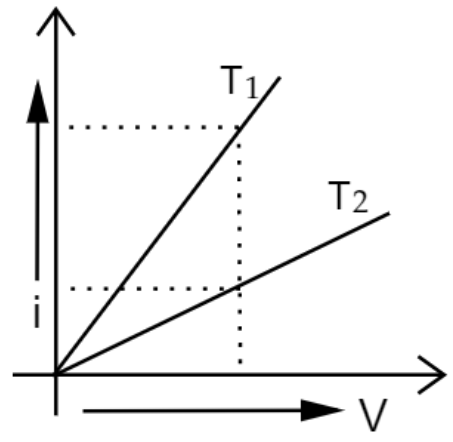
Ans : From the graph: 

$Slope=\frac{i}{V}$

It is known that, $\frac{i}{V}=\frac{1}{R}$

It means that the smaller the slope, the larger the resistance.

As the resistance increases, temperature also increases.

Temperature of ${{T}_{2}}$ is higher because ${{T}_{2}}$ has a small slope.

6. A set of n-identical resistors, each of resistance $R$ ohm when connected in series have an effective resistance of $X$ ohm and when the resistors are connected in parallel the effective resistance is $Y$ ohm. Find the relation between $R$,$X$ and $Y$? 

n-resistors connected in series 

$\Rightarrow X=nR$    ……$(1)$

n-resistors connected in parallel

$\Rightarrow Y=\frac{R}{n}$     ……$(2)$

Multiply equations $(1)$ and $(2)$

$\Rightarrow XY=nR\times \frac{R}{n}$ 

$\Rightarrow XY={{R}^{2}}$

$\Rightarrow R=\sqrt{XY}$

7. Show that the resistance of a conductor is given by $R=\frac{ml}{n{{e}^{2}}\tau A}$.

Ans: Consider a conductor of length $l$  and area $A$.

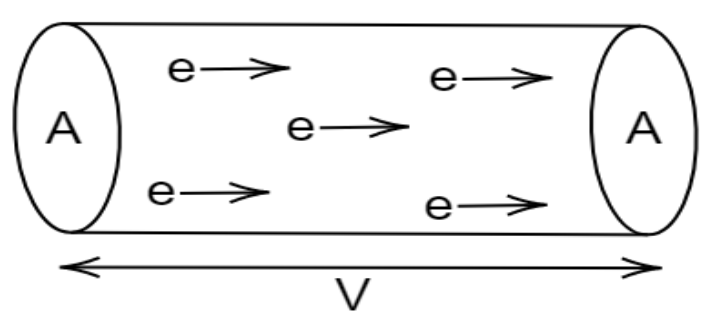
If electric field $E$ is applied across the conductor, 

The drift velocity of electrons ${{v}_{d}}$ is given by:

${{v}_{d}}=\frac{eE}{m}\tau $

It is known that, $I=neA{{v}_{d}}$

$\Rightarrow \text{I}=\operatorname{neA}\left( \frac{eE}{m}\tau  \right)$; $E=\frac{V}{l}$

$\Rightarrow \text{I}=\operatorname{neA}\left( \frac{eV}{ml}\tau  \right)$

$\Rightarrow \frac{V}{I}=\frac{ml}{n{{e}^{2}}A\tau }$;$\frac{V}{I}=R$

$\Rightarrow R=\frac{m}{n{{e}^{2}}\tau }\left( \frac{l}{A} \right)$

$\Rightarrow \text{R}=\frac{ml}{n{{e}^{2}}\tau A}$

Therefore, the resistance of the conductor, $\text{R}=\frac{ml}{n{{e}^{2}}\tau A}$

8. Figure shows a piece of pure semiconductor $S$ in series with a variable resistor $R$ and a source of constant voltage $V$. Would you increase and decrease the value of $R$ to keep the reading of ammeter $(A)$ constant, when semiconductor $S$ is heated? Give reasons.

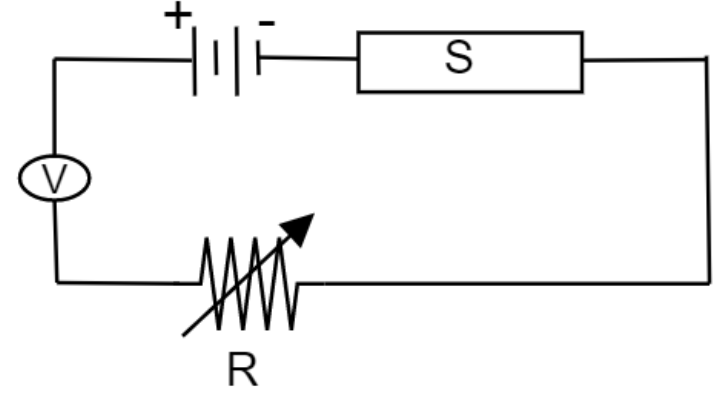
Ans: On increasing the temperature, resistance of the semiconductor decreases. So, to increase the temperature, the semiconductor $S$ is heated.

To maintain constant current in ammeter, total resistance of the circuit should remain unchanged.

Therefore, the value of $R$ has to be increased.

9. Why is constantan or manganin used for making standard resistors?

Ans: Constantan or manganin are alloys of high resistivity and low temperature coefficient of resistance. So, these are used for making standard resistors.

10. What are ohmic and non-ohmic resistors? Give one example of each?

Ans: Ohmic resistors are resistors which obey ohm’s law. Eg: Metals 

Non-ohmic resistors are resistors which do not obey ohm’s law. Eg: semiconductor diode, transistor etc.

11. The storage battery of a car has an emf of $12V$. If the internal resistance of the battery is $0.4\Omega $, what is the maximum current that can be drawn from the battery?

Emf of the battery, \[E=\text{ }12\text{ }V~\] 

Internal resistance of the battery\[,r=\text{ }0.4\text{ }\Omega ~\] 

It is known that,

To get maximum current from that battery:

$\Rightarrow E-iR=0$

$\Rightarrow E=iR$

$\Rightarrow i=\frac{E}{R}=\frac{12}{0.4}$

$\Rightarrow i=30A$

Therefore, the maximum current drawn from the given battery,$i=30A$.

12. In a potentiometer arrangement, a cell of emf $1.25V$ gives a balance point at $35.0cm$ length of the wire. If the cell is replaced by another cell and the balance point shifts to $63.0cm$, what is the emf of the second cell?

Emf of the cell, ${{E}_{1}}=1.25V$  

Balance point of the potentiometer, ${{l}_{1}}=35cm$ 

The cell is replaced by another cell of emf  ${{E}_{2}}$ 

New balance point of the potentiometer,  ${{l}_{2}}=63cm$ 

Balance condition of potentiometer: $\frac{{{E}_{1}}}{{{E}_{2}}}=\frac{{{l}_{1}}}{{{l}_{2}}}$ 

$\Rightarrow {{E}_{2}}={{E}_{1}}\times \frac{{{l}_{2}}}{{{l}_{1}}}$

$\Rightarrow {{E}_{2}}=1.25\times \frac{63}{35}=2.25~\text{V}$

Hence, the emf of the second cell $2.25V$.

13. What conclusion can you draw from the following observations on a resistor made of alloy manganin?

Current	Voltage	Current	Voltage
0.2	3.94	3	59.2
0.4	7.87	4	78.8
0.6	11.8	5	98.6
0.8	15.7	6	118.5
1.0	19.7	7	138.2
2.0	39.7	8	158.0

Ans: It can be concluded that the ratio of voltage with current is constant and is equal to $19.7$ i.e., it obeys Ohm’s law. Therefore, manganin is an ohmic conductor.

From Ohm’s law, $\frac{V}{I}=R$ i.e., the ratio of voltage with current is the resistance of the conductor. Thus, the resistance of manganin is $19.7\Omega $.

Short Answer Questions: (3 Marks)

1. What happens to the resistance of the wire when its length is increased to twice its original length?

$R=\rho \frac{l}{A}=\rho (\frac{l}{\pi {{r}^{2}}})$ 

It is given that, 

New length of the wire, $l'=2l$ 

Let, the new radius be $r'$.

As volume of the wire remains the same: $\pi {{\text{r}}^{2}}\ell =\pi {{(r')}^{2}}\ell '$ 

$\Rightarrow \pi {{r}^{2}}l=\pi {{(r')}^{2}}2\ell $

\[\Rightarrow {{(r')}^{2}}=\frac{{{r}^{2}}}{2}\]

New resistance, $R'=\rho \left( \frac{l'}{\pi r{{'}^{2}}} \right)$

$\Rightarrow R'=\rho \frac{2l}{\pi \left( \frac{{{r}^{2}}}{2} \right)}$

$\Rightarrow R'=\rho \left( \frac{4l}{\pi {{r}^{2}}} \right)$

$\Rightarrow R'=4\rho \left( \frac{l}{\pi {{r}^{2}}} \right)$

$\Rightarrow R'=4R$

Hence, new resistance becomes four times the original resistance.

2. Mark the direction of current in the circuit as per Kirchhoff’s first rule. What is the value of the main current in the shown network? 

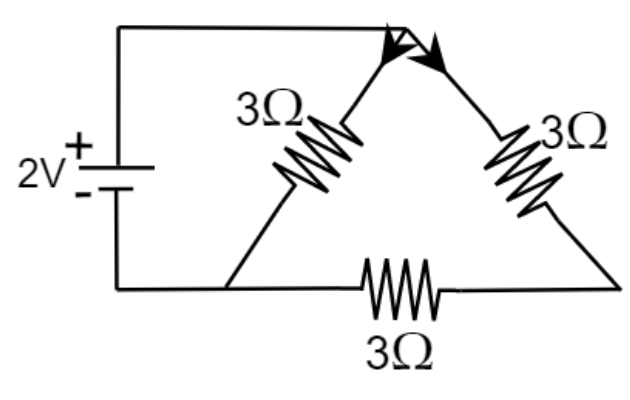
Ans: In the given figure,

${{R}_{2}}$ and ${{R}_{3}}$ are in series

$\Rightarrow R=3+3=6\Omega $ 

$R$ and ${{R}_{1}}$ are in parallel

$\frac{1}{{{R}_{net}}}=\frac{1}{R}+\frac{1}{{{R}_{1}}}$ 

$\Rightarrow \frac{1}{{{R}_{net}}}=\frac{1}{6}+\frac{1}{3}=\frac{3+6}{18}$

$\Rightarrow {{R}_{net}}=\frac{18}{9}=2\Omega $

Net current: $I=\frac{V}{R}$

$I=\frac{2}{2}=1A$ 

Therefore, net current is $1A$.

(a) Why do we prefer a potentiometer to measure the emf of a cell rather than a voltmeter?

Ans: Potentiometer is based on a null method i.e.; it draws no current from the cell. Emf of a cell is equal to the terminal potential difference when no current flows from the cell. Therefore, a potentiometer is preferred to measure the emf of a cell rather than a voltmeter.

(b) With suitable circuit diagram, show how emfs of 2 cells can be compared using a potentiometer?

Ans: Potentiometer works on the principle that when a constant current flows through the wire of uniform area of cross-section then

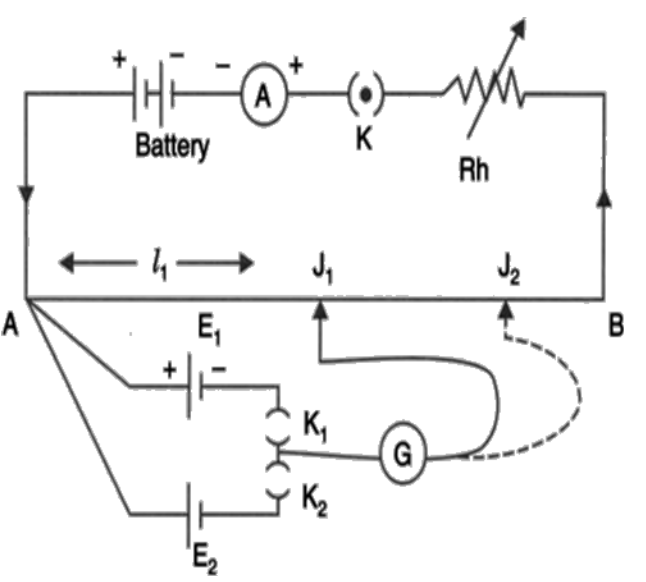
Condition: 

Close the switch 1 and 3 such that ${{E}_{1}}$comes in the circuit.

Potential Difference across AJ is ${{V}_{AJ}}<{{I}_{1}}$ 

It is known that, no current flows between ${{E}_{1}}$  and  ${{V}_{AJ}}$ 

$\Rightarrow {{V}_{AJ}}={{E}_{1}}$

${{E}_{1}}<{{l}_{1}}$

$\Rightarrow {{E}_{1}}=k{{l}_{1}}$    ……$(1)$

Condition:  

Close the switch 2 and 3 such that ${{E}_{2}}$ comes in the circuit and balance point is obtained of ${{J}_{1}}$ .

Since no current flows between $A{{J}_{1}}$ and ${{E}_{2}}$

$\Rightarrow {{V}_{A{{J}_{1}}}}={{E}_{2}}$

${{E}_{2}}<{{l}_{2}}$

$\Rightarrow {{E}_{2}}=k{{l}_{2}}$  ……$(2)$

$\Rightarrow {{V}_{AJ}}={{E}_{2}}=k{{l}_{2}}$  

Dividing equations $(1)$ and $(2)$

$\Rightarrow \frac{{{E}_{1}}}{{{E}_{2}}}=\frac{k{{l}_{1}}}{k{{l}_{2}}}$ 

$\Rightarrow \frac{{{E}_{1}}}{{{E}_{2}}}=\frac{{{l}_{1}}}{{{l}_{2}}}$

Therefore, $\frac{{{E}_{1}}}{{{E}_{2}}}=\frac{{{l}_{1}}}{{{l}_{2}}}$.

4. Potential difference $V$ is applied across the ends of copper wire of length $l$ and diameter $D$. What is the effect on drift velocity of electrons if

(a) \[V\] is doubled 

${{V}_{d}}=\frac{I}{neA}=\frac{V}{R(neA)}$

$\Rightarrow {{V}_{d}}=\frac{V}{\left( \rho \frac{\ell }{A} \right)(neA)}=\frac{V}{ne\rho \ell }$

Therefore, when $V$ is doubled, drift velocity gets doubled.

(b) $\ell $ is doubled

Ans:   It is known that,

Therefore, when $l$ is doubled, drift velocity gets halved.

(c) D is doubled 

Therefore, as $V$ is independent of $D$, drift velocity remains unchanged.

5. What is drift velocity? Derive expression for drift velocity of electrons in a good conductor in terms of relaxation time of electrons? 

Ans: Drift velocity is defined as the average velocity with which free electrons get drifted in a direction opposite to that of an electric field.

Let, $m$ be the mass of the electron and $e$ be the charge of electrons.

When electric field $E$ is applied, acceleration acquired by the electron is $a=\frac{eE}{m}$.

From, first equation of motion: $v=u+at$ 

Average initial velocity, $u=OV={{v}_{d}}$

Relaxation time, $t=\tau $

$\Rightarrow {{v}_{d}}=a\tau $ 

$\Rightarrow {{v}_{d}}=\frac{eE\tau }{m}$

$e$ is the change on electron 

$E$ is the electric field intensity 

$\tau $  is the relaxation time 

$m$ is the mass of electron

Therefore, the expression for drift velocity of electrons in a good conductor in terms of relaxation time of electrons is ${{v}_{d}}=\frac{eE\tau }{m}$.

6. The potentiometer circuit shown, the balance (null) point is at $X$. State with reason, where the balance point will be shifted when 

(Image will be uploaded soon)

(a) Resistance R is increased, keeping all parameters unchanged. 

Ans: If resistance $R$ is increased, then the current through potentiometer wire $AB$ will decrease. Therefore, the potential difference across $A$ will decrease and balance point shifts towards $B$. 

(b) Resistance S is increased, keeping R constant.

Ans:  If resistance $S$ is increased, then the terminal potential difference of the battery will decrease. Therefore, the balance point will be obtained at a smaller length and thus shifts towards $A$. 

(c) Cell P is replaced by another cell whose emf is lower than that of cell Q.

Ans: If cell $P$ is replaced by another cell whose emf is lower than that of cell Q, then the potential difference across $AB$ will be less than that of emf Q. Therefore, the balance point will not be obtained.

(a) Using the principle of Wheatstone bridge describes the method to determine the specific resistance of a wire in the laboratory. Draw the circuit diagram and write the formula used? 

Ans: Firstly, close the Key $(k)$ and move the jockey along the wire till a certain point $B$ is reached where the galvanometer shows no deflection. Therefore, the bridge is said to be balanced. 

If $Rcm$is the resistance per cm length of the wire then.

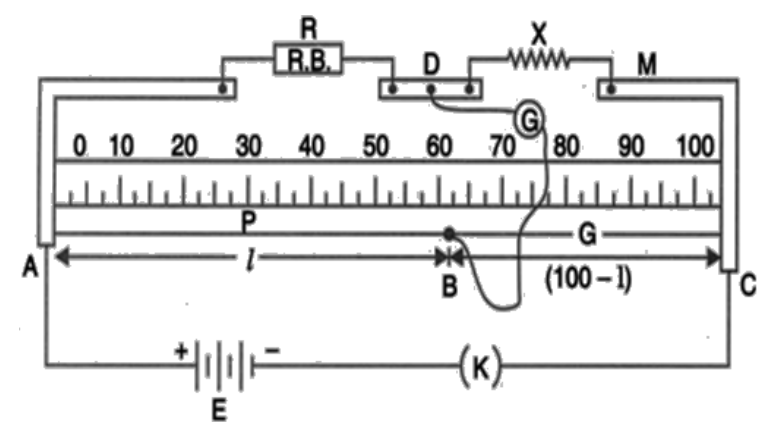
$\frac{R}{X}=\frac{lRcm}{(100-l)Rcm}$ 

$X=\frac{R(100-l)}{l}$

$P=\frac{XA}{l'}$, $l'$is the length if the wire

$P=\frac{R(100-l)A}{l(l')}$ 

Therefore, the point is located at, $P=\frac{R(100-l)A}{l(l')}$.

(b) In a Wheatstone bridge experiment, a student by mistake connects key $(k)$ in place of galvanometer and galvanometer $(G)$ in place of Key $(K)$. What will be the change in the deflection of the bridge? 

Ans: If the bridge is balanced, then there will be no current in the key. Therefore, constant current flows through the galvanometer and thus there will be no change in deflection of the bridge.

8. Two primary cells of emf ${{E}_{1}}$ and ${{E}_{2}}$  are connected to the potentiometer wire $AB$ as shown in the figure if the balancing length for the two combinations of the cells are $250cm$ and $400cm$. Find the ratio of ${{E}_{1}}$ and ${{E}_{2}}$ .

  (Image will be uploaded soon)

Ans: It is known that,$E=kl$

$\text{ }{{E}_{1}}-{{E}_{2}}=K\times 250$   ……$(1)$

${{E}_{1}}+{{E}_{2}}=K\times 400$   ……$(2)$

Adding equations $(1)$ and $(2)$

$2{{E}_{1}}=250~K+400K$

\[2{{E}_{1}}=250~K+400\] 

$2{{E}_{1}}=650K$ 

${{E}_{1}}=\frac{650}{2}K$

${{E}_{1}}=325K$

Substituting ${{E}_{1}}=325K$ in equation$(1)$

$\text{ 325K}-{{E}_{2}}=K\times 250$

${{E}_{2}}=325K-250K$

${{E}_{2}}=75K$

Divide ${{E}_{1}}$ and ${{E}_{2}}$

\[\Rightarrow \frac{{{E}_{1}}}{{{E}_{2}}}=\frac{325K}{75K}\]

\[\Rightarrow \frac{{{E}_{1}}}{{{E}_{2}}}=4.33\]

The ratio of ${{E}_{1}}$ and ${{E}_{2}}$ is $4.33$.

9. Explain with the help of a circuit diagram, how the value of an unknown resistance can be determined using a Wheatstone bridge? 

Ans: In this case \[P,\text{ }Q,\text{ }R\] are known resistance and $X$ is an unknown resistance.

Applying Kirchhoff’s law for closed path \[ABDA\]. 

${{I}_{1}}P+{{I}_{3}}G-{{I}_{2}}R=0$    ……$(1)$

For closed path \[~BCDB\]

$({{I}_{1}}-{{I}_{3}})Q-({{I}_{2}}+{{I}_{3}})X-{{I}_{3}}G=0$   …… $(2)$

The bridge is said to be balanced when no current flows through the galvanometer. 

$\Rightarrow Ig=0$ $({{I}_{g}}={{I}_{3}})$

Equation $(1)\Rightarrow {{I}_{1}}P={{I}_{2}}R$

\[\Rightarrow \frac{{{I}_{1}}}{{{I}_{2}}}=\frac{R}{P}\]      ……$(3)$

Equation $(2)\Rightarrow {{I}_{1}}Q={{I}_{2}}X$

\[\Rightarrow \frac{{{I}_{1}}}{{{I}_{2}}}=\frac{X}{Q}\]      ……$(4)$

Equating equations $(3)$and $(4)$

$\frac{R}{P}=\frac{X}{Q}\Rightarrow X=\frac{RQ}{P}$ 

10. Find the current drawn from a cell of emf  $1V$ and internal resistance \[\frac{2}{3}\Omega \] connected to the network shown in the figure. $E=1V$ , $r=\frac{2}{3}\Omega $.

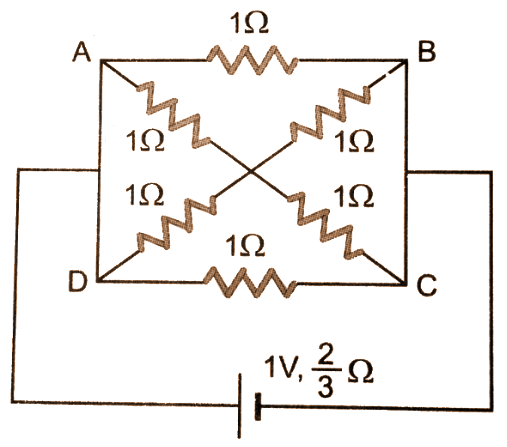
Ans: The circuit can be redrawn as follows:

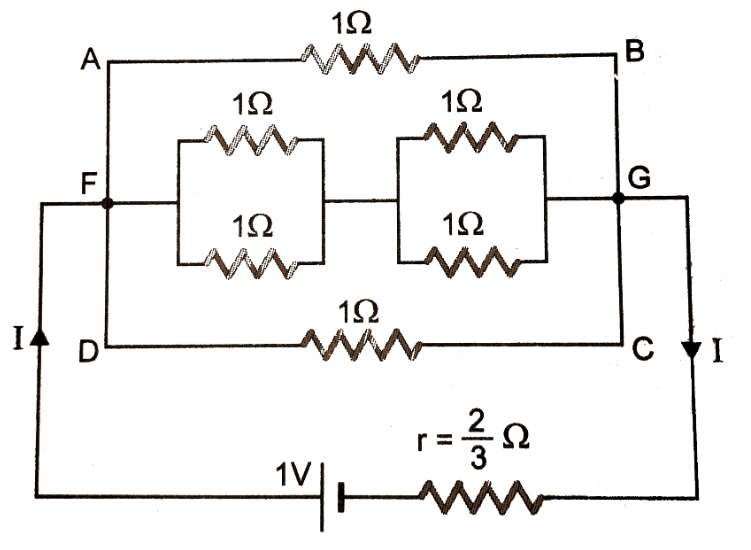
$\Rightarrow \text{ }\frac{I}{{{R}_{1}}}=\frac{1}{1}+\frac{1}{1}$ 

$\Rightarrow \frac{1}{{{R}_{1}}}=2$

$\Rightarrow {{R}_{1}}=\frac{1}{2}$

$\Rightarrow {{R}_{2}}=\frac{1}{2}$

$R={{R}_{1}}+{{R}_{2}}$

$\Rightarrow R=\frac{1}{2}+\frac{1}{2}$

$\Rightarrow R=1\Omega $

Here, \[1\Omega ,1\Omega \] and \[1\Omega \] are in parallel.

$\Rightarrow \frac{1}{{{R}_{net}}}=\frac{1}{1}+\frac{1}{1}+\frac{1}{1}$

$\Rightarrow \frac{1}{Rnet}=\frac{3}{1}$

$\Rightarrow \text{ Rnet }=\frac{3}{1}\Omega ~$

$\text{I}=\frac{E}{R+r}=\frac{1}{\frac{3}{1}+\frac{3}{3}}=\frac{3}{3}=1A$

$\Rightarrow I=1A$

Current drawn from a cell of emf  $1V$ is $I=1A$.

(a) State and explain Kirchhoff’s law? 

Ans: Kirchhoff’s first law: It states that the algebraic sum of currents at a junction in an electrical circuit is always zero. 

$\Rightarrow {{i}_{1}}-{{i}_{2}}+{{i}_{3}}-{{i}_{4}}-{{i}_{5}}-{{i}_{6}}=0$ 

Kirchhoff’s second law: It states that in any closed part of an electrical circuit, the algebraic sum of emf is equal to the algebraic sum of the products of resistances and current flowing through them. Eg: For closed path \[ABCA~\]

${{R}_{1}}{{I}_{1}}-{{R}_{3}}{{I}_{3}}+{{R}_{2}}{{I}_{2}}-{{E}_{1}}+{{E}_{2}}=0$ 

${{E}_{1}}-{{E}_{2}}={{R}_{1}}{{I}_{1}}-{{R}_{3}}{{I}_{3}}+{{R}_{2}}{{I}_{2}}$

(b) In the network shown, find the values of current ${{I}_{1}},{{I}_{2}},{{I}_{3}}$.

Ans: Applying Kirchhoff’s law at point D

${{I}_{1}}={{I}_{2}}+{{I}_{3}}$      ……$(1)$

For closed path \[ABDA\]

$2{{I}_{1}}+1-2+{{I}_{1}}+3{{I}_{2}}=0$ 

$3{{I}_{1}}+3{{I}_{2}}-1=0$

$3{{I}_{1}}+3{{I}_{2}}=1$       ……$(2)$

For closed path \[DBCD\]

$3{{I}_{2}}-1-{{I}_{3}}-3{{I}_{3}}+3=0$

$3{{I}_{2}}-4{{I}_{3}}+2=0$

$4{{I}_{3}}-3{{I}_{2}}-2=0$

$4{{I}_{3}}-3{{I}_{2}}=2$     ……$(3)$

Substituting $(1)$ in $(2)$

$(2)\Rightarrow 3({{I}_{2}}+{{I}_{3}})+3{{I}_{2}}=1$

$(2)\Rightarrow 6{{I}_{2}}+3{{I}_{3}}=1$

$(3)\Rightarrow 4{{I}_{3}}-3{{I}_{2}}=2$

$2\times (3)\Rightarrow 8{{I}_{3}}-6{{I}_{2}}=4$       ……$(4)$

$(3)+(4)=11{{I}_{3}}=5$

$\Rightarrow {{I}_{3}}=\frac{5}{11}A$

Substituting ${{I}_{3}}$ in equation $(3)$

$\Rightarrow 4(\frac{5}{11})-3{{I}_{2}}=2$

$\Rightarrow \frac{20}{11}-3{{I}_{2}}=2$

$\Rightarrow \frac{20}{11}-2=3{{I}_{2}}$

$\Rightarrow \frac{-2}{11}=3{{I}_{2}}$

$\Rightarrow {{I}_{2}}=\frac{-2}{33}A$

Substituting ${{I}_{2}}$,${{I}_{3}}$ in equation $(1)$

${{I}_{1}}=\frac{-2}{33}+\frac{5}{11}$

$\Rightarrow {{I}_{1}}=\frac{13}{33}A$

Currents are ${{I}_{1}}=\frac{13}{33}A$, ${{I}_{2}}=\frac{-2}{33}A$ and ${{I}_{3}}=\frac{5}{11}A$.

12. The variation of resistance of a metallic conductor with temperature is given in figure.

(a) Calculate the temperature coefficient of resistance from the graph.

Temperature coefficient of Resistance:$\alpha =\frac{R-{{R}_{0}}}{{{R}_{0}}\theta }$ 

where $R$ is the resistance of the conductor and $\theta $ is the temperature corresponding to point A. 

(b) State why the resistance of the conductor increases with the rise in temperature. 

Ans: It is known that, 

$R=\rho \frac{l}{A}=\frac{m}{n{{e}^{2}}\tau }(\frac{t}{A})$

where $\rho $is the resistivity.

When temperature increases, the number of collisions increases, average relaxation time decreases, therefore resistance increases. 

13. A circle ring having negligible resistance is used to connect four resistors of resistances \[\mathbf{6R},\mathbf{6R},\mathbf{6R}\] and $R$ as shown in the figure. Find the equivalent resistance between points A & B.

Ans: The given circuit can be redrawn as follows:

\[6R,6R\] and $6R$ are in parallel.

$\Rightarrow \frac{1}{{{R}_{s}}}=\frac{1}{6R}+\frac{1}{6R}+\frac{1}{6R}$ 

$\Rightarrow \frac{1}{{{R}_{s}}}=\frac{3}{6R}$

$\Rightarrow {{R}_{S}}=\frac{6R}{3}=2R$ 

${{R}_{S}}=2R$ and $R$ are in series.

${{R}_{net}}=2R+R$ 

${{R}_{net}}=3R$

14. A battery of emf $E$ and internal resistance $r$ sends a current, ${{I}_{1}},{{I}_{2}}$ when connected to an external resistance of ${{R}_{1}},{{R}_{2}}$  respectively. Find the emf. and internal resistance of the battery.

$E$ is the emf of a battery

$r$ is the internal resistance which sends currents ${{I}_{1}},{{I}_{2}}$

${{R}_{1}},{{R}_{2}}$ are external resistances

Current ${{I}_{1}}$ can be written as: ${{I}_{1}}=\frac{E}{{{R}_{1}}+r}$

$E={{I}_{1}}({{R}_{1}}+r)$  ……$(1)$

Similarly, $E={{I}_{2}}({{R}_{2}}+r)$ ……$(2)$

From equations $(1)$ and $(2)$

$\Rightarrow {{I}_{1}}({{R}_{1}}+r)={{I}_{2}}({{R}_{2}}+r)$

$\Rightarrow {{I}_{2}}r-{{I}_{1}}r={{I}_{1}}{{R}_{1}}-{{I}_{2}}{{R}_{2}}$

$\Rightarrow r\left( {{I}_{2}}-{{I}_{1}} \right)={{I}_{1}}{{R}_{1}}-{{I}_{2}}{{R}_{2}}$

${*{35}{l}} \Rightarrow r=\frac{{{I}_{1}}{{R}_{1}}-{{I}_{2}}{{R}_{2}}}{{{I}_{2}}-{{I}_{1}}}$

Emf of the battery,$E$

$\Rightarrow E={{I}_{1}}\left( {{R}_{1}}+r \right)$

$\Rightarrow E={{I}_{1}}\left[ {{R}_{1}}+\frac{{{\text{I}}_{1}}{{\text{R}}_{1}}-{{\text{I}}_{2}}{{\text{R}}_{2}}}{{{\text{I}}_{2}}-{{\text{I}}_{1}}} \right]$

$\Rightarrow E={{I}_{1}}\left[ \frac{{{\text{I}}_{2}}{{\text{R}}_{1}}-{{\text{I}}_{1}}{{R}_{1}}+{{I}_{1}}{{\text{R}}_{1}}-{{\text{I}}_{2}}{{\text{R}}_{2}}}{{{\text{I}}_{2}}-{{\text{I}}_{1}}} \right]$

$\Rightarrow E=\frac{{{I}_{1}}{{I}_{2}}\left( {{\text{R}}_{1}}-{{\text{R}}_{2}} \right)}{{{\text{I}}_{2}}-{{\text{I}}_{1}}}$

Therefore, emf and internal resistance of the battery are $E=\frac{{{I}_{1}}{{I}_{2}}\left( {{\text{R}}_{1}}-{{\text{R}}_{2}} \right)}{{{\text{I}}_{2}}-{{\text{I}}_{1}}}$ 

${*{35}{l}} r=\frac{{{I}_{1}}{{R}_{1}}-{{I}_{2}}{{R}_{2}}}{{{I}_{2}}-{{I}_{1}}}$

15. Find the value of unknown resistance $X$ in the circuit shown in the figure if no current flows through the section AO. Also calculate the current drawn by the circuit from the battery of emf. $6V$ and negligible internal resistance. 

Ans: It is given that no current flows through AO then the circuit is said to be a balanced Wheatstone bridge. 

$\Rightarrow \frac{2}{4}=\frac{3}{X}$ 

$\Rightarrow X=\frac{12}{2}=6$

$\Rightarrow X=6\Omega $

In branch AO, \[I=0\]

Resistance of $10\Omega $ between A and O is ineffective and the circuit is reduced to:

\[2\Omega \] and \[4\Omega \] are in series; \[3\Omega \] and \[6\Omega \] are in series

6Ω and 9Ω are in parallel.

$\Rightarrow \frac{1}{{{R}_{P}}}=\frac{1}{6}+\frac{1}{9}=\frac{9+6}{54}=\frac{15}{54}$ 

$\Rightarrow {{R}_{P}}=\frac{54}{15}\Omega $

${{R}_{P}}$ and \[2.4\Omega \] are in series

$\Rightarrow {{R}_{eff}}=2.4+\frac{54}{15}$ 

$\Rightarrow {{R}_{eff}}=\frac{24}{10}+\frac{54}{15}=\frac{360+540}{150}=\frac{900}{150}$

$\Rightarrow {{R}_{eff}}=6\Omega $

Current: $I=\frac{V}{R}=\frac{6}{6}=1$

Therefore, the unknown resistance $X=6\Omega $ and current drawn by the circuit from the battery is $I=1A$.

(a) Obtain ohm’s law from the expression for electrical conductivity.

$I=neA{{v}_{d}}$

$J=\frac{I}{A}=ne{{v}_{d}}$

${{V}_{d}}=\frac{eE\tau }{m}$

$\Rightarrow J=\frac{n{{e}^{2}}E\tau }{m}$ ; $J=\sigma E$

$\sigma =\frac{J}{E}=\frac{n{{e}^{2}}\tau }{m}$

Let $l$ and $A$ be the length and area of the wire.

$\Rightarrow I=\frac{n{{e}^{2}}E\tau }{m}\times A$ ; $(E=\frac{V}{l})$

$\Rightarrow I=\frac{n{{e}^{2}}V\tau }{ml}A$ 

$\Rightarrow V=\left( \frac{m}{n{{e}^{2}}\tau } \right)\left( \frac{l}{A} \right)I$ 

$\therefore V=RI$

$\Rightarrow R=\rho \frac{l}{A}$ where, $\rho =\frac{m}{n{{e}^{2}}\tau }$(Specific resistance of a wire)

(b) A cylindrical wire is stretched to increase its length by $10%$ calculate the percentage increase in resistance?

Ans:  It is given that; the length of cylindrical wire is stretched to increase its length by $10%$.

Let, the original length be $l$ and the new length be $l'$.

$\Rightarrow l'=l+\frac{10}{100}l$ 

$\Rightarrow l'=1.1l$

$\Rightarrow \frac{l'}{l}=1.1$

As the volume of the wire remains the same

$\frac{A'}{A}=\frac{l}{l'}$

It is known that, $\text{R=}\rho \frac{l}{A}$

$R'=\rho \frac{l'}{A'}$

$\Rightarrow \frac{R'}{R}=\frac{l'}{A'}\times \frac{A}{l}$

\[\Rightarrow \frac{R'}{R}=\frac{l'}{l}\times \frac{l'}{l}={{\left( \frac{l'}{l} \right)}^{2}}\]

$\Rightarrow \frac{R'}{R}={{(1.1)}^{2}}=1.21$

Thus, the percentage increase in Resistance is $\frac{R'-R}{R}\times 100=21%$.

17. The current $I$ flows through a wire of radius $r$ and the free electron drift with a velocity ${{\upsilon }_{d}}$ what is the drift velocity of electrons through a wire of same material but having double the radius, when a current of $2I$ flows through it?

$\Rightarrow {{v}_{d}}=\frac{I}{neA}=\frac{I}{ne\pi {{r}^{2}}}$  ……$(1)$

If ${{v}_{d}}'$ is the drift velocity of electrons in the second wire

$vd'=\frac{I'}{nA'e}$ 

$\Rightarrow vd'=\frac{2I}{n4\pi {{r}^{2}}e}$

$\Rightarrow vd'=\frac{1}{2}(\frac{I}{n\pi {{r}^{2}}e})$   ……$(2)$

$\Rightarrow vd'=\frac{vd}{2}$ 

Therefore, the drift velocity gets reduced to half.

18. Three identical cells, each of emf. $2V$ and unknown internal resistance are connected in parallel. This combination is connected to a $5$ ohm resistor. If the terminal voltage across the cell is \[\mathbf{1}.\mathbf{5}\] volt. What is the internal resistance of each cell? Hence define the internal resistance of a cell? 

\[E=2V,\text{ }V=1.5V,\text{ }R=5\text{ }\Omega \]

Total internal resistance =  $\frac{r}{3}$ 

Internal resistance $r$ is equal to: $r=\left( \frac{E}{V}-1 \right)R$ 

$\Rightarrow \frac{r}{3}=\left( \frac{2}{1.5}-1 \right)5$

$\Rightarrow \frac{r}{3}=\left( \frac{2-1.5}{1.5} \right)5$

$\Rightarrow r=\left( \frac{0.5}{1.5} \right)15$

$\Rightarrow r=50ohm$

The resistance offered by the electrolyte of the cell, when the electric current flows through it, is called the internal resistance of a cell. In this case, internal resistance is equal to $r=50ohm$.

19. Using Kirchhoff’s law, determine the current ${{I}_{1}},{{I}_{2}},{{I}_{3}}$  for the network shown.

Ans : In the given figure, applying junction rule at point F

$\Rightarrow {{I}_{1}}={{I}_{2}}+{{I}_{3}}$    ……$(1)$

Loop rule for \[BAFCB\]

$\Rightarrow 2{{I}_{1}}+6{{I}_{2}}-24+27=0$ 

$\Rightarrow 2{{I}_{1}}+6{{I}_{2}}+3=0~$    …… $(2)$

Loop rule for FCDEF

$\Rightarrow 27+6{{I}_{2}}-4{{I}_{3}}=0$  …….$(3)$

Substituting ${{I}_{1}}$ in equation$(2)$

$(2)\Rightarrow 2({{I}_{2}}+{{I}_{3}})+6{{I}_{2}}+3=0~$

$(2)\Rightarrow 2{{I}_{3}}+8{{I}_{2}}+3=0$

$2\times (2)\Rightarrow 2(2{{I}_{3}}+8{{I}_{2}}+3)=0$

$2\times (2)\Rightarrow 4{{I}_{3}}+16{{I}_{2}}+6=0$   …….$(4)$

$(4)+(3)\Rightarrow 27+6+22{{I}_{2}}=0$

$\Rightarrow {{I}_{2}}=\frac{-33}{22}=\frac{-3}{2}$

$\Rightarrow {{I}_{2}}=-1.5A$

Substitute ${{I}_{2}}$ in equation $(2)$

$\Rightarrow 2{{I}_{1}}+6(-1.5)+3=0~$ 

$\Rightarrow 2{{I}_{1}}=6$

$\Rightarrow {{I}_{1}}=3A$

Substitute ${{I}_{1}},{{I}_{2}}$ in equation $(1)$

$\Rightarrow 3=-1.5+{{I}_{3}}$

$\Rightarrow {{I}_{3}}=4.5A$

Therefore, the currents are ${{I}_{1}}=3A$,${{I}_{2}}=-1.5A$and ${{I}_{3}}=4.5A$.

20. Show that when a current is divided between two resistances in accordance with Kirchhoff’s laws, the heat provided is minimum.

Ans: Consider two resistances ${{R}_{1}},{{R}_{2}}$  in parallel with ${{i}_{1}},{{i}_{2}}$ currents flowing in it. Using Kirchhoff’s first law,

$i={{i}_{1}}+{{i}_{2}}$    ……$(1)$

${{i}_{1}}{{R}_{1}}-{{i}_{2}}{{R}_{2}}=0$ 

$\frac{{{i}_{1}}}{{{i}_{2}}}=\frac{{{R}_{2}}}{{{R}_{1}}}.$

Heat produced in the circuit in $t$ seconds is $H=i_{1}^{2}{{R}_{1}}t+{{i}_{2}}^{2}{{R}_{2}}t$$\Rightarrow H={{i}_{1}}^{2}{{R}_{1}}t+{{\left( i-{{i}_{1}} \right)}^{2}}{{R}_{2}}t$ 

If the heat produced is minimum then $\frac{dH}{d{{i}_{1}}}=0$ 

$\Rightarrow 2{{\text{i}}_{1}}{{\text{R}}_{1}}\text{t}+2\left( \text{i}-{{\text{i}}_{1}} \right)(-1){{\text{R}}_{2}}\text{t=0}$ 

\[\Rightarrow 2\left( \text{i}-{{\text{i}}_{1}} \right){{\text{R}}_{2}}\text{t}=2{{\text{i}}_{1}}{{\text{R}}_{1}}\text{t}\]

\[\Rightarrow \left( i-{{i}_{1}} \right){{R}_{2}}={{i}_{1}}{{R}_{1}}\]

\[\Rightarrow \frac{{{i}_{1}}}{{{i}_{2}}}=\frac{{{R}_{2}}}{{{R}_{1}}}\]

Therefore, it is proved in accordance with Kirchhoff’s law.

(a) Define emf. of a cell? On what factors does it depend? 

Ans: Emf of a cell is defined as the potential difference between the two electrodes of the cell in open Circuit (when no current is drawn).

It depends on the following factors:

(a) Nature of Electrodes 

(b) Nature and concentration of the Electrolytes 

(c) Temperature of the cell. 

(b) Figure below shows a $2.0V$ potentiometer used for the determination of internal resistance of a $1.5V$ cell. The balance point of the cell in the open circuit is $76.3cm$. When a resistance of $9.5\Omega $ is used in the external circuit of the cell the balance point shifts to $64.8cm$ length of the potentiometer. Determine the internal resistance of the cell.

Ans : It is known that,

Internal resistance of the cell, $\text{r}=\text{R}\left( \frac{{{\ell }_{1}}-{{\ell }_{2}}}{{{\ell }_{2}}} \right)$

It is given that,

${{\ell }_{1}}=76.3~\text{cm, }{{\ell }_{2}}=64.8~\text{cm, R}=9.5\Omega $

$\Rightarrow \text{r}=9.5\left( \frac{76.3-64.8}{64.8} \right)$

$\Rightarrow r=1.68\Omega $

Therefore, the internal resistance of the cell, $r=1.68\Omega $.

22. A battery of emf 10 V and internal resistance $3\Omega $ is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistance of the resistor? What is the terminal voltage of the battery when the circuit is closed?

Ans: In the above question it is given that:

Emf of the battery, E = 10 V

Internal resistance of the battery, $r=3\Omega $

Current in the circuit, $I=0.5A$ 

Consider the resistance of the resistor to be $R$.

Therefore, using Ohm’s law,

$R+r=\frac{E}{I}$

$\Rightarrow R+r=\frac{10}{0.5}$

$\Rightarrow R+r=20$

$\therefore R=20-3=17\Omega $

Let the terminal voltage of the resistor be $V$.

Using Ohm's law,

$\Rightarrow V=0.5\times 17=8.5V$

Thus, the resistance of the resistor is $17\Omega $ and the terminal voltage is $8.5V$ .

(a) Three resistors $1\Omega $ , $2\Omega $ and $3\Omega $ are combined in series. What is the total resistance of the combination?

Ans: In the above question it is given that three resistors of resistances  $1\Omega $ , $2\Omega $ and $3\Omega $  are combined in series. 

The total resistance of the combination is the algebraic sum of individual resistances.

Hence the total resistance is given by:

Total Resistance $=1+2+3=6\Omega $

(b) If the combination is connected to a battery of emf $12V$ and negligible internal resistance, obtain the potential drop across each resistor.

Ans: Consider the current flowing through the circuit to be $I$.

Emf of the battery, $E=12V$

Total resistance of the circuit, $R=6\Omega $

The relation for current using Ohm’s law is given by:

$I=\frac{E}{R}$

$\Rightarrow I=\frac{12}{6}=2A$

Consider the potential drop across $1\Omega $ resistor to be ${{V}_{1}}$ .

Using Ohm’s law, the value of ${{V}_{1}}$ can be obtained as:

${{V}_{1}}=2\times 1=2V$ …… (1)

Consider the potential drop across $2\Omega $ resistor to be ${{V}_{2}}$ .

Again, using Ohm’s law, the value of ${{V}_{2}}$ can be obtained as:

${{V}_{2}}=2\times 2=4V$ …… (2)

Consider potential drop across $3\Omega $ resistor to be ${{V}_{3}}$ .

$\therefore {{V}_{3}}=2\times 3=6V$ ...... (3)

Hence, the potential drop across $1\Omega $ , $2\Omega $ and $3\Omega $  resistors are $2V$ , $4V$ and $6V$ respectively.

24. At room temperature ${{27.0}^{\circ }}C$ , the resistance of a heating element is $100\Omega $. What is the temperature of the element if the resistance is found to be $117\Omega $, given that the temperature coefficient of the material of the resistor is $1.70\times {{10}^{-4}}^{\circ }{{C}^{-1}}$ ?

Room temperature, $T={{27.0}^{\circ }}C$

Resistance of the heating element at $T$ , $R=100\Omega $

Consider ${{T}_{1}}$ as the increased temperature of the filament.

Therefore, resistance of the heating element at ${{T}_{1}}$, ${{R}_{1}}=117\Omega $

Temperature coefficient of the material of the filament, $\alpha =1.70\times {{10}^{-4}}^{\circ }{{C}^{-1}}$

We know that,

$\alpha =\frac{{{R}_{1}}-R}{R\left( {{T}_{1}}-T \right)}$

$\therefore \left( {{T}_{1}}-T \right)=\frac{{{R}_{1}}-R}{R\alpha }$

$\Rightarrow \left( {{T}_{1}}-27 \right)=\frac{117-100}{100\times 1.70\times {{10}^{-4}}}$

$\Rightarrow \left( {{T}_{1}}-27 \right)=1000$

$\therefore {{T}_{1}}={{1027}^{\circ }}C$

Therefore, at ${{1027}^{\circ }}C$ , the resistance of the element is $117\Omega $ .

25. A negligibly small current is passed through a wire of length 15 m and uniform cross-section $6.0\times {{10}^{-7}}{{m}^{2}}$ , and its resistance is measured to be $5.0\Omega $ . What is the resistivity of the material at the temperature of the experiment?

Length of the wire, $l=15m$

Area of cross-section of the wire, $a=6.0\times {{10}^{-7}}{{m}^{2}}$

Resistance of the material of the wire, $R=5.0\Omega $

Let resistivity of the material of the wire be $\rho $

We know that resistance is related to resistivity as:

$R=\rho \frac{l}{A}$

$\Rightarrow \rho =\frac{RA}{l}$

$\Rightarrow \rho =\frac{5\times 6.0\times {{10}^{-7}}}{15}$

$\therefore \rho =2\times {{10}^{-7}}{{m}^{2}}$

Therefore, the resistivity of the material is $2\times {{10}^{-7}}{{m}^{2}}$ .

26. A silver wire has a resistance of \[2.1\Omega \] at ${{27.5}^{\circ }}C$ , and a resistance of $2.7\Omega $ at ${{100}^{\circ }}C$. Determine the temperature coefficient of resistivity of silver.

Temperature, ${{T}_{1}}={{27.5}^{\circ }}C$.

Resistance of the silver wire at ${{T}_{1}}$ is ${{R}_{1}}=2.1\Omega $ .

Temperature, ${{T}_{2}}={{100}^{\circ }}C$ .

Resistance of the silver wire at ${{T}_{2}}$ is ${{R}_{2}}=2.7\Omega $ .

Let the temperature coefficient of silver be $\alpha $ .

It is related to temperature and resistance by the formula:

$\alpha =\frac{{{R}_{2}}-{{R}_{1}}}{{{R}_{1}}\left( {{T}_{2}}-{{T}_{1}} \right)}$

$\Rightarrow \alpha =\frac{2.7-2.1}{2.1\left( 100-27.5 \right)}={{0.0039}^{\circ }}{{C}^{-1}}$

Hence the temperature coefficient of silver is ${{0.0039}^{\circ }}{{C}^{-1}}$.

27. A heating element using nichrome connected to a 230 V supply draws an initial current of 3.2A which settles after a few seconds to a steady value of 2.8 A. What is the steady temperature of the heating element if the room temperature is ${{27}^{\circ }}C$ ? Temperature coefficient of resistance of nichrome averaged over the temperature range involved is $1.70\times {{10}^{-4}}^{\circ }{{C}^{-1}}$ .

Supply voltage is $V=230V$

Initial current drawn is ${{I}_{1}}=3.2A$.

Let the initial resistance be ${{R}_{1}}$ .

${{R}_{1}}=\frac{V}{{{I}_{1}}}$

$\Rightarrow {{R}_{1}}=\frac{230}{3.2}=71.87\Omega $

Steady state value of the current is ${{I}_{2}}=2.8A$.

Let the resistance of the steady state be ${{R}_{2}}$ .

Therefore, using Ohm’s law.

${{R}_{2}}=\frac{V}{{{I}_{2}}}$

$\Rightarrow {{R}_{2}}=\frac{230}{2.8}=82.14\Omega $

Temperature coefficient of nichrome is $\alpha =1.70\times {{10}^{-4}}^{\circ }{{C}^{-1}}$ .

Initial temperature of nichrome is ${{T}_{1}}={{27}^{\circ }}C$.

Let the steady state temperature reached by nichrome be ${{T}_{2}}$ .

Now using the formula of $\alpha $,

$\Rightarrow \left( {{T}_{2}}-{{T}_{1}} \right)=\frac{{{R}_{2}}-{{R}_{1}}}{{{R}_{1}}\alpha }$

$\Rightarrow \left( {{T}_{2}}-27 \right)=\frac{82.14-71.87}{71.87\times 1.70\times {{10}^{-4}}}$

$\Rightarrow {{T}_{2}}-27=840.5$

$\therefore {{T}_{2}}={{867.5}^{\circ }}C$

Hence the steady temperature of the heating element is ${{867.5}^{\circ }}C$ .

28. A storage battery of emf 8.0 V and internal resistance $0.5\Omega $ is being charged by a 120 V DC supply using a series resistor of $15.5\Omega $. What is the terminal voltage of the battery during charging? What is the purpose of having a series resistor in the charging circuit?

Emf of the storage battery is $E=0.8V$.

Internal resistance of the battery is $r=0.5\Omega $ .

DC supply voltage is $V=120V$

Resistance of the resistor is $R=15.5\Omega $.

Consider effective voltage in the circuit to be $V'$.

$V'=120-8=112V$

Now, the current flowing in the circuit is $I$ and the resistance $R$ is connected in series to the storage battery. 

$I=\frac{V'}{R+r}$

$\therefore I=\frac{112}{15.5+0.5}=7A$

Hence voltage across resistor $R$will be:

$IR=7\times 15.5=108.5V$

DC supply voltage = Terminal voltage of battery + Voltage drop across $R$

Terminal voltage of battery $=120-108.5=11.5V$

A series resistor in a charging circuit is responsible for limiting the current drawn from the external source. The current will be extremely high in its absence which is very dangerous.

29. The number density of free electrons in a copper conductor estimated in Example is $8.5\times {{10}^{28}}{{m}^{-3}}$ . How long does an electron take to drift from one end of a wire 3.0 m long to its other end? The area of cross-section of the wire is $2.0\times {{10}^{-6}}{{m}^{2}}$ and it is carrying a current of 3.0 A.

Number density of free electrons in a copper conductor is $n=8.5\times {{10}^{28}}{{m}^{-3}}$.

Length of the copper wire is $l=3.0m$.

Area of cross-section of the wire is $A=2.0\times {{10}^{-6}}{{m}^{2}}$.

Current carried by the wire is $I=3.0A$.

Now we know that:

$I=nAe{{V}_{d}}$

$e$ is the electric charge of magnitude $1.6\times {{10}^{-19}}C$.

${{V}_{d}}$ is the drift velocity and

\[Drift\text{ }velocity=\frac{\text{Length of the wire }\left( \text{l} \right)}{\text{Time taken to cover }\left( \text{t} \right)}\]

$I=nAe\frac{l}{t}$

$\Rightarrow t=\frac{nAel}{I}$

$\Rightarrow t=\frac{3\times 8.5\times {{10}^{28}}\times 2\times {{10}^{-6}}\times 1.6\times {{10}^{-19}}}{3.0}$

$\therefore t=2.7\times {{10}^{4}}s$ .

Hence the time taken by an electron to drift from one end of the wire to the other is $2.7\times {{10}^{4}}s$.

30. The earth’s surface has a negative surface charge density of ${{10}^{-9}}C{{m}^{-2}}$ . The potential difference of $400kV$ between the top of the atmosphere and the surface results (due to the low conductivity of the lower atmosphere) in a current of only $1800A$ over the entire globe. If there were no mechanism of sustaining atmospheric electric fields, how much time (roughly) would be required to neutralize the earth’s surface? (This never happens in practice because there is a mechanism to replenish electric charges, namely the continual thunderstorms and lightning in different parts of the globe). (Radius of earth = $6.37\times {{10}^{6}}m$.)

Surface charge density of the earth is $\sigma ={{10}^{-9}}C{{m}^{-2}}$.

Current over the entire globe is $I=1800A$.

Radius of the earth is $r=6.37\times {{10}^{6}}m$.

Surface area of the earth is given by:

$A=4\pi {{r}^{2}}$

$\Rightarrow A=4\pi \times {{\left( 6.37\times {{10}^{6}} \right)}^{2}}$

$\therefore A=5.09\times {{10}^{14}}{{m}^{2}}$

Charge on the earth surface is given by:

$q=\sigma A$

$\Rightarrow q={{10}^{-9}}\times 5.09\times {{10}^{14}}$

$\therefore q=5.09\times {{10}^{5}}C$

Now if time taken to neutralize the earth’s surface is $t$, then

Current, $I=\frac{q}{t}$

$\Rightarrow t=\frac{q}{I}$

$\Rightarrow t=\frac{5.09\times {{10}^{5}}}{1800}=282.77s$

Therefore, the time taken to neutralize the earth’s surface is $282.77s$.

31. Choose the Correct Alternative:

(a) Alloys of metals usually have (greater/less) resistivity than that of their constituent metals.

Ans: Alloys of metals usually have greater resistivity than that of their constituent metals.

(b) Alloys usually have much (lower/higher) temperature coefficients of resistance than pure metals.

Ans: Alloys usually have lower temperature coefficients of resistance than pure metals.

(c) The resistivity of the alloy manganin is nearly independent of/increases rapidly with increase of temperature.

Ans: The resistivity of the alloy, manganin, is nearly independent of increase of temperature.

(d) The resistivity of a typical insulator (e.g., amber) is greater than that of a metal by a factor of the order of $\left( {{10}^{22}}/{{10}^{3}} \right)$.

Ans: The resistivity of a typical insulator is greater than that of a metal by a factor of the order of ${{10}^{22}}$ .

32. Determine the current drawn from a $12V$ supply with internal resistance $0.5\Omega $ by the infinite network shown in Figure. Each resistor has $1\Omega $ resistance.

Ans: In the above question it is given that the resistance of each resistor connected in the given circuit is $R=1\Omega $.

Let the equivalent resistance of the given circuit be $R'$.

As the network is infinite the equivalent resistance is given by the relation,

$R'=2+\frac{R'}{\left( R'+1 \right)}$

$\Rightarrow {{\left( R' \right)}^{2}}-2R'-2=0$

$\Rightarrow R'=\frac{2\pm \sqrt{12}}{2}=1\pm \sqrt{3}$

As only positive value is acceptable,

$\therefore R'=1+\sqrt{3}$

Internal resistance of the circuit is $r=0.5\Omega $.

Therefore, total resistance $=2.73+0.5=3.23\Omega $.

Using Ohm’s law,

$I=\frac{V}{R}=\frac{12}{3.23}=3.72A$.

Therefore, the current drawn is $3.72A$.

33. Figure 3.34 shows a potentiometer circuit for comparison of two resistances. The balance point with a standard resistor $R=10.0\Omega $ is found to be \[\mathbf{58}.\mathbf{3cm}\] while that with the unknown resistance $X$ is \[\mathbf{68}.\mathbf{5}\text{ }\mathbf{cm}\]. Determine the value of $X$. What might you do if you failed to find a balance point with the given cell of emf $\varepsilon $ ?

Resistance of the standard resistor is $R=10.0\Omega $ .

Balance point for this resistance is at a distance ${{l}_{1}}=58.3cm$.

Current in the potentiometer wire is $i$.

Hence, potential drop across $R$ is ${{E}_{1}}=iR$.

Resistance of the unknown resistor is $X$.

Balance point for this resistance is at a distance ${{l}_{2}}=68.5cm$.

Hence, potential drop across $X$ is ${{E}_{2}}=iX$.

The relation connecting emf and balance point is,

$\frac{{{E}_{1}}}{{{E}_{2}}}=\frac{{{l}_{1}}}{{{l}_{2}}}$

$\Rightarrow \frac{iR}{iX}=\frac{{{l}_{1}}}{{{l}_{2}}}$

$\Rightarrow X=\frac{{{l}_{1}}}{{{l}_{2}}}\times R=\frac{68.5}{58.3}\times 10=11.749\Omega $ .

Therefore, the value of the unknown resistance $X$ is $11.749\Omega $.

If we fail to find a balance point with the given cell of emf $\varepsilon $, then the potential drop across $R$and $X$ is reduced by putting a resistance in series with it. 

A balance point is obtained only if the potential drop across $R$ or $X$ is smaller than the potential drop across the potentiometer wire AB. 

34. Figure shows a $2.0V$ potentiometer used for the determination of internal resistance of $1.5V$ cell. The balance point of the cell in the open circuit is $76.3cm$. When a resistor of $9.5\Omega $ is used in the external circuit of the cell, the balance point shifts to $64.8cm$ length of the potentiometer wire. Determine the internal resistance of the cell.

Balance point of the cell in the open circuit is ${{l}_{1}}=76.3cm$.

An external resistance $R$ of resistance $9.5\Omega $ is connected to the circuit.

New balance point of the circuit is at a distance ${{l}_{2}}=64.8cm$ .

Current flowing through the circuit  $=I$ .

The relation connecting resistance and emf is:

$r=\left( \frac{{{l}_{1}}-{{l}_{2}}}{{{l}_{2}}} \right)R$

$\Rightarrow r=\left( \frac{76.3-64.8}{64.8} \right)9.5=1.68\Omega $

Hence the internal resistance of the cell is $1.68\Omega $ . 

Long Answer Questions: (5 Marks)

(a) Three resistors $2\Omega $ , $4\Omega $ and $5\Omega $  are combined in parallel. What is the total resistance of the combination?

Ans: In the above question it is given that there are three resistors of resistances $2\Omega $ , $4\Omega $ and $5\Omega $. 

They are connected in parallel. 

Hence, total resistance $R$ of the combination will be:

$\frac{1}{R}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+\frac{1}{{{R}_{3}}}$

$\Rightarrow \frac{1}{R}=\frac{1}{2}+\frac{1}{4}+\frac{1}{5}=\frac{19}{20}$

$\therefore R=\frac{20}{19}\Omega $

Therefore, total resistance of the combination is $\frac{20}{19}\Omega $ .

(b) If the combination is connected to a battery of emf $20V$ and negligible internal resistance, determine the current through each resistor, and the total current drawn from the battery.

Emf of the battery, $V=20V$

Current ${{I}_{1}}$ flowing through resistor ${{R}_{1}}$ is given by:

${{I}_{1}}=\frac{V}{{{R}_{1}}}$

$\Rightarrow {{I}_{1}}=\frac{20}{2}=10A$

Current ${{I}_{2}}$ flowing through resistor ${{R}_{2}}$ is given by:

${{I}_{2}}=\frac{V}{{{R}_{2}}}$

$\Rightarrow {{I}_{2}}=\frac{20}{4}=5A$

Current ${{I}_{3}}$ flowing through resistor ${{R}_{3}}$ is given by:

${{I}_{3}}=\frac{V}{{{R}_{3}}}$

$\Rightarrow {{I}_{3}}=\frac{20}{5}=4A$

Hence the total current will be:

$I={{I}_{1}}+{{I}_{2}}+{{I}_{3}}$

$\therefore I=10+5+4=19A$

Therefore, the current through resistors $2\Omega $ , $4\Omega $ and $5\Omega $ is $10A$ , $5A$ and $4A$ respectively and the total current is $19A$.

2. Determine the current in each branch of the network shown in figure:

Ans: Current flowing through various branches of the circuit is represented in the given figure.

${{I}_{1}}=$Current flowing through the outer circuit

${{I}_{2}}=$Current flowing through branch AB

${{I}_{3}}=$Current flowing through branch AD

${{I}_{2}}-{{I}_{4}}=$Current flowing through branch BC

${{I}_{3}}+{{I}_{4}}=$Current flowing through branch CD

${{I}_{4}}=$Current flowing through branch BD

For the closed circuit ABDA, potential is zero i.e.,

$10{{I}_{2}}+5{{I}_{4}}-5{{I}_{3}}=0$

$2{{I}_{2}}+{{I}_{4}}-{{I}_{3}}=0$

${{I}_{3}}=2{{I}_{2}}+{{I}_{4}}$ …… (1)

For the closed circuit BCDB, potential is zero i.e.,

$5\left( {{I}_{2}}-{{I}_{4}} \right)-10\left( {{I}_{3}}+{{I}_{4}} \right)-5{{I}_{4}}=0$

$5{{I}_{2}}+5{{I}_{4}}-10{{I}_{3}}-10{{I}_{4}}-5{{I}_{4}}=0$

$5{{I}_{2}}-10{{I}_{3}}-20{{I}_{4}}=0$

${{I}_{2}}=2{{I}_{3}}+4{{I}_{4}}$ …… (2)

For the closed circuit ABCFEA, potential is zero i.e.,

$-10+10\left( {{I}_{1}} \right)+10\left( {{I}_{2}} \right)+5\left( {{I}_{2}}-{{I}_{4}} \right)=0$

$10=15{{I}_{2}}+10{{I}_{1}}-5{{I}_{4}}$

$3{{I}_{3}}+2{{I}_{1}}-{{I}_{4}}=2$ …… (3)

From equations (1) and (2), we obtain

${{I}_{3}}=2\left( 2{{I}_{3}}+4{{I}_{4}} \right)+{{I}_{4}}$

${{I}_{3}}=4{{I}_{3}}+8{{I}_{4}}+{{I}_{4}}$

$-3{{I}_{3}}=9{{I}_{4}}$

$-3{{I}_{4}}=+{{I}_{3}}$ …… (4)

Putting equation (4) in equation (1), we obtain

${{I}_{3}}=2{{I}_{2}}+{{I}_{4}}$

$-4{{I}_{4}}=2{{I}_{2}}$ …… (5)

It is evident from the given figure that,

${{I}_{1}}={{I}_{3}}+{{I}_{2}}$ ……. (6)

Putting equation (6) in equation (1), we obtain

$3{{I}_{2}}+2\left( {{I}_{3}}+{{I}_{2}} \right)-{{I}_{4}}=2$

$5{{I}_{2}}+2{{I}_{3}}-{{I}_{4}}=2$ …… (7)

Putting equations (4) and (5) in equation (7), we obtain

$5\left( -2{{I}_{4}} \right)+2\left( -3{{I}_{4}} \right)-{{I}_{4}}=2$

$-10{{I}_{4}}-6{{I}_{4}}-{{I}_{4}}=2$

$17{{I}_{4}}=-2$

${{I}_{4}}=-\frac{2}{17}A$

Equation (4) reduces to

${{I}_{3}}=-3\left( {{I}_{4}} \right)$

${{I}_{3}}=-3\left( -\frac{2}{17} \right)=\frac{6}{17}A$

${{I}_{2}}=-2\left( {{I}_{4}} \right)$

${{I}_{2}}=-2\left( -\frac{2}{17} \right)=\frac{4}{17}A$

${{I}_{2}}-{{I}_{4}}=\frac{4}{17}-\left( -\frac{2}{17} \right)=\frac{6}{17}$

${{I}_{3}}+{{I}_{4}}=\frac{6}{17}+\left( \frac{-2}{17} \right)=\frac{4}{17}A$

${{I}_{1}}={{I}_{3}}+{{I}_{2}}$

$\therefore {{I}_{1}}=\frac{6}{17}+\frac{4}{17}=\frac{10}{17}A$

Therefore, current in branch AB $=\frac{4}{17}A$

Current in branch BC $=\frac{6}{17}A$

Current in branch CD $=\frac{-4}{17}A$

Current in branch AD $=\frac{6}{17}A$

Current in branch BD $=\left( \frac{-2}{17} \right)A$

Total current $=\frac{4}{17}+\frac{6}{17}+\frac{-4}{17}+\frac{6}{17}+\frac{-2}{17}=\frac{10}{17}A$ .

(a) In a metre bridge [Fig. 3.27], the balance point is found to be at $39.5cm$ from the end A, when the resistor Y is of $12.5\Omega $ . Determine the resistance of $X$. Why are the connections between resistors in a Wheatstone or meter bridge made of thick copper strips?

Ans: A metre bridge with resistors $X$ and $Y$ is represented in the given figure.

In the above question it is given that:

Balance point from end A is at distance, ${{l}_{1}}=39.5cm$

Resistance of the resistor \[Y=12.5\Omega \] .

Condition for the balance is,

$\frac{X}{Y}=\frac{100-{{l}_{1}}}{{l}_{1}}$

$\therefore X=\frac{100-39.5}{39.5}\times 12.5=8.2\Omega $

Hence, the resistance of resistor $X$ is $8.2\Omega $.

The connection between resistors in a Wheatstone or metre bridge is made of thick copper strips which helps to minimize the resistance. Hence it is not taken into consideration in the bridge formula.

(b) Determine the balance point of the bridge above if $X$ and $Y$are interchanged.

Ans: Now, if $X$ and $Y$are interchanged, then ${{l}_{1}}$ and $100-{{l}_{1}}$ also gets interchanged.

Hence the balance point of the bridge will be $100-{{l}_{1}}$ from $A$.

$\therefore 100-{{l}_{1}}=100-39.5=60.5cm$

Hence, the balance point is $60.5cm$ from $A$.

(c) What happens if the galvanometer and cell are interchanged at the balance point of the bridge? Would the galvanometer show any current?

Ans: When the galvanometer and cell are interchanged at the balance point of the bridge, the galvanometer will show no deflection. As there is zero deflection, no current would flow through the galvanometer.

(a) Six lead-acid types of secondary cells each of emf 2.0 V and internal resistance $0.015\Omega $ are joined in series to provide a supply to a resistance of $8.5\Omega$ . What is the current drawn from the supply and its terminal voltage?

Number of secondary cells is $n=6$.

Emf of each secondary cell is $E=2.0V$.

Internal resistance of each cell is $r=0.015\Omega $ .

Series resistor is connected to the combination of cells.

The resistance of the resistor $R$ is $8.5\Omega $.

If the current drawn from the supply is $I$, then 

$I=\frac{nE}{R+nr}$

$\Rightarrow I=\frac{6\times 2}{8.5+6\times 0.015}$

$\therefore I=1.39A$

Now the Terminal voltage will be

$V=IR=1.39\times 8.5=11.87V$

Therefore, the current drawn from the supply is $1.39A$ and the terminal voltage is $11.87V$.

(b) A secondary cell after long use has an emf of $1.9V$ and a large internal resistance of $380\Omega $. What maximum current can be drawn from the cell? Could the cell drive the starting motor of a car?

Ans: After long use, 

Emf of the secondary cell will be $E=1.9V$.

Internal resistance of the cell is $r=380\Omega $ .

Therefore, maximum current $=\frac{E}{r}$

$\Rightarrow \frac{E}{r}=\frac{1.9}{380}=0.005A$.

Hence the maximum current drawn from the cell is $0.005A$. Since a large current is required to start the motor of a car, the cell cannot be used to start a motor.

5. Two wires of equal length, one of aluminium and the other of copper have the same resistance. Which of the two wires is lighter? Hence explain why aluminium wires are preferred for overhead power cables.

${{\rho }_{Al}}=2.63\times {{10}^{8}}\Omega m$, ${{\rho }_{Cu}}=1.72\times {{10}^{-8}}\Omega m$, $\text{Relative density of Al}=2.7$, $\text{Relative density of Cu}=8.9$

Resistivity of aluminium is ${{\rho }_{Al}}=2.63\times {{10}^{8}}\Omega m$.

Relative density of aluminium is ${{d}_{1}}=2.7$.

Consider ${{l}_{1}}$ to be the length of aluminium wire, ${{m}_{1}}$ as its mass, resistance of the copper wire as ${{R}_{2}}$, and area of cross-section of the copper wire as ${{A}_{2}}$.

Therefore, 

${{R}_{1}}={{\rho }_{1}}\frac{{{l}_{1}}}{{{A}_{1}}}$ …… (1)

${{R}_{2}}={{\rho }_{2}}\frac{{{l}_{2}}}{{{A}_{2}}}$ …… (2)

But we have ${{R}_{1}}={{R}_{2}}$

$\therefore {{\rho }_{1}}\frac{{{l}_{1}}}{{{A}_{1}}}={{\rho }_{2}}\frac{{{l}_{2}}}{{{A}_{2}}}$

Also, we have ${{l}_{1}}={{l}_{2}}$.

\[\therefore \frac{{{\rho }_{1}}}{{{A}_{1}}}=\frac{{{\rho }_{2}}}{{{A}_{2}}}\]

i.e., $\frac{{{A}_{1}}}{{{A}_{2}}}=\frac{{{\rho }_{1}}}{{{\rho }_{2}}}$

$\therefore \frac{{{A}_{1}}}{{{A}_{2}}}=\frac{2.63\times {{10}^{8}}}{1.72\times {{10}^{-8}}}=\frac{2.63}{1.72}$

Now the mass of the aluminium wire is given by:

${{m}_{1}}=Volume\times Density$

$\therefore {{m}_{1}}={{A}_{1}}{{l}_{1}}\times {{d}_{1}}={{A}_{1}}{{l}_{1}}{{d}_{1}}$ …… (3)

Similarly, mass of the copper wire is given by:

${{m}_{2}}=Volume\times Density$

$\therefore {{m}_{2}}={{A}_{2}}{{l}_{2}}\times {{d}_{2}}={{A}_{2}}{{l}_{2}}{{d}_{2}}$ …… (4)

Dividing equation (3) by equation (4), we get:

$\frac{{{m}_{1}}}{{{m}_{2}}}=\frac{{{A}_{1}}{{l}_{1}}{{d}_{1}}}{{{A}_{2}}{{l}_{2}}{{d}_{2}}}$

As ${{l}_{1}}={{l}_{2}}$,

$\frac{{{m}_{1}}}{{{m}_{2}}}=\frac{{{A}_{1}}{{d}_{1}}}{{{A}_{2}}{{d}_{2}}}$

As \[\frac{{{A}_{1}}}{{{A}_{2}}}=\frac{2.63}{1.72}\]

$\frac{{{m}_{1}}}{{{m}_{2}}}=\frac{2.63}{1.72}\times \frac{2.7}{8.9}=0.46$

It indicated that ${{m}_{1}} < {{m}_{2}}$.

Therefore, aluminium is lighter than copper.

Since aluminium is lighter, it is preferred for overhead power cables over copper.

6. Answer the Following Questions:

a. A steady current flow in a metallic conductor of the non-uniform cross section. Which of these quantities is constant along with the conductor: current, current density, electric field, drift speed?

Ans: In the above question it is given that a steady current flows in a metallic conductor of the non-uniform cross-section. Therefore, the current flowing through the conductor is constant.

Current density, electric field, and drift speed are inversely proportional to the area of cross-section. Hence, they are not constant.

b. Is ohm’s law universally applicable for all conducting elements? If not, give examples of elements which do not obey Ohm’s law.

Ans: Ohm’s law is not universally applicable for all conducting elements.

Vacuum diode semiconductor is a non-ohmic conductor. Therefore, Ohm’s law is not valid for it.

c. A low voltage supply from which one needs high currents must have very low internal resistance. Why?

Ans: According to Ohm’s law, $V=IR$ .

It states that Voltage $\left( V \right)$  is directly proportional to current $\left( I \right)$ .

$I=\frac{V}{R}$

where, $R$ is the internal resistance of the source. 

If V is low, then R must be very low, for high current drawn from the source.

d. A high tension (HT) supply of, say, 6 kV must have a very large internal resistance. Why?

Ans: A high tension supply of a very large internal resistance is required in order to prohibit the current from exceeding the safety limit. 

If the internal resistance is very low, then the current drawn exceeds the safety limits in case of a short circuit.

(a) Given n resistors each of resistance R, how will you combine them to get the (i) maximum (ii) minimum effective resistance? What is the ratio of the maximum to minimum resistance?

Ans: In the above question it is given that the total number of resistors are $n$ where resistance of each resistor is $R$.

i. When $n$ resistors are connected in series the effective resistance will be maximum when it is a product of $nR$ . Hence, maximum resistance of the combination is given by ${{R}_{1}}=nR$ .

ii. The effective resistance is the minimum when resistors are connected in parallel. Therefore, the effective resistance ${{R}_{2}}$ is given by ${{R}_{2}}=\frac{R}{n}$ .

The ratio of the maximum to the minimum resistance will be

$\Rightarrow \frac{{{R}_{1}}}{{{R}_{2}}}=\frac{nR}{R/n}={{n}^{2}}$

(b) Given the resistances of $1\Omega ,2\Omega ,3\Omega $ , how will you combine them to get an equivalent resistance of (i) $\left( 11/3 \right)\Omega $ (ii) $\left( 11/5 \right)\Omega $ (iii) $6\Omega $ (iv) $\left( 6/11 \right)\Omega $ ?

Ans: In the above question it is given that: 

${{R}_{1}}=1\Omega ,{{R}_{2}}=2\Omega ,{{R}_{3}}=3\Omega $

(i) For equivalent resistance of $\left( 11/5 \right)\Omega $:

Consider the circuit diagram given below.

Equivalent resistance for the circuit will be:

$R'=\frac{2\times 1}{2+1}+3=\frac{2}{3}+3=\frac{11}{3}\Omega $

(ii) For equivalent resistance of $\left( 11/3 \right)\Omega $:

$R'=\frac{2\times 3}{2+3}+1=\frac{6}{5}+1=\frac{11}{5}\Omega $

(iii) For equivalent resistance of $6\Omega $:

$R'=1+2+3=6\Omega $

(iv) For equivalent resistance of $\left( 6/11 \right)\Omega $:

$R'=\frac{1\times 2\times 3}{1\times 2+2\times 3+3\times 1}=\frac{6}{11}\Omega $

Ans:  Consider first small loop, two resistors of resistance $1\Omega $ each are connected in series.

Therefore, their equivalent resistance $=1+1=2\Omega $ .

Now two resistors of resistance $2\Omega $ each are connected in series.

Therefore, their equivalent resistance $=2+2=4\Omega $ .

Hence the circuit is resolved to:(Image will be uploaded soon)

Here  $2\Omega $ and $4\Omega $ resistors are connected in parallel in all the four loops.

Therefore, equivalent resistance $R'$ is given by,

$R'=\frac{2\times 4}{2+4}=\frac{8}{6}=\frac{4}{3}\Omega $

The circuit further results into:

Four resistors are connected in series.

Therefore, equivalent resistance of the given circuit will be $\frac{4}{3}\times 4=\frac{16}{3}\Omega $ .

Ans: In the circuit it is given that five resistors of resistance $R$ are connected in series. 

Therefore, equivalent resistance of the circuit $=R+R+R+R+R=5R$ .

8. Figure shows a potentiometer with a cell of $2.0V$ and internal resistance $0.40\Omega $ maintaining a potential drop across the resistor wire AB. A standard cell which maintains a constant emf of $1.02V$ (for very moderate currents up to a few mA) gives a balance point at $67.3cm$ length of the wire. To ensure very low currents drawn from the standard cell, a very high resistance of $600k\Omega $ is put in series with it, which is shorted close to the balance point. The standard cell is then replaced by a cell of unknown emf $\varepsilon $ and the balance point found similarly, turns out to be at $82.3cm$length of the wire.

(a) What is the value of $\varepsilon $ ?

Ans: In the above question it is given that constant emf of the given standard cell is ${{E}_{1}}=1.02V$.

The balance point on the wire is at a distance ${{l}_{1}}=67.3cm$.

When the cell of unknown emf $\varepsilon $ is replaced, the standard cell new balance point shifts to $l=82.3cm$.

$\frac{{{E}_{1}}}{{{l}_{1}}}=\frac{\varepsilon }{l}$

$\Rightarrow \varepsilon =\frac{l}{{{l}_{1}}}\times {{E}_{1}}=\frac{82.3}{67.3}\times 1.02=1.247V$

Therefore, the value of unknown emf is $1.247V$.

(b) What purpose does the high resistance of $600k\Omega $ have?

Ans: The purpose of using the high resistance of $600k\Omega $ is to reduce the current through the galvanometer when the movable contact is far from the balance point.

(c) Is the balance point affected by this high resistance?

Ans: The balance point is not affected by the presence of high resistance.

(d) Is the balance point affected by the internal resistance of the driver cell?

Ans: The balance point is not affected by the internal resistance of the driver cell.

(e) Would the method work in the above situation if the driver cell of the potentiometer had an emf of $1.0V$ instead of $2.0V$?

Ans: The method would not work if the driver cell of the potentiometer had an emf of $1.0V$ instead of $2.0V$ because if the emf of the driver cell of the potentiometer is less than the emf of the other cell, then the balance point would not exist on the wire.

(f) Would the circuit work well for determining an extremely small emf, say of the order of a few mV (such as the typical emf of a thermos-couple)? If not, how will you modify the circuit?

Ans: The circuit would not work well for determining an extremely small emf. Due to the instability in the circuit, the balance point would be close to the end A. Hence, there is a large percentage error. The given circuit can be modified by connecting a series resistance with the wire AB. 

The potential drop across AB is slightly greater than the measured emf. The percentage error would be small.

Class 12 Physics Chapter 3 Important Questions- What is Ohm’s Law?

Among the set of class 12 physics ch 3 important questions, Ohm’s Law is a very crucial topic. This law determines the relationship between electric current and potential difference. The current that flows through the conductor is directly proportional to the applied voltage. Further, it provided that all the physical conditions and temperature needs to remain constant. This is important because in certain components when electricity is passed it elevates the temperature. A classic example of this Ohm’s Law violation is the light bulb’s filament. This law was verified by German physicist Georg Simon Ohm and hence the law is named after him. 

Ohm’s Law Equation = V= IR 

Where, 

V= voltage across the conductor.

I= current passing through the conductor.

R= resistance offered by the conductor in the flow of current. 

There are also class 12 physics chapter 3 extra questions provided at the end of the chapter. 

State the Factors Affecting Resistivity in Chapter 3 Physics Class 12 Important Questions?

There are certain materials in which electric charge easily passes through the object. The electric resistance evaluates how much restriction is provided in this flow of electric charge within the circuit. These are some of the factors which affect electric resistance. The following factors determine the electrical resistance of a conductor. 

The length of the conducting device.

The cross-sectional area of the conducting device.

The material of the conducting device.

The temperature of the conducting material. 

Here, the electrical resistance is directly proportional to the length of the conducting device and inversely proportional to the cross-sectional area of the conductor. The following relation is denoted by this given equation below:

p= resistivity of the material (measured in ohm meter, Ωm)

This is an important question of chapter 3 physics class 12 for students appearing in their 12th boards. 

Explain Kirchhoff's Law in Context to Physics Class 12 Chapter 3 Important Questions?

Kirchoff's law is a key idea in class 12 significant issues about current electricity. German physicist Gustav Kirchoff created a few principles in 1845 that govern the exchange of energy and current within an electrical circuit. Kirchoff's Current and Voltage Laws are the names given to both of these laws. Let's examine each of these two laws in greater detail.

Kirchhoff’s 1st Law (Current Law)

According to the 1st Law of Kirchhoff, the total current entering the node or junction is equal to the charge leaving the node or junction, as no charge is lost. This states the algebraic sum of every current entering and leaving the node is equal to zero. 

Kirchoff’s 2nd Law (Voltage Law)

According to the 2nd Law of Kirchhoff, the sum of every voltage drop is equal to the voltage around the loop in the same loop for any closed network and also equals zero. The algebraic sum of every voltage in the loop has to be zero and it is known as the conservation of energy.  

CBSE Class 12 Physics Chapter 3 Important Questions- What are the Two Types of Resistance?

There are basically two main types of resistors. This incorporates the resistors in parallel and resistors in series. In case of resistors in parallel, the difference among every resistor remains the same. Moreover, this difference is equal to the applied difference. While resistors in series the same amount of current flows through each resistor whenever there is any change.

Conclusion 

The conclusion on important questions for CBSE Class 12 Physics Chapter 3 - Current Electricity is that practicing relevant and well-curated questions is crucial for a comprehensive understanding of the chapter and for exam preparation. By solving important questions, students can enhance their problem-solving skills, reinforce the concepts learned, and become familiar with the application of theoretical knowledge in various scenarios related to current electricity. 

Important questions for CBSE Class 12 Physics Chapter 3 may cover a range of topics including electric current, Ohm's law, resistance, electrical circuits, Kirchhoff's laws, and the combination of resistors. These questions can be designed to assess students' understanding of theoretical concepts, ability to apply formulas and laws, and aptitude for solving circuit-related problems.

It is important to note that while solving important questions is helpful, it should be complemented with a thorough understanding of the underlying principles and concepts. Therefore, students are advised to focus on conceptual clarity and regular practice to excel in CBSE Class 12 Physics Chapter 3 - Current Electricity.

Important Related Links for CBSE Class 12 Physics 

CBSE Class 12 Physics Study Materials

FAQs on Important Questions for CBSE Class 12 Physics Chapter 3 - Current Electricity 2024-25

1. What is the potential difference and how is current and potential difference related to each other?

Ans: The word current means movement and electricity comes from the word electrons so basically current is the movement of free electrons in the conductor per unit time. Some conductors have a large number of free electrons whereas some have less number of free electrons. When these conductors are connected to each other, the free electrons move from high density of electrons to the low density of electrons. Thus, the current flows in the opposite direction of the flow of electrons. This difference in the density of electrons between the two conductors which promotes current electricity is called potential difference. Therefore, the current flows only when a potential difference is applied at the two ends of the conductor. According to Ohm's law, “In a conductor, potential difference applied across the conductor is directly proportional to the amount of the flow of current.”

2. What is the difference between resistance and resistivity?

Ans:   Resistance is the hindrance offered to the flow of electrons in a specific material. Resistance can be considered opposite to the potential difference across the conductor because it encourages the flow of electrons while resistance discourages it. The rate at which the charge flows between two conductors is a combination of resistance and potential difference. Resistivity of a substance is the measure it's resisting power to conduct current electricity. In other words, resistivity is a fundamental property that quantifies how strongly a specified material can resist the flow of electrons.

3. What are the topics covered in important questions for class 12 CBSE Physics Chapter 6 by Vedantu?

Ans: In the chapter current electricity, vedantu has researched the important questions for CBSE which are basically from the following topics: Resistance and resistivity, potential difference, current electricity, ohm's law, potentiometer, emf of the cell, kirchoff's rule, drift velocity, cells and its combinations, wheatstone bridge, circuit diagrams, numericals, Peltier Effect, Thomson Effect, Thermoelectric Effect and Joule’s Law Of Heating.

4. How to study current electricity for CBSE exam?

Ans: Basic ideas about the chapter are required before solving questions or getting into difficult concepts to study the theories well. You can also revise from notes to understand the concept. Note are the comprehensive way where all the topics are clubbed and related to each other in order to get the flow of the entire chapter at one go. Electricity is divided into two major sections - Static electricity and Current electricity. From static electricity revise topics like electric field, Coulomb’s Law, potential, electric flux, Gauss’s law and capacitors. Current electricity consists of topics like Ohm’s law, resistance, resistivity, conductivity, resistor combinations, etc. Once the revision is over, learn the theories, formulas and important points. To attain command over numerical questions, master Kirchoff’s rules, resistance and cell combination rules and solve maximum numerical from books, sample papers and previous year’s papers. Keep a note of all the important points so you can also make flashcards or sticky notes to help you in last-minute revision. Practice from solved papers and previous years papers as much as possible to get used to the question pattern and enhance your speed and accuracy.

5. What are the different topics covered in Chapter 3 of Class 12 Physics?

Ans: The various topics covered in Class 12 Chapter 3 Physics are:

Electric current

Electric currents in conductors 

Drift of electrons and origin of resistivity

Limitations of Ohm’s law

Resistivity of various materials

Temperature dependence of resistivity

Electrical energy, power

Combination of resistors - series and parallel

Cells, emf, internal resistance

Cells in series and parallel

Kirchhoff’s rules

Wheatstone bridge

Meter bridge

Potentiometer

All these topics are important for the student to study so that they are thorough with all that their syllabus has to offer.

These solutions are available on Vedantu's official website( vedantu.com ) and mobile app free of cost.

6. What is the name of Chapter 3 of Class 12 Physics?

Ans: The name of the third chapter in Class 12 physics is ‘Current Electricity’. This chapter is very important, as it contains many important topics. It is important that students go through all the topics of Chapter 3 and make notes accordingly, to score well in the Class 12 Physics exam. The various numerical problems that this chapter entails are also essential for practice, as it will help students not just in their upcoming board exams, but also prove to be of great value in higher education. Reading the chapter thoroughly and marking all the important portions will help students solve any questions asked in the exam.

7. Are the important questions good reference material?

Ans: Yes, Vedantu’s important questions are surely the best reference material students should access to score high marks in their exams. These questions are designed by experts and are organized to help students in every step of their preparation. The questions that these guide books provide help students in practising the various important topics that are essential for the exams. This lets the student know how the question pattern usually is.

8. Is Chapter 3 of Class 12 Physics hard?

Ans: If students are clear and confident with all the concepts of Chapter 3, they will find everything easy. Thus, it is important to read the chapter and be thorough with the concepts. The best way to do this is by marking all the important and relevant areas and practising them regularly. Students should be thorough with all the laws, formulas and theorems of Chapter 3, as most questions set in the question papers deal with the understanding of these. Thus, students must practice repeatedly to be confident in what they study. This will make the chapter easy to understand.

9. What is Ohm’s law? Is it universally applicable to all conducting elements?

Ans: The current flowing from the conductor from the two points is directly proportional to the voltage across those two points. This is what the Ohm’s law states.

Where v stands for Voltage

I stands for current

And R stands for resistance.

Ohm’s law is inapplicable universally when we think about all the conducting elements . For instance, vacuum diode semiconductor is a non-ohmic conductor and  thus the Ohm’s law is inapplicable to it. 

For more such answers and insights to the chapter, it is advisable that it focuses on the important questions and concepts. To help themselves, they can visit the website of Vedantu and look through all the important questions that are needed for the preparation of the exam.

CBSE Class 12 Physics Important Questions

Cbse study materials.

1569+ Class 12 Physics Case Study Questions PDF Download

• Post author: studyrate
• Post published:
• Post category: Class 12 / 12 board
• Post comments: 0 Comments

So, you’re in Class 12 and the concept of Physics case study questions is beginning to loom large. Are you feeling a little lost? Fear not! This article will guide you through everything you need to know to conquer these challenging yet rewarding Class 12 Physics Case Study Questions.

Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.

We have provided here Case Study questions for the Class 12 Physics for board exams. You can read these chapter-wise Case Study questions. These questions are prepared by subject experts and experienced teachers. The answer and solutions are also provided so that you can check the correct answer for each question. Practice these questions to score excellent marks in your final exams.

Physics is more than just formulas and equations, right? It’s a way to interpret the natural world, and case studies provide a perfect opportunity for students to apply theoretical knowledge to real-world situations. So, what’s the importance of case studies in class 12 Physics? Well, they help you to solidify your understanding and enhance your analytical skills, which are invaluable for exams and beyond.

Table of Contents

Case Study-Based Questions for Class 12 Physics

There are total of 14 chapters Electric Charges And Fields, Electrostatic Potential And Capacitance, Current Electricity, Moving Charges And Magnetism, Magnetism And Matter, Electromagnetic Induction, Alternating Current, Electromagnetic Waves, Ray Optics and Optical Instruments, Wave Optics, Dual Nature Of Radiation And Matter, Atoms, Nuclei, Semiconductor Electronics Materials Devices, And Simple Circuits.

• Case Study Based Questions on class 12 Physics Chapter 1 Electric Charges And Fields
• Case Study Based Questions on Class 12 Physics Chapter 2 Electrostatic Potential And Capacitance
• Case Study Based Questions on Class 12 Physics Chapter 3 Current Electricity
• Case Study Based Questions on Class 12 Physics Chapter 4 Moving Charges And Magnetism
• Case Study Based Questions on Class 12 Physics Chapter 5 Magnetism And Matter
• Case Study Based Questions on Class 12 Physics Chapter 6 Electromagnetic Induction
• Case Study Based Questions on Class 12 Physics Chapter 7 Alternating Current
• Case Study Based Questions on Class 12 Physics Chapter 8 Electromagnetic waves
• Case Study Based Questions on Class 12 Physics Chapter 9 Ray Optics and Optical Instruments
• Case Study Based Questions on class 12 Physics Chapter 10 Wave Optics
• Case Study Based Questions on class 12 Physics Chapter 11 Dual Nature of Matter and Radiation
• Case Study Based Questions on class 12 Physics Chapter 12 Atoms
• Case Study Based Questions on class 12 Physics Chapter 13 Nuclei
• Case Study Based Questions on class 12 Physics Chapter 14 Semiconductor Electronics
• Class 12 Chemistry Case Study Questions
• Class 12 Biology Case Study Questions
• Class 12 Maths Case Study Questions

Class 12 students should go through important Case Study problems for Physics before the exams. This will help them to understand the type of Case Study questions that can be asked in Grade 12 Physics examinations. Our expert faculty for standard 12 Physics have designed these questions based on the trend of questions that have been asked in last year’s exams. The solutions have been designed in a manner to help the grade 12 students understand the concepts and also easy-to-learn solutions.

How to Approach Physics Case Study Questions

Ah, the million-dollar question! How do you tackle these daunting case study questions? Let’s dive in.

Effective Reading Techniques

A vital part of cracking case study questions is understanding the problem correctly. Don’t rush through the question, take your time to fully grasp the scenario, and don’t skip over the details – they can be critical!

Conceptual Analysis

Once you’ve understood the problem, it’s time to figure out which physics principles apply. Remember, your foundational knowledge is your greatest weapon here.

Solving Strategies

Next, put pen to paper and start solving! Follow a systematic approach, check your calculations, and make sure your answer makes sense in the context of the problem.

Best Books for Class 12 Physics Exams

Class 12 Physics Syllabus 2024

Chapter–1: Electric Charges and Fields

Electric charges, Conservation of charge, Coulomb’s law-force between two point charges, forces between multiple charges; superposition principle, and continuous charge distribution.

Electric field, electric field due to a point charge, electric field lines, electric dipole, electric field due to a dipole, torque on a dipole in a uniform electric field.

Electric flux, statement of Gauss’s theorem and its applications to find field due to infinitely long straight wire, uniformly charged infinite plane sheet, and uniformly charged thin spherical shell (field inside and outside).

Chapter–2: Electrostatic Potential and Capacitance

Electric potential, potential difference, electric potential due to a point charge, a dipole and system of charges; equipotential surfaces, electrical potential energy of a system of two-point charges and of electric dipole in an electrostatic field.

Conductors and insulators, free charges and bound charges inside a conductor. Dielectrics and electric polarization, capacitors and capacitance, combination of capacitors in series and in parallel, capacitance of a parallel plate capacitor with and without dielectric medium between the plates, energy stored in a capacitor (no derivation, formulae only).

Chapter–3: Current Electricity

Electric current, flow of electric charges in a metallic conductor, drift velocity, mobility and their relation with electric current; Ohm’s law, V-I characteristics (linear and non-linear), electrical energy and power, electrical resistivity and conductivity, temperature dependence of resistance, Internal resistance of a cell, potential difference and emf of a cell, combination of cells in series and in parallel, Kirchhoff’s rules, Wheatstone bridge.

Chapter–4: Moving Charges and Magnetism

Concept of magnetic field, Oersted’s experiment.

Biot – Savart law and its application to current carrying circular loop.

Ampere’s law and its applications to infinitely long straight wire. Straight solenoid (only qualitative treatment), force on a moving charge in uniform magnetic and electric fields.

Force on a current-carrying conductor in a uniform magnetic field, force between two parallel current-carrying conductors-definition of ampere, torque experienced by a current loop in uniform magnetic field; Current loop as a magnetic dipole and its magnetic dipole moment, moving coil galvanometerits current sensitivity and conversion to ammeter and voltmeter.

Chapter–5: Magnetism and Matter

Bar magnet, bar magnet as an equivalent solenoid (qualitative treatment only), magnetic field intensity due to a magnetic dipole (bar magnet) along its axis and perpendicular to its axis (qualitative treatment only), torque on a magnetic dipole (bar magnet) in a uniform magnetic field (qualitative treatment only), magnetic field lines.

Magnetic properties of materials- Para-, dia- and ferro – magnetic substances with examples, Magnetization of materials, effect of temperature on magnetic properties.

Chapter–6: Electromagnetic Induction

Electromagnetic induction; Faraday’s laws, induced EMF and current; Lenz’s Law, Self and mutual induction.

Chapter–7: Alternating Current

Alternating currents, peak and RMS value of alternating current/voltage; reactance and impedance; LCR series circuit (phasors only), resonance, power in AC circuits, power factor, wattless current. AC generator, Transformer.

Chapter–8: Electromagnetic Waves

Basic idea of displacement current, Electromagnetic waves, their characteristics, their transverse nature (qualitative idea only). Electromagnetic spectrum (radio waves, microwaves, infrared, visible, ultraviolet, X-rays, gamma rays) including elementary facts about their uses.

Chapter–9: Ray Optics and Optical Instruments

Ray Optics:  Reflection of light, spherical mirrors, mirror formula, refraction of light, total internal reflection and optical fibers, refraction at spherical surfaces, lenses, thin lens formula, lens maker’s formula, magnification, power of a lens, combination of thin lenses in contact, refraction of light through a prism.

Optical instruments:  Microscopes and astronomical telescopes (reflecting and refracting) and their magnifying powers.

Chapter–10: Wave Optics

Wave optics: Wave front and Huygen’s principle, reflection and refraction of plane wave at a plane surface using wave fronts. Proof of laws of reflection and refraction using Huygen’s principle. Interference, Young’s double slit experiment and expression for fringe width (No derivation final expression only), coherent sources and sustained interference of light, diffraction due to a single slit, width of central maxima (qualitative treatment only).

Chapter–11: Dual Nature of Radiation and Matter

Dual nature of radiation, Photoelectric effect, Hertz and Lenard’s observations; Einstein’s photoelectric equation-particle nature of light.

Experimental study of photoelectric effect

Matter waves-wave nature of particles, de-Broglie relation.

Chapter–12: Atoms

Alpha-particle scattering experiment; Rutherford’s model of atom; Bohr model of hydrogen atom, Expression for radius of nth possible orbit, velocity and energy of electron in his orbit, of hydrogen line spectra (qualitative treatment only).

Chapter–13: Nuclei

Composition and size of nucleus, nuclear force

Mass-energy relation, mass defect; binding energy per nucleon and its variation with mass number; nuclear fission, nuclear fusion.

Chapter–14: Semiconductor Electronics: Materials, Devices and Simple Circuits

Energy bands in conductors, semiconductors and insulators (qualitative ideas only) Intrinsic and extrinsic semiconductors- p and n type, p-n junction

Semiconductor diode – I-V characteristics in forward and reverse bias, application of junction diode -diode as a rectifier.

For further information, Subscribe Our YouTube Channel, and comment below about your queries.

You can click on the chapter-wise Case Study links given above and read the Class 12th Physics Case Study questions and answers provided by us. If you face any issues or have any questions please put your questions in the comments section below. Our teachers will be happy to provide you with answers.

FAQs Class 12 Physics Case Studies Questions

What is the best website for a  case   study  of physics  class   12 .

studyrate.in is the best website for Class 12 Physics Case Study Questions for Board Exams. Here you can find various types of Study Materials, Ebooks, Notes, and much more free of cost.

What are Physics case study questions?

Physics case study questions involve applying physics principles to solve real-world scenarios or problems.

How can I prepare for Physics case study questions?

Strengthen your basic concepts, practice solving a variety of problems, and make use of resources like the Class 12 Physics Case Study Questions PDF.

You Might Also Like

Class 12 physics assertion reason questions chapter 9 ray optics and optical instruments, mcq questions class 11 english snapshots chapter 6 the ghat of the only world with answers, class 12 chemistry case study questions chapter 11 alcohols, phenols, and ethers, leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.

This site uses Akismet to reduce spam. Learn how your comment data is processed .

The Topper Combo Flashcards

• Contains the Latest NCERT in just 350 flashcards.
• Colourful and Interactive
• Summarised Important reactions according to the latest PYQs of NEET(UG) and JEE

No thanks, I’m not interested!

• Neet Online Test Pack

12th Standard stateboard question papers & Study material

தமிழ் subjects.

கணினி பயன்பாடுகள்

கணினி அறிவியல்

வணிகக் கணிதம் மற்றும் புள்ளியியல்.

கணினி தொழில்நுட்பம்

கணக்குப்பதிவியல்

English Subjects

Computer Science

Business Maths and Statistics

Accountancy

Computer Applications

Computer Technology

11th Standard stateboard question papers & Study material

9th Standard stateboard question papers & Study material

Social Science

சமூக அறிவியல்

6th standard stateboard question papers & study material.

10th Standard stateboard question papers & Study material

7th Standard stateboard question papers & Study material

8th Standard stateboard question papers & Study material

கணிதம் - old

12th Standard CBSE Subject Question Paper & Study Material

Introductory Micro and Macroeconomics

Business Studies

Indian Society

Physical Education

Bio Technology

Engineering Graphics

Entrepreneurship

Hindi Elective

Home Science

Legal Studies

Political Science

11th Standard CBSE Subject Question Paper & Study Material

Mathematics

Enterprenership

Applied Mathematics

10th standard cbse subject question paper & study material.

9th Standard CBSE Subject Question Paper & Study Material

8th Standard CBSE Subject Question Paper & Study Material

7th Standard CBSE Subject Question Paper & Study Material

6th Standard CBSE Subject Question Paper & Study Material

School Exams

Tamil Nadu State Board Exams

Scholarship Exams

Study Materials , News and Scholarships

Stateboard Tamil Nadu

Free Online Tests

Educational News

Scholarships

Entrance Exams India

Video Materials

12th Standard CBSE

CBSE 12th Standard Physics Subject Current Electricity Chapter Case Study Questions 2021

CBSE 12th Standard Physics Subject Current Electricity Chapter Case Study Questions 2021 Sharma - Kochi May-21 , 2021

QB365 Provides the updated CASE Study Questions for Class 12 , and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get  more marks in Exams 

A PHP Error was encountered

Severity: Warning

Message: in_array() expects parameter 2 to be array, null given

Filename: material/details.php

Line Number: 1436

Message: Use of undefined constant EXAM - assumed 'EXAM' (this will throw an Error in a future version of PHP)

Line Number: 1438

QB365 - Question Bank Software

Cbse 12th standard physics subject current electricity case study questions 2021.

Final Semester - June 2015

A	A
A	A

(ii) SI unit of electric current is

s

(iii) A steady current flows in a metallic conductor of non-uniform cross-section. Which of these quantities is constant along the conductor?

(v) When a current of 40 A flows through a conductor of area 10 m 2 , then the current density is

According to Ohm's law, the current flowing through a conductor is directly proportional to the potential difference across the ends of the conductor i.e  \(I \propto V \Rightarrow \frac{V}{I}=R\)  where R is resistance of the conductor Electrical resistance of a conductor is the obstruction posed by the conductor to the flow of electric current through it. It depends upon length, area of cross-section, nature of material and temperature of the conductor We can write  \(R \propto \frac{l}{A} \text { or } R=\rho \frac{l}{A}\)  where \(\rho\)  is electrical resistivity of the material of the conductor. (i) Dimensions of electric resistance is

(ii) If  \(1 \mu \mathrm{A}\)  current flows through a conductor when potential difference of2 volt is applied across its ends, then the resistance of the conductor is

(iii) Specific resistance of a wire depends upon

(iv) The slope of the graph between potential difference and current through a conductor is

(v) The resistivity of the material of a wire 1.0 m long, 0.4 mm in diameter and having a resistance of 2.0 ohm is

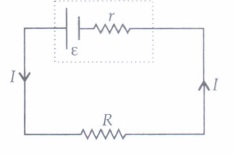
(ii) A cell of emf E and internal resistance r gives a current of 0.5 A with an external resistance of  \(12 \Omega\)  and a current of 0.25 A with an external resistance of  \(25 \Omega\)  .What is the value of internal resistance of the cell?

(iii) Choose the wrong statement.

(iv) An external resistance R is connected to a cell of internal resistance r, the maximum current flows in the external resistance, when

(v) IF external resistance connected to a cell has been increased to 5 times, the potential difference across the terminals of the cell increases from 10 V to 30 V. Then, the emf of the cell is

(ii) The total emf of the cells when n identical cells each of emf e are connected in parallel is

(iii) 4 cells each of emf 2 V and internal resistance of  \(1 \Omega\)  are connected in parallel to a load resistor of  \(2 \Omega\) . Then the current through the load resistor is

(iv) If two cells out of n number of cells each of internal resistance 'r' are wrongly connected in series, then total resistance of the cell is

(v) Two identical non-ideal batteries are connected in parallel. Consider the following statements. (i). The equivalent emf is smaller than either of the two emfs. (ii) The equivalent internal resistance is smaller than either of the two internal resistances

(ii) A current of 1.0 mA is flowing through a potentiometer wire of length 4 cm and of resistance  \(4 \Omega\)  .The potential gradient of the potentiometer wire is

(iii) Sensitivity of a potentiometer can be increased by

(iv) A potentiometer is an accurate and versatile device to make electrical measurements of EMF because the method involves

(v) In a potentiometer experiment, the balancing length is 8 m, when the two cells E l and E 2 are joined in series. When the two cells are connected in opposition the balancing length is 4 m. The ratio of the e. m. f. of two cells (E l /E 2 ) is

*****************************************

• Previous CBSE 12th Physics Wave Optics Chapter Case Study Question with Answers
• Next CBSE 12th Physics Ray Optics and Optical Instruments Chapter Case Study Question...

Reviews & Comments about CBSE 12th Standard Physics Subject Current Electricity Chapter Case Study Questions 2021

Write your Comment

12th Standard CBSE Physics Videos

CBSE 12th Physics Sample Model Question Paper with Answer Key 2023

12th Standard CBSE Physics Usefull Links

• 10th Standard

Other 12th Standard CBSE Subjects

Other 12th Standard CBSE Physics Study material

Cbse 12th physics wave optics chapter case study question with answers click to view, cbse 12th physics ray optics and optical ... click to view, cbse 12th physics nuclei chapter case study question with answers click to view, cbse 12th physics moving charges and magnetism ... click to view, cbse 12th physics electromagnetic induction chapter case ... click to view, cbse 12th physics atoms chapter case study question with answers click to view, 12th physics alternating current chapter case study question with answers cbse click to view, cbse 12th standard physics subject wave optics ... click to view, cbse 12th standard physics subject communication systems ... click to view, cbse 12th standard physics subject semiconductor electronics ... click to view, cbse 12th standard physics subject nuclei value ... click to view, cbse 12th standard physics subject atoms value ... click to view, cbse 12th standard physics subject dual nature ... click to view, cbse 12th standard physics subject electromagnetic waves ... click to view.

500+ Sample Question Papers

CBSE Class 12 - Question Papers for Practice

CBSE 2019-2020 Session

All Subjects with updated syllabus

Question Papers by Teachers

Question Posted by Teachers all over India

Register & Get the solution for CBSE 12th Standard Physics Subject Current Electricity Chapter Case Study Questions 2021

NCERT Solutions for Class 6, 7, 8, 9, 10, 11 and 12

Important Questions for Class 12 Physics Chapter 3 Current Electricity Class 12 Important Questions

December 6, 2019 by Sastry CBSE

Current Electricity Class 12 Important Questions Very Short Answer Type

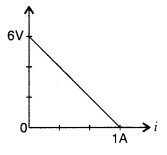
The electron proceeds from A to B, making six collisions on its path. The dotted curve shows how the random motion of the same electron gets modified when an electric field is applied.

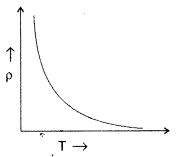
Question 10. The emf of a cell is always greater than its terminal voltage. Why? Give reason. (Delhi 2013) Answer: Emf is the p.d. when no current is drawn. When current is drawn, there will be potential drop across the internal resistance of the cell. So, terminal voltage will be less than the emf.

Question 11. A cell of emf ‘E’ and internal resistance ‘r’ draws a current ‘I’. Write the relation between terminal voltage ‘V’ in terms of E, I and r. (Delhi 2013) Answer: V = E – I

Question 13. Why is the terminal voltage of a cell less than its emf? (Comptt. All India 2013) Answer: Terminal voltage of a cell is less than emf because some curent, however small, may be is drawn to measure terminal voltage due to internal resistance of the cell.

Question 14. Two students A and B were asked to pick a resistor of 15 kΩ from a collection of carbon resis-tors. A picked a resistor with bands of colours : brown, green, orange while B chose a resistor with bands of black, green, red. Who picked the correct resistor? (Comptt. All India 2013) Answer: Student ‘A’ picked up the correct resistor of 15 kΩ.

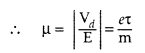
Question 19. How does the random motion of free electrons in a conductor get affected when a potential difference is applied across its ends? (Comptt. Delhi 2014) Answer: Random motion of free electrons gets directed towards the point at a higher potential.

Question 20. State the underlying principle of a potentiometer. (Comptt. Delhi 2014) Answer: When a constant current flows through a wire of uniform cross-section and of uniform composition, the potential difference across any length of wire is directly proportional to its length, i.e., V l \(\infty\) l

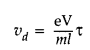
Question 23. Graph showing the variation of current versus voltage for a material GaAs is shown in the figure. Identify the region of (i) negative resistance (ii) where Ohm’s law is obeyes (Delhi 2014) versus for a GaAs is in the Identify the region of Answer: DE : Negative resistance region. AB : Where Ohm’s law is obeyed.

Question 24. I – V graph for a metallic wire at two different temperatures, T 1 and T 2 is as shown in the figure. Which of the two temperatures is lower and why? (All India 2015) Answer: The temperature T 1 is lower. Larger the slope of V-I graph, smaller the resistance. As the resistance of a metal increases with the increase of temperature, resistance at temperature T 1 is lower.

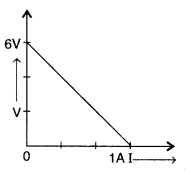
Question 26. Why is a potentiometer preferred over a voltmeter for determining the emf of a cell? (Comptt. Delhi 2016) Answer: Potentiometer does not draw any (net) current from the cell; while Voltmeter draws some current from cell, when connected across it, hence it measures terminal voltage. It is why a potentiometer is preferred over a voltmeter to measure emf.

Question 27. Nichrome and copper wires of same length and same radius are connected in series. Current I is passed through them. Which wire gets heated up more? Justify your answer. (Outside Delhi 2017) Answer: Nichrome : Nichrome wire gets heated up more because of higher resistivity of nichrome. Resistivity NI > Resistivity Cu

Question 28. Define the conductivity of a conductor. Write its SI unit. (Comptt. Outside Delhi 2017) Answer: Conductivity is defined as the reciprocal of resistivity, i.e., σ = \(\frac{1}{\rho}\) Its SI unit is S(Siemen)

Current Electricity Class 12 Important Questions Short Answer Type I

Question 31. Using the mathematical expression for the conductivity of a material, explain how it varies with temperature for (i) semiconductors, (ii) good conductors. (All India 2008) Answer: Conductivity σ = \(\frac{n e^{2} \tau}{m}\) (i) Semiconductors: With increase in temperature, conductivity of semiconductor increases. It is due to increase in V. It dominates the effect caused by decrease in ‘x’. (ii) Good conductors : With increase in temperature, conductivity of good conductors decreases. It is due to decrease in the value of relaxation time. The effect of increased value of V is negligible.

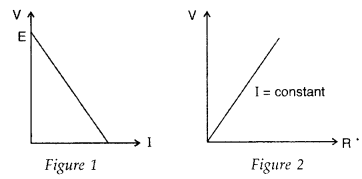
Question 56. State Kirchhoff’s rules. Explain briefly how these rules are justified. (Delhi 2014) Answer: Kirchhoff’s rules.

• Kirchhoff’s junction rule : At any junction, the sum of the currents entering the junction is equal to the sum of currents leaving the junction.
• Kirchhoff’s loop rule : The algebraic sum of changes in potential in any closed loop involving resistors and cells is zero.

These two laws are justified on the basis of law of conservation of charge and the law of conservation of energy respectively.

Question 60. Estimate the average drift speed of conduction electrons in a copper wire of cross-sectional area 2.5 × 10 -7 m 2 carrying a current of 2.7 A. Assume the density of conduction electrons to be 9 × 10 28 m -3 . (All India 2014) Answer: 0.75 × 10 -3 ms -1

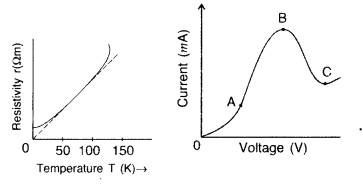
Current Electricity Class 12 Important Questions Short Answer Type II

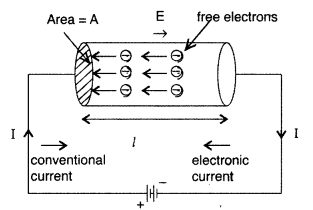
Question 100. A potentiometer wire of length 1.0 m has a resistance of 15 Ω. It is connected to a 5 V battery in series with a resistance of 5 Ω. Determine the emf of the primary cell which gives a balance point at 60 cm. (Delhi 2012) Answer:

Question 101. A potentiometer wire of length 1 m has a resistance of 5 Ω. It is connected to a 8 V battery in series with a resistance of 15 Ω. Determine the emf of the primary cell which gives a balance point at 60 cm. (Delhi 2012) Answer:

Question 102. Answer the following : (a) Why are the connections between the resistors in a meter bridge made of thick copper strips? (b) Why is it generally preferred to obtain the balance point in the middle of the meter bridge wire? (c) Which material is used for the meter bridge wire and why? (All India 2012) Answer: (a) The connections between the resistors in a meter bridge are made of thick copper strip, so as to have the minimum possible resistances. (b) It is generally preferred to obtain the balance point in the middle of the meter bridge, so as to minimise the error of balance. (c) The material used for meter bridge is an alloy ‘constantant’ or ‘manganin’ because of (i) hight resistivity and (ii) low temperature coefficient of resistivity.

Question 104. In the electric network shown in the figure, use Kirchhoffs rules to calculate the power consumed by the resistance R = 4 Ω. (Comptt. Delhi 2012) Answer: -12 + 2I 1 + 4(I 1 + I 2 ) = 0 -12 + 2I 1 + 4 I 1 + 4I 2 = 0 6I 1 + 4I 2 = 12 ⇒ 3I 1 + 2I 2 = 6 … (i) For loop ADFEA -4(I 1 + I 2 ) + 6 = 0 -4I 1 – 4I 2 = -6 ⇒ 2I 1 + 2I 2 = 3 … (ii) Solving (i) and (ii), we get I 1 = 3A and I 2 = -1.5A ∴ Power consumed in 4Ω resistance (R) = I 2 R = (I 1 + I 2 ) 2 × R = (3 – 1.5) 2 × 4 W = 9 watt

Question 105. In the electric network shown in the figure use Kirchhoffs rules to calculate the power consumed by the resistance R = 8 Ω. (Comptt. Delhi 2012) Answer: In loop BCDA, I 1 × 4 + (I 1 + I 2 ) × 8 = 12 4I 1 + 8I 1 + 8I 2 = 12 12I 1 + 8I 2 = 12 ∴ 3I 1 + 2I 2 = 3 … (Dividing by 4) … (i) In loop ADFE, (I 1 + I 2 ) × 8 = 8 => 8I 1 , + 8I 2 = 8 ∴ I 1 + I 2 = 1 …(Dividing by 8) Solving equations (i) and (ii), we get I 1 = 1A and I 2 = 0A ∴ Power consumed in 80 resistance (R) = I 2 R = (I 1 + I 2 ) 2 × R = (1 + 0) 2 × 8 = 8 watt

The distance transversed by each electron in time (t) = drift velocity × time = V d t

If we consider two planes P and Q at a distance V d t in a conductor, then the total charge flowing in time t will be equal to the total charge on the electrons present within the cylinder PQ.

The volume of this cylinder = cross sectional area × length = A V d t

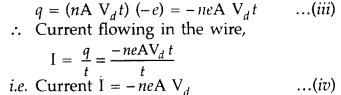
Question 113. Draw a circuit diagram of a potentiometer. State its working principle. Derive the necessary formula to describe how it is used to compare the emfs of the two cells. (Comptt. All India) Answer: (a) Principle : The basic principle of a potentiometer is that “when a constant current flows through a wire of uniform cross-sectional area and composition, the potential drop across any length of the wire is directly proportional to that length. \(v \propto l\)

Comparison of emf’s of two cells: First of all the ends of potentiometer are connected to a battery Bx, key K and rheostat Rh such that the positive terminal of battery B, is connected to end A of the wire. This completes the primary circuit.

Now the positive terminals of the cells C 1 and C 2 whose emfs are to be compared are connected to A and the negative terminals to the jockey J through a two-way key and a galvanometer (fig). This is the secondary circuit.

A number of observations are taken for different resistances taken in resistance box and S is calculated each time and the mean value of S is found.

Precautions: (i) In this experiment the resistance of the copper strips and connecting screws have not been taken into account. These resistances are called end-resistances. Therefore very small resistances cannot be found accurately by metre bridge. The resistance S should not be very small. (ii) The current should not flow in the metre bridge wire for a long time, otherwise the wire will become hot and its resistance will be changed.

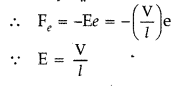
Current Electricity Class 12 Important Questions Long Answer Type

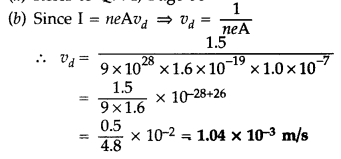
Question 126. (a) State the working principle of a potentiometer. With the help of the circuit diagram, explain how a potentiometer is used to compare the emf’s of two primary cells. Obtain the required expression used for comparing the emfs. (b) Write two possible causes for one sided deflection in a potentiometer experiment. (Delhi 2012) Answer: (a) Principle : The basic principle of a potentiometer is that “when a constant current flows through a wire of uniform cross-sectional area and composition, the potential drop across any length of the wire is directly proportional to that length. \(v \propto l\)

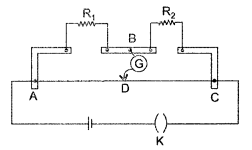
(a) Principle : The basic principle of a potentiometer is that “when a constant current flows through a wire of uniform cross-sectional area and composition, the potential drop across any length of the wire is directly proportional to that length. \(v \propto l\)

(ii) (c) Electric current will remain constant in the wire. Reason : All other quantities depend on the cross sectional area of the wire and hence will not remain constant.

Question 134. (a) Draw a circuit diagram of a meter bridge used to determine the unknown resistance R of a given wire. Hence derive the expression for R in terms of the known resistance S. (b) What does the term ‘end error’ in a metre bridge circuit mean and how is it corrected? How will the balancing point be affected, if the positions of the battery and galvanometer are interchanged in a metre bridge experiment? Give reason for your answer. (Comptt. Delhi 2016) Answer: (a)

(b) The error which arises on account of resistance of copper strips and the connecting wire at both ends of the meter bridge is called end error. It is minimized by adjusting the balance point near the middle point of the bridge. • The balancing point will not be affected, as the bridge remains balanced.

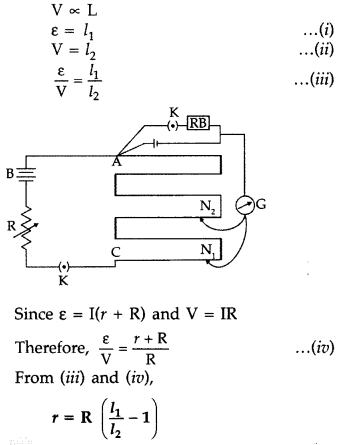
Important Questions for Class 12 Physics

Free resources.

NCERT Solutions

Quick Resources

• Andhra Pradesh
• Chhattisgarh
• West Bengal
• Madhya Pradesh
• Maharashtra
• Jammu & Kashmir
• NCERT Books 2022-23
• NCERT Solutions
• NCERT Notes
• NCERT Exemplar Books
• NCERT Exemplar Solution
• States UT Book
• School Kits & Lab Manual
• NCERT Books 2021-22
• NCERT Books 2020-21
• NCERT Book 2019-2020
• NCERT Book 2015-2016
• RD Sharma Solution
• TS Grewal Solution
• TR Jain Solution
• Selina Solution
• Frank Solution
• Lakhmir Singh and Manjit Kaur Solution
• I.E.Irodov solutions
• ICSE - Goyal Brothers Park
• ICSE - Dorothy M. Noronhe
• Sandeep Garg Textbook Solution
• Micheal Vaz Solution
• S.S. Krotov Solution
• Evergreen Science
• KC Sinha Solution
• ICSE - ISC Jayanti Sengupta, Oxford
• ICSE Focus on History
• ICSE GeoGraphy Voyage
• ICSE Hindi Solution
• ICSE Treasure Trove Solution
• Thomas & Finney Solution
• SL Loney Solution
• SB Mathur Solution
• P Bahadur Solution
• Narendra Awasthi Solution
• MS Chauhan Solution
• LA Sena Solution
• Integral Calculus Amit Agarwal Solution
• IA Maron Solution
• Hall & Knight Solution
• Errorless Solution
• Pradeep's KL Gogia Solution
• OP Tandon Solutions
• Sample Papers
• Previous Year Question Paper
• Important Question
• Value Based Questions
• CBSE Syllabus
• CBSE MCQs PDF
• Assertion & Reason
• New Revision Notes
• Revision Notes
• Question Bank
• Marks Wise Question
• Toppers Answer Sheets
• Exam Paper Aalysis
• Concept Map
• CBSE Text Book
• Additional Practice Questions
• Vocational Book
• CBSE - Concept
• KVS NCERT CBSE Worksheets
• Formula Class Wise
• Formula Chapter Wise
• JEE Previous Year Paper
• JEE Mock Test
• JEE Crash Course
• JEE Sample Papers
• Important Info
• SRM-JEEE Previous Year Paper
• SRM-JEEE Mock Test
• VITEEE Previous Year Paper
• VITEEE Mock Test
• BITSAT Previous Year Paper
• BITSAT Mock Test
• Manipal Previous Year Paper
• Manipal Engineering Mock Test
• AP EAMCET Previous Year Paper
• AP EAMCET Mock Test
• COMEDK Previous Year Paper
• COMEDK Mock Test
• GUJCET Previous Year Paper
• GUJCET Mock Test
• KCET Previous Year Paper
• KCET Mock Test
• KEAM Previous Year Paper
• KEAM Mock Test
• MHT CET Previous Year Paper
• MHT CET Mock Test
• TS EAMCET Previous Year Paper
• TS EAMCET Mock Test
• WBJEE Previous Year Paper
• WBJEE Mock Test
• AMU Previous Year Paper
• AMU Mock Test
• CUSAT Previous Year Paper
• CUSAT Mock Test
• AEEE Previous Year Paper
• AEEE Mock Test
• UPSEE Previous Year Paper
• UPSEE Mock Test
• CGPET Previous Year Paper
• Crash Course
• Previous Year Paper
• NCERT Based Short Notes
• NCERT Based Tests
• NEET Sample Paper
• Previous Year Papers
• Quantitative Aptitude
• Numerical Aptitude Data Interpretation
• General Knowledge
• Mathematics
• Agriculture
• Accountancy
• Business Studies
• Political science
• Enviromental Studies
• Mass Media Communication
• Teaching Aptitude
• NAVODAYA VIDYALAYA
• SAINIK SCHOOL (AISSEE)
• Mechanical Engineering
• Electrical Engineering
• Electronics & Communication Engineering
• Civil Engineering
• Computer Science Engineering
• CBSE Board News
• Scholarship Olympiad
• School Admissions
• Entrance Exams
• All Board Updates
• Miscellaneous
• State Wise Books
• Engineering Exam

SHARING IS CARING If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.

• NCERT Solutions for Class 12 Maths
• NCERT Solutions for Class 10 Maths
• CBSE Syllabus 2023-24
• Social Media Channels
• Login Customize Your Notification Preferences
• Electric Charges and Fields 14 April, 2021, 6:29 pm
• Electrostatic Potential And Capacitance 14 April, 2021, 6:29 pm
• Current Electricity 14 April, 2021, 6:29 pm
• Moving Charges And Magnetism 14 April, 2021, 6:29 pm
• Magnetism And Matter 14 April, 2021, 6:29 pm
• Electromagnetic Induction 14 April, 2021, 6:29 pm
• Alternating Current 14 April, 2021, 6:29 pm
• Electromagnetic Waves 14 April, 2021, 6:29 pm
• Ray Optics & Optical Instruments 14 April, 2021, 6:29 pm

• Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.

Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.

Provide prime users with access to exclusive PDF study materials that are not available to regular users.

Case Based Questions Test: Current Electricity - Grade 12 MCQ

15 questions mcq test - case based questions test: current electricity.

1 Crore+ students have signed up on EduRev. Have you?

Read the following text and answer the following questions on the basis of the same: Electric Toaster : Small Industries Service Institute Takyelpat Industrial Estate Imphal has designed an Electric toaster which is operated at 220 volts A.C., single phase and available in four different rated capacity such as 600 W, 750 W, 1000 W and 1250 W. The heating element is made of nichrome 80/20 (80% nickel, 20% chromium), since Nichrome does not get oxidise readily at high temperature and have higher resistivity, so it produces more heat. The element is wound separately on Mica sheets and fitted with body of toaster with the help of ceramic terminals. Heating element of the toaster is made of:

• B. nichrome.
• C. chromium.

Read the following text and answer the following questions on the basis of the same: Electric Toaster : Small Industries Service Institute Takyelpat Industrial Estate Imphal has designed an Electric toaster which is operated at 220 volts A.C., single phase and available in four different rated capacity such as 600 W, 750 W, 1000 W and 1250 W. The heating element is made of nichrome 80/20 (80% nickel, 20% chromium), since Nichrome does not get oxidise readily at high temperature and have higher resistivity, so it produces more heat. The element is wound separately on Mica sheets and fitted with body of toaster with the help of ceramic terminals. Which one will consume more electricity?

Read the following text and answer the following questions on the basis of the same: electric toaster : small industries service institute takyelpat industrial estate imphal has designed an electric toaster which is operated at 220 volts a.c., single phase and available in four different rated capacity such as 600 w, 750 w, 1000 w and 1250 w. the heating element is made of nichrome 80/20 (80% nickel, 20% chromium), since nichrome does not get oxidise readily at high temperature and have higher resistivity, so it produces more heat. the element is wound separately on mica sheets and fitted with body of toaster with the help of ceramic terminals. insulating materials used in the device are:.

• C. Mica, ceramic, Nichrome
• D. Mica, ceramic

Read the following text and answer the following questions on the basis of the same:

Shunt resistance: The ammeter shunt is the device which provides the low resistance path to the flow of current. It is connected in parallel with the ammeter. In some ammeter the shunt is in-built inside the instrument while in others it is externally connected to the circuit. Ammeters are designed for measurement of low current. For measuring high current, the shunt is connected in parallel to the ammeter. The significant portion of the current passes to the shunt because of the low resistance path and little amount of current passes through the ammeter. The shunt is connected in parallel to the ammeter because of which the voltage drops across the meter and shunt remain the same. Thus, the movement of the pointer is not affected by the shunt. Let us consider that the current to be measured is I. The circuit has ammeter and shunt connected parallel to each other. The ammeter is designed for measurement of small current say, Im. The magnitude of the current I passes through the meter is very high, and it will burn the meter. So, for measuring the current I the shunt is required in the circuit. As the shunt connects in parallel with the ammeter, thus the same voltage drops occur between them:

I Sh R SH = I m R m

∴ R SH = I m R m /I SH

Shunt current I SH = I – I m

So, R SH = I m R m /(I – I m )

∴ I/I m = 1 + (R m /R SH )

The ratio of the total current to the current required for the movement of the ammeter coil is called the multiplying power of the shunt.

∴ The multiplying power = m = I/Im

RSH = Rm / (m – 1)

The following are the requirements of the shunt.

• The resistance of the shunt should remain constant with time.

• The temperature of the material should remain the same even though substantial current flows through the circuit.

Manganin and Constantan are used for making the shunt of DC and AC ammeter respectively. What is multiplying power of the shunt?

• A. Total current/Current required by the movement of ammeter coil
• B. Current required by the movement of ammeter coi/Total currennt
• C. Current required by the movement of ammeter coil X Total current
• D. None of the above

Current through shunt is

• A. greater than current through ammeter coil.
• B. less than current through ammeter coil.
• C. equal to the current through ammeter coil.
• D. may be greater than or equal to or less than current through ammeter coil.

What will be the value of the shunt resistance if the ammeter coil resistance is 1Ω and multiplying power is 100?

Types of resistors Most common type of resistor is Carbon Composition Resistors. Carbon resistors are a cheap, general purpose resistor used in electrical and electronic circuits. Their resistive element is manufactured from a mixture of finely ground carbon dust or graphite and a non-conducting ceramic powder to bind it all together. The ratio of carbon dust to ceramic (conductor to insulator) determines the resistive value of the resistor. Higher the ratio of carbon, lower the overall resistance. Film Type Resistors consist of Metal Film, Carbon Film and Metal Oxide Film .Such resistors are generally made by depositing pure metals, such as nickel, or an oxide film, such as tin-oxide, on an insulating ceramic rod or substrate. The resistive value of the resistor is controlled by increasing the desired thickness of the deposited film giving them the names of either “thick-film resistors” or “thin-film resistors”. Film type resistors can achieve much higher ohmic value compared to other types. Another type of resistor, called a Wirewound Resistor, is made by winding a thin metal alloy wire (Nichrome) or similar wire on an insulating ceramic former in the form of a spiral helix. These types of resistors are generally only available in very low ohmic value with high precision . They are able to handle much higher electrical currents than other resistors of the same ohmic value with much excessive power ratings. These high power resistors are moulded into an aluminium heat sink body with fins attached to increase their overall surface area to promote heat loss and cooling.

Carbon composition resistors are made from a mixture of

• A. finely ground metal dust and ceramic powder.
• B. finely ground carbon dust or graphite and ceramic powder.
• C. finely ground carbon dust or graphite and copper powder.
• D. finely ground carbon dust or graphite.

Metal Film Type Resistors are generally made by depositing pure ______, on ______ rod or substrate.

• A. Ceramic, metal
• B. Carbon, ceramic
• C. Metal, ceramic
• D. Carbon, metal

Wire wound resistors are available in very ____ ohmic high precision values with ______ power rating.

• A. High, high
• B. Low, low
• C. High, Low
• D. Low, high

Read the following text and answer the following questions on the basis of the same: Electric Toaster : Small Industries Service Institute Takyelpat Industrial Estate Imphal has designed an Electric toaster which is operated at 220 volts A.C., single phase and available in four different rated capacity such as 600 W, 750 W, 1000 W and 1250 W. The heating element is made of nichrome 80/20 (80% nickel, 20% chromium), since Nichrome does not get oxidise readily at high temperature and have higher resistivity, so it produces more heat. The element is wound separately on Mica sheets and fitted with body of toaster with the help of ceramic terminals.

What is meant by 80/20 Nichrome?

• A. 80% Chromium and 20% Nickel
• B. 80% Nickel and 20% Chromium
• C. Purity 80%, Impurity 20%
• D. It is a mixture of Chromium and Nickel

Operating voltage of the device is:

• A. 220 V AC, single phase
• B. 220 V AC, three phase
• C. 220 V DC
• D. 220 V AC/DC

Materials used for making shunt of DC and AC ammeter are respectively

• A. Manganin and Manganin
• B. Manganin and Copper
• C. Manganin and Constantan
• D. Constantan and Manganin

How shunt is connected with a ammeter?

• A. In series when connected externally
• B. In parallel when connected externally
• C. In parallel when connected internally
• D. Both (B) and (C)

In carbon composition resistors, ______ the ratio of carbon, _____ the overall resistance.

• A. Higher, lower
• B. Lower, higher
• C. Lower, lower
• D. Higher, higher

Wirewound Resistors are made by winding a thin _____ or similar wire on an ____ former in the form of a spiral helix.

• A. Nichrome, copper
• B. Nichrome, ceramic
• C. Copper, ceramic
• D. Copper, Nichrome

--> and get INR 200 additional OFF

Top Courses for Grade 12

Important Questions for Case Based Questions Test: Current Electricity

Case based questions test: current electricity mcqs with answers, online tests for case based questions test: current electricity.

cation olution

Join the 10M+ students on EduRev

Welcome Back

Create your account for free.

Forgot Password

myCBSEguide

• Case Study Questions Class...

Case Study Questions Class 12 Physics

Table of Contents

myCBSEguide App

Download the app to get CBSE Sample Papers 2023-24, NCERT Solutions (Revised), Most Important Questions, Previous Year Question Bank, Mock Tests, and Detailed Notes.

CBSE will ask two Case Study Questions in the CBSE class 12 Physics questions paper. Question numbers 15 and 16 are case-based questions where 5 MCQs will be asked based on a paragraph. Each theme will have five questions and students will have a choice to attempt any four of them. You can download CBSE Class 12 Physics case study questions from the myCBSEguide App and our free student dashboard .

You can Score High

CBSE class 12 Physics question paper will carry questions for 70 marks. Certainly, the question paper is a bit easier this year. It is because the syllabus is already reduced and there are more internal choices. Besides this, the case study questions are a plus to winning the game with good marks.

In simple words, all circumstances are in favour of the sincere students who are working hard to score high this year. Although it has been a difficult time for students as they were not getting the personal attention of the teachers. We know that online classes have their own limits, but we still expect better scores, especially from students who are putting extra effort into their studies.

Class 12 Physics Case Study Questions

CBSE class 12 Physics question paper will have case study questions too. These case-based questions will be objective type in nature. So, class 12 Physics students must prepare themselves for such questions. First of all, you should study NCERT Textbooks line by line and then you should practice as many questions as possible.

Case Study Syllabus

We know that CBSE has reduced the syllabus. Hence, practice only relevant questions. don’t waste time on case study questions from deleted portion. It is of no use. You can download the latest class 12 Physics case study questions from the myCBSEguide App.

Physics Case Studies

Class 12 Physics has many chapters but all chapters are not important for case studies. As we know case studies are not exactly given from NCERT books but these may be extracted from some newspaper articles, magazines, journals or other books. So, it is very much important that you are studying only the most relevant case studies. Here, the myCBSEguide app helps you a lot. We have case study questions that are prepared by a team of expert teachers. These experts exactly know what types of questions can come in exams.

Case Study Questions

There are a number of study apps available over the internet. But if you are a CBSE student and willing to get an app for the CBSE curriculum, you have very limited options. And if you want an app that is specifically designed for CBSE students, your search will definitely end on finding myCBSEguide. Case study questions are the latest updates in CBSE syllabus. It is exclusively available in the myCBSEguide app.

Here are some example questions. For more questions, you can download the myCBSEguide App.

Physics Case Study -1

Read  the following source and answer any four out of the following questions: Electric charge is the physical property of matter that causes it to experience a force when placed in an electromagnetic field. There are two types of charges positive and negative charges. Also, like charges repel each other whereas unlike charges attract each other.

• -3.2  × ×  10 -18  C
• 3.2  × ×  10  18  C
• -3.2  × ×  10 -17  C
• 3.2  × ×  10  -17   C
• -1.6  × ×  10 -18  C
• 1.6  × ×  10  -18  C
• 2.6  × ×  10 -18  C
• 1.6  × ×  10 -21  C
• 9.1  × ×  10 -31  kg
• 9.1  × ×  10 -31  g
• 1.6  × ×  10 -19  kg
• 1.6  × ×  10 -19  g
• there is only a positive charge in the body
• there is positive as well as negative charge in the body but the positive charge is more than the negative charge
• there is equally positive and negative charge in the body but the positive charge lies in the outer regions
• the negative charge is displaced from its position
• valence electrons only
• electrons of inner shells
• both valence electrons and electrons of the inner shell.
• none of the above

Physics Case Study -2

Read the following source and answer any four out of the following questions: Resistance is a measure of the opposition to current flow in an electrical circuit. Resistance is measured in ohms. Also, Resistivity is the electrical resistance of a conductor of unit cross-sectional area, and unit length. … A characteristic property of each material, resistivity is useful in comparing various materials on the basis of their ability to conduct electric currents.

• nature of material
• temperature
• dimensions of material
• cross-sectional area
• length of wire
• wire’s nature
• all of the above
• more resistance
• less resistance
• same resistance

Physics Case Study -3

Read the source given below and answer any four out of the following questions: The Bohr model of the atom was proposed by Neil Bohr in 1915. It came into existence with the modification of Rutherford’s model of an atom. Rutherford’s model introduced the nuclear model of an atom, in which he explained that a nucleus (positively charged) is surrounded by negatively charged electrons.

• The energy of the electrons in the orbit is quantized
• The electron in the orbit nearest the nucleus has the lowest energy
• Electrons revolve in different orbits around the nucleus
• The position and velocity of the electrons in the orbit cannot be determined simultaneously
• Single proton
• Multiple electrons
• emitted only
• absorbed only
• both (a) and (b)
• none of these
•  It must emit a continuous spectrum
•  It loses its energy
• Gaining its energy
• A discrete spectrum
• dequantized

Physics Case Study & myCBSEguide App

We at myCBSEguide provide the best case study questions for CBSE class 12 Physics. We have Physics case study questions for every chapter in 12th class Physics. Students can access the Physics case study questions with answers on the myCBSEguide App or on the student dashboard . Here are some features that make myCBSEguide the best learning app for CBSE students:

• Updated syllabus
• Up to date question bank
• Model papers and 10-year questions
• NCERT and Exemplar sulutions
• Best quality learning videos
• Detailed revision notes

12 Physics Question Paper Design

Here is the question paper design for CBSE class 12 Physics. It shows the typology of the questions and their weightage in CBSE board exams.

QUESTION PAPER DESIGN Theory (Class: 12)

Maximum Marks: 70 Duration: 3 hrs

	Exhibit memory of previously learned material by recalling facts, terms, basic concepts, and answers.  Demonstrate understanding of facts and ideas by organizing, comparing, translating, interpreting, giving descriptions, and stating main ideas	27	38%
	Solve problems to new situations by applying acquired knowledge, facts, techniques and rules in a different way	22	32%
	Examine and break information into parts by identifying motives or causes. Make inferences and find evidence to support generalizations Present and defend opinions by making judgments about information, the validity of ideas, or quality of work based on a set of criteria. Compile information together in a different way by combining elements in a new pattern or proposing alternative solutions.	21	30%
		70	100
		30
		100

Note:  The above template is only a sample. Suitable internal variations may be made for generating similar templates keeping the overall weightage to different forms of questions and typology of questions the same.

Test Generator

Create question paper PDF and online tests with your own name & logo in minutes.

Question Bank, Mock Tests, Exam Papers, NCERT Solutions, Sample Papers, Notes

Related Posts

• Competency Based Learning in CBSE Schools
• Class 11 Physical Education Case Study Questions
• Class 11 Sociology Case Study Questions
• Class 12 Applied Mathematics Case Study Questions
• Class 11 Applied Mathematics Case Study Questions
• Class 11 Mathematics Case Study Questions
• Class 11 Biology Case Study Questions
• Class 12 Physical Education Case Study Questions

2 thoughts on “Case Study Questions Class 12 Physics”

Good question l will check answers sheet

Question 2 answer key ?

Leave a Comment

Save my name, email, and website in this browser for the next time I comment.

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Join our Telegram Channel for Free PDF Download

Assertion and Reason Questions on Class 12 Physics Chapter 3 Current Electricity

• Last modified on: 3 months ago
• Reading Time: 6 Minutes

Board	CBSE
	Class 12 Students
	Physics
	Chapter 3 Current Electricity
	Assertion and Reason Questions
	6
	Yes

Assertion Reason Questions

Directions:  These questions consist of two statements, each printed as Assertion and Reason. While answering these questions, you are required to choose any one of the following four responses. (a) If both Assertion and Reason are correct and the Reason is a correct explanation of the Assertion. (b) If both Assertion and Reason are correct but Reason is not a correct explanation of the Assertion. (c) If the Assertion is correct but Reason is incorrect. (d) If both the Assertion and Reason are incorrect.

Q.1. Assertion : In a simple battery circuit, the point of the lowest potential is positive terminal of the battery. Reason : The current flows towards the point of the higher potential, as it does in such a circuit from the negative to the positive terminal.

Q.2. Assertion : A larger dry cell has higher emf. Reason : The emf of a dry cell is proportional to its size.

Q.3. Assertion : A current continues to flow in superconducting coil even after switch is off. Reason : Superconducting coils show Meissner effect.

Q.4. Assertion : Voltmeter is connected in parallel with the circuit. Reason : Resistance of a voltmeter is very large.

Q.5. Assertion : Ohm’s law is applicable for all conducting elements. Reason : Ohm’s law is a fundamental law.

Q.6. Assertion : An electric bulb becomes dim, when the electric heater in parallel circuit is switched on. Reason : Dimness decreases after sometime.

Related Posts

• Assertion and Reason Questions on class 12 Physics Chapter 1 Electric Charges and Fields
• Assertion and Reason Questions on class 12 Physics Chapter 2 Electrostatic Potential and Capacitance
• Assertion and Reason Questions on class 12 Physics Chapter 4 Moving Charges and Magnetism
• Assertion and Reason Questions on class 12 Physics Chapter 5 Magnetism and Matter
• Assertion and Reason Questions on class 12 Physics Chapter 6 Electromagnetic Induction
• Assertion and Reason Questions on class 12 Physics Chapter 7 Alternating Current
• Assertion and Reason Questions on class 12 Physics Chapter 8 Electromagnetic waves
• Assertion and Reason Questions on class 12 Physics Chapter 9 Ray Optics and Optical Instruments
• Assertion and Reason Questions on class 12 Physics Chapter 10 Wave Optics
• Assertion and Reason Questions on class 12 Physics Chapter 11 Dual Nature of Matter and Radiation
• Assertion and Reason Questions on class 12 Physics Chapter 12 Atoms
• Assertion and Reason Questions on class 12 Physics Chapter 13 Nuclei
• Assertion and Reason Questions on class 12 Physics Chapter 14 Semiconductor Electronics

You May Also Like:

Category lists (all posts).

All categories of this website are listed below with number of posts in each category for better navigation. Visitors can click on a particular category to see all posts related to that category.

• Full Form (1)
• Biography of Scientists (1)
• Assertion Reason Questions in Biology (37)
• Case Study Questions for Class 12 Biology (14)
• DPP Biology for NEET (12)
• Blog Posts (35)
• Career Guidance (1)
• Assertion Reason Questions for Class 10 Maths (14)
• Case Study Questions for Class 10 Maths (15)
• Extra Questions for Class 10 Maths (12)
• Maths Formulas for Class 10 (1)
• MCQ Questions for Class 10 Maths (15)
• NCERT Solutions for Class 10 Maths (4)
• Quick Revision Notes for Class 10 Maths (14)
• Assertion Reason Questions for Class 10 Science (16)
• Case Study Questions for Class 10 Science (14)
• Evergreen Science Book Solutions for Class 10 (17)
• Extra Questions for Class 10 Science (23)
• HOTS for Class 10 Science (17)
• Important Questions for Class 10 Science (10)
• Lakhmir Singh Class 10 Biology Solutions (4)
• Lakhmir Singh Class 10 Chemistry Solutions (5)
• Lakhmir Singh Class 10 Physics Solutions (5)
• MCQ Questions for Class 10 Science (20)
• NCERT Exemplar Solutions for Class 10 Science (16)
• NCERT Solutions for Class 10 Science (15)
• Quick Revision Notes for Class 10 Science (4)
• Study Notes for Class 10 Science (17)
• Assertion Reason Questions for Class 10 Social Science (14)
• Case Study Questions for Class 10 Social Science (24)
• MCQ Questions for Class 10 Social Science (3)
• Topicwise Notes for Class 10 Social Science (4)
• CBSE CLASS 11 (1)
• Assertion Reason Questions for Class 11 Chemistry (14)
• Case Study Questions for Class 11 Chemistry (11)
• Free Assignments for Class 11 Chemistry (1)
• MCQ Questions for Class 11 Chemistry (8)
• Very Short Answer Questions for Class 11 Chemistry (7)
• Assertion Reason Questions for Class 11 Entrepreneurship (8)
• Important Questions for CBSE Class 11 Entrepreneurship (1)
• Assertion Reason Questions for Class 11 Geography (24)
• Case Study Questions for Class 11 Geography (24)
• Assertion Reason Questions for Class 11 History (12)
• Case Study Questions for Class 11 History (12)
• Assertion and Reason Questions for Class 11 Maths (16)
• Case Study Questions for Class 11 Maths (16)
• Formulas for Class 11 Maths (6)
• MCQ Questions for Class 11 Maths (17)
• NCERT Solutions for Class 11 Maths (8)
• Case Study Questions for Class 11 Physical Education (11)
• Assertion Reason Questions for Class 11 Physics (15)
• Case Study Questions for Class 11 Physics (12)
• Class 11 Physics Study Notes (5)
• Concept Based Notes for Class 11 Physics (2)
• Conceptual Questions for Class 11 Physics (10)
• Derivations for Class 11 Physics (3)
• Extra Questions for Class 11 Physics (13)
• MCQ Questions for Class 11 Physics (16)
• NCERT Solutions for Class 11 Physics (16)
• Numerical Problems for Class 11 Physics (4)
• Physics Formulas for Class 11 (7)
• Revision Notes for Class 11 Physics (11)
• Very Short Answer Questions for Class 11 Physics (11)
• Assertion Reason Questions for Class 11 Political Science (20)
• Case Study Questions for Class 11 Political Science (20)
• CBSE CLASS 12 (8)
• Extra Questions for Class 12 Biology (14)
• MCQ Questions for Class 12 Biology (13)
• Case Studies for CBSE Class 12 Business Studies (13)
• MCQ Questions for Class 12 Business Studies (1)
• Revision Notes for Class 12 Business Studies (10)
• Assertion Reason Questions for Class 12 Chemistry (15)
• Case Study Based Questions for Class 12 Chemistry (14)
• Extra Questions for Class 12 Chemistry (5)
• Important Questions for Class 12 Chemistry (15)
• MCQ Questions for Class 12 Chemistry (8)
• NCERT Solutions for Class 12 Chemistry (16)
• Revision Notes for Class 12 Chemistry (7)
• Assertion Reason Questions for Class 12 Economics (9)
• Case Study Questions for Class 12 Economics (9)
• MCQ Questions for Class 12 Economics (1)
• MCQ Questions for Class 12 English (2)
• Assertion Reason Questions for Class 12 Entrepreneurship (7)
• Case Study Questions for Class 12 Entrepreneurship (7)
• Case Study Questions for Class 12 Geography (18)
• Assertion Reason Questions for Class 12 History (8)
• Case Study Questions for Class 12 History (13)
• Assertion Reason Questions for Class 12 Informatics Practices (13)
• Case Study Questions for Class 12 Informatics Practices (11)
• MCQ Questions for Class 12 Informatics Practices (5)
• Assertion and Reason Questions for Class 12 Maths (14)
• Case Study Questions for Class 12 Maths (13)
• Maths Formulas for Class 12 (5)
• MCQ Questions for Class 12 Maths (14)
• Problems Based on Class 12 Maths (1)
• RD Sharma Solutions for Class 12 Maths (1)
• Assertion Reason Questions for Class 12 Physical Education (11)
• Case Study Questions for Class 12 Physical Education (11)
• MCQ Questions for Class 12 Physical Education (10)
• Assertion Reason Questions for Class 12 Physics (16)
• Case Study Based Questions for Class 12 Physics (14)
• Class 12 Physics Conceptual Questions (16)
• Class 12 Physics Discussion Questions (1)
• Class 12 Physics Latest Updates (2)
• Derivations for Class 12 Physics (8)
• Extra Questions for Class 12 Physics (4)
• Important Questions for Class 12 Physics (8)
• MCQ Questions for Class 12 Physics (14)
• NCERT Solutions for Class 12 Physics (18)
• Numerical Problems Based on Class 12 Physics (16)
• Physics Class 12 Viva Questions (1)
• Revision Notes for Class 12 Physics (7)
• Assertion Reason Questions for Class 12 Political Science (16)
• Case Study Questions for Class 12 Political Science (16)
• Notes for Class 12 Political Science (1)
• Assertion Reason Questions for Class 6 Maths (13)
• Case Study Questions for Class 6 Maths (13)
• Extra Questions for Class 6 Maths (1)
• Worksheets for Class 6 Maths (1)
• Assertion Reason Questions for Class 6 Science (16)
• Case Study Questions for Class 6 Science (16)
• Extra Questions for Class 6 Science (1)
• MCQ Questions for Class 6 Science (9)
• Assertion Reason Questions for Class 6 Social Science (1)
• Case Study Questions for Class 6 Social Science (26)
• NCERT Exemplar for Class 7 Maths (13)
• NCERT Exemplar for Class 7 Science (19)
• NCERT Exemplar Solutions for Class 7 Maths (12)
• NCERT Exemplar Solutions for Class 7 Science (18)
• NCERT Notes for Class 7 Science (18)
• Assertion Reason Questions for Class 7 Maths (14)
• Case Study Questions for Class 7 Maths (14)
• Extra Questions for Class 7 Maths (5)
• Assertion Reason Questions for Class 7 Science (18)
• Case Study Questions for Class 7 Science (17)
• Extra Questions for Class 7 Science (19)
• Assertion Reason Questions for Class 7 Social Science (1)
• Case Study Questions for Class 7 Social Science (30)
• Assertion Reason Questions for Class 8 Maths (7)
• Case Study Questions for Class 8 Maths (17)
• Extra Questions for Class 8 Maths (1)
• MCQ Questions for Class 8 Maths (6)
• Assertion Reason Questions for Class 8 Science (16)
• Case Study Questions for Class 8 Science (11)
• Extra Questions for Class 8 Science (2)
• MCQ Questions for Class 8 Science (4)
• Numerical Problems for Class 8 Science (1)
• Revision Notes for Class 8 Science (11)
• Assertion Reason Questions for Class 8 Social Science (27)
• Case Study Questions for Class 8 Social Science (23)
• CBSE Class 9 English Beehive Notes and Summary (2)
• Assertion Reason Questions for Class 9 Maths (14)
• Case Study Questions for Class 9 Maths (14)
• MCQ Questions for Class 9 Maths (11)
• NCERT Notes for Class 9 Maths (6)
• NCERT Solutions for Class 9 Maths (12)
• Revision Notes for Class 9 Maths (3)
• Study Notes for Class 9 Maths (10)
• Assertion Reason Questions for Class 9 Science (16)
• Case Study Questions for Class 9 Science (15)
• Evergreen Science Book Solutions for Class 9 (15)
• Extra Questions for Class 9 Science (22)
• MCQ Questions for Class 9 Science (11)
• NCERT Solutions for Class 9 Science (15)
• Revision Notes for Class 9 Science (1)
• Study Notes for Class 9 Science (15)
• Topic wise MCQ Questions for Class 9 Science (2)
• Topicwise Questions and Answers for Class 9 Science (15)
• Assertion Reason Questions for Class 9 Social Science (15)
• Case Study Questions for Class 9 Social Science (19)
• CHEMISTRY (8)
• Chemistry Articles (2)
• Daily Practice Problems (DPP) (3)
• Books for CBSE Class 9 (1)
• Books for ICSE Class 10 (3)
• Editable Study Materials (8)
• Exam Special for CBSE Class 10 (3)
• H. C. Verma (Concepts of Physics) (13)
• Study Materials for ICSE Class 10 Biology (14)
• Extra Questions for ICSE Class 10 Chemistry (1)
• Study Materials for ICSE Class 10 Chemistry (5)
• Study Materials for ICSE Class 10 Maths (16)
• Important Questions for ICSE Class 10 Physics (13)
• MCQ Questions for ICSE Class 10 Physics (4)
• Study Materials for ICSE Class 10 Physics (8)
• Study Materials for ICSE Class 9 Maths (7)
• Study Materials for ICSE Class 9 Physics (10)
• Topicwise Problems for IIT Foundation Mathematics (4)
• Challenging Physics Problems for JEE Advanced (2)
• Topicwise Problems for JEE Physics (1)
• DPP for JEE Main (1)
• Integer Type Questions for JEE Main (1)
• Integer Type Questions for JEE Chemistry (6)
• Chapterwise Questions for JEE Main Physics (1)
• Integer Type Questions for JEE Main Physics (8)
• Physics Revision Notes for JEE Main (4)
• JEE Mock Test Physics (1)
• JEE Study Material (1)
• JEE/NEET Physics (6)
• CBSE Syllabus (1)
• Maths Articles (2)
• NCERT Books for Class 12 Physics (1)
• NEET Chemistry (13)
• Important Questions for NEET Physics (17)
• Topicwise DPP for NEET Physics (5)
• Topicwise MCQs for NEET Physics (32)
• NTSE MAT Questions (1)
• Physics (1)
• Alternating Current (1)
• Electrostatics (6)
• Fluid Mechanics (2)
• PowerPoint Presentations (13)
• Previous Years Question Paper (3)
• Products for CBSE Class 10 (15)
• Products for CBSE Class 11 (10)
• Products for CBSE Class 12 (6)
• Products for CBSE Class 6 (2)
• Products for CBSE Class 7 (5)
• Products for CBSE Class 8 (1)
• Products for CBSE Class 9 (3)
• Products for Commerce (3)
• Products for Foundation Courses (2)
• Products for JEE Main & Advanced (10)
• Products for NEET (6)
• Products for ICSE Class 6 (1)
• Electrostatic Potential and Capacitance (1)
• Topic Wise Study Notes (Physics) (2)
• Topicwise MCQs for Physics (2)
• Uncategorized (138)

Test series for students preparing for Engineering & Medical Entrance Exams are available. We also provide test series for School Level Exams. Tests for students studying in CBSE, ICSE or any state board are available here. Just click on the link and start test.

In order to equip the students with the latest methodology of testing and evaluation in competitive exam segment in India  Physics Gurukul has introduced  successrouter.com  for Online Testing and Assessment. Try our free tests for JEE and NEET Today!

Download CBSE Books

Exam Special Series:

• Sample Question Paper for CBSE Class 10 Science (for 2024)
• Sample Question Paper for CBSE Class 10 Maths (for 2024)
• CBSE Most Repeated Questions for Class 10 Science Board Exams
• CBSE Important Diagram Based Questions Class 10 Physics Board Exams
• CBSE Important Numericals Class 10 Physics Board Exams
• CBSE Practical Based Questions for Class 10 Science Board Exams
• CBSE Important “Differentiate Between” Based Questions Class 10 Social Science
• Sample Question Papers for CBSE Class 12 Physics (for 2024)
• Sample Question Papers for CBSE Class 12 Chemistry (for 2024)
• Sample Question Papers for CBSE Class 12 Maths (for 2024)
• Sample Question Papers for CBSE Class 12 Biology (for 2024)
• CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
• Master Organic Conversions CBSE Class 12 Chemistry Board Exams
• CBSE Important Numericals Class 12 Physics Board Exams
• CBSE Important Definitions Class 12 Physics Board Exams
• CBSE Important Laws & Principles Class 12 Physics Board Exams
• 10 Years CBSE Class 12 Chemistry Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Physics Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Maths Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Biology Previous Year-Wise Solved Papers (2023-2024)
• ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
• ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
• ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
• ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
• ICSE Important Functions and Locations Based Questions Class 10 Biology
• ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)

✨ Join our Online JEE Test Series for 499/- Only (Web + App) for 1 Year

✨ Join our Online NEET Test Series for 499/- Only for 1 Year

3 thoughts on “ Assertion and Reason Questions on Class 12 Physics Chapter 3 Current Electricity ”

• Pingback: Assertion and Reason Questions on class 12 Physics Chapter 14 Semiconductor Electronics - Gurukul For JEE & NEET
• Pingback: Assertion and Reason Questions on class 12 Physics Chapter 12 Atoms - Gurukul For JEE & NEET
• Pingback: Assertion and Reason Questions on class 12 Physics Chapter 10 Wave Optics - Gurukul For JEE & NEET

Leave a Reply Cancel reply

Join our Online Test Series for CBSE, ICSE, JEE, NEET and Other Exams

Editable Study Materials for Your Institute - CBSE, ICSE, State Boards (Maharashtra & Karnataka), JEE, NEET, FOUNDATION, OLYMPIADS, PPTs

Discover more from Gurukul of Excellence

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading