means end analysis problem solving

How it works

For Business

Join Mind Tools

Article • 4 min read

Means-End Analysis

Identifying the steps needed to solve a problem.

By the Mind Tools Content Team

Means-End Analysis is a simple tool that helps you to identify the practical steps needed to solve a problem or to reach a desired state.

In this article we'll explore Means-End Analysis, and we'll look at how you can apply it.

About the Tool

Means-End Analysis is essentially an early form of Gap Analysis . It was created by researchers Allen Newell and Herbert Simon in the late 1950s, and it was then published their 1972 book, "Human Problem Solving."

Newell and Simon were creating an effective problem-solving program for early computers, and Means-End Analysis was a direct result of this research. They named the tool "Means-End" because it helps you define the means needed to reach a desired end.

Means-End Analysis might seem quite simplistic at first glance. However, when you begin using it, you'll find that it's a practical and useful method for solving simple problems.

How to Use the Tool

Step 1: define your initial state (problem).

Start by defining the problem you're trying to solve. It might help to write the problem down on a piece of paper, or even draw out a diagram.

It's important to you make sure you're trying to solve the right problem, and not just a symptom of a deeper issue. If you're struggling to do this, you can use tools such as Root Cause Analysis , Cause and Effect Analysis , CATWOE , and the 5 Whys to help define your problem, and to make sure that you're addressing the real issue.

Step 2: Visualize Your Goal State

Next, picture the ideal state you'd like to be in. This is the outcome you'd like to see, once the problem is solved.

Again, it might be helpful to write this out on paper.

Step 3: List the Differences Between States

Now, look at the differences between your initial state and your goal state. And then explore the obstacles that are stopping you from reaching this state. Make a list of these differences and obstacles.

If the obstacles seem overwhelmingly large, consider using Drill Down to break them down into easy-to-understand chunks.

Step 4: Create Sub-Goals

Once you have a list of the differences and obstacles that you need to overcome, you need to create sub-goals that will help you address each of these.

Think of these sub-goals as steps that will ultimately lead you to your desired goal state – look at each obstacle you've listed, and then create the plans you need to overcome them.

Step 5: Take Action

The last step is to take action on your analysis.

If you're dealing with a simple problem, you'll be able to identify all of the actions that you need to take to solve your problem quickly. ( Action Plans are useful here.)

However, if you're solving a difficult problem, or planning a new project, you'll likely have to do further analysis and planning. The Simplex Process is useful for solving complex problems, while our project management section will help you plan more complex projects.

Means-End Analysis is a simple problem-solving tool that you can use to solve well-defined problems, and to kick-start the planning stage of a new project.

To use the tool, first look at your initial state (the state you're in right now). Then, picture your desired goal state – this is the state you want to be in once you've solved the problem or completed the project.

Next, make a list of the obstacles that are standing in the way of your goal state, and create sub-goals that will guide you in overcoming all those obstacles.

Finally, take action on your analysis.

You've accessed 1 of your 2 free resources.

Get unlimited access

Discover more content

Creating a value proposition.

Communicating the Benefits of Your Proposition Simply and Clearly

The Rhetorical Triangle

Making Your Communications Credible and Engaging

Add comment

Comments (0)

Be the first to comment!

Gain essential management and leadership skills

Busy schedule? No problem. Learn anytime, anywhere. 

Subscribe to unlimited access to meticulously researched, evidence-based resources.

Join today and take advantage of our 30% offer, available until May 31st .

Sign-up to our newsletter

Subscribing to the Mind Tools newsletter will keep you up-to-date with our latest updates and newest resources.

Subscribe now

Business Skills

Personal Development

Leadership and Management

Member Extras

Most Popular

Latest Updates

Getting Green Done

Revolutionary Wealth

Mind Tools Store

About Mind Tools Content

Discover something new today

The first 90 days.

Michael Watkins

Expert Interviews

Gaining the Trust of Your New Team

Developing a Reputation as a Trustworthy Manager

How Emotionally Intelligent Are You?

Boosting Your People Skills

Self-Assessment

What's Your Leadership Style?

Learn About the Strengths and Weaknesses of the Way You Like to Lead

Recommended for you

Plus minus implications.

This Technique for Weighing Pros and Cons Is Useful When You’re Feeling Indecisive

Business Operations and Process Management

Strategy Tools

Customer Service

Business Ethics and Values

Handling Information and Data

Project Management

Knowledge Management

Self-Development and Goal Setting

Time Management

Presentation Skills

Learning Skills

Career Skills

Communication Skills

Negotiation, Persuasion and Influence

Working With Others

Difficult Conversations

Creativity Tools

Self-Management

Work-Life Balance

Stress Management and Wellbeing

Coaching and Mentoring

Change Management

Team Management

Managing Conflict

Delegation and Empowerment

Performance Management

Leadership Skills

Developing Your Team

Talent Management

Problem Solving

Decision Making

Member Podcast

• Memberships

Means End Analysis: the basics and example

Means End Analysis (MEA): this article explains the concept of Means End Analysis or MEA in a practical way. This article contains the general definition of the technique, and the steps involved in the process, including a means end analysis example. After reading it, you will understand the basics of this Problem Solving tool. Enjoy reading!

What is a Means End Analysis (MEA)?

Means End Analysis (MEA) is a problem-solving technique that has been used since the fifties of the last century to stimulate creativity .

Means End Analysis is also a way of looking at the organisational planning , and helps in achieving the end-goals .

With Means End Analysis, it is possible to control the entire process of problem solving. It starts from a predetermined goal, in which actions are chosen that lead to that goal.

Each action that is executed leads to the next action; everything is connected together in order to reach the end-goal. In the meantime however, problems may arise. It is often hard to determine where exactly the crux is.

With the help of Means End Analysis, both forward and backward research can be done to determine where the stagnation is occurring. This enables the larger parts of a problem to be solved first, to subsequently return to the smaller problems afterwards.

Intermediate steps

In order for Means End Analysis to be effective, it is advisable to get all relevant actions and intermediate steps leading to the goal in the picture, making them detectable.

Additionally, it is handy to be capable of tracking (small) changes, and to measure the differences between the actual and desired state of the individual actions.

If this doesn’t happen, there is a significant risk that a mistake or change will have further consequences across the series of actions following it, making it harder and harder to intervene.

Every organisation works with goals that need to be met.

Depending on the goal a short term (a week or a month), mid-long term (a year), and a long term (muliple years) are determined. It is nice both for the organisation and for the employees when these goals are successfully met.

By making an analysis of the means and the intermediate actions with the help of Means End Analysis beforehand, it is easier to focus and not lose your way. It is a fact that goals don’t just achieve themselves. Based on careful planning , action should be undertaken.

Without planning there’s a significant chance for the organisation to head in the wrong direction, deviating from its pre-determined goal.

Means End Analysis example

To successfully execute Means End Analysis it is advisable to think from large to small; the eventual goal needs to be split into smaller sub-goals, making it overseeable for all parties that are going to work towards on achieving it.

When a commercial electronic business has the end-goal to reach a turnover of 15 million euro’s within a year, that is a noble thought. It means that all actions in that year will be geared towards meeting that 15 million euro limit.

However, it will only work when it becomes clear what has to be done to meet that turnover of 15 million. With the help of Means End Analysis, the end goal is split into a few smaller goals, which will contribute to the 15 million turnover:

• A specific product, for example the newest smartphone, needs to be sold aggressively;
• A minimal selling price is set, which dealers also must comply with;
• Aside from the newest smartphone, there are some related products that will be go to market as well.

Means End Analysis : Executable steps

Regardless of the splitting into smaller sub-goals, it will still not be possible for the organisation to achieve a turnover of 15 million. The search for even smaller, more specific steps, aids in them to achieving the end-goal.

These sub-sub-goals are translated into executable steps that are deployed by the organisation and used to achieve the original goal of a turnover of 15 million. In case there is stagnation of a problem somewhere, it becomes much easier to find the problem and fix that part of the process. Prior sub-goals are elaborated upon below:

• A specific marketing plan is developed for the smartphone to give publicity to the new product, especially via social media;
• New applications will be developped by the electronic business to be sold as a by-product;
• A special discount is offered to students when they can prove that they are, in fact, registered at an institute of higher education;
• An advertisement will be placed in door-to-door newspapers, whereby a coupon can be used to obtain a substantial trade-in discount for the old mobile phone.

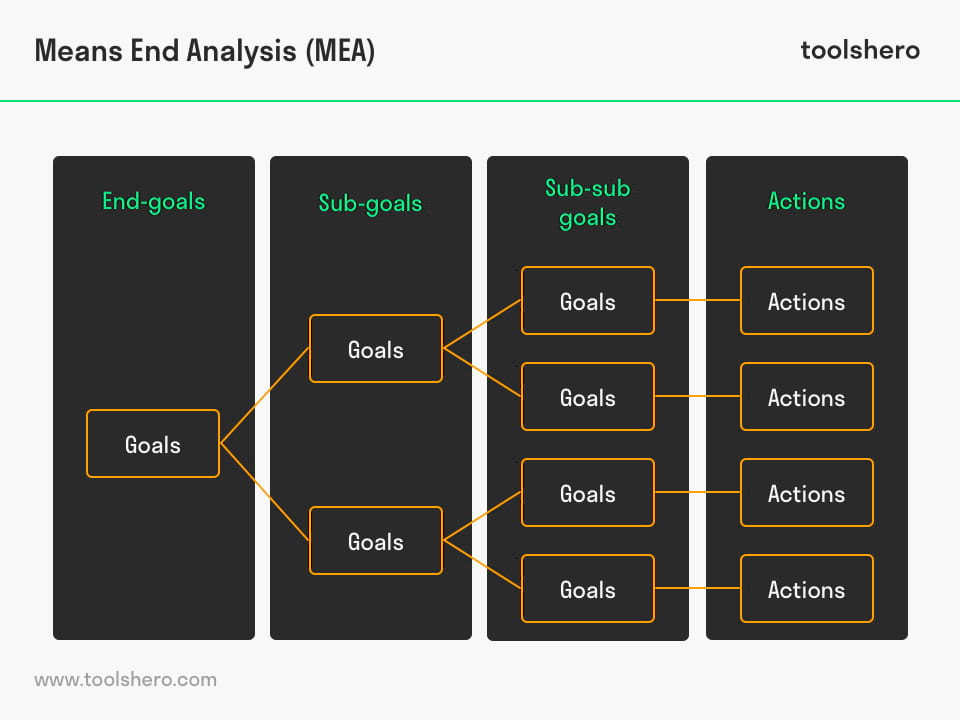
Figure 1 – an example overview of a Means End Analysis

Means End Analysis is about thoroughly thinking through which steps are needed in order to reach the end-goal.

Additionally, everyone within the organisation gets a reality check, because it shows that even the smallest steps have an impact on the overall goal that has been set .

It’s Your Turn

What do you think? Is Means End Analysis applicable in your personal or professional environment? Do you recognize the practical explanation or do you have more suggestions? What are your success factors for achieving end-goals??

Share your experience and knowledge in the comments box below.

More information

• Fikes, R. E., & Nilsson, N. J. (1971). STRIPS: A new approach to the application of theorem proving to problem solving . Artificial intelligence, 2(3-4), 189-208.
• Johnson, A. P. (2005). A short guide to action research . Boston: Pearson/ Allyn and Bacon .
• Sweller, J. (1988). Cognitive load during problem solving: Effects on learning . Cognitive science, 12(2), 257-285.

How to cite this article: Mulder, P. (2018). Means End Analysis (MEA) . Retrieved [insert date] from Toolshero: https://www.toolshero.com/problem-solving/means-end-analysis-mea/

Original publication date: 04/19/2018 | Last update: 01/25/2024

Add a link to this page on your website: <a href=”https://www.toolshero.com/problem-solving/means-end-analysis-mea/”> Toolshero: Means End Analysis (MEA)</a>

Did you find this article interesting?

Your rating is more than welcome or share this article via Social media!

Average rating 4.5 / 5. Vote count: 13

No votes so far! Be the first to rate this post.

We are sorry that this post was not useful for you!

Let us improve this post!

Tell us how we can improve this post?

Patty Mulder

Patty Mulder is an Dutch expert on Management Skills, Personal Effectiveness and Business Communication. She is also a Content writer, Business Coach and Company Trainer and lives in the Netherlands (Europe). Note: all her articles are written in Dutch and we translated her articles to English!

Related ARTICLES

Soft Systems Methodology (SSM) by Peter Checkland

Convergent Thinking: the Definition and Theory

CATWOE Analysis: theory and example

Systems Thinking: Theory and Definition

5 Whys Root Cause Analysis (Toyoda)

Positive Deviance (PD) explained

Also interesting.

Crowdsourcing: the meaning, definition and some examples

Systematic Inventive Thinking (SIT)

Linear Thinking by Edward De Bono explained

Leave a reply cancel reply.

You must be logged in to post a comment.

BOOST YOUR SKILLS

Toolshero supports people worldwide ( 10+ million visitors from 100+ countries ) to empower themselves through an easily accessible and high-quality learning platform for personal and professional development.

By making access to scientific knowledge simple and affordable, self-development becomes attainable for everyone, including you! Join our learning platform and boost your skills with Toolshero.

POPULAR TOPICS

• Change Management
• Marketing Theories
• Problem Solving Theories
• Psychology Theories

ABOUT TOOLSHERO

• Free Toolshero e-book
• Memberships & Pricing

Artificial Intelligence

Control System

• Interview Q

Intelligent Agent

Problem-solving, adversarial search, knowledge represent, uncertain knowledge r., subsets of ai, artificial intelligence mcq, related tutorials.

• Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Verbal Ability

Interview Questions

Company Questions

Trending Technologies

Cloud Computing

Data Science

Machine Learning

B.Tech / MCA

Data Structures

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

C Programming

Data Mining

Data Warehouse

Means-Ends Analysis

Means-Ends analysis is a method of solving problems. This method is useful for well-formed problems, less so for less-formed problems.

State Space [ edit ]

Problem solving occurs in a state space . Imagine first an initial state and then a goal state . We want to get from the initial state to the goal state . There might be many different paths from the initial state to the goal state .

We can talk about how to solve this problem in terms of differences between different states and the goal (end) state . I want to deduce the difference between two different states.

So I can look at my current problem, and then my end- state . I will then ask "how many differences are there between my current state and my end state ".

Imagine we start at step one, our initial state . The next step in this process is to create every possible permutation from my initial state . The next step is to calculate the difference in the states I just made and my end state .

There is an obvious method here: if I generate 6 different possible states from my initial state , I can then calculate the difference between each of those states and the end state . I would look for the option that had the least number of differences to produce the most optimal solution.

Universal method of problem solving [ edit ]

A means-ends analysis is considered a universal method of solving problems. However, there is no guarantee of success.

References [ edit ]

• ↑ http://www.flaticon.com/

Give a specific name, value or other brief answer without explanation or calculation.

Reach a conclusion from the information given.

Obtain a numerical answer showing the relevant stages in the working.

A unit of abstract mathematical system subject to the laws of arithmetic.

7.3 Problem-Solving

Learning objectives.

By the end of this section, you will be able to:

• Describe problem solving strategies
• Define algorithm and heuristic
• Explain some common roadblocks to effective problem solving

   People face problems every day—usually, multiple problems throughout the day. Sometimes these problems are straightforward: To double a recipe for pizza dough, for example, all that is required is that each ingredient in the recipe be doubled. Sometimes, however, the problems we encounter are more complex. For example, say you have a work deadline, and you must mail a printed copy of a report to your supervisor by the end of the business day. The report is time-sensitive and must be sent overnight. You finished the report last night, but your printer will not work today. What should you do? First, you need to identify the problem and then apply a strategy for solving the problem.

The study of human and animal problem solving processes has provided much insight toward the understanding of our conscious experience and led to advancements in computer science and artificial intelligence. Essentially much of cognitive science today represents studies of how we consciously and unconsciously make decisions and solve problems. For instance, when encountered with a large amount of information, how do we go about making decisions about the most efficient way of sorting and analyzing all the information in order to find what you are looking for as in visual search paradigms in cognitive psychology. Or in a situation where a piece of machinery is not working properly, how do we go about organizing how to address the issue and understand what the cause of the problem might be. How do we sort the procedures that will be needed and focus attention on what is important in order to solve problems efficiently. Within this section we will discuss some of these issues and examine processes related to human, animal and computer problem solving.

PROBLEM-SOLVING STRATEGIES

   When people are presented with a problem—whether it is a complex mathematical problem or a broken printer, how do you solve it? Before finding a solution to the problem, the problem must first be clearly identified. After that, one of many problem solving strategies can be applied, hopefully resulting in a solution.

Problems themselves can be classified into two different categories known as ill-defined and well-defined problems (Schacter, 2009). Ill-defined problems represent issues that do not have clear goals, solution paths, or expected solutions whereas well-defined problems have specific goals, clearly defined solutions, and clear expected solutions. Problem solving often incorporates pragmatics (logical reasoning) and semantics (interpretation of meanings behind the problem), and also in many cases require abstract thinking and creativity in order to find novel solutions. Within psychology, problem solving refers to a motivational drive for reading a definite “goal” from a present situation or condition that is either not moving toward that goal, is distant from it, or requires more complex logical analysis for finding a missing description of conditions or steps toward that goal. Processes relating to problem solving include problem finding also known as problem analysis, problem shaping where the organization of the problem occurs, generating alternative strategies, implementation of attempted solutions, and verification of the selected solution. Various methods of studying problem solving exist within the field of psychology including introspection, behavior analysis and behaviorism, simulation, computer modeling, and experimentation.

A problem-solving strategy is a plan of action used to find a solution. Different strategies have different action plans associated with them (table below). For example, a well-known strategy is trial and error. The old adage, “If at first you don’t succeed, try, try again” describes trial and error. In terms of your broken printer, you could try checking the ink levels, and if that doesn’t work, you could check to make sure the paper tray isn’t jammed. Or maybe the printer isn’t actually connected to your laptop. When using trial and error, you would continue to try different solutions until you solved your problem. Although trial and error is not typically one of the most time-efficient strategies, it is a commonly used one.

   Another type of strategy is an algorithm. An algorithm is a problem-solving formula that provides you with step-by-step instructions used to achieve a desired outcome (Kahneman, 2011). You can think of an algorithm as a recipe with highly detailed instructions that produce the same result every time they are performed. Algorithms are used frequently in our everyday lives, especially in computer science. When you run a search on the Internet, search engines like Google use algorithms to decide which entries will appear first in your list of results. Facebook also uses algorithms to decide which posts to display on your newsfeed. Can you identify other situations in which algorithms are used?

A heuristic is another type of problem solving strategy. While an algorithm must be followed exactly to produce a correct result, a heuristic is a general problem-solving framework (Tversky & Kahneman, 1974). You can think of these as mental shortcuts that are used to solve problems. A “rule of thumb” is an example of a heuristic. Such a rule saves the person time and energy when making a decision, but despite its time-saving characteristics, it is not always the best method for making a rational decision. Different types of heuristics are used in different types of situations, but the impulse to use a heuristic occurs when one of five conditions is met (Pratkanis, 1989):

• When one is faced with too much information
• When the time to make a decision is limited
• When the decision to be made is unimportant
• When there is access to very little information to use in making the decision
• When an appropriate heuristic happens to come to mind in the same moment

Working backwards is a useful heuristic in which you begin solving the problem by focusing on the end result. Consider this example: You live in Washington, D.C. and have been invited to a wedding at 4 PM on Saturday in Philadelphia. Knowing that Interstate 95 tends to back up any day of the week, you need to plan your route and time your departure accordingly. If you want to be at the wedding service by 3:30 PM, and it takes 2.5 hours to get to Philadelphia without traffic, what time should you leave your house? You use the working backwards heuristic to plan the events of your day on a regular basis, probably without even thinking about it.

Another useful heuristic is the practice of accomplishing a large goal or task by breaking it into a series of smaller steps. Students often use this common method to complete a large research project or long essay for school. For example, students typically brainstorm, develop a thesis or main topic, research the chosen topic, organize their information into an outline, write a rough draft, revise and edit the rough draft, develop a final draft, organize the references list, and proofread their work before turning in the project. The large task becomes less overwhelming when it is broken down into a series of small steps.

Further problem solving strategies have been identified (listed below) that incorporate flexible and creative thinking in order to reach solutions efficiently.

Additional Problem Solving Strategies :

• Abstraction – refers to solving the problem within a model of the situation before applying it to reality.
• Analogy – is using a solution that solves a similar problem.
• Brainstorming – refers to collecting an analyzing a large amount of solutions, especially within a group of people, to combine the solutions and developing them until an optimal solution is reached.
• Divide and conquer – breaking down large complex problems into smaller more manageable problems.
• Hypothesis testing – method used in experimentation where an assumption about what would happen in response to manipulating an independent variable is made, and analysis of the affects of the manipulation are made and compared to the original hypothesis.
• Lateral thinking – approaching problems indirectly and creatively by viewing the problem in a new and unusual light.
• Means-ends analysis – choosing and analyzing an action at a series of smaller steps to move closer to the goal.
• Method of focal objects – putting seemingly non-matching characteristics of different procedures together to make something new that will get you closer to the goal.
• Morphological analysis – analyzing the outputs of and interactions of many pieces that together make up a whole system.
• Proof – trying to prove that a problem cannot be solved. Where the proof fails becomes the starting point or solving the problem.
• Reduction – adapting the problem to be as similar problems where a solution exists.
• Research – using existing knowledge or solutions to similar problems to solve the problem.
• Root cause analysis – trying to identify the cause of the problem.

The strategies listed above outline a short summary of methods we use in working toward solutions and also demonstrate how the mind works when being faced with barriers preventing goals to be reached.

One example of means-end analysis can be found by using the Tower of Hanoi paradigm . This paradigm can be modeled as a word problems as demonstrated by the Missionary-Cannibal Problem :

Missionary-Cannibal Problem

Three missionaries and three cannibals are on one side of a river and need to cross to the other side. The only means of crossing is a boat, and the boat can only hold two people at a time. Your goal is to devise a set of moves that will transport all six of the people across the river, being in mind the following constraint: The number of cannibals can never exceed the number of missionaries in any location. Remember that someone will have to also row that boat back across each time.

Hint : At one point in your solution, you will have to send more people back to the original side than you just sent to the destination.

The actual Tower of Hanoi problem consists of three rods sitting vertically on a base with a number of disks of different sizes that can slide onto any rod. The puzzle starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top making a conical shape. The objective of the puzzle is to move the entire stack to another rod obeying the following rules:

• 1. Only one disk can be moved at a time.
• 2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
• 3. No disc may be placed on top of a smaller disk.

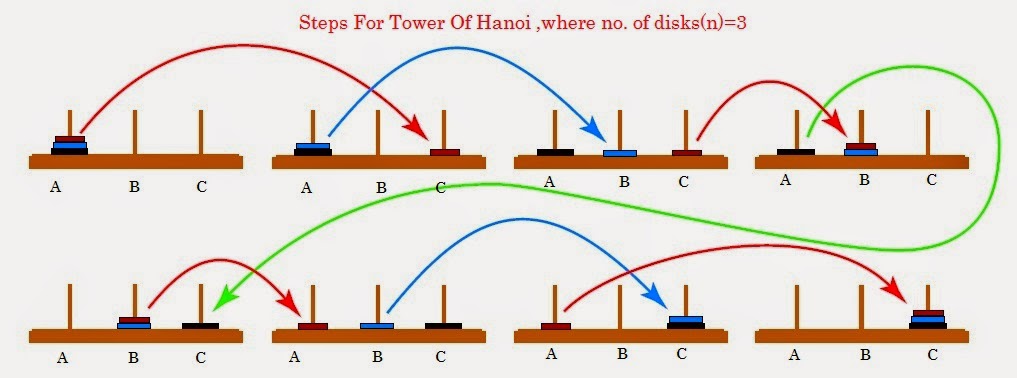
  Figure 7.02. Steps for solving the Tower of Hanoi in the minimum number of moves when there are 3 disks.

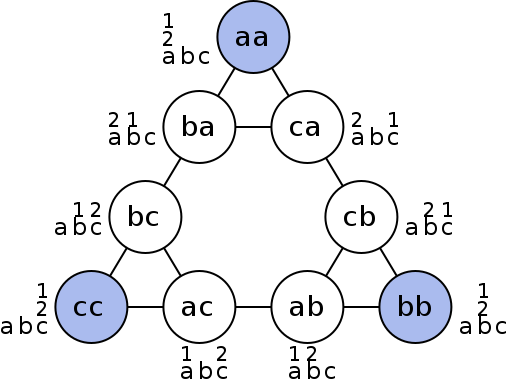
Figure 7.03. Graphical representation of nodes (circles) and moves (lines) of Tower of Hanoi.

The Tower of Hanoi is a frequently used psychological technique to study problem solving and procedure analysis. A variation of the Tower of Hanoi known as the Tower of London has been developed which has been an important tool in the neuropsychological diagnosis of executive function disorders and their treatment.

GESTALT PSYCHOLOGY AND PROBLEM SOLVING

As you may recall from the sensation and perception chapter, Gestalt psychology describes whole patterns, forms and configurations of perception and cognition such as closure, good continuation, and figure-ground. In addition to patterns of perception, Wolfgang Kohler, a German Gestalt psychologist traveled to the Spanish island of Tenerife in order to study animals behavior and problem solving in the anthropoid ape.

As an interesting side note to Kohler’s studies of chimp problem solving, Dr. Ronald Ley, professor of psychology at State University of New York provides evidence in his book A Whisper of Espionage  (1990) suggesting that while collecting data for what would later be his book  The Mentality of Apes (1925) on Tenerife in the Canary Islands between 1914 and 1920, Kohler was additionally an active spy for the German government alerting Germany to ships that were sailing around the Canary Islands. Ley suggests his investigations in England, Germany and elsewhere in Europe confirm that Kohler had served in the German military by building, maintaining and operating a concealed radio that contributed to Germany’s war effort acting as a strategic outpost in the Canary Islands that could monitor naval military activity approaching the north African coast.

While trapped on the island over the course of World War 1, Kohler applied Gestalt principles to animal perception in order to understand how they solve problems. He recognized that the apes on the islands also perceive relations between stimuli and the environment in Gestalt patterns and understand these patterns as wholes as opposed to pieces that make up a whole. Kohler based his theories of animal intelligence on the ability to understand relations between stimuli, and spent much of his time while trapped on the island investigation what he described as  insight , the sudden perception of useful or proper relations. In order to study insight in animals, Kohler would present problems to chimpanzee’s by hanging some banana’s or some kind of food so it was suspended higher than the apes could reach. Within the room, Kohler would arrange a variety of boxes, sticks or other tools the chimpanzees could use by combining in patterns or organizing in a way that would allow them to obtain the food (Kohler & Winter, 1925).

While viewing the chimpanzee’s, Kohler noticed one chimp that was more efficient at solving problems than some of the others. The chimp, named Sultan, was able to use long poles to reach through bars and organize objects in specific patterns to obtain food or other desirables that were originally out of reach. In order to study insight within these chimps, Kohler would remove objects from the room to systematically make the food more difficult to obtain. As the story goes, after removing many of the objects Sultan was used to using to obtain the food, he sat down ad sulked for a while, and then suddenly got up going over to two poles lying on the ground. Without hesitation Sultan put one pole inside the end of the other creating a longer pole that he could use to obtain the food demonstrating an ideal example of what Kohler described as insight. In another situation, Sultan discovered how to stand on a box to reach a banana that was suspended from the rafters illustrating Sultan’s perception of relations and the importance of insight in problem solving.

Grande (another chimp in the group studied by Kohler) builds a three-box structure to reach the bananas, while Sultan watches from the ground.  Insight , sometimes referred to as an “Ah-ha” experience, was the term Kohler used for the sudden perception of useful relations among objects during problem solving (Kohler, 1927; Radvansky & Ashcraft, 2013).

Solving puzzles.

   Problem-solving abilities can improve with practice. Many people challenge themselves every day with puzzles and other mental exercises to sharpen their problem-solving skills. Sudoku puzzles appear daily in most newspapers. Typically, a sudoku puzzle is a 9×9 grid. The simple sudoku below (see figure) is a 4×4 grid. To solve the puzzle, fill in the empty boxes with a single digit: 1, 2, 3, or 4. Here are the rules: The numbers must total 10 in each bolded box, each row, and each column; however, each digit can only appear once in a bolded box, row, and column. Time yourself as you solve this puzzle and compare your time with a classmate.

How long did it take you to solve this sudoku puzzle? (You can see the answer at the end of this section.)

   Here is another popular type of puzzle (figure below) that challenges your spatial reasoning skills. Connect all nine dots with four connecting straight lines without lifting your pencil from the paper:

Did you figure it out? (The answer is at the end of this section.) Once you understand how to crack this puzzle, you won’t forget.

   Take a look at the “Puzzling Scales” logic puzzle below (figure below). Sam Loyd, a well-known puzzle master, created and refined countless puzzles throughout his lifetime (Cyclopedia of Puzzles, n.d.).

What steps did you take to solve this puzzle? You can read the solution at the end of this section.

Pitfalls to problem solving.

   Not all problems are successfully solved, however. What challenges stop us from successfully solving a problem? Albert Einstein once said, “Insanity is doing the same thing over and over again and expecting a different result.” Imagine a person in a room that has four doorways. One doorway that has always been open in the past is now locked. The person, accustomed to exiting the room by that particular doorway, keeps trying to get out through the same doorway even though the other three doorways are open. The person is stuck—but she just needs to go to another doorway, instead of trying to get out through the locked doorway. A mental set is where you persist in approaching a problem in a way that has worked in the past but is clearly not working now.

Functional fixedness is a type of mental set where you cannot perceive an object being used for something other than what it was designed for. During the Apollo 13 mission to the moon, NASA engineers at Mission Control had to overcome functional fixedness to save the lives of the astronauts aboard the spacecraft. An explosion in a module of the spacecraft damaged multiple systems. The astronauts were in danger of being poisoned by rising levels of carbon dioxide because of problems with the carbon dioxide filters. The engineers found a way for the astronauts to use spare plastic bags, tape, and air hoses to create a makeshift air filter, which saved the lives of the astronauts.

   Researchers have investigated whether functional fixedness is affected by culture. In one experiment, individuals from the Shuar group in Ecuador were asked to use an object for a purpose other than that for which the object was originally intended. For example, the participants were told a story about a bear and a rabbit that were separated by a river and asked to select among various objects, including a spoon, a cup, erasers, and so on, to help the animals. The spoon was the only object long enough to span the imaginary river, but if the spoon was presented in a way that reflected its normal usage, it took participants longer to choose the spoon to solve the problem. (German & Barrett, 2005). The researchers wanted to know if exposure to highly specialized tools, as occurs with individuals in industrialized nations, affects their ability to transcend functional fixedness. It was determined that functional fixedness is experienced in both industrialized and nonindustrialized cultures (German & Barrett, 2005).

In order to make good decisions, we use our knowledge and our reasoning. Often, this knowledge and reasoning is sound and solid. Sometimes, however, we are swayed by biases or by others manipulating a situation. For example, let’s say you and three friends wanted to rent a house and had a combined target budget of $1,600. The realtor shows you only very run-down houses for $1,600 and then shows you a very nice house for $2,000. Might you ask each person to pay more in rent to get the $2,000 home? Why would the realtor show you the run-down houses and the nice house? The realtor may be challenging your anchoring bias. An anchoring bias occurs when you focus on one piece of information when making a decision or solving a problem. In this case, you’re so focused on the amount of money you are willing to spend that you may not recognize what kinds of houses are available at that price point.

The confirmation bias is the tendency to focus on information that confirms your existing beliefs. For example, if you think that your professor is not very nice, you notice all of the instances of rude behavior exhibited by the professor while ignoring the countless pleasant interactions he is involved in on a daily basis. Hindsight bias leads you to believe that the event you just experienced was predictable, even though it really wasn’t. In other words, you knew all along that things would turn out the way they did. Representative bias describes a faulty way of thinking, in which you unintentionally stereotype someone or something; for example, you may assume that your professors spend their free time reading books and engaging in intellectual conversation, because the idea of them spending their time playing volleyball or visiting an amusement park does not fit in with your stereotypes of professors.

Finally, the availability heuristic is a heuristic in which you make a decision based on an example, information, or recent experience that is that readily available to you, even though it may not be the best example to inform your decision . Biases tend to “preserve that which is already established—to maintain our preexisting knowledge, beliefs, attitudes, and hypotheses” (Aronson, 1995; Kahneman, 2011). These biases are summarized in the table below.

Were you able to determine how many marbles are needed to balance the scales in the figure below? You need nine. Were you able to solve the problems in the figures above? Here are the answers.

   Many different strategies exist for solving problems. Typical strategies include trial and error, applying algorithms, and using heuristics. To solve a large, complicated problem, it often helps to break the problem into smaller steps that can be accomplished individually, leading to an overall solution. Roadblocks to problem solving include a mental set, functional fixedness, and various biases that can cloud decision making skills.

References:

Openstax Psychology text by Kathryn Dumper, William Jenkins, Arlene Lacombe, Marilyn Lovett and Marion Perlmutter licensed under CC BY v4.0. https://openstax.org/details/books/psychology

Review Questions:

1. A specific formula for solving a problem is called ________.

a. an algorithm

b. a heuristic

c. a mental set

d. trial and error

2. Solving the Tower of Hanoi problem tends to utilize a  ________ strategy of problem solving.

a. divide and conquer

b. means-end analysis

d. experiment

3. A mental shortcut in the form of a general problem-solving framework is called ________.

4. Which type of bias involves becoming fixated on a single trait of a problem?

a. anchoring bias

b. confirmation bias

c. representative bias

d. availability bias

5. Which type of bias involves relying on a false stereotype to make a decision?

6. Wolfgang Kohler analyzed behavior of chimpanzees by applying Gestalt principles to describe ________.

a. social adjustment

b. student load payment options

c. emotional learning

d. insight learning

7. ________ is a type of mental set where you cannot perceive an object being used for something other than what it was designed for.

a. functional fixedness

c. working memory

Critical Thinking Questions:

1. What is functional fixedness and how can overcoming it help you solve problems?

2. How does an algorithm save you time and energy when solving a problem?

Personal Application Question:

1. Which type of bias do you recognize in your own decision making processes? How has this bias affected how you’ve made decisions in the past and how can you use your awareness of it to improve your decisions making skills in the future?

anchoring bias

availability heuristic

confirmation bias

functional fixedness

hindsight bias

problem-solving strategy

representative bias

trial and error

working backwards

Answers to Exercises

algorithm:  problem-solving strategy characterized by a specific set of instructions

anchoring bias:  faulty heuristic in which you fixate on a single aspect of a problem to find a solution

availability heuristic:  faulty heuristic in which you make a decision based on information readily available to you

confirmation bias:  faulty heuristic in which you focus on information that confirms your beliefs

functional fixedness:  inability to see an object as useful for any other use other than the one for which it was intended

heuristic:  mental shortcut that saves time when solving a problem

hindsight bias:  belief that the event just experienced was predictable, even though it really wasn’t

mental set:  continually using an old solution to a problem without results

problem-solving strategy:  method for solving problems

representative bias:  faulty heuristic in which you stereotype someone or something without a valid basis for your judgment

trial and error:  problem-solving strategy in which multiple solutions are attempted until the correct one is found

working backwards:  heuristic in which you begin to solve a problem by focusing on the end result

Share This Book

• Increase Font Size

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• HHS Author Manuscripts

Means-End Problem Solving in Infancy: Development, Emergence of Intentionality, and Transfer of Knowledge

Iryna babik.

1 Department of Physical Therapy, Biomechanics & Movement Science Program, University of Delaware, Newark, DE, USA

Andrea Baraldi Cunha

Samantha m. ross.

2 College of Public Health and Human Sciences, Oregon State University, Corvallis, OR, USA

Samuel W. Logan

James c. galloway.

3 Department of Psychology, University of Delaware, Newark, DE, USA

Michele A. Lobo

Associated data.

Behaviors and performance of 23 typically developing infants were assessed longitudinally at 6, 9, 12, 18, and 24 months in two means-end tasks: pulling a towel or rotating a turntable to obtain a supported object. With age, infants performed more goal-directed behaviors, leading to increased problem-solving success. Intentionality emerged earlier in the towel task than in the turntable task (6.9 vs. 10.8 months). Potential knowledge transfer between the tasks was first observed at 9 months. This study provides insight into the development of means-end learning, the emergence of intentionality, and potential transfer of knowledge in tasks involving a similar concept (support) but requiring different modes of action for success (pulling vs. rotating).

Means-end problem solving involves the intentional execution of a planned sequence of actions to achieve a goal ( Brandone, 2015 ; Lobo & Galloway, 2013a ; Piaget, 1953 ; Slater, 1995 ; Willatts, 1999 ). Examples of means-end tasks that infants learn to perform in the first years of life include removing a cover to retrieve a hidden object ( Diamond, 1985 ; Piaget, 1953 ; Shinskey & Munakata, 2003 ), pulling a cloth to retrieve a distant object supported on the cloth ( Munakata, McClelland, Johnson, & Siegler, 1997 ; Schlesinger & Langer, 1999 ; Uzgiris & Hunt, 1975 ; Willatts, 1984a , 1985 , 1999 ), using the correct switch to activate a distant toy ( Lobo & Galloway, 2008 ; Lobo & Galloway, 2013a ), and pulling the correct string attached to a distant object to retrieve the object ( Rat-Fischer, O’Regan, & Fagard, 2014 ; Richardson, 1932 ; Uzgiris & Hunt, 1975 ). In all of these means-end tasks, infants demonstrate an understanding that they can act upon one object to affect another object. Investigating these complex behaviors can provide insight into the mechanisms involved in early learning ( Bonawitz et al., 2010 ; Brandone, 2015 ; Bremner, 2000 ; Csibra & Gergely, 2007 ; Gibson & Pick, 1988 ; Lobo & Galloway, 2008 ; Munakata et al., 1997 ; Willatts, 1999 ). Means-end tasks are considered important developmental tasks and are often incorporated in standardized developmental assessments ( Bayley, 2006 ).

Requirements for Means-End Problem Solving

Means-end problem solving depends upon requisite motor skills like reaching and object manipulation, perceptual skills like visual attention to objects ( Baillargeon, 1987 ; Gibson & Pick, 2000; Johnson, Slemmer, & Amso, 2004 ; Lobo & Galloway, 2008 ; von Helmholtz, 1962 ), and motor-perceptual coupling abilities ( Case-Smith, Bigsby, & Clutter, 1998 ; Lobo & Galloway, 2008 ; Thelen, 1990 ). Means-end problem solving may also require cognitive abilities to distinguish between the means and end object, to understand the concepts of support and causal relations, to identify goals, to remember the consequences of previous behaviors on objects, and to select actions that will produce identified goals ( Bremner, 2000 ; Piaget, 1953 ; Sommerville & Woodward, 2005a ; Willatts, 1999 ).

Development of Means-End Problem Solving

Traditionally, successful means-end behaviors have been reported to emerge at about 5–6 months of age for less complex tasks, such as selecting the correct lever and visually attending to the resulting activation of a distant toy ( Lobo & Galloway, 2008 ). By 7–8 months, infants begin solving means-end problems requiring one intermediate step, such as pulling a support to retrieve a distant toy ( Clearfield, Stanger, & Jenne, 2015 ; Munakata et al., 1997 ; Willatts, 1984a , 1985 , 1999 ). At 9 months, infants are capable of solving two-step problems, such as removing an obstructing barrier and then retrieving an object by pulling a support ( Willatts, 1984a ). At 10 months, infants can solve means-end problems requiring three intermediate steps, such as removing a barrier, pulling a cloth, and then pulling a string to bring a distant object within reach (Willatts, Forsyth, DiModugno, Varma, & Colvin, 1989).

While infants may spontaneously initiate and succeed in means-end problem-solving tasks in the first year of life ( Bates, Carlson-Luden, & Bretherton, 1980 ; Diamond, 1985 ; Piaget, 1953 ; Uzgiris & Hunt, 1975 ; Willatts, 1990 ), means-end skills continue to develop and be refined throughout the second year of life ( Brown, 1990 ; Casler & Keleman, 2005 ; Chen & Siegler, 2000 ; Nielsen, 2006 ; Rat-Fischer, O’Regan, & Fagard, 2012 ; Piaget, 1953 ).

Although there has been research interest in early means-end performance, previous research has typically been cross-sectional, has covered only short periods of developmental time, and has primarily focused on infants’ trial outcome (successful/unsuccessful). Longitudinal research can uniquely serve to uncover developmental processes and underlying mechanisms of learning, while revealing rates and trajectories of change ( Singer & Willett, 2003 ).

Emergence of Intentionality in Means-End Problem Solving

Intentionality is the deliberate or purposeful projection of awareness toward some object or outcome ( Schlitz, 1996 ). Means-end problem-solving tasks can serve as effective tools for assessing intentionality in infants ( Clearfield et al., 2015 ; Piaget, 1953 ; Schlesinger & Langer, 1999 ; Uzgiris & Hunt, 1975 ; Willatts, 1984a , 1999 ). Piaget (1953 , 1955 ) suggested that 4–8 month old infants lack the concept of causality, do not distinguish means from end, and may only accidentally solve a means-end task. Although infants might perform intentional goal-directed behaviors (e.g., pulling a support to retrieve a distant object) at 8–12 months, Piaget proposed that the true understanding of means-end relations (e.g., pulling the support only if the goal object rests on it) was achieved through active exploration (operationally defined as sensorimotor interaction with objects that provides the potential for information gathering) and experimentation only by 12–18 months. However, there is evidence that Piaget may have underestimated infants’ understanding of support and means-end relations (e.g., Baillargeon, 1987 ; Goubet & Clifton, 1998 ; Hood & Willatts, 1986 ; Spelke, 1988 ; Willatts, 1999 ). For example, 7–8-month-olds have demonstrated an understanding of the concept of support and means-end relations ( Willatts, 1999 ).

Intentionality in infants’ means-end behaviors has traditionally been tested by including control trials without a toy ( Munakata et al., 1997 ; Willatts, 1984a , 1999 ), using familiar vs. unfamiliar objects ( Willatts, 1984a ), or presenting “contact” vs. “noncontact” trials with the toy either placed on or near the support ( Clearfield et al., 2015 ; Schlesinger & Langer, 1999 ; Uzgiris & Hunt, 1975 ). For example, in a task requiring cloth pulling to retrieve a distant, supported object, infants’ behaviors have been considered intentional when they pulled the cloth more often during trials when a toy was supported on the cloth than during trials without a toy present ( Willatts, 1984a , 1999 ). In this case, 7–8-month-old infants, but not 6-month-olds, have demonstrated intention in the means-end cloth-pulling task ( Willatts, 1999 ).

The emergence of infants’ intentionality in means-end problem solving may depend on the requirements of the task. It has been argued that intentionality appears earlier in means-end tasks involving supports, such as pulling a towel supporting an out-of-reach object, than in tasks involving surrounding means, such as using a hook to get an out-of-reach object ( Bates et al., 1980 ; Schlesinger & Langer, 1999 ; Uzgiris & Hunt, 1975 ). This may be explained by the fact that general exploration of the means object in support tasks, but not in surround tasks, almost always results in translation of the end object, thus providing infants with information about the means-end relation. For example, infants have demonstrated intentionality by understanding the difference between “contact” and “noncontact” trials earlier (by the age of 8 months) in the cloth task than in the hook task (by 12 months; Bates et al., 1980 ; Schlesinger & Langer, 1999 ; Uzgiris & Hunt, 1975 ; Willatts, 1999 ). However, it is not clear whether two tasks with the same relational concept might differ in the timing of the emergence of intentionality if they require different manual behaviors for goal attainment. One might expect an earlier appearance of intentionality in a support task requiring pulling vs. rotation since the latter may be a more difficult concept to grasp during infancy ( Bai & Bertenthal, 1992 ; Goldfield & Dickerson, 1981 ).

Transfer of Knowledge in Means-End Problem Solving

Transfer of knowledge is the dynamic application of cognitive and metacognitive strategies and general principles learned in one context (e.g., situation or task) to another context ( Lauder, Reynolds, & Angus, 1999 ; Prawat, 1989 ; Renkl, Mandl, & Gruber, 1996 ). This process often leads to the acquisition of new meaning and understanding, and is an important facilitator for learning and problem solving ( Coleman, Brown, & Rivkin, 1997 ; Healy et al., 2002 ; Prawat, 1989 ; Price & Driscoll, 1997 ; Renkl et al., 1996 ; Singer, 1982 ).

Previous research has demonstrated a wide variety of transfer abilities in young children (e.g., Brown, 1990 , Chen, Sanchez, & Campbell, 1997 ; Munakata et al., 1997 ; O’Connor & Russell, 2015 ). For example, Brown (1990) reported on the transfer of knowledge in problem solving by analogy in 2- and 3-year olds. The children were first trained to use a red-and-white hook to bring a distant toy within reach. Then they were presented with an analogous object retrieval task and given a choice of two tools: one similar in functional features (solid-colored hook), and the other similar in surface features (red-and-white stick). Three-year-olds, but not 2-year-olds, were able to choose the correct tool based on similarity of functional features. Chen et al. (1997) demonstrated the transfer of solution strategy in 13-month-olds, but not 10-month-olds, from modeled observation of a three-step means-end task involving a barrier, cloth, and string to a novel action task involving a similar structure but different objects.

In contrast to others who have documented transfer of knowledge between two tasks requiring the same motor actions on different objects, O’Connor and Russell (2015) documented transfer of knowledge between two tasks requiring not only different objects, but also different actions. They found that after being trained to bring a hidden toy into view by rotating a turntable, 7-month-olds were able to successfully solve the hiding-well search task. The authors suggested that infants’ experience observing and comprehending the consequences of their actions, or ‘insight into agency’, in the first task facilitated the transfer of knowledge to the novel situation. This study, however, involved the provision of training or assistance to infants, and thus, does not provide insight into the spontaneous development of knowledge transfer.

Although previous studies have evaluated infants’ performance in more than one means-end task (e.g., Clearfield et al., 2015 ; Schlesinger & Langer, 1999 ; Willatts, 1984a ), none, to our knowledge, have comprehensively analyzed the data to assess for possible transfer of knowledge between different means-end tasks. This may be because most of the previous studies have been cross-sectional, while only a longitudinal design can help address this important developmental question.

Current Study

This study is innovative because it is the first to longitudinally and comprehensively assess behaviors performed by typically developing infants throughout the first two years of life in two means-end tasks that incorporate a similar concept (object support), yet require different manual actions (pulling versus rotating) to attain the task goal (grasping the end object).

The first aim of this study was to track behavioral performance and learning in two means-end tasks. We intended to enhance our knowledge about the behaviors infants engage in at different stages of means-end learning across age and to identify behaviors associated with successful means-end performance. Based on previous research, we hypothesized that infants would display diverse exploratory behaviors toward the means and end objects and that these behaviors would become more goal-directed with age ( Willatts, 1984a , 1984b , 1999 ). We expected greater performance of goal-directed behaviors to be associated with success in the tasks ( Willatts, 1999 ).

The second aim of this study was to document the emergence of intentionality throughout the first two years of life in two means-end tasks involving the same relational concept (support) but requiring different manual behaviors (pulling versus rotating the support) to obtain the goal object. As in previous research, we measured intentionality as a shift towards more goal orientation in trials involving the end object relative to control trials without the end object present ( Munakata et al., 1997 ; Willatts, 1984a , 1999 ). Intentionality was assigned when infants engaged in behaviors with the means object that could result in attainment of the end object more often in trials involving the end object than in trials without the end object. We hypothesized that the timing of the emergence of intentionality would differ across the two means-end tasks, emerging first in the towel task that required simple pulling and then in the turntable task that required rotation, a spatial translation more difficult to understand ( Bai & Bertenthal, 1992 ; Bates et al., 1980 ; Goldfield & Dickerson, 1981 ; Schlesinger & Langer, 1999 ; Uzgiris & Hunt, 1975 ).

The third aim of this study was to determine whether infants were able to transfer their understanding of means-end relations across two tasks with a similar concept but different action requirements throughout the first two years of life. Based on previous research, we hypothesized that infants would demonstrate knowledge transfer between the two tasks within the first two years of life ( Brown, 1990 ; Chen et al., 1997 ; O’Connor & Russell, 2015 ).

Participants

Power analysis was conducted in the validated program GLIMMPSE ( http://glimmpse.samplesizeshop.org/ ) recommended for computing sample size calculations for longitudinal designs ( Guo, Logan, Glueck, & Muller, 2013 ). At the target power 0.8 and Type I error rate .05, the estimated sample size ranged from 20 to 23 participants depending on proposed variance estimates, using both the Hotelling Lawley Trace and Wilks Likelihood Ratio statistical tests.

Parents of 23 full-term typically developing infants (13 males; Gestational age Mean = 39.4 weeks; SD = 1.1; 70.8% Caucasian, 20.9% African-American, 8.3% Asian; 4.2% with $0–14,999 gross household income; 4.2% with $25,000–34,999, 4.2% with $35,000–44,999, 8.3% with $45,000–59,999, 25.0% with $60,000–79,999, 54.1% with greater than $80,000) consented to participate in this study. There was no attrition of participants; 94% of visits and 93% of trials were completed across all participants. Recruitment from the local Delaware community was performed via word of mouth and mailed advertisements. Recruitment, informed consent, and data collection were completed in accordance with the regulations set by the University of Delaware’s and Christiana Care Health System’s Institutional Review Boards [The Relationship Between Early Brain Structure & Development in Full-term & Pre-term Infants, University of Delaware IRB #128785–1, Christiana Care Health System IRB CCC# 27122, DDD# 504929]. Participants received monetary compensation for their participation in the study.

Infants were assessed in their homes at 6, 9, 12, 18, and 24 months of age as they engaged in two means-end problem-solving tasks ( Figure 1 ). Infants were in a positive or neutral behavioral state for all testing procedures to ensure the best performance. The towel task assessed their ability to retrieve a distant toy (end object) by pulling a towel (means object). Infants were seated in a high chair or on a parent’s lap at a table. Testing included one No-Toy Trial with a 14” x 23” towel folded and placed on the table in front of the infant. Researchers attempted to attract infants’ attention to the towel throughout the trial when infants were not visually attending to it for more than 5 seconds. The trial ended when 30-seconds elapsed (see Willatts, 1999 ): this time period was long enough to allow adequate exploration, and short enough to keep the infant engaged.

The Toy Trial setup for the towel (A) and turntable (B) tasks.

The No-Toy Trial was followed by 3 Toy Trials using the same towel presented as in the No-Toy Trial but now with a desirable toy placed out-of-reach on the far end of the towel ( Figure 1A ). The toy was selected from a small pool of salient similarly sized toys that were consistent across participants, and interesting across ages 6 to 24 months. Researchers attempted to attract infants’ attention to the toy at the beginning and throughout trials when infants were not visually attending to it for more than 5 seconds by touching it and saying “Get the toy”. Toy trials ended when an infant touched the toy, dropped the towel, or 30 seconds elapsed. The No-Toy trial was always presented before the Toy trials (similar to Willatts, 1984a , 1999 ) to capture behavior on the means object within sessions before infants experienced it as a potential tool to retrieve the distant end object.

The turntable task assessed infants’ ability to retrieve a distant toy (end object) by spinning the turntable (means object). Testing procedures were the same as for the towel task, except a turntable was used instead of a towel ( Figure 1B ).

Assessments were video recorded using two camcorders for time-synched frontal and side views. Behaviors were coded using OpenSHAPA software. Across all the variables described below, intra-rater agreement was 95.7±1.5% and inter-rater agreement with a primary coder was 90.3±5.2% for 20% of the coded data; both based on the equation [Agreed / (Agreed + Disagreed)] * 100.

All Toy Trials were classified as Successful or Unsuccessful. A Successful trial involved toy contact with prior visual attention to the toy in the 5 seconds before the contact (see Willatts, 1999 ); other trials were considered Unsuccessful.

Towel task.

The following behaviors were observed and coded: 1) Touching the towel – any part of the hand statically contacting the towel; 2) Lifting the towel – lifting at least half of the towel up from the surface without pulling it; 3) Mouthing the towel – towel in contact with the infant’s mouth, tongue, or lips; 4) Pulling the towel – sliding the towel on the surface; 5) Reaching for the distant toy – extending the arm(s) for the out-of-reach toy (Toy Trials only); 6) Looking at the towel – eyes directed at the towel; and 7) Looking at the toy – eyes directed at the toy (Toy Trials only). Each coded behavior was converted to percentage of trial time by dividing the cumulative duration of that behavior during a trial by the duration of the trial.

These behaviors were further categorized as Goal-directed behaviors or Non – goal-directed behaviors . We refer to the goal here as the means-end task goal of object attainment. Therefore, attention to the end object and behaviors that could potentially lead to the attainment of the end object were classified as goal-directed behaviors, while attention to the means object and behaviors that were unlikely to result in the attainment of the end object were classified as non–goal-directed. Goal-directed behaviors for the towel task included Pulling the towel and Looking at the toy . Note that although the performance of goal-directed behaviors increases the likelihood of success, it does not guarantee it per se: simply looking at the end object would not result in attainment of that object and pulling the towel could be too weak to move the end object within an infant’s reach or too forceful, causing the end object to fall off the table and ending that trial. Non – goal-directed behaviors included Touching , Lifting , Mouthing , and Looking at the towel , as well as Reaching for the distant, out-of-reach toy . Reaching was included among non–goal-directed behaviors because, although brief instances of reaching preceded end object attainment in Successful Trials, reaching was more often observed for longer periods in instances where it was not a successful strategy (e.g., attempting unsuccessfully to reach for the distant toy). Note that for No-Toy Trials, Goal-directed behaviors did not include Looking at the toy or Reaching for the toy because a toy was not present. While No-Toy Trials did not allow for a specific means-end task goal, “ Goal-directed behaviors” in this case served only as a control for comparison with the same behaviors during Toy Trials.

Turntable task.

The following behaviors were observed and coded: 1) Touching the turntable – any part of the hands statically contacting the turntable; 2) Pulling the turntable – attempting to slide the turntable on the surface; 3) Banging the turntable – hand(s) repeatedly hitting the turntable; 4) Mouthing the turntable – turntable in contact with the mouth, tongue, or lips; 5) Alternate spinning of the turntable – spinning the turntable cyclically in alternating directions through small or large ranges; 6) Unidirectional spinning of the turntable – spinning the turntable continuously in one direction; 7) Reaching for the distant toy – extending the arm(s) for the out-of-reach toy (Toy Trials only); 8) Looking at the turntable – eyes directed at the turntable; and 9) Looking at the toy – eyes directed at the toy (Toy Trials only). Goal-directed behaviors for the turntable task included Alternate spinning of the turntable , Unidirectional spinning of the turntable , and Looking at the toy . Alternate spinning of the turntable was included among goal-directed behaviors because it was often performed through a range large enough to result in end object attainment. Non – goal-directed behaviors included Touching , Pulling , Banging , Mouthing , and Looking at the turntable , as well as Reaching for the distant toy . For No-Toy Trials, Goal-directed behaviors did not include Looking at the toy or Reaching for the toy .

Statistical Analyses

Statistical analyses, unless otherwise specified, were conducted using Hierarchical Linear and Nonlinear Modeling Software (HLM; Raudenbush, Bryk, Cheong, Congdon, & du Toit, 2004 ), the most recommended tool for the analysis of longitudinal data, accounting for non-independence of multiple observations of the same participants. Linear and quadratic trends of change with age (variables Age and Age 2 ) were tested; statistically non-significant trends of change were dropped from the final models. To ensure that the observed effects in the current study are not only statistically significant, but also meaningful, Cohen’s d measures of effect size were reported: 0.2 small, 0.5 medium, 0.8 large, and 1.2 very large effects ( Cohen, 1988 ; Sawilowsky, 2009 ).

Development of Means-End Problem Solving.

To describe developmental trends of behaviors performed by infants across age in each task, data for the three Toy Trials were averaged within each visit for each infant. Preliminary analyses determined there were no significant differences in infants’ performance among the three toy trials. No-Toy Trial data were not included in these analyses. The trajectories of change in each behavior (including aggregated Goal-directed and Non – goal-directed behaviors ) across age were evaluated using HLM, while including in the multilevel model each behavior as a dependent variable, and Age and Age 2 as independent variables.

Change in trial success rate with age was analyzed by examining the raw data plots presenting the percent of successful trials out of the total number of trials performed at each age for each means-end task. In addition, binomial logistic regression was performed to determine the effect of age on the likelihood of a successful trial outcome, while entering into the logistic regression model a binomial variable Outcome specifying the trial outcome (0 = unsuccessful trial; 1 = successful trial) as a dependent variable and Age as an independent variable.

Differences in behaviors performed during “Successful” vs. “Unsuccessful” trials were analyzed next. Each Toy Trial served as a separate entry. Each behavior (including aggregated Goal-directed and Non – goal-directed behaviors ) was entered into HLM as a dependent variable, and Outcome , Age , and Age 2 as independent variables.

Emergence of Intentionality in Means-End Problem Solving.

To establish the timeline of the emergence of intentionality, we calculated a new variable ( Intentionality ) as a difference between the percent of Goal-directed and Non–goal-directed behaviors at each data point for each infant. The trajectory of change was then determined for Intentionality using HLM, which allowed us to find the estimated age when infants would be expected to shift from performing predominantly non–goal-directed behaviors towards more goal orientation ( Intentionality = 0), thus suggesting the emergence of intentionality in each means-end task.

To further assess whether the observed behavioral shifts truly represented intentionality, we compared infants’ behaviors between Toy Trials and control No-Toy Trials. Each behavior (including aggregated Goal-directed and Non – goal-directed behaviors ) was entered in HLM as a dependent variable, while a binary variable Goal specifying the type of the trial (0 = No-Toy Trials; 1 = Toy Trials), Age , and Age 2 were entered as independent variables.

Transfer of Knowledge in Means-End Problem Solving.

Only data for Toy Trials, averaged across the three trials, were included in these analyses. To determine whether the towel and turntable tasks differed in difficulty, infants’ success rates were compared between the two tasks using binomial logistic regression, while entering into the regression model Outcome as a dependent variable and a binary variable Task (0 = towel task; 1 = turntable task) and Age as independent variables.

We assessed whether the prevalence of goal-directedness would always be demonstrated first in the towel task and then in the turntable task, rather than the other way around. Next, we determined the age when the majority of infants showed understanding of the task requirements for both means-end tasks, or, in other words, were able to transfer their means-end knowledge between the two tasks. Among the infants with more than 50% of their behaviors being goal-directed during the towel task, we estimated the percent with more than 50% of their behaviors also being goal-directed in the turntable task. Transfer of knowledge was considered to take place at the first point when the majority of infants (>50%) who showed goal orientation in the towel task also demonstrated it in the turntable task.

There was very minimal trial attrition: infants completed 98.8% of the trials in the towel task and 98.5% of the trials in the turntable task. Several variables produced a large frequency of zero values (≥95%; Lifting the towel , Mouthing the towel , Mouthing the turntable ) and were excluded from the analyses of individual behaviors, but not from the analyses of aggregated behaviors. No statistically significant differences were found in infants’ performance of the coded behaviors between the three Toy Trials within each visit (e.g., infants did not improve their performance from one trial to another), which justified the averaging of the data across the tree Toy Trials.

Detailed information on statistical parameters of the following analyses is provided in online supplementary materials Table S1 . As infants got older, they significantly changed their performance of all coded behaviors. In the towel task, infants spent less time statically touching the towel ( t (88) = 5.08, p < .001, d = 1.08), and more time pulling the towel ( t (111) = 6.92, p < .001, d = 1.31) and reaching for the toy ( t (111) = 2.63, p = .010, d = 0.50) ( Figure 2A illustrates the behaviors representing about 95% of infants’ manual repertoire).

Estimated growth curves for manual behaviors in the towel (A) and turntable (B) tasks, visual attention in the two tasks (C), and goal-directed vs. non–goal-directed behaviors in the two tasks (D); Spinning = unidirectional spinning of the turntable; TW = towel task; TT = turntable task.

In the turntable task, with age infants decreased static touching ( t (108) = 5.07, p < .001, d = 0.98) and banging ( t (108) = 2.44, p = .016, d = 0.47) of the turntable, increased unidirectional spinning of the turntable ( t (86) = 2.19, p = .031, d = 0.47) and reaching for the toy ( t (108) = 3.00, p = .003, d = 0.58), and showed consistently low levels of pulling the turntable ( t (86) = 2.80, p = .006, d = 0.60), whereas alternate spinning increased until 12 months and decreased thereafter ( t (108) = 2.46, p = .016, d = 0.47) ( Figure 2B illustrates behaviors representing about 80% of infants’ manual repertoire).

Infants increased looking at the end object (Towel task: t (88) = 5.43, p < .001, d = 1.16; Turntable task: t (87) = 17.07, p < .001, d = 3.66) and decreased looking at the means object (Towel task: t (110) = 4.38, p < .001, d = 0.84; Turntable task: t (109) = 5.25, p < .001, d = 1.01) in both tasks with age ( Figure 2C ). Goal-directed behaviors increased in both the towel ( t (88) = 4.34, p < .001, d = 0.93) and the turntable ( t (87) = 12.56, p < .001, d = 2.69) tasks across age, while non–goal-directed behaviors decreased in both the towel ( t (87) = 5.35, p < .001, d = 1.15) and the turntable ( t (86) = 3.45, p < .001, d = 0.74) tasks ( Figure 2D ).

Raw data plots showed that the percent of successful trials increased across age for both tasks, with higher success rate observed in the towel task compared to the turntable task throughout the 6–18-month age period ( Figure 3 ). Furthermore, the likelihood of infants’ success in the two means-end tasks changed significantly with age. For the towel task, a binomial logistic regression model studying the effect of age on the likelihood of a successful trial outcome was significant: χ 2 (1) = 47.18, p < .0001, explaining 18.6% (Nagelkerke R 2 ; Nagelkerke, 1991 ) of variance in trial success and correctly classifying 72.5% of cases. Hosmer and Lemeshow’s test suggested the model was a good fit ( p = .448). Results suggested that a one-month increase in age made occurrence of success 1.16 times more likely. For the turntable task, a similar logistic regression model was also significant: χ 2 (1) = 113.6, p < .0001, explaining 39.4% (Nagelkerke R 2 ) of variance in trial success and correctly classifying 75.5% of cases. Hosmer and Lemeshow’s test suggested the model was a good fit ( p = .368). A one-month increase in age made occurrence of success 1.25 times more likely.

Percent of successful trials across age in the towel and turntable tasks.

Detailed information on statistical parameters of the following analyses is provided in online supplementary materials Table S2 . Statistically significant differences were found between means-end behaviors performed in successful vs. unsuccessful trials. For the towel task, infants spent more time pulling the towel ( t (22) = 5.28, p < .001, d = 2.25) and looking at the toy ( t (287) = 8.75, p < .001, d = 1.03), and less time statically touching the towel ( t (309) = 2.59, p = .010, d = 0.29) during successful compared to unsuccessful trials; there were no significant differences in other tested behaviors.

For the turntable task, infants spent more time performing alternate ( t (22) = 2.38, p = .027, d = 1.01) and unidirectional spinning ( t (22) = 5.45, p < .001, d = 2.32) of the turntable and looking at the toy ( t (22) = 5.12, p < .001, d = 2.18), and less time statically touching the turntable ( t (301) = 3.98, p < .001, d = 0.46) and reaching for the toy ( t (301) = 2.87, p = .004, d = 0.33) during successful compared to unsuccessful trials. These differences were consistent throughout the study.

Infants spent more time performing goal-directed behaviors (Towel task: t (22) = 5.68, p < .001, d = 2.42; Turntable task: t (22) = 7.80, p < .001, d = 3.33) and less time performing non–goal-directed behaviors (Towel task: t (287) = 3.19, p = .002, d = 0.38; Turntable task: t (301) = 4.02, p < .001, d = 0.46) during successful as compared to unsuccessful trials in both tasks.

Estimated statistical models (see Table S1 in online supplementary materials ) suggested that infants started performing more goal-directed than non–goal-directed behaviors at the age of 6.4 months in the towel task. This shift was observed at 10.1 months in the turntable task, suggesting that intentionality might develop sooner in the towel task than the turntable task.

To test that the performance of more goal-directed behaviors during Toy Trials reflected infants’ intentionality, we used No-Toy Trials as a control. Detailed information on statistical parameters of the following analyses is provided in online supplementary materials Table S3 . Infants’ behaviors differed significantly between the Toy and No-Toy Trials. In the towel task, in the presence of the toy, infants spent less time statically touching the towel ( t (306) = 5.25, p < .001, d = 0.60) and more time pulling the towel ( t (306) = 12.67, p < .001, d = 1.45) ( Figure 4A ). In the turntable task, the presence of the toy resulted in less time spent statically touching the turntable ( t (195) = 5.08, p < .001, d = 0.73) and more time spent in alternate ( t (195) = 2.19, p = .030, d = 0.31) and unidirectional spinning of the turntable ( t (195) = 4.91, p < .001, d = 0.70) ( Figure 4B ). These differences were consistent throughout the study duration. Visual attention towards the means object dropped on average 22.7% (29.6 to 6.9%) between No-Toy and Toy Trials for the towel task ( t (308) = 12.97, p < .001, d = 1.48) and 32.5% (41.9 to 9.4%) between No-Toy and Toy Trials for the turntable task ( t (219) = 18.25, p < .001, d = 2.47), and stayed consistent across the 9 to 24 month age period.

Estimated growth curves for manual behaviors in the towel (A) and turntable (B) tasks in trials with and without the end object; Toy = Toy Trials; No-toy = No-Toy Trials; Spinning = unidirectional spinning of the turntable.

In the presence of the end object, with age infants spent more time performing goal-directed behaviors (Towel task: t (200) = 12.58, p < .001, d = 1.78; Turntable task: t (196) = 5.37, p < .001, d = 0.77) and less time performing non–goal-directed behaviors (Towel task: t (221) = 11.55, p < .001, d = 1.55; Turntable task: t (217) = 7.89, p < .001, d = 1.07) in both tasks ( Figure 5 ). In the presence of the end object, a point was observed where infants shifted from performing mostly non–goal-directed behaviors to predominantly goal-directed behaviors (suggesting intentionality). A similar shift was not observed for No-Toy Trials in the towel task throughout the 6–24 month age period, or in the turntable task until the age of about 24 months ( Figure 5 ).

Estimated growth curves for the goal-directed and non–goal-directed behaviors in trials with or without an object present for the towel task (A) and the turntable task (B); note that in contrast to Figure 2D , goal-directed behaviors in Toy Trials here do not include Looking at the toy to ensure unbiased comparison to the No-Toy Trials; Toy = Toy Trials; No-toy = No-Toy Trials.

The likelihood of infants’ success in a means-end trial differed significantly between the two tasks. The logistic regression model studying the effect of task on the likelihood of a successful trial outcome was statistically significant: χ 2 (1) = 47.42, p < .0001, explaining 37.7% (Nagelkerke R 2 ) of variance in trial success and correctly classifying 74.5% of cases. Hosmer and Lemeshow’s test suggested that the model was a good fit ( p = .671). The odds of succeeding during the towel task were 4.40 times higher than those for the turntable task across the duration of the study.

The prevalence of goal-directedness in the towel task preceded that demonstrated in the turntable task in 100% of the infants. Of the infants who performed more goal-directed than non–goal-directed behaviors during the towel task, only 20.0% showed a similar level of goal orientation at 6 months in the turntable task, this number increased to 53.8% at 9 months, 55.0% at 12 months, 81.0% at 18 months, and 90.5% at 24 months. Thus, starting at 9 months, the majority of infants seemed to transfer their means-end problem-solving knowledge from the towel task to the turntable task.

This study was innovative because it was the first to evaluate the developmental trajectories of behaviors performed by typically developing infants in two means-end tasks, to establish the timeline for the emergence of intentionality in the two tasks, and to determine whether infants demonstrated any transfer of knowledge between the two means-end tasks throughout the first two years of life. The longitudinal design of this study provided a comprehensive picture of means-end problem-solving learning in infancy.

As expected ( Willatts, 1984a , 1984b , 1999 ), infants in this study displayed a wide range of visual and manual exploratory behaviors toward the means and end objects in the two means-end tasks from 6 through 24-months-old. Daily, infants actively explore objects using multiple modalities (e.g., proprioceptive, somatosensory, visual, tactile, and oral). This rich exploration provides rich opportunities to learn and understand object affordances, relations among objects, differences between means and end objects, the concept of support, and means-end causation, all important precursors for successful means-end problem solving ( Bremner, 2000 ; Gibson, 1988 ; Lobo & Galloway, 2008 , 2013b ; Lobo, Galloway, & Savelsbergh, 2004 ; Sommerville, Hildebrand, & Crane, 2008 ; Sommerville & Woodward, 2005a ; Sommerville, Woodward, & Needham, 2005 ; Willatts, 1999 ). Active exploration can allow for a ‘trial and error’ process through which infants learn to eliminate behaviors that do not lead to a desired goal (i.e., end object attainment) and to repeat behaviors that are likely to result in reaching the goal. With learning, a shift from more non–goal-directed behavior to predominantly goal-directed behavior would be expected.

Indeed, we found that as infants got older, they engaged in more goal-directed behavior and less non–goal-directed behavior for these tasks. For example, infants increased looking at the end object and decreased looking at the means objects with age. They also increased goal-directed towel pulling and turntable spinning and decreased performance of behaviors that would not result in attainment of the end object, such as static touching, mouthing, lifting, and banging of the means objects. Successful trials in both tasks across all ages were characterized by more goal-directed behavior, and unsuccessful trials were characterized by more non–goal-directed behavior. Therefore, the observed shift towards more goal orientation with age was accompanied by a greater rate of success in both tasks.

The timing of emergence of intentionality differed between the two means-end tasks even though they both required an understanding of the relational concept of support. Most infants expressed intentionality at the age of 6.4 months in the towel task but not until the age of 10.1 months in the turntable task. The predominant performance of goal-directed behaviors was not observed throughout the first two years of life in control No-Toy trials where an end object was not present. This confirmed that infants’ increase in goal-directed behavior during Toy Trials likely represented the emergence of intentionality in means-end problem solving ( Willatts, 1984a , 1999 ). Manual exploration of the means object coupled with visual observation of the effects on the end object may help young infants develop a means-end concept, so they can conceive and implement a correct sequence of actions ( Bower & Wishart, 1972 ; Diamond, 1991 ) and also acquire “insight into agency” as they begin understanding the possible consequences of their own actions ( O’Connor & Russell, 2015 ).

In the current study, we observed a steady increase in infants’ goal-directedness in means-end problem solving with age, suggesting no regressions in the development of intentionality. Although understanding of means-end causality emerges gradually via active trial-and-error learning, we aimed to identify a time frame when infants’ behavior became more goal-directed. Different timelines for the emergence of intentionality in the two means-end tasks suggest context-dependency of means-end causal knowledge. As infants acquire general understanding about means-end relations, they may still need specific practice to be able to implement this knowledge in a new setting or task.

The earlier appearance of intentionality in the towel task suggested it was easier for infants to solve than the turntable task. Furthermore, we found that the percent of successful trials at the age of 6 months was 3.3 times higher in the towel task than in the turntable task (43.1 vs. 12.9%). Across age, the odds of succeeding were 4.4 times higher in the towel task than in the turntable task. However, learning in the turntable task had a steeper trajectory than that in the towel task: one-month increase in age made occurrence of success 1.16 times more likely in the towel task and 1.25 times more likely in the turntable task. This resulted in similar success rates in both tasks by the age of 24 months (89.4% in the towel task, 91.9% in the turntable task).

Why would the turntable task be more difficult than the towel task, taking into account that both tasks require a seemingly similar understanding of the concept of support and means-end relations? The main distinction between the two tasks was that they required different motor actions to achieve the end goal: pulling vs. rotation of the means object. One might argue that the turntable task may be more difficult for infants because they struggle with understanding the relations between rotational surfaces and the objects they support ( Bai & Bertenthal, 1992 ; Goldfield & Dickerson, 1981 ).

Moreover, infants’ daily experiences may impact their ability to succeed in the two means-end tasks. For example, current results suggested that at the age of 6 months, pulling the towel occurred 30% of the observation time, while turntable rotation occurred only 6.7% of the time. Only after 9 months of age did infants begin performing rotation of the turntable more than other non–goal-directed exploratory behaviors, such as touching, pulling, banging, and mouthing the turntable. However, even by 24 months, a gap between the amount of towel pulling (72%) and turntable rotation (61.8%) remained. We propose that the difficulty of the turntable task may stem from the comparative novelty of this task for infants: in everyday life, infants are more likely to encounter and explore objects that afford pulling rather than rotation.

Furthermore, by the age of 9 months, the majority of infants who engaged in primarily goal-directed behavior in the towel task also performed mostly goal-directed behavior in the turntable task. We propose that by this age, infants might begin understanding the relations between the means and the end object, comprehending the consequences of their own actions on the objects and generalizing that knowledge across tasks. While the turntable task is more difficult for infants to solve, it does not appear to be more physically demanding. Rather, the turntable task may be more challenging for infants to understand the affordance of the means object and the relation between the means and the end object ( Bai & Bertenthal, 1992 ; Goldfield & Dickerson, 1981 ). However, by the age of 9 months, infants might be able to transfer their causal knowledge about pulling a support to obtain a toy to the situation of rotating a surface to obtain a toy.

Infants’ active exploration facilitates their understanding of means-end causal relations between objects ( Lobo & Galloway, 2008 ; Sommerville, Hildebrand, & Crane, 2008 ; Sommerville & Woodward, 2005a ) and gradually improves their ability to transfer this knowledge across different situations and tasks ( O’Connor & Russell, 2015 ). Although one might hypothesize that means-end understanding appears separately in different, yet related tasks, rather than being transferred from one task to another, it is more likely that infants not only learn to understand means-end relations in specific situations, but also acquire the ability to generalize that knowledge across related contexts.

Limitations of the Study

The longitudinal design of the current study resulted in infants being tested multiple times in the two means-end tasks. With repetitive testing, it was possible that infants would remember their experience and work upon this knowledge between consecutive testing sessions. Indeed, previous research has shown that active exploration of the objects involved in means-end tasks and their relations can improve infants’ means-end problem-solving ( Abravanel & Gingold, 1985 ; Provasi, Dublon, & Bloch, 2001 ; Sommerville et al., 2008 ; Sommerville, Woodward, & Needham, 2005 ). However, as infants’ knowledge about means-end causal relations does not emerge in the vacuum, but rather is a direct result of their everyday exploration of objects (e.g., Gibson, 1988 ), remembering past experiences with means-end tasks is an important part of learning to problem-solve. The non-independent data obtained across the multiple observations were appropriately analyzed in this study using multilevel hierarchical modeling.

The data did not support the performance of statistical testing to support the idea of knowledge transfer between the two means-end tasks at a particular age. Instead, we based our conclusions on the fact that the majority of infants performed a greater amount of goal-directed behavior in both tasks, and that they always succeeded first in the towel task prior to the turntable task. Future research should further investigate this topic using experimental designs.

Conclusions

This longitudinal study provides a more comprehensive picture of the behaviors infants perform with objects as they learn means-end relations. These results highlight that: 1) early learning often begins with the performance of a greater range of exploratory behaviors that become more refined and goal-directed with age and successful performance; 2) the constraints of tasks may influence infants’ level of success and the emergence of intentionality, even when the tasks require an understanding of similar relational concepts; 3) infants may begin to transfer knowledge of support relations between tasks within the first year of life, with most infants showing success in pulling and rotating tasks by 24 months of age. Future research should further explore the issue of generalizability versus specificity in the development of means-end knowledge.

Supplementary Material

Supp tables1-3, acknowledgements.

The authors would like to acknowledge the infants and their parents for their participation, time, and patience in making the current longitudinal study possible. Also, we would like to thank the research assistants who helped with the coding of data. This research was supported by the National Institute of Health, Eunice Kennedy Shriver National Institute of Child Health & Human Development (1R21HD076092–01A1, Lobo PI; 1R01HD051748, Galloway, PI).

• Abravanel E, & Gingold H (1985). Learning via observation during the second year of life . Developmental Psychology , 21 ( 4 ), 614–623. DOI: 10.1037/0012-1649.21.4.614 [ CrossRef ] [ Google Scholar ]
• Bai DL, & Bertenthal BI (1992). Locomotor status and the development of special search skills . Child Development , 63 ( 1 ), 215–226. DOI: 10.1111/j.1467-8624.1992.tb03608.x [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Baillargeon R (1987). Object permanence in 3 1/2- and 4 1/2-month-old infants . Developmental Psychology , 23 ( 5 ), 655–664. DOI: 10.1037/0012-1649.23.5.655 [ CrossRef ] [ Google Scholar ]
• Baillargeon R (1993). The object concept revisited: New directions in the investigation of infants’ physical knowledge In Granrud C (Ed.), Visual perception and cognition in infancy (pp. 265–315). Hillsdale, NJ: Erlbaum. [ Google Scholar ]
• Bates E, Carlson-Luden V, & Bretherton I (1980). Perceptual aspects of tool using in infancy . Infant Behavior and Development , 3 , 127–140. DOI: 10.1016/S0163-6383(80)80017-8 [ CrossRef ] [ Google Scholar ]
• Bayley N (2006). Bayley scales of infant and toddler development (3rd ed.). San Antonio, TX: The Psychological Corporation. [ Google Scholar ]
• Bonawitz EB, Ferranti D, Saxe R, Gopnik A, Meltzoff AN, Woodward J, & Schulz LE (2010). Just do it? Investigating the gap between prediction and action in toddlers’ causal inferences . Cognition , 115 , 104–117. DOI: 10.1016/j.cognition.2009.12.001 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Bower TGR, & Wishart JG (1972). The effects of motor skills on object permanence . Cognition , 1 ( 2–3 ), 165–172. DOI: 10.1016/0010-0277(72)90017-0 [ CrossRef ] [ Google Scholar ]
• Brandone AC (2015). Infants’ social and motor experience and the emerging understanding of intentional actions . Developmental Psychology , 51 ( 4 ), 512–523. DOI: 10.1037/a0038844 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Bremner JG (2000). Developmental relationships between perception and action in infancy . Infant Behavior and Development , 23 ( 3 ), 567–582. DOI: 10.1016/S0163-6383(01)00058-3 [ CrossRef ] [ Google Scholar ]
• Brown AL (1990). Domain-specific principles affect learning and transfer in children . Cognitive Science , 14 ( 1 ), 107–133. DOI: 10.1207/s15516709cog1401_6 [ CrossRef ] [ Google Scholar ]
• Case-Smith J, Bigsby R, & Clutter J (1998). Perceptual-motor coupling in the development of grasp . American Journal of Occupational Therapy , 52 ( 2 ), 102–110. DOI: 10.5014/ajot.52.2.102 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Casler K, & Keleman D (2005). Young children’s rapid learning about artifacts . Developmental Science , 8 ( 6 ), 472–480. DOI: 10.1111/j.1467-7687.2005.00438.x [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Chen Z, Sanchez RP, & Campbell T (1997). From beyond to within their grasp: The rudiments of analogical problem solving in 10- and 13-month-olds . Developmental Psychology , 33 ( 5 ), 790–801. DOI: 10.1037/0012-1649.33.5.790 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Chen Z, & Siegler RS (2000). Across the great divide: Bridging the gap between understanding of toddlers’ and older children’s thinking . Monographs of the Society for Research in Child Development , 65 , 1–108. DOI: 10.1111/1540-5834.00085 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Clearfield MW, Stanger SB, & Jenne HK (2015). Socioeconomic status (SES) affects means-end behavior across the first year . Journal of Applied Developmental Psychology , 38 , 22–28. DOI: 10.1016/j.appdev.2015.02.001 [ CrossRef ] [ Google Scholar ]
• Cohen J (1988). Statistical power analysis for the behavioral sciences (2nd ed.). Hillsdale, NJ: Lawrence Erlbaum Associates. [ Google Scholar ]
• Coleman EB, Brown AL, & Rivkin ID (1997). The effect of instructional explanations on learning from scientific texts . Journal of the Learning Sciences , 6 ( 4 ), 347–365. DOI: 10.1207/s15327809jls0604_1 [ CrossRef ] [ Google Scholar ]
• Csibra G, & Gergely G (2007). “Obsessed with goals”: Functions and mechanisms of teleological interpretation of actions in humans . Acta Psychologica , 124 , 60–78. DOI: 10.1016/j.actpsy.2006.09.007 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Diamond A (1985). Development of the ability to use recall to guide action, as indicated by infants’ performance on AB . Child Development , 56 ( 4 ), 868–883. DOI: 10.2307/1130099 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Diamond A (1991). Neuropsychological insights into the meaning of object concept development In Carey S & Gelman R (Eds.), The Jean Piaget Symposium series. The epigenesis of mind: Essays on biology and cognition (pp. 67–110). Hillsdale, NJ: Erlbaum. [ Google Scholar ]
• Gibson EJ (1988). Exploratory behavior in the development of perceiving, acting, and the acquiring of knowledge . Annual Review of Psychology , 39 ( 1 ), 1–41. DOI: 10.1146/annurev.ps.39.020188.000245 [ CrossRef ] [ Google Scholar ]
• Gibson EJ, & Pick AD (1988). An ecological approach to perceptual learning and development . Oxford, UK: Oxford University Press. [ Google Scholar ]
• Goldfield EC, & Dickerson DJ (1981). Keeping track of locations during movement in 8- to 10-month-old infants . Journal of Experimental Child Psychology , 32 ( 1 ), 48–64. DOI: 10.1016/0022-0965(81)90092-8 [ CrossRef ] [ Google Scholar ]
• Goubet N, & Clifton R (1998). Object and event representation in 6–1/2-month-old infants . Developmental Psychology , 34 ( 1 ), 63–76. DOI: 10.1037/0012-1649.34.1.63 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Guo Y, Logan HL, Glueck DH, & Muller KE (2013). Selecting a sample size for studies with repeated measures . BMC Medical Research Methodology , 13 ( 1 ), 100–107. DOI: 10.1186/1471-2288-13-100 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Healy AF, Buck-Gengler CJ, Barshi I, Parker JT, Schneider VI, Raymond WD, … Bourne LE Jr.(2002). Optimizing the durability and generalizability of knowledge and skills In Shohov SP (Ed.), Trends in cognitive psychology (pp. 123–192). New York: Nova Science Publishers, Inc. [ Google Scholar ]
• Hood BM, & Willatts P (1986). Reaching in the dark to an object’s remembered position: Evidence for object permanence in 5-month-old infants . British Journal of Developmental Psychology , 4 ( 1 ), 57–65. DOI: 10.1111/j.2044-835X.1986.tb00998.x [ CrossRef ] [ Google Scholar ]
• Johnson SP, Slemmer JA, & Amso D (2004). Where infants look determines how they see: Eye movements and object perception performance in 3-month-olds . Infancy , 6 ( 2 ), 185–201. DOI: 10.1207/s15327078in0602_3 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lauder W, Reynolds W, & Angus N (1999). Transfer of knowledge and skills: Some implications for nursing and nurse education . Nurse Education Today , 19 ( 6 ), 480–487. DOI: 10.1054/nedt.1999.0338 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lobo MA, & Galloway JC (2008). Postural and object-oriented experiences advance early reaching, object exploration, and means-end behavior . Child Development , 79 ( 6 ), 1869–1890. DOI: 10.1111/j.1467-8624.2008.01231.x [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lobo MA, & Galloway JC (2013a). Assessment and stability of early learning abilities in preterm and full-term infants across the first two years of life . Research in Developmental Disabilities , 34 ( 5 ), 1721–1730. DOI: 10.1016/j.ridd.2013.02.010 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lobo MA, & Galloway JC (2013b). The onset of reaching significantly impacts how infants explore both objects and their bodies . Infant Behavior and Development , 36 ( 1 ), 14–24. DOI: 10.1016/j.infbeh.2012.09.003 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lobo MA, Galloway JC, & Savelsbergh GJ (2004). General and task-related experiences affect early object interaction . Child Development , 75 ( 4 ), 1268–1281. DOI: 10.1111/j.1467-8624.2004.00738.x [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Munakata Y (1998). Infant perseveration and implications for object permanence theories: A PDP model of the AB task . Developmental Science , 1 ( 2 ), 161–184. DOI: 10.1111/1467-7687.00021 [ CrossRef ] [ Google Scholar ]
• Munakata Y, McClelland JL, Johnson MH, & Siegler RS (1997). Rethinking infant knowledge: Toward an adaptive process account of successes and failures in object permanence tasks . Psychological Review , 104 ( 4 ), 686–713. DOI: 10.1037/0033-295X.104.4.686 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Nagelkerke NJD (1991). A note on a general definition of the coefficient of determination . Biometrika , 78 ( 3 ), 691–692. [ Google Scholar ]
• Nielsen M (2006). Copying actions and copying outcomes: Social learning through the second year . Developmental Psychology , 42 ( 3 ), 555–565. DOI: 10.1037/0012-1649.42.3.555 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• O’Connor RJ, & Russell J (2015). Understanding the effects of one’s actions upon hidden objects and the development of search behaviour in 7-month-old infants . Developmental Science , 18 ( 5 ), 824–831. DOI: 10.1111/desc.12265 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Piaget J (1953). The origin of intelligence in the child . London: Routledge & Kegan Paul. [ Google Scholar ]
• Piaget J (1955). The construction of reality in the child . London: Routledge & Kegan Paul. [ Google Scholar ]
• Prawat RS (1989). Promoting access to knowledge, strategy, and disposition in students: A research synthesis . Review of Educational Research , 59 ( 1 ), 1–41. DOI: 10.3102/00346543059001001 [ CrossRef ] [ Google Scholar ]
• Price EA, & Driscoll MP (1997). An inquiry into the spontaneous transfer of problem-solving skill . Contemporary Educational Psychology , 22 ( 4 ), 472–494. DOI: 10.1006/ceps.1997.0948 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Provasi J, Dubon CD, & Bloch H (2001). Do 9- and 12-month-old infants learn means-end relations by observing? . Infant Behavior and Development , 24 ( 2 ), 195–213. DOI: 10.1016/S0163-6383(01)00072-8 [ CrossRef ] [ Google Scholar ]
• Rat-Fischer L, O’Regan JK, & Fagard J (2012). The emergence of tool use during the second year of life . Journal of Experimental Child Psychology , 113 ( 3 ), 440–446. DOI: 10.1016/j.jecp.2012.06.001 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Rat-Fischer L, O’Regan JK, & Fagard J (2014). Comparison of active and purely visual performance in a multiple-string means-end task in infants . Cognition , 133 ( 1 ), 304–316. DOI: 10.1016/j.cognition.2014.06.005 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Raudenbush S, Bryk A, Cheong YF, Congdon R, & du Toit M (2004). HLM 6: Hierarchical linear and nonlinear modeling . Lincolnwood, IL: Scientific Software International, Inc. [ Google Scholar ]
• Renkl A, Mandl H, & Gruber H (1996). Inert knowledge: Analysis and remedies . Educational Psychologist , 31 ( 2 ), 115–121. DOI: 10.1207/s15326985ep3102_3 [ CrossRef ] [ Google Scholar ]
• Richardson HM (1932). The growth of adaptive behaviour in infants: An experimental study at seven age levels . Genetic Psychology Monographs , XII , 195–357. [ Google Scholar ]
• Sawilowsky SS (2009). New effect size rules of thumb . Journal of Modern Applied Statistical Methods , 8 , 467–474. [ Google Scholar ]
• Schlesinger M, & Langer J (1999). Infants’ developing expectations of possible and impossible tool‐use events between ages 8 and 12 months . Developmental Science , 2 ( 2 ), 195–205. DOI: 10.1111/1467-7687.00068 [ CrossRef ] [ Google Scholar ]
• Schlitz M (1996). Intentionality: A program of study . Advances: The Journal of Mind-Body Health , 12 ( 3 ), 31–32. [ Google Scholar ]
• Shinskey JL, & Munakata Y (2003). Are infants in the dark about hidden objects? Developmental Science , 6 ( 3 ), 273–282. DOI: 10.1111/1467-7687.00283 [ CrossRef ] [ Google Scholar ]
• Singer JD, & Willett JB (2003). Applied longitudinal data analysis: Modeling change and event occurrence . Oxford, NY: Oxford University Press. [ Google Scholar ]
• Singer RN (1982). The learning of motor skills . New York: McMillan. [ Google Scholar ]
• Slater A (1995). Individual differences in infancy and later IQ . Journal of Child Psychology and Psychiatry , 36 ( 1 ), 69–112. DOI: 10.1111/j.1469-7610.1995.tb01656.x [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Sommerville JA, Hildebrand EA, & Crane CC (2008). Experience matters: The impact of doing versus watching on infants’ subsequent perception of tool use events . Developmental Psychology , 44 ( 5 ), 1249–1256. DOI: 10.1037/a0012296 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Sommerville JA, & Woodward AL (2005a). Infants’ sensitivity to the causal features of means-end support sequences in action and perception . Infancy , 8 ( 2 ), 119–145. DOI: 10.1207/s15327078in0802_2 [ CrossRef ] [ Google Scholar ]
• Sommerville JA, & Woodward AL (2005b). Pulling out the intentional structure of action: The relation between action processing and action production in infancy . Cognition , 95 ( 1 ), 1–30. DOI: 10.1016/j.cognition.2003.12.004 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Sommerville JA, Woodward AL, & Needham A (2005). Action experience alters 3-month-old infants’ perception of others’ actions . Cognition , 96 ( 1 ), B1–B11. DOI: 10.1016/j.cognition.2004.07.004 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Spelke ES (1988). Where perceiving ends and thinking begins: The apprehension of objects in infancy In Yonas A (Ed.), Perceptual development in infancy (pp. 197–234). Hillsdale, NJ: Erlbaum. [ Google Scholar ]
• Thelen E (1990). Coupling perception and action in the development of skill: A dynamic approach In Bloch H & Berthenthal BI (Eds.), Sensory-motor organizations and development in infancy and early childhood . Boston: Kluwer Academic. [ Google Scholar ]
• Uzgiris IC, & Hunt JMV (1975). Assessment in infancy: Ordinal scales of psychological development . Urbana: University of Illinois Press. [ Google Scholar ]
• von Helmholtz H (1962). Handbook of psychological optics (Rev. ed.). New York: Optical Society of America. [ Google Scholar ]
• Willatts P (1984a). The stage-IV infant’s solution of problems requiring the use of supports . Infant Behavior and Development , 7 ( 2 ), 125–134. DOI: 10.1016/S0163-6383(84)80053-3 [ CrossRef ] [ Google Scholar ]
• Willatts P (1984b). Stages in the development of intentional search by young infants . Developmental Psychology , 20 ( 3 ), 389–396. DOI: 10.1037/0012-1649.20.3.389 [ CrossRef ] [ Google Scholar ]
• Willatts P (1985). Adjustment of means-ends coordination and the representation of spatial relations in the production of search errors by infants . British Journal of Developmental Psychology , 3 ( 3 ), 259–272. DOI: 10.1111/j.2044-835X.1985.tb00978.x [ CrossRef ] [ Google Scholar ]
• Willatts P (1990). Development of problem-solving strategies in infancy In Bjorklund DF Ed.), Children’s strategies: Contemporary views of cognitive development (pp. 23–66). Hillsdale, NJ: Lawrence Erlbaum Associates, Inc. [ Google Scholar ]
• Willatts P (1999). Development of means-end behavior in young infants: Pulling a support to retrieve a distant object . Developmental Psychology , 35 ( 3 ), 651–667. DOI: 10.1037/0012-1649.35.3.651 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Willatts P, Forsyth JS, DiModugno MK, Varma S, & Colvin M (1998). Effect of long-chain polyunsaturated fatty acids in infant formula on problem solving at 10 months of age . Lancet , 352 ( 9129 ), 688–691. DOI: 10.1016/S0140-6736(97)11374-5 [ PubMed ] [ CrossRef ] [ Google Scholar ]

Means-End Reasoning

• Reference work entry
• First Online: 01 January 2022
• pp 4142–4147
• Cite this reference work entry

• Anastasia Krasheninnikova 3 , 4 , 5  

29 Accesses

1 Citations

Means-end behavior ; Means-end understanding

Broadly speaking means-end reasoning is concerned with finding means for achieving goals (Pollock 2002 ). More specifically, it involves the deliberate and planned execution of a chain of actions to achieve a goal and occurs in situations where an obstacle (e.g., a distance between the subject and a desirable item, person) preventing the achievement of the goal must initially be removed (Willatts 1999 ).

Introduction

In everyday life, we are regularly facing situations which require elaborate sequences of mediating actions to reach a distant goal at the end. For example, imagine a person opening a drawer to take a key to unlock a storeroom to get a ladder needed to reach the door to an out-of-reach vitrine where there is a candy box that can be opened to get some sweets. As this hypothetical problem-solving sequence illustrates (modiefied from Santos et al 2005 ), the individual steps within a sequence are often separated...

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Institutional subscriptions

Alem, S., Perry, C. J., Zhu, X., Loukola, O. J., Ingraham, T., Søvik, E., & Chittka, L. (2016). Associative mechanisms allow for social learning and cultural transmission of string pulling in an insect. PLoS Biology, 14 (10), 1–28. https://doi.org/10.1371/journal.pbio.1002564 .

Article   Google Scholar  

Auersperg, A. M. I., Gajdon, G. K., & Huber, L. (2009). Kea (Nestor notabilis) consider spatial relationships between objects in the support problem. Biology Letters, 5 (4), 455–458. https://doi.org/10.1098/rsbl.2009.0114 .

Article   PubMed   PubMed Central   Google Scholar  

Auersperg, A. M. I., Kacelnik, A., & Von Bayern, A. M. P. (2013). Explorative learning and functional inferences on a five-step means-means-end problem in Goffin’ s cockatoos ( Cacatua goffini ). PLoS One, 8 (7), e68979. https://doi.org/10.1371/journal.pone.0068979 .

Bird, C. D., & Emery, N. J. (2009). Insightful problem solving and creative tool modification by captive nontool-using rooks. Proceedings of the National Academy of Sciences, 106 (25), 10370–10375. https://doi.org/10.1073/pnas.0901008106 .

Hanus, D. (2016). Causal reasoning versus associative learning: A useful dichotomy or a strawman battle in comparative psychology? Journal of Comparative Psychology, 130 (3), 241–248. https://doi.org/10.1037/a0040235 .

Article   PubMed   Google Scholar  

Hauser, M. D., Kralik, J., & Botto-Mahan, C. (1999). Problem solving and functional design features: Experiments on cotton-top tamarins, Saguinus oedipus oedipus. Animal Behaviour, 57 , 565–582. https://doi.org/10.1006/anbe.1998.1032 .

Heinrich, B., & Bugnyar, T. (2005). Testing problem solving in ravens: String-pulling to reach food. Ethology, 111 (10), 962–976. https://doi.org/10.1111/j.1439-0310.2005.01133.x .

Herrmann, E., Wobber, V., & Call, J. (2008). Great apes’ (Pan troglodytes, Pan paniscus, Gorilla gorilla, Pongo pygmaeus) understanding of tool functional properties after limited experience. Journal of Comparative Psychology, 122 (2), 220–230. https://doi.org/10.1037/0735-7036.122.2.220 .

Irie-Sugimoto, N., Kobayashi, T., Sato, T., & Hasegawa, T. (2008). Evidence of means – End behavior in Asian elephants (Elephas maximus). Animal Cognition, 11 (2), 359–365. https://doi.org/10.1007/s10071-007-0126-z .

Jacobs, I. F., & Osvath, M. (2015). The string-pulling paradigm in comparative psychology. Journal of Comparative Psychology, 129 (2), 89–120. https://doi.org/10.1037/a0038746 .

Köhler, W. (1927). The mentality of aper (2nd ed.). New York: Vintage Books.

Google Scholar  

Krasheninnikova, A., Bräger, S., & Wanker, R. (2013). Means-end comprehension in four parrot species: Explained by social complexity. Animal Cognition, 16 (5), 755–764. https://doi.org/10.1007/s10071-013-0609-z .

Matsuzawa, T. (2001). Primate foundations of human intelligence: A view of tool use in non-human primates and fossil hominids. In T. Matsuzawa (Ed.), Primate origins of human cognition and behavior (pp. 3–25). Tokyo/Berlin/Heidelberg: Springer.

Chapter   Google Scholar  

Osthaus, B., Lea, S. E. G., & Slater, A. M. (2005). Dogs (Canis lupus familiaris) fail to show understanding of means-end connections in a string-pulling task. Animal Cognition, 8 (1), 37–47. https://doi.org/10.1007/s10071-004-0230-2 .

Piaget, J., & Cook, M. (1952). The origins of intelligence in children . New York: International Universities Press.

Book   Google Scholar  

Pollock, J. L. (2002). The logical foundations of means-end reasoning. In R. Elio (Ed.), Common sense, reasoning, and rationality (pp. 60–77). Oxford: Oxford University Press.

Povinelli, D. J. (2000). Folk physics for Apes: The Chimpanzee’s theory of how the world works. Book reviews . https://doi.org/10.1016/j.orggeochem.2014.10.015 .

Range, F., Möslinger, H., & Virányi, Z. (2012). Domestication has not affected the understanding of means-end connections in dogs. Animal Cognition, 15 (4), 597–607. https://doi.org/10.1007/s10071-012-0488-8 .

Santos, L. R., Rosati, A., Sproul, C., Spaulding, B., & Hauser, M. D. (2005). Means-means-end tool choice in cotton-top tamarins (Saguinus oedipus): Finding the limits on primates’ knowledge of tools. Animal Cognition, 8 (4), 236–246. https://doi.org/10.1007/s10071-004-0246-7 .

Schmidt, G. F., & Cook, R. G. (2006). Mind the gap: Means – End discrimination by pigeons. Animal Behaviour, 71 , 599–608. https://doi.org/10.1016/j.anbehav.2005.06.010 .

Shettleworth, S. J. (2012). Do animals have insight, and what is insight anyway? Canadian Journal of Experimental Psychology/Revue Canadienne de Psychologie Expérimentale, 66 (4), 217–226. https://doi.org/10.1037/a0030674 .

Taylor, A. H., Medina, F. S., Holzhaider, J. C., Hearne, L. J., Hunt, G. R., & Gray, R. D. (2010). An investigation into the cognition behind spontaneous string pulling in new caledonian crows. PLoS One, 5 (2), e9345. https://doi.org/10.1371/journal.pone.0009345 .

Whitt, E., Douglas, M., Osthaus, B., & Hocking, I. (2009). Domestic cats (Felis catus) do not show causal understanding in a string-pulling task. Animal Cognition, 12 (5), 739–743. https://doi.org/10.1007/s10071-009-0228-x .

Willatts, P. (1999). Development of means-end behavior in young infants: Pulling a support to retrieve a distant object. Developmental Psychology, 35 (3), 651–667. https://doi.org/10.1037/0012-1649.35.3.651 .

Wimpenny, J. H., Weir, A. A. S., Clayton, L., Rutz, C., & Kacelnik, A. (2009). Cognitive processes associated with sequential tool use in new Caledonian crows. PLoS One, 4 (8), e6471. https://doi.org/10.1371/journal.pone.0006471 .

Woodward, J. (2011). A philosopher looks at tool use and causal understanding. In T. McCormack, C. Hoerl, & S. Butterfill (Eds.), Tool use and causal cognition (pp. 1–47). Oxford: Oxford University Press.

Download references

Author information

Authors and affiliations.

Department of Behavioural Neurobiology, Max-Planck-Institute for Ornithology, Seewiesen, Germany

Anastasia Krasheninnikova

Max-Planck Comparative Cognition Research Group, Tenerife, Spain

Department of Behavioural Ecology and Evolutionary Genetics, Max-Planck-Institute for Ornithology, Seewiesen, Germany

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Anastasia Krasheninnikova .

Editor information

Editors and affiliations.

Department of Psychology, Oakland University, Rochester, MI, USA

Jennifer Vonk

Todd K. Shackelford

Section Editor information

University of Manitoba, Winnipeg, MB, Canada

Dawson Clary

Rights and permissions

Reprints and permissions

Copyright information

© 2022 Springer Nature Switzerland AG

About this entry

Cite this entry.

Krasheninnikova, A. (2022). Means-End Reasoning. In: Vonk, J., Shackelford, T.K. (eds) Encyclopedia of Animal Cognition and Behavior. Springer, Cham. https://doi.org/10.1007/978-3-319-55065-7_1539

Download citation

DOI : https://doi.org/10.1007/978-3-319-55065-7_1539

Published : 20 May 2022

Publisher Name : Springer, Cham

Print ISBN : 978-3-319-55064-0

Online ISBN : 978-3-319-55065-7

eBook Packages : Behavioral Science and Psychology Reference Module Humanities and Social Sciences Reference Module Business, Economics and Social Sciences

Share this entry

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

18.12: Chapter 14- Problem Solving, Categories and Concepts

• Last updated
• Save as PDF
• Page ID 113223

This page is a draft and under active development. Please forward any questions, comments, and/or feedback to the ASCCC OERI ( [email protected] ).

• Kenneth A. Koenigshofer
• ASCCC Open Educational Resources Initiative (OERI)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Define problem types
• Describe problem solving strategies
• Define algorithm and heuristic
• Describe the role of insight in problem solving
• Explain some common roadblocks to effective problem solving
• What is meant by a search problem
• Describe means-ends analysis
• How do analogies and restructuring contribute to problem solving
• Explain how experts solve problems and what gives them an advantage over non-experts
• Describe the brain mechanisms in problem solving

In this section we examine problem-solving strategies. People face problems every day—usually, multiple problems throughout the day. Sometimes these problems are straightforward: To double a recipe for pizza dough, for example, all that is required is that each ingredient in the recipe be doubled. Sometimes, however, the problems we encounter are more complex. For example, say you have a work deadline, and you must mail a printed copy of a report to your supervisor by the end of the business day. The report is time-sensitive and must be sent overnight. You finished the report last night, but your printer will not work today. What should you do? First, you need to identify the problem and then apply a strategy, usually a set of steps, for solving the problem.

Defining Problems

We begin this module on Problem Solving by giving a short description of what psychologists regard as a problem. Afterwards we are going to present different approaches towards problem solving, starting with gestalt psychologists and ending with modern search strategies connected to artificial intelligence. In addition we will also consider how experts do solve problems and finally we will have a closer look at two topics: The neurophysiological background on the one hand and the question what kind of role can be assigned to evolution regarding problem solving on the other.

The most basic definition is “A problem is any given situation that differs from a desired goal”. This definition is very useful for discussing problem solving in terms of evolutionary adaptation, as it allows to understand every aspect of (human or animal) life as a problem. This includes issues like finding food in harsh winters, remembering where you left your provisions, making decisions about which way to go, repeating and varying all kinds of complex movements by learning, and so on. Though all these problems were of crucial importance during the evolutionary process that created us the way we are, they are by no means solved exclusively by humans. We find a most amazing variety of different solutions for these problems of adaptation in animals as well (just consider, e.g., by which means a bat hunts its prey, compared to a spider ).

However, for this module, we will mainly focus on abstract problems that humans may encounter (e.g. playing chess or doing an assignment in college). Furthermore, we will not consider those situations as abstract problems that have an obvious solution: Imagine a college student, let's call him Knut. Knut decides to take a sip of coffee from the mug next to his right hand. He does not even have to think about how to do this. This is not because the situation itself is trivial (a robot capable of recognizing the mug, deciding whether it is full, then grabbing it and moving it to Knut’s mouth would be a highly complex machine) but because in the context of all possible situations it is so trivial that it no longer is a problem our consciousness needs to be bothered with. The problems we will discuss in the following all need some conscious effort, though some seem to be solved without us being able to say how exactly we got to the solution. Still we will find that often the strategies we use to solve these problems are applicable to more basic problems, as well as the more abstract ones such as completing a reading or writing assignment for a college class.

Non-trivial, abstract problems can be divided into two groups:

Well-defined Problems

For many abstract problems it is possible to find an algorithmic solution. We call all those problems well-defined that can be properly formalized, which comes along with the following properties:

• The problem has a clearly defined given state. This might be the line-up of a chess game, a given formula you have to solve, or the set-up of the towers of Hanoi game (which we will discuss later ).
• There is a finite set of operators, that is, of rules you may apply to the given state. For the chess game, e.g., these would be the rules that tell you which piece you may move to which position.
• Finally, the problem has a clear goal state: The equations is resolved to x, all discs are moved to the right stack, or the other player is in checkmate.

Not surprisingly, a problem that fulfills these requirements can be implemented algorithmically (also see convergent thinking ). Therefore many well-defined problems can be very effectively solved by computers, like playing chess.

Ill-defined Problems

Though many problems can be properly formalized (sometimes only if we accept an enormous complexity) there are still others where this is not the case. Good examples for this are all kinds of tasks that involve creativity , and, generally speaking, all problems for which it is not possible to clearly define a given state and a goal state: Formalizing a problem of the kind “Please paint a beautiful picture” may be impossible. Still this is a problem most people would be able to access in one way or the other, even if the result may be totally different from person to person. And while Knut might judge that picture X is gorgeous, you might completely disagree.

Nevertheless ill-defined problems often involve sub-problems that can be totally well-defined. On the other hand, many every-day problems that seem to be completely well-defined involve a great deal of creativity and many ambiguities. For example, suppose Knut has to read some technical material and then write an essay about it.

If we think of Knut's fairly ill-defined task of writing an essay, he will not be able to complete this task without first understanding the text he has to write about. This step is the first sub-goal Knut has to solve. Interestingly, ill-defined problems often involve subproblems that are well-defined.

Knut’s situation could be explained as a classical example of problem solving: He needs to get from his present state – an unfinished assignment – to a goal state - a completed assignment - and has certain operators to achieve that goal. Both Knut’s short and long term memory are active. He needs his short term memory to integrate what he is reading with the information from earlier passages of the paper. His long term memory helps him remember what he learned in the lectures he took and what he read in other books. And of course Knut’s ability to comprehend language enables him to make sense of the letters printed on the paper and to relate the sentences in a proper way.

Same place, different day. Knut is sitting at his desk again, staring at a blank paper in front of him, while nervously playing with a pen in his right hand. Just a few hours left to hand in his essay and he has not written a word. All of a sudden he smashes his fist on the table and cries out: "I need a plan!

How is a problem represented in the mind?

Generally speaking, problem representations are models of the situation as experienced by the agent. Representing a problem means to analyze it and split it into separate components:

• objects, predicates
• state space
• selection criteria

Therefore the efficiency of Problem Solving depends on the underlying representations in a person’s mind. Analyzing the problem domain according to different dimensions, i.e., changing from one representation to another, results in arriving at a new understanding of a problem. This is basically what is described as restructuring.

There are two very different ways of approaching a goal-oriented situation . In one case an organism readily reproduces the response to the given problem from past experience. This is called reproductive thinking .

The second way requires something new and different to achieve the goal, prior learning is of little help here. Such productive thinking is (sometimes) argued to involve insight . Gestalt psychologists even state that insight problems are a separate category of problems in their own right.

Tasks that might involve insight usually have certain features – they require something new and non-obvious to be done and in most cases they are difficult enough to predict that the initial solution attempt will be unsuccessful. When you solve a problem of this kind you often have a so called "AHA-experience" – the solution pops up all of a sudden. At one time you do not have any ideas of the answer to the problem, you do not even feel to make any progress trying out different ideas, but in the next second the problem is solved.

Sometimes, previous experience or familiarity can even make problem solving more difficult. This is the case whenever habitual directions get in the way of finding new directions – an effect called fixation .

Functional fixedness

Functional fixedness concerns the solution of object-use problems . The basic idea is that when the usual way of using an object is emphasised, it will be far more difficult for a person to use that object in a novel manner.

An example is the two-string problem : Knut is left in a room with a chair and a pair of pliers given the task to bind two strings together that are hanging from the ceiling. The problem he faces is that he can never reach both strings at a time because they are just too far away from each other. What can Knut do?

Figure \(\PageIndex{1}\): Put the two strings together by tying the pliers to one of the strings and then swing it toward the other one.

Mental fixedness

Functional fixedness as involved in the examples above illustrates a mental set – a person’s tendency to respond to a given task in a manner based on past experience. Because Knut maps an object to a particular function he has difficulties to vary the way of use (pliers as pendulum's weight).

Problem-Solving Strategies

When you are presented with a problem—whether it is a complex mathematical problem or a broken printer, how do you solve it? Before finding a solution to the problem, the problem must first be clearly identified. After that, one of many problem solving strategies can be applied, hopefully resulting in a solution. Regardless of strategy, you will likely be guided, consciously or unconsciously, by your knowledge of cause-effect relations among the elements of the problem and the similarity of the problem to previous problems you have solved before. As discussed in earlier sections of this chapter, innate dispositions of the brain to look for and represent causal and similarity relations are key components of general intelligence (Koenigshofer, 2017).

A problem-solving strategy is a plan of action used to find a solution. Different strategies have different action plans associated with them. For example, a well-known strategy is trial and error. The old adage, “If at first you don’t succeed, try, try again” describes trial and error. In terms of your broken printer, you could try checking the ink levels, and if that doesn’t work, you could check to make sure the paper tray isn’t jammed. Or maybe the printer isn’t actually connected to your laptop. When using trial and error, you would continue to try different solutions until you solved your problem. Although trial and error is not typically one of the most time-efficient strategies, it is a commonly used one.

Another type of strategy is an algorithm. An algorithm is a problem-solving formula that provides you with step-by-step instructions used to achieve a desired outcome (Kahneman, 2011). You can think of an algorithm as a recipe with highly detailed instructions that produce the same result every time they are performed. Algorithms are used frequently in our everyday lives, especially in computer science. When you run a search on the Internet, search engines like Google use algorithms to decide which entries will appear first in your list of results. Facebook also uses algorithms to decide which posts to display on your newsfeed. Can you identify other situations in which algorithms are used?

A heuristic is another type of problem solving strategy. While an algorithm must be followed exactly to produce a correct result, a heuristic is a general problem-solving framework (Tversky & Kahneman, 1974). You can think of these as mental shortcuts that are used to solve problems. A “rule of thumb” is an example of a heuristic. Such a rule saves the person time and energy when making a decision, but despite its time-saving characteristics, it is not always the best method for making a rational decision. Different types of heuristics are used in different types of situations, but the impulse to use a heuristic occurs when one of five conditions is met (Pratkanis, 1989):

• When one is faced with too much information
• When the time to make a decision is limited
• When the decision to be made is unimportant
• When there is access to very little information to use in making the decision
• When an appropriate heuristic happens to come to mind in the same moment

Working backwards is a useful heuristic in which you begin solving the problem by focusing on the end result. Consider this example: You live in Washington, D.C. and have been invited to a wedding at 4 PM on Saturday in Philadelphia. Knowing that Interstate 95 tends to back up any day of the week, you need to plan your route and time your departure accordingly. If you want to be at the wedding service by 3:30 PM, and it takes 2.5 hours to get to Philadelphia without traffic, what time should you leave your house? You use the working backwards heuristic to plan the events of your day on a regular basis, probably without even thinking about it.

Another useful heuristic is the practice of accomplishing a large goal or task by breaking it into a series of smaller steps. Students often use this common method to complete a large research project or long essay for school. For example, students typically brainstorm, develop a thesis or main topic, research the chosen topic, organize their information into an outline, write a rough draft, revise and edit the rough draft, develop a final draft, organize the references list, and proofread their work before turning in the project. The large task becomes less overwhelming when it is broken down into a series of small steps.

Problem Solving as a Search Problem

The idea of regarding problem solving as a search problem originated from Alan Newell and Herbert Simon while trying to design computer programs which could solve certain problems. This led them to develop a program called General Problem Solver which was able to solve any well-defined problem by creating heuristics on the basis of the user's input. This input consisted of objects and operations that could be done on them.

As we already know, every problem is composed of an initial state, intermediate states and a goal state (also: desired or final state), while the initial and goal states characterise the situations before and after solving the problem. The intermediate states describe any possible situation between initial and goal state. The set of operators builds up the transitions between the states. A solution is defined as the sequence of operators which leads from the initial state across intermediate states to the goal state.

The simplest method to solve a problem, defined in these terms, is to search for a solution by just trying one possibility after another (also called trial and error ).

As already mentioned above, an organised search, following a specific strategy, might not be helpful for finding a solution to some ill-defined problem, since it is impossible to formalise such problems in a way that a search algorithm can find a solution.

As an example we could just take Knut and his essay: he has to find out about his own opinion and formulate it and he has to make sure he understands the sources texts. But there are no predefined operators he can use, there is no panacea how to get to an opinion and even not how to write it down.

Means-End Analysis

In Means-End Analysis you try to reduce the difference between initial state and goal state by creating sub-goals until a sub-goal can be reached directly (in computer science, what is called recursion works on this basis).

An example of a problem that can be solved by Means-End Analysis is the " Towers of Hanoi "

Figure \(\PageIndex{2}\): Towers of Hanoi with 8 discs – A well defined problem (image from Wikimedia Commons; https://commons.wikimedia.org/wiki/F..._of_Hanoi.jpeg , by User:Evanherk .licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license).

The initial state of this problem is described by the different sized discs being stacked in order of size on the first of three pegs (the “start-peg“). The goal state is described by these discs being stacked on the third pegs (the “end-peg“) in exactly the same order.

Figure \(\PageIndex{3}\): This animation shows the solution of the game "Tower of Hanoi" with four discs. (image from Wikimedia Commons; https://commons.wikimedia.org/wiki/F...of_Hanoi_4.gif ; by André Karwath aka Aka ; licensed under the Creative Commons Attribution-Share Alike 2.5 Generic license).

There are three operators:

• You are allowed to move one single disc from one peg to another one
• You are only able to move a disc if it is on top of one stack
• A disc cannot be put onto a smaller one.

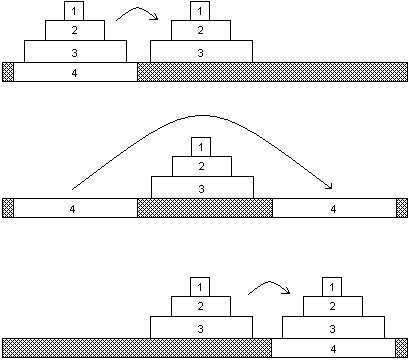
In order to use Means-End Analysis we have to create sub-goals. One possible way of doing this is described in the picture:

1. Moving the discs lying on the biggest one onto the second peg.

2. Shifting the biggest disc to the third peg.

3. Moving the other ones onto the third peg, too

You can apply this strategy again and again in order to reduce the problem to the case where you only have to move a single disc – which is then something you are allowed to do.

Strategies of this kind can easily be formulated for a computer; the respective algorithm for the Towers of Hanoi would look like this:

1. move n-1 discs from A to B

2. move disc #n from A to C

3. move n-1 discs from B to C

where n is the total number of discs, A is the first peg, B the second, C the third one. Now the problem is reduced by one with each recursive loop.

Means-end analysis is important to solve everyday-problems – like getting the right train connection: You have to figure out where you catch the first train and where you want to arrive, first of all. Then you have to look for possible changes just in case you do not get a direct connection. Third, you have to figure out what are the best times of departure and arrival, on which platforms you leave and arrive and make it all fit together.

Analogies describe similar structures and interconnect them to clarify and explain certain relations. In a recent study, for example, a song that got stuck in your head is compared to an itching of the brain that can only be scratched by repeating the song over and over again. Useful analogies appears to be based on a psychological mapping of relations between two very disparate types of problems that have abstract relations in common. Applied to STEM problems, Gray and Holyoak (2021) state: "Analogy is a powerful tool for fostering conceptual understanding and transfer in STEM and other fields. Well-constructed analogical comparisons focus attention on the causal-relational structure of STEM concepts, and provide a powerful capability to draw inferences based on a well-understood source domain that can be applied to a novel target domain." Note that similarity between problems of different types in their abstract relations, such as causation, is a key feature of reasoning, problem-solving and inference when forming and using analogies. Recall the discussion of general intelligence in module 14.2. There, similarity relations, causal relations, and predictive relations between events were identified as key components of general intelligence, along with ability to visualize in imagination possible future actions and their probable outcomes prior to commiting to actual behavior in the physical world (Koenigshofer, 2017).

Restructuring by Using Analogies

One special kind of restructuring, the way already mentioned during the discussion of the Gestalt approach, is analogical problem solving. Here, to find a solution to one problem – the so called target problem, an analogous solution to another problem – the source problem, is presented.

An example for this kind of strategy is the radiation problem posed by K. Duncker in 1945:

As a doctor you have to treat a patient with a malignant, inoperable tumour, buried deep inside the body. There exists a special kind of ray, which is perfectly harmless at a low intensity, but at the sufficient high intensity is able to destroy the tumour – as well as the healthy tissue on his way to it. What can be done to avoid the latter?

When this question was asked to participants in an experiment, most of them couldn't come up with the appropriate answer to the problem. Then they were told a story that went something like this:

A General wanted to capture his enemy's fortress. He gathered a large army to launch a full-scale direct attack, but then learned, that all the roads leading directly towards the fortress were blocked by mines. These roadblocks were designed in such a way, that it was possible for small groups of the fortress-owner's men to pass them safely, but every large group of men would initially set them off. Now the General figured out the following plan: He divided his troops into several smaller groups and made each of them march down a different road, timed in such a way, that the entire army would reunite exactly when reaching the fortress and could hit with full strength.

Here, the story about the General is the source problem, and the radiation problem is the target problem. The fortress is analogous to the tumour and the big army corresponds to the highly intensive ray. Consequently a small group of soldiers represents a ray at low intensity. The solution to the problem is to split the ray up, as the general did with his army, and send the now harmless rays towards the tumour from different angles in such a way that they all meet when reaching it. No healthy tissue is damaged but the tumour itself gets destroyed by the ray at its full intensity.

M. Gick and K. Holyoak presented Duncker's radiation problem to a group of participants in 1980 and 1983. Only 10 percent of them were able to solve the problem right away, 30 percent could solve it when they read the story of the general before. After given an additional hint – to use the story as help – 75 percent of them solved the problem.

With this results, Gick and Holyoak concluded, that analogical problem solving depends on three steps:

1. Noticing that an analogical connection exists between the source and the target problem. 2. Mapping corresponding parts of the two problems onto each other (fortress → tumour, army → ray, etc.) 3. Applying the mapping to generate a parallel solution to the target problem (using little groups of soldiers approaching from different directions → sending several weaker rays from different directions)

The concept that links the target problem with the analogy (the “source problem“) is called problem schema. Gick and Holyoak obtained the activation of a schema on their participants by giving them two stories and asking them to compare and summarize them. This activation of problem schemata is called “schema induction“.

The two presented texts were picked out of six stories which describe analogical problems and their solution. One of these stories was "The General."

After solving the task the participants were asked to solve the radiation problem. The experiment showed that in order to solve the target problem reading of two stories with analogical problems is more helpful than reading only one story: After reading two stories 52% of the participants were able to solve the radiation problem (only 30% were able to solve it after reading only one story, namely: “The General“).

The process of using a schema or analogy, i.e. applying it to a novel situation, is called transduction . One can use a common strategy to solve problems of a new kind.

To create a good schema and finally get to a solution using the schema is a problem-solving skill that requires practice and some background knowledge.

How Do Experts Solve Problems?

With the term expert we describe someone who devotes large amounts of his or her time and energy to one specific field of interest in which he, subsequently, reaches a certain level of mastery. It should not be of surprise that experts tend to be better in solving problems in their field than novices (people who are beginners or not as well trained in a field as experts) are. They are faster in coming up with solutions and have a higher success rate of right solutions. But what is the difference between the way experts and non-experts solve problems? Research on the nature of expertise has come up with the following conclusions:

When it comes to problems that are situated outside the experts' field, their performance often does not differ from that of novices.

Knowledge: An experiment by Chase and Simon (1973a, b) dealt with the question how well experts and novices are able to reproduce positions of chess pieces on chessboards when these are presented to them only briefly. The results showed that experts were far better in reproducing actual game positions, but that their performance was comparable with that of novices when the chess pieces were arranged randomly on the board. Chase and Simon concluded that the superior performance on actual game positions was due to the ability to recognize familiar patterns: A chess expert has up to 50,000 patterns stored in his memory. In comparison, a good player might know about 1,000 patterns by heart and a novice only few to none at all. This very detailed knowledge is of crucial help when an expert is confronted with a new problem in his field. Still, it is not pure size of knowledge that makes an expert more successful. Experts also organise their knowledge quite differently from novices.

Organization: In 1982 M. Chi and her co-workers took a set of 24 physics problems and presented them to a group of physics professors as well as to a group of students with only one semester of physics. The task was to group the problems based on their similarities. As it turned out the students tended to group the problems based on their surface structure (similarities of objects used in the problem, e.g. on sketches illustrating the problem), whereas the professors used their deep structure (the general physical principles that underlay the problems) as criteria. By recognizing the actual structure of a problem experts are able to connect the given task to the relevant knowledge they already have (e.g. another problem they solved earlier which required the same strategy).

Analysis: Experts often spend more time analyzing a problem before actually trying to solve it. This way of approaching a problem may often result in what appears to be a slow start, but in the long run this strategy is much more effective. A novice, on the other hand, might start working on the problem right away, but often has to realise that he reaches dead ends as he chose a wrong path in the very beginning.

Creative Cognition

Divergent thinking.

The term divergent thinking describes a way of thinking that does not lead to one goal, but is open-ended. Problems that are solved this way can have a large number of potential 'solutions' of which none is exactly 'right' or 'wrong', though some might be more suitable than others.

Solving a problem like this involves indirect and productive thinking and is mostly very helpful when somebody faces an ill-defined problem , i.e. when either initial state or goal state cannot be stated clearly and operators are either insufficient or not given at all.

The process of divergent thinking is often associated with creativity, and it undoubtedly leads to many creative ideas. Nevertheless, researches have shown that there is only modest correlation between performance on divergent thinking tasks and other measures of creativity. Additionally it was found that in processes resulting in original and practical inventions things like searching for solutions, being aware of structures and looking for analogies are heavily involved, too.

Figure \(\PageIndex{4}\): functional MRI images of the brains of musicians playing improvised jazz revealed that a large brain region involved in monitoring one's performance shuts down during creative improvisation, while a small region involved in organizing self-initiated thoughts and behaviors is highly activated (Image and modified caption from Wikimedia Commons. File:Creative Improvisation (24130148711).jpg; https://commons.wikimedia.org/wiki/F...130148711).jpg ; by NIH Image Gallery ; As a work of the U.S. federal government , the image is in the public domain .

Convergent Thinking

Convergent thinking patterns are problem solving techniques that unite different ideas or fields to find a solution. The focus of this mindset is speed, logic and accuracy, also identification of facts, reapplying existing techniques, gathering information. The most important factor of this mindset is: there is only one correct answer. You only think of two answers, namely right or wrong. This type of thinking is associated with certain science or standard procedures. People with this type of thinking have logical thinking, are able to memorize patterns, solve problems and work on scientific tests. Most school subjects sharpen this type of thinking ability.

Research shows that the creative process involves both types of thought processes.

Brain Mechanisms in Problem Solving

Presenting Neurophysiology in its entirety would be enough to fill several books. Instead, let's focus only on the aspects that are especially relevant to problem solving. Still, this topic is quite complex and problem solving cannot be attributed to one single brain area. Rather there are systems or networks of several brain areas working together to perform a specific problem solving task. This is best shown by an example, playing chess:

Table 2: Brain areas involved in a complex cognitive task.

One of the key tasks, namely planning and executing strategies , is performed by the prefrontal cortex (PFC) , which also plays an important role for several other tasks correlated with problem solving. This can be made clear from the effects of damage to the PFC on ability to solve problems.

Patients with a lesion in this brain area have difficulty switching from one behavioral pattern to another. A well known example is the wisconsin card-sorting task . A patient with a PFC lesion who is told to separate all blue cards from a deck, would continue sorting out the blue ones, even if the experimenter next told him to sort out all brown cards. Transferred to a more complex problem, this person would most likely fail, because he is not flexible enough to change his strategy after running into a dead end or when the problem changes.

Another example comes from a young homemaker, who had a tumour in the frontal lobe. Even though she was able to cook individual dishes, preparing a whole family meal was an impossible task for her.

Mushiake et al. (2009) note that to achieve a goal in a complex environment, such as problem‐solving situations like those above, we must plan multiple steps of action. When planning a series of actions, we have to anticipate future outcomes that will occur as a result of each action, and, in addition, we must mentally organize the temporal sequence of events in order to achieve the goal. These researchers investigated the role of lateral prefrontal cortex (PFC) in problem solving in monkeys. They found that "PFC neurons reflected final goals and immediate goals during the preparatory period. [They] also found some PFC neurons reflected each of all the forthcoming steps of actions during the preparatory period and they increased their [neural] activity step by step during the execution period. [Furthermore, they] found that the transient increase in synchronous activity of PFC neurons was involved in goal subgoal transformations. [They concluded] that the PFC is involved primarily in the dynamic representation of multiple future events that occur as a consequence of behavioral actions in problem‐solving situations" (Mushiake et al., 2009, p. 1). In other words, the prefrontal cortex represents in our imagination the sequence of events following each step that we take in solving a particular problem, guiding us step by step to the solution.

As the examples above illustrate, the structure of our brain is of great importance regarding problem solving, i.e. cognitive life. But how was our cognitive apparatus designed? How did perception-action integration as a central species-specific property of humans come about? The answer, as argued extensively in earlier sections of this book, is, of course, natural selection and other forces of genetic evolution. Clearly, animals and humans with genes facilitating brain organization that led to good problem solving skills would be favored by natural selection over genes responsible for brain organization less adept at solving problems. We became equipped with brains organized for effective problem solving because flexible abilities to solve a wide range of problems presented by the environment enhanced ability to survive, to compete for resources, to escape predators, and to reproduce (see chapter on Evolution and Genetics in this text).

In short, good problem solving mechanisms in brains designed for the real world gave a competitive advantage and increased biological fitness. Consequently, humans (and many other animals to a lesser degree) have "innate ability to problem-solve in the real world. Solving real world problems in real time given constraints posed by one's environment is crucial for survival . . . Real world problem solving (RWPS) is different from those that occur in a classroom or in a laboratory during an experiment. They are often dynamic and discontinuous, accompanied by many starts and stops . . . Real world problems are typically ill-defined, and even when they are well-defined, often have open-ended solutions . . . RWPS is quite messy and involves a tight interplay between problem solving, creativity, and insight . . . In psychology and neuroscience, problem-solving broadly refers to the inferential steps taken by an agent [human, animal, or computer] that leads from a given state of affairs to a desired goal state" (Sarathy, 2018, p. 261-2). According to Sarathy (2018), the initial stage of RWPS requires defining the problem and generating a representation of it in working memory. This stage involves activation of parts of the " prefrontal cortex (PFC) , default mode network (DMN) , and the dorsal anterior cingulate cortex (dACC) ." The DMN includes the medial prefrontal cortex , posterior cingulate cortex , and the inferior parietal lobule . Other structures sometimes considered part of the network are the lateral temporal cortex , hippocampal formation , and the precuneus . This network of structures is called "default mode" because these structures show increased activity when one is not engaged in focused, attentive, goal-directed actions, but rather a "resting state" (a baseline default state) and show decreased neural activity when one is focused and attentive to a particular goal-directed behavior (Raichle, et al., 2001).

Moral Reasoning

Jeurissen, et al., (2014) examined a special type of reasoning, moral reasoning, using TMS (Transcranial Magnetic Stimulation). The dorsolateral prefrontal cortex (DLPFC) and temporal-parietal junction (TPJ) have both been shown to be involved in moral judgments, but this study by Jeurissen, et al., (2014) uses TMS to tease out the different roles these brain areas play in different scenarios involving moral dilemmas.

Moral dilemmas have been categorized by researchers as moral-impersonal (e.g., trolley or switch dilemma-- save the lives of five workmen at the expense of the life of one by switching train to another track) and moral-personal dilemmas (e.g., footbridge dilemma-- push a strange r in front of a train to save the lives of five others). In the first scenario, the person just pulls a switch resulting in death of one person to save five, but in the second, the person pushes the victim to their death to save five others.

Dual-process theory proposes that moral decision-making involves two components: an automatic emotional response and a voluntary application of a utilitarian decision-rule (in this case, one death to save five people is worth it). The thought of being responsible for the death of another person elicits an aversive emotional response, but at the same time, cognitive reasoning favors the utilitarian option. Decision making and social cognition are often associated with the DLPFC. Neurons in the prefrontal cortex have been found to be involved in cost-benefit analysis and categorize stimuli based on the predicted consequences.

Theory-of-mind (TOM) is a cognitive mechanism which is used when one tries to understand and explain the knowledge, beliefs, and intention of others. TOM and empathy are often associated with TPJ functioning .

In the article by Jeurissen, et al., (2014), brain activity is measured by BOLD. BOLD refers to Blood-oxygen-level-dependent imaging , or BOLD-contrast imaging, which is a way to measure neural activity in different brain areas in MRI images .

Greene et al., 2001 (Links to an external site.) , 2004 (Links to an external site.) reported that activity in the prefrontal cortex is thought to be important for the cognitive reasoning process , which can counteract the automatic emotional response that occurs in moral dilemmas like the one in Jeurissen, et al., (2014). Greene et al. (2001) (Links to an external site.) found that the medial portions of the medial frontal gyrus, the posterior cingulate gyrus, and the bilateral angular gyrus showed a higher BOLD response in the moral-personal condition than the moral-impersonal condition. The right middle frontal gyrus and the bilateral parietal lobes showed a lower BOLD response in the moral-personal condition than in the moral impersonal. Furthermore, Greene et al. (2004) (Links to an external site.) showed an increased BOLD response for the bilateral amygdale in personal compared to the impersonal dilemmas.

Given the role of the prefrontal cortex in moral decision-making, Jeurissen, et al., (2014) hypothesized that when magnetically stimulating prefrontal cortex , they will selectively influence the decision process of the moral personal dilemmas because the cognitive reasoning for which the DLPFC is important is disrupted , thereby releasing the emotional component making it more influential in the resolution of the dilemma. Because the activity in the TPJ is related to emotional processing and theory of mind ( Saxe and Kanwisher, 2003 (Links to an external site.) ; Young et al., 2010 (Links to an external site.) ), Jeurissen, et al., (2014) hypothesized that when magnetically stimulating this area, the TPJ, during a moral decision, this will selectively influence the decision process of moral-impersonal dilemmas.

Results of this study by Jeurissen, et al., (2014) showed an important role of the TPJ in moral judgment . Experiments using fMRI ( Greene et al., 2004 (Links to an external site.) ), have found the cingulate cortex to be involved in moral judgment . In earlier studies, the cingulate cortex was found to be involved in the emotional response. Since the moral-personal dilemmas are more emotional ly salient, the higher activity observed for TPJ in the moral-personal condition (more emotional) is consistent with this view. Another area that is hypothesized to be associated with the emotional response is the temporal cortex . In this study by Jeurissen, et al., (2014) , magnetic stimulation of the right DLPFC and right TPJ shows roles for right DLPFC (reasoning and utilitarian) and right TPJ (emotion) in moral impersonal and moral personal dilemmas respectively. TMS over the right DLPFC (disrupting neural activity here) leads to behavior changes consistent with less cognitive control over emotion . After right DLPFC stimulation, participants show less feelings of regret than after magnetic stimulation of the right TPJ. This last finding indicates that the right DLPFC is involved in evaluating the outcome of the decision process. In summary, this experiment by Jeurissen, et al., (2014) adds to evidence of a critical role of right DLPFC and right TPJ in moral decision-making and supports that hypothesis that the former is involved in judgments based on cognitive reasoning and anticipation of outcomes, whereas the latter is involved in emotional processing related to moral dilemmas.

Many different strategies exist for solving problems. Typical strategies include trial and error, applying algorithms, and using heuristics. To solve a large, complicated problem, it often helps to break the problem into smaller steps that can be accomplished individually, leading to an overall solution. The brain mechanisms involved in problem solving vary to some degree depending upon the sensory modalities involved in the problem and its solution, however, the prefrontal cortex is one brain region that appears to be centrally involved in all problem-solving. The prefrontal cortex is required for flexible shifts in attention, for representing the problem in working memory, and for holding steps in problem solving in working memory along with representations of future consequences of those actions permitting planning and execution of plans. Also implicated is the Default Mode Network (DMN) including medial prefrontal cortex, posterior cingulate cortex, and the inferior parietal module, and sometimes the lateral temporal cortex, hippocampus, and the precuneus. Moral reasoning involves a different set of brain areas, primarily the dorsolateral prefrontal cortex (DLPFC) and temporal-parietal junction (TPJ).

Review Questions

• an algorithm
• a heuristic
• a mental set
• trial and error

Gray, M. E., & Holyoak, K. J. (2021). Teaching by analogy: From theory to practice. Mind, Brain, and Education , 15 (3), 250-263.

Hunt, L. T., Behrens, T. E., Hosokawa, T., Wallis, J. D., & Kennerley, S. W. (2015). Capturing the temporal evolution of choice across prefrontal cortex. Elife , 4 , e11945.

Mushiake, H., Sakamoto, K., Saito, N., Inui, T., Aihara, K., & Tanji, J. (2009). Involvement of the prefrontal cortex in problem solving. International review of neurobiology , 85 , 1-11.

Jeurissen, D., Sack, A. T., Roebroeck, A., Russ, B. E., & Pascual-Leone, A. (2014). TMS affects moral judgment, showing the role of DLPFC and TPJ in cognitive and emotional processing. Frontiers in neuroscience , 8 , 18.

Kahneman, D. (2011). Thinking, fast and slow. New York: Farrar, Straus, and Giroux.

Koenigshofer, K. A. (2017). General Intelligence: Adaptation to Evolutionarily Familiar Abstract Relational Invariants, Not to Environmental or Evolutionary Novelty. The Journal of Mind and Behavior , 119-153.

Pratkanis, A. (1989). The cognitive representation of attitudes. In A. R. Pratkanis, S. J. Breckler, & A. G. Greenwald (Eds.), Attitude structure and function (pp. 71–98). Hillsdale, NJ: Erlbaum.

Raichle, M. E., MacLeod, A. M., Snyder, A. Z., Powers, W. J., Gusnard, D. A., & Shulman, G. L. (2001). A default mode of brain function. Proceedings of the National Academy of Sciences , 98 (2), 676-682.

Sawyer, K. (2011). The cognitive neuroscience of creativity: a critical review. Creat. Res. J. 23, 137–154. doi: 10.1080/10400419.2011.571191

Tversky, A., & Kahneman, D. (1974). Judgment under uncertainty: Heuristics and biases. Science , 185 (4157), 1124–1131.

Mushiake, H., Sakamoto, K., Saito, N., Inui, T., Aihara, K., & Tanji, J. (2009). Involvement of the prefrontal cortex in problem solving. International review of neurobiology , 85 , 1-11. https://www.sciencedirect.com/scienc...74774209850010

Attributions

"Overview," "Problem Solving Strategies," adapted from Problem Solving by OpenStax Colleg licensed CC BY-NC 4.0 via OER Commons

"Defining Problems," "Problem Solving as a Search Problem," "Creative Cognition," "Brain Mechanisms in Problem-Solving" adapted by Kenneth A. Koenigshofer, Ph.D., from 2.1, 2.2, 2.3, 2.4, 2.5, 2.6 in Cognitive Psychology and Cognitive Neuroscience (Wikibooks) https://en.wikibooks.org/wiki/Cognit...e_Neuroscience ; unless otherwise noted, LibreTexts content is licensed by CC BY-NC-SA 3.0 . Legal ; the LibreTexts libraries are Powered by MindTouch

Moral Reasoning was written by Kenneth A. Koenigshofer, Ph.D, Chaffey College.

Categories and Concepts

People form mental concepts of categories of objects, which permit them to respond appropriately to new objects they encounter. Most concepts cannot be strictly defined but are organized around the “best” examples or prototypes, which have the properties most common in the category. Objects fall into many different categories, but there is usually a most salient one, called the basic-level category, which is at an intermediate level of specificity (e.g., chairs, rather than furniture or desk chairs). Concepts are closely related to our knowledge of the world, and people can more easily learn concepts that are consistent with their knowledge. Theories of concepts argue either that people learn a summary description of a whole category or else that they learn exemplars of the category. Recent research suggests that there are different ways to learn and represent concepts and that they are accomplished by different neural systems.

• Understand the problems with attempting to define categories.
• Understand typicality and fuzzy category boundaries.
• Learn about theories of the mental representation of concepts.
• Learn how knowledge may influence concept learning.

Introduction

Consider the following set of objects: some dust, papers, a computer monitor, two pens, a cup, and an orange. What do these things have in common? Only that they all happen to be on my desk as I write this. This set of things can be considered a category , a set of objects that can be treated as equivalent in some way. But, most of our categories seem much more informative—they share many properties. For example, consider the following categories: trucks, wireless devices, weddings, psychopaths, and trout. Although the objects in a given category are different from one another, they have many commonalities. When you know something is a truck, you know quite a bit about it. The psychology of categories concerns how people learn, remember, and use informative categories such as trucks or psychopaths.

The mental representations we form of categories are called concepts . There is a category of trucks in the actual physical world, and I also have a concept of trucks in my head. We assume that people’s concepts correspond more or less closely to the actual category, but it can be useful to distinguish the two, as when someone’s concept is not really correct.

Concepts are at the core of intelligent behavior . We expect people to be able to know what to do in new situations and when confronting new objects. If you go into a new classroom and see chairs, a blackboard, a projector, and a screen, you know what these things are and how they will be used. You’ll sit on one of the chairs and expect the instructor to write on the blackboard or project something onto the screen. You do this even if you have never seen any of these particular objects before , because you have concepts of classrooms, chairs, projectors, and so forth, that tell you what they are and what you’re supposed to do with them. Furthermore, if someone tells you a new fact about the projector—for example, that it has a halogen bulb—you are likely to extend this fact to other projectors you encounter. In short, concepts allow you to extend what you have learned about a limited number of objects to a potentially infinite set of entities (i.e. generalization ). Notice how categories and concepts arise from similarity, one of the abstract features of the world that has been genetically internalized into the brain during evolution , creating an innate disposition of brains to search for and to represent groupings of similar things, forming one component of general intelligence. One property of the human brain that distinguishes us from other animals is the high degrees of abstraction in similarity relations that the human brain is capable of encoding compared to the brains of non-human animals (Koenigshofer, 2017).

Simpler organisms, such as animals and human infants, also have concepts ( Mareschal, Quinn, & Lea, 2010 ). Squirrels may have a concept of predators, for example, that is specific to their own lives and experiences. However, animals likely have many fewer concepts and cannot understand complex concepts such as mortgages or musical instruments.

You know thousands of categories, most of which you have learned without careful study or instruction. Although this accomplishment may seem simple, we know that it isn’t, because it is difficult to program computers to solve such intellectual tasks. If you teach a learning program that a robin, a swallow, and a duck are all birds, it may not recognize a cardinal or peacock as a bird. However, this shortcoming in computers may be at least partially overcome when the type of processing used is parallel distributed processing as employed in artificial neural networks (Koenigshofer, 2017), discussed in this chapter. As we’ll shortly see, the problem for computers is that objects in categories are often surprisingly diverse.

Nature of Categories

Traditionally, it has been assumed that categories are well-defined . This means that you can give a definition that specifies what is in and out of the category. Such a definition has two parts. First, it provides the necessary features for category membership: What must objects have in order to be in it? Second, those features must be jointly sufficient for membership: If an object has those features, then it is in the category. For example, if I defined a dog as a four-legged animal that barks, this would mean that every dog is four-legged, an animal, and barks, and also that anything that has all those properties is a dog.

Unfortunately, it has not been possible to find definitions for many familiar categories. Definitions are neat and clear-cut; the world is messy and often unclear. For example, consider our definition of dogs. In reality, not all dogs have four legs; not all dogs bark. I knew a dog that lost her bark with age (this was an improvement); no one doubted that she was still a dog. It is often possible to find some necessary features (e.g., all dogs have blood and breathe), but these features are generally not sufficient to determine category membership (you also have blood and breathe but are not a dog).

Even in domains where one might expect to find clear-cut definitions, such as science and law, there are often problems. For example, many people were upset when Pluto was downgraded from its status as a planet to a dwarf planet in 2006. Upset turned to outrage when they discovered that there was no hard-and-fast definition of planethood: “Aren’t these astronomers scientists? Can’t they make a simple definition?” In fact, they couldn’t. After an astronomical organization tried to make a definition for planets, a number of astronomers complained that it might not include accepted planets such as Neptune and refused to use it. If everything looked like our Earth, our moon, and our sun, it would be easy to give definitions of planets, moons, and stars, but the universe has not conformed to this ideal.

Fuzzy Categories

Borderline items.

Experiments also showed that the psychological assumptions of well-defined categories were not correct. Hampton ( 1979 ) asked subjects to judge whether a number of items were in different categories. He did not find that items were either clear members or clear nonmembers. Instead, he found many items that were just barely considered category members and others that were just barely not members, with much disagreement among subjects. Sinks were barely considered as members of the kitchen utensil category, and sponges were barely excluded. People just included seaweed as a vegetable and just barely excluded tomatoes and gourds. Hampton found that members and nonmembers formed a continuum, with no obvious break in people’s membership judgments. If categories were well defined, such examples should be very rare. Many studies since then have found such borderline members that are not clearly in or clearly out of the category.

McCloskey and Glucksberg ( 1978 ) found further evidence for borderline membership by asking people to judge category membership twice, separated by two weeks. They found that when people made repeated category judgments such as “Is an olive a fruit?” or “Is a sponge a kitchen utensil?” they changed their minds about borderline items—up to 22 percent of the time. So, not only do people disagree with one another about borderline items, they disagree with themselves! As a result, researchers often say that categories are fuzzy , that is, they have unclear boundaries that can shift over time.

A related finding that turns out to be most important is that even among items that clearly are in a category, some seem to be “better” members than others ( Rosch, 1973 ). Among birds, for example, robins and sparrows are very typical . In contrast, ostriches and penguins are very atypical (meaning not typical). If someone says, “There’s a bird in my yard,” the image you have will be of a smallish passerine bird such as a robin, not an eagle or hummingbird or turkey.

You can find out which category members are typical merely by asking people. Table 1 shows a list of category members in order of their rated typicality. Typicality is perhaps the most important variable in predicting how people interact with categories. The following text box is a partial list of what typicality influences.

We can understand the two phenomena of borderline members and typicality as two sides of the same coin. Think of the most typical category member: This is often called the category prototype . Items that are less and less similar to the prototype become less and less typical. At some point, these less typical items become so atypical that you start to doubt whether they are in the category at all. Is a rug really an example of furniture? It’s in the home like chairs and tables, but it’s also different from most furniture in its structure and use. From day to day, you might change your mind as to whether this atypical example is in or out of the category. So, changes in typicality ultimately lead to borderline members.

Source of Typicality

Intuitively, it is not surprising that robins are better examples of birds than penguins are, or that a table is a more typical kind of furniture than is a rug. But given that robins and penguins are known to be birds, why should one be more typical than the other? One possible answer is the frequency with which we encounter the object: We see a lot more robins than penguins, so they must be more typical. Frequency does have some effect, but it is actually not the most important variable ( Rosch, Simpson, & Miller, 1976 ). For example, I see both rugs and tables every single day, but one of them is much more typical as furniture than the other.

The best account of what makes something typical comes from Rosch and Mervis’s ( 1975 ) family resemblance theory . They proposed that items are likely to be typical if they (a) have the features that are frequent in the category and (b) do not have features frequent in other categories. Let’s compare two extremes, robins and penguins. Robins are small flying birds that sing, live in nests in trees, migrate in winter, hop around on your lawn, and so on. Most of these properties are found in many other birds. In contrast, penguins do not fly, do not sing, do not live in nests or in trees, do not hop around on your lawn. Furthermore, they have properties that are common in other categories, such as swimming expertly and having wings that look and act like fins. These properties are more often found in fish than in birds.

According to Rosch and Mervis, then, it is not because a robin is a very common bird that makes it typical. Rather, it is because the robin has the shape, size, body parts, and behaviors that are very common (i.e. most similar) among birds—and not common among fish, mammals, bugs, and so forth.

In a classic experiment, Rosch and Mervis ( 1975 ) made up two new categories, with arbitrary features. Subjects viewed example after example and had to learn which example was in which category. Rosch and Mervis constructed some items that had features that were common in the category and other items that had features less common in the category. The subjects learned the first type of item before they learned the second type. Furthermore, they then rated the items with common features as more typical. In another experiment, Rosch and Mervis constructed items that differed in how many features were shared with a different category. The more features were shared, the longer it took subjects to learn which category the item was in. These experiments, and many later studies, support both parts of the family resemblance theory.

Category Hierarchies

Many important categories fall into hierarchies , in which more concrete categories are nested inside larger, abstract categories. For example, consider the categories: brown bear, bear, mammal, vertebrate, animal, entity. Clearly, all brown bears are bears; all bears are mammals; all mammals are vertebrates; and so on. Any given object typically does not fall into just one category—it could be in a dozen different categories, some of which are structured in this hierarchical manner. Examples of biological categories come to mind most easily, but within the realm of human artifacts, hierarchical structures can readily be found: desk chair, chair, furniture, artifact, object.

Brown ( 1958 ), a child language researcher, was perhaps the first to note that there seems to be a preference for which category we use to label things. If your office desk chair is in the way, you’ll probably say, “Move that chair,” rather than “Move that desk chair” or “piece of furniture.” Brown thought that the use of a single, consistent name probably helped children to learn the name for things. And, indeed, children’s first labels for categories tend to be exactly those names that adults prefer to use ( Anglin, 1977 ).

This preference is referred to as a preference for the basic level of categorization , and it was first studied in detail by Eleanor Rosch and her students ( Rosch, Mervis, Gray, Johnson, & Boyes-Braem, 1976 ). The basic level represents a kind of Goldilocks effect, in which the category used for something is not too small (northern brown bear) and not too big (animal), but is just right (bear). The simplest way to identify an object’s basic-level category is to discover how it would be labeled in a neutral situation. Rosch et al. ( 1976 ) showed subjects pictures and asked them to provide the first name that came to mind. They found that 1,595 names were at the basic level, with 14 more specific names ( subordinates ) used. Only once did anyone use a more general name ( superordinate ). Furthermore, in printed text, basic-level labels are much more frequent than most subordinate or superordinate labels (e.g., Wisniewski & Murphy, 1989 ).

The preference for the basic level is not merely a matter of labeling. Basic-level categories are usually easier to learn. As Brown noted, children use these categories first in language learning, and superordinates are especially difficult for children to fully acquire. [1] People are faster at identifying objects as members of basic-level categories ( Rosch et al., 1976 ).

Rosch et al. ( 1976 ) initially proposed that basic-level categories cut the world at its joints, that is, merely reflect the big differences between categories like chairs and tables or between cats and mice that exist in the world. However, it turns out that which level is basic is not universal. North Americans are likely to use names like tree, fish , and bird to label natural objects. But people in less industrialized societies seldom use these labels and instead use more specific words, equivalent to elm, trout, and finch ( Berlin, 1992 ). Because Americans and many other people living in industrialized societies know so much less than our ancestors did about the natural world, our basic level has “moved up” to what would have been the superordinate level a century ago. Furthermore, experts in a domain often have a preferred level that is more specific than that of non-experts. Birdwatchers see sparrows rather than just birds, and carpenters see roofing hammers rather than just hammers ( Tanaka & Taylor, 1991 ). This all suggests that the preferred level is not (only) based on how different categories are in the world, but that people’s knowledge and interest in the categories has an important effect.

One explanation of the basic-level preference is that basic-level categories are more differentiated: The category members are similar to one another, but they are different from members of other categories ( Murphy & Brownell, 1985 ; Rosch et al., 1976 ). (The alert reader will note a similarity to the explanation of typicality I gave above. However, here we’re talking about the entire category and not individual members.) Chairs are pretty similar to one another, sharing a lot of features (legs, a seat, a back, similar size and shape); they also don’t share that many features with other furniture. Superordinate categories are not as useful because their members are not very similar to one another. What features are common to most furniture? There are very few. Subordinate categories are not as useful, because they’re very similar to other categories: Desk chairs are quite similar to dining room chairs and easy chairs. As a result, it can be difficult to decide which subordinate category an object is in ( Murphy & Brownell, 1985 ). Experts can differ from novices in which categories are the most differentiated, because they know different things about the categories, therefore changing how similar the categories are.

[1] This is a controversial claim, as some say that infants learn superordinates before anything else (Mandler, 2004). However, if true, then it is very puzzling that older children have great difficulty learning the correct meaning of words for superordinates, as well as in learning artificial superordinate categories (Horton & Markman, 1980; Mervis, 1987). However, it seems fair to say that the answer to this question is not yet fully known.

Theories of Concept Representation

Now that we know these facts about the psychology of concepts, the question arises of how concepts are mentally represented. There have been two main answers. The first, somewhat confusingly called the prototype theory suggests that people have a summary representation of the category, a mental description that is meant to apply to the category as a whole. (The significance of summary will become apparent when the next theory is described.) This description can be represented as a set of weighted features ( Smith & Medin, 1981 ). The features are weighted by their frequency in the category. For the category of birds, having wings and feathers would have a very high weight; eating worms would have a lower weight; living in Antarctica would have a lower weight still, but not zero, as some birds do live there.

The idea behind prototype theory is that when you learn a category, you learn a general description that applies to the category as a whole: Birds have wings and usually fly; some eat worms; some swim underwater to catch fish. People can state these generalizations, and sometimes we learn about categories by reading or hearing such statements (“The kimodo dragon can grow to be 10 feet long”).

When you try to classify an item, you see how well it matches that weighted list of features. For example, if you saw something with wings and feathers fly onto your front lawn and eat a worm, you could (unconsciously) consult your concepts and see which ones contained the features you observed. This example possesses many of the highly weighted bird features, and so it should be easy to identify as a bird.

This theory readily explains the phenomena we discussed earlier. Typical category members have more, higher-weighted features. Therefore, it is easier to match them to your conceptual representation. Less typical items have fewer or lower-weighted features (and they may have features of other concepts). Therefore, they don’t match your representation as well (less similarity). This makes people less certain in classifying such items. Borderline items may have features in common with multiple categories or not be very close to any of them. For example, edible seaweed does not have many of the common features of vegetables but also is not close to any other food concept (meat, fish, fruit, etc.), making it hard to know what kind of food it is.

A very different account of concept representation is the exemplar theory ( exemplar being a fancy name for an example; Medin & Schaffer, 1978 ). This theory denies that there is a summary representation. Instead, the theory claims that your concept of vegetables is remembered examples of vegetables you have seen. This could of course be hundreds or thousands of exemplars over the course of your life, though we don’t know for sure how many exemplars you actually remember.

How does this theory explain classification? When you see an object, you (unconsciously) compare it to the exemplars in your memory, and you judge how similar it is to exemplars in different categories. For example, if you see some object on your plate and want to identify it, it will probably activate memories of vegetables, meats, fruit, and so on. In order to categorize this object, you calculate how similar it is to each exemplar in your memory. These similarity scores are added up for each category. Perhaps the object is very similar to a large number of vegetable exemplars, moderately similar to a few fruit, and only minimally similar to some exemplars of meat you remember. These similarity scores are compared, and the category with the highest score is chosen . [2]

Why would someone propose such a theory of concepts? One answer is that in many experiments studying concepts, people learn concepts by seeing exemplars over and over again until they learn to classify them correctly. Under such conditions, it seems likely that people eventually memorize the exemplars ( Smith & Minda, 1998 ). There is also evidence that close similarity to well-remembered objects has a large effect on classification . Allen and Brooks ( 1991 ) taught people to classify items by following a rule. However, they also had their subjects study the items, which were richly detailed. In a later test, the experimenters gave people new items that were very similar to one of the old items but were in a different category. That is, they changed one property so that the item no longer followed the rule. They discovered that people were often fooled by such items. Rather than following the category rule they had been taught, they seemed to recognize the new item as being very similar to an old one and so put it, incorrectly, into the same category.

Many experiments have been done to compare the prototype and exemplar theories. Overall, the exemplar theory seems to have won most of these comparisons . However, the experiments are somewhat limited in that they usually involve a small number of exemplars that people view over and over again. It is not so clear that exemplar theory can explain real-world classification in which people do not spend much time learning individual items (how much time do you spend studying squirrels? or chairs?). Also, given that some part of our knowledge of categories is learned through general statements we read or hear, it seems that there must be room for a summary description separate from exemplar memory.

Many researchers would now acknowledge that concepts are represented through multiple cognitive systems. For example, your knowledge of dogs may be in part through general descriptions such as “dogs have four legs.” But you probably also have strong memories of some exemplars (your family dog, Lassie) that influence your categorization. Furthermore, some categories also involve rules (e.g., a strike in baseball). How these systems work together is the subject of current study.

[2] Actually, the decision of which category is chosen is more complex than this, but the details are beyond this discussion.

The final topic has to do with how concepts fit with our broader knowledge of the world. We have been talking very generally about people learning the features of concepts. For example, they see a number of birds and then learn that birds generally have wings, or perhaps they remember bird exemplars. From this perspective, it makes no difference what those exemplars or features are—people just learn them. But consider two possible concepts of buildings and their features in Table 2.

Imagine you had to learn these two concepts by seeing exemplars of them, each exemplar having some of the features listed for the concept (as well as some idiosyncratic features). Learning the donker concept would be pretty easy. It seems to be a kind of underwater building, perhaps for deep-sea explorers. Its features seem to go together. In contrast, the blegdav doesn’t really make sense. If it’s in the desert, how can you get there by submarine, and why do they have polar bears as pets? Why would farmers live in the desert or use submarines? What good would steel windows do in such a building? This concept seems peculiar. In fact, if people are asked to learn new concepts that make sense, such as donkers, they learn them quite a bit faster than concepts such as blegdavs that don’t make sense ( Murphy & Allopenna, 1994 ). Furthermore, the features that seem connected to one another (such as being underwater and getting there by submarine) are learned better than features that don’t seem related to the others (such as being red).

Such effects demonstrate that when we learn new concepts, we try to connect them to the knowledge we already have about the world. If you were to learn about a new animal that doesn’t seem to eat or reproduce, you would be very puzzled and think that you must have gotten something wrong. By themselves, the prototype and exemplar theories don’t predict this. They simply say that you learn descriptions or exemplars, and they don’t put any constraints on what those descriptions or exemplars are. However, the knowledge approach to concepts emphasizes that concepts are meant to tell us about real things in the world, and so our knowledge of the world is used in learning and thinking about concepts.

We can see this effect of knowledge when we learn about new pieces of technology. For example, most people could easily learn about tablet computers (such as iPads) when they were first introduced by drawing on their knowledge of laptops, cell phones, and related technology. Of course, this reliance on past knowledge can also lead to errors, as when people don’t learn about features of their new tablet that weren’t present in their cell phone or expect the tablet to be able to do something it can’t.

One important aspect of people’s knowledge about categories is called psychological essentialism ( Gelman, 2003 ; Medin & Ortony, 1989 ). People tend to believe that some categories—most notably natural kinds such as animals, plants, or minerals—have an underlying property that is found only in that category and that causes its other features. Most categories don’t actually have essences, but this is sometimes a firmly held belief. For example, many people will state that there is something about dogs, perhaps some specific gene or set of genes, that all dogs have and that makes them bark, have fur, and look the way they do. Therefore, decisions about whether something is a dog do not depend only on features that you can easily see but also on the assumed presence of this cause.

Belief in an essence can be revealed through experiments describing fictional objects. Keil ( 1989 ) described to adults and children a fiendish operation in which someone took a raccoon, dyed its hair black with a white stripe down the middle, and implanted a “sac of super-smelly yucky stuff” under its tail. The subjects were shown a picture of a skunk and told that this is now what the animal looks like. What is it? Adults and children over the age of 4 all agreed that the animal is still a raccoon. It may look and even act like a skunk, but a raccoon cannot change its stripes (or whatever!)—it will always be a raccoon.

Importantly, the same effect was not found when Keil described a coffeepot that was operated on to look like and function as a bird feeder. Subjects agreed that it was now a bird feeder. Artifacts don’t have an essence.

Signs of essentialism include (a) objects are believed to be either in or out of the category, with no in-between; (b) resistance to change of category membership or of properties connected to the essence; and (c) for living things, the essence is passed on to progeny.

Essentialism is probably helpful in dealing with much of the natural world, but it may be less helpful when it is applied to humans. Considerable evidence suggests that people think of gender, racial, and ethnic groups as having essences, which serves to emphasize the difference between groups and even justify discrimination ( Hirschfeld, 1996 ). Historically, group differences were described by inheriting the blood of one’s family or group. “Bad blood” was not just an expression but a belief that negative properties were inherited and could not be changed. After all, if it is in the nature of “those people” to be dishonest (or clannish or athletic ...), then that could hardly be changed, any more than a raccoon can change into a skunk.

Research on categories of people is an exciting ongoing enterprise, and we still do not know as much as we would like to about how concepts of different kinds of people are learned in childhood and how they may (or may not) change in adulthood. Essentialism doesn’t apply only to person categories, but it is one important factor in how we think of groups.

Concepts are central to our everyday thought. When we are planning for the future or thinking about our past, we think about specific events and objects in terms of their categories. If you’re visiting a friend with a new baby, you have some expectations about what the baby will do, what gifts would be appropriate, how you should behave toward it, and so on. Knowing about the category of babies helps you to effectively plan and behave when you encounter this child you’ve never seen before. Such inferences from knowledge about a category are highly adaptive and an important component of thinking and intelligence.

Learning about those categories is a complex process that involves seeing exemplars (babies), hearing or reading general descriptions (“Babies like black-and-white pictures”), general knowledge (babies have kidneys), and learning the occasional rule (all babies have a rooting reflex). Current research is focusing on how these different processes take place in the brain. It seems likely that these different aspects of concepts are accomplished by different neural structures ( Maddox & Ashby, 2004 ). However, it is clear that the brain is genetically predisposed to seek out similarities in the environment and to represent groupings of things forming categories that can be used to make inferences about new instances of the category which have never been encountered before. In this way knowledge is organized and expectations from this knowledge allow improved adaptation to newly encountered environmental objects and situations by virtue of their similarity to a known category previously formed (Koenigshofer, 2017).

Another interesting topic is how concepts differ across cultures. As different cultures have different interests and different kinds of interactions with the world, it seems clear that their concepts will somehow reflect those differences. On the other hand, the structure of the physical world also imposes a strong constraint on what kinds of categories are actually useful. The interplay of culture, the environment, and basic cognitive processes in establishing concepts has yet to be fully investigated.

Discussion Questions

• Pick a couple of familiar categories and try to come up with definitions for them. When you evaluate each proposal (a) is it in fact accurate as a definition, and (b) is it a definition that people might actually use in identifying category members?
• For the same categories, can you identify members that seem to be “better” and “worse” members? What about these items makes them typical and atypical?
• Going around the room, point to some common objects (including things people are wearing or brought with them) and identify what the basic-level category is for that item. What are superordinate and subordinate categories for the same items?
• List some features of a common category such as tables. The knowledge view suggests that you know reasons for why these particular features occur together. Can you articulate some of those reasons? Do the same thing for an animal category.
• Choose three common categories: a natural kind, a human artifact, and a social event. Discuss with class members from other countries or cultures whether the corresponding categories in their cultures differ. Can you make a hypothesis about when such categories are likely to differ and when they are not?
• Allen, S. W., & Brooks, L. R. (1991). Specializing the operation of an explicit rule. Journal of Experimental Psychology: General, 120 , 3–19.
• Anglin, J. M. (1977). Word, object, and conceptual developmen t. New York, NY: W. W. Norton.
• Berlin, B. (1992). Ethnobiological classification: Principles of categorization of plants and animals in traditional societies . Princeton, NJ: Princeton University Press.
• Brown, R. (1958). How shall a thing be called? Psychological Review, 65 , 14–21.
• Gelman, S. A. (2003). The essential child: Origins of essentialism in everyday thought . Oxford, UK: Oxford University Press.
• Hampton, J. A. (1979). Polymorphous concepts in semantic memory. Journal of Verbal Learning and Verbal Behavior, 18 , 441–461.
• Hirschfeld, L. A. (1996). Race in the making: Cognition, culture, and the child's construction of human kinds . Cambridge, MA: MIT Press.
• Horton, M. S., & Markman, E. M. (1980). Developmental differences in the acquisition of basic and superordinate categories. Child Development , 51, 708–719.
• Keil, F. C. (1989). Concepts, kinds, and cognitive development . Cambridge, MA: MIT Press.
• Koenigshofer, K. A. (2017). General Intelligence: Adaptation to Evolutionarily Familiar Abstract Relational Invariants, Not to Environmental or Evolutionary Novelty. The Journal of Mind and Behavior , 38(2):119-153.
• Maddox, W. T., & Ashby, F. G. (2004). Dissociating explicit and procedural-based systems of perceptual category learning. Behavioural Processes, 66 , 309–332.
• Mandler, J. M. (2004). The foundations of mind: Origins of conceptual thought . Oxford, UK: Oxford University Press.
• Mareschal, D., Quinn, P. C., & Lea, S. E. G. (Eds.) (2010). The making of human concepts . Oxford, UK: Oxford University Press.
• McCloskey, M. E., & Glucksberg, S. (1978). Natural categories: Well defined or fuzzy sets? Memory & Cognition, 6 , 462–472.
• Medin, D. L., & Ortony, A. (1989). Psychological essentialism. In S. Vosniadou & A. Ortony (Eds.), Similarity and analogical reasoning (pp. 179–195). Cambridge, UK: Cambridge University Press.
• Medin, D. L., & Schaffer, M. M. (1978). Context theory of classification learning. Psychological Review , 85, 207–238.
• Mervis, C. B. (1987). Child-basic object categories and early lexical development. In U. Neisser (Ed.), Concepts and conceptual development: Ecological and intellectual factors in categorization (pp. 201–233). Cambridge, UK: Cambridge University Press.
• Murphy, G. L., & Allopenna, P. D. (1994). The locus of knowledge effects in concept learning. Journal of Experimental Psychology: Learning, Memory, and Cognition, 20 , 904–919.
• Murphy, G. L., & Brownell, H. H. (1985). Category differentiation in object recognition: Typicality constraints on the basic category advantage. Journal of Experimental Psychology: Learning, Memory, and Cognition, 11 , 70–84.
• Norenzayan, A., Smith, E. E., Kim, B. J., & Nisbett, R. E. (2002). Cultural preferences for formal versus intuitive reasoning. Cognitive Science, 26 , 653–684.
• Rosch, E., & Mervis, C. B. (1975). Family resemblance: Studies in the internal structure of categories. Cognitive Psychology , 7, 573–605.
• Rosch, E., Mervis, C. B., Gray, W., Johnson, D., & Boyes-Braem, P. (1976). Basic objects in natural categories. Cognitive Psychology, 8 , 382–439.
• Rosch, E., Simpson, C., & Miller, R. S. (1976). Structural bases of typicality effects. Journal of Experimental Psychology: Human Perception and Performance, 2 , 491–502.
• Rosch, E. H. (1973). On the internal structure of perceptual and semantic categories. In T. E. Moore (Ed.), Cognitive development and the acquisition of language (pp. 111–144). New York, NY: Academic Press.
• Smith, E. E., & Medin, D. L. (1981). Categories and concepts . Cambridge, MA: Harvard University Press.
• Smith, J. D., & Minda, J. P. (1998). Prototypes in the mist: The early epochs of category learning. Journal of Experimental Psychology: Learning, Memory, and Cognition, 24 , 1411–1436.
• Tanaka, J. W., & Taylor, M. E. (1991). Object categories and expertise: Is the basic level in the eye of the beholder? Cognitive Psychology, 15 , 121–149.
• Wisniewski, E. J., & Murphy, G. L. (1989). Superordinate and basic category names in discourse: A textual analysis. Discourse Processes, 12 , 245–261.

• Gregory Murphy is Professor of Psychology at New York University. He previously taught at the University of Illinois and Brown University. His research focuses on concepts and reasoning, and he is the author of The Big Book of Concepts (MIT Press, 2002).

Creative Commons License

Adapted by Kenneth Koenigshofer, PhD, from Categories and Concepts by Gregory Murphy , licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License . Permissions beyond the scope of this license may be available in our Licensing Agreement .

How to cite this noba module using apa style.

Murphy, G. (2021). Categories and concepts. In R. Biswas-Diener & E. Diener (Eds), Noba textbook series: Psychology. Champaign, IL: DEF publishers. Retrieved from http://noba.to/6vu4cpkt

Psych 256: Cognitive Psychology SP15

Making connections between theory and reality, problem solving using means-end analysis.

Everyone has had a long list of to dos or personal things to take care of.  Looking at the whole it can seem a little overwhelming and most of us get lost, depressed, or even frustrated.  Using a means-end analysis is basically looking at a goal, starting point, and the best way to get from point A to point B by breaking down the list or problems to make them more doable in our lives (Newell & Simon, 1972).  For this blog, I will pass on some tips on how to manage your homework load that you have each semester to lessen the stress.  Keeping in mind, that these tips have worked for me but can be modified to individual needs, because let’s face it, each of us have different lifestyles and means-end analysis will not necessarily work for everyone problem.

Each of us when we start a new semester, whether it is at a new school or the current one, can feel overwhelmed by the work load that looms ahead of us.  What I do to lessen the stress is I take each class syllabus and course calendar and a full size desk top calendar, the ones with the large squares for the dates, and I write down the class and what is due each week including test and quizzes.  This way I can see clearly what I have to complete. This is the process of setting subgoals which helps to move toward the overall goal of course completion (Goldstein, 2011). Once classes are taken care of I will then insert any social or work related items. With all of this in place I have a black and white picture of my life each month.  Once this is in place I can set up a realistic schedule to complete the semester and how it is broken down weekly, allows me to manage it properly without over stressing out.  I take one day at a time.  As each day passes you can cross out what has been completed and feel a sense of accomplishment.

Now we move into supplies to fulfill the semester.  I will look at each class and see if any will need something other than the usual, such as art supplies, software, etc.  Take a list to your local store and remember it is ok to over buy on paper, printer ink, and writing tools because you never can estimate what you might use up.  I find that having all the items for each class available will help keep stress levels down by not having to run to the store at the last minute.  Being well stocked will help prepare for the semester.

Next, let’s look at textbooks.  Most of us will buy them and throw them in the back of our cars.  The best thing to do is to look them over, read the index, and maybe a few chapters to get acclimated to the class.  I use colored tabs to mark out each chapter, so I can easily flip to it.  Being familiar with the classes you are taking and what is required in readings, online work, extra supplies, etc. will help you plan your weeks to come plus lower your stress levels.

Now the important thing is your study area.  Some people will study in their bedroom, but this is too tempting of a place to take a nap or simply fall asleep and then your day is over.  If all you have is your bedroom then I would suggest going to the school library or a quiet area in a coffee shop or 24 hour restaurant.  I have a desk in a room with little to no distractions.  I have everything I need in this room to complete my homework, readings, and school projects.  I have set times to do my school work according to my calendar that I discussed earlier.  Another thing that might help is turn off cell phones and any other communication or social media devices.  Let people know that you will be studying at set times so that they will not text or call to disturb you.  These types of disruptions can derail you from what you are reading or writing.  If you have children, you can do what a friend of mine does and put a sign on the door letting your children know that it is mommy/daddy study time.  Of course this doesn’t always work because children are children and that just doesn’t happen.  In that case, perhaps work it out with your partner that they handle the kids while you are studying or have a friend or relative watch the children for that bit of time.  Having a place to work just for you will increase productivity and or course lower some stress.

With some of the tips I have given, you can lower stress levels of the new semester by setting smaller goals so you can reach the finish line at the end of the semester.  This is all made possible by using a means-end analysis solution.  Keep in mind this may not work for you or you may have to modify the ideas that I have given to make it work in your life.  Whatever will work by planning out your semester so you can achieve the grades is great.  I hope you will be able to add some of or all of my tips to get you to your semester goals by breaking down the whole to more manageable pieces.

Goldstein, E. (2011). Cognitive psychology: Connecting mind, research, and everyday experience (3rd ed.). Australia: Wadsworth Cengage Learning.

Newell, A., & Simon, H. A. (1972).  Human problem solving  (Vol. 104, No. 9). Englewood Cliffs, NJ: Prentice-Hall.

Leave a Reply

You must be logged in to post a comment.

Means-Ends Analysis in Artificial Intelligence

In this page we will learn about How means-ends analysis Works, Operator Subgoaling, Algorithm for Means-Ends Analysis, Example of Mean-Ends Analysis.

• We've looked at tactics that can reason in either forward or backward directions, but a combination of the two is best for addressing a complex and vast problem. This mixed technique allows you to solve the large component of a problem first, then go back and fix the minor issues that develop while merging the major elements of the problem. Means-Ends Analysis is one such technique.
• Means-Ends Analysis is a problem-solving method used in artificial intelligence programs to limit search.
• It's a hybrid of backward and forward searching methods.
• The MEA technique was originally used in a problem-solving computer software called General Problem Solver by Allen Newell and Herbert A. Simon in 1961. (GPS).

The discrepancy between the existing state and the goal state was evaluated during the MEA analysis procedure.

How means-ends analysis Works:

The means-ends analysis approach can be used to solve a problem in a recursive manner. It's a problem-solving method for controlling search. The following are the main steps that describe how the MEA technique for problem solving works.

• To proceed, assess the difference between the initial and end states.
• Choose from a variety of operators to apply to each difference.
• Applying the operator to each difference lowers the gap between the current and desired states.

Operator Subgoaling

We detect disparities between the existing state and the goal state during the MEA process. Once these discrepancies have occurred, we can use an operator to decrease them. However, there are situations when an operator cannot be applied to the existing state. So we build a subproblem of the current state in which an operator can be applied; this sort of backward chaining, in which operators are chosen and then sub goals are established to define the operator's preconditions, is known as Operator Subgoaling.

Algorithm for Means-Ends Analysis:

Let's take Current state as CURRENT and Goal State as GOAL, then the steps for the MEA algorithm are following.

Step 1: Compare CURRENT and GOAL, and if there are no discrepancies, return Success and Exit.

• Choose a new operator O that applies to the current difference, and if no such operator exists, signal failure.
• O-Start, a state in which O?s preconditions are satisfied.
• O-Result, the state that would result if O were applied In O-start.
• If (First-Part <------ MEA (CURRENT, O-START) And (LAST-Part <----- MEA (O-Result, GOAL), are successful, then signal Success and return the result of combination of FIRST-PART, O, and LAST-PART.

The algorithm described above is better suited to tackling simple problems than it is to solving complex problems.

Example of Mean-Ends Analysis:

Let's look at an example where we know the starting state and the desired state. In this issue, we must detect differences between the beginning state and the goal state and apply operators to obtain the goal state.

To solve the problem, we will first identify the differences between starting and goal states, then construct a new state and apply the operators to each difference. For this problem, we have the following operators:

1. Evaluating the initial state: In the first step, we'll evaluate the initial state and compare it to the Goal state to see what the differences Evaluating the initial state: In the first step, we'll evaluate the initial state and compare it to the Goal state to see what the differences are.

2. Applying the Delete operator: As you can see, the first difference is that there's no dot symbol in the Goal state, whereas there is in the initial state, so we'll use the Delete operator to remove it.

3. Applying the Move Operator: After using the Delete operator, a new state appears, which we will compare to the objective state again. After comparing these states, we notice that the square is outside the circle, so we'll use the Move Operator to fix it.

4. Applying the Expand Operator: In the third phase, a new state is created, and we will compare it to the desired state. There is still one difference between the states, which is the size of the square, so we will use the Expand operator to construct the desired state.