introduction to statistics homework solutions

E | Solution Sheets

Hypothesis testing with one sample.

Class Time: __________________________ Name: _____________________________________

H 0 : _______
H a : _______
In words, CLEARLY state what your random variable X ¯ X ¯ or P ′ P ′ represents.
State the distribution to use for the test.
What is the test statistic?
What is the p -value? In one or two complete sentences, explain what the p -value means for this problem.
Alpha: _______
Decision: _______
Reason for decision: _______
Conclusion: _______

Hypothesis Testing with Two Samples

In words, clearly state what your random variable X ¯ 1 − X ¯ 2 X ¯ 1 − X ¯ 2 , P ′ 1 − P ′ 2 P ′ 1 − P ′ 2 or X ¯ d X ¯ d represents.
What is the p -value? In one to two complete sentences, explain what the p-value means for this problem.
In complete sentences, explain how you determined which distribution to use.

The Chi-Square Distribution

Class Time: __________________________ Name: ____________________________________

What are the degrees of freedom?
What is the p -value? In one to two complete sentences, explain what the p -value means for this problem.

F Distribution and One-Way ANOVA

df ( n ) = ______ df ( d ) = _______
What is the p -value?

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/introductory-statistics-2e/pages/1-introduction

Authors: Barbara Illowsky, Susan Dean
Publisher/website: OpenStax
Book title: Introductory Statistics 2e
Publication date: Dec 13, 2023
Location: Houston, Texas
Book URL: https://openstax.org/books/introductory-statistics-2e/pages/1-introduction
Section URL: https://openstax.org/books/introductory-statistics-2e/pages/e-solution-sheets

© Dec 6, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Chapter 1: Sampling and Data

Chapter 1 Homework

Homework from 1.2.

For each of the following eight exercises, identify: a. the population, b. the sample, c. the parameter, d. the statistic, e. the variable, and f. the data. Give examples where appropriate.

A fitness center is interested in the mean amount of time a client exercises in the center each week.

The population is all of the clients of the fitness center. A sample of the clients that use the fitness center for a given week. The average amount of time that all clients exercise in one week. The average amount of time that a sample of clients exercises in one week. The amount of time that a client exercises in one week. Examples are: 2 hours, 5 hours, and 7.5 hours –>

Ski resorts are interested in the mean age that children take their first ski and snowboard lessons. They need this information to plan their ski classes optimally.

all children who take ski or snowboard lessons
a group of these children
the population mean age of children who take their first snowboard lesson
the sample mean age of children who take their first snowboard lesson
X = the age of one child who takes his or her first ski or snowboard lesson
values for X , such as 3, 7, and so on

A cardiologist is interested in the mean recovery period of her patients who have had heart attacks.

the cardiologist’s patients a group of the cardiologist’s patients the mean recovery period of all of the cardiologist’s patients the mean recovery period of the group of the cardiologist’s patients X = the mean recovery period of one patient values for X, such as 10 days, 14 days, 20 days, and so on –>

Insurance companies are interested in the mean health costs each year of their clients, so that they can determine the costs of health insurance.

the clients of the insurance companies
a group of the clients
the mean health costs of the clients
the mean health costs of the sample
X = the health costs of one client
values for X , such as 34, 9, 82, and so on

A politician is interested in the proportion of voters in his district who think he is doing a good job.

all voters in the politician’s district a random selection of voters in the politician’s district the proportion of voters in this district who think this politician is doing a good job the proportion of voters in this district who think this politician is doing a good job in the sample X = the number of voters in the district who think this politician is doing a good job Yes, he is doing a good job. No, he is not doing a good job. –>

A marriage counselor is interested in the proportion of clients she counsels who stay married.

all the clients of this counselor
a group of clients of this marriage counselor
the proportion of all her clients who stay married
the proportion of the sample of the counselor’s clients who stay married
X = the number of couples who stay married

Political pollsters may be interested in the proportion of people who will vote for a particular cause.

all voters (in a certain geographic area) a random selection of all the voters the proportion of voters who are interested in this particular cause the proportion of voters who are interested in this particular cause in the sample X = the number of voters who are interested in this particular cause yes, no –>

A marketing company is interested in the proportion of people who will buy a particular product.

all people (maybe in a certain geographic area, such as the United States)
a group of the people
the proportion of all people who will buy the product
the proportion of the sample who will buy the product
X = the number of people who will buy it
buy, not buy

Use the following information to answer the next three exercises: A Lake Tahoe Community College instructor is interested in the mean number of days Lake Tahoe Community College math students are absent from class during a quarter.

What is the population she is interested in?

all Lake Tahoe Community College students
all Lake Tahoe Community College English students
all Lake Tahoe Community College students in her classes
all Lake Tahoe Community College math students

Consider the following:

[latex]X[/latex] = number of days a Lake Tahoe Community College math student is absent

In this case, X is an example of a:

population.

The instructor’s sample produces a mean number of days absent of 3.5 days. This value is an example of a:

More Homework from 1.2

For the following exercises, identify the type of data that would be used to describe a response (quantitative discrete, quantitative continuous, or qualitative), and give an example of the data.

number of tickets sold to a concert

quantitative discrete, 150

percentage of body fat

quantitative continuous, 19.2% –>

favorite baseball team

qualitative, Oakland A’s

time in line to buy groceries

quantitative continuous, 7.2 minutes –>

number of students enrolled at Evergreen Valley College

quantitative discrete, 11,234 students

most-watched television show

qualitative, Dancing with the Stars –>

brand of toothpaste

qualitative, Crest

distance to the closest movie theater

quantitative continuous, 8.32 miles –>

age of executives in Fortune 500 companies

quantitative continuous, 47.3 years

number of competing computer spreadsheet software packages

quantitative discrete, three –>

Use the following information to answer the next two exercises: A study was done to determine the age, number of times per week, and the duration (amount of time) of resident use of a local park in San Jose. The first house in the neighborhood around the park was selected randomly and then every 8th house in the neighborhood around the park was interviewed.

“Number of times per week” is what type of data?

qualitative
quantitative discrete
quantitative continuous

“Duration (amount of time)” is what type of data?

Airline companies are interested in the consistency of the number of babies on each flight, so that they have adequate safety equipment. Suppose an airline conducts a survey. Over Thanksgiving weekend, it surveys six flights from Boston to Salt Lake City to determine the number of babies on the flights. It determines the amount of safety equipment needed by the result of that study.

Using complete sentences, list three things wrong with the way the survey was conducted.
Using complete sentences, list three ways that you would improve the survey if it were to be repeated.

The survey would not be a true representation of the entire population of air travelers.

Conducting the survey on a holiday weekend will not produce representative results.

Conduct the survey during different times of the year.

Conduct the survey using flights to and from various locations.

Conduct the survey on different days of the week.

Suppose you want to determine the mean number of students per statistics class in your state. Describe a possible sampling method in three to five complete sentences. Make the description detailed.

Answers will vary. Sample Answer: Randomly choose 25 colleges in the state. Use all statistics classes from each of the chosen colleges in the sample. This can be done by listing all the colleges together with a two-digit number starting with 00 then 01, etc. The list of colleges can be found on Wikipedia. http://en.wikipedia.org/wiki/List_of_colleges_and_universities_in_California Use a random number generator to pick 25 colleges. –>

Suppose you want to determine the mean number of cans of soda drunk each month by students in their twenties at your school. Describe a possible sampling method in three to five complete sentences. Make the description detailed.

Answers will vary. Sample Answer: You could use a systematic sampling method. Stop the tenth person as they leave one of the buildings on campus at 9:50 in the morning. Then stop the tenth person as they leave a different building on campus at 1:50 in the afternoon.

List some practical difficulties involved in getting accurate results from a telephone survey.

Answers will vary. Sample Answer: Not all people have a listed phone number. Many people hang up or do not respond to phone surveys. –>

List some practical difficulties involved in getting accurate results from a mailed survey.

Answers will vary. Sample Answer: Many people will not respond to mail surveys. If they do respond to the surveys, you can’t be sure who is responding. In addition, mailing lists can be incomplete.

With your classmates, brainstorm some ways you could overcome these problems if you needed to conduct a phone or mail survey.

Ask everyone to include their age then take a random sample from the data. Include in the report how the survey was conducted and why the results may not be accurate. –>

The instructor takes her sample by gathering data on five randomly selected students from each Lake Tahoe Community College math class. The type of sampling she used is

cluster sampling
stratified sampling
simple random sampling
convenience sampling

A study was done to determine the age, number of times per week, and the duration (amount of time) of residents using a local park in San Jose. The first house in the neighborhood around the park was selected randomly and then every eighth house in the neighborhood around the park was interviewed. The sampling method was:

simple random

Name the sampling method used in each of the following situations:

convenience cluster stratified systematic simple random

A “random survey” was conducted of 3,274 people of the “microprocessor generation” (people born since 1971, the year the microprocessor was invented). It was reported that 48% of those individuals surveyed stated that if they had 💲2,000 to spend, they would use it for computer equipment. Also, 66% of those surveyed considered themselves relatively savvy computer users.

Do you consider the sample size large enough for a study of this type? Why or why not?

Additional information: The survey, reported by Intel Corporation, was filled out by individuals who visited the Los Angeles Convention Center to see the Smithsonian Institute’s road show called “America’s Smithsonian.”

With this additional information, do you feel that all demographic and ethnic groups were equally represented at the event? Why or why not?
With the additional information, comment on how accurately you think the sample statistics reflect the population parameters.

Yes, in polling, samples that are from 1,200 to 1,500 observations are considered large enough and good enough if the survey is random and is well done. We do not have enough information to decide if this is a random sample from the U.S. population. No, this is a convenience sample taken from individuals who visited an exhibition in the Angeles Convention Center. This sample is not representative of the U.S. population. It is possible that the two sample statistics, 48% and 66% are larger than the true parameters in the population at large. In any event, no conclusion about the population proportions can be inferred from this convenience sample. –>

The Gallup-Healthways Well-Being Index is a survey that follows trends of U.S. residents on a regular basis. There are six areas of health and wellness covered in the survey: Life Evaluation, Emotional Health, Physical Health, Healthy Behavior, Work Environment, and Basic Access. Some of the questions used to measure the Index are listed below.

Identify the type of data obtained from each question used in this survey: qualitative, quantitative discrete, or quantitative continuous.

Do you have any health problems that prevent you from doing any of the things people your age can normally do?
During the past 30 days, for about how many days did poor health keep you from doing your usual activities?
In the last seven days, on how many days did you exercise for 30 minutes or more?
Do you have health insurance coverage?

In advance of the 1936 Presidential Election, a magazine titled Literary Digest released the results of an opinion poll predicting that the republican candidate Alf Landon would win by a large margin. The magazine sent postcards to approximately 10,000,000 prospective voters. These prospective voters were selected from the subscription list of the magazine, from automobile registration lists, from phone lists, and from club membership lists. Approximately 2,300,000 people returned the postcards.

Think about the state of the United States in 1936. Explain why a sample chosen from magazine subscription lists, automobile registration lists, phone books, and club membership lists was not representative of the population of the United States at that time.
What effect does the low response rate have on the reliability of the sample?
Are these problems examples of sampling error or nonsampling error?
During the same year, George Gallup conducted his own poll of 30,000 prospective voters. His researchers used a method they called “quota sampling” to obtain survey answers from specific subsets of the population. Quota sampling is an example of which sampling method described in this module?

The country was in the middle of the Great Depression, and many people could not afford these “luxury” items and therefore were not able to be included in the survey. Samples that are too small can lead to sampling bias. sampling error stratified

Crime-related and demographic statistics for 47 US states in 1960 were collected from government agencies, including the FBI’s Uniform Crime Report . One analysis of this data found a strong connection between education and crime indicating that higher levels of education in a community correspond to higher crime rates.

Which of the potential problems with samples discussed in [link] could explain this connection?

Causality: The fact that two variables are related does not guarantee that one variable is influencing the other. We cannot assume that crime rate impacts education level or that education level impacts crime rate.

Confounding: There are many factors that define a community other than education level and crime rate. Communities with high crime rates and high education levels may have other lurking variables that distinguish them from communities with lower crime rates and lower education levels. Because we cannot isolate these variables of interest, we cannot draw valid conclusions about the connection between education and crime. Possible lurking variables include police expenditures, unemployment levels, region, average age, and size.

YouPolls is a website that allows anyone to create and respond to polls. One question posted April 15 asks:

“Do you feel happy paying your taxes when members of the Obama administration are allowed to ignore their tax liabilities?” 1

As of April 25, 11 people responded to this question. Each participant answered “NO!”

Which of the potential problems with samples discussed in this module could explain this connection?

Self-Selected Samples: Only people who are interested in the topic are choosing to respond. Sample Size Issues: A sample with only 11 participants will not accurately represent the opinions of a nation. Undue Influence: The question is wording in a specific way to generate a specific response. Self-Funded or Self-Interest Studies: This question was generated to support one person’s claim and it was designed to get the answer that the person desires. –>

A scholarly article about response rates begins with the following quote:

“Declining contact and cooperation rates in random digit dial (RDD) national telephone surveys raise serious concerns about the validity of estimates drawn from such research.” 2

The Pew Research Center for People and the Press admits:

“The percentage of people we interview – out of all we try to interview – has been declining over the past decade or more.” 3

What are some reasons for the decline in response rate over the past decade?
Explain why researchers are concerned with the impact of the declining response rate on public opinion polls.
Possible reasons: increased use of caller id, decreased use of landlines, increased use of private numbers, voice mail, privacy managers, hectic nature of personal schedules, decreased willingness to be interviewed
When a large number of people refuse to participate, then the sample may not have the same characteristics of the population. Perhaps the majority of people willing to participate are doing so because they feel strongly about the subject of the survey.

Bringing It Together

Seven hundred and seventy-one distance learning students at Long Beach City College responded to surveys in the 2010-11 academic year. Highlights of the summary report are listed in [link] .

What percentage of the students surveyed do not have a computer at home?
About how many students in the survey live at least 16 miles from campus?
If the same survey were done at Great Basin College in Elko, Nevada, do you think the percentages would be the same? Why?

4% 13% Not necessarily. Long Beach City is the seventh largest college in California, and it has an enrollment of approximately 27,000 students. On the other hand, Great Basin College has its campuses in rural northeastern Nevada, and its enrollment of about 3,500 students. –>

Several online textbook retailers advertise that they have lower prices than on-campus bookstores. However, an important factor is whether the Internet retailers actually have the textbooks that students need in stock. Students need to be able to get textbooks promptly at the beginning of the college term. If the book is not available, then a student would not be able to get the textbook at all, or might get a delayed delivery if the book is back ordered.

A college newspaper reporter is investigating textbook availability at online retailers. He decides to investigate one textbook for each of the following seven subjects: calculus, biology, chemistry, physics, statistics, geology, and general engineering. He consults textbook industry sales data and selects the most popular nationally used textbook in each of these subjects. He visits websites for a random sample of major online textbook sellers and looks up each of these seven textbooks to see if they are available in stock for quick delivery through these retailers. Based on his investigation, he writes an article in which he draws conclusions about the overall availability of all college textbooks through online textbook retailers.

Write an analysis of his study that addresses the following issues: Is his sample representative of the population of all college textbooks? Explain why or why not. Describe some possible sources of bias in this study, and how it might affect the results of the study. Give some suggestions about what could be done to improve the study.

Answers will vary. Sample answer: The sample is not representative of the population of all college textbooks. Two reasons why it is not representative are that he only sampled seven subjects and he only investigated one textbook in each subject. There are several possible sources of bias in the study. The seven subjects that he investigated are all in mathematics and the sciences; there are many subjects in the humanities, social sciences, and other subject areas (for example: literature, art, history, psychology, sociology, business) that he did not investigate at all. It may be that different subject areas exhibit different patterns of textbook availability, but his sample would not detect such results.

He also looked only at the most popular textbook in each of the subjects he investigated. The availability of the most popular textbooks may differ from the availability of other textbooks in one of two ways:

the most popular textbooks may be more readily available online, because more new copies are printed, and more students nationwide are selling back their used copies, OR
the most popular textbooks may be harder to find available online, because more student demand exhausts the supply more quickly.

In reality, many college students do not use the most popular textbooks in their subject, and this study gives no useful information about the situation for those less popular textbooks.

He could improve this study by:

expanding the selection of subjects he investigates so that it is more representative of all subjects studied by college students, and
expanding the selection of textbooks he investigates within each subject to include a mixed representation of both the most popular and less popular textbooks.

HOMEWORK from 1.3

Fifty part-time students were asked how many courses they were taking this term. The (incomplete) results are shown below:

Fill in the blanks in [link] .
What percent of students take exactly two courses?
What percent of students take one or two courses?

Sixty adults with gum disease were asked the number of times per week they used to floss before their diagnosis. The (incomplete) results are shown in [link] .

What percent of adults flossed six times per week?
What percentage flossed at most three times per week?

Nineteen immigrants to the U.S were asked how many years, to the nearest year, they have lived in the U.S. The data are as follows: 2 5 7 2 2 10 20 15 0 7 0 20 5 12 15 12 4 5 10 .

[link] was produced.

Fix the errors in [link] . Also, explain how someone might have arrived at the incorrect number(s).
Explain what is wrong with this statement: “47 percent of the people surveyed have lived in the U.S. for 5 years.”
Fix the statement in b to make it correct.
What fraction of the people surveyed have lived in the U.S. five or seven years?
What fraction of the people surveyed have lived in the U.S. at most 12 years?
What fraction of the people surveyed have lived in the U.S. fewer than 12 years?
What fraction of the people surveyed have lived in the U.S. from five to 20 years, inclusive?

The Frequencies for 15 and 20 should both be two and the Relative Frequencies should both be

The mistake could be due to copying the data down wrong. The Cumulative Relative Frequency for five years should be 0.4737. The mistake is due to calculating the Relative Frequency instead of the Cumulative Relative Frequency. The Cumulative Relative Frequency for 15 years should be 0.8947 The 47% is the Cumulative Relative Frequency, not the Relative Frequency. 47% of the people surveyed have lived in the U.S. for five years or less.

How much time does it take to travel to work? [link] shows the mean commute time by state for workers at least 16 years old who are not working at home. Find the mean travel time, and round off the answer properly.

The sum of the travel times is 1,173.1. Divide the sum by 50 to calculate the mean value: 23.462. Because each state’s travel time was measured to the nearest tenth, round this calculation to the nearest hundredth: 23.46.

Forbes magazine published data on the best small firms in 2012. These were firms which had been publicly traded for at least a year, have a stock price of at least 💲5 per share, and have reported annual revenue between 💲5 million and 💲1 billion. [link] shows the ages of the chief executive officers for the first 60 ranked firms.

What is the frequency for CEO ages between 54 and 65?
What percentage of CEOs are 65 years or older?
What is the relative frequency of ages under 50?
What is the cumulative relative frequency for CEOs younger than 55?
Which graph shows the relative frequency and which shows the cumulative relative frequency?

Graph A is a bar graph with 7 bars. The x-axis shows CEO's ages in intervals of 5 years starting with 40 - 44. The y-axis shows the relative frequency in intervals of 0.2 from 0 - 1. The highest relative frequency shown is 0.27.

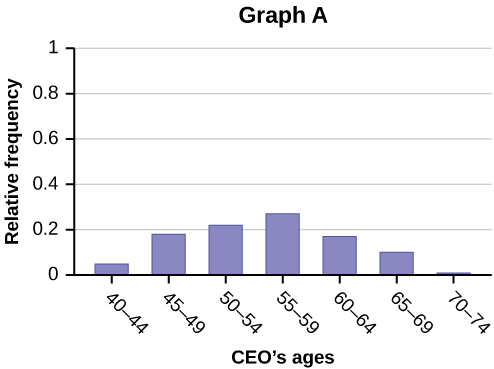
26 (This is the count of CEOs in the 55 to 59 and 60 to 64 categories.) 12% (number of CEOs age 65 or older ÷ total number of CEOs) 14/60; 0.23; 23% 0.45 Graph A represents the cumulative relative frequency, and Graph B shows the relative frequency. –>

Use the following information to answer the next two exercises: [link] contains data on hurricanes that have made direct hits on the U.S. Between 1851 and 2004. A hurricane is given a strength category rating based on the minimum wind speed generated by the storm.

What is the relative frequency of direct hits that were category 4 hurricanes?

Not enough information to calculate

What is the relative frequency of direct hits that were AT MOST a category 3 storm?

HOMEWORK from 1.4

How does sleep deprivation affect your ability to drive? A recent study measured the effects on 19 professional drivers. Each driver participated in two experimental sessions: one after normal sleep and one after 27 hours of total sleep deprivation. The treatments were assigned in random order. In each session, performance was measured on a variety of tasks including a driving simulation.

Use key terms from this module to describe the design of this experiment.

Explanatory variable: amount of sleep

Response variable: performance measured in assigned tasks

Treatments: normal sleep and 27 hours of total sleep deprivation

Experimental Units: 19 professional drivers

Lurking variables: none – all drivers participated in both treatments

Random assignment: treatments were assigned in random order; this eliminated the effect of any “learning” that may take place during the first experimental session

Control/Placebo: completing the experimental session under normal sleep conditions

Blinding: researchers evaluating subjects’ performance must not know which treatment is being applied at the time

An advertisement for Acme Investments displays the two graphs in [link] to show the value of Acme’s product in comparison with the Other Guy’s product. Describe the potentially misleading visual effect of these comparison graphs. How can this be corrected?

This is a line graph titled Acme Investments. The line graph shows a dramatic increase; neither the x-axis nor y-axis are labeled.

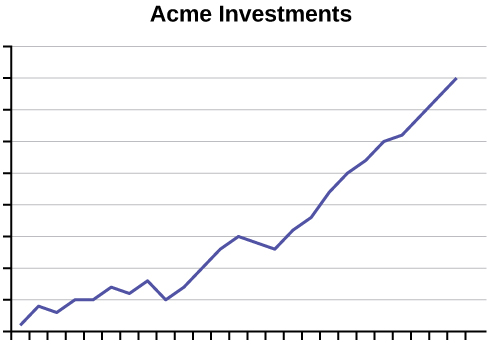
The graphs do not show scales of values. We do not know the period of time each graph represents; they may show data from different years. We also do not know if the vertical scales on each graph are equivalent. The scales may have been adjusted to exaggerate or minimize trends. There is no reliable information to be gleaned from these graphs, and setting them up as examples of performance is misleading. –>

The graph in [link] shows the number of complaints for six different airlines as reported to the US Department of Transportation in February 2013. Alaska, Pinnacle, and Airtran Airlines have far fewer complaints reported than American, Delta, and United. Can we conclude that American, Delta, and United are the worst airline carriers since they have the most complaints?

This is a bar graph with 6 different airlines on the x-axis, and number of complaints on y-axis. The graph is titled Total Passenger Complaints. Data is from an April 2013 DOT report.

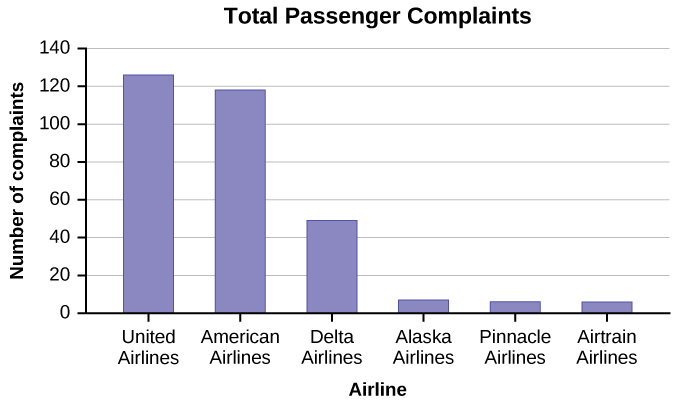
You cannot assume that the numbers of complaints reflect the quality of the airlines. The airlines shown with the greatest number of complaints are the ones with the most passengers. You must consider the appropriateness of methods for presenting data; in this case displaying totals is misleading.

Share This Book

Introductory Statistics - 2e

(35 reviews)

Barbara Illowsky, De Anza College

Susan Dean, De Anza College

Daniel Birmajer, Nazareth College

Bryan Blount, Kentucky Wesleyan College

Sheri Boyd, Rollins College

Matthew Einsohn, Prescott College

James Helmreich, Marist College

Lynette Kenyon, Collin County Community College

Sheldon Lee, Viterbo University

Jeff Taub, Maine Maritime Academy

Last Update: 2024

ISBN 13: 9781961584327

Publisher: OpenStax

Language: English

Formats Available

Conditions of use.

Learn more about reviews.

Reviewed by Ivan Temesvari, Instructor, Northeastern Illinois University on 4/4/24

Comprehensiveness rating: 4 see less

The text covers the topics of what any other introductory statistics text would cover. The example problems throughout the chapters may not be fancy, but still get the job done with well-organized and formatted tables and figures which appear to have been created using a graphics calculator. Each chapter is robust with exercises, try-it problems for the student to stop and practice/reflect on the content, a chapter review, homework problems, and solutions to the practice problems. There is an entire chapter dedicated to use of a TI-83 or TI-84 calculator with detailed instructions. The index of the text is well organized, and it is recommended to use the book in web format due to the highlighting tool available.

Content Accuracy rating: 5

I did not encounter any staggering errata in my review of the text. However, I did not read every word and cross check every exercise and solution. I'd imagine errata would be addressed periodically as the text has been updated to a 2nd edition. Also, the main page of the text has an errata page dedicated to errors found and it is currently active as I see a dated submission of the same day I happen to be writing this review 4/4/2024.

Relevance/Longevity rating: 5

Every chapter contains exercise problems that are based on real-life examples which shows a good attention to detail in how the topics are delivered. The mathematical symbols and typesetting are clear and match up with any advanced mathematical text of known importance. In fact, since this text incorporates the use of current technology (e.g., TI-84+ calculator), in some ways it is better than a more formal stats text.

Clarity rating: 4

Some statistical concepts require the use of current technology for access to graphical figures which help support the understanding of various topics throughout the text.

Consistency rating: 3

I didn't like how some of the sections go straight into a Stats Lab problem without any buildup or introduction to the relation of the problem to the topics covered in the associated chapter (e.g. 8.4 Confidence Interval (Home Costs)).

Modularity rating: 5

This text is very well organized. As I mentioned, every chapter has many sections of independent topics along with sections dedicated to Practice Problems, Homework, and even Solutions to the Practice Problems. There is even a section dedicated to References which is good to have in case you wanted to find out where some of the data was collected from, but also to delve more into the data from its source.

Organization/Structure/Flow rating: 3

Interface rating: 5

The web-based text utilizes a Highlighting feature which allows an account holder access to their previously highlighted text for a quick review of their notes. I personally would find this very useful as I prefer to highlight text as I read it for a note later. The highlight feature also allows a few different colors and a separate web page to review all of the highlighted text in one place instead of having to scroll and click around the entire text. As I mentioned before, it's best to read the book in web form, so that could be a draw back if you were using the pdf form. However, the pdf form has all of the same content as the web based form. Personally, I prefer the pdf form if I want to scroll through the pages of the chapter instead of having to click next repeatedly as I scan through the sections of the text.

Grammatical Errors rating: 5

I found that the text to be well written (in English).

Cultural Relevance rating: 5

It's a statistics text with many varied examples across a plethora of relatable topics which allow for the discovery of statistical methods. I found the examples related to food or athletics to be most interesting.

These OpenStax textbooks now have Instructor and Student Resources to supplement the experience. Also, there are now Technology Partners that have developed their own content to supplement the text with auto graded assignments and LMS interfaces.

Reviewed by Amish Mishra, Assistant Professor, Taylor University on 1/3/24

The text provides the necessary details of the most important topics in an introductory statistics course without going too deep into details or calculations. read more

Comprehensiveness rating: 5 see less

The text provides the necessary details of the most important topics in an introductory statistics course without going too deep into details or calculations.

Formula 10 in Appendix F has the bounds flipped on the gamma function’s integral. It should go from 0 to infinity.

Relevance/Longevity rating: 3

Perhaps using the TI calculators is now a thing of the past. I can understand if the authors would like to keep the statistical concepts in the focus rather than the tool, but today statistics can hardly be done in the workplace or academia without software like R or SPSS.

Clarity rating: 5

I like the dotplot introduction to give students an easy visualization and invitation to statistics

Consistency rating: 5

I found the section at the end listing the mathematical notation to be quite a helpful reference

It has a similar format to most statistics textbooks I’ve seen. Perhaps the chapter on descriptive statistics could be broken down further into a graphical chapter and a numerical chapter.

Organization/Structure/Flow rating: 5

The text has clear organization and supplements new concepts with good examples

I found it quite nice to have the book in pdf or online format. The various formats are helpful for different students’ learning styles

I did not see any

examples were great

- In the descriptive statistics section, it could also include examples of heatmaps and pictographs because those have become very popular - In the section about exponential distributions, some more justification can be provided for the memoryless property. For example, this sentence made me question the utility of the distribution: “In this case it means that an old part is not any more likely to break down at any particular time than a brand new part.” It is unintuitive for students to think this so some justification is needed for why thinking like this makes sense. - Introduction of Chapter 6: In reference to the normal distribution, the authors said, “The probability density function is a rather complicated function.” I would rather say it is surprisingly elegant so students also gain an appreciation for its formulation 😊 - Key terms section at the end of Chapter 7: not sure why there’s a paragraph for exponential distributions again when they were already discussed in 5.3 - In chapter 11, it may be worth commenting briefly on how the chi-squared test of independence is related to the chi-squared test of association - Overall, a fantastic resource that is open and free for anyone who wants to self-study statistics well. Thank you!

Reviewed by Daniel McGough, Graduate Student Instructor, Purdue University on 10/26/23

This book covers a broad category of statistics and statistical techniques, some of which I just ended up skipping. read more

This book covers a broad category of statistics and statistical techniques, some of which I just ended up skipping.

This book is very accurate.

As an instructor in a psychology department, there were a lot of things in this text that I didn't end up needing or using.

I think some of the terminology, while accurate, was difficult for some of my students to understand.

Good internal consistency in terminology and formulas.

Modularity rating: 4

Pretty good modularity, as i only assigned part of each chapter for readings.

I think the organization is great. It starts off with the background things one needs, such as what a random variable is and what distributions are, then advances through more complex information regarding inferential statistics. I might change the order of a few of the chapters towards the end of the book, but that would be all.

Interface rating: 4

There are a lot of "Box"es that almost seem necessary for students to read/interact with to get the knowledge in them. I would just make those part of the plain text.

No grammar errors that I caught.

I don't think it referred to race at all.

This book is a great resource for teaching intro stats. However, I do think that the next time I teach this material, I will be switching to Learning Statistics with R or one of its variants. That is not because I think this textbook is bad by any means, but it actually is just too general in its approach. I want an open text book that is more geared towards psychology students, rather than general statistical use.

Reviewed by Kim Proctor, Lecturer, California State University, Dominguez Hills on 12/8/22

The text covers multiple areas that are necessary for students to grasp a basic knowledge of statistics. However, I would have liked to see the inclusion of information for some kind of computer-assisted analysis of descriptive statistics, contingency tables, z-test, t-tests, ANOVA, linear regression, and chi-square. Whether these analyses were conducted via excel, SPSS, some free online calculator, or R, these would have been helpful as I end up using other resources in order to include computer-assisted analyses to familiarize my students with these processes. The index is comprehensive. However, some information included in both the main sections and glossary is somewhat confusing, e.g., the data set(s), of which there are only two, are not fully explained and are somewhat unuseful for multiple forms of analysis practice.

I did not notice any errors in the accuracy of the book. However, the supplemental materials--in particular the lecture slides had a few slight errors.

While I do believe the book has excellent longevity, I maintain that adding support information on computer-aided analyses for each of the sections using Excel, SPSS, R, or some free online calculator would make the book much more relevant and more attractive to instructors who would prefer a book that includes such information. I do believe the way the book is arranged and formatted aids in ease of updating. With that stated, some questions discuss elections, polling or other issues that do not account for the current influence and uses of social media, the internet, and smart phones.

Clarity rating: 2

The text is somewhat accessible. I do not believe the way the different areas of text, examples, and explanations are set up within the book are as accessible, clear, and readable as they could be. In fact, the format of the text and examples at times makes the book difficult to follow. As stated in a previous section, some information included in both the main sections and glossary is somewhat confusing, e.g., formulas, concepts, and the data set(s)(of which there are only two) are not fully explained and are somewhat unuseful or confusing without further explanation from the instructor and examples from other texts, this is particularly relevant to the "try this, and "let's practice" examples.

The text is extremely consistent in terms of terminology and framework. Although, in my opinion, the terminology and framework are not as accessible to college-level intro stats students as it could be.

I believe the modularity of the reading sections and the inclusion of a course pack that can be uploaded to Canvas or Blackboard is extremely helpful. I can assign students to read only one or two sections of a chapter, and I can mix and match sections from different chapters. I absolutely love the Modularity of this book.

The topics are presented in a logical and clear fashion. However, I believe the ordering of topics could be improved. For example, ANOVA should be presented after the chapter on 2-sample t-tests, and Normal Distribution should be presented after the chapter on probability.

The text is free from navigation issues and distortion of images. However, the images and other display features are not that aesthetically pleasing: most are presented as grey tables, etc.

I noted no grammatical errors in the text.

Cultural Relevance rating: 2

The text is not culturally offensive. However, the text is extremely insensitive. It does not account for alternative options for male/ female, and is not inclusive towards varied cultures and beliefs. Racial "minorities" are rarely mentioned in the text, and are not reflected in visuals.

1. I suggest alterations/ additions to the information in the text: in the form of some kind of computer-assisted analysis of descriptive statistics, contingency tables, z-test, t-tests, ANOVA, linear regression, and chi-square. 2. I do not believe the way the different areas of text, examples, and explanations are set up within the book are as accessible, clear, and readable as they could be. In fact, the format of the text and examples at times makes the book difficult to follow. 3. With regard to relevance, some questions discuss elections, polling, or other issues that do not account for the current influence and uses of social media, the internet, and smartphones. 4. The text is not culturally offensive, but it is extremely insensitive. It does not account for alternative options for male/ female, and is not inclusive towards varied cultures and beliefs. Racial "minorities" are rarely mentioned in the text and are not reflected in visuals.

Reviewed by Lauren Farr, Instructor of Mathematics, Spartanburg Community College on 9/22/22

In reviewing this material, it appears as though the text meets or exceeds the standards set for traditional textbooks for an Introductory Statistics course. The content appears to be comprehensive, accurate, and up to date. This text could be used to teach an Elementary Statistics class and covers enough topics that it could be used for an additional course in Intermediate Statistics.

I have yet to find an error in any of the material.

The problems in the book are made in such a way that the text will not become obsolete. For example, they use general topics such as heights of people on a sport’s team instead of naming a specific team or year. This is good because the book can be used for a longer period of time.

The book gives the formal definitions and applicable theorems. For clarity, it then gives problems and examples to illustrate what these definitions and theorems actually mean so students can better understand them. The examples are provide students with a reasoning behind why we "need" the theorems to begin with and how Statistics can apply to their life.

Material is presented in an orderly way. It gives the definition and applicable theorems. It then gives problems and examples to illustrate what these definitions and theorems actually mean so students can better understand them.

The glossary and the table of contents are especially important aspects of online learning tools. This text makes it extremely easy to switch between different topics and navigate around the book. The book is broken up into sections that cover a specific topic, so it is easy to find material. This divides the material into smaller sections which helps students better learn the material and to not become overwhelmed.

The glossary and the table of contents are especially important aspects of online learning tools. This text makes it extremely easy to switch between different topics and navigate around the book. The book does go in a logical fashion from basic Statistics concepts/definitions to more complex ones.

Many students do not want to write in a physical textbook. This online book allows you to highlight sections and make notes while you are reading that you can easy access later without having to flip through the book to look for where you wrote notes. I have yet to find any interface issues.

I have yet to find any grammatical errors.

Cultural Relevance rating: 3

The text is not culturally insensitive as most problems are about “people” or “doctors” or “neighbors”. There is no reference to race, ethnicities, or backgrounds.

This appears to be a fabulous textbook. I look forward to investigating it further. I am also excited to apply some of the ideas, such as the group project problems, to my classes.

Reviewed by Nels Grevstad, Professor of Statistics, Metropolitan State University of Denver on 8/18/22

Comprehensiveness rating: 3 see less

The book covers all the topics typically covered in an introductory statistics class, but the depth of the coverage is sometimes less than adequate. As an example, self-selected samples are described as "unreliable", but there's no mention of WHY. As another example, there book provides almost no intuition behind the (probability) Multiplication Rule and Addition Rule.

Content Accuracy rating: 3

The content is generally accurate, but in a few places it's just plain wrong. For example, Figs. 8.2 and 8.3 attempt to explain confidence intervals using a graph of a normal curve centered on X-bar (the SAMPLE mean) and with the CONFIDENCE INTERVAL endpoints marked on the horizontal axis capturing the middle 90% of the normal distribution. What variable is this the distribution of?

Some of the data sets will become outdated with time, but I think that's true of any statistics textbook.

Clarity rating: 3

The clarity of the book is generally adequate, but explanations are often lacking, and there are numerous places where clarity could be improved upon. An example of this is using the same symbol to represent different things -- in Try It 3.13 (a probability problem), the letter S is used to represent an event, but everywhere else in the chapter, S is used to represent the sample space.

The text is generally internally consistent, but there are several inconsistencies. For example, in Chapter 2, sometimes the symbol used for the sample standard deviation is Sx (S with subscript x), other times it's just S (no subscript). As another example, sometimes the right side of the (probability) Multiplication Rule is written as P(B)P(A|B) and other times as P(A|B)P(B).

There are not any major problems with the modularity of the book that I could see.

Organization/Structure/Flow rating: 2

The organization/structure/flow of the book is NOT well-thought-out.

There are numerous places where a term is used before it has been defined. For example, in Example 1.3 the term "simple random sample" is used before that term has even been defined. In Try It 1.10, a histogram is used before histograms have even been covered.

Furthermore, there are several instances where NEW ideas are introduced in the Chapter Review section. An example of this is describing the relative advantages and disadvantages of stem-and-leaf plots versus histograms in the Chapter 2 Review, but this isn't mentioned at all in the main body of the chapter. Another example of this (also in the Chapter 2 Review) is the introduction of grouped bar charts and stacked bar charts, neither of which is discussed in the main body of the chapter.

There are many other organizational deficiencies, too numerous to mention here.

I only saw only a few minor issues with the interface of the book, and they shouldn't distract or confuse the reader.

Grammatical Errors rating: 2

There are grammatical errors and typos, and in some cases, they can cause confusion. For example, the term "statistic of a sampling distribution" appears in multiple places (it's supposed to be "sampling distribution of a statistic"), including in a section header.

Cultural Relevance rating: 4

The text is not culturally insensitive or offensive, but it does not appear to me that the authors went out of their way to find examples that are particularly inclusive.

I do not plan on using this book for my classes in future semesters.

Reviewed by Aaron Zerhusen, Assistant Professor, Dominican University on 5/9/22

Most of the typical topics covered in an Introduction to Statistics class are all covered in reasonable detail. Basic descriptive statistics, constructing and reading various types of graphs and charts, an introduction to relevant concepts of probability, and hypotheses testing. Notably, Bayes’ Rule is absent. Instructions for use of a TI-83/84 calculator are included, but no other technology is used. The data sets used in the text (including within the homework) do not seem to be provided anywhere in a format that would allow for easy use of technology such as Excel, Minitab, or R. The inclusion of a section on ethics in statistics and experimental design in the first chapter is a welcome feature.

The content is accurate.

Relevance/Longevity rating: 4

Material is presented with some examples drawn from real-world data, but there could be more. Again, examples and homework problems utilizing data sets that are provided in a format (such as csv files) that could be read by a variety of statistics software would help greatly.

The clarity of the exposition within the sections is lacking. Explanations are terse, relying on the examples to illustrate the concepts. Definitions and theorems are not clearly indicated, but rather are often hidden within a paragraph. The key terms, chapter review, and formula review sections at the end of each chapter are helpful.

The notation and techniques introduces are consistent.

The modularity by chapter is typical of a book of this type. A flowchart of dependencies would help instructors, and is not provided.

The organization is typical of an introduction to statistics text.

The interface is standard and clear. The web version of the book takes advantage of HTML to show/hide solutions as appropriate in exercises for students to work through.

Grammatical Errors rating: 3

There are a number of errors in the mathematical typesetting which detract from the clarity of the book.

Examples are pulled from data for a range of subjects. The language used in the text is rather neutral.

If the instructor is careful to address the places where the book is not clear I think this will be a fine textbook. The inclass activities and lab assignments are very nice.

Reviewed by Lance Kruse, Adjunct Assistant Professor, Bowling Green State University on 4/17/22

The textbook addresses the foundational concepts for statistics, including a robust discussion of sampling and descriptive statistics. Even for students who may not frequently utilize inferential statistics, the beginning chapters provide a wealth of knowledge about descriptive statistics and introductory probability concepts. The inferential statistics are quite comprehensive and organized logically based on the samples and means being compared. The concepts align with the several introductory educational statistics courses I have taught.

No errors or biases were identified.

The topics used in the examples span a diverse range of topics including higher education enrollment, high school sports, technology, research projects, business, politics, health care, and many everyday life examples (e.g., pizza delivery). Some of the dates mentioned in the scenarios are a bit dated (e.g., year 2008, iPhone 4s), but these do not impact the purpose of the example. Statistics do not become out of date, so there is not a concern about the relevancy of the content moving forward. The textbook does provide support for using a TI-83/84 calculator, which is quite nice to improve accessibility to the calculations required.

The writing is clear, accessible, and approachable to any reader regardless of their prior statistics knowledge and/or experience.

Terminology is clear and consistent. There are helpful glossaries at the end of each chapter to define the key terms used. Parenthetical clarifications are provided to ensure ideas are clear.

Each section has several subheadings to more clearly identify specific sections of the reading. Those sections are accessible as separate standalone readings that do not require readings of previous sections to understand them. The text uses several examples to clarify the concepts and does not overly refer to previous sections of the text.

The flow of topics is logical and appropriate for an introductory statistics course.

The PDF download is neat and clear. There is a digital table of contents that shows all of the chapters and subsections in the chapters that automatically navigate you to those sections. This makes it very easy to jump around to various parts of text with ease.

No grammatical errors were noticed.

Gender is presented as a binary (male/female) and is not inclusive of the full spectrum of gender identity. However, this issue is not relegated to only this text and is commonly present in most statistics textbooks. I believe a standalone discussion of inclusivity in research and statistics should be presented by the instructor to discuss the importance of inclusivity in research, but yet the practical issues this may cause for statistics (e.g., having inclusive categories for self-identification that may result in very small sample sizes that violate the statistical assumptions required for an inferential test). These discussions should be happening in the classroom to ensure students are engaging in ethical and culturally responsive research while also understanding the implications of such decisions.

Reviewed by Matthew van den Berg, Professorial lecturer, American University on 1/14/22

Provides coverage of all the usual topics for an introductory statistics course along with extra topics that many courses will likely skip due to time constraints. read more

Provides coverage of all the usual topics for an introductory statistics course along with extra topics that many courses will likely skip due to time constraints.

I came across no errors or accuracy issues, and did not perceive any biases.

The text is relevant and up-to-date. It's introductory statistics, so I can't really imagine a text being "out-of-date" in this field. The one issue here may be that this text provides additional instruction for using a TI-83+ and/or TI-84 calculator. This may still be the preferred calculator for many students, but students many students may only rely on computer based analysis so the calculator instructions are less valuable.

The text is well written and comparable to the clarity of any other statistics textbook. This may be subject to students' preferred learning methods however, as this text heavily emphasizes examples to explain new concepts. Often rather than introducing the theory behind a new concept, then providing an example, the text often goes straight into an example and uses that example to show the theory.

The formulas and language are consistent throughout.

I skipped several sections within the text, and the flow of the material and explanations did not suffer from it.

Organization/Structure/Flow rating: 4

Sometimes, the text over-uses examples as an introductory tool for new concepts. This may be helpful for some students, while other students may prefer an organization structure the first provides theory and formulas, and then offers an example. I think the heavy use of examples in the text is generally a good thing, however it can lead to formulas and theoretical concepts getting somewhat lost in those examples.

I experienced no interface issues with the text.

The text was well-written and free of grammatical errors.

I noticed no cultural biases or insensitivity issues.

I was happy with the textbook for an introductory statistics course that covered: descriptive statistics, probability, hypothesis testing, and simple linear regression. Stylistically, the text relies heavily on examples to explain the concepts. This provides a lot of chances for students to read applied examples, but can sometimes obscure the core concepts, theories, and formulas.

Reviewed by Emily Breit, Professor, Fort Hays State University on 10/13/21

The textbook covers the chapters you would generally find in a one semester statistics course. It provides general coverage of the content areas including: descriptive statistics, probability, CLT, confidence intervals, hypothesis testing, and... read more

Content appears to be error-free and unbiased.

The content is up-to-date and, as with most statistics textbook, the material should remain relevant for an extended period of time.

The textbook provided simple, easy to follow examples.

Consistency rating: 4

Terminology and variables were consistent throughout the text.

The authors did a good job of providing both written and visual examples of the content.

The chapters followed from descriptive statistics and probability into more application based examples.

Charts and graphs were clear and provided additional insight into the problems presented.

Grammatical errors were not detected.

The examples were easy to follow and were based on content that is inclusive to students with diverse backgrounds.

Reviewed by Stanley Elias, Adjunct Professor, Massasoit Community College on 6/24/21

Quite comprehensive as an introductory text for non-technical students. It touches on topics not usually seen in an introductory text (hypergeometric and Poisson distributions, e.g.) The index is an effective search tool for finding specific... read more

Content Accuracy rating: 4

I noticed a very few minor inconsistencies in the tables, but on the whole the text is accurate and unbiased.

Content is in keeping with current society and technology and can be easily updated when the need arises. The modularity of the text allows for the easy rearrangement of the order of presentation.

It is easy for mathematics texts to lapse into jargon. That is not the case here. Topics are explained carefully and logically in a way that is easy to follow. The conclusions thus reached are abundantly clear.

The terminology used in the text is consistent from one chapter to the next. Especially appealing are the "Try It" problems that follow example problems, enabling the student to apply what was illustrated in the example

Each chapter follows from the one before and leads to the next, but if desired they can be rearranged without any loss in continuity. For example, I prefer to teach correlation and regression earlier in the course than it usually occurs, so I present Chapter 12 (Linear Regression and Correlation) between Chapter 3 (Probability Topics) and Chapter 4 (Discrete Random Variables). This change is mentioned in the preface as a possible rearrangement.

Topics are presented in the logical order one would expect. I especially appreciated the different problem sets (Practice, Homework and Bringing It Together) that present problems of increasing difficulty.

There are no interface issues. The charts and tables are appropriately sized and colored and easy to read.

I found no grammatical errors.

The text is apolitical. Some of the names mentioned in the problems appear to be the only cultural or ethnic references.

I have used this text the last three times I have taught the course, and I intend to use it again. I especially appreciate the inclusion of Texas Instruments calculators when appropriate. The guidelines and step-by-step procedures are a great help. Another help is the set of practice tests and finals in Appendix B. The text is not as slickly produced as those from the major publishers, but it is still complete and very accessible to students. And as an Open Source text, there is never any excuse not to have a copy!

Reviewed by Tingting Fang, Associate Professor, North Shore Community College on 6/23/21

This OER book covers all the required topics as an introductory statistics text. The content is well presented using examples, lots of exercises problems. After examples, there are Try it questions provided. This gives the students chance to check their understandings of the topics immediately. TI calculators are widely used in this text, so some formulas or complicated mathematical theories are not introduced. For Non-math majors, I would say this is good and give the students chance to focus on the application part of the theory. TI-calculator command descriptions are included within examples. Students can easily follow what is taught.

Most of the contents are accurate and presented very well.

Content is up-to-date, but not in a way that will quickly make the text obsolete within a short period of time. The text is written and/or arranged in such a way that necessary updates will be relatively easy and straightforward to implement.

It is easy for me as an instructor to read the book since I already know the fundamental concepts for probabilities and statistics. However, there are some symbols that are not commonly used in the other same level statistics book. For example, chapter 10 presents how to calculate confidence interval. EBM is used to represent” margin of error”. This 3-word symbol is not user friendly in the formulas. It is better to use a single letter E to denote it as in the other books

It is very consistent. The language of the contents is easy to follow.

In general, each model of the book is well designed. Different sections could be rearranged easily depending on the topics covered by the instructors. One thing that can be improved is in chapter 2: Descriptive Statistics. Measures of the Location (2.3) is introduced before Measures of the center (2.5). However, the concept of mean (average) is used when Percentile is calculated in sec 2.3. I would suggest to move sec 2.5 before sec 2.3.

This book is well organized. The part I like most is that each chapter includes contents part, Key terms, Chapter review, homework problems and solution keys. Students can easily find what they need. It is easy to use.

It is very easy to find the right contents.

It is well written. It is easy to understand what the book is trying to present.

The text is not culturally insensitive or offensive in any way.

As an OER book, this text is a good choice with no cost. For those who heavily rely on TI-calculators, this book is even better.

Reviewed by Isaias Sarmiento, Assistant Professor, Bunker Hill Community College on 6/7/20

This textbook is a bit different from other textbooks in its coverage of topics. Here are some observations: 1. The topic on ethics is addressed early in the textbook. (Most textbooks I have found don't pay much attention to ethics.) 2. While there is mention of experiments, I could not find any mention of observational studies. 3. Percentiles are mentioned, but there is no discussion on how to find percentiles methodically. 4. There is strong presence of the use of tree diagrams and Venn diagrams in calculating probabilities. 5. There is strong emphasis on the TI-83/84 to calculate probabilities.

I did not notice any math computation errors. I did notice some typos. In Section 1.2, there is a math example about the demographics of two colleges in the Spring 2010 quarter, but then there are references to Fall 2007.

I'm reviewing the 2018 edition of the textbook. Some of the contexts seem a little outdated. (In Chapter 8, there is an example about smartphones, and the phones listed date back to the early 2010s.) With that said, I don't think the outdated contexts detract too much from the content. At least they are still within the same decade!

The textbook sufficiently defined vocabulary terms and, where appropriate, provided examples of those terms.

In Chapter 3, there is mention of the P(A and B) probability. But I think we have to be careful about this notation. If the problem involves a single selection, then P(A and B) is really just a joint probability -- one fraction, that's it. But if the problem involves two selections (with or without replacement), now we're talking about the multiplication rule. The book mentions the multiplication rule early on in 3.2, but I just couldn't find any examples of how with/without replacement is applied within the multiplication rule.

The discussion on conditional probability could have included the intuitive approach.

It seemed that the terminology used was consistent throughout the textbook. The one time where I felt that there was an inconsistency is in the construction of histograms. In some histograms, the classes overlapped (e.g. 59.95 - 61.95, 61.95 - 63.95). In other histograms, the classes did not overlap. Also, some histograms used class boundaries (Example 2.8), while other histograms did not (Example 2.9). On page 82, the authors state that there is more than one way to create a histogram. However, I feel that the authors should stick with just one way for consistency.

The textbook does a good job in breaking down each section through Examples, a Try It! feature, Collaborative Exercises, and a Statistics Lab. Some sections discuss how to use a TI-83/84 calculator to obtain answers. At the end of each chapter, there is a Key Terms list, a Chapter Review, and a list of math exercises followed by the solution key.

Overall, the topics are presented logically. There were some instances in which I felt that specific vocabulary terms were introduced a little early. For example, the term "probability" was defined in Chapter 1, but only in Chapter 3 was the term fully addressed. The concept of sampling with or without replacement was described in Section 1.2, when its relevance was really in Chapter 3. The term "median" was mentioned in Section 2.3 as part of the larger discussion of the percentiles, but then it was formally defined in Section 2.5 as an example of a measure of central tendency. I felt that the discussion on box plots in 2.4 should have been integrated with the discussion on quartiles in 2.3. The linear regression equation was mentioned before the linear correlation coefficient, which I found unusual.

One recommendation would be to place vocabulary terms in boxes. The terms were bold-faced, but the text can sometimes be so dense that vocabulary boxes would have been helpful in breaking up the text.

The page breaks in some places seem strange. On page 138, halfway through the page, there is an instruction to find the standard deviation, but the rest of the page is blank. On page 141, there is only one line of text.

The interface was sufficiently clear. I noticed that, in the online version of the textbook, the exercises that referenced tables and figures included a hyperlink to the table/figure so that the student can easily refer to it. Also, the online version allows you to highlight text and make comments, as though you were writing notes within the book.

Grammatical Errors rating: 4

In a couple of instances did I find a grammar or spelling error. In the 1.10 Try It!, the graph should say "per Student", not "per Students". On page 181, the word "rolls", as in "rolls of a fair die", was misspelled as "roles".

The textbook was culturally sensitive. The book made an effort to use names that imply different racial/ethnic backgrounds (e.g. Rosa, Binh). The textbook was also willing to include applications that may be deemed controversial (e.g. AIDS). I did notice that, at least in the first chapter, there seemed to be a focus on California-related contexts, though I don't recall the entire textbook being that way.

If you are accustomed to using a author like Triola, this textbook might take some getting used to. You will be hard pressed to find any mention of the counting methods (factorial, permutation, combination), and this may help explain why the binomial probability distribution formula is not mentioned. Regarding hypothesis testing, the null hypothesis is not restricted to the "equal" case, as it considers the cases "less than or equal to" and "greater than or equal to". With its focus on the TI-83/84, the textbook effectively avoids other accessible tools like Excel and even normal probability tables. If you have students who do not have access to a TI-83/84, then you will need to provide extra instruction.

Reviewed by Elaine Petrocelli, Adjunct Instructor, North Shore Community College on 5/27/20

This text is comprehensive for an Elementary Statistics course that is not geared toward math or engineering majors. It covers all the typical topics found in an Intro to Statistics book. The text includes an introduction and chapter objectives at the beginning of each chapter. There are examples as well as Try It problems. At the end of each chapter included are key terms, chapter review, formula review, practice and homework problems and a StatsLab exercise. Answers to odd questions are available as well. It includes a nice glossary and index that are easy to use.

The text is complete and the formulas and key terms are accurate as well as unbiased. I did not find any errors in the calculations.

The content is up to date and will not become obsolete any time soon. The examples used are classic and ageless. Because of the structure of the book, any updates would be relatively easy to incorporate.

The text is written very clearly in a manner that students can understand. The examples and try it problems allow the student to apply what they've learned to test their understanding. The end of the chapter review, key terms and formula review are also very helpful. The instructions for the problems are clearly written and easy to follow.

The text is consistent throughout in format and in usage of industry standard terms and formulas. The framework and terminology is consistent with that of other published statistics text books.

The text can easily be divided into sections that can be taught at different times during the course. In the preface of the book it even lists alternate sequencing. There are several sections that could be left out or used as stand alone.

The topics in the book are presented in a clear logical order. The text includes an introduction and chapter objectives at the beginning of each chapter. There are examples as well as try it problems. At the end of each chapter included are key terms, chapter review, formula review, practice and homework problems and a StatsLab exercise. Answers to odd questions are available as well. The different color highlighting and bolding also help to transition from topic to topic or to the next chapter. The organization also allows for skipping sections or teaching out of order.

The interface was easy to use and had no navigation issues. The images and charts were clear and easy to understand. The highlighting and bolding made it easy to know when a new section began and easy to find what you were searching for. I didn't encounter any distortion of images or charts.

I did not find any grammatical errors.

The text appeared to be neutral regarding culture. There were no offensive or insensitive references. Examples were inclusive and diverse.

I liked the StatsLab and Try It sections. I also liked the collaborative exercises and Bringing it Together Homework. This text offers much opportunity to apply what is learned which is really important in statistics.

Reviewed by Rachel Keller, Adjunct Instructor, Radford University on 1/21/20

This book is quite comprehensive for an introductory course. Many topics that are not typically covered in a survey course are included (e.g., the geometric, hypergeometric, and exponential distributions are included in addition to the ubiquitous binomial, poisson, and normal distributions). Furthermore, there is an extensive collection of supplemental resources for both the student (e.g., calculator guide, formula sheets, descriptions of mathematical phrases and symbols) as well as the instructor (e.g., data sets, practice exams, projects).

The content of this text is adequately accurate and unbiased.

The fundamental concepts covered in this text are classic and likely to withstand the test of time. What distinguishes statistics textbooks from various decades is not the tests, distributions, or even necessarily terminology, but rather the technology and the datasets. This text illustrates data analysis with the current technological standard of the TI calculator series, which has all expectation of remaining current for some time. A majority of the provided data for examples is based on demographic/social/educational data (e.g. heights, pizza delivery times, test scores) that are unlikely to become problematically dated so as to obfuscate the underlying statistical process. When specific dates and data are provided, they seem to be largely representative of the most recent decade and updates would be straightforward to implement if desired.

The prose of the text is lucid and accessible. Key terms and formulas are offset in bold text and subsequently defined/listed (in end-of-chapter resources) in that familiar presentation that students have come to expect. The one disadvantage is that the explanations are quite succinct, but border on terse sometimes in a manner that might leave weaker students wanting more detailed descriptions in layman's terms to accompany the math jargon. On the other hand, what the text lacks in depth of prose, it makes up for in breadth of example problems which allows the author to "show" the reader how the concepts works rather than "tell" him so.

There were no issues with consistency.

Like most statistics textbooks, the topics are presented in such a manner that individual sections or chapters can be omitted freely at the instructor's discretion. There are occasional references to preceding material (with hyperlinks to another section of the text) which might direct the student to a section the instructor did not cover, but these are infrequent enough as not to be problematic. One nice feature of this text is that the practice problems and exams are subdivided by section/chapter for easy problem identification which facilitates test construction when sections/chapters have been omitted - this is in contrast to those textbook publishers who simply publish chapter reviews with a jumble of problems the instructor has to sift through when not covering all topics.

This textbook is arranged in the typical ordering/grouping of topics as most introductory texts. Most instructors will find no need to reorder, but this can be easily accomplished if desired.

Interface rating: 3

The interface of this textbook is reasonably user-friendly. Navigation within the textbook sections and supplemental resources is quite straightforward. The only issue I see here is that the there are no physical copies of statistical tables provided; rather, the reader is directed to "links to government site tables used in statistics" - which is a link to a SUNY Polytechnic Institute website with an online textbook (Engineering Statistics Handbook). The individual 'tables' present at first glance like they might be online distribution calculators, but they are not, and the table values are listed after the content in a form that is not readily conducive to printing. Arguably, a student could learn to find appropriate values within this page, but scrolling would make this needlessly annoying and the instructor could not provide exam copies of these tables from this site and would need to look elsewhere. My suggestion is that the book could be improved by directing the students to links to online distributional calculators (for use on HW and in-class) and by providing printer-ready pages (for exams) in the appendices so that both formats were available.

No obvious issues with grammatical errors.

No reason that any reasonable person would find legitimate claim that this book is culturally insensitive. Statistics is a subject that is universally relevant and the problem sets, descriptions, and examples show no intentional cultural bias or insensitivity.

Reviewed by Jamie McGill, Assistant Professor, East Tennessee State University on 10/31/19

The text is comprehensive for an Introduction to Statistics course. The topics include what is typically taught in a freshman level Probability and Statistics course. I compared the topics with those taught from our current textbook and there is... read more

The book is accurate and complete in examples and information. No errors or bias noted. A good attribute of online textbooks is that if an error is noticed, it can be fixed quickly.

The text presents the topics in a way that will not become obsolete. Because no statistical software is included in the textbook, the instructor always has the option to introduce the software preferred at the time. Various calculators are mentioned, again because there isn't only one, the textbook will withstand time.

Definitions and summaries are included in each chapter. The text is written in a clear manner and is easy to understand.

The book follows the same basic structure for all chapters, making it consistent and easy to follow within each chapter.

The chapters could easily be reorganized while still making sense. This allows the instructor some flexibility in covering the material.

The arrangement of topics is presented in a logical manner. The topics are organized for an easy flow from chapter to chapter. Within each chapter, there is the same structure and arrangement. Again, this helps with the transition from chapter to chapter.

Overall, the interface is adequate. Slight distortions of images/tables are not significant nor confusing when reading through the chapters.

I did not see any grammatical errors.

Examples are culturally inclusive. I noted no offensive or insensitive wording or examples.

Being an OER textbook, it is a much better deal for the students than the traditionally published text that is often used. This text covers the same topics and links to an online homework platform if that is desired. It appears to be comprehensive as a textbook for a non-calculus based statistics course.

Reviewed by Meryem Abouali, Adjunct lectruer, LAGCC on 5/10/19

This book does contain a table of contents and the main components necessary to cover the average course in statistics. It provides an effective index. read more

This book does contain a table of contents and the main components necessary to cover the average course in statistics. It provides an effective index.

The content is accurate. Formulas and definitions are accurate . There isn't any obvious numerical error

The book is very relevant. the context is up to date. The text is written and arranged in such a way that necessary updates will be relatively easy and straight forward to implement. An instructor can supplement this with hands-on activities. Many of the examples are universal in nature and will still remain relevant for some time to come.

The text is clear and provides adequate context for any technical terminology used. It is clearly defined in terms of the notation and symbol used.

The text is consistent in terms of terminology and framework. The layout of each chapter is consistent . The reader quickly can become familiar with how each chapter is presented and knows what to expect.

It is nicely laid out and can be no problem modularize it depending on an instructor's preference. . The text is readily divisible into smaller reading sections that can be assigned at different points within the course. On a larger scale, the chapters are organized logically and in a manner consistent with other similar texts.

The topics in the text are presented in a logical , clear fashion. The statistical concepts are presented inn a clear and logical order and the flow is logical too.

The interface is base on PDF format which is convenient for students and allows them to download the text to their laptops, tablets, ...etc

The text contains no grammatical errors.

The text is not culturally insensitive or offensive in any way . It should make use of examples that are inclusive of different races , ethnicity of different background.

Overall, the text does the job for which is written for and covering most of thee necessary topics needed for introductory statistics course.

Reviewed by Thomas Blamey, Math Faculty, University of Hawaii Maui College on 5/8/19

I felt the textbook was as good as an publishers text in this introductory field. read more

I felt the textbook was as good as an publishers text in this introductory field.

I did not see any glaring errors...and for the most part I felt is used common language an introductory text would use... Accept when the authors were introducing "Confidence Intervals". They used uncommon language such as: EBM (this is not common and they should use a more common item such as "E" or "ME") error bound (this is not common and they should uses "margin of error" as the vast majority of intro texts do) P′ =X/n (they bounce back and forth on a "cap" X or not x...it should be non cap). This would make it much easier for the majority of students who will be migrating on to the next course in this area of study.

This area of study has changed little in recent times...and the text displays a "standard" delivery of the content. I would have love to see them include multiple technologies (not just the TI calculator). I use Excel as it is the gold standard for desk-stations around the globe (although I understand many classrooms are not equipped with computing so the TI is the standard technology for "Ed").

The text is written well and has an average communication level when delivering this material.

The authors have done well to keep a consistent tone - difficulty when more than 1 author is involved.

The text does a good job of following the market and breaking the topics into chapters that can be taken or re-arranged to suit most introductory courses.

The organization is typical of this level of course - there is disagreement as to where "correlation/regression" should be placed (but the majority of texts at this level place it in the end - I would split this into "descriptive" and "inferential"). The "descriptive" could be included in Ch2 as a section.

The interface is fine - it is a "free" text so one would not expect the top shelf pictures and images.

Again...the only issues I saw here (minor) were the "cap" X or not when discussing sample proportion.

The text seemed culturally neutral...

I want to thank the authors for their work...I am actually using it in my University courses with MyOpen Math... And I am currently reworking the standard to fit my thoughts above and using data local to my community.

Reviewed by Kim Spayd, Assistant Professor, Gettysburg College on 3/11/19

The very basic topics are included and a surprisingly large number of specific probability distributions. However, inferential topics are lacking. Sampling distributions are glossed over in a very unsatisfactory manner and their connection to inferential techniques is not made clear enough. Additionally, the coverage of confidence intervals is inadequate; only three intervals are discussed. In contrast, hypothesis tests are adequately covered.

I found no factual errors.

The content is standard and updates would be infrequent, if necessary at all. However, many of the examples are disappointingly banal. It is understandable that the authors would not want to include examples or references that might need frequent updating. But there are so many options for examples that are more interesting and appealing to college students.

The prose and examples are very accessible but maybe too much so. The level of exposition is very low, leaving out many details that could explain choices made later. Such information would not necessarily be lost on an introductory statistics student; rather, I think it would make for a richer understanding of the mechanics of inferential statistics, which is the most useful part of the text.

Vocabulary is repeatedly introduced but in different contexts; this could be confusing or helpful, depending on the person reading.

Sections are short and easily divisible for reading assignments.

The organization of the material is the biggest weakness of this text. A multitude of topics are introduced quickly within the same chapter or section, one right after the other, with little connection between them. Terminology is often reintroduced. For example, the median of a data set is described in the context of quartiles and the interquartile range, then later reintroduced in the section about measures of center. The interquartile range is not addressed in the section about measures of spread. Another example is the inclusion of Type I and Type II errors before finishing the mechanics of a hypothesis test. No adequate discussion of the probabilities of these errors can take place until much later in the text. Unfortunately, there are many more examples of the seemingly haphazard organization of the material.

Overall the interface is adequate. There are some tables that are split between pages (for example, moderately sized frequency tables) and some notation that is spaced oddly (for example, sample mean and standard deviation as well as z-scores for confidence intervals). Every so often, there is a page that is mostly blank for no clear reason.

The examples generally avoid topics that could be considered even close to topical or controversial. The one caveat I have noticed, not limited to this text, is the repeated mention of gender binaries (boys and girls, men and women). Recognizing and including a category for people who identify as non-binary would be a step towards increased inclusivity.

Reviewed by Patricia Swails, Professor of Education, Oakland City University on 2/25/19

The text presents a comprehensive course in basic statistics. There is an index as well as a glossary and reference list after each chapter. Chapter sections are congruent across chapters, including collaborative exercises for group work, guiding questions a Statistics Lab, Try It guided practice, extensive practice problems based on real-world experiences, and homework. Problem solutions are also provided. Ancillary materials include an instructor manual, Get Start guide, and PowerPoint. Instruction includes key terms, statistical formulas, graphing, and calculator information. There is, however, no discussion of validity or reliability, nor is there any discussion of post hoc testing in the ANOVA chapter.

The text is predominantly error free and unbiased. There is a typo on page 456, listing both Goset and Gossett as the statistician’s name. It makes a clear distinction between data and datum, which is commendable considering the current tendency to use data as a singular term. The null and alternate hypothesis formats are a bit unusual, stating the null as less than and the alternate as more than, rather than the usual no difference or relationship for the null and increase/decrease or there is a difference or relationship leading to a two- or one-tailed discussion.

The text is a traditional presentation of statistics that strongly supports its longevity. The text is appropriate for advanced high school and bachelor levels as well as a graduate-level survey or resource for an advanced statistics course. Information is also presented on IRB and ethics, not always found in statistics instruction. Each chapter is thorough, including TI programming calculator instructions, but there is only a vague reference to statistical software with no direct mention of Excel or other statistical software such as SPSS. The instructor can easily add computer software to the Collaborative Exercises.

The instructional narrative is presented in a conversational style that helps those students intimidated by statistics. The text thorough fulfills its purpose to help students design, implement, and analyze basic statistical concepts. Key terms are presented in bold font. Each chapter states specific objectives and learner outcomes. Most importantly, the text explains the why as well as the how, much more than the basic, Do This. Further, the text includes traditional formula notation, a feature often omitted in many statistics texts.

The text is most consistent in the presentation of terminology. There are some variations, however, such as the introduction of the Independent variable but no reference to the dependent variable. Rather, the terms explanatory and response variables are used. There is no mention of control, moderator, or intervening variables and uses the term, lurking variable rather than the traditional term, extraneous variable. Skewness is presented as right or left skew with no mention of positive or negative skew except in a table. Further, the term, symmetric, is used early in the text then the term, normal, is used later in the text to describe distributions. Different terms are used in place of measures of dispersion and central tendency.

The congruency of chapter components allows instructors and students to easily organize the learning environment. Using the same sections in all chapters assures the instructor of a thorough coverage of any topic presented. Each chapter includes objectives and learning outcomes to assist the instructor in identifying specific readings for a course or for ordering the chapters in a specific sequence.

There is a logical sequence of chapters, but some instructors may find the Chi Square instruction out of place. The chapter can easily be positioned between descriptive and inferential chapters without any loss in accuracy and clarity. Chapters can be rearranged or omitted, depending on the course’s purpose. Each chapter builds in complexity of narrative, formulas, problems, etc.

The congruent structure of each chapter helps students anticipate the scope of instruction, practice, and other supports provided for each topic. This ease of navigation also serves to decrease the anxiety level of statistics-phobic students. This text would be an excellent main text or ancillary text for online course delivery formats.

The text does refer to GPA’s rather than the preferred GPAs. The balance of information is error free.

The instruction is inclusive, sensitive, and inoffensive. The example scenarios are based on diverse, authentic studies. Culturally-diverse populations, both genders, etc. are used in examples and problems throughout all chapters.

Introductory Statistics is worthy of instructor review for a variety of secondary and post-secondary course work. I am using the text for my basic statistics survey course.

Reviewed by Kay Graves, Assistant Professor, Fontbonne University on 6/19/18

This Introductory Statistics book covers all the introductory areas/concepts very thoroughly with the exception of Counting methods such as permutations and combinations. These counting methods are not covered at all in the book and thus I must... read more

Per my review and use, I have found no errors.

This book could be used for many ears without any updates. The examples are current and would continue to remain current for several more years

Overall the text/concepts are written in a very clear manner. The only concern I have is that several times when calculations are used, the formulas are not always given in the text but the reader must find the formulas at the end of the chapter.

Text is consistent.

Each section of each chapter is well organized. While many sections of this (and other) intro stats books need to be followed in a order, there are several sections that could stand alone or be left out if time is short.

The topics are presented in a typical, logical order for an introductory statistics course.

The online interactive version of the book allows the students to work example problems and then click on the link to see if their work is correct. But the biggest hang-up that I have with this book is that the homework or review problems are numbered in the truly online interactive version; the homework or review problems are only numbered in the PDF or book version. This is a bit frustrating for the student to have to go back and forth between the two versions and for the instructor to assign work.

Grammar is fine.

This book has many examples and assignments that cover many different and diverse topics without being offensive or heavy in one area.

Reviewed by Peter Orgas, Adjunct Lecturer , LaGuardia Community College on 5/21/18

Introductory Statistics is comprehensive and includes all the topics needed for an introductory course in statistics. In the preface, you are given options on how to strategical present the topics during the semester rather than follow chapter by chapter. The section on using the calculator is useful for the students, however, adding the probability tables instead of a link would be beneficial.

I found no inconsistencies, errors or bias throughout the textbook’s content.

The examples and data sets would appeal to a variety of students regardless of their major. It shows that statistical analysis is present in all areas of study. There were sections within chapters that focused too much on the use of the calculator.

The text was very clear. Students can read each section and get a good understanding of the topic due to the use of highlighted definitions and breakdown of problems. There are various examples for students to work out and get a better understanding. Chapter reviews and formulas help to sum out all the topics’ main ideas and terms before the exercises.

I found all the chapters to be consistent in both layout and breakdown.

The chapters are separated into smaller topics which makes it easy to use all parts of the chapter if necessary. Also, the preface also gives you an option to use the chapters out of order to design your class differently than just chapter 1 then 2.etc., thus the textbook is structured to use the chapters you only need without losing the concepts.

The topics are presented in an order consistent with any high priced introductory statistics textbook I have used.

I found the interface to be very consistent and there were no images distorted.

In the various chapters I reviewed. I found no grammar errors.

I found the textbook to be neutral with no insensitive or offensive materials. It appears very inclusive.

I found the textbook very useful and better than some high priced textbooks and plan on using it in upcoming semesters.

Reviewed by Jill Jamison Beals, Assistant Professor, George Fox University on 3/27/18

Introductory Statistics includes all the topics critical to a first course in college statistics designed for a wide range of majors and programs. It is complete in its coverage of the entire statistical process from sampling to application of inferential statistics to generalizing and/or making a decision about a population of interest. For a semester long course, which does not allow covering all the of chapters, the comprehensiveness allows for picking and choosing the most relevant topics for the course. One aspect that is less complete is the sole focus on using the TI-83, 83+, 84, 84+ Calculator for computations. While complete in itself, applications of spreadsheets and probability tables are missing.

I have not found anything that is inaccurate, in error or biased.

The examples and exercises are such that they will not be out of date. There many references to specific colleges and locations that may seem irrelevant to students, but the examples themselves are lasting. The text includes examples and exercises that could be considered “triggers” and instructors should be aware of these, but they are not so intense to be considered inappropriate. Overall the text includes wide ranging subjects, issues, fields, and interests to be meaningful to a wide cross section of students.

The textbook introduces new terminology, notation and formulas and concepts in each chapter while limiting excessive wordiness. This is enhanced by the key terms, chapter review and formula reviews provided at the end of each chapter. In some cases, extra notation is avoided without loss of conceptual completeness, such as using OR and AND for probability statements rather than set notation for union and intersection. The verbal descriptions are concise and dense with many examples to fill out a reader’s understanding of an idea or concept.

The text is consistent in layout and approach to topics. Terminology is used in a consistent way throughout the chapters.

Each chapter has a clear introduction with distinct objectives. And while sections and chapters are ordered in a progressive manner, the text is self-contained enough so that sections and chapters can be presented in an order (or skipped) to serve overall course objectives. Exercises within chapters are also broken out by section, facilitating the assigning of only those exercises that practice desired topics.

The text is organized such that concepts build on each other in a logical fashion. Within chapters, sections move back and forth between explanation and examples, also in a logical manner, addressing key points as appropriate to the flow of the text.

The interface is sufficient, navigating around the text with table of contents is convenient. At times page breaks chop up examples. The font choice and the layout of the online version makes for a more readable text than the PDF version and a better overall appearance.

I have not found any significant grammatical errors in the text book.

For use in the United States the text is relevant. While exercises and examples reference many different cultures (countries) most that have a culture specific reference are about US specific topics such as baseball, the US senate, presidential elections, income, etc. This enhances relevance for American students.

I have used many statistics textbooks for an introductory stats class and find this textbook to be just as good as ones with high price tags, so being free to students makes it a good choice. One of the best feature is the Stats Lab activities/assignments included for each chapter. As is, or adapted, they make for in depth exploration into the given topic.

Reviewed by Cathleen Battiste Presutti, Lecturer, Ohio University Lancaster on 2/1/18

This text covers almost all of the concepts required in an introductory or sophomore level statistics course. However, there is one topic omission that I feel should be included in a future edition is combinatorics. The inclusion of general counting techniques would be beneficial to students and could easily be included in the chapter on probability. In the current edition of the text, it seems as though the authors either assume that students already know the combination formula used in the section on binomial distributions or will be relying so heavily on their calculators that explaining the formula is not necessary.

Beyond the authors' errata which is available separately on textbook's webpage, I have found the textbook to be error-free and accurate.

For the most part, I find that the subject matter in the examples and exercises to be up-to-date. There are a couple of current "hot button" social/political topics and references to current technology that are incorporated into the exercises that I feel will be less relevant in a few years. However, they are few in number. Much of the subject matter used in the examples and exercises is timeless and would not need to be revised in order to make the text feel current.

The concepts throughout the text are explained appropriately and clearly. There is a nice balance between the clarity of the theory and the readability of the text. The prose format of definitions and theorems makes theoretical concepts more accessible to non-math major students without watering down the material.

The text is consistent in its terminology and framework.

There are a few sections in chapters one and two that didn't need to stand alone and could have been combined with other sections due to the relationship of the topics in them. These were sections on data displays. And there was no individual section that would have been improved by separating into two sections. Overall, having the topics separated into smaller sections promotes synthesis of the material.

In chapter three, it seems more appropriate to cover section five (Venn diagrams and factor trees) along with counting techniques before starting probability theory. I also believe that the topics in chapter twelve (linear regression and correlation) would be better suited to introduced before the chapters on probability distributions. Otherwise the remaining chapters of the text are appropriately and logically organized based on the material covered in an introduction to statistics course.

The text is free of any issues. There are no navigation problems nor any display issues.

There are no grammatical errors.

I found the text to be culturally respectful and inclusive with regard to gender, ethic background, etc.

This text is a good introduction to statistical methods. It presents formulas and techniques in a clear way with detailed examples. The theoretical depth of the material is at a level allowing students with a basic knowledge of algebra to understand the concepts while motivating deeper investigation for more mathematically advanced students.

Reviewed by Caitlin Finlayson, Assistant Professor, University of Mary Washington on 4/11/17

The text covers all of the major concepts students would be expected to learn in an introductory statistics course including sampling and data, descriptive statistics, and inferential statistics. While the text might be overly comprehensive for a one semester statistics course, instructors could easily pick and choose which chapters and concepts to include or extend the course over two semesters. Each chapter includes a list of key terms alongside definitions. The text also includes an index as well as multiple appendices such as data sets and review exercises, which would be beneficial for students. The end-of-chapter reviews are also quite comprehensive and include a review of each section, reviews of formulas, and practice questions.

The book appears to be accurate, error-free, and unbiased. It includes numerous examples and sample problems throughout the chapters, whose answers appear to be correct. The text also discusses common biases in statistical research, such as assumptions, sampling methods, and research ethics.

The examples and data sets presented in the book help to make statistics relevant for students. Many of the examples reference university students and all are situated within real-world problems or issues. Most of the data sets are from several years ago (such as carbon dioxide emissions from 2009 and earlier), and it would be helpful if these were updated. However, the variety of examples and data sets provided make this book relevant and applicable to a variety of disciplines.

This text emphasizes examples and sample problems over extensive narratives. The introductory text in each chapter is helpful and clear, but the descriptive text in the various sections of the chapter are often quite brief. It would be helpful if the chapter's narrative flowed a bit more cohesively from one topic to the next. That said, the emphasis on practice questions and examples would pair well with an instructor who could clearly present the concepts in class and then assign the textbook reading following the class meeting.

The book's consistency is excellent and it follows a similar structure across all of the chapters. Each chapter includes numerous examples, and students would particularly find the examples with solutions followed by the "Try It" exercises without a solution immediately listed a helpful way to learn the material, practice it with guidance, and then try it on their own.

This text includes a variety of core concepts in statistics that could easily be rearranged depending on instructor preference. As with any mathematical course, some concepts need to be introduced before others (the normal distribution, for example, is fairly critical in understanding hypothesis testing), but later concepts especially could be reorganized. In addition, less essential core concepts could be eliminated or reduced depending on the course objectives with little disruption to the reader.

The text presents topics in a clear and organized way. Each chapter is similarly structured and presents core statistical concepts in a logical way, first introducing the concept, then providing examples, and finally offering sample problems for students to complete on their own in order to test their understanding.

The text is well-presented with clear, simple diagrams and a consistent visual framework. The tables and figures enhance the concepts discussed and would aid in the reader's understanding.

The text contains no grammatical errors and is well-written.

The text contains a variety of culturally relevant examples, including many data sets and sample problems related to college students. At times, the examples could be adjusted so they are less culturally insensitive. A sample problem in Chapter 10, for example, refers to iPhones being more popular with "whites" than with "African Americans," though some people prefer the label "black," and this example overlooks or oversimplifies broader issues with income distribution. (iPhone purchases are not simply based on cultural preferences, though it's likely a contributing factor.) Perhaps instead of using different races in the example, the text could be revised to compare age groups. Otherwise, the examples include a variety of women and men as well as varying ethnicities and the issues discussed would be relevant for students of a variety of ages and life experiences.

Overall, the text is highly comprehensive, covering a wide array of statistical concepts and including numerous examples and sample problems.

Reviewed by Jonathan Bayer, Associate Professor, Virginia Western Community College on 4/11/17

This book is sufficiently comprehensive for a non-majors introductory statistics course. In terms of content, it offers an adequate number of topics and adequate explanations. However, the book offers very little regarding sampling distributions and the relationship to the normal distribution. There are enough example and homework problems to support the content. The index and glossary were also sufficiently comprehensive.

I did not find any obvious errors in the calculations or formulas.

I found the text contained an over reliance on the use of the graphing calculator. The textbook more or less requires the use of a graphing calculator. I think including a more substantial use of statistical software would have made the text more relevant. Students will find the use of data sets in the textbook and the citation of where to obtain them both relevant and helpful.

The material is presented clearly. Some of the sections are a little bit “wordy” but this does not take away from the overall clarity.

In the sections I reviewed, the notation and terminology was consistent.

The organization and chunking of material in each section is appropriate for an introductory statistics student.

The text is well organized. Each section I reviewed was presented in the same way. It begins with the objectives at the beginning of each chapter, proceeds through vocabulary and examples, and then ends with practice problems. It is organized similar to other statistics textbooks.

The interface of the online version of the textbook works very well. Working through the contents tab you can access any section of the text quickly. The show solution/hide solution option makes it easy for students to attempt examples without looking at the solution. I did have problems when I attempted to visit one of the links to an external website.

The text is “wordy”. I noticed the authors referenced certain ideas imprecisely. When referencing the outcomes of an experiment they failed to use the idea of a sample point and often used experiment interchangeably with event or in place of event when event was closer to the point. These mistakes did not take much away from the text and perhaps I am being a little too critical considering it is written for an introductory student.

The text did not seem to be particularly culturally relevant. I did not find any evidence of it being culturally offensive.

Reviewed by Sandra Porter, Math Instructor, Central Lakes College on 4/11/17

The text covers all of the topics that are included in the Minnesota Transfer Curriculum for an introductory statistics course. Calculator instructions for the TI- graphing calculator family are included in each section. The confidence interval chapter [Chapter 8] does not include finding confidence intervals based on standard deviations and variances. The hypothesis testing chapter [Chapter 9] also does not mention testing for standard deviations or variances. This chapter does spend a significant amount of time giving a good background on the concept of hypothesis testing which will improve student understanding for the rest of the topics. Type I and Type II errors are given good coverage with the introductory hypothesis testing. Table F1 includes an overview of typical English phrases that are often misinterpreted when trying to devise hypothesis statements. Phrases such as, “x is no more than 4”, is illustrated to be equivalent to x = 4. Table F2 includes a chart showing the symbols used throughout a statistics course and gives its meaning and the associated topic for its use.

The content is generally accurate. There are some minor typos which might lead to confusion for students. A few noted below: Example 5.8 P(x < 5) = 1 – e(-0.25)(5) = 0.7135 should read P(x < 5) = 1 – e^(-0.25)(5) = 0.7135 In the paragraph following Figure 12.12, “the last two items at the bottom are r2 = 0.43969” should read “the last two items at the bottom are r^2 = 0.43969” Example 12.8 Figure 12-15 r = - 0.624-0.532, therefore r is significant, should read Figure 12-15 r = - 0.624 < - 0.532, therefore r is significant.

Statistics books that utilize actual studies are meaningful and demonstrate relevance to students. This book does make use of studies and indicates where the information originates. There are some problems that are included in Chapter 9 that are contributed by students of the author and are poetic in nature. The relevance of these problems can be assessed by individual instructors. Necessary updates should be relatively easy to implement.

Overall, the text does well in explanations of the technical procedures. Terminology is defined within context of the topic being addressed and is also included in a glossary at the end of the book. The writing is at an appropriate level for this course.

There did not appear to be any issues with consistency in terminology or framework.

Modularity rating: 2

The organization of this book allows for smaller reading sections to be easily assigned. Realignment of subunits should not provide disruption to the reader.

The topics are arranged in an order that follows natural progression in a statistics course. They are addressed logically and given adequate coverage.

images/charts, and any other display features that may distract or confuse the reader. The mean of a sample, x ¯, in most of the text is written as x, with a bar written a substantial distance above it as demonstrated by the snip from the text at right. [unable to paste the snip to this document] In other places, it is written as x ¯. This makes for inconsistent spacing in the paragraph structure.

Listing the probability of A and B as P(AANDB) is not very readable. [3.1 Terminology]

I did not notice any grammatical errors, although better use of punctuation within sentences could improve readability. Example: “you do not think Jeffrey swims the 25-yard freestyle in 16.43 seconds but faster with the new goggles.” Possible revision: “you do not think Jeffrey swims the 25-yard freestyle in 16.43 seconds, but faster with the new goggles.” [Example 9.14]

Cultural Relevance rating: 1

This text refers to many different cultures and ethnic backgrounds. The examples are respectful of differences in our society.

This textbook covers all of the required topics for transfer in the MNSCU [Minnesota State College and University] system. It would work best for a lecture course, where it could be used primarily as a resource. An online student might have difficulty with the readability of the text in the absence of instructor guidance. The margins are small to maximize the information that can be contained on each page. The amount of information contained in a small space might prove intimidating for some students, especially those that are not comfortable with math as a subject matter. I would consider this text for adoption, but not without exploring other options that are available.

Reviewed by Wendy Lightheart, Mathematics Faculty, Lane Community College on 8/21/16

This textbook covers all of the usual topics you would expect to cover in an introductory statistics course for non-math majors. There is a glossary available at the end of each chapter, which is very helpful. A comprehensive index is available in this textbook at the end of the book, as you would expect. In addition, it's nice that a student may use the search option when using the pdf version of the textbook to search for specific terms.

I've went through most of the textbook, but didn't thoroughly check the Try It or homework exercises. In the content and examples, I have found several errors, most of which are minor. I will be submitting those errors to add to the errata.

The content is very relevant as it includes current studies and refers to today's modern technology and current events. It shouldn't be too difficult to update it with new studies and/or new technology and more current events in future versions.

The textbook is very clear and concise, for the most part.

Overall the book is fairly consistent in terms of terminology and framework. However, there are times when examples do not reflect the content exactly. For example, the histogram given in the solution to Example 2.9 does not follow the steps for making a histogram described previously in the content.

The text is split up into subsections and smaller reading sections quite well. The blocks of text are appropriately small and manageable and most sections could be reordered without much difficulty to the reader.

The topics are given in a very logical order. I particularly like how confidence intervals are covered for both a population mean (including t-intervals) and a population proportion before hypotheses tests for these parameters are explained. But if someone wants to cover both confidence intervals and hypotheses for a particular parameter together, then this can be easily done as well.

Most images and display features are very good. However, there are some formatting issues that should be resolved. For example, each x-bar in the text has the bar located a significant distance above the x. Also, many times what should be subscripts are not displayed that way, which can be confusing for students who are trying to learn the massive amount of notation used in a statistics course.

Of the errors I've found in this text, none of them were grammatical errors.

I haven't found any issues with cultural insensitivity or offensive material in this textbook. The examples tend to include people from various ethnic backgrounds and people of different gender and races as well.

Overall, I'm very happy with this textbook.

Reviewed by Rudolf Lublinsky, Instructor, Portland Community College, Oregon on 8/21/16

This textbook covers all of the standard topics usually covered in ? descriptive and inferential statistics textbooks for non- mathematicians. The sequence is the same used in almost every such book. All subject areas addressed in the Table of... read more

The computational technology in this textbook is based on a specific brand of calculator (TI-83, TI-84) only. For using the textbook a student has almost evitable to purchase a calculator of this brand. Forcing students to buy a specific brand of calculator contradicts the very idea of saving money using OER. The technologies offered in the text especially do not make sense for online class students who use the computer technologies and don’t need to purchase and use a calculator at all. I think some instructions for using of the Excel statistical functions have to be added in the book.

The book is mathematically accurate, as far as I can see, but there are some minor errors. For example, in the formula of the confidence interval on page 417 there are the extra parenthesis in the wrong places. It gives wrong boundaries of the confidence interval. In headlines of Ch. 9 on pages 482, 484, 503, 507, 510, and 518 words “Full hypothesis test” are misleading. I suggest that it should be “Null hypothesis test”. The definition of mutually exclusive events on page 172 is correct but it makes sense to clarify it for the case when events A and B are exhaustive events of a phenomenon.

The introductory statistics doesn’t change quickly. In general, the content is as up-to-date as any introductory probability textbook can reasonably be. Main change is in technology used for computation. The calculator references will be out of date rather quickly. For non- mathematician students a statistics course is a prerequisite and computing in this course should be supplemented by at least some simple computer technologies, Excel for example, to connect this course with using the statistics in the students’ next disciplines

The clarity in the book is very good. The language in the book is simple and clear. The instructions in the book are detailed and easy to follow.

The text is consistent in its terminology and framework. Despite a difference of topics in statistics and multiple authors of the textbook, notation, vocabulary, organization, structure and flow don’t vary widely in the chapters of the book.

Chapters of the text are rather autonomous and each contains the explanation of key terms, notation, and some information from the previous chapters. I don't see any problems to divide the textbook into the weekly modules both in descriptive and inferential statistics.

The organization is fine. The text book presents all the topics in an appropriate sequence. The structure of each chapter is done in the same fashion. This makes reading much easier. Due to the autonomy of chapters instructors can easily adjust the flow.

I like the textbook interface. It is not monotonous; headlines of the different parts of the text are highlighted, bold or have a different color. The table of contents is allows direct access to the section but not vice versa.

I’ve not found any grammatical errors in this textbook (but English is not my native language). It is well written.

There are some examples that are inclusive of a variety of races, ethnicities and back grounds. No portion of this text appeared to me to be culturally insensitive or offensive in any way, shape, or form.

The textbook is a good book for introduction to statistics. Its Stats Lab fosters active learning in the class room. There are great number of examples, exercises in “Try it” and “Practice”. The language of the book is simple and clear. The graphing calculator is well integrated into curriculum. On the other hand sometimes the main stress is done not on conceptual understanding of statistics but on details of computational procedures for the specific brand of calculator and looks like a content of a calculator manual. The ignoring of the computer technologies is a weakness of the textbook.

The textbook available to students for free and with addition of the computational computer technologies can be recommended for a community college basic statistics courses.

Reviewed by Jaejin Jang, Associate Professor, University of Wisconsin, Milwaukee on 1/7/16

A Statistics textbook mostly have a standard structure. This bookk covers major subjects of the course. Central limit theorem is given a whole chapter, which is good because of its importance. However, I would like to see these more. No... read more

No explanation for Normal and other table use. I understand we now mostly use computers for the table values; however, I believe, students still get benefit from the use of tables although it is an additional material to cover. Normality test would be needed. No Goodness-of-fit test or probability plot is explained. Normality test is important for the inference statistics. It would be good to explain mean and variance of linear combination of variables, such as E[5X+2Y]= 5E[X]+2E[Y]. It will be better to give a form of PDF (or PMF) of discrete random variables. Confidence Interval formula of F-distrbution would be better.

This book is accurate.

Elementary Statitics theory is not changed quickly. Although the application examples can be more or less current, this book is uptodated.

This book is clear in its contents. This book is actually carefully written for better understandinig of the materials.

Yes. No problem.

This book follows standard chapter layout of Statistics books (except that F-distribution is explained and used at the last part of the book). Good concise sections with many problems helps understanding the materials.

Yes. Again, the standard structure of Statistics textbooks. Explanantions are simple and clear.

No interface problems.

Looks good.

No problem.

(1) The competition of Statistics textbooks in the market is very high, and there are many good books available (at high prices). One of the important aspects of the textbooks is the presentation, such as font, page layout and color. To choose a book to review for my possible use in the near future, I selected this book because it caught my eyes among a few candidate books. For example, this book has better use of colors, colorful boxes, and arrangement of tables to better guide the reading and understanding of the materials. This book has good details of the editing and has a very competitive presentation compared with other commercial Statistics textbooks. This book is well written. This book proves “a free textbook is not necessarily worse than more expensive books.”

(2) It is hard for a Statistics textbook to be better than others due to the large number of books available. The most successful aspect of this book to me is the exercises. They are carefully made to make students easily understand the lecture materials and get feeling of real statistical analysis. The book also has very nice in-class exercises (Stats Lab) in all chapters. While this is very good for student learning, I wonder if an instructor can find time for this when covering the materials of the course. This book has many good features – such as key word summary and chapter review at the end of a chapter.

(3) This book provides instructor resources such as syllabus, assignments, quizzes, exams, lecture videos and others. Although these are popular with commercial textbooks, these features are certainly helpful. Especially, it provides nice assignments (or projects). The lecture video, which is helpful, is partially based on hand writing. I would prefer the video to be completely based on PPT. No PowerPoint lecture note is provided. This will make the preparation of lecture note time taking.

(4) The book explains the use of TI calculators; however, use of Excel will be more helpful for the students, both for descriptive Statistics and inferential Statistics. Although one book cannot have all possible contents, explanation of Minitab or Matlab will be helpful.

(5) Editing The numbers in tables can be centered for a better appearance. The “bar” notation of some variables (e.g., x_bar for sample mean) is away from the variable (e.g. x), which makes some equations less neat appearance. Solution of homework of each chapter is given in the chapter, which is nice.

Reviewed by Undupitiya Wijesiri, Professor, Southwest Minnesota State University on 6/10/15

This book covers all necessary content areas for an introduction to Statistics course for non-math majors. The text book provides an effective index, plenty of exercises, review questions, and practice tests. read more

An overwhelming majority of the content is accurate. I found only couple of errors. The formula for finding the variance using grouped data is not consistent with the definition used. Assumptions for chi-squared tests were not mentioned.

Content is up to date. It would have been better if computer software such as MINITAB or SPSS was used for the computations. This would help students learn how to interpret standard statistical outputs in practice.

The textbook is written with adequate clarity. Discussion on sampling distributions would have helped the flow of the content. Central limit theorem for a sample proportions is not included. I think the authors rely too much on the graphing calculator for simple algebraic calculations. Should have used the normal and t-tables to find probabilities.

The notation used is consistent with standard notations used in the field throughout the text. However the formula used for finding variance of grouped data is not consistent with the definition. Poor notation is used in chapter 13 in discussion of ANOVA. Students may confuse the sum of the values in each group as the standard deviation in the group since the letter s is used for the sum.

The text is divided into easily readable sections. Content is well organized and presented in a manner so that reading sections can be assigned throughout the course. Different sections could be reorganized easily without presenting too much interruption to the reader.

The material is presented with a flow consistent with a standard statistic text. Sample percentiles should have been discussed before discussing the median and quartiles. Overall content is organized and structured well.

I do not see any significant interface issues. Some of the formulas were hard to read because of distortion but it will not post any confusion for a careful reader.

I did not see any culturally insensitive material or exercises in the text.

Overall a good text for non-math majors. Basic ideas such as experimental units, sampling distributions are not discussed. Relies too much on graphing calculators for simple algebraic calculations and finding probabilities. It is better to discuss percentiles before discussing the median and quartiles since they were defined later in the chapter. Could have used statistical software for hypothesis testing, chi-squared tests, ANOVA, and regression. Plenty of examples, exercises, review questions, and practice tests were given in the textbook. Good lab assignments.

Reviewed by Vance Revennaugh, Associate Professor, University of Northwestern - Saint Paul on 6/10/15

The text covers most of the areas and ideas of an introductory statistics course, The topics are covered at an appropriate depth. I did not find any work on confidence intervals for the population variance or standard deviation, although there was a section on hypothesis teaching for a single population variance or standard deviation. Also, I did not find any discussion on non-parametic statistics. The authors do cover geometric, hypergeometric, and Poisson distributions in detail. The probability chapter did not cover Baye's Theorem or counting. Overall, the coverage and depth are satisfactory. Also, I am able to find topics using the index and Table of Contents adequately.

I could not find any typos. I feel the text was accurate, error-free, and unbiased.

Content is up-to-date. However I did notice an example using data from 1915 to 1964. I feel the authors encourage the use of a graphing calculator and do not mention any other statistical software. I feel the text is arranged in such a way that necessary updates will be relatively easy and straight forward to implement.

I believe the text is very clear and understandable for students. The authors explain and define statistic terms and concepts thoroughly. There are also a sufficient number of examples to help explain the material. The solutions to odd-numbered practice problems and homework problems are also provided at the end of each chapter

The text is consistent in terms of terminology and framework.

The text is easily and readily divisible into smaller reading sections. I noted that the authors did place a hypothesis test for a single population variance or standard deviation in the Chi-Square chapter instead of the Hypothesis Testing with One Sample chapter. The text should be easily reorganized and realigned without presenting much disruption to the reader.

The organization of the text is very similar to other introductory statistics texts. The topics are presented in a logical, clear fashion.

I reviewed with a hard-copy of the text, so I cannot comment on this item. I do plan to use the videos for the text in my online course.

I did not notice any grammatical errors.

I did not think that the text was culturally insensitive or offensive in any way. Any names of people used in the examples are inclusive of a variety of ethnicities, races, and backgrounds.

I plan to use this online text for an online course in the fall of 2015. I am planning to use the online text for day school stats classes in the spring of 2016.

Reviewed by Jacqueline Joslyn, Instructor/Teaching Assistant, University of Arizona on 6/10/15

The most important topics are covered. There are some concepts, like stem-and-leaf plots, that may be less critical for students in the social sciences to learn. Instructors can choose whether or not to skip the superfluous concepts. read more

I did not notice any glaring errors. There are some awkward word choices, which I discuss under "grammar".

The content is up-to-date. There are references to studies conducted from 2009 to 2013. Several questions discuss smartphones and other modern technologies. These questions can be easily updated, but they may lose relevance within a short period of time.

This textbook is ideal for students who learn by reading. The instructions are a bit wordy, which might be confusing for some students. It would be an excellent choice for instructors who tend to deliver concise, visual lectures. Since mathematical symbols and equations are often verbalized and instructions are reading intensive, classroom time can be used to engage students in hands-on practice (e.g. showing them how to use the graphing calculator) and to break down the concepts and exercises into visual and mathematical models (e.g. writing down the equation and explaining how to interpret the notation). The instructor can spend less time explaining concepts and more time helping students to work on their quantitative and logical thinking skills.

I appreciate that the textbook attempts to introduce students to various types of probability distribution functions in Chapter 4, but students may have trouble with some of these concepts because the information is not summarized or compared. Some chapters are written better than others. For instance, Chapter 11 is much more organized and readable. Different chi-square tests are explained separately, and then succinctly compared.

Consistency rating: 2

Examples, questions, and chapter sections are organized consistently. The “Formula Review” sections are especially useful. Important rules of thumb are usually typed in bold. There are well-organized appendices at the end of the book. However, as a reference book, it does not fulfill my expectations. The writing style is inconsistent. Sometimes formulas are stated plainly, sometimes not. Mathematical jargon is introduced with varying degrees of precision and elaboration from chapter to chapter.

It is very easy, and perhaps ideal, to pick specific chapters of this textbook to use in combination with other materials. Since the writing is inconsistent, it is not the best choice for instructors who prefer to teach from a single textbook.

The book is organized in the same way as other statistics textbooks.

Interface issues are minimal. Occasionally, there are large spaces between items (for example, page 72). This can be a little distracting.

The definitions of terms are satisfactory for the most part. However, there are segments of the book that are worded vaguely or oddly. For instance, the word “experiment” is often used to define words in the earlier chapters, which can be awkward. At one point, the authors state the tree diagrams are “used to determine the outcomes of the experiment” (188), but “event” might have been a better word to use than “experiment”. An advantage of this emphasis on statistical experiments is that it encourages the instructor to engage students in hands-on learning exercises, which introduces students to the rigors of collecting data.

The questions are culturally relevant to most U.S. students. Data on California is used fairly often. Chapter 9 includes some cute review questions written by students (sometimes in the form poems).

Reviewed by Edward Dillon, Instructor, Minneapolis Community and Technical College on 6/10/15

This textbook covers all of the standard topics usually covered in an undergradate introductory text including hyhothresis testing and ANOVA. The sequence is the same used in almost every such textbook. The index clearing describes the toppics... read more

I randomly selected one example from each of the 13 chapters and worked through these finding no errors. The book includes extensive problem sets, "Try It" problems within the text after examples to give students practice, Review sets (Appendix A, for CH 3-13), practice tests and practice final exams (Appendix B). I did not spot any errors in the answer keys, though the real only way to vet so much content is to use the text. I did not spot any particula bias.

This text is full of relavant data sets providing believeable real life examples for students. Many of the data sets are cited so that students can follow up at the original source, if they are interested. Many timely topics like wifi performance and West Nile virus are included.

The text is indeed writeen clearly, if not a little dry (as are most stats books). Key words are highlighted in bold to alert the reading to thei importance. The text is nicely chunked with examples and graphics to make it readable. The page spacing is ocassionally odd, for example there will be a title for a new sub-topic within a section and then a page break (example: p. 43 has the sub-topic title "Simple Random Sample", then the text to explain the idea is on the next page). I think they could clean this flow by simply using page breaks.

The authors do not deviate from terminology and framework that is used in any of the popular intro stats textbooks put out by mainsteam publishers. The glossaries included could be used in any undergrad stats class that I have taught.

As mentioned earlier in this review I think they do a really good job of organizing the sequence of topics and then chunking each section in a way that flows nicely so that students read about a topic, see an example and then have the opportunity to do a "Try It" example. I would be able to use it in my own stats class in the order that the chapters are given.

They have organized similar to a multiitude of undergrad stats textbooks. One feature that I think is fairly unique is that they emaphaize organization of work. Undergraduate students often have trouble keeping thier work organized in a mathematics (or stats) course. The authors include graphical organizers for doing things like hypothesis tests for example. Students are offered a checklist approach to completing tasks (literally check lists). I like this.

I did not find any real issues here other than what I mentioned earlier . . . that the flow is sometimes a bit odd with headings on one page and a misplaced page break separating the text from the heading. There is sometimes issues with the typography, usual involving symbols. For example on page 380, the bars above x-bar, the symbol for sample mean, is far away (above) the "x". This is likely to confuse students.

I did not spot and such errors. I specifically read through ALL of the end of chapter glossaries.

I did not spot any particular culturally sensitive or offensive material. I think that they could spice this text up with more examples involving issues of social justice, but that is just my personal preference in a stats text.

The text includes instruction on the use of graphing calculators to do calculations, a technology used in many undergrad programs. The Group Projects in Appedix D are interesting and well thought out. They frenquently use error finding examples, a problem that contains errors which students work through to foster critical thinking.

Reviewed by Bill Heider, Instructor, Hibbing Community College on 6/10/15

This book covers all the topics typically covered in an introductory level statistics course from an introduction to probability and the basics f study design through sampling distributions, confidence intervals, tests of one and two samples for means, proportions and variances, the typical Chi square tests including independence, goodness of fit and homogeneity, regression and ANOVA. It does not include non-parametric tests. The p-value method is the only method utilized when performing hypothesis testing. The critical value method is not utilized. One topic missing is s a discussion of determining normality of a data set. The index (and table of contents) in the pdf form of the text is especially useful as it allows the user to click on the page number in the index to scroll to the desired page.

The work is free of errors. Sample problems are drawn from a wide variety of subjects and topics.

Use of the TI 84 calculator is emphasized. Directions for performing calculations on the calculator are included in the solution of example problems. Most examples are generic in the sense that there won't be a need to update the data used. Occasionally there is some data (for example one problem uses the population of Lake Tahoe NV and another uses information from a 2006 survey) that will date the book for users. This does not in any way affect the relevance and/or appropriateness of the problem being taught, it may warrant a need to update with more current data to maintain interest of readers.

Most explanations are clear but in some cases technology is relied upon to perform calculations. For example, when performing the test for independence , it is explained how to calculate the individual terms yet to get the test statistic(the chi square) rather than showing that it is the sum of the individual terms the book states the sum is derived from use of a calculator or technology. It seems it could have been clearer to the reader had the individual terms been shown rather than just being given directions of how to do the calculation using a TI-84 calculator where it does not seem at all clear where the final value is coming from.

The book uses standard language used in statistics. The book follows the same layout from chapter to chapter. Terminology and symbols are explained. Some Examples are worked in each section (where appropriate) with a problem for students to try interspersed among the explanations. Calculator directions are included in the solution where appropriate. There is also a summary of any of the statistics commands available on the TI83/84 family of calculators. There are activities ("labs") at the end of each chapter followed by exercises for the entire chapter at the very end of each chapter (rather than the more typical problem set at the end of each section within the chapter). The answer key is provided at the end of the chapter rather than at the back of the book that does make it easier to check solutions

Each section of a chapter is easily covered in a day or two days at most. One example of where the text departs from the order of most statistics tests is that the hypthesis test for variance is delayed until after the chi square tests are introduced. If one wanted to include the topic with the other one sample tests it ould easilty be done. Diferent options for ordering are given at the begining of the text.

Each section follows the same structure. Vocabulary and an explanation of the topic to be covered in the section followed by examples. Calculator directions are included where they are needed in the solution of a problem. Activities are included at the end of each chapter followed by a summary of key terms and the key concepts/topic for each section of the chapter. A problem set for the chapter and then answers for odd exercises ended each chapter. Once one becomes familiar with the layout it does make it fairly easy for one to search for information..

The interface is wnderful. The ability to click on page numbers in both the table of contents and the index and be moved to the appropriate page in the text is nice. ALl text and imageas in the PDF format are very clear. Highlighting f key concepts and ideas draws reader attention as does bold type for key terminology

Most examples are generic. The examples were often relevent (distribution of populaitons bsed on race for a city were used once; opinion poll differrentieated by sex was used in another) but the topics were not offensive.

The book had links to external sources relevent to the topic. Some video lectures were linked in an associated website. a teaching guide is also available.

Sampling and Data
Descriptive Statistics
Probability Topics
Discrete Random Variables
Continuous Random Variables
The Normal Distribution
The Central Limit Theorem
Confidence Intervals
Hypothesis Testing with One Sample
Hypothesis Testing with Two Samples
The Chi-Square Distribution
Linear Regression and Correlation
F Distribution and One-Way ANOVA
Review Exercises (Ch 3-13)
Practice Tests (1-4) and Final Exams
Group and Partner Projects
Solution Sheets
Mathematical Phrases, Symbols, and Formulas
NOTEs for the TI-83, 83+ 84, 84+ Calculators
Tables

Ancillary Material

Instructor resources
Student resources

About the Book

Introductory Statistics 2e provides an engaging, practical, and thorough overview of the core concepts and skills taught in most one-semester statistics courses. The text focuses on diverse applications from a variety of fields and societal contexts, including business, healthcare, sciences, sociology, political science, computing, and several others. The material supports students with conceptual narratives, detailed step-by-step examples, and a wealth of illustrations, as well as collaborative exercises, technology integration problems, and statistics labs. The text assumes some knowledge of intermediate algebra, and includes thousands of problems and exercises that offer instructors and students ample opportunity to explore and reinforce useful statistical skills.

About the Contributors

Barbara Illowsky , De Anza College

Susan Dean , De Anza College

Daniel Birmajer , Nazareth College

Bryan Blount , Kentucky Wesleyan College

Sheri Boyd , Rollins College

Matthew Einsohn , Prescott College

James Helmreich , Marist College

Lynette Kenyon , Collin County Community College

Sheldon Lee , Viterbo University

Jeff Taub , Maine Maritime Academy

Contribute to this Page

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Statistics and probability

Unit 1: analyzing categorical data, unit 2: displaying and comparing quantitative data, unit 3: summarizing quantitative data, unit 4: modeling data distributions, unit 5: exploring bivariate numerical data, unit 6: study design, unit 7: probability, unit 8: counting, permutations, and combinations, unit 9: random variables, unit 10: sampling distributions, unit 11: confidence intervals, unit 12: significance tests (hypothesis testing), unit 13: two-sample inference for the difference between groups, unit 14: inference for categorical data (chi-square tests), unit 15: advanced regression (inference and transforming), unit 16: analysis of variance (anova).

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

9: End of chapter exercise solution

Last updated
Save as PDF
Page ID 278

David Diez, Christopher Barr, & Mine Çetinkaya-Rundel

David Diez, Christopher Barr, & Mine Çetinkaya-Rundel
OpenIntro Statistics

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

Introduction to data

1.1 (a) Treatment: 10/43 = 0.23 $\rightarrow$ 23%. Control: 2/46 = 0:04 ! 4%. (b) There is a 19% difference between the pain reduction rates in the two groups. At first glance, it appears patients in the treatment group are more likely to experience pain reduction from the acupuncture treatment. (c) Answers may vary but should be sensible. Two possible answers: 1 Though the groups' difference is big, I'm skeptical the results show a real difference and think this might be due to chance. 2 The difference in these rates looks pretty big, so I suspect acupuncture is having a positive impact on pain.

1.3 (a-i) 143,196 eligible study subjects born in Southern California between 1989 and 1993. (a-ii) Measurements of carbon monoxide, nitrogen dioxide, ozone, and particulate matter less than $10_{\mu m}$ (PM10) collected at air-qualitymonitoring stations as well as length of gestation. These are continuous numerical variables. (a-iii) The research question: "Is there an association between air pollution exposure and preterm births?" (b-i) 600 adult patients aged 18-69 years diagnosed and currently treated for asthma. (b-ii) The variables were whether or not the patient practiced the Buteyko method (categorical) and measures of quality of life, activity, asthma symptoms and medication reduction of the patients (categorical, ordinal). It may also be reasonable to treat the ratings on a scale of 1 to 10 as discrete numerical variables. (b-iii) The research question: "Do asthmatic patients who practice the Buteyko method experience improvement in their condition?"

1.5 (a) $50 \times 3 = 150$. (b) Four continuous numerical variables: sepal length, sepal width, petal length, and petal width. (c) One categorical variable, species, with three levels: setosa, versicolor, and virginica. 1.7 (a) Population of interest: all births in Southern California. Sample: 143,196 births between 1989 and 1993 in Southern California. If births in this time span can be considered to be representative of all births, then the results are generalizable to the population of Southern California. However, since the study is observational, the ndings do not imply causal relationships. (b) Population: all 18-69 year olds diagnosed and currently treated for asthma. Sample: 600 adult patients aged 18-69 years diagnosed and currently treated for asthma. Since the sample consists of voluntary patients, the results cannot necessarily be generalized to the population at large. However, since the study is an experiment, the ndings can be used to establish causal relationships.

1.9 (a) Explanatory: number of study hours per week. Response: GPA. (b) There is a slight positive relationship between the two variables. One respondent reported a GPA above 4.0, which is a data error. There are also a few respondents who reported unusually high study hours (60 and 70 hours/week). The variability in GPA also appears to be larger for students who study less than those who study more. Since the data become sparse as the number of study hours increases, it is somewhat difficult to evaluate the strength of the relationship and also the variability across different numbers of study hours. (c) Observational. (d) Since this is an observational study, a causal relationship is not implied.

1.11 (a) Observational. (b) The professor suspects students in a given section may have similar feelings about the course. To ensure each section is reasonably represented, she may choose to randomly select a xed number of students, say 10, from each section for a total sample size of 40 students. Since a random sample of fixed size was taken within each section in this scenario, this represents strati ed sampling.

1.13 Sampling from the phone book would miss unlisted phone numbers, so this would result in bias. People who do not have their numbers listed may share certain characteristics, e.g. consider that cell phones are not listed in phone books, so a sample from the phone book would not necessarily be a representative of the population.

1.15 The estimate will be biased, and it will tend to overestimate the true family size. For example, suppose we had just two families: the first with 2 parents and 5 children, and the second with 2 parents and 1 child. Then if we draw one of the six children at random, 5 times out of 6 we would sample the larger family

1.17 (a) No, this is an observational study. (b) This statement is not justi ed; it implies a causal association between sleep disorders and bullying. However, this was an observational study. A better conclusion would be "School children identi ed as bullies are more likely to suffer from sleep disorders than non-bullies."

1.19 (a) Experiment, as the treatment was assigned to each patient. (b) Response: Duration of the cold. Explanatory: Treatment, with 4 levels: placebo, 1g, 3g, 3g with additives. (c) Patients were blinded. (d) Double-blind with respect to the researchers evaluating the patients, but the nurses who briey interacted with patients during the distribution of the medication were not blinded. We could say the study was partly double-blind. (e) No. The patients were randomly assigned to treatment groups and were blinded, so we would expect about an equal number of patients in each group to not adhere to the treatment.

1.21 (a) Experiment. (b) Treatment is exercise twice a week. Control is no exercise. (c) Yes, the blocking variable is age. (d) No. (e) This is an experiment, so a causal conclusion is reasonable. Since the sample is random, the conclusion can be generalized to the population at large. However, we must consider that a placebo effect is possible. (f) Yes. Randomly sampled people should not be required to participate in a clinical trial, and there are also ethical concerns about the plan to instruct one group not to participate in a healthy behavior, which in this case is exercise.

1.23 (a) Positive association: mammals with longer gestation periods tend to live longer as well. (b) Association would still be positive. (c) No, they are not independent. See part (a).

1.25 (a) 1/linear and 3/nonlinear. (b) 4/some curvature (nonlinearity) may be present on the right side. "Linear" would also be acceptable for the type of relationship for plot 4. (c) 2.

1.27 (a) Decrease: the new score is smaller than the mean of the 24 previous scores. (b) Calculate a weighted mean. Use a weight of 24 for the old mean and 1 for the new mean: $\frac {(24 \times 74 + 1 \times 64)}{(24 + 1)} = 73.6$. There are other ways to solve this exercise that do not use a weighted mean. (c) The new score is more than 1 standard deviation away from the previous mean, so increase.

1.29 Both distributions are right skewed and bimodal with modes at 10 and 20 cigarettes; note that people may be rounding their answers to half a pack or a whole pack. The median of each distribution is between 10 and 15 cigarettes. The middle 50% of the data (the IQR) appears to be spread equally in each group and have a width of about 10 to 15. There are potential outliers above 40 cigarettes per day. It appears that more respondents who smoke only a few cigarettes (0 to 5) on the weekdays than on weekends.

1.31 (a) $\bar {x}_{amtWeekends} = 20, \bar {x}_{amtWeekdays} = 16$. (b) $s_{amtWeekends} = 0, s_{amtWeekdays} = 4.18$.

In this very small sample, higher on weekdays.

1.33 (a) Both distributions have the same median, 6, and the same IQR. (b) Same IQR, but second distribution has higher median. (c) Second distribution has higher median. IQRs are equal. (d) Second distribution has higher median and larger IQR.

1.37 Descriptions will vary a little. (a) 2. Unimodal, symmetric, centered at 60, standard deviation of roughly 3. (b) 3. Symmetric and approximately evenly distributed from 0 to 100. (c) 1. Right skewed, unimodal, centered at about 1.5, with most observations falling between 0 and 3. A very small fraction of observations exceed a value of 5.

1.39 The histogram shows that the distribution is bimodal, which is not apparent in the box plot. The box plot makes it easy to identify more precise values of observations outside of the whiskers.

1.41 (a) The median is better; the mean is substantially affected by the two extreme observations. (b) The IQR is better; the standard deviation, like the mean, is substantially affected by the two high salaries.

1.43 The distribution is unimodal and symmetric with a mean of about 25 minutes and a standard deviation of about 5 minutes. There does not appear to be any counties with unusually high or low mean travel times. Since the distribution is already unimodal and symmetric, a log transformation is not necessary.

1.45 Answers will vary. There are pockets of longer travel time around DC, Southeastern NY, Chicago, Minneapolis, Los Angeles, and many other big cities. There is also a large section of shorter average commute times that overlap with farmland in the Midwest. Many farmers' homes are adjacent to their farmland, so their commute would be 0 minutes, which may explain why the average commute time for these counties is relatively low.

1.47 (a) We see the order of the categories and the relative frequencies in the bar plot. (b) There are no features that are apparent in the pie chart but not in the bar plot. (c) We usually prefer to use a bar plot as we can also see the relative frequencies of the categories in this graph.

1.49 The vertical locations at which the ideological groups break into the Yes, No, and Not Sure categories differ, which indicates the variables are dependent.

1.51 (a) False. Instead of comparing counts, we should compare percentages. (b) True. (c) False. We cannot infer a causal relationship from an association in an observational study. However, we can say the drug a person is on affects his risk in this case, as he chose that drug and his choice may be associated with other variables, which is why part (b) is true. The difference in these statements is subtle but important. (d) True.

1.53 (a) Proportion who had heart attack: $\frac {7,979}{227,571} \approx 0.035$ (b) Expected number of cardiovascular problems in the rosiglitazone group if having cardiovascular problems and treatment were independent can be calculated as the number of patients in that group multiplied by the overall rate of cardiovascular problems in the study: $67,593 \times \frac {7,979}{227,571} \approx 2370$. (c-i) H0: Independence model. The treatment and cardiovascular problems are independent. They have no relationship, and the difference in incidence rates between the rosiglitazone and pioglitazone groups is due to chance. HA: Alternate model. The treatment and cardiovascular problems are not independent. The difference in the incidence rates between the rosiglitazone and pioglitazone groups is not due to chance, and rosiglitazone is associated with an increased risk of serious cardiovascular problems. (c-ii) A higher number of patients with cardiovascular problems in the rosiglitazone group than expected under the assumption of independence would provide support for the alternative hypothesis. This would suggest that rosiglitazone increases the risk of such problems. (c-iii) In the actual study, we observed 2,593 cardiovascular events in the rosiglitazone group. In the 1,000 simulations under the independence model, we observed somewhat less than 2,593 in all but one or two simulations, which suggests that the actual results did not come from the independence model. That is, the analysis provides strong evidence that the variables are not independent, and we reject the independence model in favor of the alternative. The study's results provide strong evidence that rosiglitazone is associated with an increased risk of cardiovascular problems.

Probability

2.1 (a) False. These are independent trials. (b) False. There are red face cards. (c) True. A card cannot be both a face card and an ace.

2.3 (a) 10 tosses. Fewer tosses mean more variability in the sample fraction of heads, meaning there's a better chance of getting at least 60% heads. (b) 100 tosses. More flips means the observed proportion of heads would often be closer to the average, 0.50, and therefore also above 0.40. (c) 100 tosses. With more flips, the observed proportion of heads would often be closer to the average, 0.50. (d) 10 tosses. Fewer ips would increase variability in the fraction of tosses that are heads.

2.5 (a) $0.5^{10} = 0.00098$. (b) $0.5^{10} = 0.00098$. (c) P(at least one tails) = 1 - P(no tails) = $1 - (0.5^{10}) \approx 1 - 0.001 = 0.999$.

2.7 (a) No, there are voters who are both politically Independent and also swing voters. (b) Venn diagram below: (c) 24%. (d) Add up the corresponding disjoint sections in the Venn diagram: 0.24 + 0.11 + 0.12 = 0.47. Alternatively, use the General Addition Rule: 0.35 + 0.23 - 0.11 = 0.47. (e) 1 - 0.47 = 0.53. (f) $P(Independent) \times P(swing) = 0.35 \times 0.23 = 0.08$, which does not equal P(Independent and swing) = 0.11, so the events are dependent. If you stated that this difference might be due to sampling variability in the survey, that answer would also be reasonable (we'll dive into this topic more in later chapters).

2.9 (a) If the class is not graded on a curve, they are independent. If graded on a curve, then neither independent nor disjoint (unless the instructor will only give one A, which is a situation we will ignore in parts (b) and (c)). (b) They are probably not independent: if you study together, your study habits would be related, which suggests your course performances are also related. (c) No. See the answer to part (a) when the course is not graded on a curve. More generally: if two things are unrelated (independent), then one occurring does not preclude the other from occurring.

2.11 (a) $0.16 + 0.09 = 0.25$. (b) $0.17 + 0.09 = 0.26$. (c) Assuming that the education level of the husband and wife are independent: $0.25 \times 0.26 = 0.065$. You might also notice we actually made a second assumption: that the decision to get married is unrelated to education level. (d) The husband/wife independence assumption is probably not reasonable, because people often marry another person with a comparable level of education. We will leave it to you to think about whether the second assumption noted in part (c) is reasoanble.

2.13 (a) Invalid. Sum is greater than 1. (b) Valid. Probabilities are between 0 and 1, and they sum to 1. In this class, every student gets a C. (c) Invalid. Sum is less than 1. (d) Invalid. There is a negative probability. (e) Valid. Probabilities are between 0 and 1, and they sum to 1. (f) Invalid. There is a negative probability.

2.15 (a) No, but we could if A and B are independent. (b-i) 0.21. (b-ii) 0.3+0.7-0.21 = 0.79. (b-iii) Same as P(A): 0.3. (c) No, because $0.1 \ne 0.21$, where 0.21 was the value computed under independence from part (a). (d) P(A|B) = 0.1/0.7 = 0.143.

2.17 (a) 0.60 + 0.20 - 0.18 = 0.62. (b) 0.18/0.20 = 0.90. (c) $0.11/0.33 \approx 0.33$. (d) No, otherwise the final answers of parts (b) and (c) would have been equal. (e) $0.06/0.34\approx 0.18$.

2.19 (a) 162/248 = 0.65. (b) 181/252 = 0.72 (c) Under the assumption of a dating choices being independent of hamburger preference, which on the surface seems reasonable: $0.65 \times 0.72 = 0.468$. (d) (252 + 6 - 1)/500 = 0.514

2.21 (a) The tree diagram:

(b) $P(can construct|pass) = \frac {P(can construct and pass)}{P(pass)} = \frac {0.80 \times 0.86}{0.8 \times 0.86 + 0.2 \times 0.65} = \frac {0.688}{0.818} \approx 0.84$.

2.23 First draw a tree diagram:

Then compute the probability: $P(HIV |+) = \frac {P(HIV and +)}{P(+)} = \frac {0.259 \times 0.997}{0.259 \times 0.997+0.741 \times 0.074} = \frac {0.2582}{0.3131} = 0.8247$.

2.25 A tree diagram of the situation:

$P(lupus|positive) = \frac {P(lupus and positive)}{P(positive)} = \frac {0.0196}{0.0196+0.2548} = 0.0714$. Even when a patient tests positive for lupus, there is only a 7.14% chance that he actually has lupus. While House is not exactly right - it is possible that the patient has lupus - his implied skepticism is warranted.

2.27 (a) 0.3. (b) 0.3. (c) 0.3. (d) $0.3 \times 0.3 = 0.09$. (e) Yes, the population that is being sampled from is identical in each draw.

2.29 (a) 2/9. (b) 3/9 = 1/3. (c) $(3/10) \times (2/9) \approx 0.067$. (d) No. In this small population of marbles, removing one marble meaningfully changes the probability of what might be drawn next.

2.31 For 1 leggings (L) and 2 jeans (J), there are three possible orderings: LJJ, JLJ, and JJL. The probability for LJJ is $ (5/24) \times (7/23) \times (6/22) = 0.0173$. The other two orderings have the same probability, and these three possible orderings are disjoint events. Final answer: 0.0519.

2.33 (a) 13. (b) No. The students are not a random sample.

2.35 (a) The table below summarizes the probability model:

(b) E(X-5) = E(X)-5 = 3.59-5 = -$1.41. The standard deviation is the same as the standard deviation of X: $3.37. (c) No. The expected earnings is negative, so on average you would lose money playing the game.

The expected return is a 5% increase in value for a single year.

2.39 (a) Expected: -$0.16. Variance: 8.95. SD: $2.99. (b) Expected: -$0.16. SD: $1.73. (c) Expected values are the same, but the SDs differ. The SD from the game with tripled winnings/losses is larger, since the three independent games might go in different directions (e.g.could win one game and lose two games). So the three independent games is lower risk, but in this context it just means we are likely to lose a more stable amount since the expected value is still negative.

2.41 A fair game has an expected value of zero: $$5 \times 0.46 + x \times 0.54 = 0$. Solving for x: -$4.26. You would bet $4.26 for the Padres to make the game fair.

2.43 (a) Expected: $3.90. SD: $0.34. (b) Expected: $27.30. SD: $0.89. If you computed part (b) using part (a), you should have ob-

tained an SD of $0.90.

2.45 Approximate answers are OK. Answers are only estimates based on the sample. (a) (29 + 32)/144 = 0.42. (b) 21/144 = 0.15. (c) (26 + 12 + 15)/144 = 0.37\).

Distributions of random variables

3.1 (a) 8.85%. (b) 6.94%. (c) 58.86%. (d) 4.56%.

3.3 (a) Verbal: $N(\mu = 462; \sigma = 119)$, Quant: $N(\mu = 584; \sigma = 151)$. (b) $Z_{V R} = 1.33, Z_{QR} = 0.57$.

(c) She scored 1.33 standard deviations above the mean on the Verbal Reasoning section and 0.57 standard deviations above the mean on the Quantitative Reasoning section. (d) She did better on the Verbal Reasoning section since her Z score on that section was higher. (e) $Perc_{V R} = 0.9082 \approx 91%, Perc_{QR} = 0.7157 \approx 72%$. (f) 100% - 91% = 9% did better than her on VR, and 100% - 72% = 28% did better than her on QR. (g) We cannot compare the raw scores since they are on different scales. Comparing her percentile scores is more appropriate when comparing her performance to others. (h) Answer to part (b) would not change as Z scores can be calculated for distributions that are not normal. However, we could not answer parts (c)-(f) since we cannot use the normal probability table to calculate probabilities and percentiles without a normal model.

3.5 (a) Z = 0.84, which corresponds to 711 on QR. (b) Z = -0.52, which corresponds to 400 on VR.

3.7 (a) $Z = 1.2 \approx 0.1151$. (b) $Z = -1.28 \approx $70.6 0 F or colder.

3.9 (a) N(25; 2.78). (b) $Z = 1.08 \approx 0.1401$. (c) The answers are very close because only the units were changed. (The only reason why they are a little different is because 28 0 C is 82.4 0 F, not precisely 83 0 F.)

3.11 (a) Z = 0.67. (b) $\mu$ = $1650, x = $1800. (c) $0.67 = \frac {1800-1650}{\sigma} = $223.88$.

3.13 $Z = 1.56 \approx 0.0594$, i.e. 6%.

3.15 (a) $Z = 0.73 \approx 0.2327$. (b) If you are bidding on only one auction and set a low maximum bid price, someone will probably outbid you. If you set a high maximum bid price, you may win the auction but pay more than is necessary. If bidding on more than one auction, and you set your maximum bid price very low, you probably won't win any of the auctions. However, if the maximum bid price is even modestly high, you are likely to win multiple auctions. (c) An answer roughly equal to the 10th percentile would be reasonable. Regrettably, no percentile cutoff point guarantees beyond any possible event that you win at least one auction. However, you may pick a higher percentile if you want to be more sure of winning an auction. (d) Answers will vary a little but should correspond to the answer in part (c). We use the 10th percentile: $Z = -1:28 \approx $69.80$.

3.17 14/20 = 70% are within 1 SD. Within 2 SD: 19/20 = 95%. Within 3 SD: 20/20 = 100%. They follow this rule closely.

3.19 The distribution is unimodal and symmetric. The superimposed normal curve approximates the distribution pretty well. The points on the normal probability plot also follow a relatively straight line. There is one slightly distant observation on the lower end, but it is not extreme. The data appear to be reasonably approximated by the normal distribution.

3.21 (a) No. The cards are not independent. For example, if the first card is an ace of clubs, that implies the second card cannot be an ace of clubs. Additionally, there are many possible categories, which would need to be simplified. (b) No. There are six events under consideration. The Bernoulli distribution allows for only two events or categories. Note that rolling a die could be a Bernoulli trial if we simply to two events, e.g. rolling a 6 and not rolling a 6, though specifying such details would be necessary.

3.23 (a) ${(1 - 0.471)}^2 \times 0.471 = 0.1318$. (b) $0.471^3 = 0.1045$. (c) $\mu = 1/0.471 = 2.12, \sigma = 2.38$. (d) $\mu = 1/0.30 = 3.33, \sigma = 2.79$. (e) When p is smaller, the event is rarer, meaning the expected number of trials before a success and the standard deviation of the waiting time are higher.

3.25 (a) $0.875^2 \times 0.125 = 0.096$. (b) $\mu = 8, \sigma = 7.48$.

3.27 (a) Yes. The conditions are satisfied: independence, xed number of trials, either success or failure for each trial, and probability of success being constant across trials. (b) 0.200. (c) 0.200. (d) $0.0024+0.0284+0.1323 = 0.1631$. (e) 1 - 0.0024 = 0.9976.

3.29 (a) $\mu = 35, \sigma = 3.24$. (b) Yes. Z = 3.09. Since 45 is more than 2 standard deviations from the mean, it would be considered unusual. Note that the normal model is not required to apply this rule of thumb. (c) Using a normal model: 0.0010. This does indeed appear to be an unusual observation. If using a normal model with a 0.5 correction, the probability would be calculated as 0.0017.

3.31 Want to find the probabiliy that there will be more than 1,786 enrollees. Using the normal model: 0.0537. With a 0.5 correction: 0.0559.

3.33 (a) 1 - 0.753 = 0.5781. (b) 0.1406. (c) 0.4219. (d) 1 - 0.253 = 0.9844.

3.35 (a) Geometric distribution: 0.109. (b) Binomial: 0.219. (c) Binomial: 0.137. (d) 1 - 0.8756 = 0.551. (e) Geometric: 0.084. (f) Using a binomial distribution with n = 6 and p = 0.125, we see that $\mu = 4, \sigma = 1.06$, and Z = -1.89. Since this is within 2 SD, it may not be considered unusual, though this is a borderline case, so we might say the observations is somewhat unusual.

3.37 0 wins (-$3): 0.1458. 1 win (-$1): 0.3936. 2 wins (+$1): 0.3543. 3 wins (+$3): 0.1063.

3.39 (a) $\overset {Anna}{1/5} \times \overset {Ben}{1/4} \times \overset {Carl}{1/3} \times \overset {Damian}{1/2} \times \overset {Eddy}{1/1} = 1/5! = 1/120$. (b) Since the probabilities must add to 1, there must be 5! = 120 possible orderings. (c) 8! = 40,320.

3.41 (a) Geometric: $(5/6)^4 \times (1/6) = 0.0804$. Note that the geometric distribution is just a special case of the negative binomial distribution when there is a single success on the last trial. (b) Binomial: 0.0322. (c) Negative binomial: 0.0193.

3.43 (a) Negative binomial with n = 4 and p = 0.55, where a success is defined here as a female student. The negative binomial setting is appropriate since the last trial is fixed but the order of the rst 3 trials is unknown. (b) 0.1838. (c)$\binom {3}{1} = 3$. (d) In the binomial model there are no restrictions on the outcome of the last trial. In the negative binomial model the last trial is fixed. Therefore we are interested in the number of ways of orderings of the other k -1 successes in the first n - 1 trials.

3.45 (a) Poisson with $\lambda = 75$. (b) $\mu = \lambda = 75, \sigma = \sqrt {\lambda} = 8.66$. (c) Z = -1.73. Since 60 is within 2 standard deviations of the mean, it would not generally be considered unusual. Note that we often use this rule of thumb even when the normal model does not apply.

3.47 Using Poisson with $\lambda = 75: 0.0402$.

Foundations for inference

4.1 (a) Mean. Each student reports a numerical value: a number of hours. (b) Mean. Each student reports a number, which is a percentage, and we can average over these percentages. (c) Proportion. Each student reports Yes or No, so this is a categorical variable and we use a proportion. (d) Mean. Each student reports a number, which is a percentage like in part (b). (e) Proportion. Each student reports whether or not he got a job, so this is a categorical variable and we use a proportion.

4.3 (a) Mean: 13.65. Median: 14. (b) SD: 1.91. IQR: 15 - 13 = 2. (c) Z16 = 1.23, which is not unusual since it is within 2 SD of the mean. Z18 = 2:23, which is generally considered unusual. (d) No. Point estimates that are based on samples only approximate the population parameter, and they vary from one sample to another. (e) We use the SE, which is $1.91/\sqrt {100} = 0.191$ for this sample's mean.

4.5 (a) SE = 2.89. (b) Z = 1.73, which indicates that the two values are not unusually distant from each other when accounting for the uncertainty in John's point estimate.

4.7 (a) We are 95% confident that US residents spend an average of 3.53 to 3.83 hours per day relaxing or pursuing activities they enjoy after an average work day. (b) 95% of such random samples will yield a 95% CI that contains the true average hours per day that US residents spend relaxing or pursuing activities they enjoy after an average work day. (c) They can be a little less confident in capturing the parameter, so the interval will be a little slimmer.

4.9 A common way to decrease the width of the interval without losing con dence is to increase the sample size. It may also be possible to use a more advanced sampling method, such as strati ed sampling, though the required analysis is beyond the scope of this course, and such a sampling method may be difficult in this context.

4.11 (a) False. Provided the data distribution is not very strongly skewed (n = 64 in this sample, so we can be slightly lenient with the skew), the sample mean will be nearly normal, allowing for the method normal approximation described. (b) False. Inference is made on the population parameter, not the point estimate. The point estimate is always in the confidence interval. (c) True. (d) False. The confidence interval is not about a sample mean. (e) False. To be more con dent that we capture the parameter, we need a wider interval. Think about needing a bigger net to be more sure of catching a sh in a murky lake. (f) True. Optional explanation: This is true since the normal model was used to model the sample mean. The margin of error is half the width of the interval, and the sample mean is the midpoint of the interval. (g) False. In the calculation of the standard error, we divide the standard deviation by the square root of the sample size. To cut the SE (or margin of error) in half, we would need to sample 22 = 4 times the number of people in the initial sample.

4.13 Independence: sample from < 10% of population. We must assume it is a simple random sample to move forward; in practice, we would investigate whether this is the case, but here we will just report that we are making this assumption. Notice that there are no students who have had no exclusive relationships in the sample, which suggests some student responses are likely missing (perhaps only positive values were reported). The sample size is at least 30. The skew is strong, but the sample is very large so this is not a concern. 90% CI: (2.97, 3.43). We are 90% con dent that the average number of exclusive relationships that Duke students have been in is between 2.97 and 3.43.

4.15 (a) H 0 : $\mu$ = 8 (On average, New Yorkers sleep 8 hours a night.) H A : $\mu$ < 8 (On average, New Yorkers sleep less than 8 hours a night.) (b) H 0 : $\mu$ = 15 (The average amount of company time each employee spends not working is 15 minutes for March Madness.) H A : $\mu$ > 15 (The average amount of company time each employee spends not working is greater than 15 minutes for March Madness.)

4.17 First, the hypotheses should be about the population mean ($\mu$) not the sample mean. Second, the null hypothesis should have an equal sign and the alternative hypothesis should be about the null hypothesized value, not the observed sample mean. The correct way to set up these hypotheses is shown below:

\[H_0 : \mu = \text {2 hours}\]

\[H_A : \mu > \text {2 hours}\]

The one-sided test indicates that we our only interested in showing that 2 is an underestimate. Here the interest is in only one direction, so a one-sided test seems most appropriate. If we would also be interested if the data showed strong evidence that 2 was an overestimate, then the test should be two-sided.

4.19 (a) This claim does not seem plausible since 3 hours (180 minutes) is not in the interval. (b) 2.2 hours (132 minutes) is in the 95% confidence interval, so we do not have evidence to say she is wrong. However, it would be more appropriate to use the point estimate of the sample. (c) A 99% con dence interval will be wider than a 95% con dence interval, meaning it would enclose this smaller interval. This means 132 minutes would be in the wider interval, and we would not reject her claim based on a 99% confidence level.

4.21 Independence: The sample is presumably a simple random sample, though we should verify that is the case. Generally, this is what is meant by "random sample", though it is a good idea to actually check. For all following questions and solutions, it may be assumed that "random sample" actually means "simple random sample". 75 ball bearings is smaller than 10% of the population of ball bearings. The sample size is at least 30. The data are only slightly skewed. Under the assumption that the random sample is a simple random sample, $\bar {x}$ will be normally distributed. $H_0 : \mu$ = 7 hours. $H_A : \mu \ne$ 7 hours. $Z = -1.04 \rightarrow$ p-value = $2 \times 0.1492 = 0.2984$. Since the p-value is greater than 0.05, we fail to reject H 0 . The data do not provide convincing evidence that the average lifespan of all ball bearings produced by this machine is different than 7 hours. (Comment on using a one-sided alternative: the worker may be interested in learning if the ball bearings underperforms or over-performs the manufacturer's claim, which is why we suggest a two-sided test.)

4.23 (a) Independence: The sample is random and 64 patients would almost certainly make up less than 10% of the ER residents. The sample size is at least 30. No information is provided about the skew. In practice, we would ask to see the data to check this condition, but here we will make the assumption that the skew is not very strong. (b) $H_0 : \mu = 127. H_A : \mu \ne 127$. $Z = 2.15 \approx$ p-value = $2 \times 0.0158 = 0.0316$. Since the p-value is less than $\alpha = 0.05$, we reject H 0 . The data provide convincing evidence that the the average ER wait time has increased over the last year. (c) Yes, it would change. The p-value is greater than 0.01, meaning we would fail to reject H 0 at = 0.01.

4.25 $H_0 : \mu = 130. H_A : \mu \ne 130$. Z = 1.39 $\approx$ p-value = $2 \times 0.0823 = 0.1646$, which is larger than $\alpha = 0.05$. The data do not provide convincing evidence that the true average calorie content in bags of potato chips is different than 130 calories.

4.27 (a) H 0 : Anti-depressants do not help symptoms of Fibromyalgia. H A : Antidepressants do treat symptoms of Fibromyalgia. Remark: Diana might also have taken special note if her symptoms got much worse, so a more scienti c approach would have been to use a two-sided test. While parts (b)-(d) use the onesided version, your answers will be a little different if you used a two-sided test. (b) Concluding that anti-depressants work for the treatment of Fibromyalgia symptoms when they actually do not. (c) Concluding that anti-depressants do not work for the treatment of Fibromyalgia symptoms when they actually do. (d) If she makes a Type 1 error, she will continue taking medication that does not actually treat her disorder. If she makes a Type 2 error, she will stop taking medication that could treat her disorder.

4.29 (a) If the null hypothesis is rejected in error, then the regulators concluded that the adverse effect was higher in those taking the drug than those who did not take the drug when in reality the rates are the same for the two groups. (b) If the null hypothesis is not rejected but should have been, then the regulators failed to identify that the adverse effect was higher in those taking the drug. (c) Answers may vary a little. If all 403 drugs are actually okay, then about $403 \times 0.05 \approx 20$ drugs will have a Type 1 error. Of the 42 suspect drugs, we would expect about 20/42 would represent an error while about $22/42 \approx 52%$ would actually be drugs with adverse effects. (d) There is not enough information to tell.

4.31 (a) Independence: The sample is random. In practice, we should ask whether 70 customers is less than 10% of the population (we'll assume this is the case for this exercise). The sample size is at least 30. No information is provided about the skew, so this is another item we would typically ask about. For now, we'll assume the skew is not very strong. (b) $H_0 : \mu = 18. H_A : \mu > 18$. $Z = 3.46 \approx$ p-value = 0.0003, which is less than $\alpha = 0.05$, so we reject H 0 . There is strong evidence that the average revenue per customer is greater than $18. (c) (18.65, 19.85). (d) Yes. The hypothesis test reject the notion that $\mu = 18$, and this value is not in the confidence interval. (e) Even though the increase in average revenue per customer appears to be significant, the restaurant owner may want to consider other criteria, such as total profits. With a longer happy hour, the revenue over the entire evening may actually drop since lower prices are offered for a longer time. Also, costs usually rise when prices are lowered. A better measure to consider may be an increase in total profits for the entire evening.

4.33 (a) The distribution is unimodal and strongly right skewed with a median between 5 and 10 years old. Ages range from 0 to slightly over 50 years old, and the middle 50% of the distribution is roughly between 5 and 15 years old. There are potential outliers on the higher end. (b) When the sample size is small, the sampling distribution is right skewed, just like the population distribution. As the sample size increases, the sampling distribution gets more unimodal, symmetric, and approaches normality. The variability also decreases. This is consistent with the Central Limit Theorem.

4.35 The centers are the same in each plot, and each data set is from a nearly normal distribution (see Section 4.2.6), though the histograms may not look very normal since each represents only 100 data points. The only way to tell which plot corresponds to which scenario is to examine the variability of each distribution. Plot B is the most variable, followed by Plot A, then Plot C. This means Plot B will correspond to the original data, Plot A to the sample means with size 5, and Plot C to the sample means with size 25.

4.37 (a) Right skewed. There is a long tail on the higher end of the distribution but a much shorter tail on the lower end. (b) Less than, as the median would be less than the mean in a right skewed distribution. (c) We should not. (d) Even though the population distribution is not normal, the conditions for inference are reasonably satis ed, with the possible exception of skew. If the skew isn't very strong (we should ask to see the data), then we can use the Central Limit Theorem to estimate this probability. For now, we'll assume the skew isn't very strong, though the description suggests it is at least moderate to strong. Use N(1.3; $SE_{\bar {x}} = 0.3/\sqrt {60}$): Z = 2.58 $\rightarrow$ 0.0049. (e) It would decrease it by a factor of $1/\sqrt {2}$.

4.39 (a) $Z = -3.33 \rightarrow 0.0004$. (b) The population SD is known and the data are nearly normal, so the sample mean will be nearly normal with distribution $N(\mu, \sigma / \sqrt {n}$, i.e. N(2.5; 0.0055). (c) $Z = -10.54 \rightarrow \approx 0$. (d) See below:

(e) We could not estimate (a) without a nearly normal population distribution. We also could not estimate (c) since the sample size is not sufficient to yield a nearly normal sampling distribution if the population distribution is not nearly normal.

4.41 (a) We cannot use the normal model for this calculation, but we can use the histogram. About 500 songs are shown to be longer than 5 minutes, so the probability is about $500/3000 = 0.167$. (b) Two different answers are reasonable. Option 1Since the population distribution is only slightly skewed to the right, even a small sample size will yield a nearly normal sampling distribution. We also know that the songs are sampled randomly and the sample size is less than 10% of the population, so the length of one song in the sample is independent of another. We are looking for the probability that the total length of 15 songs is more than 60 minutes, which means that the average song should last at least 60/15 = 4 minutes. Using $SE = 1.62/ \sqrt {15}$, $Z = 1.31 \rightarrow 0.0951$. Option 2Since the population distribution is not normal, a small sample size may not be sufficient to yield a nearly normal sampling distribution. Therefore, we cannot estimate the probability using the tools we have learned so far. (c) We can now be confident that the conditions are satis ed. $Z = 0.92 \rightarrow 0.1788$.

4.43 (a) $H_0 : \mu _{2009} = \mu _{2004}$. $H_A : \mu _{2009} \ne \mu _{2004}$. (b) $\bar {x}_{2009} - \bar {x}_{2004} = -3.6$ spam emails per day. (c) The null hypothesis was not rejected, and the data do not provide convincing evidence that the true average number of spam emails per day in years 2004 and 2009 are different. The observed difference is about what we might expect from sampling variability alone. (d) Yes, since the hypothesis of no difference was not rejected in part (c).

4.45 (a) $H_0 : p_{2009} = p_{2004}$. $H_A : p_{2009} \ne p_{2004}$. (b) -7%. (c) The null hypothesis was rejected. The data provide strong evidence that the true proportion of those who once a month or less frequently delete their spam email was higher in 2004 than in 2009. The difference is so large that it cannot easily be explained as being due to chance. (d) No, since the null difference, 0, was rejected in part (c).

4.47 (a) Scenario I is higher. Recall that a sample mean based on less data tends to be less accurate and have larger standard errors. (b) Scenario I is higher. The higher the confidence level, the higher the corresponding margin of error. (c) They are equal. The sample size does not affect the calculation of the p-value for a given Z score. (d) Scenario I is higher. If the null hypothesis is harder to reject (lower), then we are more likely to make a Type 2 error.

4.49 $ 10 \ge 2.58 \times \frac {102}{\sqrt {n}} \rightarrow n \ge 692.5319$. He should survey at least 693 customers.

4.51 (a) The null hypothesis would be that the mean this year is also 128 minutes. The alternative hypothesis would be that the mean is different from 128 minutes. (b) First calculate the SE: $\frac {39}{\sqrt {64}} = 4.875$. Next, identify the Z scores that would result in rejecting H 0 : $Z_{lower}$ = -1.96, $Z_{upper}$ = 1.96. In each case, calculate the corresponding sample mean cutoff: $\bar {x}_{lower}$ = 118.445 and $\bar {x}_{upper}$ = 137.555\). (c) Construct Z scores for the values from part (b) but using the supposed true distribution (i.e. $\mu$ = 135), i.e. not using the null value ($\mu$ = 128). The probability of correctly rejecting the null hypothesis would be 0.0003+0.3015 = 0.3018 using these two cutoffs, and the probability of a Type 2 error would then be 1 - 0.3018 = 0.6982.

Inference for numerical data

5.1 (a) For each observation in one data set, there is exactly one specially-corresponding observation in the other data set for the same geographic location. The data are paired. (b) H 0 : $\mu_{diff} = 0$ (There is no difference in average daily high temperature between January 1, 1968 and January 1, 2008 in the continental US.) $H_A : \mu_{diff} > 0$ (Average daily high temperature in January 1, 1968 was lower than average daily high temperature in January, 2008 in the continental US.) If you chose a two-sided test, that would also be acceptable. If this is the case, note that your p-value will be a little bigger than what is reported here in part (d). (c) Independence: locations are random and represent less than 10% of all possible locations in the US. The sample size is at least 30. We are not given the distribution to check the skew. In practice, we would ask to see the data to check this condition, but here we will move forward under the assumption that it is not strongly skewed. (d) $Z = 1.60 \rightarrow$ p-value = 0.0548. (e) Since the p-value > $\alpha$ (since not given use 0.05), fail to reject H 0 . The data do not provide strong evidence of temperature warming in the continental US. However it should be noted that the p-value is very close to 0.05. (f) Type 2, since we may have incorrectly failed to reject H 0 . There may be an increase, but we were unable to defftect it. (g) Yes, since we failed to reject H 0 , which had a null value of 0.

5.3 (a) (-0.03, 2.23). (b) We are 90% confident that the average daily high on January 1, 2008 in the continental US was 0.13 degrees lower to 2.13 degrees higher than the average daily high on January 1, 1968. (c) No, since 0 is included in the interval.

5.5 (a) Each of the 36 mothers is related to exactly one of the 36 fathers (and vice-versa), so there is a special correspondence between the mothers and fathers. (b) $H_0 : \mu _{diff}$ = 0. $H_A : \mu _{diff} \ne 0$. Independence: random sample from less than 10% of population. Sample size of at least 30. The skew of the differences is, at worst, slight. $Z = 2.72 \rightarrow$ p-value = 0.0066. Since p-value < 0.05, reject H 0 . The data provide strong evidence that the average IQ scores of mothers and fathers of gifted children are different, and the data indicate that mothers' scores are higher than fathers' scores for the parents of gifted children.

5.7 Independence: Random samples that are less than 10% of the population. Both samples are at least of size 30. In practice, we'd ask for the data to check the skew (which is not provided), but here we will move forward under the assumption that the skew is not extreme (there is some leeway in the skew for such large samples). Use z* = 1.65. 90% CI: (0.16, 5.84). We are 90% con dent that the average score in 2008 was 0.16 to 5.84 points higher than the average score in 2004.

5.9 (a) $H_0 : \mu _{2008} = \mu _{2004} \rightarrow \mu _{2004} - \mu _{2008} = 0$ (Average math score in 2008 is equal to average math score in 2004.) $H_A : \mu _{2008} \ne \mu _{2004} \rightarrow \mu _{2004} - \mu _{2008} \ne 0$ (Average math score in 2008 is different than average math score in 2004.) Conditions necessary for inference were checked in Exercise 5.7. Z = -1.74 $\rightarrow$ p-value = 0.0818. Since the p-value < $\alpha$, reject H 0 . The data provide strong evidence that the average math score for 13 year old students has changed between 2004 and 2008. (b) Yes, a Type 1 error is possible. We rejected H 0 , but it is possible H 0 is actually true. (c) No, since we rejected H 0 in part (a).

5.11 (a) We are 95% confident that those on the Paleo diet lose 0.891 pounds less to 4.891 pounds more than those in the control group. (b) No. The value representing no difference between the diets, 0, is included in the confidence interval. (c) The change would have shifted the con dence interval by 1 pound, yielding CI = (0.109; 5.891), which does not include 0. Had we observed this result, we would have rejected H 0 .

5.13 Independence and sample size conditions are satis ed. Almost any degree of skew is reasonable with such large samples. Compute the joint SE: $\sqrt {SE^2_M + SE^2_W} = 0.114$. The 95% CI: (-11.32, -10.88). We are 95% confident that the average body fat percentage in men is 11.32% to 10.88% lower than the average body fat percentage in women.

5.15 (a) df = 6 - 1 = 5, $t^*_5$ = 2.02 (column with two tails of 0.10, row with df = 5). (b) df = 21 - 1 = 5, $t^*_20 = 2.53$ (column with two tails of 0.02, row with df = 20). (c) df = 28, $t^*_28 = 2.05$. (d) df = 11, $t^*_11 = 3.11$.

5.17 The mean is the midpoint: $\bar {x} = 20$. Identify the margin of error: ME = 1.015, then use $t^*_{35} = 2.03$ and $SE = s/\sqrt {n}$ in the formula for margin of error to identify s = 3.

5.19 (a) $H_0: \mu = 8$ (New Yorkers sleep 8 hrs per night on average.) $H_A: \mu < 8$ (New Yorkers sleep less than 8 hrs per night on average.) (b) Independence: The sample is random and from less than 10% of New Yorkers. The sample is small, so we will use a t distribution. For this size sample, slight skew is acceptable, and the min/max suggest there is not much skew in the data. T = -1.75. df = 25-1 = 24. (c) 0.025 < p-value < 0.05. If in fact the true population mean of the amount New Yorkers sleep per night was 8 hours, the probability of getting a random sample of 25 New Yorkers where the average amount of sleep is 7.73 hrs per night or less is between 0.025 and 0.05. (d) Since p-value < 0.05, reject H 0 . The data provide strong evidence that New Yorkers sleep less than 8 hours per night on average. (e) No, as we rejected H 0 .

5.21 $t^*_{19}$ is 1.73 for a one-tail. We want the lower tail, so set -1.73 equal to the T score, then solve for $\bar {x}: 56.91$.

5.23 No, he should not move forward with the test since the distributions of total personal income are very strongly skewed. When sample sizes are large, we can be a bit lenient with skew. However, such strong skew observed in this exercise would require somewhat large sample sizes, somewhat higher than 30.

5.25 (a) These data are paired. For example, the Friday the 13th in say, September 1991, would probably be more similar to the Friday the 6th in September 1991 than to Friday the 6th in another month or year. (b) Let $\mu _{diff} = \mu _{sixth} - \mu _{thirteenth}$. $H_0 : \mu _{diff} = 0$. $H_A : \mu _{diff} \ne 0$. (c) Independence: The months selected are not random. However, if we think these dates are roughly equivalent to a simple random sample of all such Friday 6th/13th date pairs, then independence is reasonable. To proceed, we must make this strong assumption, though we should note this assumption in any reported results. With fewer than 10 observations, we would need to use the t distribution to model the sample mean. The normal probability plot of the differences shows an approximately straight line. There isn't a clear reason why this distribution would be skewed, and since the normal quantile plot looks reasonable, we can mark this condition as reasonably satis ed. (d) T = 4.94 for df = 10 - 1 = 9 $\rightarrow $ p-value < 0.01. (e) Since p-value < 0.05, reject H 0 . The data provide strong evidence that the average number of cars at the intersection is higher on Friday the 6th than on Friday the 13th. (We might believe this intersection is representative of all roads, i.e. there is higher traffic on Friday the 6th relative to Friday the 13th. However, we should be cautious of the required assumption for such a generalization.) (f) If the average number of cars passing the intersection actually was the same on Friday the 6th and 13th, then the probability that we would observe a test statistic so far from zero is less than 0.01. (g) We might have made a Type 1 error, i.e. incorrectly rejected the null hypothesis.

5.27 (a) $H_0 : \mu _{diff} = 0$. $H_A : \mu _{diff} \ne 0$. T = -2.71. df = 5. 0:02 < p-value < 0:05. Since p-value < 0.05, reject H 0 . The data provide strong evidence that the average number of traffic accident related emergency room admissions are different between Friday the 6th and Friday the 13th. Furthermore, the data indicate that the direction of that difference is that accidents are lower on Friday the 6th relative to Friday the 13th. (b) (-6.49, -0.17). (c) This is an observational study, not an experiment, so we cannot so easily infer a causal intervention implied by this statement. It is true that there is a difference. However, for example, this does not mean that a responsible adult going out on Friday the 13th has a higher chance of harm than on any other night.

5.29 (a) Chicken fed linseed weighed an average of 218.75 grams while those fed horsebean weighed an average of 160.20 grams. Both distributions are relatively symmetric with no apparent outliers. There is more variability in the weights of chicken fed linseed. (b) $H_0 : \mu _{ls} = \mu _{hb}$. $H_A : \mu _{ls} \ne \mu _{hb}$. We leave the conditions to you to consider. T = 3.02, df = min(11; 9) = 9 $\rightarrow$ 0.01 < p-value < 0.02. Since p-value < 0.05, reject H 0 . The data provide strong evidence that there is a significant difference between the average weights of chickens that were fed linseed and horsebean. (c) Type 1, since we rejected H 0 . (d) Yes, since p-value > 0.01, we would have failed to reject H 0 .

5.31 $H_0 : \mu _C = \mu _S$. $H_A : \mu _C \ne \mu _S$. T = 3.48, df = 11 $\rightarrow$ p-value < 0.01. Since p-value < 0.05, reject H 0 . The data provide strong evidence that the average weight of chickens that were fed casein is different than the average weight of chickens that were fed soybean (with weights from casein being higher). Since this is a randomized experiment, the observed difference are can be attributed to the diet.

5.33 $H_0 : \mu _T = \mu _C$. $H_A : \mu _T \ne \mu _C$. T = 2.24, df = 21 $\rightarrow$ 0.02 < p-value < 0.05. Since p-value < 0.05, reject H 0 . The data provide strong evidence that the average food consumption by the patients in the treatment and control groups are different. Furthermore, the data indicate patients in the distracted eating (treatment) group consume more food than patients in the control group.

5.35 Let $\mu _{diff} = \mu _{pre} - \mu _{post}$. $H_0 : \mu _{diff} = 0$: Treatment has no effect. $H_A : \mu _{diff} > 0$: Treatment is effective in reducing Pd T scores, the average pre-treatment score is higher than the average post-treatment score. Note that the reported values are pre minus post, so we are looking for a positive difference, which would correspond to a reduction in the psychopathic deviant T score. Conditions are checked as follows. Independence: The subjects are randomly assigned to treatments, so the patients in each group are independent. All three sample sizes are smaller than 30, so we use t tests.Distributions of differences are somewhat skewed. The sample sizes are small, so we cannot reliably relax this assumption. (We will proceed, but we would not report the results of this specific analysis, at least for treatment group 1.) For all three groups: $df = 13. T_1 = 1.89$ (0.025 < p-value < 0.05), $T_2 = 1.35$ (p-value = 0.10), $T_3 = -1.40$ (p-value > 0.10). The only significant test reduction is found in Treatment 1, however, we had earlier noted that this result might not be reliable due to the skew in the distribution. Note that the calculation of the p-value for Treatment 3 was unnecessary: the sample mean indicated a increase in Pd T scores under this treatment (as opposed to a decrease, which was the result of interest). That is, we could tell without formally completing the hypothesis test that the p-value would be large for this treatment group.

5.37 $H_0: \mu _1 = \mu _2 = \dots = \mu _6$. H A : The average weight varies across some (or all) groups. Independence: Chicks are randomly assigned to feed types (presumably kept separate from one another), therefore independence of observations is reasonable. Approx. normal: the distributions of weights within each feed type appear to be fairly symmetric. Constant variance: Based on the side-by-side box plots, the constant variance assumption appears to be reasonable. There are differences in the actual computed standard deviations, but these might be due to chance as these are quite small samples. $F_{5;65} = 15.36$ and the p-value is approximately 0. With such a small p-value, we reject H 0 . The data provide convincing evidence that the average weight of chicks varies across some (or all) feed supplement groups.

5.39 (a) H 0 : The mean MET for each group is equal to the others. H A : At least one pair of means is different. (b) Independence: We don't have any information on how the data were collected, so we cannot assess independence. To proceed, we must assume the subjects in each group are independent. In practice, we would inquire for more details. Approx. normal: The data are bound below by zero and the standard deviations are larger than the means, indicating very strong strong skew. However, since the sample sizes are extremely large, even extreme skew is acceptable. Constant variance: This condition is sufficiently met, as the standard deviations are reasonably consistent across groups. (c) See below, with the last column omitted:

(d) Since p-value is very small, reject H 0 . The data provide convincing evidence that the average MET differs between at least one pair of groups.

5.41 (a) H 0 : Average GPA is the same for all majors. HA: At least one pair of means are different. (b) Since p-value > 0.05, fail to reject H 0 . The data do not provide convincing evidence of a difference between the average GPAs across three groups of majors. (c) The total degrees of freedom is 195+2 = 197, so the sample size is 197 + 1 = 198.

5.43 (a) False. As the number of groups increases, so does the number of comparisons and hence the modified significance level decreases. (b) True. (c) True. (d) False. We need observations to be independent regardless of sample size.

5.45 (a) H 0 : Average score difference is the same for all treatments. H A : At least one pair of means are different. (b) We should check conditions. If we look back to the earlier exercise, we will see that the patients were randomized, so independence is satis ed. There are some minor concerns about skew, especially with the third group, though this may be acceptable. The standard deviations across the groups are reasonably similar. Since the p-value is less than 0.05, reject H 0 . The data provide convincing evidence of a difference between the average reduction in score among treatments. (c) We determined that at least two means are different in part (b), so we now conduct $K = 3 \times 2/2 = 3$ pairwise t tests that each use $\alpha = 0.05/3 = 0.0167$ for a significance level. Use the following hypotheses for each pairwise test. H 0 : The two means are equal. H A : The two means are different. The sample sizes are equal and we use the pooled SD, so we can compute SE = 3.7 with the pooled df = 39. The p-value only for Trmt 1 vs. Trmt 3 may be statistically significant: 0.01 < p-value < 0.02. Since we cannot tell, we should use a computer to get the p-value, 0.015, which is statistically significant for the adjusted significance level. That is, we have identified Treatment 1 and Treatment 3 as having different effects. Checking the other two comparisons, the differences are not statistically significant.

Inference for categorical data

6.1 (a) False. Doesn't satisfy success-failure condition. (b) True. The success-failure condition is not satis ed. In most samples we would expect $\hat {p}$ to be close to 0.08, the true population proportion. While $\hat {p}$ can be much above 0.08, it is bound below by 0, suggesting it would take on a right skewed shape. Plotting the sampling distribution would confirm this suspicion. (c) False. $SE_{\hat {p}} = 0.0243$, and $\hat {p} = 0.12$ is only $ \frac {0.12-0.08}{0.0243} = 1.65$ SEs away from the mean, which would not be considered unusual. (d) True. $\hat {p} = 0.12$ is 2.32 standard errors away from the mean, which is often considered unusual. (e) False. Decreases the SE by a factor of $1/\sqrt {2}$.

6.3 (a) True. See the reasoning of 6.1(b). (b) True. We take the square root of the sample size in the SE formula. (c) True. The independence and success-failure conditions are satisfied. (d) True. The independence and success-failure conditions are satisfied.

6.5 (a) False. A con dence interval is constructed to estimate the population proportion, not the sample proportion. (b) True. 95% CI: 70% $\pm$ 8%. (c) True. By the definition of a confidence interval. (d) True. Quadrupling the sample size decreases the SE and ME by a factor of $1/\sqrt {4}$. (e) True. The 95% CI is entirely above 50%.

6.7 With a random sample from < 10% of the population, independence is satis ed. The success-failure condition is also satis ed. ME = z*$\sqrt {\frac {\hat {p}(1- \hat {p})}{n}} = 1.96 \sqrt {\frac {0.56 \times 0.44}{600}} = 0.0397 \approx 4%$

6.9 (a) Proportion of graduates from this university who found a job within one year of graduating. $\hat {p} = 348/400 = 0.87$. (b) This is a random sample from less than 10% of the population, so the observations are independent. Success-failure condition is satisfied: 348 successes, 52 failures, both well above 10. (c) (0.8371, 0.9029). We are 95% confident that approximately 84% to 90% of graduates from this university found a job within one year of completing their undergraduate degree. (d) 95% of such random samples would produce a 95% confidence interval that includes the true proportion of students at this university who found a job within one year of graduating from college. (e) (0.8267, 0.9133). Similar interpretation as before. (f) 99% CI is wider, as we are more confident that the true proportion is within the interval and so need to cover a wider range.

6.11 (a) No. The sample only represents students who took the SAT, and this was also an online survey. (b) (0.5289, 0.5711). We are 95% confident that 53% to 57% of high school seniors are fairly certain that they will participate in a study abroad program in college. (c) 90% of such random samples would produce a 90% con dence interval that includes the true proportion. (d) Yes. The interval lies entirely above 50%.

6.13 (a) This is an appropriate setting for a hypothesis test. H 0 : p = 0.50. H A : p > 0.50. Both independence and the success-failure condition are satis ed. $Z = 1:.2 \rightarrow $ p-value = 0.1314. Since the p-value > $\alpha$ = 0.05, we fail to reject H 0 . The data do not provide strong evidence in favor of the claim. (b) Yes, since we did not reject H 0 in part (a).

6.15 (a) $H_0 : p = 0.38$. $H_A : p \ne 0.38$. Independence (random sample, < 10% of population) and the success-failure condition are satisfied. $Z = -20 \rightarrow p-value \approx 0$. Since the p-value is very small, we reject H 0 . The data provide strong evidence that the proportion of Americans who only use their cell phones to access the internet is different than the Chinese proportion of 38%, and the data indicate that the proportion is lower in the US. (b) If in fact 38% of Americans used their cell phones as a primary access point to the internet, the probability of obtaining a random sample of 2,254 Americans where 17% or less or 59% or more use their only their cell phones to access the internet would be approximately 0. (c) (0.1545, 0.1855). We are 95% confident that approximately 15.5% to 18.6% of all Americans primarily use their cell phones to browse the internet.

6.17 (a) $H_0 : p = 0.5. H_A : p > 0.5$. Independence (random sample, < 10% of population) is satisfied, as is the success-failure conditions (using p 0 = 0.5, we expect 40 successes and 40 failures). $Z = 2.91 \rightarrow p-value = 0.0018$. Since the p-value < 0.05, we reject the null hypothesis. The data provide strong evidence that the rate of correctly identifying a soda for these people is significantly better than just by random guessing. (b) If in fact people cannot tell the difference between diet and regular soda and they randomly guess, the probability of getting a random sample of 80 people where 53 or more identify a soda correctly would be 0.0018.

6.19 (a) Independence is satisfied (random sample from < 10% of the population), as is the success-failure condition (40 smokers, 160 non-smokers). The 95% CI: (0.145, 0.255). We are 95% confident that 14.5% to 25.5% of all students at this university smoke. (b) We want z*SE to be no larger than 0.02 for a 95% confidence level. We use z* = 1.96 and plug in the point estimate $\hat {p} = 0.2$ within the SE formula: $1.96 \sqrt {\frac {0.2(1 - 0.2)}{n}} \le 0.02$. The sample size n should be at least 1,537.

6.21 The margin of error, which is computed as z*SE, must be smaller than 0.01 for a 90% confidence level. We use z* = 1.65 for

a 90% confidence level, and we can use the point estimate $\hat {p} = 052$ in the formula for SE. $1.65 \sqrt {\frac {0.52(1 - 0.52)}{n}} \le 0.01$. Therefore, the sample size n must be at least 6,796.

6.23 This is not a randomized experiment, and it is unclear whether people would be affected by the behavior of their peers. That is, independence may not hold. Additionally, there are only 5 interventions under the provocative scenario, so the success-failure condition does not hold. Even if we consider a hypothesis test where we pool the proportions, the success-failure condition will not be satisfied. Since one condition is questionable and the other is not satisfied, the difference in sample proportions will not follow a nearly normal distribution.

6.25 (a) False. The entire con dence interval is above 0. (b) True. (c) True. (d) True. (e) False. It is simply the negated and reordered values: (-0.06,-0.02).

6.27 (a) (0.23, 0.33). We are 95% confident that the proportion of Democrats who support the plan is 23% to 33% higher than the proportion of Independents who do. (b) True.

6.29 (a) College grads: 23.7%. Non-college grads: 33.7%. (b) Let $p_{CG}$ and $p_{NCG}$ represent the proportion of college graduates and noncollege graduates who responded "do not know". $H_0 : p_{CG} = p_{NCG}. H_A : p_{CG} \ne p_{NCG}$. Independence is satisfied (random sample, < 10% of the population), and the success-failure condition, which we would check using the pooled proportion ($\hat {p} = 235/827 = 0.284$), is also satisfied. $Z = -3.18 \rightarrow p-value = 0.0014$. Since the p-value is very small, we reject H 0 . The data provide strong evidence that the proportion of college graduates who do not have an opinion on this issue is different than that of non-college graduates. The data also indicate that fewer college grads say they "do not know" than noncollege grads (i.e. the data indicate the direction after we reject H 0 ).

6.31 (a) College grads: 35.2%. Non-college grads: 33.9%. (b) Let pCG and pNCG represent the proportion of college graduates and non-college grads who support offshore drilling. H 0 : $p_{CG} = p_{NCG}. H_A : p_{CG} \ne p_{NCG}$. Independence is satisfied (random sample, < 10% of the population), and the success-failure condition, which we would check using the pooled proportion ($\hat {p} = 286/827 = 0.346$), is also satised. $Z = 0.39 \rightarrow p-value = 0.6966$. Since the p-value > $\alpha$ (0.05), we fail to reject H 0 . The data do not provide strong evidence of a difference between the proportions of college graduates and non-college graduates who support offshore drilling in California.

6.33 Subscript C means control group. Subscript T means truck drivers. (a) H 0 : pC = pT . H A : pC $\ne$ pT . Independence is satisfied (random samples, < 10% of the population), as is the success-failure condition, which we would check using the pooled proportion ($\hat {p} = 70/495 = 0.141$). $Z = -1.58 \rightarrow p-value = 0.1164$. Since the p-value is high, we fail to reject H 0 . The data do not provide strong evidence that the rates of sleep deprivation are different for non-transportation workers and truck drivers.

6.35 (a) Summary of the study:

(b) H 0 : pN = pL. There is no difference in virologic failure rates between the Nevaripine and Lopinavir groups. H A : pN $\ne$ pL. There is some difference in virologic failure rates between the Nevaripine and Lopinavir groups. (c) Random assignment was used, so the observations in each group are independent. If the patients in the study are representative of those in the general population (something impossible to check with the given information), then we can also confidently generalize the ndings to the population. The success-failure condition, which we would check using the pooled proportion ($\hat {p} = 36/240 = 0.15$), is satis ed. $Z = 3.04 \rightarrow p-value = 0.0024$. Since the p-value is low, we reject H 0 . There is strong evidence of a difference in virologic failure rates between the Nevaripine and Lopinavir groups do not appear to be independent.

6.37 (a) False. The chi-square distribution has one parameter called degrees of freedom. (b) True. (c) True. (d) False. As the degrees of freedom increases, the shape of the chi-square distribution becomes more symmetric.

6.39 (a) H 0 : The distribution of the format of the book used by the students follows the professor's predictions. H A : The distribution of the format of the book used by the students does not follow the professor's predictions. (b) $E_{hard copy} = 126 \times 0.60 = 75.6$. $E_{print} = 126 \times 0.25 = 31.5$. $E_{online} = 126 \times 0.15 = 18.9$. (c) Independence: The sample is not random. However, if the professor has reason to believe that the proportions are stable from one term to the next and students are not a ecting each other's study habits, independence is probably reasonable. Sample size: All expected counts are at least 5. Degrees of freedom: df = k - 1 = 3 - 1 = 2 is more than 1. (d) $X^2 = 2.32, df = 2, p-value > 0.3$. (e) Since the p-value is large, we fail to reject H 0 . The data do not provide strong evidence indicating the professor's predictions were statistically inaccurate.

6.41 (a). Two-way table:

(b-i) $E_{row_1;col_1} = \frac {(row 1 total) \times (col 1 total)}{table total} = \frac {150 \times 70}{300} = 35$. This is lower than the observed value. (b-ii) $E_{row_2;col_2} = \frac {(row 2 total) \times (col 2 total)}{table total} = \frac {150 \times 230}{300} = 115$. This is lower than the observed value.

6.43 H 0 : The opinion of college grads and nongrads is not different on the topic of drilling for oil and natural gas off the coast of California. H A : Opinions regarding the drilling for oil and natural gas off the coast of California has an association with earning a college degree.

\[E_{row 1;col 1} = 151.5 E_{row 1;col 2} = 134.5\]

\[E_{row 2;col 1} = 162.1 E_{row 2;col 2} = 143.9\]

\[E_{row 3;col 1} = 124.5 E_{row 3;col 2} = 110.5\]

Independence: The samples are both random, unrelated, and from less than 10% of the population, so independence between observations is reasonable. Sample size: All expected counts are at least 5. Degrees of freedom: $df = (R - 1) \times (C - 1) = (3 - 1) \times (2 - 1) = 2$, which is greater than 1. $X^2 = 11.47, df = 2 \rightarrow 0.001 < p-value < 0.005$. Since the p-value < \alpha\), we reject H 0 . There is strong evidence that there is an association between support for off -shore drilling and having a college degree.

6.45 (a) H 0 : There is no relationship between gender and how informed Facebook users are about adjusting their privacy settings. H A : There is a relationship between gender and how informed Facebook users are about adjusting their privacy settings. (b) The expected counts:

\[E_{row 1;col 1} = 296.6 E_{row 1;col 2} = 369.3\]

\[E_{row 2;col 1} = 162.1 E_{row 2;col 2} = 68.2\]

\[E_{row 3;col 1} = 7.6 E_{row 3;col 2} = 9.4\]

The sample is random, all expected counts are above 5, and $df = (3 - 1) \times (2 - 1) = 2 > 1$, so we may proceed with the test.

6.47 It is not appropriate. There are only 9 successes in the sample, so the success-failure condition is not met.

6.49 (a) H 0 : p = 0.69. H A : p $\ne$ 0.69. (b) $\hat {p} = \frac {17}{30} = 0.57$. (c) The success-failure condition is not satisfied; note that it is appropriate to use the null value ($p_0 = 0.69$) to compute the expected number of successes and failures. (d) Answers may vary. Each student can be represented with a card. Take 100 cards, 69 black cards representing those who follow the news about Egypt and 31 red cards representing those who do not. Shuffle the cards and draw with replacement (shuffling each time in between draws) 30 cards representing the 30 high school students. Calculate the proportion of black cards in this sample, $\hat {p} _{sim}$, i.e. the proportion of those who follow the news in the simulation. Repeat this many times (e.g. 10,000 times) and plot the resulting sample proportions. The p-value will be two times the proportion of simulations where $\hat {p}_{sim} \ge 0.57$. (Note: we would generally use a computer to perform these simulations.) (e) The p-value is about 0.001 + 0.005 + 0.020 + 0.035 + 0.075 = 0.136, meaning the two-sided p-value is about 0.272. Your p-value may vary slightly since it is based on a visual estimate. Since the p-value is greater than 0.05, we fail to reject H 0 . The data do not provide strong evidence that the proportion of high school students who followed the news about Egypt is different than the proportion of American adults who did.

6.51 The subscript pr corresponds to provocative and con to conservative. (a) $H_0 : p_{pr} = p_{con}$. $H_A : p_{pr} \ne p_{con}$. (b) -0.35. (c) The left tail for the p-value is calculated by adding up the two left bins: 0.005 + 0.015 = 0.02. Doubling the one tail, the p-value is 0.04. (Students may have approximate results, and a small number of students may have a p-value of about 0.05.) Since the p-value is low, we reject H 0 . The data provide strong evidence that people react differently under the two scenarios.

Introduction to linear regression

7.1 (a) The residual plot will show randomly distributed residuals around 0. The variance is also approximately constant. (b) The residuals will show a fan shape, with higher variability for smaller x. There will also be many points on the right above the line. There is trouble with the model being t here.

7.3 (a) Strong relationship, but a straight line would not t the data. (b) Strong relationship, and a linear t would be reasonable. (c) Weak relationship, and trying a linear fit would be reasonable. (d) Moderate relationship, but a straight line would not t the data. (e) Strong relationship, and a linear t would be reasonable. (f) Weak relationship, and trying a linear fit would be reasonable.

7.5 (a) Exam 2 since there is less of a scatter in the plot of nal exam grade versus exam 2. Notice that the relationship between Exam 1 and the Final Exam appears to be slightly nonlinear. (b) Exam 2 and the nal are relatively close to each other chronologically, or Exam 2 may be cumulative so has greater similarities in material to the nal exam. Answers may vary for part (b).

7.7 (a) $R = -0.7 \rightarrow$ (4). (b) $R = 0.45 \rightarrow$ (3). (c) $R = 0.06 \rightarrow$ (1). (d) $R = 0.92 \rightarrow$ (2).

7.9 (a) The relationship is positive, weak, and possibly linear. However, there do appear to be some anomalous observations along the left where several students have the same height that is notably far from the cloud of the other points. Additionally, there are many students who appear not to have driven a car, and they are represented by a set of points along the bottom of the scatterplot. (b) There is no obvious explanation why simply being tall should lead a person to drive faster. However, one confounding factor is gender. Males tend to be taller than females on average, and personal experiences (anecdotal) may suggest they drive faster. If we were to follow-up on this suspicion, we would nd that sociological studies con rm this suspicion. (c) Males are taller on average and they drive faster. The gender variable is indeed an important confounding variable.

7.11 (a) There is a somewhat weak, positive, possibly linear relationship between the distance traveled and travel time. There is clustering near the lower left corner that we should take special note of. (b) Changing the units will not change the form, direction or strength of the relationship between the two variables. If longer distances measured in miles are associated with longer travel time measured in minutes, longer distances measured in kilometers will be associated with longer travel time measured in hours. (c) Changing units doesn't affect correlation: R = 0.636.

7.13 (a) There is a moderate, positive, and linear relationship between shoulder girth and height. (b) Changing the units, even if just for one of the variables, will not change the form, direction or strength of the relationship between the two variables.

7.15 In each part, we may write the husband ages as a linear function of the wife ages: (a) $age_H = age_W + 3$; (b) $age_H = age_W - 2$; and (c) $age_H = age_W/2$. Therefore, the correlation will be exactly 1 in all three parts. An alternative way to gain insight into this solution is to create a mock data set, such as a data set of 5 women with ages 26, 27, 28, 29, and 30 (or some other set of ages). Then, based on the description, say for part (a), we can compute their husbands' ages as 29, 30, 31, 32, and 33. We can plot these points to see they fall on a straight line, and they always will. The same approach can be applied to the other parts as well.

7.17 (a) There is a positive, very strong, linear association between the number of tourists and spending. (b) Explanatory: number of tourists (in thousands). Response: spending (in millions of US dollars). (c)We can predict spending for a given number of tourists using a regression line. This may be useful information for determining how much the country may want to spend in advertising abroad, or to forecast expected revenues from tourism. (d) Even though the relationship appears linear in the scatterplot, the residual plot actually shows a nonlinear relationship. This is not a contradiction: residual plots can show divergences from linearity that can be difficult to see in a scatterplot. A simple linear model is inadequate for modeling these data. It is also important to consider that these data are observed sequentially, which means there may be a hidden structure that it is not evident in the current data but that is important to consider.

7.19 (a) First calculate the slope: $b_1 = R \times \frac {s_y}{s_x} = 0.636 \times \frac {113}{99} = 0.726$. Next, make use of the fact that the regression line passes through the point $(\bar {x}; \bar {y}): \bar {y} = b_0 + b_1 \times \bar {x}$. Plug in $\bar {x}, \bar {y}, and b_1$, and solve for $b_0$: 51. Solution: travdel time = $51 + 0.726 \times distance$. (b) $b_1$: For each additional mile in distance, the model predicts an additional 0.726 minutes in travel time. $b_0$: When the distance traveled is 0 miles, the travel time is expected to be 51 minutes. It does not make sense to have a travel distance of 0 miles in this context. Here, the y-intercept serves only to adjust the height of the line and is meaningless by itself. (c) $R^2 = 0.636^2 = 0.40$. About 40% of the variability in travel time is accounted for by the model, i.e. explained by the distance traveled. (d) $\hat {travdel time} = 51 + 0.726 \times distance = 51 + 0.726 \times 103 \approx 126 minutes$. (Note: we should be cautious in our predictions with this model since we have not yet evaluated whether it is a well- t model.) (e) $e_i = y_i - \hat {y}_i = 168 - 126 = 42 minutes$. A positive residual means that the model underestimates the travel time. (f) No, this calculation would require extrapolation.

7.21 The relationship between the variables is somewhat linear. However, there are two apparent outliers. The residuals do not show a random scatter around 0. A simple linear model may not be appropriate for these data, and we should investigate the two outliers.

7.23 (a) $\sqrt {R^2} = 0.849$. Since the trend is negative, R is also negative: $R = -0.849$. (b) $b_0 = 55.34. b_1 = -0.537$. (c) For a neighborhood with 0% reduced-fee lunch, we would expect 55.34% of the bike riders to wear helmets. (d) For every additional percentage point of reduced fee lunches in a neighborhood, we would expect 0.537% fewer kids to be wearing helmets. (e) $\hat {y} = 40 \times (-0.537)+55.34 = 33.86$, $e = 40 - \hat {y} = 6.14$. There are 6.14% more bike riders wearing helmets than predicted by the regression model in this neighborhood.

7.25 (a) The outlier is in the upper-left corner. Since it is horizontally far from the center of the data, it is a point with high leverage. Since the slope of the regression line would be very different if t without this point, it is also an inuential point. (b) The outlier is located in the lowerleft corner. It is horizontally far from the rest of the data, so it is a high-leverage point. The line again would look notably different if the fit excluded this point, meaning it the outlier is inuential. (c) The outlier is in the upper-middle of the plot. Since it is near the horizontal center of the data, it is not a high-leverage point. This means it also will have little or no inuence on the slope of the regression line.

7.27 (a) There is a negative, moderate-to-strong, somewhat linear relationship between percent of families who own their home and the percent of the population living in urban areas in 2010. There is one outlier: a state where 100% of the population is urban. The variability in the percent of homeownership also increases as we move from left to right in the plot. (b) The outlier is located in the bottom right corner, horizontally far from the center of the other points, so it is a point with high leverage. It is an influential point since excluding this point from the analysis would greatly affect the slope of the regression line.

7.29 (a) The relationship is positive, moderate-to-strong, and linear. There are a few outliers but no points that appear to be influential. (b) $\hat {wedight} = -105.0113+1.0176 \times height. Slope: For each additional centimeter in height, the model predicts the average weight to be 1.0176 additional kilograms (about 2.2 pounds). Intercept: People who are 0 centimeters tall are expected to weigh -105.0113 kilograms. This is obviously not possible. Here, the y-intercept serves only to adjust the height of the line and is meaningless by itself. (c) H 0 : The true slope coefficient of height is zero ( \(\beta _1$ = 0). H 0 : The true slope coefficient of height is greater than zero ( $\beta _1$ > 0). A two-sided test would also be acceptable for this application. The p-value for the two-sided alternative hypothesis ( $\beta _1 \ne 0$) is incredibly small, so the p-value for the onesided hypothesis will be even smaller. That is, we reject H 0 . The data provide convincing evidence that height and weight are positively correlated. The true slope parameter is indeed greater than 0. (d) $R^2 = 0.72^2 = 0.52$. Approximately 52% of the variability in weight can be explained by the height of individuals.

7.31 (a) $H_0: \beta _1 = 0. H_0: \beta _1 > 0$. A two-sided test would also be acceptable for this application. The p-value, as reported in the table, is incredibly small. Thus, for a one-sided test, the p-value will also be incredibly small, and we reject $H_0$. The data provide convincing evidence that wives' and husbands' heights are positively correlated. (b) $\hat {hedight} _W = 43.5755 + 0.2863 times height_H$. (c) Slope: For each additional inch in husband's height, the average wife's height is expected to be an additional 0.2863 inches on average. Intercept: Men who are 0 inches tall are expected to have wives who are, on average, 43.5755 inches tall. The intercept here is meaningless, and it serves only to adjust the height of the line. (d) The slope is positive, so R must also be positive. $R = \sqrt {0.09} = 0.30$. (e) 63.2612. Since $R^2$ is low, the prediction based on this regression model is not very reliable. (f) No, we should avoid extrapolating.

7.33 (a) 25.75. (b) $H_0: \beta _1 = 0$. $H_A: \beta _1 \ne 0$. A one-sided test also may be reasonable for this application. T = 2.23, $df = 23 \rightarrow p-value$ between 0.02 and 0.05. So we reject H 0 . There is an association between gestational age and head circumference. We can also say that the associaation is positive.

Multiple and logistic regression

8.1 (a) $\hat {baby_weight} = 123.05 \times 8.94$ smoke (b) The estimated body weight of babies born to smoking mothers is 8.94 ounces lower than babies born to non-smoking mothers. Smoker: $123.05-8.94 \times 1 = 114.11$ ounces. Non-smoker: $123.05 - 8.94 \times 0 = 123.05$ ounces. (c) $H_0: \beta _1 = 0. H_A: \beta _1 \ne 0$. $T = -8..65$, and the p-value is approximately 0. Since the p-value is very small, we reject $H_0$. The data provide strong evidence that the true slope parameter is different than 0 and that there is an association between birth weight and smoking. Furthermore, having rejected $H_0$, we can conclude that smoking is associated with lower birth weights.

8.3 (a) $\hat {baby_weight} = -80.41 + 0.44 \times gestation - 3.33 \times parity - 0.01 \times age + 1.15 \times height + 0.05 weight - 8.40$ smoke. (b) gestation: The model predicts a 0.44 ounce increase in the birth weight of the baby for each additional day of pregnancy, all else held constant. age: The model predicts a 0.01 ounce decrease in the birth weight of the baby for each additional year in mother's age, all else held constant. (c) Parity might be correlated with one of the other variables in the model, which complicates model estimation. (d) $\hat {baby_weight} = 120.58$. e = 120 - 120.58 = -0.58. The model over-predicts this baby's birth weight. (e) $R^2 = 0.2504$. $R^2_{adj} = 0.2468$.

8.5 (a) (-0.32, 0.16). We are 95% confident that male students on average have GPAs 0.32 points lower to 0.16 points higher than females when controlling for the other variables in the model. (b) Yes, since the p-value is larger than 0.05 in all cases (not including the intercept).

8.7 (a) There is not a signi cant relationship between the age of the mother. We should consider removing this variable from the model. (b) All other variables are statistically significant at the 5% level.

8.9 Based on the p-value alone, either gestation or smoke should be added to the model first. However, since the adjusted $R^2$ for the model with gestation is higher, it would be preferable to add gestation in the first step of the forwardselection algorithm. (Other explanations are possible. For instance, it would be reasonable to only use the adjusted $R^2$.)

8.11 Nearly normal residuals: The normal probability plot shows a nearly normal distribution of the residuals, however, there are some minor irregularities at the tails. With a data set so large, these would not be a concern. Constant variability of residuals: The scatterplot of the residuals versus the tted values does not show any overall structure. However, values that have very low or very high tted values appear to also have somewhat larger outliers. In addition, the residuals do appear to have constant variability between the two parity and smoking status groups, though these items are relatively minor.

Independent residuals: The scatterplot of residuals versus the order of data collection shows a random scatter, suggesting that there is no apparent structures related to the order the data were collected.

Linear relationships between the response variable and numerical explanatory variables: The residuals vs. height and weight of mother are randomly distributed around 0. The residuals vs. length of gestation plot also does not show any clear or strong remaining structures, with the possible exception of very short or long gestations. The rest of the residuals do appear to be randomly distributed around 0. All concerns raised here are relatively mild. There are some outliers, but there is so much data that the inuence of such observations will be minor.

8.13 (a) There are a few potential outliers, e.g. on the left in the total length variable, but nothing that will be of serious concern in a data set this large. (b) When coefficient estimates are sensitive to which variables are included in the model, this typically indicates that some variables are collinear. For example, a possum's gender may be related to its head length, which would explain why the coefficient (and p-value) for sex male changed when we removed the head length variable. Likewise, a possum's skull width is likely to be related to its head length, probably even much more closely related than the head length was to gender.

8.15 (a) The logistic model relating $\hat {p}_i$ to the predictors may be written as $log (\frac {\hat {p}_i}{1- \hat {p}_i}) = 33.5095 - 1.4207 \times sex male_i - 0.2787 \times skull widthi + 0.5687 total length_i$. Only total_length has a positive association with a possum being from Victoria. (b) $\hat {p} = 0.0062$. While the probability is very near zero, we have not run diagnostics on the model. We might also be a little skeptical that the model will remain accurate for a possum found in a US zoo. For example, perhaps the zoo selected a possum with specific characteristics but only looked in one region. On the other hand, it is encouraging that the possum was caught in the wild. (Answers regarding the reliability of the model probability will vary.)

Contributors

David M Diez (Google/YouTube), Christopher D Barr (Harvard School of Public Health), Mine Çetinkaya-Rundel (Duke University)

Statistics 110: Probability

Strategic Practice and Homework Problems

Actively solving practice problems is essential for learning probability. Strategic practice problems are organized by concept, to test and reinforce understanding of that concept. Homework problems usually do not say which concepts are involved, and often require combining several concepts. Each of the Strategic Practice documents here contains a set of strategic practice problems, solutions to those problems, a homework assignment, and solutions to the homework assignment. Also included here are the exercises from the book that are marked with an s, and solutions to those exercises.

IMAGES

Homework #12 Solutions
Homework solutions to introduction to probability and mathematical
Statistics 100A Homework 2 Solutions
Solved Introduction to Statistics Homework: Section 3.2
Math 8 introduction to statistics Homework 1
Introduction to Statistics

VIDEO

Introduction to Statistical Theory Part-1 Chapter 6||full exercise solution Notes For BS students
Final Example 3 Solution
Mean Solution
Introduction to Statistical Theory Part-1 Chapter 2[Presentation of Data] Complete Exercise Solution
Statistics Homework Help
Formulas

COMMENTS

Ch. 1 Solutions
Introduction; 9.1 Null and Alternative Hypotheses; 9.2 Outcomes and the Type I and Type II Errors; 9.3 Distribution Needed for Hypothesis Testing; 9.4 Rare Events, the Sample, Decision and Conclusion; 9.5 Additional Information and Full Hypothesis Test Examples; 9.6 Hypothesis Testing of a Single Mean and Single Proportion; Key Terms; Chapter Review; Formula Review ...
PDF Introductory Statistics Explained Answers to Exercises
Contents 1 Introduction1 2 GatheringData3 2.1 Introduction. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3 2.2 PopulationsandSamples ...
Introductory Statistics
Now, with expert-verified solutions from Introductory Statistics 10th Edition, you'll learn how to solve your toughest homework problems. Our resource for Introductory Statistics includes answers to chapter exercises, as well as detailed information to walk you through the process step by step. With Expert Solutions for thousands of practice ...
Introductory Statistics
Now, with expert-verified solutions from Introductory Statistics 1st Edition, you'll learn how to solve your toughest homework problems. Our resource for Introductory Statistics includes answers to chapter exercises, as well as detailed information to walk you through the process step by step. With Expert Solutions for thousands of practice ...
E Solution Sheets
Use the previous information to sketch a picture of this situation. Clearly label and scale the horizontal axis and shade the region (s) corresponding to the p -value. Figure E4. Indicate the correct decision ("reject" or "do not reject" the null hypothesis) and write appropriate conclusions, using complete sentences.
Chapter 1 Homework
HOMEWORK from 1.2. For each of the following eight exercises, identify: a. the population, b. the sample, c. the parameter, d. the statistic, e. the variable, and f. the data. Give examples where appropriate. A fitness center is interested in the mean amount of time a client exercises in the center each. week.
Introductory Statistics
Now, with expert-verified solutions from Introductory Statistics 9th Edition, you'll learn how to solve your toughest homework problems. Our resource for Introductory Statistics includes answers to chapter exercises, as well as detailed information to walk you through the process step by step. With Expert Solutions for thousands of practice ...
Introductory Statistics
Most of the typical topics covered in an Introduction to Statistics class are all covered in reasonable detail. Basic descriptive statistics, constructing and reading various types of graphs and charts, an introduction to relevant concepts of probability, and hypotheses testing. ... Solution of homework of each chapter is given in the chapter ...
Statistics and Probability
Unit 7: Probability. 0/1600 Mastery points. Basic theoretical probability Probability using sample spaces Basic set operations Experimental probability. Randomness, probability, and simulation Addition rule Multiplication rule for independent events Multiplication rule for dependent events Conditional probability and independence.
1.E: Introduction to Statistics (Exercises)
These are homework exercises to accompany the Textmap created for "Introductory Statistics" by Shafer and Zhang. Complementary General Chemistry question banks can be found for other Textmaps and can be accessed here. In addition to these publicly available questions, access to private problems bank for use in exams and homework is available to ...
1.E: Introduction to Statistics (Exercises)
These are homework exercises to accompany the Textmap created for "Introductory Statistics" by Shafer and Zhang. ... Introduction to Statistics (Exercises) is shared under a not declared license and was ... the California State University Affordable Learning Solutions Program, and Merlot. We also acknowledge previous National Science Foundation ...
Worksheets- Introductory Statistics
The student will explain the details of each procedure used. Worksheets- Introductory Statistics. 1.1.1: Central Limit Theorem- Cookie Recipes (Worksheet) The LibreTexts worksheets are documents with questions or exercises for students to complete and record answers and are intended to help a student become proficient in a particular skill that ...
Chapter 1 Solutions
Problem. 1SE. Step-by-step solution. Step 1 of 1. We are asked about the term for data that have not been particularly organized or examined. This term is raw data. Raw data have not yet been statistically analyzed; they are unprocessed. Before they are arranged or analyzed information or observations are called raw data.
Homework 10 solutions
Homework 10 solutions introduction to statistical inference homework 10 solutions due: may 30, 2020 (7pm) remember to show all your you will not receive any. Skip to document. ... Matey Neykov, Dept. of Statistics and Data Science, Carnegie Mellon University 1 Note: the estimator S 2 is independent of β̂ 1 (see Wackerly p), so the assumption ...
Introduction to Mathematical Statistics
Exercise 61. Exercise 62. Exercise 63. At Quizlet, we're giving you the tools you need to take on any subject without having to carry around solutions manuals or printing out PDFs! Now, with expert-verified solutions from Introduction to Mathematical Statistics 5th Edition, you'll learn how to solve your toughest homework problems.
STAT200 Week4 Homework Solutions new
STAT 200: Introduction to Statistics. Week 4 Homework Solutions (1 point each/10 points total) Problem 1 (6.1) The commuter trains on the Red Line for the Regional Transit Authority (RTA) in Cleveland, OH, have a waiting time during peak rush hour periods of eight minutes ("2012 annual report," 2012). a.)
9: End of chapter exercise solution
Introduction to data. 1.1 (a) Treatment: 10/43 = 0.23 $\rightarrow$ 23%. Control: 2/46 = 0:04 ! 4%. (b) There is a 19% difference between the pain reduction rates in the two groups. At first glance, it appears patients in the treatment group are more likely to experience pain reduction from the acupuncture treatment.
STAT 200
Page 1 of 18 STAT 200: Introduction to Statistics Homework #7 Solutions 1. (3 points): Table #1 contains the value of the house and the amount of rental income in a year that the house brings in ("Capital and rental," 2013). Create a scatter plot and find a regression equation between house value and rental income.
Statistics Textbook Solutions & Answers
Statistics: Informed Decisions Using Data. 5th Edition • ISBN: 9780134462134 Michael Sullivan III. 6,143 solutions. Get your Statistics homework done with Quizlet! Browse through thousands of step-by-step solutions to end-of-chapter questions from the most popular Statistics textbooks. It's never been a better time to #LearnOn.
Strategic Practice and Homework Problems
Actively solving practice problems is essential for learning probability. Strategic practice problems are organized by concept, to test and reinforce understanding of that concept. Homework problems usually do not say which concepts are involved, and often require combining several concepts.Each of the Strategic Practice documents here contains a set of strategic practice problems, solutions ...
Statistics
Find step-by-step solutions and answers to Statistics - 9780393929720, as well as thousands of textbooks so you can move forward with confidence. ... Now, with expert-verified solutions from Statistics 4th Edition, you'll learn how to solve your toughest homework problems. Our resource for Statistics includes answers to chapter exercises, as ...