If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 10: One-step and two-step equations & inequalities
Combining like terms.
- Intro to combining like terms (Opens a modal)
- Combining like terms with negative coefficients & distribution (Opens a modal)
- Combining like terms with negative coefficients (Opens a modal)
- Combining like terms with rational coefficients (Opens a modal)
- Combining like terms with negative coefficients Get 5 of 7 questions to level up!
- Combining like terms with negative coefficients & distribution Get 3 of 4 questions to level up!
- Combining like terms with rational coefficients Get 3 of 4 questions to level up!
The distributive property & equivalent expressions
- The distributive property with variables (Opens a modal)
- Factoring with the distributive property (Opens a modal)
- Equivalent expressions: negative numbers & distribution (Opens a modal)
- Distributive property with variables (negative numbers) Get 3 of 4 questions to level up!
- Equivalent expressions: negative numbers & distribution Get 5 of 7 questions to level up!
Interpreting linear expressions
- Interpreting linear expressions: diamonds (Opens a modal)
- Interpreting linear expressions: flowers (Opens a modal)
- Writing expressions word problems (Opens a modal)
- Interpreting linear expressions Get 3 of 4 questions to level up!
- Writing expressions word problems Get 5 of 7 questions to level up!
Two-step equations intro
- Same thing to both sides of equations (Opens a modal)
- Intro to two-step equations (Opens a modal)
- Two-step equations intuition (Opens a modal)
- Worked example: two-step equations (Opens a modal)
- Two-step equations Get 5 of 7 questions to level up!
Two-step equations with decimals and fractions
- Two-step equations with decimals and fractions (Opens a modal)
- Find the mistake: two-step equations (Opens a modal)
- Two-step equations review (Opens a modal)
- Two-step equations with decimals and fractions Get 5 of 7 questions to level up!
- Find the mistake: two-step equations Get 3 of 4 questions to level up!
Two-step equation word problems
- Equation word problem: super yoga (1 of 2) (Opens a modal)
- Equation word problem: super yoga (2 of 2) (Opens a modal)
- Two-step equation word problem: computers (Opens a modal)
- Two-step equation word problem: garden (Opens a modal)
- Two-step equation word problem: oranges (Opens a modal)
- Interpret two-step equation word problems Get 3 of 4 questions to level up!
- Two-step equations word problems Get 3 of 4 questions to level up!
One-step inequalities
- Testing solutions to inequalities (Opens a modal)
- One-step inequalities examples (Opens a modal)
- One-step inequalities: -5c ≤ 15 (Opens a modal)
- One-step inequality word problem (Opens a modal)
- One-step inequalities review (Opens a modal)
- Testing solutions to inequalities Get 3 of 4 questions to level up!
- One-step inequalities Get 5 of 7 questions to level up!
Two-step inequalities
- Two-step inequalities (Opens a modal)
- Two-step inequality word problem: apples (Opens a modal)
- Two-step inequality word problem: R&B (Opens a modal)
- Two-step inequalities Get 5 of 7 questions to level up!
- Two-step inequality word problems Get 3 of 4 questions to level up!
- Texas Go Math
- Big Ideas Math
- Engageny Math
- McGraw Hill My Math
- enVision Math
- 180 Days of Math
- Math in Focus Answer Key
- Math Expressions Answer Key
- Privacy Policy
Into Math Grade 7 Module 7 Lesson 3 Answer Key Write Two-Step Equations for Situations
We included HMH Into Math Grade 7 Answer Key PDF Module 7 Lesson 3 Write Two-Step Equations for Situations to make students experts in learning maths.
HMH Into Math Grade 7 Module 7 Lesson 3 Answer Key Write Two-Step Equations for Situations
I Can write two-step equations for various situations.
Spark Your Learning

Explanation: He made 6 quiches yesterday.
Scenario 2: Javier buys four dozen eggs. He saves $1.50 by using a coupon. The total he pays is $8.50. What was the cost of a dozen eggs without the coupon? Answer: $2.50
Explanation: The cost of a dozen eggs without a coupon is $2.50.
Scenario 3: Lina ate \(\frac{1}{4}\) of a quiche for lunch. Each of her two sisters split another piece equally. The three ate a total of \(\frac{7}{12}\) of the quiche. What fraction of the quiche did each of Lina’s sisters eat? Answer:
Turn and Talk Choose one of the equations you wrote. Make up another scenario that the equation could represent. Answer:
Build Understanding
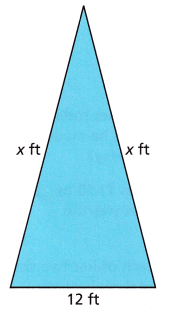
C. What is the value of the expression you wrote? Answer: x = 18 feet.
D. Use your answers from Parts B and C to write an equation that can be used to find the length of each of the two equal sides. Answer:
E. How would your equation change if the perimeter were 80 feet? Answer: 80 = 2 (x + 10).
F. What would your equation be if the perimeter were 80 feet and the base were 10 feet long? Answer: The equation is 80 = 2 (x + 10). Given Perimeter = 80 feet and base = 10 feet. Let us assume one side of the traingle is x a = x feet p = 2(a + b) 80 = 2 (x + 10)
Turn and Talk How is an equation like an expression? How is it different? Answer:
Step It Out

B. Write an equation that can be used to find the unknown information. Use x as the variable. Answer: 0.5(22 + x) = 18.55
C. What does each side of the equation represent? Answer: Each side of the equation represents before the discount and after the discount given.
D. What does the variable x represent? Answer: X represents the price of the shoes before the discount.
Check Understanding
Question 1. Each time Cheryl runs, she runs 3 miles. She rides her bike only on Saturdays and always for 10 miles. She exercises the same amount each week. She rides and runs for a total of 22 miles in a week. Write an equation that can be used to find out how many times Cheryl goes running each week. Answer: 3x + 10y = 22
Explanation: An equation that can be used to find out how many times Cheryl goes running each week is 3x + 10y = 22.
Question 2. Mrs. Wu uses a 25% off coupon to buy 1 adult ticket and 1 child ticket to a movie. She pays a total amount of $9.00. A child ticket without the coupon costs $4.00. Write an equation that can be used to find the cost of an adult ticket without the coupon. Answer: cost of an adult ticket is $7.25.
Explanation: An equation that can be used to find the cost of an adult ticket without the coupon is 11.25 – 4 = $7.25
On Your Own
Model with Mathematics For Problems 3-8, write an equation to represent the situation.
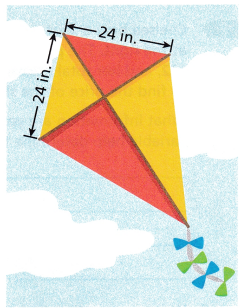
Explanation: Given, Perimeter us 120inches Sides are 24 inches + 24 inches = 48 inches Two longer sides + (24 × 2) = 120 inches (2 × x) + 48 = 120 2x = 120 – 48 2x = 72 x = 72 ÷ 2 x = 36
Question 4. Ms. Malia bought a laptop with a 10% discount. She also bought a mouse for $13.99 and spent a total of $621.49 before taxes. Write an equation to find the original cost of the laptop. Answer: $675
Explanation: The original cost of the laptop is x Given discount = 10% Price of mouse = $13.99 Total amount spent is $621.49 x – x \(\frac{10}{100}\) + 13.99 = 621.49 x – \(\frac{x}{10}\) + 13.99 = 621.99 \(\frac{9x}{10}\) + 13.99 = 621.99 \(\frac{9x}{10}\) = 621.99 -13.99 \(\frac{9x}{10}\) = 607.5 9x = 607.5 × 10 x = 6075 ÷ 9 x = $675
Question 5. Paolo is using his grandmother’s cookie recipe. He always doubles the amount of chocolate chips and oats. The recipe calls for 2\(\frac{1}{2}\) cups of chocolate chips. The total amount of chips and oats after doubling is 6\(\frac{1}{3}\) cups. Write an equation to find the original amount of oats in the recipe. Answer: x = 1 \(\frac{11}{12}\)
Explanation: Given, The total amount of chips and oats is 6\(\frac{1}{3}\) Recipe calls for 2\(\frac{1}{2}\) 6\(\frac{1}{3}\) – 2\(\frac{1}{2}\) = 2x \(\frac{19}{3}\) – \(\frac{5}{2}\) = 2x \(\frac{23}{6}\) = 2x \(\frac{23}{12}\) = x x = 1\(\frac{11}{12}\)
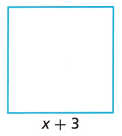
Explanation: Length = x + 3 Perimeter of the square = 4 × length = 54.8 4 (x + 3) = 54.8 x + 3 = 54.8 ÷ 4 x + 3 = 13.7 x = 13.7 – 3 x = 10.7 Each side of the length = 10.7
Question 7. Ms. Emily buys a hat and gloves with a coupon for 30% off her entire purchase. The gloves cost $35 before the discount. Her biH before tax is $44.80. Write an equation to find the original cost of the hat. Answer: ($35 + x) (1 – 0.3) 44.80
Question 8. Bo’s sister Anna is \(\frac{3}{4}\) his age minus 1 year. She is 11 years old. Write an equation to find Bo’s age. Answer: Bo’s age is 16.
Explanation: Let us solve the given question based on the given conditions. \(\frac{3}{4}\) × x – 1 = 11 Now solve the given equation \(\frac{3}{4}\)x = 11 + 1 \(\frac{3}{4}\)x = 12 x = 12 × \(\frac{4}{3}\) x = 16. Bo’s age is 16.
I’m in a Learning Mindset!
What barriers do I perceive to writing two-step equations for situations? Answer:
Lesson 7.3 More Practice/Homework
Question 1. Pierce is making a rectangular frame for a photo collage that has a perimeter of 72.2 inches. The length of the frame is 20.3 inches. Write an equation to find the width of the frame. Answer: x = \(\frac{79}{5}\).
Explanation: From the given question, 2(20.3 + x) = 72.2 Let us solve the equation Now expand the given expression 40.6 + 2x = 72.2 2x = 72.2 – 40.6 2x = 31.6 x = 31.6 ÷ 2 x = 79 ÷ 5
Question 2. Kendra is 3 times her daughter’s age plus 7 years. Kendra is 49 years old. Write an equation to find her daughter’s age. Answer: Her daughter’s age is 14.
Explanation: Let us solve the given question 7 + 3x = 49 3x = 49 – 7 3x = 42 Divide both sides x = 42 ÷ 3 simplify x = 14
Question 3. Mitchell orders a plain turkey sandwich and a drink for lunch. The drink is $2.95. Instead he is served the super sandwich with lettuce, tomato, and mayonnaise. The restaurant manager takes 15% off the price of the sandwich. Write an equation to determine the original price of Mitchell’s sandwich if his new bill is $8.05. Answer: Original price is $6
Explanation: The original price of the sandwich is $x. The drink is $2.95 $2.95 + (1 – 0.15) x = $8.05 $2.95 + 0.85 x = $8.05 0.85x = $8.05 -$2.95 0.85x = $5.1 x = $5.1 ÷ 0.85 x = $6
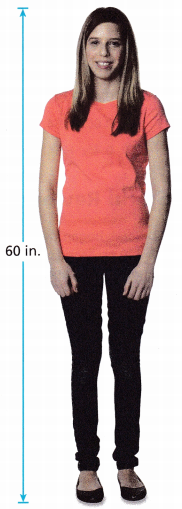
Explanation: Let us assume Bianca’s height as x. \(\frac{2}{3}\) × x + 32 = 60 \(\frac{2}{3}\) × x = 60 – 32 \(\frac{2}{3}\) × x = 28 x = (28 × 3) ÷ 2 x = 84 ÷ 2 x = 42 Therefore Bianca’s height is 42 inches.
Question 5. Health and Fitness Tyler does squats and pushups. He wants to increase the number of each type of exercise by 20% by the end of the month. He currently does 25 pushups. If Tyler meets his goal, he will do a total of 13 more squats and pushups than he does now. Write an equation to find how many squats Tyler does now. Answer: x = 40
Explanation: Let us solve the given question 25 × 20% + x × 20% = 13 5 + 0.2x = 13 0.2x = 13 – 5 0.2x = 8 x = 8 ÷ 0.2 x = 80 ÷ 2 x = 40 Therefore Tyler does 40 squats.
Question 6. Model with Mathematics An equilateral triangle has side lengths that measure x + 4 inches. The perimeter of the triangle is 18.6 inches. Write an equation to find the value of x. Answer: x = 2.2
Explanation: Given is an equilateral triangle Side is x + 4 inches Perimeter is 18.6 inches. The three sides of an equilateral traingle are equal x + 4 = 18.6 ÷ 3 x + 4 = 6.2 x = 6.2 – 4 x = 2.2
Question 7. Model with Mathematics Ms. Lynette earns $19.50 an hour when she works overtime. She worked overtime twice this week. One day she worked 3 hours of overtime. Her total overtime pay for the week is $146.25. Write an equation to find the number of overtime hours worked on the second day. Answer: 4.5 hours
Explanation: Let us assume the the number of overtime hours worked on the second day as x 3 × 19.5 + 19.5 × x = 146.25 58.5 + 19.5x = 146.25 19.5x = 146.25 -58.5 19.5x = 87.75 x = 87.75 ÷ 19.5 x = 4.5 hours
Question 8. A parallelogram has a perimeter of 50\(\frac{1}{2}\) inches. The two longer sides of the parallelogram are each 16\(\frac{1}{4}\) inches. Write an equation to find the length of each of the shorter sides. Answer:
Question 9. A baby usually gains 10% of its birth weight plus 2 pounds in the first six weeks after birth. A baby gained 2.8 pounds. Write an equation to find the baby’s birth weight. Answer: 1.1x + 2 = 2.8
Explanation: Gain 10% = 100% + 10% = 110% = 1.1 Let us assume the baby’s birth weight as x. Now let us solve the given question 1.1x + 2 = 2.8
Question 10. A rhombus has sides of length x + 6 inches and a perimeter of 49 inches. Which equation represents this situation? (A) 4x + 6 = 49 (B) 4(x + 6) – 49 (C) x + 6 = 49 (D) x + 24 = 49 Answer: (B) 4(x + 6) – 49
Explanation: Rhombus has four equal sides Perimeter = 4 × side length = x + 6 Perimeter = 49 inches Side = x + 6 4 (x + 6) = 49
Question 11. Mrs. Owens has a coupon for 40% off a pair of shoes. She pays $111.79 for a pair of shoes and a dress after using the coupon. The dress costs $64.99. Which equation can be solved for x, the retail price of the shoes? (A) 0.6x + 64.99 = 111.79 (B) 0.4x + 64.99 = 111.79 (C) 0.6(x + 64.99) = 111.79 (D) 0.4(x + 64.99) = 111.79 Answer: (A) 0.6x + 64.99 = 111.79
Explanation: From the given question Calculate the given question (64.99 + 40% of x) × (1 – 40%) = 111.79 0.6x + 64.99 = 111.79
Spiral Review
Question 12. Sarah began the school week with $2.60 in her lunch account. She deposited $20 on Monday, and then spent $4.75 each day that week for lunch. What was the balance in her lunch account at the end of the day on Friday? Answer: -1.15
Explanation: Based on the given question calculate 2.6 + 20 – 4.75 × 5 2.6 + 20 – 23.75 22.6 – 23.75 -1.15 The balance in her lunch account at the end of the day on Friday is -1.15.
Question 13. Mr. Alvarado goes shopping at the mall with $70. He buys a pair of pants for $33.76 and a shirt for $29.52. He also returns a hat he bought the previous week for $19.67. How much money does Mr. Alvarado have after he buys the pants and shirt and returns the hat? Answer: $26.39
Explanation: Mr. Alvarado went for shopping with $70. Pair of pants for $33.76 The hat he brought = $19.67 The money Mr. Alvarado have is 70 – 29.52 – 33.76 + 19.67 = 26.39
Leave a Comment Cancel Reply
You must be logged in to post a comment.

Multi-Step Equations Exercises
Multi-step equations practice problems with answers.
For this exercise, I have prepared seven (7) multi-step equations for you to practice. If you feel the need to review the techniques involved in solving multi-step equations, take a short detour to review my other lesson about it. Click the link below to take you there!

Solving Multi-Step Equations
1) Solve the multi-step equation for [latex]\large{c}[/latex].
[latex]c – 20 = 4 – 3c[/latex]
Add both sides by [latex]20[/latex]. Next, add [latex]3c[/latex] to both sides. Finally, divide both sides by the coefficient of [latex]4c[/latex] which is [latex]4[/latex] to get [latex]c=6[/latex].
2) Solve the multi-step equation for [latex]\large{n}[/latex].
[latex] – \,4\left( { – 3n – 8} \right) = 10n + 20[/latex]
- Remember to always perform the same operation on both sides of the equation.
- Subtract by [latex]32[/latex].
- Subtract by [latex]10n[/latex].
- Divide by [latex]2[/latex]
- The final solution is [latex]n=-6[/latex].
3) Solve the multi-step equation for [latex]\large{y}[/latex].
[latex]2\left( {4 – y} \right) – 3\left( {y + 3} \right) = – 11[/latex]
Apply twice the Distributive Property of Multiplication over Addition to the left side of the equation. Then combine like terms . Add both sides by [latex]1[/latex] followed by dividing both sides of the equation by [latex]-5[/latex].
4) Solve the multi-step equation for [latex]\large{k}[/latex].
[latex]{\Large{{6k + 4} \over 2}} = 2k – 11[/latex]
Multiply both sides by [latex]2[/latex]. Next, subtract [latex]4[/latex] to both sides. Then, subtract [latex]4k[/latex]. Finally, divide by [latex]2[/latex] to obtain the value of [latex]k[/latex] which is [latex]-13[/latex].
5) Solve the multi-step equation for [latex]\large{x}[/latex].
[latex] – \left( { – 8 – 3x} \right) = – 2\left( {1 – x} \right) + 6x[/latex]
Apply the Distributive Property on both sides of the equation. Be careful when multiplying expressions with the same or different signs . Next, add [latex]2[/latex] to both sides, then subtract [latex]3x[/latex], and finally finish it off by dividing [latex]5[/latex] to both sides.
6) Solve the multi-step equation for [latex]\large{m}[/latex].
[latex]{\large{3 \over 4}}m – 2\left( {m – 1} \right) = {\large{1 \over 4}}m + 5[/latex]
7) Solve the multi-step equation for [latex]\large{x}[/latex].
[latex]3\left( {3x – 8} \right) – 5\left( {3x – 8} \right) = 4\left( {x – 2} \right) – 6\left( {x – 2} \right)[/latex]
You may also be interested in these related math lessons or tutorials:
Two-Step Equations Practice Problems with Answers
- Math Lessons Online

Lesson 3 Homework Practice Solve Equations with Rational Coefficients

You’re now diving into Lesson 3 , where your mission will be to tackle equations with rational coefficients. The term ‘rational coefficients’ is intimidating. But don’t worry! We’re here to break it down. A rational coefficient is a fancy term for a number that can be formulated as a ratio of two integers. It provides a logical framework to tackle complex equations.
Overview of solving equations with rational coefficients
First up, let’s take a clear look at equations. You can think about equations like balanced see-saws. Whatever you do on one side has to be balanced out on the other side. Equations with rational coefficients can be easily simplified by manipulating the fractional coefficients to isolate the variable.
Step 1: Identify the rational coefficient. The fraction in the equation is multiplied by the variable (e.g., 2/3x = 4).
Step 2: To isolate your variable, you will perform the inverse operation to eliminate the rational coefficient. You’ll multiply both sides of your equation by the reciprocal of your rational coefficient.
Example: Let’s use the equation above. If we multiply both sides of 2/3x = 4 by 3/2 (the reciprocal of 2/3), we get 1x = 6. And voila, you have your solution.
In just a few steps, you’ve tackled equations with rational coefficients. Don’t let challenges discourage you in mathematics. It involves estimation, trial and error, and practice. But you can master it. Keep practicing, be persistent, and continue to hone your problem-solving skills . Remember, every mathematician learns at their own pace. You got this!
Practice is the key here, so nail down these steps and tackle additional problems independently. Happy solving!
The Concept of Rational Coefficients
You’ve made it to Lesson 3 , where you’ll tackle problems including rational coefficients. It might seem daunting at first, but with a systematic approach and a little practice, you’ll quickly learn how to navigate this mathematical territory.
Explanation of rational coefficients and their role in equations
In algebra, a rational coefficient is a ratio of two integers with a zero denominator. It is important to remember that these coefficients, just like any number in an algebraic equation, can be manipulated through the usual multiplication, division, addition, and subtraction.
Now, you ask, how do rational coefficients affect the equation? These coefficients play a pivotal role in determining the solution to the equation.
Here is how you can approach it:
Step 1: Simplify the equation. If you have fractions in the equation, sometimes called rational numbers , making them whole numbers is easier. You can multiply every term with the least common denominator (LCD).
Step 2: The next step is to use simple math techniques to find the variable. It is fundamentally the same as solving any basic algebraic equation –addition, subtraction, multiplication, and division are your friends.
Step 3: Remember to check if your solution is correct. Substitute the solution into the original equation and see if both sides balance.
Remember: The key to mastering equations with rational coefficients is understanding and accurately manipulating these coefficients to find your solution.
Remember, the key to success is consistent practice. Each equation you tackle improves your skill and confidence. Solving equations with rational coefficients will be easy. Good luck!
Let’s recap:
| Steps | Explanation |
|---|---|
| Step 1: Simplify the equation | Multiply every term with the least common denominator (LCD) to make them whole numbers. |
| Step 2: Solve for the variable | Use elementary operations (addition, subtraction, multiplication, and division) to solve for the variable. |
| Step 3: Check your solution | Substitute the solution back into the original equation to verify if both sides balance. |
Techniques for Solving Equations with Rational Coefficients
As an aspiring mathematician or someone trying to polish their math skills , navigating the world of equations with rational coefficients can sometimes seem daunting. Worry not! Let’s simplify the process into two easy-to-follow steps: clearing fractions and cross-multiplication.
Step-by-step methods for solving equations with rational coefficients
Step 1: Identify the equation with a rational coefficient. Rational coefficients are fractions expressed as a ratio of two integers.
Step 2: Apply one of the strategies below to solve the equation.
- Method 1: Clearing Fractions
Wherever you see fractions, simplify them!
Step 1: Multiply each term in the equation by the fraction’s denominator to clear the fractions.
Step 2: Carry out the arithmetic operations and solve the equation.
Step 3: Check your work by substituting the solution into the original equation. If it makes the equation true, then your solution is correct.
- Method 2: Cross-Multiplication
When your solution is a proportion, this method works well.
Step 1: Use cross-multiplication if two fractions are set equal.
Step 2: Multiply the terms diagonally and set the products equal.
Step 3: Solve for the variable.
Step 4: Verify your solution by plugging it into the original equation.
Please make no mistake: the key to mastering mathematical equations is through practice, and lots of it. Please don’t avoid making mistakes; use them to strengthen your understanding and sharpen your skills. Get your homework and apply the strategies you learned. You can solve these problems if you keep practicing. With unwavering dedication and practice, you can conquer any equation that comes your way.
Examples and Practice Problems
You’ll come across equations with rational terms as you learn math. At first, it might seem challenging, but after reading this blog, you can do it like a pro!
Solving equations with rational coefficients through examples and practice problems
As you embark on your mathematical journey, you are bound to encounter equations with rational coefficients. By the end of this guide, you will be a pro at solving these types of equations.
- Example 1: Clearing fractions and solving for the variable
Take this equation: 3/4x = 6. First, clear out the fraction by multiplying both sides of the equation by 4. You’ll get 3x = 24. Now, try solving for ‘x’ by dividing 24 by 3. Your answer will be x = 8.
Now let’s practice:
- Try solving 2/7y = 6.
- Keep in mind the steps followed in the example.
- Clear the fraction, isolate the variable, and solve for ‘y’.
- Example 2: Cross-multiplication to solve for the variable
Here’s our equation: 4/5 = x/10. Cross-multiplication involves multiplying the fraction’s numerator on the left by the fraction’s denominator on the right and vice versa. This gives us 4 10 = 5 x, which simplifies to 40 = 5x.
Proceed with the operation: Solve for ‘x’ by dividing both sides by 5, which leaves us with x = 8.
Time to practice: Try the same steps with the equation 3/4 = y/12. Follow this example above, and you can solve this equation effectively.
In both types of equations, remember always to check your answers. Substituting your calculated value into the original equation should give you a true statement. These tutorials can guide you in solving complex equations and hone your skills.
- Grade 1 Lessons
- Grade 2 Lessons
- Grade 3 Lessons
- Grade 4 Lessons
- Grade 5 Lessons
- Grade 6 Lessons
- Grade 7 Lessons
- Grade 8 Lessons
- Kindergarten
- Math Activities
- Math Tutorial
- Multiplication
- Subtraction
- #basic mathematic
- #Basic Mathematical Operation
- #best math online math tutor
- #Best Math OnlineTutor
- #dividing fractions
- #effective teaching
- #grade 8 math lessons
- #linear equation
- #Math Online Blog
- #mathematical rule
- #mutiplying fractions
- #odd and even numbers
- #Online Math Tutor
- #online teaching
- #order of math operations
- #pemdas rule
- #Point-Slope Form
- #Precalculus
- #Slope-Intercept Form
- #Tutoring Kids

Thank you for signing up!
GET IN TOUCH WITH US
- 888-309-8227
- 732-384-0146
New User Registration
Forgot Password
Glencoe Math Course 3, Grade: 8 Publisher: Glencoe/McGraw-Hill
Glencoe math course 3, title : glencoe math course 3, publisher : glencoe/mcgraw-hill, isbn : not available, isbn-13 : 9780021387137, use the table below to find videos, mobile apps, worksheets and lessons that supplement glencoe math course 3..
| --> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| --> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| --> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| --> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| --> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| --> |
|
|
|
|
|
|
|
|
|
|
|
|
| --> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| --> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| --> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
textbook resources
- Call us toll-free
- FAQs – Frequently Asked Questions
- Contact Lumos Learning – Proven Study Programs by Expert Teachers
Follow us: Lumos Learning -->
- 2024 © Lumos Learning
- Privacy Policy - Terms of Service - Disclaimers
PARCC® is a registered trademark of PARCC, Inc. Lumos Learning, is not owned by or affiliated in any fashion with PARCC, Inc... Read More
PARCC® is a registered trademark of PARCC, Inc. Lumos Learning, is not owned by or affiliated in any fashion with PARCC, Inc., the Partnership for the Assessment of Readiness for College and Careers, nor any state of the Union. Neither PARCC, Inc., nor The Partnership for the Assessment of Readiness for College and Careers, nor any member state has endorsed this product. No portion of any fees or charges paid for any products or services Lumos Learning offers will be paid or inure to the benefit of PARCC, Inc., or any state of the Union
SBAC is a copyright of The Regents of the University of California – Smarter Balanced Assessment Consortium, which is not aff... Read More
SBAC is a copyright of The Regents of the University of California – Smarter Balanced Assessment Consortium, which is not affiliated to Lumos Learning. The Regents of the University of California – Smarter Balanced Assessment Consortium, was not involved in the production of, and does not endorse these products or this site.
ACT® Aspire™ is a registered trademark of ACT Aspire LLC., which is not affiliated to Lumos Learning. ACT Aspire LLC, was not... Read More
ACT® Aspire™ is a registered trademark of ACT Aspire LLC., which is not affiliated to Lumos Learning. ACT Aspire LLC,was not involved in the production of, and does not endorse these products or this site.
Florida Department of Education is not affiliated to Lumos Learning. Florida department of education, was not involved in the... Read More
Florida Department of Education is not affiliated to Lumos Learning. Florida department of education, was not involved in the production of, and does not endorse these products or this site.
Indiana Department of Education is not affiliated to Lumos Learning. Indiana department of education, was not involved in the... Read More
Indiana Department of Education is not affiliated to Lumos Learning. Indiana department of education, was not involved in the production of, and does not endorse these products or this site.
Mississippi Department of Education is not affiliated to Lumos Learning. Mississippi department of education, was not involved... Read More
Mississippi Department of Education is not affiliated to Lumos Learning. Mississippi department of education, was not involved in the production of, and does not endorse these products or this site.
Ohio Department of Education is not affiliated to Lumos Learning. Ohio department of education, was not involved in the prod... Read More
Ohio Department of Education is not affiliated to Lumos Learning. Ohio department of education, was not involved in the production of, and does not endorse these products or this site.
Tennessee Department of Education is not affiliated to Lumos Learning. Tennessee department of education, was not involved... Read More
Tennessee Department of Education is not affiliated to Lumos Learning. Tennessee department of education, was not involved in the production of, and does not endorse these products or this site.
Georgia Department of Education is not affiliated to Lumos Learning. Georgia department of education, was not involved... Read More
Georgia Department of Education is not affiliated to Lumos Learning. Georgia department of education, was not involved in the production of, and does not endorse these products or this site.
Missouri Department of Education is not affiliated to Lumos Learning. Missouri department of education, was not involved... Read More
Missouri Department of Education is not affiliated to Lumos Learning. Missouri department of education, was not involved in the production of, and does not endorse these products or this site.
Louisiana Department of Education is not affiliated to Lumos Learning. Louisiana department of education, was not involved... Read More
Louisiana Department of Education is not affiliated to Lumos Learning. Louisiana department of education, was not involved in the production of, and does not endorse these products or this site.
| | > >
|
Chapter 3, Lesson 5: Solving Two-Step Equations
- Extra Examples
- Group Activity Cards
- Personal Tutor
- Self-Check Quizzes
The resource you requested requires you to enter a username and password below:
| Password: | |
Please read our Terms of Use and Privacy Notice before you explore our Web site. To report a technical problem with this Web site, please contact the site producer .


IMAGES
VIDEO
COMMENTS
Two-Step Equations Practice Problems with Answers. Hone your skills in solving two-step equations because it will serve as your foundation when solving multi-step equations. I prepared eight (8) two-step equations problems with complete solutions to get you rolling. My advice is for you to solve them by hand using a pencil or pen and paper.
12. Four less than the quotient of a number and 3 is -10. 13. Nine less than six times a number is -15. 14. Three less than the quotient of a number and 6 is 1. 15. Eight more than the quotient of a number and 5 is 3. 16. The difference between twice a number and 11 is -23. Lesson 3 Skills Practice Write Two-Step Equations Let n represent the ...
Find step-by-step solutions and answers to Glencoe Math Course 3, Volume 1 - 9780076615308, as well as thousands of textbooks so you can move forward with confidence. ... Key Concept Check. Page 101: Problem Solving. Page 102: Reflect. Page 103: Unit Project. Exercise 1. ... Section 2-3: Write Two Step Equations. Page 140: Mid-Chapter Check ...
Two step math equations are algebraic problems that require you to make two moves to find the value of the unknown variable. For example, using the equation 3x + 5 = 11 we will need to perform two steps to find the value of x. The first step would be to get the constant values of the equation by themselves. In this case 5 and 11 are our constants.
Unit test. Level up on all the skills in this unit and collect up to 1,600 Mastery points! Start Unit test. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere.
Solving Multi-Step Equations Leveled Practice. ©n 92o0P1A50 yKBuItja1 vScoyf6tywmaIrXem HL5LICv.x o PAhlVl6 EryiFgyhntlsl KrXe6sge8ravaeOda.u. LEVEL 1 (cont): Solve each 2-step equation. 7) −56 =. 9) 12 =. 11) LEVEL 2: Solve each Multi-Step equation. 13)
For Exercises 1-3, determine whether each linear function is a direct variation. If so, state the constant of variation. 1. Price, x $5 $10 $15 $20 ... Lesson 3 Skills Practice Equations in y = mx Form Direct variation. $0.082 per $1 No direct variation No direct variation y = 8
Solving Two-Step and Multi-Step Equations Fill in the blanks to solve each equation. ... Answer Key for Unit 2 SOLVING TWO-STEP AND MULTI-STEP EQUATIONS Practice A 1. 2; 10; 2 2. 3; 8; 4 ... 10. x 3 11. b 2 12. q 3 13. 4 14. 5 15. 3 x 5 2x 90; 19 16. 20 minutes Practice C 1. r 3 2. w 14 3. y 4 4. f 5 5. p 10 6. r 7 7. y 27 8. h 7 8 9. m 3 10. v ...
Chapter 2, Lesson 3: Solving Multi-Step Equations. Teacher Resources Common Core State Standards Supplement, TE Diagnostic and Placement Tests Key Concepts Math Skills Maintenance Scavenger Hunt Answer Sheet Science and Mathematics Lab Manual Technology User Guides Professional Development Research Vocabulary PuzzleMaker. Program Resources ...
Standardized Test Practice Vocabulary Review Lesson Resources ... Personal Tutor Self-Check Quizzes. Hotmath Homework Help Math Review Math Tools Multilingual eGlossary Visual Vocabulary Cards ... Concepts, Skills, and Problem Solving, Course 3. Chapter 8, Lesson 3: Writing Two-Step Equations. Extra Examples; Personal Tutor; Self-Check Quizzes ...
What barriers do I perceive to writing two-step equations for situations? Answer: Lesson 7.3 More Practice/Homework. Question 1. Pierce is making a rectangular frame for a photo collage that has a perimeter of 72.2 inches. The length of the frame is 20.3 inches. Write an equation to find the width of the frame. Answer: x = \(\frac{79}{5 ...
Multi-Step Equations Practice Problems with Answers. For this exercise, I have prepared seven (7) multi-step equations for you to practice. If you feel the need to review the techniques involved in solving multi-step equations, take a short detour to review my other lesson about it. Click the link below to take you there!
Graph each equation. 7. y = 5x + 1. 8. y = x + 2. 9. y = 3x + 3. 10. TELEPHONE A cell phone company charges $40 per month plus $2 for each minute of time used out of the service area. Write the equation that describes the amount y that a cell phone user would pay if they used the phone for x minutes out of the service area. Graph the function.
Lesson 4 Homework Practice Two Step Equations. 5.0 (1 review) Flashcards; Learn; Test; Match; Q-Chat; Flashcards; ... Students also viewed. Day 20. 15 terms. quizlette47445661. Preview. Combo with "Speakout Upper-intermediate Unit 1.2 text" and 2 others. Teacher 28 terms. alina_yagotintsewa. Preview. health final exam review. 26 terms ...
Solving multi-step equations. Learn with flashcards, games, and more — for free.
Fill Lesson 3 Homework Practice Write Two Step Equations Answer Key, Edit online. Sign, fax and printable from PC, iPad, tablet or mobile with pdfFiller Instantly. ... Create your eSignature using pdfFiller and then eSign your lesson 3 skills practice write two step equations answer key form immediately from your email with pdfFiller's Gmail ...
TAKS Test Practice Vocabulary Review Lesson Resources Extra Examples Personal Tutor Self-Check Quizzes. Hotmath Homework Help Math Review Multilingual Glossary Online Calculators Study to Go. Mathematics. Home > Chapter 3 > Lesson 5. Texas Pre-Algebra. Chapter 3, Lesson 5: Solving Two-Step Equations. Extra Examples; Personal Tutor; Self-Check ...
3 6 Skills Practice Writing Two Step Equations Answers. Check out how easy it is to complete and eSign documents online using fillable templates and a powerful editor. ... Course 2 Chapter 6 Equations And Inequalities Answer Key 2 days ago — Lesson 7 Homework Practice Solve And Write Two Step Inequalities Answers. Grade 7 McGraw Hill Glencoe ...
Step 1: Use cross-multiplication if two fractions are set equal. Step 2: Multiply the terms diagonally and set the products equal. Step 3: Solve for the variable. Step 4: Verify your solution by plugging it into the original equation. Please make no mistake: the key to mastering mathematical equations is through practice, and lots of it.
Use the table below to find videos, mobile apps, worksheets and lessons that supplement Glencoe Math Course 3. Glencoe Math Course 3 grade 8 workbook & answers help online. Grade: 8, Title: Glencoe Math Course 3, Publisher: Glencoe/McGraw-Hill, ISBN:
Standardized Test Practice Vocabulary Review Lesson Resources ... Hotmath Homework Help Math Review Math Tools Multilingual eGlossary Visual Vocabulary Cards Online Calculators Study to Go. Mathematics. Home > Chapter 3 > Lesson 5. Kentucky Math Connects: Concepts, Skills, and Problem Solving, Course 2. Chapter 3, Lesson 5: Solving Two-Step ...
Two step equations answer key: 1. p = -2. 2. r = 18. 3. d = -3. In order to solve these two-step equations, we need to isolate the variable on one side of the equation. Let's break down the steps for each equation: 1. 6p + 22 = 10. Subtract 22 from both sides: 6p = -12. Divide by 6: p = -2. 2. 1/3 r - 4 = 2. Add 4 to both sides: 1/3 r = 6 ...
Standardized Test Practice Vocabulary Review Lesson Resources ... Personal Tutor Self-Check Quizzes. Hotmath Homework Help Math Review Math Tools Multilingual eGlossary Visual Vocabulary Cards Online Calculators Study to Go. Mathematics. Home > Chapter 3 > Lesson 5. Math Connects: Concepts, Skills, and Problem Solving, Course 2. Chapter 3 ...