Have a thesis expert improve your writing
Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.
- Knowledge Base
- Null and Alternative Hypotheses | Definitions & Examples

Null and Alternative Hypotheses | Definitions & Examples
Published on 5 October 2022 by Shaun Turney . Revised on 6 December 2022.
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :
- Null hypothesis (H 0 ): There’s no effect in the population .
- Alternative hypothesis (H A ): There’s an effect in the population.
The effect is usually the effect of the independent variable on the dependent variable .
Table of contents
Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, differences between null and alternative hypotheses, how to write null and alternative hypotheses, frequently asked questions about null and alternative hypotheses.
The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”, the null hypothesis (H 0 ) answers “No, there’s no effect in the population.” On the other hand, the alternative hypothesis (H A ) answers “Yes, there is an effect in the population.”
The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample.
You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.
The null hypothesis is the claim that there’s no effect in the population.
If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.
Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept. Be careful not to say you “prove” or “accept” the null hypothesis.
Null hypotheses often include phrases such as “no effect”, “no difference”, or “no relationship”. When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).
Examples of null hypotheses
The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.
| ( ) | ||
| Does tooth flossing affect the number of cavities? | Tooth flossing has on the number of cavities. | test: The mean number of cavities per person does not differ between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ = µ . |
| Does the amount of text highlighted in the textbook affect exam scores? | The amount of text highlighted in the textbook has on exam scores. | : There is no relationship between the amount of text highlighted and exam scores in the population; β = 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression.* | test: The proportion of people with depression in the daily-meditation group ( ) is greater than or equal to the no-meditation group ( ) in the population; ≥ . |
*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .
The alternative hypothesis (H A ) is the other answer to your research question . It claims that there’s an effect in the population.
Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.
The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.
Alternative hypotheses often include phrases such as “an effect”, “a difference”, or “a relationship”. When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes > or <). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.
Examples of alternative hypotheses
The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.
| Does tooth flossing affect the number of cavities? | Tooth flossing has an on the number of cavities. | test: The mean number of cavities per person differs between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ ≠ µ . |
| Does the amount of text highlighted in a textbook affect exam scores? | The amount of text highlighted in the textbook has an on exam scores. | : There is a relationship between the amount of text highlighted and exam scores in the population; β ≠ 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression. | test: The proportion of people with depression in the daily-meditation group ( ) is less than the no-meditation group ( ) in the population; < . |
Null and alternative hypotheses are similar in some ways:
- They’re both answers to the research question
- They both make claims about the population
- They’re both evaluated by statistical tests.
However, there are important differences between the two types of hypotheses, summarized in the following table.
| A claim that there is in the population. | A claim that there is in the population. | |
|
| ||
| Equality symbol (=, ≥, or ≤) | Inequality symbol (≠, <, or >) | |
| Rejected | Supported | |
| Failed to reject | Not supported |
To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.
The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:
Does independent variable affect dependent variable ?
- Null hypothesis (H 0 ): Independent variable does not affect dependent variable .
- Alternative hypothesis (H A ): Independent variable affects dependent variable .
Test-specific
Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.
| ( ) | ||
| test
with two groups | The mean dependent variable does not differ between group 1 (µ ) and group 2 (µ ) in the population; µ = µ . | The mean dependent variable differs between group 1 (µ ) and group 2 (µ ) in the population; µ ≠ µ . |
| with three groups | The mean dependent variable does not differ between group 1 (µ ), group 2 (µ ), and group 3 (µ ) in the population; µ = µ = µ . | The mean dependent variable of group 1 (µ ), group 2 (µ ), and group 3 (µ ) are not all equal in the population. |
| There is no correlation between independent variable and dependent variable in the population; ρ = 0. | There is a correlation between independent variable and dependent variable in the population; ρ ≠ 0. | |
| There is no relationship between independent variable and dependent variable in the population; β = 0. | There is a relationship between independent variable and dependent variable in the population; β ≠ 0. | |
| Two-proportions test | The dependent variable expressed as a proportion does not differ between group 1 ( ) and group 2 ( ) in the population; = . | The dependent variable expressed as a proportion differs between group 1 ( ) and group 2 ( ) in the population; ≠ . |
Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.
The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).
The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).
A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).
A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.
Turney, S. (2022, December 06). Null and Alternative Hypotheses | Definitions & Examples. Scribbr. Retrieved 9 June 2024, from https://www.scribbr.co.uk/stats/null-and-alternative-hypothesis/
Is this article helpful?

Shaun Turney
Other students also liked, levels of measurement: nominal, ordinal, interval, ratio, the standard normal distribution | calculator, examples & uses, types of variables in research | definitions & examples.
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
AP®︎/College Statistics
Course: ap®︎/college statistics > unit 10.
- Idea behind hypothesis testing
Examples of null and alternative hypotheses
- Writing null and alternative hypotheses
- P-values and significance tests
- Comparing P-values to different significance levels
- Estimating a P-value from a simulation
- Estimating P-values from simulations
- Using P-values to make conclusions
Want to join the conversation?
- Upvote Button navigates to signup page
- Downvote Button navigates to signup page
- Flag Button navigates to signup page

Video transcript
Null Hypothesis and Alternative Hypothesis
- Inferential Statistics
- Statistics Tutorials
- Probability & Games
- Descriptive Statistics
- Applications Of Statistics
- Math Tutorials
- Pre Algebra & Algebra
- Exponential Decay
- Worksheets By Grade
- Ph.D., Mathematics, Purdue University
- M.S., Mathematics, Purdue University
- B.A., Mathematics, Physics, and Chemistry, Anderson University
Hypothesis testing involves the careful construction of two statements: the null hypothesis and the alternative hypothesis. These hypotheses can look very similar but are actually different.
How do we know which hypothesis is the null and which one is the alternative? We will see that there are a few ways to tell the difference.
The Null Hypothesis
The null hypothesis reflects that there will be no observed effect in our experiment. In a mathematical formulation of the null hypothesis, there will typically be an equal sign. This hypothesis is denoted by H 0 .
The null hypothesis is what we attempt to find evidence against in our hypothesis test. We hope to obtain a small enough p-value that it is lower than our level of significance alpha and we are justified in rejecting the null hypothesis. If our p-value is greater than alpha, then we fail to reject the null hypothesis.
If the null hypothesis is not rejected, then we must be careful to say what this means. The thinking on this is similar to a legal verdict. Just because a person has been declared "not guilty", it does not mean that he is innocent. In the same way, just because we failed to reject a null hypothesis it does not mean that the statement is true.
For example, we may want to investigate the claim that despite what convention has told us, the mean adult body temperature is not the accepted value of 98.6 degrees Fahrenheit . The null hypothesis for an experiment to investigate this is “The mean adult body temperature for healthy individuals is 98.6 degrees Fahrenheit.” If we fail to reject the null hypothesis, then our working hypothesis remains that the average adult who is healthy has a temperature of 98.6 degrees. We do not prove that this is true.
If we are studying a new treatment, the null hypothesis is that our treatment will not change our subjects in any meaningful way. In other words, the treatment will not produce any effect in our subjects.
The Alternative Hypothesis
The alternative or experimental hypothesis reflects that there will be an observed effect for our experiment. In a mathematical formulation of the alternative hypothesis, there will typically be an inequality, or not equal to symbol. This hypothesis is denoted by either H a or by H 1 .
The alternative hypothesis is what we are attempting to demonstrate in an indirect way by the use of our hypothesis test. If the null hypothesis is rejected, then we accept the alternative hypothesis. If the null hypothesis is not rejected, then we do not accept the alternative hypothesis. Going back to the above example of mean human body temperature, the alternative hypothesis is “The average adult human body temperature is not 98.6 degrees Fahrenheit.”
If we are studying a new treatment, then the alternative hypothesis is that our treatment does, in fact, change our subjects in a meaningful and measurable way.
The following set of negations may help when you are forming your null and alternative hypotheses. Most technical papers rely on just the first formulation, even though you may see some of the others in a statistics textbook.
- Null hypothesis: “ x is equal to y .” Alternative hypothesis “ x is not equal to y .”
- Null hypothesis: “ x is at least y .” Alternative hypothesis “ x is less than y .”
- Null hypothesis: “ x is at most y .” Alternative hypothesis “ x is greater than y .”
- Null Hypothesis Examples
- An Example of a Hypothesis Test
- Hypothesis Test for the Difference of Two Population Proportions
- What Is a P-Value?
- How to Conduct a Hypothesis Test
- Hypothesis Test Example
- Maslow's Hierarchy of Needs Explained
- Chi-Square Goodness of Fit Test
- What Level of Alpha Determines Statistical Significance?
- Popular Math Terms and Definitions
- How to Do Hypothesis Tests With the Z.TEST Function in Excel
- The Difference Between Type I and Type II Errors in Hypothesis Testing
- Type I and Type II Errors in Statistics
- The Runs Test for Random Sequences
- What 'Fail to Reject' Means in a Hypothesis Test
- What Is the Difference Between Alpha and P-Values?
Module 9: Hypothesis Testing With One Sample
Null and alternative hypotheses, learning outcomes.
- Describe hypothesis testing in general and in practice
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.
H a : The alternative hypothesis : It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make adecision. There are two options for a decision . They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in H 0 and H a :
| equal (=) | not equal (≠) greater than (>) less than (<) |
| greater than or equal to (≥) | less than (<) |
| less than or equal to (≤) | more than (>) |
H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30
H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.
H 0 : The drug reduces cholesterol by 25%. p = 0.25
H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:
H 0 : μ = 2.0
H a : μ ≠ 2.0
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 66 H a : μ __ 66
- H 0 : μ = 66
- H a : μ ≠ 66
We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:
H 0 : μ ≥ 5
H a : μ < 5
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 45 H a : μ __ 45
- H 0 : μ ≥ 45
- H a : μ < 45
In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.
H 0 : p ≤ 0.066
H a : p > 0.066
On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : p __ 0.40 H a : p __ 0.40
- H 0 : p = 0.40
- H a : p > 0.40
Concept Review
In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis , typically denoted with H 0 . The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality (=, ≤ or ≥) Always write the alternative hypothesis , typically denoted with H a or H 1 , using less than, greater than, or not equals symbols, i.e., (≠, >, or <). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.
Formula Review
H 0 and H a are contradictory.
- OpenStax, Statistics, Null and Alternative Hypotheses. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:58/Introductory_Statistics . License : CC BY: Attribution
- Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
- Simple hypothesis testing | Probability and Statistics | Khan Academy. Authored by : Khan Academy. Located at : https://youtu.be/5D1gV37bKXY . License : All Rights Reserved . License Terms : Standard YouTube License
Hypothesis Testing: Null Hypothesis and Alternative Hypothesis
Join over 2 million students who advanced their careers with 365 Data Science. Learn from instructors who have worked at Meta, Spotify, Google, IKEA, Netflix, and Coca-Cola and master Python, SQL, Excel, machine learning, data analysis, AI fundamentals, and more.

Figuring out exactly what the null hypothesis and the alternative hypotheses are is not a walk in the park. Hypothesis testing is based on the knowledge that you can acquire by going over what we have previously covered about statistics in our blog.
So, if you don’t want to have a hard time keeping up, make sure you have read all the tutorials about confidence intervals , distributions , z-tables and t-tables .
We've also made a video on null hypothesis vs alternative hypothesis - you can watch it below or just scroll down if you prefer reading.

Confidence intervals provide us with an estimation of where the parameters are located. You can obtain them with our confidence interval calculator and learn more about them in the related article.

However, when we are making a decision, we need a yes or no answer. The correct approach, in this case, is to use a test .
Here we will start learning about one of the fundamental tasks in statistics - hypothesis testing !
The Hypothesis Testing Process
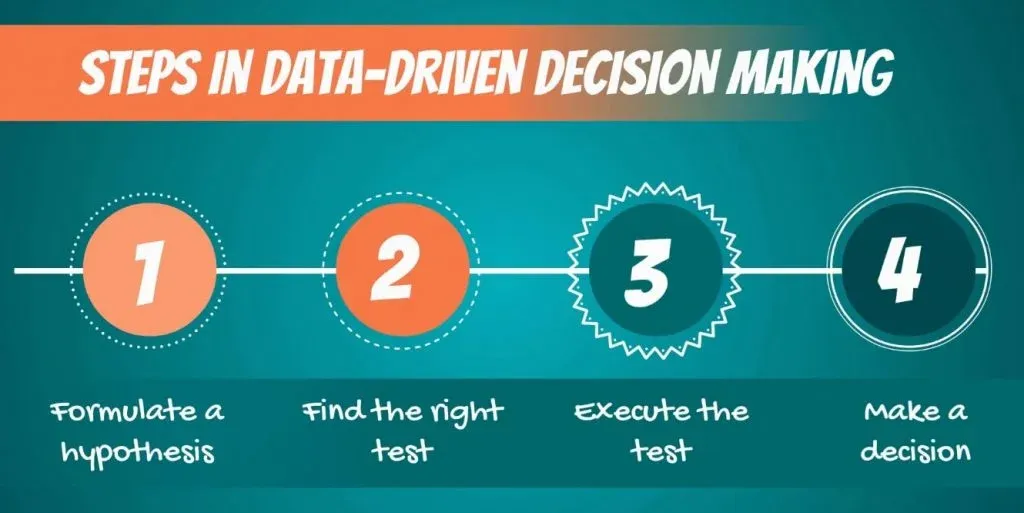
First off, let’s talk about data-driven decision-making. It consists of the following steps:
- First, we must formulate a hypothesis .
- After doing that, we have to find the right test for our hypothesis .
- Then, we execute the test.
- Finally, we make a decision based on the result.
Let’s start from the beginning.
What is a Hypothesis?
Though there are many ways to define it, the most intuitive must be:
“A hypothesis is an idea that can be tested.”

This is not the formal definition, but it explains the point very well.
So, if we say that apples in New York are expensive, this is an idea or a statement. However, it is not testable, until we have something to compare it with.

For instance, if we define expensive as: any price higher than $1.75 dollars per pound, then it immediately becomes a hypothesis .

What Cannot Be a Hypothesis?
An example may be: would the USA do better or worse under a Clinton administration, compared to a Trump administration? Statistically speaking, this is an idea , but there is no data to test it. Therefore, it cannot be a hypothesis of a statistical test.

Actually, it is more likely to be a topic of another discipline.
Conversely, in statistics, we may compare different US presidencies that have already been completed. For example, the Obama administration and the Bush administration, as we have data on both.

A Two-Sided Test
Alright, let’s get out of politics and get into hypotheses . Here’s a simple topic that CAN be tested.
According to Glassdoor (the popular salary information website), the mean data scientist salary in the US is 113,000 dollars.
So, we want to test if their estimate is correct.
The Null and Alternative Hypotheses
There are two hypotheses that are made: the null hypothesis , denoted H 0 , and the alternative hypothesis , denoted H 1 or H A .

The null hypothesis is the one to be tested and the alternative is everything else. In our example:
The null hypothesis would be: The mean data scientist salary is 113,000 dollars.

While the alternative : The mean data scientist salary is not 113,000 dollars.

Author's note: If you're interested in a data scientist career, check out our articles Data Scientist Career Path , 5 Business Basics for Data Scientists , Data Science Interview Questions , and 15 Data Science Consulting Companies Hiring Now .
An Example of a One-Sided Test
You can also form one-sided or one-tailed tests.
Say your friend, Paul, told you that he thinks data scientists earn more than 125,000 dollars per year. You doubt him, so you design a test to see who’s right.

The null hypothesis of this test would be: The mean data scientist salary is more than 125,000 dollars.
The alternative will cover everything else, thus: The mean data scientist salary is less than or equal to 125,000 dollars.

Important: The outcomes of tests refer to the population parameter rather than the sample statistic! So, the result that we get is for the population.

Important: Another crucial consideration is that, generally, the researcher is trying to reject the null hypothesis . Think about the null hypothesis as the status quo and the alternative as the change or innovation that challenges that status quo. In our example, Paul was representing the status quo, which we were challenging.

Let’s go over it once more. In statistics, the null hypothesis is the statement we are trying to reject. Therefore, the null hypothesis is the present state of affairs, while the alternative is our personal opinion.

Why Hypothesis Testing Works
Right now, you may be feeling a little puzzled. This is normal because this whole concept is counter-intuitive at the beginning. However, there is an extremely easy way to continue your journey of exploring it. By diving into the linked tutorial, you will find out why hypothesis testing actually works.
Interested in learning more? You can take your skills from good to great with our statistics course!
Try statistics course for free
Next Tutorial: Hypothesis Testing: Significance Level and Rejection Region
World-Class
Data Science
Learn with instructors from:
Iliya Valchanov
Co-founder of 365 Data Science
Iliya is a finance graduate with a strong quantitative background who chose the exciting path of a startup entrepreneur. He demonstrated a formidable affinity for numbers during his childhood, winning more than 90 national and international awards and competitions through the years. Iliya started teaching at university, helping other students learn statistics and econometrics. Inspired by his first happy students, he co-founded 365 Data Science to continue spreading knowledge. He authored several of the program’s online courses in mathematics, statistics, machine learning, and deep learning.
We Think you'll also like

Statistics Tutorials
False Positive vs. False Negative: Type I and Type II Errors in Statistical Hypothesis Testing

Hypothesis Testing with Z-Test: Significance Level and Rejection Region
Calculating and Using Covariance and Linear Correlation Coefficient

Examples of Numerical and Categorical Variables

Statistics Resources
- Excel - Tutorials
- Basic Probability Rules
- Single Event Probability
- Complement Rule
- Intersections & Unions
- Compound Events
- Levels of Measurement
- Independent and Dependent Variables
- Entering Data
- Central Tendency
- Data and Tests
- Displaying Data
- Discussing Statistics In-text
- SEM and Confidence Intervals
- Two-Way Frequency Tables
- Empirical Rule
- Finding Probability
- Accessing SPSS
- Chart and Graphs
- Frequency Table and Distribution
- Descriptive Statistics
- Converting Raw Scores to Z-Scores
- Converting Z-scores to t-scores
- Split File/Split Output
- Partial Eta Squared
- Downloading and Installing G*Power: Windows/PC
- Correlation
- Testing Parametric Assumptions
- One-Way ANOVA
- Two-Way ANOVA
- Repeated Measures ANOVA
- Goodness-of-Fit
- Test of Association
- Pearson's r
- Point Biserial
- Mediation and Moderation
- Simple Linear Regression
- Multiple Linear Regression
- Binomial Logistic Regression
- Multinomial Logistic Regression
- Independent Samples T-test
- Dependent Samples T-test
- Testing Assumptions
- T-tests using SPSS
- T-Test Practice
- Predictive Analytics This link opens in a new window
- Quantitative Research Questions
- Null & Alternative Hypotheses
- One-Tail vs. Two-Tail
- Alpha & Beta
- Associated Probability
- Decision Rule
- Statement of Conclusion
- Statistics Group Sessions
ASC Chat Hours
ASC Chat is usually available at the following times ( Pacific Time):
| Days | Hours (Pacific time) |
|---|---|
| Mon. | 9 am - 8 pm |
| Tue. | 7 am - 1 pm 3 pm - 10 pm |
| Wed. | 7 am - 1 pm 3 pm - 10 pm |
| Thurs. | 7 am - 1 pm 2 pm - 10 pm |
| Fri. | 9 am - 1 pm 3 pm - 5 pm 6 pm - 8 pm |
| Sat. | 7 am - 1 pm 6 pm - 9 pm |
| Sun. | 10 am - 1 pm 5 pm - 9 pm |
If there is not a coach on duty, submit your question via one of the below methods:
928-440-1325
Ask a Coach
Search our FAQs on the Academic Success Center's Ask a Coach page.
Once you have developed a clear and focused research question or set of research questions, you’ll be ready to conduct further research, a literature review, on the topic to help you make an educated guess about the answer to your question(s). This educated guess is called a hypothesis.
In research, there are two types of hypotheses: null and alternative. They work as a complementary pair, each stating that the other is wrong.
- Null Hypothesis (H 0 ) – This can be thought of as the implied hypothesis. “Null” meaning “nothing.” This hypothesis states that there is no difference between groups or no relationship between variables. The null hypothesis is a presumption of status quo or no change.
- Alternative Hypothesis (H a ) – This is also known as the claim. This hypothesis should state what you expect the data to show, based on your research on the topic. This is your answer to your research question.
Null Hypothesis: H 0 : There is no difference in the salary of factory workers based on gender. Alternative Hypothesis : H a : Male factory workers have a higher salary than female factory workers.
Null Hypothesis : H 0 : There is no relationship between height and shoe size. Alternative Hypothesis : H a : There is a positive relationship between height and shoe size.
Null Hypothesis : H 0 : Experience on the job has no impact on the quality of a brick mason’s work. Alternative Hypothesis : H a : The quality of a brick mason’s work is influenced by on-the-job experience.
Was this resource helpful?
- << Previous: Hypothesis Testing
- Next: One-Tail vs. Two-Tail >>
- Last Updated: May 29, 2024 9:48 AM
- URL: https://resources.nu.edu/statsresources

User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident
Keyboard Shortcuts
10.1 - setting the hypotheses: examples.
A significance test examines whether the null hypothesis provides a plausible explanation of the data. The null hypothesis itself does not involve the data. It is a statement about a parameter (a numerical characteristic of the population). These population values might be proportions or means or differences between means or proportions or correlations or odds ratios or any other numerical summary of the population. The alternative hypothesis is typically the research hypothesis of interest. Here are some examples.
Example 10.2: Hypotheses with One Sample of One Categorical Variable Section
About 10% of the human population is left-handed. Suppose a researcher at Penn State speculates that students in the College of Arts and Architecture are more likely to be left-handed than people found in the general population. We only have one sample since we will be comparing a population proportion based on a sample value to a known population value.
- Research Question : Are artists more likely to be left-handed than people found in the general population?
- Response Variable : Classification of the student as either right-handed or left-handed
State Null and Alternative Hypotheses
- Null Hypothesis : Students in the College of Arts and Architecture are no more likely to be left-handed than people in the general population (population percent of left-handed students in the College of Art and Architecture = 10% or p = .10).
- Alternative Hypothesis : Students in the College of Arts and Architecture are more likely to be left-handed than people in the general population (population percent of left-handed students in the College of Arts and Architecture > 10% or p > .10). This is a one-sided alternative hypothesis.
Example 10.3: Hypotheses with One Sample of One Measurement Variable Section

A generic brand of the anti-histamine Diphenhydramine markets a capsule with a 50 milligram dose. The manufacturer is worried that the machine that fills the capsules has come out of calibration and is no longer creating capsules with the appropriate dosage.
- Research Question : Does the data suggest that the population mean dosage of this brand is different than 50 mg?
- Response Variable : dosage of the active ingredient found by a chemical assay.
- Null Hypothesis : On the average, the dosage sold under this brand is 50 mg (population mean dosage = 50 mg).
- Alternative Hypothesis : On the average, the dosage sold under this brand is not 50 mg (population mean dosage ≠ 50 mg). This is a two-sided alternative hypothesis.
Example 10.4: Hypotheses with Two Samples of One Categorical Variable Section

Many people are starting to prefer vegetarian meals on a regular basis. Specifically, a researcher believes that females are more likely than males to eat vegetarian meals on a regular basis.
- Research Question : Does the data suggest that females are more likely than males to eat vegetarian meals on a regular basis?
- Response Variable : Classification of whether or not a person eats vegetarian meals on a regular basis
- Explanatory (Grouping) Variable: Sex
- Null Hypothesis : There is no sex effect regarding those who eat vegetarian meals on a regular basis (population percent of females who eat vegetarian meals on a regular basis = population percent of males who eat vegetarian meals on a regular basis or p females = p males ).
- Alternative Hypothesis : Females are more likely than males to eat vegetarian meals on a regular basis (population percent of females who eat vegetarian meals on a regular basis > population percent of males who eat vegetarian meals on a regular basis or p females > p males ). This is a one-sided alternative hypothesis.
Example 10.5: Hypotheses with Two Samples of One Measurement Variable Section

Obesity is a major health problem today. Research is starting to show that people may be able to lose more weight on a low carbohydrate diet than on a low fat diet.
- Research Question : Does the data suggest that, on the average, people are able to lose more weight on a low carbohydrate diet than on a low fat diet?
- Response Variable : Weight loss (pounds)
- Explanatory (Grouping) Variable : Type of diet
- Null Hypothesis : There is no difference in the mean amount of weight loss when comparing a low carbohydrate diet with a low fat diet (population mean weight loss on a low carbohydrate diet = population mean weight loss on a low fat diet).
- Alternative Hypothesis : The mean weight loss should be greater for those on a low carbohydrate diet when compared with those on a low fat diet (population mean weight loss on a low carbohydrate diet > population mean weight loss on a low fat diet). This is a one-sided alternative hypothesis.
Example 10.6: Hypotheses about the relationship between Two Categorical Variables Section
- Research Question : Do the odds of having a stroke increase if you inhale second hand smoke ? A case-control study of non-smoking stroke patients and controls of the same age and occupation are asked if someone in their household smokes.
- Variables : There are two different categorical variables (Stroke patient vs control and whether the subject lives in the same household as a smoker). Living with a smoker (or not) is the natural explanatory variable and having a stroke (or not) is the natural response variable in this situation.
- Null Hypothesis : There is no relationship between whether or not a person has a stroke and whether or not a person lives with a smoker (odds ratio between stroke and second-hand smoke situation is = 1).
- Alternative Hypothesis : There is a relationship between whether or not a person has a stroke and whether or not a person lives with a smoker (odds ratio between stroke and second-hand smoke situation is > 1). This is a one-tailed alternative.
This research question might also be addressed like example 11.4 by making the hypotheses about comparing the proportion of stroke patients that live with smokers to the proportion of controls that live with smokers.
Example 10.7: Hypotheses about the relationship between Two Measurement Variables Section
- Research Question : A financial analyst believes there might be a positive association between the change in a stock's price and the amount of the stock purchased by non-management employees the previous day (stock trading by management being under "insider-trading" regulatory restrictions).
- Variables : Daily price change information (the response variable) and previous day stock purchases by non-management employees (explanatory variable). These are two different measurement variables.
- Null Hypothesis : The correlation between the daily stock price change (\$) and the daily stock purchases by non-management employees (\$) = 0.
- Alternative Hypothesis : The correlation between the daily stock price change (\$) and the daily stock purchases by non-management employees (\$) > 0. This is a one-sided alternative hypothesis.
Example 10.8: Hypotheses about comparing the relationship between Two Measurement Variables in Two Samples Section
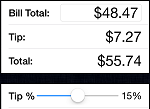
- Research Question : Is there a linear relationship between the amount of the bill (\$) at a restaurant and the tip (\$) that was left. Is the strength of this association different for family restaurants than for fine dining restaurants?
- Variables : There are two different measurement variables. The size of the tip would depend on the size of the bill so the amount of the bill would be the explanatory variable and the size of the tip would be the response variable.
- Null Hypothesis : The correlation between the amount of the bill (\$) at a restaurant and the tip (\$) that was left is the same at family restaurants as it is at fine dining restaurants.
- Alternative Hypothesis : The correlation between the amount of the bill (\$) at a restaurant and the tip (\$) that was left is the difference at family restaurants then it is at fine dining restaurants. This is a two-sided alternative hypothesis.
Null Hypothesis Definition and Examples, How to State
What is the null hypothesis, how to state the null hypothesis, null hypothesis overview.

Why is it Called the “Null”?
The word “null” in this context means that it’s a commonly accepted fact that researchers work to nullify . It doesn’t mean that the statement is null (i.e. amounts to nothing) itself! (Perhaps the term should be called the “nullifiable hypothesis” as that might cause less confusion).
Why Do I need to Test it? Why not just prove an alternate one?
The short answer is, as a scientist, you are required to ; It’s part of the scientific process. Science uses a battery of processes to prove or disprove theories, making sure than any new hypothesis has no flaws. Including both a null and an alternate hypothesis is one safeguard to ensure your research isn’t flawed. Not including the null hypothesis in your research is considered very bad practice by the scientific community. If you set out to prove an alternate hypothesis without considering it, you are likely setting yourself up for failure. At a minimum, your experiment will likely not be taken seriously.

- Null hypothesis : H 0 : The world is flat.
- Alternate hypothesis: The world is round.
Several scientists, including Copernicus , set out to disprove the null hypothesis. This eventually led to the rejection of the null and the acceptance of the alternate. Most people accepted it — the ones that didn’t created the Flat Earth Society !. What would have happened if Copernicus had not disproved the it and merely proved the alternate? No one would have listened to him. In order to change people’s thinking, he first had to prove that their thinking was wrong .
How to State the Null Hypothesis from a Word Problem
You’ll be asked to convert a word problem into a hypothesis statement in statistics that will include a null hypothesis and an alternate hypothesis . Breaking your problem into a few small steps makes these problems much easier to handle.
Step 2: Convert the hypothesis to math . Remember that the average is sometimes written as μ.
H 1 : μ > 8.2
Broken down into (somewhat) English, that’s H 1 (The hypothesis): μ (the average) > (is greater than) 8.2
Step 3: State what will happen if the hypothesis doesn’t come true. If the recovery time isn’t greater than 8.2 weeks, there are only two possibilities, that the recovery time is equal to 8.2 weeks or less than 8.2 weeks.
H 0 : μ ≤ 8.2
Broken down again into English, that’s H 0 (The null hypothesis): μ (the average) ≤ (is less than or equal to) 8.2
How to State the Null Hypothesis: Part Two
But what if the researcher doesn’t have any idea what will happen.
Example Problem: A researcher is studying the effects of radical exercise program on knee surgery patients. There is a good chance the therapy will improve recovery time, but there’s also the possibility it will make it worse. Average recovery times for knee surgery patients is 8.2 weeks.
Step 1: State what will happen if the experiment doesn’t make any difference. That’s the null hypothesis–that nothing will happen. In this experiment, if nothing happens, then the recovery time will stay at 8.2 weeks.
H 0 : μ = 8.2
Broken down into English, that’s H 0 (The null hypothesis): μ (the average) = (is equal to) 8.2
Step 2: Figure out the alternate hypothesis . The alternate hypothesis is the opposite of the null hypothesis. In other words, what happens if our experiment makes a difference?
H 1 : μ ≠ 8.2
In English again, that’s H 1 (The alternate hypothesis): μ (the average) ≠ (is not equal to) 8.2
That’s How to State the Null Hypothesis!
Check out our Youtube channel for more stats tips!
Gonick, L. (1993). The Cartoon Guide to Statistics . HarperPerennial. Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences , Wiley.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
8.2 Null and Alternative Hypotheses
Learning objectives.
- Describe hypothesis testing in general and in practice.
A hypothesis test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints and only one of these hypotheses is true. The hypothesis test determines which hypothesis is most likely true.
- The null hypothesis is a claim that a population parameter equals some value. For example, [latex]H_0: \mu=5[/latex].
- The alternative hypothesis is a claim that a population parameter is greater than, less than, or not equal to some value. For example, [latex]H_a: \mu>5[/latex], [latex]H_a: \mu<5[/latex], or [latex]H_a: \mu \neq 5[/latex]. The form of the alternative hypothesis depends on the wording of the hypothesis test.
- An alternative notation for [latex]H_a[/latex] is [latex]H_1[/latex].
Because the null and alternative hypotheses are contradictory, we must examine evidence to decide if we have enough evidence to reject the null hypothesis or not reject the null hypothesis. The evidence is in the form of sample data. After we have determined which hypothesis the sample data supports, we make a decision. There are two options for a decision . They are “ reject [latex]H_0[/latex] ” if the sample information favors the alternative hypothesis or “ do not reject [latex]H_0[/latex] ” if the sample information is insufficient to reject the null hypothesis.
Watch this video: Simple hypothesis testing | Probability and Statistics | Khan Academy by Khan Academy [6:24]
A candidate in a local election claims that 30% of registered voters voted in a recent election. Information provided by the returning office suggests that the percentage is higher than the 30% claimed.
The parameter under study is the proportion of registered voters, so we use [latex]p[/latex] in the statements of the hypotheses. The hypotheses are
[latex]\begin{eqnarray*} \\ H_0: & & p=30\% \\ \\ H_a: & & p \gt 30\% \\ \\ \end{eqnarray*}[/latex]
- The null hypothesis [latex]H_0[/latex] is the claim that the proportion of registered voters that voted equals 30%.
- The alternative hypothesis [latex]H_a[/latex] is the claim that the proportion of registered voters that voted is greater than (i.e. higher) than 30%.
A medical researcher believes that a new medicine reduces cholesterol by 25%. A medical trial suggests that the percent reduction is different than claimed. State the null and alternative hypotheses.
[latex]\begin{eqnarray*} H_0: & & p=25\% \\ \\ H_a: & & p \neq 25\% \end{eqnarray*}[/latex]
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). State the null and alternative hypotheses.
[latex]\begin{eqnarray*} H_0: & & \mu=2 \mbox{ points} \\ \\ H_a: & & \mu \neq 2 \mbox{ points} \end{eqnarray*}[/latex]
We want to test whether or not the mean height of eighth graders is 66 inches. State the null and alternative hypotheses.
[latex]\begin{eqnarray*} H_0: & & \mu=66 \mbox{ inches} \\ \\ H_a: & & \mu \neq 66 \mbox{ inches} \end{eqnarray*}[/latex]
We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:
[latex]\begin{eqnarray*} H_0: & & \mu=5 \mbox{ years} \\ \\ H_a: & & \mu \lt 5 \mbox{ years} \end{eqnarray*}[/latex]
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses.
[latex]\begin{eqnarray*} H_0: & & \mu=45 \mbox{ minutes} \\ \\ H_a: & & \mu \lt 45 \mbox{ minutes} \end{eqnarray*}[/latex]
In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.
[latex]\begin{eqnarray*} H_0: & & p=6.6\% \\ \\ H_a: & & p \gt 6.6\% \end{eqnarray*}[/latex]
On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. State the null and alternative hypotheses.
[latex]\begin{eqnarray*} H_0: & & p=40\% \\ \\ H_a: & & p \gt 40\% \end{eqnarray*}[/latex]
Concept Review
In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we evaluate the null hypothesis , typically denoted with [latex]H_0[/latex]. The null hypothesis is not rejected unless the hypothesis test shows otherwise. The null hypothesis always contain an equal sign ([latex]=[/latex]). Always write the alternative hypothesis , typically denoted with [latex]H_a[/latex] or [latex]H_1[/latex], using less than, greater than, or not equals symbols ([latex]\lt[/latex], [latex]\gt[/latex], [latex]\neq[/latex]). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. But we can never state that a claim is proven true or false. All we can conclude from the hypothesis test is which of the hypothesis is most likely true. Because the underlying facts about hypothesis testing is based on probability laws, we can talk only in terms of non-absolute certainties.
Attribution
“ 9.1 Null and Alternative Hypotheses “ in Introductory Statistics by OpenStax is licensed under a Creative Commons Attribution 4.0 International License.
Introduction to Statistics Copyright © 2022 by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Statistics Made Easy
What is an Alternative Hypothesis in Statistics?
Often in statistics we want to test whether or not some assumption is true about a population parameter .
For example, we might assume that the mean weight of a certain population of turtle is 300 pounds.
To determine if this assumption is true, we’ll go out and collect a sample of turtles and weigh each of them. Using this sample data, we’ll conduct a hypothesis test .
The first step in a hypothesis test is to define the null and alternative hypotheses .
These two hypotheses need to be mutually exclusive, so if one is true then the other must be false.
These two hypotheses are defined as follows:
Null hypothesis (H 0 ): The sample data is consistent with the prevailing belief about the population parameter.
Alternative hypothesis (H A ): The sample data suggests that the assumption made in the null hypothesis is not true. In other words, there is some non-random cause influencing the data.
Types of Alternative Hypotheses
There are two types of alternative hypotheses:
A one-tailed hypothesis involves making a “greater than” or “less than ” statement. For example, suppose we assume the mean height of a male in the U.S. is greater than or equal to 70 inches.
The null and alternative hypotheses in this case would be:
- Null hypothesis: µ ≥ 70 inches
- Alternative hypothesis: µ < 70 inches
A two-tailed hypothesis involves making an “equal to” or “not equal to” statement. For example, suppose we assume the mean height of a male in the U.S. is equal to 70 inches.
- Null hypothesis: µ = 70 inches
- Alternative hypothesis: µ ≠ 70 inches
Note: The “equal” sign is always included in the null hypothesis, whether it is =, ≥, or ≤.
Examples of Alternative Hypotheses
The following examples illustrate how to define the null and alternative hypotheses for different research problems.
Example 1: A biologist wants to test if the mean weight of a certain population of turtle is different from the widely-accepted mean weight of 300 pounds.
The null and alternative hypothesis for this research study would be:
- Null hypothesis: µ = 300 pounds
- Alternative hypothesis: µ ≠ 300 pounds
If we reject the null hypothesis, this means we have sufficient evidence from the sample data to say that the true mean weight of this population of turtles is different from 300 pounds.
Example 2: An engineer wants to test whether a new battery can produce higher mean watts than the current industry standard of 50 watts.
- Null hypothesis: µ ≤ 50 watts
- Alternative hypothesis: µ > 50 watts
If we reject the null hypothesis, this means we have sufficient evidence from the sample data to say that the true mean watts produced by the new battery is greater than the current industry standard of 50 watts.
Example 3: A botanist wants to know if a new gardening method produces less waste than the standard gardening method that produces 20 pounds of waste.
- Null hypothesis: µ ≥ 20 pounds
- Alternative hypothesis: µ < 20 pounds
If we reject the null hypothesis, this means we have sufficient evidence from the sample data to say that the true mean weight produced by this new gardening method is less than 20 pounds.
When to Reject the Null Hypothesis
Whenever we conduct a hypothesis test, we use sample data to calculate a test-statistic and a corresponding p-value.
If the p-value is less than some significance level (common choices are 0.10, 0.05, and 0.01), then we reject the null hypothesis.
This means we have sufficient evidence from the sample data to say that the assumption made by the null hypothesis is not true.
If the p-value is not less than some significance level, then we fail to reject the null hypothesis.
This means our sample data did not provide us with evidence that the assumption made by the null hypothesis was not true.
Additional Resource: An Explanation of P-Values and Statistical Significance
Featured Posts
Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Join the Statology Community
Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!
By subscribing you accept Statology's Privacy Policy.
Frequently asked questions
What are null and alternative hypotheses.
Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.
Frequently asked questions: Statistics
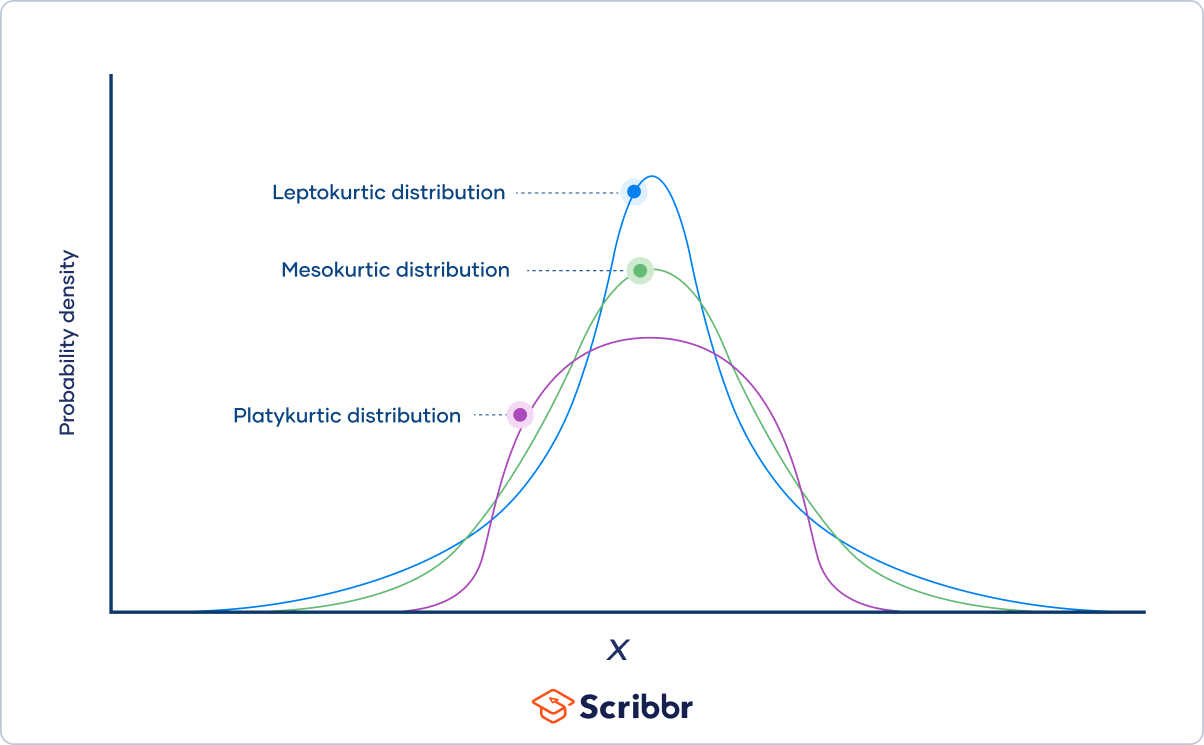
As the degrees of freedom increase, Student’s t distribution becomes less leptokurtic , meaning that the probability of extreme values decreases. The distribution becomes more and more similar to a standard normal distribution .
The three categories of kurtosis are:
- Mesokurtosis : An excess kurtosis of 0. Normal distributions are mesokurtic.
- Platykurtosis : A negative excess kurtosis. Platykurtic distributions are thin-tailed, meaning that they have few outliers .
- Leptokurtosis : A positive excess kurtosis. Leptokurtic distributions are fat-tailed, meaning that they have many outliers.
Probability distributions belong to two broad categories: discrete probability distributions and continuous probability distributions . Within each category, there are many types of probability distributions.
Probability is the relative frequency over an infinite number of trials.
For example, the probability of a coin landing on heads is .5, meaning that if you flip the coin an infinite number of times, it will land on heads half the time.
Since doing something an infinite number of times is impossible, relative frequency is often used as an estimate of probability. If you flip a coin 1000 times and get 507 heads, the relative frequency, .507, is a good estimate of the probability.
Categorical variables can be described by a frequency distribution. Quantitative variables can also be described by a frequency distribution, but first they need to be grouped into interval classes .
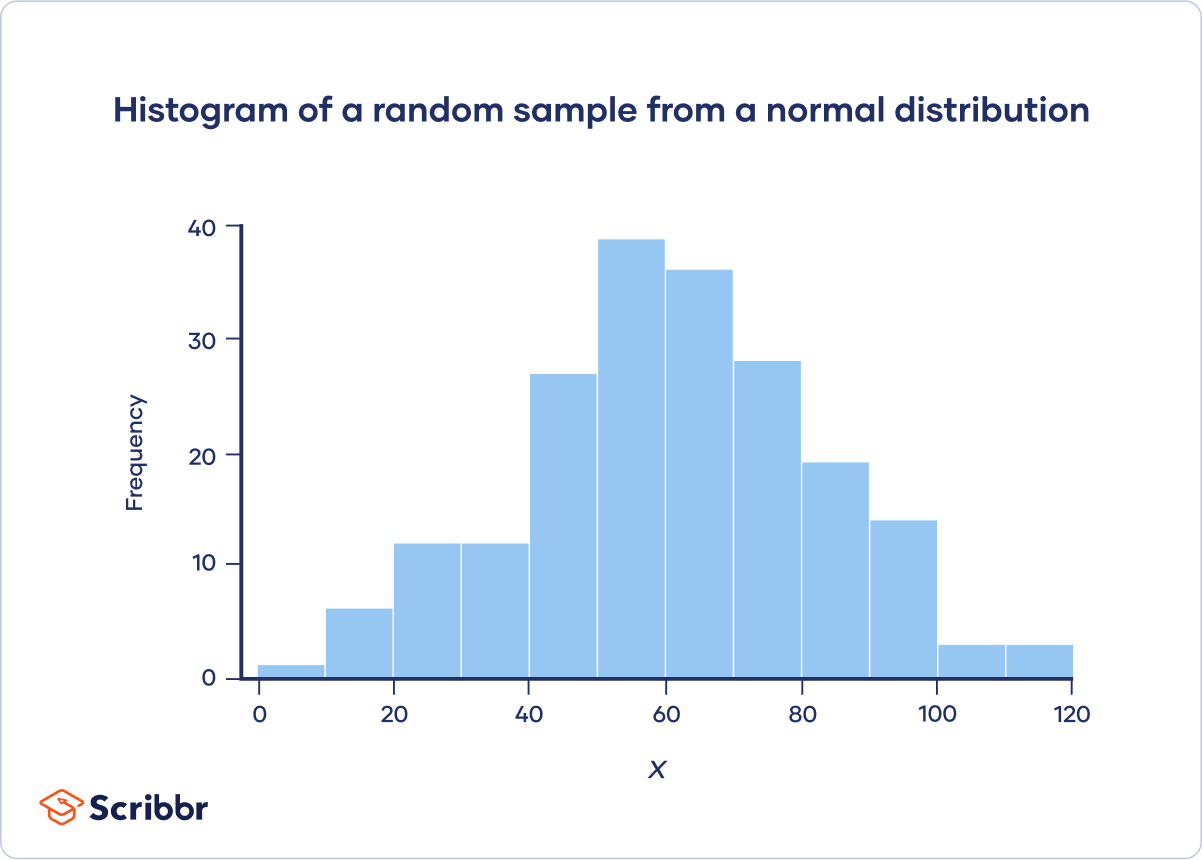
A histogram is an effective way to tell if a frequency distribution appears to have a normal distribution .
Plot a histogram and look at the shape of the bars. If the bars roughly follow a symmetrical bell or hill shape, like the example below, then the distribution is approximately normally distributed.
You can use the CHISQ.INV.RT() function to find a chi-square critical value in Excel.
For example, to calculate the chi-square critical value for a test with df = 22 and α = .05, click any blank cell and type:
=CHISQ.INV.RT(0.05,22)
You can use the qchisq() function to find a chi-square critical value in R.
For example, to calculate the chi-square critical value for a test with df = 22 and α = .05:
qchisq(p = .05, df = 22, lower.tail = FALSE)
You can use the chisq.test() function to perform a chi-square test of independence in R. Give the contingency table as a matrix for the “x” argument. For example:
m = matrix(data = c(89, 84, 86, 9, 8, 24), nrow = 3, ncol = 2)
chisq.test(x = m)
You can use the CHISQ.TEST() function to perform a chi-square test of independence in Excel. It takes two arguments, CHISQ.TEST(observed_range, expected_range), and returns the p value.
Chi-square goodness of fit tests are often used in genetics. One common application is to check if two genes are linked (i.e., if the assortment is independent). When genes are linked, the allele inherited for one gene affects the allele inherited for another gene.
Suppose that you want to know if the genes for pea texture (R = round, r = wrinkled) and color (Y = yellow, y = green) are linked. You perform a dihybrid cross between two heterozygous ( RY / ry ) pea plants. The hypotheses you’re testing with your experiment are:
- This would suggest that the genes are unlinked.
- This would suggest that the genes are linked.
You observe 100 peas:
- 78 round and yellow peas
- 6 round and green peas
- 4 wrinkled and yellow peas
- 12 wrinkled and green peas
Step 1: Calculate the expected frequencies
To calculate the expected values, you can make a Punnett square. If the two genes are unlinked, the probability of each genotypic combination is equal.
| RRYY | RrYy | RRYy | RrYY | |
| RrYy | rryy | Rryy | rrYy | |
| RRYy | Rryy | RRyy | RrYy | |
| RrYY | rrYy | RrYy | rrYY |
The expected phenotypic ratios are therefore 9 round and yellow: 3 round and green: 3 wrinkled and yellow: 1 wrinkled and green.
From this, you can calculate the expected phenotypic frequencies for 100 peas:
| Round and yellow | 78 | 100 * (9/16) = 56.25 |
| Round and green | 6 | 100 * (3/16) = 18.75 |
| Wrinkled and yellow | 4 | 100 * (3/16) = 18.75 |
| Wrinkled and green | 12 | 100 * (1/16) = 6.21 |
Step 2: Calculate chi-square
| − | − | ||||
| Round and yellow | 78 | 56.25 | 21.75 | 473.06 | 8.41 |
| Round and green | 6 | 18.75 | −12.75 | 162.56 | 8.67 |
| Wrinkled and yellow | 4 | 18.75 | −14.75 | 217.56 | 11.6 |
| Wrinkled and green | 12 | 6.21 | 5.79 | 33.52 | 5.4 |
Χ 2 = 8.41 + 8.67 + 11.6 + 5.4 = 34.08
Step 3: Find the critical chi-square value
Since there are four groups (round and yellow, round and green, wrinkled and yellow, wrinkled and green), there are three degrees of freedom .
For a test of significance at α = .05 and df = 3, the Χ 2 critical value is 7.82.
Step 4: Compare the chi-square value to the critical value
Χ 2 = 34.08
Critical value = 7.82
The Χ 2 value is greater than the critical value .
Step 5: Decide whether the reject the null hypothesis
The Χ 2 value is greater than the critical value, so we reject the null hypothesis that the population of offspring have an equal probability of inheriting all possible genotypic combinations. There is a significant difference between the observed and expected genotypic frequencies ( p < .05).
The data supports the alternative hypothesis that the offspring do not have an equal probability of inheriting all possible genotypic combinations, which suggests that the genes are linked
You can use the chisq.test() function to perform a chi-square goodness of fit test in R. Give the observed values in the “x” argument, give the expected values in the “p” argument, and set “rescale.p” to true. For example:
chisq.test(x = c(22,30,23), p = c(25,25,25), rescale.p = TRUE)
You can use the CHISQ.TEST() function to perform a chi-square goodness of fit test in Excel. It takes two arguments, CHISQ.TEST(observed_range, expected_range), and returns the p value .
Both correlations and chi-square tests can test for relationships between two variables. However, a correlation is used when you have two quantitative variables and a chi-square test of independence is used when you have two categorical variables.
Both chi-square tests and t tests can test for differences between two groups. However, a t test is used when you have a dependent quantitative variable and an independent categorical variable (with two groups). A chi-square test of independence is used when you have two categorical variables.
The two main chi-square tests are the chi-square goodness of fit test and the chi-square test of independence .
A chi-square distribution is a continuous probability distribution . The shape of a chi-square distribution depends on its degrees of freedom , k . The mean of a chi-square distribution is equal to its degrees of freedom ( k ) and the variance is 2 k . The range is 0 to ∞.
As the degrees of freedom ( k ) increases, the chi-square distribution goes from a downward curve to a hump shape. As the degrees of freedom increases further, the hump goes from being strongly right-skewed to being approximately normal.
To find the quartiles of a probability distribution, you can use the distribution’s quantile function.
You can use the quantile() function to find quartiles in R. If your data is called “data”, then “quantile(data, prob=c(.25,.5,.75), type=1)” will return the three quartiles.
You can use the QUARTILE() function to find quartiles in Excel. If your data is in column A, then click any blank cell and type “=QUARTILE(A:A,1)” for the first quartile, “=QUARTILE(A:A,2)” for the second quartile, and “=QUARTILE(A:A,3)” for the third quartile.
You can use the PEARSON() function to calculate the Pearson correlation coefficient in Excel. If your variables are in columns A and B, then click any blank cell and type “PEARSON(A:A,B:B)”.
There is no function to directly test the significance of the correlation.
You can use the cor() function to calculate the Pearson correlation coefficient in R. To test the significance of the correlation, you can use the cor.test() function.
You should use the Pearson correlation coefficient when (1) the relationship is linear and (2) both variables are quantitative and (3) normally distributed and (4) have no outliers.
The Pearson correlation coefficient ( r ) is the most common way of measuring a linear correlation. It is a number between –1 and 1 that measures the strength and direction of the relationship between two variables.
This table summarizes the most important differences between normal distributions and Poisson distributions :
| Characteristic | Normal | Poisson |
|---|---|---|
| Continuous | ||
| Mean (µ) and standard deviation (σ) | Lambda (λ) | |
| Shape | Bell-shaped | Depends on λ |
| Symmetrical | Asymmetrical (right-skewed). As λ increases, the asymmetry decreases. | |
| Range | −∞ to ∞ | 0 to ∞ |
When the mean of a Poisson distribution is large (>10), it can be approximated by a normal distribution.
In the Poisson distribution formula, lambda (λ) is the mean number of events within a given interval of time or space. For example, λ = 0.748 floods per year.
The e in the Poisson distribution formula stands for the number 2.718. This number is called Euler’s constant. You can simply substitute e with 2.718 when you’re calculating a Poisson probability. Euler’s constant is a very useful number and is especially important in calculus.
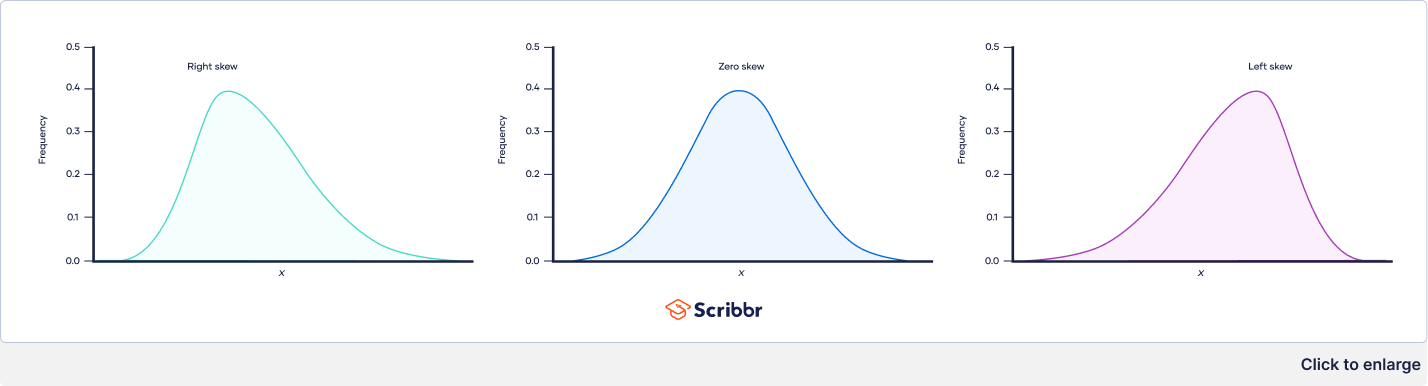
The three types of skewness are:
- Right skew (also called positive skew ) . A right-skewed distribution is longer on the right side of its peak than on its left.
- Left skew (also called negative skew). A left-skewed distribution is longer on the left side of its peak than on its right.
- Zero skew. It is symmetrical and its left and right sides are mirror images.
Skewness and kurtosis are both important measures of a distribution’s shape.
- Skewness measures the asymmetry of a distribution.
- Kurtosis measures the heaviness of a distribution’s tails relative to a normal distribution .
A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (“ x affects y because …”).
A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses . In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.
The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).
The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).
The t distribution was first described by statistician William Sealy Gosset under the pseudonym “Student.”
To calculate a confidence interval of a mean using the critical value of t , follow these four steps:
- Choose the significance level based on your desired confidence level. The most common confidence level is 95%, which corresponds to α = .05 in the two-tailed t table .
- Find the critical value of t in the two-tailed t table.
- Multiply the critical value of t by s / √ n .
- Add this value to the mean to calculate the upper limit of the confidence interval, and subtract this value from the mean to calculate the lower limit.
To test a hypothesis using the critical value of t , follow these four steps:
- Calculate the t value for your sample.
- Find the critical value of t in the t table .
- Determine if the (absolute) t value is greater than the critical value of t .
- Reject the null hypothesis if the sample’s t value is greater than the critical value of t . Otherwise, don’t reject the null hypothesis .
You can use the T.INV() function to find the critical value of t for one-tailed tests in Excel, and you can use the T.INV.2T() function for two-tailed tests.
You can use the qt() function to find the critical value of t in R. The function gives the critical value of t for the one-tailed test. If you want the critical value of t for a two-tailed test, divide the significance level by two.
You can use the RSQ() function to calculate R² in Excel. If your dependent variable is in column A and your independent variable is in column B, then click any blank cell and type “RSQ(A:A,B:B)”.
You can use the summary() function to view the R² of a linear model in R. You will see the “R-squared” near the bottom of the output.
There are two formulas you can use to calculate the coefficient of determination (R²) of a simple linear regression .
The coefficient of determination (R²) is a number between 0 and 1 that measures how well a statistical model predicts an outcome. You can interpret the R² as the proportion of variation in the dependent variable that is predicted by the statistical model.
There are three main types of missing data .
Missing completely at random (MCAR) data are randomly distributed across the variable and unrelated to other variables .
Missing at random (MAR) data are not randomly distributed but they are accounted for by other observed variables.
Missing not at random (MNAR) data systematically differ from the observed values.
To tidy up your missing data , your options usually include accepting, removing, or recreating the missing data.
- Acceptance: You leave your data as is
- Listwise or pairwise deletion: You delete all cases (participants) with missing data from analyses
- Imputation: You use other data to fill in the missing data
Missing data are important because, depending on the type, they can sometimes bias your results. This means your results may not be generalizable outside of your study because your data come from an unrepresentative sample .
Missing data , or missing values, occur when you don’t have data stored for certain variables or participants.
In any dataset, there’s usually some missing data. In quantitative research , missing values appear as blank cells in your spreadsheet.
There are two steps to calculating the geometric mean :
- Multiply all values together to get their product.
- Find the n th root of the product ( n is the number of values).
Before calculating the geometric mean, note that:
- The geometric mean can only be found for positive values.
- If any value in the data set is zero, the geometric mean is zero.
The arithmetic mean is the most commonly used type of mean and is often referred to simply as “the mean.” While the arithmetic mean is based on adding and dividing values, the geometric mean multiplies and finds the root of values.
Even though the geometric mean is a less common measure of central tendency , it’s more accurate than the arithmetic mean for percentage change and positively skewed data. The geometric mean is often reported for financial indices and population growth rates.
The geometric mean is an average that multiplies all values and finds a root of the number. For a dataset with n numbers, you find the n th root of their product.
Outliers are extreme values that differ from most values in the dataset. You find outliers at the extreme ends of your dataset.
It’s best to remove outliers only when you have a sound reason for doing so.
Some outliers represent natural variations in the population , and they should be left as is in your dataset. These are called true outliers.
Other outliers are problematic and should be removed because they represent measurement errors , data entry or processing errors, or poor sampling.
You can choose from four main ways to detect outliers :
- Sorting your values from low to high and checking minimum and maximum values
- Visualizing your data with a box plot and looking for outliers
- Using the interquartile range to create fences for your data
- Using statistical procedures to identify extreme values
Outliers can have a big impact on your statistical analyses and skew the results of any hypothesis test if they are inaccurate.
These extreme values can impact your statistical power as well, making it hard to detect a true effect if there is one.
No, the steepness or slope of the line isn’t related to the correlation coefficient value. The correlation coefficient only tells you how closely your data fit on a line, so two datasets with the same correlation coefficient can have very different slopes.
To find the slope of the line, you’ll need to perform a regression analysis .
Correlation coefficients always range between -1 and 1.
The sign of the coefficient tells you the direction of the relationship: a positive value means the variables change together in the same direction, while a negative value means they change together in opposite directions.
The absolute value of a number is equal to the number without its sign. The absolute value of a correlation coefficient tells you the magnitude of the correlation: the greater the absolute value, the stronger the correlation.
These are the assumptions your data must meet if you want to use Pearson’s r :
- Both variables are on an interval or ratio level of measurement
- Data from both variables follow normal distributions
- Your data have no outliers
- Your data is from a random or representative sample
- You expect a linear relationship between the two variables
A correlation coefficient is a single number that describes the strength and direction of the relationship between your variables.
Different types of correlation coefficients might be appropriate for your data based on their levels of measurement and distributions . The Pearson product-moment correlation coefficient (Pearson’s r ) is commonly used to assess a linear relationship between two quantitative variables.
There are various ways to improve power:
- Increase the potential effect size by manipulating your independent variable more strongly,
- Increase sample size,
- Increase the significance level (alpha),
- Reduce measurement error by increasing the precision and accuracy of your measurement devices and procedures,
- Use a one-tailed test instead of a two-tailed test for t tests and z tests.
A power analysis is a calculation that helps you determine a minimum sample size for your study. It’s made up of four main components. If you know or have estimates for any three of these, you can calculate the fourth component.
- Statistical power : the likelihood that a test will detect an effect of a certain size if there is one, usually set at 80% or higher.
- Sample size : the minimum number of observations needed to observe an effect of a certain size with a given power level.
- Significance level (alpha) : the maximum risk of rejecting a true null hypothesis that you are willing to take, usually set at 5%.
- Expected effect size : a standardized way of expressing the magnitude of the expected result of your study, usually based on similar studies or a pilot study.
Statistical analysis is the main method for analyzing quantitative research data . It uses probabilities and models to test predictions about a population from sample data.
The risk of making a Type II error is inversely related to the statistical power of a test. Power is the extent to which a test can correctly detect a real effect when there is one.
To (indirectly) reduce the risk of a Type II error, you can increase the sample size or the significance level to increase statistical power.
The risk of making a Type I error is the significance level (or alpha) that you choose. That’s a value that you set at the beginning of your study to assess the statistical probability of obtaining your results ( p value ).
The significance level is usually set at 0.05 or 5%. This means that your results only have a 5% chance of occurring, or less, if the null hypothesis is actually true.
To reduce the Type I error probability, you can set a lower significance level.
In statistics, a Type I error means rejecting the null hypothesis when it’s actually true, while a Type II error means failing to reject the null hypothesis when it’s actually false.
In statistics, power refers to the likelihood of a hypothesis test detecting a true effect if there is one. A statistically powerful test is more likely to reject a false negative (a Type II error).
If you don’t ensure enough power in your study, you may not be able to detect a statistically significant result even when it has practical significance. Your study might not have the ability to answer your research question.
While statistical significance shows that an effect exists in a study, practical significance shows that the effect is large enough to be meaningful in the real world.
Statistical significance is denoted by p -values whereas practical significance is represented by effect sizes .
There are dozens of measures of effect sizes . The most common effect sizes are Cohen’s d and Pearson’s r . Cohen’s d measures the size of the difference between two groups while Pearson’s r measures the strength of the relationship between two variables .
Effect size tells you how meaningful the relationship between variables or the difference between groups is.
A large effect size means that a research finding has practical significance, while a small effect size indicates limited practical applications.
Using descriptive and inferential statistics , you can make two types of estimates about the population : point estimates and interval estimates.
- A point estimate is a single value estimate of a parameter . For instance, a sample mean is a point estimate of a population mean.
- An interval estimate gives you a range of values where the parameter is expected to lie. A confidence interval is the most common type of interval estimate.
Both types of estimates are important for gathering a clear idea of where a parameter is likely to lie.
Standard error and standard deviation are both measures of variability . The standard deviation reflects variability within a sample, while the standard error estimates the variability across samples of a population.
The standard error of the mean , or simply standard error , indicates how different the population mean is likely to be from a sample mean. It tells you how much the sample mean would vary if you were to repeat a study using new samples from within a single population.
To figure out whether a given number is a parameter or a statistic , ask yourself the following:
- Does the number describe a whole, complete population where every member can be reached for data collection ?
- Is it possible to collect data for this number from every member of the population in a reasonable time frame?
If the answer is yes to both questions, the number is likely to be a parameter. For small populations, data can be collected from the whole population and summarized in parameters.
If the answer is no to either of the questions, then the number is more likely to be a statistic.
The arithmetic mean is the most commonly used mean. It’s often simply called the mean or the average. But there are some other types of means you can calculate depending on your research purposes:
- Weighted mean: some values contribute more to the mean than others.
- Geometric mean : values are multiplied rather than summed up.
- Harmonic mean: reciprocals of values are used instead of the values themselves.
You can find the mean , or average, of a data set in two simple steps:
- Find the sum of the values by adding them all up.
- Divide the sum by the number of values in the data set.
This method is the same whether you are dealing with sample or population data or positive or negative numbers.
The median is the most informative measure of central tendency for skewed distributions or distributions with outliers. For example, the median is often used as a measure of central tendency for income distributions, which are generally highly skewed.
Because the median only uses one or two values, it’s unaffected by extreme outliers or non-symmetric distributions of scores. In contrast, the mean and mode can vary in skewed distributions.
To find the median , first order your data. Then calculate the middle position based on n , the number of values in your data set.
A data set can often have no mode, one mode or more than one mode – it all depends on how many different values repeat most frequently.
Your data can be:
- without any mode
- unimodal, with one mode,
- bimodal, with two modes,
- trimodal, with three modes, or
- multimodal, with four or more modes.
To find the mode :
- If your data is numerical or quantitative, order the values from low to high.
- If it is categorical, sort the values by group, in any order.
Then you simply need to identify the most frequently occurring value.
The interquartile range is the best measure of variability for skewed distributions or data sets with outliers. Because it’s based on values that come from the middle half of the distribution, it’s unlikely to be influenced by outliers .
The two most common methods for calculating interquartile range are the exclusive and inclusive methods.
The exclusive method excludes the median when identifying Q1 and Q3, while the inclusive method includes the median as a value in the data set in identifying the quartiles.
For each of these methods, you’ll need different procedures for finding the median, Q1 and Q3 depending on whether your sample size is even- or odd-numbered. The exclusive method works best for even-numbered sample sizes, while the inclusive method is often used with odd-numbered sample sizes.
While the range gives you the spread of the whole data set, the interquartile range gives you the spread of the middle half of a data set.
Homoscedasticity, or homogeneity of variances, is an assumption of equal or similar variances in different groups being compared.
This is an important assumption of parametric statistical tests because they are sensitive to any dissimilarities. Uneven variances in samples result in biased and skewed test results.
Statistical tests such as variance tests or the analysis of variance (ANOVA) use sample variance to assess group differences of populations. They use the variances of the samples to assess whether the populations they come from significantly differ from each other.
Variance is the average squared deviations from the mean, while standard deviation is the square root of this number. Both measures reflect variability in a distribution, but their units differ:
- Standard deviation is expressed in the same units as the original values (e.g., minutes or meters).
- Variance is expressed in much larger units (e.g., meters squared).
Although the units of variance are harder to intuitively understand, variance is important in statistical tests .
The empirical rule, or the 68-95-99.7 rule, tells you where most of the values lie in a normal distribution :
- Around 68% of values are within 1 standard deviation of the mean.
- Around 95% of values are within 2 standard deviations of the mean.
- Around 99.7% of values are within 3 standard deviations of the mean.
The empirical rule is a quick way to get an overview of your data and check for any outliers or extreme values that don’t follow this pattern.
In a normal distribution , data are symmetrically distributed with no skew. Most values cluster around a central region, with values tapering off as they go further away from the center.
The measures of central tendency (mean, mode, and median) are exactly the same in a normal distribution.
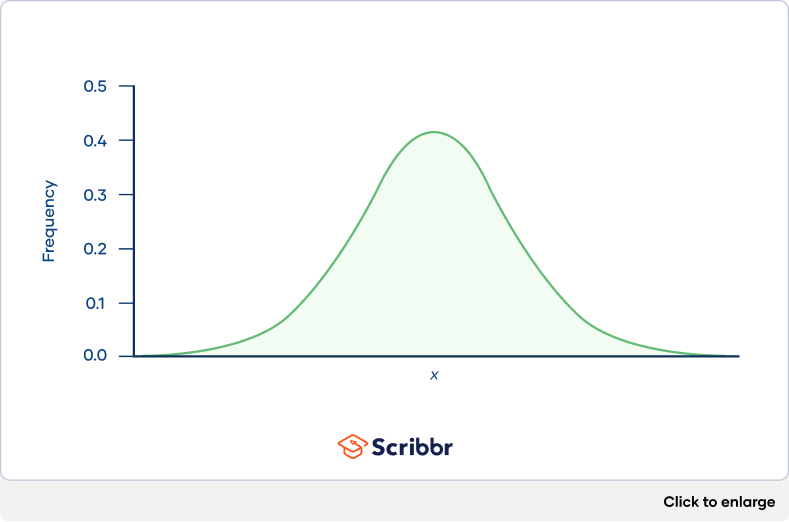
The standard deviation is the average amount of variability in your data set. It tells you, on average, how far each score lies from the mean .
In normal distributions, a high standard deviation means that values are generally far from the mean, while a low standard deviation indicates that values are clustered close to the mean.
No. Because the range formula subtracts the lowest number from the highest number, the range is always zero or a positive number.
In statistics, the range is the spread of your data from the lowest to the highest value in the distribution. It is the simplest measure of variability .
While central tendency tells you where most of your data points lie, variability summarizes how far apart your points from each other.
Data sets can have the same central tendency but different levels of variability or vice versa . Together, they give you a complete picture of your data.
Variability is most commonly measured with the following descriptive statistics :
- Range : the difference between the highest and lowest values
- Interquartile range : the range of the middle half of a distribution
- Standard deviation : average distance from the mean
- Variance : average of squared distances from the mean
Variability tells you how far apart points lie from each other and from the center of a distribution or a data set.
Variability is also referred to as spread, scatter or dispersion.
While interval and ratio data can both be categorized, ranked, and have equal spacing between adjacent values, only ratio scales have a true zero.
For example, temperature in Celsius or Fahrenheit is at an interval scale because zero is not the lowest possible temperature. In the Kelvin scale, a ratio scale, zero represents a total lack of thermal energy.
A critical value is the value of the test statistic which defines the upper and lower bounds of a confidence interval , or which defines the threshold of statistical significance in a statistical test. It describes how far from the mean of the distribution you have to go to cover a certain amount of the total variation in the data (i.e. 90%, 95%, 99%).
If you are constructing a 95% confidence interval and are using a threshold of statistical significance of p = 0.05, then your critical value will be identical in both cases.
The t -distribution gives more probability to observations in the tails of the distribution than the standard normal distribution (a.k.a. the z -distribution).
In this way, the t -distribution is more conservative than the standard normal distribution: to reach the same level of confidence or statistical significance , you will need to include a wider range of the data.
A t -score (a.k.a. a t -value) is equivalent to the number of standard deviations away from the mean of the t -distribution .
The t -score is the test statistic used in t -tests and regression tests. It can also be used to describe how far from the mean an observation is when the data follow a t -distribution.
The t -distribution is a way of describing a set of observations where most observations fall close to the mean , and the rest of the observations make up the tails on either side. It is a type of normal distribution used for smaller sample sizes, where the variance in the data is unknown.
The t -distribution forms a bell curve when plotted on a graph. It can be described mathematically using the mean and the standard deviation .
In statistics, ordinal and nominal variables are both considered categorical variables .
Even though ordinal data can sometimes be numerical, not all mathematical operations can be performed on them.
Ordinal data has two characteristics:
- The data can be classified into different categories within a variable.
- The categories have a natural ranked order.
However, unlike with interval data, the distances between the categories are uneven or unknown.
Nominal and ordinal are two of the four levels of measurement . Nominal level data can only be classified, while ordinal level data can be classified and ordered.
Nominal data is data that can be labelled or classified into mutually exclusive categories within a variable. These categories cannot be ordered in a meaningful way.
For example, for the nominal variable of preferred mode of transportation, you may have the categories of car, bus, train, tram or bicycle.
If your confidence interval for a difference between groups includes zero, that means that if you run your experiment again you have a good chance of finding no difference between groups.
If your confidence interval for a correlation or regression includes zero, that means that if you run your experiment again there is a good chance of finding no correlation in your data.
In both of these cases, you will also find a high p -value when you run your statistical test, meaning that your results could have occurred under the null hypothesis of no relationship between variables or no difference between groups.
If you want to calculate a confidence interval around the mean of data that is not normally distributed , you have two choices:
- Find a distribution that matches the shape of your data and use that distribution to calculate the confidence interval.
- Perform a transformation on your data to make it fit a normal distribution, and then find the confidence interval for the transformed data.
The standard normal distribution , also called the z -distribution, is a special normal distribution where the mean is 0 and the standard deviation is 1.
Any normal distribution can be converted into the standard normal distribution by turning the individual values into z -scores. In a z -distribution, z -scores tell you how many standard deviations away from the mean each value lies.
The z -score and t -score (aka z -value and t -value) show how many standard deviations away from the mean of the distribution you are, assuming your data follow a z -distribution or a t -distribution .
These scores are used in statistical tests to show how far from the mean of the predicted distribution your statistical estimate is. If your test produces a z -score of 2.5, this means that your estimate is 2.5 standard deviations from the predicted mean.
The predicted mean and distribution of your estimate are generated by the null hypothesis of the statistical test you are using. The more standard deviations away from the predicted mean your estimate is, the less likely it is that the estimate could have occurred under the null hypothesis .
To calculate the confidence interval , you need to know:
- The point estimate you are constructing the confidence interval for
- The critical values for the test statistic
- The standard deviation of the sample
- The sample size
Then you can plug these components into the confidence interval formula that corresponds to your data. The formula depends on the type of estimate (e.g. a mean or a proportion) and on the distribution of your data.
The confidence level is the percentage of times you expect to get close to the same estimate if you run your experiment again or resample the population in the same way.
The confidence interval consists of the upper and lower bounds of the estimate you expect to find at a given level of confidence.
For example, if you are estimating a 95% confidence interval around the mean proportion of female babies born every year based on a random sample of babies, you might find an upper bound of 0.56 and a lower bound of 0.48. These are the upper and lower bounds of the confidence interval. The confidence level is 95%.
The mean is the most frequently used measure of central tendency because it uses all values in the data set to give you an average.
For data from skewed distributions, the median is better than the mean because it isn’t influenced by extremely large values.
The mode is the only measure you can use for nominal or categorical data that can’t be ordered.
The measures of central tendency you can use depends on the level of measurement of your data.
- For a nominal level, you can only use the mode to find the most frequent value.
- For an ordinal level or ranked data, you can also use the median to find the value in the middle of your data set.
- For interval or ratio levels, in addition to the mode and median, you can use the mean to find the average value.
Measures of central tendency help you find the middle, or the average, of a data set.
The 3 most common measures of central tendency are the mean, median and mode.
- The mode is the most frequent value.
- The median is the middle number in an ordered data set.
- The mean is the sum of all values divided by the total number of values.
Some variables have fixed levels. For example, gender and ethnicity are always nominal level data because they cannot be ranked.
However, for other variables, you can choose the level of measurement . For example, income is a variable that can be recorded on an ordinal or a ratio scale:
- At an ordinal level , you could create 5 income groupings and code the incomes that fall within them from 1–5.
- At a ratio level , you would record exact numbers for income.
If you have a choice, the ratio level is always preferable because you can analyze data in more ways. The higher the level of measurement, the more precise your data is.
The level at which you measure a variable determines how you can analyze your data.
Depending on the level of measurement , you can perform different descriptive statistics to get an overall summary of your data and inferential statistics to see if your results support or refute your hypothesis .
Levels of measurement tell you how precisely variables are recorded. There are 4 levels of measurement, which can be ranked from low to high:
- Nominal : the data can only be categorized.
- Ordinal : the data can be categorized and ranked.
- Interval : the data can be categorized and ranked, and evenly spaced.
- Ratio : the data can be categorized, ranked, evenly spaced and has a natural zero.
No. The p -value only tells you how likely the data you have observed is to have occurred under the null hypothesis .
If the p -value is below your threshold of significance (typically p < 0.05), then you can reject the null hypothesis, but this does not necessarily mean that your alternative hypothesis is true.
The alpha value, or the threshold for statistical significance , is arbitrary – which value you use depends on your field of study.
In most cases, researchers use an alpha of 0.05, which means that there is a less than 5% chance that the data being tested could have occurred under the null hypothesis.
P -values are usually automatically calculated by the program you use to perform your statistical test. They can also be estimated using p -value tables for the relevant test statistic .
P -values are calculated from the null distribution of the test statistic. They tell you how often a test statistic is expected to occur under the null hypothesis of the statistical test, based on where it falls in the null distribution.
If the test statistic is far from the mean of the null distribution, then the p -value will be small, showing that the test statistic is not likely to have occurred under the null hypothesis.
A p -value , or probability value, is a number describing how likely it is that your data would have occurred under the null hypothesis of your statistical test .
The test statistic you use will be determined by the statistical test.
You can choose the right statistical test by looking at what type of data you have collected and what type of relationship you want to test.
The test statistic will change based on the number of observations in your data, how variable your observations are, and how strong the underlying patterns in the data are.
For example, if one data set has higher variability while another has lower variability, the first data set will produce a test statistic closer to the null hypothesis , even if the true correlation between two variables is the same in either data set.
The formula for the test statistic depends on the statistical test being used.
Generally, the test statistic is calculated as the pattern in your data (i.e. the correlation between variables or difference between groups) divided by the variance in the data (i.e. the standard deviation ).
- Univariate statistics summarize only one variable at a time.
- Bivariate statistics compare two variables .
- Multivariate statistics compare more than two variables .
The 3 main types of descriptive statistics concern the frequency distribution, central tendency, and variability of a dataset.
- Distribution refers to the frequencies of different responses.
- Measures of central tendency give you the average for each response.
- Measures of variability show you the spread or dispersion of your dataset.
Descriptive statistics summarize the characteristics of a data set. Inferential statistics allow you to test a hypothesis or assess whether your data is generalizable to the broader population.
In statistics, model selection is a process researchers use to compare the relative value of different statistical models and determine which one is the best fit for the observed data.
The Akaike information criterion is one of the most common methods of model selection. AIC weights the ability of the model to predict the observed data against the number of parameters the model requires to reach that level of precision.
AIC model selection can help researchers find a model that explains the observed variation in their data while avoiding overfitting.
In statistics, a model is the collection of one or more independent variables and their predicted interactions that researchers use to try to explain variation in their dependent variable.
You can test a model using a statistical test . To compare how well different models fit your data, you can use Akaike’s information criterion for model selection.
The Akaike information criterion is calculated from the maximum log-likelihood of the model and the number of parameters (K) used to reach that likelihood. The AIC function is 2K – 2(log-likelihood) .
Lower AIC values indicate a better-fit model, and a model with a delta-AIC (the difference between the two AIC values being compared) of more than -2 is considered significantly better than the model it is being compared to.
The Akaike information criterion is a mathematical test used to evaluate how well a model fits the data it is meant to describe. It penalizes models which use more independent variables (parameters) as a way to avoid over-fitting.
AIC is most often used to compare the relative goodness-of-fit among different models under consideration and to then choose the model that best fits the data.
A factorial ANOVA is any ANOVA that uses more than one categorical independent variable . A two-way ANOVA is a type of factorial ANOVA.
Some examples of factorial ANOVAs include:
- Testing the combined effects of vaccination (vaccinated or not vaccinated) and health status (healthy or pre-existing condition) on the rate of flu infection in a population.
- Testing the effects of marital status (married, single, divorced, widowed), job status (employed, self-employed, unemployed, retired), and family history (no family history, some family history) on the incidence of depression in a population.
- Testing the effects of feed type (type A, B, or C) and barn crowding (not crowded, somewhat crowded, very crowded) on the final weight of chickens in a commercial farming operation.
In ANOVA, the null hypothesis is that there is no difference among group means. If any group differs significantly from the overall group mean, then the ANOVA will report a statistically significant result.
Significant differences among group means are calculated using the F statistic, which is the ratio of the mean sum of squares (the variance explained by the independent variable) to the mean square error (the variance left over).
If the F statistic is higher than the critical value (the value of F that corresponds with your alpha value, usually 0.05), then the difference among groups is deemed statistically significant.
The only difference between one-way and two-way ANOVA is the number of independent variables . A one-way ANOVA has one independent variable, while a two-way ANOVA has two.
- One-way ANOVA : Testing the relationship between shoe brand (Nike, Adidas, Saucony, Hoka) and race finish times in a marathon.
- Two-way ANOVA : Testing the relationship between shoe brand (Nike, Adidas, Saucony, Hoka), runner age group (junior, senior, master’s), and race finishing times in a marathon.
All ANOVAs are designed to test for differences among three or more groups. If you are only testing for a difference between two groups, use a t-test instead.
Multiple linear regression is a regression model that estimates the relationship between a quantitative dependent variable and two or more independent variables using a straight line.
Linear regression most often uses mean-square error (MSE) to calculate the error of the model. MSE is calculated by:
- measuring the distance of the observed y-values from the predicted y-values at each value of x;
- squaring each of these distances;
- calculating the mean of each of the squared distances.
Linear regression fits a line to the data by finding the regression coefficient that results in the smallest MSE.
Simple linear regression is a regression model that estimates the relationship between one independent variable and one dependent variable using a straight line. Both variables should be quantitative.
For example, the relationship between temperature and the expansion of mercury in a thermometer can be modeled using a straight line: as temperature increases, the mercury expands. This linear relationship is so certain that we can use mercury thermometers to measure temperature.
A regression model is a statistical model that estimates the relationship between one dependent variable and one or more independent variables using a line (or a plane in the case of two or more independent variables).
A regression model can be used when the dependent variable is quantitative, except in the case of logistic regression, where the dependent variable is binary.
A t-test should not be used to measure differences among more than two groups, because the error structure for a t-test will underestimate the actual error when many groups are being compared.
If you want to compare the means of several groups at once, it’s best to use another statistical test such as ANOVA or a post-hoc test.
A one-sample t-test is used to compare a single population to a standard value (for example, to determine whether the average lifespan of a specific town is different from the country average).
A paired t-test is used to compare a single population before and after some experimental intervention or at two different points in time (for example, measuring student performance on a test before and after being taught the material).
A t-test measures the difference in group means divided by the pooled standard error of the two group means.
In this way, it calculates a number (the t-value) illustrating the magnitude of the difference between the two group means being compared, and estimates the likelihood that this difference exists purely by chance (p-value).
Your choice of t-test depends on whether you are studying one group or two groups, and whether you care about the direction of the difference in group means.
If you are studying one group, use a paired t-test to compare the group mean over time or after an intervention, or use a one-sample t-test to compare the group mean to a standard value. If you are studying two groups, use a two-sample t-test .
If you want to know only whether a difference exists, use a two-tailed test . If you want to know if one group mean is greater or less than the other, use a left-tailed or right-tailed one-tailed test .
A t-test is a statistical test that compares the means of two samples . It is used in hypothesis testing , with a null hypothesis that the difference in group means is zero and an alternate hypothesis that the difference in group means is different from zero.
Statistical significance is a term used by researchers to state that it is unlikely their observations could have occurred under the null hypothesis of a statistical test . Significance is usually denoted by a p -value , or probability value.
Statistical significance is arbitrary – it depends on the threshold, or alpha value, chosen by the researcher. The most common threshold is p < 0.05, which means that the data is likely to occur less than 5% of the time under the null hypothesis .
When the p -value falls below the chosen alpha value, then we say the result of the test is statistically significant.
A test statistic is a number calculated by a statistical test . It describes how far your observed data is from the null hypothesis of no relationship between variables or no difference among sample groups.
The test statistic tells you how different two or more groups are from the overall population mean , or how different a linear slope is from the slope predicted by a null hypothesis . Different test statistics are used in different statistical tests.
Statistical tests commonly assume that:
- the data are normally distributed
- the groups that are being compared have similar variance
- the data are independent
If your data does not meet these assumptions you might still be able to use a nonparametric statistical test , which have fewer requirements but also make weaker inferences.
Ask our team
Want to contact us directly? No problem. We are always here for you.
- Email [email protected]
- Start live chat
- Call +1 (510) 822-8066
- WhatsApp +31 20 261 6040

Our team helps students graduate by offering:
- A world-class citation generator
- Plagiarism Checker software powered by Turnitin
- Innovative Citation Checker software
- Professional proofreading services
- Over 300 helpful articles about academic writing, citing sources, plagiarism, and more
Scribbr specializes in editing study-related documents . We proofread:
- PhD dissertations
- Research proposals
- Personal statements
- Admission essays
- Motivation letters
- Reflection papers
- Journal articles
- Capstone projects
Scribbr’s Plagiarism Checker is powered by elements of Turnitin’s Similarity Checker , namely the plagiarism detection software and the Internet Archive and Premium Scholarly Publications content databases .
The add-on AI detector is powered by Scribbr’s proprietary software.
The Scribbr Citation Generator is developed using the open-source Citation Style Language (CSL) project and Frank Bennett’s citeproc-js . It’s the same technology used by dozens of other popular citation tools, including Mendeley and Zotero.
You can find all the citation styles and locales used in the Scribbr Citation Generator in our publicly accessible repository on Github .

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

2.1.3: The Research Hypothesis and the Null Hypothesis
- Last updated
- Save as PDF
- Page ID 44856

- Michelle Oja
- Taft College
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Hypotheses are predictions of expected findings.
The Research Hypothesis
A research hypothesis is a mathematical way of stating a research question. A research hypothesis names the groups (we'll start with a sample and a population), what was measured, and which we think will have a higher mean. The last one gives the research hypothesis a direction. In other words, a research hypothesis should include:
- The name of the groups being compared. This is sometimes considered the IV.
- What was measured. This is the DV.
- Which group are we predicting will have the higher mean.
There are two types of research hypotheses related to sample means and population means: Directional Research Hypotheses and Non-Directional Research Hypotheses
Directional Research Hypothesis
If we expect our obtained sample mean to be above or below the other group's mean (the population mean, for example), we have a directional hypothesis. There are two options:
- Symbol: \( \displaystyle \bar{X} > \mu \)
- (The mean of the sample is greater than than the mean of the population.)
- Symbol: \( \displaystyle \bar{X} < \mu \)
- (The mean of the sample is less than than mean of the population.)
Example \(\PageIndex{1}\)
A study by Blackwell, Trzesniewski, and Dweck (2007) measured growth mindset and how long the junior high student participants spent on their math homework. What’s a directional hypothesis for how scoring higher on growth mindset (compared to the population of junior high students) would be related to how long students spent on their homework? Write this out in words and symbols.
Answer in Words: Students who scored high on growth mindset would spend more time on their homework than the population of junior high students.
Answer in Symbols: \( \displaystyle \bar{X} > \mu \)
Non-Directional Research Hypothesis
A non-directional hypothesis states that the means will be different, but does not specify which will be higher. In reality, there is rarely a situation in which we actually don't want one group to be higher than the other, so we will focus on directional research hypotheses. There is only one option for a non-directional research hypothesis: "The sample mean differs from the population mean." These types of research hypotheses don’t give a direction, the hypothesis doesn’t say which will be higher or lower.
A non-directional research hypothesis in symbols should look like this: \( \displaystyle \bar{X} \neq \mu \) (The mean of the sample is not equal to the mean of the population).
Exercise \(\PageIndex{1}\)
What’s a non-directional hypothesis for how scoring higher on growth mindset higher on growth mindset (compared to the population of junior high students) would be related to how long students spent on their homework (Blackwell, Trzesniewski, & Dweck, 2007)? Write this out in words and symbols.
Answer in Words: Students who scored high on growth mindset would spend a different amount of time on their homework than the population of junior high students.
Answer in Symbols: \( \displaystyle \bar{X} \neq \mu \)
See how a non-directional research hypothesis doesn't really make sense? The big issue is not if the two groups differ, but if one group seems to improve what was measured (if having a growth mindset leads to more time spent on math homework). This textbook will only use directional research hypotheses because researchers almost always have a predicted direction (meaning that we almost always know which group we think will score higher).
The Null Hypothesis
The hypothesis that an apparent effect is due to chance is called the null hypothesis, written \(H_0\) (“H-naught”). We usually test this through comparing an experimental group to a comparison (control) group. This null hypothesis can be written as:
\[\mathrm{H}_{0}: \bar{X} = \mu \nonumber \]
For most of this textbook, the null hypothesis is that the means of the two groups are similar. Much later, the null hypothesis will be that there is no relationship between the two groups. Either way, remember that a null hypothesis is always saying that nothing is different.
This is where descriptive statistics diverge from inferential statistics. We know what the value of \(\overline{\mathrm{X}}\) is – it’s not a mystery or a question, it is what we observed from the sample. What we are using inferential statistics to do is infer whether this sample's descriptive statistics probably represents the population's descriptive statistics. This is the null hypothesis, that the two groups are similar.
Keep in mind that the null hypothesis is typically the opposite of the research hypothesis. A research hypothesis for the ESP example is that those in my sample who say that they have ESP would get more correct answers than the population would get correct, while the null hypothesis is that the average number correct for the two groups will be similar.
In general, the null hypothesis is the idea that nothing is going on: there is no effect of our treatment, no relation between our variables, and no difference in our sample mean from what we expected about the population mean. This is always our baseline starting assumption, and it is what we seek to reject. If we are trying to treat depression, we want to find a difference in average symptoms between our treatment and control groups. If we are trying to predict job performance, we want to find a relation between conscientiousness and evaluation scores. However, until we have evidence against it, we must use the null hypothesis as our starting point.
In sum, the null hypothesis is always : There is no difference between the groups’ means OR There is no relationship between the variables .
In the next chapter, the null hypothesis is that there’s no difference between the sample mean and population mean. In other words:
- There is no mean difference between the sample and population.
- The mean of the sample is the same as the mean of a specific population.
- \(\mathrm{H}_{0}: \bar{X} = \mu \nonumber \)
- We expect our sample’s mean to be same as the population mean.
Exercise \(\PageIndex{2}\)
A study by Blackwell, Trzesniewski, and Dweck (2007) measured growth mindset and how long the junior high student participants spent on their math homework. What’s the null hypothesis for scoring higher on growth mindset (compared to the population of junior high students) and how long students spent on their homework? Write this out in words and symbols.
Answer in Words: Students who scored high on growth mindset would spend a similar amount of time on their homework as the population of junior high students.
Answer in Symbols: \( \bar{X} = \mu \)
Our websites may use cookies to personalize and enhance your experience. By continuing without changing your cookie settings, you agree to this collection. For more information, please see our University Websites Privacy Notice .
Neag School of Education
Educational Research Basics by Del Siegle
Null and alternative hypotheses.
Converting research questions to hypothesis is a simple task. Take the questions and make it a positive statement that says a relationship exists (correlation studies) or a difference exists between the groups (experiment study) and you have the alternative hypothesis. Write the statement such that a relationship does not exist or a difference does not exist and you have the null hypothesis. You can reverse the process if you have a hypothesis and wish to write a research question.
When you are comparing two groups, the groups are the independent variable. When you are testing whether something affects something else, the cause is the independent variable. The independent variable is the one you manipulate.
Teachers given higher pay will have more positive attitudes toward children than teachers given lower pay. The first step is to ask yourself “Are there two or more groups being compared?” The answer is “Yes.” What are the groups? Teachers who are given higher pay and teachers who are given lower pay. The independent variable is teacher pay. The dependent variable (the outcome) is attitude towards school.
You could also approach is another way. “Is something causing something else?” The answer is “Yes.” What is causing what? Teacher pay is causing attitude towards school. Therefore, teacher pay is the independent variable (cause) and attitude towards school is the dependent variable (outcome).
By tradition, we try to disprove (reject) the null hypothesis. We can never prove a null hypothesis, because it is impossible to prove something does not exist. We can disprove something does not exist by finding an example of it. Therefore, in research we try to disprove the null hypothesis. When we do find that a relationship (or difference) exists then we reject the null and accept the alternative. If we do not find that a relationship (or difference) exists, we fail to reject the null hypothesis (and go with it). We never say we accept the null hypothesis because it is never possible to prove something does not exist. That is why we say that we failed to reject the null hypothesis, rather than we accepted it.
Del Siegle, Ph.D. Neag School of Education – University of Connecticut [email protected] www.delsiegle.com

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons

Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

10.1: Null and Alternative Hypotheses
- Last updated
- Save as PDF
- Page ID 155545

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
\(H_0\): The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.
\(H_a\): The alternative hypothesis: It is a claim about the population that is contradictory to \(H_0\) and what we conclude when we reject \(H_0\). This is usually what the researcher is trying to prove.
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject \(H_0\)" if the sample information favors the alternative hypothesis or "do not reject \(H_0\)" or "decline to reject \(H_0\)" if the sample information is insufficient to reject the null hypothesis.
| equal (=) | not equal \((\neq)\) greater than (>) less than (<) |
| greater than or equal to \((\geq)\) | less than (<) |
| less than or equal to \((\geq)\) | more than (>) |
\(H_{0}\) always has a symbol with an equal in it. \(H_{a}\) never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
Example \(\PageIndex{1}\)
- \(H_{0}\): No more than 30% of the registered voters in Santa Clara County voted in the primary election. \(p \leq 30\)
- \(H_{a}\): More than 30% of the registered voters in Santa Clara County voted in the primary election. \(p > 30\)
Exercise \(\PageIndex{1}\)
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.
- \(H_{0}\): The drug reduces cholesterol by 25%. \(p = 0.25\)
- \(H_{a}\): The drug does not reduce cholesterol by 25%. \(p \neq 0.25\)
Example \(\PageIndex{2}\)
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:
- \(H_{0}: \mu = 2.0\)
- \(H_{a}: \mu \neq 2.0\)
Exercise \(\PageIndex{2}\)
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol \((=, \neq, \geq, <, \leq, >)\) for the null and alternative hypotheses.
- \(H_{0}: \mu \_ 66\)
- \(H_{a}: \mu \_ 66\)
- \(H_{0}: \mu = 66\)
- \(H_{a}: \mu \neq 66\)
Example \(\PageIndex{3}\)
We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:
- \(H_{0}: \mu \geq 5\)
- \(H_{a}: \mu < 5\)
Exercise \(\PageIndex{3}\)
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- \(H_{0}: \mu \_ 45\)
- \(H_{a}: \mu \_ 45\)
- \(H_{0}: \mu \geq 45\)
- \(H_{a}: \mu < 45\)
Example \(\PageIndex{4}\)
In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.
- \(H_{0}: p \leq 0.066\)
- \(H_{a}: p > 0.066\)
Exercise \(\PageIndex{4}\)
On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (\(=, \neq, \geq, <, \leq, >\)) for the null and alternative hypotheses.
- \(H_{0}: p \_ 0.40\)
- \(H_{a}: p \_ 0.40\)
- \(H_{0}: p = 0.40\)
- \(H_{a}: p > 0.40\)
COLLABORATIVE EXERCISE
Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.
In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we:
- Evaluate the null hypothesis , typically denoted with \(H_{0}\). The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality \((=, \leq \text{or} \geq)\)
- Always write the alternative hypothesis , typically denoted with \(H_{a}\) or \(H_{1}\), using less than, greater than, or not equals symbols, i.e., \((\neq, >, \text{or} <)\).
- If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis.
- Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.
Formula Review
\(H_{0}\) and \(H_{a}\) are contradictory.
| equal \((=)\) | greater than or equal to \((\geq)\) | less than or equal to \((\leq)\) | |
| has: | not equal \((\neq)\) greater than \((>)\) less than \((<)\) | less than \((<)\) | greater than \((>)\) |
- If \(\alpha \leq p\)-value, then do not reject \(H_{0}\).
- If\(\alpha > p\)-value, then reject \(H_{0}\).
\(\alpha\) is preconceived. Its value is set before the hypothesis test starts. The \(p\)-value is calculated from the data.References
Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm .
9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
H 0 : The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.
H a : The alternative hypothesis: It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 . This is usually what the researcher is trying to prove.
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject H 0 " if the sample information favors the alternative hypothesis or "do not reject H 0 " or "decline to reject H 0 " if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in H 0 and H a :
| equal (=) | not equal (≠) greater than (>) less than (<) |
| greater than or equal to (≥) | less than (<) |
| less than or equal to (≤) | more than (>) |
H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
Example 9.1
H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ .30 H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.
Example 9.2
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are: H 0 : μ = 2.0 H a : μ ≠ 2.0
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 66
- H a : μ __ 66
Example 9.3
We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are: H 0 : μ ≥ 5 H a : μ < 5
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 45
- H a : μ __ 45
Example 9.4
In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066
On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : p __ 0.40
- H a : p __ 0.40
Collaborative Exercise
Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/introductory-statistics-2e/pages/1-introduction
- Authors: Barbara Illowsky, Susan Dean
- Publisher/website: OpenStax
- Book title: Introductory Statistics 2e
- Publication date: Dec 13, 2023
- Location: Houston, Texas
- Book URL: https://openstax.org/books/introductory-statistics-2e/pages/1-introduction
- Section URL: https://openstax.org/books/introductory-statistics-2e/pages/9-1-null-and-alternative-hypotheses
© Dec 6, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
Alternative hypothesis
By Jim Frost
The alternative hypothesis is one of two mutually exclusive hypotheses in a hypothesis test. The alternative hypothesis states that a population parameter does not equal a specified value. Typically, this value is the null hypothesis value associated with no effect , such as zero. If your sample contains sufficient evidence, you can reject the null hypothesis and favor the alternative hypothesis. The alternative hypothesis is often denoted as H 1 or H A .
If you are performing a two-tailed hypothesis test, the alternative hypothesis states that the population parameter does not equal the null hypothesis value. For example, when the alternative hypothesis is H A : μ ≠ 0, the test can detect differences both greater than and less than the null value.
A one-tailed alternative hypothesis can test for a difference only in one direction. For example, H A : μ > 0 can only test for differences that are greater than zero.
- How Hypothesis Tests Work: Significance Levels (Alpha) and P values
- How to Identify the Distribution of Your Data
- When Can I Use One-Tailed Hypothesis Tests?
- Examples of Hypothesis Tests: Busting Myths about the Battle of the Sexes
- Failing to Reject the Null Hypothesis
- School Guide
- Mathematics
- Number System and Arithmetic
- Trigonometry
- Probability
- Mensuration
- Maths Formulas
- Integration Formulas
- Differentiation Formulas
- Trigonometry Formulas
- Algebra Formulas
- Mensuration Formula
- Statistics Formulas
- Trigonometric Table
Null Hypothesis
- Hypothesis Testing Formula
- SQLite IS NULL
- MySQL NOT NULL Constraint
- Real-life Applications of Hypothesis Testing
- Null in JavaScript
- SQL NOT NULL Constraint
- Null Cipher
- Hypothesis in Machine Learning
- Understanding Hypothesis Testing
- Difference between Null and Alternate Hypothesis
- Hypothesis Testing in R Programming
- SQL | NULL functions
- Kotlin Null Safety
- PHP | is_null() Function
- MySQL | NULLIF( ) Function
- Null-Coalescing Operator in C#
- Nullity of a Matrix
Null Hypothesis , often denoted as H 0, is a foundational concept in statistical hypothesis testing. It represents an assumption that no significant difference, effect, or relationship exists between variables within a population. It serves as a baseline assumption, positing no observed change or effect occurring. The null is t he truth or falsity of an idea in analysis.
In this article, we will discuss the null hypothesis in detail, along with some solved examples and questions on the null hypothesis.
Table of Content
What is Null Hypothesis?
Null hypothesis symbol, formula of null hypothesis, types of null hypothesis, null hypothesis examples, principle of null hypothesis, how do you find null hypothesis, null hypothesis in statistics, null hypothesis and alternative hypothesis, null hypothesis and alternative hypothesis examples, null hypothesis – practice problems.
Null Hypothesis in statistical analysis suggests the absence of statistical significance within a specific set of observed data. Hypothesis testing, using sample data, evaluates the validity of this hypothesis. Commonly denoted as H 0 or simply “null,” it plays an important role in quantitative analysis, examining theories related to markets, investment strategies, or economies to determine their validity.
Null Hypothesis Meaning
Null Hypothesis represents a default position, often suggesting no effect or difference, against which researchers compare their experimental results. The Null Hypothesis, often denoted as H 0 asserts a default assumption in statistical analysis. It posits no significant difference or effect, serving as a baseline for comparison in hypothesis testing.
The null Hypothesis is represented as H 0 , the Null Hypothesis symbolizes the absence of a measurable effect or difference in the variables under examination.
Certainly, a simple example would be asserting that the mean score of a group is equal to a specified value like stating that the average IQ of a population is 100.
The Null Hypothesis is typically formulated as a statement of equality or absence of a specific parameter in the population being studied. It provides a clear and testable prediction for comparison with the alternative hypothesis. The formulation of the Null Hypothesis typically follows a concise structure, stating the equality or absence of a specific parameter in the population.
Mean Comparison (Two-sample t-test)
H 0 : μ 1 = μ 2
This asserts that there is no significant difference between the means of two populations or groups.
Proportion Comparison
H 0 : p 1 − p 2 = 0
This suggests no significant difference in proportions between two populations or conditions.
Equality in Variance (F-test in ANOVA)
H 0 : σ 1 = σ 2
This states that there’s no significant difference in variances between groups or populations.
Independence (Chi-square Test of Independence):
H 0 : Variables are independent
This asserts that there’s no association or relationship between categorical variables.
Null Hypotheses vary including simple and composite forms, each tailored to the complexity of the research question. Understanding these types is pivotal for effective hypothesis testing.
Equality Null Hypothesis (Simple Null Hypothesis)
The Equality Null Hypothesis, also known as the Simple Null Hypothesis, is a fundamental concept in statistical hypothesis testing that assumes no difference, effect or relationship between groups, conditions or populations being compared.
Non-Inferiority Null Hypothesis
In some studies, the focus might be on demonstrating that a new treatment or method is not significantly worse than the standard or existing one.
Superiority Null Hypothesis
The concept of a superiority null hypothesis comes into play when a study aims to demonstrate that a new treatment, method, or intervention is significantly better than an existing or standard one.
Independence Null Hypothesis
In certain statistical tests, such as chi-square tests for independence, the null hypothesis assumes no association or independence between categorical variables.
Homogeneity Null Hypothesis
In tests like ANOVA (Analysis of Variance), the null hypothesis suggests that there’s no difference in population means across different groups.
- Medicine: Null Hypothesis: “No significant difference exists in blood pressure levels between patients given the experimental drug versus those given a placebo.”
- Education: Null Hypothesis: “There’s no significant variation in test scores between students using a new teaching method and those using traditional teaching.”
- Economics: Null Hypothesis: “There’s no significant change in consumer spending pre- and post-implementation of a new taxation policy.”
- Environmental Science: Null Hypothesis: “There’s no substantial difference in pollution levels before and after a water treatment plant’s establishment.”
The principle of the null hypothesis is a fundamental concept in statistical hypothesis testing. It involves making an assumption about the population parameter or the absence of an effect or relationship between variables.
In essence, the null hypothesis (H 0 ) proposes that there is no significant difference, effect, or relationship between variables. It serves as a starting point or a default assumption that there is no real change, no effect or no difference between groups or conditions.
The null hypothesis is usually formulated to be tested against an alternative hypothesis (H 1 or H [Tex]\alpha [/Tex] ) which suggests that there is an effect, difference or relationship present in the population.
Null Hypothesis Rejection
Rejecting the Null Hypothesis occurs when statistical evidence suggests a significant departure from the assumed baseline. It implies that there is enough evidence to support the alternative hypothesis, indicating a meaningful effect or difference. Null Hypothesis rejection occurs when statistical evidence suggests a deviation from the assumed baseline, prompting a reconsideration of the initial hypothesis.
Identifying the Null Hypothesis involves defining the status quotient, asserting no effect and formulating a statement suitable for statistical analysis.
When is Null Hypothesis Rejected?
The Null Hypothesis is rejected when statistical tests indicate a significant departure from the expected outcome, leading to the consideration of alternative hypotheses. It occurs when statistical evidence suggests a deviation from the assumed baseline, prompting a reconsideration of the initial hypothesis.
In statistical hypothesis testing, researchers begin by stating the null hypothesis, often based on theoretical considerations or previous research. The null hypothesis is then tested against an alternative hypothesis (Ha), which represents the researcher’s claim or the hypothesis they seek to support.
The process of hypothesis testing involves collecting sample data and using statistical methods to assess the likelihood of observing the data if the null hypothesis were true. This assessment is typically done by calculating a test statistic, which measures the difference between the observed data and what would be expected under the null hypothesis.
In the realm of hypothesis testing, the null hypothesis (H 0 ) and alternative hypothesis (H₁ or Ha) play critical roles. The null hypothesis generally assumes no difference, effect, or relationship between variables, suggesting that any observed change or effect is due to random chance. Its counterpart, the alternative hypothesis, asserts the presence of a significant difference, effect, or relationship between variables, challenging the null hypothesis. These hypotheses are formulated based on the research question and guide statistical analyses.
Difference Between Null Hypothesis and Alternative Hypothesis
The null hypothesis (H 0 ) serves as the baseline assumption in statistical testing, suggesting no significant effect, relationship, or difference within the data. It often proposes that any observed change or correlation is merely due to chance or random variation. Conversely, the alternative hypothesis (H 1 or Ha) contradicts the null hypothesis, positing the existence of a genuine effect, relationship or difference in the data. It represents the researcher’s intended focus, seeking to provide evidence against the null hypothesis and support for a specific outcome or theory. These hypotheses form the crux of hypothesis testing, guiding the assessment of data to draw conclusions about the population being studied.
Criteria | Null Hypothesis | Alternative Hypothesis |
|---|---|---|
Definition | Assumes no effect or difference | Asserts a specific effect or difference |
Symbol | H | H (or Ha) |
Formulation | States equality or absence of parameter | States a specific value or relationship |
Testing Outcome | Rejected if evidence of a significant effect | Accepted if evidence supports the hypothesis |
Let’s envision a scenario where a researcher aims to examine the impact of a new medication on reducing blood pressure among patients. In this context:
Null Hypothesis (H 0 ): “The new medication does not produce a significant effect in reducing blood pressure levels among patients.”
Alternative Hypothesis (H 1 or Ha): “The new medication yields a significant effect in reducing blood pressure levels among patients.”
The null hypothesis implies that any observed alterations in blood pressure subsequent to the medication’s administration are a result of random fluctuations rather than a consequence of the medication itself. Conversely, the alternative hypothesis contends that the medication does indeed generate a meaningful alteration in blood pressure levels, distinct from what might naturally occur or by random chance.
People Also Read:
Mathematics Maths Formulas Probability and Statistics
Example 1: A researcher claims that the average time students spend on homework is 2 hours per night.
Null Hypothesis (H 0 ): The average time students spend on homework is equal to 2 hours per night. Data: A random sample of 30 students has an average homework time of 1.8 hours with a standard deviation of 0.5 hours. Test Statistic and Decision: Using a t-test, if the calculated t-statistic falls within the acceptance region, we fail to reject the null hypothesis. If it falls in the rejection region, we reject the null hypothesis. Conclusion: Based on the statistical analysis, we fail to reject the null hypothesis, suggesting that there is not enough evidence to dispute the claim of the average homework time being 2 hours per night.
Example 2: A company asserts that the error rate in its production process is less than 1%.
Null Hypothesis (H 0 ): The error rate in the production process is 1% or higher. Data: A sample of 500 products shows an error rate of 0.8%. Test Statistic and Decision: Using a z-test, if the calculated z-statistic falls within the acceptance region, we fail to reject the null hypothesis. If it falls in the rejection region, we reject the null hypothesis. Conclusion: The statistical analysis supports rejecting the null hypothesis, indicating that there is enough evidence to dispute the company’s claim of an error rate of 1% or higher.
Q1. A researcher claims that the average time spent by students on homework is less than 2 hours per day. Formulate the null hypothesis for this claim?
Q2. A manufacturing company states that their new machine produces widgets with a defect rate of less than 5%. Write the null hypothesis to test this claim?
Q3. An educational institute believes that their online course completion rate is at least 60%. Develop the null hypothesis to validate this assertion?
Q4. A restaurant claims that the waiting time for customers during peak hours is not more than 15 minutes. Formulate the null hypothesis for this claim?
Q5. A study suggests that the mean weight loss after following a specific diet plan for a month is more than 8 pounds. Construct the null hypothesis to evaluate this statement?
Summary – Null Hypothesis and Alternative Hypothesis
The null hypothesis (H 0 ) and alternative hypothesis (H a ) are fundamental concepts in statistical hypothesis testing. The null hypothesis represents the default assumption, stating that there is no significant effect, difference, or relationship between variables. It serves as the baseline against which the alternative hypothesis is tested. In contrast, the alternative hypothesis represents the researcher’s hypothesis or the claim to be tested, suggesting that there is a significant effect, difference, or relationship between variables. The relationship between the null and alternative hypotheses is such that they are complementary, and statistical tests are conducted to determine whether the evidence from the data is strong enough to reject the null hypothesis in favor of the alternative hypothesis. This decision is based on the strength of the evidence and the chosen level of significance. Ultimately, the choice between the null and alternative hypotheses depends on the specific research question and the direction of the effect being investigated.
FAQs on Null Hypothesis
What does null hypothesis stands for.
The null hypothesis, denoted as H 0 , is a fundamental concept in statistics used for hypothesis testing. It represents the statement that there is no effect or no difference, and it is the hypothesis that the researcher typically aims to provide evidence against.
How to Form a Null Hypothesis?
A null hypothesis is formed based on the assumption that there is no significant difference or effect between the groups being compared or no association between variables being tested. It often involves stating that there is no relationship, no change, or no effect in the population being studied.
When Do we reject the Null Hypothesis?
In statistical hypothesis testing, if the p-value (the probability of obtaining the observed results) is lower than the chosen significance level (commonly 0.05), we reject the null hypothesis. This suggests that the data provides enough evidence to refute the assumption made in the null hypothesis.
What is a Null Hypothesis in Research?
In research, the null hypothesis represents the default assumption or position that there is no significant difference or effect. Researchers often try to test this hypothesis by collecting data and performing statistical analyses to see if the observed results contradict the assumption.
What Are Alternative and Null Hypotheses?
The null hypothesis (H0) is the default assumption that there is no significant difference or effect. The alternative hypothesis (H1 or Ha) is the opposite, suggesting there is a significant difference, effect or relationship.
What Does it Mean to Reject the Null Hypothesis?
Rejecting the null hypothesis implies that there is enough evidence in the data to support the alternative hypothesis. In simpler terms, it suggests that there might be a significant difference, effect or relationship between the groups or variables being studied.
How to Find Null Hypothesis?
Formulating a null hypothesis often involves considering the research question and assuming that no difference or effect exists. It should be a statement that can be tested through data collection and statistical analysis, typically stating no relationship or no change between variables or groups.
How is Null Hypothesis denoted?
The null hypothesis is commonly symbolized as H 0 in statistical notation.
What is the Purpose of the Null hypothesis in Statistical Analysis?
The null hypothesis serves as a starting point for hypothesis testing, enabling researchers to assess if there’s enough evidence to reject it in favor of an alternative hypothesis.
What happens if we Reject the Null hypothesis?
Rejecting the null hypothesis implies that there is sufficient evidence to support an alternative hypothesis, suggesting a significant effect or relationship between variables.
What are Test for Null Hypothesis?
Various statistical tests, such as t-tests or chi-square tests, are employed to evaluate the validity of the Null Hypothesis in different scenarios.
Please Login to comment...
Similar reads.
- Geeks Premier League 2023
- Math-Concepts
- Geeks Premier League
- School Learning
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
P-Value And Statistical Significance: What It Is & Why It Matters
Saul Mcleod, PhD
Editor-in-Chief for Simply Psychology
BSc (Hons) Psychology, MRes, PhD, University of Manchester
Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.
Learn about our Editorial Process
Olivia Guy-Evans, MSc
Associate Editor for Simply Psychology
BSc (Hons) Psychology, MSc Psychology of Education
Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.
On This Page:
The p-value in statistics quantifies the evidence against a null hypothesis. A low p-value suggests data is inconsistent with the null, potentially favoring an alternative hypothesis. Common significance thresholds are 0.05 or 0.01.
Hypothesis testing
When you perform a statistical test, a p-value helps you determine the significance of your results in relation to the null hypothesis.
The null hypothesis (H0) states no relationship exists between the two variables being studied (one variable does not affect the other). It states the results are due to chance and are not significant in supporting the idea being investigated. Thus, the null hypothesis assumes that whatever you try to prove did not happen.
The alternative hypothesis (Ha or H1) is the one you would believe if the null hypothesis is concluded to be untrue.
The alternative hypothesis states that the independent variable affected the dependent variable, and the results are significant in supporting the theory being investigated (i.e., the results are not due to random chance).
What a p-value tells you
A p-value, or probability value, is a number describing how likely it is that your data would have occurred by random chance (i.e., that the null hypothesis is true).
The level of statistical significance is often expressed as a p-value between 0 and 1.
The smaller the p -value, the less likely the results occurred by random chance, and the stronger the evidence that you should reject the null hypothesis.
Remember, a p-value doesn’t tell you if the null hypothesis is true or false. It just tells you how likely you’d see the data you observed (or more extreme data) if the null hypothesis was true. It’s a piece of evidence, not a definitive proof.
Example: Test Statistic and p-Value
Suppose you’re conducting a study to determine whether a new drug has an effect on pain relief compared to a placebo. If the new drug has no impact, your test statistic will be close to the one predicted by the null hypothesis (no difference between the drug and placebo groups), and the resulting p-value will be close to 1. It may not be precisely 1 because real-world variations may exist. Conversely, if the new drug indeed reduces pain significantly, your test statistic will diverge further from what’s expected under the null hypothesis, and the p-value will decrease. The p-value will never reach zero because there’s always a slim possibility, though highly improbable, that the observed results occurred by random chance.
P-value interpretation
The significance level (alpha) is a set probability threshold (often 0.05), while the p-value is the probability you calculate based on your study or analysis.
A p-value less than or equal to your significance level (typically ≤ 0.05) is statistically significant.
A p-value less than or equal to a predetermined significance level (often 0.05 or 0.01) indicates a statistically significant result, meaning the observed data provide strong evidence against the null hypothesis.
This suggests the effect under study likely represents a real relationship rather than just random chance.
For instance, if you set α = 0.05, you would reject the null hypothesis if your p -value ≤ 0.05.
It indicates strong evidence against the null hypothesis, as there is less than a 5% probability the null is correct (and the results are random).
Therefore, we reject the null hypothesis and accept the alternative hypothesis.
Example: Statistical Significance
Upon analyzing the pain relief effects of the new drug compared to the placebo, the computed p-value is less than 0.01, which falls well below the predetermined alpha value of 0.05. Consequently, you conclude that there is a statistically significant difference in pain relief between the new drug and the placebo.
What does a p-value of 0.001 mean?
A p-value of 0.001 is highly statistically significant beyond the commonly used 0.05 threshold. It indicates strong evidence of a real effect or difference, rather than just random variation.
Specifically, a p-value of 0.001 means there is only a 0.1% chance of obtaining a result at least as extreme as the one observed, assuming the null hypothesis is correct.
Such a small p-value provides strong evidence against the null hypothesis, leading to rejecting the null in favor of the alternative hypothesis.
A p-value more than the significance level (typically p > 0.05) is not statistically significant and indicates strong evidence for the null hypothesis.
This means we retain the null hypothesis and reject the alternative hypothesis. You should note that you cannot accept the null hypothesis; we can only reject it or fail to reject it.
Note : when the p-value is above your threshold of significance, it does not mean that there is a 95% probability that the alternative hypothesis is true.
One-Tailed Test

Two-Tailed Test
How do you calculate the p-value ?
Most statistical software packages like R, SPSS, and others automatically calculate your p-value. This is the easiest and most common way.
Online resources and tables are available to estimate the p-value based on your test statistic and degrees of freedom.
These tables help you understand how often you would expect to see your test statistic under the null hypothesis.
Understanding the Statistical Test:
Different statistical tests are designed to answer specific research questions or hypotheses. Each test has its own underlying assumptions and characteristics.
For example, you might use a t-test to compare means, a chi-squared test for categorical data, or a correlation test to measure the strength of a relationship between variables.
Be aware that the number of independent variables you include in your analysis can influence the magnitude of the test statistic needed to produce the same p-value.
This factor is particularly important to consider when comparing results across different analyses.
Example: Choosing a Statistical Test
If you’re comparing the effectiveness of just two different drugs in pain relief, a two-sample t-test is a suitable choice for comparing these two groups. However, when you’re examining the impact of three or more drugs, it’s more appropriate to employ an Analysis of Variance ( ANOVA) . Utilizing multiple pairwise comparisons in such cases can lead to artificially low p-values and an overestimation of the significance of differences between the drug groups.
How to report
A statistically significant result cannot prove that a research hypothesis is correct (which implies 100% certainty).
Instead, we may state our results “provide support for” or “give evidence for” our research hypothesis (as there is still a slight probability that the results occurred by chance and the null hypothesis was correct – e.g., less than 5%).
Example: Reporting the results
In our comparison of the pain relief effects of the new drug and the placebo, we observed that participants in the drug group experienced a significant reduction in pain ( M = 3.5; SD = 0.8) compared to those in the placebo group ( M = 5.2; SD = 0.7), resulting in an average difference of 1.7 points on the pain scale (t(98) = -9.36; p < 0.001).
The 6th edition of the APA style manual (American Psychological Association, 2010) states the following on the topic of reporting p-values:
“When reporting p values, report exact p values (e.g., p = .031) to two or three decimal places. However, report p values less than .001 as p < .001.
The tradition of reporting p values in the form p < .10, p < .05, p < .01, and so forth, was appropriate in a time when only limited tables of critical values were available.” (p. 114)
- Do not use 0 before the decimal point for the statistical value p as it cannot equal 1. In other words, write p = .001 instead of p = 0.001.
- Please pay attention to issues of italics ( p is always italicized) and spacing (either side of the = sign).
- p = .000 (as outputted by some statistical packages such as SPSS) is impossible and should be written as p < .001.
- The opposite of significant is “nonsignificant,” not “insignificant.”
Why is the p -value not enough?
A lower p-value is sometimes interpreted as meaning there is a stronger relationship between two variables.
However, statistical significance means that it is unlikely that the null hypothesis is true (less than 5%).
To understand the strength of the difference between the two groups (control vs. experimental) a researcher needs to calculate the effect size .
When do you reject the null hypothesis?
In statistical hypothesis testing, you reject the null hypothesis when the p-value is less than or equal to the significance level (α) you set before conducting your test. The significance level is the probability of rejecting the null hypothesis when it is true. Commonly used significance levels are 0.01, 0.05, and 0.10.
Remember, rejecting the null hypothesis doesn’t prove the alternative hypothesis; it just suggests that the alternative hypothesis may be plausible given the observed data.
The p -value is conditional upon the null hypothesis being true but is unrelated to the truth or falsity of the alternative hypothesis.
What does p-value of 0.05 mean?
If your p-value is less than or equal to 0.05 (the significance level), you would conclude that your result is statistically significant. This means the evidence is strong enough to reject the null hypothesis in favor of the alternative hypothesis.
Are all p-values below 0.05 considered statistically significant?
No, not all p-values below 0.05 are considered statistically significant. The threshold of 0.05 is commonly used, but it’s just a convention. Statistical significance depends on factors like the study design, sample size, and the magnitude of the observed effect.
A p-value below 0.05 means there is evidence against the null hypothesis, suggesting a real effect. However, it’s essential to consider the context and other factors when interpreting results.
Researchers also look at effect size and confidence intervals to determine the practical significance and reliability of findings.
How does sample size affect the interpretation of p-values?
Sample size can impact the interpretation of p-values. A larger sample size provides more reliable and precise estimates of the population, leading to narrower confidence intervals.
With a larger sample, even small differences between groups or effects can become statistically significant, yielding lower p-values. In contrast, smaller sample sizes may not have enough statistical power to detect smaller effects, resulting in higher p-values.
Therefore, a larger sample size increases the chances of finding statistically significant results when there is a genuine effect, making the findings more trustworthy and robust.
Can a non-significant p-value indicate that there is no effect or difference in the data?
No, a non-significant p-value does not necessarily indicate that there is no effect or difference in the data. It means that the observed data do not provide strong enough evidence to reject the null hypothesis.
There could still be a real effect or difference, but it might be smaller or more variable than the study was able to detect.
Other factors like sample size, study design, and measurement precision can influence the p-value. It’s important to consider the entire body of evidence and not rely solely on p-values when interpreting research findings.
Can P values be exactly zero?
While a p-value can be extremely small, it cannot technically be absolute zero. When a p-value is reported as p = 0.000, the actual p-value is too small for the software to display. This is often interpreted as strong evidence against the null hypothesis. For p values less than 0.001, report as p < .001
Further Information
- P-values and significance tests (Kahn Academy)
- Hypothesis testing and p-values (Kahn Academy)
- Wasserstein, R. L., Schirm, A. L., & Lazar, N. A. (2019). Moving to a world beyond “ p “< 0.05”.
- Criticism of using the “ p “< 0.05”.
- Publication manual of the American Psychological Association
- Statistics for Psychology Book Download
Bland, J. M., & Altman, D. G. (1994). One and two sided tests of significance: Authors’ reply. BMJ: British Medical Journal , 309 (6958), 874.
Goodman, S. N., & Royall, R. (1988). Evidence and scientific research. American Journal of Public Health , 78 (12), 1568-1574.
Goodman, S. (2008, July). A dirty dozen: twelve p-value misconceptions . In Seminars in hematology (Vol. 45, No. 3, pp. 135-140). WB Saunders.
Lang, J. M., Rothman, K. J., & Cann, C. I. (1998). That confounded P-value. Epidemiology (Cambridge, Mass.) , 9 (1), 7-8.
Related Articles

Exploratory Data Analysis

Research Methodology , Statistics
What Is Face Validity In Research? Importance & How To Measure

Criterion Validity: Definition & Examples
Convergent Validity: Definition and Examples

Content Validity in Research: Definition & Examples

Construct Validity In Psychology Research

IMAGES
VIDEO
COMMENTS
The null hypothesis (H 0) answers "No, there's no effect in the population." The alternative hypothesis (H a) answers "Yes, there is an effect in the population." The null and alternative are always claims about the population. That's because the goal of hypothesis testing is to make inferences about a population based on a sample.
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test: Null hypothesis (H0): There's no effect in the population. Alternative hypothesis (HA): There's an effect in the population. The effect is usually the effect of the independent variable on the dependent ...
It is the opposite of your research hypothesis. The alternative hypothesis--that is, the research hypothesis--is the idea, phenomenon, observation that you want to prove. If you suspect that girls take longer to get ready for school than boys, then: Alternative: girls time > boys time. Null: girls time <= boys time.
Alternative Hypothesis H A: The correlation in the population is not zero: ρ ≠ 0. For all these cases, the analysts define the hypotheses before the study. After collecting the data, they perform a hypothesis test to determine whether they can reject the null hypothesis. The preceding examples are all for two-tailed hypothesis tests.
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0, the —null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
Review. In a hypothesis test, sample data is evaluated in order to arrive at a decision about some type of claim.If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis, typically denoted with \(H_{0}\).The null is not rejected unless the hypothesis test shows otherwise.
Alternative hypothesis " x is not equal to y .". Null hypothesis: " x is at least y .". Alternative hypothesis " x is less than y .". Null hypothesis: " x is at most y .". Alternative hypothesis " x is greater than y .". Here are the differences between the null and alternative hypotheses and how to distinguish between them.
H0: The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt. Ha: The alternative hypothesis: It is a claim about the population that is contradictory to H0 and what we conclude when we reject H0. Since the ...
The Null and Alternative Hypotheses. There are two hypotheses that are made: the null hypothesis, denoted H 0, and the alternative hypothesis, denoted H 1 or H A. The null hypothesis is the one to be tested and the alternative is everything else. In our example: The null hypothesis would be: The mean data scientist salary is 113,000 dollars.
H0: The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt. Ha: The alternative hypothesis: It is a claim about the population that is.
Examples: Null Hypothesis: H 0: There is no difference in the salary of factory workers based on gender. Alternative Hypothesis: H a: Male factory workers have a higher salary than female factory workers. Null Hypothesis: H 0: There is no relationship between height and shoe size. Alternative Hypothesis: H a: There is a positive relationship ...
10.1 - Setting the Hypotheses: Examples. A significance test examines whether the null hypothesis provides a plausible explanation of the data. The null hypothesis itself does not involve the data. It is a statement about a parameter (a numerical characteristic of the population). These population values might be proportions or means or ...
Whenever we perform a hypothesis test, we always write a null hypothesis and an alternative hypothesis, which take the following forms: H0 (Null Hypothesis): Population parameter =, ≤, ≥ some value. HA (Alternative Hypothesis): Population parameter <, >, ≠ some value. Note that the null hypothesis always contains the equal sign.
The alternative hypothesis ( Ha H a) is a claim about the population that is contradictory to H0 H 0 and what we conclude when we reject H0 H 0. Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample ...
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0: The null hypothesis: It is a statement of no difference between the variables-they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.
Step 1: Figure out the hypothesis from the problem. The hypothesis is usually hidden in a word problem, and is sometimes a statement of what you expect to happen in the experiment. The hypothesis in the above question is "I expect the average recovery period to be greater than 8.2 weeks.". Step 2: Convert the hypothesis to math.
The null hypothesis is a claim that a population parameter equals some value. For example, H 0: μ = 5 H 0: μ = 5. The alternative hypothesis is denoted H a H a. It is a claim about the population that is contradictory to the null hypothesis and is what we conclude is true when we reject H 0 H 0. The alternative hypothesis is a claim that a ...
Null hypothesis: µ ≥ 70 inches. Alternative hypothesis: µ < 70 inches. A two-tailed hypothesis involves making an "equal to" or "not equal to" statement. For example, suppose we assume the mean height of a male in the U.S. is equal to 70 inches. The null and alternative hypotheses in this case would be: Null hypothesis: µ = 70 inches.
For example, if one data set has higher variability while another has lower variability, the first data set will produce a test statistic closer to the null hypothesis, even if the true correlation between two variables is the same in either data set.
This null hypothesis can be written as: H0: X¯ = μ H 0: X ¯ = μ. For most of this textbook, the null hypothesis is that the means of the two groups are similar. Much later, the null hypothesis will be that there is no relationship between the two groups. Either way, remember that a null hypothesis is always saying that nothing is different.
If we do not find that a relationship (or difference) exists, we fail to reject the null hypothesis (and go with it). We never say we accept the null hypothesis because it is never possible to prove something does not exist. That is why we say that we failed to reject the null hypothesis, rather than we accepted it. Del Siegle, Ph.D.
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. \(H_0\): The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.
An alternative hypothesis (H1 or Ha) in a statistical inference experiment directly contradicts the null hypothesis and states that there is a relationship between two variables. While the null hypothesis presumes no change or status quo, an alternative hypothesis or the claim shows that a non-random cause influences the observations.
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0: The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.
The alternative hypothesis is often denoted as H 1 or H A. If you are performing a two-tailed hypothesis test, the alternative hypothesis states that the population parameter does not equal the null hypothesis value. For example, when the alternative hypothesis is H A: μ ≠ 0, the test can detect differences both greater than and less than ...
Null hypothesis, often denoted as H0, is a foundational concept in statistical hypothesis testing. It represents an assumption that no significant difference, effect, or relationship exists between variables within a population. Learn more about Null Hypothesis, its formula, symbol and example in this article
The alternative hypothesis (Ha or H1) is the one you would believe if the null hypothesis is concluded to be untrue. The alternative hypothesis states that the independent variable affected the dependent variable, and the results are significant in supporting the theory being investigated (i.e., the results are not due to random chance).