problem solving involving the normal curve concepts

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

6.2: Applications of the Normal Distribution

• Last updated
• Save as PDF
• Page ID 10948

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

The shaded area in the following graph indicates the area to the left of \(x\). This area is represented by the probability \(P(X < x)\). Normal tables, computers, and calculators provide or calculate the probability \(P(X < x)\).

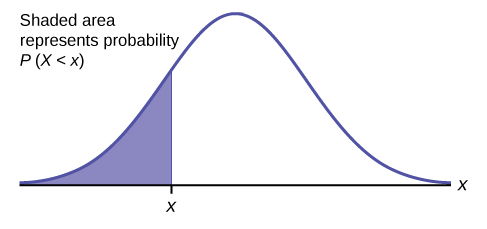
The area to the right is then \(P(X > x) = 1 – P(X < x)\). Remember, \(P(X < x) =\) Area to the left of the vertical line through \(x\). \(P(X > x) = 1 – P(X < x) =\) Area to the right of the vertical line through \(x\). \(P(X < x)\) is the same as \(P(X \leq x)\) and \(P(X > x)\) is the same as \(P(X \geq x)\) for continuous distributions.

Calculations of Probabilities

Probabilities are calculated using technology. There are instructions given as necessary for the TI-83+ and TI-84 calculators.To calculate the probability, use the probability tables provided in [link] without the use of technology. The tables include instructions for how to use them.

Example \(\PageIndex{1}\)

If the area to the left is 0.0228, then the area to the right is \(1 - 0.0228 = 0.9772\).

Exercise \(\PageIndex{1}\)

If the area to the left of \(x\) is \(0.012\), then what is the area to the right?

\(1 - 0.012 = 0.988\)

Example \(\PageIndex{2}\)

The final exam scores in a statistics class were normally distributed with a mean of 63 and a standard deviation of five.

• Find the probability that a randomly selected student scored more than 65 on the exam.
• Find the probability that a randomly selected student scored less than 85.
• Find the 90 th percentile (that is, find the score \(k\) that has 90% of the scores below k and 10% of the scores above \(k\)).
• Find the 70 th percentile (that is, find the score \(k\) such that 70% of scores are below \(k\) and 30% of the scores are above \(k\)).

a. Let \(X\) = a score on the final exam. \(X \sim N(63, 5)\), where \(\mu = 63\) and \(\sigma = 5\)

Draw a graph.

Then, find \(P(x > 65)\).

\[P(x > 65) = 0.3446\nonumber \]

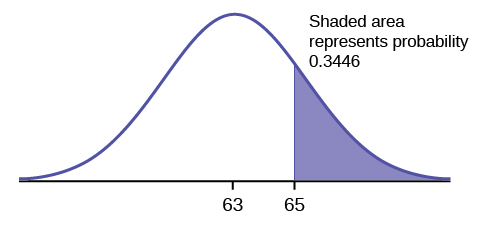
The probability that any student selected at random scores more than 65 is 0.3446.

USING THE TI-83, 83+, 84, 84+ CALCULATOR

Go into 2nd DISTR .

After pressing 2nd DISTR , press 2:normalcdf .

The syntax for the instructions are as follows:

normalcdf(lower value, upper value, mean, standard deviation) For this problem: normalcdf(65,1E99,63,5) = 0.3446. You get 1E99 (= 10 99 ) by pressing 1 , the EE key (a 2nd key) and then 99 . Or, you can enter 10^ 99 instead. The number 10 99 is way out in the right tail of the normal curve. We are calculating the area between 65 and 10 99 . In some instances, the lower number of the area might be –1E99 (= –10 99 ). The number –10 99 is way out in the left tail of the normal curve.

Historical Note

The TI probability program calculates a \(z\)-score and then the probability from the \(z\)-score. Before technology, the \(z\)-score was looked up in a standard normal probability table (because the math involved is too cumbersome) to find the probability. In this example, a standard normal table with area to the left of the \(z\)-score was used. You calculate the \(z\)-score and look up the area to the left. The probability is the area to the right.

\[z = 65 – 63565 – 635 = 0.4\nonumber \]

Area to the left is 0.6554.

\[P(x > 65) = P(z > 0.4) = 1 – 0.6554 = 0.3446\nonumber \]

Find the percentile for a student scoring 65:

*Press 2nd Distr *Press 2:normalcdf ( *Enter lower bound, upper bound, mean, standard deviation followed by ) *Press ENTER . For this Example, the steps are 2nd Distr 2:normalcdf (65,1,2nd EE,99,63,5) ENTER The probability that a selected student scored more than 65 is 0.3446. To find the probability that a selected student scored more than 65, subtract the percentile from 1.

b. Draw a graph.

Then find \(P(x < 85)\), and shade the graph.

Using a computer or calculator, find \(P(x < 85) = 1\).

\(\text{normalcdf}(0,85,63,5) = 1\) (rounds to one)

The probability that one student scores less than 85 is approximately one (or 100%).

c. Find the 90 th percentile. For each problem or part of a problem, draw a new graph. Draw the \(x\)-axis. Shade the area that corresponds to the 90 th percentile.

Let \(k =\) the 90 th percentile. The variable \(k\) is located on the \(x\)-axis. \(P(x < k)\) is the area to the left of \(k\). The 90 th percentile \(k\) separates the exam scores into those that are the same or lower than \(k\) and those that are the same or higher. Ninety percent of the test scores are the same or lower than \(k\), and ten percent are the same or higher. The variable \(k\) is often called a critical value.

\(k = 69.4\)

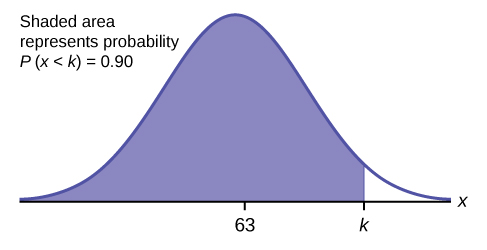
The 90 th percentile is 69.4. This means that 90% of the test scores fall at or below 69.4 and 10% fall at or above. To get this answer on the calculator, follow this step:

invNorm in 2nd DISTR . invNorm(area to the left, mean, standard deviation)

For this problem, \(\text{invNorm}(0.90,63,5) = 69.4\)

d. Find the 70 th percentile.

Draw a new graph and label it appropriately. \(k = 65.6\)

The 70 th percentile is 65.6. This means that 70% of the test scores fall at or below 65.6 and 30% fall at or above.

\(\text{invNorm}(0.70,63,5) = 65.6\)

Exercise \(\PageIndex{2}\)

The golf scores for a school team were normally distributed with a mean of 68 and a standard deviation of three. Find the probability that a randomly selected golfer scored less than 65.

\(\text{normalcdf}(10^{99},65,68,3) = 0.1587\)

Example \(\PageIndex{3}\)

A personal computer is used for office work at home, research, communication, personal finances, education, entertainment, social networking, and a myriad of other things. Suppose that the average number of hours a household personal computer is used for entertainment is two hours per day. Assume the times for entertainment are normally distributed and the standard deviation for the times is half an hour.

• Find the probability that a household personal computer is used for entertainment between 1.8 and 2.75 hours per day.
• Find the maximum number of hours per day that the bottom quartile of households uses a personal computer for entertainment.

a. Let \(X =\) the amount of time (in hours) a household personal computer is used for entertainment. \(X \sim N(2, 0.5)\) where \(\mu = 2\) and \(\sigma = 0.5\).

Find \(P(1.8 < x < 2.75)\).

The probability for which you are looking is the area between \(x = 1.8\) and \(x = 2.75\). \(P(1.8 < x < 2.75) = 0.5886\)

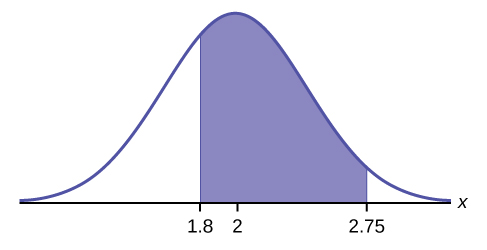
\[\text{normalcdf}(1.8,2.75,2,0.5) = 0.5886\nonumber \]

The probability that a household personal computer is used between 1.8 and 2.75 hours per day for entertainment is 0.5886.

To find the maximum number of hours per day that the bottom quartile of households uses a personal computer for entertainment, find the 25 th percentile, \(k\), where \(P(x < k) = 0.25\).

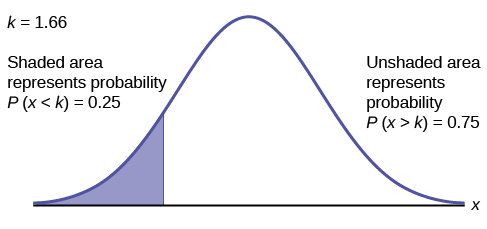
\[\text{invNorm}(0.25,2,0.5) = 1.66\nonumber \]

The maximum number of hours per day that the bottom quartile of households uses a personal computer for entertainment is 1.66 hours.

Exercise \(\PageIndex{3}\)

The golf scores for a school team were normally distributed with a mean of 68 and a standard deviation of three. Find the probability that a golfer scored between 66 and 70.

\(\text{normalcdf}(66,70,68,3) = 0.4950\)

Example \(\PageIndex{4}\)

There are approximately one billion smartphone users in the world today. In the United States the ages 13 to 55+ of smartphone users approximately follow a normal distribution with approximate mean and standard deviation of 36.9 years and 13.9 years, respectively.

• Determine the probability that a random smartphone user in the age range 13 to 55+ is between 23 and 64.7 years old.
• Determine the probability that a randomly selected smartphone user in the age range 13 to 55+ is at most 50.8 years old.
• Find the 80 th percentile of this distribution, and interpret it in a complete sentence.
• \(\text{normalcdf}(23,64.7,36.9,13.9) = 0.8186\)
• \(\text{normalcdf}(-10^{99},50.8,36.9,13.9) = 0.8413\)
• \(\text{invNorm}(0.80,36.9,13.9) = 48.6\)

The 80 th percentile is 48.6 years.

80% of the smartphone users in the age range 13 – 55+ are 48.6 years old or less.

Use the information in Example to answer the following questions.

Exercise \(\PageIndex{4}\)

• Find the 30 th percentile, and interpret it in a complete sentence.
• What is the probability that the age of a randomly selected smartphone user in the range 13 to 55+ is less than 27 years old and at least 0 years old?

Let \(X =\) a smart phone user whose age is 13 to 55+. \(X \sim N(36.9, 13.9)\)

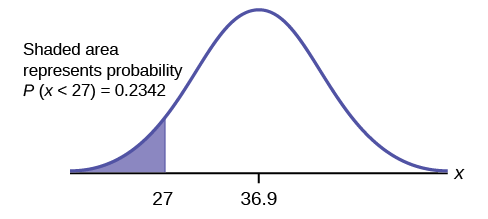
\[\text{normalcdf}(0,27,36.9,13.9) = 0.2342\nonumber \]

Example \(\PageIndex{5}\)

In the United States the ages 13 to 55+ of smartphone users approximately follow a normal distribution with approximate mean and standard deviation of 36.9 years and 13.9 years respectively. Using this information, answer the following questions (round answers to one decimal place).

• Calculate the interquartile range (\(IQR\)).
• Forty percent of the ages that range from 13 to 55+ are at least what age?

\[IQR = Q_{3} – Q_{1}\nonumber \]

Calculate \(Q_{3} =\) 75 th percentile and \(Q_{1} =\) 25 th percentile.

\[ \begin{align*} \text{invNorm}(0.75,36.9,13.9) &= Q_{3} = 46.2754 \\[4pt] \text{invNorm}(0.25,36.9,13.9) &= Q_{1} = 27.5246 \\[4pt] IQR &= Q_{3} - Q_{1} = 18.7508 \end{align*}\]

Find \(k\) where \(P(x > k) = 0.40\) ("At least" translates to "greater than or equal to.")

\(0.40 =\) the area to the right.

Area to the left \(= 1 – 0.40 = 0.60\).

The area to the left of \(k = 0.60\).

\(\text{invNorm}(0.60,36.9,13.9) = 40.4215\).

\(k = 40.42\).

Forty percent of the smartphone users from 13 to 55+ are at least 40.4 years.

Exercise \(\PageIndex{5}\)

Two thousand students took an exam. The scores on the exam have an approximate normal distribution with a mean \(\mu = 81\) points and standard deviation \(\sigma = 15\) points.

• Calculate the first- and third-quartile scores for this exam.
• The middle 50% of the exam scores are between what two values?
• \(Q_{1} =\) 25 th percentile \(= \text{invNorm}(0.25,81,15) = 70.9\) \(Q_{3} =\) 75 th percentile \(= \text{invNorm}(0.75,81,15) = 91.1\)
• The middle 50% of the scores are between 70.9 and 91.1.

Example \(\PageIndex{6}\)

A citrus farmer who grows mandarin oranges finds that the diameters of mandarin oranges harvested on his farm follow a normal distribution with a mean diameter of 5.85 cm and a standard deviation of 0.24 cm.

• Find the probability that a randomly selected mandarin orange from this farm has a diameter larger than 6.0 cm. Sketch the graph.
• The middle 20% of mandarin oranges from this farm have diameters between ______ and ______.
• Find the 90 th percentile for the diameters of mandarin oranges, and interpret it in a complete sentence.

a. \(\text{normalcdf}(6,10^{99},5.85,0.24) = 0.2660\)

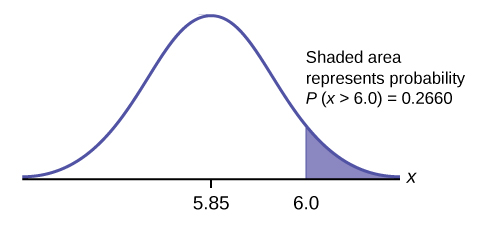
\(1 – 0.20 = 0.80\)

The tails of the graph of the normal distribution each have an area of 0.40.

Find \(k1\), the 40 th percentile, and \(k2\), the 60 th percentile (\(0.40 + 0.20 = 0.60\)).

\(k1 = \text{invNorm}(0.40,5.85,0.24) = 5.79\) cm

\(k2 = \text{invNorm}(0.60,5.85,0.24) = 5.91\) cm

c. 6.16: Ninety percent of the diameter of the mandarin oranges is at most 6.15 cm.

Exercise \(\PageIndex{6}\)

Using the information from Example, answer the following:

• The middle 45% of mandarin oranges from this farm are between ______ and ______.
• Find the 16 th percentile and interpret it in a complete sentence.

The middle area \(= 0.40\), so each tail has an area of 0.30.

\( – 0.40 = 0.60\)

The tails of the graph of the normal distribution each have an area of 0.30.

Find \(k1\), the 30 th percentile and \(k2\), the 70 th percentile (\(0.40 + 0.30 = 0.70\)).

\(k1 = \text{invNorm}(0.30,5.85,0.24) = 5.72\) cm

\(k2 = \text{invNorm}(0.70,5.85,0.24) = 5.98\) cm

\(\text{normalcdf}(5,10^{99},5.85,0.24) = 0.9998\)

• “Naegele’s rule.” Wikipedia. Available online at http://en.Wikipedia.org/wiki/Naegele's_rule (accessed May 14, 2013).
• “403: NUMMI.” Chicago Public Media & Ira Glass, 2013. Available online at www.thisamericanlife.org/radi...sode/403/nummi (accessed May 14, 2013).
• “Scratch-Off Lottery Ticket Playing Tips.” WinAtTheLottery.com, 2013. Available online at www.winatthelottery.com/publi...partment40.cfm (accessed May 14, 2013).
• “Smart Phone Users, By The Numbers.” Visual.ly, 2013. Available online at http://visual.ly/smart-phone-users-numbers (accessed May 14, 2013).
• “Facebook Statistics.” Statistics Brain. Available online at http://www.statisticbrain.com/facebo...tics/(accessed May 14, 2013).

The normal distribution, which is continuous, is the most important of all the probability distributions. Its graph is bell-shaped. This bell-shaped curve is used in almost all disciplines. Since it is a continuous distribution, the total area under the curve is one. The parameters of the normal are the mean \(\mu\) and the standard deviation σ . A special normal distribution, called the standard normal distribution is the distribution of z -scores. Its mean is zero, and its standard deviation is one.

Formula Review

• Normal Distribution: \(X \sim N(\mu, \sigma)\) where \(\mu\) is the mean and σ is the standard deviation.
• Standard Normal Distribution: \(Z \sim N(0, 1)\).
• Calculator function for probability: normalcdf (lower \(x\) value of the area, upper \(x\) value of the area, mean, standard deviation)
• Calculator function for the \(k\) th percentile: \(k = \text{invNorm}\) (area to the left of \(k\), mean, standard deviation)

Exercise \(\PageIndex{7}\)

How would you represent the area to the left of one in a probability statement?

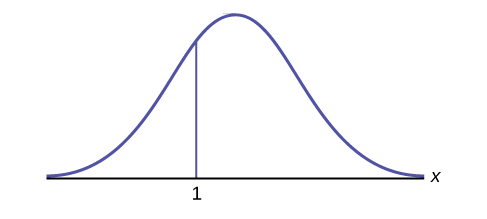
\(P(x < 1)\)

Exercise \(\PageIndex{8}\)

Is \(P(x < 1)\) equal to \(P(x \leq 1)\)? Why?

Yes, because they are the same in a continuous distribution: \(P(x = 1) = 0\)

Exercise \(\PageIndex{9}\)

How would you represent the area to the left of three in a probability statement?

Exercise \(\PageIndex{10}\)

What is the area to the right of three?

\(1 – P(x < 3)\) or \(P(x > 3)\)

Exercise \(\PageIndex{11}\)

If the area to the left of \(x\) in a normal distribution is 0.123, what is the area to the right of \(x\)?

Exercise \(\PageIndex{12}\)

If the area to the right of \(x\) in a normal distribution is 0.543, what is the area to the left of \(x\)?

\(1 - 0.543 = 0.457\)

Use the following information to answer the next four exercises:

\(X \sim N(54, 8)\)

Exercise \(\PageIndex{13}\)

Find the probability that \(x > 56\).

Exercise \(\PageIndex{14}\)

Find the probability that \(x < 30\).

Exercise \(\PageIndex{15}\)

Find the 80 th percentile.

Exercise \(\PageIndex{16}\)

Find the 60 th percentile.

Exercise \(\PageIndex{17}\)

\(X \sim N(6, 2)\)

Find the probability that \(x\) is between three and nine.

Exercise \(\PageIndex{18}\)

\(X \sim N(–3, 4)\)

Find the probability that \(x\) is between one and four.

Exercise \(\PageIndex{19}\)

\(X \sim N(4, 5)\)

Find the maximum of \(x\) in the bottom quartile.

Exercise \(\PageIndex{20}\)

Use the following information to answer the next three exercise: The life of Sunshine CD players is normally distributed with a mean of 4.1 years and a standard deviation of 1.3 years. A CD player is guaranteed for three years. We are interested in the length of time a CD player lasts. Find the probability that a CD player will break down during the guarantee period.

Figure \(\PageIndex{12}\).

• Check student’s solution.

Exercise \(\PageIndex{21}\)

Find the probability that a CD player will last between 2.8 and six years.

Figure \(\PageIndex{13}\).

Exercise \(\PageIndex{22}\)

Find the 70 th percentile of the distribution for the time a CD player lasts.

Figure \(\PageIndex{14}\).

• 0.70, 4.78 years

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

11.3: Application of Normal Distributions

• Last updated
• Save as PDF
• Page ID 59991

• Darlene Diaz
• Santiago Canyon College via ASCCC Open Educational Resources Initiative

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Apply the characteristics of a normal distribution to solving applications.

Introduction

The normal distribution is the foundation for statistical inference and will be an essential part of many of those topics in later chapters. In the meantime, this section will cover some of the types of questions that can be answered using the properties of a normal distribution. The first examples deal with more theoretical questions that will help you master basic understandings and computational skills, while the later problems will provide examples with real data, or at least a real context.

Normal Distributions with Real Data

The foundation of performing experiments by collecting surveys and samples is most often based on the normal distribution, as you will learn in greater detail in later chapters. Here are two examples to get you started.

Example \(\PageIndex{1}\)

The Information Centre of the National Health Service in Britain collects and publishes a great deal of information and statistics on health issues affecting the population. One such comprehensive data set tracks information about the health of children [1]. According to its statistics, in 2006, the mean height of 12-year-old boys was 152.9 cm, with a standard deviation estimate of approximately 8.5 cm. (These are not the exact figures for the population, and in later chapters, we will learn how they are calculated and how accurate they may be, but for now, we will assume that they are a reasonable estimate of the true parameters.) If 12-year-old Cecil is 158 cm, approximately what percentage of all 12-year-old boys in Britain is he taller than?

We first must assume that the height of 12-year-old boys in Britain is normally distributed, and this seems like a reasonable assumption to make. As always, draw a sketch and estimate a reasonable answer prior to calculating the percentage. In this case, let’s use the calculator to sketch the distribution and the shading. First, decide on an appropriate window that includes about 3 standard deviations on either side of the mean. In this case, 3 standard deviations is about 25.5 cm, so add and subtract this value to/from the mean to find the horizontal extremes. Then enter the appropriate ‘ShadeNorm(’ command as shown:

From this data, we would estimate that Cecil is taller than about 73% of 12-year-old boys. We could also phrase our assumption this way: the probability of a randomly selected British 12- year-old boy being shorter than Cecil is about 0.73. Often with data like this, we use percentiles. We would say that Cecil is in the 73 rd percentile for height among 12-year-old boys in Britain.

How tall would Cecil need to be in order to be in the top 1% of all 12-year-old boys in Britain?

Here is a sketch:

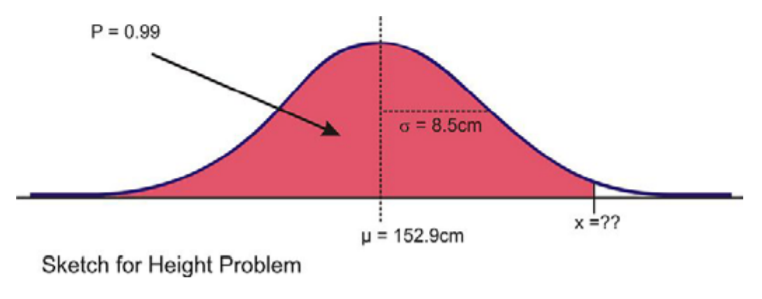
In this case, we are given the percentage, so we need to use the ‘invNorm(’ command as shown.

Our results indicate that Cecil would need to be about 173 cm tall to be in the top 1% of 12-year-old boys in Britain.

Example \(\PageIndex{2}\)

Suppose that the distribution of the masses of female marine iguanas in Puerto Villamil in the Galapagos Islands is approximately normal, with a mean mass of 950 g and a standard deviation of 325 g. There are very few young marine iguanas in the populated areas of the islands, because feral cats tend to kill them. How rare is it that we would find a female marine iguana with a mass less than 400 g in this area?

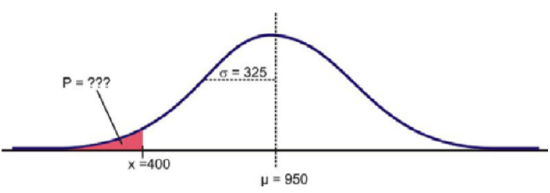
Using a graphing calculator, we can approximate the probability of a female marine iguana being less than 400 grams as follows:

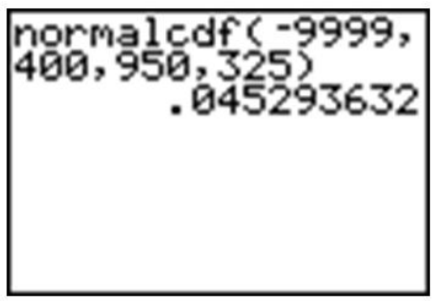
With a probability of approximately 0.045, or only about 5%, we could say it is rather unlikely that we would find an iguana this small.

Example \(\PageIndex{3}\)

The physical plant at the main campus of a large state university receives daily requests to replace florescent lightbulbs. The distribution of the number of daily requests is bell-shaped and has a mean of 59 and a standard deviation of 9. Using the Empirical rule, what is the approximate percentage of lightbulb replacement requests numbering between 59 and 77?

Since we want to use the Empirical Rule, we should draw a figure reflecting the Empirical Rule given the mean is \(59\) and the standard deviation is \(9\). Recall, 1 standard deviation from the mean is \(59 ± 9\), two standard deviations from the mean is \(59 ± 2 \cdot 9\), and 3 standard deviations from the mean is \(59 ± 3 \cdot 9\).

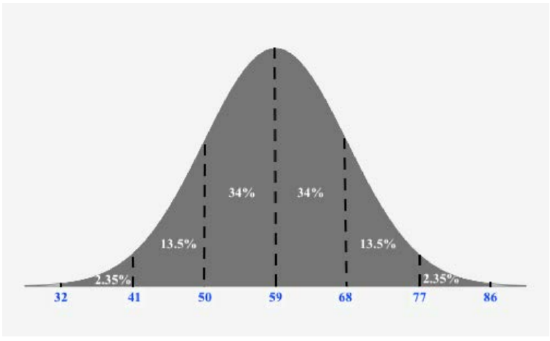
Once we make this figure, we can easily the percentage of lightbulb replacement requests numbering between 59 and 77:

\(34 \% + 13.5 \% = 47.5 \%\)

Thus, \(47.5 \%\) of lightbulb replacement requests numbering between 59 and 77.

Example \(\PageIndex{4}\)

A company has a policy of retiring company cars; this policy looks at number of miles driven, purpose of trips, style of car and other features. The distribution of the number of months in service for the fleet of cars is bell-shaped and has a mean of 41 months and a standard deviation of 5 months. Using the Empirical Rule, what is the approximate percentage of cars that remain in service between 46 and 56 months?

Since we want to use the Empirical Rule, we should draw a figure reflecting the Empirical Rule given the mean is 41 and the standard deviation is 5:

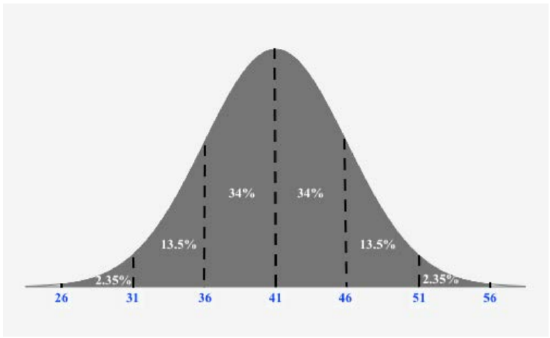
Once we make this figure, we can easily the approximate percentage of cars that remain in service between 46 and 56 months:

\(13.5 \% + 2.35 \% = 15.85 \%\)

Thus, \(15.85 \%\) of cars remain in service between 46 and 56 months.

1. Which of the following intervals contains the middle 95% of the data in a standard normal distribution?

a) \(z < 2\)

b) \(z ≤ 1.645\)

c) \(z ≤ 1.96\)

d) \(−1.645 ≤ z ≤ 1.645\)

e) \(−1.96 ≤ z ≤ 1.96\)

2. The manufacturing process at a metal-parts factory produces some slight variation in the diameter of metal ball bearings. The quality control experts claim that the bearings produced have a mean diameter of 1.4 cm. If the diameter is more than 0.0035 cm too wide or too narrow, they will not work properly. In order to maintain its reliable reputation, the company wishes to ensure that no more than one-tenth of 1% of the bearings that are made are ineffective. What would the standard deviation of the manufactured bearings need to be in order to meet this goal?

3. Suppose that the wrapper of a certain candy bar lists its weight as 2.13 ounces. Naturally, the weights of individual bars vary somewhat. Suppose that the weights of these candy bars vary according to a normal distribution, with \(µ = 2.2\) ounces and \(σ = 0.04\) ounces.

a) What proportion of the candy bars weigh less than the advertised weight?

b) What proportion of the candy bars weight between 2.2 and 2.3 ounces?

c) A candy bar of what weight would be heavier than all but 1% of the candy bars out there?

d) If the manufacturer wants to adjust the production process so that no more than 1 candy bar in 1000 weighs less than the advertised weight, what would the mean of the actual weights need to be? (Assume the standard deviation remains the same.)

e) If the manufacturer wants to adjust the production process so that the mean remains at 2.2 ounces and no more than 1 candy bar in 1000 weighs less than the advertised weight, how small does the standard deviation of the weights need to be?

4. The Acme Company manufactures widgets. The distribution of widget weights is bell-shaped. The widget weights have a mean of 51 ounces and a standard deviation of 4 ounces. Use the Empirical Rule to answer the following questions.

a) 99.7% of the widget weights lie between what two weights?

b) What percentage of the widget weights lie between 43 and 63 ounces?

c) What percentage of the widget weights lie above 47?

Module 6: Probability and Probability Distributions

Normal random variables (6 of 6), learning outcomes.

• Use a normal probability distribution to estimate probabilities and identify unusual events.

Now we use the simulation and the standard normal curve to find the probabilities associated with any normal density curve.

Length of Human Pregnancy

The length (in days) of a randomly chosen human pregnancy is a normal random variable with μ = 266, σ = 16. So X = length of pregnancy (in days)

(a) What is the probability that a randomly chosen pregnancy will last less than 246 days?

We want P ( X < 246). To find this probability, we first convert X = 246 to a z -score:

[latex]Z=\frac{246-266}{16}=\frac{-20}{16}=-1.25[/latex]

Now we can use the simulation to find P ( Z < −1.25). This is the area under the normal probability curve to the left of Z = −1.25.

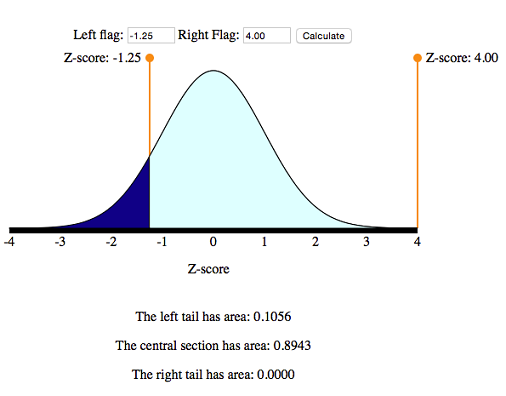
The probability that a randomly chosen pregnancy lasts less than 246 days is 0.1056. In other words, there is an 11% chance that a randomly selected pregnancy will last less than 246 days.

(b) Suppose a pregnant woman’s husband has scheduled his business trips so that he will be in town between the 235th and 295th days of her pregnancy. What is the probability that the birth will take place during that time?

Compute the z -scores for each of these x -values:

[latex]Z=\frac{235-266}{16}=\frac{-31}{16}=-1.94[/latex]

[latex]Z=\frac{295-266}{16}=\frac{29}{16}=1.81[/latex]

Use the simulation to find the area under the standard normal curve between these two z -scores.

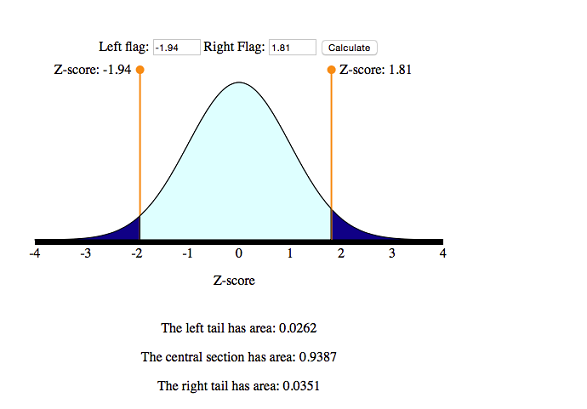
So the desired probability is 0.9387.

[latex]P(235<X<295)=P(-1.94<Z<1.81)=0.9387[/latex]

There is about a 94% probability that he will be home for the birth. Looks like he planned well.

The previous examples all followed the same general form: Given values of a normal random variable, we found an associated probability. The two basic steps in the solution process were as follows:

• Convert x -value to a z -score.
• Use the simulation to find associated probability.

The next example is a different type of problem: Given a probability, we will find the associated value of the normal random variable. The solution process will go in reverse order.

• Use a new simulation to convert statements about probabilities to statements about z -scores.
• Convert z -scores to x -values.

These types of problems are informally called “work-backwards” problems. We will use a new simulation for these types of problems. The new simulation requires us to enter a probability and then gives us the associated z-score. This is backwards from the simulation we worked with previously where we entered a z-score to find a probability. We will use this simulation in the next example.

Click here to open this simulation in its own window.

Work Backwards to Find X

Foot length (in inches) of a randomly chosen adult male is a normal random variable with a mean of 11 and standard deviation of 1.5. So X = foot length (inches).

(a) Suppose that an XL sock is designed to fit the largest 30% of men’s feet. What is the smallest foot length that fits an XL sock?

Step 1: Use the simulation to convert the probability to a statement about z -scores.

We want to mark off the largest 30% of the distribution, so the probability to the right of the z -score is 30%. This means that 70% of the area is to the left of the z -score.

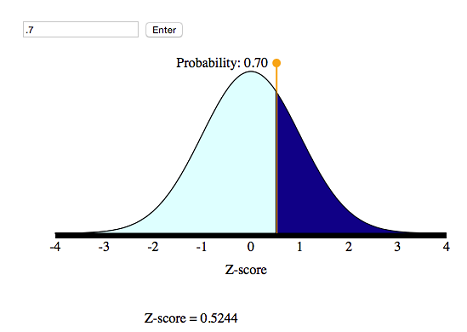
From the simulation, we can see that the corresponding z -score is 0.52.

Step 2: Now we need to convert this z -score to a foot length.

Before we calculate the length, note that the z -score is about 0.5, so the x -value will be about 0.5 standard deviations above the mean.

[latex]x=\mathrm{μ}+0.5⋅\mathrm{σ}=11+0.5(1.5)=11+0.75=11.75\text{}\mathrm{inches}[/latex]

Conclusion: A foot length of 11.75 inches is the shortest foot for an XL sock.

(b) What is the first quartile for the men’s foot lengths?

Step 1: Use the simulation to convert this probability into a statement about z -scores.

We want to mark off the smallest 25% of the distribution, so the probability to the left of the z -score is 25%.

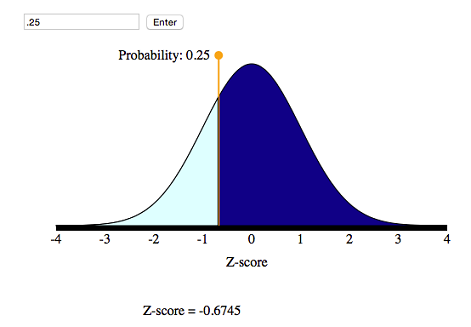
From the simulation, we can see that the corresponding z -score is −0.67.

Step 2: Convert this z -score to a foot length. If X is the foot length we seek, then X is 0.67 standard deviations below the mean. That is,

[latex]x=\mathrm{μ}-0.67⋅\mathrm{σ}=11-0.67(1.5)=11-1.005=9.995\text{}\mathrm{inches}[/latex]

Conclusion: The first quartile mark is 9.995 inches, so about 25% of the men’s feet are shorter than 10 inches.

In the preceding example (specifically step 2), we found the x -value by reasoning about the meaning of the z -score. We can also develop a formula for this process.

Recall the definition of z -score. In words, the z -score of an x -value is the number of standard deviations X is away from the mean. As a formula, this is

[latex]Z=\frac{x-\mathrm{μ}}{\mathrm{σ}}[/latex]

We can solve this equation for X as follows:

[latex]\begin{array}{l}\frac{x-\mathrm{μ}}{\mathrm{σ}}=Z\\ x-\mathrm{μ}=Z⋅\mathrm{σ}\\ x=\mathrm{μ}+Z⋅\mathrm{σ}\end{array}[/latex]

This gives us a formula for finding X from Z . You can use this formula in step 2 of a work-backwards problem.

Let’s Summarize

• In “Continuous Random Variables,” we made the transition from discrete to continuous random variables. A continuous random variable is not limited to distinct values. It is a measurement such as foot length. We cannot display the probability distribution for a continuous random variable with a table or histogram. We use a density curve to assign probabilities to intervals of x -values. We use the area under the density curve to find probabilities .
• We use a normal density curve to model the probability distribution for many variables, such as weight, shoe sizes, foot lengths, and other human physical characteristics. Normal curves are mathematical models. We use µ to represent the mean of a normal curve and σ to represent the standard deviation of a normal curve. We use Greek letters to remind us that the normal curve is not a distribution of real data. It is a mathematical model based on a mathematical equation. We use this mathematical model to represent the perfect bell-shaped distribution.
• For a normal curve, the empirical rule for normal curves tells us that 68% of the observations fall within 1 standard deviation of the mean, 95% within 2 standard deviations of the mean, and 99.7% within 3 standard deviations of the mean.
• To compare x -values from different distributions, we standardize the values by finding a z -score :  [latex]Z=\frac{x-\mathrm{μ}}{\mathrm{σ}}[/latex]
• A z -score measures how far X is from the mean in standard deviations. In other words, the z -score is the number of standard deviations X is from the mean of the distribution. For example, Z = 1 means the x -value is 1 standard deviation above the mean.
• If we convert the x -values into z -scores, the distribution of z -scores is also a normal density curve. This curve is called the standard normal distribution . We use a simulation with the standard normal curve to find probabilities for any normal distribution.
• We can also work backwards and find the x -value for a given probability. We used a different simulation to work backwards from probabilities to x -values. With this simulation, we found x -values corresponding to quartiles and percentiles.

Are You Ready for the Checkpoint?

If you completed all of the exercises in this module, you should be ready for the Checkpoint. To make sure that you are ready for the Checkpoint, use the My Response link below to evaluate your understanding of the learning outcomes for this module and to submit questions that you may have.

Contribute!

Improve this page Learn More

• Concepts in Statistics. Provided by : Open Learning Initiative. Located at : http://oli.cmu.edu . License : CC BY: Attribution

Normal Distribution Problems with Solutions

Problems and applications on normal distributions are presented. The solutions to these problems are at the bottom of the page. An online normal probability calculator and an inverse normal probability calculator may be useful to check your answers.

Problems with Solutions

• X is a normally distributed variable with mean = 30 and standard deviation = 4. Find the probabilities a) P(X < 40) b) P(X > 21) c) P(30 < X < 35)  
• A radar unit is used to measure the speeds of cars on a motorway. The speeds are normally distributed with a mean of 90 km/hr and a standard deviation of 10 km/hr. What is the probability that a car picked at random is traveling at more than 100 km/hr?  
• For certain types of computers, the length of time between charges of the battery is normally distributed with a mean of 50 hours and a standard deviation of 15 hours. John owns one of these computers and wants to know the probability that the length of time will be between 50 and 70 hours.  
• Entry to a certain University is determined by a national test. The scores on this test are normally distributed with a mean of 500 and a standard deviation of 100. Tom wants to be admitted to this university and he knows that he must score better than at least 70% of the students who took the test. Tom takes the test and scores 585. Will he be admitted to this university?  
• The length of similar components produced by a company is approximated by a normal distribution model with a mean of 5 cm and a standard deviation of 0.02 cm. If a component is chosen at random a) what is the probability that the length of this component is between 4.98 and 5.02 cm? b) What is the probability that the length of this component is between 4.96 and 5.04 cm?  
• The length of life of an instrument produced by a machine has a normal distribution with a mean of 12 months and a standard deviation of 2 months. Find the probability that an instrument produced by this machine will last a) less than 7 months. b) between 7 and 12 months.  
• The time taken to assemble a car in a certain plant is a random variable having a normal distribution of 20 hours and a standard deviation of 2 hours. What is the probability that a car can be assembled at this plant in a period of time a) less than 19.5 hours? b) between 20 and 22 hours?  
• A large group of students took a test in Physics and the final grades have a mean of 70 and a standard deviation of 10. If we can approximate the distribution of these grades by a normal distribution, what percent of the students a) scored higher than 80? b) Should pass the test (grades60)? c) Should fail the test (grades<60)?  
• The annual salaries of employees in a large company are approximately normally distributed with a mean of $50,000 and a standard deviation of $20,000. a) What percent of people earn less than $40,000? b) What percent of people earn between $45,000 and $65,000? c) What percent of people earn more than $70,000?  

Solutions to the Above Problems

• Note: What is meant here by area is the area under the standard normal curve. a) For x = 40, the z-value z = (40 - 30) / 4 = 2.5 Hence P(x < 40) = P(z < 2.5) = [area to the left of 2.5] = 0.9938 b) For x = 21, z = (21 - 30) / 4 = -2.25 Hence P(x > 21) = P(z > -2.25) = [total area] - [area to the left of -2.25] = 1 - 0.0122 = 0.9878 c) For x = 30 , z = (30 - 30) / 4 = 0 and for x = 35, z = (35 - 30) / 4 = 1.25 Hence P(30 < x < 35) = P(0 < z < 1.25) = [area to the left of z = 1.25] - [area to the left of 0] = 0.8944 - 0.5 = 0.3944  
• Let x be the random variable that represents the speed of cars. x has = 90 and = 10. We have to find the probability that x is higher than 100 or P(x > 100) For x = 100 , z = (100 - 90) / 10 = 1 P(x > 90) = P(z > 1) = [total area] - [area to the left of z = 1] = 1 - 0.8413 = 0.1587 The probability that a car selected at random has a speed greater than 100 km/hr is equal to 0.1587  
• Let x be the random variable that represents the length of time. It has a mean of 50 and a standard deviation of 15. We have to find the probability that x is between 50 and 70 or P( 50< x < 70) For x = 50 , z = (50 - 50) / 15 = 0 For x = 70 , z = (70 - 50) / 15 = 1.33 (rounded to 2 decimal places) P( 50< x < 70) = P( 0< z < 1.33) = [area to the left of z = 1.33] - [area to the left of z = 0] = 0.9082 - 0.5 = 0.4082 The probability that John's computer has a length of time between 50 and 70 hours is equal to 0.4082.  
• Let x be the random variable that represents the scores. x is normally distributed with a mean of 500 and a standard deviation of 100. The total area under the normal curve represents the total number of students who took the test. If we multiply the values of the areas under the curve by 100, we obtain percentages. For x = 585 , z = (585 - 500) / 100 = 0.85 The proportion P of students who scored below 585 is given by P = [area to the left of z = 0.85] = 0.8023 = 80.23% Tom scored better than 80.23% of the students who took the test and he will be admitted to this University.  
• a) P(4.98 < x < 5.02) = P(-1 < z < 1) = 0.6826 b) P(4.96 < x < 5.04) = P(-2 < z < 2) = 0.9544  
• a) P(x < 7) = P(z < -2.5) = 0.0062 b) P(7 < x < 12) = P(-2.5 < z < 0) = 0.4938  
• a) P(x < 19.5) = P(z < -0.25) = 0.4013 b) P(20 < x < 22) = P(0 < z < 1) = 0.3413  
• a) For x = 80, z = 1 Area to the right (higher than) z = 1 is equal to 0.1586 = 15.87% scored more that 80. b) For x = 60, z = -1 The area to the right of z = -1 is equal to 0.8413 = 84.13% should pass the test. c) 100% - 84.13% = 15.87% should fail the test.  
• a) For x = 40000, z = -0.5 The area to the left (less than) of z = -0.5 is equal to 0.3085 = 30.85% earn less than $40,000. b) For x = 45000 , z = -0.25 and for x = 65000, z = 0.75 The area between z = -0.25 and z = 0.75 is equal to 0.3720 = 37.20 earning between $45,000 and $65,000. c) For x = 70000, z = 1 The area to the right (higher) of z = 1 is equal to 0.1586 = 15.86% earning more than $70,000.

More References and links

• Normal Distribution Definition
• Elementary statistics and probabilities

• No category

APPLYING TEH NORMAL CURVE CONCEPTS IN PROBLEM SOLVING

Related documents

Add this document to collection(s)

You can add this document to your study collection(s)

Add this document to saved

You can add this document to your saved list

Suggest us how to improve StudyLib

(For complaints, use another form )

Input it if you want to receive answer

Have an account?

APPLYING THE NORMAL CURVE CONCEPTS IN PR...

Mathematics.

APPLYING THE NORMAL CURVE CONCEPTS IN PROBLEM SOLVING

10 questions

Introducing new   Paper mode

No student devices needed.   Know more

Find the area under the normal distribution curve to the left of z =0.27.

A z-score tells you...

How many standard deviations away from the mean a score lies.

The original raw score on which it is based.

The standard deviation of sampling distribution

If the distribution it comes from is normal

Find the area of the shaded region if the z-score is 0.75

This data is a normal distribution.

What percent of the data is in the shade region?

What does this symbol represent?

Standard deviation

find the area of shaded region if the z-scores is 1.25

This data is normally distributed. What percent of the data is in shaded region?

Where can we locate the mean in the normal curve?

At the center

to the right portion

to the left portion center

On the z- axis

Find the area under the standard normal curve to the right of z = -2.67

If Ms. San Juan’s score is 87, the class average is 82 and the SD is 4. What is San Juan’s score?

Explore all questions with a free account

Continue with email

Continue with phone

• f16-busad265

Lesson 10: Solving Normal Curve Problems

September 21, 2016

Wed, Sep 21

• Standard Normal Calculations with Z-Scores
• Exam 1 Part 1

Presentation :

• Find probabilities for Z-Scores with the Z-Table  (use this link or back page of textbook)
• p(X<a) = “Less Than”
• p(X>b) = “Greater Than”
• p(a<X<b) = “Between” (between 2 values)
• Draw a picture of the distribution
• Convert given values (a, b) to Z-Scores and locate on the horizontal axis
• Look up corresponding probabilities in the Z-Table
• If “Less Than”, shade under the curve to the left of Z-Score; the Z-Table probability you found is the answer.
• If “Greater Than”, shade under the curve to the right of the Z-Score; subtract the Z-Table probability from 1 to find the answer.
• Shade the area under the curve between the two Z-Scores
• Find the probability for the larger value (further to the right)
• Find the probability for the smaller value (further to the left)
• Subtract the smaller from the larger to find the “Between” probability
• Z = (x – xbar)/s
• x = xbar + Z * s
• xbar = mean
• s = standard deviation
• Step through examples 1.29, 1.30 and 1.31 on pp. 65-66
• Step through example 1.32 on pp. 67-68
• 1.103 and 1.104 on p. 66
• 1.105 and 1.106 on p. 68

Assignment :

• Read pp. 64-68
• Work on Exam 1 Part 1 Take Home

Justin Holman is CEO of Aftermarket Analytics, where he leads efforts to develop cutting edge sales forecasting and inventory optimization technology for the Automotive Aftermarket. Prior to joining Aftermarket Analytics, Justin managed corporate consulting for the Strategy & Analytics division at MapInfo Corporation, leading major projects for retail clients including The Home Depot, Darden Restaurants, Bridgestone-Firestone, Sainsbury’s and New York & Company. Before that, Justin served as Vice President of Software Development at LogicTools, now part of IBM's supply chain application software group. Justin holds a B.A. from Claremont McKenna College, a Ph.D. from the University of Oregon and an Executive Management certificate from Northwestern University's Kellogg School of Management.

[…] Normal Curve Calculations with Z-Scores […]

Leave a Reply Cancel reply

Forget password?

What are you looking for?