addition and subtraction fractions problem solving

Addition and Subtraction of Fraction: Methods, Examples, Facts, FAQs

What is addition and subtraction of fractions, methods of addition and subtraction of fractions, addition and subtraction of mixed numbers, solved examples on addition and subtraction of fractions, practice problems on addition and subtraction of fractions, frequently asked questions on addition and subtraction of fractions.

Addition and subtraction of fractions are the fundamental operations on fractions that can be studied easily using two cases:

• Addition and subtraction of like fractions (fractions with same denominators)
• Addition and subtraction of unlike fractions (fractions with different denominators)

A fraction represents parts of a whole. For example, the fraction 37 represents 3 parts out of 7 equal parts of a whole. Here, 3 is the numerator and it represents the number of parts taken. 7 is the denominator and it represents the total number of parts of the whole.

Adding and subtracting fractions is simple and straightforward when it comes to like fractions. In the case of unlike fractions, we first need to make the denominators the same. Let’s take a closer look at both these cases.

Before adding and subtracting fractions, we first need to make sure that the fractions have the same denominators. 

When the denominators are the same, we simply add the numerators and keep the denominator as it is. To add or subtract unlike fractions, we first need to learn how to make the denominators alike. Let’s learn how to add fractions and how to subtract fractions in both cases.

Related Worksheets

Addition and Subtraction of Like Fractions

The rules for adding fractions with the same denominator are really simple and straightforward. 

Let’s learn with the help of examples and visual bar models.

Addition of Like Fractions

Here are the steps to add fractions with the same denominator:

Step 1: Add the numerators of the given fractions. 

Step 2: Keep the denominator the same. 

Step 3: Simplify.          

$\frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}$  …$c \neq 0$

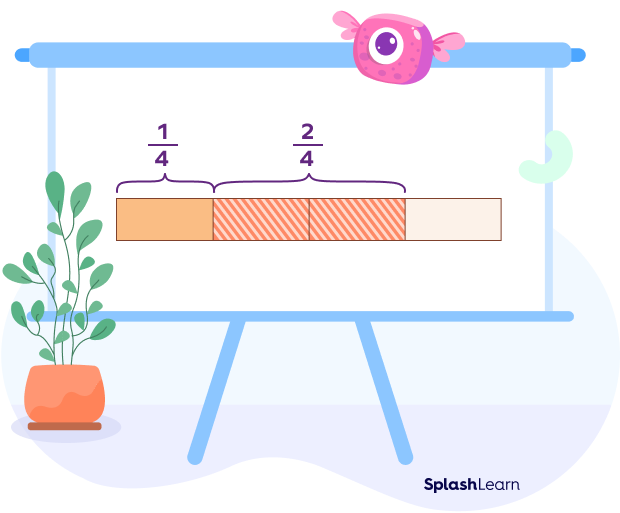
Example 1: Find $\frac{1}{4} + \frac{2}{4}$ .

$\frac{1}{4} + \frac{2}{4} = \frac{1 + 2}{4} = \frac{3}{4}$

We can visualize this addition using a bar model:

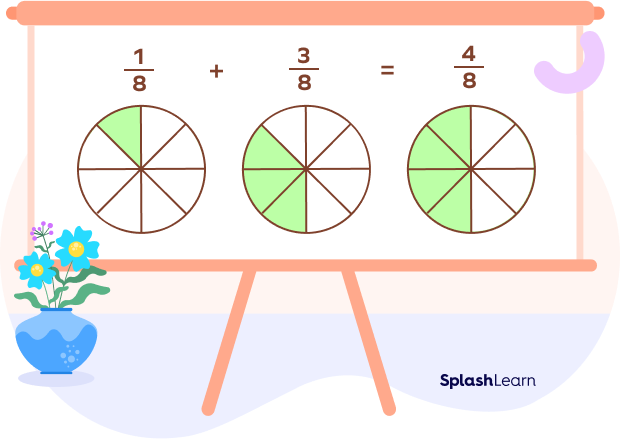
Example 2: $\frac{1}{8} + \frac{3}{8} = \frac{1 + 3}{8} = \frac{4}{8} = \frac{1}{2}$

Subtraction of Like Fractions

Here are the steps to subtract fractions with the same denominator:

Step 1: Subtract the numerators of the given fractions. 

Step 3: Simplify. 

$\frac{a}{c}\;-\;\frac{b}{c} = \frac{a \;-\; b}{c}$ …$c \neq 0$

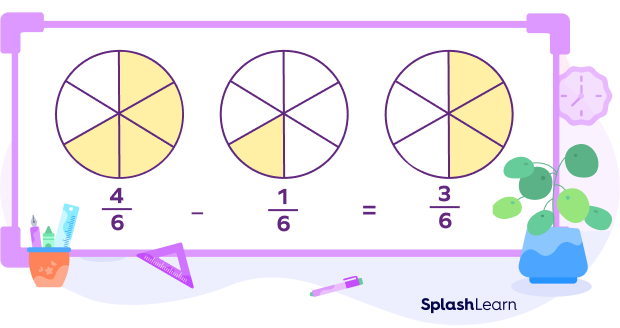
Example 1: Find $\frac{4}{6} \;-\; \frac{1}{6}$.

$\frac{4}{6}\;-\;\frac{1}{6} = \frac{4-1}{6} = \frac{3}{6} = \frac{1}{2}$

Addition and Subtraction of Unlike Fractions

Addition and subtraction of fractions with unlike denominators can be a little bit tricky since the denominators are not the same. So, we need to first convert the unlike fractions into like fractions. Let’s look at a few ways to do this!

Addition of Unlike Fractions

We can make the denominators the same by finding the LCM of the two denominators. Once we calculate the LCM, we multiply both the numerator and the denominator with an appropriate number so that we get the LCM value in the denominator. 

Example: $\frac{3}{5} + \frac{3}{2}$

Step 1: Find the LCM (Least Common Multiple) of the two denominators.

The LCM of 5 and 2 is 10.

Step 2: Convert both the fractions into like fractions by making the denominators same.  

$\frac{3 \times 2}{5 \times 2} = \frac{6}{10}$  

$\frac{3 \times 5}{2 \times 5} = \frac{15}{10}$

Step 3: Add the numerators. The denominator stays the same.

$\frac{6}{10} + \frac{15}{10} = \frac{21}{10}$

Step 4: Convert the resultant fraction to its simplest form if the GCF of the numerator and denominator is not 1. 

In this case, GCF (21,10) $= 1$

The fraction $\frac{21}{10}$ is already in its simplest form. 

Thus, $\frac{3}{5} + \frac{3}{2} = \frac{21}{10}$

Subtraction of Unlike Fractions

Let’s learn how to subtract fractions when denominators are not the same. To subtract unlike fractions, we use the LCM method. The process is similar to what we discussed in the previous example.

Example: $\frac{5}{6} \;-\; \frac{2}{9}$

Step 1: Find the LCM of the two denominators.

LCM of 6 and $9 = 18$

Step 2: Convert both the fractions into like fractions by making the denominators same.

$\frac{5 \times 3}{6 \times 3} = \frac{15}{18}$   

$\frac{2 \times 2}{9 \times 2} = \frac{4}{18}$

Step 3: Subtract the numerators. The denominator stays the same.

$\frac{15}{18} \;-\; \frac{4}{18} = \frac{11}{18}$

In this case, the GCF (11,18) $= 1$

So, it is already in its simplest form. 

Thus, $\frac{5}{6}\;-\; 29 = \frac{11}{18}$

A mixed number is a type of fraction that has two parts: a whole number and a proper fraction. It is also known as a mixed fraction. Any mixed number can be written in the form of an improper fraction and vice-versa. 

Adding and subtracting mixed fractions is done by converting mixed numbers into improper fractions .

Addition and Subtraction of Mixed Fractions with Same Denominators

The steps of adding and subtracting mixed numbers with the same denominators are the same. The only difference is the operation.

Step 1: Convert the given mixed fractions to improper fractions.

Step 2: Add/Subtract the like fractions obtained in step 1.

Step 3: Reduce the fraction to its simplest form.

Step 4: Convert the resulting fraction into a mixed number.

Example 1: $2\frac{1}{5} + 1\frac{3}{5}$

$2\frac{1}{5} = \frac{(5 \times 2) + 1}{5} = \frac{11}{5}$

$1\frac{3}{5} = \frac{(5 \times 1) + 3}{5} = \frac{8}{5}$

Thus, $2\frac{1}{5} + 1\frac{3}{5} = \frac{11}{5} + \frac{8}{5} = \frac{19}{5}$

Converting $\frac{19}{5}$ into a mixed number, we get

$\frac{19}{5} = 3\frac{4}{5}$

Example 2: $2\frac{1}{5} + 1\frac{3}{5} = \frac{11}{5} \;-\; \frac{8}{5} = \frac{3}{5}$

Addition and Subtraction of Mixed Fractions with Unlike Denominators

Step 2: Convert both the fractions into like fractions by finding the least common denominator.

Step 3: Add the fractions. (or subtract the fractions.)

Step 4: Reduce the fraction if possible or convert back to a mixed number 

Let us understand the addition of mixed numbers with unlike denominators with the help of an example.

Example 1: Find the value of $1\frac{3}{5} + 2\frac{1}{2}$.

Convert the given mixed fractions to improper fractions.

$1\frac{3}{5} = \frac{8}{5}$ and $2\frac{1}{2} = \frac{5}{2}$

Step 2: Convert both the fractions into like fractions by making the denominators the same.

Here, LCM of 5 and 2 is 10.

Thus, $\frac{8 \times 2}{5 \times 2} = \frac{16}{10}$ and $\frac{5\times 5}{2 \times 5} = \frac{25}{10}$

Step 3: Add the fractions by adding the numerators.

$\frac{16}{10} + \frac{25}{10} = \frac{41}{10}$

Step 4: Convert back into a mixed number. 

Thus, $\frac{41}{10}$ will become  $4\frac{1}{10}$

Therefore, $1\frac{3}{5} + 2\frac{1}{2} =  4\frac{1}{10}$

Here’s an example for subtraction. It follows the same steps.

Example 2 : $6\frac{1}{2} \;-\; 1\frac{3}{4}$

Step 1: Convert the mixed numbers into improper fractions.

     $6\frac{1}{2} \;-\; 1\frac{3}{4} = \frac{13}{2} \;-\; \frac{7}{4}$

Step 2: Make the denominators equal.

LCM of 2 and 4 is 4. 

   $\frac{13 \times 2}{2 \times 2} = \frac{26}{4}$ 

Step 3: Subtract the fractions.

        $\frac{26}{4} \;-\;  \frac{7}{4} = \frac{19}{4}$

Step 4: Convert the fraction as a mixed number.

            $\frac{19}{4}  = 4\frac{3}{4}$  

Thus, $6\frac{1}{2} \;-\; 1\frac{3}{4}  =   4\frac{3}{4}$  

Facts about Addition and Subtraction of Fractions

• We cannot add or subtract fractions without converting them into like fractions.
• Like fractions are fractions that have the same denominator, and unlike fractions are fractions that have different denominators.
• Equivalent fractions are two different fractions that represent the same value.
• The LCD (least common denominator) of two fractions is the LCM of the denominators.

In this article, we have learned about addition and subtraction of fractions (like fractions, unlike fractions, mixed fractions), methods of addition and subtraction of these fractions along with the steps. Let’s solve some examples on adding and subtracting fractions to understand the concept better.

• Solve: $\frac{2}{4} + \frac{1}{4}$ .

Solution: 

Here, the denominators are the same.

Thus, we add the numerators by keeping the denominators as it is.

$\frac{2}{4} + \frac{1}{4} = \frac{2 + 1}{4}$ 

$\frac{2}{4} + \frac{1}{4} = \frac{3}{4}$

2. Find the sum of the fractions $\frac{3}{5}$ and $\frac{5}{2}$ by using the LCM method.

$\frac{3}{5}$ and $\frac{5}{2}$ are unlike fractions.

The LCM of 2 and 5 is 10.

Thus, we can write

$\frac{3}{5} + \frac{5}{2} = \frac{3 \times 2}{5 \times 2} + \frac{5 \times 5}{2 \times 5}$

$= \frac{6}{10} + \frac{25}{10}$

            $= \frac{6}{10} + \frac{25}{10}$

            $= \frac{31}{10}$

Thus, $\frac{3}{5} + \frac{5}{2} =  \frac{31}{10}$

3. Find $\frac{4}{16} + \frac{5}{8}$.

Solution:  

To add two fractions with different denominators, we first need to find the LCM of the denominators.

The LCM of 16 and 8 is 16.

$\frac{4}{16} + \frac{5}{8} = \frac{4 \times 1}{16\times 1} + \frac{5 \times 2}{8 \times 2}$ 

            $= \frac{10}{16} + \frac{4}{16}$ 

            $= \frac{14}{16}$

$= \frac{7}{8}$

4. From a rope $12\frac{1}{2}$ ft. long, a $7 \frac{6}{8}\;-$ ft-long piece is cut off. Find the length of the remaining rope.

Total length of the rope $= 12\frac{1}{2}$ ft.

Length of the rope that was cut off $= 7 \frac{6}{8}$ ft. 

The length of the remaining rope $= 12\frac{1}{2} \;-\; 7 \frac{6}{8}$

$12\frac{1}{2} \;-\; 7 \frac{6}{8} = \frac{25}{2} \;-\; \frac{62}{8}$

         $= \frac{25 \times 4}{2 \times 4} \;-\; \frac{62 \times 1}{8\times 1}$

         $= \frac{100}{8} \;-\; \frac{62}{8}$

         $= \frac{38}{8}$

         $= \frac{19}{4}$

Converting it into a mixed fraction, $\frac{19}{4}$ becomes $4 \frac{3}{4}$.

Thus, the length of the remaining rope is $4\frac{3}{4}$ ft.

Attend this quiz & Test your knowledge.

Find $\frac{2}{4} + \frac{2}{4}$.

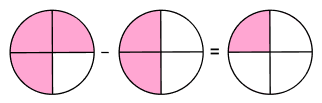
$\frac{7}{24} + \frac{5}{16} =$, what is the least common denominator of $\frac{1}{2}$ and $\frac{1}{3}$, $\frac{3}{6} \;-\; \frac{1}{6} =$, what equation does the following figure represent.

How do we add and subtract negative fractions?

Negative fractions are simply fractions with a negative sign. The steps to add and subtract the negative fractions remain the same. We need to follow the rules for addition/subtraction with negative signs.

How can we convert an improper fraction into a mixed number?

To convert an improper fraction into a mixed number, we divide the numerator by the denominator. The denominator stays the same. The quotient represents the whole number part. The remainder represents the numerator of the mixed number.

Example: $\frac{14}{3} = 4\; \text{R}\; 2$

Quotient $= 4$

Remainder $= 2$

$\frac{14}{3} = 4\frac{2}{3}$

How do we divide two fractions?

To divide one fraction by another, we multiply the first fraction by the reciprocal of the second fraction.

$\frac{A}{B} \div \frac{C}{D} = \frac{A}{B} \times \frac{D}{C}$

For example, $\frac{1}{2} \div \frac{3}{5} = \frac{1}{2} \times \frac{5}{3} = \frac{5}{6}$

What are the rules of adding and subtracting fractions?

• Before adding or subtracting, we check if the fractions have the same denominator.
• If the denominators are equal, then we add/subtract the numerators keeping the common denominator.
• If the denominators are different, then we make the denominators equal by using the LCM method. Once the fractions have the same denominator, we can add/subtract the numerators keeping the common denominator as it is.

How do we add and subtract fractions with whole numbers?

• Convert the whole number to a fraction. To do this, give the whole number a denominator of 1.
• Convert to fractions of like denominators. 
• Add/subtract the numerators. Now that the fractions have the same denominators, you can treat the numerators as a normal addition/subtraction problem.

RELATED POSTS

• Cube Numbers – Definition, Examples, Facts, Practice Problems
• Volume of Hemisphere: Definition, Formula, Examples
• CPCTC: Definition, Postulates, Theorem, Proof, Examples
• Dividend – Definition with Examples
• Reflexive Property – Definition, Equality, Examples, FAQs

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Fraction word prob.

Fraction word problems

Here you will learn about fraction word problems, including solving math word problems within a real-world context involving adding fractions, subtracting fractions, multiplying fractions, and dividing fractions.

Students will first learn about fraction word problems as part of number and operations—fractions in 4 th grade.

What are fraction word problems?

Fraction word problems are math word problems involving fractions that require students to use problem-solving skills within the context of a real-world situation.

To solve a fraction word problem, you must understand the context of the word problem, what the unknown information is, and what operation is needed to solve it. Fraction word problems may require addition, subtraction, multiplication, or division of fractions.

After determining what operation is needed to solve the problem, you can apply the rules of adding, subtracting, multiplying, or dividing fractions to find the solution.

For example,

Natalie is baking 2 different batches of cookies. One batch needs \cfrac{3}{4} cup of sugar and the other batch needs \cfrac{2}{4} cup of sugar. How much sugar is needed to bake both batches of cookies?

You can follow these steps to solve the problem:

Step-by-step guide: Adding and subtracting fractions

Step-by-step guide: Adding fractions

Step-by-step guide: Subtracting fractions

Step-by-step guide: Multiplying and dividing fractions

Step-by-step guide: Multiplying fractions

Step-by-step guide: Dividing fractions

Common Core State Standards

How does this relate to 4 th grade math to 6 th grade math?

• Grade 4: Number and Operations—Fractions (4.NF.B.3d) Solve word problems involving addition and subtraction of fractions referring to the same whole and having like denominators, e.g., by using visual fraction models and equations to represent the problem.
• Grade 4: Number and Operations—Fractions (4.NF.B.4c) Solve word problems involving multiplication of a fraction by a whole number, e.g., by using visual fraction models and equations to represent the problem. For example, if each person at a party will eat \cfrac{3}{8} of a pound of roast beef, and there will be 5 people at the party, how many pounds of roast beef will be needed? Between what two whole numbers does your answer lie?
• Grade 5: Number and Operations—Fractions (5.NF.A.2) Solve word problems involving addition and subtraction of fractions referring to the same whole, including cases of unlike denominators, e.g., by using visual fraction models or equations to represent the problem. Use benchmark fractions and number sense of fractions to estimate mentally and assess the reasonableness of answers. For example, recognize an incorrect result \cfrac{2}{5}+\cfrac{1}{2}=\cfrac{3}{7} by observing that \cfrac{3}{7}<\cfrac{1}{2} .
• Grade 5: Number and Operations—Fractions (5.NF.B.6) Solve real world problems involving multiplication of fractions and mixed numbers, e.g., by using visual fraction models or equations to represent the problem.
• Grade 5: Number and Operations—Fractions (5.NF.B.7c) Solve real world problems involving division of unit fractions by non-zero whole numbers and division of whole numbers by unit fractions, e.g., by using visual fraction models and equations to represent the problem. For example, how much chocolate will each person get if 3 people share \cfrac{1}{2} \: lb of chocolate equally? How many \cfrac{1}{3} cup servings are in 2 cups of raisins?
• Grade 6: The Number System (6.NS.A.1) Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to represent the problem. For example, create a story context for \cfrac{2}{3} \div \cfrac{4}{5} and use a visual fraction model to show the quotient; use the relationship between multiplication and division to explain that \cfrac{2}{3} \div \cfrac{4}{5}=\cfrac{8}{9} because \cfrac{3}{4} of \cfrac{8}{9} is \cfrac{2}{3}. (In general, \cfrac{a}{b} \div \cfrac{c}{d}=\cfrac{a d}{b c} \, ) How much chocolate will each person get if 3 people share \cfrac{1}{2} \: lb of chocolate equally? How many \cfrac{3}{4} cup servings are in \cfrac{2}{3} of a cup of yogurt? How wide is a rectangular strip of land with length \cfrac{3}{4} \: m and area \cfrac{1}{2} \: m^2?

[FREE] Fraction Operations Worksheet (Grade 4 to 6)

Use this quiz to check your grade 4 to 6 students’ understanding of fraction operations. 10+ questions with answers covering a range of 4th to 6th grade fraction operations topics to identify areas of strength and support!

How to solve fraction word problems

In order to solve fraction word problems:

Determine what operation is needed to solve.

Write an equation.

Solve the equation.

State your answer in a sentence.

Fraction word problem examples

Example 1: adding fractions (like denominators).

Julia ate \cfrac{3}{8} of a pizza and her brother ate \cfrac{2}{8} of the same pizza. How much of the pizza did they eat altogether?

The problem states how much pizza Julia ate and how much her brother ate. You need to find how much pizza Julia and her brother ate altogether , which means you need to add.

2 Write an equation.

3 Solve the equation.

To add fractions with like denominators, add the numerators and keep the denominators the same.

4 State your answer in a sentence.

The last step is to go back to the word problem and write a sentence to clearly say what the solution represents in the context of the problem.

Julia and her brother ate \cfrac{5}{8} of the pizza altogether.

Example 2: adding fractions (unlike denominators)

Tim ran \cfrac{5}{6} of a mile in the morning and \cfrac{1}{3} of a mile in the afternoon. How far did Tim run in total?

The problem states how far Tim ran in the morning and how far he ran in the afternoon. You need to find how far Tim ran in total , which means you need to add.

To add fractions with unlike denominators, first find a common denominator and then change the fractions accordingly before adding.

\cfrac{5}{6}+\cfrac{1}{3}= \, ?

The least common multiple of 6 and 3 is 6, so 6 can be the common denominator.

That means \cfrac{1}{3} will need to be changed so that its denominator is 6. To do this, multiply the numerator and the denominator by 2.

\cfrac{1 \times 2}{3 \times 2}=\cfrac{2}{6}

Now you can add the fractions and simplify the answer.

\cfrac{5}{6}+\cfrac{2}{6}=\cfrac{7}{6}=1 \cfrac{1}{6}

Tim ran a total of 1 \cfrac{1}{6} miles.

Example 3: subtracting fractions (like denominators)

Pia walked \cfrac{4}{7} of a mile to the park and \cfrac{3}{7} of a mile back home. How much farther did she walk to the park than back home?

The problem states how far Pia walked to the park and how far she walked home. Since you need to find the difference ( how much farther ) between the two distances, you need to subtract.

To subtract fractions with like denominators, subtract the numerators and keep the denominators the same.

\cfrac{4}{7}-\cfrac{3}{7}=\cfrac{1}{7}

Pia walked \cfrac{1}{7} of a mile farther to the park than back home.

Example 4: subtracting fractions (unlike denominators)

Henry bought \cfrac{7}{8} pound of beef from the grocery store. He used \cfrac{1}{3} of a pound of beef to make a hamburger. How much of the beef does he have left?

The problem states how much beef Henry started with and how much he used. Since you need to find how much he has left , you need to subtract.

To subtract fractions with unlike denominators, first find a common denominator and then change the fractions accordingly before subtracting.

\cfrac{7}{8}-\cfrac{1}{3}= \, ?

The least common multiple of 8 and 3 is 24, so 24 can be the common denominator.

That means both fractions will need to be changed so that their denominator is 24.

To do this, multiply the numerator and the denominator of each fraction by the same number so that it results in a denominator of 24. This will give you an equivalent fraction for each fraction in the problem.

\begin{aligned}&\cfrac{7 \times 3}{8 \times 3}=\cfrac{21}{24} \\\\ &\cfrac{1 \times 8}{3 \times 8}=\cfrac{8}{24} \end{aligned}

Now you can subtract the fractions.

\cfrac{21}{24}-\cfrac{8}{24}=\cfrac{13}{24}

Henry has \cfrac{13}{24} of a pound of beef left.

Example 5: multiplying fractions

Andre has \cfrac{3}{4} of a candy bar left. He gives \cfrac{1}{2} of the remaining bit of the candy bar to his sister. What fraction of the whole candy bar does Andre have left now?

It could be challenging to determine the operation needed for this problem; many students may automatically assume it is subtraction since you need to find how much of the candy bar is left.

However, since you know Andre started with a fraction of the candy bar and you need to find a fraction OF a fraction, you need to multiply.

The difference here is that Andre did NOT give his sister \cfrac{1}{2} of the candy bar, but he gave her \cfrac{1}{2} of \cfrac{3}{4} of a candy bar.

To solve the word problem, you can ask, “What is \cfrac{1}{2} of \cfrac{3}{4}? ” and set up the equation accordingly. Think of the multiplication sign as meaning “of.”

\cfrac{1}{2} \times \cfrac{3}{4}= \, ?

To multiply fractions, multiply the numerators and multiply the denominators.

\cfrac{1}{2} \times \cfrac{3}{4}=\cfrac{3}{8}

Andre gave \cfrac{1}{2} of \cfrac{3}{4} of a candy bar to his sister, which means he has \cfrac{1}{2} of \cfrac{3}{4} left. Therefore, Andre has \cfrac{3}{8} of the whole candy bar left.

Example 6: dividing fractions

Nia has \cfrac{7}{8} cup of trail mix. How many \cfrac{1}{4} cup servings can she make?

The problem states the total amount of trail mix Nia has and asks how many servings can be made from it.

To solve, you need to divide the total amount of trail mix (which is \cfrac{7}{8} cup) by the amount in each serving ( \cfrac{1}{4} cup) to find out how many servings she can make.

To divide fractions, multiply the dividend by the reciprocal of the divisor.

\begin{aligned}& \cfrac{7}{8} \div \cfrac{1}{4}= \, ? \\\\ & \downarrow \downarrow \downarrow \\\\ &\cfrac{7}{8} \times \cfrac{4}{1}=\cfrac{28}{8} \end{aligned}

You can simplify \cfrac{28}{8} to \cfrac{7}{2} and then 3 \cfrac{1}{2}.

Nia can make 3 \cfrac{1}{2} cup servings.

Teaching tips for fraction word problems

• Encourage students to look for key words to help determine the operation needed to solve the problem. For example, subtracting fractions word problems might ask students to find “how much is left” or “how much more” one fraction is than another.
• Provide students with an answer key to word problem worksheets to allow them to obtain immediate feedback on their solutions. Encourage students to attempt the problems independently first, then check their answers against the key to identify any mistakes and learn from them. This helps reinforce problem-solving skills and confidence.
• Be sure to incorporate real-world situations into your math lessons. Doing so allows students to better understand the relevance of fractions in everyday life.
• As students progress and build a strong foundational understanding of one-step fraction word problems, provide them with multi-step word problems that involve more than one operation to solve.
• Take note that students will not divide a fraction by a fraction as shown above until 6 th grade (middle school), but they will divide a unit fraction by a whole number and a whole number by a fraction in 5 th grade (elementary school), where the same mathematical rules apply to solving.
• There are many alternatives you can use in place of printable math worksheets to make practicing fraction word problems more engaging. Some examples are online math games and digital workbooks.

Easy mistakes to make

• Misinterpreting the problem Misreading or misunderstanding the word problem can lead to solving for the wrong quantity or using the wrong operation.
• Not finding common denominators When adding or subtracting fractions with unlike denominators, students may forget to find a common denominator, leading to an incorrect answer.
• Forgetting to simplify Unless a problem specifically says not to simplify, fractional answers should always be written in simplest form.

Related fractions operations lessons

• Fractions operations
• Multiplicative inverse
• Reciprocal math
• Fractions as divisions

Practice fraction word problem questions

1. Malia spent \cfrac{5}{6} of an hour studying for a math test. Then she spent \cfrac{1}{3} of an hour reading. How much longer did she spend studying for her math test than reading?

Malia spent \cfrac{1}{2} of an hour longer studying for her math test than reading.

Malia spent \cfrac{5}{18} of an hour longer studying for her math test than reading.

Malia spent \cfrac{1}{2} of an hour longer reading than studying for her math test.

Malia spent 1 \cfrac{1}{6} of an hour longer studying for her math test than reading.

To find the difference between the amount of time Malia spent studying for her math test than reading, you need to subtract. Since the fractions have unlike denominators, you need to find a common denominator first.

You can use 6 as the common denominator, so \cfrac{1}{3} becomes \cfrac{3}{6}. Then you can subtract.

\cfrac{3}{6} can then be simplified to \cfrac{1}{2}.

Finally, you need to choose the answer that correctly answers the question within the context of the situation. Therefore, the correct answer is “Malia spent \cfrac{1}{2} of an hour longer studying for her math test than reading.”

2. A square garden is \cfrac{3}{4} of a meter wide and \cfrac{8}{9} of a meter long. What is its area?

The area of the garden is 1\cfrac{23}{36} square meters.

The area of the garden is \cfrac{27}{32} square meters.

The area of the garden is \cfrac{2}{3} square meters.

The perimeter of the garden is \cfrac{2}{3} meters.

To find the area of a square, you multiply the length and width. So to solve, you multiply the fractional lengths by mulitplying the numerators and multiplying the denominators.

\cfrac{24}{36} can be simplified to \cfrac{2}{3}. 

Therefore, the correct answer is “The area of the garden is \cfrac{2}{3} square meters.”

3. Zoe ate \cfrac{3}{8} of a small cake. Liam ate \cfrac{1}{8} of the same cake. How much more of the cake did Zoe eat than Liam?

Zoe ate \cfrac{3}{64} more of the cake than Liam.

Zoe ate \cfrac{1}{4} more of the cake than Liam.

Zoe ate \cfrac{1}{8} more of the cake than Liam.

Liam ate \cfrac{1}{4} more of the cake than Zoe.

To find how much more cake Zoe ate than Liam, you subtract. Since the fractions have the same denominator, you subtract the numerators and keep the denominator the same.

\cfrac{2}{8} can be simplified to \cfrac{1}{4}. 

Therefore, the correct answer is “Zoe ate \cfrac{1}{4} more of the cake than Liam.”

4. Lila poured \cfrac{11}{12} cup of pineapple and \cfrac{2}{3} cup of mango juice in a bottle. How many cups of juice did she pour into the bottle altogether?

Lila poured 1 \cfrac{7}{12} cups of juice in the bottle altogether.

Lila poured \cfrac{1}{4} cups of juice in the bottle altogether.

Lila poured \cfrac{11}{18} cups of juice in the bottle altogether.

Lila poured 1 \cfrac{3}{8} cups of juice in the bottle altogether.

To find the total amount of juice that Lila poured into the bottle, you need to add. Since the fractions have unlike denominators, you need to find a common denominator first.

You can use 12 as the common denominator, so \cfrac{2}{3} becomes \cfrac{8}{12}.  Then you can add.

\cfrac{19}{12} can be simplified to 1 \cfrac{7}{12}. 

Therefore, the correct answer is “Lila poured 1 \cfrac{7}{12} cups of juice in the bottle altogether.”

5. Killian used \cfrac{9}{10} of a gallon of paint to paint his living room and \cfrac{7}{10} of a gallon to paint his bedroom. How much paint did Killian use in all?

Killian used \cfrac{2}{10} gallons of paint in all.

Killian used \cfrac{1}{5} gallons of paint in all.

Killian used \cfrac{63}{100} gallons of paint in all.

Killian used 1 \cfrac{3}{5} gallons of paint in all.

To find the total amount of paint Killian used, you add the amount he used for the living room and the amount he used for the kitchen. Since the fractions have the same denominator, you add the numerators and keep the denominators the same.

\cfrac{16}{10} can be simplified to 1 \cfrac{6}{10} and then further simplified to 1 \cfrac{3}{5}.

Therefore, the correct answer is “Killian used 1 \cfrac{3}{5} gallons of paint in all.”

6. Evan pours \cfrac{4}{5} of a liter of orange juice evenly among some cups.

He put \cfrac{1}{10} of a liter into each cup. How many cups did Evan fill?

Evan filled \cfrac{2}{25} cups.

Evan filled 8 cups.

Evan filled \cfrac{9}{10} cups.

Evan filled 7 cups.

To find the number of cups Evan filled, you need to divide the total amount of orange juice by the amount being poured into each cup. To divide fractions, you mulitply the first fraction (the dividend) by the reciprocal of the second fraction (the divisor).

\cfrac{40}{5} can be simplifed to 8.

Therefore, the correct answer is “Evan filled 8 cups.”

Fraction word problems FAQs

Fraction word problems are math word problems involving fractions that require students to use problem-solving skills within the context of a real-world situation. Fraction word problems may involve addition, subtraction, multiplication, or division of fractions.

To solve fraction word problems, first you need to determine the operation. Then you can write an equation and solve the equation based on the arithmetic rules for that operation.

Fraction word problems and decimal word problems are similar because they both involve solving math problems within real-world contexts. Both types of problems require understanding the problem, determining the operation needed to solve it (addition, subtraction, multiplication, division), and solving it based on the arithmetic rules for that operation.

The next lessons are

Still stuck.

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

We're sorry, but we don't support Internet Explorer anymore. Please use a different browser .

Add and Subtract Fractions Online practice for grades 3-7

On this page, you can practice addition and subtraction of fractions. Each practice set will automatically include both addition and subtraction problems.

The options are:

• You can limit the fractions in the problems to like fractions (fractions with the same denominator), for example: 1/6 + 4/6.
• You can limit the script to use only proper fractions—fractions that are less than 1. With this option, the script will make problems such as 1/4 + 2/5, but will not make problems such as 8/5 − 4/5.
• When you choose problems that use simplified fractions, the script will only include fractions in the problems that are in lowest terms. For example, you could get a problem such as 5/6 + 3/5, but you would not see 2/4 + 6/8.
• The last option, when chose, allows or accepts answers to not be in lowest terms. In other words, the script will accept an answer such as 8/10.

Note: ALL answers have to be given as mixed numbers, when possible. In other words, your answer cannot be left as an improper fraction.

You may use the space below to write the intermediate step. Your work in this area will not be checked.

Generate Quick Link

• Get started with computers
• Learn Microsoft Office
• Apply for a job
• Improve my work skills
• Design nice-looking docs
• Getting Started
• Smartphones & Tablets
• Typing Tutorial
• Online Learning
• Basic Internet Skills
• Online Safety
• Social Media
• Zoom Basics
• Google Docs
• Google Sheets
• Career Planning
• Resume Writing
• Cover Letters
• Job Search and Networking
• Business Communication
• Entrepreneurship 101
• Careers without College
• Job Hunt for Today
• 3D Printing
• Freelancing 101
• Personal Finance
• Sharing Economy
• Decision-Making
• Graphic Design
• Photography
• Image Editing
• Learning WordPress
• Language Learning
• Critical Thinking
• For Educators
• Translations
• Staff Picks
• English expand_more expand_less

Fractions  - Adding and Subtracting Fractions

Fractions  -, adding and subtracting fractions, fractions adding and subtracting fractions.

Fractions: Adding and Subtracting Fractions

Lesson 3: adding and subtracting fractions.

/en/fractions/comparing-and-reducing-fractions/content/

Adding and subtracting fractions

In the previous lessons, you learned that a fraction is part of a whole. Fractions show how much you have of something, like 1/2 of a tank of gas or 1/3 of a cup of water.

In real life, you might need to add or subtract fractions. For example, have you ever walked 1/2 of a mile to work and then walked another 1/2 mile back? Or drained 1/4 of a quart of gas from a gas tank that had 3/4 of a quart in it? You probably didn't think about it at the time, but these are examples of adding and subtracting fractions.

Click through the slideshow to learn how to set up addition and subtraction problems with fractions.

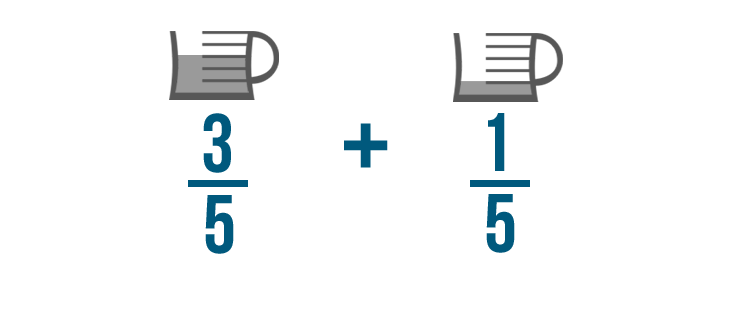
Let's imagine that a cake recipe tells you to add 3/5 of a cup of oil to the batter.

You also need 1/5 of a cup of oil to grease the pan. To see how much oil you'll need total, you can add these fractions together.

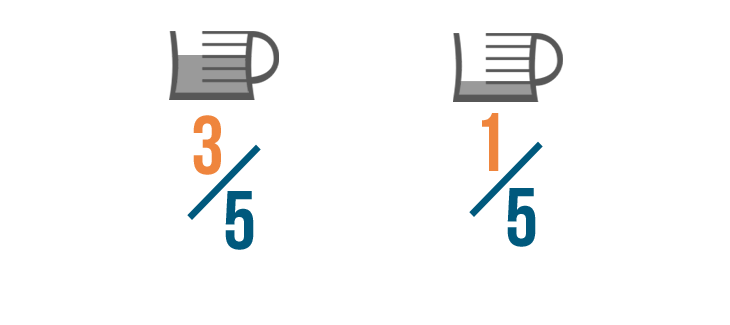
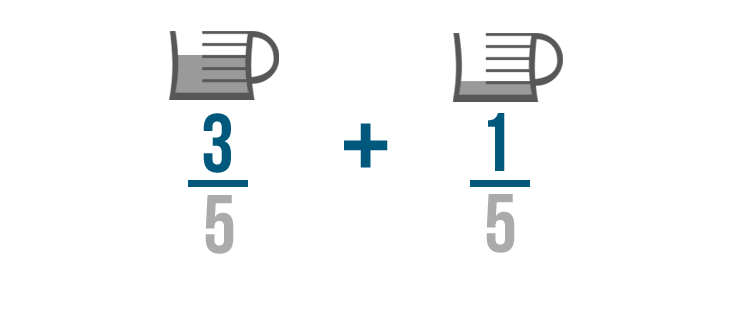
When you add fractions, you just add the top numbers, or numerators .

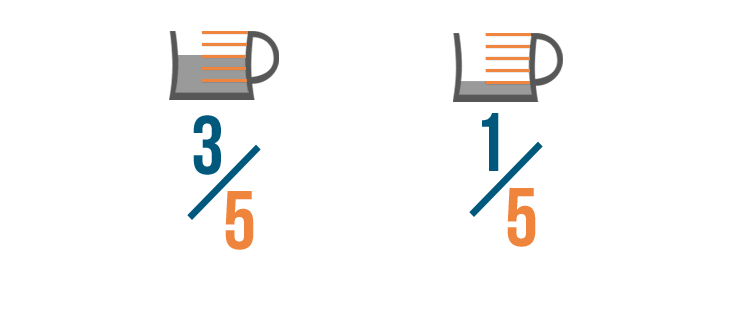
That's because the bottom numbers, or denominators , show how many parts would make a whole.

We don't want to change how many parts make a whole cup ( 5 ). We just want to find out how many parts we need total.

So we only need to add the numerators of our fractions.

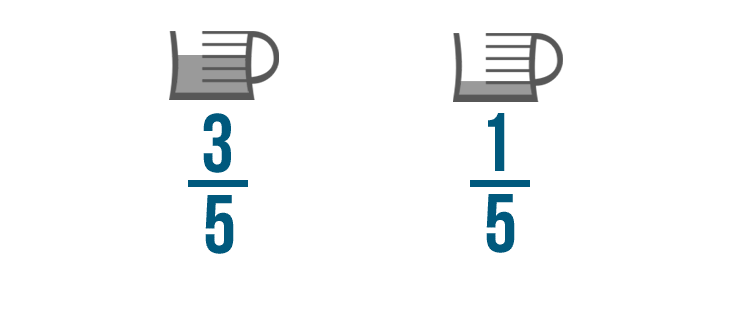
We can stack the fractions so the numerators are lined up. This will make it easier to add them.

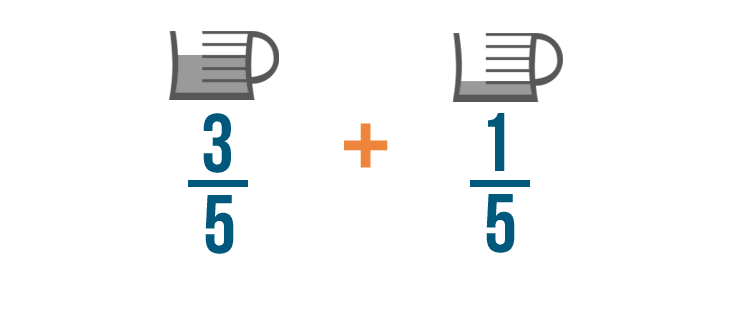
And that's all we have to do to set up an addition example with fractions. Our fractions are now ready to be added.

We'll do the same thing to set up a subtraction example. Let's say you had 3/4 of a tank of gas when you got to work.

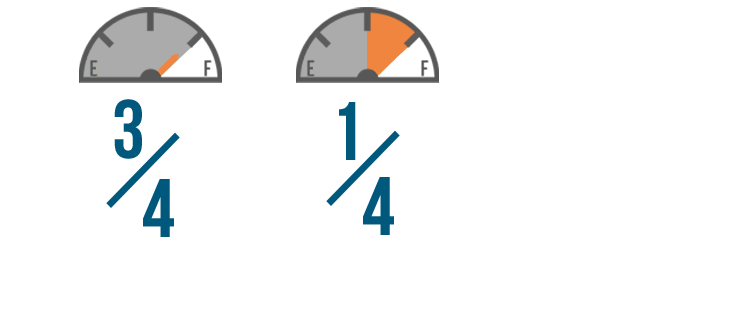
If you use 1/4 of a tank to drive home, how much will you have left? We can subtract these fractions to find out.

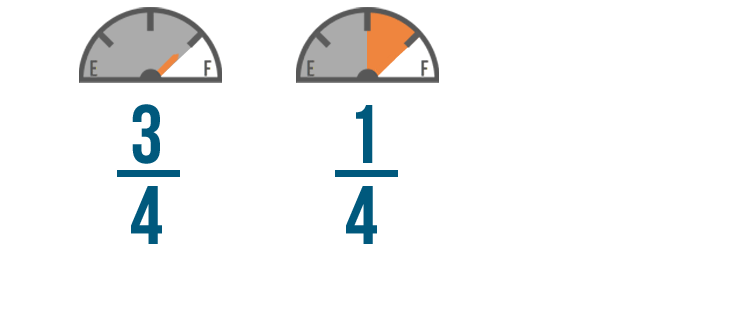
Just like when we added, we'll stack our fractions to keep the numerators lined up.

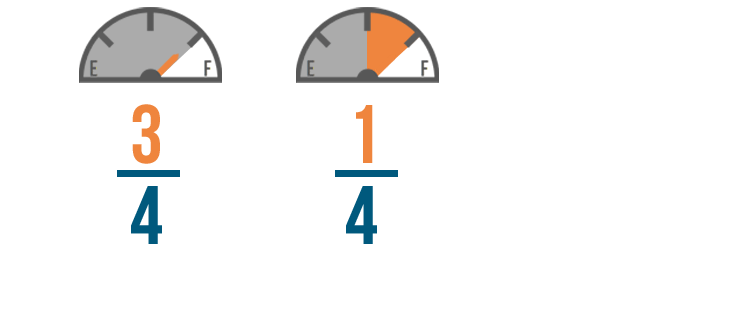
This is because we want to subtract 1 part from 3 parts.

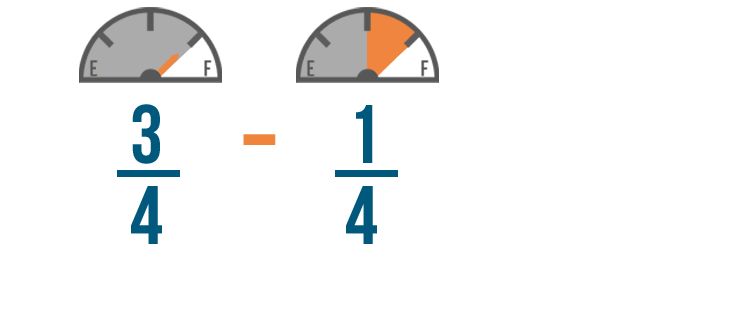
Now that our example is set up, we're ready to subtract!

Try setting up these addition and subtraction problems with fractions. Don't try solving them yet!

You run 4/10 of a mile in the morning. Later, you run for 3/10 of a mile.

You had 7/8 of a stick of butter and used 2/8 of the stick while cooking dinner.

Your gas tank is 2/5 full, and you put in another 2/5 of a tank.

Solving addition problems with fractions

Now that we know how to write addition problems with fractions, let's practice solving a few. If you can add whole numbers , you're ready to add fractions.

Click through the slideshow to learn how to add fractions.

Let's continue with our previous example and add these fractions: 3/5 of cup of oil and 1/5 of a cup of oil.

Remember, when we add fractions, we don't add the denominators.

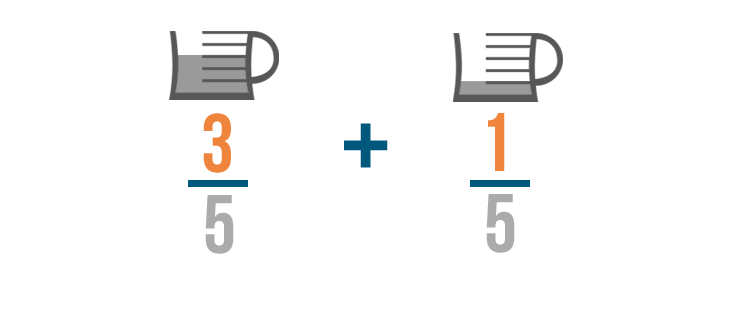
This is because we're finding how many parts we need total. The numerators show the parts we need, so we'll add 3 and 1 .

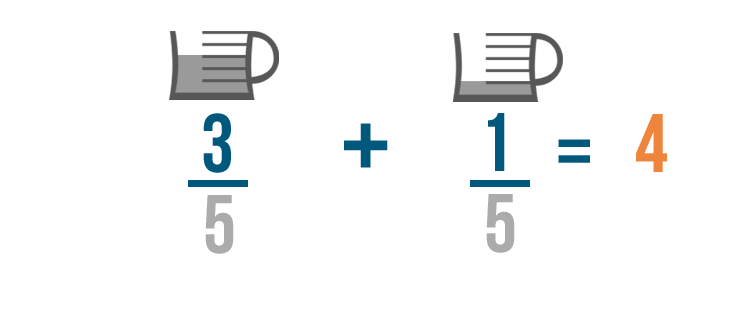
3 plus 1 equals 4 . Make sure to line up the 4 with the numbers you just added.

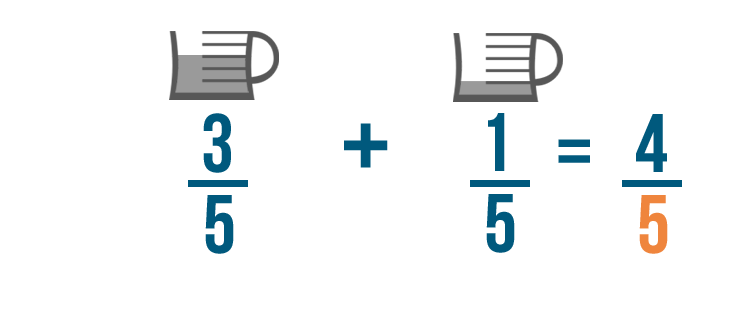
The denominators will stay the same, so we'll write 5 on the bottom of our new fraction.

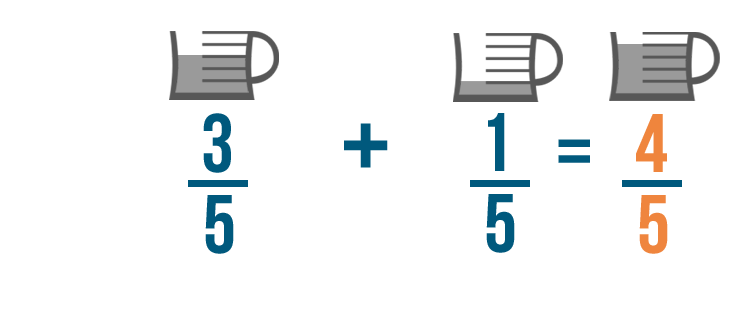
3/5 plus 1/5 equals 4/5 . So you'll need 4/5 of a cup of oil total to make your cake.

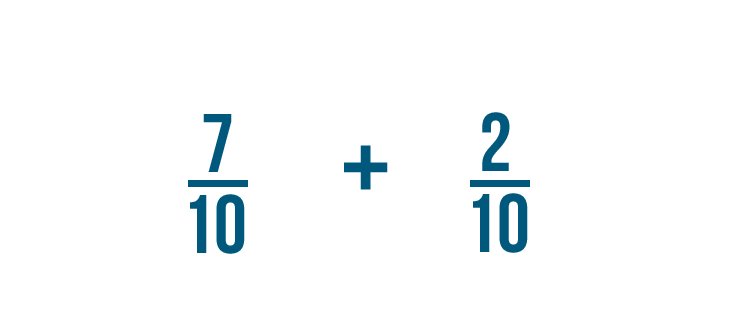
Let's try another example: 7/10 plus 2/10 .

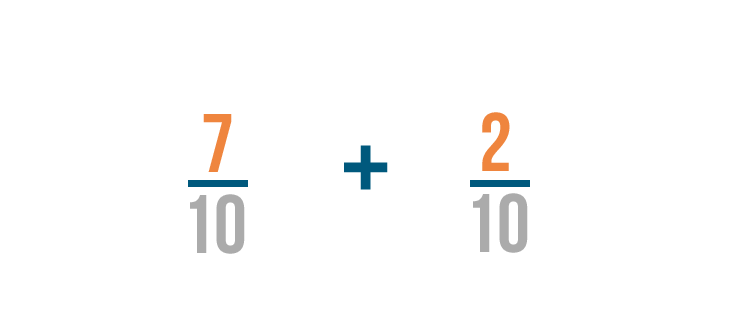
Just like before, we're only going to add the numerators. In this example, the numerators are 7 and 2 .

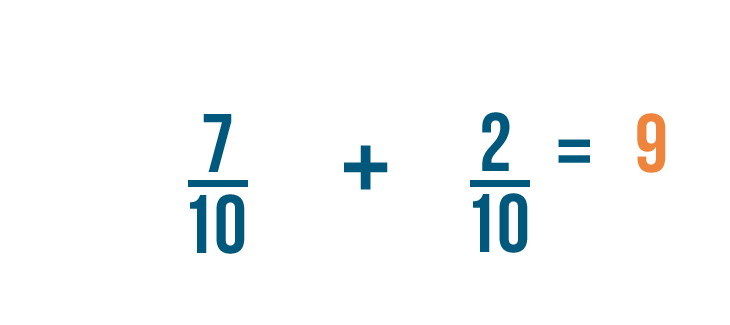
7 plus 2 equals 9 , so we'll write that to the right of the numerators.

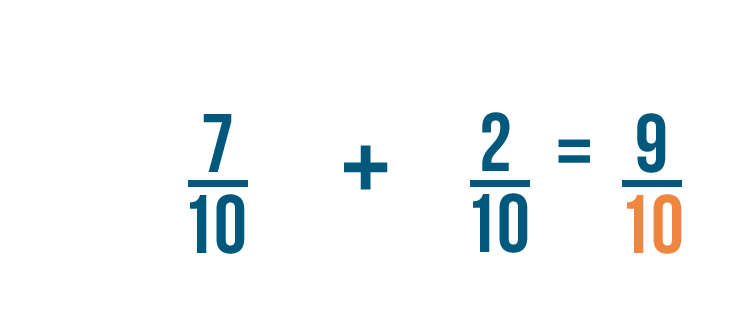
Just like in our earlier example, the denominator stays the same.

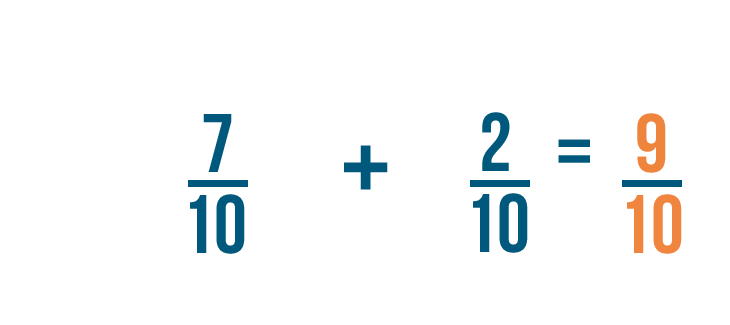
So 7/10 plus 2/10 equals 9/10 .

Try solving some of the addition problems below.

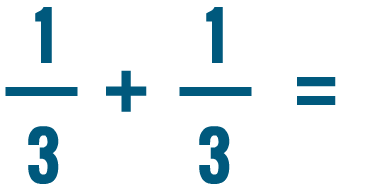
Solving subtraction problems with fractions

Subtracting fractions is a lot like regular subtraction. If you can subtract whole numbers , you can subtract fractions too!

Click through the slideshow to learn how to subtract fractions.

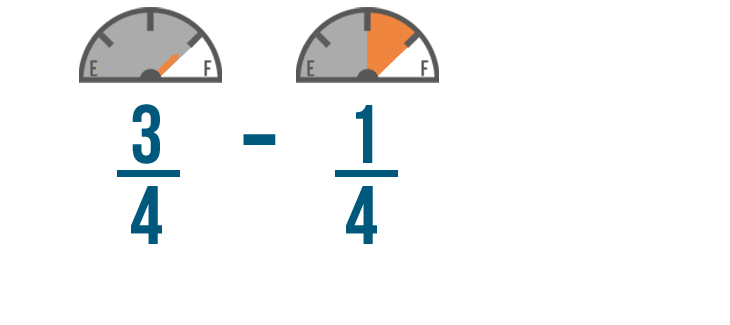
Let's use our earlier example and subtract 1/4 of a tank of gas from 3/4 of a tank.

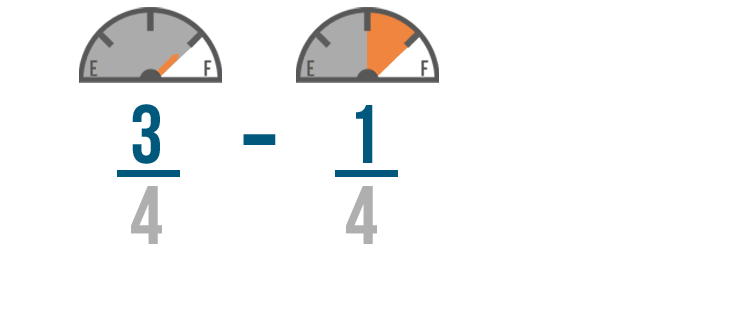
Just like in addition, we're not going to change the denominators.

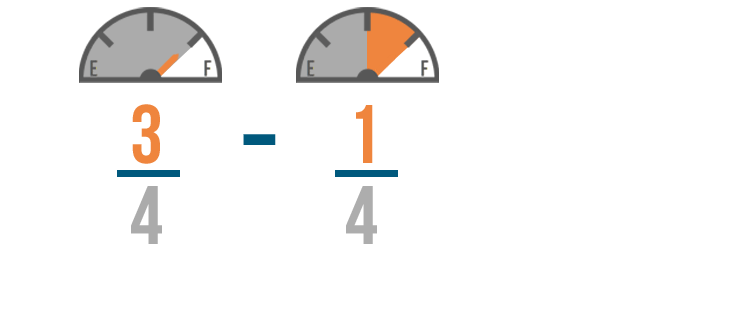
We don't want to change how many parts make a whole tank of gas. We just want to know how many parts we'll have left.

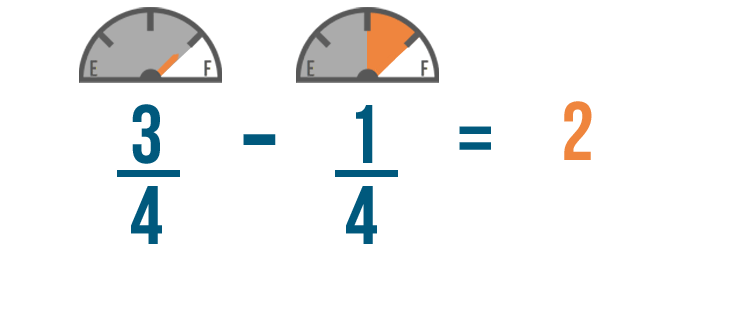
We'll start by subtracting the numerators. 3 minus 1 equals 2 , so we'll write 2 to the right of the numerators.

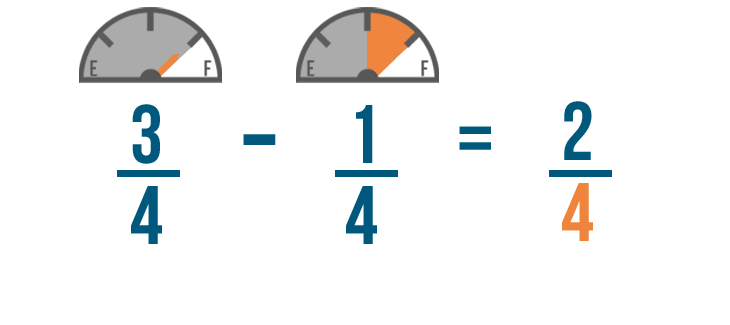
Just like when we added, the denominator of our answer will be the same as the other denominators.

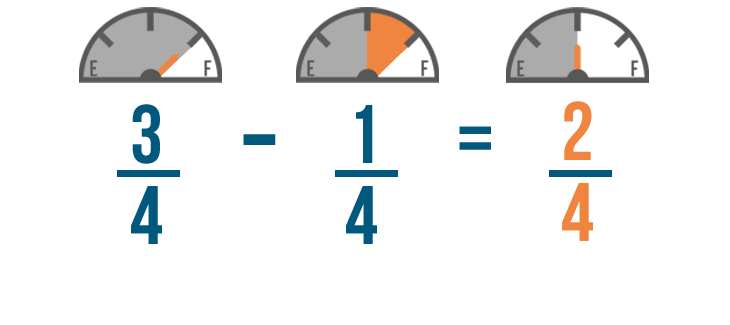
So 3/4 minus 1/4 equals 2/4 . You'll have 2/4 of a tank of gas left when you get home.

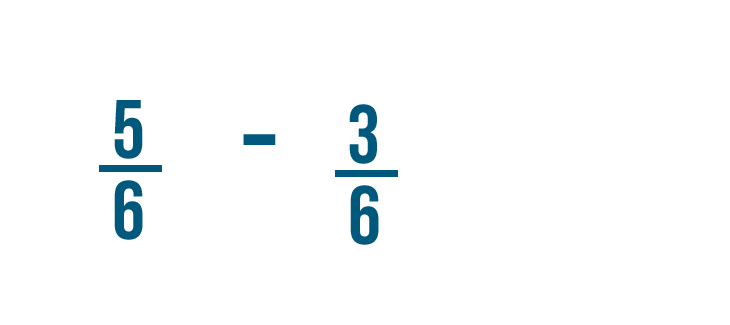
Let's try solving another problem: 5/6 minus 3/6 .

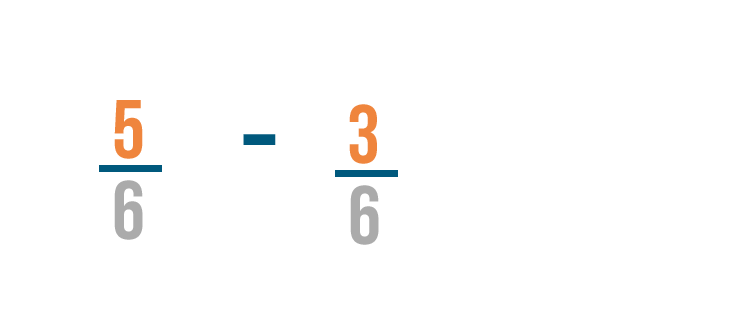
We'll start by subtracting the numerators.

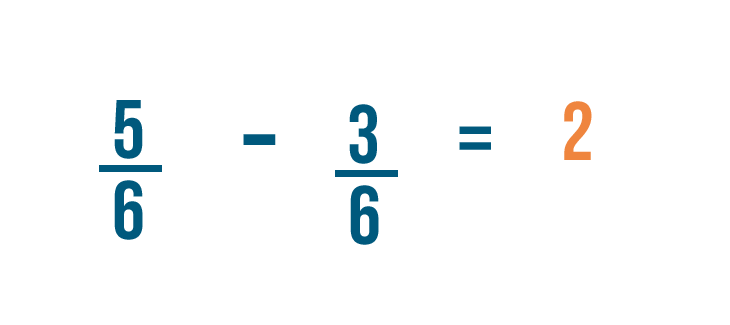
5 minus 3 equals 2 . So we'll put a 2 to the right of the numerators.

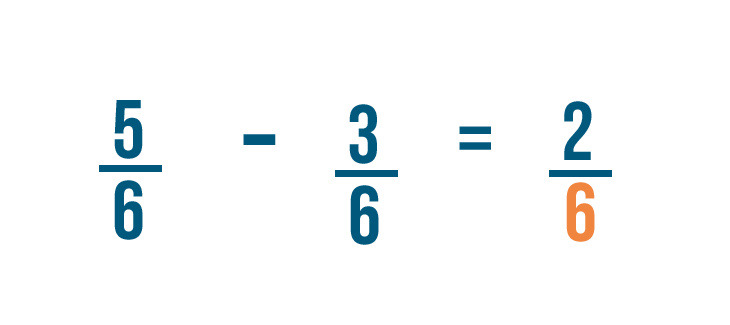
As usual, the denominator stays the same.

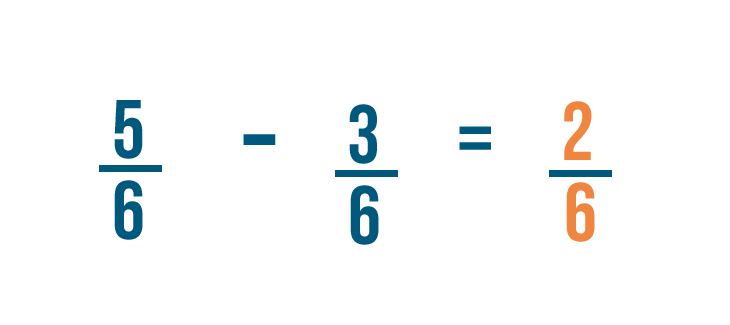
So 5/6 minus 3/6 equals 2/6 .

Try solving some of the subtraction problems below.

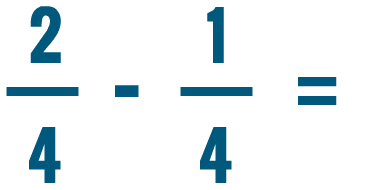
After you add or subtract fractions, you may sometimes have a fraction that can be reduced to a simpler fraction. As you learned in Comparing and Reducing Fractions , it's always best to reduce a fraction to its simplest form when you can. For example, 1/4 plus 1/4 equals 2/4 . Because 2 and 4 can both be divided 2 , we can reduce 2/4 to 1/2 .

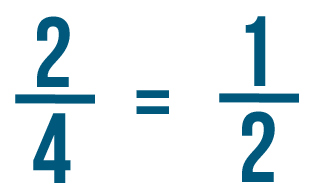
Adding fractions with different denominators

On the last page, we learned how to add fractions that have the same denominator, like 1/4 and 3/4 . But what if you needed to add fractions with different denominators? For example, our cake recipe might say to blend 1/4 cup of milk in slowly and then dump in another 1/3 of a cup.

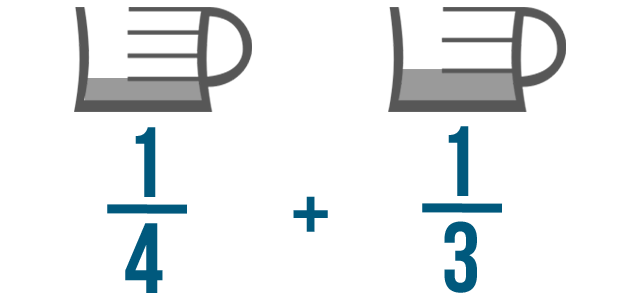
In Comparing and Reducing Fractions , we compared fractions with a different bottom number, or denominator. We had to change the fractions so their denominators were the same. To do that, we found the lowest common denominator , or LCD .

We can only add or subtract fractions if they have the same denominators. So we'll need to find the lowest common denominator before we add or subtract these fractions. Once the fractions have the same denominator, we can add or subtract as usual.

Click through the slideshow to learn how to add fractions with different denominators.

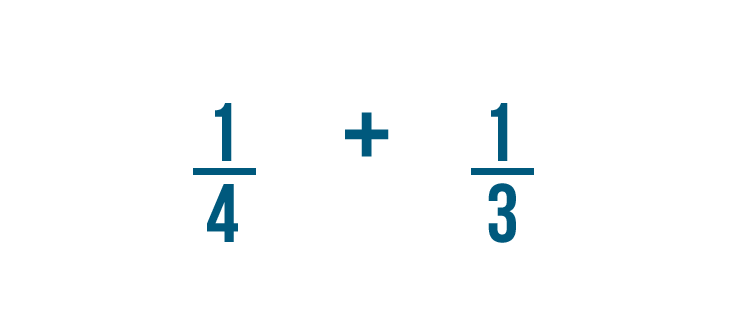
Let's add 1/4 and 1/3 .

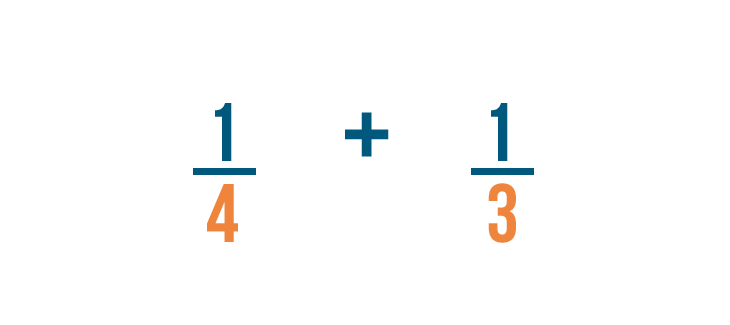
Before we can add these fractions, we'll need to change them so they have the same denominator .

To do that, we'll have to find the LCD , or lowest common denominator, of 4 and 3 .

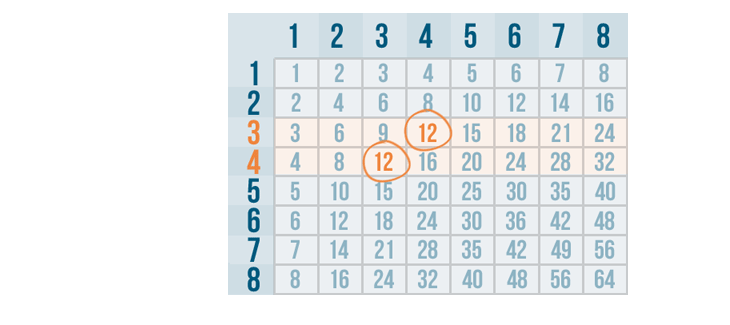
It looks like 12 is the smallest number that can be divided by both 3 and 4, so 12 is our LCD .

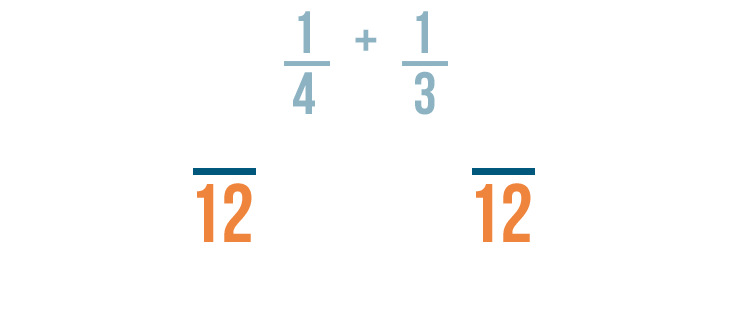
Since 12 is the LCD, it will be the new denominator for our fractions.

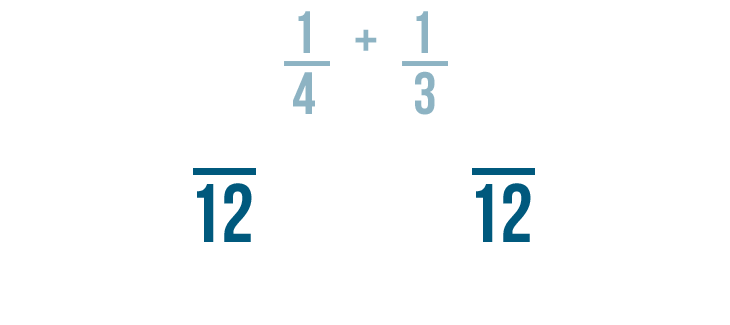
Now we'll change the numerators of the fractions, just like we changed the denominators.

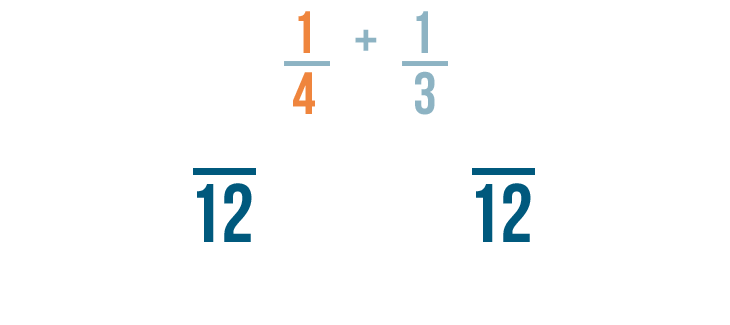
First, let's look at the fraction on the left: 1/4 .

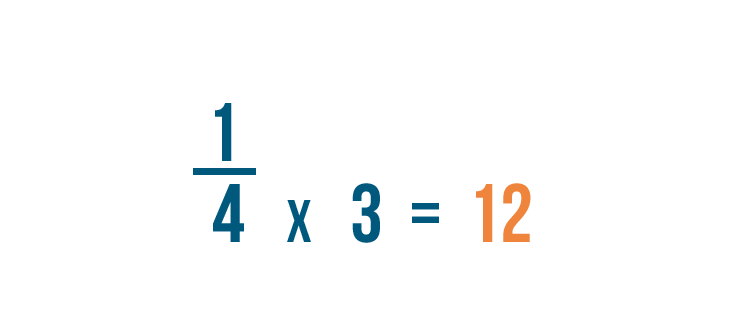
To change 4 into 12 , we multiplied it by 3 .

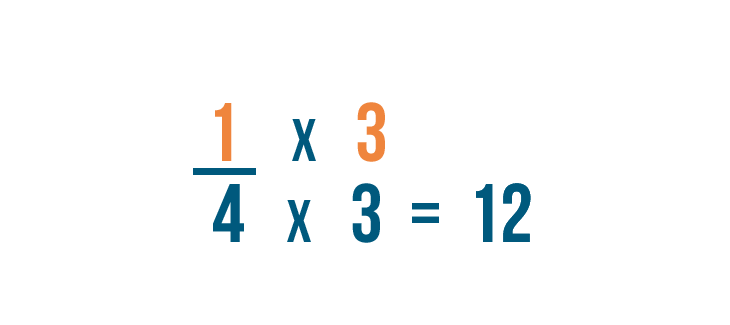
Since the denominator was multiplied by 3 , we'll also multiply the numerator by 3 .

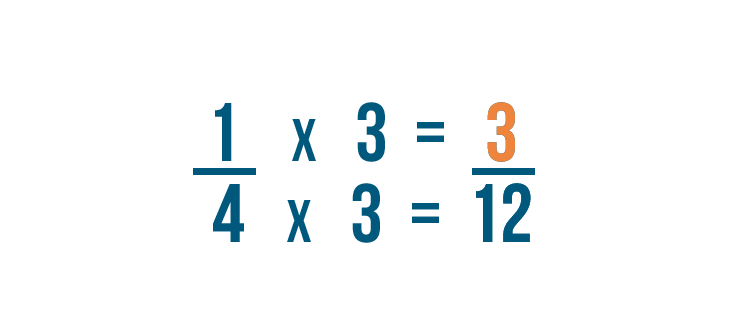
1 times 3 equals 3 .

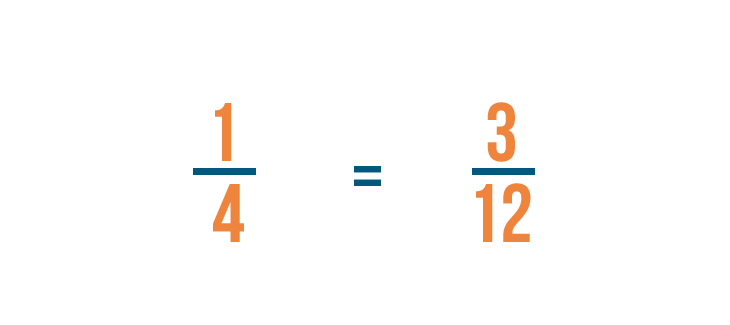
1/4 is equal to 3/12 .

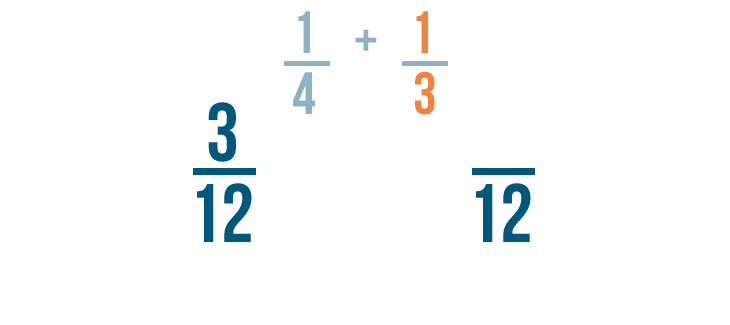
Now let's look at the fraction on the right: 1/3 . We changed its denominator to 12 as well.

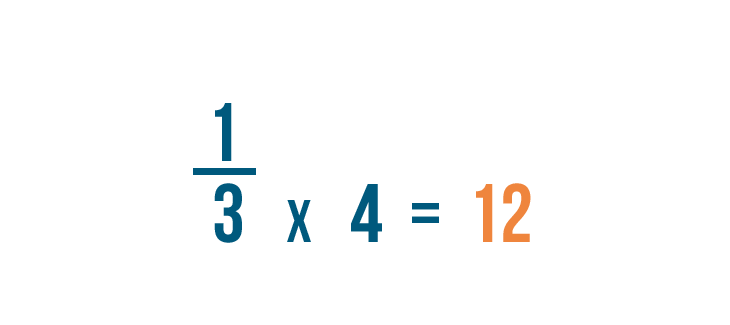
Our old denominator was 3 . We multiplied it by 4 to get 12.

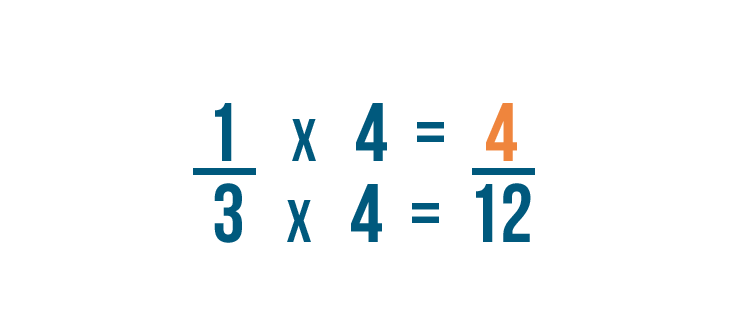
We'll also multiply the numerator by 4 . 1 times 4 equals 4 .

So 1/3 is equal to 4/12 .

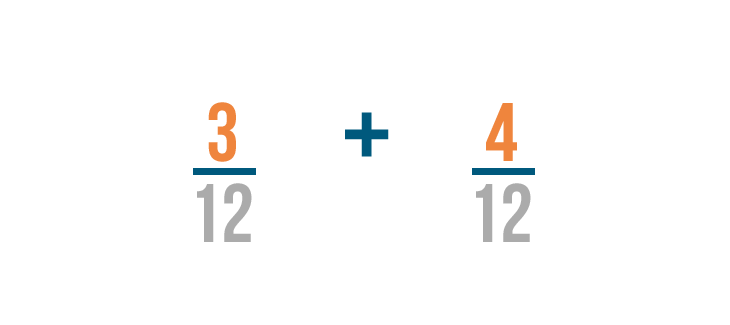
Now that our fractions have the same denominator, we can add them like we normally do.

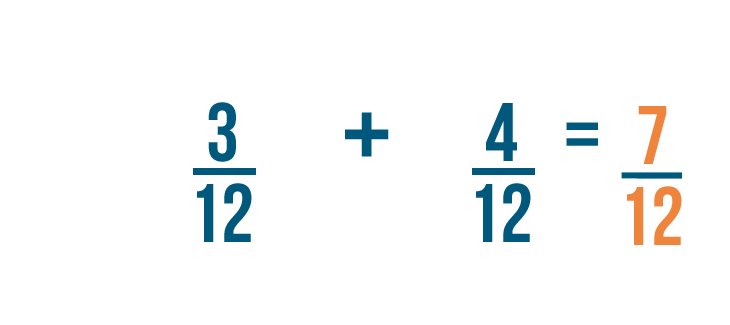
3 plus 4 equals 7 . As usual, the denominator stays the same. So 3/12 plus 4/12 equals 7/12 .

Try solving the addition problems below.

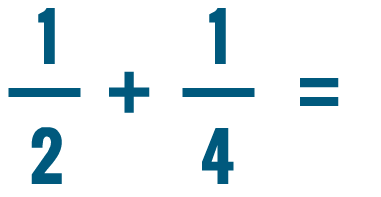
Subtracting fractions with different denominators

We just saw that fractions can only be added when they have the same denominator. The same thing is true when we're subtracting fractions. Before we can subtract, we'll have to change our fractions so they have the same denominator.

Click through the slideshow to learn how to subtract fractions with different denominators.

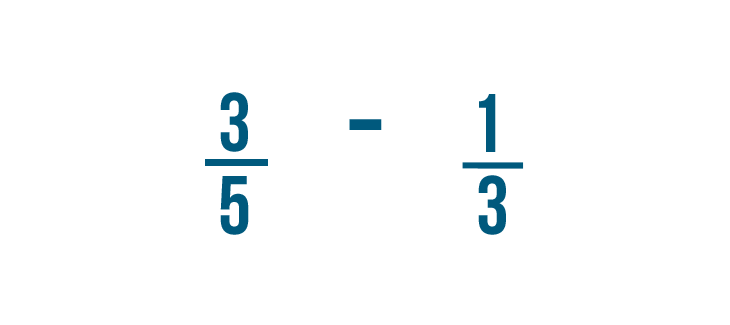
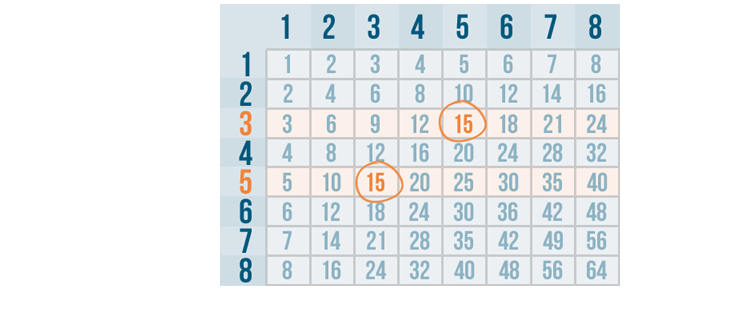
Let's try subtracting 1/3 from 3/5 .

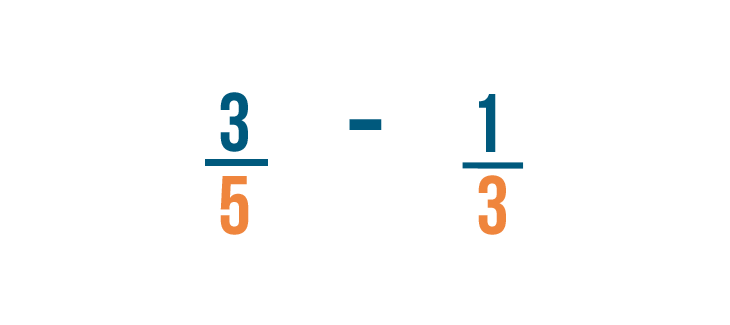
First, we'll change the denominators of both fractions to be the same by finding the lowest common denominator .

It looks like 15 is the smallest number that can be divided evenly by 3 and 5 , so 15 is our LCD.

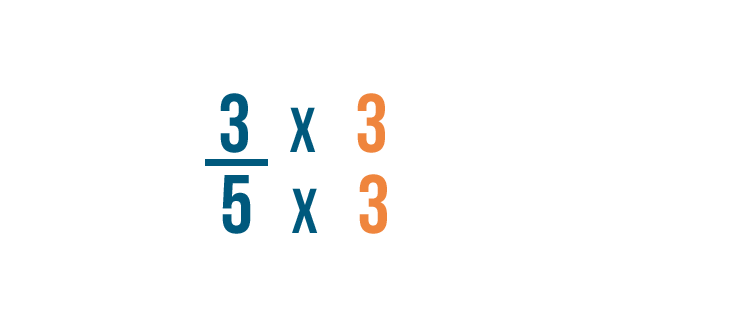
Now we'll change our first fraction. To change the denominator to 15 , we'll multiply the denominator and the numerator by 3 .

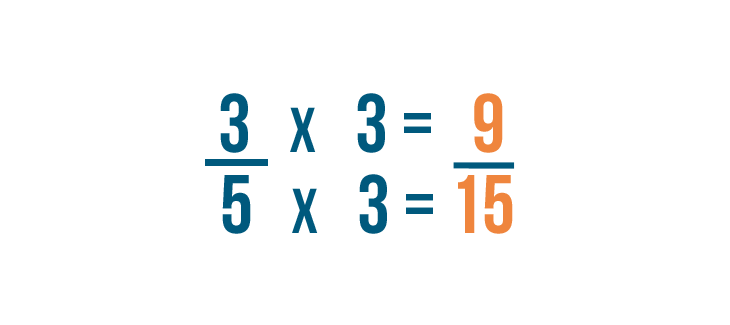
5 times 3 equals 15 . So our fraction is now 9/15 .

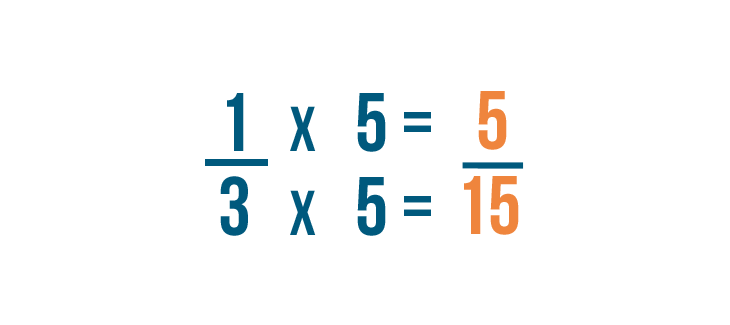
Now let's change the second fraction. To change the denominator to 15 , we'll multiply both numbers by 5 to get 5/15 .

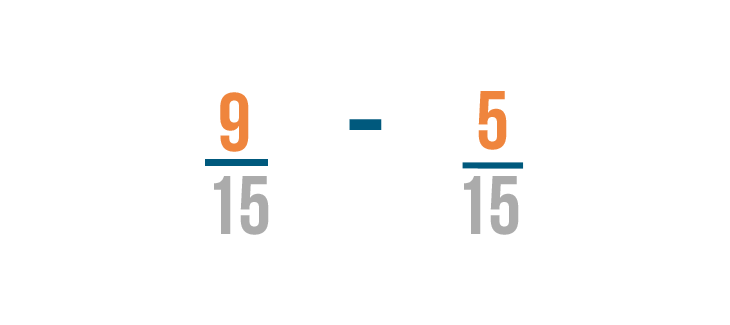
Now that our fractions have the same denominator, we can subtract like we normally do.

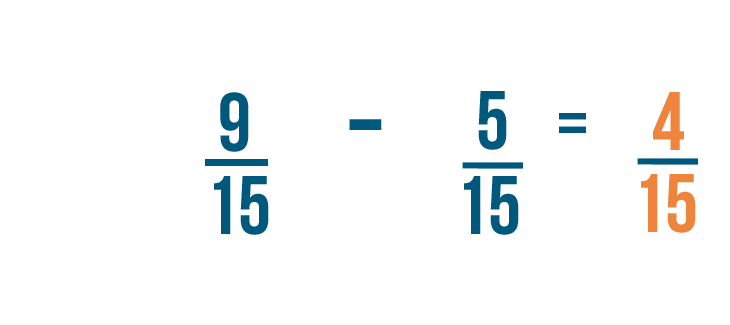
9 minus 5 equals 4 . As always, the denominator stays the same. So 9/15 minus 5/15 equals 4/15 .

Try solving the subtraction problems below.

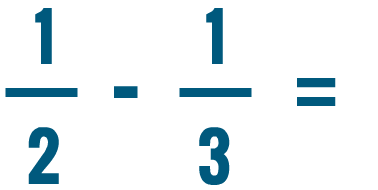
Adding and subtracting mixed numbers

Over the last few pages, you've practiced adding and subtracting different kinds of fractions. But some problems will need one extra step. For example, can you add the fractions below?

In Introduction to Fractions , you learned about mixed numbers . A mixed number has both a fraction and a whole number . An example is 2 1/2 , or two-and-a-half . Another way to write this would be 5/2 , or five-halves . These two numbers look different, but they're actually the same.

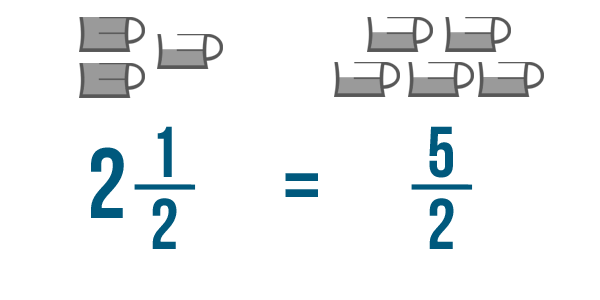
5/2 is an improper fraction . This just means the top number is larger than the bottom number. Even though improper fractions look strange, you can add and subtract them just like normal fractions. Mixed numbers aren't easy to add, so you'll have to convert them into improper fractions first.

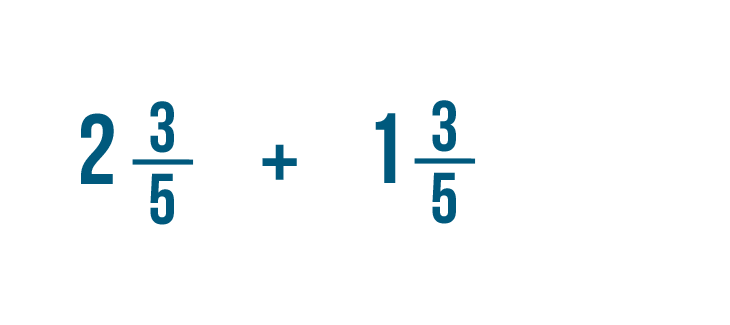
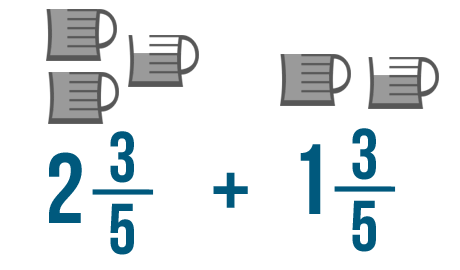
Let's add these two mixed numbers: 2 3/5 and 1 3/5 .

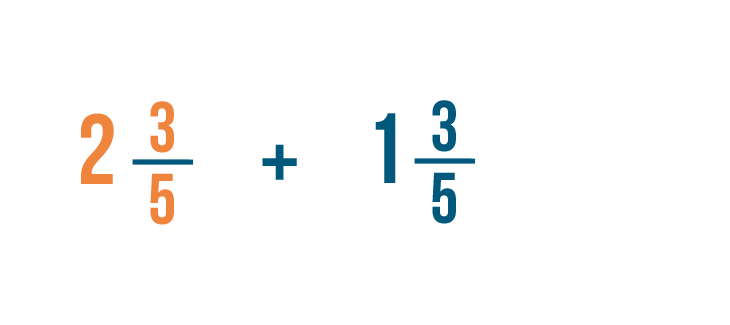
We'll need to convert these mixed numbers to improper fractions. Let's start with 2 3/5 .

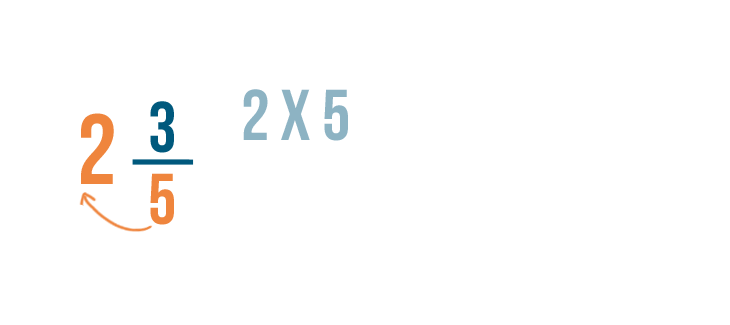
As you learned in Lesson 2 , we'll multiply the whole number, 2 , by the bottom number, 5 .

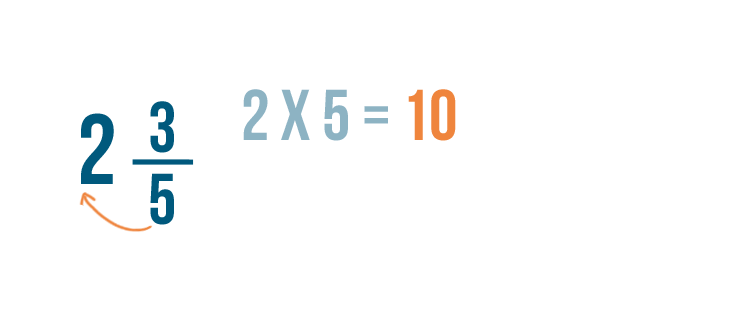
2 times 5 equals 10 .

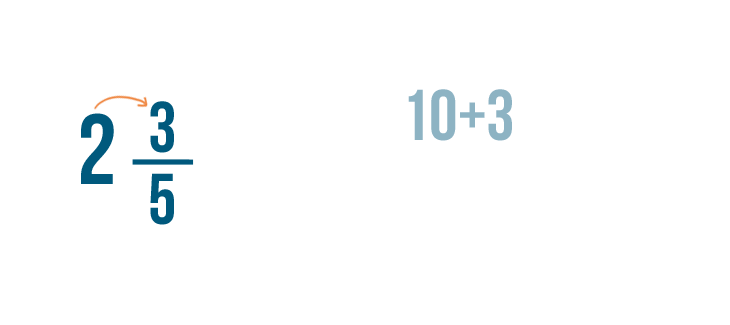
Now, let's add 10 to the numerator, 3 .

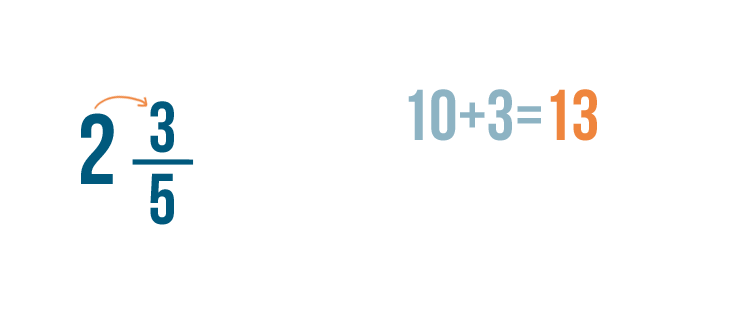
10 + 3 equals 13 .

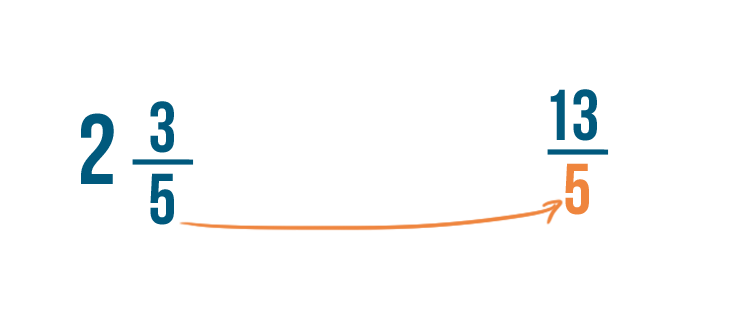
Just like when you add fractions, the denominator stays the same. Our improper fraction is 13/5 .

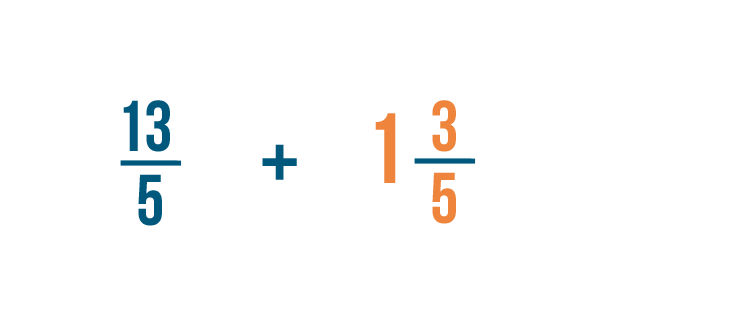
Now we'll need to convert our second mixed number: 1 3/5 .

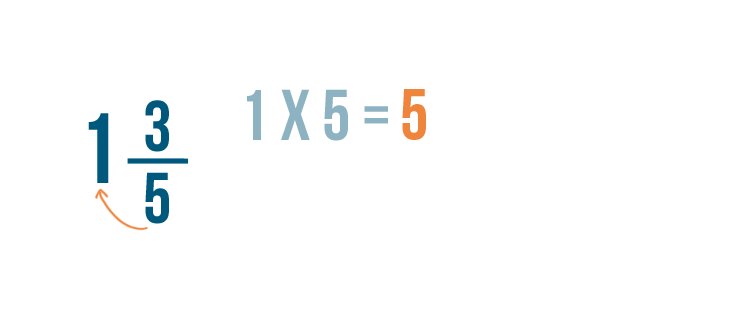
First, we'll multiply the whole number by the denominator. 1 x 5 = 5 .

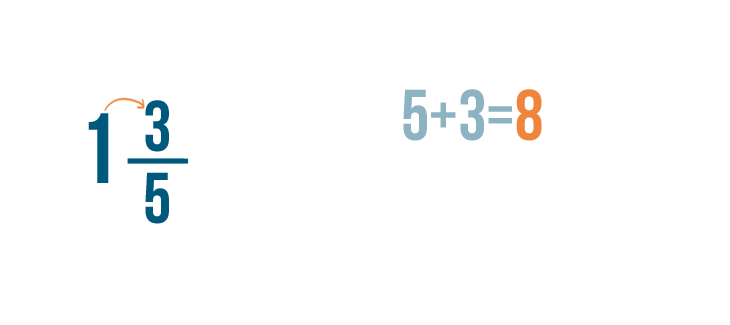
Next, we'll add 5 to the numerators. 5 + 3 = 8 .

Just like last time, the denominator remains the same. So we've changed 1 3/5 to 8/5 .

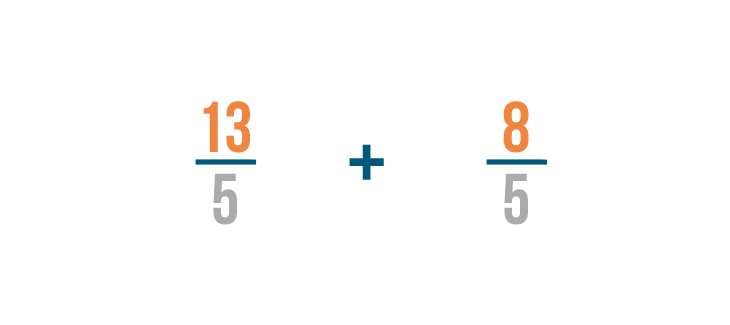
Now that we've changed our mixed numbers to improper fractions, we can add like we normally do.

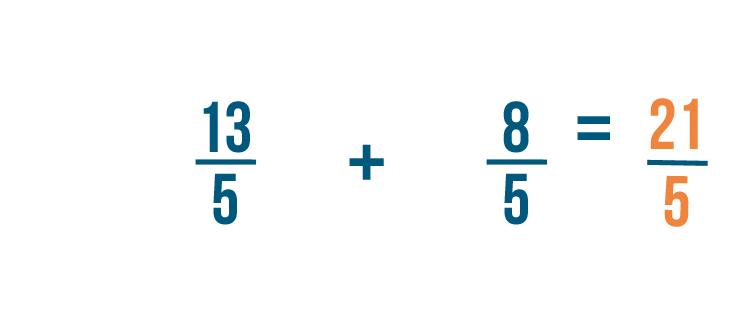
13 plus 8 equals 21 . As usual, the denominator will stay the same. So 13/5 + 8/5 = 21/5 .

Because we started with a mixed number, let's convert this improper fraction back into a mixed number.

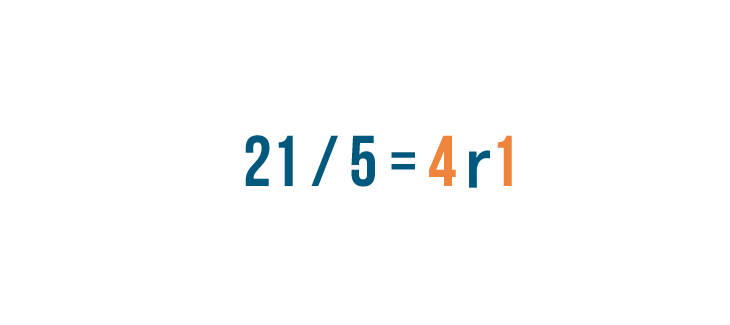
As you learned in the previous lesson , divide the top number by the bottom number. 21 divided by 5 equals 4, with a remainder of 1 .

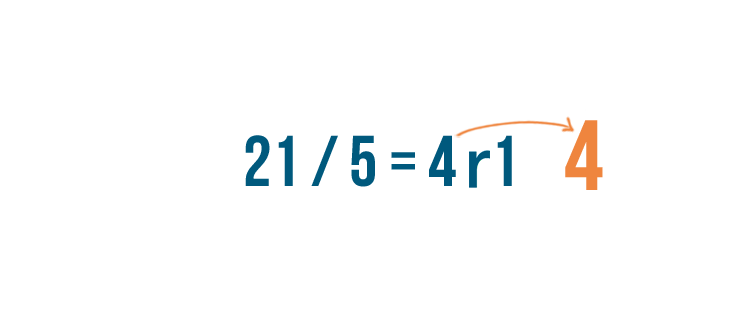
The answer, 4, will become our whole number.

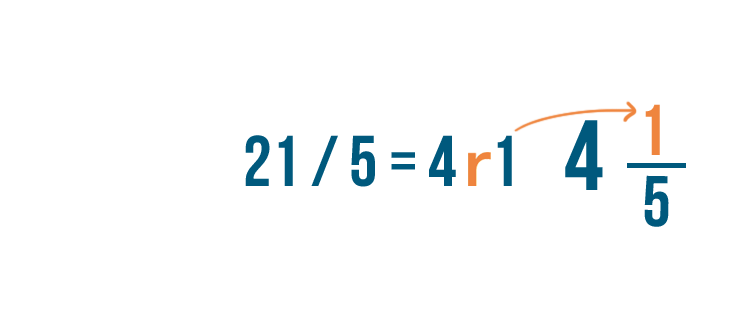
And the remainder , 1, will become the numerator of the fraction.

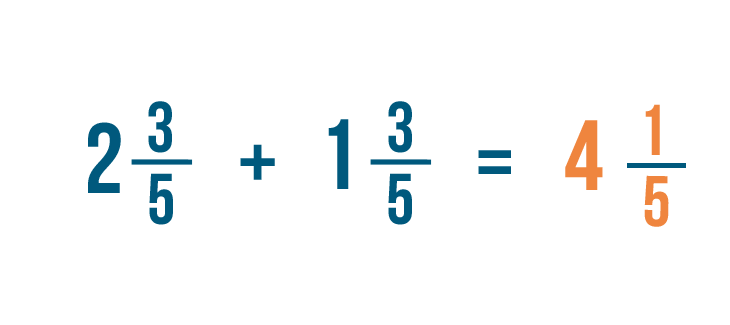
So 2 3/5 + 1 3/5 = 4 1/5 .

/en/fractions/multiplying-and-dividing-fractions/content/

• Number Charts
• Multiplication
• Long division
• Basic operations
• Telling time
• Place value
• Roman numerals
• Fractions & related
• Add, subtract, multiply,   and divide fractions
• Mixed numbers vs. fractions
• Equivalent fractions
• Prime factorization & factors
• Fraction Calculator
• Decimals & Percent
• Add, subtract, multiply,   and divide decimals
• Fractions to decimals
• Percents to decimals
• Percentage of a number
• Percent word problems
• Classify triangles
• Classify quadrilaterals
• Circle worksheets
• Area & perimeter of rectangles
• Area of triangles & polygons
• Coordinate grid, including   moves & reflections
• Volume & surface area
• Pre-algebra
• Square Roots
• Order of operations
• Scientific notation
• Proportions
• Ratio word problems
• Write expressions
• Evaluate expressions
• Simplify expressions
• Linear equations
• Linear inequalities
• Graphing & slope
• Equation calculator
• Equation editor
• Elementary Math Games
• Addition and subtraction
• Math facts practice
• The four operations
• Factoring and number theory
• Geometry topics
• Middle/High School
• Statistics & Graphs
• Probability
• Trigonometry
• Logic and proof
• For all levels
• Favorite math puzzles
• Favorite challenging puzzles
• Math in real world
• Problem solving & projects
• For gifted children
• Math history
• Math games and fun websites
• Interactive math tutorials
• Math help & online tutoring
• Assessment, review & test prep
• Online math curricula

Key to Fractions Workbooks

These workbooks by Key Curriculum Press feature a number of exercises to help your child learn about fractions. Book 1 teaches fraction concepts, Book 2 teaches multiplying and dividing, Book 3 teaches adding and subtracting, and Book 4 teaches mixed numbers. Each book has a practice test at the end.

Adding Fractions

A fraction like 3 4 says we have 3 out of the 4 parts the whole is divided into.

To add fractions there are Three Simple Steps:

• Step 1: Make sure the bottom numbers (the denominators ) are the same
• Step 2: Add the top numbers (the numerators ), put that answer over the denominator
• Step 3: Simplify the fraction (if possible)

Step 1 . The bottom numbers (the denominators) are already the same. Go straight to step 2.

Step 2 . Add the top numbers and put the answer over the same denominator:

1 4 + 1 4 = 1 + 1 4 = 2 4

Step 3 . Simplify the fraction:

In picture form it looks like this:

... and do you see how 2 4 is simpler as 1 2 ? (see Equivalent Fractions .)

Step 1 : The bottom numbers are different. See how the slices are different sizes?

We need to make them the same before we can continue, because we can't add them like that.

The number "6" is twice as big as "3", so to make the bottom numbers the same we can multiply the top and bottom of the first fraction by 2 , like this:

Important: you multiply both top and bottom by the same amount, to keep the value of the fraction the same

Now the fractions have the same bottom number ("6"), and our question looks like this:

The bottom numbers are now the same, so we can go to step 2.

Step 2 : Add the top numbers and put them over the same denominator:

2 6 + 1 6 = 2 + 1 6 = 3 6

Step 3 : Simplify the fraction:

In picture form the whole answer looks like this:

With Pen and Paper

And here is how to do it with a pen and paper (press the play button):

A Rhyme To Help You Remember

♫ "If adding or subtracting is your aim, The bottom numbers must be the same! ♫ "Change the bottom using multiply or divide, But the same to the top must be applied, ♫ "And don't forget to simplify, Before its time to say good bye"

Again, the bottom numbers are different (the slices are different sizes)!

But let us try dividing them into smaller sizes that will each be the same :

The first fraction: by multiplying the top and bottom by 5 we ended up with 5 15 :

The second fraction: by multiplying the top and bottom by 3 we ended up with 3 15 :

The bottom numbers are now the same, so we can go ahead and add the top numbers:

The result is already as simple as it can be, so that is the answer: 

1 3 + 1 5 = 8 15

Making the Denominators the Same

In the previous example how did we know to cut them into 1 / 15 ths to make the denominators the same? We simply multiplied the two denominators together (3 × 5 = 15).

Read about the two main ways to make the denominators the same here:

• Common Denominator Method , or the
• Least Common Denominator Method

They both work, use which one you prefer!

Example: Cupcakes

You want to make and sell cupcakes:

• A friend can supply the ingredients, if you give them 1 / 3 of sales
• And a market stall costs 1 / 4 of sales

How much is that altogether?

We need to add 1 / 3 and 1 / 4

First make the bottom numbers (the denominators) the same.

Multiply top and bottom of 1 / 3 by 4 :

And multiply top and bottom of 1 / 4 by 3 :

Now do the calculations:

Answer: 7 12 of sales go in ingredients and market costs.

Adding Mixed Fractions

We have a special (more advanced) page on Adding Mixed Fractions .

Fraction Word Problems (Grade 5)

These lessons, with videos, examples and solutions help Grade 5 students learn to solve word problems involving addition and subtraction of fractions referring to the same whole, including cases of unlike denominators, e.g., by using visual fraction models or equations to represent the problem. Use benchmark fractions and number sense of fractions to estimate mentally and assess the reasonableness of answers.

Related Pages Common Core for Grade 5 More Lessons for Grade 5

For example, recognize an incorrect result 2/5 + 1/2 = 3/7, by observing that 3/7 < 1/2.

Common Core: 5.NF.2

Suggested Learning Targets

• I can solve addition and subtraction word problems with fractions.
• I can estimate fractions to make sense of my answer.

Solve Fraction Word Problems with Visual Bar Models

Example: Kayla weighed her Halloween treats. She counted 1/4 of a pound of lollipops and 2/7 of a pound of gobstoppers. She also counted 1/3 of a pound of mints. How many pounds of candy did Kayla have altogether?

Add mixed numbers word problems

Example: While gardening, Jan spend 1 3/4 hours planting and 2 1/8 hours trimming. What was the total hours worked by Jan in her garden?

Solve word problems involving addition of fractions - unlike denominators

Example: Matthew ran 1/6 of a mile then took a break before running another 3/4 of a mile. How far did Matthew run in all?

Subtracting Fractions From Whole Numbers Solve a word problem using bar models.

Example: A craft store has a 9-yard spool of ribbon. In the morning, a customer buys 1/5 yard of ribbon from the spool. In the afternoon, another customer buys 7/10 yard of ribbon from the spool. How much ribbon is left?

Adding and subtracting unlike fractions word problems

• Drew and Maddy were filling the class raised garden bed with soil. Drew shoveled in 1/3 of a cubic yard, and Maddy shoveled in 1/2 of a cubic yard. How much soil did they put into the garden bed altogether?
• Caden invited Owen over to his house. Caden shared his chocolate stash from last Halloween. He still had 4/5 of a pound of chocolate. Caden asked Owen how much chocolate he would like. Owen said that he would like 1/3 of a pound of chocolate. How much chocolate does Caden have left?

Adding and subtracting mixed numbers word problems

• Jaida went gold panning and found 1 1/5 pounds of gold. The next day she found 3 1/4 pound more. How much total gold did Jaida find?
• Jonathan collected 4 1/2 kilograms of filberts. He gave 2 3/4 kilograms to his friend. How many kilograms of filberts does Jonathan have now?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Adding Fractions Practice Questions

Click here for questions, click here for answers.

Addition, Adding

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

• International
• Schools directory
• Resources Jobs Schools directory News Search

Adding and Subtracting Fraction Word Problems

Subject: Mathematics

Age range: 7-11

Resource type: Worksheet/Activity

Last updated

16 June 2015

• Share through email
• Share through twitter
• Share through linkedin
• Share through facebook
• Share through pinterest

Creative Commons "Sharealike"

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

Perfect for my year 7. Thank you for sharing.

Empty reply does not make any sense for the end user

excellent - just what I was looking for

roger_matthews

Helpful sheet for practicing wordy fraction questions. Answers can sometimes be simplified further.

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource:

• Home   |  
• About   |  
• Contact Us   |  
• Privacy   |  
• Newsletter   |  
• Shop   |  
• 🔍 Search Site
• Easter Color By Number Sheets
• Printable Easter Dot to Dot
• Easter Worksheets for kids
• Kindergarten
• All Generated Sheets
• Place Value Generated Sheets
• Addition Generated Sheets
• Subtraction Generated Sheets
• Multiplication Generated Sheets
• Division Generated Sheets
• Money Generated Sheets
• Negative Numbers Generated Sheets
• Fraction Generated Sheets
• Place Value Zones
• Number Bonds
• Addition & Subtraction
• Times Tables
• Fraction & Percent Zones
• All Calculators
• Fraction Calculators
• Percent calculators
• Area & Volume Calculators
• Age Calculator
• Height Calculator
• Roman Numeral Calculator
• Coloring Pages
• Fun Math Sheets
• Math Puzzles
• Mental Math Sheets
• Online Times Tables
• Online Addition & Subtraction
• Math Grab Packs
• All Math Quizzes
• 1st Grade Quizzes
• 2nd Grade Quizzes
• 3rd Grade Quizzes
• 4th Grade Quizzes
• 5th Grade Quizzes
• 6th Grade Math Quizzes
• Place Value
• Rounding Numbers
• Comparing Numbers
• Number Lines
• Prime Numbers
• Negative Numbers
• Roman Numerals
• Subtraction
• Add & Subtract
• Multiplication
• Fraction Worksheets
• Learning Fractions
• Fraction Printables
• Percent Worksheets & Help
• All Geometry
• 2d Shapes Worksheets
• 3d Shapes Worksheets
• Shape Properties
• Geometry Cheat Sheets
• Printable Shapes
• Coordinates
• Measurement
• Math Conversion
• Statistics Worksheets
• Bar Graph Worksheets
• Venn Diagrams
• All Word Problems
• Finding all possibilities
• Logic Problems
• Ratio Word Problems
• All UK Maths Sheets
• Year 1 Maths Worksheets
• Year 2 Maths Worksheets
• Year 3 Maths Worksheets
• Year 4 Maths Worksheets
• Year 5 Maths Worksheets
• Year 6 Maths Worksheets
• All AU Maths Sheets
• Kindergarten Maths Australia
• Year 1 Maths Australia
• Year 2 Maths Australia
• Year 3 Maths Australia
• Year 4 Maths Australia
• Year 5 Maths Australia
• Meet the Sallies
• Certificates

Second Grade Math Worksheets Hub Page

Welcome to our Second Grade Math Worksheets area. Here you will find our selection of free printable 2nd Grade math practice sheets, for your child will enjoy.

Come and take a look at our multiplication pages, or money flashcards. Perhaps you would prefer our telling the time worksheets, or identifying 2d and 3d shapes in the geometry section?

For full functionality of this site it is necessary to enable JavaScript.

Here are the instructions how to enable JavaScript in your web browser .

• This page contains links to other Math webpages where you will find a range of activities and resources.
• If you can't find what you are looking for, try searching the site using the Google search box at the top of each page.

2nd Grade Math Learning

Here are the standards for the end of the year for Second Grade.

• Know and use place value to 3 digits.
• Read, write and compare 3-digit numbers.
• Use place value to mentally add or subtract 1, 10 or 100 from any 3-digit number
• Count and skip-count within 1000 by 2s, 5s, 10s, and 100s
• Learn about odd and even numbers and find odd and even numbers to 20
• Fluently add or subtract within 20 using mental strategies.
• Use addition and subtraction facts within 100 to solve a range of one- and two-step word problems.
• Add up to four 2-digit numbers
• Add and subtract within 1000
• Add with different sets of objecs in equal groups
• Represent arrays and equal groups as repeated addition and then multiplication equations.
• Begin to learn multiplication facts up to 5x5.
• Partition a rectangle into rows and columns of the same size squares
• Partition a rectangle, square or circle into two, three or four equal shares.
• Describe the shares as halves, thirds, quarters or fourths
• Recognize that equal shares of identical whole need not have the same shape.
• Select the appropriate equipment and units for measuring.
• Measure the lengths of objects twice using different units, such as inches and cm.
• Solve measuring problems involving adding and subtracting within 100.
• Tell and write the time to the nearest 5 minutes
• Know the relationships involving time units: seconds, minutes, hours, days, weeks, months, years.
• Solve word problems involving money and use the $ and ¢ symbols appropriately.
• Draw a simple picture graph or bar graph to represent data with up to four categories
• Identify and name a range of 2D and 3D shapes.
• Identify different types of angles and find them on 2D shapes.
• Recognize and draw shapes with specific attributes: number of angles, sides, faces, corners, etc.
• Identify the faces of 3D shapes: squares, triangles, hexagons, rectangles.

Second Grade Math Worksheets

On this page you will find link to our range of math worksheets for 2nd grade.

Quicklinks to 2nd Grade ...

Second Grade Math Quiz

• Place Value & Number Sense

Word Problems Zone

Fractions zone.

• Measurement Zone

Geometry Zone

Data analysis zone.

• Fun Zone: games and puzzles
• Seasonal Math Worksheets

Summer term Math Grab Packs - out now!

Our summer term grab packs are out now.

There is a different grab pack for each grade.

Free to all of our newsletter subscribers!

• Summer term Math Grab Packs

Place Value & Number Sense Zone

Second grade place value charts.

Here you will find a range of Free Printable Number Charts for 1st and 2nd Grade.

These printable charts will help your child learn to read and write numbers.

Some of the charts are partially filled to help your child learn their place value.

Using these sheets will help your child to:

• learn to count in tens and ones;
• learn to read and write numbers.
• Printable Number Charts 0-99
• Hundred Number Charts (100 Squares)
• Number Grid up to 200
• Number Grid up to 300

Place Value & Number Sense Worksheets

Below are our selection of Place Value, Ordering and Rounding Worksheets

Using these second grade math worksheets will help your child to:

• learn to count by hundreds, tens, fives, twos and ones;
• learn their place value to Hundreds;
• order numbers to 999.
• recognise odd and even numbers up to 20
• 2nd Grade Place Value Models and Representations
• Second Grade Place Value Worksheets 3 Digits

This page will open in our sister-site 2nd-grade-math-salamanders.com in a new browser window.

• Count to 1000 by Ones
• 2nd Grade Counting Worksheets 1s 2s 5s 10s 100s
• Odd Numbers and Even Numbers Worksheets and Support
• Roman Numerals worksheets

Ordering and Rounding Worksheets (3-digits)

Once your child is confident with their place value to hundreds, they can start learning about ordering and rounding numbers.

The graded worksheets here will help your child learn to compare numbers to 999, and round numbers to the nearest 10.

• Ordering Numbers Worksheets up to 3-Digits
• Rounding to the nearest 10 Worksheets

Second Grade Number Line Worksheets

The following webpages involve correctly placing numbers on a number line.

• count by 1s 2s 5s 10s 50s and 100s;
• position numbers on a number line;
• understand place value up to 3 digits.
• Number lines up to 100 (easier)
• Number Line Worksheets 3 Digits

Top of Page

Second Grade Mental Math Zone

Here you will find a range of printable mental math 2nd grade sheets for your child to enjoy.

Each quiz tests the children on a range of math topics from number facts and mental arithmetic to geometry, fraction and measures questions.

A great way to revise topics, or use as a weekly math test or math quiz!

Using the link below will open the 2nd Grade Math Salamanders website in a new browser window.

• Second Grade Mental Math Worksheets

Addition Worksheets 2nd Grade

• learn their addition facts to 20+20
• learn how to solve addition sums where one of the addends is missing, but the total is given;
• learn to add numbers to 999 in columns.
• Number Bonds to 20
• Adding on a Number Line Worksheets
• Adding tens

This link will open our 2nd-grade-math-salamanders site in a new window.

• Add 1, 10 or 100 Worksheets
• Math Addition Facts to 20
• 3-Digit Column Addition Worksheets

These sheets involve solving a range of addition word problems within 100.

• Addition Word Problems (2nd grade)

Subtraction Worksheets 2nd Grade

The following worksheets involve using the Second Grade Math skills of subtracting numbers, and solving subtraction problems.

• know their subtraction facts to 20;
• know how addition and subtraction are related to each other;
• learn to do 3 digit column subtraction.
• Subtracting on a Number Line Worksheets
• Subtract 1, 10 or 100 Worksheets
• Subtraction Facts to 20 Worksheets
• 3 Digit Subtraction Worksheets
• Subtraction Word Problems 2nd grade

Addition & Subtraction Worksheets

You can create your own addition and subtraction worksheets with our random generator.

All you need to do is to set your number size and let the generator do the rest!

• Number Line Addition and Subtraction
• Add and Subtract Within 20 Worksheets
• Addition Subtraction Fact Worksheets (randomly generated)
• 3 Digit Addition and Subtraction Worksheets
• 2nd Grade Addition and Subtraction Word Problems

Multiplication Worksheets 2nd Grade

The following worksheets involve using the 2nd Grade Math skills of multiplying, and solving multiplication problems.

• learn their multiplication tables up to 5 x 5;
• understand multiplication as repeated addition;
• learn how multiplication and division are related to each other.

Online Times Table Practice

• Times Tables Practice Zone
• Understanding Multiplication Worksheets

Multiplication Worksheets to 5x5

• Multiplication to 5x5 Worksheets

Multiplication Word Problems

• Multiplication Word Problems 2nd Grade

Randomly Generated Multiplication Worksheets

• Times Tables Worksheets (randomly generated)

Division Worksheets 2nd Grade

The following worksheets involve using the 2nd Grade Math skills of dividing, and solving division problems.

Using these second grade math worksheets will help your child learn to:

• understand division as repeated subtraction or sharing;
• understand different models of division;
• Second Grade Division Worksheets
• Division Facts Worksheets (randomly generated)

Here are a range of problems solving sheets for 2nd graders. Most of the sheets contain 'real-life' problems related to animal facts.

Using the sheets will help your child to:

• apply their addition, subtraction, and multiplication skills;
• apply their knowledge of rounding and place value;
• solve a range of 'real life' problems.

These sheets involve solving one or two more challenging longer problems. This link opens in a new tab.

• Second Grade Math Problems

These sheets involve solving many 'real-life' problems involving data.

• 2nd Grade Math Word Problems
• Addition Word Problems 2nd grade

These sheets involve solving a range of subtraction word problems up to 100.

These sheets involve solving a range of multiplication problems.

Second Grade Fraction Worksheets

• understand what a half is;
• shade in half of a shape;
• find different numbers involving 'halves' on a number line;
• find half of different numbers up to 20.
• Fraction Math Worksheets - Understanding a half
• Fraction Riddles for kids (easier)
• Second Grade Geometry Worksheets

At a Second Grade level, children are introduced to a wider range of 2d and 3d shapes, and start to learn to reflect, flip and rotate shapes.

They are able to classify and sort two-dimensional shapes using different criteria, and they learn the properties of three-dimensional shapes.

The following worksheets will help your child to:

• Identify and name a range of 2d and 3d shapes;
• Draw 2d shapes;
• Know some of the properties of 2d shapes.

Symmetry Worksheets

• learn how to reflect simple shapes in a horizontal or vertical mirror line;
• learn how to reflect simple shapes in 2 mirror lines.
• Symmetry Worksheets - Block Symmetry

Measurement Zone, including Time & Money

• 2nd Grade Measurement Worksheets

These sheets involve reading scales going up in ones, fives, tens and hundreds to find the length, weight or liquid capacity.

Using these sheets will help children to consolidate their counting as well as learning to read a simple scale.

2nd Grade Money Worksheets

The following worksheets involve counting different amounts of money in pennies, nickels, dimes and quarters.

There is a wider range of free money worksheets at the 2nd Grade Math Salamanders (see below). These sheets will open in a new tab.

• learn the names and values of the US coins;
• learn to count up different amounts of money to $1 in coins.
• learn to count up to $10 in coins and dollar bills.

Money Worksheets

• Money Worksheets for 2nd Grade - Counting money to $1
• Counting Quarters Worksheets
• Free Money Worksheets up to $2
• Printable Money Worksheets up to $10
• Money Worksheets Canada 2nd Grade
• Money Riddles

UK Money Worksheets

• Money Worksheets UK Coins Hub Page

Printable Money Resources

• Printable Money Flashcards
• Kids Counting Money Dominoes

Time Worksheets

Here are our collection of clock worksheets for 2nd grade. These sheets cover telling the time for quarter past and quarter to times.

• read quarter past and quarter to times;
• convert analogue to digital times;
• draw clock hands in the correct place for quarter past and quarter to.
• adding and subtracting hours from different times.
• Clock Worksheets - Quarter Past and Quarter To
• Add and Subtract Time Worksheets
• Tally Chart Worksheets

Here is our selection of tally chart worksheets for 1st and 2nd graders.

These sheets involve counting and recording tallies.

Venn Diagram Worksheets

Here is our selection of venn diagram worksheets for 2nd graders.

These sheets involve sorting and analysing data in venn diagrams.

Using the link below will open the webpage on our 2nd-grade-math-salamanders website in a new browser window.

• Venn Diagram Worksheets 2nd Grade

2nd Grade Line Plots Worksheets

These sheets involve reading and interpreting a range of line plots.

Using the link below will open the 2nd grade Math Salamanders website in a new browser window.

• Line Plots 2nd Grade

2nd Grade Bar Graph Worksheets

These sheets involve reading and interpreting a range of bar graphs and picture graphs with a scale going up in ones or twos.

Draw missing bars on a bar graph to the correct height.

Use the information in a bar graph to add data into a table.

• Bar Graphs 2nd Grade

Fun Zone: Puzzles, Games and Riddles

Second grade math games.

All children like to play Math games, and you will find a good range of 2nd Grade Math Games here for your child to play and enjoy.

The following games involve different Second Grade Math activities which you and your child can enjoy together.

• Math Games Second Grade

Second Grade Math Puzzles

The puzzles will help your child practice and apply their addition, subtraction and multiplication facts as well as developing their thinking and reasoning skills in a fun and engaging way.

The Number Square Puzzles page will open a new browser window which will take you to the 2nd grade math salamanders website.

Using these puzzles will help your child to:

• learn their addition facts to 20+20;
• learn and practice subtraction facts to 20;
• pratice multiplying up to 5x5;
• develop thinking and reasoning skills;
• develop perseverance.
• 2nd Grade Math Puzzles
• Number Square Puzzles 2nd Grade
• Math Puzzles at 2nd Grade Math Salamanders

Here is our collection of Math Quizzes for 2nd grade.

Quizzes are a great way to practise math skills or to asses knowledge.

• Second Grade Math Quiz page

Math Salamanders Second Grade Math Games Ebook

Our Second Grade Math Games Ebook contains all of our fun maths games, complete with instructions and resources.

This ebooklet is available in our store - use the link below to find out more!

• Second Grade Math Games Ebook

Second Grade Seasonal Math Worksheets

We have started creating sets of seasonal worksheets for each grade.

These sheets are great for linking to a particular topic, or doing some math that relates to the time of year.

• Thanksgiving Math Worksheets 2nd Grade
• 2nd Grade Christmas Math Worksheets

Looking for a resource which is not here?

Take a look at our 2nd Grade Math Salamanders website.

On this site you will find a wider selection of 2nd grade math worksheet and free math resources.

• 2nd Grade Math Salamanders Website

How to Print or Save these sheets 🖶

Need help with printing or saving? Follow these 3 steps to get your worksheets printed perfectly!

• How to Print support

Subscribe to Math Salamanders News

Sign up for our newsletter to get free math support delivered to your inbox each month. Plus, get a seasonal math grab pack included for free!

• Newsletter Signup

Return from Second Grade Math Worksheets to Math Salamanders Homepage

Math-Salamanders.com

The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.

We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.

New! Comments

TOP OF PAGE

© 2010-2024 Math Salamanders Limited. All Rights Reserved.

• Privacy Policy
• Copyright Policy

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.8: Solving Equations Using the Subtraction and Addition Properties of Equality

• Last updated
• Save as PDF
• Page ID 41915

• Nancy Ikeda
• Fullerton College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

• Determine whether a number is a solution of an equation

Model the Subtraction Property of Equality

• Solve equations using the Subtraction Property of Equality
• Solve equations using the Addition Property of Equality
• Translate word phrases to algebraic equations
• Translate to an equation and solve

Be Prepared 2.7

Before you get started, take this readiness quiz.

Evaluatex+8whenx=11.Evaluatex+8whenx=11. If you missed this problem, review Example 2.13.

Be Prepared 2.8

Evaluate5x−3whenx=9.Evaluate5x−3whenx=9. If you missed this problem, review Example 2.14.

Be Prepared 2.9

Translate into algebra: the difference of xx and 8.8. If you missed this problem, review Example 2.24.

When some people hear the word algebra , they think of solving equations. The applications of solving equations are limitless and extend to all careers and fields. In this section, we will begin solving equations. We will start by solving basic equations, and then as we proceed through the course we will build up our skills to cover many different forms of equations.

Determine Whether a Number is a Solution of an Equation

Solving an equation is like discovering the answer to a puzzle. An algebraic equation states that two algebraic expressions are equal. To solve an equation is to determine the values of the variable that make the equation a true statement. Any number that makes the equation true is called a solution of the equation. It is the answer to the puzzle!

Solution of an Equation

A solution to an equation is a value of a variable that makes a true statement when substituted into the equation.

The process of finding the solution to an equation is called solving the equation.

To find the solution to an equation means to find the value of the variable that makes the equation true. Can you recognize the solution of x+2=7?x+2=7? If you said 5,5, you’re right! We say 55 is a solution to the equation x+2=7x+2=7 because when we substitute 55 for xx the resulting statement is true.

x+2=75+2=?77=7✓x+2=75+2=?77=7✓

Since 5+2=75+2=7 is a true statement, we know that 55 is indeed a solution to the equation.

The symbol =?=? asks whether the left side of the equation is equal to the right side. Once we know, we can change to an equal sign (=)(=) or not-equal sign (≠).(≠).

Determine whether a number is a solution to an equation.

• Step 1. Substitute the number for the variable in the equation.
• Step 2. Simplify the expressions on both sides of the equation.
• If it is true, the number is a solution.
• If it is not true, the number is not a solution.

Example 2.28

Determine whetherx=5is a solution of6x−17=16.Determine whetherx=5is a solution of6x−17=16.

So x=5x=5 is not a solution to the equation 6x−17=16.6x−17=16.

Try It 2.55

Isx=3a solution of4x−7=16?Isx=3a solution of4x−7=16?

Try It 2.56

Isx=2a solution of6x−2=10?Isx=2a solution of6x−2=10?

Example 2.29

Determine whethery=2is a solution of6y−4=5y−2.Determine whethery=2is a solution of6y−4=5y−2.

Here, the variable appears on both sides of the equation. We must substitute 22 for each y.y.

Since y=2y=2 results in a true equation, we know that 22 is a solution to the equation 6y−4=5y−2.6y−4=5y−2.

Try It 2.57

Isy=3a solution of9y−2=8y+1?Isy=3a solution of9y−2=8y+1?

Try It 2.58

Isy=4a solution of5y−3=3y+5?Isy=4a solution of5y−3=3y+5?

We will use a model to help you understand how the process of solving an equation is like solving a puzzle. An envelope represents the variable – since its contents are unknown – and each counter represents one.

Suppose a desk has an imaginary line dividing it in half. We place three counters and an envelope on the left side of desk, and eight counters on the right side of the desk as in Figure 2.3. Both sides of the desk have the same number of counters, but some counters are hidden in the envelope. Can you tell how many counters are in the envelope?

What steps are you taking in your mind to figure out how many counters are in the envelope? Perhaps you are thinking “I need to remove the 3Figure 2.4 shows this process.

What algebraic equation is modeled by this situation? Each side of the desk represents an expression and the center line takes the place of the equal sign. We will call the contents of the envelope x,x, so the number of counters on the left side of the desk is x+3.x+3. On the right side of the desk are 88 counters. We are told that x+3x+3 is equal to 88 so our equation isx+3=8.x+3=8.

Let’s write algebraically the steps we took to discover how many counters were in the envelope.

Now let’s check our solution. We substitute 55 for xx in the original equation and see if we get a true statement.

Our solution is correct. Five counters in the envelope plus three more equals eight.

Manipulative Mathematics

Example 2.30.

Write an equation modeled by the envelopes and counters, and then solve the equation:

We can see that there is one counter in the envelope. This can be shown algebraically as:

Substitute 11 for xx in the equation to check.

Since x=1x=1 makes the statement true, we know that 11 is indeed a solution.

Try It 2.59

Write the equation modeled by the envelopes and counters, and then solve the equation:

Try It 2.60

Solve Equations Using the Subtraction Property of Equality

Our puzzle has given us an idea of what we need to do to solve an equation. The goal is to isolate the variable by itself on one side of the equations. In the previous examples, we used the Subtraction Property of Equality, which states that when we subtract the same quantity from both sides of an equation, we still have equality.

Subtraction Property of Equality

For any numbers a,b,a,b, and c,c, if

a−c=b−ca−c=b−c

Think about twin brothers Andy and Bobby. They are 1717 years old. How old was Andy 33 years ago? He was 33 years less than 17,17, so his age was 17−3,17−3, or 14.14. What about Bobby’s age 33 years ago? Of course, he was 1414 also. Their ages are equal now, and subtracting the same quantity from both of them resulted in equal ages 33 years ago.

a=ba−3=b−3a=ba−3=b−3

Solve an equation using the Subtraction Property of Equality.

• Step 1. Use the Subtraction Property of Equality to isolate the variable.
• Step 3. Check the solution.

Example 2.31

Solve: x+8=17.x+8=17.

We will use the Subtraction Property of Equality to isolate x.x.

Since x=9x=9 makes x+8=17x+8=17 a true statement, we know 99 is the solution to the equation.

Try It 2.61

x+6=19x+6=19

Try It 2.62

x+9=14x+9=14

Example 2.32

Solve: 100=y+74.100=y+74.

To solve an equation, we must always isolate the variable—it doesn’t matter which side it is on. To isolate y,y, we will subtract 7474 from both sides.

Since y=26y=26 makes 100=y+74100=y+74 a true statement, we have found the solution to this equation.

Try It 2.63

95=y+6795=y+67

Try It 2.64

91=y+4591=y+45

Solve Equations Using the Addition Property of Equality

In all the equations we have solved so far, a number was added to the variable on one side of the equation. We used subtraction to “undo” the addition in order to isolate the variable.

But suppose we have an equation with a number subtracted from the variable, such as x−5=8.x−5=8. We want to isolate the variable, so to “undo” the subtraction we will add the number to both sides.

We use the Addition Property of Equality, which says we can add the same number to both sides of the equation without changing the equality. Notice how it mirrors the Subtraction Property of Equality.

Addition Property of Equality

For any numbers a,ba,b, and cc, if

a+c=b+ca+c=b+c

Remember the 17-year-old17-year-old twins, Andy and Bobby? In ten years, Andy’s age will still equal Bobby’s age. They will both be 27.27.

a=ba+10=b+10a=ba+10=b+10

We can add the same number to both sides and still keep the equality.

Solve an equation using the Addition Property of Equality.

• Step 1. Use the Addition Property of Equality to isolate the variable.

Example 2.33

Solve: x−5=8.x−5=8.

We will use the Addition Property of Equality to isolate the variable.

Try It 2.65

x−9=13x−9=13

Try It 2.66

y−1=3y−1=3

Example 2.34

Solve: 27=a−16.27=a−16.

We will add 1616 to each side to isolate the variable.

The solution to 27=a−1627=a−16 is a=43.a=43.

Try It 2.67

19=a−1819=a−18

Try It 2.68

27=n−1427=n−14

Translate Word Phrases to Algebraic Equations

Remember, an equation has an equal sign between two algebraic expressions. So if we have a sentence that tells us that two phrases are equal, we can translate it into an equation. We look for clue words that mean equals . Some words that translate to the equal sign are:

• is equal to
• is the same as

It may be helpful to put a box around the equals word(s) in the sentence to help you focus separately on each phrase. Then translate each phrase into an expression, and write them on each side of the equal sign.

We will practice translating word sentences into algebraic equations. Some of the sentences will be basic number facts with no variables to solve for. Some sentences will translate into equations with variables. The focus right now is just to translate the words into algebra.

Example 2.35

Translate the sentence into an algebraic equation: The sum of 66 and 99 is 15.15.

The word is tells us the equal sign goes between 9 and 15.

Try It 2.69

Translate the sentence into an algebraic equation:

The sum of 77 and 66 gives 13.13.

Try It 2.70

The sum of 88 and 66 is 14.14.

Example 2.36

Translate the sentence into an algebraic equation: The product of 88 and 77 is 56.56.

The location of the word is tells us that the equal sign goes between 7 and 56.

Try It 2.71

The product of 66 and 99 is 54.54.

Try It 2.72

The product of 2121 and 33 gives 63.63.

Example 2.37

Translate the sentence into an algebraic equation: Twice the difference of xx and 33 gives 18.18.

Try It 2.73

Translate the given sentence into an algebraic equation:

Twice the difference of xx and 55 gives 30.30.

Try It 2.74

Twice the difference of yy and 44 gives 16.16.

Translate to an Equation and Solve

Now let’s practice translating sentences into algebraic equations and then solving them. We will solve the equations by using the Subtraction and Addition Properties of Equality.

Example 2.38

Translate and solve: Three more than xx is equal to 47.47.

So x=44x=44 is the solution.

Try It 2.75

Translate and solve:

Seven more than xx is equal to 37.37.

Try It 2.76

Eleven more than yy is equal to 28.28.

Example 2.39

Translate and solve: The difference of yy and 1414 is 18.18.

So y=32y=32 is the solution.

Try It 2.77

The difference of zz and 1717 is equal to 37.37.

Try It 2.78

The difference of xx and 1919 is equal to 45.45.

ACCESS ADDITIONAL ONLINE RESOURCES

• Solving One Step Equations By Addition and Subtraction

Section 2.3 Exercises

Practice makes perfect.

In the following exercises, determine whether each given value is a solution to the equation.

x+13=21x+13=21

• ⓐ x=8x=8
• ⓑ x=34x=34

y+18=25y+18=25

• ⓐ y=7y=7
• ⓑ y=43y=43

m−4=13m−4=13

• ⓐ m=9m=9
• ⓑ m=17m=17

n−9=6n−9=6

• ⓐ n=3n=3
• ⓑ n=15n=15

3p+6=153p+6=15

• ⓐ p=3p=3
• ⓑ p=7p=7

8q+4=208q+4=20

• ⓐ q=2q=2
• ⓑ q=3q=3

18d−9=2718d−9=27

• ⓐ d=1d=1
• ⓑ d=2d=2

24f−12=6024f−12=60

• ⓐ f=2f=2
• ⓑ f=3f=3

8u−4=4u+408u−4=4u+40

• ⓐ u=3u=3
• ⓑ u=11u=11

7v−3=4v+367v−3=4v+36

• ⓐ v=3v=3
• ⓑ v=11v=11

20h−5=15h+3520h−5=15h+35

• ⓐ h=6h=6
• ⓑ h=8h=8

18 k − 3 = 12 k + 33 18 k − 3 = 12 k + 33

• ⓐ k=1k=1
• ⓑ k=6k=6

In the following exercises, write the equation modeled by the envelopes and counters and then solve using the subtraction property of equality.

Solve Equations using the Subtraction Property of Equality

In the following exercises, solve each equation using the subtraction property of equality.

a + 2 = 18 a + 2 = 18

b + 5 = 13 b + 5 = 13

p + 18 = 23 p + 18 = 23

q + 14 = 31 q + 14 = 31

r + 76 = 100 r + 76 = 100

s + 62 = 95 s + 62 = 95

16 = x + 9 16 = x + 9

17 = y + 6 17 = y + 6

93 = p + 24 93 = p + 24

116 = q + 79 116 = q + 79

465 = d + 398 465 = d + 398

932 = c + 641 932 = c + 641

Solve Equations using the Addition Property of Equality

In the following exercises, solve each equation using the addition property of equality.

y − 3 = 19 y − 3 = 19

x − 4 = 12 x − 4 = 12

u − 6 = 24 u − 6 = 24

v − 7 = 35 v − 7 = 35

f − 55 = 123 f − 55 = 123

g − 39 = 117 g − 39 = 117

19 = n − 13 19 = n − 13

18 = m − 15 18 = m − 15

10 = p − 38 10 = p − 38

18 = q − 72 18 = q − 72

268 = y − 199 268 = y − 199

204 = z − 149 204 = z − 149

Translate Word Phrase to Algebraic Equations

In the following exercises, translate the given sentence into an algebraic equation.

The sum of 88 and 99 is equal to 17.17.

The sum of 77 and 99 is equal to 16.16.

The difference of 2323 and 1919 is equal to 4.4.

The difference of 2929 and 1212 is equal to 17.17.

The product of 33 and 99 is equal to 27.27.

The product of 66 and 88 is equal to 48.48.

The quotient of 5454 and 66 is equal to 9.9.

The quotient of 4242 and 77 is equal to 6.6.

Twice the difference of nn and 1010 gives 52.52.

Twice the difference of mm and 1414 gives 64.64.

The sum of three times yy and 1010 is 100.100.

The sum of eight times xx and 44 is 68.68.

In the following exercises, translate the given sentence into an algebraic equation and then solve it.

Five more than pp is equal to 21.21.

Nine more than qq is equal to 40.40.

The sum of rr and 1818 is 73.73.

The sum of ss and 1313 is 68.68.

The difference of dd and 3030 is equal to 52.52.

The difference of cc and 2525 is equal to 75.75.

1212 less than uu is 89.89.

1919 less than ww is 56.56.

325325 less than cc gives 799.799.

299299 less than dd gives 850.850.

Everyday Math

Insurance Vince’s car insurance has a $500$500 deductible. Find the amount the insurance company will pay, p,p, for an $1800$1800 claim by solving the equation 500+p=1800.500+p=1800.

Insurance Marta’s homeowner’s insurance policy has a $750$750 deductible. The insurance company paid $5800$5800 to repair damages caused by a storm. Find the total cost of the storm damage, d,d, by solving the equation d−750=5800.d−750=5800.

Sale purchase Arthur bought a suit that was on sale for $120$120 off. He paid $340$340 for the suit. Find the original price, p,p, of the suit by solving the equation p−120=340.p−120=340.

Sale purchase Rita bought a sofa that was on sale for $1299.$1299. She paid a total of $1409,$1409, including sales tax. Find the amount of the sales tax, t,t, by solving the equation 1299+t=1409.1299+t=1409.

Writing Exercises

Is x=1x=1 a solution to the equation 8x−2=16−6x?8x−2=16−6x? How do you know?

Write the equation y−5=21y−5=21 in words. Then make up a word problem for this equation.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?

Subtraction Worksheets

Welcome to the Subtraction Worksheets page at Math-Drills.com where you will get less of an experience than our other pages! This page includes Subtraction worksheets on topics such as five minute frenzies, one-, two-, three- and multi-digit subtraction and subtracting across zeros.

Subtraction has been around for several years now... well maybe more than a few, so it's probably a good thing for students to learn. People experience subtraction every minute of their lives from banks and the government taking away your money to the cookies in the jar mysteriously disappearing. With a good knowledge of subtraction, you can understand why your bank account reaches zero and do something to prevent it from happening.

Some students do have difficulty with subtraction, so take it easy on them. Help them to learn their addition facts first. Once they know those, they will need a few more strategies to successfully subtract. Teaching with manipulatives like base ten blocks or cereal or insects in the park can help students gain a deeper understanding of subtraction. The subtracting worksheets on this page are meant to support good teaching practices, so only use them for independent learning if students are practising skills they already know.

We use the words, minuend, subtrahend and difference on this page. Please refer to the following, so you know which word means which part of a subtraction question.

Minuend - Subtrahend = Difference

Most Popular Subtraction Worksheets this Week

Subtraction Facts Tables

Five minute subtraction frenzies are timed practice charts that help students develop subtraction fact recall speed. These charts are similar to the addition and multiplication frenzy charts, but due to the nature of how subtraction works, we could not focus solely on the single digit fact families. For example, you might get questions like 18 - 4 = 14. You also have to be aware that you must subtract the row number from the column number to get a positive number (or zero). Other than that, they should be a nice way to practice some mental subtraction. As with most of these pages, please only use them as a timed activity with students who will experience success. If a student does not have the necessary skills to complete a frenzy in under five minutes, you may need to take a different approach to how you deliver this page. For all others, students should be able to complete this page in under five minutes with a 98% or greater accuracy and improve their time as they get more practice.

• Five Minute Subtraction Frenzies Five Minute Subtraction Frenzy (Minuends 9 to 18; Subtrahends 0 to 9) Five Minute Subtraction Frenzy (Minuends 29 to 38; Subtrahends 10 to 19) Five Minute Subtraction Frenzy (Minuends 41 to 50; Subtrahends 16 to 25)

Most of the subtraction tables in this section are meant to be used as a reference for students learning their subtraction facts. After a while, most students will remember the facts and recall them easily when completing math problems.

• Subtraction Facts Tables 0 to 11 Subtraction Facts 0 to 11 in Grey Subtraction Facts 0 to 11 in Color Subtraction Facts 0 to 11 with Facts Highlighted Subtraction Facts 0 to 11 in Montessori Colors Subtraction Facts 0 to 11 in Montessori Colors with Facts Highlighted
• Subtraction Facts Tables 1 to 12 Subtraction Facts Tables in Gray 1 to 12 Subtraction Facts Tables in Color 1 to 12 Subtraction Facts Tables in Montessori Colors 1 to 12 Subtraction Facts 1 to 12 with Facts Highlighted Subtraction Facts 1 to 12 in Montessori Colors with Facts Highlighted
• Compact Subtraction Facts Tables Compact Subtraction Table (Filled) Compact Subtraction Table (Blank)

Single-Digit Subtraction Facts

Subtracting single-digit facts is a skill that students generally learn after or while they are learning single-digit addition facts. The subtraction worksheets in this section are meant to be used for practice, testing or with teacher guidance. They will not teach students how to subtract or what the connection is between addition and subtraction; for that, students require a teacher or parent.

Some students might find it easier to start with subtraction facts with minuends (the first number) limited to 9 or lower. This way, they don't need to count across 10 eliminating that extra pesky digit... for now.

• Subtracting Single-Digit from Single-Digit Numbers 100 Subtraction Questions with Minuends up to 9 64 Subtraction Questions with Minuends up to 9 25 Subtraction Questions with Minuends up to 9

In relation to addition facts, the following worksheets cover the facts from 0 to 9, and the worksheets after that cover the addition facts from 1 to 9. The minuends are the amounts to be subtracted from, so a minuend of 18 means that both the subtrahend (the amount being subtracted) and the difference will be 9. The worksheets marked with an asterisk (*) include all possible questions in a random order on each version of the worksheet.

• Subtraction Facts from (0 − 0) to (18 − 9) Subtraction Facts from (0 − 0) to (18 − 9) (100* Questions) ✎ Subtraction Facts from (0 − 0) to (18 − 9) (81 Questions) ✎ Subtraction Facts from (0 − 0) to (18 − 9) (64 Questions) ✎ Subtraction Facts from (0 − 0) to (18 − 9) (50 Questions) ✎ Subtraction Facts from (0 − 0) to (18 − 9) (25 Large Print Questions) ✎ Subtraction Facts from (0 − 0) to (18 − 9) (12 Very Large Print Questions) ✎
• Subtraction Facts from (2 − 1) to (18 − 9) (No Zeros) Subtraction Facts from (2 − 1) to (18 − 9) (100 Questions) ✎ Subtraction Facts from (2 − 1) to (18 − 9) (81* Questions) ✎ Subtraction Facts from (2 − 1) to (18 − 9) (64 Questions) ✎ Subtraction Facts from (2 − 1) to (18 − 9) (50 Questions) ✎ Subtraction Facts from (2 − 1) to (18 − 9) (25 Large Print Questions) ✎ Subtraction Facts from (2 − 1) to (18 − 9) (12 Very Large Print Questions) ✎
• Subtraction Facts with Minuends from 10 to 18 100 Subtraction Questions with Minuends from 10 to 18 and All Regrouping (100 Questions) 64 Subtraction Questions with Minuends from 10 to 18 and All Regrouping (64 Questions) 25 Subtraction Questions with Minuends from 10 to 18 and All Regrouping (25 Large Print Questions)

Sometimes students just need to reinforce a single number at a time which is where these worksheets come in. There are three sets of worksheets in this section, each with a different number of questions. The last set is the most interesting as there are no questions repeated. Eleven and Twelve have been included as they are essentially subtracting by 10 and 1 or 2 more.

• Subtracting Individual Focus or Target Facts (50 Questions per Page) Subtracting 0 (50 Questions) ✎ Subtracting 1 (50 Questions) ✎ Subtracting 2 (50 Questions) ✎ Subtracting 3 (50 Questions) ✎ Subtracting 4 (50 Questions) ✎ Subtracting 5 (50 Questions) ✎ Subtracting 6 (50 Questions) ✎ Subtracting 7 (50 Questions) ✎ Subtracting 8 (50 Questions) ✎ Subtracting 9 (50 Questions) ✎ Subtracting 10 (50 Questions) ✎ Subtracting 11 (50 Questions) ✎ Subtracting 12 (50 Questions) ✎
• Subtracting Individual Focus or Target Facts (25 Questions per Page) Subtracting Zero (0) (25 Large Print Questions) ✎ Subtracting One (1) (25 Large Print Questions) ✎ Subtracting Two (2) (25 Large Print Questions) ✎ Subtracting Three (3) (25 Large Print Questions) ✎ Subtracting Four (4) (25 Large Print Questions) ✎ Subtracting Five (5) (25 Large Print Questions) ✎ Subtracting Six (6) (25 Large Print Questions) ✎ Subtracting Seven (7) (25 Large Print Questions) ✎ Subtracting Eight (8) (25 Large Print Questions) ✎ Subtracting Nine (9) (25 Large Print Questions) ✎
• Subtracting Individual Focus or Target Facts with Differences of 0 to 99 (100 Unique Questions per Page) Subtracting One (1) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Two (2) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Three (3) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Four (4) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Five (5) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Six (6) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Seven (7) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Eight (8) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Nine (9) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Ten (10) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Eleven (11) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Twelve (12) with Differences 0 to 99 (100 Unique Questions) ✎
• Horizontally Arranged Subtraction Facts with Minuends to 18 Horizontal Subtraction Facts with Minuends to 18 (100 Questions) ✎ Horizontal Subtraction Facts with Minuends to 18 (50 Questions) ✎ Horizontal Subtraction Facts with Minuends to 18 (25 Questions; Large Print) ✎
• Horizontally Arranged Subtracting 1 to 5 from 1 to 10 Horizontal Subtracting 1 to 5 from 1 to 10 (100 Questions) ✎ Horizontal Subtracting 1 to 5 from 1 to 10 (50 Questions) ✎ Horizontal Subtracting 1 to 5 from 1 to 10 (25 Questions; Large Print) ✎
• Horizontally Arranged Subtracting 1s and 2s from Single-Digit Minuends Horizontal Subtracting Ones from Single-Digit Minuends (25 per page) ✎ Horizontal Subtracting Twos from Single-Digit Minuends (25 per page) ✎
• Horizontally Arranged Subtracting Individual Focus Facts Horizontal Subtracting 0s (100 per page) ✎ Horizontal Subtracting 1s (100 per page) ✎ Horizontal Subtracting 2s (100 per page) ✎ Horizontal Subtracting 3s (100 per page) ✎ Horizontal Subtracting 4s (100 per page) ✎ Horizontal Subtracting 5s (100 per page) ✎ Horizontal Subtracting 6s (100 per page) ✎ Horizontal Subtracting 7s (100 per page) ✎ Horizontal Subtracting 8s (100 per page) ✎ Horizontal Subtracting 9s (100 per page) ✎
• Horizontally Arranged Subtracting Pairs of Individual Focus Facts Horizontal Subtracting 0s and 1s (100 per page) ✎ Horizontal Subtracting 2s and 3s (100 per page) ✎ Horizontal Subtracting 4s and 5s (100 per page) ✎ Horizontal Subtracting 6s and 7s (100 per page) ✎ Horizontal Subtracting 8s and 9s (100 per page) ✎
• Subtracting a Number from Itself Subtracting a Number from Itself (Range 1 to 20)

The make ten subtraction strategy involves "spliting" the subtrahend (amount being subtracted) into two parts. The first part should be the exact amount that will reduce the minuend (the first number) to ten (or multiple of ten as the case may be) and the second part is the leftover amount. The strategy helps students internalize a mental strategy for subtracting across tens. For example, with the question 15 - 9, students first recognize that they need to subtract 5 to get 10, so they split the 9 into 5 and 4. Subtracting 5 from 15 results in 10 and subtracting 4 more results in 6, so 15 - 9 = 6. This strategy can be used any time students need to subtract "over" a multiple of ten and there are many worksheets in this section to practice it. For example, subtracting 84 - 8, students recognize that they must subtract 4 from 84 to get 80 which leaves 4 more to subtract from 80 to get 76.

• Make Ten Strategy Worksheets with 10 and Multiples of 10 Make 10 Subtraction Strategy Make 20 Subtraction Strategy Make 30 Subtraction Strategy Make 40 Subtraction Strategy Make 50 Subtraction Strategy Make 60 Subtraction Strategy Make 70 Subtraction Strategy Make 80 Subtraction Strategy Make 90 Subtraction Strategy Make Multiples of 10 Subtraction Strategy

Long Subtraction Worksheets

Try teaching a mental math strategy for subtraction called counting up. Here is how it is done:

Start with the second number (the subtrahend) and count up by tens until you find the closest value to the first number (the minuend). Keep track of how many tens you counted. Add or subtract a single digit number to get the minuend exactly then adjust the tens by that amount. For the question, 84 - 35, start at 35, and count, 45, 55, 65, 75, 85 (five tens) and one down to get 84. Five tens minus one is 49. For the question 65 - 22, start at 22 and count, 32, 42, 52, 62 (four tens) and three up to get 65. Four tens and three is 43. The previous examples used two-digit numbers, but the strategy can swiftly be modified for larger numbers. How far can your students go with it? Here is an example with three-digit numbers:

Let's use the question 927 - 648. First, count up by hundreds to 948 (that's 300). Then count down by tens to 928 (that's -20). Finally count down by ones to 927 (that's one). 300 - 20 - 1 = 279. That's almost easier than adding!

The multi-digit or long subtraction worksheets in the first part of this section are classic long subtraction worksheets with randomly generated numbers. Regrouping should be necessary about half of the time. Versions with ALL regrouping and NO regrouping follow. If you would like to see numbers with thousands separators, look a little further down and choose the appropriate version for your location.

• Subtracting up to 3-Digit Numbers with Some Regrouping Subtracting 2-Digit from 2-Digit Numbers with Some Regrouping ✎ Subtracting 2-Digit from 3-Digit Numbers with Some Regrouping ✎ Subtracting 3-Digit from 3-Digit Numbers with Some Regrouping ✎ 3-Digit Expanded Form Subtraction Subtracting 3-Digit from 4-Digit Numbers with Some Regrouping ✎
• Subtracting up to 3-Digit Numbers with Some Regrouping (Large Print) Subtracting 1-Digit from 2-Digit Numbers with Some Regrouping ( Large Print ) ✎ Subtracting 2-Digit from 2-Digit Numbers with Some Regrouping ( Large Print ) ✎ Subtracting 1-Digit from 3-Digit Numbers with Some Regrouping ( Large Print ) ✎ Subtracting 2-Digit from 3-Digit Numbers with Some Regrouping ( Large Print ) ✎ Subtracting 3-Digit from 3-Digit Numbers with Some Regrouping ( Large Print ) ✎ Subtracting 1- to 3-Digit from 1- to 3-Digit Numbers with Some Regrouping ( Large Print ) ✎ Subtracting 3-Digit from 4-Digit Numbers with Some Regrouping ( Large Print ) ✎
• Subtracting 4- to 9-Digit Numbers with Some Regrouping Subtracting 4-Digit from 4-Digit Numbers with Some Regrouping ✎ Subtracting 4-Digit from 5-Digit Numbers with Some Regrouping ✎ Subtracting 5-Digit from 5-Digit Numbers with Some Regrouping ✎ Subtracting 5-Digit from 6-Digit Numbers with Some Regrouping ✎ Subtracting 6-Digit from 6-Digit Numbers with Some Regrouping ✎ Subtracting 6-Digit from 7-Digit Numbers with Some Regrouping ✎ Subtracting 7-Digit from 7-Digit Numbers with Some Regrouping ✎ Subtracting 7-Digit from 8-Digit Numbers with Some Regrouping ✎ Subtracting 8-Digit from 8-Digit Numbers with Some Regrouping ✎ Subtracting 8-Digit from 9-Digit Numbers with Some Regrouping ✎ Subtracting 9-Digit from 9-Digit Numbers with Some Regrouping ✎
• Subtracting 4- to 6-Digit Numbers with Some Regrouping (Large Print) Subtracting 4-Digit from 4-Digit Numbers with Some Regrouping ( Large Print ) ✎ Subtracting 4-Digit from 5-Digit Numbers with Some Regrouping ( Large Print ) ✎ Subtracting 5-Digit from 5-Digit Numbers with Some Regrouping ( Large Print ) ✎ Subtracting 5-Digit from 6-Digit Numbers with Some Regrouping ( Large Print ) ✎ Subtracting 6-Digit from 6-Digit Numbers with Some Regrouping ( Large Print ) ✎

For students who need a little extra help with lining things up, these long subtraction worksheets have the digits spaced farther apart on a grid. The answer keys also show the carrying values to help diagnose where things went wrong (but hopefully they won't).

• Long Subtraction Worksheets with Grid Support 2-Digit Minus 2-Digit Subtraction With Grid Support 3-Digit Minus 2-Digit Subtraction With Grid Support 3-Digit Minus 3-Digit Subtraction With Grid Support 4-Digit Minus 3-Digit Subtraction With Grid Support 4-Digit Minus 4-Digit Subtraction With Grid Support 5-Digit Minus 4-Digit Subtraction With Grid Support 5-Digit Minus 5-Digit Subtraction With Grid Support 6-Digit Minus 5-Digit Subtraction With Grid Support 6-Digit Minus 6-Digit Subtraction With Grid Support 2- to 4-Digit Minus 2- to 4-Digit Subtraction With Grid Support 3- to 6-Digit Minus 3- to 6-Digit Subtraction With Grid Support

The next long subtraction worksheets include questions that require regrouping at every step. They can be frustrating and difficult for students who are not familiar with the concept of subtraction. Try showing them with base ten blocks how regrouping works.

• Subtracting up to 3-Digit Numbers with All Regrouping Subtracting 1-Digit Numbers with ALL Regrouping ✎ Subtracting 2-Digit Numbers with ALL Regrouping ✎ Subtracting 3-Digit Numbers with ALL Regrouping ✎
• Subtracting up to 3-Digit Numbers with All Regrouping (Large Print) Subtracting 1-Digit Numbers with ALL Regrouping ( Large Print ) ✎ Subtracting 2-Digit Numbers with ALL Regrouping ( Large Print ) ✎ Subtracting 3-Digit Numbers with ALL Regrouping ( Large Print ) ✎
• Subtracting 4- to 8-Digit Numbers with All Regrouping Subtracting 4-Digit Numbers with ALL Regrouping ✎ Subtracting 5-Digit Numbers with ALL Regrouping ✎ Subtracting 6-Digit Numbers with ALL Regrouping ✎ Subtracting 7-Digit Numbers with ALL Regrouping ✎ Subtracting 8-Digit Numbers with ALL Regrouping ✎
• Subtracting 4- to 6-Digit Numbers with All Regrouping (Large Print) Subtracting 4-Digit Numbers with ALL Regrouping ( Large Print ) ✎ Subtracting 5-Digit Numbers with ALL Regrouping ( Large Print ) ✎ Subtracting 6-Digit Numbers with ALL Regrouping ( Large Print ) ✎

Some students require a little extra help when learning to subtract large numbers. These subtraction worksheets include questions where the regrouping step has been eliminated. This might help students learn a subtraction algorithm before learning about regrouping.

• Subtracting up to 3-Digit Numbers with No Regrouping Subtracting 2-Digit from 2-Digit Numbers with NO Regrouping ✎ Subtracting 2-Digit from 3-Digit Numbers with NO Regrouping ✎ Subtracting 3-Digit from 3-Digit Numbers with NO Regrouping ✎ Subtracting 2-Digit from 4-Digit Numbers with NO Regrouping ✎ Subtracting 3-Digit from 4-Digit Numbers with NO Regrouping ✎
• Subtracting up to 3-Digit Numbers with No Regrouping (Large Print) Subtracting 2-Digit from 2-Digit Numbers with NO Regrouping ( Large Print ) ✎ Subtracting 2-Digit from 3-Digit Numbers with NO Regrouping ( Large Print ) ✎ Subtracting 3-Digit from 3-Digit Numbers with NO Regrouping ( Large Print ) ✎ Subtracting 2-Digit from 4-Digit Numbers with NO Regrouping ( Large Print ) ✎ Subtracting 3-Digit from 4-Digit Numbers with NO Regrouping ( Large Print ) ✎
• Subtracting 4- to 9-Digit Numbers with No Regrouping Subtracting 4-Digit from 4-Digit Numbers with NO Regrouping ✎ Subtracting 5-Digit from 5-Digit Numbers with NO Regrouping ✎ Subtracting 6-Digit from 6-Digit Numbers with NO Regrouping ✎ Subtracting 7-Digit from 7-Digit Numbers with NO Regrouping ✎ Subtracting 8-Digit from 8-Digit Numbers with NO Regrouping ✎ Subtracting 9-Digit from 9-Digit Numbers with NO Regrouping ✎
• Subtracting 4- to 6-Digit Numbers with No Regrouping (Large Print) Subtracting 4-Digit from 4-Digit Numbers with NO Regrouping ( Large Print ) ✎ Subtracting 5-Digit from 5-Digit Numbers with NO Regrouping ( Large Print ) ✎ Subtracting 6-Digit from 6-Digit Numbers with NO Regrouping ( Large Print ) ✎

Why horizontal subtraction worksheets? Students can show their understanding of place value and number sense if they do not already have the numbers lined up. Vertical subtraction is often learned based on a student's understanding of single-digit subtraction, but looking at the whole number is lost in the algorithm.

• Horizontally Arranged 2-Digit Minus 1-Digit Questions 2-digit Minus 1-Digit Horizontal Subtraction (100 Questions) ✎ 2-digit Minus 1-Digit Horizontal Subtraction (50 Questions) ✎ 2-digit Minus 1-Digit Horizontal Subtraction (25 Questions; Large Print) ✎
• Horizontally Arranged 2-Digit Minus 2-Digit Questions 2-digit Minus 2-Digit Horizontal Subtraction (100 Questions) ✎ 2-digit Minus 2-Digit Horizontal Subtraction (50 Questions) ✎ 2-digit Minus 2-Digit Horizontal Subtraction (25 Questions; Large Print) ✎
• Horizontally Arranged 3-Digit Minus 1-Digit Questions 3-digit Minus 1-Digit Horizontal Subtraction (100 Questions) ✎ 3-digit Minus 1-Digit Horizontal Subtraction (50 Questions) ✎ 3-digit Minus 1-Digit Horizontal Subtraction (25 Questions; Large Print) ✎
• Horizontally Arranged 3-Digit Minus 2-Digit Questions 3-digit Minus 2-Digit Horizontal Subtraction (50 Questions) ✎ 3-digit Minus 2-Digit Horizontal Subtraction (25 Questions; Large Print) ✎ 3-Digit Minus 2-Digit Horizontal Subtraction ( All Regrouping ; 100 Questions)
• Horizontally Arranged 3-Digit Minus 3-Digit Questions 3-Digit Minus 3-Digit Horizontal Subtraction (50 Questions) ✎ 3-Digit Minus 3-Digit Horizontal Subtraction (25 Questions; Large Print) ✎
• Horizontally Arranged Various-Digit Minus Various-Digit Questions Various-Digit Minus Various-Digit Horizontal Subtraction (50 Questions) ✎ Various-Digit Minus Various-Digit Horizontal Subtraction (25 Questions; Large Print) ✎

Many students in English-speaking countries are used to seeing numbers with comma-separated thousands.

• Long Subtraction Worksheets with Comma Separated Thousands Subtracting 2-Digit from 4-Digit Numbers (Comma Separated) ✎ Subtracting 3-Digit from 4-Digit Numbers (Comma Separated) ✎ Subtracting 4-Digit from 4-Digit Numbers (Comma Separated) ✎ Subtracting 2-Digit from 5-Digit Numbers (Comma Separated) ✎ Subtracting 3-Digit from 5-Digit Numbers (Comma Separated) ✎ Subtracting 4-Digit from 5-Digit Numbers (Comma Separated) ✎ Subtracting 5-Digit from 5-Digit Numbers (Comma Separated) ✎ Mixture of Multi-Digit Subtraction from 2 to 4 digits (Comma Separated) ✎ Mixture of Multi-Digit Subtraction from 2 to 5 digits (Comma Separated) ✎
• Long Subtraction Worksheets with Comma Separated Thousands and All Regrouping Subtracting 4-Digit Numbers with ALL Regrouping (Comma Separated) ✎ Subtracting 5-Digit Numbers with ALL Regrouping (Comma Separated) ✎ Subtracting 6-Digit Numbers with ALL Regrouping (Comma Separated) ✎ Subtracting 7-Digit Numbers with ALL Regrouping (Comma Separated) ✎ Subtracting 8-Digit Numbers with ALL Regrouping (Comma Separated) ✎
• Long Subtraction Worksheets with Comma Separated Thousands and No Regrouping Subtracting 5-Digit from 5-Digit Numbers with NO Regrouping (Comma Separated) ✎ Subtracting 6-Digit from 6-Digit Numbers with NO Regrouping (Comma Separated) ✎ Subtracting 7-Digit from 7-Digit Numbers with NO Regrouping (Comma Separated) ✎ Subtracting 8-Digit from 8-Digit Numbers with NO Regrouping (Comma Separated) ✎ Subtracting 9-Digit from 9-Digit Numbers with NO Regrouping (Comma Separated) ✎

Space-separated thousands are becoming more widely used, including in the United States. Canadian students have used both comma separated and space separated thousands for many years.

• Long Subtraction Worksheets with Space Separated Thousands Subtracting 2-Digit from 4-Digit Numbers (Space Separated) ✎ Subtracting 3-Digit from 4-Digit Numbers (Space Separated) ✎ Subtracting 4-Digit from 4-Digit Numbers (Space Separated) ✎ Subtracting 2-Digit from 5-Digit Numbers (Space Separated) ✎ Subtracting 3-Digit from 5-Digit Numbers (Space Separated) ✎ Subtracting 4-Digit from 5-Digit Numbers (Space Separated) ✎ Subtracting 5-Digit from 5-Digit Numbers (Space Separated) ✎ Mixture of Multi-Digit Subtraction from 2 to 4 digits (Space Separated) ✎ Mixture of Multi-Digit Subtraction from 2 to 5 digits (Space Separated) ✎
• Long Subtraction Worksheets with Space Separated Thousands and All Regrouping Subtracting 4-Digit Numbers with ALL Regrouping (Space Separated) ✎ Subtracting 5-Digit Numbers with ALL Regrouping (Space Separated) ✎ Subtracting 6-Digit Numbers with ALL Regrouping (Space Separated) ✎ Subtracting 7-Digit Numbers with ALL Regrouping (Space Separated) ✎ Subtracting 8-Digit Numbers with ALL Regrouping (Space Separated) ✎
• Long Subtraction Worksheets with Space Separated Thousands and No Regrouping Subtracting 5-Digit from 5-Digit Numbers with NO Regrouping (Space Separated) ✎ Subtracting 6-Digit from 6-Digit Numbers with NO Regrouping (Space Separated) ✎ Subtracting 7-Digit from 7-Digit Numbers with NO Regrouping (Space Separated) ✎ Subtracting 8-Digit from 8-Digit Numbers with NO Regrouping (Space Separated) ✎ Subtracting 9-Digit from 9-Digit Numbers with NO Regrouping (Space Separated) ✎

Even though period separated thousands are not common in the English-speaking world, we provide these for our friends in other countries who may find them useful.

• Long Subtraction Worksheets with Period Separated Thousands Subtracting 2-Digit from 4-Digit Numbers (Period Separated) ✎ Subtracting 3-Digit from 4-Digit Numbers (Period Separated) ✎ Subtracting 4-Digit from 4-Digit Numbers (Period Separated) ✎ Subtracting 2-Digit from 5-Digit Numbers (Period Separated) ✎ Subtracting 3-Digit from 5-Digit Numbers (Period Separated) ✎ Subtracting 4-Digit from 5-Digit Numbers (Period Separated) ✎ Subtracting 5-Digit from 5-Digit Numbers (Period Separated) ✎ Mixture of Multi-Digit Subtraction from 2 to 4 digits (Period Separated) ✎ Mixture of Multi-Digit Subtraction from 2 to 5 digits (Period Separated) ✎
• Long Subtraction Worksheets with Period Separated Thousands and All Regrouping Subtracting 4-Digit Numbers with ALL Regrouping (Period Separated) ✎ Subtracting 5-Digit Numbers with ALL Regrouping (Period Separated) ✎ Subtracting 6-Digit Numbers with ALL Regrouping (Period Separated) ✎ Subtracting 7-Digit Numbers with ALL Regrouping (Period Separated) ✎ Subtracting 8-Digit Numbers with ALL Regrouping (Period Separated) ✎
• Long Subtraction Worksheets with Period Separated Thousands and No Regrouping Subtracting 5-Digit from 5-Digit Numbers with NO Regrouping (Period Separated) ✎ Subtracting 6-Digit from 6-Digit Numbers with NO Regrouping (Period Separated) ✎ Subtracting 7-Digit from 7-Digit Numbers with NO Regrouping (Period Separated) ✎ Subtracting 8-Digit from 8-Digit Numbers with NO Regrouping (Period Separated) ✎ Subtracting 9-Digit from 9-Digit Numbers with NO Regrouping (Period Separated) ✎

Various Other Long Subtraction Worksheets

Generally, a student would not regroup to determine the complements of 10, 100, 1000, etc. One strategy that could be used is as follows: working from left to right, a student would take each digit in the subtrahend and figure out its nines complement. If the digit was 3, for example, the nines complement of 3 is 6. For the last digit (ones), the student would use the tens complement. For example, a typical question is 1000 - 456. The nines complement of 4 is 5, the nines complement of 5 is 4 and the tens complement of 6 is 4. Putting it all together, the student would get 5 4 4 or 544 = 1000 - 456.

• Calculating Complements of Powers of Ten (Subtracting Across Zeros) Complements of 10 Complements of 100 Complements of 1000 Complements of 10000 Complements of 100 and 1000 Complements of 1000 and 10000 Complements of 100, 1000 and 10000

A similar strategy is employed with the next worksheets except students must adapt to calculating the largest place value number.

• Calculating Complements of Multiples of Powers of Ten (Subtracting Across Zeros) Subtracting from multiples of 10 Subtracting from multiples of 100 Subtracting from multiples of 1000 Subtracting from multiples of 10000 Subtracting from a mixture of multiples of 100 and 1000 Subtracting from a mixture of multiples of 1000 and 10000 Subtracting from a mixture of multiples of 100, 1000 and 10000

These worksheets are meant to give students practice dealing with 0's in the middles of subtraction questions. Whether using pencil and paper or mental arithmetic, it is always a good idea to make sure students know what to do when they encounter zeros.

• Subtracting Across Zeros in the Middle (Ones Always Need Regrouping) 3-Digit Subtraction across zeros in the middle ( Ones always need regrouping ) 4-Digit Subtraction across zeros in the middle ( Ones always need regrouping ) 5-Digit Subtraction across zeros in the middle ( Ones always need regrouping )
• Subtracting Across Zeros in the Middle (Ones Sometimes Need Regrouping) 3-Digit Subtraction across zeros in the middle ( Ones sometimes need regrouping ) 4-Digit Subtraction across zeros in the middle ( Ones sometimes need regrouping ) 5-Digit Subtraction across zeros in the middle ( Ones sometimes need regrouping )

Subtracting numbers in number systems other than decimal numbers including binary, quaternary, octal, duodecimal and hexadecimal numbers.

• Subtracting in Other Base Number Systems Subtracting Binary Numbers (Base 2) Subtracting Ternary Numbers (Base 3) Subtracting Quaternary Numbers (Base 4) Subtracting Quinary Numbers (Base 5) Subtracting Senary Numbers (Base 6) Subtracting Octal Numbers (Base 8) Subtracting Duodecimal Numbers (Base 12) Subtracting Hexadecimal Numbers (Base 16) Subtracting Vigesimal Numbers (Base 20) Subtracting Hexatrigesimal Numbers (Base 36) Subtracting Various Numbers (Various Bases)

Copyright © 2005-2024 Math-Drills.com You may use the math worksheets on this website according to our Terms of Use to help students learn math.

• Children's Books
• Education & Reference

Enjoy fast, free delivery, exclusive deals, and award-winning movies & TV shows with Prime Try Prime and start saving today with fast, free delivery

Amazon Prime includes:

Fast, FREE Delivery is available to Prime members. To join, select "Try Amazon Prime and start saving today with Fast, FREE Delivery" below the Add to Cart button.

• Cardmembers earn 5% Back at Amazon.com with a Prime Credit Card.
• Unlimited Free Two-Day Delivery
• Streaming of thousands of movies and TV shows with limited ads on Prime Video.
• A Kindle book to borrow for free each month - with no due dates
• Listen to over 2 million songs and hundreds of playlists
• Unlimited photo storage with anywhere access

Important:  Your credit card will NOT be charged when you start your free trial or if you cancel during the trial period. If you're happy with Amazon Prime, do nothing. At the end of the free trial, your membership will automatically upgrade to a monthly membership.

Download the free Kindle app and start reading Kindle books instantly on your smartphone, tablet, or computer - no Kindle device required .

Read instantly on your browser with Kindle for Web.

Using your mobile phone camera - scan the code below and download the Kindle app.

Image Unavailable

• To view this video download Flash Player

Follow the author

Summer Math Workbook For Grade 4 With Addition, Subtraction, Multiplication, Division, Word Problems, Fractions: Daily Math Practice Workbook For 4th ... For Grade 4 | Math Worksheets For Grade 4 Paperback – May 21, 2024

Purchase options and add-ons.

We provide you with a workbook that has numerous math exercises since we think that children improve their math skills through practice.

This book will

• help students prepare for an exam.
• developing intelligence in students.

Math Workbook comes with:

• 2000 exercises
• Subtraction
• Multiplication
• Word Problems
• large size - 8.5 x 11.
• Reading age 9 - 10 years
• Print length 100 pages
• Language English
• Dimensions 8.5 x 0.23 x 11 inches
• Publication date May 21, 2024
• ISBN-13 979-8326267276
• See all details

Product details

• ASIN ‏ : ‎ B0D4VFL92H
• Publisher ‏ : ‎ Independently published (May 21, 2024)
• Language ‏ : ‎ English
• Paperback ‏ : ‎ 100 pages
• ISBN-13 ‏ : ‎ 979-8326267276
• Reading age ‏ : ‎ 9 - 10 years
• Item Weight ‏ : ‎ 11.2 ounces
• Dimensions ‏ : ‎ 8.5 x 0.23 x 11 inches
• Best Sellers Rank: #90,953 in Books ( See Top 100 in Books )

About the author

Discover more of the author’s books, see similar authors, read author blogs and more

Customer reviews

Customer Reviews, including Product Star Ratings help customers to learn more about the product and decide whether it is the right product for them.

To calculate the overall star rating and percentage breakdown by star, we don’t use a simple average. Instead, our system considers things like how recent a review is and if the reviewer bought the item on Amazon. It also analyzed reviews to verify trustworthiness.

No customer reviews

• Amazon Newsletter
• About Amazon
• Accessibility
• Sustainability
• Press Center
• Investor Relations
• Amazon Devices
• Amazon Science
• Sell on Amazon
• Sell apps on Amazon
• Supply to Amazon
• Protect & Build Your Brand
• Become an Affiliate
• Become a Delivery Driver
• Start a Package Delivery Business
• Advertise Your Products
• Self-Publish with Us
• Become an Amazon Hub Partner
• › See More Ways to Make Money
• Amazon Visa
• Amazon Store Card
• Amazon Secured Card
• Amazon Business Card
• Shop with Points
• Credit Card Marketplace
• Reload Your Balance
• Amazon Currency Converter
• Your Account
• Your Orders
• Shipping Rates & Policies
• Amazon Prime
• Returns & Replacements
• Manage Your Content and Devices
• Recalls and Product Safety Alerts
• Conditions of Use
• Privacy Notice
• Consumer Health Data Privacy Disclosure
• Your Ads Privacy Choices

Spotify is currently not available in your country.

Follow us online to find out when we launch., spotify gives you instant access to millions of songs – from old favorites to the latest hits. just hit play to stream anything you like..

Listen everywhere

Spotify works on your computer, mobile, tablet and TV.

Unlimited, ad-free music

No ads. No interruptions. Just music.

Download music & listen offline

Keep playing, even when you don't have a connection.

Premium sounds better

Get ready for incredible sound quality.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 2: Addition and subtraction

About this unit.

In this topic, we will add and subtract whole numbers. The topic starts with 1+1=2 and goes through adding and subtracting within 1000. We will cover regrouping, borrowing, and word problems.

Basic addition and subtraction

• Basic addition (Opens a modal)
• Basic subtraction (Opens a modal)
• Add and subtract: pieces of fruit (Opens a modal)
• Relating addition and subtraction (Opens a modal)
• Add within 5 7 questions Practice
• Subtract within 5 7 questions Practice
• Add within 10 7 questions Practice
• Subtract within 10 7 questions Practice
• Relate addition and subtraction 7 questions Practice
• Getting to 10 by filling boxes (Opens a modal)
• Adding to 10 (Opens a modal)
• Make 10 (grids and number bonds) 7 questions Practice
• Make 10 7 questions Practice

Addition and subtraction word problems within 10

• Addition word problems within 10 (Opens a modal)
• Subtraction word problems within 10 (Opens a modal)
• Addition word problems within 10 7 questions Practice
• Subtraction word problems within 10 7 questions Practice

Addition and subtraction within 20

• Adding within 20 using place value blocks (Opens a modal)
• Adding within 20 using ten frames (Opens a modal)
• Adding 7 + 6 (Opens a modal)
• Adding 8 + 7 (Opens a modal)
• Adding with arrays (Opens a modal)
• Subtracting different ways (Opens a modal)
• Subtract within 20 using a number line (Opens a modal)
• Subtract within 20 using place value blocks (Opens a modal)
• Subtract within 20 using ten frames (Opens a modal)
• Subtracting 14 - 6 (Opens a modal)
• Add within 20 visually 7 questions Practice
• Add within 20 7 questions Practice
• Adding with arrays 4 questions Practice
• Subtract within 20 visually 7 questions Practice
• Subtract within 20 7 questions Practice
• Find missing number (add and subtract within 20) 7 questions Practice
• Add & subtract within 20 7 questions Practice

Word problems within 20

• Addition and subtraction word problems: superheroes (Opens a modal)
• Addition and subtraction word problems: gorillas (Opens a modal)
• Addition and subtraction word problems 1 7 questions Practice
• Addition and subtraction word problems 2 7 questions Practice
• Add and subtract within 20 word problems 7 questions Practice

Word problems with "more" and "fewer"

• Comparison word problems: marbles (Opens a modal)
• Comparison word problems: roly-polies (Opens a modal)
• Word problems with "more" and "fewer" 2 7 questions Practice

Intro to addition with 2-digit numbers

• Adding 2-digit numbers without regrouping (Opens a modal)
• Adding 2-digit numbers without regrouping 1 (Opens a modal)
• Example: Adding 2-digit numbers (no carrying) (Opens a modal)
• Breaking apart 2-digit addition problems (Opens a modal)
• Regrouping to add 1-digit number (Opens a modal)
• Adding up to four 2-digit numbers 4 questions Practice
• Break apart 2-digit addition problems 4 questions Practice
• Regroup when adding 1-digit numbers 7 questions Practice

Intro to subtraction with 2-digit numbers

• Subtracting two-digit numbers without regrouping (Opens a modal)
• Subtracting 2-digit numbers without regrouping 1 (Opens a modal)
• Subtracting a 1-digit number with regrouping (Opens a modal)
• Subtract within 100 using place value blocks 4 questions Practice
• Subtract within 100 using a number line 4 questions Practice
• Subtract 1-digit numbers with regrouping 7 questions Practice

Strategies for adding and subtracting within 100

• Adding 53+17 by making a group of 10 (Opens a modal)
• Adding by making a group of 10 (Opens a modal)
• Strategies for adding 2-digit numbers (Opens a modal)
• Addition and subtraction with number lines (Opens a modal)
• Add 2-digit numbers by making tens 4 questions Practice
• Add 2-digit numbers by making tens 2 4 questions Practice
• Select strategies for adding within 100 4 questions Practice
• Add within 100 using a number line 4 questions Practice

Addition within 100

• Understanding place value when adding ones (Opens a modal)
• Understanding place value when adding tens (Opens a modal)
• Adding with regrouping (Opens a modal)
• Add within 100 using place value blocks 4 questions Practice

Subtraction within 100

• Subtracting with regrouping (borrowing) (Opens a modal)

Word problems within 100

• Adding and subtracting on number line word problems (Opens a modal)
• Adding two digit numbers on a number line (Opens a modal)
• Subtraction word problem: tennis balls (Opens a modal)
• Addition word problem: horses (Opens a modal)
• Subtraction word problem: snow (Opens a modal)
• Subtraction word problem: crayons (Opens a modal)
• Multi step addition word problem (Opens a modal)
• Multi-step subtraction word problem (Opens a modal)
• Add and subtract on the number line word problems 4 questions Practice
• Addition word problems within 100 4 questions Practice
• Subtraction word problems within 100 4 questions Practice
• 2-step addition word problems within 100 4 questions Practice
• 2-step subtraction word problems within 100 4 questions Practice

Adding 1s, 10s, and 100s

• Adding 10 or 100 (Opens a modal)
• Adding 1s, 10s, and 100s (Opens a modal)
• Adding 3-digit numbers (no regrouping) (Opens a modal)
• Add 10s and 100s (no regrouping) 4 questions Practice
• Add within 1,000 using place value blocks 4 questions Practice

Subtracting 1s, 10s, and 100s

• Subtracting 1, 10, or 100 (Opens a modal)
• Subtracting 1s, 10s, and 100s (Opens a modal)
• Subtracting 3-digit numbers (no regrouping) (Opens a modal)
• Subtract 10s and 100s (no regrouping) 7 questions Practice
• Subtract within 1,000 using place value blocks 4 questions Practice

Strategies for adding 2- and 3-digit numbers

• Breaking apart 3-digit addition problems (Opens a modal)
• Solving 3-digit addition in your head (Opens a modal)
• Addition using groups of 10 and 100 (Opens a modal)
• Adding and subtracting on number line (Opens a modal)
• Break apart 3-digit addition problems 4 questions Practice
• Add using groups of 10 and 100 4 questions Practice
• Add on a number line 4 questions Practice
• Select strategies for adding within 1000 4 questions Practice

Addition with regrouping within 1000

• Using place value to add 3-digit numbers: part 2 (Opens a modal)
• Adding 3-digit numbers (Opens a modal)
• Add within 1000 4 questions Practice

Subtraction with regrouping within 1000

• Worked example: Subtracting 3-digit numbers (regrouping) (Opens a modal)
• Worked example: Subtracting 3-digit numbers (regrouping twice) (Opens a modal)
• Worked example: Subtracting 3-digit numbers (regrouping from 0) (Opens a modal)
• Subtracting in your head (no regrouping) (Opens a modal)
• Subtract on a number line 4 questions Practice
• Subtract within 1000 4 questions Practice

Addition and subtraction missing value problems

• Missing numbers in addition and subtraction (Opens a modal)
• Missing number for 3-digit addition within 1000 (Opens a modal)
• Find the missing number (add and subtract within 100) 4 questions Practice
• Find the missing number (add and subtract within 1000) 4 questions Practice

Addition and subtraction greater than 1000

• Relate place value to standard algorithm for multi-digit addition (Opens a modal)
• Multi-digit addition with regrouping (Opens a modal)
• Multi-digit subtraction with regrouping: 6798-3359 (Opens a modal)
• Multi-digit subtraction with regrouping: 7329-6278 (Opens a modal)
• Multi-digit subtraction with regrouping twice (Opens a modal)
• Alternate mental subtraction method (Opens a modal)
• Adding multi-digit numbers: 48,029+233,930 (Opens a modal)
• Relate place value to standard algorithm for multi-digit subtraction (Opens a modal)
• Multi-digit subtraction: 389,002-76,151 (Opens a modal)
• Multi-digit addition 4 questions Practice
• Multi-digit subtraction 4 questions Practice

Color By Number Math Addition Worksheets

34 color by number addition worksheets Addition color by number worksheets Addition color by number worksheet for 1st grade (free printable)

Addition, Elementary, Color by Number, Math Games, Centers, Early

Worksheets digit subtraction homeschool worksheethero worksheetschool algunproblemita problems centers multiplication learners 19 best images of color code math worksheets Number math color coloring addition minecraft worksheets fact transformers autobot symbol subtraction coloringsquared pages printable superhero numbers sheets via post

Addition color number worksheets kindergarten digit math double whale printables

Worksheet addition grade color number first printable math worksheets 1st pdf print aligned common coreAddition color number worksheets subtraction printable source Worksheets worksheet multiplication division abrir centers finishersAddition, elementary, color by number, math games, centers, early.

Addition color number coloring pages kidsAddition, elementary, color by number, math games, centers, early 11 easy addition color by number worksheets ~ coloring style worksheetsSubtraction kindergarten worksheetschool.

Addition number color worksheets kindergarten math printables octopus

Color by number additionAddition color number worksheet coloring pages kids Color addition worksheet4Color number worksheets code addition math worksheet printable worksheeto subtraction via.

Color addition coloring grade worksheets math 3rd number sheets pages numbers sum worksheet 1st kids first kindergarten subtraction choose boardAddition and subtraction color by number worksheets in this you can Color by number addition15 best images of superhero color by number worksheets.

Addition color by number worksheets

addition and subtraction color by number worksheets in this you can

Addition Color by Number Worksheets - Kindergarten Mom

Addition Color by Number Worksheet for 1st Grade (Free Printable)

Color by Number Addition - Best Coloring Pages For Kids

34 Color by Number Addition Worksheets - Kitty Baby Love

19 Best Images of Color Code Math Worksheets - Color by Code Math

11 Easy Addition Color by Number Worksheets ~ Coloring Style Worksheets

More Posts:

• ›   Composite Functions Worksheets
• ›   Find The Circle Printable Worksheet
• ›   Commands And Exclamations Worksheets
• ›   Coins Printable Worksheets
• ›   Composite Transformations Worksheets
• ›   Electricity And Magnetism Worksheets
• ›   Christmas Craft For 4th Graders
• ›   Direct Object Practice Worksheets
• ›   Cinco De Mayo Printable

Reading & Math for K-5

• Kindergarten
• Learning numbers
• Comparing numbers
• Place Value
• Roman numerals
• Subtraction
• Multiplication
• Order of operations
• Drills & practice
• Measurement
• Factoring & prime factors
• Proportions
• Shape & geometry
• Data & graphing
• Word problems
• Children's stories
• Leveled Stories
• Context clues
• Cause & effect
• Compare & contrast
• Fact vs. fiction
• Fact vs. opinion
• Main idea & details
• Story elements
• Conclusions & inferences
• Sounds & phonics
• Words & vocabulary
• Reading comprehension
• Early writing
• Numbers & counting
• Simple math
• Social skills
• Other activities
• Dolch sight words
• Fry sight words
• Multiple meaning words
• Prefixes & suffixes
• Vocabulary cards
• Other parts of speech
• Punctuation
• Capitalization
• Narrative writing
• Opinion writing
• Informative writing
• Cursive alphabet
• Cursive letters
• Cursive letter joins
• Cursive words
• Cursive sentences
• Cursive passages
• Grammar & Writing

Breadcrumbs

• Word Problems
• Mixed add/subtract

Download & Print Only $4.40

Addition & subtraction word problems

Add & subtract numbers < 50.

These grade 1 word problems worksheets involve the addition and subtraction of 1 and 2 digit numbers. Some problems have 3 or more terms.

These worksheets are available to members only.

Join K5 to save time, skip ads and access more content. Learn More

More word problem worksheets

Explore all of our math word problem worksheets , from kindergarten through grade 5.

What is K5?

K5 Learning offers free worksheets , flashcards  and inexpensive  workbooks  for kids in kindergarten to grade 5. Become a member  to access additional content and skip ads.

Our members helped us give away millions of worksheets last year.

We provide free educational materials to parents and teachers in over 100 countries. If you can, please consider purchasing a membership ($24/year) to support our efforts.

Members skip ads and access exclusive features.

Learn about member benefits

This content is available to members only.

• Forgot Password?