how to use hypothesis test

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

9.1: Introduction to Hypothesis Testing

Last updated
Save as PDF
Page ID 10211

Kyle Siegrist
University of Alabama in Huntsville via Random Services

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

Basic Theory

Preliminaries.

As usual, our starting point is a random experiment with an underlying sample space and a probability measure $\P$. In the basic statistical model, we have an observable random variable $\bs{X}$ taking values in a set $S$. In general, $\bs{X}$ can have quite a complicated structure. For example, if the experiment is to sample $n$ objects from a population and record various measurements of interest, then \[ \bs{X} = (X_1, X_2, \ldots, X_n) \] where $X_i$ is the vector of measurements for the $i$th object. The most important special case occurs when $(X_1, X_2, \ldots, X_n)$ are independent and identically distributed. In this case, we have a random sample of size $n$ from the common distribution.

The purpose of this section is to define and discuss the basic concepts of statistical hypothesis testing . Collectively, these concepts are sometimes referred to as the Neyman-Pearson framework, in honor of Jerzy Neyman and Egon Pearson, who first formalized them.

A statistical hypothesis is a statement about the distribution of $\bs{X}$. Equivalently, a statistical hypothesis specifies a set of possible distributions of $\bs{X}$: the set of distributions for which the statement is true. A hypothesis that specifies a single distribution for $\bs{X}$ is called simple ; a hypothesis that specifies more than one distribution for $\bs{X}$ is called composite .

In hypothesis testing , the goal is to see if there is sufficient statistical evidence to reject a presumed null hypothesis in favor of a conjectured alternative hypothesis . The null hypothesis is usually denoted $H_0$ while the alternative hypothesis is usually denoted $H_1$.

An hypothesis test is a statistical decision ; the conclusion will either be to reject the null hypothesis in favor of the alternative, or to fail to reject the null hypothesis. The decision that we make must, of course, be based on the observed value $\bs{x}$ of the data vector $\bs{X}$. Thus, we will find an appropriate subset $R$ of the sample space $S$ and reject $H_0$ if and only if $\bs{x} \in R$. The set $R$ is known as the rejection region or the critical region . Note the asymmetry between the null and alternative hypotheses. This asymmetry is due to the fact that we assume the null hypothesis, in a sense, and then see if there is sufficient evidence in $\bs{x}$ to overturn this assumption in favor of the alternative.

An hypothesis test is a statistical analogy to proof by contradiction, in a sense. Suppose for a moment that $H_1$ is a statement in a mathematical theory and that $H_0$ is its negation. One way that we can prove $H_1$ is to assume $H_0$ and work our way logically to a contradiction. In an hypothesis test, we don't prove anything of course, but there are similarities. We assume $H_0$ and then see if the data $\bs{x}$ are sufficiently at odds with that assumption that we feel justified in rejecting $H_0$ in favor of $H_1$.

Often, the critical region is defined in terms of a statistic $w(\bs{X})$, known as a test statistic , where $w$ is a function from $S$ into another set $T$. We find an appropriate rejection region $R_T \subseteq T$ and reject $H_0$ when the observed value $w(\bs{x}) \in R_T$. Thus, the rejection region in $S$ is then $R = w^{-1}(R_T) = \left\{\bs{x} \in S: w(\bs{x}) \in R_T\right\}$. As usual, the use of a statistic often allows significant data reduction when the dimension of the test statistic is much smaller than the dimension of the data vector.

The ultimate decision may be correct or may be in error. There are two types of errors, depending on which of the hypotheses is actually true.

Types of errors:

A type 1 error is rejecting the null hypothesis $H_0$ when $H_0$ is true.
A type 2 error is failing to reject the null hypothesis $H_0$ when the alternative hypothesis $H_1$ is true.

Similarly, there are two ways to make a correct decision: we could reject $H_0$ when $H_1$ is true or we could fail to reject $H_0$ when $H_0$ is true. The possibilities are summarized in the following table:

Of course, when we observe $\bs{X} = \bs{x}$ and make our decision, either we will have made the correct decision or we will have committed an error, and usually we will never know which of these events has occurred. Prior to gathering the data, however, we can consider the probabilities of the various errors.

If $H_0$ is true (that is, the distribution of $\bs{X}$ is specified by $H_0$), then $\P(\bs{X} \in R)$ is the probability of a type 1 error for this distribution. If $H_0$ is composite, then $H_0$ specifies a variety of different distributions for $\bs{X}$ and thus there is a set of type 1 error probabilities.

The maximum probability of a type 1 error, over the set of distributions specified by $ H_0 $, is the significance level of the test or the size of the critical region.

The significance level is often denoted by $\alpha$. Usually, the rejection region is constructed so that the significance level is a prescribed, small value (typically 0.1, 0.05, 0.01).

If $H_1$ is true (that is, the distribution of $\bs{X}$ is specified by $H_1$), then $\P(\bs{X} \notin R)$ is the probability of a type 2 error for this distribution. Again, if $H_1$ is composite then $H_1$ specifies a variety of different distributions for $\bs{X}$, and thus there will be a set of type 2 error probabilities. Generally, there is a tradeoff between the type 1 and type 2 error probabilities. If we reduce the probability of a type 1 error, by making the rejection region $R$ smaller, we necessarily increase the probability of a type 2 error because the complementary region $S \setminus R$ is larger.

The extreme cases can give us some insight. First consider the decision rule in which we never reject $H_0$, regardless of the evidence $\bs{x}$. This corresponds to the rejection region $R = \emptyset$. A type 1 error is impossible, so the significance level is 0. On the other hand, the probability of a type 2 error is 1 for any distribution defined by $H_1$. At the other extreme, consider the decision rule in which we always rejects $H_0$ regardless of the evidence $\bs{x}$. This corresponds to the rejection region $R = S$. A type 2 error is impossible, but now the probability of a type 1 error is 1 for any distribution defined by $H_0$. In between these two worthless tests are meaningful tests that take the evidence $\bs{x}$ into account.

If $H_1$ is true, so that the distribution of $\bs{X}$ is specified by $H_1$, then $\P(\bs{X} \in R)$, the probability of rejecting $H_0$ is the power of the test for that distribution.

Thus the power of the test for a distribution specified by $ H_1 $ is the probability of making the correct decision.

Suppose that we have two tests, corresponding to rejection regions $R_1$ and $R_2$, respectively, each having significance level $\alpha$. The test with region $R_1$ is uniformly more powerful than the test with region $R_2$ if \[ \P(\bs{X} \in R_1) \ge \P(\bs{X} \in R_2) \text{ for every distribution of } \bs{X} \text{ specified by } H_1 \]

Naturally, in this case, we would prefer the first test. Often, however, two tests will not be uniformly ordered; one test will be more powerful for some distributions specified by $H_1$ while the other test will be more powerful for other distributions specified by $H_1$.

If a test has significance level $\alpha$ and is uniformly more powerful than any other test with significance level $\alpha$, then the test is said to be a uniformly most powerful test at level $\alpha$.

Clearly a uniformly most powerful test is the best we can do.

$P$-value

In most cases, we have a general procedure that allows us to construct a test (that is, a rejection region $R_\alpha$) for any given significance level $\alpha \in (0, 1)$. Typically, $R_\alpha$ decreases (in the subset sense) as $\alpha$ decreases.

The $P$-value of the observed value $\bs{x}$ of $\bs{X}$, denoted $P(\bs{x})$, is defined to be the smallest $\alpha$ for which $\bs{x} \in R_\alpha$; that is, the smallest significance level for which $H_0$ is rejected, given $\bs{X} = \bs{x}$.

Knowing $P(\bs{x})$ allows us to test $H_0$ at any significance level for the given data $\bs{x}$: If $P(\bs{x}) \le \alpha$ then we would reject $H_0$ at significance level $\alpha$; if $P(\bs{x}) \gt \alpha$ then we fail to reject $H_0$ at significance level $\alpha$. Note that $P(\bs{X})$ is a statistic . Informally, $P(\bs{x})$ can often be thought of as the probability of an outcome as or more extreme than the observed value $\bs{x}$, where extreme is interpreted relative to the null hypothesis $H_0$.

Analogy with Justice Systems

There is a helpful analogy between statistical hypothesis testing and the criminal justice system in the US and various other countries. Consider a person charged with a crime. The presumed null hypothesis is that the person is innocent of the crime; the conjectured alternative hypothesis is that the person is guilty of the crime. The test of the hypotheses is a trial with evidence presented by both sides playing the role of the data. After considering the evidence, the jury delivers the decision as either not guilty or guilty . Note that innocent is not a possible verdict of the jury, because it is not the point of the trial to prove the person innocent. Rather, the point of the trial is to see whether there is sufficient evidence to overturn the null hypothesis that the person is innocent in favor of the alternative hypothesis of that the person is guilty. A type 1 error is convicting a person who is innocent; a type 2 error is acquitting a person who is guilty. Generally, a type 1 error is considered the more serious of the two possible errors, so in an attempt to hold the chance of a type 1 error to a very low level, the standard for conviction in serious criminal cases is beyond a reasonable doubt .

Tests of an Unknown Parameter

Hypothesis testing is a very general concept, but an important special class occurs when the distribution of the data variable $\bs{X}$ depends on a parameter $\theta$ taking values in a parameter space $\Theta$. The parameter may be vector-valued, so that $\bs{\theta} = (\theta_1, \theta_2, \ldots, \theta_n)$ and $\Theta \subseteq \R^k$ for some $k \in \N_+$. The hypotheses generally take the form \[ H_0: \theta \in \Theta_0 \text{ versus } H_1: \theta \notin \Theta_0 \] where $\Theta_0$ is a prescribed subset of the parameter space $\Theta$. In this setting, the probabilities of making an error or a correct decision depend on the true value of $\theta$. If $R$ is the rejection region, then the power function $ Q $ is given by \[ Q(\theta) = \P_\theta(\bs{X} \in R), \quad \theta \in \Theta \] The power function gives a lot of information about the test.

The power function satisfies the following properties:

$Q(\theta)$ is the probability of a type 1 error when $\theta \in \Theta_0$.
$\max\left\{Q(\theta): \theta \in \Theta_0\right\}$ is the significance level of the test.
$1 - Q(\theta)$ is the probability of a type 2 error when $\theta \notin \Theta_0$.
$Q(\theta)$ is the power of the test when $\theta \notin \Theta_0$.

If we have two tests, we can compare them by means of their power functions.

Suppose that we have two tests, corresponding to rejection regions $R_1$ and $R_2$, respectively, each having significance level $\alpha$. The test with rejection region $R_1$ is uniformly more powerful than the test with rejection region $R_2$ if $ Q_1(\theta) \ge Q_2(\theta)$ for all $ \theta \notin \Theta_0 $.

Most hypothesis tests of an unknown real parameter $\theta$ fall into three special cases:

Suppose that $ \theta $ is a real parameter and $ \theta_0 \in \Theta $ a specified value. The tests below are respectively the two-sided test , the left-tailed test , and the right-tailed test .

$H_0: \theta = \theta_0$ versus $H_1: \theta \ne \theta_0$
$H_0: \theta \ge \theta_0$ versus $H_1: \theta \lt \theta_0$
$H_0: \theta \le \theta_0$ versus $H_1: \theta \gt \theta_0$

Thus the tests are named after the conjectured alternative. Of course, there may be other unknown parameters besides $\theta$ (known as nuisance parameters ).

Equivalence Between Hypothesis Test and Confidence Sets

There is an equivalence between hypothesis tests and confidence sets for a parameter $\theta$.

Suppose that $C(\bs{x})$ is a $1 - \alpha$ level confidence set for $\theta$. The following test has significance level $\alpha$ for the hypothesis $ H_0: \theta = \theta_0 $ versus $ H_1: \theta \ne \theta_0 $: Reject $H_0$ if and only if $\theta_0 \notin C(\bs{x})$

By definition, $\P[\theta \in C(\bs{X})] = 1 - \alpha$. Hence if $H_0$ is true so that $\theta = \theta_0$, then the probability of a type 1 error is $P[\theta \notin C(\bs{X})] = \alpha$.

Equivalently, we fail to reject $H_0$ at significance level $\alpha$ if and only if $\theta_0$ is in the corresponding $1 - \alpha$ level confidence set. In particular, this equivalence applies to interval estimates of a real parameter $\theta$ and the common tests for $\theta$ given above .

In each case below, the confidence interval has confidence level $1 - \alpha$ and the test has significance level $\alpha$.

Suppose that $\left[L(\bs{X}, U(\bs{X})\right]$ is a two-sided confidence interval for $\theta$. Reject $H_0: \theta = \theta_0$ versus $H_1: \theta \ne \theta_0$ if and only if $\theta_0 \lt L(\bs{X})$ or $\theta_0 \gt U(\bs{X})$.
Suppose that $L(\bs{X})$ is a confidence lower bound for $\theta$. Reject $H_0: \theta \le \theta_0$ versus $H_1: \theta \gt \theta_0$ if and only if $\theta_0 \lt L(\bs{X})$.
Suppose that $U(\bs{X})$ is a confidence upper bound for $\theta$. Reject $H_0: \theta \ge \theta_0$ versus $H_1: \theta \lt \theta_0$ if and only if $\theta_0 \gt U(\bs{X})$.

Pivot Variables and Test Statistics

Recall that confidence sets of an unknown parameter $\theta$ are often constructed through a pivot variable , that is, a random variable $W(\bs{X}, \theta)$ that depends on the data vector $\bs{X}$ and the parameter $\theta$, but whose distribution does not depend on $\theta$ and is known. In this case, a natural test statistic for the basic tests given above is $W(\bs{X}, \theta_0)$.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 12: Significance tests (hypothesis testing)

About this unit.

Significance tests give us a formal process for using sample data to evaluate the likelihood of some claim about a population value. Learn how to conduct significance tests and calculate p-values to see how likely a sample result is to occur by random chance. You'll also see how we use p-values to make conclusions about hypotheses.

The idea of significance tests

Simple hypothesis testing (Opens a modal)
Idea behind hypothesis testing (Opens a modal)
Examples of null and alternative hypotheses (Opens a modal)
P-values and significance tests (Opens a modal)
Comparing P-values to different significance levels (Opens a modal)
Estimating a P-value from a simulation (Opens a modal)
Using P-values to make conclusions (Opens a modal)
Simple hypothesis testing Get 3 of 4 questions to level up!
Writing null and alternative hypotheses Get 3 of 4 questions to level up!
Estimating P-values from simulations Get 3 of 4 questions to level up!

Error probabilities and power

Introduction to Type I and Type II errors (Opens a modal)
Type 1 errors (Opens a modal)
Examples identifying Type I and Type II errors (Opens a modal)
Introduction to power in significance tests (Opens a modal)
Examples thinking about power in significance tests (Opens a modal)
Consequences of errors and significance (Opens a modal)
Type I vs Type II error Get 3 of 4 questions to level up!
Error probabilities and power Get 3 of 4 questions to level up!

Tests about a population proportion

Constructing hypotheses for a significance test about a proportion (Opens a modal)
Conditions for a z test about a proportion (Opens a modal)
Reference: Conditions for inference on a proportion (Opens a modal)
Calculating a z statistic in a test about a proportion (Opens a modal)
Calculating a P-value given a z statistic (Opens a modal)
Making conclusions in a test about a proportion (Opens a modal)
Writing hypotheses for a test about a proportion Get 3 of 4 questions to level up!
Conditions for a z test about a proportion Get 3 of 4 questions to level up!
Calculating the test statistic in a z test for a proportion Get 3 of 4 questions to level up!
Calculating the P-value in a z test for a proportion Get 3 of 4 questions to level up!
Making conclusions in a z test for a proportion Get 3 of 4 questions to level up!

Tests about a population mean

Writing hypotheses for a significance test about a mean (Opens a modal)
Conditions for a t test about a mean (Opens a modal)
Reference: Conditions for inference on a mean (Opens a modal)
When to use z or t statistics in significance tests (Opens a modal)
Example calculating t statistic for a test about a mean (Opens a modal)
Using TI calculator for P-value from t statistic (Opens a modal)
Using a table to estimate P-value from t statistic (Opens a modal)
Comparing P-value from t statistic to significance level (Opens a modal)
Free response example: Significance test for a mean (Opens a modal)
Writing hypotheses for a test about a mean Get 3 of 4 questions to level up!
Conditions for a t test about a mean Get 3 of 4 questions to level up!
Calculating the test statistic in a t test for a mean Get 3 of 4 questions to level up!
Calculating the P-value in a t test for a mean Get 3 of 4 questions to level up!
Making conclusions in a t test for a mean Get 3 of 4 questions to level up!

Business Insights

Harvard Business School Online's Business Insights Blog provides the career insights you need to achieve your goals and gain confidence in your business skills.

Career Development
Communication
Decision-Making
Earning Your MBA
Negotiation
News & Events
Productivity
Staff Spotlight
Student Profiles
Work-Life Balance
AI Essentials for Business
Alternative Investments
Business Analytics
Business Strategy
Business and Climate Change
Design Thinking and Innovation
Digital Marketing Strategy
Disruptive Strategy
Economics for Managers
Entrepreneurship Essentials
Financial Accounting
Global Business
Launching Tech Ventures
Leadership Principles
Leadership, Ethics, and Corporate Accountability
Leading Change and Organizational Renewal
Leading with Finance
Management Essentials
Negotiation Mastery
Organizational Leadership
Power and Influence for Positive Impact
Strategy Execution
Sustainable Business Strategy
Sustainable Investing
Winning with Digital Platforms

A Beginner’s Guide to Hypothesis Testing in Business

Business professionals performing hypothesis testing

30 Mar 2021

Becoming a more data-driven decision-maker can bring several benefits to your organization, enabling you to identify new opportunities to pursue and threats to abate. Rather than allowing subjective thinking to guide your business strategy, backing your decisions with data can empower your company to become more innovative and, ultimately, profitable.

If you’re new to data-driven decision-making, you might be wondering how data translates into business strategy. The answer lies in generating a hypothesis and verifying or rejecting it based on what various forms of data tell you.

Below is a look at hypothesis testing and the role it plays in helping businesses become more data-driven.

Access your free e-book today.

What Is Hypothesis Testing?

To understand what hypothesis testing is, it’s important first to understand what a hypothesis is.

A hypothesis or hypothesis statement seeks to explain why something has happened, or what might happen, under certain conditions. It can also be used to understand how different variables relate to each other. Hypotheses are often written as if-then statements; for example, “If this happens, then this will happen.”

Hypothesis testing , then, is a statistical means of testing an assumption stated in a hypothesis. While the specific methodology leveraged depends on the nature of the hypothesis and data available, hypothesis testing typically uses sample data to extrapolate insights about a larger population.

Hypothesis Testing in Business

When it comes to data-driven decision-making, there’s a certain amount of risk that can mislead a professional. This could be due to flawed thinking or observations, incomplete or inaccurate data , or the presence of unknown variables. The danger in this is that, if major strategic decisions are made based on flawed insights, it can lead to wasted resources, missed opportunities, and catastrophic outcomes.

The real value of hypothesis testing in business is that it allows professionals to test their theories and assumptions before putting them into action. This essentially allows an organization to verify its analysis is correct before committing resources to implement a broader strategy.

As one example, consider a company that wishes to launch a new marketing campaign to revitalize sales during a slow period. Doing so could be an incredibly expensive endeavor, depending on the campaign’s size and complexity. The company, therefore, may wish to test the campaign on a smaller scale to understand how it will perform.

In this example, the hypothesis that’s being tested would fall along the lines of: “If the company launches a new marketing campaign, then it will translate into an increase in sales.” It may even be possible to quantify how much of a lift in sales the company expects to see from the effort. Pending the results of the pilot campaign, the business would then know whether it makes sense to roll it out more broadly.

Related: 9 Fundamental Data Science Skills for Business Professionals

Key Considerations for Hypothesis Testing

1. alternative hypothesis and null hypothesis.

In hypothesis testing, the hypothesis that’s being tested is known as the alternative hypothesis . Often, it’s expressed as a correlation or statistical relationship between variables. The null hypothesis , on the other hand, is a statement that’s meant to show there’s no statistical relationship between the variables being tested. It’s typically the exact opposite of whatever is stated in the alternative hypothesis.

For example, consider a company’s leadership team that historically and reliably sees $12 million in monthly revenue. They want to understand if reducing the price of their services will attract more customers and, in turn, increase revenue.

In this case, the alternative hypothesis may take the form of a statement such as: “If we reduce the price of our flagship service by five percent, then we’ll see an increase in sales and realize revenues greater than $12 million in the next month.”

The null hypothesis, on the other hand, would indicate that revenues wouldn’t increase from the base of $12 million, or might even decrease.

Check out the video below about the difference between an alternative and a null hypothesis, and subscribe to our YouTube channel for more explainer content.

2. Significance Level and P-Value

Statistically speaking, if you were to run the same scenario 100 times, you’d likely receive somewhat different results each time. If you were to plot these results in a distribution plot, you’d see the most likely outcome is at the tallest point in the graph, with less likely outcomes falling to the right and left of that point.

With this in mind, imagine you’ve completed your hypothesis test and have your results, which indicate there may be a correlation between the variables you were testing. To understand your results' significance, you’ll need to identify a p-value for the test, which helps note how confident you are in the test results.

In statistics, the p-value depicts the probability that, assuming the null hypothesis is correct, you might still observe results that are at least as extreme as the results of your hypothesis test. The smaller the p-value, the more likely the alternative hypothesis is correct, and the greater the significance of your results.

3. One-Sided vs. Two-Sided Testing

When it’s time to test your hypothesis, it’s important to leverage the correct testing method. The two most common hypothesis testing methods are one-sided and two-sided tests , or one-tailed and two-tailed tests, respectively.

Typically, you’d leverage a one-sided test when you have a strong conviction about the direction of change you expect to see due to your hypothesis test. You’d leverage a two-sided test when you’re less confident in the direction of change.

Business Analytics | Become a data-driven leader | Learn More

4. Sampling

To perform hypothesis testing in the first place, you need to collect a sample of data to be analyzed. Depending on the question you’re seeking to answer or investigate, you might collect samples through surveys, observational studies, or experiments.

A survey involves asking a series of questions to a random population sample and recording self-reported responses.

Observational studies involve a researcher observing a sample population and collecting data as it occurs naturally, without intervention.

Finally, an experiment involves dividing a sample into multiple groups, one of which acts as the control group. For each non-control group, the variable being studied is manipulated to determine how the data collected differs from that of the control group.

A Beginner's Guide to Data and Analytics | Access Your Free E-Book | Download Now

Learn How to Perform Hypothesis Testing

Hypothesis testing is a complex process involving different moving pieces that can allow an organization to effectively leverage its data and inform strategic decisions.

If you’re interested in better understanding hypothesis testing and the role it can play within your organization, one option is to complete a course that focuses on the process. Doing so can lay the statistical and analytical foundation you need to succeed.

Do you want to learn more about hypothesis testing? Explore Business Analytics —one of our online business essentials courses —and download our Beginner’s Guide to Data & Analytics .

About the Author

Teach yourself statistics

How to Test Statistical Hypotheses

This lesson describes a general procedure that can be used to test statistical hypotheses.

How to Conduct Hypothesis Tests

All hypothesis tests are conducted the same way. The researcher states a hypothesis to be tested, formulates an analysis plan, analyzes sample data according to the plan, and accepts or rejects the null hypothesis, based on results of the analysis.

State the hypotheses. Every hypothesis test requires the analyst to state a null hypothesis and an alternative hypothesis . The hypotheses are stated in such a way that they are mutually exclusive. That is, if one is true, the other must be false; and vice versa.
Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
Test method. Typically, the test method involves a test statistic and a sampling distribution . Computed from sample data, the test statistic might be a mean score, proportion, difference between means, difference between proportions, z-score, t statistic, chi-square, etc. Given a test statistic and its sampling distribution, a researcher can assess probabilities associated with the test statistic. If the test statistic probability is less than the significance level, the null hypothesis is rejected.

Test statistic = (Statistic - Parameter) / (Standard deviation of statistic)

Test statistic = (Statistic - Parameter) / (Standard error of statistic)

P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic, assuming the null hypothesis is true.
Interpret the results. If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.

Applications of the General Hypothesis Testing Procedure

The next few lessons show how to apply the general hypothesis testing procedure to different kinds of statistical problems.

Proportions
Difference between proportions
Regression slope
Difference between means
Difference between matched pairs
Goodness of fit
Homogeneity
Independence

At this point, don't worry if the general procedure for testing hypotheses seems a little bit unclear. The procedure will be clearer as you see it applied in the next few lessons.

Test Your Understanding

In hypothesis testing, which of the following statements is always true?

I. The P-value is greater than the significance level. II. The P-value is computed from the significance level. III. The P-value is the parameter in the null hypothesis. IV. The P-value is a test statistic. V. The P-value is a probability.

(A) I only (B) II only (C) III only (D) IV only (E) V only

The correct answer is (E). The P-value is the probability of observing a sample statistic as extreme as the test statistic. It can be greater than the significance level, but it can also be smaller than the significance level. It is not computed from the significance level, it is not the parameter in the null hypothesis, and it is not a test statistic.

Quality Improvement
Talk To Minitab

What Statistical Hypothesis Test Should I Use?

Topics: Hypothesis Testing

So, you collected some data and now you want it to tell you something meaningful. Unfortunately, your last statistics class was years ago and you can't quite remember what to do with that data. You remember something about a null hypothesis and and alternative, but what's all this about testing?

Sometimes it's easier just to give a problem to the Assistant. Especially when it comes to statistics.

Don't get me wrong, I love to analyze data and see what it means...but most of us don't analyze data all day, every day. And in statistics, as in sports, if you don't use it, you lose it. If you haven't done an analysis in months it's not unreasonable to imagine you might need a little help.

In that case, you might seek out the Assistant. Specifically, the Assistant menu in Minitab Statistical Software . The Assistant's always ready to guide you through a difficult statistical task if you're not quite sure what to do.

The 2-Sample t-test

For example, suppose you want to compare two different materials for making backpacks –Cloth A and Cloth B –to determine which would make a more durable product. You sample materials from both suppliers and measure the mean amount of force needed to tear them.

If you're already up on your statistics, you know right away that you want to use a 2-sample t-test, which analyzes the difference between the means of your samples to determine whether that difference is statistically significant. You'll also know that the hypotheses of this two-tailed test would be:

Null hypothesis: H0: m1 - m2 = 0 (strengths of the material from both companies are equal)
Alternative hypothesis: H1: m1 - m2 ≠ 0 (strengths of the material from both companies are different)

And that if the test's p-value is less than your chosen significance level, you should reject the null hypothesis.

Maybe you're the type of person who remembers all of that stuff, even if you haven't done a t-test in years. If so, good for you–but I could stand to get a little help. Let's see what the assistant can do for me.

The Assistant and the Hypothesis Test

I'll start by pulling up Assistant > Hypothesis Tests... in Minitab. Up comes this dialog box:

Well, I know I have two samples that I want to compare. But I can't remember if I need a paired t-test, a % defective, or what. So I'll click "Help me choose." Now the Assistant gives me an easy-to-follow decision tree that leads me to the 2-sample t-test.

I can follow the tree straight to its conclusion, as shown on the right.

A Guided Path to the Right Hypothesis Test

But if I can't remember enough specifics to follow the decision tree from start to finish from the amount of information shown on the right, the Assistant will actually guide me through the process step-by-step so I arrive safely at the right hypothesis test to use.

In this scenario, The Assistant asks one question, then I choose the right option for my situation and proceed to the next question.

Particularly helpful is the fact that if I forget, for example, the difference between Continuous and Attribute data, all I have to do is click on a button and I'll get an explanation and an example for both.

In this situation, the questions I need to answer are:

Do you have continuous data or attribute data? (Answer: Continuous)
What are you comparing? (Answer: Two means)
Are you measuring different sets of items or the same set of items? (Answer: Different sets)

Now I know what test I need to use to compare the two means. But I'm not sure I know how to do that test.

Fortunately, the Assistant can help me with that, too. I'll show you how in my next post .

Trust Center

Terms of Use
Privacy Policy
Cookies Settings

Statistics Tutorial

Descriptive statistics, inferential statistics, stat reference, statistics - hypothesis testing.

Hypothesis testing is a formal way of checking if a hypothesis about a population is true or not.

Hypothesis Testing

A hypothesis is a claim about a population parameter .

A hypothesis test is a formal procedure to check if a hypothesis is true or not.

Examples of claims that can be checked:

The average height of people in Denmark is more than 170 cm.

The share of left handed people in Australia is not 10%.

The average income of dentists is less the average income of lawyers.

The Null and Alternative Hypothesis

Hypothesis testing is based on making two different claims about a population parameter.

The null hypothesis ($H_{0} $) and the alternative hypothesis ($H_{1}$) are the claims.

The two claims needs to be mutually exclusive , meaning only one of them can be true.

The alternative hypothesis is typically what we are trying to prove.

For example, we want to check the following claim:

"The average height of people in Denmark is more than 170 cm."

In this case, the parameter is the average height of people in Denmark ($\mu$).

The null and alternative hypothesis would be:

Null hypothesis : The average height of people in Denmark is 170 cm.

Alternative hypothesis : The average height of people in Denmark is more than 170 cm.

The claims are often expressed with symbols like this:

$H_{0}$: $\mu = 170 \: cm $

$H_{1}$: $\mu > 170 \: cm $

If the data supports the alternative hypothesis, we reject the null hypothesis and accept the alternative hypothesis.

If the data does not support the alternative hypothesis, we keep the null hypothesis.

Note: The alternative hypothesis is also referred to as ($H_{A} $).

The Significance Level

The significance level ($\alpha$) is the uncertainty we accept when rejecting the null hypothesis in the hypothesis test.

The significance level is a percentage probability of accidentally making the wrong conclusion.

Typical significance levels are:

$\alpha = 0.1$ (10%)
$\alpha = 0.05$ (5%)
$\alpha = 0.01$ (1%)

A lower significance level means that the evidence in the data needs to be stronger to reject the null hypothesis.

There is no "correct" significance level - it only states the uncertainty of the conclusion.

Note: A 5% significance level means that when we reject a null hypothesis:

We expect to reject a true null hypothesis 5 out of 100 times.

The Test Statistic

The test statistic is used to decide the outcome of the hypothesis test.

The test statistic is a standardized value calculated from the sample.

Standardization means converting a statistic to a well known probability distribution .

The type of probability distribution depends on the type of test.

Common examples are:

Standard Normal Distribution (Z): used for Testing Population Proportions
Student's T-Distribution (T): used for Testing Population Means

Note: You will learn how to calculate the test statistic for each type of test in the following chapters.

The Critical Value and P-Value Approach

There are two main approaches used for hypothesis tests:

The critical value approach compares the test statistic with the critical value of the significance level.
The p-value approach compares the p-value of the test statistic and with the significance level.

The Critical Value Approach

The critical value approach checks if the test statistic is in the rejection region .

The rejection region is an area of probability in the tails of the distribution.

The size of the rejection region is decided by the significance level ($\alpha$).

The value that separates the rejection region from the rest is called the critical value .

Here is a graphical illustration:

If the test statistic is inside this rejection region, the null hypothesis is rejected .

For example, if the test statistic is 2.3 and the critical value is 2 for a significance level ($\alpha = 0.05$):

We reject the null hypothesis ($H_{0} $) at 0.05 significance level ($\alpha$)

The P-Value Approach

The p-value approach checks if the p-value of the test statistic is smaller than the significance level ($\alpha$).

The p-value of the test statistic is the area of probability in the tails of the distribution from the value of the test statistic.

If the p-value is smaller than the significance level, the null hypothesis is rejected .

The p-value directly tells us the lowest significance level where we can reject the null hypothesis.

For example, if the p-value is 0.03:

We reject the null hypothesis ($H_{0} $) at a 0.05 significance level ($\alpha$)

We keep the null hypothesis ($H_{0}$) at a 0.01 significance level ($\alpha$)

Note: The two approaches are only different in how they present the conclusion.

Steps for a Hypothesis Test

The following steps are used for a hypothesis test:

Check the conditions
Define the claims
Decide the significance level
Calculate the test statistic

One condition is that the sample is randomly selected from the population.

The other conditions depends on what type of parameter you are testing the hypothesis for.

Common parameters to test hypotheses are:

Proportions (for qualitative data)
Mean values (for numerical data)

You will learn the steps for both types in the following pages.

COLOR PICKER

Contact Sales

If you want to use W3Schools services as an educational institution, team or enterprise, send us an e-mail: [email protected]

Report Error

If you want to report an error, or if you want to make a suggestion, send us an e-mail: [email protected]

How to Write Hypothesis Test Conclusions (With Examples)

A hypothesis test is used to test whether or not some hypothesis about a population parameter is true.

To perform a hypothesis test in the real world, researchers obtain a random sample from the population and perform a hypothesis test on the sample data, using a null and alternative hypothesis:

Null Hypothesis (H 0 ): The sample data occurs purely from chance.
Alternative Hypothesis (H A ): The sample data is influenced by some non-random cause.

If the p-value of the hypothesis test is less than some significance level (e.g. α = .05), then we reject the null hypothesis .

Otherwise, if the p-value is not less than some significance level then we fail to reject the null hypothesis .

When writing the conclusion of a hypothesis test, we typically include:

Whether we reject or fail to reject the null hypothesis.
The significance level.
A short explanation in the context of the hypothesis test.

For example, we would write:

We reject the null hypothesis at the 5% significance level. There is sufficient evidence to support the claim that…

Or, we would write:

We fail to reject the null hypothesis at the 5% significance level. There is not sufficient evidence to support the claim that…

The following examples show how to write a hypothesis test conclusion in both scenarios.

Example 1: Reject the Null Hypothesis Conclusion

Suppose a biologist believes that a certain fertilizer will cause plants to grow more during a one-month period than they normally do, which is currently 20 inches. To test this, she applies the fertilizer to each of the plants in her laboratory for one month.

She then performs a hypothesis test at a 5% significance level using the following hypotheses:

H 0 : μ = 20 inches (the fertilizer will have no effect on the mean plant growth)
H A : μ > 20 inches (the fertilizer will cause mean plant growth to increase)

Suppose the p-value of the test turns out to be 0.002.

Here is how she would report the results of the hypothesis test:

We reject the null hypothesis at the 5% significance level. There is sufficient evidence to support the claim that this particular fertilizer causes plants to grow more during a one-month period than they normally do.

Example 2: Fail to Reject the Null Hypothesis Conclusion

Suppose the manager of a manufacturing plant wants to test whether or not some new method changes the number of defective widgets produced per month, which is currently 250. To test this, he measures the mean number of defective widgets produced before and after using the new method for one month.

He performs a hypothesis test at a 10% significance level using the following hypotheses:

H 0 : μ after = μ before (the mean number of defective widgets is the same before and after using the new method)
H A : μ after ≠ μ before (the mean number of defective widgets produced is different before and after using the new method)

Suppose the p-value of the test turns out to be 0.27.

Here is how he would report the results of the hypothesis test:

We fail to reject the null hypothesis at the 10% significance level. There is not sufficient evidence to support the claim that the new method leads to a change in the number of defective widgets produced per month.

Additional Resources

The following tutorials provide additional information about hypothesis testing:

Introduction to Hypothesis Testing 4 Examples of Hypothesis Testing in Real Life How to Write a Null Hypothesis

Featured Posts

7 Best YouTube Channels to Learn Statistics for Free

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
Duis aute irure dolor in reprehenderit in voluptate
Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.3.2 hypothesis testing (p-value approach).

The P -value approach involves determining "likely" or "unlikely" by determining the probability — assuming the null hypothesis was true — of observing a more extreme test statistic in the direction of the alternative hypothesis than the one observed. If the P -value is small, say less than (or equal to) $\alpha$, then it is "unlikely." And, if the P -value is large, say more than $\alpha$, then it is "likely."

If the P -value is less than (or equal to) $\alpha$, then the null hypothesis is rejected in favor of the alternative hypothesis. And, if the P -value is greater than $\alpha$, then the null hypothesis is not rejected.

Specifically, the four steps involved in using the P -value approach to conducting any hypothesis test are:

Specify the null and alternative hypotheses.
Using the sample data and assuming the null hypothesis is true, calculate the value of the test statistic. Again, to conduct the hypothesis test for the population mean μ , we use the t -statistic $t^*=\frac{\bar{x}-\mu}{s/\sqrt{n}}$ which follows a t -distribution with n - 1 degrees of freedom.
Using the known distribution of the test statistic, calculate the P -value : "If the null hypothesis is true, what is the probability that we'd observe a more extreme test statistic in the direction of the alternative hypothesis than we did?" (Note how this question is equivalent to the question answered in criminal trials: "If the defendant is innocent, what is the chance that we'd observe such extreme criminal evidence?")
Set the significance level, $\alpha$, the probability of making a Type I error to be small — 0.01, 0.05, or 0.10. Compare the P -value to $\alpha$. If the P -value is less than (or equal to) $\alpha$, reject the null hypothesis in favor of the alternative hypothesis. If the P -value is greater than $\alpha$, do not reject the null hypothesis.

Example S.3.2.1

Mean gpa section .

In our example concerning the mean grade point average, suppose that our random sample of n = 15 students majoring in mathematics yields a test statistic t * equaling 2.5. Since n = 15, our test statistic t * has n - 1 = 14 degrees of freedom. Also, suppose we set our significance level α at 0.05 so that we have only a 5% chance of making a Type I error.

Right Tailed

The P -value for conducting the right-tailed test H 0 : μ = 3 versus H A : μ > 3 is the probability that we would observe a test statistic greater than t * = 2.5 if the population mean $\mu$ really were 3. Recall that probability equals the area under the probability curve. The P -value is therefore the area under a t n - 1 = t 14 curve and to the right of the test statistic t * = 2.5. It can be shown using statistical software that the P -value is 0.0127. The graph depicts this visually.

t-distrbution graph showing the right tail beyond a t value of 2.5

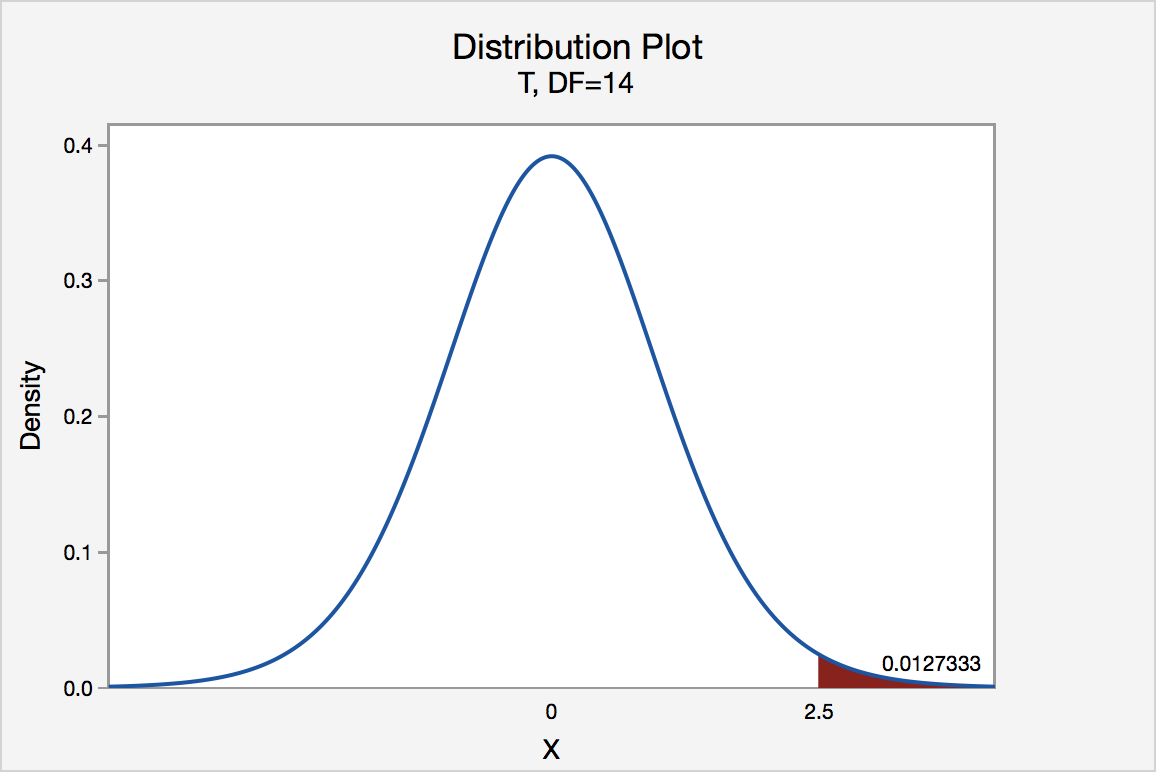
The P -value, 0.0127, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0127, is less than $\alpha$ = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ > 3.

Note that we would not reject H 0 : μ = 3 in favor of H A : μ > 3 if we lowered our willingness to make a Type I error to $\alpha$ = 0.01 instead, as the P -value, 0.0127, is then greater than $\alpha$ = 0.01.

Left Tailed

In our example concerning the mean grade point average, suppose that our random sample of n = 15 students majoring in mathematics yields a test statistic t * instead of equaling -2.5. The P -value for conducting the left-tailed test H 0 : μ = 3 versus H A : μ < 3 is the probability that we would observe a test statistic less than t * = -2.5 if the population mean μ really were 3. The P -value is therefore the area under a t n - 1 = t 14 curve and to the left of the test statistic t* = -2.5. It can be shown using statistical software that the P -value is 0.0127. The graph depicts this visually.

t distribution graph showing left tail below t value of -2.5

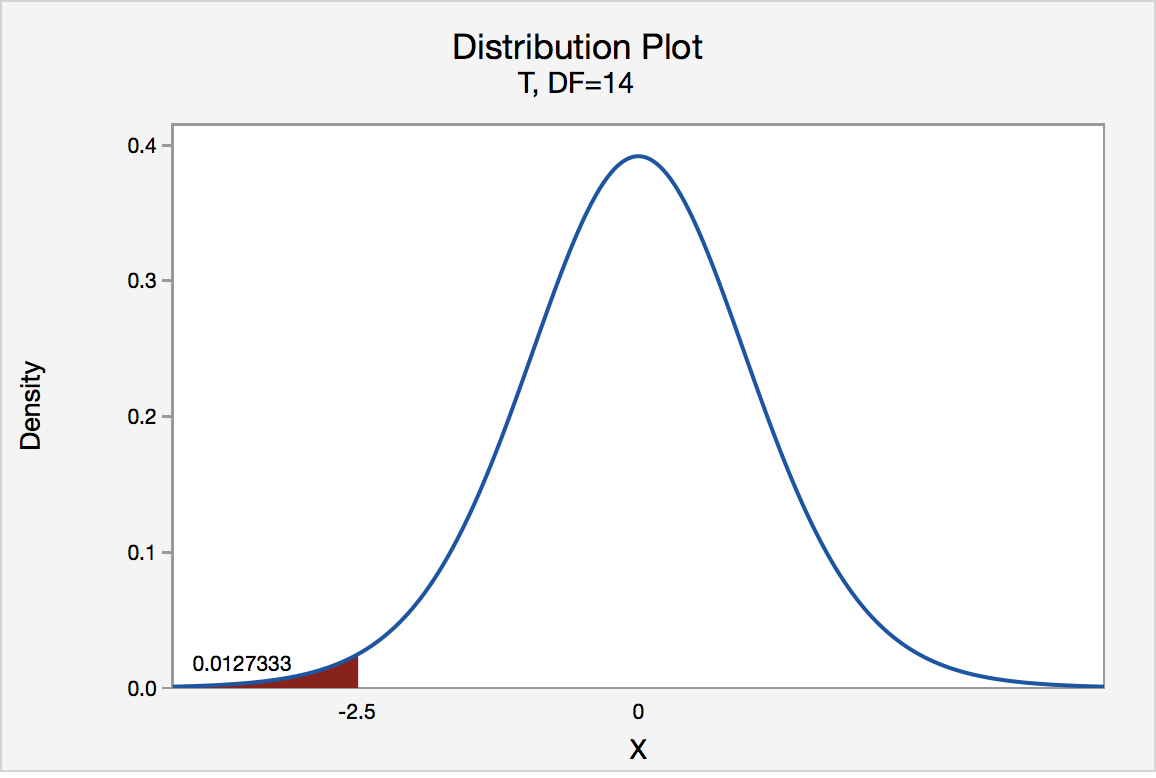
The P -value, 0.0127, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0127, is less than α = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ < 3.

Note that we would not reject H 0 : μ = 3 in favor of H A : μ < 3 if we lowered our willingness to make a Type I error to α = 0.01 instead, as the P -value, 0.0127, is then greater than $\alpha$ = 0.01.

In our example concerning the mean grade point average, suppose again that our random sample of n = 15 students majoring in mathematics yields a test statistic t * instead of equaling -2.5. The P -value for conducting the two-tailed test H 0 : μ = 3 versus H A : μ ≠ 3 is the probability that we would observe a test statistic less than -2.5 or greater than 2.5 if the population mean μ really was 3. That is, the two-tailed test requires taking into account the possibility that the test statistic could fall into either tail (hence the name "two-tailed" test). The P -value is, therefore, the area under a t n - 1 = t 14 curve to the left of -2.5 and to the right of 2.5. It can be shown using statistical software that the P -value is 0.0127 + 0.0127, or 0.0254. The graph depicts this visually.

t-distribution graph of two tailed probability for t values of -2.5 and 2.5

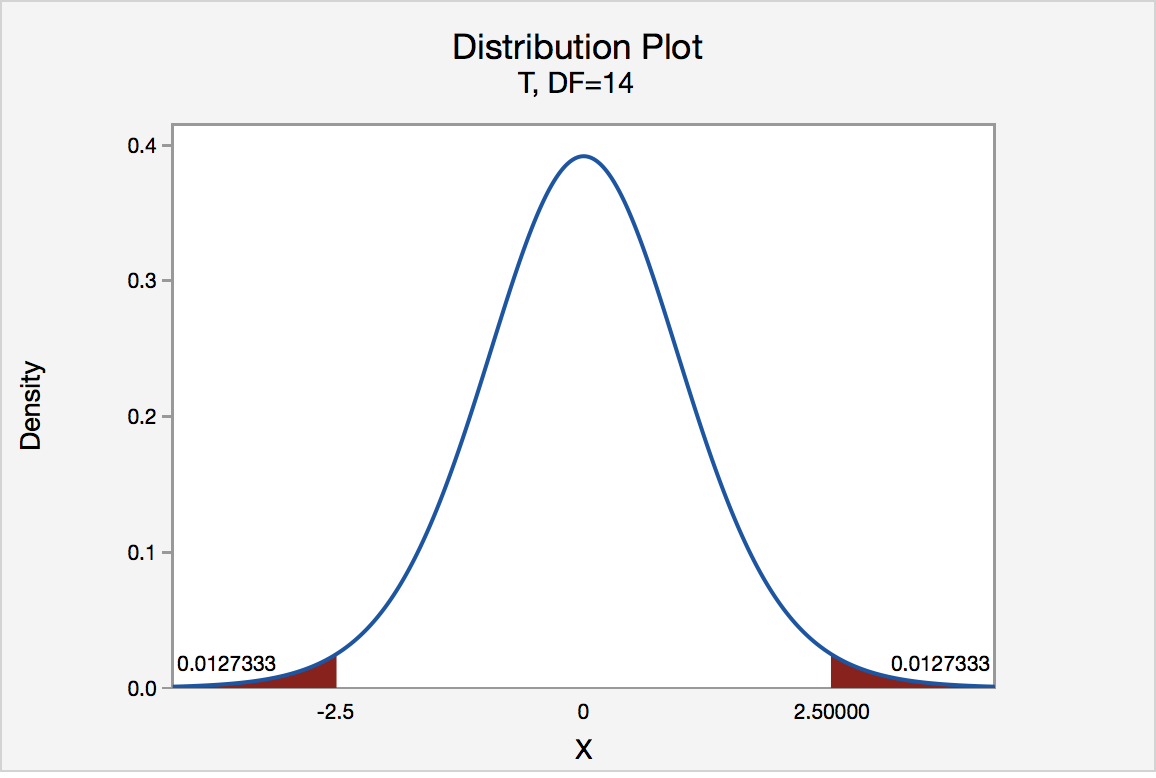
Note that the P -value for a two-tailed test is always two times the P -value for either of the one-tailed tests. The P -value, 0.0254, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0254, is less than α = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ ≠ 3.

Note that we would not reject H 0 : μ = 3 in favor of H A : μ ≠ 3 if we lowered our willingness to make a Type I error to α = 0.01 instead, as the P -value, 0.0254, is then greater than $\alpha$ = 0.01.

Now that we have reviewed the critical value and P -value approach procedures for each of the three possible hypotheses, let's look at three new examples — one of a right-tailed test, one of a left-tailed test, and one of a two-tailed test.

The good news is that, whenever possible, we will take advantage of the test statistics and P -values reported in statistical software, such as Minitab, to conduct our hypothesis tests in this course.

Mastering Hypothesis Testing in Excel: A Practical Guide for Students

Excel for Hypothesis Testing: A Practical Approach for Students

Hypothesis testing lies at the heart of statistical inference, serving as a cornerstone for drawing meaningful conclusions from data. It's a methodical process used to evaluate assumptions about a population parameter, typically based on sample data. The fundamental idea behind hypothesis testing is to assess whether observed differences or relationships in the sample are statistically significant enough to warrant generalizations to the larger population. This process involves formulating null and alternative hypotheses, selecting an appropriate statistical test, collecting sample data, and interpreting the results to make informed decisions. In the realm of statistical software, SAS stands out as a robust and widely used tool for data analysis in various fields such as academia, industry, and research. Its extensive capabilities make it particularly favored for complex analyses, large datasets, and advanced modeling techniques. However, despite its versatility and power, SAS can have a steep learning curve, especially for students who are just beginning their journey into statistics. The intricacies of programming syntax, data manipulation, and interpreting output may pose challenges for novice users, potentially hindering their understanding of statistical concepts like hypothesis testing. If you need assistance with your Excel homework , understanding hypothesis testing is essential for performing statistical analyses and drawing meaningful conclusions from data using Excel's built-in functions and tools.

Enter Excel, a ubiquitous spreadsheet software that most students are already familiar with to some extent. While Excel may not offer the same level of sophistication as SAS in terms of advanced statistical procedures, it remains a valuable tool, particularly for introductory and intermediate-level analyses. Its intuitive interface, user-friendly features, and widespread accessibility make it an attractive option for students seeking a practical approach to learning statistics. By leveraging Excel's built-in functions, data visualization tools, and straightforward formulas, students can gain hands-on experience with hypothesis testing in a familiar environment. In this blog post, we aim to bridge the gap between theoretical concepts and practical application by demonstrating how Excel can serve as a valuable companion for students tackling hypothesis testing problems, including those typically encountered in SAS assignments. We will focus on demystifying the process of hypothesis testing, breaking it down into manageable steps, and showcasing Excel's capabilities for conducting various tests commonly encountered in introductory statistics courses.

Understanding the Basics

Hypothesis testing is a fundamental concept in statistics that allows researchers to draw conclusions about a population based on sample data. At its core, hypothesis testing involves making a decision about whether a statement regarding a population parameter is likely to be true. This decision is based on the analysis of sample data and is guided by two competing hypotheses: the null hypothesis (H0) and the alternative hypothesis (Ha). The null hypothesis represents the status quo or the absence of an effect. It suggests that any observed differences or relationships in the sample data are due to random variation or chance. On the other hand, the alternative hypothesis contradicts the null hypothesis and suggests the presence of an effect or difference in the population. It reflects the researcher's belief or the hypothesis they aim to support with their analysis.

Formulating Hypotheses

In Excel, students can easily formulate hypotheses using simple formulas and logical operators. For instance, suppose a researcher wants to test whether the mean of a sample is equal to a specified value. They can use the AVERAGE function in Excel to calculate the sample mean and then compare it to the specified value using logical operators like "=" for equality. If the calculated mean is equal to the specified value, it supports the null hypothesis; otherwise, it supports the alternative hypothesis.

Excel's flexibility allows students to customize their hypotheses based on the specific parameters they are testing. Whether it's comparing means, proportions, variances, or other population parameters, Excel provides a user-friendly interface for formulating hypotheses and conducting statistical analysis.

Selecting the Appropriate Test

Excel offers a plethora of functions and tools for conducting various types of hypothesis tests, including t-tests, z-tests, chi-square tests, and ANOVA (analysis of variance). However, selecting the appropriate test requires careful consideration of the assumptions and conditions associated with each test. Students should familiarize themselves with the assumptions underlying each hypothesis test and assess whether their data meets those assumptions. For example, t-tests assume that the data follow a normal distribution, while chi-square tests require categorical data and independence between observations.

Furthermore, students should consider the nature of their research question and the type of data they are analyzing. Are they comparing means of two independent groups or assessing the association between categorical variables? By understanding the characteristics of their data and the requirements of each test, students can confidently choose the appropriate hypothesis test in Excel.

T-tests are statistical tests commonly used to compare the means of two independent samples or to compare the mean of a single sample to a known value. These tests are valuable in various fields, including psychology, biology, economics, and more. In Excel, students can employ the T.TEST function to conduct t-tests, providing them with a practical and accessible way to analyze their data and draw conclusions about population parameters based on sample statistics.

Independent Samples T-Test

The independent samples t-test, also known as the unpaired t-test, is utilized when comparing the means of two independent groups. This test is often employed in experimental and observational studies to assess whether there is a significant difference between the means of the two groups. In Excel, students can easily organize their data into separate columns representing the two groups, calculate the sample means and standard deviations for each group, and then use the T.TEST function to obtain the p-value. The p-value obtained from the T.TEST function represents the probability of observing the sample data if the null hypothesis, which typically states that there is no difference between the means of the two groups, is true.

A small p-value (typically less than the chosen significance level, commonly 0.05) indicates that there is sufficient evidence to reject the null hypothesis in favor of the alternative hypothesis, suggesting a significant difference between the group means. By conducting an independent samples t-test in Excel, students can not only assess the significance of differences between two groups but also gain valuable experience in data analysis and hypothesis testing, which are essential skills in various academic and professional settings.

Paired Samples T-Test

The paired samples t-test, also known as the dependent t-test or matched pairs t-test, is employed when comparing the means of two related groups. This test is often used in studies where participants are measured before and after an intervention or when each observation in one group is matched or paired with a specific observation in the other group. Examples include comparing pre-test and post-test scores, analyzing the performance of individuals under different conditions, and assessing the effectiveness of a treatment or intervention. In Excel, students can perform a paired samples t-test by first calculating the differences between paired observations (e.g., subtracting the before-measurement from the after-measurement). Next, they can use the one-sample t-test function, specifying the calculated differences as the sample data. This approach allows students to determine whether the mean difference between paired observations is statistically significant, indicating whether there is a meaningful change or effect between the two related groups.

Interpreting the results of a paired samples t-test involves assessing the obtained p-value in relation to the chosen significance level. A small p-value suggests that there is sufficient evidence to reject the null hypothesis, indicating a significant difference between the paired observations. This information can help students draw meaningful conclusions from their data and make informed decisions based on statistical evidence. By conducting paired samples t-tests in Excel, students can not only analyze the relationship between related groups but also develop critical thinking skills and gain practical experience in hypothesis testing, which are valuable assets in both academic and professional contexts. Additionally, mastering the application of statistical tests in Excel can enhance students' data analysis skills and prepare them for future research endeavors and real-world challenges.

Chi-Square Test

The chi-square test is a versatile statistical tool used to assess the association between two categorical variables. In essence, it helps determine whether the observed frequencies in a dataset significantly deviate from what would be expected under certain assumptions. Excel provides a straightforward means to perform chi-square tests using the CHISQ.TEST function, which calculates the probability associated with the chi-square statistic.

Goodness-of-Fit Test

One application of the chi-square test is the goodness-of-fit test, which evaluates how well the observed frequencies in a single categorical variable align with the expected frequencies dictated by a theoretical distribution. This test is particularly useful when researchers wish to ascertain whether their data conforms to a specific probability distribution. In Excel, students can organize their data into a frequency table, listing the categories of the variable of interest along with their corresponding observed frequencies. They can then specify the expected frequencies based on the theoretical distribution they are testing against. For example, if analyzing the outcomes of a six-sided die roll, where each face is expected to occur with equal probability, the expected frequency for each category would be the total number of observations divided by six.

Once the observed and expected frequencies are determined, students can employ the CHISQ.TEST function in Excel to calculate the chi-square statistic and its associated p-value. The p-value represents the probability of obtaining a chi-square statistic as extreme or more extreme than the observed value under the assumption that the null hypothesis is true (i.e., the observed frequencies match the expected frequencies). Interpreting the results of the goodness-of-fit test involves comparing the calculated p-value to a predetermined significance level (commonly denoted as α). If the p-value is less than α (e.g., α = 0.05), there is sufficient evidence to reject the null hypothesis, indicating that the observed frequencies significantly differ from the expected frequencies specified by the theoretical distribution. Conversely, if the p-value is greater than α, there is insufficient evidence to reject the null hypothesis, suggesting that the observed frequencies align well with the expected frequencies.

Test of Independence

Another important application of the chi-square test in Excel is the test of independence, which evaluates whether there is a significant association between two categorical variables in a contingency table. This test is employed when researchers seek to determine whether the occurrence of one variable is related to the occurrence of another. To conduct a test of independence in Excel, students first create a contingency table that cross-tabulates the two categorical variables of interest. Each cell in the table represents the frequency of occurrences for a specific combination of categories from the two variables.

Similar to the goodness-of-fit test, students then calculate the expected frequencies for each cell under the assumption of independence between the variables. Using the CHISQ.TEST function in Excel, students can calculate the chi-square statistic and its associated p-value based on the observed and expected frequencies in the contingency table. The interpretation of the test results follows a similar procedure to that of the goodness-of-fit test, with the p-value indicating whether there is sufficient evidence to reject the null hypothesis of independence between the two variables.

Excel, despite being commonly associated with spreadsheet tasks, offers a plethora of features that make it a versatile and powerful tool for statistical analysis, especially for students diving into the intricacies of hypothesis testing. Its widespread availability and user-friendly interface make it accessible to students at various levels of statistical proficiency. However, the true value of Excel lies not just in its accessibility but also in its ability to facilitate a hands-on learning experience that reinforces theoretical concepts.

At the core of utilizing Excel for hypothesis testing is a solid understanding of the fundamental principles of statistical inference. Students need to grasp concepts such as the null and alternative hypotheses, significance levels, p-values, and test statistics. Excel provides a practical platform for students to apply these concepts in a real-world context. Through hands-on experimentation with sample datasets, students can observe how changes in data inputs and statistical parameters affect the outcome of hypothesis tests, thus deepening their understanding of statistical theory.