which of the following is an appropriate null hypothesis

Module 9: Hypothesis Testing With One Sample

Null and alternative hypotheses, learning outcomes.

• Describe hypothesis testing in general and in practice

The actual test begins by considering two  hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.

H a : The alternative hypothesis : It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make adecision. There are two options for a  decision . They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in  H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30

H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

H 0 : The drug reduces cholesterol by 25%. p = 0.25

H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

H 0 : μ = 2.0

H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 66 H a : μ __ 66

• H 0 : μ = 66
• H a : μ ≠ 66

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

H 0 : μ ≥ 5

H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 45 H a : μ __ 45

• H 0 : μ ≥ 45
• H a : μ < 45

In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

H 0 : p ≤ 0.066

H a : p > 0.066

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : p __ 0.40 H a : p __ 0.40

• H 0 : p = 0.40
• H a : p > 0.40

Concept Review

In a  hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis , typically denoted with H 0 . The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality (=, ≤ or ≥) Always write the alternative hypothesis , typically denoted with H a or H 1 , using less than, greater than, or not equals symbols, i.e., (≠, >, or <). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

H 0 and H a are contradictory.

• OpenStax, Statistics, Null and Alternative Hypotheses. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:58/Introductory_Statistics . License : CC BY: Attribution
• Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Simple hypothesis testing | Probability and Statistics | Khan Academy. Authored by : Khan Academy. Located at : https://youtu.be/5D1gV37bKXY . License : All Rights Reserved . License Terms : Standard YouTube License

Have a thesis expert improve your writing

Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.

• Knowledge Base
• Null and Alternative Hypotheses | Definitions & Examples

Null and Alternative Hypotheses | Definitions & Examples

Published on 5 October 2022 by Shaun Turney . Revised on 6 December 2022.

The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :

• Null hypothesis (H 0 ): There’s no effect in the population .
• Alternative hypothesis (H A ): There’s an effect in the population.

The effect is usually the effect of the independent variable on the dependent variable .

Table of contents

Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, differences between null and alternative hypotheses, how to write null and alternative hypotheses, frequently asked questions about null and alternative hypotheses.

The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”, the null hypothesis (H 0 ) answers “No, there’s no effect in the population.” On the other hand, the alternative hypothesis (H A ) answers “Yes, there is an effect in the population.”

The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample.

You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.

The null hypothesis is the claim that there’s no effect in the population.

If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.

Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept. Be careful not to say you “prove” or “accept” the null hypothesis.

Null hypotheses often include phrases such as “no effect”, “no difference”, or “no relationship”. When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).

Examples of null hypotheses

The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.

*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .

The alternative hypothesis (H A ) is the other answer to your research question . It claims that there’s an effect in the population.

Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.

The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.

Alternative hypotheses often include phrases such as “an effect”, “a difference”, or “a relationship”. When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes > or <). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.

Examples of alternative hypotheses

The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.

Null and alternative hypotheses are similar in some ways:

• They’re both answers to the research question
• They both make claims about the population
• They’re both evaluated by statistical tests.

However, there are important differences between the two types of hypotheses, summarized in the following table.

To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.

The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:

Does independent variable affect dependent variable ?

• Null hypothesis (H 0 ): Independent variable does not affect dependent variable .
• Alternative hypothesis (H A ): Independent variable affects dependent variable .

Test-specific

Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.

Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.

The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).

The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

Turney, S. (2022, December 06). Null and Alternative Hypotheses | Definitions & Examples. Scribbr. Retrieved 27 May 2024, from https://www.scribbr.co.uk/stats/null-and-alternative-hypothesis/

Is this article helpful?

Shaun Turney

Other students also liked, levels of measurement: nominal, ordinal, interval, ratio, the standard normal distribution | calculator, examples & uses, types of variables in research | definitions & examples.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics   >   unit 10.

• Idea behind hypothesis testing

Examples of null and alternative hypotheses

• Writing null and alternative hypotheses
• P-values and significance tests
• Comparing P-values to different significance levels
• Estimating a P-value from a simulation
• Estimating P-values from simulations
• Using P-values to make conclusions

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Hypothesis Testing with One Sample

Null and Alternative Hypotheses

OpenStaxCollege

[latexpage]

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.

H a : The alternative hypothesis: It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

H 0 : The drug reduces cholesterol by 25%. p = 0.25

H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

H 0 : μ = 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ = 66
• H a : μ ≠ 66

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

H 0 : μ ≥ 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ ≥ 45
• H a : μ < 45

In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

H 0 : p ≤ 0.066

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p = 0.40
• H a : p > 0.40

<!– ??? –>

Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

Chapter Review

In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we:

Formula Review

H 0 and H a are contradictory.

If α ≤ p -value, then do not reject H 0 .

If α > p -value, then reject H 0 .

α is preconceived. Its value is set before the hypothesis test starts. The p -value is calculated from the data.

You are testing that the mean speed of your cable Internet connection is more than three Megabits per second. What is the random variable? Describe in words.

The random variable is the mean Internet speed in Megabits per second.

You are testing that the mean speed of your cable Internet connection is more than three Megabits per second. State the null and alternative hypotheses.

The American family has an average of two children. What is the random variable? Describe in words.

The random variable is the mean number of children an American family has.

The mean entry level salary of an employee at a company is 💲58,000. You believe it is higher for IT professionals in the company. State the null and alternative hypotheses.

A sociologist claims the probability that a person picked at random in Times Square in New York City is visiting the area is 0.83. You want to test to see if the proportion is actually less. What is the random variable? Describe in words.

The random variable is the proportion of people picked at random in Times Square visiting the city.

A sociologist claims the probability that a person picked at random in Times Square in New York City is visiting the area is 0.83. You want to test to see if the claim is correct. State the null and alternative hypotheses.

In a population of fish, approximately 42% are female. A test is conducted to see if, in fact, the proportion is less. State the null and alternative hypotheses.

Suppose that a recent article stated that the mean time spent in jail by a first–time convicted burglar is 2.5 years. A study was then done to see if the mean time has increased in the new century. A random sample of 26 first-time convicted burglars in a recent year was picked. The mean length of time in jail from the survey was 3 years with a standard deviation of 1.8 years. Suppose that it is somehow known that the population standard deviation is 1.5. If you were conducting a hypothesis test to determine if the mean length of jail time has increased, what would the null and alternative hypotheses be? The distribution of the population is normal.

A random survey of 75 death row inmates revealed that the mean length of time on death row is 17.4 years with a standard deviation of 6.3 years. If you were conducting a hypothesis test to determine if the population mean time on death row could likely be 15 years, what would the null and alternative hypotheses be?

• H 0 : __________
• H a : __________
• H 0 : μ = 15
• H a : μ ≠ 15

The National Institute of Mental Health published an article stating that in any one-year period, approximately 9.5 percent of American adults suffer from depression or a depressive illness. Suppose that in a survey of 100 people in a certain town, seven of them suffered from depression or a depressive illness. If you were conducting a hypothesis test to determine if the true proportion of people in that town suffering from depression or a depressive illness is lower than the percent in the general adult American population, what would the null and alternative hypotheses be?

Some of the following statements refer to the null hypothesis, some to the alternate hypothesis.

State the null hypothesis, H 0 , and the alternative hypothesis. H a , in terms of the appropriate parameter ( μ or p ).

• The mean number of years Americans work before retiring is 34.
• At most 60% of Americans vote in presidential elections.
• The mean starting salary for San Jose State University graduates is at least 💲100,000 per year.
• Twenty-nine percent of high school seniors get drunk each month.
• Fewer than 5% of adults ride the bus to work in Los Angeles.
• The mean number of cars a person owns in her lifetime is not more than ten.
• About half of Americans prefer to live away from cities, given the choice.
• Europeans have a mean paid vacation each year of six weeks.
• The chance of developing breast cancer is under 11% for women.
• Private universities’ mean tuition cost is more than 💲20,000 per year.
• H 0 : μ = 34; H a : μ ≠ 34
• H 0 : p ≤ 0.60; H a : p > 0.60
• H 0 : μ ≥ 100,000; H a : μ < 100,000
• H 0 : p = 0.29; H a : p ≠ 0.29
• H 0 : p = 0.05; H a : p < 0.05
• H 0 : μ ≤ 10; H a : μ > 10
• H 0 : p = 0.50; H a : p ≠ 0.50
• H 0 : μ = 6; H a : μ ≠ 6
• H 0 : p ≥ 0.11; H a : p < 0.11
• H 0 : μ ≤ 20,000; H a : μ > 20,000

Over the past few decades, public health officials have examined the link between weight concerns and teen girls’ smoking. Researchers surveyed a group of 273 randomly selected teen girls living in Massachusetts (between 12 and 15 years old). After four years the girls were surveyed again. Sixty-three said they smoked to stay thin. Is there good evidence that more than thirty percent of the teen girls smoke to stay thin? The alternative hypothesis is:

• p < 0.30
• p > 0.30

A statistics instructor believes that fewer than 20% of Evergreen Valley College (EVC) students attended the opening night midnight showing of the latest Harry Potter movie. She surveys 84 of her students and finds that 11 attended the midnight showing. An appropriate alternative hypothesis is:

• p > 0.20
• p < 0.20

Previously, an organization reported that teenagers spent 4.5 hours per week, on average, on the phone. The organization thinks that, currently, the mean is higher. Fifteen randomly chosen teenagers were asked how many hours per week they spend on the phone. The sample mean was 4.75 hours with a sample standard deviation of 2.0. Conduct a hypothesis test. The null and alternative hypotheses are:

• H o : \(\overline{x}\) = 4.5, H a : \(\overline{x}\) > 4.5
• H o : μ ≥ 4.5, H a : μ < 4.5
• H o : μ = 4.75, H a : μ > 4.75
• H o : μ = 4.5, H a : μ > 4.5

Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm.

Null and Alternative Hypotheses Copyright © 2013 by OpenStaxCollege is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

10.2: Null and Alternative Hypotheses

• Last updated
• Save as PDF
• Page ID 100392

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

The actual test begins by considering two hypotheses. They are called the null hypothesis and the alternative hypothesis. These hypotheses contain opposing viewpoints.

• The null hypothesis (\(H_{0}\)) is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.
• The alternative hypothesis (\(H_{a}\)) is a claim about the population that is contradictory to \(H_{0}\) and what we conclude when we reject \(H_{0}\).

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data. After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject \(H_{0}\)" if the sample information favors the alternative hypothesis or "do not reject \(H_{0}\)" or "decline to reject \(H_{0}\)" if the sample information is insufficient to reject the null hypothesis.

\(H_{0}\) always has a symbol with an equal in it. \(H_{a}\) never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example \(\PageIndex{1}\)

• \(H_{0}\): No more than 30% of the registered voters in Santa Clara County voted in the primary election. \(p \leq 30\)
• \(H_{a}\): More than 30% of the registered voters in Santa Clara County voted in the primary election. \(p > 30\)

Exercise \(\PageIndex{1}\)

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

• \(H_{0}\): The drug reduces cholesterol by 25%. \(p = 0.25\)
• \(H_{a}\): The drug does not reduce cholesterol by 25%. \(p \neq 0.25\)

Example \(\PageIndex{2}\)

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

• \(H_{0}: \mu = 2.0\)
• \(H_{a}: \mu \neq 2.0\)

Exercise \(\PageIndex{2}\)

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol \((=, \neq, \geq, <, \leq, >)\) for the null and alternative hypotheses.

• \(H_{0}: \mu \  \_ \  66\)
• \(H_{a}: \mu \  \_ \  66\)
• \(H_{0}: \mu = 66\)
• \(H_{a}: \mu \neq 66\)

Example \(\PageIndex{3}\)

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

• \(H_{0}: \mu \geq 5\)
• \(H_{a}: \mu < 5\)

Exercise \(\PageIndex{3}\)

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• \(H_{0}: \mu \  \_ \  45\)
• \(H_{a}: \mu \  \_ \  45\)
• \(H_{0}: \mu \geq 45\)
• \(H_{a}: \mu < 45\)

Example \(\PageIndex{4}\)

In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

• \(H_{0}: p \leq 0.066\)
• \(H_{a}: p > 0.066\)

Exercise \(\PageIndex{4}\)

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (\(=, \neq, \geq, <, \leq, >\)) for the null and alternative hypotheses.

• \(H_{0}: p \  \_ \  0.40\)
• \(H_{a}: p \  \_ \  0.40\)
• \(H_{0}: p = 0.40\)
• \(H_{a}: p > 0.40\)

COLLABORATIVE EXERCISE

Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

Chapter Review

In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we:

• Evaluate the null hypothesis , typically denoted with \(H_{0}\). The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality \((=, \leq \text{or} \geq)\)
• Always write the alternative hypothesis , typically denoted with \(H_{a}\) or \(H_{1}\), using less than, greater than, or not equals symbols, i.e., \((\neq, >, \text{or} <)\).
• If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis.
• Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

\(H_{0}\) and \(H_{a}\) are contradictory.

• If \(\alpha \leq p\)-value, then do not reject \(H_{0}\).
• If\(\alpha > p\)-value, then reject \(H_{0}\).

\(\alpha\) is preconceived. Its value is set before the hypothesis test starts. The \(p\)-value is calculated from the data.References

Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm .

Contributors

Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/[email protected] .

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• About Varsity Tutors

AP Statistics : How to establish a null hypothesis

Study concepts, example questions & explanations for ap statistics, all ap statistics resources, example questions, example question #1 : how to establish a null hypothesis.

Jimmy thinks that Josh cannot shoot more than 50 points on average in a game. Josh disputes this claim and tells Jimmy that he is going to play 10 games and prove him wrong. What is the null hypothesis? 

Josh cannot shoot exactly 50 points.

Josh cannot play 10 games.

Josh cannot shoot less than 50 points.

Josh cannot shoot more than 50 points.

The null hypothesis is what we intend to either reject or fail to reject using our sample data. In this case, the null hypothesis is that Josh cannot shoot more than 50 points on average, and Josh's performance in 10 games are the sample data we use to assess this hypothesis. 

A student is beginning an analysis to determine whether there is a relationship between temperatures and traffic accidents.  The student is trying to articulate a null hypothesis for the study.  Which of the following is an acceptable null hypothesis?

There is a positive relationship between temperatures and traffic accidents

There is a negative relationship between temperatures and traffic accidents

No variable can accurately predict whether traffic accidents will increase

Traffic accidents increase as temperatures decrease

There is no relationship between temperatures and frequency of traffic accidents

The null hypothesis is the default hypothesis and predicts that there is no relationship between the variables in question.  Each of the incorrect answer choices here either predicts a relationship between variables or makes a broad assertion that includes much more than the variables in question.

Not enough information to make a decision.

Conditionally

The statistician has determined that she will only reject the null hypothesis if she has 95% confidence that there is a relationship between variables. 

To have this level of confidence, the statistician must obtain a p value of 0.05 or lower.

Therefore, she should not reject the null hypothesis since 0.1 is greater that 0.05.

The Environmental Protection Agency (EPA) wants to test the pollution level of the Colorado River. If the pollution level is too high, the water will be stopped from going into drinking water pipelines. The EPA randomly chooses different spots along the river to collect water samples from, and then tests the samples for their pollution levels. Which of the following decisions would result from the type I error?

Keeping the drinking water pipelines open when the pollution levels are higher than the allowed limit. 

Keeping the drinking water pipelines open when the pollution levels are within the allowed limit. 

Closing the drinking water pipelines for the river when the pollution levels are within the allowed limit. 

Closing the drinking water pipelines when the pollution levels are higher than the allowed limit. 

Closing the drinking water pipelines because of the endangered frog population. 

The hypotheses tested here are: 

The type I error occurs when the null hypothesis is rejected even though it is actually true. In this case, the type I error would be deciding that the mean pollution levels are higher than the allowed limit and closing the drinking water pipelines. 

A study would like to determine whether meditation helps students improve focus time. They know that the average focus time of an American 4 th grader is 23 minutes. They then recruit 50 meditators and calculate their average focus time. What is the appropriate null hypothesis for this study?

A researcher wants to determine whether there is a significant linear relationship between time spent meditating and time spent studying. What is the appropriate null hypothesis for this study?

This question is about a linear regression between time spent meditating and time spent studying. Therefore, the hypothesis is regarding Beta1, the slope of the line. We are testing a non-directional or bi-directional claim that the relationship is significant . Therefore, the null hypothesis is that the relationship is not significant, meaning the slope of the line is equal to zero.

A researcher wants to compare 3 different treatments to see if any of the treatments affects study time. The three treatments studied are control group, a group given vitamins, and a group given a placebo.  They found that the average time spent studying with control students was 2 hours, with students given vitamins it was 3 hours, and with placebos students studied 5 hours. Which of the following is the correct null hypothesis?

Because we are comparing more than 2 groups, we must use an ANOVA for this problem. For an ANOVA problem, the null hypothesis is that all of the groups’ means are the same.

Example Question #31 : Significance

A researcher wants to investigate the claim that taking vitamins will help a student study longer. First, the researcher collects 32 students who do not take vitamins and determines their time spent studying. Then, the 32 students are given a vitamin for 1 week. After 1 week of taking vitamins, students are again tested to determine their time spent studying. Which of the following is the correct null hypothesis?

Because the same students are tested twice, this is a paired study, therefore we must use a hypothesis appropriate for a paired t-test.  The hypothesis for a paired t-test regards the average of the differences between before and after treatment, called MuD. We are testing the claim that vitamins increase study time, which would mean that study time for vitamin users would be greater than that of the control.  Therefore the null must include all other outcomes. The null hypothesis should state that the difference between before and after treatment is greater than or equal to zero.

For her school science project, Susy wants to determine whether the ants in her neighborhood have smaller colonies than average. Research tells her that the average Harvester colony has around 4,000 ants. She counts the number of ants in 5 colonies in her neighborhood and determines the average colony size to be 3,700 ants. What is the appropriate null hypothesis for her science project?

Susy wants to know whether ants in her neighborhood have smaller colonies, so that will be her alternative hypothesis. Therefore her null hypothesis needs to cover all other outcomes, that the colony sizes are greater than or equal to average colony size of 4000 ants.

For his school science project, Timmy wants to determine whether the ants in his neighborhood have colonies that are sized differently than normal. His research shows that the average Harvester colony has around 4000 ants. He counts the number of ants in 5 colonies and determines that the average colony size is 3,700 ants. What is the appropriate null hypothesis for his science project?

Timmy does not have a directional hypothesis, he only wants to know whether local ant colonies are different from average. Therefore he thinks the colonies could be bigger or smaller than average. This means his alternative hypothesis is that the ant colonies are NOT equal to the average colony size of 4000 ants. His null hypothesis must include all other outcomes, which in this case is that local ant colonies are equal to the average size of 4000 ants. 

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Contact Information

Complaint details.

Null Hypothesis Examples

ThoughtCo / Hilary Allison

• Scientific Method
• Chemical Laws
• Periodic Table
• Projects & Experiments
• Biochemistry
• Physical Chemistry
• Medical Chemistry
• Chemistry In Everyday Life
• Famous Chemists
• Activities for Kids
• Abbreviations & Acronyms
• Weather & Climate
• Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
• B.A., Physics and Mathematics, Hastings College

In statistical analysis, the null hypothesis assumes there is no meaningful relationship between two variables. Testing the null hypothesis can tell you whether your results are due to the effect of manipulating ​a dependent variable or due to chance. It's often used in conjunction with an alternative hypothesis, which assumes there is, in fact, a relationship between two variables.

The null hypothesis is among the easiest hypothesis to test using statistical analysis, making it perhaps the most valuable hypothesis for the scientific method. By evaluating a null hypothesis in addition to another hypothesis, researchers can support their conclusions with a higher level of confidence. Below are examples of how you might formulate a null hypothesis to fit certain questions.

What Is the Null Hypothesis?

The null hypothesis states there is no relationship between the measured phenomenon (the dependent variable ) and the independent variable , which is the variable an experimenter typically controls or changes. You do not​ need to believe that the null hypothesis is true to test it. On the contrary, you will likely suspect there is a relationship between a set of variables. One way to prove that this is the case is to reject the null hypothesis. Rejecting a hypothesis does not mean an experiment was "bad" or that it didn't produce results. In fact, it is often one of the first steps toward further inquiry.

To distinguish it from other hypotheses , the null hypothesis is written as ​ H 0  (which is read as “H-nought,” "H-null," or "H-zero"). A significance test is used to determine the likelihood that the results supporting the null hypothesis are not due to chance. A confidence level of 95% or 99% is common. Keep in mind, even if the confidence level is high, there is still a small chance the null hypothesis is not true, perhaps because the experimenter did not account for a critical factor or because of chance. This is one reason why it's important to repeat experiments.

Examples of the Null Hypothesis

To write a null hypothesis, first start by asking a question. Rephrase that question in a form that assumes no relationship between the variables. In other words, assume a treatment has no effect. Write your hypothesis in a way that reflects this.

Other Types of Hypotheses

In addition to the null hypothesis, the alternative hypothesis is also a staple in traditional significance tests . It's essentially the opposite of the null hypothesis because it assumes the claim in question is true. For the first item in the table above, for example, an alternative hypothesis might be "Age does have an effect on mathematical ability."

Key Takeaways

• In hypothesis testing, the null hypothesis assumes no relationship between two variables, providing a baseline for statistical analysis.
• Rejecting the null hypothesis suggests there is evidence of a relationship between variables.
• By formulating a null hypothesis, researchers can systematically test assumptions and draw more reliable conclusions from their experiments.
• Difference Between Independent and Dependent Variables
• Examples of Independent and Dependent Variables
• What Is a Hypothesis? (Science)
• What 'Fail to Reject' Means in a Hypothesis Test
• Definition of a Hypothesis
• Null Hypothesis Definition and Examples
• Scientific Method Vocabulary Terms
• Null Hypothesis and Alternative Hypothesis
• Hypothesis Test for the Difference of Two Population Proportions
• How to Conduct a Hypothesis Test
• What Is a P-Value?
• What Are the Elements of a Good Hypothesis?
• What Is the Difference Between Alpha and P-Values?
• Understanding Path Analysis
• Hypothesis Test Example
• An Example of a Hypothesis Test

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

5.2 - writing hypotheses.

The first step in conducting a hypothesis test is to write the hypothesis statements that are going to be tested. For each test you will have a null hypothesis (\(H_0\)) and an alternative hypothesis (\(H_a\)).

When writing hypotheses there are three things that we need to know: (1) the parameter that we are testing (2) the direction of the test (non-directional, right-tailed or left-tailed), and (3) the value of the hypothesized parameter.

• At this point we can write hypotheses for a single mean (\(\mu\)), paired means(\(\mu_d\)), a single proportion (\(p\)), the difference between two independent means (\(\mu_1-\mu_2\)), the difference between two proportions (\(p_1-p_2\)), a simple linear regression slope (\(\beta\)), and a correlation (\(\rho\)). 
• The research question will give us the information necessary to determine if the test is two-tailed (e.g., "different from," "not equal to"), right-tailed (e.g., "greater than," "more than"), or left-tailed (e.g., "less than," "fewer than").
• The research question will also give us the hypothesized parameter value. This is the number that goes in the hypothesis statements (i.e., \(\mu_0\) and \(p_0\)). For the difference between two groups, regression, and correlation, this value is typically 0.

Hypotheses are always written in terms of population parameters (e.g., \(p\) and \(\mu\)).  The tables below display all of the possible hypotheses for the parameters that we have learned thus far. Note that the null hypothesis always includes the equality (i.e., =).

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.4: Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 283

• David Diez, Christopher Barr, & Mine Çetinkaya-Rundel
• OpenIntro Statistics

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Is the typical US runner getting faster or slower over time? We consider this question in the context of the Cherry Blossom Run, comparing runners in 2006 and 2012. Technological advances in shoes, training, and diet might suggest runners would be faster in 2012. An opposing viewpoint might say that with the average body mass index on the rise, people tend to run slower. In fact, all of these components might be influencing run time.

In addition to considering run times in this section, we consider a topic near and dear to most students: sleep. A recent study found that college students average about 7 hours of sleep per night.15 However, researchers at a rural college are interested in showing that their students sleep longer than seven hours on average. We investigate this topic in Section 4.3.4.

Hypothesis Testing Framework

The average time for all runners who finished the Cherry Blossom Run in 2006 was 93.29 minutes (93 minutes and about 17 seconds). We want to determine if the run10Samp data set provides strong evidence that the participants in 2012 were faster or slower than those runners in 2006, versus the other possibility that there has been no change. 16 We simplify these three options into two competing hypotheses :

• H 0 : The average 10 mile run time was the same for 2006 and 2012.
• H A : The average 10 mile run time for 2012 was different than that of 2006.

We call H 0 the null hypothesis and H A the alternative hypothesis.

Null and alternative hypotheses

• The null hypothesis (H 0 ) often represents either a skeptical perspective or a claim to be tested.
• The alternative hypothesis (H A ) represents an alternative claim under consideration and is often represented by a range of possible parameter values.

15 theloquitur.com/?p=1161

16 While we could answer this question by examining the entire population data (run10), we only consider the sample data (run10Samp), which is more realistic since we rarely have access to population data.

The null hypothesis often represents a skeptical position or a perspective of no difference. The alternative hypothesis often represents a new perspective, such as the possibility that there has been a change.

Hypothesis testing framework

The skeptic will not reject the null hypothesis (H 0 ), unless the evidence in favor of the alternative hypothesis (H A ) is so strong that she rejects H 0 in favor of H A .

The hypothesis testing framework is a very general tool, and we often use it without a second thought. If a person makes a somewhat unbelievable claim, we are initially skeptical. However, if there is sufficient evidence that supports the claim, we set aside our skepticism and reject the null hypothesis in favor of the alternative. The hallmarks of hypothesis testing are also found in the US court system.

Exercise \(\PageIndex{1}\)

A US court considers two possible claims about a defendant: she is either innocent or guilty. If we set these claims up in a hypothesis framework, which would be the null hypothesis and which the alternative? 17

Jurors examine the evidence to see whether it convincingly shows a defendant is guilty. Even if the jurors leave unconvinced of guilt beyond a reasonable doubt, this does not mean they believe the defendant is innocent. This is also the case with hypothesis testing: even if we fail to reject the null hypothesis, we typically do not accept the null hypothesis as true. Failing to find strong evidence for the alternative hypothesis is not equivalent to accepting the null hypothesis.

17 H 0 : The average cost is $650 per month, \(\mu\) = $650.

In the example with the Cherry Blossom Run, the null hypothesis represents no difference in the average time from 2006 to 2012. The alternative hypothesis represents something new or more interesting: there was a difference, either an increase or a decrease. These hypotheses can be described in mathematical notation using \(\mu_{12}\) as the average run time for 2012:

• H 0 : \(\mu_{12} = 93.29\)
• H A : \(\mu_{12} \ne 93.29\)

where 93.29 minutes (93 minutes and about 17 seconds) is the average 10 mile time for all runners in the 2006 Cherry Blossom Run. Using this mathematical notation, the hypotheses can now be evaluated using statistical tools. We call 93.29 the null value since it represents the value of the parameter if the null hypothesis is true. We will use the run10Samp data set to evaluate the hypothesis test.

Testing Hypotheses using Confidence Intervals

We can start the evaluation of the hypothesis setup by comparing 2006 and 2012 run times using a point estimate from the 2012 sample: \(\bar {x}_{12} = 95.61\) minutes. This estimate suggests the average time is actually longer than the 2006 time, 93.29 minutes. However, to evaluate whether this provides strong evidence that there has been a change, we must consider the uncertainty associated with \(\bar {x}_{12}\).

1 6 The jury considers whether the evidence is so convincing (strong) that there is no reasonable doubt regarding the person's guilt; in such a case, the jury rejects innocence (the null hypothesis) and concludes the defendant is guilty (alternative hypothesis).

We learned in Section 4.1 that there is fluctuation from one sample to another, and it is very unlikely that the sample mean will be exactly equal to our parameter; we should not expect \(\bar {x}_{12}\) to exactly equal \(\mu_{12}\). Given that \(\bar {x}_{12} = 95.61\), it might still be possible that the population average in 2012 has remained unchanged from 2006. The difference between \(\bar {x}_{12}\) and 93.29 could be due to sampling variation, i.e. the variability associated with the point estimate when we take a random sample.

In Section 4.2, confidence intervals were introduced as a way to find a range of plausible values for the population mean. Based on run10Samp, a 95% confidence interval for the 2012 population mean, \(\mu_{12}\), was calculated as

\[(92.45, 98.77)\]

Because the 2006 mean, 93.29, falls in the range of plausible values, we cannot say the null hypothesis is implausible. That is, we failed to reject the null hypothesis, H 0 .

Double negatives can sometimes be used in statistics

In many statistical explanations, we use double negatives. For instance, we might say that the null hypothesis is not implausible or we failed to reject the null hypothesis. Double negatives are used to communicate that while we are not rejecting a position, we are also not saying it is correct.

Example \(\PageIndex{1}\)

Next consider whether there is strong evidence that the average age of runners has changed from 2006 to 2012 in the Cherry Blossom Run. In 2006, the average age was 36.13 years, and in the 2012 run10Samp data set, the average was 35.05 years with a standard deviation of 8.97 years for 100 runners.

First, set up the hypotheses:

• H 0 : The average age of runners has not changed from 2006 to 2012, \(\mu_{age} = 36.13.\)
• H A : The average age of runners has changed from 2006 to 2012, \(\mu _{age} 6 \ne 36.13.\)

We have previously veri ed conditions for this data set. The normal model may be applied to \(\bar {y}\) and the estimate of SE should be very accurate. Using the sample mean and standard error, we can construct a 95% con dence interval for \(\mu _{age}\) to determine if there is sufficient evidence to reject H 0 :

\[\bar{y} \pm 1.96 \times \dfrac {s}{\sqrt {100}} \rightarrow 35.05 \pm 1.96 \times 0.90 \rightarrow (33.29, 36.81)\]

This confidence interval contains the null value, 36.13. Because 36.13 is not implausible, we cannot reject the null hypothesis. We have not found strong evidence that the average age is different than 36.13 years.

Exercise \(\PageIndex{2}\)

Colleges frequently provide estimates of student expenses such as housing. A consultant hired by a community college claimed that the average student housing expense was $650 per month. What are the null and alternative hypotheses to test whether this claim is accurate? 18

H A : The average cost is different than $650 per month, \(\mu \ne\) $650.

18 Applying the normal model requires that certain conditions are met. Because the data are a simple random sample and the sample (presumably) represents no more than 10% of all students at the college, the observations are independent. The sample size is also sufficiently large (n = 75) and the data exhibit only moderate skew. Thus, the normal model may be applied to the sample mean.

Exercise \(\PageIndex{3}\)

The community college decides to collect data to evaluate the $650 per month claim. They take a random sample of 75 students at their school and obtain the data represented in Figure 4.11. Can we apply the normal model to the sample mean?

If the court makes a Type 1 Error, this means the defendant is innocent (H 0 true) but wrongly convicted. A Type 2 Error means the court failed to reject H 0 (i.e. failed to convict the person) when she was in fact guilty (H A true).

Example \(\PageIndex{2}\)

The sample mean for student housing is $611.63 and the sample standard deviation is $132.85. Construct a 95% confidence interval for the population mean and evaluate the hypotheses of Exercise 4.22.

The standard error associated with the mean may be estimated using the sample standard deviation divided by the square root of the sample size. Recall that n = 75 students were sampled.

\[ SE = \dfrac {s}{\sqrt {n}} = \dfrac {132.85}{\sqrt {75}} = 15.34\]

You showed in Exercise 4.23 that the normal model may be applied to the sample mean. This ensures a 95% confidence interval may be accurately constructed:

\[\bar {x} \pm z*SE \rightarrow 611.63 \pm 1.96 \times 15.34 \times (581.56, 641.70)\]

Because the null value $650 is not in the confidence interval, a true mean of $650 is implausible and we reject the null hypothesis. The data provide statistically significant evidence that the actual average housing expense is less than $650 per month.

Decision Errors

Hypothesis tests are not flawless. Just think of the court system: innocent people are sometimes wrongly convicted and the guilty sometimes walk free. Similarly, we can make a wrong decision in statistical hypothesis tests. However, the difference is that we have the tools necessary to quantify how often we make such errors.

There are two competing hypotheses: the null and the alternative. In a hypothesis test, we make a statement about which one might be true, but we might choose incorrectly. There are four possible scenarios in a hypothesis test, which are summarized in Table 4.12.

A Type 1 Error is rejecting the null hypothesis when H0 is actually true. A Type 2 Error is failing to reject the null hypothesis when the alternative is actually true.

Exercise 4.25

In a US court, the defendant is either innocent (H 0 ) or guilty (H A ). What does a Type 1 Error represent in this context? What does a Type 2 Error represent? Table 4.12 may be useful.

To lower the Type 1 Error rate, we might raise our standard for conviction from "beyond a reasonable doubt" to "beyond a conceivable doubt" so fewer people would be wrongly convicted. However, this would also make it more difficult to convict the people who are actually guilty, so we would make more Type 2 Errors.

Exercise 4.26

How could we reduce the Type 1 Error rate in US courts? What influence would this have on the Type 2 Error rate?

To lower the Type 2 Error rate, we want to convict more guilty people. We could lower the standards for conviction from "beyond a reasonable doubt" to "beyond a little doubt". Lowering the bar for guilt will also result in more wrongful convictions, raising the Type 1 Error rate.

Exercise 4.27

How could we reduce the Type 2 Error rate in US courts? What influence would this have on the Type 1 Error rate?

A skeptic would have no reason to believe that sleep patterns at this school are different than the sleep patterns at another school.

Exercises 4.25-4.27 provide an important lesson:

If we reduce how often we make one type of error, we generally make more of the other type.

Hypothesis testing is built around rejecting or failing to reject the null hypothesis. That is, we do not reject H 0 unless we have strong evidence. But what precisely does strong evidence mean? As a general rule of thumb, for those cases where the null hypothesis is actually true, we do not want to incorrectly reject H 0 more than 5% of the time. This corresponds to a significance level of 0.05. We often write the significance level using \(\alpha\) (the Greek letter alpha): \(\alpha = 0.05.\) We discuss the appropriateness of different significance levels in Section 4.3.6.

If we use a 95% confidence interval to test a hypothesis where the null hypothesis is true, we will make an error whenever the point estimate is at least 1.96 standard errors away from the population parameter. This happens about 5% of the time (2.5% in each tail). Similarly, using a 99% con dence interval to evaluate a hypothesis is equivalent to a significance level of \(\alpha = 0.01\).

A confidence interval is, in one sense, simplistic in the world of hypothesis tests. Consider the following two scenarios:

• The null value (the parameter value under the null hypothesis) is in the 95% confidence interval but just barely, so we would not reject H 0 . However, we might like to somehow say, quantitatively, that it was a close decision.
• The null value is very far outside of the interval, so we reject H 0 . However, we want to communicate that, not only did we reject the null hypothesis, but it wasn't even close. Such a case is depicted in Figure 4.13.

In Section 4.3.4, we introduce a tool called the p-value that will be helpful in these cases. The p-value method also extends to hypothesis tests where con dence intervals cannot be easily constructed or applied.

Formal Testing using p-Values

The p-value is a way of quantifying the strength of the evidence against the null hypothesis and in favor of the alternative. Formally the p-value is a conditional probability.

definition: p-value

The p-value is the probability of observing data at least as favorable to the alternative hypothesis as our current data set, if the null hypothesis is true. We typically use a summary statistic of the data, in this chapter the sample mean, to help compute the p-value and evaluate the hypotheses.

A poll by the National Sleep Foundation found that college students average about 7 hours of sleep per night. Researchers at a rural school are interested in showing that students at their school sleep longer than seven hours on average, and they would like to demonstrate this using a sample of students. What would be an appropriate skeptical position for this research?

This is entirely based on the interests of the researchers. Had they been only interested in the opposite case - showing that their students were actually averaging fewer than seven hours of sleep but not interested in showing more than 7 hours - then our setup would have set the alternative as \(\mu < 7\).

We can set up the null hypothesis for this test as a skeptical perspective: the students at this school average 7 hours of sleep per night. The alternative hypothesis takes a new form reflecting the interests of the research: the students average more than 7 hours of sleep. We can write these hypotheses as

• H 0 : \(\mu\) = 7.
• H A : \(\mu\) > 7.

Using \(\mu\) > 7 as the alternative is an example of a one-sided hypothesis test. In this investigation, there is no apparent interest in learning whether the mean is less than 7 hours. (The standard error can be estimated from the sample standard deviation and the sample size: \(SE_{\bar {x}} = \dfrac {s_x}{\sqrt {n}} = \dfrac {1.75}{\sqrt {110}} = 0.17\)). Earlier we encountered a two-sided hypothesis where we looked for any clear difference, greater than or less than the null value.

Always use a two-sided test unless it was made clear prior to data collection that the test should be one-sided. Switching a two-sided test to a one-sided test after observing the data is dangerous because it can inflate the Type 1 Error rate.

TIP: One-sided and two-sided tests

If the researchers are only interested in showing an increase or a decrease, but not both, use a one-sided test. If the researchers would be interested in any difference from the null value - an increase or decrease - then the test should be two-sided.

TIP: Always write the null hypothesis as an equality

We will find it most useful if we always list the null hypothesis as an equality (e.g. \(\mu\) = 7) while the alternative always uses an inequality (e.g. \(\mu \ne 7, \mu > 7, or \mu < 7)\).

The researchers at the rural school conducted a simple random sample of n = 110 students on campus. They found that these students averaged 7.42 hours of sleep and the standard deviation of the amount of sleep for the students was 1.75 hours. A histogram of the sample is shown in Figure 4.14.

Before we can use a normal model for the sample mean or compute the standard error of the sample mean, we must verify conditions. (1) Because this is a simple random sample from less than 10% of the student body, the observations are independent. (2) The sample size in the sleep study is sufficiently large since it is greater than 30. (3) The data show moderate skew in Figure 4.14 and the presence of a couple of outliers. This skew and the outliers (which are not too extreme) are acceptable for a sample size of n = 110. With these conditions veri ed, the normal model can be safely applied to \(\bar {x}\) and the estimated standard error will be very accurate.

What is the standard deviation associated with \(\bar {x}\)? That is, estimate the standard error of \(\bar {x}\). 25

The hypothesis test will be evaluated using a significance level of \(\alpha = 0.05\). We want to consider the data under the scenario that the null hypothesis is true. In this case, the sample mean is from a distribution that is nearly normal and has mean 7 and standard deviation of about 0.17. Such a distribution is shown in Figure 4.15.

The shaded tail in Figure 4.15 represents the chance of observing such a large mean, conditional on the null hypothesis being true. That is, the shaded tail represents the p-value. We shade all means larger than our sample mean, \(\bar {x} = 7.42\), because they are more favorable to the alternative hypothesis than the observed mean.

We compute the p-value by finding the tail area of this normal distribution, which we learned to do in Section 3.1. First compute the Z score of the sample mean, \(\bar {x} = 7.42\):

\[Z = \dfrac {\bar {x} - \text {null value}}{SE_{\bar {x}}} = \dfrac {7.42 - 7}{0.17} = 2.47\]

Using the normal probability table, the lower unshaded area is found to be 0.993. Thus the shaded area is 1 - 0.993 = 0.007. If the null hypothesis is true, the probability of observing such a large sample mean for a sample of 110 students is only 0.007. That is, if the null hypothesis is true, we would not often see such a large mean.

We evaluate the hypotheses by comparing the p-value to the significance level. Because the p-value is less than the significance level \((p-value = 0.007 < 0.05 = \alpha)\), we reject the null hypothesis. What we observed is so unusual with respect to the null hypothesis that it casts serious doubt on H 0 and provides strong evidence favoring H A .

p-value as a tool in hypothesis testing

The p-value quantifies how strongly the data favor H A over H 0 . A small p-value (usually < 0.05) corresponds to sufficient evidence to reject H 0 in favor of H A .

TIP: It is useful to First draw a picture to find the p-value

It is useful to draw a picture of the distribution of \(\bar {x}\) as though H 0 was true (i.e. \(\mu\) equals the null value), and shade the region (or regions) of sample means that are at least as favorable to the alternative hypothesis. These shaded regions represent the p-value.

The ideas below review the process of evaluating hypothesis tests with p-values:

• The null hypothesis represents a skeptic's position or a position of no difference. We reject this position only if the evidence strongly favors H A .
• A small p-value means that if the null hypothesis is true, there is a low probability of seeing a point estimate at least as extreme as the one we saw. We interpret this as strong evidence in favor of the alternative.
• We reject the null hypothesis if the p-value is smaller than the significance level, \(\alpha\), which is usually 0.05. Otherwise, we fail to reject H 0 .
• We should always state the conclusion of the hypothesis test in plain language so non-statisticians can also understand the results.

The p-value is constructed in such a way that we can directly compare it to the significance level ( \(\alpha\)) to determine whether or not to reject H 0 . This method ensures that the Type 1 Error rate does not exceed the significance level standard.

If the null hypothesis is true, how often should the p-value be less than 0.05?

About 5% of the time. If the null hypothesis is true, then the data only has a 5% chance of being in the 5% of data most favorable to H A .

Exercise 4.31

Suppose we had used a significance level of 0.01 in the sleep study. Would the evidence have been strong enough to reject the null hypothesis? (The p-value was 0.007.) What if the significance level was \(\alpha = 0.001\)? 27

27 We reject the null hypothesis whenever p-value < \(\alpha\). Thus, we would still reject the null hypothesis if \(\alpha = 0.01\) but not if the significance level had been \(\alpha = 0.001\).

Exercise 4.32

Ebay might be interested in showing that buyers on its site tend to pay less than they would for the corresponding new item on Amazon. We'll research this topic for one particular product: a video game called Mario Kart for the Nintendo Wii. During early October 2009, Amazon sold this game for $46.99. Set up an appropriate (one-sided!) hypothesis test to check the claim that Ebay buyers pay less during auctions at this same time. 28

28 The skeptic would say the average is the same on Ebay, and we are interested in showing the average price is lower.

Exercise 4.33

During early October, 2009, 52 Ebay auctions were recorded for Mario Kart.29 The total prices for the auctions are presented using a histogram in Figure 4.17, and we may like to apply the normal model to the sample mean. Check the three conditions required for applying the normal model: (1) independence, (2) at least 30 observations, and (3) the data are not strongly skewed. 30

30 (1) The independence condition is unclear. We will make the assumption that the observations are independent, which we should report with any nal results. (2) The sample size is sufficiently large: \(n = 52 \ge 30\). (3) The data distribution is not strongly skewed; it is approximately symmetric.

H 0 : The average auction price on Ebay is equal to (or more than) the price on Amazon. We write only the equality in the statistical notation: \(\mu_{ebay} = 46.99\).

H A : The average price on Ebay is less than the price on Amazon, \(\mu _{ebay} < 46.99\).

29 These data were collected by OpenIntro staff.

Example 4.34

The average sale price of the 52 Ebay auctions for Wii Mario Kart was $44.17 with a standard deviation of $4.15. Does this provide sufficient evidence to reject the null hypothesis in Exercise 4.32? Use a significance level of \(\alpha = 0.01\).

The hypotheses were set up and the conditions were checked in Exercises 4.32 and 4.33. The next step is to find the standard error of the sample mean and produce a sketch to help find the p-value.

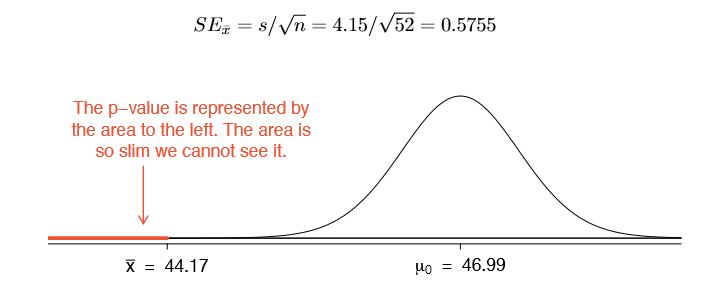
Because the alternative hypothesis says we are looking for a smaller mean, we shade the lower tail. We find this shaded area by using the Z score and normal probability table: \(Z = \dfrac {44.17 \times 46.99}{0.5755} = -4.90\), which has area less than 0.0002. The area is so small we cannot really see it on the picture. This lower tail area corresponds to the p-value.

Because the p-value is so small - specifically, smaller than = 0.01 - this provides sufficiently strong evidence to reject the null hypothesis in favor of the alternative. The data provide statistically signi cant evidence that the average price on Ebay is lower than Amazon's asking price.

Two-sided hypothesis testing with p-values

We now consider how to compute a p-value for a two-sided test. In one-sided tests, we shade the single tail in the direction of the alternative hypothesis. For example, when the alternative had the form \(\mu\) > 7, then the p-value was represented by the upper tail (Figure 4.16). When the alternative was \(\mu\) < 46.99, the p-value was the lower tail (Exercise 4.32). In a two-sided test, we shade two tails since evidence in either direction is favorable to H A .

Exercise 4.35 Earlier we talked about a research group investigating whether the students at their school slept longer than 7 hours each night. Let's consider a second group of researchers who want to evaluate whether the students at their college differ from the norm of 7 hours. Write the null and alternative hypotheses for this investigation. 31

Example 4.36 The second college randomly samples 72 students and nds a mean of \(\bar {x} = 6.83\) hours and a standard deviation of s = 1.8 hours. Does this provide strong evidence against H 0 in Exercise 4.35? Use a significance level of \(\alpha = 0.05\).

First, we must verify assumptions. (1) A simple random sample of less than 10% of the student body means the observations are independent. (2) The sample size is 72, which is greater than 30. (3) Based on the earlier distribution and what we already know about college student sleep habits, the distribution is probably not strongly skewed.

Next we can compute the standard error \((SE_{\bar {x}} = \dfrac {s}{\sqrt {n}} = 0.21)\) of the estimate and create a picture to represent the p-value, shown in Figure 4.18. Both tails are shaded.

31 Because the researchers are interested in any difference, they should use a two-sided setup: H 0 : \(\mu\) = 7, H A : \(\mu \ne 7.\)

An estimate of 7.17 or more provides at least as strong of evidence against the null hypothesis and in favor of the alternative as the observed estimate, \(\bar {x} = 6.83\).

We can calculate the tail areas by rst nding the lower tail corresponding to \(\bar {x}\):

\[Z = \dfrac {6.83 - 7.00}{0.21} = -0.81 \xrightarrow {table} \text {left tail} = 0.2090\]

Because the normal model is symmetric, the right tail will have the same area as the left tail. The p-value is found as the sum of the two shaded tails:

\[ \text {p-value} = \text {left tail} + \text {right tail} = 2 \times \text {(left tail)} = 0.4180\]

This p-value is relatively large (larger than \(\mu\)= 0.05), so we should not reject H 0 . That is, if H 0 is true, it would not be very unusual to see a sample mean this far from 7 hours simply due to sampling variation. Thus, we do not have sufficient evidence to conclude that the mean is different than 7 hours.

Example 4.37 It is never okay to change two-sided tests to one-sided tests after observing the data. In this example we explore the consequences of ignoring this advice. Using \(\alpha = 0.05\), we show that freely switching from two-sided tests to onesided tests will cause us to make twice as many Type 1 Errors as intended.

Suppose the sample mean was larger than the null value, \(\mu_0\) (e.g. \(\mu_0\) would represent 7 if H 0 : \(\mu\) = 7). Then if we can ip to a one-sided test, we would use H A : \(\mu > \mu_0\). Now if we obtain any observation with a Z score greater than 1.65, we would reject H 0 . If the null hypothesis is true, we incorrectly reject the null hypothesis about 5% of the time when the sample mean is above the null value, as shown in Figure 4.19.

Suppose the sample mean was smaller than the null value. Then if we change to a one-sided test, we would use H A : \(\mu < \mu_0\). If \(\bar {x}\) had a Z score smaller than -1.65, we would reject H 0 . If the null hypothesis is true, then we would observe such a case about 5% of the time.

By examining these two scenarios, we can determine that we will make a Type 1 Error 5% + 5% = 10% of the time if we are allowed to swap to the "best" one-sided test for the data. This is twice the error rate we prescribed with our significance level: \(\alpha = 0.05\) (!).

Caution: One-sided hypotheses are allowed only before seeing data

After observing data, it is tempting to turn a two-sided test into a one-sided test. Avoid this temptation. Hypotheses must be set up before observing the data. If they are not, the test must be two-sided.

Choosing a Significance Level

Choosing a significance level for a test is important in many contexts, and the traditional level is 0.05. However, it is often helpful to adjust the significance level based on the application. We may select a level that is smaller or larger than 0.05 depending on the consequences of any conclusions reached from the test.

• If making a Type 1 Error is dangerous or especially costly, we should choose a small significance level (e.g. 0.01). Under this scenario we want to be very cautious about rejecting the null hypothesis, so we demand very strong evidence favoring H A before we would reject H 0 .
• If a Type 2 Error is relatively more dangerous or much more costly than a Type 1 Error, then we should choose a higher significance level (e.g. 0.10). Here we want to be cautious about failing to reject H 0 when the null is actually false. We will discuss this particular case in greater detail in Section 4.6.

Significance levels should reflect consequences of errors

The significance level selected for a test should reflect the consequences associated with Type 1 and Type 2 Errors.

Example 4.38

A car manufacturer is considering a higher quality but more expensive supplier for window parts in its vehicles. They sample a number of parts from their current supplier and also parts from the new supplier. They decide that if the high quality parts will last more than 12% longer, it makes nancial sense to switch to this more expensive supplier. Is there good reason to modify the significance level in such a hypothesis test?

The null hypothesis is that the more expensive parts last no more than 12% longer while the alternative is that they do last more than 12% longer. This decision is just one of the many regular factors that have a marginal impact on the car and company. A significancelevel of 0.05 seems reasonable since neither a Type 1 or Type 2 error should be dangerous or (relatively) much more expensive.

Example 4.39

The same car manufacturer is considering a slightly more expensive supplier for parts related to safety, not windows. If the durability of these safety components is shown to be better than the current supplier, they will switch manufacturers. Is there good reason to modify the significance level in such an evaluation?

The null hypothesis would be that the suppliers' parts are equally reliable. Because safety is involved, the car company should be eager to switch to the slightly more expensive manufacturer (reject H 0 ) even if the evidence of increased safety is only moderately strong. A slightly larger significance level, such as \(\mu = 0.10\), might be appropriate.

Exercise 4.40

A part inside of a machine is very expensive to replace. However, the machine usually functions properly even if this part is broken, so the part is replaced only if we are extremely certain it is broken based on a series of measurements. Identify appropriate hypotheses for this test (in plain language) and suggest an appropriate significance level. 32

Statistics Made Easy

5 Tips for Interpreting P-Values Correctly in Hypothesis Testing

Hypothesis testing is a critical part of statistical analysis and is often the endpoint where conclusions are drawn about larger populations based on a sample or experimental dataset. Central to this process is the p-value. Broadly, the p-value quantifies the strength of evidence against the null hypothesis. Given the importance of the p-value, it is essential to ensure its interpretation is correct. Here are five essential tips for ensuring the p-value from a hypothesis test is understood correctly. 

1. Know What the P-value Represents

First, it is essential to understand what a p-value is. In hypothesis testing, the p-value is defined as the probability of observing your data, or data more extreme, if the null hypothesis is true. As a reminder, the null hypothesis states no difference between your data and the expected population. 

For example, in a hypothesis test to see if changing a company’s logo drives more traffic to the website, a null hypothesis would state that the new traffic numbers are equal to the old traffic numbers. In this context, the p-value would be the probability that the data you observed, or data more extreme, would occur if this null hypothesis were true. 

Therefore, a smaller p-value indicates that what you observed is unlikely to have occurred if the null were true, offering evidence to reject the null hypothesis. Typically, a cut-off value of 0.05 is used where any p-value below this is considered significant evidence against the null. 

2. Understand the Directionality of Your Hypothesis

Based on the research question under exploration, there are two types of hypotheses: one-sided and two-sided. A one-sided test specifies a particular direction of effect, such as traffic to a website increasing after a design change. On the other hand, a two-sided test allows the change to be in either direction and is effective when the researcher wants to see any effect of the change. 

Either way, determining the statistical significance of a p-value is the same: if the p-value is below a threshold value, it is statistically significant. However, when calculating the p-value, it is important to ensure the correct sided calculations have been completed. 

Additionally, the interpretation of the meaning of a p-value will differ based on the directionality of the hypothesis. If a one-sided test is significant, the researchers can use the p-value to support a statistically significant increase or decrease based on the direction of the test. If a two-sided test is significant, the p-value can only be used to say that the two groups are different, but not that one is necessarily greater. 

3. Avoid Threshold Thinking

A common pitfall in interpreting p-values is falling into the threshold thinking trap. The most commonly used cut-off value for whether a calculated p-value is statistically significant is 0.05. Typically, a p-value of less than 0.05 is considered statistically significant evidence against the null hypothesis. 

However, this is just an arbitrary value. Rigid adherence to this or any other predefined cut-off value can obscure business-relevant effect sizes. For example, a hypothesis test looking at changes in traffic after a website design may find that an increase of 10,000 views is not statistically significant with a p-value of 0.055 since that value is above 0.05. However, the actual increase of 10,000 may be important to the growth of the business. 

Therefore, a p-value can be practically significant while not being statistically significant. Both types of significance and the broader context of the hypothesis test should be considered when making a final interpretation. 

4. Consider the Power of Your Study

Similarly, some study conditions can result in a non-significant p-value even if practical significance exists. Statistical power is the ability of a study to detect an effect when it truly exists. In other words, it is the probability that the null hypothesis will be rejected when it is false. 

Power is impacted by a lot of factors. These include sample size, the effect size you are looking for, and variability within the data. In the example of website traffic after a design change, if the number of visits overall is too small, there may not be enough views to have enough power to detect a difference. 

Simple ways to increase the power of a hypothesis test and increase the chances of detecting an effect are increasing the sample size, looking for a smaller effect size, changing the experiment design to control for variables that can increase variability, or adjusting the type of statistical test being run.

5. Be Aware of Multiple Comparisons

Whenever multiple p-values are calculated in a single study due to multiple comparisons, there is an increased risk of false positives. This is because each individual comparison introduces random fluctuations, and each additional comparison compounds these fluctuations. 

For example, in a hypothesis test looking at traffic before and after a website redesign, the team may be interested in making more than one comparison. This can include total visits, page views, and average time spent on the website. Since multiple comparisons are being made, there must be a correction made when interpreting the p-value. 

The Bonferroni correction is one of the most commonly used methods to account for this increased probability of false positives. In this method, the significance cut-off value, typically 0.05, is divided by the number of comparisons made. The result is used as the new significance cut-off value.  Applying this correction mitigates the risk of false positives and improves the reliability of findings from a hypothesis test. 

In conclusion, interpreting p-values requires a nuanced understanding of many statistical concepts and careful consideration of the hypothesis test’s context. By following these five tips, the interpretation of the p-value from a hypothesis test can be more accurate and reliable, leading to better data-driven decision-making.

Featured Posts

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Indian J Anaesth
• v.60(9); 2016 Sep

Basic statistical tools in research and data analysis

Zulfiqar ali.

Department of Anaesthesiology, Division of Neuroanaesthesiology, Sheri Kashmir Institute of Medical Sciences, Soura, Srinagar, Jammu and Kashmir, India

S Bala Bhaskar

1 Department of Anaesthesiology and Critical Care, Vijayanagar Institute of Medical Sciences, Bellary, Karnataka, India

Statistical methods involved in carrying out a study include planning, designing, collecting data, analysing, drawing meaningful interpretation and reporting of the research findings. The statistical analysis gives meaning to the meaningless numbers, thereby breathing life into a lifeless data. The results and inferences are precise only if proper statistical tests are used. This article will try to acquaint the reader with the basic research tools that are utilised while conducting various studies. The article covers a brief outline of the variables, an understanding of quantitative and qualitative variables and the measures of central tendency. An idea of the sample size estimation, power analysis and the statistical errors is given. Finally, there is a summary of parametric and non-parametric tests used for data analysis.

INTRODUCTION

Statistics is a branch of science that deals with the collection, organisation, analysis of data and drawing of inferences from the samples to the whole population.[ 1 ] This requires a proper design of the study, an appropriate selection of the study sample and choice of a suitable statistical test. An adequate knowledge of statistics is necessary for proper designing of an epidemiological study or a clinical trial. Improper statistical methods may result in erroneous conclusions which may lead to unethical practice.[ 2 ]

Variable is a characteristic that varies from one individual member of population to another individual.[ 3 ] Variables such as height and weight are measured by some type of scale, convey quantitative information and are called as quantitative variables. Sex and eye colour give qualitative information and are called as qualitative variables[ 3 ] [ Figure 1 ].

Classification of variables

Quantitative variables

Quantitative or numerical data are subdivided into discrete and continuous measurements. Discrete numerical data are recorded as a whole number such as 0, 1, 2, 3,… (integer), whereas continuous data can assume any value. Observations that can be counted constitute the discrete data and observations that can be measured constitute the continuous data. Examples of discrete data are number of episodes of respiratory arrests or the number of re-intubations in an intensive care unit. Similarly, examples of continuous data are the serial serum glucose levels, partial pressure of oxygen in arterial blood and the oesophageal temperature.

A hierarchical scale of increasing precision can be used for observing and recording the data which is based on categorical, ordinal, interval and ratio scales [ Figure 1 ].

Categorical or nominal variables are unordered. The data are merely classified into categories and cannot be arranged in any particular order. If only two categories exist (as in gender male and female), it is called as a dichotomous (or binary) data. The various causes of re-intubation in an intensive care unit due to upper airway obstruction, impaired clearance of secretions, hypoxemia, hypercapnia, pulmonary oedema and neurological impairment are examples of categorical variables.

Ordinal variables have a clear ordering between the variables. However, the ordered data may not have equal intervals. Examples are the American Society of Anesthesiologists status or Richmond agitation-sedation scale.

Interval variables are similar to an ordinal variable, except that the intervals between the values of the interval variable are equally spaced. A good example of an interval scale is the Fahrenheit degree scale used to measure temperature. With the Fahrenheit scale, the difference between 70° and 75° is equal to the difference between 80° and 85°: The units of measurement are equal throughout the full range of the scale.

Ratio scales are similar to interval scales, in that equal differences between scale values have equal quantitative meaning. However, ratio scales also have a true zero point, which gives them an additional property. For example, the system of centimetres is an example of a ratio scale. There is a true zero point and the value of 0 cm means a complete absence of length. The thyromental distance of 6 cm in an adult may be twice that of a child in whom it may be 3 cm.

STATISTICS: DESCRIPTIVE AND INFERENTIAL STATISTICS

Descriptive statistics[ 4 ] try to describe the relationship between variables in a sample or population. Descriptive statistics provide a summary of data in the form of mean, median and mode. Inferential statistics[ 4 ] use a random sample of data taken from a population to describe and make inferences about the whole population. It is valuable when it is not possible to examine each member of an entire population. The examples if descriptive and inferential statistics are illustrated in Table 1 .

Example of descriptive and inferential statistics

Descriptive statistics

The extent to which the observations cluster around a central location is described by the central tendency and the spread towards the extremes is described by the degree of dispersion.

Measures of central tendency

The measures of central tendency are mean, median and mode.[ 6 ] Mean (or the arithmetic average) is the sum of all the scores divided by the number of scores. Mean may be influenced profoundly by the extreme variables. For example, the average stay of organophosphorus poisoning patients in ICU may be influenced by a single patient who stays in ICU for around 5 months because of septicaemia. The extreme values are called outliers. The formula for the mean is

where x = each observation and n = number of observations. Median[ 6 ] is defined as the middle of a distribution in a ranked data (with half of the variables in the sample above and half below the median value) while mode is the most frequently occurring variable in a distribution. Range defines the spread, or variability, of a sample.[ 7 ] It is described by the minimum and maximum values of the variables. If we rank the data and after ranking, group the observations into percentiles, we can get better information of the pattern of spread of the variables. In percentiles, we rank the observations into 100 equal parts. We can then describe 25%, 50%, 75% or any other percentile amount. The median is the 50 th percentile. The interquartile range will be the observations in the middle 50% of the observations about the median (25 th -75 th percentile). Variance[ 7 ] is a measure of how spread out is the distribution. It gives an indication of how close an individual observation clusters about the mean value. The variance of a population is defined by the following formula:

where σ 2 is the population variance, X is the population mean, X i is the i th element from the population and N is the number of elements in the population. The variance of a sample is defined by slightly different formula:

where s 2 is the sample variance, x is the sample mean, x i is the i th element from the sample and n is the number of elements in the sample. The formula for the variance of a population has the value ‘ n ’ as the denominator. The expression ‘ n −1’ is known as the degrees of freedom and is one less than the number of parameters. Each observation is free to vary, except the last one which must be a defined value. The variance is measured in squared units. To make the interpretation of the data simple and to retain the basic unit of observation, the square root of variance is used. The square root of the variance is the standard deviation (SD).[ 8 ] The SD of a population is defined by the following formula:

where σ is the population SD, X is the population mean, X i is the i th element from the population and N is the number of elements in the population. The SD of a sample is defined by slightly different formula:

where s is the sample SD, x is the sample mean, x i is the i th element from the sample and n is the number of elements in the sample. An example for calculation of variation and SD is illustrated in Table 2 .

Example of mean, variance, standard deviation

Normal distribution or Gaussian distribution

Most of the biological variables usually cluster around a central value, with symmetrical positive and negative deviations about this point.[ 1 ] The standard normal distribution curve is a symmetrical bell-shaped. In a normal distribution curve, about 68% of the scores are within 1 SD of the mean. Around 95% of the scores are within 2 SDs of the mean and 99% within 3 SDs of the mean [ Figure 2 ].

Normal distribution curve

Skewed distribution

It is a distribution with an asymmetry of the variables about its mean. In a negatively skewed distribution [ Figure 3 ], the mass of the distribution is concentrated on the right of Figure 1 . In a positively skewed distribution [ Figure 3 ], the mass of the distribution is concentrated on the left of the figure leading to a longer right tail.

Curves showing negatively skewed and positively skewed distribution

Inferential statistics

In inferential statistics, data are analysed from a sample to make inferences in the larger collection of the population. The purpose is to answer or test the hypotheses. A hypothesis (plural hypotheses) is a proposed explanation for a phenomenon. Hypothesis tests are thus procedures for making rational decisions about the reality of observed effects.

Probability is the measure of the likelihood that an event will occur. Probability is quantified as a number between 0 and 1 (where 0 indicates impossibility and 1 indicates certainty).

In inferential statistics, the term ‘null hypothesis’ ( H 0 ‘ H-naught ,’ ‘ H-null ’) denotes that there is no relationship (difference) between the population variables in question.[ 9 ]

Alternative hypothesis ( H 1 and H a ) denotes that a statement between the variables is expected to be true.[ 9 ]

The P value (or the calculated probability) is the probability of the event occurring by chance if the null hypothesis is true. The P value is a numerical between 0 and 1 and is interpreted by researchers in deciding whether to reject or retain the null hypothesis [ Table 3 ].

P values with interpretation

If P value is less than the arbitrarily chosen value (known as α or the significance level), the null hypothesis (H0) is rejected [ Table 4 ]. However, if null hypotheses (H0) is incorrectly rejected, this is known as a Type I error.[ 11 ] Further details regarding alpha error, beta error and sample size calculation and factors influencing them are dealt with in another section of this issue by Das S et al .[ 12 ]

Illustration for null hypothesis

PARAMETRIC AND NON-PARAMETRIC TESTS

Numerical data (quantitative variables) that are normally distributed are analysed with parametric tests.[ 13 ]

Two most basic prerequisites for parametric statistical analysis are:

• The assumption of normality which specifies that the means of the sample group are normally distributed
• The assumption of equal variance which specifies that the variances of the samples and of their corresponding population are equal.

However, if the distribution of the sample is skewed towards one side or the distribution is unknown due to the small sample size, non-parametric[ 14 ] statistical techniques are used. Non-parametric tests are used to analyse ordinal and categorical data.

Parametric tests

The parametric tests assume that the data are on a quantitative (numerical) scale, with a normal distribution of the underlying population. The samples have the same variance (homogeneity of variances). The samples are randomly drawn from the population, and the observations within a group are independent of each other. The commonly used parametric tests are the Student's t -test, analysis of variance (ANOVA) and repeated measures ANOVA.

Student's t -test

Student's t -test is used to test the null hypothesis that there is no difference between the means of the two groups. It is used in three circumstances:

where X = sample mean, u = population mean and SE = standard error of mean

where X 1 − X 2 is the difference between the means of the two groups and SE denotes the standard error of the difference.

• To test if the population means estimated by two dependent samples differ significantly (the paired t -test). A usual setting for paired t -test is when measurements are made on the same subjects before and after a treatment.

The formula for paired t -test is:

where d is the mean difference and SE denotes the standard error of this difference.

The group variances can be compared using the F -test. The F -test is the ratio of variances (var l/var 2). If F differs significantly from 1.0, then it is concluded that the group variances differ significantly.

Analysis of variance

The Student's t -test cannot be used for comparison of three or more groups. The purpose of ANOVA is to test if there is any significant difference between the means of two or more groups.

In ANOVA, we study two variances – (a) between-group variability and (b) within-group variability. The within-group variability (error variance) is the variation that cannot be accounted for in the study design. It is based on random differences present in our samples.

However, the between-group (or effect variance) is the result of our treatment. These two estimates of variances are compared using the F-test.

A simplified formula for the F statistic is:

where MS b is the mean squares between the groups and MS w is the mean squares within groups.

Repeated measures analysis of variance

As with ANOVA, repeated measures ANOVA analyses the equality of means of three or more groups. However, a repeated measure ANOVA is used when all variables of a sample are measured under different conditions or at different points in time.

As the variables are measured from a sample at different points of time, the measurement of the dependent variable is repeated. Using a standard ANOVA in this case is not appropriate because it fails to model the correlation between the repeated measures: The data violate the ANOVA assumption of independence. Hence, in the measurement of repeated dependent variables, repeated measures ANOVA should be used.

Non-parametric tests

When the assumptions of normality are not met, and the sample means are not normally, distributed parametric tests can lead to erroneous results. Non-parametric tests (distribution-free test) are used in such situation as they do not require the normality assumption.[ 15 ] Non-parametric tests may fail to detect a significant difference when compared with a parametric test. That is, they usually have less power.

As is done for the parametric tests, the test statistic is compared with known values for the sampling distribution of that statistic and the null hypothesis is accepted or rejected. The types of non-parametric analysis techniques and the corresponding parametric analysis techniques are delineated in Table 5 .

Analogue of parametric and non-parametric tests

Median test for one sample: The sign test and Wilcoxon's signed rank test

The sign test and Wilcoxon's signed rank test are used for median tests of one sample. These tests examine whether one instance of sample data is greater or smaller than the median reference value.

This test examines the hypothesis about the median θ0 of a population. It tests the null hypothesis H0 = θ0. When the observed value (Xi) is greater than the reference value (θ0), it is marked as+. If the observed value is smaller than the reference value, it is marked as − sign. If the observed value is equal to the reference value (θ0), it is eliminated from the sample.

If the null hypothesis is true, there will be an equal number of + signs and − signs.

The sign test ignores the actual values of the data and only uses + or − signs. Therefore, it is useful when it is difficult to measure the values.

Wilcoxon's signed rank test

There is a major limitation of sign test as we lose the quantitative information of the given data and merely use the + or – signs. Wilcoxon's signed rank test not only examines the observed values in comparison with θ0 but also takes into consideration the relative sizes, adding more statistical power to the test. As in the sign test, if there is an observed value that is equal to the reference value θ0, this observed value is eliminated from the sample.

Wilcoxon's rank sum test ranks all data points in order, calculates the rank sum of each sample and compares the difference in the rank sums.

Mann-Whitney test

It is used to test the null hypothesis that two samples have the same median or, alternatively, whether observations in one sample tend to be larger than observations in the other.

Mann–Whitney test compares all data (xi) belonging to the X group and all data (yi) belonging to the Y group and calculates the probability of xi being greater than yi: P (xi > yi). The null hypothesis states that P (xi > yi) = P (xi < yi) =1/2 while the alternative hypothesis states that P (xi > yi) ≠1/2.

Kolmogorov-Smirnov test

The two-sample Kolmogorov-Smirnov (KS) test was designed as a generic method to test whether two random samples are drawn from the same distribution. The null hypothesis of the KS test is that both distributions are identical. The statistic of the KS test is a distance between the two empirical distributions, computed as the maximum absolute difference between their cumulative curves.

Kruskal-Wallis test

The Kruskal–Wallis test is a non-parametric test to analyse the variance.[ 14 ] It analyses if there is any difference in the median values of three or more independent samples. The data values are ranked in an increasing order, and the rank sums calculated followed by calculation of the test statistic.

Jonckheere test

In contrast to Kruskal–Wallis test, in Jonckheere test, there is an a priori ordering that gives it a more statistical power than the Kruskal–Wallis test.[ 14 ]

Friedman test

The Friedman test is a non-parametric test for testing the difference between several related samples. The Friedman test is an alternative for repeated measures ANOVAs which is used when the same parameter has been measured under different conditions on the same subjects.[ 13 ]

Tests to analyse the categorical data

Chi-square test, Fischer's exact test and McNemar's test are used to analyse the categorical or nominal variables. The Chi-square test compares the frequencies and tests whether the observed data differ significantly from that of the expected data if there were no differences between groups (i.e., the null hypothesis). It is calculated by the sum of the squared difference between observed ( O ) and the expected ( E ) data (or the deviation, d ) divided by the expected data by the following formula:

A Yates correction factor is used when the sample size is small. Fischer's exact test is used to determine if there are non-random associations between two categorical variables. It does not assume random sampling, and instead of referring a calculated statistic to a sampling distribution, it calculates an exact probability. McNemar's test is used for paired nominal data. It is applied to 2 × 2 table with paired-dependent samples. It is used to determine whether the row and column frequencies are equal (that is, whether there is ‘marginal homogeneity’). The null hypothesis is that the paired proportions are equal. The Mantel-Haenszel Chi-square test is a multivariate test as it analyses multiple grouping variables. It stratifies according to the nominated confounding variables and identifies any that affects the primary outcome variable. If the outcome variable is dichotomous, then logistic regression is used.

SOFTWARES AVAILABLE FOR STATISTICS, SAMPLE SIZE CALCULATION AND POWER ANALYSIS

Numerous statistical software systems are available currently. The commonly used software systems are Statistical Package for the Social Sciences (SPSS – manufactured by IBM corporation), Statistical Analysis System ((SAS – developed by SAS Institute North Carolina, United States of America), R (designed by Ross Ihaka and Robert Gentleman from R core team), Minitab (developed by Minitab Inc), Stata (developed by StataCorp) and the MS Excel (developed by Microsoft).

There are a number of web resources which are related to statistical power analyses. A few are:

• StatPages.net – provides links to a number of online power calculators
• G-Power – provides a downloadable power analysis program that runs under DOS
• Power analysis for ANOVA designs an interactive site that calculates power or sample size needed to attain a given power for one effect in a factorial ANOVA design
• SPSS makes a program called SamplePower. It gives an output of a complete report on the computer screen which can be cut and paste into another document.

It is important that a researcher knows the concepts of the basic statistical methods used for conduct of a research study. This will help to conduct an appropriately well-designed study leading to valid and reliable results. Inappropriate use of statistical techniques may lead to faulty conclusions, inducing errors and undermining the significance of the article. Bad statistics may lead to bad research, and bad research may lead to unethical practice. Hence, an adequate knowledge of statistics and the appropriate use of statistical tests are important. An appropriate knowledge about the basic statistical methods will go a long way in improving the research designs and producing quality medical research which can be utilised for formulating the evidence-based guidelines.

Financial support and sponsorship

Conflicts of interest.

There are no conflicts of interest.

• Resources / Blog

Data Analysis for Quantitative Data: Techniques and Tools for Accurate Insights

Data is the lifeblood of your organization, especially in a constantly evolving marketplace. Every day, you make decisions that impact achieving your organizational goals. If your organization isn’t digging into and exploring all the data it collects, it risks becoming less relevant in your customers’ eyes. Everyone in your organization, from top-level executives to entry-level employees, must understand how to interpret data to make impactful decisions.

Without data literacy , your organization is blind to what is happening and will make decisions based on guesswork and intuition, which may or may not yield the best decisions. Whether attempting to streamline your organization’s operations, boost sales growth, or improve customer satisfaction, understanding your data is the cornerstone of success.

To become data literate, you need to understand the two distinct types of data: quantitative and qualitative. After introducing these distinct types of data, we will look specifically at quantitative data and how to analyze it.

On this page :

What is Quantitative Data?

What's the difference between quantitative and qualitative data, 10 steps to analyzing quantitative data, the role of machine learning in quantitative data analysis, real-world applications of quantitative data analysis, future trends in quantitative data analysis.

Quantitative data refers to information that can be measured and expressed numerically. This type of data deals with numbers and things that can be measured objectively, such as height, width, length, temperature, humidity, and prices. Quantitative data can be analyzed using various statistical methods to uncover patterns, relationships, and trends within the data set.

Here are several examples of quantitative data:

• Height : A person's height of 175 centimeters.
• Temperature : The temperature is 25 Celsius.
• Income : A person's monthly salary is $3000.
• Age : Someone is 35 years old.
• Test Scores : A student scores 85 out of 100 on a math test.
• Number of Items Sold : A store sells 100 product units monthly.
• Distance : A car travels 50 kilometers an hour.
• Speed : A train might travel 100 kilometers per hour.
• Population : A city’s population is 1,000,000 people.
• Time : An event lasts 2 hours and 30 minutes.

As you can see, these examples represent quantities measured and expressed using numerical values.

Quantitative and qualitative data are the two primary types of data used in research and analysis, and they differ in terms of their nature, characteristics, and how they are collected and analyzed. The table below shows the differences between both data types:

Now that you know what each data type represents, the following table illustrates the differences between quantitative and qualitative data. The 'Price' column provides quantitative information, representing the cost of each product in dollars, whereas the 'Customer Review' column contains qualitative data featuring customer feedback regarding their experiences with the products.

While the two data types represent different data, one thing to remember is that quantitative and qualitative data complement each other. Quantitative data provides you with statistical insight, while qualitative data provides you with depth and context.

Now that we have defined quantitative data let’s look at the steps you would take to perform quantitative data analysis. Analyzing quantitative data will allow you to unlock insights that can help you make informed decisions. From defining your research objectives to interpreting your analysis results, each step will help you unleash the power of quantitative data.

Following the steps above will provide you with the means to perform effective quantitative data analysis. Using the insights you uncover from your data will help guide your decision-making processes, helping your organization to meet or surpass its goals and objectives.

Any organization's picture can be more precise with more quantitative data. However, if you manually sift through gigabytes of data, you may not be able to see the forest for the trees, leading to incorrect assumptions and decisions. Machine Learning (ML), a subset of Artificial Intelligence (AI), comes to the rescue, helping you see the forest.

The power of ML is that it can identify patterns and trends using algorithms, revealing hidden insights that would take a human analyst a much longer time to discover, if at all. Additionally, ML can help predict future trends by looking at historical data. So, how does ML learn to read quantitative data and provide valuable insights? Let's look at how you teach ML.

There are many different learning methods for ML, but we will define three: supervised, unsupervised, and reinforcement learning.

• Supervised Learning uses labeled training data, which contains input-output pairs. The ML algorithms then analyze a large data set containing these pairs to learn the desired output when asked to make a prediction using new data.
• Unsupervised Learning uses unlabeled training data. The ML algorithms try to find patterns and structures in the input data without guidance on the outcomes they should predict.
• Reinforcement Learning is when an algorithm learns decision-making by performing an action and receiving reward or penalty feedback. The algorithm's overall goal is to discover a strategy that maximizes reward feedback.

While machine learning has become an indispensable tool for quantitative data analysis, it's important to recognize that it does not replace the need for human judgment and decision-making. Python, R, and specialized platforms like TensorFlow and Azure ML have made it easier than ever to integrate machine learning into the data analysis workflow, dramatically enhancing the efficiency and depth of insights that can be uncovered.

When leveraging these resources, analysts can uncover hidden patterns and transform raw data into actionable intelligence. However, rather than replacing human expertise, machine learning augments it by delivering more precise outcomes, freeing up analysts to concentrate on high-level strategic planning and choices that require a human touch. The power of machine learning lies in its ability to work in tandem with human judgment, providing the raw insights that inform critical decisions and drive meaningful change.

Example: Predictive Analytics in E-commerce

Imagine you're a data scientist working for an online retail organization that wants to improve customer retention and increase sales by predicting purchasing behavior and preferences. By leveraging predictive analytics, you can analyze historical transaction data to forecast future buying patterns and identify high-value customers.

• Data Collection and Preparation: You first collect and preprocess quantitative transactional data, including customer demographics, purchase history, purchase frequency, transaction amounts, customer lifetime value, product attributes, and website interactions. This process will also collect qualitative data such as product categories and customer feedback.
• Feature Engineering: Next, you extract meaningful features from the raw data through feature engineering, such as average purchase value or total number of orders, and you create derived variables such as recency and frequency. This information provides the inputs for predictive modeling.
• Predictive Modeling: To forecast customer churn, identify cross-selling opportunities, and create personalized product recommendations, you use ML algorithms to build predictive models. These models use historical data to predict the likelihood of customers’ purchasing in a specific timeframe or which products they will likely purchase next.
• Model Evaluation and Validation: You evaluate the performance of the predictive models using metrics such as accuracy, precision, recall, and area under the receiver operating characteristic curve (AUC-ROC). You then use cross-validation techniques and holdout validation to assess model generalization and ensure robustness against overfitting.
• Deployment and Integration: Once validated, the predictive models are deployed into production systems, integrated with the company's e-commerce platform, and used to generate real-time recommendations and personalized marketing campaigns. Customers receive targeted offers, product suggestions, and promotional discounts based on their predicted preferences and behaviors.
• Monitoring and Iteration: Continuous monitoring of model performance and customer feedback enables iterative refinement and optimization of the predictive analytics pipeline.

Quantitative data analysis is constantly evolving, driven by advancements in technology, new research methodologies, and emerging trends in data science. To remain ahead of the curve, it is crucial that you are aware of future trends that will impact how you perform data analysis. Some of the future trends that will potentially impact quantitative analysis include:

• Increased Use of Artificial Intelligence and Machine Learning : Integrating AI and ML techniques is expected to become more prevalent, enabling more sophisticated and automated data analysis.
• Growth of Big Data : As data grows in volume, variety, and velocity, quantitative analysis methods must adapt to handle larger datasets more efficiently.
• Advancements in Data Privacy Regulations : Increasing concerns and regulations around data privacy will impact how data is collected, stored, and analyzed, prompting the development of new methods that protect individual privacy.
• Rise of Edge Computing : With the rise of IoT devices, edge computing will become more critical. It will push data analysis closer to where data is generated to improve speed and reduce data transfer costs.
• Quantum Computing : The potential rise of quantum computing could revolutionize data analysis by providing the power to process enormous and complex datasets much faster than traditional computers.
• Proliferation of Data-as-a-Service (DaaS) : DaaS will provide increased access to high-quality and specialized data streams, enabling more refined and real-time analyses.
• Augmented Analytics : Augmented analytics, which incorporates natural language processing and automated algorithms, will make data analysis more accessible to non-experts and enhance decision-making processes.
• Focus on Predictive and Prescriptive Analytics : There will be a shift towards more predictive and prescriptive analytics, moving beyond descriptive analytics to offer foresight and guidance on future actions.

As quantitative data analysis evolves, it will be defined by a trifecta of innovation, integration, and integrity. Cutting-edge advancements will reshape analytical methods and tools, while the fusion of diverse data sources and techniques will unearth groundbreaking insights.

However, the true measure of success will lie in the ethical application of these capabilities, prioritizing transparency, privacy, and fairness. The future of data analysis will demand continuous learning, collaboration, and unwavering commitment to using data for the greater good, unlocking transformative opportunities for data-driven decision-making that benefits all.

Quantitative data is a powerful tool for uncovering insights, identifying patterns, and informing decision-making. We've explored the fundamental concepts of quantitative data, delved into the differences between quantitative and qualitative data, and navigated through a step-by-step guide to conducting data analysis using quantitative data. From defining research objectives to deploying advanced ML techniques, each step in the quantitative data analysis process helps you extract meaningful insights from numerical data.

The future of quantitative data analysis is bright, with advancements in technology, methodologies, and interdisciplinary collaboration driving innovation and progress. With the right tools, techniques, and mindset, the vast amount of quantitative data available to you becomes an opportunity to unlock hidden truths, drive informed decisions, and shape a better future through data-driven insights. The power of quantitative data analysis will propel you and your organization forward to greater success.

• Expand/Collapse Microsoft Office 38 RSS
• Expand/Collapse Training Trends 107 RSS
• Expand/Collapse CyberSecurity 59 RSS
• Expand/Collapse DevOps 2 RSS
• Expand/Collapse Modern Workplace 41 RSS
• Expand/Collapse Cloud 16 RSS
• Expand/Collapse Programming 10 RSS
• Expand/Collapse Artificial Intelligence (AI) 8 RSS
• Expand/Collapse ITIL 17 RSS
• Expand/Collapse Data & Analytics 26 RSS
• Expand/Collapse Business Analyst 13 RSS
• Expand/Collapse Training By Job Role 1 RSS
• Expand/Collapse Leadership and Professional Development 14 RSS
• Expand/Collapse Managed Learning Services 3 RSS
• Expand/Collapse Design & Multi-Media 1 RSS

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.

H a : The alternative hypothesis: It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 . This is usually what the researcher is trying to prove.

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject H 0 " if the sample information favors the alternative hypothesis or "do not reject H 0 " or "decline to reject H 0 " if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ .30 H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 66
• H a : μ __ 66

Example 9.3

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 45
• H a : μ __ 45

Example 9.4

In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p __ 0.40
• H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/introductory-statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Introductory Statistics
• Publication date: Sep 19, 2013
• Location: Houston, Texas
• Book URL: https://openstax.org/books/introductory-statistics/pages/1-introduction
• Section URL: https://openstax.org/books/introductory-statistics/pages/9-1-null-and-alternative-hypotheses

© Jun 23, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 29 May 2024

Final analysis of a phase II trial of daratumumab, carfilzomib, lenalidomide, and dexamethasone in newly diagnosed multiple myeloma without transplant

• Benjamin A. Derman 1 ,
• Jennifer Cooperrider 1 ,
• Jacalyn Rosenblatt 2 ,
• David E. Avigan 2 ,
• Murtuza Rampurwala 1 ,
• David Barnidge 3 ,
• Ajay Major   ORCID: orcid.org/0000-0001-7261-1335 4 ,
• Theodore Karrison 5 ,
• Ken Jiang 1 ,
• Aubrianna Ramsland 1 ,
• Tadeusz Kubicki   ORCID: orcid.org/0000-0001-7588-1453 1 &
• Andrzej J. Jakubowiak   ORCID: orcid.org/0000-0002-2597-6822 1  

Blood Cancer Journal volume  14 , Article number:  87 ( 2024 ) Cite this article

1 Altmetric

Metrics details

• Phase II trials

We evaluated the efficacy and safety of 24 cycles of Dara in combination with carfilzomib (K), lenalidomide (R), and dexamethasone (d) without autologous stem cell transplant (ASCT) in newly diagnosed multiple myeloma (NDMM) irrespective of ASCT eligibility in a single-arm, phase II study. The primary endpoint was the rate of stringent complete response (sCR) and/or measurable residual disease (MRD) < 10 −5 by next-generation sequencing (NGS) at the end of cycle 8 (C8). MRD was also assessed on peripheral blood samples using both the EXENT ® system and liquid chromatography–mass spectrometry (LC–MS). Forty-two patients entered the treatment phase; forty were evaluable for the primary endpoint. The rate of sCR and/or MRD < 10 −5 following C8 was 30/40 (75%), meeting the statistical threshold for efficacy. The 10 −6 MRD negative rate improved with treatment beyond C8. Agreement between EXENT ® and NGS was high and increased over time; agreement between LC-MS and NGS was lower. The estimated 3-year progression-free survival progression-free survival was 85%, and 3-year overall survival was 95%. Upper respiratory infections occurred in 67% (7% grade 3–4). There were no treatment-related deaths. Extended frontline Dara-KRd induced a high rate of sCR and/or MRD negativity; the rate and depth of MRD negativity improved beyond C8.

Similar content being viewed by others

Daratumumab, lenalidomide, and dexamethasone in relapsed/refractory myeloma: a cytogenetic subgroup analysis of POLLUX

Daratumumab plus lenalidomide and dexamethasone in relapsed/refractory multiple myeloma: extended follow-up of POLLUX, a randomized, open-label, phase 3 study

Daratumumab-based quadruplet therapy for transplant-eligible newly diagnosed multiple myeloma with high cytogenetic risk

Introduction.

Patients with newly diagnosed multiple myeloma (NDMM) typically receive induction therapy consisting of at least a proteasome inhibitor (PI), an immunomodulatory imide drug (IMiD), and a corticosteroid, potentially followed by autologous stem cell transplant (ASCT) and maintenance therapy. ASCT employed in the frontline setting compared to a delayed ASCT at the time of first relapse has been shown to improve progression-free survival (PFS) but to date, its association with overall survival (OS) has not been demonstrated [ 1 , 2 ].

Quadruplet induction therapy with the anti-CD38 monoclonal antibody (mAb) daratumumab (Dara) added to a PI, IMiD, and corticosteroid has led to high rates of deep and durable responses. The combination of Dara, bortezomib (V), lenalidomide (R), and dexamethasone (d) and ASCT led to a stringent complete response (sCR) rate of 69% and a minimal residual disease (MRD) negativity (10 −5 ) rate of 75% as best response in the PERSEUS trial [ 3 ]. When V was replaced with carfilzomib (K) in the MASTER trial, MRD-adapted Dara-KRd with ASCT led to an MRD negative (10 −6 ) rate of 71%; with rapid de-escalation of therapy for patients with MRD negativity, the 3-year PFS was 88%, 79%, and 50% for patients with 0, 1 or 2+ high-risk cytogenetic abnormalities (HRCA) [ 4 ]. An ASCT-free approach with Dara-KRd for up to 13 cycles led to a CR or better in 67% of patients; separately, the MANHATTAN trial found that Dara-KRd for 8 cycles led to an MRD negativity (10 −5 ) rate of 71% [ 5 , 6 ]. Some patients in both studies received post-protocol ASCT, and thus the durability of response to Dara-KRd without ASCT was not established.

In this phase II study, we sought to evaluate the efficacy of an ASCT-free approach with 24 cycles of Dara-KRd in patients with NDMM regardless of ASCT eligibility.

Study design and participants

This was an open-label, single-arm, phase II study that enrolled patients from two Multiple Myeloma Research Consortium sites in the United States. Patients aged 18 or older with NDMM were eligible irrespective of ASCT eligibility. All patients provided written informed consent; the study was conducted in accordance with the International Conference on Harmonization Guidelines for Good Clinical Practice and the Declaration of Helsinki. The study was approved by the institutional review boards of the participating institutions, and the study was registered at clinicaltrials.gov (NCT03500445). The datasets generated during the current study are available from the corresponding author upon reasonable request.

Patients with NDMM were permitted to receive up to one cycle of anti-myeloma therapy prior to enrollment. Once enrolled, patients received Dara-KRd for a planned 24 cycles at the following doses: intravenous (IV) daratumumab 16 mg/kg weekly for cycles (C) 1 & 2, every 2 weeks for C3–8, then every 4 weeks for C9–24; IV carfilzomib 20/36 mg/m 2 on days 1, 2, 8, 9, 15, and 16 for C1–8 and then 36 mg/m 2 on days 1, 2, 15, and 16 for C9–24; oral lenalidomide 25 mg on days 1–21 of a 28-day cycle for 24 cycles; and oral dexamethasone 40 mg weekly (20 mg if age > 75) for C1-8 and then 20 mg weekly for C9–24. Patients were given the option to harvest stem cells after 4–6 cycles of protocol therapy to permit ASCT in the future. Following the completion of 24 cycles of protocol therapy, single-agent lenalidomide maintenance therapy was recommended.

Assessments

Minimal residual disease (MRD) testing was performed at the end of C8, C12, and C24 by next-generation sequencing (NGS, clonoSEQ, Adaptive Biotechnologies) with a limit of detection (LoD) of 6.8 × 10 −7 with 20 µg of DNA input. Mass spectrometry (MS) of peripheral blood samples was also performed by The Binding Site (part of Thermo Fisher) using the matrix-assisted laser desorption/ionization time-of-flight (MALDI-TOF) MS-based EXENT ® system (lower limit of measuring interval (LLMI) = 15 mg/L in 200 mg/L total immunoglobulin) with EXENT ® immunoprecipitate eluates also analyzed by the more sensitive LC–MS (LLMI ≥ 0.15 mg/L) as previously described [ 7 ].

Adverse events (AEs) were graded according to the National Cancer Institute Common Terminology Criteria for Adverse Events version 4.0.

Study endpoints

The primary endpoint was the rate of sCR and/or MRD negativity at the 10 −5 threshold at the end of C8 to account for patients nonevaluable for MRD by NGS due to unavailable or untrackable clonal sequences along with the limitation of accurately distinguishing the IgG kappa mAb Dara from IgG kappa paraprotein by serum protein immunofixation. Secondary endpoints included conventional International Myeloma Working Group (IMWG) response [ 8 ], MRD status by NGS, toxicity, PFS, and OS. Peripheral blood MRD status using the EXENT ® assay and LC–MS were exploratory endpoints.

Statistical analysis

The primary analysis required forty patients to test the null hypothesis that the sCR and/or MRD negative status by NGS at the end of 8 cycles is ≤30% against the alternative that it is >30% using an exact one-sided binomial test with alpha = 0.10. The null hypothesis was to be rejected if 17 or more sCR and/or MRD negative responses were observed. Our sample size provided 85% power if the true response rate was 50%.

Efficacy analyses were performed on the intent-to-treat (ITT) population, including the MRD negativity rate as per the international consensus on MRD reporting [ 9 ]. Patients without progression nor toxicity who discontinued treatment prior to C8 were included in all analyses except the C8 response evaluation; they were ‘replaced’ by additional patients to achieve the necessary sample size. Categorical data were compared using chi-squared or Fisher’s exact tests. The Kaplan-Meier method was used for time-to-event endpoints, specifically for PFS and OS.

Patient characteristics

A total of 42 patients entered the treatment phase from March 2019 to January 2022. The data cutoff was July 15, 2023. The median age was 58 (range 39–79), including 12 (29%) age ≥ 65 years (Table 1 ). High-risk cytogenetic abnormalities (HRCA) by CD138+ selected fluorescent in situ hybridization according to IMWG criteria [ 10 ] were present in 24 (57%), including 10 (24%) with t(4;14), 3 (7%) with t(14;16), 8 (19%) with deletion 17p, and 14 (33%) with a 1q copy number abnormality (6 [14%] with 1q amplification); only 2 patients had an isolated 1q gain without any other high-risk abnormalities. Two or more HRCA were present in 10 (24%) patients.

Of the 42 patients who entered the treatment phase, 40 (95%) were evaluated for response at the end of C8. Two patients withdrew from the study before C8, one due to geographic relocation and one due to a psychological disturbance unrelated to treatment (Fig. 1 ). The median number of cycles received was 23 (range 1–24).

Forty-seven patients were assessed for eligibility, of which 42 enrolled on the study. A total of 40 patients were evaluable for the primary endpoint, though all 42 patients were followed for progression-free and overall survival.

Following 8 cycles of Dara-KRd ( n  = 40), the rate of sCR and/or MRD negativity (<10 −5 ) was 30/40 (75%, 95% confidence interval [CI] 61–89%), meeting the statistical threshold for efficacy (Table 2 ). The overall response rate at the end of 8 cycles was 38/40 (95%), with 27 (68%) achieving an sCR, 28 (70%) at least a CR, and 38 (95%) at least a very good partial response. Two (5%) patients had primary refractory disease; one had two HRCA, and the other had an insufficient sample for cytogenetics but had 15% circulating plasma cells at diagnosis that had not met the previously established criteria (≥20% plasma cells) for plasma cell leukemia.

The rate of sCR as the best response in the ITT population ( n  = 42) was 31/42 (74%) and 36/42 (86%) ≥CR. A best response of sCR and/or MRD negativity (10 −5 ) was achieved in 32/42 (76%).

Patient disposition

Among the 42 patients who entered the treatment phase, 21 (50%) reached the end of therapy, 6 (14%) of whom were off all treatment at the data cutoff. An additional 11 (26%) patients remain on protocol treatment, all past C8. A total of 7 (17%) patients experienced disease progression, including 6 (14%) while on protocol therapy (Supplemental Tables 1 and 2 ). Two deaths occurred, both early in treatment and due to primary refractory disease. Stem cell collection was performed for 37 (88%) patients, all with G-CSF and upfront plerixafor with a median of 2 (range 1–3) days of collection, for a median yield of 8.26 × 10 6 CD34 + cells/kg (range 3.1–17.5 × 10 6 CD34 + cells/kg). Four (10%) patients discontinued protocol therapy early while still in disease response; one of these patients proceeded to ASCT (Supplemental Table 1 ). Another 3 (7%) patients received ASCT following disease progression.

Clonotypic tracking for MRD by NGS was available for 34 (81%) patients; 4 (9.5%) had clonotypic tracking failure leading to a 90% calibration rate, and 4 (9.5%) had no suitable calibration material available (Supplemental Fig. 1 ). By MRD ITT [ 9 ], 20 (59%) achieved MRD negativity at the 10 −5 threshold and 12 (35%) at 10 −6 at the end of C8 (Table 2 ). Responses deepened over time (Table 2 ) among patients who reached C8: 1/10 (10%) and 6/18 (33%) patients converted from MRD positive at C8 to MRD negative at later timepoints at the 10 −5 and 10 −6 thresholds, respectively. The rate of MRD negativity at any timepoint was 22/34 (65%) at 10 −5 and 18/34 (53%) at 10 −6 . Among 33 MRD-evaluable patients from C8 onward, 6 had one MRD < 10 −5 result and less than one year of subsequent follow-up, while 11 of the remaining 27 patients (41%) had sustained 10 −5 MRD negativity (two consecutive MRD negative results ≥1 year apart).

Mass spectrometry

A trackable monoclonal light chain was identified in 39 (93%) patients; 3 patients had no baseline sample available (Supplemental Fig. 2 ). Among the same 39 patients evaluable for conventional response at C8, 22/39 (56%) were EXENT ® negative at the end of C8 and 25/39 (64%) were EXENT ® negative as the best response. By LC–MS, 7/39 (18%) were LC–MS negative following C8 and 12/39 (31%) were LC–MS negative as best response (Table 2 ; Fig. 2 ).

Longitudinal assessments for measurable residual disease using both next generation sequencing (NGS) and mass spectrometry (MS) are shown. Each paired row represents a unique patient. Black denotes patients with disease progression, including in long-term follow-up (LTFU). Four patients had neither NGS nor MS tracking results available, including two with primary refractory disease. indeterm indeterminate result, LC–MS liquid chromatography–mass spectrometry.

There was 75% agreement between 32 paired EXENT ® and NGS (10 −5 ) samples at C8 (Cohen’s kappa 0.48, 95% CI 0.18–0.79), with 3 cases NGS(+)/EXENT ® (−) and 5 cases NGS(−)/EXENT ® (+) (Fig. 3 ). Among paired EXENT ® and NGS (10 −6 ) samples at C8, the agreement was 69% (Cohen’s kappa 0.39, 0.10–0.69), with 8 cases NGS(+)/EXENT ® (−) and only 2 cases NGS(−)/EXENT ® (+). Concordance increased by the end of C24 to 84% for both EXENT ® /NGS (10 −5 ) and EXENT ® /NGS (10 −6 ).

A visual representation of concordance between mass spectrometry in the peripheral blood and next-generation sequencing in the bone marrow at the conclusion of 8 cycles of Dara-KRd. LC–MS liquid chromatography–mass spectrometry, MS mass spectrometry, NGS next-generation sequencing.

The agreement between LC–MS and NGS at both thresholds was lower. There was 50% agreement (Cohen’s kappa 0.14, 95% CI: −0.08 to 0.36) between 32 paired LC–MS and NGS (10 −5 ) samples at C8, with most discordance (15/16, 94%) due to NGS(−)/LC-MS(+) cases (Fig. 3 ). There was 63% agreement (Cohen’s kappa 0.11, 95% CI −0.21 to 0.43) between LC–MS and NGS (10 −6 ) samples at C8, with 9 cases NGS(−)/LC-MS(+) and 3 cases NGS(+)/LC-MS(−). At the end of C24, 7/8 (88%) and 5/6 (83%) discordant cases were LC–MS(+)/NGS(−) at 10 −5 and 10 −6 thresholds, respectively.

Progression-free survival and overall survival

With a median follow-up of 27 months (range 1.5–52 months), there were 7 progression events and 2 deaths (both due to progression). The estimated 3-year PFS was 85% (Fig. 4 ): 100% for standard-risk disease, 92% for 1 HRCA, and 60% for 2 + HRCA. Of the 7 patients with progression, 6 had at least one of the following: extramedullary disease ( n  = 4), 2 + HRCA ( n  = 4), or circulating plasma cells ( n  = 1). The estimated 3-year OS was 95%.

A Progression-free survival (PFS) and overall survival (OS) by intent to treat analysis. B PFS is stratified by the number of high-risk cytogenetic abnormalities (HRCA). One patient had unknown cytogenetics.

Excluding patients who experienced progression or death prior to C8 using the landmark method [ 11 ], C8 MRD status at neither 10 -5 nor 10 −6 was associated with PFS (Supplemental Fig. 3 ). None of the 11 patients with sustained MRD negativity < 10 −5 had disease progression.

Using the same landmark method [ 11 ], the EXENT ® assay and LC-MS status at C8 were not associated with PFS (logrank p  = 0.055 and p  = 0.22, respectively) (Supplemental Fig. 4 ). Excluding patients with progression before C8, EXENT ® negative status as the best response was associated with superior PFS ( p  = 0.03); only one patient with EXENT ® negativity had disease progression. None of the patients who reached LC–MS negativity experienced disease progression (Fig. 5 ).

A Progression-free survival stratified by EXENT status as the best response and B progression-free survival stratified by liquid-chromatography mass spectrometry (LC–MS) status as the best response, both using the landmark method from cycle 8 onward.

Safety and tolerability

Dose reductions occurred in 2 (5%) patients for daratumumab, both as temporary dose omissions to limit exposure at the onset of the COVID-19 pandemic. Dose reductions occurred in 11 (26%) patients for carfilzomib, 23 (55%) for lenalidomide, and 22 (52%) for dexamethasone. Hematologic AEs (Table 3 ) included neutropenia (all grade (G) 26%, G3 + 21%), anemia (G 59%, G3 + 2%), and thrombocytopenia (G 64%, G3 + 26%). The most common nonhematologic AEs were hyperglycemia (G 76%, G3 + 7%), diarrhea (G 71%, G3 + 5%), hypertension (G 57%, G3 + 17%), and neuropathy (G 40%, G3 + 0%). Upper respiratory infections occurred in 28 (67%) patients including 16 (38%) with COVID-19 infections; there were 3 (7%) total G3+ infectious events. There was one case of thrombotic microangiopathy leading to the discontinuation of carfilzomib. G3 atrial fibrillation and heart failure each occurred in 1 patient, both of which resolved. No patient discontinued treatment or died due to toxicity.

In this phase II study involving a diverse NDMM population with 57% harboring an HRCA, eight cycles of Dara-KRd without ASCT led to an sCR and/or MRD negativity rate of 75%, thereby meeting the primary endpoint. The historical comparator for this trial was KRd without ASCT, which led to sCR rates ranging widely from 6 to 62% in a variety of settings [ 12 , 13 , 14 , 15 ]. Extended Dara-KRd also compares favorably with other quadruplets; the sCR and/or MRD negativity (<10 −5 ) rate after 8 cycles of elotuzumab (Elo)-KRd was 58% [ 16 ]. Even with the more conservative ITT approach, the 59% post-induction MRD 10 − 5 negativity rate in this study was high in the context of other (sometimes shorter) quadruplet induction strategies: Dara-VRd 22% [ 17 ], Dara-VMP 28% [ 18 ], Dara-VTd 35% [ 19 ], Dara-KRd 38% [ 20 ], Isa-VRd 50% [ 21 ], Isa-KRd 45-54% [ 22 , 23 ], and Elo-KRd 53% [ 24 ].

The estimated 3-year PFS with Dara-KRd in this trial was 85%, including 100% for patients with no HRCA, 92% for 1 HRCA, and 60% for 2 + HRCA. This represents one of the highest reported rates of 3-year PFS in NDMM regardless of receipt of ASCT; for comparison, in the phase 3 PERSEUS trial, Dara-VRd and ASCT led to a 3-year PFS of 90% [ 3 ]. This study also highlights the challenge of treating patients with 2 + HRCA. A post-hoc analysis of PFS from the GRIFFIN trial revealed the 3-year PFS with Dara-VRd and ASCT to be 54% for patients with 2 + HRCA [ 25 ]. The MASTER trial involving Dara-KRd, ASCT, and MRD-guided discontinuation of therapy and the GMMG-CONCEPT trial involving extended Isa-KR post-ASCT led to a similar 3-year PFS. 4,22 A retrospective study of patients with 2 + HRCA who received ASCT was less optimistic with a median PFS of just 22.9 months [ 26 ]. The OPTIMUM MUKnine trial used an extended high-intensity therapy approach for ultra-high-risk disease, yielding a 3-year PFS of ~75% [ 27 ]. The totality of these results suggests that the current treatment approach for patients with 2 + HRCA is unsatisfactory regardless of ASCT and serves as motivation to incorporate chimeric antigen receptor (CAR) T-cell therapy and bispecific antibodies earlier into the treatment paradigm.

Extended quadruplet therapy may help compensate for the deferral of ASCT. Eight cycles of induction have been an arbitrary historical standard for patients deferring ASCT. The benefit of extending quadruplet therapy beyond 8 cycles is further exemplified by the deepening of responses over time in this study and in others [ 13 , 28 , 29 ]. The rate of MRD negativity at the 10 −6 threshold was 35% after 8 cycles of therapy but increased to 53% as a best response, which may explain why C8 MRD status was not prognostic. Importantly, no patient with sustained MRD < 10 −5 nor <10 − 6 experienced disease progression, in line with observations that sustained MRD negativity is an important prognostic marker.

Stem cell mobilization and collection did not appear to be significantly impacted by the administration of a quadruplet therapy in this study. The median stem cell yield in this study was higher than in the MASTER trial (8.26 × 10 6 vs 6.0 × 10 6 CD34 +  cells/kg), perhaps because mobilization of all patients in our study included upfront plerixafor and because a higher target stem cell dose (4 × 10 6 CD34 +  cells/kg per transplant) was used.

Mass spectrometry performed on peripheral blood also added prognostic value. Negativity as the best response using EXENT ® was associated with superior PFS, and patients negative by LC–MS did not experience disease progression. The sensitivity of LC–MS is greater than EXENT ® , which explains the lower rate of LC–MS negativity compared to EXENT ® negativity; a negative LC–MS result may serve as one of the best predictors of durable response. However, C8 does not appear to be the appropriate timepoint for prognostication by mass spectrometry, particularly for patients with an IgG heavy chain, likely due to paraprotein that persists in circulation long after eradication of the malignant plasma cells that produced it [ 30 ]. A recent analysis among patients receiving maintenance therapy found that 18 months post-ASCT was the optimal prognostication timepoint for EXENT ® [ 31 ]. Additionally, identifying the time from immunofixation negativity to negativity by mass spectrometry for each method is an area requiring further research.

No patient discontinued protocol therapy due to toxicity, suggesting extended Dara-KRd has a favorable safety profile. The 55% dose reduction rate for lenalidomide is similar to that seen in the ENDURANCE trial [ 14 ]. Rates of neutropenia were low, yet infections were still common, potentially in part due to enrollment of patients primarily during the initial years of the COVID-19 pandemic; while 38% of patients did contract COVID-19, no patient died from COVID-19. Cardiac events were rare, and no venous thromboembolic (VTE) events were reported, potentially due to omitting intravenous fluids with carfilzomib after cycle 1 day 1, close collaboration with a cardio-oncologist, and the recommendation for enhanced VTE prophylaxis with direct oral anticoagulants. The absence of treatment-related deaths in this study is notable in light of preliminary findings from the GEM2017FIT study, which included a cohort of older transplant-ineligible patients that were assigned 18 cycles of Dara-KRd, of which 8.5% died due to an adverse event [ 32 ]. In a similar vein, the PERSEUS study found that compared with VRd and ASCT, Dara-VRd and ASCT were associated with improved PFS in nearly all subgroups except patients aged 65 and older. These studies may suggest that quadruplet therapy be used with caution in older adults.

Limitations of this study include its small sample size and the use of a nonstandard primary endpoint. Twice weekly carfilzomib, as used in this study, has become less common in practice, especially as Dara-KRd with once weekly carfilzomib 56 mg/m 2 led to similarly high MRD negativity rates [ 6 ]. Extending Dara-KRd carries cost implications and time toxicity to patients but may also spare patients from frontline ASCT that is associated with short-term detriments in health-related quality of life and increased risk of second hematologic malignancies [ 33 , 34 ]. Patients who experience relapse while on Dara-KRd face more challenges in finding a suitable second-line regimen, as it is unlikely that bortezomib has activity in carfilzomib-resistant settings.

In conclusion, this study is the first to our knowledge to show that extended Dara-KRd can induce and sustain deep and durable responses without the use of ASCT. The high proportion of patients with HRCA in this study provides a signal of efficacy in a population that is typically recommended to proceed with early ASCT when possible. The success of this extended approach may be due to the deepening of MRD and MS responses beyond eight cycles, raising the question of whether ASCT could be supplanted in NDMM. Moreover, this study challenges whether the addition of an anti-CD38 mAb to KRd may lead to superior outcomes compared to KRd with or without ASCT. The phase III PERSEUS study that compared Dara-VRd vs VRd in the ASCT-intended setting has shown that Dara-VRd is associated with superior PFS [ 3 ]. An ongoing phase III randomized trial of VRd vs extended KRd (NCT03729804) may provide a signal about the duration of PI and outcomes, and the phase III CEPHEUS and IMROZ studies may further inform on the best approach to NDMM in the transplant-deferred setting. Still, other randomized studies will be needed to answer whether ASCT can be circumvented by extending quadruplet treatment for most patients with NDMM and whether extended quadruplet therapy is superior to shorter courses of quadruplet therapy in the absence of ASCT.

Data availability

The data generated in this study is available from the corresponding author upon reasonable request.

Attal M, Lauwers-Cances V, Hulin C, Leleu X, Caillot D, Escoffre M, et al. Lenalidomide, bortezomib, and dexamethasone with transplantation for myeloma. N Engl J Med. 2017;376:1311–20.

Article   CAS   PubMed   PubMed Central   Google Scholar  

Richardson PG, Jacobus SJ, Weller EA, Hassoun H, Lonial S, Raje NS, et al. Triplet therapy, transplantation, and maintenance until progression in myeloma. N Engl J Med. 2022;387:132–47.

Sonneveld P, Dimopoulos MA, Boccadoro M, Quach H, Ho PJ, Beksac M, et al. Daratumumab, Bortezomib, Lenalidomide, and Dexamethasone for Multiple Myeloma. N Engl J Med. 2024;390:301–13.

Article   CAS   PubMed   Google Scholar  

Costa LJ, Chhabra S, Medvedova E, Dholaria BR, Schmidt TM, Godby KN, et al. Minimal residual disease response-adapted therapy in newly diagnosed multiple myeloma (MASTER): final report of the multicentre, single-arm, phase 2 trial. Lancet Haematol. (2023). https://doi.org/10.1016/S2352-3026(23)00236-3 .

Jakubowiak A, Usmani SZ, Krishnan A, Lonial S, Comenzo RL, Wang J, et al. Daratumumab plus carfilzomib, lenalidomide, and dexamethasone in patients with newly diagnosed multiple myeloma. Clin Lymphoma Myeloma Leuk. 2021;21:701–10.

Landgren O, Hultcrantz M, Diamond B, Lesokhin AM, Mailankody S, Hassoun H, et al. Safety and effectiveness of weekly carfilzomib, lenalidomide, dexamethasone, and daratumumab combination therapy for patients with newly diagnosed multiple myeloma: the MANHATTAN nonrandomized clinical trial. JAMA Oncol. 2021;7:862–8.

Article   PubMed   PubMed Central   Google Scholar  

Barnidge D, Troske D, North S, Wallis G, Perkins M, Harding S. Endogenous monoclonal immunoglobulins analyzed using the EXENT® solution and LC-MS. J Mass Spectrom Adv Clin Lab. 2024;32:31–40.

Kumar S, Paiva B, Anderson KC, Durie B, Landgren O, Moreau P, et al. International Myeloma Working Group consensus criteria for response and minimal residual disease assessment in multiple myeloma. Lancet Oncol. 2016;17:e328–e346.

Article   PubMed   Google Scholar  

Costa LJ, Derman BA, Bal S, Sidana S, Chhabra S, Silbermann R, et al. International harmonization in performing and reporting minimal residual disease assessment in multiple myeloma trials. Leukemia. 2021;35:18–30.

Sonneveld P, Avet-Loiseau H, Lonial S, Usmani S, Siegel D, Anderson KC, et al. Treatment of multiple myeloma with high-risk cytogenetics: a consensus of the International Myeloma Working Group. Blood. 2016;127:2955–62.

Anderson JR, Cain KC, Gelber RD. Analysis of survival by tumor response. J Clin Oncol. 1983;1:710–9.

Gay F, Musto P, Rota-Scalabrini D, Bertamini L, Belotti A, Galli M, et al. Carfilzomib with cyclophosphamide and dexamethasone or lenalidomide and dexamethasone plus autologous transplantation or carfilzomib plus lenalidomide and dexamethasone, followed by maintenance with carfilzomib plus lenalidomide or lenalidomide alone for patients with newly diagnosed multiple myeloma (FORTE): a randomised, open-label, phase 2 trial. Lancet Oncol. 2021;22:1705–20.

Jakubowiak AJ, Dytfeld D, Griffith KA, Lebovic D, Vesole DH, Jagannath S, et al. A phase 1/2 study of carfilzomib in combination with lenalidomide and low-dose dexamethasone as a frontline treatment for multiple myeloma. Blood. 2012;120:1801–9.

Kumar SK, Jacobus SJ, Cohen AD, Weiss M, Callander N, Singh AK, et al. Carfilzomib or bortezomib in combination with lenalidomide and dexamethasone for patients with newly diagnosed multiple myeloma without intention for immediate autologous stem-cell transplantation (ENDURANCE): a multicentre, open-label, phase 3, randomised, controlled trial. Lancet Oncol. 2020;21:1317–30.

Kazandjian D, Korde N, Mailankody S, Hill E, Figg WD, Roschewski M, et al. Remission and progression-free survival in patients with newly diagnosed multiple myeloma treated with carfilzomib, lenalidomide, and dexamethasone: five-year follow-up of a phase 2 clinical trial. JAMA Oncol. 2018;4:1781–3.

Derman BA, Kansagra A, Zonder J, Stefka AT, Grinblatt DL, Anderson LD Jr, et al. Elotuzumab and weekly carfilzomib, lenalidomide, and dexamethasone in patients with newly diagnosed multiple myeloma without transplant intent: a phase 2 measurable residual disease–adapted study. JAMA Oncol. 2022;8:1278–86.

Voorhees PM, Sborov DW, Laubach J, Kaufman JL, Reeves B, Rodriguez C, et al. Addition of daratumumab to lenalidomide, bortezomib, and dexamethasone for transplantation-eligible patients with newly diagnosed multiple myeloma (GRIFFIN): final analysis of an open-label, randomised, phase 2 trial. Lancet Haematol. (2023). https://doi.org/10.1016/S2352-3026(23)00217-X .

Mateos M-V, San-Miguel J, Cavo M, Bladé Creixenti J, Suzuki K, Jakubowiak A, et al. Daratumumab plus bortezomib, melphalan, and prednisone (D-VMP) versus bortezomib, melphalan, and prednisone (VMP) alone in transplant-ineligible patients with newly diagnosed multiple myeloma (NDMM): updated analysis of the phase 3 alcyone study. Blood. 2022;140:10157–9.

Article   Google Scholar  

Avet Loiseau H, Sonneveld P, Moreau P, Offner F, van der Velden VHJ, Caillot D, et al. Daratumumab (DARA) with bortezomib, thalidomide, and dexamethasone (VTd) in transplant-eligible patients (Pts) with newly diagnosed multiple myeloma (NDMM): analysis of minimal residual disease (MRD) negativity in cassiopeia part 1 and part 2. Blood. 2021;138:82.

Costa LJ, Chhabra S, Medvedova E, Dholaria BR, Schmidt TM, Godby KN, et al. Daratumumab, carfilzomib, lenalidomide, and dexamethasone with minimal residual disease response-adapted therapy in newly diagnosed multiple myeloma. JCO. (2021). https://doi.org/10.1200/JCO.21.01935 .

Goldschmidt H, Mai EK, Bertsch U, Fenk R, Nievergall E, Tichy D, et al. Addition of isatuximab to lenalidomide, bortezomib, and dexamethasone as induction therapy for newly diagnosed, transplantation-eligible patients with multiple myeloma (GMMG-HD7): part 1 of an open-label, multicentre, randomised, active-controlled, phase 3 trial. Lancet Haematol. 2022;9:e810–e21.

Leypoldt LB, Tichy D, Besemer B, Hänel M, Raab MS, Mann C, et al. Isatuximab, carfilzomib, lenalidomide, and dexamethasone for the treatment of high-risk newly diagnosed multiple myeloma. JCO. (2023). https://doi.org/10.1200/JCO.23.01696 .

Gay F, Roeloffzen W, Dimopoulos MA, Rosiñol L, van der Klift M, Mina R, et al. Results of the phase III randomized iskia trial: isatuximab-carfilzomib-lenalidomide-dexamethasone vs carfilzomib-lenalidomide-dexamethasone as pre-transplant induction and post-transplant consolidation in newly diagnosed multiple myeloma patients. Blood. 2023;142:4.

Knop S, Stuebig T, Kull M, Greil R, Steiner N, Bassermann F, et al. Carfilzomib, lenalidomide, and dexamethasone (KRd) versus elotuzumab and KRd in transplant-eligible patients with newly diagnosed multiple myeloma: Post-induction response and MRD results from an open-label randomized phase 3 study. JCO. 2023;41:8000.

Callander N, Silbermann R, Kaufman JL, Godby KN, Laubach JP, Schmidt TM, et al. Analysis of transplant-eligible patients (Pts) who received frontline daratumumab (DARA)-based quadruplet therapy for the treatment of newly diagnosed multiple myeloma (NDMM) with High-risk Cytogenetic Abnormalities (HRCA) in the griffin and master studies. Blood. 2022;140:10144–7.

Pasvolsky O, Ghanem S, Milton DR, Masood A, Tanner MR, Bashir Q, et al. Outcomes of autologous stem cell transplant in patients with ultra high-risk multiple myeloma. Transplantat Cell Ther. (2023). https://doi.org/10.1016/j.jtct.2023.08.031 .

Kaiser MF, Hall A, Walker K, Sherborne A, De Tute RM, Newnham N, et al. Daratumumab, cyclophosphamide, bortezomib, lenalidomide, and dexamethasone as induction and extended consolidation improves outcome in ultra-high-risk multiple myeloma. JCO. (2023). https://doi.org/10.1200/JCO.22.02567 .

Voorhees PM, Kaufman JL, Laubach J, Sborov DW, Reeves B, Rodriguez C, et al. Daratumumab, lenalidomide, bortezomib, and dexamethasone for transplant-eligible newly diagnosed multiple myeloma: the GRIFFIN trial. Blood. 2020;136:936–45.

Jasielec J, Kubicki T, Raje N, Vij R, Reece D, Berdeja JG, et al. Carfilzomib, lenalidomide, and dexamethasone plus transplant in newly diagnosed multiple myeloma. Blood. (2020). https://doi.org/10.1182/blood.2020007522 .

Roopenian DC, Akilesh S. FcRn: the neonatal Fc receptor comes of age. Nat Rev Immunol. 2007;7:715–25.

Kubicki T, Dytfeld D, Barnidge D, Sakrikar D, Lakos G, Przybylowicz-Chalecka A, et al. Mass spectrometry-based assessment of M-protein in peripheral blood during maintenance therapy in multiple myeloma (MM) in the phase III ATLAS trial. Blood. 2023;142:340.

Mateos M-V, Paiva B, Cedena Romero MT, Puig N, Sureda Balari AM, Oriol A, et al. GEM2017FIT trial: induction therapy with bortezomib-melphalan and prednisone (VMP) followed by lenalidomide and dexamethasone (Rd) versus carfilzomib, lenalidomide and dexamethasone (KRd) plus/minus daratumumab (D), 18 cycles, followed by consolidation and maintenance therapy with lenalidomide and daratumumab: phase iii, multicenter, randomized trial for elderly fit newly diagnosed multiple myeloma (NDMM) patients aged between 65 and 80 years. Blood. 2023;142:209.

Chakraborty R, Hamilton BK, Hashmi SK, Kumar SK, Majhail NS. Health-related quality of life after autologous stem cell transplantation for multiple myeloma. Biol Blood Marrow Transpl. 2018;24:1546–53.

Rosenberg AS, Brunson A, Tuscano J, Jonas BA, Hoeg R, Wun T, et al. Effect of autologous hematopoietic stem cell transplant on the development of second primary malignancies in multiple myeloma patients. Blood Cancer J. 2021;11:1–11.

Download references

Acknowledgements

The authors thank the patients and their families for participating in this study. The authors thank Luis Alcantar, Evangelia Andreatos, Karson Buckley, Camila Duarte, Martha Hodges, Bernadette Libao, Sarah Major, Allison Marthaler, Amanda McIver, Samrawit Melka, Megan Whelan, and Brittany Wolfe at the University of Chicago for their assistance in conducting this study. This study was supported, in part, by Amgen, Janssen, and the Multiple Myeloma Research Consortium.

Author information

Authors and affiliations.

Section of Hematology/Oncology, University of Chicago, Chicago, IL, USA

Benjamin A. Derman, Jennifer Cooperrider, Murtuza Rampurwala, Ken Jiang, Aubrianna Ramsland, Tadeusz Kubicki & Andrzej J. Jakubowiak

Beth Israel Deaconess Medical Center, Boston, MA, USA

Jacalyn Rosenblatt & David E. Avigan

The Binding Site Group, part of Thermo Fisher, Rochester, MN, USA

David Barnidge

University of Colorado, Denver, CO, USA

Department of Public Health Sciences, University of Chicago, Chicago, IL, USA

Theodore Karrison

You can also search for this author in PubMed   Google Scholar

Contributions

AJJ was responsible for designing the protocol, statistical design, and data analysis. BAD was responsible for data analysis and initial paper drafting. DB was responsible for performing mass spectrometry analysis. KJ and AR were responsible for processing samples. ThK was responsible for statistical design and data analysis. All authors were responsible for the interpretation of results, paper revisions, and final approval.

Corresponding author

Correspondence to Andrzej J. Jakubowiak .

Ethics declarations

Competing interests.

BAD declares advisory board fees from Janssen and Cota, Inc. He serves as an independent reviewer for a clinical trial for BMS. Research funding from Amgen and GSK. JC has no disclosures. JR declares consulting/advisory board fees from Advare, Bioclinica, Bristol Myers Squibb, Karyopharm Therapeutics, Parexel, and Sanofi. DEA declares consulting/advisory board fees from Aviv Med Tech, Bristol Myers Squibb/Celgene, Chugai Pharma, Janseen, Juno Therapeutics, Karyopharm Therapeutics, Kowa Pharmaceutical, Legend Biotech, Partner Therapeutics, Sanofi, and Takeda; employment by Paraxel; research funding from Kite and Pharmacyclics. MR declares advisory board fees from AstraZeneca. DB is an employee of The Binding Site, part of Thermo Fisher, and may receive royalties from EXENT and LC–MS technology license from the Mayo Foundation. AM has no disclosures. Th.K. has no disclosures. KJ has no disclosures. TaK has no disclosures. AJJ declares honoraria and advisory board fees from Abbvie, Amgen, Bristol-Myers Squibb/Celgene, GlaxoSmithKline, Gracell, Janssen, and Sanofi.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Study protocol, supplemental material, rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Derman, B.A., Cooperrider, J., Rosenblatt, J. et al. Final analysis of a phase II trial of daratumumab, carfilzomib, lenalidomide, and dexamethasone in newly diagnosed multiple myeloma without transplant. Blood Cancer J. 14 , 87 (2024). https://doi.org/10.1038/s41408-024-01045-3

Download citation

Received : 05 February 2024

Revised : 20 March 2024

Accepted : 25 March 2024

Published : 29 May 2024

DOI : https://doi.org/10.1038/s41408-024-01045-3

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies