

Trial and Error
Trial and Error is a fundamental method of problem-solving, which involves attempting different solutions until the correct one is found. As a strategy frequently used in multiple fields, including psychology, science, and computer programming, its significance is profound and multifaceted.
Understanding the term
To fully appreciate the trial and error method’s value, let’s delve into its characteristics, process, and theoretical underpinnings.
Characteristics of the Trial and Error Method
The trial and error method is defined by two key elements: making attempts (trials) and learning from failures (errors). The process continues until a solution is found.
The Trial and Error Process
The process of trial and error consists of generating possible solutions, applying them, assessing their effectiveness, and revising the approach based on the results.
Theoretical Background
Trial and error has roots in behavioral psychology, where it’s often associated with Edward Thorndike’s Law of Effect. This law suggests that responses followed by satisfaction will be repeated, while those followed by discomfort will be discontinued.
Trial and Error in Everyday Life
The application of the trial and error method is ubiquitous, extending from our daily activities to complex scientific research.
Learning New Skills
When we learn to ride a bicycle, cook a new dish, or play a musical instrument, we use trial and error to master the skills.
Technological Advancements
In the tech industry, trial and error play a crucial role in software development and debugging, hardware design, and algorithm optimization.
Advantages and Disadvantages
The trial and error method, despite its universal application, comes with its pros and cons.
H3: Advantages
Trial and error encourages creativity and fosters resilience. It allows for the discovery of all possible solutions and can lead to unexpected yet effective outcomes.
H3: Disadvantages
However, trial and error can be time-consuming and resource-intensive. It may not be feasible when there’s a need for immediate solutions or when the risks of failure are high.
To better illustrate the concept of trial and error, let’s consider a couple of examples.
Example 1: Learning to Code
When learning to code, students often write a program, run it to see if it works, and if it doesn’t, they debug and modify their code. This is an example of trial and error.
Example 2: Medicinal Drug Discovery
In medicinal chemistry, scientists often synthesize and test numerous compounds before finding one that effectively treats a disease. This process embodies the trial and error method.
Enhancing the Trial and Error Process
While trial and error inherently involve some degree of uncertainty, some strategies can enhance its efficiency.
Learn from Each Attempt
Each trial, whether successful or unsuccessful, provides valuable information. Reflecting on each attempt can improve future trials and hasten the problem-solving process.
Embrace Failure
Viewing errors as learning opportunities rather than failures can foster resilience and creativity, essential traits for effective problem-solving.
In essence, trial and error is an indispensable problem-solving strategy that encourages creativity, resilience, and comprehensive solution discovery. By understanding its characteristics, benefits, and limitations, we can harness its potential more effectively in various domains of life. Remember, each trial brings you one step closer to a solution, and each error is a stepping stone to success.
7.3 Problem-Solving
Learning objectives.
By the end of this section, you will be able to:
- Describe problem solving strategies
- Define algorithm and heuristic
- Explain some common roadblocks to effective problem solving
People face problems every day—usually, multiple problems throughout the day. Sometimes these problems are straightforward: To double a recipe for pizza dough, for example, all that is required is that each ingredient in the recipe be doubled. Sometimes, however, the problems we encounter are more complex. For example, say you have a work deadline, and you must mail a printed copy of a report to your supervisor by the end of the business day. The report is time-sensitive and must be sent overnight. You finished the report last night, but your printer will not work today. What should you do? First, you need to identify the problem and then apply a strategy for solving the problem.
The study of human and animal problem solving processes has provided much insight toward the understanding of our conscious experience and led to advancements in computer science and artificial intelligence. Essentially much of cognitive science today represents studies of how we consciously and unconsciously make decisions and solve problems. For instance, when encountered with a large amount of information, how do we go about making decisions about the most efficient way of sorting and analyzing all the information in order to find what you are looking for as in visual search paradigms in cognitive psychology. Or in a situation where a piece of machinery is not working properly, how do we go about organizing how to address the issue and understand what the cause of the problem might be. How do we sort the procedures that will be needed and focus attention on what is important in order to solve problems efficiently. Within this section we will discuss some of these issues and examine processes related to human, animal and computer problem solving.
PROBLEM-SOLVING STRATEGIES
When people are presented with a problem—whether it is a complex mathematical problem or a broken printer, how do you solve it? Before finding a solution to the problem, the problem must first be clearly identified. After that, one of many problem solving strategies can be applied, hopefully resulting in a solution.
Problems themselves can be classified into two different categories known as ill-defined and well-defined problems (Schacter, 2009). Ill-defined problems represent issues that do not have clear goals, solution paths, or expected solutions whereas well-defined problems have specific goals, clearly defined solutions, and clear expected solutions. Problem solving often incorporates pragmatics (logical reasoning) and semantics (interpretation of meanings behind the problem), and also in many cases require abstract thinking and creativity in order to find novel solutions. Within psychology, problem solving refers to a motivational drive for reading a definite “goal” from a present situation or condition that is either not moving toward that goal, is distant from it, or requires more complex logical analysis for finding a missing description of conditions or steps toward that goal. Processes relating to problem solving include problem finding also known as problem analysis, problem shaping where the organization of the problem occurs, generating alternative strategies, implementation of attempted solutions, and verification of the selected solution. Various methods of studying problem solving exist within the field of psychology including introspection, behavior analysis and behaviorism, simulation, computer modeling, and experimentation.
A problem-solving strategy is a plan of action used to find a solution. Different strategies have different action plans associated with them (table below). For example, a well-known strategy is trial and error. The old adage, “If at first you don’t succeed, try, try again” describes trial and error. In terms of your broken printer, you could try checking the ink levels, and if that doesn’t work, you could check to make sure the paper tray isn’t jammed. Or maybe the printer isn’t actually connected to your laptop. When using trial and error, you would continue to try different solutions until you solved your problem. Although trial and error is not typically one of the most time-efficient strategies, it is a commonly used one.
Another type of strategy is an algorithm. An algorithm is a problem-solving formula that provides you with step-by-step instructions used to achieve a desired outcome (Kahneman, 2011). You can think of an algorithm as a recipe with highly detailed instructions that produce the same result every time they are performed. Algorithms are used frequently in our everyday lives, especially in computer science. When you run a search on the Internet, search engines like Google use algorithms to decide which entries will appear first in your list of results. Facebook also uses algorithms to decide which posts to display on your newsfeed. Can you identify other situations in which algorithms are used?
A heuristic is another type of problem solving strategy. While an algorithm must be followed exactly to produce a correct result, a heuristic is a general problem-solving framework (Tversky & Kahneman, 1974). You can think of these as mental shortcuts that are used to solve problems. A “rule of thumb” is an example of a heuristic. Such a rule saves the person time and energy when making a decision, but despite its time-saving characteristics, it is not always the best method for making a rational decision. Different types of heuristics are used in different types of situations, but the impulse to use a heuristic occurs when one of five conditions is met (Pratkanis, 1989):
- When one is faced with too much information
- When the time to make a decision is limited
- When the decision to be made is unimportant
- When there is access to very little information to use in making the decision
- When an appropriate heuristic happens to come to mind in the same moment
Working backwards is a useful heuristic in which you begin solving the problem by focusing on the end result. Consider this example: You live in Washington, D.C. and have been invited to a wedding at 4 PM on Saturday in Philadelphia. Knowing that Interstate 95 tends to back up any day of the week, you need to plan your route and time your departure accordingly. If you want to be at the wedding service by 3:30 PM, and it takes 2.5 hours to get to Philadelphia without traffic, what time should you leave your house? You use the working backwards heuristic to plan the events of your day on a regular basis, probably without even thinking about it.
Another useful heuristic is the practice of accomplishing a large goal or task by breaking it into a series of smaller steps. Students often use this common method to complete a large research project or long essay for school. For example, students typically brainstorm, develop a thesis or main topic, research the chosen topic, organize their information into an outline, write a rough draft, revise and edit the rough draft, develop a final draft, organize the references list, and proofread their work before turning in the project. The large task becomes less overwhelming when it is broken down into a series of small steps.
Further problem solving strategies have been identified (listed below) that incorporate flexible and creative thinking in order to reach solutions efficiently.
Additional Problem Solving Strategies :
- Abstraction – refers to solving the problem within a model of the situation before applying it to reality.
- Analogy – is using a solution that solves a similar problem.
- Brainstorming – refers to collecting an analyzing a large amount of solutions, especially within a group of people, to combine the solutions and developing them until an optimal solution is reached.
- Divide and conquer – breaking down large complex problems into smaller more manageable problems.
- Hypothesis testing – method used in experimentation where an assumption about what would happen in response to manipulating an independent variable is made, and analysis of the affects of the manipulation are made and compared to the original hypothesis.
- Lateral thinking – approaching problems indirectly and creatively by viewing the problem in a new and unusual light.
- Means-ends analysis – choosing and analyzing an action at a series of smaller steps to move closer to the goal.
- Method of focal objects – putting seemingly non-matching characteristics of different procedures together to make something new that will get you closer to the goal.
- Morphological analysis – analyzing the outputs of and interactions of many pieces that together make up a whole system.
- Proof – trying to prove that a problem cannot be solved. Where the proof fails becomes the starting point or solving the problem.
- Reduction – adapting the problem to be as similar problems where a solution exists.
- Research – using existing knowledge or solutions to similar problems to solve the problem.
- Root cause analysis – trying to identify the cause of the problem.
The strategies listed above outline a short summary of methods we use in working toward solutions and also demonstrate how the mind works when being faced with barriers preventing goals to be reached.
One example of means-end analysis can be found by using the Tower of Hanoi paradigm . This paradigm can be modeled as a word problems as demonstrated by the Missionary-Cannibal Problem :
Missionary-Cannibal Problem
Three missionaries and three cannibals are on one side of a river and need to cross to the other side. The only means of crossing is a boat, and the boat can only hold two people at a time. Your goal is to devise a set of moves that will transport all six of the people across the river, being in mind the following constraint: The number of cannibals can never exceed the number of missionaries in any location. Remember that someone will have to also row that boat back across each time.
Hint : At one point in your solution, you will have to send more people back to the original side than you just sent to the destination.
The actual Tower of Hanoi problem consists of three rods sitting vertically on a base with a number of disks of different sizes that can slide onto any rod. The puzzle starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top making a conical shape. The objective of the puzzle is to move the entire stack to another rod obeying the following rules:
- 1. Only one disk can be moved at a time.
- 2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
- 3. No disc may be placed on top of a smaller disk.
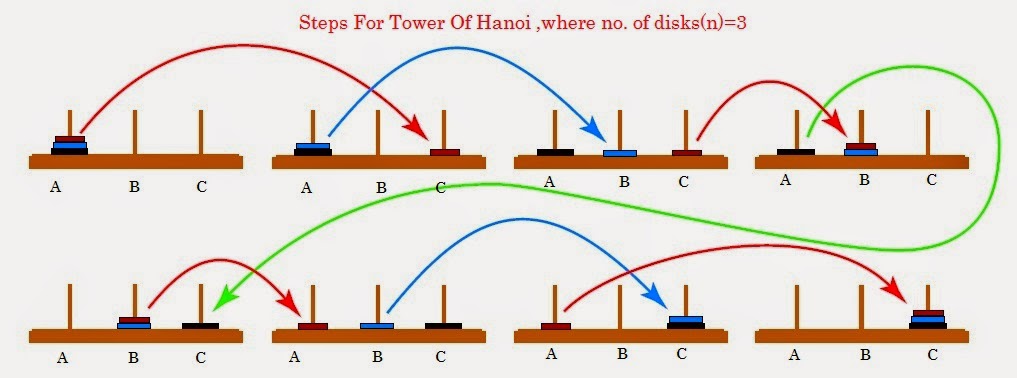
Figure 7.02. Steps for solving the Tower of Hanoi in the minimum number of moves when there are 3 disks.
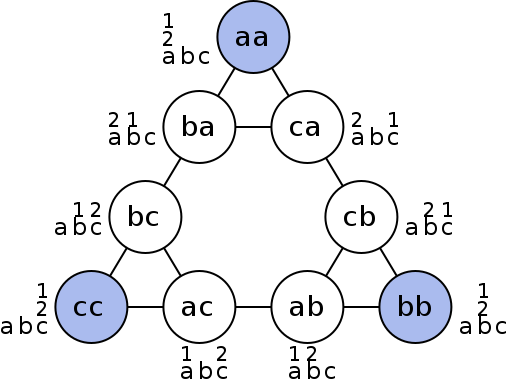
Figure 7.03. Graphical representation of nodes (circles) and moves (lines) of Tower of Hanoi.
The Tower of Hanoi is a frequently used psychological technique to study problem solving and procedure analysis. A variation of the Tower of Hanoi known as the Tower of London has been developed which has been an important tool in the neuropsychological diagnosis of executive function disorders and their treatment.
GESTALT PSYCHOLOGY AND PROBLEM SOLVING
As you may recall from the sensation and perception chapter, Gestalt psychology describes whole patterns, forms and configurations of perception and cognition such as closure, good continuation, and figure-ground. In addition to patterns of perception, Wolfgang Kohler, a German Gestalt psychologist traveled to the Spanish island of Tenerife in order to study animals behavior and problem solving in the anthropoid ape.
As an interesting side note to Kohler’s studies of chimp problem solving, Dr. Ronald Ley, professor of psychology at State University of New York provides evidence in his book A Whisper of Espionage (1990) suggesting that while collecting data for what would later be his book The Mentality of Apes (1925) on Tenerife in the Canary Islands between 1914 and 1920, Kohler was additionally an active spy for the German government alerting Germany to ships that were sailing around the Canary Islands. Ley suggests his investigations in England, Germany and elsewhere in Europe confirm that Kohler had served in the German military by building, maintaining and operating a concealed radio that contributed to Germany’s war effort acting as a strategic outpost in the Canary Islands that could monitor naval military activity approaching the north African coast.
While trapped on the island over the course of World War 1, Kohler applied Gestalt principles to animal perception in order to understand how they solve problems. He recognized that the apes on the islands also perceive relations between stimuli and the environment in Gestalt patterns and understand these patterns as wholes as opposed to pieces that make up a whole. Kohler based his theories of animal intelligence on the ability to understand relations between stimuli, and spent much of his time while trapped on the island investigation what he described as insight , the sudden perception of useful or proper relations. In order to study insight in animals, Kohler would present problems to chimpanzee’s by hanging some banana’s or some kind of food so it was suspended higher than the apes could reach. Within the room, Kohler would arrange a variety of boxes, sticks or other tools the chimpanzees could use by combining in patterns or organizing in a way that would allow them to obtain the food (Kohler & Winter, 1925).
While viewing the chimpanzee’s, Kohler noticed one chimp that was more efficient at solving problems than some of the others. The chimp, named Sultan, was able to use long poles to reach through bars and organize objects in specific patterns to obtain food or other desirables that were originally out of reach. In order to study insight within these chimps, Kohler would remove objects from the room to systematically make the food more difficult to obtain. As the story goes, after removing many of the objects Sultan was used to using to obtain the food, he sat down ad sulked for a while, and then suddenly got up going over to two poles lying on the ground. Without hesitation Sultan put one pole inside the end of the other creating a longer pole that he could use to obtain the food demonstrating an ideal example of what Kohler described as insight. In another situation, Sultan discovered how to stand on a box to reach a banana that was suspended from the rafters illustrating Sultan’s perception of relations and the importance of insight in problem solving.
Grande (another chimp in the group studied by Kohler) builds a three-box structure to reach the bananas, while Sultan watches from the ground. Insight , sometimes referred to as an “Ah-ha” experience, was the term Kohler used for the sudden perception of useful relations among objects during problem solving (Kohler, 1927; Radvansky & Ashcraft, 2013).
Solving puzzles.
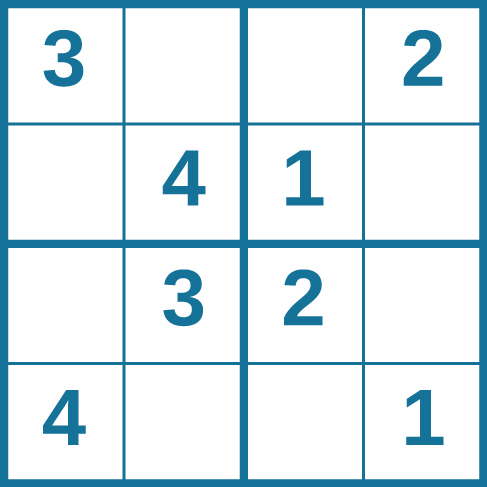
Problem-solving abilities can improve with practice. Many people challenge themselves every day with puzzles and other mental exercises to sharpen their problem-solving skills. Sudoku puzzles appear daily in most newspapers. Typically, a sudoku puzzle is a 9×9 grid. The simple sudoku below (see figure) is a 4×4 grid. To solve the puzzle, fill in the empty boxes with a single digit: 1, 2, 3, or 4. Here are the rules: The numbers must total 10 in each bolded box, each row, and each column; however, each digit can only appear once in a bolded box, row, and column. Time yourself as you solve this puzzle and compare your time with a classmate.
How long did it take you to solve this sudoku puzzle? (You can see the answer at the end of this section.)
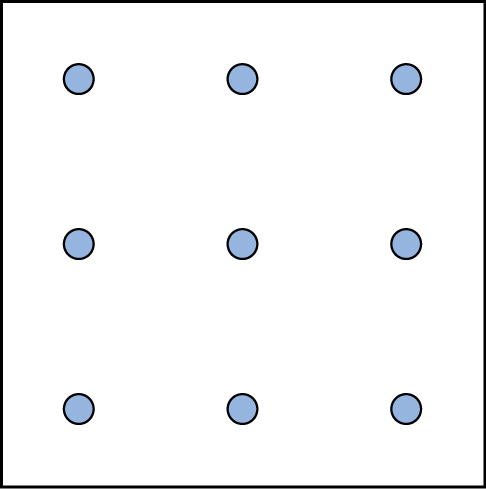
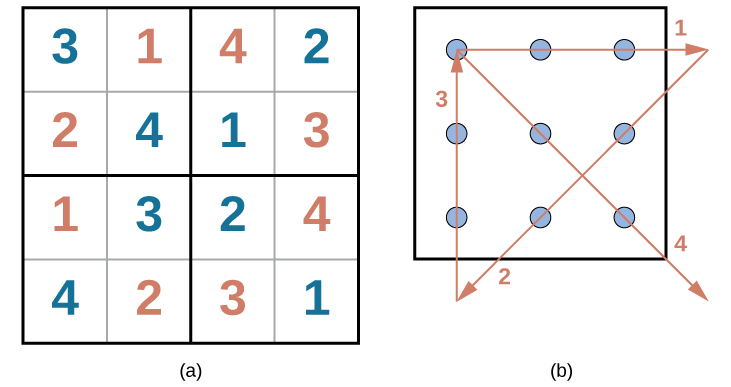
Here is another popular type of puzzle (figure below) that challenges your spatial reasoning skills. Connect all nine dots with four connecting straight lines without lifting your pencil from the paper:
Did you figure it out? (The answer is at the end of this section.) Once you understand how to crack this puzzle, you won’t forget.
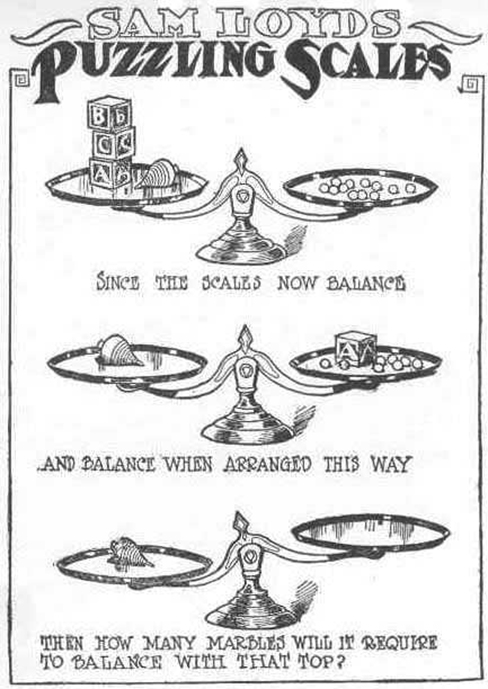
Take a look at the “Puzzling Scales” logic puzzle below (figure below). Sam Loyd, a well-known puzzle master, created and refined countless puzzles throughout his lifetime (Cyclopedia of Puzzles, n.d.).

What steps did you take to solve this puzzle? You can read the solution at the end of this section.
Pitfalls to problem solving.
Not all problems are successfully solved, however. What challenges stop us from successfully solving a problem? Albert Einstein once said, “Insanity is doing the same thing over and over again and expecting a different result.” Imagine a person in a room that has four doorways. One doorway that has always been open in the past is now locked. The person, accustomed to exiting the room by that particular doorway, keeps trying to get out through the same doorway even though the other three doorways are open. The person is stuck—but she just needs to go to another doorway, instead of trying to get out through the locked doorway. A mental set is where you persist in approaching a problem in a way that has worked in the past but is clearly not working now.
Functional fixedness is a type of mental set where you cannot perceive an object being used for something other than what it was designed for. During the Apollo 13 mission to the moon, NASA engineers at Mission Control had to overcome functional fixedness to save the lives of the astronauts aboard the spacecraft. An explosion in a module of the spacecraft damaged multiple systems. The astronauts were in danger of being poisoned by rising levels of carbon dioxide because of problems with the carbon dioxide filters. The engineers found a way for the astronauts to use spare plastic bags, tape, and air hoses to create a makeshift air filter, which saved the lives of the astronauts.
Researchers have investigated whether functional fixedness is affected by culture. In one experiment, individuals from the Shuar group in Ecuador were asked to use an object for a purpose other than that for which the object was originally intended. For example, the participants were told a story about a bear and a rabbit that were separated by a river and asked to select among various objects, including a spoon, a cup, erasers, and so on, to help the animals. The spoon was the only object long enough to span the imaginary river, but if the spoon was presented in a way that reflected its normal usage, it took participants longer to choose the spoon to solve the problem. (German & Barrett, 2005). The researchers wanted to know if exposure to highly specialized tools, as occurs with individuals in industrialized nations, affects their ability to transcend functional fixedness. It was determined that functional fixedness is experienced in both industrialized and nonindustrialized cultures (German & Barrett, 2005).
In order to make good decisions, we use our knowledge and our reasoning. Often, this knowledge and reasoning is sound and solid. Sometimes, however, we are swayed by biases or by others manipulating a situation. For example, let’s say you and three friends wanted to rent a house and had a combined target budget of $1,600. The realtor shows you only very run-down houses for $1,600 and then shows you a very nice house for $2,000. Might you ask each person to pay more in rent to get the $2,000 home? Why would the realtor show you the run-down houses and the nice house? The realtor may be challenging your anchoring bias. An anchoring bias occurs when you focus on one piece of information when making a decision or solving a problem. In this case, you’re so focused on the amount of money you are willing to spend that you may not recognize what kinds of houses are available at that price point.
The confirmation bias is the tendency to focus on information that confirms your existing beliefs. For example, if you think that your professor is not very nice, you notice all of the instances of rude behavior exhibited by the professor while ignoring the countless pleasant interactions he is involved in on a daily basis. Hindsight bias leads you to believe that the event you just experienced was predictable, even though it really wasn’t. In other words, you knew all along that things would turn out the way they did. Representative bias describes a faulty way of thinking, in which you unintentionally stereotype someone or something; for example, you may assume that your professors spend their free time reading books and engaging in intellectual conversation, because the idea of them spending their time playing volleyball or visiting an amusement park does not fit in with your stereotypes of professors.
Finally, the availability heuristic is a heuristic in which you make a decision based on an example, information, or recent experience that is that readily available to you, even though it may not be the best example to inform your decision . Biases tend to “preserve that which is already established—to maintain our preexisting knowledge, beliefs, attitudes, and hypotheses” (Aronson, 1995; Kahneman, 2011). These biases are summarized in the table below.
Were you able to determine how many marbles are needed to balance the scales in the figure below? You need nine. Were you able to solve the problems in the figures above? Here are the answers.

Many different strategies exist for solving problems. Typical strategies include trial and error, applying algorithms, and using heuristics. To solve a large, complicated problem, it often helps to break the problem into smaller steps that can be accomplished individually, leading to an overall solution. Roadblocks to problem solving include a mental set, functional fixedness, and various biases that can cloud decision making skills.
References:
Openstax Psychology text by Kathryn Dumper, William Jenkins, Arlene Lacombe, Marilyn Lovett and Marion Perlmutter licensed under CC BY v4.0. https://openstax.org/details/books/psychology
Review Questions:
1. A specific formula for solving a problem is called ________.
a. an algorithm
b. a heuristic
c. a mental set
d. trial and error
2. Solving the Tower of Hanoi problem tends to utilize a ________ strategy of problem solving.
a. divide and conquer
b. means-end analysis
d. experiment
3. A mental shortcut in the form of a general problem-solving framework is called ________.
4. Which type of bias involves becoming fixated on a single trait of a problem?
a. anchoring bias
b. confirmation bias
c. representative bias
d. availability bias
5. Which type of bias involves relying on a false stereotype to make a decision?
6. Wolfgang Kohler analyzed behavior of chimpanzees by applying Gestalt principles to describe ________.
a. social adjustment
b. student load payment options
c. emotional learning
d. insight learning
7. ________ is a type of mental set where you cannot perceive an object being used for something other than what it was designed for.
a. functional fixedness
c. working memory
Critical Thinking Questions:
1. What is functional fixedness and how can overcoming it help you solve problems?
2. How does an algorithm save you time and energy when solving a problem?
Personal Application Question:
1. Which type of bias do you recognize in your own decision making processes? How has this bias affected how you’ve made decisions in the past and how can you use your awareness of it to improve your decisions making skills in the future?
anchoring bias
availability heuristic
confirmation bias
functional fixedness
hindsight bias
problem-solving strategy
representative bias
trial and error
working backwards
Answers to Exercises
algorithm: problem-solving strategy characterized by a specific set of instructions
anchoring bias: faulty heuristic in which you fixate on a single aspect of a problem to find a solution
availability heuristic: faulty heuristic in which you make a decision based on information readily available to you
confirmation bias: faulty heuristic in which you focus on information that confirms your beliefs
functional fixedness: inability to see an object as useful for any other use other than the one for which it was intended
heuristic: mental shortcut that saves time when solving a problem
hindsight bias: belief that the event just experienced was predictable, even though it really wasn’t
mental set: continually using an old solution to a problem without results
problem-solving strategy: method for solving problems
representative bias: faulty heuristic in which you stereotype someone or something without a valid basis for your judgment
trial and error: problem-solving strategy in which multiple solutions are attempted until the correct one is found
working backwards: heuristic in which you begin to solve a problem by focusing on the end result

Share This Book
- Increase Font Size
Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Thinking and Intelligence
Problem Solving
OpenStaxCollege
[latexpage]
Learning Objectives
By the end of this section, you will be able to:
- Describe problem solving strategies
- Define algorithm and heuristic
- Explain some common roadblocks to effective problem solving
People face problems every day—usually, multiple problems throughout the day. Sometimes these problems are straightforward: To double a recipe for pizza dough, for example, all that is required is that each ingredient in the recipe be doubled. Sometimes, however, the problems we encounter are more complex. For example, say you have a work deadline, and you must mail a printed copy of a report to your supervisor by the end of the business day. The report is time-sensitive and must be sent overnight. You finished the report last night, but your printer will not work today. What should you do? First, you need to identify the problem and then apply a strategy for solving the problem.
PROBLEM-SOLVING STRATEGIES
When you are presented with a problem—whether it is a complex mathematical problem or a broken printer, how do you solve it? Before finding a solution to the problem, the problem must first be clearly identified. After that, one of many problem solving strategies can be applied, hopefully resulting in a solution.
A problem-solving strategy is a plan of action used to find a solution. Different strategies have different action plans associated with them ( [link] ). For example, a well-known strategy is trial and error . The old adage, “If at first you don’t succeed, try, try again” describes trial and error. In terms of your broken printer, you could try checking the ink levels, and if that doesn’t work, you could check to make sure the paper tray isn’t jammed. Or maybe the printer isn’t actually connected to your laptop. When using trial and error, you would continue to try different solutions until you solved your problem. Although trial and error is not typically one of the most time-efficient strategies, it is a commonly used one.
Another type of strategy is an algorithm. An algorithm is a problem-solving formula that provides you with step-by-step instructions used to achieve a desired outcome (Kahneman, 2011). You can think of an algorithm as a recipe with highly detailed instructions that produce the same result every time they are performed. Algorithms are used frequently in our everyday lives, especially in computer science. When you run a search on the Internet, search engines like Google use algorithms to decide which entries will appear first in your list of results. Facebook also uses algorithms to decide which posts to display on your newsfeed. Can you identify other situations in which algorithms are used?
A heuristic is another type of problem solving strategy. While an algorithm must be followed exactly to produce a correct result, a heuristic is a general problem-solving framework (Tversky & Kahneman, 1974). You can think of these as mental shortcuts that are used to solve problems. A “rule of thumb” is an example of a heuristic. Such a rule saves the person time and energy when making a decision, but despite its time-saving characteristics, it is not always the best method for making a rational decision. Different types of heuristics are used in different types of situations, but the impulse to use a heuristic occurs when one of five conditions is met (Pratkanis, 1989):
- When one is faced with too much information
- When the time to make a decision is limited
- When the decision to be made is unimportant
- When there is access to very little information to use in making the decision
- When an appropriate heuristic happens to come to mind in the same moment
Working backwards is a useful heuristic in which you begin solving the problem by focusing on the end result. Consider this example: You live in Washington, D.C. and have been invited to a wedding at 4 PM on Saturday in Philadelphia. Knowing that Interstate 95 tends to back up any day of the week, you need to plan your route and time your departure accordingly. If you want to be at the wedding service by 3:30 PM, and it takes 2.5 hours to get to Philadelphia without traffic, what time should you leave your house? You use the working backwards heuristic to plan the events of your day on a regular basis, probably without even thinking about it.
Another useful heuristic is the practice of accomplishing a large goal or task by breaking it into a series of smaller steps. Students often use this common method to complete a large research project or long essay for school. For example, students typically brainstorm, develop a thesis or main topic, research the chosen topic, organize their information into an outline, write a rough draft, revise and edit the rough draft, develop a final draft, organize the references list, and proofread their work before turning in the project. The large task becomes less overwhelming when it is broken down into a series of small steps.
Problem-solving abilities can improve with practice. Many people challenge themselves every day with puzzles and other mental exercises to sharpen their problem-solving skills. Sudoku puzzles appear daily in most newspapers. Typically, a sudoku puzzle is a 9×9 grid. The simple sudoku below ( [link] ) is a 4×4 grid. To solve the puzzle, fill in the empty boxes with a single digit: 1, 2, 3, or 4. Here are the rules: The numbers must total 10 in each bolded box, each row, and each column; however, each digit can only appear once in a bolded box, row, and column. Time yourself as you solve this puzzle and compare your time with a classmate.
Here is another popular type of puzzle ( [link] ) that challenges your spatial reasoning skills. Connect all nine dots with four connecting straight lines without lifting your pencil from the paper:
Take a look at the “Puzzling Scales” logic puzzle below ( [link] ). Sam Loyd, a well-known puzzle master, created and refined countless puzzles throughout his lifetime (Cyclopedia of Puzzles, n.d.).
PITFALLS TO PROBLEM SOLVING
Not all problems are successfully solved, however. What challenges stop us from successfully solving a problem? Albert Einstein once said, “Insanity is doing the same thing over and over again and expecting a different result.” Imagine a person in a room that has four doorways. One doorway that has always been open in the past is now locked. The person, accustomed to exiting the room by that particular doorway, keeps trying to get out through the same doorway even though the other three doorways are open. The person is stuck—but she just needs to go to another doorway, instead of trying to get out through the locked doorway. A mental set is where you persist in approaching a problem in a way that has worked in the past but is clearly not working now.
Functional fixedness is a type of mental set where you cannot perceive an object being used for something other than what it was designed for. During the Apollo 13 mission to the moon, NASA engineers at Mission Control had to overcome functional fixedness to save the lives of the astronauts aboard the spacecraft. An explosion in a module of the spacecraft damaged multiple systems. The astronauts were in danger of being poisoned by rising levels of carbon dioxide because of problems with the carbon dioxide filters. The engineers found a way for the astronauts to use spare plastic bags, tape, and air hoses to create a makeshift air filter, which saved the lives of the astronauts.

Check out this Apollo 13 scene where the group of NASA engineers are given the task of overcoming functional fixedness.
Researchers have investigated whether functional fixedness is affected by culture. In one experiment, individuals from the Shuar group in Ecuador were asked to use an object for a purpose other than that for which the object was originally intended. For example, the participants were told a story about a bear and a rabbit that were separated by a river and asked to select among various objects, including a spoon, a cup, erasers, and so on, to help the animals. The spoon was the only object long enough to span the imaginary river, but if the spoon was presented in a way that reflected its normal usage, it took participants longer to choose the spoon to solve the problem. (German & Barrett, 2005). The researchers wanted to know if exposure to highly specialized tools, as occurs with individuals in industrialized nations, affects their ability to transcend functional fixedness. It was determined that functional fixedness is experienced in both industrialized and nonindustrialized cultures (German & Barrett, 2005).
In order to make good decisions, we use our knowledge and our reasoning. Often, this knowledge and reasoning is sound and solid. Sometimes, however, we are swayed by biases or by others manipulating a situation. For example, let’s say you and three friends wanted to rent a house and had a combined target budget of $1,600. The realtor shows you only very run-down houses for $1,600 and then shows you a very nice house for $2,000. Might you ask each person to pay more in rent to get the $2,000 home? Why would the realtor show you the run-down houses and the nice house? The realtor may be challenging your anchoring bias. An anchoring bias occurs when you focus on one piece of information when making a decision or solving a problem. In this case, you’re so focused on the amount of money you are willing to spend that you may not recognize what kinds of houses are available at that price point.
The confirmation bias is the tendency to focus on information that confirms your existing beliefs. For example, if you think that your professor is not very nice, you notice all of the instances of rude behavior exhibited by the professor while ignoring the countless pleasant interactions he is involved in on a daily basis. Hindsight bias leads you to believe that the event you just experienced was predictable, even though it really wasn’t. In other words, you knew all along that things would turn out the way they did. Representative bias describes a faulty way of thinking, in which you unintentionally stereotype someone or something; for example, you may assume that your professors spend their free time reading books and engaging in intellectual conversation, because the idea of them spending their time playing volleyball or visiting an amusement park does not fit in with your stereotypes of professors.
Finally, the availability heuristic is a heuristic in which you make a decision based on an example, information, or recent experience that is that readily available to you, even though it may not be the best example to inform your decision . Biases tend to “preserve that which is already established—to maintain our preexisting knowledge, beliefs, attitudes, and hypotheses” (Aronson, 1995; Kahneman, 2011). These biases are summarized in [link] .
Please visit this site to see a clever music video that a high school teacher made to explain these and other cognitive biases to his AP psychology students.
Were you able to determine how many marbles are needed to balance the scales in [link] ? You need nine. Were you able to solve the problems in [link] and [link] ? Here are the answers ( [link] ).
Many different strategies exist for solving problems. Typical strategies include trial and error, applying algorithms, and using heuristics. To solve a large, complicated problem, it often helps to break the problem into smaller steps that can be accomplished individually, leading to an overall solution. Roadblocks to problem solving include a mental set, functional fixedness, and various biases that can cloud decision making skills.
Review Questions
A specific formula for solving a problem is called ________.
- an algorithm
- a heuristic
- a mental set
- trial and error
A mental shortcut in the form of a general problem-solving framework is called ________.
Which type of bias involves becoming fixated on a single trait of a problem?
- anchoring bias
- confirmation bias
- representative bias
- availability bias
Which type of bias involves relying on a false stereotype to make a decision?
Critical Thinking Questions
What is functional fixedness and how can overcoming it help you solve problems?
Functional fixedness occurs when you cannot see a use for an object other than the use for which it was intended. For example, if you need something to hold up a tarp in the rain, but only have a pitchfork, you must overcome your expectation that a pitchfork can only be used for garden chores before you realize that you could stick it in the ground and drape the tarp on top of it to hold it up.
How does an algorithm save you time and energy when solving a problem?
An algorithm is a proven formula for achieving a desired outcome. It saves time because if you follow it exactly, you will solve the problem without having to figure out how to solve the problem. It is a bit like not reinventing the wheel.
Personal Application Question
Which type of bias do you recognize in your own decision making processes? How has this bias affected how you’ve made decisions in the past and how can you use your awareness of it to improve your decisions making skills in the future?
Problem Solving Copyright © 2014 by OpenStaxCollege is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.
- Bipolar Disorder
- Therapy Center
- When To See a Therapist
- Types of Therapy
- Best Online Therapy
- Best Couples Therapy
- Best Family Therapy
- Managing Stress
- Sleep and Dreaming
- Understanding Emotions
- Self-Improvement
- Healthy Relationships
- Student Resources
- Personality Types
- Guided Meditations
- Verywell Mind Insights
- 2024 Verywell Mind 25
- Mental Health in the Classroom
- Editorial Process
- Meet Our Review Board
- Crisis Support
Problem-Solving Strategies and Obstacles
Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."
:max_bytes(150000):strip_icc():format(webp)/IMG_9791-89504ab694d54b66bbd72cb84ffb860e.jpg)
Sean is a fact-checker and researcher with experience in sociology, field research, and data analytics.
:max_bytes(150000):strip_icc():format(webp)/Sean-Blackburn-1000-a8b2229366944421bc4b2f2ba26a1003.jpg)
JGI / Jamie Grill / Getty Images
- Application
- Improvement
From deciding what to eat for dinner to considering whether it's the right time to buy a house, problem-solving is a large part of our daily lives. Learn some of the problem-solving strategies that exist and how to use them in real life, along with ways to overcome obstacles that are making it harder to resolve the issues you face.
What Is Problem-Solving?
In cognitive psychology , the term 'problem-solving' refers to the mental process that people go through to discover, analyze, and solve problems.
A problem exists when there is a goal that we want to achieve but the process by which we will achieve it is not obvious to us. Put another way, there is something that we want to occur in our life, yet we are not immediately certain how to make it happen.
Maybe you want a better relationship with your spouse or another family member but you're not sure how to improve it. Or you want to start a business but are unsure what steps to take. Problem-solving helps you figure out how to achieve these desires.
The problem-solving process involves:
- Discovery of the problem
- Deciding to tackle the issue
- Seeking to understand the problem more fully
- Researching available options or solutions
- Taking action to resolve the issue
Before problem-solving can occur, it is important to first understand the exact nature of the problem itself. If your understanding of the issue is faulty, your attempts to resolve it will also be incorrect or flawed.
Problem-Solving Mental Processes
Several mental processes are at work during problem-solving. Among them are:
- Perceptually recognizing the problem
- Representing the problem in memory
- Considering relevant information that applies to the problem
- Identifying different aspects of the problem
- Labeling and describing the problem
Problem-Solving Strategies
There are many ways to go about solving a problem. Some of these strategies might be used on their own, or you may decide to employ multiple approaches when working to figure out and fix a problem.
An algorithm is a step-by-step procedure that, by following certain "rules" produces a solution. Algorithms are commonly used in mathematics to solve division or multiplication problems. But they can be used in other fields as well.
In psychology, algorithms can be used to help identify individuals with a greater risk of mental health issues. For instance, research suggests that certain algorithms might help us recognize children with an elevated risk of suicide or self-harm.
One benefit of algorithms is that they guarantee an accurate answer. However, they aren't always the best approach to problem-solving, in part because detecting patterns can be incredibly time-consuming.
There are also concerns when machine learning is involved—also known as artificial intelligence (AI)—such as whether they can accurately predict human behaviors.
Heuristics are shortcut strategies that people can use to solve a problem at hand. These "rule of thumb" approaches allow you to simplify complex problems, reducing the total number of possible solutions to a more manageable set.
If you find yourself sitting in a traffic jam, for example, you may quickly consider other routes, taking one to get moving once again. When shopping for a new car, you might think back to a prior experience when negotiating got you a lower price, then employ the same tactics.
While heuristics may be helpful when facing smaller issues, major decisions shouldn't necessarily be made using a shortcut approach. Heuristics also don't guarantee an effective solution, such as when trying to drive around a traffic jam only to find yourself on an equally crowded route.
Trial and Error
A trial-and-error approach to problem-solving involves trying a number of potential solutions to a particular issue, then ruling out those that do not work. If you're not sure whether to buy a shirt in blue or green, for instance, you may try on each before deciding which one to purchase.
This can be a good strategy to use if you have a limited number of solutions available. But if there are many different choices available, narrowing down the possible options using another problem-solving technique can be helpful before attempting trial and error.
In some cases, the solution to a problem can appear as a sudden insight. You are facing an issue in a relationship or your career when, out of nowhere, the solution appears in your mind and you know exactly what to do.
Insight can occur when the problem in front of you is similar to an issue that you've dealt with in the past. Although, you may not recognize what is occurring since the underlying mental processes that lead to insight often happen outside of conscious awareness .
Research indicates that insight is most likely to occur during times when you are alone—such as when going on a walk by yourself, when you're in the shower, or when lying in bed after waking up.
How to Apply Problem-Solving Strategies in Real Life
If you're facing a problem, you can implement one or more of these strategies to find a potential solution. Here's how to use them in real life:
- Create a flow chart . If you have time, you can take advantage of the algorithm approach to problem-solving by sitting down and making a flow chart of each potential solution, its consequences, and what happens next.
- Recall your past experiences . When a problem needs to be solved fairly quickly, heuristics may be a better approach. Think back to when you faced a similar issue, then use your knowledge and experience to choose the best option possible.
- Start trying potential solutions . If your options are limited, start trying them one by one to see which solution is best for achieving your desired goal. If a particular solution doesn't work, move on to the next.
- Take some time alone . Since insight is often achieved when you're alone, carve out time to be by yourself for a while. The answer to your problem may come to you, seemingly out of the blue, if you spend some time away from others.
Obstacles to Problem-Solving
Problem-solving is not a flawless process as there are a number of obstacles that can interfere with our ability to solve a problem quickly and efficiently. These obstacles include:
- Assumptions: When dealing with a problem, people can make assumptions about the constraints and obstacles that prevent certain solutions. Thus, they may not even try some potential options.
- Functional fixedness : This term refers to the tendency to view problems only in their customary manner. Functional fixedness prevents people from fully seeing all of the different options that might be available to find a solution.
- Irrelevant or misleading information: When trying to solve a problem, it's important to distinguish between information that is relevant to the issue and irrelevant data that can lead to faulty solutions. The more complex the problem, the easier it is to focus on misleading or irrelevant information.
- Mental set: A mental set is a tendency to only use solutions that have worked in the past rather than looking for alternative ideas. A mental set can work as a heuristic, making it a useful problem-solving tool. However, mental sets can also lead to inflexibility, making it more difficult to find effective solutions.
How to Improve Your Problem-Solving Skills
In the end, if your goal is to become a better problem-solver, it's helpful to remember that this is a process. Thus, if you want to improve your problem-solving skills, following these steps can help lead you to your solution:
- Recognize that a problem exists . If you are facing a problem, there are generally signs. For instance, if you have a mental illness , you may experience excessive fear or sadness, mood changes, and changes in sleeping or eating habits. Recognizing these signs can help you realize that an issue exists.
- Decide to solve the problem . Make a conscious decision to solve the issue at hand. Commit to yourself that you will go through the steps necessary to find a solution.
- Seek to fully understand the issue . Analyze the problem you face, looking at it from all sides. If your problem is relationship-related, for instance, ask yourself how the other person may be interpreting the issue. You might also consider how your actions might be contributing to the situation.
- Research potential options . Using the problem-solving strategies mentioned, research potential solutions. Make a list of options, then consider each one individually. What are some pros and cons of taking the available routes? What would you need to do to make them happen?
- Take action . Select the best solution possible and take action. Action is one of the steps required for change . So, go through the motions needed to resolve the issue.
- Try another option, if needed . If the solution you chose didn't work, don't give up. Either go through the problem-solving process again or simply try another option.
You can find a way to solve your problems as long as you keep working toward this goal—even if the best solution is simply to let go because no other good solution exists.
Sarathy V. Real world problem-solving . Front Hum Neurosci . 2018;12:261. doi:10.3389/fnhum.2018.00261
Dunbar K. Problem solving . A Companion to Cognitive Science . 2017. doi:10.1002/9781405164535.ch20
Stewart SL, Celebre A, Hirdes JP, Poss JW. Risk of suicide and self-harm in kids: The development of an algorithm to identify high-risk individuals within the children's mental health system . Child Psychiat Human Develop . 2020;51:913-924. doi:10.1007/s10578-020-00968-9
Rosenbusch H, Soldner F, Evans AM, Zeelenberg M. Supervised machine learning methods in psychology: A practical introduction with annotated R code . Soc Personal Psychol Compass . 2021;15(2):e12579. doi:10.1111/spc3.12579
Mishra S. Decision-making under risk: Integrating perspectives from biology, economics, and psychology . Personal Soc Psychol Rev . 2014;18(3):280-307. doi:10.1177/1088868314530517
Csikszentmihalyi M, Sawyer K. Creative insight: The social dimension of a solitary moment . In: The Systems Model of Creativity . 2015:73-98. doi:10.1007/978-94-017-9085-7_7
Chrysikou EG, Motyka K, Nigro C, Yang SI, Thompson-Schill SL. Functional fixedness in creative thinking tasks depends on stimulus modality . Psychol Aesthet Creat Arts . 2016;10(4):425‐435. doi:10.1037/aca0000050
Huang F, Tang S, Hu Z. Unconditional perseveration of the short-term mental set in chunk decomposition . Front Psychol . 2018;9:2568. doi:10.3389/fpsyg.2018.02568
National Alliance on Mental Illness. Warning signs and symptoms .
Mayer RE. Thinking, problem solving, cognition, 2nd ed .
Schooler JW, Ohlsson S, Brooks K. Thoughts beyond words: When language overshadows insight. J Experiment Psychol: General . 1993;122:166-183. doi:10.1037/0096-3445.2.166
By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."
Problem-Solving Strategies
- First Online: 06 August 2020
Cite this chapter

- Orit Hazzan ORCID: orcid.org/0000-0002-8627-0997 4 ,
- Noa Ragonis ORCID: orcid.org/0000-0002-8163-0199 5 &
- Tami Lapidot 4
1395 Accesses
Problem-solving is generally considered as one of the most important and challenging cognitive activities in everyday as well as in any professional contexts. Specifically, it is one of the central activities performed by computer scientists as well as by computer science learners. However, it is not a uniform or linear process that can be taught as an algorithm to be followed, and the understanding of this individual process is not always clear. Computer science learners often face difficulties in performing two of the main stages of a problem-solving process: problem analysis and solution construction. Therefore, it is important that computer science educators be aware of these difficulties and acquire appropriate pedagogical tools to guide and scaffold learners in learning these skills. This chapter is dedicated to such pedagogical tools. It presents several problem-solving strategies to address in the MTCS course together with appropriate activities that mediate them to the prospective computer science teachers by enabling them to experience the different strategies.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
- Available as EPUB and PDF
- Read on any device
- Instant download
- Own it forever
- Compact, lightweight edition
- Dispatched in 3 to 5 business days
- Free shipping worldwide - see info
- Durable hardcover edition
Tax calculation will be finalised at checkout
Purchases are for personal use only
Institutional subscriptions
An algorithmic problem is defined by what is given – the initial conditions of the problem and its goals – the desired state, what should be accomplished. An algorithm problem can be solved with a series of actions formulated formally either by pseudo-code or a programming language. See Sect. 12.4.1 .
In advanced computer science classes, it is relevant to mention that in computer science, in addition to the development of problem-solving strategies, special emphasis is placed also on non-solvable problems (see Sect. 12.4.3 ).
Role of Variables in Python: http://www.cs.joensuu.fi/~saja/var_roles/stud_vers/stud_Python_eng.html
Roles of Variables with examples in Scratch: https://www.sisd.net/cms/lib/TX01001452/Centricity/domain/433/cse/1.1.5%20RolesOfVariables_UsedActivity1.2.4.pptx
The Roles of Variables home page ( http://saja.kapsi.fi/var_roles/ ) is a rich resource and contains different kinds of educational resources.
See http://www.cs.joensuu.fi/~saja/var_roles/role_intro.html
See http://www.cs.joensuu.fi/~saja/var_roles/try.html
See http://cs.uef.fi/~pgerdt/RAE/
See http://www.cs.joensuu.fi/~saja/var_roles/why_roles.html
See http://www.cs.joensuu.fi/~saja/var_roles/teaching.html
See http://saja.kapsi.fi/var_roles/literature.html
Ahrendt W, Bubel R, Hahnle R (2009) Integrated and tool-supported teaching of testing, debugging, and verification. In: Gibbons J, Oliveira JN (eds) Proceedings of the 2nd international conference on teaching formal methods (TFM ’09). Springer, Berlin/Heidelberg, pp 125–143
Google Scholar
Alqadi BS, Maletic JI (2017) An empirical study of debugging patterns among novices programmers. In: Proceedings of the 2017 ACM SIGCSE technical symposium on computer science education (SIGCSE ’17). ACM, New York, pp 15–20
Arshad N (2009) Teaching programming and problem solving to CS2 students using think-alouds. SIGCSE Bull 41(1):372–376
Astrachan O, Berry G, Cox L, Mitchener G (1998) Design patterns: an essential component of CS curricula. In: Proceeding of SIGCSE, pp 153–160
Batory D, Sarvela JN, Rauschmayer A (2004) Scaling stepwise refinement. IEEE Trans Softw Eng 30(6):355–371
Bauer A, Popović Z (2017) Collaborative problem solving in an open-ended scientific discovery game. In: Proceedings of the ACM Human-Computer Interaction 1, CSCW, Article 22 (December 2017)
Ben-Ari M, Sajaniemi J (2003) Roles of variables from the perspective of computer science educators. University of Joensuu, Department of Computer Science, Technical Report, Series A-2003–6
Börstler J, Hilburn TB (2016) Team projects in computing education. ACM Trans Comput Educ 16(2), Article 4 (March 2016)
Byckling P, Sajaniemi J (2006) Roles of variables and programming skills improvement. SIGCSE Bull 38(1):413–417
Carver S, McCoy (1988) Learning and transfer of debugging skills: applying task analysis to curriculum design and assessment. In Mayer RE (ed) Teaching and learning computer programming, multiple research perspectives. Lawrence Erlbaum Associates, Inc., Chapter 11
Celepkolu M, Boyer KE (2018) The importance of producing shared code through pair programming. In: Proceedings of the 49th ACM technical symposium on computer science education (SIGCSE ’18). ACM, New York, pp 765–770
Clancy MJ, Linn M C (1999) Patterns and pedagogy. In: Proceedings of the SIGCSE’99, pp 37–42
Cosmides L, Tooby J (1997) Evolutionary psychology: a primer. Retrieved 24 October 2004, from http://www.psych.ucsb.edu/research/cep/primer.html
Dijkstra EW (1976) A discipline of programming. Prentice-Hall, Englewood Cliffs
MATH Google Scholar
East JP, Thomas SR, Wallingford E, Beck W, Drake J (1996) Pattern-based programming instruction. In: Proceedings of ASEE annual conference and exposition, Washington, DC
Ginat D (2003) The greedy trap and learning from mistakes. SIGCSE Bull 35(1):11–15
Ginat D (2004) Algorithmic patterns and the case of the sliding delta. SIGCSE Bull 36(2):29–33
Ginat D (2008) Learning from wrong and creative algorithm design. SIGCSE Bull 40(1):26–30
Ginat D (2009) Interleaved pattern composition and scaffolded learning. In: Proceedings of the 14th Annual ACM SIGCSE Conference on Innovation and Technology in Computer Science Education – ITiCSE ‘09, Paris, France, pp 109–113
Ginat D, Shmalo R (2013) Constructive use of errors in teaching CS1. In: Proceedings of the 44th ACM technical symposium on Computer science education (SIGCSE ’13). ACM, New York, pp 353–358
Hasni TF, Lodhi F (2011) Teaching problem solving effectively. ACM Inroads 2(3):58–62
Hazzan O, Leron U (2006) Why do we resist testing? Syst Des Front Exclus Front Cover Syst Des 3(7):20–23
Johnson DW, Johanson RT (2017) Cooperative learning. Retrieved from: https://2017.congresoinnovacion.educa.aragon.es/documents/48/David_Johnson.pdf
Jonassen DH (2000) Toward a design theory of problem solving. Educ Technol Res Dev 48(4):63–85
Kiesmüller U (2009) Diagnosing learners’ problem-solving strategies using learning environments with algorithmic problems in secondary education. Trans Comput Educ 9(3), Article 17 (September 2009), 26 pages
Laakso MJ, Malmi L, Korhonen A, Rajala T, Kaila E, Salakoski T (2008) Using roles of variables to enhance novice’s debugging work. Issues Informing Sci Inf Technol 5:281–295
Lapidot T, Hazzan O (2005) Song debugging: merging content and pedagogy in computer science education. Inroads SIGCSE Bull 37(4):79–83
Lieberman H (1997) The debugging scandal and what to do about it (special section). Comm ACM 40(4):27–29
Lishinski A, Yadav A, Enbody R, Good J (2016) The influence of problem solving abilities on Students’ performance on different assessment tasks in CS1. In: Proceedings of the 47th ACM technical symposium on computing science education (SIGCSE ’16). ACM, New York, pp 329–334
Muller O (2005) Pattern oriented instruction and the enhancement of analogical reasoning. In: Proceedings of the first International Workshop on Computer Education Research ICER ‘05, Seattle, WA, USA, pp 57–67
Muller O, Haberman B, Averbuch H (2004) (An almost) pedagogical pattern for pattern-based problem solving instruction. In: Proceedings of the 9th Annual SIGCSE Conference on Innovation and Technology in Computer Science. Education, pp 102–106
Muller O, Ginat D, Haberman B (2007) Pattern-oriented instruction and its influence on problem decomposition and solution construction. ACM SIGCSE Bull 39(3):151–155
Murphy L, Lewandowski G, McCauley R, Simon B, Thomas L, Zander C (2008) Debugging: the good, the bad, and the quirky – a qualitative analysis of novices’ strategies. SIGCSE Bull 40(1):163–167
Nagvajara P, Taskin B (2007) Design-for-debug: a vital aspect in education. In: Proceedings of the 2007 IEEE international conference on microelectronic systems education (MSE ’07). IEEE Computer Society, Washington, DC, USA, pp 65–66
Papert S (1980) Mindstorms: children, computers and powerful ideas. Basic Books Inc, New York
Polya G (1957) How to solve it. Doubleday and Co., Inc, Garden City
Polya G (1981) Mathematical discovery on understanding learning and teaching problem solving. Wiley, New York
Popper KR (1992/1959) Logic of scientific discovery. Harper and Row, New York
Proulx VK (2000) Programming patterns and design patterns in the introductory computer science course. Proc SIGCSE 32(1):80–84
Ragonis N (2012) Integrating the teaching of algorithmic patterns into computer science teacher preparation programs. In: Proceedings of the 17th ACM annual conference on Innovation and technology in computer science education (ITiCSE ’12). ACM, New York, pp 339–344
Raman K, Svore KM, Gilad-Bachrach R, Burges CJC (2012) Learning from mistakes: towards a correctable learning algorithm. In: Proceedings of the 21st ACM international conference on information and knowledge management (CIKM ’12). ACM, New York, pp 1930–1934
Reed D (1999) Incorporating problem-solving patterns in CS1. J Comput Sci Edu 13(1):6–13
Reynolds RG, Maletic JI, Porvin SE (1992) Stepwise refinement and problem solving. IEEE Softw 9(5):79–88
Robins A, Rountree J, Rountree N (2003) Learning and teaching programming: a review and discussion. Comput Sci Edu 13(2):137–172
Sajaniemi J (2005) Roles of variables and learning to program. In: Jimoyiannis A (ed) Proceedings of the 3rd Panhellenic conference didactics of informatics, University of Peloponnese, Korinthos, Greece. http://cs.joensuu.fi/~saja/var_roles/abstracts/didinf05.pdf . Accessed 3 July 2010
Santos AL, Sousa J (2017) An exploratory study of how programming instructors illustrate variables and control flow. In: Proceedings of the 17th Koli calling international conference on computing education research (Koli Calling ’17). ACM, New York, pp 173–177
Schoenfeld AH (1983) Episodes and executive decisions in mathematical problem-solving. In: Lesh R, Landaue M (eds) Acquisition of mathematics concepts and processes. Academic Press Inc, New York
Schön DA (1983) The reflective practitioner. BasicBooks
Seta K, Kajino T, Umano M, Ikeda M (2006) An ontology based reflection support system to encourage learning from mistakes. In: Deved V (ed) Proceedings of the 24th IASTED international conference on artificial intelligence and applications (AIA’06). ACTA Press, Anaheim, pp 142–149
Soloway E (1986) Learning to program = learning to construct mechanisms and explanations. CACM 29(1):850–858
Spohrer JG, Soloway E (1986) Analyzing the high frequency bugs in novice programs. In: Soloway E, Iyengar S (eds) Empirical studies of programmers. Ablex, Norwood, pp 230–251
Stoeffler K, Rosen Y, von Davier A (2017) Exploring the measurement of collaborative problem solving using a human-agent educational game. In: Proceedings of the seventh international learning analytics & knowledge conference (LAK ‘17). ACM, New York, pp 570–571
Vainio V, Sajaniemi J (2007) Factors in novice programmers’ poor tracing skills. SIGCSE Bull 39(3):236–240
Vasconcelos J (2007) Basic strategy for algorithmic problem solving. http://www.cs.jhu.edu/~jorgev/cs106/ProblemSolving.html . Accessed 2 June 2010
Vírseda R d V, Orna EP, Berbis E, Guerrero S d L (2011) A logic teaching tool based on tableaux for verification and debugging of algorithms. In: Blackburn P, van Ditmarsch H, Soler-Toscano F, Manzano M (eds) Proceedings of the third international congress conference on tools for teaching logic (TICTTL’11). Springer, Berlin/Heidelberg, pp 239–248
Von Davier AA, Halpin PF (2013) Collaborative problem solving and the assessment of cognitive skills: psychometric considerations. ETS Res Rep Ser 2013(2):1–36
Wallingford E (1996) Toward a first course based on object-oriented patterns. In: Proceedings of the SIGCSE, pp 27–31
Wirth N (1971) Program development by stepwise refinement. CACM 14(4):221–227. http://sunnyday.mit.edu/16.355/wirth-refinement.html . Accessed 13 Nov 2010
Download references
Author information
Authors and affiliations.
Department of Education in Science & Technology, Technion–Israel Institute of Technology, Haifa, Israel
Orit Hazzan & Tami Lapidot
Faculty of Education, Beit Berl College, Doar Beit Berl, Israel
Noa Ragonis
You can also search for this author in PubMed Google Scholar
Rights and permissions
Reprints and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this chapter
Hazzan, O., Ragonis, N., Lapidot, T. (2020). Problem-Solving Strategies. In: Guide to Teaching Computer Science. Springer, Cham. https://doi.org/10.1007/978-3-030-39360-1_8
Download citation
DOI : https://doi.org/10.1007/978-3-030-39360-1_8
Published : 06 August 2020
Publisher Name : Springer, Cham
Print ISBN : 978-3-030-39359-5
Online ISBN : 978-3-030-39360-1
eBook Packages : Computer Science Computer Science (R0)
Share this chapter
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Trial and error
Imagine that you wake up in the morning, turn on your computer to do some study, and then discover your Wi-Fi isn’t working. First, you run a diagnostic test on your computer, but it doesn’t uncover anything. Next, you restart your computer, and still no luck. Lastly, you reboot your modem router, and… success!
The process you have just used is called trial and error, and it can be used to solve small problems like the one you had with your Wi-Fi. It can also be a powerful method in controlled situations for scientific breakthroughs, inventions, and developing new products. The idea is that you keep trying different approaches until you find one that works. The benefit of trial and error is that it allows you to test certain ideas (or hypotheses) to see if they are an effective solution to a problem. You can then take what you’ve learnt from your trials (and errors) and use it to make adjustments and to guide your next moves.
The downsides are that it can take time to conduct these trials, and this technique can’t be used in all situations. In some cases, a simple error could lead to disaster. For example, if you work as a bomb disposal expert and you need to disarm an explosive, cutting wires until you find the right one probably wouldn’t be a good idea!
- Can you think of another example of a situation in which it would not be a good idea to use trial and error?
- What about a situation in which trial and error would be a good strategy to use?
Answer the following questions to identify in which situations trial and error would be a good problem-solving technique to use.
Key Transferable Skills Copyright © 2024 by RMIT University Library is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book
Leadership & Flow
Global Research Program and Network
What is ‘trial and error’?
Trial and error is not a method of finding the best solution, nor a method of finding all solutions. It is a problem-solving technique that is used simply to find a solution.
‘ So, you screwed up? ’ – How many times have you heard this criticism when you failed? What this question often implies is that you are a loser , someone who lost its reputation or having difficulty managing a situation or a relationship. Hidden, this question sends the message: ‘You are not good enough’ .
No wonder, that it is inherently coded in us to fear failure and be ashamed when we fail. Even though every one fails sometimes in life, as failure is part of a learning process we cannot avoid. If we look deep inside, everybody would agree, that the failures that make us stronger and unique.
Studies show that the most successful people failed a lot. When testing concepts, ideas, solving new problems in the real world one cannot avoid making mistakes, or fall flat sometimes. Successful managers, leaders, and entrepreneurs all understand the importance of failure, indeed they are mastered in failing but:
- they have learned to move on; and
- learned from their mistakes, in other words, they truly understand the meaning of trial and error.
To me, failure and self-development come hand in hand. It is not a question if: ‘ Will you fail or not?’ , but rather ‘ What level of risk you take?’ when you fail . Successful managers and leaders suggest testing concepts, ideas in a low-risk environment to minimize risk associated with failure.
So, why not to use this ‘formula’ in teaching management and leadership?
Computer games and online simulations, such as FLIGBY offer to test and master leadership and management skills in a safe, low-risk environment and allows to experiment.
By playing FLIGBY the players can face with some of their lacking abilities, management or leadership skills. It is almost certain that they will fail someway or another as leaders/managers while playing the Game. Odd it might be, but true that failing in the Game motivates the player to play more in order to test and try out other alternative management and leadership styles and skills in order to succeed.
This is how FLIGBY unconsciously teaches new management and leadership skills and styles, teaches to accept failure as part of a learning process, and master in people management skills.
After all our whole life is based on ‘ trail and error’ , but no one can take away the experience we collect through truly experiencing life, including the mistakes we make!
(The author of this entry is Esztella Fazekas , member of the Leadership & Flow Research Team)

8 Effective Problem-Solving Strategies
Categories Cognition
If you need to solve a problem, there are a number of different problem-solving strategies that can help you come up with an accurate decision. Sometimes the best choice is to use a step-by-step approach that leads to the right solution, but other problems may require a trial-and-error approach.
Some helpful problem-solving strategies include: Brainstorming Step-by-step algorithms Trial-and-error Working backward Heuristics Insight Writing it down Getting some sleep
Table of Contents
Why Use Problem-Solving Strategies
While you can always make a wild guess or pick at random, that certainly isn’t the most accurate way to come up with a solution. Using a more structured approach allows you to:
- Understand the nature of the problem
- Determine how you will solve it
- Research different options
- Take steps to solve the problem and resolve the issue
There are many tools and strategies that can be used to solve problems, and some problems may require more than one of these methods in order to come up with a solution.
Problem-Solving Strategies
The problem-solving strategy that works best depends on the nature of the problem and how much time you have available to make a choice. Here are eight different techniques that can help you solve whatever type of problem you might face.
Brainstorming
Coming up with a lot of potential solutions can be beneficial, particularly early on in the process. You might brainstorm on your own, or enlist the help of others to get input that you might not have otherwise considered.
Step-by-Step
Also known as an algorithm, this approach involves following a predetermined formula that is guaranteed to produce the correct result. While this can be useful in some situations—such as solving a math problem—it is not always practical in every situation.
On the plus side, algorithms can be very accurate and reliable. Unfortunately, they can also be time-consuming.
And in some situations, you cannot follow this approach because you simply don’t have access to all of the information you would need to do so.
Trial-and-Error
This problem-solving strategy involves trying a number of different solutions in order to figure out which one works best. This requires testing steps or more options to solve the problem or pick the right solution.
For example, if you are trying to perfect a recipe, you might have to experiment with varying amounts of a certain ingredient before you figure out which one you prefer.
On the plus side, trial-and-error can be a great problem-solving strategy in situations that require an individualized solution. However, this approach can be very time-consuming and costly.
Working Backward
This problem-solving strategy involves looking at the end result and working your way back through the chain of events. It can be a useful tool when you are trying to figure out what might have led to a particular outcome.
It can also be a beneficial way to play out how you will complete a task. For example, if you know you need to have a project done by a certain date, working backward can help you figure out the steps you’ll need to complete in order to successfully finish the project.
Heuristics are mental shortcuts that allow you to come up with solutions quite quickly. They are often based on past experiences that are then applied to other situations. They are, essentially, a handy rule of thumb.
For example, imagine a student is trying to pick classes for the next term. While they aren’t sure which classes they’ll enjoy the most, they know that they tend to prefer subjects that involve a lot of creativity. They utilize this heuristic to pick classes that involve art and creative writing.
The benefit of a heuristic is that it is a fast way to make fairly accurate decisions. The trade-off is that you give up some accuracy in order to gain speed and efficiency.
Sometimes, the solution to a problem seems to come out of nowhere. You might suddenly envision a solution after struggling with the problem for a while. Or you might abruptly recognize the correct solution that you hadn’t seen before.
No matter the source, insight-based problem-solving relies on following your gut instincts. While this may not be as objective or accurate as some other problem-solving strategies, it can be a great way to come up with creative, novel solutions.
Write It Down
Sometimes putting the problem and possible solutions down in paper can be a useful way to visualize solutions. Jot down whatever might help you envision your options. Draw a picture, create a mind map, or just write some notes to clarify your thoughts.
Get Some Sleep
If you’re facing a big problem or trying to make an important decision, try getting a good night’s sleep before making a choice. Sleep plays an essential role in memory consolidation, so getting some rest may help you access the information or insight you need to make the best choice.
Other Considerations
Even with an arsenal of problem-solving strategies at your disposal, coming up with solutions isn’t always easy. Certain challenges can make the process more difficult. A few issues that might emerge include:
- Mental set : When people form a mental set, they only rely on things that have worked in the last. Sometimes this can be useful, but in other cases, it can severely hinder the problem-solving process.
- Cognitive biases : Unconscious cognitive biases can make it difficult to see situations clearly and objectively. As a result, you may not consider all of your options or ignore relevant information.
- Misinformation : Poorly sourced clues and irrelevant details can add more complications. Being able to sort out what’s relevant and what’s not is essential for solving problems accurately.
- Functional fixedness : Functional fixedness happens when people only think of customary solutions to problems. It can hinder out-of-the-box thinking and prevents insightful, creative solutions.
Important Problem-Solving Skills
Becoming a good problem solver can be useful in a variety of domains, from school to work to interpersonal relationships. Important problem-solving skills encompass being able to identify problems, coming up with effective solutions, and then implementing these solutions.
According to a 2023 survey by the National Association of Colleges and Employers, 61.4% of employers look for problem-solving skills on applicant resumes.
Some essential problem-solving skills include:
- Research skills
- Analytical abilities
- Decision-making skills
- Critical thinking
- Communication
- Time management
- Emotional intelligence
Solving a problem is complex and requires the ability to recognize the issue, collect and analyze relevant data, and make decisions about the best course of action. It can also involve asking others for input, communicating goals, and providing direction to others.
How to Become a Better Problem-Solver
If you’re ready to strengthen your problem-solving abilities, here are some steps you can take:
Identify the Problem
Before you can practice your problem-solving skills, you need to be able to recognize that there is a problem. When you spot a potential issue, ask questions about when it started and what caused it.
Do Your Research
Instead of jumping right in to finding solutions, do research to make sure you fully understand the problem and have all the background information you need. This helps ensure you don’t miss important details.
Hone Your Skills
Consider signing up for a class or workshop focused on problem-solving skill development. There are also books that focus on different methods and approaches.
The best way to strengthen problem-solving strategies is to give yourself plenty of opportunities to practice. Look for new challenges that allow you to think critically, analytically, and creatively.
Final Thoughts
If you have a problem to solve, there are plenty of strategies that can help you make the right choice. The key is to pick the right one, but also stay flexible and willing to shift gears.
In many cases, you might find that you need more than one strategy to make the choices that are right for your life.
Brunet, J. F., McNeil, J., Doucet, É., & Forest, G. (2020). The association between REM sleep and decision-making: Supporting evidences. Physiology & Behavior , 225, 113109. https://doi.org/10.1016/j.physbeh.2020.113109
Chrysikou, E. G, Motyka, K., Nigro, C., Yang, S. I. , & Thompson-Schill, S. L. (2016). Functional fixedness in creative thinking tasks depends on stimulus modality. Psychol Aesthet Creat Arts , 10(4):425‐435. https://doi.org/10.1037/aca0000050
Sarathy, V. (2018). Real world problem-solving. Front Hum Neurosci , 12:261. https://doi.org/10.3389/fnhum.2018.00261
Chapter 7: Thinking and Intelligence
Problem solving, learning objectives.
By the end of this section, you will be able to:
- Describe problem solving strategies
- Define algorithm and heuristic
- Explain some common roadblocks to effective problem solving
People face problems every day—usually, multiple problems throughout the day. Sometimes these problems are straightforward: To double a recipe for pizza dough, for example, all that is required is that each ingredient in the recipe be doubled. Sometimes, however, the problems we encounter are more complex. For example, say you have a work deadline, and you must mail a printed copy of a report to your supervisor by the end of the business day. The report is time-sensitive and must be sent overnight. You finished the report last night, but your printer will not work today. What should you do? First, you need to identify the problem and then apply a strategy for solving the problem.
PROBLEM-SOLVING STRATEGIES
When you are presented with a problem—whether it is a complex mathematical problem or a broken printer, how do you solve it? Before finding a solution to the problem, the problem must first be clearly identified. After that, one of many problem solving strategies can be applied, hopefully resulting in a solution.
A problem-solving strategy is a plan of action used to find a solution. Different strategies have different action plans associated with them ( [link] ). For example, a well-known strategy is trial and error . The old adage, “If at first you don’t succeed, try, try again” describes trial and error. In terms of your broken printer, you could try checking the ink levels, and if that doesn’t work, you could check to make sure the paper tray isn’t jammed. Or maybe the printer isn’t actually connected to your laptop. When using trial and error, you would continue to try different solutions until you solved your problem. Although trial and error is not typically one of the most time-efficient strategies, it is a commonly used one.
Another type of strategy is an algorithm. An algorithm is a problem-solving formula that provides you with step-by-step instructions used to achieve a desired outcome (Kahneman, 2011). You can think of an algorithm as a recipe with highly detailed instructions that produce the same result every time they are performed. Algorithms are used frequently in our everyday lives, especially in computer science. When you run a search on the Internet, search engines like Google use algorithms to decide which entries will appear first in your list of results. Facebook also uses algorithms to decide which posts to display on your newsfeed. Can you identify other situations in which algorithms are used?
A heuristic is another type of problem solving strategy. While an algorithm must be followed exactly to produce a correct result, a heuristic is a general problem-solving framework (Tversky & Kahneman, 1974). You can think of these as mental shortcuts that are used to solve problems. A “rule of thumb” is an example of a heuristic. Such a rule saves the person time and energy when making a decision, but despite its time-saving characteristics, it is not always the best method for making a rational decision. Different types of heuristics are used in different types of situations, but the impulse to use a heuristic occurs when one of five conditions is met (Pratkanis, 1989):
- When one is faced with too much information
- When the time to make a decision is limited
- When the decision to be made is unimportant
- When there is access to very little information to use in making the decision
- When an appropriate heuristic happens to come to mind in the same moment
Working backwards is a useful heuristic in which you begin solving the problem by focusing on the end result. Consider this example: You live in Washington, D.C. and have been invited to a wedding at 4 PM on Saturday in Philadelphia. Knowing that Interstate 95 tends to back up any day of the week, you need to plan your route and time your departure accordingly. If you want to be at the wedding service by 3:30 PM, and it takes 2.5 hours to get to Philadelphia without traffic, what time should you leave your house? You use the working backwards heuristic to plan the events of your day on a regular basis, probably without even thinking about it.
Another useful heuristic is the practice of accomplishing a large goal or task by breaking it into a series of smaller steps. Students often use this common method to complete a large research project or long essay for school. For example, students typically brainstorm, develop a thesis or main topic, research the chosen topic, organize their information into an outline, write a rough draft, revise and edit the rough draft, develop a final draft, organize the references list, and proofread their work before turning in the project. The large task becomes less overwhelming when it is broken down into a series of small steps.
Problem-solving abilities can improve with practice. Many people challenge themselves every day with puzzles and other mental exercises to sharpen their problem-solving skills. Sudoku puzzles appear daily in most newspapers. Typically, a sudoku puzzle is a 9×9 grid. The simple sudoku below ( [link] ) is a 4×4 grid. To solve the puzzle, fill in the empty boxes with a single digit: 1, 2, 3, or 4. Here are the rules: The numbers must total 10 in each bolded box, each row, and each column; however, each digit can only appear once in a bolded box, row, and column. Time yourself as you solve this puzzle and compare your time with a classmate.
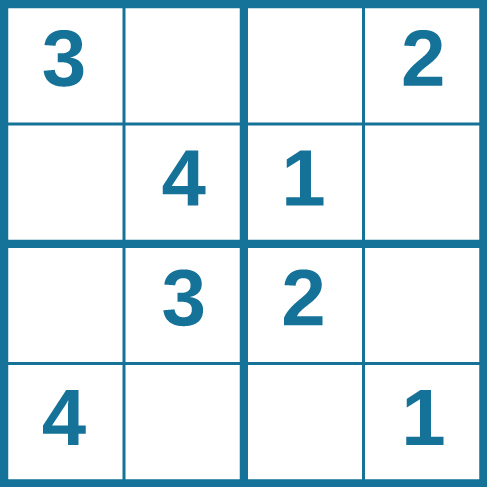
How long did it take you to solve this sudoku puzzle? (You can see the answer at the end of this section.)
Here is another popular type of puzzle ( [link] ) that challenges your spatial reasoning skills. Connect all nine dots with four connecting straight lines without lifting your pencil from the paper:
Did you figure it out? (The answer is at the end of this section.) Once you understand how to crack this puzzle, you won’t forget.
Take a look at the “Puzzling Scales” logic puzzle below ( [link] ). Sam Loyd, a well-known puzzle master, created and refined countless puzzles throughout his lifetime (Cyclopedia of Puzzles, n.d.).
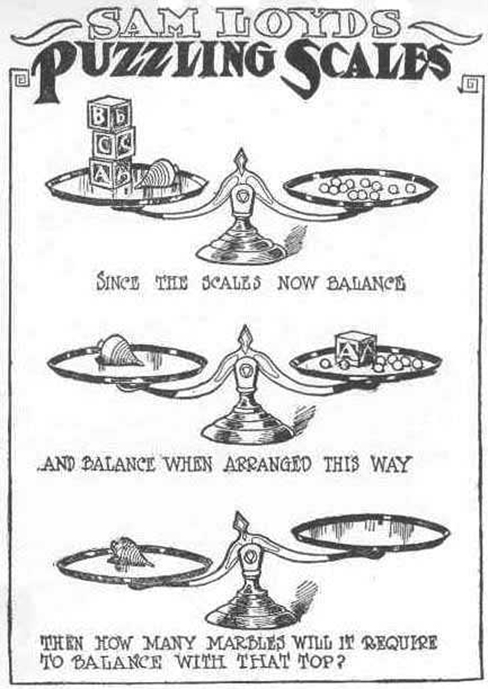
PITFALLS TO PROBLEM SOLVING
Not all problems are successfully solved, however. What challenges stop us from successfully solving a problem? Albert Einstein once said, “Insanity is doing the same thing over and over again and expecting a different result.” Imagine a person in a room that has four doorways. One doorway that has always been open in the past is now locked. The person, accustomed to exiting the room by that particular doorway, keeps trying to get out through the same doorway even though the other three doorways are open. The person is stuck—but she just needs to go to another doorway, instead of trying to get out through the locked doorway. A mental set is where you persist in approaching a problem in a way that has worked in the past but is clearly not working now.
Functional fixedness is a type of mental set where you cannot perceive an object being used for something other than what it was designed for. During the Apollo 13 mission to the moon, NASA engineers at Mission Control had to overcome functional fixedness to save the lives of the astronauts aboard the spacecraft. An explosion in a module of the spacecraft damaged multiple systems. The astronauts were in danger of being poisoned by rising levels of carbon dioxide because of problems with the carbon dioxide filters. The engineers found a way for the astronauts to use spare plastic bags, tape, and air hoses to create a makeshift air filter, which saved the lives of the astronauts.
Link to Learning
Check out this Apollo 13 scene where the group of NASA engineers are given the task of overcoming functional fixedness.
Researchers have investigated whether functional fixedness is affected by culture. In one experiment, individuals from the Shuar group in Ecuador were asked to use an object for a purpose other than that for which the object was originally intended. For example, the participants were told a story about a bear and a rabbit that were separated by a river and asked to select among various objects, including a spoon, a cup, erasers, and so on, to help the animals. The spoon was the only object long enough to span the imaginary river, but if the spoon was presented in a way that reflected its normal usage, it took participants longer to choose the spoon to solve the problem. (German & Barrett, 2005). The researchers wanted to know if exposure to highly specialized tools, as occurs with individuals in industrialized nations, affects their ability to transcend functional fixedness. It was determined that functional fixedness is experienced in both industrialized and nonindustrialized cultures (German & Barrett, 2005).
In order to make good decisions, we use our knowledge and our reasoning. Often, this knowledge and reasoning is sound and solid. Sometimes, however, we are swayed by biases or by others manipulating a situation. For example, let’s say you and three friends wanted to rent a house and had a combined target budget of $1,600. The realtor shows you only very run-down houses for $1,600 and then shows you a very nice house for $2,000. Might you ask each person to pay more in rent to get the $2,000 home? Why would the realtor show you the run-down houses and the nice house? The realtor may be challenging your anchoring bias. An anchoring bias occurs when you focus on one piece of information when making a decision or solving a problem. In this case, you’re so focused on the amount of money you are willing to spend that you may not recognize what kinds of houses are available at that price point.
The confirmation bias is the tendency to focus on information that confirms your existing beliefs. For example, if you think that your professor is not very nice, you notice all of the instances of rude behavior exhibited by the professor while ignoring the countless pleasant interactions he is involved in on a daily basis. Hindsight bias leads you to believe that the event you just experienced was predictable, even though it really wasn’t. In other words, you knew all along that things would turn out the way they did. Representative bias describes a faulty way of thinking, in which you unintentionally stereotype someone or something; for example, you may assume that your professors spend their free time reading books and engaging in intellectual conversation, because the idea of them spending their time playing volleyball or visiting an amusement park does not fit in with your stereotypes of professors.
Finally, the availability heuristic is a heuristic in which you make a decision based on an example, information, or recent experience that is that readily available to you, even though it may not be the best example to inform your decision . Biases tend to “preserve that which is already established—to maintain our preexisting knowledge, beliefs, attitudes, and hypotheses” (Aronson, 1995; Kahneman, 2011). These biases are summarized in [link] .
Please visit this site to see a clever music video that a high school teacher made to explain these and other cognitive biases to his AP psychology students.
Were you able to determine how many marbles are needed to balance the scales in [link] ? You need nine. Were you able to solve the problems in [link] and [link] ? Here are the answers ( [link] ).
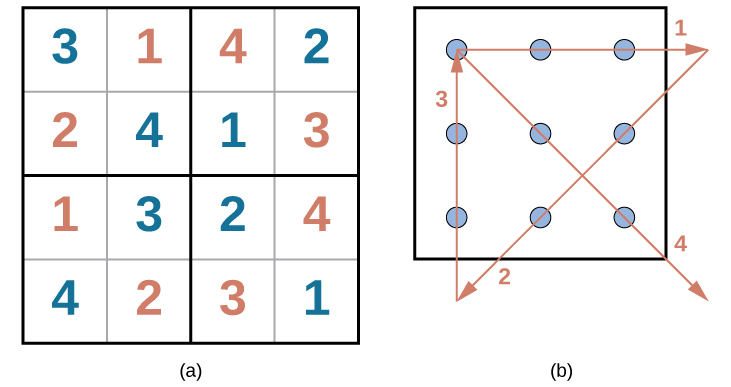
Many different strategies exist for solving problems. Typical strategies include trial and error, applying algorithms, and using heuristics. To solve a large, complicated problem, it often helps to break the problem into smaller steps that can be accomplished individually, leading to an overall solution. Roadblocks to problem solving include a mental set, functional fixedness, and various biases that can cloud decision making skills.
Self Check Questions
Critical thinking questions.
1. What is functional fixedness and how can overcoming it help you solve problems?
2. How does an algorithm save you time and energy when solving a problem?
Personal Application Question
3. Which type of bias do you recognize in your own decision making processes? How has this bias affected how you’ve made decisions in the past and how can you use your awareness of it to improve your decisions making skills in the future?
1. Functional fixedness occurs when you cannot see a use for an object other than the use for which it was intended. For example, if you need something to hold up a tarp in the rain, but only have a pitchfork, you must overcome your expectation that a pitchfork can only be used for garden chores before you realize that you could stick it in the ground and drape the tarp on top of it to hold it up.
2. An algorithm is a proven formula for achieving a desired outcome. It saves time because if you follow it exactly, you will solve the problem without having to figure out how to solve the problem. It is a bit like not reinventing the wheel.
- Psychology. Authored by : OpenStax College. Located at : http://cnx.org/contents/[email protected]:1/Psychology . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/content/col11629/latest/.

Privacy Policy
35 problem-solving techniques and methods for solving complex problems

Design your next session with SessionLab
Join the 150,000+ facilitators using SessionLab.
Recommended Articles
A step-by-step guide to planning a workshop, how to create an unforgettable training session in 8 simple steps, 47 useful online tools for workshop planning and meeting facilitation.
All teams and organizations encounter challenges as they grow. There are problems that might occur for teams when it comes to miscommunication or resolving business-critical issues . You may face challenges around growth , design , user engagement, and even team culture and happiness. In short, problem-solving techniques should be part of every team’s skillset.
Problem-solving methods are primarily designed to help a group or team through a process of first identifying problems and challenges , ideating possible solutions , and then evaluating the most suitable .
Finding effective solutions to complex problems isn’t easy, but by using the right process and techniques, you can help your team be more efficient in the process.
So how do you develop strategies that are engaging, and empower your team to solve problems effectively?
In this blog post, we share a series of problem-solving tools you can use in your next workshop or team meeting. You’ll also find some tips for facilitating the process and how to enable others to solve complex problems.
Let’s get started!
How do you identify problems?
How do you identify the right solution.
- Tips for more effective problem-solving
Complete problem-solving methods
- Problem-solving techniques to identify and analyze problems
- Problem-solving techniques for developing solutions
Problem-solving warm-up activities
Closing activities for a problem-solving process.
Before you can move towards finding the right solution for a given problem, you first need to identify and define the problem you wish to solve.
Here, you want to clearly articulate what the problem is and allow your group to do the same. Remember that everyone in a group is likely to have differing perspectives and alignment is necessary in order to help the group move forward.
Identifying a problem accurately also requires that all members of a group are able to contribute their views in an open and safe manner. It can be scary for people to stand up and contribute, especially if the problems or challenges are emotive or personal in nature. Be sure to try and create a psychologically safe space for these kinds of discussions.
Remember that problem analysis and further discussion are also important. Not taking the time to fully analyze and discuss a challenge can result in the development of solutions that are not fit for purpose or do not address the underlying issue.
Successfully identifying and then analyzing a problem means facilitating a group through activities designed to help them clearly and honestly articulate their thoughts and produce usable insight.
With this data, you might then produce a problem statement that clearly describes the problem you wish to be addressed and also state the goal of any process you undertake to tackle this issue.
Finding solutions is the end goal of any process. Complex organizational challenges can only be solved with an appropriate solution but discovering them requires using the right problem-solving tool.
After you’ve explored a problem and discussed ideas, you need to help a team discuss and choose the right solution. Consensus tools and methods such as those below help a group explore possible solutions before then voting for the best. They’re a great way to tap into the collective intelligence of the group for great results!
Remember that the process is often iterative. Great problem solvers often roadtest a viable solution in a measured way to see what works too. While you might not get the right solution on your first try, the methods below help teams land on the most likely to succeed solution while also holding space for improvement.
Every effective problem solving process begins with an agenda . A well-structured workshop is one of the best methods for successfully guiding a group from exploring a problem to implementing a solution.
In SessionLab, it’s easy to go from an idea to a complete agenda . Start by dragging and dropping your core problem solving activities into place . Add timings, breaks and necessary materials before sharing your agenda with your colleagues.
The resulting agenda will be your guide to an effective and productive problem solving session that will also help you stay organized on the day!
Tips for more effective problem solving
Problem-solving activities are only one part of the puzzle. While a great method can help unlock your team’s ability to solve problems, without a thoughtful approach and strong facilitation the solutions may not be fit for purpose.
Let’s take a look at some problem-solving tips you can apply to any process to help it be a success!
Clearly define the problem
Jumping straight to solutions can be tempting, though without first clearly articulating a problem, the solution might not be the right one. Many of the problem-solving activities below include sections where the problem is explored and clearly defined before moving on.
This is a vital part of the problem-solving process and taking the time to fully define an issue can save time and effort later. A clear definition helps identify irrelevant information and it also ensures that your team sets off on the right track.
Don’t jump to conclusions
It’s easy for groups to exhibit cognitive bias or have preconceived ideas about both problems and potential solutions. Be sure to back up any problem statements or potential solutions with facts, research, and adequate forethought.
The best techniques ask participants to be methodical and challenge preconceived notions. Make sure you give the group enough time and space to collect relevant information and consider the problem in a new way. By approaching the process with a clear, rational mindset, you’ll often find that better solutions are more forthcoming.

Try different approaches
Problems come in all shapes and sizes and so too should the methods you use to solve them. If you find that one approach isn’t yielding results and your team isn’t finding different solutions, try mixing it up. You’ll be surprised at how using a new creative activity can unblock your team and generate great solutions.
Don’t take it personally
Depending on the nature of your team or organizational problems, it’s easy for conversations to get heated. While it’s good for participants to be engaged in the discussions, ensure that emotions don’t run too high and that blame isn’t thrown around while finding solutions.
You’re all in it together, and even if your team or area is seeing problems, that isn’t necessarily a disparagement of you personally. Using facilitation skills to manage group dynamics is one effective method of helping conversations be more constructive.
Get the right people in the room
Your problem-solving method is often only as effective as the group using it. Getting the right people on the job and managing the number of people present is important too!
If the group is too small, you may not get enough different perspectives to effectively solve a problem. If the group is too large, you can go round and round during the ideation stages.
Creating the right group makeup is also important in ensuring you have the necessary expertise and skillset to both identify and follow up on potential solutions. Carefully consider who to include at each stage to help ensure your problem-solving method is followed and positioned for success.
Document everything
The best solutions can take refinement, iteration, and reflection to come out. Get into a habit of documenting your process in order to keep all the learnings from the session and to allow ideas to mature and develop. Many of the methods below involve the creation of documents or shared resources. Be sure to keep and share these so everyone can benefit from the work done!
Bring a facilitator
Facilitation is all about making group processes easier. With a subject as potentially emotive and important as problem-solving, having an impartial third party in the form of a facilitator can make all the difference in finding great solutions and keeping the process moving. Consider bringing a facilitator to your problem-solving session to get better results and generate meaningful solutions!
Develop your problem-solving skills
It takes time and practice to be an effective problem solver. While some roles or participants might more naturally gravitate towards problem-solving, it can take development and planning to help everyone create better solutions.
You might develop a training program, run a problem-solving workshop or simply ask your team to practice using the techniques below. Check out our post on problem-solving skills to see how you and your group can develop the right mental process and be more resilient to issues too!
Design a great agenda
Workshops are a great format for solving problems. With the right approach, you can focus a group and help them find the solutions to their own problems. But designing a process can be time-consuming and finding the right activities can be difficult.
Check out our workshop planning guide to level-up your agenda design and start running more effective workshops. Need inspiration? Check out templates designed by expert facilitators to help you kickstart your process!
In this section, we’ll look at in-depth problem-solving methods that provide a complete end-to-end process for developing effective solutions. These will help guide your team from the discovery and definition of a problem through to delivering the right solution.
If you’re looking for an all-encompassing method or problem-solving model, these processes are a great place to start. They’ll ask your team to challenge preconceived ideas and adopt a mindset for solving problems more effectively.
- Six Thinking Hats
- Lightning Decision Jam
- Problem Definition Process
- Discovery & Action Dialogue
Design Sprint 2.0
- Open Space Technology
1. Six Thinking Hats
Individual approaches to solving a problem can be very different based on what team or role an individual holds. It can be easy for existing biases or perspectives to find their way into the mix, or for internal politics to direct a conversation.
Six Thinking Hats is a classic method for identifying the problems that need to be solved and enables your team to consider them from different angles, whether that is by focusing on facts and data, creative solutions, or by considering why a particular solution might not work.
Like all problem-solving frameworks, Six Thinking Hats is effective at helping teams remove roadblocks from a conversation or discussion and come to terms with all the aspects necessary to solve complex problems.
2. Lightning Decision Jam
Featured courtesy of Jonathan Courtney of AJ&Smart Berlin, Lightning Decision Jam is one of those strategies that should be in every facilitation toolbox. Exploring problems and finding solutions is often creative in nature, though as with any creative process, there is the potential to lose focus and get lost.
Unstructured discussions might get you there in the end, but it’s much more effective to use a method that creates a clear process and team focus.
In Lightning Decision Jam, participants are invited to begin by writing challenges, concerns, or mistakes on post-its without discussing them before then being invited by the moderator to present them to the group.
From there, the team vote on which problems to solve and are guided through steps that will allow them to reframe those problems, create solutions and then decide what to execute on.
By deciding the problems that need to be solved as a team before moving on, this group process is great for ensuring the whole team is aligned and can take ownership over the next stages.
Lightning Decision Jam (LDJ) #action #decision making #problem solving #issue analysis #innovation #design #remote-friendly The problem with anything that requires creative thinking is that it’s easy to get lost—lose focus and fall into the trap of having useless, open-ended, unstructured discussions. Here’s the most effective solution I’ve found: Replace all open, unstructured discussion with a clear process. What to use this exercise for: Anything which requires a group of people to make decisions, solve problems or discuss challenges. It’s always good to frame an LDJ session with a broad topic, here are some examples: The conversion flow of our checkout Our internal design process How we organise events Keeping up with our competition Improving sales flow
3. Problem Definition Process
While problems can be complex, the problem-solving methods you use to identify and solve those problems can often be simple in design.
By taking the time to truly identify and define a problem before asking the group to reframe the challenge as an opportunity, this method is a great way to enable change.
Begin by identifying a focus question and exploring the ways in which it manifests before splitting into five teams who will each consider the problem using a different method: escape, reversal, exaggeration, distortion or wishful. Teams develop a problem objective and create ideas in line with their method before then feeding them back to the group.
This method is great for enabling in-depth discussions while also creating space for finding creative solutions too!
Problem Definition #problem solving #idea generation #creativity #online #remote-friendly A problem solving technique to define a problem, challenge or opportunity and to generate ideas.
4. The 5 Whys
Sometimes, a group needs to go further with their strategies and analyze the root cause at the heart of organizational issues. An RCA or root cause analysis is the process of identifying what is at the heart of business problems or recurring challenges.
The 5 Whys is a simple and effective method of helping a group go find the root cause of any problem or challenge and conduct analysis that will deliver results.
By beginning with the creation of a problem statement and going through five stages to refine it, The 5 Whys provides everything you need to truly discover the cause of an issue.
The 5 Whys #hyperisland #innovation This simple and powerful method is useful for getting to the core of a problem or challenge. As the title suggests, the group defines a problems, then asks the question “why” five times, often using the resulting explanation as a starting point for creative problem solving.
5. World Cafe
World Cafe is a simple but powerful facilitation technique to help bigger groups to focus their energy and attention on solving complex problems.
World Cafe enables this approach by creating a relaxed atmosphere where participants are able to self-organize and explore topics relevant and important to them which are themed around a central problem-solving purpose. Create the right atmosphere by modeling your space after a cafe and after guiding the group through the method, let them take the lead!
Making problem-solving a part of your organization’s culture in the long term can be a difficult undertaking. More approachable formats like World Cafe can be especially effective in bringing people unfamiliar with workshops into the fold.
World Cafe #hyperisland #innovation #issue analysis World Café is a simple yet powerful method, originated by Juanita Brown, for enabling meaningful conversations driven completely by participants and the topics that are relevant and important to them. Facilitators create a cafe-style space and provide simple guidelines. Participants then self-organize and explore a set of relevant topics or questions for conversation.
6. Discovery & Action Dialogue (DAD)
One of the best approaches is to create a safe space for a group to share and discover practices and behaviors that can help them find their own solutions.
With DAD, you can help a group choose which problems they wish to solve and which approaches they will take to do so. It’s great at helping remove resistance to change and can help get buy-in at every level too!
This process of enabling frontline ownership is great in ensuring follow-through and is one of the methods you will want in your toolbox as a facilitator.
Discovery & Action Dialogue (DAD) #idea generation #liberating structures #action #issue analysis #remote-friendly DADs make it easy for a group or community to discover practices and behaviors that enable some individuals (without access to special resources and facing the same constraints) to find better solutions than their peers to common problems. These are called positive deviant (PD) behaviors and practices. DADs make it possible for people in the group, unit, or community to discover by themselves these PD practices. DADs also create favorable conditions for stimulating participants’ creativity in spaces where they can feel safe to invent new and more effective practices. Resistance to change evaporates as participants are unleashed to choose freely which practices they will adopt or try and which problems they will tackle. DADs make it possible to achieve frontline ownership of solutions.
7. Design Sprint 2.0
Want to see how a team can solve big problems and move forward with prototyping and testing solutions in a few days? The Design Sprint 2.0 template from Jake Knapp, author of Sprint, is a complete agenda for a with proven results.
Developing the right agenda can involve difficult but necessary planning. Ensuring all the correct steps are followed can also be stressful or time-consuming depending on your level of experience.
Use this complete 4-day workshop template if you are finding there is no obvious solution to your challenge and want to focus your team around a specific problem that might require a shortcut to launching a minimum viable product or waiting for the organization-wide implementation of a solution.
8. Open space technology
Open space technology- developed by Harrison Owen – creates a space where large groups are invited to take ownership of their problem solving and lead individual sessions. Open space technology is a great format when you have a great deal of expertise and insight in the room and want to allow for different takes and approaches on a particular theme or problem you need to be solved.
Start by bringing your participants together to align around a central theme and focus their efforts. Explain the ground rules to help guide the problem-solving process and then invite members to identify any issue connecting to the central theme that they are interested in and are prepared to take responsibility for.
Once participants have decided on their approach to the core theme, they write their issue on a piece of paper, announce it to the group, pick a session time and place, and post the paper on the wall. As the wall fills up with sessions, the group is then invited to join the sessions that interest them the most and which they can contribute to, then you’re ready to begin!
Everyone joins the problem-solving group they’ve signed up to, record the discussion and if appropriate, findings can then be shared with the rest of the group afterward.
Open Space Technology #action plan #idea generation #problem solving #issue analysis #large group #online #remote-friendly Open Space is a methodology for large groups to create their agenda discerning important topics for discussion, suitable for conferences, community gatherings and whole system facilitation
Techniques to identify and analyze problems
Using a problem-solving method to help a team identify and analyze a problem can be a quick and effective addition to any workshop or meeting.
While further actions are always necessary, you can generate momentum and alignment easily, and these activities are a great place to get started.
We’ve put together this list of techniques to help you and your team with problem identification, analysis, and discussion that sets the foundation for developing effective solutions.
Let’s take a look!
- The Creativity Dice
- Fishbone Analysis
- Problem Tree
- SWOT Analysis
- Agreement-Certainty Matrix
- The Journalistic Six
- LEGO Challenge
- What, So What, Now What?
- Journalists
Individual and group perspectives are incredibly important, but what happens if people are set in their minds and need a change of perspective in order to approach a problem more effectively?
Flip It is a method we love because it is both simple to understand and run, and allows groups to understand how their perspectives and biases are formed.
Participants in Flip It are first invited to consider concerns, issues, or problems from a perspective of fear and write them on a flip chart. Then, the group is asked to consider those same issues from a perspective of hope and flip their understanding.
No problem and solution is free from existing bias and by changing perspectives with Flip It, you can then develop a problem solving model quickly and effectively.
Flip It! #gamestorming #problem solving #action Often, a change in a problem or situation comes simply from a change in our perspectives. Flip It! is a quick game designed to show players that perspectives are made, not born.
10. The Creativity Dice
One of the most useful problem solving skills you can teach your team is of approaching challenges with creativity, flexibility, and openness. Games like The Creativity Dice allow teams to overcome the potential hurdle of too much linear thinking and approach the process with a sense of fun and speed.
In The Creativity Dice, participants are organized around a topic and roll a dice to determine what they will work on for a period of 3 minutes at a time. They might roll a 3 and work on investigating factual information on the chosen topic. They might roll a 1 and work on identifying the specific goals, standards, or criteria for the session.
Encouraging rapid work and iteration while asking participants to be flexible are great skills to cultivate. Having a stage for idea incubation in this game is also important. Moments of pause can help ensure the ideas that are put forward are the most suitable.
The Creativity Dice #creativity #problem solving #thiagi #issue analysis Too much linear thinking is hazardous to creative problem solving. To be creative, you should approach the problem (or the opportunity) from different points of view. You should leave a thought hanging in mid-air and move to another. This skipping around prevents premature closure and lets your brain incubate one line of thought while you consciously pursue another.
11. Fishbone Analysis
Organizational or team challenges are rarely simple, and it’s important to remember that one problem can be an indication of something that goes deeper and may require further consideration to be solved.
Fishbone Analysis helps groups to dig deeper and understand the origins of a problem. It’s a great example of a root cause analysis method that is simple for everyone on a team to get their head around.
Participants in this activity are asked to annotate a diagram of a fish, first adding the problem or issue to be worked on at the head of a fish before then brainstorming the root causes of the problem and adding them as bones on the fish.
Using abstractions such as a diagram of a fish can really help a team break out of their regular thinking and develop a creative approach.
Fishbone Analysis #problem solving ##root cause analysis #decision making #online facilitation A process to help identify and understand the origins of problems, issues or observations.
12. Problem Tree
Encouraging visual thinking can be an essential part of many strategies. By simply reframing and clarifying problems, a group can move towards developing a problem solving model that works for them.
In Problem Tree, groups are asked to first brainstorm a list of problems – these can be design problems, team problems or larger business problems – and then organize them into a hierarchy. The hierarchy could be from most important to least important or abstract to practical, though the key thing with problem solving games that involve this aspect is that your group has some way of managing and sorting all the issues that are raised.
Once you have a list of problems that need to be solved and have organized them accordingly, you’re then well-positioned for the next problem solving steps.
Problem tree #define intentions #create #design #issue analysis A problem tree is a tool to clarify the hierarchy of problems addressed by the team within a design project; it represents high level problems or related sublevel problems.
13. SWOT Analysis
Chances are you’ve heard of the SWOT Analysis before. This problem-solving method focuses on identifying strengths, weaknesses, opportunities, and threats is a tried and tested method for both individuals and teams.
Start by creating a desired end state or outcome and bare this in mind – any process solving model is made more effective by knowing what you are moving towards. Create a quadrant made up of the four categories of a SWOT analysis and ask participants to generate ideas based on each of those quadrants.
Once you have those ideas assembled in their quadrants, cluster them together based on their affinity with other ideas. These clusters are then used to facilitate group conversations and move things forward.
SWOT analysis #gamestorming #problem solving #action #meeting facilitation The SWOT Analysis is a long-standing technique of looking at what we have, with respect to the desired end state, as well as what we could improve on. It gives us an opportunity to gauge approaching opportunities and dangers, and assess the seriousness of the conditions that affect our future. When we understand those conditions, we can influence what comes next.
14. Agreement-Certainty Matrix
Not every problem-solving approach is right for every challenge, and deciding on the right method for the challenge at hand is a key part of being an effective team.
The Agreement Certainty matrix helps teams align on the nature of the challenges facing them. By sorting problems from simple to chaotic, your team can understand what methods are suitable for each problem and what they can do to ensure effective results.
If you are already using Liberating Structures techniques as part of your problem-solving strategy, the Agreement-Certainty Matrix can be an invaluable addition to your process. We’ve found it particularly if you are having issues with recurring problems in your organization and want to go deeper in understanding the root cause.
Agreement-Certainty Matrix #issue analysis #liberating structures #problem solving You can help individuals or groups avoid the frequent mistake of trying to solve a problem with methods that are not adapted to the nature of their challenge. The combination of two questions makes it possible to easily sort challenges into four categories: simple, complicated, complex , and chaotic . A problem is simple when it can be solved reliably with practices that are easy to duplicate. It is complicated when experts are required to devise a sophisticated solution that will yield the desired results predictably. A problem is complex when there are several valid ways to proceed but outcomes are not predictable in detail. Chaotic is when the context is too turbulent to identify a path forward. A loose analogy may be used to describe these differences: simple is like following a recipe, complicated like sending a rocket to the moon, complex like raising a child, and chaotic is like the game “Pin the Tail on the Donkey.” The Liberating Structures Matching Matrix in Chapter 5 can be used as the first step to clarify the nature of a challenge and avoid the mismatches between problems and solutions that are frequently at the root of chronic, recurring problems.
Organizing and charting a team’s progress can be important in ensuring its success. SQUID (Sequential Question and Insight Diagram) is a great model that allows a team to effectively switch between giving questions and answers and develop the skills they need to stay on track throughout the process.
Begin with two different colored sticky notes – one for questions and one for answers – and with your central topic (the head of the squid) on the board. Ask the group to first come up with a series of questions connected to their best guess of how to approach the topic. Ask the group to come up with answers to those questions, fix them to the board and connect them with a line. After some discussion, go back to question mode by responding to the generated answers or other points on the board.
It’s rewarding to see a diagram grow throughout the exercise, and a completed SQUID can provide a visual resource for future effort and as an example for other teams.
SQUID #gamestorming #project planning #issue analysis #problem solving When exploring an information space, it’s important for a group to know where they are at any given time. By using SQUID, a group charts out the territory as they go and can navigate accordingly. SQUID stands for Sequential Question and Insight Diagram.
16. Speed Boat
To continue with our nautical theme, Speed Boat is a short and sweet activity that can help a team quickly identify what employees, clients or service users might have a problem with and analyze what might be standing in the way of achieving a solution.
Methods that allow for a group to make observations, have insights and obtain those eureka moments quickly are invaluable when trying to solve complex problems.
In Speed Boat, the approach is to first consider what anchors and challenges might be holding an organization (or boat) back. Bonus points if you are able to identify any sharks in the water and develop ideas that can also deal with competitors!
Speed Boat #gamestorming #problem solving #action Speedboat is a short and sweet way to identify what your employees or clients don’t like about your product/service or what’s standing in the way of a desired goal.
17. The Journalistic Six
Some of the most effective ways of solving problems is by encouraging teams to be more inclusive and diverse in their thinking.
Based on the six key questions journalism students are taught to answer in articles and news stories, The Journalistic Six helps create teams to see the whole picture. By using who, what, when, where, why, and how to facilitate the conversation and encourage creative thinking, your team can make sure that the problem identification and problem analysis stages of the are covered exhaustively and thoughtfully. Reporter’s notebook and dictaphone optional.
The Journalistic Six – Who What When Where Why How #idea generation #issue analysis #problem solving #online #creative thinking #remote-friendly A questioning method for generating, explaining, investigating ideas.
18. LEGO Challenge
Now for an activity that is a little out of the (toy) box. LEGO Serious Play is a facilitation methodology that can be used to improve creative thinking and problem-solving skills.
The LEGO Challenge includes giving each member of the team an assignment that is hidden from the rest of the group while they create a structure without speaking.
What the LEGO challenge brings to the table is a fun working example of working with stakeholders who might not be on the same page to solve problems. Also, it’s LEGO! Who doesn’t love LEGO!
LEGO Challenge #hyperisland #team A team-building activity in which groups must work together to build a structure out of LEGO, but each individual has a secret “assignment” which makes the collaborative process more challenging. It emphasizes group communication, leadership dynamics, conflict, cooperation, patience and problem solving strategy.
19. What, So What, Now What?
If not carefully managed, the problem identification and problem analysis stages of the problem-solving process can actually create more problems and misunderstandings.
The What, So What, Now What? problem-solving activity is designed to help collect insights and move forward while also eliminating the possibility of disagreement when it comes to identifying, clarifying, and analyzing organizational or work problems.
Facilitation is all about bringing groups together so that might work on a shared goal and the best problem-solving strategies ensure that teams are aligned in purpose, if not initially in opinion or insight.
Throughout the three steps of this game, you give everyone on a team to reflect on a problem by asking what happened, why it is important, and what actions should then be taken.
This can be a great activity for bringing our individual perceptions about a problem or challenge and contextualizing it in a larger group setting. This is one of the most important problem-solving skills you can bring to your organization.
W³ – What, So What, Now What? #issue analysis #innovation #liberating structures You can help groups reflect on a shared experience in a way that builds understanding and spurs coordinated action while avoiding unproductive conflict. It is possible for every voice to be heard while simultaneously sifting for insights and shaping new direction. Progressing in stages makes this practical—from collecting facts about What Happened to making sense of these facts with So What and finally to what actions logically follow with Now What . The shared progression eliminates most of the misunderstandings that otherwise fuel disagreements about what to do. Voila!
20. Journalists
Problem analysis can be one of the most important and decisive stages of all problem-solving tools. Sometimes, a team can become bogged down in the details and are unable to move forward.
Journalists is an activity that can avoid a group from getting stuck in the problem identification or problem analysis stages of the process.
In Journalists, the group is invited to draft the front page of a fictional newspaper and figure out what stories deserve to be on the cover and what headlines those stories will have. By reframing how your problems and challenges are approached, you can help a team move productively through the process and be better prepared for the steps to follow.
Journalists #vision #big picture #issue analysis #remote-friendly This is an exercise to use when the group gets stuck in details and struggles to see the big picture. Also good for defining a vision.
Problem-solving techniques for developing solutions
The success of any problem-solving process can be measured by the solutions it produces. After you’ve defined the issue, explored existing ideas, and ideated, it’s time to narrow down to the correct solution.
Use these problem-solving techniques when you want to help your team find consensus, compare possible solutions, and move towards taking action on a particular problem.
- Improved Solutions
- Four-Step Sketch
- 15% Solutions
- How-Now-Wow matrix
- Impact Effort Matrix
21. Mindspin
Brainstorming is part of the bread and butter of the problem-solving process and all problem-solving strategies benefit from getting ideas out and challenging a team to generate solutions quickly.
With Mindspin, participants are encouraged not only to generate ideas but to do so under time constraints and by slamming down cards and passing them on. By doing multiple rounds, your team can begin with a free generation of possible solutions before moving on to developing those solutions and encouraging further ideation.
This is one of our favorite problem-solving activities and can be great for keeping the energy up throughout the workshop. Remember the importance of helping people become engaged in the process – energizing problem-solving techniques like Mindspin can help ensure your team stays engaged and happy, even when the problems they’re coming together to solve are complex.
MindSpin #teampedia #idea generation #problem solving #action A fast and loud method to enhance brainstorming within a team. Since this activity has more than round ideas that are repetitive can be ruled out leaving more creative and innovative answers to the challenge.
22. Improved Solutions
After a team has successfully identified a problem and come up with a few solutions, it can be tempting to call the work of the problem-solving process complete. That said, the first solution is not necessarily the best, and by including a further review and reflection activity into your problem-solving model, you can ensure your group reaches the best possible result.
One of a number of problem-solving games from Thiagi Group, Improved Solutions helps you go the extra mile and develop suggested solutions with close consideration and peer review. By supporting the discussion of several problems at once and by shifting team roles throughout, this problem-solving technique is a dynamic way of finding the best solution.
Improved Solutions #creativity #thiagi #problem solving #action #team You can improve any solution by objectively reviewing its strengths and weaknesses and making suitable adjustments. In this creativity framegame, you improve the solutions to several problems. To maintain objective detachment, you deal with a different problem during each of six rounds and assume different roles (problem owner, consultant, basher, booster, enhancer, and evaluator) during each round. At the conclusion of the activity, each player ends up with two solutions to her problem.
23. Four Step Sketch
Creative thinking and visual ideation does not need to be confined to the opening stages of your problem-solving strategies. Exercises that include sketching and prototyping on paper can be effective at the solution finding and development stage of the process, and can be great for keeping a team engaged.
By going from simple notes to a crazy 8s round that involves rapidly sketching 8 variations on their ideas before then producing a final solution sketch, the group is able to iterate quickly and visually. Problem-solving techniques like Four-Step Sketch are great if you have a group of different thinkers and want to change things up from a more textual or discussion-based approach.
Four-Step Sketch #design sprint #innovation #idea generation #remote-friendly The four-step sketch is an exercise that helps people to create well-formed concepts through a structured process that includes: Review key information Start design work on paper, Consider multiple variations , Create a detailed solution . This exercise is preceded by a set of other activities allowing the group to clarify the challenge they want to solve. See how the Four Step Sketch exercise fits into a Design Sprint
24. 15% Solutions
Some problems are simpler than others and with the right problem-solving activities, you can empower people to take immediate actions that can help create organizational change.
Part of the liberating structures toolkit, 15% solutions is a problem-solving technique that focuses on finding and implementing solutions quickly. A process of iterating and making small changes quickly can help generate momentum and an appetite for solving complex problems.
Problem-solving strategies can live and die on whether people are onboard. Getting some quick wins is a great way of getting people behind the process.
It can be extremely empowering for a team to realize that problem-solving techniques can be deployed quickly and easily and delineate between things they can positively impact and those things they cannot change.
15% Solutions #action #liberating structures #remote-friendly You can reveal the actions, however small, that everyone can do immediately. At a minimum, these will create momentum, and that may make a BIG difference. 15% Solutions show that there is no reason to wait around, feel powerless, or fearful. They help people pick it up a level. They get individuals and the group to focus on what is within their discretion instead of what they cannot change. With a very simple question, you can flip the conversation to what can be done and find solutions to big problems that are often distributed widely in places not known in advance. Shifting a few grains of sand may trigger a landslide and change the whole landscape.
25. How-Now-Wow Matrix
The problem-solving process is often creative, as complex problems usually require a change of thinking and creative response in order to find the best solutions. While it’s common for the first stages to encourage creative thinking, groups can often gravitate to familiar solutions when it comes to the end of the process.
When selecting solutions, you don’t want to lose your creative energy! The How-Now-Wow Matrix from Gamestorming is a great problem-solving activity that enables a group to stay creative and think out of the box when it comes to selecting the right solution for a given problem.
Problem-solving techniques that encourage creative thinking and the ideation and selection of new solutions can be the most effective in organisational change. Give the How-Now-Wow Matrix a go, and not just for how pleasant it is to say out loud.
How-Now-Wow Matrix #gamestorming #idea generation #remote-friendly When people want to develop new ideas, they most often think out of the box in the brainstorming or divergent phase. However, when it comes to convergence, people often end up picking ideas that are most familiar to them. This is called a ‘creative paradox’ or a ‘creadox’. The How-Now-Wow matrix is an idea selection tool that breaks the creadox by forcing people to weigh each idea on 2 parameters.
26. Impact and Effort Matrix
All problem-solving techniques hope to not only find solutions to a given problem or challenge but to find the best solution. When it comes to finding a solution, groups are invited to put on their decision-making hats and really think about how a proposed idea would work in practice.
The Impact and Effort Matrix is one of the problem-solving techniques that fall into this camp, empowering participants to first generate ideas and then categorize them into a 2×2 matrix based on impact and effort.
Activities that invite critical thinking while remaining simple are invaluable. Use the Impact and Effort Matrix to move from ideation and towards evaluating potential solutions before then committing to them.
Impact and Effort Matrix #gamestorming #decision making #action #remote-friendly In this decision-making exercise, possible actions are mapped based on two factors: effort required to implement and potential impact. Categorizing ideas along these lines is a useful technique in decision making, as it obliges contributors to balance and evaluate suggested actions before committing to them.
27. Dotmocracy
If you’ve followed each of the problem-solving steps with your group successfully, you should move towards the end of your process with heaps of possible solutions developed with a specific problem in mind. But how do you help a group go from ideation to putting a solution into action?
Dotmocracy – or Dot Voting -is a tried and tested method of helping a team in the problem-solving process make decisions and put actions in place with a degree of oversight and consensus.
One of the problem-solving techniques that should be in every facilitator’s toolbox, Dot Voting is fast and effective and can help identify the most popular and best solutions and help bring a group to a decision effectively.
Dotmocracy #action #decision making #group prioritization #hyperisland #remote-friendly Dotmocracy is a simple method for group prioritization or decision-making. It is not an activity on its own, but a method to use in processes where prioritization or decision-making is the aim. The method supports a group to quickly see which options are most popular or relevant. The options or ideas are written on post-its and stuck up on a wall for the whole group to see. Each person votes for the options they think are the strongest, and that information is used to inform a decision.
All facilitators know that warm-ups and icebreakers are useful for any workshop or group process. Problem-solving workshops are no different.
Use these problem-solving techniques to warm up a group and prepare them for the rest of the process. Activating your group by tapping into some of the top problem-solving skills can be one of the best ways to see great outcomes from your session.
- Check-in/Check-out
- Doodling Together
- Show and Tell
- Constellations
- Draw a Tree
28. Check-in / Check-out
Solid processes are planned from beginning to end, and the best facilitators know that setting the tone and establishing a safe, open environment can be integral to a successful problem-solving process.
Check-in / Check-out is a great way to begin and/or bookend a problem-solving workshop. Checking in to a session emphasizes that everyone will be seen, heard, and expected to contribute.
If you are running a series of meetings, setting a consistent pattern of checking in and checking out can really help your team get into a groove. We recommend this opening-closing activity for small to medium-sized groups though it can work with large groups if they’re disciplined!
Check-in / Check-out #team #opening #closing #hyperisland #remote-friendly Either checking-in or checking-out is a simple way for a team to open or close a process, symbolically and in a collaborative way. Checking-in/out invites each member in a group to be present, seen and heard, and to express a reflection or a feeling. Checking-in emphasizes presence, focus and group commitment; checking-out emphasizes reflection and symbolic closure.
29. Doodling Together
Thinking creatively and not being afraid to make suggestions are important problem-solving skills for any group or team, and warming up by encouraging these behaviors is a great way to start.
Doodling Together is one of our favorite creative ice breaker games – it’s quick, effective, and fun and can make all following problem-solving steps easier by encouraging a group to collaborate visually. By passing cards and adding additional items as they go, the workshop group gets into a groove of co-creation and idea development that is crucial to finding solutions to problems.
Doodling Together #collaboration #creativity #teamwork #fun #team #visual methods #energiser #icebreaker #remote-friendly Create wild, weird and often funny postcards together & establish a group’s creative confidence.
30. Show and Tell
You might remember some version of Show and Tell from being a kid in school and it’s a great problem-solving activity to kick off a session.
Asking participants to prepare a little something before a workshop by bringing an object for show and tell can help them warm up before the session has even begun! Games that include a physical object can also help encourage early engagement before moving onto more big-picture thinking.
By asking your participants to tell stories about why they chose to bring a particular item to the group, you can help teams see things from new perspectives and see both differences and similarities in the way they approach a topic. Great groundwork for approaching a problem-solving process as a team!
Show and Tell #gamestorming #action #opening #meeting facilitation Show and Tell taps into the power of metaphors to reveal players’ underlying assumptions and associations around a topic The aim of the game is to get a deeper understanding of stakeholders’ perspectives on anything—a new project, an organizational restructuring, a shift in the company’s vision or team dynamic.
31. Constellations
Who doesn’t love stars? Constellations is a great warm-up activity for any workshop as it gets people up off their feet, energized, and ready to engage in new ways with established topics. It’s also great for showing existing beliefs, biases, and patterns that can come into play as part of your session.
Using warm-up games that help build trust and connection while also allowing for non-verbal responses can be great for easing people into the problem-solving process and encouraging engagement from everyone in the group. Constellations is great in large spaces that allow for movement and is definitely a practical exercise to allow the group to see patterns that are otherwise invisible.
Constellations #trust #connection #opening #coaching #patterns #system Individuals express their response to a statement or idea by standing closer or further from a central object. Used with teams to reveal system, hidden patterns, perspectives.
32. Draw a Tree
Problem-solving games that help raise group awareness through a central, unifying metaphor can be effective ways to warm-up a group in any problem-solving model.
Draw a Tree is a simple warm-up activity you can use in any group and which can provide a quick jolt of energy. Start by asking your participants to draw a tree in just 45 seconds – they can choose whether it will be abstract or realistic.
Once the timer is up, ask the group how many people included the roots of the tree and use this as a means to discuss how we can ignore important parts of any system simply because they are not visible.
All problem-solving strategies are made more effective by thinking of problems critically and by exposing things that may not normally come to light. Warm-up games like Draw a Tree are great in that they quickly demonstrate some key problem-solving skills in an accessible and effective way.
Draw a Tree #thiagi #opening #perspectives #remote-friendly With this game you can raise awarness about being more mindful, and aware of the environment we live in.
Each step of the problem-solving workshop benefits from an intelligent deployment of activities, games, and techniques. Bringing your session to an effective close helps ensure that solutions are followed through on and that you also celebrate what has been achieved.
Here are some problem-solving activities you can use to effectively close a workshop or meeting and ensure the great work you’ve done can continue afterward.
- One Breath Feedback
- Who What When Matrix
- Response Cards
How do I conclude a problem-solving process?
All good things must come to an end. With the bulk of the work done, it can be tempting to conclude your workshop swiftly and without a moment to debrief and align. This can be problematic in that it doesn’t allow your team to fully process the results or reflect on the process.
At the end of an effective session, your team will have gone through a process that, while productive, can be exhausting. It’s important to give your group a moment to take a breath, ensure that they are clear on future actions, and provide short feedback before leaving the space.
The primary purpose of any problem-solving method is to generate solutions and then implement them. Be sure to take the opportunity to ensure everyone is aligned and ready to effectively implement the solutions you produced in the workshop.
Remember that every process can be improved and by giving a short moment to collect feedback in the session, you can further refine your problem-solving methods and see further success in the future too.
33. One Breath Feedback
Maintaining attention and focus during the closing stages of a problem-solving workshop can be tricky and so being concise when giving feedback can be important. It’s easy to incur “death by feedback” should some team members go on for too long sharing their perspectives in a quick feedback round.
One Breath Feedback is a great closing activity for workshops. You give everyone an opportunity to provide feedback on what they’ve done but only in the space of a single breath. This keeps feedback short and to the point and means that everyone is encouraged to provide the most important piece of feedback to them.
One breath feedback #closing #feedback #action This is a feedback round in just one breath that excels in maintaining attention: each participants is able to speak during just one breath … for most people that’s around 20 to 25 seconds … unless of course you’ve been a deep sea diver in which case you’ll be able to do it for longer.
34. Who What When Matrix
Matrices feature as part of many effective problem-solving strategies and with good reason. They are easily recognizable, simple to use, and generate results.
The Who What When Matrix is a great tool to use when closing your problem-solving session by attributing a who, what and when to the actions and solutions you have decided upon. The resulting matrix is a simple, easy-to-follow way of ensuring your team can move forward.
Great solutions can’t be enacted without action and ownership. Your problem-solving process should include a stage for allocating tasks to individuals or teams and creating a realistic timeframe for those solutions to be implemented or checked out. Use this method to keep the solution implementation process clear and simple for all involved.
Who/What/When Matrix #gamestorming #action #project planning With Who/What/When matrix, you can connect people with clear actions they have defined and have committed to.
35. Response cards
Group discussion can comprise the bulk of most problem-solving activities and by the end of the process, you might find that your team is talked out!
Providing a means for your team to give feedback with short written notes can ensure everyone is head and can contribute without the need to stand up and talk. Depending on the needs of the group, giving an alternative can help ensure everyone can contribute to your problem-solving model in the way that makes the most sense for them.
Response Cards is a great way to close a workshop if you are looking for a gentle warm-down and want to get some swift discussion around some of the feedback that is raised.
Response Cards #debriefing #closing #structured sharing #questions and answers #thiagi #action It can be hard to involve everyone during a closing of a session. Some might stay in the background or get unheard because of louder participants. However, with the use of Response Cards, everyone will be involved in providing feedback or clarify questions at the end of a session.
Save time and effort discovering the right solutions
A structured problem solving process is a surefire way of solving tough problems, discovering creative solutions and driving organizational change. But how can you design for successful outcomes?
With SessionLab, it’s easy to design engaging workshops that deliver results. Drag, drop and reorder blocks to build your agenda. When you make changes or update your agenda, your session timing adjusts automatically , saving you time on manual adjustments.
Collaborating with stakeholders or clients? Share your agenda with a single click and collaborate in real-time. No more sending documents back and forth over email.
Explore how to use SessionLab to design effective problem solving workshops or watch this five minute video to see the planner in action!

Over to you
The problem-solving process can often be as complicated and multifaceted as the problems they are set-up to solve. With the right problem-solving techniques and a mix of creative exercises designed to guide discussion and generate purposeful ideas, we hope we’ve given you the tools to find the best solutions as simply and easily as possible.
Is there a problem-solving technique that you are missing here? Do you have a favorite activity or method you use when facilitating? Let us know in the comments below, we’d love to hear from you!
thank you very much for these excellent techniques
Certainly wonderful article, very detailed. Shared!
Your list of techniques for problem solving can be helpfully extended by adding TRIZ to the list of techniques. TRIZ has 40 problem solving techniques derived from methods inventros and patent holders used to get new patents. About 10-12 are general approaches. many organization sponsor classes in TRIZ that are used to solve business problems or general organiztational problems. You can take a look at TRIZ and dwonload a free internet booklet to see if you feel it shound be included per your selection process.
Leave a Comment Cancel reply
Your email address will not be published. Required fields are marked *
Going from a mere idea to a workshop that delivers results for your clients can feel like a daunting task. In this piece, we will shine a light on all the work behind the scenes and help you learn how to plan a workshop from start to finish. On a good day, facilitation can feel like effortless magic, but that is mostly the result of backstage work, foresight, and a lot of careful planning. Read on to learn a step-by-step approach to breaking the process of planning a workshop into small, manageable chunks. The flow starts with the first meeting with a client to define the purposes of a workshop.…

How does learning work? A clever 9-year-old once told me: “I know I am learning something new when I am surprised.” The science of adult learning tells us that, in order to learn new skills (which, unsurprisingly, is harder for adults to do than kids) grown-ups need to first get into a specific headspace. In a business, this approach is often employed in a training session where employees learn new skills or work on professional development. But how do you ensure your training is effective? In this guide, we'll explore how to create an effective training session plan and run engaging training sessions. As team leader, project manager, or consultant,…

Effective online tools are a necessity for smooth and engaging virtual workshops and meetings. But how do you choose the right ones? Do you sometimes feel that the good old pen and paper or MS Office toolkit and email leaves you struggling to stay on top of managing and delivering your workshop? Fortunately, there are plenty of online tools to make your life easier when you need to facilitate a meeting and lead workshops. In this post, we’ll share our favorite online tools you can use to make your job as a facilitator easier. In fact, there are plenty of free online workshop tools and meeting facilitation software you can…
Design your next workshop with SessionLab
Join the 150,000 facilitators using SessionLab
Sign up for free

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
8.2 Problem-Solving: Heuristics and Algorithms
Learning objectives.
- Describe the differences between heuristics and algorithms in information processing.
When faced with a problem to solve, should you go with intuition or with more measured, logical reasoning? Obviously, we use both of these approaches. Some of the decisions we make are rapid, emotional, and automatic. Daniel Kahneman (2011) calls this “fast” thinking. By definition, fast thinking saves time. For example, you may quickly decide to buy something because it is on sale; your fast brain has perceived a bargain, and you go for it quickly. On the other hand, “slow” thinking requires more effort; applying this in the same scenario might cause us not to buy the item because we have reasoned that we don’t really need it, that it is still too expensive, and so on. Using slow and fast thinking does not guarantee good decision-making if they are employed at the wrong time. Sometimes it is not clear which is called for, because many decisions have a level of uncertainty built into them. In this section, we will explore some of the applications of these tendencies to think fast or slow.
We will look further into our thought processes, more specifically, into some of the problem-solving strategies that we use. Heuristics are information-processing strategies that are useful in many cases but may lead to errors when misapplied. A heuristic is a principle with broad application, essentially an educated guess about something. We use heuristics all the time, for example, when deciding what groceries to buy from the supermarket, when looking for a library book, when choosing the best route to drive through town to avoid traffic congestion, and so on. Heuristics can be thought of as aids to decision making; they allow us to reach a solution without a lot of cognitive effort or time.
The benefit of heuristics in helping us reach decisions fairly easily is also the potential downfall: the solution provided by the use of heuristics is not necessarily the best one. Let’s consider some of the most frequently applied, and misapplied, heuristics in the table below.
In many cases, we base our judgments on information that seems to represent, or match, what we expect will happen, while ignoring other potentially more relevant statistical information. When we do so, we are using the representativeness heuristic . Consider, for instance, the data presented in the table below. Let’s say that you went to a hospital, and you checked the records of the babies that were born on that given day. Which pattern of births do you think you are most likely to find?
Most people think that list B is more likely, probably because list B looks more random, and matches — or is “representative of” — our ideas about randomness, but statisticians know that any pattern of four girls and four boys is mathematically equally likely. Whether a boy or girl is born first has no bearing on what sex will be born second; these are independent events, each with a 50:50 chance of being a boy or a girl. The problem is that we have a schema of what randomness should be like, which does not always match what is mathematically the case. Similarly, people who see a flipped coin come up “heads” five times in a row will frequently predict, and perhaps even wager money, that “tails” will be next. This behaviour is known as the gambler’s fallacy . Mathematically, the gambler’s fallacy is an error: the likelihood of any single coin flip being “tails” is always 50%, regardless of how many times it has come up “heads” in the past.
The representativeness heuristic may explain why we judge people on the basis of appearance. Suppose you meet your new next-door neighbour, who drives a loud motorcycle, has many tattoos, wears leather, and has long hair. Later, you try to guess their occupation. What comes to mind most readily? Are they a teacher? Insurance salesman? IT specialist? Librarian? Drug dealer? The representativeness heuristic will lead you to compare your neighbour to the prototypes you have for these occupations and choose the one that they seem to represent the best. Thus, your judgment is affected by how much your neibour seems to resemble each of these groups. Sometimes these judgments are accurate, but they often fail because they do not account for base rates , which is the actual frequency with which these groups exist. In this case, the group with the lowest base rate is probably drug dealer.
Our judgments can also be influenced by how easy it is to retrieve a memory. The tendency to make judgments of the frequency or likelihood that an event occurs on the basis of the ease with which it can be retrieved from memory is known as the availability heuristic (MacLeod & Campbell, 1992; Tversky & Kahneman, 1973). Imagine, for instance, that I asked you to indicate whether there are more words in the English language that begin with the letter “R” or that have the letter “R” as the third letter. You would probably answer this question by trying to think of words that have each of the characteristics, thinking of all the words you know that begin with “R” and all that have “R” in the third position. Because it is much easier to retrieve words by their first letter than by their third, we may incorrectly guess that there are more words that begin with “R,” even though there are in fact more words that have “R” as the third letter.
The availability heuristic may explain why we tend to overestimate the likelihood of crimes or disasters; those that are reported widely in the news are more readily imaginable, and therefore, we tend to overestimate how often they occur. Things that we find easy to imagine, or to remember from watching the news, are estimated to occur frequently. Anything that gets a lot of news coverage is easy to imagine. Availability bias does not just affect our thinking. It can change behaviour. For example, homicides are usually widely reported in the news, leading people to make inaccurate assumptions about the frequency of murder. In Canada, the murder rate has dropped steadily since the 1970s (Statistics Canada, 2018), but this information tends not to be reported, leading people to overestimate the probability of being affected by violent crime. In another example, doctors who recently treated patients suffering from a particular condition were more likely to diagnose the condition in subsequent patients because they overestimated the prevalence of the condition (Poses & Anthony, 1991).
The anchoring and adjustment heuristic is another example of how fast thinking can lead to a decision that might not be optimal. Anchoring and adjustment is easily seen when we are faced with buying something that does not have a fixed price. For example, if you are interested in a used car, and the asking price is $10,000, what price do you think you might offer? Using $10,000 as an anchor, you are likely to adjust your offer from there, and perhaps offer $9000 or $9500. Never mind that $10,000 may not be a reasonable anchoring price. Anchoring and adjustment does not just happen when we’re buying something. It can also be used in any situation that calls for judgment under uncertainty, such as sentencing decisions in criminal cases (Bennett, 2014), and it applies to groups as well as individuals (Rutledge, 1993).
In contrast to heuristics, which can be thought of as problem-solving strategies based on educated guesses, algorithms are problem-solving strategies that use rules. Algorithms are generally a logical set of steps that, if applied correctly, should be accurate. For example, you could make a cake using heuristics — relying on your previous baking experience and guessing at the number and amount of ingredients, baking time, and so on — or using an algorithm. The latter would require a recipe which would provide step-by-step instructions; the recipe is the algorithm. Unless you are an extremely accomplished baker, the algorithm should provide you with a better cake than using heuristics would. While heuristics offer a solution that might be correct, a correctly applied algorithm is guaranteed to provide a correct solution. Of course, not all problems can be solved by algorithms.
As with heuristics, the use of algorithmic processing interacts with behaviour and emotion. Understanding what strategy might provide the best solution requires knowledge and experience. As we will see in the next section, we are prone to a number of cognitive biases that persist despite knowledge and experience.
Key Takeaways
- We use a variety of shortcuts in our information processing, such as the representativeness, availability, and anchoring and adjustment heuristics. These help us to make fast judgments but may lead to errors.
- Algorithms are problem-solving strategies that are based on rules rather than guesses. Algorithms, if applied correctly, are far less likely to result in errors or incorrect solutions than heuristics. Algorithms are based on logic.
Bennett, M. W. (2014). Confronting cognitive ‘anchoring effect’ and ‘blind spot’ biases in federal sentencing: A modest solution for reforming and fundamental flaw. Journal of Criminal Law and Criminology , 104 (3), 489-534.
Kahneman, D. (2011). Thinking, fast and slow. New York, NY: Farrar, Straus and Giroux.
MacLeod, C., & Campbell, L. (1992). Memory accessibility and probability judgments: An experimental evaluation of the availability heuristic. Journal of Personality and Social Psychology, 63 (6), 890–902.
Poses, R. M., & Anthony, M. (1991). Availability, wishful thinking, and physicians’ diagnostic judgments for patients with suspected bacteremia. Medical Decision Making, 11 , 159-68.
Rutledge, R. W. (1993). The effects of group decisions and group-shifts on use of the anchoring and adjustment heuristic. Social Behavior and Personality, 21 (3), 215-226.
Statistics Canada. (2018). Ho micide in Canada, 2017 . Retrieved from https://www150.statcan.gc.ca/n1/en/daily-quotidien/181121/dq181121a-eng.pdf
Tversky, A., & Kahneman, D. (1973). Availability: A heuristic for judging frequency and probability. Cognitive Psychology, 5 , 207–232.
Psychology - 1st Canadian Edition Copyright © 2020 by Sally Walters is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

18.12: Chapter 14- Problem Solving, Categories and Concepts
- Last updated
- Save as PDF
- Page ID 113223
This page is a draft and under active development. Please forward any questions, comments, and/or feedback to the ASCCC OERI ( [email protected] ).

- Kenneth A. Koenigshofer
- ASCCC Open Educational Resources Initiative (OERI)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Learning Objectives
- Define problem types
- Describe problem solving strategies
- Define algorithm and heuristic
- Describe the role of insight in problem solving
- Explain some common roadblocks to effective problem solving
- What is meant by a search problem
- Describe means-ends analysis
- How do analogies and restructuring contribute to problem solving
- Explain how experts solve problems and what gives them an advantage over non-experts
- Describe the brain mechanisms in problem solving
In this section we examine problem-solving strategies. People face problems every day—usually, multiple problems throughout the day. Sometimes these problems are straightforward: To double a recipe for pizza dough, for example, all that is required is that each ingredient in the recipe be doubled. Sometimes, however, the problems we encounter are more complex. For example, say you have a work deadline, and you must mail a printed copy of a report to your supervisor by the end of the business day. The report is time-sensitive and must be sent overnight. You finished the report last night, but your printer will not work today. What should you do? First, you need to identify the problem and then apply a strategy, usually a set of steps, for solving the problem.
Defining Problems
We begin this module on Problem Solving by giving a short description of what psychologists regard as a problem. Afterwards we are going to present different approaches towards problem solving, starting with gestalt psychologists and ending with modern search strategies connected to artificial intelligence. In addition we will also consider how experts do solve problems and finally we will have a closer look at two topics: The neurophysiological background on the one hand and the question what kind of role can be assigned to evolution regarding problem solving on the other.
The most basic definition is “A problem is any given situation that differs from a desired goal”. This definition is very useful for discussing problem solving in terms of evolutionary adaptation, as it allows to understand every aspect of (human or animal) life as a problem. This includes issues like finding food in harsh winters, remembering where you left your provisions, making decisions about which way to go, repeating and varying all kinds of complex movements by learning, and so on. Though all these problems were of crucial importance during the evolutionary process that created us the way we are, they are by no means solved exclusively by humans. We find a most amazing variety of different solutions for these problems of adaptation in animals as well (just consider, e.g., by which means a bat hunts its prey, compared to a spider ).
However, for this module, we will mainly focus on abstract problems that humans may encounter (e.g. playing chess or doing an assignment in college). Furthermore, we will not consider those situations as abstract problems that have an obvious solution: Imagine a college student, let's call him Knut. Knut decides to take a sip of coffee from the mug next to his right hand. He does not even have to think about how to do this. This is not because the situation itself is trivial (a robot capable of recognizing the mug, deciding whether it is full, then grabbing it and moving it to Knut’s mouth would be a highly complex machine) but because in the context of all possible situations it is so trivial that it no longer is a problem our consciousness needs to be bothered with. The problems we will discuss in the following all need some conscious effort, though some seem to be solved without us being able to say how exactly we got to the solution. Still we will find that often the strategies we use to solve these problems are applicable to more basic problems, as well as the more abstract ones such as completing a reading or writing assignment for a college class.
Non-trivial, abstract problems can be divided into two groups:
Well-defined Problems
For many abstract problems it is possible to find an algorithmic solution. We call all those problems well-defined that can be properly formalized, which comes along with the following properties:
- The problem has a clearly defined given state. This might be the line-up of a chess game, a given formula you have to solve, or the set-up of the towers of Hanoi game (which we will discuss later ).
- There is a finite set of operators, that is, of rules you may apply to the given state. For the chess game, e.g., these would be the rules that tell you which piece you may move to which position.
- Finally, the problem has a clear goal state: The equations is resolved to x, all discs are moved to the right stack, or the other player is in checkmate.
Not surprisingly, a problem that fulfills these requirements can be implemented algorithmically (also see convergent thinking ). Therefore many well-defined problems can be very effectively solved by computers, like playing chess.
Ill-defined Problems
Though many problems can be properly formalized (sometimes only if we accept an enormous complexity) there are still others where this is not the case. Good examples for this are all kinds of tasks that involve creativity , and, generally speaking, all problems for which it is not possible to clearly define a given state and a goal state: Formalizing a problem of the kind “Please paint a beautiful picture” may be impossible. Still this is a problem most people would be able to access in one way or the other, even if the result may be totally different from person to person. And while Knut might judge that picture X is gorgeous, you might completely disagree.
Nevertheless ill-defined problems often involve sub-problems that can be totally well-defined. On the other hand, many every-day problems that seem to be completely well-defined involve a great deal of creativity and many ambiguities. For example, suppose Knut has to read some technical material and then write an essay about it.
If we think of Knut's fairly ill-defined task of writing an essay, he will not be able to complete this task without first understanding the text he has to write about. This step is the first sub-goal Knut has to solve. Interestingly, ill-defined problems often involve subproblems that are well-defined.
Knut’s situation could be explained as a classical example of problem solving: He needs to get from his present state – an unfinished assignment – to a goal state - a completed assignment - and has certain operators to achieve that goal. Both Knut’s short and long term memory are active. He needs his short term memory to integrate what he is reading with the information from earlier passages of the paper. His long term memory helps him remember what he learned in the lectures he took and what he read in other books. And of course Knut’s ability to comprehend language enables him to make sense of the letters printed on the paper and to relate the sentences in a proper way.
Same place, different day. Knut is sitting at his desk again, staring at a blank paper in front of him, while nervously playing with a pen in his right hand. Just a few hours left to hand in his essay and he has not written a word. All of a sudden he smashes his fist on the table and cries out: "I need a plan!
How is a problem represented in the mind?
Generally speaking, problem representations are models of the situation as experienced by the agent. Representing a problem means to analyze it and split it into separate components:
- objects, predicates
- state space
- selection criteria
Therefore the efficiency of Problem Solving depends on the underlying representations in a person’s mind. Analyzing the problem domain according to different dimensions, i.e., changing from one representation to another, results in arriving at a new understanding of a problem. This is basically what is described as restructuring.
There are two very different ways of approaching a goal-oriented situation . In one case an organism readily reproduces the response to the given problem from past experience. This is called reproductive thinking .
The second way requires something new and different to achieve the goal, prior learning is of little help here. Such productive thinking is (sometimes) argued to involve insight . Gestalt psychologists even state that insight problems are a separate category of problems in their own right.
Tasks that might involve insight usually have certain features – they require something new and non-obvious to be done and in most cases they are difficult enough to predict that the initial solution attempt will be unsuccessful. When you solve a problem of this kind you often have a so called "AHA-experience" – the solution pops up all of a sudden. At one time you do not have any ideas of the answer to the problem, you do not even feel to make any progress trying out different ideas, but in the next second the problem is solved.
Sometimes, previous experience or familiarity can even make problem solving more difficult. This is the case whenever habitual directions get in the way of finding new directions – an effect called fixation .
Functional fixedness
Functional fixedness concerns the solution of object-use problems . The basic idea is that when the usual way of using an object is emphasised, it will be far more difficult for a person to use that object in a novel manner.
An example is the two-string problem : Knut is left in a room with a chair and a pair of pliers given the task to bind two strings together that are hanging from the ceiling. The problem he faces is that he can never reach both strings at a time because they are just too far away from each other. What can Knut do?
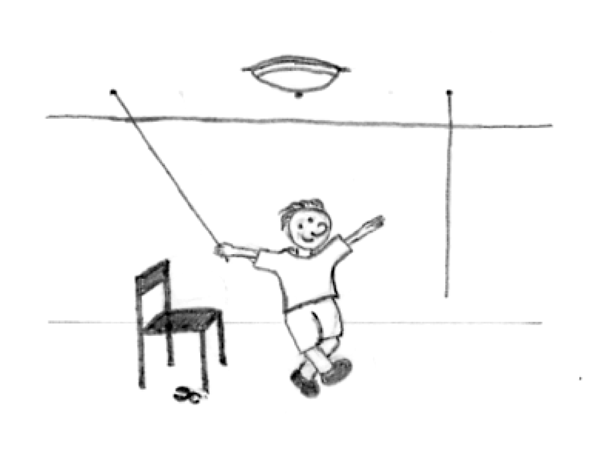
Figure \(\PageIndex{1}\): Put the two strings together by tying the pliers to one of the strings and then swing it toward the other one.
Mental fixedness
Functional fixedness as involved in the examples above illustrates a mental set – a person’s tendency to respond to a given task in a manner based on past experience. Because Knut maps an object to a particular function he has difficulties to vary the way of use (pliers as pendulum's weight).
Problem-Solving Strategies
When you are presented with a problem—whether it is a complex mathematical problem or a broken printer, how do you solve it? Before finding a solution to the problem, the problem must first be clearly identified. After that, one of many problem solving strategies can be applied, hopefully resulting in a solution. Regardless of strategy, you will likely be guided, consciously or unconsciously, by your knowledge of cause-effect relations among the elements of the problem and the similarity of the problem to previous problems you have solved before. As discussed in earlier sections of this chapter, innate dispositions of the brain to look for and represent causal and similarity relations are key components of general intelligence (Koenigshofer, 2017).
A problem-solving strategy is a plan of action used to find a solution. Different strategies have different action plans associated with them. For example, a well-known strategy is trial and error. The old adage, “If at first you don’t succeed, try, try again” describes trial and error. In terms of your broken printer, you could try checking the ink levels, and if that doesn’t work, you could check to make sure the paper tray isn’t jammed. Or maybe the printer isn’t actually connected to your laptop. When using trial and error, you would continue to try different solutions until you solved your problem. Although trial and error is not typically one of the most time-efficient strategies, it is a commonly used one.
Another type of strategy is an algorithm. An algorithm is a problem-solving formula that provides you with step-by-step instructions used to achieve a desired outcome (Kahneman, 2011). You can think of an algorithm as a recipe with highly detailed instructions that produce the same result every time they are performed. Algorithms are used frequently in our everyday lives, especially in computer science. When you run a search on the Internet, search engines like Google use algorithms to decide which entries will appear first in your list of results. Facebook also uses algorithms to decide which posts to display on your newsfeed. Can you identify other situations in which algorithms are used?
A heuristic is another type of problem solving strategy. While an algorithm must be followed exactly to produce a correct result, a heuristic is a general problem-solving framework (Tversky & Kahneman, 1974). You can think of these as mental shortcuts that are used to solve problems. A “rule of thumb” is an example of a heuristic. Such a rule saves the person time and energy when making a decision, but despite its time-saving characteristics, it is not always the best method for making a rational decision. Different types of heuristics are used in different types of situations, but the impulse to use a heuristic occurs when one of five conditions is met (Pratkanis, 1989):
- When one is faced with too much information
- When the time to make a decision is limited
- When the decision to be made is unimportant
- When there is access to very little information to use in making the decision
- When an appropriate heuristic happens to come to mind in the same moment
Working backwards is a useful heuristic in which you begin solving the problem by focusing on the end result. Consider this example: You live in Washington, D.C. and have been invited to a wedding at 4 PM on Saturday in Philadelphia. Knowing that Interstate 95 tends to back up any day of the week, you need to plan your route and time your departure accordingly. If you want to be at the wedding service by 3:30 PM, and it takes 2.5 hours to get to Philadelphia without traffic, what time should you leave your house? You use the working backwards heuristic to plan the events of your day on a regular basis, probably without even thinking about it.
Another useful heuristic is the practice of accomplishing a large goal or task by breaking it into a series of smaller steps. Students often use this common method to complete a large research project or long essay for school. For example, students typically brainstorm, develop a thesis or main topic, research the chosen topic, organize their information into an outline, write a rough draft, revise and edit the rough draft, develop a final draft, organize the references list, and proofread their work before turning in the project. The large task becomes less overwhelming when it is broken down into a series of small steps.
Problem Solving as a Search Problem
The idea of regarding problem solving as a search problem originated from Alan Newell and Herbert Simon while trying to design computer programs which could solve certain problems. This led them to develop a program called General Problem Solver which was able to solve any well-defined problem by creating heuristics on the basis of the user's input. This input consisted of objects and operations that could be done on them.
As we already know, every problem is composed of an initial state, intermediate states and a goal state (also: desired or final state), while the initial and goal states characterise the situations before and after solving the problem. The intermediate states describe any possible situation between initial and goal state. The set of operators builds up the transitions between the states. A solution is defined as the sequence of operators which leads from the initial state across intermediate states to the goal state.
The simplest method to solve a problem, defined in these terms, is to search for a solution by just trying one possibility after another (also called trial and error ).
As already mentioned above, an organised search, following a specific strategy, might not be helpful for finding a solution to some ill-defined problem, since it is impossible to formalise such problems in a way that a search algorithm can find a solution.
As an example we could just take Knut and his essay: he has to find out about his own opinion and formulate it and he has to make sure he understands the sources texts. But there are no predefined operators he can use, there is no panacea how to get to an opinion and even not how to write it down.
Means-End Analysis
In Means-End Analysis you try to reduce the difference between initial state and goal state by creating sub-goals until a sub-goal can be reached directly (in computer science, what is called recursion works on this basis).
An example of a problem that can be solved by Means-End Analysis is the " Towers of Hanoi "
Figure \(\PageIndex{2}\): Towers of Hanoi with 8 discs – A well defined problem (image from Wikimedia Commons; https://commons.wikimedia.org/wiki/F..._of_Hanoi.jpeg , by User:Evanherk .licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license).
The initial state of this problem is described by the different sized discs being stacked in order of size on the first of three pegs (the “start-peg“). The goal state is described by these discs being stacked on the third pegs (the “end-peg“) in exactly the same order.
Figure \(\PageIndex{3}\): This animation shows the solution of the game "Tower of Hanoi" with four discs. (image from Wikimedia Commons; https://commons.wikimedia.org/wiki/F...of_Hanoi_4.gif ; by André Karwath aka Aka ; licensed under the Creative Commons Attribution-Share Alike 2.5 Generic license).
There are three operators:
- You are allowed to move one single disc from one peg to another one
- You are only able to move a disc if it is on top of one stack
- A disc cannot be put onto a smaller one.
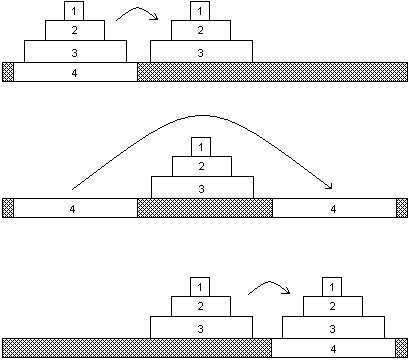
In order to use Means-End Analysis we have to create sub-goals. One possible way of doing this is described in the picture:
1. Moving the discs lying on the biggest one onto the second peg.
2. Shifting the biggest disc to the third peg.
3. Moving the other ones onto the third peg, too
You can apply this strategy again and again in order to reduce the problem to the case where you only have to move a single disc – which is then something you are allowed to do.
Strategies of this kind can easily be formulated for a computer; the respective algorithm for the Towers of Hanoi would look like this:
1. move n-1 discs from A to B
2. move disc #n from A to C
3. move n-1 discs from B to C
where n is the total number of discs, A is the first peg, B the second, C the third one. Now the problem is reduced by one with each recursive loop.
Means-end analysis is important to solve everyday-problems – like getting the right train connection: You have to figure out where you catch the first train and where you want to arrive, first of all. Then you have to look for possible changes just in case you do not get a direct connection. Third, you have to figure out what are the best times of departure and arrival, on which platforms you leave and arrive and make it all fit together.
Analogies describe similar structures and interconnect them to clarify and explain certain relations. In a recent study, for example, a song that got stuck in your head is compared to an itching of the brain that can only be scratched by repeating the song over and over again. Useful analogies appears to be based on a psychological mapping of relations between two very disparate types of problems that have abstract relations in common. Applied to STEM problems, Gray and Holyoak (2021) state: "Analogy is a powerful tool for fostering conceptual understanding and transfer in STEM and other fields. Well-constructed analogical comparisons focus attention on the causal-relational structure of STEM concepts, and provide a powerful capability to draw inferences based on a well-understood source domain that can be applied to a novel target domain." Note that similarity between problems of different types in their abstract relations, such as causation, is a key feature of reasoning, problem-solving and inference when forming and using analogies. Recall the discussion of general intelligence in module 14.2. There, similarity relations, causal relations, and predictive relations between events were identified as key components of general intelligence, along with ability to visualize in imagination possible future actions and their probable outcomes prior to commiting to actual behavior in the physical world (Koenigshofer, 2017).
Restructuring by Using Analogies
One special kind of restructuring, the way already mentioned during the discussion of the Gestalt approach, is analogical problem solving. Here, to find a solution to one problem – the so called target problem, an analogous solution to another problem – the source problem, is presented.
An example for this kind of strategy is the radiation problem posed by K. Duncker in 1945:
As a doctor you have to treat a patient with a malignant, inoperable tumour, buried deep inside the body. There exists a special kind of ray, which is perfectly harmless at a low intensity, but at the sufficient high intensity is able to destroy the tumour – as well as the healthy tissue on his way to it. What can be done to avoid the latter?
When this question was asked to participants in an experiment, most of them couldn't come up with the appropriate answer to the problem. Then they were told a story that went something like this:
A General wanted to capture his enemy's fortress. He gathered a large army to launch a full-scale direct attack, but then learned, that all the roads leading directly towards the fortress were blocked by mines. These roadblocks were designed in such a way, that it was possible for small groups of the fortress-owner's men to pass them safely, but every large group of men would initially set them off. Now the General figured out the following plan: He divided his troops into several smaller groups and made each of them march down a different road, timed in such a way, that the entire army would reunite exactly when reaching the fortress and could hit with full strength.
Here, the story about the General is the source problem, and the radiation problem is the target problem. The fortress is analogous to the tumour and the big army corresponds to the highly intensive ray. Consequently a small group of soldiers represents a ray at low intensity. The solution to the problem is to split the ray up, as the general did with his army, and send the now harmless rays towards the tumour from different angles in such a way that they all meet when reaching it. No healthy tissue is damaged but the tumour itself gets destroyed by the ray at its full intensity.
M. Gick and K. Holyoak presented Duncker's radiation problem to a group of participants in 1980 and 1983. Only 10 percent of them were able to solve the problem right away, 30 percent could solve it when they read the story of the general before. After given an additional hint – to use the story as help – 75 percent of them solved the problem.
With this results, Gick and Holyoak concluded, that analogical problem solving depends on three steps:
1. Noticing that an analogical connection exists between the source and the target problem. 2. Mapping corresponding parts of the two problems onto each other (fortress → tumour, army → ray, etc.) 3. Applying the mapping to generate a parallel solution to the target problem (using little groups of soldiers approaching from different directions → sending several weaker rays from different directions)
The concept that links the target problem with the analogy (the “source problem“) is called problem schema. Gick and Holyoak obtained the activation of a schema on their participants by giving them two stories and asking them to compare and summarize them. This activation of problem schemata is called “schema induction“.
The two presented texts were picked out of six stories which describe analogical problems and their solution. One of these stories was "The General."
After solving the task the participants were asked to solve the radiation problem. The experiment showed that in order to solve the target problem reading of two stories with analogical problems is more helpful than reading only one story: After reading two stories 52% of the participants were able to solve the radiation problem (only 30% were able to solve it after reading only one story, namely: “The General“).
The process of using a schema or analogy, i.e. applying it to a novel situation, is called transduction . One can use a common strategy to solve problems of a new kind.
To create a good schema and finally get to a solution using the schema is a problem-solving skill that requires practice and some background knowledge.
How Do Experts Solve Problems?
With the term expert we describe someone who devotes large amounts of his or her time and energy to one specific field of interest in which he, subsequently, reaches a certain level of mastery. It should not be of surprise that experts tend to be better in solving problems in their field than novices (people who are beginners or not as well trained in a field as experts) are. They are faster in coming up with solutions and have a higher success rate of right solutions. But what is the difference between the way experts and non-experts solve problems? Research on the nature of expertise has come up with the following conclusions:
When it comes to problems that are situated outside the experts' field, their performance often does not differ from that of novices.
Knowledge: An experiment by Chase and Simon (1973a, b) dealt with the question how well experts and novices are able to reproduce positions of chess pieces on chessboards when these are presented to them only briefly. The results showed that experts were far better in reproducing actual game positions, but that their performance was comparable with that of novices when the chess pieces were arranged randomly on the board. Chase and Simon concluded that the superior performance on actual game positions was due to the ability to recognize familiar patterns: A chess expert has up to 50,000 patterns stored in his memory. In comparison, a good player might know about 1,000 patterns by heart and a novice only few to none at all. This very detailed knowledge is of crucial help when an expert is confronted with a new problem in his field. Still, it is not pure size of knowledge that makes an expert more successful. Experts also organise their knowledge quite differently from novices.
Organization: In 1982 M. Chi and her co-workers took a set of 24 physics problems and presented them to a group of physics professors as well as to a group of students with only one semester of physics. The task was to group the problems based on their similarities. As it turned out the students tended to group the problems based on their surface structure (similarities of objects used in the problem, e.g. on sketches illustrating the problem), whereas the professors used their deep structure (the general physical principles that underlay the problems) as criteria. By recognizing the actual structure of a problem experts are able to connect the given task to the relevant knowledge they already have (e.g. another problem they solved earlier which required the same strategy).
Analysis: Experts often spend more time analyzing a problem before actually trying to solve it. This way of approaching a problem may often result in what appears to be a slow start, but in the long run this strategy is much more effective. A novice, on the other hand, might start working on the problem right away, but often has to realise that he reaches dead ends as he chose a wrong path in the very beginning.
Creative Cognition
Divergent thinking.
The term divergent thinking describes a way of thinking that does not lead to one goal, but is open-ended. Problems that are solved this way can have a large number of potential 'solutions' of which none is exactly 'right' or 'wrong', though some might be more suitable than others.
Solving a problem like this involves indirect and productive thinking and is mostly very helpful when somebody faces an ill-defined problem , i.e. when either initial state or goal state cannot be stated clearly and operators are either insufficient or not given at all.
The process of divergent thinking is often associated with creativity, and it undoubtedly leads to many creative ideas. Nevertheless, researches have shown that there is only modest correlation between performance on divergent thinking tasks and other measures of creativity. Additionally it was found that in processes resulting in original and practical inventions things like searching for solutions, being aware of structures and looking for analogies are heavily involved, too.
Figure \(\PageIndex{4}\): functional MRI images of the brains of musicians playing improvised jazz revealed that a large brain region involved in monitoring one's performance shuts down during creative improvisation, while a small region involved in organizing self-initiated thoughts and behaviors is highly activated (Image and modified caption from Wikimedia Commons. File:Creative Improvisation (24130148711).jpg; https://commons.wikimedia.org/wiki/F...130148711).jpg ; by NIH Image Gallery ; As a work of the U.S. federal government , the image is in the public domain .
Convergent Thinking
Convergent thinking patterns are problem solving techniques that unite different ideas or fields to find a solution. The focus of this mindset is speed, logic and accuracy, also identification of facts, reapplying existing techniques, gathering information. The most important factor of this mindset is: there is only one correct answer. You only think of two answers, namely right or wrong. This type of thinking is associated with certain science or standard procedures. People with this type of thinking have logical thinking, are able to memorize patterns, solve problems and work on scientific tests. Most school subjects sharpen this type of thinking ability.
Research shows that the creative process involves both types of thought processes.
Brain Mechanisms in Problem Solving
Presenting Neurophysiology in its entirety would be enough to fill several books. Instead, let's focus only on the aspects that are especially relevant to problem solving. Still, this topic is quite complex and problem solving cannot be attributed to one single brain area. Rather there are systems or networks of several brain areas working together to perform a specific problem solving task. This is best shown by an example, playing chess:
Table 2: Brain areas involved in a complex cognitive task.
One of the key tasks, namely planning and executing strategies , is performed by the prefrontal cortex (PFC) , which also plays an important role for several other tasks correlated with problem solving. This can be made clear from the effects of damage to the PFC on ability to solve problems.
Patients with a lesion in this brain area have difficulty switching from one behavioral pattern to another. A well known example is the wisconsin card-sorting task . A patient with a PFC lesion who is told to separate all blue cards from a deck, would continue sorting out the blue ones, even if the experimenter next told him to sort out all brown cards. Transferred to a more complex problem, this person would most likely fail, because he is not flexible enough to change his strategy after running into a dead end or when the problem changes.
Another example comes from a young homemaker, who had a tumour in the frontal lobe. Even though she was able to cook individual dishes, preparing a whole family meal was an impossible task for her.
Mushiake et al. (2009) note that to achieve a goal in a complex environment, such as problem‐solving situations like those above, we must plan multiple steps of action. When planning a series of actions, we have to anticipate future outcomes that will occur as a result of each action, and, in addition, we must mentally organize the temporal sequence of events in order to achieve the goal. These researchers investigated the role of lateral prefrontal cortex (PFC) in problem solving in monkeys. They found that "PFC neurons reflected final goals and immediate goals during the preparatory period. [They] also found some PFC neurons reflected each of all the forthcoming steps of actions during the preparatory period and they increased their [neural] activity step by step during the execution period. [Furthermore, they] found that the transient increase in synchronous activity of PFC neurons was involved in goal subgoal transformations. [They concluded] that the PFC is involved primarily in the dynamic representation of multiple future events that occur as a consequence of behavioral actions in problem‐solving situations" (Mushiake et al., 2009, p. 1). In other words, the prefrontal cortex represents in our imagination the sequence of events following each step that we take in solving a particular problem, guiding us step by step to the solution.
As the examples above illustrate, the structure of our brain is of great importance regarding problem solving, i.e. cognitive life. But how was our cognitive apparatus designed? How did perception-action integration as a central species-specific property of humans come about? The answer, as argued extensively in earlier sections of this book, is, of course, natural selection and other forces of genetic evolution. Clearly, animals and humans with genes facilitating brain organization that led to good problem solving skills would be favored by natural selection over genes responsible for brain organization less adept at solving problems. We became equipped with brains organized for effective problem solving because flexible abilities to solve a wide range of problems presented by the environment enhanced ability to survive, to compete for resources, to escape predators, and to reproduce (see chapter on Evolution and Genetics in this text).
In short, good problem solving mechanisms in brains designed for the real world gave a competitive advantage and increased biological fitness. Consequently, humans (and many other animals to a lesser degree) have "innate ability to problem-solve in the real world. Solving real world problems in real time given constraints posed by one's environment is crucial for survival . . . Real world problem solving (RWPS) is different from those that occur in a classroom or in a laboratory during an experiment. They are often dynamic and discontinuous, accompanied by many starts and stops . . . Real world problems are typically ill-defined, and even when they are well-defined, often have open-ended solutions . . . RWPS is quite messy and involves a tight interplay between problem solving, creativity, and insight . . . In psychology and neuroscience, problem-solving broadly refers to the inferential steps taken by an agent [human, animal, or computer] that leads from a given state of affairs to a desired goal state" (Sarathy, 2018, p. 261-2). According to Sarathy (2018), the initial stage of RWPS requires defining the problem and generating a representation of it in working memory. This stage involves activation of parts of the " prefrontal cortex (PFC) , default mode network (DMN) , and the dorsal anterior cingulate cortex (dACC) ." The DMN includes the medial prefrontal cortex , posterior cingulate cortex , and the inferior parietal lobule . Other structures sometimes considered part of the network are the lateral temporal cortex , hippocampal formation , and the precuneus . This network of structures is called "default mode" because these structures show increased activity when one is not engaged in focused, attentive, goal-directed actions, but rather a "resting state" (a baseline default state) and show decreased neural activity when one is focused and attentive to a particular goal-directed behavior (Raichle, et al., 2001).
Moral Reasoning
Jeurissen, et al., (2014) examined a special type of reasoning, moral reasoning, using TMS (Transcranial Magnetic Stimulation). The dorsolateral prefrontal cortex (DLPFC) and temporal-parietal junction (TPJ) have both been shown to be involved in moral judgments, but this study by Jeurissen, et al., (2014) uses TMS to tease out the different roles these brain areas play in different scenarios involving moral dilemmas.
Moral dilemmas have been categorized by researchers as moral-impersonal (e.g., trolley or switch dilemma-- save the lives of five workmen at the expense of the life of one by switching train to another track) and moral-personal dilemmas (e.g., footbridge dilemma-- push a strange r in front of a train to save the lives of five others). In the first scenario, the person just pulls a switch resulting in death of one person to save five, but in the second, the person pushes the victim to their death to save five others.
Dual-process theory proposes that moral decision-making involves two components: an automatic emotional response and a voluntary application of a utilitarian decision-rule (in this case, one death to save five people is worth it). The thought of being responsible for the death of another person elicits an aversive emotional response, but at the same time, cognitive reasoning favors the utilitarian option. Decision making and social cognition are often associated with the DLPFC. Neurons in the prefrontal cortex have been found to be involved in cost-benefit analysis and categorize stimuli based on the predicted consequences.
Theory-of-mind (TOM) is a cognitive mechanism which is used when one tries to understand and explain the knowledge, beliefs, and intention of others. TOM and empathy are often associated with TPJ functioning .
In the article by Jeurissen, et al., (2014), brain activity is measured by BOLD. BOLD refers to Blood-oxygen-level-dependent imaging , or BOLD-contrast imaging, which is a way to measure neural activity in different brain areas in MRI images .
Greene et al., 2001 (Links to an external site.) , 2004 (Links to an external site.) reported that activity in the prefrontal cortex is thought to be important for the cognitive reasoning process , which can counteract the automatic emotional response that occurs in moral dilemmas like the one in Jeurissen, et al., (2014). Greene et al. (2001) (Links to an external site.) found that the medial portions of the medial frontal gyrus, the posterior cingulate gyrus, and the bilateral angular gyrus showed a higher BOLD response in the moral-personal condition than the moral-impersonal condition. The right middle frontal gyrus and the bilateral parietal lobes showed a lower BOLD response in the moral-personal condition than in the moral impersonal. Furthermore, Greene et al. (2004) (Links to an external site.) showed an increased BOLD response for the bilateral amygdale in personal compared to the impersonal dilemmas.
Given the role of the prefrontal cortex in moral decision-making, Jeurissen, et al., (2014) hypothesized that when magnetically stimulating prefrontal cortex , they will selectively influence the decision process of the moral personal dilemmas because the cognitive reasoning for which the DLPFC is important is disrupted , thereby releasing the emotional component making it more influential in the resolution of the dilemma. Because the activity in the TPJ is related to emotional processing and theory of mind ( Saxe and Kanwisher, 2003 (Links to an external site.) ; Young et al., 2010 (Links to an external site.) ), Jeurissen, et al., (2014) hypothesized that when magnetically stimulating this area, the TPJ, during a moral decision, this will selectively influence the decision process of moral-impersonal dilemmas.
Results of this study by Jeurissen, et al., (2014) showed an important role of the TPJ in moral judgment . Experiments using fMRI ( Greene et al., 2004 (Links to an external site.) ), have found the cingulate cortex to be involved in moral judgment . In earlier studies, the cingulate cortex was found to be involved in the emotional response. Since the moral-personal dilemmas are more emotional ly salient, the higher activity observed for TPJ in the moral-personal condition (more emotional) is consistent with this view. Another area that is hypothesized to be associated with the emotional response is the temporal cortex . In this study by Jeurissen, et al., (2014) , magnetic stimulation of the right DLPFC and right TPJ shows roles for right DLPFC (reasoning and utilitarian) and right TPJ (emotion) in moral impersonal and moral personal dilemmas respectively. TMS over the right DLPFC (disrupting neural activity here) leads to behavior changes consistent with less cognitive control over emotion . After right DLPFC stimulation, participants show less feelings of regret than after magnetic stimulation of the right TPJ. This last finding indicates that the right DLPFC is involved in evaluating the outcome of the decision process. In summary, this experiment by Jeurissen, et al., (2014) adds to evidence of a critical role of right DLPFC and right TPJ in moral decision-making and supports that hypothesis that the former is involved in judgments based on cognitive reasoning and anticipation of outcomes, whereas the latter is involved in emotional processing related to moral dilemmas.
Many different strategies exist for solving problems. Typical strategies include trial and error, applying algorithms, and using heuristics. To solve a large, complicated problem, it often helps to break the problem into smaller steps that can be accomplished individually, leading to an overall solution. The brain mechanisms involved in problem solving vary to some degree depending upon the sensory modalities involved in the problem and its solution, however, the prefrontal cortex is one brain region that appears to be centrally involved in all problem-solving. The prefrontal cortex is required for flexible shifts in attention, for representing the problem in working memory, and for holding steps in problem solving in working memory along with representations of future consequences of those actions permitting planning and execution of plans. Also implicated is the Default Mode Network (DMN) including medial prefrontal cortex, posterior cingulate cortex, and the inferior parietal module, and sometimes the lateral temporal cortex, hippocampus, and the precuneus. Moral reasoning involves a different set of brain areas, primarily the dorsolateral prefrontal cortex (DLPFC) and temporal-parietal junction (TPJ).
Review Questions
- an algorithm
- a heuristic
- a mental set
- trial and error
Gray, M. E., & Holyoak, K. J. (2021). Teaching by analogy: From theory to practice. Mind, Brain, and Education , 15 (3), 250-263.
Hunt, L. T., Behrens, T. E., Hosokawa, T., Wallis, J. D., & Kennerley, S. W. (2015). Capturing the temporal evolution of choice across prefrontal cortex. Elife , 4 , e11945.
Mushiake, H., Sakamoto, K., Saito, N., Inui, T., Aihara, K., & Tanji, J. (2009). Involvement of the prefrontal cortex in problem solving. International review of neurobiology , 85 , 1-11.
Jeurissen, D., Sack, A. T., Roebroeck, A., Russ, B. E., & Pascual-Leone, A. (2014). TMS affects moral judgment, showing the role of DLPFC and TPJ in cognitive and emotional processing. Frontiers in neuroscience , 8 , 18.
Kahneman, D. (2011). Thinking, fast and slow. New York: Farrar, Straus, and Giroux.
Koenigshofer, K. A. (2017). General Intelligence: Adaptation to Evolutionarily Familiar Abstract Relational Invariants, Not to Environmental or Evolutionary Novelty. The Journal of Mind and Behavior , 119-153.
Pratkanis, A. (1989). The cognitive representation of attitudes. In A. R. Pratkanis, S. J. Breckler, & A. G. Greenwald (Eds.), Attitude structure and function (pp. 71–98). Hillsdale, NJ: Erlbaum.
Raichle, M. E., MacLeod, A. M., Snyder, A. Z., Powers, W. J., Gusnard, D. A., & Shulman, G. L. (2001). A default mode of brain function. Proceedings of the National Academy of Sciences , 98 (2), 676-682.
Sawyer, K. (2011). The cognitive neuroscience of creativity: a critical review. Creat. Res. J. 23, 137–154. doi: 10.1080/10400419.2011.571191
Tversky, A., & Kahneman, D. (1974). Judgment under uncertainty: Heuristics and biases. Science , 185 (4157), 1124–1131.
Mushiake, H., Sakamoto, K., Saito, N., Inui, T., Aihara, K., & Tanji, J. (2009). Involvement of the prefrontal cortex in problem solving. International review of neurobiology , 85 , 1-11. https://www.sciencedirect.com/scienc...74774209850010
Attributions
"Overview," "Problem Solving Strategies," adapted from Problem Solving by OpenStax Colleg licensed CC BY-NC 4.0 via OER Commons
"Defining Problems," "Problem Solving as a Search Problem," "Creative Cognition," "Brain Mechanisms in Problem-Solving" adapted by Kenneth A. Koenigshofer, Ph.D., from 2.1, 2.2, 2.3, 2.4, 2.5, 2.6 in Cognitive Psychology and Cognitive Neuroscience (Wikibooks) https://en.wikibooks.org/wiki/Cognit...e_Neuroscience ; unless otherwise noted, LibreTexts content is licensed by CC BY-NC-SA 3.0 . Legal ; the LibreTexts libraries are Powered by MindTouch
Moral Reasoning was written by Kenneth A. Koenigshofer, Ph.D, Chaffey College.
Categories and Concepts
People form mental concepts of categories of objects, which permit them to respond appropriately to new objects they encounter. Most concepts cannot be strictly defined but are organized around the “best” examples or prototypes, which have the properties most common in the category. Objects fall into many different categories, but there is usually a most salient one, called the basic-level category, which is at an intermediate level of specificity (e.g., chairs, rather than furniture or desk chairs). Concepts are closely related to our knowledge of the world, and people can more easily learn concepts that are consistent with their knowledge. Theories of concepts argue either that people learn a summary description of a whole category or else that they learn exemplars of the category. Recent research suggests that there are different ways to learn and represent concepts and that they are accomplished by different neural systems.
- Understand the problems with attempting to define categories.
- Understand typicality and fuzzy category boundaries.
- Learn about theories of the mental representation of concepts.
- Learn how knowledge may influence concept learning.
Introduction

Consider the following set of objects: some dust, papers, a computer monitor, two pens, a cup, and an orange. What do these things have in common? Only that they all happen to be on my desk as I write this. This set of things can be considered a category , a set of objects that can be treated as equivalent in some way. But, most of our categories seem much more informative—they share many properties. For example, consider the following categories: trucks, wireless devices, weddings, psychopaths, and trout. Although the objects in a given category are different from one another, they have many commonalities. When you know something is a truck, you know quite a bit about it. The psychology of categories concerns how people learn, remember, and use informative categories such as trucks or psychopaths.
The mental representations we form of categories are called concepts . There is a category of trucks in the actual physical world, and I also have a concept of trucks in my head. We assume that people’s concepts correspond more or less closely to the actual category, but it can be useful to distinguish the two, as when someone’s concept is not really correct.
Concepts are at the core of intelligent behavior . We expect people to be able to know what to do in new situations and when confronting new objects. If you go into a new classroom and see chairs, a blackboard, a projector, and a screen, you know what these things are and how they will be used. You’ll sit on one of the chairs and expect the instructor to write on the blackboard or project something onto the screen. You do this even if you have never seen any of these particular objects before , because you have concepts of classrooms, chairs, projectors, and so forth, that tell you what they are and what you’re supposed to do with them. Furthermore, if someone tells you a new fact about the projector—for example, that it has a halogen bulb—you are likely to extend this fact to other projectors you encounter. In short, concepts allow you to extend what you have learned about a limited number of objects to a potentially infinite set of entities (i.e. generalization ). Notice how categories and concepts arise from similarity, one of the abstract features of the world that has been genetically internalized into the brain during evolution , creating an innate disposition of brains to search for and to represent groupings of similar things, forming one component of general intelligence. One property of the human brain that distinguishes us from other animals is the high degrees of abstraction in similarity relations that the human brain is capable of encoding compared to the brains of non-human animals (Koenigshofer, 2017).
Simpler organisms, such as animals and human infants, also have concepts ( Mareschal, Quinn, & Lea, 2010 ). Squirrels may have a concept of predators, for example, that is specific to their own lives and experiences. However, animals likely have many fewer concepts and cannot understand complex concepts such as mortgages or musical instruments.
You know thousands of categories, most of which you have learned without careful study or instruction. Although this accomplishment may seem simple, we know that it isn’t, because it is difficult to program computers to solve such intellectual tasks. If you teach a learning program that a robin, a swallow, and a duck are all birds, it may not recognize a cardinal or peacock as a bird. However, this shortcoming in computers may be at least partially overcome when the type of processing used is parallel distributed processing as employed in artificial neural networks (Koenigshofer, 2017), discussed in this chapter. As we’ll shortly see, the problem for computers is that objects in categories are often surprisingly diverse.
Nature of Categories

Traditionally, it has been assumed that categories are well-defined . This means that you can give a definition that specifies what is in and out of the category. Such a definition has two parts. First, it provides the necessary features for category membership: What must objects have in order to be in it? Second, those features must be jointly sufficient for membership: If an object has those features, then it is in the category. For example, if I defined a dog as a four-legged animal that barks, this would mean that every dog is four-legged, an animal, and barks, and also that anything that has all those properties is a dog.
Unfortunately, it has not been possible to find definitions for many familiar categories. Definitions are neat and clear-cut; the world is messy and often unclear. For example, consider our definition of dogs. In reality, not all dogs have four legs; not all dogs bark. I knew a dog that lost her bark with age (this was an improvement); no one doubted that she was still a dog. It is often possible to find some necessary features (e.g., all dogs have blood and breathe), but these features are generally not sufficient to determine category membership (you also have blood and breathe but are not a dog).
Even in domains where one might expect to find clear-cut definitions, such as science and law, there are often problems. For example, many people were upset when Pluto was downgraded from its status as a planet to a dwarf planet in 2006. Upset turned to outrage when they discovered that there was no hard-and-fast definition of planethood: “Aren’t these astronomers scientists? Can’t they make a simple definition?” In fact, they couldn’t. After an astronomical organization tried to make a definition for planets, a number of astronomers complained that it might not include accepted planets such as Neptune and refused to use it. If everything looked like our Earth, our moon, and our sun, it would be easy to give definitions of planets, moons, and stars, but the universe has not conformed to this ideal.
Fuzzy Categories
Borderline items.
Experiments also showed that the psychological assumptions of well-defined categories were not correct. Hampton ( 1979 ) asked subjects to judge whether a number of items were in different categories. He did not find that items were either clear members or clear nonmembers. Instead, he found many items that were just barely considered category members and others that were just barely not members, with much disagreement among subjects. Sinks were barely considered as members of the kitchen utensil category, and sponges were barely excluded. People just included seaweed as a vegetable and just barely excluded tomatoes and gourds. Hampton found that members and nonmembers formed a continuum, with no obvious break in people’s membership judgments. If categories were well defined, such examples should be very rare. Many studies since then have found such borderline members that are not clearly in or clearly out of the category.
McCloskey and Glucksberg ( 1978 ) found further evidence for borderline membership by asking people to judge category membership twice, separated by two weeks. They found that when people made repeated category judgments such as “Is an olive a fruit?” or “Is a sponge a kitchen utensil?” they changed their minds about borderline items—up to 22 percent of the time. So, not only do people disagree with one another about borderline items, they disagree with themselves! As a result, researchers often say that categories are fuzzy , that is, they have unclear boundaries that can shift over time.
A related finding that turns out to be most important is that even among items that clearly are in a category, some seem to be “better” members than others ( Rosch, 1973 ). Among birds, for example, robins and sparrows are very typical . In contrast, ostriches and penguins are very atypical (meaning not typical). If someone says, “There’s a bird in my yard,” the image you have will be of a smallish passerine bird such as a robin, not an eagle or hummingbird or turkey.
You can find out which category members are typical merely by asking people. Table 1 shows a list of category members in order of their rated typicality. Typicality is perhaps the most important variable in predicting how people interact with categories. The following text box is a partial list of what typicality influences.
We can understand the two phenomena of borderline members and typicality as two sides of the same coin. Think of the most typical category member: This is often called the category prototype . Items that are less and less similar to the prototype become less and less typical. At some point, these less typical items become so atypical that you start to doubt whether they are in the category at all. Is a rug really an example of furniture? It’s in the home like chairs and tables, but it’s also different from most furniture in its structure and use. From day to day, you might change your mind as to whether this atypical example is in or out of the category. So, changes in typicality ultimately lead to borderline members.

Source of Typicality
Intuitively, it is not surprising that robins are better examples of birds than penguins are, or that a table is a more typical kind of furniture than is a rug. But given that robins and penguins are known to be birds, why should one be more typical than the other? One possible answer is the frequency with which we encounter the object: We see a lot more robins than penguins, so they must be more typical. Frequency does have some effect, but it is actually not the most important variable ( Rosch, Simpson, & Miller, 1976 ). For example, I see both rugs and tables every single day, but one of them is much more typical as furniture than the other.
The best account of what makes something typical comes from Rosch and Mervis’s ( 1975 ) family resemblance theory . They proposed that items are likely to be typical if they (a) have the features that are frequent in the category and (b) do not have features frequent in other categories. Let’s compare two extremes, robins and penguins. Robins are small flying birds that sing, live in nests in trees, migrate in winter, hop around on your lawn, and so on. Most of these properties are found in many other birds. In contrast, penguins do not fly, do not sing, do not live in nests or in trees, do not hop around on your lawn. Furthermore, they have properties that are common in other categories, such as swimming expertly and having wings that look and act like fins. These properties are more often found in fish than in birds.

According to Rosch and Mervis, then, it is not because a robin is a very common bird that makes it typical. Rather, it is because the robin has the shape, size, body parts, and behaviors that are very common (i.e. most similar) among birds—and not common among fish, mammals, bugs, and so forth.
In a classic experiment, Rosch and Mervis ( 1975 ) made up two new categories, with arbitrary features. Subjects viewed example after example and had to learn which example was in which category. Rosch and Mervis constructed some items that had features that were common in the category and other items that had features less common in the category. The subjects learned the first type of item before they learned the second type. Furthermore, they then rated the items with common features as more typical. In another experiment, Rosch and Mervis constructed items that differed in how many features were shared with a different category. The more features were shared, the longer it took subjects to learn which category the item was in. These experiments, and many later studies, support both parts of the family resemblance theory.
Category Hierarchies
Many important categories fall into hierarchies , in which more concrete categories are nested inside larger, abstract categories. For example, consider the categories: brown bear, bear, mammal, vertebrate, animal, entity. Clearly, all brown bears are bears; all bears are mammals; all mammals are vertebrates; and so on. Any given object typically does not fall into just one category—it could be in a dozen different categories, some of which are structured in this hierarchical manner. Examples of biological categories come to mind most easily, but within the realm of human artifacts, hierarchical structures can readily be found: desk chair, chair, furniture, artifact, object.
Brown ( 1958 ), a child language researcher, was perhaps the first to note that there seems to be a preference for which category we use to label things. If your office desk chair is in the way, you’ll probably say, “Move that chair,” rather than “Move that desk chair” or “piece of furniture.” Brown thought that the use of a single, consistent name probably helped children to learn the name for things. And, indeed, children’s first labels for categories tend to be exactly those names that adults prefer to use ( Anglin, 1977 ).
This preference is referred to as a preference for the basic level of categorization , and it was first studied in detail by Eleanor Rosch and her students ( Rosch, Mervis, Gray, Johnson, & Boyes-Braem, 1976 ). The basic level represents a kind of Goldilocks effect, in which the category used for something is not too small (northern brown bear) and not too big (animal), but is just right (bear). The simplest way to identify an object’s basic-level category is to discover how it would be labeled in a neutral situation. Rosch et al. ( 1976 ) showed subjects pictures and asked them to provide the first name that came to mind. They found that 1,595 names were at the basic level, with 14 more specific names ( subordinates ) used. Only once did anyone use a more general name ( superordinate ). Furthermore, in printed text, basic-level labels are much more frequent than most subordinate or superordinate labels (e.g., Wisniewski & Murphy, 1989 ).
The preference for the basic level is not merely a matter of labeling. Basic-level categories are usually easier to learn. As Brown noted, children use these categories first in language learning, and superordinates are especially difficult for children to fully acquire. [1] People are faster at identifying objects as members of basic-level categories ( Rosch et al., 1976 ).
Rosch et al. ( 1976 ) initially proposed that basic-level categories cut the world at its joints, that is, merely reflect the big differences between categories like chairs and tables or between cats and mice that exist in the world. However, it turns out that which level is basic is not universal. North Americans are likely to use names like tree, fish , and bird to label natural objects. But people in less industrialized societies seldom use these labels and instead use more specific words, equivalent to elm, trout, and finch ( Berlin, 1992 ). Because Americans and many other people living in industrialized societies know so much less than our ancestors did about the natural world, our basic level has “moved up” to what would have been the superordinate level a century ago. Furthermore, experts in a domain often have a preferred level that is more specific than that of non-experts. Birdwatchers see sparrows rather than just birds, and carpenters see roofing hammers rather than just hammers ( Tanaka & Taylor, 1991 ). This all suggests that the preferred level is not (only) based on how different categories are in the world, but that people’s knowledge and interest in the categories has an important effect.
One explanation of the basic-level preference is that basic-level categories are more differentiated: The category members are similar to one another, but they are different from members of other categories ( Murphy & Brownell, 1985 ; Rosch et al., 1976 ). (The alert reader will note a similarity to the explanation of typicality I gave above. However, here we’re talking about the entire category and not individual members.) Chairs are pretty similar to one another, sharing a lot of features (legs, a seat, a back, similar size and shape); they also don’t share that many features with other furniture. Superordinate categories are not as useful because their members are not very similar to one another. What features are common to most furniture? There are very few. Subordinate categories are not as useful, because they’re very similar to other categories: Desk chairs are quite similar to dining room chairs and easy chairs. As a result, it can be difficult to decide which subordinate category an object is in ( Murphy & Brownell, 1985 ). Experts can differ from novices in which categories are the most differentiated, because they know different things about the categories, therefore changing how similar the categories are.
[1] This is a controversial claim, as some say that infants learn superordinates before anything else (Mandler, 2004). However, if true, then it is very puzzling that older children have great difficulty learning the correct meaning of words for superordinates, as well as in learning artificial superordinate categories (Horton & Markman, 1980; Mervis, 1987). However, it seems fair to say that the answer to this question is not yet fully known.
Theories of Concept Representation
Now that we know these facts about the psychology of concepts, the question arises of how concepts are mentally represented. There have been two main answers. The first, somewhat confusingly called the prototype theory suggests that people have a summary representation of the category, a mental description that is meant to apply to the category as a whole. (The significance of summary will become apparent when the next theory is described.) This description can be represented as a set of weighted features ( Smith & Medin, 1981 ). The features are weighted by their frequency in the category. For the category of birds, having wings and feathers would have a very high weight; eating worms would have a lower weight; living in Antarctica would have a lower weight still, but not zero, as some birds do live there.
The idea behind prototype theory is that when you learn a category, you learn a general description that applies to the category as a whole: Birds have wings and usually fly; some eat worms; some swim underwater to catch fish. People can state these generalizations, and sometimes we learn about categories by reading or hearing such statements (“The kimodo dragon can grow to be 10 feet long”).
When you try to classify an item, you see how well it matches that weighted list of features. For example, if you saw something with wings and feathers fly onto your front lawn and eat a worm, you could (unconsciously) consult your concepts and see which ones contained the features you observed. This example possesses many of the highly weighted bird features, and so it should be easy to identify as a bird.
This theory readily explains the phenomena we discussed earlier. Typical category members have more, higher-weighted features. Therefore, it is easier to match them to your conceptual representation. Less typical items have fewer or lower-weighted features (and they may have features of other concepts). Therefore, they don’t match your representation as well (less similarity). This makes people less certain in classifying such items. Borderline items may have features in common with multiple categories or not be very close to any of them. For example, edible seaweed does not have many of the common features of vegetables but also is not close to any other food concept (meat, fish, fruit, etc.), making it hard to know what kind of food it is.
A very different account of concept representation is the exemplar theory ( exemplar being a fancy name for an example; Medin & Schaffer, 1978 ). This theory denies that there is a summary representation. Instead, the theory claims that your concept of vegetables is remembered examples of vegetables you have seen. This could of course be hundreds or thousands of exemplars over the course of your life, though we don’t know for sure how many exemplars you actually remember.
How does this theory explain classification? When you see an object, you (unconsciously) compare it to the exemplars in your memory, and you judge how similar it is to exemplars in different categories. For example, if you see some object on your plate and want to identify it, it will probably activate memories of vegetables, meats, fruit, and so on. In order to categorize this object, you calculate how similar it is to each exemplar in your memory. These similarity scores are added up for each category. Perhaps the object is very similar to a large number of vegetable exemplars, moderately similar to a few fruit, and only minimally similar to some exemplars of meat you remember. These similarity scores are compared, and the category with the highest score is chosen . [2]
Why would someone propose such a theory of concepts? One answer is that in many experiments studying concepts, people learn concepts by seeing exemplars over and over again until they learn to classify them correctly. Under such conditions, it seems likely that people eventually memorize the exemplars ( Smith & Minda, 1998 ). There is also evidence that close similarity to well-remembered objects has a large effect on classification . Allen and Brooks ( 1991 ) taught people to classify items by following a rule. However, they also had their subjects study the items, which were richly detailed. In a later test, the experimenters gave people new items that were very similar to one of the old items but were in a different category. That is, they changed one property so that the item no longer followed the rule. They discovered that people were often fooled by such items. Rather than following the category rule they had been taught, they seemed to recognize the new item as being very similar to an old one and so put it, incorrectly, into the same category.
Many experiments have been done to compare the prototype and exemplar theories. Overall, the exemplar theory seems to have won most of these comparisons . However, the experiments are somewhat limited in that they usually involve a small number of exemplars that people view over and over again. It is not so clear that exemplar theory can explain real-world classification in which people do not spend much time learning individual items (how much time do you spend studying squirrels? or chairs?). Also, given that some part of our knowledge of categories is learned through general statements we read or hear, it seems that there must be room for a summary description separate from exemplar memory.
Many researchers would now acknowledge that concepts are represented through multiple cognitive systems. For example, your knowledge of dogs may be in part through general descriptions such as “dogs have four legs.” But you probably also have strong memories of some exemplars (your family dog, Lassie) that influence your categorization. Furthermore, some categories also involve rules (e.g., a strike in baseball). How these systems work together is the subject of current study.
[2] Actually, the decision of which category is chosen is more complex than this, but the details are beyond this discussion.
The final topic has to do with how concepts fit with our broader knowledge of the world. We have been talking very generally about people learning the features of concepts. For example, they see a number of birds and then learn that birds generally have wings, or perhaps they remember bird exemplars. From this perspective, it makes no difference what those exemplars or features are—people just learn them. But consider two possible concepts of buildings and their features in Table 2.

Imagine you had to learn these two concepts by seeing exemplars of them, each exemplar having some of the features listed for the concept (as well as some idiosyncratic features). Learning the donker concept would be pretty easy. It seems to be a kind of underwater building, perhaps for deep-sea explorers. Its features seem to go together. In contrast, the blegdav doesn’t really make sense. If it’s in the desert, how can you get there by submarine, and why do they have polar bears as pets? Why would farmers live in the desert or use submarines? What good would steel windows do in such a building? This concept seems peculiar. In fact, if people are asked to learn new concepts that make sense, such as donkers, they learn them quite a bit faster than concepts such as blegdavs that don’t make sense ( Murphy & Allopenna, 1994 ). Furthermore, the features that seem connected to one another (such as being underwater and getting there by submarine) are learned better than features that don’t seem related to the others (such as being red).
Such effects demonstrate that when we learn new concepts, we try to connect them to the knowledge we already have about the world. If you were to learn about a new animal that doesn’t seem to eat or reproduce, you would be very puzzled and think that you must have gotten something wrong. By themselves, the prototype and exemplar theories don’t predict this. They simply say that you learn descriptions or exemplars, and they don’t put any constraints on what those descriptions or exemplars are. However, the knowledge approach to concepts emphasizes that concepts are meant to tell us about real things in the world, and so our knowledge of the world is used in learning and thinking about concepts.
We can see this effect of knowledge when we learn about new pieces of technology. For example, most people could easily learn about tablet computers (such as iPads) when they were first introduced by drawing on their knowledge of laptops, cell phones, and related technology. Of course, this reliance on past knowledge can also lead to errors, as when people don’t learn about features of their new tablet that weren’t present in their cell phone or expect the tablet to be able to do something it can’t.
One important aspect of people’s knowledge about categories is called psychological essentialism ( Gelman, 2003 ; Medin & Ortony, 1989 ). People tend to believe that some categories—most notably natural kinds such as animals, plants, or minerals—have an underlying property that is found only in that category and that causes its other features. Most categories don’t actually have essences, but this is sometimes a firmly held belief. For example, many people will state that there is something about dogs, perhaps some specific gene or set of genes, that all dogs have and that makes them bark, have fur, and look the way they do. Therefore, decisions about whether something is a dog do not depend only on features that you can easily see but also on the assumed presence of this cause.
Belief in an essence can be revealed through experiments describing fictional objects. Keil ( 1989 ) described to adults and children a fiendish operation in which someone took a raccoon, dyed its hair black with a white stripe down the middle, and implanted a “sac of super-smelly yucky stuff” under its tail. The subjects were shown a picture of a skunk and told that this is now what the animal looks like. What is it? Adults and children over the age of 4 all agreed that the animal is still a raccoon. It may look and even act like a skunk, but a raccoon cannot change its stripes (or whatever!)—it will always be a raccoon.
Importantly, the same effect was not found when Keil described a coffeepot that was operated on to look like and function as a bird feeder. Subjects agreed that it was now a bird feeder. Artifacts don’t have an essence.
Signs of essentialism include (a) objects are believed to be either in or out of the category, with no in-between; (b) resistance to change of category membership or of properties connected to the essence; and (c) for living things, the essence is passed on to progeny.
Essentialism is probably helpful in dealing with much of the natural world, but it may be less helpful when it is applied to humans. Considerable evidence suggests that people think of gender, racial, and ethnic groups as having essences, which serves to emphasize the difference between groups and even justify discrimination ( Hirschfeld, 1996 ). Historically, group differences were described by inheriting the blood of one’s family or group. “Bad blood” was not just an expression but a belief that negative properties were inherited and could not be changed. After all, if it is in the nature of “those people” to be dishonest (or clannish or athletic ...), then that could hardly be changed, any more than a raccoon can change into a skunk.
Research on categories of people is an exciting ongoing enterprise, and we still do not know as much as we would like to about how concepts of different kinds of people are learned in childhood and how they may (or may not) change in adulthood. Essentialism doesn’t apply only to person categories, but it is one important factor in how we think of groups.
Concepts are central to our everyday thought. When we are planning for the future or thinking about our past, we think about specific events and objects in terms of their categories. If you’re visiting a friend with a new baby, you have some expectations about what the baby will do, what gifts would be appropriate, how you should behave toward it, and so on. Knowing about the category of babies helps you to effectively plan and behave when you encounter this child you’ve never seen before. Such inferences from knowledge about a category are highly adaptive and an important component of thinking and intelligence.
Learning about those categories is a complex process that involves seeing exemplars (babies), hearing or reading general descriptions (“Babies like black-and-white pictures”), general knowledge (babies have kidneys), and learning the occasional rule (all babies have a rooting reflex). Current research is focusing on how these different processes take place in the brain. It seems likely that these different aspects of concepts are accomplished by different neural structures ( Maddox & Ashby, 2004 ). However, it is clear that the brain is genetically predisposed to seek out similarities in the environment and to represent groupings of things forming categories that can be used to make inferences about new instances of the category which have never been encountered before. In this way knowledge is organized and expectations from this knowledge allow improved adaptation to newly encountered environmental objects and situations by virtue of their similarity to a known category previously formed (Koenigshofer, 2017).
Another interesting topic is how concepts differ across cultures. As different cultures have different interests and different kinds of interactions with the world, it seems clear that their concepts will somehow reflect those differences. On the other hand, the structure of the physical world also imposes a strong constraint on what kinds of categories are actually useful. The interplay of culture, the environment, and basic cognitive processes in establishing concepts has yet to be fully investigated.
Discussion Questions
- Pick a couple of familiar categories and try to come up with definitions for them. When you evaluate each proposal (a) is it in fact accurate as a definition, and (b) is it a definition that people might actually use in identifying category members?
- For the same categories, can you identify members that seem to be “better” and “worse” members? What about these items makes them typical and atypical?
- Going around the room, point to some common objects (including things people are wearing or brought with them) and identify what the basic-level category is for that item. What are superordinate and subordinate categories for the same items?
- List some features of a common category such as tables. The knowledge view suggests that you know reasons for why these particular features occur together. Can you articulate some of those reasons? Do the same thing for an animal category.
- Choose three common categories: a natural kind, a human artifact, and a social event. Discuss with class members from other countries or cultures whether the corresponding categories in their cultures differ. Can you make a hypothesis about when such categories are likely to differ and when they are not?
- Allen, S. W., & Brooks, L. R. (1991). Specializing the operation of an explicit rule. Journal of Experimental Psychology: General, 120 , 3–19.
- Anglin, J. M. (1977). Word, object, and conceptual developmen t. New York, NY: W. W. Norton.
- Berlin, B. (1992). Ethnobiological classification: Principles of categorization of plants and animals in traditional societies . Princeton, NJ: Princeton University Press.
- Brown, R. (1958). How shall a thing be called? Psychological Review, 65 , 14–21.
- Gelman, S. A. (2003). The essential child: Origins of essentialism in everyday thought . Oxford, UK: Oxford University Press.
- Hampton, J. A. (1979). Polymorphous concepts in semantic memory. Journal of Verbal Learning and Verbal Behavior, 18 , 441–461.
- Hirschfeld, L. A. (1996). Race in the making: Cognition, culture, and the child's construction of human kinds . Cambridge, MA: MIT Press.
- Horton, M. S., & Markman, E. M. (1980). Developmental differences in the acquisition of basic and superordinate categories. Child Development , 51, 708–719.
- Keil, F. C. (1989). Concepts, kinds, and cognitive development . Cambridge, MA: MIT Press.
- Koenigshofer, K. A. (2017). General Intelligence: Adaptation to Evolutionarily Familiar Abstract Relational Invariants, Not to Environmental or Evolutionary Novelty. The Journal of Mind and Behavior , 38(2):119-153.
- Maddox, W. T., & Ashby, F. G. (2004). Dissociating explicit and procedural-based systems of perceptual category learning. Behavioural Processes, 66 , 309–332.
- Mandler, J. M. (2004). The foundations of mind: Origins of conceptual thought . Oxford, UK: Oxford University Press.
- Mareschal, D., Quinn, P. C., & Lea, S. E. G. (Eds.) (2010). The making of human concepts . Oxford, UK: Oxford University Press.
- McCloskey, M. E., & Glucksberg, S. (1978). Natural categories: Well defined or fuzzy sets? Memory & Cognition, 6 , 462–472.
- Medin, D. L., & Ortony, A. (1989). Psychological essentialism. In S. Vosniadou & A. Ortony (Eds.), Similarity and analogical reasoning (pp. 179–195). Cambridge, UK: Cambridge University Press.
- Medin, D. L., & Schaffer, M. M. (1978). Context theory of classification learning. Psychological Review , 85, 207–238.
- Mervis, C. B. (1987). Child-basic object categories and early lexical development. In U. Neisser (Ed.), Concepts and conceptual development: Ecological and intellectual factors in categorization (pp. 201–233). Cambridge, UK: Cambridge University Press.
- Murphy, G. L., & Allopenna, P. D. (1994). The locus of knowledge effects in concept learning. Journal of Experimental Psychology: Learning, Memory, and Cognition, 20 , 904–919.
- Murphy, G. L., & Brownell, H. H. (1985). Category differentiation in object recognition: Typicality constraints on the basic category advantage. Journal of Experimental Psychology: Learning, Memory, and Cognition, 11 , 70–84.
- Norenzayan, A., Smith, E. E., Kim, B. J., & Nisbett, R. E. (2002). Cultural preferences for formal versus intuitive reasoning. Cognitive Science, 26 , 653–684.
- Rosch, E., & Mervis, C. B. (1975). Family resemblance: Studies in the internal structure of categories. Cognitive Psychology , 7, 573–605.
- Rosch, E., Mervis, C. B., Gray, W., Johnson, D., & Boyes-Braem, P. (1976). Basic objects in natural categories. Cognitive Psychology, 8 , 382–439.
- Rosch, E., Simpson, C., & Miller, R. S. (1976). Structural bases of typicality effects. Journal of Experimental Psychology: Human Perception and Performance, 2 , 491–502.
- Rosch, E. H. (1973). On the internal structure of perceptual and semantic categories. In T. E. Moore (Ed.), Cognitive development and the acquisition of language (pp. 111–144). New York, NY: Academic Press.
- Smith, E. E., & Medin, D. L. (1981). Categories and concepts . Cambridge, MA: Harvard University Press.
- Smith, J. D., & Minda, J. P. (1998). Prototypes in the mist: The early epochs of category learning. Journal of Experimental Psychology: Learning, Memory, and Cognition, 24 , 1411–1436.
- Tanaka, J. W., & Taylor, M. E. (1991). Object categories and expertise: Is the basic level in the eye of the beholder? Cognitive Psychology, 15 , 121–149.
- Wisniewski, E. J., & Murphy, G. L. (1989). Superordinate and basic category names in discourse: A textual analysis. Discourse Processes, 12 , 245–261.

- Gregory Murphy is Professor of Psychology at New York University. He previously taught at the University of Illinois and Brown University. His research focuses on concepts and reasoning, and he is the author of The Big Book of Concepts (MIT Press, 2002).
Creative Commons License

Adapted by Kenneth Koenigshofer, PhD, from Categories and Concepts by Gregory Murphy , licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License . Permissions beyond the scope of this license may be available in our Licensing Agreement .
How to cite this noba module using apa style.
Murphy, G. (2021). Categories and concepts. In R. Biswas-Diener & E. Diener (Eds), Noba textbook series: Psychology. Champaign, IL: DEF publishers. Retrieved from http://noba.to/6vu4cpkt

4 Problem Solving Techniques: How to Solve Problems at Work
Table of Contents
Problems are nothing but wake-up calls for creativity. —Gerhard Gschwandtner
All life is problem solving. —Karl Popper
W hen you think about it, most jobs are all about problem solving.
Customers or clients have a problem, and it’s up to the business and employees to solve it.
These problems can be relatively simple (“I am hungry and need something good to eat”) or very complicated (“ I don’t know what to do with my life , and I need someone to teach me”).
No matter where you end up working in the future, knowing how to tackle and solve problems will serve you well.
In fact, problem solving is one of the most important soft skills for a lot of employers—which means that if you hone your ability to solve complex problems efficiently and intelligently, it will be much easier to get ahead in your career.
And if you ever plan to start your own business , you better believe your problem solving skills will come in handy.
Here’s the catch: There is no single problem solving method that can be applied to every issue you’ll encounter at work. Different issues require different solutions.
In this article, I’m going to show you some of the most common problem solving techniques and how you can start applying them to your work (or day-to-day life) right away.
1. Rubber duck problem solving

In software engineering, rubber duck debugging or rubber ducking is a method of debugging code.
The name references to a story in the book The Pragmatic Programmer, where a programmer would carry around a rubber duck and debug their code by forcing themselves to explain it, line-by-line, to the duck.
Many other terms exist for this technique, often involving different inanimate objects. Still, the point is the same: Taking the time to explain your problem out loud—to a rubber duck, your dog, or just yourself—is a good way to see the problem from a new angle and eventually solve it. If talking out loud to yourself doesn’t work for you, you can also try writing out the problem in detail.
The key is to slow down and think your way through the problem before you run to someone else for a solution.
Your future bosses will love you for this. When you encounter a problem at your job, if you work through it and think of solutions before bringing it up to your boss, you’ll be practicing the fine art of managing up . (Another great way to advance your career.)
The critical part of rubber duck problem solving is to commit to asking thorough, detailed questions of an imaginary person or inanimate object .
Try this process:
1. Describe the problem in detail. Imagine how you’d explain the issue to a friend or colleague. Don’t think about solutions yet—just get the issue all laid out.
2. Explain what you’ve already discovered. Assuming you’ve already researched the issue, explain everything you already know that will factor into a solution.
3. List out the questions you still have. Now explain to the inanimate object where there’s missing information—what don’t you know or understand that prevents you from getting to the root of the problem?
4. Explain why some solutions won’t work. What solutions to your problem can be ruled out because they won’t work? What have you tried already, and why didn’t it work out?
Now take a break, and come back to read over your notes. If you haven’t already, you’ll probably be struck by a few ideas (and maybe even full solutions) that you didn’t think of previously.
2. Lateral thinking
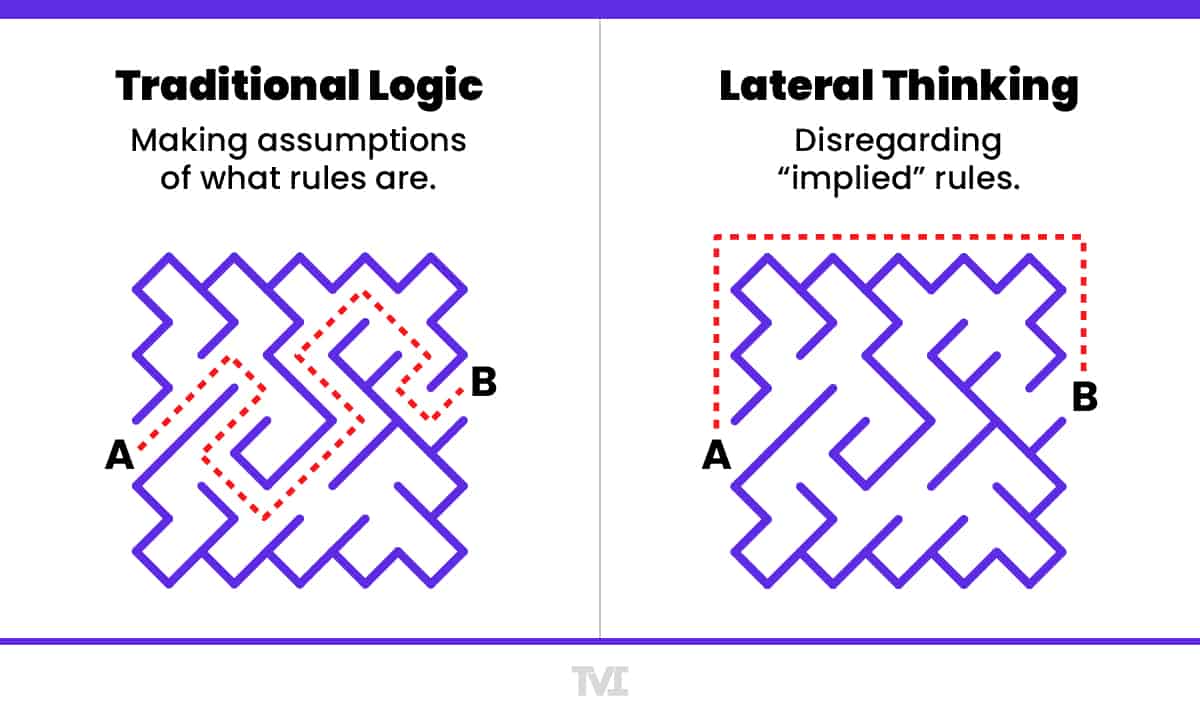
Here’s a common brainteaser, originated in Shane Snow’s book Smartcuts :
“Pretend you are driving a car in the middle of a thunderstorm, and you happen upon three people on the side of the road.
One of them is a frail old woman who looks on the verge of collapse. Another is a friend who once saved your life. The other is the romantic interest of your dreams, and this is a once-in-a-lifetime opportunity to meet them.
You have only one other seat in the car.
Who do you pick up?
There’s a good reason to choose any of the three.
The old woman needs help.
The friend deserves your payback.
And clearly, a happy future with the person of your dreams will have an enormous long-term impact on your life.
So, who should you pick?
[Dramatic pause]
The old woman, of course. Then, give the car keys to your friend, and stay behind with the romantic interest to wait for the bus! ”
This puzzle is one of the greatest examples of the problem solving method known as lateral thinking. That’s a fancy term for using creative, unexpected solutions to solve a problem, rather than more traditional and pragmatic methods.
Lateral thinking can be tricky because it requires you to cast aside assumptions (and it’s not always easy to know when you have made an assumption).
But if you’re able to do that, then new solutions to the problem you’re facing will emerge. In the example above, you may have assumed that you can only put one person in your car or that only you can drive your car. Remove these assumptions, and suddenly the problem is much easier to see.
So how do you put this into practice? Let’s use a work-related example.
Imagine your boss has put you in charge of a project that requires you to coordinate meetings between the marketing team and the tech support team.
But there’s a problem: The marketing team is in Dubai, and the tech support team is in Dallas. There are over 100 people on those two teams, and there’s no easy way to get them in the same room, let alone the same time zone.
That problem might seem impossible until you pause and consider some of the assumptions already being made:
Assumption 1: The meetings have to be held in person.
Assumption 2: The meetings have to happen live.
Assumption 3: All team members have to be present for all meetings.
Assumption 4: These meetings are necessary to complete the project.
Now, take each of these assumptions, and see what happens when you take them out of the equation.
What would happen if the meetings were held virtually? Or using collaboration software?
Could you pre-record some of the sessions to cut down on meetings?
What if your company flew a few representatives from each team to a central location rather than making everyone travel?
What if you skipped these meetings altogether, and instead…
You get the idea. The more assumptions you can find in the problem, as you’ve approached it, the more solutions you can come up with until you find the right one.
3. Trial and error

So far, the tactics on this list have required you to be patient and thoughtful, but the problem solving method commonly known as trial and error is far more action-oriented (even if it is more tedious and time-consuming).
When you take the trial and error approach, you commit to simply going ahead and trying different options to solve any given problem. When one fails, you stop and start over with another option.
The trial and error method is incredibly common, and you may sometimes make use of it without realizing it. For example, let’s imagine you’re starting a new job, and you’re trying to find the most efficient way to get there on time.
The first day you walk through the park…
The next day you take your bike…
Then you try the bus route…
Eventually, you’ve tried every option (that’s the trial) and discovered which ones take too long (that’s the error).
A word of warning: Stay away from this method if your situation has too many options because it won’t be feasible to test every single solution. Depending on the task, trial and error can either be the fastest way to do something or the slowest. So, think carefully before you decide this is how you want to solve a problem.
While the trial and error approach affords you numerous chances to find a solution, it’s not meant to help you learn why something works a certain way. That being said, the underlying cause can often reveal itself once you hit on the right solution.
So who uses this technique?
- Chemists. It’s how they discover new drugs, such as antibiotics. They simply try chemicals randomly until they find one with the desired effect.
- Gamers. Video game players often use trial and error to succeed in a game.
- Sports teams. They use it to qualify for and/or progress through the playoffs and win the championship by testing different tactics—plays, lineups, and formations—to defeat everyone along the way to victory. This is especially crucial in playoff series in which multiple wins are required to advance. A team that loses a game will have the opportunity to try new tactics to find a way to win, if they are not eliminated.
- Scientists. The scientific method is regarded as a trial and error strategy because scientists create and test hypotheses.
4. The 5 Whys

If you have little siblings or have spent time babysitting, then you’ll be familiar with how infuriating the question, “Why?” can be.
But there’s a reason little kids are constantly asking why . They’re relatively new here on planet Earth, and there are A LOT of problems to understand and solve!
Asking “why” is one of the most effective ways to solve a tricky problem, and it’s even been developed into an official problem solving technique known as “The 5 Whys.”
The concept was originally developed by Sakichi Toyoda, for the Toyota Industries Corporation, according to a report from Asian Development Bank .
Unlike the trial and error problem solving method, “The 5 Whys” is all about getting to the very root cause of any given issue, so you can solve it once and for all.
The concept is pretty simple. You take any given problem, and you ask yourself, “Why is this problem happening?”
From there, you ask, “Why is that problem happening?”
As you follow this line of questioning, you’ll eventually come to a point where you can no longer ask “why” and still get a meaningful answer. When that happens, you know you’ve found the root cause of the issue—and discovering that is half the battle in finding a solution.
Face problems head-on
Look at your problems as fun puzzles that always have a solution, no matter how hard it may be to find it.
By not bugging your co-workers or boss and solving problems yourself, you’ll become the most loved problem solver in the office.
You’re welcome. 😉
Hi there! Such a wonderful write-up, thanks!
You’re welcome – glad you enjoyed it!
Thanks for giving us important information
You’re welcome – glad it was helpful!
very help full boss
Glad to hear it!
Thanks so much. This’s so helpful.
You’re welcome!
thanks for the good subject
Glad you enjoyed it!
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
Privacy Policy

IMAGES
VIDEO
COMMENTS
In insight problem-solving, the cognitive processes that help you solve a problem happen outside your conscious awareness. 4. Working backward. Working backward is a problem-solving approach often ...
Main page; Contents; Current events; Random article; About Wikipedia; Contact us; Donate; Pages for logged out editors learn more
Understanding the Concept of Trial and Error: An Accessible Guide in Everyday Language, Crafted by Expert Psychologists, Professors, and Advanced Students. Join us in enhancing clarity.
Additional Problem Solving Strategies:. Abstraction - refers to solving the problem within a model of the situation before applying it to reality.; Analogy - is using a solution that solves a similar problem.; Brainstorming - refers to collecting an analyzing a large amount of solutions, especially within a group of people, to combine the solutions and developing them until an optimal ...
Problem-solving abilities can improve with practice. Many people challenge themselves every day with puzzles and other mental exercises to sharpen their problem-solving skills. Sudoku puzzles appear daily in most newspapers. Typically, a sudoku puzzle is a 9×9 grid. The simple sudoku below is a 4×4 grid. To solve the puzzle, fill in the empty ...
means-ends analysis, heuristic, or trial-and-error, problem-solving strategy in which an end goal is identified and then fulfilled via the generation of subgoals and action plans that help overcome obstacles encountered along the way. Solving a problem with means-ends analysis typically begins by examining the end goal and breaking it down into ...
A heuristic is another type of problem solving strategy. While an algorithm must be followed exactly to produce a correct result, a heuristic is a general problem-solving framework (Tversky & Kahneman, 1974). You can think of these as mental shortcuts that are used to solve problems. A "rule of thumb" is an example of a heuristic.
Problem-solving is a vital skill for coping with various challenges in life. This webpage explains the different strategies and obstacles that can affect how you solve problems, and offers tips on how to improve your problem-solving skills. Learn how to identify, analyze, and overcome problems with Verywell Mind.
Problem-solving skills are essential in our daily lives. The video explains different problem-solving methods, including trial and error, algorithm strategy, and heuristics. It also discusses concepts like means-end analysis, working backwards, fixation, and insight. These techniques help us tackle both well-defined and ill-defined problems ...
Common recognized stages of problem-solving processes are listed below. Needless to say that in most cases, problem-solving processes are not linear and intertwine the different stages described below not necessarily in the order they are presented here. 1. Problem analysis. Understand and identify the problem; understand what the problem is about.
The process you have just used is called trial and error, and it can be used to solve small problems like the one you had with your Wi-Fi. It can also be a powerful method in controlled situations for scientific breakthroughs, inventions, and developing new products. The idea is that you keep trying different approaches until you find one that ...
Trial and error is really a primitive experience-based technique for problem-solving, learning, and discovery. With trial and error any "so-called" solution is ...
Try Different Solutions Until One Works (Trial and Error) This technique involves attempting various potential solutions sequentially until finding one that successfully solves the problem. ... What are the most common problem-solving techniques? The most common techniques include brainstorming, the 5 Whys, mind mapping, SWOT analysis, and ...
Studies show that the most successful people failed a lot. When testing concepts, ideas, solving new problems in the real world one cannot avoid making mistakes, or fall flat sometimes. Successful managers, leaders, and entrepreneurs all understand the importance of failure, indeed they are mastered in failing but: they have learned to move on; and
Communication. Time management. Emotional intelligence. Solving a problem is complex and requires the ability to recognize the issue, collect and analyze relevant data, and make decisions about the best course of action. It can also involve asking others for input, communicating goals, and providing direction to others.
Many people challenge themselves every day with puzzles and other mental exercises to sharpen their problem-solving skills. Sudoku puzzles appear daily in most newspapers. Typically, a sudoku puzzle is a 9×9 grid. The simple sudoku below ( [link]) is a 4×4 grid. To solve the puzzle, fill in the empty boxes with a single digit: 1, 2, 3, or 4.
The trial and error method is a problem-solving technique that involves trying different approaches or solutions until you find the one that works best.
All teams and organizations encounter challenges as they grow. There are problems that might occur for teams when it comes to miscommunication or resolving business-critical issues.You may face challenges around growth, design, user engagement, and even team culture and happiness.In short, problem-solving techniques should be part of every team's skillset.
Algorithms. In contrast to heuristics, which can be thought of as problem-solving strategies based on educated guesses, algorithms are problem-solving strategies that use rules. Algorithms are generally a logical set of steps that, if applied correctly, should be accurate. For example, you could make a cake using heuristics — relying on your ...
A heuristic is another type of problem solving strategy. While an algorithm must be followed exactly to produce a correct result, a heuristic is a general problem-solving framework (Tversky & Kahneman, 1974). You can think of these as mental shortcuts that are used to solve problems. A "rule of thumb" is an example of a heuristic.
Here's the catch: There is no single problem solving method that can be applied to every issue you'll encounter at work. Different issues require different solutions. In this article, I'm going to show you some of the most common problem solving techniques and how you can start applying them to your work (or day-to-day life) right away. 1.
A set of step-by-step procedure that provides the correct answer to a particular problem. By following the instructions correctly, you are guaranteed to arrive at the right answer. Example: When you are solving problems for your math homework, you don't want to risk your grade on a guess. By following an algorithm, you can ensure that you will ...
Ian must use the formula, a^2 + b^2 = c^2. Ian plugs in 3 into a and 4 into b, and after he solves the problem algebraically, Ian finds out that the hypotenuse is 5 inches. 3. Heuristics. A problem solving strategy that involves following a general rule-of-thumb to reduce the number of possible solutions.