concept of unbalanced assignment problem

Unbalanced Assignment Problem: Definition, Formulation, and Solution Methods

Table of Contents

Are you familiar with the assignment problem in Operations Research (OR)? This problem deals with assigning tasks to workers in a way that minimizes the total cost or time needed to complete the tasks. But what if the number of tasks and workers is not equal? In this case, we face the Unbalanced Assignment Problem (UAP). This blog will help you understand what the UAP is, how to formulate it, and how to solve it.

What is the Unbalanced Assignment Problem?

The Unbalanced Assignment Problem is an extension of the Assignment Problem in OR, where the number of tasks and workers is not equal. In the UAP, some tasks may remain unassigned, while some workers may not be assigned any task. The objective is still to minimize the total cost or time required to complete the assigned tasks, but the UAP has additional constraints that make it more complex than the traditional assignment problem.

Formulation of the Unbalanced Assignment Problem

To formulate the UAP, we start with a matrix that represents the cost or time required to assign each task to each worker. If the matrix is square, we can use the Hungarian algorithm to solve the problem. But when the matrix is not square, we need to add dummy tasks or workers to balance the matrix. These dummy tasks or workers have zero costs and are used to make the matrix square.

Once we have a square matrix, we can apply the Hungarian algorithm to find the optimal assignment. However, we need to be careful in interpreting the results, as the assignment may include dummy tasks or workers that are not actually assigned to anything.

Solutions for the Unbalanced Assignment Problem

Besides the Hungarian algorithm, there are other methods to solve the UAP, such as the transportation algorithm and the auction algorithm. The transportation algorithm is based on transforming the UAP into a transportation problem, which can be solved with the transportation simplex method. The auction algorithm is an iterative method that simulates a bidding process between the tasks and workers to find the optimal assignment.

In summary, the Unbalanced Assignment Problem is a variant of the traditional Assignment Problem in OR that deals with assigning tasks to workers when the number of tasks and workers is not equal. To solve the UAP, we need to balance the matrix by adding dummy tasks or workers and then apply algorithms such as the Hungarian algorithm, the transportation algorithm, or the auction algorithm. Understanding the UAP can help businesses and organizations optimize their resource allocation and improve their operational efficiency.

How useful was this post?

Click on a star to rate it!

Average rating 1.5 / 5. Vote count: 2

No votes so far! Be the first to rate this post.

We are sorry that this post was not useful for you! 😔

Let us improve this post!

Tell us how we can improve this post?

Operations Research

1 Operations Research-An Overview

• History of O.R.
• Approach, Techniques and Tools
• Phases and Processes of O.R. Study
• Typical Applications of O.R
• Limitations of Operations Research
• Models in Operations Research
• O.R. in real world

2 Linear Programming: Formulation and Graphical Method

• General formulation of Linear Programming Problem
• Optimisation Models
• Basics of Graphic Method
• Important steps to draw graph
• Multiple, Unbounded Solution and Infeasible Problems
• Solving Linear Programming Graphically Using Computer
• Application of Linear Programming in Business and Industry

3 Linear Programming-Simplex Method

• Principle of Simplex Method
• Computational aspect of Simplex Method
• Simplex Method with several Decision Variables
• Two Phase and M-method
• Multiple Solution, Unbounded Solution and Infeasible Problem
• Sensitivity Analysis
• Dual Linear Programming Problem

4 Transportation Problem

• Basic Feasible Solution of a Transportation Problem
• Modified Distribution Method
• Stepping Stone Method
• Unbalanced Transportation Problem
• Degenerate Transportation Problem
• Transhipment Problem
• Maximisation in a Transportation Problem

5 Assignment Problem

• Solution of the Assignment Problem
• Unbalanced Assignment Problem
• Problem with some Infeasible Assignments
• Maximisation in an Assignment Problem
• Crew Assignment Problem

6 Application of Excel Solver to Solve LPP

• Building Excel model for solving LP: An Illustrative Example

7 Goal Programming

• Concepts of goal programming
• Goal programming model formulation
• Graphical method of goal programming
• The simplex method of goal programming
• Using Excel Solver to Solve Goal Programming Models
• Application areas of goal programming

8 Integer Programming

• Some Integer Programming Formulation Techniques
• Binary Representation of General Integer Variables
• Unimodularity
• Cutting Plane Method
• Branch and Bound Method
• Solver Solution

9 Dynamic Programming

• Dynamic Programming Methodology: An Example
• Definitions and Notations
• Dynamic Programming Applications

10 Non-Linear Programming

• Solution of a Non-linear Programming Problem
• Convex and Concave Functions
• Kuhn-Tucker Conditions for Constrained Optimisation
• Quadratic Programming
• Separable Programming
• NLP Models with Solver

11 Introduction to game theory and its Applications

• Important terms in Game Theory
• Saddle points
• Mixed strategies: Games without saddle points
• 2 x n games
• Exploiting an opponent’s mistakes

12 Monte Carlo Simulation

• Reasons for using simulation
• Monte Carlo simulation
• Limitations of simulation
• Steps in the simulation process
• Some practical applications of simulation
• Two typical examples of hand-computed simulation
• Computer simulation

13 Queueing Models

• Characteristics of a queueing model
• Notations and Symbols
• Statistical methods in queueing
• The M/M/I System
• The M/M/C System
• The M/Ek/I System
• Decision problems in queueing

Assignment Problem: Meaning, Methods and Variations | Operations Research

After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:

An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.

The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.

Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.

Definition of Assignment Problem:

ADVERTISEMENTS:

Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.

The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:

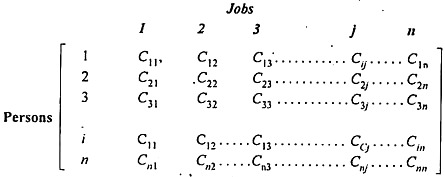
Check it out now on O’Reilly

Dive in for free with a 10-day trial of the O’Reilly learning platform—then explore all the other resources our members count on to build skills and solve problems every day.

Unbalanced Assignment Problem

In the previous section, the number of persons and the number of jobs were assumed to be the same. In this section, we remove this assumption and consider a situation where the number of persons is not equal to the number of jobs . In all such cases, fictitious rows and/or columns are added in the matrix to make it a square matrix.

• Maximization Problem
• Multiple Optimal Solutions

Example: Unbalanced Assignment Problem

Since the number of persons is less than the number of jobs, we introduce a dummy person (D) with zero values. The revised assignment problem is given below:

Use Horizontal Scrollbar to View Full Table Calculation.

Now use the Hungarian method to obtain the optimal solution yourself. Ans. = 20 + 17 + 17 + 0 = 54.

Share and Recommend

Operations Research Simplified Back Next

Goal programming Linear programming Simplex Method Transportation Problem

the intact one

Read MBA, BBA, B.COM Notes

Unbalanced Assignment Problems

Whenever the cost matrix of an assignment problem is not a square matrix, that is, whenever the number of sources is not equal to the number of destinations, the assignment problem is called an unbalanced assignment problem. In such problems, dummy rows (or columns) are added in the matrix so as to complete it to form a square matrix. The dummy rows or columns will contain all costs elements as zeroes. The Hungarian method may be used to solve the problem.

Example :  A company has five machines that are used for four jobs. Each job can be assigned to one and only one machine. The cost of each job on each machine is given in the following Table.

Unbalanced Maximization Assignment problem example

Assignment Problem

Solution:  Convert the 4 × 5 matrix into a square matrix by adding a dummy row D5.

Dummy Row D5 Added

Row-wise Reduction of the Matrix

Column-wise reduction is not necessary since all columns contain a single zero. Now, draw minimum number of lines to cover all the zeros, as shown in Table.

All Zeros in the Matrix Covered

Number of lines drawn ≠ Order of matrix. Hence not optimal.

Select the least uncovered element, i.e., 1, subtract it from other uncovered elements, add to the elements at intersection of lines and leave the elements that are covered with single line unchanged as shown in Table.

Subtracted or Added to Elements

Again Added or Subtracted 1 from Elements

Number of lines drawn = Order of matrix. Hence optimality is reached. Now assign the jobs to machines, as shown in Table.

Assigning Jobs to Machines

Example :  In a plant layout, four different machines M1, M2, M3 and M4 are to be erected in a machine shop. There are five vacant areas A, B, C, D and E. Because of limited space, Machine M2 cannot be erected at area C and Machine M4 cannot be erected at area A. The cost of erection of machines is given in the Table.

Find the optimal assignment plan.

Solution:  As the given matrix is not balanced, add a dummy row D5 with zero cost values. Assign a high cost H for (M2, C) and (M4, A). While selecting the lowest cost element neglect the high cost assigned H, as shown in Table below.

– Row-wise reduction of the matrix is shown in Table.

Matrix Reduced Row-wise

Note:  Column-wise reduction is not necessary, as each column has at least one single zero. Now, draw minimum number of lines to cover all the zeros, see Table.

Lines Drawn to Cover all Zeros

Number of lines drawn ≠ Order of matrix. Hence not Optimal. Select the smallest uncovered element, in this case 1. Subtract 1 from all other uncovered element and add 1 with the elements at the intersection. The element covered by single line remains unchanged. These changes are shown in Table. Now try to draw minimum number of lines to cover all the zeros.

Added or Subtracted 1 from Elements

Now number of lines drawn = Order of matrix, hence optimality is reached. Optimal assignment of machines to areas are shown in Table.

Optimal Assignment

Hence, the optimal solution is:

Share this:

You might also like, economic problems magnitude, causes, effects and measurement tool, introduction to logistic management, takeover code, 2 thoughts on “ unbalanced assignment problems ”.

• Pingback: GGSIPU(NEW DELHI) QUANTITATIVE TECHNIQUE – 2ND SEMESTER – STUDY MBA & BBA NOTES
• Pingback: CCSU(BBA) 406 Operation Research – Home | Management

Leave a Reply Cancel reply

Nash Balanced Assignment Problem

• Conference paper
• First Online: 21 November 2022
• Cite this conference paper

• Minh Hieu Nguyen 11 ,
• Mourad Baiou 11 &
• Viet Hung Nguyen 11  

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 13526))

Included in the following conference series:

• International Symposium on Combinatorial Optimization

360 Accesses

2 Citations

In this paper, we consider a variant of the classic Assignment Problem (AP), called the Balanced Assignment Problem (BAP) [ 2 ]. The BAP seeks to find an assignment solution which has the smallest value of max-min distance : the difference between the maximum assignment cost and the minimum one. However, by minimizing only the max-min distance, the total cost of the BAP solution is neglected and it may lead to an inefficient solution in terms of total cost. Hence, we propose a fair way based on Nash equilibrium [ 1 , 3 , 4 ] to inject the total cost into the objective function of the BAP for finding assignment solutions having a better trade-off between the two objectives: the first aims at minimizing the total cost and the second aims at minimizing the max-min distance. For this purpose, we introduce the concept of Nash Fairness (NF) solutions based on the definition of proportional-fair scheduling adapted in the context of the AP: a transfer of utilities between the total cost and the max-min distance is considered to be fair if the percentage increase in the total cost is smaller than the percentage decrease in the max-min distance and vice versa.

We first show the existence of a NF solution for the AP which is exactly the optimal solution minimizing the product of the total cost and the max-min distance. However, finding such a solution may be difficult as it requires to minimize a concave function. The main result of this paper is to show that finding all NF solutions can be done in polynomial time. For that, we propose a Newton-based iterative algorithm converging to NF solutions in polynomial time. It consists in optimizing a sequence of linear combinations of the two objective based on Weighted Sum Method [ 5 ]. Computational results on various instances of the AP are presented and commented.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Bertsimas, D., Farias, V.F., Trichakis, N.: The price of fairness. Oper. Res. January–February 59 (1), 17–31 (2011)

MathSciNet   MATH   Google Scholar  

Martello, S., Pulleyblank, W.R., Toth, P., De Werra, D.: Balanced optimization problems. Oper. Res. Lett. 3 (5), 275–278 (1984)

Article   MathSciNet   MATH   Google Scholar  

Kelly, F.P., Maullo, A.K., Tan, D.K.H.: Rate control for communication networks: shadow prices, proportional fairness and stability. J. Oper. Res. Soc. 49 (3), 237–252 (1997). https://doi.org/10.1057/palgrave.jors.2600523

Article   Google Scholar  

Ogryczak, W., Luss, H., Pioro, M., Nace, D., Tomaszewski, A.: Fair optimization and networks: a survey. J. Appl. Math. 2014 , 1–26 (2014)

Marler, R.T., Arora, J.S.: The weighted sum method for multi-objective optimization: new insights. Struct. Multi. Optim. 41 (6), 853–862 (2010)

Heller, I., Tompkins, C.B.: An extension of a theorem of Dantzig’s. Ann. Math. Stud. (38), 247–254 (1956)

Google Scholar  

Kuhn, H.W.: The Hungarian method for assignment problem. Naval Res. Logist. Q. 2 (1–2), 83–97 (1955)

Martello, S.: Most and least uniform spanning trees. Discrete Appl. Math. 15 (2), 181–197 (1986)

Beasley, J.E.: Linear programming on Clay supercomputer. J. Oper. Res. Soc. 41 , 133–139 (1990)

Nguyen, M.H, Baiou, M., Nguyen, V.H., Vo, T.Q.T.: Nash fairness solutions for balanced TSP. In: International Network Optimization Conference (INOC2022) (2022)

Download references

Author information

Authors and affiliations.

INP Clermont Auvergne, Univ Clermont Auvergne, Mines Saint-Etienne, CNRS, UMR 6158 LIMOS, 1 Rue de la Chebarde, Aubiere Cedex, France

Minh Hieu Nguyen, Mourad Baiou & Viet Hung Nguyen

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Viet Hung Nguyen .

Editor information

Editors and affiliations.

ESSEC Business School of Paris, Cergy Pontoise Cedex, France

Ivana Ljubić

IBM TJ Watson Research Center, Yorktown Heights, NY, USA

Francisco Barahona

Georgia Institute of Technology, Atlanta, GA, USA

Santanu S. Dey

Université Paris-Dauphine, Paris, France

A. Ridha Mahjoub

Proposition 1 . There may be more than one NF solution for the AP.

Let us illustrate this by an instance of the AP having the following cost matrix

By verifying all feasible assignment solutions in this instance, we obtain easily three assignment solutions \((1-1, 2-2, 3-3), (1-2, 2-3, 3-1)\) , \((1-3, 2-2, 3-1)\) and \((1-3, 2-1, 3-2)\) corresponding to 4 NF solutions (280, 36), (320, 32), (340, 30) and (364, 28). Note that \(i-j\) where \(1 \le i,j \le 3\) represents the assignment between worker i and job j in the solution of this instance.     \(\square \)

We recall below the proofs of some recent results that we have published in [ 10 ]. They are needed to prove the new results presented in this paper.

Theorem 2 [ 10 ] . \((P^{*},Q^{*}) = {{\,\mathrm{arg\,min}\,}}_{(P,Q) \in \mathcal {S}} PQ\) is a NF solution.

Obviously, there always exists a solution \((P^{*},Q^{*}) \in \mathcal {S}\) such that

Now \(\forall (P',Q') \in \mathcal {S}\) we have \(P'Q' \ge P^{*}Q^{*}\) . Then

The first inequality holds by the Cauchy-Schwarz inequality.

Hence, \((P^{*},Q^{*})\) is a NF solution.     \(\square \)

Theorem 3 [ 10 ] . \((P^{*},Q^{*}) \in \mathcal {S}\) is a NF solution if and only if \((P^{*},Q^{*})\) is an optimal solution of \(\mathcal {P(\alpha ^{*})}\) where \(\alpha ^{*} = \frac{Q^{*}}{P^{*}}\) .

Firstly, let \((P^{*},Q^{*})\) be a NF solution and \(\alpha ^{*} = \frac{Q^{*}}{P^{*}}\) . We will show that \((P^{*},Q^{*})\) is an optimal solution of \(\mathcal {P(\alpha ^{*})}\) .

Since \((P^{*},Q^{*})\) is a NF solution, we have

Since \(\alpha ^{*} = \frac{Q^{*}}{P^{*}}\) , we have \(\alpha ^{*}P^{*}+Q^{*} = 2Q^{*}\) .

Dividing two sides of ( 6 ) by \(P^{*} > 0\) we obtain

So we deduce from ( 7 )

Hence, \((P^{*},Q^{*})\) is an optimal solution of \(\mathcal {P}(\alpha ^{*})\) .

Now suppose \(\alpha ^{*} = \frac{Q^{*}}{P^{*}}\) and \((P^{*},Q^{*})\) is an optimal solution of \(\mathcal {P}(\alpha ^{*})\) , we show that \((P^{*},Q^{*})\) is a NF solution.

If \((P^{*},Q^{*})\) is not a NF solution, there exists a solution \((P',Q') \in \mathcal {S}\) such that

We have then

which contradicts the optimality of \((P^{*},Q^{*})\) .     \(\square \)

Lemma 3 [ 10 ] . Let \(\alpha , \alpha ' \in \mathbb {R}_+\) and \((P_{\alpha }, Q_{\alpha })\) , \((P_{\alpha '}, Q_{\alpha '})\) be the optimal solutions of \(\mathcal {P(\alpha )}\) and \(\mathcal {P(\alpha ')}\) respectively, if \(\alpha \le \alpha '\) then \(P_{\alpha } \ge P_{\alpha '}\) and \(Q_{\alpha } \le Q_{\alpha '}\) .

The optimality of \((P_{\alpha }, Q_{\alpha })\) and \((P_{\alpha '}, Q_{\alpha '})\) gives

By adding both sides of ( 8a ) and ( 8b ), we obtain \((\alpha - \alpha ') (P_{\alpha } - P_{\alpha '}) \le 0\) . Since \(\alpha \le \alpha '\) , it follows that \(P_{\alpha } \ge P_{\alpha '}\) .

On the other hand, inequality ( 8a ) implies \(Q_{\alpha '} - Q_{\alpha } \ge \alpha (P_{\alpha } - P_{\alpha '}) \ge 0\) that leads to \(Q_{\alpha } \le Q_{\alpha '}\) .     \(\square \)

Lemma 4 [ 10 ] . During the execution of Procedure Find ( \(\alpha _{0})\) in Algorithm 1 , \(\alpha _{i} \in [0,1], \, \forall i \ge 1\) . Moreover, if \(T_{0} \ge 0\) then the sequence \(\{\alpha _i\}\) is non-increasing and \(T_{i} \ge 0, \, \forall i \ge 0\) . Otherwise, if \(T_{0} \le 0\) then the sequence \(\{\alpha _i\}\) is non-decreasing and \(T_{i} \le 0, \, \forall i \ge 0\) .

Since \(P \ge Q \ge 0, \, \forall (P, Q) \in \mathcal {S}\) , it follows that \(\alpha _{i+1} = \frac{Q_i}{P_i} \in [0,1], \, \forall i \ge 0\) .

We first consider \(T_{0} \ge 0\) . We proof \(\alpha _i \ge \alpha _{i+1}, \, \forall i \ge 0\) by induction on i . For \(i = 0\) , we have \(T_{0} = \alpha _{0} P_{0} - Q_{0} = P_{0}(\alpha _{0}-\alpha _{1}) \ge 0\) , it follows that \(\alpha _{0} \ge \alpha _{1}\) . Suppose that our hypothesis is true until \(i = k \ge 0\) , we will prove that it is also true with \(i = k+1\) .

Indeed, we have

The inductive hypothesis gives \(\alpha _k \ge \alpha _{k+1}\) that implies \(P_{k+1} \ge P_k > 0\) and \(Q_{k} \ge Q_{k+1} \ge 0\) according to Lemma 3 . It leads to \(Q_{k}P_{k+1} - P_{k}Q_{k+1} \ge 0\) and then \(\alpha _{k+1} - \alpha _{k+2} \ge 0\) .

Hence, we have \(\alpha _{i} \ge \alpha _{i+1}, \, \forall i \ge 0\) .

Consequently, \(T_{i} = \alpha _{i}P_{i} - Q_{i} = P_{i}(\alpha _{i}-\alpha _{i+1}) \ge 0, \, \forall i \ge 0\) .

Similarly, if \(T_{0} \le 0\) we obtain that the sequence \(\{\alpha _i\}\) is non-decreasing and \(T_{i} \le 0, \, \forall i \ge 0\) . That concludes the proof.     \(\square \)

Lemma 5 [ 10 ] . From each \(\alpha _{0} \in [0,1]\) , Procedure Find \((\alpha _{0})\) converges to a coefficient \(\alpha _{k} \in \mathcal {C}_{0}\) satisfying \(\alpha _{k}\) is the unique element \(\in \mathcal {C}_{0}\) between \(\alpha _{0}\) and \(\alpha _{k}\) .

As a consequence of Lemma 4 , Procedure \(\textit{Find}(\alpha _{0})\) converges to a coefficient \(\alpha _{k} \in [0,1], \forall \alpha _{0} \in [0,1]\) .

By the stopping criteria of Procedure Find \((\alpha _{0})\) , when \(T_{k} = \alpha _{k} P_{k} - Q_{k} = 0\) we obtain \(\alpha _{k} \in C_{0}\) and \((P_{k},Q_{k})\) is a NF solution. (Theorem 3 )

If \(T_{0} = 0\) then obviously \(\alpha _{k} = \alpha _{0}\) . We consider \(T_{0} > 0\) and the sequence \(\{\alpha _i\}\) is now non-negative, non-increasing. We will show that \([\alpha _{k},\alpha _{0}] \cap \mathcal {C}_{0} = \alpha _{k}\) .

Suppose that we have \(\alpha \in (\alpha _{k},\alpha _{0}]\) and \(\alpha \in \mathcal {C}_{0}\) corresponding to a NF solution ( P ,  Q ). Then there exists \(1 \le i \le k\) such that \(\alpha \in (\alpha _{i}, \alpha _{i-1}]\) . Since \(\alpha \le \alpha _{i-1}\) , \(P \ge P_{i-1}\) and \(Q \le Q_{i-1}\) due to Lemma 3 . Thus, we get

By the definitions of \(\alpha \) and \(\alpha _{i}\) , inequality ( 9 ) is equivalent to \(\alpha \le \alpha _{i}\) which leads to a contradiction.

By repeating the same argument for \(T_{0} < 0\) , we also have a contradiction.     \(\square \)

Rights and permissions

Reprints and permissions

Copyright information

© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this paper

Cite this paper.

Nguyen, M.H., Baiou, M., Nguyen, V.H. (2022). Nash Balanced Assignment Problem. In: Ljubić, I., Barahona, F., Dey, S.S., Mahjoub, A.R. (eds) Combinatorial Optimization. ISCO 2022. Lecture Notes in Computer Science, vol 13526. Springer, Cham. https://doi.org/10.1007/978-3-031-18530-4_13

Download citation

DOI : https://doi.org/10.1007/978-3-031-18530-4_13

Published : 21 November 2022

Publisher Name : Springer, Cham

Print ISBN : 978-3-031-18529-8

Online ISBN : 978-3-031-18530-4

eBook Packages : Computer Science Computer Science (R0)

Share this paper

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Balanced and Unbalanced Transportation Problems

The two categories of transportation problems are balanced and unbalanced transportation problems . As we all know, a transportation problem is a type of Linear Programming Problem (LPP) in which items are carried from a set of sources to a set of destinations based on the supply and demand of the sources and destinations, with the goal of minimizing the total transportation cost. It is also known as the Hitchcock problem.

Introduction to Balanced and Unbalanced Transportation Problems

Balanced transportation problem.

The problem is considered to be a balanced transportation problem when both supplies and demands are equal.

Unbalanced Transportation Problem

Unbalanced transportation problem is defined as a situation in which supply and demand are not equal. A dummy row or a dummy column is added to this type of problem, depending on the necessity, to make it a balanced problem. The problem can then be addressed in the same way as the balanced problem.

Methods of Solving Transportation Problems

There are three ways for determining the initial basic feasible solution. They are

1. NorthWest Corner Cell Method.

2. Vogel’s Approximation Method (VAM).

3. Least Call Cell Method.

The following is the basic framework of the balanced transportation problem:

The destinations D1, D2, D3, and D4 in the above table are where the products/goods will be transported from various sources O1, O2, O3, and O4. The supply from the source Oi is represented by S i . The demand for the destination Dj is d j . If a product is delivered from source Si to destination Dj, then the cost is called C ij .

Let us now explore the process of solving the balanced transportation problem using one of the ways known as the NorthWest Corner Method in this article.

Solving Balanced Transportation problem by Northwest Corner Method

Consider this scenario:

With three sources (O1, O2, and O3) and four destinations (D1, D2, D3, and D4), what is the best way to solve this problem? The supply for the sources O1, O2, and O3 are 300, 400, and 500, respectively. Demands for the destination D1, D2, D3, and D4 are 250, 350, 400, and 200, respectively.

The starting point for the North West Corner technique is (O1, D1), which is the table’s northwest corner. The cost of transportation is calculated for each value in the cell. As indicated in the diagram, compare the demand for column D1 with the supply from source O1 and assign a minimum of two to the cell (O1, D1).

Column D1’s demand has been met, hence the entire column will be canceled. The supply from the source O1 is still 300 – 250 = 50.

Analyze the northwest corner, i.e. (O1, D2), of the remaining table, excluding column D1, and assign the lowest among the supply for the appropriate column and rows. Because the supply from O1 is 50 and the demand for D2 is 350, allocate 50 to the cell (O1, D2).

Now, row O1 is canceled because the supply from row O1 has been completed. Hence, the demand for Column D2 has become 350 – 50 = 50.

The northwest corner cell in the remaining table is (O2, D2). The shortest supply from source O2 (400) and the demand for column D2 (300) is 300, thus putting 300 in the cell (O2, D2). Because the demand for column D2 has been met, the column can be deleted, and the remaining supply from source O2 is 400 – 300 = 100.

Again, find the northwest corner of the table, i.e. (O2, D3), and compare the O2 supply (i.e. 100) to the D2 demand (i.e. 400) and assign the smaller (i.e. 100) to the cell (O2, D2). Row O2 has been canceled because the supply from O2 has been completed. Column D3 has a leftover demand of 400 – 100 = 300.

Continuing in the same manner, the final cell values will be:

It should be observed that the demand for the relevant columns and rows is equal in the last remaining cell, which was cell (O3, D4). In this situation, the supply from O3 was 200, and the demand for D4 was 200, therefore this cell was assigned to it. Nothing was left for any row or column at the end.

To achieve the basic solution, multiply the allotted value by the respective cell value (i.e. the cost) and add them all together.

I.e., (250 × 3) + (50 × 1) + (300 × 6) + (100 × 5) + (300 × 3) + (200 × 2) = 4400.

Solving Unbalanced Transportation Problem

An unbalanced transportation problem is provided below. Because the sum of all the supplies, O1, O2, O3, and O4, does not equal the sum of all the demands, D1, D2, D3, D4, and D5, the situation is unbalanced.

The idea of a dummy row or dummy column will be applied in this type of scenario. Because the supply is more than the demand in this situation, a fake demand column will be inserted, with a demand of (total supply – total demand), i.e. 117 – 95 = 22, as seen in the image below. A fake supply row would have been introduced if demand was greater than supply.

Now this problem has been changed to a balanced transportation problem, and it can be addressed using any of the ways listed below to solve a balanced transportation problem, such as the northwest corner method mentioned earlier.

Frequently Asked Questions on Balanced and Unbalanced Transportation Problems

What is meant by balanced and unbalanced transportation problems.

The problem is referred to as a balanced transportation problem when both supplies and demands are equal. Unbalanced transportation is defined as a situation where supply and demand are not equal.

What is called a transportation problem?

The transportation problem is a type of Linear Programming Problem in which commodities are carried from a set of sources to a set of destinations while taking into account the supply and demand of the sources and destinations, respectively, in order to reduce the total cost of transportation.

What are the different methods to solve transportation problems?

The following are three approaches to solve the transportation issue:

• NorthWest Corner Cell Method.
• Least Call Cell Method.
• Vogel’s Approximation Method (VAM).

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.