what is randomization in research design

• Search Menu
• Advance Articles
• Author Guidelines
• Open Access Policy
• Self-Archiving Policy
• About Significance
• About The Royal Statistical Society
• Editorial Board
• Advertising & Corporate Services
• Journals on Oxford Academic
• Books on Oxford Academic

Article Contents

What is randomisation, why do we randomise, choosing a randomisation method, implementing the chosen randomisation method.

• < Previous

Randomisation: What, Why and How?

• Article contents
• Figures & tables
• Supplementary Data

Zoë Hoare, Randomisation: What, Why and How?, Significance , Volume 7, Issue 3, September 2010, Pages 136–138, https://doi.org/10.1111/j.1740-9713.2010.00443.x

• Permissions Icon Permissions

Randomisation is a fundamental aspect of randomised controlled trials, but how many researchers fully understand what randomisation entails or what needs to be taken into consideration to implement it effectively and correctly? Here, for students or for those about to embark on setting up a trial, Zoë Hoare gives a basic introduction to help approach randomisation from a more informed direction.

Most trials of new medical treatments, and most other trials for that matter, now implement some form of randomisation. The idea sounds so simple that defining it becomes almost a joke: randomisation is “putting participants into the treatment groups randomly”. If only it were that simple. Randomisation can be a minefield, and not everyone understands what exactly it is or why they are doing it.

A key feature of a randomised controlled trial is that it is genuinely not known whether the new treatment is better than what is currently offered. The researchers should be in a state of equipoise; although they may hope that the new treatment is better, there is no definitive evidence to back this hypothesis up. This evidence is what the trial is trying to provide.

You will have, at its simplest, two groups: patients who are getting the new treatment, and those getting the control or placebo. You do not hand-select which patient goes into which group, because that would introduce selection bias. Instead you allocate your patients randomly. In its simplest form this can be done by the tossing of a fair coin: heads, the patient gets the trial treatment; tails, he gets the control. Simple randomisation is a fair way of ensuring that any differences that occur between the treatment groups arise completely by chance. But – and this is the first but of many here – simple randomisation can lead to unbalanced groups, that is, groups of unequal size. This is particularly true if the trial is only small. For example, tossing a fair coin 10 times will only result in five heads and five tails about 25% of the time. We would have a 66% chance of getting 6 heads and 4 tails, 5 and 5, or 4 and 6; 33% of the time we would get an even larger imbalance, with 7, 8, 9 or even all 10 patients in one group and the other group correspondingly undersized.

The impact of an imbalance like this is far greater for a small trial than for a larger trial. Tossing a fair coin 100 times will result in imbalance larger than 60–40 less than 1% of the time. One important part of the trial design process is the statement of intention of using randomisation; then we need to establish which method to use, when it will be used, and whether or not it is in fact random.

Randomisation needs to be controlled: You would not want all the males under 30 to be in one trial group and all the women over 70 in the other

It is partly true to say that we do it because we have to. The Consolidated Standards of Reporting Trials (CONSORT) 1 , to which we should all adhere, tells us: “Ideally, participants should be assigned to comparison groups in the trial on the basis of a chance (random) process characterized by unpredictability.” The requirement is there for a reason. Randomisation of the participants is crucial because it allows the principles of statistical theory to stand and as such allows a thorough analysis of the trial data without bias. The exact method of randomisation can have an impact on the trial analyses, and this needs to be taken into account when writing the statistical analysis plan.

Ideally, simple randomisation would always be the preferred option. However, in practice there often needs to be some control of the allocations to avoid severe imbalances within treatments or within categories of patient. You would not want, for example, all the males under 30 to be in one group and all the females over 70 in the other. This is where restricted or stratified randomisation comes in.

Restricted randomisation relates to using any method to control the split of allocations to each of the treatment groups based on certain criteria. This can be as simple as generating a random list, such as AAABBBABABAABB …, and allocating each participant as they arrive to the next treatment on the list. At certain points within the allocations we know that the groups will be balanced in numbers – here at the sixth, eighth, tenth and 14th participants – and we can control the maximum imbalance at any one time.

Stratified randomisation sets out to control the balance in certain baseline characteristics of the participants – such as sex or age. This can be thought of as producing an individual randomisation list for each of the characteristics concerned.

© iStockphoto.com/dra_schwartz

Stratification variables are the baseline characteristics that you think might influence the outcome your trial is trying to measure. For example, if you thought gender was going to have an effect on the efficacy of the treatment then you would use it as one of your stratification variables. A stratified randomisation procedure would aim to ensure a balance of the two gender groups between the two treatment groups.

If you also thought age would be affecting the treatment then you could also stratify by age (young/old) with some sensible limits on what old and young are. Once you start stratifying by age and by gender, you have to start taking care. You will need to use a stratified randomisation process that balances at the stratum level (i.e. at the level of those characteristics) to ensure that all four strata (male/young, male/old, female/young and female/old) have equivalent numbers of each of the treatment groups represented.

“Great”, you might think. “I'll just stratify by all my baseline characteristics!” Better not. Stop and consider what this would mean. As the number of stratification variables increases linearly, the number of strata increases exponentially. This reduces the number of participants that would appear in each stratum. In our example above, with our two stratification variables of age and sex we had four strata; if we added, say “blue-eyed” and “overweight” to our criteria to give four stratification variables each with just two levels we would get 16 represented strata. How likely is it that each of those strata will be represented in the population targeted by the trial? In other words, will we be sure of finding a blue-eyed young male who is also overweight among our patients? And would one such overweight possible Adonis be statistically enough? It becomes evident that implementing pre-generated lists within each stratification level or stratum and maintaining an overall balance of group sizes becomes much more complicated with many stratification variables and the uncertainty of what type of participant will walk through the door next.

Does it matter? There are a wide variety of methods for randomisation, and which one you choose does actually matter. It needs to be able to do everything that is required of it. Ask yourself these questions, and others:

Can the method accommodate enough treatment groups? Some methods are limited to two treatment groups; many trials involve three or more.

What type of randomness, if any, is injected into the method? The level of randomness dictates how predictable a method is.

A deterministic method has no randomness, meaning that with all the previous information you can tell in advance which group the next patient to appear will be allocated to. Allocating alternate participants to the two treatments using ABABABABAB … would be an example.

A static random element means that each allocation is made with a pre-defined probability. The coin-toss method does this.

With a dynamic element the probability of allocation is always changing in relation to the information received, meaning that the probability of allocation can only be worked out with knowledge of the algorithm together with all its settings. A biased coin toss does this where the bias is recalculated for each participant.

Can the method accommodate stratification variables, and if so how many? Not all of them can. And can it cope with continuous stratification variables? Most variables are divided into mutually exclusive categories (e.g. male or female), but sometimes it may be necessary (or preferable) to use a continuous scale of the variable – such as weight, or body mass index.

Can the method use an unequal allocation ratio? Not all trials require equal-sized treatment groups. There are many reasons why it might be wise to have more patients receiving treatment A than treatment B 2 . However, an allocation ratio being something other than 1:1 does impact on the study design and on the calculation of the sample size, so is not something to be changing mid-trial. Not all allocation methods can cope with this inequality.

Is thresholding used in the method? Thresholding handles imbalances in allocation. A threshold is set and if the imbalance becomes greater than the threshold then the allocation becomes deterministic to reduce the imbalance back below the threshold.

Can the method be implemented sequentially? In other words, does it require that the total number of participants be known at the beginning of the allocations? Some methods generate lists requiring exactly N participants to be recruited in order to be effective – and recruiting participants is often one of the more problematic parts of a trial.

Is the method complex? If so, then its practical implementation becomes an issue for the day-to-day running of the trial.

Is the method suitable to apply to a cluster randomisation? Cluster randomisations are used when randomising groups of individuals to a treatment rather than the individuals themselves. This can be due to the nature of the treatment, such as a new teaching method for schools or a dietary intervention for families. Using clusters is a big part of the trial design and the randomisation needs to be handled slightly differently.

Should a response-adaptive method be considered? If there is some evidence that one treatment is better than another, then a response-adaptive method works by taking into account the outcomes of previous allocations and works to minimise the number of participants on the “wrong” treatment.

For multi-centred trials, how to handle the randomisations across the centres should be considered at this point. Do all centres need to be completely balanced? Are all centres the same size? Considering the various centres as stratification variables is one way of dealing with more than one centre.

Once the method of randomisation has been established the next important step is to consider how to implement it. The recommended way is to enlist the services of a central randomisation office that can offer robust, validated techniques with the security and back-up needed to implement many of the methods proposed today. How the method is implemented must be as clearly reported as the method chosen. As part of the implementation it is important to keep the allocations concealed, both those already done and any future ones, from as many people as possible. This helps prevent selection bias: a clinician may withhold a participant if he believes that based on previous allocations the next allocations would not be the “preferred” ones – see the section below on subversion.

Part of the trial design will be to note exactly who should know what about how each participant has been allocated. Researchers and participants may be equally blinded, but that is not always the case.

For example, in a blinded trial there may be researchers who do not know which group the participants have been allocated to. This enables them to conduct the assessments without any bias for the allocation. They may, however, start to guess, on the basis of the results they see. A measure of blinding may be incorporated for the researchers to indicate whether they have remained blind to the treatment allocated. This can be in the form of a simple scale tool for the researcher to indicate how confident they are in knowing which allocated group the participant is in by the end of an assessment. With psychosocial interventions it is often impossible to hide from the participants, let alone the clinicians, which treatment group they have been allocated to.

In a drug trial where a placebo can be prescribed a coded system can ensure that neither patients nor researchers know which group is which until after the analysis stage.

With any level of blinding there may be a requirement to unblind participants or clinicians at any point in the trial, and there should be a documented procedure drawn up on how to unblind a particular participant without risking the unblinding of a trial. For drug trials in particular, the methods for unblinding a participant must be stated in the trial protocol. Wherever possible the data analysts and statisticians should remain blind to the allocation until after the main analysis has taken place.

Blinding should not be confused with allocation concealment. Blinding prevents performance and ascertainment bias within a trial, while allocation concealment prevents selection bias. Bias introduced by poor allocation concealment may be thought of as a predictive bias, trying to influence the results from the outset, while the biases introduced by non-blinding can be thought of as a reactive bias, creating causal links in outcomes because of being in possession of information about the treatment group.

In the literature on randomisation there are numerous tales of how allocation schemes have been subverted by clinicians trying to do the best for the trial or for their patient or both. This includes anecdotal tales of clinicians holding sealed envelopes containing the allocations up to X-ray lights and confessing to breaking into locked filing cabinets to get at the codes 3 . This type of behaviour has many explanations and reasons, but does raise the question whether these clinicians were in a state of equipoise with regard to the trial, and whether therefore they should really have been involved with the trial. Randomisation schemes and their implications must be signed up to by the whole team and are not something that only the participants need to consent to.

Clinicians have been known to X-ray sealed allocation envelopes to try to get their patients into the preferred group in a trial

The 2010 CONSORT statement can be found at http://www.consort-statement.org/consort-statement/ .

Dumville , J. C. , Hahn , S. , Miles , J. N. V. and Torgerson , D. J. ( 2006 ) The use of unequal randomisation ratios in clinical trials: A review . Contemporary Clinical Trials , 27 , 1 – 12 .

Google Scholar

Shulz , K. F. ( 1995 ) Subverting randomisation in controlled trials . Journal of the American Medical Association , 274 , 1456 – 1458 .

Email alerts

Citing articles via.

• Recommend to Your Librarian
• Advertising & Corporate Services
• Journals Career Network

Affiliations

• Online ISSN 1740-9713
• Print ISSN 1740-9705
• Copyright © 2024 Royal Statistical Society
• About Oxford Academic
• Publish journals with us
• University press partners
• What we publish
• New features  
• Open access
• Institutional account management
• Rights and permissions
• Get help with access
• Accessibility
• Advertising
• Media enquiries
• Oxford University Press
• Oxford Languages
• University of Oxford

Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide

• Copyright © 2024 Oxford University Press
• Cookie settings
• Cookie policy
• Privacy policy
• Legal notice

This Feature Is Available To Subscribers Only

Sign In or Create an Account

This PDF is available to Subscribers Only

For full access to this pdf, sign in to an existing account, or purchase an annual subscription.

• Open access
• Published: 16 August 2021

A roadmap to using randomization in clinical trials

• Vance W. Berger 1 ,
• Louis Joseph Bour 2 ,
• Kerstine Carter 3 ,
• Jonathan J. Chipman   ORCID: orcid.org/0000-0002-3021-2376 4 , 5 ,
• Colin C. Everett   ORCID: orcid.org/0000-0002-9788-840X 6 ,
• Nicole Heussen   ORCID: orcid.org/0000-0002-6134-7206 7 , 8 ,
• Catherine Hewitt   ORCID: orcid.org/0000-0002-0415-3536 9 ,
• Ralf-Dieter Hilgers   ORCID: orcid.org/0000-0002-5945-1119 7 ,
• Yuqun Abigail Luo 10 ,
• Jone Renteria 11 , 12 ,
• Yevgen Ryeznik   ORCID: orcid.org/0000-0003-2997-8566 13 ,
• Oleksandr Sverdlov   ORCID: orcid.org/0000-0002-1626-2588 14 &
• Diane Uschner   ORCID: orcid.org/0000-0002-7858-796X 15

for the Randomization Innovative Design Scientific Working Group

BMC Medical Research Methodology volume  21 , Article number:  168 ( 2021 ) Cite this article

26k Accesses

38 Citations

14 Altmetric

Metrics details

Randomization is the foundation of any clinical trial involving treatment comparison. It helps mitigate selection bias, promotes similarity of treatment groups with respect to important known and unknown confounders, and contributes to the validity of statistical tests. Various restricted randomization procedures with different probabilistic structures and different statistical properties are available. The goal of this paper is to present a systematic roadmap for the choice and application of a restricted randomization procedure in a clinical trial.

We survey available restricted randomization procedures for sequential allocation of subjects in a randomized, comparative, parallel group clinical trial with equal (1:1) allocation. We explore statistical properties of these procedures, including balance/randomness tradeoff, type I error rate and power. We perform head-to-head comparisons of different procedures through simulation under various experimental scenarios, including cases when common model assumptions are violated. We also provide some real-life clinical trial examples to illustrate the thinking process for selecting a randomization procedure for implementation in practice.

Restricted randomization procedures targeting 1:1 allocation vary in the degree of balance/randomness they induce, and more importantly, they vary in terms of validity and efficiency of statistical inference when common model assumptions are violated (e.g. when outcomes are affected by a linear time trend; measurement error distribution is misspecified; or selection bias is introduced in the experiment). Some procedures are more robust than others. Covariate-adjusted analysis may be essential to ensure validity of the results. Special considerations are required when selecting a randomization procedure for a clinical trial with very small sample size.

Conclusions

The choice of randomization design, data analytic technique (parametric or nonparametric), and analysis strategy (randomization-based or population model-based) are all very important considerations. Randomization-based tests are robust and valid alternatives to likelihood-based tests and should be considered more frequently by clinical investigators.

Peer Review reports

Various research designs can be used to acquire scientific medical evidence. The randomized controlled trial (RCT) has been recognized as the most credible research design for investigations of the clinical effectiveness of new medical interventions [ 1 , 2 ]. Evidence from RCTs is widely used as a basis for submissions of regulatory dossiers in request of marketing authorization for new drugs, biologics, and medical devices. Three important methodological pillars of the modern RCT include blinding (masking), randomization, and the use of control group [ 3 ].

While RCTs provide the highest standard of clinical evidence, they are laborious and costly, in terms of both time and material resources. There are alternative designs, such as observational studies with either a cohort or case–control design, and studies using real world evidence (RWE). When properly designed and implemented, observational studies can sometimes produce similar estimates of treatment effects to those found in RCTs, and furthermore, such studies may be viable alternatives to RCTs in many settings where RCTs are not feasible and/or not ethical. In the era of big data, the sources of clinically relevant data are increasingly rich and include electronic health records, data collected from wearable devices, health claims data, etc. Big data creates vast opportunities for development and implementation of novel frameworks for comparative effectiveness research [ 4 ], and RWE studies nowadays can be implemented rapidly and relatively easily. But how credible are the results from such studies?

In 1980, D. P. Byar issued warnings and highlighted potential methodological problems with comparison of treatment effects using observational databases [ 5 ]. Many of these issues still persist and actually become paramount during the ongoing COVID-19 pandemic when global scientific efforts are made to find safe and efficacious vaccines and treatments as soon as possible. While some challenges pertinent to RWE studies are related to the choice of proper research methodology, some additional challenges arise from increasing requirements of health authorities and editorial boards of medical journals for the investigators to present evidence of transparency and reproducibility of their conducted clinical research. Recently, two top medical journals, the New England Journal of Medicine and the Lancet, retracted two COVID-19 studies that relied on observational registry data [ 6 , 7 ]. The retractions were made at the request of the authors who were unable to ensure reproducibility of the results [ 8 ]. Undoubtedly, such cases are harmful in many ways. The already approved drugs may be wrongly labeled as “toxic” or “inefficacious”, and the reputation of the drug developers could be blemished or destroyed. Therefore, the highest standards for design, conduct, analysis, and reporting of clinical research studies are now needed more than ever. When treatment effects are modest, yet still clinically meaningful, a double-blind, randomized, controlled clinical trial design helps detect these differences while adjusting for possible confounders and adequately controlling the chances of both false positive and false negative findings.

Randomization in clinical trials has been an important area of methodological research in biostatistics since the pioneering work of A. Bradford Hill in the 1940’s and the first published randomized trial comparing streptomycin with a non-treatment control [ 9 ]. Statisticians around the world have worked intensively to elaborate the value, properties, and refinement of randomization procedures with an incredible record of publication [ 10 ]. In particular, a recent EU-funded project ( www.IDeAl.rwth-aachen.de ) on innovative design and analysis of small population trials has “randomization” as one work package. In 2020, a group of trial statisticians around the world from different sectors formed a subgroup of the Drug Information Association (DIA) Innovative Designs Scientific Working Group (IDSWG) to raise awareness of the full potential of randomization to improve trial quality, validity and rigor ( https://randomization-working-group.rwth-aachen.de/ ).

The aims of the current paper are three-fold. First, we describe major recent methodological advances in randomization, including different restricted randomization designs that have superior statistical properties compared to some widely used procedures such as permuted block designs. Second, we discuss different types of experimental biases in clinical trials and explain how a carefully chosen randomization design can mitigate risks of these biases. Third, we provide a systematic roadmap for evaluating different restricted randomization procedures and selecting an “optimal” one for a particular trial. We also showcase application of these ideas through several real life RCT examples.

The target audience for this paper would be clinical investigators and biostatisticians who are tasked with the design, conduct, analysis, and interpretation of clinical trial results, as well as regulatory and scientific/medical journal reviewers. Recognizing the breadth of the concept of randomization, in this paper we focus on a randomized, comparative, parallel group clinical trial design with equal (1:1) allocation, which is typically implemented using some restricted randomization procedure, possibly stratified by some important baseline prognostic factor(s) and/or study center. Some of our findings and recommendations are generalizable to more complex clinical trial settings. We shall highlight these generalizations and outline additional important considerations that fall outside the scope of the current paper.

The paper is organized as follows. The “ Methods ” section provides some general background on the methodology of randomization in clinical trials, describes existing restricted randomization procedures, and discusses some important criteria for comparison of these procedures in practice. In the “ Results ” section, we present our findings from four simulation studies that illustrate the thinking process when evaluating different randomization design options at the study planning stage. The “ Conclusions ” section summarizes the key findings and important considerations on restricted randomization procedures, and it also highlights some extensions and further topics on randomization in clinical trials.

What is randomization and what are its virtues in clinical trials?

Randomization is an essential component of an experimental design in general and clinical trials in particular. Its history goes back to R. A. Fisher and his classic book “The Design of Experiments” [ 11 ]. Implementation of randomization in clinical trials is due to A. Bradford Hill who designed the first randomized clinical trial evaluating the use of streptomycin in treating tuberculosis in 1946 [ 9 , 12 , 13 ].

Reference [ 14 ] provides a good summary of the rationale and justification for the use of randomization in clinical trials. The randomized controlled trial (RCT) has been referred to as “the worst possible design (except for all the rest)” [ 15 ], indicating that the benefits of randomization should be evaluated in comparison to what we are left with if we do not randomize. Observational studies suffer from a wide variety of biases that may not be adequately addressed even using state-of-the-art statistical modeling techniques.

The RCT in the medical field has several features that distinguish it from experimental designs in other fields, such as agricultural experiments. In the RCT, the experimental units are humans, and in the medical field often diagnosed with a potentially fatal disease. These subjects are sequentially enrolled for participation in the study at selected study centers, which have relevant expertise for conducting clinical research. Many contemporary clinical trials are run globally, at multiple research institutions. The recruitment period may span several months or even years, depending on a therapeutic indication and the target patient population. Patients who meet study eligibility criteria must sign the informed consent, after which they are enrolled into the study and, for example, randomized to either experimental treatment E or the control treatment C according to the randomization sequence. In this setup, the choice of the randomization design must be made judiciously, to protect the study from experimental biases and ensure validity of clinical trial results.

The first virtue of randomization is that, in combination with allocation concealment and masking, it helps mitigate selection bias due to an investigator’s potential to selectively enroll patients into the study [ 16 ]. A non-randomized, systematic design such as a sequence of alternating treatment assignments has a major fallacy: an investigator, knowing an upcoming treatment assignment in a sequence, may enroll a patient who, in their opinion, would be best suited for this treatment. Consequently, one of the groups may contain a greater number of “sicker” patients and the estimated treatment effect may be biased. Systematic covariate imbalances may increase the probability of false positive findings and undermine the integrity of the trial. While randomization alleviates the fallacy of a systematic design, it does not fully eliminate the possibility of selection bias (unless we consider complete randomization for which each treatment assignment is determined by a flip of a coin, which is rarely, if ever used in practice [ 17 ]). Commonly, RCTs employ restricted randomization procedures which sequentially balance treatment assignments while maintaining allocation randomness. A popular choice is the permuted block design that controls imbalance by making treatment assignments at random in blocks. To minimize potential for selection bias, one should avoid overly restrictive randomization schemes such as permuted block design with small block sizes, as this is very similar to alternating treatment sequence.

The second virtue of randomization is its tendency to promote similarity of treatment groups with respect to important known, but even more importantly, unknown confounders. If treatment assignments are made at random, then by the law of large numbers, the average values of patient characteristics should be approximately equal in the experimental and the control groups, and any observed treatment difference should be attributed to the treatment effects, not the effects of the study participants [ 18 ]. However, one can never rule out the possibility that the observed treatment difference is due to chance, e.g. as a result of random imbalance in some patient characteristics [ 19 ]. Despite that random covariate imbalances can occur in clinical trials of any size, such imbalances do not compromise the validity of statistical inference, provided that proper statistical techniques are applied in the data analysis.

Several misconceptions on the role of randomization and balance in clinical trials were documented and discussed by Senn [ 20 ]. One common misunderstanding is that balance of prognostic covariates is necessary for valid inference. In fact, different randomization designs induce different extent of balance in the distributions of covariates, and for a given trial there is always a possibility of observing baseline group differences. A legitimate approach is to pre-specify in the protocol the clinically important covariates to be adjusted for in the primary analysis, apply a randomization design (possibly accounting for selected covariates using pre-stratification or some other approach), and perform a pre-planned covariate-adjusted analysis (such as analysis of covariance for a continuous primary outcome), verifying the model assumptions and conducting additional supportive/sensitivity analyses, as appropriate. Importantly, the pre-specified prognostic covariates should always be accounted for in the analysis, regardless whether their baseline differences are present or not [ 20 ].

It should be noted that some randomization designs (such as covariate-adaptive randomization procedures) can achieve very tight balance of covariate distributions between treatment groups [ 21 ]. While we address randomization within pre-specified stratifications, we do not address more complex covariate- and response-adaptive randomization in this paper.

Finally, randomization plays an important role in statistical analysis of the clinical trial. The most common approach to inference following the RCT is the invoked population model [ 10 ]. With this approach, one posits that there is an infinite target population of patients with the disease, from which \(n\) eligible subjects are sampled in an unbiased manner for the study and are randomized to the treatment groups. Within each group, the responses are assumed to be independent and identically distributed (i.i.d.), and inference on the treatment effect is performed using some standard statistical methodology, e.g. a two sample t-test for normal outcome data. The added value of randomization is that it makes the assumption of i.i.d. errors more feasible compared to a non-randomized study because it introduces a real element of chance in the allocation of patients.

An alternative approach is the randomization model , in which the implemented randomization itself forms the basis for statistical inference [ 10 ]. Under the null hypothesis of the equality of treatment effects, individual outcomes (which are regarded as not influenced by random variation, i.e. are considered as fixed) are not affected by treatment. Treatment assignments are permuted in all possible ways consistent with the randomization procedure actually used in the trial. The randomization-based p- value is the sum of null probabilities of the treatment assignment permutations in the reference set that yield the test statistic values greater than or equal to the experimental value. A randomization-based test can be a useful supportive analysis, free of assumptions of parametric tests and protective against spurious significant results that may be caused by temporal trends [ 14 , 22 ].

It is important to note that Bayesian inference has also become a common statistical analysis in RCTs [ 23 ]. Although the inferential framework relies upon subjective probabilities, a study analyzed through a Bayesian framework still relies upon randomization for the other aforementioned virtues [ 24 ]. Hence, the randomization considerations discussed herein have broad application.

What types of randomization methodologies are available?

Randomization is not a single methodology, but a very broad class of design techniques for the RCT [ 10 ]. In this paper, we consider only randomization designs for sequential enrollment clinical trials with equal (1:1) allocation in which randomization is not adapted for covariates and/or responses. The simplest procedure for an RCT is complete randomization design (CRD) for which each subject’s treatment is determined by a flip of a fair coin [ 25 ]. CRD provides no potential for selection bias (e.g. based on prediction of future assignments) but it can result, with non-negligible probability, in deviations from the 1:1 allocation ratio and covariate imbalances, especially in small samples. This may lead to loss of statistical efficiency (decrease in power) compared to the balanced design. In practice, some restrictions on randomization are made to achieve balanced allocation. Such randomization designs are referred to as restricted randomization procedures [ 26 , 27 ].

Suppose we plan to randomize an even number of subjects \(n\) sequentially between treatments E and C. Two basic designs that equalize the final treatment numbers are the random allocation rule (Rand) and the truncated binomial design (TBD), which were discussed in the 1957 paper by Blackwell and Hodges [ 28 ]. For Rand, any sequence of exactly \(n/2\) E’s and \(n/2\) C’s is equally likely. For TBD, treatment assignments are made with probability 0.5 until one of the treatments receives its quota of \(n/2\) subjects; thereafter all remaining assignments are made deterministically to the opposite treatment.

A common feature of both Rand and TBD is that they aim at the final balance, whereas at intermediate steps it is still possible to have substantial imbalances, especially if \(n\) is large. A long run of a single treatment in a sequence may be problematic if there is a time drift in some important covariate, which can lead to chronological bias [ 29 ]. To mitigate this risk, one can further restrict randomization so that treatment assignments are balanced over time. One common approach is the permuted block design (PBD) [ 30 ], for which random treatment assignments are made in blocks of size \(2b\) ( \(b\) is some small positive integer), with exactly \(b\) allocations to each of the treatments E and C. The PBD is perhaps the oldest (it can be traced back to A. Bradford Hill’s 1951 paper [ 12 ]) and the most widely used randomization method in clinical trials. Often its choice in practice is justified by simplicity of implementation and the fact that it is referenced in the authoritative ICH E9 guideline on statistical principles for clinical trials [ 31 ]. One major challenge with PBD is the choice of the block size. If \(b=1\) , then every pair of allocations is balanced, but every even allocation is deterministic. Larger block sizes increase allocation randomness. The use of variable block sizes has been suggested [ 31 ]; however, PBDs with variable block sizes are also quite predictable [ 32 ]. Another problematic feature of the PBD is that it forces periodic return to perfect balance, which may be unnecessary from the statistical efficiency perspective and may increase the risk of prediction of upcoming allocations.

More recent and better alternatives to the PBD are the maximum tolerated imbalance (MTI) procedures [ 33 , 34 , 35 , 36 , 37 , 38 , 39 , 40 , 41 ]. These procedures provide stronger encryption of the randomization sequence (i.e. make it more difficult to predict future treatment allocations in the sequence even knowing the current sizes of the treatment groups) while controlling treatment imbalance at a pre-defined threshold throughout the experiment. A general MTI procedure specifies a certain boundary for treatment imbalance, say \(b>0\) , that cannot be exceeded. If, at a given allocation step the absolute value of imbalance is equal to \(b\) , then one next allocation is deterministically forced toward balance. This is in contrast to PBD which, after reaching the target quota of allocations for either treatment within a block, forces all subsequent allocations to achieve perfect balance at the end of the block. Some notable MTI procedures are the big stick design (BSD) proposed by Soares and Wu in 1983 [ 37 ], the maximal procedure proposed by Berger, Ivanova and Knoll in 2003 [ 35 ], the block urn design (BUD) proposed by Zhao and Weng in 2011 [ 40 ], just to name a few. These designs control treatment imbalance within pre-specified limits and are more immune to selection bias than the PBD [ 42 , 43 ].

Another important class of restricted randomization procedures is biased coin designs (BCDs). Starting with the seminal 1971 paper of Efron [ 44 ], BCDs have been a hot research topic in biostatistics for 50 years. Efron’s BCD is very simple: at any allocation step, if treatment numbers are balanced, the next assignment is made with probability 0.5; otherwise, the underrepresented treatment is assigned with probability \(p\) , where \(0.5<p\le 1\) is a fixed and pre-specified parameter that determines the tradeoff between balance and randomness. Note that \(p=1\) corresponds to PBD with block size 2. If we set \(p<1\) (e.g. \(p=2/3\) ), then the procedure has no deterministic assignments and treatment allocation will be concentrated around 1:1 with high probability [ 44 ]. Several extensions of Efron’s BCD providing better tradeoff between treatment balance and allocation randomness have been proposed [ 45 , 46 , 47 , 48 , 49 ]; for example, a class of adjustable biased coin designs introduced by Baldi Antognini and Giovagnoli in 2004 [ 49 ] unifies many BCDs in a single framework. A comprehensive simulation study comparing different BCDs has been published by Atkinson in 2014 [ 50 ].

Finally, urn models provide a useful mechanism for RCT designs [ 51 ]. Urn models apply some probabilistic rules to sequentially add/remove balls (representing different treatments) in the urn, to balance treatment assignments while maintaining the randomized nature of the experiment [ 39 , 40 , 52 , 53 , 54 , 55 ]. A randomized urn design for balancing treatment assignments was proposed by Wei in 1977 [ 52 ]. More novel urn designs, such as the drop-the-loser urn design developed by Ivanova in 2003 [ 55 ] have reduced variability and can attain the target treatment allocation more efficiently. Many urn designs involve parameters that can be fine-tuned to obtain randomization procedures with desirable balance/randomness tradeoff [ 56 ].

What are the attributes of a good randomization procedure?

A “good” randomization procedure is one that helps successfully achieve the study objective(s). Kalish and Begg [ 57 ] state that the major objective of a comparative clinical trial is to provide a precise and valid comparison. To achieve this, the trial design should be such that it: 1) prevents bias; 2) ensures an efficient treatment comparison; and 3) is simple to implement to minimize operational errors. Table 1 elaborates on these considerations, focusing on restricted randomization procedures for 1:1 randomized trials.

Before delving into a detailed discussion, let us introduce some important definitions. Following [ 10 ], a randomization sequence is a random vector \({{\varvec{\updelta}}}_{n}=({\delta }_{1},\dots ,{\delta }_{n})\) , where \({\delta }_{i}=1\) , if the i th subject is assigned to treatment E or \({\delta }_{i}=0\) , if the \(i\) th subject is assigned to treatment C. A restricted randomization procedure can be defined by specifying a probabilistic rule for the treatment assignment of the ( i +1)st subject, \({\delta }_{i+1}\) , given the past allocations \({{\varvec{\updelta}}}_{i}\) for \(i\ge 1\) . Let \({N}_{E}\left(i\right)={\sum }_{j=1}^{i}{\delta }_{j}\) and \({N}_{C}\left(i\right)=i-{N}_{E}\left(i\right)\) denote the numbers of subjects assigned to treatments E and C, respectively, after \(i\) allocation steps. Then \(D\left(i\right)={N}_{E}\left(i\right)-{N}_{C}(i)\) is treatment imbalance after \(i\) allocations. For any \(i\ge 1\) , \(D\left(i\right)\) is a random variable whose probability distribution is determined by the chosen randomization procedure.

Balance and randomness

Treatment balance and allocation randomness are two competing requirements in the design of an RCT. Restricted randomization procedures that provide a good tradeoff between these two criteria are desirable in practice.

Consider a trial with sample size \(n\) . The absolute value of imbalance, \(\left|D(i)\right|\) \((i=1,\dots,n)\) , provides a measure of deviation from equal allocation after \(i\) allocation steps. \(\left|D(i)\right|=0\) indicates that the trial is perfectly balanced. One can also consider \(\Pr(\vert D\left(i\right)\vert=0)\) , the probability of achieving exact balance after \(i\) allocation steps. In particular \(\Pr(\vert D\left(n\right)\vert=0)\) is the probability that the final treatment numbers are balanced. Two other useful summary measures are the expected imbalance at the \(i\mathrm{th}\)  step, \(E\left|D(i)\right|\) and the expected value of the maximum imbalance of the entire randomization sequence, \(E\left(\underset{1\le i\le n}{\mathrm{max}}\left|D\left(i\right)\right|\right)\) .

Greater forcing of balance implies lack of randomness. A procedure that lacks randomness may be susceptible to selection bias [ 16 ], which is a prominent issue in open-label trials with a single center or with randomization stratified by center, where the investigator knows the sequence of all previous treatment assignments. A classic approach to quantify the degree of susceptibility of a procedure to selection bias is the Blackwell-Hodges model [ 28 ]. Let \({G}_{i}=1\) (or 0), if at the \(i\mathrm{th}\)  allocation step an investigator makes a correct (or incorrect) guess on treatment assignment \({\delta }_{i}\) , given past allocations \({{\varvec{\updelta}}}_{i-1}\) . Then the predictability of the design at the \(i\mathrm{th}\)  step is the expected value of \({G}_{i}\) , i.e. \(E\left(G_i\right)=\Pr(G_i=1)\) . Blackwell and Hodges [ 28 ] considered the expected bias factor , the difference between expected total number of correct guesses of a given sequence of random assignments and the similar quantity obtained from CRD for which treatment assignments are made independently with equal probability: \(E(F)=E\left({\sum }_{i=1}^{n}{G}_{i}\right)-n/2\) . This quantity is zero for CRD, and it is positive for restricted randomization procedures (greater values indicate higher expected bias). Matts and Lachin [ 30 ] suggested taking expected proportion of deterministic assignments in a sequence as another measure of lack of randomness.

In the literature, various restricted randomization procedures have been compared in terms of balance and randomness [ 50 , 58 , 59 ]. For instance, Zhao et al. [ 58 ] performed a comprehensive simulation study of 14 restricted randomization procedures with different choices of design parameters, for sample sizes in the range of 10 to 300. The key criteria were the maximum absolute imbalance and the correct guess probability. The authors found that the performance of the designs was within a closed region with the boundaries shaped by Efron’s BCD [ 44 ] and the big stick design [ 37 ], signifying that the latter procedure with a suitably chosen MTI boundary can be superior to other restricted randomization procedures in terms of balance/randomness tradeoff. Similar findings confirming the utility of the big stick design were recently reported by Hilgers et al. [ 60 ].

Validity and efficiency

Validity of a statistical procedure essentially means that the procedure provides correct statistical inference following an RCT. In particular, a chosen statistical test is valid, if it controls the chance of a false positive finding, that is, the pre-specified probability of a type I error of the test is achieved but not exceeded. The strong control of type I error rate is a major prerequisite for any confirmatory RCT. Efficiency means high statistical power for detecting meaningful treatment differences (when they exist), and high accuracy of estimation of treatment effects.

Both validity and efficiency are major requirements of any RCT, and both of these aspects are intertwined with treatment balance and allocation randomness. Restricted randomization designs, when properly implemented, provide solid ground for valid and efficient statistical inference. However, a careful consideration of different options can help an investigator to optimize the choice of a randomization procedure for their clinical trial.

Let us start with statistical efficiency. Equal (1:1) allocation frequently maximizes power and estimation precision. To illustrate this, suppose the primary outcomes in the two groups are normally distributed with respective means \({\mu }_{E}\) and \({\mu }_{C}\) and common standard deviation \(\sigma >0\) . Then the variance of an efficient estimator of the treatment difference \({\mu }_{E}-{\mu }_{C}\) is equal to \(V=\frac{4{\sigma }^{2}}{n-{L}_{n}}\) , where \({L}_{n}=\frac{{\left|D(n)\right|}^{2}}{n}\) is referred to as loss [ 61 ]. Clearly, \(V\) is minimized when \({L}_{n}=0\) , or equivalently, \(D\left(n\right)=0\) , i.e. the balanced trial.

When the primary outcome follows a more complex statistical model, optimal allocation may be unequal across the treatment groups; however, 1:1 allocation is still nearly optimal for binary outcomes [ 62 , 63 ], survival outcomes [ 64 ], and possibly more complex data types [ 65 , 66 ]. Therefore, a randomization design that balances treatment numbers frequently promotes efficiency of the treatment comparison.

As regards inferential validity, it is important to distinguish two approaches to statistical inference after the RCT – an invoked population model and a randomization model [ 10 ]. For a given randomization procedure, these two approaches generally produce similar results when the assumption of normal random sampling (and some other assumptions) are satisfied, but the randomization model may be more robust when model assumptions are violated; e.g. when outcomes are affected by a linear time trend [ 67 , 68 ]. Another important issue that may interfere with validity is selection bias. Some authors showed theoretically that PBDs with small block sizes may result in serious inflation of the type I error rate under a selection bias model [ 69 , 70 , 71 ]. To mitigate risk of selection bias, one should ideally take preventative measures, such as blinding/masking, allocation concealment, and avoidance of highly restrictive randomization designs. However, for already completed studies with evidence of selection bias [ 72 ], special statistical adjustments are warranted to ensure validity of the results [ 73 , 74 , 75 ].

Implementation aspects

With the current state of information technology, implementation of randomization in RCTs should be straightforward. Validated randomization systems are emerging, and they can handle randomization designs of increasing complexity for clinical trials that are run globally. However, some important points merit consideration.

The first point has to do with how a randomization sequence is generated and implemented. One should distinguish between advance and adaptive randomization [ 16 ]. Here, by “adaptive” randomization we mean “in-real-time” randomization, i.e. when a randomization sequence is generated not upfront, but rather sequentially, as eligible subjects enroll into the study. Restricted randomization procedures are “allocation-adaptive”, in the sense that the treatment assignment of an individual subject is adapted to the history of previous treatment assignments. While in practice the majority of trials with restricted and stratified randomization use randomization schedules pre-generated in advance, there are some circumstances under which “in-real-time” randomization schemes may be preferred; for instance, clinical trials with high cost of goods and/or shortage of drug supply [ 76 ].

The advance randomization approach includes the following steps: 1) for the chosen randomization design and sample size \(n\) , specify the probability distribution on the reference set by enumerating all feasible randomization sequences of length \(n\) and their corresponding probabilities; 2) select a sequence at random from the reference set according to the probability distribution; and 3) implement this sequence in the trial. While enumeration of all possible sequences and their probabilities is feasible and may be useful for trials with small sample sizes, the task becomes computationally prohibitive (and unnecessary) for moderate or large samples. In practice, Monte Carlo simulation can be used to approximate the probability distribution of the reference set of all randomization sequences for a chosen randomization procedure.

A limitation of advance randomization is that a sequence of treatment assignments must be generated upfront, and proper security measures (e.g. blinding/masking) must be in place to protect confidentiality of the sequence. With the adaptive or “in-real-time” randomization, a sequence of treatment assignments is generated dynamically as the trial progresses. For many restricted randomization procedures, the randomization rule can be expressed as \(\Pr(\delta_{i+1}=1)=\left|F\left\{D\left(i\right)\right\}\right|\) , where \(F\left\{\cdot \right\}\) is some non-increasing function of \(D\left(i\right)\) for any \(i\ge 1\) . This is referred to as the Markov property [ 77 ], which makes a procedure easy to implement sequentially. Some restricted randomization procedures, e.g. the maximal procedure [ 35 ], do not have the Markov property.

The second point has to do with how the final data analysis is performed. With an invoked population model, the analysis is conditional on the design and the randomization is ignored in the analysis. With a randomization model, the randomization itself forms the basis for statistical inference. Reference [ 14 ] provides a contemporaneous overview of randomization-based inference in clinical trials. Several other papers provide important technical details on randomization-based tests, including justification for control of type I error rate with these tests [ 22 , 78 , 79 ]. In practice, Monte Carlo simulation can be used to estimate randomization-based p- values [ 10 ].

A roadmap for comparison of restricted randomization procedures

The design of any RCT starts with formulation of the trial objectives and research questions of interest [ 3 , 31 ]. The choice of a randomization procedure is an integral part of the study design. A structured approach for selecting an appropriate randomization procedure for an RCT was proposed by Hilgers et al. [ 60 ]. Here we outline the thinking process one may follow when evaluating different candidate randomization procedures. Our presented roadmap is by no means exhaustive; its main purpose is to illustrate the logic behind some important considerations for finding an “optimal” randomization design for the given trial parameters.

Throughout, we shall assume that the study is designed as a randomized, two-arm comparative trial with 1:1 allocation, with a fixed sample size \(n\) that is pre-determined based on budgetary and statistical considerations to obtain a definitive assessment of the treatment effect via the pre-defined hypothesis testing. We start with some general considerations which determine the study design:

Sample size ( \(n\) ). For small or moderate studies, exact attainment of the target numbers per group may be essential, because even slight imbalance may decrease study power. Therefore, a randomization design in such studies should equalize well the final treatment numbers. For large trials, the risk of major imbalances is less of a concern, and more random procedures may be acceptable.

The length of the recruitment period and the trial duration. Many studies are short-term and enroll participants fast, whereas some other studies are long-term and may have slow patient accrual. In the latter case, there may be time drifts in patient characteristics, and it is important that the randomization design balances treatment assignments over time.

Level of blinding (masking): double-blind, single-blind, or open-label. In double-blind studies with properly implemented allocation concealment the risk of selection bias is low. By contrast, in open-label studies the risk of selection bias may be high, and the randomization design should provide strong encryption of the randomization sequence to minimize prediction of future allocations.

Number of study centers. Many modern RCTs are implemented globally at multiple research institutions, whereas some studies are conducted at a single institution. In the former case, the randomization is often stratified by center and/or clinically important covariates. In the latter case, especially in single-institution open-label studies, the randomization design should be chosen very carefully, to mitigate the risk of selection bias.

An important point to consider is calibration of the design parameters. Many restricted randomization procedures involve parameters, such as the block size in the PBD, the coin bias probability in Efron’s BCD, the MTI threshold, etc. By fine-tuning these parameters, one can obtain designs with desirable statistical properties. For instance, references [ 80 , 81 ] provide guidance on how to justify the block size in the PBD to mitigate the risk of selection bias or chronological bias. Reference [ 82 ] provides a formal approach to determine the “optimal” value of the parameter \(p\) in Efron’s BCD in both finite and large samples. The calibration of design parameters can be done using Monte Carlo simulations for the given trial setting.

Another important consideration is the scope of randomization procedures to be evaluated. As we mentioned already, even one method may represent a broad class of randomization procedures that can provide different levels of balance/randomness tradeoff; e.g. Efron’s BCD covers a wide spectrum of designs, from PBD(2) (if \(p=1\) ) to CRD (if \(p=0.5\) ). One may either prefer to focus on finding the “optimal” parameter value for the chosen design, or be more general and include various designs (e.g. MTI procedures, BCDs, urn designs, etc.) in the comparison. This should be done judiciously, on a case-by-case basis, focusing only on the most reasonable procedures. References [ 50 , 58 , 60 ] provide good examples of simulation studies to facilitate comparisons among various restricted randomization procedures for a 1:1 RCT.

In parallel with the decision on the scope of randomization procedures to be assessed, one should decide upon the performance criteria against which these designs will be compared. Among others, one might think about the two competing considerations: treatment balance and allocation randomness. For a trial of size \(n\) , at each allocation step \(i=1,\dots ,n\) one can calculate expected absolute imbalance \(E\left|D(i)\right|\) and the probability of correct guess \(\Pr(G_i=1)\) as measures of lack of balance and lack of randomness, respectively. These measures can be either calculated analytically (when formulae are available) or through Monte Carlo simulations. Sometimes it may be useful to look at cumulative measures up to the \(i\mathrm{th}\)  allocation step ( \(i=1,\dots ,n\) ); e.g. \(\frac{1}{i}{\sum }_{j=1}^{i}E\left|D(j)\right|\) and \(\frac1i\sum\nolimits_{j=1}^i\Pr(G_j=1)\) . For instance, \(\frac{1}{n}{\sum }_{j=1}^{n}{\mathrm{Pr}}({G}_{j}=1)\) is the average correct guess probability for a design with sample size \(n\) . It is also helpful to visualize the selected criteria. Visualizations can be done in a number of ways; e.g. plots of a criterion vs. allocation step, admissibility plots of two chosen criteria [ 50 , 59 ], etc. Such visualizations can help evaluate design characteristics, both overall and at intermediate allocation steps. They may also provide insights into the behavior of a particular design for different values of the tuning parameter, and/or facilitate a comparison among different types of designs.

Another way to compare the merits of different randomization procedures is to study their inferential characteristics such as type I error rate and power under different experimental conditions. Sometimes this can be done analytically, but a more practical approach is to use Monte Carlo simulation. The choice of the modeling and analysis strategy will be context-specific. Here we outline some considerations that may be useful for this purpose:

Data generating mechanism . To simulate individual outcome data, some plausible statistical model must be posited. The form of the model will depend on the type of outcomes (e.g. continuous, binary, time-to-event, etc.), covariates (if applicable), the distribution of the measurement error terms, and possibly some additional terms representing selection and/or chronological biases [ 60 ].

True treatment effects . At least two scenarios should be considered: under the null hypothesis ( \({H}_{0}\) : treatment effects are the same) to evaluate the type I error rate, and under an alternative hypothesis ( \({H}_{1}\) : there is some true clinically meaningful difference between the treatments) to evaluate statistical power.

Randomization designs to be compared . The choice of candidate randomization designs and their parameters must be made judiciously.

Data analytic strategy . For any study design, one should pre-specify the data analysis strategy to address the primary research question. Statistical tests of significance to compare treatment effects may be parametric or nonparametric, with or without adjustment for covariates.

The approach to statistical inference: population model-based or randomization-based . These two approaches are expected to yield similar results when the population model assumptions are met, but they may be different if some assumptions are violated. Randomization-based tests following restricted randomization procedures will control the type I error at the chosen level if the distribution of the test statistic under the null hypothesis is fully specified by the randomization procedure that was used for patient allocation. This is always the case unless there is a major flaw in the design (such as selection bias whereby the outcome of any individual participant is dependent on treatment assignments of the previous participants).

Overall, there should be a well-thought plan capturing the key questions to be answered, the strategy to address them, the choice of statistical software for simulation and visualization of the results, and other relevant details.

In this section we present four examples that illustrate how one may approach evaluation of different randomization design options at the study planning stage. Example 1 is based on a hypothetical 1:1 RCT with \(n=50\) and a continuous primary outcome, whereas Examples 2, 3, and 4 are based on some real RCTs.

Example 1: Which restricted randomization procedures are robust and efficient?

Our first example is a hypothetical RCT in which the primary outcome is assumed to be normally distributed with mean \({\mu }_{E}\) for treatment E, mean \({\mu }_{C}\) for treatment C, and common variance \({\sigma }^{2}\) . A total of \(n\) subjects are to be randomized equally between E and C, and a two-sample t-test is planned for data analysis. Let \(\Delta ={\mu }_{E}-{\mu }_{C}\) denote the true mean treatment difference. We are interested in testing a hypothesis \({H}_{0}:\Delta =0\) (treatment effects are the same) vs. \({H}_{1}:\Delta \ne 0\) .

The total sample size \(n\) to achieve given power at some clinically meaningful treatment difference \({\Delta }_{c}\) while maintaining the chance of a false positive result at level \(\alpha\) can be obtained using standard statistical methods [ 83 ]. For instance, if \({\Delta }_{c}/\sigma =0.95\) , then a design with \(n=50\) subjects (25 per arm) provides approximately 91% power of a two-sample t-test to detect a statistically significant treatment difference using 2-sided \(\alpha =\) 5%. We shall consider 12 randomization procedures to sequentially randomize \(n=50\) subjects in a 1:1 ratio.

Random allocation rule – Rand.

Truncated binomial design – TBD.

Permuted block design with block size of 2 – PBD(2).

Permuted block design with block size of 4 – PBD(4).

Big stick design [ 37 ] with MTI = 3 – BSD(3).

Biased coin design with imbalance tolerance [ 38 ] with p  = 2/3 and MTI = 3 – BCDWIT(2/3, 3).

Efron’s biased coin design [ 44 ] with p  = 2/3 – BCD(2/3).

Adjustable biased coin design [ 49 ] with a = 2 – ABCD(2).

Generalized biased coin design (GBCD) with \(\gamma =1\) [ 45 ] – GBCD(1).

GBCD with \(\gamma =2\) [ 46 ] – GBCD(2).

GBCD with \(\gamma =5\) [ 47 ] – GBCD(5).

Complete randomization design – CRD.

These 12 procedures can be grouped into five major types. I) Procedures 1, 2, 3, and 4 achieve exact final balance for a chosen sample size (provided the total sample size is a multiple of the block size). II) Procedures 5 and 6 ensure that at any allocation step the absolute value of imbalance is capped at MTI = 3. III) Procedures 7 and 8 are biased coin designs that sequentially adjust randomization according to imbalance measured as the difference in treatment numbers. IV) Procedures 9, 10, and 11 (GBCD’s with \(\gamma =\) 1, 2, and 5) are adaptive biased coin designs, for which randomization probability is modified according to imbalance measured as the difference in treatment allocation proportions (larger \(\gamma\) implies greater forcing of balance). V) Procedure 12 (CRD) is the most random procedure that achieves balance for large samples.

Balance/randomness tradeoff

We first compare the procedures with respect to treatment balance and allocation randomness. To quantify imbalance after \(i\) allocations, we consider two measures: expected value of absolute imbalance \(E\left|D(i)\right|\) , and expected value of loss \(E({L}_{i})=E{\left|D(i)\right|}^{2}/i\) [ 50 , 61 ]. Importantly, for procedures 1, 2, and 3 the final imbalance is always zero, thus \(E\left|D(n)\right|\equiv 0\) and \(E({L}_{n})\equiv 0\) , but at intermediate steps one may have \(E\left|D(i)\right|>0\) and \(E\left({L}_{i}\right)>0\) , for \(1\le i<n\) . For procedures 5 and 6 with MTI = 3, \(E\left({L}_{i}\right)\le 9/i\) . For procedures 7 and 8, \(E\left({L}_{n}\right)\) tends to zero as \(n\to \infty\) [ 49 ]. For procedures 9, 10, 11, and 12, as \(n\to \infty\) , \(E\left({L}_{n}\right)\) tends to the positive constants 1/3, 1/5, 1/11, and 1, respectively [ 47 ]. We take the cumulative average loss after \(n\) allocations as an aggregate measure of imbalance: \(Imb\left(n\right)=\frac{1}{n}{\sum }_{i=1}^{n}E\left({L}_{i}\right)\) , which takes values in the 0–1 range.

To measure lack of randomness, we consider two measures: expected proportion of correct guesses up to the \(i\mathrm{th}\)  step, \(PCG\left(i\right)=\frac1i\sum\nolimits_{j=1}^i\Pr(G_j=1)\) ,  \(i=1,\dots ,n\) , and the forcing index [ 47 , 84 ], \(FI(i)=\frac{{\sum }_{j=1}^{i}E\left|{\phi }_{j}-0.5\right|}{i/4}\) , where \(E\left|{\phi }_{j}-0.5\right|\) is the expected deviation of the conditional probability of treatment E assignment at the \(j\mathrm{th}\)  allocation step ( \({\phi }_{j}\) ) from the unconditional target value of 0.5. Note that \(PCG\left(i\right)\) takes values in the range from 0.5 for CRD to 0.75 for PBD(2) assuming \(i\) is even, whereas \(FI(i)\) takes values in the 0–1 range. At the one extreme, we have CRD for which \(FI(i)\equiv 0\) because for CRD \({\phi }_{i}=0.5\) for any \(i\ge 1\) . At the other extreme, we have PBD(2) for which every odd allocation is made with probability 0.5, and every even allocation is deterministic, i.e. made with probability 0 or 1. For PBD(2), assuming \(i\) is even, there are exactly \(i/2\) pairs of allocations, and so \({\sum }_{j=1}^{i}E\left|{\phi }_{j}-0.5\right|=0.5\cdot i/2=i/4\) , which implies that \(FI(i)=1\) for PBD(2). For all other restricted randomization procedures one has \(0<FI(i)<1\) .

A “good” randomization procedure should have low values of both loss and forcing index. Different randomization procedures can be compared graphically. As a balance/randomness tradeoff metric, one can calculate the quadratic distance to the origin (0,0) for the chosen sample size, e.g. \(d(n)=\sqrt{{\left\{Imb(n)\right\}}^{2}+{\left\{FI(n)\right\}}^{2}}\) (in our example \(n=50\) ), and the randomization designs can then be ranked such that designs with lower values of \(d(n)\) are preferable.

We ran a simulation study of the 12 randomization procedures for an RCT with \(n=50\) . Monte Carlo average values of absolute imbalance, loss, \(Imb\left(i\right)\) , \(FI\left(i\right)\) , and \(d(i)\) were calculated for each intermediate allocation step ( \(i=1,\dots ,50\) ), based on 10,000 simulations.

Figure  1 is a plot of expected absolute imbalance vs. allocation step. CRD, GBCD(1), and GBCD(2) show increasing patterns. For TBD and Rand, the final imbalance (when \(n=50\) ) is zero; however, at intermediate steps is can be quite large. For other designs, absolute imbalance is expected to be below 2 at any allocation step up to \(n=50\) . Note the periodic patterns of PBD(2) and PBD(4); for instance, for PBD(2) imbalance is 0 (or 1) for any even (or odd) allocation.

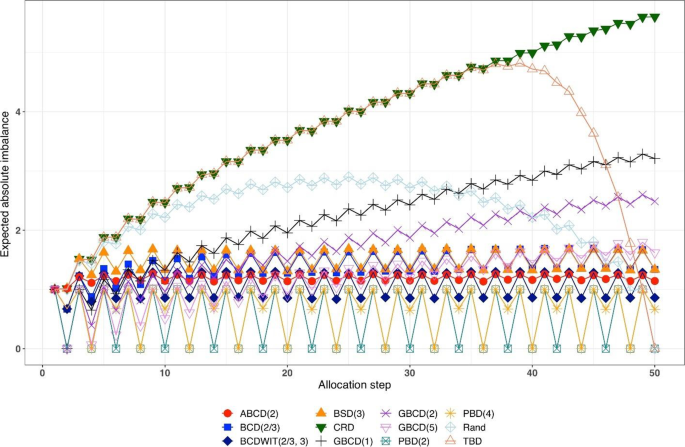
Simulated expected absolute imbalance vs. allocation step for 12 restricted randomization procedures for n  = 50. Note: PBD(2) and PBD(4) have forced periodicity absolute imbalance of 0, which distinguishes them from MTI procedures

Figure  2 is a plot of expected proportion of correct guesses vs. allocation step. One can observe that for CRD it is a flat pattern at 0.5; for PBD(2) it fluctuates while reaching the upper limit of 0.75 at even allocation steps; and for ten other designs the values of proportion of correct guesses fall between those of CRD and PBD(2). The TBD has the same behavior up to ~ 40 th allocation step, at which the pattern starts increasing. Rand exhibits an increasing pattern with overall fewer correct guesses compared to other randomization procedures. Interestingly, BSD(3) is uniformly better (less predictable) than ABCD(2), BCD(2/3), and BCDWIT(2/3, 3). For the three GBCD procedures, there is a rapid initial increase followed by gradual decrease in the pattern; this makes good sense, because GBCD procedures force greater balance when the trial is small and become more random (and less prone to correct guessing) as the sample size increases.

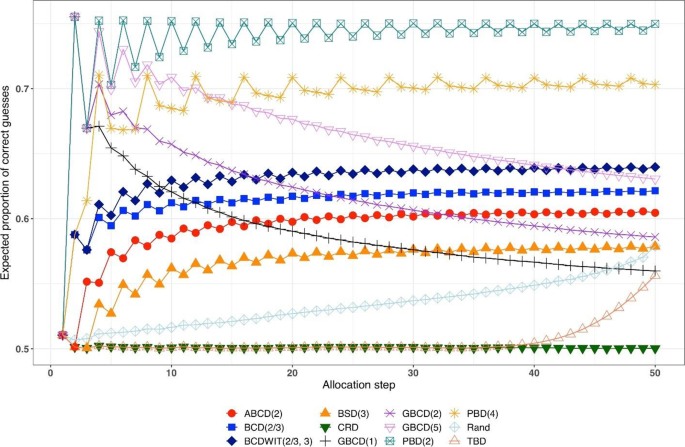
Simulated expected proportion of correct guesses vs. allocation step for 12 restricted randomization procedures for n  = 50

Table 2 shows the ranking of the 12 designs with respect to the overall performance metric \(d(n)=\sqrt{{\left\{Imb(n)\right\}}^{2}+{\left\{FI(n)\right\}}^{2}}\) for \(n=50\) . BSD(3), GBCD(2) and GBCD(1) are the top three procedures, whereas PBD(2) and CRD are at the bottom of the list.

Figure  3 is a plot of \(FI\left(n\right)\) vs. \(Imb\left(n\right)\) for \(n=50\) . One can see the two extremes: CRD that takes the value (0,1), and PBD(2) with the value (1,0). The other ten designs are closer to (0,0).

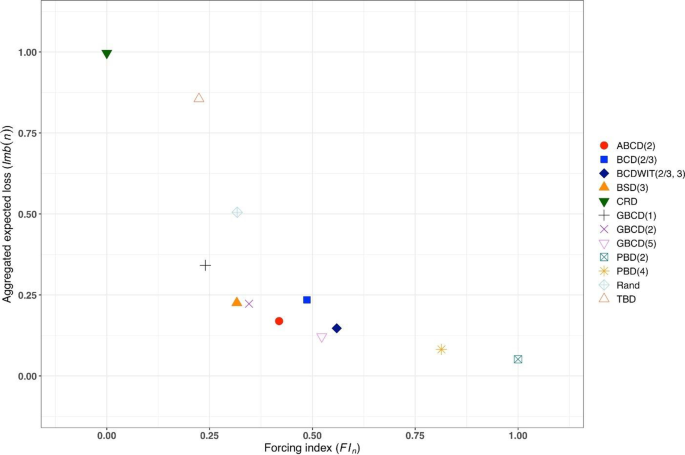
Simulated forcing index (x-axis) vs. aggregate expected loss (y-axis) for 12 restricted randomization procedures for n  = 50

Figure  4 is a heat map plot of the metric \(d(i)\) for \(i=1,\dots ,50\) . BSD(3) seems to provide overall best tradeoff between randomness and balance throughout the study.

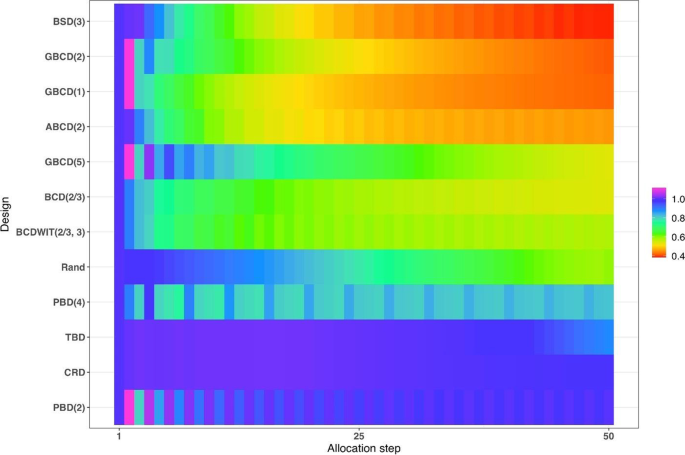
Heatmap of the balance/randomness tradeoff \(d\left(i\right)=\sqrt{{\left\{Imb(i)\right\}}^{2}+{\left\{FI(i)\right\}}^{2}}\) vs. allocation step ( \(i=1,\dots ,50\) ) for 12 restricted randomization procedures. The procedures are ordered by value of d(50), with smaller values (more red) indicating more optimal performance

Inferential characteristics: type I error rate and power

Our next goal is to compare the chosen randomization procedures in terms of validity (control of the type I error rate) and efficiency (power). For this purpose, we assumed the following data generating mechanism: for the \(i\mathrm{th}\)  subject, conditional on the treatment assignment \({\delta }_{i}\) , the outcome \({Y}_{i}\) is generated according to the model

where \({u}_{i}\) is an unknown term associated with the \(i\mathrm{th}\)  subject and \({\varepsilon }_{i}\) ’s are i.i.d. measurement errors. We shall explore the following four models:

M1: Normal random sampling :  \({u}_{i}\equiv 0\) and \({\varepsilon }_{i}\sim\) i.i.d. N(0,1), \(i=1,\dots ,n\) . This corresponds to a standard setup for a two-sample t-test under a population model.

M2: Linear trend :  \({u}_{i}=\frac{5i}{n+1}\) and \({\varepsilon }_{i}\sim\) i.i.d. N(0,1), \(i=1,\dots ,n\) . In this model, the outcomes are affected by a linear trend over time [ 67 ].

M3: Cauchy errors :  \({u}_{i}\equiv 0\) and \({\varepsilon }_{i}\sim\) i.i.d. Cauchy(0,1), \(i=1,\dots ,n\) . In this setup, we have a misspecification of the distribution of measurement errors.

M4: Selection bias :  \({u}_{i+1}=-\nu \cdot sign\left\{D\left(i\right)\right\}\) , \(i=0,\dots ,n-1\) , with the convention that \(D\left(0\right)=0\) . Here, \(\nu >0\) is the “bias effect” (in our simulations we set \(\nu =0.5\) ). We also assume that \({\varepsilon }_{i}\sim\) i.i.d. N(0,1), \(i=1,\dots ,n\) . In this setup, at each allocation step the investigator attempts to intelligently guess the upcoming treatment assignment and selectively enroll a patient who, in their view, would be most suitable for the upcoming treatment. The investigator uses the “convergence” guessing strategy [ 28 ], that is, guess the treatment as one that has been less frequently assigned thus far, or make a random guess in case the current treatment numbers are equal. Assuming that the investigator favors the experimental treatment and is interested in demonstrating its superiority over the control, the biasing mechanism is as follows: at the \((i+1)\) st step, a “healthier” patient is enrolled, if \(D\left(i\right)<0\) ( \({u}_{i+1}=0.5\) ); a “sicker” patient is enrolled, if \(D\left(i\right)>0\) ( \({u}_{i+1}=-0.5\) ); or a “regular” patient is enrolled, if \(D\left(i\right)=0\) ( \({u}_{i+1}=0\) ).

We consider three statistical test procedures:

T1: Two-sample t-test : The test statistic is \(t=\frac{{\overline{Y} }_{E}-{\overline{Y} }_{C}}{\sqrt{{S}_{p}^{2}\left(\frac{1}{{N}_{E}\left(n\right)}+\frac{1}{{N}_{C}\left(n\right)}\right)}}\) , where \({\overline{Y} }_{E}=\frac{1}{{N}_{E}\left(n\right)}{\sum }_{i=1}^{n}{{\delta }_{i}Y}_{i}\) and \({\overline{Y} }_{C}=\frac{1}{{N}_{C}\left(n\right)}{\sum }_{i=1}^{n}{(1-\delta }_{i}){Y}_{i}\) are the treatment sample means,  \({N}_{E}\left(n\right)={\sum }_{i=1}^{n}{\delta }_{i}\) and \({N}_{C}\left(n\right)=n-{N}_{E}\left(n\right)\) are the observed group sample sizes, and \({S}_{p}^{2}\) is a pooled estimate of variance, where \({S}_{p}^{2}=\frac{1}{n-2}\left({\sum }_{i=1}^{n}{\delta }_{i}{\left({Y}_{i}-{\overline{Y} }_{E}\right)}^{2}+{\sum }_{i=1}^{n}(1-{\delta }_{i}){\left({Y}_{i}-{\overline{Y} }_{C}\right)}^{2}\right)\) . Then \({H}_{0}:\Delta =0\) is rejected at level \(\alpha\) , if \(\left|t\right|>{t}_{1-\frac{\alpha }{2}, n-2}\) , the 100( \(1-\frac{\alpha }{2}\) )th percentile of the t-distribution with \(n-2\) degrees of freedom.

T2: Randomization-based test using mean difference : Let \({{\varvec{\updelta}}}_{obs}\) and \({{\varvec{y}}}_{obs}\) denote, respectively the observed sequence of treatment assignments and responses, obtained from the trial using randomization procedure \(\mathfrak{R}\) . We first compute the observed mean difference \({S}_{obs}=S\left({{\varvec{\updelta}}}_{obs},{{\varvec{y}}}_{obs}\right)={\overline{Y} }_{E}-{\overline{Y} }_{C}\) . Then we use Monte Carlo simulation to generate \(L\) randomization sequences of length \(n\) using procedure \(\mathfrak{R}\) , where \(L\) is some large number. For the \(\ell\mathrm{th}\)  generated sequence, \({{\varvec{\updelta}}}_{\ell}\) , compute \({S}_{\ell}=S({{\varvec{\updelta}}}_{\ell},{{\varvec{y}}}_{obs})\) , where \({\ell}=1,\dots ,L\) . The proportion of sequences for which \({S}_{\ell}\) is at least as extreme as \({S}_{obs}\) is computed as \(\widehat{P}=\frac{1}{L}{\sum }_{{\ell}=1}^{L}1\left\{\left|{S}_{\ell}\right|\ge \left|{S}_{obs}\right|\right\}\) . Statistical significance is declared, if \(\widehat{P}<\alpha\) .

T3: Randomization-based test based on ranks : This test procedure follows the same logic as T2, except that the test statistic is calculated based on ranks. Given the vector of observed responses \({{\varvec{y}}}_{obs}=({y}_{1},\dots ,{y}_{n})\) , let \({a}_{jn}\) denote the rank of \({y}_{j}\) among the elements of \({{\varvec{y}}}_{obs}\) . Let \({\overline a}_n\) denote the average of \({a}_{jn}\) ’s, and let \({\boldsymbol a}_n=\left(a_{1n}-{\overline a}_n,...,\alpha_{nn}-{\overline a}_n\right)\boldsymbol'\) . Then a linear rank test statistic has the form \({S}_{obs}={{\varvec{\updelta}}}_{obs}^{\boldsymbol{^{\prime}}}{{\varvec{a}}}_{n}={\sum }_{i=1}^{n}{\delta }_{i}({a}_{in}-{\overline{a} }_{n})\) .

We consider four scenarios of the true mean difference  \(\Delta ={\mu }_{E}-{\mu }_{C}\) , which correspond to the Null case ( \(\Delta =0\) ), and three choices of \(\Delta >0\) which correspond to Alternative 1 (power ~ 70%), Alternative 2 (power ~ 80%), and Alternative 3 (power ~ 90%). In all cases, \(n=50\) was used.

Figure  5 summarizes the results of a simulation study comparing 12 randomization designs, under 4 models for the outcome (M1, M2, M3, and M4), 4 scenarios for the mean treatment difference (Null, and Alternatives 1, 2, and 3), using 3 statistical tests (T1, T2, and T3). The operating characteristics of interest are the type I error rate under the Null scenario and the power under the Alternative scenarios. Each scenario was simulated 10,000 times, and each randomization-based test was computed using \(L=\mathrm{10,000}\) sequences.

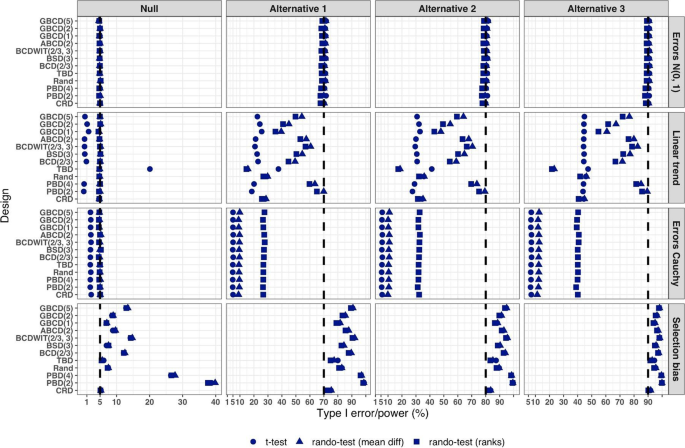
Simulated type I error rate and power of 12 restricted randomization procedures. Four models for the data generating mechanism of the primary outcome (M1: Normal random sampling; M2: Linear trend; M3: Errors Cauchy; and M4: Selection bias). Four scenarios for the treatment mean difference (Null; Alternatives 1, 2, and 3). Three statistical tests (T1: two-sample t-test; T2: randomization-based test using mean difference; T3: randomization-based test using ranks)

From Fig.  5 , under the normal random sampling model (M1), all considered randomization designs have similar performance: they maintain the type I error rate and have similar power, with all tests. In other words, when population model assumptions are satisfied, any combination of design and analysis should work well and yield reliable and consistent results.

Under the “linear trend” model (M2), the designs have differential performance. First of all, under the Null scenario, only Rand and CRD maintain the type I error rate at 5% with all three tests. For TBD, the t-test is anticonservative, with type I error rate ~ 20%, whereas for nine other procedures the t-test is conservative, with type I error rate in the range 0.1–2%. At the same time, for all 12 designs the two randomization-based tests maintain the nominal type I error rate at 5%. These results are consistent with some previous findings in the literature [ 67 , 68 ]. As regards power, it is reduced significantly compared to the normal random sampling scenario. The t-test seems to be most affected and the randomization-based test using ranks is most robust for a majority of the designs. Remarkably, for CRD the power is similar with all three tests. This signifies the usefulness of randomization-based inference in situations when outcome data are subject to a linear time trend, and the importance of applying randomization-based tests at least as supplemental analyses to likelihood-based test procedures.

Under the “Cauchy errors” model (M3), all designs perform similarly: the randomization-based tests maintain the type I error rate at 5%, whereas the t-test deflates the type I error to 2%. As regards power, all designs also have similar, consistently degraded performance: the t-test is least powerful, and the randomization-based test using ranks has highest power. Overall, under misspecification of the error distribution a randomization-based test using ranks is most appropriate; yet one should acknowledge that its power is still lower than expected.

Under the “selection bias” model (M4), the 12 designs have differential performance. The only procedure that maintained the type I error rate at 5% with all three tests was CRD. For eleven other procedures, inflations of the type I error were observed. In general, the more random the design, the less it was affected by selection bias. For instance, the type I error rate for TBD was ~ 6%; for Rand, BSD(3), and GBCD(1) it was ~ 7.5%; for GBCD(2) and ABCD(2) it was ~ 8–9%; for Efron’s BCD(2/3) it was ~ 12.5%; and the most affected design was PBD(2) for which the type I error rate was ~ 38–40%. These results are consistent with the theory of Blackwell and Hodges [ 28 ] which posits that TBD is least susceptible to selection bias within a class of restricted randomization designs that force exact balance. Finally, under M4, statistical power is inflated by several percentage points compared to the normal random sampling scenario without selection bias.

We performed additional simulations to assess the impact of the bias effect \(\nu\) under selection bias model. The same 12 randomization designs and three statistical tests were evaluated for a trial with \(n=50\) under the Null scenario ( \(\Delta =0\) ), for \(\nu\) in the range of 0 (no bias) to 1 (strong bias). Figure S1 in the Supplementary Materials shows that for all designs but CRD, the type I error rate is increasing in \(\nu\) , with all three tests. The magnitude of the type I error inflation is different across the restricted randomization designs; e.g. for TBD it is minimal, whereas for more restrictive designs it may be large, especially for \(\nu \ge 0.4\) . PBD(2) is particularly vulnerable: for \(\nu\) in the range 0.4–1, its type I error rate is in the range 27–90% (for the nominal \(\alpha =5\) %).

In summary, our Example 1 includes most of the key ingredients of the roadmap for assessment of competing randomization designs which was described in the “ Methods ” section. For the chosen experimental scenarios, we evaluated CRD and several restricted randomization procedures, some of which belonged to the same class but with different values of the parameter (e.g. GBCD with \(\gamma =1, 2, 5\) ). We assessed two measures of imbalance, two measures of lack of randomness (predictability), and a metric that quantifies balance/randomness tradeoff. Based on these criteria, we found that BSD(3) provides overall best performance. We also evaluated type I error and power of selected randomization procedures under several treatment response models. We have observed important links between balance, randomness, type I error rate and power. It is beneficial to consider all these criteria simultaneously as they may complement each other in characterizing statistical properties of randomization designs. In particular, we found that a design that lacks randomness, such as PBD with blocks of 2 or 4, may be vulnerable to selection bias and lead to inflations of the type I error. Therefore, these designs should be avoided, especially in open-label studies. As regards statistical power, since all designs in this example targeted 1:1 allocation ratio (which is optimal if the outcomes are normally distributed and have between-group constant variance), they had very similar power of statistical tests in most scenarios except for the one with chronological bias. In the latter case, randomization-based tests were more robust and more powerful than the standard two-sample t-test under the population model assumption.

Overall, while Example 1 is based on a hypothetical 1:1 RCT, its true purpose is to showcase the thinking process in the application of our general roadmap. The following three examples are considered in the context of real RCTs.

Example 2: How can we reduce predictability of a randomization procedure and lower the risk of selection bias?

Selection bias can arise if the investigator can intelligently guess at least part of the randomization sequence yet to be allocated and, on that basis, preferentially and strategically assigns study subjects to treatments. Although it is generally not possible to prove that a particular study has been infected with selection bias, there are examples of published RCTs that do show some evidence to have been affected by it. Suspect trials are, for example, those with strong observed baseline covariate imbalances that consistently favor the active treatment group [ 16 ]. In what follows we describe an example of an RCT where the stratified block randomization procedure used was vulnerable to potential selection biases, and discuss potential alternatives that may reduce this vulnerability.

Etanercept was studied in patients aged 4 to 17 years with polyarticular juvenile rheumatoid arthritis [ 85 ]. The trial consisted of two parts. During the first, open-label part of the trial, patients received etanercept twice weekly for up to three months. Responders from this initial part of the trial were then randomized, at a 1:1 ratio, in the second, double-blind, placebo-controlled part of the trial to receive etanercept or placebo for four months or until a flare of the disease occurred. The primary efficacy outcome, the proportion of patients with disease flare, was evaluated in the double-blind part. Among the 51 randomized patients, 21 of the 26 placebo patients (81%) withdrew because of disease flare, compared with 7 of the 25 etanercept patients (28%), yielding a p- value of 0.003.

Regulatory review by the Food and Drug Administrative (FDA) identified vulnerability to selection biases in the study design of the double-blind part and potential issues in study conduct. These findings were succinctly summarized in [ 16 ] (pp.51–52).

Specifically, randomization was stratified by study center and number of active joints (≤ 2 vs. > 2, referred to as “few” or “many” in what follows), with blocked randomization within each stratum using a block size of two. Furthermore, randomization codes in corresponding “few” and “many” blocks within each study center were mirror images of each other. For example, if the first block within the “few” active joints stratum of a given center is “placebo followed by etanercept”, then the first block within the “many” stratum of the same center would be “etanercept followed by placebo”. While this appears to be an attempt to improve treatment balance in this small trial, unblinding of one treatment assignment may lead to deterministic predictability of three upcoming assignments. While the double-blind nature of the trial alleviated this concern to some extent, it should be noted that all patients did receive etanercept previously in the initial open-label part of the trial. Chances of unblinding may not be ignorable if etanercept and placebo have immediately evident different effects or side effects. The randomized withdrawal design was appropriate in this context to improve statistical power in identifying efficacious treatments, but the specific randomization procedure used in the trial increased vulnerability to selection biases if blinding cannot be completely maintained.

FDA review also identified that four patients were randomized from the wrong “few” or “many” strata, in three of which (3/51 = 5.9%) it was foreseeable that the treatment received could have been reversed compared to what the patient would have received if randomized in the correct stratum. There were also some patients randomized out of order. Imbalance in baseline characteristics were observed in age (mean ages of 8.9 years in the etanercept arm vs. that of 12.2 years in the placebo arm) and corticosteroid use at baseline (50% vs. 24%).

While the authors [ 85 ] concluded that “The unequal randomization did not affect the study results”, and indeed it was unknown whether the imbalance was a chance occurrence or in part caused by selection biases, the trial could have used better alternative randomization procedures to reduce vulnerability to potential selection bias. To illustrate the latter point, let us compare predictability of two randomization procedures – permuted block design (PBD) and big stick design (BSD) for several values of the maximum tolerated imbalance (MTI). We use BSD here for the illustration purpose because it was found to provide a very good balance/randomness tradeoff based on our simulations in Example 1 . In essence, BSD provides the same level of imbalance control as PBD but with stronger encryption.

Table 3 reports two metrics for PBD and BSD: proportion of deterministic assignments within a randomization sequence, and excess correct guess probability. The latter metric is the absolute increase in proportion of correct guesses for a given procedure over CRD that has 50% probability of correct guesses under the “optimal guessing strategy”. Footnote 1 Note that for MTI = 1, BSD is equivalent to PBD with blocks of two. However, by increasing MTI, one can substantially decrease predictability. For instance, going from MTI = 1 in the BSD to an MTI of 2 or 3 (two bottom rows), the proportion of deterministic assignments decreases from 50% to 25% and 16.7%, respectively, and excess correct guess probability decreases from 25% to 12.5% and 8.3%, which is a substantial reduction in risk of selection bias. In addition to simplicity and lower predictability for the same level of MTI control, BSD has another important advantage: investigators are not accustomed to it (as they are to the PBD), and therefore it has potential for complete elimination of prediction through thwarting enough early prediction attempts.

Our observations here are also generalizable to other MTI randomization methods, such as the maximal procedure [ 35 ], Chen’s designs [ 38 , 39 ], block urn design [ 40 ], just to name a few. MTI randomization procedures can be also used as building elements for more complex stratified randomization schemes [ 86 ].

Example 3: How can we mitigate risk of chronological bias?

Chronological bias may occur if a trial recruitment period is long, and there is a drift in some covariate over time that is subsequently not accounted for in the analysis [ 29 ]. To mitigate risk of chronological bias, treatment assignments should be balanced over time. In this regard, the ICH E9 guideline has the following statement [ 31 ]:

“...Although unrestricted randomisation is an acceptable approach, some advantages can generally be gained by randomising subjects in blocks. This helps to increase the comparability of the treatment groups, particularly when subject characteristics may change over time, as a result, for example, of changes in recruitment policy. It also provides a better guarantee that the treatment groups will be of nearly equal size...”

While randomization in blocks of two ensures best balance, it is highly predictable. In practice, a sensible tradeoff between balance and randomness is desirable. In the following example, we illustrate the issue of chronological bias in the context of a real RCT.

Altman and Royston [ 87 ] gave several examples of clinical studies with hidden time trends. For instance, an RCT to compare azathioprine versus placebo in patients with primary biliary cirrhosis (PBC) with respect to overall survival was an international, double-blind, randomized trial including 248 patients of whom 127 received azathioprine and 121 placebo [ 88 ]. The study had a recruitment period of 7 years. A major prognostic factor for survival was the serum bilirubin level on entry to the trial. Altman and Royston [ 87 ] provided a cusum plot of log bilirubin which showed a strong decreasing trend over time – patients who entered the trial later had, on average, lower bilirubin levels, and therefore better prognosis. Despite that the trial was randomized, there was some evidence of baseline imbalance with respect to serum bilirubin between azathioprine and placebo groups. The analysis using Cox regression adjusted for serum bilirubin showed that the treatment effect of azathioprine was statistically significant ( p  = 0.01), with azathioprine reducing the risk of dying to 59% of that observed during the placebo treatment.

The azathioprine trial [ 88 ] provides a very good example for illustrating importance of both the choice of a randomization design and a subsequent statistical analysis. We evaluated several randomization designs and analysis strategies under the given time trend through simulation. Since we did not have access to the patient level data from the azathioprine trial, we simulated a dataset of serum bilirubin values from 248 patients that resembled that in the original paper (Fig.  1 in [ 87 ]); see Fig.  6 below.

reproduced from Fig.  1 of Altman and Royston [ 87 ]

Cusum plot of baseline log serum bilirubin level of 248 subjects from the azathioprine trial,

For the survival outcomes, we use the following data generating mechanism [ 71 , 89 ]: let \({h}_{i}(t,{\delta }_{i})\) denote the hazard function of the \(i\mathrm{th}\)  patient at time \(t\) such that

where \({h}_{c}(t)\) is an unspecified baseline hazard, \(\log HR\) is the true value of the log-transformed hazard ratio, and \({u}_{i}\) is the log serum bilirubin of the \(i\mathrm{th}\)  patient at study entry.

Our main goal is to evaluate the impact of the time trend in bilirubin on the type I error rate and power. We consider seven randomization designs: CRD, Rand, TBD, PBD(2), PBD(4), BSD(3), and GBCD(2). The latter two designs were found to be the top two performing procedures based on our simulation results in Example 1 (cf. Table 2 ). PBD(4) is the most commonly used procedure in clinical trial practice. Rand and TBD are two designs that ensure exact balance in the final treatment numbers. CRD is the most random design, and PBD(2) is the most balanced design.

To evaluate both type I error and power, we consider two values for the true treatment effect: \(HR=1\) (Null) and \(HR=0.6\) (Alternative). For data analysis, we use the Cox regression model, either with or without adjustment for serum bilirubin. Furthermore, we assess two approaches to statistical inference: population model-based and randomization-based. For the sake of simplicity, we let \({h}_{c}\left(t\right)\equiv 1\) (exponential distribution) and assume no censoring when simulating the data.

For each combination of the design, experimental scenario, and data analysis strategy, a trial with 248 patients was simulated 10,000 times. Each randomization-based test was computed using \(L=\mathrm{1,000}\) sequences. In each simulation, we used the same time trend in serum bilirubin as described. Through simulation, we estimated the probability of a statistically significant baseline imbalance in serum bilirubin between azathioprine and placebo groups, type I error rate, and power.

First, we observed that the designs differ with respect to their potential to achieve baseline covariate balance under the time trend. For instance, probability of a statistically significant group difference on serum bilirubin (two-sided P  < 0.05) is ~ 24% for TBD, ~ 10% for CRD, ~ 2% for GBCD(2), ~ 0.9% for Rand, and ~ 0% for BSD(3), PBD(4), and PBD(2).

Second, a failure to adjust for serum bilirubin in the analysis can negatively impact statistical inference. Table 4 shows the type I error and power of statistical analyses unadjusted and adjusted for serum bilirubin, using population model-based and randomization-based approaches.

If we look at the type I error for the population model-based, unadjusted analysis, we can see that only CRD and Rand are valid (maintain the type I error rate at 5%), whereas TBD is anticonservative (~ 15% type I error) and PBD(2), PBD(4), BSD(3), and GBCD(2) are conservative (~ 1–2% type I error). These findings are consistent with the ones for the two-sample t-test described earlier in the current paper, and they agree well with other findings in the literature [ 67 ]. By contrast, population model-based covariate-adjusted analysis is valid for all seven randomization designs. Looking at the type I error for the randomization-based analyses, all designs yield consistent valid results (~ 5% type I error), with or without adjustment for serum bilirubin.

As regards statistical power, unadjusted analyses are substantially less powerful then the corresponding covariate-adjusted analysis, for all designs with either population model-based or randomization-based approaches. For the population model-based, unadjusted analysis, the designs have ~ 59–65% power, whereas than the corresponding covariate-adjusted analyses have ~ 97% power. The most striking results are observed with the randomization-based approach: the power of unadjusted analysis is quite different across seven designs: it is ~ 37% for TBD, ~ 60–61% for CRD and Rand, ~ 80–87% for BCD(3), GBCD(2), and PBD(4), and it is ~ 90% for PBD(2). Thus, PBD(2) is the most powerful approach if a time trend is present, statistical analysis strategy is randomization-based, and no adjustment for time trend is made. Furthermore, randomization-based covariate-adjusted analyses have ~ 97% power for all seven designs. Remarkably, the power of covariate-adjusted analysis is identical for population model-based and randomization-based approaches.

Overall, this example highlights the importance of covariate-adjusted analysis, which should be straightforward if a covariate affected by a time trend is known (e.g. serum bilirubin in our example). If a covariate is unknown or hidden, then unadjusted analysis following a conventional test may have reduced power and distorted type I error (although the designs such as CRD and Rand do ensure valid statistical inference). Alternatively, randomization-based tests can be applied. The resulting analysis will be valid but may be potentially less powerful. The degree of loss in power following randomization-based test depends on the randomization design: designs that force greater treatment balance over time will be more powerful. In fact, PBD(2) is shown to be most powerful under such circumstances; however, as we have seen in Example 1 and Example 2, a major deficiency of PBD(2) is its vulnerability to selection bias. From Table 4 , and taking into account the earlier findings in this paper, BSD(3) seems to provide a very good risk mitigation strategy against unknown time trends.

Example 4: How do we design an RCT with a very small sample size?

In our last example, we illustrate the importance of the careful choice of randomization design and subsequent statistical analysis in a nonstandard RCT with small sample size. Due to confidentiality and because this study is still in conduct, we do not disclose all details here except for that the study is an ongoing phase II RCT in a very rare and devastating autoimmune disease in children.

The study includes three periods: an open-label single-arm active treatment for 28 weeks to identify treatment responders (Period 1), a 24-week randomized treatment withdrawal period to primarily assess the efficacy of the active treatment vs. placebo (Period 2), and a 3-year long-term safety, open-label active treatment (Period 3). Because of a challenging indication and the rarity of the disease, the study plans to enroll up to 10 male or female pediatric patients in order to randomize 8 patients (4 per treatment arm) in Period 2 of the study. The primary endpoint for assessing the efficacy of active treatment versus placebo is the proportion of patients with disease flare during the 24-week randomized withdrawal phase. The two groups will be compared using Fisher’s exact test. In case of a successful outcome, evidence of clinical efficacy from this study will be also used as part of a package to support the claim for drug effectiveness.

Very small sample sizes are not uncommon in clinical trials of rare diseases [ 90 , 91 ]. Naturally, there are several methodological challenges for this type of study. A major challenge is generalizability of the results from the RCT to a population. In this particular indication, no approved treatment exists, and there is uncertainty on disease epidemiology and the exact number of patients with the disease who would benefit from treatment (patient horizon). Another challenge is the choice of the randomization procedure and the primary statistical analysis. In this study, one can enumerate upfront all 25 possible outcomes: {0, 1, 2, 3, 4} responders on active treatment, and {0, 1, 2, 3, 4} responders on placebo, and create a chart quantifying the level of evidence ( p- value) for each experimental outcome, and the corresponding decision. Before the trial starts, a discussion with the regulatory agency is warranted to agree upon on what level of evidence must be achieved in order to declare the study a “success”.

Let us perform a hypothetical planning for the given study. Suppose we go with a standard population-based approach, for which we test the hypothesis \({H}_{0}:{p}_{E}={p}_{C}\) vs. \({H}_{0}:{p}_{E}>{p}_{C}\) (where \({p}_{E}\) and \({p}_{C}\) stand for the true success rates for the experimental and control group, respectively) using Fisher’s exact test. Table 5 provides 1-sided p- values of all possible experimental outcomes. One could argue that a p- value < 0.1 may be viewed as a convincing level of evidence for this study. There are only 3 possibilities that can lead to this outcome: 3/4 vs. 0/4 successes ( p  = 0.0714); 4/4 vs. 0/4 successes ( p  = 0.0143); and 4/4 vs. 1/4 successes ( p  = 0.0714). For all other outcomes, p  ≥ 0.2143, and thus the study would be regarded as a “failure”.

Now let us consider a randomization-based inference approach. For illustration purposes, we consider four restricted randomization procedures—Rand, TBD, PBD(4), and PBD(2)—that exactly achieve 4:4 allocation. These procedures are legitimate choices because all of them provide exact sample sizes (4 per treatment group), which is essential in this trial. The reference set of either Rand or TBD includes \(70=\left(\begin{array}{c}8\\ 4\end{array}\right)\) unique sequences though with different probabilities of observing each sequence. For Rand, these sequences are equiprobable, whereas for TBD, some sequences are more likely than others. For PBD( \(2b\) ), the size of the reference set is \({\left\{\left(\begin{array}{c}2b\\ b\end{array}\right)\right\}}^{B}\) , where \(B=n/2b\) is the number of blocks of length \(2b\) for a trial of size \(n\) (in our example \(n=8\) ). This results in in a reference set of \({2}^{4}=16\) unique sequences with equal probability of 1/16 for PBD(2), and of \({6}^{2}=36\) unique sequences with equal probability of 1/36 for PBD(4).

In practice, the study statistician picks a treatment sequence at random from the reference set according to the chosen design. The details (randomization seed, chosen sequence, etc.) are carefully documented and kept confidential. For the chosen sequence and the observed outcome data, a randomization-based p- value is the sum of probabilities of all sequences in the reference set that yield the result at least as large in favor of the experimental treatment as the one observed. This p- value will depend on the randomization design, the observed randomization sequence and the observed outcomes, and it may also be different from the population-based analysis p- value.

To illustrate this, suppose the chosen randomization sequence is CEECECCE (C stands for control and E stands for experimental), and the observed responses are FSSFFFFS (F stands for failure and S stands for success). Thus, we have 3/4 successes on experimental and 0/4 successes on control. Then, the randomization-based p- value is 0.0714 for Rand; 0.0469 for TBD, 0.1250 for PBD(2); 0.0833 for PBD(4); and it is 0.0714 for the population-based analysis. The coincidence of the randomization-based p- value for Rand and the p- value of the population-based analysis is not surprising. Fisher's exact test is a permutation test and in the case of Rand as randomization procedure, the p- value of a permutation test and of a randomization test are always equal. However, despite the numerical equality, we should be mindful of different assumptions (population/randomization model).

Likewise, randomization-based p- values can be derived for other combinations of observed randomization sequences and responses. All these details (the chosen randomization design, the analysis strategy, and corresponding decisions) would have to be fully specified upfront (before the trial starts) and agreed upon by both the sponsor and the regulator. This would remove any ambiguity when the trial data become available.

As the example shows, the level of evidence in the randomization-based inference approach depends on the chosen randomization procedure and the resulting decisions may be different depending on the specific procedure. For instance, if the level of significance is set to 10% as a criterion for a “successful trial”, then with the observed data (3/4 vs. 0/4), there would be a significant test result for TBD, Rand, PBD(4), but not for PBD(2).

Summary and discussion

Randomization is the foundation of any RCT involving treatment comparison. Randomization is not a single technique, but a very broad class of statistical methodologies for design and analysis of clinical trials [ 10 ]. In this paper, we focused on the randomized controlled two-arm trial designed with equal allocation, which is the gold standard research design to generate clinical evidence in support of regulatory submissions. Even in this relatively simple case, there are various restricted randomization procedures with different probabilistic structures and different statistical properties, and the choice of a randomization design for any RCT must be made judiciously.

For the 1:1 RCT, there is a dual goal of balancing treatment assignments while maintaining allocation randomness. Final balance in treatment totals frequently maximizes statistical power for treatment comparison. It is also important to maintain balance at intermediate steps during the trial, especially in long-term studies, to mitigate potential for chronological bias. At the same time, a procedure should have high degree of randomness so that treatment assignments within the sequence are not easily predictable; otherwise, the procedure may be vulnerable to selection bias, especially in open-label studies. While balance and randomness are competing criteria, it is possible to find restricted randomization procedures that provide a sensible tradeoff between these criteria, e.g. the MTI procedures, of which the big stick design (BSD) [ 37 ] with a suitably chosen MTI limit, such as BSD(3), has very appealing statistical properties. In practice, the choice of a randomization procedure should be made after a systematic evaluation of different candidate procedures under different experimental scenarios for the primary outcome, including cases when model assumptions are violated.

In our considered examples we showed that the choice of randomization design, data analytic technique (e.g. parametric or nonparametric model, with or without covariate adjustment), and the decision on whether to include randomization in the analysis (e.g. randomization-based or population model-based analysis) are all very important considerations. Furthermore, these examples highlight the importance of using randomization designs that provide strong encryption of the randomization sequence, importance of covariate adjustment in the analysis, and the value of statistical thinking in nonstandard RCTs with very small sample sizes and small patient horizon. Finally, in this paper we have discussed randomization-based tests as robust and valid alternatives to likelihood-based tests. Randomization-based inference is a useful approach in clinical trials and should be considered by clinical researchers more frequently [ 14 ].

Further topics on randomization

Given the breadth of the subject of randomization, many important topics have been omitted from the current paper. Here we outline just a few of them.

In this paper, we have focused on the 1:1 RCT. However, clinical trials may involve more than two treatment arms. Extensions of equal randomization to the case of multiple treatment arms is relatively straightforward for many restricted randomization procedures [ 10 ]. Some trials with two or more treatment arms use unequal allocation (e.g. 2:1). Randomization procedures with unequal allocation ratios require careful consideration. For instance, an important and desirable feature is the allocation ratio preserving property (ARP). A randomization procedure targeting unequal allocation is said to be ARP, if at each allocation step the unconditional probability of a particular treatment assignment is the same as the target allocation proportion for this treatment [ 92 ]. Non-ARP procedures may have fluctuations in the unconditional randomization probability from allocation to allocation, which may be problematic [ 93 ]. Fortunately, some randomization procedures naturally possess the ARP property, and there are approaches to correct for a non-ARP deficiency – these should be considered in the design of RCTs with unequal allocation ratios [ 92 , 93 , 94 ].

In many RCTs, investigators may wish to prospectively balance treatment assignments with respect to important prognostic covariates. For a small number of categorical covariates one can use stratified randomization by applying separate MTI randomization procedures within strata [ 86 ]. However, a potential advantage of stratified randomization decreases as the number of stratification variables increases [ 95 ]. In trials where balance over a large number of covariates is sought and the sample size is small or moderate, one can consider covariate-adaptive randomization procedures that achieve balance within covariate margins, such as the minimization procedure [ 96 , 97 ], optimal model-based procedures [ 46 ], or some other covariate-adaptive randomization technique [ 98 ]. To achieve valid and powerful results, covariate-adaptive randomization design must be followed by covariate-adjusted analysis [ 99 ]. Special considerations are required for covariate-adaptive randomization designs with more than two treatment arms and/or unequal allocation ratios [ 100 ].

In some clinical research settings, such as trials for rare and/or life threatening diseases, there is a strong ethical imperative to increase the chance of a trial participant to receive an empirically better treatment. Response-adaptive randomization (RAR) has been increasingly considered in practice, especially in oncology [ 101 , 102 ]. Very extensive methodological research on RAR has been done [ 103 , 104 ]. RAR is increasingly viewed as an important ingredient of complex clinical trials such as umbrella and platform trial designs [ 105 , 106 ]. While RAR, when properly applied, has its merit, the topic has generated a lot of controversial discussions over the years [ 107 , 108 , 109 , 110 , 111 ]. Amid the ongoing COVID-19 pandemic, RCTs evaluating various experimental treatments for critically ill COVID-19 patients do incorporate RAR in their design; see, for example, the I-SPY COVID-19 trial ( https://clinicaltrials.gov/ct2/show/NCT04488081 ).

Randomization can also be applied more broadly than in conventional RCT settings where randomization units are individual subjects. For instance, in a cluster randomized trial, not individuals but groups of individuals (clusters) are randomized among one or more interventions or the control [ 112 ]. Observations from individuals within a given cluster cannot be regarded as independent, and special statistical techniques are required to design and analyze cluster-randomized experiments. In some clinical trial designs, randomization is applied within subjects. For instance, the micro-randomized trial (MRT) is a novel design for development of mobile treatment interventions in which randomization is applied to select different treatment options for individual participants over time to optimally support individuals’ health behaviors [ 113 ].

Finally, beyond the scope of the present paper are the regulatory perspectives on randomization and practical implementation aspects, including statistical software and information systems to generate randomization schedules in real time. We hope to cover these topics in subsequent papers.

Availability of data and materials

All results reported in this paper are based either on theoretical considerations or simulation evidence. The computer code (using R and Julia programming languages) is fully documented and is available upon reasonable request.

Guess the next allocation as the treatment with fewest allocations in the sequence thus far, or make a random guess if the treatment numbers are equal.

Byar DP, Simon RM, Friedewald WT, Schlesselman JJ, DeMets DL, Ellenberg JH, Gail MH, Ware JH. Randomized clinical trials—perspectives on some recent ideas. N Engl J Med. 1976;295:74–80.

Article   CAS   PubMed   Google Scholar  

Collins R, Bowman L, Landray M, Peto R. The magic of randomization versus the myth of real-world evidence. N Engl J Med. 2020;382:674–8.

Article   PubMed   Google Scholar  

ICH Harmonised tripartite guideline. General considerations for clinical trials E8. 1997.

Hernán MA, Robins JM. Using big data to emulate a target trial when a randomized trial is not available. Am J Epidemiol. 2016;183(8):758–64.

Article   PubMed   PubMed Central   Google Scholar  

Byar DP. Why data bases should not replace randomized clinical trials. Biometrics. 1980;36:337–42.

Mehra MR, Desai SS, Kuy SR, Henry TD, Patel AN. Cardiovascular disease, drug therapy, and mortality in Covid-19. N Engl J Med. 2020;382:e102. https://www.nejm.org/doi/10.1056/NEJMoa2007621 .

Mehra MR, Desai SS, Ruschitzka F, Patel AN. Hydroxychloroquine or chloroquine with or without a macrolide for treatment of COVID-19: a multinational registry analysis. Lancet. 2020. https://www.sciencedirect.com/science/article/pii/S0140673620311806?via%3Dihub .

Mehra MR, Desai SS, Kuy SR, Henry TD, Patel AN. Retraction: Cardiovascular disease, drug therapy, and mortality in Covid-19. N Engl J Med. 2020. https://doi.org/10.1056/NEJMoa2007621 . https://www.nejm.org/doi/10.1056/NEJMc2021225 .

Medical Research Council. Streptomycin treatment of pulmonary tuberculosis. BMJ. 1948;2:769–82.

Article   Google Scholar  

Rosenberger WF, Lachin J. Randomization in clinical trials: theory and practice. 2nd ed. New York: Wiley; 2015.

Google Scholar  

Fisher RA. The design of experiments. Edinburgh: Oliver and Boyd; 1935.

Hill AB. The clinical trial. Br Med Bull. 1951;7(4):278–82.

Hill AB. Memories of the British streptomycin trial in tuberculosis: the first randomized clinical trial. Control Clin Trials. 1990;11:77–9.

Rosenberger WF, Uschner D, Wang Y. Randomization: The forgotten component of the randomized clinical trial. Stat Med. 2019;38(1):1–30 (with discussion).

Berger VW. Trials: the worst possible design (except for all the rest). Int J Person Centered Med. 2011;1(3):630–1.

Berger VW. Selection bias and covariate imbalances in randomized clinical trials. New York: Wiley; 2005.

Book   Google Scholar  

Berger VW. The alleged benefits of unrestricted randomization. In: Berger VW, editor. Randomization, masking, and allocation concealment. Boca Raton: CRC Press; 2018. p. 39–50.

Altman DG, Bland JM. Treatment allocation in controlled trials: why randomise? BMJ. 1999;318:1209.

Article   CAS   PubMed   PubMed Central   Google Scholar  

Senn S. Testing for baseline balance in clinical trials. Stat Med. 1994;13:1715–26.

Senn S. Seven myths of randomisation in clinical trials. Stat Med. 2013;32:1439–50.

Rosenberger WF, Sverdlov O. Handling covariates in the design of clinical trials. Stat Sci. 2008;23:404–19.

Proschan M, Dodd L. Re-randomization tests in clinical trials. Stat Med. 2019;38:2292–302.

Spiegelhalter DJ, Freedman LS, Parmar MK. Bayesian approaches to randomized trials. J R Stat Soc A Stat Soc. 1994;157(3):357–87.

Berry SM, Carlin BP, Lee JJ, Muller P. Bayesian adaptive methods for clinical trials. Boca Raton: CRC Press; 2010.

Lachin J. Properties of simple randomization in clinical trials. Control Clin Trials. 1988;9:312–26.

Pocock SJ. Allocation of patients to treatment in clinical trials. Biometrics. 1979;35(1):183–97.

Simon R. Restricted randomization designs in clinical trials. Biometrics. 1979;35(2):503–12.

Blackwell D, Hodges JL. Design for the control of selection bias. Ann Math Stat. 1957;28(2):449–60.

Matts JP, McHugh R. Analysis of accrual randomized clinical trials with balanced groups in strata. J Chronic Dis. 1978;31:725–40.

Matts JP, Lachin JM. Properties of permuted-block randomization in clinical trials. Control Clin Trials. 1988;9:327–44.

ICH Harmonised Tripartite Guideline. Statistical principles for clinical trials E9. 1998.

Shao H, Rosenberger WF. Properties of the random block design for clinical trials. In: Kunert J, Müller CH, Atkinson AC, eds. mODa 11 – Advances in model-oriented design and analysis. Springer International Publishing Switzerland; 2016. 225–233.

Zhao W. Evolution of restricted randomization with maximum tolerated imbalance. In: Berger VW, editor. Randomization, masking, and allocation concealment. Boca Raton: CRC Press; 2018. p. 61–81.

Bailey RA, Nelson PR. Hadamard randomization: a valid restriction of random permuted blocks. Biom J. 2003;45(5):554–60.

Berger VW, Ivanova A, Knoll MD. Minimizing predictability while retaining balance through the use of less restrictive randomization procedures. Stat Med. 2003;22:3017–28.

Zhao W, Berger VW, Yu Z. The asymptotic maximal procedure for subject randomization in clinical trials. Stat Methods Med Res. 2018;27(7):2142–53.

Soares JF, Wu CFJ. Some restricted randomization rules in sequential designs. Commun Stat Theory Methods. 1983;12(17):2017–34.

Chen YP. Biased coin design with imbalance tolerance. Commun Stat Stochastic Models. 1999;15(5):953–75.

Chen YP. Which design is better? Ehrenfest urn versus biased coin. Adv Appl Probab. 2000;32:738–49.

Zhao W, Weng Y. Block urn design—A new randomization algorithm for sequential trials with two or more treatments and balanced or unbalanced allocation. Contemp Clin Trials. 2011;32:953–61.

van der Pas SL. Merged block randomisation: A novel randomisation procedure for small clinical trials. Clin Trials. 2019;16(3):246–52.

Zhao W. Letter to the Editor – Selection bias, allocation concealment and randomization design in clinical trials. Contemp Clin Trials. 2013;36:263–5.

Berger VW, Bejleri K, Agnor R. Comparing MTI randomization procedures to blocked randomization. Stat Med. 2016;35:685–94.

Efron B. Forcing a sequential experiment to be balanced. Biometrika. 1971;58(3):403–17.

Wei LJ. The adaptive biased coin design for sequential experiments. Ann Stat. 1978;6(1):92–100.

Atkinson AC. Optimum biased coin designs for sequential clinical trials with prognostic factors. Biometrika. 1982;69(1):61–7.

Smith RL. Sequential treatment allocation using biased coin designs. J Roy Stat Soc B. 1984;46(3):519–43.

Ball FG, Smith AFM, Verdinelli I. Biased coin designs with a Bayesian bias. J Stat Planning Infer. 1993;34(3):403–21.

BaldiAntognini A, Giovagnoli A. A new ‘biased coin design’ for the sequential allocation of two treatments. Appl Stat. 2004;53(4):651–64.

Atkinson AC. Selecting a biased-coin design. Stat Sci. 2014;29(1):144–63.

Rosenberger WF. Randomized urn models and sequential design. Sequential Anal. 2002;21(1&2):1–41 (with discussion).

Wei LJ. A class of designs for sequential clinical trials. J Am Stat Assoc. 1977;72(358):382–6.

Wei LJ, Lachin JM. Properties of the urn randomization in clinical trials. Control Clin Trials. 1988;9:345–64.

Schouten HJA. Adaptive biased urn randomization in small strata when blinding is impossible. Biometrics. 1995;51(4):1529–35.

Ivanova A. A play-the-winner-type urn design with reduced variability. Metrika. 2003;58:1–13.

Kundt G. A new proposal for setting parameter values in restricted randomization methods. Methods Inf Med. 2007;46(4):440–9.

Kalish LA, Begg CB. Treatment allocation methods in clinical trials: a review. Stat Med. 1985;4:129–44.

Zhao W, Weng Y, Wu Q, Palesch Y. Quantitative comparison of randomization designs in sequential clinical trials based on treatment balance and allocation randomness. Pharm Stat. 2012;11:39–48.

Flournoy N, Haines LM, Rosenberger WF. A graphical comparison of response-adaptive randomization procedures. Statistics in Biopharmaceutical Research. 2013;5(2):126–41.

Hilgers RD, Uschner D, Rosenberger WF, Heussen N. ERDO – a framework to select an appropriate randomization procedure for clinical trials. BMC Med Res Methodol. 2017;17:159.

Burman CF. On sequential treatment allocations in clinical trials. PhD Thesis Dept. Mathematics, Göteborg. 1996.

Azriel D, Mandel M, Rinott Y. Optimal allocation to maximize the power of two-sample tests for binary response. Biometrika. 2012;99(1):101–13.

Begg CB, Kalish LA. Treatment allocation for nonlinear models in clinical trials: the logistic model. Biometrics. 1984;40:409–20.

Kalish LA, Harrington DP. Efficiency of balanced treatment allocation for survival analysis. Biometrics. 1988;44(3):815–21.

Sverdlov O, Rosenberger WF. On recent advances in optimal allocation designs for clinical trials. J Stat Theory Practice. 2013;7(4):753–73.

Sverdlov O, Ryeznik Y, Wong WK. On optimal designs for clinical trials: an updated review. J Stat Theory Pract. 2020;14:10.

Rosenkranz GK. The impact of randomization on the analysis of clinical trials. Stat Med. 2011;30:3475–87.

Galbete A, Rosenberger WF. On the use of randomization tests following adaptive designs. J Biopharm Stat. 2016;26(3):466–74.

Proschan M. Influence of selection bias on type I error rate under random permuted block design. Stat Sin. 1994;4:219–31.

Kennes LN, Cramer E, Hilgers RD, Heussen N. The impact of selection bias on test decisions in randomized clinical trials. Stat Med. 2011;30:2573–81.

PubMed   Google Scholar  

Rückbeil MV, Hilgers RD, Heussen N. Assessing the impact of selection bias on test decisions in trials with a time-to-event outcome. Stat Med. 2017;36:2656–68.

Berger VW, Exner DV. Detecting selection bias in randomized clinical trials. Control Clin Trials. 1999;25:515–24.

Ivanova A, Barrier RC, Berger VW. Adjusting for observable selection bias in block randomized trials. Stat Med. 2005;24:1537–46.

Kennes LN, Rosenberger WF, Hilgers RD. Inference for blocked randomization under a selection bias model. Biometrics. 2015;71:979–84.

Hilgers RD, Manolov M, Heussen N, Rosenberger WF. Design and analysis of stratified clinical trials in the presence of bias. Stat Methods Med Res. 2020;29(6):1715–27.

Hamilton SA. Dynamically allocating treatment when the cost of goods is high and drug supply is limited. Control Clin Trials. 2000;21(1):44–53.

Zhao W. Letter to the Editor – A better alternative to the inferior permuted block design is not necessarily complex. Stat Med. 2016;35:1736–8.

Berger VW. Pros and cons of permutation tests in clinical trials. Stat Med. 2000;19:1319–28.

Simon R, Simon NR. Using randomization tests to preserve type I error with response adaptive and covariate adaptive randomization. Statist Probab Lett. 2011;81:767–72.

Tamm M, Cramer E, Kennes LN, Hilgers RD. Influence of selection bias on the test decision. Methods Inf Med. 2012;51:138–43.

Tamm M, Hilgers RD. Chronological bias in randomized clinical trials arising from different types of unobserved time trends. Methods Inf Med. 2014;53:501–10.

BaldiAntognini A, Rosenberger WF, Wang Y, Zagoraiou M. Exact optimum coin bias in Efron’s randomization procedure. Stat Med. 2015;34:3760–8.

Chow SC, Shao J, Wang H, Lokhnygina. Sample size calculations in clinical research. 3rd ed. Boca Raton: CRC Press; 2018.

Heritier S, Gebski V, Pillai A. Dynamic balancing randomization in controlled clinical trials. Stat Med. 2005;24:3729–41.

Lovell DJ, Giannini EH, Reiff A, et al. Etanercept in children with polyarticular juvenile rheumatoid arthritis. N Engl J Med. 2000;342(11):763–9.

Zhao W. A better alternative to stratified permuted block design for subject randomization in clinical trials. Stat Med. 2014;33:5239–48.

Altman DG, Royston JP. The hidden effect of time. Stat Med. 1988;7:629–37.

Christensen E, Neuberger J, Crowe J, et al. Beneficial effect of azathioprine and prediction of prognosis in primary biliary cirrhosis. Gastroenterology. 1985;89:1084–91.

Rückbeil MV, Hilgers RD, Heussen N. Randomization in survival trials: An evaluation method that takes into account selection and chronological bias. PLoS ONE. 2019;14(6):e0217964.

Article   CAS   Google Scholar  

Hilgers RD, König F, Molenberghs G, Senn S. Design and analysis of clinical trials for small rare disease populations. J Rare Dis Res Treatment. 2016;1(3):53–60.

Miller F, Zohar S, Stallard N, Madan J, Posch M, Hee SW, Pearce M, Vågerö M, Day S. Approaches to sample size calculation for clinical trials in rare diseases. Pharm Stat. 2017;17:214–30.

Kuznetsova OM, Tymofyeyev Y. Preserving the allocation ratio at every allocation with biased coin randomization and minimization in studies with unequal allocation. Stat Med. 2012;31(8):701–23.

Kuznetsova OM, Tymofyeyev Y. Brick tunnel and wide brick tunnel randomization for studies with unequal allocation. In: Sverdlov O, editor. Modern adaptive randomized clinical trials: statistical and practical aspects. Boca Raton: CRC Press; 2015. p. 83–114.

Kuznetsova OM, Tymofyeyev Y. Expansion of the modified Zelen’s approach randomization and dynamic randomization with partial block supplies at the centers to unequal allocation. Contemp Clin Trials. 2011;32:962–72.

EMA. Guideline on adjustment for baseline covariates in clinical trials. 2015.

Taves DR. Minimization: A new method of assigning patients to treatment and control groups. Clin Pharmacol Ther. 1974;15(5):443–53.

Pocock SJ, Simon R. Sequential treatment assignment with balancing for prognostic factors in the controlled clinical trial. Biometrics. 1975;31(1):103–15.

Hu F, Hu Y, Ma Z, Rosenberger WF. Adaptive randomization for balancing over covariates. Wiley Interdiscipl Rev Computational Stat. 2014;6(4):288–303.

Senn S. Statistical issues in drug development. 2nd ed. Wiley-Interscience; 2007.

Kuznetsova OM, Tymofyeyev Y. Covariate-adaptive randomization with unequal allocation. In: Sverdlov O, editor. Modern adaptive randomized clinical trials: statistical and practical aspects. Boca Raton: CRC Press; 2015. p. 171–97.

Berry DA. Adaptive clinical trials: the promise and the caution. J Clin Oncol. 2011;29(6):606–9.

Trippa L, Lee EQ, Wen PY, Batchelor TT, Cloughesy T, Parmigiani G, Alexander BM. Bayesian adaptive randomized trial design for patients with recurrent glioblastoma. J Clin Oncol. 2012;30(26):3258–63.

Hu F, Rosenberger WF. The theory of response-adaptive randomization in clinical trials. New York: Wiley; 2006.

Atkinson AC, Biswas A. Randomised response-adaptive designs in clinical trials. Boca Raton: CRC Press; 2014.

Rugo HS, Olopade OI, DeMichele A, et al. Adaptive randomization of veliparib–carboplatin treatment in breast cancer. N Engl J Med. 2016;375:23–34.

Berry SM, Petzold EA, Dull P, et al. A response-adaptive randomization platform trial for efficient evaluation of Ebola virus treatments: a model for pandemic response. Clin Trials. 2016;13:22–30.

Ware JH. Investigating therapies of potentially great benefit: ECMO. (with discussion). Stat Sci. 1989;4(4):298–340.

Hey SP, Kimmelman J. Are outcome-adaptive allocation trials ethical? (with discussion). Clin Trials. 2005;12(2):102–27.

Proschan M, Evans S. Resist the temptation of response-adaptive randomization. Clin Infect Dis. 2020;71(11):3002–4. https://doi.org/10.1093/cid/ciaa334 .

Villar SS, Robertson DS, Rosenberger WF. The temptation of overgeneralizing response-adaptive randomization. Clinical Infectious Diseases. 2020; ciaa1027; doi: https://doi.org/10.1093/cid/ciaa1027 .

Proschan M. Reply to Villar, et al. Clinical infectious diseases. 2020; ciaa1029; doi: https://doi.org/10.1093/cid/ciaa1029 .

Donner A, Klar N. Design and Analysis of Cluster Randomization Trials in Health Research. London: Arnold Publishers Limited; 2000.

Klasnja P, Hekler EB, Shiffman S, Boruvka A, Almirall D, Tewari A, Murphy SA. Micro-randomized trials: An experimental design for developing just-in-time adaptive interventions. Health Psychol. 2015;34:1220–8.

Article   PubMed Central   Google Scholar  

Download references

Acknowledgements

The authors are grateful to Robert A. Beckman for his continuous efforts coordinating Innovative Design Scientific Working Groups, which is also a networking research platform for the Randomization ID SWG. We would also like to thank the editorial board and the two anonymous reviewers for the valuable comments which helped to substantially improve the original version of the manuscript.

None. The opinions expressed in this article are those of the authors and may not reflect the opinions of the organizations that they work for.

Author information

Authors and affiliations.

National Institutes of Health, Bethesda, MD, USA

Vance W. Berger

Boehringer Ingelheim Pharma GmbH & Co. KG, Biberach, Germany

Louis Joseph Bour

Boehringer-Ingelheim Pharmaceuticals Inc, Ridgefield, CT, USA

Kerstine Carter

Population Health Sciences, University of Utah School of Medicine, Salt Lake City UT, USA

Jonathan J. Chipman

Cancer Biostatistics, University of Utah Huntsman Cancer Institute, Salt Lake City UT, USA

Clinical Trials Research Unit, University of Leeds, Leeds, UK

Colin C. Everett

RWTH Aachen University, Aachen, Germany

Nicole Heussen & Ralf-Dieter Hilgers

Medical School, Sigmund Freud University, Vienna, Austria

Nicole Heussen

York Trials Unit, Department of Health Sciences, University of York, York, UK

Catherine Hewitt

Food and Drug Administration, Silver Spring, MD, USA

Yuqun Abigail Luo

Open University of Catalonia (UOC) and the University of Barcelona (UB), Barcelona, Spain

Jone Renteria

Department of Human Development and Quantitative Methodology, University of Maryland, College Park, MD, USA

BioPharma Early Biometrics & Statistical Innovations, Data Science & AI, R&D BioPharmaceuticals, AstraZeneca, Gothenburg, Sweden

Yevgen Ryeznik

Early Development Analytics, Novartis Pharmaceuticals Corporation, NJ, East Hanover, USA

Oleksandr Sverdlov

Biostatistics Center & Department of Biostatistics and Bioinformatics, George Washington University, DC, Washington, USA

Diane Uschner

You can also search for this author in PubMed   Google Scholar

• Robert A Beckman

Contributions

Conception: VWB, KC, NH, RDH, OS. Writing of the main manuscript: OS, with contributions from VWB, KC, JJC, CE, NH, and RDH. Design of simulation studies: OS, YR. Development of code and running simulations: YR. Digitization and preparation of data for Fig.  5 : JR. All authors reviewed the original manuscript and the revised version. The authors read and approved the final manuscript.

Corresponding author

Correspondence to Oleksandr Sverdlov .

Ethics declarations

Ethics approval and consent to participate.

Not applicable.

Consent for publication

Competing interests, additional information, publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Additional file 1: figure s1.

. Type I error rate under selection bias model with bias effect ( \(\nu\) ) in the range 0 (no bias) to 1 (strong bias) for 12 randomization designs and three statistical tests.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Berger, V., Bour, L., Carter, K. et al. A roadmap to using randomization in clinical trials. BMC Med Res Methodol 21 , 168 (2021). https://doi.org/10.1186/s12874-021-01303-z

Download citation

Received : 24 December 2020

Accepted : 14 April 2021

Published : 16 August 2021

DOI : https://doi.org/10.1186/s12874-021-01303-z

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Randomization-based test
• Restricted randomization design

BMC Medical Research Methodology

ISSN: 1471-2288

• General enquiries: [email protected]

• Yale Directories

Institution for Social and Policy Studies

Advancing research • shaping policy • developing leaders, why randomize.

About Randomized Field Experiments Randomized field experiments allow researchers to scientifically measure the impact of an intervention on a particular outcome of interest.

What is a randomized field experiment? In a randomized experiment, a study sample is divided into one group that will receive the intervention being studied (the treatment group) and another group that will not receive the intervention (the control group). For instance, a study sample might consist of all registered voters in a particular city. This sample will then be randomly divided into treatment and control groups. Perhaps 40% of the sample will be on a campaign’s Get-Out-the-Vote (GOTV) mailing list and the other 60% of the sample will not receive the GOTV mailings. The outcome measured –voter turnout– can then be compared in the two groups. The difference in turnout will reflect the effectiveness of the intervention.

What does random assignment mean? The key to randomized experimental research design is in the random assignment of study subjects – for example, individual voters, precincts, media markets or some other group – into treatment or control groups. Randomization has a very specific meaning in this context. It does not refer to haphazard or casual choosing of some and not others. Randomization in this context means that care is taken to ensure that no pattern exists between the assignment of subjects into groups and any characteristics of those subjects. Every subject is as likely as any other to be assigned to the treatment (or control) group. Randomization is generally achieved by employing a computer program containing a random number generator. Randomization procedures differ based upon the research design of the experiment. Individuals or groups may be randomly assigned to treatment or control groups. Some research designs stratify subjects by geographic, demographic or other factors prior to random assignment in order to maximize the statistical power of the estimated effect of the treatment (e.g., GOTV intervention). Information about the randomization procedure is included in each experiment summary on the site.

What are the advantages of randomized experimental designs? Randomized experimental design yields the most accurate analysis of the effect of an intervention (e.g., a voter mobilization phone drive or a visit from a GOTV canvasser, on voter behavior). By randomly assigning subjects to be in the group that receives the treatment or to be in the control group, researchers can measure the effect of the mobilization method regardless of other factors that may make some people or groups more likely to participate in the political process. To provide a simple example, say we are testing the effectiveness of a voter education program on high school seniors. If we allow students from the class to volunteer to participate in the program, and we then compare the volunteers’ voting behavior against those who did not participate, our results will reflect something other than the effects of the voter education intervention. This is because there are, no doubt, qualities about those volunteers that make them different from students who do not volunteer. And, most important for our work, those differences may very well correlate with propensity to vote. Instead of letting students self-select, or even letting teachers select students (as teachers may have biases in who they choose), we could randomly assign all students in a given class to be in either a treatment or control group. This would ensure that those in the treatment and control groups differ solely due to chance. The value of randomization may also be seen in the use of walk lists for door-to-door canvassers. If canvassers choose which houses they will go to and which they will skip, they may choose houses that seem more inviting or they may choose houses that are placed closely together rather than those that are more spread out. These differences could conceivably correlate with voter turnout. Or if house numbers are chosen by selecting those on the first half of a ten page list, they may be clustered in neighborhoods that differ in important ways from neighborhoods in the second half of the list. Random assignment controls for both known and unknown variables that can creep in with other selection processes to confound analyses. Randomized experimental design is a powerful tool for drawing valid inferences about cause and effect. The use of randomized experimental design should allow a degree of certainty that the research findings cited in studies that employ this methodology reflect the effects of the interventions being measured and not some other underlying variable or variables.

Study Design 101

• Helpful formulas
• Finding specific study types
• Randomized Controlled Trial
• Meta- Analysis
• Systematic Review
• Practice Guideline
• Cohort Study
• Case Control Study
• Case Reports

A study design that randomly assigns participants into an experimental group or a control group. As the study is conducted, the only expected difference between the control and experimental groups in a randomized controlled trial (RCT) is the outcome variable being studied.

• Good randomization will "wash out" any population bias
• Easier to blind/mask than observational studies
• Results can be analyzed with well known statistical tools
• Populations of participating individuals are clearly identified

Disadvantages

• Expensive in terms of time and money
• Volunteer biases: the population that participates may not be representative of the whole
• Loss to follow-up attributed to treatment

Design pitfalls to look out for

An RCT should be a study of one population only.

Was the randomization actually "random", or are there really two populations being studied?

The variables being studied should be the only variables between the experimental group and the control group.

Are there any confounding variables between the groups?

Fictitious Example

To determine how a new type of short wave UVA-blocking sunscreen affects the general health of skin in comparison to a regular long wave UVA-blocking sunscreen, 40 trial participants were randomly separated into equal groups of 20: an experimental group and a control group. All participants' skin health was then initially evaluated. The experimental group wore the short wave UVA-blocking sunscreen daily, and the control group wore the long wave UVA-blocking sunscreen daily.

After one year, the general health of the skin was measured in both groups and statistically analyzed. In the control group, wearing long wave UVA-blocking sunscreen daily led to improvements in general skin health for 60% of the participants. In the experimental group, wearing short wave UVA-blocking sunscreen daily led to improvements in general skin health for 75% of the participants.

Real-life Examples

van Der Horst, N., Smits, D., Petersen, J., Goedhart, E., & Backx, F. (2015). The preventive effect of the nordic hamstring exercise on hamstring injuries in amateur soccer players: a randomized controlled trial. The American Journal of Sports Medicine, 43 (6), 1316-1323. https://doi.org/10.1177/0363546515574057

This article reports on the research investigating whether the Nordic Hamstring Exercise is effective in preventing both the incidence and severity of hamstring injuries in male amateur soccer players. Over the course of a year, there was a statistically significant reduction in the incidence of hamstring injuries in players performing the NHE, but for those injured, there was no difference in severity of injury. There was also a high level of compliance in performing the NHE in that group of players.

Natour, J., Cazotti, L., Ribeiro, L., Baptista, A., & Jones, A. (2015). Pilates improves pain, function and quality of life in patients with chronic low back pain: a randomized controlled trial. Clinical Rehabilitation, 29 (1), 59-68. https://doi.org/10.1177/0269215514538981

This study assessed the effect of adding pilates to a treatment regimen of NSAID use for individuals with chronic low back pain. Individuals who included the pilates method in their therapy took fewer NSAIDs and experienced statistically significant improvements in pain, function, and quality of life.

Related Formulas

• Relative Risk

Related Terms

Blinding/Masking

When the groups that have been randomly selected from a population do not know whether they are in the control group or the experimental group.

Being able to show that an independent variable directly causes the dependent variable. This is generally very difficult to demonstrate in most study designs.

Confounding Variables

Variables that cause/prevent an outcome from occurring outside of or along with the variable being studied. These variables render it difficult or impossible to distinguish the relationship between the variable and outcome being studied).

Correlation

A relationship between two variables, but not necessarily a causation relationship.

Double Blinding/Masking

When the researchers conducting a blinded study do not know which participants are in the control group of the experimental group.

Null Hypothesis

That the relationship between the independent and dependent variables the researchers believe they will prove through conducting a study does not exist. To "reject the null hypothesis" is to say that there is a relationship between the variables.

Population/Cohort

A group that shares the same characteristics among its members (population).

Population Bias/Volunteer Bias

A sample may be skewed by those who are selected or self-selected into a study. If only certain portions of a population are considered in the selection process, the results of a study may have poor validity.

Randomization

Any of a number of mechanisms used to assign participants into different groups with the expectation that these groups will not differ in any significant way other than treatment and outcome.

Research (alternative) Hypothesis

The relationship between the independent and dependent variables that researchers believe they will prove through conducting a study.

Sensitivity

The relationship between what is considered a symptom of an outcome and the outcome itself; or the percent chance of not getting a false positive (see formulas).

Specificity

The relationship between not having a symptom of an outcome and not having the outcome itself; or the percent chance of not getting a false negative (see formulas).

Type 1 error

Rejecting a null hypothesis when it is in fact true. This is also known as an error of commission.

Type 2 error

The failure to reject a null hypothesis when it is in fact false. This is also known as an error of omission.

Now test yourself!

1. Having a volunteer bias in the population group is a good thing because it means the study participants are eager and make the study even stronger.

a) True b) False

2. Why is randomization important to assignment in an RCT?

a) It enables blinding/masking b) So causation may be extrapolated from results c) It balances out individual characteristics between groups. d) a and c e) b and c

← Previous Next →

© 2011-2019, The Himmelfarb Health Sciences Library Questions? Ask us .

• Himmelfarb Intranet
• Privacy Notice
• Terms of Use
• GW is committed to digital accessibility. If you experience a barrier that affects your ability to access content on this page, let us know via the Accessibility Feedback Form .

A simplified guide to randomized controlled trials

Affiliations.

• 1 Fetal Medicine Unit, St. Georges University Hospital, London, UK.
• 2 Division of Neonatology, Department of Pediatrics, Mount Sinai Hospital, Toronto, ON, Canada.
• 3 Institute of Health Policy, Management and Evaluation, University of Toronto, Toronto, ON, Canada.
• 4 Department of Clinical Science, Intervention and Technology, Karolinska Institute and Center for Fetal Medicine, Karolinska University Hospital, Stockholm, Sweden.
• 5 Women's Health and Perinatology Research Group, Department of Clinical Medicine, UiT-The Arctic University of Norway, Tromsø, Norway.
• 6 Department of Obstetrics and Gynecology, University Hospital of North Norway, Tromsø, Norway.
• PMID: 29377058
• DOI: 10.1111/aogs.13309

A randomized controlled trial is a prospective, comparative, quantitative study/experiment performed under controlled conditions with random allocation of interventions to comparison groups. The randomized controlled trial is the most rigorous and robust research method of determining whether a cause-effect relation exists between an intervention and an outcome. High-quality evidence can be generated by performing an randomized controlled trial when evaluating the effectiveness and safety of an intervention. Furthermore, randomized controlled trials yield themselves well to systematic review and meta-analysis providing a solid base for synthesizing evidence generated by such studies. Evidence-based clinical practice improves patient outcomes and safety, and is generally cost-effective. Therefore, randomized controlled trials are becoming increasingly popular in all areas of clinical medicine including perinatology. However, designing and conducting an randomized controlled trial, analyzing data, interpreting findings and disseminating results can be challenging as there are several practicalities to be considered. In this review, we provide simple descriptive guidance on planning, conducting, analyzing and reporting randomized controlled trials.

Keywords: Clinical trial; good clinical practice; random allocation; randomized controlled trial; research methods; study design.

© 2018 Nordic Federation of Societies of Obstetrics and Gynecology.

Publication types

• Systematic Review
• Randomized Controlled Trials as Topic / methods*
• Research Design*

What is a Randomized Control Trial (RCT)?

Julia Simkus

Editor at Simply Psychology

BA (Hons) Psychology, Princeton University

Julia Simkus is a graduate of Princeton University with a Bachelor of Arts in Psychology. She is currently studying for a Master's Degree in Counseling for Mental Health and Wellness in September 2023. Julia's research has been published in peer reviewed journals.

Learn about our Editorial Process

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

A randomized control trial (RCT) is a type of study design that involves randomly assigning participants to either an experimental group or a control group to measure the effectiveness of an intervention or treatment.

Randomized Controlled Trials (RCTs) are considered the “gold standard” in medical and health research due to their rigorous design.

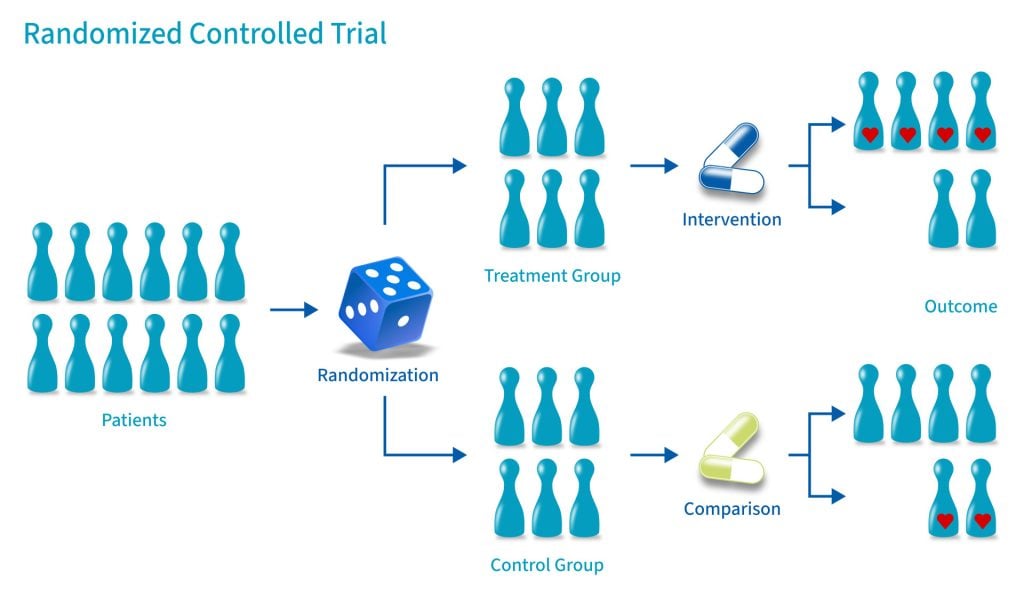
Control Group

A control group consists of participants who do not receive any treatment or intervention but a placebo or reference treatment. The control participants serve as a comparison group.

The control group is matched as closely as possible to the experimental group, including age, gender, social class, ethnicity, etc.

Because the participants are randomly assigned, the characteristics between the two groups should be balanced, enabling researchers to attribute any differences in outcome to the study intervention.

Since researchers can be confident that any differences between the control and treatment groups are due solely to the effects of the treatments, scientists view RCTs as the gold standard for clinical trials.

Random Allocation

Random allocation and random assignment are terms used interchangeably in the context of a randomized controlled trial (RCT).

Both refer to assigning participants to different groups in a study (such as a treatment group or a control group) in a way that is completely determined by chance.

The process of random assignment controls for confounding variables , ensuring differences between groups are due to chance alone.

Without randomization, researchers might consciously or subconsciously assign patients to a particular group for various reasons.

Several methods can be used for randomization in a Randomized Control Trial (RCT). Here are a few examples:

• Simple Randomization: This is the simplest method, like flipping a coin. Each participant has an equal chance of being assigned to any group. This can be achieved using random number tables, computerized random number generators, or drawing lots or envelopes.
• Block Randomization: In this method, participants are randomized within blocks, ensuring that each block has an equal number of participants in each group. This helps to balance the number of participants in each group at any given time during the study.
• Stratified Randomization: This method is used when researchers want to ensure that certain subgroups of participants are equally represented in each group. Participants are divided into strata, or subgroups, based on characteristics like age or disease severity, and then randomized within these strata.
• Cluster Randomization: In this method, groups of participants (like families or entire communities), rather than individuals, are randomized.
• Adaptive Randomization: In this method, the probability of being assigned to each group changes based on the participants already assigned to each group. For example, if more participants have been assigned to the control group, new participants will have a higher probability of being assigned to the experimental group.

Computer software can generate random numbers or sequences that can be used to assign participants to groups in a simple randomization process.

For more complex methods like block, stratified, or adaptive randomization, computer algorithms can be used to consider the additional parameters and ensure that participants are assigned to groups appropriately.

Using a computerized system can also help to maintain the integrity of the randomization process by preventing researchers from knowing in advance which group a participant will be assigned to (a principle known as allocation concealment). This can help to prevent selection bias and ensure the validity of the study results .

Allocation Concealment

Allocation concealment is a technique to ensure the random allocation process is truly random and unbiased.

RCTs use allocation concealment to decide which patients get the real medicine and which get a placebo (a fake medicine)

It involves keeping the sequence of group assignments (i.e., who gets assigned to the treatment group and who gets assigned to the control group next) hidden from the researchers before a participant has enrolled in the study.

This helps to prevent the researchers from consciously or unconsciously selecting certain participants for one group or the other based on their knowledge of which group is next in the sequence.

Allocation concealment ensures that the investigator does not know in advance which treatment the next person will get, thus maintaining the integrity of the randomization process.

Blinding (Masking)

Binding, or masking, refers to withholding information regarding the group assignments (who is in the treatment group and who is in the control group) from the participants, the researchers, or both during the study .

A blinded study prevents the participants from knowing about their treatment to avoid bias in the research. Any information that can influence the subjects is withheld until the completion of the research.

Blinding can be imposed on any participant in an experiment, including researchers, data collectors, evaluators, technicians, and data analysts.

Good blinding can eliminate experimental biases arising from the subjects’ expectations, observer bias, confirmation bias, researcher bias, observer’s effect on the participants, and other biases that may occur in a research test.

In a double-blind study , neither the participants nor the researchers know who is receiving the drug or the placebo. When a participant is enrolled, they are randomly assigned to one of the two groups. The medication they receive looks identical whether it’s the drug or the placebo.

Figure 1 . Evidence-based medicine pyramid. The levels of evidence are appropriately represented by a pyramid as each level, from bottom to top, reflects the quality of research designs (increasing) and quantity (decreasing) of each study design in the body of published literature. For example, randomized control trials are higher quality and more labor intensive to conduct, so there is a lower quantity published.

Prevents bias

In randomized control trials, participants must be randomly assigned to either the intervention group or the control group, such that each individual has an equal chance of being placed in either group.

This is meant to prevent selection bias and allocation bias and achieve control over any confounding variables to provide an accurate comparison of the treatment being studied.

Because the distribution of characteristics of patients that could influence the outcome is randomly assigned between groups, any differences in outcome can be explained only by the treatment.

High statistical power

Because the participants are randomized and the characteristics between the two groups are balanced, researchers can assume that if there are significant differences in the primary outcome between the two groups, the differences are likely to be due to the intervention.

This warrants researchers to be confident that randomized control trials will have high statistical power compared to other types of study designs.

Since the focus of conducting a randomized control trial is eliminating bias, blinded RCTs can help minimize any unconscious information bias.

In a blinded RCT, the participants do not know which group they are assigned to or which intervention is received. This blinding procedure should also apply to researchers, health care professionals, assessors, and investigators when possible.

“Single-blind” refers to an RCT where participants do not know the details of the treatment, but the researchers do.

“ Double-blind ” refers to an RCT where both participants and data collectors are masked of the assigned treatment.

Limitations

Costly and timely.

Some interventions require years or even decades to evaluate, rendering them expensive and time-consuming.

It might take an extended period of time before researchers can identify a drug’s effects or discover significant results.

Requires large sample size

There must be enough participants in each group of a randomized control trial so researchers can detect any true differences or effects in outcomes between the groups.

Researchers cannot detect clinically important results if the sample size is too small.

Change in population over time

Because randomized control trials are longitudinal in nature, it is almost inevitable that some participants will not complete the study, whether due to death, migration, non-compliance, or loss of interest in the study.

This tendency is known as selective attrition and can threaten the statistical power of an experiment.

Randomized control trials are not always practical or ethical, and such limitations can prevent researchers from conducting their studies.

For example, a treatment could be too invasive, or administering a placebo instead of an actual drug during a trial for treating a serious illness could deny a participant’s normal course of treatment. Without ethical approval, a randomized control trial cannot proceed.

Fictitious Example

An example of an RCT would be a clinical trial comparing a drug’s effect or a new treatment on a select population.

The researchers would randomly assign participants to either the experimental group or the control group and compare the differences in outcomes between those who receive the drug or treatment and those who do not.

Real-life Examples

• Preventing illicit drug use in adolescents: Long-term follow-up data from a randomized control trial of a school population (Botvin et al., 2000).
• A prospective randomized control trial comparing medical and surgical treatment for early pregnancy failure (Demetroulis et al., 2001).
• A randomized control trial to evaluate a paging system for people with traumatic brain injury (Wilson et al., 2009).
• Prehabilitation versus Rehabilitation: A Randomized Control Trial in Patients Undergoing Colorectal Resection for Cancer (Gillis et al., 2014).
• A Randomized Control Trial of Right-Heart Catheterization in Critically Ill Patients (Guyatt, 1991).
• Berry, R. B., Kryger, M. H., & Massie, C. A. (2011). A novel nasal excitatory positive airway pressure (EPAP) device for the treatment of obstructive sleep apnea: A randomized controlled trial. Sleep , 34, 479–485.
• Gloy, V. L., Briel, M., Bhatt, D. L., Kashyap, S. R., Schauer, P. R., Mingrone, G., . . . Nordmann, A. J. (2013, October 22). Bariatric surgery versus non-surgical treatment for obesity: A systematic review and meta-analysis of randomized controlled trials. BMJ , 347.
• Streeton, C., & Whelan, G. (2001). Naltrexone, a relapse prevention maintenance treatment of alcohol dependence: A meta-analysis of randomized controlled trials. Alcohol and Alcoholism, 36 (6), 544–552.

How Should an RCT be Reported?

Reporting of a Randomized Controlled Trial (RCT) should be done in a clear, transparent, and comprehensive manner to allow readers to understand the design, conduct, analysis, and interpretation of the trial.

The Consolidated Standards of Reporting Trials ( CONSORT ) statement is a widely accepted guideline for reporting RCTs.

Further Information

• Cocks, K., & Torgerson, D. J. (2013). Sample size calculations for pilot randomized trials: a confidence interval approach. Journal of clinical epidemiology, 66(2), 197-201.
• Kendall, J. (2003). Designing a research project: randomised controlled trials and their principles. Emergency medicine journal: EMJ, 20(2), 164.

Akobeng, A.K., Understanding randomized controlled trials. Archives of Disease in Childhood , 2005; 90: 840-844.

Bell, C. C., Gibbons, R., & McKay, M. M. (2008). Building protective factors to offset sexually risky behaviors among black youths: a randomized control trial. Journal of the National Medical Association, 100 (8), 936-944.

Bhide, A., Shah, P. S., & Acharya, G. (2018). A simplified guide to randomized controlled trials. Acta obstetricia et gynecologica Scandinavica, 97 (4), 380-387.

Botvin, G. J., Griffin, K. W., Diaz, T., Scheier, L. M., Williams, C., & Epstein, J. A. (2000). Preventing illicit drug use in adolescents: Long-term follow-up data from a randomized control trial of a school population. Addictive Behaviors, 25 (5), 769-774.

Demetroulis, C., Saridogan, E., Kunde, D., & Naftalin, A. A. (2001). A prospective randomized control trial comparing medical and surgical treatment for early pregnancy failure. Human Reproduction, 16 (2), 365-369.

Gillis, C., Li, C., Lee, L., Awasthi, R., Augustin, B., Gamsa, A., … & Carli, F. (2014). Prehabilitation versus rehabilitation: a randomized control trial in patients undergoing colorectal resection for cancer. Anesthesiology, 121 (5), 937-947.

Globas, C., Becker, C., Cerny, J., Lam, J. M., Lindemann, U., Forrester, L. W., … & Luft, A. R. (2012). Chronic stroke survivors benefit from high-intensity aerobic treadmill exercise: a randomized control trial. Neurorehabilitation and Neural Repair, 26 (1), 85-95.

Guyatt, G. (1991). A randomized control trial of right-heart catheterization in critically ill patients. Journal of Intensive Care Medicine, 6 (2), 91-95.

MediLexicon International. (n.d.). Randomized controlled trials: Overview, benefits, and limitations. Medical News Today. Retrieved from https://www.medicalnewstoday.com/articles/280574#what-is-a-randomized-controlled-trial

Wilson, B. A., Emslie, H., Quirk, K., Evans, J., & Watson, P. (2005). A randomized control trial to evaluate a paging system for people with traumatic brain injury. Brain Injury, 19 (11), 891-894.

Related Articles

Research Methodology

Qualitative Data Coding

What Is a Focus Group?

Cross-Cultural Research Methodology In Psychology

What Is Internal Validity In Research?

Research Methodology , Statistics

What Is Face Validity In Research? Importance & How To Measure

Criterion Validity: Definition & Examples

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.2: Completely Randomized Design

• Last updated
• Save as PDF
• Page ID 33889

• Penn State's Department of Statistics
• The Pennsylvania State University

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

After identifying the experimental unit and the number of replications that will be used, the next step is to assign the treatments (i.e. factor levels or factor level combinations) to experimental units.

In a completely randomized design, treatments are assigned to experimental units at random. This is typically done by listing the treatments and assigning a random number to each.

In the greenhouse experiment discussed in Chapter 1, there was a single factor (fertilizer) with 4 levels (i.e. 4 treatments), six replications, and a total of 24 experimental units (each unit a potted plant). Suppose the image below is the Greenhouse Floor plan and bench that was used for the experiment (as viewed from above).

We need to be able to randomly assign each of the treatment levels to 6 potted plants. To do this, assign physical position numbers on the bench for placing the pots.

Using Technology

Minitab example.

In Minitab, this assignment can be done by manually creating two columns: one with each treatment level repeated 6 times (order not important) and the other with a position number 1 to \(N\), where \(N\) is the total number of experimental units to be used (i.e. \(N=24\) in this example). The third column will store the treatment assignment.

Next, select Calc > Sample from Columns , fill in the dialog box as seen below, and click OK .

Be sure to have the "Sample with Replacement" box unchecked so that all treatment levels will be assigned to the same number of pots, giving rise to a proper completely randomized design for a specified number of replicates.

This will result in a completely random assignment.

This assignment can then be used to apply the treatment levels appropriately to pots on the greenhouse bench.

SAS Example

To make the assignments in SAS we can utilize the SAS surveyselect procedure as below:

The output would be as below. In practice, it is recommended to specify a seed to ensure the results are reproducible.

Completely Randomized Design

To randomly assign treatment levels to each of our plants we can use the following commands:

This means that the first experimental unit will get Fertilizer 3, the second experimental unit will get Fertilizer 2, etc.

Randomized Complete Block Design

Obtain the block design. Load the greenhouse data and obtain the ANOVA table.

To obtain the block design we can use the following commands:

To load the greenhouse data and obtain the ANOVA table ( lmer() and aov( )) we use the following commands:

For comparison the ANOVA table for the completely randomized design is given below:

Using Power Analysis to Choose the Unit of Randomization, Outcome, and Approach for Subgroup Analysis for a Multilevel Randomized Controlled Clinical Trial to Reduce Disparities in Cardiovascular Health

• Open access
• Published: 20 May 2024

Cite this article

You have full access to this open access article

• Kylie K. Harrall   ORCID: orcid.org/0000-0003-4467-2282 1 ,
• Katherine A. Sauder 2 ,
• Deborah H. Glueck 3 ,
• Elizabeth A. Shenkman 1 &
• Keith E. Muller 1  

We give examples of three features in the design of randomized controlled clinical trials which can increase power and thus decrease sample size and costs. We consider an example multilevel trial with several levels of clustering. For a fixed number of independent sampling units, we show that power can vary widely with the choice of the level of randomization. We demonstrate that power and interpretability can improve by testing a multivariate outcome rather than an unweighted composite outcome. Finally, we show that using a pooled analytic approach, which analyzes data for all subgroups in a single model, improves power for testing the intervention effect compared to a stratified analysis, which analyzes data for each subgroup in a separate model. The power results are computed for a proposed prevention research study. The trial plans to randomize adults to either telehealth (intervention) or in-person treatment (control) to reduce cardiovascular risk factors. The trial outcomes will be measures of the Essential Eight, a set of scores for cardiovascular health developed by the American Heart Association which can be combined into a single composite score. The proposed trial is a multilevel study, with outcomes measured on participants, participants treated by the same provider, providers nested within clinics, and clinics nested within hospitals. Investigators suspect that the intervention effect will be greater in rural participants, who live farther from clinics than urban participants. The results use published, exact analytic methods for power calculations with continuous outcomes. We provide example code for power analyses using validated software.

Avoid common mistakes on your manuscript.

Introduction

This manuscript provides a discussion about three design choices that can increase power for randomized controlled trials with multiple levels of clustering. A Glossary provides definitions for many terms used in the text.

First, we demonstrate that, for a fixed number of independent sampling units, power depends on the choice of level of randomization. Second, we show that testing a multivariate hypothesis, rather than a hypothesis about an unweighted composite outcome, can increase power and interpretability. Finally, we show that using a pooled analytic approach, which analyzes data for all subgroups in a single model, can improve power compared to a stratified analysis, which analyzes data for each subgroup in a separate model (Buckley et al., 2017 ). The goal of the manuscript is to allow designers facing similar design questions to conduct careful power calculations during the design of their trials.

The design questions are answered for a specific example study. The study is a proposed multilevel randomized controlled prevention research trial. The trial will be an extension of the Agency for Healthcare Research and Quality (AHRQ)-funded observational study R01HS028283 (E. A. Shenkman PI). In the proposed trial, the investigators plan to randomize adults to either telehealth or in person treatment. The goal is to reduce cardiovascular risk factors. The trial outcomes will be measures of the Essential Eight (Lloyd-Jones et al., 2022 ), an approach to quantify cardiovascular health developed by the American Heart Association. The Essential Eight includes definitions for scores for diet, physical activity, nicotine exposure, sleep health, body mass index, blood lipids, blood glucose, and blood pressure. The scores can be combined into a single unweighted composite score by averaging the domain-specific scores, as suggested on page e28 in Lloyd-Jones et al. ( 2022 ). The proposed trial will have multiple levels of clustering, with outcomes measured on participants, participants treated by the same provider, providers nested within clinics, and clinics nested within hospitals. The number of independent sampling units, the hospitals, will be fixed by design. Investigators suspect risk reduction will be higher in rural participants, who live farther from clinics than urban participants.

The proposed trial will have two goals. The first goal will be to assess the effect of intervention on cardiovascular health. The second goal will be to determine whether there were differences in intervention effects between subgroups. Subgroups will be defined by the location of hospitals in rural or urban areas.

During the design process for the proposed trial, three questions about design were raised.

First, researchers wondered whether to randomize participants, providers, clinics, or hospitals. The researchers were curious about the implication of the choice of level of randomization on power.

Second, researchers were curious whether testing intervention effects on the unweighted composite outcome would yield more power than assessing whether there was a multivariate response. An unweighted composite score is the sum of a set of variables. A weighted composite multiplies each element of the set of variables by a number, called a weight, and then sums the results. A multivariate response corresponds to an intervention-related change in at least one of the Essential Eight component scores.

Third, researchers were not certain as to the best way to analyze potential differences in intervention effects between hospitals in rural or urban regions. Some researchers wished to split the data into two sets, one with rural hospitals only and the other with urban hospitals only. These researchers planned to assess intervention effects in each subgroup using separate models. Other researchers argued that estimating intervention effects in both subgroups in the same model was more efficient. Researchers questioned which analytic approach provided the most power. Answering the question required comparing power calculations for two different approaches for analyzing data with subgroups.

To answer the design questions, the investigators for the proposed trial iteratively considered the effect on power of several design alternatives. The researchers worked with statisticians to evaluate the effect of analytic strategies and choices of outcome variables. As in all clinical trials, power was only one of multiple considerations driving design decisions. Researchers also considered costs, ethics, feasibility of recruitment, noncompliance, and the chance of contamination, an event which occurs when those randomized to one intervention receive a different intervention. Multilevel trials are particularly subject to contamination, because participants often share the same classroom, clinic, or other grouping and thus may hear about or participate in a different intervention condition. Costs, ethics, feasibility of recruitment, noncompliance, and the chance of contamination are discussed in depth in other publications, e.g., Cuzick et al. ( 1997 ). The goal of this manuscript was to provide information about how to conduct power calculations for three specific design questions which arise in multilevel clinical trials.

Several simplifying assumptions were made. The example uses the Essential Eight as a measure of cardiovascular health. The scoring suggested by Lloyd-Jones et al. ( 2022 ) produces continuous outcomes, with a Gaussian (normal) distribution rather than a binary (yes/no), count, negative binomial, or right truncated distribution. For simplicity, the cluster size at each level is assumed to be the same. With balanced cluster sizes at each level, cluster means of continuous data have an asymptotically normal distribution. In turn, the distribution of the test statistic is known exactly, and the test achieves the claimed Type I error rate. No missing outcome data is allowed for any participant. The intraclass correlation coefficient, a measure of correlation between elements in a cluster, is assumed to be the same for each cluster element within a single level and across intervention assignments and subgroups. No covariates are used. The researchers planned to use a general linear mixed model (Laird & Ware, 1982 ) rather than generalized estimating equations.

The nomenclature used in this manuscript for describing the structure of factors in randomized controlled clinical trials follows a commonly used convention, which describes both nesting and clustering, as used in Moerbeek ( 2005 ), Heo and Leon ( 2008 ), and Moerbeek and Teerenstra ( 2015 ). For the example described above, outcomes are measured on participants, participants are treated by the same provider, providers work together in clinics, and clinics are located within hospitals. Outcomes are nested within participants. Participants are nested within provider. Providers are nested within clinics. Clinics are nested within hospitals. The design thus has four levels of nesting. Because participants are nested within a provider, it is a reasonable assumption that they will have correlated outcomes. A similar assumption holds for providers in a clinic, and clinics in a hospital. Thus, the design has three levels of clustering.

In a multilevel trial, randomization can occur at the level of the independent sampling unit or within independent sampling units at any level. This is shown schematically for the example study in Fig. 1 . For clarity, although the example study will include multiple hospitals, clinics, providers, and participants, the figure shows only two hospitals, two clinics per hospital, two providers per clinic, and two participants per provider. Hospitals appear at the top level. Within each hospital, at the next level, are two clinics. Within each clinic, at the next level, are two providers. Finally, within each provider, at the bottom level, are two participants. Hospitals are considered to be independent sampling units.

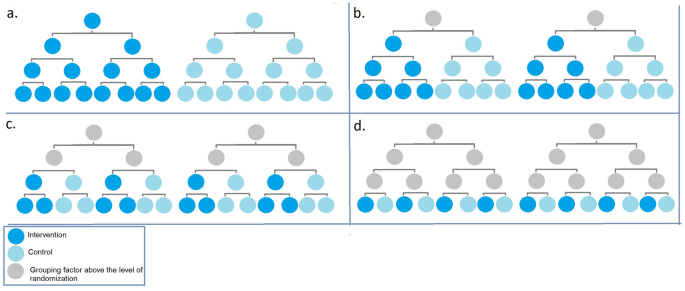
Four levels of randomization in a multilevel trial with four levels of nesting and three levels of clustering ( a hospital level randomization; b clinic-level randomization; c provider-level randomization; and d study participant-level randomization). For ease of display in the figure, only two independent sampling units, the hospitals, are shown, with two clinics in each hospital, two providers in each clinic, and two study participants per provider. The power calculations have more study participants, providers, clinics, and hospitals. Intervention is shown in azure, with control in Alice blue. Grouping factors above the level of randomization are shown in gray

There are many possible randomization schemes for designs with clusters. The unit of randomization is the name given to the element of a study design which is randomized. The unit of randomization and the independent sampling unit may be the same, or they may be different, depending on the study design. The difference between unit of randomization and independent sampling unit can be seen in two types of studies with a single level of clustering: the randomized complete block design and the group-randomized design. In a randomized complete block design, randomization occurs within independent clusters. In a group-randomized trial, there is a single level of grouping or clustering, and each independent group or cluster is randomly assigned to an intervention. For group-randomized trials, the independent sampling unit is the same as the unit of randomization.

For designs with multiple levels of clustering, there are many possible ways to conduct randomization. Figure 1 shows four possible levels of randomization for the example multilevel trial. In panel a, the randomization is at the level of the hospital. The entire hospital is randomized to intervention or control. The randomization is between independent sampling units. In panel b, the randomization is at the level of the clinic. It is a randomization within independent sampling units. In panel c, the randomization is at the level of the provider. Again, the randomization is within the independent sampling units. Finally, in panel d, the randomization is at the level of the participant, within the independent sampling units. Gray circles above the level of randomization show how grouping or clustering still creates correlation, no matter where the randomization occurs.

This manuscript provides example power analyses for a single example trial for three design choices: level of randomization, form of the outcome, and analytic approach for assessing subgroup differences. A literature review provides background on power and sample size software and methodology for randomized clinical control trials with multiple levels of clustering. The results section provides power curves for each of the three design choices. The discussion section summarizes limitations and strengths of the approach and outlines implications for future research. A detailed mathematical presentation of the predictors, outcomes, covariance structure, models, and hypotheses tests appears in Online Resource 1 .

Software Review Methods

The introduction section lists assumptions made for the example. The assumptions led to exclusion and inclusion criteria for a review of software packages. The goal of the literature review was to find software which could be used for the power analyses. Software packages had to compute power for the general linear mixed model, with Gaussian outcomes. Packages designed for use for binary, count, or right truncated outcomes were excluded. Packages designed for computing power for generalized estimating equations were also excluded.

The review of software packages was not an exhaustive or structured literature review. Both Google Scholar and PubMed were searched, using the keywords “multilevel,” “cluster,” and “power” with a Boolean “or”.

The resulting website hits were examined in order of relevance, until the same package appeared in both searches. A Ph.D. statistician (KEM) downloaded the software and read the accompanying documentation. He also reviewed peer-reviewed publications on the software packages, if available, published analytic methods or both, to obtain more detail. Software packages were then judged as being able to compute power for the three design choices.

Power Methods

The power calculations presented in this study use published analytic power results (Chi et al., 2019 ) for the Wald test in the mixed model (Laird & Ware, 1982 ). The calculations were implemented in POWERLIB, a free, validated, open-source SAS \(/\) IML package (SAS Institute Inc, 2020 ) described in Johnson et al. ( 2009 ). POWERLIB was chosen because it has the ability to address all three design choices considered in this study. POWERLIB was initially designed to provide power calculations only for the general linear multivariate model. Chi et al. ( 2019 ) showed that under certain conditions, the mixed model Wald test with Kenward and Roger ( 2009 ) degrees of freedom coincides with the Hotelling-Lawley trace statistic for the general linear multivariate model using the McKeon ( 1974 ) reference distribution. Designs with clusters fit the restrictions if (1) all the clusters at each level are the same size, (2) there are no repeated measurements of predictors over time, and (3) there are no missing data in the predictors or outcomes. Under the restrictions, exact or very accurate power approximations for the mixed model can be calculated using results presented by Muller et al. ( 1992 ). For the examples and assumptions considered in this manuscript, the results are exact.

The power calculations require seven inputs: the Type I error rate, the covariance of the errors, the between-independent sampling unit contrast, the within-independent sampling unit contrast, the population values of the parameters for a specified alternative hypothesis, the corresponding values for the null hypothesis, and the sample size in each group. Inputs for the power calculations shown in this paper appear in Online Resource 1 . Power curves were produced from the points generated from POWERLIB using SAS SGPLOT. Approximately 100 power values were calculated for each power curve in order to accurately reflect the smoothness of the underlying function.

Contamination

The occurrence, in a randomized controlled clinical trial, of an event in which a cluster, independent sampling unit, or both, are exposed to an intervention other than that assigned by the randomization scheme.

A group, with membership determined by common exposures, experiences, background, or interactions among group members.

A variable formed by summing or averaging the possibly weighted values of other variables.

Exchangeability

An assumption about the joint distribution of a set of random variables, each of which has a number, which indicates that the joint distribution does not change if the variables are renumbered. In cluster sampling, the assumption of exchangeability leads to elements of a cluster having equal variance and equal correlation.

Intraclass Correlation Coefficient or ICC

The common correlation among any two items due to a single level of clustering.

Independent Sampling Unit

Generically, a unit in a study design which is statistically independent of all other units of the same sort. In a multilevel study, a group or cluster which is statistically independent from all other groups or clusters at the same level. Often, the level in a multilevel trial in which all the other levels are nested, but that itself is not nested in another level.

A study involving data structures with more than one dimension of grouping or clustering, often with clusters nested within clusters. Here, multilevel indicates multiple levels in a hierarchical design, rather than describing a multilevel intervention, which is applied at many levels of a study.

A feature of study designs which occurs when levels of one factor appear only within levels of another factor.

The probability of rejecting the null hypothesis, evaluated for a particular alternative hypothesis.

Treatment Effect Heterogeneity

Differences in the effect of intervention between subgroups.

Unit of Randomization

Generically, the unit in a study design which is randomly assigned to an intervention or control group. In a multilevel trial, it indicates the level at which randomization takes place.

Unweighted Composite

A variable formed by summing the unweighted values of other variables.

Answering the Design Questions

Assumptions used for all design questions.

A power analysis for each design question is described in each of the next three subsections. Each subsection explains the question at hand, describes the hypothesis of interest, the data analysis planned, and the aligned power analysis. An aligned power analysis matches the planned data analysis in terms of model, hypothesis, statistical hypothesis tests, reference distributions, and Type I error rate (Muller et al., 1992 ). For analysts who want more information, mathematical details appear in Online Resource 1 . The Online Resource 1 details matrices defining the predictors, outcomes, models, and between- and within-independent sampling unit hypotheses.

The example power analyses assumed 20 hospitals, 8 clinics per hospital, 6 providers per clinic, and 6 participants per provider. All examples assume that all 8 outcomes are measured on all participants. For the subgroup analysis, it is assumed that there are 10 urban hospitals and 10 rural hospitals. The power analysis also assumed an equal number assigned to intervention and control.

The sampling design of a study dictates the correlation and variance of the outcomes. By convention, single measurements on elements in a cluster are assumed to be exchangeable, which means that their sampling distribution does not change if the elements are renamed or renumbered. In cluster sampling, the assumption of exchangeability leads to elements of a cluster having equal variance and equal correlation. The three-level cluster correlation model (Longford, 1987 ) assumed the intraclass correlations are 0.05 for provider, 0.01 for clinic, and 0.01 for hospital. Therefore, the hypothesized correlation between any two participants seeing the same provider in the same clinic in the same hospital should be \(0.05+0.01+0.01=0.07\) .

The variance of the outcomes arises from two sources. One source is the clustering of participants within providers, providers within clinics, and clinics within hospitals. Another source is the covariance between the Essential Eight outcomes. As detailed in Online Resource 1 , all models with the multivariate outcomes used a Kronecker product of the three level cluster covariance model and an unstructured covariance model among the eight outcomes for data analysis. In order to simplify the narrative, the power analyses assumed the subscales of the Essential Eight were independent with variances of 1. For models with the unweighted composite outcome, the variance model is a Kronecker product of the three-level cluster covariance model, with the scalar variance of the unweighted composite outcome.

For each design question, researchers planned to fit a general linear mixed model which varied with the level of randomization. The investigators planned to use the Wald test with Kenward and Roger ( 2009 ) degrees of freedom at an alpha level of 0.05.

Design Consideration 1: Level of Randomization

Researchers conducted a power analysis to examine the effect of choice of level of randomization on power. The four randomization schemes considered are shown in Fig. 1 . Changing randomization level changes the distributions of the estimates of means, as well as their variances and correlations. Accurate power analysis requires correctly accounting for the differences.

Researchers sought to examine the effect of intervention on a single, unweighted composite outcome, formed by averaging the Essential Eight outcomes. The scientific question was whether intervention would alter the average response for the unweighted outcome more for those randomized to intervention, compared to control. The null hypothesis was that there would be no intervention effect on the unweighted composite outcome. The alternative hypothesis was that the composite outcome would change, as a result of the intervention effect.

Any power calculation computes power for a specified pattern of results. In most cases, there are a variety of patterns which are plausible. In this case, the researchers computed power supposing that intervention caused a change in only one of the eight outcomes, thinking that the intervention would change diet, but no other of the Essential Eight.

Design Consideration 2: Unweighted Composite Versus Multivariate

Researchers conducted a power analysis to examine the effect of the choice of outcome type on power. Randomization was assumed to occur at the level of the independent sampling unit, the hospital (see Fig. 1 a).

The scientific question for the multivariate outcome is whether intervention has an effect on any of the Essential Eight outcomes. The grand null hypothesis is that there is no difference in any of the eight subscores between those randomized to intervention or control. It is a grand null, rather than a single null, because it involves the combination of eight hypotheses. The alternative hypothesis is that there is at least one mean subscore which differs between those randomized to intervention or control.

The scientific question for the composite outcome is whether intervention has an effect on the average Essential Eight. The null hypothesis is that there would be no effect of intervention on the composite outcome. The alternative hypothesis was that there would be an intervention effect on the composite outcome.

The researchers considered two mixed models: one with a multivariate outcome and one with an unweighted composite outcome. Both models included fixed effect predictors for an intercept and an indicator variable for treatment. The variance models are described above.

The specific alternative considered for both power analyses was that there was exactly one subscore which differed between the intervention and control groups. As we shall note in the Discussion, power depends on the alternative chosen. The power calculations would certainly change if more subscores differed between the intervention and control groups.

Design Consideration 3: Stratified Versus Pooled Subgroup Analysis

We considered two approaches for analyzing data with subgroups. A stratified approach, described by Buckley et al. ( 2017 ), splits the example trial data into two separate sets, one with rural hospitals and the other with urban hospitals. Modeling and hypothesis testing are reported separately for each set. If the subgroups are of equal size, the separate sets each have half the number of independent sampling units as the original data set. The stratified analysis has two hypothesis tests. In each subset, the investigators planned to test separately the null hypothesis that, for the subgroup considered, there is no difference in the average of the single outcome between those randomized to intervention or control. The alternative hypothesis assumed is that, for the subgroup considered, there is some difference in the average of the single outcome for those randomized to intervention or control.

A pooled analysis conducts modeling and hypothesis testing in the full data set. The approach was described in Muller and Fetterman ( 2003 ). They recommended the pooled approach because it generally has more power. In the pooled analysis, investigators planned to test the null hypothesis that there is no difference in the average of the single outcome between those randomized to intervention or control, averaged over subgroup. The alternative hypothesis is that there was a difference in the average of the single outcome between those randomized to intervention or control, averaging over subgroup. The hypothesis test is conducted under the implicit assumption that there is no difference in treatment effects between the subgroups.

For both the stratified and pooled analyses, the researcher fit a general linear mixed model, with the unweighted composite as the outcome. For the pooled analysis, the fixed effect predictors included an intercept, an indicator variable for intervention, an indicator variable for subgroup, and the subgroup-by-intervention interaction. The approach was adopted because of the belief that including the effect modifier (the interaction term) generally leads to an efficiency gain, at least in single level trials as shown by Tong et al. ( 2022 ) and Tong et al. ( 2023 ). For the stratified analysis, the fixed effect predictors included an intercept and an indicator variable for subgroup. The covariance model was as described above. Estimates of mean effect were computed for the urban hospitals randomized to intervention, the urban hospitals randomized to control, the rural hospitals randomized to intervention, and the rural hospitals randomized to control. Variances were estimated in the entire sample.

Power for the pooled approach was computed similarly as for the stratified approach. One additional assumption was made. Power is always computed for a specified alternative hypothesis. The approach adopted here was to assume that there was no interaction. The power computation thus assumed that the interaction parameter was included in the model, but that interaction term was zero.

An alternative power calculation would have been to consider a model with no fixed effect interaction term and to compute power for the intervention effect in that model. Because each fixed effect in the model reduces the error degrees of freedom by one, the approach we chose is slightly more conservative.

Software Review

A literature review of current methods and software for power analysis showed that only one power calculation method, and associated software package, provides power computations for all three design choices considered, under the restrictive assumptions about design, model, hypothesis test, and reference distribution. A summary of the review appears in Table 1 . Software packages were included in the table if they could compute power for trials with four or more levels of nesting and three or more levels of clustering. Most existing software packages lacked applicability to at least one of the three cases discussed in this paper. Most packages provide results for single outcomes, but do not account for both multilevel design and multiple outcomes. In many software packages, comparison of power at different levels of randomization was not straightforward. Some packages could not provide power for subgroup factors.

To arrive at the set of software packages included in Table 1 , we reviewed many other power and sample size software packages. Specific examples of packages limited to two or fewer levels of nesting included the Research Methods Resources (National Institutes of Health, 2022 ) and a variety of R packages, such as Kleinman et al. ( 2021 ). The Mplus package (Muthén & Muthén, 2023 ) allows specifying a data analysis and conducting a simulation for a specific design in order to assess power. Finch and Bolin ( 2016 ) described how to allow up to three more levels of nesting and up to two levels of clustering in Mplus. The commercial software packages NCSS \(/\) PASS (NCSS, 2008 ), SAS (SAS Institute Inc, 2011 ), and STATA (StataCorp, 1985 ) have power methods that explicitly account for only one level of clustering (two levels of nesting).

Several manuscripts were found, some with accompanying software, which provided power for analytic approaches or outcomes other than that considered in this manuscript. A general review appears in Turner et al. ( 2017 ). Subsequently, Li et al. ( 2019 ) discussed power and sample size methods for analysis of cluster-randomized cross-over trials with generalized estimating equations. Wang et al. ( 2022 ) provided power for generalized estimating equations for four level cluster-randomized trials. Candel and Van Breukelen ( 2010 ) provided sample size for varying cluster sizes in cluster randomized trials with binary outcomes. The relative efficiency of cluster randomized designs or multicenter trials with equal or unequal cluster sizes was discussed by van Breukelen et al. ( 2007 ). Tong et al. ( 2022 ) also discussed unequal cluster sizes in analyses of treatment effect heterogeneity.

Power Results

Power curves for the three design considerations are shown in Figs. 2 , 3 , and 4 . Power curves for randomization at one of four levels of nesting of the example multilevel study are shown in Fig. 2 . The curves show that power is highest for randomization at the level of participant. Power decreases when moving to an outer level of clustering. Power curves for an unweighted composite versus multivariate outcomes are shown in Fig. 3 . The curve shows that power for the multivariate approach is higher than the power for the composite outcome. Power curves for stratified versus pooled modeling to assess treatment are shown in Fig. 4 . Because the sample size for the stratified models is half that of the sample size for the pooled approach, the power is higher for the pooled approach.

Code to create the power curves appears in Online Resource 2 , with an index to the files in Index.txt. Online Resource 2 contains programs (.sas), code modules (.iml), associated data (.sas7bdat), result files (.lst), and plots (.png). All.sas,.iml, and.lst files are text format.

Power for randomization at level of study participant, provider, clinic, or hospital. The gray reference line at 0.05 is the Type I error rate, a lower limit for power. The gray reference line at 0.9 indicates a common target power for clinical trial design

Power for unweighted composite outcome versus multivariate outcome. The 1.0 on the horizontal axis corresponds to a difference between the intervention and the control groups of one standard deviation of one of the Essential Eight variables. The gray reference line at 0.05 is the Type I error rate, a lower limit for power. The gray reference line at 0.9 indicates a common target power for clinical trial design

Power for stratified analysis of subgroups, versus pooled analysis, for a single outcome variable of the Essential Eight. There are two subgroups, so the sample size for the stratified analysis is half that of the pooled analysis. The 1.0 on the horizontal axis corresponds to a difference between the intervention and the control groups of one standard deviation of one of the Essential Eight variables. The gray reference line at 0.05 is the Type I error rate, a lower limit for power. The gray reference line at 0.9 indicates a common target power for clinical trial design

This manuscript provided a discussion of three questions about the design of a particular multilevel randomized controlled clinical trial. For this example, there were three conclusions. First, for the example considered, the choice of unit of randomization can change the power, with power the highest for the choice of unit of randomization at the lowest level of nesting. For the example, power is highest for randomization of participants, rather than hospitals. Second, for the example considered, using a multivariate hypothesis, rather than a hypothesis about an unweighted composite outcome, can substantially increase power. Third, for the example considered, there can be a substantial gain in power by using a pooled analysis strategy, rather than splitting the sample by subgroup and evaluating the intervention effect in each subgroup-specific sample.

It is our hope that readers will find it useful to have solution strategies to all three design questions in the same place. The manuscript provides a unique discussion about the selection of multivariate versus composite outcomes, illustrating that the best analysis strongly depends on the choice of test and the underlying patterns of data. Our power analyses utilized peer-reviewed validated software (Johnson et al., 2009 ) and methods, including those of Muller et al. ( 1992 ), Muller et al. ( 2007 ), and Chi et al. ( 2019 ). So that other researchers may replicate our designs, we have provided straightforward and annotated code for each design.

In general, a tenet of power analysis is that higher sample sizes lead to more power. Two of our findings are consistent with this tenet. We showed that randomization of participants, instead of hospitals, increases power. The result occurs because there are more participants than hospitals in the study. We also showed that pooled, rather than stratified, analysis approaches have more power. The result occurs because there are more units of randomization in the pooled analysis.

There are both ethical and economic reasons to conduct careful power calculations and make considered design choices in multilevel randomized controlled clinical trials. Like all randomized controlled clinical trials, multilevel randomized controlled clinical trials can take a huge amount of time and money. Recruiting and retaining participants in a randomized controlled clinical trial require substantial investment by study staff. In addition, any trial with human participants can incur ethical costs. Study participants may experience potential harms from research, in addition to the inconvenience and time costs for participating in a trial. Studies which are too large place more participants than necessary at potential risk. Studies which are too small to have sufficient power place participants at risk for little or no chance of being able to adequately test a hypothesis.

This manuscript considered each design question separately. An alternative approach would have been to consider more complicated designs with combinations of design features, which is typical of actual research. For example, the manuscript could have considered the effects on power of changing both level of randomization, and whether the outcome was composite or multivariate, at the same time. We avoided complex designs in order to make the results easier to understand. It is important to note that the methods used do accommodate any combination of the study design features considered.

The goal of this manuscript was to encourage careful calculation of power during the design of every study. Conclusions from the example considered may not generalize to other designs. The example considered was a design with outcomes measured on participants, participants treated by the same provider, providers nested within clinics, and clinics nested within hospitals. Conclusions for this manuscript only are true for a design which matches this study in terms of sample size, levels of nesting, levels of clustering, number of independent sampling units and clusters, sample size within clusters, intraclass correlations, covariances among outcomes, pattern of means, and statistical test procedure. Specifically, the example design has four levels of nesting, three levels of clustering, certain dimensions, variances, correlations, means, statistical model, statistical test, reference distribution, and null and alternative hypotheses. Changing any feature will change the power values.

In general, multilevel studies require special methods for power and data analysis. Failure to align power and data analysis approaches with the study design can result in misspecification of power, incorrect choices of sample size, and increased rates of decision errors (Muller et al., 1992 ). There are extensive treatments of analytic approaches for multilevel studies. See, e.g., Verbeke and Molenberghs ( 2009 ) and Cheng et al. ( 2010 ) for data analysis with the general linear mixed model and Muller and Stewart ( 2006 ) for the theory of the general linear univariate, multivariate, and mixed models. Accurate analytic approximate and exact power and sample size calculations are also available for a wide swath of hypotheses using the general linear multivariate model (Muller et al., 1992 ) or using the general linear mixed model (Muller et al., 2007 ; Chi et al., 2019 ).

This paper used the general linear mixed model, the general linear hypothesis, and the Wald test with Kenward and Roger ( 2009 ) degrees of freedom. Other authors have suggested instead using generalized estimating equation-based approaches, with data analytic approaches using small sample corrections for small numbers of independent sampling units (Kauermann & Carroll, 2001 ; Mancl & DeRouen, 2001 ). Parallel results for binary outcomes are described by Li and Redden ( 2015 ).

The number of independent sampling units is often fixed by the funding agency. For example, a multi-center trial funded by the National Institutes of Health may make awards to a certain number of clinical centers. The number is usually determined by the funds available and by the number of clinical centers who submit well-scored grants. When the number of independent sampling units is fixed by design, one reasonable approach to maximize power is by considering the effect of changing the level of randomization.

Statistical and power concerns should only be indulged when changing the level of randomization will not cause ancillary changes to the study results. In some cases, pragmatic considerations must supersede power considerations. One example occurs when contamination is a concern. Contamination occurs when those randomized to one intervention receive a different intervention than planned. Contamination tends to bias the results of a study towards the null when the study is analyzed as randomized. Multilevel studies are particularly subject to contamination, because the close relationship among members of clusters leads to cross-over between randomization arms. For example, participants in a single clinic may discuss their treatment in a waiting room. Those who were randomized to placebo, rather than intervention, may demand breaking the masking and receiving the intervention instead. Thus, both pragmatic implementation questions and power considerations should be considered when deciding on the level of randomization.

This manuscript presents code and mathematical detail for computing power for multivariate or composite outcomes. However, power is just one concern when choosing outcomes. Testing intervention effects on either a multivariate or a composite outcome evaluates different scientific questions. The multivariate hypothesis tests whether there is a difference between randomization groups in any outcome. It is important to note that a rejection of a multivariate test does not guarantee the randomization groups differ for any single outcome, but for some weighted combination of the outcomes. Considering an unweighted composite outcome asks whether the average level of the outcomes differs between the randomization groups. A potential deficit of an unweighted composite outcome is the possibility that an intervention may lead to an increase in some univariate outcomes and a concomitant decrease in other outcomes. If increases match decreases, the combination may lead to a misleading null result. If there is uncertainty about the direction of the effect for one or more univariate outcomes, a composite outcome should be viewed with caution.

Whether a multivariate outcome leads to more power than an unweighted composite depends on the hypotheses tested, the pattern of means, the covariance pattern, and the dimensions of the design. In the scenario considered, the researchers compared two different hypotheses. For the unweighted composite outcome, they planned to test whether those randomized to intervention had different average levels of the unweighted composite outcome. For the multivariate outcome, the researchers planned to test whether there was any difference in any of the univariate outcomes. An unweighted composite can have more power than a multivariate test if the unweighted composite components (1) share a common scale and (2) have equal magnitudes and directions of association with the outcome. In other cases, the unweighted composite can have lower power, as demonstrated by the example. The conclusion can also vary with the choice of covariance pattern among the outcomes.

The study assumed that the investigators wished to examine only intervention effects, not examine interaction. In general, in studies with subgroups and an intervention, investigators can test at least three distinct hypotheses. Researchers may want to test the interaction hypothesis and find out whether the intervention effect differs within subgroups. Researchers may wish to test the intervention main effect and see if randomization to intervention or control affects the outcome, assuming no interaction. Rarely, researchers may want to test the subgroup effect and see if, for example, urban hospitals have different responses than rural hospitals, again assuming no interaction. Because power depends on what hypothesis is of scientific interest, researchers must compute power for the correct hypothesis. In a randomized controlled clinical trial, with an intervention and a subgroup, analysts must decide how to model and test for interaction. Interaction occurs when the intervention has a differential effect within different subgroups.

For a clinical trial with subgroups, a common approach to test differences in intervention effects between subgroups is to use a planned cascade of hypothesis tests (Muller & Fetterman, 2003 ). First, the subgroup-by-intervention interaction is tested. If the subgroup-by-intervention interaction hypothesis is significant, the hypothesis test result is reported, and further hypothesis testing is used to examine the intervention effects which are distinct within each subgroup. If the subgroup-by-intervention interaction hypothesis is non-significant, the interaction term may be removed from the model. A more conservative approach is to leave the non-significant interaction term in the model and then test the intervention effect.

A different approach for studies with subgroups is to stratify the data and to examine the intervention effect separately within each subgroup (Buckley et al., 2017 ). We demonstrate that this approach has much less power because it has a much smaller sample size. It also precludes the ability to test for treatment-by-subgroup interaction and to estimate the size of the differences in treatment effect among subgroups. For that reason, we, like Muller and Fetterman ( 2003 ), suggest always using the pooled analysis. In particular, because there may be disparities among cardiovascular health among subgroups, it is important to design studies with sufficient power to examine differences in treatment effect.

The study considered in this manuscript had several limitations. First, the study used examples, rather than general mathematical proofs, to show results for one study design, rather than for many study designs. A higher standard of evidence would be to use derivations to obtain closed-form results for multiple study designs. Second, the calculations for the study used POWERLIB (Johnson et al., 2009 ). Although POWERLIB is open source, it is inaccessible to most scientists, because it requires a paid license for SAS \(/\) IML (SAS Institute Inc, 2020 ), and assumes a knowledge of matrices and multivariate linear models sufficient to state the model, alternative, and hypothesis. In addition, the use of POWERLIB requires assumptions about the study design which rarely hold in multilevel studies. Rarely, if ever, are all the clusters at each level the same size. Covariates may be measured repeatedly over time. Missing data is the norm, rather than the exception, in studies in prevention science. However, even under departures from these assumptions, the power results can provide good guidance. Clearly, further work is needed to develop power and sample size methods allowing unequal cluster sizes in complex cluster designs.

The manuscript was focused on a specific example, with three design choices. To simplify the discussion, several restrictive assumptions were made. This meant that the great generality of possible models, analyses, and tests were not considered. The study did not consider computing power for confirmatory analyses of treatment effect heterogeneity (Li et al., 2022 ). In addition, the example study did not include covariates, which obviated discussion of covariate intraclass correlation (Yang et al., 2020 ).

In addition, the study considered only one possible alternative hypothesis for the comparison of power for unweighted composite versus multivariate outcomes. Power depends strongly on the alternative of interest. For this reason, we urge analysts to compute power for all plausible alternatives for their study design. In addition, the study only considered one analytic alternative to examining intervention effects on an unweighted composite outcome, i.e., using a multivariate test. It is possible that a gated analytic approach such as that suggested by Shaffer ( 1986 ) or separate Bonferroni-corrected tests (Bonferroni, 1936 ) for each outcome would perform better. Using the Bonferroni-corrected tests corresponds to considering a joint set of univariate hypotheses. Each hypothesis states that there is no intervention effect for a particular outcome, out of the set of eight outcomes. This approach is typically used if the univariate outcomes are co-primary.

The power calculation used standardized inputs and made the assumption that subscales for the Essential Eight were independent for the power analysis. The assumption is likely inadequate, because outcomes such as smoking, exercise, blood pressure, and lipids are often correlated. POWERLIB does allow computing power for correlated outcomes and accepts the correlation and variance of the error matrix as inputs. However, authors often do not provide sufficient information in publications to obtain this input. Power results differ for independent and non-independent outcomes. Thus, finding better inputs improves power estimates. Harrall et al. ( 2023 ) recommended approaches for finding inputs for power and sample size analysis from published articles or existing data. The updated scoring system for the Essential Eight (Lloyd-Jones et al., 2022 ) has only recently been published, meaning that accurate inputs for power analysis have not been published, to our knowledge, as of this writing. Estimates of variances but not covariances for the Essential Eight subscores did appear in supplemental material for Shetty et al. ( 2022 ). The power analyses presented in the present paper assume standard deviations of a single observation for a single participant was 1.0. This approach was critiqued by Lenth ( 2001 ) who suggested computing power in actual units of the data to be collected. In general, we strive to follow Lenth’s recommendations, but admit defeat when estimates are not available.

One design question considered in the study was whether a pooled or stratified data analytic approach had more power. The analytic approach used for the pooled analysis included fixed effect predictors for an intercept, an indicator variable for intervention, an indicator variable for the subgroup, and an intervention-by-subgroup interaction term. Power was computed for the main effect of intervention, while setting the interaction parameter to zero. An alternative approach would have been to compute power for the interaction hypothesis. For single-level (rather than multilevel) cluster randomized designs, such power calculations have already been studied by Tong et al. ( 2022 ) and Tong et al. ( 2023 ).

One goal of this study was to encourage investigators considering multilevel designs to conduct accurate power analysis and consider design alternatives. Power analysis takes time and care to do right and is frequently conducted before funding arrives. However, the results presented here demonstrate that large power differences can occur with what appear to be minor design decisions. The amount of time and money spent on a power analysis will, in retrospect, pale in comparison with the monetary costs and psychic regret engendered by a failed trial.

The study also had several strengths. Use of a published and validated software package (Johnson et al., 2009 ) based on published power and sample size approximations (Muller et al., 1992 ) guarantees accuracy of results. The approximations reduced to exact results for all designs evaluated in the present paper. While simulation-based power approximations can be accurate, without industry-standard unit-checking, published validation, and peer-reviewed and publicly available code, simulation results do not meet National Academy of Science standards for reproducibility (National Academies of Sciences, Engineering, & Medicine, 2019 ). Finally, the study used an approach we have described elsewhere, including in Section 16.4 in Muller et al. ( 1992 ) and in Chi et al. ( 2019 ). The approach centers on transforming the original models to power equivalent models which simplify the presentation and computations. A power equivalent analysis provides exactly the same power, using a simplified model, hypothesis, or both. As detailed in Online Resource 1 , all of the power computations for the study used power equivalent models.

The results of this study show that with increasing study design complexity comes the requirement for more intensive study planning. While more research is needed to generalize the results, to evaluate the utility of different analytic approaches, and to provide analytic results for power at various choices of levels of randomization, this study provides first steps towards the goals. Once the analytic results are published and validated, adding the resulting methods into a free, open-source, validated, point-and-click, wizard-style program such as GLIMMPSE ( www.SampleSizeShop.org .), described in Guo et al. ( 2013 ) and Kreidler et al. ( 2013 ), will provide greater access and dissemination.

Data Availability

No data nor materials were used in this manuscript.

Code Availability

All code used to generate the results appears in Online Resource 2 .

Buckley, J. P., Doherty, B. T., Keil, A. P., & Engel, S. M. (2017). Statistical approaches for estimating sex-specific effects in endocrine disruptors research. Environmental Health Perspectives, 125 (6), 067013. https://doi.org/10.1289/EHP334

Article   PubMed   PubMed Central   Google Scholar  

Bonferroni, C. E. (1936). Teoria Statistica delle Classi e Calcolo delle Probabilitá. Pubblicazioni del R Istituto Superiore di Scienze Economiche e Commerciali di Firenze, Florence, Italy.

Borenstein, M., Hedges, L., & Rothstein, H. (2023). CRT-Power. Biostat. Inc., Englewood, NJ. Accessed March 17, 2023, from https://www.crt-power.com/

Candel, M. J. J. M., & Van Breukelen, G. J. P. (2010). Sample size adjustments for varying cluster sizes in cluster randomized trials with binary outcomes analyzed with second-order PQL mixed logistic regression. Statistics in Medicine, 29 (14), 1488–1501. https://doi.org/10.1002/sim.3857

Article   PubMed   Google Scholar  

Cheng, J., Edwards, L. J., Maldonado-Molina, M. M., Komro, K. A., & Muller, K. E. (2010). Real longitudinal data analysis for real people: Building a good enough mixed model. Statistics in Medicine, 29 (4), 504–520.

Chi, Y.-Y., Glueck, D. H., & Muller, K. E. (2019). Power and sample size for fixed-effects inference in reversible linear mixed models. The American Statistician, 73 (4), 350–359. https://doi.org/10.1080/00031305.2017.1415972

Cuzick, J., Edwards, R., & Segnan, N. (1997). Adjusting for non-compliance and contamination in randomized clinical trials. Statistics in Medicine, 16 (9), 1017–1029. https://doi.org/10.1002/(SICI)1097-0258(19970515)16:9<1017::AID-SIM508>3.0.CO;2-V

Article   CAS   PubMed   Google Scholar  

Dong, N., & Maynard, R. (2013). PowerUp!: A tool for calculating minimum detectable effect sizes and minimum required sample sizes for experimental and quasi-experimental design studies. Journal of Research on Educational Effectiveness, 6 (1), 24–67. https://doi.org/10.1080/19345747.2012.673143

Article   Google Scholar  

Finch, H., & Bolin, J. (2016). Multilevel modeling using Mplus, 1st edn. Chapman and Hall/CRC, Boca Raton, FL.

Guo, Y., Logan, H. L., Glueck, D. H., & Muller, K. E. (2013). Selecting a sample size for studies with repeated measures. BMC Medical Research Methodology, 13 , 100. https://doi.org/10.1186/1471-2288-13-100

Harrall, K. K., Muller, K. E., Starling, A. P., Dabelea, D., Barton, K. E., Adgate, J. L., & Glueck, D. H. (2023). Power and sample size analysis for longitudinal mixed models of health in populations exposed to environmental contaminants: a tutorial. BMC Medical Research Methodology, 23 (1), 12. https://doi.org/10.1186/s12874-022-01819-y

Heo, M., & Leon, A. C. (2008). Statistical power and sample size requirements for three level hierarchical cluster randomized trials. Biometrics, 64 (4), 1256–1262. https://doi.org/10.1111/j.1541-0420.2008.00993.x

Johnson, J. L., Muller, K. E., Slaughter, J. C., Gurka, M. J., Gribbin, M. J., & Simpson, S. L. (2009). POWERLIB: SAS/IML software for computing power in multivariate linear models. Journal of Statistical Software, 30 (5), 30–05. https://doi.org/10.18637/jss.v030.i05

Kauermann, G., & Carroll, R. J. (2001). A note on the efficiency of sandwich covariance matrix estimation. Journal of the American Statistical Association, 96 (456), 1387–1396. https://doi.org/10.1198/016214501753382309

Kenward, M. G., & Roger, J. H. (2009). An improved approximation to the precision of fixed effects from restricted maximum likelihood. Computational Statistics & Data Analysis, 53 (7), 2583–2595. https://doi.org/10.1016/j.csda.2008.12.013

Kleinman, K., Sakrejda, A., Moyer, J., Nugent, J., Reich, N., & Obeng, D. (2021). clusterPower: Power calculations for cluster-randomized and cluster-randomized crossover trials. Accessed March 17, 2023, from https://CRAN.R-project.org/package=clusterPower

Kreidler, S. M., Muller, K. E., Grunwald, G. K., Ringham, B. M., Coker-Dukowitz, Z. T., Sakhadeo, U. R., Barón, A. E., & Glueck, D. H. (2013). GLIMMPSE: Online power computation for linear models with and without a baseline covariate. Journal of Statistical Software, 54 (10), 10. https://doi.org/10.18637/jss.v054.i10

Laird, N. M., & Ware, J. H. (1982). Random-effects models for longitudinal data. Biometrics, 38 (4), 963–974. https://doi.org/10.2307/2529876

Lenth, R. V. (2001). Some practical guidelines for effective sample size determination. The American Statistician, 55 (3), 187–193. https://doi.org/10.1198/000313001317098149

Li, F., Chen, X., Tian, Z., Esserman, D., Heagerty, P. J., & Wang, R. (2022). Designing three-level cluster randomized trials to assess treatment effect heterogeneity. Biostatistics (Oxford, England), 026. https://doi.org/10.1093/biostatistics/kxac026

Li, F., Forbes, A. B., Turner, E. L., & Preisser, J. S. (2019). Power and sample size requirements for GEE analyses of cluster randomized crossover trials. Statistics in Medicine, 38 (4), 636–649. https://doi.org/10.1002/sim.7995

Li, P., & Redden, D. T. (2015). Small sample performance of bias-corrected sandwich estimators for cluster-randomized trials with binary outcomes. Statistics in Medicine, 34 (2), 281–296. https://doi.org/10.1002/sim.6344

Lloyd-Jones, D. M., Allen, N. B., Anderson, C. A. M., Black, T., Brewer, L. C., Foraker, R. E., Grandner, M. A., Lavretsky, H., Perak, A. M., Sharma, G., Rosamond, W., & Null, N. (2022). Life’s essential 8: Updating and enhancing the American Heart Association’s construct of cardiovascular Health: A presidential advisory from the American Heart Association. Circulation, 146 (5), 18–43. https://doi.org/10.1161/CIR.0000000000001078

Longford, N. T. (1987). A fast scoring algorithm for maximum likelihood estimation in unbalanced mixed models with nested random effects. Biometrika, 74 (4), 817–827. https://doi.org/10.2307/2336476

Mancl, L. A., & DeRouen, T. A. (2001). A covariance estimator for GEE with improved small-sample properties. Biometrics, 57 (1), 126–134. https://doi.org/10.1111/j.0006-341x.2001.00126.x

McKeon, J. J. (1974). F approximations to the distribution of Hotelling’s T-squared. Biometrika, 61 (2), 381–383. https://doi.org/10.2307/2334369

Moerbeek, M. (2005). Randomization of clusters versus randomization of persons within clusters. The American Statistician, 59 (2), 173–179. https://doi.org/10.1198/000313005X43542

Moerbeek, M., & Teerenstra, S. (2015). Power analysis of trials with multilevel data, 1st edition edn. Chapman and Hall/CRC, Boca Raton.

Muller, K. E., Edwards, L. J., Simpson, S. L., & Taylor, D. J. (2007). Statistical tests with accurate size and power for balanced linear mixed models. Statistics in Medicine, 26 (19), 3639–3660. https://doi.org/10.1002/sim.2827

Muller, K. E., & Fetterman, B. A. (2003). Regression and ANOVA: An integrated approach using SAS software. John Wiley & Sons, Inc.

Muller, K. E., Lavange, L. M., Ramey, S. L., & Ramey, C. T. (1992). Power calculations for general linear multivariate models including repeated measures applications. Journal of the American Statistical Association, 87 (420), 1209–1226. https://doi.org/10.1080/01621459.1992.10476281

Muller, K. E., & Stewart, P. W. (2006). Linear model theory: Univariate, multivariate, and mixed models. John Wiley & Sons, New York, New York. Google-Books-ID: bLwRX4S676QC.

Muthén, L. K., & Muthén, B. O. (2023). Mplus programs. statmodel.com, Los Angeles, CA. Accessed March 17, 2023, from https://www.statmodel.com

National Academies of Sciences, Engineering, and Medicine. (2019). Reproducibility and Replicability in Science. National Academies Press (US), Washington (DC).

National Institutes of Health (2022) Research methods resources. Accessed March 17, 2023, from https://researchmethodsresources.nih.gov/

NCSS. (2008). PASS: Power analysis and sample size, Kaysville, UT. http://www.ncss.com/pass.html

Raudenbush, S. W., Spybrook, J., Congdon, R., Liu, X., Martinez, A., Bloom, H., & Hill, C. (2011). Optimal Design Software. Accessed March 17, 2023, from https://wtgrantfoundation.org/resource/optimal-design-with-empirical-information-od

SAS Institute Inc. (2020). SAS IML: Programming guide, Cary, North Carolina, USA.

SAS Institute Inc. (2011). SAS 9.4 Software: Version 9.4, Cary, NC. http://www.sas.com/software/sas9/

StataCorp, L. P. (1985). Stata. StataCorp, L.P., College Station, TX.

Shaffer, J. P. (1986). Modified sequentially rejective multiple test procedures. Journal of the American Statistical Association, 81 (395), 826–831. https://doi.org/10.2307/2289016

Shetty, N. S., Parcha, V., Patel, N., Yadav, I., Basetty, C., Li, C., Pandey, A., Kalra, R., Li, P., Arora, G., & Arora, P. (2022). AHA life’s essential 8 and ideal cardiovascular health among young adults. American Journal of Preventive Cardiology, 13 , 100452. https://doi.org/10.1016/j.ajpc.2022.100452

Tong, G., Esserman, D., & Li, F. (2022). Accounting for unequal cluster sizes in designing cluster randomized trials to detect treatment effect heterogeneity. Statistics in Medicine, 41 (8), 1376–1396. https://doi.org/10.1002/sim.9283

Tong, G., Taljaard, M., & Li, F. (2023). Sample size considerations for assessing treatment effect heterogeneity in randomized trials with heterogeneous intracluster correlations and variances. Statistics in Medicine, 42 (19), 3392–3412. https://doi.org/10.1002/sim.9811

Turner, E. L., Li, F., Gallis, J. A., Prague, M., & Murray, D. M. (2017). Review of recent methodological developments in group-randomized trials: Part 1-design. American Journal of Public Health, 107 (6), 907–915. https://doi.org/10.2105/AJPH.2017.303706

van Breukelen, G. J. P., Candel, M. J. J. M., & Berger, M. P. F. (2007). Relative efficiency of unequal versus equal cluster sizes in cluster randomized and multicentre trials. Statistics in Medicine, 26 (13), 2589–2603. https://doi.org/10.1002/sim.2740

Verbeke, G., & Molenberghs, G. (2009). Linear mixed models for longitudinal data. Springer.

Wang, X., Turner, E. L., Preisser, J. S., & Li, F. (2022). Power considerations for generalized estimating equations analyses of four-level cluster randomized trials. Biometrical Journal. Biometrische Zeitschrift, 64 (4), 663–680. https://doi.org/10.1002/bimj.202100081

Yang, S., Li, F., Starks, M. A., Hernandez, A. F., Mentz, R. J., & Choudhury, K. R. (2020). Sample size requirements for detecting treatment effect heterogeneity in cluster randomized trials. Statistics in Medicine, 39 (28), 4218–4237. https://doi.org/10.1002/sim.8721

Download references

KKH, DHG, and KEM were supported by NIH/NIGMS funded grants 5R01GM121081-08, 3R25GM111901, and 3R25GM111901-04S1. EAS was supported by AHRQ-funded grant R01HS028283.

Author information

Authors and affiliations.

Department of Health Outcomes and Biomedical Informatics, University of Florida College of Medicine, 2004 Mowry Road, Gainesville, 32606, FL, USA

Kylie K. Harrall, Elizabeth A. Shenkman & Keith E. Muller

Department of Implementation Science, Wake Forest University School of Medicine, 475 Vine Street, Winston-Salem, 27101, NC, USA

Katherine A. Sauder

Department of Pediatrics, University of Colorado School of Medicine, 13123 E. 16th Ave., Aurora, 80045, CO, USA

Deborah H. Glueck

You can also search for this author in PubMed   Google Scholar

Contributions

KKH conceptualized the idea and wrote the first draft of the power analyses, for a trial similar to the one described in the manuscript. DHG created the initial and subsequent drafts of the manuscript, with supervision from KKH and KEM. DHG and KEM obtained funding. KEM created code, following initial code drafts from KKH and DHG. KEM created the mathematical derivations in Online Resource 1 , with results and notation checked by DHG. EAS suggested the theoretical example described in the manuscript. KAS served as a site principal investigator for a randomized controlled clinical trial, the power analysis for which initially raised the questions answered in the manuscript. In addition, KAS critically reviewed the document for utility to non-statistical investigators. All authors reviewed the manuscript and approved the submission.

Corresponding author

Correspondence to Kylie K. Harrall .

Ethics declarations

Ethical approval.

The manuscript did not involve any data. Thus, no institutional review board was involved.

Consent to Participate

The research did not involve human study participants. Thus, no informed consent was required.

Consent for Publication

All authors approved the final submitted manuscript.

Conflict of Interest

The authors declare no competing interests.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary file1 (PDF 257 KB)

Supplementary file2 (zip 303 kb), rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Harrall, K.K., Sauder, K.A., Glueck, D.H. et al. Using Power Analysis to Choose the Unit of Randomization, Outcome, and Approach for Subgroup Analysis for a Multilevel Randomized Controlled Clinical Trial to Reduce Disparities in Cardiovascular Health. Prev Sci (2024). https://doi.org/10.1007/s11121-024-01673-y

Download citation

Accepted : 11 March 2024

Published : 20 May 2024

DOI : https://doi.org/10.1007/s11121-024-01673-y

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Multilevel randomized controlled trial
• Composite outcome
• Subgroup analysis
• Heterogeneity of treatment effect
• Find a journal
• Publish with us
• Track your research

• Open access
• Published: 10 May 2024

Novice providers’ success in performing lumbar puncture: a randomized controlled phantom study between a conventional spinal needle and a novel bioimpedance needle

• Helmiina Lilja 1   na1 ,
• Maria Talvisara 1   na1 ,
• Vesa Eskola 2 , 3 ,
• Paula Heikkilä 2 , 3 ,
• Harri Sievänen 4 &
• Sauli Palmu 2 , 3  

BMC Medical Education volume  24 , Article number:  520 ( 2024 ) Cite this article

183 Accesses

Metrics details

Lumbar puncture (LP) is an important yet difficult skill in medical practice. In recent years, the number of LPs in clinical practice has steadily decreased, which reduces residents’ clinical exposure and may compromise their skills and attitude towards LP. Our study aims to assess whether the novel bioimpedance needle is of assistance to a novice provider and thus compensates for this emerging knowledge gap.

This randomized controlled study, employing a partly blinded design, involved 60 s- and third-year medical students with no prior LP experience. The students were randomly assigned to two groups consisting of 30 students each. They performed LP on an anatomical lumbar model either with the conventional spinal needle or the bioimpedance needle. Success in LP was analysed using the independent samples proportion procedure. Additionally, the usability of the needles was evaluated with pertinent questions.

With the conventional spinal needle, 40% succeeded in performing the LP procedure, whereas with the bioimpedance needle, 90% were successful ( p  < 0.001). The procedures were successful at the first attempt in 5 (16.7%) and 15 (50%) cases ( p  = 0.006), respectively. Providers found the bioimpedance needle more useful and felt more confident using it.

Conclusions

The bioimpedance needle was beneficial in training medical students since it significantly facilitated the novice provider in performing LP on a lumbar phantom. Further research is needed to show whether the observed findings translate into clinical skills and benefits in hospital settings.

Peer Review reports

Lumbar puncture (LP) is one of the essential skills of physicians in medical practice, especially in the fields of neurology, neurosurgery, emergency medicine and pediatrics. It is one of the procedures that medical students practice in their training. LP is an important clinical procedure for diagnosing neurological infections and inflammatory diseases and excluding subarachnoid hemorrhage [ 1 ]. LP can also be used for examining the spread of cancer cells to the central nervous system in diagnosing acute lymphoblastic leukemia (ALL) and for delivering intrathecal administration of chemotherapy in patients with ALL [ 2 ]. In recent years, the number of LPs in clinical practice has steadily decreased [ 3 , 4 ]. Over the past decade, a 37% decrease in LPs was observed across US children’s hospitals [ 3 ]. Similar trends have also been observed in emergency medicine [ 4 ]. Stricter criteria in practice guidelines, changes in patient demographics, and development in medical imaging have likely contributed to this decrease. This trend presumably reduces residents’ clinical exposure and may compromise their skills and attitude towards LP.

When performed by an experienced physician, LP is a relatively safe procedure, albeit not always straightforward or free from complications [ 4 ]. The spinal needle used in LP is thin and flexible, making its insertion into the spinal canal without seeing the location of the needle tip or destination challenging. The physician performing the procedure must master the specific lumbar anatomy to avoid complications [ 5 ]. The LP technique is not the only thing that matters, but patients’ size and comfort also affect the success of the procedure [ 6 ]. Hence, a practitioner lacking adequate experience in LP should be appropriately supervised when performing the procedure [ 4 ]. Nevertheless, there are situations in which such supervision is not possible.

Little experience in performing LPs may require more attempts to obtain cerebrospinal fluid (CSF) samples [ 7 ]. Because of several attempts, blood can be introduced to CSF and result in a traumatic LP. Success at the first attempt is associated with a lower incidence of traumatic LPs [ 2 , 8 , 9 , 10 , 11 , 12 ]. A bloody CSF sample complicates the diagnostics [ 8 ]. It has also been shown that a high number of attempts increases the incidence of postdural puncture headache (PDPH), the most common complication of LP, in addition to other adverse effects [ 9 ].

Considering the possible complications and difficulties of performing LP, a concern arises regarding whether inexperienced physicians can perform LP with adequate confidence and safety. The use of a novel bioimpedance-based spinal needle system could offer a solution. This needle provides real-time feedback from the needle tip when penetrating the lumbar tissues and informs the physician when the needle tip reaches CSF with an audio-visual alarm. This information may make performing the LP procedure smoother, thus decreasing the incidence of the most common complications [ 13 ]. A bioimpedance-based spinal needle system has been recently found clinically feasible in LPs among adults, adolescents, and children, including neonates [ 2 , 14 , 15 ].

The current phantom study aimed to assess whether the novel needle technology can compensate for the lack of experience when a medical student performs LP for the first time. In particular, we compared the performance of the bioimpedance spinal needle and conventional spinal needle in terms of the overall success rate of the LP procedure, success rate at the first attempt, duration of the procedure, and number of stylet removals. We hypothesized that novice users would find the bioimpedance needle more useful in performing LPs than a conventional spinal needle. If so proven, the use of this novel device can contribute to training medical students in this important skill and facilitate situations when an inexperienced physician needs to perform LP without the supervision and guidance of an experienced physician [ 4 ].

We planned to recruit 60 medical students from Tampere University in this randomized controlled trial. Students who were studying medicine for their third year or less were considered eligible for the study. At this stage of studies, they were expected to have no clinical experience and be thus naïve in performing an LP. All students had the same baseline knowledge regarding lumbar spine anatomy.

The participants were recruited by sending an invitation e-mail to all potentially eligible medical students. The email provided information about the study. Of the 177 students who responded to the invitation, 60 students were included on a first-come-first-serve basis. The participants were rewarded with a 10€ voucher to the university campus cafeteria.

Randomization lists in blocks of six were generated for two groups (A and B) before recruitment by an independent person who was not involved in recruitment or data collection. Participants assigned to group A used a conventional spinal needle (90 mm long 22G Quincke-type needle), and those to group B used the bioimpedance needle system (IQ-Tip system with a 90 mm long IQ-Tip needle, Injeq Plc, Tampere, Finland).

The study LPs were performed on an adult-size anatomical lumbar phantom (Blue Phantom BPLP2201, CAE Healthcare, FL, USA) intended for medical training and practising. The phantom is made of a tissue-simulating elastomer material that looks and feels like human soft tissue. Skeletal structures made of hard material and a plastic tube mimicking the spinal canal are embedded in the phantom. The saline inside the tube mimics CSF and is under hydrostatic pressure. The phantom offers a relatively realistic feel in palpating the lumbar anatomy and getting haptic feedback from the advancing needle.

The study LPs were performed in February 2023 in ten different sessions, with 6 participants in each session. Two separate rooms were used to conduct the study. The participants were first admitted to a waiting room and then separately to another room where each student performed the study LP with the assigned spinal needle under supervision (HL and MT). By having these two rooms, we ensured that no information was exchanged after or during the procedure.

Before the study LPs, the participants were shown an instructional video on how to perform an LP from the widely used Finnish medical database Terveysportti [ 16 ] and a video on the operation of the bioimpedance needle [ 13 ]. The first video (duration 3 min) describes the indications, contraindications and a step-by-step instruction on how the procedure is performed. The latter is a 25- second animation showing how the bioimpedance system operates and guides the procedure. In addition, the supervisor gave each participant the following instructions before starting the study LP: When you think you have reached the subarachnoid space, remove the stylet from the needle. If you are in the correct place, the fluid will start flowing from the needle. You may redirect the needle as many times as you wish, but you are only allowed to remove the needle and do a new attempt five times. Please wait a while when you have removed the stylet because it may take a while before the fluid starts dropping. These instructions were given to all participants irrespective of the study group to standardize the information in all sessions.

After watching the videos and listening to the instructions, the participants became aware of their assigned study group. Participants were allowed five attempts, while redirections of the needle and stylet removals could be performed as many times as needed. We measured the duration of the LP procedure and collected data on the number of stylet removals, the number of attempts, and whether the LP was successful.

The duration of the procedure was defined from the point when the needle penetrated the phantom surface to either when the first drop of fluid fell from the needle, or the participant wanted to stop or had used all five attempts. There was no maximum time for completing the LP procedure. The procedure was defined as successful if the participant succeeded in obtaining a drop of fluid from the needle.

In addition, seven relevant statements to this study were chosen from the System Usability Scale (SUS) [ 17 ], which is an industry standard for evaluating the usability of various devices and systems. The seven statements, slightly modified from the original statements, are shown in Table  1 . After performing the study LP and irrespective of their success, all participants were asked to respond to the statements using a 5-point Likert scale (1 = strongly disagree, 5 = strongly agree).

Statistical analysis

For the estimation of statistical power, we assumed that the overall success rate would be 60% with the conventional needle (group A) and 90% with the bioimpedance needle (group B). Then, the sample size of 60 participants divided randomly into two equal-sized groups would be sufficient to detect a between-group at a significance level of p  < 0.05 and with 80% statistical power if such a difference truly exists.

Overall success in performing the lumbar puncture and success at the first attempt in the groups were analysed by the independent samples proportion procedure. The median number of attempts and stylet removals in the successful procedures were compared by independent samples Mann‒Whitney U test. Responses to the seven usability statements were compared by this test as well.

Statistical analyses were performed with IBM SPSS Statistics for Windows, version 29.0 (IBM Corp., Armonk, NY, USA). A p value less than 0.05 was considered statistically significant.

Sixty medical students were randomly assigned into two groups, 30 performing the LP procedure on the lumbar phantom using a conventional spinal needle and 30 using the bioimpedance needle. None of the participants had previous experience in performing an LP.

With the conventional spinal needle (group A), 12 out of 30 participants (40%) succeeded in performing the LP procedure, whereas with the bioimpedance needle (group B), 27 out of 30 participants (90%) were successful ( p  < 0.001). The procedures were successful at the first attempt in 5 (16.7%) and 15 (50%) cases ( p  = 0.006), respectively.

Figure  1 illustrates the number of attempts and stylet removals in the study groups. Regarding the success of the procedure at any attempt, the median number of attempts was 2 (range 1–5) for the conventional needle and 1 [ 1 , 2 , 3 , 4 , 5 ] for the bioimpedance needle ( p  = 0.56).

In the successful procedures, the median number of stylet removals was 4 [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18 , 19 , 20 , 21 , 22 , 23 , 24 , 25 , 26 ] and 1 (1–33) ( p  = 0.001), respectively. The mean duration of a successful procedure was 3:51 (SD 3:43) with the conventional needle and 1:59 (2:25) with the bioimpedance needle ( p  = 0.068).

The responses to the seven usability statements are illustrated in Fig.  2 . Regarding the statements on regular use, ease of use, need for support from an experienced user, learning to use, and cumbersomeness, the responses differed significantly between groups, consistently favouring the bioimpedance needle ( p  < 0.001). Regarding the feeling of confidence in use, the responses significantly favoured the bioimpedance needle ( p  = 0.012). Likewise, the responses significantly favoured the bioimpedance needle to less need to learn many things before its use.

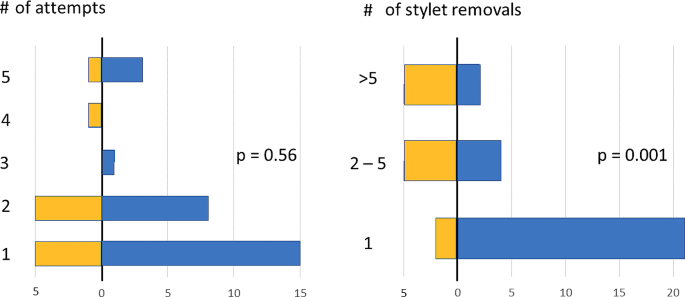
Distributions of the number of attempts in successful LP procedures (left panel) with the conventional spinal needle (group A, yellow bars) and with the bioimpedance needle (group B, blue bars). Respective distributions of the number of stylet removals (right panel) in groups A and B

After performing the LP, the provider answered seven statements about the usability of the needle in question on a scale of 1 (strongly disagree) to 5 (strongly agree). Distributions of responses to every seven usability statements in group A (conventional spinal needle, yellow bars) and in group B (bioimpedance needle, blue bars) using the System Usability Scale (SUS)

The decline in the number of LPs during the last decade [ 3 , 4 ] likely weakening the practical knowledge and skills of novice physicians served as the rationale for the current study. Using a solid randomized controlled study design, we assessed whether bioimpedance-based tissue detection technology could help an inexperienced provider perform LP. Our study was conducted among early-stage medical students who had no previous experience with LPs. Following our hypothesis, we found that the use of a bioimpedance needle in simulated phantom LPs was useful to novice providers. The bioimpedance needle decreased not only the number of attempts to achieve a successful LP but also its time, in addition to the significantly lower number of stylet removals during the procedure. Furthermore, the usability of the bioimpedance needle was found to be significantly better than that of the spinal needle used currently in clinical practice.

The users of the bioimpedance needle found the novel device easy and intuitive to learn and use while feeling more confident in performing LP compared to those using the conventional needle. They also expressed their interest in using the bioimpedance needle regularly. It is recalled that the present providers were all novices without earlier experience in LP, and therefore, the observed between-group differences in performance could have been smaller with more experienced providers.

Of common bedside procedures in clinical practice, LP was recently found to be associated with the lowest baseline levels of experience and confidence among 4 th− to 6th -year medical students. However, a single seminar with standardized simulation training brought more confidence to the LP procedure among these students [ 18 ]. Other recent studies have also shown that simulation-based education can improve procedural competence and skills in performing LP [ 19 , 20 , 21 , 22 ]. In these studies, the participants had more experience than in our study, but the benefits of simulation-based learning were significant. A recent study assessing a mixed reality simulator found this approach helpful in learning of LP among residents, faculty, interns, and medical students, approximately 60% having no previous experience in LP [ 23 ]. After mixed reality training, the success rate of LP increased while the time of the procedure decreased [ 23 ], which is in line with our findings. Virtual reality-based training in LP learning has also been studied, and it might have beneficial results in the provider’s skills and confidence [ 24 , 25 ]. All these findings speak for the utility of various simulation approaches in adopting essential (new) clinical skills for LP at different stages of medical studies and careers.

Lumbar puncture is commonly considered a difficult and possibly frightening procedure to perform. In addition to the physician’s experience and skills, there are other factors that affect the success of LP, including patient size, spinal deformities, lumbar anatomy, cooperation and comfort [ 6 ]. Occasionally, a physician may have to insert the needle more than once to succeed in LP. However, repeated attempts are associated with several complications, such as PDPH and traumatic LP [ 7 , 10 , 11 , 12 , 26 , 27 , 28 ]. In our study, the median number of attempts was two for the conventional spinal needle and one for the bioimpedance needle. The low number of attempts may have also contributed to the low incidence of traumatic LP and PDPH observed in pediatric patients with leukemia, whose intrathecal therapy was administered using the bioimpedance needle [ 15 ]. Since the basic use of a bioimpedance needle is virtually similar to that of a conventional spinal needle with no need for additional devices (e.g., ultrasound imaging), it may offer a notable option for effective teaching of LP among medical students. Its real-time CSF detection ability is likely to consolidate the learning experience and increase confidence in one’s skills.

In this study, we found a significantly higher success rate and confidence in procedural skills of medical students associated with using the bioimpedance needle compared to the conventional spinal needle. Should these benefits translate into the real clinical world and manifest as a lower incidence of failed LP procedures and procedure-related complications, a higher incidence of high-quality CSF samples, a lower need for repeated procedures, a lower need for experienced and more expensive physicians to supervise, perform, or complete the LP procedure, substantial savings in the total costs of the lumbar puncture procedure are possible despite the initially higher unit cost of the bioimpedance needle system compared to conventional spinal needles. Further clinical studies on the benefits of the bioimpedance needle system in clinical LP procedures are needed to confirm these speculations.

The major strengths of the present study are the randomized controlled, partly blinded design and adequate sample size. The random assignment of participants to study groups and data analysis were performed by an independent person who was not involved in recruitment or data collection. The participants received the same instructions and information before performing their assigned LP procedure and were asked not to study LP in advance to keep the participants as naïve in performing LP as possible. Obviously, we could not control for this and have full certainty about the prior information on retrieval of the participants. However, the participants were not told before the study session which type of spinal needle they would use in their assigned LP.

During the LP sessions, there were a few technical issues concerning the lumbar phantom and bioimpedance needle. First, since the pressure inside the phantom spinal canal (plastic tube) affects the fluid flow through the needle, we attempted to keep the height of the hydrostatic saline column constant by adding new saline as needed, but slight variation in pressure may have occurred, and concerned all study LP procedures. Second, when the plastic tube and surrounding phantom material are pierced multiple times in succession, it is possible that the leakage of saline moistens the rubbery material and increases markedly its electrical conductivity despite the self-healing property of the material. Had this happened, consequent false detections may have led to unnecessary removals of the stylet in the LP procedures performed with the bioimpedance needle system. Therefore, as a precaution, the maximum number of participants at each session was limited to six to mitigate the risk of moistening of material. Third, in two cases, the bioimpedance needle system did not detect saline, although the needle tip was in the correct place, confirmed by saline flow after stylet removal. This rate of missed detections in line with clinical experience [ 2 , 15 ] and may be due to elastomer remnants stuck at the needle tip compromising the bioimpedance measurement and saline detection. However, despite the failed functionality, the mechanical performance of the bioimpedance needle as a spinel needle is maintained and LP could be performed as usual. Regarding the credibility of the present findings, the bioimpedance needle did not get any undue benefit from these technical issues compared to the conventional spinal needle.

Given that the participants were clinically inexperienced early-stage medical students, the study was conducted using an anatomical lumbar phantom, not on actual patients. Obviously, the haptic feedback from the phantom and anatomic variation in the lumbar region do not fully correspond to a real patient. On the other hand, the use of phantom takes off the pressure from a novice provider and possibly eases the procedure, not having to take thought on a patient’s comfort, anatomy, and condition. Although the LP procedure was performed for the first time without the guidance of an experienced physician, the users of the bioimpedance needle felt more confident and performed significantly better than those with the conventional spinal needle. If used for teaching purposes, the bioimpedance needle and the anatomical lumbar phantom could offer a positive experience of the LP procedure and raise confidence in one’s own skills before the first real patient encounter. Whether the present promising results of a phantom study would translate into improved performance in actual clinical work calls for further investigation.

Lumbar puncture is a widely used but demanding procedure needed for the diagnosis and treatment of several diseases. It is relatively safe when performed correctly, but due to the decreasing trend of performed LP procedures, a concern has arisen concerning novice physicians’ expertise in LP. The bioimpedance needle could offer a solution to this problem and facilitate practical training of LP among early-stage medical students. The present randomized controlled phantom study showed that providers with no previous experience in LP perceived the bioimpedance needle as more useful, became confident, and achieved significantly higher success rates both overall and at the first attempt with fewer stylet removals compared to those using a conventional spinal needle. Further research is needed to show whether the observed findings translate into clinical skills and benefits in hospital settings.

Data availability

The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.

Abbreviations

Acute lymphoblastic leukemia

Cerebrospinal fluid

• Lumbar puncture

Postdural puncture headache

Ellenby MS, Tegtmeyer K, Lai S, Braner DAV. Videos in clinical medicine. Lumbar puncture. N Engl J Med. 2006;355(13):e12.

Article   Google Scholar  

Långström S, Huurre A, Kari J, Lohi O, Sievänen H, Palmu S. Bioimpedance spinal needle provides high success and low complication rate in lumbar punctures of pediatric patients with acute lymphoblastic leukemia. Sci Rep. 2022;12(1):6799.

Geanacopoulos AT, Porter JJ, Michelson KA, Green RS, Chiang VW, Monuteaux MC, et al. Declines in the Number of Lumbar Punctures Performed at United States children’s hospitals, 2009–2019. J Pediatr. 2021;231:87–e931.

Gottlieb M, Jordan J, Krzyzaniak S, Mannix A, King A, Cooney R, et al. Trends in emergency medicine resident procedural reporting over a 10-year period. AEM Educ Train. 2023;7(1):e10841.

Boon JM, Abrahams PH, Meiring JH, Welch T. Lumbar puncture: anatomical review of a clinical skill. Clin Anat. 2004;17(7):544–53.

Thieme E-. Journals - Seminars in Neurology/Abstract [Internet]. [cited 2023 Sep 19]. https://www.thieme-connect.com/products/ejournals/abstract/10.1055/s -2003-40758.

Howard SC, Gajjar AJ, Cheng C, Kritchevsky SB, Somes GW, Harrison PL, et al. Risk factors for traumatic and bloody lumbar puncture in children with acute lymphoblastic leukemia. JAMA. 2002;288(16):2001–7.

Coughlan S, Elbadry M, Salama M, Divilley R, Stokes HK, O’Neill MB. The current use of lumbar puncture in a General Paediatric Unit. Ir Med J. 2021;114(5):354.

Google Scholar  

Jaime-Pérez JC, Sotomayor-Duque G, Aguilar-Calderón P, Salazar-Cavazos L, Gómez-Almaguer D. Impact of obesity on lumbar puncture outcomes in adults with Acute Lymphoblastic Leukemia and Lymphoma: experience at an academic reference Center. Int J Hematol Oncol Stem Cell Res. 2019;13(3):146–52.

Flores-Jimenez JA, Gutierrez-Aguirre CH, Cantu-Rodriguez OG, Jaime-Perez JC, Gonzalez-Llano O, Sanchez-Cardenas M, et al. Safety and cost-effectiveness of a simplified method for lumbar puncture in patients with hematologic malignancies. Acta Haematol. 2015;133(2):168–71.

Barreras P, Benavides DR, Barreras JF, Pardo CA, Jani A, Faigle R, et al. A dedicated lumbar puncture clinic: performance and short-term patient outcomes. J Neurol. 2017;264(10):2075–80.

Renard D, Thouvenot E. CSF RBC count in successful first-attempt lumbar puncture: the interest of atraumatic needle use. Neurol Sci. 2017;38(12):2189–93.

Injeq. [Internet]. [accessed 2024 Apr 9]. FAQ. Available from Question 1: https://injeq.com/faq/ .

Halonen S, Annala K, Kari J, Jokinen S, Lumme A, Kronström K, et al. Detection of spine structures with Bioimpedance Probe (BIP) needle in clinical lumbar punctures. J Clin Monit Comput. 2017;31(5):1065–72.

Sievänen H, Kari J, Halonen S, Elomaa T, Tammela O, Soukka H, et al. Real-time detection of cerebrospinal fluid with bioimpedance needle in paediatric lumbar puncture. Clin Physiol Funct Imaging. 2021;41(4):303–9.

Terveysportti. [Internet]. [accessed 2024 Apr 9]. Available from (in Finnish): https://www.terveysportti.fi/terveysportti/koti .

Bangor A, Kortum P, Miller J. Determining what individual SUS scores mean: adding an adjective rating scale. J Usabil Stud. 2009;4:114–23.

von Cranach M, Backhaus T, Brich J. Medical students’ attitudes toward lumbar puncture—and how to change. Brain Behav. 2019;9(6):e01310.

Barsuk JH, Cohen ER, Caprio T, McGaghie WC, Simuni T, Wayne DB. Simulation-based education with mastery learning improves residents’ lumbar puncture skills. Neurology. 2012;79(2):132–7.

McMillan HJ, Writer H, Moreau KA, Eady K, Sell E, Lobos AT, et al. Lumbar puncture simulation in pediatric residency training: improving procedural competence and decreasing anxiety. BMC Med Educ. 2016;16:198.

Gaubert S, Blet A, Dib F, Ceccaldi PF, Brock T, Calixte M, et al. Positive effects of lumbar puncture simulation training for medical students in clinical practice. BMC Med Educ. 2021;21(1):18.

Toy S, McKay RS, Walker JL, Johnson S, Arnett JL. Using Learner-Centred, Simulation-based training to Improve Medical Students’ procedural skills. J Med Educ Curric Dev. 2017;4:2382120516684829.

Huang X, Yan Z, Gong C, Zhou Z, Xu H, Qin C, et al. A mixed-reality stimulator for lumbar puncture training: a pilot study. BMC Med Educ. 2023;23(1):178.

Vrillon A, Gonzales-Marabal L, Ceccaldi PF, Plaisance P, Desrentes E, Paquet C, et al. Using virtual reality in lumbar puncture training improves students learning experience. BMC Med Educ. 2022;22(1):244.

Roehr M, Wu T, Maykowski P, Munter B, Hoebee S, Daas E, et al. The feasibility of virtual reality and student-led Simulation Training as methods of lumbar puncture instruction. Med Sci Educ. 2021;31(1):117–24.

Seeberger MD, Kaufmann M, Staender S, Schneider M, Scheidegger D. Repeated Dural Punctures increase the incidence of Postdural puncture headache. Anaesth Analgesia. 1996;82(2):302.

Glatstein MM, Zucker-Toledano M, Arik A, Scolnik D, Oren A, Reif S. Incidence of traumatic lumbar puncture: experience of a large, tertiary care pediatric hospital. Clin Pediatr (Phila). 2011;50(11):1005–9.

Shah KH, Richard KM, Nicholas S, Edlow JA. Incidence of traumatic lumbar puncture. Acad Emerg Med. 2003;10(2):151–4.

Download references

No external funding.

Open access funding provided by Tampere University (including Tampere University Hospital).

Author information

Helmiina Lilja and Maria Talvisara contributed equally to this work.

Authors and Affiliations

Faculty of Medicine and Health Technology, Tampere University, Arvo Ylpön katu 34, Tampere, 33520, Finland

Helmiina Lilja & Maria Talvisara

Tampere Center for Child, Adolescent and Maternal Health Research, Faculty of Medicine and Health Technology, Tampere University, Arvo Ylpön katu 34, Tampere, 33520, Finland

Vesa Eskola, Paula Heikkilä & Sauli Palmu

Tampere University Hospital, Elämänaukio 2, Tampere, 33520, Finland

Injeq Plc, Biokatu 8, Tampere, Tampere, 33520, Finland

Harri Sievänen

You can also search for this author in PubMed   Google Scholar

Contributions

H.L. and M.T.: data collection, data analysis, drafting the manuscript, editing the manuscript. V.E. and P.H.: planning the study, editing the manuscript. H.S. and S.P.: conceptualizing and planning the study, data analysis, editing the manuscript.

Corresponding author

Correspondence to Sauli Palmu .

Ethics declarations

Ethics approval and consent to participate.

The protocol was approved by the university medical education board which acts as the licensing committee for trials performed in our institute. The participants gave their informed consent to participate.

Consent for publication

Not applicable.

Competing interests

H.S. is an employee of Injeq Plc.

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Lilja, H., Talvisara, M., Eskola, V. et al. Novice providers’ success in performing lumbar puncture: a randomized controlled phantom study between a conventional spinal needle and a novel bioimpedance needle. BMC Med Educ 24 , 520 (2024). https://doi.org/10.1186/s12909-024-05505-z

Download citation

Received : 06 October 2023

Accepted : 02 May 2024

Published : 10 May 2024

DOI : https://doi.org/10.1186/s12909-024-05505-z

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Spinal needle
• Clinical skill
• Bioimpedance

BMC Medical Education

ISSN: 1472-6920

• Submission enquiries: [email protected]
• General enquiries: [email protected]

• Open access
• Published: 15 May 2024

Factors and management techniques in odontogenic keratocysts: a systematic review

• Mario Dioguardi 1 ,
• Cristian Quarta 1 ,
• Diego Sovereto 1 ,
• Giorgia Apollonia Caloro 2 ,
• Andrea Ballini 1 ,
• Riccardo Aiuto 3 ,
• Angelo Martella 4 ,
• Lorenzo Lo Muzio 1 &
• Michele Di Cosola 1  

European Journal of Medical Research volume  29 , Article number:  287 ( 2024 ) Cite this article

107 Accesses

Metrics details

Odontogenic keratocysts exhibit frequent recurrence, distinctive histopathological traits, a tendency towards aggressive clinical behavior, and a potential linkage to the nevoid basal cell carcinoma syndrome. The aim of this systematic review is to compile insights concerning the control of this condition and assess the effectiveness of various treatment approaches in reducing the likelihood of recurrence.

Materials and methods

The following systematic review adhered to the PRISMA guidelines. The systematic revision was registered on PROSPERO and  structured around the questions related to the population, intervention, control, outcome and study design (PICOS).

After conducting a search on the PubMed database, we initially identified 944 records. After using end-note software to remove duplicate entries, results totally with 462 distinct records. A thorough review of the titles and abstracts of these articles led to the selection of 50 papers for in-depth examination. Ultimately, following the application of our eligibility criteria, we incorporated 11 articles into our primary outcome analysis.

Among the studies examined, the most common location for these lesions was found to be in the area of the mandibular ramus and the posterior region of the mandible. In cases where the exact location wasn’t specified, the mandible emerged as the predominant site. When we considered the characteristics of these lesions in studies that mentioned locularity, most were described as unilocular in two studies, while in two other studies, the prevalence of multilocular lesions was observed. Risk factors associated with keratocyst recurrence include younger patient age, the presence of multilocular lesions, larger lesion size, and a longer anteroposterior dimension. Certain treatment methods have demonstrated a lack of relapses. These include the use of 5-fluorouracil, marsupialization, enucleation with peripheral ostectomy or resection, enucleation and curettage, as well as resection without creating continuity defects. However, it is important to note that further research is essential. Prospective studies and randomized trials are needed to collect more comprehensive evidence regarding the effectiveness of various treatment approaches and follow-up protocols for managing odontogenic keratocysts.

Clinical relevance

Odontogenic keratocysts still enter into differential diagnoses with other lesions that affect the jaw bones such as ameloblastama and other tumor forms, furthermore it is not free from recurrence, therefore the therapeutic approach to the lesion aimed at its elimination can influence both the possible recurrence and complications, knowledge of the surgical methods that offer the most predictable and clinically relevant result for the management of follow-up and recurrences.

Introduction

The odontogenic keratocyst (OKC) is a developmental cyst that originates from remnants of the dental lamina within the jawbones [ 1 ]. Several studies have reported a preference for males [ 1 , 2 , 3 ], with an incidence peak around the third decade [ 4 ] and a nearly equal distribution in other decades, with another small peak between 50 and 70 years of age [ 1 ]. It can occur in any area of the jawbones but is most commonly found in the mandible, with a particular preference for the mandibular angle extending to the mandibular ramus [ 4 ].

Diagnosis of OKC is typically  radiological. Radiographs commonly reveal well-defined radiolucent areas with  rounded or scalloped margins that are well demarcated; these areas can present as either multilocular or unilocular [ 5 ].

In the 2022 classification, OKC remains classified as a cyst; molecular studies have detected frequent mutations in the tumor suppressor gene PTCH1, a gene that activates the SHH pathway, leading to aberrant epithelial proliferation [ 1 ], sparking debates on whether OKC is a cyst or a cystic neoplasm. It was labeled as a keratocystic odontogenic tumor in 2005 [ 5 ], thus considered a cystic neoplasm, and later reclassified as a cyst in the 2017 classification [ 1 ].

Keratocysts are characterized by a high recurrence rate, specific histological features, aggressive clinical behavior, and can be associated with the nevoid basal cell carcinoma syndrome [ 6 ].

The mechanism of recurrence was proposed by Brannon [ 7 ] in 1976, suggesting it was due to three different mechanisms:

Incomplete removal of the cyst,

Growth of new keratocysts from satellite cysts,

Development of a new keratocyst in the area adjacent to the site of the primary keratocyst, interpreted as recurrence.

Odontogenic keratocysts can be treated with various surgical methods, which can be divided into conservative approaches and invasive approaches or a combination thereof [ 8 ]; in the literature, enucleation, marsupialization, resection, and the use of adjunct therapies such as Carnoy’s solution and cryotherapy are reported [ 1 , 4 , 9 ].

Despite many studies in the literature examining several therapeutic approaches in managing this lesion, it is still not clear which method provides lower recurrence rates without causing significant morbidity [ 10 ]; the purpose of this systematic review is to gather information on the management of this lesion and evaluate which treatment method results in fewer recurrences.

The following systematic review adhered to the PRISMA (Preferred Reporting Items for Systematic review and Meta-Analysis) protocol guidelines [ 11 ].

The systematic revision was registered on PROSPERO with number of: CRD42023480051.

The study was structured around the questions related to the population, intervention, control, outcome and study design (PICOS):

Population (P): individuals with non-syndromic or syndromic odontogenic keratocyst (initial cases) diagnosed histologically;

Intervention (I): surgical interventions for patients with odontogenic keratocystic, such as enucleation, enucleation coupled with curettage, enucleation with additional therapeutic measures (such as Carnoy's solution application, cryotherapy), marsupialization or decompression, with or without subsequent cystectomy and adjunctive therapy, and resection;

Control (C): not applicable;

Outcome (O): recurrence of KOT (Keratocystic Odontogenic Tumor) associated with distinct surgical treatments and characteristics of the keratocysts analyzed;

Study design (S): prospective randomized controlled clinical trials, controlled clinical investigations (either prospective or retrospective), and case series that explored and compared the diverse surgical approaches concerning recurrence over a suitable follow-up period (minimum of 1 year).

The formulation of the PICOS question can be summarized as follows: “What characteristics do the odontogenic keratocysts analyzed in the studies have? Which surgeries had the least recurrences during the follow-up?”.

Following the initial selection phase of records identified in various databases, potentially eligible articles were qualitatively assessed. This assessment aimed to investigate which surgical treatment was the most reliable in giving the least number of recurrences.

Eligibility criteria

This text discusses the process of selecting research articles for a study related to the recurrence of KOT associated with distinct surgical interventions, such as enucleation, with or without curettage and additional therapeutic measures, marsupialization or decompression, with or without subsequent cystectomy and adjunctive therapy, and resection.

The process involved initially identifying potentially eligible articles based on their abstracts. These articles were then subjected to a thorough examination of their full content to determine their suitability for both qualitative and quantitative analyses.

The criteria for including articles in the full-text analysis were studies relating to KOT treatments in which the number of recurrences and the general characteristics of the lesions are reported.

The exclusion criteria were applied to exclude the following types of studies:

Studies involving animals or conducted in a laboratory setting (in vitro)

Letters to the editor

Articles that did not adequately specify the type of surgical method used

Studies with an inadequate follow-up period (less than 1 year)

Clinical studies conducted more than 30 years ago (only studies from the last 30 years were included because classifications and surgical and therapeutic techniques have been constantly changing and improving, with generally earlier diagnoses and more suitable treatments with lower recurrence rates. Therefore, to avoid increasing the heterogeneity of the included studies and to prevent bias in the aggregated treatment results, the reviewers collectively decided to include only studies from 1989 onwards)

Review articles

Research methodology

Studies have been identified through bibliographic research on electronic databases.

The literature search was conducted on the search engines “PubMed”. The search on the providers was conducted between 02.09.2023 and 12.09.2023, and the last search for a partial update of the literature was conducted on 18.09.2023.

The following search terms were used on PubMed: “KOT” AND “Recurrence” (37 records), “odontogenic keratocyst marsupialization” (285 records), “odontogenic keratocyst enucleation” (622 records).

Screening methodology

The selection criteria and their combinations for searching were established prior to the record identification stage through mutual consensus between the two reviewers  (M.D. and M.D.C.) responsible for choosing potentially eligible articles. Following this, the records acquired were then assessed separately by the two independent reviewers, with a third reviewer  (A.B.) serving as an decision-maker in cases of uncertainty.

The screening process involved evaluating the titles and abstracts of articles, and in cases where there was uncertainty, a more in-depth examination of the article's content was conducted to remove records that were not relevant to the topics under review.

Following a search in the PubMed database, 944 records were initially located. Subsequently, after applying end-note software to eliminate duplications, 462 unique records remained. Upon reviewing the titles and abstracts of these articles, after this initial screening, a total of 50 articles were selected for a thorough examination of their full text by two reviewers. From these 50 articles, the ones that met the criteria for qualitative analysis for the outcome were identified. Finally, applying the eligibility criteria, we included 16 articles for the primary outcome analysis (Fig.  1 ).

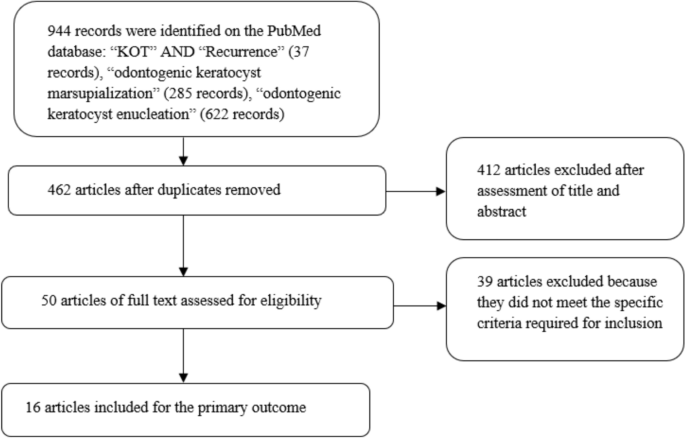
Flowchart of the different phases of the systematic review

Study characteristics and data extraction

The included studies for the quantitative analysis were: Maurette et al. [ 12 ]; Nakamura et al. [ 13 ]; Bataineh and al Qudah [ 14 ]; Leung et al. [ 15 ]; Kolokythas et al. [ 9 ]; Berge et al. [ 16 ]; Pogrel and Jordan, [ 17 ]; Tabrizi et al. [ 18 ]; Zecha et al. [ 19 ]; Moellmann et al. [ 20 ]; Caminiti et al.[ 21 ], Stoelinga [ 4 ]; Dammer et al. [ 2 ]; Marker et.al. [ 22 ]; August et al.[ 23 ]; Brøndum and Jensen [ 24 ].

The extracted data included the journal (author, data, and reference); study design; number of patients (males/females); number of lesions; number of lesions associated with basal cell naevus syndrome (BCNS); mean age (range); site where the lesions were diagnosed; locularity (multilocular or unilocular); type of treatment; mean follow-up.

Finally, for each study, the number of relapses relating to each treatment was observed.

The data extracted are shown in Table  1 and 2 .

Risk of bias

The risk of bias was assessed using the Newcastle–Ottawa Scale (NOS) for cohort studies, assigning a value from 0 to 3 for each item, the assessment of the risk of bias was assessed by the first reviewer, and was deemed acceptable for all included studies, details are shown in Table  3

The articles included in this review analyze different types of keratocyst treatment and lesion characteristics.

Among the first to coin the term 'odontogenic keratocyst' was Philipsen in 1956, who, in a literature review, proposed the term 'odontogenic keratocyst' for all odontogenic cysts that exhibit epithelial keratinization [ 25 ].

The terminology, as adopted by Pindborg in 1962 and 1963 and also used by Toller in 1967, replaced the term ‘primordial cyst’ with ‘odontogenic keratocyst’, identifying 33 odontogenic keratocysts (study not included in this review) [ 26 , 27 , 28 , 29 ]

One of the early retrospective studies conducted on odontogenic keratocysts was performed by Pindborg, who retrospectively identified 26 keratinized cysts out of a total of 791 odontogenic cysts in 1962 [ 27 ].

The odontogenic keratocysts are often described in literature as benign cysts occurring within the bones, and they exhibit a propensity for infiltrative and aggressive growth patterns. These cysts make up an estimated 2–21.8% of all cysts affecting the jaw [ 24 , 25 ]. Moreover, there is a potential association between these cysts and genetic mutations, notably linked to nevoid basal cell carcinoma syndrome (NBCCS), a condition characterized by the presence of multiple OKCs in the jaw region [ 26 ]; this is also found in one of the articles included in this review [ 13 ], while in others the association was not specified [ 14 , 17 ] or there was no association at all [ 9 , 12 , 15 , 16 , 18 , 19 , 20 , 21 ]; many of these studies have placed the correlation with this syndrome in the exclusion criteria, as in the patients who are affected by it the probability that these cysts will reappear is high, and therefore it would be difficult to distinguish a recurrent event from the appearance of a new cyst [ 21 ]

These cysts are notorious for their tendency to grow aggressively in their immediate prossimity and for having a notably high rate of recurrence. Several contributing factors underpin this recurrence, including the use of inadequate treatment methods, incomplete elimination of the cyst, a high rate of cell division (mitotic index) within the cyst's epithelial cells, a larger cyst size, and the specific location of the cyst. The latter factor becomes especially problematic if it is challenging to access surgically [ 25 , 27 ]. Although they exhibit hostile conduct, OKC generally induce limited bone enlargement as they tend to proliferate within the intramedullary region, effectively growing within the bone [ 30 ].

Substantial lesions marked by substantial cortical plate erosion and engagement with neighboring structures may not produce symptoms in individuals, resulting in a delayed diagnosis [ 31 ].

The most frequent location of the lesions in the studies analyzed is at the level of the mandibular ramus and in the posterior mandible [ 12 , 13 , 14 , 15 , 16 , 19 ], and where the precise localization of the lesions is not specified, the mandible is the most frequent site [ 9 , 18 , 20 , 21 ]. In the studies in which locularity is specified among the characteristics of the lesions, the majority of the lesions were unilocular in two studies [ 13 , 21 ], while in two other studies the quantity of multilocular lesions was greater [ 14 , 15 ]. Younger patient age, multilocularity of the lesion, larger size, and longer anteroposterior dimension of the keratocyst have been identified as risk factors for keratocyst recurrence [ 15 ].

The treatments that have not had relapses are that with 5-fluorouracil [ 21 ], marsupialization [ 13 , 17 , 18 ], enucleation with peripheral ostectomy or resection [ 9 ], enucleation and curettage [ 12 ], and resection without continuity defects [ 14 ].

Decompression has been studied in 5 articles [ 9 , 12 , 22 , 23 , 24 ]; this method has the advantage of having minimal surgical morbidity and reduced risk to anatomical structures associated with the lesion, such as developing nerves or teeth [ 22 ]. Decompression and marsupialization techniques involve creating a communication between the cyst and the oral cavity, relieving pressure and allowing cyst shrinkage and bone apposition [ 12 ]. Clinical and radiographic resolution of OKCs after marsupialization is relatively rapid, typically within 19 months [ 17 ]. In studies where marsupialization alone was used for treatment, there were no relapses in two studies [ 17 , 18 ], while Zecha et al. [ 19 ] found four cases of relapse in ten patients treated with marsupialization.

Decompression and marsupialization are non-invasive treatment options for keratocysts, but require patient cooperation, including regular irrigation and follow-up [ 17 , 18 ].

Topical 5-fluorouracil is known for its antiproliferative effects on keratocystic epithelium and satellite cysts; furthermore, its use has some advantages, such as technical ease and the lack of neurotoxicity [ 21 ] and, in the only study of this review in which it were used in the treatment, there were no relapses [ 21 ].

Other treatment modalities used to reduce keratocyst recurrence are resection of the affected maxillary segment and enucleation with additional treatments such as curettage or ostectomy [ 9 , 14 ], which in these studies have not given recurrences, which, as regards resection, is a similar result to other studies in the literature [ 4 , 8 , 32 ]. However, despite the remarkably high success rate of this approach, resection is not widely embraced as a standard procedure, primarily due to concerns regarding its aggressiveness and associated postoperative complications, including morbidity [ 33 ]. Enucleation, often combined with curettage (the process of scraping the walls of the lesion cavity) or ostectomy (the surgical removal of bone tissue), is commonly used to treat keratocysts; although a more conservative treatment than resection, the effectiveness of this modality may be limited in cases where vital structures, such as the exposed inferior alveolar nerve, are at risk or when there is a perforation of the bony wall exposing the overlying mucosal tissue [ 15 ].

Carnoy’s solution was used in three studies [ 15 , 20 , 21 ] and of these studies one used the modified Carnoy’s solution [ 21 ]. The FDA avoid the use of Carnoy's solution containing chloroform in the United States, leading to the adoption of a modified formula. However, the modified formula has been found to have a higher relapse rate, suggesting the potential role that traditional Carnoy’s solution may have in treatment [ 34 ].

There are risk factors associated with the recurrence of odontogenic keratocyst, such as age, multilocularity, lesion size and radiographic characteristics.

The various surgical techniques used to treat keratocysts have potential benefits, including preservation of jaw function, reduction of the potential for recurrence, and eradication of the cystic lesion.

Marsupialization or decompression are advantageous conservative treatment options that aim to minimize surgical invasiveness while effectively managing keratocysts.

Long-term follow-up and monitoring of patients treated for these lesions is important to detect recurrence early.

There is a need for further research, prospective studies and randomized trials to gather more evidence on the effectiveness of different treatment methods and follow-up protocols for odontogenic keratocysts.

Availability of data and materials

All data generated or analyzed during this study are included in this published article.

Speight PM, Takata T. New tumour entities in the 4th edition of the World Health Organization Classification of Head and Neck tumours: odontogenic and maxillofacial bone tumours. Virchows Arch 2018;472:331–9. https://doi.org/10.1007/s00428-017-2182-3

Dammer R, Niederdellmann H, Dammer P, Nuebler-Moritz M. Conservative or radical treatment of keratocysts: a retrospective review. Br J Oral Maxillofac Surg. 1997;35:46–8. https://doi.org/10.1016/s0266-4356(97)90009-7 .

Article   CAS   PubMed   Google Scholar  

Ahlfors E, Larsson A, Sjögren S. The odontogenic keratocyst: a benign cystic tumor? J Oral Maxillofac Surg. 1984;42:10–9. https://doi.org/10.1016/0278-2391(84)90390-2 .

Stoelinga PJ. Long-term follow-up on keratocysts treated according to a defined protocol. Int J Oral Maxillofac Surg. 2001;30:14–25. https://doi.org/10.1054/ijom.2000.0027 .

Barnes L. Pathology and genetics of head and neck tumours; IARC.2005;9.

Soluk-Tekkesin M, Wright JM. The World Health Organization classification of odontogenic lesions: a summary of the changes of the 2022 (5th) edition. Turk Patoloji Derg. 2022;38:168–84. https://doi.org/10.5146/tjpath.2022.01573 .

Article   PubMed   PubMed Central   Google Scholar  

Brannon RB. The odontogenic keratocyst. A clinicopathologic study of 312 cases. Part I. Clinical features. Oral Surg Oral Med Oral Pathol. 1976;42:54–72. https://doi.org/10.1016/0030-4220(76)90031-1 .

Titinchi F. Protocol for management of odontogenic keratocysts considering recurrence according to treatment methods. J Korean Assoc Oral Maxillofac Surg. 2020;46:358–60. https://doi.org/10.5125/jkaoms.2020.46.5.358 .

Kolokythas A, Fernandes RP, Pazoki A, Ord RA. Odontogenic keratocyst: to decompress or not to decompress? A comparative study of decompression and enucleation versus resection/peripheral ostectomy. J Oral Maxillofac Surg. 2007;65:640–4. https://doi.org/10.1016/j.joms.2006.06.284 .

Article   PubMed   Google Scholar  

Troiano G, Dioguardi M, Cocco A, Laino L, Cervino G, Cicciu M, Ciavarella D, Lo Muzio L. Conservative vs radical approach for the treatment of solid/multicystic ameloblastoma: a systematic review and meta-analysis of the last decade. Oral Health Prev Dent. 2017;15:421–6. https://doi.org/10.3290/j.ohpd.a38732 .

Liberati A, Altman DG, Tetzlaff J, Mulrow C, Gøtzsche PC, Ioannidis JP, Clarke M, Devereaux PJ, Kleijnen J, Moher D. The PRISMA statement for reporting systematic reviews and meta-analyses of studies that evaluate health care interventions: explanation and elaboration. J Clin Epidemiol. 2009;62:e1-34. https://doi.org/10.1016/j.jclinepi.2009.06.006 .

Maurette PE, Jorge J, de Moraes M. Conservative treatment protocol of odontogenic keratocyst: a preliminary study. J Oral Maxillofac Surg. 2006;64:379–83. https://doi.org/10.1016/j.joms.2005.11.007 .

Nakamura N, Mitsuyasu T, Mitsuyasu Y, Taketomi T, Higuchi Y, Ohishi M. Marsupialization for odontogenic keratocysts: long-term follow-up analysis of the effects and changes in growth characteristics. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 2002;94:543–53. https://doi.org/10.1067/moe.2002.128022 .

Bataineh AB, Al Qudah M. Treatment of mandibular odontogenic keratocysts. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 1998;86:42–7. https://doi.org/10.1016/s1079-2104(98)90148-2 .

Leung YY, Lau SL, Tsoi KY, Ma HL, Ng CL. Results of the treatment of keratocystic odontogenic tumours using enucleation and treatment of the residual bony defect with carnoy’s solution. Int J Oral Maxillofac Surg. 2016;45:1154–8. https://doi.org/10.1016/j.ijom.2016.02.002 .

Berge TI, Helland SB, Sælen A, Øren M, Johannessen AC, Skartveit L, Grung B. Pattern of recurrence of nonsyndromic keratocystic odontogenic tumors. Oral Surg Oral Med Oral Pathol Oral Radiol. 2016;122:10–6. https://doi.org/10.1016/j.oooo.2016.01.004 .

Pogrel MA, Jordan RC. Marsupialization as a definitive treatment for the odontogenic keratocyst. J Oral Maxillofac Surg. 2004;62:651–65. https://doi.org/10.1016/j.joms.2003.08.029 .

Tabrizi R, Özkan BT, Dehgani A, Langner NJ. Marsupialization as a treatment option for the odontogenic keratocyst. J Craniofac Surg. 2012;23:e459-461. https://doi.org/10.1097/SCS.0b013e31825b3308 .

Zecha JA, Mendes RA, Lindeboom VB, van der Waal I. Recurrence rate of keratocystic odontogenic tumor after conservative surgical treatment without adjunctive therapies-a 35 year single institution experience. Oral Oncol. 2010;46:740–2. https://doi.org/10.1016/j.oraloncology.2010.07.004 .

Moellmann HL, Parviz A, Goldmann-Kirn M, Rana M, Rana M. Comparison of five different treatment approaches of mandibular keratocystic odontogenic keratocyst (OKC): a retrospective recurrence analysis of clinical and radiographic parameters. J Maxillofac Oral Surg. 2023. https://doi.org/10.1007/s12663-023-01929-0 .

Caminiti MF, El-Rabbany M, Jeon J, Bradley G. 5-fluorouracil is associated with a decreased recurrence risk in odontogenic keratocyst management: a retrospective cohort study. J Oral Maxillofac Surg. 2021;79:814–21. https://doi.org/10.1016/j.joms.2020.07.215 .

Marker P, Brøndum N, Clausen PP, Bastian HL. Treatment of large odontogenic keratocysts by decompression and later cystectomy: a long-term follow-up and a histologic study of 23 cases. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 1996;82:122–31. https://doi.org/10.1016/s1079-2104(96)80214-9 .

August M, Faquin WC, Troulis MJ, Kaban LB. Dedifferentiation of odontogenic keratocyst epithelium after cyst decompression. J Oral Maxillofac Surg. 2003;61:678–83. https://doi.org/10.1053/joms.2003.50137 .

Brøndum N, Jensen VJ. Recurrence of keratocysts and decompression treatment. a long-term follow-up of forty-four cases. Oral Surg Oral Med Oral Pathol. 1991;72:265–9. https://doi.org/10.1016/0030-4220(91)90211-t .

HP P. Om keratocyster (kolesten tomer) in the jaws. Tandlaegebladet. 1956;60:963–81.

Google Scholar  

Toller P. Origin and growth of cysts of the jaws. Ann R Coll Surg Engl. 1967;40:306–36.

CAS   PubMed   PubMed Central   Google Scholar  

Pindborg JJ, Hansen J. Studies on odontogenic cyst epithelium. 2. clinical and roentgenologic aspects of odontogenic keratocysts. Acta Pathol Microbiol Scand. 1963;58:283–94.

Rud J, Pindborg JJ. Odontogenic keratocysts: a follow-up study of 21 cases. J Oral Surg. 1969;27:323–30.

CAS   PubMed   Google Scholar  

Panders AK, Haddlers HN. Solitary keratocysts of the jaws. J Oral Surg. 1969;27:931–8.

Scarfe WC, Toghyani S, Azevedo B. Imaging of benign odontogenic lesions. Radiol Clin North Am. 2018;56:45–62. https://doi.org/10.1016/j.rcl.2017.08.004 .

Eryilmaz T, Ozmen S, Findikcioglu K, Kandal S, Aral M. Odontogenic keratocyst: an unusual location and review of the literature. Ann Plast Surg. 2009;62:210–2. https://doi.org/10.1097/SAP.0b013e31817dad9c .

Pitak-Arnnop P, Chaine A, Oprean N, Dhanuthai K, Bertrand JC, Bertolus C. Management of odontogenic keratocysts of the jaws: a 10 year experience with 120 consecutive lesions. J Craniomaxillofac Surg. 2010;38:358–64. https://doi.org/10.1016/j.jcms.2009.10.006 .

Kaczmarzyk T, Mojsa I, Stypulkowska J. A systematic review of the recurrence rate for keratocystic odontogenic tumour in relation to treatment modalities. Int J Oral Maxillofac Surg. 2012;41:756–67. https://doi.org/10.1016/j.ijom.2012.02.008 .

Dashow JE, McHugh JB, Braun TM, Edwards SP, Helman JI, Ward BB. Significantly decreased recurrence rates in keratocystic odontogenic tumor with simple enucleation and curettage using carnoy’s versus modified carnoy’s solution. J Oral Maxillofac Surg. 2015;73:2132–5. https://doi.org/10.1016/j.joms.2015.05.005 .

Download references

Acknowledgements

Not applicable

This research received no external funding.

Author information

Authors and affiliations.

Department of Clinical and Experimental Medicine, University of Foggia, Via Rovelli 50, 71122, Foggia, Italy

Mario Dioguardi, Cristian Quarta, Diego Sovereto, Andrea Ballini, Lorenzo Lo Muzio & Michele Di Cosola

Unità Operativa Nefrologia e Dialisi, Presidio Ospedaliero Scorrano, ASL (Azienda Sanitaria Locale) Lecce, Via Giuseppina Delli Ponti, 73020, Scorrano, Italy

Giorgia Apollonia Caloro

Department of Biomedical, Surgical, and Dental Science, University of Milan, 20122, Milan, Italy

Riccardo Aiuto

DataLab, Department of Engineering for Innovation, University of Salento, Lecce, Italy

Angelo Martella

You can also search for this author in PubMed   Google Scholar

Contributions

Conceptualization, M.D.and C.Q.; methodology, M.D.; software, M.D. and D.S.; validation, M.D. and A.B.; formal analysis, M.D.; investigation, M.D. and C.Q.; data curation, M.D. and D.S.; bibliographic reserach, C.Q. and R.A.; writing—original draft preparation, M.D. and C.Q.; writing—review and editing, M.D. and A.B.; visualization, D.S and M.D..; supervision L.L.M.., and M.D.C.; Critical revision of the manuscript for important intellectual content M.D., C.Q.; and A.B.; Bioinformatic analysis review, A.M.; project administration, L.L.M. All authors have read and agreed to the published version of the manuscript.

Corresponding author

Correspondence to Mario Dioguardi .

Ethics declarations

Ethics approval and consent to participate.

Not applicable.

Institutional Review Board Statement

Consent for publication, competing interests.

The authors declare no conflict of interest.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Dioguardi, M., Quarta, C., Sovereto, D. et al. Factors and management techniques in odontogenic keratocysts: a systematic review. Eur J Med Res 29 , 287 (2024). https://doi.org/10.1186/s40001-024-01854-z

Download citation

Received : 26 January 2024

Accepted : 22 April 2024

Published : 15 May 2024

DOI : https://doi.org/10.1186/s40001-024-01854-z

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

European Journal of Medical Research

ISSN: 2047-783X

• Submission enquiries: [email protected]
• General enquiries: [email protected]

• Open access
• Published: 17 May 2024

Behavioral skills training for teaching safety skills to mental health service providers compared to training-as-usual: a pragmatic randomized control trial

• Elizabeth Lin 1 ,
• Mais Malhas 1 ,
• Emmanuel Bratsalis 1 ,
• Kendra Thomson 1 , 2 ,
• Fabienne Hargreaves 1 ,
• Kayle Donner 1 ,
• Heba Baig 1 ,
• Rhonda Boateng 1 ,
• Rajlaxmi Swain 1 ,
• Mary Benisha Benadict 1 &
• Louis Busch 1  

BMC Health Services Research volume  24 , Article number:  639 ( 2024 ) Cite this article

63 Accesses

Metrics details

Violence in the healthcare workplace has been a global concern for over two decades, with a high prevalence of violence towards healthcare workers reported. Workplace violence has become a healthcare quality indicator and embedded in quality improvement initiatives of many healthcare organizations. The Centre for Addiction and Mental Health (CAMH), Canada’s largest mental health hospital, provides all clinical staff with mandated staff safety training for self-protection and team-control skills. These skills are to be used as a last resort when a patient is at imminent risk of harm to self or others. The purpose of this study is to compare the effectiveness of two training methods of this mandated staff safety training for workplace violence in a large psychiatric hospital setting.

Using a pragmatic randomized control trial design, this study compares two approaches to teaching safety skills CAMH’s training-as-usual (TAU) using the 3D approach (description, demonstration and doing) and behavioural skills training (BST), from the field of applied behaviour analysis, using instruction, modeling, practice and feedback loop. Staff were assessed on three outcome measures (competency, mastery and confidence), across three time points: before training (baseline), immediately after training (post-training) and one month later (follow-up). This study was registered with the ISRCTN registry on 06/09/2023 (ISRCTN18133140).

With a sample size of 99 new staff, results indicate that BST was significantly better than TAU in improving observed performance of self-protection and team-control skills. Both methods were associated with improved skills and confidence. However, there was a decrease in skill performance levels at the one-month follow-up for both methods, with BST remaining higher than TAU scores across all three time points. The impact of training improved staff confidence in both training methods and remained high across all three time points.

Conclusions

The study findings suggest that BST is more effective than TAU in improving safety skills among healthcare workers. However, the retention of skills over time remains a concern, and therefore a single training session without on-the-job-feedback or booster sessions based on objective assessments of skill may not be sufficient. Further research is needed to confirm and expand upon these findings in different settings.

Peer Review reports

Introduction

Violence in the healthcare workplace has been a global concern for over two decades. In 2002, a joint task force of the International Labour Office (ILO), World Health Organization, Public Services International, and the International Council of Nurses created an initiative to address this issue [ 1 ]. One result was the documentation of a high international prevalence of violence towards healthcare workers showing that as many as half or more experienced physical or psychological violence in the previous year [ 2 , 3 ]. Since then, workplace violence has become a healthcare quality indicator and been embedded in the quality improvement initiatives of many healthcare organizations (for example, Health Quality Ontario [ 4 ]). Conceptually, it is also reflected in the expansion of the Triple Aim framework to the Quintuple Aim to include staff work-life experience [ 5 ].

Despite these efforts, the high prevalence of workplace violence in healthcare persists [ 6 ]. Two meta-analyses, representing 393,344 healthcare workers, found a 19.3% pooled prevalence of workplace violence in the past year among which 24.4% and 42.5% reported physical and psychological violence experiences, respectively [ 7 , 8 ]. The literature also highlighted that workers in mental health settings were at particular risk [ 8 , 9 ]. A systematic review of violence in U.S. psychiatric hospitals found between 25 to 85 percent of staff encountering physical aggression in the past year [ 10 ]. Partial explanations for this wide range include methodological, population, and setting differences. For example, Gerberich and colleagues [ 11 ] surveyed nearly 4,000 Minnesota nurses and found 13 percent reporting physical assault and 38 percent reporting verbal or other non-physical violence in the previous year. Further analyses showed that nurses on psychiatric or behavioral units were twice as likely as those on medical/surgical units to experience physical violence and nearly three times as likely to experience non-physical violence. Ridenour, et al., [ 12 ] in a hospital-record study of acute locked psychiatric wards in U.S. Veteran’s Hospitals found that 85 percent of nurses had experienced aggression in a 30-day period (85 percent verbal; 81 percent physical). And, in a prospective study of a Canadian psychiatric hospital, Cooper and Mendonca [ 13 ] found over 200 physical assaults on nurses within 27 months. While they do not indicate what percentage of nurses were assaulted, their results are consistent with a frequency of between 1 and 2 assaults per week.

Workplace violence has been associated with negative psychological, physical, emotional, financial, and social consequences which impact staff’s ability to provide care and function at work [ 14 , 15 , 16 ]. A 7-year, population-based, follow-up study in Denmark highlighted the long-term impact of physical and psychological health issues owing to physical workplace violence [ 17 ]. Two studies, one in Italy [ 18 ] and one in Pakistan [ 19 ], have linked workplace violence to demoralization and declining quality of healthcare delivery and job satisfaction among healthcare workers.

Building on these efforts, the ILO published a 2020 report recommending the need for national and organizational work environment policies and workplace training “…on the identified hazards and risks of violence and harassment and the associated prevention and protection measures….” ([ 20 ], p. 55). Consequently, many countries [ 21 , 22 , 23 ] have committed to creating a safe work environment. In Ontario, Canada, the government has provided guidelines for preventing workplace violence in healthcare [ 4 , 24 ], and our institution, the Centre for Addiction and Mental Health, launched a major initiative in 2018 to address the physical and psychological safety of patients and staff [ 25 ]. A priority component of this initiative is mandatory training for all new clinical staff on trauma-informed crisis prevention, de-escalation skills, and, in particular, safe physical intervention skills [ 26 , 27 ].

However, the effects of such training, especially for managing aggressive behaviour, are only partially understood. A 2015 systematic review on training for mental health staff [ 28 ] and a more recent Cochrane review on training for healthcare staff [ 29 ] reported remarkably similar findings. Both noted the inconsistent evidence (due to methodological issues, small numbers of studies, heterogenous results) which made definitive conclusions about the merits and efficacy of training difficult. The more consistent impacts found by Price and colleagues [ 28 ] were improved knowledge and staff confidence in their ability to manage aggression. There was some evidence of improved de-escalation skills including the ability to deal with physical aggression [ 30 , 31 ] and verbal abuse [ 32 ]. However, these studies were limited because they used unvalidated scales or simulated, rather than real-world, scenarios. For outcomes such as assault rates, injuries, the incidence of aggressive events, and the use of physical restraints, the findings were mixed or difficult to generalize due to the inconsistent evidence.

Similarly, Geoffrion and colleagues [ 29 ] found some positive effect of skills-training on knowledge and attitudes, at least short-term, but noted that support for longer-term effects was less sure. The evidence for impacts on skills or the incidence of aggressive behaviour was even more uncertain. They also noted that the literature was limited because it focused largely on nurses. They concluded, “education combined with training may not have an effect on workplace aggression directed toward healthcare workers, even though education and training may increase personal knowledge and positive attitudes” ([ 29 ], p. 2). Among their recommendations were the need to evaluate training in higher-risk settings such as mental healthcare, include other healthcare professionals who also have direct patient contact in addition to nurses, and use more robust study designs. In addition, the literature evaluating training procedures focussed on self-reported rather than objective measures of performance.

Given the concerns with demonstrating effectiveness, the violence prevention literature has tended to focus on training modalities and immediate post-training assessment rather than on skill retention over time. In a systematic review of prevention interventions in the emergency room, Wirth et al. [ 21 ] found only five out of 15 included studies that noted any kind of evaluation in the period after training (generally two to nine months post-training) while Geoffrion, et al. [ 29 ] identified only two among the nine studies in their meta-analysis that had follow-up skills assessments. However, for both of these reviews, the studies doing follow-up evaluations focused on subjective, self-reported outcomes (empathy, confidence, self-reported knowledge) with no objective behavioral skills measures. Both Wirth et al. [ 21 ] and Leach et al. [ 33 ] cite studies noting a loss of effectiveness of prevention skills (between three to six months post-training), but specific percentages of retention were not provided.

The present study sought to address these gaps by comparing two approaches to teaching safety skills for managing aggressive patient/client behaviour. The setting was a large psychiatric teaching hospital; the sample was drawn from all new clinical staff attending their mandated on-boarding training; and we used a pragmatic randomized control trial design. In addition, we added a 1-month post-training assessment to evaluate skill retention. Our control intervention was the current training-as-usual (TAU) in which trainers “describe” and “demonstrate”, and trainees “do” by practicing the demonstrated skill but without objective checklist-guided performance assessment by the trainer. Our test intervention was behavioural skills training (BST) [ 34 , 35 ] drawn from the field of applied behaviour analysis [ 36 ]. BST is a performance- and competency-based training model that uses an instructional, modeling, practice, and feedback loop to teach targeted skills to a predetermined performance level. Checklists guide the instructional sequence and the determination of whether or not the predetermined performance threshold has been reached. Considerable evidence indicates that BST can yield significant improvement in skills post-training, over time, and across different settings [ 37 , 38 , 39 ]. It has been used to train a wide range of participants, including behavior analysts, parents, and educators, to build safety-related skills and manage aggressive behavior [ 37 , 40 , 41 ].

As previously described [ 42 ], our objective was to compare the effectiveness of TAU against BST. Our hypotheses, stated in null form, were that these methods would not differ significantly in:

Observer assessment of self-protection and team-control physical skills.

Self-assessed confidence in using those skills.

Study participants were recruited from all newly-hired clinical staff attending a mandatory two-week orientation. Staff were required to register beforehand for a half-day, in-person, physical safety skills session. They were randomized to a session at the time of registration, and the sessions were then randomized to TAU or BST. All randomization was performed by RB using GraphPad software [ 43 ].

The physical skills training was scheduled for a 3.5 h session on one day of the mandatory onboarding. At the end of the previous day, attendees were introduced to the study (including the fact that it was a randomized study) and asked for consent to email them a copy of the informed consent. On the morning of the physical skills training, a research team member met with attendees to answer questions and then meet privately with each individual to ascertain if they wished to participate and sign the informed consent. The trainers and session attendees were thus unaware of who was or was not in the study. Recruitment began January 2021, after ethics approval, and continued until September 2021 when the target of at least 40 study participants completing all assessments for each training condition was reached. The target sample size was chosen to allow 80-percent power to detect a medium to large effect size [ 44 ].

Both methods taught the same 11 target skills for safely responding to patients/clients that may exhibit harm to self or others (e.g., aggressive behaviour) during their hospital admission. These skills, defined by the hospital as mandatory for all newly hired staff, included six self-protection and five team-control (physical restraint) skills (see Appendix A ). Each target skill had defined components and a specific sequence in which they were taught as outlined on performance checklists (see Appendix B for a checklist example).

The two methods differed in how these sequences were administered. For BST, the trainers used the performance checklists to guide the training sequence (instruction, modeling, rehearsal, and feedback) and to indicate when the trainee was ready to move on to the next skill [ 34 ] (see Appendix C for BST sequence). In BST, common practice is to define successful performance criteria a priori (e.g., up to three correct, consecutive executions at 100% [ 45 ]). However, because the physical skills training session in our study had to be completed within the scheduled 3.5 h, the criterion was lowered for practical reasons to one correct performance (defined as 80% of the components comprising that skill) with the added goal of aiming for up to 5 times in a row if time allowed before moving on to the next skill. In contrast, while TAU included elements of modeling, practice, and feedback, it did not systematically assess skill acquisition nor impose any specific level of success before proceeding to the next skill.

There were three outcome measures, two observer-based assessments of skill acquisition (competence and mastery) and one self-reported confidence measure. Competence was defined as the percentage of components comprising an individual skill that were correctly executed (e.g., if a skill had 10 components and only six were executed properly, the competence score for that skill would be 60%). Mastery was the threshold defining when a competence score was felt to indicate successful achievement of a skill and to indicate some degree of the durability of the skill acquisition [ 46 ]. For our study, we expanded mastery to apply to the two categories of self-protection and team-control (rather than to each individual skill) using the average competence scores for the skills within each category. Mastery was pre-defined as 80-percent, a commonly used threshold [ 28 , 47 ].

The outcome measures were assessed at three time points: immediately before training (baseline), immediately after training (post-training), and one month later (follow-up). The hospital provided limited descriptive information (professional role, department) for all registrants for administrative purposes but for confidentiality reasons did not provide personal information such as age or gender/sex. The research team elected not to collect personal information for two reasons. First, the primary study concern was to evaluate the main effect of training method rather than developing predictive models, and the expected result of the randomization process was that potential covariates would not be systematically biased in the two study groups. Second, we would not be able to use this information to compare participants with non-participants to identify biases in who consented to be in the study. We were able to compare them on department role and profession by subtracting the aggregated study-participant information from the aggregated hospital-provided information – the only form of the hospital-provided information available to the research team (see Table 1  below). In addition, since degree of patient contact was an important factor in the likelihood of needing to exercise safety skills, the research team also created an algorithm estimating which combinations of professional role and department were likely to have direct, less direct, or rare/low patient contact.

Participants were also asked at baseline and follow-up how many events they encountered in the previous month that required the use of these skills. This information was collected because of our interest in testing a post-hoc hypothesis that those with actual experience would score higher than those who did not.

All assessments were carried out following a standardized protocol. To ensure that registrants remained blinded to which colleagues were in the study, each registrant’s skill acquisition was assessed privately by a research team member at baseline and post-training using the performance checklists. Only assessments for those consenting to participate were videotaped. Study participants were then asked to return one month later for a follow-up assessment which was also videotaped. For the purposes of post-hoc analyses, participants completing all three assessments were defined as ‘completers’ while those completing baseline and post-training assessments but not the one-month follow-up were ‘non-completers.’

The same performance checklists used by the BST trainers were then used by trained observers blinded to the participant’s training method to assess the videotapes. As described previously [ 42 ], interobserver agreement (IOA) was routinely evaluated throughout the study with the final value being 96% across the 33% of the performance assessment videos scored for the IOA calculation.

Skill acquisition outcomes were calculated using the checklist-based observer assessments of the videotapes. The percentage of correctly executed components for each target skill was established. Then, these percentages were averaged across the six self-protection target skills and across the five team-control target skills to create competence scores. Finally, the predefined threshold of 80% was applied to the competence scores to determine which participants met the mastery threshold [ 47 , 48 ].

Self-reported confidence was assessed on a 10-point Likert scale (‘not at all’ to ‘extremely’ confident) using a version of our institution’s standard assessment questions adapted for this study (See Appendix D ).

Statistical analysis

R software was used to generate descriptive statistics (frequencies, percentages) and test our hypotheses [ 49 ]. Generalized linear mixed models (GLMM) were used to test nested main and interaction effects using likelihood-ratio chi-square statistics for the post-training and follow-up results as there were no baseline differences. GLMM was also used to evaluate BST-TAU differences at the three study time points [ 50 , 51 ]. For the BST-TAU comparisons, we used Cohen’s d as a guide for evaluating the practical significance of the differences for the continuous measures (competence, confidence). We used Cohen’s suggested thresholds [ 52 ] of 0.2, 0.5, and 0.8 for small, medium, and large effect sizes conservatively by applying them to both the point estimates and 95% confidence intervals. Thus, for example, a Cohen’s d where the confidence interval went below 0.2 would be interpreted as non-meaningful. For the categorical measure of mastery, we used BST-TAU risk ratios. Confidence intervals for all effect size measures were obtained using bootstrapping. Independent-samples t -tests were used for the post-hoc analyses and, along with chi-square tests, to compare the completers and non-completers.

One hundred ninety-nine staff consented to participate in the study out of a total of 360 session attendees (55%). Of these, 108 (54%) had been randomly assigned to a BST session and 91 (46%) to a TAU session. Half ( n  = 99) completed assessments at all three time points (44% TAU; 55% BST). These 99 (hereafter ‘study completers’) constituted 28 percent of all session attendees.

Among the non-completers, 53 had been assigned to BST and 47 to TAU. Eight were classified as incomplete because of technical software issues when video-recording one of their assessments and one (the first participant) because the IOA process prompted substantive changes to the assessment checklist. The primary reason for the remaining non-completers was missing the follow-up assessment (91 individuals: 50/53 BST, 41/47 TAU) largely due to difficulties scheduling a non-mandatory event during the pandemic (e.g., units restricting staff from leaving because of clinical staff shortages or patient outbreaks, staff illness).

Descriptive information for the expected degree of patient contact and for hospital department is shown in Table  1 for study participants (completers, non-completers), non-participants, and the total group of session attendees. No significant differences were found when comparing participants versus non-participants or study completers versus non-completers in terms of expected patient contact ( χ 2 (2) = 0.36, n.s.; χ 2 (2) = 2.22, n.s.; respectively) or department type ( χ 2 (3) = 4.40; ( χ 2 (3) = 1.00, n.s.; respectively).

Figure  1 depicts the self-protection and team-control competence scores for the study completers (left and right sides, respectively). The hypothesis-testing results showed a significant difference by training Method (self-protection: χ 2 (1) = 34.46, p  < 0.001; team-control: χ 2 (1) = 50.42, p  < 0.001). There was also a significant decline between post-training and follow-up (Time) for both skill categories independent of Method (self-protection: χ 2 (1) = 81.29, p  < 0.001; team-control: χ 2 (1) = 56.51, p  < 0.001), and a significant Method-by-Time interaction independent of Method and Time for team-control skills ( χ 2 (1) = 17.41, p  < 0.001). BST-TAU comparisons showed no difference at baseline for either type of skill (not shown). However, BST was significantly better than TAU at both post-training (self-protection: Cohen’s d  = 1.45 [1.02, 1.87], large effect size; team-control: Cohen’s d  = 2.55 [2.08, 3.02]; large effect size) and follow-up (respectively – Cohen’s d  = 0.82 [0.40, 1.23]; Cohen’s d  = 0.62 [0.21, 1.03], both small effect sizes). For both methods, competence scores dropped between post-training and follow-up although not to the original baseline levels.

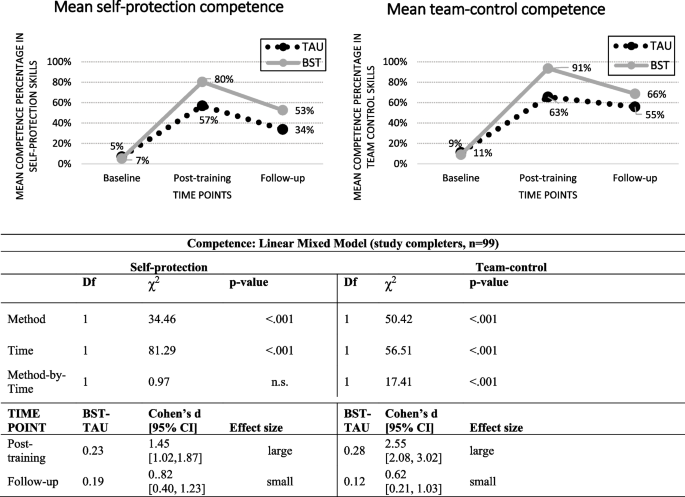
Observer-rated self-protection and team-control competence skills in TAU and BST across time-points

The skill mastery results for the study completers are shown in Fig.  2 . The mastery patterns paralleled the competence patterns in that BST was significantly better than TAU (self protection: χ 2 (1) = 28.82, p  < 0.001; team-control: χ 2 (1) = 72.87, p  < 0.001). There was also a significant Time effect independent of Method (self-protection: χ 2 (1) = 27.54, p  < 0.001; team-control: χ 2 (1) = 33.03, p  < 0.001). There were no significant interactions for either type of skill once the effects of Method and Time were accounted for. BST-TAU comparisons showed no difference in percent achieving Mastery at baseline (not shown) but large risk ratios at both post-training (self-protection: 13.43 [4.01, > 1000]; team-control: 31.24 [8.45, > 1000] and follow-up [self-protection: 12.30 [1.58, > 1000]; team-control: 30.60 [6.75. > 1000]).

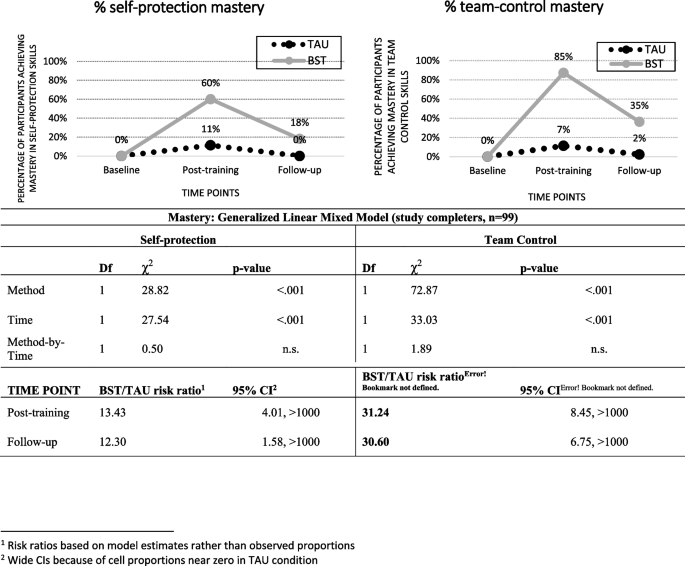
Observer-rated self-protection and team-control mastery (Predefined as 80% or better competence) by TAU and BST across time-points

Confidence scores for the study completers are shown in Fig.  3 . The only significant main effect was for Time (self-protection: χ 2 (1) = 36.87, p  < 0.001; team-control: χ 2 (1) = 21.08, p  < 0.001). For both skill categories, the scores increased between baseline and post-training and then dropped at follow-up but not to the original baseline levels.

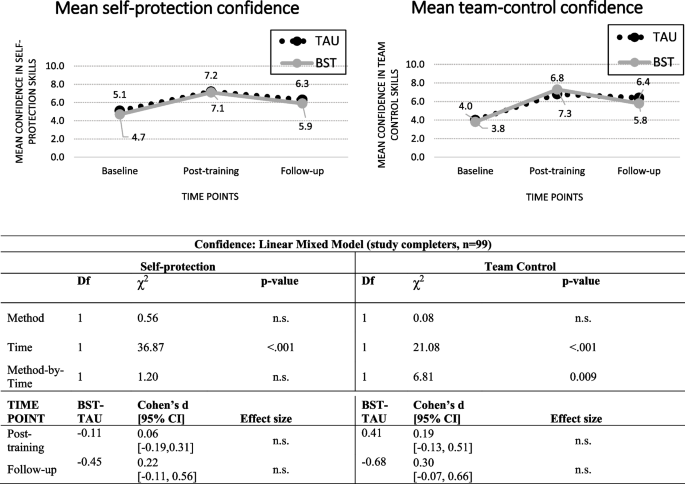
Self-rated self-protection and team-control confidence in TAU and BST across time-points

To assess what impact the high no-show rate for the one-month follow-up could have had, we compared the completers and the non-completers on the six post-training outcomes (competence, mastery, and confidence for self-protection and for team-control). Non-completers had slightly lower scores than completers except for the two confidence measures where their self-assessments were higher (not shown). However, the only significant difference between the two groups was for self-protection competence means (0.70 vs 0.63, completers vs non- completers, t (195) = 2.40, p  = 0.017).

In terms of past-month experience, few study completers reported events requiring self-protection (19 at baseline, 9 at follow-up) or team-control skills (14 at baseline, 14 at follow-up). Consequently, we only examined the presence or absence of experience without breaking it down by training method. We found non-significant results for both competence and mastery (not shown) but a potential impact on confidence for self-protection skills at follow-up and for team-control skills at baseline and post-training (Fig.  4 ).

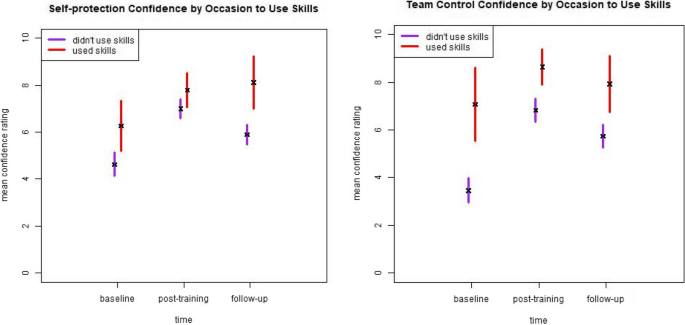
Self-rated self-protection and team-control confidence by occasion to use skills in the past month across time-points

4. Summary and discussion.

Our strongest finding was that BST was significantly better than TAU in improving the observed performance of self-protection and team-control skills. While follow-up scores decreased for both methods, BST scores remained higher than TAU scores. The impact of training on staff confidence differs from these patterns in that confidence scores improved noticeably at post-training and remained relatively high at follow-up. Further, our post-hoc analyses suggested that recent experience using safety skills might have a greater impact on confidence than on observed skill performance. We also found that training, regardless of method, was independently associated with improved observer-scored skills and self-reported confidence.

The better performance of BST is consistent with the fact that it incorporates training elements that are supported both by current educational and learning theories and evidence of effectiveness [ 46 , 53 , 54 , 55 ]. While both BST and TAU can be considered ‘outcomes based’ [ 54 ], the key difference is the BST’s use of the checklist. Based directly on the desired behavioral outcomes, this tool simultaneously creates a common understanding because it is shared with the trainees, ensures consistent and systematic training across all BST trainees, pinpoints where immediate and personalized feedback is needed to either correct or reinforce performance, and tracks the number of correct repetitions required to meet mastery criteria as well as support retention [ 46 , 56 , 57 ]. By contrast, TAU does not use a checklist and the kind and amount of feedback or practice repetitions is left to the trainer’s discretion.

However, there are at least two questions regarding whether BST produced the expected results. The BST framework requires continued rehearsal and feedback until a specified performance criterion is reached [ 34 ]. However, our mandatory safety training had practical, unmodifiable constraints. The institution required the safety-training sessions be completed in 3.5 h which meant that BST trainers were limited in their ability to use the more stringent performance criteria described in the literature. For example, it was not practical to set the performance criterion at higher than 80 percent. In addition, all BST completers were able to demonstrate 80-percent correct performance for each skill at least once, but not all were able to demonstrate five consecutive, correct executions within the allotted time. If the requirement of five in a row at 80% or higher had been implemented, then the post-training scores (and potentially the 1-month follow-up scores) for the BST completers could have been higher.

A second question is what level of skill retention should be expected at follow-up. The BST scores at one-month follow-up constituted 66% and 73% of the competence scores at post-training (self-protection and team-control, respectively) and 30% and 41% of the mastery percentages at post-training (self-protection and team-control, respectively). Although BST and elements of performance feedback models have been found to be effective in staff training with successful retention over time [ 58 , 59 , 60 , 61 , 62 ], finding appropriate comparators for our study was challenging because there are no studies where BST has been used for training such a large and diverse group of staff. Further, as noted above, the body of workplace violence prevention literature has not consistently focussed on retention. However, the broader training and education literature does suggest that our results are consistent with or somewhat lower than those from other studies. Offiah et al. [ 63 ] found that 45 percent of medical students retained the full set of clinical skills 18 months after completing simulation training, and Bruno and colleagues [ 64 ] found published retention rates ranging between 75 and 85 percent across time periods between four to 24 months and across diverse disciplinary fields. Regardless of the comparators, the loss in skill performance after one-month post-training is a concern.

Our interpretation is that reliance on a single session, even with highly structured and competency-based methods, is not adequate particularly in the context of managing distressing events. Efforts should be made to allow for flexibility with respect to setting higher thresholds for success despite organizational restraints for staff training. Furthermore, settings that require these skills to be performed more reliably for both patient and staff safety (e.g., emergency departments, acute care settings, security services) should consider on-the-job feedback or booster sessions based on objective assessments of skill rather than on pre-set amounts of time (e.g. annual refresher). This would be more consistent with the BST literature, as on-the-job training should occur based on an evidence-based approach.

Our finding of a differential impact of training on confidence versus demonstrable skills is consistent with a long-standing, substantial body of research examining the relationship between self-assessment and objective measures of learning [ 28 , 65 , 66 ]. The pattern of non-existent, weak, or even inverse relationships between the two has been shown for a variety of medical staff trainee and education learner groups [ 28 , 29 , 67 , 68 , 69 , 70 , 71 , 72 ]. Consequently, many researchers recommend either not using self-assessments at all or at least ensuring that objective measures are also collected (e.g.,[ 64 , 65 ]).

The literature does offer some hypotheses for why this discrepancy occurs and, further, why self-assessment continues to be used in medical education and training despite the robust evidence that it does not accurately reflect learning. Katowa-Mukwato and Banda [ 70 ] in a study of Zambian medical students suggest that fear of revealing their weaknesses led to a negative correlation between self- and objective-ratings. Persky, et al. [ 69 ] reference the theory of ‘metacognition’ – defined as ‘thinking about thinking’ (p. 993, [ 69 ] – and the ‘Dunning-Kruger’ effect that the ability to recognize competence (i.e., accurate metacognition) is unevenly distributed. There is also discussion as to why these measures continue to be used and suggestions of how best to use them. Yates et al. [ 65 ] suggest that ease of collecting this information is a factor. More complex and nuanced explanations are offered by Lu, et al. [ 66 ] and Tavares, et al. [ 73 ] who note that self-assessment is an important component in theories of learning and evaluation and that self-perception and self-reflection (particularly when objective findings are shared) are critical ingredients for supporting medical and continuing profession education in a self-regulating profession.

Because the goal of our study was to assess the effectiveness of two training methods, we did not collect information or have the opportunity to explore any of these potential reasons for why self-reported and objective measures are discrepant or to evaluate the best use of that discrepancy. The modest contributions that our study adds are that selecting a higher-risk setting, including non-nursing healthcare professionals, using a more rigorous study design (as recommended by Geoffrion, et al. [ 29 ]), and attempting to account for recent experience do not appear to alter this pattern.

The major strength of our study is its design. Currently, we have identified only one other study evaluating the impact of BST training for clinical staff using a randomized control trial design [ 41 ]. Other strengths are our inclusion of a large percentage of non-nursing, direct-care staff, our use of both self-reported and observer-assessed outcome measures, and our findings regarding retention. These strengths allow us to add to the evidence base already established in the literature.

However, interpretation of our results should consider several limitations. Conducting a research study on full-time clinical staff during a pandemic meant that a high percentage of those consenting to be in the study did not complete their 1-month follow-up assessment. The reported reasons for missing the third assessment (unit restrictions or short staffing because of the pandemic) are consistent with the demographic differences between completers and non-completers in that they were more likely to be nurses or working on inpatient units. Our comparison of the post-training scores of the completers and non-completers suggested that the no-shows had slightly lower post-training observed skill performance (but slightly better confidence ratings). If we had managed to assess the non-completers at follow-up, our reported findings may have been diluted although it is unlikely that this would have completely negated the large effect sizes.

The time constraints on the mandatory training meant that we were unable to fully apply either the BST mastery criteria commonly reported in the literature (i.e., three correct, consecutive executions [ 28 , 47 ] or the one we would have preferred (i.e., five correct executions). While this type of limitation is consistent with the pragmatic nature of our design, it likely had an impact on our findings in terms of potentially lowering the post-training BST competency and mastery scores and, perhaps more importantly, contributing to the lower retention rates at 1-month follow-up [ 56 ].

The 45-percent refusal rate by the training registrants is another concerning issue. Anecdotal reports from the training team were that the response rate was very low at the start of the study because many of the new hires were nervous about being videotaped (a specific comment reported was that it reminded some of the new graduates of ‘nursing school.’) and were unsure of the purpose of the study. The team then changed to a more informal, conversational introduction describing the need for the study as well as reassuring attendees that it was the training, not the participants, that was being evaluated. The team’s impression was that this improved the participation rate. The participants and non-participants were not statistically different in terms of their expected patient contact and department role. However, we cannot preclude that there may have been systematic biases for other unmeasured characteristics.

Another limitation, as identified by Price, et al. [ 28 ], is that we used artificial training scenarios, though this may be unavoidable given the low frequency of aggressive events and the ethics of deliberately exposing staff to these events. Also, we only measured the skills directly related to handling client/patient events. We were not able to access information on event frequency or severity, staff distress and complaints, or institutional-level measures such as lost workdays due to sick leave, staff turnover, or expenditures [ 29 , 33 ]. A further gap, which is important but difficult to assess, is whether there is any impact of staff safety training on the clients or patients who are involved.

Given these strengths and limitations, we see our study as adding one piece of evidence that needs to be a) confirmed or disconfirmed by other researchers in both the same and different settings and b) understood as part of a complex mix of ingredients. Specific areas for further research arising directly out of our findings include evaluating whether less constrained training time would improve attainment of skill mastery, exploration and evaluation of methods to increase skill retention over time, and, most importantly but also more difficult to assess, the impact on patients and clients of staff safety skills training. More evidence on these fronts will hopefully contribute to maintaining and improving workplace safety.

Availability of data and materials

The dataset generated and analysed during the current study is not publicly available due to the fact that it is part of a larger internal administrative data collection but is available from the corresponding author on reasonable request.

International Labour Organization. Joint Programme Launches New Initiative Against Workplace Violence in the Health Sector. 2002. Available from: https://www.ilo.org/global/about-the-ilo/newsroom/news/WCMS_007817/lang--en/index.htm . Cited 2022 Aug 5.

Di Martino V. Workplace violence in the health sector. Country case studies Brazil, Bulgaria, Lebanon, Portugal, South Africa, Thailand and an Additional Australian Study. Geneva: ILO/ICN/WHO/PSI Joint Programme on Workplace Violence in the Health Sector; 2002.

Needham I, Kingma M, O’Brien-Pallas L, McKenna K, Tucker R, Oud N, editors. Workplace Violence in the Health Sector. In: Proceedings of the First International Conference on Workplace Violence in the Health Sector - Together, Creating a Safe Work Environment. The Netherlands: Kavanah; 2008. p. 383.

Health Quality Ontario. Quality Improvement Plan Guidance: Workplace Violence Prevention. 2019.

Google Scholar  

Bodenheimer T, Sinsky C. From triple to quadruple aim: care of the patient requires care of the provider. Ann Fam Med. 2014;12(6):573–6.

Article   PubMed   PubMed Central   Google Scholar  

Somani R, Muntaner C, Hillan E, Velonis AJ, Smith P. A Systematic review: effectiveness of interventions to de-escalate workplace violence against nurses in healthcare settings. Saf Health Work. 2021;12(3):289–95. https://doi.org/10.1016/j.shaw.2021.04.004 .

Li Y, Li RQ, Qiu D, Xiao SY. Prevalence of workplace physical violence against health care professionals by patients and visitors: a systematic review and meta-analysis. Int J Environ Res Public Health. 2020;17(1):299.

Liu J, Gan Y, Jiang H, Li L, Dwyer R, Lu K, et al. Prevalence of workplace violence against healthcare workers: a systematic review and meta-analysis. Occup Environ Med. 2019;76(12):927–37.

Article   PubMed   Google Scholar  

O’Rourke M, Wrigley C, Hammond S. Violence within mental health services: how to enhance risk management. Risk Manag Healthc Policy. 2018;11:159–67.

Odes R, Chapman S, Harrison R, Ackerman S, Hong OS. Frequency of violence towards healthcare workers in the United States’ inpatient psychiatric hospitals: a systematic review of literature. Int J Ment Health Nurs. 2021;30(1):27–46.

Gerberich SG, Church TR, McGovern PM, Hansen HE, Nachreiner NM, Geisser MS, et al. An epidemiological study of the magnitude and consequences of work related violence: the minnesota nurses’ study. Occup Environ Med. 2004;61(6):495–503.

Article   CAS   PubMed   PubMed Central   Google Scholar  

Ridenour M, Lanza M, Hendricks S, Hartley D, Rierdan J, Zeiss R, et al. Incidence and risk factors of workplace violence on psychiatric staff. Work. 2015;51(1):19–28.

Cooper AJ, Mendonca JD. A prospective study of patient assaults on nurses in a provincial psychiatric hospital in Canada. Acta Psychiatr Scand. 1991;84(2):163–6.

Article   CAS   PubMed   Google Scholar  

Hiebert BJ, Care WD, Udod SA, Waddell CM. Psychiatric nurses’ lived experiences of workplace violence in acute care psychiatric Units in Western Canada. Issues Ment Health Nurs. 2022;43(2):146–53.

Lim M, Jeffree M, Saupin S, Giloi N, Lukman K. Workplace violence in healthcare settings: the risk factors, implications and collaborative preventive measures. Ann Med Surg. 2022;78:103727.

Article   Google Scholar  

Lanctôt N, Guay S. The aftermath of workplace violence among healthcare workers: a systematic literature review of the consequences. Aggress Violent Behav. 2014;19(5):492–501.

Friis K, Pihl-Thingvad J, Larsen FB, Christiansen J, Lasgaard M. Long-term adverse health outcomes of physical workplace violence: a 7-year population-based follow-up study. Eur J Work Organ Psychol. 2019;28(1):101–9.

Berlanda S, Pedrazza M, Fraizzoli M, de Cordova F. Addressing risks of violence against healthcare staff in emergency departments: the effects of job satisfaction and attachment style. Biomed Res Int. 2019;28(5430870):1–12.

Baig LA, Ali SK, Shaikh S, Polkowski MM. Multiple dimensions of violence against healthcare providers in Karachi: results from a multicenter study from Karachi. J Pakistani Med Assoc. 2018;68(8):1157–65.

International Labour Organization. Safe and healthy working environments free from violence and harassment. International Labour Organization. Geneva: International Labour Organization; 2020. Available from: https://www.ilo.org/global/topics/safety-and-health-at-work/resources-library/publications/WCMS_751832/lang--en/index.htm .

Wirth T, Peters C, Nienhaus A, Schablon A. Interventions for workplace violence prevention in emergency departments: a systematic review. Int J Environ Res Public Health. 2021;18(16):8459.

U.S. Congress. Workplace Violence Prevention for Health Care and Social Service Workers Act. U.S.A.; 2020. Available from: https://www.congress.gov/bill/116th-congress/house-bill/1309 .

Lu A, Ren S, Xu Y, Lai J, Hu J, Lu J, et al. China legislates against violence to medical workers. TneLancet Psychiatry. 2020;7(3):E9.

PubMed   Google Scholar  

Government of Ontario Ministry of Labour T and SD. Preventing workplace violence in the health care sector | ontario.ca. 2020. Available from: https://www.ontario.ca/page/preventing-workplace-violence-health-care-sector . Cited 2020 Jul 28.

Safe and Well Committee. Safe & Well Newsletter. 2018. Available from: http://insite.camh.net/files/SafeWell_Newsletter_October2018_107833.pdf .

Patel MX, Sethi FN, Barnes TR, Dix R, Dratcu L, Fox B, et al. Joint BAP NAPICU evidence-based consensus guidelines for the clinical management of acute disturbance: de-escalation and rapid tranquillisation. J Psychiatr Intensive Care. 2018;14(2):89–132.

Heckemann B, Zeller A, Hahn S, Dassen T, Schols JMGA, Halfens RJG. The effect of aggression management training programmes for nursing staff and students working in an acute hospital setting. A narrative review of current literature. Nurse Educ Today. 2015;35(1):212–9.

Price O, Baker J, Bee P, Lovell K. Learning and performance outcomes of mental health staff training in de-escalation techniques for the management of violence and aggression. Br J Psychiatry. 2015;206:447–55.

Geoffrion S, Hills DJ, Ross HM, Pich J, Hill AT, Dalsbø TK, et al. Education and training for preventing and minimizing workplace aggression directed toward healthcare workers. Cochrane Database Syst Rev. 2020;9(Art. No.: CD011860). Available from: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC8094156/ . Cited 2021 Dec 3.

Paterson B, Turnbull J, Aitken I. An evaluation of a training course in the short-term management of violence. Nurse Educ Today. 1992;12(5):368–75.

Rice ME, Helzel MF, Varney GW, Quinsey VL. Crisis prevention and intervention training for psychiatric hospital staff. Am J Community Psychol. 1985;13(3):289–304.

Wondrak R, Dolan B. Dealing with verbal abuse: evaluation of the efficacy of a workshop for student nurses. Nurse Educ Today. 1992;12(2):108–15.

Leach B, Gloinson ER, Sutherland A, Whitmore M. Reviewing the evidence base for de-escalation training: a rapid evidence assessment. RAND research reports. RAND Corporation; 2019. Available from: https://www.rand.org/pubs/research_reports/RR3148.html . Cited 2021 Nov 26.

Parsons MB, Rollyson JH, Reid DH. Evidence-based staff training: a guide for practitioners. Behav Anal Pract. 2012;5(2):2–11.

Miltenberger RG, Flessner C, Gatheridge B, Johnson B, Satterlund M, Egemo K. Evaluation of behavioral skills training to prevent gun play in children. J Appl Bahavior Anal. 2004;37:513–6.

Baer DM, Wolf MM, Risley TR. Some still-current dimensions of applied behavior analysis. J Appl Behav Anal. 1987;20(4):313–27.

Dillenburger K. Staff training. Handbook of treatments for autism spectrum disorder. In: Matson JL, editor. Handbook of treatments for autism spectrum disorder. Switzerland: Springer Nature; 2017. p. 95–107.

Kirkpatrick M, Akers J, Rivera G. Use of behavioral skills training with teachers: a systematic review. J Behav Educ. 2019;28(3):344–61.

Sun X. Behavior skills training for family caregivers of people with intellectual or developmental disabilities: a systematic review of literature. Int J Dev Disabil. 2020:68(3):247-73.

Davis S, Thomson K, Magnacca C. Evaluation of a caregiver training program to teach help-seeking behavior to children with autism spectrum disorder. Int J Dev Disailities. 2020;66(5):348–57.

Gormley L, Healy O, O’Sullivan B, O’Regan D, Grey I, Bracken M. The impact of behavioural skills training on the knowledge, skills and well-being of front line staff in the intellectual disability sector: a clustered randomised control trial. J Intellect Disabil Res. 2019;63(11):1291–304.

Lin E, Malhas M, Bratsalis E, Thomson K, Boateng R, Hargreaves F, et al. Behavioural skills training for teaching safety skills to mental health clinicians: A protocol for a pragmatic randomized control trial. JMIR Res Protoc. 2022;11(12):e39672.

GraphPad. Randomly assign subjects to treatment groups. Available from: https://www.graphpad.com/quickcalcs/randomize1.cfm . Cited 2023 June 6.

Van Voorhis CRW, Morgan BL. Understanding power and rules of thumb for determining sample sizes. Tutor Quant Methods Psychol. 2007;3(2):43–50.

Erath TG, DiGennaro Reed FD, Sundermeyer HW, Brand D, Novak MD, Harbison MJ, et al. Enhancing the training integrity of human service staff using pyramidal behavioral skills training. J Appl Behav Anal. 2020;53(1):449–64.

Wong KK, Fienup DM, Richling SM, Keen A, Mackay K. Systematic review of acquisition mastery criteria and statistical analysis of associations with response maintenance and generalization. Behav Interv. 2022;37(4):993–1012.

Richling SM, Williams WL, Carr JE. The effects of different mastery criteria on the skill maintenance of children with developmental disabilities. J Appl Behav Anal. 2019;52(3):701–17 (Available from: https://pubmed.ncbi.nlm.nih.gov/31155708/ ). Cited 2022 Oct 14.

Pitts L, Hoerger ML. Mastery criteria and the maintenance of skills in children with developmental disabilities. Behav Interv. 2021;36(2):522–31. Available from: https://doi.org/10.1002/bin.1778 . Cited 2022 Oct 17.

R Core Team. R: A language and environment for statistical computing. Vienna: R Foundation for Statistical Computing; 2021.

Pinheiro J, Bates D. Mixed-effects models in S and S-PLUS. New York: Springer Science+Business Media; 2006.

Bosker R, Snijders TA. Multilevel analysis: An introduction to basic and advanced multilevel modeling. In: Analysis M, editor. London. UK: Sage Publishers; 2012. p. 1–368.

Cohen J. Statistical power analysis for the behavioral sciences. 2nd ed. Hillsdale, NJ: Lawrence Erlbaum Associates; 1988.

Taylor DCM, Hamdy H. Adult learning theories: Implications for learningand teaching in medical education: AMEEGuide No. 83. Med Teach. 2013;35(11):e1561-72.

Nodine TR. How did we get here? A brief history of competency-based higher education in the United States. Competency Based Educ. 2016;1:5–11.

Novak MD, Reed FDD, Erath TG, Blackman AL, Ruby SA, Pellegrino AJ. Evidence-Based Performance Management: Applying behavioral science to support practitioners. Perspect Behav Sci. 2019;42:955–72.

Fienup DM, Broadsky J. Effects of mastery criterion on the emergence of derived equivalence relations. J Appl Behav Anal. 2017;40:843–8.

Fuller JL, Fienup DM. A preliminary analysis of mastery criterion level: effects on response maintenance. Behav Anal Pract. 2018;11(1):1–8.

Alavosius MP, Sulzer-Azaroff B. The effects of performance feedback on the safety of client lifting and transfer. J Appl Behav Anal. 1986;19:261–7.

Hogan A, Knez N, Kahng S. Evaluating the use of behavioral skills training to improve school staffs’ implementation of behavior intervention plans. J Behav Educ. 2015;24(2):242–54.

Nabeyama B, Sturmey P. Using behavioral skills training to promote safe and correct staff guarding and ambulation distance of students with multiple physical disabilities. J Appl Behav Anal. 2010;43(2):341–5.

Parsons MB, Rollyson JH, Reid DH. Teaching practitioners to conduct behavioral skills training: a pyramidal approach for training multiple human service staff. Behav Anal Pract. 2013;6(2):4–16.

Sarakoff RA, Sturmey P. The effects of behavioral skills training on staff implementation of discrete-trial teaching. J Appl Behav Anal. 2004;37(4):535–8.

Offiah G, Ekpotu LP, Murphy S, Kane D, Gordon A, O’Sullivan M, et al. Evaluation of medical student retention of clinical skills following simulation training. BMC Med Educ. 2019;19:263.

Bruno P, Ongaro A, Fraser I. Long-term retention of material taught and examined in chiropractic curricula: its relevance to education and clinical practice. J Can Chiropr Assoc. 2007;51(1):14–8.

PubMed   PubMed Central   Google Scholar  

Yates N, Gough S, Brazil V. Self-assessment: With all its limitations, why are we still measuring and teaching it? Lessons from a scoping review. Med Teach. 2022;44(11):1296–302. https://doi.org/10.1080/0142159X.2022.2093704 .

Lu FI, Takahashi SG, Kerr C. Myth or reality: self-assessment is central to effective curriculum in anatomical pathology graduate medical education. Acad Pathol. 2021;8:23742895211013530.

Magnacca C, Thomson K, Marcinkiewicz A, Davis S, Steel L, Lunsky Y, et al. A telecommunication model to teach facilitators to deliver acceptance and commitment training. Behav Anal Pract. 2022;15(3):752–752.

Naughton CA, Friesner DL. Comparison of pharmacy students’ perceived and actual knowledge using the pharmacy curricular outcomes assessment. Am J Pharm Educ. 2012;76(4):63.

Persky AM, Ee E, Schlesselman LS. Perception of learning versus performance as outcome measures of educational research. Am J Pharm. 2020;84(7):993–1000.

Katowa-Mukwato P, Sekelani SB. Self-perceived versus objectively measured competence in performing clinical pratical procedures by final medical students. Int J Med Educ. 2016;7:122–9.

Barsuk JH, Cohen ER, Feinglass J, McGaghie WC, Wayne DB. Residents’ procedural experience does not ensure competence: a research synthesis. J Grad Med Educ. 2017;9(2):201–8.

Choudhry NK, Fletcher RH, Soumerai SB. Systematic review: the relationship between clinical experience and quality of health care. Ann Intern Med. 2005;142(4):260–73.

Tavares W, Sockalingam S, Valanci S, Giuliani M, Davis D, Campbell C, et al. Performance Data Advocacy for Continuing Professional Development in Health Professions. Acad Med. 2024;99(2):153-8. https://doi.org/10.1097/ACM.0000000000005490 .

Download references

Acknowledgements

We thank Sanjeev Sockalingam, Asha Maharaj, Katie Hodgson, Erin Ledrew, Sophie Soklaridis, and Stephanie Sliekers for their guidance and for dedicating the human and financial resources needed to support this study. We also want to express our sincere gratitude to the following individuals for facilitating physical skills sessions and for volunteering as actors in the physical skills demonstrations: Kate Van den Borre, Steven Hughes, Paul Martin Demers, Ross Violo, Genevieve Poulin, Stacy de Souza, Narendra Deonauth, Joanna Zygmunt, Tessa Donnelly, Lawren Taylor, and Bobby Bonner. Finally, we are grateful to Marcos Sanchez for statistical consultation and Quincy Vaz for research support.

This research was funded internally by the Centre for Addiction and Mental Health.

Author information

Authors and affiliations.

Department of Education, Centre for Addiction and Mental Health, Toronto, ON, Canada

Elizabeth Lin, Mais Malhas, Emmanuel Bratsalis, Kendra Thomson, Fabienne Hargreaves, Kayle Donner, Heba Baig, Rhonda Boateng, Rajlaxmi Swain, Mary Benisha Benadict & Louis Busch

Department of Applied Disability Studies, Brock University, St. Catharines, ON, Canada

Kendra Thomson

You can also search for this author in PubMed   Google Scholar

Contributions

All authors were involved in the study design, monitoring and implementing the study, and review of manuscript drafts. EL was responsible for the original study design and drafting of the full manuscript. MM, EB, and FH led the implementation of the training sessions. EB, FH, HB, KT, and LB were involved in the reliability assessments (IOA). KD and HB were primarily responsible for data analysis. HB and RB monitored the data collection and the ongoing study procedures. RS and MBB assisted in the literature review.

Corresponding author

Correspondence to Elizabeth Lin .

Ethics declarations

Ethics approval and consent to participate.

This study was approved by the Research Ethics Board of the Centre for Addiction and Mental Health (#101/2020). Informed consent was obtained from all subjects participating in the study. All interventions were performed in accordance with the Declaration of Helsinki. This study was registered with the ISRCTN registry on 06/01/2023 (ISRCTN18133140).

Consent for publication

Not applicable.

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Additional file 1., additional file 2., rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Lin, E., Malhas, M., Bratsalis, E. et al. Behavioral skills training for teaching safety skills to mental health service providers compared to training-as-usual: a pragmatic randomized control trial. BMC Health Serv Res 24 , 639 (2024). https://doi.org/10.1186/s12913-024-10994-1

Download citation

Received : 06 September 2023

Accepted : 16 April 2024

Published : 17 May 2024

DOI : https://doi.org/10.1186/s12913-024-10994-1

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Workplace violence
• Violence prevention
• Behavioural skills training
• Performance and competency-based staff training

BMC Health Services Research

ISSN: 1472-6963

• General enquiries: [email protected]

• Open access
• Published: 14 May 2024

A novel dance intervention program for children and adolescents with developmental disabilities: a pilot randomized control trial

• Jeffrey T. Anderson 1 , 4 ,
• Christina Toolan 2 ,
• Emily Coker 3 ,
• Hannah Singer 1 , 4 ,
• Derek Pham 1 ,
• Nicholas Jackson 1 ,
• Catherine Lord 1 , 4 &
• Rujuta B. Wilson 1 , 4  

BMC Sports Science, Medicine and Rehabilitation volume  16 , Article number:  109 ( 2024 ) Cite this article

105 Accesses

Metrics details

Organized physical activity programs have been shown to provide wide benefits to participants, though there are relatively few studies examining the impact of these programs for individuals with developmental disabilities. This pilot study was conducted to determine the feasibility and impact of an undergraduate-led dance intervention program for children and adolescents with developmental disabilities. We evaluated the impact of the dance program on motor ability and social skills.

The study design was a waitlist control clinical trial in which participants were randomized to active and control groups. Eligible participants included male and female children and adolescents between the ages of 4 and 17 years with neurodevelopmental disabilities. The Motor Assessment Battery for Children Checklist and the Social Responsiveness Scale were used to assess change in motor and social skills, respectively. After gathering baseline data, the active group completed 1 h of online dance classes per week for 10 weeks, while the control group entered a 10-week waiting period. All participants then returned for a follow-up visit. Pre- and post-intervention data were analyzed using linear mixed-effects modeling adjusting for age and class attendance with subject random intercept.

We recruited and randomized 43 participants with neurodevelopmental disabilities (mean age = 8.63, SD = 2.98), of which 30 participated in dance classes. The attendance rate was 82.6% for the active group and 61.7% for the control group. The active group demonstrated a significant improvement in motor skills in an unpredictable environment, as indicated on the Motor Assessment Battery for Children Checklist ( n  = 21, p  = 0.05). We also observed positive trends in social skills that did not reach significance.

Conclusions

Our results indicate that it is feasible to develop and implement a fully digital dance intervention program for individuals with developmental disabilities. Further, we find that change in motor skills can be detected after just 10 h of low-intensity participation. However, a lack of significant change in social skills coupled with limitations in study implementation suggests further research is needed to determine the full impact of this dance program.

Trial Registration

ClinicalTrials.gov Protocol Registration System: Protocol ID 20-001680-AM-00005, registered 17/2/2021 – Retrospectively Registered, https://clinicaltrials.gov/study/NCT04762290 .

Peer Review reports

Organized physical activity (OPA), which is structured physical activity led by a coach or instructor, has wide benefits for physical health and wellbeing. It is well established that routine physical activity reduces risk for multiple chronic conditions and improves health outcomes [ 1 ]. Physical activity is also associated with the formation of fundamental motor skills in early childhood, highlighting its importance for motor development [ 2 ]. The World Health Organization echoed the importance of daily physical activity for children and adolescents to strengthen muscles and reduce sedentary behavior [ 3 ]. In addition, physical activity may provide benefits to the psychological wellbeing of adolescents through strengthening cognitive function networks in the brain [ 4 ]. Importantly, not all types of physical activity provide the same array of benefits; this distinction, however, has not yet been thoroughly explored. One study which investigated the relationship between structured and unstructured physical activity found that structured physical activity with guided opportunities for practice proved to be the most beneficial for motor skill development [ 5 ]. Similarly, structured indoor and outdoor activities have been shown to reduce the yearly increase of body mass index for developing children. Researchers have found a smaller increase in BMI during what is described as the adiposity rebound period of childhood for children who participate in these activities compared to those who do not [ 6 ]. These findings illustrate that within the broader context of physical activity, participation in OPA is a particularly effective way for children and adolescents to improve their physical health and wellbeing.

Despite OPA’s known benefits, much of the research around OPA focuses on typically developing children. Comparatively fewer studies investigated the benefits of OPA programs for children with neurodevelopmental disabilities (NDD), despite the fact that these children often face greater barriers to participation in physical activity. NDD, as defined in the Diagnostic and Statistical Manual, 5th edition, refers to a group of conditions including autism, attention deficit/hyperactivity disorder (ADHD), and cerebral palsy, that often emerge before grade school and are characterized by developmental deficits in personal, social, academic, or occupational domains [ 7 ]. Furthermore, it is not uncommon for children and adolescents to be diagnosed with more than one NDD [ 8 ]. Literature has shown that adolescents with NDDs are less likely to engage in OPA than neurotypical peers [ 9 , 10 , 11 ]. It is well known that individuals with NDDs often have difficulties in physical movement and mobility. In autistic patients, this can include as praxis, object manipulation, and postural stability [ 12 ], while cerebral palsy is characterized by high muscle tone and missed motor milestones. Motor challenges also have broad negative impacts on adaptive function and quality of life. Adolescents with cerebral palsy have reported higher physical quality of life, social quality of life, and overall happiness when able to be more physically active [ 13 ]. Likewise, motor difficulties in autism are negatively correlated with social skills [ 14 ]. This is significant because social challenges can lead to further barriers, including negative social interactions with peers [ 15 ] and higher feelings of loneliness [ 16 ].

In addition, there is a lack of programs led by physical education coaches with the training and knowledge to adapt the program to individual needs. Limited education for coaches regarding disability has a significant impact on the number of available and adequately trained coaches, and may negatively affect disabled individuals’ participation in sports and other forms of physical activity [ 17 ]. Semi-structured interviews with coaches of autistic athletes have shown that the coach-athlete relationship is a particularly important theme, suggesting that adapting teaching styles according to the experience of autistic individuals is an effective coaching strategy [ 18 ]. While research into this topic is sparse, these findings offer evidence that encouraging coaches to adopt adaptive teaching styles may reduce barriers to participating in physical activity programs for individuals with NDDs.

There are several examples of physical activity programs which have been successfully implemented for individuals with NDDs and have shown benefits across domains. Previous research has shown that following participation in group OPA programs, autistic children had improved overall motor skills, including aiming, catching, and balance, as well as improved social communication and social motivation [ 19 , 20 ]. Another review of movement interventions for children with intellectual disabilities found improvements in fundamental motor skills and balance [ 21 ]. Researchers have also explored dance-based OPA programs as interventions for children with NDDs, and found techniques such as mirroring and exploratory movement to benefit social and communication skills, motor skills, and behavioral domains [ 22 , 23 ]. The success of these programs demonstrates the need to further reduce the barriers individuals with NDDs face by developing and evaluating new OPA programs that are adapted for their needs.

To address this gap, we established an organized dance intervention program called the Expressive Movement Initiative (EMI) at the University of California, Los Angeles (UCLA). The course model was designed to achieve meaningful participation for each dancer by creating an adaptable framework which acknowledges individual needs. To achieve that goal, each dancer was paired individually with an undergraduate buddy who had been trained about NDDs, inclusive language, neurodiversity, and adaptive dance and movement teaching styles. Using a strength-based approach [ 18 , 24 ], this framework ensured that each dancer had the support of an individual who was equipped to support their needs. Furthermore, the use of student buddies to carry out the program greatly increased the feasibility of maintaining one-to-one pairings which in turn provided adequate support for participants and increased opportunities for meaningful social interactions. A document detailing the structure of the dance classes and the protocol for the study at the time of this publication can be found on the clinicaltrials.gov website ( https://clinicaltrials.gov/study/NCT04762290?tab=history&a=3 ). Here we present interim analysis of our study protocol. We choose to present interim analysis due to impacts of the COVID-19 global pandemic on the delivery of the intervention and participant retention. Our goals are to present [ 1 ] the feasibility of developing and implementing the EMI program, and [ 2 ] the results of two of our standardized outcome measures that were not affected by data attrition. This includes one primary outcome measure – the Motor Assessment Battery for Children Checklist (mABC-C), and one secondary outcome measure – the Social Responsiveness Scale (SRS). Other measures described in our study protocol are not presented due to attrition that resulted in incomplete datasets and will be presented when the full sample is collected and complete. We hypothesized that participants would show improvements in motor and social skills following participation in this program as indicated by the mABC-C and SRS, respectively.

Our study design and research methods were reviewed and approved by the University of California, Los Angeles Institutional Review Board (IRB#20-001680). Due to the age of the participant population and/or diagnoses that affect cognitive abilities, a legally authorized representative of all participants provided written informed consent for their data to be used in related research.

Participants

Eligible participants were between the ages of 4 and 17 with a diagnosed NDD from a healthcare provider, which was reported by parents during eligibility screening. Exclusion criteria was previous participation in EMI dance classes. There were no exclusion criteria related to the degree of intellectual/physical disability or co-occurring health conditions. Participants living in the United States were recruited for this study through flyers and social media listings. Interested families contacted the study team directly and all prospective participants were screened until recruitment goals were met. In instances where parents reported more than one diagnosed NDD, e.g., autism and co-occurring ADHD, or a NDD with a co-occurring condition that falls into a different diagnostic category, e.g., anxiety, this information was recorded onto the participant ID key by a researcher at study entry. Furthermore, parents were asked to report racial and ethnic affiliation.

All potential participants were screened in January and February of 2021. Pre-testing took place from February 15, 2021 to March 5, 2021 and follow-up visits occurred from May 2, 2021 to May 9, 2021. The trial, which was originally planned to conclude in March 2024, was interrupted after one year to perform an interim analysis on the data collected during the COVID-19 pandemic. This decision was made in order to perform a feasibility assessment and adjust the study protocol to include direct in-person measures upon resuming the trial.

Intervention design

The intervention was designed as a longitudinal waitlist-control study in which participants were randomized into active and control groups using permuted block randomization with a 2:1 active to control randomization scheme. Study data were collected and managed using Research Electronic Data Capture (REDCap) hosted at UCLA [ 25 ]. REDCap is a secure, web-based software platform designed to support data capture for research studies, providing (1) an intuitive interface for validated data capture; (2) audit trails for tracking data manipulation and export procedures; (3) automated export procedures for seamless data downloads to common statistical packages; and (4) procedures for data integration and interoperability with external sources. REDCap was also used to complete the randomization, with the allocation sequence being generated by author six and participants being enrolled by author eight. The randomization list was concealed by REDCap, with the assignment group only being known once an intervention group was assigned. Additionally, participants were stratified by language level (complex speech, phrased speech, or minimally verbal) in order to ensure an even distribution of baseline communication skills. The treatment period was 10 weeks with weekly 1-hour classes. The active and control group completed pre and post intervention surveys online via Zoom in an interview format. Whereas participants were aware of which group they had been placed in, assessments were conducted by trained research staff who were blinded to assignment group. The control group was offered participation in the dance classes after the post-intervention data collection (Fig.  1 ).

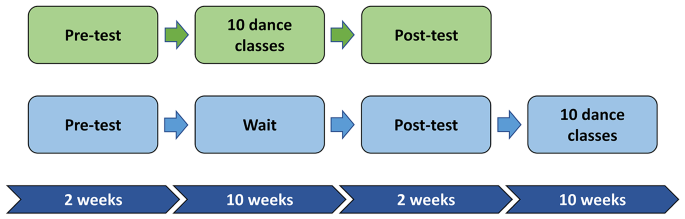
Graphical representation of the longitudinal study design. The timeline for study events as they relate to the dance intervention

The EMI dance intervention classes were carried out by trained undergraduate students. Each session consisted of an artistic director to lead the class and buddies that were paired 1:1 to each participant. Buddies received training around NDD, accessible language, and how to adapt their teaching for their buddy. This training included attending speaker presentations and reviewing weekly feedback provided by a class instructor. Due to the COVID-19 pandemic, all classes were held virtually on Zoom. To ensure the quality of virtual instruction, artistic directors and buddies received training in adapting movements for Zoom delivery. Additionally, artistic directors provided buddies with written feedback on a weekly basis to provide strategies for adjusting teaching styles to their dancer.

The structure of each class could take one of two forms, group class or buddy class, which alternated each week. Dancers started each group class with a warm up consisting of stretches and other movements, followed by an “across the floors” exercise which involved more exaggerated movement. Across the floor movements were commonly based in ballet techniques, such as “relevé walks”, “step, prep, passé,” and “reach chassé.” A short break was incorporated into every class to encourage hydration and resting. After the break, the instructor taught a short choreography to the dancers, which would first be practiced at a pace best for the participant before being paired with music. To close out group time, a musical game was played. These games would require dancers to follow a particular objective, such as balance a tissue on their head while dancing, or follow instructions embedded within a song, such as the hokey-pokey. Following this, dancers were sent into Zoom breakout rooms for a few minutes to work with their buddies. Upon their return, they were given the opportunity to share what they did with their buddy and engage in a cooldown before ending class. A visual representation of a typical group class can be seen in Fig.  2 .

Buddy classes began with a warm up and an across the floors series similar to group class. However, after this point they would be sent directly into breakout rooms with their buddies for the remainder of class, which usually lasted 40–45 min. Class plans would provide buddies with objectives to accomplish during their one-on-one session, such as play a musical game or come up with specific dance skills to practice. This structure allowed dancers to receive more individualized attention and work on learned movement skills. Much like group classes, buddy classes ended with dancers coming back to the main room, sharing what they did with their buddy, and engaging in a cooldown activity.

Group Class Agenda. The typical order of activities that occur during group class. During buddy class, dancers would spend additional time with their buddy in lieu of learning new choreography or playing a game

Measures used pre- and post-intervention

Social Skills : Social skills were assessed through parent responses to the Social Responsiveness Scale 2nd edition (SRS-2) [ 26 ]. The SRS-2 is a continuous measure of social behaviors that is normed and validated for use across the lifespan in autistic individuals as well as non-autistic individuals who may show various impairments. It captures behaviors related to 5 subscales: (a) social awareness, (b) social cognition, (c) social communication, (d) social motivation, and (e) restricted interested and repetitive behavior. The instrument contains 65 items that took parents approximately 15 min to complete.

Motor Function. Motor function was assessed via parent responses to the Movement Assessment Battery for Children Checklist (mABC-C) [ 27 ]. This checklist is intended to be completed by a teacher or parent and contains questions pertaining to a variety of motor tasks. The mABC-C contains 30 items, which took parents approximately 10 min to complete. It is validated for use in children ages 5 through 12 with or without motor challenges as a screening tool for Developmental Coordination Disorder (DCD) [ 28 , 29 ]. The instrument yields a total motor score, wherein a higher score indicates worse motor skills as more characteristics meet criteria for DCD. The mABC-C is associated with a direct assessment battery, the Movement Assessment Battery for Children –second edition (mABC-2), which is commonly used as a tool for assessing children with suspected motor skill impairment [ 30 ]. As we were unable to conduct in-person visits due to the COVID-19 pandemic, the mABC-C was used to target relevant motor domains.

Statistical analysis

The primary analysis was intention-to-treat and included all randomly assigned participants who completed the mABC-C and the SRS in at least one study visit. Dance class attendance rate was calculated independently for the active and control groups. Linear mixed-effects modeling adjusted for age and class attendance with subject random intercept was used to evaluate the change in motor function and social skill scores after undergoing EMI dance classes. Between group differences in change over time were assessed using a group-by-time interaction term. All statistical significance was determined using a two-sided alpha level less than 0.05, and all analyses were conducted using R Version 4.2.1 [ 31 ].

A total of 43 participants were recruited and randomized for this study, of which 61 percent were male. Speech level in this sample ranged from non-speaking to fully-verbal. All participants had a diagnosed NDD, with a majority of participants having a diagnosis of autism (Table 1 ). A summary of parental racial and ethnic affiliation can be seen in Table 2 .

Out of the 43 participants who were allocated to an intervention group, 36 completed the mABC-C and SRS at baseline (n active = 21, n control = 15) and 26 participants completed them at follow-up (n active = 14, n control = 12). 30 participants received the allocated intervention (Fig.  3 ). On average, participants in the active group had an attendance rate of 82.6% while participants in the control group had an attendance rate of 61.7%. There was only one protocol deviation for a participant in the active group. This participant was lost to follow-up and did not provide post-assessment data. However, they re-engaged the study team and were given the opportunity to participate in the dance classes with the control group. The pre-assessment data for this participant is included in the intention-to-treat analysis and they have been counted as not having received the allocated intervention.

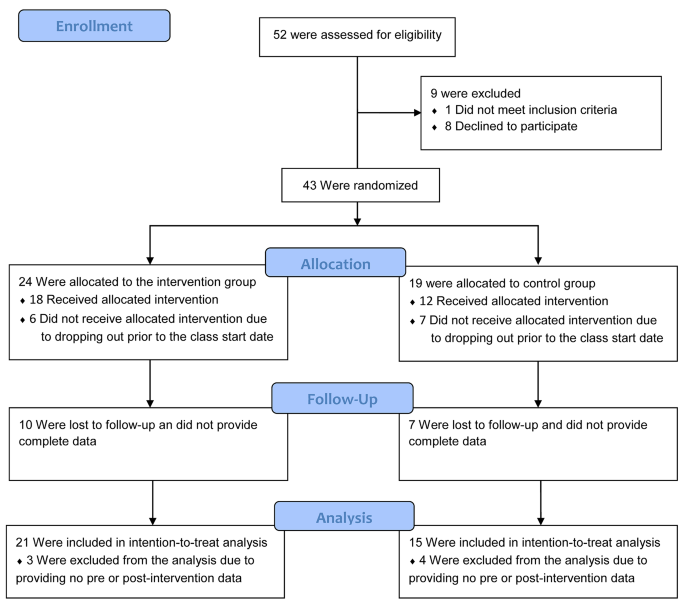
Participant Flow Diagram. Figure  3 Shows the number of participants that were screened, randomized, and ultimately included in the analysis. A power analysis was performed on the full sample size projected over the multi-year study. No power analysis was performed on the sample reported in this interim analysis

There was no significant change in either the active group ( n  = 21, p  = 0.11) or the control group ( n  = 15, p  = 0.82) on the mABC-C total score, although the active group showed a positive trend. The active group displayed a significant improvement on the “movement in an unpredictable environment” domain of the mABC-C ( n  = 21, p  = 0.05), while the control group did not show any significant change in this domain ( n  = 15, p  = 0.64). A summary of the data can be seen in Table  3 .

Across the domains of the SRS, the active group demonstrated positive trends for improvement in social communication and social motivation, neither of which were significant. We did not observe any notable changes in social awareness, social cognition, or restricted interest and repetitive behavior for the active group. There were no significant changes across any of the domains nor the total score of the SRS for the control group (Fig.  4 ).

Individual and Mean Scores for mABC-C and SRS Subscales. Figure  4   Individual scores (grayscale) and means calculated using linear mixed-effects modeling (color) are plotted for subscales of the mABC-C and the SRS. The social communication and social motivation subscales of the SRS are displayed to visualize the change in scores

The aim of this pilot study was to investigate the feasibility and impact of a novel movement-based dance intervention program for children and adolescents with NDD. Consistent with our hypothesis, we found that children in the active group showed a statistically significant improvement in movement in dynamic environments, as measured by the mABC-C, and we observed a trend of improvements in social skills on the SRS.

We measured movement skills that are related to movement in dynamic environments, which are targeted through the EMI program activities. Examples of dynamic movement activities include self-care/classroom skills, ball skills, and PE/recreational skills. Examples of specific items covered in this section of the mABC-C include, “moves body in time with music or other people,” “keeps time to a musical beat by clapping hands or tapping feet,” and, “maintains balance when frequent adjustments are required.” This type of movement occurs in a dance class setting in which students are learning how to express themselves using movement through space and time. As such, the expressive movement component of EMI likely accounts for the improvements to movement in dynamic environments. This finding is in line with other movement-based intervention studies which have found similar results on the mABC-2 when assessing the impact of their program on motor skills [ 20 ]. Motor skills are integral to many developmental and behavioral domains because they influence how one interacts with their environment. Namely, better motor skills could enhance or improve opportunities to participate in peer interactions by allowing for participation in a broader range of activities, such as sports or active games. Better motor skills may also lead to an increase in active behavior and exercise, which has benefits for social wellbeing, mental health, and cognitive benefits, including a reduction in sedentary behavior [ 32 ]. Importantly, improvements in motor skills reported in this study resulted from a relatively low-intensity program that put minimal burden on participating families. One hour of class per week in an online setting offers a more accessible option for families compared to other interventions, as it does not require transportation for participation. Thus, our findings are promising for the viability of OPA programs for children and adolescents with NDDs.

Changes in social skills were characterized by positive trends for social communication and social motivation that were not statistically significant. Participants were given opportunities for social engagement through one-to-one pairings with buddies, which were reinforced by weeks dedicating greater amount of time to buddy interactions. During group time, the instructor also frequently encouraged participants to verbally share their thoughts or experiences, such as their favorite song or what they did during buddy time. These social interactions likely account for the positive trend in social skills noted on the SRS. This result also mirrors similar works that have investigated the impact of OPA on social skills, which have yielded a mix of significant and non-significant results [ 19 ]. As will be further discussed in study limitations, several factors such as small sample size and heterogeneity of the participant sample may have impacted our ability to measure significant change in these areas. Considering the impact that negative social interactions can have on individuals with NDD [ 15 ], future research is warranted to investigate the impact of OPA programs on social skills and subsequent changes in quality of life. For example, it is possible that positive social interactions during OPA programs increase both one’s motivation to interact with peers and the effectiveness of the communication, which in turn could reduce feelings of loneliness [ 16 ].

One strength of the present study was the enrollment of individuals with varying NDDs and co-occurring diagnoses, which served to increase the generalizability of the program. Across participants of EMI, there were diagnoses of autism, ADHD, cerebral palsy, genetic syndromes, and other disabilities. As participants included males and females between the ages of 4 and 17 with no prerequisite for dancing ability, it follows that a wide range of children and adolescents with a diagnosed NDD can benefit from the presented program. This flexibility could be attributed to the training given to buddies, which emphasized adaptable teaching for the specific needs of each student. Furthermore, the decision to use a student-supported structure for class instruction increases the accessibility of the program by allowing for one-to-one pairings between buddies and dancers while remaining cost-free to families who participate.

We acknowledge that there were also several limitations in our implementation, which should be considered when interpreting the results. As a pilot study, our sample size was small and may have limited our ability to identify all effects. Furthermore, the heterogeneity of our participant sample, while positive for the reach and impact of the EMI program, may have constrained our ability to measure significant results related to social communication and social motivation. The reliance on parent reported diagnoses rather than medical records or clinical assessments is another potential limitation. In addition, the quality of our data was affected by a high amount of attrition in the second half of the study, which led to missing data. These factors could lead to a degree of sampling bias in our study population, although it is likely that global changes in the pandemic played a significant role in engagement levels, in part due to a shift back to in-person social, educational, and leisure activities after a prolonged period of these activities being restricted. Several families who did not complete the study reported that they wanted to travel or have their child return to other programs that had been on a hiatus during the pandemic. Indeed, class attendance rate, which was roughly 80% for the active group when COVID-19 restrictions remained in effect, dropped to nearly 60% for the control group after many restrictions were lifted. Finally, it was necessary for our protocol to be transitioned to fully remote due to the pandemic, which did not allow us to conduct direct measures of participants in person. Direct assessment of more detailed motor skills and social skills may have allowed us to detect changes secondary to participation in the dance intervention. Despite opportunities for one-on-one engagement, the program’s effects on social engagement may have also been attenuated due to the online format of the classes.

In this pilot study, we demonstrate the feasibility of developing and implementing an online dance intervention for individuals with NDDs. Furthermore, this intervention shows benefits in motor skills after a 10-week period with a dose of 1 h per week. Moving forward, we are utilizing direct standardized and quantitative measures of motor skills and social communication to further examine the impact of this dance intervention. Future studies will include an IQ assessment to understand whether this differentially affects the results of the intervention. Future work could also assess the impact of EMI participation on teachers and buddies in order to provide further insight into the efficacy of this approach. Our preliminary results support the growing body of research that OPA is a promising intervention for motor skills among children and adolescents with NDDs.

Data availability

The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request. Full details of the trial protocol version that is reported in this paper can be found on the ClinicalTrials.gov Protocol Registration System, available at https://clinicaltrials.gov/study/NCT04762290?tab=history&a=3 .

Abbreviations

Attention deficit/hyperactivity disorder

Autism Intervention Research Network on Physical Health

Expressive Movement Initiative

Health Services and Resources Administration

Movement Assessment Battery for Children Checklist

Movement Assessment Battery for Children – second edition

Developmental coordination disorder

Neurodevelopmental disability

Organized physical activity

Social Responsiveness Scale

University of California, Los Angeles

Rhodes RE, Janssen I, Bredin SSD, Warburton DER, Bauman A. Physical activity: Health impact, prevalence, correlates and interventions. Psychol Health. 2017;32(8):942–75.

Article   PubMed   Google Scholar  

Jones D, Innerd A, Giles EL, Azevedo LB. Association between fundamental motor skills and physical activity in the early years: a systematic review and meta-analysis. J Sport Health Sci. 2020;9(6):542–52.

Article   PubMed   PubMed Central   Google Scholar  

Bull FC, Al-Ansari SS, Biddle S, Borodulin K, Buman MP, Cardon G, et al. World Health Organization 2020 guidelines on physical activity and sedentary behaviour. Br J Sports Med. 2020;54(24):1451–62.

Rodriguez-Ayllon M, Cadenas-Sánchez C, Estévez-López F, Muñoz NE, Mora-Gonzalez J, Migueles JH, et al. Role of physical activity and sedentary behavior in the Mental Health of Preschoolers, children and adolescents: a systematic review and Meta-analysis. Sports Med. 2019;49(9):1383–410.

Dapp LC, Gashaj V, Roebers CM. Physical activity and motor skills in children: a differentiated approach. Psychol Sport Exerc. 2021;54:101916.

Article   Google Scholar  

Dunton G, McConnell R, Jerrett M, Wolch J, Lam C, Gilliland F, et al. Organized Physical Activity in Young School Children and subsequent 4-Year change in body Mass Index. Arch Pediatr Adolesc Med. 2012;166(8):713–8.

Diagnostic and Statistical Manual of Mental Disorders [Internet]. 5th ed, American Psychiatric Association. 2013 [cited 2023 Dec 6]. https://dsm.psychiatryonline.org/doi/book/10.1176/appi.books.9780890425596 .

Dewey D. What is comorbidity and why does it Matter in Neurodevelopmental disorders? Curr Dev Disord Rep. 2018;5(4):235–42.

Cook BG, Li D, Heinrich KM, Obesity. Physical activity, and sedentary behavior of Youth with learning disabilities and ADHD. J Learn Disabil. 2015;48(6):563–76.

McCoy SM, Morgan K. Obesity, physical activity, and sedentary behaviors in adolescents with autism spectrum disorder compared with typically developing peers. Autism. 2020;24(2):387–99.

Papadopoulos NV, Whelan M, Skouteris H, Williams K, McGinley J, Shih STF, et al. An examination of parent-reported facilitators and barriers to Organized Physical Activity Engagement for Youth with Neurodevelopmental disorders, Physical, and medical conditions. Front Psychol. 2020;11:568723.

Zampella CJ, Wang LAL, Haley M, Hutchinson AG, de Marchena A. Motor Skill differences in Autism Spectrum Disorder: a clinically focused review. Curr Psychiatry Rep. 2021;23(10):64.

Gulati S, Sondhi V. Cerebral palsy: an overview. Indian J Pediatr. 2018;85(11):1006–16.

Wang LAL, Petrulla V, Zampella CJ, Waller R, Schultz RT. Gross Motor Impairment and its relation to Social skills in Autism Spectrum disorder: a systematic review and two Meta-analyses. Psychol Bull. 2022;148(3–4):273–300.

Hymas R, Badcock JC, Milne E. Loneliness in Autism and Its Association with Anxiety and Depression: A Systematic Review with Meta-Analyses. Rev J Autism Dev Disord [Internet]. 2022 Jul 16 [cited 2023 Feb 17]; https://doi.org/10.1007/s40489-022-00330-w .

Bauminger N, Shulman C, Agam G. Peer Interaction and Loneliness in High-Functioning Children with Autism. 2003.

Townsend RC, Huntley TD, Cushion CJ, Culver D. Infusing disability into coach education and development: a critical review and agenda for change. Phys Educ Sport Pedagogy. 2022;27(3):247–60.

Kimber A, Burns J, Murphy M. It’s all about knowing the young person: best practice in coaching autistic athletes. Sports Coaching Rev. 2021;0(0):1–21.

Google Scholar  

Howells K, Sivaratnam C, May T, Lindor E, McGillivray J, Rinehart N. Efficacy of Group-based organised physical activity participation for Social outcomes in children with Autism Spectrum disorder: a systematic review and Meta-analysis. J Autism Dev Disord. 2019;49(8):3290–308.

Howells K, Sivaratnam C, Lindor E, He J, Hyde C, McGillivray J, et al. Can a community-based football Program Benefit Motor ability in children with Autism Spectrum Disorder? A pilot evaluation considering the role of Social impairments. J Autism Dev Disord. 2022;52(1):402–13.

Maïano C, Hue O, April J. Effects of motor skill interventions on fundamental movement skills in children and adolescents with intellectual disabilities: a systematic review. J Intellect Disabil Res. 2019;63(9):1163–79.

Aithal S, Karkou V, Makris S, Karaminis T, Powell J. A Dance Movement psychotherapy intervention for the wellbeing of children with an Autism Spectrum disorder: a pilot intervention study. Front Psychol. 2021;12:588418.

Pontone M, Vause T, Zonneveld KLM. Benefits of recreational dance and behavior analysis for individuals with neurodevelopmental disorders: a literature review. Behav Interv. 2021;36(1):195–210.

Urbanowicz A, Nicolaidis C, den Houting J, Shore SM, Gaudion K, Girdler S, et al. An Expert discussion on strengths-based approaches in Autism. Autism Adulthood. 2019;1(2):82–9.

Harris PA, Taylor R, Thielke R, Payne J, Gonzalez N, Conde JG. Research electronic data capture (REDCap)--a metadata-driven methodology and workflow process for providing translational research informatics support. J Biomed Inf. 2009;42(2):377–81.

Constantno J, Gruber C. Social Responsiveness Scale, Second Edition (SRS-2) | Center for Autism Research [Internet]. 2012 [cited 2022 May 13]. https://www.carautismroadmap.org/social-responsiveness-scale/ .

Henderson SE, Sugden D, Barnett AL. Movement Assessment Battery for Children-2. 2007.

Schoemaker MM, Smits-Engelsman BCM, Jongmans MJ. Psychometric properties of the Movement Assessment Battery for Children-Checklist as a screening instrument for children with a developmental co-ordination disorder. Br J Educ Psychol. 2003;73(3):425–41.

Schoemaker MM, Niemeijer AS, Flapper BCT, Smits-Engelsman BCM. Validity and reliability of the Movement Assessment Battery for Children-2 Checklist for children with and without motor impairments. Dev Med Child Neurol. 2012;54(4):368–75.

Brown T, Lalor A. The Movement Assessment Battery for Children—Second Edition (MABC-2): a review and critique. Phys Occup Ther Pediatr. 2009;29(1):86–103.

RStudio Team. Posit. 2020 [cited 2023 May 31]. RStudio: Integrated Development for R. http://www.rstudio.com/ .

Webster EK, Martin CK, Staiano AE. Fundamental motor skills, screen-time, and physical activity in preschoolers. J Sport Health Sci. 2019;8(2):114–21.

Download references

Acknowledgements

We acknowledge the Expressive Movement Initiative group at UCLA for their invaluable role as organizers and teachers of the dance program used in this research. We also acknowledge the Autism Intervention Research network on Physical health (AIR-P) for supporting this project.

This study was funded by the Health Resources and Services Administration (HRSA) (Grant NO.: UT2MC39440). The funding agency did not play a role in the design of the study, the collection, analysis, and interpretation of the data, nor in the writing of this manuscript. Additional funding support was received from the Department of Health and Human Services, Administration for Community Living (Grant NO.: 90DDUC0129) and the National Institute of Child Health and Human Development (Grant NO.: K23HD099275).

Author information

Authors and affiliations.

University of California, Los Angeles, Los Angeles, CA, USA

Jeffrey T. Anderson, Hannah Singer, Derek Pham, Nicholas Jackson, Catherine Lord & Rujuta B. Wilson

California State University, Dominguez Hills, Carson, CA, USA

Christina Toolan

Stanford School of Medicine, Stanford, CA, USA

Emily Coker

Semel Institute for Neuroscience and Human Behavior, 760 Westwood Plaza, Los Angeles, CA, 90024, USA

Jeffrey T. Anderson, Hannah Singer, Catherine Lord & Rujuta B. Wilson

You can also search for this author in PubMed   Google Scholar

Contributions

JA entered and interpreted data collected during the study and drafted the manuscript. CT and HS assisted with the collection of data and data entry. EC made significant contributions to the design of the dance intervention and the randomized control trial. NJ generated the allocation sequence for randomization. DP and NJ conducted the statistical analysis for the study and advised on interpreting and reporting results. CL advised on the study design and data collection methods. RW oversaw the design and implantation of the study, the analysis and interpretation of the results, and was a major contributor in writing the manuscript. All authors read and approved the final version of this manuscript.

Corresponding author

Correspondence to Rujuta B. Wilson .

Ethics declarations

Ethics approval and consent to participate.

Our study design and research methods were reviewed and approved by the University of California, Los Angeles Institutional Review Board (IRB#20-001680). Due to the age of the participant population as well as diagnoses that affect cognitive abilities, a legally authorized representative of all participants provided written informed consent for their data to be used in related research. All research was performed in accordance with the guidelines and regulations in the Declaration of Helsinki.

Consent for publication

Not applicable.

Competing interests

The authors declare that they have no competing interests.

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Anderson, J.T., Toolan, C., Coker, E. et al. A novel dance intervention program for children and adolescents with developmental disabilities: a pilot randomized control trial. BMC Sports Sci Med Rehabil 16 , 109 (2024). https://doi.org/10.1186/s13102-024-00897-3

Download citation

Received : 11 August 2023

Accepted : 02 May 2024

Published : 14 May 2024

DOI : https://doi.org/10.1186/s13102-024-00897-3

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Intervention
• Developmental
• Randomized Control Trial

BMC Sports Science, Medicine and Rehabilitation

ISSN: 2052-1847

• General enquiries: [email protected]

Metabolic Responses to an Acute Glucose Challenge: The Differential Effects of Eight Weeks of Almond vs. Cracker Consumption in Young Adults

• Find this author on Google Scholar
• Find this author on PubMed
• Search for this author on this site
• For correspondence: [email protected]
• Info/History
• Supplementary material
• Preview PDF

This study investigated the dynamic responses to an acute glucose challenge following chronic almond versus cracker consumption for 8 weeks (clinicaltrials.gov ID: NCT03084003 ). Seventy-three young adults (age: 18-19 years, BMI: 18-41 kg/m2) participated in an 8-week randomized, controlled, parallel-arm intervention and were randomly assigned to consume either almonds (2 oz/d, n=38) or an isocaloric control snack of graham crackers (325 kcal/d, n=35) daily for 8 weeks. Twenty participants from each group underwent a 2-hour oral glucose tolerance test (oGTT) at the end of the 8-week intervention. Metabolite abundances in the oGTT serum samples were quantified using untargeted metabolomics, and targeted analyses for free PUFAs, total fatty acids, oxylipins, and endocannabinoids. Multivariate, univariate, and chemical enrichment analyses were conducted to identify significant metabolic shifts. Findings exhibit a biphasic lipid response distinguished by higher levels of unsaturated triglycerides in the earlier periods of the oGTT followed by lower levels in the latter period in the almond versus cracker group (p-value<0.05, chemical enrichment analyses). Almond (vs. cracker) consumption was also associated with higher AUC120 min of aminomalonate, and oxylipins (p-value<0.05), but lower AUC120 min of L-cystine, N-acetylmannosamine, and isoheptadecanoic acid (p-value<0.05). Additionally, the Matsuda Index in the almond group correlated with AUC120 min of CE 22:6 (r=-0.46; p-value<0.05) and 12,13 DiHOME (r=0.45; p-value<0.05). Almond consumption for 8 weeks leads to dynamic, differential shifts in response to an acute glucose challenge, marked by alterations in lipid and amino acid mediators involved in metabolic and physiological pathways.

Competing Interest Statement

RMO and JD disclose grant support from Almond Board of California. SP, OF, and JWN have no conflicts of interest.

Clinical Trial

NCT03084003

Funding Statement

The present study was supported by the Almond Board of California (PI: RMO). JD was supported by the National Institute On Minority Health And Health Disparities of the National Institutes of Health under award numbers K99MD012815 and R00MD012815, and by a separate Almond Board of California grant at the time of this work. Additional support was provided by USDA Project 2032-51530-025-00D (JWN). The USDA is an equal opportunity provider and employer. The content is solely the responsibility of the authors and does not necessarily represent the official views of the funders. Moreover, mention of commercial products is solely for the purpose of providing specific information and does not imply recommendation or endorsement by the USDA or NIH. The funders had no role in the study design and implementation, data collection, data analysis, or interpretation of results.

Author Declarations

I confirm all relevant ethical guidelines have been followed, and any necessary IRB and/or ethics committee approvals have been obtained.

The details of the IRB/oversight body that provided approval or exemption for the research described are given below:

IRB of University of California, Merced gave ethical approval for this work

I confirm that all necessary patient/participant consent has been obtained and the appropriate institutional forms have been archived, and that any patient/participant/sample identifiers included were not known to anyone (e.g., hospital staff, patients or participants themselves) outside the research group so cannot be used to identify individuals.

I understand that all clinical trials and any other prospective interventional studies must be registered with an ICMJE-approved registry, such as ClinicalTrials.gov. I confirm that any such study reported in the manuscript has been registered and the trial registration ID is provided (note: if posting a prospective study registered retrospectively, please provide a statement in the trial ID field explaining why the study was not registered in advance).

I have followed all appropriate research reporting guidelines, such as any relevant EQUATOR Network research reporting checklist(s) and other pertinent material, if applicable.

Data Availability

Data is available upon request

View the discussion thread.

Supplementary Material

Thank you for your interest in spreading the word about medRxiv.

NOTE: Your email address is requested solely to identify you as the sender of this article.

Citation Manager Formats

• EndNote (tagged)
• EndNote 8 (xml)
• RefWorks Tagged
• Ref Manager
• Tweet Widget
• Facebook Like
• Google Plus One
• Addiction Medicine (324)
• Allergy and Immunology (628)
• Anesthesia (165)
• Cardiovascular Medicine (2383)
• Dentistry and Oral Medicine (289)
• Dermatology (207)
• Emergency Medicine (380)
• Endocrinology (including Diabetes Mellitus and Metabolic Disease) (839)
• Epidemiology (11777)
• Forensic Medicine (10)
• Gastroenterology (703)
• Genetic and Genomic Medicine (3751)
• Geriatric Medicine (350)
• Health Economics (635)
• Health Informatics (2401)
• Health Policy (935)
• Health Systems and Quality Improvement (900)
• Hematology (341)
• HIV/AIDS (782)
• Infectious Diseases (except HIV/AIDS) (13323)
• Intensive Care and Critical Care Medicine (769)
• Medical Education (366)
• Medical Ethics (105)
• Nephrology (398)
• Neurology (3513)
• Nursing (198)
• Nutrition (528)
• Obstetrics and Gynecology (675)
• Occupational and Environmental Health (665)
• Oncology (1825)
• Ophthalmology (538)
• Orthopedics (219)
• Otolaryngology (287)
• Pain Medicine (233)
• Palliative Medicine (66)
• Pathology (446)
• Pediatrics (1035)
• Pharmacology and Therapeutics (426)
• Primary Care Research (422)
• Psychiatry and Clinical Psychology (3181)
• Public and Global Health (6150)
• Radiology and Imaging (1281)
• Rehabilitation Medicine and Physical Therapy (749)
• Respiratory Medicine (828)
• Rheumatology (379)
• Sexual and Reproductive Health (372)
• Sports Medicine (323)
• Surgery (402)
• Toxicology (50)
• Transplantation (172)
• Urology (146)

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• J Hum Reprod Sci
• v.4(1); Jan-Apr 2011

This article has been retracted.

An overview of randomization techniques: an unbiased assessment of outcome in clinical research.

Department of Biostatics, National Institute of Animal Nutrition & Physiology (NIANP), Adugodi, Bangalore, India

Randomization as a method of experimental control has been extensively used in human clinical trials and other biological experiments. It prevents the selection bias and insures against the accidental bias. It produces the comparable groups and eliminates the source of bias in treatment assignments. Finally, it permits the use of probability theory to express the likelihood of chance as a source for the difference of end outcome. This paper discusses the different methods of randomization and use of online statistical computing web programming ( www.graphpad.com /quickcalcs or www.randomization.com ) to generate the randomization schedule. Issues related to randomization are also discussed in this paper.

INTRODUCTION

A good experiment or trial minimizes the variability of the evaluation and provides unbiased evaluation of the intervention by avoiding confounding from other factors, which are known and unknown. Randomization ensures that each patient has an equal chance of receiving any of the treatments under study, generate comparable intervention groups, which are alike in all the important aspects except for the intervention each groups receives. It also provides a basis for the statistical methods used in analyzing the data. The basic benefits of randomization are as follows: it eliminates the selection bias, balances the groups with respect to many known and unknown confounding or prognostic variables, and forms the basis for statistical tests, a basis for an assumption of free statistical test of the equality of treatments. In general, a randomized experiment is an essential tool for testing the efficacy of the treatment.

In practice, randomization requires generating randomization schedules, which should be reproducible. Generation of a randomization schedule usually includes obtaining the random numbers and assigning random numbers to each subject or treatment conditions. Random numbers can be generated by computers or can come from random number tables found in the most statistical text books. For simple experiments with small number of subjects, randomization can be performed easily by assigning the random numbers from random number tables to the treatment conditions. However, in the large sample size situation or if restricted randomization or stratified randomization to be performed for an experiment or if an unbalanced allocation ratio will be used, it is better to use the computer programming to do the randomization such as SAS, R environment etc.[ 1 – 6 ]

REASON FOR RANDOMIZATION

Researchers in life science research demand randomization for several reasons. First, subjects in various groups should not differ in any systematic way. In a clinical research, if treatment groups are systematically different, research results will be biased. Suppose that subjects are assigned to control and treatment groups in a study examining the efficacy of a surgical intervention. If a greater proportion of older subjects are assigned to the treatment group, then the outcome of the surgical intervention may be influenced by this imbalance. The effects of the treatment would be indistinguishable from the influence of the imbalance of covariates, thereby requiring the researcher to control for the covariates in the analysis to obtain an unbiased result.[ 7 , 8 ]

Second, proper randomization ensures no a priori knowledge of group assignment (i.e., allocation concealment). That is, researchers, subject or patients or participants, and others should not know to which group the subject will be assigned. Knowledge of group assignment creates a layer of potential selection bias that may taint the data.[ 9 ] Schul and Grimes stated that trials with inadequate or unclear randomization tended to overestimate treatment effects up to 40% compared with those that used proper randomization. The outcome of the research can be negatively influenced by this inadequate randomization.

Statistical techniques such as analysis of covariance (ANCOVA), multivariate ANCOVA, or both, are often used to adjust for covariate imbalance in the analysis stage of the clinical research. However, the interpretation of this post adjustment approach is often difficult because imbalance of covariates frequently leads to unanticipated interaction effects, such as unequal slopes among subgroups of covariates.[ 1 ] One of the critical assumptions in ANCOVA is that the slopes of regression lines are the same for each group of covariates. The adjustment needed for each covariate group may vary, which is problematic because ANCOVA uses the average slope across the groups to adjust the outcome variable. Thus, the ideal way of balancing covariates among groups is to apply sound randomization in the design stage of a clinical research (before the adjustment procedure) instead of post data collection. In such instances, random assignment is necessary and guarantees validity for statistical tests of significance that are used to compare treatments.

TYPES OF RANDOMIZATION

Many procedures have been proposed for the random assignment of participants to treatment groups in clinical trials. In this article, common randomization techniques, including simple randomization, block randomization, stratified randomization, and covariate adaptive randomization, are reviewed. Each method is described along with its advantages and disadvantages. It is very important to select a method that will produce interpretable and valid results for your study. Use of online software to generate randomization code using block randomization procedure will be presented.

Simple randomization

Randomization based on a single sequence of random assignments is known as simple randomization.[ 3 ] This technique maintains complete randomness of the assignment of a subject to a particular group. The most common and basic method of simple randomization is flipping a coin. For example, with two treatment groups (control versus treatment), the side of the coin (i.e., heads - control, tails - treatment) determines the assignment of each subject. Other methods include using a shuffled deck of cards (e.g., even - control, odd - treatment) or throwing a dice (e.g., below and equal to 3 - control, over 3 - treatment). A random number table found in a statistics book or computer-generated random numbers can also be used for simple randomization of subjects.

This randomization approach is simple and easy to implement in a clinical research. In large clinical research, simple randomization can be trusted to generate similar numbers of subjects among groups. However, randomization results could be problematic in relatively small sample size clinical research, resulting in an unequal number of participants among groups.

Block randomization

The block randomization method is designed to randomize subjects into groups that result in equal sample sizes. This method is used to ensure a balance in sample size across groups over time. Blocks are small and balanced with predetermined group assignments, which keeps the numbers of subjects in each group similar at all times.[ 1 , 2 ] The block size is determined by the researcher and should be a multiple of the number of groups (i.e., with two treatment groups, block size of either 4, 6, or 8). Blocks are best used in smaller increments as researchers can more easily control balance.[ 10 ]

After block size has been determined, all possible balanced combinations of assignment within the block (i.e., equal number for all groups within the block) must be calculated. Blocks are then randomly chosen to determine the patients’ assignment into the groups.

Although balance in sample size may be achieved with this method, groups may be generated that are rarely comparable in terms of certain covariates. For example, one group may have more participants with secondary diseases (e.g., diabetes, multiple sclerosis, cancer, hypertension, etc.) that could confound the data and may negatively influence the results of the clinical trial.[ 11 ] Pocock and Simon stressed the importance of controlling for these covariates because of serious consequences to the interpretation of the results. Such an imbalance could introduce bias in the statistical analysis and reduce the power of the study. Hence, sample size and covariates must be balanced in clinical research.

Stratified randomization

The stratified randomization method addresses the need to control and balance the influence of covariates. This method can be used to achieve balance among groups in terms of subjects’ baseline characteristics (covariates). Specific covariates must be identified by the researcher who understands the potential influence each covariate has on the dependent variable. Stratified randomization is achieved by generating a separate block for each combination of covariates, and subjects are assigned to the appropriate block of covariates. After all subjects have been identified and assigned into blocks, simple randomization is performed within each block to assign subjects to one of the groups.

The stratified randomization method controls for the possible influence of covariates that would jeopardize the conclusions of the clinical research. For example, a clinical research of different rehabilitation techniques after a surgical procedure will have a number of covariates. It is well known that the age of the subject affects the rate of prognosis. Thus, age could be a confounding variable and influence the outcome of the clinical research. Stratified randomization can balance the control and treatment groups for age or other identified covariates. Although stratified randomization is a relatively simple and useful technique, especially for smaller clinical trials, it becomes complicated to implement if many covariates must be controlled.[ 12 ] Stratified randomization has another limitation; it works only when all subjects have been identified before group assignment. However, this method is rarely applicable because clinical research subjects are often enrolled one at a time on a continuous basis. When baseline characteristics of all subjects are not available before assignment, using stratified randomization is difficult.[ 10 ]

Covariate adaptive randomization

One potential problem with small to moderate size clinical research is that simple randomization (with or without taking stratification of prognostic variables into account) may result in imbalance of important covariates among treatment groups. Imbalance of covariates is important because of its potential to influence the interpretation of a research results. Covariate adaptive randomization has been recommended by many researchers as a valid alternative randomization method for clinical research.[ 8 , 13 ] In covariate adaptive randomization, a new participant is sequentially assigned to a particular treatment group by taking into account the specific covariates and previous assignments of participants.[ 7 ] Covariate adaptive randomization uses the method of minimization by assessing the imbalance of sample size among several covariates.

Using the online randomization http://www.graphpad.com/quickcalcs/index.cfm , researcher can generate randomization plan for treatment assignment to patients. This online software is very simple and easy to implement. Up to 10 treatments can be allocated to patients and the replication of treatment can also be performed up to 9 times. The major limitations of this software is that once the randomization plan is generated, same randomization plan cannot be generated as this uses the seed point of local computer clock and is not displayed for further use. Other limitation of this online software Maximum of only 10 treatments can be assigned to patients. Entering the web address http://www.graphpad.com/quickcalcs/index.cfm on address bar of any browser, the page of graphpad appears with number of options. Select the option of “Random Numbers” and then press continue, Random Number Calculator with three options appears. Select the tab “Randomly assign subjects to groups” and press continue. In the next page, enter the number of subjects in each group in the tab “Assign” and select the number of groups from the tab “Subjects to each group” and keep number 1 in repeat tab if there is no replication in the study. For example, the total number of patients in a three group experimental study is 30 and each group will assigned to 10 patients. Type 10 in the “Assign” tab and select 3 in the tab “Subjects to each group” and then press “do it” button. The results is obtained as shown as below (partial output is presented)

Another randomization online software, which can be used to generate randomization plan is http://www.randomization.com . The seed for the random number generator[ 14 , 15 ] (Wichmann and Hill, 1982, as modified by McLeod, 1985) is obtained from the clock of the local computer and is printed at the bottom of the randomization plan. If a seed is included in the request, it overrides the value obtained from the clock and can be used to reproduce or verify a particular plan. Up to 20 treatments can be specified. The randomization plan is not affected by the order in which the treatments are entered or the particular boxes left blank if not all are needed. The program begins by sorting treatment names internally. The sorting is case sensitive, however, so the same capitalization should be used when recreating an earlier plan. Example of 10 patients allocating to two groups (each with 5 patients), first the enter the treatment labels in the boxes, and enter the total number of patients that is 10 in the tab “Number of subjects per block” and enter the 1 in the tab “Number of blocks” for simple randomization or more than one for Block randomization. The output of this online software is presented as follows.

The benefits of randomization are numerous. It ensures against the accidental bias in the experiment and produces comparable groups in all the respect except the intervention each group received. The purpose of this paper is to introduce the randomization, including concept and significance and to review several randomization techniques to guide the researchers and practitioners to better design their randomized clinical trials. Use of online randomization was effectively demonstrated in this article for benefit of researchers. Simple randomization works well for the large clinical trails ( n >100) and for small to moderate clinical trials ( n <100) without covariates, use of block randomization helps to achieve the balance. For small to moderate size clinical trials with several prognostic factors or covariates, the adaptive randomization method could be more useful in providing a means to achieve treatment balance.

Source of Support: Nil

Conflict of Interest: None declared.