what is variable in research and its types

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, automatically generate references for free.

• Knowledge Base
• Methodology
• Types of Variables in Research | Definitions & Examples

Types of Variables in Research | Definitions & Examples

Published on 19 September 2022 by Rebecca Bevans . Revised on 28 November 2022.

In statistical research, a variable is defined as an attribute of an object of study. Choosing which variables to measure is central to good experimental design .

You need to know which types of variables you are working with in order to choose appropriate statistical tests and interpret the results of your study.

You can usually identify the type of variable by asking two questions:

• What type of data does the variable contain?
• What part of the experiment does the variable represent?

Table of contents

Types of data: quantitative vs categorical variables, parts of the experiment: independent vs dependent variables, other common types of variables, frequently asked questions about variables.

Data is a specific measurement of a variable – it is the value you record in your data sheet. Data is generally divided into two categories:

• Quantitative data represents amounts.
• Categorical data represents groupings.

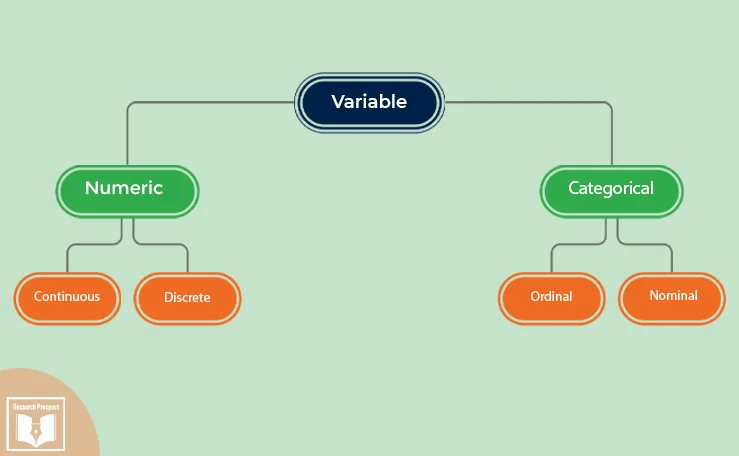
A variable that contains quantitative data is a quantitative variable ; a variable that contains categorical data is a categorical variable . Each of these types of variable can be broken down into further types.

Quantitative variables

When you collect quantitative data, the numbers you record represent real amounts that can be added, subtracted, divided, etc. There are two types of quantitative variables: discrete and continuous .

Categorical variables

Categorical variables represent groupings of some kind. They are sometimes recorded as numbers, but the numbers represent categories rather than actual amounts of things.

There are three types of categorical variables: binary , nominal , and ordinal variables.

*Note that sometimes a variable can work as more than one type! An ordinal variable can also be used as a quantitative variable if the scale is numeric and doesn’t need to be kept as discrete integers. For example, star ratings on product reviews are ordinal (1 to 5 stars), but the average star rating is quantitative.

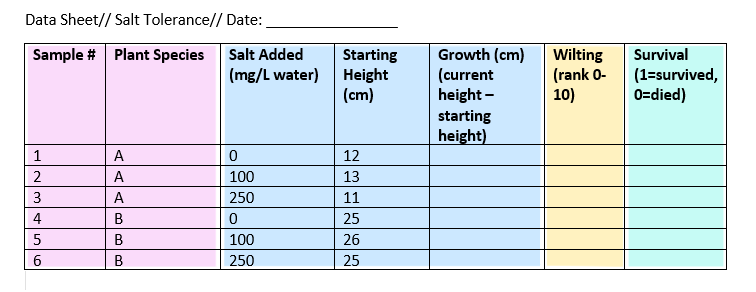
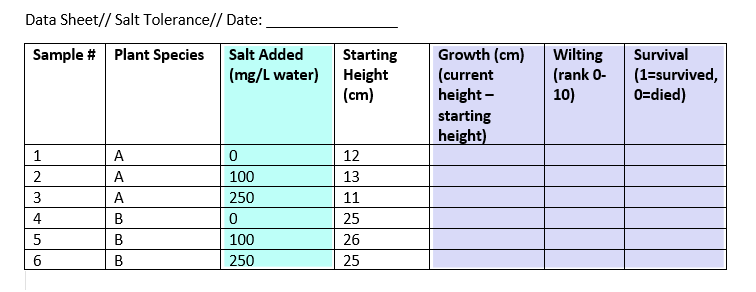
Example data sheet

To keep track of your salt-tolerance experiment, you make a data sheet where you record information about the variables in the experiment, like salt addition and plant health.

To gather information about plant responses over time, you can fill out the same data sheet every few days until the end of the experiment. This example sheet is colour-coded according to the type of variable: nominal , continuous , ordinal , and binary .

Prevent plagiarism, run a free check.

Experiments are usually designed to find out what effect one variable has on another – in our example, the effect of salt addition on plant growth.

You manipulate the independent variable (the one you think might be the cause ) and then measure the dependent variable (the one you think might be the effect ) to find out what this effect might be.

You will probably also have variables that you hold constant ( control variables ) in order to focus on your experimental treatment.

In this experiment, we have one independent and three dependent variables.

The other variables in the sheet can’t be classified as independent or dependent, but they do contain data that you will need in order to interpret your dependent and independent variables.

What about correlational research?

When you do correlational research , the terms ‘dependent’ and ‘independent’ don’t apply, because you are not trying to establish a cause-and-effect relationship.

However, there might be cases where one variable clearly precedes the other (for example, rainfall leads to mud, rather than the other way around). In these cases, you may call the preceding variable (i.e., the rainfall) the predictor variable and the following variable (i.e., the mud) the outcome variable .

Once you have defined your independent and dependent variables and determined whether they are categorical or quantitative, you will be able to choose the correct statistical test .

But there are many other ways of describing variables that help with interpreting your results. Some useful types of variable are listed below.

A confounding variable is closely related to both the independent and dependent variables in a study. An independent variable represents the supposed cause , while the dependent variable is the supposed effect . A confounding variable is a third variable that influences both the independent and dependent variables.

Failing to account for confounding variables can cause you to wrongly estimate the relationship between your independent and dependent variables.

Discrete and continuous variables are two types of quantitative variables :

• Discrete variables represent counts (e.g., the number of objects in a collection).
• Continuous variables represent measurable amounts (e.g., water volume or weight).

You can think of independent and dependent variables in terms of cause and effect: an independent variable is the variable you think is the cause , while a dependent variable is the effect .

In an experiment, you manipulate the independent variable and measure the outcome in the dependent variable. For example, in an experiment about the effect of nutrients on crop growth:

• The  independent variable  is the amount of nutrients added to the crop field.
• The  dependent variable is the biomass of the crops at harvest time.

Defining your variables, and deciding how you will manipulate and measure them, is an important part of experimental design .

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

Bevans, R. (2022, November 28). Types of Variables in Research | Definitions & Examples. Scribbr. Retrieved 14 May 2024, from https://www.scribbr.co.uk/research-methods/variables-types/

Is this article helpful?

Rebecca Bevans

Other students also liked, a quick guide to experimental design | 5 steps & examples, quasi-experimental design | definition, types & examples, construct validity | definition, types, & examples.

Variables: Definition, Examples, Types of Variables in Research

What is a Variable?

Within the context of a research investigation, concepts are generally referred to as variables. A variable is, as the name applies, something that varies.

Examples of Variable

These are all examples of variables because each of these properties varies or differs from one individual to another.

• income and expenses,
• family size,
• country of birth,
• capital expenditure,
• class grades,
• blood pressure readings,
• preoperative anxiety levels,
• eye color, and
• vehicle type.

What is Variable in Research?

A variable is any property, characteristic, number, or quantity that increases or decreases over time or can take on different values (as opposed to constants, such as n , that do not vary) in different situations.

When conducting research, experiments often manipulate variables. For example, an experimenter might compare the effectiveness of four types of fertilizers.

In this case, the variable is the ‘type of fertilizers.’ A social scientist may examine the possible effect of early marriage on divorce. Her early marriage is variable.

A business researcher may find it useful to include the dividend in determining the share prices . Here, the dividend is the variable.

Effectiveness, divorce, and share prices are variables because they also vary due to manipulating fertilizers, early marriage, and dividends.

11 Types of Variables in Research

Qualitative variables.

An important distinction between variables is the qualitative and quantitative variables.

Qualitative variables are those that express a qualitative attribute, such as hair color, religion, race, gender, social status, method of payment, and so on. The values of a qualitative variable do not imply a meaningful numerical ordering.

The value of the variable ‘religion’ (Muslim, Hindu.., etc..) differs qualitatively; no ordering of religion is implied. Qualitative variables are sometimes referred to as categorical variables.

For example, the variable sex has two distinct categories: ‘male’ and ‘female.’ Since the values of this variable are expressed in categories, we refer to this as a categorical variable.

Similarly, the place of residence may be categorized as urban and rural and thus is a categorical variable.

Categorical variables may again be described as nominal and ordinal.

Ordinal variables can be logically ordered or ranked higher or lower than another but do not necessarily establish a numeric difference between each category, such as examination grades (A+, A, B+, etc., and clothing size (Extra large, large, medium, small).

Nominal variables are those that can neither be ranked nor logically ordered, such as religion, sex, etc.

A qualitative variable is a characteristic that is not capable of being measured but can be categorized as possessing or not possessing some characteristics.

Quantitative Variables

Quantitative variables, also called numeric variables, are those variables that are measured in terms of numbers. A simple example of a quantitative variable is a person’s age.

Age can take on different values because a person can be 20 years old, 35 years old, and so on. Likewise, family size is a quantitative variable because a family might be comprised of one, two, or three members, and so on.

Each of these properties or characteristics referred to above varies or differs from one individual to another. Note that these variables are expressed in numbers, for which we call quantitative or sometimes numeric variables.

A quantitative variable is one for which the resulting observations are numeric and thus possess a natural ordering or ranking.

Discrete and Continuous Variables

Quantitative variables are again of two types: discrete and continuous.

Variables such as some children in a household or the number of defective items in a box are discrete variables since the possible scores are discrete on the scale.

For example, a household could have three or five children, but not 4.52 children.

Other variables, such as ‘time required to complete an MCQ test’ and ‘waiting time in a queue in front of a bank counter,’ are continuous variables.

The time required in the above examples is a continuous variable, which could be, for example, 1.65 minutes or 1.6584795214 minutes.

Of course, the practicalities of measurement preclude most measured variables from being continuous.

Discrete Variable

A discrete variable, restricted to certain values, usually (but not necessarily) consists of whole numbers, such as the family size and a number of defective items in a box. They are often the results of enumeration or counting.

A few more examples are;

• The number of accidents in the twelve months.
• The number of mobile cards sold in a store within seven days.
• The number of patients admitted to a hospital over a specified period.
• The number of new branches of a bank opened annually during 2001- 2007.
• The number of weekly visits made by health personnel in the last 12 months.

Continuous Variable

A continuous variable may take on an infinite number of intermediate values along a specified interval. Examples are:

• The sugar level in the human body;
• Blood pressure reading;
• Temperature;
• Height or weight of the human body;
• Rate of bank interest;
• Internal rate of return (IRR),
• Earning ratio (ER);
• Current ratio (CR)

No matter how close two observations might be, if the instrument of measurement is precise enough, a third observation can be found, falling between the first two.

A continuous variable generally results from measurement and can assume countless values in the specified range.

Dependent Variables and Independent Variable

In many research settings, two specific classes of variables need to be distinguished from one another: independent variable and dependent variable.

Many research studies aim to reveal and understand the causes of underlying phenomena or problems with the ultimate goal of establishing a causal relationship between them.

Look at the following statements:

• Low intake of food causes underweight.
• Smoking enhances the risk of lung cancer.
• Level of education influences job satisfaction.
• Advertisement helps in sales promotion.
• The drug causes improvement of health problems.
• Nursing intervention causes more rapid recovery.
• Previous job experiences determine the initial salary.
• Blueberries slow down aging.
• The dividend per share determines share prices.

In each of the above queries, we have two independent and dependent variables. In the first example, ‘low intake of food’ is believed to have caused the ‘problem of being underweight.’

It is thus the so-called independent variable. Underweight is the dependent variable because we believe this ‘problem’ (the problem of being underweight) has been caused by ‘the low intake of food’ (the factor).

Similarly, smoking, dividend, and advertisement are all independent variables, and lung cancer, job satisfaction, and sales are dependent variables.

In general, an independent variable is manipulated by the experimenter or researcher, and its effects on the dependent variable are measured.

Independent Variable

The variable that is used to describe or measure the factor that is assumed to cause or at least to influence the problem or outcome is called an independent variable.

The definition implies that the experimenter uses the independent variable to describe or explain its influence or effect of it on the dependent variable.

Variability in the dependent variable is presumed to depend on variability in the independent variable.

Depending on the context, an independent variable is sometimes called a predictor variable, regressor, controlled variable, manipulated variable, explanatory variable, exposure variable (as used in reliability theory), risk factor (as used in medical statistics), feature (as used in machine learning and pattern recognition) or input variable.

The explanatory variable is preferred by some authors over the independent variable when the quantities treated as independent variables may not be statistically independent or independently manipulable by the researcher.

If the independent variable is referred to as an explanatory variable, then the term response variable is preferred by some authors for the dependent variable.

Dependent Variable

The variable used to describe or measure the problem or outcome under study is called a dependent variable.

In a causal relationship, the cause is the independent variable, and the effect is the dependent variable. If we hypothesize that smoking causes lung cancer, ‘smoking’ is the independent variable and cancer the dependent variable.

A business researcher may find it useful to include the dividend in determining the share prices. Here dividend is the independent variable, while the share price is the dependent variable.

The dependent variable usually is the variable the researcher is interested in understanding, explaining, or predicting.

In lung cancer research, the carcinoma is of real interest to the researcher, not smoking behavior per se. The independent variable is the presumed cause of, antecedent to, or influence on the dependent variable.

Depending on the context, a dependent variable is sometimes called a response variable, regressand, predicted variable, measured variable, explained variable, experimental variable, responding variable, outcome variable, output variable, or label.

An explained variable is preferred by some authors over the dependent variable when the quantities treated as dependent variables may not be statistically dependent.

If the dependent variable is referred to as an explained variable, then the term predictor variable is preferred by some authors for the independent variable.

Levels of an Independent Variable

If an experimenter compares an experimental treatment with a control treatment, then the independent variable (a type of treatment) has two levels: experimental and control.

If an experiment were to compare five types of diets, then the independent variables (types of diet) would have five levels.

In general, the number of levels of an independent variable is the number of experimental conditions.

Background Variable

In almost every study, we collect information such as age, sex, educational attainment, socioeconomic status, marital status, religion, place of birth, and the like. These variables are referred to as background variables.

These variables are often related to many independent variables, so they indirectly influence the problem. Hence they are called background variables.

The background variables should be measured if they are important to the study. However, we should try to keep the number of background variables as few as possible in the interest of the economy.

Moderating Variable

In any statement of relationships of variables, it is normally hypothesized that in some way, the independent variable ’causes’ the dependent variable to occur.

In simple relationships, all other variables are extraneous and are ignored.

In actual study situations, such a simple one-to-one relationship needs to be revised to take other variables into account to explain the relationship better.

This emphasizes the need to consider a second independent variable that is expected to have a significant contributory or contingent effect on the originally stated dependent-independent relationship.

Such a variable is termed a moderating variable.

Suppose you are studying the impact of field-based and classroom-based training on the work performance of health and family planning workers. You consider the type of training as the independent variable.

If you are focusing on the relationship between the age of the trainees and work performance, you might use ‘type of training’ as a moderating variable.

Extraneous Variable

Most studies concern the identification of a single independent variable and measuring its effect on the dependent variable.

But still, several variables might conceivably affect our hypothesized independent-dependent variable relationship, thereby distorting the study. These variables are referred to as extraneous variables.

Extraneous variables are not necessarily part of the study. They exert a confounding effect on the dependent-independent relationship and thus need to be eliminated or controlled for.

An example may illustrate the concept of extraneous variables. Suppose we are interested in examining the relationship between the work status of mothers and breastfeeding duration.

It is not unreasonable in this instance to presume that the level of education of mothers as it influences work status might have an impact on breastfeeding duration too.

Education is treated here as an extraneous variable. In any attempt to eliminate or control the effect of this variable, we may consider this variable a confounding variable.

An appropriate way of dealing with confounding variables is to follow the stratification procedure, which involves a separate analysis of the different levels of lies in confounding variables.

For this purpose, one can construct two cross­tables for illiterate mothers and the other for literate mothers.

Suppose we find a similar association between work status and duration of breast­feeding in both the groups of mothers. In that case, we conclude that mothers’ educational level is not a confounding variable.

Intervening Variable

Often an apparent relationship between two variables is caused by a third variable.

For example, variables X and Y may be highly correlated, but only because X causes the third variable, Z, which in turn causes Y. In this case, Z is the intervening variable.

An intervening variable theoretically affects the observed phenomena but cannot be seen, measured, or manipulated directly; its effects can only be inferred from the effects of the independent and moderating variables on the observed phenomena.

We might view motivation or counseling as the intervening variable in the work-status and breastfeeding relationship.

Thus, motive, job satisfaction, responsibility, behavior, and justice are some of the examples of intervening variables.

Suppressor Variable

In many cases, we have good reasons to believe that the variables of interest have a relationship, but our data fail to establish any such relationship. Some hidden factors may suppress the true relationship between the two original variables.

Such a factor is referred to as a suppressor variable because it suppresses the relationship between the other two variables.

The suppressor variable suppresses the relationship by being positively correlated with one of the variables in the relationship and negatively correlated with the other. The true relationship between the two variables will reappear when the suppressor variable is controlled for.

Thus, for example, low age may pull education up but income down. In contrast, a high age may pull income up but education down, effectively canceling the relationship between education and income unless age is controlled for.

4 Relationships Between Variables

In dealing with relationships between variables in research, we observe a variety of dimensions in these relationships.

Positive and Negative Relationship

Symmetrical relationship, causal relationship, linear and non-linear relationship.

Two or more variables may have a positive, negative, or no relationship. In the case of two variables, a positive relationship is one in which both variables vary in the same direction.

However, they are said to have a negative relationship when they vary in opposite directions.

When a change in the other variable does not accompany the change or movement of one variable, we say that the variables in question are unrelated.

For example, if an increase in wage rate accompanies one’s job experience, the relationship between job experience and the wage rate is positive.

If an increase in an individual’s education level decreases his desire for additional children, the relationship is negative or inverse.

If the level of education does not have any bearing on the desire, we say that the variables’ desire for additional children and ‘education’ are unrelated.

Strength of Relationship

Once it has been established that two variables are related, we want to ascertain how strongly they are related.

A common statistic to measure the strength of a relationship is the so-called correlation coefficient symbolized by r. r is a unit-free measure, lying between -1 and +1 inclusive, with zero signifying no linear relationship.

As far as the prediction of one variable from the knowledge of the other variable is concerned, a value of r= +1 means a 100% accuracy in predicting a positive relationship between the two variables, and a value of r = -1 means a 100% accuracy in predicting a negative relationship between the two variables.

So far, we have discussed only symmetrical relationships in which a change in the other variable accompanies a change in either variable.

This relationship does not indicate which variable is the independent variable and which variable is the dependent variable.

In other words, you can label either of the variables as the independent variable.

Such a relationship is a symmetrical  relationship. In an asymmetrical relationship, a change in variable X (say) is accompanied by a change in variable Y, but not vice versa.

The amount of rainfall, for example, will increase productivity, but productivity will not affect the rainfall. This is an asymmetrical relationship.

Similarly, the relationship between smoking and lung cancer would be asymmetrical because smoking could cause cancer, but lung cancer could not cause smoking.

Indicating a relationship between two variables does not automatically ensure that changes in one variable cause changes in another.

It is, however, very difficult to establish the existence of causality between variables. While no one can ever be certain that variable A causes variable B , one can gather some evidence that increases our belief that A leads to B.

In an attempt to do so, we seek the following evidence:

• Is there a relationship between A and B?  When such evidence exists, it indicates a possible causal link between the variables.
• Is the relationship asymmetrical so that a change in A results in B but not vice-versa? In other words, does A occur before B? If we find that B occurs before A, we can have little confidence that A causes.
• Does a change in A result in a change in B regardless of the actions of other factors? Or, is it possible to eliminate other possible causes of B? Can one determine that C, D, and E (say) do not co-vary with B in a way that suggests possible causal connections?

A linear relationship is a straight-line relationship between two variables, where the variables vary at the same rate regardless of whether the values are low, high, or intermediate.

This is in contrast with the non-linear (or curvilinear) relationships, where the rate at which one variable changes in value may differ for different values of the second variable.

Whether a variable is linearly related to the other variable or not can simply be ascertained by plotting the K values against X values.

If the values, when plotted, appear to lie on a straight line, the existence of a linear relationship between X and Y is suggested.

Height and weight almost always have an approximately linear relationship, while age and fertility rates have a non-linear relationship.

Frequently Asked Questions about Variable

What is a variable within the context of a research investigation.

A variable, within the context of a research investigation, refers to concepts that vary. It can be any property, characteristic, number, or quantity that can increase or decrease over time or take on different values.

How is a variable used in research?

In research, a variable is any property or characteristic that can take on different values. Experiments often manipulate variables to compare outcomes. For instance, an experimenter might compare the effectiveness of different types of fertilizers, where the variable is the ‘type of fertilizers.’

What distinguishes qualitative variables from quantitative variables?

Qualitative variables express a qualitative attribute, such as hair color or religion, and do not imply a meaningful numerical ordering. Quantitative variables, on the other hand, are measured in terms of numbers, like a person’s age or family size.

How do discrete and continuous variables differ in terms of quantitative variables?

Discrete variables are restricted to certain values, often whole numbers, resulting from enumeration or counting, like the number of children in a household. Continuous variables can take on an infinite number of intermediate values along a specified interval, such as the time required to complete a test.

What are the roles of independent and dependent variables in research?

In research, the independent variable is manipulated by the researcher to observe its effects on the dependent variable. The independent variable is the presumed cause or influence, while the dependent variable is the outcome or effect that is being measured.

What is a background variable in a study?

Background variables are information collected in a study, such as age, sex, or educational attainment. These variables are often related to many independent variables and indirectly influence the main problem or outcome, hence they are termed background variables.

How does a suppressor variable affect the relationship between two other variables?

A suppressor variable can suppress or hide the true relationship between two other variables. It does this by being positively correlated with one of the variables and negatively correlated with the other. When the suppressor variable is controlled for, the true relationship between the two original variables can be observed.

Variables in Research | Types, Definiton & Examples

Introduction

What is a variable, what are the 5 types of variables in research, other variables in research.

Variables are fundamental components of research that allow for the measurement and analysis of data. They can be defined as characteristics or properties that can take on different values. In research design , understanding the types of variables and their roles is crucial for developing hypotheses , designing methods , and interpreting results .

This article outlines the the types of variables in research, including their definitions and examples, to provide a clear understanding of their use and significance in research studies. By categorizing variables into distinct groups based on their roles in research, their types of data, and their relationships with other variables, researchers can more effectively structure their studies and achieve more accurate conclusions.

A variable represents any characteristic, number, or quantity that can be measured or quantified. The term encompasses anything that can vary or change, ranging from simple concepts like age and height to more complex ones like satisfaction levels or economic status. Variables are essential in research as they are the foundational elements that researchers manipulate, measure, or control to gain insights into relationships, causes, and effects within their studies. They enable the framing of research questions, the formulation of hypotheses, and the interpretation of results.

Variables can be categorized based on their role in the study (such as independent and dependent variables ), the type of data they represent (quantitative or categorical), and their relationship to other variables (like confounding or control variables). Understanding what constitutes a variable and the various variable types available is a critical step in designing robust and meaningful research.

ATLAS.ti makes complex data easy to understand

Turn to our powerful data analysis tools to make the most of your research. Get started with a free trial.

Variables are crucial components in research, serving as the foundation for data collection , analysis , and interpretation . They are attributes or characteristics that can vary among subjects or over time, and understanding their types is essential for any study. Variables can be broadly classified into five main types, each with its distinct characteristics and roles within research.

This classification helps researchers in designing their studies, choosing appropriate measurement techniques, and analyzing their results accurately. The five types of variables include independent variables, dependent variables, categorical variables, continuous variables, and confounding variables. These categories not only facilitate a clearer understanding of the data but also guide the formulation of hypotheses and research methodologies.

Independent variables

Independent variables are foundational to the structure of research, serving as the factors or conditions that researchers manipulate or vary to observe their effects on dependent variables. These variables are considered "independent" because their variation does not depend on other variables within the study. Instead, they are the cause or stimulus that directly influences the outcomes being measured. For example, in an experiment to assess the effectiveness of a new teaching method on student performance, the teaching method applied (traditional vs. innovative) would be the independent variable.

The selection of an independent variable is a critical step in research design, as it directly correlates with the study's objective to determine causality or association. Researchers must clearly define and control these variables to ensure that observed changes in the dependent variable can be attributed to variations in the independent variable, thereby affirming the reliability of the results. In experimental research, the independent variable is what differentiates the control group from the experimental group, thereby setting the stage for meaningful comparison and analysis.

Dependent variables

Dependent variables are the outcomes or effects that researchers aim to explore and understand in their studies. These variables are called "dependent" because their values depend on the changes or variations of the independent variables.

Essentially, they are the responses or results that are measured to assess the impact of the independent variable's manipulation. For instance, in a study investigating the effect of exercise on weight loss, the amount of weight lost would be considered the dependent variable, as it depends on the exercise regimen (the independent variable).

The identification and measurement of the dependent variable are crucial for testing the hypothesis and drawing conclusions from the research. It allows researchers to quantify the effect of the independent variable , providing evidence for causal relationships or associations. In experimental settings, the dependent variable is what is being tested and measured across different groups or conditions, enabling researchers to assess the efficacy or impact of the independent variable's variation.

To ensure accuracy and reliability, the dependent variable must be defined clearly and measured consistently across all participants or observations. This consistency helps in reducing measurement errors and increases the validity of the research findings. By carefully analyzing the dependent variables, researchers can derive meaningful insights from their studies, contributing to the broader knowledge in their field.

Categorical variables

Categorical variables, also known as qualitative variables, represent types or categories that are used to group observations. These variables divide data into distinct groups or categories that lack a numerical value but hold significant meaning in research. Examples of categorical variables include gender (male, female, other), type of vehicle (car, truck, motorcycle), or marital status (single, married, divorced). These categories help researchers organize data into groups for comparison and analysis.

Categorical variables can be further classified into two subtypes: nominal and ordinal. Nominal variables are categories without any inherent order or ranking among them, such as blood type or ethnicity. Ordinal variables, on the other hand, imply a sort of ranking or order among the categories, like levels of satisfaction (high, medium, low) or education level (high school, bachelor's, master's, doctorate).

Understanding and identifying categorical variables is crucial in research as it influences the choice of statistical analysis methods. Since these variables represent categories without numerical significance, researchers employ specific statistical tests designed for a nominal or ordinal variable to draw meaningful conclusions. Properly classifying and analyzing categorical variables allow for the exploration of relationships between different groups within the study, shedding light on patterns and trends that might not be evident with numerical data alone.

Continuous variables

Continuous variables are quantitative variables that can take an infinite number of values within a given range. These variables are measured along a continuum and can represent very precise measurements. Examples of continuous variables include height, weight, temperature, and time. Because they can assume any value within a range, continuous variables allow for detailed analysis and a high degree of accuracy in research findings.

The ability to measure continuous variables at very fine scales makes them invaluable for many types of research, particularly in the natural and social sciences. For instance, in a study examining the effect of temperature on plant growth, temperature would be considered a continuous variable since it can vary across a wide spectrum and be measured to several decimal places.

When dealing with continuous variables, researchers often use methods incorporating a particular statistical test to accommodate a wide range of data points and the potential for infinite divisibility. This includes various forms of regression analysis, correlation, and other techniques suited for modeling and analyzing nuanced relationships between variables. The precision of continuous variables enhances the researcher's ability to detect patterns, trends, and causal relationships within the data, contributing to more robust and detailed conclusions.

Confounding variables

Confounding variables are those that can cause a false association between the independent and dependent variables, potentially leading to incorrect conclusions about the relationship being studied. These are extraneous variables that were not considered in the study design but can influence both the supposed cause and effect, creating a misleading correlation.

Identifying and controlling for a confounding variable is crucial in research to ensure the validity of the findings. This can be achieved through various methods, including randomization, stratification, and statistical control. Randomization helps to evenly distribute confounding variables across study groups, reducing their potential impact. Stratification involves analyzing the data within strata or layers that share common characteristics of the confounder. Statistical control allows researchers to adjust for the effects of confounders in the analysis phase.

Properly addressing confounding variables strengthens the credibility of research outcomes by clarifying the direct relationship between the dependent and independent variables, thus providing more accurate and reliable results.

Beyond the primary categories of variables commonly discussed in research methodology , there exists a diverse range of other variables that play significant roles in the design and analysis of studies. Below is an overview of some of these variables, highlighting their definitions and roles within research studies:

• Discrete variables : A discrete variable is a quantitative variable that represents quantitative data , such as the number of children in a family or the number of cars in a parking lot. Discrete variables can only take on specific values.
• Categorical variables : A categorical variable categorizes subjects or items into groups that do not have a natural numerical order. Categorical data includes nominal variables, like country of origin, and ordinal variables, such as education level.
• Predictor variables : Often used in statistical models, a predictor variable is used to forecast or predict the outcomes of other variables, not necessarily with a causal implication.
• Outcome variables : These variables represent the results or outcomes that researchers aim to explain or predict through their studies. An outcome variable is central to understanding the effects of predictor variables.
• Latent variables : Not directly observable, latent variables are inferred from other, directly measured variables. Examples include psychological constructs like intelligence or socioeconomic status.
• Composite variables : Created by combining multiple variables, composite variables can measure a concept more reliably or simplify the analysis. An example would be a composite happiness index derived from several survey questions .
• Preceding variables : These variables come before other variables in time or sequence, potentially influencing subsequent outcomes. A preceding variable is crucial in longitudinal studies to determine causality or sequences of events.

Master qualitative research with ATLAS.ti

Turn data into critical insights with our data analysis platform. Try out a free trial today.

• How it works

Types of Variables – A Comprehensive Guide

Published by Carmen Troy at August 14th, 2021 , Revised On October 26, 2023

A variable is any qualitative or quantitative characteristic that can change and have more than one value, such as age, height, weight, gender, etc.

Before conducting research, it’s essential to know what needs to be measured or analysed and choose a suitable statistical test to present your study’s findings. 

In most cases, you can do it by identifying the key issues/variables related to your research’s main topic.

Example:  If you want to test whether the hybridisation of plants harms the health of people. You can use the key variables like agricultural techniques, type of soil, environmental factors, types of pesticides used, the process of hybridisation, type of yield obtained after hybridisation, type of yield without hybridisation, etc.

Variables are broadly categorised into:

• Independent variables
• Dependent variable
• Control variable

Independent Vs. Dependent Vs. Control Variable

The research includes finding ways:

• To change the independent variables.
• To prevent the controlled variables from changing.
• To measure the dependent variables.

Note:  The term dependent and independent is not applicable in  correlational research  as this is not a  controlled experiment.  A researcher doesn’t have control over the variables. The association and between two or more variables are measured. If one variable affects another one, then it’s called the predictor variable and outcome variable.

Example:  Correlation between investment (predictor variable) and profit (outcome variable)

What data collection best suits your research?

• Find out by hiring an expert from ResearchProspect today!
• Despite how challenging the subject may be, we are here to help you.

Types of Variables Based on the Types of Data

A data is referred to as the information and statistics gathered for analysis of a research topic. Data is broadly divided into two categories, such as:

Quantitative/Numerical data  is associated with the aspects of measurement, quantity, and extent. 

Categorial data  is associated with groupings.

A qualitative variable consists of qualitative data, and a quantitative variable consists of a quantitative variable.

Quantitative Variable

The quantitative variable is associated with measurement, quantity, and extent, like how many . It follows the statistical, mathematical, and computational techniques in numerical data such as percentages and statistics. The research is conducted on a large group of population.

Example:  Find out the weight of students of the fifth standard studying in government schools.

The quantitative variable can be further categorised into continuous and discrete.

Categorial Variable

The categorical variable includes measurements that vary in categories such as names but not in terms of rank or degree. It means one level of a categorical variable cannot be considered better or greater than another level. 

Example: Gender, brands, colors, zip codes

The categorical variable is further categorised into three types:

Note:  Sometimes, an ordinal variable also acts as a quantitative variable. Ordinal data has an order, but the intervals between scale points may be uneven.

Example: Numbers on a rating scale represent the reviews’ rank or range from below average to above average. However, it also represents a quantitative variable showing how many stars and how much rating is given.

Not sure which statistical tests to use for your data?

Let the experts at researchprospect do the daunting work for you..

Using our approach, we illustrate how to collect data, sample sizes, validity, reliability, credibility, and ethics, so you won’t have to do it all by yourself!

Other Types of Variables

It’s important to understand the difference between dependent and independent variables and know whether they are quantitative or categorical to choose the appropriate statistical test.

There are many other types of variables to help you differentiate and understand them.

Also, read a comprehensive guide written about inductive and deductive reasoning .

• Entertainment
• Online education
• Database management, storage, and retrieval

Frequently Asked Questions

What are the 10 types of variables in research.

The 10 types of variables in research are:

• Independent
• Confounding
• Categorical
• Extraneous.

What is an independent variable?

An independent variable, often termed the predictor or explanatory variable, is the variable manipulated or categorized in an experiment to observe its effect on another variable, called the dependent variable. It’s the presumed cause in a cause-and-effect relationship, determining if changes in it produce changes in the observed outcome.

What is a variable?

In research, a variable is any attribute, quantity, or characteristic that can be measured or counted. It can take on various values, making it “variable.” Variables can be classified as independent (manipulated), dependent (observed outcome), or control (kept constant). They form the foundation for hypotheses, observations, and data analysis in studies.

What is a dependent variable?

A dependent variable is the outcome or response being studied in an experiment or investigation. It’s what researchers measure to determine the effect of changes in the independent variable. In a cause-and-effect relationship, the dependent variable is presumed to be influenced or caused by the independent variable.

What is a variable in programming?

In programming, a variable is a symbolic name for a storage location that holds data or values. It allows data storage and retrieval for computational operations. Variables have types, like integer or string, determining the nature of data they can hold. They’re fundamental in manipulating and processing information in software.

What is a control variable?

A control variable in research is a factor that’s kept constant to ensure that it doesn’t influence the outcome. By controlling these variables, researchers can isolate the effects of the independent variable on the dependent variable, ensuring that other factors don’t skew the results or introduce bias into the experiment.

What is a controlled variable in science?

In science, a controlled variable is a factor that remains constant throughout an experiment. It ensures that any observed changes in the dependent variable are solely due to the independent variable, not other factors. By keeping controlled variables consistent, researchers can maintain experiment validity and accurately assess cause-and-effect relationships.

How many independent variables should an investigation have?

Ideally, an investigation should have one independent variable to clearly establish cause-and-effect relationships. Manipulating multiple independent variables simultaneously can complicate data interpretation.

However, in advanced research, experiments with multiple independent variables (factorial designs) are used, but they require careful planning to understand interactions between variables.

You May Also Like

This article provides the key advantages of primary research over secondary research so you can make an informed decision.

The authenticity of dissertation is largely influenced by the research method employed. Here we present the most notable research methods for dissertation.

A meta-analysis is a formal, epidemiological, quantitative study design that uses statistical methods to generalise the findings of the selected independent studies.

USEFUL LINKS

LEARNING RESOURCES

COMPANY DETAILS

• How It Works

Types of Variable

All experiments examine some kind of variable(s). A variable is not only something that we measure, but also something that we can manipulate and something we can control for. To understand the characteristics of variables and how we use them in research, this guide is divided into three main sections. First, we illustrate the role of dependent and independent variables. Second, we discuss the difference between experimental and non-experimental research. Finally, we explain how variables can be characterised as either categorical or continuous.

Dependent and Independent Variables

An independent variable, sometimes called an experimental or predictor variable, is a variable that is being manipulated in an experiment in order to observe the effect on a dependent variable, sometimes called an outcome variable.

Imagine that a tutor asks 100 students to complete a maths test. The tutor wants to know why some students perform better than others. Whilst the tutor does not know the answer to this, she thinks that it might be because of two reasons: (1) some students spend more time revising for their test; and (2) some students are naturally more intelligent than others. As such, the tutor decides to investigate the effect of revision time and intelligence on the test performance of the 100 students. The dependent and independent variables for the study are:

Dependent Variable: Test Mark (measured from 0 to 100)

Independent Variables: Revision time (measured in hours) Intelligence (measured using IQ score)

The dependent variable is simply that, a variable that is dependent on an independent variable(s). For example, in our case the test mark that a student achieves is dependent on revision time and intelligence. Whilst revision time and intelligence (the independent variables) may (or may not) cause a change in the test mark (the dependent variable), the reverse is implausible; in other words, whilst the number of hours a student spends revising and the higher a student's IQ score may (or may not) change the test mark that a student achieves, a change in a student's test mark has no bearing on whether a student revises more or is more intelligent (this simply doesn't make sense).

Therefore, the aim of the tutor's investigation is to examine whether these independent variables - revision time and IQ - result in a change in the dependent variable, the students' test scores. However, it is also worth noting that whilst this is the main aim of the experiment, the tutor may also be interested to know if the independent variables - revision time and IQ - are also connected in some way.

In the section on experimental and non-experimental research that follows, we find out a little more about the nature of independent and dependent variables.

Experimental and Non-Experimental Research

• Experimental research : In experimental research, the aim is to manipulate an independent variable(s) and then examine the effect that this change has on a dependent variable(s). Since it is possible to manipulate the independent variable(s), experimental research has the advantage of enabling a researcher to identify a cause and effect between variables. For example, take our example of 100 students completing a maths exam where the dependent variable was the exam mark (measured from 0 to 100), and the independent variables were revision time (measured in hours) and intelligence (measured using IQ score). Here, it would be possible to use an experimental design and manipulate the revision time of the students. The tutor could divide the students into two groups, each made up of 50 students. In "group one", the tutor could ask the students not to do any revision. Alternately, "group two" could be asked to do 20 hours of revision in the two weeks prior to the test. The tutor could then compare the marks that the students achieved.
• Non-experimental research : In non-experimental research, the researcher does not manipulate the independent variable(s). This is not to say that it is impossible to do so, but it will either be impractical or unethical to do so. For example, a researcher may be interested in the effect of illegal, recreational drug use (the independent variable(s)) on certain types of behaviour (the dependent variable(s)). However, whilst possible, it would be unethical to ask individuals to take illegal drugs in order to study what effect this had on certain behaviours. As such, a researcher could ask both drug and non-drug users to complete a questionnaire that had been constructed to indicate the extent to which they exhibited certain behaviours. Whilst it is not possible to identify the cause and effect between the variables, we can still examine the association or relationship between them. In addition to understanding the difference between dependent and independent variables, and experimental and non-experimental research, it is also important to understand the different characteristics amongst variables. This is discussed next.

Categorical and Continuous Variables

Categorical variables are also known as discrete or qualitative variables. Categorical variables can be further categorized as either nominal , ordinal or dichotomous .

• Nominal variables are variables that have two or more categories, but which do not have an intrinsic order. For example, a real estate agent could classify their types of property into distinct categories such as houses, condos, co-ops or bungalows. So "type of property" is a nominal variable with 4 categories called houses, condos, co-ops and bungalows. Of note, the different categories of a nominal variable can also be referred to as groups or levels of the nominal variable. Another example of a nominal variable would be classifying where people live in the USA by state. In this case there will be many more levels of the nominal variable (50 in fact).
• Dichotomous variables are nominal variables which have only two categories or levels. For example, if we were looking at gender, we would most probably categorize somebody as either "male" or "female". This is an example of a dichotomous variable (and also a nominal variable). Another example might be if we asked a person if they owned a mobile phone. Here, we may categorise mobile phone ownership as either "Yes" or "No". In the real estate agent example, if type of property had been classified as either residential or commercial then "type of property" would be a dichotomous variable.
• Ordinal variables are variables that have two or more categories just like nominal variables only the categories can also be ordered or ranked. So if you asked someone if they liked the policies of the Democratic Party and they could answer either "Not very much", "They are OK" or "Yes, a lot" then you have an ordinal variable. Why? Because you have 3 categories, namely "Not very much", "They are OK" and "Yes, a lot" and you can rank them from the most positive (Yes, a lot), to the middle response (They are OK), to the least positive (Not very much). However, whilst we can rank the levels, we cannot place a "value" to them; we cannot say that "They are OK" is twice as positive as "Not very much" for example.

Continuous variables are also known as quantitative variables. Continuous variables can be further categorized as either interval or ratio variables.

• Interval variables are variables for which their central characteristic is that they can be measured along a continuum and they have a numerical value (for example, temperature measured in degrees Celsius or Fahrenheit). So the difference between 20°C and 30°C is the same as 30°C to 40°C. However, temperature measured in degrees Celsius or Fahrenheit is NOT a ratio variable.
• Ratio variables are interval variables, but with the added condition that 0 (zero) of the measurement indicates that there is none of that variable. So, temperature measured in degrees Celsius or Fahrenheit is not a ratio variable because 0°C does not mean there is no temperature. However, temperature measured in Kelvin is a ratio variable as 0 Kelvin (often called absolute zero) indicates that there is no temperature whatsoever. Other examples of ratio variables include height, mass, distance and many more. The name "ratio" reflects the fact that you can use the ratio of measurements. So, for example, a distance of ten metres is twice the distance of 5 metres.

Ambiguities in classifying a type of variable

In some cases, the measurement scale for data is ordinal, but the variable is treated as continuous. For example, a Likert scale that contains five values - strongly agree, agree, neither agree nor disagree, disagree, and strongly disagree - is ordinal. However, where a Likert scale contains seven or more value - strongly agree, moderately agree, agree, neither agree nor disagree, disagree, moderately disagree, and strongly disagree - the underlying scale is sometimes treated as continuous (although where you should do this is a cause of great dispute).

It is worth noting that how we categorise variables is somewhat of a choice. Whilst we categorised gender as a dichotomous variable (you are either male or female), social scientists may disagree with this, arguing that gender is a more complex variable involving more than two distinctions, but also including measurement levels like genderqueer, intersex and transgender. At the same time, some researchers would argue that a Likert scale, even with seven values, should never be treated as a continuous variable.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

Types of Variables

• Last updated
• Save as PDF
• Page ID 31273

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

CO-4: Distinguish among different measurement scales, choose the appropriate descriptive and inferential statistical methods based on these distinctions, and interpret the results.

CO-7: Use statistical software to analyze public health data.

Classifying Types of Variables

Learning objectives.

LO 4.1: Determine the type (categorical or quantitative) of a given variable.

LO 4.2: Classify a given variable as nominal, ordinal, discrete, or continuous.

Types of Variables (3 Parts; 13:25 total time)

Variables can be broadly classified into one of two types :

• Quantitative
• Categorical

Below we define these two main types of variables and provide further sub-classifications for each type.

Categorical variables take category or label values, and place an individual into one of several groups .

Categorical variables are often further classified as either:

• Nominal, when there is no natural ordering among the categories .

Common examples would be gender, eye color, or ethnicity.

• Ordinal , when there is a natural order among the categories , such as, ranking scales or letter grades.

However, ordinal variables are still categorical and do not provide precise measurements.

Differences are not precisely meaningful, for example, if one student scores an A and another a B on an assignment, we cannot say precisely the difference in their scores, only that an A is larger than a B.

Quantitative variables take numerical values, and represent some kind of measurement .

Quantitative variables are often further classified as either:

• Discrete , when the variable takes on a countable number of values.

Most often these variables indeed represent some kind of count such as the number of prescriptions an individual takes daily.

• Continuous , when the variable can take on any value in some range of values .

Our precision in measuring these variables is often limited by our instruments.

Units should be provided.

Common examples would be height (inches), weight (pounds), or time to recovery (days).

One special variable type occurs when a variable has only two possible values.

A variable is said to be Binary or Dichotomous , when there are only two possible levels.

These variables can usually be phrased in a “yes/no” question. Whether nor not someone is a smoker is an example of a binary variable.

Currently we are primarily concerned with classifying variables as either categorical or quantitative.

Sometimes, however, we will need to consider further and sub-classify these variables as defined above.

These concepts will be discussed and reviewed as needed but here is a quick practice on sub-classifying categorical and quantitative variables.

Did I Get This?

Example: medical records.

Let’s revisit the dataset showing medical records for a sample of patients

In our example of medical records, there are several variables of each type:

• Age, Weight, and Height are quantitative variables.
• Race, Gender, and Smoking are categorical variables.
• Notice that the values of the categorical variable Smoking have been coded as the numbers 0 or 1.

It is quite common to code the values of a categorical variable as numbers, but you should remember that these are just codes.

They have no arithmetic meaning (i.e., it does not make sense to add, subtract, multiply, divide, or compare the magnitude of such values).

Usually, if such a coding is used, all categorical variables will be coded and we will tend to do this type of coding for datasets in this course.

• Sometimes, quantitative variables are divided into groups for analysis, in such a situation, although the original variable was quantitative, the variable analyzed is categorical.

A common example is to provide information about an individual’s Body Mass Index by stating whether the individual is underweight, normal, overweight, or obese.

This categorized BMI is an example of an ordinal categorical variable.

• Categorical variables are sometimes called qualitative variables, but in this course we’ll use the term “categorical.”

Software Activity

LO 7.1: View a dataset in EXCEL, text editor, or other spreadsheet or statistical software.

Learn By Doing:

Exploring a Dataset using Software

Why Does the Type of Variable Matter?

The types of variables you are analyzing directly relate to the available descriptive and inferential statistical methods .

It is important to:

• assess how you will measure the effect of interest and
• know how this determines the statistical methods you can use.

As we proceed in this course, we will continually emphasize the types of variables that are appropriate for each method we discuss .

For example:

To compare the number of polio cases in the two treatment arms of the Salk Polio vaccine trial, you could use

• Fisher’s Exact Test
• Chi-Square Test

To compare blood pressures in a clinical trial evaluating two blood pressure-lowering medications, you could use

• Two-sample t-Test
• Wilcoxon Rank-Sum Test

(Optional) Great Resource: : UCLA Institute for Digital Research and Education – What statistical analysis should I use?

• USC Libraries
• Research Guides

Organizing Your Social Sciences Research Paper

• Independent and Dependent Variables
• Purpose of Guide
• Design Flaws to Avoid
• Glossary of Research Terms
• Reading Research Effectively
• Narrowing a Topic Idea
• Broadening a Topic Idea
• Extending the Timeliness of a Topic Idea
• Academic Writing Style
• Applying Critical Thinking
• Choosing a Title
• Making an Outline
• Paragraph Development
• Research Process Video Series
• Executive Summary
• The C.A.R.S. Model
• Background Information
• The Research Problem/Question
• Theoretical Framework
• Citation Tracking
• Content Alert Services
• Evaluating Sources
• Primary Sources
• Secondary Sources
• Tiertiary Sources
• Scholarly vs. Popular Publications
• Qualitative Methods
• Quantitative Methods
• Insiderness
• Using Non-Textual Elements
• Limitations of the Study
• Common Grammar Mistakes
• Writing Concisely
• Avoiding Plagiarism
• Footnotes or Endnotes?
• Further Readings
• Generative AI and Writing
• USC Libraries Tutorials and Other Guides
• Bibliography

Definitions

Dependent Variable The variable that depends on other factors that are measured. These variables are expected to change as a result of an experimental manipulation of the independent variable or variables. It is the presumed effect.

Independent Variable The variable that is stable and unaffected by the other variables you are trying to measure. It refers to the condition of an experiment that is systematically manipulated by the investigator. It is the presumed cause.

Cramer, Duncan and Dennis Howitt. The SAGE Dictionary of Statistics . London: SAGE, 2004; Penslar, Robin Levin and Joan P. Porter. Institutional Review Board Guidebook: Introduction . Washington, DC: United States Department of Health and Human Services, 2010; "What are Dependent and Independent Variables?" Graphic Tutorial.

Identifying Dependent and Independent Variables

Don't feel bad if you are confused about what is the dependent variable and what is the independent variable in social and behavioral sciences research . However, it's important that you learn the difference because framing a study using these variables is a common approach to organizing the elements of a social sciences research study in order to discover relevant and meaningful results. Specifically, it is important for these two reasons:

• You need to understand and be able to evaluate their application in other people's research.
• You need to apply them correctly in your own research.

A variable in research simply refers to a person, place, thing, or phenomenon that you are trying to measure in some way. The best way to understand the difference between a dependent and independent variable is that the meaning of each is implied by what the words tell us about the variable you are using. You can do this with a simple exercise from the website, Graphic Tutorial. Take the sentence, "The [independent variable] causes a change in [dependent variable] and it is not possible that [dependent variable] could cause a change in [independent variable]." Insert the names of variables you are using in the sentence in the way that makes the most sense. This will help you identify each type of variable. If you're still not sure, consult with your professor before you begin to write.

Fan, Shihe. "Independent Variable." In Encyclopedia of Research Design. Neil J. Salkind, editor. (Thousand Oaks, CA: SAGE, 2010), pp. 592-594; "What are Dependent and Independent Variables?" Graphic Tutorial; Salkind, Neil J. "Dependent Variable." In Encyclopedia of Research Design , Neil J. Salkind, editor. (Thousand Oaks, CA: SAGE, 2010), pp. 348-349;

Structure and Writing Style

The process of examining a research problem in the social and behavioral sciences is often framed around methods of analysis that compare, contrast, correlate, average, or integrate relationships between or among variables . Techniques include associations, sampling, random selection, and blind selection. Designation of the dependent and independent variable involves unpacking the research problem in a way that identifies a general cause and effect and classifying these variables as either independent or dependent.

The variables should be outlined in the introduction of your paper and explained in more detail in the methods section . There are no rules about the structure and style for writing about independent or dependent variables but, as with any academic writing, clarity and being succinct is most important.

After you have described the research problem and its significance in relation to prior research, explain why you have chosen to examine the problem using a method of analysis that investigates the relationships between or among independent and dependent variables . State what it is about the research problem that lends itself to this type of analysis. For example, if you are investigating the relationship between corporate environmental sustainability efforts [the independent variable] and dependent variables associated with measuring employee satisfaction at work using a survey instrument, you would first identify each variable and then provide background information about the variables. What is meant by "environmental sustainability"? Are you looking at a particular company [e.g., General Motors] or are you investigating an industry [e.g., the meat packing industry]? Why is employee satisfaction in the workplace important? How does a company make their employees aware of sustainability efforts and why would a company even care that its employees know about these efforts?

Identify each variable for the reader and define each . In the introduction, this information can be presented in a paragraph or two when you describe how you are going to study the research problem. In the methods section, you build on the literature review of prior studies about the research problem to describe in detail background about each variable, breaking each down for measurement and analysis. For example, what activities do you examine that reflect a company's commitment to environmental sustainability? Levels of employee satisfaction can be measured by a survey that asks about things like volunteerism or a desire to stay at the company for a long time.

The structure and writing style of describing the variables and their application to analyzing the research problem should be stated and unpacked in such a way that the reader obtains a clear understanding of the relationships between the variables and why they are important. This is also important so that the study can be replicated in the future using the same variables but applied in a different way.

Fan, Shihe. "Independent Variable." In Encyclopedia of Research Design. Neil J. Salkind, editor. (Thousand Oaks, CA: SAGE, 2010), pp. 592-594; "What are Dependent and Independent Variables?" Graphic Tutorial; “Case Example for Independent and Dependent Variables.” ORI Curriculum Examples. U.S. Department of Health and Human Services, Office of Research Integrity; Salkind, Neil J. "Dependent Variable." In Encyclopedia of Research Design , Neil J. Salkind, editor. (Thousand Oaks, CA: SAGE, 2010), pp. 348-349; “Independent Variables and Dependent Variables.” Karl L. Wuensch, Department of Psychology, East Carolina University [posted email exchange]; “Variables.” Elements of Research. Dr. Camille Nebeker, San Diego State University.

• << Previous: Design Flaws to Avoid
• Next: Glossary of Research Terms >>
• Last Updated: May 20, 2024 9:47 AM
• URL: https://libguides.usc.edu/writingguide

• Bipolar Disorder
• Therapy Center
• When To See a Therapist
• Types of Therapy
• Best Online Therapy
• Best Couples Therapy
• Best Family Therapy
• Managing Stress
• Sleep and Dreaming
• Understanding Emotions
• Self-Improvement
• Healthy Relationships
• Student Resources
• Personality Types
• Guided Meditations
• Verywell Mind Insights
• 2024 Verywell Mind 25
• Mental Health in the Classroom
• Editorial Process
• Meet Our Review Board
• Crisis Support

Types of Variables in Psychology Research

Examples of Independent and Dependent Variables

Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

 James Lacy, MLS, is a fact-checker and researcher.

Dependent and Independent Variables

• Intervening Variables
• Extraneous Variables
• Controlled Variables
• Confounding Variables
• Operationalizing Variables

Frequently Asked Questions

Variables in psychology are things that can be changed or altered, such as a characteristic or value. Variables are generally used in psychology experiments to determine if changes to one thing result in changes to another.

Variables in psychology play a critical role in the research process. By systematically changing some variables in an experiment and measuring what happens as a result, researchers are able to learn more about cause-and-effect relationships.

The two main types of variables in psychology are the independent variable and the dependent variable. Both variables are important in the process of collecting data about psychological phenomena.

This article discusses different types of variables that are used in psychology research. It also covers how to operationalize these variables when conducting experiments.

Students often report problems with identifying the independent and dependent variables in an experiment. While this task can become more difficult as the complexity of an experiment increases, in a psychology experiment:

• The independent variable is the variable that is manipulated by the experimenter. An example of an independent variable in psychology: In an experiment on the impact of sleep deprivation on test performance, sleep deprivation would be the independent variable. The experimenters would have some of the study participants be sleep-deprived while others would be fully rested.
• The dependent variable is the variable that is measured by the experimenter. In the previous example, the scores on the test performance measure would be the dependent variable.

So how do you differentiate between the independent and dependent variables? Start by asking yourself what the experimenter is manipulating. The things that change, either naturally or through direct manipulation from the experimenter, are generally the independent variables. What is being measured? The dependent variable is the one that the experimenter is measuring.

Intervening Variables in Psychology

Intervening variables, also sometimes called intermediate or mediator variables, are factors that play a role in the relationship between two other variables. In the previous example, sleep problems in university students are often influenced by factors such as stress. As a result, stress might be an intervening variable that plays a role in how much sleep people get, which may then influence how well they perform on exams.

Extraneous Variables in Psychology

Independent and dependent variables are not the only variables present in many experiments. In some cases, extraneous variables may also play a role. This type of variable is one that may have an impact on the relationship between the independent and dependent variables.

For example, in our previous example of an experiment on the effects of sleep deprivation on test performance, other factors such as age, gender, and academic background may have an impact on the results. In such cases, the experimenter will note the values of these extraneous variables so any impact can be controlled for.

There are two basic types of extraneous variables:

• Participant variables : These extraneous variables are related to the individual characteristics of each study participant that may impact how they respond. These factors can include background differences, mood, anxiety, intelligence, awareness, and other characteristics that are unique to each person.
• Situational variables : These extraneous variables are related to things in the environment that may impact how each participant responds. For example, if a participant is taking a test in a chilly room, the temperature would be considered an extraneous variable. Some participants may not be affected by the cold, but others might be distracted or annoyed by the temperature of the room.

Other extraneous variables include the following:

• Demand characteristics : Clues in the environment that suggest how a participant should behave
• Experimenter effects : When a researcher unintentionally suggests clues for how a participant should behave

Controlled Variables in Psychology

In many cases, extraneous variables are controlled for by the experimenter. A controlled variable is one that is held constant throughout an experiment.

In the case of participant variables, the experiment might select participants that are the same in background and temperament to ensure that these factors don't interfere with the results. Holding these variables constant is important for an experiment because it allows researchers to be sure that all other variables remain the same across all conditions.  

Using controlled variables means that when changes occur, the researchers can be sure that these changes are due to the manipulation of the independent variable and not caused by changes in other variables.

It is important to also note that a controlled variable is not the same thing as a control group . The control group in a study is the group of participants who do not receive the treatment or change in the independent variable.

All other variables between the control group and experimental group are held constant (i.e., they are controlled). The dependent variable being measured is then compared between the control group and experimental group to see what changes occurred because of the treatment.

Confounding Variables in Psychology

If a variable cannot be controlled for, it becomes what is known as a confounding variabl e. This type of variable can have an impact on the dependent variable, which can make it difficult to determine if the results are due to the influence of the independent variable, the confounding variable, or an interaction of the two.

Operationalizing Variables in Psychology

An operational definition describes how the variables are measured and defined in the study. Before conducting a psychology experiment , it is essential to create firm operational definitions for both the independent variable and dependent variables.

For example, in our imaginary experiment on the effects of sleep deprivation on test performance, we would need to create very specific operational definitions for our two variables. If our hypothesis is "Students who are sleep deprived will score significantly lower on a test," then we would have a few different concepts to define:

• Students : First, what do we mean by "students?" In our example, let’s define students as participants enrolled in an introductory university-level psychology course.
• Sleep deprivation : Next, we need to operationally define the "sleep deprivation" variable. In our example, let’s say that sleep deprivation refers to those participants who have had less than five hours of sleep the night before the test.
• Test variable : Finally, we need to create an operational definition for the test variable. For this example, the test variable will be defined as a student’s score on a chapter exam in the introductory psychology course.

Once all the variables are operationalized, we're ready to conduct the experiment.

Variables play an important part in psychology research. Manipulating an independent variable and measuring the dependent variable allows researchers to determine if there is a cause-and-effect relationship between them.

A Word From Verywell

Understanding the different types of variables used in psychology research is important if you want to conduct your own psychology experiments. It is also helpful for people who want to better understand what the results of psychology research really mean and become more informed consumers of psychology information .

Independent and dependent variables are used in experimental research. Unlike some other types of research (such as correlational studies ), experiments allow researchers to evaluate cause-and-effect relationships between two variables.

Researchers can use statistical analyses to determine the strength of a relationship between two variables in an experiment. Two of the most common ways to do this are to calculate a p-value or a correlation. The p-value indicates if the results are statistically significant while the correlation can indicate the strength of the relationship.

In an experiment on how sugar affects short-term memory, sugar intake would be the independent variable and scores on a short-term memory task would be the independent variable.

In an experiment looking at how caffeine intake affects test anxiety, the amount of caffeine consumed before a test would be the independent variable and scores on a test anxiety assessment would be the dependent variable.

Just as with other types of research, the independent variable in a cognitive psychology study would be the variable that the researchers manipulate. The specific independent variable would vary depending on the specific study, but it might be focused on some aspect of thinking, memory, attention, language, or decision-making.

American Psychological Association. Operational definition . APA Dictionary of Psychology.

American Psychological Association. Mediator . APA Dictionary of Psychology.

Altun I, Cınar N, Dede C. The contributing factors to poor sleep experiences in according to the university students: A cross-sectional study .  J Res Med Sci . 2012;17(6):557-561. PMID:23626634

Skelly AC, Dettori JR, Brodt ED. Assessing bias: The importance of considering confounding .  Evid Based Spine Care J . 2012;3(1):9-12. doi:10.1055/s-0031-1298595

• Evans, AN & Rooney, BJ. Methods in Psychological Research. Thousand Oaks, CA: SAGE Publications; 2014.
• Kantowitz, BH, Roediger, HL, & Elmes, DG. Experimental Psychology. Stamfort, CT: Cengage Learning; 2015.

By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

The Plagiarism Checker Online For Your Academic Work

Start Plagiarism Check

Editing & Proofreading for Your Research Paper

Get it proofread now

Online Printing & Binding with Free Express Delivery

Configure binding now

• Academic essay overview
• The writing process
• Structuring academic essays
• Types of academic essays
• Academic writing overview
• Sentence structure
• Academic writing process
• Improving your academic writing
• Titles and headings
• APA style overview
• APA citation & referencing
• APA structure & sections
• Citation & referencing
• Structure and sections
• APA examples overview
• Commonly used citations
• Other examples
• British English vs. American English
• Chicago style overview
• Chicago citation & referencing
• Chicago structure & sections
• Chicago style examples
• Citing sources overview
• Citation format
• Citation examples
• College essay overview
• Application
• How to write a college essay
• Types of college essays
• Commonly confused words
• Definitions
• Dissertation overview
• Dissertation structure & sections
• Dissertation writing process
• Graduate school overview
• Application & admission
• Study abroad
• Master degree
• Harvard referencing overview
• Language rules overview
• Grammatical rules & structures
• Parts of speech
• Punctuation
• Methodology overview
• Analyzing data
• Experiments
• Observations
• Inductive vs. Deductive
• Qualitative vs. Quantitative
• Types of validity
• Types of reliability
• Sampling methods
• Theories & Concepts
• Types of research studies
• Types of variables
• MLA style overview
• MLA examples
• MLA citation & referencing
• MLA structure & sections
• Plagiarism overview
• Plagiarism checker
• Types of plagiarism
• Printing production overview
• Research bias overview
• Types of research bias
• Example sections
• Types of research papers
• Research process overview
• Problem statement
• Research proposal
• Research topic
• Statistics overview
• Levels of measurment
• Frequency distribution
• Measures of central tendency
• Measures of variability
• Hypothesis testing
• Parameters & test statistics
• Types of distributions
• Correlation
• Effect size
• Hypothesis testing assumptions
• Types of ANOVAs
• Types of chi-square
• Statistical data
• Statistical models
• Spelling mistakes
• Tips overview
• Academic writing tips
• Dissertation tips
• Sources tips
• Working with sources overview
• Evaluating sources
• Finding sources
• Including sources
• Types of sources

Your Step to Success

Plagiarism Check within 10min

Printing & Binding with 3D Live Preview

Types of Variables in Research – Definition & Examples

How do you like this article cancel reply.

Save my name, email, and website in this browser for the next time I comment.

A fundamental component in statistical investigations is the methodology you employ in selecting your research variables. The careful selection of appropriate variable types can significantly enhance the robustness of your experimental design . This piece explores the diverse array of variable classifications within the field of statistical research. Additionally, understanding the different types of variables in research can greatly aid in shaping your experimental hypotheses and outcomes.

Inhaltsverzeichnis

• 1 Types of Variables in Research – In a Nutshell
• 2 Definition: Types of variables in research
• 3 Types of variables in research – Quantitative vs. Categorical
• 4 Types of variables in research – Independent vs. Dependent
• 5 Other useful types of variables in research

Types of Variables in Research – In a Nutshell

• A variable is an attribute of an item of analysis in research.
• The types of variables in research can be categorized into: independent vs. dependent , or categorical vs. quantitative .
• The types of variables in research (correlational) can be classified into predictor or outcome variables.
• Other types of variables in research are confounding variables , latent variables , and composite variables.

Definition: Types of variables in research

A variable is a trait of an item of analysis in research. Types of variables in research are imperative, as they describe and measure places, people, ideas , or other research objects . There are many types of variables in research. Therefore, you must choose the right types of variables in research for your study.

Note that the correct variable will help with your research design , test selection, and result interpretation.

In a study testing whether some genders are more stress-tolerant than others, variables you can include are the level of stressors in the study setting, male and female subjects, and productivity levels in the presence of stressors.

Also, before choosing which types of variables in research to use, you should know how the various types work and the ideal statistical tests and result interpretations you will use for your study. The key is to determine the type of data the variable contains and the part of the experiment the variable represents.

Types of variables in research – Quantitative vs. Categorical

Data is the precise extent of a variable in statistical research that you record in a data sheet. It is generally divided into quantitative and categorical classes.

Quantitative or numerical data represents amounts, while categorical data represents collections or groupings.

The type of data contained in your variable will determine the types of variables in research. For instance, variables consisting of quantitative data are called quantitative variables, while those containing categorical data are called categorical variables. The section below explains these two types of variables in research better.

Quantitative variables

The scores you record when collecting quantitative data usually represent real values you can add, divide , subtract , or multiply . There are two types of quantitative variables: discrete variables and continuous variables .

The table below explains the elements that set apart discrete and continuous types of variables in research:

Categorical variables

Categorical variables contain data representing groupings. Additionally, the data in categorical variables is sometimes recorded as numbers . However, the numbers represent categories instead of real amounts.

There are three categorical types of variables in research: nominal variables, ordinal variables , and binary variables . Here is a tabular summary.

It is worth mentioning that some categorical variables can function as multiple types. For example, in some studies, you can use ordinal variables as quantitative variables if the scales are numerical and not discrete.

Data sheet of quantitative and categorical variables

A data sheet is where you record the data on the variables in your experiment.

In a study of the salt-tolerance levels of various plant species, you can record the data on salt addition and how the plant responds in your datasheet.

The key is to gather the information and draw a conclusion over a specific period and filling out a data sheet along the process.

Below is an example of a data sheet containing binary, nominal, continuous , and ordinal types of variables in research.

Types of variables in research – Independent vs. Dependent

The purpose of experiments is to determine how the variables affect each other. As stated in our experiment above, the study aims to find out how the quantity of salt introduce in the water affects the plant’s growth and survival.

Therefore, the researcher manipulates the independent variables and measures the dependent variables . Additionally, you may have control variables that you hold constant.

The table below summarizes independent variables, dependent variables , and control variables .

Data sheet of independent and dependent variables

In salt-tolerance research, there is one independent variable (salt amount) and three independent variables. All other variables are neither dependent nor independent.

Below is a data sheet based on our experiment:

Types of variables in correlational research

The types of variables in research may differ depending on the study.

In correlational research , dependent and independent variables do not apply because the study objective is not to determine the cause-and-effect link between variables.

However, in correlational research, one variable may precede the other, as illness leads to death, and not vice versa. In such an instance, the preceding variable, like illness, is the predictor variable, while the other one is the outcome variable.

Other useful types of variables in research

The key to conducting effective research is to define your types of variables as independent and dependent. Next, you must determine if they are categorical or numerical types of variables in research so you can choose the proper statistical tests for your study.

Below are other types of variables in research worth understanding.

What is the definition for independent and dependent variables?

An autonomous or independent variable is the one you believe is the origin of the outcome, while the dependent variable is the one you believe affects the outcome of your study.

What are quantitative and categorical variables?

Knowing the types of variables in research that you can work with will help you choose the best statistical tests and result representation techniques. It will also help you with your study design.

Discrete and continuous variables: What is their difference?

Discrete variables are types of variables in research that represent counts, like the quantities of objects. In contrast, continuous variables are types of variables in research that represent measurable quantities like age, volume, and weight.

We use cookies on our website. Some of them are essential, while others help us to improve this website and your experience.

• External Media

Individual Privacy Preferences

Cookie Details Privacy Policy Imprint

Here you will find an overview of all cookies used. You can give your consent to whole categories or display further information and select certain cookies.

Accept all Save

Essential cookies enable basic functions and are necessary for the proper function of the website.

Show Cookie Information Hide Cookie Information

Statistics cookies collect information anonymously. This information helps us to understand how our visitors use our website.

Content from video platforms and social media platforms is blocked by default. If External Media cookies are accepted, access to those contents no longer requires manual consent.

Privacy Policy Imprint

Stats and R

Variable types and examples, different types of variables for different types of statistical analysis, big picture, from continuous to discrete, from quantitative to qualitative, misleading data encoding, introduction.

If you happen to work with datasets frequently, you probably know that each row of your dataset represents a different experimental unit (also called observation ) and each column represents a different characteristic (called variable ):

If you do some research on the weight and height of 100 students of your university, for example, you will most likely have a dataset containing 100 rows and 3 columns:

• one for the student’s ID (could be anonymized or not),
• one for the weight,
• and one for the height.

These three columns represent three characteristics of the 100 students. They are called variables .

In this article, we are going to focus on variables, and in particular on the different types of variable that exist in statistics. (To learn about the different data types in R, read “ Data types in R ”.)

First, one may wonder why we are interested in defining the types of our variables of interest.

The reason why we often class variables into different types is because not all statistical analyses can be performed on all variable types. For instance, it is impossible to compute the mean of the variable “hair color” as you cannot sum brown and blond hair.

On the other hand, finding the mode of a continuous variable does not really make any sense because most of the time there will not be two exact same values, so there will be no mode. And even in the case there is a mode, there will be very few observations with this value. As an example, try finding the mode of the height of the students in your class. If you are lucky, a couple of students will have the same size. However, most of the time, every student will have a different size (especially if heights have been measured in millimeters) and thus there will be no mode. To see what kind of analysis is possible on each type of variable, see more details in the articles “ Descriptive statistics by hand ” and “ Descriptive statistics in R ”.

Similarly, some statistical tests can only be performed on certain type of variables. For example, the Pearson correlation is usually computed on two quantitative variables, while a Chi-square test of independence is done with two qualitative variables, and a Student t-test or ANOVA requires a mix of one quantitative and one qualitative variable.

In statistics, variables are classified into 4 different types:

We present each type together with examples in the following sections.

Quantitative

A quantitative variable is a variable that reflects a notion of magnitude , that is, if the values it can take are numbers . A quantitative variable represents thus a measure and is numerical.

Quantitative variables are divided into two types: discrete and continuous . The difference is explained in the following two sections.

Quantitative discrete variables are variables for which the values it can take are countable and have a finite number of possibilities . The values are often (but not always) integers. Here are some examples of discrete variables:

• Number of children per family
• Number of students in a class
• Number of citizens of a country

Even if it would take a long time to count the citizens of a large country, it is still technically doable. Moreover, for all examples, the number of possibilities is finite . Whatever the number of children in a family, it will never be 3.58 or 7.912 so the number of possibilities is a finite number and thus countable.

On the other hand, quantitative continuous variables are variables for which the values are not countable and have an infinite number of possibilities . For example:

For simplicity, we usually referred to years, kilograms (or pounds) and centimeters (or feet and inches) for age, weight and height respectively. However, a 28-year-old man could actually be 28 years, 7 months, 16 days, 3 hours, 4 minutes, 5 seconds, 31 milliseconds, 9 nanoseconds old.

For all measurements, we usually stop at a standard level of granularity, but nothing (except our measurement tools) prevents us from going deeper, leading to an infinite number of potential values . The fact that the values can take an infinite number of possibilities makes it uncountable.

Qualitative

In opposition to quantitative variables, qualitative variables (also referred as categorical variables or factors in R) are variables that are not numerical and which values fit into categories .

In other words, a qualitative variable is a variable which takes as its values modalities, categories or even levels, in contrast to quantitative variables which measure a quantity on each individual.

Qualitative variables are divided into two types: nominal and ordinal .

A qualitative nominal variable is a qualitative variable where no ordering is possible or implied in the levels.

For example, the variable gender is nominal because there is no order in the levels (no matter how many levels you consider for the gender—only two with female/male, or more than two with female/male/ungendered/others, levels are un ordered). Eye color is another example of a nominal variable because there is no order among blue, brown or green eyes.

A nominal variable can have:

• two levels (e.g., do you smoke? Yes/No, or are you pregnant? Yes/No), or
• a large number of levels (what is your college major? Each major is a level in that case).

Note that a qualitative variable with exactly 2 levels is also referred as a binary or dichotomous variable.

On the other hand, a qualitative ordinal variable is a qualitative variable with an order implied in the levels . For instance, if the severity of road accidents has been measured on a scale such as light, moderate and fatal accidents, this variable is a qualitative ordinal variable because there is a clear order in the levels.

Another good example is health, which can take values such as poor, reasonable, good, or excellent. Again, there is a clear order in these levels so health is in this case a qualitative ordinal variable.

Variable transformations

There are two main variable transformations:

• From a continuous to a discrete variable
• From a quantitative to a qualitative variable

Let’s say we are interested in babies’ ages. The data collected is the age of the babies, so a quantitative continuous variable. However, we may work with only the number of weeks since birth and thus transforming the age into a discrete variable. The variable age remains a quantitative continuous variable but the variable we are working on (i.e., the number of weeks since birth) can be seen as a quantitative discrete variable.

Let’s say we are interested in the Body Mass Index (BMI). For this, a researcher collects data on height and weight of individuals and computes the BMI. The BMI is a quantitative continuous variable but the researcher may want to turn it into a qualitative variable by categorizing individuals below a certain threshold as underweighted, above a certain threshold as overweighted and the rest as normal weighted. The raw BMI is a quantitative continuous variable but the categorization of the BMI makes the transformed variable a qualitative (ordinal) variable, where the levels are in this case underweighted < normal < overweighted.

Same goes for age when age is transformed to a qualitative ordinal variable with levels such as minors, adults and seniors. It is also often the case (especially in surveys) that the variable salary (quantitative continuous) is transformed into a qualitative ordinal variable with different range of salaries (e.g., < 1000€, 1000 - 2000€, > 2000€).

Additional notes

Last but not least, in datasets it is very often the case that numbers are used for qualitative variables. For instance, a researcher may assign the number “1” to women and the number “2” to men (or “0” to the answer “No” and “1” to the answer “Yes”). Despite the numerical classification, the variable gender is still a qualitative variable and not a discrete variable as it may look. The numerical classification is only used to facilitate data collection and data management. It is indeed easier to write the number “1” or “2” instead of “women” or “men”, and thus less prone to encoding errors.

The same goes for the identification of each observation. Suppose you collected information on 100 students. You may use their student’s ID to identify them in the dataset (so that you can trace them back). Most of the time, students’ ID (or ID in general) are encoded as numeric values. At first sight, it may thus look like a quantitative variable (because it goes from 1 to 100 for example). However, ID is clearly not a quantitative variable because it actually corresponds to an anonymized version of the student’s first and last name. If you think about it, it would make no sense to compute the mean or median on the IDs, as it does not represent a numerical measurement (but rather just an easier way to identify students than with their names).

If you face this kind of setup, do not forget to transform your variable into the right type before performing any statistical analyses. Usually, a basic descriptive analysis (and knowledge about the variables which have been measured) prior to the main statistical analyses is enough to check that all variable types are correct.

Thanks for reading.

I hope this article helped you to understand the different types of variable. If you would like to learn more about the different data types in R, read the article “ Data types in R ”.

As always, if you have a question or a suggestion related to the topic covered in this article, please add it as a comment so other readers can benefit from the discussion.

Related articles

• Pearson, Spearman and Kendall correlation coefficients by hand
• How to: one-way ANOVA by hand
• One-sample Wilcoxon test in R
• What statistical test should I do?
• Hypothesis test by hand

Liked this post?

• Get updates every time a new article is published (no spam and unsubscribe anytime):

Yes, receive new posts by email

• Support the blog

Consulting FAQ Contribute Sitemap

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Indian Dermatol Online J
• v.10(1); Jan-Feb 2019

Types of Variables, Descriptive Statistics, and Sample Size

Feroze kaliyadan.

Department of Dermatology, King Faisal University, Al Hofuf, Saudi Arabia

Vinay Kulkarni

1 Department of Dermatology, Prayas Amrita Clinic, Pune, Maharashtra, India

This short “snippet” covers three important aspects related to statistics – the concept of variables , the importance, and practical aspects related to descriptive statistics and issues related to sampling – types of sampling and sample size estimation.

What is a variable?[ 1 , 2 ] To put it in very simple terms, a variable is an entity whose value varies. A variable is an essential component of any statistical data. It is a feature of a member of a given sample or population, which is unique, and can differ in quantity or quantity from another member of the same sample or population. Variables either are the primary quantities of interest or act as practical substitutes for the same. The importance of variables is that they help in operationalization of concepts for data collection. For example, if you want to do an experiment based on the severity of urticaria, one option would be to measure the severity using a scale to grade severity of itching. This becomes an operational variable. For a variable to be “good,” it needs to have some properties such as good reliability and validity, low bias, feasibility/practicality, low cost, objectivity, clarity, and acceptance. Variables can be classified into various ways as discussed below.

Quantitative vs qualitative

A variable can collect either qualitative or quantitative data. A variable differing in quantity is called a quantitative variable (e.g., weight of a group of patients), whereas a variable differing in quality is called a qualitative variable (e.g., the Fitzpatrick skin type)

A simple test which can be used to differentiate between qualitative and quantitative variables is the subtraction test. If you can subtract the value of one variable from the other to get a meaningful result, then you are dealing with a quantitative variable (this of course will not apply to rating scales/ranks).

Quantitative variables can be either discrete or continuous

Discrete variables are variables in which no values may be assumed between the two given values (e.g., number of lesions in each patient in a sample of patients with urticaria).

Continuous variables, on the other hand, can take any value in between the two given values (e.g., duration for which the weals last in the same sample of patients with urticaria). One way of differentiating between continuous and discrete variables is to use the “mid-way” test. If, for every pair of values of a variable, a value exactly mid-way between them is meaningful, the variable is continuous. For example, two values for the time taken for a weal to subside can be 10 and 13 min. The mid-way value would be 11.5 min which makes sense. However, for a number of weals, suppose you have a pair of values – 5 and 8 – the midway value would be 6.5 weals, which does not make sense.

Under the umbrella of qualitative variables, you can have nominal/categorical variables and ordinal variables

Nominal/categorical variables are, as the name suggests, variables which can be slotted into different categories (e.g., gender or type of psoriasis).

Ordinal variables or ranked variables are similar to categorical, but can be put into an order (e.g., a scale for severity of itching).

Dependent and independent variables

In the context of an experimental study, the dependent variable (also called outcome variable) is directly linked to the primary outcome of the study. For example, in a clinical trial on psoriasis, the PASI (psoriasis area severity index) would possibly be one dependent variable. The independent variable (sometime also called explanatory variable) is something which is not affected by the experiment itself but which can be manipulated to affect the dependent variable. Other terms sometimes used synonymously include blocking variable, covariate, or predictor variable. Confounding variables are extra variables, which can have an effect on the experiment. They are linked with dependent and independent variables and can cause spurious association. For example, in a clinical trial for a topical treatment in psoriasis, the concomitant use of moisturizers might be a confounding variable. A control variable is a variable that must be kept constant during the course of an experiment.

Descriptive Statistics

Statistics can be broadly divided into descriptive statistics and inferential statistics.[ 3 , 4 ] Descriptive statistics give a summary about the sample being studied without drawing any inferences based on probability theory. Even if the primary aim of a study involves inferential statistics, descriptive statistics are still used to give a general summary. When we describe the population using tools such as frequency distribution tables, percentages, and other measures of central tendency like the mean, for example, we are talking about descriptive statistics. When we use a specific statistical test (e.g., Mann–Whitney U-test) to compare the mean scores and express it in terms of statistical significance, we are talking about inferential statistics. Descriptive statistics can help in summarizing data in the form of simple quantitative measures such as percentages or means or in the form of visual summaries such as histograms and box plots.

Descriptive statistics can be used to describe a single variable (univariate analysis) or more than one variable (bivariate/multivariate analysis). In the case of more than one variable, descriptive statistics can help summarize relationships between variables using tools such as scatter plots.

Descriptive statistics can be broadly put under two categories:

• Sorting/grouping and illustration/visual displays
• Summary statistics.

Sorting and grouping

Sorting and grouping is most commonly done using frequency distribution tables. For continuous variables, it is generally better to use groups in the frequency table. Ideally, group sizes should be equal (except in extreme ends where open groups are used; e.g., age “greater than” or “less than”).

Another form of presenting frequency distributions is the “stem and leaf” diagram, which is considered to be a more accurate form of description.

Suppose the weight in kilograms of a group of 10 patients is as follows:

56, 34, 48, 43, 87, 78, 54, 62, 61, 59

The “stem” records the value of the “ten's” place (or higher) and the “leaf” records the value in the “one's” place [ Table 1 ].

Stem and leaf plot

Illustration/visual display of data

The most common tools used for visual display include frequency diagrams, bar charts (for noncontinuous variables) and histograms (for continuous variables). Composite bar charts can be used to compare variables. For example, the frequency distribution in a sample population of males and females can be illustrated as given in Figure 1 .

Composite bar chart

A pie chart helps show how a total quantity is divided among its constituent variables. Scatter diagrams can be used to illustrate the relationship between two variables. For example, global scores given for improvement in a condition like acne by the patient and the doctor [ Figure 2 ].

Scatter diagram

Summary statistics

The main tools used for summary statistics are broadly grouped into measures of central tendency (such as mean, median, and mode) and measures of dispersion or variation (such as range, standard deviation, and variance).

Imagine that the data below represent the weights of a sample of 15 pediatric patients arranged in ascending order:

30, 35, 37, 38, 38, 38, 42, 42, 44, 46, 47, 48, 51, 53, 86

Just having the raw data does not mean much to us, so we try to express it in terms of some values, which give a summary of the data.

The mean is basically the sum of all the values divided by the total number. In this case, we get a value of 45.

The problem is that some extreme values (outliers), like “'86,” in this case can skew the value of the mean. In this case, we consider other values like the median, which is the point that divides the distribution into two equal halves. It is also referred to as the 50 th percentile (50% of the values are above it and 50% are below it). In our previous example, since we have already arranged the values in ascending order we find that the point which divides it into two equal halves is the 8 th value – 42. In case of a total number of values being even, we choose the two middle points and take an average to reach the median.

The mode is the most common data point. In our example, this would be 38. The mode as in our case may not necessarily be in the center of the distribution.

The median is the best measure of central tendency from among the mean, median, and mode. In a “symmetric” distribution, all three are the same, whereas in skewed data the median and mean are not the same; lie more toward the skew, with the mean lying further to the skew compared with the median. For example, in Figure 3 , a right skewed distribution is seen (direction of skew is based on the tail); data values' distribution is longer on the right-hand (positive) side than on the left-hand side. The mean is typically greater than the median in such cases.

Location of mode, median, and mean

Measures of dispersion

The range gives the spread between the lowest and highest values. In our previous example, this will be 86-30 = 56.

A more valuable measure is the interquartile range. A quartile is one of the values which break the distribution into four equal parts. The 25 th percentile is the data point which divides the group between the first one-fourth and the last three-fourth of the data. The first one-fourth will form the first quartile. The 75 th percentile is the data point which divides the distribution into a first three-fourth and last one-fourth (the last one-fourth being the fourth quartile). The range between the 25 th percentile and 75 th percentile is called the interquartile range.

Variance is also a measure of dispersion. The larger the variance, the further the individual units are from the mean. Let us consider the same example we used for calculating the mean. The mean was 45.

For the first value (30), the deviation from the mean will be 15; for the last value (86), the deviation will be 41. Similarly we can calculate the deviations for all values in a sample. Adding these deviations and averaging will give a clue to the total dispersion, but the problem is that since the deviations are a mix of negative and positive values, the final total becomes zero. To calculate the variance, this problem is overcome by adding squares of the deviations. So variance would be the sum of squares of the variation divided by the total number in the population (for a sample we use “n − 1”). To get a more realistic value of the average dispersion, we take the square root of the variance, which is called the “standard deviation.”

The box plot

The box plot is a composite representation that portrays the mean, median, range, and the outliers [ Figure 4 ].

The concept of skewness and kurtosis

Skewness is a measure of the symmetry of distribution. Basically if the distribution curve is symmetric, it looks the same on either side of the central point. When this is not the case, it is said to be skewed. Kurtosis is a representation of outliers. Distributions with high kurtosis tend to have “heavy tails” indicating a larger number of outliers, whereas distributions with low kurtosis have light tails, indicating lesser outliers. There are formulas to calculate both skewness and kurtosis [Figures ​ [Figures5 5 – 8 ].

Positive skew

High kurtosis (positive kurtosis – also called leptokurtic)

Negative skew

Low kurtosis (negative kurtosis – also called “Platykurtic”)

Sample Size

In an ideal study, we should be able to include all units of a particular population under study, something that is referred to as a census.[ 5 , 6 ] This would remove the chances of sampling error (difference between the outcome characteristics in a random sample when compared with the true population values – something that is virtually unavoidable when you take a random sample). However, it is obvious that this would not be feasible in most situations. Hence, we have to study a subset of the population to reach to our conclusions. This representative subset is a sample and we need to have sufficient numbers in this sample to make meaningful and accurate conclusions and reduce the effect of sampling error.

We also need to know that broadly sampling can be divided into two types – probability sampling and nonprobability sampling. Examples of probability sampling include methods such as simple random sampling (each member in a population has an equal chance of being selected), stratified random sampling (in nonhomogeneous populations, the population is divided into subgroups – followed be random sampling in each subgroup), systematic (sampling is based on a systematic technique – e.g., every third person is selected for a survey), and cluster sampling (similar to stratified sampling except that the clusters here are preexisting clusters unlike stratified sampling where the researcher decides on the stratification criteria), whereas nonprobability sampling, where every unit in the population does not have an equal chance of inclusion into the sample, includes methods such as convenience sampling (e.g., sample selected based on ease of access) and purposive sampling (where only people who meet specific criteria are included in the sample).

An accurate calculation of sample size is an essential aspect of good study design. It is important to calculate the sample size much in advance, rather than have to go for post hoc analysis. A sample size that is too less may make the study underpowered, whereas a sample size which is more than necessary might lead to a wastage of resources.

We will first go through the sample size calculation for a hypothesis-based design (like a randomized control trial).

The important factors to consider for sample size calculation include study design, type of statistical test, level of significance, power and effect size, variance (standard deviation for quantitative data), and expected proportions in the case of qualitative data. This is based on previous data, either based on previous studies or based on the clinicians' experience. In case the study is something being conducted for the first time, a pilot study might be conducted which helps generate these data for further studies based on a larger sample size). It is also important to know whether the data follow a normal distribution or not.

Two essential aspects we must understand are the concept of Type I and Type II errors. In a study that compares two groups, a null hypothesis assumes that there is no significant difference between the two groups, and any observed difference being due to sampling or experimental error. When we reject a null hypothesis, when it is true, we label it as a Type I error (also denoted as “alpha,” correlating with significance levels). In a Type II error (also denoted as “beta”), we fail to reject a null hypothesis, when the alternate hypothesis is actually true. Type II errors are usually expressed as “1- β,” correlating with the power of the test. While there are no absolute rules, the minimal levels accepted are 0.05 for α (corresponding to a significance level of 5%) and 0.20 for β (corresponding to a minimum recommended power of “1 − 0.20,” or 80%).

Effect size and minimal clinically relevant difference

For a clinical trial, the investigator will have to decide in advance what clinically detectable change is significant (for numerical data, this is could be the anticipated outcome means in the two groups, whereas for categorical data, it could correlate with the proportions of successful outcomes in two groups.). While we will not go into details of the formula for sample size calculation, some important points are as follows:

In the context where effect size is involved, the sample size is inversely proportional to the square of the effect size. What this means in effect is that reducing the effect size will lead to an increase in the required sample size.

Reducing the level of significance (alpha) or increasing power (1-β) will lead to an increase in the calculated sample size.

An increase in variance of the outcome leads to an increase in the calculated sample size.

A note is that for estimation type of studies/surveys, sample size calculation needs to consider some other factors too. This includes an idea about total population size (this generally does not make a major difference when population size is above 20,000, so in situations where population size is not known we can assume a population of 20,000 or more). The other factor is the “margin of error” – the amount of deviation which the investigators find acceptable in terms of percentages. Regarding confidence levels, ideally, a 95% confidence level is the minimum recommended for surveys too. Finally, we need an idea of the expected/crude prevalence – either based on previous studies or based on estimates.

Sample size calculation also needs to add corrections for patient drop-outs/lost-to-follow-up patients and missing records. An important point is that in some studies dealing with rare diseases, it may be difficult to achieve desired sample size. In these cases, the investigators might have to rework outcomes or maybe pool data from multiple centers. Although post hoc power can be analyzed, a better approach suggested is to calculate 95% confidence intervals for the outcome and interpret the study results based on this.

Financial support and sponsorship

Conflicts of interest.

There are no conflicts of interest.

• Privacy Policy

Home » Categorical Variable – Definition, Types and Examples

Categorical Variable – Definition, Types and Examples

Table of Contents

Categorical Variable

Definition:

Categorical variable is a type of variable used in statistics and research, which represents data that can be divided into categories or groups based on specific characteristics. These categories are often non-numerical and are used to represent qualitative data, such as gender, color, or type of car.

Types of Categorical Variables

There are two main types of categorical variables:

Nominal Variables

Nominal variables are those that describe a characteristic or quality without any specific order or ranking. They represent data that can be divided into distinct categories, but these categories do not have any inherent hierarchy or ranking. Examples of nominal variables include gender, race, religion, or type of vehicle.

Ordinal Variables

Ordinal variables, on the other hand, have categories that can be ordered or ranked based on their value. They represent data that can be divided into distinct categories, and these categories have an inherent order or hierarchy. Examples of ordinal variables include levels of education, income brackets, or survey responses that use a Likert scale (e.g., strongly agree, agree, neutral, disagree, strongly disagree).

Applications of Categorical Variable

Categorical variables are widely used in various fields, including statistics, social sciences, market research, and data analysis. Here are some common applications of categorical variables:

• Surveys : Categorical variables are commonly used to gather information about people’s opinions and attitudes on various topics. Surveys often include questions that ask respondents to choose from a list of options or categories, such as political affiliation, favorite color, or preferred mode of transportation.
• Market research: Categorical variables are used in market research to segment customers into different groups based on their characteristics, preferences, and buying behavior. This helps businesses to tailor their products, services, and marketing strategies to specific customer segments.
• Medical research : Categorical variables are used to categorize patients based on their medical conditions, symptoms, or treatments. This helps researchers to analyze data and identify patterns, risk factors, and treatment outcomes.
• Education : Categorical variables are used in education to track and analyze student performance, attendance, and demographic data. This helps educators to identify achievement gaps, target interventions, and improve teaching strategies.
• Political science : Categorical variables are used in political science to analyze voting behavior, party affiliation, and public opinion. This helps researchers to understand political trends, voter preferences, and the impact of policies and campaigns.

Examples of Categorical Variable

Here are some examples of categorical variables:

• Gender : This is a nominal variable that categorizes people into two distinct categories – male and female.
• Marital Status: This is a nominal variable that categorizes people into different categories, such as married, single, divorced, or widowed.
• Education Level: This is an ordinal variable that categorizes people into different levels of education, such as high school, college, or graduate school.
• Language Spoken at Home : This is a nominal variable that categorizes people based on the language they speak at home, such as English, Spanish, French, or Mandarin.
• Car Make: This is a nominal variable that categorizes cars into different makes, such as Toyota, Ford, BMW, or Honda.
• Likert Scale Responses: This is an ordinal variable that categorizes survey responses based on a scale of agreement or disagreement, such as strongly agree, agree, neutral, disagree, or strongly disagree.
• Country of Origin : This is a nominal variable that categorizes people based on their country of origin, such as the United States, Canada, Mexico, or India.

Purpose of Categorical Variable

The purpose of categorical variables is to represent data that can be divided into distinct categories or groups based on specific characteristics. Categorical variables are used to organize and analyze data into meaningful groups, which can help to identify patterns, trends, and relationships in the data. Here are some specific purposes of categorical variables:

• Data organization: Categorical variables are used to organize data into meaningful groups, which can help to simplify data analysis and interpretation.
• Data segmentation: Categorical variables are used to segment data into distinct groups based on specific characteristics, such as age, gender, or location. This helps to identify differences and similarities between groups and target specific interventions or marketing strategies.
• Data visualization: Categorical variables are often visualized using charts, such as bar charts or pie charts, which help to visually display the distribution of data across the different categories. This makes it easier to communicate data and identify patterns or trends.
• Statistical analysis: Categorical variables are used in statistical analysis to test hypotheses, identify correlations, and make predictions. Statistical methods such as chi-square tests, contingency tables, and logistic regression are commonly used to analyze categorical data.

When to use Categorical Variable

Categorical variables should be used when data can be divided into distinct categories or groups based on specific characteristics or attributes. Here are some specific situations when categorical variables are appropriate:

• Qualitative data: Categorical variables are commonly used to represent qualitative data, such as opinions, attitudes, or preferences. For example, survey responses that ask people to choose between different options or categories are often represented using categorical variables.
• Nominal data : Nominal data is data that can be divided into distinct categories without any specific order or ranking. Categorical variables are appropriate for representing nominal data, such as race, gender, or religion.
• Ordinal data: Ordinal data is data that can be divided into distinct categories with an inherent order or ranking. Categorical variables can also be used to represent ordinal data, such as levels of education, income brackets, or customer satisfaction ratings.
• Segmentation : Categorical variables are often used for data segmentation, where data is divided into groups based on specific characteristics or attributes. For example, customer data can be segmented based on demographics, behavior, or buying patterns.
• Analysis : Categorical variables are commonly used in statistical analysis, where they can be used to test hypotheses, identify correlations, and make predictions. For example, chi-square tests can be used to test the association between two categorical variables.

Characteristics of Categorical Variable

Here are some of the key characteristics of categorical variables:

• Discrete : Categorical variables are discrete, meaning they can only take on a limited number of values or categories. For example, a variable representing hair color might have categories such as black, brown, blonde, or red.
• Nominal or ordinal: Categorical variables can be nominal or ordinal. Nominal variables have categories that are not inherently ordered or ranked, such as eye color or country of origin. Ordinal variables have categories that are ordered or ranked, such as education level or income bracket.
• Non-numeric: Categorical variables are non-numeric, meaning they cannot be measured or represented by numbers. Instead, they are represented by labels or categories.
• Qualitative : Categorical variables represent qualitative data, such as opinions, preferences, or characteristics. They do not represent quantitative data, such as measurements or counts.
• Mutually exclusive: Categorical variables are mutually exclusive, meaning each observation can only belong to one category. For example, a variable representing political affiliation would have categories such as Democrat, Republican, or Independent, and each person can only belong to one of those categories.
• Counted or calculated as percentages: Categorical variables are often counted or calculated as percentages to understand the distribution of data across different categories. For example, a survey result might show that 45% of respondents prefer vanilla ice cream, while 30% prefer chocolate and 25% prefer strawberry.

Advantages of Categorical Variable

Categorical variables have several advantages in data analysis and interpretation. Here are some of the key advantages:

• Easy to understand and interpret: Categorical variables are easy to understand and interpret, as they represent data in discrete categories or groups. This makes it easy to summarize and visualize data, and to communicate findings to others.
• Useful for data segmentation: Categorical variables are useful for data segmentation, where data is divided into distinct groups based on specific characteristics or attributes. This can help to identify differences and similarities between groups, and to target interventions or marketing strategies to specific groups.
• Useful for statistical analysis : Categorical variables are commonly used in statistical analysis, where they can be used to test hypotheses, identify correlations, and make predictions. There are many statistical methods available for analyzing categorical data, such as chi-square tests, contingency tables, and logistic regression.
• Useful for data reduction: Categorical variables can be used to reduce the complexity of data, by grouping similar observations into categories. This can help to simplify data analysis and interpretation, and to identify patterns or trends in the data.
• Useful for exploratory data analysis: Categorical variables are useful for exploratory data analysis, as they can help to identify relationships and patterns in the data. For example, a bar chart showing the distribution of a categorical variable can help to identify the most common categories and any outliers.

Limitations of Categorical Variable

Categorical variables also have some limitations that should be considered when using them in data analysis. Here are some of the key limitations:

• Limited information: Categorical variables provide limited information compared to continuous variables, as they only represent data in discrete categories or groups. This can make it more difficult to identify patterns or trends in the data, and to make accurate predictions or forecasts.
• Potential loss of information: Categorical variables can also lead to a loss of information, as observations within each category are treated as equal. This can obscure important differences between observations within each category, and can lead to incorrect conclusions or predictions.
• Limited statistical methods: While there are many statistical methods available for analyzing categorical data, they are more limited than those available for continuous data. For example, there are fewer options for modeling relationships between categorical variables and continuous outcomes.
• Limited ability to measure change: Categorical variables are less sensitive to change than continuous variables, as they only represent data in discrete categories or groups. This can make it more difficult to measure small changes in the data, and to identify the factors that drive these changes.
• Potential for bias: Categorical variables can also introduce bias into data analysis, as the categories used to represent data are often subjective and may not accurately reflect the underlying data. This can lead to incorrect conclusions or predictions, and can limit the generalizability of findings.

About the author

Muhammad Hassan

Researcher, Academic Writer, Web developer

You may also like

Control Variable – Definition, Types and Examples

Moderating Variable – Definition, Analysis...

Qualitative Variable – Types and Examples

Variables in Research – Definition, Types and...

Independent Variable – Definition, Types and...

Ratio Variable – Definition, Purpose and Examples

A .gov website belongs to an official government organization in the United States.

A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Talking with Your Healthcare Provider
• Birth Defects Statistics
• Birth Defects Resources
• Birth Defects Awareness Month
• Living with Down Syndrome
• Conversation Tips
• Growth Charts for Down Syndrome
• Accessing NBDPS and BD-STEPS Data
• Birth Defects Awareness Month Social Media Resources
• About Alcohol Use During Pregnancy

About Down Syndrome

• Down syndrome is a genetic condition where a person is born with an extra chromosome.
• This can affect how their brain and body develop.
• People diagnosed with Down syndrome can lead healthy lives with supportive care.

Down syndrome is a condition in which a person has an extra copy of chromosome 21. Chromosomes are small "packages" of genes in the body's cells, which determine how the body forms and functions.

When babies are growing, the extra chromosome changes how their body and brain develop. This can cause both physical and mental challenges.

People with Down syndrome often have developmental challenges, such as being slower to learn to speak than other children.

Distinct physical signs of Down syndrome are usually present at birth and become more apparent as the baby grows. They can include facial features, such as:

• A flattened face, especially the bridge of the nose
• Almond-shaped eyes that slant up
• A tongue that tends to stick out of the mouth

Other physical signs can include:

• A short neck
• Small ears, hands, and feet
• A single line across the palm of the hand (palmar crease)
• Small pinky fingers
• Poor muscle tone or loose joints
• Shorter-than-average height

Some people with Down syndrome have other medical problems as well. Common health problems include:

• Congenital heart defects
• Hearing loss
• Obstructive sleep apnea

Down syndrome is the most common chromosomal condition diagnosed in the United States. Each year, about 5,700 babies born in the US have Down syndrome. 1

There are three types of Down syndrome. The physical features and behaviors are similar for all three types.

With Trisomy 21, each cell in the body has three separate copies of chromosome 21. About 95% of people with Down syndrome have Trisomy 21.

Translocation Down syndrome

In this type, an extra part or a whole extra chromosome 21 is present. However, the extra chromosome is attached or "trans-located" to a different chromosome rather than being a separate chromosome 21. This type accounts for about 3% of people with Down syndrome.

Mosaic Down syndrome

Mosaic means mixture or combination. In this type, some cells have three copies of chromosome 21, but other cells have the typical two copies. People with mosaic Down syndrome may have fewer features of the condition. This type accounts for about 2% of people with Down syndrome.

Risk factors

We don't know for sure why Down syndrome occurs or how many different factors play a role. We do know that some things can affect your risk of having a baby with Down syndrome.

One factor is your age when you get pregnant. The risk of having a baby with Down syndrome increases with age, especially if you are 35 years or older when you get pregnant. 2 3 4

However, the majority of babies with Down syndrome are still born to mothers less than 35 years old. This is because there are many more births among younger women. 5 6

Regardless of age, parents who have one child with Down syndrome are at an increased risk of having another child with Down syndrome. 7

Screening and diagnosis

There are two types of tests available to detect Down syndrome during pregnancy: screening tests and diagnostic tests. A screening test can tell you if your pregnancy has a higher chance of being affected Down syndrome. Screening tests don't provide an absolute diagnosis.

Diagnostic tests can typically detect if a baby will have Down syndrome, but they carry more risk. Neither screening nor diagnostic tests can predict the full impact of Down syndrome on a baby.

The views of these organizations are their own and do not reflect the official position of CDC.

Down Syndrome Resource Foundation (DSRF) : The DSRF supports people living with Down syndrome and their families with individualized and leading-edge educational programs, health services, information resources, and rich social connections so each person can flourish in their own right.

GiGi's Playhouse : GiGi's Playhouse provides free educational, therapeutic-based, and career development programs for individuals with Down syndrome, their families, and the community, through a replicable playhouse model.

Global Down Syndrome Foundation : This foundation is dedicated to significantly improving the lives of people with Down syndrome through research, medical care, education and advocacy.

National Association for Down Syndrome : The National Association for Down Syndrome supports all persons with Down syndrome in achieving their full potential. They seek to help families, educate the public, address social issues and challenges, and facilitate active participation.

National Down Syndrome Society (NDSS) : NDSS seeks to increase awareness and acceptance of those with Down syndrome.

• Stallings, E. B., Isenburg, J. L., Rutkowski, R. E., Kirby, R. S., Nembhard, W.N., Sandidge, T., Villavicencio, S., Nguyen, H. H., McMahon, D. M., Nestoridi, E., Pabst, L. J., for the National Birth Defects Prevention Network. National population-based estimates for major birth defects, 2016–2020. Birth Defects Research. 2024 Jan;116(1), e2301.
• Allen EG, Freeman SB, Druschel C, et al. Maternal age and risk for trisomy 21 assessed by the origin of chromosome nondisjunction: a report from the Atlanta and National Down Syndrome Projects. Hum Genet. 2009 Feb;125(1):41-52.
• Ghosh S, Feingold E, Dey SK. Etiology of Down syndrome: Evidence for consistent association among altered meiotic recombination, nondisjunction, and maternal age across populations. Am J Med Genet A. 2009 Jul;149A(7):1415-20.
• Sherman SL, Allen EG, Bean LH, Freeman SB. Epidemiology of Down syndrome. Ment Retard Dev Disabil Res Rev. 2007;13(3):221-7.
• Olsen CL, Cross PK, Gensburg LJ, Hughes JP. The effects of prenatal diagnosis, population ageing, and changing fertility rates on the live birth prevalence of Down syndrome in New York State, 1983-1992. Prenat Diagn. 1996 Nov;16(11):991-1002.
• Adams MM, Erickson JD, Layde PM, Oakley GP. Down's syndrome. Recent trends in the United States. JAMA. 1981 Aug 14;246(7):758-60.
• Morris JK, Mutton DE, Alberman E. Recurrences of free trisomy 21: analysis of data from the National Down Syndrome Cytogenetic Register. Prenatal Diagnosis: Published in Affiliation With the International Society for Prenatal Diagnosis. 2005 Dec 15;25(12):1120-8.

Birth Defects

About one in every 33 babies is born with a birth defect. Although not all birth defects can be prevented, people can increase their chances of having a healthy baby by managing health conditions and adopting healthy behaviors before becoming pregnant.

For Everyone

Health care providers, public health.

R news and tutorials contributed by hundreds of R bloggers

Count function in r i dplyr::count().

Posted on May 18, 2024 by Zubair Goraya in R bloggers | 0 Comments

Data analysis is all about turning raw data into actionable insights. I was working on a research project analyzing survey data from thousands of respondents. The clock was ticking, and I needed to summarize responses to hundreds of questions quickly. Manually counting each response would have taken days, if not weeks. 

Then, I discovered the magic of the  count  function in R. In a matter of minutes, I transformed a messy dataset into a neatly summarized table, revealing patterns and trends that were previously hidden. That’s the power of the  count  function – it’s a game-changer for data analysts of all levels. You can read more about count function.

• The count function in R’s dplyr package summarises the frequency of values within a dataset. Forget manual counting; count does the heavy lifting for you.  
• Count effortlessly adapts to your data’s structure when dealing with categorical factors like car models or numeric variables like horsepower. 
• Count  seamlessly integrates with other dplyr functions, allowing you to filter, group, and transform your data fluently and intuitively. 
• Don’t let incorrect data types or missing values trip you up. With some know-how, you can easily troubleshoot common issues and ensure accurate results.
• Beyond simple counting, the count function is your gateway to uncovering patterns, trends, and relationships hidden within your data. 

What is the Count Function in R?

The count function in R from the  dplyr package empowers you to swiftly summarize and tabulate the frequency or number of values that occur within a dataset. It’s just like a magnifying glass that zooms in on the distribution of values, allowing you to answer critical questions effortlessly: 

• How many cars in the mtcars dataset have  4  cylinders?
• What’s the distribution of transmission types (am vs. automatic)?
• How many observations fall into each combination of cylinder count and transmission type?

This function operates like a frequency calculator, adeptly identifying and quantifying unique values within your data. It generates a new data frame that lists each distinct value and its corresponding count, offering a clear and concise distribution summary.

The dplyr package also provides a family of related functions that complement count:

Required Libraries for count function in R

In this tutorial, we will use the following libraries and data set.

Read more how to install libraries in R

tally () in R

A function that directly prints the count results to your console, perfect for quick checks.

In the R code above, we use tally() in conjunction with count() to count the number of cars based on the number of cylinders and print the result directly to the console.

add_count() in R

Instead of creating a separate data frame, it seamlessly adds a new column to your existing dataset, recording the count for each group or value.

Here, add_count() adds a new column named “n” to the  mtcars  dataset, showing the number of cars with a given number of cylinders.

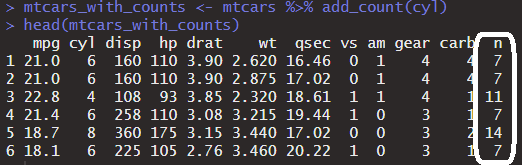
add_tally() in R

Specifically designed for grouped data, this function works in harmony with group_by(), enabling you to add counts within pre-defined groups effortlessly.

We first use the group_by() function in the R code to group the data set by the number of cylinders, and then we count the number of cars in each group using add_tally().

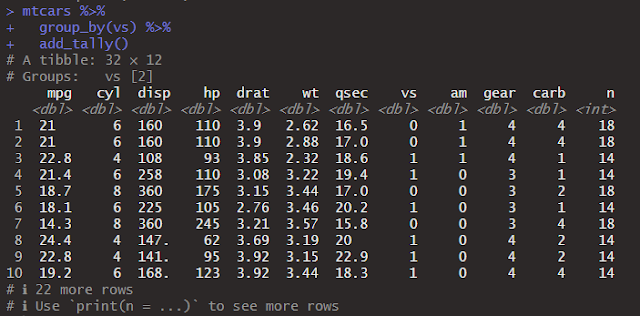
Whether you’re exploring categorical variables, analyzing grouped data, or delving into weighted counts, the count function and its counterparts offer a flexible and efficient toolkit for uncovering the hidden patterns within your data.

Why Choose the Count Function? 

• Efficiency and Speed:  Compared to manual counting or writing custom loops, counting significantly streamlines the process of summarizing frequencies. It’s designed to operate efficiently on large datasets, saving you valuable time and effort.
• Simplicity and Readability:  The syntax of count is concise and intuitive, making your code easier to read and understand. This clarity is especially beneficial when collaborating with others or revisiting your analysis later.
• Versatility Across Data Types:  Whether your data includes categorical factors (e.g., car models, survey responses), numeric variables (e.g., ages, sales figures), or a combination of both, count handles it all with ease. This adaptability makes it a versatile tool for various data analysis tasks.
• Seamless Integration with Tidyverse:  If you’re already familiar with the dplyr package and the tidyverse philosophy, count fits right into your existing workflow. You can seamlessly combine it with other dplyr functions like filter, group_by, and mutate to create powerful data manipulation pipelines.
• Clear and Informative Output:  The count function generates a tidy data frame as its output, making it easy to visualize, interpret, and further analyze the summarized results. You can readily create bar charts, tables, or other visualizations to communicate your findings.
• Handling Missing Values:  By default, count excludes missing values (NA) from its calculations, ensuring that your summaries are accurate and relevant. However, you can also include missing values if they are meaningful in your analysis.

How Does the Count Function Work?

Think of the count function as a helpful tally counter. It looks at your data and counts how often each unique item appears.

Step 1: Load the dplyr Package

Before using count, you must have the dplyr package loaded into R. It gives you access to a whole set of tools for working with data.

• Comprehensive Guide: How to install RStudio
• How to Import and Install Packages in R: A Comprehensive Guide
• No interest in Coding? Try our Shiny Apps

Step 2: Use count function to Count Unique Values

Let’s say you want to know how many cars in the mtcars dataset have different numbers of cylinders. Here’s the code:

• It takes your mtcars dataset.
• The %>% symbol (called a “pipe”) sends the data into the count function.
• The count(cyl) part tells the count to look at the cyl column (number of cylinders) and count how many times each unique value appears.

This means there are 11 cars with four cylinders, seven with six cylinders, and 14 with eight cylinders.

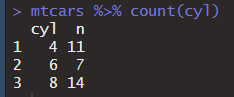
Step 3: Counting with Groups

Want to get learn some advance? 

You can count within groups. For example, how many cars have automatic or manual transmissions (am) for each number of cylinders (cyl).

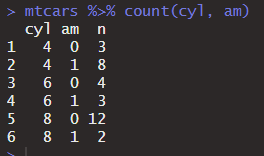
Step 4: Handling Missing Values (NA)

By default, the  count  doesn’t include any rows where the value you’re counting is missing (NA). If you want to include those missing values in your count, add na.rm = FALSE to the count function.

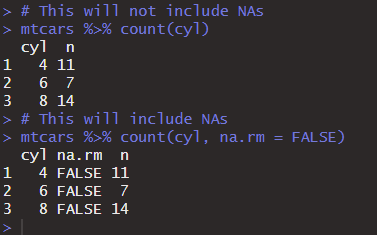
Key Points to Remember

• The count function makes counting things in your data super easy.
• You can count how often different values appear in one column or across multiple columns.
• By default, count ignores missing values, but you can change that if necessary.

Overview of Count Functions in R

Common errors and solutions with the count function in r.

Even with its user-friendly design, the count function can sometimes throw a curveball. Let’s tackle some common hiccups you might encounter and provide solutions to get you back on track:

Incorrect Data Types

Imagine counting unique values in a column that’s not a factor or character variable. You might get an error or unexpected results.

Always double-check your data types. Use functions like class() or str() to verify that the column you’re working with is suitable for counting unique values. If needed, convert the column to a factor using as.factor().

Let’s say we want to count the unique values in the hp (horsepower) column of the mtcars dataset. Before proceeding, we check the data type:

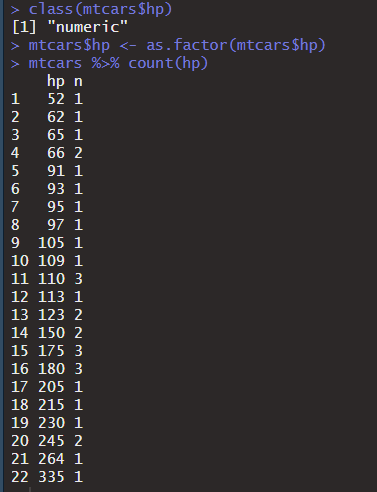
Missing Values (NA):

By default, count excludes rows with missing (NA) values in the column you’re counting. This can lead to undercounting if those missing values are meaningful.

To include missing values in your count, add the argument na.rm = FALSE to the count function.

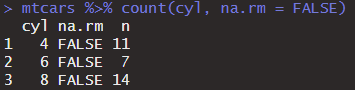
Unexpected Results (Grouping Gone Wrong)

Sometimes, you might get results that don’t match your expectations, especially when working with grouped data.

Carefully review your group_by() statement. Ensure you’re grouping by the correct variables and in the desired order. Double-check for typos or incorrect variable names.

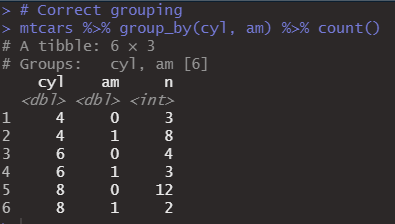
General Troubleshooting Tips

• Read the Error Messages:  Error messages are your friends! They often provide valuable clues about what went wrong.
• Consult the Documentation:  The official dplyr documentation is a treasure trove of information. Look up the count function to clarify its usage and arguments.
• Seek  Help  Online:  If you’re still stuck, don’t hesitate to ask for  help  on online forums like Stack Overflow. The R community is known for its helpfulness and expertise.

By being mindful of these common errors and following the suggested solutions, you’ll be well on your way to mastering the count function and confidently summarizing your data in R.

The count function in R is an adaptable and necessary tool for any data analyst. Its ability to quickly and efficiently summarize the frequency of values within datasets makes it a true workhorse in data wrangling. The count function seamlessly adapts to various data types and scenarios, from counting unique values to analysing grouped data .

We’ve delved into the inner workings of the count, highlighting its simplicity and integration with the powerful dplyr package. By understanding its core purpose, you’re equipped to easily tackle a wide range of data summarization tasks. We’ve also explored common pitfalls and provided practical solutions, ensuring you can navigate potential challenges confidently.

Remember, the count function isn’t just about numbers; it’s about extracting meaning and insights from your data. Whether exploring the characteristics of cars in the mtcars dataset or analyzing complex survey responses, count enables you to uncover patterns, trends, and relationships that might otherwise remain hidden.

So, the next time you’re faced with a dataset waiting to be deciphered, don’t hesitate to reach for the count function. Its efficiency, versatility, and intuitive syntax make it your trusted ally in the quest for data-driven discoveries.

Frequently Asked Questions (FAQs)

Is there a counting function in r.

Yes, R offers several counting functions. The most versatile and commonly used is the count function, which is part of the dplyr package. It efficiently summarizes the frequency of values within a dataset.

What is count() used for?

The count() function is used to tally the occurrences of unique values within a variable or combination of variables. It’s your go-to tool for quickly understanding the distribution of data.

What package is  count  in R?

The count function is in the dplyr package, a core component of the tidyverse, a collection of R packages designed for data science.

How to count rows in R?

To count the total number of rows in a data frame (like the mtcars dataset), you can use the  nrow () function:

nrow (mtcars) # This will show us there are 32 rows in  mtcars  dataset

How do you count characters in R?

The  nchar () function counts the number of characters in a string:

nchar (“Hello, R!”) # Returns 8

How to use count if?

The count function doesn’t have an “if” condition built in. However, you can combine it with a filter from dplyr to achieve conditional counting:

mtcars %>% filter(cyl == 4) %>% count() 

This will count only the rows where there are four cylinders (cyl = 4)

What’s an n()?

Within dplyr, n() is a special function used to count the number of observations (rows) in a group or the entire dataset when used with summarize. It’s often paired with group_by to count observations per group.

# Example Counting with Grouped Data

  group_by(cyl) %>% 

  summarize(Count = n())

What is the use of count() and count_*?

• count (): As discussed earlier, count() creates a new data frame with the unique values and corresponding counts.
• The count_* family (add_count, add_tally) adds a new column to your existing data frame, showing the count for each group or value. This is useful to keep the original data structure while adding count information.

What is the count method?

In R, “count” typically refers to functions like count(), table(), or length() rather than a specific “method.” These functions provide different ways to count elements within data structures.

What is %>% in R?

The %>%  symbol,  called the “pipe” operator, is a handy tool from the  magrittr  package (included in the  tidyverse ). It allows you to chain functions together, passing the output of one function as the input to the next. This makes your code more readable and easier to follow.

Which function in RStudio?

RStudio is an integrated development environment (IDE) for R, not a function itself. The functions we’ve discussed (like count, n(), nrow(), nchar()) are all part of R and can be used within RStudio.

What is the sum() function in R?

The sum() function adds up numeric values. You can use it to calculate the total of a column in a data frame:

sum(mtcars$mpg) # Calculates the total miles per gallon across all cars

How to count observations in R?

• For the total number of observations (rows) in a data frame, use  nrow ().
• To count observations within groups, use group_by() followed by summarize(n = n()) (or tally()).

Which function gives the count of levels in R?

The  nlevels () function tells you how many unique levels (categories) a factor variable has:

nlevels(mtcars$cyl)

This will return the number of unique levels in the cyl variable.

How do I count the number of values in a list in R?

Use the length() function to find the number of elements in a list.

What is the difference between N and count in R?

• N: Within dplyr, N is a special symbol representing the total number of rows in a data frame. It’s often used within summarize() for calculations based on the total count.
• count : The count function is a specialized tool from dplyr designed to efficiently count unique values and create summary tables.

Transform your raw data into actionable insights. Let my expertise in R and advanced data analysis techniques unlock the power of your information. Get a personalized consultation and see how I can streamline your projects, saving you time and driving better decision-making. Contact me today at [email protected] or  visit  to schedule your discovery call.

Copyright © 2024 | MH Corporate basic by MH Themes

Never miss an update! Subscribe to R-bloggers to receive e-mails with the latest R posts. (You will not see this message again.)

• {{subColumn.name}}

AIMS Mathematics

• {{newsColumn.name}}
• Share facebook twitter google linkedin

Unraveling multivariable Hermite-Apostol-type Frobenius-Genocchi polynomials via fractional operators

• Mohra Zayed 1 , 
• Shahid Ahmad Wani 2 ,  ,  , 
• Georgia Irina Oros 3 , 
• William Ramírez 4,5 ,  , 
• 1. Mathematics Department, College of Science, King Khalid University, Abha 61413, Saudi Arabia
• 2. Symbiosis Institute of Technology, Symbiosis International (Deemed) University, (SIU), Pune, Maharashtra, India
• 3. Department of Mathematics and Computer Science, Faculty of Informatics and Sciences, University of Oradea, Oradea 410087, Romania
• 4. Section of Mathematics International Telematic University Uninettuno, Rome 00186, Italy
• 5. Department of Natural and Exact Sciences, Universidad de la Costa, Barranquilla 080002, Colombia
• Received: 05 March 2024 Revised: 22 April 2024 Accepted: 30 April 2024 Published: 20 May 2024

MSC : 11T23, 33B10, 33C45, 33E20, 33E30

• Full Text(HTML)
• Download PDF

This study explores the evolution and application of integral transformations, initially rooted in mathematical physics but now widely employed across diverse mathematical disciplines. Integral transformations offer a comprehensive framework comprising recurrence relations, generating expressions, operational formalism, and special functions, enabling the construction and analysis of specialized polynomials. Specifically, the research investigates a novel extended family of Frobenius-Genocchi polynomials of the Hermite-Apostol-type, incorporating multivariable variables defined through fractional operators. It introduces an operational rule for this generalized family, establishes a generating connection, and derives recurring relations. Moreover, the study highlights the practical applications of this generalized family, demonstrating its potential to provide solutions for specific scenarios.

• operational connection ,
• fractional operators ,
• Eulers' integral ,
• multivariable special polynomials ,
• explicit form ,
• applications

Citation: Mohra Zayed, Shahid Ahmad Wani, Georgia Irina Oros, William Ramírez. Unraveling multivariable Hermite-Apostol-type Frobenius-Genocchi polynomials via fractional operators[J]. AIMS Mathematics, 2024, 9(7): 17291-17304. doi: 10.3934/math.2024840

Related Papers:

• This work is licensed under a Creative Commons Attribution-NonCommercial-Share Alike 4.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/ -->

Supplements

Access history.

• Corresponding authors: Email: [email protected] , [email protected] , [email protected] , [email protected] ;  Email: [email protected] , [email protected] , [email protected] , [email protected]

Reader Comments

• © 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License ( http://creativecommons.org/licenses/by/4.0 )

通讯作者: 陈斌, [email protected]

沈阳化工大学材料科学与工程学院 沈阳 110142

Article views( 3 ) PDF downloads( 1 ) Cited by( 0 )

Associated material

Other articles by authors.

• Mohra Zayed
• Shahid Ahmad Wani
• Georgia Irina Oros
• William Ramírez

Related pages

• on Google Scholar
• Email to a friend
• Order reprints

Export File