case study questions class 12 physics chapter 4

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Join our Telegram Channel for Free PDF Download

Case Study Question for Class 12 Physics Chapter 4 Moving Charges and Magnetism

• Last modified on: 2 years ago
• Reading Time: 4 Minutes

Case Study Question 1:

Moving coil galvanometer operates on Permanent Magnet Moving Coll (PMMC) mechanism and was designed by the scientist Darsonval.

Moving coil galvanometers are of two types (i) Suspended coll (ii) Pivoted coil type or tangent galvanometer,

Its working is based on the fact that when a current carrying coil is placed in a magnetic field, it experiences a torque. This torque tends to rotate the coil about its axis of suspension in such a way that the magnetic flux passing through the coil is maximum.

(i) A moving coil galvanometer is an instrument which (a) is used to measure emf (b) is used to measure potential difference (c) is used to measure resistance (d) is a deflection instrument which gives a deflection when a current flows through its coil

(ii) To make the field radial in a moving coil galvanometer. (a) number of turns of coil is kept small (b) magnet is taken in the form of horse-shoe (c) poles are of very strong magnets (d) poles are cylindrically cut

(iii) The deflection in a moving coil galvanometer is (a) directly proportional to torsional constant of spring (b) directly proportional to the number of turns in the coil (c) inversely proportional to the area of the coil (d) inversely proportional to the current in the coil

(iv) In a moving coil galvanometer, having a coil of N-turns of area A and carrying current I is placed in a radial field of strength B. The torque acting on the coil is (a) NA 2 B 2 I (b) NABI 2 (c) N 2 ABI (d) NABI

(v) To increase the current sensitivity of a moving coil galvanometer, we should decrease (a) strength of magnet (b) torsional constant of spring (c) number of turns in coil (d) area of coil

Download CBSE Books

Exam Special Series:

• Sample Question Paper for CBSE Class 10 Science (for 2024)
• Sample Question Paper for CBSE Class 10 Maths (for 2024)
• CBSE Most Repeated Questions for Class 10 Science Board Exams
• CBSE Important Diagram Based Questions Class 10 Physics Board Exams
• CBSE Important Numericals Class 10 Physics Board Exams
• CBSE Practical Based Questions for Class 10 Science Board Exams
• CBSE Important “Differentiate Between” Based Questions Class 10 Social Science
• Sample Question Papers for CBSE Class 12 Physics (for 2024)
• Sample Question Papers for CBSE Class 12 Chemistry (for 2024)
• Sample Question Papers for CBSE Class 12 Maths (for 2024)
• Sample Question Papers for CBSE Class 12 Biology (for 2024)
• CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
• Master Organic Conversions CBSE Class 12 Chemistry Board Exams
• CBSE Important Numericals Class 12 Physics Board Exams
• CBSE Important Definitions Class 12 Physics Board Exams
• CBSE Important Laws & Principles Class 12 Physics Board Exams
• 10 Years CBSE Class 12 Chemistry Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Physics Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Maths Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Biology Previous Year-Wise Solved Papers (2023-2024)
• ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
• ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
• ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
• ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
• ICSE Important Functions and Locations Based Questions Class 10 Biology
• ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)

✨ Join our Online JEE Test Series for 499/- Only (Web + App) for 1 Year

✨ Join our Online NEET Test Series for 499/- Only for 1 Year

Leave a Reply Cancel reply

Join our Online Test Series for CBSE, ICSE, JEE, NEET and Other Exams

Editable Study Materials for Your Institute - CBSE, ICSE, State Boards (Maharashtra & Karnataka), JEE, NEET, FOUNDATION, OLYMPIADS, PPTs

Discover more from Gurukul of Excellence

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading

CBSE Expert

CBSE Class 12 Physics Case Study Questions PDF Download

Case Study questions for the Class 12 Physics board exams are available here. You can read the Class 12 Physics Case Study Questions broken down by chapter. Subject matter specialists and seasoned teachers created these quizzes. You can verify the right response to each question by referring to the answer key, which is also provided. To achieve success on your final exams, practice the following questions.

CBSE (Central Board of Secondary Education) is a renowned educational board in India that designs the curriculum for Class 12 Physics with the goal of promoting a scientific temperament and nurturing critical thinking among students. As part of their Physics examination, CBSE includes case study questions to assess students’ ability to apply theoretical knowledge to real-world scenarios effectively.

Chapter-wise Solved Case Study Questions for Class 12 Physics

Before the exams, students in class 12 should review crucial Physics Case Study issues. They will gain a better understanding of the kinds of Case Study questions that may be asked in Physics exams for Grade 12. These questions were created by our highly qualified standard 12 Physics staff based on the questions that appeared most frequently in last year’s exams. The solutions have been written in a way that will make them simple to grasp and will aid students in grade 12 in understanding the topics.

Best Books for Class 12 Physics Exams

Strictly in accordance with the new term-by-term curriculum for the class 12 board exams to be held in the academic year 2023–2024, which will include multiple choice questions based on new board typologies including stand-alone MCQs and case-based MCQs with an assertion–reason. Included are inquiries from the official CBSE Question Bank that was released in April 2024. What changes have been made to the book: strictly in accordance with the term-by-term syllabus for the board exams that will be held during the 2024 academic year? Chapter- and topic-based Questions with multiple choices that are based on the unique evaluation method used for the Class 12th Physics Final Board Exams.

Key Benefits of Solving CBSE Class 12 Physics Case Study Questions

• Application of Concepts: Case study questions demand the application of theoretical knowledge in practical scenarios, preparing students for real-world challenges and professional pursuits.
• Critical Thinking: By evaluating and analyzing case studies, students develop critical thinking abilities, enabling them to approach complex problems with a logical mindset.
• In-Depth Understanding: Addressing case study questions necessitates a thorough understanding of physics concepts, leading to a more profound comprehension of the subject matter.
• Holistic Evaluation: CBSE adopts case study questions as they provide a holistic evaluation of a student’s aptitude and proficiency in physics, moving beyond rote memorization.
• Preparation for Competitive Exams: Since competitive exams often include similar application-based questions, practicing case study questions equips students for various entrance tests.

How to Approach CBSE Class 12 Physics Case Study Questions

• Read and Analyze Thoroughly: Carefully read the case study to grasp its context and identify the underlying physics principles involved.
• Identify Relevant Concepts: Highlight the physics theories and concepts applicable to the given scenario.
• Create a Systematic Solution: Formulate a step-by-step solution using the identified concepts, explaining each step with clarity.
• Include Diagrams and Charts: If relevant, incorporate diagrams, charts, or graphs to visually represent the situation, aiding better comprehension.
• Double-Check Answers: Always review your answers for accuracy, ensuring that they align with the principles of physics.

Tips for Excelling in CBSE Class 12 Physics

• Conceptual Clarity: Focus on building a strong foundation of physics concepts, as this will enable you to apply them effectively to case study questions.
• Practice Regularly: Dedicate time to solving case study questions regularly, enhancing your proficiency in handling real-world scenarios.
• Seek Guidance: Don’t hesitate to seek guidance from teachers, peers, or online resources to gain additional insights into challenging concepts.
• Time Management: During exams, practice efficient time management to ensure you allocate enough time to each case study question without rushing.
• Stay Positive: Approach case study questions with a positive mindset, embracing them as opportunities to showcase your skills and knowledge.

CBSE Class 12 Physics case study questions play a pivotal role in promoting practical understanding and critical thinking among students. By embracing these questions as opportunities for growth, students can excel in their physics examinations and beyond.

Leave a Comment Cancel reply

Save my name, email, and website in this browser for the next time I comment.

Download India's best Exam Preparation App Now.

Key Features

• Revision Notes
• Important Questions
• Previous Years Questions
• Case-Based Questions
• Assertion and Reason Questions

No thanks, I’m not interested!

• New QB365-SLMS
• NEET Materials
• JEE Materials
• Banking first yr Materials
• TNPSC Materials
• DIPLOMA COURSE Materials
• 5th Standard Materials
• 12th Standard Materials
• 11th Standard Materials
• 10th Standard Materials
• 9th Standard Materials
• 8th Standard Materials
• 7th Standard Materials
• 6th Standard Materials
• 12th Standard CBSE Materials
• 11th Standard CBSE Materials
• 10th Standard CBSE Materials
• 9th Standard CBSE Materials
• 8th Standard CBSE Materials
• 7th Standard CBSE Materials
• 6th Standard CBSE Materials
• Tamilnadu Stateboard
• Scholarship Exams
• Scholarships

CBSE 12th Standard Physics Subject Moving Charges And Magnetism Chapter Case Study Questions 2021

By QB365 on 21 May, 2021

QB365 Provides the updated CASE Study Questions for Class 12 , and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get  more marks in Exams 

QB365 - Question Bank Software

Cbse 12th standard physics subject moving charges and magnetism case study questions 2021.

12th Standard CBSE

Final Semester - June 2015

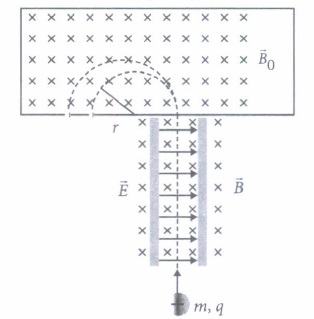
(ii) Radius of particle in second magnetic field B o is

(iii) Which of the following will trace a circular trajectory wit largest radius?

(iv) Mass of the particle in terms q, B o,  B,r and E is

(v) The particle comes out of velocity selector along a straight line, because

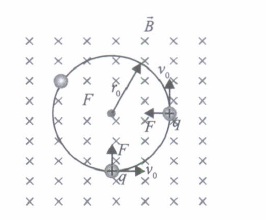
(ii) If v o = 2v o  then the time required for one revolution of the electron will change to

(iii) A charged particles is projected in a magnetic field  \(\vec{B}=(2 \hat{i}+4 \hat{j}) \times 10^{2} \mathrm{~T}\)  The acceleration of the particle is found to be  \(\vec{a}=(x \hat{i}+2 \hat{j}) \mathrm{m} \mathrm{s}^{-2}\) . Find the value of x.

(iv) If the given electron has a velocity not perpendicular to B, then trajectory of the electron is

(v) If this electron of charge (e) is moving parallel to uniform magnetic field with constant velocity v, the force acting on the electron is

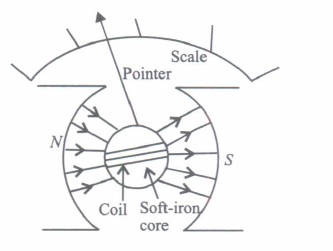
(ii) To make the field radial in a moving coil galvanometer

(iii) The deflection in a moving coil galvanometer is

(iv) In a moving coil galvanometer, having a coil of N-turns of area A and carrying current I is placed in a radial field of strength B. The torque acting on the coil is

(v) To increase the current sensitivity of a moving coil galvanometer, we should decrease

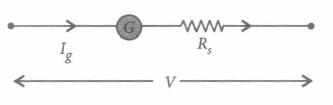
(ii) There are 3 voltmeter A, B, C having the same range but their resistance are  \(15,000 \Omega, 10,000 \Omega\)  and  \(5,000 \Omega\)  respectively. The best voltmeter amongst them is the one whose resistance is

(iii) A milliammeter of range 0 to 25 mA and resistance of  \(10 \Omega\)  is to be converted into a voltmeter with a range of 0 to 25 V. The resistance that should be connected in series will be

(iv) To convert a moving coil galvanometer (MCG) into a voltmeter

(v) The resistance of an ideal voltmeter is

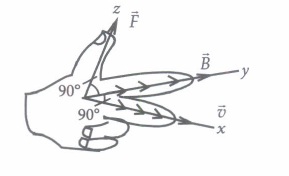
(ii) A proton is projected with a uniform velocity v along the axis of a current carrying solenoid, then

(iii) A charged particle experiences magnetic force in the presence of magnetic field. Which of the following statement is correct?

(iv) A charge q moves with a velocity 2 ms -1 along x-axis in a uniform magnetic field  \(\vec{B}=(\hat{i}+2 \hat{j}+3 \hat{k}) \mathrm{T}\)  then charge will experience a force

(v) Moving charge will produce

*****************************************

Cbse 12th standard physics subject moving charges and magnetism case study questions 2021 answer keys.

(i) (c): In mass spectrometer, the ions are sorted out by accelerating them through electric and magnetic field. (ii) (c):  As  \(\frac{m v^{2}}{r}=q v B_{0} \therefore r=\frac{m v}{q B_{0}}\) (iii) (b): As radius  \(r \propto \frac{m}{q}\) \(\therefore\)  r will be maximum for  \(\alpha\)  - particle. (iv) (b) : Here,  \(r=\frac{m v}{q B_{0}} \text { or } m=\frac{r q B_{0}}{v}\) As  \(v=\frac{E}{B}, \therefore m=\frac{q B_{0} B r}{E}\) (v) (c): From the relation v = E/B, it is clear electric and magnetic force balance each other.

(i) (b) : As  \(r_{0}=\frac{m v}{q B} \Rightarrow r^{\prime}=\frac{m\left(2 v_{0}\right)}{q B}=2 r_{0}\) (ii) (c): As,  \(T=\frac{2 \pi m}{q B}\) Thus, it remains same as it is in dependent of velocity (iii) (b) : As  \(F \perp B\) Hence,  \(a \perp B\) \(\therefore \vec{a} \cdot \vec{B}=0\) \(\Rightarrow \quad(x \hat{i}+2 \hat{j}) \cdot(2 \hat{i}+4 \hat{j})=0\) \(2 x+8=0 \Rightarrow x=-4 \mathrm{~m} \mathrm{~s}^{-2}\) (iv) (c): If the charged particle has a velocity not perpendicular to  \(\vec{B},\)  then component of velocity along  \(\vec{B}\)  remains unchanged as the motion along the  \(\vec{B}\)  will not be affected by  \(\vec{B}\) . Then, the motion of the particle in a plane perpendicular to  \(\vec{B}\)  is as before circular one. Thereby, producing helical motion. (v) (d): The force on electron  \(F=q v B \sin \theta\) As the electron is moving parallel to B So, \(\theta=0^{\circ} \Rightarrow q v B \sin 0^{\circ}=0\)

(I) (d): A moving coil galvanometer is a sensitive instrument which is used to measure a deflection when a current flows through its coil. (ii) (d) : Uniform field is made radial by cutting pole pieces cylindrically. (iii) (b): The deflection in a moving coil galvanometer  \(\phi=\frac{N A B}{k} \cdot I \text { or } \phi \propto N\)  where Nis number of turns in a coil, B is magnetic field and A is area of cross-section. (iv) (d): The deflecting torque acting on the coil  \(\tau_{\text {deflection }}=N I A B\) (v) (b): Current sensitivity of galvanometer \(\frac{\phi}{I}=S_{i}=\frac{N B A}{k}\) Hence, to increase (current sensitivity) S i  (torsional constant of spring) k must be decrease.

(i) (d) : A galvanometer can be converted into a voltmeter of given range by connecting a suitable high resistance R in series of galvanometer, which is given by  \(R=\frac{V}{I_{g}}-G=\frac{100}{10 \times 10^{-3}}-25=10000-25=9975 \Omega\) (ii) (c): An ideal voltmeter should have a very high resistance. (iii) (c): Resistance of voltmeter  \(=\frac{25}{25 \times 10^{-3}}=1000 \Omega\) \(\therefore \quad X=1000-10=990 \Omega\) (iv) (d) : To convert a moving coil galvanometer into a voltmeter, it is connected with a high resistance in series. The voltmeter is connected in parallel to measure the potential difference. As the resistance is high, the voltmeter itself does not consume current. (v) (d): The resistance of an ideal voltmeter is infinity.

(i) (a): For stationary electron, \(\vec{v}=0\) \(\therefore\)  Force on the electron is  \(\vec{F}_{m}=-e(\vec{v} \times \vec{B})=0\) (ii) (d) : Force on the proton  \(\vec{F}_{B}=e(\vec{v} \times \vec{B})\) Since,  \(\vec{v}\)  is parallel to  \(\vec{B}\) \(\therefore \quad \vec{F}_{B} \doteq 0\) Hence proton will continue to move with velocity v along the axis of solenoid. (iii) (b): Magnetic force on the charged particle q is  \(\vec{F}_{m}=q(\vec{v} \times \vec{B}) \text { or } F_{m}=q v B \sin \theta\) where  \(\theta\)  is the angle between  \(\vec{v} \text { and } \vec{B}\) Out of the given cases, only in case (b) it will experience the force while in other cases it will experience no force (iv) (a) :  \(\vec{F}=q(\vec{v} \times \vec{B})\) \(=q[(2 \hat{i} \times(\hat{i}+2 \hat{j}+3 \hat{k})]=(4 q) \hat{k}-(6 q) \hat{j}\) (v) (c): When an electric charge is moving both electric and magnetic fields are produced, whereas a static charge produces only electric field.

Related 12th Standard CBSE Physics Materials

12th standard cbse syllabus & materials, 12th maths vector algebra chapter case study question with answers cbse, 12th maths three dimensional geometry chapter case study question with answers cbse, 12th maths probability chapter case study question with answers cbse, 12th maths linear programming chapter case study question with answers cbse, 12th maths differential equations chapter case study question with answers cbse, 12th maths continuity and differentiability chapter case study question with answers cbse, 12th maths application of integrals chapter case study question with answers cbse, 12th chemistry the d and f block elements chapter case study question with answers cbse, 12th chemistry haloalkanes and haloarenes chapter case study question with answers cbse, 12th chemistry coordination compounds chapter case study question with answers cbse, 12th chemistry chemical kinetics chapter case study question with answers cbse, 12th chemistry biomolecules chapter case study question with answers cbse, 12th chemistry amines chapter case study question with answers cbse, 12th aldehydes ketones and carboxylic acids chapter case study question with answers cbse, 12th chemistry alcohols phenols and ethers chapter case study question with answers cbse.

Class VI to XII

Tn state board / cbse, 3000+ q&a's per subject, score high marks.

12th Standard CBSE Study Materials

12th Standard CBSE Subjects

myCBSEguide

• Case Study Questions Class...

Case Study Questions Class 12 Physics

Table of Contents

myCBSEguide App

Download the app to get CBSE Sample Papers 2023-24, NCERT Solutions (Revised), Most Important Questions, Previous Year Question Bank, Mock Tests, and Detailed Notes.

CBSE will ask two Case Study Questions in the CBSE class 12 Physics questions paper. Question numbers 15 and 16 are case-based questions where 5 MCQs will be asked based on a paragraph. Each theme will have five questions and students will have a choice to attempt any four of them. You can download CBSE Class 12 Physics case study questions from the myCBSEguide App and our free student dashboard .

You can Score High

CBSE class 12 Physics question paper will carry questions for 70 marks. Certainly, the question paper is a bit easier this year. It is because the syllabus is already reduced and there are more internal choices. Besides this, the case study questions are a plus to winning the game with good marks.

In simple words, all circumstances are in favour of the sincere students who are working hard to score high this year. Although it has been a difficult time for students as they were not getting the personal attention of the teachers. We know that online classes have their own limits, but we still expect better scores, especially from students who are putting extra effort into their studies.

Class 12 Physics Case Study Questions

CBSE class 12 Physics question paper will have case study questions too. These case-based questions will be objective type in nature. So, class 12 Physics students must prepare themselves for such questions. First of all, you should study NCERT Textbooks line by line and then you should practice as many questions as possible.

Case Study Syllabus

We know that CBSE has reduced the syllabus. Hence, practice only relevant questions. don’t waste time on case study questions from deleted portion. It is of no use. You can download the latest class 12 Physics case study questions from the myCBSEguide App.

Physics Case Studies

Class 12 Physics has many chapters but all chapters are not important for case studies. As we know case studies are not exactly given from NCERT books but these may be extracted from some newspaper articles, magazines, journals or other books. So, it is very much important that you are studying only the most relevant case studies. Here, the myCBSEguide app helps you a lot. We have case study questions that are prepared by a team of expert teachers. These experts exactly know what types of questions can come in exams.

Case Study Questions

There are a number of study apps available over the internet. But if you are a CBSE student and willing to get an app for the CBSE curriculum, you have very limited options. And if you want an app that is specifically designed for CBSE students, your search will definitely end on finding myCBSEguide. Case study questions are the latest updates in CBSE syllabus. It is exclusively available in the myCBSEguide app.

Here are some example questions. For more questions, you can download the myCBSEguide App.

Physics Case Study -1

Read  the following source and answer any four out of the following questions: Electric charge is the physical property of matter that causes it to experience a force when placed in an electromagnetic field. There are two types of charges positive and negative charges. Also, like charges repel each other whereas unlike charges attract each other.

• -3.2  × ×  10 -18  C
• 3.2  × ×  10  18  C
• -3.2  × ×  10 -17  C
• 3.2  × ×  10  -17   C
• -1.6  × ×  10 -18  C
• 1.6  × ×  10  -18  C
• 2.6  × ×  10 -18  C
• 1.6  × ×  10 -21  C
• 9.1  × ×  10 -31  kg
• 9.1  × ×  10 -31  g
• 1.6  × ×  10 -19  kg
• 1.6  × ×  10 -19  g
• there is only a positive charge in the body
• there is positive as well as negative charge in the body but the positive charge is more than the negative charge
• there is equally positive and negative charge in the body but the positive charge lies in the outer regions
• the negative charge is displaced from its position
• valence electrons only
• electrons of inner shells
• both valence electrons and electrons of the inner shell.
• none of the above

Physics Case Study -2

Read the following source and answer any four out of the following questions: Resistance is a measure of the opposition to current flow in an electrical circuit. Resistance is measured in ohms. Also, Resistivity is the electrical resistance of a conductor of unit cross-sectional area, and unit length. … A characteristic property of each material, resistivity is useful in comparing various materials on the basis of their ability to conduct electric currents.

• nature of material
• temperature
• dimensions of material
• cross-sectional area
• length of wire
• wire’s nature
• all of the above
• more resistance
• less resistance
• same resistance

Physics Case Study -3

Read the source given below and answer any four out of the following questions: The Bohr model of the atom was proposed by Neil Bohr in 1915. It came into existence with the modification of Rutherford’s model of an atom. Rutherford’s model introduced the nuclear model of an atom, in which he explained that a nucleus (positively charged) is surrounded by negatively charged electrons.

• The energy of the electrons in the orbit is quantized
• The electron in the orbit nearest the nucleus has the lowest energy
• Electrons revolve in different orbits around the nucleus
• The position and velocity of the electrons in the orbit cannot be determined simultaneously
• Single proton
• Multiple electrons
• emitted only
• absorbed only
• both (a) and (b)
• none of these
•  It must emit a continuous spectrum
•  It loses its energy
• Gaining its energy
• A discrete spectrum
• dequantized

Physics Case Study & myCBSEguide App

We at myCBSEguide provide the best case study questions for CBSE class 12 Physics. We have Physics case study questions for every chapter in 12th class Physics. Students can access the Physics case study questions with answers on the myCBSEguide App or on the student dashboard . Here are some features that make myCBSEguide the best learning app for CBSE students:

• Updated syllabus
• Up to date question bank
• Model papers and 10-year questions
• NCERT and Exemplar sulutions
• Best quality learning videos
• Detailed revision notes

12 Physics Question Paper Design

Here is the question paper design for CBSE class 12 Physics. It shows the typology of the questions and their weightage in CBSE board exams.

QUESTION PAPER DESIGN Theory (Class: 12)

Maximum Marks: 70 Duration: 3 hrs

Note:  The above template is only a sample. Suitable internal variations may be made for generating similar templates keeping the overall weightage to different forms of questions and typology of questions the same.

Test Generator

Create question paper PDF and online tests with your own name & logo in minutes.

Question Bank, Mock Tests, Exam Papers, NCERT Solutions, Sample Papers, Notes

Related Posts

• Competency Based Learning in CBSE Schools
• Class 11 Physical Education Case Study Questions
• Class 11 Sociology Case Study Questions
• Class 12 Applied Mathematics Case Study Questions
• Class 11 Applied Mathematics Case Study Questions
• Class 11 Mathematics Case Study Questions
• Class 11 Biology Case Study Questions
• Class 12 Physical Education Case Study Questions

2 thoughts on “Case Study Questions Class 12 Physics”

Good question l will check answers sheet

Question 2 answer key ?

Leave a Comment

Save my name, email, and website in this browser for the next time I comment.

NCERT Books and Solutions for all classes

Class 12 Physics Case Study Questions

Please refer to the chapter-wise Class 12 Physics Case Study Questions given below. These questions are expected to come in your class 12 Physics board exams. Our expert teachers have developed these Case Study questions and answers based on the latest examination guidelines and updated syllabus issued by CBSE, NCERT, and KVS. These will help you to understand all topics too and bet way to write answers in your exams. Revise these solved problems prior to your exams to score better marks in Class 12 exams.

Case Study Questions Class 12 Physics

Please click on the links below to access free important Case Study questions and answers for Grade 12 Physics. All solved questions have been designed based on the latest pattern of questions asked in recent examinations.

Chapter-wise Solved Case Study Questions for Class 12 Physics

Class 12 students should go through important Case Study problems for Physics before the exams. This will help them to understand the type of Case Study questions that can be asked in Grade 12 Physics examinations. Our expert faculty for standard 12 Physics have designed these questions based on the trend of questions that have been asked in last year’s exams. The solutions have been designed in a manner to help the grade 12 students understand the concepts and also easy to learn solutions.

You can click on the chapter-wise Case Study links given above and read the Class 12th Physics Case Study questions and answers provided by us. If you face any issues or have any questions please put your questions in the comments section below. Our teachers will be happy to provide you answers.

Related Posts:

Related Posts

Relations and functions class 12 mathematics exam questions.

Evans Tries an O level Class 12 English Exam Questions

Linear programming class 12 mathematics exam questions.

Talk to our experts

1800-120-456-456

• Important Questions for CBSE Class 12 Physics Chapter 4 - Moving Charges and Magnetism 2024-25

CBSE Class 12 Physics Chapter- 4 Important Questions - Free PDF Download

Important Questions of Chapter 4 Physics Class 12 PDF available on the Vedantu website will help students in their preparation for the board examinations and any entrance examinations. Among all the science subjects, Physics is always found to be difficult for most students. The only key to excelling in Physics is to study with dedication and with quality materials. Chapter 4 of Physics Class 12 deals with Moving Charges and Magnetism. The Class 12 Physics Chapter 4 important questions will be useful for students in their preparation.

Download CBSE Class 12 Physics Important Questions 2024-25 PDF

Also, check CBSE Class 12 Physics Important Questions for other chapters:

Important Topics Covered in Chapter 4

The following is a list of the important topics covered under the chapter on Moving Charges and Magnetism:

Ampere's Circuital Law

Biot-Savart Law, Magnetic Field Due to a Current Element 

The Moving Coil Galvanometer

The Toroid and the Solenoid

Magnetic Field and Magnetic Force

Magnetic Field and Motion in Combined Electric 

Magnetic Dipole, Torque on Current Loop

Related Chapters

Study Important Questions for Class 12 Physics Chapter 4 - Moving Charges and Magnetism

Very Short Answer Questions  1 Mark

1. State two properties of the material of the wire used for suspension of the coil in a moving coil galvanometer.  

Ans: Two properties of the material of the wire used for suspension of the coil in a moving coil galvanometer are:

Non-Brittle conductor 

Restoring Torque per unit twist should be small. 

2. What will be the path of a charged particle moving along the direction of a uniform magnetic field? 

Ans: The path of a charged particle moving along the direction of a uniform magnetic field would be a straight line path as no force would act on the particle. 

3. Two wires of equal lengths are bent in the form of two loops. One of the loops is square shaped whereas the other loop is circular. These are suspended in a uniform magnetic field and the same current is passed through them. Which loop will experience greater torque? Give reasons.  

Ans : We know the expression for torque as, 

$\tau =\text{NIAB}$

\[\Rightarrow \tau \propto A\]

Since, we know that the area of circular loops is more than that of a square loop, torque which is directly proportional to area would experience greater torque than the square loop.  

Therefore, torque experienced by a circular loop is greater.

4. A cyclotron is not suitable to accelerate electron. Why? 

Ans: A cyclotron is not suitable to accelerate electron as its mass is known to be less due to which they gain speed and step out of the dee immediately.

Short Answer Questions 2 Marks

1. A steady current flows in the network shown in the figure. What will be the magnetic field at the center of the network?

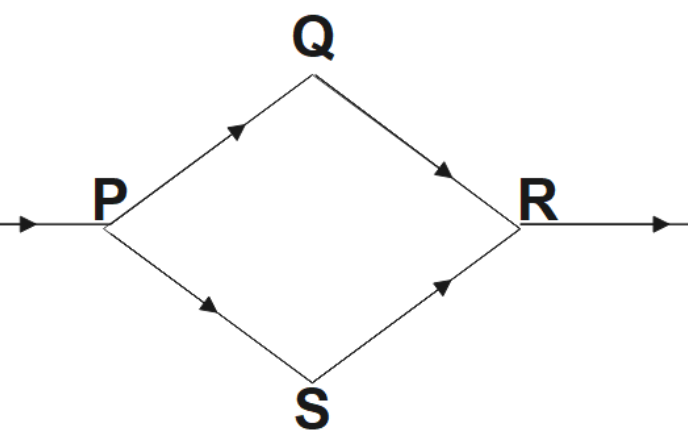
Ans:   The magnetic field at the center of the network is zero. This is because, the magnetic field at the center of the loop would just be equal and opposite i.e., magnetic field due \[\text{PQR}\] is equal and opposite to that due to \[\text{PSR}\].

2. An $\alpha $ - particle and a proton are moving in the plane of paper in a region where there is uniform magnetic field B directed normal to the plane of paper. If two particles have equal linear momenta, what will be the ratio of the radii of their trajectories in the field? 

Ans : We know the radius of the path to be given by, 

 \[R=\frac{mv}{Bq}\]

\[\Rightarrow R\propto \frac{1}{q}\] 

\[\Rightarrow \frac{{{R}_{\alpha }}}{{{R}_{p}}}=\frac{{{q}_{p}}}{{{q}_{\alpha }}}=\frac{e}{2e}=\frac{1}{2}\] 

Where, ${{R}_{\alpha }}\text{ and }{{\text{R}}_{p}}$are radii of $\alpha $-particle and proton respectively and ${{q}_{\alpha }}\text{ and }{{\text{q}}_{p}}$ are their respective charges. 

$\therefore {{R}_{\alpha }}:{{R}_{p}}=1:2$ 

Therefore, we find the required ratio to be 1:2. 

3. Give one difference each between diamagnetic and ferromagnetic substances. Give one example of each. 

Ans: Diamagnetic substances are the ones that are weakly repelled by a magnet. For example, gold. Ferromagnetic materials are the ones that are strongly attracted by a magnet. For example, iron. 

4. Write the expression for the force acting on a charged particle of charge q moving with velocity is in the presence of magnetic field B. Show that in the presence of this force,

The K.E. of the particle does not change. 

Ans : We know the expression for magnetic force as, $F=q(\vec{v}\times \vec{B})$

Since direction of force is perpendicular to the plane containing $(\vec{v}\times \vec{B})$, 

$F=qvB\sin 90{}^\circ =qvB$

Here, we find the force and displacement to be perpendicular to each other. So, 

$W=FS\cos \theta $ 

$\Rightarrow W=FS\cos 90{}^\circ =0$ 

$\Rightarrow \text{KE}=0$ 

Therefore, we find the kinetic energy to be constant at the given condition. 

Its instantaneous power is zero. 

Ans:   We have the expression for instantaneous power given by,

$p=Fv\cos \theta $ 

When force and velocity are perpendicular to each other, 

$p=Fv\cos 90{}^\circ =0$

Therefore, we find the instantaneous power to be zero.

5. An electron of kinetic energy \[25\mathbf{KeV}\]moves perpendicular to the direction of a uniform magnetic field of \[0.2\mathbf{millitesla}\]. Calculate the time period of rotation of the electron in the magnetic field.  

Ans : We are given the magnetic field to be, $B=0.2T=0.2\times {{10}^{-3}}T$ 

We know the expression for Time Period to be, $T=\frac{2\pi M}{QB}$

Substituting the given values, 

$\Rightarrow T=\frac{2\times 3.14\times 9.1\times {{10}^{-31}}}{1.6\times {{10}^{-17}}\times 0.2\times {{10}^{-3}}}$ 

$\Rightarrow T=1.787\times {{10}^{-7}}\text{ second}$ 

We find the time period of rotation of the electron in the magnetic field to be $T=1.787\times {{10}^{-7}}\text{ second}$. 

6. It is desired to pass only \[10%\] of the current through a galvanometer of resistance $90\Omega $. How much shunt resistance should be connected across the galvanometer?   

Ans: Current through galvanometer, 

${{I}_{G}}=10%\text{ of I}=\frac{10}{100}\times I$  

Galvanometer resistance is given to be, $G=90\Omega $ 

Now, we could find the shunt resistance as, 

S $=\frac{\frac{9I}{10I-I}}{100}$ 

$\Rightarrow S=\frac{90I}{90I}=10$ 

$\Rightarrow S=10\Omega $ 

Therefore, we found the shunt resistance to be $S=10\Omega $. 

Short Answer Question 3 Marks

1. Derive an expression for the force acting on a current carrying conductor placed in a uniform magnetic field. Name the rule which gives the direction of the force. Write the condition for which this force will have (1) maximum (2) minimum value.  

Ans : Let us consider a conductor that is placed in a uniform magnetic field \[\vec{B}\]making an angle $\theta $ with \[\vec{B}\]. Let \[I\] be the current that flows through the conductor.

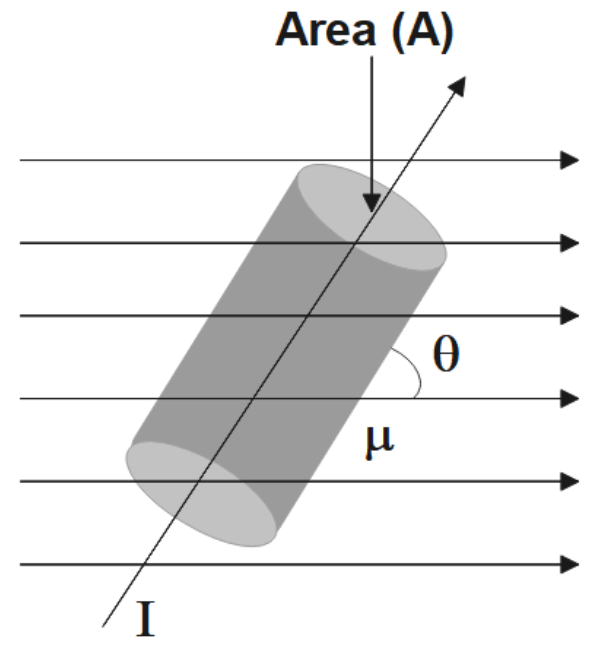
If $n$ is the number of electrons per unit volume of the conductor, then the total number of electrons in the small current element \[dl,\text{ N}=nAdl\].

We have, 

$\theta =Ne$ 

$\Rightarrow \theta =nAdle$ 

Let $\vec{f}$ be the force experienced by each electron, then, 

$\vec{f}=e({{\vec{v}}_{d}}\times \vec{B})$ 

Now, force experienced by a small current element would be, 

\[d\vec{f}=neAdl({{\vec{v}}_{d}}\times \vec{B})\] 

$d\vec{f}=neAdlB\sin \theta $ 

But we have, $I=neAvd$ 

$\Rightarrow d\vec{f}=IdlB\sin \theta $ 

Now, the total force experienced will be,

\[F=\int_{0}^{1}{df}=\int_{0}^{1}{IdlB\sin \theta }\] 

$\Rightarrow F=IBl\sin \theta $ 

In vector form total force could be given by, $\vec{F}=I(\vec{l}\times \vec{B})$ 

Force will be maximum when $\theta =90{}^\circ $ 

Force will be minimum when $\theta =0{}^\circ $

2. A straight wire carries a current of \[\mathbf{10}\]A. An electron moving at ${{10}^{7}}\text{ m/s}$is at distance \[\mathbf{2}.\mathbf{0}\] cm from the wire. Find the force acting on the electron if its velocity is directed towards the wire.

Ans : We are given the current through the straight wire to be, \[I\text{ }=\text{ }10A\] 

Speed of the electron, $v={{10}^{7}}\text{ m/s}$ 

Distance of electron from the wire, $R=2.0\text{ cm}=2\times {{10}^{-2}}\text{ m}$ 

Force acting on a moving electron would be,  \[F=qVB\sin \theta \] 

We have the expression for magnetic field as, 

\[B=\frac{{{\mu }_{0}}}{4\pi }\frac{2I}{r}\] 

$B=\frac{{{10}^{-7}}\times 2\times 10}{2\times {{10}^{-2}}}={{10}^{-4}}T$ and it is given to be $\bot $ to the plane of paper and directed towards.

Now, force acting on the electron could be given by, $\Rightarrow F=1.6\times {{10}^{-19}}\times {{10}^{7}}\times {{10}^{-4}}\sin 90{}^\circ $ 

$\Rightarrow F=1.6\times {{10}^{-16}}N$ 

Therefore, we find the force to be, $F=1.6\times {{10}^{-16}}N$. 

3. State Biot-Savart's law. Derive an expression for the magnetic field at the center of a circular coil of \[\mathbf{n}\] -turns carrying current – I. 

Ans: Biot – Savart law states that the magnetic field $dB$ due to a current element $\overrightarrow{dl}$ at any point would be as following:

$dB\propto I$ 

$dB\propto dl$ 

$dB\propto \sin \theta $ 

$dB\propto \frac{1}{{{r}^{2}}}$ 

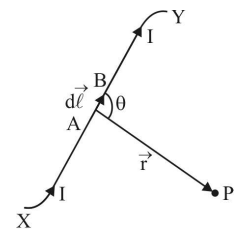
Combining all the above conditions, we get, 

$dB\propto \frac{Idl\sin \theta }{{{r}^{2}}}$ 

\[\Rightarrow dB=\frac{{{\mu }_{0}}}{4\pi }\frac{Idl\sin \theta }{{{r}^{2}}}\]

Consider a circular loop of radius $r$ that is carrying a current $I$, 

Since $dl\bot \vec{r}$ , 

$\Rightarrow \theta =90{}^\circ $ 

Now, on applying Biot Savart law 

$dB=\frac{{{\mu }_{0}}}{4\pi }\frac{Idl\sin 90{}^\circ }{{{r}^{2}}}$ 

For entire closed circular loop, 

$B=\int_{0}^{2\pi r}{\frac{{{\mu }_{0}}}{4\pi }\frac{Idl\sin 90{}^\circ }{{{r}^{2}}}}$ 

$\Rightarrow B=\frac{{{\mu }_{0}}}{4\pi }\frac{I}{{{r}^{2}}}\int_{0}^{2\pi r}{dl}=\frac{{{\mu }_{0}}}{4\pi }\frac{I}{{{r}^{2}}}\times 2\pi r$ 

For $n$ turns of a coil we would get, 

$\Rightarrow B=\frac{{{\mu }_{0}}}{4\pi }\frac{2\pi nI}{r}$ 

Therefore, we find the expression for magnetic field at the center of a circular coil of n -turns carrying current – I to be, 

$B=\frac{{{\mu }_{0}}}{4\pi }\frac{2\pi nI}{r}$

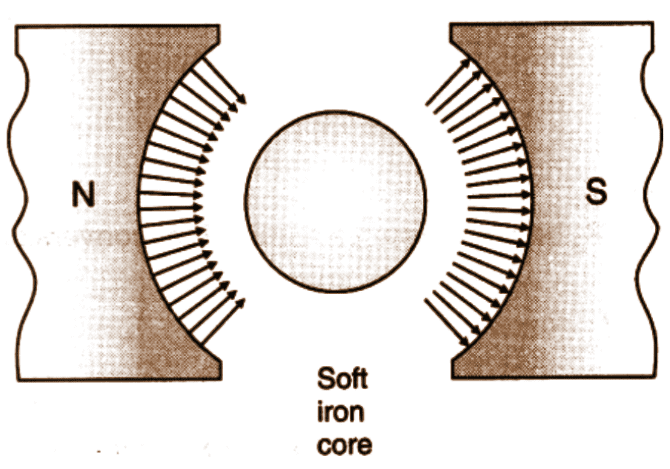
4. What is a radial magnetic field? How is it obtained in a moving coil galvanometer?

Ans : A radial magnetic field is the magnetic field in which the plane of the coil always lies in the direction of the magnetic field. It can be obtained by the following ways:

Properly cutting the pole pieces concave in shape. 

Placing soft iron cylindrical core between the pole pieces.

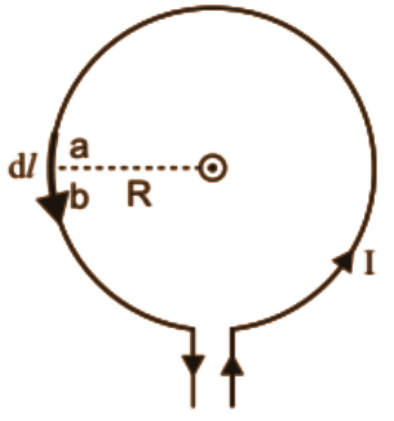
5. Two straight parallel current carrying conductors are kept at a distance r from each other in air. The direction for current in both the conductors is the same. Find the magnitude and direction of the force between them. Hence define one ampere. 

Ans: Let us consider two parallel conductors carrying current ${{I}_{1}}\,\text{ and }{{I}_{2}}$ and is separated by a distance \[d\], 

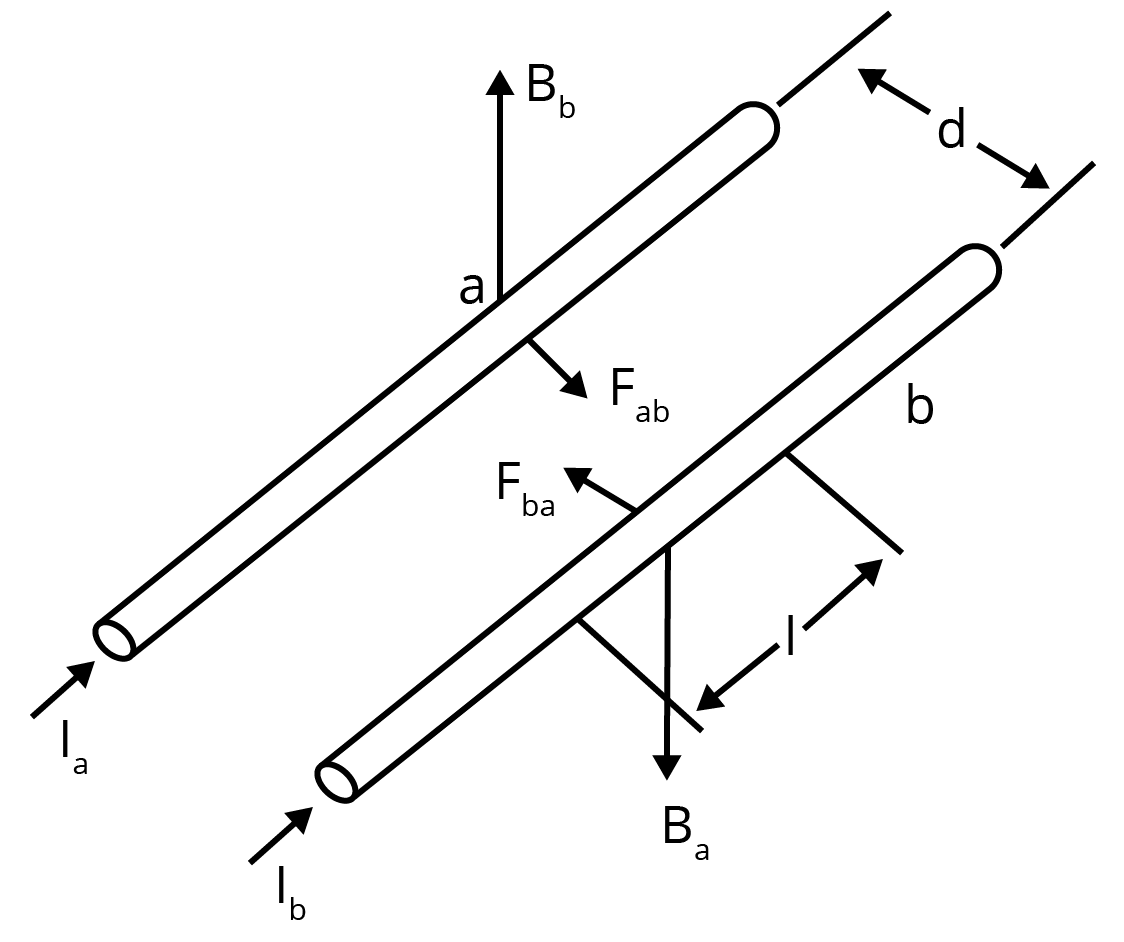
Magnetic field due to current ${{I}_{1}}$ at any point on conductor 2 could be given by, 

\[{{B}_{1}}=\frac{{{\mu }_{0}}}{4\pi }\frac{2Il}{d}\,\] ……………………….. (1)

($\bot $ to the plane and downwards $(\times )$)

Since current carrying conductor is placed at right angles with the magnetic field, we get the magnetic force to be, 

$F=BIl\sin 90{}^\circ $ 

$\Rightarrow F=BIl$ ………………………… (2) 

This would be the Force experienced per unit length of conductor. 

Now, we have, 

${{F}_{2}}=\frac{{{\mu }_{0}}}{4\pi }\frac{2{{I}_{1}}{{I}_{2}}}{d}$…………………………… (3) 

Fleming’s left hand Rule says ${{F}_{2}}$ is directed towards conductor 1.

Similarly, ${{F}_{1}}=\frac{{{\mu }_{0}}}{4\pi }\frac{2{{I}_{1}}{{I}_{2}}}{d}$ (Directed Towards conductor $2$)

Since ${{F}_{1}}\text{ and }{{F}_{2}}$ are equal in magnitude and directed opposite, two parallel current carrying conductors would attract each other.

Since, $F=\frac{{{\mu }_{0}}}{4\pi }\left( \frac{2{{I}_{1}}{{I}_{2}}}{d} \right)$ 

If ${{I}_{1}}={{I}_{2}}=1\text{ A}$  and $d=1\text{m}$ , then, 

$F=2\times {{10}^{-7}}\,\text{m}$ 

Hence, we found that one ampere is that current which is flowing in two infinitely long parallel conductors that are separated by a distance of $1$ meter in vacuum and experiences a force of $F=2\times {{10}^{-2}}\,\text{m}$ on each meter of the other wire.

6. A circular coil of wire consisting of $100$ turns, each of radius $8.0$ cm carries a current of $0.40\,\text{A}$. What is the magnitude of the magnetic field B at the centre of the coil?

Ans: We are given:

Number of turns on the circular coils, $n=100$ 

Radius of each turn, $r=8.0\text{ cm}=0.08\text{ m}$ 

Current flowing in the coil, $I=0.4\,\text{A}$ 

Magnitude of the magnetic field at the centre of the coil could be given by the relation,

$\left| B \right|=\frac{{{\mu }_{0}}}{4\pi }\frac{2\pi nl}{r}$ 

Where, Permeability of free space, \[{{\mu }_{0}}=4\pi \times {{10}^{-7}}\,\text{T m }{{\text{A}}^{-1}}\] 

$\Rightarrow \left| B \right|=\frac{4\pi \times {{10}^{-7}}}{4\pi }\times \frac{2\pi \times 100\times 0.4}{0.08}$ 

$\Rightarrow \left| B \right|=3.14\times {{10}^{-4}}T$ 

Hence, the magnitude of the magnetic field is found to be $3.14\times {{10}^{-4}}T$.

7. A long straight wire carries a current of $35\,\text{A}$. What is the magnitude of the field B at a point $20$ cm from the wire?

Ans: We are given the following:

Current in the wire, $I=35\text{ A}$ 

Distance of a point from the wire, $r=20\text{ cm}=0.2\,\text{m}$ 

Magnitude of the magnetic field at this point could be given as:

$B=\frac{{{\mu }_{0}}}{4\pi }\frac{2l}{r}$ 

Where, ${{\mu }_{0}}=$ Permeability of free space $=4\pi \times {{10}^{-7}}\,\text{T m }{{\text{A}}^{-1}}$ 

$\Rightarrow B=\frac{4\pi \times {{10}^{-7}}\times 2\times 35}{4\pi \times 0.2}$ 

$\Rightarrow B=3.5\times {{10}^{-5}}\,\text{T}$ 

Hence, the magnitude of the magnetic field at a point $20\,\text{cm}$ from the wire is found to be $3.5\times {{10}^{-5}}\,\text{T}$.

8. A long straight wire in the horizontal plane carries a current of \[50\text{ A}\] in the north to south direction. Give the magnitude and direction of B at a point \[2.5\]m east of the wire. 

Current in the wire, \[I\text{ }=\text{ }50\text{ A}\] 

A point is said to be \[2.5\]m away from the East of the wire. 

Magnitude of the distance of the point from the wire is given as, \[r\text{ }=\text{ }2.5\text{ m}\]. 

Magnitude of the magnetic field at that point could be given by the relation, \[B=\frac{{{\mu }_{0}}2I}{4\pi r}\] 

$\Rightarrow B=\frac{4\pi \times {{10}^{-7}}\times 2\times 50}{4\pi \times 2.5}$ 

$\Rightarrow B=4\times {{10}^{-6}}\,\text{T}$

Since, the point is located normal to the wire length at a distance of $2.5\text{ m}$and the direction of the current in the wire is vertically downward, by using Maxwell’s right hand thumb rule we get the direction of the magnetic field at the given point as vertically upward.

9. A horizontal overhead power line carries a current of \[\mathbf{90}\text{ }\mathbf{A}\]in an east to west direction. What is the magnitude and direction of the magnetic field due to the current \[\mathbf{1}.\mathbf{5}\text{ }\mathbf{m}\] below the line? 

Ans: We are given the following: 

Current in the power line, \[I\text{ }=\text{ }90\,\text{A}\] 

A Point is located below the power line that is at distance, \[r\text{ }=\text{ }1.5\text{ m}\] 

Now, the magnetic field at that point could be given by the relation,

\[B=\frac{{{\mu }_{0}}2I}{4\pi r}\]

$\Rightarrow B=\frac{4\pi \times {{10}^{-7}}\times 2\times 50}{4\pi \times 1.5}$ 

$\Rightarrow B=1.2\times {{10}^{-5}}\,\text{T}$

Since, the current is flowing from East to West and the point is given to be below the power line, by using Maxwell’s right hand thumb rule we get the direction of the magnetic field to be towards the South.

10. What is the magnitude of magnetic force per unit length on a wire carrying a current of \[8\text{ A}\] and making an angle of \[30{}^\text{o}\]  with the direction of a uniform magnetic field of \[0.15\text{ T}\] ? 

Current in the wire, \[I\text{ }=\text{ }8\text{ A}\] 

Magnitude of the uniform magnetic field, \[B\text{ }=\text{ }0.15\text{ T}\] 

Angle between the wire and magnetic field, $\theta =\text{ }30{}^\circ $ 

Magnetic force per unit length on the wire is given as:

$f=BI\sin \theta $ 

\[\Rightarrow f=0.15\times 8\times 1\times \sin 30{}^\circ \] 

\[\Rightarrow f=0.6\,\text{N }{{\text{m}}^{-1}}\] 

Therefore, the magnetic force per unit length on the wire is found to be $0.6\,\text{N }{{\text{m}}^{-1}}$.

11. A \[\mathbf{3}.\mathbf{0}\] cm wire carrying a current of \[\mathbf{10}\]A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be \[\mathbf{0}.\mathbf{27}\] T. What is the magnetic force on the wire? 

Length of the wire, \[l\text{ }=\text{ }3\text{ cm }=\text{ }0.03\text{ m}\] 

Current flowing in the wire, \[I\text{ }=\text{ }10\text{ A}\] 

Magnetic field, \[B\text{ }=\text{ }0.27\text{ T}\] 

Angle between the current and magnetic field, $\theta =\text{ }90{}^\circ $ 

Magnetic force exerted on the wire could be given as:

$F=BIl\sin \theta $ 

Substituting the given values, we get, 

\[\Rightarrow F=0.27\times 10\times 0.03\sin 90{}^\circ \] 

\[\Rightarrow F=8.1\times {{10}^{-2}}\,\text{N}\] 

Therefore, the magnetic force on the wire is found to be \[8.1\times {{10}^{-2}}\,\text{N}\] and the direction of the force can be obtained using Fleming’s left-hand rule.

12. Two long and parallel straight wires A and B carrying currents of \[\mathbf{8}.\mathbf{0}\] A and \[\mathbf{5}.\mathbf{0}\] A in the same direction are separated by a distance of \[\mathbf{4}.\mathbf{0}\] cm. Estimate the force on a \[\mathbf{10}\] cm section of wire A. 

Current flowing in wire A, ${{I}_{A}}=8.0\,\text{A}$ 

Current flowing in wire B, ${{I}_{B}}=5.0\text{ A}$ 

Distance between the two wires, \[r\text{ }=\text{ }4.0\text{ cm }=\text{ }0.04\text{ m}\] 

Length of a section of wire A, \[l\text{ }=\text{ }10\text{ cm }=\text{ }0.1\text{ m}\] 

Force exerted on length l due to the magnetic field could be given as:

$B=\frac{{{\mu }_{0}}2{{I}_{A}}{{I}_{B}}l}{4\pi r}$ 

Where, ${{\mu }_{0}}=$ Permeability of free space $=4\pi \times {{10}^{-7}}\,\text{T m }{{\text{A}}^{-1}}$

$\Rightarrow B=\frac{4\pi \times {{10}^{-7}}\times 2\times 8\times 5\times 0.1}{4\pi \times 0.04}$ 

$\Rightarrow B=2\times {{10}^{-5}}\,\text{N}$ 

The magnitude of force is found to be $2\times {{10}^{-5}}\,\text{N}$. This is an attractive force that is normal to A towards B because the direction of the currents in the wires are the same.

13. A closely wound solenoid $80cm$long has $5$ layers of windings of $400$ turns each. The diameter of the solenoid is $1.8cm$. If the current carried is $8.0A$, estimate the magnitude of B inside the solenoid near its centre. 

Length of the solenoid, $l=80cm=0.8m$

Since there are five layers of windings of 400 turns each on the solenoid; 

Total number of turns on the solenoid would be, $N=5\times 400=2000$

Diameter of the solenoid, $D=1.8cm=0.018m$

Current carried by the solenoid, $I=8.0A$

We have the magnitude of the magnetic field inside the solenoid near its centre given by the relation, 

$B=\frac{{{\mu }_{0}}NI}{l}$

Where, ${{\mu }_{0}}=4\pi \times {{10}^{-4}}Tm{{A}^{-1}}$is the permeability of free space. 

On substituting the given values we get, 

$B=\frac{4\pi \times {{10}^{-7}}\times 2000\times 8}{0.8}$

$\Rightarrow B=2.512\times {{10}^{-2}}T$

Therefore, the magnitude of the magnetic field inside the solenoid near its centre is found to be $2.512\times {{10}^{-2}}T$.

14. A square coil of side $10cm$consists of 20 turns and carries a current of $12A$. The coil is suspended vertically and the normal to the plane of the coil makes an angle of $30{}^\circ $with the direction of a uniform horizontal magnetic field of magnitude $0.80T$. What is the magnitude of torque experienced by the coil?

Ans: We are given,

Length of a side of the square coil, $l=10cm=0.1m$

Area of the square, $A={{l}^{2}}={{\left( 0.1 \right)}^{2}}=0.01{{m}^{2}}$

Current flowing in the coil, $I=12A$

Number of turns on the coil, $n=20$

Angle made by the plane of the coil with magnetic field, $\theta =30{}^\circ $

Strength of magnetic field, $B=0.80T$

Magnitude of the magnetic torque experienced by the coil in the magnetic field is given by the relation,

$\tau =nIAB\sin \theta $

Substituting the given values, we get,

$\tau =20\times 0.8\times 12\times 0.01\times \sin 30{}^\circ $

$\Rightarrow \tau =0.96Nm$

Therefore, the magnitude of the torque experienced by the coil is 0.96Nm.

A circular coil of \[\mathbf{30}\] turns and radius \[\mathbf{8}.\mathbf{0}cm\] carrying a current of \[\mathbf{6}.\mathbf{0}A\] is suspended vertically in a uniform horizontal magnetic field of magnitude \[\mathbf{1}.\mathbf{0}T\]. The field lines make an angle of with the normal of the coil. Calculate the magnitude of the counter torque that must be applied to prevent the coil from turning.

Ans: Given that, number of turns on the circular coil, \[n=30\] 

Radius of the coil, \[r=8.0\text{ cm}=0.08\text{ m}\] 

Area of the coil $=\pi {{r}^{2}}=\pi {{(0.08)}^{2}}=0.0201\text{ }{{\text{m}}^{2}}$ 

Current flowing in the coil, \[I=6.0\text{ A}\] 

Magnetic field strength, \[B=1\text{ T}\] 

Angle between the field lines and normal with the coil surface, $\theta =60{}^\circ $ 

The coil experiences a torque in the magnetic field. So, it turns. The counter torque applied to prevent the coil from turning is given by the relation,

$T=nIBA\sin \theta \,$ ……………………. (1)

$\Rightarrow T=30\times 6\times 1\times 0.0201\times \sin 60{}^\circ $ 

$\Rightarrow T=3.133\text{Nm}$ 

Therefore, counter torque to be applied against coil turning is $3.133\text{Nm}$.

Would your answer change, if the circular coil in (a) were replaced by a planar coil of some irregular shape that encloses the same area? (All other particulars are also unaltered.) 

Ans: It can be inferred from relation (1) that the magnitude of the applied torque is not dependent on the shape of the coil. It depends on the area of the coil. Hence, the answer would not change if the circular coil in the above case is replaced by a planar coil of some irregular shape that encloses the same area.

16. A magnetic field of $100G$$\left( where,\text{ }1G={{10}^{-4}}T \right)$ is required which is uniform in a region of linear dimension about $10cm$ and area of cross-section about${{10}^{-3}}{{m}^{2}}$. The maximum current carrying capacity of a given coil of wire is $15A$ and the number of turns per unit length that can be wound a core is at most $1000\text{ turns per m}$. Suggest some appropriate design particulars to a solenoid for the required purpose. Assume the core is not ferromagnetic.

Magnetic field strength,$B=100G=100\times {{10}^{-4}}T$

Number of turns per unit length,$n=1000turns\text{ per m}$

Current flowing in the coil,$I=15A$

Permeability of free space, ${{\mu }_{0}}=4\pi \times {{10}^{-7}}Tm{{A}^{-1}}$

Magnetic field is given the relation,

$B={{\mu }_{0}}nI$

$\Rightarrow nI=\frac{B}{{{\mu }_{0}}}=\frac{100\times {{10}^{-4}}}{4\pi \times {{10}^{-7}}}$

$\Rightarrow nI\approx 8000A/m$

So, if the length of the coil is taken as 50 cm, radius 4 cm, number of turns 400, and current 10 A, then these values are not unique for the given purpose. There is always a Possibility of some adjustments with limits.

17. A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are wound. If the current in the wire is 11 A, what is the magnetic field 

outside the toroid 

Inner radius of the toroid, ${{r}_{1}}=25cm=0.25m$

Outer radius of the toroid, ${{r}_{2}}=26cm=0.26m$

Number of turns on the coil, $N=3500$

Current in the coil, $I=11A$

So, we know, the magnetic field outside a toroid is zero. It is non-zero only inside the core of a toroid.

inside the core of the toroid.

Ans: Magnetic field inside the core of a toroid is given by the relation,

Where, Permeability of free space ${{\mu }_{0}}=4\pi \times {{10}^{-7}}Tm{{A}^{-1}}$

$l$ is the length of toroid

$l=2\pi \left( \frac{{{r}_{1}}+{{r}_{2}}}{2} \right)=\pi \left( 0.25+0.26 \right)=0.51\pi $

$\Rightarrow B=\frac{4\pi \times {{10}^{-7}}\times 3500\times 11}{0.51\pi }\approx 3.0\times {{10}^{-2}}T$

Therefore, the magnetic field inside the core of the toroid is approximately $3.0\times {{10}^{-2}}T$.

in the empty space surrounded by the toroid.

Ans: Magnetic field in the empty space that is surrounded by the toroid is zero. 

18. Answer the following questions: 

A magnetic field that varies in magnitude from point to point but has a constant direction (east to west) is set up in a chamber. A charged particle enters the chamber and travels undeflected along a straight path with constant speed. What can you say about the initial velocity of the particle?

Ans: The initial velocity of the particle could either be parallel or be anti-parallel to the magnetic field. So, it travels along a straight path without suffering any deflection in the field.

A charged particle enters an environment of a strong and non-uniform magnetic field varying from point to point both in magnitude and direction, and comes out of it following a complicated trajectory. Would its final speed equal the initial speed if it suffered no collisions with the environment? 

Ans: Yes, the final speed of the charged particle would be equal to its initial speed because the magnetic force can change direction of velocity, but not its magnitude.

An electron travelling west to east enters a chamber having a uniform electrostatic field in north to south direction. Specify the direction in which a uniform magnetic field should be set up to prevent the electron from deflecting from its straight line path. 

Ans: An electron travelling from West to East enters a chamber having a uniform electrostatic field along the North-South direction. This moving electron remains undeflected if the electric force acting on it is equal and opposite to the magnetic field. Magnetic force would be directed towards the South. Also, according to Fleming’s left hand rule, the magnetic field should be applied in a vertically downward direction.

19. A straight horizontal conducting rod of length $0.45m$ and mass $60g$is suspended by two vertical wires at its ends. A current of $5.0A$ is set up in the rod through the wires.

What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero?

Length of the rod, $l=0.45m$

Mass suspended by the wires, $m=60g=60\times {{10}^{-3}}kg$

Acceleration due to gravity, $g=9.8m{{s}^{-2}}$

Current in the rod flowing through the wire, $I=5A$

We could say that magnetic field (B) is equal and opposite to the weight of the wire i.e.,

$\Rightarrow B=\frac{mg}{Il}=\frac{60\times {{10}^{-3}}\times 9.8}{5\times 0.45}$

$\Rightarrow B=0.26T$

Therefore, a horizontal magnetic field of 0.26 T normal to the length of the conductor should be set up.

What will be the total tension in the wires if the direction of current is reversed keeping the magnetic field same as before? (Ignore the mass of the wires.) $g=9.8m{{s}^{-2}}$

Ans: When the direction of the current is reversed, $BIl$ and $mg$ will act downwards. So, the effective tension in the wires is found to be, 

$T=0.26\times 5\times 0.45+\left( 60\times {{10}^{-3}} \right)\times 9.8$

$\Rightarrow T=1.176N$

Therefore, total tension in the wires is $1.176N$. 

20. The wires which connect the battery of an automobile to its starting motor carry a current of $300A$(for a short time). What is the force per unit length between the wires if they are $70cm$long and $1.5cm$ apart? Is the force attractive or repulsive?

Ans: Given that,

Current in both wires, $I=300A$

Distance between the wires, $r=1.5cm=0.015m$

Length of the two wires, $l=70cm=0.7m$

We know that, Force between the two wires is given by the relation,

$F=\frac{{{\mu }_{0}}{{I}^{2}}}{2\pi r}$

Where, Permeability of free space${{\mu }_{0}}=4\pi \times 10Tm{{A}^{-1}}$

$\Rightarrow F=\frac{4\pi \times {{10}^{-7}}\times {{300}^{2}}}{2\pi \times 0.015}$

$\Rightarrow F=1.2N$

Since the direction of the current in the wires is found to be opposite, a repulsive force exists between them.

21. A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, what is the: (The coil is made of copper wire of cross-sectional area ${{10}^{-5}}{{m}^{2}}$, and the free electron density in copper is given to be about${{10}^{29}}{{m}^{-3}}$).

total torque on the coil?

Number of turns on the circular coil, $n=20$

Radius of the coil, $r=10cm=0.1m$

Magnetic field strength, $B=0.10T$

Current in the coil, $I=5.0A$

Since, the angle between force and the normal to the loop, the total torque on the coil is zero. So, $\tau =NIAB\sin \theta $ is zero.

total force on the coil,  

Ans: The total force on the coil is zero as the field is uniform.

average force on each electron in the coil due to the magnetic field?

Ans: Number of free electrons per cubic meter in copper, $N={{10}^{29}}/{{m}^{3}}$

Charge on the electron would be, $e=1.6\times {{10}^{-19}}C$

Magnetic force, $F=Be{{v}_{d}}$

Where, ${{v}_{d}}$ is Drift velocity of electrons.

${{v}_{d}}=\frac{I}{neA}=\frac{5}{{{10}^{29}}\times 1.6\times {{10}^{-19}}\times {{10}^{-5}}}=3.125\times {{10}^{-5}}m/s$

$\Rightarrow F=0.10\times 1.6\times {{10}^{-19}}\times 3.125\times {{10}^{-5}}$

$\Rightarrow F=5\times {{10}^{-25}}N$

Therefore, the average force on each electron is found to be $5\times {{10}^{-25}}N$.

22. A galvanometer coil has a resistance of $12\Omega $and the metre shows full scale deflection for a current of $3mA$. How will you convert the metre into a voltmeter of range $0$ to $18V$?

Ans: Given that, 

Resistance of the galvanometer coil, $G=12\Omega $

Current for which there is full scale deflection, ${{I}_{g}}=3mA=3\times {{10}^{-3}}A$

Range of the voltmeter needs to be converted to $18V$.

Let a resistor of resistance R be connected in series with the galvanometer to convert it into a voltmeter. This resistance can be given as:

$R=\frac{V}{{{I}_{g}}}-G$

Substituting the given values we get, 

$R=\frac{18}{3\times {{10}^{-3}}}-12=6000-12$

$\Rightarrow R=5988\Omega $

Therefore, we found that a resistor of resistance $5988\Omega $ is to be connected in series with the given galvanometer. 

23. A galvanometer coil has a resistance of $15\Omega $ and the metre shows full scale deflection for a current of $4mA$. How will you convert the metre into an ammeter of range $0$ to $6A$?

Resistance of the galvanometer coil, $G=15\Omega $

Current for which the galvanometer shows full scale deflection, ${{I}_{g}}=4mA=4\times {{10}^{-3}}A$

We said that, Range of the ammeter needs to be $6A$.

In order to convert the given galvanometer into an ammeter, a shunt resistor of resistance S is to be connected in parallel with the galvanometer. 

The value of S could be given as:

$S=\frac{{{I}_{g}}G}{I-{{I}_{g}}}$

Substituting the values, 

$S=\frac{4\times {{10}^{-3}}\times 15}{6-4\times {{10}^{-3}}}=\frac{0.06}{5.996}\approx 0.01\Omega $

$\Rightarrow S=10m\Omega $

Therefore, we found that a $10m\Omega $ shunt resistor is to be connected in parallel with the galvanometer.

Long Answer Questions                                                                                   5 Marks

What is a cyclotron? Explain its working principle.

Ans: Cyclotron is a device used to accelerate charged particles like protons, deuterons, $\alpha $ - particles, etc. 

It works on the basis of the principle that a charged particle can be accelerated to very high energies by making it pass through a moderate electric field a number of times and applying a strong magnetic field at the same time. 

A cyclotron’s oscillator frequency is \[10\,\text{MHz}\], what should be the operating magnetic field for accelerating protons? If radius is \[20\,\text{cm}\], what is the K.E. of the proton beam produced by the accelerator? \[\left( e=1.6\times {{10}^{-19}}\text{ c},mp=1.6\times {{10}^{-27}}\text{ kg},1\text{ MeV}=1.602\times {{10}^{-13}}\text{ J} \right)\]

Ans: Given that, \[v=10\,\text{MHz}=10\times {{10}^{6}}\text{ Hz}\] 

\[e=1.6\times {{10}^{-19}}\text{ c}\]

\[mp=1.6\times {{10}^{-27}}\text{ kg}\]

\[r=20\,\text{cm}=20\times {{10}^{-2}}\,\text{m}\] 

We have the expression for kinetic energy, 

KE $=\frac{{{q}^{2}}{{B}^{2}}{{r}^{2}}}{2m}$ 

Using $v=\frac{qB}{2\pi }$ 

$B=\frac{2\pi mV}{q}$ 

$\Rightarrow B=\frac{2\times 3.14\times 1.6\times {{10}^{-27}}\times {{10}^{7}}}{1.6\times {{10}^{-19}}}$ 

$\Rightarrow B=0.628\text{ T}$ 

Therefore, the operating magnetic field for accelerating protons is $0.628\text{ T}$.

KE $=\frac{{{\left( 1.6\times {{10}^{-19}} \right)}^{2}}\times {{\left( 0.66 \right)}^{2}}\times {{\left( 0.2 \right)}^{2}}}{2\times 1.67\times {{10}^{-27}}}$ 

KE $=13.35\times {{10}^{-13}}\text{ J}$ 

But we have, $1.602\times {{10}^{-13}}\text{ Joules}=1\text{ MeV}$ 

Since $12.02\times {{10}^{-13}}\text{ J}$ has $\frac{12.02\times {{10}^{-13}}}{1.602\times {{10}^{-13}}}\text{ MeV}$ 

$\Rightarrow KE=8.3\text{ MeV}$

Therefore, the K.E. of the proton beam produced by the accelerator is $8.3\text{ MeV}$.

Draw a labelled diagram of a moving coil galvanometer. Prove that in a radial magnetic field, the deflection of the coil is directly proportional to the current flowing in the coil. 

Ans: When a current $I$ is passed through a coil two equal and opposite forces act on the arms of a coil to form a couple which exerts a Torque on the coil. 

\[\tau =NIAB\sin \theta \] 

If $\theta =90{}^\circ \left( \sin 90{}^\circ =1 \right)$ 

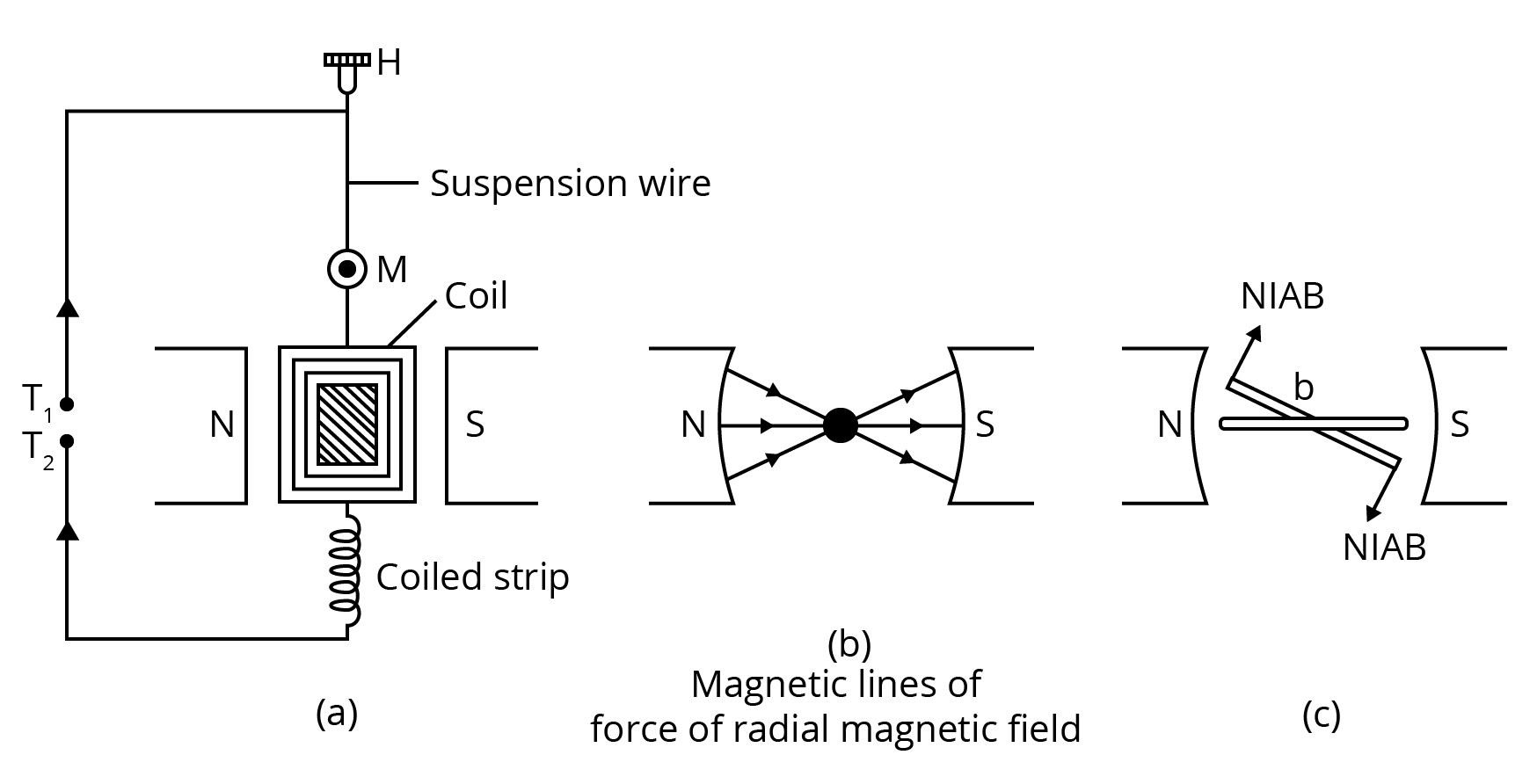
$\theta $ is the angle made by the normal to the plane of coil with B 

$\tau =NIAB\text{ }$ ……………………………….. (1)

This is called as deflecting torque 

As the coil deflected the spring is twisted and a restoring torque per unit twist then the restoring torque for the deflecting & is given by 

${\tau }'=k\phi $ ……………………….. (2)

In equilibrium 

\[\text{Deflecting Torque}=\text{Restoring Torque}\] 

\[NIAB=K\phi \] 

\[I=\frac{K\phi }{NAB}\phi \] 

\[I=G\phi \] where \[G=\frac{K}{NAB}\] (galvanometer constant) 

$\Rightarrow I\propto \phi $ 

Therefore, deflection of the coil is directly proportional to the current flowing in the coil.

A galvanometer can be converted into a voltmeter to measure upto 

$V$ volt by connecting a resistance ${{R}_{1}}$ series with the coil 

\[\frac{V}{2}\] volt by connecting a resistance ${{R}_{2}}$ in series with a coil. Find \[R\] in terms of ${{R}_{1}}\text{ and }{{R}_{2}}$ required to convert – it into a voltmeter that can read up to \['2V'\] volt. 

Ans: We know that, ${{I}_{g}}=\frac{V}{R+{{R}_{G}}}$ 

\[\Rightarrow {{I}_{g}}\text{=}\frac{V}{{{R}_{1}}+{{R}_{G}}}\] …………………………….. (1)

And ${{I}_{g}}=\frac{\frac{V}{2}}{{{R}_{2}}+{{R}_{G}}}$  ……………………………. (2)

Equating \[\left( 1 \right)\text{ }\And \text{ }\left( 2 \right)\] 

$\frac{V}{{{R}_{1}}+{{R}_{G}}}=\frac{\frac{V}{2}}{{{R}_{2}}+{{R}_{G}}}$ 

That is, ${{R}_{1}}+{{R}_{G}}=2\left( {{R}_{2}}+{{R}_{G}} \right)$

${{R}_{G}}=-2{{R}_{2}}+{{R}_{1}}$ 

For conversion ${{I}_{g}}=\frac{2V}{R+{{R}_{G}}}$ 

$\Rightarrow {{I}_{g}}\frac{V}{{{R}_{1}}+{{R}_{G}}}=\frac{2V}{R+{{R}_{G}}}$ 

$\Rightarrow {{I}_{g}}=2{{R}_{1}}+2{{R}_{G}}=R+{{R}_{G}}$ 

$\Rightarrow R=2{{R}_{1}}+{{R}_{G}}$ 

$\Rightarrow R=2{{R}_{1}}+{{R}_{1}}-2{{R}_{2}}$ 

$\Rightarrow R=3{{R}_{1}}-2{{R}_{2}}$ 

Therefore, R in the case can be written as, $R=3{{R}_{1}}-2{{R}_{2}}$.

3. Two moving coil meters, ${{M}_{1}}$ and ${{M}_{2}}$ have the following particulars:

${{R}_{1}}=10\,\Omega ,$ ${{N}_{1}}=30,$${{A}_{1}}=3.6\times {{10}^{-3}}\text{ }{{\text{m}}^{2}},$ ${{B}_{1}}=0.25\text{ T}$

\[{{R}_{2}}=14\,\Omega ,\] \[{{N}_{2}}=42\],${{A}_{2}}=1.8\times {{10}^{-3}}\text{ }{{\text{m}}^{2}},$ ${{B}_{2}}=0.50\text{ T}$

(The spring constants are identical for the two meters). 

Determine the ratio of (a) current sensitivity and (b) Voltage sensitivity of ${{M}_{1}}$ and  ${{M}_{2}}$.

a) current sensitivity of ${{M}_{1}}$ and  ${{M}_{2}}$:

Ans: From given data, moving coil meter ${{M}_{1}}$, 

Resistance, ${{R}_{1}}=10\,\Omega $ 

Number of turns, ${{N}_{1}}=30$ 

Area of cross-section, ${{A}_{1}}=3.6\times {{10}^{-3}}\text{ }{{\text{m}}^{2}}$

Magnetic field strength, ${{B}_{1}}=0.25\text{ T}$

Spring constant ${{K}_{1}}=K$ 

For moving coil meter ${{M}_{2}}$ : 

Resistance, \[{{R}_{2}}=14\,\Omega \]

Number of turns, \[{{N}_{2}}=42\]

Area of cross-section, ${{A}_{2}}=1.8\times {{10}^{-3}}\text{ }{{\text{m}}^{2}}$

Magnetic field strength, ${{B}_{2}}=0.50\text{ T}$

Spring constant, ${{K}_{2}}=K$ 

Current sensitivity of ${{M}_{1}}$ is given as:

${{I}_{s1}}=\frac{{{N}_{1}}{{B}_{1}}{{A}_{1}}}{{{K}_{1}}}$ 

And, the current sensitivity of ${{M}_{2}}$ is given as:

${{I}_{s2}}=\frac{{{N}_{2}}{{B}_{2}}{{A}_{2}}}{{{K}_{2}}}$ 

$\therefore $ Ratio $\frac{{{I}_{s2}}}{{{I}_{s1}}}=\frac{{{N}_{2}}{{B}_{2}}{{A}_{2}}{{K}_{1}}}{{{N}_{1}}{{B}_{1}}{{A}_{1}}{{K}_{2}}}$ $=\frac{42\times 0.5\times 1.8\times {{10}^{-3}}\times K}{K\times 30\times 0.25\times 3.6\times {{10}^{-3}}}=1.4$

Hence, the ratio of current sensitivity of ${{M}_{2}}\text{ to }{{M}_{1}}$ is $1.4$.

(b) voltage sensitivity of ${{M}_{2}}\text{ and }{{M}_{1}}$ 

Ans: Voltage sensitivity for ${{M}_{2}}$ is given as:

${{V}_{s2}}=\frac{{{N}_{2}}{{B}_{2}}{{A}_{2}}}{{{K}_{2}}{{R}_{2}}}$ 

And, voltage sensitivity for ${{M}_{1}}$ is given as:

${{V}_{s1}}=\frac{{{N}_{1}}{{B}_{1}}{{A}_{1}}}{{{K}_{1}}{{R}_{1}}}$

On taking the ratio we get, 

$\frac{{{V}_{S2}}}{{{V}_{S1}}}=\frac{{{N}_{2}}{{B}_{2}}{{A}_{2}}{{K}_{1}}{{R}_{1}}}{{{K}_{2}}{{R}_{2}}{{N}_{1}}{{B}_{1}}{{A}_{1}}}$

$\therefore \frac{{{V}_{S2}}}{{{V}_{S1}}}=\frac{42\times 0.5\times 1.8\times {{10}^{-3}}\times 10\times K}{K\times 14\times 30\times 0.25\times 3.6\times {{10}^{-3}}}=1$

Therefore, the ratio of voltage sensitivity of ${{M}_{2}}\text{ and }{{\text{M}}_{1}}$is 1. 

4. In a chamber, a uniform magnetic field of $6.5G\left( 1G={{10}^{-4}}T \right)$is maintained. An electron is shot into the field with a speed of $4.8\times {{10}^{6}}m{{s}^{-1}}$ normal to the field. Explain why the path of the electron is a circle. Determine the radius of the circular orbit.$\left( e=1.6\times {{10}^{-19}}C,{{m}_{e}}=9.1\times {{10}^{-31}}kg \right)$

Ans: Given that, magnetic field strength, \[B=6.5\text{ G}=6.5\times {{10}^{-4}}\text{ T}\]

Speed of the electron, \[v=4.8\times {{10}^{6}}\text{ m/s}\]

Charge on the electron, $e=1.6\times {{10}^{-19}}\text{ C}$ 

Mass of the electron, ${{m}_{e}}=9.1\times {{10}^{-31}}\text{ kg}$

Angle between the shot electron and magnetic field, $\theta =90{}^\circ $ 

Magnetic force exerted on the electron in the magnetic field is given as: 

\[F=evB\sin \theta \] 

This force provides centripetal force to the moving electron. Hence, the electron starts moving in a circular path of radius $r$. 

Therefore, centripetal force exerted on the electron, 

${{F}_{c}}=\frac{m{{v}^{2}}}{r}$ 

In equilibrium, the centripetal force exerted on the electron is equal to the magnetic force, 

That is, ${{F}_{c}}=F$ 

$\frac{m{{v}^{2}}}{r}=evB\sin \theta $ 

$\Rightarrow r=\frac{mv}{Be\sin \theta }$ 

$\Rightarrow r=\frac{9.1\times {{10}^{-31}}\times 4.8\times {{10}^{6}}}{6.5\times {{10}^{-4}}\times 1.6\times {{10}^{-19}}\times \sin 90{}^\circ }$ 

$\Rightarrow r=4.2\times {{10}^{-2}}\text{ m}$ 

\[\Rightarrow r=4.2\text{ cm}\] 

Therefore, the radius of the circular orbit of the electron is \[4.2\text{ cm}\].

5. In Exercise \[4.11\] obtain the frequency of revolution of the electron in its circular orbit. Does the answer depend on the speed of the electron? Explain. 

Ans: Given that, magnetic field strength, $B=6.5\times {{10}^{-4}}\text{ T}$ 

Charge of the electron, $e=1.6\times {{10}^{-19}}\text{ C}$ 

Mass of the electron, ${{m}_{e}}=9.1\times {{10}^{-31}}\text{ kg}$ 

Velocity of the electron, \[v=4.8\times {{10}^{6}}\text{ m/s}\] 

Radius of the orbit, \[r=4.2\text{ cm}=0.042\text{ m}\] 

Frequency of revolution of the electron $=\upsilon $ 

Angular frequency of the electron, $\omega =2n\upsilon $  

Velocity of the electron is related to the angular frequency as:

 $v=r\omega $ 

In the circular orbit, the magnetic force on the electron is balanced by the centripetal force. So, 

$evB=\frac{m{{v}^{2}}}{R}$ 

$\Rightarrow eB=\frac{m}{r}\left( r\omega  \right)=\frac{m}{r}\left( r2\pi \upsilon  \right)$ 

$\Rightarrow \upsilon =\frac{Be}{2\pi m}$ 

This expression for frequency is independent of the speed of the electron. 

On substituting, frequency, 

$\Rightarrow \upsilon =\frac{6.5\times {{10}^{-4}}\times 1.6\times {{10}^{-19}}}{2\times 3.14\times 9.1\times {{10}^{-31}}}$ 

$\Rightarrow \upsilon =18.2\times {{10}^{6}}\text{ Hz}$ 

$\Rightarrow \upsilon \approx 18\text{ MHz}$ 

Therefore, the frequency of the electron is around \[18\text{ MHz}\] and is independent of the speed of the electron.

6. Two concentric circular coils X and Y radii 16 cm and 10 cm, respectively, lie in the same vertical plane containing the north to south direction. Coil X has 20 turns and carries a current of 16 A; coil Y has 25 turns and carries a current of 18 A. The sense of the current in X is anticlockwise, and clockwise in Y, for an observer looking at the coils facing west. Give the magnitude and direction of the net magnetic field due to the coils at their centre.

Radius of coil X, ${{r}_{1}}=16cm=0.16m$

Radius of coil Y, ${{r}_{2}}=10cm=0.1m$

Number of turns of on coil X,${{n}_{1}}=20$

Number of turns of on coil Y,${{n}_{2}}=25$

Current in coil X, ${{I}_{1}}=16A$

Current in coil Y,${{I}_{2}}=18A$

Magnetic field due to coil X at their centre is given by the relation,

${{B}_{1}}=\frac{{{\mu }_{0}}{{n}_{1}}{{I}_{1}}}{2{{r}_{1}}}$

Where, Permeability of free space, ${{\mu }_{0}}=4\pi \times {{10}^{-4}}Tm{{A}^{-1}}$

${{B}_{1}}=\frac{4\pi \times {{10}^{-7}}\times 20\times 16}{2\times 0.16}$

$\therefore {{B}_{1}}=4\pi \times {{10}^{-4}}T$(towards East)

Magnetic field due to coil Y at their centre is given by the relation,

${{B}_{2}}=\frac{{{\mu }_{0}}{{n}_{2}}{{I}_{2}}}{2{{r}_{2}}}$

$\Rightarrow {{B}_{2}}=\frac{4\pi \times {{10}^{-7}}\times 25\times 18}{2\times 0.10}$

$\Rightarrow {{B}_{2}}=9\pi \times {{10}^{-4}}T$(towards West)

So, net magnetic field could be obtained as,

$B={{B}_{2}}-{{B}_{1}}=9\pi \times {{10}^{-4}}-4\pi \times {{10}^{-4}}$

$\Rightarrow B=1.57\times {{10}^{-3}}T$(towards West)

Therefore, net magnetic field is $1.57\times {{10}^{-3}}T$ towards west.

7. For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,

Show that this reduces to the familiar result for the field at the centre of the coil.

Radius of circular coil = R

Number of turns on the coil = N

Current in the coil = I

Magnetic field at a point on its axis at distance x is given by the relation,

Where,${{\mu }_{0}}=4\pi \times {{10}^{-4}}Tm{{A}^{-1}}$Permeability of free space

If the magnetic field at the centre of the coil is considered, then $x=0$

$\therefore B=\frac{{{\mu }_{0}}I{{R}^{2}}N}{2{{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\frac{3}{2}}}}$

Therefore, this is the familiar result for the magnetic field at the centre of the coil.

Consider two parallel coaxial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the midpoint between the coils is uniform over a distance that is small as compared to R, and is given by, approximately, (Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.)

Ans: Radii of two parallel coaxial circular coils = R

Number of turns on each coil = N

Current in both coils = I

Distance between both the coils = R

Let us consider point Q at distance d from the centre.

Then, one coil is at a distance of $\frac{R}{2}+d$from point Q.

Magnetic field at point Q could be given as:

$B=\frac{{{\mu }_{0}}I{{R}^{2}}N}{2{{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\frac{3}{2}}}}$

Also, the other coil is at a distance of  $\frac{R}{2}+d$from point Q.

Magnetic field due to this coil is given as:

${{B}_{2}}=\frac{{{\mu }_{0}}NI{{R}^{2}}}{2{{\left[ {{\left( \frac{R}{2}-d \right)}^{2}}+{{R}^{2}} \right]}^{\frac{3}{2}}}}$

Now we have the total magnetic field as, 

$B={{B}_{1}}+{{B}_{2}}$

$\Rightarrow B=\frac{{{\mu }_{0}}I{{R}^{2}}}{2}\left[ \left\{ {{\left\{ \left. {{\left( \frac{R}{2}-d \right)}^{2}}+{{R}^{2}} \right\} \right.}^{\frac{-3}{2}}}+{{\left. \left\{ {{\left( \frac{R}{2}+d \right)}^{2}}+{{R}^{2}} \right. \right\}}^{\frac{-3}{2}}}\times N \right. \right]$

$\Rightarrow B=\frac{{{\mu }_{0}}I{{R}^{2}}}{2}\left[ \left\{ {{\left\{ \left. \frac{5{{R}^{2}}}{4}+{{d}^{2}}-Rd \right\} \right.}^{\frac{-3}{2}}}+{{\left. \left\{ \frac{5{{R}^{2}}}{4}+{{d}^{2}}+Rd \right. \right\}}^{\frac{-3}{2}}}\times N \right. \right]$

$\Rightarrow B=\frac{{{\mu }_{0}}I{{R}^{2}}}{2}\left[ \left\{ {{\left\{ \left. 1+\frac{4{{d}^{2}}}{5{{R}^{2}}}-\frac{4d}{5R} \right\} \right.}^{\frac{-3}{2}}}+{{\left\{ 1+\frac{4{{d}^{2}}}{5{{R}^{2}}}+\frac{4d}{5R} \right\}}^{\frac{-3}{2}}}\times N \right. \right]$

Now for $d\ll R$, we could neglect the factor $\frac{{{d}^{2}}}{{{R}^{2}}}$, we get, 

$B\approx \frac{{{\mu }_{0}}I{{R}^{2}}}{2}\times {{\left( \frac{5{{R}^{2}}}{4} \right)}^{\frac{-3}{2}}}\left[ {{\left( 1-\frac{4d}{5R} \right)}^{\frac{-3}{2}}}+{{\left( 1+\frac{4d}{5R} \right)}^{\frac{-3}{2}}} \right]\times N$

$\Rightarrow B\approx \frac{{{\mu }_{0}}I{{R}^{2}}}{2}\times {{\left( \frac{5{{R}^{2}}}{4} \right)}^{\frac{-3}{2}}}\left[ 1-\frac{6d}{5R}+1+\frac{6d}{5R} \right]$

$\Rightarrow B\approx {{\left( \frac{4}{5} \right)}^{\frac{3}{2}}}\frac{{{\mu }_{0}}IN}{R}=0.72\left( \frac{{{\mu }_{0}}IN}{R} \right)$

Therefore, we proved that the field along the axis around the mid-point between the coils is uniform. 

8. An electron emitted by a heated cathode and accelerated through a potential difference of $2.0kV$, enters a region with a uniform magnetic field of $0.15T$. Determine the trajectory of the electron if the field 

is transverse to its initial velocity. 

Ans: We are given, 

Magnetic field strength, $B=0.15T$

Charge on the electron, $e=1.6\times {{10}^{-19}}C$

Mass of the electron, $m=9.1\times {{10}^{-31}}kg$

Potential difference, $V=2.0kV=2\times {{10}^{3}}V$

Now we have the kinetic energy of the electron given by, 

$eV=\frac{1}{2}m{{v}^{2}}$

$\Rightarrow v=\sqrt{\frac{2eV}{m}}$…………………….. (1)

Where, $v$is the velocity of the electron

Since the magnetic force on the electron provides the required centripetal force of the electron, the electron traces a circular path of radius $r$.

Now, the magnetic force on the electron is given by the relation, 

Centripetal force, 

${{F}_{C}}=\frac{m{{v}^{2}}}{r}$

$\Rightarrow Bev=\frac{m{{v}^{2}}}{r}$

$\Rightarrow r=\frac{mv}{Be}$………………….. (2)

From the equations (1) and (2), we get, 

$r=\frac{m}{Be}{{\left[ \frac{2eV}{m} \right]}^{\frac{1}{2}}}$

$\Rightarrow r=\frac{9.1\times {{10}^{-31}}}{0.15\times 1.6\times {{10}^{-19}}}{{\left( \frac{2\times 1.6\times {{10}^{-19}}\times 2\times {{10}^{3}}}{9.1\times {{10}^{-31}}} \right)}^{\frac{1}{2}}}$

$\Rightarrow r=100.55\times {{10}^{-5}}$

$\Rightarrow r=1mm$

Therefore, we found that the electron has a circular trajectory of radius 1.0 mm normal to the magnetic field.

makes an angle of $30{}^\circ $with the initial velocity.

Ans: When the field makes an angle $\theta $ of $30{}^\circ $with initial velocity, the initial velocity will be,

${{v}_{1}}=v\sin \theta $

From equation (2), we can write the following expression:

${{r}_{1}}=\frac{m{{v}_{1}}}{Be}$

$\Rightarrow {{r}_{1}}=\frac{mv\sin \theta }{Be}$

$\Rightarrow {{r}_{1}}=\frac{9.1\times {{10}^{-31}}}{0.15\times 1.6\times {{10}^{-19}}}\left[ \frac{2\times 1.6\times {{10}^{-19}}\times 2\times {{10}^{3}}}{9\times {{10}^{-31}}} \right]\sin 30{}^\circ $

$\Rightarrow r=0.5\times {{10}^{-3}}m=0.5mm$

Therefore, we found that the electron has a helical trajectory of radius $0.5mm$, with the axis of the solenoid along the magnetic field direction.

9. A magnetic field set up using Helmholtz coils (described in Exercise $4.16$) is uniform in a small region and has a magnitude of $0.75T$. In the same region, a uniform electrostatic field is maintained in a direction normal to the common axis of the coils. A narrow beam of (single species) charged particles all accelerated through $15kV$enters this region in a direction perpendicular to both the axis of the coils and the electrostatic field. If the beam remains undeflected when the electrostatic field is $9.0\times {{10}^{-5}}V{{m}^{-1}}$ make a simple guess as to what the beam contains. Why is the answer not unique?

Magnetic field, $B=0.75T$

Accelerating voltage, $V=15kV=15\times {{10}^{3}}V$

Electrostatic field, $E=9\times {{10}^{5}}V{{m}^{-1}}$

Mass of the electron$=m$

Charge of the electron $=e$

Velocity of the electron $=v$

Kinetic energy of the electron $=eV$

Thus, 

$\frac{1}{2}m{{v}^{2}}=eV$

$\Rightarrow \frac{e}{m}=\frac{{{v}^{2}}}{2V}$…………………….. (1)

Since the particle remains undeflected by electric and magnetic fields, we could infer that the electric field is balancing the magnetic field.

$\Rightarrow v=\frac{E}{B}$……………………….. (2)

Now we could substitute equation (2) in equation (1) to get,

$\Rightarrow \frac{e}{m}=\frac{1}{2}\frac{{{\left( \frac{E}{B} \right)}^{2}}}{V}=\frac{{{E}^{2}}}{2V{{B}^{2}}}$

$\Rightarrow \frac{e}{m}=\frac{{{\left( 9.0\times {{10}^{5}} \right)}^{2}}}{2\times 15000\times {{\left( 0.75 \right)}^{2}}}=4.8\times {{10}^{7}}C/kg$

This value of the specific charge $\left( \frac{e}{m} \right)$ is equal to the value of deuteron or deuterium ions. This is not a unique answer. Other possible answers are $H{{e}^{++}}$, $L{{i}^{+++}}$

10. A uniform magnetic field of $1.5T$ exists in a cylindrical region of radius $10.0cm$, its direction parallel to the axis along east to west. A wire carrying a current of $7.0A$ in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if,

The wire intersects the axis,

Magnetic field strength, $B=1.5T$

Radius of the cylindrical region, $r=10cm=0.1m$

Current in the wire passing through the cylindrical region, $I=7A$

If the wire intersects the axis, then the length of the wire is the diameter of the cylindrical region. Thus, $l=2r=0.2m$

Angle between magnetic field and current, $\theta =90{}^\circ $

We know that, Magnetic force acting on the wire is given by the relation,

$F=BIl\sin \theta $

$\Rightarrow F=1.5\times 7\times 0.2\times \sin 90{}^\circ $

$\Rightarrow F=2.1N$

Therefore, a force of 2.1 N acts on the wire in a vertically downward direction.

The wire is turned from N-S to northeast-northwest direction,

Ans: New length of the wire after turning it to the northeast-northwest direction can be given as:

${{l}_{1}}=\frac{l}{\sin \theta }$

Angle between magnetic field and current, $\theta =45{}^\circ $

Force on the wire,

$F=BI{{l}_{1}}\sin \theta =BIl=1.5\times 7\times 0.2$

Therefore, a force of 2.1 N acts vertically downward on the wire. This is independent of angle $\theta $ as $l\sin \theta $ is fixed.

The wire in the N-S direction is lowered from the axis by a distance of $6.0cm$?

Ans: The wire is lowered from the axis by distance, $d=6.0cm$

Let ${{l}_{2}}$be the new length of the wire, 

${{\left( \frac{{{l}_{2}}}{2} \right)}^{2}}=4\left( d+r \right)=4\left( 10+6 \right)=4\times 16$

$\Rightarrow {{l}_{2}}=8\times 2=16cm=0.16m$

Magnetic force that is exerted on the wire is, 

${{F}_{2}}=BI{{l}_{2}}=1.5\times 7\times 0.16$

$\Rightarrow F=1.68N$

Therefore, a force of $1.68N$acts in a vertically downward direction on the wire.

11. A uniform magnetic field of $3000G$ is established along the positive z-direction. A rectangular loop of sides $10cm$ and $5cm$ carries a current of $12A$. What is the torque on the loop in the different cases shown in Figure? What is the force on each case? Which case corresponds to stable equilibrium?

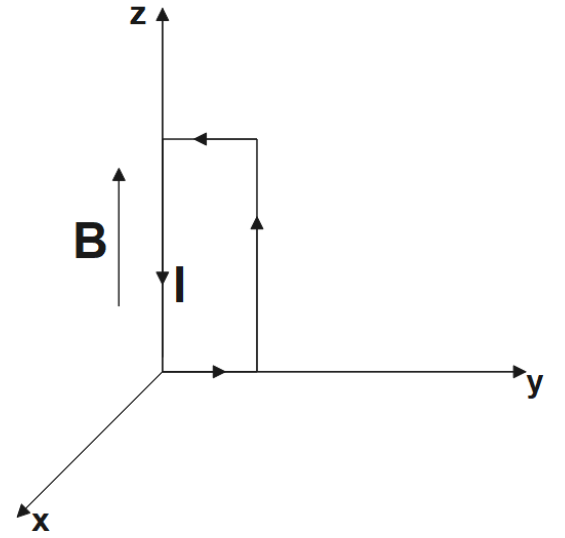
Magnetic field strength, $B=3000G=3000\times {{10}^{-4}}T=0.3T$

Length of the rectangular loop, $l=10cm$

Width of the rectangular loop, $b=5cm$

Area of the loop, $A=l\times b=\left( 10\times 5 \right)c{{m}^{2}}=50\times {{10}^{-4}}{{m}^{2}}$

Current in the loop, $I=12A$

Now, we could take the anti-clockwise direction of the current as positive and vice-versa, 

We have the expression for torque given as,

\[\vec{\tau }=I\vec{A}\times \vec{B}\]

We could see from the given figure that A is normal to the y-z plane and B is directed along the z-axis. Substituting the given values, 

$\tau =12\times \left( 50\times {{10}^{-4}} \right)\hat{i}\times 0.3\hat{k}$

$\Rightarrow \tau =-1.8\times {{10}^{-2}}\hat{j}Nm$

Now the torque is found to be directed along a negative y-direction. Since the external magnetic field is uniform, the force on the loop would be zero. 

(Image will be uploaded soon)

Ans: This case is very similar to case (a), so, the answer here would be same as (a). 

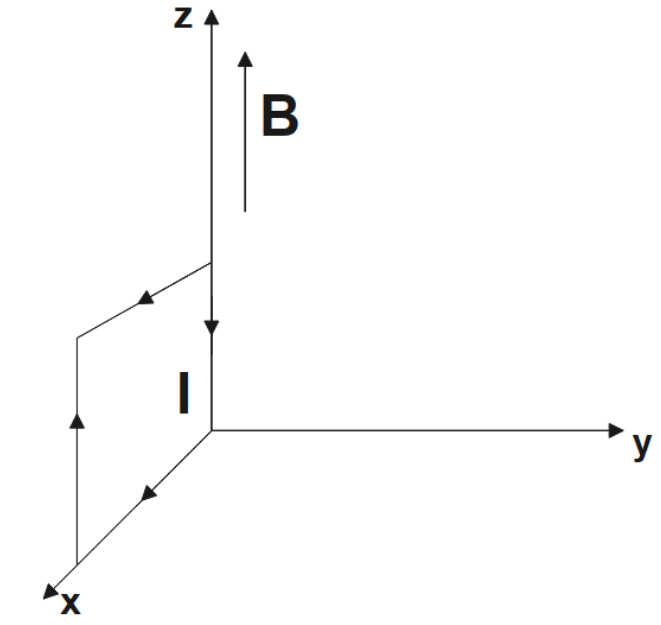
Ans: Torque here would be, 

$\Rightarrow \tau =-12\left( 50\times {{10}^{-4}} \right)\hat{j}\times 0.3\hat{k}$

$\Rightarrow \tau =-1.8\times {{10}^{-2}}\hat{i}Nm$

The direction here is along the negative x direction and the force is zero. 

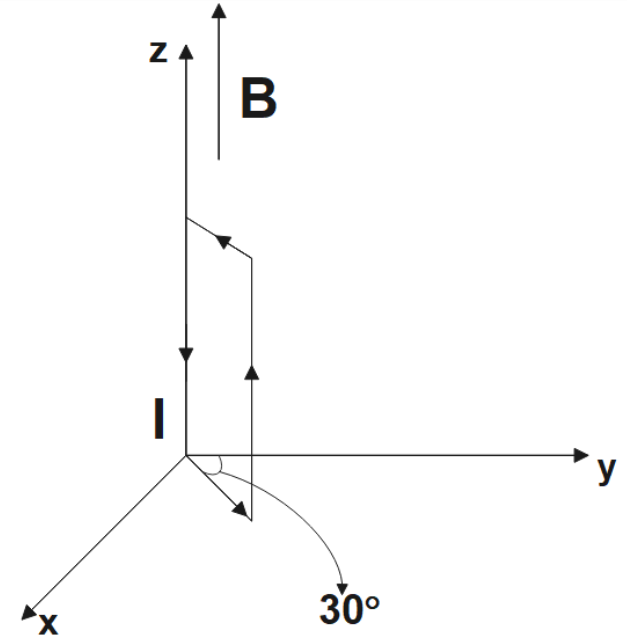
$\left| \tau  \right|=IAB$

$\Rightarrow \tau =12\times \left( 50\times {{10}^{-4}} \right)\times 0.3$

$\Rightarrow \left| \tau  \right|=1.8\times {{10}^{-2}}Nm$

Here, the direction is found to be at $240{}^\circ $with positive x-direction and the force is zero.

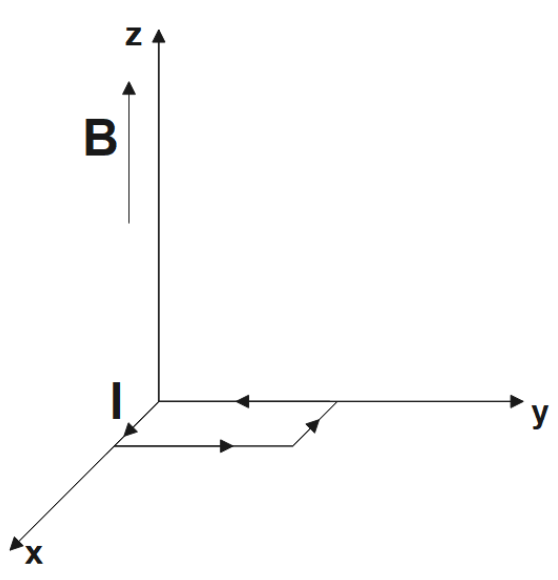
Ans: Torque, 

$\tau =I\vec{A}\times \vec{B}$

$\Rightarrow \tau =\left( 50\times {{10}^{-4}}\times 12 \right)\hat{k}\times 0.3\hat{k}$

$\Rightarrow \tau =0$

Here, both torque and force are found to be zero. For this case, the direction $I\vec{A}$and $\vec{B}$is the same and the angle between them is zero. They would come back to equilibrium on being displaced and so the equilibrium is stable.

(image will be uploaded soon)

Ans: Torque is given by, 

Here also both torque and force are found to be zero. 

For this case, the direction of $I\vec{A}$ and $\vec{B}$ are opposite and the angle between them is $180{}^\circ $. Here it doesn’t come back to its original position on being disturbed and hence, the equilibrium is unstable. 

12. A solenoid $60cm$ long and has a radius $4.0cm$ has 3 layers of windings of 300turns each. A $2.0cm$ long wire of mass $2.5g$ lies inside the solenoid (near its centre) normal to its axis; both the wire and the axis of the solenoid are in the horizontal plane. The wire is connected through two leads parallel to the axis of the solenoid to an external battery which supplies a current of $6.0A$ in the wire. What value of current (with appropriate sense of circulation) in the windings of the solenoid can support the weight of the wire? $g=9.8m{{s}^{-2}}$

Length of the solenoid, $L=60cm=0.6m$

Radius of the solenoid, $r=4.0cm=0.04m$

It is given that there are 3 layers of windings of 300 turns each.

Total number of turns, $n=3\times 300=900$

Length of the wire, $l=2cm=0.02m$

Mass of the wire, $m=2.5g=2.5\times {{10}^{-3}}kg$

Current flowing through the wire, $i=6A$

Magnetic field produced inside the solenoid, $B=\frac{{{\mu }_{0}}nI}{L}$

Current flowing through the windings of the solenoid, $I$

Magnetic force is given by the relation,

$F=Bil=\frac{{{\mu }_{0}}nI}{L}il$

Now, we have the force on the wire equal to the weight of the wire.

$mg=\frac{{{\mu }_{0}}nIil}{L}$

$\Rightarrow I=\frac{mgL}{{{\mu }_{0}}nil}=\frac{2.5\times {{10}^{-3}}\times 9.8\times 0.6}{4\pi \times {{10}^{-7}}\times 900\times 0.02\times 6}$

$\Rightarrow I=108A$

Therefore, the current flowing through the solenoid is 108 A.

Download Important Questions Of Chapter 4 Physics Class 12 PDF

Class 12 physics chapter 4 important questions.

The Class 12 Physics Chapter 4 important questions PDF is highly beneficial for the students who are targeting good grades in competitive exams. The textbook prescribed by NCERT for Class 12 Physics consists of many topics. For elevating the grades and to improve their knowledge in the subject students are suggested to download chapter wise notes available on Vedantu for detailed explanation along with exercise problems. 

For thorough preparation, students should start with Chapter 4 Physics Class 12 important questions . The important questions of Chapter 4 Physics Class 12 are prepared with deep insight into the syllabus according to CBSE board exams , previous year’s questions. The Chapter 4 Physics Class 12 important questions included all the textbook exercises along with many Class 12 Physics Chapter 4 extra questions prepared by experts and the master teachers.

Chapter 4 Moving Charges and Magnetism has good marks allotment in the Board exams. The Moving charges and Magnetism include many interesting topics like magnetic forces, magnetic field, the direction of magnetic force in the current-carrying coil with different cases, etc. These concepts are not only important in the point of board exam but also for students who are aiming for IIT-JEE , NEET exams as well.

Students must start with Class 12 Physics Chapter 4 important questions after revising the chapter. Students must be thoroughly familiar with all the concepts of Chapter 4 for solving Class 12 Physics Chapter 4 extra questions. Let us have a look at some key points of Chapter 4:

The chapter consists of many direct derivations like ampere circuital law, the force between two parallel current-carrying wires, etc.

Chapter 4 mainly focused on explaining the idea that electric and magnetic fields are interrelated to one another. Because since the beginning it was assumed that electric fields and magnetic fields are independent of each other.

We come across the concepts like a magnetic force, Lorentz force which is a piece of evidence about electric and magnetic fields that are related to each other.

We study the effects of magnetic fields on current. We study a few devices that use the principle of magnetic induction.

We study cyclotrons, solenoids, moving coil galvanometers, etc.

These are a few key points to be remembered while jumping into the practice of Chapter 4 Physics Class 12 important questions .

Key Features of Vedantu’s CBSE Class 12 Important Questions for Physics Chapter 4 - Moving Charges and Magnetism

The following are the reasons why you should choose Vedantu’s Important Questions for Class 12 CBSE Physics Chapter 4 - Moving Charges and Magnetism:

Vedantu’s Important Questions for Class 12 CBSE Physics Chapter 4 - Moving Charges and Magnetism are aligned with the CBSE Board guidelines and answering pattern.

Our questions are prepared in a manner that will serve the purpose of revising the entire chapter to be able to solve any kind of question that is asked in the exam.

The questions adhere to the strict norms of the CBSE Class 12 Physics syllabus . The answers have also been framed in a straightforward manner using simple language. 

The set of important questions for CBSE Class 12 Physics Chapter 4 - Moving Charges and Magnetism for the academic year 2024-25 prove to be a valuable tool for students' exam preparation. These questions cover vital concepts such as magnetic fields, Ampere's law, and applications of moving charges in magnetic fields. By practicing these questions, students can strengthen their understanding of the topic and improve problem-solving abilities. The comprehensive nature of these questions ensures thorough coverage of the chapter, enabling students to excel in their examinations. With these resources at their disposal, students can confidently approach the subject and achieve academic success in the upcoming academic year.

Important Related Links for CBSE Class 12 Physics 

FAQs on Important Questions for CBSE Class 12 Physics Chapter 4 - Moving Charges and Magnetism 2024-25

1. What is Biot Savart’s law, according to Chapter 4 of Class 12 Physics?

This law is solely concerned with current sources and magnetic fields. The magnetic field is determined once the current involving vector products is spread. The distance between the field points and the current changes all the time, and this is the calculus problem. Aerodynamics and magnetic effects at the atomic and molecular levels are calculated. Visit Vedantu to learn more about this law.

2. What is Ampere's circuital law, according to Chapter 4 of Class 12 Physics?

Relation between the magnetic field and source current is discussed in ampere's circuital law. The density of a magnetic field in an imaginary path is studied in ampere's circuital law. For more information, visit Vedantu's official website. There you will find the important questions which will be helpful in your exams. These questions will cover all the important topics curated together from the exam's point of view. You can download these questions and save them on your PC for future reference free of cost from the Vedantu website and the Vedantu app.

3. What are the Different Applications of Ampere's Circuital Law, according to Chapter 4 of Class 12 Physics?

Different applications of ampere’s circuital law are:

Long current-carrying induced magnetism

Current carrying cylinder creating a magnetic field

Current carrying hollow cylinder creating magnetic fields

Vedantu has all the physics questions that are solved, so you do not have to take the pressure of solving them, especially when you have to submit the homework and have not read the chapter thoroughly. Also, in exams, you can go through these questions quickly and remember them till your exam day.

4. What is Understood by a Cyclotron, according to Chapter 4 of Class 12 Physics?

The first particle accelerator is responsible for accelerating charged particles to high energies. The charged particle accelerates outwards from the spiral routes alongside the spiral particles. Physics is a difficult topic that requires careful attention. All notes and content may be found on Vedantu. It also includes all of the practice examinations that will be useful in your board exams. Hence, if you want to get high grades, you should consult Vedantu.

5. What are the limitations to a cyclotron, according to Chapter 4 of Class 12 Physics?

The limitations of cyclotron are :

The electron cannot be accelerated by a cyclotron as they are of very small size.

Neutral particles cannot be accelerated.

Cannot accelerate large positive charged particles. 

Board exams are crucial for students. For these exams, a lot of practice is required. Vedantu has previous year's question papers which you can solve and then appear for the main exams. So, visit Vedantu for all such material.

CBSE Class 12 Physics Important Questions

Cbse study materials.

1569+ Class 12 Physics Case Study Questions PDF Download

• Post author: studyrate
• Post published:
• Post category: Class 12 / 12 board
• Post comments: 0 Comments

So, you’re in Class 12 and the concept of Physics case study questions is beginning to loom large. Are you feeling a little lost? Fear not! This article will guide you through everything you need to know to conquer these challenging yet rewarding Class 12 Physics Case Study Questions.

Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.

We have provided here Case Study questions for the Class 12 Physics for board exams. You can read these chapter-wise Case Study questions. These questions are prepared by subject experts and experienced teachers. The answer and solutions are also provided so that you can check the correct answer for each question. Practice these questions to score excellent marks in your final exams.

Physics is more than just formulas and equations, right? It’s a way to interpret the natural world, and case studies provide a perfect opportunity for students to apply theoretical knowledge to real-world situations. So, what’s the importance of case studies in class 12 Physics? Well, they help you to solidify your understanding and enhance your analytical skills, which are invaluable for exams and beyond.

Table of Contents

Case Study-Based Questions for Class 12 Physics

There are total of 14 chapters Electric Charges And Fields, Electrostatic Potential And Capacitance, Current Electricity, Moving Charges And Magnetism, Magnetism And Matter, Electromagnetic Induction, Alternating Current, Electromagnetic Waves, Ray Optics and Optical Instruments, Wave Optics, Dual Nature Of Radiation And Matter, Atoms, Nuclei, Semiconductor Electronics Materials Devices, And Simple Circuits.

• Case Study Based Questions on class 12 Physics Chapter 1 Electric Charges And Fields
• Case Study Based Questions on Class 12 Physics Chapter 2 Electrostatic Potential And Capacitance
• Case Study Based Questions on Class 12 Physics Chapter 3 Current Electricity
• Case Study Based Questions on Class 12 Physics Chapter 4 Moving Charges And Magnetism
• Case Study Based Questions on Class 12 Physics Chapter 5 Magnetism And Matter
• Case Study Based Questions on Class 12 Physics Chapter 6 Electromagnetic Induction
• Case Study Based Questions on Class 12 Physics Chapter 7 Alternating Current
• Case Study Based Questions on Class 12 Physics Chapter 8 Electromagnetic waves
• Case Study Based Questions on Class 12 Physics Chapter 9 Ray Optics and Optical Instruments
• Case Study Based Questions on class 12 Physics Chapter 10 Wave Optics
• Case Study Based Questions on class 12 Physics Chapter 11 Dual Nature of Matter and Radiation
• Case Study Based Questions on class 12 Physics Chapter 12 Atoms
• Case Study Based Questions on class 12 Physics Chapter 13 Nuclei
• Case Study Based Questions on class 12 Physics Chapter 14 Semiconductor Electronics
• Class 12 Chemistry Case Study Questions
• Class 12 Biology Case Study Questions
• Class 12 Maths Case Study Questions

Class 12 students should go through important Case Study problems for Physics before the exams. This will help them to understand the type of Case Study questions that can be asked in Grade 12 Physics examinations. Our expert faculty for standard 12 Physics have designed these questions based on the trend of questions that have been asked in last year’s exams. The solutions have been designed in a manner to help the grade 12 students understand the concepts and also easy-to-learn solutions.

How to Approach Physics Case Study Questions

Ah, the million-dollar question! How do you tackle these daunting case study questions? Let’s dive in.

Effective Reading Techniques

A vital part of cracking case study questions is understanding the problem correctly. Don’t rush through the question, take your time to fully grasp the scenario, and don’t skip over the details – they can be critical!

Conceptual Analysis

Once you’ve understood the problem, it’s time to figure out which physics principles apply. Remember, your foundational knowledge is your greatest weapon here.

Solving Strategies

Next, put pen to paper and start solving! Follow a systematic approach, check your calculations, and make sure your answer makes sense in the context of the problem.

Best Books for Class 12 Physics Exams

Class 12 Physics Syllabus 2024

Chapter–1: Electric Charges and Fields

Electric charges, Conservation of charge, Coulomb’s law-force between two point charges, forces between multiple charges; superposition principle, and continuous charge distribution.

Electric field, electric field due to a point charge, electric field lines, electric dipole, electric field due to a dipole, torque on a dipole in a uniform electric field.

Electric flux, statement of Gauss’s theorem and its applications to find field due to infinitely long straight wire, uniformly charged infinite plane sheet, and uniformly charged thin spherical shell (field inside and outside).

Chapter–2: Electrostatic Potential and Capacitance

Electric potential, potential difference, electric potential due to a point charge, a dipole and system of charges; equipotential surfaces, electrical potential energy of a system of two-point charges and of electric dipole in an electrostatic field.

Conductors and insulators, free charges and bound charges inside a conductor. Dielectrics and electric polarization, capacitors and capacitance, combination of capacitors in series and in parallel, capacitance of a parallel plate capacitor with and without dielectric medium between the plates, energy stored in a capacitor (no derivation, formulae only).

Chapter–3: Current Electricity

Electric current, flow of electric charges in a metallic conductor, drift velocity, mobility and their relation with electric current; Ohm’s law, V-I characteristics (linear and non-linear), electrical energy and power, electrical resistivity and conductivity, temperature dependence of resistance, Internal resistance of a cell, potential difference and emf of a cell, combination of cells in series and in parallel, Kirchhoff’s rules, Wheatstone bridge.

Chapter–4: Moving Charges and Magnetism

Concept of magnetic field, Oersted’s experiment.

Biot – Savart law and its application to current carrying circular loop.

Ampere’s law and its applications to infinitely long straight wire. Straight solenoid (only qualitative treatment), force on a moving charge in uniform magnetic and electric fields.

Force on a current-carrying conductor in a uniform magnetic field, force between two parallel current-carrying conductors-definition of ampere, torque experienced by a current loop in uniform magnetic field; Current loop as a magnetic dipole and its magnetic dipole moment, moving coil galvanometerits current sensitivity and conversion to ammeter and voltmeter.

Chapter–5: Magnetism and Matter

Bar magnet, bar magnet as an equivalent solenoid (qualitative treatment only), magnetic field intensity due to a magnetic dipole (bar magnet) along its axis and perpendicular to its axis (qualitative treatment only), torque on a magnetic dipole (bar magnet) in a uniform magnetic field (qualitative treatment only), magnetic field lines.

Magnetic properties of materials- Para-, dia- and ferro – magnetic substances with examples, Magnetization of materials, effect of temperature on magnetic properties.

Chapter–6: Electromagnetic Induction

Electromagnetic induction; Faraday’s laws, induced EMF and current; Lenz’s Law, Self and mutual induction.

Chapter–7: Alternating Current

Alternating currents, peak and RMS value of alternating current/voltage; reactance and impedance; LCR series circuit (phasors only), resonance, power in AC circuits, power factor, wattless current. AC generator, Transformer.

Chapter–8: Electromagnetic Waves

Basic idea of displacement current, Electromagnetic waves, their characteristics, their transverse nature (qualitative idea only). Electromagnetic spectrum (radio waves, microwaves, infrared, visible, ultraviolet, X-rays, gamma rays) including elementary facts about their uses.

Chapter–9: Ray Optics and Optical Instruments

Ray Optics:  Reflection of light, spherical mirrors, mirror formula, refraction of light, total internal reflection and optical fibers, refraction at spherical surfaces, lenses, thin lens formula, lens maker’s formula, magnification, power of a lens, combination of thin lenses in contact, refraction of light through a prism.

Optical instruments:  Microscopes and astronomical telescopes (reflecting and refracting) and their magnifying powers.

Chapter–10: Wave Optics

Wave optics: Wave front and Huygen’s principle, reflection and refraction of plane wave at a plane surface using wave fronts. Proof of laws of reflection and refraction using Huygen’s principle. Interference, Young’s double slit experiment and expression for fringe width (No derivation final expression only), coherent sources and sustained interference of light, diffraction due to a single slit, width of central maxima (qualitative treatment only).

Chapter–11: Dual Nature of Radiation and Matter

Dual nature of radiation, Photoelectric effect, Hertz and Lenard’s observations; Einstein’s photoelectric equation-particle nature of light.

Experimental study of photoelectric effect

Matter waves-wave nature of particles, de-Broglie relation.

Chapter–12: Atoms

Alpha-particle scattering experiment; Rutherford’s model of atom; Bohr model of hydrogen atom, Expression for radius of nth possible orbit, velocity and energy of electron in his orbit, of hydrogen line spectra (qualitative treatment only).

Chapter–13: Nuclei

Composition and size of nucleus, nuclear force

Mass-energy relation, mass defect; binding energy per nucleon and its variation with mass number; nuclear fission, nuclear fusion.

Chapter–14: Semiconductor Electronics: Materials, Devices and Simple Circuits

Energy bands in conductors, semiconductors and insulators (qualitative ideas only) Intrinsic and extrinsic semiconductors- p and n type, p-n junction

Semiconductor diode – I-V characteristics in forward and reverse bias, application of junction diode -diode as a rectifier.

For further information, Subscribe Our YouTube Channel, and comment below about your queries.

You can click on the chapter-wise Case Study links given above and read the Class 12th Physics Case Study questions and answers provided by us. If you face any issues or have any questions please put your questions in the comments section below. Our teachers will be happy to provide you with answers.

FAQs Class 12 Physics Case Studies Questions

What is the best website for a  case   study  of physics  class   12 .

studyrate.in is the best website for Class 12 Physics Case Study Questions for Board Exams. Here you can find various types of Study Materials, Ebooks, Notes, and much more free of cost.

What are Physics case study questions?

Physics case study questions involve applying physics principles to solve real-world scenarios or problems.

How can I prepare for Physics case study questions?

Strengthen your basic concepts, practice solving a variety of problems, and make use of resources like the Class 12 Physics Case Study Questions PDF.

You Might Also Like

Mcq class 12 english evans tries an o-level questions with answers english chapter 7, class 12 physics case study questions chapter 4 moving charges and magnetism, mcq questions class 12 economics chapter 5 government budget and the economy with answers, leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.

This site uses Akismet to reduce spam. Learn how your comment data is processed .

The Topper Combo Flashcards

• Contains the Latest NCERT in just 350 flashcards.
• Colourful and Interactive
• Summarised Important reactions according to the latest PYQs of NEET(UG) and JEE

No thanks, I’m not interested!

• Physics Important Questions
• Class 12 Physics
• Chapter 4: Moving Charges Magnetism

Important Questions for Class 12 Physics Chapter 4 – Moving Charges and Magnetism

Magnetism is a physical characteristic caused by magnetic fields that produce attractive and repulsive effects on other objects. A magnetic field is generated by electric currents and magnetic moments of particles and influences other currents and magnetic moments. Ferromagnetic materials, which are strongly drawn to magnetic fields and can become permanent magnets themselves, are the most well-known materials that exhibit magnetism. Only a limited number of substances are ferromagnetic, including iron, cobalt, nickel and their alloys, which are the most common. The less common ferromagnetic substances include the rare-earth metals neodymium and samarium. Ferro- refers to iron as the permanent magnetism that was first found in lodestone, a type of iron ore called magnetite (Fe3O4).

A magnetic field is a field of vectors representing magnetism’s impact on moving electric charges, electric currents, and magnetic materials. A force perpendicular to both the velocity and magnetic field is experienced by a moving charge in a magnetic field. A permanent magnet’s magnetic field attracts ferromagnetic materials like iron and other magnets. Nonuniform magnetic fields can also apply tiny forces to “nonmagnetic” materials through paramagnetism, diamagnetism, and antiferromagnetism, but these forces are usually so weak that they can only be measured with laboratory equipment. Magnetised materials are surrounded by magnetic fields generated by electric currents in electromagnets and changing electric fields. As the strength and direction of magnetic fields can vary in different locations, they are described mathematically with a vector field function assigning a vector to each point in space.

Magnetic fields are produced by the movement of electric charges and the inherent magnetic moments of particles connected to their spin, a fundamental quantum property. Magnetic and electric fields are related, and both are part of the electromagnetic force, one of nature’s four fundamental forces. Magnetic fields are widely utilised in modern technology, especially in electrical engineering and electromechanics. Rotating magnetic fields are applied in electric motors and generators. The study of magnetic fields in electrical devices like transformers is called magnetic circuits. The Hall effect shows the presence of charge carriers in a material through magnetic forces. The Earth generates its own magnetic field, protecting the ozone layer from solar wind and crucial for compass navigation.

Important Questions For Class 12 – Physics – Chapter 4 – Moving Charges and Magnetism are provided here. Students must go through these questions and solve them to prepare for their Physics papers. They can also refer to these questions for quick revision. These questions are more likely to be asked in the exam; hence, students must practise them thoroughly.

Very Short Answer Type Questions

1. How does the radius of the path of a charged particle moving in a cyclotron change when the radio frequency field’s frequency is doubled?

(a) It will be halved.

(b) It will be doubled.

(c) It will remain unchanged.

(d) It will be increased by four times.

Answer: (c) It will remain unchanged.

2. Which of the following statements about a cyclotron is not true?

(a) A cyclotron is a device that uses high energies to accelerate ions or charged particles.

(b) Cyclotron combines electric and magnetic fields to accelerate charged particles and increase their energy.

(c) The cyclotron works by utilising the principle that the time it takes for an ion to complete one revolution is not affected by its speed or the radius of its orbit.

(d) In a cyclotron, the path of charged particles and ions is not fixed and can be arbitrary.

Answer: (d) In a cyclotron, the path of charged particles and ions is not fixed and can be arbitrary.

3. If an electron is travelling with velocity ν, it generates a magnetic field B, then

(a) the direction of field B will align with the direction of velocity ν.

(b) the direction of field B will be in the opposite direction to the direction of velocity ν.

(c) the direction of field B will be at a right angle to the direction of velocity ν.

(d) the direction of field B is independent of the direction of velocity ν.

Answer: (c) the direction of field B will be at a right angle to the direction of velocity ν.

4. If the magnetic compass needle is brought close to a straight wire bearing current, then

(I) the straight wire results in a significant deviation of the compass needle.

(II) The needle tangentially aligns to an imaginary circle whose centre is the straight wire and whose plane is perpendicular to the wire.

(a) (II) is correct

(b) (I) is correct

(c) neither (I) nor (II) is correct

(d) both (I) and (II) are correct

Answer: (d) both (I) and (II) are correct

5. Which statement about magnetic forces is correct?

(a) Magnetic forces always obey Newton’s third law.

(b) Magnetic forces do not follow Newton’s third law.

(c) Magnetic forces adhere to Newton’s third law when the current is very high.

(d) Magnetic forces comply with Newton’s third law in a low magnetic field environment.

Answer: (b) Magnetic forces do not follow Newton’s third law.

6. Converting a moving coil galvanometer into a voltmeter is achieved by

(a) placing a high resistance in series.

(b) placing a low resistance in parallel.

(c) placing a high resistance in parallel.

(d) placing a low resistance in series.

Answer: (a) placing a high resistance in series.

7. Converting a moving coil galvanometer into an ammeter is done by

(a) placing a high shunt resistance in series.

(b) placing a low shunt resistance in parallel.

(c) placing a low resistance in series.

(d) placing a high resistance in parallel.

Answer: (b) placing a low shunt resistance in parallel.

Short Answer Type Questions

1. Verify that the cyclotron frequency = eB/m has the correct dimensions of [T] -1

When a charged particle travels normal to the magnetic field, then

\(\begin{array}{l}\frac{ mv^2 }{ r } = qvB\end{array} \)

\(\begin{array}{l}\textup{Therefore, dimensions of } \omega = \frac{qB}{m} = \frac{v}{r} = \frac{LT^{-1}}{L} = [T^{-1}]\end{array} \)

2. Show that a force that does no work and is a velocity-dependent force.

Work is a scalar product of displacement and force. Hence work done at any instant is given by the following formula:

\(\begin{array}{l}dW = \vec{F}. \vec{ds}\end{array} \)

Where displacement is given as:

\(\begin{array}{l}\textup{Displacement, } \vec{ds} = \vec{v} dt \end{array} \)

According to the question, the work done by the force is:

\(\begin{array}{l}dW = 0\end{array} \)

\(\begin{array}{l}\Rightarrow \vec{ F }. \vec{v}dt = 0\end{array} \)

\(\begin{array}{l}\vec{F}.\vec{v} = 0\end{array} \)

This shows that the angle between force and velocity will be 90 o . If the direction of velocity changes, then the direction of the force will also vary.

3. The magnetic force depends on v, which depends on the inertial frame of reference. Does then the magnetic force differ from inertial frame to frame? Is it reasonable that the net acceleration has a different value in different frames of reference?

The magnetic force relies on vector v, which depends on the inertial reference frame. Magnetic force on a charged particle,

\(\begin{array}{l}F = q ( \vec{v} \times \vec{B} ) \end{array} \)

\(\begin{array}{l} F = qvBsin \theta \end{array} \)

Thus, the magnetic force is velocity-dependent. It varies from one inertial frame to another inertial frame.

4. Describe the motion of a charged particle in a cyclotron if the frequency of the radio (rf) field was doubled.

When the frequency of the radio frequency (rf) field is doubled, then the resonance condition is violated, and the time period of the radio frequency (rf) field is halved.

Therefore, the duration in which a particle completes half revolution inside the dees, radio frequency completes the cycle. As a result, particles will accelerate and decelerate alternatively.

5. Two long wires carrying current I 1 and 1 2 are arranged as shown in the figure. The one carrying current I 1 is along the x-axis. The other carrying current, I 2 is along a line parallel to the y-axis given by x = 0 and z =d. Find the force exerted at 0 2 because of the wire along the x-axis.

Magnetic field at the point O 2 due to current I 1 in long wire along the x-axis is

\(\begin{array}{l} B_{O_{2}} = \frac{ \mu_0 }{ 4 \pi } \frac{ 2I }{ d } \end{array} \)

It will be along the y-axis. Since the second wire is along the y-axis, the angle between the direction of

\(\begin{array}{l} I_2 \vec{l} \textup{ and } \vec{B}_{O_{2}} \textup{ is zero.} \end{array} \)

\(\begin{array}{l} \theta = 0^o \end{array} \)

Force on the wire existing along the y-axis is,

\(\begin{array}{l} f = I_2 | \vec{ l } \times \vec{B}_{O_{2}} | = I_2 l B_{O_{2}} sin 0^o = 0 \end{array} \)

Long Answer Type Questions

1. A current carrying loop consists of 3 identical quarter circles of radius R, lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin, joined together. Find the direction and magnitude of B at the origin.

Solution: Draw a rough diagram.

The equation used is

\(\begin{array}{l}B = \frac{ \mu_0 I \theta }{ 4 \pi R }\end{array} \)

It is given that

\(\begin{array}{l} \textup{Quarter Circles } \theta = \frac{ \pi }{ 2 } \end{array} \)

The electric current in circular arc = I, Radius = R

The magnetic field at the origin point due to the electric current carrying arc existing in x-y plane:

\(\begin{array}{l} \vec{ B } _ { xy } = \frac{ \mu _ { 0 } I ( \pi / 2 ) }{ 4 \pi R } \hat{ k } \end{array} \)

\(\begin{array}{l} = \frac{ \mu _ { 0 } I }{ 8 R } \hat{ k } \end{array} \)

Likewise, the Magnetic field at the origin point due to the electric current circular arc existing in the y-z plane:

\(\begin{array}{l} \vec{ B } _ { xy } = \frac{ \mu _ { 0 } I ( \pi /2 ) } { 4 \pi R } \hat{ i } \end{array} \)

\(\begin{array}{l} = \frac{ \mu _ { 0 } I }{ 8 R } \hat{ i } \end{array} \)

Likewise, the magnetic field at origin due to the electric current carrying a circular arc existing in the y-x plane:

\(\begin{array}{l} \vec{ B } _ { zx } = \frac{ \mu _ { 0 }I ( \pi / 2 ) }{ 4 \pi R } \hat{ j } \end{array} \)

\(\begin{array}{l} = \frac{ \mu _ { 0 } I }{ 8R } \hat{ j } \end{array} \)

The total vector sum of the magnetic field at the origin point due to each quarter circle,

\(\begin{array}{l} \vec{ B } = \vec{ B } _ { xy } + \vec{ B } _ { yz } + \vec{ B } _ { zx } \end{array} \)

\(\begin{array}{l} \vec{ B } _ { net } = \left ( \frac{ \mu I }{ 8 R } \right ) ( \hat{ i } + \hat{ j } + \hat{ k } ) \end{array} \)

2. A charged particle of charge e and mass m is moving in an electric field E, and magnetic field B. Construct dimensionless quantities and quantities of dimension [T] -1 .

No dimensionless quantity made using the given quantities. In the case of a charged particle travelling normally to the magnetic field, the magnetic Lorentz forces lend the required circular or centripetal force for revolution.

\(\begin{array}{l} \frac{ mv ^ { 2 } }{ R } = qvB \end{array} \)

By simplifying the equation, we get,

\(\begin{array}{l} \frac{ q B }{ m } = \frac{ v }{ R } = \omega \end{array} \)

The dimensional form of angular frequency

\(\begin{array}{l} [\omega] = \left [ \frac{ qB }{ m } \right ] = \frac{ v } { R } = [T] ^ { -1 } \end{array} \)

3. An electron enters with a velocity v = V o i into a cubical region (faces parallel to coordinate planes) in which there are uniform electric and magnetic fields. The orbit of the is found to spiral down inside the cube in the plane parallel to the x-y plane. Suggest a configuration of fields E and B that can lead to it.

If a charged particle is positioned in an electric field and magnetic field, then it begins moving in a spiral trajectory where magnetic field B and electric field E is perpendicular to the direction of motion. The electric field applies force on the charged particle, which results in the particle’s deceleration or acceleration and the centripetal force works due to the magnetic force. Assume that a magnetic field B = B 0 exists in the area, and an electron enters with a velocity of into the cubical region.

Using magnetic Lorentz force, the net force on the electron is represented by

\(\begin{array}{l} \vec{ F} _ { m } = – e ( v _ { 0 } \hat{ i } \times B _ { 0 } \hat{ k } ) \end{array} \)

\(\begin{array}{l} = e v _ { 0 } B _ { 0 } \hat{ j } \end{array} \)

The orbit of the electron circles around down inside the cube in the plane parallel to the x-y plane. So, E should be along the x-axis, and magnetic field B should be along the +z direction.

\(\begin{array}{l} \vec{ B } = B _ { 0 } \hat{ k } \textup{ and } \vec{ E } = E _ { 0 } \hat{ i } \end{array} \)

(where E 0 > 0)

4. Do magnetic forces obey Newton’s third law? Verify for two current elements dl 1 – dl i (unit vector) located at the origin and dl 2 = dl j (unit vector) located at (O, R, O). Both carry current I.

Here, it is required to find the magnetic field’s direction due to one wire at the point on a different wire, then the magnetic force on the current bearing wire.

As per Biot-Savart’s law, the magnetic field is parallel to idl × r, and idl is the current bearing element which has its direction along the current flow’s direction.

In the case of the magnetic field direction, at dl 2 , positioned at (0, R, 0) due to wire dl s represented by B || idl × r or i × j (point (0, r, 0) lies on the y-axis) and i × j = k. Therefore, the magnetic field at dl 2 is along the z-direction.

The magnetic force direction exerted at dl 2 due to the magnetic field of the first wire is along the x-axis.

F -i(I × ), i.e., F || (i × k) or along the -j direction.

Thus, the force due to dl 1 and dl 2 is non-zero.

Hence, magnetic forces do not follow Newton’s third law. But they follow Newton’s third law if the current carrying sections are placed parallel to each other.

5. A multirange voltmeter can be constructed by using a galvanometer circuit, as shown in the figure. We want to construct a voltmeter that can measure 2V, 20V and 200V using a galvanometer of resistance 10Ω and produce maximum deflection for a current of 1 mA. Find R 1 , R 2 , and R 3 that have to be used.

In this scenario,

\(\begin{array}{l} G = 10\Omega \end{array} \)

\(\begin{array}{l} I _ { g } = 1 m A = 10 ^ { -3 } A \end{array} \)

\(\begin{array}{l} \textup{ Case (i): } V = 2V \end{array} \)

\(\begin{array}{l}R _ { 1 } = \frac{ V }{ I _ g } – G \end{array} \)

\(\begin{array}{l} \frac{ 2 }{ 10 ^ { -3 } } -10 \end{array} \)

\(\begin{array}{l} 1990 \Omega \approx 2\Omega \end{array} \)

\(\begin{array}{l} \textup{ Case (b): } V = 20V \end{array} \)

\(\begin{array}{l} ( R _ { 1 } + R _ { 2 } ) = \frac{ 20 }{ 10 ^ { -3 } } – 10 \end{array} \)

\(\begin{array}{l} 20, 000 – 10 \approx 20k\Omega \end{array} \)

\(\begin{array}{l} R_2 = 20k \Omega – 2 k \Omega = 18 k \Omega \end{array} \)

\(\begin{array}{l} \textup{ Case(c): } V = 200V \end{array} \)

\(\begin{array}{l} R _ { 1 } + R _ { 2 } + R _ { 3 } = \frac{ 200 }{ 10 ^ { -3 } } – 10 \end{array} \)

\(\begin{array}{l} \approx 200 k \Omega \end{array} \)

\(\begin{array}{l} \therefore R _ { 3 } = 200 k \Omega – 20 k \Omega \approx 180 k \Omega \end{array} \)

6. A long straight wire carrying a current of 25A rests on a table, as shown in the figure. Another wire PQ of length 1m, mass 2.5g, carries the same current but in the opposite direction. The wire PQ is free to slide up and down. To what height will PQ rise?

In this case,

\(\begin{array}{l} I _ { 1 } = 25 A \end{array} \)

\(\begin{array}{l} I _ { 2 } = 25 A \end{array} \)

\(\begin{array}{l} l = 1m \end{array} \)

\(\begin{array}{l} m = 2.5g = 2.5 \times 10 ^ { -3 } kg \end{array} \)

In the equilibrium position,

\(\begin{array}{l} m g = \frac{ \mu _ { 0 } }{ 4 \pi } \frac{ 2 l _ { 1 } l _ { 2 } l }{ h } \end{array} \)

\(\begin{array}{l} h = \frac{ \mu _ { 0 } }{ 4 \pi } \frac{ 2 l _ { 1 } l _ { 2 } l }{ mg } \end{array} \)

\(\begin{array}{l} = \frac{ 10 ^ { -7 } \times 2 \times 25 \times 25 \times 1 }{ (2.5 \times 10 ^ { -3 }) \times 9.8 } = 51 \times 10 ^ { -4 } m = 0.51 cm \end{array} \)

7. A 100-turn rectangular coil, ABCD (in XY plane), is hung from one arm of a balance. A mass of 500g is added to the other arm to balance the weight of the coil. A current 4.9 A passes through the coil, and a constant magnetic field of 0.2 T acting inward (in xz plane) is switched on such that only arm CD of length 1 cm lies in the field. How much additional mass ‘m’ must be added to regain the balance?

If the magnetic field is zero and the weight is added to one balance pan, balance the rectangular coil in the other balance pan. Then

\(\begin{array}{l} M g l = W _ { coil } l \textup{ or } W _ { coil } = M g = 500 \times 9.8 N \end{array} \)

When the current (I) is passed through the coil and the magnetic field is switched on, let ‘m’ be the mass added in a pan to counterbalance the beam. Then

\(\begin{array}{l} M g l + mgl + = W _ { coil } l + I B L \, sin 90 ^ { 0 } \, l \end{array} \)

\(\begin{array}{l} m g l = I B L I \textup{ or } m = \frac{ I B L }{ 9 } \end{array} \)

\(\begin{array}{l} \therefore m = \frac{ 4.9 \times 0.2 \times ( 1 \times 10 ^ {-2} ) }{ 9.8 } = 10 ^ {-3} kg = 1g \end{array} \)

8. A rectangular conducting loop consists of two wires on two opposite sides of length ‘I’ joined together by a rod of length ‘d’. The wires are each of the same material but with cross-sections differing by a factor of 2. The thicker wire has a resistance E, and the rods are of low resistance, which in turn are connected to a constant voltage source V 0 . The loop is placed in uniform a magnetic field B at 45 o to its plane. Find τ, the torque exerted by the magnetic field on the loop about an axis through the centres of rods.

Equation used: \(\begin{array}{l}B = B_0 \hat{i} \end{array} \)

\(\begin{array}{l} \vec{ \tau } = \vec{ r } + \vec{ F } \end{array} \)

Force on current bearing wire placed in a magnetic field,

\(\begin{array}{l} \vec{ F } = i ( \vec{ I } \times \vec{ B } ) \end{array} \)

The force on the thicker wire (wire 1) is

\(\begin{array}{l} F _ { 1 } = i _ { 1 } I B = \left ( \frac{ V _ { O } }{ R } \right ) I B \end{array} \)

\(\begin{array}{l} \textup{Since resistance of wire } R = \frac{ \rho I}{ A } \end{array} \)

\(\begin{array}{l} \textup{Each wire is of the same material } R \propto \frac{ 1 }{ A} \end{array} \)

\(\begin{array}{l} \textup{ Force on another wire } \vec{ F } _ { 2 } = ( \vec{ I } \times \vec{ B } ) \end{array} \)

\(\begin{array}{l} F _ { 2 } = i _ { 2 } I B = \left ( \frac{ V _ 0 }{ 2 R } \right ) I B \end{array} \)

Torque on wire on wire 1 due to F 1 ,

\(\begin{array}{l} \vec{ \tau } _ { 1 }\left ( \frac{d}{2} \right ) \left ( \frac{ V _ {0} }{ R } \right ) I B \, sin 45 ^ { o } = \left ( \frac{ V _ { 0 } d }{ 2 \sqrt{ 2 } } \right ) I B \end{array} \)

Torque on the wire 2 due to F 2 ,

\(\begin{array}{l} \vec{ \tau } _ { 2 } = \vec{ r } \times \vec{ F } _ { 2 } = \left ( \frac{ d }{ 2 } \right ) F _ { 2 } \, sin \theta \end{array} \)

\(\begin{array}{l} \tau _ { 2 } = \left ( \frac{ d }{ 2 } \right ) \left ( \frac{ V _ { 0 } }{ 2 R } \right ) I B sin 45 ^ { o } = \left ( \frac{ V _ { 0 } d }{ 4 \sqrt{ 2 } } \right ) I B \end{array} \)

\(\begin{array}{l} \textup{Net torque } \tau = \tau _ 1 – \tau _ 2 \end{array} \)

\(\begin{array}{l} \tau = \frac{ 1 }{ 4 \sqrt{ 2 } } \frac{ V _ { 0 } I d B }{ R } \end{array} \)

(A = Id = Area of loop)

9. An electron and a positron are released from (0, 0, 0) and (0, 0, 1.5R), respectively, in a uniform magnetic field, each with an equal momentum of magnitude p = e BR. Under what conditions on the directions of momentum will the orbits be non-intersecting circles?

Since B is along the x-axis, for a circular orbit, the memento of the two particles is in the y-z plane. Assume p 1 and p 2 as the moment of the electron and positron, respectively. Both of them are defined as a circle of radius R. Assume p 1 makes an angle θ with the y-axis, and p 2 should make the same angle. The centre of the circles should be normal to the momenta and at a distance of R.

The circles of the two shall not overlap if the length between the two centres is more than 2R.

Let d be the length between Ce and Cp.

\(\begin{array}{l} d ^ { 2 } = [ R sin \theta – ( – R sin \theta ) ^ 2 ] \left [ R cos \theta \left ( \frac{ 3 }{ 2 } – R cos \theta \right ) \right ] ^ { 2 } \end{array} \)

\(\begin{array}{l} d ^ { 2 } = ( 2 R sin \theta ) ^ { 2 } + \left ( \frac{ 3 }{ 2 } R – 2 R cos \theta \right ) ^ { 2 } \end{array} \)

\(\begin{array}{l} = 4 R ^ { 2 } sin ^ { 2 } \theta + \frac{ 9 ^ { 2 } }{ 4 } r – 6 R ^ { 2 } cos \theta + 4 R ^ 2 cos ^ 2 \theta \end{array} \)

\(\begin{array}{l} = 4 R ^ { 2 } + \frac{ 9 }{ 4 } R ^ { 2 } – 6 R ^ { 2 } cos \theta \end{array} \)

As ‘d’ has to be larger than 2R

\(\begin{array}{l} d ^ { 2 } > 4 R ^ { 2 } \end{array} \)

\(\begin{array}{l} \Rightarrow 4 R ^ { 2 } + \frac{ 9 }{ 4 } R ^ { 2 } – 6 R ^ { 2 } cos \theta > 4 R ^ { 2 } \end{array} \)

\(\begin{array}{l} \frac{ 9 }{ 4 } > 6 cos \theta \textup{ or } cos \theta < \frac{ 3 }{ 8 } \end{array} \)

10. A uniform conducting wire of length 12a and resistance R is wound as a current-carrying coil in the shape of (i) an equilateral triangle of side a; (ii) a square of sides a, and (iii) a regular hexagon of sides a. The coil is connected to a voltage source V 0 . Find the magnetic moment of the coil in each case.

(i) No. of turns, n = 4

\(\begin{array}{l}\textup{ Area of triangle A} = \frac{ 1 }{ 2 } a \times \alpha \, sin 60 ^ { o } \end{array} \)

\(\begin{array}{l} = a ^ { 2 } \sqrt{ 3 } / 4 \end{array} \)

(ii) \(\begin{array}{l} n = 3, \, \textup{area A} = a \times a = a ^ { 2 } \end{array} \)

(iii) \(\begin{array}{l} n = 2, \textup{ area A} = 6 [\frac{ a }{ 2 } \times \frac{ a }{ 2 } tan 60 ^ { o }] = \frac{ 3 \sqrt{ 3 } }{ 2 } a ^ { 2 } \end{array} \)

Magnetic moment, M = nIA

\(\begin{array}{l} \textup{For (i), } M _ { 1 } = 4 \times I \times a ^ { 2 } \sqrt{ 3 } / 4 = \sqrt{ 3 } a ^ { 2 } I \end{array} \)

\(\begin{array}{l} \textup{For (ii), } M _2 = 3 \times I \times a ^ { a } = 3 a ^ { 2 } I \end{array} \)

\(\begin{array}{l} \textup{For (iii), } M _ { 3 } = 2 \times \frac{ 3 \sqrt{ 3 } }{ 2 } a ^ { 2 } = 3 \sqrt{ 3 } a ^ { 2 } I \end{array} \)

(a) Show that ζ(L) monotonically increases with L.

(b) Use an appropriate Amperian loop to show that ζ(∞)=μ 0 I, where I is the current in the wire.

(c) Verify directly the above result.

(d) Suppose we replace the circular coil with a square coil of sides R carrying the same current I. What can you say about ζ(L) and ζ(∞)?

Since the circular loop carrying an electric current is lying in the x-y plane, the magnetic field is along the z-axis, in the line integral direction,

\(\begin{array}{l} \xi ( L ) = \left| \int _ { – L } ^ { + L } \vec{ B } . \vec{ dl } \right| \end{array} \)

\(\begin{array}{l} = \int _ { – L } ^ { + L } B d l \cos 0 ^ { o } \end{array} \)

\(\begin{array}{l} = \int _ { -L } ^ { +L } B d l = 2 B L \end{array} \)

So, ζ(L) is monotonically rising with L.

(b) Take a closed amperian path PQRP as represented in the figure.

As per the Ampere circuital law, the integral of B over the closed trajectory PQRP is

\(\begin{array}{l} \oint _ { P Q R P } \vec{ B } . \vec{ dl } = \int _ { P Q R } \vec{ B } . \vec{d l} + \int _ { R P } \vec{ B } . \vec{ d l } \end{array} \)

\(\begin{array}{l} = \int _ { P Q R } \vec{ B } . \vec{ d l } + \int _ { – L } ^ { + L } \vec{ B } . \vec{ d l } = \mu _ { 0 } I \end{array} \)

\(\begin{array}{l} \int _ { P Q R } \vec{ B } . \vec{ d l } + \zeta ( L ) = \mu _ { 0 } I \end{array} \)

If L → ∞, then the value of B → 0 (as B ∝ 1 / r3)

\(\begin{array}{l} \therefore \int _ { P Q R } \vec{ B } . \vec{ d l } = 0 \textup{, from (i), } 0 + \zeta ( \infty ) = \mu _ { 0 } I \textup{ or } \zeta ( \infty ) = \mu _ { 0 } I \end{array} \)

(c) Magnet field B at a point on the circular coil axis at a distance z from the centre of a circular coil of radius R bearing current I is

\(\begin{array}{l} B _ { z } = \frac{ \mu _ { 0 } I R ^ { 2 } }{ 2 ( z ^ { 2 } + R ^ { 2 } ) ^ { 3/2} } \end{array} \)

\(\begin{array}{l} \therefore \int _ { – \infty } ^ { + \infty } B _ { z } dz = \int _ { -\infty } ^ { + \infty } \frac{ \mu _ { 0 } I R ^ { 2 } }{ 2 ( z ^ { 2 } + R ^ { 2 } ) ^ { 3/2 } } dz \end{array} \)

\(\begin{array}{l} \textup{Put }z = R \tan \theta, \,\, dz = R \sec ^ { 2 } \theta d \theta \end{array} \)

\(\begin{array}{l} \therefore \int _ { – \infty } ^ { + \infty } B _ { z } dz = \frac{ \mu _ { 0 } I }{ 2 } \int _ { \pi / 2 } ^ { + \pi / 2 } \cos \theta d \theta = \mu _ { 0 } I \end{array} \)

(d) If the circular coil is replaced by a square coil of side R, bearing the same current I, then

\(\begin{array}{l} B ( z ) _ { \textup{square} } < B ( z ) _ { \textup{circular coil } } \end{array} \)

\(\begin{array}{l} \therefore \zeta ( L ) _ { \textup{square }} < \zeta ( L ) _ { \textup{circular coil } } \end{array} \)

Utilising arguments as in (b)

\(\begin{array}{l} \zeta ( \infty ) _ { \textup{square } } = \zeta ( \infty ) _ { \textup{ circular } } = \mu _ { 0 } I \end{array} \)

12. A multi-range current metre can be constructed by using a galvanometer circuit, as shown in the figure. We want a current metre that can measure 10mA, 100mA and 1A using a galvanometer of resistance 10Ω and that produces maximum deflection for a current of 1mA. Find S 1 , S 2 and S 3 that have to be used.

\(\begin{array}{l} G = 10 \Omega \end{array} \)

In order to convert a galvanometer into an ammeter of the given current range 0 to 1, the shunt resistance needed is

\(\begin{array}{l} S = \frac{ I _ { g } }{ I – I _ { g } } \end{array} \)

\(\begin{array}{l} I = 10 m A = 10 \times 10 ^ { -3 } A \end{array} \)

S = S _ { 1 } + S _ { 2 } + S _ { 3 }

\(\begin{array}{l} \therefore S _ { 1 } + S _ { 2 } + S _ { 3 } = \frac{ 1 m A \times 10 \Omega }{ (10 – 1) m A } = \frac{ 10 }{ 9 } \Omega \end{array} \)

\(\begin{array}{l} \textup{When } I = 100 m A \end{array} \)

\(\begin{array}{l} S = S _ { 2 } + S _ { 3 } \end{array} \)

\(\begin{array}{l} \textup{Galvanometer Resistance } = G + S _ { 1 } \end{array} \)

\(\begin{array}{l} \therefore S _ { 2 } + S _ { 3 } = \frac{ I _ { g } (G + S _ { 1 }) }{ I – { l _ { g } } } \end{array} \)

\(\begin{array}{l} = \frac{ 1 m A \times ( 10 + S _ { 1 } ) }{ (100 – 1) m A } = \frac{ 10 + S _ { 1 } }{ 99 } \textup{ …. (ii)} \end{array} \)

Case (iii) If I – 1A, then S = S 3

Galvanometer Resistance = (G + S 1 + S 2 )

\(\begin{array}{l} \therefore S _ { 3 } = \frac{ I _ { g ( G + S + S _ { 2 } ) } }{ I – I _ { g } } \end{array} \)

\(\begin{array}{l} = \frac{ 1 m A [ 10 + S _ { 1 } + S _ { 2 } ] }{ ( 1000 – 1) m A } \end{array} \)

\(\begin{array}{l} \frac{ 10 + S _ { 1 } + S _ { 2 } }{ 999 } \textup{ …. (iii)} \end{array} \)

By inserting the value (ii) in (i), we get

\(\begin{array}{l} S _ { 1 } + \frac{ 10 + S _ { 1 } }{ 99 } = \frac{ 10 }{ 9 } \end{array} \)

\(\begin{array}{l} \textup{or } S _ { 1 } \left ( 1 + \frac{1}{99} \right ) = \frac{10}{9} – \frac{ 10 }{ 99 } = \frac{ 100 }{ 99 } \end{array} \)

\(\begin{array}{l} \therefore S _ { 1 } \times \frac{ 100 }{ 99 } = \frac{ 100 }{ 99 } \textup{ or } S _ { 1 } = 1 \Omega \end{array} \)

From equation (ii)

\(\begin{array}{l} S _ { 2 } + S _ { 3 } = \frac{ 1 }{ 99 } ( 10 + 1 ) = \frac{ 1 }{ 9 } \textup{ ….(iv)} \end{array} \)

From equation (iii)

\(\begin{array}{l} S _ { 3 } = \frac{ 10 + 1 + S _ { 2 } }{ 999 } = \frac{ 11 + S _ { 2 } }{ 999 } \end{array} \)

\(\begin{array}{l} \textup{Or } S _ { 3 } – \frac{ S _ { 2 } }{ 999 } = \frac{ 11 }{ 999 } \textup{ ….(iv)} \end{array} \)

Minusing equation (v) from equation (iv), we get

\(\begin{array}{l} S _ { 2 } = \frac{ S _ { 2 } }{ 999 } = \frac{ 1 }{ 9 } – \frac{ 11 }{ 999 } = \frac{ 1000 }{ 999 } \end{array} \)

\(\begin{array}{l} \textup{Or } \frac{ S _ { 2 } \times 1000}{ 999 } = \frac{ 1000 }{ 999 } or S _ { 2 } = \frac{1}{10} = 0.1 \Omega \end{array} \)

From equation (iv)

\(\begin{array}{l} \frac{1}{10} + s _ { 3 } = \frac{ 1 }{ 9 } \end{array} \)

\(\begin{array}{l} \textup{Or } \frac{ 1 }{ 9 } – \frac{ 1 }{ 10 } = \frac{ 1 }{ 90 } \end{array} \)

\(\begin{array}{l} \textup{Or } S _ { 3 } = 0.011 \omega \end{array} \)

13. Five long wires, A, B, C, D, and E, each carrying current I, are arranged to form the edges of a pentagonal prism, as shown in the figure. Each carries current out of the plane of the paper.

(a) What will be magnetic induction at a point on the axis O? Axis is at a distance R from each wire.

(b) What will be the field if the current in one of the wires (say A) is switched off?

(c) What if the current in one of the wires (say) A is reversed?

(a) The five wires A, B, C, D and E are positioned perpendicular to the plane of the paper, as shown in the figure. The total magnetic field induction at point O resulting from the current flowing through all five wires is zero, as it can be represented by the sides of a closed pentagon in the plane of the paper.

(b) The overall magnetic field induction at point O caused by the currents flowing through wires A, B, C, D, and E is the same as, but opposite in direction, to the magnetic field induction at O due to the current through wire A alone.

Therefore, the magnetic field induction at O due to the electric current flowing through wire A is

\(\begin{array}{l} B = \frac{ \mu _ { 0 } }{ 4 \pi } \frac{ 2 I }{ R } \textup{ acting }\perp \, \, r \, \, \textup{to AO towards right. } \end{array} \)

Therefore, the magnetic field induction at point O due to currents through the wires E, D, C, and B is

\(\begin{array}{l} \frac{ \mu _ { 0 } }{ 4 \pi } \frac{ 2 I }{ R } \textup{, acting} \perp \, \, r \textup{ to AO towards left. } \end{array} \)

(c) When the electric current flowing wire A is reversed, then the net magnetic field induction at point O is equal to mag. The magnetic field induction due to wires E, D, C, and B is

\(\begin{array}{l} \frac{ \mu _ { 0 } }{ 4 \pi } \frac{ 2 I }{ R } \,\, (\textup{ acting } \perp \, \, r \,\, \textup{AO towards left}) + \frac{ \mu _ { 0 } }{ 4 \pi } \frac{ 2 I }{ R } (\textup{acting} \, \, \perp r \, \, \textup{AO towards left} ) \end{array} \)

\(\begin{array}{l} = \frac{ \mu _ { 0 } I }{ \pi R } \textup{ acting } \perp \,\, r \textup{ AO towards left.} \end{array} \)

14. What are the applications of magnetism?

• Although we frequently use computers in our daily lives, we may not have considered the presence of a magnet inside them. Magnets play a crucial role in storing data on a hard disk and allow the computer to retrieve information.
• Magnets are also utilised in various electronic devices such as TVs, speakers, and radios. The combination of a small coil of wire and a magnet in a speaker converts electronic signals into sound waves.
• Magnets are used within generators to convert mechanical energy into electrical energy. In contrast, certain motors also use magnets to transform electrical energy into mechanical energy.
• Additionally, a powerful magnet is used by cranes to move large metal objects.
• Magnet technology is utilised in various industries, including ore processing, for separating metallic materials from other substances.
• Magnets also play a crucial role in medical imaging, such as MRI machines, to create detailed images of the body’s internal structures.
• Magnet usage can be found in everyday household items such as refrigerator magnets and magnetic bottle openers.
• A compass, which uses a magnetic needle to indicate a direction, is commonly used in outdoor activities.
• Additionally, magnets are used in technology, such as credit and debit cards, as the dark strip on the back is magnetic and stores data.

15. Write an essay on Galvanometer.

A galvanometer is an instrument that measures electric current and the direction of the current. The early versions of this instrument were not precise, but later models, known as ammeters, were calibrated and able to give more accurate measurements of the current flow. A galvanometer is an instrument that uses the interaction between an electric current and a magnetic field to measure current. It deflects a pointer in reaction to the current moving through a conducting coil in a fixed magnetic field.

Galvanometers are considered a type of actuator and were the first to measure small amounts of electric current. They were discovered by Hans Christian Ørsted in 1820 and were named after Luigi Galvani, who, in 1791, observed that electric current causes the legs of a dead frog to move. André-Marie Ampère mathematically described Ørsted’s discovery and named the instrument after Galvani’s discovery. Galvanometers have been crucial in advancing science and technology across various fields. In the 19th century, they were used to establish long-distance communication via submarine cables, such as the first transatlantic telegraph cables. They also played a vital role in discovering electrical activity in the heart and brain through their precise current measurement.

Galvanometers have been utilised as display elements in other types of analogue metres, such as light and VU metres, by measuring the output of their sensors. The most commonly used galvanometer type today is the D’Arsonval/Weston type. It operates by deflecting a pointer in response to an electric current flowing through a coil in a fixed magnetic field and can be considered a type of actuator. It is important to note that ammeters, calibrated and accurate instruments for measuring current, cannot be compared with values from a galvanometer.

Suggested Videos

Top 10 important questions from moving charges & magnetism class 12 physics.

Moving Charges and Magnetism Class 12 Physics One Shot

Moving Charges and Magnetism Class 12 Physics Full Chapter Revision

Moving Charges and Magnetism Class 12 Physics JEE Important Questions

Stay tuned to BYJU’S and Fall in Love with Learning!

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• Andhra Pradesh
• Chhattisgarh
• West Bengal
• Madhya Pradesh
• Maharashtra
• Jammu & Kashmir
• NCERT Books 2022-23
• NCERT Solutions
• NCERT Notes
• NCERT Exemplar Books
• NCERT Exemplar Solution
• States UT Book
• School Kits & Lab Manual
• NCERT Books 2021-22
• NCERT Books 2020-21
• NCERT Book 2019-2020
• NCERT Book 2015-2016
• RD Sharma Solution
• TS Grewal Solution
• TR Jain Solution
• Selina Solution
• Frank Solution
• ML Aggarwal Solution
• Lakhmir Singh and Manjit Kaur Solution
• I.E.Irodov solutions
• ICSE - Goyal Brothers Park
• ICSE - Dorothy M. Noronhe
• Sandeep Garg Textbook Solution
• Micheal Vaz Solution
• S.S. Krotov Solution
• Evergreen Science
• KC Sinha Solution
• ICSE - ISC Jayanti Sengupta, Oxford
• ICSE Focus on History
• ICSE GeoGraphy Voyage
• ICSE Hindi Solution
• ICSE Treasure Trove Solution
• Thomas & Finney Solution
• SL Loney Solution
• SB Mathur Solution
• P Bahadur Solution
• Narendra Awasthi Solution
• MS Chauhan Solution
• LA Sena Solution
• Integral Calculus Amit Agarwal Solution
• IA Maron Solution
• Hall & Knight Solution
• Errorless Solution
• Pradeep's KL Gogia Solution
• OP Tandon Solutions
• Sample Papers
• Previous Year Question Paper
• Value Based Questions
• CBSE Syllabus
• CBSE MCQs PDF
• Assertion & Reason
• New Revision Notes
• Revision Notes
• HOTS Question
• Marks Wise Question
• Toppers Answer Sheets
• Exam Paper Aalysis
• Concept Map
• CBSE Text Book
• Additional Practice Questions
• Vocational Book
• CBSE - Concept
• KVS NCERT CBSE Worksheets
• Formula Class Wise
• Formula Chapter Wise
• JEE Crash Course
• JEE Previous Year Paper
• Important Info
• JEE Mock Test
• JEE Sample Papers
• SRM-JEEE Mock Test
• VITEEE Mock Test
• BITSAT Mock Test
• Manipal Engineering Mock Test
• AP EAMCET Previous Year Paper
• COMEDK Previous Year Paper
• GUJCET Previous Year Paper
• KCET Previous Year Paper
• KEAM Previous Year Paper
• Manipal Previous Year Paper
• MHT CET Previous Year Paper
• WBJEE Previous Year Paper
• AMU Previous Year Paper
• TS EAMCET Previous Year Paper
• SRM-JEEE Previous Year Paper
• VITEEE Previous Year Paper
• BITSAT Previous Year Paper
• UPSEE Previous Year Paper
• CGPET Previous Year Paper
• CUSAT Previous Year Paper
• AEEE Previous Year Paper
• Crash Course
• Previous Year Paper
• NCERT Based Short Notes
• NCERT Based Tests
• NEET Sample Paper
• Previous Year Papers
• Quantitative Aptitude
• Numerical Aptitude Data Interpretation
• General Knowledge
• Mathematics
• Agriculture
• Accountancy
• Business Studies
• Political science
• Enviromental Studies
• Mass Media Communication
• Teaching Aptitude
• NAVODAYA VIDYALAYA
• SAINIK SCHOOL (AISSEE)
• Mechanical Engineering
• Electrical Engineering
• Electronics & Communication Engineering
• Civil Engineering
• Computer Science Engineering
• CBSE Board News
• Scholarship Olympiad
• School Admissions
• Entrance Exams
• All Board Updates
• Miscellaneous
• State Wise Books
• Engineering Exam

SHARING IS CARING If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.

CBSE Class 12th - PHYSICS : Chapterwise Case Study Question & Solution

CBSE will ask two Case Study Questions in the CBSE class 12 Physics questions paper. Question numbers 15 and 16 are cased-based questions where 5 MCQs will be asked based on a paragraph. Each theme will have five questions and students will have a choice to attempt any four of them.

• NCERT Solutions for Class 12 Maths
• NCERT Solutions for Class 10 Maths
• CBSE Syllabus 2023-24
• Social Media Channels
• Login Customize Your Notification Preferences
• CBSE 12th 2024-25 : Biology Official Competency Focused Practice Questions released by CBSE 7 May, 2024, 4:29 pm
• CBSE 12th 2024-25 : Mathematics Official Competency Focused Practice Questions released by CBSE 7 May, 2024, 3:51 pm
• CBSE Board Class 12 Computer Science Answer Key 2024 and Question Papers, Download PDF All SETs 2 April, 2024, 1:51 pm
• CBSE Class 12 Computer Science Exam 2024 : Important MCQs with Answers For Last Minute Revision 1 April, 2024, 5:42 pm
• CBSE Board Class 12 History Answer Key 2024 and Question Papers, Download PDF All SETs 28 March, 2024, 1:18 pm
• CBSE Board 12th History Exam 2024 : Chapterwise Most Important Question with Answers 27 March, 2024, 4:57 pm
• CBSE Board Class 12 Business Studies Answer Key 2024 and Question Papers, Download PDF All SETs 27 March, 2024, 1:05 pm
• CBSE Class 12th Exam 2024: Business Studies Important MCQs & Assertion-Reason Questions 26 March, 2024, 3:39 pm
• CBSE Board Class 12 Political Science Answer Key 2024 and Question Papers, Download PDF All SETs 22 March, 2024, 1:36 pm

• Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.

Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.

Provide prime users with access to exclusive PDF study materials that are not available to regular users.