Bluetree Education Group

- Primary Math


Must-Know Ratio Concepts for P5 & P6 Math Students
- September 25, 2023
- Primary Math - Heuristics
As a parent, you might have noticed that Primary Math Ratio Concepts can often pose a challenge for students in Primary 5 and 6. To alleviate your concerns and provide guidance, we’ve compiled a comprehensive guide on the four most essential ratio concepts your child should master. So, let’s delve into these must-know ratio concepts :
1. One side unchanged or Constant Part
2. total unchanged or constant total, 3. difference unchanged or constant difference.
4. Everything Changed

You must be familiar with these concepts as they are routinely evaluated in Primary Math exams, including PSLE.
Let’s learn the applications of these important Primary concepts:
This question is more challenging as it consists of 2 concepts in one problem sums.
Concept 1: Total Stays the Same
Concept 2: Repeated Identity
It is important that one is able to recognise that the total number of items for A, B and C stays the same too.
A, B and C are repeated in both ratios , except that they are grouped differently in each ratios.
Watch the 2 videos to find out how these questions are solved.
When will the difference stays the same
1) When equal number of items are added
2) When equal number of items are removed
3) Age question when the question is comparing 2 people’s ages.
The age of mother is 60 years old. Her daughter is 35 years old.
The age difference between mother and daughter is 60 – 35 = 25 years.
4. Everything Changed
Watch the video to find out how you can solve the question easily with the use of the Tic – Tac – Toe Table.
Understanding Primary Math Ratio concepts proves essential for your child’s exam success. These fundamental principles serve as the cornerstone for various mathematical problems and frequently feature in assessments.
At BlueTree, our specialized classes are meticulously crafted to equip your child with a profound comprehension of these concepts. This approach ensures their ability to confidently tackle a myriad of math questions, including those related to ratios in their exams. With our expert guidance, comprehensive curriculum, and tailored instruction, your child will acquire the skills and knowledge essential for excelling in Primary/PSLE Math exams, securing top grades, and gaining a competitive edge for a brighter academic future with BlueTree’s P5 & P6 Math classes.
To learn more, please don’t hesitate to reach out to us via WhatsApp by clicking here .
Read Also: Unlocking the Secrets of Equal Concept: Mastering Popular Problem Sums Questions for Primary/ PSLE Math
Like what you see?
Register for a trial class and see what more we can provide for your child today, recent articles.

Interactions Within the Environment (Let’s Attempt 2023 WA2 from MGS Q2, Q12)

How Plants Have Babies: Important PSLE Concept on Plant Reproduction

2023 PSLE Science Paper Analysis

Plant Adaptation in Action: The Fascinating World of Carnivorous Plants
Secondary blog.

Resources & Topics Overview
Post: must-know ratio concepts for p5 & p6 math students.
WhatsApp us
4 Must Know Concepts of Ratio Math Problems

PSLE Ratio Math problems consist of many marks in the exam and you cannot afford to lose them.
No matter how the questions twist and turn, here are 4 PSLE Ratio concepts which the questions will test.
1. Constant Part
Constant part means one of the parts remained the same while the other part changed.
In this case, you will need to make the part which remained the same to be equal to each other.
Example: Ali and Billy have money in the ratio of 5 : 6. After Billy spent $16, the ratio became 3 : 2. How much money does Billy have in the end?
18u – 10u = 8u
10u = $20 (Ans)
2. Constant Total
Constant Total means the total remained the same. Usually, this concept applies for question related to “Internal Transfer”.
If A transfer an amount to B, A will decrease while B will increase by the same amount. So the total will stay the same.
Example: Ali and Billy have money in the ratio of 5 : 4. After Ali gave Billy $20, they have an equal amount of money. How much money does Billy have in the end?
A : B : Total
= 5 : 4 : 9
= 10 : 8 : 18
= 1 : 1 : 2
= 9 : 9 : 18
1 unit = $20
9 units = $180 (Ans)
3. Constant Difference
Constant Difference means the difference remained the same. Usually, this concept applies for question related to “Age”.
As years go by, the age difference between 2 people will always be the same, because both will grow old together.
Example: The ages of Ali and Billy are in the ratio of 4 : 7. In 3 years time, their ages will be in the ratio of 3 : 5. How old is Billy now?
A : B : Difference
= 4 : 7 : 3
= 8 : 14 : 6
= 3 : 5 : 2
= 9 : 15 : 6
1 unit = 3 years
14 units = 42 years old (Ans)
4. Everything Changed
As the name says, everything changed! Every part changed, the difference changed, the total changed… Nothing remained the same.
This type of questions are usually the last few 5 marks questions in the paper. So make sure you know how to do this type of questions.
There are a few methods to solve this type of question. I will use an example below to show a method which you can use.
Example: The ratio of Ali’s money to Billy’s money was 2 : 1. After Ali saved another $60 and Billy spent $150, the ratio became 4 : 1. How much money did Ali have at first?
Step 1: Write down the starting ratio and apply the changes.

Step 2: Compare the final units with the final ratio.
A : B
= 2u + 60 : 1u – 150
= 4 : 1
Step 3: Cross Multiply the final units with the final ratio
1 × (2u + 60) = 4 × (1u – 150)
2u + 60 = 4u – 600
Step 4: Solve for 1 unit
2 units = 60 + 600 = $660 (Ans)
These are the 4 must-know concepts of PSLE Ratio Math problems. Make sure you know when to apply the concept and how to use them correctly.
Free Download: 80 Useful Tricks to Solve Math Problems Easily
We hope that this article has helped your child to better understand how to solve these 4 types of ratio Math problems.
Before you go, download this eBook for free to learn to solve other types of Math problems.
The 80 tricks taught in this eBook will be very useful in helping your child solve Math problem sums!

Follow Jimmy Maths on Telegram here!

How to Solve Simultaneous Equations
Different types of rates questions in psle math papers.
Cancel reply
You must be logged in to post a comment.
Leave a Reply Cancel reply
YOU HAVE THE FOLLOWING POINTS
- PRIMARY SCHOOL
- SECONDARY SCHOOL
- LOGIN / REGISTER
One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
This topic is relevant for:

Ratio Problem Solving
Here we will learn about ratio problem solving, including how to set up and solve problems. We will also look at real life ratio problems.
There are also ratio problem solving worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is ratio problem solving?
Ratio problem solving is a collection of word problems that link together aspects of ratio and proportion into more real life questions. This requires you to be able to take key information from a question and use your knowledge of ratios (and other areas of the curriculum) to solve the problem.
A ratio is a relationship between two or more quantities . They are usually written in the form a:b where a and b are two quantities. When problem solving with a ratio, the key facts that you need to know are,
- What is the ratio involved?
- What order are the quantities in the ratio?
- What is the total amount / what is the part of the total amount known?
- What are you trying to calculate ?
As with all problem solving, there is not one unique method to solve a problem. However, this does not mean that there aren’t similarities between different problems that we can use to help us find an answer.
The key to any problem solving is being able to draw from prior knowledge and use the correct piece of information to allow you to get to the next step and then the solution.
Let’s look at a couple of methods we can use when given certain pieces of information.
When solving ratio problems it is very important that you are able to use ratios. This includes being able to use ratio notation.
For example, Charlie and David share some sweets in the ratio of 3:5. This means that for every 3 sweets Charlie gets, David receives 5 sweets.
Charlie and David share 40 sweets, how many sweets do they each get?
We use the ratio to divide 40 sweets into 8 equal parts.
Then we multiply each part of the ratio by 5.
3 x 5:5 x 5 = 15:25
This means that Charlie will get 15 sweets and David will get 25 sweets.
- Dividing ratios
Step-by-step guide: Dividing ratios (coming soon)
| You have been given And you want to | Step 1: Add the parts of the ratio together. Step 2: Divide the quantity by the sum of the parts. Step 3: Multiply the share value by each part in the ratio. | For example Share £100 in the ratio 4:1 . (£80:£20) |
|---|---|---|
| You have been given And you want to find | Step 1: Identify which part of the ratio has been given. Step 2: Calculate the individual share value. Step 3: Multiply the other quantities in the ratio by the share value. | For example A bag of sweets is shared between boys and girls in the ratio of 5:6. Each person receives the same number of sweets. If there are 15 boys, how many girls are there? (18) |
Ratios and fractions (proportion problems)
We also need to consider problems involving fractions. These are usually proportion questions where we are stating the proportion of the total amount as a fraction.
| You have been given And you want to find | Step 1: Add the parts of the ratio for the denominator. Step 2: State the required part of the ratio as the numerator. | For example The ratio of red to green counters is 3:5. What fraction of the counters are green? (\frac{5}{8}) |
|---|---|---|
| You have been given And you want to find | Step 1: Subtract the numerator from the denominator of the fraction. Step 2: State the parts of the ratio in the correct order. | For example if \frac{9}{10} students are right handed, write the ratio of right handed students to left handed students. (9:1) |
Simplifying and equivalent ratios
- Simplifying ratios
| You have been given And you want to find | Step 1: Calculate the highest common factor of the parts of the ratio. Step 2: Divide each part of the ratio by the highest common factor. | For example Simplify the ratio 10:15. (2:3) |
|---|---|---|
Equivalent ratios
| You have been given And you want to find | Step 1: Identify which part of the ratio is to equal 1. Step 2: Divide all parts of the ratio by this value. | For example Write the ratio 4:15 in the form 1:n. (1:3.75) |
|---|---|---|
| You have been given And you want to find | Step 1: Multiply all parts of the ratio by the same amount. | For example A map uses the scale 1:500. How many centimetres in real life is 3cm on the map? (1:500 = 3:1500, so 1500 cm) |
Units and conversions ratio questions
Units and conversions are usually equivalent ratio problems (see above).
- If £1:\$1.37 and we wanted to convert £10 into dollars, we would multiply both sides of the ratio by 10 to get £10 is equivalent to \$13.70.
- The scale on a map is 1:25,000. I measure 12cm on the map. How far is this in real life, in kilometres? After multiplying both parts of the ratio by 12 you must then convert 12 \times 25000=300000 \ cm to km by dividing the solution by 100 \ 000 to get 3km.
Notice that for all three of these examples, the units are important. For example if we write the mapping example as the ratio 4cm:1km, this means that 4cm on the map is 1km in real life.
Top tip: if you are converting units, always write the units in your ratio.
Usually with ratio problem solving questions, the problems are quite wordy . They can involve missing values , calculating ratios , graphs , equivalent fractions , negative numbers , decimals and percentages .
Highlight the important pieces of information from the question, know what you are trying to find or calculate , and use the steps above to help you start practising how to solve problems involving ratios.
How to do ratio problem solving
In order to solve problems including ratios:
Identify key information within the question.
Know what you are trying to calculate.
Use prior knowledge to structure a solution.
Explain how to do ratio problem solving

Ratio problem solving worksheet
Get your free ratio problem solving worksheet of 20+ questions and answers. Includes reasoning and applied questions.
Related lessons on ratio
Ratio problem solving is part of our series of lessons to support revision on ratio . You may find it helpful to start with the main ratio lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
- How to work out ratio
- Ratio to fraction
- Ratio scale
- Ratio to percentage
Ratio problem solving examples
Example 1: part:part ratio.
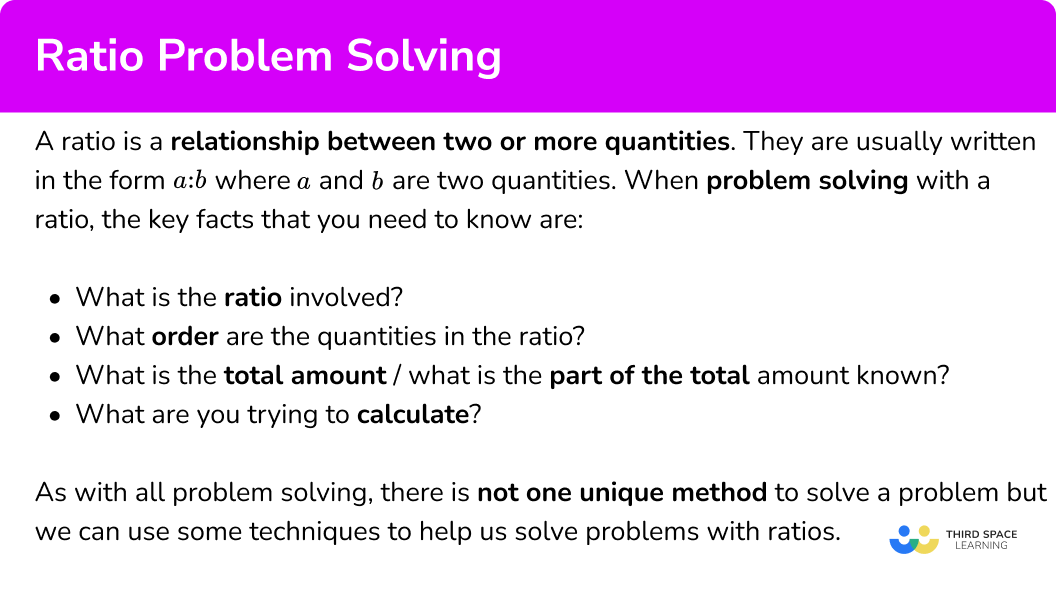
Within a school, the number of students who have school dinners to packed lunches is 5:7. If 465 students have a school dinner, how many students have a packed lunch?
Within a school, the number of students who have school dinners to packed lunches is \bf{5:7.} If \bf{465} students have a school dinner , how many students have a packed lunch ?
Here we can see that the ratio is 5:7 where the first part of the ratio represents school dinners (S) and the second part of the ratio represents packed lunches (P).
We could write this as

Where the letter above each part of the ratio links to the question.
We know that 465 students have school dinner.
2 Know what you are trying to calculate.
From the question, we need to calculate the number of students that have a packed lunch, so we can now write a ratio below the ratio 5:7 that shows that we have 465 students who have school dinners, and p students who have a packed lunch.
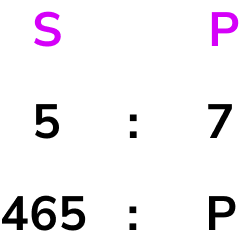
We need to find the value of p.
3 Use prior knowledge to structure a solution.
We are looking for an equivalent ratio to 5:7. So we need to calculate the multiplier. We do this by dividing the known values on the same side of the ratio by each other.
So the value of p is equal to 7 \times 93=651.
There are 651 students that have a packed lunch.
Example 2: unit conversions
The table below shows the currency conversions on one day.
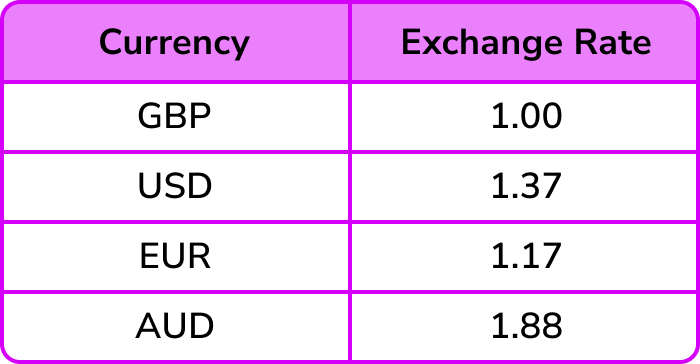
Use the table above to convert £520 (GBP) to Euros € (EUR).
Use the table above to convert \bf{£520} (GBP) to Euros \bf{€} (EUR).
The two values in the table that are important are GBP and EUR. Writing this as a ratio, we can state
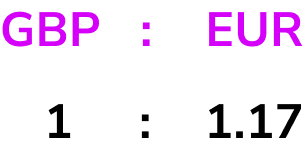
We know that we have £520.
We need to convert GBP to EUR and so we are looking for an equivalent ratio with GBP = £520 and EUR = E.

To get from 1 to 520, we multiply by 520 and so to calculate the number of Euros for £520, we need to multiply 1.17 by 520.
1.17 \times 520=608.4
So £520 = €608.40.
Example 3: writing a ratio 1:n
Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the 500ml of concentrated plant food must be diluted into 2l of water. Express the ratio of plant food to water respectively in the ratio 1:n.
Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the \bf{500ml} of concentrated plant food must be diluted into \bf{2l} of water . Express the ratio of plant food to water respectively as a ratio in the form 1:n.
Using the information in the question, we can now state the ratio of plant food to water as 500ml:2l. As we can convert litres into millilitres, we could convert 2l into millilitres by multiplying it by 1000.
2l = 2000ml
So we can also express the ratio as 500:2000 which will help us in later steps.
We want to simplify the ratio 500:2000 into the form 1:n.
We need to find an equivalent ratio where the first part of the ratio is equal to 1. We can only do this by dividing both parts of the ratio by 500 (as 500 \div 500=1 ).
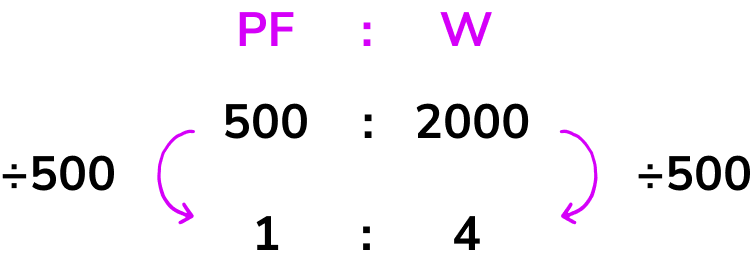
So the ratio of plant food to water in the form 1:n is 1:4.
Example 4: forming and solving an equation
Three siblings, Josh, Kieran and Luke, receive pocket money per week proportional to their age. Kieran is 3 years older than Josh. Luke is twice Josh’s age. If Josh receives £8 pocket money, how much money do the three siblings receive in total?
Three siblings, Josh, Kieran and Luke, receive pocket money per week proportional to their ages. Kieran is \bf{3} years older than Josh . Luke is twice Josh’s age. If Luke receives \bf{£8} pocket money, how much money do the three siblings receive in total ?
We can represent the ages of the three siblings as a ratio. Taking Josh as x years old, Kieran would therefore be x+3 years old, and Luke would be 2x years old. As a ratio, we have
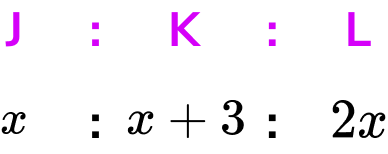
We also know that Luke receives £8.
We want to calculate the total amount of pocket money for the three siblings.
We need to find the value of x first. As Luke receives £8, we can state the equation 2x=8 and so x=4.
Now we know the value of x, we can substitute this value into the other parts of the ratio to obtain how much money the siblings each receive.
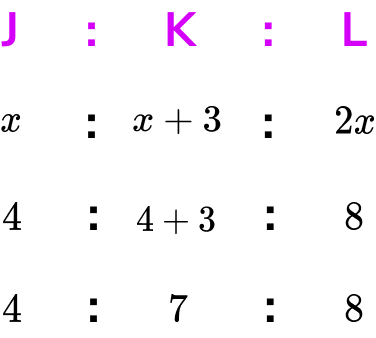
The total amount of pocket money is therefore 4+7+8=£19.
Example 5: simplifying ratios
Below is a bar chart showing the results for the colours of counters in a bag.
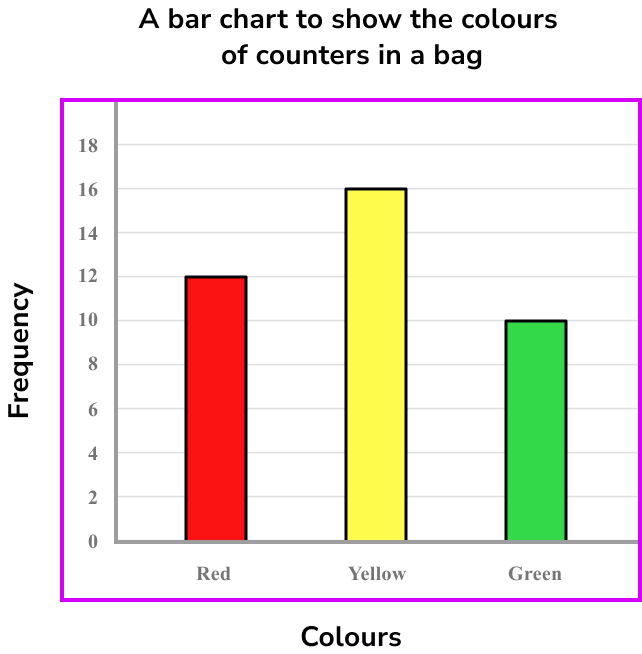
Express this data as a ratio in its simplest form.
From the bar chart, we can read the frequencies to create the ratio.
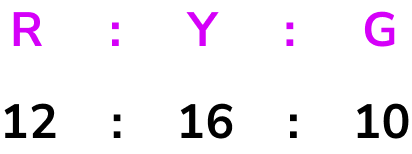
We need to simplify this ratio.
To simplify a ratio, we need to find the highest common factor of all the parts of the ratio. By listing the factors of each number, you can quickly see that the highest common factor is 2.
\begin{aligned} &12 = 1, {\color{red} 2}, 3, 4, 6, 12 \\\\ &16 = 1, {\color{red} 2}, 4, 8, 16 \\\\ &10 = 1, {\color{red} 2}, 5, 10 \end{aligned}
HCF (12,16,10) = 2
Dividing all the parts of the ratio by 2 , we get

Our solution is 6:8:5 .
Example 6: combining two ratios
Glass is made from silica, lime and soda. The ratio of silica to lime is 15:2. The ratio of silica to soda is 5:1. State the ratio of silica:lime:soda.
Glass is made from silica, lime and soda. The ratio of silica to lime is \bf{15:2.} The ratio of silica to soda is \bf{5:1.} State the ratio of silica:lime:soda .
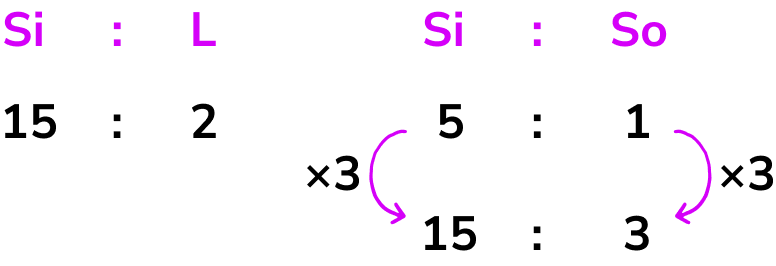
We know the two ratios

We are trying to find the ratio of all 3 components: silica, lime and soda.
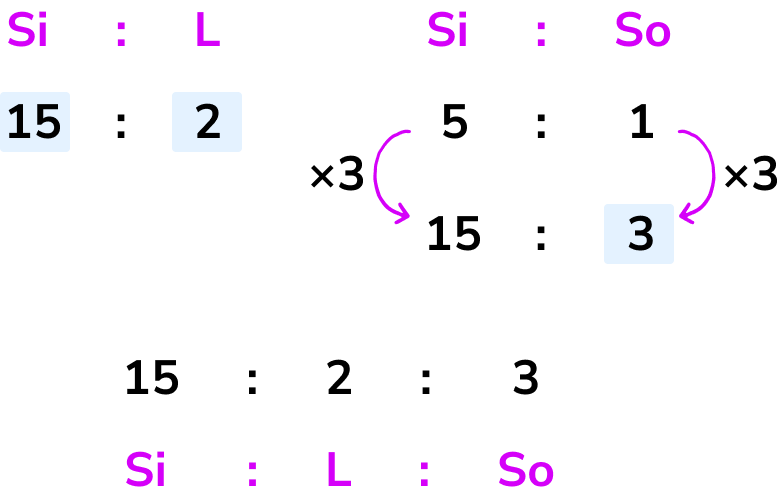
Using equivalent ratios we can say that the ratio of silica:soda is equivalent to 15:3 by multiplying the ratio by 3.
We now have the same amount of silica in both ratios and so we can now combine them to get the ratio 15:2:3.
Example 7: using bar modelling
India and Beau share some popcorn in the ratio of 5:2. If India has 75g more popcorn than Beau, what was the original quantity?
India and Beau share some popcorn in the ratio of \bf{5:2.} If India has \bf{75g} more popcorn than Beau , what was the original quantity?
We know that the initial ratio is 5:2 and that India has three more parts than Beau.
We want to find the original quantity.
Drawing a bar model of this problem, we have

Where India has 5 equal shares, and Beau has 2 equal shares.
Each share is the same value and so if we can find out this value, we can then find the total quantity.
From the question, India’s share is 75g more than Beau’s share so we can write this on the bar model.
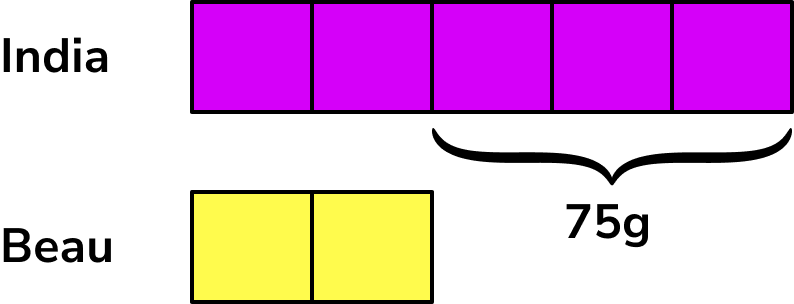
We can find the value of one share by working out 75 \div 3=25g.
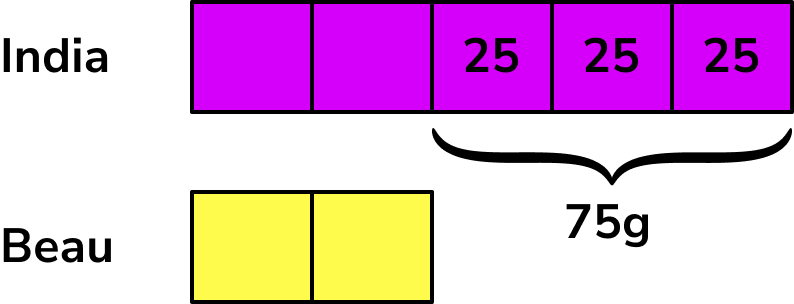
We can fill in each share to be 25g.
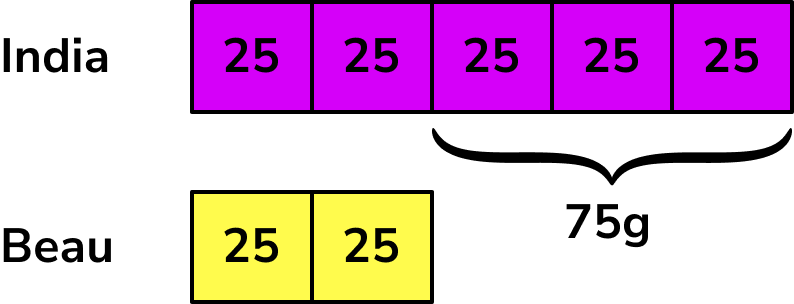
Adding up each share, we get
India = 5 \times 25=125g
Beau = 2 \times 25=50g
The total amount of popcorn was 125+50=175g.
Common misconceptions
- Mixing units
Make sure that all the units in the ratio are the same. For example, in example 6 , all the units in the ratio were in millilitres. We did not mix ml and l in the ratio.
- Ratio written in the wrong order
For example the number of dogs to cats is given as the ratio 12:13 but the solution is written as 13:12.
- Ratios and fractions confusion
Take care when writing ratios as fractions and vice-versa. Most ratios we come across are part:part. The ratio here of red:yellow is 1:2. So the fraction which is red is \frac{1}{3} (not \frac{1}{2} ).

- Counting the number of parts in the ratio, not the total number of shares
For example, the ratio 5:4 has 9 shares, and 2 parts. This is because the ratio contains 2 numbers but the sum of these parts (the number of shares) is 5+4=9. You need to find the value per share, so you need to use the 9 shares in your next line of working.
- Ratios of the form \bf{1:n}
The assumption can be incorrectly made that n must be greater than 1 , but n can be any number, including a decimal.
Practice ratio problem solving questions
1. An online shop sells board games and computer games. The ratio of board games to the total number of games sold in one month is 3:8. What is the ratio of board games to computer games?

8-3=5 computer games sold for every 3 board games.
2. The volume of gas is directly proportional to the temperature (in degrees Kelvin). A balloon contains 2.75l of gas and has a temperature of 18^{\circ}K. What is the volume of gas if the temperature increases to 45^{\circ}K?
3. The ratio of prime numbers to non-prime numbers from 1-200 is 45:155. Express this as a ratio in the form 1:n.
4. The angles in a triangle are written as the ratio x:2x:3x. Calculate the size of each angle.
5. A clothing company has a sale on tops, dresses and shoes. \frac{1}{3} of sales were for tops, \frac{1}{5} of sales were for dresses, and the rest were for shoes. Write a ratio of tops to dresses to shoes sold in its simplest form.
6. During one month, the weather was recorded into 3 categories: sunshine, cloud and rain. The ratio of sunshine to cloud was 2:3 and the ratio of cloud to rain was 9:11. State the ratio that compares sunshine:cloud:rain for the month.
Ratio problem solving GCSE questions
1. One mole of water weighs 18 grams and contains 6.02 \times 10^{23} water molecules.
Write this in the form 1gram:n where n represents the number of water molecules in standard form.
2. A plank of wood is sawn into three pieces in the ratio 3:2:5. The first piece is 36cm shorter than the third piece.
Calculate the length of the plank of wood.
5-3=2 \ parts = 36cm so 1 \ part = 18cm
3. (a) Jenny is x years old. Sally is 4 years older than Jenny. Kim is twice Jenny’s age. Write their ages in a ratio J:S:K.
(b) Sally is 16 years younger than Kim. Calculate the sum of their ages.
Learning checklist
You have now learned how to:
- Relate the language of ratios and the associated calculations to the arithmetic of fractions and to linear functions
- Develop their mathematical knowledge, in part through solving problems and evaluating the outcomes, including multi-step problems
- Make and use connections between different parts of mathematics to solve problems
The next lessons are
- Compound measures
- Best buy maths
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.
Privacy Overview
2021 PSLE Maths Questions & Answers

Was the PSLE math 2021 paper really more difficult as compared to the 2020 PSLE math paper ?
The difficulty of the PSLE mathematics exam paper has always been a concern amongst Primary 6 students and parents in Singapore.
With multiple discussions about the PSLE math paper on-going and a particular Math problem on Helen’s and Ivan’s coins getting on the news , you might be how tough these PSLE Math questions really are.
Today, let’s look at a few of these primary 6 math problems and hopefully, this would act as a guide to help you with your P6 math revision.
Here’s what we will cover:
- Helen and Ivan coin question
- Area and perimeter question
- Big books small books questions

Past PSLE questions and answers
- 2023 PSLE math questions
- 2022 PSLE math questions
- 2021 PSLE math questions
- 2020 PSLE math questions
- 2019 PSLE math questions
- 2017 PSLE math questions
PSLE-related information
- Important PSLE exam dates
- PSLE scoring system
- PSLE math paper format
- Approved calculator list
1. 2021 PSLE Math coin question on Helen and Ivan
This Helen and Ivan coin question goes somewhat like this:
Helen and Ivan had the same number of coins. Each of them had a mix of twenty-cent coins and fifty-cent coins. Helen had 64 twenty-cent coins and Ivan had 104 twenty-cent coins. The total mass of Helen’s coins was 1.134 kg. a) Who had more money? How much more did the person have? b) If a fifty-cent coin is 2.7g heavier than a twenty-cent coin, what is the mass of Ivan’s coins in kilograms?
*Note that this might not be the actual phrasing of the question in PSLE.

How to solve this PSLE 2021 coin question
Here’s a step-by-step video solution for this math question to help you with the answer!
To get the answer to part a of this PSLE coin question, you will first need to recognize that the total number of coins between Helen and Ivan is the same.
Knowing this would help us infer that the difference in the value of the coins between Helen and Ivan depends on how many fifty-cent coins and twenty-cent coins each of them had, which leads to the difference in the mass of the coins in part b.
Why this Helen and Ivan coin question may be difficult to Primary 6 children:
This coin question sounds fairly straightforward. All our Primary 6 children have to do is to compare the number of twenty-cent coins and fifty-cent coins between Helen and Ivan and name the person with more money.
So…where’s the tough part?
The complexity comes in when our 12-year-olds find difficulty distinguishing between the number of coins, the value of the coins (20-cent versus 50-cent) and the mass of the coins.
If your child has solved similar math problems that involves coins and understands how number and value works, they’ll have no problem solving this question.
Back to top
2. 2021 PSLE Math question on Area and Perimeter
This perimeter and area question in the PSLE paper looks somewhat like this:
The perimeter of the shaded part is 4 cm more than that of the unshaded part. a) What is the length of AB? b) What is the area of the shaded part?
How to solve this PSLE 2021 Math problem on Area and perimeter
When it comes to making use of the perimeter of shaded and unshaded parts to find the unknown length AB, the trick is to make use of the knowledge of rectilinear figures and move some lines around to simplify the problem. Being able to do that will help children see the relationship between the given lengths and solve part a of the question easily.
As for part b, the trick is to think about how the shaded part is can be derived from basic shapes that are familiar to you.
Once a Primary 6 child can tell that the shaded area is formed by putting 3 rectangles together and subtracting a triangle from it, they are well on their way to solving this area and perimeter problem in PSLE.
Why this area and perimeter Math question may be difficult to Primary 6 children:
Looking at the side of the figure with the length AB on it, our P6 children are used to having the length of a part of the side.
However, that length doesn’t correspond to the opposite side of 7 cm in this PSLE Math problem.
In fact, it is an unknown part of that 7 cm, so the problem isn’t as direct to solve.
3. 2021 PSLE Math big books small books question
This big book small book question in the PSLE exam goes somewhat like this:
A bookshelf can fit either 30 big books or 45 small books. There are 3 big books and 23 small books on the bookshelf. What is the maximum number of big books that can be added onto the bookshelf?

How to solve this big books small books PSLE question
To solve this PSLE Math question, you need to be able to see the relationship between the space the big books take up on the bookshelf and the space the small books take up.
When you are able to make use of a ratio to see that, the next part then depends on how you play with the ratio to get the information that you need.
Why this Math question on big and small books may be difficult for some Primary 6 children:
The main reason lies in the number 23. Some P6 children might feel less confident working with such a prime number and start to doubt themselves when they get a “weird” ratio/fraction.
Now that we’ve had a look at some of the tougher question in the 2021 PSLE Math paper, do you think they are really that hard?
Let us know in the comments below if this post has been useful in helping you prepare for your P6 primary school leaving exam .
Practicle is an online gamified Singapore Math adaptive learning platform that helps primary school children master Math through understanding and fun.
- EAF Certification
- Privacy policy
- Terms of use
- Math heuristics guide
- Math problem sum guide
© 2024 Practicle. All Rights Reserved,
- A.I. Math Tutor
- Math Vision: Our video tutorials

Reading & Math for K-5
- Kindergarten
- Learning numbers
- Comparing numbers
- Place Value
- Roman numerals
- Subtraction
- Multiplication
- Order of operations
- Drills & practice
- Measurement
- Factoring & prime factors
- Proportions
- Shape & geometry
- Data & graphing
- Word problems
- Children's stories
- Leveled Stories
- Context clues
- Cause & effect
- Compare & contrast
- Fact vs. fiction
- Fact vs. opinion
- Main idea & details
- Story elements
- Conclusions & inferences
- Sounds & phonics
- Words & vocabulary
- Reading comprehension
- Early writing
- Numbers & counting
- Simple math
- Social skills
- Other activities
- Dolch sight words
- Fry sight words
- Multiple meaning words
- Prefixes & suffixes
- Vocabulary cards
- Other parts of speech
- Punctuation
- Capitalization
- Narrative writing
- Opinion writing
- Informative writing
- Cursive alphabet
- Cursive letters
- Cursive letter joins
- Cursive words
- Cursive sentences
- Cursive passages
- Grammar & Writing
Breadcrumbs
Ratio word problems

Download & Print Only $7.90
Use ratios to solve these word problems
Students can use simple ratios to solve these word problems ; the arithmetic is kept simple so as to focus on the understanding of the use of ratios.

These worksheets are available to members only.
Join K5 to save time, skip ads and access more content. Learn More
What is K5?
K5 Learning offers free worksheets , flashcards and inexpensive workbooks for kids in kindergarten to grade 5. Become a member to access additional content and skip ads.
Our members helped us give away millions of worksheets last year.
We provide free educational materials to parents and teachers in over 100 countries. If you can, please consider purchasing a membership ($24/year) to support our efforts.
Members skip ads and access exclusive features.
Learn about member benefits
This content is available to members only.
- Forgot Password?

www.learnbrill.com
P6 - solving fraction, ratio, percentages word problems.
for Primary 6 students
Course Description

This course is targeted at Singapore primary school level 6 , but is also suitable for primary school level 5 students.
Based on feedback, many parents have used the videos to learn the methods to help their children to learn faster.
Math Arena students gain an edge using techniques that we teach here in our videos, these methods provide accuracy and speed. We believe it also provides better understanding of their solution to the question that they are solving.
It can also be used as independent learning or for revision.
There are a total of 5 PDF sets for this series. They are arranged by similarity for easy question pattern recognition.
The Number of stars indicates level of difficulty. One star is fundamental, 2 stars are moderate. 3 and 4 stars are difficult and challenging. Note due to the student’s ability he may experience difficult questions as easy and easy questions as difficult. So do not be over anxious, if an “easy question” stumped you, just keep practicing.
Course Content
- get 5 (Set A, B, C, D and E) PDF files on FRP which you can print for practice
- be able to watch and learn from 100 videos
- learn fast, accurate methods in solving Fraction, Ratio Percentage Questions
Course Pre-requisites
You will need to know:
- Fundamental Heuristic Concepts of Fraction, Ratio and Percentages
- How to watch videos on your computer
- PDF files contain the questions, the videos are the solutions to the questions.
- Question header may not contain the full question as it it limited to 255 characters.
- Our Videos complements the student’s math lessons in Math Arena.
- Fraction, Ratio, Percentages (FRP) are the main bulk of of questions for PSLE.
- It is common that parents do learn from our videos and work with their children too.
- The bar model is good for understanding but may be less useful for more complicated questions. It can also lead to harder transition to algebra in their secondary schools.
Take a moment to ...

Course curriculum
Introduction.
P6FRPV1-A - learnbrill
1) 40% of a group of 800 pupils are girls. 30% of the girls have long hair. How many girls have short hair?
2) There were a total of 1080 roses of the tulips were pink. The rest were red roses and tulips. If the total number of pink roses and pink tulips was 200, how many roses were there in the garden?
3) There are blue, red, and pink balls in a box. 40% of the balls are blue. The number of blue balls is 20 more than the number of pink balls. There are 50 red balls. What is the number of pink balls in the box?
4) In Jin’s Bike Shop, 30% of the tires were black and the rest were white. 40% of the black tires and 20% of the white tires were sold. If Jin had 148 tires left in the shop, how many white tires were there at first?
5) The mass of a bottle when it was 14 filled with syrup was 960 g. Mary added more syrup into the bottle to make it 23 full and the mass increased to 1.86kg. Find the mass of the bottle when it is completely filled with syrup.
6) There were 3808 biscuits, cookies and brownies on a tray. If Tim took away 1/3 of the biscuits, 1/3 of the cookies and 2/5 of the brownies, there would be an equal number of each type of snacks left.
7) Salimah bought some roses, tulips and carnations. 1/4 of them were roses, 5/12 of the remainder were tulips and the remaining flowers were carnations. Each rose cost $2.50. Each tulip cost $3 and each carnation cost $1.50.
8) Michelle spends 35% of her salary every month. Her salary for June was 20% more than that of May. As a result, her expenditure in June increased by $175. How much was Michelle’s expenditure in May?
9) Mark was training for a marathon. Each week, he jogged a distance of 10% more than the previous week. He jogged 36.3 km in Week 3. a. What distance did he jog in Week 1? b. What was the total distance Mark jog in 3 weeks?
10) The original selling price of a computer was $2800. A shop sold it at a discount of 20% during a sale. If the shop charged a 7% GST on the discounted price , a. How much was the GST?
11) The bill for a dinner for 4 friends at Sedap Restaurant is shown below. A service charge of 10% was included in the bill before a GST of 7% is added.
12) A store was having a 20% storewide discount. a. If Mrs Chan paid $55 for a blouse, what was the original price of the blouse? b. Mrs Goh wanted to buy a dress that cost $200 originally.
13) On Friday, shirts in a shop were sold at $30 each. On Saturday, a discount was given on all the shirts, and the number of shirts sold increased by 20%.
14) At a sale, Mr Chua bought an electric kettle and a fan at a discount. He paid a total of $105 for these two items. The amount paid for the electric kettle is 2/3 as much as that for the fan. How much did he pay for the fan?
15) 40% of the people who joined a newly opened fitness club were female. After one year, the number of female members decreased by 20% and the number of male members increased by 45%. In the end, the fitness club had 228 more members than a year ago.
16) DIZ Orchestra performed at the concert hall on two evenings. On the first evening, there were 70 more men than women in the audience. On the second evening, the number of men decreased by 10 % and the number of women increased by 20%.
17) Fiona had $480 more than Shixiu. Shixiu gave Fiona 20% of her money. Fiona then gave 75% of her money to Shixiu. In the end, Shixiu had $1892 more than Fiona. How much did Shixiu have at first?
18) Ted had $300 less than Amy. Amy decided to give 1/5 of her money to Ted. Ted gave 1/3 of his money back to Amy. Amy now has $400 more than Ted. How much money did Ted have at first?
19) The table below shows the number of coloured beads that Jane and Dinah had.
20) At first, jolly had 5/8 of the number of stickers Kelly had. When Kelly gave 36 stickers to Jolly, both had the same number of stickers. How many more stickers did Kelly have than Jolly at first? How many stickers were there altogether?
21) Jara used 70 beads to make a bracelet and 75% of her remaining beads to make a necklace. If she had 20% of her original number of beads left, how many beads does she have at first?
22) Jeff spent 1/4 of his salary on an Ipad and2/9 of the remainder on a watch. If he spent $360 on his watch, what was his salary?
23) A fishmonger sold 40% of his salmon at $30 per kg on Saturday. He sold 25% of the remaining salmon on Sunday at a discount of 10%. He collected a total of $1765.50. How much salmon was left after the weekend?
24) Larry read 2/7 of a book in the morning and 2/5 of the remainder in the afternoon. He then read 3/4 of the remaining pages in the evening and found that there were still another 60 unread pages. Find the total number of pages in the book.
25) Ken spent 1/4 of his money and an additional $6 on a number of CDs. He then spent 3/5 of the remaining money and an additional $12 on magazines. Given that he was left with $18, what fraction of his money was spent on magazines?
P6FRPV1-B - learnbrill
1) How many three-fifths are there in 9 wholes?
2) How many times of 1 2/5 is 7?
3) What is the value of 3/a2 when a = 1/2 ?
4) The difference between two numbers is 54. The sum of 1/3 the smaller number and 2/9 the bigger number is 102. Find the sum of the two numbers.
5) A television set sold at $450 incurred a loss of 10%. AT what price had the television set to be sold in order to make a profit of 10%?
6) An MP3 player was sold at $240 after a discount of 20%. This yielded a profit of 20%. What would the profit be if the MP3 player was sold at the original price?
7) Mrs Lee bought a diamond bracelet during a sale. The store was giving a discount of 30%. Mrs Lee, being a regular customer, received an additional 10% member’s discount off the discounted price. She paid $645.75 for the bracelet.
8) A shop gave different discounts at different time of the day. In the morning, Mr Lim bought a sofa for $1050 after a discount of 25%. In the afternoon, Mr Tan bought a similar sofa for $1120. Find the percentage discount given to Mr Tan.
9) At Shop A, Mr Tang bought a laptop for $2400 which was 20% more than the price that Shop B sold it for. a. How much did Shop B sell the laptop at? b. During a sale, both shops offered an equal percentage discount on the same laptop.
10) The number of girls at a camp is 3/7 the number of boys. If there are 210 children at the camp, how many more boys than girls are there?
11) In a toy shop, 46% of the toys are stuffed toys. 5/9 of the remaining toys are toy trains and the rest are toy cars. There are 280 stuffed toys and toy cars. How many toy cars are there in the shop?
12) There were 3220 spectators at a stadium. 3/7 of the male and 3/4 of the female spectators did not wear sunglasses. The number of male spectators who wore sunglasses was the same as the number of female spectators who wore sunglasses.
13. In a train, the ratio of female passengers to male passengers was 5 : 3. When 16 female passengers alighted the train, the new ratio of female passengers to that of male passengers became 11 : 9.
14) There were 369 roses and lilies at a flower shop. After 2/5 of the roses and 3/7 of the lilies were sold, there was an equal number of roses and lilies left. How many roses were left?
15) There are 1023 pupils in Ubi Primary School. 2/3 of the girls and 5/6 of the boys participated in a mass run. A total of 795 pupils took part in the mass run.
16) At a sports carnival, the ratio of the number of pupils sent by School A, School B and School C to the event was 1:2:3, The number of boys from School A and the number of girls from School B were the same.
17) There are 2300 pupils in a school this year and this number is 15% more than the number of students last year. The number of boys is 25% more than that of last year but the number of girls is 25% less than that of last year.
18) Last month, the number of workers in Restaurant A was twice that of Restaurant B. The ratio of the number of male walkers to the number of female walkers in Restaurant A and Restaurant B was 5 : 4 and 2 : 7 respectively.
19) At a concert, 3/8 of the audience were boys, 1/2 of the remaining audience were girls. There were 120 women and the number of men was 2/3 the number of women. How many people were there in the audience?
20) There were 42 people at a party. 8 of them were men and 15 of them were women. The number of women was thrice the number of girls and the remaining were boys. How many males were there at the party?
21) Melissa collected some beads. 20% of them were golden beads. 9/20 of them were silver beads and the rest were bronze beads. There were 300 more bronze beads than golden beads. How many beads did she collect altogether?
22) At a party, there were twice as many boys as adults, thrice as many adults as girls. Every boy was given 12 sweets, every girl was given 26 sweets and the adults were not given any.
23) A group of pupils registered for a mass run conducted by their school. There were 9 fewer pupils in the lower primary than the upper primary who registered for it. 2/3 of all those registered were boys. 3/7 of the lower primary pupils were girls.
24) In a boutique, 40% of the clothing are dresses. 70% of the remainder are skirts and the rest are pants. There are 30 more skirts than dresses. After some dresses are sold, 25% of the remaining clothing in the boutique are dresses.
25) The number of students who do not wear spectacles is 80% of the number of students who wear spectacles. 36% of the students who wear spectacles are girls and 2/5 of the students who do not wear spectacles are boys.
26) There were some people in a school hall attending a talk. 70% of the people were adults. 3/5 of the children were girls. There were 174 more adults than boys.
27) There are roses and carnations altogether. 6/7 of the roses and 5/6 of the carnations are pink. There are 39 pink flowers in total. How many roses are not pink? How many carnations are pink?
P6FRPV1-C - learnbrill
1) Joseph had a collection of toys. He gave half of his toys to his sister and 1/5 of the remaining toys to his brother. If he had 48 toys left, how many toys did he have at first?
2) Shawn spent $120 on a bag and 1/3 of the remaining money on a cap. If he had 2/5 of the original sum of money left, how much money did he have at first?
3) Patrick spent 25% of his savings on a bag and 40% of the remainder on a pair of shorts. He was left with $135. How much savings did Patrick have at first?
4) Mrs Gupta spent $8 more than 1/5 of her original amount of money on a book. She then spent $4 more than 3/4 of her remaining money on stationery. Given that Mrs Gupta had $12 left, how much did the book cost?
5) Mr Koh had some money. He spent 1/5 of it on a watch and 3/8 of the remainder on a golf set. The amount of money left was $1492 more than the golf set.
6) I have $495 in the form of dollar notes. 1/6 of them are $2 notes and 1/10 of the remainder are $5 notes. The rest are $10 notes. How many $10 notes do I have?
7) Shirley weights 30% more than Alice. If Shirley weighs 6 kg more than Alice, what is their average weight?
8) Kaden is 6 times as old as John. Haikal is 2/3 the age of Kaden. What fraction of Haikal’s age is John’s age?
9) 1/4 of Abdullah’s age is equal to 2/3 of Hussein’s age. The ratio of Hussein’s age to Siti’s age is 2 : 3. Abdullah is 42 years older than Siti. How old is Hussein?
10) Aysha has 1/2 as much money as Keira. Keira has 1/2 as much money as Hairul. What is the ratio of Hairul’s money to Keira’s money to Aysha’s money? How much more money does Hairul have than Aysha if Hairul has $792?
11) Ronn’s savings was 2/7 that of Wayne’s savings in January. In February, Ronn saved another $37 and Wayne saved another $82. Wayne’s savings then became thrice that of Ronn’s. What was Wayne’s savings at the end of February?
12) Alice’s salary was 45% less than Bella’s salary at first. After Alice spent $668 and Bella spent $752, Bella had 4 times as much left as Alice. What was the sum of their salaries?
13) Sally had 3/4 as much money as Zoey. Sally and Zoey shared the cost of a present in the ratio 2 : 3 respectively. Sally used 50% of her money to pay for her share. Zoey had $84 left after paying for her share.
14) A shopkeeper has some $2 notes and $5 notes in his cash register. At first, he had 2/7 as many $5 notes as $2 notes. After exchanging 10 of the $2 notes for $5 notes, he had 2/5 as many $5 notes as $2 notes.
15) Gerald had some green and yellow beads. The number of green beads was 1/3 the number of yellow beads. He gave each of his friends 2 green beads and 3 yellow beads. He then had 42 green beads and 270 yellow beads left.
16) At a fruit stall, the number of watermelons was 3/5 of the number of pineapples. In the morning, 1/3 of the watermelons and 1/3 of the pineapples were sold. In the afternoon, 8 watermelons and 8 pineapples were sold.
17) At first, Frank had 7/12 of the number of cards Gary had. Then, Gary gave Frank 70 cards and both had the same number of cards
18) Alice, Beth and Charles shared a sum of money. Alice received 4/9 of what Beth received. Charles received 2/3 as much as Beth. Beth gave $420 to Alice and another sum of money to Charles. As a result, all the three had the same amount of money.
19. Mel, Nancy and Omega shared some shiny cards. Mel had one-third of what Nancy and Omega had. Nancy had one-fifth of what Mel and Omega had. Mel had 32 fewer shiny cards then Omega. a. What is the ratio of shiny cards between Mel, Nancy and Omega?
20) A sum of $2345 was distributed to Aaron, Bill and Cavin. 1/2 of Aaron’s share was 1/3 of Bill’s share. 1/4 of Bill’s share was 1/5 of Cavin’s share. What was the ratio of Aaron’s share to Bill’s share to Cavin’s share? How much did Bill get?
21) 4/5 of David’s cards is equal to 2 1/2 of Ali’s cards. When David lost 400 cards and Ali bought another 75 cards, the ratio of David’s cards to Ali’s cards became 5:3. How many cards did David have at first?
22) At first, Huimin had only ten-dollar notes and Jim had only two-dollar notes. The number of notes Huimin had was 2/3 the number of notes Jim had. After Huimin gave Jim $3600, the number of notes Huimin had became 1/6 the number of notes Jim had.
23) 4 poles of different lengths were found in a park. The length of pole A is 1/8 of the total length of poles B, C and D. The length of pole B is 2/3 of the total length of poles C and D. The length of pole C is 1/5 of the length of pole D.
P6FRPV1-D - learnbrill
1) The pie chart represents the number fruits sold at a fruit stall. 650 apples were sold. How many oranges were sold?
2) The pie chart below shows the number of different coloured beads Jenny bought. Jenny bought 57 more blue beads than green beads. How many beads did Jenny buy altogether?
3) The pie chart shows the different nationalities of tourists at the River Safari on a particular day. If there are 135 Korean tourists, how many European and Indian tourists are there altogether?
4) The pie chart below shows the amount of money collected from the sales of different types of items in a supermarket in a week.
5) Some people participated in a survey to select their favourite of ice-cream flavour. The pie chart below shows the results of the survey. The ratio of the number of people who prefer vanilla to chocolate flavour is 1 : 3.
6) The bar graph below shows the number of food items sold at a carnival.
7) The graph below shows the number of cars sold from July to December.
8) The table below shows Mrs Lau’s expenditure on groceries and transportation from January to May in a year. a. In which month was the expenditure on groceries 150% of that in May?
9) There were some pies and cakes for sale in a pastry shop. 1/4 of the pastries were pies. The pastry chef then baked an equal number of pies.
10) On a farm, the number of cows was 4/5 the number of goats. After some goat were sold, the number of goats decreased by 60% and there were 360 cows and goats left. How many goats were sold?
11. The ratio of the mass of sugar in packet A to the mass of sugar in packet B is 5 : 6. After the mass of sugar in packet A is increased by 30%, by what percentage must the mass of sugar in packet B be decreased
12) In a factory, the first batch of toy cars and toy bears were produced in the ratio 5: 8. In the second batch of production, the number of toy bears produced increased by 40%. If 455 toys were produced during the first batch,
13) The ratio of Anna’s salary to Ben’s salary to Colin’s salary is 4 : 7 : 10. If Anna’s salary is increased by 20% and Ben’s salary is reduced by 20%, the new total salary is $5100. Find the total salary of the three children.
14) Last year, there were 120 pupils in the computer club. 40% of the pupils were boys. Some boys joined the computer club this year. The percentage of the pupils who are boys has increased to 52%. How many boys joined the computer club this year?
15) Mr Ng earned a fixed monthly salary last year. He spent 25% of his salary in November. In December, he spent 50% less than what he spent in November.
16) Aishah had a collection of coins from Malaysia, India and China. She had 248 from Malaysia. 30% of her coins were from India. She had 24 fewer coins from China than from India. a. What was the total number of coins in Aishah’s collection?
17) Mr Lin always saves 30% of his monthly salary. When his salary increased by 10%, his savings increased by $189. Find Mr Lin’s salary before the increase.
18) Mrs. Chan baked chocolate, strawberry and vanilla puffs. She baked 132 chocolate puffs. 35% of her puffs were strawberry puffs. She baked 12 more vanilla puffs than strawberry puffs.
19) 35% of the marbles in a box are blue. The rest of the marbles are green, red and black in the ratio of 3 : 5 : 4. There are 78 more red marbles than green marbles. How many marbles are in the box altogether?
20) Stella bought some red, yellow and white bows. The ratio of the number of red bows to the number of yellow bows was 4 : 1. The ratio of the number of red bows to the number of white bows was 5 : 2. If there were 165 more red bows than yellow bows,
21) In a basket, there were balls of three different sizes: large, medium and small. 2/3 of the balls were large, 1/5 of the balls were medium and the rest were small. There were 128 more large balls than small balls. How many small balls were there?
22) Last month, the number of supervisors was 3/14 of the number of workers in a factory. This month, the company employed 12 more supervisors and 42 more workers. As a result, the number of supervisors became 25% of the number of workers.
23) Sally had some money at first and she spent 1/7 of her money on a wallet. She spent the rest of the money on 2 chairs and a fan. The 2 chairs cost $491 more than the wallet. The fan cost $97 more than the wallet. How much did the fan cost?
24) Lili, Ariel, Elsa and Kolette bought a present for Mr Kumar. Lili paid 1/5 of the total amount paid by Ariel, Elsa and Kolette. Finally, Lili and Ariel paid $84 altogether while Elsa paid 20% more than Kolette.
25) A train left the terminal with some passengers. At Station A, 1/3 of them alighted and 50 others boarded the train. At Station B, 114 passengers alighted and 15 passengers boarded the train. Then,
26) Mr Lee had some apples and Mangoes. On Day 1, he sold 136 mangoes and threw away 30 rotten ones. Three-quarters of the mangoes were left. On Day 2, he sold three-fifths of the apples.
27) Charlotte and Su Ying had a total of 864 tokens. Charlotte lost 2/5 of her tokens to Su Ying and then Su Ying lost 1/4 of the total number of tokens she had to Charlotte.
P6FRPV1-E - learnbrill
1) The ratio of Ken’s savings to Belle’s savings is 2 : 3. After each of them had spent $18 on food, Ken has 3/5 as much money as Belle. Find their total savings at the end.
2) Sally and Dahua had some stamps in the ratio of 5 : 6. After Sally gave away 20 stamps and Dahua bought 32 stamps, the ratio became 3 : 5. How many stamps did Sally have at first?
3) Bee Heng spent 1/4 of his money and Calvin spent 1/6 of his money. They had the same amount of money left. If Bee Heng has $36 more than Calvin at first, how much does Calvin have at first?
4) Ann and Susan went for a dinner. Ann paid 25% of the bill and Susan paid the rest. After paying for the dinner, Susan had 1/4 of her money left and Ann had $63 left.
5) Mr Ng had a total of 150 red pens and blue pens. After he bought another 50 more red pens and gave away 1/3 of his blue pens, he had the same number of red pens and blue pens lefts.
6) Mary and Jane each had a sticker album. After Jane gave away 30% of her stickers and Mary lost 25% of her stickers, they had the same number of stickers left. If Jane had 6 more stickers than Mary at first,
7) Jane and Iris had 255 sweets altogether. Jane had 15 more sweets than Iris. Jane gave away 25% as many sweets as Iris and was left with twice as many sweets as Iris. How many sweets did Iris give away?
8) Mrs Bala had a total of 128 apples, oranges and mangoes in the ratio of 7 : 5 : 4 respectively. After she gave away some apples and 15 mangoes, the ratio of the number of oranges to the total number of fruits left became 1 : 2.
9) Justina had 72 more Singapore stamps than Malaysian stamps. She gave away some Singapore and Malaysian stamps. The number of Singapore stamps she gave away was 3/4 of the number of Malaysian stamps she had at first.
10) There were 156 more silver balloons than gold balloons at a party. After 5/6 of the silver balloons and 3/4 of the gold balloons burst, there were 106 balloons left. How many balloons were there altogether at first?
11) Jason and Eileen had a total of 255 goldfish. After Jason gave away 1/4 of his goldfish and Eileen gave away 34 of hers, the ratio of the number of goldfish Jason had left to that of Eileen’s became 1:3.
12) Alex and Benson each have some stickers. If Alex used 12 stickers, Benson would have half as many stickers as Alex. If Benson used 18 stickers, Alex would have 5 times as many stickers as Benson. How many stickers did they have altogether?
13) Edison is reading a novel. The ratio of the number of pages he has read to the number of pages he has not read is 3 : 8. If he reads another 182 pages, the number of pages he has read will become 70% of the number of pages he has not read.
14) At a conference, when 10 women left for the washroom, the ratio of the number of men to the number of women that remained became 1 : 1. If 10 men were to leave for the washroom instead,
15) Janice and Marissa had some money. If Janice spends $40 per day and Marissa spends $80 per day, Marissa would have $500 left by the time Janice spends all her money. If Janice spends $80 per day and Marissa spends $40 per day,
16) A fruit seller has some apples and pears. If he sells twice as many pears as the apples, he would have 207 apples left when all the pears are sold. If he sells twice as many apples as the pears,
17) Two groups of people, A and B are working on a project. If 18 people move from group A to group B, then group B will have 3 more people than group A. If we take away 18 people from both groups,
18) Maxie had, 1900 ml more fruit juice than Nick. After Maxie gave Nick 500 ml. of fruit juice, the ratio of Maxie's juice to Nick's juice became 5: 2. How much fruit juice did Maxie have at first?
19) The ratio of Charlie’s stickers to Mary’s stickers was 7:4 at first. If Charlie gives 1/3 of his stickers to Mary, what will be the ratio of Charlie’s stickers to Mary’s stickers in the end?
20) Douglas had some stamps. He sold 2/7 of the stamps and then gave 162 stamps to his best friend. He was left with 1/5 of the stamps he had at first. How many stamps did Douglas have at first?
21) Mrs Tan’s ribbon was 300 m longer than Mrs Ng’s. When Mrs Ng gave 120m of her ribbon to Mrs Tan, the length of Mrs Ng’s ribbon became 1/5 of the length of Mrs Tan’s ribbon. Find the length of Mrs Ng’s ribbon at first.
22) The number of toy cars Keith had was 1/5 the number of paper aeroplanes. After he gave 1/2 of his paper aeroplanes and 1/3 of his toy cars to his brother, he had 286 more paper aeroplanes than toy cars.
23) At first, Jane had 160 more beads than Olivia. Jane first gave 25% of her beads to Olivia, and then Olivia gave 60% of her beads to Jane. In the end, Jane had 200 more beads than Olivia. How many beads did Jane have at first?
24) Four children, Angela, Belinda, Christobel and Dorothy shared $450. Angela received 1/2 of the total amount of money received by Belinda, Christobel and Dorothy. Belinda received 4/11 of the total amount of money received by Angela,
25) Mark and Tina shared some stickers. Mark gave 25% of his stickers to Tina. Then Tina gave 50% of her stickers to Mark. In the end, the ratio of the number of stickers Mark had to the number of stickers Tina had was 14 : 5.
26) Joy and Ken earned $7960 altogether. Joy earned $600 less than Ken. Joy gave 4 times as much money as the amount Ken gave to their mother. Then Ken had twice the amount of money that Joy had left.
27) Jake had some gold coins and gave one-third to Clubby. Clubby had some silver coins and gave one-third to Jake. Jake lost 64 of his gold coins, while Clubby lost 52 of his silver coins. After that,
Subscribe $5.00 / month

Ratio Practice Questions
Click here for questions, click here for answers, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy
Terms and Conditions
Corbettmaths © 2012 – 2024
Chang's Math blog
Compilation of math questions by pupils
Tuesday, January 26, 2016
P6 ratio, age problem (fr pak wai).

Ratio Word Problems
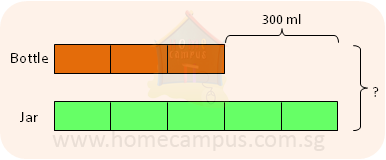
1. the difference between the capacities of a jar and a bottle is 300 ml. if the capacities of the bottle and the jar are in the ratio 3 : 5, what is the maximum volume of water in ml that they can hold together.
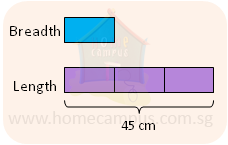
2. The ratio of the breadth of a rectangle to its perimeter is 1 : 8. Find the area of the rectangle if its length is 45 cm.
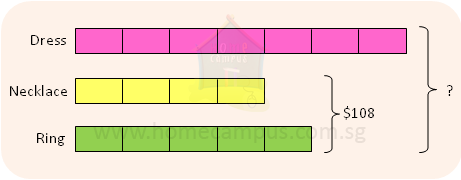
3. Sally had $200 at first. She spent a sum of money on a dress, a necklace and a ring in the ratio 7 : 4 : 5. If she spent $108 on the jewellery, how much money had she left?
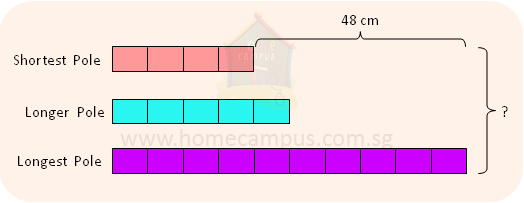
4. The lengths of 3 poles are in the ratio 4 : 5 : 10. The shortest pole is 48 cm shorter than the longest pole. What is the length of the poles altogether?
5. Pam travelled 1 11 of the distance of her journey by car while the rest by bus and train in the ratio 1 : 4. If she travelled 532 km more by train than by car, how far did she travel?

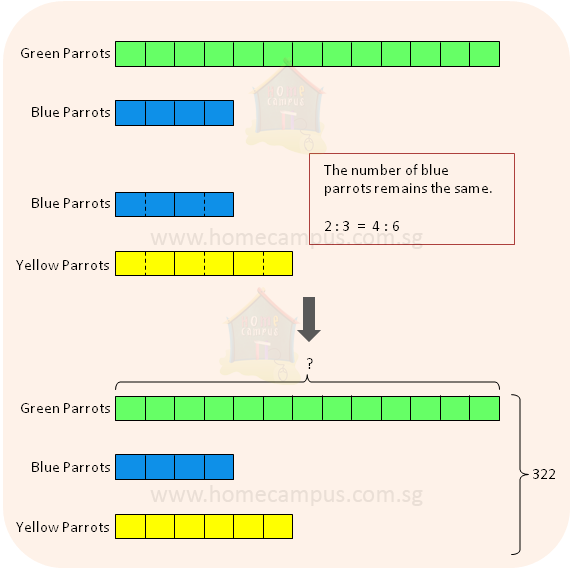
6. A pet parrot shop has 322 parrots that are coloured either green or blue or yellow. The ratio of the number of green parrots to the number of blue parrots is 13 : 4. The ratio of the number of blue parrots to the number of yellow parrots is 2 : 3.
7. In a school, for every 5 children born in January there were 3 born in February and for every 2 children born in February there were 5 born in March.
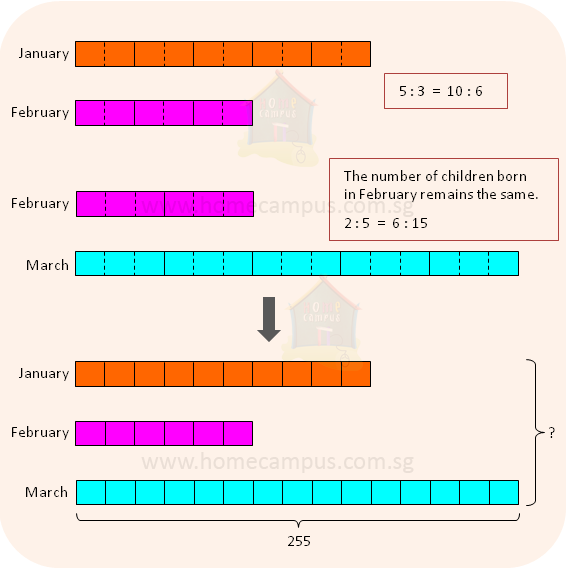
8. Rayan received twice as much pocket money as Falaq. After Rayan spent $5 on animal cards, the ratio of Rayan's amount to that of Falaq's became 3 : 2. Find the amount of pocket money that Falaq received.
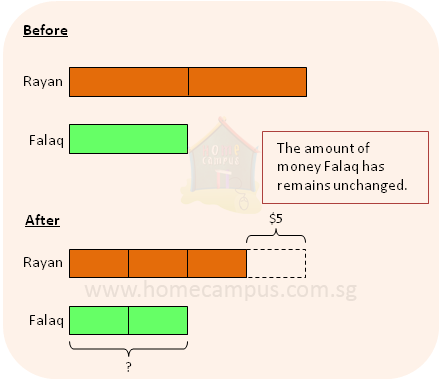
9. The ratio of Grace's mass to Laura's mass was 7 : 5 at first. Then, Laura fell sick and lost 1 10 of her mass. The new difference between their body masses was 25 kg.
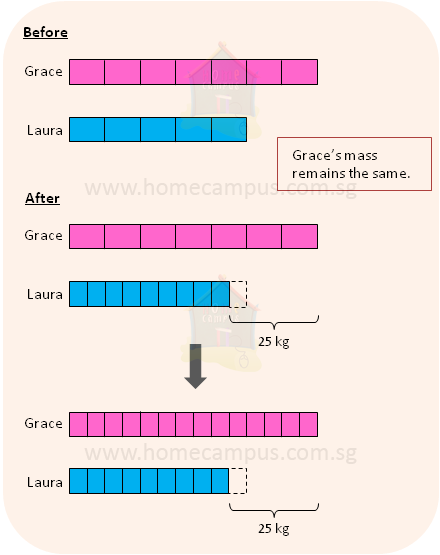
10. Abby and Nina share a sum of money in the ratio 2 : 3. Then, Nina gives a sixth of her share to Abby.
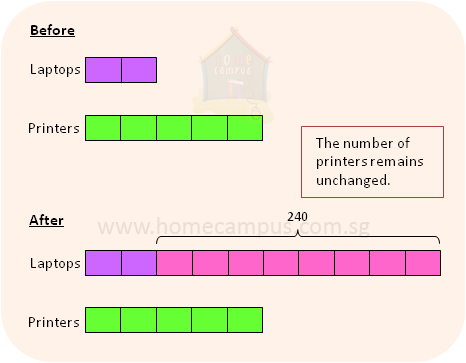
11. The ratio of the number of laptops to the number of printers in an electronics store was 2 : 5 at first. After a shipment of 240 new laptops arrived at the store, there were twice as many laptops as printers.
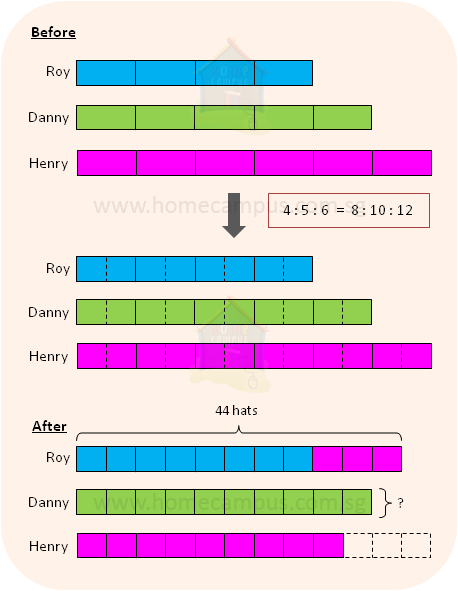
12. Roy, Danny and Henry had a collection of hats. The ratio of the number of hats that Roy had to the number of hats that Danny had to the number of hats that Henry had was 4 : 5 : 6. Then, Henry gave 1 4 of his hats to Roy.
- Kindergarten
- Greater Than Less Than
- Measurement
- Multiplication
- Place Value
- Subtraction
- Punctuation
- 1st Grade Reading
- 2nd Grade Reading
- 3rd Grade Reading
- Cursive Writing
Ratio P6 - Displaying top 8 worksheets found for this concept.
Some of the worksheets for this concept are Ratios word problems, Ratio word problems work, P6 briefing for parents, Chij katong primary p3 semestral assessment 1 2019, Work word problems, User manual overview function, Year 6 booster booklet fractions, Work out each of the show your workings clearly.
Found worksheet you are looking for? To download/print, click on pop-out icon or print icon to worksheet to print or download. Worksheet will open in a new window. You can & download or print using the browser document reader options.
1. Ratios Word Problems
2. ratio word problems worksheet, 3. p6 briefing for parents -, 4. chij (katong) primary p3 semestral assessment 1 (2019 ..., 5. work word problems -, 6. user manual // overview & function, 7. year 6 booster booklet fractions, 8. work out each of the following. show your workings clearly ....
Primary 6 Ratio Questions
These are problems that other students can't solve. Your future exam questions are probably inside so use these to practice! 1) Snap homework photo 2) Upload and wait 3) Solution emailed to you free!

{{notification.title}}

360 Tutoring Program
*If you qualify, the Free 360 Tutoring Program will be extended to you at no extra charge.
On top of the tutor you are getting, ManyTutors will provide unlimited free tutors to help you with any questions you may have for other subjects. Just snap a photo of your homework, post, and someone will provide the solution for free.
You will get a complimentary premium account on Ask ManyTutors that allows you to ask English, Chinese, Malay, Math, Science, Geography and History homework questions free of charge.
Under the 360 Program, the tutor will receive a different rate from what you are paying to ManyTutors.

P5/6. 40 Must-Know Problem Sums (Volume 6 out of 6)
$ 35.00
The one BIG difference about this problem sums guidebook is it covers one of the MOST Challenging topical problem sums that many children and parents often face. Questions involving shapes (such as triangles, slanted triangles, rectangles and squares) and ratio, percentages, and fractions.
The P5/6 problem sums are also getting tougher. We have compiled the more advanced problem sums so your child can have them at her fingertips. Over 60 questions in this final volume (Vol. 6) of the 40-sum-series!
Planning to get one? Would you want to know the difference between 40 Sums Vol 1 to 6?
- Vol 1 covers 11 must-know level 1/ basic problem sums types.
- Vol 2 contains tips and tricks on the very challenging questions involving speed and algebra and it has the more challenging level 2 problem sums types.
- Vol 3 covers percentages problem sums too. It comes with an 8-page summary with the must-know smart tips on solving percentages problem sums fast.
- Vol 4 cover challenging problem sums on circles, volume/ rate, angles/ folding angles and much much more.
- Vol 5 covers number patterns too along with other tougher problem sums which P6s will eventually see in their exam papers.
- Vol 6 covers questions involving shapes (such as triangles, slanted triangles, rectangles and squares) and ratio, percentages, and fractions.
134 in stock
Description

Here is our “ 40 Must-Know Problem Sums for PSLE Students Volume 6 “.
Many P5/6 children and parents have told us that Area and perimeter questions (involving ratio, percentage and fraction with shapes like triangles, rectangles and squares) and the advanced problem sums are getting more challenging.
They seemed to be endless!
Using the last 4 months, our math team has worked really very hard going through all the top school papers and compiled this set of must-know 40 sums.
This is book your “formula” book to solve these problem sums – fast.
Many children are confused by these very common and yet challenging problem sums. Others find them tough and even frustrating to solve.😱
Is your child one of them?😭
This book comes with the step-by-step solving process . No more buying of more books or papers just to do them for the sake of doing.

Here are what you will find helpful in this book once you get hold of it.
Problem sums on …
– 2 ifs – Area (Fraction) – Area (Percent) – Area (Ratio) – Area (Units)
– Circle Square – Equivalent Ratio – Frame – Grouping – More Than – Path
– Perimeter and Value – Rectangle – Remainder
– Same Difference – Same One – Same Total
– Slanted Triangle – Triangle Rectangle – Triangle Rectangle Square – Triangle Square – Triangle – Triangles X2
– Units and Parts – Working Backwards
Do you think this compilation is going to make your child’s learning sooo much easier?
One of our parents told us this 40-sums series is saving her life 😀

Wait! There are limited copies.
Because of the logistics issue, we can only print 50 copies.
Special price for the first 15 copies is $35! (Usual is $42)
All you need to do now is click on the “Add to Cart” button below to order now .
Related products

P1-6. Problem Sums Formula Sheets

P5. 51 Must Know Problem Sums (Volume 1 out of 3) for CA1 & SA1

P5/6. 40 Must-Know Problem Sums (Volume 4 out of 6)
Order now for a free Model Fraction Cards (worth $29!) with code “lob10” for 10% off Pri levels books. "We have limited stock. If you don't see it in your package, it means we have run out. While supplies last." Dismiss
WhatsApp us

IMAGES
VIDEO
COMMENTS
Master essential Primary Math Ratio concepts for P5 & P6 Math in our must-read guide. Boost your child's exam success here!
Word Problem Worksheet - Part 1 (Fractions, Percentages, Ratios) P6 Mathematics CA1 2015 References: P6 2015 Math CA1 papers of NHPS, RS . Compiled by: 2 www.sgtestpaper.com Show your workings clearly in the space below it and write your answer in the space provided.
Ratio Math problems consist of many marks in the exam and you cannot afford to lose them. Here are 4 common types of ratio math problems.
Ratio. In this article, we are going to learn about the ratios and the fractions as per the Primary 6 Maths level. The learning objectives are. Relationship between ratio and fraction. Simple word problems involving ratios. This article can serve as a refresher for the ratios and fractions concepts as taught in P5.
Free ratio problem solving math topic guide, including step-by-step examples, free practice questions, teaching tips and more!
PSLE Maths Problem Solving Strategies for Primary 5 and Primary 6 - Part 1 (Fractions, Ratio)#1 Repeated Identity Concept#2 Equal Fractions Concept#3 Externa...
In this first part of Types of Changing Ratios, determine which questions fall under an Unchanged Total in a given Ratio and find out how to solve them.Don't...
Free ratio problem solving GCSE maths revision guide, including step by step examples, exam questions and free worksheet.
Be better prepared for PSLE 2023. Learn from these hard math questions from the PSLE Math 2021 paper with this P6 math revision guide!
Next: Reflections Textbook Exercise. The Corbettmaths Textbook Exercise on Ratio: Problem Solving.
Connect with us!💜 Instagram: https://www.instagram.com/askteacherjoseph🖤 Tiktok: https://www.tiktok.com/@askteacherjoseph💌 Email: theimpactacademysg@gmail...
Ratio word problems. Students can use simple ratios to solve these word problems; the arithmetic is kept simple so as to focus on the understanding of the use of ratios. Free, printable math worksheets from K5 Learning.
Learn how to solve fraction, ratio, and percentage problems for Primary 6 with clear videos and quizzes. Enroll now and ace your exams.
Practice Questions. Previous: Percentages of an Amount (Non Calculator) Practice Questions. Next: Rotations Practice Questions. The Corbettmaths Practice Questions on Ratio.
Compilation of math questions by pupils. Tuesday, January 26, 2016. P6 ratio, age problem (fr Pak Wai) Posted by ChangCL's Site at 5:37 PM. ... P6 ratio, age problem (fr Pak Wai) P6 fractions (fr PCS remedial WS) P6 numbers (fr PCS remedial WS) Sec1 or sec2 Sch geom / trigo ( accidentally creat...
For more Singapore Math problems check out my channel at https://www.youtube.com/@inspiredLearningThis video shows how to resolve the ratio word problems of ...
Ratio Word Problems. 1. The difference between the capacities of a jar and a bottle is 300 ml. If the capacities of the bottle and the jar are in the ratio 3 : 5, what is the maximum volume of water in ml that they can hold together? 2 units = 300 ml. 1 unit = 300 ml ÷ 2 = 150 ml. 8 units = 150 ml × 8 = 1200 ml.
P6 Topics (Term 1) Fraction: •4 operations with fractions •Dividing a fraction by a proper fraction •Solving word problems involving fractions ... •Compare ratios •Solve word problems involving ratio. P6 Topics (Term 1) Percentage: •Express a decimal or fraction as a percentage and vice versa
Ratio P6 - Displaying top 8 worksheets found for this concept. Some of the worksheets for this concept are Ratios word problems, Ratio word problems work, P6 briefing for parents, Chij katong primary p3 semestral assessment 1 2019, Work word problems, User manual overview function, Year 6 booster booklet fractions, Work out each of the show ...
This question is taken from a practise paper from Bedok Green Primary School. Solution as requested by my student. Teacher David Ng is a Maths assessment boo...
This is a collection of Singapore primary 6 Ratio practice questions. Snap a photo of your homework and a few Singapore will provide the solution to your question in a few hours. Suitable for primary, secondary and JC levels.
Conversational learning is part of the teaching pedagogy in our classes as demonstrated in the videos. The benefits includes 1.Better info application, 2.Fas...
The one BIG difference about this problem sums guidebook is it covers one of the MOST Challenging topical problem sums that many children and parents often face. Questions involving shapes (such as triangles, slanted triangles, rectangles and squares) and ratio, percentages, and fractions. The P5/6 problem sums are also getting tougher. We have compiled the more advanced problem sums so your ...