xrd slide presentation

$X-ray Diffraction SEF logo$

X-ray Diffraction SEF

Search form

Request new password

XRD Literature

View (active tab)

X-ray Powder Diffraction (XRD)

Barbara L Dutrow, Louisiana State University , Christine M. Clark, Eastern Michigan University

What is X-ray Powder Diffraction (XRD)

X-ray powder diffraction (XRD) is a rapid analytical technique primarily used for phase identification of a crystalline material and can provide information on unit cell dimensions. The analyzed material is finely ground, homogenized, and average bulk composition is determined.

Fundamental Principles of X-ray Powder Diffraction (XRD)

Max von Laue, in 1912, discovered that crystalline substances act as three-dimensional diffraction gratings for X-ray wavelengths similar to the spacing of planes in a crystal lattice. X-ray diffraction is now a common technique for the study of crystal structures and atomic spacing.

X-ray diffraction is based on constructive interference of monochromatic X-rays and a crystalline sample. These X-rays are generated by a cathode ray tube, filtered to produce monochromatic radiation, collimated to concentrate, and directed toward the sample. The interaction of the incident rays with the sample produces constructive interference (and a diffracted ray) when conditions satisfy Bragg's Law ( n λ =2 d sin θ ). This law relates the wavelength of electromagnetic radiation to the diffraction angle and the lattice spacing in a crystalline sample. These diffracted X-rays are then detected, processed and counted. By scanning the sample through a range of 2 θ angles, all possible diffraction directions of the lattice should be attained due to the random orientation of the powdered material. Conversion of the diffraction peaks to d-spacings allows identification of the mineral because each mineral has a set of unique d-spacings. Typically, this is achieved by comparison of d-spacings with standard reference patterns.

All diffraction methods are based on generation of X-rays in an X-ray tube. These X-rays are directed at the sample, and the diffracted rays are collected. A key component of all diffraction is the angle between the incident and diffracted rays. Powder and single crystal diffraction vary in instrumentation beyond this.

X-ray Powder Diffraction (XRD) Instrumentation - How Does It Work?

$X-ray Diffraction Instrument$

The geometry of an X-ray diffractometer is such that the sample rotates in the path of the collimated X-ray beam at an angle θ while the X-ray detector is mounted on an arm to collect the diffracted X-rays and rotates at an angle of 2 θ . The instrument used to maintain the angle and rotate the sample is termed a goniometer . For typical powder patterns, data is collected at 2 θ from ~5 ° to 70 ° , angles that are preset in the X-ray scan.

Applications

X-ray powder diffraction is most widely used for the identification of unknown crystalline materials (e.g. minerals, inorganic compounds). Determination of unknown solids is critical to studies in geology, environmental science, material science, engineering and biology.

Other applications include:

characterization of crystalline materials
identification of fine-grained minerals such as clays and mixed layer clays that are difficult to determine optically
determination of unit cell dimensions
measurement of sample purity

With specialized techniques, XRD can be used to:

determine crystal structures using Rietveld refinement
determine of modal amounts of minerals (quantitative analysis)
determining lattice mismatch between film and substrate and to inferring stress and strain
determining dislocation density and quality of the film by rocking curve measurements
measuring superlattices in multilayered epitaxial structures
determining the thickness, roughness and density of the film using glancing incidence X-ray reflectivity measurements
make textural measurements, such as the orientation of grains, in a polycrystalline sample

Strengths and Limitations of X-ray Powder Diffraction (XRD)?

Powerful and rapid (< 20 min) technique for identification of an unknown mineral
In most cases, it provides an unambiguous mineral determination
Minimal sample preparation is required
XRD units are widely available
Data interpretation is relatively straight forward

Limitations

Homogeneous and single phase material is best for identification of an unknown
Must have access to a standard reference file of inorganic compounds (d-spacings, hkl s)
Requires tenths of a gram of material which must be ground into a powder
For mixed materials, detection limit is ~ 2% of sample
For unit cell determinations, indexing of patterns for non-isometric crystal systems is complicated
Peak overlay may occur and worsens for high angle 'reflections'

User's Guide - Sample Collection and Preparation

Determination of an unknown requires: the material, an instrument for grinding, and a sample holder.

Obtain a few tenths of a gram (or more) of the material, as pure as possible
Grind the sample to a fine powder, typically in a fluid to minimize inducing extra strain (surface energy) that can offset peak positions, and to randomize orientation. Powder less than ~10 μ m(or 200-mesh) in size is preferred

smear uniformly onto a glass slide, assuring a flat upper surface
pack into a sample container
sprinkle on double sticky tape
Care must be taken to create a flat upper surface and to achieve a random distribution of lattice orientations unless creating an oriented smear.
For analysis of clays which require a single orientation, specialized techniques for preparation of clay samples are given by USGS .
For unit cell determinations, a small amount of a standard with known peak positions (that do not interfere with the sample) can be added and used to correct peak positions.

Data Collection, Results and Presentation

Data Collection The intensity of diffracted X-rays is continuously recorded as the sample and detector rotate through their respective angles. A peak in intensity occurs when the mineral contains lattice planes with d-spacings appropriate to diffract X-rays at that value of θ . Although each peak consists of two separate reflections (K α 1 and K α 2 ), at small values of 2 θ the peak locations overlap with K α 2 appearing as a hump on the side of K α 1 . Greater separation occurs at higher values of θ . Typically these combined peaks are treated as one. The 2 λ position of the diffraction peak is typically measured as the center of the peak at 80% peak height.

Data Reduction

Results are commonly presented as peak positions at 2 θ and X-ray counts (intensity) in the form of a table or an x-y plot (shown above). Intensity ( I ) is either reported as peak height intensity, that intensity above background, or as integrated intensity, the area under the peak. The relative intensity is recorded as the ratio of the peak intensity to that of the most intense peak ( relative intensity = I/I 1 x 100 ).

Determination of an Unknown

The d-spacing of each peak is then obtained by solution of the Bragg equation for the appropriate value of λ . Once all d-spacings have been determined, automated search/match routines compare the d s of the unknown to those of known materials. Because each mineral has a unique set of d-spacings, matching these d-spacings provides an identification of the unknown sample. A systematic procedure is used by ordering the d-spacings in terms of their intensity beginning with the most intense peak. Files of d-spacings for hundreds of thousands of inorganic compounds are available from the International Centre for Diffraction Data as the Powder Diffraction File (PDF). Many other sites contain d-spacings of minerals such as the American Mineralogist Crystal Structure Database . Commonly this information is an integral portion of the software that comes with the instrumentation.

Determination of Unit Cell Dimensions

For determination of unit cell parameters, each reflection must be indexed to a specific hkl .

The following literature can be used to further explore X-ray Powder Diffraction (XRD)

Bish, DL and Post, JE, editors. 1989. Modern Powder Diffraction. Reviews in Mienralogy, v. 20. Mineralogical Society of America.
Cullity, B. D. 1978. Elements of X-ray diffraction. 2nd ed. Addison-Wesley, Reading, Mass.
Klug, H. P., and L. E. Alexander. 1974. X-ray diffraction procedures for polycrystalline and amorphous materials. 2nd ed. Wiley, New York.
Moore, D. M. and R. C. Reynolds, Jr. 1997. X-Ray diffraction and the identification and analysis of clay minerals. 2nd Ed. Oxford University Press, New York.

Teaching Activities and Resources

Teaching activities, labs, and resources pertaining to X-ray Powder Diffraction (XRD).

X-ray techniques lab exercises from the SERC Teaching Mineralogy Collections
Weathering of Igneous, Metamorphic, and Sedimentary Rocks in a Semi-Arid Climate - An Engineering Application of Petrology - This problem develops skills in X-ray diffraction analysis as applied to clay mineralogy, reinforces lecture material on the geochemistry of weathering, and demonstrates the role of petrologic characterization in site engineering.
Teaching Guide to X-ray Diffraction at Cambridge
A Powerpoint presentation on use of XRD in Soil Science (PowerPoint 1.6MB Sep7 07) by Melody Bergeron, Image and Chemical Analysis Laboratory at Montana State University.
Brady, John B., and Boardman, Shelby J., 1995, Introducing Mineralogy Students to X-ray Diffraction Through Optical Diffraction Experiments Using Lasers. Jour. Geol. Education, v. 43 #5, 471-476.
Brady, John B., Newton, Robert M., and Boardman, Shelby J., 1995, New Uses for Powder X-ray Diffraction Experiments in the Undergraduate Curriculum. Jour. Geol. Education, v. 43 #5, 466-470.
Dutrow, Barb, 1997, Better Living Through Minerals X-ray Diffraction of Household Products, in: Brady, J., Mogk, D., and Perkins D. (eds.) Teaching Mineralogy, Mineralogical Society of America, p. 349-359.
Hovis, Guy, L., 1997, Determination of Chemical Composition, State of Order, Molar Volume, and Density of a Monoclinic Alkali Feldspar Using X-ray Diffraction, in: Brady, J., Mogk, D., and Perkins D. (eds.) Teaching Mineralogy, Mineralogical Society of America, p. 107-118.
Brady, John B., 1997, Making Solid Solutions with Alkali Halides (and Breaking Them) , in: Brady, J., Mogk, D., and Perkins D. (eds.) Teaching Mineralogy, Mineralogical Society of America, p. 91-95.
Perkins, Dexter, III, and Sorensen, Paul, Mineral Synthesis and X-ray Diffraction Experiments, in: Brady, J., Mogk, D., and Perkins D. (eds.) Teaching Mineralogy, Mineralogical Society of America, p. 81-90.
Hollecher, Kurt, A Long-Term Mineralogy Practical Exam, in: Brady, J., Mogk, D., and Perkins D. (eds.) Teaching Mineralogy, Mineralogical Society of America, p. 43-46.
Moecher, David, 2004, Characterization and Identification of Mineral Unknowns: A Mineralogy Term Project, Jour. Geoscience Education, v 52 #1, p. 5-9.
Hluchy, M.M., 1999, The Value of Teaching X-ray Techniques and Clay Mineralogy to Undergraduates, Jour. Geoscience Education, v. 47, p. 236-240.

« Scanning Electron Microscopy (SEM) X-ray Computed Tomography (CT) »

Crystallography
Environmental Health Risk Assessment
Geochemical Instrumentation and Analysis
Browse Collection
Contribute Teaching Activities
Hurricane Katrina
Impacts on American Indian Lands
Montana Geoscience Data Project
Teaching Phase Equilibria
Teaching with GeoPads
Yellowstone REU
Advances in Paleontology
Montana Geoheritage Project
Yellowstone

About this Site
Accessibility

Citing and Terms of Use

Material on this page is offered under a Creative Commons license unless otherwise noted below.

Show terms of use for text on this page »

Show terms of use for media on this page »

$X-ray Diffraction Instrument$

Last Modified: May 05, 2024
Short URL: https://serc.carleton.edu/18400 What's This?

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

X-ray diffraction (XRD) basics and application

Last updated
Save as PDF
Page ID 148442

How the Technique Works

X-ray diffraction is a common technique that determine a sample's composition or crystalline structure. For larger crystals such as macromolecules and inorganic compounds, it can be used to determine the structure of atoms within the sample. If the crystal size is too small, it can determine sample composition, crystallinity, and phase purity. This technique sends x-ray beams through it. X-ray beams are chosen because their wavelength is similar to the spacing between atoms in the sample, so the angle of diffraction will be affected by the spacing of the atoms in the molecule, as opposed to using much larger wavelengths, which would be unaltered by the spacing between atoms. The x-rays then pass through the sample, “bouncing” off of the atoms in the structure, and changing the direction of the beam at some different angle, theta, from the original beam. This is the angle of diffraction. Some of these diffracted beams cancel each other out, but if the beams have similar wavelengths, then constructive interference occurs. Constructive interference is when the x-ray beams that are whole number integers of the same wavelength add together to create a new beam with a higher amplitude. The greater amplitude of the wave translates into a greater signal for this specific angle of diffraction. The angle of diffraction can then be used to determine the difference between atomic planes using Bragg’s law , $sin Θ = nλ / 2d$ where lambda is the wavelength added, theta is the angle of diffraction, and d is the distance between atomic planes. The distance between atomic plates can then be used to determine composition or crystalline structure.

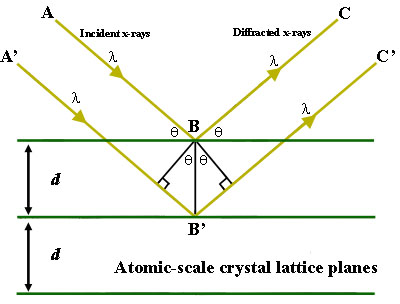
Figure 1. Bragg's Law reflection. The diffracted X-rays exhibit constructive interference when the distance between paths ABC and A'B'C' differs by an integer number of wavelengths (λ). Figure Courtesy of Creative Commons license and found on https://serc. carleton. edu/msu_nanotech/methods/BraggsLaw. html

Useful Visualization of X-ray Diffraction

https://www. doitpoms. ac. uk/tlplib/xray-diffraction/bragg. php

How to interpret the data

The result of X-ray diffraction plots the intensity of the signal for various angles of diffraction at their respective two theta positions. The two theta positions correspond to a certain spacing between the crystals or atoms in the samples, determined by the angle of diffraction from the incident x-ray beam sent into the sample. The intensity of the peaks is related to the amount of molecules in that phase or with that spacing. The greater the intensity of the peak, the greater the amount of crystals or molecules with that distinct spacing.

The width of the peaks is inversely proportional to the crystal size. A thinner peak corresponds to a bigger crystal. A broader peak means that there may be a smaller crystal, defect in the crystalline structure, or that the sample might be amorphous in nature, a solid lacking perfect crystallinity. For smaller samples, the patterns determined using XRD analysis can be used to determine a sample’s composition. There is a large database of elements, compounds, and minerals that contain the diffraction patterns for elements, compounds, and minerals. The pattern for an unknown compound can be compared to the literature and experimentally determined values to verify the identity of an element, matching both the location, width, and relative heights of the diffraction patterns.

HqtX6uVvZQnap3esoJiDP5RqaCD42ZwhhSDhXzMg5udZ6NiHyzm2fi-1YvHYartS3RYKqaFsKqyGgrVVC0634qxZmqkDSQjESjdb8WE9OulMKLHIyb1f5p0RKTufjNn9LtYzZPtg

Figure "2" Figure courtesy of Creative Commons license and can be found at https://serc. carleton. edu/details/images/20376. html

Good literature examples

https://www. ncbi. nlm. nih. gov/pubmed/25459903
https://link. springer. com/article/10. 1186/2228-5326-3-8

Works cited

X-ray Diffraction @ McGill http://eps. mcgill. ca/xrd/howxrdworks. html (accessed May 3, 2019).
BraggsLaw https://serc. carleton. edu/msu_nanote. . . BraggsLaw. html (accessed May 3, 2019).
DoITPoMS - TLP Library X-ray Diffraction Techniques - Relationship between crystalline structure and X-ray data https://www. doitpoms. ac. uk/tlplib/xr. . . ction/peak. php (accessed May 3, 2019).
Diffraction Basics | Chemical Instrumentation Facility | Iowa State University https://www. cif. iastate. edu/acide/xrd-tutorial/xrd (accessed May 3, 2019)

Preferences

X-ray Diffraction (XRD) - PowerPoint PPT Presentation

X-ray Diffraction (XRD)

... this kind of texture arises from all sorts of treatments, e.g. casting, cold working, annealing, etc. if the crystallites (or grains) ... wood, quite thick ... – powerpoint ppt presentation.

What is X-ray Diffraction
Properties and generation of X-ray
Basics of Crystallography
XRD Pattern
Powder Diffraction
Applications of XRD
X-rays are electromagnetic radiation with very short wavelength (? 10-8 -10-12 m)
The energy of the x-ray can be calculated with the equation
e.g. the x-ray photon with wavelength 1Å has energy 12.5 keV
A spectrum of x-ray is produced as a result of the interaction between the incoming electrons and the nucleus or inner shell electrons of the target element.
Two components of the spectrum can be identified, namely, the continuous spectrum caused by bremsstrahlung (German word braking radiation) and the characteristic spectrum.
The short-wavelength limit (SWL or ?SWL) corresponds to those x-ray photons generated when an incoming electron yield all its energy in one impact.
Sharp peaks in the spectrum can be seen if the accelerating voltage is high (e.g. 25 kV for molybdenum target).
These peaks fall into sets which are given the names, K, L, M. lines with increasing wavelength.
If an incoming electron has sufficient kinetic energy for knocking out an electron of the K shell (the inner-most shell), it may excite the atom to an high-energy state (K state).
One of the outer electron falls into the K-shell vacancy, emitting the excess energy as a x-ray photon.
Characteristic x-ray energy
Ex-rayEfinal-Einitial
All x-rays are absorbed to some extent in passing through matter due to electron ejection or scattering.
The absorption follows the equation
where I is the transmitted intensity
I0 is the incident intensity
x is the thickness of the matter
is the linear absorption coefficient
(element dependent)
? is the density of the matter
(?/?) is the mass absorption coefficient (cm2/gm).
The mass absorption coefficient is also wavelength dependent.
Discontinuities or Absorption edges can be seen on the absorption coefficient vs. wavelength plot.
These absorption edges mark the point on the wavelength scale where the x-rays possess sufficient energy to eject an electron from one of the shells.
The absorption behavior of x-ray by matter can be used as a means for producing quasi- monochromatic x-ray which is essential for XRD experiments.
The rule Choose for the filter an element whose K absorption edge is just to the short-wavelength side of the K? line of the target material.
A common example is the use of nickel to cut down the K? peak in the copper x-ray spectrum.
The thickness of the filter to achieve the desired intensity ratio of the peaks can be calculated with the absorption equation shown in the last section.
nl 2dsin(?)
Peak position
Peak intensity
Sometimes, even though the Braggs condition is satisfied, a strong diffraction peak is not observed at the expected angle.
Consider the diffraction peak of (001) plane of a FCC crystal.
Owing to the existence of the (002) plane in between, complications occur.
ray 1 and ray 3 have path difference of ?
but ray 1 and ray 2 have path difference of ?/2. So do ray 2 and ray 3.
It turns out that it is in fact a destructive condition, i.e. having an intensity of 0.
the diffraction peak of a (001) plane in a FCC crystal can never be observed.
e.g., Aluminium (FCC), all atoms are the same in the unit cell
four atoms at positions, (uvw)
A(0,0,0), B(½,0,½),
C(½,½,0) D(0,½,½)
For a certain set of plane, (hkl)
F ? f (?) exp2?i(hukvlw)
f (?) ? exp2?i(hukvlw)
f (?)exp2?i(0) exp2?i(h/2 l/2)
exp2?i(h/2 k/2) exp2?i(k/2 l/2)
f (?)1 e?i(hk) e?i(kl) e?i(lh)
Since e2n?i 1 and e(2n1)?i -1,
?if h, k l are all odd or all even, then (hk), (kl), and (lh) are all even and F 4f otherwise, F 0
Particle or
2. Residual
A powder sample is in fact an assemblage of small crystallites, oriented at random in space.
x-ray detectors (e.g. Geiger counters) is used instead of the film to record both the position and intensity of the x-ray peaks
The sample holder and the x-ray detector are mechanically linked
If the sample holder turns ?, the detector turns 2?, so that the detector is always ready to detect the Bragg diffracted
One of the most important uses of XRD
Obtain XRD pattern
Measure d-spacings
Obtain integrated intensities
Compare data with known standards in the JCPDS file, which are for random orientations (there are more than 50,000 JCPDS cards of inorganic materials).
To identify crystalline phases
To determine structural properties
Lattice parameters (10-4Å), strain, grain size, expitaxy,
phase composition, preferred orientation
order-disorder transformation, thermal expansion
To measure thickness of thin films and multilayers
To determine atomic arrangement
To image and characterize defects
Detection limits 3 in a two phase mixture can be
0.1 with synchrotron radiation.
Lateral resolution normally none
b. Tetragonal
ab?c (a and c)
c. Orthorhombic
a?b?c (a, b and c)
Number of reflection
Peak splitting
The intensity of diffraction peaks depends on the amount of the substance
By comparing the peak intensities of various components in a mixture, the relative amount of each components in the mixture can be worked out
In common polycrystalline materials, the grains may not be oriented randomly. (We are not talking about the grain shape, but the orientation of the unit cell of each grain, )
This kind of texture arises from all sorts of treatments, e.g. casting, cold working, annealing, etc.
If the crystallites (or grains) are not oriented randomly, the diffraction cone will not be a complete cone
By rotating the specimen about three major axes as shown, these spatial variations in diffraction intensity can be measured.
Temperature
Electric Field

PowerShow.com is a leading presentation sharing website. It has millions of presentations already uploaded and available with 1,000s more being uploaded by its users every day. Whatever your area of interest, here you’ll be able to find and view presentations you’ll love and possibly download. And, best of all, it is completely free and easy to use.

You might even have a presentation you’d like to share with others. If so, just upload it to PowerShow.com. We’ll convert it to an HTML5 slideshow that includes all the media types you’ve already added: audio, video, music, pictures, animations and transition effects. Then you can share it with your target audience as well as PowerShow.com’s millions of monthly visitors. And, again, it’s all free.

About the Developers

PowerShow.com is brought to you by CrystalGraphics , the award-winning developer and market-leading publisher of rich-media enhancement products for presentations. Our product offerings include millions of PowerPoint templates, diagrams, animated 3D characters and more.

X RAY DIFFRACTION- XRD

Mar 17, 2019

640 likes | 1.23k Views

X RAY DIFFRACTION- XRD. SOLID MATTER- AMORPHOUS: Atoms arranged in a random manner , like in liquids- eg: Glass CRYSTALLINE :

Share Presentation

diffraction
ray diffraction
scattering techniques
end window tubes
ray rocking curve analysis

Presentation Transcript

X RAY DIFFRACTION- XRD SOLID MATTER- AMORPHOUS: Atoms arranged in a random manner , like in liquids- eg: Glass CRYSTALLINE: Atoms arranged in a regular pattern. Smallest volume element repeats in three dimensions describing the crystal. The smallest volume element is UNIT CELL. Dimensions of the unit cell described by the edges a,b, and c and the angles between them alpha, beta and gamma.

X - RAYS • German scientist Rontgen discovered X-rays in 1895 accidentally when working with discharge tube. • Barium platinocyanide screen placed near the tube began to glow, Glow continued even when a wooden screen was placed between them. • As cause was not known, called as X-rays. • It could pass through opaque bodies. Wave length shorter than that of ultraviolet light.

Essential elements of a coolidge X- ray vacuum tube: • Cathode- tungsten filament heated to incandescence by a low voltage AC from a step down transformer/ storage battery. • Emits large number of electrons known as thermions focused on a target using cylindrical shields (molybdenum) • Shield maintained at a negative potential surrounding the cathode. • Electrons accelerated to very high speeds by DC potential difference about 50kV to 100kV applied between cathode and anode (anticathode). The high DC from a step up transformer. Electrons Tungsten filament Shield Cooling water X rays

The Coolidge tube (1913) is also called hot cathode tube • It works with a very good quality vacuum (about 10-4 Pa, or 10-6 Torr). • The filament is the cathode of the tube. The high voltage potential is between the cathode and the anode, the electrons are accelerated and then hit the anode. • There are two designs: end-window tubes and side-window tubes. • In the end-window tubes, the filament is around the anode, the electrons have a curved path. • Special about side-window tubes is: • An Electrostatic lens focuses the beam onto a very small spot on the anode • The anode is specially designed to dissipate the heat and wear resulting from this intense focused barrage of electrons: • Mechanically spun to increase the area heated by the beam. • Cooled by circulating coolant. • The anode is precisely angled at 1-20 degrees off perpendicular to the electron current so as to allow escape of some of the X-ray photons which are emitted essentially perpendicular to the direction of the electron current. • The anode is usually made out of tungsten or molybdenum. • The tube has a window designed for escape of the generated X-ray photons. • The power of a Coolidge tube usually ranges from 1 to 4 kW

Introduction to X-ray Diffraction • References: • Elements of Modern X-ray Physics, Jens Als-Nielsen and Des McMorrow, John Wiley & Sons, Ltd., 2001 (Modern x-ray physics & new developments) • X-ray Diffraction, by B.E. Warren, General Publishing Company, 1969, 1990 (Classic x-ray physics book) • Elements of X-ray Diffraction,2nd Ed., by B.D. Cullity, Addison-Wesley, 1978 (Covers most techniques used in traditional material characterization) • High Resolution X-ray Diffractometry and Topography, by D. Keith Bowen and Brian K. Tanner, Taylor & Francis, Ltd., 1998 (Semiconductors and thin film analysis) • Modern Aspects of Small-Angle Scattering, by H. Brumberger, Editor, Kluwer Academic Publishers, 1993 (SAXS techniques) • Principles of Protein X-ray Crystallography, by Jan Drenth, Springer, 1994 (Crystallography)

The incoming beam (coming from upper left) causes each scatterer to re-radiate a small portion of its energy as a spherical wave. If scatterers are arranged symmetrically with a separation d, these spherical waves will be in synch only in directions where their path-length difference 2 d sin θ equals an integer multiple of the wavelength λ. In that case, part of the incoming beam is deflected by an angle 2θ, producing a reflection spot in the diffraction pattern

An intuitive understanding of XRD can be obtained from the Bragg Model of Diffraction. • In this model, a given reflection is associated with a set of evenly spaced sheets running through the crystal, usually passing through the centers of the atoms of the crystal lattice. • The orientation of a particular set of sheets is identified by its three MILLER INDICES (h, k, l), and let their spacing be noted by d. • WILLIAM LAWARENCE BRAGG proposed a model in which the incoming X-rays are scattered specularly (mirror-like) from each plane; from that assumption, X-rays scattered from adjacent planes will combine constructively when the angle θ between the plane and the X-ray results in a path-length difference that is an integer multiple n of the X-ray wave length λ.

A reflection is said to be indexed when its Miller indices have been identified from the known wavelength and the scattering angle 2θ. Such indexing gives the unit cell parameters, the lengths and angles of the unit-cell, as well as its space group. Since BRAGG’S LAW does not interpret the relative intensities of the reflections, however, it is generally inadequate to solve for the arrangement of atoms within the unit-cell; for that, a Fourier transform method must be carried out.

BRAGG’S LAW

Theoretical Considerations

An X-ray diffraction pattern formed when X-rays are focused on a crystalline material, (a protein). Each dot, called a reflection, forms from the coherent interference of scattered X-rays passing through the crystal. X-ray scattering techniques are a family of non-destructive analytical techniques which reveal information about the crystallographic structure, chemical composition, and physical properties of materials and thin films. These techniques are based on observing the scattered intensity of an X-RAY beam hitting a sample as a function of incident and scattered angle, polarization, and wavelength or energy.

X-ray diffraction techniques • X-ray diffraction finds the geometry or shape of a molecule using x-rays. X-ray diffraction techniques are based on the elastic scattering of x-rays from structures that have long range order. • Single-crystal X-ray diffraction is a technique used to solve the complete structure of crystalline materials, ranging from simple inorganic solids to complex macromolecules, such as proteins. • Powder diffraction (XRD) is a technique used to characterize the crystallographic structure, crystallite size (grain size), and preferred orientation in polycrystalline or powdered solid samples. Powder diffraction is commonly used to identify unknown substances, by comparing diffraction data against a database maintained by the International Centre for Diffraction Data. It may also be used to characterize heterogeneous solid mixtures to determine relative abundance of crystalline compounds and, when coupled with lattice refinement techniques, such as Rietveld refinement, can provide structural information on unknown materials. Powder diffraction is also a common method for determining strains in crystalline materials.

Thin film diffraction and grazing incidence x-ray diffraction may be used to characterize the crystallographic structure and preferred orientation of substrate-anchored thin films. • High-resolution x-ray diffraction is used to characterize thickness, crystallographic structure, and strain in thin epitaxial films. It employs parallel-beam optics. • X-ray pole figure analysis enables one to analyze and determine the distribution of crystalline orientations within a crystalline thin-film sample. • X-ray rocking curve analysis is used to quantify grain

Scattering techniques Elastic scattering • Materials that do not have long range order may also be studied by scattering methods that rely on elastic scattering of monochromatic x-rays. • Small angle X-ray scattering (SAXS) probes structure in the nanometer to micrometer range by measuring scattering intensity at scattering angles 2θ close to 0°. • X-ray reflectivity is an analytical technique for determining thickness, roughness, and density of single layer and multilayer thin films. • Wide angle X-ray scattering (WAXS), a technique concentrating on scattering angles 2θ larger than 5°. Inelastic scattering • When the energy and angle of the inelastically scattered x-rays are monitored scattering techniques can be used to probe the electronic band structure of materials. • Compton scattering • Resonant inelastic x-ray scattering (RIXS) • X-ray Raman scattering

X-ray Generation & Properties • Lattice Planes and Bragg's Law • Powder Diffraction • Thin Film Diffraction • Texture Measurement (Pole Figures) • Residual Stress Measurements • Small Angle X-ray Scattering (SAXS) • X-ray Crystallography

1. X-ray Generation & Properties • X-rays are electromagnetic radiation with typical photon energies in the range of 100 eV - 100 keV. For diffraction applications, only short wavelength x-rays (hard x-rays) in the range of a few angstroms to 0.1 angstrom (1 keV - 120 keV) are used. • Because the wavelength of x-rays is comparable to the size of atoms, they are ideally suited for probing the structural arrangement of atoms and molecules in a wide range of materials. The energetic x-rays can penetrate deep into the materials and provide information about the bulk structure. • X-rays are produced generally by either x-ray tubes or synchrotron radiation. In a x-ray tube, which is the primary x-ray source used in laboratory x-ray instruments, x-rays are generated when a focused electron beam accelerated across a high voltage field bombards a stationary or rotating solid target. As electrons collide with atoms in the target and slow down, a continuous spectrum of x-rays are emitted, which are termed Bremsstrahlung radiation. The high energy electrons also eject inner shell electrons in atoms through the ionization process. When a free electron fills the shell, a x-ray photon with energy characteristic of the target material is emitted.

Common targets used in x-ray tubes include Cu and Mo, which emit 8 keV and 14 keV x-rays with corresponding wavelengths of 1.54 Å and 0.8 Å, respectively. (The energy E of a x-ray photon and it's wavelength is related by the equation E = hc/l, where h is Planck's constant and c the speed of light) • In recent years synchrotron facilities have become widely used as preferred sources for x-ray diffraction measurements. Synchrotron radiation is emitted by electrons or positrons travelling at near light speed in a circular storage ring. These powerful sources, which are thousands to millions of times more intense than laboratory x-ray tubes, have become indispensable tools for a wide range of structural investigations and brought advances in numerous fields of science and technology.

2. Lattice Planes and Bragg's Law • X-rays primarily interact with electrons in atoms. When x-ray photons collide with electrons, some photons from the incident beam will be deflected away from the direction where they original travel, much like billiard balls bouncing off one anther. If the wavelength of these scattered x-rays did not change (meaning that x-ray photons did not lose any energy), the process is called elastic scattering (Thompson Scattering) in that only momentum has been transferred in the scattering process. These are the x-rays that we measure in diffraction experiments, as the scattered x-rays carry information about the electron distribution in materials. On the other hand, In the inelastic scattering process (Compton Scattering), x-rays transfer some of their energy to the electrons and the scattered x-rays will have different wavelength than the incident x-rays.

Diffracted waves from different atoms can interfere with each other and the resultant intensity distribution is strongly modulated by this interaction. If the atoms are arranged in a periodic fashion, as in crystals, the diffracted waves will consist of sharp interference maxima (peaks) with the same symmetry as in the distribution of atoms. Measuring the diffraction pattern therefore allows us to deduce the distribution of atoms in a material.

The peaks in a x-ray diffraction pattern are directly related to the atomic distances. Consider an incident x-ray beam interacting with the atoms arranged in a periodic manner as shown in 2 dimensions • The atoms, represented as green spheres in the graph, can be viewed as forming different sets of planes in the crystal (colored lines). For a given set of lattice plane with an inter-plane distance of d, the condition for a diffraction (peak) to occur can be written as known as the Bragg's law, after W.L. Bragg, who first proposed it. n is an integer representing the order of the diffraction peak. The Bragg's Law is one of most important laws used for interpreting x-ray diffraction data. • Here, atoms are used as scattering points in this example, Bragg's Law applies to scattering centers consisting of any periodic distribution of electron density. Ie., the law holds true if the atoms are replaced by molecules or collections of molecules, such as colloids, polymers, proteins and virus particles

3. Powder Diffraction • Powder XRD (X-ray Diffraction) is perhaps the most widely used x-ray diffraction technique for characterizing materials. As the name suggests, the sample is usually in a powdery form, consisting of fine grains of single crystalline material to be studied. The technique is used also widely for studying particles in liquid suspensions or polycrystalline solids (bulk or thin film materials).

The term 'powder' really means that the crytalline domains are randomly oriented in the sample. Therefore when the 2-D diffraction pattern is recorded, it shows concentric rings of scattering peaks corresponding to the various d spacings in the crystal lattice. The positions and the intensities of the peaks are used for identifying the underlying structure (or phase) of the material. For example, the diffraction lines of graphite would be different from diamond even though they both are made of carbon atoms. This phase identification is important because the material properties are highly dependent on structure (just think of graphite and diamond). • .

Powder diffraction data can be collected using either transmission or reflection geometry, as shown below. Because the particles in the powder sample are randomly oriented, these two methods will yield the same data. In the MRL x-ray facility, powder diffraction data are measured using the Philips XPERT MPD diffractometer, which measures data in reflection mode and is used mostly with solid samples, or the custom built 4-circle diffractometer, which operates in transmission mode and is more suitable for liquid phase samples

MOUNTING THE CRYSTAL DIFFRACTOMETER

A powder XRD scan from a K2Ta2O6 sample is as shown -as a plot of scattering intensity v/s. the scattering angle 2theta or the corresponding d-spacing. The peak positions, intensities, widths and shapes all provide important information about the structure of the material.

4. Thin Film Diffraction • Thin film diffraction refers not to a specific technique but rather a collection of XRD techniques used to characterize thin film samples grown on substrates. These materials have important technological applications in microelectronic and optoelectronic devices, where high quality epitaxial films are critical for device performance. Thin film diffraction methods are used as important process development and control tools, as hard x-rays can penetrate through the epitaxial layers and measure the properties of both the film and the substrate. • There are several special considerations for using XRD to characterize thin film samples. (i) reflection geometry is used for these measurements as the substrates are generally too thick for transmission. (ii) high angular resolution is required because the peaks from semiconductor materials are sharp due to very low defect densities in the material. Multiple bounce crystal monochromators are used to provide a highly collimated x-ray beam for these measurements. Eg: in the Philips MRD used in the x-ray facility, a 4-crystal monochromator made from Ge is used to produce an incident beam with less than 5 arc seconds of angular divergence.

Basic XRD measurements made on thin film samples include: • Precise lattice constants measurements derived from 2q - q scans, which provide information about lattice mismatch between the film and the substrate and therefore is indicative of strain & stress • Rocking curve measurements made by doing a q scan at a fixed 2q angle, the width of which is inversely proportionally to the dislocation density in the film and is therefore used as a gauge of the quality of the film. • Superlattice measurements in multilayered heteroepitaxial structures, which manifest as satellite peaks surrounding the main diffraction peak from the film. Film thickness and quality can be deduced from the data. • Glancing incidence x-ray reflectivity measurements, which can determine the thickness, roughness, and density of the film. This technique does not require crystalline film and works even with amorphous materials. • Texture measurements-(discussed separately)

The graph shows the high resolution XRD data of the superlattice peaks on the GaN (002) reflections. Red line denotes results of computer simulation of the structure.

5. Texture Measurement (Pole Figure) • Texture measurements are used to determine the orientation distribution of crystalline grains in a polycrystalline sample. A material is termed textured if the grains are aligned in a preferred orientation along certain lattice planes. One can view the textured state of a material (typically in the form of thin films) as an intermediate state in between a completely randomly oriented polycrystalline powder and a completely oriented single crystal. The texture is usually introduced in the fabrication process (e.g. rolling of thin sheet metal, deposition,etc.) and affect the material properties by introducing structural anisotropy.

A texture measurement is also referred to as a pole figure as it is often plotted in polar coordinates consisting of the tilt and rotation angles with respect to a given crytallographic orientation. A pole figure is measured at a fixed scattering angle (constant d spacing) and consists of a series of f -scans (in- plane rotation around the center of the sample) at different tilt or Y -(azimuth) angles, as illustrated below.

The pole figure data are displayed as contour plots or elevation graphs with zero angle in the center. Below we show two pole figure plots using the same data set. An orientation distribution function (ODF) can be calculated using the pole figure data.

6. Residual Stress Measurement • Structural and residual stress in materials can be determined from precision lattice constants measurements. For polycrystalline samples high resolution powder diffraction measurements generally will provide adequate accuracy for stress evaluation. For textured (oriented) and single crystalline materials, 4-circle diffractometry is needed in which the sample is rotated so that measurements on multiple diffraction peaks can be carried out. The interpretation of stress measurement data is complicated and model dependent. Consult the reference literature for more details

7. Small Angle X-ray Scattering (SAXS) • SAXS measurements typically are concerned with scattering angles < 1o. As dictated by Bragg's Law, the diffraction information about structures with large d-spacings lies in the region. Therefore the SAXS technique is commonly used for probing large length scale structures such as high molecular weight polymers, biological macromolecules (proteins, nucleic acids, etc.), and self-assembled superstructures (e.g. surfactant templated mesoporous materials). • SAXS measurements are technically challenging because of the small angular separation of the direct beam (which is very intense) and the scattered beam. Large specimen-to-detector distances (0.5 m - 10 m) and high quality collimating optics are used to achieve good signal-to-noise ratio in the SAXS measurement.

The MRL x-ray facility has cutting edge capabilities for SAXS measurements with three custom-built SAXS instruments including one 3.5-meter long ultra-small angle SAXS instrument with state-of-the-art optics and area detector for low scattering density samples (see instrumentation section for more details)

8. X-ray Crystallography • X-ray crystallography is a standard technique for solving crystal structures. Its basic theory was developed soon after x-rays were first discovered more than a century ago. However, over the years it has gone through continual development in data collection instrumentation and data reduction methods. In recent years, the advent of synchrotron radiation sources, area detector based data collection instruments, and high speed computers has dramatically enhanced the efficiency of crystallographic structural determination. Today x-ray crystallography is widely used in materials and biological research. Structures of very large biological machinery (e.g. protein and DNA complexes, virus particles) have been solved using this method.

In x-ray crystallography, integrated intensities of the diffraction peaks are used to reconstruct the electron density map within the unit cell in the crystal. To achieve high accuracy in the reconstruction, which is done by Fourier transforming the diffraction intensities with appropriate phase assignment, a high degree of completeness as well as redundancy in diffraction data is necessary, meaning that all possible reflections are measured multiple times to reduce systematic and statistical error. The most efficient way to do this is by using an area detector which can collect diffraction data in a large solid angle. The use of high intensity x-ray sources, such as synchrotron radiation, is an effective way to reduce data collection time.

One of the central difficulties in structural determination using x-ray crystallography is referred to as the "phase problem", which arises from the fact that the diffraction data contains information only on the amplitude but not the phase of the structure factor. Over the years many methods have been developed to deduce the phases for reflections, including computationally based direct methods, isomorphous replacement, and multi-wavelength anormalous diffraction (MAD) methods.

X-ray crystallography

Procedure • The technique of single-crystal X-ray crystallography has three basic steps. The first — and often most difficult — step is to obtain an adequate crystal of the material under study. The crystal should be sufficiently large (typically larger than 100 micrometres in all dimensions), pure in composition and regular in structure, with no significant internal imperfections such as cracks or twinning. A small or irregular crystal will give fewer and less reliable data, from which it may be impossible to determine the atomic arrangement.

In the second step, the crystal is placed in an intense beam of X-rays, usually of a single wavelength (monochromatic X-rays), producing the regular pattern of reflections. As the crystal is gradually rotated, previous reflections disappear and new ones appear; the intensity of every spot is recorded at every orientation of the crystal. Multiple data sets may have to be collected, with each set covering slightly more than half a full rotation of the crystal and typically containing tens of thousands of reflection intensities.

In the third step, these data are combined computationally with complementary chemical information to produce and refine a model of the arrangement of atoms within the crystal. The final, refined model of the atomic arrangement — now called a crystal structure — is usually stored in a public database.

A real 3-dimensional crystal contains many sets of planes. For diffraction, crystal must have the correct orientation with respect to the incoming beam. • Perfect, infinite crystal and perfectly collimated beam: diffraction condition must be satisfied ``exactly.'' • Strains, defects, finite size effects, instrumental resolution: diffraction peaks are broadened. More formally, the scattered intensity is proportional to the square of the Fourier transform of the charge density:

where is the charge density. For perfect crystals, I(q) consists of delta functions (perfectly sharp scattering). For imperfect crystals, the peaks are broadened. For liquids and glasses, it is a continuous, slowly varying function

Features of Electron, X-ray, or Neutron Diffraction • For a known structure, pattern can be calculated exactly. • Symmetry of the diffraction pattern given by symmetry of the lattice. • Intensities of spots determined by basis of atoms at each lattice point. • Sharpness and shape of spots determined by perfection of crystal. • Liquids, glasses, and other disordered materials produce broad fuzzy rings instead of sharp spots. • Defects and disorder in crystals also result in diffuse scattering.

The ``Ultimate'' (Technically Challenging) Experiment • Sample is tiny (micron-sized). • The effect is weak (light elements, small modulations, subtle modifications of the long-range order). • Instrumental resolution (angle and energy) is ``perfect'' allowing detailed measure- ments of structural disorder. • Measurement is time-resolved (nanosecond time scale). • To achieve all of the above, will need lots of intensity in the primary beam together with sensitive detection systems.

Powder vs. Single Crystal X-ray Diffraction SINGLE CRYSTAL • Put a crystal in the beam, observe what reflections come out at what angles for what orientations of the crystal with what intensities. • Advantages • In principle you can learn everything there is to know about the structure. • Disadvantages • You may not have a single crystal. It is time-consuming and difficult to orient the crystal. If more than one phase is present, you will not necessarily realize that there is more than one set of reflections.

POWDER • Samples consists of a collection of many small crystallites with random orientations. Average over crystal orientations and measure the scattered intensity as a function of outgoing angle. • Disadvantage • Inversion of the measured intensities to find the structure is more difficult and less reliable. • Advantages • It is usually much easier to prepare a powder sample. You are guaranteed to see all reflections. The best way to follow phase changes as a function of temperature, pressure, or some other variable.

More by User

$X-ray Diffraction (XRD)$

X-ray Diffraction (XRD)

X-ray Diffraction (XRD). What is X-ray Diffraction Properties and generation of X-ray Bragg’s Law Basics of Crystallography XRD Pattern Powder Diffraction Applications of XRD . X-ray and X-ray Diffraction.

6.31k views • 64 slides

$CHAPTER 3: CRYSTAL STRUCTURES X-Ray Diffraction (XRD)$

CHAPTER 3: CRYSTAL STRUCTURES X-Ray Diffraction (XRD)

CHAPTER 3: CRYSTAL STRUCTURES X-Ray Diffraction (XRD). ISSUES TO ADDRESS. • Historical retrospective Henry Bragg Equation XRD-analysis How to read XRD patterns? Exclusions What questions can be answered by XRD method?. Scale of Structure Organization. Sir William Henry Bragg :

367 views • 15 slides

$X-ray Diffraction$

X-ray Diffraction

Instrument Report:. X-ray Diffraction. Guanghui Zhu. Contents. Diffraction Mechanism C onstruction of the Diffractometer Applications of XRD Data A nalysis and Explanation 2D XRD XRD Simulation. Diffraction Mechanism.

1.81k views • 63 slides

$X-ray diffraction$

X-ray diffraction

X-ray diffraction. Submitted By:- Nardev Kumar Bajaj Roll NO-12025138 Group-C. Submitted To:- Dr.Mandeep Singh. Contents. Introduction to X-rays Bragg’s law Scherrer law XRD Definition Working Why XRD Applications References. Introduction to X-rays.

2.09k views • 19 slides

$X-ray Diffraction$

X-ray Diffraction. X-ray Generation. X-ray tube (sealed) Pure metal target (Cu) Electrons remover inner-shell electrons from target. Other electrons “fall” into hole. X-ray Generation. The incoming electron must have enough energy to remove inner 1 s electrons from the copper atoms.

452 views • 21 slides

$X-ray Diffraction$

X-ray Diffraction. Frequency (Hz). 10 12. 10 9. 10 24. 10 21. 10 18. 10 15. 10 6. 10 3. 10 -12. 10 -9. 10 -6. 10 -3. 1.0. 10 3. 10 -15. 10 6. Wavelength (m). Electromagnetic Spectrum. Gamma Rays. UV. IR. Long Radio Waves. X-rays. Micro. TV. FM. AM. What are X-rays?.

754 views • 24 slides

$X-Ray Diffraction$

X-Ray Diffraction

X-Ray Diffraction. Emily Day and Sage Ross Advanced Lab 1 Spring 2004. Outline. Introduction History How Diffraction Works Demonstration Analyzing Diffraction Patterns Solving DNA Applications Summary and Conclusions. Introduction. Motivation:

609 views • 22 slides

$X-ray diffraction$

X-ray diffraction. Equipment. Bruker D8 Analytical X-ray Systems. X-ray beam source.

1.92k views • 57 slides

$X-Ray Diffraction (XRD)$

X-Ray Diffraction (XRD)

X-Ray Diffraction (XRD). Principle. In XRD, an incident wave is directed into a material and a detector is typically moved about to record the directions and intensities of the outgoing diffracted waves. X-ray diffraction has acted as the corner stone of the twentieth century science.

1.22k views • 77 slides

$X-Ray Diffraction (XRD)$

X-Ray Diffraction (XRD). What is XRD?. X-ray diffraction is a method of X-ray crystallography , in which a beam of X-rays strikes a sample (crystalline solid), land on a piece of film or other detector to produce scattered beams.

6.55k views • 48 slides

$X-Ray Diffraction$

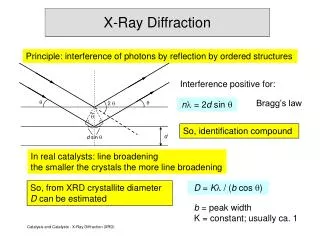
X-Ray Diffraction. Principle: interference of photons by reflection by ordered structures. Interference positive for:. Bragg’s law. . n  = 2 d sin . . 2 . . So, identification compound. d. d sin . In real catalysts: line broadening

1.7k views • 10 slides

X-RAY DIFFRACTION

X-RAY DIFFRACTION. X- Ray Sources Diffraction: Bragg’s Law Crystal Structure Determination. Elements of X-Ray Diffraction B.D. Cullity & S.R. Stock Prentice Hall, Upper Saddle River (2001).

2.88k views • 80 slides

$X-Ray Diffraction$

X-Ray Diffraction. Dr. T. Ramlochan March 2010. Public service announcement…. Radiation warning symbol. New IAEA Radiation warning symbol. Radiation is dangerous, so run away!. Crystals.

606 views • 17 slides

$Lecture 20 X-Ray Diffraction (XRD)$

Lecture 20 X-Ray Diffraction (XRD)

Lecture 20 X-Ray Diffraction (XRD). Theory and Analytical Technique. X-Ray Analysis. X-rays discovered in 1895 Fundamental to understanding of crystal structure and symmetry

562 views • 14 slides

$XRD X-ray diffraction$

XRD X-ray diffraction

XRD X-ray diffraction. Dr. Karin Habermehl-Cwirzen. 1895- Röntgen publishes the discovery of X-rays 1912- Laue observes diffraction of X-rays from a crystal (Nobel prize 1914).

965 views • 25 slides

$X-ray Diffraction (XRD)$

2.34k views • 62 slides

$X-Ray Diffraction (XRD)$

878 views • 77 slides

$X-ray diffraction$

X-ray diffraction. Muhannad Alzahrani. Supervisor: Dr. Akhtar Naqvi. Presentation Outline. Introduction Theoretical Background Experimantal Procedure Results and Discussion Conclusion. Introduction (1). X-ray was first discovered by Wilhelm Rontgen in 1895

408 views • 14 slides

1.95k views • 80 slides

IMAGES

PPT
Slide ea XRD Glass Microscope
XRD
xrd slide presentation
Xrd Presentation Basics
xrd slide presentation

VIDEO

Monsters University Toxicity Challenge Stage 30 ios iphone gameplay
குடியிருப்புக்குள் புகுந்த சிறுத்தை
Amazing French Manicures with Nail Stamping!
PlatinumWorldTeamBuild
Apple iOS Development: Modernizing Your App Architecture with UIKit
Pokémon Stadium Free Battle 40

COMMENTS

Xrd (X-ray Diffraction) presentation
The document summarizes a seminar on X-ray diffraction (XRD) techniques. It introduces Bragg's law which relates the wavelength of X-rays to the diffraction pattern produced when X-rays interact with a crystal lattice. Three common XRD methods are described: the Laue method for single crystals, the rotating crystal method, and the powder method.
PPT
X-ray diffraction is a method of X-ray crystallography , in which a beam of X-rays strikes a sample (crystalline solid), land on a piece of film or other detector to produce scattered beams. Slideshow 4024666 by jaron.
PPT
The atomic planes of a crystal cause an incident beam of x-rays (if wavelength is approximately the magnitude of the interatomic distance) to interfere with one another as they leave the crystal. The phenomenon is called x-ray diffraction. Bragg's Law: n = 2dsin ( ) ~ d 2 B atomic plane B X-ray of I d.
PDF X-Ray Diffraction (XRD)
Summary & Conclusion. X-ray diffraction is a technique for. analyzing structures of biological molecules. X-ray beam hits a crystal, scattering the beam in a manner characterized by the. atomic structure. Even complex structures can be analyzed by x-ray diffraction, such as. DNA and proteins.
PPT
Oct 23, 2014. 1.44k likes | 2.85k Views. X-ray Diffraction: Principles and Practice. Ashish Garg and Nilesh Gurao Department of Materials Science and Engineering Indian Institute of Technology Kanpur. Layout of the Lecture. Materials Characterization Importance of X-ray Diffraction Basics Diffraction X-ray Diffraction. Download Presentation.
PDF X-ray Diffraction (XRD)
constants or parameters which can be determined by XRD. Beryl crystals smallest building block Unit cell (cm) Lattice (Å) CsCl d 1 d 2 d 3 a b c b a g. Seven Crystal Systems - Review. Miller Indices: hkl - Review ... Glass slide Powders: 0.1mm < particle size <40 mm Peak broadening less diffraction occurring Bulks: smooth surface after ...
XRD Literature
The slides that I use when training new users in the X-Ray SEF at MIT. Scott Speakman. Crystallographic Teaching Pamphlets. Series of online tutorials for a wide range of topics in crystallography and diffraction. IUCr. Lab Manual for X-Ray Powder Diffraction. Introduction to XRD, specimen preparation, and lab practices (primarily for clay ...
X-ray Powder Diffraction (XRD)
A Powerpoint presentation on use of XRD in Soil Science (PowerPoint 1.6MB Sep7 07) by Melody Bergeron, Image and Chemical Analysis Laboratory at Montana State University. Brady, John B., and Boardman, Shelby J., 1995, Introducing Mineralogy Students to X-ray Diffraction Through Optical Diffraction Experiments Using Lasers. Jour. Geol.
X ray diffraction
X ray diffraction. Aug 21, 2013 • Download as PPT, PDF •. 441 likes • 267,608 views. Nani Karnam Vinayakam. It helps for the undergraduate and post graduate students of pharmacy and ayurveda to know the basics and application of the xrd. Technology Education. 1 of 27.
X-ray diffraction (XRD) basics and application
X-ray diffraction is a common technique that determine a sample's composition or crystalline structure. For larger crystals such as macromolecules and inorganic compounds, it can be used to determine the structure of atoms within the sample. If the crystal size is too small, it can determine sample composition, crystallinity, and phase purity.
Intro to powder XRD webinar series
Join our free series of webinars: "Ask our Expert: Better XRD data analysis": - Webinar 1: Introduction to powder XRD. - Webinar 2: XRD Phase quantification: step-by-step tutorial. More info. - Webinar 3: Transmission vs reflection measurements: practical tips on when to use which.
XRD basics to advanced experiments
12.15pm: Lunch. 2.00pm: Advanced XRD analysis and applications: Thin films and nanomaterials research by Dr Sandeep Nagar, XRD Application Specialist, Malvern Panalytical. 3.00pm: Break. 3.15pm: (Demo) Advanced XRD experiments on the intelligent multi-purpose Empyrean series 3 with multi-core optics by Dr Sandeep Nagar, XRD Application ...
X-Ray Diffraction (XRD)
What is XRD? X-ray diffraction is a method of X-ray crystallography, in which a beam of X-rays strikes a sample (crystalline solid), land on a piece of film or other detector to produce scattered beams. These beams make a diffraction pattern of spots; the strengths and angles of these beams are recorded as the sample is gradually rotated. X-ray crystallography is a method of determining the ...
PPT
Properties and Generation of X-ray • X-rays are electromagneticradiation with very short wavelength ( 10-8 -10-12 m) • The energy of the x-ray can be calculated with the equation E = h = hc/ • e.g. the x-ray photon with wavelength 1Å has energy 12.5 keV.
X-ray Diffraction Techniques
15 X-Ray Powder Diffraction (XRPD) uses information about the position, intensity, width, and shape of diffraction peaks in a pattern from a polycrystalline sample. The x-axis, 2theta, corresponds to the angular position of the detector that rotates around the sample. 16 Monochromatic and Broad Spectrum of X-rays.
X-ray Diffraction (XRD)
The PowerPoint PPT presentation: "X-ray Diffraction (XRD)" is the property of its rightful owner. Do you have PowerPoint slides to share? If so, share your PPT presentation slides online with PowerShow.com. It's FREE!
XRD 2023
XRD_2023 - Free download as Powerpoint Presentation (.ppt), PDF File (.pdf), Text File (.txt) or view presentation slides online. Scribd is the world's largest social reading and publishing site.
Clarivate Plc 2024 Q1
The following slide deck was published by Clarivate Plc in conjunction with their 2024 Q1 earnings call. ... Earnings Call Presentation. May 08, 2024 11:30 AM ET Clarivate Plc (CLVT) Stock, CLVT ...
PPT
X-Ray Diffraction (XRD) X-Ray Diffraction (XRD). Principle. In XRD, an incident wave is directed into a material and a detector is typically moved about to record the directions and intensities of the outgoing diffracted waves. X-ray diffraction has acted as the corner stone of the twentieth century science. 1.22k views • 77 slides
XRD Applications in Science & Engineering
XRD Applications in Science & Engineering. 1. X-ray Diffraction and Its Applications in Science & Engineering. 2. CONVENTIONS OF LATTICE DESCRIPTION Unit cell is the smallest unit of a crystal, which, if repeated, could generate the whole crystal. A crystal's unit cell dimensions are defined by six numbers, the lengths of the 3 axes, a, b ...
Esperion Therapeutics, Inc. 2024 Q1
The following slide deck was published by Esperion Therapeutics, Inc. ... Earnings Call Presentation. May 07, 2024 8:32 AM ET Esperion Therapeutics, Inc. (ESPR) Stock. SA Transcripts.
QuidelOrtho Corporation 2024 Q1
The following slide deck was published by QuidelOrtho Corporation in conjunction with their 2024 Q1 earnings call. ... Earnings Call Presentation. May 08, 2024 6:18 PM ET QuidelOrtho Corporation ...

X-ray Diffraction SEF

Search form

XRD Literature

X-ray Powder Diffraction (XRD)

What is X-ray Powder Diffraction (XRD)

Fundamental Principles of X-ray Powder Diffraction (XRD)

X-ray Powder Diffraction (XRD) Instrumentation - How Does It Work?

Applications

Strengths and Limitations of X-ray Powder Diffraction (XRD)?

Limitations

User's Guide - Sample Collection and Preparation

Data Collection, Results and Presentation

Related Links

Teaching Activities and Resources

Margin Size

X-ray diffraction (XRD) basics and application

How the Technique Works

Useful Visualization of X-ray Diffraction

How to interpret the data

Good literature examples

Works cited

X-ray Diffraction (XRD) - PowerPoint PPT Presentation

X-ray Diffraction (XRD)

X RAY DIFFRACTION- XRD

Share Presentation

Presentation Transcript

X-ray Diffraction (XRD)

CHAPTER 3: CRYSTAL STRUCTURES X-Ray Diffraction (XRD)

X-ray Diffraction

X-ray diffraction

X-Ray Diffraction

X-Ray Diffraction (XRD)

X-RAY DIFFRACTION

Lecture 20 X-Ray Diffraction (XRD)

XRD X-ray diffraction

IMAGES

VIDEO

COMMENTS