symmetry problem solving tes

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Resources tagged with: Symmetry

There are 71 NRICH Mathematical resources connected to Symmetry , you may find related items under Transformations and constructions .

Always, Sometimes or Never? Shape

Are these statements always true, sometimes true or never true?

Use the information on these cards to draw the shape that is being described.

National Flags

This problem explores the shapes and symmetries in some national flags.

Poly Plug Pattern

Create a pattern on the small grid. How could you extend your pattern on the larger grid?

Exploded Squares

This practical activity challenges you to create symmetrical designs by cutting a square into strips.

Attractive Rotations

Here is a chance to create some attractive images by rotating shapes through multiples of 90 degrees, or 30 degrees, or 72 degrees or...

Counters in the Middle

This task depends on groups working collaboratively, discussing and reasoning to agree a final product.

Reflector ! Rotcelfer

Can you place the blocks so that you see the reflection in the picture?

Coordinate Challenge

Use the clues about the symmetrical properties of these letters to place them on the grid.

Stringy Quads

This practical problem challenges you to make quadrilaterals with a loop of string. You'll need some friends to help!

Octa-flower

Join some regular octahedra, face touching face and one vertex of each meeting at a point. How many octahedra can you fit around this point?

Symmetry Challenge

How many symmetric designs can you make on this grid? Can you find them all?

Shady Symmetry

How many different symmetrical shapes can you make by shading triangles or squares?

Reflecting Squarely

In how many ways can you fit all three pieces together to make shapes with line symmetry?

A Cartesian Puzzle

Find the missing coordinates which will form these eight quadrilaterals. These coordinates themselves will then form a shape with rotational and line symmetry.

Attractive Tablecloths

Charlie likes tablecloths that use as many colours as possible, but insists that his tablecloths have some symmetry. Can you work out how many colours he needs for different tablecloth designs?

Each of the following shapes is made from arcs of a circle of radius r. What is the perimeter of a shape with 3, 4, 5 and n "nodes".

Witch of Agnesi

Sketch the members of the family of graphs given by y = a^3/(x^2+a^2) for a=1, 2 and 3.

Folium of Descartes

Investigate the family of graphs given by the equation x^3+y^3=3axy for different values of the constant a.

Logosquares

Ten squares form regular rings either with adjacent or opposite vertices touching. Calculate the inner and outer radii of the rings that surround the squares.

Mean Geometrically

A and B are two points on a circle centre O. Tangents at A and B cut at C. CO cuts the circle at D. What is the relationship between areas of ADBO, ABO and ACBO?

Colouring Triangles

Explore ways of colouring this set of triangles. Can you make symmetrical patterns?

Symmetric Trace

Points off a rolling wheel make traces. What makes those traces have symmetry?

Building Patterns

Can you deduce the pattern that has been used to lay out these bottle tops?

Emmy Noether

Find out about Emmy Noether, whose ideas linked physics and algebra, and whom Einstein described as a 'creative mathematical genius'.

Watch Those Wheels

Have you ever noticed the patterns in car wheel trims? These questions will make you look at car wheels in a different way!

What mathematical words can be used to describe this floor covering? How many different shapes can you see inside this photograph?

Plot the graph of x^y = y^x in the first quadrant and explain its properties.

An irregular tetrahedron has two opposite sides the same length a and the line joining their midpoints is perpendicular to these two edges and is of length b. What is the volume of the tetrahedron?

Symmetrical Semaphore

Someone at the top of a hill sends a message in semaphore to a friend in the valley. A person in the valley behind also sees the same message. What is it?

Hidden Meaning

What is the missing symbol? Can you decode this in a similar way?

Pattern Power

Mathematics is the study of patterns. Studying pattern is an opportunity to observe, hypothesise, experiment, discover and create.

Two Triangles in a Square

Given that ABCD is a square, M is the mid point of AD and CP is perpendicular to MB with P on MB, prove DP = DC.

Some local pupils lost a geometric opportunity recently as they surveyed the cars in the car park. Did you know that car tyres, and the wheels that they on, are a rich source of geometry?

Tournament Scheduling

Scheduling games is a little more challenging than one might desire. Here are some tournament formats that sport schedulers use.

Classifying Solids Using Angle Deficiency

Toni Beardon has chosen this article introducing a rich area for practical exploration and discovery in 3D geometry

The Frieze Tree

Patterns that repeat in a line are strangely interesting. How many types are there and how do you tell one type from another?

Frieze Patterns in Cast Iron

A gallery of beautiful photos of cast ironwork friezes in Australia with a mathematical discussion of the classification of frieze patterns.

A red square and a blue square overlap. Is the area of the overlap always the same?

Square Pizza

Can you show that you can share a square pizza equally between two people by cutting it four times using vertical, horizontal and diagonal cuts through any point inside the square?

Prime Magic

Place the numbers 1, 2, 3,..., 9 one on each square of a 3 by 3 grid so that all the rows and columns add up to a prime number. How many different solutions can you find?

Rhombicubocts

Each of these solids is made up with 3 squares and a triangle around each vertex. Each has a total of 18 square faces and 8 faces that are equilateral triangles. How many faces, edges and vertices does each solid have?

An equilateral triangle is sitting on top of a square. What is the radius of the circle that circumscribes this shape?

The ten arcs forming the edges of the "holly leaf" are all arcs of circles of radius 1 cm. Find the length of the perimeter of the holly leaf and the area of its surface.

Eight Dominoes

Using the 8 dominoes make a square where each of the columns and rows adds up to 8

A Problem of Time

Consider a watch face which has identical hands and identical marks for the hours. It is opposite to a mirror. When is the time as read direct and in the mirror exactly the same between 6 and 7?

Maltese Cross

Sketch the graph of $xy(x^2 - y^2) = x^2 + y^2$ consisting of four curves and a single point at the origin. Convert to polar form. Describe the symmetries of the graph.

Sketch the graphs for this implicitly defined family of functions.

Find the shape and symmetries of the two pieces of this cut cube.

This activity investigates how you might make squares and pentominoes from Polydron.

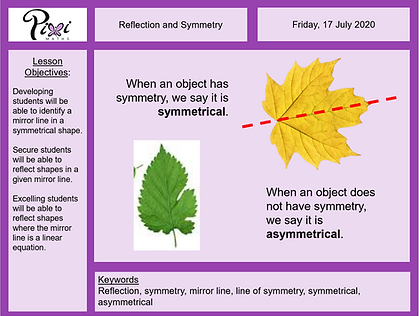
Reflection and Symmetry

Two lessons on reflection:

An introduction which focuses on symmetry and reflecting simple shapes with a fully differentiated main task.

The second lesson is more advanced and features linear graphs as lines of symmetry.   Extension task is credit of TES user TristanJones.

Line Symmetry Practice Questions

Click here for questions, click here for answers, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

• Home   |  
• About   |  
• Contact Us   |  
• Privacy   |  
• Newsletter   |  
• Shop   |  
• 🔍 Search Site
• Easter Color By Number Sheets
• Printable Easter Dot to Dot
• Easter Worksheets for kids
• Kindergarten
• All Generated Sheets
• Place Value Generated Sheets
• Addition Generated Sheets
• Subtraction Generated Sheets
• Multiplication Generated Sheets
• Division Generated Sheets
• Money Generated Sheets
• Negative Numbers Generated Sheets
• Fraction Generated Sheets
• Place Value Zones
• Number Bonds
• Addition & Subtraction
• Times Tables
• Fraction & Percent Zones
• All Calculators
• Fraction Calculators
• Percent calculators
• Area & Volume Calculators
• Age Calculator
• Height Calculator
• Roman Numeral Calculator
• Coloring Pages
• Fun Math Sheets
• Math Puzzles
• Mental Math Sheets
• Online Times Tables
• Online Addition & Subtraction
• Math Grab Packs
• All Math Quizzes
• 1st Grade Quizzes
• 2nd Grade Quizzes
• 3rd Grade Quizzes
• 4th Grade Quizzes
• 5th Grade Quizzes
• 6th Grade Math Quizzes
• Place Value
• Rounding Numbers
• Comparing Numbers
• Number Lines
• Prime Numbers
• Negative Numbers
• Roman Numerals
• Subtraction
• Add & Subtract
• Multiplication
• Fraction Worksheets
• Learning Fractions
• Fraction Printables
• Percent Worksheets & Help
• All Geometry
• 2d Shapes Worksheets
• 3d Shapes Worksheets
• Shape Properties
• Geometry Cheat Sheets
• Printable Shapes
• Coordinates
• Measurement
• Math Conversion
• Statistics Worksheets
• Bar Graph Worksheets
• Venn Diagrams
• All Word Problems
• Finding all possibilities
• Logic Problems
• Ratio Word Problems
• All UK Maths Sheets
• Year 1 Maths Worksheets
• Year 2 Maths Worksheets
• Year 3 Maths Worksheets
• Year 4 Maths Worksheets
• Year 5 Maths Worksheets
• Year 6 Maths Worksheets
• All AU Maths Sheets
• Kindergarten Maths Australia
• Year 1 Maths Australia
• Year 2 Maths Australia
• Year 3 Maths Australia
• Year 4 Maths Australia
• Year 5 Maths Australia
• Meet the Sallies
• Certificates

Symmetry Worksheets Line Symmetry Easier

Welcome to the Math Salamanders Line Symmetry Worksheets page. Here you will find a range of free printable symmetry worksheets, which will help your child to practice their reflecting and flipping skills.

For full functionality of this site it is necessary to enable JavaScript.

Here are the instructions how to enable JavaScript in your web browser .

Symmetry Help

The Math Salamanders have a large bank of free printable symmetry worksheets. Each symmetry sheet comes complete with answers for support.

Handy Hints

Each point or block that has been reflected must remain the same distance from the mirror line as the original point. So if point A is 3 squares away from the mirror line, then the reflection of point A must also be 3 squares away.

When reflecting a shape, look at the corners of the shape and reflect each corner first as a dot in the mirror line. The dots can then be joined up (in the correct order!)

For lines of symmetry at angles of 45°, it is often better to rotate your paper so that the line of symmetry is vertical or horizontal, and the rest of the paper is at an angle.

The basis and understanding of symmetry starts at about Grade 2, and then develops further in Grades 3,4 and 5.

Line Symmetry Worksheets

On this webpage you will find our range of line symmetry sheets for kids.

The sheets have been carefully graded with the easier sheets coming first. The first 3 worksheets involve only horizontal and vertical lines only. The next 3 worksheets involve reflecting diagonal lines as well.

There are also some templates at the end of this section for you to create your own shapes for your child to reflect, or, even better, for your child to create their own symmetric patterns!

Using these sheets will help your child to:

• learn to reflect a shape in a vertical or horizontal mirror line;
• learn to reflect a shape in both a vertical and horizontal mirror line;

Reflecting in 1 mirror line

Horizontal and vertical lines only.

• Line Symmetry 1
• PDF version
• Line Symmetry 2
• Line Symmetry 3
• Line Symmetry 4
• Line Symmetry 5
• Line Symmetry 6

Reflecting in Diagonal mirror lines

• Line Symmetry 9
• Line Symmetry 10

Reflecting in vertical, horizontal and diagonal lines

• Line Symmetry 11

Reflecting in 2 mirror lines

• Line Symmetry 7
• Sheet 7 Answers
• Line Symmetry 8
• Sheet 8 Answers

Reflecting in vertical and horizontal or 2 diagonal lines

• Line Symmetry 12

Line Symmetry templates

• Line Symmetry Template 1
• Line Symmetry Template 2
• Line Symmetry Template 3
• Line Symmetry Template 4
• Line Symmetry Template 5
• Line Symmetry Template 6

Looking for something harder?

Here you will find a range of line symmetry activity sheets with one or two mirror lines.

The sheets in this section are similar to those on this page, but are more complicated and at a harder level.

• Harder Symmetry Activities

More Recommended Math Worksheets

Take a look at some more of our worksheets similar to these.

Block Symmetry Worksheets

Here you will find a range of symmetry worksheets reflecting blocks instead of lines.

These sheets are at an easier level than the ones on this page.

• Symmetry Worksheets - Block Symmetry
• Explore 2d Shapes Worksheets

Looking for some geometry worksheets to get children thinking and reasoning about 2d shapes?

The shapes on this page are all about children really understanding what 2d shapes are all about, and using their reasoning skills to justify their thinking.

• know the properties of a range of 2d shapes;
• recognise that some shapes can also be described as being other shapes; e.g. a square is also a rhombus;
• recognise and understand right angles, parallel lines, lines of symmetry;
• develop their geometric reasoning skills.

Coordinate Sheets

Here is our collection of printable coordinate plane grids and coordinate worksheets.

Using these fun coordinate sheets is a great way to learn math in an enjoyable way.

• plot and write coordinates.
• Coordinate Plane Grid templates
• Coordinate Worksheets (1st Quadrant)
• Coordinate Plane Worksheets (All 4 Quadrants)

Captain Recommends

Have a look at these online symmetry games - a great way to learn symmetry and get instant feedback!

• Softschools Symmetry Game
• Sheppard Software Symmetry Activities

How to Print or Save these sheets 🖶

Need help with printing or saving? Follow these 3 steps to get your worksheets printed perfectly!

• How to Print support

Subscribe to Math Salamanders News

Sign up for our newsletter to get free math support delivered to your inbox each month. Plus, get a seasonal math grab pack included for free!

• Newsletter Signup

Return to Geometry Section

Return from Symmetry Worksheets to Math Salamanders Homepage

Math-Salamanders.com

The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.

We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.

New! Comments

TOP OF PAGE

© 2010-2024 Math Salamanders Limited. All Rights Reserved.

• Privacy Policy
• Copyright Policy

Lines of Symmetry Worksheet

FREE DOWNLOAD

Help your students prepare for their Maths GCSE with this free lines of symmetry worksheet of 34 questions and answers

• Section 1 of the lines of symmetry worksheet contains 27 skills-based lines of symmetry questions, in 3 groups to support differentiation
• Section 2 contains 4 applied lines of symmetry questions with a mix of worded symmetry activities and deeper problem solving questions
• Section 3 contains 3 foundation and higher level GCSE exam style lines of symmetry questions 
• Answers and a mark scheme for all lines of symmetry questions are provided
• Questions follow variation theory with plenty of opportunities for students to work independently at their own level
• All questions created by fully qualified expert secondary maths teachers
• Suitable for GCSE maths revision for AQA, OCR and Edexcel exam boards

Unlock access to download your free resource

To receive this printable resource and regular emails with more free resources, blog posts and other Third Space updates, enter your email address and click below.

To receive this resource and regular emails with more free resources, blog posts and other Third Space updates, enter your email address and click below.

• Job Title * Job title Headteacher Deputy Head Assistant Head Head of Maths Deputy Head of Maths Trust Leader Primary SLT Other SLT Secondary Maths Teacher Primary Teacher Teaching Assistant Tutor Parent Student Other
• Phone This field is for validation purposes and should be left unchanged.

You can unsubscribe at any time (each email we send will contain an easy way to unsubscribe). To find out more about how we use your data, see our privacy policy .

Raise maths attainment across your school with hundreds of flexible and easy to use GCSE maths worksheets and lessons designed by teachers for teachers.

Lines of symmetry at a glance

A shape has a line of symmetry if a line can be drawn through the shape so that each half of the shape is an exact mirror image of the other half (identical halves). Some 2D shapes have multiple lines of symmetry, some have one and others don’t have any.

We might be asked to draw lines of symmetry on different shapes or to identify the number of lines of symmetry a polygon may have. We could also be asked to create symmetrical shapes by adding sections or shading parts of a diagram. 

Regular polygons have a number of lines of symmetry equal to their number of sides. For example, an equilateral triangle has three lines of symmetry and a regular hexagon has six lines of symmetry. Drawing a symmetric figure in different orientations will not change its lines of symmetry. 

Usually diagrams are placed on grids or a set of xy axes. 

Vertical lines of symmetry can be labelled as x=a where a is an integer or a decimal.

Horizontal lines of symmetry can be labelled as y=b where b is an integer or a decimal.

Two types of shape symmetry include line symmetry and rotational symmetry.

Looking forward, students can then progress to additional symmetry worksheets and other geometry worksheets , for example a simplifying expressions worksheet or simultaneous equations worksheet .

For more teaching and learning support on Geometry our GCSE maths lessons provide step by step support for all GCSE maths concepts.

Related worksheets

Volume And Surface Area Of Pyramids Exam Questions

Vector Problems Exam Questions

2D Shapes Exam Questions

Loci And Construction Exam Questions

Popular for gcse.

Do you have students who need additional support to achieve their target GCSE maths grade?

There will be students in your class who require individual attention to help them succeed in their maths GCSEs. In a class of 30, it’s not always easy to provide.

Help your students feel confident with exam-style questions and the strategies they’ll need to answer them correctly with personalised online one to one tutoring from Third Space Learning

Lessons are selected to provide support where each student needs it most, and specially-trained GCSE maths tutors adapt the pitch and pace of each lesson. This ensures a personalised revision programme that raises grades and boosts confidence.

Privacy Overview

• £ 0.00 0 items

Year 4 Lines of Symmetry Maths Challenge

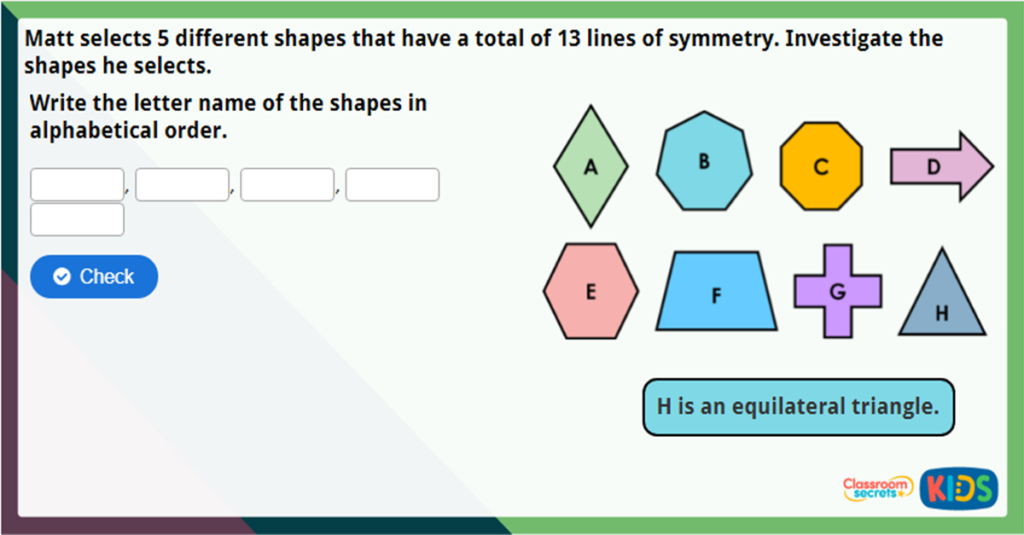
This Year 4 Lines of Symmetry Challenge checks children’s understanding of finding lines of symmetry. Children will help Matt to select the correct shapes to find a given number of lines of symmetry.

If you would like to access  additional resources which link to this maths challenge, you can purchase a subscription for only £5.31 per month on our sister site, Classroom Secrets .

Teacher Specific Information

This Year 4 Lines of Symmetry Challenge checks pupils’ understanding of finding lines of symmetry. Pupils will help Matt to select the correct shapes to find a given number of lines of symmetry.

National Curriculum Objectives

Properties of Shapes

Mathematics Year 4: (4G2b) Identify lines of symmetry in 2-D shapes presented in different orientations

Have you visited our sister site yet?

Primary resources for teachers

Classroom Secrets provides high-quality, affordable teaching resources that children love, and teachers trust.

Stay in touch

01422 419608

[email protected]

Interested in getting weekly updates from us? Then sign up to our newsletter here!

Information

• Cookie Policy
• Privacy Settings
• Terms and Conditions
• End User License Agreement

Copyright: Classroom Secrets 2024

Company number: 8401067

VAT number: 248824574

Designed by Classroom Secrets

Bootstrap Modal Title

Bootstrap modal body text should be here.

• International
• Schools directory
• Resources Jobs Schools directory News Search

Outstanding Maths Lesson for Interview/Lesson Observation Problem Solving - Years 5 and 6

Subject: Mathematics

Age range: 7-11

Resource type: Lesson (complete)

Last updated

10 May 2024

• Share through email
• Share through twitter
• Share through linkedin
• Share through facebook
• Share through pinterest

An exceptional maths problem solving lesson, complete with written lesson plan and interactive slides. Crafted to engage and challenge high-ability Year 5/6 students, this lesson offers a rich tapestry of activities and tasks designed to ignite mathematical thinking.

Perfect for a lesson observation or job interview, these comprehensive materials will impress all observers and demonstrate your expertise in delivering high-quality maths education.

Tes paid licence How can I reuse this?

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

This resource hasn't been reviewed yet

To ensure quality for our reviews, only customers who have purchased this resource can review it

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource:

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 15 May 2024

Wavefunction matching for solving quantum many-body problems

• Serdar Elhatisari   ORCID: orcid.org/0000-0002-7951-1991 1 , 2 ,
• Lukas Bovermann   ORCID: orcid.org/0000-0001-7765-1643 3 ,
• Yuan-Zhuo Ma   ORCID: orcid.org/0000-0002-0892-4457 4 , 5 ,
• Evgeny Epelbaum   ORCID: orcid.org/0000-0002-7613-0210 3 ,
• Dillon Frame 6 , 7 ,
• Fabian Hildenbrand 6 , 7 ,
• Myungkuk Kim 8 ,
• Youngman Kim 8 ,
• Hermann Krebs 3 ,
• Timo A. Lähde   ORCID: orcid.org/0000-0003-3251-1035 6 , 7 ,
• Dean Lee   ORCID: orcid.org/0000-0002-3630-567X 4 ,
• Ning Li 9 ,
• Bing-Nan Lu 10 ,
• Ulf-G. Meißner   ORCID: orcid.org/0000-0003-1254-442X 2 , 6 , 7 , 11 ,
• Gautam Rupak 12 ,
• Shihang Shen   ORCID: orcid.org/0000-0002-8051-6466 6 , 7 ,
• Young-Ho Song   ORCID: orcid.org/0000-0003-0361-3251 13 &
• Gianluca Stellin 14  

Nature ( 2024 ) Cite this article

4210 Accesses

116 Altmetric

Metrics details

• Quantum simulation
• Theoretical nuclear physics
• Theoretical physics
• Ultracold gases

Ab initio calculations have an essential role in our fundamental understanding of quantum many-body systems across many subfields, from strongly correlated fermions 1 , 2 , 3 to quantum chemistry 4 , 5 , 6 and from atomic and molecular systems 7 , 8 , 9 to nuclear physics 10 , 11 , 12 , 13 , 14 . One of the primary challenges is to perform accurate calculations for systems where the interactions may be complicated and difficult for the chosen computational method to handle. Here we address the problem by introducing an approach called wavefunction matching. Wavefunction matching transforms the interaction between particles so that the wavefunctions up to some finite range match that of an easily computable interaction. This allows for calculations of systems that would otherwise be impossible owing to problems such as Monte Carlo sign cancellations. We apply the method to lattice Monte Carlo simulations 15 , 16 of light nuclei, medium-mass nuclei, neutron matter and nuclear matter. We use high-fidelity chiral effective field theory interactions 17 , 18 and find good agreement with empirical data. These results are accompanied by insights on the nuclear interactions that may help to resolve long-standing challenges in accurately reproducing nuclear binding energies, charge radii and nuclear-matter saturation in ab initio calculations 19 , 20 .

Similar content being viewed by others

A linear response framework for quantum simulation of bosonic and fermionic correlation functions

Exact exchange-correlation potentials from ground-state electron densities

Beyond the RPA and GW methods with adiabatic xc-kernels for accurate ground state and quasiparticle energies

Quantum Monte Carlo simulations are a powerful and efficient ab initio method for describing quantum many-body systems using stochastic processes 1 , 9 , 15 , 16 , 21 , 22 , 23 . If the Monte Carlo amplitudes are positive, then the computational effort grows only as a low power of the number of particles. For many problems of interest, a simple Hamiltonian H S can be found that is easily computable using Monte Carlo methods and describes the energies and other observable properties of the many-body system in fair agreement with empirical data 24 , 25 , 26 , 27 . However, realistic high-fidelity Hamiltonians usually suffer from severe sign problems with positive and negative contributions cancelling each other so that Monte Carlo calculations become impractical. Here we solve the problem using an approach called wavefunction matching. While keeping the observable physics unchanged, wavefunction matching creates a new high-fidelity Hamiltonian H ′ such that the two-body wavefunctions up to some finite range match that of a simple Hamiltonian H S , which is easily computed. This allows for a rapidly converging expansion in powers of the difference H ′ −  H S . Although wavefunction matching can be used with any computational scheme, we focus here on quantum Monte Carlo simulations where the method presents a practical strategy for evading sign oscillations in high-fidelity calculations. While H S and H ′ act on many-body systems, the wavefunction-matching process is done at the two-body level only. For the sake of clarity, we define H S and H ′ as containing only two-body interactions. Later we also consider the inclusion of three-body interactions. However, that analysis is separate from wavefunction matching.

A unitary transformation U is a linear transformation that maps normalized orthogonal states to other normalized orthogonal states. Starting from a high-fidelity Hamiltonian H with only two-body interactions, wavefunction matching defines a new Hamiltonian H ′ =  U † HU , where U † is the Hermitian conjugate of U . The unitary transformation is performed at the two-body level. In each two-body angular momentum channel, the unitary transformation U is active only when the separation distance between two particles is less than some chosen distance R . For the calculations presented here, the value R  = 3.72 fm is used. The dependence on R is extensively discussed in  Supplementary Information .

Let us write ψ 0 ( r ), \({\psi }_{0}^{{\prime} }(r)\) and \({\psi }_{0}^{{\rm{S}}}(r)\) for the two-body ground-state wavefunctions of H , H ′ and the simple Hamiltonian H S , respectively. Here r is the distance between the two particles. The transformation U is defined such that \({\psi }_{0}^{{\prime} }(r)\) is proportional to \({\psi }_{0}^{{\rm{S}}}(r)\) for r  <  R . The simple Hamiltonian is chosen so that the constant of proportionality is close to 1. For r  >  R , however, U is not active and so \({\psi }_{0}^{{\prime} }(r)\) remains equal to ψ 0 ( r ). The key point to notice here is that \({\psi }_{0}^{{\prime} }(r)\) and \({\psi }_{0}^{{\rm{S}}}(r)\) are numerically close to each other for all values of r . This can be seen visually in Fig. 1a and is the reason why perturbation theory in powers of H ′ −  H S converges quickly when starting from low-energy states of H S .

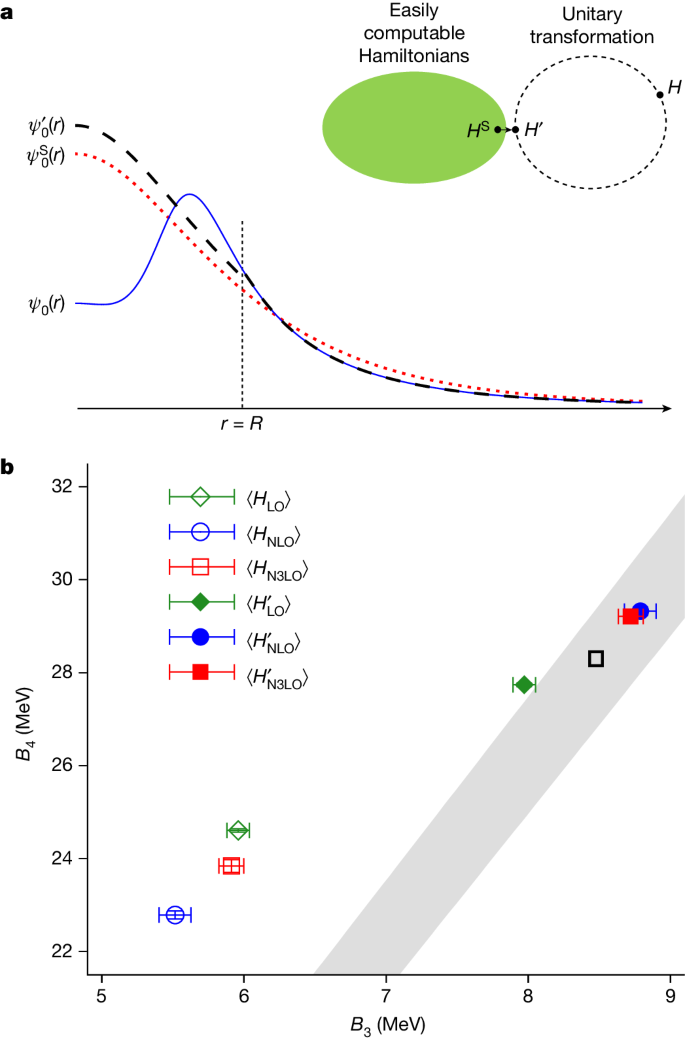
a , Pictorial representation of wavefunction matching. The simple Hamiltonian H S is an easily computable Hamiltonian whereas the high-fidelity Hamiltonian H is not. A unitary transformation on the two-nucleon interaction with finite range R is used to produce a new Hamiltonian H ′ that is close to H S . In each two-body channel, the ground-state wavefunction of H ′ matches the ground-state wavefunction of H for r  >  R and is proportional to the ground-state wavefunction of H S for r  <  R . b , The Tjon band correlation between the binding energies of 3 H ( B 3 ) and 4 He ( B 4 ). The grey band is the predicted result from ref. 31 . The black open box shows the empirical point. The green diamond, blue circle and red square points show the results at LO, NLO and N3LO in chiral effective field theory, respectively. The open points show the results from the first-order perturbative calculations using the Hamiltonian H and the filled points are the results of the first-order perturbative calculations using the Hamiltonian H ′. The error bars show standard deviations.

Wavefunction matching will now be applied to ab initio Monte Carlo nuclear lattice simulations 15 , 16 , 25 , 26 , 28 using the framework of chiral effective field theory (χEFT) 17 , 29 . For our realistic Hamiltonian H , we use χEFT two-nucleon interactions at next-to-next-to-next-to-leading order (N3LO) with lattice spacing a  = 1.32 fm using a low-energy scheme described in  Supplementary Information . For our simple Hamiltonian H S , we use a χEFT interaction at leading order. Details of the interactions can be found in  Supplementary Information . In the following, we use the term ‘local’ for interactions that do not change the positions of particles and ‘non-local’ refers to interactions that do change the relative positions of particles. The ‘range’ of the interaction refers to the separation distance beyond which the interaction between particles becomes negligible.

We calculate all quantities up to first order in perturbation theory, which corresponds to one power in the difference H ′ −  H S . As a first test, we consider the energy of the deuteron, 2 H. The wavefunction-matching calculation gives a binding energy of 2.02 MeV, compared with 2.21 MeV for the true binding energy of H and 2.22 MeV for the experimentally observed value. The residual error of 0.1 MeV per nucleon is due to corrections beyond first order in powers of H ′ −  H S . If one does not use wavefunction matching and instead performs the analogous calculation to first order in H  −  H S , the result is a much less accurate binding energy of 0.68 MeV.

As a second test of wavefunction matching, we calculate the binding energies of 3 H and 4 He. The Tjon band describes the universal correlations between the 3 H and 4 He binding energies 30 , 31 . Provided that there are no long-range non-local interactions, any realistic two-nucleon interaction produces binding energies that lie on the Tjon band. The inclusion of any short-range three-nucleon interaction also preserves this universal relation. In Fig. 1 , we show wavefunction-matching calculations using two-nucleon interactions only. At leading order (LO) the calculated point falls outside the Tjon band as the Coulomb interaction is not included, whereas the next-to-leading order (NLO) and N3LO results lie squarely in the middle of the band. We are using a low-energy scheme where the two-nucleon interaction is the same at NLO and next-to-next-to-leading order (NNLO) 32 . The empirical point is also shown in Fig. 1 . The good agreement with the Tjon band suggests a residual error of 0.1 MeV per nucleon or less for 3 H and 4 He. In  Supplementary Information , we present numerical evidence that the estimate of 0.1 MeV error per nucleon is also valid for light and medium-mass nuclei. This can be compared with the substantial deviation from the Tjon line if one does not use wavefunction matching and performs the analogous calculation to first order in H  −  H S . Before proceeding to larger nuclei and many-body systems, we first comment on the current status of ab initio calculations of nuclear structure using χEFT. The following analysis is not directly connected to wavefunction matching. Instead, it is a separate theoretical framework designed to help push beyond the current limitations of ab initio nuclear structure theory.

There has been tremendous progress in the past few years towards producing accurate results for nuclear structure across much of the nuclear chart using a variety of different computational approaches 33 , 34 , 35 , 36 , 37 , 38 , 39 , 40 , 41 , 42 , 43 , 44 . But there is also ample evidence that the calculations are sensitive to the manner in which the short-distance features of the interactions are regulated 20 , 45 , 46 , 47 , 48 , a warning sign that systematic errors are not fully under control. Current ab initio calculations have difficulty simultaneously maintaining high-fidelity two-nucleon phase shifts and mixing angles and describing the saturation energy and density of symmetric nuclear matter as well as the binding energies and charge radii of light and medium-mass nuclei. Previous ab initio nuclear structure calculations have either not addressed some of the relevant observables or require further improvement in one or more of these areas. We aim to identify the problem and point to a viable solution.

The results in refs. 49 , 50 showed that the range and locality of the nuclear interactions have a strong influence on nuclear binding and that the α–α interaction is highly sensitive to the range and locality of the nucleonic interactions as well as omitted higher-order interactions. These same arguments apply to other interactions involving α particles and nucleons. In  Supplementary Information , we use the formalism of cluster effective field theory 51 , 52 , 53 , 54 for α-particles and nucleons to provide a simple counting argument for the number of parameters that require tuning to reduce unwanted errors. Our strategy is to tune the short-distance features of the three-nucleon interactions to achieve this error cancellation. We should emphasize that our calculations are full A -body calculations, and cluster effective field theory is only used to diagnose sensitivities to short-distance physics.

In χEFT, three-nucleon forces first appear at order NNLO. These include terms associated with the exchange of two pions and whose coefficients are determined from pion–nucleon scattering. There are also two interactions with singular short-distance properties that must be regulated and the corresponding couplings fitted to empirical data. As shown in Fig. 2a , c D corresponds to the short-range interaction of two nucleons linked to a third nucleon through the exchange of a pion, and c E corresponds to the short-range interaction of all three nucleons. At N3LO, there are additional terms associated with the exchange of two pions as well as readjustments of the c D and c E coefficients 55 , 56 , 57 . Four-nucleon interactions also appear at N3LO but are not considered in this work.

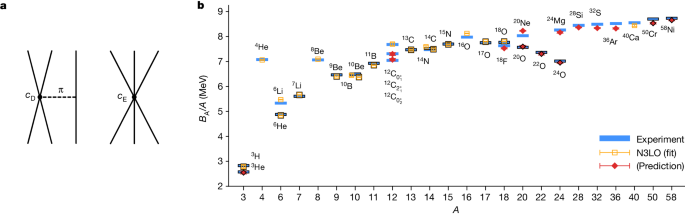
a , Short-range three-nucleon forces at NNLO. The first is the one-pion exchange term c D shown on the left. The other is the purely short-range term c E shown on the right. At order N3LO, there are additional three-nucleon interactions associated with the exchange of two pions, as well as the corrections from the renormalization of the c D and c E terms. b , Results for nuclear binding energies ( B A ) using wavefunction matching. Calculated ground-state and excited-state energies of some selected nuclei with up to A  = 58 at N3LO in χ EFT and comparison with experimental data. The symbols with a black border indicate nuclei with unequal numbers of protons and neutrons. The nuclei used in the fit of the higher-order three-nucleon interactions are labelled with open squares and the other nuclei are predictions denoted with filled diamonds. The error bars show standard deviations.

We tune the short-distance features of the c D and c E three-nucleon interactions to minimize errors in the binding energies of selected light and medium-mass nuclei. A total of six additional three-nucleon parameters are adjusted, and in  Supplementary Information we present the details of these parameters along with a detailed description of the fitting procedure and the resulting uncertainty. We find that with just one parameter, the root-mean-square-deviation (RMSD) for the energy per nucleon drops from 1.2 MeV down to 0.4 MeV. With the addition of a few additional parameters, the RMSD per nucleon drops further to about 0.1 MeV. These results are consistent with the hypothesis that the α–α interaction has a key role in nuclear binding and that there are several additional cluster interactions that are sensitive to short-distance physics.

In Fig. 2b , we present the results for the nuclear binding energies using wavefunction matching. We show ground-state and excited-state energies of selected nuclei with up to A  = 58 nucleons and comparison with experimental data. The symbols with a black border indicate nuclei with unequal numbers of protons and neutrons. The nuclei used in the fit of the three-nucleon interactions are labelled with open squares, and the other nuclei are predictions denoted with filled diamonds. The one-standard-deviation error bars shown in Fig. 2 represent uncertainties due to Monte Carlo errors, infinite-volume extrapolations and infinite projection time extrapolations. As described in  Supplementary Information , we estimate the additional systematic errors due to truncation of the expansion in powers of H ′ −  H S to be approximately 0.1 MeV per nucleon. However, this source of systematic error can be significantly reduced by allowing for variational optimization of the Hamiltonian used to prepare the nuclear many-body wavefunction. We perform this variational optimization so that the remaining systematic error is smaller than the estimated computational error due to other sources. In  Supplementary Information , we also compute the additional systematic errors due to uncertainties in the chiral interactions.

In Fig. 3a , we present the results for the charge radii of nuclei with up to A  = 58 nucleons. No charge radii data were used to fit any interaction parameters. The one-standard-deviation point estimate error bars shown in Fig. 3 represent computational uncertainties due to Monte Carlo errors, infinite-volume extrapolation and infinite-time extrapolation. The agreement with empirical results is quite good, with an RMSD of about 0.03 fm. An extended analysis for selected nuclei that also includes uncertainties from the interactions are presented in  Supplementary Information . We note that the larger errors for the heaviest nuclei are statistical and can be decreased by utilizing greater computational resources. The specific terms included in the calculations of the charge radii are detailed in  Supplementary Information .

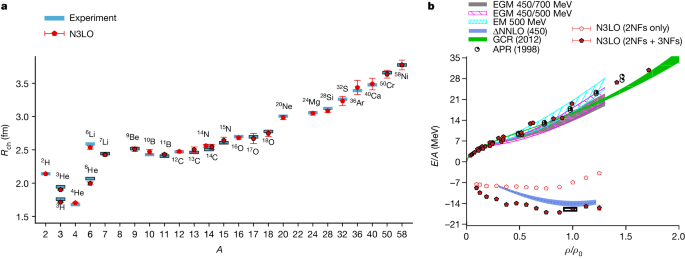
a , Predictions for charge radii ( R ch ) of nuclei up to A  = 58 at N3LO in χEFT and comparison with experimental data. The symbols with a black border indicate nuclei with unequal numbers of protons and neutrons. b , Predictions for pure neutron-matter energy per neutron and symmetric nuclear-matter energy per nucleon as a function of density at N3LO in χEFT. For pure neutron matter, we use the number of neutrons from 14 to 80 and various box sizes from 6.58 fm to 13.2 fm. For symmetric nuclear matter, we use nucleon numbers from 12 to 160 and a periodic box of length 9.21 fm. For comparison, we show the results from variational calculations (APR) 65 , auxiliary-field diffusion Monte Carlo simulations (GCR) 66 , many-body perturbation theory using N3LO/NNLO (two-nucleon (2NF)/three-nucleon (3NF)) chiral interactions (EM 500 MeV, EGM 450/500 MeV and EGM 450/700 MeV) 67 and coupled cluster theory using NNLO chiral interactions with explicit delta degrees of freedom (ΔNNLO) 68 . The empirical saturation point is labelled with a black rectangular box. E denotes energy, ρ is the nucleon density, and ρ 0 is the saturation density of symmetric nuclear matter. The error bars show standard deviations.

In Fig. 3b , we present lattice results for the energy per nucleon versus density for pure neutron matter and symmetric nuclear matter. None of the neutron-matter and symmetric nuclear-matter data were used to fit any interaction parameters. The density is expressed as a fraction of the saturation density for nuclear matter, ρ 0  = 0.16 fm −3 . For the neutron-matter calculations, we consider 14 to 80 neutrons in periodic box lengths ranging from 6.58 fm to 13.2 fm. For the symmetric nuclear-matter calculations, we use system sizes from 12 to 160 nucleons in a periodic box of length 9.21 fm. The comparisons with several other published works are shown and detailed in the figure caption. We see that the neutron-matter calculations agree well with previous calculations. Within the uncertainties due to finite system size corrections, the symmetric nuclear-matter calculations show saturation at an energy and density consistent with the empirical saturation point labelled with the black rectangular box. The relative uncertainties due to finite system size are at the 10% level for the energy. Additional calculations with larger systems are needed to reduce the thermodynamic extrapolation error further.

The one-standard-deviation point estimate error bars shown represent computational uncertainties due to Monte Carlo errors and infinite projection time extrapolation. These lattice simulations of symmetric nuclear matter are qualitatively different to other theoretical calculations that assume a homogeneous phase. The lattice simulations show phase separation and cluster formation, just as in the real physical system. Owing to the finite number of nucleons in these calculations, some oscillations due to nuclear shell effects can be seen in the energy per nucleon.

Another interesting feature of the lattice results is that symmetric nuclear matter without three-nucleon forces is underbound rather than overbound. This is different from what is found in other calculations using renormalization-group methods 58 , 59 , 60 . As discussed in  Supplementary Information , wavefunction matching is very different from renormalization-group transformations. Wavefunction matching implements a unitary transformation that has finite range, and the process can be viewed as defining a new χEFT two-nucleon Hamiltonian H ′. The interaction in H ′ has a range no larger than that of H and H S for the low-energy interactions. Therefore, one does not need to reconstruct the many-body forces induced by the unitary transformation and can simply treat H ′ as the new χEFT two-nucleon Hamiltonian. Wavefunction matching has some characteristics similar to the unitary correlation operator method (UCOM) 61 , 62 , 63 . However, the unitary transformation in UCOM has properties that are more similar to renormalization-group transformations and, therefore, is also quite different from wavefunction matching. The induced forces generated by wavefunction matching have been investigated in a toy model 64 . A detailed discussion of the theory and applications of wavefunction matching and its implementation in continuous space are presented in  Supplementary Information .

In summary, we have presented an approach for solving quantum many-body systems called wavefunction matching. Wavefunction matching uses a transformation of the particle interactions to allow for calculations of systems that would otherwise be difficult or impossible. We have applied the method to lattice Monte Carlo simulations of light nuclei, medium-mass nuclei, neutron matter and nuclear matter using high-fidelity chiral interactions and found good agreement with empirical data. Judging from the accuracy of the predictions, we have been successful in cancelling systematic errors in nuclear structure calculations by tuning the short-distance features of the three-nucleon interactions. These developments may help resolve long-standing challenges in ab initio nuclear structure theory.

Although we have focused on Monte Carlo simulations for nuclear physics here, wavefunction matching can be used with any computational method and applied to any quantum many-body system. This also includes quantum computing algorithms where wavefunction matching can be used to reduce the number of quantum gates required. All that is needed is a simple Hamiltonian H S that produces fair agreement with empirical data for the many-body system of interest and is easily computable using the method of choice. Further details on the implementation and theory of wavefunction matching are given in  Supplementary Information .

Data availability

All of the data produced in association with this work have been stored and are publicly available at https://drive.google.com/drive/folders/1MByuG6NMagcgmURe4py-kwr9vksnHCl4 .

Code availability

All of the codes produced in association with this work have been stored and can be obtained upon request from the corresponding author, subject to possible export control constraints.

Assaad, F. & Evertz, H. in Computational Many-Particle Physics (eds Fehske, H., Weiße, A. & Schneider, R.) 277–356 (Springer, 2008).

Schollwöck, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 326 , 96–192 (2011).

Article   ADS   MathSciNet   Google Scholar  

Orús, R. A practical introduction to tensor networks: matrix product states and projected entangled pair states. Ann. Phys. 349 , 117–158 (2014).

Dovesi, R., Civalleri, B., Roetti, C., Saunders, V. R. & Orlando, R. Ab initio quantum simulation in solid state chemistry. Rev. Comput. Chem. 21 , 1–125 (2005).

Article   CAS   Google Scholar  

Friesner, R. A. Ab initio quantum chemistry: methodology and applications. Proc. Natl Acad. Sci. USA 102 , 6648–6653 (2005).

Article   ADS   CAS   PubMed   PubMed Central   Google Scholar  

Bartlett, R. J. & Musiał, M. Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 79 , 291 (2007).

Article   ADS   CAS   Google Scholar  

Aymar, M., Greene, C. H. & Luc-Koenig, E. Multichannel Rydberg spectroscopy of complex atoms. Rev. Mod. Phys. 68 , 1015 (1996).

Stone, A. & Misquitta, A. Atom–atom potentials from ab initio calculations. Int. Rev. Phys. Chem. 26 , 193–222 (2007).

Motta, M. & Zhang, S. Ab initio computations of molecular systems by the auxiliary-field quantum Monte Carlo method. Wiley Interdiscip. Rev. Comput. Mol. Sci. 8 , e1364 (2018).

Article   Google Scholar  

Barrett, B. R., Navrátil, P. & Vary, J. P. Ab initio no core shell model. Prog. Part. Nucl. Phys. 69 , 131–181 (2013).

Hagen, G., Papenbrock, T., Hjorth-Jensen, M. & Dean, D. J. Coupled-cluster computations of atomic nuclei. Rep. Prog. Phys. 77 , 096302 (2014).

Article   ADS   CAS   PubMed   Google Scholar  

Carlson, J. et al. Quantum Monte Carlo methods for nuclear physics. Rev. Mod. Phys. 87 , 1067 (2015).

Article   ADS   MathSciNet   CAS   Google Scholar  

Hergert, H., Bogner, S. K., Morris, T. D., Schwenk, A. & Tsukiyama, K. The in-medium similarity renormalization group: a novel ab initio method for nuclei. Phys. Rep. 621 , 165–222 (2016).

Stroberg, S., Holt, J., Schwenk, A. & Simonis, J. Ab initio limits of atomic nuclei. Phys. Rev. Lett. 126 , 022501 (2021).

Lee, D. Lattice simulations for few- and many-body systems. Prog. Part. Nucl. Phys. 63 , 117–154 (2009).

Lähde, T. A. & Meißner, U.-G. Nuclear Lattice Effective Field Theory: An Introduction Vol. 975 (Springer, 2019).

Epelbaum, E., Hammer, H.-W. & Meißner, U.-G. Modern theory of nuclear forces. Rev. Mod. Phys. 81 , 1773–1825 (2009).

Machleidt, R. & Entem, D. Chiral effective field theory and nuclear forces. Phys. Rep. 503 , 1–75 (2011).

Ekström, A. et al. What is ab initio in nuclear theory? Front. Phys. 11 , 1129094 (2023).

Machleidt, R. What is ab initio? Few Body Syst. 64 , 77 (2023).

Article   ADS   Google Scholar  

Carlson, J. et al. Quantum Monte Carlo methods for nuclear physics. Rev. Mod. Phys. 87 , 1067–1118 (2015).

Pastore, S. et al. Quantum Monte Carlo calculations of weak transitions in A  = 6–10 nuclei. Phys. Rev. C 97 , 022501 (2018).

Gandolfi, S., Lonardoni, D., Lovato, A. & Piarulli, M. Atomic nuclei from quantum Monte Carlo calculations with chiral EFT interactions. Front. Phys. 8 , 117 (2020).

Lu, B.-N. et al. Essential elements for nuclear binding. Phys. Lett. B 797 , 134863 (2019).

Lu, B.-N. et al. Ab initio nuclear thermodynamics. Phys. Rev. Lett. 125 , 192502 (2020).

Shen, S. et al. Emergent geometry and duality in the carbon nucleus. Nat. Commun. 14 , 2777 (2023).

Gnech, A., Fore, B. & Lovato, A. Distilling the essential elements of nuclear binding via neural-network quantum states. Preprint at https://arxiv.org/abs/2308.16266 (2023).

Lu, B.-N. et al. Perturbative quantum Monte Carlo method for nuclear physics. Phys. Rev. Lett. 128 , 242501 (2022).

Machleidt, R. & Sammarruca, F. Chiral EFT based nuclear forces: achievements and challenges. Phys. Scr. 91 , 083007 (2016).

Tjon, J. A. Bound states of 4 He with local interactions. Phys. Lett. B 56 , 217–220 (1975).

Platter, L., Hammer, H. W. & Meißner, U.-G. On the correlation between the binding energies of the triton and the alpha-particle. Phys. Lett. B 607 , 254–258 (2005).

Li, N. et al. Neutron–proton scattering with lattice chiral effective field theory at next-to-next-to-next-to-leading order. Phys. Rev. C 98 , 044002 (2018).

Ekström, A. et al. Accurate nuclear radii and binding energies from a chiral interaction. Phys. Rev. C 91 , 051301 (2015).

Drischler, C., Hebeler, K. & Schwenk, A. Chiral interactions up to next-to-next-to-next-to-leading order and nuclear saturation. Phys. Rev. Lett. 122 , 042501 (2019).

Lonardoni, D. et al. Properties of nuclei up to A  = 16 using local chiral interactions. Phys. Rev. Lett. 120 , 122502 (2018).

Morris, T. D. et al. Structure of the lightest tin isotopes. Phys. Rev. Lett. 120 , 152503 (2018).

Piarulli, M. et al. Light-nuclei spectra from chiral dynamics. Phys. Rev. Lett. 120 , 052503 (2018).

Somà, V., Navrátil, P., Raimondi, F., Barbieri, C. & Duguet, T. Novel chiral Hamiltonian and observables in light and medium-mass nuclei. Phys. Rev. C 101 , 014318 (2020).

Gysbers, P. et al. Discrepancy between experimental and theoretical β-decay rates resolved from first principles. Nat. Phys. 15 , 428–431 (2019).

Maris, P. et al. Light nuclei with semilocal momentum-space regularized chiral interactions up to third order. Phys. Rev. C 103 , 054001 (2021).

Hebeler, K. Three-nucleon forces: implementation and applications to atomic nuclei and dense matter. Phys. Rep. 890 , 1–116 (2021).

Jiang, W. G. et al. Accurate bulk properties of nuclei from A  = 2 to ∞ from potentials with Δ isobars. Phys. Rev. C 102 , 054301 (2020).

Wirth, R., Yao, J. M. & Hergert, H. Ab initio calculation of the contact operator contribution in the standard mechanism for neutrinoless double beta decay. Phys. Rev. Lett. 127 , 242502 (2021).

Hu, B. et al. Ab initio predictions link the neutron skin of 208 Pb to nuclear forces. Nat. Phys. 18 , 1196–1200 (2022).

Article   CAS   PubMed   PubMed Central   Google Scholar  

Stroberg, S. R. et al. A nucleus-dependent valence-space approach to nuclear structure. Phys. Rev. Lett. 118 , 032502 (2017).

Hüther, T., Vobig, K., Hebeler, K., Machleidt, R. & Roth, R. Family of chiral two- plus three-nucleon interactions for accurate nuclear structure studies. Phys. Lett. B 808 , 135651 (2020).

Hoppe, J., Drischler, C., Hebeler, K., Schwenk, A. & Simonis, J. Probing chiral interactions up to next-to-next-to-next-to-leading order in medium-mass nuclei. Phys. Rev. C 100 , 024318 (2019).

Nosyk, Y., Entem, D. R. & Machleidt, R. Nucleon–nucleon potentials from Δ-full chiral effective-field-theory and implications. Phys. Rev. C 104 , 054001 (2021).

Elhatisari, S. et al. Nuclear binding near a quantum phase transition. Phys. Rev. Lett. 117 , 132501 (2016).

Article   ADS   PubMed   Google Scholar  

Kanada-En’yo, Y. & Lee, D. Effective interactions between nuclear clusters. Phys. Rev. C 103 , 024318 (2021).

Bertulani, C. A., Hammer, H. W. & Van Kolck, U. Effective field theory for halo nuclei. Nucl. Phys. A 712 , 37–58 (2002).

Higa, R., Hammer, H. W. & van Kolck, U. Alpha alpha scattering in halo effective field theory. Nucl. Phys. A 809 , 171–188 (2008).

Rotureau, J. & van Kolck, U. Effective field theory and the Gamow shell model: the 6 He halo nucleus. Few Body Syst. 54 , 725–735 (2013).

Hammer, H. W., Ji, C. & Phillips, D. R. Effective field theory description of halo nuclei. J. Phys. G 44 , 103002 (2017).

Ishikawa, S. & Robilotta, M. R. Two-pion exchange three-nucleon potential: O ( q 4 ) chiral expansion. Phys. Rev. C 76 , 014006 (2007).

Bernard, V., Epelbaum, E., Krebs, H. & Meißner, U.-G. Subleading contributions to the chiral three-nucleon force. I. Long-range terms. Phys. Rev. C 77 , 064004 (2008).

Bernard, V., Epelbaum, E., Krebs, H. & Meißner, U. G. Subleading contributions to the chiral three-nucleon force II: short-range terms and relativistic corrections. Phys. Rev. C 84 , 054001 (2011).

Bogner, S. K., Kuo, T. T. S., Schwenk, A., Entem, D. R. & Machleidt, R. Towards a model independent low momentum nucleon nucleon interaction. Phys. Lett. B 576 , 265–272 (2003).

Bogner, S. K., Furnstahl, R. J. & Perry, R. J. Similarity renormalization group for nucleon–nucleon interactions. Phys. Rev. C 75 , 061001 (2007).

Bogner, S., Furnstahl, R. & Schwenk, A. From low-momentum interactions to nuclear structure. Prog. Part. Nucl. Phys. 65 , 94–147 (2010).

Feldmeier, H., Neff, T., Roth, R. & Schnack, J. A unitary correlation operator method. Nucl. Phys. A 632 , 61–95 (1998).

Neff, T. & Feldmeier, H. Tensor correlations in the unitary correlation operator method. Nucl. Phys. A 713 , 311–371 (2003).

Roth, R., Neff, T. & Feldmeier, H. Nuclear structure in the framework of the unitary correlation operator method. Prog. Part. Nucl. Phys. 65 , 50–93 (2010).

Bovermann, L., Epelbaum, E., Krebs, H. & Lee, D. Lattice improvement of nuclear shape calculations using unitary transformations. Proc. Sci. https://doi.org/10.22323/1.396.0369 (2022).

Google Scholar  

Akmal, A., Pandharipande, V. R. & Ravenhall, D. G. The equation of state of nucleon matter and neutron star structure. Phys. Rev. C 58 , 1804–1828 (1998).

Gandolfi, S., Carlson, J. & Reddy, S. The maximum mass and radius of neutron stars and the nuclear symmetry energy. Phys. Rev. C 85 , 032801 (2012).

Tews, I., Krüger, T., Hebeler, K. & Schwenk, A. Neutron matter at next-to-next-to-next-to-leading order in chiral effective field theory. Phys. Rev. Lett. 110 , 032504 (2013).

Ekström, A., Hagen, G., Morris, T. D., Papenbrock, T. & Schwartz, P. D. Δ isobars and nuclear saturation. Phys. Rev. C 97 , 024332 (2018).

Download references

Acknowledgements

We thank members and partners of the Nuclear Lattice Effective Field Theory Collaboration (J. Drut, G. Jansen, S. Krieg, Z. Ren, A. Sarkar and Q. Wang) and S. Bogner, A. Ekström, H. Hergert, M. Hjorth-Jensen, D. Phillips, A. Schwenk and W. Nazarewicz for discussions. We acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) and the NSFC through the funds provided to the Sino-German Collaborative Research Center TRR110 ‘Symmetries and the Emergence of Structure in QCD’ (DFG project ID 196253076 - TRR 110, NSFC grant number 12070131001), the Chinese Academy of Sciences (CAS) President’s International Fellowship Initiative (PIFI) (grant number 2018DM0034), Volkswagen Stiftung (grant number 93562), the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (ERC AdG EXOTIC, grant agreement number 101018170, and ERC AdG NuclearTheory, grant agreement number 885150), the Scientific and Technological Research Council of Turkey (TUBITAK project number 120F341), the National Natural Science Foundation of China (grants numbers 12105106 and 12275259), NSAF No.U2330401, US National Science Foundation (PHY-1913620, PHY-2209184, PHY-2310620), US Department of Energy (DE-SC0021152, DE-SC0013365, DE-SC0023658, DE-SC0024586, NUCLEI SciDAC-5 project DE-SC0023175), the Rare Isotope Science Project of the Institute for Basic Science funded by the Ministry of Science and ICT (MSICT), the National Research Foundation of Korea (2013M7A1A1075764, RS-2022-00165168), the Institute for Basic Science (IBS-R031-D1, IBS-I001-D1) and the Espace de Structure et de réactions Nucléaires Théorique (ESNT) of the CEA DSM/DAM. Computational resources provided by the Gauss Centre for Supercomputing e.V. ( www.gauss-centre.eu ) for computing time on the GCS Supercomputer JUWELS at Jülich Supercomputing Centre (JSC) and special GPU time allocated on JURECA-DC as well as the Oak Ridge Leadership Computing Facility through the INCITE award ‘Ab-initio nuclear structure and nuclear reactions’, and partially provided by TUBITAK ULAKBIM High Performance and Grid Computing Center (TRUBA resources). Computational resources were also partly provided by the National Supercomputing Center of Korea with supercomputing resources including technical support (KSC-2021-CRE-0429, KSC-2022-CHA-0003, KSC-2023-CHA-0005), and the Southern Nuclear Science Computing Center in the South China Normal University. We have complied with community standards for authorship and all relevant recommendations with regard to inclusion and ethics.

Author information

Authors and affiliations.

Faculty of Natural Sciences and Engineering, Gaziantep Islam Science and Technology University, Gaziantep, Turkey

Serdar Elhatisari

Helmholtz-Institut für Strahlen- und Kernphysik and Bethe Center for Theoretical Physics, Universität Bonn, Bonn, Germany

Serdar Elhatisari & Ulf-G. Meißner

Institut für Theoretische Physik II, Ruhr-Universität Bochum, Bochum, Germany

Lukas Bovermann, Evgeny Epelbaum & Hermann Krebs

Facility for Rare Isotope Beams and Department of Physics and Astronomy, Michigan State University, East Lansing, MI, USA

Yuan-Zhuo Ma & Dean Lee

Guangdong Provincial Key Laboratory of Nuclear Science, Institute of Quantum Matter, South China Normal University, Guangzhou, China

Yuan-Zhuo Ma

Institut für Kernphysik, Institute for Advanced Simulation, Jülich Center for Hadron Physics, Jülich, Germany

Dillon Frame, Fabian Hildenbrand, Timo A. Lähde, Ulf-G. Meißner & Shihang Shen

Center for Advanced Simulation and Analytics (CASA), Forschungszentrum Jülich, Jülich, Germany

Center for Exotic Nuclear Studies, Institute for Basic Science, Daejeon, Korea

Myungkuk Kim & Youngman Kim

School of Physics, Sun Yat-Sen University, Guangzhou, China

Graduate School of China Academy of Engineering Physics, Beijing, China

Bing-Nan Lu

Tbilisi State University, Tbilisi, Georgia

Ulf-G. Meißner

Department of Physics and Astronomy and HPC2 Center for Computational Sciences, Mississippi State University, Mississippi State, MI, USA

Gautam Rupak

Institute for Rare Isotope Science, Institute for Basic Science (IBS), Daejeon, Korea

Young-Ho Song

ESNT, DRF/IRFU/DPhN/LENA, CEA Paris-Saclay and Université Paris-Saclay, Gif-sur-Yvette, France

Gianluca Stellin

You can also search for this author in PubMed   Google Scholar

Contributions

Code development, testing, optimization and production runs were led by S.E. with contributions from F.H., M.K., T.A.L., D.L., N.L., B.-N.L., Y.-Z.M., G.R., S.S. and Y.-H.S. Conceptual work and tests were led by L.B. with contributions from S.E., E.E., D.F., H.K. and D.L. S.E., T.L., D.L., U.-G.M. and Y.K. supervised the research effort. Additional code development, testing, optimization and production runs in response to reviewer comments were performed by Y.-Z.M. The literature search was led by G.S. All authors contributed to the writing, editing and review of this work.

Corresponding author

Correspondence to Dean Lee .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Peer review

Peer review information.

Nature thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary information.

Supplementary Sections 1–18, including Supplementary Figs. 1–16, Tables 1–19 and References.

Peer Review File

Rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Elhatisari, S., Bovermann, L., Ma, YZ. et al. Wavefunction matching for solving quantum many-body problems. Nature (2024). https://doi.org/10.1038/s41586-024-07422-z

Download citation

Received : 23 November 2022

Accepted : 15 April 2024

Published : 15 May 2024

DOI : https://doi.org/10.1038/s41586-024-07422-z

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.