An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .
- Advanced Search
- Journal List
- Ind Psychiatry J
- v.19(1); Jan-Jun 2010

Statistics without tears: Populations and samples
Amitav banerjee.
Department of Community Medicine, D Y Patil Medical College, Pune, India
Suprakash Chaudhury
1 Department of Psychiatry, RINPAS, Kanke, Ranchi, India
Research studies are usually carried out on sample of subjects rather than whole populations. The most challenging aspect of fieldwork is drawing a random sample from the target population to which the results of the study would be generalized. In actual practice, the task is so difficult that some sampling bias occurs in almost all studies to a lesser or greater degree. In order to assess the degree of this bias, the informed reader of medical literature should have some understanding of the population from which the sample was drawn. The ultimate decision on whether the results of a particular study can be generalized to a larger population depends on this understanding. The subsequent deliberations dwell on sampling strategies for different types of research and also a brief description of different sampling methods.
Research workers in the early 19th century endeavored to survey entire populations. This feat was tedious, and the research work suffered accordingly. Current researchers work only with a small portion of the whole population (a sample) from which they draw inferences about the population from which the sample was drawn.
This inferential leap or generalization from samples to population, a feature of inductive or empirical research, can be full of pitfalls. In clinical medicine, it is not sufficient merely to describe a patient without assessing the underlying condition by a detailed history and clinical examination. The signs and symptoms are then interpreted against the total background of the patient's history and clinical examination including mental state examination. Similarly, in inferential statistics, it is not enough to just describe the results in the sample. One has to critically appraise the real worth or representativeness of that particular sample. The following discussion endeavors to explain the inputs required for making a correct inference from a sample to the target population.
TARGET POPULATION
Any inferences from a sample refer only to the defined population from which the sample has been properly selected. We may call this the target population. For example, if in a sample of lawyers from Delhi High Court it is found that 5% are having alcohol dependence syndrome, can we say that 5% of all lawyers all over the world are alcoholics? Obviously not, as the lawyers of Delhi High Court may be an institution by themselves and may not represent the global lawyers′ community. The findings of this study, therefore, apply only to Delhi High Court lawyers from which a representative sample was taken. Of course, this finding may nevertheless be interesting, but only as a pointer to further research. The data on lawyers in a particular city tell us nothing about lawyers in other cities or countries.
POPULATIONS IN INFERENTIAL STATISTICS
In statistics, a population is an entire group about which some information is required to be ascertained. A statistical population need not consist only of people. We can have population of heights, weights, BMIs, hemoglobin levels, events, outcomes, so long as the population is well defined with explicit inclusion and exclusion criteria. In selecting a population for study, the research question or purpose of the study will suggest a suitable definition of the population to be studied, in terms of location and restriction to a particular age group, sex or occupation. The population must be fully defined so that those to be included and excluded are clearly spelt out (inclusion and exclusion criteria). For example, if we say that our study populations are all lawyers in Delhi, we should state whether those lawyers are included who have retired, are working part-time, or non-practicing, or those who have left the city but still registered at Delhi.
Use of the word population in epidemiological research does not correspond always with its demographic meaning of an entire group of people living within certain geographic or political boundaries. A population for a research study may comprise groups of people defined in many different ways, for example, coal mine workers in Dhanbad, children exposed to German measles during intrauterine life, or pilgrims traveling to Kumbh Mela at Allahabad.
GENERALIZATION (INFERENCES) FROM A POPULATION
When generalizing from observations made on a sample to a larger population, certain issues will dictate judgment. For example, generalizing from observations made on the mental health status of a sample of lawyers in Delhi to the mental health status of all lawyers in Delhi is a formalized procedure, in so far as the errors (sampling or random) which this may hazard can, to some extent, be calculated in advance. However, if we attempt to generalize further, for instance, about the mental statuses of all lawyers in the country as a whole, we hazard further pitfalls which cannot be specified in advance. We do not know to what extent the study sample and population of Delhi is typical of the larger population – that of the whole country – to which it belongs.
The dilemmas in defining populations differ for descriptive and analytic studies.
POPULATION IN DESCRIPTIVE STUDIES
In descriptive studies, it is customary to define a study population and then make observations on a sample taken from it. Study populations may be defined by geographic location, age, sex, with additional definitions of attributes and variables such as occupation, religion and ethnic group.[ 1 ]
Geographic location
In field studies, it may be desirable to use a population defined by an administrative boundary such as a district or a state. This may facilitate the co-operation of the local administrative authorities and the study participants. Moreover, basic demographic data on the population such as population size, age, gender distribution (needed for calculating age- and sex-specific rates) available from census data or voters’ list are easier to obtain from administrative headquarters. However, administrative boundaries do not always consist of homogenous group of people. Since it is desirable that a modest descriptive study does not cover a number of different groups of people, with widely differing ways of life or customs, it may be necessary to restrict the study to a particular ethnic group, and thus ensure better genetic or cultural homogeneity. Alternatively, a population may be defined in relation to a prominent geographic feature, such as a river, or mountain, which imposes a certain uniformity of ways of life, attitudes, and behavior upon the people who live in the vicinity.
If cases of a disease are being ascertained through their attendance at a hospital outpatient department (OPD), rather than by field surveys in the community, it will be necessary to define the population according to the so-called catchment area of the hospital OPD. For administrative purposes, a dispensary, health center or hospital is usually considered to serve a population within a defined geographic area. But these catchment areas may only represent in a crude manner with the actual use of medical facilities by the local people. For example, in OPD study of psychiatric illnesses in a particular hospital with a defined catchment area, many people with psychiatric illnesses may not visit the particular OPD and may seek treatment from traditional healers or religious leaders.
Catchment areas depend on the demography of the area and the accessibility of the health center or hospital. Accessibility has three dimensions – physical, economic and social.[ 2 ] Physical accessibility is the time required to travel to the health center or medical facility. It depends on the topography of the area (e.g. hill and tribal areas with poor roads have problems of physical accessibility). Economic accessibility is the paying capacity of the people for services. Poverty may limit health seeking behavior if the person cannot afford the bus fare to the health center even if the health services may be free of charge. It may also involve absence from work which, for daily wage earners, is a major economic disincentive. Social factors such as caste, culture, language, etc. may adversely affect accessibility to health facility if the treating physician is not conversant with the local language and customs. In such situations, the patient may feel more comfortable with traditional healers.
Ascertainment of a particular disease within a particular area may be incomplete either because some patient may seek treatment elsewhere or some patients do not seek treatment at all. Focus group discussions (qualitative study) with local people, especially those residing away from the health center, may give an indication whether serious underreporting is occurring.
When it is impossible to relate cases of a disease to a population, perhaps because the cases were ascertained through a hospital with an undefined catchment area, proportional morbidity rates may be used. These rates have been widely used in cancer epidemiology where the number of cases of one form of cancer is expressed as a proportion of the number of cases of all forms of cancer among patients attending the same hospital during the same period.
POPULATIONS IN ANALYTIC STUDIES
Case control studies.
As opposed to descriptive studies where a study population is defined and then observations are made on a representative sample from it, in case control studies observations are made on a group of patients. This is known as the study group , which usually is not selected by sampling of a defined larger group. For instance, a study on patients of bipolar disorder may include every patient with this disorder attending the psychiatry OPD during the study period. One should not forget, however, that in this situation also, there is a hypothetical population consisting of all patients with bipolar disorder in the universe (which may be a certain region, a country or globally depending on the extent of the generalization intended from the findings of the study). Case control studies are often carried out in hospital settings because this is more convenient and accessible group than cases in the community at large. However, the two groups of cases may differ in many respects. At the outset of the study, it should be deliberated whether these differences would affect the external validity (generalization) of the study. Usually, analytic studies are not carried out in groups containing atypical cases of the disorder, unless there is a special indication to do so.
Populations in cohort studies
Basically, cohort studies compare two groups of people (cohorts) and demonstrate whether or not there are more cases of the disease among the cohort exposed to the suspected cause than among the cohort not exposed. To determine whether an association exists between positive family history of schizophrenia and subsequent schizophrenia in persons having such a history, two cohorts would be required: first, the exposed group, that is, people with a family history of mental disorders (the suspected cause) and second, the unexposed group, that is, people without a family history of mental disorders. These two cohorts would need to be followed up for a number of years and cases of schizophrenia in either group would be recorded. If a positive family history is associated with development of schizophrenia, then more cases would occur in the first group than in the second group.
The crucial challenges in a cohort study are that it should include participants exposed to a particular cause being investigated and that it should consist of persons who can be followed up for the period of time between exposure (cause) and development of the disorder. It is vital that the follow-up of a cohort should be complete as far as possible. If more than a small proportion of persons in the cohort cannot be traced (loss to follow-up or attrition), the findings will be biased , in case these persons differ significantly from those remaining in the study.
Depending on the type of exposure being studied, there may or may not be a range of choice of cohort populations exposed to it who may form a larger population from which one has to select a study sample. For instance, if one is exploring association between occupational hazard such as job stress in health care workers in intensive care units (ICUs) and subsequent development of drug addiction, one has to, by the very nature of the research question, select health care workers working in ICUs. On the other hand, cause effect study for association between head injury and epilepsy offers a much wider range of possible cohorts.
Difficulties in making repeated observations on cohorts depend on the length of time of the study. In correlating maternal factors (pregnancy cohort) with birth weight, the period of observation is limited to 9 months. However, if in a study it is tried to find the association between maternal nutrition during pregnancy and subsequent school performance of the child, the study will extend to years. For such long duration investigations, it is wise to select study cohorts that are firstly, not likely to migrate, cooperative and likely to be so throughout the duration of the study, and most importantly, easily accessible to the investigator so that the expense and efforts are kept within reasonable limits. Occupational groups such as the armed forces, railways, police, and industrial workers are ideal for cohort studies. Future developments facilitating record linkage such as the Unique Identification Number Scheme may give a boost to cohort studies in the wider community.
A sample is any part of the fully defined population. A syringe full of blood drawn from the vein of a patient is a sample of all the blood in the patient's circulation at the moment. Similarly, 100 patients of schizophrenia in a clinical study is a sample of the population of schizophrenics, provided the sample is properly chosen and the inclusion and exclusion criteria are well defined.
To make accurate inferences, the sample has to be representative. A representative sample is one in which each and every member of the population has an equal and mutually exclusive chance of being selected.
Sample size
Inputs required for sample size calculation have been dealt from a clinical researcher's perspective avoiding the use of intimidating formulae and statistical jargon in an earlier issue of the journal.[ 1 ]
Target population, study population and study sample
A population is a complete set of people with a specialized set of characteristics, and a sample is a subset of the population. The usual criteria we use in defining population are geographic, for example, “the population of Uttar Pradesh”. In medical research, the criteria for population may be clinical, demographic and time related.
- Clinical and demographic characteristics define the target population, the large set of people in the world to which the results of the study will be generalized (e.g. all schizophrenics).
- The study population is the subset of the target population available for study (e.g. schizophrenics in the researcher's town).
- The study sample is the sample chosen from the study population.
METHODS OF SAMPLING
Purposive (non-random samples).
- Volunteers who agree to participate
- Snowball sample, where one case identifies others of his kind (e.g. intravenous drug users)
- Convenient sample such as captive medical students or other readily available groups
- Quota sampling, at will selection of a fixed number from each group
- Referred cases who may be under pressure to participate
- Haphazard with combination of the above methods
Non-random samples have certain limitations. The larger group (target population) is difficult to identify. This may not be a limitation when generalization of results is not intended. The results would be valid for the sample itself (internal validity). They can, nevertheless, provide important clues for further studies based on random samples. Another limitation of non-random samples is that statistical inferences such as confidence intervals and tests of significance cannot be estimated from non-random samples. However, in some situations, the investigator has to make crucial judgments. One should remember that random samples are the means but representativeness is the goal. When non-random samples are representative (compare the socio-demographic characteristics of the sample subjects with the target population), generalization may be possible.
Random sampling methods
Simple random sampling.
A sample may be defined as random if every individual in the population being sampled has an equal likelihood of being included. Random sampling is the basis of all good sampling techniques and disallows any method of selection based on volunteering or the choice of groups of people known to be cooperative.[ 3 ]
In order to select a simple random sample from a population, it is first necessary to identify all individuals from whom the selection will be made. This is the sampling frame. In developing countries, listings of all persons living in an area are not usually available. Census may not catch nomadic population groups. Voters’ and taxpayers’ lists may be incomplete. Whether or not such deficiencies are major barriers in random sampling depends on the particular research question being investigated. To undertake a separate exercise of listing the population for the study may be time consuming and tedious. Two-stage sampling may make the task feasible.
The usual method of selecting a simple random sample from a listing of individuals is to assign a number to each individual and then select certain numbers by reference to random number tables which are published in standard statistical textbooks. Random number can also be generated by statistical software such as EPI INFO developed by WHO and CDC Atlanta.
Systematic sampling
A simple method of random sampling is to select a systematic sample in which every n th person is selected from a list or from other ordering. A systematic sample can be drawn from a queue of people or from patients ordered according to the time of their attendance at a clinic. Thus, a sample can be drawn without an initial listing of all the subjects. Because of this feasibility, a systematic sample may have some advantage over a simple random sample.
To fulfill the statistical criteria for a random sample, a systematic sample should be drawn from subjects who are randomly ordered. The starting point for selection should be randomly chosen. If every fifth person from a register is being chosen, then a random procedure must be used to determine whether the first, second, third, fourth, or fifth person should be chosen as the first member of the sample.
Multistage sampling
Sometimes, a strictly random sample may be difficult to obtain and it may be more feasible to draw the required number of subjects in a series of stages. For example, suppose we wish to estimate the number of CATSCAN examinations made of all patients entering a hospital in a given month in the state of Maharashtra. It would be quite tedious to devise a scheme which would allow the total population of patients to be directly sampled. However, it would be easier to list the districts of the state of Maharashtra and randomly draw a sample of these districts. Within this sample of districts, all the hospitals would then be listed by name, and a random sample of these can be drawn. Within each of these hospitals, a sample of the patients entering in the given month could be chosen randomly for observation and recording. Thus, by stages, we draw the required sample. If indicated, we can introduce some element of stratification at some stage (urban/rural, gender, age).
It should be cautioned that multistage sampling should only be resorted to when difficulties in simple random sampling are insurmountable. Those who take a simple random sample of 12 hospitals, and within each of these hospitals select a random sample of 10 patients, may believe they have selected 120 patients randomly from all the 12 hospitals. In statistical sense, they have in fact selected a sample of 12 rather than 120.[ 4 ]
Stratified sampling
If a condition is unevenly distributed in a population with respect to age, gender, or some other variable, it may be prudent to choose a stratified random sampling method. For example, to obtain a stratified random sample according to age, the study population can be divided into age groups such as 0–5, 6–10, 11–14, 15–20, 21–25, and so on, depending on the requirement. A different proportion of each group can then be selected as a subsample either by simple random sampling or systematic sampling. If the condition decreases with advancing age, then to include adequate number in the older age groups, one may select more numbers in older subsamples.
Cluster sampling
In many surveys, studies may be carried out on large populations which may be geographically quite dispersed. To obtain the required number of subjects for the study by a simple random sample method will require large costs and will be cumbersome. In such cases, clusters may be identified (e.g. households) and random samples of clusters will be included in the study; then, every member of the cluster will also be part of the study. This introduces two types of variations in the data – between clusters and within clusters – and this will have to be taken into account when analyzing data.
Cluster sampling may produce misleading results when the disease under study itself is distributed in a clustered fashion in an area. For example, suppose we are studying malaria in a population. Malaria incidence may be clustered in villages having stagnant water collections which may serve as a source of mosquito breeding. In villages without such water stagnation, there will be lesser malaria cases. The choice of few villages in cluster sampling may give erroneous results. The selection of villages as a cluster may be quite unrepresentative of the whole population by chance.[ 5 ]
Lot quality assurance sampling
Lot quality assurance sampling (LQAS), which originated in the manufacturing industry for quality control purposes, was used in the nineties to assess immunization coverage, estimate disease prevalence, and evaluate control measures and service coverage in different health programs.[ 6 ] Using only a small sample size, LQAS can effectively differentiate between areas that have or have not met the performance targets. Thus, this method is used not only to estimate the coverage of quality care but also to identify the exact subdivisions where it is deficient so that appropriate remedial measures can be implemented.
The choice of sampling methods is usually dictated by feasibility in terms of time and resources. Field research is quite messy and difficult like actual battle. It may be sometimes difficult to get a sample which is truly random. Most samples therefore tend to get biased. To estimate the magnitude of this bias, the researcher should have some idea about the population from which the sample is drawn. In conclusion, the following quote cited by Bradford Hill[ 4 ] elegantly sums up the benefit of random sampling:
…The actual practice of medicine is virtually confined to those members of the population who either are ill, or think they are ill, or are thought by somebody to be ill, and these so amply fill up the working day that in the course of time one comes unconsciously to believe that they are typical of the whole. This is not the case. The use of a random sample brings to light the individuals who are ill and know they are ill but have no intention of doing anything about it, as well as those who have never been ill, and probably never will be until their final illness. These would have been inaccessible to any other method of approach but that of the random sample… . J. H. Sheldon
Source of Support: Nil.
Conflict of Interest: None declared.
Study Population
- Reference work entry
- pp 6412–6414
- Cite this reference work entry

3435 Accesses
Study population is a subset of the target population from which the sample is actually selected. It is broader than the concept sample frame . It may be appropriate to say that sample frame is an operationalized form of study population. For example, suppose that a study is going to conduct a survey of high school students on their social well-being . High school students all over the world might be considered as the target population. Because of practicalities, researchers decide to only recruit high school students studying in China who are the study population in this example. Suppose there is a list of high school students of China, this list is used as the sample frame .
Description
Study population is the operational definition of target population (Henry, 1990 ; Bickman & Rog, 1998 ). Researchers are seldom in a position to study the entire target population, which is not always readily accessible. Instead, only part of it—respondents who are both eligible for the study...
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
- Available as PDF
- Read on any device
- Instant download
- Own it forever
- Available as EPUB and PDF
- Durable hardcover edition
- Dispatched in 3 to 5 business days
- Free shipping worldwide - see info
Tax calculation will be finalised at checkout
Purchases are for personal use only
Institutional subscriptions
Babbie, E. R. (2010). The practice of social research . Belmont, CA: Wadsworth Publishing Company.
Google Scholar
Bickman, L., & Rog, D. J. (1998). Handbook of applied social research methods . Thousand Oaks, CA: Sage Publications.
Friedman, L. M., Furberg, C. D., & DeMets, D. L. (2010). Fundamentals of clinical trials . New York: Springer.
Gerrish, K., & Lacey, A. (2010). The research process in nursing . West Sussex: Wiley-Blackwell.
Henry, G. T. (1990). Practical sampling . Newbury Park, CA: Sage Publications.
Kumar, R. (2011). Research methodology: A step-by-step guide for beginners . London: Sage Publications Limited.
Riegelman, R. K. (2005). Studying a study and testing a test: How to read the medical evidence . Philadelphia: Lippincott Williams & Wilkins.
Download references
Author information
Authors and affiliations.
Sociology Department, National University of Singapore, 11 Arts Link, 117570, Singapore, Singapore
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Shu Hu .
Editor information
Editors and affiliations.
University of Northern British Columbia, Prince George, BC, Canada
Alex C. Michalos
(residence), Brandon, MB, Canada
Rights and permissions
Reprints and permissions
Copyright information
© 2014 Springer Science+Business Media Dordrecht
About this entry
Cite this entry.
Hu, S. (2014). Study Population. In: Michalos, A.C. (eds) Encyclopedia of Quality of Life and Well-Being Research. Springer, Dordrecht. https://doi.org/10.1007/978-94-007-0753-5_2893
Download citation
DOI : https://doi.org/10.1007/978-94-007-0753-5_2893
Publisher Name : Springer, Dordrecht
Print ISBN : 978-94-007-0752-8
Online ISBN : 978-94-007-0753-5
eBook Packages : Humanities, Social Sciences and Law
Share this entry
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
Methodology
- Sampling Methods | Types, Techniques & Examples
Sampling Methods | Types, Techniques & Examples
Published on September 19, 2019 by Shona McCombes . Revised on June 22, 2023.
When you conduct research about a group of people, it’s rarely possible to collect data from every person in that group. Instead, you select a sample . The sample is the group of individuals who will actually participate in the research.
To draw valid conclusions from your results, you have to carefully decide how you will select a sample that is representative of the group as a whole. This is called a sampling method . There are two primary types of sampling methods that you can use in your research:
- Probability sampling involves random selection, allowing you to make strong statistical inferences about the whole group.
- Non-probability sampling involves non-random selection based on convenience or other criteria, allowing you to easily collect data.
You should clearly explain how you selected your sample in the methodology section of your paper or thesis, as well as how you approached minimizing research bias in your work.
Table of contents
Population vs. sample, probability sampling methods, non-probability sampling methods, other interesting articles, frequently asked questions about sampling.
First, you need to understand the difference between a population and a sample , and identify the target population of your research.
- The population is the entire group that you want to draw conclusions about.
- The sample is the specific group of individuals that you will collect data from.
The population can be defined in terms of geographical location, age, income, or many other characteristics.
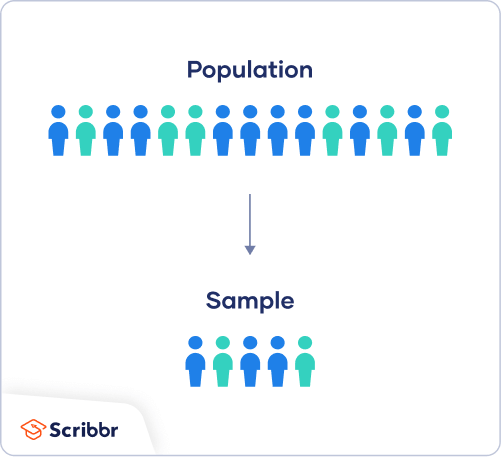
It is important to carefully define your target population according to the purpose and practicalities of your project.
If the population is very large, demographically mixed, and geographically dispersed, it might be difficult to gain access to a representative sample. A lack of a representative sample affects the validity of your results, and can lead to several research biases , particularly sampling bias .
Sampling frame
The sampling frame is the actual list of individuals that the sample will be drawn from. Ideally, it should include the entire target population (and nobody who is not part of that population).

Sample size
The number of individuals you should include in your sample depends on various factors, including the size and variability of the population and your research design. There are different sample size calculators and formulas depending on what you want to achieve with statistical analysis .
Here's why students love Scribbr's proofreading services
Discover proofreading & editing
Probability sampling means that every member of the population has a chance of being selected. It is mainly used in quantitative research . If you want to produce results that are representative of the whole population, probability sampling techniques are the most valid choice.
There are four main types of probability sample.
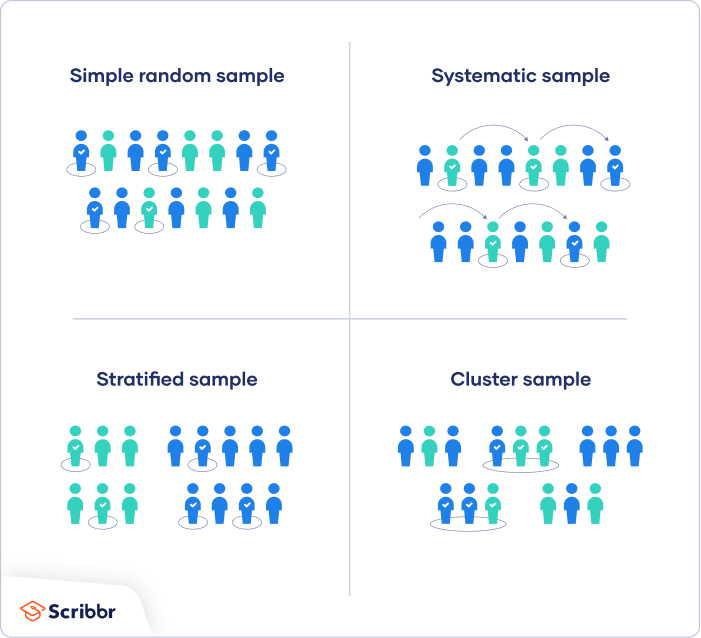
1. Simple random sampling
In a simple random sample, every member of the population has an equal chance of being selected. Your sampling frame should include the whole population.
To conduct this type of sampling, you can use tools like random number generators or other techniques that are based entirely on chance.
2. Systematic sampling
Systematic sampling is similar to simple random sampling, but it is usually slightly easier to conduct. Every member of the population is listed with a number, but instead of randomly generating numbers, individuals are chosen at regular intervals.
If you use this technique, it is important to make sure that there is no hidden pattern in the list that might skew the sample. For example, if the HR database groups employees by team, and team members are listed in order of seniority, there is a risk that your interval might skip over people in junior roles, resulting in a sample that is skewed towards senior employees.
3. Stratified sampling
Stratified sampling involves dividing the population into subpopulations that may differ in important ways. It allows you draw more precise conclusions by ensuring that every subgroup is properly represented in the sample.
To use this sampling method, you divide the population into subgroups (called strata) based on the relevant characteristic (e.g., gender identity, age range, income bracket, job role).
Based on the overall proportions of the population, you calculate how many people should be sampled from each subgroup. Then you use random or systematic sampling to select a sample from each subgroup.
4. Cluster sampling
Cluster sampling also involves dividing the population into subgroups, but each subgroup should have similar characteristics to the whole sample. Instead of sampling individuals from each subgroup, you randomly select entire subgroups.
If it is practically possible, you might include every individual from each sampled cluster. If the clusters themselves are large, you can also sample individuals from within each cluster using one of the techniques above. This is called multistage sampling .
This method is good for dealing with large and dispersed populations, but there is more risk of error in the sample, as there could be substantial differences between clusters. It’s difficult to guarantee that the sampled clusters are really representative of the whole population.
In a non-probability sample, individuals are selected based on non-random criteria, and not every individual has a chance of being included.
This type of sample is easier and cheaper to access, but it has a higher risk of sampling bias . That means the inferences you can make about the population are weaker than with probability samples, and your conclusions may be more limited. If you use a non-probability sample, you should still aim to make it as representative of the population as possible.
Non-probability sampling techniques are often used in exploratory and qualitative research . In these types of research, the aim is not to test a hypothesis about a broad population, but to develop an initial understanding of a small or under-researched population.
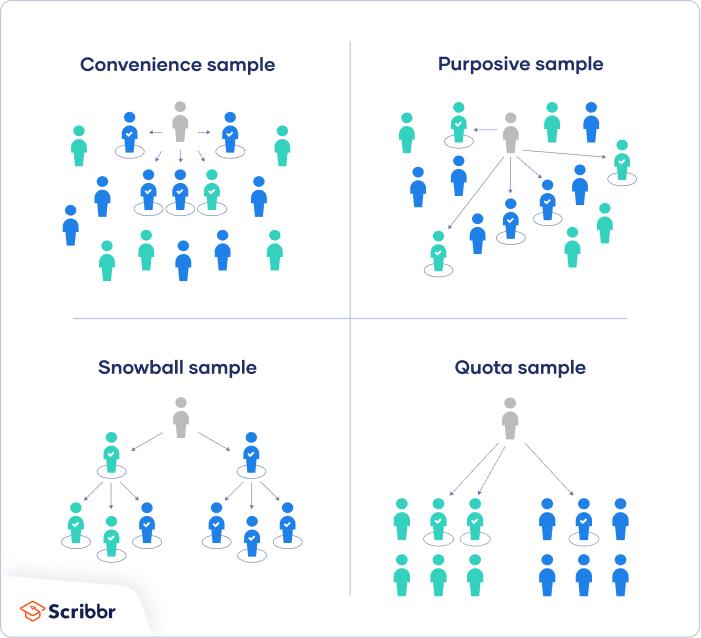
1. Convenience sampling
A convenience sample simply includes the individuals who happen to be most accessible to the researcher.
This is an easy and inexpensive way to gather initial data, but there is no way to tell if the sample is representative of the population, so it can’t produce generalizable results. Convenience samples are at risk for both sampling bias and selection bias .
2. Voluntary response sampling
Similar to a convenience sample, a voluntary response sample is mainly based on ease of access. Instead of the researcher choosing participants and directly contacting them, people volunteer themselves (e.g. by responding to a public online survey).
Voluntary response samples are always at least somewhat biased , as some people will inherently be more likely to volunteer than others, leading to self-selection bias .
3. Purposive sampling
This type of sampling, also known as judgement sampling, involves the researcher using their expertise to select a sample that is most useful to the purposes of the research.
It is often used in qualitative research , where the researcher wants to gain detailed knowledge about a specific phenomenon rather than make statistical inferences, or where the population is very small and specific. An effective purposive sample must have clear criteria and rationale for inclusion. Always make sure to describe your inclusion and exclusion criteria and beware of observer bias affecting your arguments.
4. Snowball sampling
If the population is hard to access, snowball sampling can be used to recruit participants via other participants. The number of people you have access to “snowballs” as you get in contact with more people. The downside here is also representativeness, as you have no way of knowing how representative your sample is due to the reliance on participants recruiting others. This can lead to sampling bias .
5. Quota sampling
Quota sampling relies on the non-random selection of a predetermined number or proportion of units. This is called a quota.
You first divide the population into mutually exclusive subgroups (called strata) and then recruit sample units until you reach your quota. These units share specific characteristics, determined by you prior to forming your strata. The aim of quota sampling is to control what or who makes up your sample.
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Student’s t -distribution
- Normal distribution
- Null and Alternative Hypotheses
- Chi square tests
- Confidence interval
- Quartiles & Quantiles
- Cluster sampling
- Stratified sampling
- Data cleansing
- Reproducibility vs Replicability
- Peer review
- Prospective cohort study
Research bias
- Implicit bias
- Cognitive bias
- Placebo effect
- Hawthorne effect
- Hindsight bias
- Affect heuristic
- Social desirability bias
A sample is a subset of individuals from a larger population . Sampling means selecting the group that you will actually collect data from in your research. For example, if you are researching the opinions of students in your university, you could survey a sample of 100 students.
In statistics, sampling allows you to test a hypothesis about the characteristics of a population.
Samples are used to make inferences about populations . Samples are easier to collect data from because they are practical, cost-effective, convenient, and manageable.
Probability sampling means that every member of the target population has a known chance of being included in the sample.
Probability sampling methods include simple random sampling , systematic sampling , stratified sampling , and cluster sampling .
In non-probability sampling , the sample is selected based on non-random criteria, and not every member of the population has a chance of being included.
Common non-probability sampling methods include convenience sampling , voluntary response sampling, purposive sampling , snowball sampling, and quota sampling .
In multistage sampling , or multistage cluster sampling, you draw a sample from a population using smaller and smaller groups at each stage.
This method is often used to collect data from a large, geographically spread group of people in national surveys, for example. You take advantage of hierarchical groupings (e.g., from state to city to neighborhood) to create a sample that’s less expensive and time-consuming to collect data from.
Sampling bias occurs when some members of a population are systematically more likely to be selected in a sample than others.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
McCombes, S. (2023, June 22). Sampling Methods | Types, Techniques & Examples. Scribbr. Retrieved June 9, 2024, from https://www.scribbr.com/methodology/sampling-methods/
Is this article helpful?
Shona McCombes
Other students also liked, population vs. sample | definitions, differences & examples, simple random sampling | definition, steps & examples, sampling bias and how to avoid it | types & examples, what is your plagiarism score.
- DOI: 10.26685/URNCST.16
- Corpus ID: 133595801
Research Fundamentals: Study Design, Population, and Sample Size
- Umair Majid
- Published 10 January 2018
- Education, Medicine
Tables from this paper

Ask This Paper BETA AI-Powered
86 citations, research fundamentals: data collection, data analysis, and ethics, making research more accessible: the research empowerment & development (red) fellowship program, introduction to qualitative research for novice investigators, participant recruitment among vulnerable populations: an experience from a qualitative study among refugee adolescents in germany, organizing the three forms of qualitative inquiry: a book review of qualitative inquiry – thematic, narrative and arts-based perspectives, the effects of emotional intelligence on teachers’ classroom performance: a case of primary schools in southeast region of botswana, the effectiveness of geography learning in the 2013 curriculum, launching a new brand in the multi-brand portfolio: real world observational study evaluating mediating role of detailing priority and detailing time on physicians’ prescription behavior, the correlation study between students’ vocabulary mastery and descriptive reading comprehension, bibliographic coupling networks of global research on data literacy by documents, sources and authors, 21 references, research fundamentals: the research question, outcomes, and background, sample size calculation for epidemiologic studies: principles and methods., the recruitment, sampling, and enrollment plan, re-calculating the sample size in internal pilot study designs with control of the type i error rate., observational research methods. research design ii: cohort, cross sectional, and case-control studies, sample size calculation for a proof of concept study, are randomized clinical trials good for us (in the short term) evidence for a "trial effect"., descriptive versus interpretive phenomenology: their contributions to nursing knowledge, bias and causal associations in observational research, deconstructing the placebo effect and finding the meaning response, related papers.
Showing 1 through 3 of 0 Related Papers
3. Populations and samples
Populations, unbiasedness and precision, randomisation, variation between samples, standard error of the mean.
Select if the data is a sample of a large or unlimited population and you wish to make a statement about the entire population.', '');" onmouseout="tooltip.hide();">
Related Probability Calculator | Sample Size Calculator | Statistics Calculator
Standard deviation in statistics, typically denoted by σ , is a measure of variation or dispersion (refers to a distribution's extent of stretching or squeezing) between values in a set of data. The lower the standard deviation, the closer the data points tend to be to the mean (or expected value), μ . Conversely, a higher standard deviation indicates a wider range of values. Similar to other mathematical and statistical concepts, there are many different situations in which standard deviation can be used, and thus many different equations. In addition to expressing population variability, the standard deviation is also often used to measure statistical results such as the margin of error. When used in this manner, standard deviation is often called the standard error of the mean, or standard error of the estimate with regard to a mean. The calculator above computes population standard deviation and sample standard deviation, as well as confidence interval approximations.
Population Standard Deviation
The population standard deviation, the standard definition of σ , is used when an entire population can be measured, and is the square root of the variance of a given data set. In cases where every member of a population can be sampled, the following equation can be used to find the standard deviation of the entire population:
| Where is an individual value is the mean/expected value is the total number of values |
For those unfamiliar with summation notation, the equation above may seem daunting, but when addressed through its individual components, this summation is not particularly complicated. The i=1 in the summation indicates the starting index, i.e. for the data set 1, 3, 4, 7, 8, i=1 would be 1, i=2 would be 3, and so on. Hence the summation notation simply means to perform the operation of (x i - μ) 2 on each value through N , which in this case is 5 since there are 5 values in this data set.
EX: μ = (1+3+4+7+8) / 5 = 4.6 σ = √ [(1 - 4.6) 2 + (3 - 4.6) 2 + ... + (8 - 4.6) 2 )]/5 σ = √ (12.96 + 2.56 + 0.36 + 5.76 + 11.56)/5 = 2.577
Sample Standard Deviation
In many cases, it is not possible to sample every member within a population, requiring that the above equation be modified so that the standard deviation can be measured through a random sample of the population being studied. A common estimator for σ is the sample standard deviation, typically denoted by s . It is worth noting that there exist many different equations for calculating sample standard deviation since, unlike sample mean, sample standard deviation does not have any single estimator that is unbiased, efficient, and has a maximum likelihood. The equation provided below is the "corrected sample standard deviation." It is a corrected version of the equation obtained from modifying the population standard deviation equation by using the sample size as the size of the population, which removes some of the bias in the equation. Unbiased estimation of standard deviation, however, is highly involved and varies depending on the distribution. As such, the "corrected sample standard deviation" is the most commonly used estimator for population standard deviation, and is generally referred to as simply the "sample standard deviation." It is a much better estimate than its uncorrected version, but still has a significant bias for small sample sizes (N<10).
| Where is one sample value is the sample mean is the sample size |
Refer to the "Population Standard Deviation" section for an example of how to work with summations. The equation is essentially the same excepting the N-1 term in the corrected sample deviation equation, and the use of sample values.
Applications of Standard Deviation
Standard deviation is widely used in experimental and industrial settings to test models against real-world data. An example of this in industrial applications is quality control for some products. Standard deviation can be used to calculate a minimum and maximum value within which some aspect of the product should fall some high percentage of the time. In cases where values fall outside the calculated range, it may be necessary to make changes to the production process to ensure quality control.
Standard deviation is also used in weather to determine differences in regional climate. Imagine two cities, one on the coast and one deep inland, that have the same mean temperature of 75°F. While this may prompt the belief that the temperatures of these two cities are virtually the same, the reality could be masked if only the mean is addressed and the standard deviation ignored. Coastal cities tend to have far more stable temperatures due to regulation by large bodies of water, since water has a higher heat capacity than land; essentially, this makes water far less susceptible to changes in temperature, and coastal areas remain warmer in winter, and cooler in summer due to the amount of energy required to change the temperature of the water. Hence, while the coastal city may have temperature ranges between 60°F and 85°F over a given period of time to result in a mean of 75°F, an inland city could have temperatures ranging from 30°F to 110°F to result in the same mean.
Another area in which standard deviation is largely used is finance, where it is often used to measure the associated risk in price fluctuations of some asset or portfolio of assets. The use of standard deviation in these cases provides an estimate of the uncertainty of future returns on a given investment. For example, in comparing stock A that has an average return of 7% with a standard deviation of 10% against stock B, that has the same average return but a standard deviation of 50%, the first stock would clearly be the safer option, since the standard deviation of stock B is significantly larger, for the exact same return. That is not to say that stock A is definitively a better investment option in this scenario, since standard deviation can skew the mean in either direction. While Stock A has a higher probability of an average return closer to 7%, Stock B can potentially provide a significantly larger return (or loss).
These are only a few examples of how one might use standard deviation, but many more exist. Generally, calculating standard deviation is valuable any time it is desired to know how far from the mean a typical value from a distribution can be.
| Search | |
A .gov website belongs to an official government organization in the United States.
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.
- Divisions and Offices
- Organization Chart
- Chronic Disease Interventions
- Budget and Funding
- Social Media Resources
- Show All Home
- Chronic Disease
National Center for Chronic Disease Prevention and Health Promotion (NCCDPHP)

Health and Economic Benefits of Chronic Disease Interventions
Interventions that work

Our Impact on Chronic Diseases and Risk Behaviors

About Chronic Diseases
Fast Facts: Health and Economic Costs of Chronic Conditions

Chronic Disease Data and Surveillance
CDC's work to prevent chronic diseases across the lifespan and help people manage their chronic diseases to prevent complications.
World Population Prospects 2022
- Download Center
- Data Portal
- Data Sources
- Graphs / Profiles
- Definition of Regions
- Glossary of Demographic Terms
- Methodology
- Definition of Projection Scenarios
- Frequently Asked Questions
- Publications
- World Urbanization Prospects
- Population Division
The 2022 Revision of World Population Prospects is the twenty-seventh edition of official United Nations population estimates and projections that have been prepared by the Population Division of the Department of Economic and Social Affairs of the United Nations Secretariat. It presents population estimates from 1950 to the present for 237 countries or areas, underpinned by analyses of historical demographic trends. This latest assessment considers the results of 1,758 national population censuses conducted between 1950 and 2022, as well as information from vital registration systems and from 2,890 nationally representative sample surveys The 2022 revision also presents population projections to the year 2100 that reflect a range of plausible outcomes at the global, regional and national levels.
The main results are presented in a series of Excel files displaying key demographic indicators for each UN development group, World Bank income group, geographic region, Sustainable Development Goals (SDGs) region, subregion and country or area for selected periods or dates within 1950-2100. An online database (Data Portal) provides access to a subset of key indicators and interactive data visualization, including an open API for programmatic access. For advanced users who need to use these data in a database form or statistical software, we recommend to use the CSV format for bulk download. Special Aggregates also provide additional groupings of countries. For the first time, the estimates and projections are presented in one-year intervals of age and time instead of the five-year intervals used previously. The various datasets disaggregated by age are available in two forms: by standard 5-year age groups and single ages.
Additional outputs, including results from the probabilistic projections, and more detailed metadata will be posted soon after the initial public release.

Disclaimer: This web site contains data tables, figures, maps, analyses and technical notes from the current revision of the World Population Prospects. These documents do not imply the expression of any opinion whatsoever on the part of the Secretariat of the United Nations concerning the legal status of any country, territory, city or area or of its authorities, or concerning the delimitation of its frontiers or boundaries.
Purdue Online Writing Lab Purdue OWL® College of Liberal Arts
APA Sample Paper

Welcome to the Purdue OWL
This page is brought to you by the OWL at Purdue University. When printing this page, you must include the entire legal notice.
Copyright ©1995-2018 by The Writing Lab & The OWL at Purdue and Purdue University. All rights reserved. This material may not be published, reproduced, broadcast, rewritten, or redistributed without permission. Use of this site constitutes acceptance of our terms and conditions of fair use.
Note: This page reflects the latest version of the APA Publication Manual (i.e., APA 7), which released in October 2019. The equivalent resource for the older APA 6 style can be found here .
Media Files: APA Sample Student Paper , APA Sample Professional Paper
This resource is enhanced by Acrobat PDF files. Download the free Acrobat Reader
Note: The APA Publication Manual, 7 th Edition specifies different formatting conventions for student and professional papers (i.e., papers written for credit in a course and papers intended for scholarly publication). These differences mostly extend to the title page and running head. Crucially, citation practices do not differ between the two styles of paper.
However, for your convenience, we have provided two versions of our APA 7 sample paper below: one in student style and one in professional style.
Note: For accessibility purposes, we have used "Track Changes" to make comments along the margins of these samples. Those authored by [AF] denote explanations of formatting and [AWC] denote directions for writing and citing in APA 7.
APA 7 Student Paper:
Apa 7 professional paper:.

IMAGES
VIDEO
COMMENTS
A part of population that repre sents it completely is known as sample. It means, the units, selected from the population as a sample, must represent all kind of characteristics of different ...
The sampling frame intersects the target population. The sam-ple and sampling frame described extends outside of the target population and population of interest as occa-sionally the sampling frame may include individuals not qualified for the study. Figure 1. The relationship between populations within research.
• Define a research population; • Select a sample from a population; • Explain how the choice and design of data collection method(s) used in the research project are fundamentally influenced by: 1. the aim of the research being undertaken, 2. the population of the study, 3. the kind of data required for the study 4. the location of that ...
Target population, study population and study sample. A population is a complete set of people with a specialized set of characteristics, and a sample is a subset of the population. The usual criteria we use in defining population are geographic, for example, "the population of Uttar Pradesh".
The population of interest is the study's target population that it intends to study or treat. In clinical research studies, it is often not appropriate or feasible to recruit the entire population of interest. Instead, investigators will recruit a sample from the population of interest to include in their study.
A population is a complete set of people with specified characteristics, while a sample is a subset of the population. 1 In general, most people think of the defining characteristic of a population in terms of geographic location. However, in research, other characteristics will define a population.
scientific research, it is impossible (from both a strategic and a resource perspective) to study . all. the members of a population for a research project. It just costs too much and takes too much time. Instead, a selected few par-ticipants (who make up the sample) are chosen to ensure that the sample is representative of the population.
sample is of the population. The degree of generalizability can be discussed in sta tistical terms, depending on the type of sampling strategy that the researcher uses. For example, the researchers who select the 300 students might want to general ize their results to the 3,000 students in the population. In qualitative research, the
Population and sample are fundamental concepts in research that shape the validity and generalizability of study findings. In the realm of research, understanding the concepts of population and sample is paramount to unlocking a treasure trove of knowledge. The population represents the entire group of , , 5. , .
Study population is a subset of the target population from which the sample is actually selected. It is broader than the concept sample frame. It may be appropriate to say that sample frame is an operationalized form of study population. For example, suppose that a study is going to conduct a survey of high school students on their social well ...
While this may be a population, it is even more specific; it is the target population. The aim of the research is to generalize the findings to the target population via your sample. In research, there are 2 kinds of populations: the target pop-ulation and the accessible population. The accessible popula-
A population is the entire group that you want to draw conclusions about. A sample is the specific group that you will collect data from. The size of the sample is always less than the total size of the population. In research, a population doesn't always refer to people. It can mean a group containing elements of anything you want to study ...
A sample is a subset of a population selected to participate in the study, it is a fraction of the whole, selected to participate in the research project (Brink 1996:133; Polit & Hungler 1999:227). In this survey, a subset of 55 women was selected out of the entire population of women who requested TOPs in the Gert Sibande District.
Population vs. sample. First, you need to understand the difference between a population and a sample, and identify the target population of your research.. The population is the entire group that you want to draw conclusions about.; The sample is the specific group of individuals that you will collect data from.; The population can be defined in terms of geographical location, age, income, or ...
Research Fundamentals: Study Design, Population, and Sample Size. Umair Majid. Published 10 January 2018. Education, Medicine. TLDR. In this editorial, the author discusses some considerations for including information in a research protocol on the study design and approach of a research study. Expand.
Answers Chapter 3 Q3.pdf. Populations In statistics the term "population" has a slightly different meaning from the one given to it in ordinary speech. It need not refer only to people or to animate creatures - the population of Britain, for instance or the dog population of London. Statisticians also speak of a population.
A sample that is larger than necessary will be better representative of the population and will hence provide more accurate results. However, beyond a certain point, the increase in accuracy will be small and hence not worth the effort and expense involved in recruiting the extra patients. Furthermore, an overly large sample.
Sample Frames. The sample frame is the source of the sample. A well-designed, well-implemented random sample can be generalized to a sample frame. A sample frame can be a list, or a set of procedures that could generate a list if needed. Not all records in a sample frame will lead to eligible survey respondents.
The (N-n)/(N-1) term in the finite population equation is referred to as the finite population correction factor, and is necessary because it cannot be assumed that all individuals in a sample are independent. For example, if the study population involves 10 people in a room with ages ranging from 1 to 100, and one of those chosen has an age of ...
Sample size is the number of observations or individuals included in a study or experiment. It is the number of individuals, items, or data points selected from a larger population to represent it statistically. The sample size is a crucial consideration in research because it directly impacts the reliability and extent to which you can ...
Sample Standard Deviation. In many cases, it is not possible to sample every member within a population, requiring that the above equation be modified so that the standard deviation can be measured through a random sample of the population being studied. A common estimator for σ is the sample standard deviation, typically denoted by s. It is ...
National Center for Chronic Disease Prevention and Health Promotion (NCCDPHP) CDC's work to prevent chronic diseases across the lifespan and help people manage their chronic diseases to prevent complications.
Appendix B: Comparison of sample characteristics to official population statistics for each country Table B1. Comparison of sample age groups to official population statistics. United States United Kingdom France Canada 18-24 Official 12% 11% 10% 11% Survey 2021 12% 11% 10% 11% Difference 0% 0% 0% 0%
The 2022 Revision of World Population Prospects is the twenty-seventh edition of official United Nations population estimates and projections that have been prepared by the Population Division of the Department of Economic and Social Affairs of the United Nations Secretariat. It presents population estimates from 1950 to the present for 237 countries or areas, underpinned by analyses of ...
Media Files: APA Sample Student Paper , APA Sample Professional Paper This resource is enhanced by Acrobat PDF files. Download the free Acrobat Reader. Note: The APA Publication Manual, 7 th Edition specifies different formatting conventions for student and professional papers (i.e., papers written for credit in a course and papers intended for scholarly publication).
Title. Training Requirements in OSHA Standards. Created Date. 12/21/2016 1:50:51 PM.