problem solving mathematical investigation and modeling

• Our Mission

Using Mathematical Modeling to Get Real With Students

Unlike canned word problems, mathematical modeling plunges students into the messy complexities of real-world problem solving.  

How do you bring math to life for kids? Illustrating the boundless possibilities of mathematics can be difficult if students are only asked to examine hypothetical situations like divvying up a dessert equally or determining how many apples are left after sharing with friends, writes third- and fourth- grade teacher Matthew Kandel for Mathematics Teacher: Learning and Teaching PK-12 .

In the early years of instruction, it’s not uncommon for students to think they’re learning math for the sole purpose of being able to solve word problems or help fictional characters troubleshoot issues in their imaginary lives, Kandel says. “A word problem is a one-dimensional world,” he writes. “Everything is distilled down to the quantities of interest. To solve a word problem, students can pick out the numbers and decide on an operation.” 

But through the use of mathematical modeling, students are plucked out of the hypothetical realm and plunged into the complexities of reality—presented with opportunities to help solve real-world problems with many variables by generating questions, making assumptions, learning and applying new skills, and ultimately arriving at an answer.

In Kandel’s classroom, this work begins with breaking students into small groups, providing them with an unsharpened pencil and a simple, guiding question: “How many times can a pencil be sharpened before it is too small to use?”

Setting the Stage for Inquiry 

The process of tackling the pencil question is not unlike the scientific method. After defining a question to investigate, students begin to wonder and hypothesize—what information do we need to know?—in order to identify a course of action. This step is unique to mathematical modeling: Whereas a word problem is formulaic, leading students down a pre-existing path toward a solution, a modeling task is “free-range,” empowering students to use their individual perspectives to guide them as they progress through their investigation, Kandel says. 

Modeling problems also have a number of variables, and students themselves have the agency to determine what to ignore and what to focus their attention on. 

After inter-group discussions, students in Kandel’s classroom came to the conclusion that they’d need answers to a host of other questions to proceed with answering their initial inquiry: 

• How much does the pencil sharpener remove? 
• What is the length of a brand new, unsharpened pencil? 
• Does the pencil sharpener remove the same amount of pencil each time it is used?

Introducing New Skills in Context

Once students have determined the first mathematical question they’d like to tackle (does the pencil sharpener remove the same amount of pencil each time it is used?), they are met with a roadblock. How were they to measure the pencil if the length did not fall conveniently on an inch or half inch? Kandel took the opportunity to introduce a new target skill which the class could begin using immediately: measuring to the nearest quarter inch. 

“One group of students was not satisfied with the precision of measuring to the nearest quarter inch and asked to learn how to measure to the nearest eighth of an inch,” Kandel explains. “The attention and motivation exhibited by students is unrivaled by the traditional class in which the skill comes first, the problem second.” 

Students reached a consensus and settled on taking six measurements total: the initial length of the new, unsharpened pencil as well as the lengths of the pencil after each of five sharpenings. To ensure all students can practice their newly acquired skill, Kandel tells the class that “all group members must share responsibility, taking turns measuring and checking the measurements of others.” 

Next, each group created a simple chart to record their measurements, then plotted their data as a line graph—though exploring other data visualization techniques or engaging students in alternative followup activities would work as well.

“We paused for a quick lesson on the number line and the introduction of a new term—mixed numbers,” Kandel explains. “Armed with this new information, students had no trouble marking their y-axis in half- or quarter-inch increments.” 

Sparking Mathematical Discussions

Mathematical modeling presents a multitude of opportunities for class-wide or small-group discussions, some which evolve into debates in which students state their hypotheses, then subsequently continue working to confirm or refute them. 

Kandel’s students, for example, had a wide range of opinions when it came to answering the question of how small of a pencil would be deemed unusable. Eventually, the class agreed that once a pencil reached 1 ¼ inch, it could no longer be sharpened—though some students said they would be able to still write with it. 

“This discussion helped us better understand what it means to make an assumption and how our assumptions affected our mathematical outcomes,” Kandel writes. Students then indicated the minimum size with a horizontal line across their respective graphs. 

Many students independently recognized the final step of extending their line while looking at their graphs. With each of the six points representing their measurements, the points descended downward toward the newly added horizontal “line of inoperability.” 

With mathematical modeling, Kandel says, there are no right answers, only models that are “more or less closely aligned with real-world observations.” Each group of students may come to a different conclusion, which can lead to a larger class discussion about accuracy. To prove their group had the most accurate conclusion, students needed to compare and contrast their methods as well as defend their final result. 

Developing Your Own Mathematical Models

The pencil problem is a great starting point for introducing mathematical modeling and free-range problem solving to your students, but you can customize based on what you have available and the particular needs of each group of students.

Depending on the type of pencil sharpener you have, for example, students can determine what constitutes a “fair test” and set the terms of their own inquiry. 

Additionally, Kandel suggests putting scaffolds in place to allow students who are struggling with certain elements to participate: Simplified rulers can be provided for students who need accommodations; charts can be provided for students who struggle with data collection; graphs with prelabeled x- and y-axes can be prepared in advance.

.css-1sk4066:hover{background:#d1ecfa;} 7 Real-World Math Strategies

Students can also explore completely different free-range problem solving and real world applications for math . At North Agincourt Jr. Public School in Scarborough, Canada, kids in grades 1-6 learn to conduct water audits. By adding, subtracting, finding averages, and measuring liquids—like the flow rate of all the water foundations, toilets, and urinals—students measure the amount of water used in their school or home in a single day. 

Or you can ask older students to bring in common household items—anything from a measuring cup to a recipe card—and identify three ways the item relates to math. At Woodrow Petty Elementary School in Taft, Texas, fifth-grade students display their chosen objects on the class’s “real-world math wall.” Even acting out restaurant scenarios can provide students with an opportunity to reinforce critical mathematical skills like addition and subtraction, while bolstering an understanding of decimals and percentages. At Suzhou Singapore International School in China, third- to fifth- graders role play with menus, ordering fictional meals and learning how to split the check when the bill arrives. 

Mathematics for Teaching

This site is NOT about making mathematics easy because it isn't. It is about making it make sense because it does.

What is mathematical investigation?

Mathematical investigation refers to the sustained exploration of a mathematical situation. It distinguishes itself from problem solving because it is open-ended.

I first heard about math investigations in 1990 when I attended a postgraduate course in Australia.  I love it right away and it has since become one of my favorite mathematical activity for my students who were so proud of themselves when they finished their first investigation.

Problem solving is a convergent activity. It has definite goal – the solution of the problem. Mathematical investigation on the other hand is more of a divergent activity. In mathematical investigations, students are expected to pose their own problems after initial exploration of the mathematical situation. The exploration of the situation, the formulation of problems and its solution give opportunity for the development of independent mathematical thinking and in engaging in mathematical processes such as organizing and recording data, pattern searching, conjecturing, inferring, justifying and explaining conjectures and generalizations. It is these thinking processes which enable an individual to learn more mathematics, apply mathematics in other discipline and in everyday situation and to solve mathematical (and non-mathematical) problems.

Teaching through mathematical investigation allows  for students to learn about mathematics, especially the nature of mathematical activity and thinking. It also make them realize that learning mathematics involves intuition, systematic exploration, conjecturing and reasoning, etc and not about memorizing and following existing procedures. The ultimate aim of mathematical investigation is develop students’ mathematical habits of mind .

Although  students may do the same mathematical investigation, it is not expected that all of them will consider the same problem from a particular starting point.  The “open-endedness” of many investigation also means that students may not completely cover the entire situation. However, at least for a student’s own satisfaction, the achievement of some specific results for an investigation is desirable. What is essential is that the students will experience the following mathematical processes which are the emphasis of mathematical investigation:

• systematic exploration of the given situation
• formulating problems and conjectures
• attempting to provide mathematical justifications for the conjectures.

In this kind of activity and teaching, students are given more opportunity to direct their own learning experiences. Note that a problem solving task can be turned into an investigation task by extending the problem by varying for example one of the conditions. To know more about problem solving and how they differ with math investigation read my post on Exercises, Problem Solving and Math Investigation .

Some parents and even teachers complain that students are not learning mathematics in this kind of activity. Indeed they won’t if the teacher will not discuss the results of the investigation, highlight and correct the misconceptions, synthesize students’ findings and help students make connection among the math concepts covered in the investigation. This goes without saying that teachers should try the investigation first before giving it to the students.

I think mathematical investigation is constructivist teaching at its finest. For a sample lesson, read Polygons and algebraic expressions .

• Click to share on Facebook (Opens in new window)
• Click to share on LinkedIn (Opens in new window)
• Click to share on Twitter (Opens in new window)
• Click to share on Reddit (Opens in new window)
• Click to email a link to a friend (Opens in new window)

View All Posts

23 thoughts on “ What is mathematical investigation? ”

Can anyone give me an example of it?

I think there’s a need for students to conduct investigations, especially in math, in order for them to really learn the language of mathematics. We also have to note that those young ones have their own way of doing things; which in some ways may simplify processes. Naci John

Is it possible to teach all math topics using investigation method?

No. Only those topics in math that involves generalizing and conjecturing using the mathematics students at that grade level know may be taught by math investigation. However, you can always start any topic by math investigation but it doesn’t have to be an investigation all the way. The students may see patterns and be able to state a conjecture but they will not always have the capability to explain or justify it mathematically. Doing math investigation is more for developing disposition to think mathematically. Don’t overdo it.

I find this article very informative. I hope UP NISMED can organize a workshop for teachers and students for this essential undertaking in Math. I think reconciling LS and MI will be a great boost in the teaching strats of teachers and mathematical abilities of the students.

• Pingback: Top 20 Math Posts and Pages in 2012 - Mathematics for Teaching

Thank you for posting it.

• Pingback: What is good mathematics? - Mathematics for Teaching
• Pingback: Investigation | The SPIDER Web
• Pingback: Making generalizations in mathematics - Mathematics for Teaching
• Pingback: Bloom's Taxonomy and iPad Apps - Mathematics for Teaching
• Pingback: » Theories and ideas behind the math lessons in this blog » Mathematics for Teaching

In elementary school I had to take investigations. In all 956 lessons standard addition is mentionedONCE and not truly taught. same sor addition and multiplication. long division is never properly taught. they never even mentioned how to do it. they teach a guess and check method leaving you with a remainder- no decimals. This lleaves students with lower grades on timed tests because they are rushed due to the innefficient method they first learned. The board of education deemed the program “sub standard”. Many students who used the program in elementary school needed help with math in middle school. So answer this, why do we continually use investigations?

• Pingback: » Math Lessons in Mathematics for Teaching » Mathematics for Teaching
• Pingback: » Teaching systems of linear equations using elimination method – an introductory investigation » Mathematics for Teaching
• Pingback: » What is reasoning? How can we teach it? » Mathematics for Teaching
• Pingback: Exercises, Problems, and Math Investigations

please, pki investigate naman to: How many other rectangles can be made with twelve tiles?

To me, Math investigation is an ally of constructivism. Students are engaged in tasks that allow them to put in more on what they know as they tinker on a math problem. They do exploration and research to be able to shed more light to the problem. Creative and critical thinking come to the fore. The investigation may take time. But, at the end of the process, students defend what they got, defend it, and share it.

Math investigation takes time. It is quality time. The teacher stands by for consultation and extends assistance, as needed by the students.

My book “High School Geometry with Practical Work and Portfolio Making” is rich on math investigations. My other book “Science Research and Statistics” has much more on investigations particularly on Science Investigatory projects.

hello! i am trying to teach my students to appreciate the process of mathematical investigation and to develop the skills needed. however, i am having a hard time organizing my lessons. i want to them to develop the thinking skills necessary for them to create their own math IPs or math research papers later on. 1. do you have any suggestions or activities or lesson plans that i can refer to so that the skills can be developed gradually? 2.can you recommend any textbook that can be used for this purpose alone including different mathematical model?

i hope that you could answer my queries. thank you very much.

It’s best to expose students to problems with many solutions/answers first before giving them mathematical investigation tasks. You can also convert some of your exercises to problems and mathematical investigation. Check out my post on exercises, problems and math investigations .

I think our use of the Connected Math series really falls in line with this post. Curriclum planning needs to become as strignent as lessons planning that we as teachers work extremely hard on.

• Pingback: Making connections through math investigation: polygons and operations with algebraic expressions- Part 1 « assessing and teaching K-10 mathematics

Comments are closed.

• All courses
• For Teachers
• For Students

Problem Solving, Mathematical Investigation, and Modeling (6081)

This course intends to enhance the students’ knowledge and skills in dealing with real-life and/or non-routine applications of mathematics. Students will have the opportunity to explore the use of problem-solving strategies or heuristics as they engage in mathematical investigations, formulate and justify conjectures, make generalizations, and communicate mathematical ideas.

• Teacher: MELANIE GURAT
• Enrolled students: 2

Problem Solving and Mathematical Modeling

• First Online: 11 January 2023

Cite this chapter

• Parikshit Narendra Mahalle 7 ,
• Nancy Ambritta P. 8 ,
• Sachin R. Sakhare 9 &
• Atul P. Kulkarni 10  

Part of the book series: Studies in Autonomic, Data-driven and Industrial Computing ((SADIC))

184 Accesses

A problem is a puzzle or task that requires a logical thought process or fundamental mathematical steps to solve it. The puzzle generally represents the set of questions on the underlined use case which also consist of complete description of the use case along with the set of constraints about the use case. Logic is very importantly used to solve the puzzle or problem. Logic is defined as a method of human thought that involves thinking in a linear, step-by-step manner about how a problem can be solved. Logic is a subjective matter and varies from person to person. Logic is directly linked to the natural intelligence of human being and is a language of reasoning. Logic also represents the set of rules we use when we do reasoning. It is observed that majority of the employment of fresh engineering graduates across the globe is in software and information technology sector.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info
• Durable hardcover edition

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Rao ORS Hiring trends of fresh engineering graduates. Report in engineering special

Google Scholar  

https://www.linkedin.com/pulse/story-fresh-engineering-graduate-indrani-mukherjee/

Joshi SA, Mahalle PN (2016) Design and analysis of algorithms: a problem solving approach. Cambridge University Press, India, p 209

TOCICO Board of Directors—Theory of constraints international certification organization. www.tocico.org . Retrieved 17 Mar 2018

Dettmer HW (2007) The logical thinking process: a systems approach to complex problem solving. ISBN: 978-0-87389-723-5

Pólya G (1945) How to solve it. Princeton University Press. ISBN: 0-691-08097-6

Dormy RG (2005) How to solve it by computers. Prentice Hall

Levitin A (2005) Introduction to design and analysis of algorithms. Pearson Education Press

Frejd P (2014) Modes of mathematical modelling: an analysis of how modelling is used and interpreted in and out of school settings. Linköping University

Blum W (2015) Quality teaching of mathematical modelling: what do we know, what can we do? In: Cho S (eds) The proceedings of the 12th international congress on mathematical education. Springer, Cham. https://doi.org/10.1007/978-3-319-12688-3_9

Ball DL, Hill HC, Bass H (2005) Knowing mathematics for teaching. Am Educ 29(3):14–46

Biccard P, Wessels DCJ (2011) Documenting the development of modelling competencies of grade 7 students. In: Kaiser G et al (eds) Trends in teaching and learning of mathematical modelling (ICTMA 14). Springer, Dordrecht, pp 375–383

Chapter   Google Scholar  

Kantner J (2008) The only absolute truth in mathematics is the myth of mathematics as universal. Perspect: N Y J Adult Learn 6(2). Retrieved from http://www.eric.ed.gov/PDFS/ED501486.pdf

Download references

Author information

Authors and affiliations.

Department of Artificial Intelligence and Data Science, Vishwakarma Institute of Information Technology, Pune, India

Parikshit Narendra Mahalle

Glareal Software Solutions PTE. Ltd., Singapore, Singapore

Nancy Ambritta P.

Department of Computer Engineering, Vishwakarma Institute of Information Technology, Pune, India

Sachin R. Sakhare

Department of Mechanical Engineering, Vishwakarma Institute of Information Technology, Pune, India

Atul P. Kulkarni

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Nancy Ambritta P. .

Rights and permissions

Reprints and permissions

Copyright information

© 2023 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.

About this chapter

Mahalle, P.N., Ambritta P., N., Sakhare, S.R., Kulkarni, A.P. (2023). Problem Solving and Mathematical Modeling. In: Foundations of Mathematical Modelling for Engineering Problem Solving. Studies in Autonomic, Data-driven and Industrial Computing. Springer, Singapore. https://doi.org/10.1007/978-981-19-8828-8_2

Download citation

DOI : https://doi.org/10.1007/978-981-19-8828-8_2

Published : 11 January 2023

Publisher Name : Springer, Singapore

Print ISBN : 978-981-19-8827-1

Online ISBN : 978-981-19-8828-8

eBook Packages : Intelligent Technologies and Robotics Intelligent Technologies and Robotics (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

• STEM Ambassadors
• School trusts
• ITE and governors
• Invest in schools
• STEM careers inspiration
• Benefits and impact
• Our supporters
• Become a STEM Ambassador
• Request a STEM Ambassador
• Employer information
• Training and support
• STEM Ambassadors Partners
• Working with community groups
• Search icon
• Join the STEM Community

Mathematics: Problem Solving and Investigations

A list of resources containing activities which could be integrated into your scheme of work with the purpose of integrating problem solving and investigational maths work into the natural process of learning mathematics and not just as a bolt-on added extra.

The first few resources are aimed at primary mathematics with the remainder aimed at Key Stages 3 & 4.

Making Molecules

Quality Assured Category: Mathematics Publisher: cre8ate maths

This activity asks students to investigate the structure of hydrocarbons.  A printed sheet representing carbon and hydrogen atoms is cut up and used by students to build as many isomers as they can for two chemical formulae.

Students are then challenged to discover a 3-D shape with 60 vertices, made from regular pentagons and hexagons. Teachers may choose to give 12 pentagons and 20 hexagons to groups of students for them to build the model or make up the shape from its net.

Problem Cards

Quality Assured Collection Category: Mathematics Publisher: Nuffield Foundation

This collection contains two packs of problem cards that have been designed for use by students in conjunction with the main work described in the Teachers' Guides. It is intended that the majority of students should at least be able to 'have a go' at most of the questions, but should also be encouraged, to the full extent of their individual abilities, to think around a problem and to devise alternatives and generalisations.

There are two packs of problem cards, purple and red, each accompanied by a teachers' guide.

Starting Investigations

Quality Assured Category: Mathematics Publisher: Collins Educational

A book of mathematical investigations aimed at students working at National Curriculum levels 1 to 3.

Contains forty simple investigations covering topics such as Odds and Evens, Place Value, Number patterns and many more.

Badger Maths problem solving

Quality Assured Category: Mathematics Publisher: Badger

A series of resources aimed at years one through to six aimed at developing problem solving skills. Each resource gives an example of a four step problem solving approach and task cards split into levels.

Problem solving with EYFS, Key Stage One and Key Stage Two children

Quality Assured Category: Computing Publisher: Department for Education

A set of resources from the National Strategies aimed at years one to six designed to help students become proficient problem solvers in mathematics.

Problem Solving Tasks

Quality Assured Collection Category: Mathematics Publisher:

The Spode Group have produced a number of resources to support problem solving in mathematics through real life problems.

The resources contain a wide range of open-ended tasks, practical tasks, investigations and real life problems still useful today to place the mathematics learnt in the classroom into a real world context.

Bowland Maths: Assessment Tasks

Quality Assured Collection Category: Mathematics Publisher: Bowland Charitable Trust

Bowland Maths includes over thirty tasks designed to help assess students’ achievements and progression against key processes. To help with this assessment, each task contains sample work, and a 'progression table' showing how students’ work on the task can provide evidence of their progress with the four key processes: representing, analysing, communicating and reflecting.

These materials are also ideal for formative assessment that concentrates on providing the types of rich feedback that have been proven to help students improve their reasoning.

Graded Assessment in Mathematics (GAIM)

Quality Assured Collection Category: Mathematics Publisher: Nelson Thornes

GAIM is a teacher assessment scheme for Key Stages Three and Four. The scheme is designed to encourage teaching and learning through practical problem solving and investigations,  involve students in all assessment and record keeping and introduce continuous assessment into normal classroom practice.

Investigative and Problem-Solving Approaches to Mathematics and Their Assessment

Quality Assured Category: Mathematics Publisher: Institute of Physics

This resource was written in response to the Cockroft Report to address the recommendation that all mathematics teaching should include opportunities for exposition by the teacher, discussion between teachers and students and between students themselves, practical work, consolidation and practice, problem solving and investigational work. The purpose of the pack was to address these issues and support their introduction and assessment.

Design a Board Game

Quality Assured Category: Mathematics Publisher: Shell Centre for Mathematical Education

In this Shell Centre module, groups carefully design and produce their own board games. These games are then played and evaluated by other class members.

Plan a Trip

In this Shell Centre module students plan and undertake a class trip using costings, scheduling, surveys and everyday arithmetic.

Produce a Quiz Show

In this Shell Centre modlue, Produce a Quiz Show, students devise, schedule, run and evaluate their own classroom quizzes.

Pure Investigations

These two books from the Shell centre focus on the pure investigations.

Let's Connect

Contact details.

Brgy. Atabay, Hilongos, Leyte, Philippines 6524

+639 17-306-5169

Get in Touch

Your Phone Number

Your E-mail

• Glenn’s Memoir
• Online Admission

Want to receive push notifications for all major on-site activities?

This Area is Widget-Ready

You can place here any widget you want!

You can also display any layout saved in Divi Library.

Let’s try with contact form:

Insert/edit link

Enter the destination URL

Or link to existing content

• Open supplemental data
• Reference Manager
• Simple TEXT file

People also looked at

Original research article, mathematical problem-solving through cooperative learning—the importance of peer acceptance and friendships.

• 1 Department of Education, Uppsala University, Uppsala, Sweden
• 2 Department of Education, Culture and Communication, Malardalen University, Vasteras, Sweden
• 3 School of Natural Sciences, Technology and Environmental Studies, Sodertorn University, Huddinge, Sweden
• 4 Faculty of Education, Gothenburg University, Gothenburg, Sweden

Mathematical problem-solving constitutes an important area of mathematics instruction, and there is a need for research on instructional approaches supporting student learning in this area. This study aims to contribute to previous research by studying the effects of an instructional approach of cooperative learning on students’ mathematical problem-solving in heterogeneous classrooms in grade five, in which students with special needs are educated alongside with their peers. The intervention combined a cooperative learning approach with instruction in problem-solving strategies including mathematical models of multiplication/division, proportionality, and geometry. The teachers in the experimental group received training in cooperative learning and mathematical problem-solving, and implemented the intervention for 15 weeks. The teachers in the control group received training in mathematical problem-solving and provided instruction as they would usually. Students (269 in the intervention and 312 in the control group) participated in tests of mathematical problem-solving in the areas of multiplication/division, proportionality, and geometry before and after the intervention. The results revealed significant effects of the intervention on student performance in overall problem-solving and problem-solving in geometry. The students who received higher scores on social acceptance and friendships for the pre-test also received higher scores on the selected tests of mathematical problem-solving. Thus, the cooperative learning approach may lead to gains in mathematical problem-solving in heterogeneous classrooms, but social acceptance and friendships may also greatly impact students’ results.

Introduction

The research on instruction in mathematical problem-solving has progressed considerably during recent decades. Yet, there is still a need to advance our knowledge on how teachers can support their students in carrying out this complex activity ( Lester and Cai, 2016 ). Results from the Program for International Student Assessment (PISA) show that only 53% of students from the participating countries could solve problems requiring more than direct inference and using representations from different information sources ( OECD, 2019 ). In addition, OECD (2019) reported a large variation in achievement with regard to students’ diverse backgrounds. Thus, there is a need for instructional approaches to promote students’ problem-solving in mathematics, especially in heterogeneous classrooms in which students with diverse backgrounds and needs are educated together. Small group instructional approaches have been suggested as important to promote learning of low-achieving students and students with special needs ( Kunsch et al., 2007 ). One such approach is cooperative learning (CL), which involves structured collaboration in heterogeneous groups, guided by five principles to enhance group cohesion ( Johnson et al., 1993 ; Johnson et al., 2009 ; Gillies, 2016 ). While CL has been well-researched in whole classroom approaches ( Capar and Tarim, 2015 ), few studies of the approach exist with regard to students with special educational needs (SEN; McMaster and Fuchs, 2002 ). This study contributes to previous research by studying the effects of the CL approach on students’ mathematical problem-solving in heterogeneous classrooms, in which students with special needs are educated alongside with their peers.

Group collaboration through the CL approach is structured in accordance with five principles of collaboration: positive interdependence, individual accountability, explicit instruction in social skills, promotive interaction, and group processing ( Johnson et al., 1993 ). First, the group tasks need to be structured so that all group members feel dependent on each other in the completion of the task, thus promoting positive interdependence. Second, for individual accountability, the teacher needs to assure that each group member feels responsible for his or her share of work, by providing opportunities for individual reports or evaluations. Third, the students need explicit instruction in social skills that are necessary for collaboration. Fourth, the tasks and seat arrangements should be designed to promote interaction among group members. Fifth, time needs to be allocated to group processing, through which group members can evaluate their collaborative work to plan future actions. Using these principles for cooperation leads to gains in mathematics, according to Capar and Tarim (2015) , who conducted a meta-analysis on studies of cooperative learning and mathematics, and found an increase of .59 on students’ mathematics achievement scores in general. However, the number of reviewed studies was limited, and researchers suggested a need for more research. In the current study, we focused on the effect of CL approach in a specific area of mathematics: problem-solving.

Mathematical problem-solving is a central area of mathematics instruction, constituting an important part of preparing students to function in modern society ( Gravemeijer et al., 2017 ). In fact, problem-solving instruction creates opportunities for students to apply their knowledge of mathematical concepts, integrate and connect isolated pieces of mathematical knowledge, and attain a deeper conceptual understanding of mathematics as a subject ( Lester and Cai, 2016 ). Some researchers suggest that mathematics itself is a science of problem-solving and of developing theories and methods for problem-solving ( Hamilton, 2007 ; Davydov, 2008 ).

Problem-solving processes have been studied from different perspectives ( Lesh and Zawojewski, 2007 ). Problem-solving heuristics Pólya, (1948) has largely influenced our perceptions of problem-solving, including four principles: understanding the problem, devising a plan, carrying out the plan, and looking back and reflecting upon the suggested solution. Schoenfield, (2016) suggested the use of specific problem-solving strategies for different types of problems, which take into consideration metacognitive processes and students’ beliefs about problem-solving. Further, models and modelling perspectives on mathematics ( Lesh and Doerr, 2003 ; Lesh and Zawojewski, 2007 ) emphasize the importance of engaging students in model-eliciting activities in which problem situations are interpreted mathematically, as students make connections between problem information and knowledge of mathematical operations, patterns, and rules ( Mousoulides et al., 2010 ; Stohlmann and Albarracín, 2016 ).

Not all students, however, find it easy to solve complex mathematical problems. Students may experience difficulties in identifying solution-relevant elements in a problem or visualizing appropriate solution to a problem situation. Furthermore, students may need help recognizing the underlying model in problems. For example, in two studies by Degrande et al. (2016) , students in grades four to six were presented with mathematical problems in the context of proportional reasoning. The authors found that the students, when presented with a word problem, could not identify an underlying model, but rather focused on superficial characteristics of the problem. Although the students in the study showed more success when presented with a problem formulated in symbols, the authors pointed out a need for activities that help students distinguish between different proportional problem types. Furthermore, students exhibiting specific learning difficulties may need additional support in both general problem-solving strategies ( Lein et al., 2020 ; Montague et al., 2014 ) and specific strategies pertaining to underlying models in problems. The CL intervention in the present study focused on supporting students in problem-solving, through instruction in problem-solving principles ( Pólya, 1948 ), specifically applied to three models of mathematical problem-solving—multiplication/division, geometry, and proportionality.

Students’ problem-solving may be enhanced through participation in small group discussions. In a small group setting, all the students have the opportunity to explain their solutions, clarify their thinking, and enhance understanding of a problem at hand ( Yackel et al., 1991 ; Webb and Mastergeorge, 2003 ). In fact, small group instruction promotes students’ learning in mathematics by providing students with opportunities to use language for reasoning and conceptual understanding ( Mercer and Sams, 2006 ), to exchange different representations of the problem at hand ( Fujita et al., 2019 ), and to become aware of and understand groupmates’ perspectives in thinking ( Kazak et al., 2015 ). These opportunities for learning are created through dialogic spaces characterized by openness to each other’s perspectives and solutions to mathematical problems ( Wegerif, 2011 ).

However, group collaboration is not only associated with positive experiences. In fact, studies show that some students may not be given equal opportunities to voice their opinions, due to academic status differences ( Langer-Osuna, 2016 ). Indeed, problem-solvers struggling with complex tasks may experience negative emotions, leading to uncertainty of not knowing the definite answer, which places demands on peer support ( Jordan and McDaniel, 2014 ; Hannula, 2015 ). Thus, especially in heterogeneous groups, students may need additional support to promote group interaction. Therefore, in this study, we used a cooperative learning approach, which, in contrast to collaborative learning approaches, puts greater focus on supporting group cohesion through instruction in social skills and time for reflection on group work ( Davidson and Major, 2014 ).

Although cooperative learning approach is intended to promote cohesion and peer acceptance in heterogeneous groups ( Rzoska and Ward, 1991 ), previous studies indicate that challenges in group dynamics may lead to unequal participation ( Mulryan, 1992 ; Cohen, 1994 ). Peer-learning behaviours may impact students’ problem-solving ( Hwang and Hu, 2013 ) and working in groups with peers who are seen as friends may enhance students’ motivation to learn mathematics ( Deacon and Edwards, 2012 ). With the importance of peer support in mind, this study set out to investigate whether the results of the intervention using the CL approach are associated with students’ peer acceptance and friendships.

The Present Study

In previous research, the CL approach has shown to be a promising approach in teaching and learning mathematics ( Capar and Tarim, 2015 ), but fewer studies have been conducted in whole-class approaches in general and students with SEN in particular ( McMaster and Fuchs, 2002 ). This study aims to contribute to previous research by investigating the effect of CL intervention on students’ mathematical problem-solving in grade 5. With regard to the complexity of mathematical problem-solving ( Lesh and Zawojewski, 2007 ; Degrande et al., 2016 ; Stohlmann and Albarracín, 2016 ), the CL approach in this study was combined with problem-solving principles pertaining to three underlying models of problem-solving—multiplication/division, geometry, and proportionality. Furthermore, considering the importance of peer support in problem-solving in small groups ( Mulryan, 1992 ; Cohen, 1994 ; Hwang and Hu, 2013 ), the study investigated how peer acceptance and friendships were associated with the effect of the CL approach on students’ problem-solving abilities. The study aimed to find answers to the following research questions:

a) What is the effect of CL approach on students’ problem-solving in mathematics?

b) Are social acceptance and friendship associated with the effect of CL on students’ problem-solving in mathematics?

Participants

The participants were 958 students in grade 5 and their teachers. According to power analyses prior to the start of the study, 1,020 students and 51 classes were required, with an expected effect size of 0.30 and power of 80%, provided that there are 20 students per class and intraclass correlation is 0.10. An invitation to participate in the project was sent to teachers in five municipalities via e-mail. Furthermore, the information was posted on the website of Uppsala university and distributed via Facebook interest groups. As shown in Figure 1 , teachers of 1,165 students agreed to participate in the study, but informed consent was obtained only for 958 students (463 in the intervention and 495 in the control group). Further attrition occurred at pre- and post-measurement, resulting in 581 students’ tests as a basis for analyses (269 in the intervention and 312 in the control group). Fewer students (n = 493) were finally included in the analyses of the association of students’ social acceptance and friendships and the effect of CL on students’ mathematical problem-solving (219 in the intervention and 274 in the control group). The reasons for attrition included teacher drop out due to sick leave or personal circumstances (two teachers in the control group and five teachers in the intervention group). Furthermore, some students were sick on the day of data collection and some teachers did not send the test results to the researchers.

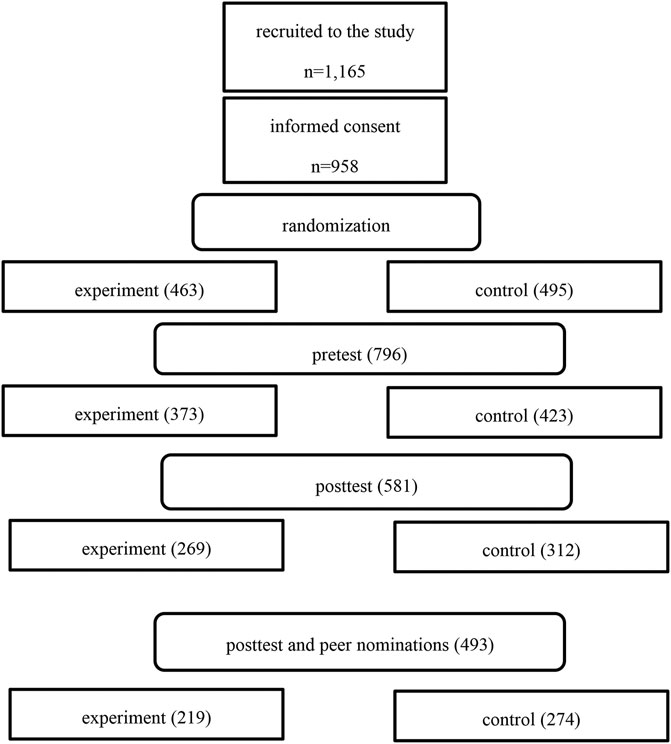
FIGURE 1 . Flow chart for participants included in data collection and data analysis.

As seen in Table 1 , classes in both intervention and control groups included 27 students on average. For 75% of the classes, there were 33–36% of students with SEN. In Sweden, no formal medical diagnosis is required for the identification of students with SEN. It is teachers and school welfare teams who decide students’ need for extra adaptations or special support ( Swedish National Educational Agency, 2014 ). The information on individual students’ type of SEN could not be obtained due to regulations on the protection of information about individuals ( SFS 2009 ). Therefore, the information on the number of students with SEN on class level was obtained through teacher reports.

TABLE 1 . Background characteristics of classes and teachers in intervention and control groups.

Intervention

The intervention using the CL approach lasted for 15 weeks and the teachers worked with the CL approach three to four lessons per week. First, the teachers participated in two-days training on the CL approach, using an especially elaborated CL manual ( Klang et al., 2018 ). The training focused on the five principles of the CL approach (positive interdependence, individual accountability, explicit instruction in social skills, promotive interaction, and group processing). Following the training, the teachers introduced the CL approach in their classes and focused on group-building activities for 7 weeks. Then, 2 days of training were provided to teachers, in which the CL approach was embedded in activities in mathematical problem-solving and reading comprehension. Educational materials containing mathematical problems in the areas of multiplication and division, geometry, and proportionality were distributed to the teachers ( Karlsson and Kilborn, 2018a ). In addition to the specific problems, adapted for the CL approach, the educational materials contained guidance for the teachers, in which problem-solving principles ( Pólya, 1948 ) were presented as steps in problem-solving. Following the training, the teachers applied the CL approach in mathematical problem-solving lessons for 8 weeks.

Solving a problem is a matter of goal-oriented reasoning, starting from the understanding of the problem to devising its solution by using known mathematical models. This presupposes that the current problem is chosen from a known context ( Stillman et al., 2008 ; Zawojewski, 2010 ). This differs from the problem-solving of the textbooks, which is based on an aim to train already known formulas and procedures ( Hamilton, 2007 ). Moreover, it is important that students learn modelling according to their current abilities and conditions ( Russel, 1991 ).

In order to create similar conditions in the experiment group and the control group, the teachers were supposed to use the same educational material ( Karlsson and Kilborn, 2018a ; Karlsson and Kilborn, 2018b ), written in light of the specified view of problem-solving. The educational material is divided into three areas—multiplication/division, geometry, and proportionality—and begins with a short teachers’ guide, where a view of problem solving is presented, which is based on the work of Polya (1948) and Lester and Cai (2016) . The tasks are constructed in such a way that conceptual knowledge was in focus, not formulas and procedural knowledge.

Implementation of the Intervention

To ensure the implementation of the intervention, the researchers visited each teachers’ classroom twice during the two phases of the intervention period, as described above. During each visit, the researchers observed the lesson, using a checklist comprising the five principles of the CL approach. After the lesson, the researchers gave written and oral feedback to each teacher. As seen in Table 1 , in 18 of the 23 classes, the teachers implemented the intervention in accordance with the principles of CL. In addition, the teachers were asked to report on the use of the CL approach in their teaching and the use of problem-solving activities embedding CL during the intervention period. As shown in Table 1 , teachers in only 11 of 23 classes reported using the CL approach and problem-solving activities embedded in the CL approach at least once a week.

Control Group

The teachers in the control group received 2 days of instruction in enhancing students’ problem-solving and reading comprehension. The teachers were also supported with educational materials including mathematical problems Karlsson and Kilborn (2018b) and problem-solving principles ( Pólya, 1948 ). However, none of the activities during training or in educational materials included the CL approach. As seen in Table 1 , only 10 of 25 teachers reported devoting at least one lesson per week to mathematical problem-solving.

Tests of Mathematical Problem-Solving

Tests of mathematical problem-solving were administered before and after the intervention, which lasted for 15 weeks. The tests were focused on the models of multiplication/division, geometry, and proportionality. The three models were chosen based on the syllabus of the subject of mathematics in grades 4 to 6 in the Swedish National Curriculum ( Swedish National Educational Agency, 2018 ). In addition, the intention was to create a variation of types of problems to solve. For each of these three models, there were two tests, a pre-test and a post-test. Each test contained three tasks with increasing difficulty ( Supplementary Appendix SA ).

The tests of multiplication and division (Ma1) were chosen from different contexts and began with a one-step problem, while the following two tasks were multi-step problems. Concerning multiplication, many students in grade 5 still understand multiplication as repeated addition, causing significant problems, as this conception is not applicable to multiplication beyond natural numbers ( Verschaffel et al., 2007 ). This might be a hindrance in developing multiplicative reasoning ( Barmby et al., 2009 ). The multi-step problems in this study were constructed to support the students in multiplicative reasoning.

Concerning the geometry tests (Ma2), it was important to consider a paradigm shift concerning geometry in education that occurred in the mid-20th century, when strict Euclidean geometry gave way to other aspects of geometry like symmetry, transformation, and patterns. van Hiele (1986) prepared a new taxonomy for geometry in five steps, from a visual to a logical level. Therefore, in the tests there was a focus on properties of quadrangles and triangles, and how to determine areas by reorganising figures into new patterns. This means that structure was more important than formulas.

The construction of tests of proportionality (M3) was more complicated. Firstly, tasks on proportionality can be found in many different contexts, such as prescriptions, scales, speeds, discounts, interest, etc. Secondly, the mathematical model is complex and requires good knowledge of rational numbers and ratios ( Lesh et al., 1988 ). It also requires a developed view of multiplication, useful in operations with real numbers, not only as repeated addition, an operation limited to natural numbers ( Lybeck, 1981 ; Degrande et al., 2016 ). A linear structure of multiplication as repeated addition leads to limitations in terms of generalization and development of the concept of multiplication. This became evident in a study carried out in a Swedish context ( Karlsson and Kilborn, 2018c ). Proportionality can be expressed as a/b = c/d or as a/b = k. The latter can also be expressed as a = b∙k, where k is a constant that determines the relationship between a and b. Common examples of k are speed (km/h), scale, and interest (%). An important pre-knowledge in order to deal with proportions is to master fractions as equivalence classes like 1/3 = 2/6 = 3/9 = 4/12 = 5/15 = 6/18 = 7/21 = 8/24 … ( Karlsson and Kilborn, 2020 ). It was important to take all these aspects into account when constructing and assessing the solutions of the tasks.

The tests were graded by an experienced teacher of mathematics (4 th author) and two students in their final year of teacher training. Prior to grading, acceptable levels of inter-rater reliability were achieved by independent rating of students’ solutions and discussions in which differences between the graders were resolved. Each student response was to be assigned one point when it contained a correct answer and two points when the student provided argumentation for the correct answer and elaborated on explanation of his or her solution. The assessment was thus based on quality aspects with a focus on conceptual knowledge. As each subtest contained three questions, it generated three student solutions. So, scores for each subtest ranged from 0 to 6 points and for the total scores from 0 to 18 points. To ascertain that pre- and post-tests were equivalent in degree of difficulty, the tests were administered to an additional sample of 169 students in grade 5. Test for each model was conducted separately, as students participated in pre- and post-test for each model during the same lesson. The order of tests was switched for half of the students in order to avoid the effect of the order in which the pre- and post-tests were presented. Correlation between students’ performance on pre- and post-test was .39 ( p < 0.000) for tests of multiplication/division; .48 ( p < 0.000) for tests of geometry; and .56 ( p < 0.000) for tests of proportionality. Thus, the degree of difficulty may have differed between pre- and post-test.

Measures of Peer Acceptance and Friendships

To investigate students’ peer acceptance and friendships, peer nominations rated pre- and post-intervention were used. Students were asked to nominate peers who they preferred to work in groups with and who they preferred to be friends with. Negative peer nominations were avoided due to ethical considerations raised by teachers and parents ( Child and Nind, 2013 ). Unlimited nominations were used, as these are considered to have high ecological validity ( Cillessen and Marks, 2017 ). Peer nominations were used as a measure of social acceptance, and reciprocated nominations were used as a measure of friendship. The number of nominations for each student were aggregated and divided by the number of nominators to create a proportion of nominations for each student ( Velásquez et al., 2013 ).

Statistical Analyses

Multilevel regression analyses were conducted in R, lme4 package Bates et al. (2015) to account for nestedness in the data. Students’ classroom belonging was considered as a level 2 variable. First, we used a model in which students’ results on tests of problem-solving were studied as a function of time (pre- and post) and group belonging (intervention and control group). Second, the same model was applied to subgroups of students who performed above and below median at pre-test, to explore whether the CL intervention had a differential effect on student performance. In this second model, the results for subgroups of students could not be obtained for geometry tests for subgroup below median and for tests of proportionality for subgroup above median. A possible reason for this must have been the skewed distribution of the students in these subgroups. Therefore, another model was applied that investigated students’ performances in math at both pre- and post-test as a function of group belonging. Third, the students’ scores on social acceptance and friendships were added as an interaction term to the first model. In our previous study, students’ social acceptance changed as a result of the same CL intervention ( Klang et al., 2020 ).

The assumptions for the multilevel regression were assured during the analyses ( Snijders and Bosker, 2012 ). The assumption of normality of residuals were met, as controlled by visual inspection of quantile-quantile plots. For subgroups, however, the plotted residuals deviated somewhat from the straight line. The number of outliers, which had a studentized residual value greater than ±3, varied from 0 to 5, but none of the outliers had a Cook’s distance value larger than 1. The assumption of multicollinearity was met, as the variance inflation factors (VIF) did not exceed a value of 10. Before the analyses, the cases with missing data were deleted listwise.

What Is the Effect of the CL Approach on Students’ Problem-Solving in Mathematics?

As seen in the regression coefficients in Table 2 , the CL intervention had a significant effect on students’ mathematical problem-solving total scores and students’ scores in problem solving in geometry (Ma2). Judging by mean values, students in the intervention group appeared to have low scores on problem-solving in geometry but reached the levels of problem-solving of the control group by the end of the intervention. The intervention did not have a significant effect on students’ performance in problem-solving related to models of multiplication/division and proportionality.

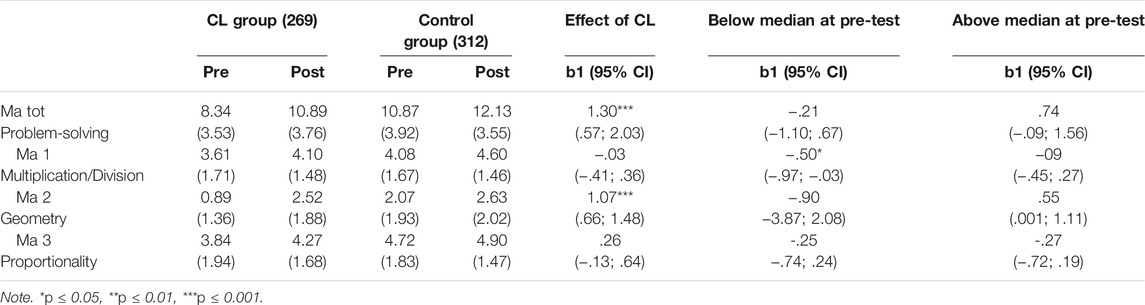
TABLE 2 . Mean scores (standard deviation in parentheses) and unstandardized multilevel regression estimates for tests of mathematical problem-solving.

The question is, however, whether CL intervention affected students with different pre-test scores differently. Table 2 includes the regression coefficients for subgroups of students who performed below and above median at pre-test. As seen in the table, the CL approach did not have a significant effect on students’ problem-solving, when the sample was divided into these subgroups. A small negative effect was found for intervention group in comparison to control group, but confidence intervals (CI) for the effect indicate that it was not significant.

Is Social Acceptance and Friendships Associated With the Effect of CL on Students’ Problem-Solving in Mathematics?

As seen in Table 3 , students’ peer acceptance and friendship at pre-test were significantly associated with the effect of the CL approach on students’ mathematical problem-solving scores. Changes in students’ peer acceptance and friendships were not significantly associated with the effect of the CL approach on students’ mathematical problem-solving. Consequently, it can be concluded that being nominated by one’s peers and having friends at the start of the intervention may be an important factor when participation in group work, structured in accordance with the CL approach, leads to gains in mathematical problem-solving.

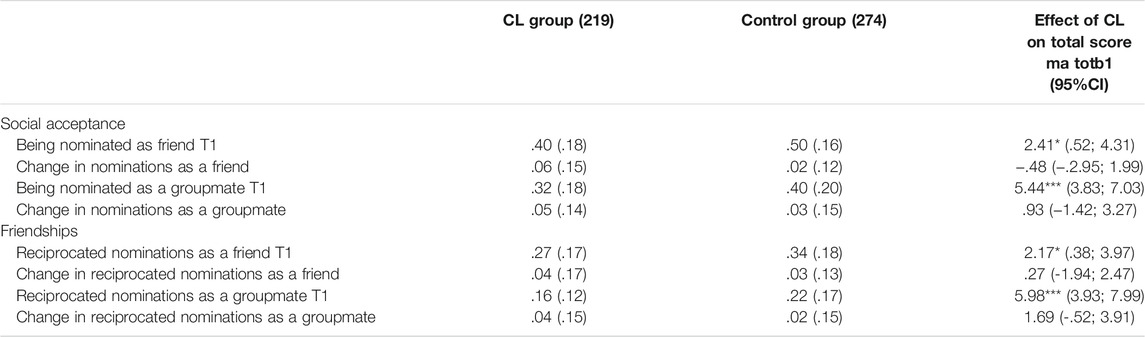
TABLE 3 . Mean scores (standard deviation in parentheses) and unstandardized multilevel regression estimates for tests of mathematical problem-solving, including scores of social acceptance and friendship in the model.

In light of the limited number of studies on the effects of CL on students’ problem-solving in whole classrooms ( Capar and Tarim, 2015 ), and for students with SEN in particular ( McMaster and Fuchs, 2002 ), this study sought to investigate whether the CL approach embedded in problem-solving activities has an effect on students’ problem-solving in heterogeneous classrooms. The need for the study was justified by the challenge of providing equitable mathematics instruction to heterogeneous student populations ( OECD, 2019 ). Small group instructional approaches as CL are considered as promising approaches in this regard ( Kunsch et al., 2007 ). The results showed a significant effect of the CL approach on students’ problem-solving in geometry and total problem-solving scores. In addition, with regard to the importance of peer support in problem-solving ( Deacon and Edwards, 2012 ; Hwang and Hu, 2013 ), the study explored whether the effect of CL on students’ problem-solving was associated with students’ social acceptance and friendships. The results showed that students’ peer acceptance and friendships at pre-test were significantly associated with the effect of the CL approach, while change in students’ peer acceptance and friendships from pre- to post-test was not.

The results of the study confirm previous research on the effect of the CL approach on students’ mathematical achievement ( Capar and Tarim, 2015 ). The specific contribution of the study is that it was conducted in classrooms, 75% of which were composed of 33–36% of students with SEN. Thus, while a previous review revealed inconclusive findings on the effects of CL on student achievement ( McMaster and Fuchs, 2002 ), the current study adds to the evidence of the effect of the CL approach in heterogeneous classrooms, in which students with special needs are educated alongside with their peers. In a small group setting, the students have opportunities to discuss their ideas of solutions to the problem at hand, providing explanations and clarifications, thus enhancing their understanding of problem-solving ( Yackel et al., 1991 ; Webb and Mastergeorge, 2003 ).

In this study, in accordance with previous research on mathematical problem-solving ( Lesh and Zawojewski, 2007 ; Degrande et al., 2016 ; Stohlmann and Albarracín, 2016 ), the CL approach was combined with training in problem-solving principles Pólya (1948) and educational materials, providing support in instruction in underlying mathematical models. The intention of the study was to provide evidence for the effectiveness of the CL approach above instruction in problem-solving, as problem-solving materials were accessible to teachers of both the intervention and control groups. However, due to implementation challenges, not all teachers in the intervention and control groups reported using educational materials and training as expected. Thus, it is not possible to draw conclusions of the effectiveness of the CL approach alone. However, in everyday classroom instruction it may be difficult to separate the content of instruction from the activities that are used to mediate this content ( Doerr and Tripp, 1999 ; Gravemeijer, 1999 ).

Furthermore, for successful instruction in mathematical problem-solving, scaffolding for content needs to be combined with scaffolding for dialogue ( Kazak et al., 2015 ). From a dialogical perspective ( Wegerif, 2011 ), students may need scaffolding in new ways of thinking, involving questioning their understandings and providing arguments for their solutions, in order to create dialogic spaces in which different solutions are voiced and negotiated. In this study, small group instruction through CL approach aimed to support discussions in small groups, but the study relies solely on quantitative measures of students’ mathematical performance. Video-recordings of students’ discussions may have yielded important insights into the dialogic relationships that arose in group discussions.

Despite the positive findings of the CL approach on students’ problem-solving, it is important to note that the intervention did not have an effect on students’ problem-solving pertaining to models of multiplication/division and proportionality. Although CL is assumed to be a promising instructional approach, the number of studies on its effect on students’ mathematical achievement is still limited ( Capar and Tarim, 2015 ). Thus, further research is needed on how CL intervention can be designed to promote students’ problem-solving in other areas of mathematics.

The results of this study show that the effect of the CL intervention on students’ problem-solving was associated with students’ initial scores of social acceptance and friendships. Thus, it is possible to assume that students who were popular among their classmates and had friends at the start of the intervention also made greater gains in mathematical problem-solving as a result of the CL intervention. This finding is in line with Deacon and Edwards’ study of the importance of friendships for students’ motivation to learn mathematics in small groups ( Deacon and Edwards, 2012 ). However, the effect of the CL intervention was not associated with change in students’ social acceptance and friendship scores. These results indicate that students who were nominated by a greater number of students and who received a greater number of friends did not benefit to a great extent from the CL intervention. With regard to previously reported inequalities in cooperation in heterogeneous groups ( Cohen, 1994 ; Mulryan, 1992 ; Langer Osuna, 2016 ) and the importance of peer behaviours for problem-solving ( Hwang and Hu, 2013 ), teachers should consider creating inclusive norms and supportive peer relationships when using the CL approach. The demands of solving complex problems may create negative emotions and uncertainty ( Hannula, 2015 ; Jordan and McDaniel, 2014 ), and peer support may be essential in such situations.

Limitations

The conclusions from the study must be interpreted with caution, due to a number of limitations. First, due to the regulation of protection of individuals ( SFS 2009 ), the researchers could not get information on type of SEN for individual students, which limited the possibilities of the study for investigating the effects of the CL approach for these students. Second, not all teachers in the intervention group implemented the CL approach embedded in problem-solving activities and not all teachers in the control group reported using educational materials on problem-solving. The insufficient levels of implementation pose a significant challenge to the internal validity of the study. Third, the additional investigation to explore the equivalence in difficulty between pre- and post-test, including 169 students, revealed weak to moderate correlation in students’ performance scores, which may indicate challenges to the internal validity of the study.

Implications

The results of the study have some implications for practice. Based on the results of the significant effect of the CL intervention on students’ problem-solving, the CL approach appears to be a promising instructional approach in promoting students’ problem-solving. However, as the results of the CL approach were not significant for all subtests of problem-solving, and due to insufficient levels of implementation, it is not possible to conclude on the importance of the CL intervention for students’ problem-solving. Furthermore, it appears to be important to create opportunities for peer contacts and friendships when the CL approach is used in mathematical problem-solving activities.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The studies involving human participants were reviewed and approved by the Uppsala Ethical Regional Committee, Dnr. 2017/372. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.

Author Contributions

NiK was responsible for the project, and participated in data collection and data analyses. NaK and WK were responsible for intervention with special focus on the educational materials and tests in mathematical problem-solving. PE participated in the planning of the study and the data analyses, including coordinating analyses of students’ tests. MK participated in the designing and planning the study as well as data collection and data analyses.

The project was funded by the Swedish Research Council under Grant 2016-04,679.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to express our gratitude to teachers who participated in the project.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2021.710296/full#supplementary-material

Barmby, P., Harries, T., Higgins, S., and Suggate, J. (2009). The array representation and primary children's understanding and reasoning in multiplication. Educ. Stud. Math. 70 (3), 217–241. doi:10.1007/s10649-008-914510.1007/s10649-008-9145-1

CrossRef Full Text | Google Scholar

Bates, D., Mächler, M., Bolker, B., and Walker, S. (2015). Fitting Linear Mixed-Effects Models Usinglme4. J. Stat. Soft. 67 (1), 1–48. doi:10.18637/jss.v067.i01

Capar, G., and Tarim, K. (2015). Efficacy of the cooperative learning method on mathematics achievement and attitude: A meta-analysis research. Educ. Sci-theor Pract. 15 (2), 553–559. doi:10.12738/estp.2015.2.2098

Child, S., and Nind, M. (2013). Sociometric methods and difference: A force for good - or yet more harm. Disabil. Soc. 28 (7), 1012–1023. doi:10.1080/09687599.2012.741517

Cillessen, A. H. N., and Marks, P. E. L. (2017). Methodological choices in peer nomination research. New Dir. Child Adolesc. Dev. 2017, 21–44. doi:10.1002/cad.20206

PubMed Abstract | CrossRef Full Text | Google Scholar

Clarke, B., Cheeseman, J., and Clarke, D. (2006). The mathematical knowledge and understanding young children bring to school. Math. Ed. Res. J. 18 (1), 78–102. doi:10.1007/bf03217430

Cohen, E. G. (1994). Restructuring the classroom: Conditions for productive small groups. Rev. Educ. Res. 64 (1), 1–35. doi:10.3102/00346543064001001

Davidson, N., and Major, C. H. (2014). Boundary crossings: Cooperative learning, collaborative learning, and problem-based learning. J. Excell. Coll. Teach. 25 (3-4), 7.

Google Scholar

Davydov, V. V. (2008). Problems of developmental instructions. A Theoretical and experimental psychological study . New York: Nova Science Publishers, Inc .

Deacon, D., and Edwards, J. (2012). Influences of friendship groupings on motivation for mathematics learning in secondary classrooms. Proc. Br. Soc. Res. into Learn. Math. 32 (2), 22–27.

Degrande, T., Verschaffel, L., and van Dooren, W. (2016). “Proportional word problem solving through a modeling lens: a half-empty or half-full glass?,” in Posing and Solving Mathematical Problems, Research in Mathematics Education . Editor P. Felmer.

Doerr, H. M., and Tripp, J. S. (1999). Understanding how students develop mathematical models. Math. Thinking Learn. 1 (3), 231–254. doi:10.1207/s15327833mtl0103_3

Fujita, T., Doney, J., and Wegerif, R. (2019). Students' collaborative decision-making processes in defining and classifying quadrilaterals: a semiotic/dialogic approach. Educ. Stud. Math. 101 (3), 341–356. doi:10.1007/s10649-019-09892-9

Gillies, R. (2016). Cooperative learning: Review of research and practice. Ajte 41 (3), 39–54. doi:10.14221/ajte.2016v41n3.3

Gravemeijer, K. (1999). How Emergent Models May Foster the Constitution of Formal Mathematics. Math. Thinking Learn. 1 (2), 155–177. doi:10.1207/s15327833mtl0102_4

Gravemeijer, K., Stephan, M., Julie, C., Lin, F.-L., and Ohtani, M. (2017). What mathematics education may prepare students for the society of the future? Int. J. Sci. Math. Educ. 15 (S1), 105–123. doi:10.1007/s10763-017-9814-6

Hamilton, E. (2007). “What changes are needed in the kind of problem-solving situations where mathematical thinking is needed beyond school?,” in Foundations for the Future in Mathematics Education . Editors R. Lesh, E. Hamilton, and Kaput (Mahwah, NJ: Lawrence Erlbaum ), 1–6.

Hannula, M. S. (2015). “Emotions in problem solving,” in Selected Regular Lectures from the 12 th International Congress on Mathematical Education . Editor S. J. Cho. doi:10.1007/978-3-319-17187-6_16

Hwang, W.-Y., and Hu, S.-S. (2013). Analysis of peer learning behaviors using multiple representations in virtual reality and their impacts on geometry problem solving. Comput. Edu. 62, 308–319. doi:10.1016/j.compedu.2012.10.005

Johnson, D. W., Johnson, R. T., and Johnson Holubec, E. (2009). Circle of Learning: Cooperation in the Classroom . Gurgaon: Interaction Book Company .

Johnson, D. W., Johnson, R. T., and Johnson Holubec, E. (1993). Cooperation in the Classroom . Gurgaon: Interaction Book Company .

Jordan, M. E., and McDaniel, R. R. (2014). Managing uncertainty during collaborative problem solving in elementary school teams: The role of peer influence in robotics engineering activity. J. Learn. Sci. 23 (4), 490–536. doi:10.1080/10508406.2014.896254

Karlsson, N., and Kilborn, W. (2018a). Inclusion through learning in group: tasks for problem-solving. [Inkludering genom lärande i grupp: uppgifter för problemlösning] . Uppsala: Uppsala University .

Karlsson, N., and Kilborn, W. (2018c). It's enough if they understand it. A study of teachers 'and students' perceptions of multiplication and the multiplication table [Det räcker om de förstår den. En studie av lärares och elevers uppfattningar om multiplikation och multiplikationstabellen]. Södertörn Stud. Higher Educ. , 175.

Karlsson, N., and Kilborn, W. (2018b). Tasks for problem-solving in mathematics. [Uppgifter för problemlösning i matematik] . Uppsala: Uppsala University .

Karlsson, N., and Kilborn, W. (2020). “Teacher’s and student’s perception of rational numbers,” in Interim Proceedings of the 44 th Conference of the International Group for the Psychology of Mathematics Education , Interim Vol., Research Reports . Editors M. Inprasitha, N. Changsri, and N. Boonsena (Khon Kaen, Thailand: PME ), 291–297.

Kazak, S., Wegerif, R., and Fujita, T. (2015). Combining scaffolding for content and scaffolding for dialogue to support conceptual breakthroughs in understanding probability. ZDM Math. Edu. 47 (7), 1269–1283. doi:10.1007/s11858-015-0720-5

Klang, N., Olsson, I., Wilder, J., Lindqvist, G., Fohlin, N., and Nilholm, C. (2020). A cooperative learning intervention to promote social inclusion in heterogeneous classrooms. Front. Psychol. 11, 586489. doi:10.3389/fpsyg.2020.586489

Klang, N., Fohlin, N., and Stoddard, M. (2018). Inclusion through learning in group: cooperative learning [Inkludering genom lärande i grupp: kooperativt lärande] . Uppsala: Uppsala University .

Kunsch, C. A., Jitendra, A. K., and Sood, S. (2007). The effects of peer-mediated instruction in mathematics for students with learning problems: A research synthesis. Learn. Disabil Res Pract 22 (1), 1–12. doi:10.1111/j.1540-5826.2007.00226.x

Langer-Osuna, J. M. (2016). The social construction of authority among peers and its implications for collaborative mathematics problem solving. Math. Thinking Learn. 18 (2), 107–124. doi:10.1080/10986065.2016.1148529

Lein, A. E., Jitendra, A. K., and Harwell, M. R. (2020). Effectiveness of mathematical word problem solving interventions for students with learning disabilities and/or mathematics difficulties: A meta-analysis. J. Educ. Psychol. 112 (7), 1388–1408. doi:10.1037/edu0000453

Lesh, R., and Doerr, H. (2003). Beyond Constructivism: Models and Modeling Perspectives on Mathematics Problem Solving, Learning and Teaching . Mahwah, NJ: Erlbaum .

Lesh, R., Post, T., and Behr, M. (1988). “Proportional reasoning,” in Number Concepts and Operations in the Middle Grades . Editors J. Hiebert, and M. Behr (Hillsdale, N.J.: Lawrence Erlbaum Associates ), 93–118.

Lesh, R., and Zawojewski, (2007). “Problem solving and modeling,” in Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics . Editor L. F. K. Lester (Charlotte, NC: Information Age Pub ), vol. 2.

Lester, F. K., and Cai, J. (2016). “Can mathematical problem solving be taught? Preliminary answers from 30 years of research,” in Posing and Solving Mathematical Problems. Research in Mathematics Education .

Lybeck, L. (1981). “Archimedes in the classroom. [Arkimedes i klassen],” in Göteborg Studies in Educational Sciences (Göteborg: Acta Universitatis Gotoburgensis ), 37.

McMaster, K. N., and Fuchs, D. (2002). Effects of Cooperative Learning on the Academic Achievement of Students with Learning Disabilities: An Update of Tateyama-Sniezek's Review. Learn. Disabil Res Pract 17 (2), 107–117. doi:10.1111/1540-5826.00037

Mercer, N., and Sams, C. (2006). Teaching children how to use language to solve maths problems. Lang. Edu. 20 (6), 507–528. doi:10.2167/le678.0

Montague, M., Krawec, J., Enders, C., and Dietz, S. (2014). The effects of cognitive strategy instruction on math problem solving of middle-school students of varying ability. J. Educ. Psychol. 106 (2), 469–481. doi:10.1037/a0035176

Mousoulides, N., Pittalis, M., Christou, C., and Stiraman, B. (2010). “Tracing students’ modeling processes in school,” in Modeling Students’ Mathematical Modeling Competencies . Editor R. Lesh (Berlin, Germany: Springer Science+Business Media ). doi:10.1007/978-1-4419-0561-1_10

Mulryan, C. M. (1992). Student passivity during cooperative small groups in mathematics. J. Educ. Res. 85 (5), 261–273. doi:10.1080/00220671.1992.9941126

OECD (2019). PISA 2018 Results (Volume I): What Students Know and Can Do . Paris: OECD Publishing . doi:10.1787/5f07c754-en

CrossRef Full Text

Pólya, G. (1948). How to Solve it: A New Aspect of Mathematical Method . Princeton, N.J.: Princeton University Press .

Russel, S. J. (1991). “Counting noses and scary things: Children construct their ideas about data,” in Proceedings of the Third International Conference on the Teaching of Statistics . Editor I. D. Vere-Jones (Dunedin, NZ: University of Otago ), 141–164., s.

Rzoska, K. M., and Ward, C. (1991). The effects of cooperative and competitive learning methods on the mathematics achievement, attitudes toward school, self-concepts and friendship choices of Maori, Pakeha and Samoan Children. New Zealand J. Psychol. 20 (1), 17–24.

Schoenfeld, A. H. (2016). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics (reprint). J. Edu. 196 (2), 1–38. doi:10.1177/002205741619600202

SFS 2009:400. Offentlighets- och sekretesslag. [Law on Publicity and confidentiality] . Retrieved from https://www.riksdagen.se/sv/dokument-lagar/dokument/svensk-forfattningssamling/offentlighets--och-sekretesslag-2009400_sfs-2009-400 on the 14th of October .

Snijders, T. A. B., and Bosker, R. J. (2012). Multilevel Analysis. An Introduction to Basic and Advanced Multilevel Modeling . 2nd Ed. London: SAGE .

Stillman, G., Brown, J., and Galbraith, P. (2008). Research into the teaching and learning of applications and modelling in Australasia. In H. Forgasz, A. Barkatas, A. Bishop, B. Clarke, S. Keast, W. Seah, and P. Sullivan (red.), Research in Mathematics Education in Australasiae , 2004-2007 , p.141–164. Rotterdam: Sense Publishers .doi:10.1163/9789087905019_009

Stohlmann, M. S., and Albarracín, L. (2016). What is known about elementary grades mathematical modelling. Edu. Res. Int. 2016, 1–9. doi:10.1155/2016/5240683

Swedish National Educational Agency (2014). Support measures in education – on leadership and incentives, extra adaptations and special support [Stödinsatser I utbildningen – om ledning och stimulans, extra anpassningar och särskilt stöd] . Stockholm: Swedish National Agency of Education .

Swedish National Educational Agency (2018). Syllabus for the subject of mathematics in compulsory school . Retrieved from https://www.skolverket.se/undervisning/grundskolan/laroplan-och-kursplaner-for-grundskolan/laroplan-lgr11-for-grundskolan-samt-for-forskoleklassen-och-fritidshemmet?url=-996270488%2Fcompulsorycw%2Fjsp%2Fsubject.htm%3FsubjectCode%3DGRGRMAT01%26tos%3Dgr&sv.url=12.5dfee44715d35a5cdfa219f ( on the 32nd of July, 2021).

van Hiele, P. (1986). Structure and Insight. A Theory of Mathematics Education . London: Academic Press .

Velásquez, A. M., Bukowski, W. M., and Saldarriaga, L. M. (2013). Adjusting for Group Size Effects in Peer Nomination Data. Soc. Dev. 22 (4), a–n. doi:10.1111/sode.12029

Verschaffel, L., Greer, B., and De Corte, E. (2007). “Whole number concepts and operations,” in Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics . Editor F. K. Lester (Charlotte, NC: Information Age Pub ), 557–628.

Webb, N. M., and Mastergeorge, A. (2003). Promoting effective helping behavior in peer-directed groups. Int. J. Educ. Res. 39 (1), 73–97. doi:10.1016/S0883-0355(03)00074-0

Wegerif, R. (2011). “Theories of Learning and Studies of Instructional Practice,” in Theories of learning and studies of instructional Practice. Explorations in the learning sciences, instructional systems and Performance technologies . Editor T. Koschmann (Berlin, Germany: Springer ). doi:10.1007/978-1-4419-7582-9

Yackel, E., Cobb, P., and Wood, T. (1991). Small-group interactions as a source of learning opportunities in second-grade mathematics. J. Res. Math. Edu. 22 (5), 390–408. doi:10.2307/749187

Zawojewski, J. (2010). Problem Solving versus Modeling. In R. Lesch, P. Galbraith, C. R. Haines, and A. Hurford (red.), Modelling student’s mathematical modelling competencies: ICTMA , p. 237–243. New York, NY: Springer .doi:10.1007/978-1-4419-0561-1_20

Keywords: cooperative learning, mathematical problem-solving, intervention, heterogeneous classrooms, hierarchical linear regression analysis

Citation: Klang N, Karlsson N, Kilborn W, Eriksson P and Karlberg M (2021) Mathematical Problem-Solving Through Cooperative Learning—The Importance of Peer Acceptance and Friendships. Front. Educ. 6:710296. doi: 10.3389/feduc.2021.710296

Received: 15 May 2021; Accepted: 09 August 2021; Published: 24 August 2021.

Reviewed by:

Copyright © 2021 Klang, Karlsson, Kilborn, Eriksson and Karlberg. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Nina Klang, [email protected]

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• 14 May 2024

Why mathematics is set to be revolutionized by AI

• Thomas Fink 0

Thomas Fink is the director of the London Institute for Mathematical Sciences, UK.

You can also search for this author in PubMed   Google Scholar

You have full access to this article via your institution.

Giving birth to a conjecture — a proposition that is suspected to be true, but needs definitive proof — can feel to a mathematician like a moment of divine inspiration. Mathematical conjectures are not merely educated guesses. Formulating them requires a combination of genius, intuition and experience. Even a mathematician can struggle to explain their own discovery process. Yet, counter-intuitively, I think that this is the realm in which machine intelligence will initially be most transformative.

In 2017, researchers at the London Institute for Mathematical Sciences, of which I am director, began applying machine learning to mathematical data as a hobby. During the COVID-19 pandemic, they discovered that simple artificial intelligence (AI) classifiers can predict an elliptic curve’s rank 1 — a measure of its complexity. Elliptic curves are fundamental to number theory, and understanding their underlying statistics is a crucial step towards solving one of the seven Millennium Problems, which are selected by the Clay Mathematics Institute in Providence, Rhode Island, and carry a prize of US$1 million each. Few expected AI to make a dent in this high-stakes arena.

AI now beats humans at basic tasks — new benchmarks are needed, says major report

AI has made inroads in other areas, too. A few years ago, a computer program called the Ramanujan Machine produced new formulae for fundamental constants 2 , such as π and e . It did so by exhaustively searching through families of continued fractions — a fraction whose denominator is a number plus a fraction whose denominator is also a number plus a fraction and so on. Some of these conjectures have since been proved, whereas others remain open problems.

Another example pertains to knot theory, a branch of topology in which a hypothetical piece of string is tangled up before the ends are glued together. Researchers at Google DeepMind, based in London, trained a neural network on data for many different knots and discovered an unexpected relationship between their algebraic and geometric structures 3 .

How has AI made a difference in areas of mathematics in which human creativity was thought to be essential?

First, there are no coincidences in maths. In real-world experiments, false negatives and false positives abound. But in maths, a single counterexample leaves a conjecture dead in the water. For example, the Pólya conjecture states that most integers below any given integer have an odd number of prime factors. But in 1960, it was found that the conjecture does not hold for the number 906,180,359. In one fell swoop, the conjecture was falsified.

Second, mathematical data — on which AI can be trained — are cheap. Primes, knots and many other types of mathematical object are abundant. The On-Line Encyclopedia of Integer Sequences (OEIS) contains almost 375,000 sequences — from the familiar Fibonacci sequence (1, 1, 2, 3, 5, 8, 13, ...) to the formidable Busy Beaver sequence (0, 1, 4, 6, 13, …), which grows faster than any computable function. Scientists are already using machine-learning tools to search the OEIS database to find unanticipated relationships.

DeepMind AI outdoes human mathematicians on unsolved problem

AI can help us to spot patterns and form conjectures. But not all conjectures are created equal. They also need to advance our understanding of mathematics. In his 1940 essay A Mathematician’s Apology , G. H. Hardy explains that a good theorem “should be one which is a constituent in many mathematical constructs, which is used in the proof of theorems of many different kinds”. In other words, the best theorems increase the likelihood of discovering new theorems. Conjectures that help us to reach new mathematical frontiers are better than those that yield fewer insights. But distinguishing between them requires an intuition for how the field itself will evolve. This grasp of the broader context will remain out of AI’s reach for a long time — so the technology will struggle to spot important conjectures.

But despite the caveats, there are many upsides to wider adoption of AI tools in the maths community. AI can provide a decisive edge and open up new avenues for research.

Mainstream mathematics journals should also publish more conjectures. Some of the most significant problems in maths — such as Fermat’s Last Theorem, the Riemann hypothesis, Hilbert’s 23 problems and Ramanujan’s many identities — and countless less-famous conjectures have shaped the course of the field. Conjectures speed up research by pointing us in the right direction. Journal articles about conjectures, backed up by data or heuristic arguments, will accelerate discovery.

Last year, researchers at Google DeepMind predicted 2.2 million new crystal structures 4 . But it remains to be seen how many of these potential new materials are stable, can be synthesized and have practical applications. For now, this is largely a task for human researchers, who have a grasp of the broad context of materials science.

Similarly, the imagination and intuition of mathematicians will be required to make sense of the output of AI tools. Thus, AI will act only as a catalyst of human ingenuity, rather than a substitute for it.

Nature 629 , 505 (2024)

doi: https://doi.org/10.1038/d41586-024-01413-w

He, Y.-H., Lee, K.-H., Oliver, T. & Pozdnyakov, A. Preprint at arXiv https://doi.org/10.48550/arXiv.2204.10140 (2024).

Raayoni, G. et al. Nature 590 , 67–73 (2021).

Article   PubMed   Google Scholar  

Davies, A. et al. Nature 600 , 70–74 (2021).

Merchant, A. et al. Nature 624 , 80–85 (2023).

Download references

Reprints and permissions

Competing Interests

The author declares no competing interests.

Related Articles

• Machine learning
• Mathematics and computing

How does ChatGPT ‘think’? Psychology and neuroscience crack open AI large language models

News Feature 14 MAY 24

The US Congress is taking on AI — this computer scientist is helping

News Q&A 09 MAY 24

Accurate structure prediction of biomolecular interactions with AlphaFold 3

Article 08 MAY 24

The dream of electronic newspapers becomes a reality — in 1974

News & Views 07 MAY 24

3D genomic mapping reveals multifocality of human pancreatic precancers

Article 01 MAY 24

AI’s keen diagnostic eye

Outlook 18 APR 24

Research Associate - Metabolism

Houston, Texas (US)

Baylor College of Medicine (BCM)

Postdoc Fellowships

Train with world-renowned cancer researchers at NIH? Consider joining the Center for Cancer Research (CCR) at the National Cancer Institute

Bethesda, Maryland

NIH National Cancer Institute (NCI)

Faculty Recruitment, Westlake University School of Medicine

Faculty positions are open at four distinct ranks: Assistant Professor, Associate Professor, Full Professor, and Chair Professor.

Hangzhou, Zhejiang, China

Westlake University

PhD/master's Candidate

PhD/master's Candidate    Graduate School of Frontier Science Initiative, Kanazawa University is seeking candidates for PhD and master's students i...

Kanazawa University

Senior Research Assistant in Human Immunology (wet lab)

Senior Research Scientist in Human Immunology, high-dimensional (40+) cytometry, ICS and automated robotic platforms.

Boston, Massachusetts (US)

Boston University Atomic Lab

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies