model with assignment

Assignment Model | Linear Programming Problem (LPP) | Introduction

What is assignment model.

→ Assignment model is a special application of Linear Programming Problem (LPP) , in which the main objective is to assign the work or task to a group of individuals such that;

i) There is only one assignment.

ii) All the assignments should be done in such a way that the overall cost is minimized (or profit is maximized, incase of maximization).

→ In assignment problem, the cost of performing each task by each individual is known. → It is desired to find out the best assignments, such that overall cost of assigning the work is minimized.

For example:

Suppose there are 'n' tasks, which are required to be performed using 'n' resources.

The cost of performing each task by each resource is also known (shown in cells of matrix)

• In the above asignment problem, we have to provide assignments such that there is one to one assignments and the overall cost is minimized.

How Assignment Problem is related to LPP? OR Write mathematical formulation of Assignment Model.

→ Assignment Model is a special application of Linear Programming (LP).

→ The mathematical formulation for Assignment Model is given below:

→ Let, C i j \text {C}_{ij} C ij ​ denotes the cost of resources 'i' to the task 'j' ; such that

→ Now assignment problems are of the Minimization type. So, our objective function is to minimize the overall cost.

→ Subjected to constraint;

(i) For all j t h j^{th} j t h task, only one i t h i^{th} i t h resource is possible:

(ii) For all i t h i^{th} i t h resource, there is only one j t h j^{th} j t h task possible;

(iii) x i j x_{ij} x ij ​ is '0' or '1'.

Types of Assignment Problem:

(i) balanced assignment problem.

• It consist of a suqare matrix (n x n).
• Number of rows = Number of columns

(ii) Unbalanced Assignment Problem

• It consist of a Non-square matrix.
• Number of rows ≠ \not=  = Number of columns

Methods to solve Assignment Model:

(i) integer programming method:.

In assignment problem, either allocation is done to the cell or not.

So this can be formulated using 0 or 1 integer.

While using this method, we will have n x n decision varables, and n+n equalities.

So even for 4 x 4 matrix problem, it will have 16 decision variables and 8 equalities.

So this method becomes very lengthy and difficult to solve.

(ii) Transportation Methods:

As assignment problem is a special case of transportation problem, it can also be solved using transportation methods.

In transportation methods ( NWCM , LCM & VAM), the total number of allocations will be (m+n-1) and the solution is known as non-degenerated. (For eg: for 3 x 3 matrix, there will be 3+3-1 = 5 allocations)

But, here in assignment problems, the matrix is a square matrix (m=n).

So total allocations should be (n+n-1), i.e. for 3 x 3 matrix, it should be (3+3-1) = 5

But, we know that in 3 x 3 assignment problem, maximum possible possible assignments are 3 only.

So, if are we will use transportation methods, then the solution will be degenerated as it does not satisfy the condition of (m+n-1) allocations.

So, the method becomes lengthy and time consuming.

(iii) Enumeration Method:

It is a simple trail and error type method.

Consider a 3 x 3 assignment problem. Here the assignments are done randomly and the total cost is found out.

For 3 x 3 matrix, the total possible trails are 3! So total 3! = 3 x 2 x 1 = 6 trails are possible.

The assignments which gives minimum cost is selected as optimal solution.

But, such trail and error becomes very difficult and lengthy.

If there are more number of rows and columns, ( For eg: For 6 x 6 matrix, there will be 6! trails. So 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720 trails possible) then such methods can't be applied for solving assignments problems.

(iv) Hungarian Method:

It was developed by two mathematicians of Hungary. So, it is known as Hungarian Method.

It is also know as Reduced matrix method or Flood's technique.

There are two main conditions for applying Hungarian Method:

(1) Square Matrix (n x n). (2) Problem should be of minimization type.

Suggested Notes:

Modified Distribution Method (MODI) | Transportation Problem | Transportation Model

Stepping Stone | Transportation Problem | Transportation Model

Vogel’s Approximation Method (VAM) | Method to Solve Transportation Problem | Transportation Model

Transportation Model - Introduction

North West Corner Method | Method to Solve Transportation Problem | Transportation Model

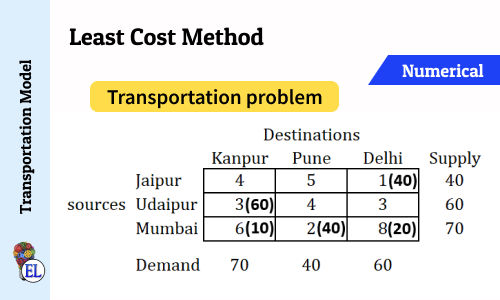
Least Cost Method | Method to Solve Transportation Problem | Transportation Model

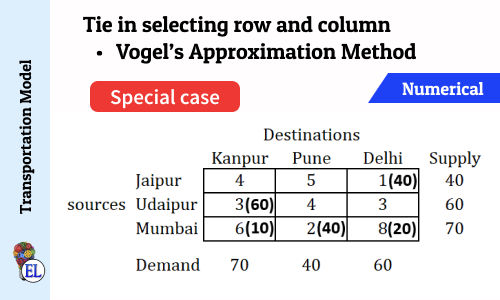
Tie in selecting row and column (Vogel's Approximation Method - VAM) | Numerical | Solving Transportation Problem | Transportation Model

Crashing Special Case - Multiple (Parallel) Critical Paths

Crashing Special Case - Indirect cost less than Crash Cost

Basics of Program Evaluation and Review Technique (PERT)

Numerical on PERT (Program Evaluation and Review Technique)

Network Analysis - Dealing with Network Construction Basics

Construct a project network with predecessor relationship | Operation Research | Numerical

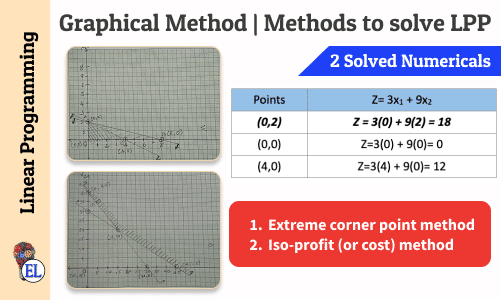
Graphical Method | Methods to solve LPP | Linear Programming

Basics of Linear Programming

Linear Programming Problem (LPP) Formulation with Numericals

All comments that you add will await moderation. We'll publish all comments that are topic related, and adhere to our Code of Conduct .

Want to tell us something privately? Contact Us

Post comment

Education Lessons

Stay in touch, [notes] operation research, [notes] dynamics of machinery, [notes] maths, [notes] science, [notes] computer aided design.

• MapReduce Algorithm
• Linear Programming using Pyomo
• Networking and Professional Development for Machine Learning Careers in the USA
• Predicting Employee Churn in Python
• Airflow Operators

Solving Assignment Problem using Linear Programming in Python

Learn how to use Python PuLP to solve Assignment problems using Linear Programming.

In earlier articles, we have seen various applications of Linear programming such as transportation, transshipment problem, Cargo Loading problem, and shift-scheduling problem. Now In this tutorial, we will focus on another model that comes under the class of linear programming model known as the Assignment problem. Its objective function is similar to transportation problems. Here we minimize the objective function time or cost of manufacturing the products by allocating one job to one machine.

If we want to solve the maximization problem assignment problem then we subtract all the elements of the matrix from the highest element in the matrix or multiply the entire matrix by –1 and continue with the procedure. For solving the assignment problem, we use the Assignment technique or Hungarian method, or Flood’s technique.

The transportation problem is a special case of the linear programming model and the assignment problem is a special case of transportation problem, therefore it is also a special case of the linear programming problem.

In this tutorial, we are going to cover the following topics:

Assignment Problem

A problem that requires pairing two sets of items given a set of paired costs or profit in such a way that the total cost of the pairings is minimized or maximized. The assignment problem is a special case of linear programming.

For example, an operation manager needs to assign four jobs to four machines. The project manager needs to assign four projects to four staff members. Similarly, the marketing manager needs to assign the 4 salespersons to 4 territories. The manager’s goal is to minimize the total time or cost.

Problem Formulation

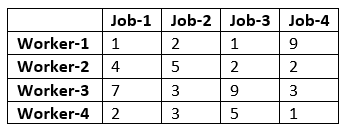
A manager has prepared a table that shows the cost of performing each of four jobs by each of four employees. The manager has stated his goal is to develop a set of job assignments that will minimize the total cost of getting all 4 jobs.  

Initialize LP Model

In this step, we will import all the classes and functions of pulp module and create a Minimization LP problem using LpProblem class.

Define Decision Variable

In this step, we will define the decision variables. In our problem, we have two variable lists: workers and jobs. Let’s create them using  LpVariable.dicts()  class.  LpVariable.dicts()  used with Python’s list comprehension.  LpVariable.dicts()  will take the following four values:

• First, prefix name of what this variable represents.
• Second is the list of all the variables.
• Third is the lower bound on this variable.
• Fourth variable is the upper bound.
• Fourth is essentially the type of data (discrete or continuous). The options for the fourth parameter are  LpContinuous  or  LpInteger .

Let’s first create a list route for the route between warehouse and project site and create the decision variables using LpVariable.dicts() the method.

Define Objective Function

In this step, we will define the minimum objective function by adding it to the LpProblem  object. lpSum(vector)is used here to define multiple linear expressions. It also used list comprehension to add multiple variables.

Define the Constraints

Here, we are adding two types of constraints: Each job can be assigned to only one employee constraint and Each employee can be assigned to only one job. We have added the 2 constraints defined in the problem by adding them to the LpProblem  object.

Solve Model

In this step, we will solve the LP problem by calling solve() method. We can print the final value by using the following for loop.

From the above results, we can infer that Worker-1 will be assigned to Job-1, Worker-2 will be assigned to job-3, Worker-3 will be assigned to Job-2, and Worker-4 will assign with job-4.

In this article, we have learned about Assignment problems, Problem Formulation, and implementation using the python PuLp library. We have solved the Assignment problem using a Linear programming problem in Python. Of course, this is just a simple case study, we can add more constraints to it and make it more complicated. You can also run other case studies on Cargo Loading problems , Staff scheduling problems . In upcoming articles, we will write more on different optimization problems such as transshipment problem, balanced diet problem. You can revise the basics of mathematical concepts in  this article  and learn about Linear Programming  in this article .

• Solving Blending Problem in Python using Gurobi
• Transshipment Problem in Python Using PuLP

You May Also Like

Solving Staff Scheduling Problem using Linear Programming

Text Analytics for Beginner using Python TextBlob

Pandas Series

• Google OR-Tools
• Español – América Latina
• Português – Brasil
• Tiếng Việt

One of the most well-known combinatorial optimization problems is the assignment problem . Here's an example: suppose a group of workers needs to perform a set of tasks, and for each worker and task, there is a cost for assigning the worker to the task. The problem is to assign each worker to at most one task, with no two workers performing the same task, while minimizing the total cost.

You can visualize this problem by the graph below, in which there are four workers and four tasks. The edges represent all possible ways to assign workers to tasks. The labels on the edges are the costs of assigning workers to tasks.

An assignment corresponds to a subset of the edges, in which each worker has at most one edge leading out, and no two workers have edges leading to the same task. One possible assignment is shown below.

The total cost of the assignment is 70 + 55 + 95 + 45 = 265 .

The next section shows how solve an assignment problem, using both the MIP solver and the CP-SAT solver.

Other tools for solving assignment problems

OR-Tools also provides a couple of other tools for solving assignment problems, which can be faster than the MIP or CP solvers:

• Linear sum assignment solver
• Minimum cost flow solver

However, these tools can only solve simple types of assignment problems. So for general solvers that can handle a wide variety of problems (and are fast enough for most applications), we recommend the MIP and CP-SAT solvers.

Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.

Last updated 2023-01-02 UTC.

Looking for something?

Six Characteristics of a Model Assignment

How many times have you had a student submit an assignment with few sources, poorly written and several days late? Probably happens more times than not. There are six characteristics of a model assignment which will not only alleviate instructor frustration, but also strengthen student writing and time management skills.

• Create assignments which directly relate to accomplishing the course objective. A model assignment maintains a clear goal toward accomplishing a course objective. For adult online learners, course goals relate less to theory or original research and more to practical approaches for day-to-day application or career advancement.
• More details equals higher quality of student final product. Since adult online learners come from diverse backgrounds, do not assume students will understand the purpose of the assignment. Be prepared to tell students what you expect (e.g. word count, citation format, number of sources, etc.) and how it should be done (e.g. upload to Moodle versus email attachment).
• Give incremental due dates. Large comprehensive assignments due at the course finality leads to unfocused, or even plagiarized, writing. Break down a large assignment into several smaller assignments due sporadically throughout the term. In turn, students receive valuable feedback incrementally as they progress throughout the course.
• Allow students to brainstorm for topics. Allow students to brainstorm topics or share with other students using the Moodle Discussion Board form. Or consider offering students a choice among 3-4 essay questions, case scenarios, or case studies. By allowing student choice, students will find a greater connection in their writing which in turn will lead to better final submissions.
• Give examples. In addition to clear directions, students also appreciate a visual piece of the final product. If you decide to use another student’s work, be sure to ask permission to use from the student. Post model assignments on your Moodle course shell.
• Share student evaluation tools. Share rubrics, or other evaluation tool, early in the assignment rather than at the end so students may clarify expectations firsthand. Post rubrics or evaluation tools on your Moodle course shell so students may refer to it when necessary.

The assignment problem revisited

• Original Paper
• Published: 16 August 2021
• Volume 16 , pages 1531–1548, ( 2022 )

Cite this article

• Carlos A. Alfaro   ORCID: orcid.org/0000-0001-9783-8587 1 ,
• Sergio L. Perez 2 ,
• Carlos E. Valencia 3 &
• Marcos C. Vargas 1  

999 Accesses

4 Citations

4 Altmetric

Explore all metrics

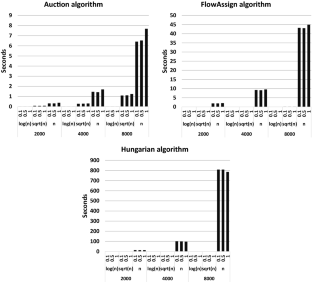
First, we give a detailed review of two algorithms that solve the minimization case of the assignment problem, the Bertsekas auction algorithm and the Goldberg & Kennedy algorithm. It was previously alluded that both algorithms are equivalent. We give a detailed proof that these algorithms are equivalent. Also, we perform experimental results comparing the performance of three algorithms for the assignment problem: the \(\epsilon \) - scaling auction algorithm , the Hungarian algorithm and the FlowAssign algorithm . The experiment shows that the auction algorithm still performs and scales better in practice than the other algorithms which are harder to implement and have better theoretical time complexity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

Parameterized Approximation Algorithms and Lower Bounds for k-Center Clustering and Variants

The DIRECT algorithm: 25 years Later

A review and comparison of solvers for convex MINLP

Bertsekas, D.P.: The auction algorithm: a distributed relaxation method for the assignment problem. Annal Op. Res. 14 , 105–123 (1988)

Article   MathSciNet   Google Scholar  

Bertsekas, D.P., Castañon, D.A.: Parallel synchronous and asynchronous implementations of the auction algorithm. Parallel Comput. 17 , 707–732 (1991)

Article   Google Scholar  

Bertsekas, D.P.: Linear network optimization: algorithms and codes. MIT Press, Cambridge, MA (1991)

MATH   Google Scholar  

Bertsekas, D.P.: The auction algorithm for shortest paths. SIAM J. Optim. 1 , 425–477 (1991)

Bertsekas, D.P.: Auction algorithms for network flow problems: a tutorial introduction. Comput. Optim. Appl. 1 , 7–66 (1992)

Bertsekas, D.P., Castañon, D.A., Tsaknakis, H.: Reverse auction and the solution of inequality constrained assignment problems. SIAM J. Optim. 3 , 268–299 (1993)

Bertsekas, D.P., Eckstein, J.: Dual coordinate step methods for linear network flow problems. Math. Progr., Ser. B 42 , 203–243 (1988)

Bertsimas, D., Tsitsiklis, J.N.: Introduction to linear optimization. Athena Scientific, Belmont, MA (1997)

Google Scholar  

Burkard, R., Dell’Amico, M., Martello, S.: Assignment Problems. Revised reprint. SIAM, Philadelphia, PA (2011)

Gabow, H.N., Tarjan, R.E.: Faster scaling algorithms for network problems. SIAM J. Comput. 18 (5), 1013–1036 (1989)

Goldberg, A.V., Tarjan, R.E.: A new approach to the maximum flow problem. J. Assoc. Comput. Mach. 35 , 921–940 (1988)

Goldberg, A.V., Tarjan, R.E.: Finding minimum-cost circulations by successive approximation. Math. Op. Res. 15 , 430–466 (1990)

Goldberg, A.V., Kennedy, R.: An efficient cost scaling algorithm for the assignment problem. Math. Programm. 71 , 153–177 (1995)

MathSciNet   MATH   Google Scholar  

Goldberg, A.V., Kennedy, R.: Global price updates help. SIAM J. Discr. Math. 10 (4), 551–572 (1997)

Kuhn, H.W.: The Hungarian method for the assignment problem. Naval Res. Logist. Quart. 2 , 83–97 (1955)

Kuhn, H.W.: Variants of the Hungarian method for the assignment problem. Naval Res. Logist. Quart. 2 , 253–258 (1956)

Lawler, E.L.: Combinatorial optimization: networks and matroids, Holt. Rinehart & Winston, New York (1976)

Orlin, J.B., Ahuja, R.K.: New scaling algorithms for the assignment ad minimum mean cycle problems. Math. Programm. 54 , 41–56 (1992)

Ramshaw, L., Tarjan, R.E., Weight-Scaling Algorithm, A., for Min-Cost Imperfect Matchings in Bipartite Graphs, : IEEE 53rd Annual Symposium on Foundations of Computer Science. New Brunswick, NJ 2012 , 581–590 (2012)

Zaki, H.: A comparison of two algorithms for the assignment problem. Comput. Optim. Appl. 4 , 23–45 (1995)

Download references

Acknowledgements

This research was partially supported by SNI and CONACyT.

Author information

Authors and affiliations.

Banco de México, Mexico City, Mexico

Carlos A. Alfaro & Marcos C. Vargas

Mountain View, CA, 94043, USA

Sergio L. Perez

Departamento de Matemáticas, CINVESTAV del IPN, Apartado postal 14-740, 07000, Mexico City, Mexico

Carlos E. Valencia

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Carlos A. Alfaro .

Ethics declarations

Conflict of interest.

There is no conflict of interest.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The authors were partially supported by SNI and CONACyT.

Rights and permissions

Reprints and permissions

About this article

Alfaro, C.A., Perez, S.L., Valencia, C.E. et al. The assignment problem revisited. Optim Lett 16 , 1531–1548 (2022). https://doi.org/10.1007/s11590-021-01791-4

Download citation

Received : 26 March 2020

Accepted : 03 August 2021

Published : 16 August 2021

Issue Date : June 2022

DOI : https://doi.org/10.1007/s11590-021-01791-4

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Assignment problem
• Bertsekas auction algorithm
• Combinatorial optimization and matching
• Find a journal
• Publish with us
• Track your research

Quantitative Techniques: Theory and Problems by P. C. Tulsian, Vishal Pandey

Get full access to Quantitative Techniques: Theory and Problems and 60K+ other titles, with a free 10-day trial of O'Reilly.

There are also live events, courses curated by job role, and more.

WHAT IS ASSIGNMENT PROBLEM

Assignment Problem is a special type of linear programming problem where the objective is to minimise the cost or time of completing a number of jobs by a number of persons.

The assignment problem in the general form can be stated as follows:

“Given n facilities, n jobs and the effectiveness of each facility for each job, the problem is to assign each facility to one and only one job in such a way that the measure of effectiveness is optimised (Maximised or Minimised).”

Several problems of management has a structure identical with the assignment problem.

Example I A manager has four persons (i.e. facilities) available for four separate jobs (i.e. jobs) and the cost of assigning (i.e. effectiveness) each job to each ...

Get Quantitative Techniques: Theory and Problems now with the O’Reilly learning platform.

O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

Don’t leave empty-handed

Get Mark Richards’s Software Architecture Patterns ebook to better understand how to design components—and how they should interact.

It’s yours, free.

Check it out now on O’Reilly

Dive in for free with a 10-day trial of the O’Reilly learning platform—then explore all the other resources our members count on to build skills and solve problems every day.

Copyright © 2003 by Robert Fourer, David M. Gay and Brian W. Kernighan

The Assignment Model

The linear programming formulation of the assignment model is similar to the formulation of the transportation model, except all the supply values for each source equal one, and all the demand values at each destination equal one. Thus, our example is formulated as follows :

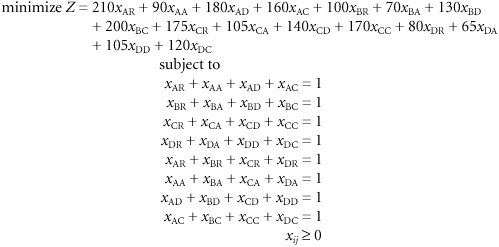
This is a balanced assignment model. An unbalanced model exists when supply exceeds demand or demand exceeds supply.

• Configuration Identification
• Configuration Status Accounting
• Configuration Change Management
• Appendix E Test Plan
• Appendix N Corrective Action Processing (CAP)
• EIGRP Route Summarization
• Using NBAR Classification
• Using Access Lists to Protect SNMP Access
• Changing the Default Log Facility
• Route Redistribution
• Understanding Solution Kits for Crystal Enterprise
• Recently Added or Changed OLAP Features in Crystal Reports
• Creating Crystal Analysis Reports
• Configuring the Application Server
• COM Reporting Components
• Project Value: The Source of all Quantitative Measures
• Risk-Adjusted Financial Management
• Expense Accounting and Earned Value
• Quantitative Time Management
• Quantitative Methods in Project Contracts
• Overview of the Oracle RDBMS
• Attacking the Authentication Process
• Indirect Privilege Escalation
• Defeating Virtual Private Databases
• Accessing the Network
• GDI+ Namespaces and Classes in .NET
• Transforming Text
• Working with Images
• Advanced Imaging
• The Matrix Class and Transformation

MBA Knowledge Base

Business • Management • Technology

Home » Management Science » Transportation and Assignment Models in Operations Research

Transportation and Assignment Models in Operations Research

Transportation and assignment models are special purpose algorithms of the linear programming. The simplex method of Linear Programming Problems(LPP) proves to be inefficient is certain situations like determining optimum assignment of jobs to persons, supply of materials from several supply points to several destinations and the like. More effective solution models have been evolved and these are called assignment and transportation models.

The transportation model is concerned with selecting the routes between supply and demand points in order to minimize costs of transportation subject to constraints of supply at any supply point and demand at any demand point. Assume a company has 4 manufacturing plants with different capacity levels, and 5 regional distribution centres. 4 x 5 = 20 routes are possible. Given the transportation costs per load of each of 20 routes between the manufacturing (supply) plants and the regional distribution (demand) centres, and supply and demand constraints, how many loads can be transported through different routes so as to minimize transportation costs? The answer to this question is obtained easily through the transportation algorithm.

Similarly, how are we to assign different jobs to different persons/machines, given cost of job completion for each pair of job machine/person? The objective is minimizing total cost. This is best solved through assignment algorithm.

Uses of Transportation and Assignment Models in Decision Making

The broad purposes of Transportation and Assignment models in LPP are just mentioned above. Now we have just enumerated the different situations where we can make use of these models.

Transportation model is used in the following:

• To decide the transportation of new materials from various centres to different manufacturing plants. In the case of multi-plant company this is highly useful.
• To decide the transportation of finished goods from different manufacturing plants to the different distribution centres. For a multi-plant-multi-market company this is useful.
• To decide the transportation of finished goods from different manufacturing plants to the different distribution centres. For a multi-plant-multi-market company this is useful. These two are the uses of transportation model. The objective is minimizing transportation cost.

Assignment model is used in the following:

• To decide the assignment of jobs to persons/machines, the assignment model is used.
• To decide the route a traveling executive has to adopt (dealing with the order inn which he/she has to visit different places).
• To decide the order in which different activities performed on one and the same facility be taken up.

In the case of transportation model, the supply quantity may be less or more than the demand. Similarly the assignment model, the number of jobs may be equal to, less or more than the number of machines/persons available. In all these cases the simplex method of LPP can be adopted, but transportation and assignment models are more effective, less time consuming and easier than the LPP.

Related posts:

• Operations Research approach of problem solving
• Introduction to Transportation Problem
• Procedure for finding an optimum solution for transportation problem
• Initial basic feasible solution of a transportation problem
• Top 7 Best Ways of Getting MBA Assignment Writing Help
• Introduction to Decision Models
• Transportation Cost Elements
• Modes of Transportation in Logistics
• Factors Affecting Transportation in Logistics
• Export/Import Transportation Systems

One thought on “ Transportation and Assignment Models in Operations Research ”

Exclussive dff. And easy understude

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Assignment Problem: Meaning, Methods and Variations | Operations Research

After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:

An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.

The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.

Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.

Definition of Assignment Problem:

ADVERTISEMENTS:

Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.

The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:

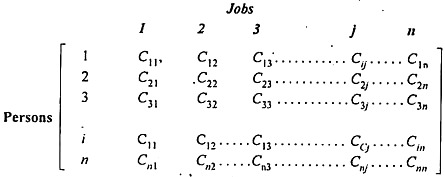
nab-Paclitaxel

Cohort 1 (direct rollover), subcutaneous, varenicline solution, calcium fructoborate, 3d model of heart, digital cognitive-behavioral therapy for insomnia (dcbti), popular categories.

Tymlos Clinical Trials

Paid Clinical Trials in Kansas City, MO

Paid Clinical Trials in Dallas, TX

Paid Clinical Trials in Tucson, AZ

Paid Clinical Trials in Spokane, WA

Paid Clinical Trials in Glendale, AZ

Paid Clinical Trials in Madison, WI

Apixaban Clinical Trials

Cellulite Clinical Trials 2023

Adrenal Insufficiency Clinical Trials 2023

Popular guides.