what is a t test in research methods

Popular searches

• How to Get Participants For Your Study
• How to Do Segmentation?
• Conjoint Preference Share Simulator
• MaxDiff Analysis
• Likert Scales
• Reliability & Validity

Request consultation

Do you need support in running a pricing or product study? We can help you with agile consumer research and conjoint analysis.

Looking for an online survey platform?

Conjointly offers a great survey tool with multiple question types, randomisation blocks, and multilingual support. The Basic tier is always free.

Research Methods Knowledge Base

• Navigating the Knowledge Base
• Foundations
• Measurement
• Research Design
• Conclusion Validity
• Data Preparation
• Descriptive Statistics
• Dummy Variables
• General Linear Model
• Posttest-Only Analysis
• Factorial Design Analysis
• Randomized Block Analysis
• Analysis of Covariance
• Nonequivalent Groups Analysis
• Regression-Discontinuity Analysis
• Regression Point Displacement
• Table of Contents

Fully-functional online survey tool with various question types, logic, randomisation, and reporting for unlimited number of surveys.

Completely free for academics and students .

The t-test assesses whether the means of two groups are statistically different from each other. This analysis is appropriate whenever you want to compare the means of two groups, and especially appropriate as the analysis for the posttest-only two-group randomized experimental design .

Figure 1 shows the distributions for the treated (blue) and control (green) groups in a study. Actually, the figure shows the idealized distribution – the actual distribution would usually be depicted with a histogram or bar graph . The figure indicates where the control and treatment group means are located. The question the t-test addresses is whether the means are statistically different.

What does it mean to say that the averages for two groups are statistically different? Consider the three situations shown in Figure 2. The first thing to notice about the three situations is that the difference between the means is the same in all three . But, you should also notice that the three situations don’t look the same – they tell very different stories. The top example shows a case with moderate variability of scores within each group. The second situation shows the high variability case. the third shows the case with low variability. Clearly, we would conclude that the two groups appear most different or distinct in the bottom or low-variability case. Why? Because there is relatively little overlap between the two bell-shaped curves. In the high variability case, the group difference appears least striking because the two bell-shaped distributions overlap so much.

This leads us to a very important conclusion: when we are looking at the differences between scores for two groups, we have to judge the difference between their means relative to the spread or variability of their scores. The t-test does just this.

Statistical Analysis of the t-test

The formula for the t-test is a ratio. The top part of the ratio is just the difference between the two means or averages. The bottom part is a measure of the variability or dispersion of the scores. This formula is essentially another example of the signal-to-noise metaphor in research: the difference between the means is the signal that, in this case, we think our program or treatment introduced into the data; the bottom part of the formula is a measure of variability that is essentially noise that may make it harder to see the group difference. Figure 3 shows the formula for the t-test and how the numerator and denominator are related to the distributions.

The top part of the formula is easy to compute – just find the difference between the means. The bottom part is called the standard error of the difference . To compute it, we take the variance for each group and divide it by the number of people in that group. We add these two values and then take their square root. The specific formula for the standard error of the difference between the means is:

Remember, that the variance is simply the square of the standard deviation .

The final formula for the t-test is:

The t -value will be positive if the first mean is larger than the second and negative if it is smaller. Once you compute the t -value you have to look it up in a table of significance to test whether the ratio is large enough to say that the difference between the groups is not likely to have been a chance finding. To test the significance, you need to set a risk level (called the alpha level ). In most social research, the “rule of thumb” is to set the alpha level at .05 . This means that five times out of a hundred you would find a statistically significant difference between the means even if there was none (i.e. by “chance”). You also need to determine the degrees of freedom (df) for the test. In the t-test , the degrees of freedom is the sum of the persons in both groups minus 2 . Given the alpha level, the df, and the t -value, you can look the t -value up in a standard table of significance (available as an appendix in the back of most statistics texts) to determine whether the t -value is large enough to be significant. If it is, you can conclude that the difference between the means for the two groups is different (even given the variability). Fortunately, statistical computer programs routinely print the significance test results and save you the trouble of looking them up in a table.

The t-test, one-way Analysis of Variance (ANOVA) and a form of regression analysis are mathematically equivalent (see the statistical analysis of the posttest-only randomized experimental design ) and would yield identical results.

Cookie Consent

Conjointly uses essential cookies to make our site work. We also use additional cookies in order to understand the usage of the site, gather audience analytics, and for remarketing purposes.

For more information on Conjointly's use of cookies, please read our Cookie Policy .

Which one are you?

I am new to conjointly, i am already using conjointly.

JMP | Statistical Discovery.™ From SAS.

Statistics Knowledge Portal

A free online introduction to statistics

What is a t- test?

A t -test (also known as Student's t -test) is a tool for evaluating the means of one or two populations using hypothesis testing. A t-test may be used to evaluate whether a single group differs from a known value ( a one-sample t-test ), whether two groups differ from each other ( an independent two-sample t-test ), or whether there is a significant difference in paired measurements ( a paired, or dependent samples t-test ).

How are t -tests used?

First, you define the hypothesis you are going to test and specify an acceptable risk of drawing a faulty conclusion. For example, when comparing two populations, you might hypothesize that their means are the same, and you decide on an acceptable probability of concluding that a difference exists when that is not true. Next, you calculate a test statistic from your data and compare it to a theoretical value from a  t- distribution. Depending on the outcome, you either reject or fail to reject your null hypothesis. 

What if I have more than two groups?

You cannot use a t -test. Use a multiple comparison method. Examples are analysis of variance ( ANOVA ) , Tukey-Kramer pairwise comparison, Dunnett's comparison to a control, and analysis of means (ANOM).  

t -Test assumptions

While t -tests are relatively robust to deviations from assumptions, t -tests do assume that:

• The data are continuous.
• The sample data have been randomly sampled from a population.
• There is homogeneity of variance (i.e., the variability of the data in each group is similar).
• The distribution is approximately normal.

For two-sample t -tests, we must have independent samples. If the samples are not independent, then a paired t -test may be appropriate.

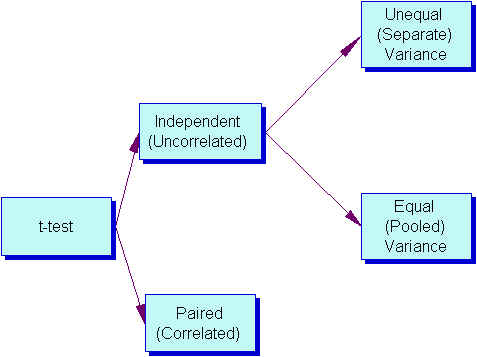
Types of t -tests

There are three t -tests to compare means: a one-sample t -test, a two-sample t -test and a paired t -test. The table below summarizes the characteristics of each and provides guidance on how to choose the correct test. Visit the individual pages for each type of t -test for examples along with details on assumptions and calculations.

The table above shows only the t -tests for population means. Another common t -test is for correlation coefficients .  You use this t -test to decide if the correlation coefficient is significantly different from zero. 

One-tailed vs. two-tailed tests

When you define the hypothesis, you also define whether you have a one-tailed or a two-tailed test. You should make this decision before collecting your data or doing any calculations. You make this decision for all three of the t -tests for means.

To explain, let’s use the one-sample t -test. Suppose we have a random sample of protein bars, and the label for the bars advertises 20 grams of protein per bar. The null hypothesis is that the unknown population mean is 20. Suppose we simply want to know if the data shows we have a different population mean. In this situation, our hypotheses are:

$ \mathrm H_o: \mu = 20 $

$ \mathrm H_a: \mu \neq 20 $

Here, we have a two-tailed test. We will use the data to see if the sample average differs sufficiently from 20 – either higher or lower – to conclude that the unknown population mean is different from 20.

Suppose instead that we want to know whether the advertising on the label is correct. Does the data support the idea that the unknown population mean is at least 20? Or not? In this situation, our hypotheses are:

$ \mathrm H_o: \mu >= 20 $

$ \mathrm H_a: \mu < 20 $

Here, we have a one-tailed test. We will use the data to see if the sample average is sufficiently less than 20 to reject the hypothesis that the unknown population mean is 20 or higher.

See the "tails for hypotheses tests" section on the t -distribution page for images that illustrate the concepts for one-tailed and two-tailed tests.

How to perform a t -test

For all of the t -tests involving means, you perform the same steps in analysis:

• Define your null ($ \mathrm H_o $) and alternative ($ \mathrm H_a $) hypotheses before collecting your data.
• Decide on the alpha value (or α value). This involves determining the risk you are willing to take of drawing the wrong conclusion. For example, suppose you set α=0.05 when comparing two independent groups. Here, you have decided on a 5% risk of concluding the unknown population means are different when they are not.
• Check the data for errors.
• Check the assumptions for the test.
• Perform the test and draw your conclusion. All t -tests for means involve calculating a test statistic. You compare the test statistic to a theoretical value from the t- distribution . The theoretical value involves both the α value and the degrees of freedom for your data. For more detail, visit the pages for one-sample t -test , two-sample t -test and paired t -test .

An open portfolio of interoperable, industry leading products

The Dotmatics digital science platform provides the first true end-to-end solution for scientific R&D, combining an enterprise data platform with the most widely used applications for data analysis, biologics, flow cytometry, chemicals innovation, and more.

Statistical analysis and graphing software for scientists

Bioinformatics, cloning, and antibody discovery software

Plan, visualize, & document core molecular biology procedures

Electronic Lab Notebook to organize, search and share data

Proteomics software for analysis of mass spec data

Modern cytometry analysis platform

Analysis, statistics, graphing and reporting of flow cytometry data

Software to optimize designs of clinical trials

The Ultimate Guide to T Tests

Get all of your t test questions answered here

The ultimate guide to t tests

The t test is one of the simplest statistical techniques that is used to evaluate whether there is a statistical difference between the means from up to two different samples. The t test is especially useful when you have a small number of sample observations (under 30 or so), and you want to make conclusions about the larger population.

The characteristics of the data dictate the appropriate type of t test to run. All t tests are used as standalone analyses for very simple experiments and research questions as well as to perform individual tests within more complicated statistical models such as linear regression. In this guide, we’ll lay out everything you need to know about t tests, including providing a simple workflow to determine what t test is appropriate for your particular data or if you’d be better suited using a different model.

What is a t test?

A t test is a statistical technique used to quantify the difference between the mean (average value) of a variable from up to two samples (datasets). The variable must be numeric. Some examples are height, gross income, and amount of weight lost on a particular diet.

A t test tells you if the difference you observe is “surprising” based on the expected difference. They use t-distributions to evaluate the expected variability. When you have a reasonable-sized sample (over 30 or so observations), the t test can still be used, but other tests that use the normal distribution (the z test) can be used in its place.

Sometimes t tests are called “Student’s” t tests, which is simply a reference to their unusual history.

It got its name because a brewer from the Guinness Brewery, William Gosset , published about the method under the pseudonym "Student". He wanted to get information out of very small sample sizes (often 3-5) because it took so much effort to brew each keg for his samples.

When should I use a t test?

A t test is appropriate to use when you’ve collected a small, random sample from some statistical “population” and want to compare the mean from your sample to another value. The value for comparison could be a fixed value (e.g., 10) or the mean of a second sample.

For example, if your variable of interest is the average height of sixth graders in your region, then you might measure the height of 25 or 30 randomly-selected sixth graders. A t test could be used to answer questions such as, “Is the average height greater than four feet?”

How does a t test work?

Based on your experiment, t tests make enough assumptions about your experiment to calculate an expected variability, and then they use that to determine if the observed data is statistically significant. To do this, t tests rely on an assumed “null hypothesis.” With the above example, the null hypothesis is that the average height is less than or equal to four feet.

Say that we measure the height of 5 randomly selected sixth graders and the average height is five feet. Does that mean that the “true” average height of all sixth graders is greater than four feet or did we randomly happen to measure taller than average students?

To evaluate this, we need a distribution that shows every possible average value resulting from a sample of five individuals in a population where the true mean is four. That may seem impossible to do, which is why there are particular assumptions that need to be made to perform a t test.

With those assumptions, then all that’s needed to determine the “sampling distribution of the mean” is the sample size (5 students in this case) and standard deviation of the data (let’s say it’s 1 foot).

That’s enough to create a graphic of the distribution of the mean, which is:

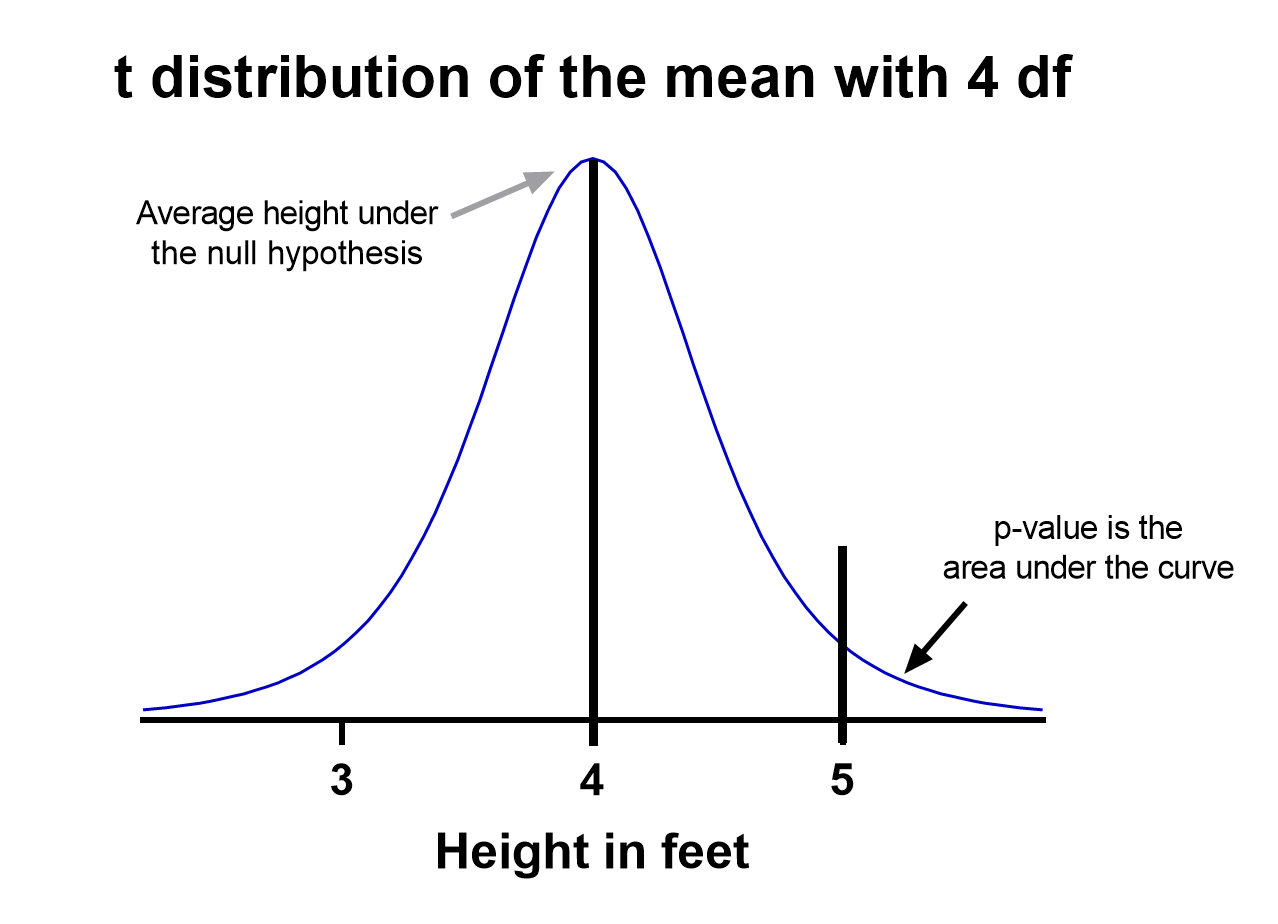
Notice the vertical line at x = 5, which was our sample mean. We (use software to) calculate the area to the right of the vertical line, which gives us the P value (0.09 in this case). Note that because our research question was asking if the average student is greater than four feet, the distribution is centered at four. Since we’re only interested in knowing if the average is greater than four feet, we use a one-tailed test in this case.

Using the standard confidence level of 0.05 with this example, we don’t have evidence that the true average height of sixth graders is taller than 4 feet.

What are the assumptions for t tests?

• One variable of interest : This is not correlation or regression, where you are interested in the relationship between multiple variables. With a t test, you can have different samples, but they are all measuring the same variable (e.g., height).
• Numeric data: You are dealing with a list of measurements that can be averaged. This means you aren’t just counting occurrences in various categories (e.g., eye color or political affiliation).
• Two groups or less: If you have more than two samples of data, a t test is the wrong technique. You most likely need to try ANOVA.
• Random sample : You need a random sample from your statistical “population of interest” in order to draw valid conclusions about the larger population. If your population is so small that you can measure everything, then you have a “census” and don’t need statistics. This is because you don’t need to estimate the truth, since you have measured the truth without variability.
• Normally Distributed : The smaller your sample size, the more important it is that your data come from a normal, Gaussian distribution bell curve. If you have reason to believe that your data are not normally distributed, consider nonparametric t test alternatives . This isn’t necessary for larger samples (usually 25 or 30 unless the data is heavily skewed). The reason is that the Central Limit Theorem applies in this case, which says that even if the distribution of your data is not normal, the distribution of the mean of your data is, so you can use a z-test rather than a t test.

How do I know which t test to use?

There are many types of t tests to choose from, but you don’t necessarily have to understand every detail behind each option.

You just need to be able to answer a few questions, which will lead you to pick the right t test. To that end, we put together this workflow for you to figure out which test is appropriate for your data.

Do you have one or two samples?

Are you comparing the means of two different samples, or comparing the mean from one sample to a fixed value? An example research question is, “Is the average height of my sample of sixth grade students greater than four feet?”

If you only have one sample of data, you can click here to skip to a one-sample t test example, otherwise your next step is to ask: 

Are observations in the two samples matched up or related in some way?

This could be as before-and-after measurements of the same exact subjects, or perhaps your study split up “pairs” of subjects (who are technically different but share certain characteristics of interest) into the two samples. The same variable is measured in both cases.

If so, you are looking at some kind of paired samples t test . The linked section will help you dial in exactly which one in that family is best for you, either difference (most common) or ratio.

If you aren’t sure paired is right, ask yourself another question:

Are you comparing different observations in each of the two samples?

If the answer is yes, then you have an unpaired or independent samples t test. The two samples should measure the same variable (e.g., height), but are samples from two distinct groups (e.g., team A and team B). 

The goal is to compare the means to see if the groups are significantly different. For example, “Is the average height of team A greater than team B?” Unlike paired, the only relationship between the groups in this case is that we measured the same variable for both. There are two versions of unpaired samples t tests (pooled and unpooled) depending on whether you assume the same variance for each sample.

Have you run the same experiment multiple times on the same subject/observational unit?

If so, then you have a nested t test (unless you have more than two sample groups). This is a trickier concept to understand. One example is if you are measuring how well Fertilizer A works against Fertilizer B. Let’s say you have 12 pots to grow plants in (6 pots for each fertilizer), and you grow 3 plants in each pot.

In this case you have 6 observational units for each fertilizer, with 3 subsamples from each pot. You would want to analyze this with a nested t test . The “nested” factor in this case is the pots. It’s important to note that we aren’t interested in estimating the variability within each pot, we just want to take it into account.

You might be tempted to run an unpaired samples t test here, but that assumes you have 6*3 = 18 replicates for each fertilizer. However, the three replicates within each pot are related, and an unpaired samples t test wouldn’t take that into account.

What if none of these sound like my experiment?

If you’re not seeing your research question above, note that t tests are very basic statistical tools. Many experiments require more sophisticated techniques to evaluate differences. If the variable of interest is a proportion (e.g., 10 of 100 manufactured products were defective), then you’d use z-tests. If you take before and after measurements and have more than one treatment (e.g., control vs a treatment diet), then you need ANOVA.

How do I perform a t test using software?

If you’re wondering how to do a t test, the easiest way is with statistical software such as Prism or an online t test calculator .

If you’re using software, then all you need to know is which t test is appropriate ( use the workflow here ) and understand how to interpret the output. To do that, you’ll also need to:

• Determine whether your test is one or two-tailed
• Choose the level of significance

Is my test one or two-tailed? 

Whether or not you have a one- or two-tailed test depends on your research hypothesis. Choosing the appropriately tailed test is very important and requires integrity from the researcher. This is because you have more “power” with one-tailed tests, meaning that you can detect a statistically significant difference more easily. Unless you have written out your research hypothesis as one directional before you run your experiment, you should use a two-tailed test.

Two-tailed tests

Two-tailed tests are the most common, and they are applicable when your research question is simply asking, “is there a difference?”

One-tailed tests

Contrast that with one-tailed tests, where the research questions are directional, meaning that either the question is, “is it greater than ” or the question is, “is it less than ”. These tests can only detect a difference in one direction.

Choosing the level of significance

All t tests estimate whether a mean of a population is different than some other value, and with all estimates come some variability, or what statisticians call “error.” Before analyzing your data, you want to choose a level of significance, usually denoted by the Greek letter alpha, 𝛼. The scientific standard is setting alpha to be 0.05.

An alpha of 0.05 results in 95% confidence intervals, and determines the cutoff for when P values are considered statistically significant.

One sample t test

If you only have one sample of a list of numbers, you are doing a one-sample t test. All you are interested in doing is comparing the mean from this group with some known value to test if there is evidence, that it is significantly different from that standard. Use our free one-sample t test calculator for this.

A one sample t test example research question is, “Is the average fifth grader taller than four feet?”

It is the simplest version of a t test, and has all sorts of applications within hypothesis testing. Sometimes the “known value” is called the “null value”. While the null value in t tests is often 0, it could be any value. The name comes from being the value which exactly represents the null hypothesis, where no significant difference exists. 

Any time you know the exact number you are trying to compare your sample of data against, this could work well. And of course: it can be either one or two-tailed.

One sample t test formula

Statistical software handles this for you, but if you want the details, the formula for a one sample t test is:

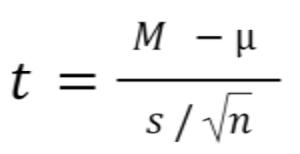
• M: Calculated mean of your sample
• μ: Hypothetical mean you are testing against
• s: The standard deviation of your sample
• n: The number of observations in your sample.

In a one-sample t test, calculating degrees of freedom is simple: one less than the number of objects in your dataset (you’ll see it written as n-1 ).

Example of a one sample t test

For our example within Prism, we have a dataset of 12 values from an experiment labeled “% of control”. Perhaps these are heights of a sample of plants that have been treated with a new fertilizer. A value of 100 represents the industry-standard control height. Likewise, 123 represents a plant with a height 123% that of the control (that is, 23% larger).

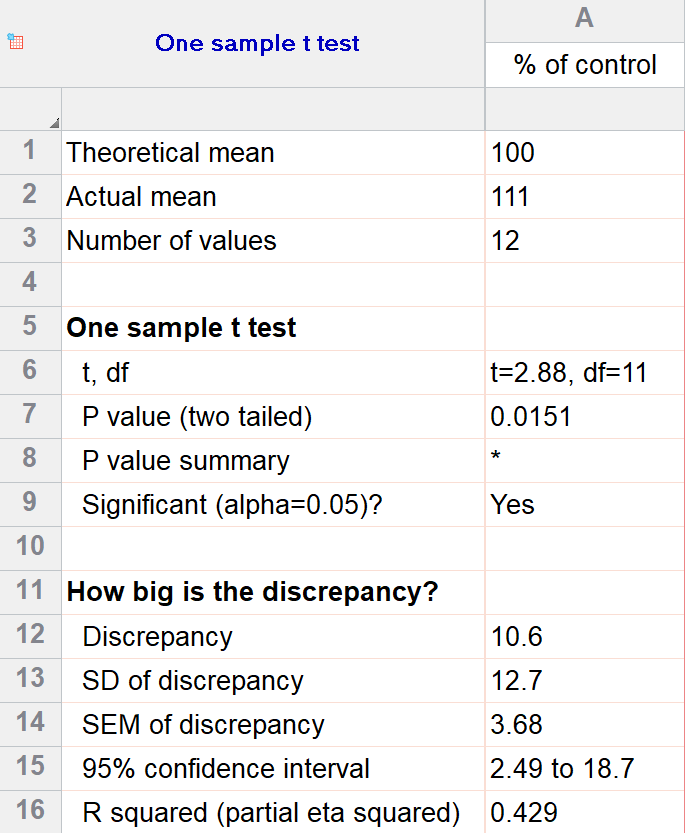
We’ll perform a two-tailed, one-sample t test to see if plants are shorter or taller on average with the fertilizer. We will use a significance threshold of 0.05. Here is the output:

You can see in the output that the actual sample mean was 111. Is that different enough from the industry standard (100) to conclude that there is a statistical difference?

The quick answer is yes, there’s strong evidence that the height of the plants with the fertilizer is greater than the industry standard (p=0.015). The nice thing about using software is that it handles some of the trickier steps for you. In this case, it calculates your test statistic (t=2.88), determines the appropriate degrees of freedom (11), and outputs a P value.

More informative than the P value is the confidence interval of the difference, which is 2.49 to 18.7. The confidence interval tells us that, based on our data, we are confident that the true difference between our sample and the baseline value of 100 is somewhere between 2.49 and 18.7. As long as the difference is statistically significant, the interval will not contain zero.

You can follow these tips for interpreting your own one-sample test.

Graphing a one-sample t test

For some techniques (like regression), graphing the data is a very helpful part of the analysis. For t tests, making a chart of your data is still useful to spot any strange patterns or outliers, but the small sample size means you may already be familiar with any strange things in your data.

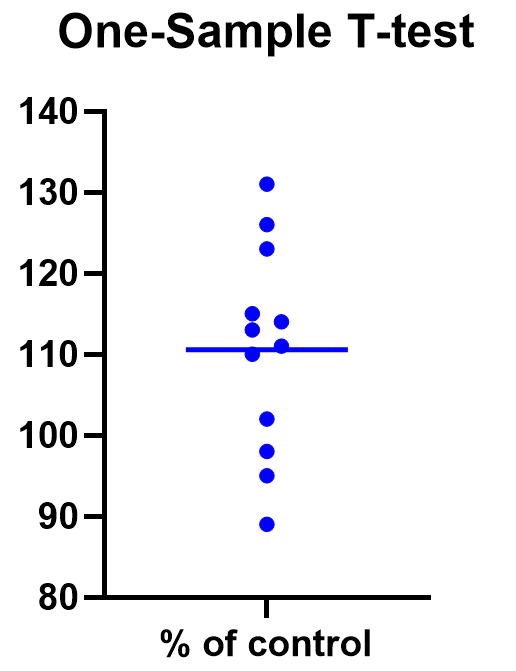
Here we have a simple plot of the data points, perhaps with a mark for the average. We’ve made this as an example, but the truth is that graphing is usually more visually telling for two-sample t tests than for just one sample.

Two sample t tests

There are several kinds of two sample t tests, with the two main categories being paired and unpaired (independent) samples.

Paired samples t test

In a paired samples t test, also called dependent samples t test, there are two samples of data, and each observation in one sample is “paired” with an observation in the second sample. The most common example is when measurements are taken on each subject before and after a treatment. A paired t test example research question is, “Is there a statistical difference between the average red blood cell counts before and after a treatment?”

Having two samples that are closely related simplifies the analysis. Statistical software, such as this paired t test calculator , will simply take a difference between the two values, and then compare that difference to 0.

In some (rare) situations, taking a difference between the pairs violates the assumptions of a t test, because the average difference changes based on the size of the before value (e.g., there’s a larger difference between before and after when there were more to start with). In this case, instead of using a difference test, use a ratio of the before and after values, which is referred to as ratio t tests .

Paired t test formula

The formula for paired samples t test is:

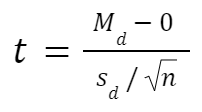
• Md: Mean difference between the samples
• sd: The standard deviation of the differences
• n: The number of differences

Degrees of freedom are the same as before. If you’re studying for an exam, you can remember that the degrees of freedom are still n-1 (not n-2) because we are converting the data into a single column of differences rather than considering the two groups independently.

Also note that the null value here is simply 0. There is no real reason to include “minus 0” in an equation other than to illustrate that we are still doing a hypothesis test. After you take the difference between the two means, you are comparing that difference to 0.

For our example data, we have five test subjects and have taken two measurements from each: before (“control”) and after a treatment (“treated”). If we set alpha = 0.05 and perform a two-tailed test, we observe a statistically significant difference between the treated and control group (p=0.0160, t=4.01, df = 4). We are 95% confident that the true mean difference between the treated and control group is between 0.449 and 2.47.

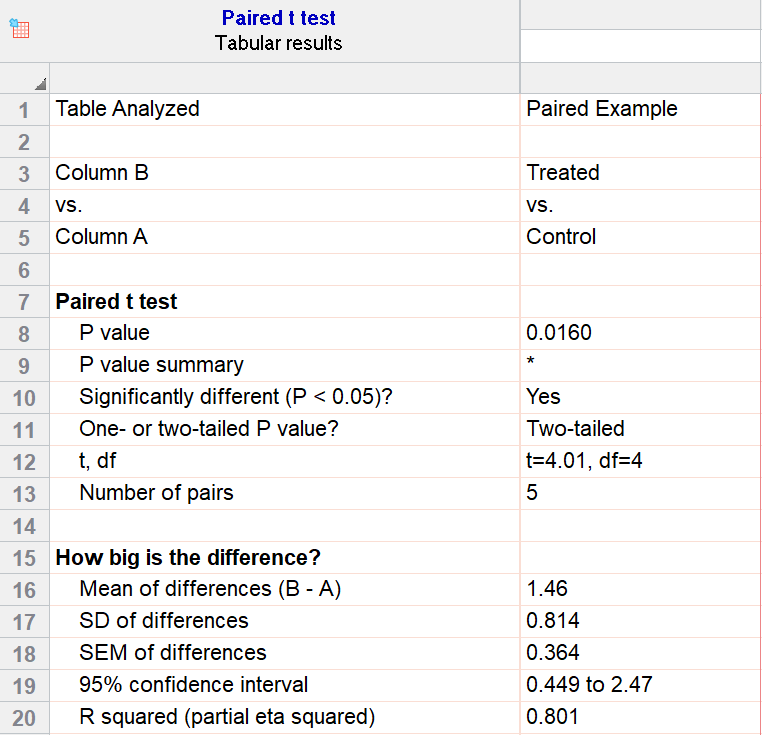
Graphing a paired t test

The significant result of the P value suggests evidence that the treatment had some effect, and we can also look at this graphically. The lines that connect the observations can help us spot a pattern, if it exists. In this case the lines show that all observations increased after treatment. While not all graphics are this straightforward, here it is very consistent with the outcome of the t test. 

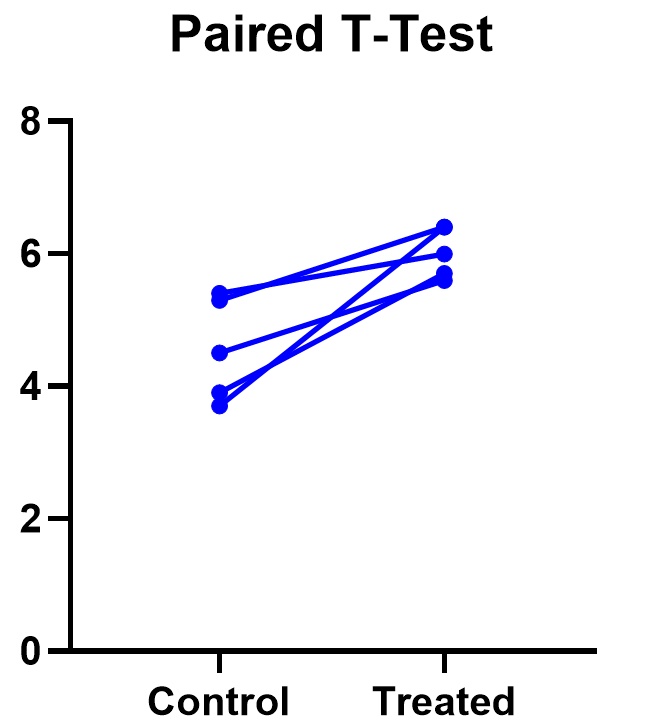
Prism’s estimation plot is even more helpful because it shows both the data (like above) and the confidence interval for the difference between means. You can easily see the evidence of significance since the confidence interval on the right does not contain zero.

Here are some more graphing tips for paired t tests .

Unpaired samples t test

Unpaired samples t test, also called independent samples t test, is appropriate when you have two sample groups that aren’t correlated with one another. A pharma example is testing a treatment group against a control group of different subjects. Compare that with a paired sample, which might be recording the same subjects before and after a treatment.

With unpaired t tests, in addition to choosing your level of significance and a one or two tailed test, you need to determine whether or not to assume that the variances between the groups are the same or not. If you assume equal variances, then you can “pool” the calculation of the standard error between the two samples. Otherwise, the standard choice is Welch’s t test which corrects for unequal variances. This choice affects the calculation of the test statistic and the power of the test, which is the test’s sensitivity to detect statistical significance. 

It’s best to choose whether or not you’ll use a pooled or unpooled (Welch’s) standard error before running your experiment, because the standard statistical test is notoriously problematic. See more details about unequal variances here .

As long as you’re using statistical software, such as this two-sample t test calculator , it’s just as easy to calculate a test statistic whether or not you assume that the variances of your two samples are the same. If you’re doing it by hand, however, the calculations get more complicated with unequal variances.

Unpaired (independent) samples t test formula

The general two-sample t test formula is:

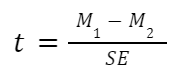
• M1 and M2: Two means you are comparing, one from each dataset
• SE : The combined standard error of the two samples (calculated using pooled or unpooled standard error)

The denominator (standard error) calculation can be complicated, as can the degrees of freedom. If the groups are not balanced (the same number of observations in each), you will need to account for both when determining n for the test as a whole.

As an example for this family, we conduct a paired samples t test assuming equal variances (pooled). Based on our research hypothesis, we’ll conduct a two-tailed test, and use alpha=0.05 for our level of significance. Our samples were unbalanced, with two samples of 6 and 5 observations respectively. 

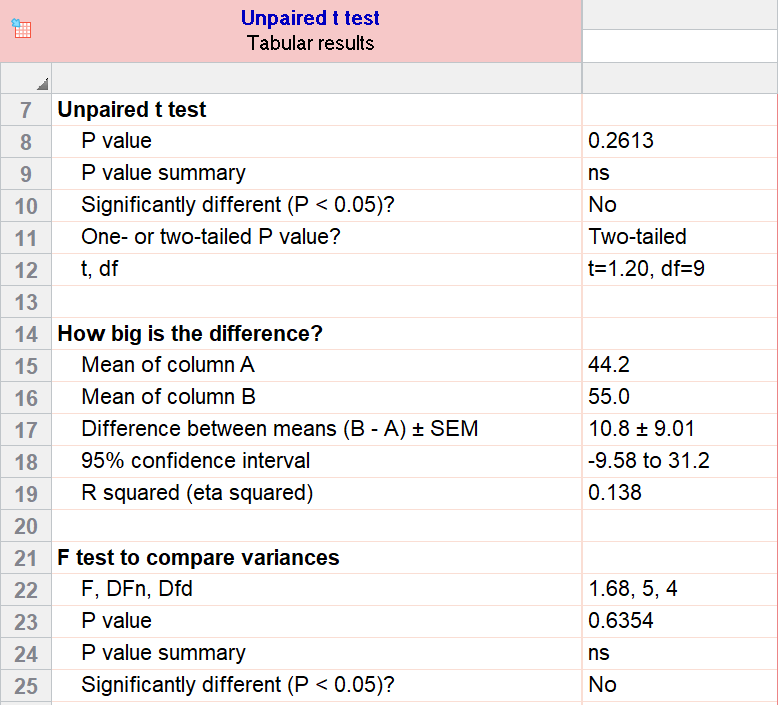
The P value (p=0.261, t = 1.20, df = 9) is higher than our threshold of 0.05. We have not found sufficient evidence to suggest a significant difference. You can see the confidence interval of the difference of the means is -9.58 to 31.2.

Note that the F-test result shows that the variances of the two groups are not significantly different from each other.

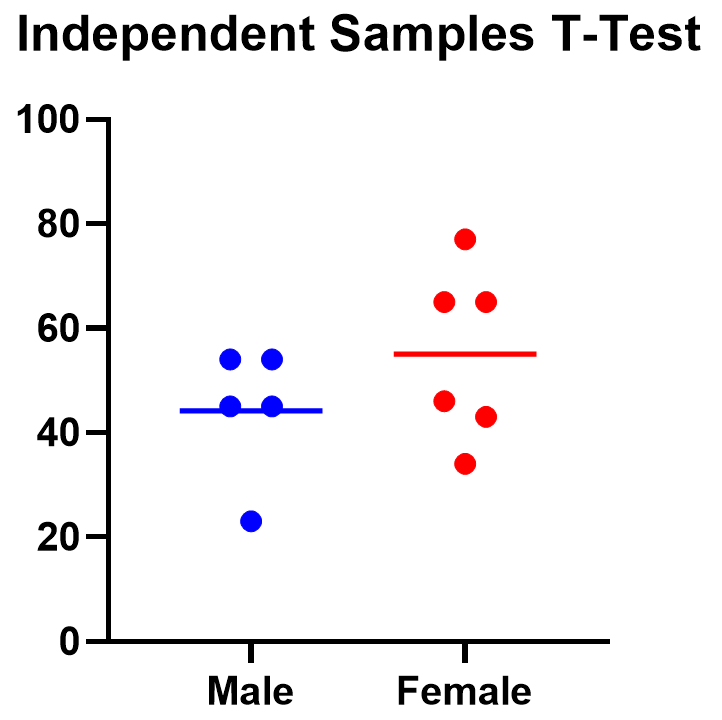
Graphing an unpaired samples t test

For an unpaired samples t test, graphing the data can quickly help you get a handle on the two groups and how similar or different they are. Like the paired example, this helps confirm the evidence (or lack thereof) that is found by doing the t test itself.

Below you can see that the observed mean for females is higher than that for males. But because of the variability in the data, we can’t tell if the means are actually different or if the difference is just by chance. 

Nonparametric alternatives for t tests

If your data comes from a normal distribution (or something close enough to a normal distribution), then a t test is valid. If that assumption is violated, you can use nonparametric alternatives.

T tests evaluate whether the mean is different from another value, whereas nonparametric alternatives compare either the median or the rank. Medians are well-known to be much more robust to outliers than the mean.

The downside to nonparametric tests is that they don’t have as much statistical power, meaning a larger difference is required in order to determine that it’s statistically significant.

Wilcoxon signed-rank test

The Wilcoxon signed-rank test is the nonparametric cousin to the one-sample t test. This compares a sample median to a hypothetical median value. It is sometimes erroneously even called the Wilcoxon t test (even though it calculates a “W” statistic).

And if you have two related samples, you should use the Wilcoxon matched pairs test instead. The two versions of Wilcoxon are different, and the matched pairs version is specifically for comparing the median difference for paired samples. 

Mann-Whitney and Kolmogorov-Smirnov tests

For unpaired (independent) samples, there are multiple options for nonparametric testing. Mann-Whitney is more popular and compares the mean ranks (the ordering of values from smallest to largest) of the two samples. Mann-Whitney is often misrepresented as a comparison of medians, but that’s not always the case. Kolmogorov-Smirnov tests if the overall distributions differ between the two samples. 

More t test FAQs

What is the formula for a t test.

The exact formula depends on which type of t test you are running, although there is a basic structure that all t tests have in common. All t test statistics will have the form:

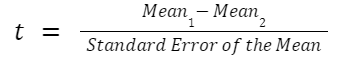
• t : The t test statistic you calculate for your test
• Mean1 and Mean2: Two means you are comparing, at least 1 from your own dataset
• Standard Error of the Mean : The standard error of the mean , also called the standard deviation of the mean, which takes into account the variance and size of your dataset

The exact formula for any t test can be slightly different, particularly the calculation of the standard error. Not only does it matter whether one or two samples are being compared, the relationship between the samples can make a difference too.

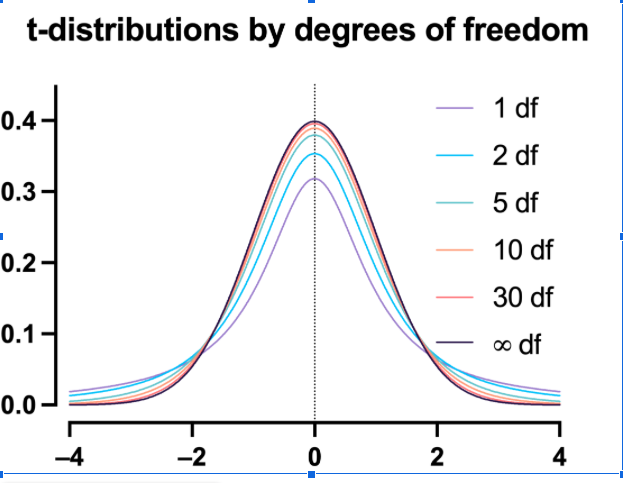
What is a t-distribution?

A t-distribution is similar to a normal distribution. It’s a bell-shaped curve, but compared to a normal it has fatter tails, which means that it’s more common to observe extremes. T-distributions are identified by the number of degrees of freedom. The higher the number, the closer the t-distribution gets to a normal distribution. After about 30 degrees of freedom, a t and a standard normal are practically the same.

What are degrees of freedom?

Degrees of freedom are a measure of how large your dataset is. They aren’t exactly the number of observations, because they also take into account the number of parameters (e.g., mean, variance) that you have estimated.

What is the difference between paired vs unpaired t tests?

Both paired and unpaired t tests involve two sample groups of data. With a paired t test, the values in each group are related (usually they are before and after values measured on the same test subject). In contrast, with unpaired t tests, the observed values aren’t related between groups. An unpaired, or independent t test, example is comparing the average height of children at school A vs school B. 

When do I use a z-test versus a t test?

Z-tests, which compare data using a normal distribution rather than a t-distribution, are primarily used for two situations. The first is when you’re evaluating proportions (number of failures on an assembly line). The second is when your sample size is large enough (usually around 30) that you can use a normal approximation to evaluate the means.

When should I use ANOVA instead of a t test?

Use ANOVA if you have more than two group means to compare.

What are the differences between t test vs chi square?

Chi square tests are used to evaluate contingency tables , which record a count of the number of subjects that fall into particular categories (e.g., truck, SUV, car). t tests compare the mean(s) of a variable of interest (e.g., height, weight).

What are P values?

P values are the probability that you would get data as or more extreme than the observed data given that the null hypothesis is true. It’s a mouthful, and there are a lot of issues to be aware of with P values.

What are t test critical values?

Critical values are a classical form (they aren’t used directly with modern computing) of determining if a statistical test is significant or not. Historically you could calculate your test statistic from your data, and then use a t-table to look up the cutoff value (critical value) that represented a “significant” result. You would then compare your observed statistic against the critical value.

How do I calculate degrees of freedom for my t test?

In most practical usage, degrees of freedom are the number of observations you have minus the number of parameters you are trying to estimate. The calculation isn’t always straightforward and is approximated for some t tests.

Statistical software calculates degrees of freedom automatically as part of the analysis, so understanding them in more detail isn’t needed beyond assuaging any curiosity.

Perform your own t test

Are you ready to calculate your own t test? Start your 30 day free trial of Prism and get access to:

• A step by step guide on how to perform a t test
• Sample data to save you time
• More tips on how Prism can help your research

With Prism, in a matter of minutes you learn how to go from entering data to performing statistical analyses and generating high-quality graphs.

• Search Search Please fill out this field.

What Is a T-Test?

Understanding the t-test, using a t-test, which t-test to use.

• T-Test FAQs
• Fundamental Analysis

T-Test: What It Is With Multiple Formulas and When To Use Them

Read how this calculation can be used for hypothesis testing in statistics

Adam Hayes, Ph.D., CFA, is a financial writer with 15+ years Wall Street experience as a derivatives trader. Besides his extensive derivative trading expertise, Adam is an expert in economics and behavioral finance. Adam received his master's in economics from The New School for Social Research and his Ph.D. from the University of Wisconsin-Madison in sociology. He is a CFA charterholder as well as holding FINRA Series 7, 55 & 63 licenses. He currently researches and teaches economic sociology and the social studies of finance at the Hebrew University in Jerusalem.

A t-test is an inferential statistic used to determine if there is a significant difference between the means of two groups and how they are related. T-tests are used when the data sets follow a normal distribution and have unknown variances, like the data set recorded from flipping a coin 100 times.

The t-test is a test used for hypothesis testing in statistics and uses the t-statistic, the t-distribution values, and the degrees of freedom to determine statistical significance.

Key Takeaways

• A t-test is an inferential statistic used to determine if there is a statistically significant difference between the means of two variables.
• The t-test is a test used for hypothesis testing in statistics.
• Calculating a t-test requires three fundamental data values including the difference between the mean values from each data set, the standard deviation of each group, and the number of data values.
• T-tests can be dependent or independent.

Investopedia / Sabrina Jiang

A t-test compares the average values of two data sets and determines if they came from the same population. In the above examples, a sample of students from class A and a sample of students from class B would not likely have the same mean and standard deviation. Similarly, samples taken from the placebo-fed control group and those taken from the drug prescribed group should have a slightly different mean and standard deviation.

Mathematically, the t-test takes a sample from each of the two sets and establishes the problem statement. It assumes a null hypothesis that the two means are equal.

Using the formulas, values are calculated and compared against the standard values. The assumed null hypothesis is accepted or rejected accordingly. If the null hypothesis qualifies to be rejected, it indicates that data readings are strong and are probably not due to chance.

The t-test is just one of many tests used for this purpose. Statisticians use additional tests other than the t-test to examine more variables and larger sample sizes. For a large sample size, statisticians use a  z-test . Other testing options include the chi-square test and the f-test.

Consider that a drug manufacturer tests a new medicine. Following standard procedure, the drug is given to one group of patients and a placebo to another group called the control group. The placebo is a substance with no therapeutic value and serves as a benchmark to measure how the other group, administered the actual drug, responds.

After the drug trial, the members of the placebo-fed control group reported an increase in average life expectancy of three years, while the members of the group who are prescribed the new drug reported an increase in average life expectancy of four years.

Initial observation indicates that the drug is working. However, it is also possible that the observation may be due to chance. A t-test can be used to determine if the results are correct and applicable to the entire population.

Four assumptions are made while using a t-test. The data collected must follow a continuous or ordinal scale, such as the scores for an IQ test, the data is collected from a randomly selected portion of the total population, the data will result in a normal distribution of a bell-shaped curve, and equal or homogenous variance exists when the standard variations are equal.

T-Test Formula

Calculating a t-test requires three fundamental data values. They include the difference between the mean values from each data set, or the mean difference, the standard deviation of each group, and the number of data values of each group.

This comparison helps to determine the effect of chance on the difference, and whether the difference is outside that chance range. The t-test questions whether the difference between the groups represents a true difference in the study or merely a random difference.

The t-test produces two values as its output: t-value and degrees of freedom . The t-value, or t-score, is a ratio of the difference between the mean of the two sample sets and the variation that exists within the sample sets.

The numerator value is the difference between the mean of the two sample sets. The denominator is the variation that exists within the sample sets and is a measurement of the dispersion or variability.

This calculated t-value is then compared against a value obtained from a critical value table called the T-distribution table. Higher values of the t-score indicate that a large difference exists between the two sample sets. The smaller the t-value, the more similarity exists between the two sample sets.

A large t-score, or t-value, indicates that the groups are different while a small t-score indicates that the groups are similar.

Degrees of freedom refer to the values in a study that has the freedom to vary and are essential for assessing the importance and the validity of the null hypothesis. Computation of these values usually depends upon the number of data records available in the sample set.

Paired Sample T-Test

The correlated t-test, or paired t-test, is a dependent type of test and is performed when the samples consist of matched pairs of similar units, or when there are cases of repeated measures. For example, there may be instances where the same patients are repeatedly tested before and after receiving a particular treatment. Each patient is being used as a control sample against themselves.

This method also applies to cases where the samples are related or have matching characteristics, like a comparative analysis involving children, parents, or siblings.

The formula for computing the t-value and degrees of freedom for a paired t-test is:

T = mean 1 − mean 2 s ( diff ) ( n ) where: mean 1  and  mean 2 = The average values of each of the sample sets s ( diff ) = The standard deviation of the differences of the paired data values n = The sample size (the number of paired differences) n − 1 = The degrees of freedom \begin{aligned}&T=\frac{\textit{mean}1 - \textit{mean}2}{\frac{s(\text{diff})}{\sqrt{(n)}}}\\&\textbf{where:}\\&\textit{mean}1\text{ and }\textit{mean}2=\text{The average values of each of the sample sets}\\&s(\text{diff})=\text{The standard deviation of the differences of the paired data values}\\&n=\text{The sample size (the number of paired differences)}\\&n-1=\text{The degrees of freedom}\end{aligned} ​ T = ( n ) ​ s ( diff ) ​ mean 1 − mean 2 ​ where: mean 1  and  mean 2 = The average values of each of the sample sets s ( diff ) = The standard deviation of the differences of the paired data values n = The sample size (the number of paired differences) n − 1 = The degrees of freedom ​

Equal Variance or Pooled T-Test

The equal variance t-test is an independent t-test and is used when the number of samples in each group is the same, or the variance of the two data sets is similar.

The formula used for calculating t-value and degrees of freedom for equal variance t-test is:

T-value = m e a n 1 − m e a n 2 ( n 1 − 1 ) × v a r 1 2 + ( n 2 − 1 ) × v a r 2 2 n 1 + n 2 − 2 × 1 n 1 + 1 n 2 where: m e a n 1  and  m e a n 2 = Average values of each of the sample sets v a r 1  and  v a r 2 = Variance of each of the sample sets n 1  and  n 2 = Number of records in each sample set \begin{aligned}&\text{T-value} = \frac{ mean1 - mean2 }{\frac {(n1 - 1) \times var1^2 + (n2 - 1) \times var2^2 }{ n1 +n2 - 2}\times \sqrt{ \frac{1}{n1} + \frac{1}{n2}} } \\&\textbf{where:}\\&mean1 \text{ and } mean2 = \text{Average values of each} \\&\text{of the sample sets}\\&var1 \text{ and } var2 = \text{Variance of each of the sample sets}\\&n1 \text{ and } n2 = \text{Number of records in each sample set} \end{aligned} ​ T-value = n 1 + n 2 − 2 ( n 1 − 1 ) × v a r 1 2 + ( n 2 − 1 ) × v a r 2 2 ​ × n 1 1 ​ + n 2 1 ​ ​ m e an 1 − m e an 2 ​ where: m e an 1  and  m e an 2 = Average values of each of the sample sets v a r 1  and  v a r 2 = Variance of each of the sample sets n 1  and  n 2 = Number of records in each sample set ​

Degrees of Freedom = n 1 + n 2 − 2 where: n 1  and  n 2 = Number of records in each sample set \begin{aligned} &\text{Degrees of Freedom} = n1 + n2 - 2 \\ &\textbf{where:}\\ &n1 \text{ and } n2 = \text{Number of records in each sample set} \\ \end{aligned} ​ Degrees of Freedom = n 1 + n 2 − 2 where: n 1  and  n 2 = Number of records in each sample set ​

Unequal Variance T-Test

The unequal variance t-test is an independent t-test and is used when the number of samples in each group is different, and the variance of the two data sets is also different. This test is also called Welch's t-test.

The formula used for calculating t-value and degrees of freedom for an unequal variance t-test is:

T-value = m e a n 1 − m e a n 2 ( v a r 1 n 1 + v a r 2 n 2 ) where: m e a n 1  and  m e a n 2 = Average values of each of the sample sets v a r 1  and  v a r 2 = Variance of each of the sample sets n 1  and  n 2 = Number of records in each sample set \begin{aligned}&\text{T-value}=\frac{mean1-mean2}{\sqrt{\bigg(\frac{var1}{n1}{+\frac{var2}{n2}\bigg)}}}\\&\textbf{where:}\\&mean1 \text{ and } mean2 = \text{Average values of each} \\&\text{of the sample sets} \\&var1 \text{ and } var2 = \text{Variance of each of the sample sets} \\&n1 \text{ and } n2 = \text{Number of records in each sample set} \end{aligned} ​ T-value = ( n 1 v a r 1 ​ + n 2 v a r 2 ​ ) ​ m e an 1 − m e an 2 ​ where: m e an 1  and  m e an 2 = Average values of each of the sample sets v a r 1  and  v a r 2 = Variance of each of the sample sets n 1  and  n 2 = Number of records in each sample set ​

Degrees of Freedom = ( v a r 1 2 n 1 + v a r 2 2 n 2 ) 2 ( v a r 1 2 n 1 ) 2 n 1 − 1 + ( v a r 2 2 n 2 ) 2 n 2 − 1 where: v a r 1  and  v a r 2 = Variance of each of the sample sets n 1  and  n 2 = Number of records in each sample set \begin{aligned} &\text{Degrees of Freedom} = \frac{ \left ( \frac{ var1^2 }{ n1 } + \frac{ var2^2 }{ n2 } \right )^2 }{ \frac{ \left ( \frac{ var1^2 }{ n1 } \right )^2 }{ n1 - 1 } + \frac{ \left ( \frac{ var2^2 }{ n2 } \right )^2 }{ n2 - 1}} \\ &\textbf{where:}\\ &var1 \text{ and } var2 = \text{Variance of each of the sample sets} \\ &n1 \text{ and } n2 = \text{Number of records in each sample set} \\ \end{aligned} ​ Degrees of Freedom = n 1 − 1 ( n 1 v a r 1 2 ​ ) 2 ​ + n 2 − 1 ( n 2 v a r 2 2 ​ ) 2 ​ ( n 1 v a r 1 2 ​ + n 2 v a r 2 2 ​ ) 2 ​ where: v a r 1  and  v a r 2 = Variance of each of the sample sets n 1  and  n 2 = Number of records in each sample set ​

The following flowchart can be used to determine which t-test to use based on the characteristics of the sample sets. The key items to consider include the similarity of the sample records, the number of data records in each sample set, and the variance of each sample set.

Image by Julie Bang © Investopedia 2019

Example of an Unequal Variance T-Test

Assume that the diagonal measurement of paintings received in an art gallery is taken. One group of samples includes 10 paintings, while the other includes 20 paintings. The data sets, with the corresponding mean and variance values, are as follows:

Though the mean of Set 2 is higher than that of Set 1, we cannot conclude that the population corresponding to Set 2 has a higher mean than the population corresponding to Set 1.

Is the difference from 19.4 to 21.6 due to chance alone, or do differences exist in the overall populations of all the paintings received in the art gallery? We establish the problem by assuming the null hypothesis that the mean is the same between the two sample sets and conduct a t-test to test if the hypothesis is plausible.

Since the number of data records is different (n1 = 10 and n2 = 20) and the variance is also different, the t-value and degrees of freedom are computed for the above data set using the formula mentioned in the Unequal Variance T-Test section.

The t-value is -2.24787. Since the minus sign can be ignored when comparing the two t-values, the computed value is 2.24787.

The degrees of freedom value is 24.38 and is reduced to 24, owing to the formula definition requiring rounding down of the value to the least possible integer value.

One can specify a level of probability (alpha level, level of significance,  p ) as a criterion for acceptance. In most cases, a 5% value can be assumed.

Using the degree of freedom value as 24 and a 5% level of significance, a look at the t-value distribution table gives a value of 2.064. Comparing this value against the computed value of 2.247 indicates that the calculated t-value is greater than the table value at a significance level of 5%. Therefore, it is safe to reject the null hypothesis that there is no difference between means. The population set has intrinsic differences, and they are not by chance.

How Is the T-Distribution Table Used?

The T-Distribution Table is available in one-tail and two-tails formats. The former is used for assessing cases that have a fixed value or range with a clear direction, either positive or negative. For instance, what is the probability of the output value remaining below -3, or getting more than seven when rolling a pair of dice? The latter is used for range-bound analysis, such as asking if the coordinates fall between -2 and +2.

What Is an Independent T-Test?

The samples of independent t-tests are selected independent of each other where the data sets in the two groups don’t refer to the same values. They may include a group of 100 randomly unrelated patients split into two groups of 50 patients each. One of the groups becomes the control group and is administered a placebo, while the other group receives a prescribed treatment. This constitutes two independent sample groups that are unpaired and unrelated to each other.

What Does a T-Test Explain and How Are They Used?

A t-test is a statistical test that is used to compare the means of two groups. It is often used in hypothesis testing to determine whether a process or treatment has an effect on the population of interest, or whether two groups are different from one another.

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

Our websites may use cookies to personalize and enhance your experience. By continuing without changing your cookie settings, you agree to this collection. For more information, please see our University Websites Privacy Notice .

Neag School of Education

Educational Research Basics by Del Siegle

An introduction to statistics usually covers t tests, anovas, and chi-square. for this course we will concentrate on t tests, although background information will be provided on anovas and chi-square., a powerpoint presentation on t tests has been created for your use..

The t test is one type of inferential statistics. It is used to determine whether there is a significant difference between the means of two groups. With all inferential statistics, we assume the dependent variable fits a normal distribution . When we assume a normal distribution exists, we can identify the probability of a particular outcome. We specify the level of probability (alpha level, level of significance, p ) we are willing to accept before we collect data ( p < .05 is a common value that is used). After we collect data we calculate a test statistic with a formula. We compare our test statistic with a critical value found on a table to see if our results fall within the acceptable level of probability. Modern computer programs calculate the test statistic for us and also provide the exact probability of obtaining that test statistic with the number of subjects we have.

Student’s test ( t test) Notes

When the difference between two population averages is being investigated, a t test is used. In other words, a t test is used when we wish to compare two means (the scores must be measured on an interval or ratio measurement scale ). We would use a t test if we wished to compare the reading achievement of boys and girls. With a t test, we have one independent variable and one dependent variable. The independent variable (gender in this case) can only have two levels (male and female). The dependent variable would be reading achievement. If the independent had more than two levels, then we would use a one-way analysis of variance (ANOVA).

The test statistic that a t test produces is a t -value. Conceptually, t -values are an extension of z -scores. In a way, the t -value represents how many standard units the means of the two groups are apart.

With a t tes t, the researcher wants to state with some degree of confidence that the obtained difference between the means of the sample groups is too great to be a chance event and that some difference also exists in the population from which the sample was drawn. In other words, the difference that we might find between the boys’ and girls’ reading achievement in our sample might have occurred by chance, or it might exist in the population. If our t test produces a t -value that results in a probability of .01, we say that the likelihood of getting the difference we found by chance would be 1 in a 100 times. We could say that it is unlikely that our results occurred by chance and the difference we found in the sample probably exists in the populations from which it was drawn.

Five factors contribute to whether the difference between two groups’ means can be considered significant:

• How large is the difference between the means of the two groups? Other factors being equal, the greater the difference between the two means, the greater the likelihood that a statistically significant mean difference exists. If the means of the two groups are far apart, we can be fairly confident that there is a real difference between them.
• How much overlap is there between the groups? This is a function of the variation within the groups. Other factors being equal, the smaller the variances of the two groups under consideration, the greater the likelihood that a statistically significant mean difference exists. We can be more confident that two groups differ when the scores within each group are close together.
• How many subjects are in the two samples? The size of the sample is extremely important in determining the significance of the difference between means. With increased sample size, means tend to become more stable representations of group performance. If the difference we find remains constant as we collect more and more data, we become more confident that we can trust the difference we are finding.
• What alpha level is being used to test the mean difference (how confident do you want to be about your statement that there is a mean difference). A larger alpha level requires less difference between the means. It is much harder to find differences between groups when you are only willing to have your results occur by chance 1 out of a 100 times ( p < .01) as compared to 5 out of 100 times ( p < .05).
• Is a directional (one-tailed) or non-directional (two-tailed) hypothesis being tested? Other factors being equal, smaller mean differences result in statistical significance with a directional hypothesis. For our purposes we will use non-directional (two-tailed) hypotheses.

I have created an Excel spreadsheet that performs t-tests (with a PowerPoint presentation that explains how enter data and read it) and a PowerPoint presentation on t tests   (you will probably find this useful).

Assumptions underlying the t test.

• The samples have been randomly drawn from their respective populations
• The scores in the population are normally distributed
• The scores in the populations have the same variance (s1=s2) Note: We use a different calculation for the standard error if they are not.

Three Types of t tests

• Pair-difference t test (a.k.a. t-test for dependent groups, correlated t test) df = n (number of pairs) -1

This is concerned with the difference between the average scores of a single sample of individuals who are assessed at two different times (such as before treatment and after treatment). It can also compare average scores of samples of individuals who are paired in some way (such as siblings, mothers, daughters, persons who are matched in terms of a particular characteristics).

• Equal Variance (Pooled-variance t-test) df=n (total of both groups) -2      Note: Used when both samples have the same number of subject or when s1=s2 (Levene or F-max tests have p > .05).
• Unequal Variance (Separate-variance t test) df dependents on a formula, but a rough estimate is one less than the smallest group    Note: Used when the samples have different numbers of subjects and they have different variances —  s1<>s2 (Levene or F-max tests have p < .05).

How do I decide which type of t test to use?

Note: The F-Max test can be substituted for the Levene test. The   t test Excel spreadsheet that I created for our class uses the F -Max.

Type I and II errors

• Type I error — reject a null hypothesis that is really true (with tests of difference this means that you say there was a difference between the groups when there really was not a difference). The probability of making a Type I error is the alpha level you choose. If you set your probability (alpha level) at p   < 05, then there is a 5% chance that you will make a Type I error. You can reduce the chance of making a Type I error by setting a smaller alpha level ( p < .01). The problem with this is that as you lower the chance of making a Type I error, you increase the chance of making a Type II error.
• Type II error — fail to reject a null hypothesis that is false (with tests of differences this means that you say there was no difference between the groups when there really was one)

Hypotheses (some ideas…)

• Non directional (two-tailed) Research Question: Is there a (statistically) significant difference between males and females with respect to math achievement? H0: There is no (statistically) significant difference between males and females with respect to math achievement. HA: There is a (statistically) significant difference between males and females with respect to math achievement.
• Directional (one-tailed) Research Question: Do males score significantly higher than females with respect to math achievement? H0: Males do not score significantly higher than females with respect to math achievement. HA: Males score significantly higher than females with respect to math achievement. The basic idea for calculating a t-test is to find the difference between the means of the two groups and divide it by the STANDARD ERROR (OF THE DIFFERENCE) — which is the standard deviation of the distribution of differences. Just for your information: A CONFIDENCE INTERVAL for a two-tailed t-test is calculated by multiplying the CRITICAL VALUE times the STANDARD ERROR and adding and subtracting that to and from the difference of the two means. EFFECT SIZE is used to calculate practical difference.   If you have several thousand subjects, it is very easy to find a statistically significant difference. Whether that difference is practical or meaningful is another questions. This is where effect size becomes important. With studies involving group differences, effect size is the difference of the two means divided by the standard deviation of the control group (or the average standard deviation of both groups if you do not have a control group). Generally, effect size is only important if you have statistical significance. An effect size of .2 is considered small, .5 is considered medium, and .8 is considered large.

A bit of history… William Sealy Gosset (1905) first published a t-test. He worked at the Guiness Brewery in Dublin and published under the name Student. The test was called Studen t Test (later shortened to t test).

t tests can be easily computed with the Excel or SPSS computer  application. I have created an Excel Spreadsheet that does a very nice job of calculating t values and other pertinent information.

Root out friction in every digital experience, super-charge conversion rates, and optimize digital self-service

Uncover insights from any interaction, deliver AI-powered agent coaching, and reduce cost to serve

Increase revenue and loyalty with real-time insights and recommendations delivered to teams on the ground

Know how your people feel and empower managers to improve employee engagement, productivity, and retention

Take action in the moments that matter most along the employee journey and drive bottom line growth

Whatever they’re are saying, wherever they’re saying it, know exactly what’s going on with your people

Get faster, richer insights with qual and quant tools that make powerful market research available to everyone

Run concept tests, pricing studies, prototyping + more with fast, powerful studies designed by UX research experts

Track your brand performance 24/7 and act quickly to respond to opportunities and challenges in your market

Explore the platform powering Experience Management

• Free Account
• For Digital
• For Customer Care
• For Human Resources
• For Researchers
• Financial Services
• All Industries

Popular Use Cases

• Customer Experience
• Employee Experience
• Net Promoter Score
• Voice of Customer
• Customer Success Hub
• Product Documentation
• Training & Certification
• XM Institute
• Popular Resources
• Customer Stories
• Artificial Intelligence
• Market Research
• Partnerships
• Marketplace

The annual gathering of the experience leaders at the world’s iconic brands building breakthrough business results, live in Salt Lake City.

• English/AU & NZ
• Español/Europa
• Español/América Latina
• Português Brasileiro
• REQUEST DEMO
• Experience Management
• Survey Data Analysis & Reporting
• Survey Analysis Methods
• T-Test Analysis

Try Qualtrics for free

An introduction to t-test theory for surveys.

8 min read What are t-tests, when should you use them, and what are their strengths and weaknesses for analyzing survey data?

What is a t-test?

The t-test, also known as t-statistic or sometimes t-distribution, is a popular statistical tool used to test differences between the means (averages) of two groups, or the difference between one group’s mean and a standard value. Running a t-test helps you to understand whether the differences are statistically significant (i.e. they didn’t just happen by a fluke).

For example, let’s say you surveyed two sample groups of 500 customers in two different cities about their experiences at your stores. Group A in Los Angeles gave you on average 8 out of 10 for customer service, while Group B in Boston gave you an average score of 5 out of 10. Was your customer service really better in LA, or was it just chance that your LA sample group happened to contain a lot of customers who had positive experiences?

T-tests give you an answer to that question. They tell you what the probability is that the differences you found were down to chance. If that probability is very small, then you can be confident that the difference is meaningful (or statistically significant).

In a t-test, you start with a null hypothesis – an assumption that the two populations are the same and there is no meaningful difference between them. The t-test will prove or disprove your null hypothesis.

Free IDC report: The new era of market research is about intelligence

Different kinds of t-tests

So far we’ve talked about testing whether there’s a difference between two independent populations, aka a 2-sample t-test. But there are some other common variations of the t-test worth knowing about too.

1-sample t-test

Instead of a second population, you run a test to see if the average of your population is significantly different from a certain number or value.

Example: Is the average monthly spend among my customers significantly more or less than $50?

2-sample t-test

The classic example we’ve described above, where the means of two independent populations are compared to see if there is a significant difference.

Example: Do Iowan shoppers spend more per store visit than Alaskan ones?

Paired t-test

With a paired t-test, you’re testing two dependent (paired) groups to see if they are significantly different. This can be useful for “before and after” scenarios.

Example: Did the average monthly spend per customer significantly increase after I ran my last marketing campaign?

You can also choose between one-tailed or two-tailed t-tests.

• Two-tailed t-tests tell you only whether or not the difference between the means is significant.
• One-tailed t-tests tell you which mean is the greater of the two.

When should I use a t-test?

A t-test is used when there are two or fewer groups. If you have more than two groups, another option, such as ANOVA , may be a better fit.

There are a couple more conditions for using a 2 sample t-test, which are:

• Your data is expressed on an interval or ordinal scale (such as ranking or numerical scores)
• The two groups you’re comparing are independent of each other (one doesn’t affect the other). This one doesn’t apply if you’re doing a paired t-test.
• Your sample is random
• The distribution is normal (the results form a bell curve with the average in the middle)
• There is a similar amount of variance in each group (i.e. how far the data points are scattered from the average is similar for each group)

You also need to have a big enough sample size to make sure the results are sound. However, one of the benefits of the t-test is that it allows you to work with relatively small quantities of data, since it relies on the mean and variance of the sample, not the population as a whole.

The table shows alternative statistical techniques that can be used to analyze this type of data when different levels of measurement are available.

Why is it called the Student’s t-test?

You may sometimes hear the t-test referred to as the “Student’s t-test”. Although it is regularly used by students, that’s not where the name comes from.

The t-distribution was developed by W. S. Gosset (1908), an employee of the Guinness brewery in Dublin. Gosset was not allowed to publish research findings in his own name, so he adopted the pseudonym “Student”. The t-distribution, as it was first designated, has been known under a variety of names, including the Student’s distribution and Student’s t-distribution.

How to run a t-test

In order to run a t-test, you need 5 things:

• The difference between the mean values of your data sets (known as the mean difference)
• The standard deviation for each one (that’s the amount of variance)
• The number of data values in each group
• An 𝝰 (alpha) value. This is a parameter for how much risk of getting it wrong you’re prepared to accept. An 𝝰 of 0.05 means a 5% risk.
• For manual calculations, you’ll need a critical value table, which will help you interpret your results. These are widely available online, for example from university websites .

From there, you can either use formulae to run your t-test manually (we’ve provided formulae at the end of this article), or use a stats software package such as SPSS or Minitab to compute your results.

The outputs of a t-test are:

This is made up of two elements: the difference between the means in your two groups, and the variance between them. These two elements are expressed as a ratio. If it’s small, there isn’t much difference between the groups. If it’s larger, there is more difference.

b) Degrees of freedom

This relates to the size of the sample and how much the values within it could vary while still maintaining the same average. Numerically, it’s the sample size minus one. You can also think of it as the number of values you’d need to find out in order to know all of the values. (The final one could be deduced by knowing the others and the total.)

Going the manual route, with these two numbers in hand, you can use your critical value table to find:

c) the p-value

This is the heart of the matter – it tells you the probability of your t-value happening by chance. The smaller the p-value, the surer you can be of the statistical significance of your results.

Stats iQ – statistically backed results in plain English

We know not everyone running survey software is a statistician, or wants to spend time learning statistical concepts and methods. That’s why we developed Stats iQ. It’s a powerful computational tool that gives you results equivalent to methods like the t-test, expressed in a few simple sentences.

Formulae for manual t-test calculation

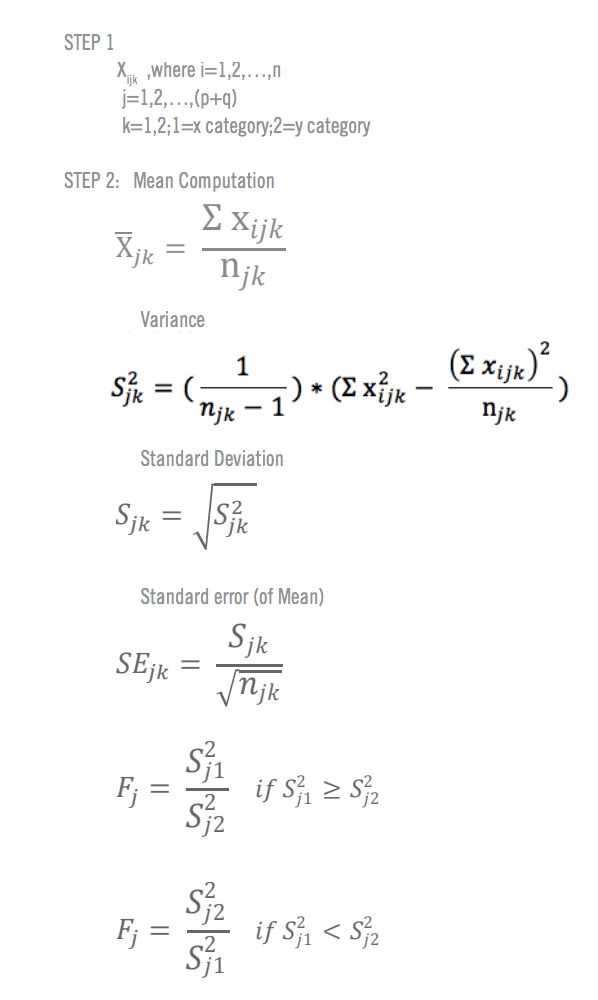
Related resources

Analysis & Reporting

Margin of error 11 min read

Data saturation in qualitative research 8 min read, thematic analysis 11 min read, behavioral analytics 12 min read, statistical significance calculator: tool & complete guide 18 min read, regression analysis 19 min read, data analysis 31 min read, request demo.

Ready to learn more about Qualtrics?

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Korean J Anesthesiol
• v.68(6); 2015 Dec

T test as a parametric statistic

Tae kyun kim.

Department of Anesthesia and Pain Medicine, Pusan National University School of Medicine, Busan, Korea.

In statistic tests, the probability distribution of the statistics is important. When samples are drawn from population N (µ, σ 2 ) with a sample size of n, the distribution of the sample mean X ̄ should be a normal distribution N (µ, σ 2 / n ). Under the null hypothesis µ = µ 0 , the distribution of statistics z = X ¯ - µ 0 σ / n should be standardized as a normal distribution. When the variance of the population is not known, replacement with the sample variance s 2 is possible. In this case, the statistics X ¯ - µ 0 s / n follows a t distribution ( n-1 degrees of freedom). An independent-group t test can be carried out for a comparison of means between two independent groups, with a paired t test for paired data. As the t test is a parametric test, samples should meet certain preconditions, such as normality, equal variances and independence.

Introduction

A t test is a type of statistical test that is used to compare the means of two groups. It is one of the most widely used statistical hypothesis tests in pain studies [ 1 ]. There are two types of statistical inference: parametric and nonparametric methods. Parametric methods refer to a statistical technique in which one defines the probability distribution of probability variables and makes inferences about the parameters of the distribution. In cases in which the probability distribution cannot be defined, nonparametric methods are employed. T tests are a type of parametric method; they can be used when the samples satisfy the conditions of normality, equal variance, and independence.

T tests can be divided into two types. There is the independent t test, which can be used when the two groups under comparison are independent of each other, and the paired t test, which can be used when the two groups under comparison are dependent on each other. T tests are usually used in cases where the experimental subjects are divided into two independent groups, with one group treated with A and the other group treated with B. Researchers can acquire two types of results for each group (i.e., prior to treatment and after the treatment): preA and postA, and preB and postB. An independent t test can be used for an intergroup comparison of postA and postB or for an intergroup comparison of changes in preA to postA (postA-preA) and changes in preB to postB (postB-preB) ( Table 1 ).

ID: individual identification, preA, preB: before the treatment A or B, postA, postB: after the treatment A or B, ΔA, ΔB: difference between before and after the treatment A or B.

On the other hand, paired t tests are used in different experimental environments. For example, the experimental subjects are not divided into two groups, and all of them are treated initially with A. The amount of change (postA-preA) is then measured for all subjects. After all of the effects of A disappear, the subjects are treated with B, and the amount of change (postB-preB) is measured for all of the subjects. A paired t test is used in such crossover test designs to compare the amount of change of A to that of B for the same subjects ( Table 2 ).

Statistic and Probability

Statistics is basically about probabilities. A statistical conclusion of a large or small difference between two groups is not based on an absolute standard but is rather an evaluation of the probability of an event. For example, a clinical test is performed to determine whether or not a patient has a certain disease. If the test results are either higher or lower than the standard, clinicians will determine that the patient has the disease despite the fact that the patient may or may not actually have the disease. This conclusion is based on the statistical concept which holds that it is more statistically valid to conclude that the patient has the disease than to declare that the patient is a rare case among people without the disease because such test results are statistically rare in normal people.

The test results and the probability distribution of the results must be known in order for the results to be determined as statistically rare. The criteria for clinical indicators have been established based on data collected from an entire population or at least from a large number of people. Here, we examine a case in which a clinical indicator exhibits a normal distribution with a mean of µ and a variance of σ 2 . If a patient's test result is χ, is this statistically rare against the criteria (e.g., 5 or 1%)? Probability is represented as the surface area in a probability distribution, and the z score that represents either 5 or 1%, near the margins of the distribution, becomes the reference value. The test result χ can be determined to be statistically rare compared to the reference probability if it lies in a more marginal area than the z score, that is, if the value of χ is located in the marginal ends of the distribution ( Fig. 1 ).

This is done to compare one individual's clinical indicator value. This however raises the question of how we would compare the mean of a sample group (consisting of more than one individual) against the population mean. Again, it is meaningless to compare each individual separately; we must compare the means of the two groups. Thus, do we make a statistical inference using only the distribution of the clinical indicators of the entire population and the mean of the sample? No. In order to infer a statistical possibility, we must know the indicator of interest and its probability distribution. In other words, we must know the mean of the sample and the distribution of the mean. We can then determine how far the sample mean varies from the population mean by knowing the sampling distribution of the means.

Sampling Distribution (Sample Mean Distribution)

The sample mean we can get from a study is one of means of all possible samples which could be drawn from a population. This sample mean from a study was already acquired from a real experiment, however, how could we know the distribution of the means of all possible samples including studied sample? Do we need to experiment it over and over again? The simulation in which samples are drawn repeatedly from a population is shown in Fig. 2 . If samples are drawn with sample size n from population of normal distribution (µ, σ 2 ), the sampling distribution shows normal distribution with mean of µ and variance of σ 2 / n . The number of samples affects the shape of the sampling distribution. That is, the shape of the distribution curve becomes a narrower bell curve with a smaller variance as the number of samples increases, because the variance of sampling distribution is σ 2 / n . The formation of a sampling distribution is well explained in Lee et al. [ 2 ] in a form of a figure.

T Distribution

Now that the sampling distribution of the means is known, we can locate the position of the mean of a specific sample against the distribution data. However, one problem remains. As we noted earlier, the sampling distribution exhibits a normal distribution with a variance of σ 2 / n , but in reality we do not know σ 2 , the variance of the population. Therefore, we use the sample variance instead of the population variance to determine the sampling distribution of the mean. The sample variance is defined as follows:

In such cases in which the sample variance is used, the sampling distribution follows a t distribution that depends on the 0degree of freedom of each sample rather than a normal distribution ( Fig. 3 ).

Independent T test

A t test is also known as Student's t test. It is a statistical analysis technique that was developed by William Sealy Gosset in 1908 as a means to control the quality of dark beers. A t test used to test whether there is a difference between two independent sample means is not different from a t test used when there is only one sample (as mentioned earlier). However, if there is no difference in the two sample means, the difference will be close to zero. Therefore, in such cases, an additional statistical test should be performed to verify whether the difference could be said to be equal to zero.

Let's extract two independent samples from a population that displays a normal distribution and compute the difference between the means of the two samples. The difference between the sample means will not always be zero, even if the samples are extracted from the same population, because the sampling process is randomized, which results in a sample with a variety of combinations of subjects. We extracted two samples with a size of 6 from a population N (150, 5 2 ) and found the difference in the means. If this process is repeated 1,000 times, the sampling distribution exhibits the shape illustrated in Fig. 4 . When the distribution is displayed in terms of a histogram and a density line, it is almost identical to the theoretical sampling distribution: N(0, 2 × 5 2 /6) ( Fig. 4 ).

However, it is difficult to define the distribution of the difference in the two sample means because the variance of the population is unknown. If we use the variance of the sample instead, the distribution of the difference of the samples means would follow a t distribution. It should be noted, however, that the two samples display a normal distribution and have an equal variance because they were independently extracted from an identical population that has a normal distribution.

Under the assumption that the two samples display a normal distribution and have an equal variance, the t statistic is as follows:

population mean difference (µ 1 - µ 2 ) was assumed to be 0; thus:

The population variance was unknown and so a pooled variance of the two samples was used:

However, if the population variance is not equal, the t statistic of the t test would be

and the degree of freedom is calculated based on the Welch Satterthwaite equation.

It is apparent that if n 1 and n 2 are sufficiently large, the t statistic resembles a normal distribution ( Fig. 3 ).

A statistical test is performed to verify the position of the difference in the sample means in the sampling distribution of the mean ( Fig. 4 ). It is statistically very rare for the difference in two sample means to lie on the margins of the distribution. Therefore, if the difference does lie on the margins, it is statistically significant to conclude that the samples were extracted from two different populations, even if they were actually extracted from the same population.

Paired T test

Paired t tests are can be categorized as a type of t test for a single sample because they test the difference between two paired results. If there is no difference between the two treatments, the difference in the results would be close to zero; hence, the difference in the sample means used for a paired t test would be 0.

Let's go back to the sampling distribution that was used in the independent t test discussed earlier. The variance of the difference between two independent sample means was represented as the sum of each variance. If the samples were not independent, the variance of the difference of two variables A and B, Var (A-B), can be shown as follows,

where σ 1 2 is the variance of variable A, σ 2 2 is the variance of variable B, and ρ is the correlation coefficient for the two variables. In an independent t test, the correlation coefficient is 0 because the two groups are independent. Thus, it is logical to show the variance of the difference between the two variables simply as the sum of the two variances. However, for paired variables, the correlation coefficient may not equal 0. Thus, the t statistic for two dependent samples must be different, meaning the following t statistic,

must be changed. First, the number of samples are paired; thus, n 1 = n 2 = n , and their variance can be represented as s 1 2 + s 2 2 - 2ρ s 1 s 2 considering the correlation coefficient. Therefore, the t statistic for a paired t test is as follows:

In this equation, the t statistic is increased if the correlation coefficient is greater than 0 because the denominator becomes smaller, which increases the statistical power of the paired t test compared to that of an independent t test. On the other hand, if the correlation coefficient is less than 0, the statistical power is decreased and becomes lower than that of an independent t test. It is important to note that if one misunderstands this characteristic and uses an independent t test when the correlation coefficient is less than 0, the generated results would be incorrect, as the process ignores the paired experimental design.

Assumptions

As previously explained, if samples are extracted from a population that displays a normal distribution but the population variance is unknown, we can use the sample variance to examine the sampling distribution of the mean, which will resemble a t distribution. Therefore, in order to reach a statistical conclusion about a sample mean with a t distribution, certain conditions must be satisfied: the two samples for comparison must be independently sampled from the same population, satisfying the conditions of normality, equal variance, and independence.

Shapiro's test or the Kolmogorov-Smirnov test can be performed to verify the assumption of normality. If the condition of normality is not met, the Wilcoxon rank sum test (Mann-Whitney U test) is used for independent samples, and the Wilcoxon sign rank test is used for paired samples for an additional nonparametric test.

The condition of equal variance is verified using Levene's test or Bartlett's test. If the condition of equal variance is not met, nonparametric test can be performed or the following statistic which follows a t distribution can is used.

However, this statistics has different degree of freedom which was calculated by the Welch-Satterthwaite [ 3 , 4 ] equation.

Owing to user-friendly statistics software programs, the rich pool of statistics information on the Internet, and expert advice from statistics professionals at every hospital, using and processing statistics data is no longer an intractable task. However, it remains the researchers' responsibility to design experiments to fulfill all of the conditions of their statistic methods of choice and to ensure that their statistical assumptions are appropriate. In particular, parametric statistical methods confer reasonable statistical conclusions only when the statistical assumptions are fully met. Some researchers often regard these statistical assumptions inconvenient and neglect them. Even some statisticians argue on the basic assumptions, based on the central limit theory, that sampling distributions display a normal distribution regardless of the fact that the population distribution may or may not follow a normal distribution, and that t tests have sufficient statistical power even if they do not satisfy the condition of normality [ 5 ]. Moreover, they contend that the condition of equal variance is not so strict because even if there is a ninefold difference in the variance, the α level merely changes from 0.5 to 0.6 [ 6 ]. However, the arguments regarding the conditions of normality and the limit to which the condition of equal variance may be violated are still bones of contention. Therefore, researchers who unquestioningly accept these arguments and neglect the basic assumptions of a t test when submitting papers will face critical comments from editors. Moreover, it will be difficult to persuade the editors to neglect the basic assumptions regardless of how solid the evidence in the paper is. Hence, researchers should sufficiently test basic statistical assumptions and employ methods that are widely accepted so as to draw valid statistical conclusions.

The results of independent and paired t tests of the examples are illustrated in Tables 1 and 2. The tests were conducted using the SPSS Statistics Package (IBM® SPSS® Statistics 21, SPSS Inc., Chicago, IL, USA).

Independent T test (Table 1)

First, we need to examine the degree of normality by confirming the Kolmogorov-Smirnov or Shapiro-Wilk test in the second table. We can determine that the samples satisfy the condition of normality because the P value is greater than 0.05. Next, we check the results of Levene's test to examine the equality of variance. The P value is again greater than 0.05; hence, the condition of equal variance is also met. Finally, we read the significance probability for the "equal variance assumed" line. If the condition of equal variance is not met (i.e., if the P value is less than 0.05 for Levene's test), we reach a conclusion by referring to the significance probability for the "equal variance not assumed" line, or we perform a nonparametric test.

Paired T test (Table 2)

A paired t test is identical to a single-sample t test. Therefore, we test the normality of the difference in the amount of change for treatment A and treatment B (ΔA-ΔB). The normality is verified based on the results of Kolmogorov-Smirnov and Shapiro-Wilk tests, as shown in the second table. In conclusion, there is a significant difference between the two treatments (i.e., the P value is less than 0.001).