scientific way of problem solving

What is the Scientific Method: How does it work and why is it important?

The scientific method is a systematic process involving steps like defining questions, forming hypotheses, conducting experiments, and analyzing data. It minimizes biases and enables replicable research, leading to groundbreaking discoveries like Einstein's theory of relativity, penicillin, and the structure of DNA. This ongoing approach promotes reason, evidence, and the pursuit of truth in science.

Updated on November 18, 2023

Beginning in elementary school, we are exposed to the scientific method and taught how to put it into practice. As a tool for learning, it prepares children to think logically and use reasoning when seeking answers to questions.

Rather than jumping to conclusions, the scientific method gives us a recipe for exploring the world through observation and trial and error. We use it regularly, sometimes knowingly in academics or research, and sometimes subconsciously in our daily lives.

In this article we will refresh our memories on the particulars of the scientific method, discussing where it comes from, which elements comprise it, and how it is put into practice. Then, we will consider the importance of the scientific method, who uses it and under what circumstances.

What is the scientific method?

The scientific method is a dynamic process that involves objectively investigating questions through observation and experimentation . Applicable to all scientific disciplines, this systematic approach to answering questions is more accurately described as a flexible set of principles than as a fixed series of steps.

The following representations of the scientific method illustrate how it can be both condensed into broad categories and also expanded to reveal more and more details of the process. These graphics capture the adaptability that makes this concept universally valuable as it is relevant and accessible not only across age groups and educational levels but also within various contexts.

Steps in the scientific method

While the scientific method is versatile in form and function, it encompasses a collection of principles that create a logical progression to the process of problem solving:

• Define a question : Constructing a clear and precise problem statement that identifies the main question or goal of the investigation is the first step. The wording must lend itself to experimentation by posing a question that is both testable and measurable.
• Gather information and resources : Researching the topic in question to find out what is already known and what types of related questions others are asking is the next step in this process. This background information is vital to gaining a full understanding of the subject and in determining the best design for experiments. 
• Form a hypothesis : Composing a concise statement that identifies specific variables and potential results, which can then be tested, is a crucial step that must be completed before any experimentation. An imperfection in the composition of a hypothesis can result in weaknesses to the entire design of an experiment.
• Perform the experiments : Testing the hypothesis by performing replicable experiments and collecting resultant data is another fundamental step of the scientific method. By controlling some elements of an experiment while purposely manipulating others, cause and effect relationships are established.
• Analyze the data : Interpreting the experimental process and results by recognizing trends in the data is a necessary step for comprehending its meaning and supporting the conclusions. Drawing inferences through this systematic process lends substantive evidence for either supporting or rejecting the hypothesis.
• Report the results : Sharing the outcomes of an experiment, through an essay, presentation, graphic, or journal article, is often regarded as a final step in this process. Detailing the project's design, methods, and results not only promotes transparency and replicability but also adds to the body of knowledge for future research.
• Retest the hypothesis : Repeating experiments to see if a hypothesis holds up in all cases is a step that is manifested through varying scenarios. Sometimes a researcher immediately checks their own work or replicates it at a future time, or another researcher will repeat the experiments to further test the hypothesis.

Where did the scientific method come from?

Oftentimes, ancient peoples attempted to answer questions about the unknown by:

• Making simple observations
• Discussing the possibilities with others deemed worthy of a debate
• Drawing conclusions based on dominant opinions and preexisting beliefs

For example, take Greek and Roman mythology. Myths were used to explain everything from the seasons and stars to the sun and death itself.

However, as societies began to grow through advancements in agriculture and language, ancient civilizations like Egypt and Babylonia shifted to a more rational analysis for understanding the natural world. They increasingly employed empirical methods of observation and experimentation that would one day evolve into the scientific method . 

In the 4th century, Aristotle, considered the Father of Science by many, suggested these elements , which closely resemble the contemporary scientific method, as part of his approach for conducting science:

• Study what others have written about the subject.
• Look for the general consensus about the subject.
• Perform a systematic study of everything even partially related to the topic.

By continuing to emphasize systematic observation and controlled experiments, scholars such as Al-Kindi and Ibn al-Haytham helped expand this concept throughout the Islamic Golden Age . 

In his 1620 treatise, Novum Organum , Sir Francis Bacon codified the scientific method, arguing not only that hypotheses must be tested through experiments but also that the results must be replicated to establish a truth. Coming at the height of the Scientific Revolution, this text made the scientific method accessible to European thinkers like Galileo and Isaac Newton who then put the method into practice.

As science modernized in the 19th century, the scientific method became more formalized, leading to significant breakthroughs in fields such as evolution and germ theory. Today, it continues to evolve, underpinning scientific progress in diverse areas like quantum mechanics, genetics, and artificial intelligence.

Why is the scientific method important?

The history of the scientific method illustrates how the concept developed out of a need to find objective answers to scientific questions by overcoming biases based on fear, religion, power, and cultural norms. This still holds true today.

By implementing this standardized approach to conducting experiments, the impacts of researchers’ personal opinions and preconceived notions are minimized. The organized manner of the scientific method prevents these and other mistakes while promoting the replicability and transparency necessary for solid scientific research.

The importance of the scientific method is best observed through its successes, for example: 

• “ Albert Einstein stands out among modern physicists as the scientist who not only formulated a theory of revolutionary significance but also had the genius to reflect in a conscious and technical way on the scientific method he was using.” Devising a hypothesis based on the prevailing understanding of Newtonian physics eventually led Einstein to devise the theory of general relativity .
• Howard Florey “Perhaps the most useful lesson which has come out of the work on penicillin has been the demonstration that success in this field depends on the development and coordinated use of technical methods.” After discovering a mold that prevented the growth of Staphylococcus bacteria, Dr. Alexander Flemimg designed experiments to identify and reproduce it in the lab, thus leading to the development of penicillin .
• James D. Watson “Every time you understand something, religion becomes less likely. Only with the discovery of the double helix and the ensuing genetic revolution have we had grounds for thinking that the powers held traditionally to be the exclusive property of the gods might one day be ours. . . .” By using wire models to conceive a structure for DNA, Watson and Crick crafted a hypothesis for testing combinations of amino acids, X-ray diffraction images, and the current research in atomic physics, resulting in the discovery of DNA’s double helix structure .

Final thoughts

As the cases exemplify, the scientific method is never truly completed, but rather started and restarted. It gave these researchers a structured process that was easily replicated, modified, and built upon. 

While the scientific method may “end” in one context, it never literally ends. When a hypothesis, design, methods, and experiments are revisited, the scientific method simply picks up where it left off. Each time a researcher builds upon previous knowledge, the scientific method is restored with the pieces of past efforts.

By guiding researchers towards objective results based on transparency and reproducibility, the scientific method acts as a defense against bias, superstition, and preconceived notions. As we embrace the scientific method's enduring principles, we ensure that our quest for knowledge remains firmly rooted in reason, evidence, and the pursuit of truth.

The AJE Team

See our "Privacy Policy"

How it works

For Business

Join Mind Tools

Article • 5 min read

Using the Scientific Method to Solve Problems

How the scientific method and reasoning can help simplify processes and solve problems.

By the Mind Tools Content Team

The processes of problem-solving and decision-making can be complicated and drawn out. In this article we look at how the scientific method, along with deductive and inductive reasoning can help simplify these processes.

‘It is a capital mistake to theorize before one has information. Insensibly one begins to twist facts to suit our theories, instead of theories to suit facts.’ Sherlock Holmes

The Scientific Method

The scientific method is a process used to explore observations and answer questions. Originally used by scientists looking to prove new theories, its use has spread into many other areas, including that of problem-solving and decision-making.

The scientific method is designed to eliminate the influences of bias, prejudice and personal beliefs when testing a hypothesis or theory. It has developed alongside science itself, with origins going back to the 13th century. The scientific method is generally described as a series of steps.

• observations/theory
• explanation/conclusion

The first step is to develop a theory about the particular area of interest. A theory, in the context of logic or problem-solving, is a conjecture or speculation about something that is not necessarily fact, often based on a series of observations.

Once a theory has been devised, it can be questioned and refined into more specific hypotheses that can be tested. The hypotheses are potential explanations for the theory.

The testing, and subsequent analysis, of these hypotheses will eventually lead to a conclus ion which can prove or disprove the original theory.

Applying the Scientific Method to Problem-Solving

How can the scientific method be used to solve a problem, such as the color printer is not working?

1. Use observations to develop a theory.

In order to solve the problem, it must first be clear what the problem is. Observations made about the problem should be used to develop a theory. In this particular problem the theory might be that the color printer has run out of ink. This theory is developed as the result of observing the increasingly faded output from the printer.

2. Form a hypothesis.

Note down all the possible reasons for the problem. In this situation they might include:

• The printer is set up as the default printer for all 40 people in the department and so is used more frequently than necessary.
• There has been increased usage of the printer due to non-work related printing.
• In an attempt to reduce costs, poor quality ink cartridges with limited amounts of ink in them have been purchased.
• The printer is faulty.

All these possible reasons are hypotheses.

3. Test the hypothesis.

Once as many hypotheses (or reasons) as possible have been thought of, then each one can be tested to discern if it is the cause of the problem. An appropriate test needs to be devised for each hypothesis. For example, it is fairly quick to ask everyone to check the default settings of the printer on each PC, or to check if the cartridge supplier has changed.

4. Analyze the test results.

Once all the hypotheses have been tested, the results can be analyzed. The type and depth of analysis will be dependant on each individual problem, and the tests appropriate to it. In many cases the analysis will be a very quick thought process. In others, where considerable information has been collated, a more structured approach, such as the use of graphs, tables or spreadsheets, may be required.

5. Draw a conclusion.

Based on the results of the tests, a conclusion can then be drawn about exactly what is causing the problem. The appropriate remedial action can then be taken, such as asking everyone to amend their default print settings, or changing the cartridge supplier.

Inductive and Deductive Reasoning

The scientific method involves the use of two basic types of reasoning, inductive and deductive.

Inductive reasoning makes a conclusion based on a set of empirical results. Empirical results are the product of the collection of evidence from observations. For example:

‘Every time it rains the pavement gets wet, therefore rain must be water’.

There has been no scientific determination in the hypothesis that rain is water, it is purely based on observation. The formation of a hypothesis in this manner is sometimes referred to as an educated guess. An educated guess, whilst not based on hard facts, must still be plausible, and consistent with what we already know, in order to present a reasonable argument.

Deductive reasoning can be thought of most simply in terms of ‘If A and B, then C’. For example:

• if the window is above the desk, and
• the desk is above the floor, then
• the window must be above the floor

It works by building on a series of conclusions, which results in one final answer.

Social Sciences and the Scientific Method

The scientific method can be used to address any situation or problem where a theory can be developed. Although more often associated with natural sciences, it can also be used to develop theories in social sciences (such as psychology, sociology and linguistics), using both quantitative and qualitative methods.

Quantitative information is information that can be measured, and tends to focus on numbers and frequencies. Typically quantitative information might be gathered by experiments, questionnaires or psychometric tests. Qualitative information, on the other hand, is based on information describing meaning, such as human behavior, and the reasons behind it. Qualitative information is gathered by way of interviews and case studies, which are possibly not as statistically accurate as quantitative methods, but provide a more in-depth and rich description.

The resultant information can then be used to prove, or disprove, a hypothesis. Using a mix of quantitative and qualitative information is more likely to produce a rounded result based on the factual, quantitative information enriched and backed up by actual experience and qualitative information.

In terms of problem-solving or decision-making, for example, the qualitative information is that gained by looking at the ‘how’ and ‘why’ , whereas quantitative information would come from the ‘where’, ‘what’ and ‘when’.

It may seem easy to come up with a brilliant idea, or to suspect what the cause of a problem may be. However things can get more complicated when the idea needs to be evaluated, or when there may be more than one potential cause of a problem. In these situations, the use of the scientific method, and its associated reasoning, can help the user come to a decision, or reach a solution, secure in the knowledge that all options have been considered.

Join Mind Tools and get access to exclusive content.

This resource is only available to Mind Tools members.

Already a member? Please Login here

Gain essential management and leadership skills

Busy schedule? No problem. Learn anytime, anywhere. 

Subscribe to unlimited access to meticulously researched, evidence-based resources.

Join today and take advantage of our 30% offer, available until May 31st .

Sign-up to our newsletter

Subscribing to the Mind Tools newsletter will keep you up-to-date with our latest updates and newest resources.

Subscribe now

Business Skills

Personal Development

Leadership and Management

Member Extras

Most Popular

Latest Updates

Winning Body Language

Business Stripped Bare

Mind Tools Store

About Mind Tools Content

Discover something new today

Nine ways to get the best from x (twitter).

Growing Your Business Quickly and Safely on Social Media

Managing Your Emotions at Work

Controlling Your Feelings... Before They Control You

How Emotionally Intelligent Are You?

Boosting Your People Skills

Self-Assessment

What's Your Leadership Style?

Learn About the Strengths and Weaknesses of the Way You Like to Lead

Recommended for you

Top tips for engaging your team in the green agenda.

Follow these practical suggestions to help your team become greener.

Business Operations and Process Management

Strategy Tools

Customer Service

Business Ethics and Values

Handling Information and Data

Project Management

Knowledge Management

Self-Development and Goal Setting

Time Management

Presentation Skills

Learning Skills

Career Skills

Communication Skills

Negotiation, Persuasion and Influence

Working With Others

Difficult Conversations

Creativity Tools

Self-Management

Work-Life Balance

Stress Management and Wellbeing

Coaching and Mentoring

Change Management

Team Management

Managing Conflict

Delegation and Empowerment

Performance Management

Leadership Skills

Developing Your Team

Talent Management

Problem Solving

Decision Making

Member Podcast

Choose Your Test

Sat / act prep online guides and tips, the 6 scientific method steps and how to use them.

General Education

When you’re faced with a scientific problem, solving it can seem like an impossible prospect. There are so many possible explanations for everything we see and experience—how can you possibly make sense of them all? Science has a simple answer: the scientific method.

The scientific method is a method of asking and answering questions about the world. These guiding principles give scientists a model to work through when trying to understand the world, but where did that model come from, and how does it work?

In this article, we’ll define the scientific method, discuss its long history, and cover each of the scientific method steps in detail.

What Is the Scientific Method?

At its most basic, the scientific method is a procedure for conducting scientific experiments. It’s a set model that scientists in a variety of fields can follow, going from initial observation to conclusion in a loose but concrete format.

The number of steps varies, but the process begins with an observation, progresses through an experiment, and concludes with analysis and sharing data. One of the most important pieces to the scientific method is skepticism —the goal is to find truth, not to confirm a particular thought. That requires reevaluation and repeated experimentation, as well as examining your thinking through rigorous study.

There are in fact multiple scientific methods, as the basic structure can be easily modified.  The one we typically learn about in school is the basic method, based in logic and problem solving, typically used in “hard” science fields like biology, chemistry, and physics. It may vary in other fields, such as psychology, but the basic premise of making observations, testing, and continuing to improve a theory from the results remain the same.

The History of the Scientific Method

The scientific method as we know it today is based on thousands of years of scientific study. Its development goes all the way back to ancient Mesopotamia, Greece, and India.

The Ancient World

In ancient Greece, Aristotle devised an inductive-deductive process , which weighs broad generalizations from data against conclusions reached by narrowing down possibilities from a general statement. However, he favored deductive reasoning, as it identifies causes, which he saw as more important.

Aristotle wrote a great deal about logic and many of his ideas about reasoning echo those found in the modern scientific method, such as ignoring circular evidence and limiting the number of middle terms between the beginning of an experiment and the end. Though his model isn’t the one that we use today, the reliance on logic and thorough testing are still key parts of science today.

The Middle Ages

The next big step toward the development of the modern scientific method came in the Middle Ages, particularly in the Islamic world. Ibn al-Haytham, a physicist from what we now know as Iraq, developed a method of testing, observing, and deducing for his research on vision. al-Haytham was critical of Aristotle’s lack of inductive reasoning, which played an important role in his own research.

Other scientists, including Abū Rayhān al-Bīrūnī, Ibn Sina, and Robert Grosseteste also developed models of scientific reasoning to test their own theories. Though they frequently disagreed with one another and Aristotle, those disagreements and refinements of their methods led to the scientific method we have today.

Following those major developments, particularly Grosseteste’s work, Roger Bacon developed his own cycle of observation (seeing that something occurs), hypothesis (making a guess about why that thing occurs), experimentation (testing that the thing occurs), and verification (an outside person ensuring that the result of the experiment is consistent).

After joining the Franciscan Order, Bacon was granted a special commission to write about science; typically, Friars were not allowed to write books or pamphlets. With this commission, Bacon outlined important tenets of the scientific method, including causes of error, methods of knowledge, and the differences between speculative and experimental science. He also used his own principles to investigate the causes of a rainbow, demonstrating the method’s effectiveness.

Scientific Revolution

Throughout the Renaissance, more great thinkers became involved in devising a thorough, rigorous method of scientific study. Francis Bacon brought inductive reasoning further into the method, whereas Descartes argued that the laws of the universe meant that deductive reasoning was sufficient. Galileo’s research was also inductive reasoning-heavy, as he believed that researchers could not account for every possible variable; therefore, repetition was necessary to eliminate faulty hypotheses and experiments.

All of this led to the birth of the Scientific Revolution , which took place during the sixteenth and seventeenth centuries. In 1660, a group of philosophers and physicians joined together to work on scientific advancement. After approval from England’s crown , the group became known as the Royal Society, which helped create a thriving scientific community and an early academic journal to help introduce rigorous study and peer review.

Previous generations of scientists had touched on the importance of induction and deduction, but Sir Isaac Newton proposed that both were equally important. This contribution helped establish the importance of multiple kinds of reasoning, leading to more rigorous study.

As science began to splinter into separate areas of study, it became necessary to define different methods for different fields. Karl Popper was a leader in this area—he established that science could be subject to error, sometimes intentionally. This was particularly tricky for “soft” sciences like psychology and social sciences, which require different methods. Popper’s theories furthered the divide between sciences like psychology and “hard” sciences like chemistry or physics.

Paul Feyerabend argued that Popper’s methods were too restrictive for certain fields, and followed a less restrictive method hinged on “anything goes,” as great scientists had made discoveries without the Scientific Method. Feyerabend suggested that throughout history scientists had adapted their methods as necessary, and that sometimes it would be necessary to break the rules. This approach suited social and behavioral scientists particularly well, leading to a more diverse range of models for scientists in multiple fields to use.

The Scientific Method Steps

Though different fields may have variations on the model, the basic scientific method is as follows:

#1: Make Observations 

Notice something, such as the air temperature during the winter, what happens when ice cream melts, or how your plants behave when you forget to water them.

#2: Ask a Question

Turn your observation into a question. Why is the temperature lower during the winter? Why does my ice cream melt? Why does my toast always fall butter-side down?

This step can also include doing some research. You may be able to find answers to these questions already, but you can still test them!

#3: Make a Hypothesis

A hypothesis is an educated guess of the answer to your question. Why does your toast always fall butter-side down? Maybe it’s because the butter makes that side of the bread heavier.

A good hypothesis leads to a prediction that you can test, phrased as an if/then statement. In this case, we can pick something like, “If toast is buttered, then it will hit the ground butter-first.”

#4: Experiment

Your experiment is designed to test whether your predication about what will happen is true. A good experiment will test one variable at a time —for example, we’re trying to test whether butter weighs down one side of toast, making it more likely to hit the ground first.

The unbuttered toast is our control variable. If we determine the chance that a slice of unbuttered toast, marked with a dot, will hit the ground on a particular side, we can compare those results to our buttered toast to see if there’s a correlation between the presence of butter and which way the toast falls.

If we decided not to toast the bread, that would be introducing a new question—whether or not toasting the bread has any impact on how it falls. Since that’s not part of our test, we’ll stick with determining whether the presence of butter has any impact on which side hits the ground first.

#5: Analyze Data

After our experiment, we discover that both buttered toast and unbuttered toast have a 50/50 chance of hitting the ground on the buttered or marked side when dropped from a consistent height, straight down. It looks like our hypothesis was incorrect—it’s not the butter that makes the toast hit the ground in a particular way, so it must be something else.

Since we didn’t get the desired result, it’s back to the drawing board. Our hypothesis wasn’t correct, so we’ll need to start fresh. Now that you think about it, your toast seems to hit the ground butter-first when it slides off your plate, not when you drop it from a consistent height. That can be the basis for your new experiment.

#6: Communicate Your Results

Good science needs verification. Your experiment should be replicable by other people, so you can put together a report about how you ran your experiment to see if other peoples’ findings are consistent with yours.

This may be useful for class or a science fair. Professional scientists may publish their findings in scientific journals, where other scientists can read and attempt their own versions of the same experiments. Being part of a scientific community helps your experiments be stronger because other people can see if there are flaws in your approach—such as if you tested with different kinds of bread, or sometimes used peanut butter instead of butter—that can lead you closer to a good answer.

A Scientific Method Example: Falling Toast

We’ve run through a quick recap of the scientific method steps, but let’s look a little deeper by trying again to figure out why toast so often falls butter side down.

#1: Make Observations

At the end of our last experiment, where we learned that butter doesn’t actually make toast more likely to hit the ground on that side, we remembered that the times when our toast hits the ground butter side first are usually when it’s falling off a plate.

The easiest question we can ask is, “Why is that?”

We can actually search this online and find a pretty detailed answer as to why this is true. But we’re budding scientists—we want to see it in action and verify it for ourselves! After all, good science should be replicable, and we have all the tools we need to test out what’s really going on.

Why do we think that buttered toast hits the ground butter-first? We know it’s not because it’s heavier, so we can strike that out. Maybe it’s because of the shape of our plate?

That’s something we can test. We’ll phrase our hypothesis as, “If my toast slides off my plate, then it will fall butter-side down.”

Just seeing that toast falls off a plate butter-side down isn’t enough for us. We want to know why, so we’re going to take things a step further—we’ll set up a slow-motion camera to capture what happens as the toast slides off the plate.

We’ll run the test ten times, each time tilting the same plate until the toast slides off. We’ll make note of each time the butter side lands first and see what’s happening on the video so we can see what’s going on.

When we review the footage, we’ll likely notice that the bread starts to flip when it slides off the edge, changing how it falls in a way that didn’t happen when we dropped it ourselves.

That answers our question, but it’s not the complete picture —how do other plates affect how often toast hits the ground butter-first? What if the toast is already butter-side down when it falls? These are things we can test in further experiments with new hypotheses!

Now that we have results, we can share them with others who can verify our results. As mentioned above, being part of the scientific community can lead to better results. If your results were wildly different from the established thinking about buttered toast, that might be cause for reevaluation. If they’re the same, they might lead others to make new discoveries about buttered toast. At the very least, you have a cool experiment you can share with your friends!

Key Scientific Method Tips

Though science can be complex, the benefit of the scientific method is that it gives you an easy-to-follow means of thinking about why and how things happen. To use it effectively, keep these things in mind!

Don’t Worry About Proving Your Hypothesis

One of the important things to remember about the scientific method is that it’s not necessarily meant to prove your hypothesis right. It’s great if you do manage to guess the reason for something right the first time, but the ultimate goal of an experiment is to find the true reason for your observation to occur, not to prove your hypothesis right.

Good science sometimes means that you’re wrong. That’s not a bad thing—a well-designed experiment with an unanticipated result can be just as revealing, if not more, than an experiment that confirms your hypothesis.

Be Prepared to Try Again

If the data from your experiment doesn’t match your hypothesis, that’s not a bad thing. You’ve eliminated one possible explanation, which brings you one step closer to discovering the truth.

The scientific method isn’t something you’re meant to do exactly once to prove a point. It’s meant to be repeated and adapted to bring you closer to a solution. Even if you can demonstrate truth in your hypothesis, a good scientist will run an experiment again to be sure that the results are replicable. You can even tweak a successful hypothesis to test another factor, such as if we redid our buttered toast experiment to find out whether different kinds of plates affect whether or not the toast falls butter-first. The more we test our hypothesis, the stronger it becomes!

What’s Next?

Want to learn more about the scientific method? These important high school science classes will no doubt cover it in a variety of different contexts.

Test your ability to follow the scientific method using these at-home science experiments for kids !

Need some proof that science is fun? Try making slime

Melissa Brinks graduated from the University of Washington in 2014 with a Bachelor's in English with a creative writing emphasis. She has spent several years tutoring K-12 students in many subjects, including in SAT prep, to help them prepare for their college education.

Ask a Question Below

Have any questions about this article or other topics? Ask below and we'll reply!

Improve With Our Famous Guides

• For All Students

The 5 Strategies You Must Be Using to Improve 160+ SAT Points

How to Get a Perfect 1600, by a Perfect Scorer

Series: How to Get 800 on Each SAT Section:

Score 800 on SAT Math

Score 800 on SAT Reading

Score 800 on SAT Writing

Series: How to Get to 600 on Each SAT Section:

Score 600 on SAT Math

Score 600 on SAT Reading

Score 600 on SAT Writing

Free Complete Official SAT Practice Tests

What SAT Target Score Should You Be Aiming For?

15 Strategies to Improve Your SAT Essay

The 5 Strategies You Must Be Using to Improve 4+ ACT Points

How to Get a Perfect 36 ACT, by a Perfect Scorer

Series: How to Get 36 on Each ACT Section:

36 on ACT English

36 on ACT Math

36 on ACT Reading

36 on ACT Science

Series: How to Get to 24 on Each ACT Section:

24 on ACT English

24 on ACT Math

24 on ACT Reading

24 on ACT Science

What ACT target score should you be aiming for?

ACT Vocabulary You Must Know

ACT Writing: 15 Tips to Raise Your Essay Score

How to Get Into Harvard and the Ivy League

How to Get a Perfect 4.0 GPA

How to Write an Amazing College Essay

What Exactly Are Colleges Looking For?

Is the ACT easier than the SAT? A Comprehensive Guide

Should you retake your SAT or ACT?

When should you take the SAT or ACT?

Stay Informed

Get the latest articles and test prep tips!

Looking for Graduate School Test Prep?

Check out our top-rated graduate blogs here:

GRE Online Prep Blog

GMAT Online Prep Blog

TOEFL Online Prep Blog

Holly R. "I am absolutely overjoyed and cannot thank you enough for helping me!”

When you choose to publish with PLOS, your research makes an impact. Make your work accessible to all, without restrictions, and accelerate scientific discovery with options like preprints and published peer review that make your work more Open.

• PLOS Biology
• PLOS Climate
• PLOS Complex Systems
• PLOS Computational Biology
• PLOS Digital Health
• PLOS Genetics
• PLOS Global Public Health
• PLOS Medicine
• PLOS Mental Health
• PLOS Neglected Tropical Diseases
• PLOS Pathogens
• PLOS Sustainability and Transformation
• PLOS Collections
• About This Blog
• Official PLOS Blog
• EveryONE Blog
• Speaking of Medicine
• PLOS Biologue
• Absolutely Maybe
• DNA Science
• PLOS ECR Community
• All Models Are Wrong
• About PLOS Blogs

A Guide to Using the Scientific Method in Everyday Life

The  scientific method —the process used by scientists to understand the natural world—has the merit of investigating natural phenomena in a rigorous manner. Working from hypotheses, scientists draw conclusions based on empirical data. These data are validated on large-scale numbers and take into consideration the intrinsic variability of the real world. For people unfamiliar with its intrinsic jargon and formalities, science may seem esoteric. And this is a huge problem: science invites criticism because it is not easily understood. So why is it important, then, that every person understand how science is done?

Because the scientific method is, first of all, a matter of logical reasoning and only afterwards, a procedure to be applied in a laboratory.

Individuals without training in logical reasoning are more easily victims of distorted perspectives about themselves and the world. An example is represented by the so-called “ cognitive biases ”—systematic mistakes that individuals make when they try to think rationally, and which lead to erroneous or inaccurate conclusions. People can easily  overestimate the relevance  of their own behaviors and choices. They can  lack the ability to self-estimate the quality of their performances and thoughts . Unconsciously, they could even end up selecting only the arguments  that support their hypothesis or beliefs . This is why the scientific framework should be conceived not only as a mechanism for understanding the natural world, but also as a framework for engaging in logical reasoning and discussion.

A brief history of the scientific method

The scientific method has its roots in the sixteenth and seventeenth centuries. Philosophers Francis Bacon and René Descartes are often credited with formalizing the scientific method because they contrasted the idea that research should be guided by metaphysical pre-conceived concepts of the nature of reality—a position that, at the time,  was highly supported by their colleagues . In essence, Bacon thought that  inductive reasoning based on empirical observation was critical to the formulation of hypotheses  and the  generation of new understanding : general or universal principles describing how nature works are derived only from observations of recurring phenomena and data recorded from them. The inductive method was used, for example, by the scientist Rudolf Virchow to formulate the third principle of the notorious  cell theory , according to which every cell derives from a pre-existing one. The rationale behind this conclusion is that because all observations of cell behavior show that cells are only derived from other cells, this assertion must be always true. 

Inductive reasoning, however, is not immune to mistakes and limitations. Referring back to cell theory, there may be rare occasions in which a cell does not arise from a pre-existing one, even though we haven’t observed it yet—our observations on cell behavior, although numerous, can still benefit from additional observations to either refute or support the conclusion that all cells arise from pre-existing ones. And this is where limited observations can lead to erroneous conclusions reasoned inductively. In another example, if one never has seen a swan that is not white, they might conclude that all swans are white, even when we know that black swans do exist, however rare they may be.  

The universally accepted scientific method, as it is used in science laboratories today, is grounded in  hypothetico-deductive reasoning . Research progresses via iterative empirical testing of formulated, testable hypotheses (formulated through inductive reasoning). A testable hypothesis is one that can be rejected (falsified) by empirical observations, a concept known as the  principle of falsification . Initially, ideas and conjectures are formulated. Experiments are then performed to test them. If the body of evidence fails to reject the hypothesis, the hypothesis stands. It stands however until and unless another (even singular) empirical observation falsifies it. However, just as with inductive reasoning, hypothetico-deductive reasoning is not immune to pitfalls—assumptions built into hypotheses can be shown to be false, thereby nullifying previously unrejected hypotheses. The bottom line is that science does not work to prove anything about the natural world. Instead, it builds hypotheses that explain the natural world and then attempts to find the hole in the reasoning (i.e., it works to disprove things about the natural world).

How do scientists test hypotheses?

Controlled experiments

The word “experiment” can be misleading because it implies a lack of control over the process. Therefore, it is important to understand that science uses controlled experiments in order to test hypotheses and contribute new knowledge. So what exactly is a controlled experiment, then? 

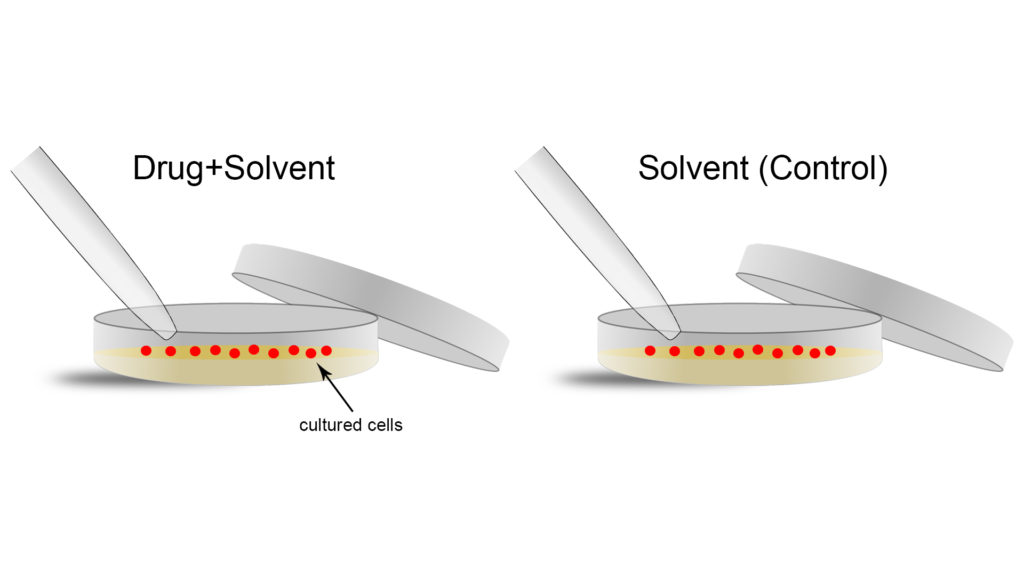
Let us take a practical example. Our starting hypothesis is the following: we have a novel drug that we think inhibits the division of cells, meaning that it prevents one cell from dividing into two cells (recall the description of cell theory above). To test this hypothesis, we could treat some cells with the drug on a plate that contains nutrients and fuel required for their survival and division (a standard cell biology assay). If the drug works as expected, the cells should stop dividing. This type of drug might be useful, for example, in treating cancers because slowing or stopping the division of cells would result in the slowing or stopping of tumor growth.

Although this experiment is relatively easy to do, the mere process of doing science means that several experimental variables (like temperature of the cells or drug, dosage, and so on) could play a major role in the experiment. This could result in a failed experiment when the drug actually does work, or it could give the appearance that the drug is working when it is not. Given that these variables cannot be eliminated, scientists always run control experiments in parallel to the real ones, so that the effects of these other variables can be determined.  Control experiments  are designed so that all variables, with the exception of the one under investigation, are kept constant. In simple terms, the conditions must be identical between the control and the actual experiment.     

Coming back to our example, when a drug is administered it is not pure. Often, it is dissolved in a solvent like water or oil. Therefore, the perfect control to the actual experiment would be to administer pure solvent (without the added drug) at the same time and with the same tools, where all other experimental variables (like temperature, as mentioned above) are the same between the two (Figure 1). Any difference in effect on cell division in the actual experiment here can be attributed to an effect of the drug because the effects of the solvent were controlled.

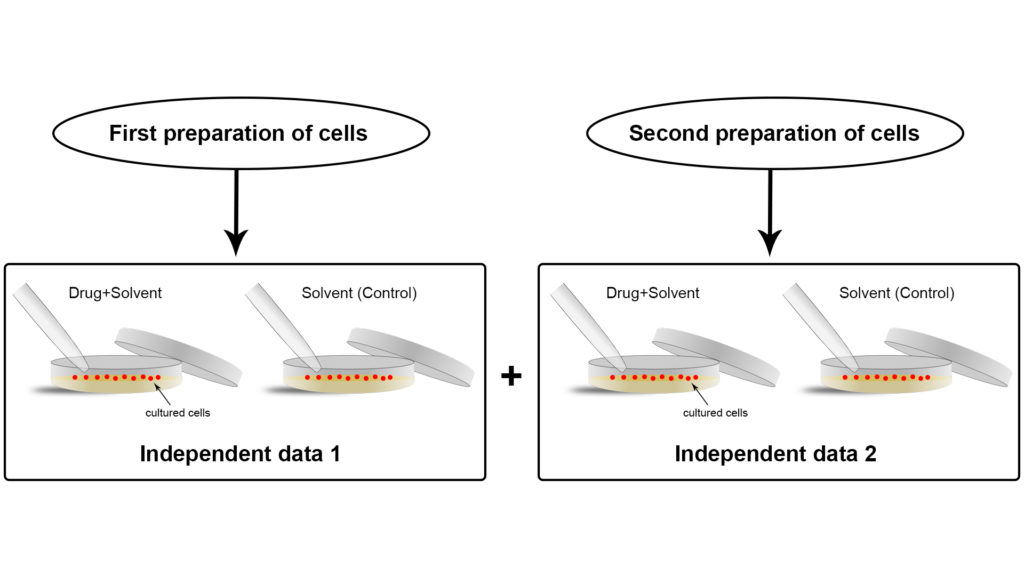
In order to provide evidence of the quality of a single, specific experiment, it needs to be performed multiple times in the same experimental conditions. We call these multiple experiments “replicates” of the experiment (Figure 2). The more replicates of the same experiment, the more confident the scientist can be about the conclusions of that experiment under the given conditions. However, multiple replicates under the same experimental conditions  are of no help  when scientists aim at acquiring more empirical evidence to support their hypothesis. Instead, they need  independent experiments  (Figure 3), in their own lab and in other labs across the world, to validate their results. 

Often times, especially when a given experiment has been repeated and its outcome is not fully clear, it is better  to find alternative experimental assays  to test the hypothesis. 

Applying the scientific approach to everyday life

So, what can we take from the scientific approach to apply to our everyday lives?

A few weeks ago, I had an agitated conversation with a bunch of friends concerning the following question: What is the definition of intelligence?

Defining “intelligence” is not easy. At the beginning of the conversation, everybody had a different, “personal” conception of intelligence in mind, which – tacitly – implied that the conversation could have taken several different directions. We realized rather soon that someone thought that an intelligent person is whoever is able to adapt faster to new situations; someone else thought that an intelligent person is whoever is able to deal with other people and empathize with them. Personally, I thought that an intelligent person is whoever displays high cognitive skills, especially in abstract reasoning. 

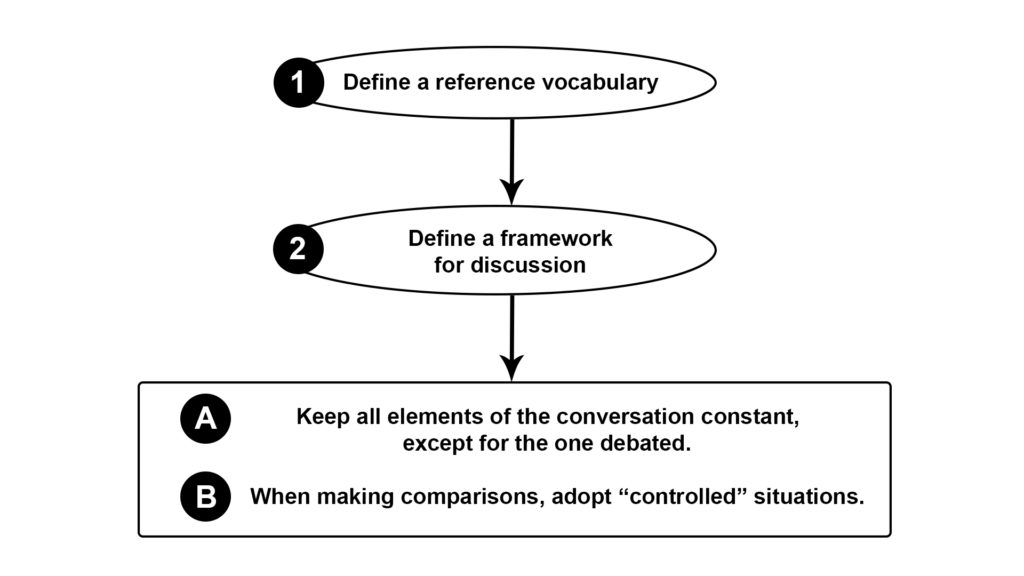
The scientific method has the merit of providing a reference system, with precise protocols and rules to follow. Remember: experiments must be reproducible, which means that an independent scientists in a different laboratory, when provided with the same equipment and protocols, should get comparable results.  Fruitful conversations as well need precise language, a kind of reference vocabulary everybody should agree upon, in order to discuss about the same “content”. This is something we often forget, something that was somehow missing at the opening of the aforementioned conversation: even among friends, we should always agree on premises, and define them in a rigorous manner, so that they are the same for everybody. When speaking about “intelligence”, we must all make sure we understand meaning and context of the vocabulary adopted in the debate (Figure 4, point 1).  This is the first step of “controlling” a conversation.

There is another downside that a discussion well-grounded in a scientific framework would avoid. The mistake is not structuring the debate so that all its elements, except for the one under investigation, are kept constant (Figure 4, point 2). This is particularly true when people aim at making comparisons between groups to support their claim. For example, they may try to define what intelligence is by comparing the  achievements in life of different individuals: “Stephen Hawking is a brilliant example of intelligence because of his great contribution to the physics of black holes”. This statement does not help to define what intelligence is, simply because it compares Stephen Hawking, a famous and exceptional physicist, to any other person, who statistically speaking, knows nothing about physics. Hawking first went to the University of Oxford, then he moved to the University of Cambridge. He was in contact with the most influential physicists on Earth. Other people were not. All of this, of course, does not disprove Hawking’s intelligence; but from a logical and methodological point of view, given the multitude of variables included in this comparison, it cannot prove it. Thus, the sentence “Stephen Hawking is a brilliant example of intelligence because of his great contribution to the physics of black holes” is not a valid argument to describe what intelligence is. If we really intend to approximate a definition of intelligence, Steven Hawking should be compared to other physicists, even better if they were Hawking’s classmates at the time of college, and colleagues afterwards during years of academic research. 

In simple terms, as scientists do in the lab, while debating we should try to compare groups of elements that display identical, or highly similar, features. As previously mentioned, all variables – except for the one under investigation – must be kept constant.

This insightful piece  presents a detailed analysis of how and why science can help to develop critical thinking.

In a nutshell

Here is how to approach a daily conversation in a rigorous, scientific manner:

• First discuss about the reference vocabulary, then discuss about the content of the discussion.  Think about a researcher who is writing down an experimental protocol that will be used by thousands of other scientists in varying continents. If the protocol is rigorously written, all scientists using it should get comparable experimental outcomes. In science this means reproducible knowledge, in daily life this means fruitful conversations in which individuals are on the same page. 
• Adopt “controlled” arguments to support your claims.  When making comparisons between groups, visualize two blank scenarios. As you start to add details to both of them, you have two options. If your aim is to hide a specific detail, the better is to design the two scenarios in a completely different manner—it is to increase the variables. But if your intention is to help the observer to isolate a specific detail, the better is to design identical scenarios, with the exception of the intended detail—it is therefore to keep most of the variables constant. This is precisely how scientists ideate adequate experiments to isolate new pieces of knowledge, and how individuals should orchestrate their thoughts in order to test them and facilitate their comprehension to others.   

Not only the scientific method should offer individuals an elitist way to investigate reality, but also an accessible tool to properly reason and discuss about it.

Edited by Jason Organ, PhD, Indiana University School of Medicine.

Simone is a molecular biologist on the verge of obtaining a doctoral title at the University of Ulm, Germany. He is Vice-Director at Culturico (https://culturico.com/), where his writings span from Literature to Sociology, from Philosophy to Science. His writings recently appeared in Psychology Today, openDemocracy, Splice Today, Merion West, Uncommon Ground and The Society Pages. Follow Simone on Twitter: @simredaelli

• Pingback: Case Studies in Ethical Thinking: Day 1 | Education & Erudition

This has to be the best article I have ever read on Scientific Thinking. I am presently writing a treatise on how Scientific thinking can be adopted to entreat all situations.And how, a 4 year old child can be taught to adopt Scientific thinking, so that, the child can look at situations that bothers her and she could try to think about that situation by formulating the right questions. She may not have the tools to find right answers? But, forming questions by using right technique ? May just make her find a way to put her mind to rest even at that level. That is why, 4 year olds are often “eerily: (!)intelligent, I have iften been intimidated and plain embarrassed to see an intelligent and well spoken 4 year old deal with celibrity ! Of course, there are a lot of variables that have to be kept in mind in order to train children in such controlled thinking environment, as the screenplay of little Sheldon shows. Thanking the author with all my heart – #ershadspeak #wearescience #weareallscientists Ershad Khandker

Simone, thank you for this article. I have the idea that I want to apply what I learned in Biology to everyday life. You addressed this issue, and have given some basic steps in using the scientific method.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name and email for the next time I comment.

By Ashley Moses, edited by Andrew S. Cale Each year, millions of scientific research papers are published. Virtually none of them can…

By Ana Santos-Carvalho and Carolina Lebre, edited by Andrew S. Cale Excessive use of technical jargon can be a significant barrier to…

By Ryan McRae and Briana Pobiner, edited by Andrew S. Cale In 2023, the field of human evolution benefited from a plethora…

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.12: Scientific Problem Solving

• Last updated
• Save as PDF
• Page ID 52325

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

How can we use problem solving in our everyday routines?

One day you wake up and realize your clock radio did not turn on to get you out of bed. You are puzzled, so you decide to find out what happened. You list three possible explanations:

• There was a power failure and your radio cannot turn on.
• Your little sister turned it off as a joke.
• You did not set the alarm last night.

Upon investigation, you find that the clock is on, so there is no power failure. Your little sister was spending the night with a friend and could not have turned the alarm off. You notice that the alarm is not set—your forgetfulness made you late. You have used the scientific method to answer a question.

Scientific Problem Solving

Humans have always wondered about the world around them. One of the questions of interest was (and still is): what is this world made of? Chemistry has been defined in various ways as the study of matter. What matter consists of has been a source of debate over the centuries. One of the key areas for this debate in the Western world was Greek philosophy.

The basic approach of the Greek philosophers was to discuss and debate the questions they had about the world. There was no gathering of information to speak of, just talking. As a result, several ideas about matter were put forth, but never resolved. The first philosopher to carry out the gathering of data was Aristotle (384-322 B.C.). He recorded many observations on the weather, on plant and animal life and behavior, on physical motions, and a number of other topics. Aristotle could probably be considered the first "real" scientist, because he made systematic observations of nature and tried to understand what he was seeing.

Inductive and Deductive Reasoning

Two approaches to logical thinking developed over the centuries. These two methods are inductive reasoning and deductive reasoning . Inductive reasoning involves getting a collection of specific examples and drawing a general conclusion from them. Deductive reasoning takes a general principle and then draws a specific conclusion from the general concept. Both are used in the development of scientific ideas.

Inductive reasoning first involves the collection of data: "If I add sodium metal to water, I observe a very violent reaction. Every time I repeat the process, I see the same thing happen." A general conclusion is drawn from these observations: the addition of sodium to water results in a violent reaction.

In deductive reasoning, a specific prediction is made based on a general principle. One general principle is that acids turn blue litmus paper red. Using the deductive reasoning process, one might predict: "If I have a bottle of liquid labeled 'acid', I expect the litmus paper to turn red when I immerse it in the liquid."

The Idea of the Experiment

Inductive reasoning is at the heart of what is now called the " scientific method ." In European culture, this approach was developed mainly by Francis Bacon (1561-1626), a British scholar. He advocated the use of inductive reasoning in every area of life, not just science. The scientific method, as developed by Bacon and others, involves several steps:

• Ask a question - identify the problem to be considered.
• Make observations - gather data that pertains to the question.
• Propose an explanation (a hypothesis) for the observations.
• Make new observations to test the hypothesis further.

Note that this should not be considered a "cookbook" for scientific research. Scientists do not sit down with their daily "to do" list and write down these steps. The steps may not necessarily be followed in order. But this does provide a general idea of how scientific research is usually done.

When a hypothesis is confirmed repeatedly, it eventually becomes a theory—a general principle that is offered to explain natural phenomena. Note a key word— explain , or  explanation . A theory offers a description of why something happens. A law, on the other hand, is a statement that is always true, but offers no explanation as to why. The law of gravity says a rock will fall when dropped, but does not explain why (gravitational theory is very complex and incomplete at present). The kinetic molecular theory of gases, on the other hand, states what happens when a gas is heated in a closed container (the pressure increases), but also explains why (the motions of the gas molecules are increased due to the change in temperature). Theories do not get "promoted" to laws, because laws do not answer the "why" question.

• The early Greek philosophers spent their time talking about nature, but did little or no actual exploration or investigation.
• Inductive reasoning - to develop a general conclusion from a collection of observations.
• Deductive reasoning - to make a specific statement based on a general principle.
• Scientific method - a process of observation, developing a hypothesis, and testing that hypothesis.
• What was the basic shortcoming of the Greek philosophers approach to studying the material world?
• How did Aristotle improve the approach?
• Define “inductive reasoning” and give an example.
• Define “deductive reasoning” and give an example.
• What is the difference between a hypothesis and a theory?
• What is the difference between a theory and a law?

Problem Solving in Science Learning

• Reference work entry
• First Online: 01 January 2015
• Cite this reference work entry

• Edit Yerushalmi 2 &
• Bat-Sheva Eylon 3  

244 Accesses

1 Citations

3 Altmetric

Introduction: Problem Solving in the Science Classroom

Problem solving plays a central role in school science, serving both as a learning goal and as an instructional tool. As a learning goal, problem-solving expertise is considered as a means of promoting both proficiency in solving practice problems and competency in tackling novel problems, a hallmark of successful scientists and engineers. As an instructional tool, problem solving attempts to situate the learning of scientific ideas and practices in an applicative context, thus providing an opportunity to transform science learning into an active, relevant, and motivating experience. Problem solving is also frequently a central strategy in the assessment of students’ performance on various measures (e.g., mastery of procedural skills, conceptual understanding, as well as scientific and learning practices).

A problem is often defined as an unfamiliar task that requires one to make judicious decisions when searching through a problem...

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Durable hardcover edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Chi MTH (2000) Self-explaining expository texts: the dual processes of generating inferences and repairing mental models. In: Glaser R (ed) Advances in instructional psychology. Lawrence Erlbaum Associates, Mahwah, pp 161–238

Google Scholar  

Greeno JG, Simon HA (1984) Problem solving and reasoning. In: Atkinson RC, Herrnstein R, Lindzey G, Lute RD (eds) Stevens’ handbook of experimental psychology. Wiley, New York

Paas F, van Gog T, Sweller J (2010) Cognitive load theory: new conceptualizations, specifications, and integrated research perspectives. Educ Psychol Rev 22:115–121

Article   Google Scholar  

Reif F (2008) Applying cognitive science to education: thinking and learning in scientific or other complex domains. MIT Press, Cambridge

Reiser BJ (2004) Scaffolding complex learning: the mechanisms of structuring and problematizing student work. J Learn Sci 13:273–304

Smith JP, DiSessa AA, Roschelle J (1993) Misconceptions reconceived: a constructivist analysis of knowledge in transition. J Learn Sci 3:115–163

Download references

Author information

Authors and affiliations.

The Weizmann Institute of Science, Rehovot, Israel

Edit Yerushalmi

The Science Teaching Department, The Weizmann Institute of Science, Rehovot, Israel

Bat-Sheva Eylon

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Bat-Sheva Eylon .

Editor information

Editors and affiliations.

Emeritus Professor of Science and Technology Education, Faculty of Education Monash University, Clayton, VIC, Australia

Richard Gunstone

Rights and permissions

Reprints and permissions

Copyright information

© 2015 Springer Science+Business Media Dordrecht

About this entry

Cite this entry.

Yerushalmi, E., Eylon, BS. (2015). Problem Solving in Science Learning. In: Gunstone, R. (eds) Encyclopedia of Science Education. Springer, Dordrecht. https://doi.org/10.1007/978-94-007-2150-0_129

Download citation

DOI : https://doi.org/10.1007/978-94-007-2150-0_129

Published : 04 January 2015

Publisher Name : Springer, Dordrecht

Print ISBN : 978-94-007-2149-4

Online ISBN : 978-94-007-2150-0

eBook Packages : Humanities, Social Sciences and Law

Share this entry

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

• Bipolar Disorder
• Therapy Center
• When To See a Therapist
• Types of Therapy
• Best Online Therapy
• Best Couples Therapy
• Best Family Therapy
• Managing Stress
• Sleep and Dreaming
• Understanding Emotions
• Self-Improvement
• Healthy Relationships
• Student Resources
• Personality Types
• Guided Meditations
• Verywell Mind Insights
• 2024 Verywell Mind 25
• Mental Health in the Classroom
• Editorial Process
• Meet Our Review Board
• Crisis Support

Overview of the Problem-Solving Mental Process

Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Rachel Goldman, PhD FTOS, is a licensed psychologist, clinical assistant professor, speaker, wellness expert specializing in eating behaviors, stress management, and health behavior change.

• Identify the Problem
• Define the Problem
• Form a Strategy
• Organize Information
• Allocate Resources
• Monitor Progress
• Evaluate the Results

Frequently Asked Questions

Problem-solving is a mental process that involves discovering, analyzing, and solving problems. The ultimate goal of problem-solving is to overcome obstacles and find a solution that best resolves the issue.

The best strategy for solving a problem depends largely on the unique situation. In some cases, people are better off learning everything they can about the issue and then using factual knowledge to come up with a solution. In other instances, creativity and insight are the best options.

It is not necessary to follow problem-solving steps sequentially, It is common to skip steps or even go back through steps multiple times until the desired solution is reached.

In order to correctly solve a problem, it is often important to follow a series of steps. Researchers sometimes refer to this as the problem-solving cycle. While this cycle is portrayed sequentially, people rarely follow a rigid series of steps to find a solution.

The following steps include developing strategies and organizing knowledge.

1. Identifying the Problem

While it may seem like an obvious step, identifying the problem is not always as simple as it sounds. In some cases, people might mistakenly identify the wrong source of a problem, which will make attempts to solve it inefficient or even useless.

Some strategies that you might use to figure out the source of a problem include :

• Asking questions about the problem
• Breaking the problem down into smaller pieces
• Looking at the problem from different perspectives
• Conducting research to figure out what relationships exist between different variables

2. Defining the Problem

After the problem has been identified, it is important to fully define the problem so that it can be solved. You can define a problem by operationally defining each aspect of the problem and setting goals for what aspects of the problem you will address

At this point, you should focus on figuring out which aspects of the problems are facts and which are opinions. State the problem clearly and identify the scope of the solution.

3. Forming a Strategy

After the problem has been identified, it is time to start brainstorming potential solutions. This step usually involves generating as many ideas as possible without judging their quality. Once several possibilities have been generated, they can be evaluated and narrowed down.

The next step is to develop a strategy to solve the problem. The approach used will vary depending upon the situation and the individual's unique preferences. Common problem-solving strategies include heuristics and algorithms.

• Heuristics are mental shortcuts that are often based on solutions that have worked in the past. They can work well if the problem is similar to something you have encountered before and are often the best choice if you need a fast solution.
• Algorithms are step-by-step strategies that are guaranteed to produce a correct result. While this approach is great for accuracy, it can also consume time and resources.

Heuristics are often best used when time is of the essence, while algorithms are a better choice when a decision needs to be as accurate as possible.

4. Organizing Information

Before coming up with a solution, you need to first organize the available information. What do you know about the problem? What do you not know? The more information that is available the better prepared you will be to come up with an accurate solution.

When approaching a problem, it is important to make sure that you have all the data you need. Making a decision without adequate information can lead to biased or inaccurate results.

5. Allocating Resources

Of course, we don't always have unlimited money, time, and other resources to solve a problem. Before you begin to solve a problem, you need to determine how high priority it is.

If it is an important problem, it is probably worth allocating more resources to solving it. If, however, it is a fairly unimportant problem, then you do not want to spend too much of your available resources on coming up with a solution.

At this stage, it is important to consider all of the factors that might affect the problem at hand. This includes looking at the available resources, deadlines that need to be met, and any possible risks involved in each solution. After careful evaluation, a decision can be made about which solution to pursue.

6. Monitoring Progress

After selecting a problem-solving strategy, it is time to put the plan into action and see if it works. This step might involve trying out different solutions to see which one is the most effective.

It is also important to monitor the situation after implementing a solution to ensure that the problem has been solved and that no new problems have arisen as a result of the proposed solution.

Effective problem-solvers tend to monitor their progress as they work towards a solution. If they are not making good progress toward reaching their goal, they will reevaluate their approach or look for new strategies .

7. Evaluating the Results

After a solution has been reached, it is important to evaluate the results to determine if it is the best possible solution to the problem. This evaluation might be immediate, such as checking the results of a math problem to ensure the answer is correct, or it can be delayed, such as evaluating the success of a therapy program after several months of treatment.

Once a problem has been solved, it is important to take some time to reflect on the process that was used and evaluate the results. This will help you to improve your problem-solving skills and become more efficient at solving future problems.

A Word From Verywell​

It is important to remember that there are many different problem-solving processes with different steps, and this is just one example. Problem-solving in real-world situations requires a great deal of resourcefulness, flexibility, resilience, and continuous interaction with the environment.

Get Advice From The Verywell Mind Podcast

Hosted by therapist Amy Morin, LCSW, this episode of The Verywell Mind Podcast shares how you can stop dwelling in a negative mindset.

Follow Now : Apple Podcasts / Spotify / Google Podcasts

You can become a better problem solving by:

• Practicing brainstorming and coming up with multiple potential solutions to problems
• Being open-minded and considering all possible options before making a decision
• Breaking down problems into smaller, more manageable pieces
• Asking for help when needed
• Researching different problem-solving techniques and trying out new ones
• Learning from mistakes and using them as opportunities to grow

It's important to communicate openly and honestly with your partner about what's going on. Try to see things from their perspective as well as your own. Work together to find a resolution that works for both of you. Be willing to compromise and accept that there may not be a perfect solution.

Take breaks if things are getting too heated, and come back to the problem when you feel calm and collected. Don't try to fix every problem on your own—consider asking a therapist or counselor for help and insight.

If you've tried everything and there doesn't seem to be a way to fix the problem, you may have to learn to accept it. This can be difficult, but try to focus on the positive aspects of your life and remember that every situation is temporary. Don't dwell on what's going wrong—instead, think about what's going right. Find support by talking to friends or family. Seek professional help if you're having trouble coping.

Davidson JE, Sternberg RJ, editors.  The Psychology of Problem Solving .  Cambridge University Press; 2003. doi:10.1017/CBO9780511615771

Sarathy V. Real world problem-solving .  Front Hum Neurosci . 2018;12:261. Published 2018 Jun 26. doi:10.3389/fnhum.2018.00261

By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

• Future Students
• Current Students
• Faculty/Staff

News and Media

• News & Media Home
• Research Stories
• School's In
• In the Media

You are here

Softening the sharp edges in mathematics.

For everyone whose relationship with mathematics is distant or broken, Jo Boaler , a professor at Stanford Graduate School of Education (GSE), has ideas for repairing it. She particularly wants young people to feel comfortable with numbers from the start — to approach the subject with playfulness and curiosity, not anxiety or dread.

“Most people have only ever experienced what I call narrow mathematics — a set of procedures they need to follow, at speed,” Boaler says. “Mathematics should be flexible, conceptual, a place where we play with ideas and make connections. If we open it up and invite more creativity, more diverse thinking, we can completely transform the experience.”

“Mathematics should be flexible, conceptual, a place where we play with ideas and make connections," says Professor Jo Boaler. (Photo: Robert Houser Photography)

Boaler, the Nomellini and Olivier Professor of Education at the GSE, is the co-founder and faculty director of Youcubed , a Stanford research center that provides resources for math learning that has reached more than 230 million students in over 140 countries. In 2013 Boaler, a former high school math teacher, produced “How to Learn Math,” the first massive open online course (MOOC) on mathematics education. She leads workshops and leadership summits for teachers and administrators, and her online courses have been taken by over a million users. 

In her new book, Math-ish: Finding Creativity, Diversity, and Meaning in Mathematics , Boaler argues for a broad, inclusive approach to math education, offering strategies and activities for learners at any age. We spoke with her about why creativity is an important part of mathematics, the impact of representing numbers visually and physically, and how what she calls “ishing” a math problem can help students make better sense of the answer. 

What do you mean by “math-ish” thinking?

It’s a way of thinking about numbers in the real world, which are usually imprecise estimates. If someone asks how old you are, how warm it is outside, how long it takes to drive to the airport – these are generally answered with what I call “ish” numbers, and that’s very different from the way we use and learn numbers in school.

In the book I share an example of a multiple-choice question from a nationwide exam where students are asked to estimate the sum of two fractions: 12/13 + 7/8. They’re given four choices for the closest answer: 1, 2, 19, or 21. Each of the fractions in the question is very close to 1, so the answer would be 2 — but the most common answer 13-year-olds gave was 19. The second most common was 21. 

I’m not surprised, because when students learn fractions, they often don’t learn to think conceptually or to consider the relationship between the numerator or denominator. They learn rules about creating common denominators and adding or subtracting the numerators, without making sense of the fraction as a whole. But stepping back and judging whether a calculation is reasonable might be the most valuable mathematical skill a person can develop.

But don’t you also risk sending the message that mathematical precision isn’t important? 

I’m not saying precision isn’t important. What I’m suggesting is that we ask students to estimate before they calculate, so when they come up with a precise answer, they’ll have a real sense for whether it makes sense. This also helps students learn how to move between big-picture and focused thinking, which are two different but equally important modes of reasoning.

Some people ask me, “Isn’t ‘ishing’ just estimating?” It is, but when we ask students to estimate, they often groan, thinking it’s yet another mathematical method. But when we ask them to “ish” a number, they're more willing to offer their thinking.

Ishing helps students develop a sense for numbers and shapes. It can help soften the sharp edges in mathematics, making it easier for kids to jump in and engage. It can buffer students against the dangers of perfectionism, which we know can be a damaging mind-set. I think we all need a little more ish in our lives. 

You also argue that mathematics should be taught in more visual ways. What do you mean by that? 

For most people, mathematics is an almost entirely symbolic, numerical experience. Any visuals are usually sterile images in a textbook, showing bisecting angles, or circles divided into slices. But the way we function in life is by developing models of things in our minds. Take a stapler: Knowing what it looks like, what it feels and sounds like, how to interact with it, how it changes things — all of that contributes to our understanding of how it works. 

There’s an activity we do with middle-school students where we show them an image of a 4 x 4 x 4 cm cube made up of smaller 1 cm cubes, like a Rubik’s Cube. The larger cube is dipped into a can of blue paint, and we ask the students, if they could take apart the little cubes, how many sides would be painted blue? Sometimes we give the students sugar cubes and have them physically build a larger 4 x 4 x 4 cube. This is an activity that leads into algebraic thinking. 

Some years back we were interviewing students a year after they’d done that activity in our summer camp and asked what had stayed with them. One student said, ‘I’m in geometry class now, and I still remember that  sugar cube, what it looked like and felt like.’ His class had been asked to estimate the volume of their shoes, and he said he’d imagined his shoes filled with 1 cm sugar cubes in order to solve that question. He had built a mental model of a cube.

When we learn about cubes, most of us don’t get to see and manipulate them. When we learn about square roots, we don’t take squares and look at their diagonals. We just manipulate numbers.

I wonder if people consider the physical representations more appropriate for younger kids.

That’s the thing — elementary school teachers are amazing at giving kids those experiences, but it dies out in middle school, and by high school it’s all symbolic. There’s a myth that there’s a hierarchy of sophistication where you start out with visual and physical representations and then build up to the symbolic. But so much of high-level mathematical work now is visual. Here in Silicon Valley, if you look at Tesla engineers, they're drawing, they're sketching, they're building models, and nobody says that's elementary mathematics.

Click to enlarge: A depiction of various ways to calculate 38 x 5, numerically and visually. (Image: Courtesy of Jo Boaler)

There’s an example in the book where you’ve asked students how they would calculate 38 x 5 in their heads, and they come up with several different ways of arriving at the same answer. The creativity is fascinating, but wouldn’t it be easier to teach students one standard method?

That narrow, rigid version of mathematics where there’s only one right approach is what most students experience, and it’s a big part of why people have such math trauma. It keeps them from realizing the full range and power of mathematics. When you only have students blindly memorizing math facts, they’re not developing number sense. They don’t learn how to use numbers flexibly in different situations. It also makes students who think differently believe there’s something wrong with them. 

When we open mathematics to acknowledge the different ways a concept or problem can be viewed, we also open the subject to many more students. Mathematical diversity, to me, is a concept that includes both the value of diversity in people and the diverse ways we can see and learn mathematics. When we bring those forms of diversity together, it’s powerful. If we want to value different ways of thinking and problem-solving in the world, we need to embrace mathematical diversity.

More Stories

⟵ Go to all Research Stories

Get the Educator

Subscribe to our monthly newsletter.

Stanford Graduate School of Education

482 Galvez Mall Stanford, CA 94305-3096 Tel: (650) 723-2109

• Contact Admissions
• GSE Leadership
• Site Feedback
• Web Accessibility
• Career Resources
• Faculty Open Positions
• Explore Courses
• Academic Calendar
• Office of the Registrar
• Cubberley Library
• StanfordWho
• StanfordYou

Improving lives through learning

• Stanford Home
• Maps & Directions
• Search Stanford
• Emergency Info
• Terms of Use
• Non-Discrimination
• Accessibility

© Stanford University , Stanford , California 94305 .

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

Suggestions or feedback?

MIT News | Massachusetts Institute of Technology

• Machine learning
• Social justice
• Black holes
• Classes and programs

Departments

• Aeronautics and Astronautics
• Brain and Cognitive Sciences
• Architecture
• Political Science
• Mechanical Engineering

Centers, Labs, & Programs

• Abdul Latif Jameel Poverty Action Lab (J-PAL)
• Picower Institute for Learning and Memory
• Lincoln Laboratory
• School of Architecture + Planning
• School of Engineering
• School of Humanities, Arts, and Social Sciences
• Sloan School of Management
• School of Science
• MIT Schwarzman College of Computing

Scientists use generative AI to answer complex questions in physics

Press contact :, media download.

*Terms of Use:

Images for download on the MIT News office website are made available to non-commercial entities, press and the general public under a Creative Commons Attribution Non-Commercial No Derivatives license . You may not alter the images provided, other than to crop them to size. A credit line must be used when reproducing images; if one is not provided below, credit the images to "MIT."

Previous image Next image

When water freezes, it transitions from a liquid phase to a solid phase, resulting in a drastic change in properties like density and volume. Phase transitions in water are so common most of us probably don’t even think about them, but phase transitions in novel materials or complex physical systems are an important area of study.

To fully understand these systems, scientists must be able to recognize phases and detect the transitions between. But how to quantify phase changes in an unknown system is often unclear, especially when data are scarce.

Researchers from MIT and the University of Basel in Switzerland applied generative artificial intelligence models to this problem, developing a new machine-learning framework that can automatically map out phase diagrams for novel physical systems.

Their physics-informed machine-learning approach is more efficient than laborious, manual techniques which rely on theoretical expertise. Importantly, because their approach leverages generative models, it does not require huge, labeled training datasets used in other machine-learning techniques.

Such a framework could help scientists investigate the thermodynamic properties of novel materials or detect entanglement in quantum systems, for instance. Ultimately, this technique could make it possible for scientists to discover unknown phases of matter autonomously.

“If you have a new system with fully unknown properties, how would you choose which observable quantity to study? The hope, at least with data-driven tools, is that you could scan large new systems in an automated way, and it will point you to important changes in the system. This might be a tool in the pipeline of automated scientific discovery of new, exotic properties of phases,” says Frank Schäfer, a postdoc in the Julia Lab in the Computer Science and Artificial Intelligence Laboratory (CSAIL) and co-author of a paper on this approach.

Joining Schäfer on the paper are first author Julian Arnold, a graduate student at the University of Basel; Alan Edelman, applied mathematics professor in the Department of Mathematics and leader of the Julia Lab; and senior author Christoph Bruder, professor in the Department of Physics at the University of Basel. The research is published today in Physical Review Letters.

Detecting phase transitions using AI

While water transitioning to ice might be among the most obvious examples of a phase change, more exotic phase changes, like when a material transitions from being a normal conductor to a superconductor, are of keen interest to scientists.

These transitions can be detected by identifying an “order parameter,” a quantity that is important and expected to change. For instance, water freezes and transitions to a solid phase (ice) when its temperature drops below 0 degrees Celsius. In this case, an appropriate order parameter could be defined in terms of the proportion of water molecules that are part of the crystalline lattice versus those that remain in a disordered state.

In the past, researchers have relied on physics expertise to build phase diagrams manually, drawing on theoretical understanding to know which order parameters are important. Not only is this tedious for complex systems, and perhaps impossible for unknown systems with new behaviors, but it also introduces human bias into the solution.

More recently, researchers have begun using machine learning to build discriminative classifiers that can solve this task by learning to classify a measurement statistic as coming from a particular phase of the physical system, the same way such models classify an image as a cat or dog.

The MIT researchers demonstrated how generative models can be used to solve this classification task much more efficiently, and in a physics-informed manner.

The Julia Programming Language , a popular language for scientific computing that is also used in MIT’s introductory linear algebra classes, offers many tools that make it invaluable for constructing such generative models, Schäfer adds.

Generative models, like those that underlie ChatGPT and Dall-E, typically work by estimating the probability distribution of some data, which they use to generate new data points that fit the distribution (such as new cat images that are similar to existing cat images).

However, when simulations of a physical system using tried-and-true scientific techniques are available, researchers get a model of its probability distribution for free. This distribution describes the measurement statistics of the physical system.

A more knowledgeable model

The MIT team’s insight is that this probability distribution also defines a generative model upon which a classifier can be constructed. They plug the generative model into standard statistical formulas to directly construct a classifier instead of learning it from samples, as was done with discriminative approaches.

“This is a really nice way of incorporating something you know about your physical system deep inside your machine-learning scheme. It goes far beyond just performing feature engineering on your data samples or simple inductive biases,” Schäfer says.

This generative classifier can determine what phase the system is in given some parameter, like temperature or pressure. And because the researchers directly approximate the probability distributions underlying measurements from the physical system, the classifier has system knowledge.

This enables their method to perform better than other machine-learning techniques. And because it can work automatically without the need for extensive training, their approach significantly enhances the computational efficiency of identifying phase transitions.

At the end of the day, similar to how one might ask ChatGPT to solve a math problem, the researchers can ask the generative classifier questions like “does this sample belong to phase I or phase II?” or “was this sample generated at high temperature or low temperature?”

Scientists could also use this approach to solve different binary classification tasks in physical systems, possibly to detect entanglement in quantum systems (Is the state entangled or not?) or determine whether theory A or B is best suited to solve a particular problem. They could also use this approach to better understand and improve large language models like ChatGPT by identifying how certain parameters should be tuned so the chatbot gives the best outputs.

In the future, the researchers also want to study theoretical guarantees regarding how many measurements they would need to effectively detect phase transitions and estimate the amount of computation that would require.

This work was funded, in part, by the Swiss National Science Foundation, the MIT-Switzerland Lockheed Martin Seed Fund, and MIT International Science and Technology Initiatives.

Share this news article on:

Press mentions.

Researchers at MIT and elsewhere have developed a new machine-learning model capable of “predicting a physical system’s phase or state,” report Kyle Wiggers and Devin Coldewey for TechCrunch . 

Previous item Next item

Related Links

• Frank Schäfer
• Alan Edelman
• Computer Science and Artificial Intelligence Laboratory
• Department of Mathematics
• Department of Electrical Engineering and Computer Science

Related Topics

• Mathematics
• Computer science and technology
• Artificial intelligence
• Computer modeling
• Computer Science and Artificial Intelligence Laboratory (CSAIL)
• Electrical Engineering & Computer Science (eecs)

Related Articles

Technique could efficiently solve partial differential equations for numerous applications

Computational model captures the elusive transition states of chemical reactions

Explained: Generative AI

From physics to generative AI: An AI model for advanced pattern generation

More mit news.

Understanding why autism symptoms sometimes improve amid fever

Read full story →

School of Engineering welcomes new faculty

Study explains why the brain can robustly recognize images, even without color

Turning up the heat on next-generation semiconductors

Sarah Millholland receives 2024 Vera Rubin Early Career Award

A community collaboration for progress

• More news on MIT News homepage →

Massachusetts Institute of Technology 77 Massachusetts Avenue, Cambridge, MA, USA

• Map (opens in new window)
• Events (opens in new window)
• People (opens in new window)
• Careers (opens in new window)
• Accessibility
• Social Media Hub
• MIT on Facebook
• MIT on YouTube
• MIT on Instagram

A new theory of quantum gravity could explain the biggest puzzle in cosmology, study suggests

A new theory of quantum gravity, which attempts to unite quantum physics with Einstein's relativity, could help solve the puzzle of the universe's expansion, a theoretical paper suggests.

A variation on the theory of quantum gravity — the unification of quantum mechanics and Einstein's general relativity — could help solve one of the biggest puzzles in cosmology, new research suggests.

For nearly a century, scientists have known that the universe is expanding. But in recent decades, physicists have found that different types of measurements of the expansion rate — called the Hubble parameter — produce puzzling inconsistencies.

To resolve this paradox, a new study suggests incorporating quantum effects into one prominent theory used to determine the expansion rate.

"We tried to resolve and explain the mismatch between the values of the Hubble parameter from two different prominent types of observations," study co-author P.K. Suresh , a professor of physics at the University of Hyderabad in India, told Live Science via email.

An expanding problem

The universe's expansion was first identified by Edwin Hubble in 1929. His observations with the largest telescope of that time revealed that galaxies farther from us appear to move away at faster speeds. Although Hubble initially overestimated the expansion rate, subsequent measurements have refined our understanding, establishing the current Hubble parameter as highly reliable.

Later in the 20th century, astrophysicists introduced a novel technique to gauge the expansion rate by examining the cosmic microwave background, the pervasive "afterglow" of the Big Bang .

However, a serious problem arose with these two types of measurements. Specifically, the newer method produced a Hubble parameter value almost 10% lower than the one deduced from the astronomical observations of distant cosmic objects. Such discrepancies between different measurements, called the Hubble tension, signal potential flaws in our understanding of the universe's evolution.

Sign up for the Live Science daily newsletter now

Get the world’s most fascinating discoveries delivered straight to your inbox.

Related: Newfound 'glitch' in Einstein's relativity could rewrite the rules of the universe, study suggests

In a study published in the journal Classical and Quantum Gravity , Suresh and his colleague from the University of Hyderabad, B. Anupama, proposed a solution to align these disparate results. They underscored that physicists infer the Hubble parameter indirectly, employing our universe's evolutionary model based on Einstein's theory of general relativity.

The team argued for revising this theory to incorporate quantum effects. These effects, intrinsic to fundamental interactions, encompass random field fluctuations and the spontaneous creation of particles from the vacuum of space.

Despite scientists' ability to integrate quantum effects into theories of other fields, quantum gravity remains elusive, making detailed calculations extremely difficult or even impossible. To make matters worse, experimental studies of these effects require reaching temperatures or energies many orders of magnitude higher than those achievable in a lab.

Acknowledging these challenges, Suresh and Anupama focused on broad quantum-gravity effects common to many proposed theories.

"Our equation doesn't need to account for everything, but that does not prevent us from testing quantum gravity or its effects experimentally," Suresh said.

Their theoretical exploration revealed that accounting for quantum effects when describing the gravitational interactions in the earliest stage of the universe's expansion, called cosmic inflation, could indeed alter the theory's predictions regarding the properties of the microwave background at present, making the two types of Hubble parameter measurements consistent.

Of course, final conclusions can be drawn only when a full-fledged theory of quantum gravity is known, but even the preliminary findings are encouraging. Moreover, the link between the cosmic microwave background and quantum gravitational effects opens the way to experimentally studying these effects in the near future, the team said.

"Quantum gravity is supposed to play a role in the dynamics of the early universe; thus its effect can be observed through measurements of the properties of the cosmic microwave background," Suresh said.

— Mysterious 'unparticles' may be pushing the universe apart, new theoretical study suggests

— 'It could be profound': How astronomer Wendy Freedman is trying to fix the universe

— James Webb telescope discovers oldest black hole in the universe  

"Some of the future missions devoted to studying this electromagnetic background are highly probable and promising to test quantum gravity. … It provides a promising suggestion to resolve and validate the inflationary models of cosmology in conjunction with quantum gravity."

Additionally, the authors posit that quantum gravitational phenomena in the early universe might have shaped the properties of gravitational waves emitted during that period. Detecting these waves with future gravitational-wave observatories could further illuminate quantum gravitational characteristics.

"Gravitational waves from various astrophysical sources have only been observed so far, but gravitational waves from the early universe have not yet been detected," Suresh said. "Hopefully, our work will help in identifying the correct inflationary model and detecting the primordial gravitational waves with quantum gravity features."

Andrey got his B.Sc. and M.Sc. degrees in elementary particle physics from Novosibirsk State University in Russia, and a Ph.D. in string theory from the Weizmann Institute of Science in Israel. He works as a science writer, specializing in physics, space, and technology. His articles have been published in  Elements ,  N+1 , and  AdvancedScienceNews .

Euclid space telescope reveals more than 300,000 new objects in 1st 24 hours of observations (photos)

Can a commercial airplane do a barrel roll?

This year's hurricane season could see 25 named storms, NOAA says in record-breaking forecast

Most Popular

• 2 James Webb telescope confirms there is something seriously wrong with our understanding of the universe
• 3 Some of the oldest stars in the universe found hiding near the Milky Way's edge — and they may not be alone
• 4 The mystery of the disappearing Neanderthal Y chromosome
• 5 Can a commercial airplane do a barrel roll?
• 2 The same genetic mutations behind gorillas' small penises may hinder fertility in men
• 3 Scientists grow diamonds from scratch in 15 minutes thanks to groundbreaking new process
• 4 22 jobs artificial general intelligence (AGI) may replace — and 10 jobs it could create
• 5 No two are alike: The colossal stone heads of Olmec in Mexico

Wavefunction matching for solving quantum many-body problems

Strongly interacting systems play an important role in quantum physics and quantum chemistry. Stochastic methods such as Monte Carlo simulations are a proven method for investigating such systems. However, these methods reach their limits when so-called sign oscillations occur. This problem has now been solved by an international team of researchers from Germany, Turkey, the USA, China, South Korea and France using the new method of wavefunction matching. As an example, the masses and radii of all nuclei up to mass number 50 were calculated using this method. The results agree with the measurements, the researchers now report in the journal " Nature ."

All matter on Earth consists of tiny particles known as atoms. Each atom contains even smaller particles: protons, neutrons and electrons. Each of these particles follows the rules of quantum mechanics. Quantum mechanics forms the basis of quantum many-body theory, which describes systems with many particles, such as atomic nuclei.

One class of methods used by nuclear physicists to study atomic nuclei is the ab initio approach. It describes complex systems by starting from a description of their elementary components and their interactions. In the case of nuclear physics, the elementary components are protons and neutrons. Some key questions that ab initio calculations can help answer are the binding energies and properties of atomic nuclei and the link between nuclear structure and the underlying interactions between protons and neutrons.

However, these ab initio methods have difficulties in performing reliable calculations for systems with complex interactions. One of these methods is quantum Monte Carlo simulations. Here, quantities are calculated using random or stochastic processes. Although quantum Monte Carlo simulations can be efficient and powerful, they have a significant weakness: the sign problem. It arises in processes with positive and negative weights, which cancel each other. This cancellation leads to inaccurate final predictions.

A new approach, known as wavefunction matching, is intended to help solve such calculation problems for ab initio methods. "This problem is solved by the new method of wavefunction matching by mapping the complicated problem in a first approximation to a simple model system that does not have such sign oscillations and then treating the differences in perturbation theory," says Prof. Ulf-G. Meißner from the Helmholtz Institute for Radiation and Nuclear Physics at the University of Bonn and from the Institute of Nuclear Physics and the Center for Advanced Simulation and Analytics at Forschungszentrum Jülich. "As an example, the masses and radii of all nuclei up to mass number 50 were calculated -- and the results agree with the measurements," reports Meißner, who is also a member of the Transdisciplinary Research Areas "Modeling" and "Matter" at the University of Bonn.

"In quantum many-body theory, we are often faced with the situation that we can perform calculations using a simple approximate interaction, but realistic high-fidelity interactions cause severe computational problems," says Dean Lee, Professor of Physics from the Facility for Rare Istope Beams and Department of Physics and Astronomy (FRIB) at Michigan State University and head of the Department of Theoretical Nuclear Sciences.

Wavefunction matching solves this problem by removing the short-distance part of the high-fidelity interaction and replacing it with the short-distance part of an easily calculable interaction. This transformation is done in a way that preserves all the important properties of the original realistic interaction. Since the new wavefunctions are similar to those of the easily computable interaction, the researchers can now perform calculations with the easily computable interaction and apply a standard procedure for handling small corrections -- called perturbation theory.

The research team applied this new method to lattice quantum Monte Carlo simulations for light nuclei, medium-mass nuclei, neutron matter and nuclear matter. Using precise ab initio calculations, the results closely matched real-world data on nuclear properties such as size, structure and binding energy. Calculations that were once impossible due to the sign problem can now be performed with wavefunction matching.

While the research team focused exclusively on quantum Monte Carlo simulations, wavefunction matching should be useful for many different ab initio approaches. "This method can be used in both classical computing and quantum computing, for example to better predict the properties of so-called topological materials, which are important for quantum computing," says Meißner.

The first author is Prof. Dr. Serdar Elhatisari, who worked for two years as a Fellow in Prof. Meißner's ERC Advanced Grant EXOTIC. According to Meißner, a large part of the work was carried out during this time. Part of the computing time on supercomputers at Forschungszentrum Jülich was provided by the IAS-4 institute, which Meißner heads.

• Quantum Computers
• Computers and Internet
• Computer Modeling
• Spintronics Research
• Mathematics
• Quantum mechanics
• Quantum entanglement
• Introduction to quantum mechanics
• Computer simulation
• Quantum computer
• Quantum dot
• Quantum tunnelling
• Security engineering

Story Source:

Materials provided by University of Bonn . Note: Content may be edited for style and length.

Journal Reference :

• Serdar Elhatisari, Lukas Bovermann, Yuan-Zhuo Ma, Evgeny Epelbaum, Dillon Frame, Fabian Hildenbrand, Myungkuk Kim, Youngman Kim, Hermann Krebs, Timo A. Lähde, Dean Lee, Ning Li, Bing-Nan Lu, Ulf-G. Meißner, Gautam Rupak, Shihang Shen, Young-Ho Song, Gianluca Stellin. Wavefunction matching for solving quantum many-body problems . Nature , 2024; DOI: 10.1038/s41586-024-07422-z

Cite This Page :

Explore More

• Birth of Universe's Earliest Galaxies
• Why the Brain Can Robustly Recognize B&W Images
• Birth Control Pill for Men?
• Intriguing World Sized Between Earth, Venus
• Billions of Orphan Stars Revealed
• Massive Catalog of Strange Worlds
• Mental Disorders May Spread Thru Social Networks
• Global Clean Water Crisis Looms Large
• 'Exo-Venus' With Earth-Like Temps
• Ants Forage Better When Given a Little Caffeine

Trending Topics

Strange & offbeat.