

Free Mathematics Tutorials
Grade 8 math problems with solutions.
Grade 8 Maths questions and problems for deep understanding of Maths concepts and skills are presented. Solutions and answers are provided.
Grade 8 Math
- Algebra Questions with Answers and Solutions for Grade 8
- Grade 8 Math Practice Test with detailed solutions and explanations.
- Grade 8 Geometry Problems and Questions with Answers . Also solutions and explanations are included.
- Grade 8 Problems and Questions on Triangles with Answers . Also solutions and explanations are included.
- Rectangular Coordinate System in a Plane
- Relations in Mathematics
- Functions in Mathematics
- Grade 8 Questions with Answers on Angles in Triangles . Also solutions with explanations included.
- Video on Solving Linear Inequalities
- Functions Represented by Equations
- Distance and Midpoint Formulas with examples, questions and solutions and
- Distance and Midpoint Calculator
- Introduction to Polynomials
- Divisibility Rules Examples and Questions .
- Divisibility Rule for 7 Examples and Questions . .
- Applications of Linear Equations - Problems with Answers for Grade 8 with solutions and explanations included
- Fractions Questions and Problems with Solutions
- Grade 8 questions on simplifying expressions with negative exponents with solutions and explanations included Online Trigonometry Calculators and Solvers
- quadratic equations problems for Grade 8 with solutions and explanations included
- Multiply and Simplify Monomials
- Grade 8 Maths word Problems With Answers Also solutions and explanations are included.
- Grade 8 Problems and Questions on Circles with Answers . Also solutions and explanations are included.
- Simplify Square Root Calculator
- What are Radicals in Math? ; examples and questions with detailed solutions are included.
- Geometry Problems
- Units Conversion and Calculators
- Convert Units of Measurements
- Number to Words Converter
Online Calculators to Practice and Understand Concepts
- Divisibility Test Calculator. An online calculator that tests whole numbers for visibility by 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13.
- Lowest Common Multiple (lcm) Calculator. Calculate the lowest common multiple of two positive integers.
- Greatest Common Factor (gcf) Calculator. Calculate the greatest common factor of two positive integers. Linear Equations Solver Calculator
- Units Conversions Calculators
- Prime Factors Calculator. Factor a positive integer into prime factors.
- Fractions Addition Calculator. Add 2 or 3 fractions and reduce the final answer.
- fraction calculator that helps you further develop the skills of how to reduce, add and multiply fractions.
- Multiply Fractions Calculator. Multiply 2 fractions and reduce the answer.
- Divide Fractions Calculator. Divide 2 fractions and reduce the answer.
- Reduce Fractions Calculator. Rewrite Fractions in reduced form.
Popular Pages
Stay in touch.
- Privacy Policy

Solve Equations (Grade 8)
Suggested learning targets.
- I can solve linear equations with rational number coefficients.
- I can solve equations whose solutions require expanding expressions using the distributive property and/or collecting like terms.


We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Build Confidence with Math Problem Solving
Daily Problem Solving will help your 8th grade students master the skills they need to be successful with challenging word problems...and have fun doing it .
What you'll get with this download:
Your download includes a full week of Daily Problem Solving for Grade 8 to try out in your own classroom. Developed with the brain in mind, these multi-step word problems will challenge your learners without overwhelming them. Best of all, you'll be able to watch their skills and confidence grow as they begin to internalize strategies for conquering this difficult math skill.
FUN & ENGAGING
Themed-problems and a weekly fun fact make it easy to keep learners engaged
MINIMAL PREP
Formatted for quick & easy implementation that won't add stress to your planning
PRINT & DIGITAL
Includes both print and digital student options for added flexibility
I've been using this with my extremely anxious learner and it works wonders to build confidence because we see the improvement.
These have given me such an insight into my students' abilities, and I've watched them improve their skills and successfully solve multi-step word problems.
Jilliana D.
STUDENT PRINTABLES
You'll receive a full week of printable Daily Problem Solving practice for your students. This format includes:
- Paper-saving format that fits a full week on one page
- Space for student work, feedback, and self-reflection
- Themed problems & weekly fun fact to engage
DIGITAL SLIDES
Daily digital slides offer your remote or online learners the opportunity to build problem-solving skills in a structured format designed for success.
- Single slide per day prevents overwhelm or distraction
- Organized with clear space to solve & answer
- Engaging graphics, themed problems, & fun facts
Don’t wait, get started helping your learners master word problems today!
© Differentiated Teaching | Back to the Blog
- Inspiration
Please ensure that your password is at least 8 characters and contains each of the following:
- a special character: @$#!%*?&

- Join for FREE
- Printable Worksheets
- Online Lessons
- Test Maker™
- Printable Games
- Worksheet Generator
- Plans & Pricing
Printable & online resources for educators
- Test Maker TM
- Browse All Questions
- Questions With Images
- Advanced Search

Share/Like This Page
Filter By Grade
You are browsing Grade 8 questions. View questions in All Grades .
Grade 2 Grade 3 Grade 4 Grade 5 Grade 6 Grade 7 Grade 8 Grade 10
Browse Questions
- All Subjects w/ Images (7032)
- By ELA/Literacy Standard
- By Math Standard
- All Subjects (19248)
- English Language Arts (5347)
- English as a Second Language ESL (3319)
- Health and Medicine (408)
- Life Skills (126)
Arithmetic and Number Concepts
Function and algebra concepts, geometry and measurement, mathematical process, logical thinking, problem solving strategies, statistics and probability concepts.
- Physical Education (403)
- Science (6481)
- Social Studies (3927)
- Study Skills and Strategies (19)
- Technology (124)
Eighth Grade (Grade 8) Problem Solving Strategies Questions
You can create printable tests and worksheets from these Grade 8 Problem Solving Strategies questions! Select one or more questions using the checkboxes above each question. Then click the add selected questions to a test button before moving to another page.
- 15 yrs and 25 yrs
- 30 yrs and 70 yrs
- 25 yrs and 50 yrs
- 15 yrs and 45 yrs
- Who has the most money?
- Does their money total more or less than $9.95?
- How much does their money plus the cost of the pizza equal?
- What is the average contribution each person is making?
- Figure out what question you are being asked.
- Determine the facts needed to solve the problem.
- Pick a strategy to solve the problem.
- Add up all the numbers to solve the problem.
- Privacy Policy
- Terms of Use
- FREE Printable Worksheets
- Common Core ELA Worksheets
- Common Core Math Worksheets
CEMC Gauss (Grade 8) Problems and Solutions
Problems and solutions.
CEMC Gauss (Grade 8) problems and solutions by test:
- 1998 CEMC Gauss (Grade 8)
- 1999 CEMC Gauss (Grade 8)
- 2000 CEMC Gauss (Grade 8)
- 2001 CEMC Gauss (Grade 8)
- 2002 CEMC Gauss (Grade 8)
- 2003 CEMC Gauss (Grade 8)
- 2004 CEMC Gauss (Grade 8)
- 2005 CEMC Gauss (Grade 8)
- 2006 CEMC Gauss (Grade 8)
- 2007 CEMC Gauss (Grade 8)
- 2008 CEMC Gauss (Grade 8)
- 2009 CEMC Gauss (Grade 8)
- 2010 CEMC Gauss (Grade 8)
- 2011 CEMC Gauss (Grade 8)
- 2012 CEMC Gauss (Grade 8)
- 2013 CEMC Gauss (Grade 8)
- 2014 CEMC Gauss (Grade 8)
| Preceded by | Followed by ' | |
- Math Contest Problems
Something appears to not have loaded correctly.
Click to refresh .
Free Printable Identifying Problems and Solutions in Reading Worksheets for 8th Grade
Identifying Problems and Solutions in Reading & Writing: Discover a collection of free printable worksheets for Grade 8 students, designed to enhance their reading comprehension and writing skills.

Recommended Topics for you
- Identifying Problems and Solutions in Fiction
- Identifying Problems and Solutions in Nonfiction

Explore Identifying Problems and Solutions in Reading Worksheets by Grades
- kindergarten
Explore Identifying Problems and Solutions in Reading Worksheets for grade 8 by Topic
Explore other subject worksheets for grade 8.
- Social studies
- Social emotional
- Foreign language
- Reading & Writing
Explore printable Identifying Problems and Solutions in Reading worksheets for 8th Grade
Identifying Problems and Solutions in Reading worksheets for Grade 8 is an essential aspect of teaching Reading & Writing to students. These worksheets are designed to help students develop their reading comprehension strategies, which are crucial for understanding complex texts and improving overall literacy skills. Teachers can use these worksheets to assess students' abilities in identifying problems within a text and determining appropriate solutions. By incorporating these worksheets into their lesson plans, educators can effectively target specific areas of improvement for each student, ensuring that they are well-prepared for the challenges of higher-level reading and writing tasks. Additionally, these worksheets can be easily adapted to suit various learning styles and preferences, making them a versatile and valuable resource for any Grade 8 classroom. Identifying Problems and Solutions in Reading worksheets for Grade 8 is a must-have tool for teachers looking to enhance their students' reading comprehension skills.
Quizizz is an innovative platform that offers a variety of resources for teachers, including worksheets and other educational materials. In the context of Identifying Problems and Solutions in Reading worksheets for Grade 8, Quizizz provides an interactive and engaging way for students to practice their reading comprehension strategies. Teachers can create customized quizzes and activities based on the content of these worksheets, allowing students to test their understanding of the material in a fun and interactive way. Additionally, Quizizz offers real-time feedback and analytics, enabling teachers to monitor student progress and identify areas where additional support may be needed. By incorporating Quizizz into their lesson plans, educators can effectively supplement their use of Identifying Problems and Solutions in Reading worksheets for Grade 8, ensuring that students receive a well-rounded and comprehensive approach to improving their reading and writing skills.

Age Problems
Age word problems.
Every now and then, we encounter word problems that require us to find the relationship between the ages of different people. Age word problems typically involve comparing two people’s ages at different points in time, i.e. at present, in the past, or in the future.
This lesson is divided into two parts. Part I involves age word problems that can be solved using a single variable while Part II contains age word problems that need to be solved using two variables .
Let’s get familiar with age word problems by working through some examples.
PART I: Age Word Problems Solvable with One Variable
Example 1: Tanya is 28 years older than Marcus. In 6 years, Tanya will be three times as old as Marcus. How old is Tanya now?
In this problem, we are only asked to find Tanya’s current age. However, the problem also gave us a lot of other information which can be overwhelming. To help us organize the important details, let’s create a table to list what we know so far.
Since we are only given details about their current ages and what they will be 6 years from now, we’ll go ahead and gray out the Past column.
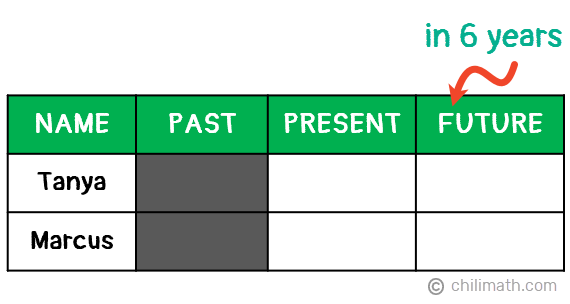
You may notice that Tanya’s current age is defined using the age of Marcus. However, Marcus’s present age is currently unknown. So let’s express Marcus’s age using the variable [latex]x[/latex]. Since Tanya is 28 years older than Marcus , then Tanya’s present age must be [latex]x+28[/latex].

Next, let’s fill in the Future column which will consist of their ages in 6 years. All we have to do is add 6 to Tanya and Marcus’s present or current ages. Therefore, we have:
- Tanya: [latex]\left( {x + 28} \right) {\color{red}+ 6} = x + 34[/latex]
- Marcus: [latex]x {\color{red}+ 6}[/latex]

Now that our table is filled out, we can go ahead and create our equation based on the information provided. The problem states the following:
In 6 years , Tanya will be three times as old as Marcus.
Here we are trying to find the relationship between their ages in the future. We can simply say that,
Tanya’s age in 6 years = 3( Marcus’s age in 6 years )
With that in mind, we can easily construct our equation.
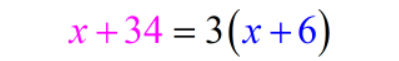
Our next step now is to solve for [latex]x[/latex]. But before that, remember that our problem is asking us to find Tanya’s current age. Since Tanya’s age is defined using Marcus’s current age (which is [latex]x[/latex]), we have to find his age first in order to determine what Tanya’s present age is.
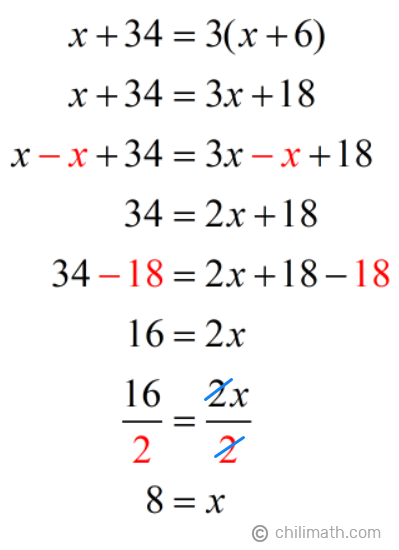
Now that we have the value for [latex]x[/latex], let’s find out what Tanya and Marcus’s current ages are. We can do this by simply replacing the [latex]x[/latex]’s with [latex]8[/latex].
CURRENT AGES (present)
- Marcus: [latex]x = {\textbf{8}}[/latex] years old
- Tanya: [latex]x + 28 = {\color{red}8} + 28 = {\textbf{36}}[/latex] years old
Going back to the problem’s question, how old is Tanya now?
Answer: Tanya is 36 years old.
Answer Check:
At this point, we are confident that our answer is correct. But, how can we be 100% sure? Well, it’s always a good idea especially in math, to check our answers so we’re certain that we got the correct values.
For this problem, we can simply verify if our answer makes our future statement true. Do you remember this statement?
In 6 years, Tanya will be three times as old as Marcus.
We know the present ages of Marcus and Tanya which are [latex]8[/latex] and [latex]36[/latex], respectively. Hence in 6 years, Marcus will be [latex]14[/latex] years old while Tanya will be [latex]42[/latex] years old.
So, will Tanya be three times as old as Marcus in 6 years? The answer is Yes .

Example 2: Bruce is 4 years younger than Hector. Twenty years ago, Hector’s age was 13 years more than half the age of Bruce. How old are they now?
By just reading the problem, we can already tell that there is a great deal of information that we have to sort through and that this problem includes a fraction. Most students easily get lost in all the given information, let alone solving equations that involve fractions. But, don’t fret! As long as you stick with the basic principles and steps on how to solve age word problems, you’ll be fine.
Right now, we don’t know Bruce or Hector’s current age. But since Bruce’s age is expressed in relation to Hector’s age, then our unknown variable will be based on Hector’s age. In other words,
- Let [latex]{\textbf{\textit{h}}} =[/latex] Hector’s age
- [latex]{\textbf{\textit{h} – 4}} =[/latex] Bruce’s age, since he is 4 years younger than Hector
Let’s organize all these important data into a table. We’re only given details about their present and past (20 years ago) ages so we’ll gray out the Future column.
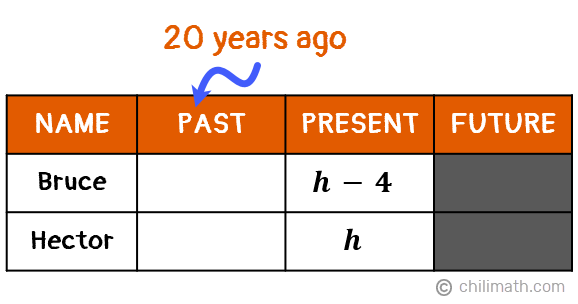
Twenty years ago, both Bruce and Hector were 20 years younger so we’ll subtract 20 from each of their present ages.
- Bruce: [latex]\left( {h – 4} \right) {\color{red}- 20} = h – 24[/latex]
- Hector: [latex]h {\color{red}- 20}[/latex]
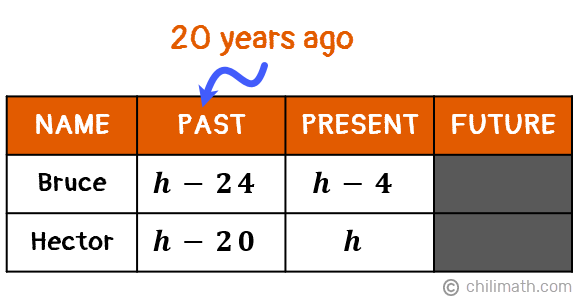
Our table is now ready so we can proceed to create our equation. As you can see under the Past column, we were able to create algebraic expressions for Bruce and Hector’s ages 20 years ago. But our problem also told us that,
Twenty years ago , Hector’s age was 13 years more than half the age of Bruce.
Since Hector’s age 20 years ago is also 13 years more than half of Bruce’s age, we can take these two algebraic expressions and set them equal to each other, to create an equation.
Hector’s age 20 years ago = [latex]\Large{1 \over 2}[/latex]( Bruce’s age 20 years ago )[latex]+ 13[/latex]
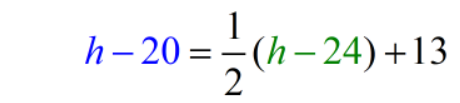
We’re now ready to solve for the unknown variable, [latex]h[/latex].
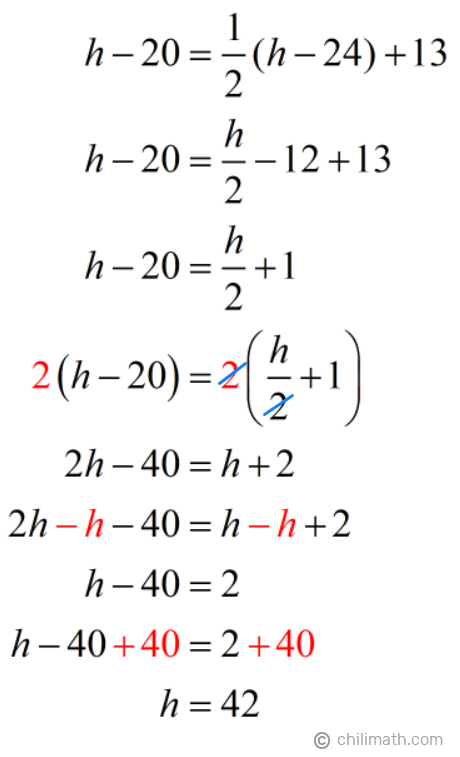
Therefore, Hector’s present age is [latex]{\textbf{42}}[/latex] years old.
On the other hand, you may recall that Bruce’s current age is: [latex]h – 4[/latex]. Since [latex]h = 42[/latex], then Bruce’s current age is [latex]42 – 4 = {\textbf{38}}[/latex].
So, how old are they now?
Answer: Hector is 42 years old and Bruce is 38 years old .
The final step is to check our answers by substituting the unknown values into our original equation to verify if each side of the equation equals the other.
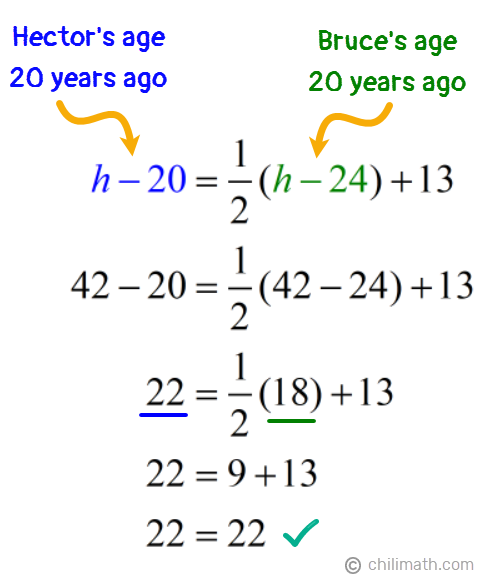
Great! Our answer checks. This just showed us that if we take Bruce’s age twenty years ago, which is 18, and divide it in half, we get 9. Adding 13 to that ([latex]9 + 13[/latex]), we get 22 which was Hector’s age twenty years ago.
Therefore, we are able to confirm that twenty years ago when Hector was 22 years old and Bruce was 18 years old, Hector’s age was 13 years more than half the age of Bruce.
Example 3: Stella is 13 years younger than Kwame. Nine years from now, the sum of their ages will be 43. Find the present age of each.
This problem is a little different from our previous two examples as we are given the sum of their ages in 9 years. But right off the bat, we can see that Stella’s age is defined in terms of Kwame’s age. Therefore, we’ll select a variable to represent Kwame’s current age. In this instance, let’s use “[latex]k[/latex]”.
- Let [latex]{\textbf{\textit{k}}} =[/latex] Kwame’s age
- [latex]{\textbf{\textit{k} – 13}} =[/latex] Stella’s age, since she is 13 years younger than Kwame

Nine years from now, both Kwame and Stella will be 9 years older. So we’ll simply add 9 to their present ages above to show their future ages.
- Kwame: [latex]k {\color{red}+ 9}[/latex]
- Stella: [latex]\left( {k – 13} \right) {\color{red}+ 9} = k – 4[/latex]
Let’s complete our table.

Now that we have the algebraic expressions for both their ages in 9 years, we can add these expressions to create our equation. We were given the following details:
Nine years from now , the sum of their ages will be 43 .
So we have,
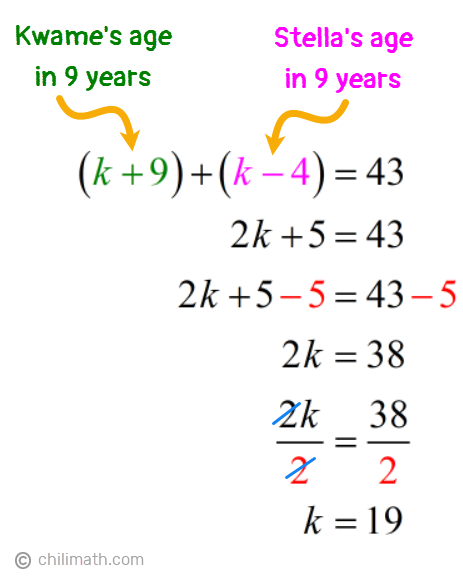
Checking back at our table, [latex]k[/latex] stands for Kwame’s age. But since our problem asked us to find the current ages for both, let’s do a little bit more solving.
- Kwame: [latex]k = {\textbf{19}}[/latex] years old
- Stella: [latex]k – 13 = {\color{red}19} – 13 = {\textbf{6}}[/latex] years old
Answer: Kwame is 19 years old and Stella is 6 years old .
Let’s now verify if indeed the sum of Kwame and Stella’s ages in 9 years will be 43.
- Kwame’s age in 9 years: [latex]k + 9 = {\color{red}19} + 9 = {\textbf{28}}[/latex]
- Stella’s age in 9 years: [latex]k – 4 = {\color{red}19} – 4 = {\textbf{15}}[/latex]
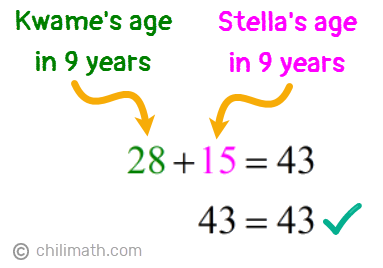
Perfect! The total of their ages nine years from now is 43 so our answers are correct.
Example 4: Mr. Cook is 34 years old. His son is 22 years younger than him. In how many years will Mr. Cook’s age be 24 years less than three times as old as his son?
We already know their current ages, so before we delve any further, let’s start filling in our table.
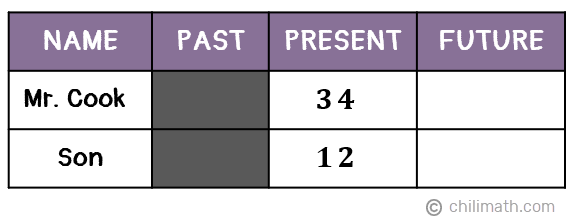
Note that since the son is 22 years younger than Mr. Cook, we subtracted 22 from 34 to get his son’s current age, [latex]34 – {\color{red}22} = 12[/latex].
This problem is unique because it’s not asking us for their ages at a certain point in time like usual. Instead, it asks us to find out the number of years when Mr. Cook’s age will meet a certain relationship with his son’s age in the future.
But at this point, we don’t know how long it will take for Mr. Cook to be 24 years less than three times as old as his son. So, let’s assign the unknown variable “[latex]x[/latex]” to stand for the number of years then add [latex]x[/latex] to both of their current ages to create algebraic expressions that will represent how old they will be after [latex]x[/latex] years.
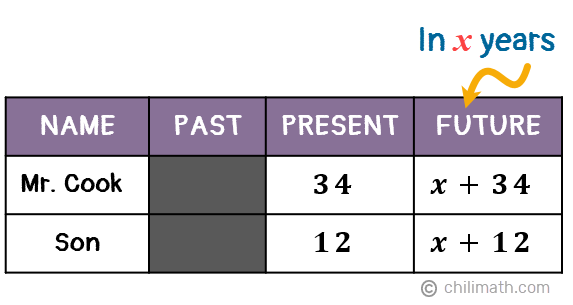
Since Mr. Cook’s age after [latex]x[/latex] number of years ([latex]x + 34[/latex]) will also be 24 years less than three times as old as his son , we can set these two algebraic expressions equal to each other, thus creating our equation.
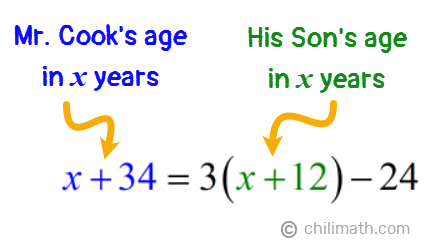
Now that we have our equation, let’s solve for [latex]x[/latex].
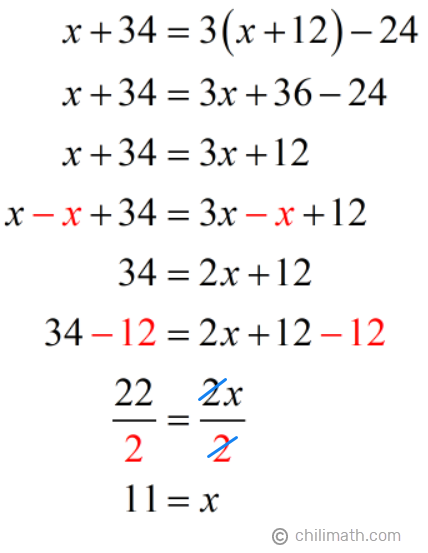
As you may recall, [latex]x[/latex] stands for the number of years from now that will take for Mr. Cook to be 24 years less than three times as old as his son. Therefore,
Answer: In 11 years , Mr. Cook’s age will be 24 years less than three times as old as his son.
To check if our answer is correct, we must first find out how old will Mr. Cook and his son be in 11 years. Substituting the value of [latex]x[/latex] which is 11 into our algebraic expressions, we get:
- Mr. Cooks’s age in 11 years: [latex]x + 34 = {\color{red}11} + 34 = {\textbf{45}}[/latex]
- Son’s age in 11 years: [latex]x + 12 = {\color{red}11} + 12 = {\textbf{23}}[/latex]
So in 11 years, Mr. Cook will be 45 years old while his son will be 23 years old.
This time, I’ll leave it up to you to verify if indeed during that time, his age of 45 years old will be 24 years less than three times as old as his son. If it meets the condition, then our answer is correct.
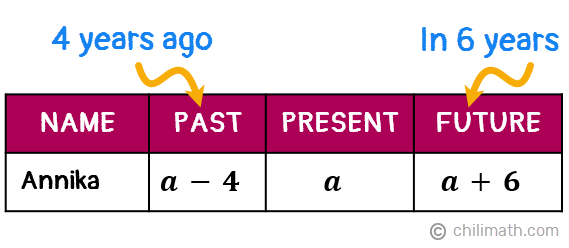
Example 5: The sum of one-fifth of Annika’s age four years ago and half of her age in six years is 33. How old is she now?
Compared to our previous exercises, this problem only involves one person. Also, instead of comparing the ages of two people at a certain point in time, we will be comparing Annika’s ages at different points in time, i.e. 4 years ago and in 6 years.
We don’t know Annika’s current age so let’s select the variable [latex]{\textbf{\textit{a}}}[/latex] to represent this unknown value. We’ll use this variable as well to create algebraic expressions that will stand for her past and future ages.
- Let [latex]{\textbf{\textit{a}}} =[/latex] Annika’s current age
- [latex]{\textbf{\textit{a} – 4}} =[/latex] Annika’s age 4 years ago
- [latex]{\textbf{\textit{a} + 6}} =[/latex] Annika’s age 6 years from now
Our problem also told us that if we add [latex]\Large{1 \over 5}[/latex] of Annika’s age 4 years ago and [latex]\Large{1 \over 2}[/latex] of her age 6 years from now , the sum is 33 .
With this information, it’s easy for us to write our equation.

Our next step is to solve for the unknown variable, [latex]a[/latex].
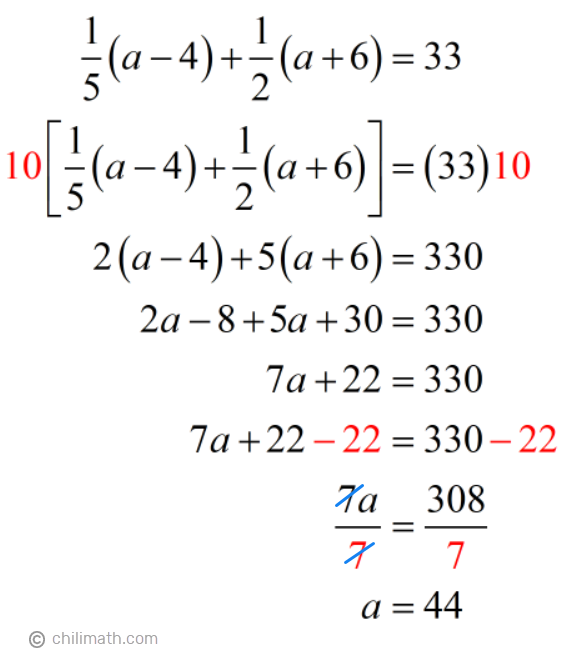
So, how old is Annika now?
Answer: Annika is currently 44 years old.
As I mentioned before, it’s always a good practice to verify if you got the correct answer. To start, let’s find out what Annika’s past and future ages are.
- Annika’s age 4 years ago : [latex]a – 4 = {\color{red}44} – 4 = {\textbf{40}}[/latex]
- Annika’s age 6 years from now : [latex]a + 6 = {\color{red}44} + 6 = {\textbf{50}}[/latex]
Now that we know how old she was 4 years ago and how old she’ll be in 6 years, we’ll plug in these values into our original equation to see if both sides of the equation equal each other.
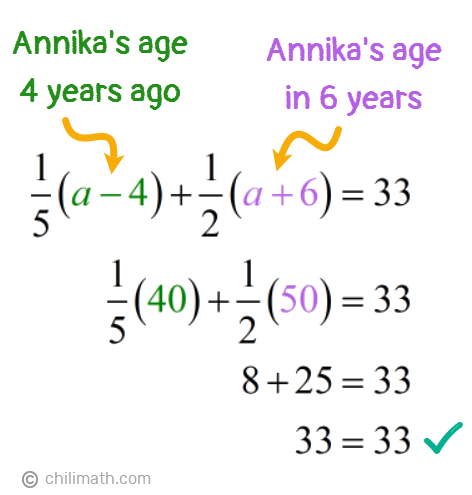
And they did! We were able to prove that the sum of [latex]\Large{1 \over 5}[/latex] of Annika’s age 4 years ago and [latex]\Large{1 \over 2}[/latex] of her age 6 years from now is indeed 33.
PART II: Age Word Problems Solvable with Two Variables
Example 6: The sum of Aaliyah and Harald’s ages is 28. Four years from now, Aaliyah will be three times as old as Harald. Find their present ages.
Neither Aaliyah nor Harald’s age is expressed in terms of the other. So for this problem, we will be using more than one variable to represent the unknown values. To start,
- Let [latex]{\textbf{\textit{a}}}[/latex] be Aaliyah’s age
- Let [latex]{\textbf{\textit{h}}}[/latex] be Harald’s age
Since they will be 4 years older in the next 4 years, we simply have to add 4 to their current ages to represent their future ages.
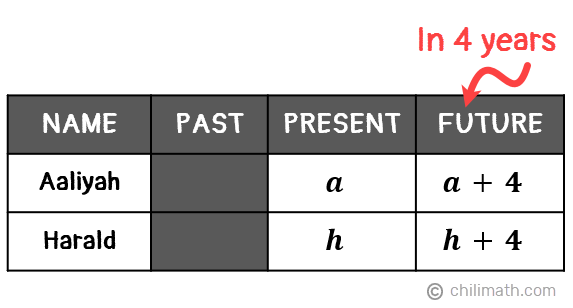
Looking back at our problem, there are two significant statements that can help us find our answers.
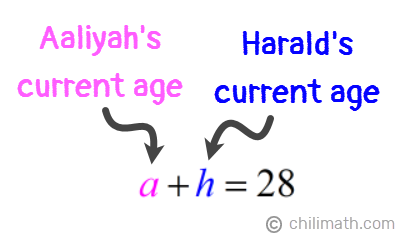
1) The sum of Aaliyah and Harald’s ages is 28.
From this statement, we can create the equation below:
2) Four years from now, Aaliyah will be three times as old as Harald.
Meanwhile, the statement above can be translated into the following equation:
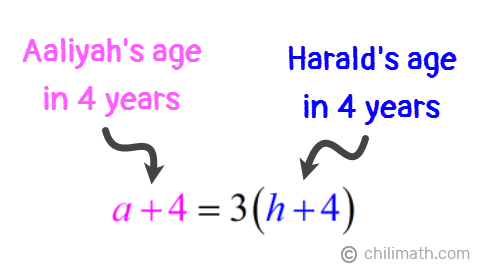
We now have two equations to solve.
- Equation 1: [latex]a + h = 28[/latex]
- Equation 2: [latex]a + 4 = 3(h + 4)[/latex]
First, we’ll use equation 1 to solve for [latex]a[/latex].
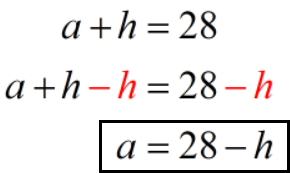
Next, we’ll replace [latex]a[/latex] with [latex]28 – h[/latex] in equation 2 .
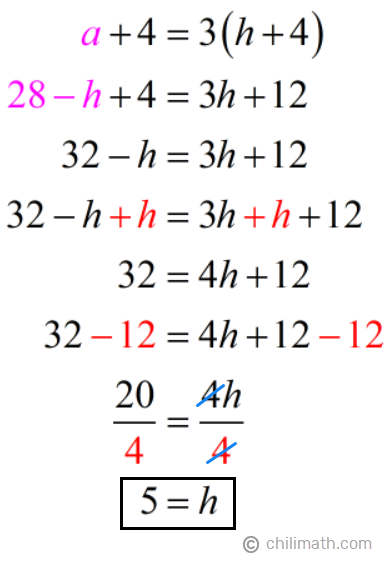
Perfect! We are able to find the values for both our unknown variables, [latex]a[/latex] and [latex]h[/latex], which also stand for the present ages for Aaliyah and Harald. So we have,
- Aaliyah’s present age: [latex]a = 28 – h = 28 – {\color{red}5} = {\textbf{23}}[/latex]
- Harald’s present age: [latex]h = {\textbf{5}}[/latex]
Answer: Currently, Aaliyah is 23 years old while Harald is 5 years old.
I’ll leave it up to you to check if our answers are correct. But as you can see, even with just using mental computation, we can already tell that the sum of Aaliyah and Harald’s ages is 28 ([latex]23 + 5 = 28[/latex]) which makes our first statement true. You may further check our answers by plugging in the values of [latex]a[/latex] and [latex]h[/latex] into equation 2 to verify if the left side of the equation equals the right, thus making our second statement true as well.
Example 7: The sum of the ages of Jaya and Nadia is three times Nadia’s age. Seven years ago, Jaya was three less than four times as old as Nadia. How old are they now?
This problem is similar to our previous example. However, for this one, we are not given the exact number for the sum. We first have to find out each of their current ages so we can determine what the sum is.
- Let [latex]{\textbf{\textit{y}}}[/latex] be Jaya’s age
- Let [latex]{\textbf{\textit{n}}}[/latex] be Nadia’s age
We then need to subtract 7 from their current ages to represent how old they were seven years ago.
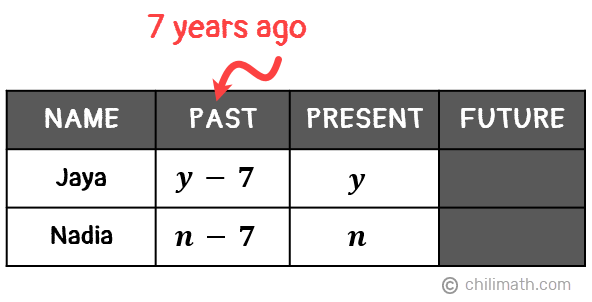
Now that we’ve organized our data, let’s go through the significant statements given in our problem and translate each into an equation.
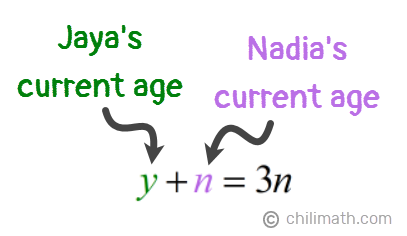
1) The sum of the ages of Jaya and Nadia is three times Nadia’s age.
2) Seven years ago, Jaya was three less than four times as old as Nadia.
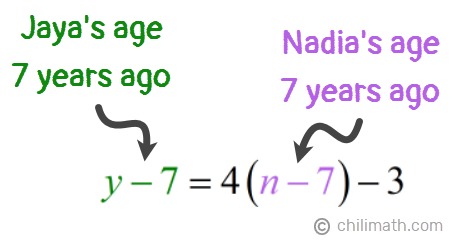
Therefore, our two equations are:
- Equation 1: [latex]y + n = 3n[/latex]
- Equation 2: [latex]y – 7 = 4(n – 7) – 3[/latex]
Let’s first focus on equation 1 and solve for [latex]y[/latex].
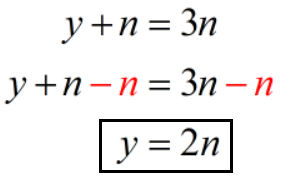
Now we’ll solve for [latex]n[/latex] using the value of [latex]y[/latex] from equation 1. We’ll do this by replacing [latex]y[/latex] with [latex]2n[/latex] in equation 2 .
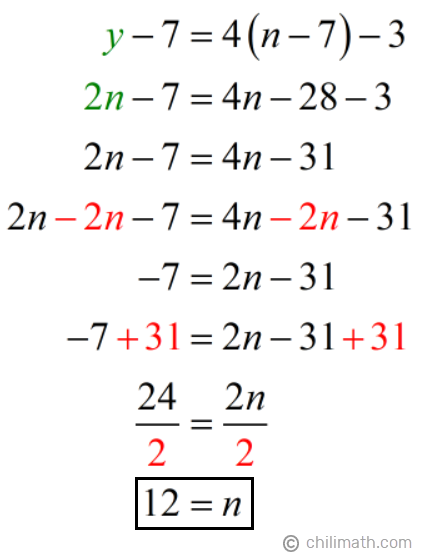
Taking the values of [latex]y[/latex] and [latex]n[/latex], we have:
- Jaya’s present age: [latex]y = 2n = 2({\color{red}12}) = {\textbf{24}}[/latex]
- Nadia’s present age: [latex]n = {\textbf{12}}[/latex]
So, going back to our problem. How old are they now?
Answer: Jaya is 24 years old and Nadia is 12 years old.
To check our answers, we’ll replace the values of [latex]y[/latex] and [latex]n[/latex] in equation 1 and equation 2. Again, I’ll leave it up to you to solve both equations and verify if each side of the equation equals the other. Once you’re done with your solutions, you’ll see that we are able to prove that both statements from our problem are true.
Example 8: The difference between the ages of Penelope and her son, Zack, is 34. In six years, Penelope will be four times as old as Zack’s age two years ago. How old are they now?
It’s easy to get lost in all the information given so we’ll focus first on assigning variables that will stand for the unknown values.
- Let [latex]{\textbf{\textit{p}}}[/latex] be Penelope’s current age
- Let [latex]{\textbf{\textit{z}}}[/latex] be Zack’s current age
One thing that’s unique about this problem is that it involves three different points in time. We are given not only the relationship between Penelope and her son’s age in the present time but also how their ages in 6 years are related to their ages two years ago.
To show this, we’ll subtract 2 from their ages now for their ages 2 years ago then add 6 to their current ages for their ages 6 years later .
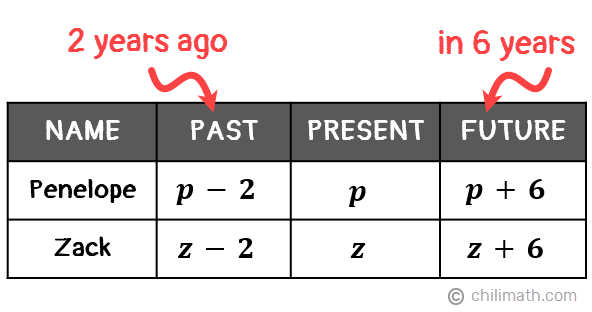
Great! We now have variables and algebraic expressions to represent Penelope and Zack’s current ages as well as their ages in the past and in the future. Moving forward, let’s go through the important details given in the problem and create an equation from each statement.
1) The difference between the ages of Penelope and her son, Zack, is 34 .
Remember that Penelope is Zack’s mother so she’s definitely older than him. Therefore, we are subtracting Zack’s age from Penelope’s age to find the difference.

2) In six years, Penelope will be four times as old as Zack’s age two years ago.
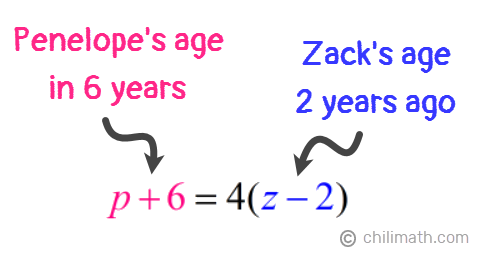
Here are our two equations:
- Equation 1: [latex]p – z = 34[/latex]
- Equation 2: [latex]p + 6 = 4(z – 2)[/latex]
Let’s now work on equation 1 to solve for [latex]p[/latex].
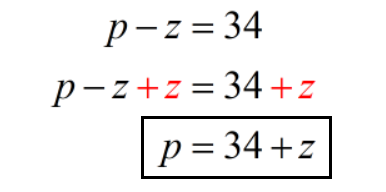
Next, we’ll replace [latex]p[/latex] with [latex]34 + z[/latex] in equation 2 then solve for [latex]z[/latex].
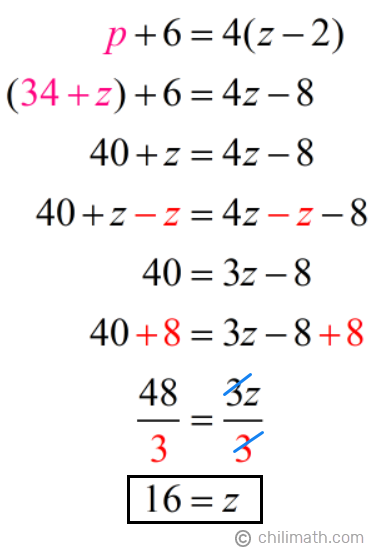
- Penelope’s current age: [latex]p = 34 + z = 34 + ({\color{red}16}) = {\textbf{50}}[/latex]
- Zack’s current age: [latex]z = {\textbf{16}}[/latex]
How about we replace the unknown values in our table and also find out what their past and future ages are?

Going back to our original question, how old are they now?
Answer: Penelope is currently 50 years old while her son, Zack, is 16 years old.
- Solve equations and inequalities
- Simplify expressions
- Factor polynomials
- Graph equations and inequalities
- Advanced solvers
- All solvers
- Arithmetics
- Determinant
- Percentages
- Scientific Notation
- Inequalities
What can QuickMath do?
QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.
- The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
- The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
- The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
- The calculus section will carry out differentiation as well as definite and indefinite integration.
- The matrices section contains commands for the arithmetic manipulation of matrices.
- The graphs section contains commands for plotting equations and inequalities.
- The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.
Math Topics
More solvers.
- Add Fractions
- Simplify Fractions

J a c o b ′ s s a v i n g s i n W e e k 2 = 3 2 {\color{#4257b2} Jacob's\ savings\ in\ Week\ 2 } = {\color{#c34632} 3^2 } J a co b ′ s s a v in g s in W ee k 2 = 3 2
J a c o b ′ s s a v i n g s i n W e e k 3 = 3 3 {\color{#4257b2} Jacob's\ savings\ in\ Week\ 3 } = {\color{#c34632} 3^3 } J a co b ′ s s a v in g s in W ee k 3 = 3 3
Create a free account to view solutions for this book
- NCERT Solutions
- NCERT Class 8
- NCERT 8 Maths
NCERT Solutions for Class 8 Maths
Ncert solutions for class 8 maths cbse 2023-24 edition – free pdf download.

NCERT Solutions for Class 8 Maths includes all the questions provided in the textbook that is prescribed in accordance with the CBSE Board. The syllabus given for all the classes is completely based on the NCERT curriculum. Hence, preparing for exams using NCERT Solutions will definitely provide students with an advantage.
BYJU’S NCERT Class 8 Solutions for Maths has been designed to help students solve problems with ease. The CBSE 8th Class Solutions for Maths provided here come with well-prepared exercises along with detailed explanations given by our expert teachers that further make learning and understanding concepts an easy task. So, if students have been looking for the most detailed and accurate Class 8 NCERT Solutions for Maths, which is also free, this is the right place.
| NCERT Solutions for Maths Class 8 Chapter-Wise – Free PDF Download |
|---|

Chapter-Wise NCERT Solutions for Class 8 Maths
NCERT Solutions for Class 8th Maths provided here are very beneficial for students. They can use these NCERT Solutions for Class 8 as a reference while practising the problems and developing better skills along with preparing efficiently for the exams. The exercises are given at the end of every chapter to practise the concepts learned in the chapter.
NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers
In this chapter, students will be learning properties related to real numbers, integers, whole numbers, rational numbers and natural numbers – independent, associative and closure. The chapter deals with the role of zero and one, multiplication over addition, representation of rational Numbers on the number line , and searching for rational numbers between two rational numbers. The topics of additive identity (0) and multiplicative identity (1) are also covered in this chapter. There are 2 exercises in this chapter, which contain questions from all the topics present in the chapter.
| Maths Class 8 NCERT Solutions Chapter 1 Exercises |
|---|
| – 11 Questions (11 Short Answers) |
| – 7 Questions (7 Short Answers) |
Also, access the following resources for Class 8 Chapter 1 Rational Numbers at BYJU’S:
- Rational Numbers Class 8 Notes – Chapter 1
- NCERT Exemplar Class 8 Maths Solutions for Chapter 1 – Rational Numbers
- RD Sharma Solutions for Class 8 Maths Chapter 1 – Rational Numbers
NCERT Solutions for Class 8 Maths Chapter 2 Linear Equations in One Variable
The chapter, Linear Equations in One Variable, deals with linear expression in one variable alone. Such equations are known as linear equations in one variable . There are six exercises in this chapter with a total of 65 questions in them. The chapter includes different concepts, including solving linear equations in one variable, some of its applications, reducing equations to a simpler form and word problems related to linear equations in one variable.
| Maths Class 8 NCERT Solutions Chapter 2 Exercises |
|---|
| – 12 Questions (12 Short Answers) |
| – 16 Questions (6 Long Answers, 10 Short Answers) |
| – 10 Questions (3 Long Answers, 7 Short Answers) |
| – 10 Questions (4 Long Answers, 6 Short Answers) |
| – 10 Questions (1 Long Answer, 9 Short Answers) |
| – 7 Questions (1 Long Answer, 6 Short Answers) |
Also, access the following resources for Class 8 Chapter 2 Linear Equations in One Variable at BYJU’S:
- Linear Equations In One Variable Class 8 Notes- Chapter 2
- NCERT Exemplar Class 8 Maths Solutions for Chapter 4 – Linear Equations In One Variable
- RD Sharma Solutions for Class 8 Maths Chapter 9 Linear Equation in One Variable
NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals
The chapter Understanding Quadrilaterals of Class 8 Maths provides the students with a proper understanding of the quadrilaterals . The chapter also covers different kinds of polygons, including triangles, quadrilaterals, pentagons, hexagons, etc. The chapter contains 4 exercises which aid the students in understanding these shapes properly.
| Maths Class 8 NCERT Solutions Chapter 3 Exercises |
|---|
| – 7 Questions (1 Long Answer, 6 Short Answers) |
| – 6 Questions (6 Short Answers) |
| – 12 Questions (6 Long Answers, 6 Short Answers) |
| – 6 Questions (1 Long Answer, 5 Short Answers) |
Also, access the following resources for Class 8 Chapter 3 Understanding Quadrilaterals at BYJU’S:
- Understanding Quadrilaterals Class 8 Notes – Chapter 3
- Important Questions for Maths Class 8 Chapter 3 Understanding Quadrilaterals
- NCERT Exemplar Class 8 Maths Solutions for Chapter 5 – Understanding Quadrilaterals Practical Geometry
- RD Sharma Solutions for Class 8 Maths Chapter 16 Understanding Shapes- II (Quadrilaterals)
NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry
The chapter, Practical Geometry, includes the method of constructing a quadrilateral with various parameters given. The chapter consists of 5 exercises, each dealing with different methods of constructing the quadrilateral. For instance, the first exercise deals with the construction of quadrilaterals when the length of four sides and a diagonal are given; similarly, the second exercise involves the method of construction of quadrilaterals when two diagonals and three sides are given, and so on. Hence, we can conclude that learning this chapter will make the students well-versed in all the concepts of quadrilateral for further classes.
| Maths Class 8 NCERT Solutions Chapter 4 Exercises |
|---|
| – 1 Question (1 Long Answer) |
| – 1 Question (1 Long Answer) |
| – 1 Question (1 Long Answer) |
| – 1 Question (1 Long Answer) |
| – 4 Questions (4 Long Answers) |
Also, access the following resources for Class 8 Chapter 4 Practical Geometry at BYJU’S:
- Practical Geometry Class 8 Notes – Chapter 4
- Important Questions Maths Class 8 Chapter 4: Practical Geometry
- RD Sharma Solutions for Class 8 Maths Chapter 18 Practical Geometry (Constructions)
NCERT Solutions for Class 8 Maths Chapter 5 Data Handling
The collection of information that can be used for analysis is known as data. In this chapter, students learn about the organisation and representation of data. Organising the data in a systematic method is referred to as data handling . In this chapter, students learn to represent these data diagrammatically as a pictograph, a bar graph, a double bar graph, a pie chart and a histogram. During the course of this chapter, students will be briefed about the concept of probability or likelihood. There are 3 exercises in this chapter that deal with all the concepts covered in the chapter.
| Class 8 NCERT Solutions Maths Chapter 5 Exercises |
|---|
| – 5 Questions (5 Short Answers) |
| – 5 Questions (3 Long Answers, 2 Short Answers) |
| – 6 Questions (2 Long Answers, 4 Short Answers) |
Also, access the following resources for Class 8 Chapter 5 Data Handling at BYJU’S:
- Data Handling Class 8 Notes- Chapter 5
- Important Questions Class 8 Maths Chapter 5 Data Handling
- NCERT Exemplar Class 8 Maths Solutions for Chapter 2 – Data Handling
- RD Sharma Solutions for Class 8 Maths Chapter 23 Data Handling – I (Classification and Tabulation of Data)
NCERT Solutions for Class 8 Maths Chapter 6 Square and Square Roots
This chapter, Squares and Square Roots, helps the students learn about the concept of square numbers and the square root of a number. The chapter deals with properties of square numbers, interesting patterns that could be learnt using square numbers, finding the square of a number, Pythagorean triplets , finding square roots through various methods, square roots of decimals and much more.
| Maths Class 8 NCERT Solutions Chapter 6 Exercises |
|---|
| – 9 Questions (9 Short Answers) |
| – 2 Questions (2 Short Answers) |
| – 10 Questions (3 Long Answers, 7 Short Answers) |
| – 9 Questions (3 Long Answers, 6 Short Answers) |
Also, access the following resources for Class 8 Chapter 6 Square and Square Roots at BYJU’S:
- Squares and Square Roots Class 8 Notes: Chapter 6
- RD Sharma Solutions for Class 8 Maths Chapter 3 – Squares and Square Roots
- NCERT Exemplar Class 8 Maths Solutions for Chapter 3 – Squares And Square Roots Cubes And Cube Roots
- Important Questions Class 8 Maths Chapter 6- Squares and Square Roots
NCERT Solutions for Class 8 Maths Chapter 7 Cube and Cube Roots
In the chapter, Cubes and Cube Roots, students learn about numerous strategies to find out the cubes and cube roots of a number. The chapter discusses finding the cubes of different numbers, some interesting patterns that could be learnt using cubes and finding the cube roots . There are 2 exercises in the chapter that will help the students understand the basics of cubes and cube roots in depth.
| Maths Class 8 NCERT Solutions Chapter 7 Exercises |
|---|
| – 4 Questions (4 Short Answers) |
| – 3 Questions (2 Long Answers,1 Short Answer) |
Also, access the following resources for Class 8 Chapter 7 Cube and Cube Roots at BYJU’S:
- Cubes and Cube Roots Class 8 Notes: Chapter 7
- Important Questions Class 8 Maths Chapter 7: Cubes and Cube Roots
- RD Sharma Solutions for Class 8 Maths Chapter 4 – Cubes and Cube Roots
NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities
The chapter, Comparing Quantities, helps the students in learning the comparison between the rise and decrease of percentages, market value, sales value, discount, etc. The chapter deals with an important concept that can be used in day-to-day life, Interest. Students learn about simple interest , compound interest calculated half-yearly, quarterly, monthly or yearly, and much more. There are 3 exercises in this chapter which help the students in learning the concept of comparing quantities.
| Maths Class 8 NCERT Solutions Chapter 8 Exercises |
|---|
| – 6 Questions (1 Long Answer, 5 Short Answers) |
| – 10 Questions (4 Long Answers, 6 Short Answers) |
| – 12 Questions (6 Long Answers, 6 Short Answers) |
Also, access the following resources for Class 8 Chapter 8 Comparing Quantities at BYJU’S:
- Important Question Class 8 Maths Chapter 8: Comparing Quantities
- NCERT Exemplar Class 8 Maths Solutions for Chapter 9 – Comparing Quantities
- Comparing Quantities Class 8 Notes: Chapter 8
NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities
This chapter, Algebraic Expressions and Identities, helps the students understand the concepts like terms, factors and coefficients related to algebraic expressions. A brief on the basics of monomials , binomials and polynomials is also given in the chapter. Students learn the addition, subtraction and multiplication of algebraic expressions. The concept of identity is also covered in the chapter. The 5 exercises in the chapter cover all the concepts present in algebraic expressions and identities.
| Maths Class 8 NCERT Solutions Chapter 9 Exercises |
|---|
| – 4 Questions (4 Short Answers) |
| – 5 Questions (5 Short Answers) |
| – 5 Questions (5 Short Answers) |
| – 3 Questions (3 Short Answers) |
| – 8 Questions (8 Short Answers) |
Also access the following resources for Class 8 Chapter 9 Algebraic Expressions and Identities at BYJU’S:
- Algebraic Expressions and Identities Class 8 Notes: Chapter 9
- RD Sharma Solutions for Class 8 Maths Chapter 6 – Algebraic Expressions and Identities
- NCERT Exemplar Class 8 Maths Solutions for Chapter 7 – Algebraic Expressions And Identities Factorisation
- Important Questions Class 8 Maths Chapter 9 Algebraic Expressions and Identities
NCERT Solutions for Class 8 Maths Chapter 10 Visualizing Solid Shapes
In this chapter, with the help of 3 exercises present, students learn to visualize solid shapes in different dimensions. The chapter is very interesting since it deals with viewing 3D shapes, mapping the space around us, and learning about faces, edges and vertices. The chapter also discusses Euler’s formula , which states that F + V – E = 2, where F is Faces, V is Vertices, and E is Edges, along with its application.
| Class 8 NCERT Solutions Maths Chapter 10 Exercises |
|---|
| – 4 Questions (4 Short Answers) |
| – 4 Questions (3 Short Answers, 1 Long Answer) |
| – 8 Questions (8 Short Answers) |
Also, access the following resources for Class 8 Chapter 10 Visualizing Solid Shapes at BYJU’S:
- Visualising Solid Shapes Class 8 Notes: Chapter 10
- Important Questions Class 8 Maths Chapter 10 Visualising Solid Shapes
- RD Sharma Solutions for Class 8 Maths Chapter 19 Visualising Shapes
- NCERT Exemplar Class 8 Maths Solutions for Chapter 6 – Visualising Solid Shapes
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration
Students in lower classes must have learnt about the area and perimeter of various closed plane figures such as triangles, rectangles, circles, etc. In this chapter, Mensuration , students will learn to solve problems related to the perimeter and area of other plane closed figures like quadrilaterals. Eventually, the students will learn about the surface area and volume of different solid shapes such as a cube, cuboids and cylinders. A total of 4 exercises are present in this chapter.
| Maths Class 8 NCERT Solutions Chapter 11 Exercises |
|---|
| – 5 Questions (5 Long Answers) |
| – 11 Questions (11 Long Answers) |
| – 10 Questions (2 Short Answers, 8 Long Answers) |
| – 8 Questions (2 Short Answers, 6 Long Answers) |
Also, access the following resources for Class 8 Chapter 11 Mensuration at BYJU’S:
- Mensuration Class 8 Notes- Chapter 11
- Important Questions Class 8 Maths Chapter 11 Mensuration
- RD Sharma Solutions for Class 8 Maths Chapter 20 Mensuration – I (Area of a Trapezium and a Polygon)
- NCERT Exemplar Class 8 Maths Solutions for Chapter 11 – Mensuration
NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers
In the chapter, Exponents and Powers, students learn different concepts, including powers with negative exponents, laws of exponents , use of exponents to express the numbers in standard form and comparison of extremely large numbers with small numbers. The chapter consists of 2 exercises to help the students learn about the topics of exponents and powers.
| Maths Class 8 NCERT Solutions Chapter 12 Exercises |
|---|
| – 7 Questions (7 Short Answers) |
| – 4 Questions (4 Short Answers) |
Also, access the following resources for Class 8 Chapter 12 Exponents and Powers at BYJU’S:
- NCERT Exemplar Class 8 Maths Solutions for Chapter 8 – Exponents And Powers
- Important Questions Class 8 Maths Chapter 12 Exponents And Powers
- RD Sharma Solutions for Class 8 Maths Chapter 2 – Powers
NCERT Solutions for Class 8 Maths Chapter 13 Direct and Inverse Proportions
This chapter contains 2 exercises with questions based on the concepts of direct proportion and inverse proportion. Two quantities, x and y are said to be in direct proportion if they increase (decrease) together in such a manner that the ratio of their corresponding values remains constant. On the other hand, two quantities, x and y, are said to be in inverse proportion if an increase in x causes a proportional decrease in y (and vice-versa) in such a manner that the product of their corresponding values remains constant.
| Maths Class 8 NCERT Solutions Chapter 13 Exercises |
|---|
| – 10 Questions (10 Short Answers) |
| – 11 Questions (11 Long Answers) |
Also, access the following resources for Class 8 Chapter 13 Direct and Inverse Proportions at BYJU’S:
- Direct and Inverse Proportions Class 8 Maths Notes – Chapter 13
- NCERT Exemplar Class 8 Maths Solutions for Chapter 10 – Direct And Inverse Proportions
- Important Questions Class 8 Maths Chapter 13 Direct and Inverse Proportions
- RD Sharma Solutions for Class 8 Maths Chapter 10 Direct and Inverse Variations
NCERT Solutions for Class 8 Maths Chapter 14 Factorization
In this chapter, students learn to perform Factorization. The topics covered in this chapter include factors of natural numbers and algebraic expressions , factorisation by regrouping terms and factorisation using identities. The chapter also deals with the division of algebraic expressions that, includes division of a monomial by another monomial, division of a polynomial by a monomial, etc. There are 4 exercises in this chapter that contain questions covering all the topics present in the chapter.
| Maths Class 8 NCERT Solutions Chapter 14 Exercises |
|---|
| – 3 Questions (3 Short Answers) |
| – 5 Questions (5 Short Answers) |
| – 5 Questions (5 Short Answers) |
| – 21 Questions (21 Short Answers) |
Also, access the following resources for Class 8 Chapter 14 Factorization at BYJU’S:
- RD Sharma Solutions for Class 8 Maths Chapter – 7 Factorization
- Factorisation Class 8 Notes- Chapter 14
- Important Questions Class 8 Maths Chapter 14 Factorization
NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs
In the chapter, Introduction to Graphs, students learn to represent different types of data with various kinds of graphs. The different types of graphs include bar graphs , pie graphs, line graphs and linear graphs. The chapter will help the students in learning how to locate a point and coordinate in a graph. A total of 3 exercises are present in the chapter that will help the students understand the concepts of Graphs.
| Class 8 NCERT Solutions Maths Chapter 15 Exercises |
|---|
| – 7 Questions (7 Long Answers) |
| – 4 Questions (4 Short Answers) |
| – 2 Questions (2 Short Answers) |
Also, access the following resources for Class 8 Chapter 15 Introduction to Graphs at BYJU’S:
- Introduction To Graphs Class 8 Notes- Chapter 15
- Important Questions Class 8 Maths Chapter 15: Introduction to Graphs
- NCERT Exemplar Class 8 Maths Solutions for Chapter 12 – Introduction To Graphs
- RD Sharma Solutions for Class 8 Maths Chapter 27 Introduction to Graphs
NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers
Students, so far, have studied various types of numbers, such as natural numbers, whole numbers, integers and rational numbers . They might have also studied a number of interesting properties of these numbers, finding factors, multiples and the relationships among them. Likewise, in this chapter, students can explore the vast genres of numbers in detail. These ideas can help the students in justifying tests of divisibility. There are 2 exercises in this chapter that covers the topic of playing with numbers.
| Class 8 NCERT Solutions Maths Chapter 16 Exercises |
|---|
| – 10 Questions (Short Answers) |
| – 4 Questions (Short Answers) |
Also, access the following resources for Class 8 Chapter 16 Playing with Numbers at BYJU’S:
- Playing With Numbers Class 8 Notes- Chapter 16
- Important Questions Class 8 Maths Chapter 16: Playing with Numbers
- NCERT Exemplar Class 8 Maths Solutions for Chapter 13 – Playing with Numbers
- RD Sharma Solutions for Class 8 Maths Chapter 5 – Playing with Numbers
CBSE Class 8 Maths Solutions of NCERT Book
We are providing chapter-wise NCERT Maths Solutions for Class 8. The solutions provided on this page will help students understand and solve all the NCERT Class 8 mathematics book questions. These solutions are free, and students can view them online on the website or download the PDF.
Solving NCERT Maths question papers and sample papers will also help the students to understand different types of questions as well as the marking scheme. Also, students can learn from NCERT Exemplar Class 8 to practise exemplar problems.
Key Features of BYJU’S NCERT Class 8 Maths Solutions
- These solutions cover all the chapters that are included in the Class 8 Maths book.
- The solutions are given in easy steps to help students understand the concepts better.
- These solutions can be downloaded and referred to at any time and at any place.
- These CBSE 8th Class Maths solutions are available for free, and any student can access them.
These are just a few benefits of using the Solutions of Maths NCERT 8th Class . Students can register with BYJU’S and get the opportunity to learn topics of CBSE or NCERT syllabus for Class 8 Maths or any other Class more effectively. They can learn different topics right from their homes using the internet, where they can browse content on their PCs. Moving on, students can customize their learning experience, and they can do it all at their own pace without worrying about deadlines or any stress. Further, we are providing the best subject experts or mentors who will guide students to learn the subject and its concepts in a more simple and fun manner.
Another benefit that students can experience with BYJU’S is that they can opt to learn NCERT subjects by accessing our solutions anywhere and at any time of the day. In addition, BYJU’S is keen on tracking the progress that students make. Feedback and counselling are provided via periodic assessments. In case students face any doubts while going through the CBSE Class 8 Maths NCERT Solutions , they can always approach our BYJU’S support team to clear all their doubts. Besides, students can bring in all their queries regarding Maths as well as other subjects, including Physics, Chemistry, and Biology. Our responsive team is always ready to answer all types of questions.
Students can also download the BYJU’S app and get complete assistance for Class 8 with a new method of learning through educational videos.
Frequently Asked Questions on NCERT Solutions for Class 8 Maths
Which chapters in ncert solutions for class 8 maths are important to prepare for the exams, do ncert solutions for class 8 maths pdfs help you to prepare for your exams, how do i start practising the syllabus of ncert solutions for class 8 maths , where can i get the chapter-wise answers of the ncert solutions for class 8 maths , leave a comment cancel reply.
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
It is helpful for us
Good and thanks byjus
It is helpful
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
Home » Games » 17 Fun Problem Solving Activities & Games [for Kids, Adults and Teens]
17 Fun Problem Solving Activities & Games [for Kids, Adults and Teens]
Everyone should learn problem solving, as it is important in both our personal and professional lives. Problems occur all around us and many people react with spontaneous emotion. Instead, effective use of problem solving skills can lead to rational thinking, a component of any successful endeavor.
Creative problem involves using one or more of the basic steps of problem solving in exercises designed to challenge the thinking. Problem solving activities work for every age group. In this article, we will present problem-solving activities for adults and kids. We will also provide you with group and team building problem solving ideas.
Table of Contents
There are four basic steps in problem solving:
- define the problem
- generate possible solutions
- evaluate and select possible solutions
- implement solutions
Problem solving activities use one of more of these steps.
Group Problem Solving Activities
Group activities provide an effective way to learn problem-solving skills. The following list of activities present problem solving skills in the form of games, a non-threatening and fun way.
Divide your group into teams of equal numbers. Give each team a ball of yarn. Instruct the teams to create a web using only the yarn. Once the teams have finished (you may have to set an amount of time for completion), switch the teams around so that every team has a web other than their own. Each team then blindfolds one team member. The goal is for the blindfolded individual to unwind the web following the verbal instruction of their teammates. In order to be successful, team members must concentrate, and give/follow directions. The first team that has dismantled the web wins this game.
To Do Scavenger Hunt
This scavenger hunt game involves solving a list of problem activities. Begin by dividing your group into teams. Give each group a list of to do activities. The list should begin with some simple tasks, with increasingly more difficult activities. Some suggested activities are:
- Write a one hundred word poem on a given theme.
- Find an object readily available in the area in which you are playing
- Drink a whole can or glass of a liquid
- Solve a Sudoku or cross word puzzle
- Write out all the lyrics of a song (a Christmas carol works well at holiday time)
The team that completes all the activities first, wins.
Impromptu Skits
Prior to playing this game, write down a few appropriate situations that deal events in the venue in which you are playing. For example, for a group involved in customer service, use dealing with an angry customer on the phone. If you have a large group, divide them into teams of six to eight members. Have each group choose a folded piece of paper on which you have written the subject of a skit they must create. Give a set amount of time to prepare the skit and then have each team present their skit to the group. If you have a small group, have each person create one side of a conversation dealing with the problem for presentation to everyone.
Block Duplicating
Build a model out of building blocks. Provide each group member (or divide into teams for a large group ) enough blocks to duplicate the model. Set a specific amount of time for completing the duplicated model. The team that is the first to finish – or gets the furthest on completing their model – wins. The more difficult the original model, the longer this task will take.
Team Building Problem Solving Activities
When choosing team building problem solving activities, make sure the game you use suits the group of people – their ages and interests. The activities we have listed will help with not only problem solving, but also build decision making, collaboration, and listening skills.
Tower Building
Although there are many variations to this game, this one using spaghetti and marsh mellows is our favorite. Divide you group into teams with an equal number of players. Provide each team with an equal amount of spaghetti and marsh mellows. The goal is to see which team can build the highest tower within a set amount of time.
Personalized Crossword
For this game to be effective, you need one or more teams of 8 to 10 people. Have each team list the first and last names of their group members. The goal is to create a crossword puzzle with clues composed of hints about the person, for example, if only one team member has red hair, the two clues for her first and last name could be, “Red hair,” and “Ginger.” It should take each team 20 to 30 minutes to complete their puzzle. When all the teams are finished, trade puzzles so that every team has a different one. Make sure you provide a list of names for the puzzle solvers.
Picture Pieces Puzzle Game
Prepare for this problem solving activity by choosing a well-known picture or cartoon full of detail. Cut the picture into equal sized squares and give one to each member of the group. You will need as many pieces as you have participants. Additionally, give each person a pencil, ruler for help enlarging the picture, colored markers, and a clean sheet of paper. Instruct them to make the puzzle piece five times larger.
Problem Solving Activities for Adults
Divide your group into two teams. Line up the two teams front to back. Have the two groups face each other. Using chalk, spray paint, or masking tape (depending on the play surface) mark a square space for each person to stand on with one extra empty space between the two facing rows. You may also use a piece of paper for each person. The goal is for the two facing lines of players to change places.
Place these restrictions on movement:
- Only one person may move at a time.
- A person may not move around anyone facing the same direction.
- A person may not move backward.
- A person may not move around more than one person on the other team at a time.
Playing Card Mix-up
Divide your group into teams of six to eight participants. Give each team two decks of cards randomly mixed together. Tell the group they must sort them out without talking. As they working at the task, after a few minutes, change the way in which they are doing so using one of the following:
- If a team is sorting by suits from ace to king (4 stacks), tell them to collect the suits together by number (13 stacks).
- If a team begins by collecting the suits together, i.e. all the ones, twos, threes, etc., tell them to sort the suits from ace to king.
The team(s) that do so successfully by the end of a given time (depending on the size of your group) share what methods they used to accomplish the task.
Blindfolded games are always fun and provide the perfect challenge for adult problem solving. We have provided two for you.
Blind Formations
Have your group of adults put on blindfolds and form a large circle. Tie the ends of a rope together and lay in it a circle in the middle of the group, close enough that each person can reach down and pick up the rope. Tell them they must create a shape – a square, triangle, pentagon, etc. If you have a very large group, divide them into teams and provide a rope for each team. Let them compete to see who forms a particular shape quickest.
Line up Blind
Blindfold everyone and number the group by whispering a number to each individual beginning at one. Tell them to line up in numerical order without talking. Variations are many, with some of the favorites not requiring the whispering step being to line up according to height, birthday, surname, color of hair, etc.
Balloon Tower
Divide you group into teams of three and provide ten balloons and four 3-foot long strips of masking tape for each team. The object of this problem solving activity is to build the tallest freestanding tower in ten minutes. They can break the balloons if they wish. However, they may not use any additional materials and the tower must be built on a table or the floor. If you wish, you may add the following instructions:
- No talking.
- Each team member may use only one hand.
- One team member may not touch the materials and only give directions.
You can use one or more of these limitations in 60-second intervals. The first team to complete their tower wins this challenge.
Problem Solving Activities for Kids
The purpose of problem solving activities for kids is to get kids to think about a problem in a different way and have fun while solving it. Children will develop their creativity as they seek to implement a solution.
Walking the Plank
For this problem solving activity for older kids or teens, you will need four 2×6 boards. Divide your group into two teams with an equal number of children on each team. Place two of the four boards end to end on the ground or floor. Set the other two parallel to the first two about two or three feet apart. The goal is for each team to pass one board forward while standing on the other board in single file. If someone steps off a board, the team must start over. The team that succeeds in passing the boards a set number of times, or reaches a predetermined spot is the winner.
“Laser” Web
Use a large ball of string to create a giant web from one end of a room to the other. The goal is for individuals or teams to move through the web without touching the string. If they do so, they have been “zapped by a laser” and must try again. For greater suspense and for older players, use blindfolds or turn off the lights, allowing players to touch the string, but not pull it down or out of its original shape.
Group Drawing
Divide your group of kids into teams of three. Each person on the team has a one of the following roles:
- Drawer . The drawer attempts to recreate a pre-drawn design they cannot see. They take directions from the talker. They stand with their back to the talker and viewer and may not talk.
- Talker . The talker describes the design to the drawer, without seeing the design. They may question the viewer. They may not use hand gestures.
- Viewer . The viewer sees the design. However, they are not allowed to talk and must communicate nonverbally to the talker. Additionally, they must not draw the design in the air or actually show the design with their gestures.
The activity ends when the viewers say they are satisfied with the drawings. You may wish to award a prize to the best drawing.
Prior to playing this game, write on individual slips of paper the names of animal pairs, one name on each slip. Distribute the slips of paper to each group, instructing them not to share which animal name they received. The kids then move around performing activities their animal might do. The goal is for the kids to get into pairs successfully in a set amount of time without talking or making any noises. Suggest the following activities:
- Cleaning or grooming
- Eating and drinking
- Walking or running
Alphabet Game
Have your players sit or stand in a circle. The goal is to shout out words in alphabetical order. Give the kids one of the following categories (or choose your own):
If a player takes longer than five seconds to think of a word, they are out. The last player remaining wins the game.
People achieve more when they solve problems and make decisions together. Our problem solving activities teach participants how to work out a solution, a talent useful in many different environments. Problem solving:
- Improves team work
- Helps participants address complex situations
- Utilizes different thinking styles
- Increases creativity
- Collectively leads to decision making
- Teaches both negotiation and cooperation
After completing a problem solving activity, encourage participants to discuss what process(es) they used in the exercise. Even kids are able to participate in such discussions. Also ask what was learned and if they have any opinions about how they could have solved the problem more efficiently.
Team-building exercises can improve problem solving and decision making in a new or established team. They work with every age group and in many different environments. Use our exercises to help solve problems and have some fun doing so.
Susan majored in English with a double minor in Humanities and Business at Arizona State University and earned a Master’s degree in Educational Administration from Liberty University. She taught grades four through twelve in both public and private schools. Subjects included English, U.S. and world history and geography, math, earth and physical science, Bible, information technologies, and creative writing.
Susan has been freelance writing for over ten years, during which time she has written and edited books, newspaper articles, biographies, book reviews, guidelines, neighborhood descriptions for realtors, Power Point presentations, resumes, and numerous other projects.
Read full bio
Related posts
Thanks for your help!!
excellent ideas – thanks !
Excellent ideas.
Thank you. My students have requested we do team-building activities; I thought we would start with problem-solving.

Leave a Comment Cancel Reply
Recent posts, 30 best coach gift ideas [for any sport].
June 1st, 2024
109 Challenging Chicago Trivia & Facts
May 15th, 2024
101 Best Pixar Trivia Questions And Answers
May 1st, 2024
78 Funny Shoe Game Wedding Questions (For Bride & Groom)
April 15th, 2024
81 Fun Multiple Choice Trivia Questions (with Answers)
April 1st, 2024
32 Creative Corporate Event Ideas
March 15th, 2024
72 Challenging Taylor Swift Trivia Questions And Answers
February 28th, 2024

Game Central
Reciprocals, related concepts.

Melody's Adventure

Low's Adventures 3

Space Survival

Electron Dash

Chromatic Pathway

Icy Super Slide

X Trench Run

Winding Road

Epic City Driver

Rambling Racer

Superbike Hero

Head Soccer

Puppet Hockey

Skateboard Hero

Arcade Golf

Pro Bowling

Touchdown Rush

Orbit Escape

Obstacle Race

Tower of Colors

Rise Higher

Cake Topping

Neon Rocket

Alien Cubes

Maze Control

Koala Sling

Red Ball 4 v 1

Rolling Hero

Sweet Drmzzz

Monkey Bubbles

Fluffy Cuddlies

Snoring Pirates

Cut for Cat

Pingu and Friends

Cookie Trail

Robot Islands PLUS

Code Builder

Follow the Code

Draw in Code
Pin Cracker

Rainbow Tower

The Way Home

Charlotte Valley

Islands Of Creatures

Maze Collapse
Happy Filled Glass 4

Big Tall Small

Gravisquare

Red Block Returns

Zero Numbers

Logic Steps
Overlap Sums

Prodigy Math
Prodigy english.
- Is a Premium Membership Worth It?
- Promote a Growth Mindset
- Help Your Child Who's Struggling with Math
- Parent's Guide to Prodigy
- Assessments
- Math Curriculum Coverage
- English Curriculum Coverage
- Administrators
- Game Portal
Make Math and English fun for kids
With Prodigy, kids practice standards-aligned skills in Math and English as they play our fun, adaptive learning games. All with teacher and parent tools to support their learning in class and at home.
Master Math Grades 1-8 & English Grades 1-6
91% of parents said their children enjoy using Prodigy Math*
" Prodigy is a great way to get kids who don't like math into math. "
Caralena Luthi

" In less than 12 months... I’ve got kids that have elevated two to three grade levels. That’s huge when you look at those kids who’ve grown three grade levels with everything that’s going on. "
5th Grade Teacher

" Having access to Prodigy really helps supplement our math learning and tells me what areas of the curriculum I need to add more focus on. I think all teachers should use Prodigy if possible because it is an amazing learning tool. "
6th Grade Teacher

*In one survey of parents commissioned by Prodigy Education.
Our mission is to help every student in the world love learning!
That’s why all of our standards-aligned educational content is free and students can play prodigy at school or at home..
Here's how nearly one million teachers use Prodigy in the classroom at no cost!
Help students master math standards with a fun and engaging gameplay experience
Adjust and align Prodigy's in-game math content with your lesson plans
Track student development to decide where to best spend your time
No trial period, no hidden costs for educators. Our optional parent memberships ensure Prodigy stays free for all teachers.
Students reported an average of twice the level of math enjoyment in just a few months.
In one school district, students mastered an average of 68% more math skills per month .
96%** of parents and teachers were satisfied with the educational impact of Prodigy Math.
**Based on a survey of parents and a survey of teachers commissioned by Prodigy Education.
Invest in your child's learning journey with engaging games that make learning fun!
Help your child improve their math skills and confidence in a fun, safe and secure environment
Motivate learning, track their progress and inspire them to practice new skills
Get insights into their classroom progress with a Prodigy parent account
Optional Prodigy memberships provide additional features that are engaging and promote more math practice - and they also help us keep Prodigy free for all teachers!
Learning made fun, in more ways than one
Our safe, curriculum-aligned games make online learning an adventure!
Discover the magic of math! Players embark on a journey filled with quests, battles, spells and rewards. Every battle brings more skill-building math questions for students to solve.
Power your imagination! Create a custom-built world through reading and language practice. Every correct answer gives students more energy to gather supplies and build up your village.

Aligned to your curriculum
Prodigy Math provides comprehensive math curriculum coverage, including Common Core, TEKS and many more state-specific standards. Prodigy English also aligns with Common Core, with more skills and coverage on the way!
Ready to kickstart a learning adventure?

If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Unit 1: Algebra foundations
Unit 2: solving equations & inequalities, unit 3: working with units, unit 4: linear equations & graphs, unit 5: forms of linear equations, unit 6: systems of equations, unit 7: inequalities (systems & graphs), unit 8: functions, unit 9: sequences, unit 10: absolute value & piecewise functions, unit 11: exponents & radicals, unit 12: exponential growth & decay, unit 13: quadratics: multiplying & factoring, unit 14: quadratic functions & equations, unit 15: irrational numbers, unit 16: creativity in algebra.

IMAGES
VIDEO
COMMENTS
The ultimate collection of free 8th grade math worksheets. All of our 8th grade math worksheets are topic-specific, printable (they are available as pdf files), and include a complete answer key. This is the only 8th grade math worksheets library you will ever need--simply pick your topic, select a worksheet, click and download.
Up next for you: Course challenge Test your knowledge of the skills in this course. Start Course challenge. Square roots review. Community questions. Learn eighth grade math—functions, linear equations, geometric transformations, and more. (aligned with Common Core standards)
Fractions Questions and Problems with Solutions. Grade 8 questions on simplifying expressions with negative exponents with solutions and explanations included Online Trigonometry Calculators and Solvers. quadratic equations problems for Grade 8 with solutions and explanations included. Multiply and Simplify Monomials.
Show Video Lesson. Grade 8 number word problems - common core. How to write word problems into systems of linear equations and solve systems of linear equations using elimination and substitution methods? Example 1: The sum of two numbers is 361 and the difference between the two numbers is 173.
Unit test. Level up on all the skills in this unit and collect up to 700 Mastery points! Start Unit test. Let's take your equation-solving skills to the next level! You'll learn all the strategies you need to confidently tackle problems with variables on both sides, parentheses, and more. Plus, you'll get plenty of practice with word problems ...
Unit 8: Pythagorean theorem and irrational numbers. 0/2000 Mastery points. Lesson 2: Side lengths and areas Lesson 3: Rational and irrational numbers Lesson 4: Square roots on the number line Lesson 5: Reasoning about square roots Extra practice: Irrational numbers Lesson 6: Finding side lengths of triangles Lesson 7: A proof of the Pythagorean ...
Examples, solutions, videos and lessons to help Grade 8 students learn how to solve linear equations in one variable. A. Give examples of linear equations in one variable with one solution, infinitely many solutions, or no solutions. Show which of these possibilities is the case by successively transforming the given equation into simpler forms ...
Learn eighth grade math skills for free! Choose from hundreds of topics including linear equations, geometric transformations, congruence, and more. ... Solve proportions: word problems 3. Estimate population size using proportions 4. Scale drawings: word problems 5. Scale drawings: scale factor word problems ... Graph solutions to multi-step ...
Teaching Through Problems Worth Solving - Grade 8 (Version 1.0) - Inquiry-based, Curriculum-linked, Differentiated Math Problems for Grade 8 Alicia Burdess Daniel Student ... photos of work, written solutions that tell the story of how the problem was solved, etc. This can be done individually or in partners or groups. This allows students to show
Daily Problem Solving will help your 8th grade students master the skills they need to be successful with challenging word problems ... You'll receive a full week of printable Daily Problem Solving practice for your students. This format includes: Paper-saving format that fits a full week on one page; Space for student work, feedback, and self ...
IXL plans. Virginia state standards. Textbooks. Test prep. Awards. Improve your math knowledge with free questions in "Solve percent word problems" and thousands of other math skills.
Free math problem solver answers your algebra homework questions with step-by-step explanations.
You can create printable tests and worksheets from these Grade 8 Problem Solving Strategies questions! Select one or more questions using the checkboxes above each question. Then click the add selected questions to a test button before moving to another page. Select All Questions. Grade 8 Problem Solving Strategies CCSS: 8.EE.C.8, 8.EE.C.8c.
Now, with expert-verified solutions from Ready Mathematics Practice and Problem Solving Grade 8 , you'll learn how to solve your toughest homework problems. Our resource for Ready Mathematics Practice and Problem Solving Grade 8 includes answers to chapter exercises, as well as detailed information to walk you through the process step by step.
CEMC Gauss (Grade 8) problems and solutions by test: 1998 CEMC Gauss (Grade 8) 1999 CEMC Gauss (Grade 8) 2000 CEMC Gauss (Grade 8) 2001 CEMC Gauss (Grade 8) ... Art of Problem Solving is an ACS WASC Accredited School. aops programs. AoPS Online. Beast Academy. AoPS Academy. About. About AoPS. Our Team. Our History. Jobs. AoPS Blog. Site Info.
Additionally, these worksheets can be easily adapted to suit various learning styles and preferences, making them a versatile and valuable resource for any Grade 8 classroom. Identifying Problems and Solutions in Reading worksheets for Grade 8 is a must-have tool for teachers looking to enhance their students' reading comprehension skills.
Solution: Now that we have the value for [latex]x[/latex], let's find out what Tanya and Marcus's current ages are. We can do this by simply replacing the [latex]x[/latex]'s with [latex]8[/latex]. ... As long as you stick with the basic principles and steps on how to solve age word problems, you'll be fine. Right now, we don't know ...
QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students. The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and ...
Find step-by-step solutions and answers to Exercise 1 from Ready Mathematics Practice and Problem Solving Grade 8 - 9781495704857, as well as thousands of textbooks so you can move forward with confidence. ... Ready Mathematics Practice and Problem Solving Grade 8 (9781495704857) Exercise 1. Chapter 1, Section Lesson 1, Page 3. Ready ...
Math; 8th grade; Unit 4: Systems of equations. 700 possible mastery points. Mastered. Proficient. Familiar. Attempted. Not started. Quiz. Unit test. ... System of equations word problem: no solution (Opens a modal) System of equations word problem: infinite solutions (Opens a modal) Systems of equations with substitution: coins
Chapter-Wise NCERT Solutions for Class 8 Maths. NCERT Solutions for Class 8th Maths provided here are very beneficial for students. They can use these NCERT Solutions for Class 8 as a reference while practising the problems and developing better skills along with preparing efficiently for the exams. The exercises are given at the end of every chapter to practise the concepts learned in the ...
For this problem solving activity for older kids or teens, you will need four 2×6 boards. Divide your group into two teams with an equal number of children on each team. Place two of the four boards end to end on the ground or floor. Set the other two parallel to the first two about two or three feet apart.
Problem 6. Math Playground has hundreds of interactive math word problems for kids in grades 1-6. Solve problems with Thinking Blocks, Jake and Astro, IQ and more. Model your word problems, draw a picture, and organize information!
Polynomial. In mathematics, a polynomial is a mathematical expression consisting of indeterminates and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate x is x² − 4x + 7. An example with three indeterminates ...
Learn. Linear graphs word problems. Modeling with tables, equations, and graphs. Linear graphs word problem: cats. Linear equations word problems: volcano. Linear equations word problems: earnings. Modeling with linear equations: snow. Linear function example: spending money. Fitting a line to data.
The outer zone is worth 1 point, then 2, 3, etc. The center is worth 10 points. 5 + 8 + 8 + 9 = 30. Strike. BrainSnack. Which pins must be knocked over to score exactly 100 points? (Hint: There ...
Trigonometry is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical ...
Puzzles, skill games, adventure, racing and more at Math Playground!
Master Math Grades 1-8 & English Grades 1-6. ... "In less than 12 months... I've got kids that have elevated two to three grade levels. That's huge when you look at those kids who've grown three grade levels with everything that's going on." Stephen P. ... Solutions. Play Prodigy Math memberships English memberships.
The Algebra 1 course, often taught in the 9th grade, covers Linear equations, inequalities, functions, and graphs; Systems of equations and inequalities; Extension of the concept of a function; Exponential models; and Quadratic equations, functions, and graphs. Khan Academy's Algebra 1 course is built to deliver a comprehensive, illuminating, engaging, and Common Core aligned experience!