homework and practice 7 2 factors

• Home   |  
• About   |  
• Contact Us   |  
• Privacy   |  
• Newsletter   |  
• Shop   |  
• 🔍 Search Site
• Easter Color By Number Sheets
• Printable Easter Dot to Dot
• Easter Worksheets for kids
• Kindergarten
• All Generated Sheets
• Place Value Generated Sheets
• Addition Generated Sheets
• Subtraction Generated Sheets
• Multiplication Generated Sheets
• Division Generated Sheets
• Money Generated Sheets
• Negative Numbers Generated Sheets
• Fraction Generated Sheets
• Place Value Zones
• Number Bonds
• Addition & Subtraction
• Times Tables
• Fraction & Percent Zones
• All Calculators
• Fraction Calculators
• Percent calculators
• Area & Volume Calculators
• Age Calculator
• Height Calculator
• Roman Numeral Calculator
• Coloring Pages
• Fun Math Sheets
• Math Puzzles
• Mental Math Sheets
• Online Times Tables
• Online Addition & Subtraction
• Math Grab Packs
• All Math Quizzes
• 1st Grade Quizzes
• 2nd Grade Quizzes
• 3rd Grade Quizzes
• 4th Grade Quizzes
• 5th Grade Quizzes
• 6th Grade Math Quizzes
• Place Value
• Rounding Numbers
• Comparing Numbers
• Number Lines
• Prime Numbers
• Negative Numbers
• Roman Numerals
• Subtraction
• Add & Subtract
• Multiplication
• Fraction Worksheets
• Learning Fractions
• Fraction Printables
• Percent Worksheets & Help
• All Geometry
• 2d Shapes Worksheets
• 3d Shapes Worksheets
• Shape Properties
• Geometry Cheat Sheets
• Printable Shapes
• Coordinates
• Measurement
• Math Conversion
• Statistics Worksheets
• Bar Graph Worksheets
• Venn Diagrams
• All Word Problems
• Finding all possibilities
• Logic Problems
• Ratio Word Problems
• All UK Maths Sheets
• Year 1 Maths Worksheets
• Year 2 Maths Worksheets
• Year 3 Maths Worksheets
• Year 4 Maths Worksheets
• Year 5 Maths Worksheets
• Year 6 Maths Worksheets
• All AU Maths Sheets
• Kindergarten Maths Australia
• Year 1 Maths Australia
• Year 2 Maths Australia
• Year 3 Maths Australia
• Year 4 Maths Australia
• Year 5 Maths Australia
• Meet the Sallies
• Certificates

Factors and Multiples Worksheets

Welcome to our Factors and Multiples Worksheets. Here you will find a wide range of free Math Worksheets which will help your child to learn to use multiples and factors at a 4th Grade/ 5th Grade level.

For full functionality of this site it is necessary to enable JavaScript.

Here are the instructions how to enable JavaScript in your web browser .

Factors and Multiples Worksheet

These sheets have been designed to support your child with their learning of multiples and factors.

The sheets are graded in order of difficulty with the easiest sheet coming first in each section.

Using these sheets will help your child to:

• Know and understand what multiples and factors are;
• apply knowledge of multiples and factors to solve problems;
• Develop and practice their mental calculation skills.

Want to test yourself to see how well you have understood this skill?.

• Try our NEW quick quiz at the bottom of this page.

Quicklinks to ...

Multiples and Factors Help

Multiples worksheets, factors worksheets.

• Factors and Multiples Riddles
• Easier/Harder Worksheets
• More related resources

Factors and Multiples Online Quiz

If a number is a multiple of another number, it means that it can be made out of adding groups of the other number together.

12 is a multiple of 4 because 4 + 4 + 4 = 12 (or 4 x 3 = 12)

27 is a multiple of 9 because 9 + 9 + 9 = 27 (or 9 x 3 = 27)

17 is not a multiple of 4 because it cannot be made by adding groups of 4 together.

A factor is a number that divides into another number with no remainder.

In other words every number is divisible by each of its factors.

1 is a factor of every whole number, because every integer is divisible by one.

3 and 7 are both factors of 21 because 3 x 7 = 21

10 and 6 are both factors of 60 because 10 x 6 = 60

7 is not a factor of 24 because 24 is not divisible by 7 (24 ÷ 7 = 3 remainder 3).

Multiples and Factors are connected with each other:

• if we know that 3 is a factor of 12, then 12 is a multiple of 3
• if we know that 33 is a multiple of 11, then 11 is a factor of 33.
• also, if we know that 24 is not a multiple of 7, then 7 is not factor of 24.

The example below shows the relationship visually.

If we know that 3 is a factor of 24, then 24 must be a multiple of 3.

If we know that 24 is a multiple of 3, then 3 must be a factor of 24.

Multiples and Factors Worksheets

We have split our worksheets into 3 different sections:

• the first section contains only worksheets about Multiples
• the second section contains only worksheets about Factors
• the third section contains worksheets with both Factors and Multiples
• Multiples Sheet 4:1
• PDF version
• Multiples Sheet 4:2
• Multiples Sheet 4:3
• Multiples Sheet 4:4

We have two worksheets on finding Factor Pairs up to 100.

We have two worksheets which involve finding all the factors of different numbers.

• Factor Pairs Worksheet 1
• Factor Pairs Worksheet 2
• Factors Worksheet 4:1
• Factors Worksheet 4:2
• Factors and Multiples Worksheet 4:1
• Factors and Multiples Worksheet 4:2
• Factors and Multiples Worksheet 4:3

Factor and Multiples Riddles

Using riddles is a great way to get children to apply their knowledge of factors and multiples to solve problems.

It is also a good way to get children working collaboratively and talking about the language together.

Each riddle consists of some clues and a selection of possible answers.

Solving the clues gradually eliminates all the incorrect answers leaving just one solution.

• Factors and Multiples Riddles 1
• Factors and Multiples Riddles 2

Looking for some easier Multiples Sheets

The sheets in this section cover similar areas to the worksheets on this page but are at an easier level.

• round a number to the nearest 10, 100 or 1000;
• use the > and < symbols correctly for inequalities;
• use multiples and apply them to solve problems.
• Rounding Inequalities Multiples Worksheets

Looking for some harder Factors and Multiples Worksheets

We also have some more advanced worksheets about multiples and factors.

The worksheets below are more suitable for 6th graders and above.

• Greatest Common Factor Worksheets
• Least Common Multiple Worksheets
• Factor Tree Worksheets (easier)
• Prime Factorization Worksheets (harder)

More Recommended Math Resources

Take a look at some more of our worksheets similar to these.

Divisibility Rules 1-10 Chart

We have a range of charts which can help you determine whether a number between 1 and 10 is a factor of a number.

• Divisibility Rules 1-10 Charts

Balancing Math Equations Worksheets

The sheets in this area will help your child understand the use and purpose of the equals sign (=) in an equation.

It will also help children learn to start manipulating and calculating numerical expressions so that they are equivalent.

This will stand them in good stead for when they start to learn algebra, and manipulate algebraic equations.

• Balancing Math Equations

Sieve of Erastosthenes

The Sieve of Erastosthenes is a method for finding what is a prime numbers between 2 and any given number.

Eratosthenes was a Greek mathematician (as well as being a poet, an astronomer and musician) who lived from about 276BC to 194BC.

If you want to find out more about his sieve for finding primes, and print out some Sieve of Eratosthenes worksheets, use the link below.

• Sieve of Eratosthenes page

Want to find out more about primes?

Take a look at our Prime Number page which clearly describes what a prime numbers is and what they are not.

There are also many different questions about prime numbers answered, as well as information about the density of primes.

• What is a Prime Number

Our quizzes have been created using Google Forms.

At the end of the quiz, you will get the chance to see your results by clicking 'See Score'.

This will take you to a new webpage where your results will be shown. You can print a copy of your results from this page, either as a pdf or as a paper copy.

For incorrect responses, we have added some helpful learning points to explain which answer was correct and why.

We do not collect any personal data from our quizzes, except in the 'First Name' and 'Group/Class' fields which are both optional and only used for teachers to identify students within their educational setting.

We also collect the results from the quizzes which we use to help us to develop our resources and give us insight into future resources to create.

For more information on the information we collect, please take a look at our Privacy Policy

We would be grateful for any feedback on our quizzes, please let us know using our Contact Us link, or use the Facebook Comments form at the bottom of the page.

This quick quiz tests your knowledge and skill with factors and multiples here!

Fun Quiz Facts

• This quiz was attempted 1,569 times last academic year. The average (mean) score was 14.8 out of 20 marks.
• Can you beat the mean score?

How to Print or Save these sheets 🖶

Need help with printing or saving? Follow these 3 steps to get your worksheets printed perfectly!

• How to Print support

Subscribe to Math Salamanders News

Sign up for our newsletter to get free math support delivered to your inbox each month. Plus, get a seasonal math grab pack included for free!

• Newsletter Signup

Return to 4th Grade Math Worksheets

Return from Factors and Multiples Worksheets to Math Salamanders Homepage

Math-Salamanders.com

The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.

We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.

New! Comments

TOP OF PAGE

© 2010-2024 Math Salamanders Limited. All Rights Reserved.

• Privacy Policy
• Copyright Policy

• Kindergarten
• Greater Than Less Than
• Measurement
• Multiplication
• Place Value
• Subtraction
• Punctuation
• 1st Grade Reading
• 2nd Grade Reading
• 3rd Grade Reading
• Cursive Writing

Homework Practice 7 2 Factors

Showing top 8 worksheets in the category - Homework Practice 7 2 Factors .

Some of the worksheets displayed are Homework practice and problem solving practice workbook, Name date period lesson 1 homework practice, Practice and homework name lesson compare mixed number, Homework practice and problem solving practice workbook, Word problem practice workbook, Finding factors, Prime and composite, Grade 6 factoring work.

Once you find your worksheet, click on pop-out icon or print icon to worksheet to print or download. Worksheet will open in a new window. You can & download or print using the browser document reader options.

Homework Practice and Problem-Solving Practice Workbook

Name date period lesson 1 homework practice, practice and homework name lesson 7.8 compare mixed number ..., word problem practice workbook, finding factors, prime and composite, grade 6 factoring worksheet.

• Kindergarten
• Greater Than Less Than
• Measurement
• Multiplication
• Place Value
• Subtraction
• Punctuation
• 1st Grade Reading
• 2nd Grade Reading
• 3rd Grade Reading
• Cursive Writing
• Alphabet Coloring
• Animals Coloring
• Birthday Coloring
• Boys Coloring
• Buildings Coloring
• Cartoons Coloring
• Christmas Coloring
• Country Flag Coloring
• Country Map Coloring
• Disney Coloring
• Fantasy Coloring
• Food Coloring
• Girls Coloring
• Holidays Coloring
• Music Coloring
• Nature Coloring
• New Year Coloring
• People Coloring
• Religious Coloring
• Sports Coloring
• Toys Coloring
• Transportation Coloring
• US Sports Team Coloring
• Valentine Day Coloring

Homework Practice 7 2 Factors

Displaying top 8 worksheets found for - Homework Practice 7 2 Factors .

Some of the worksheets for this concept are Homework practice and problem solving practice workbook, Name date period lesson 1 homework practice, Practice and homework name lesson compare mixed number, Homework practice and problem solving practice workbook, Word problem practice workbook, Finding factors, Prime and composite, Grade 6 factoring work.

Found worksheet you are looking for? To download/print, click on pop-out icon or print icon to worksheet to print or download. Worksheet will open in a new window. You can & download or print using the browser document reader options.

1. Homework Practice and Problem-Solving Practice Workbook

2. name date period lesson 1 homework practice, 3. practice and homework name lesson 7.8 compare mixed number ..., 4. homework practice and problem-solving practice workbook, 5. word problem practice workbook, 6. finding factors, 7. prime and composite, 8. grade 6 factoring worksheet.

• Kindergarten
• Greater Than Less Than
• Measurement
• Multiplication
• Place Value
• Subtraction
• Punctuation
• 1st Grade Reading
• 2nd Grade Reading
• 3rd Grade Reading
• Cursive Writing

7 2 Factors

7 2 Factors - Displaying top 8 worksheets found for this concept.

Some of the worksheets for this concept are Work factoring by grouping, Transcription and gene expression, Factors, Factors, Factors and factorization, Work 2 6 factorizing algebraic expressions, A resource pack from educationcity factors, Factors multiples primes prime factors lcm and hcf.

Found worksheet you are looking for? To download/print, click on pop-out icon or print icon to worksheet to print or download. Worksheet will open in a new window. You can & download or print using the browser document reader options.

1. Worksheet 7.2: Factoring by Grouping

2. 7.2 transcription and gene expression, 5. factors and factorization -, 6. worksheet 2 6 factorizing algebraic expressions, 7. a free resource pack from educationcity factors, 8. factors, multiples, primes, prime factors, lcm and hcf.

• Art & Design
• Design & Technology
• Physical Education
• Foreign Languages
• Greater Than Less Than
• Measurement
• Multiplication
• Place Value
• Subtraction
• Punctuation
• 1st Grade Reading
• 2nd Grade Reading
• 3rd Grade Reading
• Cursive Writing

Homework Practice 7 2 Factors

Showing top 8 worksheets in the category - Homework Practice 7 2 Factors .

Some of the worksheets displayed are Homework practice and problem solving practice workbook, Name date period lesson 1 homework practice, Practice and homework name lesson compare mixed number, Homework practice and problem solving practice workbook, Word problem practice workbook, Finding factors, Prime and composite, Grade 6 factoring work.

Once you find your worksheet, click on pop-out icon or print icon to worksheet to print or download. Worksheet will open in a new window. You can & download or print using the browser document reader options.

1. Homework Practice and Problem-Solving Practice Workbook

2. name date period lesson 1 homework practice, 3. practice and homework name lesson 7.8 compare mixed number ..., 4. homework practice and problem-solving practice workbook, 5. word problem practice workbook, 6. finding factors, 7. prime and composite, 8. grade 6 factoring worksheet.

Addition (Basic)

Addition (Multi-Digit)

Algebra & Pre-Algebra

Comparing Numbers

Daily Math Review

Division (Basic)

Division (Long Division)

Hundreds Charts

Measurement

Multiplication (Basic)

Multiplication (Multi-Digit)

Order of Operations

Place Value

Probability

Skip Counting

Subtraction

Telling Time

Word Problems (Daily)

More Math Worksheets

Reading Comprehension

Reading Comprehension Gr. 1

Reading Comprehension Gr. 2

Reading Comprehension Gr. 3

Reading Comprehension Gr. 4

Reading Comprehension Gr. 5

Reading Comprehension Gr. 6

Reading & Writing

Reading Worksheets

Cause & Effect

Fact & Opinion

Fix the Sentences

Graphic Organizers

Synonyms & Antonyms

Writing Prompts

Writing Story Pictures

Writing Worksheets

More ELA Worksheets

Consonant Sounds

Vowel Sounds

Consonant Blends

Consonant Digraphs

Word Families

More Phonics Worksheets

Early Literacy

Build Sentences

Sight Word Units

Sight Words (Individual)

More Early Literacy

Punctuation

Subjects and Predicates

More Grammar Worksheets

Spelling Lists

Spelling Grade 1

Spelling Grade 2

Spelling Grade 3

Spelling Grade 4

Spelling Grade 5

Spelling Grade 6

More Spelling Worksheets

Chapter Books

Charlotte's Web

Magic Tree House #1

Boxcar Children

More Literacy Units

Animal (Vertebrate) Groups

Butterfly Life Cycle

Electricity

Matter (Solid, Liquid, Gas)

Simple Machines

Space - Solar System

More Science Worksheets

Social Studies

Maps (Geography)

Maps (Map Skills)

More Social Studies

Mother's Day

Father's Day

More Holiday Worksheets

Puzzles & Brain Teasers

Brain Teasers

Logic:  Addition Squares

Mystery Graph Pictures

Number Detective

Lost in the USA

More Thinking Puzzles

Teacher Helpers

Teaching Tools

Award Certificates

More Teacher Helpers

Pre-K and Kindergarten

Alphabet (ABCs)

Numbers and Counting

Shapes (Basic)

More Kindergarten

Worksheet Generator

Word Search Generator

Multiple Choice Generator

Fill-in-the-Blanks Generator

More Generator Tools

Full Website Index

A collection of math worksheets on finding factors, greatest common factors, and factor trees, as well as prime numbers & composite numbers.

Logged in members can use the Super Teacher Worksheets filing cabinet to save their favorite worksheets.

Quickly access your most used files AND your custom generated worksheets!

Please login to your account or become a member and join our community today to utilize this helpful feature.

Factor Trees

Prime Numbers

Greatest common factor (gcf), proper factors and perfect numbers.

Worksheets in which students determine the least common multiple, or LCM, for each number set

Here you'll find resources to help students review multiples of given numbers.

Simplifying fractions, equivalent fractions, operations with fractions. Also includes adding, subtracting, multiplying, and dividing fractions.

Practice basic multiplication skills with these printable worksheets and games

Worksheet Images

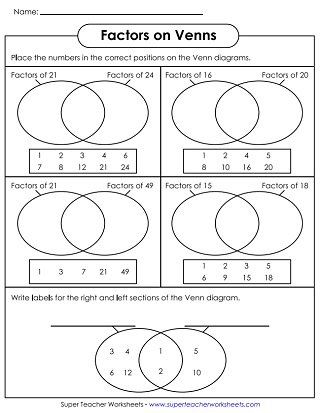
PDF with answer key:

PDF no answer key:

• Kindergarten
• Greater Than Less Than
• Measurement
• Multiplication
• Place Value
• Subtraction
• Punctuation
• 1st Grade Reading
• 2nd Grade Reading
• 3rd Grade Reading
• Cursive Writing

Homework Practice 7 2 Factors

Homework Practice 7 2 Factors - Displaying top 8 worksheets found for this concept.

Some of the worksheets for this concept are Homework practice and problem solving practice workbook, Name date period lesson 1 homework practice, Practice and homework name lesson compare mixed number, Homework practice and problem solving practice workbook, Word problem practice workbook, Finding factors, Prime and composite, Grade 6 factoring work.

Found worksheet you are looking for? To download/print, click on pop-out icon or print icon to worksheet to print or download. Worksheet will open in a new window. You can & download or print using the browser document reader options.

1. Homework Practice and Problem-Solving Practice Workbook

2. name date period lesson 1 homework practice, 3. practice and homework name lesson 7.8 compare mixed number ..., 4. homework practice and problem-solving practice workbook, 5. word problem practice workbook, 6. finding factors, 7. prime and composite, 8. grade 6 factoring worksheet.

6.4 General Strategy for Factoring Polynomials

Learning objectives.

By the end of this section, you will be able to:

• Recognize and use the appropriate method to factor a polynomial completely

Recognize and Use the Appropriate Method to Factor a Polynomial Completely

You have now become acquainted with all the methods of factoring that you will need in this course. The following chart summarizes all the factoring methods we have covered, and outlines a strategy you should use when factoring polynomials.

General Strategy for Factoring Polynomials

Use a general strategy for factoring polynomials..

• Step 1. Is there a greatest common factor? Factor it out.
• Is it a sum? Of squares? Sums of squares do not factor. Of cubes? Use the sum of cubes pattern.
• Is it a difference? Of squares? Factor as the product of conjugates. Of cubes? Use the difference of cubes pattern.
• Is it of the form x 2 + b x + c ? x 2 + b x + c ? Undo FOIL.
• Is it of the form a x 2 + b x + c ? a x 2 + b x + c ? If a and c are squares, check if it fits the trinomial square pattern. Use the trial and error or “ac” method.
• Use the grouping method.
• Step 3. Check. Is it factored completely? Do the factors multiply back to the original polynomial?

Remember, a polynomial is completely factored if, other than monomials, its factors are prime !

Example 6.35

Factor completely: 7 x 3 − 21 x 2 − 70 x . 7 x 3 − 21 x 2 − 70 x .

Try It 6.69

Factor completely: 8 y 3 + 16 y 2 − 24 y . 8 y 3 + 16 y 2 − 24 y .

Try It 6.70

Factor completely: 5 y 3 − 15 y 2 − 270 y . 5 y 3 − 15 y 2 − 270 y .

Be careful when you are asked to factor a binomial as there are several options!

Example 6.36

Factor completely: 24 y 2 − 150 . 24 y 2 − 150 .

Try It 6.71

Factor completely: 16 x 3 − 36 x . 16 x 3 − 36 x .

Try It 6.72

Factor completely: 27 y 2 − 48 . 27 y 2 − 48 .

The next example can be factored using several methods. Recognizing the trinomial squares pattern will make your work easier.

Example 6.37

Factor completely: 4 a 2 − 12 a b + 9 b 2 . 4 a 2 − 12 a b + 9 b 2 .

Try It 6.73

Factor completely: 4 x 2 + 20 x y + 25 y 2 . 4 x 2 + 20 x y + 25 y 2 .

Try It 6.74

Factor completely: 9 x 2 − 24 x y + 16 y 2 . 9 x 2 − 24 x y + 16 y 2 .

Remember, sums of squares do not factor, but sums of cubes do!

Example 6.38

Factor completely 12 x 3 y 2 + 75 x y 2 . 12 x 3 y 2 + 75 x y 2 .

Try It 6.75

Factor completely: 50 x 3 y + 72 x y . 50 x 3 y + 72 x y .

Try It 6.76

Factor completely: 27 x y 3 + 48 x y . 27 x y 3 + 48 x y .

When using the sum or difference of cubes pattern, being careful with the signs.

Example 6.39

Factor completely: 24 x 3 + 81 y 3 . 24 x 3 + 81 y 3 .

Try It 6.77

Factor completely: 250 m 3 + 432 n 3 . 250 m 3 + 432 n 3 .

Try It 6.78

Factor completely: 2 p 3 + 54 q 3 . 2 p 3 + 54 q 3 .

Example 6.40

Factor completely: 3 x 5 y − 48 x y . 3 x 5 y − 48 x y .

Try It 6.79

Factor completely: 4 a 5 b − 64 a b . 4 a 5 b − 64 a b .

Try It 6.80

Factor completely: 7 x y 5 − 7 x y . 7 x y 5 − 7 x y .

Example 6.41

Factor completely: 4 x 2 + 8 b x − 4 a x − 8 a b . 4 x 2 + 8 b x − 4 a x − 8 a b .

Try It 6.81

Factor completely: 6 x 2 − 12 x c + 6 b x − 12 b c . 6 x 2 − 12 x c + 6 b x − 12 b c .

Try It 6.82

Factor completely: 16 x 2 + 24 x y − 4 x − 6 y . 16 x 2 + 24 x y − 4 x − 6 y .

Taking out the complete GCF in the first step will always make your work easier.

Example 6.42

Factor completely: 40 x 2 y + 44 x y − 24 y . 40 x 2 y + 44 x y − 24 y .

Try It 6.83

Factor completely: 4 p 2 q − 16 p q + 12 q . 4 p 2 q − 16 p q + 12 q .

Try It 6.84

Factor completely: 6 p q 2 − 9 p q − 6 p . 6 p q 2 − 9 p q − 6 p .

When we have factored a polynomial with four terms, most often we separated it into two groups of two terms. Remember that we can also separate it into a trinomial and then one term.

Example 6.43

Factor completely: 9 x 2 − 12 x y + 4 y 2 − 49 . 9 x 2 − 12 x y + 4 y 2 − 49 .

Try It 6.85

Factor completely: 4 x 2 − 12 x y + 9 y 2 − 25 . 4 x 2 − 12 x y + 9 y 2 − 25 .

Try It 6.86

Factor completely: 16 x 2 − 24 x y + 9 y 2 − 64 . 16 x 2 − 24 x y + 9 y 2 − 64 .

Section 6.4 Exercises

Practice makes perfect.

In the following exercises, factor completely.

2 n 2 + 13 n − 7 2 n 2 + 13 n − 7

8 x 2 − 9 x − 3 8 x 2 − 9 x − 3

a 5 + 9 a 3 a 5 + 9 a 3

75 m 3 + 12 m 75 m 3 + 12 m

121 r 2 − s 2 121 r 2 − s 2

49 b 2 − 36 a 2 49 b 2 − 36 a 2

8 m 2 − 32 8 m 2 − 32

36 q 2 − 100 36 q 2 − 100

25 w 2 − 60 w + 36 25 w 2 − 60 w + 36

49 b 2 − 112 b + 64 49 b 2 − 112 b + 64

m 2 + 14 m n + 49 n 2 m 2 + 14 m n + 49 n 2

64 x 2 + 16 x y + y 2 64 x 2 + 16 x y + y 2

7 b 2 + 7 b − 42 7 b 2 + 7 b − 42

30 n 2 + 30 n + 72 30 n 2 + 30 n + 72

3 x 4 y − 81 x y 3 x 4 y − 81 x y

4 x 5 y − 32 x 2 y 4 x 5 y − 32 x 2 y

k 4 − 16 k 4 − 16

m 4 − 81 m 4 − 81

5 x 5 y 2 − 80 x y 2 5 x 5 y 2 − 80 x y 2

48 x 5 y 2 − 243 x y 2 48 x 5 y 2 − 243 x y 2

15 p q − 15 p + 12 q − 12 15 p q − 15 p + 12 q − 12

12 a b − 6 a + 10 b − 5 12 a b − 6 a + 10 b − 5

4 x 2 + 40 x + 84 4 x 2 + 40 x + 84

5 q 2 − 15 q − 90 5 q 2 − 15 q − 90

4 u 5 + 4 u 2 v 3 4 u 5 + 4 u 2 v 3

5 m 4 n + 320 m n 4 5 m 4 n + 320 m n 4

4 c 2 + 20 c d + 81 d 2 4 c 2 + 20 c d + 81 d 2

25 x 2 + 35 x y + 49 y 2 25 x 2 + 35 x y + 49 y 2

10 m 4 − 6250 10 m 4 − 6250

3 v 4 − 768 3 v 4 − 768

36 x 2 y + 15 x y − 6 y 36 x 2 y + 15 x y − 6 y

60 x 2 y − 75 x y + 30 y 60 x 2 y − 75 x y + 30 y

8 x 3 − 27 y 3 8 x 3 − 27 y 3

64 x 3 + 125 y 3 64 x 3 + 125 y 3

y 6 − 1 y 6 − 1

y 6 + 1 y 6 + 1

9 x 2 − 6 x y + y 2 − 49 9 x 2 − 6 x y + y 2 − 49

16 x 2 − 24 x y + 9 y 2 − 64 16 x 2 − 24 x y + 9 y 2 − 64

( 3 x + 1 ) 2 − 6 ( 3 x + 1 ) + 9 ( 3 x + 1 ) 2 − 6 ( 3 x + 1 ) + 9

( 4 x − 5 ) 2 − 7 ( 4 x − 5 ) + 12 ( 4 x − 5 ) 2 − 7 ( 4 x − 5 ) + 12

Writing Exercises

Explain what it mean to factor a polynomial completely.

The difference of squares y 4 − 625 y 4 − 625 can be factored as ( y 2 − 25 ) ( y 2 + 25 ) . ( y 2 − 25 ) ( y 2 + 25 ) . But it is not completely factored. What more must be done to completely factor.

Of all the factoring methods covered in this chapter (GCF, grouping, undo FOIL, ‘ac’ method, special products) which is the easiest for you? Which is the hardest? Explain your answers.

Create three factoring problems that would be good test questions to measure your knowledge of factoring. Show the solutions.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ On a scale of 1-10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Intermediate Algebra 2e
• Publication date: May 6, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/6-4-general-strategy-for-factoring-polynomials

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Factoring Calculator

Enter the expression you want to factor in the editor.

Difference of Squares : a 2   –   b 2   =   ( a   +   b ) ( a   –   b )

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.1: Greatest Common Factor and Factor by Grouping

• Last updated
• Save as PDF
• Page ID 18970

Learning Objectives

By the end of this section, you will be able to:

• Find the greatest common factor of two or more expressions
• Factor the greatest common factor from a polynomial
• Factor by grouping

BE PREPARED

Before you get started, take this readiness quiz.

• Factor 56 into primes. If you missed this problem, review Example 1.2.19 .
• Find the least common multiple of 18 and 24. If you missed this problem, review Example 1.2.28 .
• Simplify \(−3(6a+11)\). If you missed this problem, review Example 1.10.40 .

Find the Greatest Common Factor of Two or More Expressions

Earlier we multiplied factors together to get a product. Now, we will be reversing this process; we will start with a product and then break it down into its factors. Splitting a product into factors is called factoring .

We have learned how to factor numbers to find the least common multiple (LCM) of two or more numbers. Now we will factor expressions and find the greatest common factor of two or more expressions. The method we use is similar to what we used to find the LCM.

GREATEST COMMON FACTOR

The greatest common factor (GCF) of two or more expressions is the largest expression that is a factor of all the expressions.

First we’ll find the GCF of two numbers.

Example \(\PageIndex{1}\): HOW TO FIND THE GREATEST COMMON FACTOR OF TWO OR MORE EXPRESSIONS

Find the GCF of 54 and 36.

Notice that, because the GCF is a factor of both numbers, 54 and 36 can be written as multiples of 18.

\[\begin{array}{l}{54=18 \cdot 3} \\ {36=18 \cdot 2}\end{array}\]

Try It \(\PageIndex{2}\)

Find the GCF of 48 and 80.

Try It \(\PageIndex{3}\)

Find the GCF of 18 and 40.

We summarize the steps we use to find the GCF below.

Find the Greatest Common Factor (GCF) of two expressions.

• Step 1. Factor each coefficient into primes. Write all variables with exponents in expanded form.
• Step 2. List all factors—matching common factors in a column. In each column, circle the common factors.
• Step 3. Bring down the common factors that all expressions share.
• Step 4. Multiply the factors.

In the first example, the GCF was a constant. In the next two examples, we will get variables in the greatest common factor.

Example \(\PageIndex{4}\)

Find the greatest common factor of \(27x^3\) and \(18x^4\).

Try It \(\PageIndex{5}\)

Find the GCF: \(12 x^{2}, 18 x^{3}\)

Try It \(\PageIndex{6}\)

Find the GCF: \(16 y^{2}, 24 y^{3}\)

Example \(\PageIndex{7}\)

Find the GCF of \(4 x^{2} y, 6 x y^{3}\)

Try It \(\PageIndex{8}\)

Find the GCF: \(6 a b^{4}, 8 a^{2} b\)

Try It \(\PageIndex{9}\)

Find the GCF: \(9 m^{5} n^{2}, 12 m^{3} n\)

Example \(\PageIndex{10}\)

Find the GCF of: \(21 x^{3}, 9 x^{2}, 15 x\)

Try It \(\PageIndex{11}\)

Find the greatest common factor: \(25 m^{4}, 35 m^{3}, 20 m^{2}\)

Try It \(\PageIndex{12}\)

Find the greatest common factor: \(14 x^{3}, 70 x^{2}, 105 x\)

Factor the Greatest Common Factor from a Polynomial

Just like in arithmetic, where it is sometimes useful to represent a number in factored form (for example, 12 as 2·6or3·4),2·6or3·4), in algebra, it can be useful to represent a polynomial in factored form. One way to do this is by finding the GCF of all the terms. Remember, we multiply a polynomial by a monomial as follows:

\[\begin{array}{cc}{2(x+7)} & {\text { factors }} \\ {2 \cdot x+2 \cdot 7} & { } \\ {2 x+14} & {\text { product }}\end{array}\]

Now we will start with a product, like \(2 x+14\), and end with its factors, 2\((x+7)\). To do this we apply the Distributive Property “in reverse.”

We state the Distributive Property here just as you saw it in earlier chapters and “in reverse.”

DISTRIBUTIVE PROPERTY

If \(a,b,c\) are real numbers, then

\[a(b+c)=a b+a c \quad\text{ and }\quad a b+a c=a(b+c)\]

The form on the left is used to multiply. The form on the right is used to factor.

So how do you use the Distributive Property to factor a polynomial? You just find the GCF of all the terms and write the polynomial as a product!

Example \(\PageIndex{13}\): HOW TO FACTOR THE GREATEST COMMON FACTOR FROM A POLYNOMIAL

Factor: \(4 x+12\)

Try It \(\PageIndex{14}\)

Factor: \(6 a+24\)

Try It \(\PageIndex{15}\)

Factor: \(2 b+14\)

Factor the greatest common factor from a polynomial.

Step 1. Find the GCF of all the terms of the polynomial.

Step 2. Rewrite each term as a product using the GCF.

Step 3. Use the “reverse” Distributive Property to factor the expression.

Step 4. Check by multiplying the factors.

FACTOR AS A NOUN AND A VERB

We use “factor” as both a noun and a verb.

Example \(\PageIndex{16}\)

Factor: \(5 a+5\)

Try It \(\PageIndex{17}\)

Factor: \(14 x+14\)

\(14(x+1)\)

Try It \(\PageIndex{18}\)

Factor: \(12 p+12\)

\(12(p+1)\)

The expressions in the next example have several factors in common. Remember to write the GCF as the product of all the common factors.

Example \(\PageIndex{19}\)

Factor: \(12 x-60\)

Try It \(\PageIndex{20}\)

Factor: \(18 u-36\)

Try It \(\PageIndex{21}\)

Factor: \(30 y-60\)

\(30(y-2)\)

Now we’ll factor the greatest common factor from a trinomial. We start by finding the GCF of all three terms.

Example \(\PageIndex{22}\)

Factor: \(4 y^{2}+24 y+28\)

We start by finding the GCF of all three terms.

Try It \(\PageIndex{23}\)

Factor: \(5 x^{2}-25 x+15\)

\(5\left(x^{2}-5 x+3\right)\)

Try It \(\PageIndex{24}\)

Factor: \(3 y^{2}-12 y+27\)

\(3\left(y^{2}-4 y+9\right)\)

Example \(\PageIndex{25}\)

Factor: \(5 x^{3}-25 x^{2}\)

Try It \(\PageIndex{26}\)

Factor: \(2 x^{3}+12 x^{2}\)

\(2x^2(x+6)\)

Try It \(\PageIndex{27}\)

Factor: \(6 y^{3}-15 y^{2}\)

\(3y^2(2y-5)\)

Example \(\PageIndex{28}\)

Factor: \(21 x^{3}-9 x^{2}+15 x\)

In a previous example we found the GCF of \(21 x^{3}, 9 x^{2}, 15 x\) to be 3\(x\).

Try It \(\PageIndex{29}\)

Factor: \(20 x^{3}-10 x^{2}+14 x\)

\(2x(10x^2-5x+7)\)

Try It \(\PageIndex{30}\)

Factor: \(24 y^{3}-12 y^{2}-20 y\)

\(4y(6y^2-3y-5)\)

Example \(\PageIndex{31}\)

Factor: \(8 m^{3}-12 m^{2} n+20 m n^{2}\)

Try It \(\PageIndex{32}\)

Factor: \(9 x y^{2}+6 x^{2} y^{2}+21 y^{3}\)

\(3y^2(3x+2x^2+7y)\)

Try It \(\PageIndex{33}\)

Factor: \(3 p^{3}-6 p^{2} q+9 p q^{3}\)

\(3p(p^2-2pq+3q^2\)

When the leading coefficient is negative, we factor the negative out as part of the GCF.

Example \(\PageIndex{34}\)

Factor: \(-8 y-24\)

When the leading coefficient is negative, the GCF will be negative.

Try It \(\PageIndex{35}\)

Factor: \(-16 z-64\)

\(-16(z+4)\)

Try It \(\PageIndex{36}\)

Factor: \(-9 y-27\)

\(-9(y+3)\)

Example \(\PageIndex{37}\)

Factor: \(-6 a^{2}+36 a\)

The leading coefficient is negative, so the GCF will be negative.?

Try It \(\PageIndex{38}\)

Factor: \(-4 b^{2}+16 b\)

\(-4b(b-4)\)

Try It \(\PageIndex{39}\)

Factor: \(-7 a^{2}+21 a\)

\(-7a(a-3)\)

Example \(\PageIndex{40}\)

Factor: \(5 q(q+7)-6(q+7)\)

The GCF is the binomial q+7.

Try It \(\PageIndex{41}\)

Factor: \(4 m(m+3)-7(m+3)\)

\( (m+3)(4m-7) \)

Try It \(\PageIndex{42}\)

Factor: \(8 n(n-4)+5(n-4)\)

\( (n-4)(8n+5) \)

Factor by Grouping

When there is no common factor of all the terms of a polynomial, look for a common factor in just some of the terms. When there are four terms, a good way to start is by separating the polynomial into two parts with two terms in each part. Then look for the GCF in each part. If the polynomial can be factored, you will find a common factor emerges from both parts.

(Not all polynomials can be factored. Just like some numbers are prime, some polynomials are prime.)

Example \(\PageIndex{43}\)

Factor: \(x y+3 y+2 x+6\)

Try It \(\PageIndex{44}\)

Factor: \(x y+8 y+3 x+24\)

\( (x+8)(y+3) \)

Try It \(\PageIndex{45}\)

Factor: \(a b+7 b+8 a+56\)

\( (a+7)(b+8) \)

Factor by grouping.

Step 1. Group terms with common factors.

Step 2. Factor out the common factor in each group.

Step 3. Factor the common factor from the expression.

Example \(\PageIndex{46}\)

Factor: \(x^{2}+3 x-2 x-6\)

\(\begin{array}{ll}{\text { There is no GCF in all four terms. }} & x^{2}+3 x-2 x-6\\ {\text { Separate into two parts. }} & \underbrace{x^{2}+3 x}\underbrace{-2 x-6} \\ \\ {\text { Factor the GCF from both parts. Be careful }} \\ {\text { with the signs when factoring the GCF from }}& \begin{array}{c}{x(x+3)-2(x+3)} \\ {(x+3)(x-2)}\end{array} \\ {\text { the last two terms. }} \\ \\ \text { Check on your own by multinlying. }\end{array}\)

Try It \(\PageIndex{47}\)

Factor: \(x^{2}+2 x-5 x-10\)

\( (x-5)(x+2) \)

Try It \(\PageIndex{48}\)

Factor: \(y^{2}+4 y-7 y-28\)

\( (y+4)(y-7) \)

MEDIA ACCESS ADDITIONAL ONLINE RESOURCES

Access these online resources for additional instruction and practice with greatest common factors (GFCs) and factoring by grouping.

• Greatest Common Factor (GCF)
• Factoring Out the GCF of a Binomial
• Greatest Common Factor (GCF) of Polynomials

Cookies! We use them. Om Nom Nom ...

Allene W. Leflore

Rebecca Geach

Our writers always follow the customers' requirements very carefully