statistical treatment thesis definition

Research Paper Statistical Treatment of Data: A Primer

We can all agree that analyzing and presenting data effectively in a research paper is critical, yet often challenging.

This primer on statistical treatment of data will equip you with the key concepts and procedures to accurately analyze and clearly convey research findings.

You'll discover the fundamentals of statistical analysis and data management, the common quantitative and qualitative techniques, how to visually represent data, and best practices for writing the results - all framed specifically for research papers.

If you are curious on how AI can help you with statistica analysis for research, check Hepta AI .

Introduction to Statistical Treatment in Research

Statistical analysis is a crucial component of both quantitative and qualitative research. Properly treating data enables researchers to draw valid conclusions from their studies. This primer provides an introductory guide to fundamental statistical concepts and methods for manuscripts.

Understanding the Importance of Statistical Treatment

Careful statistical treatment demonstrates the reliability of results and ensures findings are grounded in robust quantitative evidence. From determining appropriate sample sizes to selecting accurate analytical tests, statistical rigor adds credibility. Both quantitative and qualitative papers benefit from precise data handling.

Objectives of the Primer

This primer aims to equip researchers with best practices for:

Statistical tools to apply during different research phases

Techniques to manage, analyze, and present data

Methods to demonstrate the validity and reliability of measurements

By covering fundamental concepts ranging from descriptive statistics to measurement validity, it enables both novice and experienced researchers to incorporate proper statistical treatment.

Navigating the Primer: Key Topics and Audience

The primer spans introductory topics including:

Research planning and design

Data collection, management, analysis

Result presentation and interpretation

While useful for researchers at any career stage, earlier-career scientists with limited statistical exposure will find it particularly valuable as they prepare manuscripts.

How do you write a statistical method in a research paper?

Statistical methods are a critical component of research papers, allowing you to analyze, interpret, and draw conclusions from your study data. When writing the statistical methods section, you need to provide enough detail so readers can evaluate the appropriateness of the methods you used.

Here are some key things to include when describing statistical methods in a research paper:

Type of Statistical Tests Used

Specify the types of statistical tests performed on the data, including:

Parametric vs nonparametric tests

Descriptive statistics (means, standard deviations)

Inferential statistics (t-tests, ANOVA, regression, etc.)

Statistical significance level (often p < 0.05)

For example: We used t-tests and one-way ANOVA to compare means across groups, with statistical significance set at p < 0.05.

Analysis of Subgroups

If you examined subgroups or additional variables, describe the methods used for these analyses.

For example: We stratified data by gender and used chi-square tests to analyze differences between subgroups.

Software and Versions

List any statistical software packages used for analysis, including version numbers. Common programs include SPSS, SAS, R, and Stata.

For example: Data were analyzed using SPSS version 25 (IBM Corp, Armonk, NY).

The key is to give readers enough detail to assess the rigor and appropriateness of your statistical methods. The methods should align with your research aims and design. Keep explanations clear and concise using consistent terminology throughout the paper.

What are the 5 statistical treatment in research?

The five most common statistical treatments used in academic research papers include:

The mean, or average, is used to describe the central tendency of a dataset. It provides a singular value that represents the middle of a distribution of numbers. Calculating means allows researchers to characterize typical observations within a sample.

Standard Deviation

Standard deviation measures the amount of variability in a dataset. A low standard deviation indicates observations are clustered closely around the mean, while a high standard deviation signifies the data is more spread out. Reporting standard deviations helps readers contextualize means.

Regression Analysis

Regression analysis models the relationship between independent and dependent variables. It generates an equation that predicts changes in the dependent variable based on changes in the independents. Regressions are useful for hypothesizing causal connections between variables.

Hypothesis Testing

Hypothesis testing evaluates assumptions about population parameters based on statistics calculated from a sample. Common hypothesis tests include t-tests, ANOVA, and chi-squared. These quantify the likelihood of observed differences being due to chance.

Sample Size Determination

Sample size calculations identify the minimum number of observations needed to detect effects of a given size at a desired statistical power. Appropriate sampling ensures studies can uncover true relationships within the constraints of resource limitations.

These five statistical analysis methods form the backbone of most quantitative research processes. Correct application allows researchers to characterize data trends, model predictive relationships, and make probabilistic inferences regarding broader populations. Expertise in these techniques is fundamental for producing valid, reliable, and publishable academic studies.

How do you know what statistical treatment to use in research?

The selection of appropriate statistical methods for the treatment of data in a research paper depends on three key factors:

The Aim and Objective of the Study

The aim and objectives that the study seeks to achieve will determine the type of statistical analysis required.

Descriptive research presenting characteristics of the data may only require descriptive statistics like measures of central tendency (mean, median, mode) and dispersion (range, standard deviation).

Studies aiming to establish relationships or differences between variables need inferential statistics like correlation, t-tests, ANOVA, regression etc.

Predictive modeling research requires methods like regression, discriminant analysis, logistic regression etc.

Thus, clearly identifying the research purpose and objectives is the first step in planning appropriate statistical treatment.

Type and Distribution of Data

The type of data (categorical, numerical) and its distribution (normal, skewed) also guide the choice of statistical techniques.

Parametric tests have assumptions related to normality and homogeneity of variance.

Non-parametric methods are distribution-free and better suited for non-normal or categorical data.

Testing data distribution and characteristics is therefore vital.

Nature of Observations

Statistical methods also differ based on whether the observations are paired or unpaired.

Analyzing changes within one group requires paired tests like paired t-test, Wilcoxon signed-rank test etc.

Comparing between two or more independent groups needs unpaired tests like independent t-test, ANOVA, Kruskal-Wallis test etc.

Thus the nature of observations is pivotal in selecting suitable statistical analyses.

In summary, clearly defining the research objectives, testing the collected data, and understanding the observational units guides proper statistical treatment and interpretation.

What is statistical techniques in research paper?

Statistical methods are essential tools in scientific research papers. They allow researchers to summarize, analyze, interpret and present data in meaningful ways.

Some key statistical techniques used in research papers include:

Descriptive statistics: These provide simple summaries of the sample and the measures. Common examples include measures of central tendency (mean, median, mode), measures of variability (range, standard deviation) and graphs (histograms, pie charts).

Inferential statistics: These help make inferences and predictions about a population from a sample. Common techniques include estimation of parameters, hypothesis testing, correlation and regression analysis.

Analysis of variance (ANOVA): This technique allows researchers to compare means across multiple groups and determine statistical significance.

Factor analysis: This technique identifies underlying relationships between variables and latent constructs. It allows reducing a large set of variables into fewer factors.

Structural equation modeling: This technique estimates causal relationships using both latent and observed factors. It is widely used for testing theoretical models in social sciences.

Proper statistical treatment and presentation of data are crucial for the integrity of any quantitative research paper. Statistical techniques help establish validity, account for errors, test hypotheses, build models and derive meaningful insights from the research.

Fundamental Concepts and Data Management

Exploring basic statistical terms.

Understanding key statistical concepts is essential for effective research design and data analysis. This includes defining key terms like:

Statistics : The science of collecting, organizing, analyzing, and interpreting numerical data to draw conclusions or make predictions.

Variables : Characteristics or attributes of the study participants that can take on different values.

Measurement : The process of assigning numbers to variables based on a set of rules.

Sampling : Selecting a subset of a larger population to estimate characteristics of the whole population.

Data types : Quantitative (numerical) or qualitative (categorical) data.

Descriptive vs. inferential statistics : Descriptive statistics summarize data while inferential statistics allow making conclusions from the sample to the larger population.

Ensuring Validity and Reliability in Measurement

When selecting measurement instruments, it is critical they demonstrate:

Validity : The extent to which the instrument measures what it intends to measure.

Reliability : The consistency of measurement over time and across raters.

Researchers should choose instruments aligned to their research questions and study methodology .

Data Management Essentials

Proper data management requires:

Ethical collection procedures respecting autonomy, justice, beneficence and non-maleficence.

Handling missing data through deletion, imputation or modeling procedures.

Data cleaning by identifying and fixing errors, inconsistencies and duplicates.

Data screening via visual inspection and statistical methods to detect anomalies.

Data Management Techniques and Ethical Considerations

Ethical data management includes:

Obtaining informed consent from all participants.

Anonymization and encryption to protect privacy.

Secure data storage and transfer procedures.

Responsible use of statistical tools free from manipulation or misrepresentation.

Adhering to ethical guidelines preserves public trust in the integrity of research.

Statistical Methods and Procedures

This section provides an introduction to key quantitative analysis techniques and guidance on when to apply them to different types of research questions and data.

Descriptive Statistics and Data Summarization

Descriptive statistics summarize and organize data characteristics such as central tendency, variability, and distributions. Common descriptive statistical methods include:

Measures of central tendency (mean, median, mode)

Measures of variability (range, interquartile range, standard deviation)

Graphical representations (histograms, box plots, scatter plots)

Frequency distributions and percentages

These methods help describe and summarize the sample data so researchers can spot patterns and trends.

Inferential Statistics for Generalizing Findings

While descriptive statistics summarize sample data, inferential statistics help generalize findings to the larger population. Common techniques include:

Hypothesis testing with t-tests, ANOVA

Correlation and regression analysis

Nonparametric tests

These methods allow researchers to draw conclusions and make predictions about the broader population based on the sample data.

Selecting the Right Statistical Tools

Choosing the appropriate analyses involves assessing:

The research design and questions asked

Type of data (categorical, continuous)

Data distributions

Statistical assumptions required

Matching the correct statistical tests to these elements helps ensure accurate results.

Statistical Treatment of Data for Quantitative Research

For quantitative research, common statistical data treatments include:

Testing data reliability and validity

Checking assumptions of statistical tests

Transforming non-normal data

Identifying and handling outliers

Applying appropriate analyses for the research questions and data type

Examples and case studies help demonstrate correct application of statistical tests.

Approaches to Qualitative Data Analysis

Qualitative data is analyzed through methods like:

Thematic analysis

Content analysis

Discourse analysis

Grounded theory

These help researchers discover concepts and patterns within non-numerical data to derive rich insights.

Data Presentation and Research Method

Crafting effective visuals for data presentation.

When presenting analyzed results and statistics in a research paper, well-designed tables, graphs, and charts are key for clearly showcasing patterns in the data to readers. Adhering to formatting standards like APA helps ensure professional data presentation. Consider these best practices:

Choose the appropriate visual type based on the type of data and relationship being depicted. For example, bar charts for comparing categorical data, line graphs to show trends over time.

Label the x-axis, y-axis, legends clearly. Include informative captions.

Use consistent, readable fonts and sizing. Avoid clutter with unnecessary elements. White space can aid readability.

Order data logically. Such as largest to smallest values, or chronologically.

Include clear statistical notations, like error bars, where applicable.

Following academic standards for visuals lends credibility while making interpretation intuitive for readers.

Writing the Results Section with Clarity

When writing the quantitative Results section, aim for clarity by balancing statistical reporting with interpretation of findings. Consider this structure:

Open with an overview of the analysis approach and measurements used.

Break down results by logical subsections for each hypothesis, construct measured etc.

Report exact statistics first, followed by interpretation of their meaning. For example, “Participants exposed to the intervention had significantly higher average scores (M=78, SD=3.2) compared to controls (M=71, SD=4.1), t(115)=3.42, p = 0.001. This suggests the intervention was highly effective for increasing scores.”

Use present verb tense. And scientific, formal language.

Include tables/figures where they aid understanding or visualization.

Writing results clearly gives readers deeper context around statistical findings.

Highlighting Research Method and Design

With a results section full of statistics, it's vital to communicate key aspects of the research method and design. Consider including:

Brief overview of study variables, materials, apparatus used. Helps reproducibility.

Descriptions of study sampling techniques, data collection procedures. Supports transparency.

Explanations around approaches to measurement, data analysis performed. Bolsters methodological rigor.

Noting control variables, attempts to limit biases etc. Demonstrates awareness of limitations.

Covering these methodological details shows readers the care taken in designing the study and analyzing the results obtained.

Acknowledging Limitations and Addressing Biases

Honestly recognizing methodological weaknesses and limitations goes a long way in establishing credibility within the published discussion section. Consider transparently noting:

Measurement errors and biases that may have impacted findings.

Limitations around sampling methods that constrain generalizability.

Caveats related to statistical assumptions, analysis techniques applied.

Attempts made to control/account for biases and directions for future research.

Rather than detracting value, acknowledging limitations demonstrates academic integrity regarding the research performed. It also gives readers deeper insight into interpreting the reported results and findings.

Conclusion: Synthesizing Statistical Treatment Insights

Recap of statistical treatment fundamentals.

Statistical treatment of data is a crucial component of high-quality quantitative research. Proper application of statistical methods and analysis principles enables valid interpretations and inferences from study data. Key fundamentals covered include:

Descriptive statistics to summarize and describe the basic features of study data

Inferential statistics to make judgments of the probability and significance based on the data

Using appropriate statistical tools aligned to the research design and objectives

Following established practices for measurement techniques, data collection, and reporting

Adhering to these core tenets ensures research integrity and allows findings to withstand scientific scrutiny.

Key Takeaways for Research Paper Success

When incorporating statistical treatment into a research paper, keep these best practices in mind:

Clearly state the research hypothesis and variables under examination

Select reliable and valid quantitative measures for assessment

Determine appropriate sample size to achieve statistical power

Apply correct analytical methods suited to the data type and distribution

Comprehensively report methodology procedures and statistical outputs

Interpret results in context of the study limitations and scope

Following these guidelines will bolster confidence in the statistical treatment and strengthen the research quality overall.

Encouraging Continued Learning and Application

As statistical techniques continue advancing, it is imperative for researchers to actively further their statistical literacy. Regularly reviewing new methodological developments and learning advanced tools will augment analytical capabilities. Persistently putting enhanced statistical knowledge into practice through research projects and manuscript preparations will cement competencies. Statistical treatment mastery is a journey requiring persistent effort, but one that pays dividends in research proficiency.

Antonio Carlos Filho @acfilho_dev

Community Blog

Keep up-to-date on postgraduate related issues with our quick reads written by students, postdocs, professors and industry leaders.

Statistical Treatment of Data – Explained & Example

• By DiscoverPhDs
• September 8, 2020

‘Statistical treatment’ is when you apply a statistical method to a data set to draw meaning from it. Statistical treatment can be either descriptive statistics, which describes the relationship between variables in a population, or inferential statistics, which tests a hypothesis by making inferences from the collected data.

Introduction to Statistical Treatment in Research

Every research student, regardless of whether they are a biologist, computer scientist or psychologist, must have a basic understanding of statistical treatment if their study is to be reliable.

This is because designing experiments and collecting data are only a small part of conducting research. The other components, which are often not so well understood by new researchers, are the analysis, interpretation and presentation of the data. This is just as important, if not more important, as this is where meaning is extracted from the study .

What is Statistical Treatment of Data?

Statistical treatment of data is when you apply some form of statistical method to a data set to transform it from a group of meaningless numbers into meaningful output.

Statistical treatment of data involves the use of statistical methods such as:

• regression,
• conditional probability,
• standard deviation and
• distribution range.

These statistical methods allow us to investigate the statistical relationships between the data and identify possible errors in the study.

In addition to being able to identify trends, statistical treatment also allows us to organise and process our data in the first place. This is because when carrying out statistical analysis of our data, it is generally more useful to draw several conclusions for each subgroup within our population than to draw a single, more general conclusion for the whole population. However, to do this, we need to be able to classify the population into different subgroups so that we can later break down our data in the same way before analysing it.

Statistical Treatment Example – Quantitative Research

For a statistical treatment of data example, consider a medical study that is investigating the effect of a drug on the human population. As the drug can affect different people in different ways based on parameters such as gender, age and race, the researchers would want to group the data into different subgroups based on these parameters to determine how each one affects the effectiveness of the drug. Categorising the data in this way is an example of performing basic statistical treatment.

Type of Errors

A fundamental part of statistical treatment is using statistical methods to identify possible outliers and errors. No matter how careful we are, all experiments are subject to inaccuracies resulting from two types of errors: systematic errors and random errors.

Systematic errors are errors associated with either the equipment being used to collect the data or with the method in which they are used. Random errors are errors that occur unknowingly or unpredictably in the experimental configuration, such as internal deformations within specimens or small voltage fluctuations in measurement testing instruments.

These experimental errors, in turn, can lead to two types of conclusion errors: type I errors and type II errors . A type I error is a false positive which occurs when a researcher rejects a true null hypothesis. On the other hand, a type II error is a false negative which occurs when a researcher fails to reject a false null hypothesis.

Find out the different dissertation and thesis binding options, which is best, advantages and disadvantages, typical costs, popular services and more.

The purpose of research is to enhance society by advancing knowledge through developing scientific theories, concepts and ideas – find out more on what this involves.

This post gives you the best questions to ask at a PhD interview, to help you work out if your potential supervisor and lab is a good fit for you.

Join thousands of other students and stay up to date with the latest PhD programmes, funding opportunities and advice.

Browse PhDs Now

A well written figure legend will explain exactly what a figure means without having to refer to the main text. Our guide explains how to write one.

You’ll come across many academics with PhD, some using the title of Doctor and others using Professor. This blog post helps you understand the differences.

Priya’s a 1st year PhD student University College Dublin. Her project involves investigating a novel seaweed-ensiling process as an alternative to drying to preserve seaweeds nutritional and monetary value.

Dr Manning gained his PhD in Chemical Engineering from the University of Sheffield in 2019. He is now a postdoc researcher studying molecular simulations on nanomaterials at the University of Bath.

Join Thousands of Students

• Foundations
• Write Paper

Search form

• Experiments
• Anthropology
• Self-Esteem
• Social Anxiety
• Statistics >

Statistical Treatment Of Data

Statistical treatment of data is essential in order to make use of the data in the right form. Raw data collection is only one aspect of any experiment; the organization of data is equally important so that appropriate conclusions can be drawn. This is what statistical treatment of data is all about.

This article is a part of the guide:

• Statistics Tutorial
• Branches of Statistics
• Statistical Analysis
• Discrete Variables

Browse Full Outline

• 1 Statistics Tutorial
• 2.1 What is Statistics?
• 2.2 Learn Statistics
• 3 Probability
• 4 Branches of Statistics
• 5 Descriptive Statistics
• 6 Parameters
• 7.1 Data Treatment
• 7.2 Raw Data
• 7.3 Outliers
• 7.4 Data Output
• 8 Statistical Analysis
• 9 Measurement Scales
• 10 Variables and Statistics
• 11 Discrete Variables

There are many techniques involved in statistics that treat data in the required manner. Statistical treatment of data is essential in all experiments, whether social, scientific or any other form. Statistical treatment of data greatly depends on the kind of experiment and the desired result from the experiment.

For example, in a survey regarding the election of a Mayor, parameters like age, gender, occupation, etc. would be important in influencing the person's decision to vote for a particular candidate. Therefore the data needs to be treated in these reference frames.

An important aspect of statistical treatment of data is the handling of errors. All experiments invariably produce errors and noise. Both systematic and random errors need to be taken into consideration.

Depending on the type of experiment being performed, Type-I and Type-II errors also need to be handled. These are the cases of false positives and false negatives that are important to understand and eliminate in order to make sense from the result of the experiment.

Treatment of Data and Distribution

Trying to classify data into commonly known patterns is a tremendous help and is intricately related to statistical treatment of data. This is because distributions such as the normal probability distribution occur very commonly in nature that they are the underlying distributions in most medical, social and physical experiments.

Therefore if a given sample size is known to be normally distributed, then the statistical treatment of data is made easy for the researcher as he would already have a lot of back up theory in this aspect. Care should always be taken, however, not to assume all data to be normally distributed, and should always be confirmed with appropriate testing.

Statistical treatment of data also involves describing the data. The best way to do this is through the measures of central tendencies like mean , median and mode . These help the researcher explain in short how the data are concentrated. Range, uncertainty and standard deviation help to understand the distribution of the data. Therefore two distributions with the same mean can have wildly different standard deviation, which shows how well the data points are concentrated around the mean.

Statistical treatment of data is an important aspect of all experimentation today and a thorough understanding is necessary to conduct the right experiments with the right inferences from the data obtained.

• Psychology 101
• Flags and Countries
• Capitals and Countries

Siddharth Kalla (Apr 10, 2009). Statistical Treatment Of Data. Retrieved Jun 07, 2024 from Explorable.com: https://explorable.com/statistical-treatment-of-data

You Are Allowed To Copy The Text

The text in this article is licensed under the Creative Commons-License Attribution 4.0 International (CC BY 4.0) .

This means you're free to copy, share and adapt any parts (or all) of the text in the article, as long as you give appropriate credit and provide a link/reference to this page.

That is it. You don't need our permission to copy the article; just include a link/reference back to this page. You can use it freely (with some kind of link), and we're also okay with people reprinting in publications like books, blogs, newsletters, course-material, papers, wikipedia and presentations (with clear attribution).

Want to stay up to date? Follow us!

Save this course for later.

Don't have time for it all now? No problem, save it as a course and come back to it later.

Footer bottom

• Privacy Policy

• Subscribe to our RSS Feed
• Like us on Facebook
• Follow us on Twitter

Statistical Methods in Theses: Guidelines and Explanations

Signed August 2018 Naseem Al-Aidroos, PhD, Christopher Fiacconi, PhD Deborah Powell, PhD, Harvey Marmurek, PhD, Ian Newby-Clark, PhD, Jeffrey Spence, PhD, David Stanley, PhD, Lana Trick, PhD

Version:  2.00

This document is an organizational aid, and workbook, for students. We encourage students to take this document to meetings with their advisor and committee. This guide should enhance a committee’s ability to assess key areas of a student’s work. 

In recent years a number of well-known and apparently well-established findings have  failed to replicate , resulting in what is commonly referred to as the replication crisis. The APA Publication Manual 6 th Edition notes that “The essence of the scientific method involves observations that can be repeated and verified by others.” (p. 12). However, a systematic investigation of the replicability of psychology findings published in  Science  revealed that over half of psychology findings do not replicate (see a related commentary in  Nature ). Even more disturbing, a  Bayesian reanalysis of the reproducibility project  showed that 64% of studies had sample sizes so small that strong evidence for or against the null or alternative hypotheses did not exist. Indeed, Morey and Lakens (2016) concluded that most of psychology is statistically unfalsifiable due to small sample sizes and correspondingly low power (see  article ). Our discipline’s reputation is suffering. News of the replication crisis has reached the popular press (e.g.,  The Atlantic ,   The Economist ,   Slate , Last Week Tonight ).

An increasing number of psychologists have responded by promoting new research standards that involve open science and the elimination of  Questionable Research Practices . The open science perspective is made manifest in the  Transparency and Openness Promotion (TOP) guidelines  for journal publications. These guidelines were adopted some time ago by the  Association for Psychological Science . More recently, the guidelines were adopted by American Psychological Association journals ( see details ) and journals published by Elsevier ( see details ). It appears likely that, in the very near future, most journals in psychology will be using an open science approach. We strongly advise readers to take a moment to inspect the  TOP Guidelines Summary Table . 

A key aspect of open science and the TOP guidelines is the sharing of data associated with published research (with respect to medical research, see point #35 in the  World Medical Association Declaration of Helsinki ). This practice is viewed widely as highly important. Indeed, open science is recommended by  all G7 science ministers . All Tri-Agency grants must include a data-management plan that includes plans for sharing: “ research data resulting from agency funding should normally be preserved in a publicly accessible, secure and curated repository or other platform for discovery and reuse by others.”  Moreover, a 2017 editorial published in the  New England Journal of Medicine announced that the  International Committee of Medical Journal Editors believes there is  “an ethical obligation to responsibly share data.”  As of this writing,  60% of highly ranked psychology journals require or encourage data sharing .

The increasing importance of demonstrating that findings are replicable is reflected in calls to make replication a requirement for the promotion of faculty (see details in  Nature ) and experts in open science are now refereeing applications for tenure and promotion (see details at the  Center for Open Science  and  this article ). Most dramatically, in one instance, a paper resulting from a dissertation was retracted due to misleading findings attributable to Questionable Research Practices. Subsequent to the retraction, the Ohio State University’s Board of Trustees unanimously revoked the PhD of the graduate student who wrote the dissertation ( see details ). Thus, the academic environment is changing and it is important to work toward using new best practices in lieu of older practices—many of which are synonymous with Questionable Research Practices. Doing so should help you avoid later career regrets and subsequent  public mea culpas . One way to achieve your research objectives in this new academic environment is  to incorporate replications into your research . Replications are becoming more common and there are even websites dedicated to helping students conduct replications (e.g.,  Psychology Science Accelerator ) and indexing the success of replications (e.g., Curate Science ). You might even consider conducting a replication for your thesis (subject to committee approval).

As early-career researchers, it is important to be aware of the changing academic environment. Senior principal investigators may be  reluctant to engage in open science  (see this student perspective in a  blog post  and  podcast ) and research on resistance to data sharing indicates that one of the barriers to sharing data is that researchers do not feel that they have knowledge of  how to share data online . This document is an educational aid and resource to provide students with introductory knowledge of how to participate in open science and online data sharing to start their education on these subjects. 

Guidelines and Explanations

In light of the changes in psychology, faculty members who teach statistics/methods have reviewed the literature and generated this guide for graduate students. The guide is intended to enhance the quality of student theses by facilitating their engagement in open and transparent research practices and by helping them avoid Questionable Research Practices, many of which are now deemed unethical and covered in the ethics section of textbooks.

This document is an informational tool.

How to Start

In order to follow best practices, some first steps need to be followed. Here is a list of things to do:

• Get an Open Science account. Registration at  osf.io  is easy!
• If conducting confirmatory hypothesis testing for your thesis, pre-register your hypotheses (see Section 1-Hypothesizing). The Open Science Foundation website has helpful  tutorials  and  guides  to get you going.
• Also, pre-register your data analysis plan. Pre-registration typically includes how and when you will stop collecting data, how you will deal with violations of statistical assumptions and points of influence (“outliers”), the specific measures you will use, and the analyses you will use to test each hypothesis, possibly including the analysis script. Again, there is a lot of help available for this. 

Exploratory and Confirmatory Research Are Both of Value, But Do Not Confuse the Two

We note that this document largely concerns confirmatory research (i.e., testing hypotheses). We by no means intend to devalue exploratory research. Indeed, it is one of the primary ways that hypotheses are generated for (possible) confirmation. Instead, we emphasize that it is important that you clearly indicate what of your research is exploratory and what is confirmatory. Be clear in your writing and in your preregistration plan. You should explicitly indicate which of your analyses are exploratory and which are confirmatory. Please note also that if you are engaged in exploratory research, then Null Hypothesis Significance Testing (NHST) should probably be avoided (see rationale in  Gigerenzer  (2004) and  Wagenmakers et al., (2012) ). 

This document is structured around the stages of thesis work:  hypothesizing, design, data collection, analyses, and reporting – consistent with the headings used by Wicherts et al. (2016). We also list the Questionable Research Practices associated with each stage and provide suggestions for avoiding them. We strongly advise going through all of these sections during thesis/dissertation proposal meetings because a priori decisions need to be made prior to data collection (including analysis decisions). 

To help to ensure that the student has informed the committee about key decisions at each stage, there are check boxes at the end of each section.

How to Use This Document in a Proposal Meeting

• Print off a copy of this document and take it to the proposal meeting.
• During the meeting, use the document to seek assistance from faculty to address potential problems.
• Revisit responses to issues raised by this document (especially the Analysis and Reporting Stages) when you are seeking approval to proceed to defense.

Consultation and Help Line

Note that the Center for Open Science now has a help line (for individual researchers and labs) you can call for help with open science issues. They also have training workshops. Please see their  website  for details.

• Hypothesizing
• Data Collection
• Printer-friendly version
• PDF version

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Indian J Crit Care Med
• v.25(Suppl 2); 2021 May

An Introduction to Statistics: Choosing the Correct Statistical Test

Priya ranganathan.

1 Department of Anaesthesiology, Critical Care and Pain, Tata Memorial Centre, Homi Bhabha National Institute, Mumbai, Maharashtra, India

The choice of statistical test used for analysis of data from a research study is crucial in interpreting the results of the study. This article gives an overview of the various factors that determine the selection of a statistical test and lists some statistical testsused in common practice.

How to cite this article: Ranganathan P. An Introduction to Statistics: Choosing the Correct Statistical Test. Indian J Crit Care Med 2021;25(Suppl 2):S184–S186.

In a previous article in this series, we looked at different types of data and ways to summarise them. 1 At the end of the research study, statistical analyses are performed to test the hypothesis and either prove or disprove it. The choice of statistical test needs to be carefully performed since the use of incorrect tests could lead to misleading conclusions. Some key questions help us to decide the type of statistical test to be used for analysis of study data. 2

W hat is the R esearch H ypothesis ?

Sometimes, a study may just describe the characteristics of the sample, e.g., a prevalence study. Here, the statistical analysis involves only descriptive statistics . For example, Sridharan et al. aimed to analyze the clinical profile, species distribution, and susceptibility pattern of patients with invasive candidiasis. 3 They used descriptive statistics to express the characteristics of their study sample, including mean (and standard deviation) for normally distributed data, median (with interquartile range) for skewed data, and percentages for categorical data.

Studies may be conducted to test a hypothesis and derive inferences from the sample results to the population. This is known as inferential statistics . The goal of inferential statistics may be to assess differences between groups (comparison), establish an association between two variables (correlation), predict one variable from another (regression), or look for agreement between measurements (agreement). Studies may also look at time to a particular event, analyzed using survival analysis.

A re the C omparisons M atched (P aired ) or U nmatched (U npaired )?

Observations made on the same individual (before–after or comparing two sides of the body) are usually matched or paired . Comparisons made between individuals are usually unpaired or unmatched . Data are considered paired if the values in one set of data are likely to be influenced by the other set (as can happen in before and after readings from the same individual). Examples of paired data include serial measurements of procalcitonin in critically ill patients or comparison of pain relief during sequential administration of different analgesics in a patient with osteoarthritis.

W hat are the T ype of D ata B eing M easured ?

The test chosen to analyze data will depend on whether the data are categorical (and whether nominal or ordinal) or numerical (and whether skewed or normally distributed). Tests used to analyze normally distributed data are known as parametric tests and have a nonparametric counterpart that is used for data, which is distribution-free. 4 Parametric tests assume that the sample data are normally distributed and have the same characteristics as the population; nonparametric tests make no such assumptions. Parametric tests are more powerful and have a greater ability to pick up differences between groups (where they exist); in contrast, nonparametric tests are less efficient at identifying significant differences. Time-to-event data requires a special type of analysis, known as survival analysis.

H ow M any M easurements are B eing C ompared ?

The choice of the test differs depending on whether two or more than two measurements are being compared. This includes more than two groups (unmatched data) or more than two measurements in a group (matched data).

T ests for C omparison

( Table 1 lists the tests commonly used for comparing unpaired data, depending on the number of groups and type of data. As an example, Megahed and colleagues evaluated the role of early bronchoscopy in mechanically ventilated patients with aspiration pneumonitis. 5 Patients were randomized to receive either early bronchoscopy or conventional treatment. Between groups, comparisons were made using the unpaired t test for normally distributed continuous variables, the Mann–Whitney U -test for non-normal continuous variables, and the chi-square test for categorical variables. Chowhan et al. compared the efficacy of left ventricular outflow tract velocity time integral (LVOTVTI) and carotid artery velocity time integral (CAVTI) as predictors of fluid responsiveness in patients with sepsis and septic shock. 6 Patients were divided into three groups— sepsis, septic shock, and controls. Since there were three groups, comparisons of numerical variables were done using analysis of variance (for normally distributed data) or Kruskal–Wallis test (for skewed data).

Tests for comparison of unpaired data

A common error is to use multiple unpaired t -tests for comparing more than two groups; i.e., for a study with three treatment groups A, B, and C, it would be incorrect to run unpaired t -tests for group A vs B, B vs C, and C vs A. The correct technique of analysis is to run ANOVA and use post hoc tests (if ANOVA yields a significant result) to determine which group is different from the others.

( Table 2 lists the tests commonly used for comparing paired data, depending on the number of groups and type of data. As discussed above, it would be incorrect to use multiple paired t -tests to compare more than two measurements within a group. In the study by Chowhan, each parameter (LVOTVTI and CAVTI) was measured in the supine position and following passive leg raise. These represented paired readings from the same individual and comparison of prereading and postreading was performed using the paired t -test. 6 Verma et al. evaluated the role of physiotherapy on oxygen requirements and physiological parameters in patients with COVID-19. 7 Each patient had pretreatment and post-treatment data for heart rate and oxygen supplementation recorded on day 1 and day 14. Since data did not follow a normal distribution, they used Wilcoxon's matched pair test to compare the prevalues and postvalues of heart rate (numerical variable). McNemar's test was used to compare the presupplemental and postsupplemental oxygen status expressed as dichotomous data in terms of yes/no. In the study by Megahed, patients had various parameters such as sepsis-related organ failure assessment score, lung injury score, and clinical pulmonary infection score (CPIS) measured at baseline, on day 3 and day 7. 5 Within groups, comparisons were made using repeated measures ANOVA for normally distributed data and Friedman's test for skewed data.

Tests for comparison of paired data

T ests for A ssociation between V ariables

( Table 3 lists the tests used to determine the association between variables. Correlation determines the strength of the relationship between two variables; regression allows the prediction of one variable from another. Tyagi examined the correlation between ETCO 2 and PaCO 2 in patients with chronic obstructive pulmonary disease with acute exacerbation, who were mechanically ventilated. 8 Since these were normally distributed variables, the linear correlation between ETCO 2 and PaCO 2 was determined by Pearson's correlation coefficient. Parajuli et al. compared the acute physiology and chronic health evaluation II (APACHE II) and acute physiology and chronic health evaluation IV (APACHE IV) scores to predict intensive care unit mortality, both of which were ordinal data. Correlation between APACHE II and APACHE IV score was tested using Spearman's coefficient. 9 A study by Roshan et al. identified risk factors for the development of aspiration pneumonia following rapid sequence intubation. 10 Since the outcome was categorical binary data (aspiration pneumonia— yes/no), they performed a bivariate analysis to derive unadjusted odds ratios, followed by a multivariable logistic regression analysis to calculate adjusted odds ratios for risk factors associated with aspiration pneumonia.

Tests for assessing the association between variables

T ests for A greement between M easurements

( Table 4 outlines the tests used for assessing agreement between measurements. Gunalan evaluated concordance between the National Healthcare Safety Network surveillance criteria and CPIS for the diagnosis of ventilator-associated pneumonia. 11 Since both the scores are examples of ordinal data, Kappa statistics were calculated to assess the concordance between the two methods. In the previously quoted study by Tyagi, the agreement between ETCO 2 and PaCO 2 (both numerical variables) was represented using the Bland–Altman method. 8

Tests for assessing agreement between measurements

T ests for T ime-to -E vent D ata (S urvival A nalysis )

Time-to-event data represent a unique type of data where some participants have not experienced the outcome of interest at the time of analysis. Such participants are considered to be “censored” but are allowed to contribute to the analysis for the period of their follow-up. A detailed discussion on the analysis of time-to-event data is beyond the scope of this article. For analyzing time-to-event data, we use survival analysis (with the Kaplan–Meier method) and compare groups using the log-rank test. The risk of experiencing the event is expressed as a hazard ratio. Cox proportional hazards regression model is used to identify risk factors that are significantly associated with the event.

Hasanzadeh evaluated the impact of zinc supplementation on the development of ventilator-associated pneumonia (VAP) in adult mechanically ventilated trauma patients. 12 Survival analysis (Kaplan–Meier technique) was used to calculate the median time to development of VAP after ICU admission. The Cox proportional hazards regression model was used to calculate hazard ratios to identify factors significantly associated with the development of VAP.

The choice of statistical test used to analyze research data depends on the study hypothesis, the type of data, the number of measurements, and whether the data are paired or unpaired. Reviews of articles published in medical specialties such as family medicine, cytopathology, and pain have found several errors related to the use of descriptive and inferential statistics. 12 – 15 The statistical technique needs to be carefully chosen and specified in the protocol prior to commencement of the study, to ensure that the conclusions of the study are valid. This article has outlined the principles for selecting a statistical test, along with a list of tests used commonly. Researchers should seek help from statisticians while writing the research study protocol, to formulate the plan for statistical analysis.

Priya Ranganathan https://orcid.org/0000-0003-1004-5264

Source of support: Nil

Conflict of interest: None

R eferences

Have a thesis expert improve your writing

Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.

• Knowledge Base

The Beginner's Guide to Statistical Analysis | 5 Steps & Examples

Statistical analysis means investigating trends, patterns, and relationships using quantitative data . It is an important research tool used by scientists, governments, businesses, and other organisations.

To draw valid conclusions, statistical analysis requires careful planning from the very start of the research process . You need to specify your hypotheses and make decisions about your research design, sample size, and sampling procedure.

After collecting data from your sample, you can organise and summarise the data using descriptive statistics . Then, you can use inferential statistics to formally test hypotheses and make estimates about the population. Finally, you can interpret and generalise your findings.

This article is a practical introduction to statistical analysis for students and researchers. We’ll walk you through the steps using two research examples. The first investigates a potential cause-and-effect relationship, while the second investigates a potential correlation between variables.

Table of contents

Step 1: write your hypotheses and plan your research design, step 2: collect data from a sample, step 3: summarise your data with descriptive statistics, step 4: test hypotheses or make estimates with inferential statistics, step 5: interpret your results, frequently asked questions about statistics.

To collect valid data for statistical analysis, you first need to specify your hypotheses and plan out your research design.

Writing statistical hypotheses

The goal of research is often to investigate a relationship between variables within a population . You start with a prediction, and use statistical analysis to test that prediction.

A statistical hypothesis is a formal way of writing a prediction about a population. Every research prediction is rephrased into null and alternative hypotheses that can be tested using sample data.

While the null hypothesis always predicts no effect or no relationship between variables, the alternative hypothesis states your research prediction of an effect or relationship.

• Null hypothesis: A 5-minute meditation exercise will have no effect on math test scores in teenagers.
• Alternative hypothesis: A 5-minute meditation exercise will improve math test scores in teenagers.
• Null hypothesis: Parental income and GPA have no relationship with each other in college students.
• Alternative hypothesis: Parental income and GPA are positively correlated in college students.

Planning your research design

A research design is your overall strategy for data collection and analysis. It determines the statistical tests you can use to test your hypothesis later on.

First, decide whether your research will use a descriptive, correlational, or experimental design. Experiments directly influence variables, whereas descriptive and correlational studies only measure variables.

• In an experimental design , you can assess a cause-and-effect relationship (e.g., the effect of meditation on test scores) using statistical tests of comparison or regression.
• In a correlational design , you can explore relationships between variables (e.g., parental income and GPA) without any assumption of causality using correlation coefficients and significance tests.
• In a descriptive design , you can study the characteristics of a population or phenomenon (e.g., the prevalence of anxiety in U.S. college students) using statistical tests to draw inferences from sample data.

Your research design also concerns whether you’ll compare participants at the group level or individual level, or both.

• In a between-subjects design , you compare the group-level outcomes of participants who have been exposed to different treatments (e.g., those who performed a meditation exercise vs those who didn’t).
• In a within-subjects design , you compare repeated measures from participants who have participated in all treatments of a study (e.g., scores from before and after performing a meditation exercise).
• In a mixed (factorial) design , one variable is altered between subjects and another is altered within subjects (e.g., pretest and posttest scores from participants who either did or didn’t do a meditation exercise).
• Experimental
• Correlational

First, you’ll take baseline test scores from participants. Then, your participants will undergo a 5-minute meditation exercise. Finally, you’ll record participants’ scores from a second math test.

In this experiment, the independent variable is the 5-minute meditation exercise, and the dependent variable is the math test score from before and after the intervention. Example: Correlational research design In a correlational study, you test whether there is a relationship between parental income and GPA in graduating college students. To collect your data, you will ask participants to fill in a survey and self-report their parents’ incomes and their own GPA.

Measuring variables

When planning a research design, you should operationalise your variables and decide exactly how you will measure them.

For statistical analysis, it’s important to consider the level of measurement of your variables, which tells you what kind of data they contain:

• Categorical data represents groupings. These may be nominal (e.g., gender) or ordinal (e.g. level of language ability).
• Quantitative data represents amounts. These may be on an interval scale (e.g. test score) or a ratio scale (e.g. age).

Many variables can be measured at different levels of precision. For example, age data can be quantitative (8 years old) or categorical (young). If a variable is coded numerically (e.g., level of agreement from 1–5), it doesn’t automatically mean that it’s quantitative instead of categorical.

Identifying the measurement level is important for choosing appropriate statistics and hypothesis tests. For example, you can calculate a mean score with quantitative data, but not with categorical data.

In a research study, along with measures of your variables of interest, you’ll often collect data on relevant participant characteristics.

In most cases, it’s too difficult or expensive to collect data from every member of the population you’re interested in studying. Instead, you’ll collect data from a sample.

Statistical analysis allows you to apply your findings beyond your own sample as long as you use appropriate sampling procedures . You should aim for a sample that is representative of the population.

Sampling for statistical analysis

There are two main approaches to selecting a sample.

• Probability sampling: every member of the population has a chance of being selected for the study through random selection.
• Non-probability sampling: some members of the population are more likely than others to be selected for the study because of criteria such as convenience or voluntary self-selection.

In theory, for highly generalisable findings, you should use a probability sampling method. Random selection reduces sampling bias and ensures that data from your sample is actually typical of the population. Parametric tests can be used to make strong statistical inferences when data are collected using probability sampling.

But in practice, it’s rarely possible to gather the ideal sample. While non-probability samples are more likely to be biased, they are much easier to recruit and collect data from. Non-parametric tests are more appropriate for non-probability samples, but they result in weaker inferences about the population.

If you want to use parametric tests for non-probability samples, you have to make the case that:

• your sample is representative of the population you’re generalising your findings to.
• your sample lacks systematic bias.

Keep in mind that external validity means that you can only generalise your conclusions to others who share the characteristics of your sample. For instance, results from Western, Educated, Industrialised, Rich and Democratic samples (e.g., college students in the US) aren’t automatically applicable to all non-WEIRD populations.

If you apply parametric tests to data from non-probability samples, be sure to elaborate on the limitations of how far your results can be generalised in your discussion section .

Create an appropriate sampling procedure

Based on the resources available for your research, decide on how you’ll recruit participants.

• Will you have resources to advertise your study widely, including outside of your university setting?
• Will you have the means to recruit a diverse sample that represents a broad population?
• Do you have time to contact and follow up with members of hard-to-reach groups?

Your participants are self-selected by their schools. Although you’re using a non-probability sample, you aim for a diverse and representative sample. Example: Sampling (correlational study) Your main population of interest is male college students in the US. Using social media advertising, you recruit senior-year male college students from a smaller subpopulation: seven universities in the Boston area.

Calculate sufficient sample size

Before recruiting participants, decide on your sample size either by looking at other studies in your field or using statistics. A sample that’s too small may be unrepresentative of the sample, while a sample that’s too large will be more costly than necessary.

There are many sample size calculators online. Different formulas are used depending on whether you have subgroups or how rigorous your study should be (e.g., in clinical research). As a rule of thumb, a minimum of 30 units or more per subgroup is necessary.

To use these calculators, you have to understand and input these key components:

• Significance level (alpha): the risk of rejecting a true null hypothesis that you are willing to take, usually set at 5%.
• Statistical power : the probability of your study detecting an effect of a certain size if there is one, usually 80% or higher.
• Expected effect size : a standardised indication of how large the expected result of your study will be, usually based on other similar studies.
• Population standard deviation: an estimate of the population parameter based on a previous study or a pilot study of your own.

Once you’ve collected all of your data, you can inspect them and calculate descriptive statistics that summarise them.

Inspect your data

There are various ways to inspect your data, including the following:

• Organising data from each variable in frequency distribution tables .
• Displaying data from a key variable in a bar chart to view the distribution of responses.
• Visualising the relationship between two variables using a scatter plot .

By visualising your data in tables and graphs, you can assess whether your data follow a skewed or normal distribution and whether there are any outliers or missing data.

A normal distribution means that your data are symmetrically distributed around a center where most values lie, with the values tapering off at the tail ends.

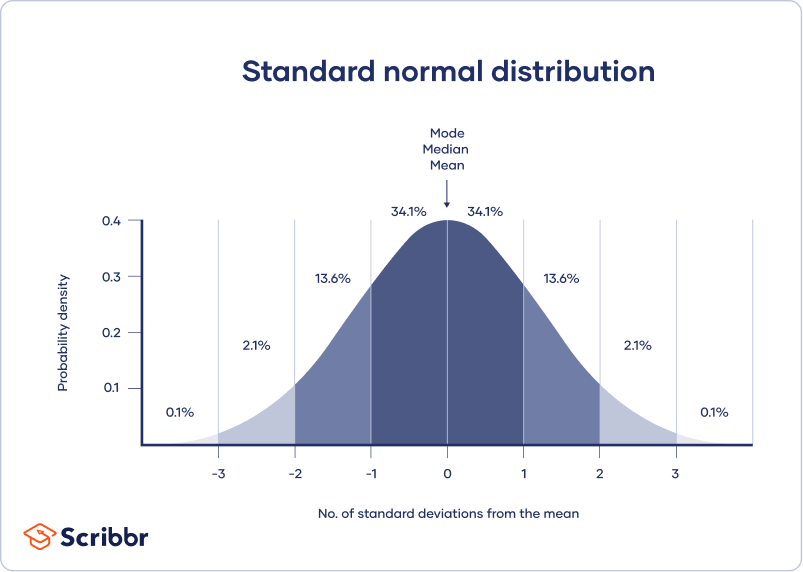
In contrast, a skewed distribution is asymmetric and has more values on one end than the other. The shape of the distribution is important to keep in mind because only some descriptive statistics should be used with skewed distributions.

Extreme outliers can also produce misleading statistics, so you may need a systematic approach to dealing with these values.

Calculate measures of central tendency

Measures of central tendency describe where most of the values in a data set lie. Three main measures of central tendency are often reported:

• Mode : the most popular response or value in the data set.
• Median : the value in the exact middle of the data set when ordered from low to high.
• Mean : the sum of all values divided by the number of values.

However, depending on the shape of the distribution and level of measurement, only one or two of these measures may be appropriate. For example, many demographic characteristics can only be described using the mode or proportions, while a variable like reaction time may not have a mode at all.

Calculate measures of variability

Measures of variability tell you how spread out the values in a data set are. Four main measures of variability are often reported:

• Range : the highest value minus the lowest value of the data set.
• Interquartile range : the range of the middle half of the data set.
• Standard deviation : the average distance between each value in your data set and the mean.
• Variance : the square of the standard deviation.

Once again, the shape of the distribution and level of measurement should guide your choice of variability statistics. The interquartile range is the best measure for skewed distributions, while standard deviation and variance provide the best information for normal distributions.

Using your table, you should check whether the units of the descriptive statistics are comparable for pretest and posttest scores. For example, are the variance levels similar across the groups? Are there any extreme values? If there are, you may need to identify and remove extreme outliers in your data set or transform your data before performing a statistical test.

From this table, we can see that the mean score increased after the meditation exercise, and the variances of the two scores are comparable. Next, we can perform a statistical test to find out if this improvement in test scores is statistically significant in the population. Example: Descriptive statistics (correlational study) After collecting data from 653 students, you tabulate descriptive statistics for annual parental income and GPA.

It’s important to check whether you have a broad range of data points. If you don’t, your data may be skewed towards some groups more than others (e.g., high academic achievers), and only limited inferences can be made about a relationship.

A number that describes a sample is called a statistic , while a number describing a population is called a parameter . Using inferential statistics , you can make conclusions about population parameters based on sample statistics.

Researchers often use two main methods (simultaneously) to make inferences in statistics.

• Estimation: calculating population parameters based on sample statistics.
• Hypothesis testing: a formal process for testing research predictions about the population using samples.

You can make two types of estimates of population parameters from sample statistics:

• A point estimate : a value that represents your best guess of the exact parameter.
• An interval estimate : a range of values that represent your best guess of where the parameter lies.

If your aim is to infer and report population characteristics from sample data, it’s best to use both point and interval estimates in your paper.

You can consider a sample statistic a point estimate for the population parameter when you have a representative sample (e.g., in a wide public opinion poll, the proportion of a sample that supports the current government is taken as the population proportion of government supporters).

There’s always error involved in estimation, so you should also provide a confidence interval as an interval estimate to show the variability around a point estimate.

A confidence interval uses the standard error and the z score from the standard normal distribution to convey where you’d generally expect to find the population parameter most of the time.

Hypothesis testing

Using data from a sample, you can test hypotheses about relationships between variables in the population. Hypothesis testing starts with the assumption that the null hypothesis is true in the population, and you use statistical tests to assess whether the null hypothesis can be rejected or not.

Statistical tests determine where your sample data would lie on an expected distribution of sample data if the null hypothesis were true. These tests give two main outputs:

• A test statistic tells you how much your data differs from the null hypothesis of the test.
• A p value tells you the likelihood of obtaining your results if the null hypothesis is actually true in the population.

Statistical tests come in three main varieties:

• Comparison tests assess group differences in outcomes.
• Regression tests assess cause-and-effect relationships between variables.
• Correlation tests assess relationships between variables without assuming causation.

Your choice of statistical test depends on your research questions, research design, sampling method, and data characteristics.

Parametric tests

Parametric tests make powerful inferences about the population based on sample data. But to use them, some assumptions must be met, and only some types of variables can be used. If your data violate these assumptions, you can perform appropriate data transformations or use alternative non-parametric tests instead.

A regression models the extent to which changes in a predictor variable results in changes in outcome variable(s).

• A simple linear regression includes one predictor variable and one outcome variable.
• A multiple linear regression includes two or more predictor variables and one outcome variable.

Comparison tests usually compare the means of groups. These may be the means of different groups within a sample (e.g., a treatment and control group), the means of one sample group taken at different times (e.g., pretest and posttest scores), or a sample mean and a population mean.

• A t test is for exactly 1 or 2 groups when the sample is small (30 or less).
• A z test is for exactly 1 or 2 groups when the sample is large.
• An ANOVA is for 3 or more groups.

The z and t tests have subtypes based on the number and types of samples and the hypotheses:

• If you have only one sample that you want to compare to a population mean, use a one-sample test .
• If you have paired measurements (within-subjects design), use a dependent (paired) samples test .
• If you have completely separate measurements from two unmatched groups (between-subjects design), use an independent (unpaired) samples test .
• If you expect a difference between groups in a specific direction, use a one-tailed test .
• If you don’t have any expectations for the direction of a difference between groups, use a two-tailed test .

The only parametric correlation test is Pearson’s r . The correlation coefficient ( r ) tells you the strength of a linear relationship between two quantitative variables.

However, to test whether the correlation in the sample is strong enough to be important in the population, you also need to perform a significance test of the correlation coefficient, usually a t test, to obtain a p value. This test uses your sample size to calculate how much the correlation coefficient differs from zero in the population.

You use a dependent-samples, one-tailed t test to assess whether the meditation exercise significantly improved math test scores. The test gives you:

• a t value (test statistic) of 3.00
• a p value of 0.0028

Although Pearson’s r is a test statistic, it doesn’t tell you anything about how significant the correlation is in the population. You also need to test whether this sample correlation coefficient is large enough to demonstrate a correlation in the population.

A t test can also determine how significantly a correlation coefficient differs from zero based on sample size. Since you expect a positive correlation between parental income and GPA, you use a one-sample, one-tailed t test. The t test gives you:

• a t value of 3.08
• a p value of 0.001

The final step of statistical analysis is interpreting your results.

Statistical significance

In hypothesis testing, statistical significance is the main criterion for forming conclusions. You compare your p value to a set significance level (usually 0.05) to decide whether your results are statistically significant or non-significant.

Statistically significant results are considered unlikely to have arisen solely due to chance. There is only a very low chance of such a result occurring if the null hypothesis is true in the population.

This means that you believe the meditation intervention, rather than random factors, directly caused the increase in test scores. Example: Interpret your results (correlational study) You compare your p value of 0.001 to your significance threshold of 0.05. With a p value under this threshold, you can reject the null hypothesis. This indicates a statistically significant correlation between parental income and GPA in male college students.

Note that correlation doesn’t always mean causation, because there are often many underlying factors contributing to a complex variable like GPA. Even if one variable is related to another, this may be because of a third variable influencing both of them, or indirect links between the two variables.

Effect size

A statistically significant result doesn’t necessarily mean that there are important real life applications or clinical outcomes for a finding.

In contrast, the effect size indicates the practical significance of your results. It’s important to report effect sizes along with your inferential statistics for a complete picture of your results. You should also report interval estimates of effect sizes if you’re writing an APA style paper .

With a Cohen’s d of 0.72, there’s medium to high practical significance to your finding that the meditation exercise improved test scores. Example: Effect size (correlational study) To determine the effect size of the correlation coefficient, you compare your Pearson’s r value to Cohen’s effect size criteria.

Decision errors

Type I and Type II errors are mistakes made in research conclusions. A Type I error means rejecting the null hypothesis when it’s actually true, while a Type II error means failing to reject the null hypothesis when it’s false.

You can aim to minimise the risk of these errors by selecting an optimal significance level and ensuring high power . However, there’s a trade-off between the two errors, so a fine balance is necessary.

Frequentist versus Bayesian statistics

Traditionally, frequentist statistics emphasises null hypothesis significance testing and always starts with the assumption of a true null hypothesis.

However, Bayesian statistics has grown in popularity as an alternative approach in the last few decades. In this approach, you use previous research to continually update your hypotheses based on your expectations and observations.

Bayes factor compares the relative strength of evidence for the null versus the alternative hypothesis rather than making a conclusion about rejecting the null hypothesis or not.

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

The research methods you use depend on the type of data you need to answer your research question .

• If you want to measure something or test a hypothesis , use quantitative methods . If you want to explore ideas, thoughts, and meanings, use qualitative methods .
• If you want to analyse a large amount of readily available data, use secondary data. If you want data specific to your purposes with control over how they are generated, collect primary data.
• If you want to establish cause-and-effect relationships between variables , use experimental methods. If you want to understand the characteristics of a research subject, use descriptive methods.

Statistical analysis is the main method for analyzing quantitative research data . It uses probabilities and models to test predictions about a population from sample data.

Is this article helpful?

Other students also liked, a quick guide to experimental design | 5 steps & examples, controlled experiments | methods & examples of control, between-subjects design | examples, pros & cons, more interesting articles.

• Central Limit Theorem | Formula, Definition & Examples
• Central Tendency | Understanding the Mean, Median & Mode
• Correlation Coefficient | Types, Formulas & Examples
• Descriptive Statistics | Definitions, Types, Examples
• How to Calculate Standard Deviation (Guide) | Calculator & Examples
• How to Calculate Variance | Calculator, Analysis & Examples
• How to Find Degrees of Freedom | Definition & Formula
• How to Find Interquartile Range (IQR) | Calculator & Examples
• How to Find Outliers | Meaning, Formula & Examples
• How to Find the Geometric Mean | Calculator & Formula
• How to Find the Mean | Definition, Examples & Calculator
• How to Find the Median | Definition, Examples & Calculator
• How to Find the Range of a Data Set | Calculator & Formula
• Inferential Statistics | An Easy Introduction & Examples
• Levels of measurement: Nominal, ordinal, interval, ratio
• Missing Data | Types, Explanation, & Imputation
• Normal Distribution | Examples, Formulas, & Uses
• Null and Alternative Hypotheses | Definitions & Examples
• Poisson Distributions | Definition, Formula & Examples
• Skewness | Definition, Examples & Formula
• T-Distribution | What It Is and How To Use It (With Examples)
• The Standard Normal Distribution | Calculator, Examples & Uses
• Type I & Type II Errors | Differences, Examples, Visualizations
• Understanding Confidence Intervals | Easy Examples & Formulas
• Variability | Calculating Range, IQR, Variance, Standard Deviation
• What is Effect Size and Why Does It Matter? (Examples)
• What Is Interval Data? | Examples & Definition
• What Is Nominal Data? | Examples & Definition
• What Is Ordinal Data? | Examples & Definition
• What Is Ratio Data? | Examples & Definition
• What Is the Mode in Statistics? | Definition, Examples & Calculator

• About English Wizard Online
• Parts of Speech, Phrases, Sentences
• Spelling/ Vocabulary
• Research/ Thesis Writing
• Lesson Plans
• Worksheets, eBooks, Workbooks, Printables
• Poems (Text and Video)
• Speech/ Pronunciation Lessons
• Classroom Ideas/ Materials
• Teacher's Comments
• Creative and Technical Writing
• Teaching Articles/ Teaching Strategies
• Essays/ Book and Movie Reviews
• Yearbook/ Student Publication/ Magazine/ Newsletter

Sample Statistical Treatment of Data in Chapter 3 (Thesis Writing)

No comments:

Post a comment.

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to  upgrade your browser .

Enter the email address you signed up with and we'll email you a reset link.

• We're Hiring!
• Help Center

CERTIFICATION OF STATISTICAL TREATMENT

Related Papers

Academies of Entrepreneurship Journal

John Bagcal

The purpose of this research is to provide owners and latent investors of resorts, with a bulletin of preferred resort facilities–as their market research tool. This supports the posit of Tumwebaze (2015) stating, that there is a prevalent 80% MSMEs mortality rate (MMR) everywhere. Albeit a handful of grounds for high MMR, the primary reason is the non-onduct of market research of most entrepreneurship, particularly micro and small enterprises. The facilities utilized in this study emerged from the TRACER variables of the travel and tourism industry as attributes of which levels are identified through focus group discussion–leading to the generation of the Attribute-Level Frame (ALF). Out of the ALF, 20 orthogonal profiles (OPs) including holdouts are generated from the 243 total combinations. These OPs exactly form-part the survey questionnaire rated by 500 local tourists from first-class municipalities, component and highly urbanized cities of Davao Region. Using additive conjoint analysis, importance values, utilities, and probabilities of the preferred resort facilities (PRFs) are uncovered, provincially and regionally. The most PRFs of the provinces and the region are: point-to-point aircon bus, minibus, and van transport; cottages and boarding houses; budget inns; full-service catering; live bands and concerts; zipline, hiking, and camping; and, swimming pools. Further, this research recommended the following: provision of PRFs as a bulletin to stakeholders; conduct of seminal studies on: the PRFs of other provinces or regions; the amenities as inclusion in the classification and rating tool for resorts other than facilities; and, ICT- support system

Jurnal Ilmiah Hospitality Management

Ryan O Tayco , Vito Carlo Genove

The state of the hotels, resorts, and restaurant industry is dependent upon the quality of service exhibited by its frontliners and personnel. This study is to measure the service quality of selected resorts in the Municipality of Dauin, province of Negros Oriental, Philippines using a descriptive-correlational design. 120 customers of the six selected resorts that served as the respondents of this research. This study aims to measure the levels of customer satisfaction using the five dimensions of service quality: tangibility, reliability, responsiveness, assurance, and empathy. Data were collected mainly from the six selected resorts, after which results were tabulated, presented, analyzed, and interpreted. The findings show that tangibility is the weakest dimension while assurance is the strongest dimension of service quality. This implies that the level of satisfaction in all dimensions is yielding a positive SERVQUAL response. Hence, customers were satisfied with all dimensions of service quality. Keywords – tourism and hospitality industry, service quality, resorts, descriptive-correlational design, Central Philippines

Philippine Institute for Development Studies, …

Divina Edralin

Ian McDonnell

Serafeim Polyzos

Tourism Review

Davide Provenzano

Purpose The purpose of this paper is to provide an overview of past perspectives and future trends in tourism and hospitality research. Design/methodology/approach The study grounds the discussion on the timeline evolution of quantitative research methods. Findings Although still under-recognized by scholars, mixed methods represent the future of research in tourism and hospitality. Research limitations/implications The investigation is confined to quantitative methods. Originality/value No other surveys sketch a period of 150 years of quantitative analyses in tourism and hospitality.

Patricio Aroca

Mazilu Mirela

Abstract: Statistics represent an essential element of the information system and occupies a special place in the information supply regarding the status and trends of country's economic, social, demographic and tourism development. The transformations of the global economy driven by the liberalization of the global trade and modern information technologies, lead to a globalization, where the notion of national statistical territory leaves gradually, place to the regional or global statistical area.

Cognizance Journal of Multidisciplinary Studies

JANICE ALEJANDRINO

This study presents the findings conducted on the profile of respondents and the extent of quality services in selected hot spring resorts in Benguet. The study utilizes mix method approach combining quantitative and qualitative methods. There were one hundred fourteen (114) total respondents from six (6) resorts in Benguet province. The respondents were predominantly adult males with a mix of educational backgrounds, including college-level and college graduate respondents. The majority of the respondents were local tourists from various provinces in the Philippines, with a significant number being employed. The study made use of survey questionnaires and structured interview. The study revealed that the selected resorts provided high-quality services in terms of tangibles, responsiveness, assurance, and empathy, with excellent reliability. Importantly, there was no significant difference in perception between resort guests and management regarding the extent of quality services ac...

RELATED PAPERS

Bolskan: Revista de …

Josep Gallart

Nadejda (Nadya) Komendantova

Developing a Global Pandemic Exit Strategy and Framework for Global Health Security

budi heryanto

Biochimica et Biophysica Acta (BBA) - General Subjects

Mike Hughes

Monitoring of Marine Pollution

STEPHEN MWANGI

The New England journal of medicine

Jay Mandrekar

James Shevock

快速制作unbc毕业证书 北英属哥伦比亚大学毕业证本科学历原版一模一样

Amin Roshani

Applied Cognitive Psychology

Cleotilde Gonzalez

ines bravo victorino

Jozsef Botos

Food Chemistry

Müfit Bahadir

Sakarya University Journal of Education

Ali R . GÜNDÜZ

Journal of Solid Mechanics

Firouz Matloubi Moghaddam

Revista Electrónica Interuniversitaria de Formación del Profesorado

Antonio Manuel Rodríguez González

原版复制ufv毕业证书 菲莎河谷大学毕业证硕士学历原版一模一样

Navya Engineers & Equipments

•   We're Hiring!
•   Help Center
• Find new research papers in:
• Health Sciences
• Earth Sciences
• Cognitive Science
• Mathematics
• Computer Science
• Academia ©2024